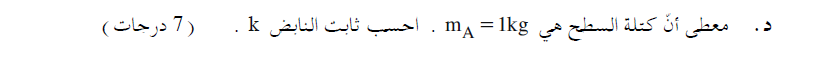
حلول ومنتديات لألبوم الحلول – الحركة التوافقية البسيطة: 2019,5-حركة توافقية رأسية لقياس الكتلة

1. 2019,5-حركة توافقية رأسية لقياس الكتلة

______________________________________________________________________________________

...

كلما كانت قيمة الكمية المقاسة أكبر، كلما كان الخطأ النسبي أصغر.

موضوع الأخطاء، الخطأ النسبي.

يتم تحديد جودة القياس من خلال الخطأ النسبي، والذي يتناسب عكسيا مع قيمة الكمية المقاسة.
لذلك، عند قياس 10 دورات، يكون الخطأ النسبي أصغر وتكون جودة القياس أعلى.

1. ومن المهم التمييز بين خطأ القياس (الخطأ المطلق) والخطأ النسبي.

يُحدَّد خطأ القياس بواسطة أداة القياس. لكل أداة قياس خطأ قياس ناتج عن دقتها المحدودة. على سبيل المثال، الحد الأقصى لدقة المسطرة هو 1 ملم، وبالتالي فإن خطأ القياس في المسطرة هو 1 ملم.

يعتبر قياس سمك الشعر بالمسطرة قياسًا رديء الجودة. ومن ناحية أخرى، يعتبر قياس طول الشخص بخطأ قياس يبلغ مليمترًا واحدًا ذا جودة أعلى بكثير.

لتحديد جودة القياس، تم تعريف الخطأ النسبي على النحو التالي:

«math xmlns=¨http://www.w3.org/1998/Math/MathML¨»«mi mathvariant=¨bold¨ mathcolor=¨#FF0000¨»§#1606;§#1587;§#1576;§#1610;«/mi»«mo mathvariant=¨bold¨ mathcolor=¨#FF0000¨»§#160;«/mo»«mi mathvariant=¨bold¨ mathcolor=¨#FF0000¨»§#1582;§#1591;§#1571;«/mi»«mo mathvariant=¨bold¨ mathcolor=¨#FF0000¨»§#160;«/mo»«mo mathvariant=¨bold¨ mathcolor=¨#FF0000¨»=«/mo»«mo mathvariant=¨bold¨ mathcolor=¨#FF0000¨»§#160;«/mo»«mfrac mathcolor=¨#FF0000¨»«mrow»«mi mathvariant=¨bold¨»§#1575;§#1604;§#1602;§#1610;§#1575;§#1587;«/mi»«mo mathvariant=¨bold¨»§#160;«/mo»«mi mathvariant=¨bold¨»§#1582;§#1591;§#1571;«/mi»«mo mathvariant=¨bold¨»§#160;«/mo»«/mrow»«mrow»«mi mathvariant=¨bold¨»§#1575;§#1604;§#1605;§#1602;§#1575;§#1587;§#1577;«/mi»«mo mathvariant=¨bold¨»§#160;«/mo»«mi mathvariant=¨bold¨»§#1575;§#1604;§#1602;§#1610;§#1605;§#1577;«/mi»«/mrow»«/mfrac»«mo mathvariant=¨bold¨ mathcolor=¨#FF0000¨»§#160;«/mo»«mo mathvariant=¨bold¨ mathcolor=¨#FF0000¨»§#215;«/mo»«mn mathvariant=¨bold¨ mathcolor=¨#FF0000¨»100«/mn»«mo mathvariant=¨bold¨ mathcolor=¨#FF0000¨»%«/mo»«/math»

في أي سؤال يتناول أخطاء القياس، من المهم أن نتذكر معنى خطأ القياس والخطأ النسبي والعلاقة بينهما.

2. يمكن أن يظهر موضوع أخطاء القياس في أسئلة البجروت في جميع المواد في الميكانيكا والكهرباء.

שגיאת המדידה נקבעת על ידי מכשיר המדידה , לכל מכשיר מדידה קיימת שגיאת מדידה הנובעת מהדיוק המוגבל של מכשיר המדידה. כך למשל הדיוק המקסימאלי בסרגל הוא 1 מ"מ , לכן שגיאת המדידה של סרגל היא 1 מילי מטר.

מדידת עובי של שערה עם סרגל נחשבת למדידה לא איכותית . לעומת זאת מדידה גובה של אדם עם שגיאת מדידה של מילי מטר נחשבת להרבה יותר איכותית.

כדי לקבוע את איכות המדידה הוגדרה השגיאה היחסית, באופן הבא:

«math xmlns=¨http://www.w3.org/1998/Math/MathML¨»«mi mathvariant=¨bold¨ mathcolor=¨#FF0000¨»§#1497;§#1495;§#1505;§#1497;§#1514;«/mi»«mo mathvariant=¨bold¨ mathcolor=¨#FF0000¨»§#160;«/mo»«mi mathvariant=¨bold¨ mathcolor=¨#FF0000¨»§#1513;§#1490;§#1497;§#1488;§#1492;«/mi»«mo mathvariant=¨bold¨ mathcolor=¨#FF0000¨»§#160;«/mo»«mo mathvariant=¨bold¨ mathcolor=¨#FF0000¨»=«/mo»«mo mathvariant=¨bold¨ mathcolor=¨#FF0000¨»§#160;«/mo»«mfrac mathcolor=¨#FF0000¨»«mrow»«mi mathvariant=¨bold¨»§#1502;§#1491;§#1497;§#1491;§#1492;«/mi»«mo mathvariant=¨bold¨»§#160;«/mo»«mi mathvariant=¨bold¨»§#1513;§#1490;§#1497;§#1488;§#1514;«/mi»«mo mathvariant=¨bold¨»§#160;«/mo»«/mrow»«mrow»«mi mathvariant=¨bold¨»§#1504;§#1502;§#1491;§#1491;«/mi»«mo mathvariant=¨bold¨»§#160;«/mo»«mi mathvariant=¨bold¨»§#1490;§#1493;§#1491;§#1500;«/mi»«/mrow»«/mfrac»«mo mathvariant=¨bold¨ mathcolor=¨#FF0000¨»§#160;«/mo»«mo mathvariant=¨bold¨ mathcolor=¨#FF0000¨»§#215;«/mo»«mn mathvariant=¨bold¨ mathcolor=¨#FF0000¨»100«/mn»«mo mathvariant=¨bold¨ mathcolor=¨#FF0000¨»%«/mo»«/math»

בכל שאלה העוסקת בשגיאות מדידה חשוב לעשות סדר ,להיזכר במשמעות של שגיאת מדידה ושגיאה יחסית והקשר ביניהם.

2. נושא שגיאות המדידה יכול להופיע בשאלות הבגרות בכל הנושאים במכניקה ובחשמל.

______________________________________________________________________________________

...

«math xmlns=¨http://www.w3.org/1998/Math/MathML¨»«msub»«mi mathvariant=¨bold¨»m«/mi»«mi mathvariant=¨bold¨»B«/mi»«/msub»«mo mathvariant=¨bold¨»=«/mo»«mfrac»«mrow»«msup»«mi mathvariant=¨bold¨»T«/mi»«mn mathvariant=¨bold¨»2«/mn»«/msup»«mo mathvariant=¨bold¨»§#183;«/mo»«mi mathvariant=¨bold¨»K«/mi»«/mrow»«mrow»«mn mathvariant=¨bold¨»4«/mn»«mo mathvariant=¨bold¨»§#183;«/mo»«msup»«mi mathvariant=¨bold¨»§#960;«/mi»«mn mathvariant=¨bold¨»2«/mn»«/msup»«/mrow»«/mfrac»«mo mathvariant=¨bold¨»-«/mo»«msub»«mi mathvariant=¨bold¨»m«/mi»«mi mathvariant=¨bold¨»A«/mi»«/msub»«/math»

يتم الحصول على تعبير كتلة الجسم B من زمن دورة الحركة التوافقية البسيطة.

نعبر عن كتلة الجسم B من خلال تعبير زمن دورة الحركة التوافقية البسيطة.

«math xmlns=¨http://www.w3.org/1998/Math/MathML¨»«mi mathvariant=¨bold-italic¨ mathcolor=¨#0000FF¨»T«/mi»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»=«/mo»«mn mathvariant=¨bold¨ mathcolor=¨#0000FF¨»2«/mn»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»§#183;«/mo»«mi mathvariant=¨bold¨ mathcolor=¨#0000FF¨»§#960;«/mi»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»§#183;«/mo»«msqrt mathcolor=¨#0000FF¨»«mfrac»«mi mathvariant=¨bold¨»m«/mi»«mi mathvariant=¨bold¨»k«/mi»«/mfrac»«/msqrt»«mspace linebreak=¨newline¨»«/mspace»«mspace linebreak=¨newline¨»«/mspace»«mi mathvariant=¨bold¨ mathcolor=¨#0000FF¨»T«/mi»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»=«/mo»«mn mathvariant=¨bold¨ mathcolor=¨#0000FF¨»2«/mn»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»§#183;«/mo»«mi mathvariant=¨bold¨ mathcolor=¨#0000FF¨»§#960;«/mi»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»§#183;«/mo»«msqrt mathcolor=¨#0000FF¨»«mfrac»«mrow»«msub»«mi mathvariant=¨bold¨»m«/mi»«mi mathvariant=¨bold¨»A«/mi»«/msub»«mo mathvariant=¨bold¨»+«/mo»«msub»«mi mathvariant=¨bold¨»m«/mi»«mi mathvariant=¨bold¨»B«/mi»«/msub»«/mrow»«mi mathvariant=¨bold¨»k«/mi»«/mfrac»«/msqrt»«mspace linebreak=¨newline¨»«/mspace»«msup»«mi mathvariant=¨bold¨ mathcolor=¨#0000FF¨»T«/mi»«mn mathvariant=¨bold¨ mathcolor=¨#0000FF¨»2«/mn»«/msup»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»=«/mo»«mn mathvariant=¨bold¨ mathcolor=¨#0000FF¨»4«/mn»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»§#183;«/mo»«msup»«mi mathvariant=¨bold¨ mathcolor=¨#0000FF¨»§#960;«/mi»«mn mathvariant=¨bold¨ mathcolor=¨#0000FF¨»2«/mn»«/msup»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»§#183;«/mo»«mrow mathcolor=¨#0000FF¨»«mo mathvariant=¨bold¨»(«/mo»«mfrac»«mrow»«msub»«mi mathvariant=¨bold¨»m«/mi»«mi mathvariant=¨bold¨»A«/mi»«/msub»«mo mathvariant=¨bold¨»+«/mo»«msub»«mi mathvariant=¨bold¨»m«/mi»«mi mathvariant=¨bold¨»B«/mi»«/msub»«/mrow»«mi mathvariant=¨bold¨»k«/mi»«/mfrac»«mo mathvariant=¨bold¨»)«/mo»«/mrow»«mspace linebreak=¨newline¨»«/mspace»«msub»«mi mathvariant=¨bold¨ mathcolor=¨#0000FF¨»m«/mi»«mi mathvariant=¨bold¨ mathcolor=¨#0000FF¨»A«/mi»«/msub»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»+«/mo»«msub»«mi mathvariant=¨bold¨ mathcolor=¨#0000FF¨»m«/mi»«mi mathvariant=¨bold¨ mathcolor=¨#0000FF¨»B«/mi»«/msub»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»=«/mo»«mfrac mathcolor=¨#0000FF¨»«mrow»«msup»«mi mathvariant=¨bold¨»T«/mi»«mn mathvariant=¨bold¨»2«/mn»«/msup»«mo mathvariant=¨bold¨»§#183;«/mo»«mi mathvariant=¨bold¨»K«/mi»«/mrow»«mrow»«mn mathvariant=¨bold¨»4«/mn»«mo mathvariant=¨bold¨»§#183;«/mo»«msup»«mi mathvariant=¨bold¨»§#960;«/mi»«mn mathvariant=¨bold¨»2«/mn»«/msup»«/mrow»«/mfrac»«mspace linebreak=¨newline¨»«/mspace»«mspace linebreak=¨newline¨»«/mspace»«menclose mathcolor=¨#0000FF¨ notation=¨circle¨»«msub»«mi mathvariant=¨bold¨»m«/mi»«mi mathvariant=¨bold¨»B«/mi»«/msub»«mo mathvariant=¨bold¨»=«/mo»«mfrac»«mrow»«msup»«mi mathvariant=¨bold¨»T«/mi»«mn mathvariant=¨bold¨»2«/mn»«/msup»«mo mathvariant=¨bold¨»§#183;«/mo»«mi mathvariant=¨bold¨»K«/mi»«/mrow»«mrow»«mn mathvariant=¨bold¨»4«/mn»«mo mathvariant=¨bold¨»§#183;«/mo»«msup»«mi mathvariant=¨bold¨»§#960;«/mi»«mn mathvariant=¨bold¨»2«/mn»«/msup»«/mrow»«/mfrac»«mo mathvariant=¨bold¨»-«/mo»«msub»«mi mathvariant=¨bold¨»m«/mi»«mi mathvariant=¨bold¨»A«/mi»«/msub»«/menclose»«/math»

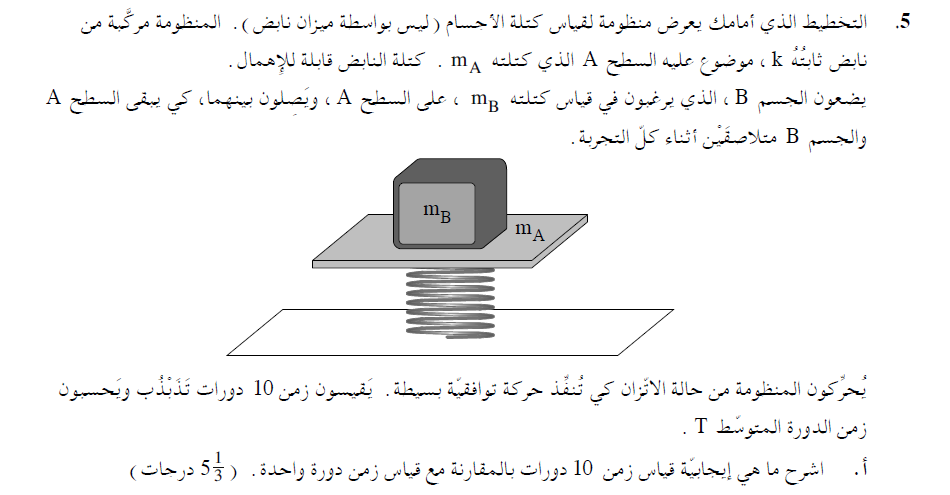
1. الحركة التوافقية الرأسية لجسم معلق بنابض. مماثل لحركة جسم ملقى على نابض رأسي.
2. السؤال يتناول فقط كتلة الجسم B، ومن المهم أيضًا أن نأخذ في الاعتبار كتلة الجسم A.

2. נוסחת זמן המחזור של תה"פ תלויה במסת הגוף הנע, השאלה עוסקת במסת גוף B , חשוב להתייחס גם למסת גוף A.

______________________________________________________________________________________

...

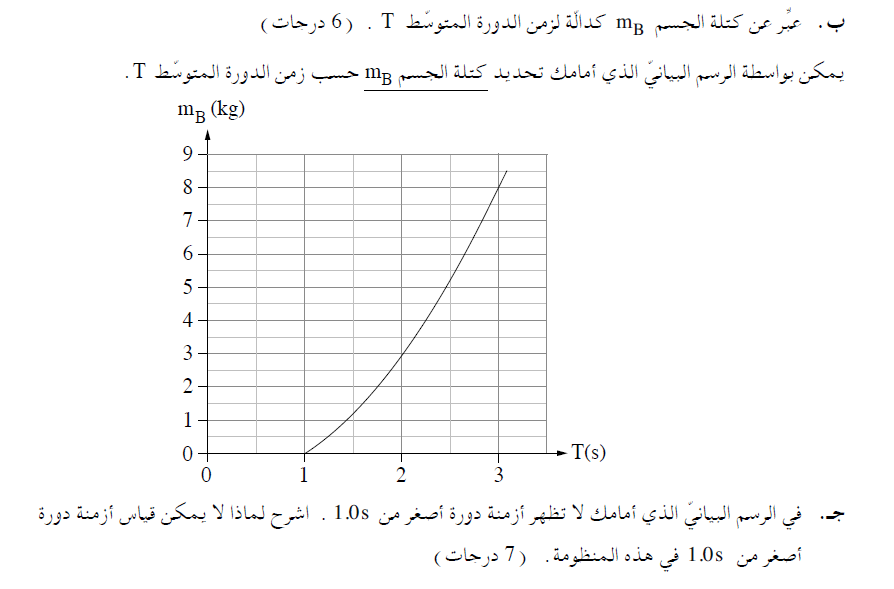
طالما أن كتلة الجسم A لم تقل، فإن زمن الدورة لن يقل عن ثانية واحدة. لذلك، في هذه المنظومة، لا يمكن قياس أزمنة الدورة التي تقل عن ثانية واحدة.

التمييز بين كتلة الجسم B والكتلة الكلية.

ومن الرسم البياني، يمكننا أن نرى أنه عندما تكون كتلة الجسم B تساوي صفرًا، فإن زمن الدورة هو ثانية واحدة. يتم تحديد هذا الزمن حسب كتلة الجسم A.

طالما أن كتلة الجسم A لم تقل، فإن زمن الدورة لن يقل عن ثانية واحدة. لذلك، في هذا المنظومة، لا يمكن قياس أزمنة الدورة التي تقل عن ثانية واحدة.

כל עוד מסת גוף A לא תקטן , זמן המחזור לא יפחת משנייה אחת.

عندما تقرأ السؤال لأول مرة، لن يكون واضحًا لك ما الذي تريده بالضبط في السؤال...

يجب عليك أن تقرأ مرارا وتكرارا، وتمنحه الوقت، وببطء يتبدد الضباب ويصبح فهمك للسؤال أفضل.

צריך לקרוא שוב ושוב לתת לזה זמן ,לאט לאט הערפל מתפוגג וההבנה נעשית טובה יותר.

______________________________________________________________________________________

...

«math xmlns=¨http://www.w3.org/1998/Math/MathML¨»«mi mathvariant=¨bold¨»K«/mi»«mo mathvariant=¨bold¨»=«/mo»«mn mathvariant=¨bold¨»39«/mn»«mo mathvariant=¨bold¨».«/mo»«mn mathvariant=¨bold¨»47«/mn»«mfrac»«mi mathvariant=¨bold¨»N«/mi»«mi mathvariant=¨bold¨»m«/mi»«/mfrac»«/math»

يمكن التعبير عن ثابت النابض من صيغة زمن الدورة، ويمكن استخدام إحدى النقاط الموجودة على الرسم البياني.

نُعبّر عن ثابت النابض من صيغة زمن دورة الحركة التوافقية البسيطة.
«math xmlns=¨http://www.w3.org/1998/Math/MathML¨»«mi mathvariant=¨bold-italic¨ mathcolor=¨#0000FF¨»T«/mi»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»=«/mo»«mn mathvariant=¨bold¨ mathcolor=¨#0000FF¨»2«/mn»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»§#183;«/mo»«mi mathvariant=¨bold¨ mathcolor=¨#0000FF¨»§#960;«/mi»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»§#183;«/mo»«msqrt mathcolor=¨#0000FF¨»«mfrac»«mi mathvariant=¨bold¨»m«/mi»«mi mathvariant=¨bold¨»K«/mi»«/mfrac»«/msqrt»«mspace linebreak=¨newline¨»«/mspace»«mspace linebreak=¨newline¨»«/mspace»«mi mathvariant=¨bold¨ mathcolor=¨#0000FF¨»T«/mi»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»`«/mo»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»=«/mo»«mn mathvariant=¨bold¨ mathcolor=¨#0000FF¨»2«/mn»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»§#183;«/mo»«mi mathvariant=¨bold¨ mathcolor=¨#0000FF¨»§#960;«/mi»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»§#183;«/mo»«msqrt mathcolor=¨#0000FF¨»«mfrac»«msub»«mi mathvariant=¨bold¨»m«/mi»«mi mathvariant=¨bold¨»A«/mi»«/msub»«mi mathvariant=¨bold¨»K«/mi»«/mfrac»«/msqrt»«mspace linebreak=¨newline¨»«/mspace»«mi mathvariant=¨bold¨ mathcolor=¨#0000FF¨»T«/mi»«msup»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»`«/mo»«mn mathvariant=¨bold¨ mathcolor=¨#0000FF¨»2«/mn»«/msup»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»=«/mo»«mn mathvariant=¨bold¨ mathcolor=¨#0000FF¨»4«/mn»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»§#183;«/mo»«msup»«mi mathvariant=¨bold¨ mathcolor=¨#0000FF¨»§#960;«/mi»«mn mathvariant=¨bold¨ mathcolor=¨#0000FF¨»2«/mn»«/msup»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»§#183;«/mo»«mrow mathcolor=¨#0000FF¨»«mo mathvariant=¨bold¨»(«/mo»«mfrac»«msub»«mi mathvariant=¨bold¨»m«/mi»«mi mathvariant=¨bold¨»A«/mi»«/msub»«mi mathvariant=¨bold¨»K«/mi»«/mfrac»«mo mathvariant=¨bold¨»)«/mo»«/mrow»«mspace linebreak=¨newline¨»«/mspace»«mspace linebreak=¨newline¨»«/mspace»«mi mathvariant=¨bold¨ mathcolor=¨#0000FF¨»K«/mi»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»=«/mo»«mfrac mathcolor=¨#0000FF¨»«mrow»«mn mathvariant=¨bold¨»4«/mn»«mo mathvariant=¨bold¨»§#183;«/mo»«msup»«mi mathvariant=¨bold¨»§#960;«/mi»«mn mathvariant=¨bold¨»2«/mn»«/msup»«mo mathvariant=¨bold¨»§#183;«/mo»«msub»«mi mathvariant=¨bold¨»m«/mi»«mi mathvariant=¨bold¨»A«/mi»«/msub»«/mrow»«mrow»«mi mathvariant=¨bold¨»T«/mi»«msup»«mo mathvariant=¨bold¨»`«/mo»«mn mathvariant=¨bold¨»2«/mn»«/msup»«/mrow»«/mfrac»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»=«/mo»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»§#160;«/mo»«mfrac mathcolor=¨#0000FF¨»«mrow»«mn mathvariant=¨bold¨»4«/mn»«mo mathvariant=¨bold¨»§#183;«/mo»«msup»«mi mathvariant=¨bold¨»§#960;«/mi»«mn mathvariant=¨bold¨»2«/mn»«/msup»«mo mathvariant=¨bold¨»§#183;«/mo»«mn mathvariant=¨bold¨»1«/mn»«/mrow»«msup»«mn mathvariant=¨bold¨»1«/mn»«mn mathvariant=¨bold¨»2«/mn»«/msup»«/mfrac»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»=«/mo»«mn mathvariant=¨bold¨ mathcolor=¨#0000FF¨»39«/mn»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨».«/mo»«mn mathvariant=¨bold¨ mathcolor=¨#0000FF¨»47«/mn»«mfrac mathcolor=¨#0000FF¨»«mi mathvariant=¨bold¨»N«/mi»«mi mathvariant=¨bold¨»m«/mi»«/mfrac»«mspace linebreak=¨newline¨»«/mspace»«/math»

وبالتالي فإن قيمة ثابت النابض هي 39.47 نيوتن لكل متر.

«math xmlns=¨http://www.w3.org/1998/Math/MathML¨»«mi mathvariant=¨bold-italic¨ mathcolor=¨#0000FF¨»T«/mi»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»=«/mo»«mn mathvariant=¨bold¨ mathcolor=¨#0000FF¨»2«/mn»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»§#183;«/mo»«mi mathvariant=¨bold¨ mathcolor=¨#0000FF¨»§#960;«/mi»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»§#183;«/mo»«msqrt mathcolor=¨#0000FF¨»«mfrac»«mi mathvariant=¨bold¨»m«/mi»«mi mathvariant=¨bold¨»K«/mi»«/mfrac»«/msqrt»«mspace linebreak=¨newline¨»«/mspace»«mspace linebreak=¨newline¨»«/mspace»«mi mathvariant=¨bold¨ mathcolor=¨#0000FF¨»T«/mi»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»`«/mo»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»=«/mo»«mn mathvariant=¨bold¨ mathcolor=¨#0000FF¨»2«/mn»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»§#183;«/mo»«mi mathvariant=¨bold¨ mathcolor=¨#0000FF¨»§#960;«/mi»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»§#183;«/mo»«msqrt mathcolor=¨#0000FF¨»«mfrac»«msub»«mi mathvariant=¨bold¨»m«/mi»«mi mathvariant=¨bold¨»A«/mi»«/msub»«mi mathvariant=¨bold¨»K«/mi»«/mfrac»«/msqrt»«mspace linebreak=¨newline¨»«/mspace»«mi mathvariant=¨bold¨ mathcolor=¨#0000FF¨»T«/mi»«msup»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»`«/mo»«mn mathvariant=¨bold¨ mathcolor=¨#0000FF¨»2«/mn»«/msup»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»=«/mo»«mn mathvariant=¨bold¨ mathcolor=¨#0000FF¨»4«/mn»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»§#183;«/mo»«msup»«mi mathvariant=¨bold¨ mathcolor=¨#0000FF¨»§#960;«/mi»«mn mathvariant=¨bold¨ mathcolor=¨#0000FF¨»2«/mn»«/msup»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»§#183;«/mo»«mrow mathcolor=¨#0000FF¨»«mo mathvariant=¨bold¨»(«/mo»«mfrac»«msub»«mi mathvariant=¨bold¨»m«/mi»«mi mathvariant=¨bold¨»A«/mi»«/msub»«mi mathvariant=¨bold¨»K«/mi»«/mfrac»«mo mathvariant=¨bold¨»)«/mo»«/mrow»«mspace linebreak=¨newline¨»«/mspace»«mspace linebreak=¨newline¨»«/mspace»«mi mathvariant=¨bold¨ mathcolor=¨#0000FF¨»K«/mi»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»=«/mo»«mfrac mathcolor=¨#0000FF¨»«mrow»«mn mathvariant=¨bold¨»4«/mn»«mo mathvariant=¨bold¨»§#183;«/mo»«msup»«mi mathvariant=¨bold¨»§#960;«/mi»«mn mathvariant=¨bold¨»2«/mn»«/msup»«mo mathvariant=¨bold¨»§#183;«/mo»«msub»«mi mathvariant=¨bold¨»m«/mi»«mi mathvariant=¨bold¨»A«/mi»«/msub»«/mrow»«mrow»«mi mathvariant=¨bold¨»T«/mi»«msup»«mo mathvariant=¨bold¨»`«/mo»«mn mathvariant=¨bold¨»2«/mn»«/msup»«/mrow»«/mfrac»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»=«/mo»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»§#160;«/mo»«mfrac mathcolor=¨#0000FF¨»«mrow»«mn mathvariant=¨bold¨»4«/mn»«mo mathvariant=¨bold¨»§#183;«/mo»«msup»«mi mathvariant=¨bold¨»§#960;«/mi»«mn mathvariant=¨bold¨»2«/mn»«/msup»«mo mathvariant=¨bold¨»§#183;«/mo»«mn mathvariant=¨bold¨»1«/mn»«/mrow»«msup»«mn mathvariant=¨bold¨»1«/mn»«mn mathvariant=¨bold¨»2«/mn»«/msup»«/mfrac»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»=«/mo»«mn mathvariant=¨bold¨ mathcolor=¨#0000FF¨»39«/mn»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨».«/mo»«mn mathvariant=¨bold¨ mathcolor=¨#0000FF¨»47«/mn»«mfrac mathcolor=¨#0000FF¨»«mi mathvariant=¨bold¨»N«/mi»«mi mathvariant=¨bold¨»m«/mi»«/mfrac»«mspace linebreak=¨newline¨»«/mspace»«/math»

לכן ערכו של קבוע הקפיץ הוא 39.47 ניוטון למטר.

1. في كل تجربة يوجد خطأ في القياس، وليس من الصحيح الوصول إلى نتيجة من نقطة واحدة على الرسم البياني.
ومن المهم التوصل إلى النتيجة من خط الاتجاه (الخط الأكثر احتمالا) والذي يمثل كافة نتائج القياس.
في هذه الحالة، الدالة الموضحة في الرسم البياني غير خطية. لا يمكن استخدام خط الاتجاه،
بدون أي خيار، نصل إلى استنتاج أن نستعمل نقطة على الرسم البياني.

2. إذا وصفنا كتلة الجسم B كدالة لزمن الدورة، نحصل على دالة خطية. ومن الميل يمكننا الاستنتاج.
لكن السؤال يقول: "باستخدام الرسم البياني أمامك..."

חשוב להגיע למסקנה מהישר המסתבר ביותר המייצג את כל תוצאות המדידות.

במקרה הזה הפונקציה המתוארת בגרף היא לא ליניארית. לא ניתן להשתמש בישר המסתבר ביותר ,

בלית ברירה מגיעים למסקנה מנקודה בגרף.

2. אם נתאר את מסת גוף B בתלות בזמן המחזור נקבל פונקציה ליניארית. ונוכל להגיע למסקנה מהשיפוע .

אך בשאלה כתוב: " באמצעות הגרף שלפניך..."

______________________________________________________________________________________

...

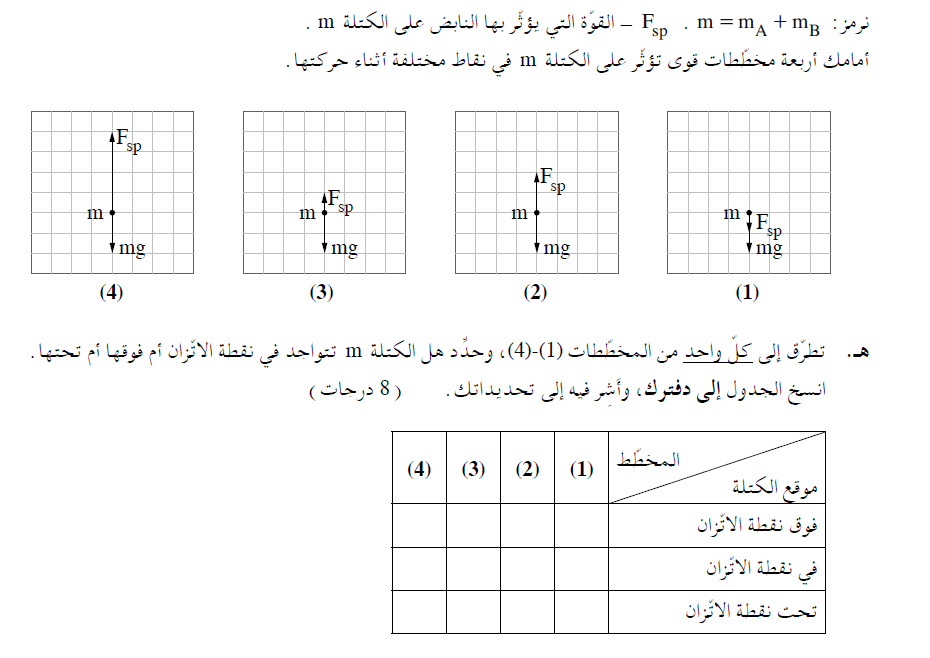
الديناميكية، معرفة قوة النابض.

قوة النابض هي قوة مُعيدة، تعمل باتجاه النقطة التي يكون فيها الجسم عندما يكون النابض مسترخيًا أي نحو نقطة الاتزان،

طالما أن النابض مضغوط، فإن قوة النابض تعمل للأعلى. عندما يستطيل النابض، تعمل قوة النابض إلى الأسفل.

نقطة الاتزان - نقطة الاتزان هي النقطة التي تكون فيها القوة المؤثرة على الجسم تساوي صفرًا.

الشكل 2 يتوافق مع نقطة الاتزان.

تحت نقطة الاتزان - عندما يكون الجسم تحت نقطة الاتزان، تكون قوة النابض أكبر من قوة النابض في نقطة الاتزان.

الشكل 4 يتوافق مع نقطة الاتزان.

فوق نقطة الاتزان - عندما يكون الجسم فوق نقطة الاتزان، هناك حالتان محتملتان:

الحالة الأولى هي أن النابض لا يزال مضغوطًا - ستكون قوة النابض أقل من قوة الزنبرك في نقطة الاتزان ولكنها لا تزال تعمل للأعلى.

الحالة الثانية: يصل الجسم إلى ارتفاع كبير، فوق النقطة التي يكون فيها النابض في حالة استرخاء والنابض استطال - في هذه الحالة تعمل قوة النابض إلى الأسفل.

لذلك، فإن الشكل 1 والشكل 3 يتوافقان مع الحالة التي يكون فيه الجسم فوق نقطة الاتزان.

سنقوم بملء الجدول الوارد في السؤال وفقًا لذلك:

כל עוד הקפיץ מכווץ כוח הקפיץ פועל כלפי מעלה. כאשר הקפיץ מתארך כוח הקפיץ פועל כלפי מטה.

נקודת שיווי משקל- נקודת שיווי משקל היא נקודה בה שקול הכוחות הפועלים על הגוף שווה לאפס.

איור 2 מתאים לנקודת שיווי משקל.

מתחת לנקודת שיווי משקל - כאשר הגוף נמצא מתחת לנקודת שיווי משקל כוח הקפיץ גדול יותר מכוח הקפיץ בנקודת שיווי משקל.

איור 4 מתאים לנקודת שיווי משקל.

מעל לנקודת שיווי משקל- כאשר הגוף נמצא מעל לנקודת שיווי משקל , יש שני מצבים אפשריים:

מצב אחד הקפיץ עדיין מכווץ- כוח הקפיץ יהיה קטן מכוח הקפיץ בנקודת שיווי משקל אך הוא עדיין פועל כלפי מעלה.

מצב שני הגוף הגיע לגובה רב , מעל לנקודה הקפיץ רפוי והקפיץ התארך- במקרה כזה כוח הקפיץ פועל כלפי מטה.

לכן איור 1 ואיור 3 מתאימים למצב שבו הגוף נמצא מעל לנקודת שיווי משקל.

נמלא בהתאם את הטבלה הנתונה בשאלה:

1. يتعلق مقدار واتجاه قوة النابض على بُعد الجسم من النقطة التي يكون فيها النابض مسترخيًا. بغض النظر عن نقطة الاتزان.

2. من المستحسن البدء بالأماكن الأكثر بساطة: نقطة الاتزان وأسفل نقطة الاتزان.
يمكن أن يساعد هذا في بناء الفهم للبنود التالية.

3. من الغريب بعض الشيء أن يوضع جسم على نابض وتأتي لحظة يستطيل فيها النابض ولا ينقبض،
يعتمد ذلك على مدى انحراف الجسم عن نقطة اتزانه.

إذا وضعنا الجسم على النابض وهبط من وضع الاسترخاء مليمترًا واحدًا إلى نقطة الاتزان.
إذا حركنا الجسم 10 سم إلى الأسفل من نقطة الاتزان فإنه سيتحرك حركة توافقية بسعة 10 سم.
في جزء من زمن حركته سيكون النابض في حالة استطالة.

في أي حركة توافقية بسيطة في نابض رأسي، يمكن للنابض أن يكون في حالة استطالة.

4. لا تحتاج إلى كتابة السبب في حل السؤال، كل ما عليك فعله هو نسخ الجدول وتحديده.
إذا كانت الإجابة غير صحيحة وكان السبب صحيحًا جزئيًا، فمن المحتمل أنك ستحصل على جزء من النقاط.

2. מומלץ להתחיל עם המקומות היותר פשוטים : נקודת שיווי משקל ומתחת לנקודת שיווי משקל.

זה יכול לעזור לבנות את ההבנה לסעיפים הבאים.

3. קצת מוזר שגוף מונח על קפיץ ויש רגע שבו הקפיץ מוארך ולא מכווץ,

זה תלוי במידה בה מסיטים את הגוף מנקודת שיווי משקל.

אם מניחים את הגוף על הקפיץ והוא יורד ממצבו הרפוי מילי מטר עד נקודת שיווי המשקל .

אם נסיט את הגוף מנקודת שיווי המשקל 10 ס"מ כלפי מטה והוא ינוע בתה"פ עם משרעת של 10 ס"מ

חלק מזמן התנועה הקפיץ יהיה מוארך.

בכל תנועה הרמונית פשוטה בקפיץ אנכי , הקפיץ יכול להיות מוארך.

4. לא צריך לכתוב נימוק בפתרון השאלה , צריך רק להעתיק את הטבלה ולקבוע .

אם התשובה לא נכונה והנימוק יהיה נכון חלקית רוב הסיכויים שתקבלו חלק מהניקוד .

______________________________________________________________________________________