حلول ومنتديات لألبوم الحلول – الحركة التوافقية البسيطة
| الموقع: | YouCube |
| المقرر: | תנועה הרמונית פשוטה - ערבית |
| كتاب: | حلول ومنتديات لألبوم الحلول – الحركة التوافقية البسيطة |
| طبع بواسطة: | משתמש אורח |
| التاريخ: | الأربعاء، 4 فبراير 2026، 12:46 AM |
جدول المحتويات
- 1. 2019,5-حركة توافقية رأسية لقياس الكتلة
- 2. 2018,5- حركة توافقية بسيطة لعربة مربوطة بنابض
- 3. 2017,7- حركة توافقية بسيطة لعربه في اتجاه أفقي
- 4. 2007,5 مُعططى رسم بياني v(t) لحركة توافقية بسيطة لنابض عمودي
- 5. 2005,5- قفزة البانجي
- 6. 2003,4 - ثلاث كرات وثلاثة رسوم بيانية
- 7. 2003,3-البندوال الرياضي
- 8. 2002,5 - عربة تصطدم بنابض أفقي.
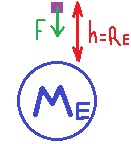
- 9. 2001,5- قياس كتلة داخل قمر اصطناعي بالاعتماد على الحركة التوافقية البسيطة
- 10. 1998,4- ايجاد g بواسطة البندول الرياضي
- 11. 1994,4- تعريف الحركة التوافقية البسيطة العمودية
- 12. 1993,5 حركة توافقية بسيطة مع نابض عمودي، مُعطى y(t)
- 13. 1993,3 -رصاصة تخترق جسمًا ويتحركان بحركة بندول بسيط.
- 14. 1992,3- سلة مع أوزان تتحرك في حركة توافقية بسيطة
- 15. 1990,4- يتحرك ثقل مربوط بنابض عمودي في في حركة توافقية بسيطة ثم ينفصل.
- 16. 1989,4 - رسم بياني للقوة كدالة للموقع
- 17. 1988,4- خرزة داخل طوق
- 18. 1987,4 - جسم مربوط بنابض أفقي ويتحرك في حركة توافقية بسيطة
- 19. 1986,2- يتحرك جسمين معًا في حركة توافقية بسيطة بين نابضين.
- 20. 1985,2 - تتأرجح الأجسام على ستة نوابض عمودية
- 21. 1983,19- جسمان معلقان على نابض عمودي.
- 22. 1981,3- البندول البسيط
- 23. 1980,3
1. 2019,5-حركة توافقية رأسية لقياس الكتلة
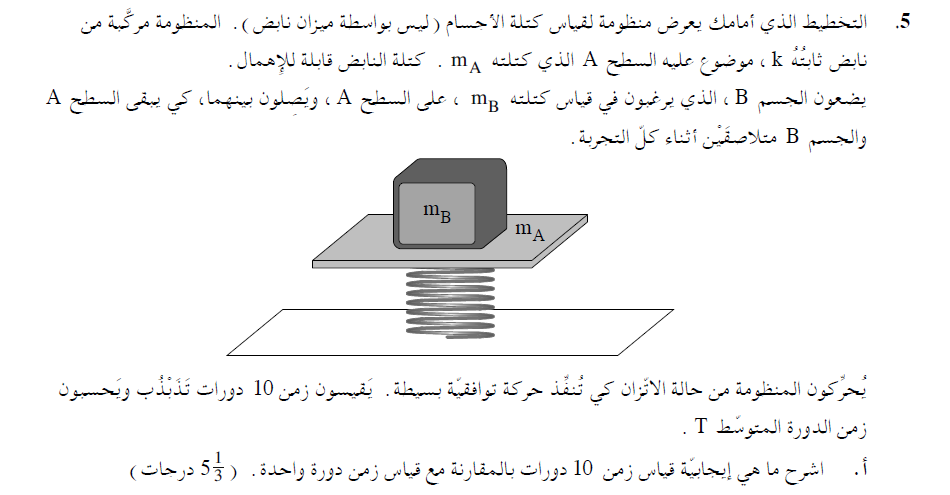
______________________________________________________________________________________
______________________________________________________________________________________

______________________________________________________________________________________
______________________________________________________________________________________
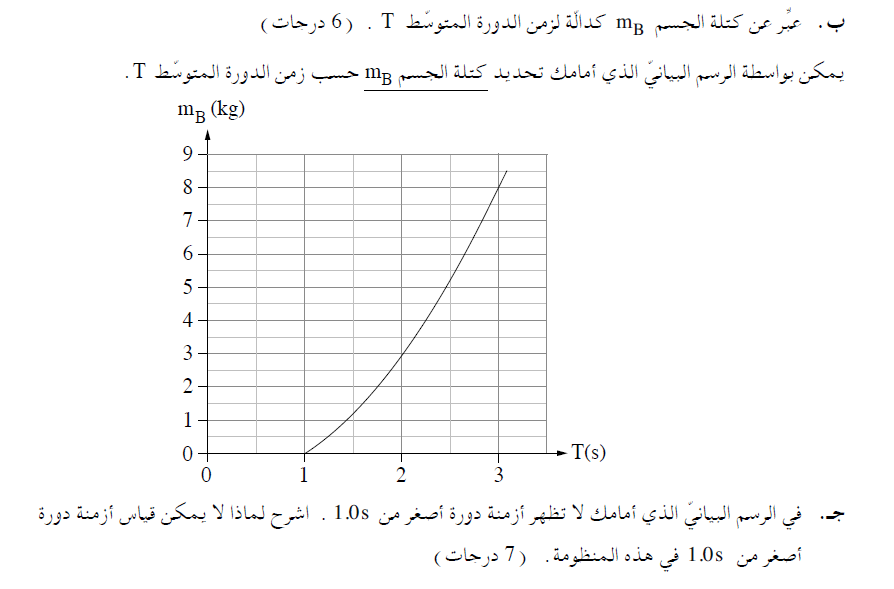
______________________________________________________________________________________
______________________________________________________________________________________
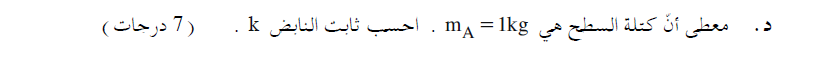
______________________________________________________________________________________
لكن السؤال يقول: "باستخدام الرسم البياني أمامك..."
______________________________________________________________________________________
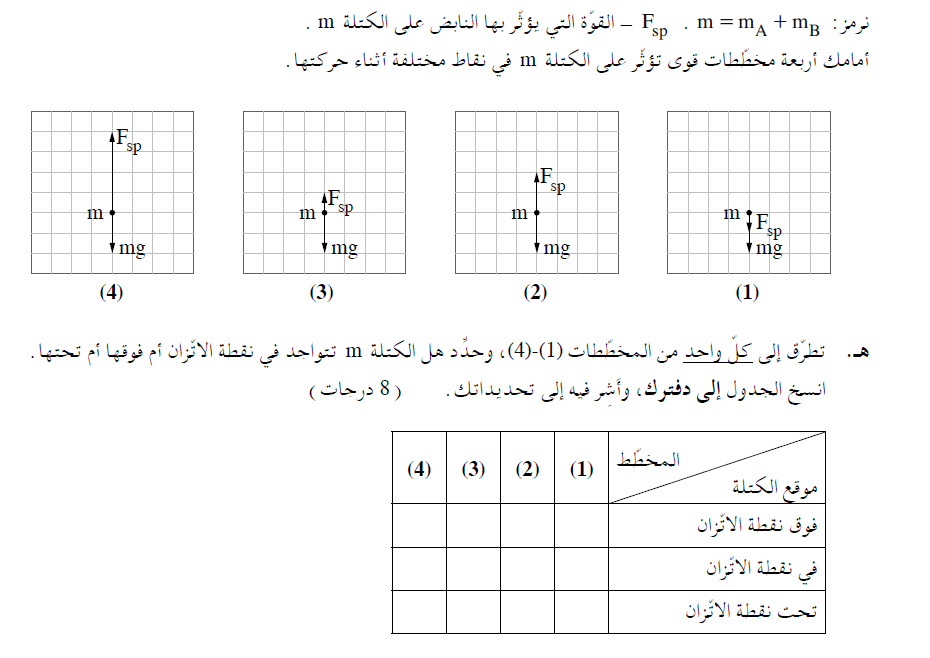
______________________________________________________________________________________
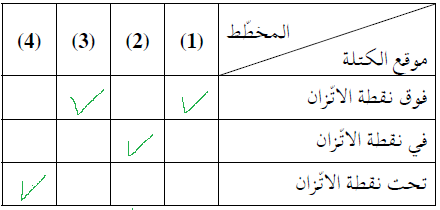

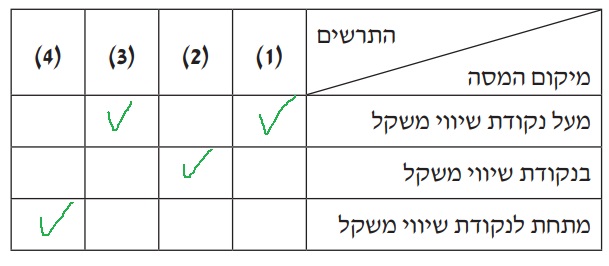
يمكن أن يساعد هذا في بناء الفهم للبنود التالية.
يعتمد ذلك على مدى انحراف الجسم عن نقطة اتزانه.
إذا كانت الإجابة غير صحيحة وكان السبب صحيحًا جزئيًا، فمن المحتمل أنك ستحصل على جزء من النقاط.
______________________________________________________________________________________
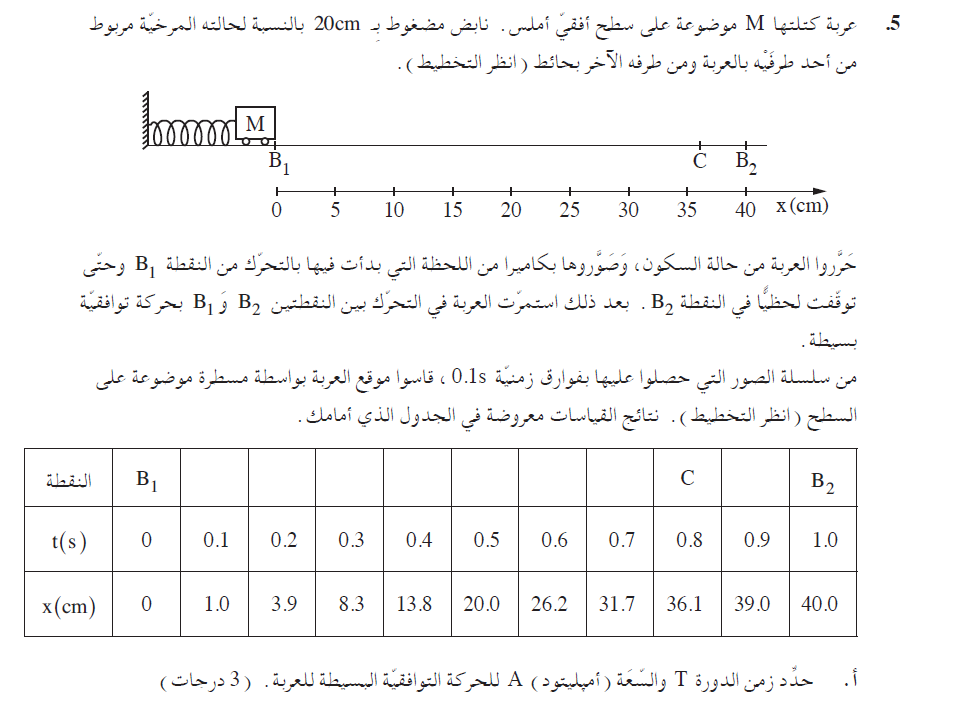
2. 2018,5- حركة توافقية بسيطة لعربة مربوطة بنابض
 ______________________________________________________________________________________
______________________________________________________________________________________
زمن الدورة في الحركة التوافقية البسيطة هو الزمن الذي يمر من لحظة بدء الجسم في الحركة حتى يعود إلى نقطة بداية الحركة، وهو الزمن ذهابًا وإيابًا.
السعة تساوي بعد نقطة احدى طرفي الحركة عن نقطة الاتزان.
زمن الدورة هو الزمن الذي يمر من لحظة بدء الحركة حتى عودة الجسم إلى نقطة بداية الحركة.
ومن الجدول يمكن فهم أن الزمن الذي يمر من لحظة بدء الحركة عند نقطة النهاية اليسرى حتى يصل الجسم إلى نقطة النهاية اليمنى هو ثانية واحدة، وبالتالي فإن الزمن الذي يمر من لحظة بدء الحركة حتى عودة العربة إلى نقطة بداية الحركة هو ثانيتين.
السعة تساوي البعد بين نقطة الاتزان وإحدى نقاط طرفي الحركة. يتم ضغط النابض بمقدار 20 سم، وبالتالي فإن النقطة التي يسترخي فيها النابض هي x=20cm، ويتحرك الجسم بين نقطة النهاية اليسرى x=0cm وx=40cm.
البعد بين نقطة الاتزان ونقطة النهاية هي 20 سم. هذا البعد هو سعة الحركة.
1. بحسب السؤال، ليست هناك حاجة للتفسير، حتى لو كتب الطالب الإجابات النهائية بدون تفسير، إذا كانت الإجابات صحيحة. سيحصل على النقاط الكاملة، ولكن إذا كانت الإجابات غير صحيحة، فلن يحصل على أي نقاط على إجاباته. لذلك فمن المستحسن أن تكتب تفسيرًا مختصرًا حتى لو لم يكن التفسير مطلوبًا.
2. يتم إعطاء القيم في الجدول بوحدات غير قياسية. يمكن وصف الحركة بوحدات غير قياسية، ولكن لا يمكن استخدام الوحدات غير القياسية في التعبيرات الفيزيائية.
______________________________________________________________________________________
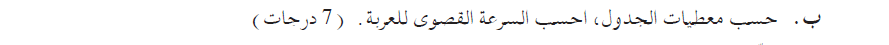
______________________________________________________________________________________
يساوي حاصل ضرب السرعة الزاوية في السعة:
في الحركة التوافقية البسيطة، لا يتحرك الجسم بتسارع ثابت، لذا فإن الإجابة ليست دقيقة (بالإضافة إلى أننا اعتمدنا على نتائج القياس).
______________________________________________________________________________________

______________________________________________________________________________________
ويتعلق زمن الدورة على C وفقًا لـلتعبير:
______________________________________________________________________________________

______________________________________________________________________________________
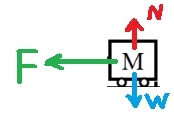
نرسم مخطط القوى:
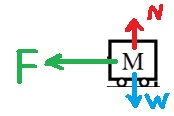
لإيجاد قوة النابض واستخدام دوال الحركة التوافقية البسيطة، سنقوم بتحديد محور حركة جديد يبدأ في نقطة الاتزان.
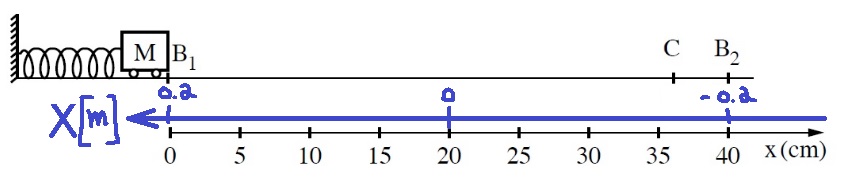
سوف نستخدم دالة الموقع كدالة للزمن الملائمة للحركة التوافقية البسيطة:


يجب تحديد محور جديد، بدءًا من النقطة التي يكون فيها الجسم في حالة اتزان.
وسيكون من الممكن استخدام دوال الحركة التوافقية البسيطة بدون زاوية طور ابتدائية.
إن الزمن الذي يمر بين لحظة مرور الجسم بنقطة ما للمرة الأولى والمرة الثانية عبر تلك النقطة ليس زمن دورة ولا نصف دورة.
______________________________________________________________________________________

______________________________________________________________________________________
هناك تعبيرات "غير محدودة"، ويجب فحص العلاقة لكل من الكميات الفيزيائية التي تظهر في التعبير.
______________________________________________________________________________________
3. 2017,7- حركة توافقية بسيطة لعربه في اتجاه أفقي

______________________________________________________________________________________
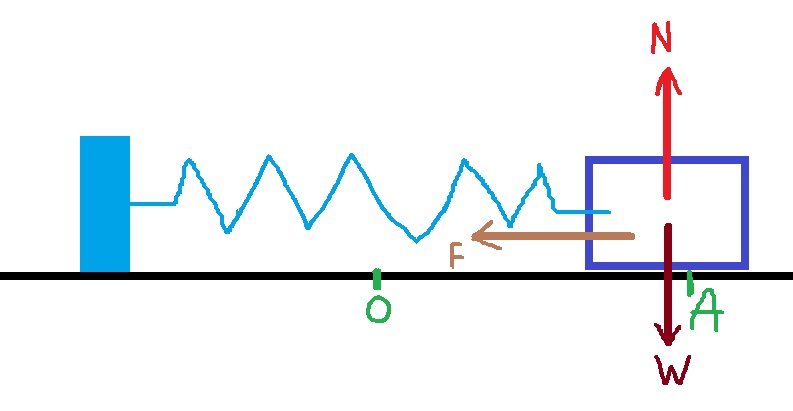
______________________________________________________________________________________

______________________________________________________________________________________
لاستخدام الدوال الأخرى في الحركة التوافقية البسيطة، يجب عليك أولاً تحديد محور الحركة.
______________________________________________________________________________________

______________________________________________________________________________________
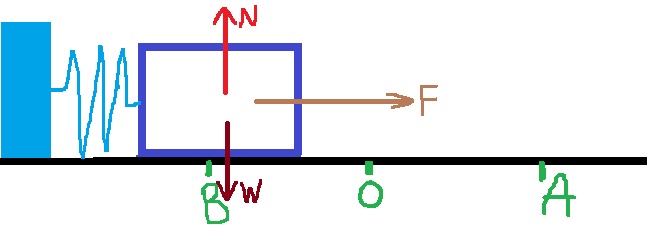
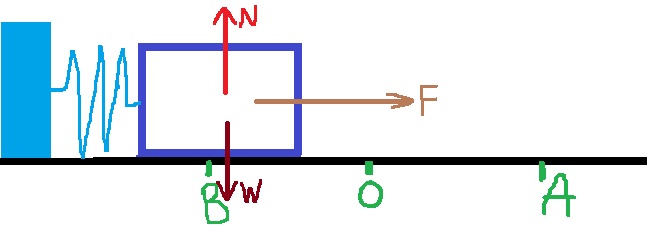
______________________________________________________________________________________

______________________________________________________________________________________
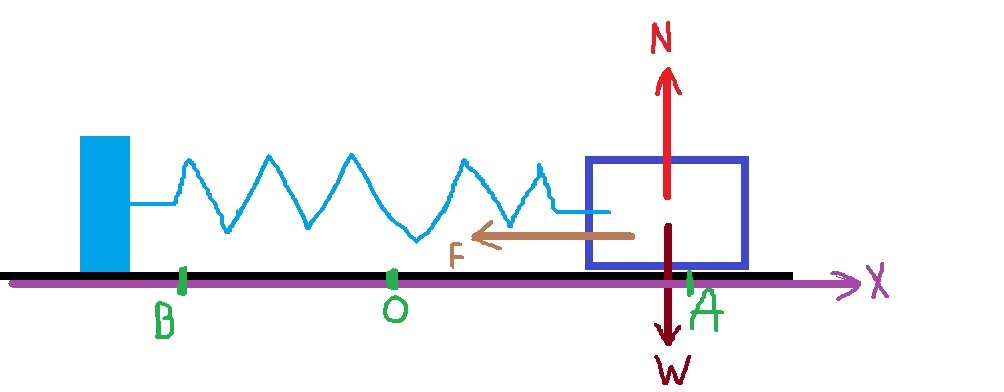

في نقطة الاتزان يكون صفرًا:
______________________________________________________________________________________

______________________________________________________________________________________
______________________________________________________________________________________
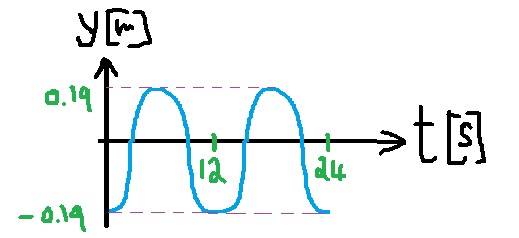
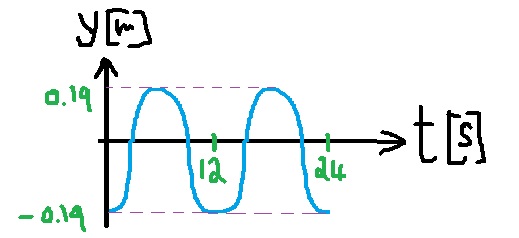
4. 2007,5 مُعططى رسم بياني v(t) لحركة توافقية بسيطة لنابض عمودي
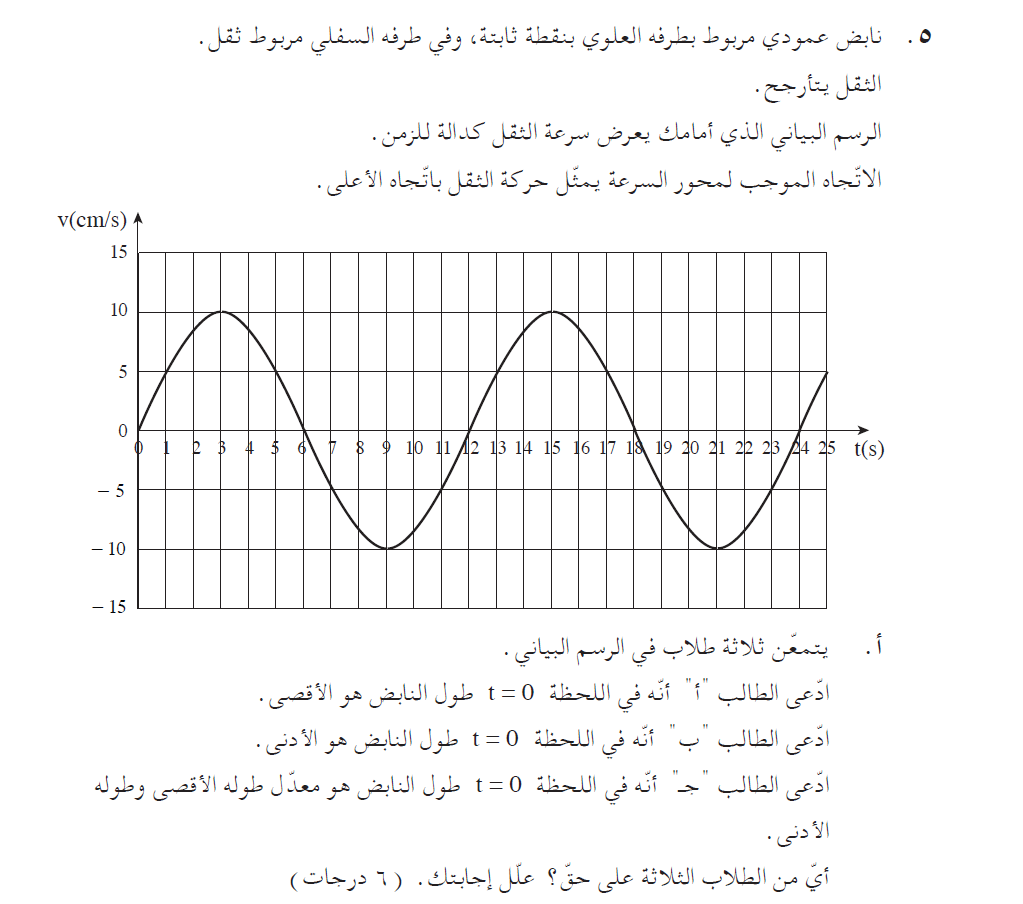
______________________________________________________________________________________
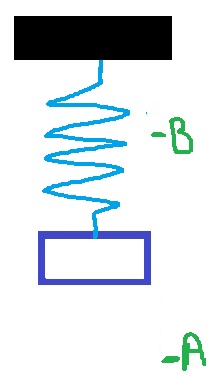

المقصود أنه عندما تكون قيمة السرعة موجبة، يتحرك الثقل إلى الأعلى.:
______________________________________________________________________________________
______________________________________________________________________________________
______________________________________________________________________________________
______________________________________________________________________________________
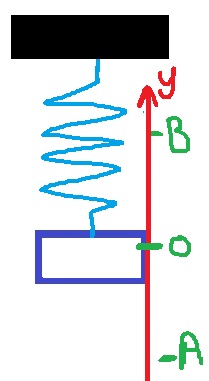

أو اضرب دالة الموقع-الزمن، والسرعة-الزمن، والتسارع-الزمن في ناقص واحد.
______________________________________________________________________________________

______________________________________________________________________________________

______________________________________________________________________________________

______________________________________________________________________________________
______________________________________________________________________________________
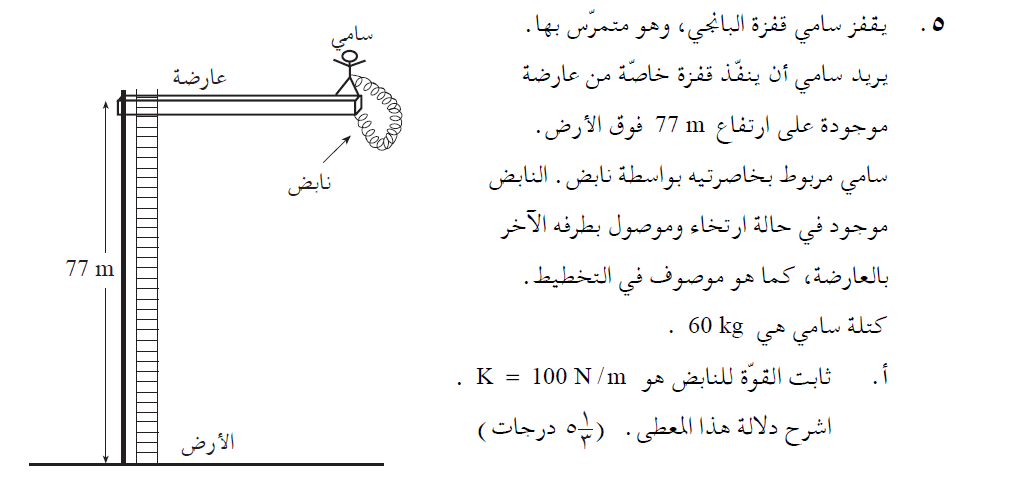
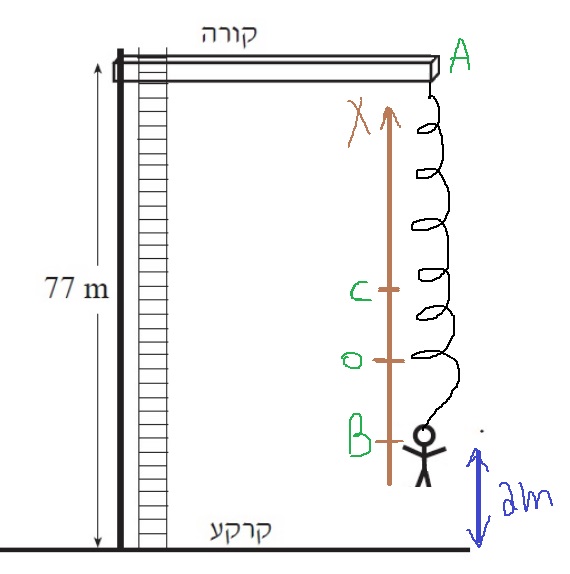
5. 2005,5- قفزة البانجي
______________________________________________________________________________________
______________________________________________________________________________________

______________________________________________________________________________________
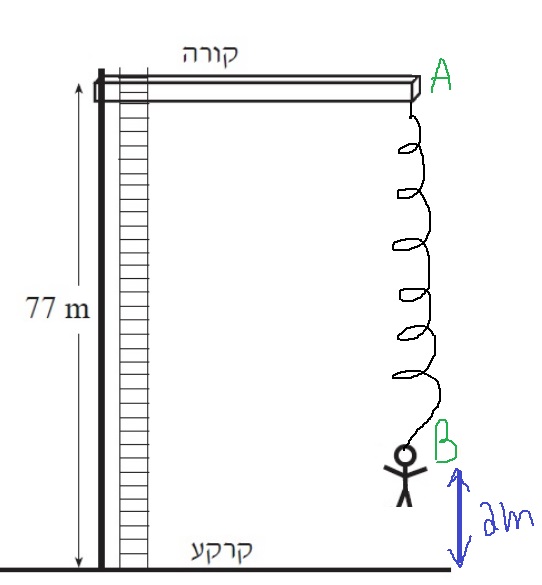

حتى لو قفز إلى أسفل أو إلى أعلى، فهو لا يزال سقوطًا حرًا. ومن المفترض أن القصد هو أنه بدأ التحرك من السكون.
______________________________________________________________________________________

______________________________________________________________________________________

______________________________________________________________________________________

______________________________________________________________________________________
______________________________________________________________________________________

______________________________________________________________________________________

______________________________________________________________________________________
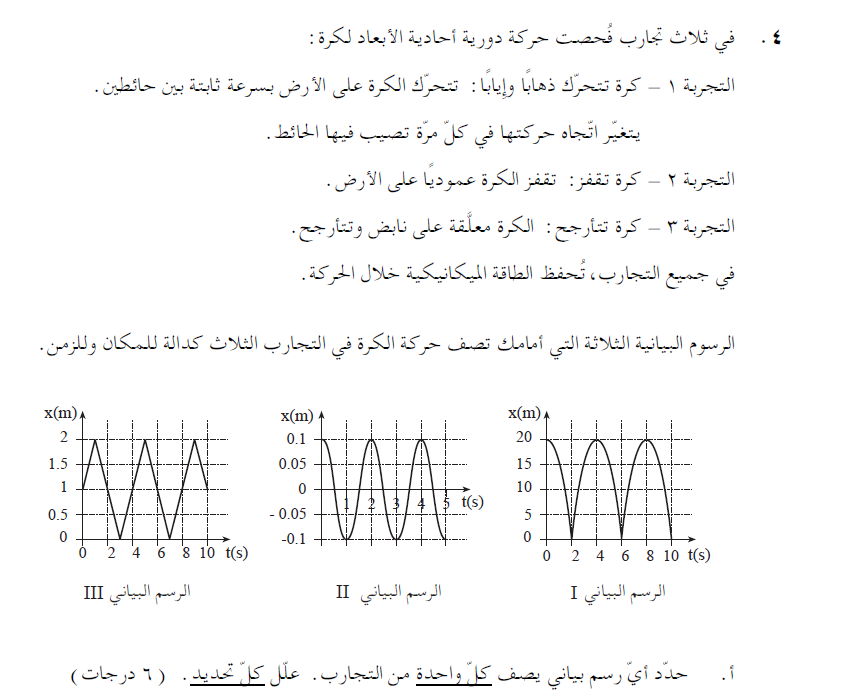
6. 2003,4 - ثلاث كرات وثلاثة رسوم بيانية
______________________________________________________________________________________
في فترة من الزمن يكون الميل ثابتًا وموجبًا. وفي فترة أخرى يكون الميل سالبًا ثابتًا - والرسم البياني الملائم هو الرسم البياني 3.
في لحظة الاصطدام، تغير الكرة اتجاه حركتها، وتغير السرعة إشارتها - والرسم البياني الملائم هو الرسم البياني 1.
شكله العام دالة جيب التمام، والرسم البياني الملائم هو الرسم البياني 2.
______________________________________________________________________________________
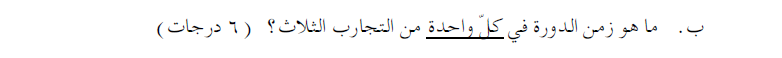
______________________________________________________________________________________
على سبيل المثال، في الكرة المتحركة ذهابًا وإيابًا، تصل الكرة إلى نفس النقطة كل ثانية، ولكن زمن الدورة هو ثانيتين.
______________________________________________________________________________________
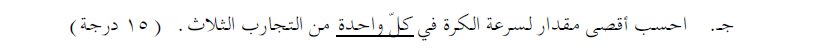
______________________________________________________________________________________
وبعد ذلك فقط يمكنك استخدام دوال الحركة التوافقية البسيطة.
______________________________________________________________________________________

______________________________________________________________________________________
______________________________________________________________________________________
7. 2003,3-البندوال الرياضي

______________________________________________________________________________________
2. هناك أسئلة بسيطة، وهذا أمر جيد. عندما لا يكون هناك داعي للخوف، فمن الأفضل عدم الخوف.
______________________________________________________________________________________
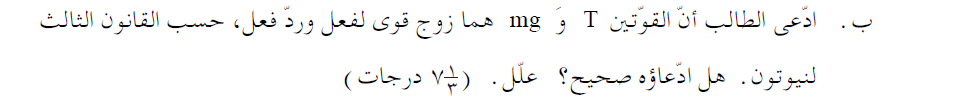
______________________________________________________________________________________
______________________________________________________________________________________

______________________________________________________________________________________
______________________________________________________________________________________

______________________________________________________________________________________
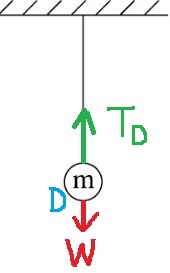
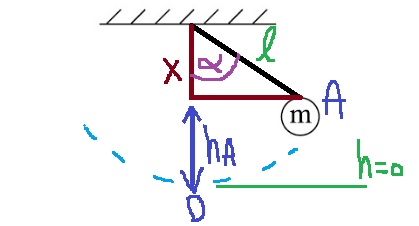
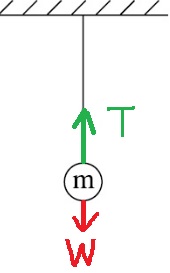
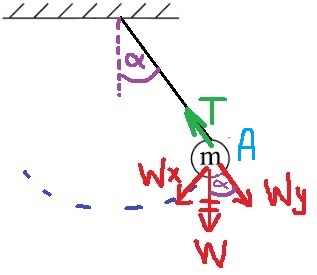
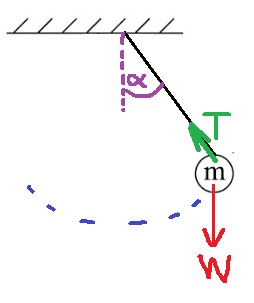
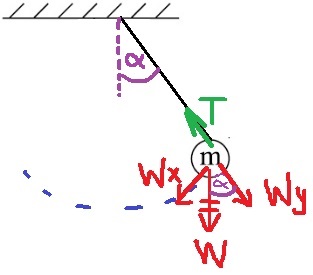
على الرغم من أن هذه مجرد مواقع مختلفة، فإن كل موقع له خصائصه الخاصة، ويتطور مسار الحل في البندين بشكل مختلف.
______________________________________________________________________________________
8. 2002,5 - عربة تصطدم بنابض أفقي.
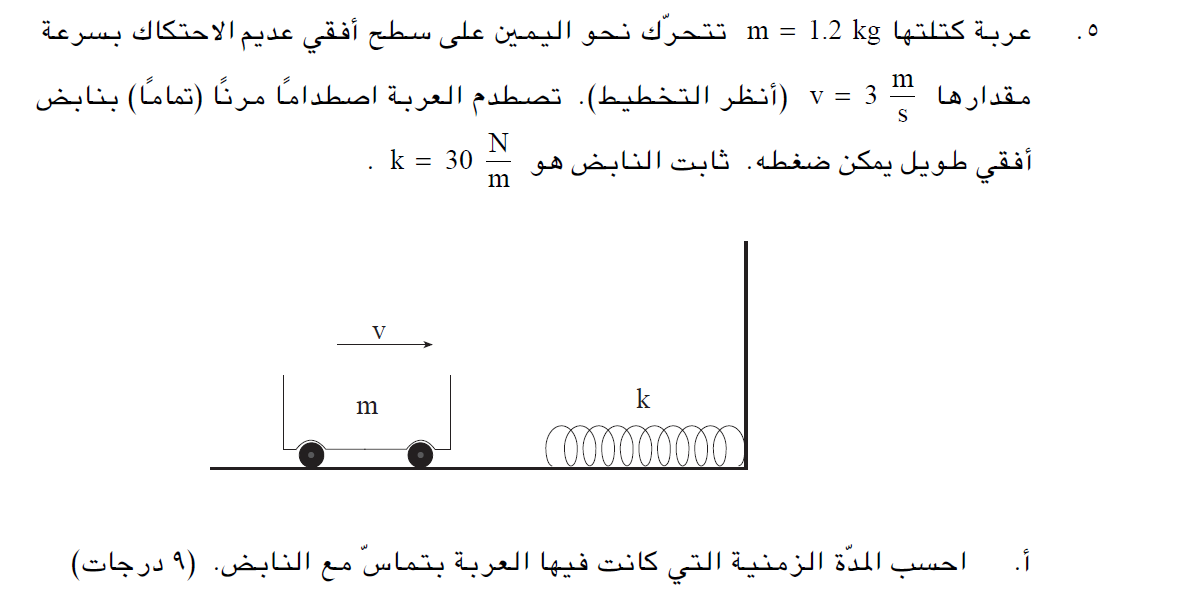
______________________________________________________________________________________
______________________________________________________________________________________

______________________________________________________________________________________
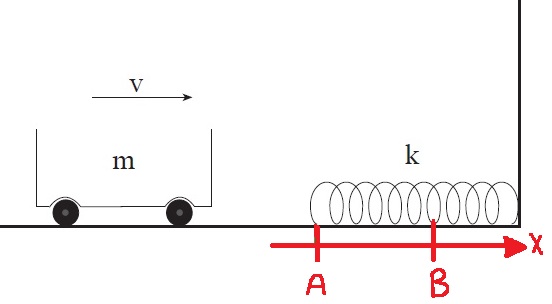

______________________________________________________________________________________

______________________________________________________________________________________
______________________________________________________________________________________

______________________________________________________________________________________
______________________________________________________________________________________
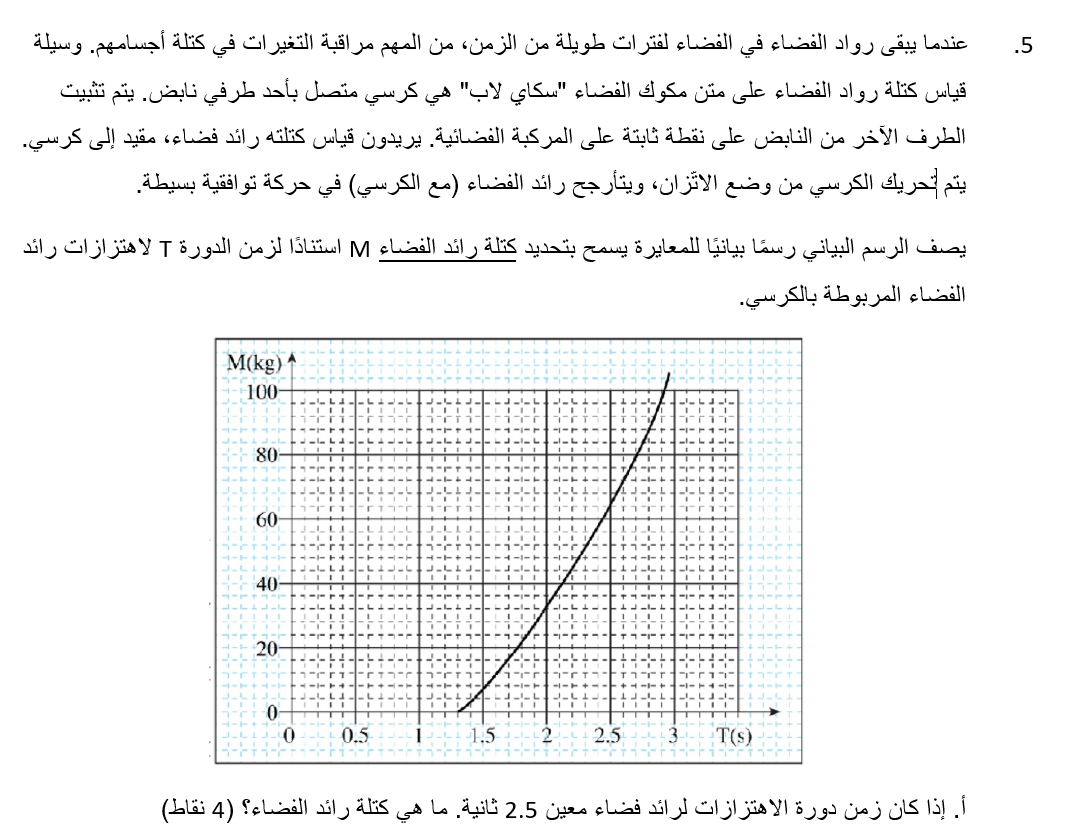
9. 2001,5- قياس كتلة داخل قمر اصطناعي بالاعتماد على الحركة التوافقية البسيطة
______________________________________________________________________________________
______________________________________________________________________________________

______________________________________________________________________________________
______________________________________________________________________________________

______________________________________________________________________________________
______________________________________________________________________________________

______________________________________________________________________________________
______________________________________________________________________________________

______________________________________________________________________________________
______________________________________________________________________________________

______________________________________________________________________________________
______________________________________________________________________________________
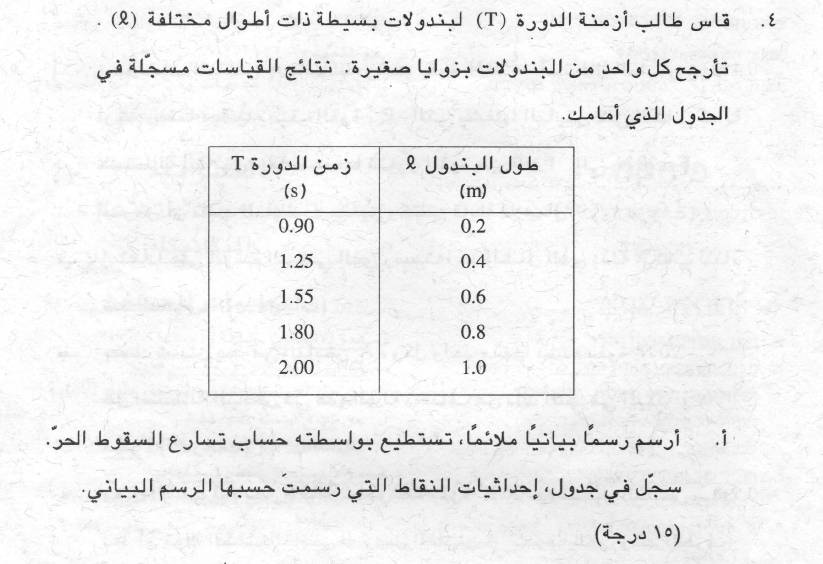
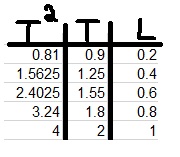
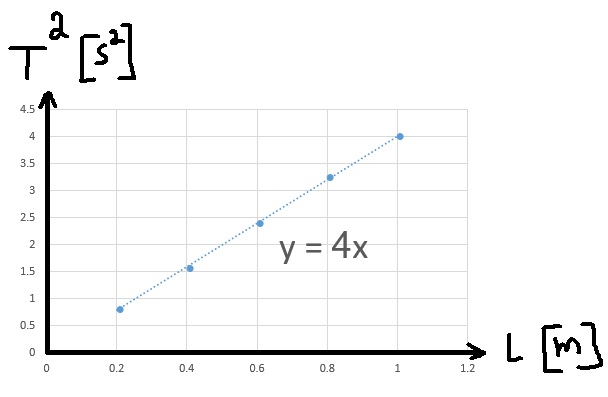
10. 1998,4- ايجاد g بواسطة البندول الرياضي
______________________________________________________________________________________


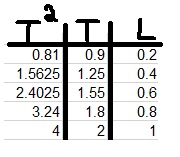
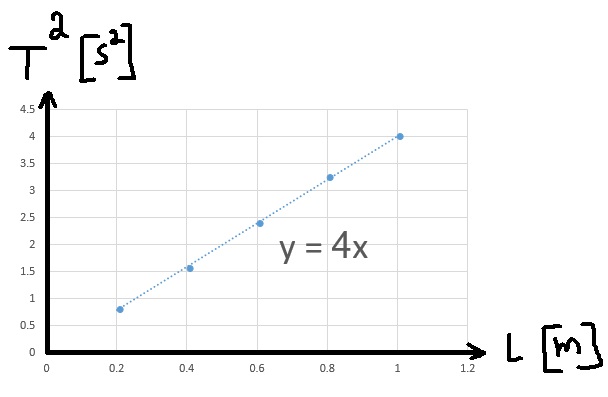


______________________________________________________________________________________

______________________________________________________________________________________
______________________________________________________________________________________
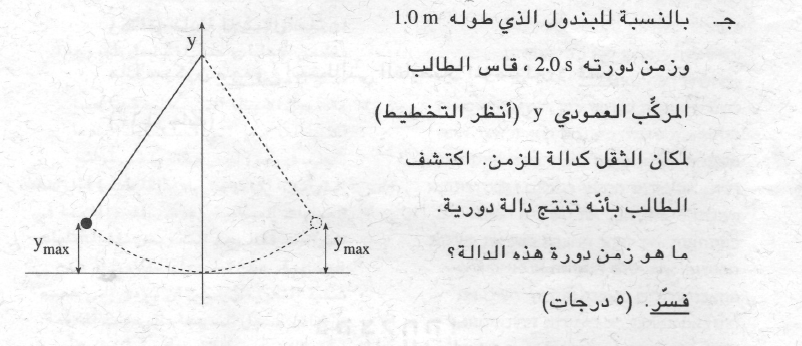
______________________________________________________________________________________
______________________________________________________________________________________
11. 1994,4- تعريف الحركة التوافقية البسيطة العمودية

______________________________________________________________________________________
______________________________________________________________________________________
أ.
_ _____________________________________________________________________________________
_____________________________________________________________________________________
______________________________________________________________________________________

______________________________________________________________________________________
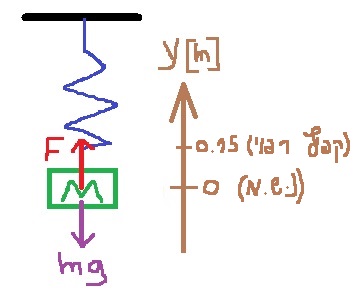
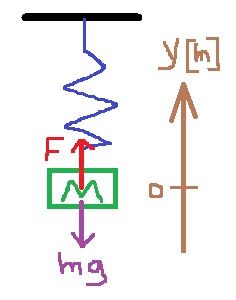
______________________________________________________________________________________
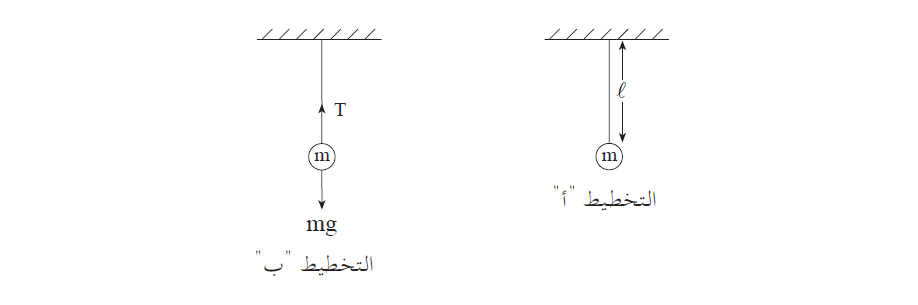
ب.

______________________________________________________________________________________
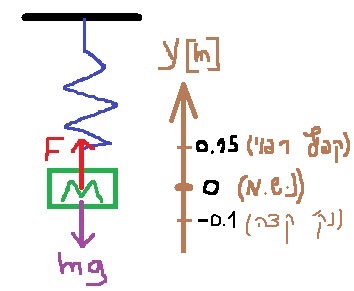
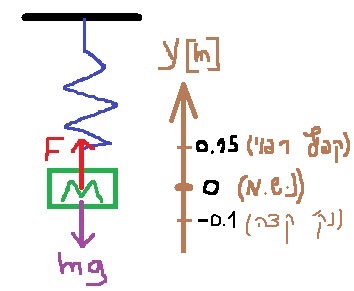
______________________________________________________________________________________
ب.

______________________________________________________________________________________
______________________________________________________________________________________
12. 1993,5 حركة توافقية بسيطة مع نابض عمودي، مُعطى y(t)
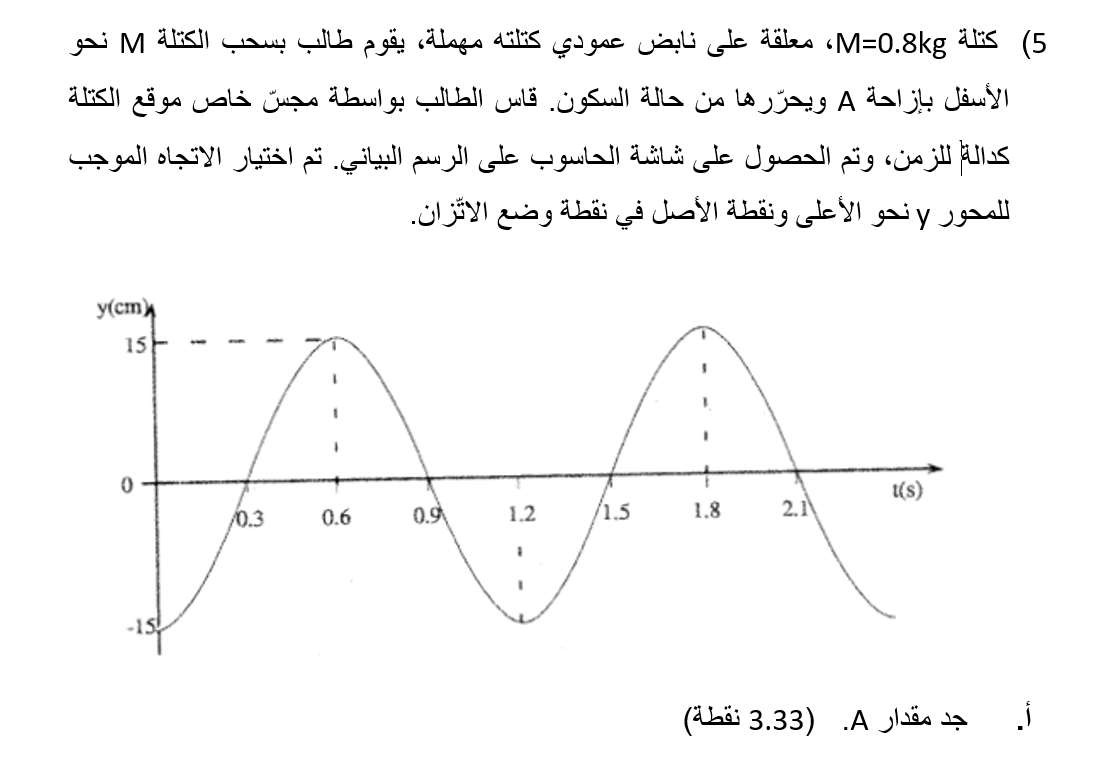
______________________________________________________________________________________
______________________________________________________________________________________

______________________________________________________________________________________
______________________________________________________________________________________
______________________________________________________________________________________
______________________________________________________________________________________

______________________________________________________________________________________
______________________________________________________________________________________
______________________________________________________________________________________
______________________________________________________________________________________

______________________________________________________________________________________
______________________________________________________________________________________
13. 1993,3 -رصاصة تخترق جسمًا ويتحركان بحركة بندول بسيط.

______________________________________________________________________________________
- تعود الأجسام المصطدمة إلى شكلها الأصلي (يجب أن تكون الأجسام مصنوعة من مواد مرنة).
______________________________________________________________________________________

______________________________________________________________________________________
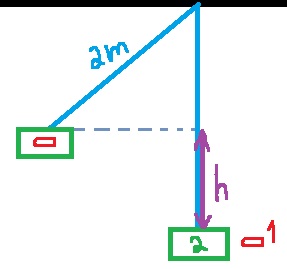
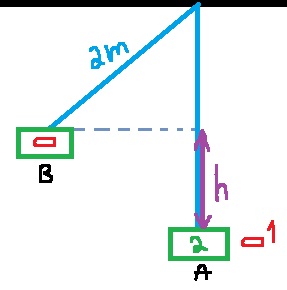


الحل الأفضل هو الإشارة لكل من الكتلتين بـ m1 m2 وبالتالي V1،V2،U1،U2.
وبالتالي هناك مرحلتين مختلفتين، مرحلة الاصطدام التي يكون فيها حفظ لكمية الحركة . ومرحلة الحركة التي يتم فيها حفظ الطاقة.
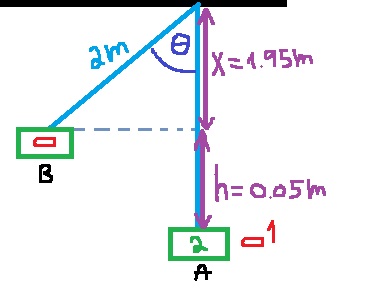
هي سرعة الصندوق والرصاصة في النقطة A، ويشار إليها بـ VA.
______________________________________________________________________________________

______________________________________________________________________________________
حتى القوة العمودية المؤثرة على السطح لا تؤثر دائمًا بشكل عمودي على الحركة. يجب فحص كل حالة على حدة.
______________________________________________________________________________________

______________________________________________________________________________________

______________________________________________________________________________________
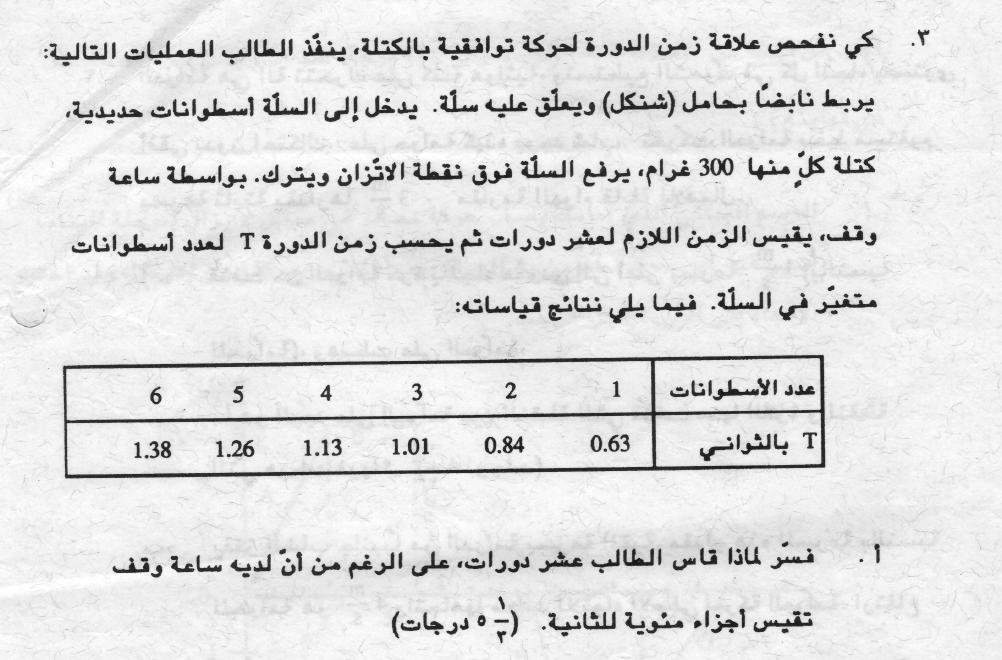
14. 1992,3- سلة مع أوزان تتحرك في حركة توافقية بسيطة
______________________________________________________________________________________
______________________________________________________________________________________

______________________________________________________________________________________


______________________________________________________________________________________

______________________________________________________________________________________

______________________________________________________________________________________

______________________________________________________________________________________
______________________________________________________________________________________
15. 1990,4- يتحرك ثقل مربوط بنابض عمودي في في حركة توافقية بسيطة ثم ينفصل.

______________________________________________________________________________________
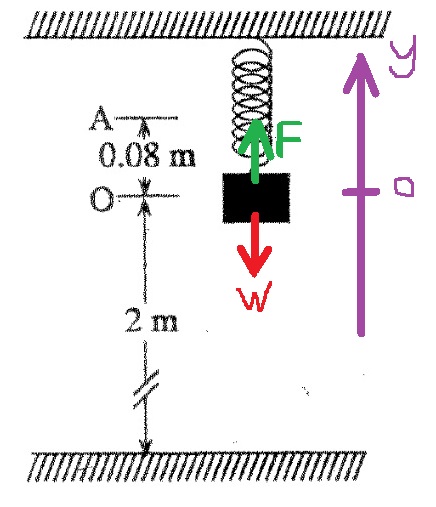

يجب إثبات أن القوة المحصّلة تتناسب خطيًا مع الموقع، قبل استخدام إحدى دوال الحركة التوافقية البسيطة.
______________________________________________________________________________________

______________________________________________________________________________________
______________________________________________________________________________________

______________________________________________________________________________________
______________________________________________________________________________________
16. 1989,4 - رسم بياني للقوة كدالة للموقع
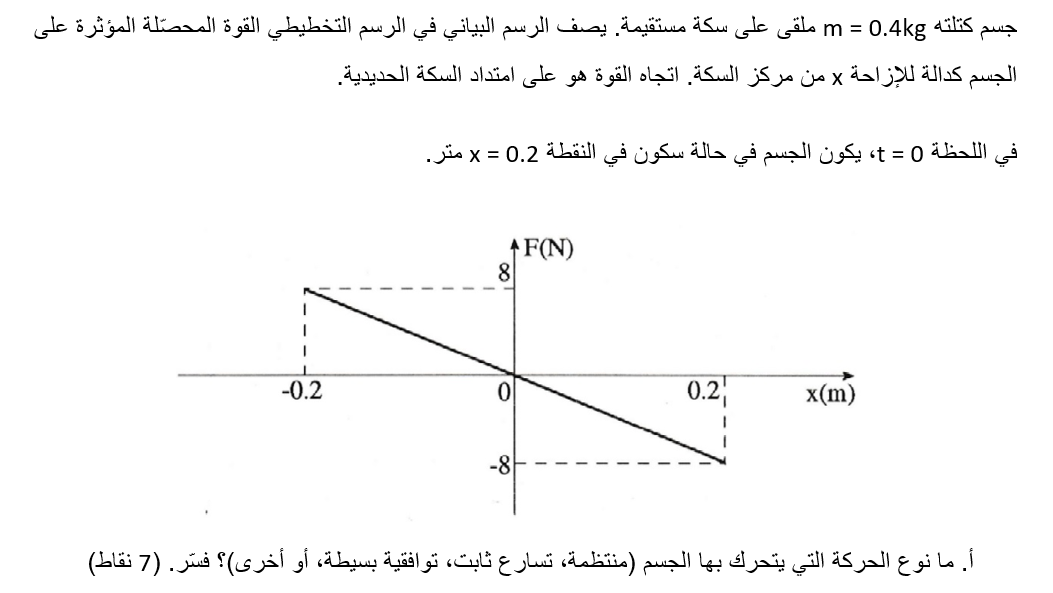
______________________________________________________________________________________
______________________________________________________________________________________

______________________________________________________________________________________
وبالتالي، فإن الميل سالب وثابت النابض موجب.
______________________________________________________________________________________
______________________________________________________________________________________
______________________________________________________________________________________
______________________________________________________________________________________
______________________________________________________________________________________

______________________________________________________________________________________
______________________________________________________________________________________
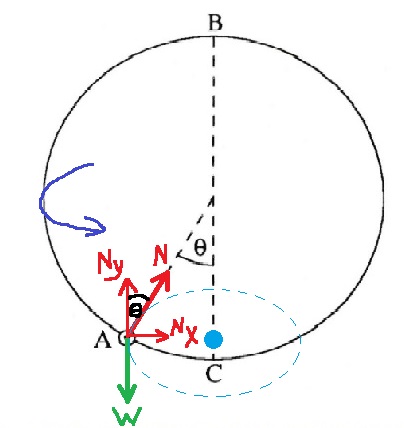
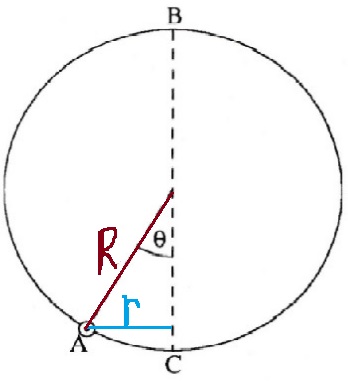
17. 1988,4- خرزة داخل طوق

______________________________________________________________________________________
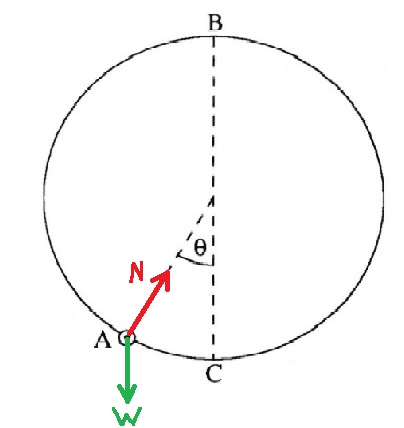

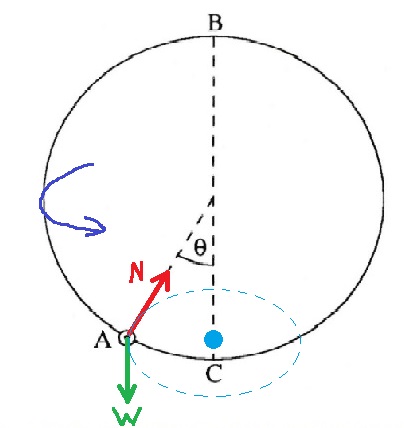
القوة العمودية تؤثر على الخرزة بشكل مشابه لقوة الشد المؤثرة على الجسم المتحرك في منظومة البندول البسيط.
______________________________________________________________________________________

______________________________________________________________________________________
______________________________________________________________________________________

______________________________________________________________________________________



______________________________________________________________________________________
18. 1987,4 - جسم مربوط بنابض أفقي ويتحرك في حركة توافقية بسيطة

______________________________________________________________________________________
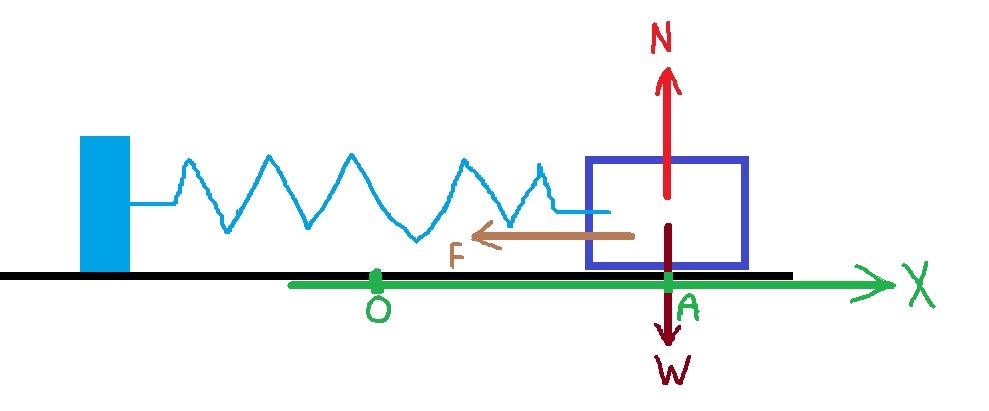

يمكن مقارنة قيمة الطاقة الميكانيكية الكلية بتعبير الطاقة في نقطة ما.
______________________________________________________________________________________

______________________________________________________________________________________
______________________________________________________________________________________

______________________________________________________________________________________
______________________________________________________________________________________

______________________________________________________________________________________
إذا كان السؤال هو ما هو المكان الذي يتحقق فيه الشرط، فسيكون هناك إجابتان صحيحتان.
______________________________________________________________________________________
19. 1986,2- يتحرك جسمين معًا في حركة توافقية بسيطة بين نابضين.

______________________________________________________________________________________
______________________________________________________________________________________

______________________________________________________________________________________
سنقوم بوصف حركة الجسمين بالنسبة للمحور الذي يشير إلى اليمين.
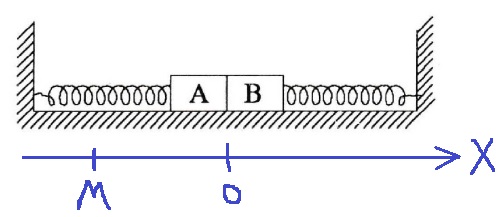

اعتمادًا على المحور المختار في الحل، يجب إضافة زاوية طور ابتدائية مقدارها «math xmlns=¨http://www.w3.org/1998/Math/MathML¨»«mtext mathvariant=¨bold¨ mathcolor=¨#FF0000¨»§#960;«/mtext»«/math» راديان.
______________________________________________________________________________________
ب.
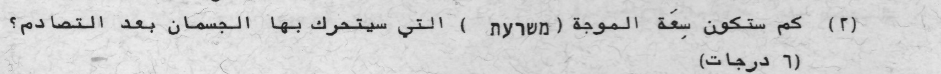
______________________________________________________________________________________
بعد الاصطدام، يتحرك الجسمان معًا كجسم واحد.
عندما يتحرك الجسمان معًا متر واحد إلى اليمين، ينكمش النابض الأيمن بمقدار متر واحد ويُشغل قوة مقدارها 30 نيوتن لكل متر على الجسم الأيسر.
من ناحية أخرى، يتم تمدّد النابض الأيسر بمقدار متر ويُشغل أيضًا قوة إلى اليسار مقدارها 30 نيوتن لكل متر.
يمكن التعامل مع النابضين كنابض واحد مع ثابت نابض 60 نيوتن لكل متر.
نستخدم دالة السرعة كدالة للموقع، في اللحظة التي يمر فيها الجسم بنقطة الاتّزان.
نعبر من هذا التعبير عن السعة، وفقًا للكتلة المشتركة. ومعامل النابض المحصّل مقداره 60 نيوتن لكل متر:
«math xmlns=¨http://www.w3.org/1998/Math/MathML¨»«mi mathvariant=¨bold¨ mathcolor=¨#0000FF¨»V«/mi»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»(«/mo»«mi mathvariant=¨bold¨ mathcolor=¨#0000FF¨»x«/mi»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»)«/mo»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»=«/mo»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»§#177;«/mo»«mi mathvariant=¨bold¨ mathcolor=¨#0000FF¨»§#969;«/mi»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»§#183;«/mo»«msqrt mathcolor=¨#0000FF¨»«msup»«mi mathvariant=¨bold¨»A«/mi»«mn mathvariant=¨bold¨»2«/mn»«/msup»«mo mathvariant=¨bold¨»-«/mo»«msup»«mi mathvariant=¨bold¨»X«/mi»«mn mathvariant=¨bold¨»2«/mn»«/msup»«/msqrt»«mspace linebreak=¨newline¨»«/mspace»«mspace linebreak=¨newline¨»«/mspace»«mi mathvariant=¨bold¨ mathcolor=¨#0000FF¨»V«/mi»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»(«/mo»«mn mathvariant=¨bold¨ mathcolor=¨#0000FF¨»0«/mn»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»)«/mo»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»=«/mo»«mi mathvariant=¨bold¨ mathcolor=¨#0000FF¨»§#969;«/mi»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»§#183;«/mo»«mi mathvariant=¨bold¨ mathcolor=¨#0000FF¨»A«/mi»«mspace linebreak=¨newline¨»«/mspace»«mspace linebreak=¨newline¨»«/mspace»«mi mathvariant=¨bold¨ mathcolor=¨#0000FF¨»A«/mi»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»=«/mo»«mfrac mathcolor=¨#0000FF¨»«mrow»«mi mathvariant=¨bold¨»V«/mi»«mo mathvariant=¨bold¨»(«/mo»«mn mathvariant=¨bold¨»0«/mn»«mo mathvariant=¨bold¨»)«/mo»«/mrow»«mi mathvariant=¨bold¨»§#969;«/mi»«/mfrac»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»=«/mo»«mfrac mathcolor=¨#0000FF¨»«mrow»«mi mathvariant=¨bold¨»V«/mi»«mo mathvariant=¨bold¨»(«/mo»«mn mathvariant=¨bold¨»0«/mn»«mo mathvariant=¨bold¨»)«/mo»«/mrow»«mstyle displaystyle=¨true¨»«mfrac»«menclose notation=¨updiagonalstrike¨»«mn mathvariant=¨bold¨»2«/mn»«mo mathvariant=¨bold¨»§#183;«/mo»«mi mathvariant=¨bold¨»§#960;«/mi»«/menclose»«mrow»«menclose notation=¨updiagonalstrike¨»«mn mathvariant=¨bold¨»2«/mn»«mo mathvariant=¨bold¨»§#183;«/mo»«mi mathvariant=¨bold¨»§#960;«/mi»«/menclose»«mo mathvariant=¨bold¨»§#183;«/mo»«msqrt»«mstyle mathvariant=¨bold¨»«mfrac»«msub»«mi»m«/mi»«mi»T«/mi»«/msub»«msub»«mi»K«/mi»«mi»T«/mi»«/msub»«/mfrac»«/mstyle»«/msqrt»«/mrow»«/mfrac»«/mstyle»«/mfrac»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»=«/mo»«mi mathvariant=¨bold¨ mathcolor=¨#0000FF¨»V«/mi»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»(«/mo»«mn mathvariant=¨bold¨ mathcolor=¨#0000FF¨»0«/mn»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»)«/mo»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»§#183;«/mo»«msqrt mathcolor=¨#0000FF¨»«mfrac»«msub»«mi mathvariant=¨bold¨»K«/mi»«mi mathvariant=¨bold¨»T«/mi»«/msub»«msub»«mi mathvariant=¨bold¨»m«/mi»«mi mathvariant=¨bold¨»T«/mi»«/msub»«/mfrac»«/msqrt»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»=«/mo»«mn mathvariant=¨bold¨ mathcolor=¨#0000FF¨»0«/mn»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨».«/mo»«mn mathvariant=¨bold¨ mathcolor=¨#0000FF¨»1«/mn»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»§#183;«/mo»«msqrt mathcolor=¨#0000FF¨»«mstyle mathvariant=¨bold¨»«mfrac»«mn»15«/mn»«mn»60«/mn»«/mfrac»«/mstyle»«/msqrt»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»=«/mo»«mn mathvariant=¨bold¨ mathcolor=¨#0000FF¨»0«/mn»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨».«/mo»«mn mathvariant=¨bold¨ mathcolor=¨#0000FF¨»05«/mn»«mi mathvariant=¨bold¨ mathcolor=¨#0000FF¨»m«/mi»«/math»
سيتحرك الجسمان بسعة مقدارها 5 سم.
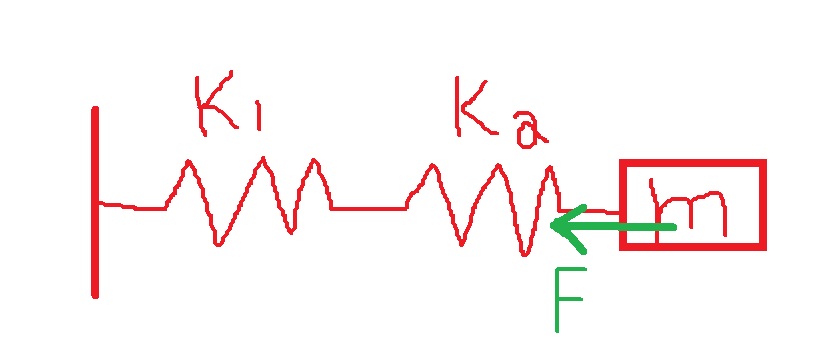
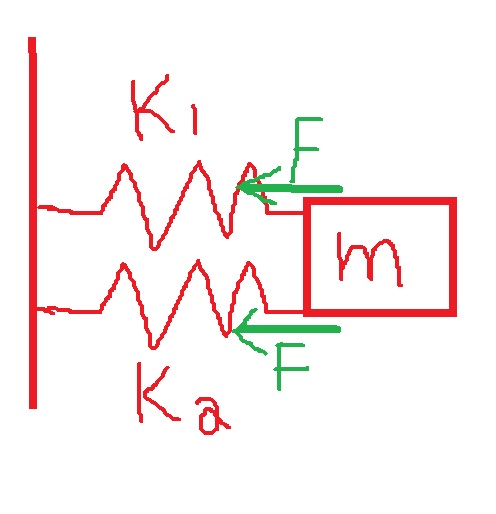
وليس لتوصيل النوابض على التوالي.


______________________________________________________________________________________

______________________________________________________________________________________
ليس من المستغرب أن محرري امتحان البجروت يحبون السؤال عن علاقة زمن الدورة بالسعة.
______________________________________________________________________________________
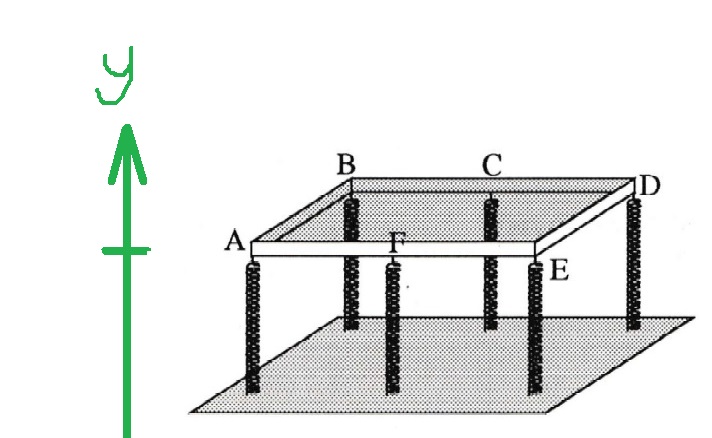
20. 1985,2 - تتأرجح الأجسام على ستة نوابض عمودية

______________________________________________________________________________________

«math xmlns=¨http://www.w3.org/1998/Math/MathML¨»«mi mathvariant=¨bold-italic¨ mathcolor=¨#0000FF¨»§#931;«/mi»«msub»«mi mathvariant=¨bold-italic¨ mathcolor=¨#0000FF¨»F«/mi»«mi mathvariant=¨bold¨ mathcolor=¨#0000FF¨»Y«/mi»«/msub»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»=«/mo»«mn mathvariant=¨bold¨ mathcolor=¨#0000FF¨»0«/mn»«mspace linebreak=¨newline¨»«/mspace»«msub»«mi mathvariant=¨bold-italic¨ mathcolor=¨#0000FF¨»F«/mi»«mn mathvariant=¨bold¨ mathcolor=¨#0000FF¨»0«/mn»«/msub»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»=«/mo»«mi mathvariant=¨bold-italic¨ mathcolor=¨#0000FF¨»M«/mi»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»§#183;«/mo»«mi mathvariant=¨bold-italic¨ mathcolor=¨#0000FF¨»g«/mi»«mspace linebreak=¨newline¨»«/mspace»«menclose mathcolor=¨#0000FF¨ notation=¨box¨»«mi mathvariant=¨bold¨»K«/mi»«mo mathvariant=¨bold¨»§#183;«/mo»«mo mathvariant=¨bold¨»§#8710;«/mo»«msub»«mi mathvariant=¨bold¨»X«/mi»«mn mathvariant=¨bold¨»0«/mn»«/msub»«mo mathvariant=¨bold¨»=«/mo»«mi mathvariant=¨bold¨»M«/mi»«mo mathvariant=¨bold¨»§#183;«/mo»«mi mathvariant=¨bold¨»g«/mi»«/menclose»«/math»
نرسم مخطط القوى للحالة الثانية - عندما تتم إضافة الكتلة الصغيرة إلى النوابض، نرمز لها بـ m .
نرمز إلى القوة التي تشغلها النوابض في هذه الحالة بـ «math xmlns=¨http://www.w3.org/1998/Math/MathML¨»«mi mathvariant=¨bold¨ mathcolor=¨#0000FF¨»F«/mi»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»`«/mo»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»§#160;«/mo»«/math» واستطالة النابض بـ «math xmlns=¨http://www.w3.org/1998/Math/MathML¨»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»§#8710;«/mo»«mi mathvariant=¨bold-italic¨ mathcolor=¨#0000FF¨»X«/mi»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»`«/mo»«/math»:

«math xmlns=¨http://www.w3.org/1998/Math/MathML¨»«mi mathvariant=¨bold-italic¨ mathcolor=¨#0000FF¨»§#931;«/mi»«msub»«mi mathvariant=¨bold-italic¨ mathcolor=¨#0000FF¨»F«/mi»«mi mathvariant=¨bold¨ mathcolor=¨#0000FF¨»Y«/mi»«/msub»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»=«/mo»«mn mathvariant=¨bold¨ mathcolor=¨#0000FF¨»0«/mn»«mspace linebreak=¨newline¨»«/mspace»«mi mathvariant=¨bold-italic¨ mathcolor=¨#0000FF¨»F«/mi»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»`«/mo»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»=«/mo»«mrow mathcolor=¨#0000FF¨»«mo mathvariant=¨bold¨»(«/mo»«mi mathvariant=¨bold¨»M«/mi»«mo mathvariant=¨bold¨»+«/mo»«mi mathvariant=¨bold¨»m«/mi»«mo mathvariant=¨bold¨»)«/mo»«/mrow»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»§#183;«/mo»«mi mathvariant=¨bold-italic¨ mathcolor=¨#0000FF¨»g«/mi»«mspace linebreak=¨newline¨»«/mspace»«mspace linebreak=¨newline¨»«/mspace»«menclose mathcolor=¨#0000FF¨ notation=¨box¨»«mi mathvariant=¨bold¨»K«/mi»«mo mathvariant=¨bold¨»§#183;«/mo»«mo mathvariant=¨bold¨»§#8710;«/mo»«mi mathvariant=¨bold¨»X«/mi»«mo mathvariant=¨bold¨»`«/mo»«mo mathvariant=¨bold¨»=«/mo»«mrow»«mo mathvariant=¨bold¨»(«/mo»«mi mathvariant=¨bold¨»M«/mi»«mo mathvariant=¨bold¨»+«/mo»«mi mathvariant=¨bold¨»m«/mi»«mo mathvariant=¨bold¨»)«/mo»«/mrow»«mo mathvariant=¨bold¨»§#183;«/mo»«mi mathvariant=¨bold¨»g«/mi»«/menclose»«/math»
معطى أن الفرق بين الاستطالة النهائية والاستطالة الابتدائية هو 10 سم : «math xmlns=¨http://www.w3.org/1998/Math/MathML¨»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»§#8710;«/mo»«mi mathvariant=¨bold¨ mathcolor=¨#0000FF¨»X«/mi»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»`«/mo»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»-«/mo»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»§#8710;«/mo»«msub»«mi mathvariant=¨bold¨ mathcolor=¨#0000FF¨»X«/mi»«mn mathvariant=¨bold¨ mathcolor=¨#0000FF¨»0«/mn»«/msub»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»§#160;«/mo»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»=«/mo»«mn mathvariant=¨bold¨ mathcolor=¨#0000FF¨»0«/mn»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨».«/mo»«mn mathvariant=¨bold¨ mathcolor=¨#0000FF¨»1«/mn»«/math»
سنقوم بإجراء عملية طرح بين معادلة الحركة في الحالة النهائية ومعادلة الحركة في الحالة الابتدائية:
«math xmlns=¨http://www.w3.org/1998/Math/MathML¨»«msub»«mi mathvariant=¨bold¨ mathcolor=¨#0000FF¨»K«/mi»«mi mathvariant=¨bold¨ mathcolor=¨#0000FF¨»T«/mi»«/msub»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»§#183;«/mo»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»§#8710;«/mo»«mi mathvariant=¨bold¨ mathcolor=¨#0000FF¨»X«/mi»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»`«/mo»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»=«/mo»«mrow mathcolor=¨#0000FF¨»«mo mathvariant=¨bold¨»(«/mo»«mi mathvariant=¨bold¨»M«/mi»«mo mathvariant=¨bold¨»+«/mo»«mi mathvariant=¨bold¨»m«/mi»«mo mathvariant=¨bold¨»)«/mo»«/mrow»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»§#183;«/mo»«mi mathvariant=¨bold¨ mathcolor=¨#0000FF¨»g«/mi»«mspace linebreak=¨newline¨»«/mspace»«msub»«mi mathvariant=¨bold¨ mathcolor=¨#0000FF¨»K«/mi»«mi mathvariant=¨bold¨ mathcolor=¨#0000FF¨»T«/mi»«/msub»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»§#183;«/mo»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»§#8710;«/mo»«msub»«mi mathvariant=¨bold¨ mathcolor=¨#0000FF¨»X«/mi»«mn mathvariant=¨bold¨ mathcolor=¨#0000FF¨»0«/mn»«/msub»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»=«/mo»«mi mathvariant=¨bold¨ mathcolor=¨#0000FF¨»M«/mi»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»§#183;«/mo»«mi mathvariant=¨bold¨ mathcolor=¨#0000FF¨»g«/mi»«mspace linebreak=¨newline¨»«/mspace»«mspace linebreak=¨newline¨»«/mspace»«msub»«mi mathvariant=¨bold¨ mathcolor=¨#0000FF¨»K«/mi»«mi mathvariant=¨bold¨ mathcolor=¨#0000FF¨»T«/mi»«/msub»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»§#183;«/mo»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»§#8710;«/mo»«mi mathvariant=¨bold¨ mathcolor=¨#0000FF¨»X«/mi»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»`«/mo»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»-«/mo»«mi mathvariant=¨bold¨ mathcolor=¨#0000FF¨»K«/mi»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»§#183;«/mo»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»§#8710;«/mo»«msub»«mi mathvariant=¨bold¨ mathcolor=¨#0000FF¨»X«/mi»«mn mathvariant=¨bold¨ mathcolor=¨#0000FF¨»0«/mn»«/msub»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»=«/mo»«mrow mathcolor=¨#0000FF¨»«mo mathvariant=¨bold¨»(«/mo»«mi mathvariant=¨bold¨»M«/mi»«mo mathvariant=¨bold¨»+«/mo»«mi mathvariant=¨bold¨»m«/mi»«mo mathvariant=¨bold¨»)«/mo»«/mrow»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»§#183;«/mo»«mi mathvariant=¨bold¨ mathcolor=¨#0000FF¨»g«/mi»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»-«/mo»«mi mathvariant=¨bold¨ mathcolor=¨#0000FF¨»M«/mi»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»§#183;«/mo»«mi mathvariant=¨bold¨ mathcolor=¨#0000FF¨»g«/mi»«mspace linebreak=¨newline¨»«/mspace»«msub»«mi mathvariant=¨bold¨ mathcolor=¨#0000FF¨»K«/mi»«mi mathvariant=¨bold¨ mathcolor=¨#0000FF¨»T«/mi»«/msub»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»§#183;«/mo»«mrow mathcolor=¨#0000FF¨»«mo mathvariant=¨bold¨»(«/mo»«mo mathvariant=¨bold¨»§#8710;«/mo»«mi mathvariant=¨bold¨»X«/mi»«mo mathvariant=¨bold¨»`«/mo»«mo mathvariant=¨bold¨»-«/mo»«mo mathvariant=¨bold¨»§#8710;«/mo»«msub»«mi mathvariant=¨bold¨»X«/mi»«mn mathvariant=¨bold¨»0«/mn»«/msub»«mo mathvariant=¨bold¨»)«/mo»«/mrow»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»=«/mo»«menclose mathcolor=¨#0000FF¨ notation=¨updiagonalstrike¨»«mi mathvariant=¨bold¨»M«/mi»«mo mathvariant=¨bold¨»§#183;«/mo»«mi mathvariant=¨bold¨»g«/mi»«/menclose»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»+«/mo»«mi mathvariant=¨bold¨ mathcolor=¨#0000FF¨»m«/mi»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»§#183;«/mo»«mi mathvariant=¨bold¨ mathcolor=¨#0000FF¨»g«/mi»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»-«/mo»«menclose mathcolor=¨#0000FF¨ notation=¨updiagonalstrike¨»«mi mathvariant=¨bold¨»M«/mi»«mo mathvariant=¨bold¨»§#183;«/mo»«mi mathvariant=¨bold¨»g«/mi»«/menclose»«mspace linebreak=¨newline¨»«/mspace»«mspace linebreak=¨newline¨»«/mspace»«msub»«mi mathvariant=¨bold¨ mathcolor=¨#0000FF¨»K«/mi»«mi mathvariant=¨bold¨ mathcolor=¨#0000FF¨»T«/mi»«/msub»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»=«/mo»«mfrac mathcolor=¨#0000FF¨»«mrow»«mi mathvariant=¨bold¨»m«/mi»«mo mathvariant=¨bold¨»§#183;«/mo»«mi mathvariant=¨bold¨»g«/mi»«/mrow»«mrow»«mo mathvariant=¨bold¨»§#8710;«/mo»«mi mathvariant=¨bold¨»X«/mi»«mo mathvariant=¨bold¨»`«/mo»«mo mathvariant=¨bold¨»-«/mo»«mo mathvariant=¨bold¨»§#8710;«/mo»«msub»«mi mathvariant=¨bold¨»X«/mi»«mn mathvariant=¨bold¨»0«/mn»«/msub»«/mrow»«/mfrac»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»=«/mo»«mfrac mathcolor=¨#0000FF¨»«mrow»«mn mathvariant=¨bold¨»10«/mn»«mo mathvariant=¨bold¨»§#183;«/mo»«mn mathvariant=¨bold¨»10«/mn»«/mrow»«mrow»«mn mathvariant=¨bold¨»0«/mn»«mo mathvariant=¨bold¨».«/mo»«mn mathvariant=¨bold¨»1«/mn»«/mrow»«/mfrac»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»=«/mo»«mn mathvariant=¨bold¨ mathcolor=¨#0000FF¨»1000«/mn»«mfrac mathcolor=¨#0000FF¨»«mi mathvariant=¨bold¨»N«/mi»«mi mathvariant=¨bold¨»m«/mi»«/mfrac»«/math»
ثابت النابض لكل من النوابض الستة يساوي سدس ثابت النابض المحصل: 166.66 نيوتن لكل متر.
ونظرا لزيادة الاستطالة وزيادة الكتلة فإن زيادة الكتلة تكون تبعا لذلك.
______________________________________________________________________________________

______________________________________________________________________________________
______________________________________________________________________________________

______________________________________________________________________________________
ليست هناك حاجة لحساب القيمة الجديدة لزمن الدورة.
______________________________________________________________________________________
21. 1983,19- جسمان معلقان على نابض عمودي.

______________________________________________________________________________________
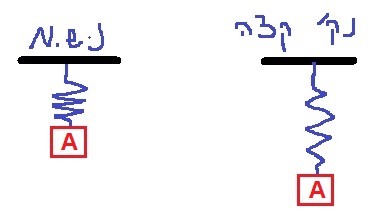
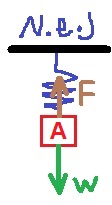
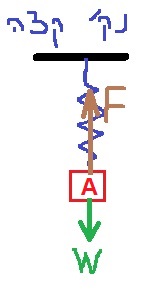
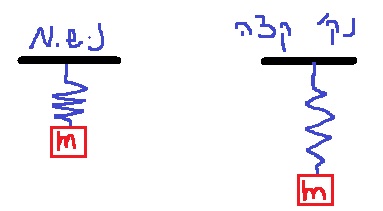
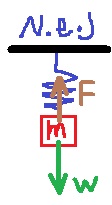
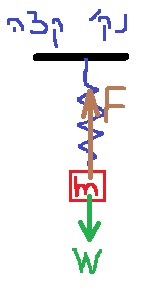
في السؤال صراحة وقسم لا.
ليس واضحا من السؤال كيفية التعبير عن قيمة السعة.
______________________________________________________________________________________

______________________________________________________________________________________
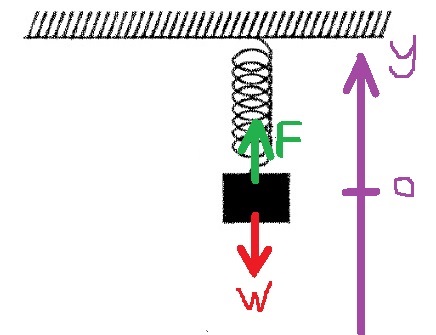
إذا لم يكن هناك وقت أثناء الامتحان، فيمكنك ترك تعبير زمن الدورة كما هو بعد التعويض:
______________________________________________________________________________________
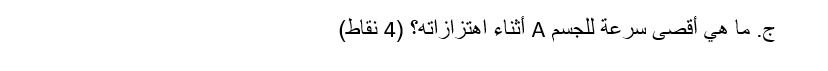
______________________________________________________________________________________
______________________________________________________________________________________
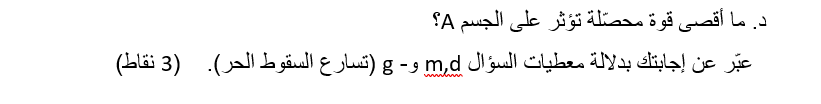
______________________________________________________________________________________
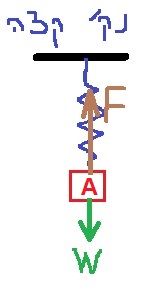
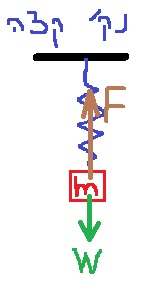
وهذا ينطبق أيضًا على القسم السابق.
محصلة كل القوى الأخرى المؤثرة على الجسم A يساوي mg لأعلى. بعد انقطاع الخيط، يبقى فقط مجموع القوى mg. إلى الأعلى. مجموع هذه القوى هو أقصى قوة محصلة بعد قطع الخيط.
أو استخدم مبادئ الحركة التوافقية البسيطة والقانون الثاني. يوصى بطريقة الحل هذه للتمرين فقط.
______________________________________________________________________________________
22. 1981,3- البندول البسيط

______________________________________________________________________________________
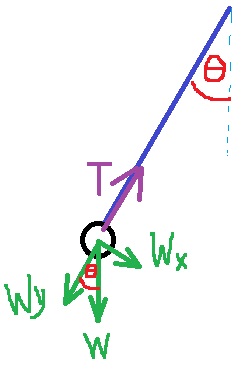
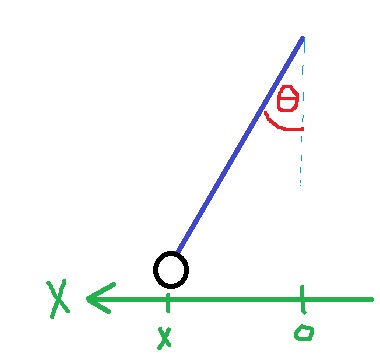


وليس فقط القوة المحصّلة في الاتجاه الأفقي.
الحركة التوافقية للنابض الأفقي، والحركة التوافقية للنابض الرأسي، والحركة التوافقية للبندول البسيطة بزوايا صغيرة.
لذلك، فإن تعبير زمن الدورة في الحركة التوافقية في نابض أفقي هو نفس تعبير تعبير زمن الدورة في الحركة التوافقية في نابض رأسي.
من المهم إظهار أن الحركة هي حركة توافقية بسيطة قبل استخدام دوال الحركة التوافقية البسيطة.
______________________________________________________________________________________

______________________________________________________________________________________
______________________________________________________________________________________

______________________________________________________________________________________
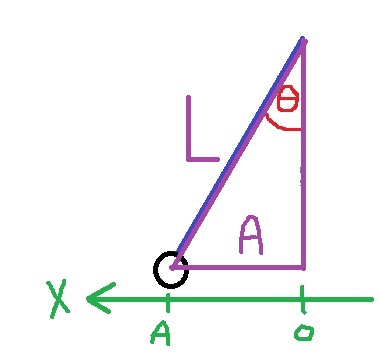
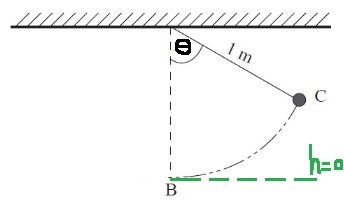
«math xmlns=¨http://www.w3.org/1998/Math/MathML¨»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»§#160;«/mo»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»§#160;«/mo»«mo mathvariant=¨bold¨ mathcolor=¨#FF0000¨»§#160;«/mo»«mo mathvariant=¨bold¨ mathcolor=¨#FF0000¨»§#160;«/mo»«mo mathvariant=¨bold¨ mathcolor=¨#FF0000¨»§#160;«/mo»«mo mathvariant=¨bold¨ mathcolor=¨#FF0000¨»§#160;«/mo»«mo mathvariant=¨bold¨ mathcolor=¨#FF0000¨»§#160;«/mo»«mo mathvariant=¨bold¨ mathcolor=¨#FF0000¨»§#160;«/mo»«mo mathvariant=¨bold¨ mathcolor=¨#FF0000¨»§#160;«/mo»«mo mathvariant=¨bold¨ mathcolor=¨#FF0000¨»§#160;«/mo»«msub»«mi mathvariant=¨bold¨ mathcolor=¨#FF0000¨»E«/mi»«mi mathvariant=¨bold¨ mathcolor=¨#FF0000¨»C«/mi»«/msub»«mo mathvariant=¨bold¨ mathcolor=¨#FF0000¨»=«/mo»«msub»«mi mathvariant=¨bold¨ mathcolor=¨#FF0000¨»E«/mi»«mi mathvariant=¨bold¨ mathcolor=¨#FF0000¨»B«/mi»«/msub»«mspace linebreak=¨newline¨»«/mspace»«msub»«mi mathvariant=¨bold¨ mathcolor=¨#FF0000¨»E«/mi»«msub mathcolor=¨#FF0000¨»«mi mathvariant=¨bold¨»K«/mi»«mi mathvariant=¨bold¨»C«/mi»«/msub»«/msub»«mo mathvariant=¨bold¨ mathcolor=¨#FF0000¨»+«/mo»«msub»«mi mathvariant=¨bold¨ mathcolor=¨#FF0000¨»U«/mi»«mi mathvariant=¨bold¨ mathcolor=¨#FF0000¨»C«/mi»«/msub»«mo mathvariant=¨bold¨ mathcolor=¨#FF0000¨»=«/mo»«msub»«mi mathvariant=¨bold¨ mathcolor=¨#FF0000¨»E«/mi»«msub mathcolor=¨#FF0000¨»«mi mathvariant=¨bold¨»K«/mi»«mi mathvariant=¨bold¨»B«/mi»«/msub»«/msub»«mo mathvariant=¨bold¨ mathcolor=¨#FF0000¨»+«/mo»«msub»«mi mathvariant=¨bold¨ mathcolor=¨#FF0000¨»U«/mi»«mi mathvariant=¨bold¨ mathcolor=¨#FF0000¨»B«/mi»«/msub»«/math»
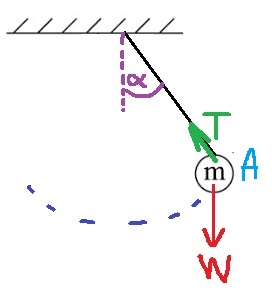
في النقطة C يكون الجسم في حالة سكون، ولا توجد طاقة حركية للجسم في النقطة C. تكون النقطة B على ارتفاع صفر بالنسبة للمستوى المرجعي.
نكتب معادلة حفظ الطاقة وفقًا لذلك، ونعبر منها عن السرعة في النقطة B :
«math xmlns=¨http://www.w3.org/1998/Math/MathML¨»«msub»«mi mathvariant=¨bold¨ mathcolor=¨#FF0000¨»E«/mi»«msub mathcolor=¨#FF0000¨»«mi mathvariant=¨bold¨»K«/mi»«mi mathvariant=¨bold¨»C«/mi»«/msub»«/msub»«mo mathvariant=¨bold¨ mathcolor=¨#FF0000¨»+«/mo»«msub»«mi mathvariant=¨bold¨ mathcolor=¨#FF0000¨»U«/mi»«mi mathvariant=¨bold¨ mathcolor=¨#FF0000¨»C«/mi»«/msub»«mo mathvariant=¨bold¨ mathcolor=¨#FF0000¨»=«/mo»«msub»«mi mathvariant=¨bold¨ mathcolor=¨#FF0000¨»E«/mi»«msub mathcolor=¨#FF0000¨»«mi mathvariant=¨bold¨»K«/mi»«mi mathvariant=¨bold¨»B«/mi»«/msub»«/msub»«mo mathvariant=¨bold¨ mathcolor=¨#FF0000¨»+«/mo»«msub»«mi mathvariant=¨bold¨ mathcolor=¨#FF0000¨»U«/mi»«mi mathvariant=¨bold¨ mathcolor=¨#FF0000¨»B«/mi»«/msub»«mspace linebreak=¨newline¨»«/mspace»«menclose mathcolor=¨#FF0000¨ notation=¨updiagonalstrike¨»«msub»«mi mathvariant=¨bold¨»E«/mi»«msub»«mi mathvariant=¨bold¨»K«/mi»«mi mathvariant=¨bold¨»C«/mi»«/msub»«/msub»«/menclose»«mo mathvariant=¨bold¨ mathcolor=¨#FF0000¨»+«/mo»«msub»«mi mathvariant=¨bold¨ mathcolor=¨#FF0000¨»U«/mi»«mi mathvariant=¨bold¨ mathcolor=¨#FF0000¨»C«/mi»«/msub»«mo mathvariant=¨bold¨ mathcolor=¨#FF0000¨»=«/mo»«msub»«mi mathvariant=¨bold¨ mathcolor=¨#FF0000¨»E«/mi»«msub mathcolor=¨#FF0000¨»«mi mathvariant=¨bold¨»K«/mi»«mi mathvariant=¨bold¨»B«/mi»«/msub»«/msub»«mo mathvariant=¨bold¨ mathcolor=¨#FF0000¨»+«/mo»«menclose mathcolor=¨#FF0000¨ notation=¨downdiagonalstrike¨»«msub»«mi mathvariant=¨bold¨»U«/mi»«mi mathvariant=¨bold¨»B«/mi»«/msub»«/menclose»«mspace linebreak=¨newline¨»«/mspace»«mspace linebreak=¨newline¨»«/mspace»«menclose mathcolor=¨#FF0000¨ notation=¨downdiagonalstrike¨»«mi mathvariant=¨bold¨»m«/mi»«/menclose»«mo mathvariant=¨bold¨ mathcolor=¨#FF0000¨»§#183;«/mo»«mi mathvariant=¨bold¨ mathcolor=¨#FF0000¨»g«/mi»«mo mathvariant=¨bold¨ mathcolor=¨#FF0000¨»§#183;«/mo»«msub»«mi mathvariant=¨bold¨ mathcolor=¨#FF0000¨»h«/mi»«mi mathvariant=¨bold¨ mathcolor=¨#FF0000¨»c«/mi»«/msub»«mo mathvariant=¨bold¨ mathcolor=¨#FF0000¨»=«/mo»«mfrac mathcolor=¨#FF0000¨»«mn mathvariant=¨bold¨»1«/mn»«mn mathvariant=¨bold¨»2«/mn»«/mfrac»«mo mathvariant=¨bold¨ mathcolor=¨#FF0000¨»§#183;«/mo»«menclose mathcolor=¨#FF0000¨ notation=¨downdiagonalstrike¨»«mi mathvariant=¨bold¨»m«/mi»«/menclose»«mo mathvariant=¨bold¨ mathcolor=¨#FF0000¨»§#183;«/mo»«msup»«msub mathcolor=¨#FF0000¨»«mi mathvariant=¨bold¨»V«/mi»«mi mathvariant=¨bold¨»B«/mi»«/msub»«mn mathvariant=¨bold¨ mathcolor=¨#FF0000¨»2«/mn»«/msup»«mspace linebreak=¨newline¨»«/mspace»«mspace linebreak=¨newline¨»«/mspace»«msub»«mi mathvariant=¨bold¨ mathcolor=¨#FF0000¨»V«/mi»«mi mathvariant=¨bold¨ mathcolor=¨#FF0000¨»B«/mi»«/msub»«mo mathvariant=¨bold¨ mathcolor=¨#FF0000¨»=«/mo»«msqrt mathcolor=¨#FF0000¨»«mn mathvariant=¨bold¨»2«/mn»«mo mathvariant=¨bold¨»§#183;«/mo»«mi mathvariant=¨bold¨»g«/mi»«mo mathvariant=¨bold¨»§#183;«/mo»«msub»«mi mathvariant=¨bold¨»h«/mi»«mi mathvariant=¨bold¨»c«/mi»«/msub»«/msqrt»«/math»
نعبر عن hc، بدلالة طول الخيط وزاوية ميل الخيط الابتدائية:
«math xmlns=¨http://www.w3.org/1998/Math/MathML¨»«msub»«mi mathvariant=¨bold¨ mathcolor=¨#FF0000¨»h«/mi»«mi mathvariant=¨bold¨ mathcolor=¨#FF0000¨»c«/mi»«/msub»«mo mathvariant=¨bold¨ mathcolor=¨#FF0000¨»=«/mo»«mi mathvariant=¨bold¨ mathcolor=¨#FF0000¨»L«/mi»«mo mathvariant=¨bold¨ mathcolor=¨#FF0000¨»-«/mo»«mi mathvariant=¨bold¨ mathcolor=¨#FF0000¨»L«/mi»«mo mathvariant=¨bold¨ mathcolor=¨#FF0000¨»§#183;«/mo»«mi mathvariant=¨bold¨ mathcolor=¨#FF0000¨»cos«/mi»«mo mathvariant=¨bold¨ mathcolor=¨#FF0000¨»(«/mo»«mi mathvariant=¨bold¨ mathcolor=¨#FF0000¨»§#952;«/mi»«mo mathvariant=¨bold¨ mathcolor=¨#FF0000¨»)«/mo»«mo mathvariant=¨bold¨ mathcolor=¨#FF0000¨»=«/mo»«mi mathvariant=¨bold¨ mathcolor=¨#FF0000¨»L«/mi»«mo mathvariant=¨bold¨ mathcolor=¨#FF0000¨»(«/mo»«mn mathvariant=¨bold¨ mathcolor=¨#FF0000¨»1«/mn»«mo mathvariant=¨bold¨ mathcolor=¨#FF0000¨»-«/mo»«mi mathvariant=¨bold¨ mathcolor=¨#FF0000¨»cos«/mi»«mo mathvariant=¨bold¨ mathcolor=¨#FF0000¨»(«/mo»«mi mathvariant=¨bold¨ mathcolor=¨#FF0000¨»§#952;«/mi»«mo mathvariant=¨bold¨ mathcolor=¨#FF0000¨»)«/mo»«mo mathvariant=¨bold¨ mathcolor=¨#FF0000¨»)«/mo»«/math»
نجد السرعة VB:
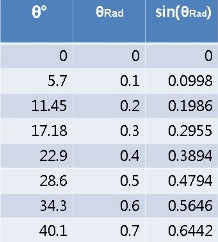
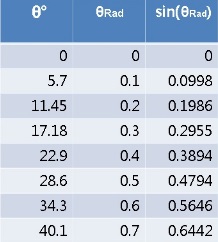
«math xmlns=¨http://www.w3.org/1998/Math/MathML¨»«msub»«mi mathvariant=¨bold¨ mathcolor=¨#FF0000¨»V«/mi»«mi mathvariant=¨bold¨ mathcolor=¨#FF0000¨»B«/mi»«/msub»«mo mathvariant=¨bold¨ mathcolor=¨#FF0000¨»=«/mo»«msqrt mathcolor=¨#FF0000¨»«mn mathvariant=¨bold¨»2«/mn»«mo mathvariant=¨bold¨»§#183;«/mo»«mi mathvariant=¨bold¨»g«/mi»«mo mathvariant=¨bold¨»§#183;«/mo»«msub»«mi mathvariant=¨bold¨»h«/mi»«mi mathvariant=¨bold¨»c«/mi»«/msub»«/msqrt»«mo mathvariant=¨bold¨ mathcolor=¨#FF0000¨»=«/mo»«msqrt mathcolor=¨#FF0000¨»«mn mathvariant=¨bold¨»2«/mn»«mo mathvariant=¨bold¨»§#183;«/mo»«mi mathvariant=¨bold¨»g«/mi»«mo mathvariant=¨bold¨»§#183;«/mo»«mi mathvariant=¨bold¨»L«/mi»«mo mathvariant=¨bold¨»(«/mo»«mn mathvariant=¨bold¨»1«/mn»«mo mathvariant=¨bold¨»-«/mo»«mi mathvariant=¨bold¨»cos«/mi»«mo mathvariant=¨bold¨»(«/mo»«mi mathvariant=¨bold¨»§#952;«/mi»«mo mathvariant=¨bold¨»)«/mo»«mo mathvariant=¨bold¨»)«/mo»«/msqrt»«mo mathvariant=¨bold¨ mathcolor=¨#FF0000¨»§#160;«/mo»«mo mathvariant=¨bold¨ mathcolor=¨#FF0000¨»=«/mo»«msqrt mathcolor=¨#FF0000¨»«mn mathvariant=¨bold¨»2«/mn»«mo mathvariant=¨bold¨»§#183;«/mo»«mn mathvariant=¨bold¨»10«/mn»«mo mathvariant=¨bold¨»§#183;«/mo»«mn mathvariant=¨bold¨»1«/mn»«mo mathvariant=¨bold¨»(«/mo»«mn mathvariant=¨bold¨»1«/mn»«mo mathvariant=¨bold¨»-«/mo»«mi mathvariant=¨bold¨»cos«/mi»«mo mathvariant=¨bold¨»(«/mo»«mn mathvariant=¨bold¨»5«/mn»«mo mathvariant=¨bold¨»)«/mo»«mo mathvariant=¨bold¨»)«/mo»«/msqrt»«mo mathvariant=¨bold¨ mathcolor=¨#FF0000¨»§#160;«/mo»«mo mathvariant=¨bold¨ mathcolor=¨#FF0000¨»=«/mo»«msqrt mathcolor=¨#FF0000¨»«mn mathvariant=¨bold¨»0«/mn»«mo mathvariant=¨bold¨».«/mo»«mn mathvariant=¨bold¨»076«/mn»«/msqrt»«mo mathvariant=¨bold¨ mathcolor=¨#FF0000¨»§#160;«/mo»«mo mathvariant=¨bold¨ mathcolor=¨#FF0000¨»=«/mo»«mo mathvariant=¨bold¨ mathcolor=¨#FF0000¨»§#160;«/mo»«mn mathvariant=¨bold¨ mathcolor=¨#FF0000¨»0«/mn»«mo mathvariant=¨bold¨ mathcolor=¨#FF0000¨».«/mo»«mn mathvariant=¨bold¨ mathcolor=¨#FF0000¨»27«/mn»«mfrac mathcolor=¨#FF0000¨»«mi mathvariant=¨bold¨»m«/mi»«mi mathvariant=¨bold¨»s«/mi»«/mfrac»«mspace linebreak=¨newline¨»«/mspace»«/math»

«math xmlns=¨http://www.w3.org/1998/Math/MathML¨»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»§#160;«/mo»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»§#160;«/mo»«mo mathvariant=¨bold¨ mathcolor=¨#FF0000¨»§#160;«/mo»«mo mathvariant=¨bold¨ mathcolor=¨#FF0000¨»§#160;«/mo»«mo mathvariant=¨bold¨ mathcolor=¨#FF0000¨»§#160;«/mo»«mo mathvariant=¨bold¨ mathcolor=¨#FF0000¨»§#160;«/mo»«mo mathvariant=¨bold¨ mathcolor=¨#FF0000¨»§#160;«/mo»«mo mathvariant=¨bold¨ mathcolor=¨#FF0000¨»§#160;«/mo»«mo mathvariant=¨bold¨ mathcolor=¨#FF0000¨»§#160;«/mo»«mo mathvariant=¨bold¨ mathcolor=¨#FF0000¨»§#160;«/mo»«msub»«mi mathvariant=¨bold¨ mathcolor=¨#FF0000¨»E«/mi»«mi mathvariant=¨bold¨ mathcolor=¨#FF0000¨»C«/mi»«/msub»«mo mathvariant=¨bold¨ mathcolor=¨#FF0000¨»=«/mo»«msub»«mi mathvariant=¨bold¨ mathcolor=¨#FF0000¨»E«/mi»«mi mathvariant=¨bold¨ mathcolor=¨#FF0000¨»B«/mi»«/msub»«mspace linebreak=¨newline¨»«/mspace»«msub»«mi mathvariant=¨bold¨ mathcolor=¨#FF0000¨»E«/mi»«msub mathcolor=¨#FF0000¨»«mi mathvariant=¨bold¨»K«/mi»«mi mathvariant=¨bold¨»C«/mi»«/msub»«/msub»«mo mathvariant=¨bold¨ mathcolor=¨#FF0000¨»+«/mo»«msub»«mi mathvariant=¨bold¨ mathcolor=¨#FF0000¨»U«/mi»«mi mathvariant=¨bold¨ mathcolor=¨#FF0000¨»C«/mi»«/msub»«mo mathvariant=¨bold¨ mathcolor=¨#FF0000¨»=«/mo»«msub»«mi mathvariant=¨bold¨ mathcolor=¨#FF0000¨»E«/mi»«msub mathcolor=¨#FF0000¨»«mi mathvariant=¨bold¨»K«/mi»«mi mathvariant=¨bold¨»B«/mi»«/msub»«/msub»«mo mathvariant=¨bold¨ mathcolor=¨#FF0000¨»+«/mo»«msub»«mi mathvariant=¨bold¨ mathcolor=¨#FF0000¨»U«/mi»«mi mathvariant=¨bold¨ mathcolor=¨#FF0000¨»B«/mi»«/msub»«/math»
בנקודה C הגוף נח, אין אנרגיה קינטית בנקודה C . הנקודה B נמצאת בגובה אפס ביחס למישור הייחוס.
נכתוב בהתאם את משוואת שימור האנרגיה ,ונבטא ממנה את המהירות בנקודה B:
«math xmlns=¨http://www.w3.org/1998/Math/MathML¨»«msub»«mi mathvariant=¨bold¨ mathcolor=¨#FF0000¨»E«/mi»«msub mathcolor=¨#FF0000¨»«mi mathvariant=¨bold¨»K«/mi»«mi mathvariant=¨bold¨»C«/mi»«/msub»«/msub»«mo mathvariant=¨bold¨ mathcolor=¨#FF0000¨»+«/mo»«msub»«mi mathvariant=¨bold¨ mathcolor=¨#FF0000¨»U«/mi»«mi mathvariant=¨bold¨ mathcolor=¨#FF0000¨»C«/mi»«/msub»«mo mathvariant=¨bold¨ mathcolor=¨#FF0000¨»=«/mo»«msub»«mi mathvariant=¨bold¨ mathcolor=¨#FF0000¨»E«/mi»«msub mathcolor=¨#FF0000¨»«mi mathvariant=¨bold¨»K«/mi»«mi mathvariant=¨bold¨»B«/mi»«/msub»«/msub»«mo mathvariant=¨bold¨ mathcolor=¨#FF0000¨»+«/mo»«msub»«mi mathvariant=¨bold¨ mathcolor=¨#FF0000¨»U«/mi»«mi mathvariant=¨bold¨ mathcolor=¨#FF0000¨»B«/mi»«/msub»«mspace linebreak=¨newline¨»«/mspace»«menclose mathcolor=¨#FF0000¨ notation=¨updiagonalstrike¨»«msub»«mi mathvariant=¨bold¨»E«/mi»«msub»«mi mathvariant=¨bold¨»K«/mi»«mi mathvariant=¨bold¨»C«/mi»«/msub»«/msub»«/menclose»«mo mathvariant=¨bold¨ mathcolor=¨#FF0000¨»+«/mo»«msub»«mi mathvariant=¨bold¨ mathcolor=¨#FF0000¨»U«/mi»«mi mathvariant=¨bold¨ mathcolor=¨#FF0000¨»C«/mi»«/msub»«mo mathvariant=¨bold¨ mathcolor=¨#FF0000¨»=«/mo»«msub»«mi mathvariant=¨bold¨ mathcolor=¨#FF0000¨»E«/mi»«msub mathcolor=¨#FF0000¨»«mi mathvariant=¨bold¨»K«/mi»«mi mathvariant=¨bold¨»B«/mi»«/msub»«/msub»«mo mathvariant=¨bold¨ mathcolor=¨#FF0000¨»+«/mo»«menclose mathcolor=¨#FF0000¨ notation=¨downdiagonalstrike¨»«msub»«mi mathvariant=¨bold¨»U«/mi»«mi mathvariant=¨bold¨»B«/mi»«/msub»«/menclose»«mspace linebreak=¨newline¨»«/mspace»«mspace linebreak=¨newline¨»«/mspace»«menclose mathcolor=¨#FF0000¨ notation=¨downdiagonalstrike¨»«mi mathvariant=¨bold¨»m«/mi»«/menclose»«mo mathvariant=¨bold¨ mathcolor=¨#FF0000¨»§#183;«/mo»«mi mathvariant=¨bold¨ mathcolor=¨#FF0000¨»g«/mi»«mo mathvariant=¨bold¨ mathcolor=¨#FF0000¨»§#183;«/mo»«msub»«mi mathvariant=¨bold¨ mathcolor=¨#FF0000¨»h«/mi»«mi mathvariant=¨bold¨ mathcolor=¨#FF0000¨»c«/mi»«/msub»«mo mathvariant=¨bold¨ mathcolor=¨#FF0000¨»=«/mo»«mfrac mathcolor=¨#FF0000¨»«mn mathvariant=¨bold¨»1«/mn»«mn mathvariant=¨bold¨»2«/mn»«/mfrac»«mo mathvariant=¨bold¨ mathcolor=¨#FF0000¨»§#183;«/mo»«menclose mathcolor=¨#FF0000¨ notation=¨downdiagonalstrike¨»«mi mathvariant=¨bold¨»m«/mi»«/menclose»«mo mathvariant=¨bold¨ mathcolor=¨#FF0000¨»§#183;«/mo»«msup»«msub mathcolor=¨#FF0000¨»«mi mathvariant=¨bold¨»V«/mi»«mi mathvariant=¨bold¨»B«/mi»«/msub»«mn mathvariant=¨bold¨ mathcolor=¨#FF0000¨»2«/mn»«/msup»«mspace linebreak=¨newline¨»«/mspace»«mspace linebreak=¨newline¨»«/mspace»«msub»«mi mathvariant=¨bold¨ mathcolor=¨#FF0000¨»V«/mi»«mi mathvariant=¨bold¨ mathcolor=¨#FF0000¨»B«/mi»«/msub»«mo mathvariant=¨bold¨ mathcolor=¨#FF0000¨»=«/mo»«msqrt mathcolor=¨#FF0000¨»«mn mathvariant=¨bold¨»2«/mn»«mo mathvariant=¨bold¨»§#183;«/mo»«mi mathvariant=¨bold¨»g«/mi»«mo mathvariant=¨bold¨»§#183;«/mo»«msub»«mi mathvariant=¨bold¨»h«/mi»«mi mathvariant=¨bold¨»c«/mi»«/msub»«/msqrt»«/math»
נבטא את hc , בתלות באורך החוט ובזווית נטיית החוט ההתחלתית :
«math xmlns=¨http://www.w3.org/1998/Math/MathML¨»«msub»«mi mathvariant=¨bold¨ mathcolor=¨#FF0000¨»h«/mi»«mi mathvariant=¨bold¨ mathcolor=¨#FF0000¨»c«/mi»«/msub»«mo mathvariant=¨bold¨ mathcolor=¨#FF0000¨»=«/mo»«mi mathvariant=¨bold¨ mathcolor=¨#FF0000¨»L«/mi»«mo mathvariant=¨bold¨ mathcolor=¨#FF0000¨»-«/mo»«mi mathvariant=¨bold¨ mathcolor=¨#FF0000¨»L«/mi»«mo mathvariant=¨bold¨ mathcolor=¨#FF0000¨»§#183;«/mo»«mi mathvariant=¨bold¨ mathcolor=¨#FF0000¨»cos«/mi»«mo mathvariant=¨bold¨ mathcolor=¨#FF0000¨»(«/mo»«mi mathvariant=¨bold¨ mathcolor=¨#FF0000¨»§#952;«/mi»«mo mathvariant=¨bold¨ mathcolor=¨#FF0000¨»)«/mo»«mo mathvariant=¨bold¨ mathcolor=¨#FF0000¨»=«/mo»«mi mathvariant=¨bold¨ mathcolor=¨#FF0000¨»L«/mi»«mo mathvariant=¨bold¨ mathcolor=¨#FF0000¨»(«/mo»«mn mathvariant=¨bold¨ mathcolor=¨#FF0000¨»1«/mn»«mo mathvariant=¨bold¨ mathcolor=¨#FF0000¨»-«/mo»«mi mathvariant=¨bold¨ mathcolor=¨#FF0000¨»cos«/mi»«mo mathvariant=¨bold¨ mathcolor=¨#FF0000¨»(«/mo»«mi mathvariant=¨bold¨ mathcolor=¨#FF0000¨»§#952;«/mi»«mo mathvariant=¨bold¨ mathcolor=¨#FF0000¨»)«/mo»«mo mathvariant=¨bold¨ mathcolor=¨#FF0000¨»)«/mo»«/math»
נמצא את VB:
«math xmlns=¨http://www.w3.org/1998/Math/MathML¨»«msub»«mi mathvariant=¨bold¨ mathcolor=¨#FF0000¨»V«/mi»«mi mathvariant=¨bold¨ mathcolor=¨#FF0000¨»B«/mi»«/msub»«mo mathvariant=¨bold¨ mathcolor=¨#FF0000¨»=«/mo»«msqrt mathcolor=¨#FF0000¨»«mn mathvariant=¨bold¨»2«/mn»«mo mathvariant=¨bold¨»§#183;«/mo»«mi mathvariant=¨bold¨»g«/mi»«mo mathvariant=¨bold¨»§#183;«/mo»«msub»«mi mathvariant=¨bold¨»h«/mi»«mi mathvariant=¨bold¨»c«/mi»«/msub»«/msqrt»«mo mathvariant=¨bold¨ mathcolor=¨#FF0000¨»=«/mo»«msqrt mathcolor=¨#FF0000¨»«mn mathvariant=¨bold¨»2«/mn»«mo mathvariant=¨bold¨»§#183;«/mo»«mi mathvariant=¨bold¨»g«/mi»«mo mathvariant=¨bold¨»§#183;«/mo»«mi mathvariant=¨bold¨»L«/mi»«mo mathvariant=¨bold¨»(«/mo»«mn mathvariant=¨bold¨»1«/mn»«mo mathvariant=¨bold¨»-«/mo»«mi mathvariant=¨bold¨»cos«/mi»«mo mathvariant=¨bold¨»(«/mo»«mi mathvariant=¨bold¨»§#952;«/mi»«mo mathvariant=¨bold¨»)«/mo»«mo mathvariant=¨bold¨»)«/mo»«/msqrt»«mo mathvariant=¨bold¨ mathcolor=¨#FF0000¨»§#160;«/mo»«mo mathvariant=¨bold¨ mathcolor=¨#FF0000¨»=«/mo»«msqrt mathcolor=¨#FF0000¨»«mn mathvariant=¨bold¨»2«/mn»«mo mathvariant=¨bold¨»§#183;«/mo»«mn mathvariant=¨bold¨»10«/mn»«mo mathvariant=¨bold¨»§#183;«/mo»«mn mathvariant=¨bold¨»1«/mn»«mo mathvariant=¨bold¨»(«/mo»«mn mathvariant=¨bold¨»1«/mn»«mo mathvariant=¨bold¨»-«/mo»«mi mathvariant=¨bold¨»cos«/mi»«mo mathvariant=¨bold¨»(«/mo»«mn mathvariant=¨bold¨»5«/mn»«mo mathvariant=¨bold¨»)«/mo»«mo mathvariant=¨bold¨»)«/mo»«/msqrt»«mo mathvariant=¨bold¨ mathcolor=¨#FF0000¨»§#160;«/mo»«mo mathvariant=¨bold¨ mathcolor=¨#FF0000¨»=«/mo»«msqrt mathcolor=¨#FF0000¨»«mn mathvariant=¨bold¨»0«/mn»«mo mathvariant=¨bold¨».«/mo»«mn mathvariant=¨bold¨»076«/mn»«/msqrt»«mo mathvariant=¨bold¨ mathcolor=¨#FF0000¨»§#160;«/mo»«mo mathvariant=¨bold¨ mathcolor=¨#FF0000¨»=«/mo»«mo mathvariant=¨bold¨ mathcolor=¨#FF0000¨»§#160;«/mo»«mn mathvariant=¨bold¨ mathcolor=¨#FF0000¨»0«/mn»«mo mathvariant=¨bold¨ mathcolor=¨#FF0000¨».«/mo»«mn mathvariant=¨bold¨ mathcolor=¨#FF0000¨»27«/mn»«mfrac mathcolor=¨#FF0000¨»«mi mathvariant=¨bold¨»m«/mi»«mi mathvariant=¨bold¨»s«/mi»«/mfrac»«mspace linebreak=¨newline¨»«/mspace»«/math»
______________________________________________________________________________________

______________________________________________________________________________________

______________________________________________________________________________________

______________________________________________________________________________________

______________________________________________________________________________________
23. 1980,3

______________________________________________________________________________________
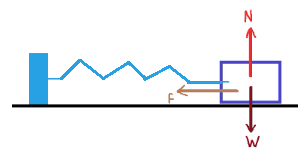

3. أي حركة في خط مستقيم حيث تتناسب فيها القوة المحصّلة تناسبًا طرديًا مع موقع الجسم هي حركة توافقية بسيطة.
______________________________________________________________________________________

______________________________________________________________________________________
من دالة السرعة كدالة للزمن «math xmlns=¨http://www.w3.org/1998/Math/MathML¨»«mi mathvariant=¨bold¨ mathcolor=¨#0000FF¨»V«/mi»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»(«/mo»«mi mathvariant=¨bold¨ mathcolor=¨#0000FF¨»t«/mi»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»)«/mo»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»=«/mo»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»-«/mo»«mi mathvariant=¨bold¨ mathcolor=¨#0000FF¨»§#969;A«/mi»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»§#183;«/mo»«mi mathvariant=¨bold¨ mathcolor=¨#0000FF¨»sin«/mi»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»(«/mo»«mi mathvariant=¨bold¨ mathcolor=¨#0000FF¨»§#969;t«/mi»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»+«/mo»«msub»«mi mathvariant=¨bold¨ mathcolor=¨#0000FF¨»§#1012;«/mi»«mn mathvariant=¨bold¨ mathcolor=¨#0000FF¨»0«/mn»«/msub»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»)«/mo»«/math» يمكن تحديد قيمة السرعة القصوى : «math xmlns=¨http://www.w3.org/1998/Math/MathML¨»«mstyle mathsize=¨20px¨»«msub»«mi mathvariant=¨bold¨ mathcolor=¨#0000FF¨»V«/mi»«mi mathvariant=¨bold¨ mathcolor=¨#0000FF¨»max«/mi»«/msub»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»=«/mo»«mi mathvariant=¨bold¨ mathcolor=¨#0000FF¨»§#969;«/mi»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»§#183;«/mo»«mi mathvariant=¨bold¨ mathcolor=¨#0000FF¨»A«/mi»«/mstyle»«/math»
نحسب التردد الزاوي:
«math xmlns=¨http://www.w3.org/1998/Math/MathML¨»«mstyle mathsize=¨20px¨»«mi mathvariant=¨bold¨ mathcolor=¨#0000FF¨»T«/mi»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»=«/mo»«mn mathvariant=¨bold¨ mathcolor=¨#0000FF¨»2«/mn»«mi mathvariant=¨bold¨ mathcolor=¨#0000FF¨»§#960;«/mi»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»§#183;«/mo»«msqrt mathcolor=¨#0000FF¨»«mfrac»«mi mathvariant=¨bold¨»m«/mi»«mi mathvariant=¨bold¨»k«/mi»«/mfrac»«/msqrt»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»§#160;«/mo»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»§#160;«/mo»«mspace linebreak=¨newline¨/»«mi mathvariant=¨bold¨ mathcolor=¨#0000FF¨»§#969;«/mi»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»=«/mo»«mfrac mathcolor=¨#0000FF¨»«mrow»«mn mathvariant=¨bold¨»2«/mn»«mi mathvariant=¨bold¨»§#960;«/mi»«/mrow»«mi mathvariant=¨bold¨»T«/mi»«/mfrac»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»=«/mo»«mfrac mathcolor=¨#0000FF¨»«mrow»«mn mathvariant=¨bold¨»2«/mn»«mi mathvariant=¨bold¨»§#960;«/mi»«/mrow»«mrow»«mn mathvariant=¨bold¨»2«/mn»«mi mathvariant=¨bold¨»§#960;«/mi»«mo mathvariant=¨bold¨»§#183;«/mo»«msqrt»«mfrac»«mi mathvariant=¨bold¨»m«/mi»«mi mathvariant=¨bold¨»k«/mi»«/mfrac»«/msqrt»«/mrow»«/mfrac»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»=«/mo»«msqrt mathcolor=¨#0000FF¨»«mfrac»«mi mathvariant=¨bold¨»k«/mi»«mi mathvariant=¨bold¨»m«/mi»«/mfrac»«/msqrt»«/mstyle»«/math»
نحسب قيمة ثابت النابض بناءً على القوة المؤثرة على النابض واستطالته.
يتم تشغيل قوة مقدارها 20 نيوتن على النابض، فيزداد طوله بمقدار 10 سم. يمكن حساب قيمة ثابت النابض من قانون هوك:
«math xmlns=¨http://www.w3.org/1998/Math/MathML¨»«mstyle mathsize=¨20px¨»«mi mathvariant=¨bold¨ mathcolor=¨#0000FF¨»F«/mi»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»=«/mo»«mi mathvariant=¨bold¨ mathcolor=¨#0000FF¨»K«/mi»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»§#183;«/mo»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»§#8710;«/mo»«mi mathvariant=¨bold¨ mathcolor=¨#0000FF¨»X«/mi»«mspace linebreak=¨newline¨/»«mspace linebreak=¨newline¨/»«mi mathvariant=¨bold¨ mathcolor=¨#0000FF¨»K«/mi»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»=«/mo»«mfrac mathcolor=¨#0000FF¨»«mi mathvariant=¨bold¨»F«/mi»«mrow»«mo mathvariant=¨bold¨»§#8710;«/mo»«mi mathvariant=¨bold¨»X«/mi»«/mrow»«/mfrac»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»=«/mo»«mfrac mathcolor=¨#0000FF¨»«mn mathvariant=¨bold¨»20«/mn»«mrow»«mn mathvariant=¨bold¨»0«/mn»«mo mathvariant=¨bold¨».«/mo»«mn mathvariant=¨bold¨»1«/mn»«/mrow»«/mfrac»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»=«/mo»«mn mathvariant=¨bold¨ mathcolor=¨#0000FF¨»200«/mn»«mfrac mathcolor=¨#0000FF¨»«mi mathvariant=¨bold¨»N«/mi»«mi mathvariant=¨bold¨»m«/mi»«/mfrac»«/mstyle»«/math»
نعبر عن مقدار السرعة القصوى ونحسب قيمتها:
«math xmlns=¨http://www.w3.org/1998/Math/MathML¨»«mstyle mathsize=¨20px¨»«msub»«mi mathvariant=¨bold¨ mathcolor=¨#0000FF¨»V«/mi»«mi mathvariant=¨bold¨ mathcolor=¨#0000FF¨»max«/mi»«/msub»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»=«/mo»«mi mathvariant=¨bold¨ mathcolor=¨#0000FF¨»§#969;«/mi»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»§#183;«/mo»«mi mathvariant=¨bold¨ mathcolor=¨#0000FF¨»A«/mi»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»=«/mo»«msqrt mathcolor=¨#0000FF¨»«mfrac»«mi mathvariant=¨bold¨»k«/mi»«mi mathvariant=¨bold¨»m«/mi»«/mfrac»«/msqrt»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»§#183;«/mo»«mi mathvariant=¨bold¨ mathcolor=¨#0000FF¨»A«/mi»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»=«/mo»«msqrt mathcolor=¨#0000FF¨»«mfrac»«mn mathvariant=¨bold¨»200«/mn»«mn mathvariant=¨bold¨»2«/mn»«/mfrac»«/msqrt»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»§#183;«/mo»«mn mathvariant=¨bold¨ mathcolor=¨#0000FF¨»0«/mn»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨».«/mo»«mn mathvariant=¨bold¨ mathcolor=¨#0000FF¨»1«/mn»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»=«/mo»«msqrt mathcolor=¨#0000FF¨»«mn mathvariant=¨bold¨»100«/mn»«/msqrt»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»§#183;«/mo»«mn mathvariant=¨bold¨ mathcolor=¨#0000FF¨»0«/mn»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨».«/mo»«mn mathvariant=¨bold¨ mathcolor=¨#0000FF¨»1«/mn»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»=«/mo»«mn mathvariant=¨bold¨ mathcolor=¨#0000FF¨»10«/mn»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»§#183;«/mo»«mn mathvariant=¨bold¨ mathcolor=¨#0000FF¨»0«/mn»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨».«/mo»«mn mathvariant=¨bold¨ mathcolor=¨#0000FF¨»1«/mn»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»=«/mo»«mn mathvariant=¨bold¨ mathcolor=¨#0000FF¨»1«/mn»«mfrac mathcolor=¨#0000FF¨»«mi mathvariant=¨bold¨»m«/mi»«mi mathvariant=¨bold¨»s«/mi»«/mfrac»«/mstyle»«/math»
______________________________________________________________________________________

______________________________________________________________________________________
רבע זמן מחזור ראשון: מרגע שחרור הגוף ועד שהוא מגיע לנקודת ראשית הציר בפעם הראשונה.
רבע זמן מחזור שני: מרגע שהגוף חולף בפעם הראשונה בנקודת ראשית הציר ועד שהוא מגיע לנקודת הקצה השלילית.
רבע זמן מחזור שלישי: מרגע שהגוף נמצא בנקודת הקצה השלילית ועד שהוא חולף בנקודת ראשית הציר בפעם השנייה.
______________________________________________________________________________________

______________________________________________________________________________________
وتكون قيمة التسارع قصوى.
سعة الاهتزاز هي (القيمة القصوى) ومقدار التسارع هو الحد الأقصى.
דוגמה להמחשה, יכול להיות חשבון בנק עם מיליארדי שקלים וברגע מסוים אין שינוי בערך הכסף בחשבון.
3. כל סעיפי השאלה עוסקים בתנעת הגוף בנקודת קצה או בנקודת הראשית , ניתן לענות על השאלות מהבנת התנועה הרמונית
______________________________________________________________________________________