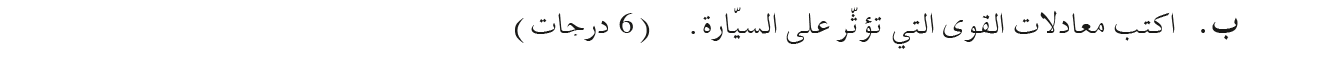
______________________________________________________________________________________
...
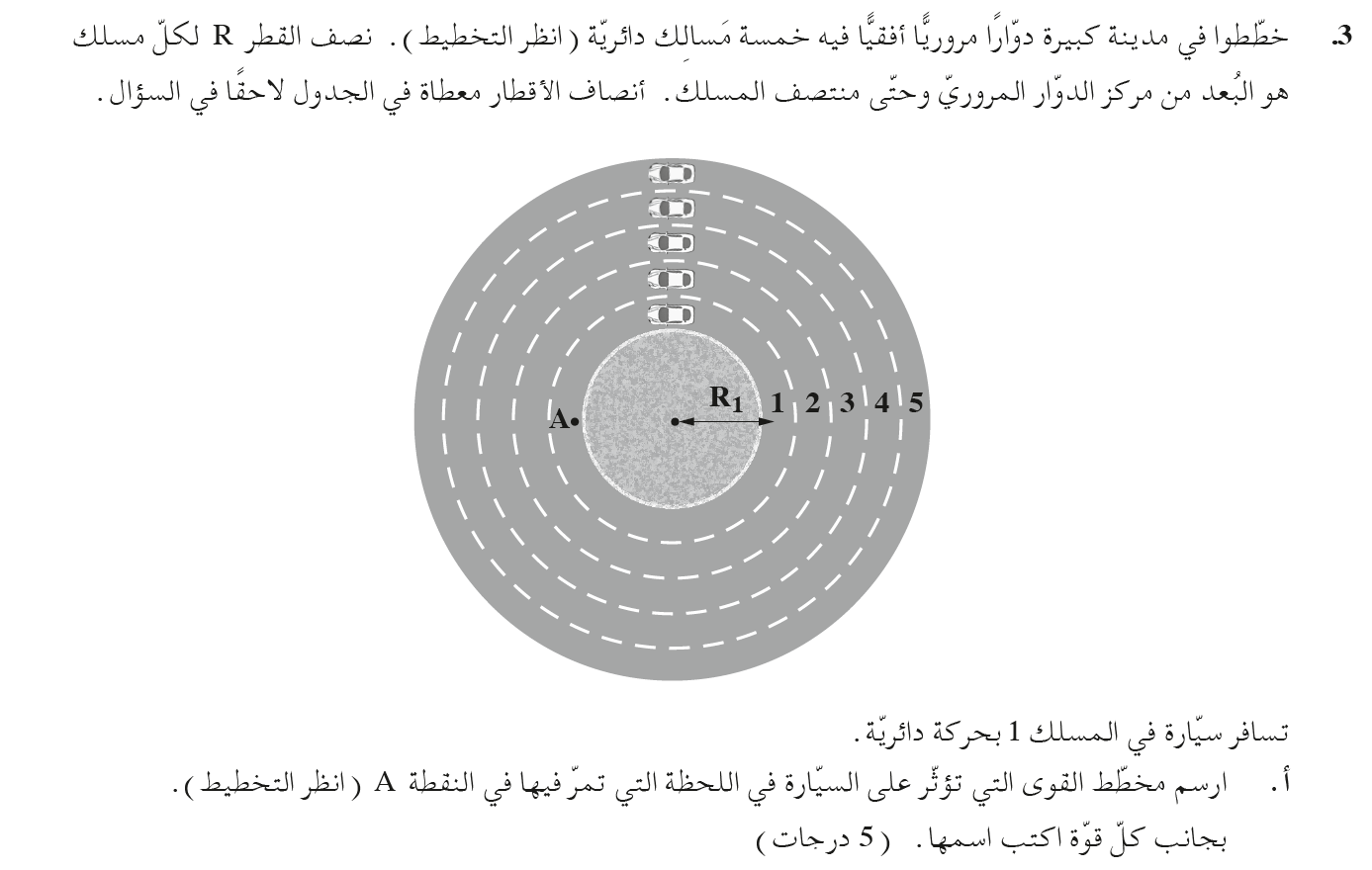
معرفة القوى المؤثرة على السيارة.
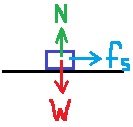
نرسم مخطط القوى المؤثرة على السيارة عندما تمر في النقطة A.
نصف القوى نسبة لوجهة نظر مراقب على الطريق:
נתאר את הכוחות ביחס לנקודת מבטו של מתבונן הנמצא על הכביש:
1. يتم عرض الرسم البياني الموضح في السؤال من مسقط علوي، ومن الناحية العملية ليس من السهل رسم قوة الجاذبية والقوة العمودية في هذا التخطيط.
يجب رسم مخطط جديد من وجهة نظر أكثر عملية لوصف القوى المؤثرة على السيارة.
2. ليست هناك حاجة لوصف شكل السيارة في الرسم التخطيطي. من الأفضل عدم قضاء وقت ثمين في أشياء غير ضرورية.
3. لا توجد معلومات تفيد بأن قوة الاحتكاك المؤثرة على السيارة هي أقصى قوة احتكاك ساكنة. وتجدر الإشارة إلى أن الاحتكاك هو احتكاك ساكن.
יש לערוך תרשים חדש מנקודת מבט יותר מעשי לתיאור הכוחות הפועלים על המכונית.
2. אין צורך לתאר בתרשים את צורת המכונית. עדיף לא להשקיע זמן יקר על דברים מיותרים.
3. לא קיים מידע לפי כוח החיכוך הפועל על המכונית הוא כוח חיכוך סטטי מקסימאלי . יש לציין שהחיכוך הוא חיכוך סטטי.
______________________________________________________________________________________
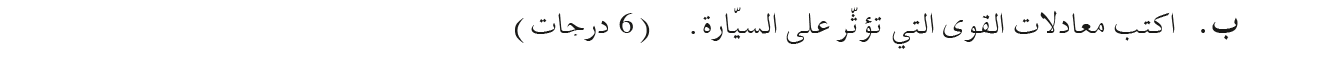
______________________________________________________________________________________
...
معادلات الحركة:
«math xmlns=¨http://www.w3.org/1998/Math/MathML¨»«msub»«mi mathvariant=¨bold¨ mathcolor=¨#0000FF¨»§#931;F«/mi»«mi mathvariant=¨bold¨ mathcolor=¨#0000FF¨»R«/mi»«/msub»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»=«/mo»«mfrac mathcolor=¨#0000FF¨»«mrow»«mi mathvariant=¨bold¨»m«/mi»«mo mathvariant=¨bold¨»§#183;«/mo»«msup»«mi mathvariant=¨bold¨»V«/mi»«mn mathvariant=¨bold¨»2«/mn»«/msup»«/mrow»«mi mathvariant=¨bold¨»R«/mi»«/mfrac»«mspace linebreak=¨newline¨»«/mspace»«mspace linebreak=¨newline¨»«/mspace»«menclose mathcolor=¨#0000FF¨ notation=¨box¨»«msub»«mi mathvariant=¨bold¨»f«/mi»«mi mathvariant=¨bold¨»s«/mi»«/msub»«mo mathvariant=¨bold¨»=«/mo»«mfrac»«mrow»«mi mathvariant=¨bold¨»m«/mi»«mo mathvariant=¨bold¨»§#183;«/mo»«msup»«mi mathvariant=¨bold¨»V«/mi»«mn mathvariant=¨bold¨»2«/mn»«/msup»«/mrow»«mi mathvariant=¨bold¨»R«/mi»«/mfrac»«/menclose»«/math» «math xmlns=¨http://www.w3.org/1998/Math/MathML¨»«msub»«mi mathvariant=¨bold¨ mathcolor=¨#0000FF¨»§#931;F«/mi»«mi mathvariant=¨bold¨ mathcolor=¨#0000FF¨»Y«/mi»«/msub»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»=«/mo»«mn mathvariant=¨bold¨ mathcolor=¨#0000FF¨»0«/mn»«mspace linebreak=¨newline¨»«/mspace»«mi mathvariant=¨bold¨ mathcolor=¨#0000FF¨»N«/mi»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»=«/mo»«mi mathvariant=¨bold¨ mathcolor=¨#0000FF¨»W«/mi»«mspace linebreak=¨newline¨»«/mspace»«menclose mathcolor=¨#0000FF¨ notation=¨box¨»«mi mathvariant=¨bold¨»N«/mi»«mo mathvariant=¨bold¨»=«/mo»«mi mathvariant=¨bold¨»m«/mi»«mo mathvariant=¨bold¨»§#183;«/mo»«mi mathvariant=¨bold¨»g«/mi»«/menclose»«/math»
«math xmlns=¨http://www.w3.org/1998/Math/MathML¨»«msub»«mi mathvariant=¨bold¨ mathcolor=¨#0000FF¨»§#931;F«/mi»«mi mathvariant=¨bold¨ mathcolor=¨#0000FF¨»R«/mi»«/msub»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»=«/mo»«mfrac mathcolor=¨#0000FF¨»«mrow»«mi mathvariant=¨bold¨»m«/mi»«mo mathvariant=¨bold¨»§#183;«/mo»«msup»«mi mathvariant=¨bold¨»V«/mi»«mn mathvariant=¨bold¨»2«/mn»«/msup»«/mrow»«mi mathvariant=¨bold¨»R«/mi»«/mfrac»«mspace linebreak=¨newline¨»«/mspace»«mspace linebreak=¨newline¨»«/mspace»«menclose mathcolor=¨#0000FF¨ notation=¨box¨»«msub»«mi mathvariant=¨bold¨»f«/mi»«mi mathvariant=¨bold¨»s«/mi»«/msub»«mo mathvariant=¨bold¨»=«/mo»«mfrac»«mrow»«mi mathvariant=¨bold¨»m«/mi»«mo mathvariant=¨bold¨»§#183;«/mo»«msup»«mi mathvariant=¨bold¨»V«/mi»«mn mathvariant=¨bold¨»2«/mn»«/msup»«/mrow»«mi mathvariant=¨bold¨»R«/mi»«/mfrac»«/menclose»«/math» «math xmlns=¨http://www.w3.org/1998/Math/MathML¨»«msub»«mi mathvariant=¨bold¨ mathcolor=¨#0000FF¨»§#931;F«/mi»«mi mathvariant=¨bold¨ mathcolor=¨#0000FF¨»Y«/mi»«/msub»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»=«/mo»«mn mathvariant=¨bold¨ mathcolor=¨#0000FF¨»0«/mn»«mspace linebreak=¨newline¨»«/mspace»«mi mathvariant=¨bold¨ mathcolor=¨#0000FF¨»N«/mi»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»=«/mo»«mi mathvariant=¨bold¨ mathcolor=¨#0000FF¨»W«/mi»«mspace linebreak=¨newline¨»«/mspace»«menclose mathcolor=¨#0000FF¨ notation=¨box¨»«mi mathvariant=¨bold¨»N«/mi»«mo mathvariant=¨bold¨»=«/mo»«mi mathvariant=¨bold¨»m«/mi»«mo mathvariant=¨bold¨»§#183;«/mo»«mi mathvariant=¨bold¨»g«/mi»«/menclose»«/math»
«math xmlns=¨http://www.w3.org/1998/Math/MathML¨»«msub»«mi mathvariant=¨bold¨ mathcolor=¨#0000FF¨»§#931;F«/mi»«mi mathvariant=¨bold¨ mathcolor=¨#0000FF¨»R«/mi»«/msub»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»=«/mo»«mfrac mathcolor=¨#0000FF¨»«mrow»«mi mathvariant=¨bold¨»m«/mi»«mo mathvariant=¨bold¨»§#183;«/mo»«msup»«mi mathvariant=¨bold¨»V«/mi»«mn mathvariant=¨bold¨»2«/mn»«/msup»«/mrow»«mi mathvariant=¨bold¨»R«/mi»«/mfrac»«mspace linebreak=¨newline¨»«/mspace»«mspace linebreak=¨newline¨»«/mspace»«menclose mathcolor=¨#0000FF¨ notation=¨box¨»«msub»«mi mathvariant=¨bold¨»f«/mi»«mi mathvariant=¨bold¨»s«/mi»«/msub»«mo mathvariant=¨bold¨»=«/mo»«mfrac»«mrow»«mi mathvariant=¨bold¨»m«/mi»«mo mathvariant=¨bold¨»§#183;«/mo»«msup»«mi mathvariant=¨bold¨»V«/mi»«mn mathvariant=¨bold¨»2«/mn»«/msup»«/mrow»«mi mathvariant=¨bold¨»R«/mi»«/mfrac»«/menclose»«/math» «math xmlns=¨http://www.w3.org/1998/Math/MathML¨»«msub»«mi mathvariant=¨bold¨ mathcolor=¨#0000FF¨»§#931;F«/mi»«mi mathvariant=¨bold¨ mathcolor=¨#0000FF¨»Y«/mi»«/msub»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»=«/mo»«mn mathvariant=¨bold¨ mathcolor=¨#0000FF¨»0«/mn»«mspace linebreak=¨newline¨»«/mspace»«mi mathvariant=¨bold¨ mathcolor=¨#0000FF¨»N«/mi»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»=«/mo»«mi mathvariant=¨bold¨ mathcolor=¨#0000FF¨»W«/mi»«mspace linebreak=¨newline¨»«/mspace»«menclose mathcolor=¨#0000FF¨ notation=¨box¨»«mi mathvariant=¨bold¨»N«/mi»«mo mathvariant=¨bold¨»=«/mo»«mi mathvariant=¨bold¨»m«/mi»«mo mathvariant=¨bold¨»§#183;«/mo»«mi mathvariant=¨bold¨»g«/mi»«/menclose»«/math»
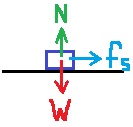
كتابة معادلات الحركة حسب قوانين نيوتن.
تتحرك السيارة على مستوى أفقي ، في الاتجاه الرأسي تكون السيارة ساكنة.
من القانون الأول لنيوتن، محصلة القوى المؤثرة على السيارة في الاتجاه الرأسي يساوي صفرًا:
«math xmlns=¨http://www.w3.org/1998/Math/MathML¨»«msub»«mi mathvariant=¨bold¨ mathcolor=¨#0000FF¨»§#931;F«/mi»«mi mathvariant=¨bold¨ mathcolor=¨#0000FF¨»R«/mi»«/msub»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»=«/mo»«mfrac mathcolor=¨#0000FF¨»«mrow»«mi mathvariant=¨bold¨»m«/mi»«mo mathvariant=¨bold¨»§#183;«/mo»«msup»«mi mathvariant=¨bold¨»V«/mi»«mn mathvariant=¨bold¨»2«/mn»«/msup»«/mrow»«mi mathvariant=¨bold¨»R«/mi»«/mfrac»«mspace linebreak=¨newline¨»«/mspace»«mspace linebreak=¨newline¨»«/mspace»«menclose mathcolor=¨#0000FF¨ notation=¨box¨»«msub»«mi mathvariant=¨bold¨»f«/mi»«mi mathvariant=¨bold¨»s«/mi»«/msub»«mo mathvariant=¨bold¨»=«/mo»«mfrac»«mrow»«mi mathvariant=¨bold¨»m«/mi»«mo mathvariant=¨bold¨»§#183;«/mo»«msup»«mi mathvariant=¨bold¨»V«/mi»«mn mathvariant=¨bold¨»2«/mn»«/msup»«/mrow»«mi mathvariant=¨bold¨»R«/mi»«/mfrac»«/menclose»«/math» «math xmlns=¨http://www.w3.org/1998/Math/MathML¨»«msub»«mi mathvariant=¨bold¨ mathcolor=¨#0000FF¨»§#931;F«/mi»«mi mathvariant=¨bold¨ mathcolor=¨#0000FF¨»Y«/mi»«/msub»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»=«/mo»«mn mathvariant=¨bold¨ mathcolor=¨#0000FF¨»0«/mn»«mspace linebreak=¨newline¨»«/mspace»«mi mathvariant=¨bold¨ mathcolor=¨#0000FF¨»N«/mi»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»=«/mo»«mi mathvariant=¨bold¨ mathcolor=¨#0000FF¨»W«/mi»«mspace linebreak=¨newline¨»«/mspace»«menclose mathcolor=¨#0000FF¨ notation=¨box¨»«mi mathvariant=¨bold¨»N«/mi»«mo mathvariant=¨bold¨»=«/mo»«mi mathvariant=¨bold¨»m«/mi»«mo mathvariant=¨bold¨»§#183;«/mo»«mi mathvariant=¨bold¨»g«/mi»«/menclose»«/math»
מהחוק הראשון של ניוטון שקול הכוחות הפועלים על המכונית בכיוון האנכי שווה לאפס:
«math xmlns=¨http://www.w3.org/1998/Math/MathML¨»«msub»«mi mathvariant=¨bold¨ mathcolor=¨#0000FF¨»§#931;F«/mi»«mi mathvariant=¨bold¨ mathcolor=¨#0000FF¨»Y«/mi»«/msub»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»=«/mo»«mn mathvariant=¨bold¨ mathcolor=¨#0000FF¨»0«/mn»«mspace linebreak=¨newline¨»«/mspace»«mi mathvariant=¨bold¨ mathcolor=¨#0000FF¨»N«/mi»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»=«/mo»«mi mathvariant=¨bold¨ mathcolor=¨#0000FF¨»W«/mi»«mspace linebreak=¨newline¨»«/mspace»«menclose mathcolor=¨#0000FF¨ notation=¨box¨»«mi mathvariant=¨bold¨»N«/mi»«mo mathvariant=¨bold¨»=«/mo»«mi mathvariant=¨bold¨»m«/mi»«mo mathvariant=¨bold¨»§#183;«/mo»«mi mathvariant=¨bold¨»g«/mi»«/menclose»«/math» «math xmlns=¨http://www.w3.org/1998/Math/MathML¨»«msub»«mi mathvariant=¨bold¨ mathcolor=¨#0000FF¨»§#931;F«/mi»«mi mathvariant=¨bold¨ mathcolor=¨#0000FF¨»R«/mi»«/msub»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»=«/mo»«mfrac mathcolor=¨#0000FF¨»«mrow»«mi mathvariant=¨bold¨»m«/mi»«mo mathvariant=¨bold¨»§#183;«/mo»«msup»«mi mathvariant=¨bold¨»V«/mi»«mn mathvariant=¨bold¨»2«/mn»«/msup»«/mrow»«mi mathvariant=¨bold¨»R«/mi»«/mfrac»«mspace linebreak=¨newline¨»«/mspace»«mspace linebreak=¨newline¨»«/mspace»«menclose mathcolor=¨#0000FF¨ notation=¨box¨»«msub»«mi mathvariant=¨bold¨»f«/mi»«mi mathvariant=¨bold¨»s«/mi»«/msub»«mo mathvariant=¨bold¨»=«/mo»«mfrac»«mrow»«mi mathvariant=¨bold¨»m«/mi»«mo mathvariant=¨bold¨»§#183;«/mo»«msup»«mi mathvariant=¨bold¨»V«/mi»«mn mathvariant=¨bold¨»2«/mn»«/msup»«/mrow»«mi mathvariant=¨bold¨»R«/mi»«/mfrac»«/menclose»«/math»
1. يجب كتابة معادلات القوة لحالة عامة، وليس لحالة وشك الحركة.
لذلك ، تجدر الإشارة إلى أن قوة الاحتكاك ساكنة وليست سكنة قصوى.
2. في معادلة القوة نحو المركز، يجب أن تختار بين السرعة الخطية والسرعة الزاوية.
في هذه الحالة ، لا يتعامل القسم السابق مع السرعات. لهذا السبب يجب أن ترى الأقسام التالية قبل كتابة معادلة القوة.
بالطبع ، سيتم أيضًا قبول معادلة مع السرعة الزاوية كإجابة صحيحة.
3. السؤال يقود الممتحن بطريقة متدرجة. يبدأ برسم مخطط القوى ويستمر بكتابة معادلات الحركة.
ليست كل الأسئلة على هذا النحو.
4. معادلات القوة هي معادلات الحركة.
לכן, יש לציין שכוח החיכוך הוא סטטי ולא סטטי מקסימאלי.
2. במשוואת הכוחות הרדיאלית, יש לבחור בין מהירות קווית למהירות זוויתית .
במקרה זה, הסעיף הקודם לא עוסק במהירויות . לכן כדאי לראות את הסעיפים הבאים לפני כתיבת משוואת הכוחות.
כמובן, גם משוואה עם מהירות זוויתית תתקבל כתשובה נכונה.
3. השאלה מובילה את הנבחן בצורה מדורגת. מתחילה בעריכת תרשים כוחות וממשיכה בכתיבת משוואות תנועה .
לא כל השאלות הן כאלו.
4. משוואות הכוחות הן משוואות התנועה.
______________________________________________________________________________________
______________________________________________________________________________________
...
«math xmlns=¨http://www.w3.org/1998/Math/MathML¨»«msub»«msup»«mi mathvariant=¨bold¨ mathcolor=¨#0000FF¨»V«/mi»«mn mathvariant=¨bold¨ mathcolor=¨#0000FF¨»2«/mn»«/msup»«mi mathvariant=¨bold¨ mathcolor=¨#0000FF¨»max«/mi»«/msub»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»=«/mo»«msub»«mi mathvariant=¨bold¨ mathcolor=¨#0000FF¨»§#956;«/mi»«mi mathvariant=¨bold¨ mathcolor=¨#0000FF¨»s«/mi»«/msub»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»§#183;«/mo»«mi mathvariant=¨bold¨ mathcolor=¨#0000FF¨»g«/mi»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»§#183;«/mo»«mi mathvariant=¨bold¨ mathcolor=¨#0000FF¨»R«/mi»«/math»
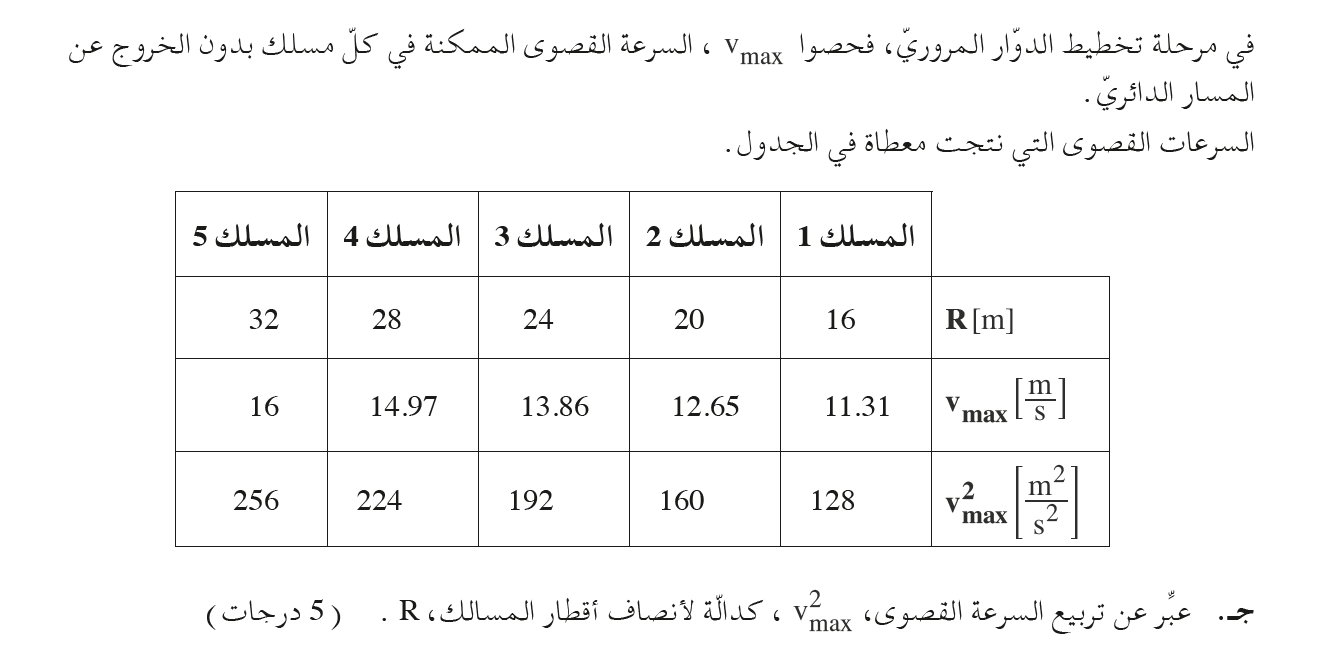
تطور التعبير من معادلات الحركة عند وشك الحركة.
تكون سرعة السيارة قصوى عندما تكون على وشك الحركة.
نرسم مخطط القوى للسيارة عندما تكون على وشك الحركة:
نكتب معادلات الحركة لحالة وشك الحركة:
«math xmlns=¨http://www.w3.org/1998/Math/MathML¨»«msub»«mi mathvariant=¨bold¨ mathcolor=¨#0000FF¨»§#931;F«/mi»«mi mathvariant=¨bold¨ mathcolor=¨#0000FF¨»R«/mi»«/msub»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»=«/mo»«mfrac mathcolor=¨#0000FF¨»«mrow»«mi mathvariant=¨bold¨»m«/mi»«mo mathvariant=¨bold¨»§#183;«/mo»«msup»«mi mathvariant=¨bold¨»V«/mi»«mn mathvariant=¨bold¨»2«/mn»«/msup»«/mrow»«mi mathvariant=¨bold¨»R«/mi»«/mfrac»«mspace linebreak=¨newline¨»«/mspace»«mspace linebreak=¨newline¨»«/mspace»«menclose mathcolor=¨#0000FF¨ notation=¨box¨»«msub»«mi mathvariant=¨bold¨»f«/mi»«msub»«mi mathvariant=¨bold¨»s«/mi»«mi mathvariant=¨bold¨»max«/mi»«/msub»«/msub»«mo mathvariant=¨bold¨»=«/mo»«mfrac»«mrow»«mi mathvariant=¨bold¨»m«/mi»«mo mathvariant=¨bold¨»§#183;«/mo»«msup»«msub»«mi mathvariant=¨bold¨»V«/mi»«mi mathvariant=¨bold¨»max«/mi»«/msub»«mn mathvariant=¨bold¨»2«/mn»«/msup»«/mrow»«mi mathvariant=¨bold¨»R«/mi»«/mfrac»«/menclose»«/math» «math xmlns=¨http://www.w3.org/1998/Math/MathML¨»«msub»«mi mathvariant=¨bold¨ mathcolor=¨#0000FF¨»§#931;F«/mi»«mi mathvariant=¨bold¨ mathcolor=¨#0000FF¨»Y«/mi»«/msub»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»=«/mo»«mn mathvariant=¨bold¨ mathcolor=¨#0000FF¨»0«/mn»«mspace linebreak=¨newline¨»«/mspace»«mi mathvariant=¨bold¨ mathcolor=¨#0000FF¨»N«/mi»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»=«/mo»«mi mathvariant=¨bold¨ mathcolor=¨#0000FF¨»W«/mi»«mspace linebreak=¨newline¨»«/mspace»«menclose mathcolor=¨#0000FF¨ notation=¨box¨»«mi mathvariant=¨bold¨»N«/mi»«mo mathvariant=¨bold¨»=«/mo»«mi mathvariant=¨bold¨»m«/mi»«mo mathvariant=¨bold¨»§#183;«/mo»«mi mathvariant=¨bold¨»g«/mi»«/menclose»«/math»
نكتب أقصى قوة احتكاك ساكنة في صورة مفصلة في معادلة الحركة نحو المركز. و نعوّض القوة العمودية من معادلة الحركة العمودية :
«math xmlns=¨http://www.w3.org/1998/Math/MathML¨»«msub»«mi mathvariant=¨bold¨ mathcolor=¨#0000FF¨»f«/mi»«msub mathcolor=¨#0000FF¨»«mi mathvariant=¨bold¨»s«/mi»«mi mathvariant=¨bold¨»max«/mi»«/msub»«/msub»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»=«/mo»«mfrac mathcolor=¨#0000FF¨»«mrow»«mi mathvariant=¨bold¨»m«/mi»«mo mathvariant=¨bold¨»§#183;«/mo»«msup»«msub»«mi mathvariant=¨bold¨»V«/mi»«mi mathvariant=¨bold¨»max«/mi»«/msub»«mn mathvariant=¨bold¨»2«/mn»«/msup»«/mrow»«mi mathvariant=¨bold¨»R«/mi»«/mfrac»«mspace linebreak=¨newline¨»«/mspace»«mspace linebreak=¨newline¨»«/mspace»«msub»«mi mathvariant=¨bold¨ mathcolor=¨#0000FF¨»§#956;«/mi»«mi mathvariant=¨bold¨ mathcolor=¨#0000FF¨»s«/mi»«/msub»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»§#183;«/mo»«mi mathvariant=¨bold¨ mathcolor=¨#FF0000¨»N«/mi»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»=«/mo»«mfrac mathcolor=¨#0000FF¨»«mrow»«mi mathvariant=¨bold¨»m«/mi»«mo mathvariant=¨bold¨»§#183;«/mo»«msup»«msub»«mi mathvariant=¨bold¨»V«/mi»«mi mathvariant=¨bold¨»max«/mi»«/msub»«mn mathvariant=¨bold¨»2«/mn»«/msup»«/mrow»«mi mathvariant=¨bold¨»R«/mi»«/mfrac»«mspace linebreak=¨newline¨»«/mspace»«mspace linebreak=¨newline¨»«/mspace»«msub»«mi mathvariant=¨bold¨ mathcolor=¨#0000FF¨»§#956;«/mi»«mi mathvariant=¨bold¨ mathcolor=¨#0000FF¨»s«/mi»«/msub»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»§#183;«/mo»«mi mathvariant=¨bold¨ mathcolor=¨#FF0000¨»m«/mi»«mo mathvariant=¨bold¨ mathcolor=¨#FF0000¨»§#183;«/mo»«mi mathvariant=¨bold¨ mathcolor=¨#FF0000¨»g«/mi»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»=«/mo»«mfrac mathcolor=¨#0000FF¨»«mrow»«mi mathvariant=¨bold¨»m«/mi»«mo mathvariant=¨bold¨»§#183;«/mo»«msup»«msub»«mi mathvariant=¨bold¨»V«/mi»«mi mathvariant=¨bold¨»max«/mi»«/msub»«mn mathvariant=¨bold¨»2«/mn»«/msup»«/mrow»«mi mathvariant=¨bold¨»R«/mi»«/mfrac»«/math»
نختزل الكتلة, ونعبّر عن السرعة:
«math xmlns=¨http://www.w3.org/1998/Math/MathML¨»«msub»«mi mathvariant=¨bold¨ mathcolor=¨#0000FF¨»§#956;«/mi»«mi mathvariant=¨bold¨ mathcolor=¨#0000FF¨»s«/mi»«/msub»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»§#183;«/mo»«menclose mathcolor=¨#0000FF¨ notation=¨updiagonalstrike¨»«mi mathvariant=¨bold¨»m«/mi»«/menclose»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»§#183;«/mo»«mi mathvariant=¨bold¨ mathcolor=¨#0000FF¨»g«/mi»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»=«/mo»«mfrac mathcolor=¨#0000FF¨»«mrow»«menclose notation=¨updiagonalstrike¨»«mi mathvariant=¨bold¨»m«/mi»«/menclose»«mo mathvariant=¨bold¨»§#183;«/mo»«msup»«msub»«mi mathvariant=¨bold¨»V«/mi»«mi mathvariant=¨bold¨»max«/mi»«/msub»«mn mathvariant=¨bold¨»2«/mn»«/msup»«/mrow»«mi mathvariant=¨bold¨»R«/mi»«/mfrac»«mspace linebreak=¨newline¨»«/mspace»«mspace linebreak=¨newline¨»«/mspace»«menclose mathcolor=¨#0000FF¨ notation=¨circle¨»«msub»«msup»«mi mathvariant=¨bold¨»V«/mi»«mn mathvariant=¨bold¨»2«/mn»«/msup»«mi mathvariant=¨bold¨»max«/mi»«/msub»«mo mathvariant=¨bold¨»=«/mo»«msub»«mi mathvariant=¨bold¨»§#956;«/mi»«mi mathvariant=¨bold¨»s«/mi»«/msub»«mo mathvariant=¨bold¨»§#183;«/mo»«mi mathvariant=¨bold¨»g«/mi»«mo mathvariant=¨bold¨»§#183;«/mo»«mi mathvariant=¨bold¨»R«/mi»«/menclose»«/math»
נערוך תרשים כוחות למכונית כאשר היא נמצאת בסף תנועה:
נכתוב את משוואות התנועה למצב של סף תנועה:
«math xmlns=¨http://www.w3.org/1998/Math/MathML¨»«msub»«mi mathvariant=¨bold¨ mathcolor=¨#0000FF¨»§#931;F«/mi»«mi mathvariant=¨bold¨ mathcolor=¨#0000FF¨»R«/mi»«/msub»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»=«/mo»«mfrac mathcolor=¨#0000FF¨»«mrow»«mi mathvariant=¨bold¨»m«/mi»«mo mathvariant=¨bold¨»§#183;«/mo»«msup»«mi mathvariant=¨bold¨»V«/mi»«mn mathvariant=¨bold¨»2«/mn»«/msup»«/mrow»«mi mathvariant=¨bold¨»R«/mi»«/mfrac»«mspace linebreak=¨newline¨»«/mspace»«mspace linebreak=¨newline¨»«/mspace»«menclose mathcolor=¨#0000FF¨ notation=¨box¨»«msub»«mi mathvariant=¨bold¨»f«/mi»«mi mathvariant=¨bold¨»s«/mi»«/msub»«mo mathvariant=¨bold¨»=«/mo»«mfrac»«mrow»«mi mathvariant=¨bold¨»m«/mi»«mo mathvariant=¨bold¨»§#183;«/mo»«msup»«mi mathvariant=¨bold¨»V«/mi»«mn mathvariant=¨bold¨»2«/mn»«/msup»«/mrow»«mi mathvariant=¨bold¨»R«/mi»«/mfrac»«/menclose»«/math» «math xmlns=¨http://www.w3.org/1998/Math/MathML¨»«msub»«mi mathvariant=¨bold¨ mathcolor=¨#0000FF¨»§#931;F«/mi»«mi mathvariant=¨bold¨ mathcolor=¨#0000FF¨»Y«/mi»«/msub»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»=«/mo»«mn mathvariant=¨bold¨ mathcolor=¨#0000FF¨»0«/mn»«mspace linebreak=¨newline¨»«/mspace»«mi mathvariant=¨bold¨ mathcolor=¨#0000FF¨»N«/mi»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»=«/mo»«mi mathvariant=¨bold¨ mathcolor=¨#0000FF¨»W«/mi»«mspace linebreak=¨newline¨»«/mspace»«menclose mathcolor=¨#0000FF¨ notation=¨box¨»«mi mathvariant=¨bold¨»N«/mi»«mo mathvariant=¨bold¨»=«/mo»«mi mathvariant=¨bold¨»m«/mi»«mo mathvariant=¨bold¨»§#183;«/mo»«mi mathvariant=¨bold¨»g«/mi»«/menclose»«/math»
1. يتعامل السؤال مع خمس حركات. لكن هذا القسم هو قسم عام يتعامل عندما تكون السيارة التي تسير على سطح أفقي غير أملس على وشك الحركة.
2. يجب كتابة تعبير لمربع السرعة القصوى وليس للسرعة القصوى.
2. יש לכתוב ביטוי לריבוע המהירות המקסימאלית ולא למהירות המקסימאלית .
______________________________________________________________________________________

______________________________________________________________________________________
...
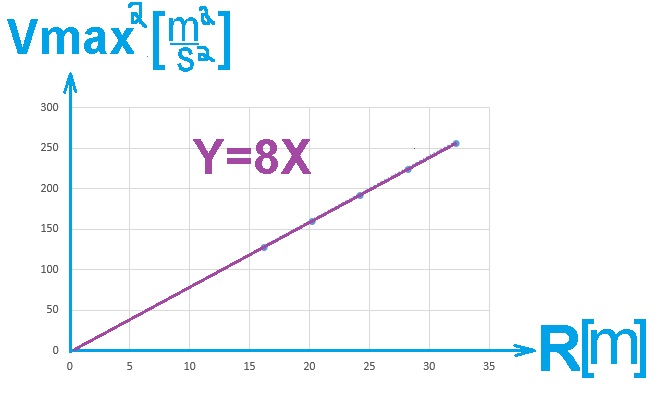
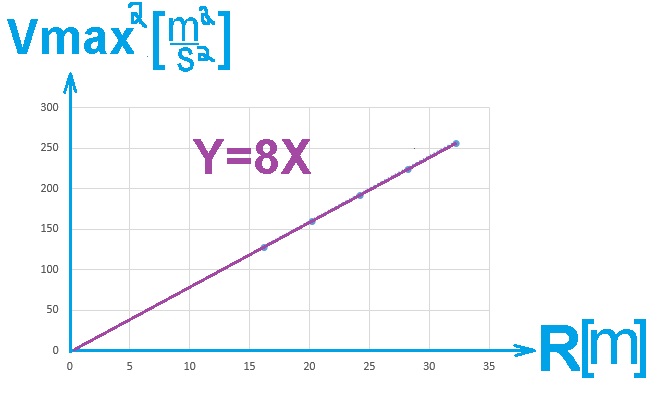
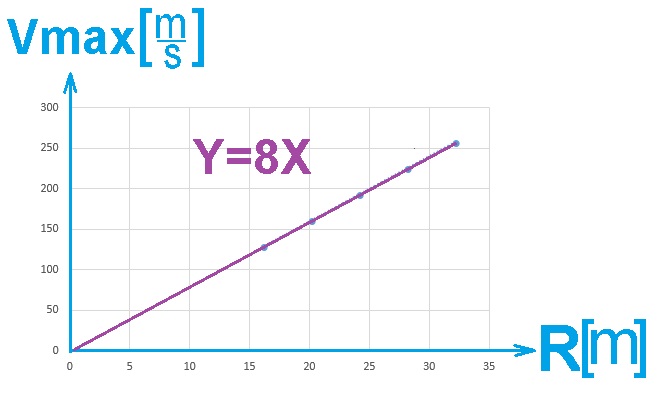
أرسم رسم بياني حسب المعطيات الموجودة في الجدول.
وفقًا للمعطيات الموجودة في الجدول ، نقوم برسم رسمًا بيانيًا يصف مربع السرعة القصوى كدالة لنصف قطر المسار.
1. تظهر القيم التربيعية للسرعات في الجدول. هناك أسئلة تظهر فيها قيم القياس فقط ويجب حساب مربع السرعة. أو كل قيمة أخرى مطلوبة.
2. خط التوجّه هو الخط المستقيم الأكثر احتمالًا. بعد تعليم النقاط ، استخدم المسطرة لتحديد الخط المستقيم الأكثر احتمالًا.
3. في هذه الحالة ، تكون جميع النقاط بالضبط على الخط المستقيم لأن القيم المعطاة في الجدول ليست قيمًا مُقاسة. تم الحصول عليهم خلال مرحلة التخطيط
على ما يبدو عن طريق الحساب.
ערך נדרש אחר.
2. קו המגמה הוא הישר המסתבר ביותר. לאחר סימון הנקודות יש להשתמש בסרגל לקביעת הישר המסתבר ביותר.
3. בהנחיות משרד החינוך לבוחנים קיימת הנחיה להוריד ציון על אי שימוש בסרגל.
אם הקו לא נראה ישר לרוב מורידים נקודה אחת.
4. במקרה זה כל הנקודות נמצאות בדיוק על הישר מכיוון שהערכים בטבלה אינם ערכי מדידות. הן התקבלו בשלב התכנון
ככל הנראה על ידי חישוב.
______________________________________________________________________________________

______________________________________________________________________________________
...
الميل مساوٍ لـ 8m/s2 .
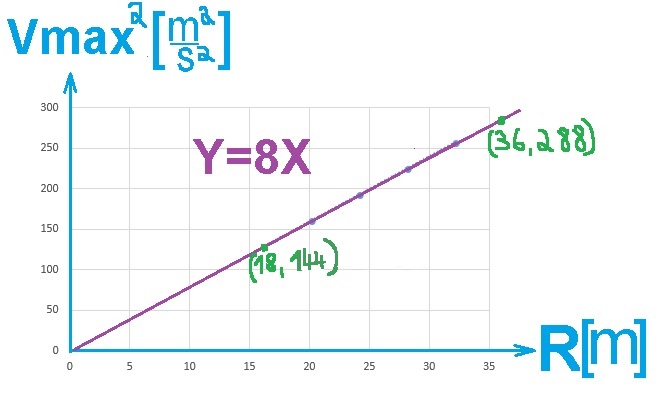
إيجاد النقطة R=36m , وحساب الميل باستخدام النقطتين.
نأخذ نقطتين على الرسم البياني:
يتم حساب ميل الخط وفقًا للنقطتين:
«math xmlns=¨http://www.w3.org/1998/Math/MathML¨»«mi mathvariant=¨bold¨ mathcolor=¨#0000FF¨»§#1513;§#1497;§#1508;§#1493;§#1506;«/mi»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»=«/mo»«mfrac mathcolor=¨#0000FF¨»«mrow»«mo mathvariant=¨bold¨»§#8710;«/mo»«msub»«mi mathvariant=¨bold¨»V«/mi»«mi mathvariant=¨bold¨»max«/mi»«/msub»«/mrow»«mrow»«mo mathvariant=¨bold¨»§#8710;«/mo»«mi mathvariant=¨bold¨»R«/mi»«/mrow»«/mfrac»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»=«/mo»«mfrac mathcolor=¨#0000FF¨»«mrow»«mn mathvariant=¨bold¨»288«/mn»«mo mathvariant=¨bold¨»-«/mo»«mn mathvariant=¨bold¨»144«/mn»«/mrow»«mrow»«mn mathvariant=¨bold¨»36«/mn»«mo mathvariant=¨bold¨»-«/mo»«mn mathvariant=¨bold¨»18«/mn»«/mrow»«/mfrac»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»=«/mo»«mfrac mathcolor=¨#0000FF¨»«mn mathvariant=¨bold¨»144«/mn»«mn mathvariant=¨bold¨»18«/mn»«/mfrac»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»=«/mo»«mn mathvariant=¨bold¨ mathcolor=¨#0000FF¨»8«/mn»«mfrac mathcolor=¨#0000FF¨»«mi mathvariant=¨bold¨»m«/mi»«msup»«mi mathvariant=¨bold¨»S«/mi»«mn mathvariant=¨bold¨»2«/mn»«/msup»«/mfrac»«/math»
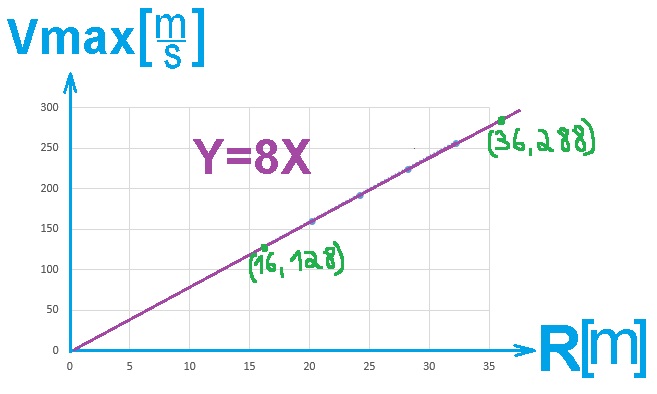
נחשב בהתאם לשתי הנקודות את שיפוע הישר:
«math xmlns=¨http://www.w3.org/1998/Math/MathML¨»«mi mathvariant=¨bold¨ mathcolor=¨#0000FF¨»§#1513;§#1497;§#1508;§#1493;§#1506;«/mi»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»=«/mo»«mfrac mathcolor=¨#0000FF¨»«mrow»«mo mathvariant=¨bold¨»§#8710;«/mo»«msub»«mi mathvariant=¨bold¨»V«/mi»«mi mathvariant=¨bold¨»max«/mi»«/msub»«/mrow»«mrow»«mo mathvariant=¨bold¨»§#8710;«/mo»«mi mathvariant=¨bold¨»R«/mi»«/mrow»«/mfrac»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»=«/mo»«mfrac mathcolor=¨#0000FF¨»«mrow»«mn mathvariant=¨bold¨»288«/mn»«mo mathvariant=¨bold¨»-«/mo»«mn mathvariant=¨bold¨»128«/mn»«/mrow»«mrow»«mn mathvariant=¨bold¨»36«/mn»«mo mathvariant=¨bold¨»-«/mo»«mn mathvariant=¨bold¨»16«/mn»«/mrow»«/mfrac»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»=«/mo»«mfrac mathcolor=¨#0000FF¨»«mn mathvariant=¨bold¨»160«/mn»«mn mathvariant=¨bold¨»20«/mn»«/mfrac»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»=«/mo»«mn mathvariant=¨bold¨ mathcolor=¨#0000FF¨»8«/mn»«mfrac mathcolor=¨#0000FF¨»«mn mathvariant=¨bold¨»1«/mn»«mi mathvariant=¨bold¨»S«/mi»«/mfrac»«/math»
1. يوجد لميل الرسم البياني وحدات. من تعريف الميل، فإن وحدات الميل تساوي النسبة بين وحدات المحور الرأسي ووحدات المحور الأفقي.
في هذه الحالة :
«math xmlns=¨http://www.w3.org/1998/Math/MathML¨»«mfrac mathcolor=¨#FF0000¨»«mrow»«mo mathvariant=¨bold¨»[«/mo»«mstyle displaystyle=¨true¨»«mfrac»«msup»«mi mathvariant=¨bold¨»m«/mi»«menclose notation=¨updiagonalstrike¨»«mn mathvariant=¨bold¨»2«/mn»«/menclose»«/msup»«msup»«mi mathvariant=¨bold¨»s«/mi»«mn mathvariant=¨bold¨»2«/mn»«/msup»«/mfrac»«/mstyle»«mo mathvariant=¨bold¨»]«/mo»«/mrow»«mstyle mathvariant=¨bold¨»«mo»[«/mo»«menclose notation=¨updiagonalstrike¨»«mi»m«/mi»«/menclose»«mo»]«/mo»«/mstyle»«/mfrac»«mo mathvariant=¨bold¨ mathcolor=¨#FF0000¨»=«/mo»«mo mathvariant=¨bold¨ mathcolor=¨#FF0000¨»[«/mo»«mfrac mathcolor=¨#FF0000¨»«mi mathvariant=¨bold¨»m«/mi»«msup»«mi mathvariant=¨bold¨»s«/mi»«mn mathvariant=¨bold¨»2«/mn»«/msup»«/mfrac»«mo mathvariant=¨bold¨ mathcolor=¨#FF0000¨»]«/mo»«/math»
يتم خصم نقاط لعدم كتابة الوحدات.
حتى لو كانت درجة كل قسم 3 نقاط ، يتم خصم نقطة واحدة على الأقل لعدم كتابة وحدات الميل.
2. يمكن الإشارة لميل المنحدر بـ m أو a ، كما يمكن ببساطة كتابة الميل. في الفيزياء ، m و a لهما معنى.
لذلك ، من الأفضل كتابة الميل بالعربية.
3. النقطة R = 36m ليست في الجدول ، يجب إيجاد قيمة المحور الرأسي للنقطة رياضياً أو بيانياً.
במקרה זה :
«math xmlns=¨http://www.w3.org/1998/Math/MathML¨»«mfrac mathcolor=¨#FF0000¨»«mrow»«mo mathvariant=¨bold¨»[«/mo»«mstyle displaystyle=¨true¨»«mfrac»«msup»«mi mathvariant=¨bold¨»m«/mi»«menclose notation=¨updiagonalstrike¨»«mn mathvariant=¨bold¨»2«/mn»«/menclose»«/msup»«msup»«mi mathvariant=¨bold¨»s«/mi»«mn mathvariant=¨bold¨»2«/mn»«/msup»«/mfrac»«/mstyle»«mo mathvariant=¨bold¨»]«/mo»«/mrow»«mstyle mathvariant=¨bold¨»«mo»[«/mo»«menclose notation=¨updiagonalstrike¨»«mi»m«/mi»«/menclose»«mo»]«/mo»«/mstyle»«/mfrac»«mo mathvariant=¨bold¨ mathcolor=¨#FF0000¨»=«/mo»«mo mathvariant=¨bold¨ mathcolor=¨#FF0000¨»[«/mo»«mfrac mathcolor=¨#FF0000¨»«mi mathvariant=¨bold¨»m«/mi»«msup»«mi mathvariant=¨bold¨»s«/mi»«mn mathvariant=¨bold¨»2«/mn»«/msup»«/mfrac»«mo mathvariant=¨bold¨ mathcolor=¨#FF0000¨»]«/mo»«/math»
על אי כתיבת יחידות מורידים ציון.
גם אם הניקוד של כל סעיף הוא 3 נקודות , על אי כתיבת יחידות בשיפוע מורידים לפחות נקודה אחת.
2. אפשר לסמן את השיפוע בעזרת m או a אפשר גם פשוט לכתוב שיפוע . בפיזיקה יש משמעות ל m ול a .
לכן, עדיף לכתוב בעברית שיפוע.
3. הנקודה R=36m לא נמצאת בטבלה, יש למצוא מתמטית או גרפית את הערך של הציר האנכי של הנקודה.
______________________________________________________________________________________
هـ.

______________________________________________________________________________________
...
«math xmlns=¨http://www.w3.org/1998/Math/MathML¨»«msub»«mi mathvariant=¨bold¨ mathcolor=¨#0000FF¨»§#956;«/mi»«mi mathvariant=¨bold¨ mathcolor=¨#0000FF¨»S«/mi»«/msub»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»=«/mo»«mn mathvariant=¨bold¨ mathcolor=¨#0000FF¨»0«/mn»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨».«/mo»«mn mathvariant=¨bold¨ mathcolor=¨#0000FF¨»8«/mn»«/math»
تعبير المعامل من ميل الخط المستقيم.
من التعبير عن مربع السرعة ، يمكنك كتابة تعبير لميل الخط المستقيم.
«math xmlns=¨http://www.w3.org/1998/Math/MathML¨»«msub»«msup»«mi mathvariant=¨bold¨ mathcolor=¨#0000FF¨»V«/mi»«mn mathvariant=¨bold¨ mathcolor=¨#0000FF¨»2«/mn»«/msup»«mi mathvariant=¨bold¨ mathcolor=¨#0000FF¨»max«/mi»«/msub»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»=«/mo»«munder mathcolor=¨#FF0000¨»«munder»«mrow»«msub»«mi mathvariant=¨bold¨»§#956;«/mi»«mi mathvariant=¨bold¨»s«/mi»«/msub»«mo mathvariant=¨bold¨»§#183;«/mo»«mi mathvariant=¨bold¨»g«/mi»«/mrow»«mo mathvariant=¨bold¨»§#9183;«/mo»«/munder»«mi mathvariant=¨bold¨»§#1605;§#1610;§#1604;«/mi»«/munder»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»§#183;«/mo»«mi mathvariant=¨bold¨ mathcolor=¨#0000FF¨»R«/mi»«/math»
نكتب تعبيرًا للميل ، ونحسب منه معامل الاحتكاك الساكن:
«math xmlns=¨http://www.w3.org/1998/Math/MathML¨»«mi mathvariant=¨bold¨ mathcolor=¨#0000FF¨»§#1575;§#1604;§#1605;§#1610;§#1604;«/mi»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»§#160;«/mo»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»=«/mo»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»§#160;«/mo»«msub»«mi mathvariant=¨bold¨ mathcolor=¨#0000FF¨»§#956;«/mi»«mi mathvariant=¨bold¨ mathcolor=¨#0000FF¨»s«/mi»«/msub»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»§#183;«/mo»«mi mathvariant=¨bold¨ mathcolor=¨#0000FF¨»g«/mi»«mspace linebreak=¨newline¨/»«mspace linebreak=¨newline¨/»«msub»«mi mathvariant=¨bold¨ mathcolor=¨#0000FF¨»§#956;«/mi»«mi mathvariant=¨bold¨ mathcolor=¨#0000FF¨»s«/mi»«/msub»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»=«/mo»«mfrac mathcolor=¨#0000FF¨»«mi mathvariant=¨bold¨»§#1575;§#1604;§#1605;§#1610;§#1604;«/mi»«mi mathvariant=¨bold¨»g«/mi»«/mfrac»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»=«/mo»«mfrac mathcolor=¨#0000FF¨»«mn mathvariant=¨bold¨»8«/mn»«mn mathvariant=¨bold¨»10«/mn»«/mfrac»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»=«/mo»«mn mathvariant=¨bold¨ mathcolor=¨#0000FF¨»0«/mn»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨».«/mo»«mn mathvariant=¨bold¨ mathcolor=¨#0000FF¨»8«/mn»«/math»
لذلك ، فإن قيمة معامل الاحتكاك الساكن هي 0.8
«math xmlns=¨http://www.w3.org/1998/Math/MathML¨»«msub»«msup»«mi mathvariant=¨bold¨ mathcolor=¨#0000FF¨»V«/mi»«mn mathvariant=¨bold¨ mathcolor=¨#0000FF¨»2«/mn»«/msup»«mi mathvariant=¨bold¨ mathcolor=¨#0000FF¨»max«/mi»«/msub»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»=«/mo»«munder mathcolor=¨#FF0000¨»«munder»«mrow»«msub»«mi mathvariant=¨bold¨»§#956;«/mi»«mi mathvariant=¨bold¨»s«/mi»«/msub»«mo mathvariant=¨bold¨»§#183;«/mo»«mi mathvariant=¨bold¨»g«/mi»«/mrow»«mo mathvariant=¨bold¨»§#9183;«/mo»«/munder»«mi mathvariant=¨bold¨»§#1513;§#1497;§#1508;§#1493;§#1506;«/mi»«/munder»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»§#183;«/mo»«mi mathvariant=¨bold¨ mathcolor=¨#0000FF¨»R«/mi»«/math»
נכתוב ביטוי לשיפוע, ונחשב ממנו את מקדם החיכוך הסטטי:
«math xmlns=¨http://www.w3.org/1998/Math/MathML¨»«msub»«msup»«mi mathvariant=¨bold¨ mathcolor=¨#0000FF¨»V«/mi»«mn mathvariant=¨bold¨ mathcolor=¨#0000FF¨»2«/mn»«/msup»«mi mathvariant=¨bold¨ mathcolor=¨#0000FF¨»max«/mi»«/msub»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»=«/mo»«munder mathcolor=¨#FF0000¨»«munder»«mrow»«msub»«mi mathvariant=¨bold¨»§#956;«/mi»«mi mathvariant=¨bold¨»s«/mi»«/msub»«mo mathvariant=¨bold¨»§#183;«/mo»«mi mathvariant=¨bold¨»g«/mi»«/mrow»«mo mathvariant=¨bold¨»§#9183;«/mo»«/munder»«mi mathvariant=¨bold¨»§#1513;§#1497;§#1508;§#1493;§#1506;«/mi»«/munder»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»§#183;«/mo»«mi mathvariant=¨bold¨ mathcolor=¨#0000FF¨»R«/mi»«/math»
מהלך פתרון קלאסי בשאלות הבגרות - פיתחנו ביטוי לפונקציה המתוארת בגרף וחשבנו את ערך שיפוע הפונקציה בגרף.
והתשובה לסעיף זה מבוססת על ביטוי שיפוע הפונקציה ועל ערך שיפוע הפונקציה.
שואלים שאלה שהתשובה שלה מבוססת על ביטוי שיפוע הפונקציה.
______________________________________________________________________________________

______________________________________________________________________________________
...
القول الصحيح هو القول 2.
مبادئ الحركة الدائرية .
بشكل عام ، من مبادئ الحركة الدائرية الثابتة ، يتعلق زمن الدورة على نصف قطر المسار والسرعة فقط ، وفقًا لما يلي:
«math xmlns=¨http://www.w3.org/1998/Math/MathML¨»«mi mathvariant=¨bold¨ mathcolor=¨#0000FF¨»V«/mi»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»=«/mo»«mfrac mathcolor=¨#0000FF¨»«mrow»«mo mathvariant=¨bold¨»§#8710;«/mo»«mi mathvariant=¨bold¨»s«/mi»«/mrow»«mrow»«mo mathvariant=¨bold¨»§#8710;«/mo»«mi mathvariant=¨bold¨»t«/mi»«/mrow»«/mfrac»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»=«/mo»«mfrac mathcolor=¨#0000FF¨»«mrow»«mn mathvariant=¨bold¨»2«/mn»«mo mathvariant=¨bold¨»§#183;«/mo»«mi mathvariant=¨bold¨»§#960;«/mi»«mo mathvariant=¨bold¨»§#183;«/mo»«mi mathvariant=¨bold¨»R«/mi»«/mrow»«mi mathvariant=¨bold¨»T«/mi»«/mfrac»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»§#160;«/mo»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»§#8658;«/mo»«mi mathvariant=¨bold¨ mathcolor=¨#0000FF¨»T«/mi»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»=«/mo»«mfrac mathcolor=¨#0000FF¨»«mrow»«mn mathvariant=¨bold¨»2«/mn»«mo mathvariant=¨bold¨»§#183;«/mo»«mi mathvariant=¨bold¨»§#960;«/mi»«mo mathvariant=¨bold¨»§#183;«/mo»«mi mathvariant=¨bold¨»R«/mi»«/mrow»«mi mathvariant=¨bold¨»V«/mi»«/mfrac»«mspace linebreak=¨newline¨/»«mspace linebreak=¨newline¨/»«mspace linebreak=¨newline¨/»«mspace linebreak=¨newline¨/»«/math»
تتعلق سرعة السيارات على نصف قطر المسار وفقًا للتعبير : «math xmlns=¨http://www.w3.org/1998/Math/MathML¨»«msub»«mi mathvariant=¨bold¨ mathcolor=¨#0000FF¨»V«/mi»«mi mathvariant=¨bold¨ mathcolor=¨#0000FF¨»max«/mi»«/msub»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»=«/mo»«msqrt mathcolor=¨#0000FF¨»«msub»«mi mathvariant=¨bold¨»§#956;«/mi»«mi mathvariant=¨bold¨»s«/mi»«/msub»«mo mathvariant=¨bold¨»§#183;«/mo»«mi mathvariant=¨bold¨»g«/mi»«mo mathvariant=¨bold¨»§#183;«/mo»«mi mathvariant=¨bold¨»R«/mi»«/msqrt»«/math».
لذلك ، في هذه الحالة ، من الممكن التعبير عن وقت الدورة كدالة لنصف قطر المسار فقط:
«math xmlns=¨http://www.w3.org/1998/Math/MathML¨»«mi mathvariant=¨bold¨ mathcolor=¨#0000FF¨»T«/mi»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»=«/mo»«mfrac mathcolor=¨#0000FF¨»«mrow»«mn mathvariant=¨bold¨»2«/mn»«mo mathvariant=¨bold¨»§#183;«/mo»«mi mathvariant=¨bold¨»§#960;«/mi»«mo mathvariant=¨bold¨»§#183;«/mo»«mi mathvariant=¨bold¨»R«/mi»«/mrow»«mi mathvariant=¨bold¨»V«/mi»«/mfrac»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»=«/mo»«mfrac mathcolor=¨#0000FF¨»«mrow»«mn mathvariant=¨bold¨»2«/mn»«mo mathvariant=¨bold¨»§#183;«/mo»«mi mathvariant=¨bold¨»§#960;«/mi»«mo mathvariant=¨bold¨»§#183;«/mo»«mi mathvariant=¨bold¨»R«/mi»«/mrow»«msqrt»«msub»«mi mathvariant=¨bold¨»§#956;«/mi»«mi mathvariant=¨bold¨»S«/mi»«/msub»«mo mathvariant=¨bold¨»§#183;«/mo»«mi mathvariant=¨bold¨»g«/mi»«mo mathvariant=¨bold¨»§#183;«/mo»«mi mathvariant=¨bold¨»R«/mi»«/msqrt»«/mfrac»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»=«/mo»«mfrac mathcolor=¨#0000FF¨»«mrow»«mn mathvariant=¨bold¨»2«/mn»«mo mathvariant=¨bold¨»§#183;«/mo»«mi mathvariant=¨bold¨»§#960;«/mi»«mo mathvariant=¨bold¨»§#183;«/mo»«msqrt»«mi mathvariant=¨bold¨»R«/mi»«/msqrt»«/mrow»«msqrt»«msub»«mi mathvariant=¨bold¨»§#956;«/mi»«mi mathvariant=¨bold¨»S«/mi»«/msub»«mo mathvariant=¨bold¨»§#183;«/mo»«mi mathvariant=¨bold¨»g«/mi»«/msqrt»«/mfrac»«mspace linebreak=¨newline¨/»«mspace linebreak=¨newline¨/»«menclose mathcolor=¨#0000FF¨ notation=¨circle¨»«mi mathvariant=¨bold¨»T«/mi»«mo mathvariant=¨bold¨»=«/mo»«mn mathvariant=¨bold¨»2«/mn»«mo mathvariant=¨bold¨»§#183;«/mo»«mi mathvariant=¨bold¨»§#960;«/mi»«mo mathvariant=¨bold¨»§#183;«/mo»«msqrt»«mfrac»«mi mathvariant=¨bold¨»R«/mi»«mrow»«msub»«mi mathvariant=¨bold¨»§#956;«/mi»«mi mathvariant=¨bold¨»S«/mi»«/msub»«mo mathvariant=¨bold¨»§#183;«/mo»«mi mathvariant=¨bold¨»g«/mi»«/mrow»«/mfrac»«/msqrt»«/menclose»«mspace linebreak=¨newline¨/»«/math»
من تعبير زمن الدورة ، يمكن ملاحظة أنه كلما زاد نصف قطر المسار ، زاد زمن الدورة. لذلك فإن العبارة الصحيحة هي العبارة 2.
«math xmlns=¨http://www.w3.org/1998/Math/MathML¨»«mi mathvariant=¨bold¨ mathcolor=¨#0000FF¨»V«/mi»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»=«/mo»«mfrac mathcolor=¨#0000FF¨»«mrow»«mo mathvariant=¨bold¨»§#8710;«/mo»«mi mathvariant=¨bold¨»s«/mi»«/mrow»«mrow»«mo mathvariant=¨bold¨»§#8710;«/mo»«mi mathvariant=¨bold¨»t«/mi»«/mrow»«/mfrac»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»=«/mo»«mfrac mathcolor=¨#0000FF¨»«mrow»«mn mathvariant=¨bold¨»2«/mn»«mo mathvariant=¨bold¨»§#183;«/mo»«mi mathvariant=¨bold¨»§#960;«/mi»«mo mathvariant=¨bold¨»§#183;«/mo»«mi mathvariant=¨bold¨»R«/mi»«/mrow»«mi mathvariant=¨bold¨»T«/mi»«/mfrac»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»§#160;«/mo»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»§#8658;«/mo»«mi mathvariant=¨bold¨ mathcolor=¨#0000FF¨»T«/mi»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»=«/mo»«mfrac mathcolor=¨#0000FF¨»«mrow»«mn mathvariant=¨bold¨»2«/mn»«mo mathvariant=¨bold¨»§#183;«/mo»«mi mathvariant=¨bold¨»§#960;«/mi»«mo mathvariant=¨bold¨»§#183;«/mo»«mi mathvariant=¨bold¨»R«/mi»«/mrow»«mi mathvariant=¨bold¨»V«/mi»«/mfrac»«mspace linebreak=¨newline¨/»«mspace linebreak=¨newline¨/»«mspace linebreak=¨newline¨/»«mspace linebreak=¨newline¨/»«/math»
מהירות המכוניות תלויה ברדיוס המסלול בהתאם לביטוי: «math xmlns=¨http://www.w3.org/1998/Math/MathML¨»«msub»«mi mathvariant=¨bold¨ mathcolor=¨#0000FF¨»V«/mi»«mi mathvariant=¨bold¨ mathcolor=¨#0000FF¨»max«/mi»«/msub»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»=«/mo»«msqrt mathcolor=¨#0000FF¨»«msub»«mi mathvariant=¨bold¨»§#956;«/mi»«mi mathvariant=¨bold¨»s«/mi»«/msub»«mo mathvariant=¨bold¨»§#183;«/mo»«mi mathvariant=¨bold¨»g«/mi»«mo mathvariant=¨bold¨»§#183;«/mo»«mi mathvariant=¨bold¨»R«/mi»«/msqrt»«/math».
לכן במקרה זה , ניתן לבטא את זמן ההקפה בתלות ברדיוס המסלול בלבד:
«math xmlns=¨http://www.w3.org/1998/Math/MathML¨»«mi mathvariant=¨bold¨ mathcolor=¨#0000FF¨»T«/mi»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»=«/mo»«mfrac mathcolor=¨#0000FF¨»«mrow»«mn mathvariant=¨bold¨»2«/mn»«mo mathvariant=¨bold¨»§#183;«/mo»«mi mathvariant=¨bold¨»§#960;«/mi»«mo mathvariant=¨bold¨»§#183;«/mo»«mi mathvariant=¨bold¨»R«/mi»«/mrow»«mi mathvariant=¨bold¨»V«/mi»«/mfrac»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»=«/mo»«mfrac mathcolor=¨#0000FF¨»«mrow»«mn mathvariant=¨bold¨»2«/mn»«mo mathvariant=¨bold¨»§#183;«/mo»«mi mathvariant=¨bold¨»§#960;«/mi»«mo mathvariant=¨bold¨»§#183;«/mo»«mi mathvariant=¨bold¨»R«/mi»«/mrow»«msqrt»«msub»«mi mathvariant=¨bold¨»§#956;«/mi»«mi mathvariant=¨bold¨»S«/mi»«/msub»«mo mathvariant=¨bold¨»§#183;«/mo»«mi mathvariant=¨bold¨»g«/mi»«mo mathvariant=¨bold¨»§#183;«/mo»«mi mathvariant=¨bold¨»R«/mi»«/msqrt»«/mfrac»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»=«/mo»«mfrac mathcolor=¨#0000FF¨»«mrow»«mn mathvariant=¨bold¨»2«/mn»«mo mathvariant=¨bold¨»§#183;«/mo»«mi mathvariant=¨bold¨»§#960;«/mi»«mo mathvariant=¨bold¨»§#183;«/mo»«msqrt»«mi mathvariant=¨bold¨»R«/mi»«/msqrt»«/mrow»«msqrt»«msub»«mi mathvariant=¨bold¨»§#956;«/mi»«mi mathvariant=¨bold¨»S«/mi»«/msub»«mo mathvariant=¨bold¨»§#183;«/mo»«mi mathvariant=¨bold¨»g«/mi»«/msqrt»«/mfrac»«mspace linebreak=¨newline¨/»«mspace linebreak=¨newline¨/»«menclose mathcolor=¨#0000FF¨ notation=¨circle¨»«mi mathvariant=¨bold¨»T«/mi»«mo mathvariant=¨bold¨»=«/mo»«mn mathvariant=¨bold¨»2«/mn»«mo mathvariant=¨bold¨»§#183;«/mo»«mi mathvariant=¨bold¨»§#960;«/mi»«mo mathvariant=¨bold¨»§#183;«/mo»«msqrt»«mfrac»«mi mathvariant=¨bold¨»R«/mi»«mrow»«msub»«mi mathvariant=¨bold¨»§#956;«/mi»«mi mathvariant=¨bold¨»S«/mi»«/msub»«mo mathvariant=¨bold¨»§#183;«/mo»«mi mathvariant=¨bold¨»g«/mi»«/mrow»«/mfrac»«/msqrt»«/menclose»«mspace linebreak=¨newline¨/»«/math»
מביטוי זמן המחזור ניתן לראות שככל שרדיוס המסלול גדול יותר, כך זמן ההקפה יותר גדול. לכן ההיגד הנכון הוא היגד 2.
1. في البداية عندما ترى خمس حركات دائرية ، يبدو السؤال صعبًا بعض الشيء.
عندما تقرأ السؤال بأكمله ، تدرك أن القسم الأخير فقط يتعامل مع جميع السيارات الخمس. وهو ليس صعبًا للغاية أيضًا.
لذلك ، يوصى بقراءة السؤال بالكامل حتى لو كانت هناك بعض المخاوف في البداية.
2. كلما زاد نصف قطر المسار ، زاد طول المسار.
ومن ناحية أخرى ، كلما زاد نصف قطر المسار ، زادت السرعة القصوى.
اتضح أنه كلما زاد نصف القطر ، زاد طول المسار ، ولكن أيضًا زادت السرعة.
لذلك لا يمكن الإجابة على السؤال بمنطق عام.
3. بشكل عام ، لا يجب أن تجيب على الأسئلة المبنية على المنطق العام وحده. في كثير من الأحيان لا يرى الطلاب الصورة الكاملة
وجميع الجوانب.
هذا السؤال هو مثال على كيف أنه حتى عندما ترى الصورة كاملة لا يمكنك الوصول إلى نتيجة مبنية على المنطق العام وحده.
يجب تطوير التعبير الذي يجيب على السؤال ، في هذه الحالة تعبير عن زمن الدورة كدالة لنصف قطر المسار.
כשקוראים את כל השאלה מבינים שרק הסעיף האחרון עוסק בכל חמשת המכוניות.
לכן, מומלץ לקרא את כל השאלה גם אם יש מעט חששות בהתחלה.
2. ככל שרדיוס המסלול גדול יותר כך המסלול יותר ארוך, מצד שני המכוניות נעות במהירות המקסימאלית האפשרית .
וככל שרדיוס המסלול גדול יותר כך המהירות המקסימאלית יותר גדולה.
יוצא שככל שהרדיוס גדול יותר המסלול יותר ארוך אבל גם המהירות יותר גדולה.
3. באופן כללי לא כדאי לענות על השאלה על סמך היגיון כללי בלבד, פעמים רבות תלמידים לא רואים את התמונה המלאה
ואת כל ההביטים.
שאלה זו היא דוגמה לכך שגם כאשר רואים את כל התמונה המלאה לא ניתן להגיע למסקנה על סמך היגיון כללי בלבד.
יש לפתוח ביטוי העונה על השאלה , במקרה זה ביטוי לזמן המחזור בתלות ברדיוס המסלול.
______________________________________________________________________________________
+
-