حلول ومنتديات لـ"ألبوم الحلول" – الحركة الدائرية المنتظمة.
| الموقع: | YouCube |
| المقرر: | תנועה מעגלית - ערבית |
| كتاب: | حلول ومنتديات لـ"ألبوم الحلول" – الحركة الدائرية المنتظمة. |
| طبع بواسطة: | משתמש אורח |
| التاريخ: | الأربعاء، 4 فبراير 2026، 12:47 AM |
جدول المحتويات
- 1. 2020,3- خمس سيارات تتحركن بمسالك دائرية أفقية
- 2. 2019,3 - صبي يقف على الأرض داخل اسطوانة دوارة
- 3. 2012,5- قطعة نقديّة على قرص
- 4. 2010,2- خرزة داخل مخروط
- 5. 2009,3 - البندول المخروطي
- 6. 2006,4-منعطف أفقي مائل
- 7. 2004,3- بندول مع ذراع أفقي
- 8. 2000,2- شارع أفقي مائل
- 9. 1997,2-بندول مع ذراع أفقي
- 10. 1992,4- عربة تدور بنابض
- 11. 1991,4-بندول مخروطي
- 12. 1985,19- جسم موضوع في أنبوب دوار
- 13. 1983,18-بندول مع ذراع أفقي
1. 2020,3- خمس سيارات تتحركن بمسالك دائرية أفقية
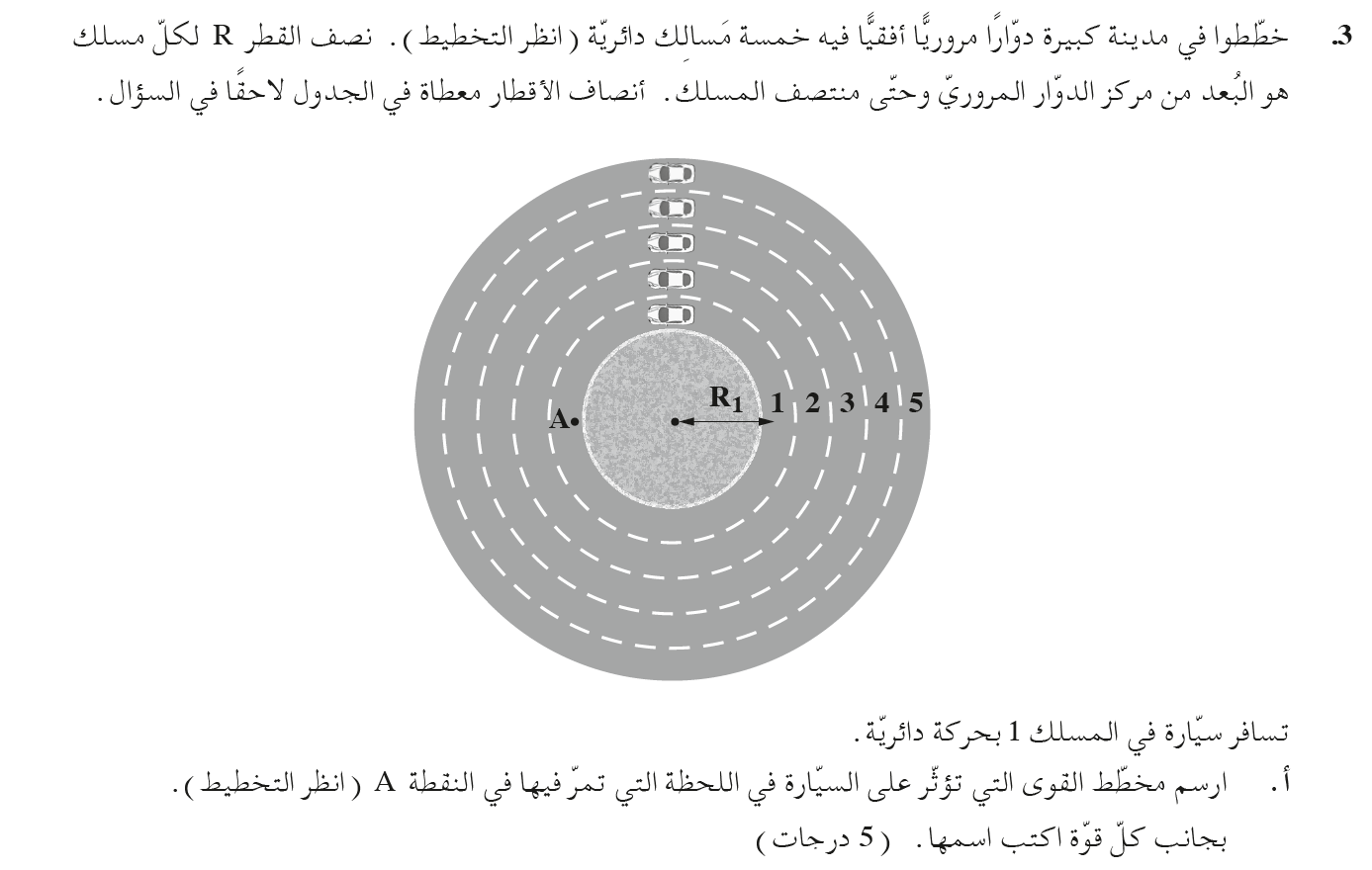
______________________________________________________________________________________
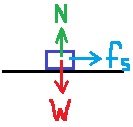
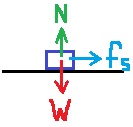

______________________________________________________________________________________
______________________________________________________________________________________
______________________________________________________________________________________
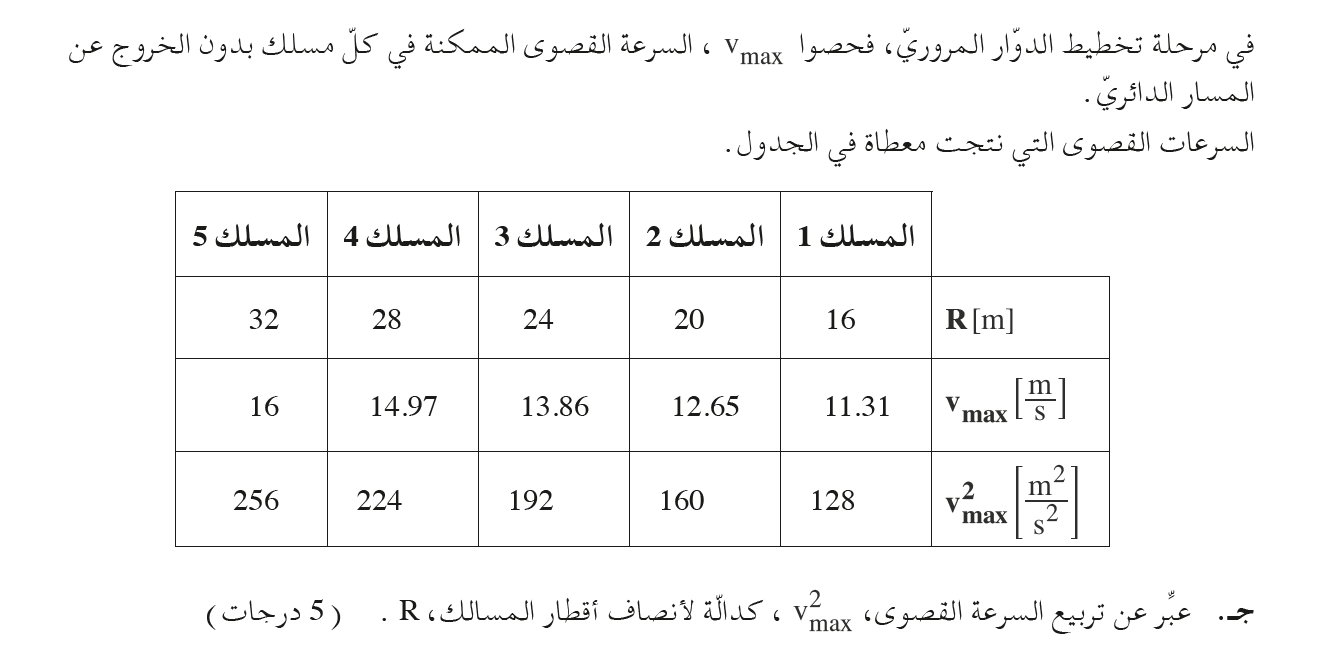
______________________________________________________________________________________
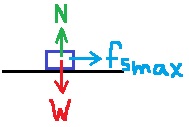

______________________________________________________________________________________

______________________________________________________________________________________
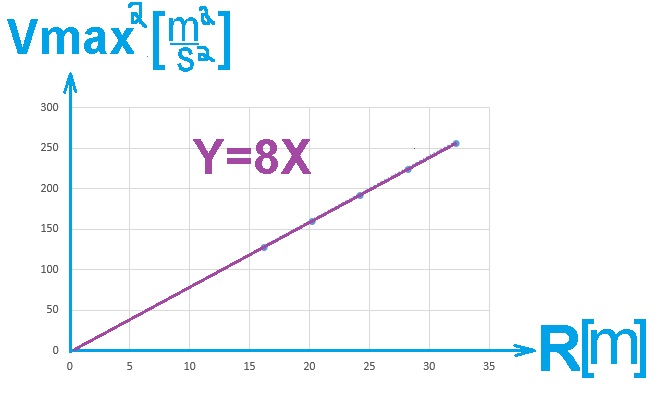
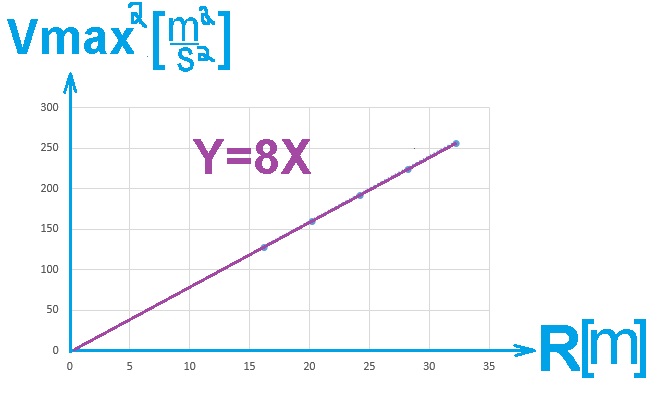
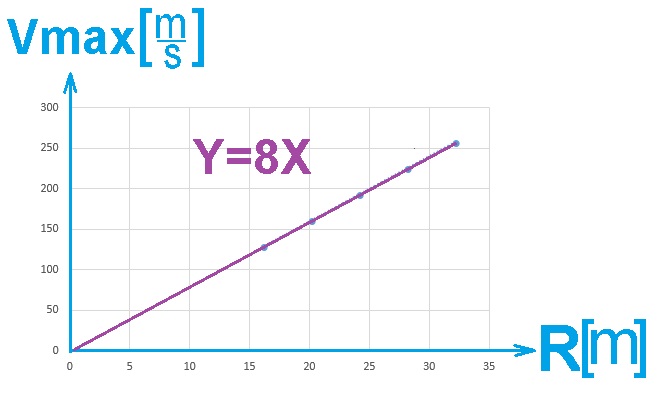
______________________________________________________________________________________

______________________________________________________________________________________
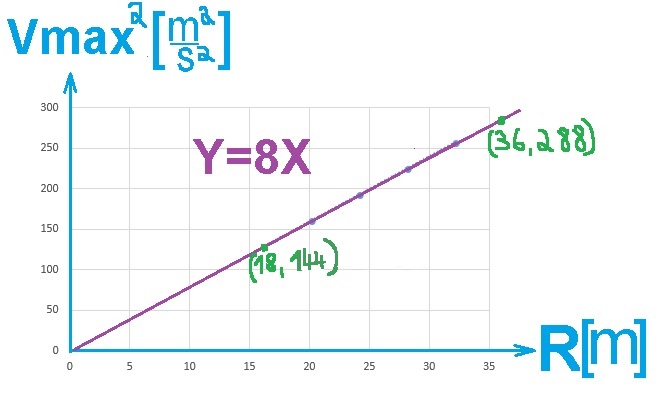
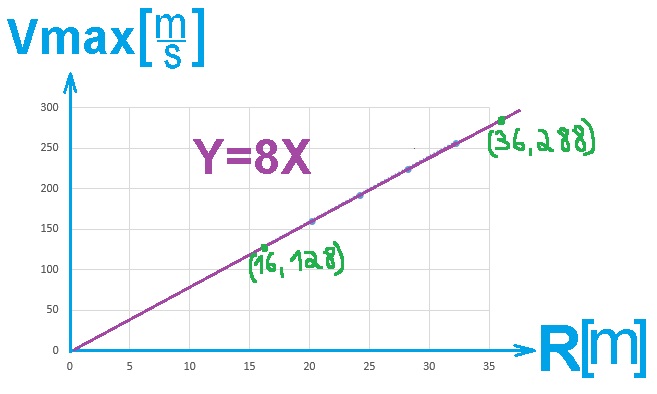
______________________________________________________________________________________
هـ.

______________________________________________________________________________________
______________________________________________________________________________________

______________________________________________________________________________________
______________________________________________________________________________________
+
-
2. 2019,3 - صبي يقف على الأرض داخل اسطوانة دوارة
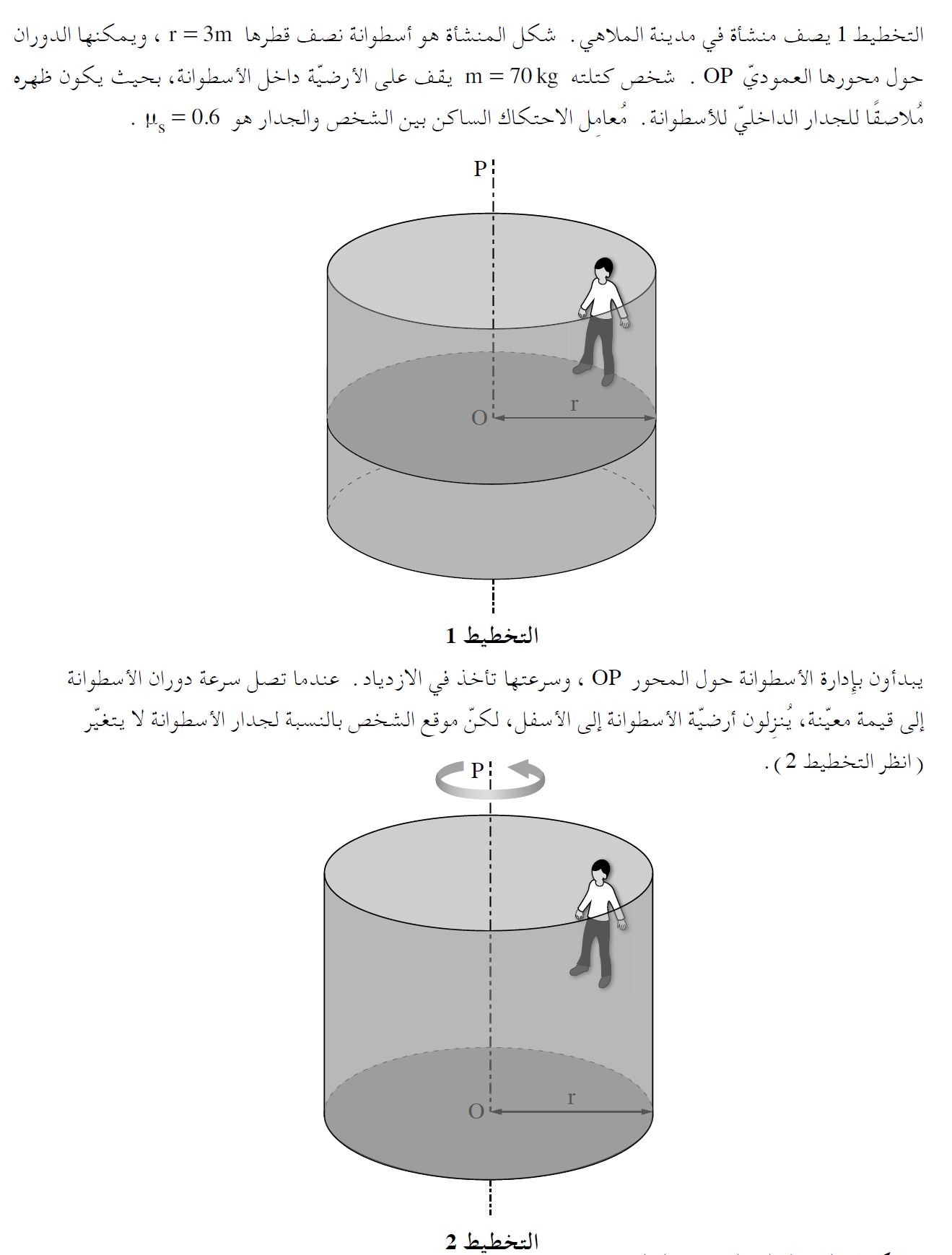

______________________________________________________________________________________
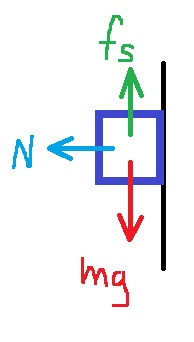
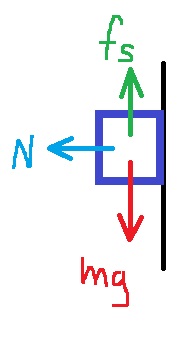

______________________________________________________________________________________

______________________________________________________________________________________
______________________________________________________________________________________

______________________________________________________________________________________
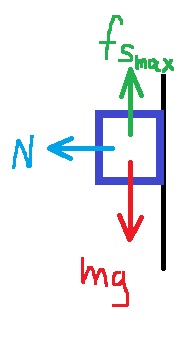

______________________________________________________________________________________

______________________________________________________________________________________
______________________________________________________________________________________

______________________________________________________________________________________
______________________________________________________________________________________
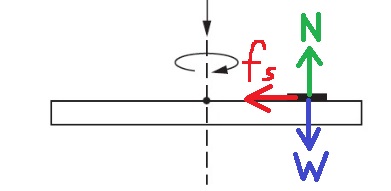
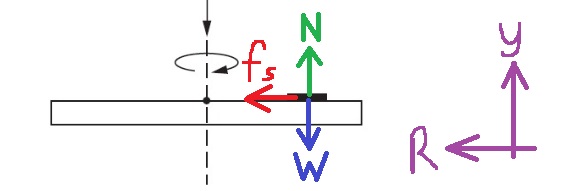
3. 2012,5- قطعة نقديّة على قرص
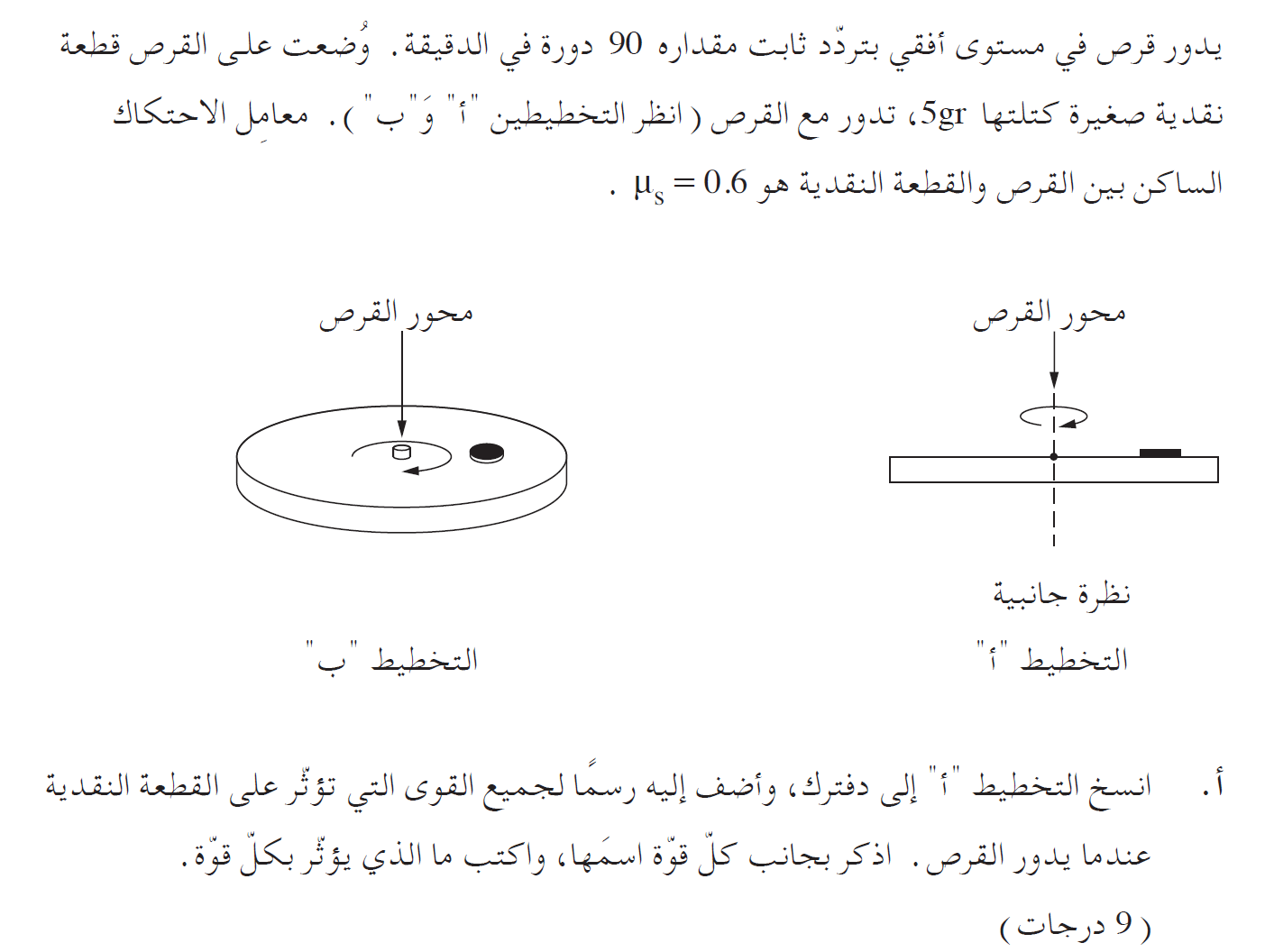
______________________________________________________________________________________

______________________________________________________________________________________

______________________________________________________________________________________

______________________________________________________________________________________

______________________________________________________________________________________
______________________________________________________________________________________

______________________________________________________________________________________
______________________________________________________________________________________
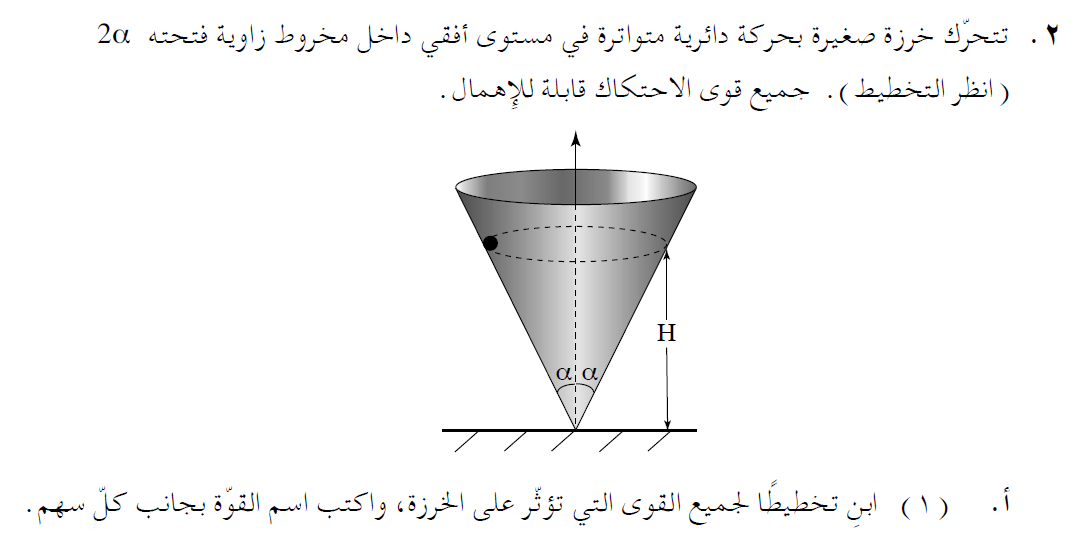
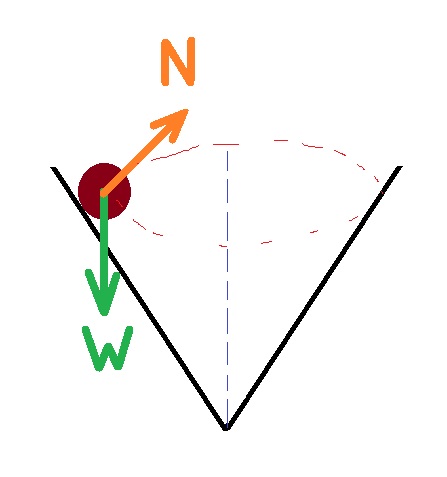
4. 2010,2- خرزة داخل مخروط
______________________________________________________________________________________
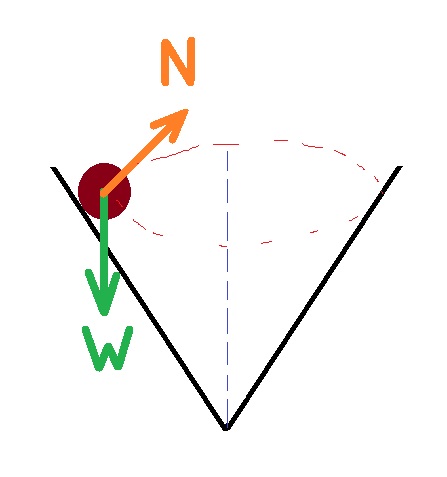

______________________________________________________________________________________
أ. 
______________________________________________________________________________________
______________________________________________________________________________________

______________________________________________________________________________________
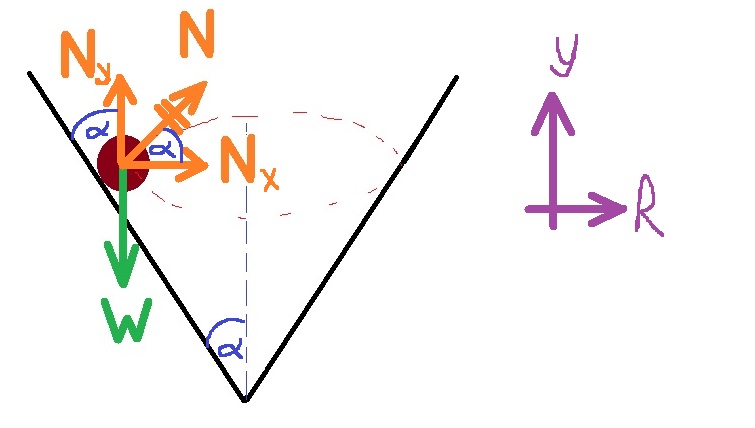
______________________________________________________________________________________

______________________________________________________________________________________

______________________________________________________________________________________

______________________________________________________________________________________
______________________________________________________________________________________

______________________________________________________________________________________
______________________________________________________________________________________
هـ.

______________________________________________________________________________________
______________________________________________________________________________________
5. 2009,3 - البندول المخروطي
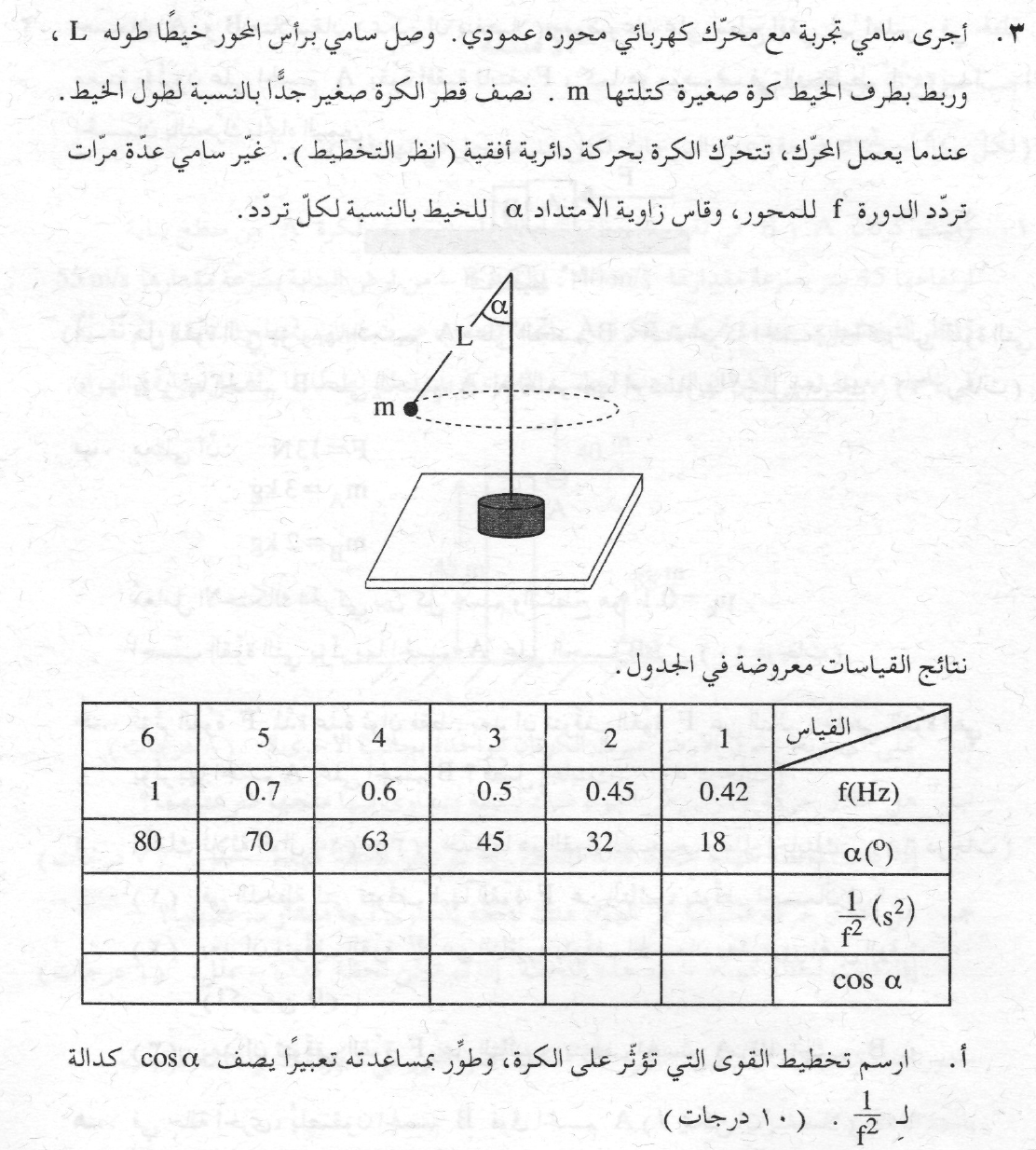
______________________________________________________________________________________
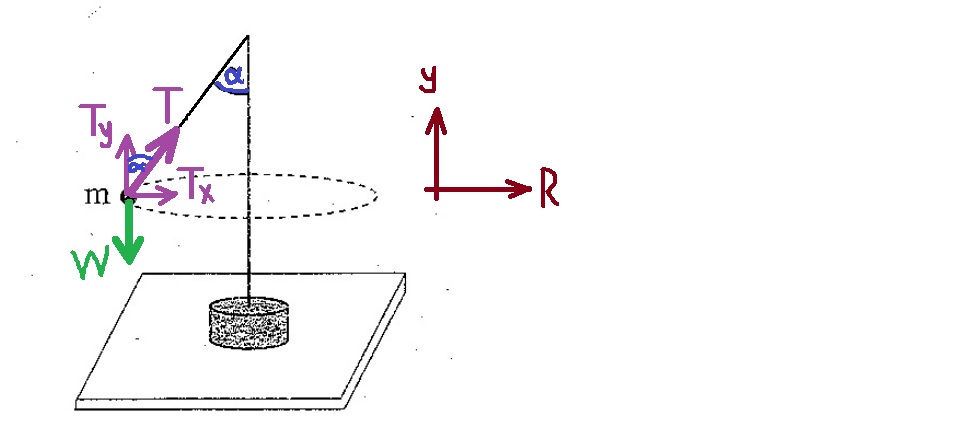
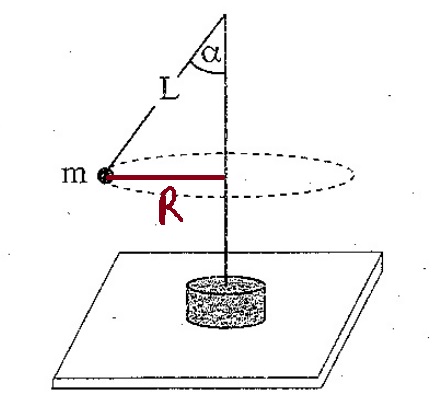

______________________________________________________________________________________

______________________________________________________________________________________
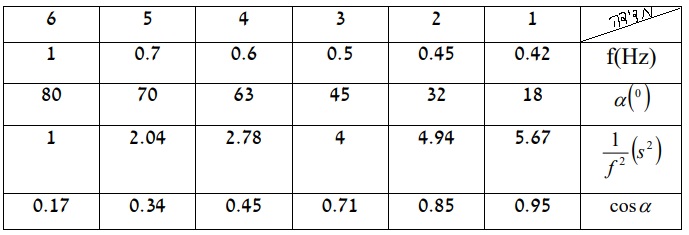
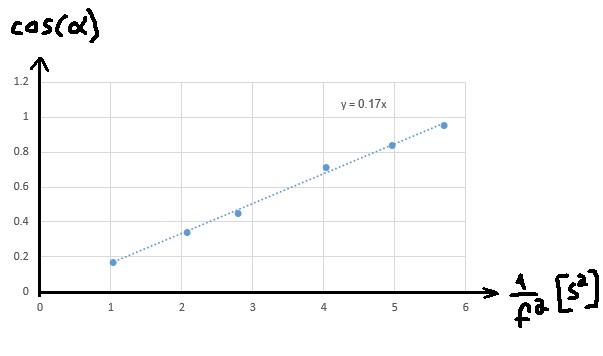


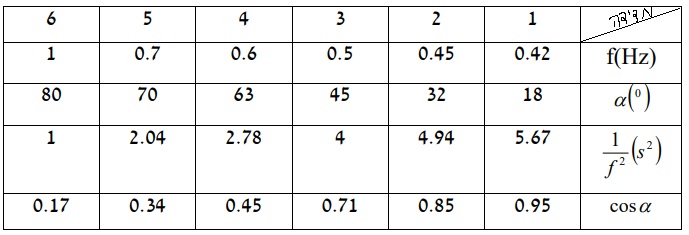
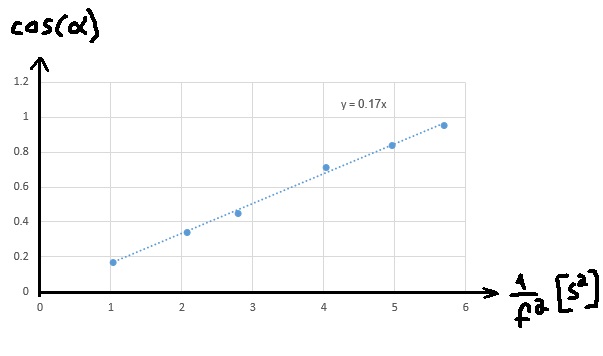


______________________________________________________________________________________

______________________________________________________________________________________
______________________________________________________________________________________

______________________________________________________________________________________
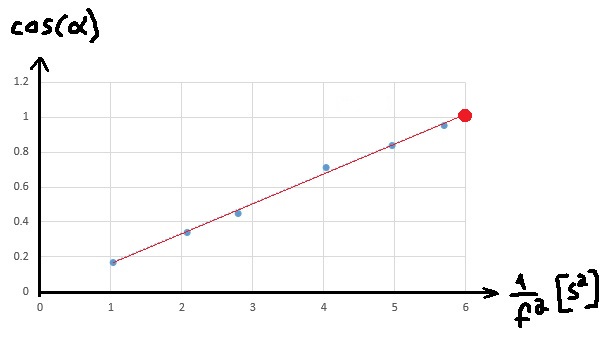

______________________________________________________________________________________
6. 2006,4-منعطف أفقي مائل

______________________________________________________________________________________
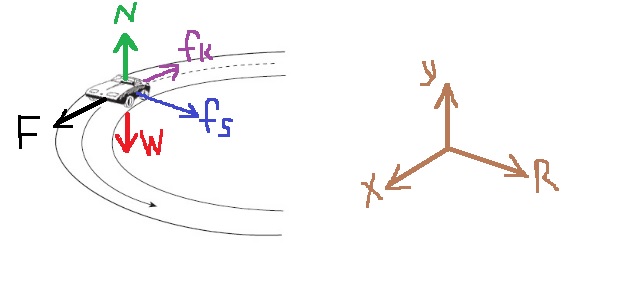

______________________________________________________________________________________

______________________________________________________________________________________
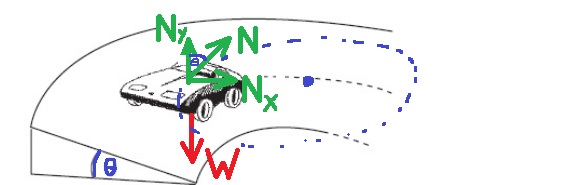

______________________________________________________________________________________
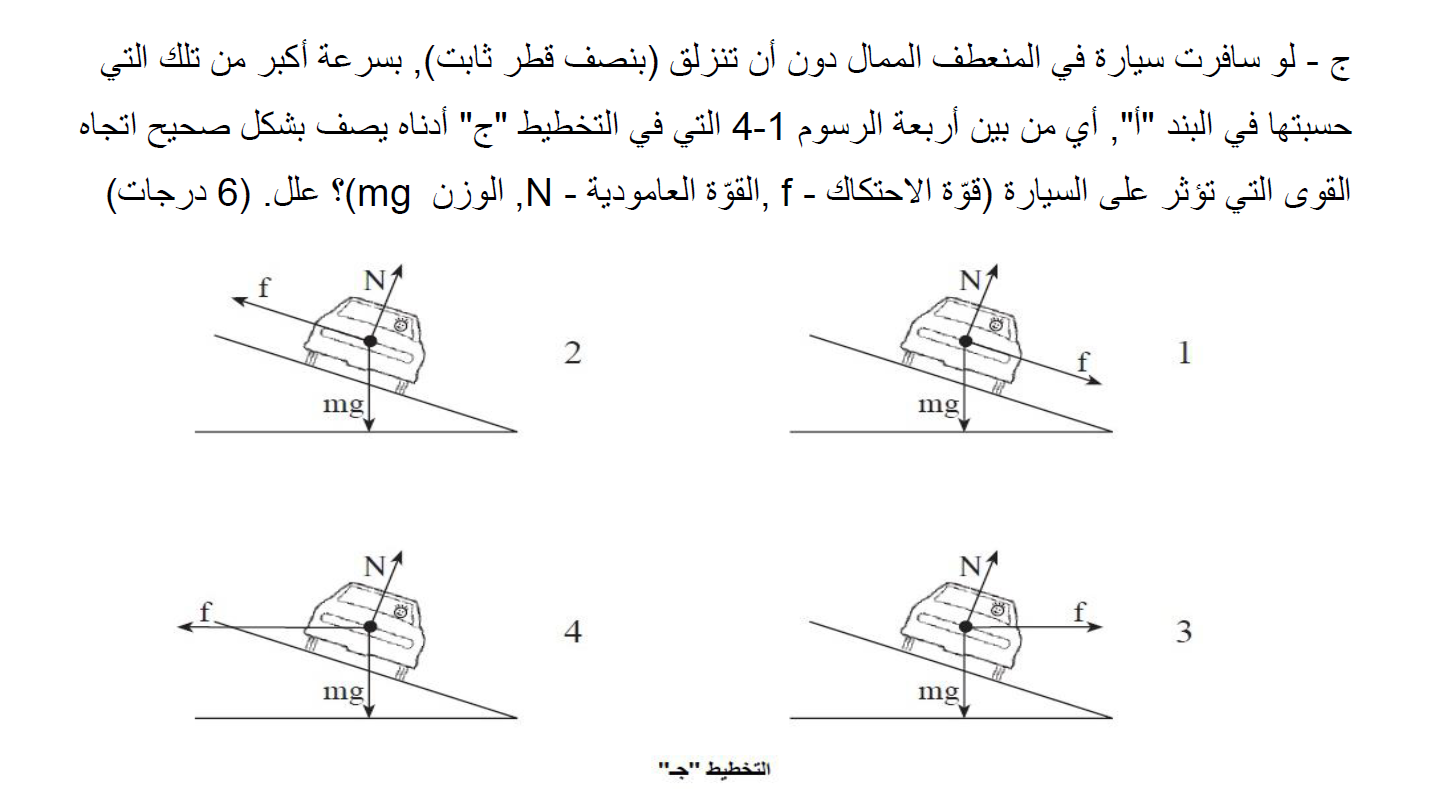
______________________________________________________________________________________
______________________________________________________________________________________

______________________________________________________________________________________
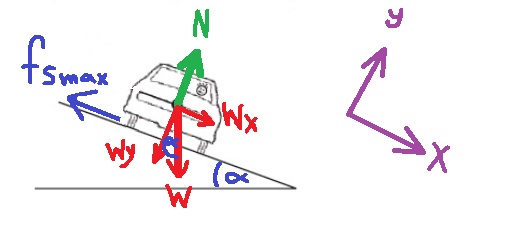

______________________________________________________________________________________
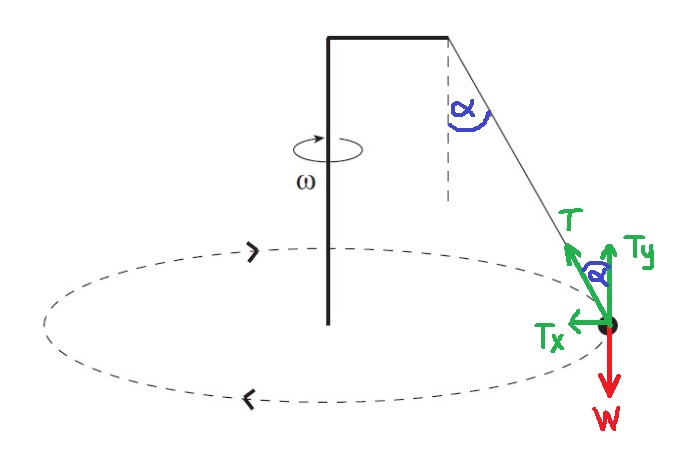
7. 2004,3- بندول مع ذراع أفقي
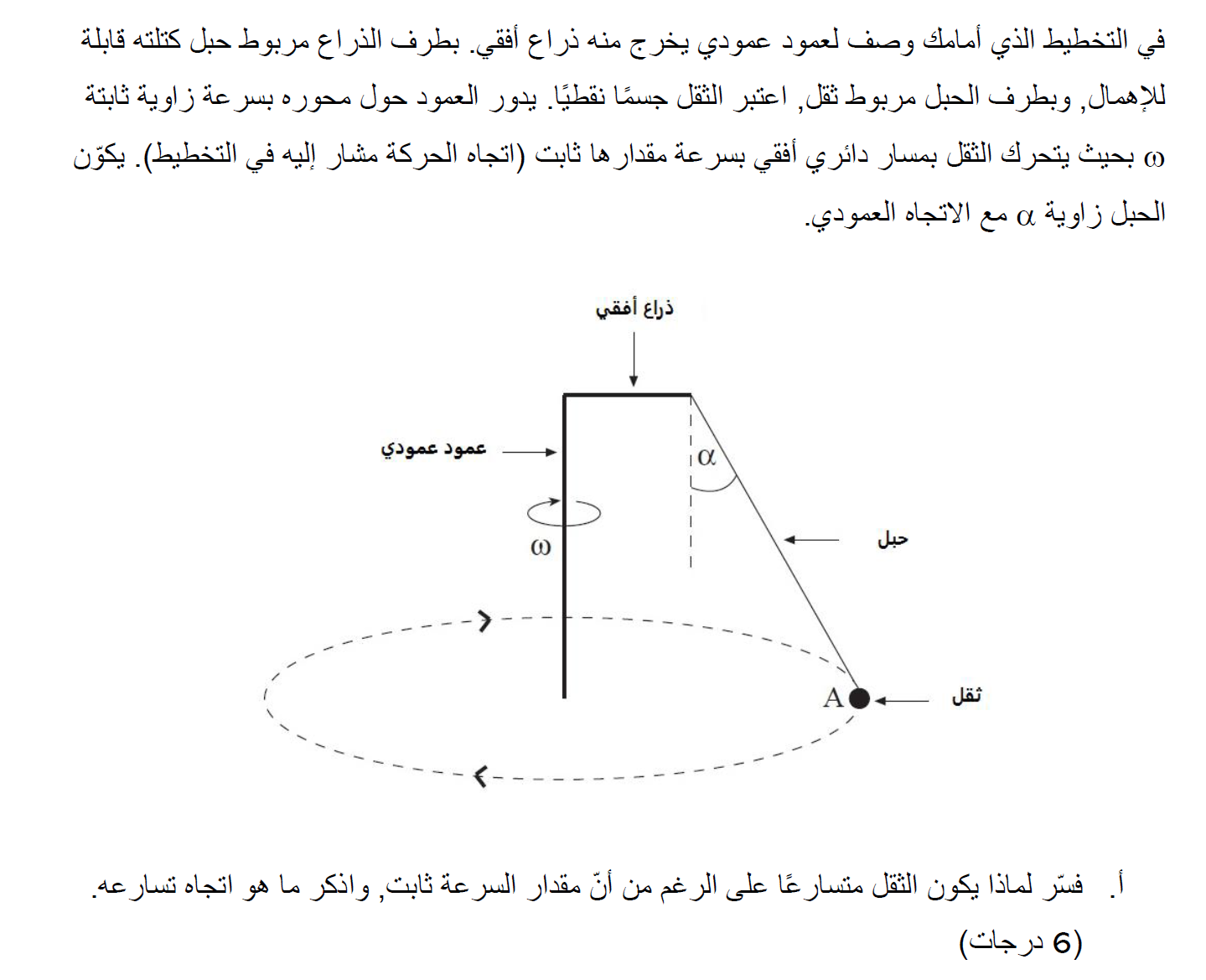
______________________________________________________________________________________
______________________________________________________________________________________

______________________________________________________________________________________
______________________________________________________________________________________

______________________________________________________________________________________
______________________________________________________________________________________

______________________________________________________________________________________

______________________________________________________________________________________

______________________________________________________________________________________
______________________________________________________________________________________
8. 2000,2- شارع أفقي مائل

______________________________________________________________________________________
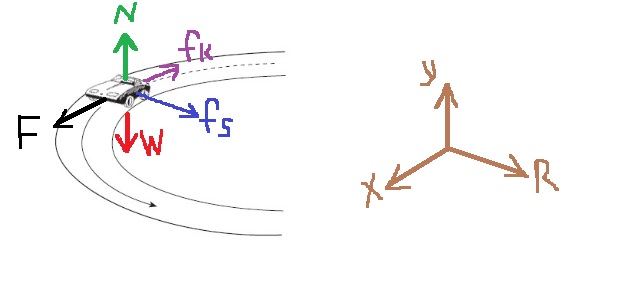
______________________________________________________________________________________
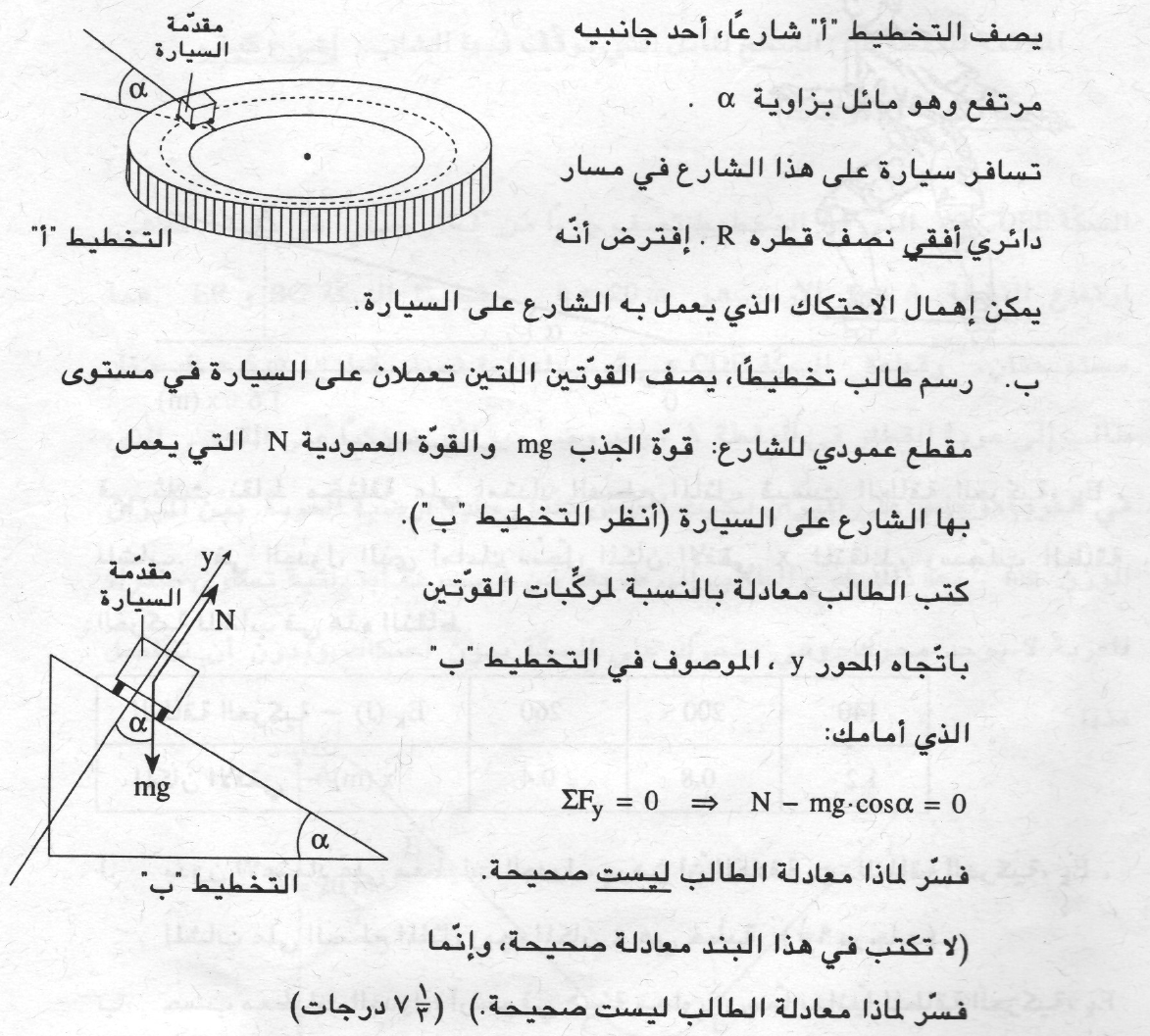
______________________________________________________________________________________
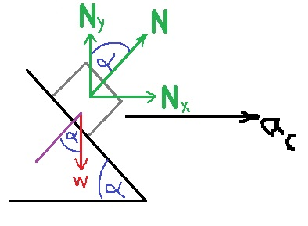
______________________________________________________________________________________

______________________________________________________________________________________
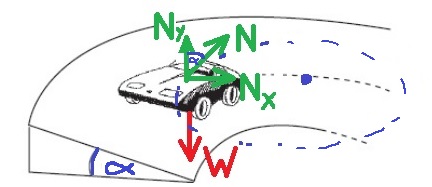
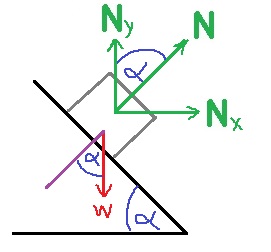
______________________________________________________________________________________
9. 1997,2-بندول مع ذراع أفقي
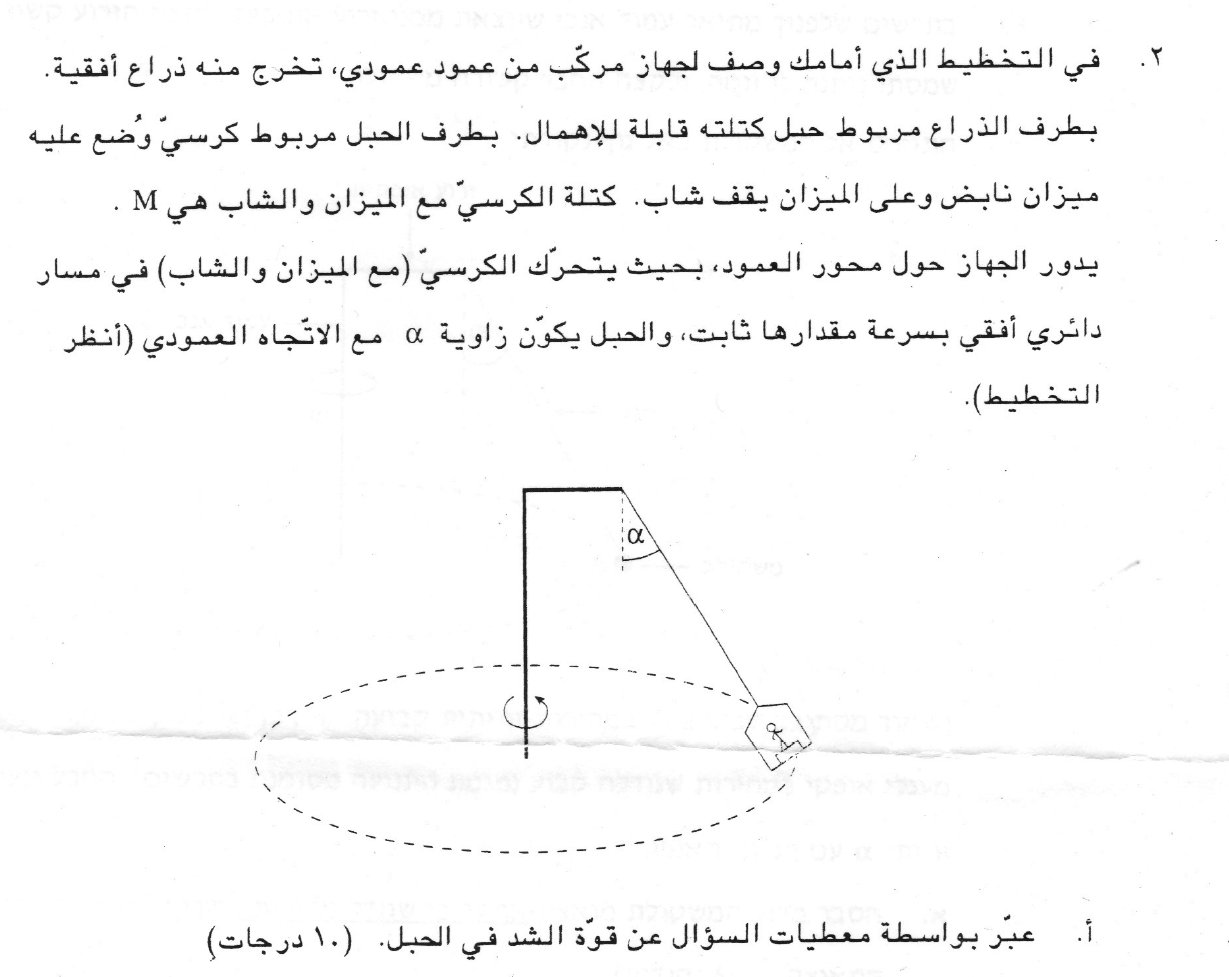
______________________________________________________________________________________
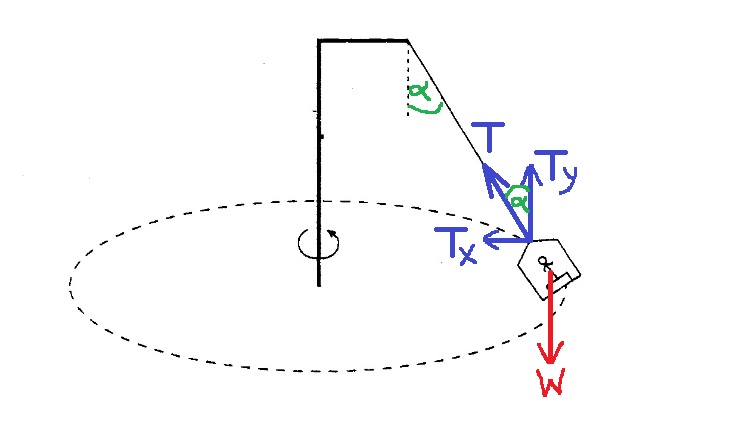
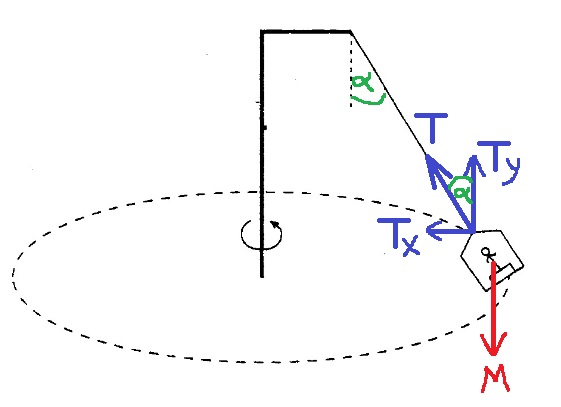
______________________________________________________________________________________

______________________________________________________________________________________
______________________________________________________________________________________

______________________________________________________________________________________
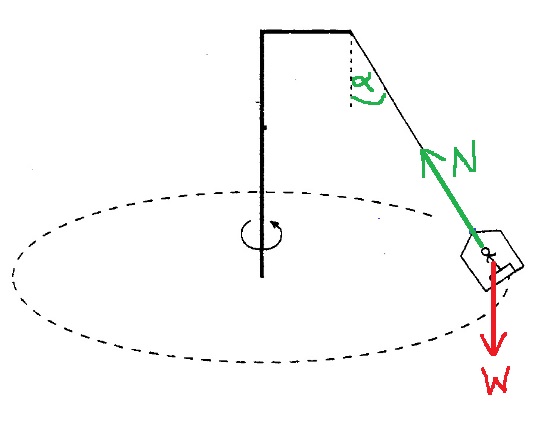

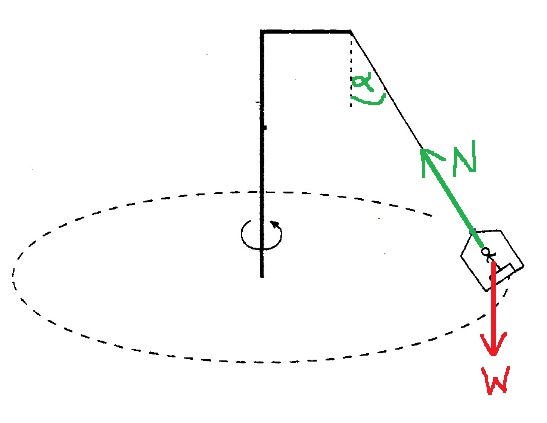

______________________________________________________________________________________

______________________________________________________________________________________
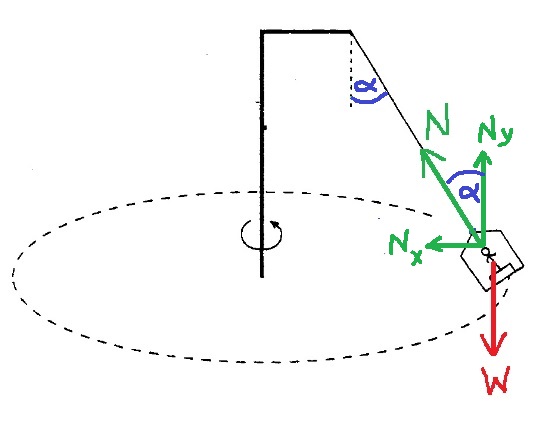

______________________________________________________________________________________
10. 1992,4- عربة تدور بنابض
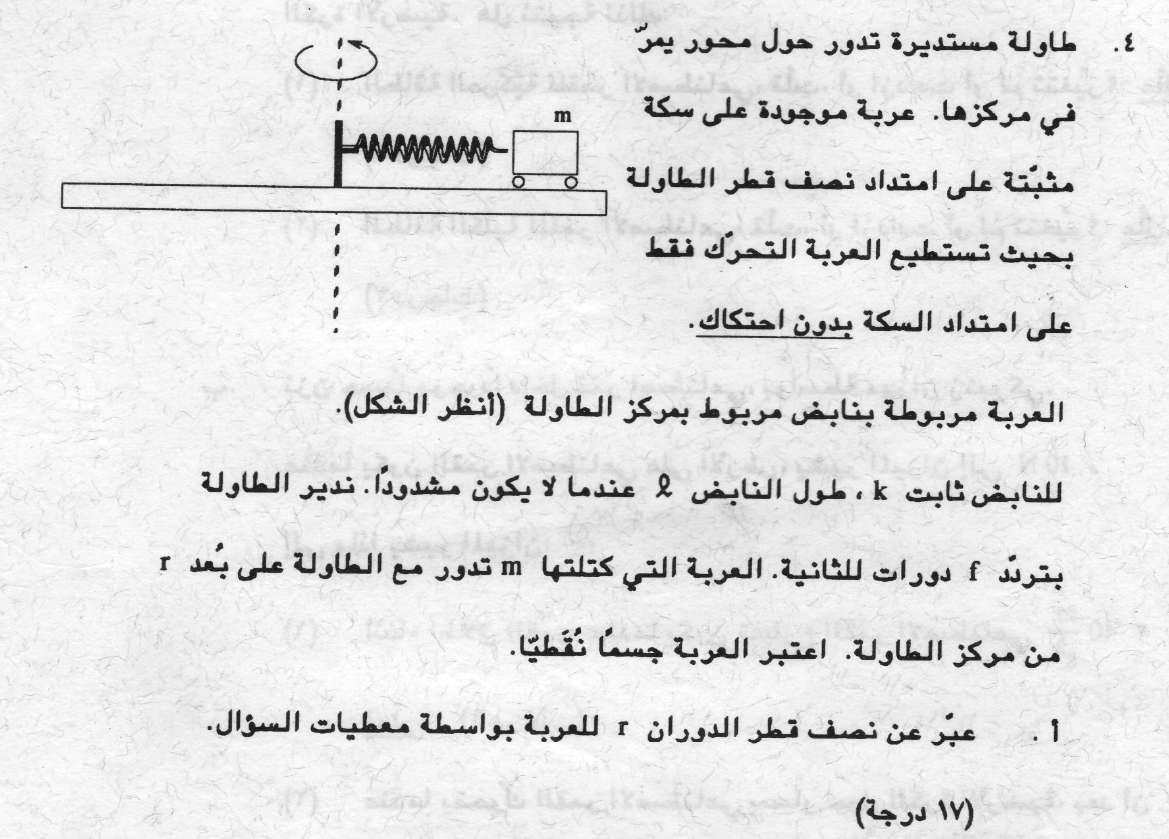
______________________________________________________________________________________
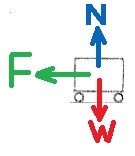

______________________________________________________________________________________

______________________________________________________________________________________
لا يوجد معنى لنصف قطر الدوران السالب، أو نصف قطر الدوران اللانهائي، لذلك لكي يكون للتعبير معنى فيزيائي، يجب أن يكون المقام في التعبير الذي تلقيناه أكبر من الصفر.
يجب الإشارة أيضًا على
أن التعبير الذي حصلنا عليه سابقًا نتج عندما كانت قوة النابض تتناسب طرديًا مع
استطالته وهذا الأمر يتم شرط أن يبقى النابض في مجال المرونة، حتى يكون لهذا
التعبير الذي حصلنا عليه معنى فيزيائي يجب أن يبقى النابض في مجال المرونة
حتى يكون معنى فيزيائي للنتيجة يجب أن تبقى العربة على سطح الطاولة أي لا تسقط عن الطاولة أي يجب أن يتحقق أيضًا الشرط أن نصف قطر الدوران r أصغر من نصف قطر الطاولة.
______________________________________________________________________________________

______________________________________________________________________________________
______________________________________________________________________________________
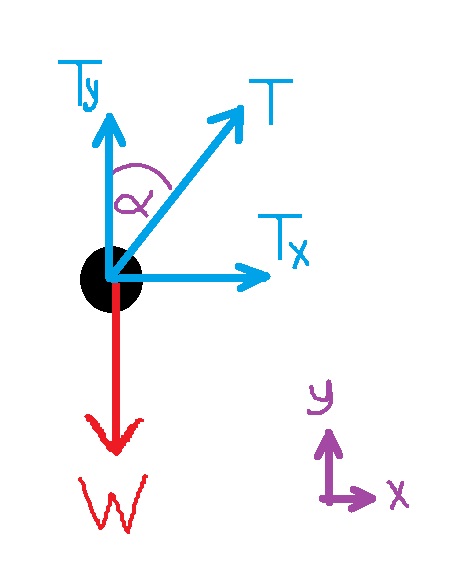
11. 1991,4-بندول مخروطي
 _____________________________________________________________________________________
_____________________________________________________________________________________
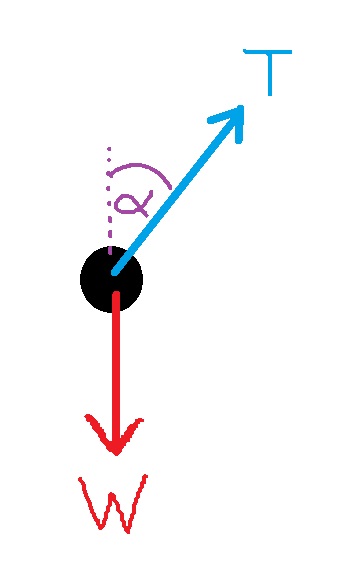

______________________________________________________________________________________
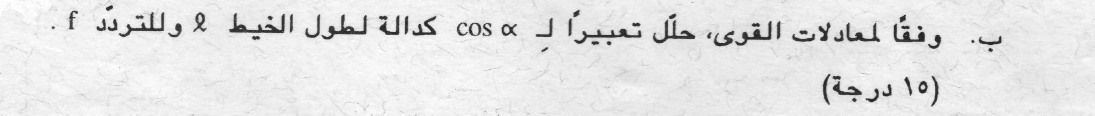
______________________________________________________________________________________
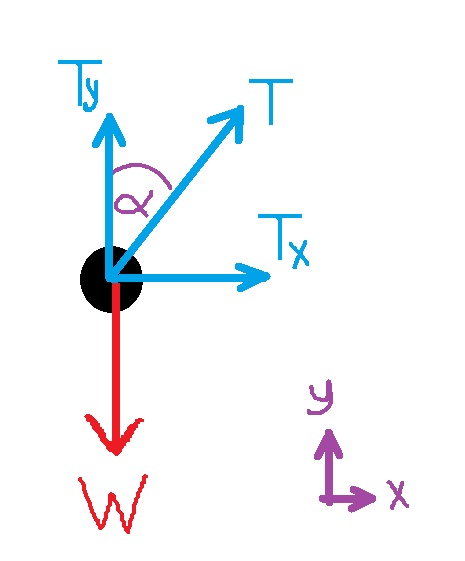
 «math xmlns=¨http://www.w3.org/1998/Math/MathML¨»«mi mathvariant=¨bold¨ mathcolor=¨#0000FF¨»sin«/mi»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»(«/mo»«mi mathvariant=¨bold¨ mathcolor=¨#0000FF¨»§#945;«/mi»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»)«/mo»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»=«/mo»«mfrac mathcolor=¨#0000FF¨»«mi mathvariant=¨bold¨»R«/mi»«mi mathvariant=¨bold¨»L«/mi»«/mfrac»«mspace linebreak=¨newline¨»«/mspace»«mspace linebreak=¨newline¨»«/mspace»«menclose mathcolor=¨#0000FF¨ notation=¨circle¨»«mi mathvariant=¨bold¨»R«/mi»«mo mathvariant=¨bold¨»=«/mo»«mi mathvariant=¨bold¨»L«/mi»«mo mathvariant=¨bold¨»§#183;«/mo»«mi mathvariant=¨bold¨»sin«/mi»«mo mathvariant=¨bold¨»(«/mo»«mi mathvariant=¨bold¨»§#945;«/mi»«mo mathvariant=¨bold¨»)«/mo»«/menclose»«/math»
«math xmlns=¨http://www.w3.org/1998/Math/MathML¨»«mi mathvariant=¨bold¨ mathcolor=¨#0000FF¨»sin«/mi»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»(«/mo»«mi mathvariant=¨bold¨ mathcolor=¨#0000FF¨»§#945;«/mi»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»)«/mo»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»=«/mo»«mfrac mathcolor=¨#0000FF¨»«mi mathvariant=¨bold¨»R«/mi»«mi mathvariant=¨bold¨»L«/mi»«/mfrac»«mspace linebreak=¨newline¨»«/mspace»«mspace linebreak=¨newline¨»«/mspace»«menclose mathcolor=¨#0000FF¨ notation=¨circle¨»«mi mathvariant=¨bold¨»R«/mi»«mo mathvariant=¨bold¨»=«/mo»«mi mathvariant=¨bold¨»L«/mi»«mo mathvariant=¨bold¨»§#183;«/mo»«mi mathvariant=¨bold¨»sin«/mi»«mo mathvariant=¨bold¨»(«/mo»«mi mathvariant=¨bold¨»§#945;«/mi»«mo mathvariant=¨bold¨»)«/mo»«/menclose»«/math» 
 «math xmlns=¨http://www.w3.org/1998/Math/MathML¨»«mi mathvariant=¨bold¨ mathcolor=¨#0000FF¨»sin«/mi»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»(«/mo»«mi mathvariant=¨bold¨ mathcolor=¨#0000FF¨»§#945;«/mi»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»)«/mo»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»=«/mo»«mfrac mathcolor=¨#0000FF¨»«mi mathvariant=¨bold¨»R«/mi»«mi mathvariant=¨bold¨»L«/mi»«/mfrac»«mspace linebreak=¨newline¨»«/mspace»«mspace linebreak=¨newline¨»«/mspace»«menclose mathcolor=¨#0000FF¨ notation=¨circle¨»«mi mathvariant=¨bold¨»R«/mi»«mo mathvariant=¨bold¨»=«/mo»«mi mathvariant=¨bold¨»L«/mi»«mo mathvariant=¨bold¨»§#183;«/mo»«mi mathvariant=¨bold¨»sin«/mi»«mo mathvariant=¨bold¨»(«/mo»«mi mathvariant=¨bold¨»§#945;«/mi»«mo mathvariant=¨bold¨»)«/mo»«/menclose»«/math»
«math xmlns=¨http://www.w3.org/1998/Math/MathML¨»«mi mathvariant=¨bold¨ mathcolor=¨#0000FF¨»sin«/mi»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»(«/mo»«mi mathvariant=¨bold¨ mathcolor=¨#0000FF¨»§#945;«/mi»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»)«/mo»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»=«/mo»«mfrac mathcolor=¨#0000FF¨»«mi mathvariant=¨bold¨»R«/mi»«mi mathvariant=¨bold¨»L«/mi»«/mfrac»«mspace linebreak=¨newline¨»«/mspace»«mspace linebreak=¨newline¨»«/mspace»«menclose mathcolor=¨#0000FF¨ notation=¨circle¨»«mi mathvariant=¨bold¨»R«/mi»«mo mathvariant=¨bold¨»=«/mo»«mi mathvariant=¨bold¨»L«/mi»«mo mathvariant=¨bold¨»§#183;«/mo»«mi mathvariant=¨bold¨»sin«/mi»«mo mathvariant=¨bold¨»(«/mo»«mi mathvariant=¨bold¨»§#945;«/mi»«mo mathvariant=¨bold¨»)«/mo»«/menclose»«/math» ______________________________________________________________________________________

______________________________________________________________________________________
______________________________________________________________________________________

______________________________________________________________________________________
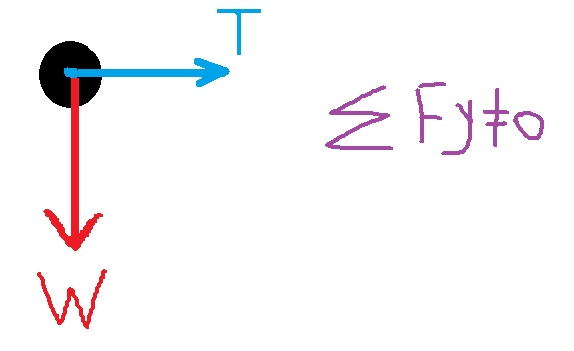

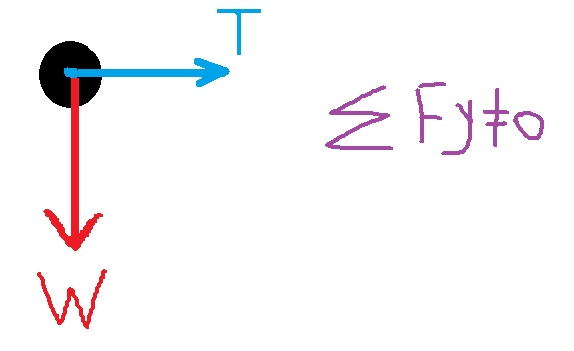
______________________________________________________________________________________
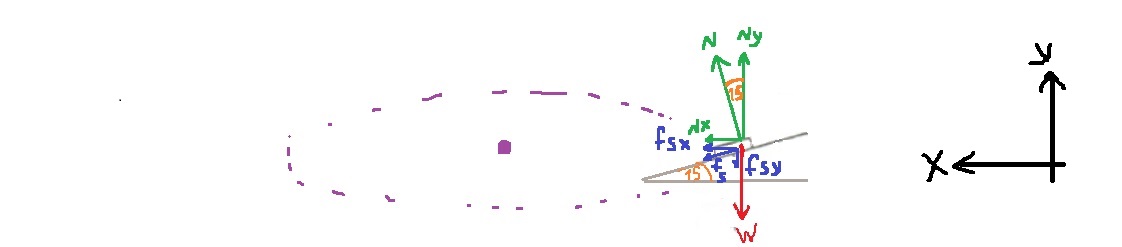
12. 1985,19- جسم موضوع في أنبوب دوار
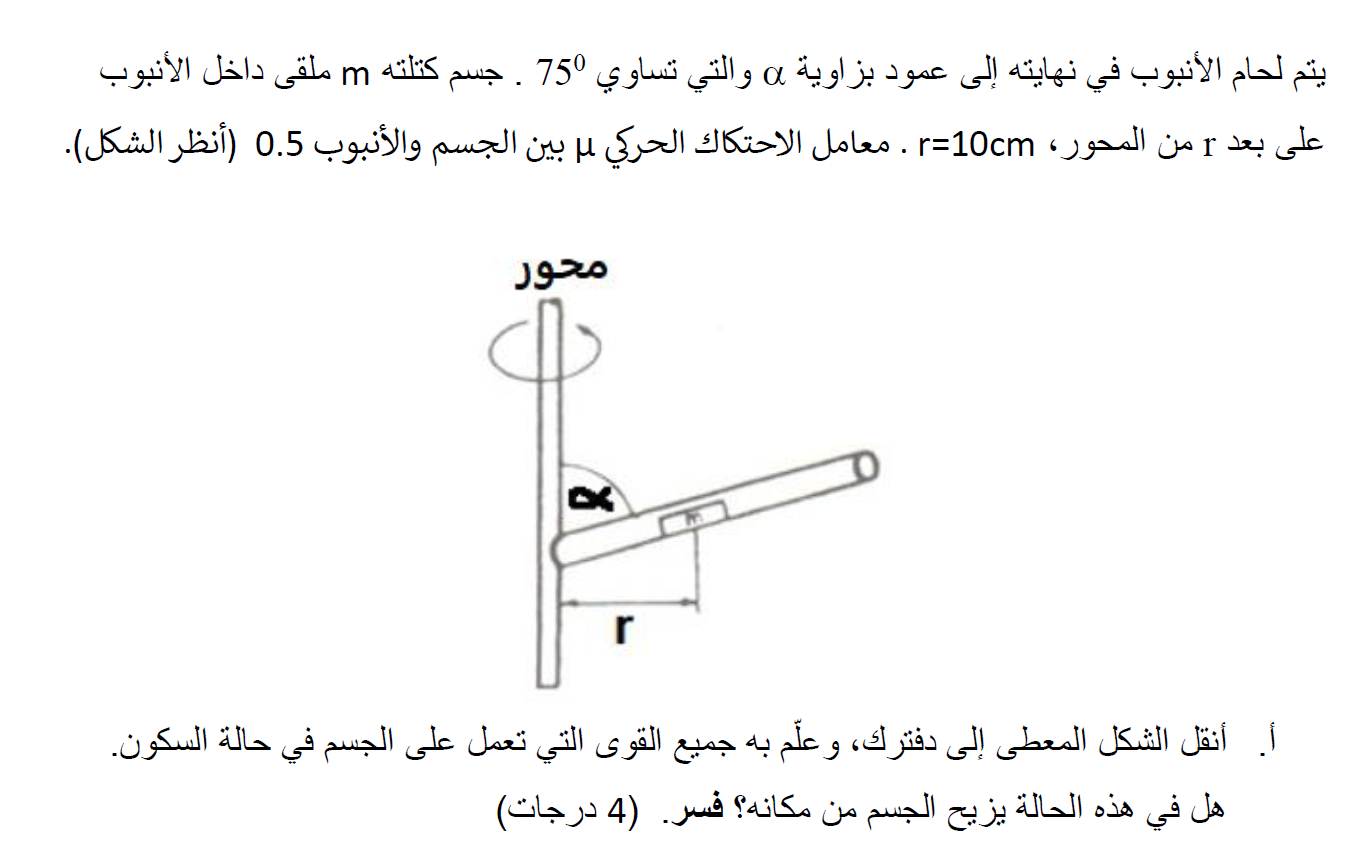
______________________________________________________________________________________
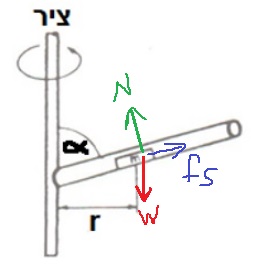

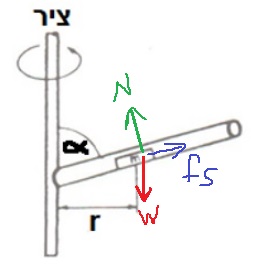
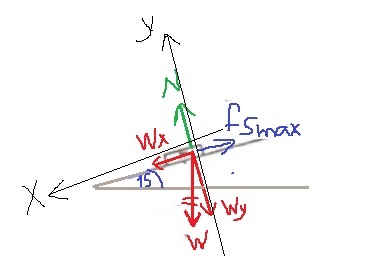

______________________________________________________________________________________

______________________________________________________________________________________
______________________________________________________________________________________

______________________________________________________________________________________

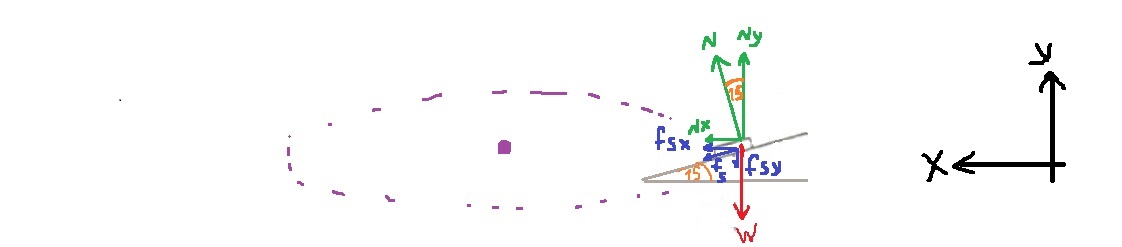
«math xmlns=¨http://www.w3.org/1998/Math/MathML¨»«mfrac mathcolor=¨#0000FF¨»«mrow»«menclose notation=¨updiagonalstrike¨»«mi mathvariant=¨bold¨»N«/mi»«/menclose»«mo mathvariant=¨bold¨»§#183;«/mo»«mfenced open=¨[¨ close=¨]¨»«mrow»«mi mathvariant=¨bold¨»sin«/mi»«mo mathvariant=¨bold¨»(«/mo»«mn mathvariant=¨bold¨»15«/mn»«mo mathvariant=¨bold¨»)«/mo»«mo mathvariant=¨bold¨»+«/mo»«msub»«mi mathvariant=¨bold¨»§#956;«/mi»«mi mathvariant=¨bold¨»s«/mi»«/msub»«mo mathvariant=¨bold¨»§#183;«/mo»«mi mathvariant=¨bold¨»cos«/mi»«mo mathvariant=¨bold¨»(«/mo»«mn mathvariant=¨bold¨»15«/mn»«mo mathvariant=¨bold¨»)«/mo»«/mrow»«/mfenced»«mo mathvariant=¨bold¨»§#160;«/mo»«/mrow»«mrow»«menclose notation=¨updiagonalstrike¨»«mi mathvariant=¨bold¨»N«/mi»«/menclose»«mo mathvariant=¨bold¨»§#183;«/mo»«mfenced open=¨[¨ close=¨]¨»«mrow»«mi mathvariant=¨bold¨»cos«/mi»«mo mathvariant=¨bold¨»(«/mo»«mn mathvariant=¨bold¨»15«/mn»«mo mathvariant=¨bold¨»)«/mo»«mo mathvariant=¨bold¨»-«/mo»«msub»«mi mathvariant=¨bold¨»§#956;«/mi»«mi mathvariant=¨bold¨»s«/mi»«/msub»«mo mathvariant=¨bold¨»§#183;«/mo»«mi mathvariant=¨bold¨»sin«/mi»«mo mathvariant=¨bold¨»(«/mo»«mn mathvariant=¨bold¨»15«/mn»«mo mathvariant=¨bold¨»)«/mo»«/mrow»«/mfenced»«/mrow»«/mfrac»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»=«/mo»«mfrac mathcolor=¨#0000FF¨»«mrow»«menclose notation=¨downdiagonalstrike¨»«mi mathvariant=¨bold¨»m«/mi»«/menclose»«mo mathvariant=¨bold¨»§#183;«/mo»«msup»«msub»«mi mathvariant=¨bold¨»§#969;«/mi»«mi mathvariant=¨bold¨»min«/mi»«/msub»«mn mathvariant=¨bold¨»2«/mn»«/msup»«mo mathvariant=¨bold¨»§#183;«/mo»«mi mathvariant=¨bold¨»R«/mi»«/mrow»«mrow»«menclose notation=¨downdiagonalstrike¨»«mi mathvariant=¨bold¨»m«/mi»«/menclose»«mo mathvariant=¨bold¨»§#183;«/mo»«mi mathvariant=¨bold¨»g«/mi»«/mrow»«/mfrac»«mspace linebreak=¨newline¨»«/mspace»«/math»
نعبّر عن السرعة الزاوية من التعبير الذي تم الحصول عليه:
«math xmlns=¨http://www.w3.org/1998/Math/MathML¨»«msub»«mi mathvariant=¨bold¨ mathcolor=¨#0000FF¨»§#969;«/mi»«mi mathvariant=¨bold¨ mathcolor=¨#0000FF¨»min«/mi»«/msub»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»=«/mo»«msqrt mathcolor=¨#0000FF¨»«mfrac»«mrow»«mi mathvariant=¨bold¨»g«/mi»«mo mathvariant=¨bold¨»§#183;«/mo»«mfenced open=¨[¨ close=¨]¨»«mrow»«mi mathvariant=¨bold¨»sin«/mi»«mo mathvariant=¨bold¨»(«/mo»«mn mathvariant=¨bold¨»15«/mn»«mo mathvariant=¨bold¨»)«/mo»«mo mathvariant=¨bold¨»+«/mo»«msub»«mi mathvariant=¨bold¨»§#956;«/mi»«mi mathvariant=¨bold¨»s«/mi»«/msub»«mo mathvariant=¨bold¨»§#183;«/mo»«mi mathvariant=¨bold¨»cos«/mi»«mo mathvariant=¨bold¨»(«/mo»«mn mathvariant=¨bold¨»15«/mn»«mo mathvariant=¨bold¨»)«/mo»«/mrow»«/mfenced»«mo mathvariant=¨bold¨»§#160;«/mo»«/mrow»«mrow»«mi mathvariant=¨bold¨»r«/mi»«mo mathvariant=¨bold¨»§#183;«/mo»«mfenced open=¨[¨ close=¨]¨»«mrow»«mi mathvariant=¨bold¨»cos«/mi»«mo mathvariant=¨bold¨»(«/mo»«mn mathvariant=¨bold¨»15«/mn»«mo mathvariant=¨bold¨»)«/mo»«mo mathvariant=¨bold¨»-«/mo»«msub»«mi mathvariant=¨bold¨»§#956;«/mi»«mi mathvariant=¨bold¨»s«/mi»«/msub»«mo mathvariant=¨bold¨»§#183;«/mo»«mi mathvariant=¨bold¨»sin«/mi»«mo mathvariant=¨bold¨»(«/mo»«mn mathvariant=¨bold¨»15«/mn»«mo mathvariant=¨bold¨»)«/mo»«/mrow»«/mfenced»«/mrow»«/mfrac»«/msqrt»«mspace linebreak=¨newline¨»«/mspace»«/math»
نعوّض المعطيات ونوجد الحد الأدنى للسرعة الزاوية التي ينفصل بها الجسم عن موقعه:
«math xmlns=¨http://www.w3.org/1998/Math/MathML¨»«msub»«mi mathvariant=¨bold¨ mathcolor=¨#0000FF¨»§#969;«/mi»«mi mathvariant=¨bold¨ mathcolor=¨#0000FF¨»min«/mi»«/msub»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»=«/mo»«msqrt mathcolor=¨#0000FF¨»«mfrac»«mrow»«mi mathvariant=¨bold¨»g«/mi»«mo mathvariant=¨bold¨»§#183;«/mo»«mfenced open=¨[¨ close=¨]¨»«mrow»«mi mathvariant=¨bold¨»sin«/mi»«mo mathvariant=¨bold¨»(«/mo»«mn mathvariant=¨bold¨»15«/mn»«mo mathvariant=¨bold¨»)«/mo»«mo mathvariant=¨bold¨»+«/mo»«msub»«mi mathvariant=¨bold¨»§#956;«/mi»«mi mathvariant=¨bold¨»s«/mi»«/msub»«mo mathvariant=¨bold¨»§#183;«/mo»«mi mathvariant=¨bold¨»cos«/mi»«mo mathvariant=¨bold¨»(«/mo»«mn mathvariant=¨bold¨»15«/mn»«mo mathvariant=¨bold¨»)«/mo»«/mrow»«/mfenced»«mo mathvariant=¨bold¨»§#160;«/mo»«/mrow»«mrow»«mi mathvariant=¨bold¨»r«/mi»«mo mathvariant=¨bold¨»§#183;«/mo»«mfenced open=¨[¨ close=¨]¨»«mrow»«mi mathvariant=¨bold¨»cos«/mi»«mo mathvariant=¨bold¨»(«/mo»«mn mathvariant=¨bold¨»15«/mn»«mo mathvariant=¨bold¨»)«/mo»«mo mathvariant=¨bold¨»-«/mo»«msub»«mi mathvariant=¨bold¨»§#956;«/mi»«mi mathvariant=¨bold¨»s«/mi»«/msub»«mo mathvariant=¨bold¨»§#183;«/mo»«mi mathvariant=¨bold¨»sin«/mi»«mo mathvariant=¨bold¨»(«/mo»«mn mathvariant=¨bold¨»25«/mn»«mo mathvariant=¨bold¨»)«/mo»«/mrow»«/mfenced»«/mrow»«/mfrac»«/msqrt»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»=«/mo»«msqrt mathcolor=¨#0000FF¨»«mfrac»«mrow»«mn mathvariant=¨bold¨»10«/mn»«mo mathvariant=¨bold¨»§#183;«/mo»«mfenced open=¨[¨ close=¨]¨»«mrow»«mi mathvariant=¨bold¨»sin«/mi»«mo mathvariant=¨bold¨»(«/mo»«mn mathvariant=¨bold¨»15«/mn»«mo mathvariant=¨bold¨»)«/mo»«mo mathvariant=¨bold¨»+«/mo»«mn mathvariant=¨bold¨»0«/mn»«mo mathvariant=¨bold¨».«/mo»«mn mathvariant=¨bold¨»5«/mn»«mo mathvariant=¨bold¨»§#183;«/mo»«mi mathvariant=¨bold¨»cos«/mi»«mo mathvariant=¨bold¨»(«/mo»«mn mathvariant=¨bold¨»15«/mn»«mo mathvariant=¨bold¨»)«/mo»«/mrow»«/mfenced»«mo mathvariant=¨bold¨»§#160;«/mo»«/mrow»«mrow»«mn mathvariant=¨bold¨»0«/mn»«mo mathvariant=¨bold¨».«/mo»«mn mathvariant=¨bold¨»1«/mn»«mo mathvariant=¨bold¨»§#183;«/mo»«mfenced open=¨[¨ close=¨]¨»«mrow»«mi mathvariant=¨bold¨»cos«/mi»«mo mathvariant=¨bold¨»(«/mo»«mn mathvariant=¨bold¨»15«/mn»«mo mathvariant=¨bold¨»)«/mo»«mo mathvariant=¨bold¨»-«/mo»«mn mathvariant=¨bold¨»0«/mn»«mo mathvariant=¨bold¨».«/mo»«mn mathvariant=¨bold¨»5«/mn»«mo mathvariant=¨bold¨»§#183;«/mo»«mi mathvariant=¨bold¨»sin«/mi»«mo mathvariant=¨bold¨»(«/mo»«mn mathvariant=¨bold¨»15«/mn»«mo mathvariant=¨bold¨»)«/mo»«/mrow»«/mfenced»«/mrow»«/mfrac»«/msqrt»«mspace linebreak=¨newline¨»«/mspace»«msub»«mi mathvariant=¨bold¨ mathcolor=¨#0000FF¨»§#969;«/mi»«mi mathvariant=¨bold¨ mathcolor=¨#0000FF¨»min«/mi»«/msub»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»=«/mo»«msqrt mathcolor=¨#0000FF¨»«mfrac»«mrow»«mn mathvariant=¨bold¨»10«/mn»«mo mathvariant=¨bold¨»§#183;«/mo»«mfenced open=¨[¨ close=¨]¨»«mrow»«mn mathvariant=¨bold¨»0«/mn»«mo mathvariant=¨bold¨».«/mo»«mn mathvariant=¨bold¨»258«/mn»«mo mathvariant=¨bold¨»+«/mo»«mn mathvariant=¨bold¨»0«/mn»«mo mathvariant=¨bold¨».«/mo»«mn mathvariant=¨bold¨»48«/mn»«/mrow»«/mfenced»«mo mathvariant=¨bold¨»§#160;«/mo»«/mrow»«mrow»«mn mathvariant=¨bold¨»0«/mn»«mo mathvariant=¨bold¨».«/mo»«mn mathvariant=¨bold¨»1«/mn»«mo mathvariant=¨bold¨»§#183;«/mo»«mfenced open=¨[¨ close=¨]¨»«mrow»«mn mathvariant=¨bold¨»0«/mn»«mo mathvariant=¨bold¨».«/mo»«mn mathvariant=¨bold¨»96«/mn»«mo mathvariant=¨bold¨»-«/mo»«mn mathvariant=¨bold¨»0«/mn»«mo mathvariant=¨bold¨».«/mo»«mn mathvariant=¨bold¨»129«/mn»«/mrow»«/mfenced»«/mrow»«/mfrac»«/msqrt»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»=«/mo»«msqrt mathcolor=¨#0000FF¨»«mfrac»«mrow»«mn mathvariant=¨bold¨»7«/mn»«mo mathvariant=¨bold¨».«/mo»«mn mathvariant=¨bold¨»41«/mn»«/mrow»«mrow»«mn mathvariant=¨bold¨»0«/mn»«mo mathvariant=¨bold¨».«/mo»«mn mathvariant=¨bold¨»0831«/mn»«/mrow»«/mfrac»«/msqrt»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»=«/mo»«msqrt mathcolor=¨#0000FF¨»«mn mathvariant=¨bold¨»89«/mn»«mo mathvariant=¨bold¨».«/mo»«mn mathvariant=¨bold¨»17«/mn»«/msqrt»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»=«/mo»«mn mathvariant=¨bold¨ mathcolor=¨#0000FF¨»9«/mn»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨».«/mo»«mn mathvariant=¨bold¨ mathcolor=¨#0000FF¨»44«/mn»«mfrac mathcolor=¨#0000FF¨»«mrow»«mi mathvariant=¨bold¨»r«/mi»«mi mathvariant=¨bold¨»a«/mi»«mi mathvariant=¨bold¨»d«/mi»«/mrow»«mi mathvariant=¨bold¨»s«/mi»«/mfrac»«mspace linebreak=¨newline¨»«/mspace»«/math»
لذلك ، فإن أقل سرعة زاوية مطلوبة لتحرك الجسم من موقعه هي 9.44 راديان في الثانية.

«math xmlns=¨http://www.w3.org/1998/Math/MathML¨»«mfrac mathcolor=¨#0000FF¨»«mrow»«menclose notation=¨updiagonalstrike¨»«mi mathvariant=¨bold¨»N«/mi»«/menclose»«mo mathvariant=¨bold¨»§#183;«/mo»«mfenced open=¨[¨ close=¨]¨»«mrow»«mi mathvariant=¨bold¨»sin«/mi»«mo mathvariant=¨bold¨»(«/mo»«mn mathvariant=¨bold¨»25«/mn»«mo mathvariant=¨bold¨»)«/mo»«mo mathvariant=¨bold¨»+«/mo»«msub»«mi mathvariant=¨bold¨»§#956;«/mi»«mi mathvariant=¨bold¨»s«/mi»«/msub»«mo mathvariant=¨bold¨»§#183;«/mo»«mi mathvariant=¨bold¨»cos«/mi»«mo mathvariant=¨bold¨»(«/mo»«mi mathvariant=¨bold¨»§#945;«/mi»«mo mathvariant=¨bold¨»)«/mo»«/mrow»«/mfenced»«mo mathvariant=¨bold¨»§#160;«/mo»«/mrow»«mrow»«menclose notation=¨updiagonalstrike¨»«mi mathvariant=¨bold¨»N«/mi»«/menclose»«mo mathvariant=¨bold¨»§#183;«/mo»«mfenced open=¨[¨ close=¨]¨»«mrow»«mi mathvariant=¨bold¨»cos«/mi»«mo mathvariant=¨bold¨»(«/mo»«mn mathvariant=¨bold¨»25«/mn»«mo mathvariant=¨bold¨»)«/mo»«mo mathvariant=¨bold¨»-«/mo»«msub»«mi mathvariant=¨bold¨»§#956;«/mi»«mi mathvariant=¨bold¨»s«/mi»«/msub»«mo mathvariant=¨bold¨»§#183;«/mo»«mi mathvariant=¨bold¨»sin«/mi»«mo mathvariant=¨bold¨»(«/mo»«mn mathvariant=¨bold¨»25«/mn»«mo mathvariant=¨bold¨»)«/mo»«/mrow»«/mfenced»«/mrow»«/mfrac»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»=«/mo»«mfrac mathcolor=¨#0000FF¨»«mrow»«menclose notation=¨downdiagonalstrike¨»«mi mathvariant=¨bold¨»m«/mi»«/menclose»«mo mathvariant=¨bold¨»§#183;«/mo»«msup»«mi mathvariant=¨bold¨»§#969;«/mi»«mn mathvariant=¨bold¨»2«/mn»«/msup»«mo mathvariant=¨bold¨»§#183;«/mo»«mi mathvariant=¨bold¨»R«/mi»«/mrow»«mrow»«menclose notation=¨downdiagonalstrike¨»«mi mathvariant=¨bold¨»m«/mi»«/menclose»«mo mathvariant=¨bold¨»§#183;«/mo»«mi mathvariant=¨bold¨»g«/mi»«/mrow»«/mfrac»«mspace linebreak=¨newline¨»«/mspace»«/math»
13. 1983,18-بندول مع ذراع أفقي
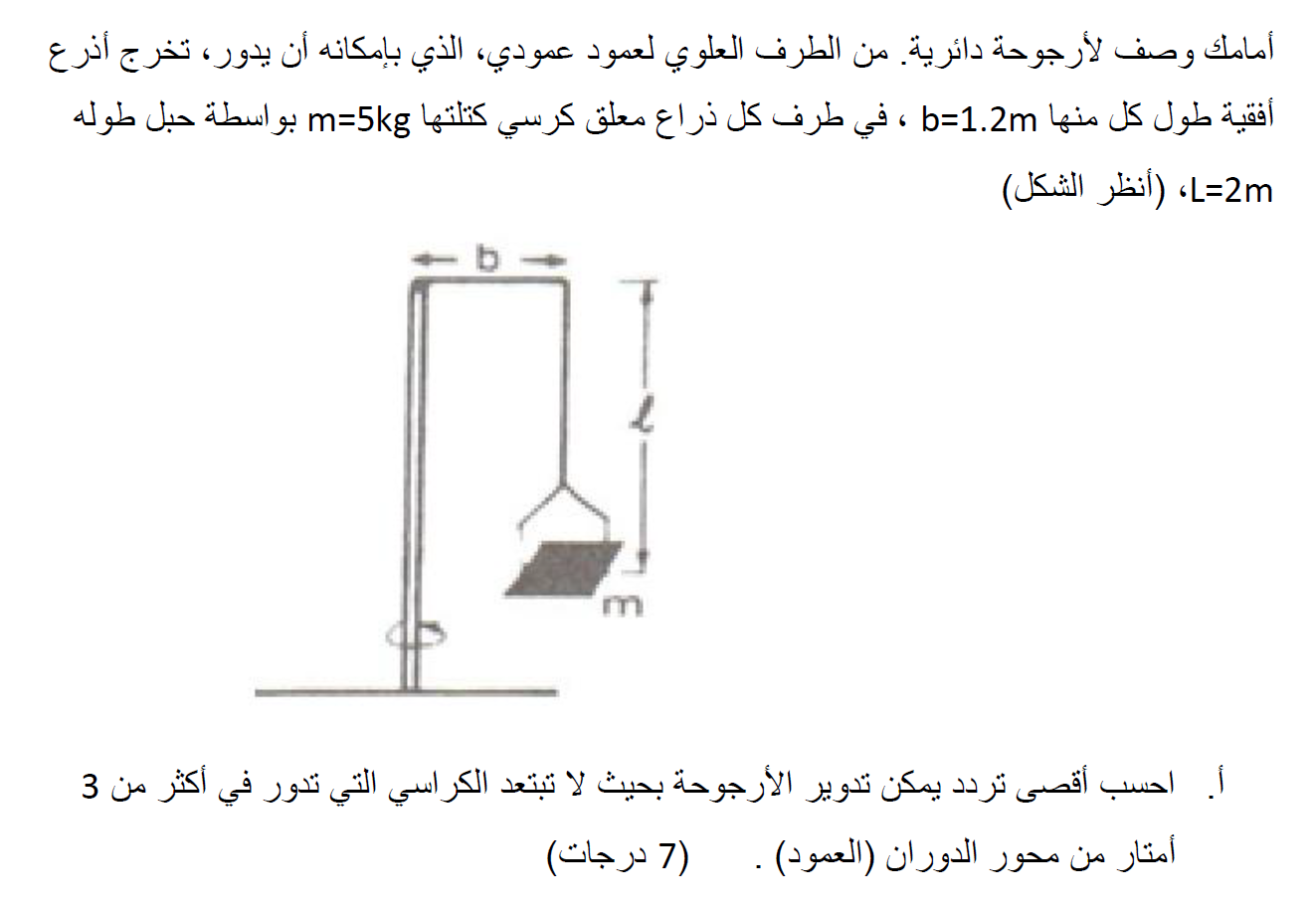
______________________________________________________________________________________
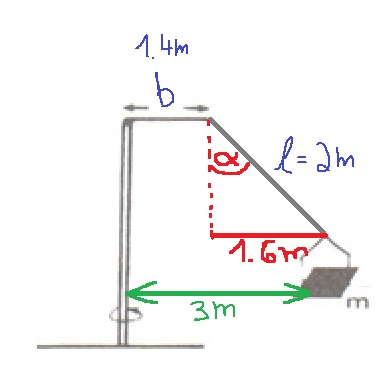
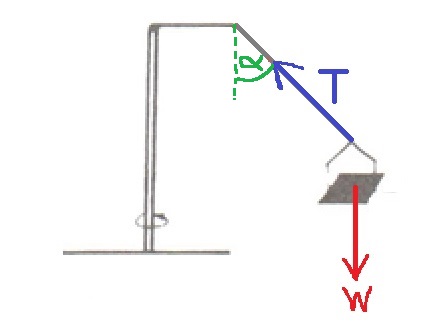
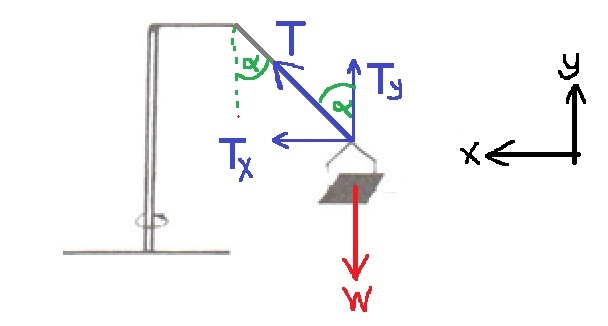
______________________________________________________________________________________

______________________________________________________________________________________
______________________________________________________________________________________

______________________________________________________________________________________
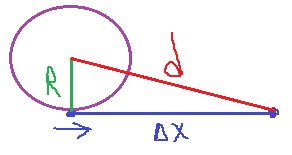

______________________________________________________________________________________