حلول التدريبات العملية في الدوائر الكهربائية: ד.5

24. ד.5

أ-الدائرة المعطاة عبارة عن دائرة مختلطة، نكتب تعبيرًا للمقاومة المحصلة :

«math xmlns=¨http://www.w3.org/1998/Math/MathML¨»«mstyle mathsize=¨20px¨»«msub»«mi mathvariant=¨bold¨ mathcolor=¨#0000FF¨»R«/mi»«mi mathvariant=¨bold¨ mathcolor=¨#0000FF¨»T«/mi»«/msub»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»=«/mo»«mrow mathcolor=¨#0000FF¨»«mo stretchy=¨true¨ mathvariant=¨bold¨»[«/mo»«mrow»«mo mathvariant=¨bold¨»(«/mo»«msub»«mi mathvariant=¨bold¨»R«/mi»«mn mathvariant=¨bold¨»2«/mn»«/msub»«mo mathvariant=¨bold¨»|«/mo»«mo mathvariant=¨bold¨»|«/mo»«msub»«mi mathvariant=¨bold¨»R«/mi»«mn mathvariant=¨bold¨»3«/mn»«/msub»«mo mathvariant=¨bold¨»)«/mo»«mo mathvariant=¨bold¨»+«/mo»«msub»«mi mathvariant=¨bold¨»R«/mi»«mn mathvariant=¨bold¨»1«/mn»«/msub»«/mrow»«mo stretchy=¨true¨ mathvariant=¨bold¨»]«/mo»«/mrow»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»+«/mo»«mi mathvariant=¨bold¨ mathcolor=¨#0000FF¨»r«/mi»«mspace linebreak=¨newline¨/»«mspace linebreak=¨newline¨/»«msub»«mi mathvariant=¨bold¨ mathcolor=¨#0000FF¨»R«/mi»«mi mathvariant=¨bold¨ mathcolor=¨#0000FF¨»T«/mi»«/msub»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»=«/mo»«mfrac mathcolor=¨#0000FF¨»«mrow»«mn mathvariant=¨bold¨»10«/mn»«mo mathvariant=¨bold¨»§#183;«/mo»«mn mathvariant=¨bold¨»10«/mn»«/mrow»«mrow»«mn mathvariant=¨bold¨»10«/mn»«mo mathvariant=¨bold¨»+«/mo»«mn mathvariant=¨bold¨»10«/mn»«/mrow»«/mfrac»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»+«/mo»«mn mathvariant=¨bold¨ mathcolor=¨#0000FF¨»10«/mn»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»+«/mo»«mn mathvariant=¨bold¨ mathcolor=¨#0000FF¨»1«/mn»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»=«/mo»«mn mathvariant=¨bold¨ mathcolor=¨#0000FF¨»16«/mn»«mi mathvariant=¨bold¨ mathcolor=¨#0000FF¨»§#937;«/mi»«/mstyle»«/math»

ب- نحسب شدة التيار بالمصدر باستخدام قانون أوم للدائرة بأكملها:

«math style=¨font-family:Tahoma¨ xmlns=¨http://www.w3.org/1998/Math/MathML¨»«mstyle mathsize=¨20px¨»«mi mathvariant=¨bold¨ mathcolor=¨#0000FF¨»I«/mi»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»=«/mo»«mfrac mathcolor=¨#0000FF¨»«mi mathvariant=¨bold¨»§#949;«/mi»«msub»«mi mathvariant=¨bold¨»R«/mi»«mi mathvariant=¨bold¨»T«/mi»«/msub»«/mfrac»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»=«/mo»«mfrac mathcolor=¨#0000FF¨»«mn mathvariant=¨bold¨»12«/mn»«mn mathvariant=¨bold¨»16«/mn»«/mfrac»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»=«/mo»«mn mathvariant=¨bold¨ mathcolor=¨#0000FF¨»0«/mn»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨».«/mo»«mn mathvariant=¨bold¨ mathcolor=¨#0000FF¨»75«/mn»«mi mathvariant=¨bold¨ mathcolor=¨#0000FF¨»A«/mi»«/mstyle»«/math»

ج- نحسب فرق جهد الأقطاب بمساعدة تعبير فرق جهد الأقطاب :

«math style=¨font-family:Tahoma¨ xmlns=¨http://www.w3.org/1998/Math/MathML¨»«mi mathvariant=¨bold¨ mathcolor=¨#0000FF¨ mathsize=¨20px¨»Vab«/mi»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨ mathsize=¨20px¨»=«/mo»«mi mathvariant=¨bold¨ mathcolor=¨#0000FF¨ mathsize=¨20px¨»§#949;«/mi»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨ mathsize=¨20px¨»-«/mo»«mi mathvariant=¨bold¨ mathcolor=¨#0000FF¨ mathsize=¨20px¨»I«/mi»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨ mathsize=¨20px¨»§#183;«/mo»«mi mathvariant=¨bold¨ mathcolor=¨#0000FF¨ mathsize=¨20px¨»r«/mi»«mspace linebreak=¨newline¨/»«mi mathvariant=¨bold¨ mathcolor=¨#0000FF¨ mathsize=¨20px¨»Vab«/mi»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨ mathsize=¨20px¨»=«/mo»«mn mathvariant=¨bold¨ mathcolor=¨#0000FF¨ mathsize=¨20px¨»12«/mn»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨ mathsize=¨20px¨»-«/mo»«mn mathvariant=¨bold¨ mathcolor=¨#0000FF¨ mathsize=¨20px¨»0«/mn»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨ mathsize=¨20px¨».«/mo»«mn mathvariant=¨bold¨ mathcolor=¨#0000FF¨ mathsize=¨20px¨»75«/mn»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨ mathsize=¨20px¨»§#183;«/mo»«mn mathvariant=¨bold¨ mathcolor=¨#0000FF¨ mathsize=¨20px¨»1«/mn»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨ mathsize=¨20px¨»=«/mo»«mn mathvariant=¨bold¨ mathcolor=¨#0000FF¨ mathsize=¨20px¨»11«/mn»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨ mathsize=¨20px¨».«/mo»«mn mathvariant=¨bold¨ mathcolor=¨#0000FF¨ mathsize=¨20px¨»25«/mn»«mi mathvariant=¨bold¨ mathcolor=¨#0000FF¨ mathsize=¨20px¨»V«/mi»«/math»

د- لحساب فرق الجهد على R₂، نجد التيار المار عبره.

نشير للتيار المار عبر المصدر بـ I ، والتيار عبر R₃ بـ I₁ والتيار عبر R₂ في I₂، تظهر التيارات الثلاثة في الشكل التالي:

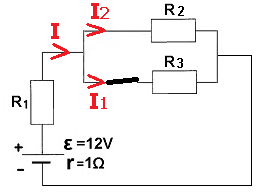
لأن مقاومة المقاوم R₂ مساوٍ لمقاومة المقاوم R₃. يمكن تحديد أن تيار المصدر سينقسم في نقطة التقاطع بنفس النسبة، لذا سيتدفق نصف تيار المصدر عبر المقاومR₂ ونصف التيار عبر المقاوم R3.

نحسب شدة التيار عبر R₂:

«math style=¨font-family:Tahoma¨ xmlns=¨http://www.w3.org/1998/Math/MathML¨»«mstyle mathsize=¨20px¨»«msub»«mi mathvariant=¨bold¨ mathcolor=¨#0000FF¨»I«/mi»«mn mathvariant=¨bold¨ mathcolor=¨#0000FF¨»2«/mn»«/msub»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»=«/mo»«mfrac mathcolor=¨#0000FF¨»«mi mathvariant=¨bold¨»I«/mi»«mn mathvariant=¨bold¨»2«/mn»«/mfrac»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»=«/mo»«mfrac mathcolor=¨#0000FF¨»«mrow»«mn mathvariant=¨bold¨»0«/mn»«mo mathvariant=¨bold¨».«/mo»«mn mathvariant=¨bold¨»75«/mn»«/mrow»«mn mathvariant=¨bold¨»2«/mn»«/mfrac»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»=«/mo»«mn mathvariant=¨bold¨ mathcolor=¨#0000FF¨»0«/mn»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨».«/mo»«mn mathvariant=¨bold¨ mathcolor=¨#0000FF¨»375«/mn»«mi mathvariant=¨bold¨ mathcolor=¨#0000FF¨»A«/mi»«/mstyle»«/math»

نحسب فرق الجهد على R₂ باستخدام قانون أوم:

طريقة أخرى: المقاومتان R2 و- R3 موصولتان على التوازي، فرق الجهد عليهم متساوٍ.

من مبادئ الدائرة على التوالي، يمكن تحديد أن فرق جهد الأقطاب يساوي مجموع فرقي الجهد على R₁ و R₂.

«math style=¨font-family:Tahoma¨ xmlns=¨http://www.w3.org/1998/Math/MathML¨»«mstyle mathsize=¨20px¨»«mi mathvariant=¨bold¨ mathcolor=¨#0000FF¨»Vab«/mi»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»=«/mo»«msub»«mi mathvariant=¨bold¨ mathcolor=¨#0000FF¨»U«/mi»«msub mathcolor=¨#0000FF¨»«mi mathvariant=¨bold¨»R«/mi»«mn mathvariant=¨bold¨»1«/mn»«/msub»«/msub»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»+«/mo»«msub»«mi mathvariant=¨bold¨ mathcolor=¨#0000FF¨»U«/mi»«msub mathcolor=¨#0000FF¨»«mi mathvariant=¨bold¨»R«/mi»«mn mathvariant=¨bold¨»2«/mn»«/msub»«/msub»«/mstyle»«/math»

نعبر عن فرق الجهد على R₂

«math style=¨font-family:Tahoma¨ xmlns=¨http://www.w3.org/1998/Math/MathML¨»«mstyle mathsize=¨20px¨»«msub»«mi mathvariant=¨bold¨ mathcolor=¨#0000FF¨»U«/mi»«msub mathcolor=¨#0000FF¨»«mi mathvariant=¨bold¨»R«/mi»«mn mathvariant=¨bold¨»2«/mn»«/msub»«/msub»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»=«/mo»«mi mathvariant=¨bold¨ mathcolor=¨#0000FF¨»Vab«/mi»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»-«/mo»«msub»«mi mathvariant=¨bold¨ mathcolor=¨#0000FF¨»U«/mi»«msub mathcolor=¨#0000FF¨»«mi mathvariant=¨bold¨»R«/mi»«mn mathvariant=¨bold¨»1«/mn»«/msub»«/msub»«mspace linebreak=¨newline¨/»«msub»«mi mathvariant=¨bold¨ mathcolor=¨#0000FF¨»U«/mi»«msub mathcolor=¨#0000FF¨»«mi mathvariant=¨bold¨»R«/mi»«mn mathvariant=¨bold¨»2«/mn»«/msub»«/msub»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»=«/mo»«mi mathvariant=¨bold¨ mathcolor=¨#0000FF¨»Vab«/mi»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»-«/mo»«mi mathvariant=¨bold¨ mathcolor=¨#0000FF¨»I«/mi»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»§#183;«/mo»«mi mathvariant=¨bold¨ mathcolor=¨#0000FF¨»R«/mi»«mn mathvariant=¨bold¨ mathcolor=¨#0000FF¨»1«/mn»«mspace linebreak=¨newline¨/»«msub»«mi mathvariant=¨bold¨ mathcolor=¨#0000FF¨»U«/mi»«msub mathcolor=¨#0000FF¨»«mi mathvariant=¨bold¨»R«/mi»«mn mathvariant=¨bold¨»2«/mn»«/msub»«/msub»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»=«/mo»«mn mathvariant=¨bold¨ mathcolor=¨#0000FF¨»11«/mn»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨».«/mo»«mn mathvariant=¨bold¨ mathcolor=¨#0000FF¨»25«/mn»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»-«/mo»«mn mathvariant=¨bold¨ mathcolor=¨#0000FF¨»0«/mn»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨».«/mo»«mn mathvariant=¨bold¨ mathcolor=¨#0000FF¨»75«/mn»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»§#183;«/mo»«mn mathvariant=¨bold¨ mathcolor=¨#0000FF¨»10«/mn»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»=«/mo»«mn mathvariant=¨bold¨ mathcolor=¨#0000FF¨»11«/mn»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨».«/mo»«mn mathvariant=¨bold¨ mathcolor=¨#0000FF¨»25«/mn»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»-«/mo»«mn mathvariant=¨bold¨ mathcolor=¨#0000FF¨»7«/mn»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨».«/mo»«mn mathvariant=¨bold¨ mathcolor=¨#0000FF¨»5«/mn»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»=«/mo»«mn mathvariant=¨bold¨ mathcolor=¨#0000FF¨»3«/mn»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨».«/mo»«mn mathvariant=¨bold¨ mathcolor=¨#0000FF¨»75«/mn»«mi mathvariant=¨bold¨ mathcolor=¨#0000FF¨»V«/mi»«/mstyle»«/math»