حلول التدريبات العملية في الدوائر الكهربائية
| الموقع: | YouCube |
| المقرر: | מעגלי זרם - ערבית |
| كتاب: | حلول التدريبات العملية في الدوائر الكهربائية |
| طبع بواسطة: | משתמש אורח |
| التاريخ: | الأربعاء، 4 فبراير 2026، 2:37 AM |
جدول المحتويات
- 1. א.1
- 2. א.2
- 3. א.3
- 4. א.4
- 5. ב.1
- 6. ב.2
- 7. ב.3
- 8. ב.4
- 9. ב.5
- 10. ב.6
- 11. ג.1
- 12. ג.2
- 13. ג.3
- 14. ג.4
- 15. ג.5
- 16. ג.6
- 17. ג.7
- 18. ג.8
- 19. ג.9
- 20. ד.1
- 21. ד.2
- 22. ד.3
- 23. ד.4
- 24. ד.5
- 25. ד.6
- 26. ד.7
- 27. ד.8
- 28. ד.9
- 29. ד.10
- 30. ד.11
- 31. ד.12
- 32. ד.13
- 33. ה.1
- 34. ה.2
- 35. ה.3
- 36. ה.4
- 37. ה.5
- 38. ה.6
- 39. ה.7
- 40. ה.8
- 41. ו.1
- 42. ו.2
- 43. ו.3
- 44. ו.4
- 45. ו.5
- 46. ו.6
- 47. ו.7
1. א.1
أ- يتدفق التيار من الجهد العالي إلى الجهد المنخفض، خارج البطارية.
لذلك، يكون اتجاه التيار عبر المستهلك من اليسار إلى اليمين. كما ترى في الشكل التالي:
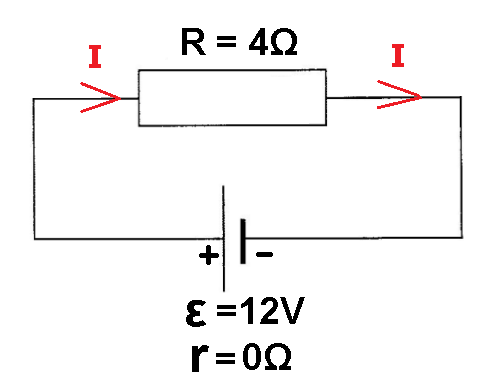
ب- من تعبير فرق جهد الأقطاب: «math style=¨font-family:Tahoma¨ xmlns=¨http://www.w3.org/1998/Math/MathML¨»«mi mathvariant=¨bold¨ mathcolor=¨#0000FF¨ mathsize=¨20px¨»Vab«/mi»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨ mathsize=¨20px¨»=«/mo»«mi mathvariant=¨bold¨ mathcolor=¨#0000FF¨ mathsize=¨20px¨»§#949;«/mi»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨ mathsize=¨20px¨»-«/mo»«mi mathvariant=¨bold¨ mathcolor=¨#0000FF¨ mathsize=¨20px¨»I«/mi»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨ mathsize=¨20px¨»§#183;«/mo»«mi mathvariant=¨bold¨ mathcolor=¨#0000FF¨ mathsize=¨20px¨»r«/mi»«/math» ، يمكن ملاحظة أنه عندما تكون المقاومة الداخلية للبطارية مساوية للصفر، فإن فرق جهد الأقطاب يساوي القوة الكهربائية الدافعة للبطارية، لذلك فإن فرق جهد الأقطاب يساوي 12 فولط.
ج- يتم توصيل المستهلك مباشرة بأقطاب البطارية، وفرق الجهد على المستهلك يساوي فرق جهد أقطاب البطارية 12 فولط.
د- نجد شدة التيار المار في الدائرة باستخدام قانون أوم:
«math style=¨font-family:Tahoma¨ xmlns=¨http://www.w3.org/1998/Math/MathML¨»«mstyle mathsize=¨20px¨»«mi mathvariant=¨bold¨ mathcolor=¨#0000FF¨»I«/mi»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»=«/mo»«mfrac mathcolor=¨#0000FF¨»«msub»«mi mathvariant=¨bold¨»U«/mi»«mi mathvariant=¨bold¨»R«/mi»«/msub»«mi mathvariant=¨bold¨»R«/mi»«/mfrac»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»=«/mo»«mfrac mathcolor=¨#0000FF¨»«mn mathvariant=¨bold¨»12«/mn»«mn mathvariant=¨bold¨»4«/mn»«/mfrac»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»=«/mo»«mn mathvariant=¨bold¨ mathcolor=¨#0000FF¨»3«/mn»«mi mathvariant=¨bold¨ mathcolor=¨#0000FF¨»A«/mi»«/mstyle»«/math»
2. א.2
أ- طالما أن مصدر فرق الجهد مثالي (المقاومة الداخلية تساوي صفر أوم) ، من تعبير فرق جهد الأقطاب والقوة الكهربائية الدافعة: «math style=¨font-family:Tahoma¨ xmlns=¨http://www.w3.org/1998/Math/MathML¨»«mi mathvariant=¨bold¨ mathcolor=¨#0000FF¨ mathsize=¨20px¨»Vab«/mi»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨ mathsize=¨20px¨»=«/mo»«mi mathvariant=¨bold¨ mathcolor=¨#0000FF¨ mathsize=¨20px¨»§#949;«/mi»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨ mathsize=¨20px¨»-«/mo»«mi mathvariant=¨bold¨ mathcolor=¨#0000FF¨ mathsize=¨20px¨»I«/mi»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨ mathsize=¨20px¨»§#183;«/mo»«mi mathvariant=¨bold¨ mathcolor=¨#0000FF¨ mathsize=¨20px¨»r«/mi»«/math»
سيكون فرق جهد الأقطاب مساويًا للقوة الكهربائية الدافعة للبطارية بغض النظر عن التيار في الدائرة.
لذلك، حتى عند تغيير مقاومة المستهلك، يبقى فرق جهد الأقطاب 12 فولط.
ب. يتم توصيل المستهلك مباشرة بأقطاب البطارية، وبالتالي فإن فرق الجهد الكهربائي على المستهلك يساوي 12 فولط.
ج- نجد شدة التيار في الدائرة باستخدام قانون أوم:
«math style=¨font-family:Tahoma¨ xmlns=¨http://www.w3.org/1998/Math/MathML¨»«mstyle mathsize=¨20px¨»«mi mathvariant=¨bold¨ mathcolor=¨#0000FF¨»I«/mi»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»=«/mo»«mfrac mathcolor=¨#0000FF¨»«msub»«mi mathvariant=¨bold¨»U«/mi»«mi mathvariant=¨bold¨»R«/mi»«/msub»«mi mathvariant=¨bold¨»R«/mi»«/mfrac»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»=«/mo»«mfrac mathcolor=¨#0000FF¨»«mn mathvariant=¨bold¨»12«/mn»«mn mathvariant=¨bold¨»4«/mn»«/mfrac»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»=«/mo»«mn mathvariant=¨bold¨ mathcolor=¨#0000FF¨»3«/mn»«mi mathvariant=¨bold¨ mathcolor=¨#0000FF¨»A«/mi»«/mstyle»«/math»
3. א.3
أ- النقطة A موجودة على سلك موصل سلك موصول بالطرف الموجب للبطارية. النقطة D موجودة على سلك موصل موصول بالطرف السالب للبطارية.
لذلك، فإن فرق الجهد VAD يساوي فرق جهد الأقطاب، حيث أن فرق جهد الأقطاب لبطارية مثالية يساوي 12 فولط.
ب- النقطة C موجودة على سلك موصل موصول بالطرف السالب لمصدر الجهد. النقطة B موجودة على سلك موصل موصول بالطرف الموجب لمصدر الجهد.
فرق الجهد VBC يساوي جهد القطب السالب للبطارية مطروحًا منه جهد القطب الموجب للبطارية، وبالتالي فإن فرق الجهد VBC يساوي سالب 12 فولط.
جـ- النقطتان A و B تقعان على نفس السلك الموصل، بافتراض أن مقاومة السلك الموصل مهملة، فإن الجهد في النقطة A هو نفس الجهد في النقطة B.
لذلك فإن فرق الجهد VAB يساوي صفرًا.
4. א.4
أ- فرق جهد الأقطاب للبطارية هو 12 فولط. (الجهد على القطب الموجب أكبر من الجهد على القطب السالب بـ 12 فولط ).
لذلك، فإن الجهد في النقطة A أكبر من الجهد في النقطة D بمقدار 12 فولط.
بما أن الجهد في النقطة D هو 5 فولط، فإن الجهد في النقطة A هو 17 فولط.
ب- الجهد في النقطة B هو نفس الجهد في النقطة A ويساوي 17 فولط.
جـ- الجهد في النقطة C هو نفس الجهد عند النقطة D ويساوي 5 فولط.
5. ב.1
أ- نجد شدة التيار في الدائرة باستخدام قانون أوم للدائرة بأكملها:
«math style=¨font-family:Tahoma¨ xmlns=¨http://www.w3.org/1998/Math/MathML¨»«mstyle mathsize=¨20px¨»«mi mathvariant=¨bold¨ mathcolor=¨#0000FF¨»I«/mi»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»=«/mo»«mfrac mathcolor=¨#0000FF¨»«mi mathvariant=¨bold¨»§#949;«/mi»«msub»«mi mathvariant=¨bold¨»R«/mi»«mi mathvariant=¨bold¨»T«/mi»«/msub»«/mfrac»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»=«/mo»«mfrac mathcolor=¨#0000FF¨»«mi mathvariant=¨bold¨»§#949;«/mi»«mrow»«mi mathvariant=¨bold¨»R«/mi»«mo mathvariant=¨bold¨»+«/mo»«mi mathvariant=¨bold¨»r«/mi»«/mrow»«/mfrac»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»=«/mo»«mfrac mathcolor=¨#0000FF¨»«mn mathvariant=¨bold¨»12«/mn»«mrow»«mn mathvariant=¨bold¨»4«/mn»«mo mathvariant=¨bold¨»+«/mo»«mn mathvariant=¨bold¨»1«/mn»«/mrow»«/mfrac»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»=«/mo»«mn mathvariant=¨bold¨ mathcolor=¨#0000FF¨»2«/mn»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨».«/mo»«mn mathvariant=¨bold¨ mathcolor=¨#0000FF¨»4«/mn»«mi mathvariant=¨bold¨ mathcolor=¨#0000FF¨»A«/mi»«/mstyle»«/math»
ب- نحسب فرق جهد الأقطاب بدلالة التعبير : «math style=¨font-family:Tahoma¨ xmlns=¨http://www.w3.org/1998/Math/MathML¨»«mi mathvariant=¨bold¨ mathcolor=¨#0000FF¨ mathsize=¨20px¨»Vab«/mi»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨ mathsize=¨20px¨»=«/mo»«mi mathvariant=¨bold¨ mathcolor=¨#0000FF¨ mathsize=¨20px¨»§#949;«/mi»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨ mathsize=¨20px¨»-«/mo»«mi mathvariant=¨bold¨ mathcolor=¨#0000FF¨ mathsize=¨20px¨»I«/mi»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨ mathsize=¨20px¨»§#183;«/mo»«mi mathvariant=¨bold¨ mathcolor=¨#0000FF¨ mathsize=¨20px¨»r«/mi»«/math»
«math style=¨font-family:Tahoma¨ xmlns=¨http://www.w3.org/1998/Math/MathML¨»«mi mathvariant=¨bold¨ mathcolor=¨#0000FF¨ mathsize=¨20px¨»Vab«/mi»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨ mathsize=¨20px¨»=«/mo»«mi mathvariant=¨bold¨ mathcolor=¨#0000FF¨ mathsize=¨20px¨»§#949;«/mi»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨ mathsize=¨20px¨»-«/mo»«mi mathvariant=¨bold¨ mathcolor=¨#0000FF¨ mathsize=¨20px¨»I«/mi»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨ mathsize=¨20px¨»§#183;«/mo»«mi mathvariant=¨bold¨ mathcolor=¨#0000FF¨ mathsize=¨20px¨»r«/mi»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨ mathsize=¨20px¨»=«/mo»«mn mathvariant=¨bold¨ mathcolor=¨#0000FF¨ mathsize=¨20px¨»12«/mn»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨ mathsize=¨20px¨»-«/mo»«mn mathvariant=¨bold¨ mathcolor=¨#0000FF¨ mathsize=¨20px¨»2«/mn»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨ mathsize=¨20px¨».«/mo»«mn mathvariant=¨bold¨ mathcolor=¨#0000FF¨ mathsize=¨20px¨»4«/mn»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨ mathsize=¨20px¨»§#183;«/mo»«mn mathvariant=¨bold¨ mathcolor=¨#0000FF¨ mathsize=¨20px¨»1«/mn»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨ mathsize=¨20px¨»=«/mo»«mn mathvariant=¨bold¨ mathcolor=¨#0000FF¨ mathsize=¨20px¨»9«/mn»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨ mathsize=¨20px¨».«/mo»«mn mathvariant=¨bold¨ mathcolor=¨#0000FF¨ mathsize=¨20px¨»6«/mn»«mi mathvariant=¨bold¨ mathcolor=¨#0000FF¨ mathsize=¨20px¨»V«/mi»«/math»
جـ- فرق الجهد على المستهلك يساوي فرق جهد الأقطاب، 9.6 فولط.
6. ב.2
أ- نستخدم قانون أوم للدائرة بأكملها:
«math style=¨font-family:Tahoma¨ xmlns=¨http://www.w3.org/1998/Math/MathML¨»«mstyle mathsize=¨20px¨»«mi mathvariant=¨bold¨ mathcolor=¨#0000FF¨»I«/mi»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»=«/mo»«mfrac mathcolor=¨#0000FF¨»«mi mathvariant=¨bold¨»§#949;«/mi»«msub»«mi mathvariant=¨bold¨»R«/mi»«mi mathvariant=¨bold¨»T«/mi»«/msub»«/mfrac»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»=«/mo»«mfrac mathcolor=¨#0000FF¨»«mi mathvariant=¨bold¨»§#949;«/mi»«mrow»«mi mathvariant=¨bold¨»R«/mi»«mo mathvariant=¨bold¨»+«/mo»«mi mathvariant=¨bold¨»r«/mi»«/mrow»«/mfrac»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»=«/mo»«mfrac mathcolor=¨#0000FF¨»«mn mathvariant=¨bold¨»12«/mn»«mrow»«mn mathvariant=¨bold¨»2«/mn»«mo mathvariant=¨bold¨»+«/mo»«mn mathvariant=¨bold¨»1«/mn»«/mrow»«/mfrac»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»=«/mo»«mn mathvariant=¨bold¨ mathcolor=¨#0000FF¨»4«/mn»«mi mathvariant=¨bold¨ mathcolor=¨#0000FF¨»A«/mi»«/mstyle»«/math»
ب - احسب فرق جهد الأقطاب باستخدام تعبير فرق جهد الأقطاب:
«math style=¨font-family:Tahoma¨ xmlns=¨http://www.w3.org/1998/Math/MathML¨»«mi mathvariant=¨bold¨ mathcolor=¨#0000FF¨ mathsize=¨20px¨»Vab«/mi»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨ mathsize=¨20px¨»=«/mo»«mi mathvariant=¨bold¨ mathcolor=¨#0000FF¨ mathsize=¨20px¨»§#949;«/mi»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨ mathsize=¨20px¨»-«/mo»«mi mathvariant=¨bold¨ mathcolor=¨#0000FF¨ mathsize=¨20px¨»I«/mi»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨ mathsize=¨20px¨»§#183;«/mo»«mi mathvariant=¨bold¨ mathcolor=¨#0000FF¨ mathsize=¨20px¨»r«/mi»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨ mathsize=¨20px¨»=«/mo»«mn mathvariant=¨bold¨ mathcolor=¨#0000FF¨ mathsize=¨20px¨»12«/mn»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨ mathsize=¨20px¨»-«/mo»«mn mathvariant=¨bold¨ mathcolor=¨#0000FF¨ mathsize=¨20px¨»4«/mn»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨ mathsize=¨20px¨»§#183;«/mo»«mn mathvariant=¨bold¨ mathcolor=¨#0000FF¨ mathsize=¨20px¨»1«/mn»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨ mathsize=¨20px¨»=«/mo»«mn mathvariant=¨bold¨ mathcolor=¨#0000FF¨ mathsize=¨20px¨»8«/mn»«mi mathvariant=¨bold¨ mathcolor=¨#0000FF¨ mathsize=¨20px¨»V«/mi»«/math»
عندما يكون مصدر الجهد غير مثاليًا، يختلف فرق جهد الأقطاب عن القوة الكهربائية الدافعة، ويتعلق بشدة التيار في الدائرة.
7. ב.3
أ. يكون أقصى تيار في البطارية عند تكون في حالة تماس كهربائي، وتكون المقاومة المحصلة للدائرة مساوية للمقاومة الداخلية للبطارية.
لكي يمر أقصى تيار في البطارية ، يجب وضع نقطة التماس في النقطة N.
ب. نحسب شدة التيار عند وضع نقطة التماس المتنقلة في النقطة N ، باستخدام قانون أوم:
«math style=¨font-family:Tahoma¨ xmlns=¨http://www.w3.org/1998/Math/MathML¨»«mstyle mathsize=¨20px¨»«mi mathvariant=¨bold¨ mathcolor=¨#0000FF¨»I«/mi»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»=«/mo»«mfrac mathcolor=¨#0000FF¨»«mi mathvariant=¨bold¨»§#949;«/mi»«msub»«mi mathvariant=¨bold¨»R«/mi»«mi mathvariant=¨bold¨»T«/mi»«/msub»«/mfrac»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»=«/mo»«mfrac mathcolor=¨#0000FF¨»«mi mathvariant=¨bold¨»§#949;«/mi»«mi mathvariant=¨bold¨»r«/mi»«/mfrac»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»=«/mo»«mfrac mathcolor=¨#0000FF¨»«mn mathvariant=¨bold¨»12«/mn»«mn mathvariant=¨bold¨»1«/mn»«/mfrac»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»=«/mo»«mn mathvariant=¨bold¨ mathcolor=¨#0000FF¨»12«/mn»«mi mathvariant=¨bold¨ mathcolor=¨#0000FF¨»A«/mi»«/mstyle»«/math»
جـ. نحسب قيمة فرق جهد الأقطاب عندما تكون شدة التيار قصوى:
«math style=¨font-family:Tahoma¨ xmlns=¨http://www.w3.org/1998/Math/MathML¨»«mi mathvariant=¨bold¨ mathcolor=¨#0000FF¨ mathsize=¨20px¨»Vab«/mi»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨ mathsize=¨20px¨»=«/mo»«mi mathvariant=¨bold¨ mathcolor=¨#0000FF¨ mathsize=¨20px¨»§#949;«/mi»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨ mathsize=¨20px¨»-«/mo»«mi mathvariant=¨bold¨ mathcolor=¨#0000FF¨ mathsize=¨20px¨»I«/mi»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨ mathsize=¨20px¨»§#183;«/mo»«mi mathvariant=¨bold¨ mathcolor=¨#0000FF¨ mathsize=¨20px¨»r«/mi»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨ mathsize=¨20px¨»=«/mo»«mn mathvariant=¨bold¨ mathcolor=¨#0000FF¨ mathsize=¨20px¨»12«/mn»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨ mathsize=¨20px¨»-«/mo»«mn mathvariant=¨bold¨ mathcolor=¨#0000FF¨ mathsize=¨20px¨»12«/mn»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨ mathsize=¨20px¨»§#183;«/mo»«mn mathvariant=¨bold¨ mathcolor=¨#0000FF¨ mathsize=¨20px¨»1«/mn»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨ mathsize=¨20px¨»=«/mo»«mn mathvariant=¨bold¨ mathcolor=¨#0000FF¨ mathsize=¨20px¨»0«/mn»«mi mathvariant=¨bold¨ mathcolor=¨#0000FF¨ mathsize=¨20px¨»V«/mi»«/math»
د. تكون أدنى شدة تيار في البطارية عندما تكون المقاومة المحصلة في الدائرة مساوية لما لا نهاية.
لكي تكون مقاومة الدائرة لا نهائية، يجب وضع نقطة التماس المتنقلة في النقطة M.
هـ. نحسب الحد الأدنى للتيار (عندما تكون نقطة التماس في النقطة M) باستخدام قانون أوم:
«math style=¨font-family:Tahoma¨ xmlns=¨http://www.w3.org/1998/Math/MathML¨»«mstyle mathsize=¨20px¨»«mi mathvariant=¨bold¨ mathcolor=¨#0000FF¨»I«/mi»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»=«/mo»«mfrac mathcolor=¨#0000FF¨»«mi mathvariant=¨bold¨»§#949;«/mi»«msub»«mi mathvariant=¨bold¨»R«/mi»«mi mathvariant=¨bold¨»T«/mi»«/msub»«/mfrac»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»=«/mo»«mfrac mathcolor=¨#0000FF¨»«mi mathvariant=¨bold¨»§#949;«/mi»«mrow»«mi mathvariant=¨bold¨»r«/mi»«mo mathvariant=¨bold¨»+«/mo»«mi mathvariant=¨bold¨»R«/mi»«/mrow»«/mfrac»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»=«/mo»«mfrac mathcolor=¨#0000FF¨»«mn mathvariant=¨bold¨»12«/mn»«mrow»«mn mathvariant=¨bold¨»1«/mn»«mo mathvariant=¨bold¨»+«/mo»«mo mathvariant=¨bold¨»§#8734;«/mo»«/mrow»«/mfrac»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»=«/mo»«mn mathvariant=¨bold¨ mathcolor=¨#0000FF¨»0«/mn»«mi mathvariant=¨bold¨ mathcolor=¨#0000FF¨»A«/mi»«/mstyle»«/math»
و. نحسب قيمة فرق جهد الأقطاب عندما يكون التيار أصغر قيمة له.
«math style=¨font-family:Tahoma¨ xmlns=¨http://www.w3.org/1998/Math/MathML¨»«mi mathvariant=¨bold¨ mathcolor=¨#0000FF¨ mathsize=¨20px¨»Vab«/mi»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨ mathsize=¨20px¨»=«/mo»«mi mathvariant=¨bold¨ mathcolor=¨#0000FF¨ mathsize=¨20px¨»§#949;«/mi»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨ mathsize=¨20px¨»-«/mo»«mi mathvariant=¨bold¨ mathcolor=¨#0000FF¨ mathsize=¨20px¨»I«/mi»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨ mathsize=¨20px¨»§#183;«/mo»«mi mathvariant=¨bold¨ mathcolor=¨#0000FF¨ mathsize=¨20px¨»r«/mi»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨ mathsize=¨20px¨»=«/mo»«mn mathvariant=¨bold¨ mathcolor=¨#0000FF¨ mathsize=¨20px¨»12«/mn»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨ mathsize=¨20px¨»-«/mo»«mn mathvariant=¨bold¨ mathcolor=¨#0000FF¨ mathsize=¨20px¨»0«/mn»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨ mathsize=¨20px¨»§#183;«/mo»«mn mathvariant=¨bold¨ mathcolor=¨#0000FF¨ mathsize=¨20px¨»1«/mn»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨ mathsize=¨20px¨»=«/mo»«mi mathvariant=¨bold-italic¨ mathcolor=¨#0000FF¨ mathsize=¨20px¨»§#949;«/mi»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨ mathsize=¨20px¨»=«/mo»«mn mathvariant=¨bold¨ mathcolor=¨#0000FF¨ mathsize=¨20px¨»12«/mn»«mi mathvariant=¨bold¨ mathcolor=¨#0000FF¨ mathsize=¨20px¨»V«/mi»«/math»
عندما تكون البطارية في حالة تماس، يتدفق عبرها تيار يدعى تيار التماس، ويكون فرق جهد الأقطاب للبطارية في هذه الحالة يساوي صفرًا.
وعندما يتم فصل البطارية، لا يوجد تيار في البطارية، فرق جهد الأقطاب للبطارية يساوي القوة الكهربائية الدافعة للبطارية.
8. ב.4
أ- في الرسم البياني لفرق جهد الأقطاب كدالة للتيار، فإن قيمة المقاومة الداخلية للبطارية تساوي ناقص ميل الدالة في الرسم البياني.
نحسب ميل الدالة للرسم البياني:
«math style=¨font-family:Tahoma¨ xmlns=¨http://www.w3.org/1998/Math/MathML¨»«mstyle mathsize=¨20px¨»«mi mathvariant=¨bold¨ mathcolor=¨#0000FF¨»§#1575;§#1604;§#1605;§#1610;§#1604;«/mi»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»=«/mo»«mfrac mathcolor=¨#0000FF¨»«mrow»«mo mathvariant=¨bold¨»§#8710;«/mo»«mi mathvariant=¨bold¨»Vab«/mi»«/mrow»«mrow»«mo mathvariant=¨bold¨»§#8710;«/mo»«mi mathvariant=¨bold¨»I«/mi»«/mrow»«/mfrac»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»=«/mo»«mfrac mathcolor=¨#0000FF¨»«mrow»«mn mathvariant=¨bold¨»0«/mn»«mo mathvariant=¨bold¨»-«/mo»«mn mathvariant=¨bold¨»1«/mn»«mo mathvariant=¨bold¨».«/mo»«mn mathvariant=¨bold¨»5«/mn»«/mrow»«mrow»«mn mathvariant=¨bold¨»3«/mn»«mo mathvariant=¨bold¨»-«/mo»«mn mathvariant=¨bold¨»0«/mn»«/mrow»«/mfrac»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»=«/mo»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»-«/mo»«mn mathvariant=¨bold¨ mathcolor=¨#0000FF¨»0«/mn»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨».«/mo»«mn mathvariant=¨bold¨ mathcolor=¨#0000FF¨»5«/mn»«mi mathvariant=¨bold¨ mathcolor=¨#0000FF¨»§#937;«/mi»«/mstyle»«/math»
لذلك ، المقاومة الداخلية للبطارية 0.5 أوم.
ب- في الرسم البياني لفرق جهد الأقطاب كدالة للتيار، فإن نقطة التقاطع مع المحور الرأسي تساوي القوة الكهربائية الدافعة للبطارية.
من الرسم البياني يمكن تحديد أن قيمة القوة الكهربائية الدافعة للبطارية هي 1.5 فولط.
ج- تصل شدة التيار إلى أقصى حد عندما تكون مقاومة المقاوم المتغير صفراً.
نجد شدة التيار باستخدام قانون أوم: «math style=¨font-family:Tahoma¨ xmlns=¨http://www.w3.org/1998/Math/MathML¨»«mstyle mathsize=¨20px¨»«mi mathvariant=¨bold¨ mathcolor=¨#0000FF¨»I«/mi»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»=«/mo»«mfrac mathcolor=¨#0000FF¨»«mi mathvariant=¨bold¨»§#949;«/mi»«msub»«mi mathvariant=¨bold¨»R«/mi»«mi mathvariant=¨bold¨»T«/mi»«/msub»«/mfrac»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»=«/mo»«mfrac mathcolor=¨#0000FF¨»«mi mathvariant=¨bold¨»§#949;«/mi»«mrow»«mi mathvariant=¨bold¨»R«/mi»«mo mathvariant=¨bold¨»+«/mo»«mi mathvariant=¨bold¨»r«/mi»«/mrow»«/mfrac»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»=«/mo»«mfrac mathcolor=¨#0000FF¨»«mrow»«mn mathvariant=¨bold¨»1«/mn»«mo mathvariant=¨bold¨».«/mo»«mn mathvariant=¨bold¨»5«/mn»«/mrow»«mrow»«mn mathvariant=¨bold¨»0«/mn»«mo mathvariant=¨bold¨»+«/mo»«mn mathvariant=¨bold¨»0«/mn»«mo mathvariant=¨bold¨».«/mo»«mn mathvariant=¨bold¨»5«/mn»«/mrow»«/mfrac»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»=«/mo»«mn mathvariant=¨bold¨ mathcolor=¨#0000FF¨»3«/mn»«mi mathvariant=¨bold¨ mathcolor=¨#0000FF¨»A«/mi»«/mstyle»«/math»
د- فرق جهد الأقطاب يساوي صفر عندما تكون البطارية في حالة تماس.
حتى تكون البطارية في حالة تماس، يجب أن تكون مقاومة المقاوم المتغير صفرًا.
هـ- نجد مقاومة RX عندما يكون فرق جهد الأقطاب مساويًا لنصف القوة الكهربائية الدافعة للبطارية باستخدام تعبير فرق جهد الأقطاب:
«math style=¨font-family:Tahoma¨ xmlns=¨http://www.w3.org/1998/Math/MathML¨»«mi mathvariant=¨bold¨ mathcolor=¨#0000FF¨ mathsize=¨20px¨»Vab«/mi»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨ mathsize=¨20px¨»=«/mo»«mi mathvariant=¨bold¨ mathcolor=¨#0000FF¨ mathsize=¨20px¨»§#949;«/mi»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨ mathsize=¨20px¨»-«/mo»«mi mathvariant=¨bold¨ mathcolor=¨#0000FF¨ mathsize=¨20px¨»I«/mi»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨ mathsize=¨20px¨»§#183;«/mo»«mi mathvariant=¨bold¨ mathcolor=¨#0000FF¨ mathsize=¨20px¨»r«/mi»«mspace linebreak=¨newline¨/»«/math»
نعبر عن شدة التيار باستخدام قانون أوم ونعوض قيمة نصف القوة الكهربائية الدافعة للبطارية في تعبير فرق جهد الأقطاب.
«math style=¨font-family:Tahoma¨ xmlns=¨http://www.w3.org/1998/Math/MathML¨»«mi mathvariant=¨bold¨ mathcolor=¨#0000FF¨ mathsize=¨20px¨»Vab«/mi»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨ mathsize=¨20px¨»=«/mo»«mi mathvariant=¨bold¨ mathcolor=¨#0000FF¨ mathsize=¨20px¨»§#949;«/mi»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨ mathsize=¨20px¨»-«/mo»«mi mathvariant=¨bold¨ mathcolor=¨#0000FF¨ mathsize=¨20px¨»I«/mi»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨ mathsize=¨20px¨»§#183;«/mo»«mi mathvariant=¨bold¨ mathcolor=¨#0000FF¨ mathsize=¨20px¨»r«/mi»«mspace linebreak=¨newline¨/»«mspace linebreak=¨newline¨/»«mfrac mathcolor=¨#0000FF¨»«mi mathvariant=¨bold¨ mathsize=¨20px¨»§#949;«/mi»«mn mathvariant=¨bold¨ mathsize=¨20px¨»2«/mn»«/mfrac»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨ mathsize=¨20px¨»=«/mo»«mi mathvariant=¨bold¨ mathcolor=¨#0000FF¨ mathsize=¨20px¨»§#949;«/mi»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨ mathsize=¨20px¨»-«/mo»«mfrac mathcolor=¨#0000FF¨»«mi mathvariant=¨bold¨ mathsize=¨20px¨»§#949;«/mi»«mrow»«mi mathvariant=¨bold¨ mathsize=¨20px¨»r«/mi»«mo mathvariant=¨bold¨ mathsize=¨20px¨»+«/mo»«msub»«mi mathvariant=¨bold¨ mathsize=¨20px¨»R«/mi»«mi mathvariant=¨bold¨ mathsize=¨20px¨»X«/mi»«/msub»«/mrow»«/mfrac»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨ mathsize=¨20px¨»§#183;«/mo»«mi mathvariant=¨bold¨ mathcolor=¨#0000FF¨ mathsize=¨20px¨»r«/mi»«mspace linebreak=¨newline¨/»«mspace linebreak=¨newline¨/»«/math»
نختزل القوة الكهربائية الدافعة للبطارية ونعبر عن مقاومة المقاوم المتغير RX:
«math style=¨font-family:Tahoma¨ xmlns=¨http://www.w3.org/1998/Math/MathML¨»«mfrac mathcolor=¨#0000FF¨»«menclose notation=¨downdiagonalstrike¨»«mi mathvariant=¨bold¨ mathsize=¨20px¨»§#949;«/mi»«/menclose»«mn mathvariant=¨bold¨ mathsize=¨20px¨»2«/mn»«/mfrac»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨ mathsize=¨20px¨»=«/mo»«menclose mathcolor=¨#0000FF¨ notation=¨downdiagonalstrike¨»«mi mathvariant=¨bold¨ mathsize=¨20px¨»§#949;«/mi»«/menclose»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨ mathsize=¨20px¨»-«/mo»«mfrac mathcolor=¨#0000FF¨»«menclose notation=¨downdiagonalstrike¨»«mi mathvariant=¨bold¨ mathsize=¨20px¨»§#949;«/mi»«/menclose»«mrow»«mi mathvariant=¨bold¨ mathsize=¨20px¨»r«/mi»«mo mathvariant=¨bold¨ mathsize=¨20px¨»+«/mo»«msub»«mi mathvariant=¨bold¨ mathsize=¨20px¨»R«/mi»«mi mathvariant=¨bold¨ mathsize=¨20px¨»X«/mi»«/msub»«/mrow»«/mfrac»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨ mathsize=¨20px¨»§#183;«/mo»«mi mathvariant=¨bold¨ mathcolor=¨#0000FF¨ mathsize=¨20px¨»r«/mi»«mspace linebreak=¨newline¨/»«mspace linebreak=¨newline¨/»«mfrac mathcolor=¨#0000FF¨»«mi mathvariant=¨bold¨ mathsize=¨20px¨»r«/mi»«mrow»«mi mathvariant=¨bold¨ mathsize=¨20px¨»r«/mi»«mo mathvariant=¨bold¨ mathsize=¨20px¨»+«/mo»«msub»«mi mathvariant=¨bold¨ mathsize=¨20px¨»R«/mi»«mi mathvariant=¨bold¨ mathsize=¨20px¨»X«/mi»«/msub»«/mrow»«/mfrac»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨ mathsize=¨20px¨»=«/mo»«mfrac mathcolor=¨#0000FF¨»«mn mathvariant=¨bold¨ mathsize=¨20px¨»1«/mn»«mn mathvariant=¨bold¨ mathsize=¨20px¨»2«/mn»«/mfrac»«mspace linebreak=¨newline¨/»«mspace linebreak=¨newline¨/»«mi mathvariant=¨bold¨ mathcolor=¨#0000FF¨ mathsize=¨20px¨»r«/mi»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨ mathsize=¨20px¨»+«/mo»«msub»«mi mathvariant=¨bold¨ mathcolor=¨#0000FF¨ mathsize=¨20px¨»R«/mi»«mi mathvariant=¨bold¨ mathcolor=¨#0000FF¨ mathsize=¨20px¨»X«/mi»«/msub»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨ mathsize=¨20px¨»=«/mo»«mn mathvariant=¨bold¨ mathcolor=¨#0000FF¨ mathsize=¨20px¨»2«/mn»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨ mathsize=¨20px¨»§#183;«/mo»«mi mathvariant=¨bold¨ mathcolor=¨#0000FF¨ mathsize=¨20px¨»r«/mi»«mspace linebreak=¨newline¨/»«mspace linebreak=¨newline¨/»«msub»«mi mathvariant=¨bold¨ mathcolor=¨#0000FF¨ mathsize=¨20px¨»R«/mi»«mi mathvariant=¨bold¨ mathcolor=¨#0000FF¨ mathsize=¨20px¨»X«/mi»«/msub»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨ mathsize=¨20px¨»=«/mo»«mi mathvariant=¨bold¨ mathcolor=¨#0000FF¨ mathsize=¨20px¨»r«/mi»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨ mathsize=¨20px¨»=«/mo»«mn mathvariant=¨bold¨ mathcolor=¨#0000FF¨ mathsize=¨20px¨»0«/mn»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨ mathsize=¨20px¨».«/mo»«mn mathvariant=¨bold¨ mathcolor=¨#0000FF¨ mathsize=¨20px¨»5«/mn»«mi mathvariant=¨bold-italic¨ mathcolor=¨#0000FF¨ mathsize=¨20px¨»§#937;«/mi»«mspace linebreak=¨newline¨/»«mspace linebreak=¨newline¨/»«/math»
و- شدة التيار القصوى هي 3 أمبير.
نستخدم قانون أوم لإيجاد المقاومة RX عندما يكون التيار في الدائرة 1.5 أمبير.
«math style=¨font-family:Tahoma¨ xmlns=¨http://www.w3.org/1998/Math/MathML¨»«mstyle mathsize=¨20px¨»«mi mathvariant=¨bold¨ mathcolor=¨#0000FF¨»I«/mi»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»`«/mo»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»=«/mo»«mfrac mathcolor=¨#0000FF¨»«mi mathvariant=¨bold¨»§#949;«/mi»«mrow»«msub»«mi mathvariant=¨bold¨»R«/mi»«mi mathvariant=¨bold¨»T«/mi»«/msub»«mo mathvariant=¨bold¨»`«/mo»«/mrow»«/mfrac»«mspace linebreak=¨newline¨/»«mi mathvariant=¨bold¨ mathcolor=¨#0000FF¨»I«/mi»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»`«/mo»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»=«/mo»«mfrac mathcolor=¨#0000FF¨»«mi mathvariant=¨bold¨»§#949;«/mi»«mrow»«msub»«mi mathvariant=¨bold¨»R«/mi»«mi mathvariant=¨bold¨»X«/mi»«/msub»«mo mathvariant=¨bold¨»+«/mo»«mi mathvariant=¨bold¨»r«/mi»«/mrow»«/mfrac»«mspace linebreak=¨newline¨/»«mspace linebreak=¨newline¨/»«msub»«mi mathvariant=¨bold¨ mathcolor=¨#0000FF¨»R«/mi»«mi mathvariant=¨bold¨ mathcolor=¨#0000FF¨»X«/mi»«/msub»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»+«/mo»«mi mathvariant=¨bold¨ mathcolor=¨#0000FF¨»r«/mi»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»=«/mo»«mfrac mathcolor=¨#0000FF¨»«mi mathvariant=¨bold¨»§#949;«/mi»«mrow»«mi mathvariant=¨bold¨»I«/mi»«mo mathvariant=¨bold¨»`«/mo»«/mrow»«/mfrac»«mspace linebreak=¨newline¨/»«mspace linebreak=¨newline¨/»«msub»«mi mathvariant=¨bold¨ mathcolor=¨#0000FF¨»R«/mi»«mi mathvariant=¨bold¨ mathcolor=¨#0000FF¨»X«/mi»«/msub»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»=«/mo»«mfrac mathcolor=¨#0000FF¨»«mi mathvariant=¨bold¨»§#949;«/mi»«mrow»«mi mathvariant=¨bold¨»I«/mi»«mo mathvariant=¨bold¨»`«/mo»«/mrow»«/mfrac»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»-«/mo»«mi mathvariant=¨bold¨ mathcolor=¨#0000FF¨»r«/mi»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»=«/mo»«mfrac mathcolor=¨#0000FF¨»«mrow»«mn mathvariant=¨bold¨»1«/mn»«mo mathvariant=¨bold¨».«/mo»«mn mathvariant=¨bold¨»5«/mn»«/mrow»«mrow»«mn mathvariant=¨bold¨»1«/mn»«mo mathvariant=¨bold¨».«/mo»«mn mathvariant=¨bold¨»5«/mn»«/mrow»«/mfrac»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»-«/mo»«mn mathvariant=¨bold¨ mathcolor=¨#0000FF¨»0«/mn»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨».«/mo»«mn mathvariant=¨bold¨ mathcolor=¨#0000FF¨»5«/mn»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»=«/mo»«mn mathvariant=¨bold¨ mathcolor=¨#0000FF¨»0«/mn»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨».«/mo»«mn mathvariant=¨bold¨ mathcolor=¨#0000FF¨»5«/mn»«mi mathvariant=¨bold-italic¨ mathcolor=¨#0000FF¨»§#937;«/mi»«/mstyle»«/math»
9. ב.5
أ- ميل خط الاتجاه في الرسم البياني لفرق جهد الأقطاب كدالة للتيار يساوي ناقص المقاومة الداخلية.لن تؤثر إضافة المقاوم على المقاومة الداخلية للبطارية وبالتالي لن تؤثر على ميل خط الاتجاه أيضًا..
ب- قيمة النقطة التي يقطع فيها خط الاتجاه المحور الرأسي تساوي القوة الكهربائية الدافعة للبطارية ، ولا تتغير القوة الكهربائية الدافعة للبطارية، وبالتالي لن تتغير نقطة تقاطع الدالة مع المحور الرأسي. نظرًا لأن الميل لن يتغير أيضًا ، فلن تتغير النقطة على المحور الأفقي أيضًا.
ج,د,هـ- طالما أن القوة الكهربائية الدافعة للبطارية ومقاومتها الداخلية لا يتغيران ، فلن يتغير الرسم البياني، ستتغير القيم التي قيست لكنها ستبقى جميعها على نفس خط الاتجاه.
10. ב.6
أ- نستعمل تعبير فرق جهد الأقطاب بدلالة القوة الكهربائية الدافعة: «math style=¨font-family:Tahoma¨ xmlns=¨http://www.w3.org/1998/Math/MathML¨»«mi mathvariant=¨bold¨ mathcolor=¨#0000FF¨ mathsize=¨20px¨»Vab«/mi»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨ mathsize=¨20px¨»=«/mo»«mi mathvariant=¨bold¨ mathcolor=¨#0000FF¨ mathsize=¨20px¨»§#949;«/mi»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨ mathsize=¨20px¨»-«/mo»«mi mathvariant=¨bold¨ mathcolor=¨#0000FF¨ mathsize=¨20px¨»I«/mi»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨ mathsize=¨20px¨»§#183;«/mo»«mi mathvariant=¨bold¨ mathcolor=¨#0000FF¨ mathsize=¨20px¨»r«/mi»«/math»، فرق جهد الأقطاب مساوٍ لفرق الجهد على المقاوم RX. نعبر عن فرق جهد الأقطاب باستخدام قانون أوم والتيار والمقاومة RX.
«math style=¨font-family:Tahoma¨ xmlns=¨http://www.w3.org/1998/Math/MathML¨»«mi mathvariant=¨bold¨ mathcolor=¨#0000FF¨ mathsize=¨20px¨»Vab«/mi»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨ mathsize=¨20px¨»=«/mo»«mi mathvariant=¨bold¨ mathcolor=¨#0000FF¨ mathsize=¨20px¨»§#949;«/mi»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨ mathsize=¨20px¨»-«/mo»«mi mathvariant=¨bold¨ mathcolor=¨#0000FF¨ mathsize=¨20px¨»I«/mi»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨ mathsize=¨20px¨»§#183;«/mo»«mi mathvariant=¨bold¨ mathcolor=¨#0000FF¨ mathsize=¨20px¨»r«/mi»«mspace linebreak=¨newline¨/»«mi mathvariant=¨bold¨ mathcolor=¨#0000FF¨ mathsize=¨20px¨»I«/mi»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨ mathsize=¨20px¨»§#183;«/mo»«msub»«mi mathvariant=¨bold¨ mathcolor=¨#0000FF¨ mathsize=¨20px¨»R«/mi»«mi mathvariant=¨bold¨ mathsize=¨20px¨ mathcolor=¨#0000FF¨»X«/mi»«/msub»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨ mathsize=¨20px¨»=«/mo»«mi mathvariant=¨bold¨ mathcolor=¨#0000FF¨ mathsize=¨20px¨»§#949;«/mi»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨ mathsize=¨20px¨»-«/mo»«mi mathvariant=¨bold¨ mathcolor=¨#0000FF¨ mathsize=¨20px¨»I«/mi»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨ mathsize=¨20px¨»§#183;«/mo»«mi mathvariant=¨bold¨ mathcolor=¨#0000FF¨ mathsize=¨20px¨»r«/mi»«/math»
للحصول على التعبير المطلوب نقسم المعادلة على التيار:
«math style=¨font-family:Tahoma¨ xmlns=¨http://www.w3.org/1998/Math/MathML¨»«mstyle mathsize=¨20px¨»«mfrac mathcolor=¨#0000FF¨»«mrow»«mi mathvariant=¨bold¨»I«/mi»«mo mathvariant=¨bold¨»§#183;«/mo»«msub»«mi mathvariant=¨bold¨»R«/mi»«mi mathvariant=¨bold¨»X«/mi»«/msub»«/mrow»«mi mathvariant=¨bold¨»I«/mi»«/mfrac»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»=«/mo»«mfrac mathcolor=¨#0000FF¨»«mi mathvariant=¨bold¨»§#949;«/mi»«mi mathvariant=¨bold¨»I«/mi»«/mfrac»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»-«/mo»«mfrac mathcolor=¨#0000FF¨»«mrow»«mi mathvariant=¨bold¨»I«/mi»«mo mathvariant=¨bold¨»§#183;«/mo»«mi mathvariant=¨bold¨»r«/mi»«/mrow»«mi mathvariant=¨bold¨»I«/mi»«/mfrac»«mspace linebreak=¨newline¨/»«mspace linebreak=¨newline¨/»«menclose mathcolor=¨#0000FF¨ notation=¨circle¨»«msub»«mi mathvariant=¨bold¨»R«/mi»«mi mathvariant=¨bold¨»X«/mi»«/msub»«mo mathvariant=¨bold¨»=«/mo»«mi mathvariant=¨bold¨»§#949;«/mi»«mo mathvariant=¨bold¨»§#183;«/mo»«mfrac»«mn mathvariant=¨bold¨»1«/mn»«mi mathvariant=¨bold¨»I«/mi»«/mfrac»«mo mathvariant=¨bold¨»-«/mo»«mi mathvariant=¨bold¨»r«/mi»«/menclose»«/mstyle»«/math»
ب- من التعبير الذي طوّرناه، يمكن ملاحظة أنه في الرسم البياني الذي يصف RX كدالة لـ «math style=¨font-family:Tahoma¨ xmlns=¨http://www.w3.org/1998/Math/MathML¨»«mstyle mathsize=¨20px¨»«mfrac mathcolor=¨#0000FF¨»«mn mathvariant=¨bold¨»1«/mn»«mi mathvariant=¨bold¨»I«/mi»«/mfrac»«/mstyle»«/math» قيمة ميل الرسم البياني تساوي القوة الكهربائية الدافعة للبطارية.
نحسب ميل الرسم البياني:
«math xmlns=¨http://www.w3.org/1998/Math/MathML¨»«mstyle mathsize=¨20px¨»«mi mathvariant=¨bold¨ mathcolor=¨#0000FF¨»§#1575;§#1604;§#1605;§#1610;§#1604;«/mi»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»=«/mo»«mfrac mathcolor=¨#0000FF¨»«mrow»«mn mathvariant=¨bold¨»3«/mn»«mo mathvariant=¨bold¨»-«/mo»«mn mathvariant=¨bold¨»0«/mn»«/mrow»«mrow»«mn mathvariant=¨bold¨»2«/mn»«mo mathvariant=¨bold¨»-«/mo»«mn mathvariant=¨bold¨»0«/mn»«mo mathvariant=¨bold¨».«/mo»«mn mathvariant=¨bold¨»2«/mn»«/mrow»«/mfrac»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»=«/mo»«mfrac mathcolor=¨#0000FF¨»«mn mathvariant=¨bold¨»3«/mn»«mrow»«mn mathvariant=¨bold¨»1«/mn»«mo mathvariant=¨bold¨».«/mo»«mn mathvariant=¨bold¨»8«/mn»«/mrow»«/mfrac»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»=«/mo»«mn mathvariant=¨bold¨ mathcolor=¨#0000FF¨»1«/mn»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨».«/mo»«mn mathvariant=¨bold¨ mathcolor=¨#0000FF¨»66«/mn»«mi mathvariant=¨bold¨ mathcolor=¨#0000FF¨»V«/mi»«/mstyle»«/math»
لذلك ، فإن القوة الكهربائية الدافعة للبطارية يساوي 1.66 فولط.
ج- لحساب قيمة المقاومة الداخلية نعوّض قيمة القوة الكهربائية الدافعة وقيم إحدى النقاط.
نأخذ النقطة: «math style=¨font-family:Tahoma¨ xmlns=¨http://www.w3.org/1998/Math/MathML¨»«mstyle mathsize=¨20px¨»«mfrac mathcolor=¨#0000FF¨»«mn mathvariant=¨bold¨»1«/mn»«mi mathvariant=¨bold¨»I«/mi»«/mfrac»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»=«/mo»«mn mathvariant=¨bold¨ mathcolor=¨#0000FF¨»2«/mn»«mfrac mathcolor=¨#0000FF¨»«mn mathvariant=¨bold¨»1«/mn»«mi mathvariant=¨bold¨»A«/mi»«/mfrac»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»§#160;«/mo»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»§#160;«/mo»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»§#160;«/mo»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»§#160;«/mo»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»§#160;«/mo»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»§#160;«/mo»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»§#160;«/mo»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»§#160;«/mo»«msub»«mi mathvariant=¨bold¨ mathcolor=¨#0000FF¨»R«/mi»«mi mathvariant=¨bold¨ mathcolor=¨#0000FF¨»X«/mi»«/msub»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»=«/mo»«mn mathvariant=¨bold¨ mathcolor=¨#0000FF¨»3«/mn»«mi mathvariant=¨bold¨ mathcolor=¨#0000FF¨»§#937;«/mi»«/mstyle»«/math».
نعبر عن المقاومة الداخلية من التعبير المعطى، ونحسب قيمتها:
«math style=¨font-family:Tahoma¨ xmlns=¨http://www.w3.org/1998/Math/MathML¨»«mstyle mathsize=¨20px¨»«msub»«mi mathvariant=¨bold¨ mathcolor=¨#0000FF¨»R«/mi»«mi mathvariant=¨bold¨ mathcolor=¨#0000FF¨»X«/mi»«/msub»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»=«/mo»«mi mathvariant=¨bold¨ mathcolor=¨#0000FF¨»§#949;«/mi»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»§#183;«/mo»«mfrac mathcolor=¨#0000FF¨»«mn mathvariant=¨bold¨»1«/mn»«mi mathvariant=¨bold¨»I«/mi»«/mfrac»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»-«/mo»«mi mathvariant=¨bold¨ mathcolor=¨#0000FF¨»r«/mi»«mspace linebreak=¨newline¨/»«mspace linebreak=¨newline¨/»«mi mathvariant=¨bold¨ mathcolor=¨#0000FF¨»r«/mi»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»=«/mo»«mi mathvariant=¨bold¨ mathcolor=¨#0000FF¨»§#949;«/mi»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»§#183;«/mo»«mfrac mathcolor=¨#0000FF¨»«mn mathvariant=¨bold¨»1«/mn»«mi mathvariant=¨bold¨»I«/mi»«/mfrac»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»-«/mo»«msub»«mi mathvariant=¨bold¨ mathcolor=¨#0000FF¨»R«/mi»«mi mathvariant=¨bold¨ mathcolor=¨#0000FF¨»X«/mi»«/msub»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»=«/mo»«mn mathvariant=¨bold¨ mathcolor=¨#0000FF¨»1«/mn»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨».«/mo»«mn mathvariant=¨bold¨ mathcolor=¨#0000FF¨»66«/mn»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»§#183;«/mo»«mn mathvariant=¨bold¨ mathcolor=¨#0000FF¨»2«/mn»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»-«/mo»«mn mathvariant=¨bold¨ mathcolor=¨#0000FF¨»3«/mn»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»=«/mo»«mn mathvariant=¨bold¨ mathcolor=¨#0000FF¨»0«/mn»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨».«/mo»«mn mathvariant=¨bold¨ mathcolor=¨#0000FF¨»33«/mn»«mi mathvariant=¨bold¨ mathcolor=¨#0000FF¨»§#937;«/mi»«/mstyle»«/math»
د- من التعبير المطور، يمكن ملاحظة أن في الرسم البياني الذي يصف RX كدالة لـ «math style=¨font-family:Tahoma¨ xmlns=¨http://www.w3.org/1998/Math/MathML¨»«mstyle mathsize=¨20px¨»«mfrac mathcolor=¨#0000FF¨»«mn mathvariant=¨bold¨»1«/mn»«mi mathvariant=¨bold¨»I«/mi»«/mfrac»«/mstyle»«/math» , عندما يكون «math style=¨font-family:Tahoma¨ xmlns=¨http://www.w3.org/1998/Math/MathML¨»«mstyle mathsize=¨20px¨»«mfrac mathcolor=¨#0000FF¨»«mn mathvariant=¨bold¨»1«/mn»«mi mathvariant=¨bold¨»I«/mi»«/mfrac»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»=«/mo»«mn mathvariant=¨bold¨ mathcolor=¨#0000FF¨»0«/mn»«/mstyle»«/math»يتحقق: «math style=¨font-family:Tahoma¨ xmlns=¨http://www.w3.org/1998/Math/MathML¨»«mstyle mathsize=¨20px¨»«msub»«mi mathvariant=¨bold¨ mathcolor=¨#0000FF¨»R«/mi»«mi mathvariant=¨bold¨ mathcolor=¨#0000FF¨»X«/mi»«/msub»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»=«/mo»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»-«/mo»«mi mathvariant=¨bold¨ mathcolor=¨#0000FF¨»r«/mi»«/mstyle»«/math».
بمعنى آخر، نقطة تقاطع الدالة مع المحو العمودي تساوي ناقص المقاومة الداخلية.
نمد الرسم البياني على استقامته حتى نقطة تقاطعه مع المحور العمودي
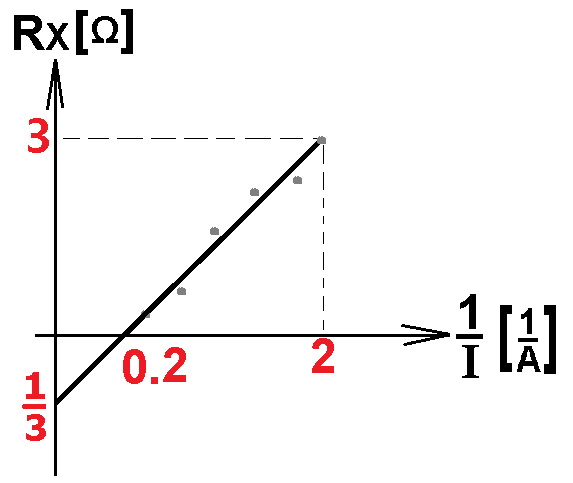
ملاحظة: يمكن ايجاد النقطة التي يتقاطع فيها خط الاتجاه مع المحور باستخدام رسم بياني كمي يحتوي بالكامل على قيم في المحاور، أو رياضيًا من معادلة الخط المستقيم.
هـ- الحد الأقصى للتيار يكون عندما تكون البطارية في حالة تماس ، «math xmlns=¨http://www.w3.org/1998/Math/MathML¨»«mstyle mathsize=¨20px¨»«msub»«mi mathvariant=¨bold¨ mathcolor=¨#0000FF¨»R«/mi»«mi mathvariant=¨bold¨ mathcolor=¨#0000FF¨»X«/mi»«/msub»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»=«/mo»«mn mathvariant=¨bold¨ mathcolor=¨#0000FF¨»0«/mn»«mi mathvariant=¨bold¨ mathcolor=¨#0000FF¨»§#937;«/mi»«/mstyle»«/math». المقاومة المحصلة للدائرة تساوي المقاومة الداخلية. نحسب شدة التيار من قانون أوم في هذه الحالة:
«math style=¨font-family:Tahoma¨ xmlns=¨http://www.w3.org/1998/Math/MathML¨»«mstyle mathsize=¨20px¨»«mi mathvariant=¨bold¨ mathcolor=¨#0000FF¨»I«/mi»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»=«/mo»«mfrac mathcolor=¨#0000FF¨»«mi mathvariant=¨bold¨»§#949;«/mi»«msub»«mi mathvariant=¨bold¨»R«/mi»«mi mathvariant=¨bold¨»T«/mi»«/msub»«/mfrac»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»=«/mo»«mfrac mathcolor=¨#0000FF¨»«mi mathvariant=¨bold¨»§#949;«/mi»«mi mathvariant=¨bold¨»r«/mi»«/mfrac»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»=«/mo»«mfrac mathcolor=¨#0000FF¨»«mrow»«mn mathvariant=¨bold¨»1«/mn»«mo mathvariant=¨bold¨».«/mo»«mn mathvariant=¨bold¨»66«/mn»«/mrow»«mrow»«mn mathvariant=¨bold¨»0«/mn»«mo mathvariant=¨bold¨».«/mo»«mn mathvariant=¨bold¨»33«/mn»«/mrow»«/mfrac»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»=«/mo»«mn mathvariant=¨bold¨ mathcolor=¨#0000FF¨»5«/mn»«mi mathvariant=¨bold¨ mathcolor=¨#0000FF¨»A«/mi»«/mstyle»«/math»
و- عندما تكون قيمة «math style=¨font-family:Tahoma¨ xmlns=¨http://www.w3.org/1998/Math/MathML¨»«mstyle mathsize=¨20px¨»«mfrac mathcolor=¨#0000FF¨»«mn mathvariant=¨bold¨»1«/mn»«mi mathvariant=¨bold¨»I«/mi»«/mfrac»«/mstyle»«/math» صغرى يكون أقصى قيمة للتيار, من الرسم البياني يمكن ملاحظة أن أصغر قيمة لـ«math style=¨font-family:Tahoma¨ xmlns=¨http://www.w3.org/1998/Math/MathML¨»«mstyle mathsize=¨20px¨»«mfrac mathcolor=¨#0000FF¨»«mn mathvariant=¨bold¨»1«/mn»«mi mathvariant=¨bold¨»I«/mi»«/mfrac»«/mstyle»«/math» هي «math xmlns=¨http://www.w3.org/1998/Math/MathML¨»«mstyle mathsize=¨20px¨»«mn mathvariant=¨bold¨ mathcolor=¨#0000FF¨»0«/mn»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨».«/mo»«mn mathvariant=¨bold¨ mathcolor=¨#0000FF¨»2«/mn»«mfrac mathcolor=¨#0000FF¨»«mn mathvariant=¨bold¨»1«/mn»«mi mathvariant=¨bold¨»A«/mi»«/mfrac»«/mstyle»«/math»
احسب القيمة القصوى للتيار :
«math style=¨font-family:Tahoma¨ xmlns=¨http://www.w3.org/1998/Math/MathML¨»«mstyle mathsize=¨20px¨»«mfrac mathcolor=¨#0000FF¨»«mn mathvariant=¨bold¨»1«/mn»«msub»«mi mathvariant=¨bold¨»I«/mi»«mi mathvariant=¨bold¨»max«/mi»«/msub»«/mfrac»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»=«/mo»«mn mathvariant=¨bold¨ mathcolor=¨#0000FF¨»0«/mn»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨».«/mo»«mn mathvariant=¨bold¨ mathcolor=¨#0000FF¨»2«/mn»«mspace linebreak=¨newline¨/»«mspace linebreak=¨newline¨/»«msub»«mi mathvariant=¨bold¨ mathcolor=¨#0000FF¨»I«/mi»«mi mathvariant=¨bold¨ mathcolor=¨#0000FF¨»max«/mi»«/msub»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»=«/mo»«mfrac mathcolor=¨#0000FF¨»«mn mathvariant=¨bold¨»1«/mn»«mrow»«mn mathvariant=¨bold¨»0«/mn»«mo mathvariant=¨bold¨».«/mo»«mn mathvariant=¨bold¨»2«/mn»«/mrow»«/mfrac»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»=«/mo»«mn mathvariant=¨bold¨ mathcolor=¨#0000FF¨»5«/mn»«mi mathvariant=¨bold¨ mathcolor=¨#0000FF¨»A«/mi»«/mstyle»«/math»
11. ג.1
أ- نحسب المقاومة المحصلة للمقاومتين الخارجيتين:
«math xmlns=¨http://www.w3.org/1998/Math/MathML¨»«mstyle mathsize=¨20px¨»«msub»«mi mathvariant=¨bold¨ mathcolor=¨#0000FF¨»R«/mi»«mi mathvariant=¨bold¨ mathcolor=¨#0000FF¨»T«/mi»«/msub»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»=«/mo»«msub»«mi mathvariant=¨bold¨ mathcolor=¨#0000FF¨»R«/mi»«mn mathvariant=¨bold¨ mathcolor=¨#0000FF¨»1«/mn»«/msub»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»+«/mo»«msub»«mi mathvariant=¨bold¨ mathcolor=¨#0000FF¨»R«/mi»«mn mathvariant=¨bold¨ mathcolor=¨#0000FF¨»2«/mn»«/msub»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»=«/mo»«mn mathvariant=¨bold¨ mathcolor=¨#0000FF¨»2«/mn»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»+«/mo»«mn mathvariant=¨bold¨ mathcolor=¨#0000FF¨»4«/mn»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»=«/mo»«mn mathvariant=¨bold¨ mathcolor=¨#0000FF¨»6«/mn»«mi mathvariant=¨bold¨ mathcolor=¨#0000FF¨»§#937;«/mi»«/mstyle»«/math»
ب - نحسب شدة التيار في الدائرة حسب قانون أوم للدائرة بأكملها:
«math style=¨font-family:Tahoma¨ xmlns=¨http://www.w3.org/1998/Math/MathML¨»«mstyle mathsize=¨20px¨»«mi mathvariant=¨bold¨ mathcolor=¨#0000FF¨»I«/mi»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»=«/mo»«mfrac mathcolor=¨#0000FF¨»«mi mathvariant=¨bold¨»§#949;«/mi»«msub»«mi mathvariant=¨bold¨»R«/mi»«mi mathvariant=¨bold¨»T«/mi»«/msub»«/mfrac»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»=«/mo»«mfrac mathcolor=¨#0000FF¨»«mn mathvariant=¨bold¨»12«/mn»«mn mathvariant=¨bold¨»6«/mn»«/mfrac»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»=«/mo»«mn mathvariant=¨bold¨ mathcolor=¨#0000FF¨»2«/mn»«mi mathvariant=¨bold¨ mathcolor=¨#0000FF¨»A«/mi»«/mstyle»«/math»
ج- نستخدم قانون أوم لحساب فرق الجهد على كل مقاوم:
«math style=¨font-family:Tahoma¨ xmlns=¨http://www.w3.org/1998/Math/MathML¨»«mstyle mathsize=¨20px¨»«msub»«mi mathvariant=¨bold¨ mathcolor=¨#0000FF¨»U«/mi»«msub mathcolor=¨#0000FF¨»«mi mathvariant=¨bold¨»R«/mi»«mn mathvariant=¨bold¨»1«/mn»«/msub»«/msub»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»=«/mo»«mi mathvariant=¨bold¨ mathcolor=¨#0000FF¨»I«/mi»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»§#183;«/mo»«msub»«mi mathvariant=¨bold¨ mathcolor=¨#0000FF¨»R«/mi»«mn mathvariant=¨bold¨ mathcolor=¨#0000FF¨»1«/mn»«/msub»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»=«/mo»«mn mathvariant=¨bold¨ mathcolor=¨#0000FF¨»2«/mn»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»§#183;«/mo»«mn mathvariant=¨bold¨ mathcolor=¨#0000FF¨»2«/mn»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»=«/mo»«mn mathvariant=¨bold¨ mathcolor=¨#0000FF¨»4«/mn»«mi mathvariant=¨bold¨ mathcolor=¨#0000FF¨»V«/mi»«mspace linebreak=¨newline¨/»«msub»«mi mathvariant=¨bold¨ mathcolor=¨#0000FF¨»U«/mi»«msub mathcolor=¨#0000FF¨»«mi mathvariant=¨bold¨»R«/mi»«mn mathvariant=¨bold¨»2«/mn»«/msub»«/msub»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»=«/mo»«mi mathvariant=¨bold¨ mathcolor=¨#0000FF¨»I«/mi»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»§#183;«/mo»«msub»«mi mathvariant=¨bold¨ mathcolor=¨#0000FF¨»R«/mi»«mn mathvariant=¨bold¨ mathcolor=¨#0000FF¨»2«/mn»«/msub»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»=«/mo»«mn mathvariant=¨bold¨ mathcolor=¨#0000FF¨»2«/mn»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»§#183;«/mo»«mn mathvariant=¨bold¨ mathcolor=¨#0000FF¨»4«/mn»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»=«/mo»«mn mathvariant=¨bold¨ mathcolor=¨#0000FF¨»8«/mn»«mi mathvariant=¨bold¨ mathcolor=¨#0000FF¨»V«/mi»«/mstyle»«/math»
د.1- نتيجة لزيادة مقاومة R2، ستزداد المقاومة المحصلة، حسب قانون أوم سيقل التيار في الدائرة. لذلك سيقل فرق الجهد على R1 أيضًا.
د.2- حسب تعبير فرق جهد الأقطاب: «math style=¨font-family:Tahoma¨ xmlns=¨http://www.w3.org/1998/Math/MathML¨»«mi mathvariant=¨bold¨ mathcolor=¨#0000FF¨ mathsize=¨20px¨»Vab«/mi»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨ mathsize=¨20px¨»=«/mo»«mi mathvariant=¨bold¨ mathcolor=¨#0000FF¨ mathsize=¨20px¨»§#949;«/mi»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨ mathsize=¨20px¨»-«/mo»«mi mathvariant=¨bold¨ mathcolor=¨#0000FF¨ mathsize=¨20px¨»I«/mi»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨ mathsize=¨20px¨»§#183;«/mo»«mi mathvariant=¨bold¨ mathcolor=¨#0000FF¨ mathsize=¨20px¨»r«/mi»«/math»، نظرًا لأن البطارية مثالية ، فلن يتغير فرق جهد الأقطاب.
12. ג.2
أ- نحسب المقاومة المحصلة للمقاومين الموصولين على التوازي:
«math style=¨font-family:Tahoma¨ xmlns=¨http://www.w3.org/1998/Math/MathML¨»«mstyle mathsize=¨20px¨»«msub»«mi mathvariant=¨bold¨ mathcolor=¨#0000FF¨»R«/mi»«mi mathvariant=¨bold¨ mathcolor=¨#0000FF¨»T«/mi»«/msub»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»=«/mo»«mfrac mathcolor=¨#0000FF¨»«mrow»«msub»«mi mathvariant=¨bold¨»R«/mi»«mn mathvariant=¨bold¨»1«/mn»«/msub»«mo mathvariant=¨bold¨»§#183;«/mo»«msub»«mi mathvariant=¨bold¨»R«/mi»«mn mathvariant=¨bold¨»2«/mn»«/msub»«/mrow»«mrow»«msub»«mi mathvariant=¨bold¨»R«/mi»«mn mathvariant=¨bold¨»1«/mn»«/msub»«mo mathvariant=¨bold¨»+«/mo»«msub»«mi mathvariant=¨bold¨»R«/mi»«mn mathvariant=¨bold¨»2«/mn»«/msub»«/mrow»«/mfrac»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»=«/mo»«mfrac mathcolor=¨#0000FF¨»«mrow»«mn mathvariant=¨bold¨»2«/mn»«mo mathvariant=¨bold¨»§#183;«/mo»«mn mathvariant=¨bold¨»4«/mn»«/mrow»«mrow»«mn mathvariant=¨bold¨»2«/mn»«mo mathvariant=¨bold¨»+«/mo»«mn mathvariant=¨bold¨»4«/mn»«/mrow»«/mfrac»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»=«/mo»«mfrac mathcolor=¨#0000FF¨»«mn mathvariant=¨bold¨»8«/mn»«mn mathvariant=¨bold¨»6«/mn»«/mfrac»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»=«/mo»«mn mathvariant=¨bold¨ mathcolor=¨#0000FF¨»1«/mn»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨».«/mo»«mn mathvariant=¨bold¨ mathcolor=¨#0000FF¨»33«/mn»«mi mathvariant=¨bold¨ mathcolor=¨#0000FF¨»§#937;«/mi»«/mstyle»«/math»
ب- نحسب شدة التيار في الدائرة من قانون أوم على الدائرة بأكملها: «math style=¨font-family:Tahoma¨ xmlns=¨http://www.w3.org/1998/Math/MathML¨»«mstyle mathsize=¨20px¨»«mi mathvariant=¨bold¨ mathcolor=¨#0000FF¨»I«/mi»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»=«/mo»«mfrac mathcolor=¨#0000FF¨»«mi mathvariant=¨bold¨»§#949;«/mi»«msub»«mi mathvariant=¨bold¨»R«/mi»«mi mathvariant=¨bold¨»T«/mi»«/msub»«/mfrac»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»=«/mo»«mfrac mathcolor=¨#0000FF¨»«mn mathvariant=¨bold¨»12«/mn»«mrow»«mn mathvariant=¨bold¨»1«/mn»«mo mathvariant=¨bold¨».«/mo»«mn mathvariant=¨bold¨»33«/mn»«/mrow»«/mfrac»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»=«/mo»«mn mathvariant=¨bold¨ mathcolor=¨#0000FF¨»9«/mn»«mi mathvariant=¨bold¨ mathcolor=¨#0000FF¨»A«/mi»«/mstyle»«/math»
ج- المقاومان موصولان على التوازي مباشرة مع أقطاب البطارية، وبالتالي فإن فرق الجهد على المقاومين يساوي فرق جهد الأقطاب للبطارية.
«math xmlns=¨http://www.w3.org/1998/Math/MathML¨»«mstyle mathsize=¨20px¨»«msub»«mi mathvariant=¨bold¨ mathcolor=¨#0000FF¨»U«/mi»«msub mathcolor=¨#0000FF¨»«mi mathvariant=¨bold¨»R«/mi»«mn mathvariant=¨bold¨»1«/mn»«/msub»«/msub»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»=«/mo»«msub»«mi mathvariant=¨bold¨ mathcolor=¨#0000FF¨»U«/mi»«msub mathcolor=¨#0000FF¨»«mi mathvariant=¨bold¨»R«/mi»«mn mathvariant=¨bold¨»2«/mn»«/msub»«/msub»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»=«/mo»«mn mathvariant=¨bold¨ mathcolor=¨#0000FF¨»12«/mn»«mi mathvariant=¨bold¨ mathcolor=¨#0000FF¨»V«/mi»«/mstyle»«/math»
طريقة أخرى: يمكن حساب فرق الجهد على كل مقاوم باستخدام قانون أوم، اعتمادًا على مقاومة المقاوم والتيار المار من خلاله.
نشير إلى التيار من خلال المقاوم R1 بواسطة I1 والتيار عبر المقاوم R2 بواسطة I2. ونضف التيارات إلى الدائرة كما هو مبين في الشكل التالي:
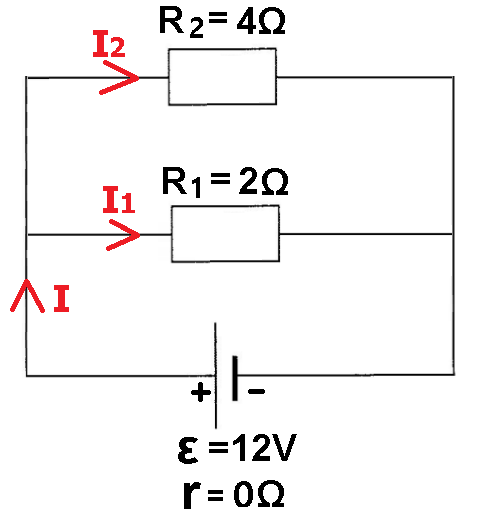
مقاومة R1 أصغر بمرتين من مقاومة R2، وبالتالي فإن شدة التيار خلال R1 ستكون أكبر بمرتين من شدة التيار عبر R2.
تيار المصدر 9 أمبير. لذلك ، سوف يتدفق تيار 6 أمبير عبر R1 ويتدفق تيار 3 أمبير عبر R2.
احسب فرق الجهد عبر كل مقاوم باستخدام قانون أوم:
«math style=¨font-family:Tahoma¨ xmlns=¨http://www.w3.org/1998/Math/MathML¨»«mstyle mathsize=¨20px¨»«msub»«mi mathvariant=¨bold¨ mathcolor=¨#0000FF¨»U«/mi»«msub mathcolor=¨#0000FF¨»«mi mathvariant=¨bold¨»R«/mi»«mn mathvariant=¨bold¨»1«/mn»«/msub»«/msub»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»=«/mo»«msub»«mi mathvariant=¨bold¨ mathcolor=¨#0000FF¨»I«/mi»«mn mathvariant=¨bold¨ mathcolor=¨#0000FF¨»1«/mn»«/msub»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»§#183;«/mo»«msub»«mi mathvariant=¨bold¨ mathcolor=¨#0000FF¨»R«/mi»«mn mathvariant=¨bold¨ mathcolor=¨#0000FF¨»1«/mn»«/msub»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»=«/mo»«mn mathvariant=¨bold¨ mathcolor=¨#0000FF¨»6«/mn»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»§#183;«/mo»«mn mathvariant=¨bold¨ mathcolor=¨#0000FF¨»2«/mn»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»=«/mo»«mn mathvariant=¨bold¨ mathcolor=¨#0000FF¨»12«/mn»«mi mathvariant=¨bold¨ mathcolor=¨#0000FF¨»V«/mi»«mspace linebreak=¨newline¨/»«msub»«mi mathvariant=¨bold¨ mathcolor=¨#0000FF¨»U«/mi»«msub mathcolor=¨#0000FF¨»«mi mathvariant=¨bold¨»R«/mi»«mn mathvariant=¨bold¨»2«/mn»«/msub»«/msub»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»=«/mo»«msub»«mi mathvariant=¨bold¨ mathcolor=¨#0000FF¨»I«/mi»«mn mathvariant=¨bold¨ mathcolor=¨#0000FF¨»2«/mn»«/msub»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»§#183;«/mo»«msub»«mi mathvariant=¨bold¨ mathcolor=¨#0000FF¨»R«/mi»«mn mathvariant=¨bold¨ mathcolor=¨#0000FF¨»2«/mn»«/msub»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»=«/mo»«mn mathvariant=¨bold¨ mathcolor=¨#0000FF¨»3«/mn»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»§#183;«/mo»«mn mathvariant=¨bold¨ mathcolor=¨#0000FF¨»4«/mn»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»=«/mo»«mn mathvariant=¨bold¨ mathcolor=¨#0000FF¨»12«/mn»«mi mathvariant=¨bold¨ mathcolor=¨#0000FF¨»V«/mi»«/mstyle»«/math»
د- لن يتغير فرق الجهد على R1. يتم توصيل المقاوم R1 مباشرة بأطراف البطارية وبالتالي فإن فرق الجهد على R1 يساوي فرق جهد أقطاب البطارية.
في الدائرة على التوازي، يتم توصيل المقاومتين بقطبي البطارية، وبالتالي فإن فرق الجهد عليهما هو نفس فرق جهد الأقطاب بغض النظر عن مقاومة المقاومات الأخرى.
(هذا هو السبب في أن جميع الأجهزة الكهربائية في المنزل موصولة على التوازي، بحيث أن على كل مستهلك فرق جهد مساوٍ لفرق جهد المصدر دون أن يتعلق على المستهلكين الآخرين).
13. ג.3
أ- يتم توصيل المقاومتين الخارجيتين والمقاومة الداخلية على التوالي.
نحسب المقاومة المحصلة للدائرة، حسب المقاومة المحصلة للمقاومات الموصولة على التوالي:
«math xmlns=¨http://www.w3.org/1998/Math/MathML¨»«mstyle mathsize=¨24px¨»«msub»«mi mathvariant=¨bold¨ mathcolor=¨#0000FF¨»R«/mi»«mi mathvariant=¨bold¨ mathcolor=¨#0000FF¨»T«/mi»«/msub»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»=«/mo»«msub»«mi mathvariant=¨bold¨ mathcolor=¨#0000FF¨»R«/mi»«mn mathvariant=¨bold¨ mathcolor=¨#0000FF¨»1«/mn»«/msub»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»+«/mo»«msub»«mi mathvariant=¨bold¨ mathcolor=¨#0000FF¨»R«/mi»«mn mathvariant=¨bold¨ mathcolor=¨#0000FF¨»2«/mn»«/msub»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»+«/mo»«mi mathvariant=¨bold¨ mathcolor=¨#0000FF¨»r«/mi»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»=«/mo»«mn mathvariant=¨bold¨ mathcolor=¨#0000FF¨»2«/mn»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»+«/mo»«mn mathvariant=¨bold¨ mathcolor=¨#0000FF¨»4«/mn»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»+«/mo»«mn mathvariant=¨bold¨ mathcolor=¨#0000FF¨»1«/mn»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»=«/mo»«mn mathvariant=¨bold¨ mathcolor=¨#0000FF¨»7«/mn»«mi mathvariant=¨bold¨ mathcolor=¨#0000FF¨»§#937;«/mi»«/mstyle»«/math»
ب- نحسب شدة التيار في الدائرة، من قانون أوم على الدائرة بأكملها:
«math style=¨font-family:Tahoma¨ xmlns=¨http://www.w3.org/1998/Math/MathML¨»«mstyle mathsize=¨20px¨»«mi mathvariant=¨bold¨ mathcolor=¨#0000FF¨»I«/mi»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»=«/mo»«mfrac mathcolor=¨#0000FF¨»«mi mathvariant=¨bold¨»§#949;«/mi»«msub»«mi mathvariant=¨bold¨»R«/mi»«mi mathvariant=¨bold¨»T«/mi»«/msub»«/mfrac»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»=«/mo»«mfrac mathcolor=¨#0000FF¨»«mn mathvariant=¨bold¨»12«/mn»«mn mathvariant=¨bold¨»7«/mn»«/mfrac»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»=«/mo»«mn mathvariant=¨bold¨ mathcolor=¨#0000FF¨»1«/mn»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨».«/mo»«mn mathvariant=¨bold¨ mathcolor=¨#0000FF¨»71«/mn»«mi mathvariant=¨bold¨ mathcolor=¨#0000FF¨»A«/mi»«/mstyle»«/math»
ج- نحسب فرق الجهد على كل مقاوم باستخدام قانون أوم:
«math style=¨font-family:Tahoma¨ xmlns=¨http://www.w3.org/1998/Math/MathML¨»«mstyle mathsize=¨20px¨»«msub»«mi mathvariant=¨bold¨ mathcolor=¨#0000FF¨»U«/mi»«msub mathcolor=¨#0000FF¨»«mi mathvariant=¨bold¨»R«/mi»«mn mathvariant=¨bold¨»1«/mn»«/msub»«/msub»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»=«/mo»«mi mathvariant=¨bold¨ mathcolor=¨#0000FF¨»I«/mi»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»§#183;«/mo»«msub»«mi mathvariant=¨bold¨ mathcolor=¨#0000FF¨»R«/mi»«mn mathvariant=¨bold¨ mathcolor=¨#0000FF¨»1«/mn»«/msub»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»=«/mo»«mn mathvariant=¨bold¨ mathcolor=¨#0000FF¨»1«/mn»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨».«/mo»«mn mathvariant=¨bold¨ mathcolor=¨#0000FF¨»71«/mn»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»§#183;«/mo»«mn mathvariant=¨bold¨ mathcolor=¨#0000FF¨»2«/mn»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»=«/mo»«mn mathvariant=¨bold¨ mathcolor=¨#0000FF¨»3«/mn»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨».«/mo»«mn mathvariant=¨bold¨ mathcolor=¨#0000FF¨»42«/mn»«mi mathvariant=¨bold¨ mathcolor=¨#0000FF¨»V«/mi»«mspace linebreak=¨newline¨/»«msub»«mi mathvariant=¨bold¨ mathcolor=¨#0000FF¨»U«/mi»«msub mathcolor=¨#0000FF¨»«mi mathvariant=¨bold¨»R«/mi»«mn mathvariant=¨bold¨»2«/mn»«/msub»«/msub»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»=«/mo»«mi mathvariant=¨bold¨ mathcolor=¨#0000FF¨»I«/mi»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»§#183;«/mo»«msub»«mi mathvariant=¨bold¨ mathcolor=¨#0000FF¨»R«/mi»«mn mathvariant=¨bold¨ mathcolor=¨#0000FF¨»2«/mn»«/msub»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»=«/mo»«mn mathvariant=¨bold¨ mathcolor=¨#0000FF¨»1«/mn»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨».«/mo»«mn mathvariant=¨bold¨ mathcolor=¨#0000FF¨»71«/mn»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»§#183;«/mo»«mn mathvariant=¨bold¨ mathcolor=¨#0000FF¨»4«/mn»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»=«/mo»«mn mathvariant=¨bold¨ mathcolor=¨#0000FF¨»6«/mn»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨».«/mo»«mn mathvariant=¨bold¨ mathcolor=¨#0000FF¨»85«/mn»«mi mathvariant=¨bold¨ mathcolor=¨#0000FF¨»V«/mi»«/mstyle»«/math»
د- نتيجة لزيادة مقاومة المقاوم R2 ، ستزداد المقاومة المحصلة ويقل التيار في الدائرة. من قانون أوم على المقاوم R1 سينخفض فرق الجهد على R1.
هـ- نظرًا لأن البطارية ليست مثالية، لها مقاومة داخلية. من تعبير فرق جهد الأقطاب: «math style=¨font-family:Tahoma¨ xmlns=¨http://www.w3.org/1998/Math/MathML¨»«mi mathvariant=¨bold¨ mathcolor=¨#0000FF¨ mathsize=¨20px¨»Vab«/mi»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨ mathsize=¨20px¨»=«/mo»«mi mathvariant=¨bold¨ mathcolor=¨#0000FF¨ mathsize=¨20px¨»§#949;«/mi»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨ mathsize=¨20px¨»-«/mo»«mi mathvariant=¨bold¨ mathcolor=¨#0000FF¨ mathsize=¨20px¨»I«/mi»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨ mathsize=¨20px¨»§#183;«/mo»«mi mathvariant=¨bold¨ mathcolor=¨#0000FF¨ mathsize=¨20px¨»r«/mi»«/math» عندما يقل التيار يزداد فرق جهد الأقطاب.
14. ג.4
أ- المقاومتان الخارجيتان والمقاومة الداخلية موصولة على التوالي وعلى التوازي، نحسب المقاومة المحصلة للدائرة:
«math xmlns=¨http://www.w3.org/1998/Math/MathML¨»«mstyle mathsize=¨20px¨»«msub»«mi mathvariant=¨bold¨ mathcolor=¨#0000FF¨»R«/mi»«mi mathvariant=¨bold¨ mathcolor=¨#0000FF¨»T«/mi»«/msub»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»=«/mo»«mstyle mathvariant=¨bold¨ mathcolor=¨#0000FF¨»«mo stretchy=¨true¨»(«/mo»«mrow»«msub»«mi»R«/mi»«mn»1«/mn»«/msub»«mo»|«/mo»«mo»|«/mo»«msub»«mi»R«/mi»«mn»2«/mn»«/msub»«/mrow»«mo stretchy=¨true¨»)«/mo»«/mstyle»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»+«/mo»«mi mathvariant=¨bold¨ mathcolor=¨#0000FF¨»r«/mi»«mspace linebreak=¨newline¨/»«msub»«mi mathvariant=¨bold¨ mathcolor=¨#0000FF¨»R«/mi»«mi mathvariant=¨bold¨ mathcolor=¨#0000FF¨»T«/mi»«/msub»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»=«/mo»«mfrac mathcolor=¨#0000FF¨»«mrow»«msub»«mi mathvariant=¨bold¨»R«/mi»«mn mathvariant=¨bold¨»1«/mn»«/msub»«mo mathvariant=¨bold¨»§#183;«/mo»«msub»«mi mathvariant=¨bold¨»R«/mi»«mn mathvariant=¨bold¨»2«/mn»«/msub»«/mrow»«mrow»«msub»«mi mathvariant=¨bold¨»R«/mi»«mn mathvariant=¨bold¨»1«/mn»«/msub»«mo mathvariant=¨bold¨»+«/mo»«msub»«mi mathvariant=¨bold¨»R«/mi»«mn mathvariant=¨bold¨»2«/mn»«/msub»«/mrow»«/mfrac»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»+«/mo»«mi mathvariant=¨bold¨ mathcolor=¨#0000FF¨»r«/mi»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»=«/mo»«mfrac mathcolor=¨#0000FF¨»«mrow»«mn mathvariant=¨bold¨»2«/mn»«mo mathvariant=¨bold¨»§#183;«/mo»«mn mathvariant=¨bold¨»4«/mn»«/mrow»«mrow»«mn mathvariant=¨bold¨»2«/mn»«mo mathvariant=¨bold¨»+«/mo»«mn mathvariant=¨bold¨»4«/mn»«/mrow»«/mfrac»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»+«/mo»«mn mathvariant=¨bold¨ mathcolor=¨#0000FF¨»1«/mn»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»=«/mo»«mn mathvariant=¨bold¨ mathcolor=¨#0000FF¨»2«/mn»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨».«/mo»«mn mathvariant=¨bold¨ mathcolor=¨#0000FF¨»33«/mn»«mi mathvariant=¨bold¨ mathcolor=¨#0000FF¨»§#937;«/mi»«/mstyle»«/math»
ب- نحسب شدة التيار في الدائرة من قانون أوم على الدائرة بأكملها:
«math style=¨font-family:Tahoma¨ xmlns=¨http://www.w3.org/1998/Math/MathML¨»«mstyle mathsize=¨20px¨»«mi mathvariant=¨bold¨ mathcolor=¨#0000FF¨»I«/mi»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»=«/mo»«mfrac mathcolor=¨#0000FF¨»«mi mathvariant=¨bold¨»§#949;«/mi»«msub»«mi mathvariant=¨bold¨»R«/mi»«mi mathvariant=¨bold¨»T«/mi»«/msub»«/mfrac»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»=«/mo»«mfrac mathcolor=¨#0000FF¨»«mn mathvariant=¨bold¨»12«/mn»«mrow»«mn mathvariant=¨bold¨»2«/mn»«mo mathvariant=¨bold¨».«/mo»«mn mathvariant=¨bold¨»33«/mn»«/mrow»«/mfrac»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»=«/mo»«mn mathvariant=¨bold¨ mathcolor=¨#0000FF¨»5«/mn»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨».«/mo»«mn mathvariant=¨bold¨ mathcolor=¨#0000FF¨»14«/mn»«mi mathvariant=¨bold¨ mathcolor=¨#0000FF¨»A«/mi»«/mstyle»«/math»
ג- المقاومتان موصولتان ببعضهما البعض على التوازي، وفرق الجهد عليهما هو نفسه ويساوي فرق جهد أقطاب مصدر فرق الجهد.
نحسب فرق جهد الأقطاب:
«math style=¨font-family:Tahoma¨ xmlns=¨http://www.w3.org/1998/Math/MathML¨»«mi mathvariant=¨bold¨ mathcolor=¨#0000FF¨ mathsize=¨20px¨»Vab«/mi»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨ mathsize=¨20px¨»=«/mo»«mi mathvariant=¨bold¨ mathcolor=¨#0000FF¨ mathsize=¨20px¨»§#949;«/mi»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨ mathsize=¨20px¨»-«/mo»«mi mathvariant=¨bold¨ mathcolor=¨#0000FF¨ mathsize=¨20px¨»I«/mi»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨ mathsize=¨20px¨»§#183;«/mo»«mi mathvariant=¨bold¨ mathcolor=¨#0000FF¨ mathsize=¨20px¨»r«/mi»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨ mathsize=¨20px¨»=«/mo»«mn mathvariant=¨bold¨ mathcolor=¨#0000FF¨ mathsize=¨20px¨»12«/mn»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨ mathsize=¨20px¨»-«/mo»«mn mathvariant=¨bold¨ mathcolor=¨#0000FF¨ mathsize=¨20px¨»5«/mn»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨ mathsize=¨20px¨».«/mo»«mn mathvariant=¨bold¨ mathcolor=¨#0000FF¨ mathsize=¨20px¨»14«/mn»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨ mathsize=¨20px¨»§#183;«/mo»«mn mathvariant=¨bold¨ mathcolor=¨#0000FF¨ mathsize=¨20px¨»1«/mn»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨ mathsize=¨20px¨»=«/mo»«mn mathvariant=¨bold¨ mathcolor=¨#0000FF¨ mathsize=¨20px¨»6«/mn»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨ mathsize=¨20px¨».«/mo»«mn mathvariant=¨bold¨ mathcolor=¨#0000FF¨ mathsize=¨20px¨»86«/mn»«mi mathvariant=¨bold¨ mathcolor=¨#0000FF¨ mathsize=¨20px¨»V«/mi»«/math»
لذلك: «math style=¨font-family:Tahoma¨ xmlns=¨http://www.w3.org/1998/Math/MathML¨»«mstyle mathsize=¨20px¨»«msub»«mi mathvariant=¨bold¨ mathcolor=¨#0000FF¨»U«/mi»«msub mathcolor=¨#0000FF¨»«mi mathvariant=¨bold¨»R«/mi»«mn mathvariant=¨bold¨»1«/mn»«/msub»«/msub»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»=«/mo»«msub»«mi mathvariant=¨bold¨ mathcolor=¨#0000FF¨»U«/mi»«msub mathcolor=¨#0000FF¨»«mi mathvariant=¨bold¨»R«/mi»«mn mathvariant=¨bold¨»2«/mn»«/msub»«/msub»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»=«/mo»«mn mathvariant=¨bold¨ mathcolor=¨#0000FF¨»6«/mn»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨».«/mo»«mn mathvariant=¨bold¨ mathcolor=¨#0000FF¨»86«/mn»«mi mathvariant=¨bold¨ mathcolor=¨#0000FF¨»V«/mi»«/mstyle»«/math»
طريقة أخرى: يمكن حساب فرق الجهد على كل مقاوم باستخدام قانون أوم، اعتمادًا على مقاومة المقاوم والتيار المار من خلاله.
نشير إلى التيار بالمقاوم R1 بواسطة I1 والتيار عبر المقاوم R2 بواسطة I2. ونضف التيارات إلى الدائرة كما مبين في الشكل التالي:
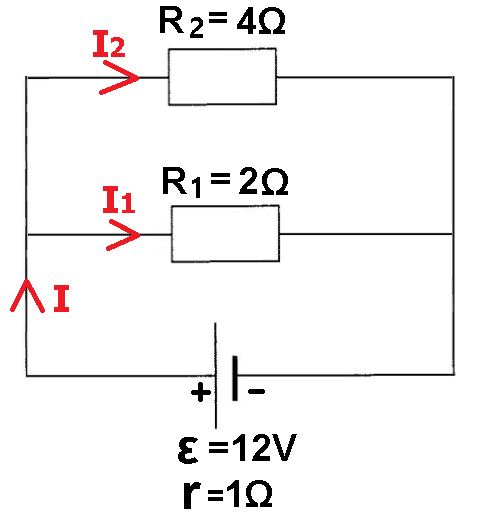
مقاومة R1 أصغر بمرتين من مقاومة R2، وبالتالي فإن شدة التيار خلال R1 ستكون أكبر بمرتين من شدة التيار عبر R2.
تيار المصدر 5.14 أمبير. لذلك ، سوف يتدفق تيار مقداره 3.41 أمبير عبر R1 وتيارمقداره 1.71 أمبير سيتدفق عبر R2.
نحسب فرق الجهد عبر كل مقاوم باستخدام قانون أوم:
«math style=¨font-family:Tahoma¨ xmlns=¨http://www.w3.org/1998/Math/MathML¨»«mstyle mathsize=¨20px¨»«msub»«mi mathvariant=¨bold¨ mathcolor=¨#0000FF¨»U«/mi»«msub mathcolor=¨#0000FF¨»«mi mathvariant=¨bold¨»R«/mi»«mn mathvariant=¨bold¨»1«/mn»«/msub»«/msub»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»=«/mo»«msub»«mi mathvariant=¨bold¨ mathcolor=¨#0000FF¨»I«/mi»«mn mathvariant=¨bold¨ mathcolor=¨#0000FF¨»1«/mn»«/msub»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»§#183;«/mo»«msub»«mi mathvariant=¨bold¨ mathcolor=¨#0000FF¨»R«/mi»«mn mathvariant=¨bold¨ mathcolor=¨#0000FF¨»1«/mn»«/msub»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»=«/mo»«mn mathvariant=¨bold¨ mathcolor=¨#0000FF¨»3«/mn»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨».«/mo»«mn mathvariant=¨bold¨ mathcolor=¨#0000FF¨»4«/mn»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»§#183;«/mo»«mn mathvariant=¨bold¨ mathcolor=¨#0000FF¨»2«/mn»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»=«/mo»«mn mathvariant=¨bold¨ mathcolor=¨#0000FF¨»6«/mn»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨».«/mo»«mn mathvariant=¨bold¨ mathcolor=¨#0000FF¨»8«/mn»«mi mathvariant=¨bold¨ mathcolor=¨#0000FF¨»V«/mi»«mspace linebreak=¨newline¨/»«msub»«mi mathvariant=¨bold¨ mathcolor=¨#0000FF¨»U«/mi»«msub mathcolor=¨#0000FF¨»«mi mathvariant=¨bold¨»R«/mi»«mn mathvariant=¨bold¨»2«/mn»«/msub»«/msub»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»=«/mo»«msub»«mi mathvariant=¨bold¨ mathcolor=¨#0000FF¨»I«/mi»«mn mathvariant=¨bold¨ mathcolor=¨#0000FF¨»2«/mn»«/msub»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»§#183;«/mo»«msub»«mi mathvariant=¨bold¨ mathcolor=¨#0000FF¨»R«/mi»«mn mathvariant=¨bold¨ mathcolor=¨#0000FF¨»2«/mn»«/msub»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»=«/mo»«mn mathvariant=¨bold¨ mathcolor=¨#0000FF¨»1«/mn»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨».«/mo»«mn mathvariant=¨bold¨ mathcolor=¨#0000FF¨»7«/mn»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»§#183;«/mo»«mn mathvariant=¨bold¨ mathcolor=¨#0000FF¨»4«/mn»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»=«/mo»«mn mathvariant=¨bold¨ mathcolor=¨#0000FF¨»6«/mn»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨».«/mo»«mn mathvariant=¨bold¨ mathcolor=¨#0000FF¨»8«/mn»«mi mathvariant=¨bold¨ mathcolor=¨#0000FF¨»V«/mi»«/mstyle»«/math»
د.1- ستؤدي زيادة مقاومة R2 إلى زيادة المقاومة المحصلة، من قانون أوم في الدائرة بأكملها سيقل تيار المصدر.
من تعبير فرق جهد الأقطاب: «math style=¨font-family:Tahoma¨ xmlns=¨http://www.w3.org/1998/Math/MathML¨»«mi mathvariant=¨bold¨ mathcolor=¨#0000FF¨ mathsize=¨20px¨»Vab«/mi»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨ mathsize=¨20px¨»=«/mo»«mi mathvariant=¨bold¨ mathcolor=¨#0000FF¨ mathsize=¨20px¨»§#949;«/mi»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨ mathsize=¨20px¨»-«/mo»«mi mathvariant=¨bold¨ mathcolor=¨#0000FF¨ mathsize=¨20px¨»I«/mi»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨ mathsize=¨20px¨»§#183;«/mo»«mi mathvariant=¨bold¨ mathcolor=¨#0000FF¨ mathsize=¨20px¨»r«/mi»«/math» يمكن تحديد أنه عندما يقل التيار، يزداد فرق جهد الأقطاب.
د.2- المقاومان R1 و R2 موصولان على التوازي, فرق الجهد على كل منهما متساوٍ ويساوي لفرق جهد الأقطاب للمصدر.
مع زيادة فرق جهد الأقطاب، سيزداد فرق الجهد على R1 أيضًا.
15. ג.5
أ- لإيجاد مقاومة RX بحيث يكون فرق الجهد الكهربائي على المصباح 3 فولط، نفترض أن المصباح يضيئ بضوء كامل وفرق الجهد عليه هو 3 فولط.
سنجد التيار في الدائرة في هذه الحالة بواسطة قانون أوم على المصباح:
«math style=¨font-family:Tahoma¨ xmlns=¨http://www.w3.org/1998/Math/MathML¨»«mstyle mathsize=¨20px¨»«mi mathvariant=¨bold¨ mathcolor=¨#0000FF¨»I«/mi»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»=«/mo»«mfrac mathcolor=¨#0000FF¨»«msub»«mi mathvariant=¨bold¨»U«/mi»«mi mathvariant=¨bold¨»RL«/mi»«/msub»«mi mathvariant=¨bold¨»RL«/mi»«/mfrac»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»=«/mo»«mfrac mathcolor=¨#0000FF¨»«mn mathvariant=¨bold¨»3«/mn»«mn mathvariant=¨bold¨»10«/mn»«/mfrac»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»=«/mo»«mn mathvariant=¨bold¨ mathcolor=¨#0000FF¨»0«/mn»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨».«/mo»«mn mathvariant=¨bold¨ mathcolor=¨#0000FF¨»3«/mn»«mi mathvariant=¨bold¨ mathcolor=¨#0000FF¨»A«/mi»«/mstyle»«/math»
نجد المقاومة المحصلة للدائرة من قانون أوم للدائرة بأكملها:
«math style=¨font-family:Tahoma¨ xmlns=¨http://www.w3.org/1998/Math/MathML¨»«mstyle mathsize=¨20px¨»«mi mathvariant=¨bold¨ mathcolor=¨#0000FF¨»I«/mi»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»=«/mo»«mfrac mathcolor=¨#0000FF¨»«mi mathvariant=¨bold¨»§#949;«/mi»«msub»«mi mathvariant=¨bold¨»R«/mi»«mi mathvariant=¨bold¨»T«/mi»«/msub»«/mfrac»«mspace linebreak=¨newline¨/»«msub»«mi mathvariant=¨bold¨ mathcolor=¨#0000FF¨»R«/mi»«mi mathvariant=¨bold¨ mathcolor=¨#0000FF¨»T«/mi»«/msub»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»=«/mo»«mfrac mathcolor=¨#0000FF¨»«mi mathvariant=¨bold¨»§#949;«/mi»«mi mathvariant=¨bold¨»I«/mi»«/mfrac»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»=«/mo»«mfrac mathcolor=¨#0000FF¨»«mn mathvariant=¨bold¨»12«/mn»«mrow»«mn mathvariant=¨bold¨»0«/mn»«mo mathvariant=¨bold¨».«/mo»«mn mathvariant=¨bold¨»3«/mn»«/mrow»«/mfrac»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»=«/mo»«mn mathvariant=¨bold¨ mathcolor=¨#0000FF¨»40«/mn»«mi mathvariant=¨bold¨ mathcolor=¨#0000FF¨»§#937;«/mi»«/mstyle»«/math»
نكتب تعبيرًا للمقاومة المحصلة ونعبر عن المقاومة الداخلية لـ r من التعبير عن المقاومة المحصلة:
«math xmlns=¨http://www.w3.org/1998/Math/MathML¨»«mstyle mathsize=¨20px¨»«msub»«mi mathvariant=¨bold¨ mathcolor=¨#0000FF¨»R«/mi»«mi mathvariant=¨bold¨ mathcolor=¨#0000FF¨»T«/mi»«/msub»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»=«/mo»«msub»«mi mathvariant=¨bold¨ mathcolor=¨#0000FF¨»R«/mi»«mi mathvariant=¨bold¨ mathcolor=¨#0000FF¨»L«/mi»«/msub»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»+«/mo»«msub»«mi mathvariant=¨bold¨ mathcolor=¨#0000FF¨»R«/mi»«mi mathvariant=¨bold¨ mathcolor=¨#0000FF¨»X«/mi»«/msub»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»+«/mo»«mi mathvariant=¨bold¨ mathcolor=¨#0000FF¨»r«/mi»«mspace linebreak=¨newline¨/»«msub»«mi mathvariant=¨bold¨ mathcolor=¨#0000FF¨»R«/mi»«mi mathvariant=¨bold¨ mathcolor=¨#0000FF¨»X«/mi»«/msub»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»=«/mo»«msub»«mi mathvariant=¨bold¨ mathcolor=¨#0000FF¨»R«/mi»«mi mathvariant=¨bold¨ mathcolor=¨#0000FF¨»T«/mi»«/msub»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»-«/mo»«msub»«mi mathvariant=¨bold¨ mathcolor=¨#0000FF¨»R«/mi»«mi mathvariant=¨bold¨ mathcolor=¨#0000FF¨»L«/mi»«/msub»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»-«/mo»«mi mathvariant=¨bold¨ mathcolor=¨#0000FF¨»r«/mi»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»=«/mo»«mn mathvariant=¨bold¨ mathcolor=¨#0000FF¨»40«/mn»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»-«/mo»«mn mathvariant=¨bold¨ mathcolor=¨#0000FF¨»10«/mn»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»-«/mo»«mn mathvariant=¨bold¨ mathcolor=¨#0000FF¨»1«/mn»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»=«/mo»«mn mathvariant=¨bold¨ mathcolor=¨#0000FF¨»29«/mn»«mi mathvariant=¨bold¨ mathcolor=¨#0000FF¨»§#937;«/mi»«/mstyle»«/math»
ب- الطول الكلي للمقاوم المتغير 10 سم ومقاومته القصوى 40 أوم، لذلك فإن مقاومة المقاوم المتغير لكل وحدة طول هي 4 أوم لكل سم. نشير إلى مقاومة المقاوم المتغير لكل وحدة طول ب «math xmlns=¨http://www.w3.org/1998/Math/MathML¨»«mstyle mathsize=¨20px¨»«mi mathvariant=¨bold¨ mathcolor=¨#0000FF¨»§#955;«/mi»«/mstyle»«/math».
نكتب تعبيرًا لمقاومة المقاوم المتغير R بدلالة مقاومته لكل وحدة طول «math xmlns=¨http://www.w3.org/1998/Math/MathML¨»«mstyle mathsize=¨20px¨»«mi mathvariant=¨bold¨ mathcolor=¨#0000FF¨»§#955;«/mi»«/mstyle»«/math» وبطوله L:
«math xmlns=¨http://www.w3.org/1998/Math/MathML¨»«mstyle mathsize=¨20px¨»«mi mathvariant=¨bold¨ mathcolor=¨#0000FF¨»R«/mi»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»=«/mo»«mi mathvariant=¨bold¨ mathcolor=¨#0000FF¨»§#955;«/mi»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»§#183;«/mo»«mi mathvariant=¨bold¨ mathcolor=¨#0000FF¨»L«/mi»«/mstyle»«/math»
نجد طول المقاوم المتغير بحيث تكون مقاومته 29 أوم.
«math xmlns=¨http://www.w3.org/1998/Math/MathML¨»«mstyle mathsize=¨20px¨»«mi mathvariant=¨bold¨ mathcolor=¨#0000FF¨»R«/mi»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»=«/mo»«mi mathvariant=¨bold¨ mathcolor=¨#0000FF¨»§#955;«/mi»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»§#183;«/mo»«mi mathvariant=¨bold¨ mathcolor=¨#0000FF¨»L«/mi»«mspace linebreak=¨newline¨/»«mi mathvariant=¨bold¨ mathcolor=¨#0000FF¨»L«/mi»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»=«/mo»«mfrac mathcolor=¨#0000FF¨»«mi mathvariant=¨bold¨»R«/mi»«mi mathvariant=¨bold¨»§#955;«/mi»«/mfrac»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»=«/mo»«mfrac mathcolor=¨#0000FF¨»«mn mathvariant=¨bold¨»29«/mn»«mn mathvariant=¨bold¨»4«/mn»«/mfrac»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»=«/mo»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»§#160;«/mo»«mn mathvariant=¨bold¨ mathcolor=¨#0000FF¨»7«/mn»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨».«/mo»«msub»«mn mathvariant=¨bold¨ mathcolor=¨#0000FF¨»25«/mn»«mi mathvariant=¨bold¨ mathcolor=¨#0000FF¨»CM«/mi»«/msub»«/mstyle»«/math»
لكي تكون مقاومة المقاوم المتغير 29 أوم ، يجب أن يكون طول المقاوم المتغير 7.25 سم.
ج- يجب تحديد الموقع الابتدائي لنقطة التماس المتحركة التي تكون فيها شدة التيار صغرى في البداية بحيث تأخذ بالازدياد مع ازاحة نقطة التماس هذه، لذلك يجب وضع نقطة التماس المتحركة في البداية في الطرف الأيمن.
إذا تم وضع نقطة التماس المتحركة أولاً في الطرف الأيسر، فسيكون التيار في البداية ذو قيمة قصوى، وقد يحترق المصباح.
16. ג.6
أ- لإيجاد مقاومة المقاوم المتغير RX بحيث يكون فرق الجهد على المصباح 3 فولط، نفترض أن فرق الجهد على المصباح هو 3 فولط ونحسب مقاومة المقاوم المتغير RX في هذه الحالة.
نظرًا لأن المصباح موصول مباشرة بقطبي مصدر فرق الجهد، فإن فرق جهد الأقطاب هو نفس فرق الجهد الموجود على المصباح ويساوي 3 فولط.
نشير إلى التيار من خلال المصباح«math style=¨font-family:Tahoma¨ xmlns=¨http://www.w3.org/1998/Math/MathML¨»«mstyle mathsize=¨20px¨»«msub»«mi mathvariant=¨bold¨ mathcolor=¨#0000FF¨»I«/mi»«mn mathvariant=¨bold¨ mathcolor=¨#0000FF¨»1«/mn»«/msub»«/mstyle»«/math» والتيار من خلال المقاوم المتغير بـ «math style=¨font-family:Tahoma¨ xmlns=¨http://www.w3.org/1998/Math/MathML¨»«mstyle mathsize=¨20px¨»«msub»«mi mathvariant=¨bold¨ mathcolor=¨#0000FF¨»I«/mi»«mn mathvariant=¨bold¨ mathcolor=¨#0000FF¨»2«/mn»«/msub»«/mstyle»«/math».
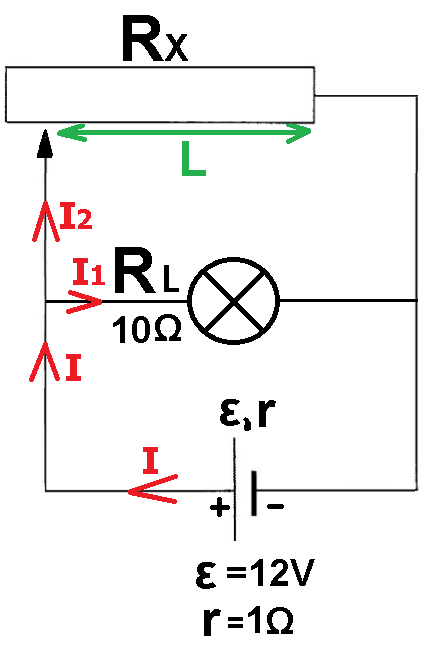
نكتب تعبير فرق جهد الأقطاب ونجد منه التيار بالمصدر «math style=¨font-family:Tahoma¨ xmlns=¨http://www.w3.org/1998/Math/MathML¨»«mstyle mathsize=¨20px¨»«mi mathvariant=¨bold¨ mathcolor=¨#0000FF¨»I«/mi»«/mstyle»«/math»:
«math style=¨font-family:Tahoma¨ xmlns=¨http://www.w3.org/1998/Math/MathML¨»«mi mathvariant=¨bold¨ mathcolor=¨#0000FF¨ mathsize=¨20px¨»Vab«/mi»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨ mathsize=¨20px¨»=«/mo»«mi mathvariant=¨bold¨ mathcolor=¨#0000FF¨ mathsize=¨20px¨»§#949;«/mi»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨ mathsize=¨20px¨»-«/mo»«mi mathvariant=¨bold¨ mathcolor=¨#0000FF¨ mathsize=¨20px¨»I«/mi»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨ mathsize=¨20px¨»§#183;«/mo»«mi mathvariant=¨bold¨ mathcolor=¨#0000FF¨ mathsize=¨20px¨»r«/mi»«mspace linebreak=¨newline¨/»«mspace linebreak=¨newline¨/»«mi mathvariant=¨bold¨ mathcolor=¨#0000FF¨ mathsize=¨20px¨»I«/mi»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨ mathsize=¨20px¨»§#183;«/mo»«mi mathvariant=¨bold¨ mathcolor=¨#0000FF¨ mathsize=¨20px¨»r«/mi»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨ mathsize=¨20px¨»=«/mo»«mi mathvariant=¨bold¨ mathcolor=¨#0000FF¨ mathsize=¨20px¨»§#949;«/mi»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨ mathsize=¨20px¨»-«/mo»«mi mathvariant=¨bold¨ mathcolor=¨#0000FF¨ mathsize=¨20px¨»Vab«/mi»«mspace linebreak=¨newline¨/»«mspace linebreak=¨newline¨/»«mi mathvariant=¨bold¨ mathcolor=¨#0000FF¨ mathsize=¨20px¨»I«/mi»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨ mathsize=¨20px¨»=«/mo»«mfrac mathcolor=¨#0000FF¨»«mrow»«mi mathvariant=¨bold¨ mathsize=¨20px¨»§#949;«/mi»«mo mathvariant=¨bold¨ mathsize=¨20px¨»-«/mo»«mi mathvariant=¨bold¨ mathsize=¨20px¨»Vab«/mi»«/mrow»«mi mathvariant=¨bold¨ mathsize=¨20px¨»r«/mi»«/mfrac»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨ mathsize=¨20px¨»=«/mo»«mfrac mathcolor=¨#0000FF¨»«mrow»«mn mathvariant=¨bold¨ mathsize=¨20px¨»12«/mn»«mo mathvariant=¨bold¨ mathsize=¨20px¨»-«/mo»«mn mathvariant=¨bold¨ mathsize=¨20px¨»3«/mn»«/mrow»«mn mathvariant=¨bold¨ mathsize=¨20px¨»1«/mn»«/mfrac»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨ mathsize=¨20px¨»=«/mo»«mn mathvariant=¨bold¨ mathcolor=¨#0000FF¨ mathsize=¨20px¨»9«/mn»«mi mathvariant=¨bold¨ mathcolor=¨#0000FF¨ mathsize=¨20px¨»A«/mi»«mspace linebreak=¨newline¨/»«/math»
يتم حساب التيار عبر المصباح باستخدام قانون أوم «math style=¨font-family:Tahoma¨ xmlns=¨http://www.w3.org/1998/Math/MathML¨»«mstyle mathsize=¨20px¨»«msub»«mi mathvariant=¨bold¨ mathcolor=¨#0000FF¨»I«/mi»«mn mathvariant=¨bold¨ mathcolor=¨#0000FF¨»1«/mn»«/msub»«/mstyle»«/math» :
«math style=¨font-family:Tahoma¨ xmlns=¨http://www.w3.org/1998/Math/MathML¨»«mstyle mathsize=¨20px¨»«msub»«mi mathvariant=¨bold¨ mathcolor=¨#0000FF¨»I«/mi»«mn mathvariant=¨bold¨ mathcolor=¨#0000FF¨»1«/mn»«/msub»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»=«/mo»«mfrac mathcolor=¨#0000FF¨»«msub»«mi mathvariant=¨bold¨»U«/mi»«mi mathvariant=¨bold¨»RL«/mi»«/msub»«mi mathvariant=¨bold¨»RL«/mi»«/mfrac»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»=«/mo»«mfrac mathcolor=¨#0000FF¨»«mn mathvariant=¨bold¨»3«/mn»«mn mathvariant=¨bold¨»10«/mn»«/mfrac»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»=«/mo»«mn mathvariant=¨bold¨ mathcolor=¨#0000FF¨»0«/mn»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨».«/mo»«mn mathvariant=¨bold¨ mathcolor=¨#0000FF¨»3«/mn»«mi mathvariant=¨bold¨ mathcolor=¨#0000FF¨»§#937;«/mi»«/mstyle»«/math»
نحسب التيار خلال المقاوم المتغير باستخدام قانون العقدة «math style=¨font-family:Tahoma¨ xmlns=¨http://www.w3.org/1998/Math/MathML¨»«mstyle mathsize=¨20px¨»«msub»«mi mathvariant=¨bold¨ mathcolor=¨#0000FF¨»I«/mi»«mn mathvariant=¨bold¨ mathcolor=¨#0000FF¨»2«/mn»«/msub»«/mstyle»«/math» :
«math style=¨font-family:Tahoma¨ xmlns=¨http://www.w3.org/1998/Math/MathML¨»«mstyle mathsize=¨20px¨»«mi mathvariant=¨bold¨ mathcolor=¨#0000FF¨»I«/mi»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»=«/mo»«msub»«mi mathvariant=¨bold¨ mathcolor=¨#0000FF¨»I«/mi»«mn mathvariant=¨bold¨ mathcolor=¨#0000FF¨»1«/mn»«/msub»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»+«/mo»«msub»«mi mathvariant=¨bold¨ mathcolor=¨#0000FF¨»I«/mi»«mn mathvariant=¨bold¨ mathcolor=¨#0000FF¨»2«/mn»«/msub»«mspace linebreak=¨newline¨/»«msub»«mi mathvariant=¨bold¨ mathcolor=¨#0000FF¨»I«/mi»«mn mathvariant=¨bold¨ mathcolor=¨#0000FF¨»2«/mn»«/msub»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»=«/mo»«mi mathvariant=¨bold¨ mathcolor=¨#0000FF¨»I«/mi»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»-«/mo»«msub»«mi mathvariant=¨bold¨ mathcolor=¨#0000FF¨»I«/mi»«mn mathvariant=¨bold¨ mathcolor=¨#0000FF¨»1«/mn»«/msub»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»=«/mo»«mn mathvariant=¨bold¨ mathcolor=¨#0000FF¨»9«/mn»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»-«/mo»«mn mathvariant=¨bold¨ mathcolor=¨#0000FF¨»0«/mn»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨».«/mo»«mn mathvariant=¨bold¨ mathcolor=¨#0000FF¨»3«/mn»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»=«/mo»«mn mathvariant=¨bold¨ mathcolor=¨#0000FF¨»8«/mn»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨».«/mo»«mn mathvariant=¨bold¨ mathcolor=¨#0000FF¨»7«/mn»«mi mathvariant=¨bold¨ mathcolor=¨#0000FF¨»A«/mi»«/mstyle»«/math»
نحسب مقاومة المقاوم المتغير RX باستخدام قانون أوم:
«math style=¨font-family:Tahoma¨ xmlns=¨http://www.w3.org/1998/Math/MathML¨»«mstyle mathsize=¨20px¨»«mi mathvariant=¨bold¨ mathcolor=¨#0000FF¨»I«/mi»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»=«/mo»«mfrac mathcolor=¨#0000FF¨»«msub»«mi mathvariant=¨bold¨»U«/mi»«mi mathvariant=¨bold¨»RX«/mi»«/msub»«msub»«mi mathvariant=¨bold¨»R«/mi»«mi mathvariant=¨bold¨»X«/mi»«/msub»«/mfrac»«mspace linebreak=¨newline¨/»«mspace linebreak=¨newline¨/»«msub»«mi mathvariant=¨bold¨ mathcolor=¨#0000FF¨»R«/mi»«mi mathvariant=¨bold¨ mathcolor=¨#0000FF¨»X«/mi»«/msub»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»=«/mo»«mfrac mathcolor=¨#0000FF¨»«msub»«mi mathvariant=¨bold¨»U«/mi»«mi mathvariant=¨bold¨»RX«/mi»«/msub»«msub»«mi mathvariant=¨bold¨»I«/mi»«mn mathvariant=¨bold¨»2«/mn»«/msub»«/mfrac»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»=«/mo»«mfrac mathcolor=¨#0000FF¨»«mn mathvariant=¨bold¨»3«/mn»«mrow»«mn mathvariant=¨bold¨»8«/mn»«mo mathvariant=¨bold¨».«/mo»«mn mathvariant=¨bold¨»7«/mn»«/mrow»«/mfrac»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»=«/mo»«mn mathvariant=¨bold¨ mathcolor=¨#0000FF¨»0«/mn»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨».«/mo»«mn mathvariant=¨bold¨ mathcolor=¨#0000FF¨»34«/mn»«mi mathvariant=¨bold¨ mathcolor=¨#0000FF¨»§#937;«/mi»«/mstyle»«/math»
لذلك ، لكي يكون فرق الجهد على المصباح 3 فولط، يجب أن تكون مقاومة المقاوم المتغير 0.34 أوم.
ب. مقاومة المقاوم المتغير لكل وحدة طول هي 4 أوم لكل سم. نشير إلى مقاومة المقاوم المتغير لكل وحدة طول «math xmlns=¨http://www.w3.org/1998/Math/MathML¨»«mstyle mathsize=¨20px¨»«mi mathvariant=¨bold¨ mathcolor=¨#0000FF¨»§#955;«/mi»«/mstyle»«/math».
نكتب تعبيرًا لمقاومة المقاوم المتغير R بدلالة مقاومته لكل وحدة طول «math xmlns=¨http://www.w3.org/1998/Math/MathML¨»«mstyle mathsize=¨20px¨»«mi mathvariant=¨bold¨ mathcolor=¨#0000FF¨»§#955;«/mi»«/mstyle»«/math» وبطوله L:
«math xmlns=¨http://www.w3.org/1998/Math/MathML¨»«mstyle mathsize=¨20px¨»«mi mathvariant=¨bold¨ mathcolor=¨#0000FF¨»R«/mi»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»=«/mo»«mi mathvariant=¨bold¨ mathcolor=¨#0000FF¨»§#955;«/mi»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»§#183;«/mo»«mi mathvariant=¨bold¨ mathcolor=¨#0000FF¨»L«/mi»«/mstyle»«/math»
نجد طول المقاوم المتغير بحيث تكون مقاومته 0.34 أوم.
«math xmlns=¨http://www.w3.org/1998/Math/MathML¨»«mstyle mathsize=¨20px¨»«mi mathvariant=¨bold¨ mathcolor=¨#0000FF¨»R«/mi»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»=«/mo»«mi mathvariant=¨bold¨ mathcolor=¨#0000FF¨»§#955;«/mi»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»§#183;«/mo»«mi mathvariant=¨bold¨ mathcolor=¨#0000FF¨»L«/mi»«mspace linebreak=¨newline¨/»«mi mathvariant=¨bold¨ mathcolor=¨#0000FF¨»L«/mi»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»=«/mo»«mfrac mathcolor=¨#0000FF¨»«mi mathvariant=¨bold¨»R«/mi»«mi mathvariant=¨bold¨»§#955;«/mi»«/mfrac»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»=«/mo»«mfrac mathcolor=¨#0000FF¨»«mrow»«mn mathvariant=¨bold¨»0«/mn»«mo mathvariant=¨bold¨».«/mo»«mn mathvariant=¨bold¨»34«/mn»«/mrow»«mn mathvariant=¨bold¨»4«/mn»«/mfrac»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»=«/mo»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»§#160;«/mo»«mn mathvariant=¨bold¨ mathcolor=¨#0000FF¨»0«/mn»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨».«/mo»«msub»«mn mathvariant=¨bold¨ mathcolor=¨#0000FF¨»085«/mn»«mi mathvariant=¨bold¨ mathcolor=¨#0000FF¨»CM«/mi»«/msub»«/mstyle»«/math»
ج. حتى لا يحترق المصباح، يجب ضبط قيمة المقاومة الابتدائية للمقاوم المتغير على قيمة قصوى، أي في الطرف الأيسر، بحيث تكون شدة تيار المصدر في البداية أصغر ما يمكن، وبالتالي فإن التيار الابتدائي خلال المصباح سيكون أيضًا أصغرقيمة له.
من المهم ملاحظة أن المقاوم المتغير موصول بتوصيل ريئوستاتي وليس توصيل بوتانسيومتري.
17. ג.7
أ- يتم توصيل المقاوم المتغير على شكل توصيل بوتانسيومتري، طرف واحد من الفولطميتر موصول بالنقطة A الموصولة بالقطب الموجب لمصدر فرق الجهد.
والطرف الآخر من الفولطميتر موصول مع نقطة التماس المتحركة Q.
يشير الفولطميتر إلى الحد الأدنى من فرق الجهد عند توصيل نقطة التماس المتحركة Q بالنقطة M. في هذه الحالة، يشير الفولطميتر إلى فرق جهد يساوي صفر فولط.
ب- حتى يُشير مقياس فرق الجهد على أقصى فرق جهد، يجب توصيل نقطة التماس المتحركة بالنقطة N. في هذا الوضع، يشير الفولطميتر إلى فرق جهد أقطاب البطارية.
ج- المقاومة الداخلية للفولطميتر تقترب إلى اللانهاية ، ولا يؤثر موقع نقطة التماس المتحركة Q على التيار في الدائرة.
نحسب شدة التيار في الدائرة من قانون أوم على الدائرة بأكملها:
«math style=¨font-family:Tahoma¨ xmlns=¨http://www.w3.org/1998/Math/MathML¨»«mstyle mathsize=¨20px¨»«mi mathvariant=¨bold¨ mathcolor=¨#0000FF¨»I«/mi»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»=«/mo»«mfrac mathcolor=¨#0000FF¨»«mi mathvariant=¨bold¨»§#949;«/mi»«msub»«mi mathvariant=¨bold¨»R«/mi»«mi mathvariant=¨bold¨»X«/mi»«/msub»«/mfrac»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»=«/mo»«mfrac mathcolor=¨#0000FF¨»«mn mathvariant=¨bold¨»12«/mn»«mn mathvariant=¨bold¨»40«/mn»«/mfrac»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»=«/mo»«mn mathvariant=¨bold¨ mathcolor=¨#0000FF¨»0«/mn»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨».«/mo»«mn mathvariant=¨bold¨ mathcolor=¨#0000FF¨»3«/mn»«mi mathvariant=¨bold¨ mathcolor=¨#0000FF¨»A«/mi»«/mstyle»«/math»
فرق الجهد المطلوب في جزء المقاومة «math xmlns=¨http://www.w3.org/1998/Math/MathML¨»«mstyle mathsize=¨20px¨»«msub»«mi mathvariant=¨bold¨ mathcolor=¨#0000FF¨»R«/mi»«mi mathvariant=¨bold¨ mathcolor=¨#0000FF¨»QM«/mi»«/msub»«/mstyle»«/math» هو 3 فولط، نجد المقاومة «math xmlns=¨http://www.w3.org/1998/Math/MathML¨»«mstyle mathsize=¨20px¨»«msub»«mi mathvariant=¨bold¨ mathcolor=¨#0000FF¨»R«/mi»«mi mathvariant=¨bold¨ mathcolor=¨#0000FF¨»QM«/mi»«/msub»«/mstyle»«/math» بواسطة قانون أوم:
«math style=¨font-family:Tahoma¨ xmlns=¨http://www.w3.org/1998/Math/MathML¨»«mstyle mathsize=¨20px¨»«mi mathvariant=¨bold¨ mathcolor=¨#0000FF¨»I«/mi»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»=«/mo»«mfrac mathcolor=¨#0000FF¨»«msub»«mi mathvariant=¨bold¨»U«/mi»«mi mathvariant=¨bold¨»RQM«/mi»«/msub»«msub»«mrow/»«mi mathvariant=¨bold¨»RQM«/mi»«/msub»«/mfrac»«mspace linebreak=¨newline¨/»«msub»«mspace linebreak=¨newline¨/»«mi mathvariant=¨bold¨ mathcolor=¨#0000FF¨»RQM«/mi»«/msub»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»=«/mo»«mfrac mathcolor=¨#0000FF¨»«msub»«mi mathvariant=¨bold¨»U«/mi»«mi mathvariant=¨bold¨»RQM«/mi»«/msub»«mi mathvariant=¨bold¨»I«/mi»«/mfrac»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»=«/mo»«mfrac mathcolor=¨#0000FF¨»«mn mathvariant=¨bold¨»3«/mn»«mrow»«mn mathvariant=¨bold¨»0«/mn»«mo mathvariant=¨bold¨».«/mo»«mn mathvariant=¨bold¨»3«/mn»«/mrow»«/mfrac»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»=«/mo»«mn mathvariant=¨bold¨ mathcolor=¨#0000FF¨»10«/mn»«mi mathvariant=¨bold¨ mathcolor=¨#0000FF¨»§#937;«/mi»«/mstyle»«/math»
طريقة أخرى: عندما يكون فرق الجهد بين النقطة Q والنقطة M يساوي 3 فولط. يجب أن يكون الجهد بين النقطة Q والنقطة N مساوٍ لـ 9 فولط (مجموع هذين فرقي الجهد يساوي 12 فولط).
يمكن القول أن المقاومتين «math xmlns=¨http://www.w3.org/1998/Math/MathML¨»«mstyle mathsize=¨20px¨»«msub»«mi mathvariant=¨bold¨ mathcolor=¨#0000FF¨»R«/mi»«mi mathvariant=¨bold¨ mathcolor=¨#0000FF¨»QM«/mi»«/msub»«/mstyle»«/math» و- «math xmlns=¨http://www.w3.org/1998/Math/MathML¨»«mstyle mathsize=¨20px¨»«msub»«mi mathvariant=¨bold¨ mathcolor=¨#0000FF¨»R«/mi»«mi mathvariant=¨bold¨ mathcolor=¨#0000FF¨»QN«/mi»«/msub»«/mstyle»«/math» موصولتان على التوالي، لذلك ، فإن النسبة بين المقاومتين هي نفس النسبة بين فرقي الجهد عليهما ويتحقق:
«math xmlns=¨http://www.w3.org/1998/Math/MathML¨»«mstyle mathsize=¨20px¨»«mfrac mathcolor=¨#0000FF¨»«msub»«mi mathvariant=¨bold¨»R«/mi»«mi mathvariant=¨bold¨»QN«/mi»«/msub»«msub»«mi mathvariant=¨bold¨»R«/mi»«mi mathvariant=¨bold¨»QM«/mi»«/msub»«/mfrac»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»=«/mo»«mfrac mathcolor=¨#0000FF¨»«mn mathvariant=¨bold¨»3«/mn»«mn mathvariant=¨bold¨»9«/mn»«/mfrac»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»=«/mo»«mn mathvariant=¨bold¨ mathcolor=¨#0000FF¨»3«/mn»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»§#160;«/mo»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»§#160;«/mo»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»§#160;«/mo»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»§#8658;«/mo»«menclose mathcolor=¨#0000FF¨ notation=¨box¨»«msub»«mi mathvariant=¨bold¨»R«/mi»«mi mathvariant=¨bold¨»QN«/mi»«/msub»«mo mathvariant=¨bold¨»=«/mo»«mn mathvariant=¨bold¨»3«/mn»«mo mathvariant=¨bold¨»§#183;«/mo»«msub»«mi mathvariant=¨bold¨»R«/mi»«mi mathvariant=¨bold¨»QM«/mi»«/msub»«/menclose»«/mstyle»«/math»
يمكن كتابة معادلة أخرى لمجموع المقاومتين : «math xmlns=¨http://www.w3.org/1998/Math/MathML¨»«mstyle mathsize=¨20px¨»«menclose mathcolor=¨#0000FF¨ notation=¨box¨»«msub»«mi mathvariant=¨bold¨»R«/mi»«mi mathvariant=¨bold¨»QN«/mi»«/msub»«mo mathvariant=¨bold¨»+«/mo»«msub»«mi mathvariant=¨bold¨»R«/mi»«mi mathvariant=¨bold¨»QM«/mi»«/msub»«mo mathvariant=¨bold¨»=«/mo»«mn mathvariant=¨bold¨»40«/mn»«/menclose»«/mstyle»«/math»
نجد المقاومة «math xmlns=¨http://www.w3.org/1998/Math/MathML¨»«mstyle mathsize=¨20px¨»«msub»«mi mathvariant=¨bold¨ mathcolor=¨#0000FF¨»R«/mi»«mi mathvariant=¨bold¨ mathcolor=¨#0000FF¨»QM«/mi»«/msub»«/mstyle»«/math» بواسطة حل معادلين بمجولين:
«math xmlns=¨http://www.w3.org/1998/Math/MathML¨»«mstyle mathsize=¨20px¨»«msub»«mi mathvariant=¨bold¨ mathcolor=¨#FF0000¨»R«/mi»«mi mathvariant=¨bold¨ mathcolor=¨#FF0000¨»QN«/mi»«/msub»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»=«/mo»«mn mathvariant=¨bold¨ mathcolor=¨#0000FF¨»3«/mn»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»§#183;«/mo»«msub»«mi mathvariant=¨bold¨ mathcolor=¨#0000FF¨»R«/mi»«mi mathvariant=¨bold¨ mathcolor=¨#0000FF¨»QM«/mi»«/msub»«mspace linebreak=¨newline¨/»«mn mathvariant=¨bold¨ mathcolor=¨#FF0000¨»40«/mn»«mo mathvariant=¨bold¨ mathcolor=¨#FF0000¨»-«/mo»«msub»«mi mathvariant=¨bold¨ mathcolor=¨#FF0000¨»R«/mi»«mi mathvariant=¨bold¨ mathcolor=¨#FF0000¨»QM«/mi»«/msub»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»=«/mo»«mn mathvariant=¨bold¨ mathcolor=¨#0000FF¨»3«/mn»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»§#183;«/mo»«msub»«mi mathvariant=¨bold¨ mathcolor=¨#0000FF¨»R«/mi»«mi mathvariant=¨bold¨ mathcolor=¨#0000FF¨»QM«/mi»«/msub»«mspace linebreak=¨newline¨/»«mn mathvariant=¨bold¨ mathcolor=¨#0000FF¨»4«/mn»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»§#183;«/mo»«msub»«mi mathvariant=¨bold¨ mathcolor=¨#0000FF¨»R«/mi»«mi mathvariant=¨bold¨ mathcolor=¨#0000FF¨»QM«/mi»«/msub»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»=«/mo»«mn mathvariant=¨bold¨ mathcolor=¨#0000FF¨»40«/mn»«mspace linebreak=¨newline¨/»«msub»«mi mathvariant=¨bold¨ mathcolor=¨#0000FF¨»R«/mi»«mi mathvariant=¨bold¨ mathcolor=¨#0000FF¨»QM«/mi»«/msub»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»=«/mo»«mfrac mathcolor=¨#0000FF¨»«mn mathvariant=¨bold¨»40«/mn»«mn mathvariant=¨bold¨»4«/mn»«/mfrac»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»=«/mo»«mn mathvariant=¨bold¨ mathcolor=¨#0000FF¨»10«/mn»«mi mathvariant=¨bold¨ mathcolor=¨#0000FF¨»§#937;«/mi»«mspace linebreak=¨newline¨/»«/mstyle»«/math»
د- مقاومة المقاوم المتغير لكل وحدة طول «math xmlns=¨http://www.w3.org/1998/Math/MathML¨»«mstyle mathsize=¨22px¨»«mi mathvariant=¨bold¨ mathcolor=¨#0000FF¨»§#955;«/mi»«/mstyle»«/math» هي 4 أوم لكل سم. نجد الطول L لقسم المقاومة«math xmlns=¨http://www.w3.org/1998/Math/MathML¨»«mstyle mathsize=¨20px¨»«msub»«mi mathvariant=¨bold¨ mathcolor=¨#0000FF¨»R«/mi»«mi mathvariant=¨bold¨ mathcolor=¨#0000FF¨»QM«/mi»«/msub»«/mstyle»«/math»
«math xmlns=¨http://www.w3.org/1998/Math/MathML¨»«mstyle mathsize=¨20px¨»«msub»«mi mathvariant=¨bold¨ mathcolor=¨#0000FF¨»R«/mi»«mi mathvariant=¨bold¨ mathcolor=¨#0000FF¨»QM«/mi»«/msub»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»=«/mo»«mi mathvariant=¨bold¨ mathcolor=¨#0000FF¨»§#955;«/mi»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»§#183;«/mo»«mi mathvariant=¨bold¨ mathcolor=¨#0000FF¨»L«/mi»«mspace linebreak=¨newline¨/»«mi mathvariant=¨bold¨ mathcolor=¨#0000FF¨»L«/mi»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»=«/mo»«mfrac mathcolor=¨#0000FF¨»«msub»«mi mathvariant=¨bold¨»R«/mi»«mi mathvariant=¨bold¨»QM«/mi»«/msub»«mi mathvariant=¨bold¨»§#955;«/mi»«/mfrac»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»=«/mo»«mfrac mathcolor=¨#0000FF¨»«mn mathvariant=¨bold¨»10«/mn»«mn mathvariant=¨bold¨»4«/mn»«/mfrac»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»=«/mo»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»§#160;«/mo»«mn mathvariant=¨bold¨ mathcolor=¨#0000FF¨»2«/mn»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨».«/mo»«msub»«mn mathvariant=¨bold¨ mathcolor=¨#0000FF¨»5«/mn»«mi mathvariant=¨bold¨ mathcolor=¨#0000FF¨»CM«/mi»«/msub»«/mstyle»«/math»
18. ג.8
نشير إلى التيار بالمصدر بواسطة I ، التيار عبر المصباح بواسطة «math style=¨font-family:Tahoma¨ xmlns=¨http://www.w3.org/1998/Math/MathML¨»«mstyle mathsize=¨20px¨»«msub»«mi mathvariant=¨bold¨ mathcolor=¨#0000FF¨»I«/mi»«mn mathvariant=¨bold¨ mathcolor=¨#0000FF¨»1«/mn»«/msub»«/mstyle»«/math» والتيار عبر المقاوم RMQ بواسطة «math style=¨font-family:Tahoma¨ xmlns=¨http://www.w3.org/1998/Math/MathML¨»«mstyle mathsize=¨20px¨»«msub»«mi mathvariant=¨bold¨ mathcolor=¨#0000FF¨»I«/mi»«mn mathvariant=¨bold¨ mathcolor=¨#0000FF¨»2«/mn»«/msub»«/mstyle»«/math» .
يتم وصف التيارات الثلاثة في الشكل التالي:
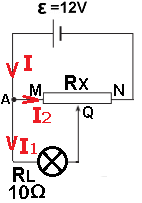
نحسب التيار المار خلال المصباح -«math style=¨font-family:Tahoma¨ xmlns=¨http://www.w3.org/1998/Math/MathML¨»«mstyle mathsize=¨24px¨»«msub»«mi mathvariant=¨bold¨ mathcolor=¨#0000FF¨»I«/mi»«mn mathvariant=¨bold¨ mathcolor=¨#0000FF¨»1«/mn»«/msub»«/mstyle»«/math»:
«math style=¨font-family:Tahoma¨ xmlns=¨http://www.w3.org/1998/Math/MathML¨»«mstyle mathsize=¨20px¨»«msub»«mi mathvariant=¨bold¨ mathcolor=¨#0000FF¨»I«/mi»«mn mathvariant=¨bold¨ mathcolor=¨#0000FF¨»1«/mn»«/msub»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»=«/mo»«mfrac mathcolor=¨#0000FF¨»«msub»«mi mathvariant=¨bold¨»U«/mi»«mi mathvariant=¨bold¨»RL«/mi»«/msub»«mi mathvariant=¨bold¨»RL«/mi»«/mfrac»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»=«/mo»«mfrac mathcolor=¨#0000FF¨»«mn mathvariant=¨bold¨»3«/mn»«mn mathvariant=¨bold¨»10«/mn»«/mfrac»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»=«/mo»«mn mathvariant=¨bold¨ mathcolor=¨#0000FF¨»0«/mn»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨».«/mo»«mn mathvariant=¨bold¨ mathcolor=¨#0000FF¨»3«/mn»«mi mathvariant=¨bold¨ mathcolor=¨#0000FF¨»A«/mi»«/mstyle»«/math»
نعبر عن شدة التيار المار خلال المقاوم RMQ- «math style=¨font-family:Tahoma¨ xmlns=¨http://www.w3.org/1998/Math/MathML¨»«mstyle mathsize=¨24px¨»«msub»«mi mathvariant=¨bold¨ mathcolor=¨#0000FF¨»I«/mi»«mn mathvariant=¨bold¨ mathcolor=¨#0000FF¨»2«/mn»«/msub»«/mstyle»«/math»:
المقاوم RMQ موصول على التوازي مع المصباح، وبالتالي فإن فرق الجهد على RMQ يساوي فرق الجهد على المصباح (3 فولط).
«math style=¨font-family:Tahoma¨ xmlns=¨http://www.w3.org/1998/Math/MathML¨»«mstyle mathsize=¨20px¨»«msub»«mi mathvariant=¨bold¨ mathcolor=¨#0000FF¨»I«/mi»«mn mathvariant=¨bold¨ mathcolor=¨#0000FF¨»2«/mn»«/msub»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»=«/mo»«mfrac mathcolor=¨#0000FF¨»«msub»«mi mathvariant=¨bold¨»U«/mi»«msub»«mi mathvariant=¨bold¨»R«/mi»«mi mathvariant=¨bold¨»MQ«/mi»«/msub»«/msub»«msub»«mi mathvariant=¨bold¨»R«/mi»«mi mathvariant=¨bold¨»MQ«/mi»«/msub»«/mfrac»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»=«/mo»«mfrac mathcolor=¨#0000FF¨»«mn mathvariant=¨bold¨»3«/mn»«msub»«mi mathvariant=¨bold¨»R«/mi»«mi mathvariant=¨bold¨»MQ«/mi»«/msub»«/mfrac»«/mstyle»«/math»
نعبر عن شدة التيار المار خلال المقاوم RQN - «math style=¨font-family:Tahoma¨ xmlns=¨http://www.w3.org/1998/Math/MathML¨»«mstyle mathsize=¨24px¨»«mi mathvariant=¨bold¨ mathcolor=¨#0000FF¨»I«/mi»«/mstyle»«/math» :
من قانون كيرخوف يمكن تحديد:
«math xmlns=¨http://www.w3.org/1998/Math/MathML¨»«mstyle mathsize=¨20px¨»«msub»«mi mathvariant=¨bold¨ mathcolor=¨#0000FF¨»U«/mi»«msub mathcolor=¨#0000FF¨»«mi mathvariant=¨bold¨»R«/mi»«mi mathvariant=¨bold¨»MQ«/mi»«/msub»«/msub»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»+«/mo»«msub»«mi mathvariant=¨bold¨ mathcolor=¨#0000FF¨»U«/mi»«msub mathcolor=¨#0000FF¨»«mi mathvariant=¨bold¨»R«/mi»«mi mathvariant=¨bold¨»QN«/mi»«/msub»«/msub»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»=«/mo»«mn mathvariant=¨bold¨ mathcolor=¨#0000FF¨»12«/mn»«mspace linebreak=¨newline¨/»«msub»«mi mathvariant=¨bold¨ mathcolor=¨#0000FF¨»U«/mi»«msub mathcolor=¨#0000FF¨»«mi mathvariant=¨bold¨»R«/mi»«mi mathvariant=¨bold¨»QN«/mi»«/msub»«/msub»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»=«/mo»«mn mathvariant=¨bold¨ mathcolor=¨#0000FF¨»12«/mn»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»-«/mo»«msub»«mi mathvariant=¨bold¨ mathcolor=¨#0000FF¨»U«/mi»«msub mathcolor=¨#0000FF¨»«mi mathvariant=¨bold¨»R«/mi»«mi mathvariant=¨bold¨»MQ«/mi»«/msub»«/msub»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»=«/mo»«mn mathvariant=¨bold¨ mathcolor=¨#0000FF¨»12«/mn»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»-«/mo»«mn mathvariant=¨bold¨ mathcolor=¨#0000FF¨»3«/mn»«mspace linebreak=¨newline¨/»«msub»«mi mathvariant=¨bold¨ mathcolor=¨#0000FF¨»U«/mi»«msub mathcolor=¨#0000FF¨»«mi mathvariant=¨bold¨»R«/mi»«mi mathvariant=¨bold¨»QN«/mi»«/msub»«/msub»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»=«/mo»«mn mathvariant=¨bold¨ mathcolor=¨#0000FF¨»9«/mn»«mi mathvariant=¨bold-italic¨ mathcolor=¨#0000FF¨»V«/mi»«/mstyle»«/math»
نعبر عن التيار المار بالمصدر:
«math style=¨font-family:Tahoma¨ xmlns=¨http://www.w3.org/1998/Math/MathML¨»«mstyle mathsize=¨20px¨»«mi mathvariant=¨bold¨ mathcolor=¨#0000FF¨»I«/mi»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»=«/mo»«mfrac mathcolor=¨#0000FF¨»«msub»«mi mathvariant=¨bold¨»U«/mi»«msub»«mi mathvariant=¨bold¨»R«/mi»«mi mathvariant=¨bold¨»QN«/mi»«/msub»«/msub»«msub»«mi mathvariant=¨bold¨»R«/mi»«mi mathvariant=¨bold¨»QN«/mi»«/msub»«/mfrac»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»=«/mo»«mfrac mathcolor=¨#0000FF¨»«mn mathvariant=¨bold¨»9«/mn»«msub»«mi mathvariant=¨bold¨»R«/mi»«mi mathvariant=¨bold¨»QN«/mi»«/msub»«/mfrac»«/mstyle»«/math»
نكتب قاعدة العقدة (المفترق) بالنسبة للعقدة A :
«math style=¨font-family:Tahoma¨ xmlns=¨http://www.w3.org/1998/Math/MathML¨»«mstyle mathsize=¨20px¨»«mi mathvariant=¨bold¨ mathcolor=¨#0000FF¨»I«/mi»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»=«/mo»«msub»«mi mathvariant=¨bold¨ mathcolor=¨#0000FF¨»I«/mi»«mn mathvariant=¨bold¨ mathcolor=¨#0000FF¨»1«/mn»«/msub»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»+«/mo»«msub»«mi mathvariant=¨bold¨ mathcolor=¨#0000FF¨»I«/mi»«mn mathvariant=¨bold¨ mathcolor=¨#0000FF¨»2«/mn»«/msub»«mspace linebreak=¨newline¨/»«menclose mathcolor=¨#0000FF¨ notation=¨box¨»«mfrac»«mn mathvariant=¨bold¨»9«/mn»«msub»«mi mathvariant=¨bold¨»R«/mi»«mi mathvariant=¨bold¨»QN«/mi»«/msub»«/mfrac»«mo mathvariant=¨bold¨»=«/mo»«mn mathvariant=¨bold¨»0«/mn»«mo mathvariant=¨bold¨».«/mo»«mn mathvariant=¨bold¨»3«/mn»«mo mathvariant=¨bold¨»+«/mo»«mfrac»«mn mathvariant=¨bold¨»3«/mn»«msub»«mi mathvariant=¨bold¨»R«/mi»«mi mathvariant=¨bold¨»MQ«/mi»«/msub»«/mfrac»«/menclose»«/mstyle»«/math»
نكتب معادلة مقاومة أخرى، وفقًا للمقاومة الكلية للمقاوم المتغير:
«math style=¨font-family:Tahoma¨ xmlns=¨http://www.w3.org/1998/Math/MathML¨»«mstyle mathsize=¨20px¨»«menclose mathcolor=¨#0000FF¨ notation=¨box¨»«msub»«mi mathvariant=¨bold¨»R«/mi»«mi mathvariant=¨bold¨»MQ«/mi»«/msub»«mo mathvariant=¨bold¨»+«/mo»«msub»«mi mathvariant=¨bold¨»R«/mi»«mi mathvariant=¨bold¨»QN«/mi»«/msub»«mo mathvariant=¨bold¨»=«/mo»«mn mathvariant=¨bold¨»40«/mn»«/menclose»«/mstyle»«/math»
نحل هيئة المعادلات المكونة من معادلتين بمجهولين اثنين:
«math style=¨font-family:Tahoma¨ xmlns=¨http://www.w3.org/1998/Math/MathML¨»«mstyle mathsize=¨20px¨»«mn mathvariant=¨bold¨ mathcolor=¨#0000FF¨»1«/mn»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»)«/mo»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»§#160;«/mo»«mfrac mathcolor=¨#0000FF¨»«mn mathvariant=¨bold¨»9«/mn»«msub»«mi mathvariant=¨bold¨»R«/mi»«mi mathvariant=¨bold¨»QN«/mi»«/msub»«/mfrac»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»=«/mo»«mn mathvariant=¨bold¨ mathcolor=¨#0000FF¨»0«/mn»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨».«/mo»«mn mathvariant=¨bold¨ mathcolor=¨#0000FF¨»3«/mn»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»+«/mo»«mfrac mathcolor=¨#0000FF¨»«mn mathvariant=¨bold¨»3«/mn»«msub»«mi mathvariant=¨bold¨»R«/mi»«mi mathvariant=¨bold¨»MQ«/mi»«/msub»«/mfrac»«/mstyle»«/math»
«math style=¨font-family:Tahoma¨ xmlns=¨http://www.w3.org/1998/Math/MathML¨»«mstyle mathsize=¨20px¨»«mrow»«mn mathvariant=¨bold¨ mathcolor=¨#0000FF¨»2«/mn»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»)«/mo»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»§#160;«/mo»«msub»«mi mathvariant=¨bold¨ mathcolor=¨#0000FF¨»R«/mi»«mi mathvariant=¨bold¨ mathcolor=¨#0000FF¨»MQ«/mi»«/msub»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»+«/mo»«msub»«mi mathvariant=¨bold¨ mathcolor=¨#0000FF¨»R«/mi»«mi mathvariant=¨bold¨ mathcolor=¨#0000FF¨»QN«/mi»«/msub»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»=«/mo»«mn mathvariant=¨bold¨ mathcolor=¨#0000FF¨»40«/mn»«/mrow»«mo»§#160;«/mo»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»§#8658;«/mo»«msub»«mi mathvariant=¨bold¨ mathcolor=¨#FF0000¨»R«/mi»«mi mathvariant=¨bold¨ mathcolor=¨#FF0000¨»QN«/mi»«/msub»«mo mathvariant=¨bold¨ mathcolor=¨#FF0000¨»=«/mo»«mn mathvariant=¨bold¨ mathcolor=¨#FF0000¨»40«/mn»«mo mathvariant=¨bold¨ mathcolor=¨#FF0000¨»-«/mo»«msub»«mi mathvariant=¨bold¨ mathcolor=¨#FF0000¨»R«/mi»«mi mathvariant=¨bold¨ mathcolor=¨#FF0000¨»MQ«/mi»«/msub»«/mstyle»«/math»
نعوّض التعبير RQN من المعادلة 2 بالمعادلة 1.
«math style=¨font-family:Tahoma¨ xmlns=¨http://www.w3.org/1998/Math/MathML¨»«mstyle mathsize=¨20px¨»«mfrac mathcolor=¨#0000FF¨»«mn mathvariant=¨bold¨»9«/mn»«msub»«mi mathvariant=¨bold¨ mathcolor=¨#FF0000¨»R«/mi»«mi mathvariant=¨bold¨ mathcolor=¨#FF0000¨»QN«/mi»«/msub»«/mfrac»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»=«/mo»«mn mathvariant=¨bold¨ mathcolor=¨#0000FF¨»0«/mn»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨».«/mo»«mn mathvariant=¨bold¨ mathcolor=¨#0000FF¨»3«/mn»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»+«/mo»«mfrac mathcolor=¨#0000FF¨»«mn mathvariant=¨bold¨»3«/mn»«msub»«mi mathvariant=¨bold¨»R«/mi»«mi mathvariant=¨bold¨»MQ«/mi»«/msub»«/mfrac»«mspace linebreak=¨newline¨/»«mspace linebreak=¨newline¨/»«mfrac mathcolor=¨#0000FF¨»«mn mathvariant=¨bold¨»9«/mn»«mrow»«mn mathvariant=¨bold¨ mathcolor=¨#FF0000¨»40«/mn»«mo mathvariant=¨bold¨ mathcolor=¨#FF0000¨»-«/mo»«msub»«mi mathvariant=¨bold¨ mathcolor=¨#FF0000¨»R«/mi»«mi mathvariant=¨bold¨ mathcolor=¨#FF0000¨»MQ«/mi»«/msub»«/mrow»«/mfrac»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»=«/mo»«mn mathvariant=¨bold¨ mathcolor=¨#0000FF¨»0«/mn»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨».«/mo»«mn mathvariant=¨bold¨ mathcolor=¨#0000FF¨»3«/mn»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»+«/mo»«mfrac mathcolor=¨#0000FF¨»«mn mathvariant=¨bold¨»3«/mn»«msub»«mi mathvariant=¨bold¨»R«/mi»«mi mathvariant=¨bold¨»MQ«/mi»«/msub»«/mfrac»«/mstyle»«/math»
نضرب المعادلة بـ «math style=¨font-family:Tahoma¨ xmlns=¨http://www.w3.org/1998/Math/MathML¨»«mstyle mathsize=¨20px¨»«msub»«mi mathvariant=¨bold¨ mathcolor=¨#0000FF¨»R«/mi»«mi mathvariant=¨bold¨ mathcolor=¨#0000FF¨»MQ«/mi»«/msub»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»§#183;«/mo»«mstyle mathvariant=¨bold¨ mathcolor=¨#0000FF¨»«mo stretchy=¨true¨»(«/mo»«mrow»«mn»40«/mn»«mo»-«/mo»«msub»«mi»R«/mi»«mi»MQ«/mi»«/msub»«/mrow»«mo stretchy=¨true¨»)«/mo»«/mstyle»«/mstyle»«/math»:
«math style=¨font-family:Tahoma¨ xmlns=¨http://www.w3.org/1998/Math/MathML¨»«mstyle mathsize=¨20px¨»«mfrac mathcolor=¨#0000FF¨»«mn mathvariant=¨bold¨»9«/mn»«mrow»«mn mathvariant=¨bold¨»40«/mn»«mo mathvariant=¨bold¨»-«/mo»«msub»«mi mathvariant=¨bold¨»R«/mi»«mi mathvariant=¨bold¨»MQ«/mi»«/msub»«/mrow»«/mfrac»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»=«/mo»«mn mathvariant=¨bold¨ mathcolor=¨#0000FF¨»0«/mn»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨».«/mo»«mn mathvariant=¨bold¨ mathcolor=¨#0000FF¨»3«/mn»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»+«/mo»«mfrac mathcolor=¨#0000FF¨»«mn mathvariant=¨bold¨»3«/mn»«msub»«mi mathvariant=¨bold¨»R«/mi»«mi mathvariant=¨bold¨»MQ«/mi»«/msub»«/mfrac»«mspace linebreak=¨newline¨/»«mspace linebreak=¨newline¨/»«mn mathvariant=¨bold¨ mathcolor=¨#0000FF¨»9«/mn»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»§#183;«/mo»«msub»«mi mathvariant=¨bold¨ mathcolor=¨#0000FF¨»R«/mi»«mi mathvariant=¨bold¨ mathcolor=¨#0000FF¨»MQ«/mi»«/msub»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»=«/mo»«mn mathvariant=¨bold¨ mathcolor=¨#0000FF¨»0«/mn»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨».«/mo»«mn mathvariant=¨bold¨ mathcolor=¨#0000FF¨»3«/mn»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»§#183;«/mo»«msub»«mi mathvariant=¨bold¨ mathcolor=¨#0000FF¨»R«/mi»«mi mathvariant=¨bold¨ mathcolor=¨#0000FF¨»MQ«/mi»«/msub»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»§#183;«/mo»«mrow mathcolor=¨#0000FF¨»«mo stretchy=¨true¨ mathvariant=¨bold¨»(«/mo»«mn mathvariant=¨bold¨»40«/mn»«mo mathvariant=¨bold¨»-«/mo»«msub»«mi mathvariant=¨bold¨»R«/mi»«mi mathvariant=¨bold¨»MQ«/mi»«/msub»«mo stretchy=¨true¨ mathvariant=¨bold¨»)«/mo»«/mrow»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»+«/mo»«mn mathvariant=¨bold¨ mathcolor=¨#0000FF¨»3«/mn»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»§#183;«/mo»«mrow mathcolor=¨#0000FF¨»«mo mathvariant=¨bold¨ stretchy=¨true¨»(«/mo»«mn mathvariant=¨bold¨»40«/mn»«mo mathvariant=¨bold¨»-«/mo»«msub»«mi mathvariant=¨bold¨»R«/mi»«mi mathvariant=¨bold¨»MQ«/mi»«/msub»«mo mathvariant=¨bold¨ stretchy=¨true¨»)«/mo»«/mrow»«mspace linebreak=¨newline¨/»«mspace linebreak=¨newline¨/»«mn mathvariant=¨bold¨ mathcolor=¨#0000FF¨»9«/mn»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»§#183;«/mo»«msub»«mi mathvariant=¨bold¨ mathcolor=¨#0000FF¨»R«/mi»«mi mathvariant=¨bold¨ mathcolor=¨#0000FF¨»MQ«/mi»«/msub»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»=«/mo»«mn mathvariant=¨bold¨ mathcolor=¨#0000FF¨»12«/mn»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»§#183;«/mo»«mi mathvariant=¨bold¨ mathcolor=¨#0000FF¨»R«/mi»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»-«/mo»«mn mathvariant=¨bold¨ mathcolor=¨#0000FF¨»0«/mn»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨».«/mo»«mn mathvariant=¨bold¨ mathcolor=¨#0000FF¨»3«/mn»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»§#183;«/mo»«msup»«msub»«mi mathvariant=¨bold¨ mathcolor=¨#0000FF¨»R«/mi»«mi mathvariant=¨bold¨ mathcolor=¨#0000FF¨»MQ«/mi»«/msub»«mn mathvariant=¨bold¨ mathcolor=¨#0000FF¨»2«/mn»«/msup»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»+«/mo»«mn mathvariant=¨bold¨ mathcolor=¨#0000FF¨»120«/mn»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»-«/mo»«mn mathvariant=¨bold¨ mathcolor=¨#0000FF¨»3«/mn»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»§#183;«/mo»«msub»«mi mathvariant=¨bold¨ mathcolor=¨#0000FF¨»R«/mi»«mi mathvariant=¨bold¨ mathcolor=¨#0000FF¨»MQ«/mi»«/msub»«mspace linebreak=¨newline¨/»«mspace linebreak=¨newline¨/»«mn mathvariant=¨bold¨ mathcolor=¨#0000FF¨»0«/mn»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨».«/mo»«mn mathvariant=¨bold¨ mathcolor=¨#0000FF¨»3«/mn»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»§#183;«/mo»«msup»«msub mathcolor=¨#0000FF¨»«mi mathvariant=¨bold¨»R«/mi»«mi mathvariant=¨bold¨»MQ«/mi»«/msub»«mn mathvariant=¨bold¨ mathcolor=¨#0000FF¨»2«/mn»«/msup»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»=«/mo»«mn mathvariant=¨bold¨ mathcolor=¨#0000FF¨»120«/mn»«mspace linebreak=¨newline¨/»«mspace linebreak=¨newline¨/»«msup»«msub mathcolor=¨#0000FF¨»«mi mathvariant=¨bold¨»R«/mi»«mi mathvariant=¨bold¨»MQ«/mi»«/msub»«mn mathvariant=¨bold¨ mathcolor=¨#0000FF¨»2«/mn»«/msup»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»=«/mo»«mfrac mathcolor=¨#0000FF¨»«mn mathvariant=¨bold¨»120«/mn»«mrow»«mn mathvariant=¨bold¨»0«/mn»«mo mathvariant=¨bold¨».«/mo»«mn mathvariant=¨bold¨»3«/mn»«/mrow»«/mfrac»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»=«/mo»«mn mathvariant=¨bold¨ mathcolor=¨#0000FF¨»400«/mn»«mspace linebreak=¨newline¨/»«mspace linebreak=¨newline¨/»«msub»«mi mathvariant=¨bold¨ mathcolor=¨#0000FF¨»R«/mi»«mi mathvariant=¨bold¨ mathcolor=¨#0000FF¨»MQ«/mi»«/msub»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»=«/mo»«msqrt mathcolor=¨#0000FF¨»«mn mathvariant=¨bold¨»400«/mn»«/msqrt»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»§#160;«/mo»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»=«/mo»«mn mathvariant=¨bold¨ mathcolor=¨#0000FF¨»20«/mn»«mi mathvariant=¨bold¨ mathcolor=¨#0000FF¨»§#937;«/mi»«mspace linebreak=¨newline¨/»«/mstyle»«/math»
لذلك، لكي يضيء المصباح بضوءه الكامل، يجب وضع نقطة التماس المتحركة في نقطة تكون فيها المقاومة RMQ مساوية 20 أوم.
طريقة اخرى:
نتعامل مع الدائرة المعطاة على أنها دائرة مختلطة (على التوازي وعلى التوالي)، تتكون من مقاومة RMQ موصولة على التوازي مع المصباح. المقاومة المحصلة لكليهما تكون موصولة على التوالي مع المقاومة RQN، كما هو موضح في الشكل التالي:
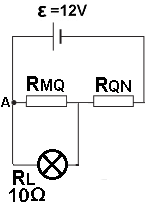
من مبادئ الدائرة التوالي، لكي يكون فرق الجهد على المصباح 3 فولط وفرق الجهد على RQN مساويًا لـ 9 فولط ، يجب أن تكون المقاومة المحصلة للمصباح و RMQ أصغر بثلاث مرات من مقاومة RQN. نكتب معادلة مقاومة وفقًا لذلك:
«math xmlns=¨http://www.w3.org/1998/Math/MathML¨»«mstyle mathsize=¨20px¨»«mfrac mathcolor=¨#0000FF¨»«mrow»«msub»«mi mathvariant=¨bold¨»R«/mi»«mi mathvariant=¨bold¨»MQ«/mi»«/msub»«mo mathvariant=¨bold¨»§#183;«/mo»«mn mathvariant=¨bold¨»10«/mn»«/mrow»«mrow»«msub»«mi mathvariant=¨bold¨»R«/mi»«mi mathvariant=¨bold¨»MQ«/mi»«/msub»«mo mathvariant=¨bold¨»+«/mo»«mn mathvariant=¨bold¨»10«/mn»«/mrow»«/mfrac»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»§#160;«/mo»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»=«/mo»«mfrac mathcolor=¨#0000FF¨»«mrow»«mo mathvariant=¨bold¨»§#160;«/mo»«msub»«mi mathvariant=¨bold¨»R«/mi»«mi mathvariant=¨bold¨»QN«/mi»«/msub»«/mrow»«mn mathvariant=¨bold¨»3«/mn»«/mfrac»«/mstyle»«/math»
نرتب المعادلة:
«math xmlns=¨http://www.w3.org/1998/Math/MathML¨»«mstyle mathsize=¨20px¨»«mfrac mathcolor=¨#0000FF¨»«mrow»«msub»«mi mathvariant=¨bold¨»R«/mi»«mi mathvariant=¨bold¨»MQ«/mi»«/msub»«mo mathvariant=¨bold¨»§#183;«/mo»«mn mathvariant=¨bold¨»10«/mn»«/mrow»«mrow»«msub»«mi mathvariant=¨bold¨»R«/mi»«mi mathvariant=¨bold¨»MQ«/mi»«/msub»«mo mathvariant=¨bold¨»+«/mo»«mn mathvariant=¨bold¨»10«/mn»«/mrow»«/mfrac»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»§#160;«/mo»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»=«/mo»«mfrac mathcolor=¨#0000FF¨»«mrow»«mo mathvariant=¨bold¨»§#160;«/mo»«msub»«mi mathvariant=¨bold¨»R«/mi»«mi mathvariant=¨bold¨»QN«/mi»«/msub»«/mrow»«mn mathvariant=¨bold¨»3«/mn»«/mfrac»«mspace linebreak=¨newline¨/»«mspace linebreak=¨newline¨/»«mn mathvariant=¨bold¨ mathcolor=¨#0000FF¨»3«/mn»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»§#183;«/mo»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»(«/mo»«msub»«mi mathvariant=¨bold¨ mathcolor=¨#0000FF¨»R«/mi»«mi mathvariant=¨bold¨ mathcolor=¨#0000FF¨»MQ«/mi»«/msub»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»§#183;«/mo»«mn mathvariant=¨bold¨ mathcolor=¨#0000FF¨»10«/mn»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»)«/mo»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»=«/mo»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»§#160;«/mo»«msub»«mi mathvariant=¨bold¨ mathcolor=¨#0000FF¨»R«/mi»«mi mathvariant=¨bold¨ mathcolor=¨#0000FF¨»QN«/mi»«/msub»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»§#183;«/mo»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»(«/mo»«msub»«mi mathvariant=¨bold¨ mathcolor=¨#0000FF¨»R«/mi»«mi mathvariant=¨bold¨ mathcolor=¨#0000FF¨»MQ«/mi»«/msub»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»+«/mo»«mn mathvariant=¨bold¨ mathcolor=¨#0000FF¨»10«/mn»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»)«/mo»«mspace linebreak=¨newline¨/»«mspace linebreak=¨newline¨/»«menclose mathcolor=¨#0000FF¨ notation=¨box¨»«mn mathvariant=¨bold¨»30«/mn»«mo mathvariant=¨bold¨»§#183;«/mo»«msub»«mi mathvariant=¨bold¨»R«/mi»«mi mathvariant=¨bold¨»MQ«/mi»«/msub»«mo mathvariant=¨bold¨»=«/mo»«msub»«mi mathvariant=¨bold¨»R«/mi»«mi mathvariant=¨bold¨»QN«/mi»«/msub»«mo mathvariant=¨bold¨»§#183;«/mo»«msub»«mi mathvariant=¨bold¨»R«/mi»«mi mathvariant=¨bold¨»MQ«/mi»«/msub»«mo mathvariant=¨bold¨»+«/mo»«mn mathvariant=¨bold¨»10«/mn»«mo mathvariant=¨bold¨»§#183;«/mo»«msub»«mi mathvariant=¨bold¨»R«/mi»«mi mathvariant=¨bold¨»QN«/mi»«/msub»«/menclose»«/mstyle»«/math»
المقاومة الكلية للمقاوم المتغير تساوي 40 أوم ، وبالتالي نكتب معادلة مقاومة اضافية:
«math style=¨font-family:Tahoma¨ xmlns=¨http://www.w3.org/1998/Math/MathML¨»«mstyle mathsize=¨20px¨»«menclose mathcolor=¨#0000FF¨ notation=¨box¨»«msub»«mi mathvariant=¨bold¨»R«/mi»«mi mathvariant=¨bold¨»MQ«/mi»«/msub»«mo mathvariant=¨bold¨»+«/mo»«msub»«mi mathvariant=¨bold¨»R«/mi»«mi mathvariant=¨bold¨»QN«/mi»«/msub»«mo mathvariant=¨bold¨»=«/mo»«mn mathvariant=¨bold¨»40«/mn»«/menclose»«/mstyle»«/math»
نحل هيئة المعادلات المكونة من معادلتين بمجهولين اثنين:
«math xmlns=¨http://www.w3.org/1998/Math/MathML¨»«mstyle mathsize=¨20px¨»«mrow mathcolor=¨#0000FF¨»«mn mathvariant=¨bold¨»1«/mn»«mo mathvariant=¨bold¨»)«/mo»«mo mathvariant=¨bold¨»§#160;«/mo»«mn mathvariant=¨bold¨»30«/mn»«mo mathvariant=¨bold¨»§#183;«/mo»«msub»«mi mathvariant=¨bold¨»R«/mi»«mi mathvariant=¨bold¨»MQ«/mi»«/msub»«mo mathvariant=¨bold¨»=«/mo»«msub»«mi mathvariant=¨bold¨»R«/mi»«mi mathvariant=¨bold¨»QN«/mi»«/msub»«mo mathvariant=¨bold¨»§#183;«/mo»«msub»«mi mathvariant=¨bold¨»R«/mi»«mi mathvariant=¨bold¨»MQ«/mi»«/msub»«mo mathvariant=¨bold¨»+«/mo»«mn mathvariant=¨bold¨»10«/mn»«mo mathvariant=¨bold¨»§#183;«/mo»«msub»«mi mathvariant=¨bold¨»R«/mi»«mi mathvariant=¨bold¨»QN«/mi»«/msub»«/mrow»«mspace linebreak=¨newline¨/»«mn mathvariant=¨bold¨ mathcolor=¨#0000FF¨»2«/mn»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»)«/mo»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»§#160;«/mo»«msub»«mi mathvariant=¨bold¨ mathcolor=¨#0000FF¨»R«/mi»«mi mathvariant=¨bold¨ mathcolor=¨#0000FF¨»MQ«/mi»«/msub»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»+«/mo»«msub»«mi mathvariant=¨bold¨ mathcolor=¨#0000FF¨»R«/mi»«mi mathvariant=¨bold¨ mathcolor=¨#0000FF¨»QN«/mi»«/msub»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»=«/mo»«mn mathvariant=¨bold¨ mathcolor=¨#0000FF¨»40«/mn»«/mstyle»«/math»
نعوّض التعبير RQN من المعادلة 2 بالمعادلة 1.
«math xmlns=¨http://www.w3.org/1998/Math/MathML¨»«mstyle mathsize=¨20px¨»«mrow»«mn mathvariant=¨bold¨ mathcolor=¨#0000FF¨»2«/mn»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»)«/mo»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»§#160;«/mo»«msub»«mi mathvariant=¨bold¨ mathcolor=¨#0000FF¨»R«/mi»«mi mathvariant=¨bold¨ mathcolor=¨#0000FF¨»MQ«/mi»«/msub»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»+«/mo»«msub»«mi mathvariant=¨bold¨ mathcolor=¨#0000FF¨»R«/mi»«mi mathvariant=¨bold¨ mathcolor=¨#0000FF¨»QN«/mi»«/msub»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»=«/mo»«mn mathvariant=¨bold¨ mathcolor=¨#0000FF¨»40«/mn»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»§#160;«/mo»«mo mathvariant=¨bold¨ mathcolor=¨#FF0000¨»§#8658;«/mo»«msub»«mi mathvariant=¨bold¨ mathcolor=¨#FF0000¨»R«/mi»«mi mathvariant=¨bold¨ mathcolor=¨#FF0000¨»QN«/mi»«/msub»«mo mathvariant=¨bold¨ mathcolor=¨#FF0000¨»=«/mo»«mn mathvariant=¨bold¨ mathcolor=¨#FF0000¨»40«/mn»«mo mathvariant=¨bold¨ mathcolor=¨#FF0000¨»-«/mo»«msub»«mi mathvariant=¨bold¨ mathcolor=¨#FF0000¨»R«/mi»«mi mathvariant=¨bold¨ mathcolor=¨#FF0000¨»MQ«/mi»«/msub»«/mrow»«mspace linebreak=¨newline¨/»«mspace linebreak=¨newline¨/»«mn mathvariant=¨bold¨ mathcolor=¨#0000FF¨»30«/mn»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»§#183;«/mo»«msub»«mi mathvariant=¨bold¨ mathcolor=¨#0000FF¨»R«/mi»«mi mathvariant=¨bold¨ mathcolor=¨#0000FF¨»MQ«/mi»«/msub»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»=«/mo»«mstyle mathvariant=¨bold¨ mathcolor=¨#FF0000¨»«mo stretchy=¨true¨»(«/mo»«mrow»«mn»40«/mn»«mo»-«/mo»«msub»«mi»R«/mi»«mi mathcolor=¨#FF0000¨»MQ«/mi»«/msub»«/mrow»«mo stretchy=¨true¨»)«/mo»«/mstyle»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»§#183;«/mo»«msub»«mi mathvariant=¨bold¨ mathcolor=¨#0000FF¨»R«/mi»«mi mathvariant=¨bold¨ mathcolor=¨#0000FF¨»MQ«/mi»«/msub»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»+«/mo»«mn mathvariant=¨bold¨ mathcolor=¨#0000FF¨»10«/mn»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»§#183;«/mo»«mstyle mathvariant=¨bold¨ mathcolor=¨#FF0000¨»«mo stretchy=¨true¨»(«/mo»«mrow»«mn»40«/mn»«mo»-«/mo»«msub»«mi»R«/mi»«mi mathcolor=¨#FF0000¨»MQ«/mi»«/msub»«/mrow»«mo stretchy=¨true¨»)«/mo»«/mstyle»«mspace linebreak=¨newline¨/»«mn mathvariant=¨bold¨ mathcolor=¨#0000FF¨»30«/mn»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»§#183;«/mo»«msub»«mi mathvariant=¨bold¨ mathcolor=¨#0000FF¨»R«/mi»«mi mathvariant=¨bold¨ mathcolor=¨#0000FF¨»MQ«/mi»«/msub»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»=«/mo»«mstyle mathvariant=¨bold¨ mathcolor=¨#FF0000¨»«mrow mathcolor=¨#0000FF¨»«mo stretchy=¨true¨»(«/mo»«mn»40«/mn»«mo»-«/mo»«msub»«mi»R«/mi»«mi»MQ«/mi»«/msub»«mo stretchy=¨true¨»)«/mo»«/mrow»«/mstyle»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»§#183;«/mo»«msub»«mi mathvariant=¨bold¨ mathcolor=¨#0000FF¨»R«/mi»«mi mathvariant=¨bold¨ mathcolor=¨#0000FF¨»MQ«/mi»«/msub»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»+«/mo»«mn mathvariant=¨bold¨ mathcolor=¨#0000FF¨»10«/mn»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»§#183;«/mo»«mstyle mathvariant=¨bold¨ mathcolor=¨#FF0000¨»«mo mathcolor=¨#0000FF¨ stretchy=¨true¨»(«/mo»«mn mathcolor=¨#0000FF¨»40«/mn»«mo mathcolor=¨#0000FF¨»-«/mo»«msub»«mi mathcolor=¨#0000FF¨»R«/mi»«mi mathcolor=¨#0000FF¨»MQ«/mi»«/msub»«mo mathcolor=¨#0000FF¨ stretchy=¨true¨»)«/mo»«/mstyle»«mspace linebreak=¨newline¨/»«mspace linebreak=¨newline¨/»«mn mathvariant=¨bold¨ mathcolor=¨#0000FF¨»30«/mn»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»§#183;«/mo»«msub»«mi mathvariant=¨bold¨ mathcolor=¨#0000FF¨»R«/mi»«mi mathvariant=¨bold¨ mathcolor=¨#0000FF¨»MQ«/mi»«/msub»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»=«/mo»«mstyle mathvariant=¨bold¨ mathcolor=¨#FF0000¨»«mn mathcolor=¨#0000FF¨»40«/mn»«mo mathcolor=¨#0000FF¨»§#183;«/mo»«msub»«mi mathcolor=¨#0000FF¨»R«/mi»«mi mathcolor=¨#0000FF¨»MQ«/mi»«/msub»«mo mathcolor=¨#0000FF¨»-«/mo»«msup»«msub mathcolor=¨#0000FF¨»«mi»R«/mi»«mi»MQ«/mi»«/msub»«mn mathcolor=¨#0000FF¨»2«/mn»«/msup»«/mstyle»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»+«/mo»«mn mathvariant=¨bold¨ mathcolor=¨#0000FF¨»400«/mn»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»-«/mo»«mstyle mathvariant=¨bold¨ mathcolor=¨#FF0000¨»«mn mathcolor=¨#0000FF¨»10«/mn»«mo mathcolor=¨#0000FF¨»§#183;«/mo»«msub»«mi mathcolor=¨#0000FF¨»R«/mi»«mi mathcolor=¨#0000FF¨»MQ«/mi»«/msub»«/mstyle»«mspace linebreak=¨newline¨/»«mspace linebreak=¨newline¨/»«msup»«msub mathcolor=¨#0000FF¨»«mi mathvariant=¨bold¨»R«/mi»«mi mathvariant=¨bold¨»MQ«/mi»«/msub»«mn mathcolor=¨#0000FF¨ mathvariant=¨bold¨»2«/mn»«/msup»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»=«/mo»«mn mathvariant=¨bold¨ mathcolor=¨#0000FF¨»400«/mn»«mspace linebreak=¨newline¨/»«mspace linebreak=¨newline¨/»«msub mathcolor=¨#0000FF¨»«mi mathvariant=¨bold¨»R«/mi»«mi mathvariant=¨bold¨»MQ«/mi»«/msub»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»=«/mo»«msqrt mathcolor=¨#0000FF¨»«mn mathvariant=¨bold¨»400«/mn»«/msqrt»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»=«/mo»«mn mathvariant=¨bold¨ mathcolor=¨#0000FF¨»20«/mn»«mfrac mathcolor=¨#0000FF¨»«mi mathvariant=¨bold¨»m«/mi»«mi mathvariant=¨bold¨»s«/mi»«/mfrac»«mspace linebreak=¨newline¨/»«msub»«mi mathvariant=¨bold¨ mathcolor=¨#0000FF¨»R«/mi»«mi mathvariant=¨bold¨ mathcolor=¨#0000FF¨»MQ«/mi»«/msub»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»=«/mo»«mn mathvariant=¨bold¨ mathcolor=¨#0000FF¨»20«/mn»«mfrac mathcolor=¨#0000FF¨»«mi mathvariant=¨bold¨»m«/mi»«mi mathvariant=¨bold¨»s«/mi»«/mfrac»«/mstyle»«/math»
لذلك، لكي يضيء المصباح بضوءه الكامل، يجب وضع نقطة التماس المتحركة في نقطة تكون فيها المقاومة RMQ مساوية 20 أوم.
19. ג.9
1. في الدائرة على التوالي، يتدفق نفس التيار عبر جميع المصابيح. نجد عدد المصابيح n التي يجب توصيلها على التوالي بحيث يكون التيار في الدائرة مساويًا للتيار المطلوب لإضاءة المصباح.
نجد شدة التيار المطلوب لإضاءة المصباح:
«math style=¨font-family:Tahoma¨ xmlns=¨http://www.w3.org/1998/Math/MathML¨»«mstyle mathsize=¨20px¨»«mi mathvariant=¨bold¨ mathcolor=¨#0000FF¨»I«/mi»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»=«/mo»«mfrac mathcolor=¨#0000FF¨»«msub»«mi mathvariant=¨bold¨»U«/mi»«msub»«mi mathvariant=¨bold¨»R«/mi»«mi mathvariant=¨bold¨»L«/mi»«/msub»«/msub»«msub»«mi mathvariant=¨bold¨»R«/mi»«mi mathvariant=¨bold¨»L«/mi»«/msub»«/mfrac»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»=«/mo»«mfrac mathcolor=¨#0000FF¨»«mn mathvariant=¨bold¨»10«/mn»«mn mathvariant=¨bold¨»5«/mn»«/mfrac»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»=«/mo»«mn mathvariant=¨bold¨ mathcolor=¨#0000FF¨»2«/mn»«mi mathvariant=¨bold¨ mathcolor=¨#0000FF¨»A«/mi»«/mstyle»«/math»
وف نعبر عن شدة التيار بدلالة عدد المصابيح الموصولة على التوالي n.
«math style=¨font-family:Tahoma¨ xmlns=¨http://www.w3.org/1998/Math/MathML¨»«mstyle mathsize=¨20px¨»«mi mathvariant=¨bold¨ mathcolor=¨#0000FF¨»I«/mi»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»=«/mo»«mfrac mathcolor=¨#0000FF¨»«mi mathvariant=¨bold¨»§#949;«/mi»«msub»«mi mathvariant=¨bold¨»R«/mi»«mi mathvariant=¨bold¨»T«/mi»«/msub»«/mfrac»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»=«/mo»«mfrac mathcolor=¨#0000FF¨»«mi mathvariant=¨bold¨»§#949;«/mi»«mrow»«mi mathvariant=¨bold¨»n«/mi»«mo mathvariant=¨bold¨»§#183;«/mo»«msub»«mi mathvariant=¨bold¨»R«/mi»«mi mathvariant=¨bold¨»L«/mi»«/msub»«mo mathvariant=¨bold¨»+«/mo»«mi mathvariant=¨bold¨»r«/mi»«/mrow»«/mfrac»«/mstyle»«/math»
نعبر عن عدد المصابيح n بدلالة شدة التيار:
«math style=¨font-family:Tahoma¨ xmlns=¨http://www.w3.org/1998/Math/MathML¨»«mstyle mathsize=¨20px¨»«mi mathvariant=¨bold¨ mathcolor=¨#0000FF¨»I«/mi»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»=«/mo»«mfrac mathcolor=¨#0000FF¨»«mi mathvariant=¨bold¨»§#949;«/mi»«mrow»«mi mathvariant=¨bold¨»n«/mi»«mo mathvariant=¨bold¨»§#183;«/mo»«msub»«mi mathvariant=¨bold¨»R«/mi»«mi mathvariant=¨bold¨»L«/mi»«/msub»«mo mathvariant=¨bold¨»+«/mo»«mi mathvariant=¨bold¨»r«/mi»«/mrow»«/mfrac»«mspace linebreak=¨newline¨/»«mspace linebreak=¨newline¨/»«mi mathvariant=¨bold¨ mathcolor=¨#0000FF¨»n«/mi»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»§#183;«/mo»«msub»«mi mathvariant=¨bold¨ mathcolor=¨#0000FF¨»R«/mi»«mi mathvariant=¨bold¨ mathcolor=¨#0000FF¨»L«/mi»«/msub»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»+«/mo»«mi mathvariant=¨bold¨ mathcolor=¨#0000FF¨»r«/mi»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»=«/mo»«mfrac mathcolor=¨#0000FF¨»«mi mathvariant=¨bold¨»§#949;«/mi»«mi mathvariant=¨bold¨»I«/mi»«/mfrac»«mspace linebreak=¨newline¨/»«mspace linebreak=¨newline¨/»«mi mathvariant=¨bold¨ mathcolor=¨#0000FF¨»n«/mi»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»§#183;«/mo»«msub»«mi mathvariant=¨bold¨ mathcolor=¨#0000FF¨»R«/mi»«mi mathvariant=¨bold¨ mathcolor=¨#0000FF¨»L«/mi»«/msub»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»=«/mo»«mfrac mathcolor=¨#0000FF¨»«mi mathvariant=¨bold¨»§#949;«/mi»«mi mathvariant=¨bold¨»I«/mi»«/mfrac»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»-«/mo»«mi mathvariant=¨bold¨ mathcolor=¨#0000FF¨»r«/mi»«mspace linebreak=¨newline¨/»«mspace linebreak=¨newline¨/»«mi mathvariant=¨bold¨ mathcolor=¨#0000FF¨»n«/mi»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»=«/mo»«mfrac mathcolor=¨#0000FF¨»«mi mathvariant=¨bold¨»§#949;«/mi»«mrow»«mi mathvariant=¨bold¨»I«/mi»«mo mathvariant=¨bold¨»§#183;«/mo»«msub»«mi mathvariant=¨bold¨»R«/mi»«mi mathvariant=¨bold¨»L«/mi»«/msub»«/mrow»«/mfrac»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»-«/mo»«mfrac mathcolor=¨#0000FF¨»«mi mathvariant=¨bold¨»r«/mi»«msub»«mi mathvariant=¨bold¨»R«/mi»«mi mathvariant=¨bold¨»L«/mi»«/msub»«/mfrac»«/mstyle»«/math»
نحسب عدد المصابيح الكهربائية n وفقًا لشدة التيار المطلوب لتشغيل المصابيح في ضوءهم الكامل:
«math style=¨font-family:Tahoma¨ xmlns=¨http://www.w3.org/1998/Math/MathML¨»«mstyle mathsize=¨20px¨»«mi mathvariant=¨bold¨ mathcolor=¨#0000FF¨»n«/mi»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»=«/mo»«mfrac mathcolor=¨#0000FF¨»«mi mathvariant=¨bold¨»§#949;«/mi»«mrow»«mi mathvariant=¨bold¨»I«/mi»«mo mathvariant=¨bold¨»§#183;«/mo»«msub»«mi mathvariant=¨bold¨»R«/mi»«mi mathvariant=¨bold¨»L«/mi»«/msub»«/mrow»«/mfrac»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»-«/mo»«mfrac mathcolor=¨#0000FF¨»«mi mathvariant=¨bold¨»r«/mi»«msub»«mi mathvariant=¨bold¨»R«/mi»«mi mathvariant=¨bold¨»L«/mi»«/msub»«/mfrac»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»=«/mo»«mfrac mathcolor=¨#0000FF¨»«mn mathvariant=¨bold¨»22«/mn»«mrow»«mn mathvariant=¨bold¨»2«/mn»«mo mathvariant=¨bold¨»§#183;«/mo»«mn mathvariant=¨bold¨»5«/mn»«/mrow»«/mfrac»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»-«/mo»«mfrac mathcolor=¨#0000FF¨»«mn mathvariant=¨bold¨»1«/mn»«mn mathvariant=¨bold¨»5«/mn»«/mfrac»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»=«/mo»«mn mathvariant=¨bold¨ mathcolor=¨#0000FF¨»2«/mn»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨».«/mo»«mn mathvariant=¨bold¨ mathcolor=¨#0000FF¨»2«/mn»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»-«/mo»«mn mathvariant=¨bold¨ mathcolor=¨#0000FF¨»0«/mn»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨».«/mo»«mn mathvariant=¨bold¨ mathcolor=¨#0000FF¨»2«/mn»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»=«/mo»«mn mathvariant=¨bold¨ mathcolor=¨#0000FF¨»2«/mn»«/mstyle»«/math»
لذلك ، لكي تضيء المصابيح في ضوء كامل، يجب توصيل مصباحين بمصدر فرق الجهد.
2. في الدائرة على التوازي، يكون فرق الجهد على المصابيح متماثل ويساوي فرق جهد الأقطاب. لكي يضيء المصباح بضوءه الكامل، يجب أن يكون فرق الجهد الكهربائي عليه 10 فولط.
نكتب تعبيرًا لفرق جهد الأقطاب بدلالة عدد المصابيح n:
«math style=¨font-family:Tahoma¨ xmlns=¨http://www.w3.org/1998/Math/MathML¨»«mstyle mathsize=¨20px¨»«mi mathvariant=¨bold¨ mathcolor=¨#0000FF¨»Vab«/mi»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»=«/mo»«mi mathvariant=¨bold¨ mathcolor=¨#0000FF¨»§#949;«/mi»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»-«/mo»«mi mathvariant=¨bold¨ mathcolor=¨#0000FF¨»I«/mi»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»§#183;«/mo»«mi mathvariant=¨bold¨ mathcolor=¨#0000FF¨»r«/mi»«mspace linebreak=¨newline¨/»«mspace linebreak=¨newline¨/»«mi mathvariant=¨bold¨ mathcolor=¨#0000FF¨»Vab«/mi»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»=«/mo»«mi mathvariant=¨bold¨ mathcolor=¨#0000FF¨»§#949;«/mi»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»-«/mo»«mfrac mathcolor=¨#0000FF¨»«mi mathvariant=¨bold¨»§#949;«/mi»«msub»«mi mathvariant=¨bold¨»R«/mi»«mi mathvariant=¨bold¨»T«/mi»«/msub»«/mfrac»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»§#183;«/mo»«mi mathvariant=¨bold¨ mathcolor=¨#0000FF¨»r«/mi»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»=«/mo»«mi mathvariant=¨bold¨ mathcolor=¨#0000FF¨»§#949;«/mi»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»-«/mo»«mfrac mathcolor=¨#0000FF¨»«mi mathvariant=¨bold¨»§#949;«/mi»«mrow»«mstyle displaystyle=¨true¨»«mfrac»«msub»«mi mathvariant=¨bold¨»R«/mi»«mi mathvariant=¨bold¨»L«/mi»«/msub»«mi mathvariant=¨bold¨»n«/mi»«/mfrac»«/mstyle»«mo mathvariant=¨bold¨»+«/mo»«mi mathvariant=¨bold¨»r«/mi»«/mrow»«/mfrac»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»§#183;«/mo»«mi mathvariant=¨bold¨ mathcolor=¨#0000FF¨»r«/mi»«mspace linebreak=¨newline¨/»«mfrac mathcolor=¨#0000FF¨»«mrow»«mi mathvariant=¨bold¨»§#949;«/mi»«mo mathvariant=¨bold¨»§#183;«/mo»«mi mathvariant=¨bold¨»r«/mi»«/mrow»«mstyle displaystyle=¨true¨ mathvariant=¨bold¨»«mfrac»«msub»«mi»R«/mi»«mi»L«/mi»«/msub»«mi»n«/mi»«/mfrac»«mo»+«/mo»«mi»r«/mi»«/mstyle»«/mfrac»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»=«/mo»«mi mathvariant=¨bold¨ mathcolor=¨#0000FF¨»§#949;«/mi»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»-«/mo»«mi mathvariant=¨bold¨ mathcolor=¨#0000FF¨»Vab«/mi»«mspace linebreak=¨newline¨/»«mspace linebreak=¨newline¨/»«mfrac mathcolor=¨#0000FF¨»«msub»«mi mathvariant=¨bold¨»R«/mi»«mi mathvariant=¨bold¨»L«/mi»«/msub»«mi mathvariant=¨bold¨»n«/mi»«/mfrac»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»+«/mo»«mi mathvariant=¨bold¨ mathcolor=¨#0000FF¨»r«/mi»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»=«/mo»«mfrac mathcolor=¨#0000FF¨»«mrow»«mi mathvariant=¨bold¨»§#949;«/mi»«mo mathvariant=¨bold¨»§#183;«/mo»«mi mathvariant=¨bold¨»r«/mi»«/mrow»«mrow»«mi mathvariant=¨bold¨»§#949;«/mi»«mo mathvariant=¨bold¨»-«/mo»«mi mathvariant=¨bold¨»Vab«/mi»«/mrow»«/mfrac»«mspace linebreak=¨newline¨/»«mspace linebreak=¨newline¨/»«mfrac mathcolor=¨#0000FF¨»«msub»«mi mathvariant=¨bold¨»R«/mi»«mi mathvariant=¨bold¨»L«/mi»«/msub»«mi mathvariant=¨bold¨»n«/mi»«/mfrac»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»=«/mo»«mfrac mathcolor=¨#0000FF¨»«mrow»«mi mathvariant=¨bold¨»§#949;«/mi»«mo mathvariant=¨bold¨»§#183;«/mo»«mi mathvariant=¨bold¨»r«/mi»«/mrow»«mrow»«mi mathvariant=¨bold¨»§#949;«/mi»«mo mathvariant=¨bold¨»-«/mo»«mi mathvariant=¨bold¨»Vab«/mi»«/mrow»«/mfrac»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»-«/mo»«mi mathvariant=¨bold¨ mathcolor=¨#0000FF¨»r«/mi»«mspace linebreak=¨newline¨/»«mspace linebreak=¨newline¨/»«mi mathvariant=¨bold¨ mathcolor=¨#0000FF¨»n«/mi»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»=«/mo»«mfrac mathcolor=¨#0000FF¨»«msub»«mi mathvariant=¨bold¨»R«/mi»«mi mathvariant=¨bold¨»L«/mi»«/msub»«mrow»«mfrac»«mrow»«mi mathvariant=¨bold¨»§#949;«/mi»«mo mathvariant=¨bold¨»§#183;«/mo»«mi mathvariant=¨bold¨»r«/mi»«/mrow»«mrow»«mi mathvariant=¨bold¨»§#949;«/mi»«mo mathvariant=¨bold¨»-«/mo»«mi mathvariant=¨bold¨»Vab«/mi»«/mrow»«/mfrac»«mo mathvariant=¨bold¨»-«/mo»«mi mathvariant=¨bold¨»r«/mi»«/mrow»«/mfrac»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»=«/mo»«mfrac mathcolor=¨#0000FF¨»«mn mathvariant=¨bold¨»5«/mn»«mrow»«mfrac»«mrow»«mn mathvariant=¨bold¨»22«/mn»«mo mathvariant=¨bold¨»§#183;«/mo»«mn mathvariant=¨bold¨»1«/mn»«/mrow»«mrow»«mn mathvariant=¨bold¨»22«/mn»«mo mathvariant=¨bold¨»-«/mo»«mn mathvariant=¨bold¨»10«/mn»«/mrow»«/mfrac»«mo mathvariant=¨bold¨»-«/mo»«mn mathvariant=¨bold¨»1«/mn»«/mrow»«/mfrac»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»=«/mo»«mfrac mathcolor=¨#0000FF¨»«mn mathvariant=¨bold¨»5«/mn»«mrow»«mfrac»«mn mathvariant=¨bold¨»22«/mn»«mn mathvariant=¨bold¨»12«/mn»«/mfrac»«mo mathvariant=¨bold¨»-«/mo»«mn mathvariant=¨bold¨»1«/mn»«/mrow»«/mfrac»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»=«/mo»«mfrac mathcolor=¨#0000FF¨»«mn mathvariant=¨bold¨»5«/mn»«mrow»«mn mathvariant=¨bold¨»1«/mn»«mo mathvariant=¨bold¨».«/mo»«mn mathvariant=¨bold¨»833«/mn»«mo mathvariant=¨bold¨»-«/mo»«mn mathvariant=¨bold¨»1«/mn»«/mrow»«/mfrac»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»=«/mo»«mfrac mathcolor=¨#0000FF¨»«mn mathvariant=¨bold¨»5«/mn»«mrow»«mn mathvariant=¨bold¨»0«/mn»«mo mathvariant=¨bold¨».«/mo»«mn mathvariant=¨bold¨»833«/mn»«/mrow»«/mfrac»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»=«/mo»«mn mathvariant=¨bold¨ mathcolor=¨#0000FF¨»6«/mn»«/mstyle»«/math»
لذلك ، لكي تضيء المصابيح في ضوءها الكامل، يجب توصيل ستة مصابيح على التوازي بمصدر فرق الجهد.
20. ד.1
أ- الدائرة المعطاة هي دائرة مختلطة - موصولة على التوازي وعلى التوالي، نكتب تعبيرًا للمقاومة المحصلة:
«math xmlns=¨http://www.w3.org/1998/Math/MathML¨»«mstyle mathsize=¨20px¨»«msub»«mi mathvariant=¨bold¨ mathcolor=¨#0000FF¨»R«/mi»«mi mathvariant=¨bold¨ mathcolor=¨#0000FF¨»T«/mi»«/msub»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»=«/mo»«mstyle mathvariant=¨bold¨ mathcolor=¨#0000FF¨»«mo stretchy=¨true¨»[«/mo»«mrow»«mo»(«/mo»«msub»«mi»R«/mi»«mn»2«/mn»«/msub»«mo»+«/mo»«msub»«mi»R«/mi»«mn»3«/mn»«/msub»«mo»)«/mo»«mo»|«/mo»«mo»|«/mo»«msub»«mi»R«/mi»«mn»1«/mn»«/msub»«/mrow»«mo stretchy=¨true¨»]«/mo»«/mstyle»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»+«/mo»«mi mathvariant=¨bold¨ mathcolor=¨#0000FF¨»r«/mi»«mspace linebreak=¨newline¨/»«mspace linebreak=¨newline¨/»«msub»«mi mathvariant=¨bold¨ mathcolor=¨#0000FF¨»R«/mi»«mi mathvariant=¨bold¨ mathcolor=¨#0000FF¨»T«/mi»«/msub»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»=«/mo»«mfrac mathcolor=¨#0000FF¨»«mrow»«mn mathvariant=¨bold¨»20«/mn»«mo mathvariant=¨bold¨»§#183;«/mo»«mn mathvariant=¨bold¨»10«/mn»«/mrow»«mrow»«mn mathvariant=¨bold¨»20«/mn»«mo mathvariant=¨bold¨»+«/mo»«mn mathvariant=¨bold¨»10«/mn»«/mrow»«/mfrac»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»+«/mo»«mn mathvariant=¨bold¨ mathcolor=¨#0000FF¨»1«/mn»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»=«/mo»«mn mathvariant=¨bold¨ mathcolor=¨#0000FF¨»7«/mn»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨».«/mo»«mn mathvariant=¨bold¨ mathcolor=¨#0000FF¨»66«/mn»«mi mathvariant=¨bold¨ mathcolor=¨#0000FF¨»§#937;«/mi»«/mstyle»«/math»
ب- نحسب شدة التيار بمصدر فرق الجهد باستخدام قانون أوم للدائرة بأكملها:
«math style=¨font-family:Tahoma¨ xmlns=¨http://www.w3.org/1998/Math/MathML¨»«mstyle mathsize=¨20px¨»«mi mathvariant=¨bold¨ mathcolor=¨#0000FF¨»I«/mi»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»=«/mo»«mfrac mathcolor=¨#0000FF¨»«mi mathvariant=¨bold¨»§#949;«/mi»«msub»«mi mathvariant=¨bold¨»R«/mi»«mi mathvariant=¨bold¨»T«/mi»«/msub»«/mfrac»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»=«/mo»«mfrac mathcolor=¨#0000FF¨»«mn mathvariant=¨bold¨»12«/mn»«mrow»«mn mathvariant=¨bold¨»7«/mn»«mo mathvariant=¨bold¨».«/mo»«mn mathvariant=¨bold¨»66«/mn»«/mrow»«/mfrac»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»=«/mo»«mn mathvariant=¨bold¨ mathcolor=¨#0000FF¨»1«/mn»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨».«/mo»«mn mathvariant=¨bold¨ mathcolor=¨#0000FF¨»57«/mn»«mi mathvariant=¨bold¨ mathcolor=¨#0000FF¨»A«/mi»«/mstyle»«/math»
ج- نحسب فرق جهد الأقطاب بمساعدة تعبير فرق جهد الأقطاب:
«math style=¨font-family:Tahoma¨ xmlns=¨http://www.w3.org/1998/Math/MathML¨»«mi mathvariant=¨bold¨ mathcolor=¨#0000FF¨ mathsize=¨20px¨»Vab«/mi»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨ mathsize=¨20px¨»=«/mo»«mi mathvariant=¨bold¨ mathcolor=¨#0000FF¨ mathsize=¨20px¨»§#949;«/mi»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨ mathsize=¨20px¨»-«/mo»«mi mathvariant=¨bold¨ mathcolor=¨#0000FF¨ mathsize=¨20px¨»I«/mi»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨ mathsize=¨20px¨»§#183;«/mo»«mi mathvariant=¨bold¨ mathcolor=¨#0000FF¨ mathsize=¨20px¨»r«/mi»«mspace linebreak=¨newline¨/»«mi mathvariant=¨bold¨ mathcolor=¨#0000FF¨ mathsize=¨20px¨»Vab«/mi»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨ mathsize=¨20px¨»=«/mo»«mn mathvariant=¨bold¨ mathcolor=¨#0000FF¨ mathsize=¨20px¨»12«/mn»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨ mathsize=¨20px¨»-«/mo»«mn mathvariant=¨bold¨ mathcolor=¨#0000FF¨ mathsize=¨20px¨»1«/mn»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨ mathsize=¨20px¨».«/mo»«mn mathvariant=¨bold¨ mathcolor=¨#0000FF¨ mathsize=¨20px¨»57«/mn»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨ mathsize=¨20px¨»§#183;«/mo»«mn mathvariant=¨bold¨ mathcolor=¨#0000FF¨ mathsize=¨20px¨»1«/mn»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨ mathsize=¨20px¨»=«/mo»«mn mathvariant=¨bold¨ mathcolor=¨#0000FF¨ mathsize=¨20px¨»10«/mn»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨ mathsize=¨20px¨».«/mo»«mn mathvariant=¨bold¨ mathcolor=¨#0000FF¨ mathsize=¨20px¨»43«/mn»«mi mathvariant=¨bold¨ mathcolor=¨#0000FF¨ mathsize=¨20px¨»V«/mi»«mspace linebreak=¨newline¨/»«mspace linebreak=¨newline¨/»«mspace linebreak=¨newline¨/»«/math»
د- لحساب فرق الجهد على R2، نجد شدة التيار المار عبره.
نشير لشدة تيار المصدر بـ I ، التيار عبر R1 بـ I1 والتيار عبر R2 بـ I2 ، تظهر التيارات الثلاثة في الشكل التالي:
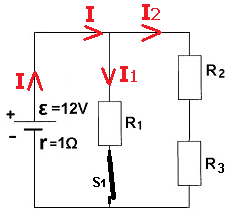
من قانون العقدة يتحقق:
«math style=¨font-family:Tahoma¨ xmlns=¨http://www.w3.org/1998/Math/MathML¨»«mstyle mathsize=¨20px¨»«mi mathvariant=¨bold¨ mathcolor=¨#0000FF¨»I«/mi»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»=«/mo»«msub»«mi mathvariant=¨bold¨ mathcolor=¨#0000FF¨»I«/mi»«mn mathvariant=¨bold¨ mathcolor=¨#0000FF¨»1«/mn»«/msub»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»+«/mo»«msub»«mi mathvariant=¨bold¨ mathcolor=¨#0000FF¨»I«/mi»«mn mathvariant=¨bold¨ mathcolor=¨#0000FF¨»2«/mn»«/msub»«mspace linebreak=¨newline¨/»«menclose mathcolor=¨#0000FF¨ notation=¨box¨»«mn mathvariant=¨bold¨»1«/mn»«mo mathvariant=¨bold¨».«/mo»«mn mathvariant=¨bold¨»57«/mn»«mo mathvariant=¨bold¨»=«/mo»«msub»«mi mathvariant=¨bold¨»I«/mi»«mn mathvariant=¨bold¨»1«/mn»«/msub»«mo mathvariant=¨bold¨»+«/mo»«msub»«mi mathvariant=¨bold¨»I«/mi»«mn mathvariant=¨bold¨»2«/mn»«/msub»«/menclose»«/mstyle»«/math»
المقاومة المحصلة للمقاومين R2 و R3 أكبر بمرتين من مقاومة المقاوم R1 ، وبالتالي فإن التيار المتدفق عبر R1 أكبر بمرتين من التيار المتدفق عبر R23 :
وبناءً عليه، تتحقق المعادلة التالية للتيارات :
«math style=¨font-family:Tahoma¨ xmlns=¨http://www.w3.org/1998/Math/MathML¨»«mstyle mathsize=¨20px¨»«menclose mathcolor=¨#0000FF¨ notation=¨box¨»«msub»«mi mathvariant=¨bold¨»I«/mi»«mn mathvariant=¨bold¨»1«/mn»«/msub»«mo mathvariant=¨bold¨»=«/mo»«mn mathvariant=¨bold¨»2«/mn»«mo mathvariant=¨bold¨»§#183;«/mo»«msub»«mi mathvariant=¨bold¨»I«/mi»«mn mathvariant=¨bold¨»2«/mn»«/msub»«/menclose»«/mstyle»«/math»
نحل هيئة المعادلات المكونة من معادلتين بمجهولين:
«math style=¨font-family:Tahoma¨ xmlns=¨http://www.w3.org/1998/Math/MathML¨»«mstyle mathsize=¨20px¨»«mrow»«mn mathvariant=¨bold¨ mathcolor=¨#0000FF¨»1«/mn»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»)«/mo»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»§#160;«/mo»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»§#160;«/mo»«mn mathvariant=¨bold¨ mathcolor=¨#0000FF¨»1«/mn»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨».«/mo»«mn mathvariant=¨bold¨ mathcolor=¨#0000FF¨»57«/mn»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»=«/mo»«msub»«mi mathvariant=¨bold¨ mathcolor=¨#0000FF¨»I«/mi»«mn mathvariant=¨bold¨ mathcolor=¨#0000FF¨»1«/mn»«/msub»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»+«/mo»«msub»«mi mathvariant=¨bold¨ mathcolor=¨#0000FF¨»I«/mi»«mn mathvariant=¨bold¨ mathcolor=¨#0000FF¨»2«/mn»«/msub»«/mrow»«mspace linebreak=¨newline¨/»«mn mathvariant=¨bold¨ mathcolor=¨#0000FF¨»2«/mn»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»)«/mo»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»§#160;«/mo»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»§#160;«/mo»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»§#160;«/mo»«msub»«mi mathvariant=¨bold¨ mathcolor=¨#0000FF¨»I«/mi»«mn mathvariant=¨bold¨ mathcolor=¨#0000FF¨»1«/mn»«/msub»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»=«/mo»«mn mathvariant=¨bold¨ mathcolor=¨#0000FF¨»2«/mn»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»§#183;«/mo»«msub»«mi mathvariant=¨bold¨ mathcolor=¨#0000FF¨»I«/mi»«mn mathvariant=¨bold¨ mathcolor=¨#0000FF¨»2«/mn»«/msub»«/mstyle»«/math»
نعوّض I1 من المعادلة الأولى في المعادلة الثانية، ونجد I2:
«math style=¨font-family:Tahoma¨ xmlns=¨http://www.w3.org/1998/Math/MathML¨»«mstyle mathsize=¨20px¨»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»§#160;«/mo»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»§#160;«/mo»«mn mathvariant=¨bold¨ mathcolor=¨#0000FF¨»1«/mn»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨».«/mo»«mn mathvariant=¨bold¨ mathcolor=¨#0000FF¨»57«/mn»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»=«/mo»«mn mathvariant=¨bold¨ mathcolor=¨#FF0000¨»2«/mn»«mo mathvariant=¨bold¨ mathcolor=¨#FF0000¨»§#183;«/mo»«msub»«mi mathvariant=¨bold¨ mathcolor=¨#FF0000¨»I«/mi»«mn mathvariant=¨bold¨ mathcolor=¨#FF0000¨»2«/mn»«/msub»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»+«/mo»«msub»«mi mathvariant=¨bold¨ mathcolor=¨#0000FF¨»I«/mi»«mn mathvariant=¨bold¨ mathcolor=¨#0000FF¨»2«/mn»«/msub»«mspace linebreak=¨newline¨/»«mspace linebreak=¨newline¨/»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»§#160;«/mo»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»§#160;«/mo»«mn mathvariant=¨bold¨ mathcolor=¨#0000FF¨»1«/mn»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨».«/mo»«mn mathvariant=¨bold¨ mathcolor=¨#0000FF¨»57«/mn»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»=«/mo»«mn mathvariant=¨bold¨ mathcolor=¨#0000FF¨»3«/mn»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»§#183;«/mo»«msub»«mi mathvariant=¨bold¨ mathcolor=¨#0000FF¨»I«/mi»«mn mathvariant=¨bold¨ mathcolor=¨#0000FF¨»2«/mn»«/msub»«mspace linebreak=¨newline¨/»«mspace linebreak=¨newline¨/»«msub»«mi mathvariant=¨bold¨ mathcolor=¨#0000FF¨»I«/mi»«mn mathvariant=¨bold¨ mathcolor=¨#0000FF¨»2«/mn»«/msub»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»=«/mo»«mfrac mathcolor=¨#0000FF¨»«mrow»«mn mathvariant=¨bold¨»1«/mn»«mo mathvariant=¨bold¨».«/mo»«mn mathvariant=¨bold¨»57«/mn»«/mrow»«mn mathvariant=¨bold¨»3«/mn»«/mfrac»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»=«/mo»«mn mathvariant=¨bold¨ mathcolor=¨#0000FF¨»0«/mn»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨».«/mo»«mn mathvariant=¨bold¨ mathcolor=¨#0000FF¨»52«/mn»«mi mathvariant=¨bold¨ mathcolor=¨#0000FF¨»A«/mi»«/mstyle»«/math»
نحسب فرق الجهد على R2 بواسطة قانون أوم:
«math xmlns=¨http://www.w3.org/1998/Math/MathML¨»«mstyle mathsize=¨20px¨»«msub»«mi mathvariant=¨bold¨ mathcolor=¨#0000FF¨»U«/mi»«msub mathcolor=¨#0000FF¨»«mi mathvariant=¨bold¨»R«/mi»«mn mathvariant=¨bold¨»2«/mn»«/msub»«/msub»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»=«/mo»«msub»«mi mathvariant=¨bold¨ mathcolor=¨#0000FF¨»I«/mi»«mn mathvariant=¨bold¨ mathcolor=¨#0000FF¨»2«/mn»«/msub»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»§#183;«/mo»«msub»«mi mathvariant=¨bold¨ mathcolor=¨#0000FF¨»R«/mi»«mn mathvariant=¨bold¨ mathcolor=¨#0000FF¨»2«/mn»«/msub»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»=«/mo»«mn mathvariant=¨bold¨ mathcolor=¨#0000FF¨»0«/mn»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨».«/mo»«mn mathvariant=¨bold¨ mathcolor=¨#0000FF¨»52«/mn»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»§#183;«/mo»«mn mathvariant=¨bold¨ mathcolor=¨#0000FF¨»10«/mn»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»=«/mo»«mn mathvariant=¨bold¨ mathcolor=¨#0000FF¨»5«/mn»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨».«/mo»«mn mathvariant=¨bold¨ mathcolor=¨#0000FF¨»2«/mn»«mi mathvariant=¨bold¨ mathcolor=¨#0000FF¨»V«/mi»«/mstyle»«/math»
طريقة أخرى: مجموع فرقي الجهد على المقاومتين R2 و R3 يساوي فرق الجهد الأقطاب. نظرًا لأن مقاومة المقاومتين R2 و R3 متساوية، فإن فرق الجهد على المقاومتين متماثل ويساوي نصف فرق جهد الأقطاب.
«math xmlns=¨http://www.w3.org/1998/Math/MathML¨»«mstyle mathsize=¨20px¨»«msub»«mi mathvariant=¨bold¨ mathcolor=¨#0000FF¨»U«/mi»«msub mathcolor=¨#0000FF¨»«mi mathvariant=¨bold¨»R«/mi»«mn mathvariant=¨bold¨»2«/mn»«/msub»«/msub»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»=«/mo»«mfrac mathcolor=¨#0000FF¨»«mi mathvariant=¨bold¨»Vab«/mi»«mn mathvariant=¨bold¨»2«/mn»«/mfrac»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»=«/mo»«mfrac mathcolor=¨#0000FF¨»«mrow»«mn mathvariant=¨bold¨»10«/mn»«mo mathvariant=¨bold¨».«/mo»«mn mathvariant=¨bold¨»4«/mn»«/mrow»«mn mathvariant=¨bold¨»2«/mn»«/mfrac»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»=«/mo»«mn mathvariant=¨bold¨ mathcolor=¨#0000FF¨»5«/mn»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨».«/mo»«mn mathvariant=¨bold¨ mathcolor=¨#0000FF¨»2«/mn»«mi mathvariant=¨bold¨ mathcolor=¨#0000FF¨»V«/mi»«/mstyle»«/math»
21. ד.2
أ.1- المعادلة الصحيحة - النقطتان R و Q موجودتان على موصل مقاومته مهملة، وبالتالي فإن النقطتين لهما نفس الجهد.
أ.2-معادلة غير صحيحة - بين النقطتين P و Q يوجد مقاوم مقاومته غير مهملة، وفرق الجهد بين النقطتين P و Q يساوي فرق الجهد على R1.
أ.3-معادلة غير صحيحة - بين النقطتين P و M يوجد مقاوم مقاومته غير مهملة، وفرق الجهد بين النقطتين P و M يساوي فرق الجهد على R2..
ب.1- المعادلة صحيحة - الجهد في النقطة P هو نفس الجهد في النقطة K، والجهد في النقطة Q هو نفس الجهد في النقطة N.
لذلك فإن فرق الجهد على المقاوم R1 هو مساوٍ لمجموع فرقي الجهد على R2 و R3.
ب.2- المعادلة غير صحيحة - الجهد في النقطة Q هو نفس الجهد في النقطة R ويساوي جهد القطب السالب للمصدر.
فرق الجهد بين النقطتين Q و R يساوي صفر ولا يساوي فرق جهد الأقطاب.
ب.3- المعادلة صحيحة - الجهد في النقطة Q هو نفس جهد القطب السالب للبطارية، والجهد في النقطة P هو نفس جهد القطب الموجب، وبالتالي فإن فرق الجهد بين النقطتين P و Q يساوي فرق جهد الأقطاب للبطارية.
ج- الجهد في النقطتين P و K يساوي الجهد الموجب (أعلى جهد).
الجهد في النقاط Q و R و N هو نفس الجهد ويساوي جهد القطب السالب (أدنى جهد).
ينتقل التيار من الجهد العالي إلى الجهد المنخفض، وفقًا لاتجاه التيار، يكون الجهد في النقطة M أصغر من الجهد في النقطة K وأكبر
من الجهد في النقطة N.
تدريج الجهود: «math xmlns=¨http://www.w3.org/1998/Math/MathML¨»«mstyle mathsize=¨20px¨»«msub»«mi mathvariant=¨bold¨ mathcolor=¨#7F007F¨»V«/mi»«mi mathvariant=¨bold¨ mathcolor=¨#7F007F¨»P«/mi»«/msub»«mo mathvariant=¨bold¨ mathcolor=¨#7F007F¨»=«/mo»«msub»«mi mathvariant=¨bold¨ mathcolor=¨#7F007F¨»V«/mi»«mi mathvariant=¨bold¨ mathcolor=¨#7F007F¨»K«/mi»«/msub»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»§#62;«/mo»«msub»«mi mathvariant=¨bold¨»V«/mi»«mi mathvariant=¨bold¨»M«/mi»«/msub»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»§#62;«/mo»«msub»«mi mathvariant=¨bold¨ mathcolor=¨#007F00¨»V«/mi»«mi mathvariant=¨bold¨ mathcolor=¨#007F00¨»N«/mi»«/msub»«mo mathvariant=¨bold¨ mathcolor=¨#007F00¨»=«/mo»«msub»«mi mathvariant=¨bold¨ mathcolor=¨#007F00¨»V«/mi»«mi mathvariant=¨bold¨ mathcolor=¨#007F00¨»R«/mi»«/msub»«mo mathvariant=¨bold¨ mathcolor=¨#007F00¨»=«/mo»«msub»«mi mathvariant=¨bold¨ mathcolor=¨#007F00¨»V«/mi»«mi mathvariant=¨bold¨ mathcolor=¨#007F00¨»Q«/mi»«/msub»«/mstyle»«/math»
22. ד.3
أ - نتيجة لفتح قاطع الدائرة، يتم الحصول على دائرة على التوالي تكون مقاومتها أكبر من مقاومة الدائرة المعطاة في القسم السابق.
مع زيادة المقاومة المحصلة، ستنخفض شدة التيار في الدائرة.
من تعبير فرق جهد الأقطاب: «math style=¨font-family:Tahoma¨ xmlns=¨http://www.w3.org/1998/Math/MathML¨»«mi mathvariant=¨bold¨ mathcolor=¨#0000FF¨ mathsize=¨20px¨»Vab«/mi»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨ mathsize=¨20px¨»=«/mo»«mi mathvariant=¨bold¨ mathcolor=¨#0000FF¨ mathsize=¨20px¨»§#949;«/mi»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨ mathsize=¨20px¨»-«/mo»«mi mathvariant=¨bold¨ mathcolor=¨#0000FF¨ mathsize=¨20px¨»I«/mi»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨ mathsize=¨20px¨»§#183;«/mo»«mi mathvariant=¨bold¨ mathcolor=¨#0000FF¨ mathsize=¨20px¨»r«/mi»«/math» عندما يقل التيار، يزداد فرق جهد الأقطاب.
ب- نحسب شدة التيار في الدائرة بعد فتح القاطع:
«math style=¨font-family:Tahoma¨ xmlns=¨http://www.w3.org/1998/Math/MathML¨»«mstyle mathsize=¨20px¨»«mi mathvariant=¨bold¨ mathcolor=¨#0000FF¨»I«/mi»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»=«/mo»«mfrac mathcolor=¨#0000FF¨»«mi mathvariant=¨bold¨»§#949;«/mi»«msub»«mi mathvariant=¨bold¨»R«/mi»«mi mathvariant=¨bold¨»T«/mi»«/msub»«/mfrac»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»=«/mo»«mfrac mathcolor=¨#0000FF¨»«mi mathvariant=¨bold¨»§#949;«/mi»«mrow»«msub»«mi mathvariant=¨bold¨»R«/mi»«mn mathvariant=¨bold¨»2«/mn»«/msub»«mo mathvariant=¨bold¨»+«/mo»«msub»«mi mathvariant=¨bold¨»R«/mi»«mn mathvariant=¨bold¨»3«/mn»«/msub»«mo mathvariant=¨bold¨»+«/mo»«mi mathvariant=¨bold¨»r«/mi»«/mrow»«/mfrac»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»=«/mo»«mfrac mathcolor=¨#0000FF¨»«mn mathvariant=¨bold¨»12«/mn»«mrow»«mn mathvariant=¨bold¨»1«/mn»«mo mathvariant=¨bold¨»+«/mo»«mn mathvariant=¨bold¨»10«/mn»«mo mathvariant=¨bold¨»+«/mo»«mn mathvariant=¨bold¨»10«/mn»«/mrow»«/mfrac»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»=«/mo»«mfrac mathcolor=¨#0000FF¨»«mn mathvariant=¨bold¨»12«/mn»«mn mathvariant=¨bold¨»21«/mn»«/mfrac»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»=«/mo»«mn mathvariant=¨bold¨ mathcolor=¨#0000FF¨»0«/mn»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨».«/mo»«mn mathvariant=¨bold¨ mathcolor=¨#0000FF¨»57«/mn»«mi mathvariant=¨bold¨ mathcolor=¨#0000FF¨»A«/mi»«/mstyle»«/math»
نحسب فرق الجهد على R2 ، باستخدام قانون أوم على المقاوم R2:
«math xmlns=¨http://www.w3.org/1998/Math/MathML¨»«mstyle mathsize=¨20px¨»«msub»«mi mathvariant=¨bold¨ mathcolor=¨#0000FF¨»U«/mi»«mrow mathcolor=¨#0000FF¨»«mi mathvariant=¨bold¨»R«/mi»«mn mathvariant=¨bold¨»2«/mn»«/mrow»«/msub»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»=«/mo»«mi mathvariant=¨bold¨ mathcolor=¨#0000FF¨»I«/mi»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»§#183;«/mo»«msub»«mi mathvariant=¨bold¨ mathcolor=¨#0000FF¨»R«/mi»«mn mathvariant=¨bold¨ mathcolor=¨#0000FF¨»2«/mn»«/msub»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»=«/mo»«mn mathvariant=¨bold¨ mathcolor=¨#0000FF¨»0«/mn»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨».«/mo»«mn mathvariant=¨bold¨ mathcolor=¨#0000FF¨»57«/mn»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»§#183;«/mo»«mn mathvariant=¨bold¨ mathcolor=¨#0000FF¨»10«/mn»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»=«/mo»«mn mathvariant=¨bold¨ mathcolor=¨#0000FF¨»5«/mn»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨».«/mo»«mn mathvariant=¨bold¨ mathcolor=¨#0000FF¨»7«/mn»«mi mathvariant=¨bold¨ mathcolor=¨#0000FF¨»V«/mi»«/mstyle»«/math»
لذلك ، سيزداد فرق الجهد على R2.
23. ד.4
أ.1- معادلة غير صحيحة - النقطتان R و Q على موصلات مختلفة ، لذلك الجهد مختلف في النقطتين.
أ.2- المعادلة الصحيحة - نتيجة لفتح قاطع الدائرة، لا يتدفق التيار عبر المقاوم R1، وفرق الجهد على R1 يساوي صفر. الجهد في النقطة P يساوي الجهد في النقطة Q.
أ.3- معادلة غير صحيحة - بين النقطتين P و M يوجد مقاوم مقاومته غير مهملة، وفرق الجهد بين النقطتين P و M يساوي فرق الجهد على R2.
ب.1- المعادلة غير صحيحة - الجهد في النقطة Q مختلف عن الجهد في النقطة N.
فرق الجهد بين النقطتين P و- Q يساوي صفرًا. فرق الجهد بين النقطتين K و- N لا يساوي صفر.
ب.2- المعادلة صحيحة - الجهد في النقطة Q يساوي جهد القطب الموجب للبطارية.
الجهد في النقطة R هو نفس جهد القطب السالب.
لذلك فإن فرق الجهد بين النقطتين Q و- R يساوي فرق جهد الأقطاب.
ب.3- المعادلة غير صحيحة - الجهد في النقطة P هو نفس الجهد في النقطة Q. هاذان الجهدان يساويان الجهد على القطب الموجب.
فرق الجهد بين النقطتين P و- Q يساوي صفرًا، من ناحية أخرى، فرق جهد الأقطاب لا يساوي الصفر.
ج- الجهد في النقاط Q P و K يساوي جهد القطب الموجب (أعلى جهد).
الجهد في النقطتين R و N هو نفس الجهد ويساوي جهد القطب السالب (أدنى جهد).
ينتقل التيار من الجهد العالي إلى الجهد المنخفض، وفقًا لاتجاه التيار، يكون الجهد في النقطة M أصغر من الجهد في النقطة K وأكبر
من الجهد في النقطة N.
لذلك، تدريج الجهود: «math xmlns=¨http://www.w3.org/1998/Math/MathML¨»«mstyle mathsize=¨20px¨»«msub»«mi mathvariant=¨bold¨ mathcolor=¨#7F007F¨»V«/mi»«mi mathvariant=¨bold¨ mathcolor=¨#7F007F¨»P«/mi»«/msub»«mo mathvariant=¨bold¨ mathcolor=¨#7F007F¨»=«/mo»«msub»«mi mathvariant=¨bold¨ mathcolor=¨#7F007F¨»V«/mi»«mi mathvariant=¨bold¨ mathcolor=¨#7F007F¨»K«/mi»«/msub»«mo mathvariant=¨bold¨ mathcolor=¨#7F007F¨»=«/mo»«msub»«mi mathvariant=¨bold¨ mathcolor=¨#7F007F¨»V«/mi»«mi mathvariant=¨bold¨ mathcolor=¨#7F007F¨»Q«/mi»«/msub»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»§#62;«/mo»«msub»«mi mathvariant=¨bold¨»V«/mi»«mi mathvariant=¨bold¨»M«/mi»«/msub»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»§#62;«/mo»«msub»«mi mathvariant=¨bold¨ mathcolor=¨#007F00¨»V«/mi»«mi mathvariant=¨bold¨ mathcolor=¨#007F00¨»N«/mi»«/msub»«mo mathvariant=¨bold¨ mathcolor=¨#007F00¨»=«/mo»«msub»«mi mathvariant=¨bold¨ mathcolor=¨#007F00¨»V«/mi»«mi mathvariant=¨bold¨ mathcolor=¨#007F00¨»R«/mi»«/msub»«mo mathvariant=¨bold¨ mathcolor=¨#007F00¨»=«/mo»«msub»«mi mathvariant=¨bold¨ mathcolor=¨#007F00¨»V«/mi»«mi mathvariant=¨bold¨ mathcolor=¨#007F00¨»Q«/mi»«/msub»«/mstyle»«/math»
24. ד.5
أ-الدائرة المعطاة عبارة عن دائرة مختلطة، نكتب تعبيرًا للمقاومة المحصلة :
«math xmlns=¨http://www.w3.org/1998/Math/MathML¨»«mstyle mathsize=¨20px¨»«msub»«mi mathvariant=¨bold¨ mathcolor=¨#0000FF¨»R«/mi»«mi mathvariant=¨bold¨ mathcolor=¨#0000FF¨»T«/mi»«/msub»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»=«/mo»«mrow mathcolor=¨#0000FF¨»«mo stretchy=¨true¨ mathvariant=¨bold¨»[«/mo»«mrow»«mo mathvariant=¨bold¨»(«/mo»«msub»«mi mathvariant=¨bold¨»R«/mi»«mn mathvariant=¨bold¨»2«/mn»«/msub»«mo mathvariant=¨bold¨»|«/mo»«mo mathvariant=¨bold¨»|«/mo»«msub»«mi mathvariant=¨bold¨»R«/mi»«mn mathvariant=¨bold¨»3«/mn»«/msub»«mo mathvariant=¨bold¨»)«/mo»«mo mathvariant=¨bold¨»+«/mo»«msub»«mi mathvariant=¨bold¨»R«/mi»«mn mathvariant=¨bold¨»1«/mn»«/msub»«/mrow»«mo stretchy=¨true¨ mathvariant=¨bold¨»]«/mo»«/mrow»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»+«/mo»«mi mathvariant=¨bold¨ mathcolor=¨#0000FF¨»r«/mi»«mspace linebreak=¨newline¨/»«mspace linebreak=¨newline¨/»«msub»«mi mathvariant=¨bold¨ mathcolor=¨#0000FF¨»R«/mi»«mi mathvariant=¨bold¨ mathcolor=¨#0000FF¨»T«/mi»«/msub»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»=«/mo»«mfrac mathcolor=¨#0000FF¨»«mrow»«mn mathvariant=¨bold¨»10«/mn»«mo mathvariant=¨bold¨»§#183;«/mo»«mn mathvariant=¨bold¨»10«/mn»«/mrow»«mrow»«mn mathvariant=¨bold¨»10«/mn»«mo mathvariant=¨bold¨»+«/mo»«mn mathvariant=¨bold¨»10«/mn»«/mrow»«/mfrac»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»+«/mo»«mn mathvariant=¨bold¨ mathcolor=¨#0000FF¨»10«/mn»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»+«/mo»«mn mathvariant=¨bold¨ mathcolor=¨#0000FF¨»1«/mn»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»=«/mo»«mn mathvariant=¨bold¨ mathcolor=¨#0000FF¨»16«/mn»«mi mathvariant=¨bold¨ mathcolor=¨#0000FF¨»§#937;«/mi»«/mstyle»«/math»
ب- نحسب شدة التيار بالمصدر باستخدام قانون أوم للدائرة بأكملها:
«math style=¨font-family:Tahoma¨ xmlns=¨http://www.w3.org/1998/Math/MathML¨»«mstyle mathsize=¨20px¨»«mi mathvariant=¨bold¨ mathcolor=¨#0000FF¨»I«/mi»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»=«/mo»«mfrac mathcolor=¨#0000FF¨»«mi mathvariant=¨bold¨»§#949;«/mi»«msub»«mi mathvariant=¨bold¨»R«/mi»«mi mathvariant=¨bold¨»T«/mi»«/msub»«/mfrac»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»=«/mo»«mfrac mathcolor=¨#0000FF¨»«mn mathvariant=¨bold¨»12«/mn»«mn mathvariant=¨bold¨»16«/mn»«/mfrac»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»=«/mo»«mn mathvariant=¨bold¨ mathcolor=¨#0000FF¨»0«/mn»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨».«/mo»«mn mathvariant=¨bold¨ mathcolor=¨#0000FF¨»75«/mn»«mi mathvariant=¨bold¨ mathcolor=¨#0000FF¨»A«/mi»«/mstyle»«/math»
ج- نحسب فرق جهد الأقطاب بمساعدة تعبير فرق جهد الأقطاب :
«math style=¨font-family:Tahoma¨ xmlns=¨http://www.w3.org/1998/Math/MathML¨»«mi mathvariant=¨bold¨ mathcolor=¨#0000FF¨ mathsize=¨20px¨»Vab«/mi»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨ mathsize=¨20px¨»=«/mo»«mi mathvariant=¨bold¨ mathcolor=¨#0000FF¨ mathsize=¨20px¨»§#949;«/mi»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨ mathsize=¨20px¨»-«/mo»«mi mathvariant=¨bold¨ mathcolor=¨#0000FF¨ mathsize=¨20px¨»I«/mi»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨ mathsize=¨20px¨»§#183;«/mo»«mi mathvariant=¨bold¨ mathcolor=¨#0000FF¨ mathsize=¨20px¨»r«/mi»«mspace linebreak=¨newline¨/»«mi mathvariant=¨bold¨ mathcolor=¨#0000FF¨ mathsize=¨20px¨»Vab«/mi»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨ mathsize=¨20px¨»=«/mo»«mn mathvariant=¨bold¨ mathcolor=¨#0000FF¨ mathsize=¨20px¨»12«/mn»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨ mathsize=¨20px¨»-«/mo»«mn mathvariant=¨bold¨ mathcolor=¨#0000FF¨ mathsize=¨20px¨»0«/mn»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨ mathsize=¨20px¨».«/mo»«mn mathvariant=¨bold¨ mathcolor=¨#0000FF¨ mathsize=¨20px¨»75«/mn»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨ mathsize=¨20px¨»§#183;«/mo»«mn mathvariant=¨bold¨ mathcolor=¨#0000FF¨ mathsize=¨20px¨»1«/mn»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨ mathsize=¨20px¨»=«/mo»«mn mathvariant=¨bold¨ mathcolor=¨#0000FF¨ mathsize=¨20px¨»11«/mn»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨ mathsize=¨20px¨».«/mo»«mn mathvariant=¨bold¨ mathcolor=¨#0000FF¨ mathsize=¨20px¨»25«/mn»«mi mathvariant=¨bold¨ mathcolor=¨#0000FF¨ mathsize=¨20px¨»V«/mi»«/math»
د- لحساب فرق الجهد على R2، نجد التيار المار عبره.
نشير للتيار المار عبر المصدر بـ I ، والتيار عبر R3 بـ I1 والتيار عبر R2 في I2، تظهر التيارات الثلاثة في الشكل التالي:
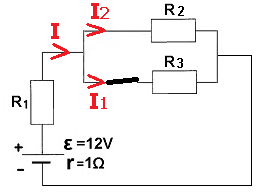
لأن مقاومة المقاوم R2 مساوٍ لمقاومة المقاوم R3. يمكن تحديد أن تيار المصدر سينقسم في نقطة التقاطع بنفس النسبة، لذا سيتدفق نصف تيار المصدر عبر المقاوم R2 ونصف التيار عبر المقاوم R3.
نحسب شدة التيار عبر R2:
«math style=¨font-family:Tahoma¨ xmlns=¨http://www.w3.org/1998/Math/MathML¨»«mstyle mathsize=¨20px¨»«msub»«mi mathvariant=¨bold¨ mathcolor=¨#0000FF¨»I«/mi»«mn mathvariant=¨bold¨ mathcolor=¨#0000FF¨»2«/mn»«/msub»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»=«/mo»«mfrac mathcolor=¨#0000FF¨»«mi mathvariant=¨bold¨»I«/mi»«mn mathvariant=¨bold¨»2«/mn»«/mfrac»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»=«/mo»«mfrac mathcolor=¨#0000FF¨»«mrow»«mn mathvariant=¨bold¨»0«/mn»«mo mathvariant=¨bold¨».«/mo»«mn mathvariant=¨bold¨»75«/mn»«/mrow»«mn mathvariant=¨bold¨»2«/mn»«/mfrac»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»=«/mo»«mn mathvariant=¨bold¨ mathcolor=¨#0000FF¨»0«/mn»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨».«/mo»«mn mathvariant=¨bold¨ mathcolor=¨#0000FF¨»375«/mn»«mi mathvariant=¨bold¨ mathcolor=¨#0000FF¨»A«/mi»«/mstyle»«/math»
نحسب فرق الجهد على R2 باستخدام قانون أوم:
«math style=¨font-family:Tahoma¨ xmlns=¨http://www.w3.org/1998/Math/MathML¨»«mstyle mathsize=¨20px¨»«msub»«mi mathvariant=¨bold¨ mathcolor=¨#0000FF¨»U«/mi»«msub mathcolor=¨#0000FF¨»«mi mathvariant=¨bold¨»R«/mi»«mn mathvariant=¨bold¨»2«/mn»«/msub»«/msub»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»=«/mo»«msub»«mi mathvariant=¨bold¨ mathcolor=¨#0000FF¨»I«/mi»«mn mathvariant=¨bold¨ mathcolor=¨#0000FF¨»2«/mn»«/msub»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»§#183;«/mo»«msub»«mi mathvariant=¨bold¨ mathcolor=¨#0000FF¨»R«/mi»«mn mathvariant=¨bold¨ mathcolor=¨#0000FF¨»2«/mn»«/msub»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»=«/mo»«mn mathvariant=¨bold¨ mathcolor=¨#0000FF¨»0«/mn»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨».«/mo»«mn mathvariant=¨bold¨ mathcolor=¨#0000FF¨»375«/mn»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»§#183;«/mo»«mn mathvariant=¨bold¨ mathcolor=¨#0000FF¨»10«/mn»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»=«/mo»«mn mathvariant=¨bold¨ mathcolor=¨#0000FF¨»3«/mn»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨».«/mo»«mn mathvariant=¨bold¨ mathcolor=¨#0000FF¨»75«/mn»«mi mathvariant=¨bold¨ mathcolor=¨#0000FF¨»V«/mi»«/mstyle»«/math»
طريقة أخرى: المقاومتان R2 و- R3 موصولتان على التوازي، فرق الجهد عليهم متساوٍ.
من مبادئ الدائرة على التوالي، يمكن تحديد أن فرق جهد الأقطاب يساوي مجموع فرقي الجهد على R1 و R2.
«math style=¨font-family:Tahoma¨ xmlns=¨http://www.w3.org/1998/Math/MathML¨»«mstyle mathsize=¨20px¨»«mi mathvariant=¨bold¨ mathcolor=¨#0000FF¨»Vab«/mi»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»=«/mo»«msub»«mi mathvariant=¨bold¨ mathcolor=¨#0000FF¨»U«/mi»«msub mathcolor=¨#0000FF¨»«mi mathvariant=¨bold¨»R«/mi»«mn mathvariant=¨bold¨»1«/mn»«/msub»«/msub»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»+«/mo»«msub»«mi mathvariant=¨bold¨ mathcolor=¨#0000FF¨»U«/mi»«msub mathcolor=¨#0000FF¨»«mi mathvariant=¨bold¨»R«/mi»«mn mathvariant=¨bold¨»2«/mn»«/msub»«/msub»«/mstyle»«/math»
نعبر عن فرق الجهد على R2
«math style=¨font-family:Tahoma¨ xmlns=¨http://www.w3.org/1998/Math/MathML¨»«mstyle mathsize=¨20px¨»«msub»«mi mathvariant=¨bold¨ mathcolor=¨#0000FF¨»U«/mi»«msub mathcolor=¨#0000FF¨»«mi mathvariant=¨bold¨»R«/mi»«mn mathvariant=¨bold¨»2«/mn»«/msub»«/msub»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»=«/mo»«mi mathvariant=¨bold¨ mathcolor=¨#0000FF¨»Vab«/mi»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»-«/mo»«msub»«mi mathvariant=¨bold¨ mathcolor=¨#0000FF¨»U«/mi»«msub mathcolor=¨#0000FF¨»«mi mathvariant=¨bold¨»R«/mi»«mn mathvariant=¨bold¨»1«/mn»«/msub»«/msub»«mspace linebreak=¨newline¨/»«msub»«mi mathvariant=¨bold¨ mathcolor=¨#0000FF¨»U«/mi»«msub mathcolor=¨#0000FF¨»«mi mathvariant=¨bold¨»R«/mi»«mn mathvariant=¨bold¨»2«/mn»«/msub»«/msub»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»=«/mo»«mi mathvariant=¨bold¨ mathcolor=¨#0000FF¨»Vab«/mi»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»-«/mo»«mi mathvariant=¨bold¨ mathcolor=¨#0000FF¨»I«/mi»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»§#183;«/mo»«mi mathvariant=¨bold¨ mathcolor=¨#0000FF¨»R«/mi»«mn mathvariant=¨bold¨ mathcolor=¨#0000FF¨»1«/mn»«mspace linebreak=¨newline¨/»«msub»«mi mathvariant=¨bold¨ mathcolor=¨#0000FF¨»U«/mi»«msub mathcolor=¨#0000FF¨»«mi mathvariant=¨bold¨»R«/mi»«mn mathvariant=¨bold¨»2«/mn»«/msub»«/msub»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»=«/mo»«mn mathvariant=¨bold¨ mathcolor=¨#0000FF¨»11«/mn»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨».«/mo»«mn mathvariant=¨bold¨ mathcolor=¨#0000FF¨»25«/mn»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»-«/mo»«mn mathvariant=¨bold¨ mathcolor=¨#0000FF¨»0«/mn»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨».«/mo»«mn mathvariant=¨bold¨ mathcolor=¨#0000FF¨»75«/mn»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»§#183;«/mo»«mn mathvariant=¨bold¨ mathcolor=¨#0000FF¨»10«/mn»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»=«/mo»«mn mathvariant=¨bold¨ mathcolor=¨#0000FF¨»11«/mn»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨».«/mo»«mn mathvariant=¨bold¨ mathcolor=¨#0000FF¨»25«/mn»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»-«/mo»«mn mathvariant=¨bold¨ mathcolor=¨#0000FF¨»7«/mn»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨».«/mo»«mn mathvariant=¨bold¨ mathcolor=¨#0000FF¨»5«/mn»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»=«/mo»«mn mathvariant=¨bold¨ mathcolor=¨#0000FF¨»3«/mn»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨».«/mo»«mn mathvariant=¨bold¨ mathcolor=¨#0000FF¨»75«/mn»«mi mathvariant=¨bold¨ mathcolor=¨#0000FF¨»V«/mi»«/mstyle»«/math»
25. ד.6
أ- نتيجة لفتح قاطع الدائرة يتم الحصول على دائرة على التوالي، تزداد المقاومة المحصلة.
حسب قاعدة أوم ، لأن المقاومة المحصلة تزداد فإن تيار المصدر سوف يقل.
من تعبير فرق جهد الأقطاب، عندما يقل تيار المصدر، يزداد فرق جهد الأقطاب.
نحسب فرق جهد الأقطاب بعد فتح قاطع الدائرة.
نجد المقاومة المحصلة لدائرة على التوالي:
«math xmlns=¨http://www.w3.org/1998/Math/MathML¨»«mstyle mathsize=¨20px¨»«msub»«mi mathvariant=¨bold¨ mathcolor=¨#0000FF¨»R«/mi»«mi mathvariant=¨bold¨ mathcolor=¨#0000FF¨»T«/mi»«/msub»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»=«/mo»«msub»«mi mathvariant=¨bold¨ mathcolor=¨#0000FF¨»R«/mi»«mn mathvariant=¨bold¨ mathcolor=¨#0000FF¨»2«/mn»«/msub»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»+«/mo»«msub»«mi mathvariant=¨bold¨ mathcolor=¨#0000FF¨»R«/mi»«mn mathvariant=¨bold¨ mathcolor=¨#0000FF¨»1«/mn»«/msub»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»+«/mo»«mi mathvariant=¨bold¨ mathcolor=¨#0000FF¨»r«/mi»«mspace linebreak=¨newline¨/»«mspace linebreak=¨newline¨/»«msub»«mi mathvariant=¨bold¨ mathcolor=¨#0000FF¨»R«/mi»«mi mathvariant=¨bold¨ mathcolor=¨#0000FF¨»T«/mi»«/msub»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»=«/mo»«mn mathvariant=¨bold¨ mathcolor=¨#0000FF¨»10«/mn»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»+«/mo»«mn mathvariant=¨bold¨ mathcolor=¨#0000FF¨»10«/mn»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»+«/mo»«mn mathvariant=¨bold¨ mathcolor=¨#0000FF¨»1«/mn»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»=«/mo»«mn mathvariant=¨bold¨ mathcolor=¨#0000FF¨»21«/mn»«mi mathvariant=¨bold¨ mathcolor=¨#0000FF¨»§#937;«/mi»«/mstyle»«/math»
نحسب التيار بالمصدر:
«math style=¨font-family:Tahoma¨ xmlns=¨http://www.w3.org/1998/Math/MathML¨»«mstyle mathsize=¨20px¨»«mi mathvariant=¨bold¨ mathcolor=¨#0000FF¨»I«/mi»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»=«/mo»«mfrac mathcolor=¨#0000FF¨»«mi mathvariant=¨bold¨»§#949;«/mi»«msub»«mi mathvariant=¨bold¨»R«/mi»«mi mathvariant=¨bold¨»T«/mi»«/msub»«/mfrac»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»=«/mo»«mfrac mathcolor=¨#0000FF¨»«mn mathvariant=¨bold¨»12«/mn»«mn mathvariant=¨bold¨»21«/mn»«/mfrac»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»=«/mo»«mn mathvariant=¨bold¨ mathcolor=¨#0000FF¨»0«/mn»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨».«/mo»«mn mathvariant=¨bold¨ mathcolor=¨#0000FF¨»57«/mn»«mi mathvariant=¨bold¨ mathcolor=¨#0000FF¨»A«/mi»«/mstyle»«/math»
نحسب فرق جهد الأقطاب في هذا الوضع:
«math style=¨font-family:Tahoma¨ xmlns=¨http://www.w3.org/1998/Math/MathML¨»«mi mathvariant=¨bold¨ mathcolor=¨#0000FF¨ mathsize=¨20px¨»Vab«/mi»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨ mathsize=¨20px¨»=«/mo»«mi mathvariant=¨bold¨ mathcolor=¨#0000FF¨ mathsize=¨20px¨»§#949;«/mi»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨ mathsize=¨20px¨»-«/mo»«mi mathvariant=¨bold¨ mathcolor=¨#0000FF¨ mathsize=¨20px¨»I«/mi»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨ mathsize=¨20px¨»§#183;«/mo»«mi mathvariant=¨bold¨ mathcolor=¨#0000FF¨ mathsize=¨20px¨»r«/mi»«mspace linebreak=¨newline¨/»«mi mathvariant=¨bold¨ mathcolor=¨#0000FF¨ mathsize=¨20px¨»Vab«/mi»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨ mathsize=¨20px¨»=«/mo»«mn mathvariant=¨bold¨ mathcolor=¨#0000FF¨ mathsize=¨20px¨»12«/mn»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨ mathsize=¨20px¨»-«/mo»«mn mathvariant=¨bold¨ mathcolor=¨#0000FF¨ mathsize=¨20px¨»0«/mn»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨ mathsize=¨20px¨».«/mo»«mn mathvariant=¨bold¨ mathcolor=¨#0000FF¨ mathsize=¨20px¨»57«/mn»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨ mathsize=¨20px¨»§#183;«/mo»«mn mathvariant=¨bold¨ mathcolor=¨#0000FF¨ mathsize=¨20px¨»1«/mn»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨ mathsize=¨20px¨»=«/mo»«mn mathvariant=¨bold¨ mathcolor=¨#0000FF¨ mathsize=¨20px¨»11«/mn»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨ mathsize=¨20px¨».«/mo»«mn mathvariant=¨bold¨ mathcolor=¨#0000FF¨ mathsize=¨20px¨»43«/mn»«mi mathvariant=¨bold¨ mathcolor=¨#0000FF¨ mathsize=¨20px¨»V«/mi»«/math»
عند إغلاق القاطع، كان فرق جهد الأقطاب 11.25 فولط، ونتيجة لإغلاق القاطع زاد فرق جهد الأقطاب إلى 11.43 فولط.
ب- عندما تم إغلاق القاطع، تقل المقاومة المحصلة ويزداد تيار المصدر، لكن نصفه فقط مرّ عبر R2.
بعد فتح قاطع الدائرة ، تزداد المقاومة المحصلة ويقل تيار المصدر، لكن كل التيار يمر عبر R2.
لذلك ، لا يمكن تحديد كيفية تغير فرق الجهد على R2 نتيجة فتح قاطع الدائرة بدون عمليات حسابية.
نحسب فرق الجهد على R2 عندما يكون القاطع مفتوحًا. باستخدام قانون أوم على R2:
«math style=¨font-family:Tahoma¨ xmlns=¨http://www.w3.org/1998/Math/MathML¨»«mstyle mathsize=¨20px¨»«msub»«mi mathvariant=¨bold¨ mathcolor=¨#0000FF¨»U«/mi»«msub mathcolor=¨#0000FF¨»«mi mathvariant=¨bold¨»R«/mi»«mn mathvariant=¨bold¨»2«/mn»«/msub»«/msub»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»=«/mo»«mi mathvariant=¨bold¨ mathcolor=¨#0000FF¨»I«/mi»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»§#183;«/mo»«msub»«mi mathvariant=¨bold¨ mathcolor=¨#0000FF¨»R«/mi»«mn mathvariant=¨bold¨ mathcolor=¨#0000FF¨»2«/mn»«/msub»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»=«/mo»«mn mathvariant=¨bold¨ mathcolor=¨#0000FF¨»0«/mn»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨».«/mo»«mn mathvariant=¨bold¨ mathcolor=¨#0000FF¨»57«/mn»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»§#183;«/mo»«mn mathvariant=¨bold¨ mathcolor=¨#0000FF¨»10«/mn»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»=«/mo»«mn mathvariant=¨bold¨ mathcolor=¨#0000FF¨»5«/mn»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨».«/mo»«mn mathvariant=¨bold¨ mathcolor=¨#0000FF¨»7«/mn»«mi mathvariant=¨bold¨ mathcolor=¨#0000FF¨»V«/mi»«/mstyle»«/math»
في القسم السابق رأينا أنه عند إغلاق القاطع، فإن فرق الجهد على R2 يساوي 3.75 فولط.
لذلك، نتيجة لإغلاق القاطع، يزداد فرق الجهد على R2.
26. ד.7
أ- من أجل عدم حرق المصباح، يجب على الطالب أولاً وضع نقطة التماس المتحركة Q في الطرف N وليس في الطرف M ، بحيث تكون قيمة المقاومة المحصلة الابتدائية قيمة قصوى ويكون التيار الابتدائي ذو أصغر قيمة له.
ب- لايجاد مقاومة المقاوم المتغير عندما تكون المصابيح مضاءة بضوءها الكامل، نفترض أن فرق الجهد على كل مصباح هو 3 فولط وأن المصابيح مضاءة بضوءها الكامل ونجد مقاومة المقاوم المتغير في هذه الحالة.
نحسب التيار من خلال كل مصباح من المصابيح عندما تضاء بضوءها الكامل:
«math style=¨font-family:Tahoma¨ xmlns=¨http://www.w3.org/1998/Math/MathML¨»«mstyle mathsize=¨20px¨»«msub»«mi mathvariant=¨bold¨ mathcolor=¨#0000FF¨»I«/mi»«msub mathcolor=¨#0000FF¨»«mi mathvariant=¨bold¨»L«/mi»«mn mathvariant=¨bold¨»1«/mn»«/msub»«/msub»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»=«/mo»«msub»«mi mathvariant=¨bold¨ mathcolor=¨#0000FF¨»I«/mi»«msub mathcolor=¨#0000FF¨»«mi mathvariant=¨bold¨»L«/mi»«mn mathvariant=¨bold¨»2«/mn»«/msub»«/msub»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»=«/mo»«mfrac mathcolor=¨#0000FF¨»«msub»«mi mathvariant=¨bold¨»U«/mi»«msub»«mi mathvariant=¨bold¨»L«/mi»«mn mathvariant=¨bold¨»2«/mn»«/msub»«/msub»«msub»«mi mathvariant=¨bold¨»R«/mi»«msub»«mi mathvariant=¨bold¨»L«/mi»«mn mathvariant=¨bold¨»2«/mn»«/msub»«/msub»«/mfrac»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»=«/mo»«mfrac mathcolor=¨#0000FF¨»«mn mathvariant=¨bold¨»3«/mn»«mn mathvariant=¨bold¨»6«/mn»«/mfrac»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»=«/mo»«mn mathvariant=¨bold¨ mathcolor=¨#0000FF¨»0«/mn»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨».«/mo»«mn mathvariant=¨bold¨ mathcolor=¨#0000FF¨»5«/mn»«mi mathvariant=¨bold¨ mathcolor=¨#0000FF¨»A«/mi»«/mstyle»«/math»
نجد تيار المصدر باستخدام قانون أوم:
«math style=¨font-family:Tahoma¨ xmlns=¨http://www.w3.org/1998/Math/MathML¨»«mstyle mathsize=¨20px¨»«mi mathvariant=¨bold¨ mathcolor=¨#0000FF¨»I«/mi»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»=«/mo»«msub»«mi mathvariant=¨bold¨ mathcolor=¨#0000FF¨»I«/mi»«msub mathcolor=¨#0000FF¨»«mi mathvariant=¨bold¨»L«/mi»«mn mathvariant=¨bold¨»1«/mn»«/msub»«/msub»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»+«/mo»«msub»«mi mathvariant=¨bold¨ mathcolor=¨#0000FF¨»I«/mi»«msub mathcolor=¨#0000FF¨»«mi mathvariant=¨bold¨»L«/mi»«mn mathvariant=¨bold¨»2«/mn»«/msub»«/msub»«mspace linebreak=¨newline¨/»«mi mathvariant=¨bold¨ mathcolor=¨#0000FF¨»I«/mi»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»=«/mo»«mn mathvariant=¨bold¨ mathcolor=¨#0000FF¨»0«/mn»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨».«/mo»«mn mathvariant=¨bold¨ mathcolor=¨#0000FF¨»5«/mn»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»+«/mo»«mn mathvariant=¨bold¨ mathcolor=¨#0000FF¨»0«/mn»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨».«/mo»«mn mathvariant=¨bold¨ mathcolor=¨#0000FF¨»5«/mn»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»=«/mo»«mn mathvariant=¨bold¨ mathcolor=¨#0000FF¨»1«/mn»«mi mathvariant=¨bold¨ mathcolor=¨#0000FF¨»A«/mi»«/mstyle»«/math»
نحسب المقاومة المحصلة باستخدام قانون أوم للدائرة بأكملها:
«math style=¨font-family:Tahoma¨ xmlns=¨http://www.w3.org/1998/Math/MathML¨»«mstyle mathsize=¨20px¨»«mi mathvariant=¨bold¨ mathcolor=¨#0000FF¨»I«/mi»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»=«/mo»«mfrac mathcolor=¨#0000FF¨»«mi mathvariant=¨bold¨»§#949;«/mi»«msub»«mi mathvariant=¨bold¨»R«/mi»«mi mathvariant=¨bold¨»T«/mi»«/msub»«/mfrac»«mspace linebreak=¨newline¨/»«mspace linebreak=¨newline¨/»«msub»«mi mathvariant=¨bold¨ mathcolor=¨#0000FF¨»R«/mi»«mi mathvariant=¨bold¨ mathcolor=¨#0000FF¨»T«/mi»«/msub»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»=«/mo»«mfrac mathcolor=¨#0000FF¨»«mi mathvariant=¨bold¨»§#949;«/mi»«mi mathvariant=¨bold¨»I«/mi»«/mfrac»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»=«/mo»«mfrac mathcolor=¨#0000FF¨»«mn mathvariant=¨bold¨»12«/mn»«mn mathvariant=¨bold¨»1«/mn»«/mfrac»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»=«/mo»«mn mathvariant=¨bold¨ mathcolor=¨#0000FF¨»12«/mn»«mi mathvariant=¨bold¨ mathcolor=¨#0000FF¨»§#937;«/mi»«/mstyle»«/math»
نحسب مقاومة المقاوم المتغير من تعبير المقاومة المحصلة:
«math xmlns=¨http://www.w3.org/1998/Math/MathML¨»«mstyle mathsize=¨20px¨»«msub»«mi mathvariant=¨bold¨ mathcolor=¨#0000FF¨»R«/mi»«mi mathvariant=¨bold¨ mathcolor=¨#0000FF¨»T«/mi»«/msub»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»=«/mo»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»(«/mo»«msub»«mi mathvariant=¨bold¨ mathcolor=¨#0000FF¨»R«/mi»«msub mathcolor=¨#0000FF¨»«mi mathvariant=¨bold¨»L«/mi»«mn mathvariant=¨bold¨»1«/mn»«/msub»«/msub»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»|«/mo»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»|«/mo»«msub»«mi mathvariant=¨bold¨ mathcolor=¨#0000FF¨»R«/mi»«msub mathcolor=¨#0000FF¨»«mi mathvariant=¨bold¨»L«/mi»«mn mathvariant=¨bold¨»2«/mn»«/msub»«/msub»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»)«/mo»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»+«/mo»«msub»«mi mathvariant=¨bold¨ mathcolor=¨#0000FF¨»R«/mi»«mi mathvariant=¨bold¨ mathcolor=¨#0000FF¨»X«/mi»«/msub»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»+«/mo»«mi mathvariant=¨bold¨ mathcolor=¨#0000FF¨»r«/mi»«mspace linebreak=¨newline¨/»«mspace linebreak=¨newline¨/»«msub»«mi mathvariant=¨bold¨ mathcolor=¨#0000FF¨»R«/mi»«mi mathvariant=¨bold¨ mathcolor=¨#0000FF¨»X«/mi»«/msub»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»=«/mo»«msub»«mi mathvariant=¨bold¨ mathcolor=¨#0000FF¨»R«/mi»«mi mathvariant=¨bold¨ mathcolor=¨#0000FF¨»T«/mi»«/msub»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»-«/mo»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»(«/mo»«msub»«mi mathvariant=¨bold¨ mathcolor=¨#0000FF¨»R«/mi»«msub mathcolor=¨#0000FF¨»«mi mathvariant=¨bold¨»L«/mi»«mn mathvariant=¨bold¨»1«/mn»«/msub»«/msub»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»|«/mo»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»|«/mo»«msub»«mi mathvariant=¨bold¨ mathcolor=¨#0000FF¨»R«/mi»«msub mathcolor=¨#0000FF¨»«mi mathvariant=¨bold¨»L«/mi»«mn mathvariant=¨bold¨»2«/mn»«/msub»«/msub»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»)«/mo»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»-«/mo»«mi mathvariant=¨bold¨ mathcolor=¨#0000FF¨»r«/mi»«mspace linebreak=¨newline¨/»«mspace linebreak=¨newline¨/»«msub»«mi mathvariant=¨bold¨ mathcolor=¨#0000FF¨»R«/mi»«mi mathvariant=¨bold¨ mathcolor=¨#0000FF¨»X«/mi»«/msub»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»=«/mo»«msub»«mi mathvariant=¨bold¨ mathcolor=¨#0000FF¨»R«/mi»«mi mathvariant=¨bold¨ mathcolor=¨#0000FF¨»T«/mi»«/msub»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»-«/mo»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»(«/mo»«mfrac mathcolor=¨#0000FF¨»«mrow»«msub»«mi mathvariant=¨bold¨»R«/mi»«msub»«mi mathvariant=¨bold¨»L«/mi»«mn mathvariant=¨bold¨»1«/mn»«/msub»«/msub»«mo mathvariant=¨bold¨»§#183;«/mo»«msub»«mi mathvariant=¨bold¨»R«/mi»«msub»«mi mathvariant=¨bold¨»L«/mi»«mn mathvariant=¨bold¨»2«/mn»«/msub»«/msub»«/mrow»«mrow»«msub»«mi mathvariant=¨bold¨»R«/mi»«msub»«mi mathvariant=¨bold¨»L«/mi»«mn mathvariant=¨bold¨»1«/mn»«/msub»«/msub»«mo mathvariant=¨bold¨»+«/mo»«msub»«mi mathvariant=¨bold¨»R«/mi»«msub»«mi mathvariant=¨bold¨»L«/mi»«mn mathvariant=¨bold¨»2«/mn»«/msub»«/msub»«/mrow»«/mfrac»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»)«/mo»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»-«/mo»«mi mathvariant=¨bold¨ mathcolor=¨#0000FF¨»r«/mi»«mspace linebreak=¨newline¨/»«mspace linebreak=¨newline¨/»«msub»«mi mathvariant=¨bold¨ mathcolor=¨#0000FF¨»R«/mi»«mi mathvariant=¨bold¨ mathcolor=¨#0000FF¨»X«/mi»«/msub»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»=«/mo»«mn mathvariant=¨bold¨ mathcolor=¨#0000FF¨»12«/mn»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»-«/mo»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»(«/mo»«mfrac mathcolor=¨#0000FF¨»«mrow»«mn mathvariant=¨bold¨»6«/mn»«mo mathvariant=¨bold¨»§#183;«/mo»«mn mathvariant=¨bold¨»6«/mn»«/mrow»«mrow»«mn mathvariant=¨bold¨»6«/mn»«mo mathvariant=¨bold¨»+«/mo»«mn mathvariant=¨bold¨»6«/mn»«/mrow»«/mfrac»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»)«/mo»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»-«/mo»«mn mathvariant=¨bold¨ mathcolor=¨#0000FF¨»1«/mn»«mspace linebreak=¨newline¨/»«mspace linebreak=¨newline¨/»«msub»«mi mathvariant=¨bold¨ mathcolor=¨#0000FF¨»R«/mi»«mi mathvariant=¨bold¨ mathcolor=¨#0000FF¨»X«/mi»«/msub»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»=«/mo»«mn mathvariant=¨bold¨ mathcolor=¨#0000FF¨»12«/mn»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»-«/mo»«mn mathvariant=¨bold¨ mathcolor=¨#0000FF¨»3«/mn»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»-«/mo»«mn mathvariant=¨bold¨ mathcolor=¨#0000FF¨»1«/mn»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»=«/mo»«mn mathvariant=¨bold¨ mathcolor=¨#0000FF¨»8«/mn»«mi mathvariant=¨bold¨ mathcolor=¨#0000FF¨»§#937;«/mi»«mspace linebreak=¨newline¨/»«/mstyle»«/math»
ج- نحسب فرق جهد الأقطاب بمساعدة تعبير القوة الكهربائية الدافعة وفرق جهد الأقطاب:
«math style=¨font-family:Tahoma¨ xmlns=¨http://www.w3.org/1998/Math/MathML¨»«mi mathvariant=¨bold¨ mathcolor=¨#0000FF¨ mathsize=¨20px¨»Vab«/mi»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨ mathsize=¨20px¨»=«/mo»«mi mathvariant=¨bold¨ mathcolor=¨#0000FF¨ mathsize=¨20px¨»§#949;«/mi»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨ mathsize=¨20px¨»-«/mo»«mi mathvariant=¨bold¨ mathcolor=¨#0000FF¨ mathsize=¨20px¨»I«/mi»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨ mathsize=¨20px¨»§#183;«/mo»«mi mathvariant=¨bold¨ mathcolor=¨#0000FF¨ mathsize=¨20px¨»r«/mi»«mspace linebreak=¨newline¨/»«mi mathvariant=¨bold¨ mathcolor=¨#0000FF¨ mathsize=¨20px¨»Vab«/mi»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨ mathsize=¨20px¨»=«/mo»«mn mathvariant=¨bold¨ mathcolor=¨#0000FF¨ mathsize=¨20px¨»12«/mn»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨ mathsize=¨20px¨»-«/mo»«mn mathvariant=¨bold¨ mathcolor=¨#0000FF¨ mathsize=¨20px¨»1«/mn»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨ mathsize=¨20px¨»§#183;«/mo»«mn mathvariant=¨bold¨ mathcolor=¨#0000FF¨ mathsize=¨20px¨»1«/mn»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨ mathsize=¨20px¨»=«/mo»«mn mathvariant=¨bold¨ mathcolor=¨#0000FF¨ mathsize=¨20px¨»11«/mn»«mi mathvariant=¨bold¨ mathcolor=¨#0000FF¨ mathsize=¨20px¨»V«/mi»«/math»
27. ד.8
أ- بعد فتح قاطع الدائرة، نحصل على دائرة موصولة على التوالي بحيث يتم فصل المصباح L1 عن الدائرة ويكون التيار المار عبر المصباح L2 نفس تيار المصدر.
نحسب مقاومة المقاوم المتغير RX اللازم لتشغيل المصباح L2 في الإضاءة الكاملة عندما يكون القاطع مفتوحًا
وبناءً على ذلك، يتم تحديد الاتجاه الذي يجب تحريك نقطة التماس المتحركة Q اليه.
نحسب شدة التيار بالمصدر من قانون أوم على المصباح الكهربائي L2:
«math style=¨font-family:Tahoma¨ xmlns=¨http://www.w3.org/1998/Math/MathML¨»«mstyle mathsize=¨20px¨»«mi mathvariant=¨bold¨ mathcolor=¨#0000FF¨»I«/mi»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»=«/mo»«msub»«mi mathvariant=¨bold¨ mathcolor=¨#0000FF¨»I«/mi»«msub mathcolor=¨#0000FF¨»«mi mathvariant=¨bold¨»L«/mi»«mn mathvariant=¨bold¨»2«/mn»«/msub»«/msub»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»=«/mo»«mfrac mathcolor=¨#0000FF¨»«msub»«mi mathvariant=¨bold¨»U«/mi»«msub»«mi mathvariant=¨bold¨»L«/mi»«mn mathvariant=¨bold¨»2«/mn»«/msub»«/msub»«msub»«mi mathvariant=¨bold¨»R«/mi»«msub»«mi mathvariant=¨bold¨»L«/mi»«mn mathvariant=¨bold¨»2«/mn»«/msub»«/msub»«/mfrac»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»=«/mo»«mfrac mathcolor=¨#0000FF¨»«mn mathvariant=¨bold¨»3«/mn»«mn mathvariant=¨bold¨»6«/mn»«/mfrac»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»=«/mo»«mn mathvariant=¨bold¨ mathcolor=¨#0000FF¨»0«/mn»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨».«/mo»«mn mathvariant=¨bold¨ mathcolor=¨#0000FF¨»5«/mn»«mi mathvariant=¨bold¨ mathcolor=¨#0000FF¨»A«/mi»«/mstyle»«/math»
نحسب المقاومة المحصلة باستخدام قانون أوم للدائرة بأكملها:
«math style=¨font-family:Tahoma¨ xmlns=¨http://www.w3.org/1998/Math/MathML¨»«mstyle mathsize=¨20px¨»«mi mathvariant=¨bold¨ mathcolor=¨#0000FF¨»I«/mi»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»=«/mo»«mfrac mathcolor=¨#0000FF¨»«mi mathvariant=¨bold¨»§#949;«/mi»«msub»«mi mathvariant=¨bold¨»R«/mi»«mi mathvariant=¨bold¨»T«/mi»«/msub»«/mfrac»«mspace linebreak=¨newline¨/»«mspace linebreak=¨newline¨/»«msub»«mi mathvariant=¨bold¨ mathcolor=¨#0000FF¨»R«/mi»«mi mathvariant=¨bold¨ mathcolor=¨#0000FF¨»T«/mi»«/msub»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»=«/mo»«mfrac mathcolor=¨#0000FF¨»«mi mathvariant=¨bold¨»§#949;«/mi»«mi mathvariant=¨bold¨»I«/mi»«/mfrac»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»=«/mo»«mfrac mathcolor=¨#0000FF¨»«mn mathvariant=¨bold¨»12«/mn»«mrow»«mn mathvariant=¨bold¨»0«/mn»«mo mathvariant=¨bold¨».«/mo»«mn mathvariant=¨bold¨»5«/mn»«/mrow»«/mfrac»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»=«/mo»«mn mathvariant=¨bold¨ mathcolor=¨#0000FF¨»24«/mn»«mi mathvariant=¨bold¨ mathcolor=¨#0000FF¨»§#937;«/mi»«/mstyle»«/math»
نحسب مقاومة المقاوم المتغير من تعبير المقاومة المحصلة:
«math xmlns=¨http://www.w3.org/1998/Math/MathML¨»«mstyle mathsize=¨20px¨»«msub»«mi mathvariant=¨bold¨ mathcolor=¨#0000FF¨»R«/mi»«mi mathvariant=¨bold¨ mathcolor=¨#0000FF¨»T«/mi»«/msub»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»=«/mo»«msub»«mi mathvariant=¨bold¨ mathcolor=¨#0000FF¨»R«/mi»«msub mathcolor=¨#0000FF¨»«mi mathvariant=¨bold¨»L«/mi»«mn mathvariant=¨bold¨»2«/mn»«/msub»«/msub»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»+«/mo»«msub»«mi mathvariant=¨bold¨ mathcolor=¨#0000FF¨»R«/mi»«mi mathvariant=¨bold¨ mathcolor=¨#0000FF¨»X«/mi»«/msub»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»+«/mo»«mi mathvariant=¨bold¨ mathcolor=¨#0000FF¨»r«/mi»«mspace linebreak=¨newline¨/»«mspace linebreak=¨newline¨/»«msub»«mi mathvariant=¨bold¨ mathcolor=¨#0000FF¨»R«/mi»«mi mathvariant=¨bold¨ mathcolor=¨#0000FF¨»X«/mi»«/msub»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»=«/mo»«msub»«mi mathvariant=¨bold¨ mathcolor=¨#0000FF¨»R«/mi»«mi mathvariant=¨bold¨ mathcolor=¨#0000FF¨»T«/mi»«/msub»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»-«/mo»«msub»«mi mathvariant=¨bold¨ mathcolor=¨#0000FF¨»R«/mi»«msub mathcolor=¨#0000FF¨»«mi mathvariant=¨bold¨»L«/mi»«mn mathvariant=¨bold¨»2«/mn»«/msub»«/msub»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»-«/mo»«mi mathvariant=¨bold¨ mathcolor=¨#0000FF¨»r«/mi»«mspace linebreak=¨newline¨/»«mspace linebreak=¨newline¨/»«msub»«mi mathvariant=¨bold¨ mathcolor=¨#0000FF¨»R«/mi»«mi mathvariant=¨bold¨ mathcolor=¨#0000FF¨»X«/mi»«/msub»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»=«/mo»«mn mathvariant=¨bold¨ mathcolor=¨#0000FF¨»24«/mn»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»-«/mo»«mn mathvariant=¨bold¨ mathcolor=¨#0000FF¨»6«/mn»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»-«/mo»«mn mathvariant=¨bold¨ mathcolor=¨#0000FF¨»1«/mn»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»=«/mo»«mn mathvariant=¨bold¨ mathcolor=¨#0000FF¨»17«/mn»«mi mathvariant=¨bold¨ mathcolor=¨#0000FF¨»§#937;«/mi»«/mstyle»«/math»
في القسم السابق (عند إغلاق قاطع الدائرة) وجدنا أنه لكي يضيء كلا المصباحين في ضوءهما الكامل، يجب أن تكون مقاومة المقاوم المتغير 8 أوم.
في هذا القسم (عندما يكون قاطع الدائرة مفتوحًا) لكي يضيء المصباح في الضوء الكامل، يجب أن تكون مقاومة المقاوم المتغير 17 أوم. لذلك ، يجب زيادة مقاومة المقاوم المتغير.
لزيادة المقاومة المتغيرة، نحرك نقطة التماس المتحركة باتجاه الطرف N.
ب- بعد فتح قاطع الدائرة، يتم الحصول على دائرةعلى التوالي، تزداد المقاومة المحصلة للدائرة. التيار بالمصدر سوف يقل، من تعبير فرق جهد الأقطاب يمكن تحديد أن فرق جهد الأقطاب سيزداد.
ج- بعد فتح القاطع، يكون التيار عبر المصباح 1 أمبير. المصباح مصمم لتيار 0.5 أمبير. لذلك ، قد يحترق المصباح.
28. ד.9
أ- الدائرة المعطاة هي دائرة مختلطة موصولة على التوازي وعلى التوالي، كما يظهر في الشكل التالي:
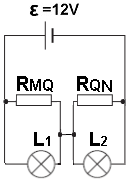
مقاومة كل المقاوم المتغير «math xmlns=¨http://www.w3.org/1998/Math/MathML¨»«mstyle mathsize=¨20px¨»«msub»«mi mathvariant=¨bold¨ mathcolor=¨#0000FF¨»R«/mi»«mi mathvariant=¨bold¨ mathcolor=¨#0000FF¨»MN«/mi»«/msub»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»=«/mo»«mn mathvariant=¨bold¨ mathcolor=¨#0000FF¨»20«/mn»«mi mathvariant=¨bold¨ mathcolor=¨#0000FF¨»§#937;«/mi»«/mstyle»«/math» نظرًا لأن نقطة التماس المتحركة Q تقع تمامًا في منتصف المقاوم المتغير، يتحقق:
«math xmlns=¨http://www.w3.org/1998/Math/MathML¨»«mstyle mathsize=¨20px¨»«msub»«mi mathvariant=¨bold¨ mathcolor=¨#0000FF¨»R«/mi»«mi mathvariant=¨bold¨ mathcolor=¨#0000FF¨»MQ«/mi»«/msub»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»=«/mo»«msub»«mi mathvariant=¨bold¨ mathcolor=¨#0000FF¨»R«/mi»«mi mathvariant=¨bold¨ mathcolor=¨#0000FF¨»QN«/mi»«/msub»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»=«/mo»«mn mathvariant=¨bold¨ mathcolor=¨#0000FF¨»10«/mn»«mi mathvariant=¨bold¨ mathcolor=¨#0000FF¨»§#937;«/mi»«/mstyle»«/math»
نحسب المقاومة المحصلة:
«math xmlns=¨http://www.w3.org/1998/Math/MathML¨»«mstyle mathsize=¨20px¨»«mrow»«msub»«mi mathvariant=¨bold¨ mathcolor=¨#0000FF¨»R«/mi»«mi mathvariant=¨bold¨ mathcolor=¨#0000FF¨»T«/mi»«/msub»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»=«/mo»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»(«/mo»«msub»«mi mathvariant=¨bold¨ mathcolor=¨#0000FF¨»R«/mi»«mi mathvariant=¨bold¨ mathcolor=¨#0000FF¨»MQ«/mi»«/msub»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»|«/mo»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»|«/mo»«msub»«mi mathvariant=¨bold¨ mathcolor=¨#0000FF¨»R«/mi»«msub mathcolor=¨#0000FF¨»«mi mathvariant=¨bold¨»L«/mi»«mn mathvariant=¨bold¨»1«/mn»«/msub»«/msub»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»)«/mo»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»+«/mo»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»(«/mo»«msub»«mi mathvariant=¨bold¨ mathcolor=¨#0000FF¨»R«/mi»«mi mathvariant=¨bold¨ mathcolor=¨#0000FF¨»QN«/mi»«/msub»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»|«/mo»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»|«/mo»«msub»«mi mathvariant=¨bold¨ mathcolor=¨#0000FF¨»R«/mi»«msub mathcolor=¨#0000FF¨»«mi mathvariant=¨bold¨»L«/mi»«mn mathvariant=¨bold¨»2«/mn»«/msub»«/msub»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»)«/mo»«mspace linebreak=¨newline¨/»«mspace linebreak=¨newline¨/»«msub»«mi mathvariant=¨bold¨ mathcolor=¨#0000FF¨»R«/mi»«mi mathvariant=¨bold¨ mathcolor=¨#0000FF¨»T«/mi»«/msub»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»=«/mo»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»(«/mo»«mfrac mathcolor=¨#0000FF¨»«mrow»«msub»«mi mathvariant=¨bold¨»R«/mi»«mi mathvariant=¨bold¨»MQ«/mi»«/msub»«mo mathvariant=¨bold¨»§#183;«/mo»«msub»«mi mathvariant=¨bold¨»R«/mi»«msub»«mi mathvariant=¨bold¨»L«/mi»«mn mathvariant=¨bold¨»1«/mn»«/msub»«/msub»«/mrow»«mrow»«msub»«mi mathvariant=¨bold¨»R«/mi»«mi mathvariant=¨bold¨»MQ«/mi»«/msub»«mo mathvariant=¨bold¨»+«/mo»«msub»«mi mathvariant=¨bold¨»R«/mi»«msub»«mi mathvariant=¨bold¨»L«/mi»«mn mathvariant=¨bold¨»1«/mn»«/msub»«/msub»«/mrow»«/mfrac»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»)«/mo»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»+«/mo»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»(«/mo»«mfrac mathcolor=¨#0000FF¨»«mrow»«msub»«mi mathvariant=¨bold¨»R«/mi»«mi mathvariant=¨bold¨»QN«/mi»«/msub»«mo mathvariant=¨bold¨»§#183;«/mo»«msub»«mi mathvariant=¨bold¨»R«/mi»«msub»«mi mathvariant=¨bold¨»L«/mi»«mn mathvariant=¨bold¨»2«/mn»«/msub»«/msub»«/mrow»«mrow»«msub»«mi mathvariant=¨bold¨»R«/mi»«mi mathvariant=¨bold¨»QN«/mi»«/msub»«mo mathvariant=¨bold¨»+«/mo»«msub»«mi mathvariant=¨bold¨»R«/mi»«msub»«mi mathvariant=¨bold¨»L«/mi»«mn mathvariant=¨bold¨»2«/mn»«/msub»«/msub»«/mrow»«/mfrac»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»)«/mo»«mspace linebreak=¨newline¨/»«/mrow»«mspace linebreak=¨newline¨/»«mspace linebreak=¨newline¨/»«msub»«mi mathvariant=¨bold¨ mathcolor=¨#0000FF¨»R«/mi»«mi mathvariant=¨bold¨ mathcolor=¨#0000FF¨»T«/mi»«/msub»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»=«/mo»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»(«/mo»«mfrac mathcolor=¨#0000FF¨»«mrow»«mn mathvariant=¨bold¨»10«/mn»«mo mathvariant=¨bold¨»§#183;«/mo»«mn mathvariant=¨bold¨»5«/mn»«/mrow»«mrow»«mn mathvariant=¨bold¨»10«/mn»«mo mathvariant=¨bold¨»+«/mo»«mn mathvariant=¨bold¨»5«/mn»«/mrow»«/mfrac»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»)«/mo»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»+«/mo»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»(«/mo»«mfrac mathcolor=¨#0000FF¨»«mrow»«mn mathvariant=¨bold¨»10«/mn»«mo mathvariant=¨bold¨»§#183;«/mo»«mn mathvariant=¨bold¨»5«/mn»«/mrow»«mrow»«mn mathvariant=¨bold¨»10«/mn»«mo mathvariant=¨bold¨»+«/mo»«mn mathvariant=¨bold¨»5«/mn»«/mrow»«/mfrac»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»)«/mo»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»=«/mo»«mn mathvariant=¨bold¨ mathcolor=¨#0000FF¨»3«/mn»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨».«/mo»«mn mathvariant=¨bold¨ mathcolor=¨#0000FF¨»33«/mn»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»+«/mo»«mn mathvariant=¨bold¨ mathcolor=¨#0000FF¨»3«/mn»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨».«/mo»«mn mathvariant=¨bold¨ mathcolor=¨#0000FF¨»33«/mn»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»=«/mo»«mn mathvariant=¨bold¨ mathcolor=¨#0000FF¨»6«/mn»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨».«/mo»«mn mathvariant=¨bold¨ mathcolor=¨#0000FF¨»66«/mn»«mi mathvariant=¨bold¨ mathcolor=¨#0000FF¨»§#937;«/mi»«/mstyle»«/math»
ب- المقاومة المحصلة للطرف الأيسر RMQ والمصباح L1 لها نفس المقاومة المحصلة للطرف الأيمن RQN والمصباح L2.
سيتم تقسيم فرق جهد الأقطاب بالتساوي بين الطرفين، لأن البطارية مثالية وقوتها الكهربائية الدافعة 12 فولط، وفرق الجهد على كل طرف سيكون 6 فولط ، وسوف تضيء المصابيح بضوءها الكامل.
نثبت ذلك عن طريق الحساب: نجد فرق الجهد على المصباح L2 من حساب التيارات في الدائرة.
نشير إلى تيار المصدر بـ I ، والتيار عبر المصباح L1 بـ I1 ، والتيار عبر RMQ بـ I2 ، والعقدة اليسرى كعقدة A.
كما موضح في الشكل التالي:
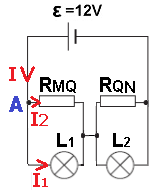
نحسب تيار المصدر من قانون أوم للدائرة بأكملها:
«math style=¨font-family:Tahoma¨ xmlns=¨http://www.w3.org/1998/Math/MathML¨»«mstyle mathsize=¨20px¨»«mi mathvariant=¨bold¨ mathcolor=¨#0000FF¨»I«/mi»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»=«/mo»«mfrac mathcolor=¨#0000FF¨»«mi mathvariant=¨bold¨»§#949;«/mi»«msub»«mi mathvariant=¨bold¨»R«/mi»«mi mathvariant=¨bold¨»T«/mi»«/msub»«/mfrac»«mspace linebreak=¨newline¨/»«mspace linebreak=¨newline¨/»«mi mathvariant=¨bold¨ mathcolor=¨#0000FF¨»I«/mi»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»=«/mo»«mfrac mathcolor=¨#0000FF¨»«mi mathvariant=¨bold¨»§#949;«/mi»«msub»«mi mathvariant=¨bold¨»R«/mi»«mi mathvariant=¨bold¨»T«/mi»«/msub»«/mfrac»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»=«/mo»«mfrac mathcolor=¨#0000FF¨»«mn mathvariant=¨bold¨»12«/mn»«mrow»«mn mathvariant=¨bold¨»6«/mn»«mo mathvariant=¨bold¨».«/mo»«mn mathvariant=¨bold¨»66«/mn»«/mrow»«/mfrac»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»=«/mo»«mn mathvariant=¨bold¨ mathcolor=¨#0000FF¨»1«/mn»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨».«/mo»«mn mathvariant=¨bold¨ mathcolor=¨#0000FF¨»8«/mn»«mi mathvariant=¨bold¨ mathcolor=¨#0000FF¨»A«/mi»«/mstyle»«/math»
نظرًا لأن مقاومة المصباح L1 أقل بمرتين من المقاومة RMQ، فإن التيار عبر المصباح سيكون أكبر بمرتين من التيار عبر RMQ.
سوف يتدفق تيار 1.2 أمبير عبر المصباح ، ويتدفق تيار 0.6 أمبير عبر المقاومة RMQ.
نحسب فرق الجهد على المصباح L1 باستخدام قانون أوم:
«math style=¨font-family:Tahoma¨ xmlns=¨http://www.w3.org/1998/Math/MathML¨»«mstyle mathsize=¨20px¨»«msub»«mi mathvariant=¨bold¨ mathcolor=¨#0000FF¨»U«/mi»«msub mathcolor=¨#0000FF¨»«mi mathvariant=¨bold¨»L«/mi»«mn mathvariant=¨bold¨»1«/mn»«/msub»«/msub»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»=«/mo»«msub»«mi mathvariant=¨bold¨ mathcolor=¨#0000FF¨»I«/mi»«msub mathcolor=¨#0000FF¨»«mi mathvariant=¨bold¨»L«/mi»«mn mathvariant=¨bold¨»1«/mn»«/msub»«/msub»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»§#183;«/mo»«msub»«mi mathvariant=¨bold¨ mathcolor=¨#0000FF¨»R«/mi»«msub mathcolor=¨#0000FF¨»«mi mathvariant=¨bold¨»L«/mi»«mn mathvariant=¨bold¨»1«/mn»«/msub»«/msub»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»=«/mo»«mn mathvariant=¨bold¨ mathcolor=¨#0000FF¨»1«/mn»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨».«/mo»«mn mathvariant=¨bold¨ mathcolor=¨#0000FF¨»2«/mn»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»§#183;«/mo»«mn mathvariant=¨bold¨ mathcolor=¨#0000FF¨»5«/mn»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»=«/mo»«mn mathvariant=¨bold¨ mathcolor=¨#0000FF¨»6«/mn»«mi mathvariant=¨bold¨ mathcolor=¨#0000FF¨»V«/mi»«/mstyle»«/math»
يتدفق التيار إلى الطرف الأيمن وينقسم بطريقة مماثلة بحيث يكون فرق الجهد على المصباح L2 أيضًا 6 فولط.
ج- بعد احتراق المصباح L2 ، ستكون مقاومة الطرف الأيسر أصغر، وسيكون فرق الجهد الكهربائي على المصباح L1 أصغر.
سنثبت ذلك بمساعدة عملية حسابية: نجد فرق الجهد على المصباح L2 من حساب التيارات في الدائرة. نرسم رسم تخطيطي للدائرة:
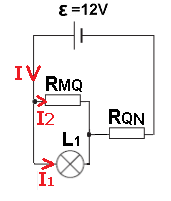
نحسب المقاومة المحصلة:
«math xmlns=¨http://www.w3.org/1998/Math/MathML¨»«mstyle mathsize=¨20px¨»«mrow»«msub»«mi mathvariant=¨bold¨ mathcolor=¨#0000FF¨»R«/mi»«mi mathvariant=¨bold¨ mathcolor=¨#0000FF¨»T«/mi»«/msub»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»=«/mo»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»(«/mo»«msub»«mi mathvariant=¨bold¨ mathcolor=¨#0000FF¨»R«/mi»«mi mathvariant=¨bold¨ mathcolor=¨#0000FF¨»MQ«/mi»«/msub»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»|«/mo»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»|«/mo»«msub»«mi mathvariant=¨bold¨ mathcolor=¨#0000FF¨»R«/mi»«msub mathcolor=¨#0000FF¨»«mi mathvariant=¨bold¨»L«/mi»«mn mathvariant=¨bold¨»1«/mn»«/msub»«/msub»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»)«/mo»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»+«/mo»«msub»«mi mathvariant=¨bold¨ mathcolor=¨#0000FF¨»R«/mi»«mi mathvariant=¨bold¨ mathcolor=¨#0000FF¨»QN«/mi»«/msub»«mspace linebreak=¨newline¨/»«mspace linebreak=¨newline¨/»«msub»«mi mathvariant=¨bold¨ mathcolor=¨#0000FF¨»R«/mi»«mi mathvariant=¨bold¨ mathcolor=¨#0000FF¨»T«/mi»«/msub»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»=«/mo»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»(«/mo»«mfrac mathcolor=¨#0000FF¨»«mrow»«msub»«mi mathvariant=¨bold¨»R«/mi»«mi mathvariant=¨bold¨»MQ«/mi»«/msub»«mo mathvariant=¨bold¨»§#183;«/mo»«msub»«mi mathvariant=¨bold¨»R«/mi»«msub»«mi mathvariant=¨bold¨»L«/mi»«mn mathvariant=¨bold¨»1«/mn»«/msub»«/msub»«/mrow»«mrow»«msub»«mi mathvariant=¨bold¨»R«/mi»«mi mathvariant=¨bold¨»MQ«/mi»«/msub»«mo mathvariant=¨bold¨»+«/mo»«msub»«mi mathvariant=¨bold¨»R«/mi»«msub»«mi mathvariant=¨bold¨»L«/mi»«mn mathvariant=¨bold¨»1«/mn»«/msub»«/msub»«/mrow»«/mfrac»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»)«/mo»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»+«/mo»«msub»«mi mathvariant=¨bold¨ mathcolor=¨#0000FF¨»R«/mi»«mi mathvariant=¨bold¨ mathcolor=¨#0000FF¨»QN«/mi»«/msub»«mspace linebreak=¨newline¨/»«/mrow»«mspace linebreak=¨newline¨/»«mspace linebreak=¨newline¨/»«msub»«mi mathvariant=¨bold¨ mathcolor=¨#0000FF¨»R«/mi»«mi mathvariant=¨bold¨ mathcolor=¨#0000FF¨»T«/mi»«/msub»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»=«/mo»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»(«/mo»«mfrac mathcolor=¨#0000FF¨»«mrow»«mn mathvariant=¨bold¨»10«/mn»«mo mathvariant=¨bold¨»§#183;«/mo»«mn mathvariant=¨bold¨»5«/mn»«/mrow»«mrow»«mn mathvariant=¨bold¨»10«/mn»«mo mathvariant=¨bold¨»+«/mo»«mn mathvariant=¨bold¨»5«/mn»«/mrow»«/mfrac»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»)«/mo»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»+«/mo»«mn mathvariant=¨bold¨ mathcolor=¨#0000FF¨»5«/mn»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»=«/mo»«mn mathvariant=¨bold¨ mathcolor=¨#0000FF¨»3«/mn»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨».«/mo»«mn mathvariant=¨bold¨ mathcolor=¨#0000FF¨»33«/mn»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»+«/mo»«mn mathvariant=¨bold¨ mathcolor=¨#0000FF¨»5«/mn»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»=«/mo»«mn mathvariant=¨bold¨ mathcolor=¨#0000FF¨»8«/mn»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨».«/mo»«mn mathvariant=¨bold¨ mathcolor=¨#0000FF¨»33«/mn»«mi mathvariant=¨bold¨ mathcolor=¨#0000FF¨»§#937;«/mi»«/mstyle»«/math»
نحسب تيار المصدر من قانون أوم للدائرة بأكملها:
«math style=¨font-family:Tahoma¨ xmlns=¨http://www.w3.org/1998/Math/MathML¨»«mstyle mathsize=¨20px¨»«mi mathvariant=¨bold¨ mathcolor=¨#0000FF¨»I«/mi»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»=«/mo»«mfrac mathcolor=¨#0000FF¨»«mi mathvariant=¨bold¨»§#949;«/mi»«msub»«mi mathvariant=¨bold¨»R«/mi»«mi mathvariant=¨bold¨»T«/mi»«/msub»«/mfrac»«mspace linebreak=¨newline¨/»«mspace linebreak=¨newline¨/»«mi mathvariant=¨bold¨ mathcolor=¨#0000FF¨»I«/mi»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»=«/mo»«mfrac mathcolor=¨#0000FF¨»«mi mathvariant=¨bold¨»§#949;«/mi»«msub»«mi mathvariant=¨bold¨»R«/mi»«mi mathvariant=¨bold¨»T«/mi»«/msub»«/mfrac»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»=«/mo»«mfrac mathcolor=¨#0000FF¨»«mn mathvariant=¨bold¨»12«/mn»«mrow»«mn mathvariant=¨bold¨»8«/mn»«mo mathvariant=¨bold¨».«/mo»«mn mathvariant=¨bold¨»33«/mn»«/mrow»«/mfrac»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»=«/mo»«mn mathvariant=¨bold¨ mathcolor=¨#0000FF¨»1«/mn»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨».«/mo»«mn mathvariant=¨bold¨ mathcolor=¨#0000FF¨»44«/mn»«mi mathvariant=¨bold¨ mathcolor=¨#0000FF¨»A«/mi»«/mstyle»«/math»
نظرًا لأن مقاومة المصباح L1 أقل بمرتين من المقاومة RMQ ، فإن التيار عبر المصباح سيكون أكبر بمرتين من التيار عبر RMQ.
تيار 0.96 أمبير سوف يتدفق عبر المصباح، و تيار 0.48 أمبير سوف يتدفق عبر المقاومة RMQ.
نحسب فرق الجهد على المصباح L1 باستخدام قانون أوم:
«math style=¨font-family:Tahoma¨ xmlns=¨http://www.w3.org/1998/Math/MathML¨»«mstyle mathsize=¨20px¨»«msub»«mi mathvariant=¨bold¨ mathcolor=¨#0000FF¨»U«/mi»«msub mathcolor=¨#0000FF¨»«mi mathvariant=¨bold¨»L«/mi»«mn mathvariant=¨bold¨»1«/mn»«/msub»«/msub»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»=«/mo»«msub»«mi mathvariant=¨bold¨ mathcolor=¨#0000FF¨»I«/mi»«msub mathcolor=¨#0000FF¨»«mi mathvariant=¨bold¨»L«/mi»«mn mathvariant=¨bold¨»1«/mn»«/msub»«/msub»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»§#183;«/mo»«msub»«mi mathvariant=¨bold¨ mathcolor=¨#0000FF¨»R«/mi»«msub mathcolor=¨#0000FF¨»«mi mathvariant=¨bold¨»L«/mi»«mn mathvariant=¨bold¨»1«/mn»«/msub»«/msub»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»=«/mo»«mn mathvariant=¨bold¨ mathcolor=¨#0000FF¨»0«/mn»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨».«/mo»«mn mathvariant=¨bold¨ mathcolor=¨#0000FF¨»96«/mn»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»§#183;«/mo»«mn mathvariant=¨bold¨ mathcolor=¨#0000FF¨»5«/mn»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»=«/mo»«mn mathvariant=¨bold¨ mathcolor=¨#0000FF¨»4«/mn»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨».«/mo»«mn mathvariant=¨bold¨ mathcolor=¨#0000FF¨»8«/mn»«mi mathvariant=¨bold¨ mathcolor=¨#0000FF¨»V«/mi»«/mstyle»«/math»
يمكن ملاحظة أنه نتيجة لانقطاع الدائرة نتيجة لاحتراق المصباح، سيقل فرق الجهد على المصباح L1.
د- نرسم مخططًا للدائرة عندما يكون المصباح L2 في حالة تماس كهربائي.
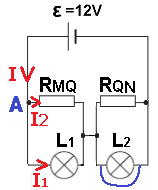
بسبب موصل التماس، ستكون مقاومة الطرف الأيمن صفراً (حتى إذا لم يتم احتراق المصباح) ، فلن يكون هناك فرق جهد على الطرف الأيمن.
وفرق الجهد على الجانب الأيسر سيكون مساويا لفرق جهد الأقطاب. لذلك ، فإن فرق الجهد على المصباح في هذه الحالة سيزداد ويصبح مساويًا لـ 12 فولط.
سنثبت ذلك بمساعدة عملية حسابية: نجد فرق الجهد في المصباح L2 من حساب التيارات في الدائرة. لنقم بعمل رسم تخطيطي للدائرة:
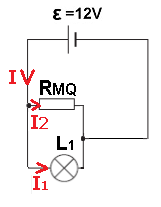
نحسب المقاومة المحصلة:
«math xmlns=¨http://www.w3.org/1998/Math/MathML¨»«mstyle mathsize=¨20px¨»«mrow»«msub»«mi mathvariant=¨bold¨ mathcolor=¨#0000FF¨»R«/mi»«mi mathvariant=¨bold¨ mathcolor=¨#0000FF¨»T«/mi»«/msub»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»=«/mo»«msub»«mi mathvariant=¨bold¨ mathcolor=¨#0000FF¨»R«/mi»«mi mathvariant=¨bold¨ mathcolor=¨#0000FF¨»MQ«/mi»«/msub»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»|«/mo»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»|«/mo»«msub»«mi mathvariant=¨bold¨ mathcolor=¨#0000FF¨»R«/mi»«msub mathcolor=¨#0000FF¨»«mi mathvariant=¨bold¨»L«/mi»«mn mathvariant=¨bold¨»1«/mn»«/msub»«/msub»«mspace linebreak=¨newline¨/»«mspace linebreak=¨newline¨/»«msub»«mi mathvariant=¨bold¨ mathcolor=¨#0000FF¨»R«/mi»«mi mathvariant=¨bold¨ mathcolor=¨#0000FF¨»T«/mi»«/msub»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»=«/mo»«mfrac mathcolor=¨#0000FF¨»«mrow»«msub»«mi mathvariant=¨bold¨»R«/mi»«mi mathvariant=¨bold¨»MQ«/mi»«/msub»«mo mathvariant=¨bold¨»§#183;«/mo»«msub»«mi mathvariant=¨bold¨»R«/mi»«msub»«mi mathvariant=¨bold¨»L«/mi»«mn mathvariant=¨bold¨»1«/mn»«/msub»«/msub»«/mrow»«mrow»«msub»«mi mathvariant=¨bold¨»R«/mi»«mi mathvariant=¨bold¨»MQ«/mi»«/msub»«mo mathvariant=¨bold¨»+«/mo»«msub»«mi mathvariant=¨bold¨»R«/mi»«msub»«mi mathvariant=¨bold¨»L«/mi»«mn mathvariant=¨bold¨»1«/mn»«/msub»«/msub»«/mrow»«/mfrac»«mspace linebreak=¨newline¨/»«/mrow»«mspace linebreak=¨newline¨/»«mspace linebreak=¨newline¨/»«msub»«mi mathvariant=¨bold¨ mathcolor=¨#0000FF¨»R«/mi»«mi mathvariant=¨bold¨ mathcolor=¨#0000FF¨»T«/mi»«/msub»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»=«/mo»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»(«/mo»«mfrac mathcolor=¨#0000FF¨»«mrow»«mn mathvariant=¨bold¨»10«/mn»«mo mathvariant=¨bold¨»§#183;«/mo»«mn mathvariant=¨bold¨»5«/mn»«/mrow»«mrow»«mn mathvariant=¨bold¨»10«/mn»«mo mathvariant=¨bold¨»+«/mo»«mn mathvariant=¨bold¨»5«/mn»«/mrow»«/mfrac»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»)«/mo»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»=«/mo»«mn mathvariant=¨bold¨ mathcolor=¨#0000FF¨»3«/mn»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨».«/mo»«mn mathvariant=¨bold¨ mathcolor=¨#0000FF¨»33«/mn»«mi mathvariant=¨bold¨ mathcolor=¨#0000FF¨»§#937;«/mi»«/mstyle»«/math»
نحسب تيار المصدر من قانون أوم للدائرة بأكملها:
«math style=¨font-family:Tahoma¨ xmlns=¨http://www.w3.org/1998/Math/MathML¨»«mstyle mathsize=¨20px¨»«mi mathvariant=¨bold¨ mathcolor=¨#0000FF¨»I«/mi»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»=«/mo»«mfrac mathcolor=¨#0000FF¨»«mi mathvariant=¨bold¨»§#949;«/mi»«msub»«mi mathvariant=¨bold¨»R«/mi»«mi mathvariant=¨bold¨»T«/mi»«/msub»«/mfrac»«mspace linebreak=¨newline¨/»«mspace linebreak=¨newline¨/»«mi mathvariant=¨bold¨ mathcolor=¨#0000FF¨»I«/mi»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»=«/mo»«mfrac mathcolor=¨#0000FF¨»«mi mathvariant=¨bold¨»§#949;«/mi»«msub»«mi mathvariant=¨bold¨»R«/mi»«mi mathvariant=¨bold¨»T«/mi»«/msub»«/mfrac»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»=«/mo»«mfrac mathcolor=¨#0000FF¨»«mn mathvariant=¨bold¨»12«/mn»«mrow»«mn mathvariant=¨bold¨»3«/mn»«mo mathvariant=¨bold¨».«/mo»«mn mathvariant=¨bold¨»33«/mn»«/mrow»«/mfrac»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»=«/mo»«mn mathvariant=¨bold¨ mathcolor=¨#0000FF¨»3«/mn»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨».«/mo»«mn mathvariant=¨bold¨ mathcolor=¨#0000FF¨»6«/mn»«mi mathvariant=¨bold¨ mathcolor=¨#0000FF¨»A«/mi»«/mstyle»«/math»
نظرًا لأن مقاومة المصباح L1 أقل بمرتين من المقاومة RMQ ، فإن التيار عبر المصباح سيكون أكبر بمرتين من التيار عبر RMQ.
سوف يتدفق تيار 2.4 أمبير عبر المصباح، ويتدفق تيار 1.2 أمبير عبر المقاومة RMQ.
نحسب فرق الجهد على المصباح L1 باستخدام قانون أوم:
«math style=¨font-family:Tahoma¨ xmlns=¨http://www.w3.org/1998/Math/MathML¨»«mstyle mathsize=¨20px¨»«msub»«mi mathvariant=¨bold¨ mathcolor=¨#0000FF¨»U«/mi»«msub mathcolor=¨#0000FF¨»«mi mathvariant=¨bold¨»L«/mi»«mn mathvariant=¨bold¨»1«/mn»«/msub»«/msub»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»=«/mo»«msub»«mi mathvariant=¨bold¨ mathcolor=¨#0000FF¨»I«/mi»«msub mathcolor=¨#0000FF¨»«mi mathvariant=¨bold¨»L«/mi»«mn mathvariant=¨bold¨»1«/mn»«/msub»«/msub»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»§#183;«/mo»«msub»«mi mathvariant=¨bold¨ mathcolor=¨#0000FF¨»R«/mi»«msub mathcolor=¨#0000FF¨»«mi mathvariant=¨bold¨»L«/mi»«mn mathvariant=¨bold¨»1«/mn»«/msub»«/msub»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»=«/mo»«mn mathvariant=¨bold¨ mathcolor=¨#0000FF¨»2«/mn»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨».«/mo»«mn mathvariant=¨bold¨ mathcolor=¨#0000FF¨»4«/mn»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»§#183;«/mo»«mn mathvariant=¨bold¨ mathcolor=¨#0000FF¨»5«/mn»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»=«/mo»«mn mathvariant=¨bold¨ mathcolor=¨#0000FF¨»12«/mn»«mi mathvariant=¨bold¨ mathcolor=¨#0000FF¨»V«/mi»«/mstyle»«/math»
يمكن ملاحظة أنه نتيجة لوجود المصباح المحترق في حالة تماس، سيزداد فرق الجهد على المصباح L1.
هـ- طالما أن التماس المتحرك Q في منتصف المقاوم المتغير، سيكون هناك تماثل بين الطرفين الأيمن والأيسر، سيكون فرق الجهد في المصابيح 6 فولط. سوف تضيء المصابيح بضوءها الكاملة.
سوف نثبت ذلك بالحساب:
نجد فرق الجهد في المصباح L2 من حساب التيارات في الدائرة.

المقاومة الكلية للمقاوم المتغير 200 أوم. مقاومة RMQ و RQN تساوي 100 أوم.
نحسب المقاومة المحصلة:
«math xmlns=¨http://www.w3.org/1998/Math/MathML¨»«mstyle mathsize=¨20px¨»«mrow»«msub»«mi mathvariant=¨bold¨ mathcolor=¨#0000FF¨»R«/mi»«mi mathvariant=¨bold¨ mathcolor=¨#0000FF¨»T«/mi»«/msub»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»=«/mo»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»(«/mo»«msub»«mi mathvariant=¨bold¨ mathcolor=¨#0000FF¨»R«/mi»«mi mathvariant=¨bold¨ mathcolor=¨#0000FF¨»MQ«/mi»«/msub»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»|«/mo»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»|«/mo»«msub»«mi mathvariant=¨bold¨ mathcolor=¨#0000FF¨»R«/mi»«msub mathcolor=¨#0000FF¨»«mi mathvariant=¨bold¨»L«/mi»«mn mathvariant=¨bold¨»1«/mn»«/msub»«/msub»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»)«/mo»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»+«/mo»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»(«/mo»«msub»«mi mathvariant=¨bold¨ mathcolor=¨#0000FF¨»R«/mi»«mi mathvariant=¨bold¨ mathcolor=¨#0000FF¨»QN«/mi»«/msub»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»|«/mo»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»|«/mo»«msub»«mi mathvariant=¨bold¨ mathcolor=¨#0000FF¨»R«/mi»«msub mathcolor=¨#0000FF¨»«mi mathvariant=¨bold¨»L«/mi»«mn mathvariant=¨bold¨»2«/mn»«/msub»«/msub»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»)«/mo»«mspace linebreak=¨newline¨/»«mspace linebreak=¨newline¨/»«msub»«mi mathvariant=¨bold¨ mathcolor=¨#0000FF¨»R«/mi»«mi mathvariant=¨bold¨ mathcolor=¨#0000FF¨»T«/mi»«/msub»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»=«/mo»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»(«/mo»«mfrac mathcolor=¨#0000FF¨»«mrow»«msub»«mi mathvariant=¨bold¨»R«/mi»«mi mathvariant=¨bold¨»MQ«/mi»«/msub»«mo mathvariant=¨bold¨»§#183;«/mo»«msub»«mi mathvariant=¨bold¨»R«/mi»«msub»«mi mathvariant=¨bold¨»L«/mi»«mn mathvariant=¨bold¨»1«/mn»«/msub»«/msub»«/mrow»«mrow»«msub»«mi mathvariant=¨bold¨»R«/mi»«mi mathvariant=¨bold¨»MQ«/mi»«/msub»«mo mathvariant=¨bold¨»+«/mo»«msub»«mi mathvariant=¨bold¨»R«/mi»«msub»«mi mathvariant=¨bold¨»L«/mi»«mn mathvariant=¨bold¨»1«/mn»«/msub»«/msub»«/mrow»«/mfrac»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»)«/mo»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»+«/mo»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»(«/mo»«mfrac mathcolor=¨#0000FF¨»«mrow»«msub»«mi mathvariant=¨bold¨»R«/mi»«mi mathvariant=¨bold¨»QN«/mi»«/msub»«mo mathvariant=¨bold¨»§#183;«/mo»«msub»«mi mathvariant=¨bold¨»R«/mi»«msub»«mi mathvariant=¨bold¨»L«/mi»«mn mathvariant=¨bold¨»2«/mn»«/msub»«/msub»«/mrow»«mrow»«msub»«mi mathvariant=¨bold¨»R«/mi»«mi mathvariant=¨bold¨»QN«/mi»«/msub»«mo mathvariant=¨bold¨»+«/mo»«msub»«mi mathvariant=¨bold¨»R«/mi»«msub»«mi mathvariant=¨bold¨»L«/mi»«mn mathvariant=¨bold¨»2«/mn»«/msub»«/msub»«/mrow»«/mfrac»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»)«/mo»«mspace linebreak=¨newline¨/»«/mrow»«mspace linebreak=¨newline¨/»«mspace linebreak=¨newline¨/»«msub»«mi mathvariant=¨bold¨ mathcolor=¨#0000FF¨»R«/mi»«mi mathvariant=¨bold¨ mathcolor=¨#0000FF¨»T«/mi»«/msub»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»=«/mo»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»(«/mo»«mfrac mathcolor=¨#0000FF¨»«mrow»«mn mathvariant=¨bold¨»100«/mn»«mo mathvariant=¨bold¨»§#183;«/mo»«mn mathvariant=¨bold¨»5«/mn»«/mrow»«mrow»«mn mathvariant=¨bold¨»100«/mn»«mo mathvariant=¨bold¨»+«/mo»«mn mathvariant=¨bold¨»5«/mn»«/mrow»«/mfrac»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»)«/mo»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»+«/mo»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»(«/mo»«mfrac mathcolor=¨#0000FF¨»«mrow»«mn mathvariant=¨bold¨»100«/mn»«mo mathvariant=¨bold¨»§#183;«/mo»«mn mathvariant=¨bold¨»5«/mn»«/mrow»«mrow»«mn mathvariant=¨bold¨»100«/mn»«mo mathvariant=¨bold¨»+«/mo»«mn mathvariant=¨bold¨»5«/mn»«/mrow»«/mfrac»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»)«/mo»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»=«/mo»«mn mathvariant=¨bold¨ mathcolor=¨#0000FF¨»4«/mn»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨».«/mo»«mn mathvariant=¨bold¨ mathcolor=¨#0000FF¨»76«/mn»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»+«/mo»«mn mathvariant=¨bold¨ mathcolor=¨#0000FF¨»4«/mn»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨».«/mo»«mn mathvariant=¨bold¨ mathcolor=¨#0000FF¨»76«/mn»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»=«/mo»«mn mathvariant=¨bold¨ mathcolor=¨#0000FF¨»9«/mn»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨».«/mo»«mn mathvariant=¨bold¨ mathcolor=¨#0000FF¨»52«/mn»«mi mathvariant=¨bold¨ mathcolor=¨#0000FF¨»§#937;«/mi»«/mstyle»«/math»
نحسب التيار بالمصدر من قانون أوم للدائرة بأكملها:
«math style=¨font-family:Tahoma¨ xmlns=¨http://www.w3.org/1998/Math/MathML¨»«mstyle mathsize=¨20px¨»«mi mathvariant=¨bold¨ mathcolor=¨#0000FF¨»I«/mi»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»=«/mo»«mfrac mathcolor=¨#0000FF¨»«mi mathvariant=¨bold¨»§#949;«/mi»«msub»«mi mathvariant=¨bold¨»R«/mi»«mi mathvariant=¨bold¨»T«/mi»«/msub»«/mfrac»«mspace linebreak=¨newline¨/»«mspace linebreak=¨newline¨/»«mi mathvariant=¨bold¨ mathcolor=¨#0000FF¨»I«/mi»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»=«/mo»«mfrac mathcolor=¨#0000FF¨»«mi mathvariant=¨bold¨»§#949;«/mi»«msub»«mi mathvariant=¨bold¨»R«/mi»«mi mathvariant=¨bold¨»T«/mi»«/msub»«/mfrac»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»=«/mo»«mfrac mathcolor=¨#0000FF¨»«mn mathvariant=¨bold¨»12«/mn»«mrow»«mn mathvariant=¨bold¨»9«/mn»«mo mathvariant=¨bold¨».«/mo»«mn mathvariant=¨bold¨»52«/mn»«/mrow»«/mfrac»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»=«/mo»«mn mathvariant=¨bold¨ mathcolor=¨#0000FF¨»1«/mn»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨».«/mo»«mn mathvariant=¨bold¨ mathcolor=¨#0000FF¨»26«/mn»«mi mathvariant=¨bold¨ mathcolor=¨#0000FF¨»A«/mi»«/mstyle»«/math»
نظرًا لأن مقاومة المصباح L1 أقل بـ 20 مرة من المقاومة RMQ ، فإن التيار عبر المصباح سيكون أكبر بـ 20 مرة من التيار عبر RMQ.
سوف يتدفق تيار 1.2 أمبير عبر المصباح، ويتدفق تيار شدته 0.06 أمبير عبر المقاومة RMQ.
نحسب فرق الجهد على المصباح L1 باستخدام قانون أوم:
«math style=¨font-family:Tahoma¨ xmlns=¨http://www.w3.org/1998/Math/MathML¨»«mstyle mathsize=¨20px¨»«msub»«mi mathvariant=¨bold¨ mathcolor=¨#0000FF¨»U«/mi»«msub mathcolor=¨#0000FF¨»«mi mathvariant=¨bold¨»L«/mi»«mn mathvariant=¨bold¨»1«/mn»«/msub»«/msub»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»=«/mo»«msub»«mi mathvariant=¨bold¨ mathcolor=¨#0000FF¨»I«/mi»«msub mathcolor=¨#0000FF¨»«mi mathvariant=¨bold¨»L«/mi»«mn mathvariant=¨bold¨»1«/mn»«/msub»«/msub»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»§#183;«/mo»«msub»«mi mathvariant=¨bold¨ mathcolor=¨#0000FF¨»R«/mi»«msub mathcolor=¨#0000FF¨»«mi mathvariant=¨bold¨»L«/mi»«mn mathvariant=¨bold¨»1«/mn»«/msub»«/msub»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»=«/mo»«mn mathvariant=¨bold¨ mathcolor=¨#0000FF¨»1«/mn»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨».«/mo»«mn mathvariant=¨bold¨ mathcolor=¨#0000FF¨»2«/mn»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»§#183;«/mo»«mn mathvariant=¨bold¨ mathcolor=¨#0000FF¨»5«/mn»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»=«/mo»«mn mathvariant=¨bold¨ mathcolor=¨#0000FF¨»6«/mn»«mi mathvariant=¨bold¨ mathcolor=¨#0000FF¨»V«/mi»«/mstyle»«/math»
يتدفق التيار إلى الطرف الأيمن وينقسم بطريقة مماثلة بحيث يكون فرق الجهد على المصباح L2 أيضًا 6 فولط.
و- بطارية غير مثالية هي بطارية ذات مقاومة داخلية. من تعبير فرق جهد الأقطاب، سيكون فرق جهد الأقطاب أقل من 12 فولط. وفقًا لذلك ، سيكون فرق الجهد في كل مصباح أقل من 6 فولط.
لذلك، إذا لم تكن البطارية مثالية ، فلن تضيء المصابيح بكامل إضاءتها.
29. ד.10
أ- نحسب المقاومة المحصلة للدائرة.
«math xmlns=¨http://www.w3.org/1998/Math/MathML¨»«msub»«mi mathvariant=¨bold¨ mathcolor=¨#0000FF¨ mathsize=¨20px¨»R«/mi»«mi mathvariant=¨bold¨ mathcolor=¨#0000FF¨ mathsize=¨20px¨»T«/mi»«/msub»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨ mathsize=¨20px¨»=«/mo»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨ mathsize=¨20px¨»[«/mo»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨ mathsize=¨20px¨»(«/mo»«msub»«mi mathvariant=¨bold¨ mathcolor=¨#0000FF¨ mathsize=¨20px¨»R«/mi»«mn mathvariant=¨bold¨ mathcolor=¨#0000FF¨ mathsize=¨20px¨»2«/mn»«/msub»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨ mathsize=¨20px¨»+«/mo»«msub»«mi mathvariant=¨bold¨ mathcolor=¨#0000FF¨ mathsize=¨20px¨»R«/mi»«mn mathvariant=¨bold¨ mathcolor=¨#0000FF¨ mathsize=¨20px¨»3«/mn»«/msub»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨ mathsize=¨20px¨»)«/mo»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨ mathsize=¨20px¨»|«/mo»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨ mathsize=¨20px¨»|«/mo»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨ mathsize=¨20px¨»(«/mo»«msub»«mi mathvariant=¨bold¨ mathcolor=¨#0000FF¨ mathsize=¨20px¨»R«/mi»«mn mathvariant=¨bold¨ mathcolor=¨#0000FF¨ mathsize=¨20px¨»4«/mn»«/msub»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨ mathsize=¨20px¨»+«/mo»«msub»«mi mathvariant=¨bold¨ mathcolor=¨#0000FF¨ mathsize=¨20px¨»R«/mi»«mn mathvariant=¨bold¨ mathcolor=¨#0000FF¨ mathsize=¨20px¨»5«/mn»«/msub»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨ mathsize=¨20px¨»)«/mo»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨ mathsize=¨20px¨»]«/mo»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨ mathsize=¨20px¨»+«/mo»«msub»«mi mathvariant=¨bold¨ mathcolor=¨#0000FF¨ mathsize=¨20px¨»R«/mi»«mn mathvariant=¨bold¨ mathcolor=¨#0000FF¨ mathsize=¨20px¨»1«/mn»«/msub»«mspace linebreak=¨newline¨/»«mspace linebreak=¨newline¨/»«msub»«mi mathvariant=¨bold¨ mathcolor=¨#0000FF¨ mathsize=¨20px¨»R«/mi»«mi mathvariant=¨bold¨ mathsize=¨20px¨ mathcolor=¨#0000FF¨»T«/mi»«/msub»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨ mathsize=¨20px¨»=«/mo»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨ mathsize=¨20px¨»[«/mo»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨ mathsize=¨20px¨»(«/mo»«mn mathvariant=¨bold¨ mathcolor=¨#0000FF¨ mathsize=¨20px¨»10«/mn»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨ mathsize=¨20px¨»+«/mo»«mn mathvariant=¨bold¨ mathcolor=¨#0000FF¨ mathsize=¨20px¨»10«/mn»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨ mathsize=¨20px¨»)«/mo»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨ mathsize=¨20px¨»|«/mo»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨ mathsize=¨20px¨»|«/mo»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨ mathsize=¨20px¨»(«/mo»«mn mathvariant=¨bold¨ mathcolor=¨#0000FF¨ mathsize=¨20px¨»10«/mn»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨ mathsize=¨20px¨»+«/mo»«mn mathvariant=¨bold¨ mathcolor=¨#0000FF¨ mathsize=¨20px¨»10«/mn»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨ mathsize=¨20px¨»)«/mo»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨ mathsize=¨20px¨»]«/mo»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨ mathsize=¨20px¨»+«/mo»«mn mathvariant=¨bold¨ mathcolor=¨#0000FF¨ mathsize=¨20px¨»10«/mn»«mspace linebreak=¨newline¨/»«mspace linebreak=¨newline¨/»«msub»«mi mathvariant=¨bold¨ mathcolor=¨#0000FF¨ mathsize=¨20px¨»R«/mi»«mi mathvariant=¨bold¨ mathsize=¨20px¨ mathcolor=¨#0000FF¨»T«/mi»«/msub»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨ mathsize=¨20px¨»=«/mo»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨ mathsize=¨20px¨»[«/mo»«mfrac mathcolor=¨#0000FF¨»«mrow»«mn mathvariant=¨bold¨ mathsize=¨20px¨»20«/mn»«mo mathvariant=¨bold¨ mathsize=¨20px¨»§#183;«/mo»«mn mathvariant=¨bold¨ mathsize=¨20px¨»20«/mn»«/mrow»«mrow»«mn mathvariant=¨bold¨ mathsize=¨20px¨»20«/mn»«mo mathvariant=¨bold¨ mathsize=¨20px¨»+«/mo»«mn mathvariant=¨bold¨ mathsize=¨20px¨»20«/mn»«/mrow»«/mfrac»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨ mathsize=¨20px¨»]«/mo»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨ mathsize=¨20px¨»+«/mo»«mn mathvariant=¨bold¨ mathcolor=¨#0000FF¨ mathsize=¨20px¨»10«/mn»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨ mathsize=¨20px¨»=«/mo»«mn mathvariant=¨bold¨ mathcolor=¨#0000FF¨ mathsize=¨20px¨»20«/mn»«mi mathvariant=¨bold¨ mathcolor=¨#0000FF¨ mathsize=¨20px¨»§#937;«/mi»«/math»
ب- نحسب تيار المصدر من قانون أوم للدائرة بأكملها:
«math style=¨font-family:Tahoma¨ xmlns=¨http://www.w3.org/1998/Math/MathML¨»«mstyle mathsize=¨20px¨»«mi mathvariant=¨bold¨ mathcolor=¨#0000FF¨»I«/mi»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»=«/mo»«mfrac mathcolor=¨#0000FF¨»«mi mathvariant=¨bold¨»§#949;«/mi»«msub»«mi mathvariant=¨bold¨»R«/mi»«mi mathvariant=¨bold¨»T«/mi»«/msub»«/mfrac»«mspace linebreak=¨newline¨/»«mspace linebreak=¨newline¨/»«mi mathvariant=¨bold¨ mathcolor=¨#0000FF¨»I«/mi»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»=«/mo»«mfrac mathcolor=¨#0000FF¨»«mi mathvariant=¨bold¨»§#949;«/mi»«msub»«mi mathvariant=¨bold¨»R«/mi»«mi mathvariant=¨bold¨»T«/mi»«/msub»«/mfrac»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»=«/mo»«mfrac mathcolor=¨#0000FF¨»«mn mathvariant=¨bold¨»30«/mn»«mn mathvariant=¨bold¨»20«/mn»«/mfrac»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»=«/mo»«mn mathvariant=¨bold¨ mathcolor=¨#0000FF¨»1«/mn»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨».«/mo»«mn mathvariant=¨bold¨ mathcolor=¨#0000FF¨»5«/mn»«mi mathvariant=¨bold¨ mathcolor=¨#0000FF¨»A«/mi»«/mstyle»«/math»
ج- نحسب فرق الجهد على المقاوم R1 باستخدام قانون أوم:
«math style=¨font-family:Tahoma¨ xmlns=¨http://www.w3.org/1998/Math/MathML¨»«mstyle mathsize=¨20px¨»«msub»«mi mathvariant=¨bold¨ mathcolor=¨#0000FF¨»U«/mi»«msub mathcolor=¨#0000FF¨»«mi mathvariant=¨bold¨»R«/mi»«mn mathvariant=¨bold¨»1«/mn»«/msub»«/msub»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»=«/mo»«mi mathvariant=¨bold¨ mathcolor=¨#0000FF¨»I«/mi»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»§#183;«/mo»«msub»«mi mathvariant=¨bold¨ mathcolor=¨#0000FF¨»R«/mi»«msub mathcolor=¨#0000FF¨»«mrow/»«mn mathvariant=¨bold¨»1«/mn»«/msub»«/msub»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»=«/mo»«mn mathvariant=¨bold¨ mathcolor=¨#0000FF¨»1«/mn»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨».«/mo»«mn mathvariant=¨bold¨ mathcolor=¨#0000FF¨»5«/mn»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»§#183;«/mo»«mn mathvariant=¨bold¨ mathcolor=¨#0000FF¨»10«/mn»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»=«/mo»«mn mathvariant=¨bold¨ mathcolor=¨#0000FF¨»15«/mn»«mi mathvariant=¨bold¨ mathcolor=¨#0000FF¨»V«/mi»«/mstyle»«/math»
د- لحساب فرق الجهد بين طرفي القاطع في الدائرة، نجد التيارات في الدائرة. نشير إلى التيار بالمصدر بواسطة I.
التيار عبر R4 بـ I1 ، والتيار عبر R2 بـ I2. نُشير إلى العقدتين في الدائرة بـ A و B. كما ترى في الشكل التالي:
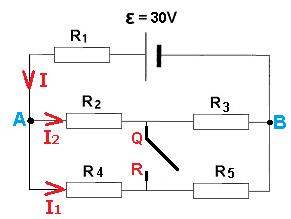
وجدنا في القسم ج أن شدةة التيار بالمصدر 1.5 أمبير.
المقاومة المحصلة للمقاومتين R2 و R3 هي نفس المقاومة المحصلة للمقاومتين R4 و R5. لذلك ينقسم التيار I في العقدة A بصورة متماثلة.
ويتحقق: «math style=¨font-family:Tahoma¨ xmlns=¨http://www.w3.org/1998/Math/MathML¨»«mstyle mathsize=¨20px¨»«msub»«mi mathvariant=¨bold¨ mathcolor=¨#0000FF¨»I«/mi»«mn mathvariant=¨bold¨ mathcolor=¨#0000FF¨»1«/mn»«/msub»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»=«/mo»«msub»«mi mathvariant=¨bold¨ mathcolor=¨#0000FF¨»I«/mi»«mn mathvariant=¨bold¨ mathcolor=¨#0000FF¨»2«/mn»«/msub»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»=«/mo»«mn mathvariant=¨bold¨ mathcolor=¨#0000FF¨»0«/mn»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨».«/mo»«mn mathvariant=¨bold¨ mathcolor=¨#0000FF¨»75«/mn»«mi mathvariant=¨bold¨ mathcolor=¨#0000FF¨»A«/mi»«/mstyle»«/math» .
نحسب فرق الجهد على المفاومتين R2 ו- R4 .
«math style=¨font-family:Tahoma¨ xmlns=¨http://www.w3.org/1998/Math/MathML¨»«mstyle mathsize=¨20px¨»«msub»«mi mathvariant=¨bold¨ mathcolor=¨#0000FF¨»U«/mi»«msub mathcolor=¨#0000FF¨»«mi mathvariant=¨bold¨»R«/mi»«mn mathvariant=¨bold¨»2«/mn»«/msub»«/msub»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»=«/mo»«msub»«mi mathvariant=¨bold¨ mathcolor=¨#0000FF¨»I«/mi»«mn mathvariant=¨bold¨ mathcolor=¨#0000FF¨»2«/mn»«/msub»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»§#183;«/mo»«msub»«mi mathvariant=¨bold¨ mathcolor=¨#0000FF¨»R«/mi»«mn mathvariant=¨bold¨ mathcolor=¨#0000FF¨»2«/mn»«/msub»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»=«/mo»«mn mathvariant=¨bold¨ mathcolor=¨#0000FF¨»0«/mn»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨».«/mo»«mn mathvariant=¨bold¨ mathcolor=¨#0000FF¨»75«/mn»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»§#183;«/mo»«mn mathvariant=¨bold¨ mathcolor=¨#0000FF¨»10«/mn»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»=«/mo»«mn mathvariant=¨bold¨ mathcolor=¨#0000FF¨»7«/mn»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨».«/mo»«mn mathvariant=¨bold¨ mathcolor=¨#0000FF¨»5«/mn»«mi mathvariant=¨bold¨ mathcolor=¨#0000FF¨»V«/mi»«mspace linebreak=¨newline¨/»«msub»«mi mathvariant=¨bold¨ mathcolor=¨#0000FF¨»U«/mi»«msub mathcolor=¨#0000FF¨»«mi mathvariant=¨bold¨»R«/mi»«mn mathvariant=¨bold¨»4«/mn»«/msub»«/msub»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»=«/mo»«msub»«mi mathvariant=¨bold¨ mathcolor=¨#0000FF¨»I«/mi»«mn mathvariant=¨bold¨ mathcolor=¨#0000FF¨»1«/mn»«/msub»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»§#183;«/mo»«msub»«mi mathvariant=¨bold¨ mathcolor=¨#0000FF¨»R«/mi»«mn mathvariant=¨bold¨ mathcolor=¨#0000FF¨»4«/mn»«/msub»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»=«/mo»«mn mathvariant=¨bold¨ mathcolor=¨#0000FF¨»0«/mn»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨».«/mo»«mn mathvariant=¨bold¨ mathcolor=¨#0000FF¨»75«/mn»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»§#183;«/mo»«mn mathvariant=¨bold¨ mathcolor=¨#0000FF¨»10«/mn»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»=«/mo»«mn mathvariant=¨bold¨ mathcolor=¨#0000FF¨»7«/mn»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨».«/mo»«mn mathvariant=¨bold¨ mathcolor=¨#0000FF¨»5«/mn»«mi mathvariant=¨bold¨ mathcolor=¨#0000FF¨»V«/mi»«/mstyle»«/math»
وفقًا لاتجاه التيار I2 ، يمكن تحديد أن الجهد في النقطة Q أقل من الجهد في النقطة A بمقدار 7.5 فولط.
وحسب اتجاه التيار I1 ، يمكن تحديد أن الجهد في النقطة R يقل 7.5 فولط عن الجهد في النقطة A.
لذلك فإن الجهد في النقطة Q يساوي الجهد في النقطة R وفرق الجهد VQR يساوي صفر فولط.
30. ד.11
أ- نحسب المقاومة المحصلة للدائرة.
«math xmlns=¨http://www.w3.org/1998/Math/MathML¨»«msub»«mi mathvariant=¨bold¨ mathcolor=¨#0000FF¨ mathsize=¨20px¨»R«/mi»«mi mathvariant=¨bold¨ mathcolor=¨#0000FF¨ mathsize=¨20px¨»T«/mi»«/msub»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨ mathsize=¨20px¨»=«/mo»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨ mathsize=¨20px¨»[«/mo»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨ mathsize=¨20px¨»(«/mo»«msub»«mi mathvariant=¨bold¨ mathcolor=¨#0000FF¨ mathsize=¨20px¨»R«/mi»«mn mathvariant=¨bold¨ mathcolor=¨#0000FF¨ mathsize=¨20px¨»2«/mn»«/msub»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨ mathsize=¨20px¨»|«/mo»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨ mathsize=¨20px¨»|«/mo»«msub»«mi mathvariant=¨bold¨ mathcolor=¨#0000FF¨ mathsize=¨20px¨»R«/mi»«mn mathvariant=¨bold¨ mathcolor=¨#0000FF¨ mathsize=¨20px¨»4«/mn»«/msub»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨ mathsize=¨20px¨»)«/mo»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨ mathsize=¨20px¨»+«/mo»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨ mathsize=¨20px¨»(«/mo»«msub»«mi mathvariant=¨bold¨ mathcolor=¨#0000FF¨ mathsize=¨20px¨»R«/mi»«mn mathvariant=¨bold¨ mathcolor=¨#0000FF¨ mathsize=¨20px¨»3«/mn»«/msub»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨ mathsize=¨20px¨»|«/mo»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨ mathsize=¨20px¨»|«/mo»«msub»«mi mathvariant=¨bold¨ mathcolor=¨#0000FF¨ mathsize=¨20px¨»R«/mi»«mn mathvariant=¨bold¨ mathcolor=¨#0000FF¨ mathsize=¨20px¨»5«/mn»«/msub»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨ mathsize=¨20px¨»)«/mo»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨ mathsize=¨20px¨»]«/mo»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨ mathsize=¨20px¨»+«/mo»«msub»«mi mathvariant=¨bold¨ mathcolor=¨#0000FF¨ mathsize=¨20px¨»R«/mi»«mn mathvariant=¨bold¨ mathcolor=¨#0000FF¨ mathsize=¨20px¨»1«/mn»«/msub»«mspace linebreak=¨newline¨/»«mspace linebreak=¨newline¨/»«msub»«mi mathvariant=¨bold¨ mathcolor=¨#0000FF¨ mathsize=¨20px¨»R«/mi»«mi mathvariant=¨bold¨ mathsize=¨20px¨ mathcolor=¨#0000FF¨»T«/mi»«/msub»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨ mathsize=¨20px¨»=«/mo»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨ mathsize=¨20px¨»[«/mo»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨ mathsize=¨20px¨»(«/mo»«mfrac mathcolor=¨#0000FF¨»«mrow»«msub»«mi mathvariant=¨bold¨ mathsize=¨20px¨»R«/mi»«mn mathvariant=¨bold¨ mathsize=¨20px¨»2«/mn»«/msub»«mo mathvariant=¨bold¨ mathsize=¨20px¨»§#183;«/mo»«msub»«mi mathvariant=¨bold¨ mathsize=¨20px¨»R«/mi»«mn mathvariant=¨bold¨ mathsize=¨20px¨»4«/mn»«/msub»«/mrow»«mrow»«msub»«mi mathvariant=¨bold¨ mathsize=¨20px¨»R«/mi»«mn mathvariant=¨bold¨ mathsize=¨20px¨»2«/mn»«/msub»«mo mathvariant=¨bold¨ mathsize=¨20px¨»+«/mo»«msub»«mi mathvariant=¨bold¨ mathsize=¨20px¨»R«/mi»«mn mathvariant=¨bold¨ mathsize=¨20px¨»4«/mn»«/msub»«/mrow»«/mfrac»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨ mathsize=¨20px¨»)«/mo»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨ mathsize=¨20px¨»+«/mo»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨ mathsize=¨20px¨»(«/mo»«mfrac mathcolor=¨#0000FF¨»«mrow»«msub»«mi mathvariant=¨bold¨ mathsize=¨20px¨»R«/mi»«mn mathvariant=¨bold¨ mathsize=¨20px¨»3«/mn»«/msub»«mo mathvariant=¨bold¨ mathsize=¨20px¨»§#183;«/mo»«msub»«mi mathvariant=¨bold¨ mathsize=¨20px¨»R«/mi»«mn mathvariant=¨bold¨ mathsize=¨20px¨»5«/mn»«/msub»«/mrow»«mrow»«msub»«mi mathvariant=¨bold¨ mathsize=¨20px¨»R«/mi»«mn mathvariant=¨bold¨ mathsize=¨20px¨»3«/mn»«/msub»«mo mathvariant=¨bold¨ mathsize=¨20px¨»+«/mo»«msub»«mi mathvariant=¨bold¨ mathsize=¨20px¨»R«/mi»«mn mathvariant=¨bold¨ mathsize=¨20px¨»5«/mn»«/msub»«/mrow»«/mfrac»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨ mathsize=¨20px¨»)«/mo»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨ mathsize=¨20px¨»]«/mo»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨ mathsize=¨20px¨»+«/mo»«msub»«mi mathvariant=¨bold¨ mathcolor=¨#0000FF¨ mathsize=¨20px¨»R«/mi»«mn mathvariant=¨bold¨ mathsize=¨20px¨ mathcolor=¨#0000FF¨»1«/mn»«/msub»«mspace linebreak=¨newline¨/»«mspace linebreak=¨newline¨/»«msub»«mi mathvariant=¨bold¨ mathcolor=¨#0000FF¨ mathsize=¨20px¨»R«/mi»«mi mathvariant=¨bold¨ mathcolor=¨#0000FF¨ mathsize=¨20px¨»T«/mi»«/msub»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨ mathsize=¨20px¨»=«/mo»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨ mathsize=¨20px¨»[«/mo»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨ mathsize=¨20px¨»(«/mo»«mfrac mathcolor=¨#0000FF¨»«mrow»«mn mathvariant=¨bold¨ mathsize=¨20px¨»10«/mn»«mo mathvariant=¨bold¨ mathsize=¨20px¨»§#183;«/mo»«mn mathvariant=¨bold¨ mathsize=¨20px¨»10«/mn»«/mrow»«mrow»«mn mathvariant=¨bold¨ mathsize=¨20px¨»10«/mn»«mo mathvariant=¨bold¨ mathsize=¨20px¨»+«/mo»«mn mathvariant=¨bold¨ mathsize=¨20px¨»10«/mn»«/mrow»«/mfrac»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨ mathsize=¨20px¨»)«/mo»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨ mathsize=¨20px¨»+«/mo»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨ mathsize=¨20px¨»(«/mo»«mfrac mathcolor=¨#0000FF¨»«mrow»«mn mathvariant=¨bold¨ mathsize=¨20px¨»10«/mn»«mo mathvariant=¨bold¨ mathsize=¨20px¨»§#183;«/mo»«mn mathvariant=¨bold¨ mathsize=¨20px¨»10«/mn»«/mrow»«mrow»«mn mathvariant=¨bold¨ mathsize=¨20px¨»10«/mn»«mo mathvariant=¨bold¨ mathsize=¨20px¨»+«/mo»«mn mathvariant=¨bold¨ mathsize=¨20px¨»10«/mn»«/mrow»«/mfrac»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨ mathsize=¨20px¨»)«/mo»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨ mathsize=¨20px¨»]«/mo»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨ mathsize=¨20px¨»+«/mo»«mn mathvariant=¨bold¨ mathcolor=¨#0000FF¨ mathsize=¨20px¨»10«/mn»«mspace linebreak=¨newline¨/»«mspace linebreak=¨newline¨/»«msub»«mi mathvariant=¨bold¨ mathcolor=¨#0000FF¨ mathsize=¨20px¨»R«/mi»«mi mathvariant=¨bold¨ mathsize=¨20px¨ mathcolor=¨#0000FF¨»T«/mi»«/msub»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨ mathsize=¨20px¨»=«/mo»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨ mathsize=¨20px¨»[«/mo»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨ mathsize=¨20px¨»(«/mo»«mfrac mathcolor=¨#0000FF¨»«mn mathvariant=¨bold¨ mathsize=¨20px¨»100«/mn»«mn mathvariant=¨bold¨ mathsize=¨20px¨»20«/mn»«/mfrac»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨ mathsize=¨20px¨»)«/mo»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨ mathsize=¨20px¨»+«/mo»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨ mathsize=¨20px¨»(«/mo»«mfrac mathcolor=¨#0000FF¨»«mn mathvariant=¨bold¨ mathsize=¨20px¨»100«/mn»«mn mathvariant=¨bold¨ mathsize=¨20px¨»20«/mn»«/mfrac»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨ mathsize=¨20px¨»)«/mo»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨ mathsize=¨20px¨»]«/mo»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨ mathsize=¨20px¨»+«/mo»«mn mathvariant=¨bold¨ mathcolor=¨#0000FF¨ mathsize=¨20px¨»10«/mn»«mspace linebreak=¨newline¨/»«mspace linebreak=¨newline¨/»«msub»«mi mathvariant=¨bold¨ mathcolor=¨#0000FF¨ mathsize=¨20px¨»R«/mi»«mi mathvariant=¨bold¨ mathsize=¨20px¨ mathcolor=¨#0000FF¨»T«/mi»«/msub»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨ mathsize=¨20px¨»=«/mo»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨ mathsize=¨20px¨»[«/mo»«mn mathvariant=¨bold¨ mathcolor=¨#0000FF¨ mathsize=¨20px¨»5«/mn»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨ mathsize=¨20px¨»+«/mo»«mn mathvariant=¨bold¨ mathcolor=¨#0000FF¨ mathsize=¨20px¨»5«/mn»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨ mathsize=¨20px¨»]«/mo»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨ mathsize=¨20px¨»+«/mo»«mn mathvariant=¨bold¨ mathcolor=¨#0000FF¨ mathsize=¨20px¨»10«/mn»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨ mathsize=¨20px¨»=«/mo»«mn mathvariant=¨bold¨ mathcolor=¨#0000FF¨ mathsize=¨20px¨»20«/mn»«mi mathvariant=¨bold-italic¨ mathcolor=¨#0000FF¨ mathsize=¨20px¨»§#937;«/mi»«mspace linebreak=¨newline¨/»«mspace linebreak=¨newline¨/»«/math»
ب- نحسب التيار بالمصدر من قانون أوم للدائرة بأكملها:
«math style=¨font-family:Tahoma¨ xmlns=¨http://www.w3.org/1998/Math/MathML¨»«mstyle mathsize=¨20px¨»«mi mathvariant=¨bold¨ mathcolor=¨#0000FF¨»I«/mi»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»=«/mo»«mfrac mathcolor=¨#0000FF¨»«mi mathvariant=¨bold¨»§#949;«/mi»«msub»«mi mathvariant=¨bold¨»R«/mi»«mi mathvariant=¨bold¨»T«/mi»«/msub»«/mfrac»«mspace linebreak=¨newline¨/»«mspace linebreak=¨newline¨/»«mi mathvariant=¨bold¨ mathcolor=¨#0000FF¨»I«/mi»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»=«/mo»«mfrac mathcolor=¨#0000FF¨»«mi mathvariant=¨bold¨»§#949;«/mi»«msub»«mi mathvariant=¨bold¨»R«/mi»«mi mathvariant=¨bold¨»T«/mi»«/msub»«/mfrac»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»=«/mo»«mfrac mathcolor=¨#0000FF¨»«mn mathvariant=¨bold¨»30«/mn»«mn mathvariant=¨bold¨»20«/mn»«/mfrac»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»=«/mo»«mn mathvariant=¨bold¨ mathcolor=¨#0000FF¨»1«/mn»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨».«/mo»«mn mathvariant=¨bold¨ mathcolor=¨#0000FF¨»5«/mn»«mi mathvariant=¨bold¨ mathcolor=¨#0000FF¨»A«/mi»«/mstyle»«/math»
ج- نحسب فرق الجهد على المقاوم R1 باستخدام قانون أوم:
«math style=¨font-family:Tahoma¨ xmlns=¨http://www.w3.org/1998/Math/MathML¨»«mstyle mathsize=¨20px¨»«msub»«mi mathvariant=¨bold¨ mathcolor=¨#0000FF¨»U«/mi»«msub mathcolor=¨#0000FF¨»«mi mathvariant=¨bold¨»R«/mi»«mn mathvariant=¨bold¨»1«/mn»«/msub»«/msub»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»=«/mo»«mi mathvariant=¨bold¨ mathcolor=¨#0000FF¨»I«/mi»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»§#183;«/mo»«msub»«mi mathvariant=¨bold¨ mathcolor=¨#0000FF¨»R«/mi»«msub mathcolor=¨#0000FF¨»«mrow/»«mn mathvariant=¨bold¨»1«/mn»«/msub»«/msub»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»=«/mo»«mn mathvariant=¨bold¨ mathcolor=¨#0000FF¨»1«/mn»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨».«/mo»«mn mathvariant=¨bold¨ mathcolor=¨#0000FF¨»5«/mn»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»§#183;«/mo»«mn mathvariant=¨bold¨ mathcolor=¨#0000FF¨»10«/mn»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»=«/mo»«mn mathvariant=¨bold¨ mathcolor=¨#0000FF¨»15«/mn»«mi mathvariant=¨bold¨ mathcolor=¨#0000FF¨»V«/mi»«/mstyle»«/math»
د- مقاومة قاطع الدائرة صفر. من قانون أوم ، فرق الجهد على سلك موصل مقاومته صفرًا يساوي صفرًا (لا يهم ما إذا كان يتدفق خلاله تيار أم لا ، ولا يهم ماهي شدة التيار).
«math style=¨font-family:Tahoma¨ xmlns=¨http://www.w3.org/1998/Math/MathML¨»«mstyle mathsize=¨20px¨»«msub»«mi mathvariant=¨bold¨ mathcolor=¨#0000FF¨»V«/mi»«mi mathvariant=¨bold¨ mathcolor=¨#0000FF¨»QR«/mi»«/msub»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»=«/mo»«mi mathvariant=¨bold¨ mathcolor=¨#0000FF¨»I«/mi»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»§#183;«/mo»«msub»«mi mathvariant=¨bold¨ mathcolor=¨#0000FF¨»R«/mi»«mi mathvariant=¨bold¨ mathcolor=¨#0000FF¨»QR«/mi»«/msub»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»=«/mo»«mi mathvariant=¨bold¨ mathcolor=¨#0000FF¨»I«/mi»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»§#183;«/mo»«msub»«mi mathvariant=¨bold¨ mathcolor=¨#0000FF¨»R«/mi»«mi mathvariant=¨bold¨ mathcolor=¨#0000FF¨»QR«/mi»«/msub»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»=«/mo»«mi mathvariant=¨bold¨ mathcolor=¨#0000FF¨»I«/mi»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»§#183;«/mo»«mn mathvariant=¨bold¨ mathcolor=¨#0000FF¨»0«/mn»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»=«/mo»«mn mathvariant=¨bold¨ mathcolor=¨#0000FF¨»0«/mn»«mi mathvariant=¨bold¨ mathcolor=¨#0000FF¨»V«/mi»«/mstyle»«/math»
لذلك فإن فرق الجهد بين طرفي قاطع الدائرة المغلقة يساوي صفر فولط.
31. ד.12
أ- نحسب المقاومة المحصلة للدائرة.
«math xmlns=¨http://www.w3.org/1998/Math/MathML¨»«msub»«mi mathvariant=¨bold¨ mathcolor=¨#0000FF¨ mathsize=¨20px¨»R«/mi»«mi mathvariant=¨bold¨ mathcolor=¨#0000FF¨ mathsize=¨20px¨»T«/mi»«/msub»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨ mathsize=¨20px¨»=«/mo»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨ mathsize=¨20px¨»(«/mo»«msub»«mi mathvariant=¨bold¨ mathcolor=¨#0000FF¨ mathsize=¨20px¨»R«/mi»«mn mathvariant=¨bold¨ mathcolor=¨#0000FF¨ mathsize=¨20px¨»2«/mn»«/msub»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨ mathsize=¨20px¨»|«/mo»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨ mathsize=¨20px¨»|«/mo»«msub»«mi mathvariant=¨bold¨ mathcolor=¨#0000FF¨ mathsize=¨20px¨»R«/mi»«mn mathvariant=¨bold¨ mathcolor=¨#0000FF¨ mathsize=¨20px¨»3«/mn»«/msub»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨ mathsize=¨20px¨»)«/mo»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨ mathsize=¨20px¨»+«/mo»«msub»«mi mathvariant=¨bold¨ mathcolor=¨#0000FF¨ mathsize=¨20px¨»R«/mi»«mn mathvariant=¨bold¨ mathcolor=¨#0000FF¨ mathsize=¨20px¨»1«/mn»«/msub»«mspace linebreak=¨newline¨/»«mspace linebreak=¨newline¨/»«msub»«mi mathvariant=¨bold¨ mathcolor=¨#0000FF¨ mathsize=¨20px¨»R«/mi»«mi mathvariant=¨bold¨ mathsize=¨20px¨ mathcolor=¨#0000FF¨»T«/mi»«/msub»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨ mathsize=¨20px¨»=«/mo»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨ mathsize=¨20px¨»(«/mo»«mfrac mathcolor=¨#0000FF¨»«mrow»«msub»«mi mathvariant=¨bold¨ mathsize=¨20px¨»R«/mi»«mn mathvariant=¨bold¨ mathsize=¨20px¨»2«/mn»«/msub»«mo mathvariant=¨bold¨ mathsize=¨20px¨»§#183;«/mo»«msub»«mi mathvariant=¨bold¨ mathsize=¨20px¨»R«/mi»«mn mathvariant=¨bold¨ mathsize=¨20px¨»3«/mn»«/msub»«/mrow»«mrow»«msub»«mi mathvariant=¨bold¨ mathsize=¨20px¨»R«/mi»«mn mathvariant=¨bold¨ mathsize=¨20px¨»2«/mn»«/msub»«mo mathvariant=¨bold¨ mathsize=¨20px¨»+«/mo»«msub»«mi mathvariant=¨bold¨ mathsize=¨20px¨»R«/mi»«mn mathvariant=¨bold¨ mathsize=¨20px¨»3«/mn»«/msub»«/mrow»«/mfrac»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨ mathsize=¨20px¨»)«/mo»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨ mathsize=¨20px¨»+«/mo»«msub»«mi mathvariant=¨bold¨ mathcolor=¨#0000FF¨ mathsize=¨20px¨»R«/mi»«mn mathvariant=¨bold¨ mathsize=¨20px¨ mathcolor=¨#0000FF¨»1«/mn»«/msub»«mspace linebreak=¨newline¨/»«mspace linebreak=¨newline¨/»«msub»«mi mathvariant=¨bold¨ mathcolor=¨#0000FF¨ mathsize=¨20px¨»R«/mi»«mi mathvariant=¨bold¨ mathcolor=¨#0000FF¨ mathsize=¨20px¨»T«/mi»«/msub»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨ mathsize=¨20px¨»=«/mo»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨ mathsize=¨20px¨»[«/mo»«mfrac mathcolor=¨#0000FF¨»«mrow»«mn mathvariant=¨bold¨ mathsize=¨20px¨»10«/mn»«mo mathvariant=¨bold¨ mathsize=¨20px¨»§#183;«/mo»«mn mathvariant=¨bold¨ mathsize=¨20px¨»10«/mn»«/mrow»«mrow»«mn mathvariant=¨bold¨ mathsize=¨20px¨»10«/mn»«mo mathvariant=¨bold¨ mathsize=¨20px¨»+«/mo»«mn mathvariant=¨bold¨ mathsize=¨20px¨»10«/mn»«/mrow»«/mfrac»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨ mathsize=¨20px¨»]«/mo»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨ mathsize=¨20px¨»+«/mo»«mn mathvariant=¨bold¨ mathcolor=¨#0000FF¨ mathsize=¨20px¨»10«/mn»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨ mathsize=¨20px¨»=«/mo»«mn mathvariant=¨bold¨ mathcolor=¨#0000FF¨ mathsize=¨20px¨»20«/mn»«mi mathvariant=¨bold¨ mathcolor=¨#0000FF¨ mathsize=¨20px¨»§#937;«/mi»«mspace linebreak=¨newline¨/»«mspace linebreak=¨newline¨/»«mspace linebreak=¨newline¨/»«msub»«mi mathvariant=¨bold¨ mathcolor=¨#0000FF¨ mathsize=¨20px¨»R«/mi»«mi mathvariant=¨bold¨ mathsize=¨20px¨ mathcolor=¨#0000FF¨»T«/mi»«/msub»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨ mathsize=¨20px¨»=«/mo»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨ mathsize=¨20px¨»[«/mo»«mfrac mathcolor=¨#0000FF¨»«mn mathvariant=¨bold¨ mathsize=¨20px¨»100«/mn»«mn mathvariant=¨bold¨ mathsize=¨20px¨»20«/mn»«/mfrac»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨ mathsize=¨20px¨»]«/mo»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨ mathsize=¨20px¨»+«/mo»«mn mathvariant=¨bold¨ mathcolor=¨#0000FF¨ mathsize=¨20px¨»10«/mn»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨ mathsize=¨20px¨»=«/mo»«mn mathvariant=¨bold¨ mathcolor=¨#0000FF¨ mathsize=¨20px¨»5«/mn»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨ mathsize=¨20px¨»+«/mo»«mn mathvariant=¨bold¨ mathcolor=¨#0000FF¨ mathsize=¨20px¨»10«/mn»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨ mathsize=¨20px¨»=«/mo»«mn mathvariant=¨bold¨ mathcolor=¨#0000FF¨ mathsize=¨20px¨»15«/mn»«mi mathvariant=¨bold¨ mathcolor=¨#0000FF¨ mathsize=¨20px¨»§#937;«/mi»«/math»
ب- نحسب التيار بالمصدر من قانون أوم للدائرة بأكملها:
«math style=¨font-family:Tahoma¨ xmlns=¨http://www.w3.org/1998/Math/MathML¨»«mstyle mathsize=¨20px¨»«mi mathvariant=¨bold¨ mathcolor=¨#0000FF¨»I«/mi»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»=«/mo»«mfrac mathcolor=¨#0000FF¨»«mi mathvariant=¨bold¨»§#949;«/mi»«msub»«mi mathvariant=¨bold¨»R«/mi»«mi mathvariant=¨bold¨»T«/mi»«/msub»«/mfrac»«mspace linebreak=¨newline¨/»«mspace linebreak=¨newline¨/»«mi mathvariant=¨bold¨ mathcolor=¨#0000FF¨»I«/mi»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»=«/mo»«mfrac mathcolor=¨#0000FF¨»«mi mathvariant=¨bold¨»§#949;«/mi»«msub»«mi mathvariant=¨bold¨»R«/mi»«mi mathvariant=¨bold¨»T«/mi»«/msub»«/mfrac»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»=«/mo»«mfrac mathcolor=¨#0000FF¨»«mn mathvariant=¨bold¨»30«/mn»«mn mathvariant=¨bold¨»15«/mn»«/mfrac»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»=«/mo»«mn mathvariant=¨bold¨ mathcolor=¨#0000FF¨»2«/mn»«mi mathvariant=¨bold¨ mathcolor=¨#0000FF¨»A«/mi»«/mstyle»«/math»
ج- نحسب فرق الجهد على المقاوم R1 باستخدام قانون أوم:
«math style=¨font-family:Tahoma¨ xmlns=¨http://www.w3.org/1998/Math/MathML¨»«mstyle mathsize=¨20px¨»«msub»«mi mathvariant=¨bold¨ mathcolor=¨#0000FF¨»U«/mi»«msub mathcolor=¨#0000FF¨»«mi mathvariant=¨bold¨»R«/mi»«mn mathvariant=¨bold¨»1«/mn»«/msub»«/msub»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»=«/mo»«mi mathvariant=¨bold¨ mathcolor=¨#0000FF¨»I«/mi»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»§#183;«/mo»«msub»«mi mathvariant=¨bold¨ mathcolor=¨#0000FF¨»R«/mi»«msub mathcolor=¨#0000FF¨»«mrow/»«mn mathvariant=¨bold¨»1«/mn»«/msub»«/msub»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»=«/mo»«mn mathvariant=¨bold¨ mathcolor=¨#0000FF¨»2«/mn»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»§#183;«/mo»«mn mathvariant=¨bold¨ mathcolor=¨#0000FF¨»10«/mn»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»=«/mo»«mn mathvariant=¨bold¨ mathcolor=¨#0000FF¨»20«/mn»«mi mathvariant=¨bold¨ mathcolor=¨#0000FF¨»V«/mi»«/mstyle»«/math»
د- الجهد في النقطة Q تساوي الجهد الموجودة على الطرف الأيسر للمقاوم R3. والجهد في النقطة R يساوي الجهد الموجود على الطرف الأيمن للمقاوم R3. لذلك، فإن فرق الجهد بين أطراف قاطع الدائرة المفتوحة VQR يساوي فرق الجهد عبر المقاوم R3.
ينقسم تيار المصدر بشكل متماثل في نقطة تقاطع المقاومتين R2 و R3. لذلك ، التيار عبر R3 يساوي 1 أمبير (نصف تيار المصدر)
نحسب فرق الجهد على المقاوم R3 بواسطة قانون أوم:
نحسب فرق الجهد على المقاوم R3 باستخدام قانون أوم:
«math style=¨font-family:Tahoma¨ xmlns=¨http://www.w3.org/1998/Math/MathML¨»«mstyle mathsize=¨20px¨»«msub»«mi mathvariant=¨bold¨ mathcolor=¨#0000FF¨»U«/mi»«msub mathcolor=¨#0000FF¨»«mi mathvariant=¨bold¨»R«/mi»«mn mathvariant=¨bold¨»3«/mn»«/msub»«/msub»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»=«/mo»«msub»«mi mathvariant=¨bold¨ mathcolor=¨#0000FF¨»I«/mi»«msub»«mi mathvariant=¨bold-italic¨ mathcolor=¨#0000FF¨»R«/mi»«mn mathvariant=¨bold¨ mathcolor=¨#0000FF¨»3«/mn»«/msub»«/msub»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»§#183;«/mo»«msub»«mi mathvariant=¨bold¨ mathcolor=¨#0000FF¨»R«/mi»«mn mathvariant=¨bold¨ mathcolor=¨#0000FF¨»3«/mn»«/msub»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»=«/mo»«mn mathvariant=¨bold¨ mathcolor=¨#0000FF¨»1«/mn»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»§#183;«/mo»«mn mathvariant=¨bold¨ mathcolor=¨#0000FF¨»10«/mn»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»=«/mo»«mn mathvariant=¨bold¨ mathcolor=¨#0000FF¨»10«/mn»«mi mathvariant=¨bold¨ mathcolor=¨#0000FF¨»V«/mi»«/mstyle»«/math»
لذلك فإن فرق الجهد VQR يساوي 10V.
32. ד.13
أ- بعد إغلاق القاطع، نحصل على دائرة كهربائية يكون فيها المقاوم R2 وكذلك المقاوم R3 في حالة تماس.
المقاومة المحصلة للدائرة تساوي مقاومة المقاوم R1.
ب- نحسب تيار المصدر من قانون أوم:
«math style=¨font-family:Tahoma¨ xmlns=¨http://www.w3.org/1998/Math/MathML¨»«mstyle mathsize=¨20px¨»«mi mathvariant=¨bold¨ mathcolor=¨#0000FF¨»I«/mi»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»=«/mo»«mfrac mathcolor=¨#0000FF¨»«mi mathvariant=¨bold¨»§#949;«/mi»«msub»«mi mathvariant=¨bold¨»R«/mi»«mi mathvariant=¨bold¨»T«/mi»«/msub»«/mfrac»«mspace linebreak=¨newline¨/»«mspace linebreak=¨newline¨/»«mi mathvariant=¨bold¨ mathcolor=¨#0000FF¨»I«/mi»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»=«/mo»«mfrac mathcolor=¨#0000FF¨»«mi mathvariant=¨bold¨»§#949;«/mi»«msub»«mi mathvariant=¨bold¨»R«/mi»«mn mathvariant=¨bold¨»1«/mn»«/msub»«/mfrac»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»=«/mo»«mfrac mathcolor=¨#0000FF¨»«mn mathvariant=¨bold¨»30«/mn»«mn mathvariant=¨bold¨»10«/mn»«/mfrac»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»=«/mo»«mn mathvariant=¨bold¨ mathcolor=¨#0000FF¨»3«/mn»«mi mathvariant=¨bold¨ mathcolor=¨#0000FF¨»A«/mi»«/mstyle»«/math»
ج- يتم توصيل الطرف الأيمن للمقاوم R1 بالجهد الموجب للبطارية.
والجهد على الطرف الأيسر للمقاوم R1 يساوي جهد القطب السالب للبطارية.
لذلك، فرق الجهد على المقاوم R1 يساوي فرق جهد الأقطاب للبطارية المثالية، ويساوي القوة الكهربائية الدافعة للبطارية، 30 فولط.
طريقة أخرى: نحسب فرق الجهد على R1 باستخدام قانون أوم:
«math style=¨font-family:Tahoma¨ xmlns=¨http://www.w3.org/1998/Math/MathML¨»«mstyle mathsize=¨20px¨»«msub»«mi mathvariant=¨bold¨ mathcolor=¨#0000FF¨»U«/mi»«msub mathcolor=¨#0000FF¨»«mi mathvariant=¨bold¨»R«/mi»«mn mathvariant=¨bold¨»1«/mn»«/msub»«/msub»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»=«/mo»«mi mathvariant=¨bold¨ mathcolor=¨#0000FF¨»I«/mi»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»§#183;«/mo»«msub»«mi mathvariant=¨bold¨ mathcolor=¨#0000FF¨»R«/mi»«msub mathcolor=¨#0000FF¨»«mrow/»«mn mathvariant=¨bold¨»1«/mn»«/msub»«/msub»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»=«/mo»«mn mathvariant=¨bold¨ mathcolor=¨#0000FF¨»3«/mn»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»§#183;«/mo»«mn mathvariant=¨bold¨ mathcolor=¨#0000FF¨»10«/mn»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»=«/mo»«mn mathvariant=¨bold¨ mathcolor=¨#0000FF¨»30«/mn»«mi mathvariant=¨bold¨ mathcolor=¨#0000FF¨»V«/mi»«/mstyle»«/math»
د- مقاومة قاطع الدائرة صفر. من قانون أوم ، فرق الجهد على سلك موصل الذي تكون مقاومته صفرًا يساوي صفرًا (لا يهم ما إذا كان يتدفق خلاله تيار أم لا ، ولا يهم ماهي شدة التيار المار عبره).
«math style=¨font-family:Tahoma¨ xmlns=¨http://www.w3.org/1998/Math/MathML¨»«mstyle mathsize=¨20px¨»«msub»«mi mathvariant=¨bold¨ mathcolor=¨#0000FF¨»V«/mi»«mi mathvariant=¨bold¨ mathcolor=¨#0000FF¨»QR«/mi»«/msub»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»=«/mo»«mi mathvariant=¨bold¨ mathcolor=¨#0000FF¨»I«/mi»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»§#183;«/mo»«msub»«mi mathvariant=¨bold¨ mathcolor=¨#0000FF¨»R«/mi»«mi mathvariant=¨bold¨ mathcolor=¨#0000FF¨»QR«/mi»«/msub»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»=«/mo»«mi mathvariant=¨bold¨ mathcolor=¨#0000FF¨»I«/mi»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»§#183;«/mo»«msub»«mi mathvariant=¨bold¨ mathcolor=¨#0000FF¨»R«/mi»«mi mathvariant=¨bold¨ mathcolor=¨#0000FF¨»QR«/mi»«/msub»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»=«/mo»«mi mathvariant=¨bold¨ mathcolor=¨#0000FF¨»I«/mi»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»§#183;«/mo»«mn mathvariant=¨bold¨ mathcolor=¨#0000FF¨»0«/mn»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»=«/mo»«mn mathvariant=¨bold¨ mathcolor=¨#0000FF¨»0«/mn»«mi mathvariant=¨bold¨ mathcolor=¨#0000FF¨»V«/mi»«/mstyle»«/math»
لذلك فإن فرق الجهد بين طرفي قاطع الدائرة المغلقة يساوي صفر فولط.
33. ה.1
أ- مصدر الجهد مثالي، وفرق جهد أقطاب البطارية يساوي القوة الكهربائية الدافعة للبطارية، والمستهلك موصول مباشرة بقطبي البطارية، وبالتالي فإن فرق الجهد على المستهلك هو 12 فولط.
ب- نحسب التيار عبر المستهلك حسب قانون أوم:
«math style=¨font-family:Tahoma¨ xmlns=¨http://www.w3.org/1998/Math/MathML¨»«mstyle mathsize=¨20px¨»«mi mathvariant=¨bold¨ mathcolor=¨#0000FF¨»I«/mi»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»=«/mo»«mfrac mathcolor=¨#0000FF¨»«msub»«mi mathvariant=¨bold¨»U«/mi»«msub»«mi mathvariant=¨bold¨»R«/mi»«mn mathvariant=¨bold¨»1«/mn»«/msub»«/msub»«msub»«mi mathvariant=¨bold¨»R«/mi»«mn mathvariant=¨bold¨»1«/mn»«/msub»«/mfrac»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»=«/mo»«mfrac mathcolor=¨#0000FF¨»«mn mathvariant=¨bold¨»12«/mn»«mn mathvariant=¨bold¨»10«/mn»«/mfrac»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»=«/mo»«mn mathvariant=¨bold¨ mathcolor=¨#0000FF¨»1«/mn»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨».«/mo»«mn mathvariant=¨bold¨ mathcolor=¨#0000FF¨»2«/mn»«mi mathvariant=¨bold¨ mathcolor=¨#0000FF¨»A«/mi»«/mstyle»«/math»
ج- نحسب قدرة المستهلك باستخدام كل من التعبيرات الثلاثة التالية:
«math style=¨font-family:Tahoma¨ xmlns=¨http://www.w3.org/1998/Math/MathML¨»«mstyle mathsize=¨20px¨»«mi mathvariant=¨bold¨ mathcolor=¨#0000FF¨»P«/mi»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»=«/mo»«mi mathvariant=¨bold¨ mathcolor=¨#0000FF¨»V«/mi»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»§#183;«/mo»«mi mathvariant=¨bold¨ mathcolor=¨#0000FF¨»I«/mi»«mspace linebreak=¨newline¨/»«msub»«mi mathvariant=¨bold¨ mathcolor=¨#0000FF¨»P«/mi»«mi mathvariant=¨bold¨ mathcolor=¨#0000FF¨»R«/mi»«/msub»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»=«/mo»«msub»«mi mathvariant=¨bold¨ mathcolor=¨#0000FF¨»U«/mi»«mi mathvariant=¨bold¨ mathcolor=¨#0000FF¨»R«/mi»«/msub»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»§#183;«/mo»«mi mathvariant=¨bold¨ mathcolor=¨#0000FF¨»I«/mi»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»=«/mo»«mn mathvariant=¨bold¨ mathcolor=¨#0000FF¨»12«/mn»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»§#183;«/mo»«mn mathvariant=¨bold¨ mathcolor=¨#0000FF¨»1«/mn»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨».«/mo»«mn mathvariant=¨bold¨ mathcolor=¨#0000FF¨»2«/mn»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»=«/mo»«mn mathvariant=¨bold¨ mathcolor=¨#0000FF¨»14«/mn»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨».«/mo»«mn mathvariant=¨bold¨ mathcolor=¨#0000FF¨»4«/mn»«mi mathvariant=¨bold¨ mathcolor=¨#0000FF¨»W«/mi»«/mstyle»«/math»
«math xmlns=¨http://www.w3.org/1998/Math/MathML¨»«mi mathvariant=¨bold¨ mathcolor=¨#0000FF¨ mathsize=¨20px¨»P«/mi»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨ mathsize=¨20px¨»=«/mo»«mfrac mathcolor=¨#0000FF¨»«msup»«mi mathvariant=¨bold¨ mathsize=¨20px¨»V«/mi»«mn mathvariant=¨bold¨ mathsize=¨20px¨»2«/mn»«/msup»«mi mathvariant=¨bold¨ mathsize=¨20px¨»R«/mi»«/mfrac»«mspace linebreak=¨newline¨/»«msub»«mi mathvariant=¨bold¨ mathcolor=¨#0000FF¨ mathsize=¨20px¨»P«/mi»«mi mathvariant=¨bold¨ mathcolor=¨#0000FF¨ mathsize=¨20px¨»R«/mi»«/msub»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨ mathsize=¨20px¨»=«/mo»«mfrac mathcolor=¨#0000FF¨»«msup»«msub»«mi mathvariant=¨bold¨ mathsize=¨20px¨»U«/mi»«mi mathvariant=¨bold¨ mathsize=¨20px¨»R«/mi»«/msub»«mn mathvariant=¨bold¨ mathsize=¨20px¨»2«/mn»«/msup»«mi mathvariant=¨bold¨ mathsize=¨20px¨»R«/mi»«/mfrac»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨ mathsize=¨20px¨»=«/mo»«mfrac mathcolor=¨#0000FF¨»«msup»«mn mathvariant=¨bold¨ mathsize=¨20px¨»12«/mn»«mn mathvariant=¨bold¨ mathsize=¨20px¨»2«/mn»«/msup»«mn mathvariant=¨bold¨ mathsize=¨20px¨»10«/mn»«/mfrac»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨ mathsize=¨20px¨»=«/mo»«mn mathvariant=¨bold¨ mathcolor=¨#0000FF¨ mathsize=¨20px¨»14«/mn»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨ mathsize=¨20px¨».«/mo»«mn mathvariant=¨bold¨ mathcolor=¨#0000FF¨ mathsize=¨20px¨»4«/mn»«mi mathvariant=¨bold¨ mathcolor=¨#0000FF¨ mathsize=¨20px¨»W«/mi»«/math»
«math style=¨font-family:Tahoma¨ xmlns=¨http://www.w3.org/1998/Math/MathML¨»«mstyle mathsize=¨20px¨»«mi mathvariant=¨bold¨ mathcolor=¨#0000FF¨»P«/mi»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»=«/mo»«msup»«mi mathvariant=¨bold¨ mathcolor=¨#0000FF¨»I«/mi»«mn mathvariant=¨bold¨ mathcolor=¨#0000FF¨»2«/mn»«/msup»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»§#183;«/mo»«mi mathvariant=¨bold¨ mathcolor=¨#0000FF¨»R«/mi»«mspace linebreak=¨newline¨/»«msub»«mi mathvariant=¨bold¨ mathcolor=¨#0000FF¨»P«/mi»«mi mathvariant=¨bold¨ mathcolor=¨#0000FF¨»R«/mi»«/msub»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»=«/mo»«msup»«mi mathvariant=¨bold¨ mathcolor=¨#0000FF¨»I«/mi»«mn mathvariant=¨bold¨ mathcolor=¨#0000FF¨»2«/mn»«/msup»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»§#183;«/mo»«mi mathvariant=¨bold¨ mathcolor=¨#0000FF¨»R«/mi»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»=«/mo»«mn mathvariant=¨bold¨ mathcolor=¨#0000FF¨»1«/mn»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨».«/mo»«msup»«mn mathvariant=¨bold¨ mathcolor=¨#0000FF¨»2«/mn»«mn mathvariant=¨bold¨ mathcolor=¨#0000FF¨»2«/mn»«/msup»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»§#183;«/mo»«mn mathvariant=¨bold¨ mathcolor=¨#0000FF¨»10«/mn»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»=«/mo»«mn mathvariant=¨bold¨ mathcolor=¨#0000FF¨»14«/mn»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨».«/mo»«mn mathvariant=¨bold¨ mathcolor=¨#0000FF¨»4«/mn»«mi mathvariant=¨bold¨ mathcolor=¨#0000FF¨»W«/mi»«/mstyle»«/math»
د- نحسب قدرة المصدر:
«math style=¨font-family:Tahoma¨ xmlns=¨http://www.w3.org/1998/Math/MathML¨»«mstyle mathsize=¨20px¨»«mmultiscripts»«mi mathvariant=¨bold¨ mathcolor=¨#0000FF¨»P«/mi»«mprescripts/»«mi mathvariant=¨bold¨ mathcolor=¨#0000FF¨»§#1605;§#1589;§#1583;§#1585;«/mi»«none/»«/mmultiscripts»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»=«/mo»«mi mathvariant=¨bold¨ mathcolor=¨#0000FF¨»§#949;«/mi»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»§#183;«/mo»«mi mathvariant=¨bold¨ mathcolor=¨#0000FF¨»I«/mi»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»=«/mo»«mn mathvariant=¨bold¨ mathcolor=¨#0000FF¨»12«/mn»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»§#183;«/mo»«mn mathvariant=¨bold¨ mathcolor=¨#0000FF¨»1«/mn»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨».«/mo»«mn mathvariant=¨bold¨ mathcolor=¨#0000FF¨»2«/mn»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»=«/mo»«mn mathvariant=¨bold¨ mathcolor=¨#0000FF¨»14«/mn»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨».«/mo»«mn mathvariant=¨bold¨ mathcolor=¨#0000FF¨»4«/mn»«mi mathvariant=¨bold¨ mathcolor=¨#0000FF¨»W«/mi»«/mstyle»«/math»
هـ - البطارية مثالية (مقاومتها الداخلية مهملة) كل الطاقة المستهلكة من مصدر فرق الجهد تصل للمستهلك ، كفاءة الدائرة تكون 100 بالمائة.
نحسب كفاءة الدائرة باستخدام تعبير الكفاءة .
نحسب كفاءة الدائرة باستخدام تعبيرات الكفاءة
«math xmlns=¨http://www.w3.org/1998/Math/MathML¨»«mstyle mathsize=¨20px¨»«mi mathvariant=¨bold¨ mathcolor=¨#0000FF¨»§#951;«/mi»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»=«/mo»«mfrac mathcolor=¨#0000FF¨»«mi mathvariant=¨bold¨»R«/mi»«mrow»«mi mathvariant=¨bold¨»r«/mi»«mo mathvariant=¨bold¨»+«/mo»«mi mathvariant=¨bold¨»R«/mi»«/mrow»«/mfrac»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»§#183;«/mo»«mn mathvariant=¨bold¨ mathcolor=¨#0000FF¨»100«/mn»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»%«/mo»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»=«/mo»«mfrac mathcolor=¨#0000FF¨»«mn mathvariant=¨bold¨»10«/mn»«mrow»«mn mathvariant=¨bold¨»0«/mn»«mo mathvariant=¨bold¨»+«/mo»«mn mathvariant=¨bold¨»10«/mn»«/mrow»«/mfrac»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»§#183;«/mo»«mn mathvariant=¨bold¨ mathcolor=¨#0000FF¨»100«/mn»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»%«/mo»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»=«/mo»«mn mathvariant=¨bold¨ mathcolor=¨#0000FF¨»100«/mn»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»%«/mo»«mspace linebreak=¨newline¨/»«mspace linebreak=¨newline¨/»«mi mathvariant=¨bold¨ mathcolor=¨#0000FF¨»§#951;«/mi»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»=«/mo»«mfrac mathcolor=¨#0000FF¨»«msub»«mi mathvariant=¨bold¨»V«/mi»«mi mathvariant=¨bold¨»AB«/mi»«/msub»«mi mathvariant=¨bold¨»§#949;«/mi»«/mfrac»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»§#183;«/mo»«mn mathvariant=¨bold¨ mathcolor=¨#0000FF¨»100«/mn»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»%«/mo»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»=«/mo»«mfrac mathcolor=¨#0000FF¨»«mn mathvariant=¨bold¨»12«/mn»«mn mathvariant=¨bold¨»12«/mn»«/mfrac»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»§#183;«/mo»«mn mathvariant=¨bold¨ mathcolor=¨#0000FF¨»100«/mn»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»%«/mo»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»=«/mo»«mn mathvariant=¨bold¨ mathcolor=¨#0000FF¨»100«/mn»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»%«/mo»«mspace linebreak=¨newline¨/»«mspace linebreak=¨newline¨/»«mi mathvariant=¨bold¨ mathcolor=¨#0000FF¨»§#951;«/mi»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»=«/mo»«mfrac mathcolor=¨#0000FF¨»«msub»«mi mathvariant=¨bold¨»P«/mi»«mi mathvariant=¨bold¨»R«/mi»«/msub»«mrow»«mi mathvariant=¨bold¨»§#1502;§#1511;§#1493;§#1512;«/mi»«mi mathvariant=¨bold¨»P«/mi»«/mrow»«/mfrac»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»§#183;«/mo»«mn mathvariant=¨bold¨ mathcolor=¨#0000FF¨»100«/mn»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»%«/mo»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»=«/mo»«mfrac mathcolor=¨#0000FF¨»«mrow»«mn mathvariant=¨bold¨»14«/mn»«mo mathvariant=¨bold¨».«/mo»«mn mathvariant=¨bold¨»4«/mn»«/mrow»«mrow»«mn mathvariant=¨bold¨»14«/mn»«mo mathvariant=¨bold¨».«/mo»«mn mathvariant=¨bold¨»4«/mn»«/mrow»«/mfrac»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»§#183;«/mo»«mn mathvariant=¨bold¨ mathcolor=¨#0000FF¨»100«/mn»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»%«/mo»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»=«/mo»«mn mathvariant=¨bold¨ mathcolor=¨#0000FF¨»100«/mn»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»%«/mo»«/mstyle»«/math»
34. ה.2
أ- نحسب تيار المصدر من قانون أوم:
«math style=¨font-family:Tahoma¨ xmlns=¨http://www.w3.org/1998/Math/MathML¨»«mstyle mathsize=¨20px¨»«mi mathvariant=¨bold¨ mathcolor=¨#0000FF¨»I«/mi»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»=«/mo»«mfrac mathcolor=¨#0000FF¨»«mi mathvariant=¨bold¨»§#949;«/mi»«msub»«mi mathvariant=¨bold¨»R«/mi»«mi mathvariant=¨bold¨»T«/mi»«/msub»«/mfrac»«mspace linebreak=¨newline¨/»«mspace linebreak=¨newline¨/»«mi mathvariant=¨bold¨ mathcolor=¨#0000FF¨»I«/mi»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»=«/mo»«mfrac mathcolor=¨#0000FF¨»«mi mathvariant=¨bold¨»§#949;«/mi»«mrow»«mi mathvariant=¨bold¨»r«/mi»«mo mathvariant=¨bold¨»+«/mo»«mi mathvariant=¨bold¨»R«/mi»«/mrow»«/mfrac»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»=«/mo»«mfrac mathcolor=¨#0000FF¨»«mn mathvariant=¨bold¨»12«/mn»«mrow»«mn mathvariant=¨bold¨»2«/mn»«mo mathvariant=¨bold¨»+«/mo»«mn mathvariant=¨bold¨»10«/mn»«/mrow»«/mfrac»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»=«/mo»«mfrac mathcolor=¨#0000FF¨»«mn mathvariant=¨bold¨»12«/mn»«mn mathvariant=¨bold¨»12«/mn»«/mfrac»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»=«/mo»«mn mathvariant=¨bold¨ mathcolor=¨#0000FF¨»1«/mn»«mi mathvariant=¨bold¨ mathcolor=¨#0000FF¨»A«/mi»«/mstyle»«/math»
ب- نحسب فرق الجهد على المستهلك باستخدام قانون أوم على المستهلك:
«math style=¨font-family:Tahoma¨ xmlns=¨http://www.w3.org/1998/Math/MathML¨»«mstyle mathsize=¨20px¨»«msub»«mi mathvariant=¨bold¨ mathcolor=¨#0000FF¨»U«/mi»«mi mathvariant=¨bold¨ mathcolor=¨#0000FF¨»R«/mi»«/msub»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»=«/mo»«mi mathvariant=¨bold¨ mathcolor=¨#0000FF¨»I«/mi»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»§#183;«/mo»«mi mathvariant=¨bold¨ mathcolor=¨#0000FF¨»R«/mi»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»=«/mo»«mn mathvariant=¨bold¨ mathcolor=¨#0000FF¨»1«/mn»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»§#183;«/mo»«mn mathvariant=¨bold¨ mathcolor=¨#0000FF¨»10«/mn»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»=«/mo»«mn mathvariant=¨bold¨ mathcolor=¨#0000FF¨»10«/mn»«mi mathvariant=¨bold¨ mathcolor=¨#0000FF¨»V«/mi»«/mstyle»«/math»
طريقة أخرى: المستهلك موصول مباشرة بأطراف البطارية، فرق الجهد على المستهلك يساوي فرق جهد الأقطاب، نحسب فرق جهد الأقطاب:
«math style=¨font-family:Tahoma¨ xmlns=¨http://www.w3.org/1998/Math/MathML¨»«mi mathvariant=¨bold¨ mathcolor=¨#0000FF¨ mathsize=¨20px¨»Vab«/mi»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨ mathsize=¨20px¨»=«/mo»«mi mathvariant=¨bold¨ mathcolor=¨#0000FF¨ mathsize=¨20px¨»§#949;«/mi»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨ mathsize=¨20px¨»-«/mo»«mi mathvariant=¨bold¨ mathcolor=¨#0000FF¨ mathsize=¨20px¨»I«/mi»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨ mathsize=¨20px¨»§#183;«/mo»«mi mathvariant=¨bold¨ mathcolor=¨#0000FF¨ mathsize=¨20px¨»r«/mi»«mspace linebreak=¨newline¨/»«mi mathvariant=¨bold¨ mathcolor=¨#0000FF¨ mathsize=¨20px¨»Vab«/mi»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨ mathsize=¨20px¨»=«/mo»«mn mathvariant=¨bold¨ mathcolor=¨#0000FF¨ mathsize=¨20px¨»12«/mn»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨ mathsize=¨20px¨»-«/mo»«mn mathvariant=¨bold¨ mathcolor=¨#0000FF¨ mathsize=¨20px¨»1«/mn»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨ mathsize=¨20px¨»§#183;«/mo»«mn mathvariant=¨bold¨ mathcolor=¨#0000FF¨ mathsize=¨20px¨»2«/mn»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨ mathsize=¨20px¨»=«/mo»«mn mathvariant=¨bold¨ mathcolor=¨#0000FF¨ mathsize=¨20px¨»10«/mn»«mi mathvariant=¨bold¨ mathcolor=¨#0000FF¨ mathsize=¨20px¨»V«/mi»«mspace linebreak=¨newline¨/»«mspace linebreak=¨newline¨/»«mspace linebreak=¨newline¨/»«/math»
ج- نحسب قدرة المستهلك باستخدام قانون جول:
«math style=¨font-family:Tahoma¨ xmlns=¨http://www.w3.org/1998/Math/MathML¨»«mstyle mathsize=¨20px¨»«msub»«mi mathvariant=¨bold¨ mathcolor=¨#0000FF¨»P«/mi»«mi mathvariant=¨bold¨ mathcolor=¨#0000FF¨»R«/mi»«/msub»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»=«/mo»«msub»«mi mathvariant=¨bold¨ mathcolor=¨#0000FF¨»U«/mi»«mi mathvariant=¨bold¨ mathcolor=¨#0000FF¨»R«/mi»«/msub»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»§#183;«/mo»«mi mathvariant=¨bold¨ mathcolor=¨#0000FF¨»I«/mi»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»=«/mo»«mn mathvariant=¨bold¨ mathcolor=¨#0000FF¨»10«/mn»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»§#183;«/mo»«mn mathvariant=¨bold¨ mathcolor=¨#0000FF¨»1«/mn»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»=«/mo»«mn mathvariant=¨bold¨ mathcolor=¨#0000FF¨»10«/mn»«mi mathvariant=¨bold¨ mathcolor=¨#0000FF¨»W«/mi»«/mstyle»«/math»
د- نحسب القدرة على المقاومة الداخلية باستخدام قانون جول الموسع:
«math style=¨font-family:Tahoma¨ xmlns=¨http://www.w3.org/1998/Math/MathML¨»«mstyle mathsize=¨20px¨»«msub»«mi mathvariant=¨bold¨ mathcolor=¨#0000FF¨»P«/mi»«mi mathvariant=¨bold¨ mathcolor=¨#0000FF¨»r«/mi»«/msub»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»=«/mo»«msup»«mi mathvariant=¨bold-italic¨ mathcolor=¨#0000FF¨»I«/mi»«mn mathvariant=¨bold¨ mathcolor=¨#0000FF¨»2«/mn»«/msup»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»§#183;«/mo»«mi mathvariant=¨bold¨ mathcolor=¨#0000FF¨»r«/mi»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»=«/mo»«msup»«mn mathvariant=¨bold¨ mathcolor=¨#0000FF¨»1«/mn»«mn mathvariant=¨bold¨ mathcolor=¨#0000FF¨»2«/mn»«/msup»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»§#183;«/mo»«mn mathvariant=¨bold¨ mathcolor=¨#0000FF¨»2«/mn»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»=«/mo»«mn mathvariant=¨bold¨ mathcolor=¨#0000FF¨»2«/mn»«mi mathvariant=¨bold¨ mathcolor=¨#0000FF¨»W«/mi»«/mstyle»«/math»
هـ- نحسب قدرة المستهلك باستخدام قانون جول:
«math style=¨font-family:Tahoma¨ xmlns=¨http://www.w3.org/1998/Math/MathML¨»«mstyle mathsize=¨20px¨»«mmultiscripts»«mi mathvariant=¨bold¨ mathcolor=¨#0000FF¨»P«/mi»«mprescripts/»«mi mathvariant=¨bold¨ mathcolor=¨#0000FF¨»§#1605;§#1589;§#1583;§#1585;«/mi»«none/»«/mmultiscripts»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»=«/mo»«mi mathvariant=¨bold¨ mathcolor=¨#0000FF¨»§#949;«/mi»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»§#183;«/mo»«mi mathvariant=¨bold¨ mathcolor=¨#0000FF¨»I«/mi»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»=«/mo»«mn mathvariant=¨bold¨ mathcolor=¨#0000FF¨»12«/mn»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»§#183;«/mo»«mn mathvariant=¨bold¨ mathcolor=¨#0000FF¨»1«/mn»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»=«/mo»«mn mathvariant=¨bold¨ mathcolor=¨#0000FF¨»12«/mn»«mi mathvariant=¨bold¨ mathcolor=¨#0000FF¨»W«/mi»«/mstyle»«/math»
و- نحسب كفاءة الدائرة باستخدام النسبة بين القدرة المستهلكة والقدرة المبذولة:
«math style=¨font-family:Tahoma¨ xmlns=¨http://www.w3.org/1998/Math/MathML¨»«mstyle mathsize=¨20px¨»«mi mathvariant=¨bold¨ mathcolor=¨#0000FF¨»§#951;«/mi»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»=«/mo»«mfrac mathcolor=¨#0000FF¨»«mi mathvariant=¨bold¨»Peff«/mi»«mi mathvariant=¨bold¨»Pin«/mi»«/mfrac»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»§#183;«/mo»«mn mathvariant=¨bold¨ mathcolor=¨#0000FF¨»100«/mn»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»%«/mo»«mspace linebreak=¨newline¨/»«mi mathvariant=¨bold¨ mathcolor=¨#0000FF¨»§#951;«/mi»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»=«/mo»«mfrac mathcolor=¨#0000FF¨»«msub»«mi mathvariant=¨bold¨»P«/mi»«mi mathvariant=¨bold¨»R«/mi»«/msub»«mmultiscripts»«mi mathvariant=¨bold¨»P«/mi»«mprescripts/»«mi mathvariant=¨bold¨»§#1605;§#1589;§#1583;§#1585;«/mi»«none/»«/mmultiscripts»«/mfrac»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»§#183;«/mo»«mn mathvariant=¨bold¨ mathcolor=¨#0000FF¨»100«/mn»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»%«/mo»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»=«/mo»«mfrac mathcolor=¨#0000FF¨»«mn mathvariant=¨bold¨»10«/mn»«mn mathvariant=¨bold¨»12«/mn»«/mfrac»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»§#183;«/mo»«mn mathvariant=¨bold¨ mathcolor=¨#0000FF¨»100«/mn»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»%«/mo»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»=«/mo»«mn mathvariant=¨bold¨ mathcolor=¨#0000FF¨»83«/mn»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨».«/mo»«mn mathvariant=¨bold¨ mathcolor=¨#0000FF¨»33«/mn»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»%«/mo»«/mstyle»«/math»
نحسب كفاءة الدائرة باستخدام تعبير الكفاءة بدلالة المقاومة:
«math style=¨font-family:Tahoma¨ xmlns=¨http://www.w3.org/1998/Math/MathML¨»«mstyle mathsize=¨20px¨»«mi mathvariant=¨bold¨ mathcolor=¨#0000FF¨»§#951;«/mi»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»=«/mo»«mfrac mathcolor=¨#0000FF¨»«mi mathvariant=¨bold¨»R«/mi»«mrow»«mi mathvariant=¨bold¨»R«/mi»«mo mathvariant=¨bold¨»+«/mo»«mi mathvariant=¨bold¨»r«/mi»«/mrow»«/mfrac»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»§#183;«/mo»«mn mathvariant=¨bold¨ mathcolor=¨#0000FF¨»100«/mn»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»%«/mo»«mspace linebreak=¨newline¨/»«mi mathvariant=¨bold¨ mathcolor=¨#0000FF¨»§#951;«/mi»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»=«/mo»«mfrac mathcolor=¨#0000FF¨»«mn mathvariant=¨bold¨»10«/mn»«mrow»«mn mathvariant=¨bold¨»10«/mn»«mo mathvariant=¨bold¨»+«/mo»«mn mathvariant=¨bold¨»2«/mn»«/mrow»«/mfrac»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»§#183;«/mo»«mn mathvariant=¨bold¨ mathcolor=¨#0000FF¨»100«/mn»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»%«/mo»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»=«/mo»«mfrac mathcolor=¨#0000FF¨»«mn mathvariant=¨bold¨»10«/mn»«mn mathvariant=¨bold¨»12«/mn»«/mfrac»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»§#183;«/mo»«mn mathvariant=¨bold¨ mathcolor=¨#0000FF¨»100«/mn»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»%«/mo»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»=«/mo»«mn mathvariant=¨bold¨ mathcolor=¨#0000FF¨»83«/mn»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨».«/mo»«mn mathvariant=¨bold¨ mathcolor=¨#0000FF¨»33«/mn»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»%«/mo»«/mstyle»«/math»
نحسب كفاءة الدائرة باستخدام النسبة بين فرق جهد الأقطاب والقوة الكهربائية الدافعة للبطارية:
«math style=¨font-family:Tahoma¨ xmlns=¨http://www.w3.org/1998/Math/MathML¨»«mstyle mathsize=¨20px¨»«mi mathvariant=¨bold¨ mathcolor=¨#0000FF¨»§#951;«/mi»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»=«/mo»«mfrac mathcolor=¨#0000FF¨»«mi mathvariant=¨bold¨»Vab«/mi»«mi mathvariant=¨bold¨»§#949;«/mi»«/mfrac»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»§#183;«/mo»«mn mathvariant=¨bold¨ mathcolor=¨#0000FF¨»100«/mn»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»%«/mo»«mspace linebreak=¨newline¨/»«mi mathvariant=¨bold¨ mathcolor=¨#0000FF¨»§#951;«/mi»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»=«/mo»«mfrac mathcolor=¨#0000FF¨»«mrow»«mi»§#949;«/mi»«mo»-«/mo»«mi»I«/mi»«mo»§#183;«/mo»«mi»r«/mi»«/mrow»«mmultiscripts»«mi mathvariant=¨bold¨»P«/mi»«mprescripts/»«mi mathvariant=¨bold¨»§#1502;§#1511;§#1493;§#1512;«/mi»«none/»«/mmultiscripts»«/mfrac»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»§#183;«/mo»«mn mathvariant=¨bold¨ mathcolor=¨#0000FF¨»100«/mn»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»%«/mo»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»=«/mo»«mfrac mathcolor=¨#0000FF¨»«mrow»«mn mathvariant=¨bold¨»12«/mn»«mo mathvariant=¨bold¨»-«/mo»«mn mathvariant=¨bold¨»1«/mn»«mo mathvariant=¨bold¨»§#183;«/mo»«mn mathvariant=¨bold¨»2«/mn»«/mrow»«mn mathvariant=¨bold¨»12«/mn»«/mfrac»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»§#183;«/mo»«mn mathvariant=¨bold¨ mathcolor=¨#0000FF¨»100«/mn»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»%«/mo»«mspace linebreak=¨newline¨/»«mi mathvariant=¨bold¨ mathcolor=¨#0000FF¨»§#951;«/mi»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»=«/mo»«mfrac mathcolor=¨#0000FF¨»«mn mathvariant=¨bold¨»10«/mn»«mn mathvariant=¨bold¨»12«/mn»«/mfrac»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»§#183;«/mo»«mn mathvariant=¨bold¨ mathcolor=¨#0000FF¨»100«/mn»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»%«/mo»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»=«/mo»«mn mathvariant=¨bold¨ mathcolor=¨#0000FF¨»83«/mn»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨».«/mo»«mn mathvariant=¨bold¨ mathcolor=¨#0000FF¨»33«/mn»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»%«/mo»«/mstyle»«/math»
35. ה.3
أ- يحدد زمن تشغيل الدائرة كمية الطاقة التي يبذلها المصدر وكمية الطاقة المستهلكة.
لكن النسبة بين الطاقة المستهلكة والطاقة المبذولة ثابتة، غير متعلقة بزمن تشغيل الدائرة.
لذلك، فإن كفاءة الدائرة لا تتعلق بزمن تشغيل الدائرة.
ب- الطاقة التي يستهلكها المستهلك تساوي شغل المستهلك، نحسب شغل المستهلك لمدة ثلاث دقائق:
وجدنا في السؤال السابق أن قدرة المستهلك هي 10 واط. سنجد شغلل المستهلك باستخدام تعريف الطاقة:
«math xmlns=¨http://www.w3.org/1998/Math/MathML¨»«mstyle mathsize=¨20px¨»«mi mathvariant=¨bold¨ mathcolor=¨#0000FF¨»P«/mi»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»=«/mo»«mfrac mathcolor=¨#0000FF¨»«mi mathvariant=¨bold¨»W«/mi»«mi mathvariant=¨bold¨»t«/mi»«/mfrac»«mspace linebreak=¨newline¨/»«msub»«mo»§#160;«/mo»«mi mathvariant=¨bold¨ mathcolor=¨#0000FF¨»§#1605;§#1587;§#1578;§#1607;§#1604;§#1603;«/mi»«/msub»«mi mathvariant=¨bold¨ mathcolor=¨#0000FF¨»E«/mi»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»=«/mo»«msub»«mi mathvariant=¨bold¨ mathcolor=¨#0000FF¨»W«/mi»«mi mathvariant=¨bold¨ mathcolor=¨#0000FF¨»R«/mi»«/msub»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»=«/mo»«msub»«mi mathvariant=¨bold¨ mathcolor=¨#0000FF¨»P«/mi»«mi mathvariant=¨bold¨ mathcolor=¨#0000FF¨»R«/mi»«/msub»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»§#183;«/mo»«mi mathvariant=¨bold¨ mathcolor=¨#0000FF¨»t«/mi»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»=«/mo»«mn mathvariant=¨bold¨ mathcolor=¨#0000FF¨»10«/mn»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»§#183;«/mo»«mn mathvariant=¨bold¨ mathcolor=¨#0000FF¨»3«/mn»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»§#183;«/mo»«mn mathvariant=¨bold¨ mathcolor=¨#0000FF¨»60«/mn»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»=«/mo»«mn mathvariant=¨bold¨ mathcolor=¨#0000FF¨»1«/mn»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»,«/mo»«mn mathvariant=¨bold¨ mathcolor=¨#0000FF¨»800«/mn»«mi mathvariant=¨bold¨ mathcolor=¨#0000FF¨»J«/mi»«/mstyle»«/math»
ج- الطاقة المستهلكة من مصدر فرق الجهد تساوي شغل مصدر فرق الجهد.
وجدنا في السؤال السابق أن قدرة مصدر الجهد هو 12 واط. نحسب شغل المصدر لمدة ثلاث دقائق، باستخدام تعريف قدرة مصدر فرق الجهد:
«math xmlns=¨http://www.w3.org/1998/Math/MathML¨»«mstyle mathsize=¨20px¨»«mi mathvariant=¨bold¨ mathcolor=¨#0000FF¨»P«/mi»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»=«/mo»«mfrac mathcolor=¨#0000FF¨»«mi mathvariant=¨bold¨»W«/mi»«mi mathvariant=¨bold¨»t«/mi»«/mfrac»«mspace linebreak=¨newline¨/»«msub»«maction actiontype=¨argument¨»«mrow/»«/maction»«mi mathvariant=¨bold¨ mathcolor=¨#0000FF¨»§#1605;§#1589;§#1583;§#1585;«/mi»«/msub»«mi mathvariant=¨bold¨ mathcolor=¨#0000FF¨»E«/mi»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»=«/mo»«mmultiscripts»«mi mathvariant=¨bold¨ mathcolor=¨#0000FF¨»W«/mi»«mprescripts/»«mi mathvariant=¨bold¨ mathcolor=¨#0000FF¨»§#1605;§#1589;§#1583;§#1585;«/mi»«none/»«/mmultiscripts»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»=«/mo»«mmultiscripts»«mi mathvariant=¨bold¨ mathcolor=¨#0000FF¨»P«/mi»«mprescripts/»«mi mathvariant=¨bold¨ mathcolor=¨#0000FF¨»§#1605;§#1589;§#1583;§#1585;«/mi»«none/»«/mmultiscripts»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»§#183;«/mo»«mi mathvariant=¨bold¨ mathcolor=¨#0000FF¨»t«/mi»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»=«/mo»«mn mathvariant=¨bold¨ mathcolor=¨#0000FF¨»12«/mn»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»§#183;«/mo»«mn mathvariant=¨bold¨ mathcolor=¨#0000FF¨»3«/mn»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»§#183;«/mo»«mn mathvariant=¨bold¨ mathcolor=¨#0000FF¨»60«/mn»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»=«/mo»«mn mathvariant=¨bold¨ mathcolor=¨#0000FF¨»2«/mn»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»,«/mo»«mn mathvariant=¨bold¨ mathcolor=¨#0000FF¨»160«/mn»«mi mathvariant=¨bold¨ mathcolor=¨#0000FF¨»J«/mi»«/mstyle»«/math»
ד- نحسب كفاءة الدائرة باستخدام النسبة بين الطاقة المستهلكة والطاقة المبذولة
النسبة بين طاقة المستهلك وطاقة المصدر:
«math xmlns=¨http://www.w3.org/1998/Math/MathML¨»«mstyle mathsize=¨20px¨»«mi mathvariant=¨bold¨ mathcolor=¨#0000FF¨»§#951;«/mi»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»=«/mo»«mfrac mathcolor=¨#0000FF¨»«mrow»«mi mathvariant=¨bold¨»§#1605;§#1587;§#1578;§#1607;§#1604;§#1603;§#1577;«/mi»«mi mathvariant=¨bold¨»E«/mi»«/mrow»«mrow»«mi mathvariant=¨bold¨»§#1605;§#1576;§#1584;§#1608;§#1604;§#1577;«/mi»«mi mathvariant=¨bold¨»E«/mi»«/mrow»«/mfrac»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»§#183;«/mo»«mn mathvariant=¨bold¨ mathcolor=¨#0000FF¨»100«/mn»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»%«/mo»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»=«/mo»«mfrac mathcolor=¨#0000FF¨»«mmultiscripts»«mi mathvariant=¨bold¨»E«/mi»«mprescripts/»«mi mathvariant=¨bold¨»§#1605;§#1587;§#1578;§#1607;§#1604;§#1603;«/mi»«none/»«/mmultiscripts»«mrow»«mi mathvariant=¨bold¨»§#1605;§#1589;§#1583;§#1585;«/mi»«mi mathvariant=¨bold¨»E«/mi»«/mrow»«/mfrac»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»§#183;«/mo»«mn mathvariant=¨bold¨ mathcolor=¨#0000FF¨»100«/mn»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»%«/mo»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»=«/mo»«mfrac mathcolor=¨#0000FF¨»«mn mathvariant=¨bold¨»1800«/mn»«mn mathvariant=¨bold¨»2160«/mn»«/mfrac»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»§#183;«/mo»«mn mathvariant=¨bold¨ mathcolor=¨#0000FF¨»100«/mn»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»%«/mo»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»=«/mo»«mn mathvariant=¨bold¨ mathcolor=¨#0000FF¨»83«/mn»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨».«/mo»«mn mathvariant=¨bold¨ mathcolor=¨#0000FF¨»33«/mn»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»%«/mo»«/mstyle»«/math»
36. ה.4
أ- تكون قدرة المستهلك قصوى عندما تكون مقاومته مساوية للمقاومة الداخلية للبطارية. ( R = r)
كلما كانت مقاومة المستهلك أقرب إلى المقاومة الداخلية للبطارية ، زادت قدرته.
مقاومة المستهلك 10 أوم والمقاومة الداخلية للبطارية 2 أوم.
لذلك، من أجل زيادة قدرة المستهلك، يجب تقليل مقاومته.
ب- تكون قدرة المستهلك قصوى عندما تكون مقاومته مساوية للمقاومة الداخلية للبطارية.
لكي تكون قدرة المستهلك قصوى، يجب أن تكون مقاومته 10 أوم.
ج- من التعبير عن كفاءة الدائرة بدلالة مقاومة المستهلك والمقاومة الداخلية ، يمكن ملاحظة أنه عندما تكون قدرة المستهلك قصوى (R = r)
تكون كفاءة الدائرة 50 بالمائة فقط.
«math style=¨font-family:Tahoma¨ xmlns=¨http://www.w3.org/1998/Math/MathML¨»«mstyle mathsize=¨20px¨»«mi mathvariant=¨bold¨ mathcolor=¨#0000FF¨»§#951;«/mi»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»=«/mo»«mfrac mathcolor=¨#0000FF¨»«mi mathvariant=¨bold¨»R«/mi»«mrow»«mi mathvariant=¨bold¨»R«/mi»«mo mathvariant=¨bold¨»+«/mo»«mi mathvariant=¨bold¨»r«/mi»«/mrow»«/mfrac»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»§#183;«/mo»«mn mathvariant=¨bold¨ mathcolor=¨#0000FF¨»100«/mn»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»%«/mo»«mspace linebreak=¨newline¨/»«mi mathvariant=¨bold¨ mathcolor=¨#0000FF¨»§#951;«/mi»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»=«/mo»«mfrac mathcolor=¨#0000FF¨»«mi mathvariant=¨bold¨»R«/mi»«mrow»«mi mathvariant=¨bold¨»R«/mi»«mo mathvariant=¨bold¨»+«/mo»«mi mathvariant=¨bold¨»R«/mi»«/mrow»«/mfrac»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»§#183;«/mo»«mn mathvariant=¨bold¨ mathcolor=¨#0000FF¨»100«/mn»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»%«/mo»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»=«/mo»«mfrac mathcolor=¨#0000FF¨»«mi mathvariant=¨bold-italic¨»R«/mi»«mrow»«mn mathvariant=¨bold¨»2«/mn»«mi mathvariant=¨bold-italic¨»R«/mi»«/mrow»«/mfrac»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»§#183;«/mo»«mn mathvariant=¨bold¨ mathcolor=¨#0000FF¨»100«/mn»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»%«/mo»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»=«/mo»«mn mathvariant=¨bold¨ mathcolor=¨#0000FF¨»50«/mn»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»%«/mo»«/mstyle»«/math»
انتبهوا: الكفاءة القصوى شيء والقدرة القصوى شيء آخر.
على سبيل المثال: يضغط السائق على دواسة البنزين "على طول الطريق" بحيث تكون قوة المحرك قصوى، وفي هذه الحالة تكون كفاءة المحرك منخفضة نسبيًا.
د- أقصى تيار يمكن أن توفره البطارية هو تيار التماس.
تيار التماس هو التيار الذي توفره البطارية عندما لا يكون هناك مستهلك في الدائرة وتكون المقاومة الوحيدة في الدائرة هي المقاومة الداخلية للبطارية.
نحسب التيار عندما تكون قدرة المستهلك القصوى:
«math style=¨font-family:Tahoma¨ xmlns=¨http://www.w3.org/1998/Math/MathML¨»«mstyle mathsize=¨20px¨»«mi mathvariant=¨bold¨ mathcolor=¨#0000FF¨»I«/mi»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»=«/mo»«mfrac mathcolor=¨#0000FF¨»«mi mathvariant=¨bold¨»§#949;«/mi»«msub»«mi mathvariant=¨bold¨»R«/mi»«mi mathvariant=¨bold¨»T«/mi»«/msub»«/mfrac»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»=«/mo»«mfrac mathcolor=¨#0000FF¨»«mi mathvariant=¨bold¨»§#949;«/mi»«mrow»«mi mathvariant=¨bold¨»r«/mi»«mo mathvariant=¨bold¨»+«/mo»«mi mathvariant=¨bold¨»R«/mi»«/mrow»«/mfrac»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»=«/mo»«mfrac mathcolor=¨#0000FF¨»«mi mathvariant=¨bold¨»§#949;«/mi»«mrow»«mi mathvariant=¨bold¨»R«/mi»«mo mathvariant=¨bold¨»+«/mo»«mi mathvariant=¨bold¨»R«/mi»«/mrow»«/mfrac»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»=«/mo»«mfrac mathcolor=¨#0000FF¨»«mn mathvariant=¨bold¨»12«/mn»«mn mathvariant=¨bold¨»20«/mn»«/mfrac»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»=«/mo»«mn mathvariant=¨bold¨ mathcolor=¨#0000FF¨»0«/mn»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨».«/mo»«mn mathvariant=¨bold¨ mathcolor=¨#0000FF¨»6«/mn»«mi mathvariant=¨bold¨ mathcolor=¨#0000FF¨»A«/mi»«/mstyle»«/math»
نحسب تيار التماس:
«math style=¨font-family:Tahoma¨ xmlns=¨http://www.w3.org/1998/Math/MathML¨»«mstyle mathsize=¨20px¨»«mi mathvariant=¨bold¨ mathcolor=¨#0000FF¨»I«/mi»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»=«/mo»«mfrac mathcolor=¨#0000FF¨»«mi mathvariant=¨bold¨»§#949;«/mi»«msub»«mi mathvariant=¨bold¨»R«/mi»«mi mathvariant=¨bold¨»T«/mi»«/msub»«/mfrac»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»=«/mo»«mfrac mathcolor=¨#0000FF¨»«mi mathvariant=¨bold¨»§#949;«/mi»«mi mathvariant=¨bold¨»r«/mi»«/mfrac»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»=«/mo»«mfrac mathcolor=¨#0000FF¨»«mn mathvariant=¨bold¨»12«/mn»«mn mathvariant=¨bold¨»2«/mn»«/mfrac»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»=«/mo»«mn mathvariant=¨bold¨ mathcolor=¨#0000FF¨»6«/mn»«mi mathvariant=¨bold¨ mathcolor=¨#0000FF¨»A«/mi»«/mstyle»«/math»
انتبهوا: من أجل أن تكون قدرة المستهلك قصىوى، يجب أن يكون التيار المار عبر المستهلك أقصى قيمة له.
يجب التمييز بين الحد الأقصى للتيار الذي يمكن أن يتدفق في المستهلك والتيار الأقصى الذي يمكن أن توفره البطارية.
37. ה.5
أ- هذا يعني أن المصباح مصمّم للعمل بفرق جهد 3 فولط، وعندما يكون فرق الجهد على المصباح 3 فولط ، فإن قدرة المصباح ستكون 0.9 واط وعندها يضيء في ضوءه الكامل.
ب- نحسب مقاومة المصباح، وفقًا لمعطيات المصباح، باستخدام قانون جول الموسع:
«math style=¨font-family:Tahoma¨ xmlns=¨http://www.w3.org/1998/Math/MathML¨»«mstyle mathsize=¨20px¨»«msub»«mi mathvariant=¨bold¨ mathcolor=¨#0000FF¨»P«/mi»«mi mathvariant=¨bold¨ mathcolor=¨#0000FF¨»L«/mi»«/msub»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»=«/mo»«mfrac mathcolor=¨#0000FF¨»«msup»«msub»«mi mathvariant=¨bold¨»U«/mi»«mi mathvariant=¨bold¨»L«/mi»«/msub»«mn mathvariant=¨bold¨»2«/mn»«/msup»«msub»«mi mathvariant=¨bold¨»R«/mi»«mi mathvariant=¨bold¨»L«/mi»«/msub»«/mfrac»«mspace linebreak=¨newline¨/»«mspace linebreak=¨newline¨/»«msub»«mi mathvariant=¨bold¨ mathcolor=¨#0000FF¨»R«/mi»«mi mathvariant=¨bold¨ mathcolor=¨#0000FF¨»L«/mi»«/msub»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»=«/mo»«mfrac mathcolor=¨#0000FF¨»«msup»«msub»«mi mathvariant=¨bold¨»U«/mi»«mi mathvariant=¨bold¨»L«/mi»«/msub»«mn mathvariant=¨bold¨»2«/mn»«/msup»«msub»«mi mathvariant=¨bold¨»P«/mi»«mi mathvariant=¨bold¨»L«/mi»«/msub»«/mfrac»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»=«/mo»«mfrac mathcolor=¨#0000FF¨»«msup»«mn mathvariant=¨bold¨»3«/mn»«mn mathvariant=¨bold¨»2«/mn»«/msup»«mrow»«mn mathvariant=¨bold¨»0«/mn»«mo mathvariant=¨bold¨».«/mo»«mn mathvariant=¨bold¨»9«/mn»«/mrow»«/mfrac»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»=«/mo»«mfrac mathcolor=¨#0000FF¨»«mn mathvariant=¨bold¨»9«/mn»«mrow»«mn mathvariant=¨bold¨»0«/mn»«mo mathvariant=¨bold¨».«/mo»«mn mathvariant=¨bold¨»9«/mn»«/mrow»«/mfrac»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»=«/mo»«mn mathvariant=¨bold¨ mathcolor=¨#0000FF¨»10«/mn»«mi mathvariant=¨bold¨ mathcolor=¨#0000FF¨»§#937;«/mi»«/mstyle»«/math»
ج- الدائرة المعطاة هي دائرة على التوالي، نحسب قدرة التيار في الدائرة عندما يضيء المصباح في ضوءه الكامل.
نستخدم قانون أوم على المصباح الكهربائي:
«math style=¨font-family:Tahoma¨ xmlns=¨http://www.w3.org/1998/Math/MathML¨»«mstyle mathsize=¨20px¨»«mi mathvariant=¨bold¨ mathcolor=¨#0000FF¨»I«/mi»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»=«/mo»«mfrac mathcolor=¨#0000FF¨»«mi mathvariant=¨normal¨»U«/mi»«mi mathvariant=¨bold¨»R«/mi»«/mfrac»«mspace linebreak=¨newline¨/»«mspace linebreak=¨newline¨/»«mi mathvariant=¨bold¨ mathcolor=¨#0000FF¨»I«/mi»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»=«/mo»«mfrac mathcolor=¨#0000FF¨»«msub»«mi mathvariant=¨bold¨»U«/mi»«mi mathvariant=¨bold¨»L«/mi»«/msub»«msub»«mi mathvariant=¨bold¨»R«/mi»«mi mathvariant=¨bold¨»L«/mi»«/msub»«/mfrac»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»=«/mo»«mfrac mathcolor=¨#0000FF¨»«mn mathvariant=¨bold¨»3«/mn»«mn mathvariant=¨bold¨»10«/mn»«/mfrac»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»=«/mo»«mn mathvariant=¨bold¨ mathcolor=¨#0000FF¨»0«/mn»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨».«/mo»«mn mathvariant=¨bold¨ mathcolor=¨#0000FF¨»3«/mn»«mi mathvariant=¨bold¨ mathcolor=¨#0000FF¨»A«/mi»«/mstyle»«/math»
نحسب المقاومة المحصلة ، من قانون أوم للدائرة بأكملها:
«math style=¨font-family:Tahoma¨ xmlns=¨http://www.w3.org/1998/Math/MathML¨»«mstyle mathsize=¨20px¨»«mi mathvariant=¨bold¨ mathcolor=¨#0000FF¨»I«/mi»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»=«/mo»«mfrac mathcolor=¨#0000FF¨»«mi mathvariant=¨normal¨»§#949;«/mi»«msub»«mi mathvariant=¨bold¨»R«/mi»«mi mathvariant=¨bold¨»T«/mi»«/msub»«/mfrac»«mspace linebreak=¨newline¨/»«mspace linebreak=¨newline¨/»«msub»«mi mathvariant=¨bold¨ mathcolor=¨#0000FF¨»R«/mi»«mi mathvariant=¨bold¨ mathcolor=¨#0000FF¨»T«/mi»«/msub»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»=«/mo»«mfrac mathcolor=¨#0000FF¨»«mi mathvariant=¨bold¨»§#949;«/mi»«mi mathvariant=¨bold¨»I«/mi»«/mfrac»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»=«/mo»«mfrac mathcolor=¨#0000FF¨»«mn mathvariant=¨bold¨»12«/mn»«mrow»«mn mathvariant=¨bold¨»0«/mn»«mo mathvariant=¨bold¨».«/mo»«mn mathvariant=¨bold¨»3«/mn»«/mrow»«/mfrac»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»=«/mo»«mn mathvariant=¨bold¨ mathcolor=¨#0000FF¨»40«/mn»«mi mathvariant=¨bold¨ mathcolor=¨#0000FF¨»§#937;«/mi»«/mstyle»«/math»
نحسب مقاومة المقاوم المتغير RX من التعبير عن المقاومة المحصلة:
«math style=¨font-family:Tahoma¨ xmlns=¨http://www.w3.org/1998/Math/MathML¨»«mstyle mathsize=¨20px¨»«msub»«mi mathvariant=¨bold¨ mathcolor=¨#0000FF¨»R«/mi»«mi mathvariant=¨bold¨ mathcolor=¨#0000FF¨»T«/mi»«/msub»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»=«/mo»«msub»«mi mathvariant=¨bold¨ mathcolor=¨#0000FF¨»R«/mi»«mi mathvariant=¨bold¨ mathcolor=¨#0000FF¨»L«/mi»«/msub»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»+«/mo»«mi mathvariant=¨bold¨ mathcolor=¨#0000FF¨»r«/mi»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»+«/mo»«msub»«mi mathvariant=¨bold¨ mathcolor=¨#0000FF¨»R«/mi»«mi mathvariant=¨bold¨ mathcolor=¨#0000FF¨»X«/mi»«/msub»«mspace linebreak=¨newline¨/»«msub»«mi mathvariant=¨bold¨ mathcolor=¨#0000FF¨»R«/mi»«mi mathvariant=¨bold¨ mathcolor=¨#0000FF¨»X«/mi»«/msub»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»=«/mo»«msub»«mi mathvariant=¨bold¨ mathcolor=¨#0000FF¨»R«/mi»«mi mathvariant=¨bold¨ mathcolor=¨#0000FF¨»T«/mi»«/msub»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»-«/mo»«msub»«mi mathvariant=¨bold¨ mathcolor=¨#0000FF¨»R«/mi»«mi mathvariant=¨bold¨ mathcolor=¨#0000FF¨»L«/mi»«/msub»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»-«/mo»«mi mathvariant=¨bold¨ mathcolor=¨#0000FF¨»r«/mi»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»=«/mo»«mn mathvariant=¨bold¨ mathcolor=¨#0000FF¨»40«/mn»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»-«/mo»«mn mathvariant=¨bold¨ mathcolor=¨#0000FF¨»10«/mn»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»-«/mo»«mn mathvariant=¨bold¨ mathcolor=¨#0000FF¨»2«/mn»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»=«/mo»«mn mathvariant=¨bold¨ mathcolor=¨#0000FF¨»28«/mn»«mi mathvariant=¨bold-italic¨ mathcolor=¨#0000FF¨»§#937;«/mi»«/mstyle»«/math»
د- نحسب القدرات المطلوبة:
«math style=¨font-family:Tahoma¨ xmlns=¨http://www.w3.org/1998/Math/MathML¨»«mstyle mathsize=¨20px¨»«msub»«mi mathvariant=¨bold¨ mathcolor=¨#0000FF¨»P«/mi»«msub»«mi mathvariant=¨bold¨ mathcolor=¨#0000FF¨»R«/mi»«mi mathvariant=¨bold¨ mathcolor=¨#0000FF¨»X«/mi»«/msub»«/msub»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»=«/mo»«msup»«mi mathvariant=¨bold¨ mathcolor=¨#0000FF¨»I«/mi»«mn mathvariant=¨bold¨ mathcolor=¨#0000FF¨»2«/mn»«/msup»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»§#183;«/mo»«msub»«mi mathvariant=¨bold¨ mathcolor=¨#0000FF¨»R«/mi»«mi mathvariant=¨bold¨ mathcolor=¨#0000FF¨»X«/mi»«/msub»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»=«/mo»«mn mathvariant=¨bold¨ mathcolor=¨#0000FF¨»0«/mn»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨».«/mo»«msup»«mn mathvariant=¨bold¨ mathcolor=¨#0000FF¨»3«/mn»«mn mathvariant=¨bold¨ mathcolor=¨#0000FF¨»2«/mn»«/msup»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»§#183;«/mo»«mn mathvariant=¨bold¨ mathcolor=¨#0000FF¨»28«/mn»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»=«/mo»«mn mathvariant=¨bold¨ mathcolor=¨#0000FF¨»2«/mn»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨».«/mo»«mn mathvariant=¨bold¨ mathcolor=¨#0000FF¨»52«/mn»«mi mathvariant=¨bold¨ mathcolor=¨#0000FF¨»W«/mi»«mspace linebreak=¨newline¨/»«mspace linebreak=¨newline¨/»«msub»«mi mathvariant=¨bold¨ mathcolor=¨#0000FF¨»P«/mi»«msub mathcolor=¨#0000FF¨»«mi mathvariant=¨bold¨»R«/mi»«mi mathvariant=¨bold¨»L«/mi»«/msub»«/msub»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»=«/mo»«msup»«mi mathvariant=¨bold¨ mathcolor=¨#0000FF¨»I«/mi»«mn mathvariant=¨bold¨ mathcolor=¨#0000FF¨»2«/mn»«/msup»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»§#183;«/mo»«msub»«mi mathvariant=¨bold¨ mathcolor=¨#0000FF¨»R«/mi»«mi mathvariant=¨bold¨ mathcolor=¨#0000FF¨»L«/mi»«/msub»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»=«/mo»«mn mathvariant=¨bold¨ mathcolor=¨#0000FF¨»0«/mn»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨».«/mo»«msup»«mn mathvariant=¨bold¨ mathcolor=¨#0000FF¨»3«/mn»«mn mathvariant=¨bold¨ mathcolor=¨#0000FF¨»2«/mn»«/msup»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»§#183;«/mo»«mn mathvariant=¨bold¨ mathcolor=¨#0000FF¨»10«/mn»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»=«/mo»«mn mathvariant=¨bold¨ mathcolor=¨#0000FF¨»0«/mn»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨».«/mo»«mn mathvariant=¨bold¨ mathcolor=¨#0000FF¨»9«/mn»«mi mathvariant=¨bold¨ mathcolor=¨#0000FF¨»W«/mi»«mspace linebreak=¨newline¨/»«mspace linebreak=¨newline¨/»«msub»«mi mathvariant=¨bold¨ mathcolor=¨#0000FF¨»P«/mi»«mi mathvariant=¨bold¨ mathcolor=¨#0000FF¨»r«/mi»«/msub»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»=«/mo»«msup»«mi mathvariant=¨bold¨ mathcolor=¨#0000FF¨»I«/mi»«mn mathvariant=¨bold¨ mathcolor=¨#0000FF¨»2«/mn»«/msup»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»§#183;«/mo»«mi mathvariant=¨bold¨ mathcolor=¨#0000FF¨»r«/mi»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»=«/mo»«mn mathvariant=¨bold¨ mathcolor=¨#0000FF¨»0«/mn»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨».«/mo»«msup»«mn mathvariant=¨bold¨ mathcolor=¨#0000FF¨»3«/mn»«mn mathvariant=¨bold¨ mathcolor=¨#0000FF¨»2«/mn»«/msup»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»§#183;«/mo»«mn mathvariant=¨bold¨ mathcolor=¨#0000FF¨»2«/mn»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»=«/mo»«mn mathvariant=¨bold¨ mathcolor=¨#0000FF¨»0«/mn»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨».«/mo»«mn mathvariant=¨bold¨ mathcolor=¨#0000FF¨»18«/mn»«mi mathvariant=¨bold¨ mathcolor=¨#0000FF¨»W«/mi»«mspace linebreak=¨newline¨/»«mspace linebreak=¨newline¨/»«mmultiscripts»«mi mathvariant=¨bold¨ mathcolor=¨#0000FF¨»P«/mi»«mprescripts/»«mi mathcolor=¨#0000FF¨»§#1605;§#1589;§#1583;§#1585;«/mi»«none/»«/mmultiscripts»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»=«/mo»«mi mathvariant=¨bold¨ mathcolor=¨#0000FF¨»§#949;«/mi»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»§#183;«/mo»«mi mathvariant=¨bold¨ mathcolor=¨#0000FF¨»I«/mi»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»=«/mo»«mn mathvariant=¨bold¨ mathcolor=¨#0000FF¨»12«/mn»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»§#183;«/mo»«mn mathvariant=¨bold¨ mathcolor=¨#0000FF¨»0«/mn»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨».«/mo»«mn mathvariant=¨bold¨ mathcolor=¨#0000FF¨»3«/mn»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»=«/mo»«mn mathvariant=¨bold¨ mathcolor=¨#0000FF¨»3«/mn»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨».«/mo»«mn mathvariant=¨bold¨ mathcolor=¨#0000FF¨»6«/mn»«mi mathvariant=¨bold¨ mathcolor=¨#0000FF¨»W«/mi»«mspace linebreak=¨newline¨/»«/mstyle»«/math»
يمكن ملاحظة أن مجموع كل القدرات الناتجة في الدائرة يساوي القدرة التي ينتجها المصدر.
«math xmlns=¨http://www.w3.org/1998/Math/MathML¨»«mmultiscripts»«mi mathvariant=¨bold¨ mathcolor=¨#0000FF¨ mathsize=¨20px¨»P«/mi»«mprescripts/»«mi mathvariant=¨bold¨ mathcolor=¨#0000FF¨»§#1605;§#1589;§#1583;§#1585;«/mi»«none/»«/mmultiscripts»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»=«/mo»«msub»«mi mathvariant=¨bold¨ mathcolor=¨#0000FF¨ mathsize=¨20px¨»P«/mi»«msub mathcolor=¨#0000FF¨»«mi mathvariant=¨bold¨ mathsize=¨20px¨»R«/mi»«mi mathvariant=¨bold¨ mathsize=¨20px¨»X«/mi»«/msub»«/msub»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨ mathsize=¨20px¨»+«/mo»«msub»«mi mathvariant=¨bold¨ mathcolor=¨#0000FF¨ mathsize=¨20px¨»P«/mi»«msub mathcolor=¨#0000FF¨»«mi mathvariant=¨bold¨ mathsize=¨20px¨»R«/mi»«mi mathvariant=¨bold¨ mathsize=¨20px¨»L«/mi»«/msub»«/msub»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨ mathsize=¨20px¨»+«/mo»«msub»«mi mathvariant=¨bold¨ mathcolor=¨#0000FF¨ mathsize=¨20px¨»P«/mi»«mi mathvariant=¨bold¨ mathcolor=¨#0000FF¨ mathsize=¨20px¨»r«/mi»«/msub»«mspace linebreak=¨newline¨/»«mspace linebreak=¨newline¨/»«mn mathvariant=¨bold¨ mathcolor=¨#0000FF¨ mathsize=¨20px¨»3«/mn»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨ mathsize=¨20px¨».«/mo»«mn mathvariant=¨bold¨ mathcolor=¨#0000FF¨ mathsize=¨20px¨»6«/mn»«mi mathvariant=¨bold¨ mathcolor=¨#0000FF¨ mathsize=¨20px¨»W«/mi»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨ mathsize=¨20px¨»=«/mo»«mn mathvariant=¨bold¨ mathcolor=¨#0000FF¨ mathsize=¨20px¨»2«/mn»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨ mathsize=¨20px¨».«/mo»«mn mathvariant=¨bold¨ mathcolor=¨#0000FF¨ mathsize=¨20px¨»52«/mn»«mi mathvariant=¨bold¨ mathcolor=¨#0000FF¨ mathsize=¨20px¨»W«/mi»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨ mathsize=¨20px¨»+«/mo»«mn mathvariant=¨bold¨ mathcolor=¨#0000FF¨ mathsize=¨20px¨»0«/mn»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨ mathsize=¨20px¨».«/mo»«mn mathvariant=¨bold¨ mathcolor=¨#0000FF¨ mathsize=¨20px¨»9«/mn»«mi mathvariant=¨bold¨ mathcolor=¨#0000FF¨ mathsize=¨20px¨»W«/mi»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨ mathsize=¨20px¨»+«/mo»«mn mathvariant=¨bold¨ mathcolor=¨#0000FF¨ mathsize=¨20px¨»0«/mn»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨ mathsize=¨20px¨».«/mo»«mn mathvariant=¨bold¨ mathcolor=¨#0000FF¨ mathsize=¨20px¨»18«/mn»«mi mathvariant=¨bold¨ mathcolor=¨#0000FF¨ mathsize=¨20px¨»W«/mi»«mspace linebreak=¨newline¨/»«mspace linebreak=¨newline¨/»«mn mathvariant=¨bold¨ mathcolor=¨#0000FF¨ mathsize=¨20px¨»3«/mn»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨ mathsize=¨20px¨».«/mo»«mn mathvariant=¨bold¨ mathcolor=¨#0000FF¨ mathsize=¨20px¨»6«/mn»«mi mathvariant=¨bold¨ mathcolor=¨#0000FF¨ mathsize=¨20px¨»W«/mi»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨ mathsize=¨20px¨»=«/mo»«mn mathvariant=¨bold¨ mathcolor=¨#0000FF¨ mathsize=¨20px¨»3«/mn»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨ mathsize=¨20px¨».«/mo»«mn mathvariant=¨bold¨ mathcolor=¨#0000FF¨ mathsize=¨20px¨»6«/mn»«mi mathvariant=¨bold¨ mathcolor=¨#0000FF¨ mathsize=¨20px¨»W«/mi»«/math»
هـ- من مبدأ حفظ الطاقة، في أي دائرة كهربائية، يكون مجموع الطاقات الناتجة في فترة زمنية معينة مساويًا للطاقة التي يبذلها مصدر فرق الجهد في تلك الفترة الزمنية. لذلك ، في أي دائرة كهربائية، تكون القدرة المبذولة من قبل المصدر مساوية لمجموع القدرات المستهلكة في الدائرة.
و- لحساب كفاءة الدائرة، من الضروري تحديد الطاقة المستهلكة وما هي الطاقة المبذولة.
يتم بذل الطاقة بواسطة مصدر فرق الجهد ، ويتم استهلاكلها في المصباح.
المقاوم المتغير مخصص فقط لـ "تنظيم" التيار في الدائرة، والطاقة الناتجة بالمقاوم المتغير تعتبر طاقة مهدرة.
نحسب كفاءة الدائرة وفقًا للنسبة بين قدرة المصباح وقدرة المصدر:
«math style=¨font-family:Tahoma¨ xmlns=¨http://www.w3.org/1998/Math/MathML¨»«mstyle mathsize=¨20px¨»«mi mathvariant=¨bold¨ mathcolor=¨#0000FF¨»§#951;«/mi»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»=«/mo»«mfrac mathcolor=¨#0000FF¨»«mi mathvariant=¨bold¨»Peff«/mi»«mi mathvariant=¨bold¨»Pin«/mi»«/mfrac»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»§#183;«/mo»«mn mathvariant=¨bold¨ mathcolor=¨#0000FF¨»100«/mn»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»%«/mo»«mspace linebreak=¨newline¨/»«mi mathvariant=¨bold¨ mathcolor=¨#0000FF¨»§#951;«/mi»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»=«/mo»«mfrac mathcolor=¨#0000FF¨»«msub»«mi mathvariant=¨bold¨»P«/mi»«mi mathvariant=¨bold¨»RL«/mi»«/msub»«mrow»«mi mathvariant=¨bold¨»§#1605;§#1589;§#1583;§#1585;«/mi»«mi mathvariant=¨bold¨»P«/mi»«/mrow»«/mfrac»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»§#183;«/mo»«mn mathvariant=¨bold¨ mathcolor=¨#0000FF¨»100«/mn»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»%«/mo»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»=«/mo»«mfrac mathcolor=¨#0000FF¨»«mrow»«mn mathvariant=¨bold¨»0«/mn»«mo mathvariant=¨bold¨».«/mo»«mn mathvariant=¨bold¨»9«/mn»«/mrow»«mrow»«mn mathvariant=¨bold¨»3«/mn»«mo mathvariant=¨bold¨».«/mo»«mn mathvariant=¨bold¨»6«/mn»«/mrow»«/mfrac»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»§#183;«/mo»«mn mathvariant=¨bold¨ mathcolor=¨#0000FF¨»100«/mn»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»%«/mo»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»=«/mo»«mn mathvariant=¨bold¨ mathcolor=¨#0000FF¨»25«/mn»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»%«/mo»«/mstyle»«/math»
38. ה.6
أ- من تعبير القدرة «math style=¨font-family:Tahoma¨ xmlns=¨http://www.w3.org/1998/Math/MathML¨»«mstyle mathsize=¨20px¨»«mi mathvariant=¨bold¨ mathcolor=¨#0000FF¨»P«/mi»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»=«/mo»«msup»«mi mathvariant=¨bold¨ mathcolor=¨#0000FF¨»I«/mi»«mn mathvariant=¨bold¨ mathcolor=¨#0000FF¨»2«/mn»«/msup»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»§#183;«/mo»«mi mathvariant=¨bold¨ mathcolor=¨#0000FF¨»R«/mi»«/mstyle»«/math» يمكن ملاحظة أنه من أجل زيادة قدرة المصباح، يجب زيادة التيار في الدائرة.
للقيام بذلك، يجب تقليل المقاومة الكلية ، لذلك يجب تحريك نقطة التماس المتحركة نحو الطرف M للمقاوم المتغير.
ب- نجد شدة التيار في الدائرة بحيث تكون قدرة المصباح مساوية 1 واط :
«math style=¨font-family:Tahoma¨ xmlns=¨http://www.w3.org/1998/Math/MathML¨»«mstyle mathsize=¨20px¨»«mi mathvariant=¨bold¨ mathcolor=¨#0000FF¨»P«/mi»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»=«/mo»«msup»«mi mathvariant=¨bold¨ mathcolor=¨#0000FF¨»I«/mi»«mn mathvariant=¨bold¨ mathcolor=¨#0000FF¨»2«/mn»«/msup»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»§#183;«/mo»«mi mathvariant=¨bold¨ mathcolor=¨#0000FF¨»R«/mi»«mspace linebreak=¨newline¨/»«mspace linebreak=¨newline¨/»«mi mathvariant=¨bold¨ mathcolor=¨#0000FF¨»I«/mi»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»=«/mo»«msqrt mathcolor=¨#0000FF¨»«mfrac»«msub»«mi mathvariant=¨bold¨»P«/mi»«msub»«mi mathvariant=¨bold¨»R«/mi»«mi mathvariant=¨bold¨»L«/mi»«/msub»«/msub»«msub»«mi mathvariant=¨bold¨»R«/mi»«mi mathvariant=¨bold¨»L«/mi»«/msub»«/mfrac»«/msqrt»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»=«/mo»«msqrt mathcolor=¨#0000FF¨»«mfrac»«mn mathvariant=¨bold¨»1«/mn»«mn mathvariant=¨bold¨»10«/mn»«/mfrac»«/msqrt»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»=«/mo»«mn mathvariant=¨bold¨ mathcolor=¨#0000FF¨»0«/mn»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨».«/mo»«mn mathvariant=¨bold¨ mathcolor=¨#0000FF¨»316«/mn»«mi mathvariant=¨bold¨ mathcolor=¨#0000FF¨»A«/mi»«/mstyle»«/math»
نحسب المقاومة المحصلة التي سيكون فيها التيار في الدائرة 0.316 أمبير.
«math style=¨font-family:Tahoma¨ xmlns=¨http://www.w3.org/1998/Math/MathML¨»«mstyle mathsize=¨20px¨»«mi mathvariant=¨bold¨ mathcolor=¨#0000FF¨»I«/mi»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»=«/mo»«mfrac mathcolor=¨#0000FF¨»«mi mathvariant=¨normal¨»§#949;«/mi»«msub»«mi mathvariant=¨bold¨»R«/mi»«mi mathvariant=¨bold¨»T«/mi»«/msub»«/mfrac»«mspace linebreak=¨newline¨/»«mspace linebreak=¨newline¨/»«msub»«mi mathvariant=¨bold¨ mathcolor=¨#0000FF¨»R«/mi»«mi mathvariant=¨bold¨ mathcolor=¨#0000FF¨»T«/mi»«/msub»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»=«/mo»«mfrac mathcolor=¨#0000FF¨»«mi mathvariant=¨bold¨»§#949;«/mi»«mi mathvariant=¨bold¨»I«/mi»«/mfrac»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»=«/mo»«mfrac mathcolor=¨#0000FF¨»«mn mathvariant=¨bold¨»12«/mn»«mrow»«mn mathvariant=¨bold¨»0«/mn»«mo mathvariant=¨bold¨».«/mo»«mn mathvariant=¨bold¨»316«/mn»«/mrow»«/mfrac»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»=«/mo»«mn mathvariant=¨bold¨ mathcolor=¨#0000FF¨»37«/mn»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨».«/mo»«mn mathvariant=¨bold¨ mathcolor=¨#0000FF¨»94«/mn»«mi mathvariant=¨bold¨ mathcolor=¨#0000FF¨»§#937;«/mi»«/mstyle»«/math»
نحسب مقاومة المقاوم المتغير RX من تعبير المقاومة المحصلة:
«math style=¨font-family:Tahoma¨ xmlns=¨http://www.w3.org/1998/Math/MathML¨»«mstyle mathsize=¨20px¨»«msub»«mi mathvariant=¨bold¨ mathcolor=¨#0000FF¨»R«/mi»«mi mathvariant=¨bold¨ mathcolor=¨#0000FF¨»T«/mi»«/msub»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»=«/mo»«msub»«mi mathvariant=¨bold¨ mathcolor=¨#0000FF¨»R«/mi»«mi mathvariant=¨bold¨ mathcolor=¨#0000FF¨»L«/mi»«/msub»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»+«/mo»«mi mathvariant=¨bold¨ mathcolor=¨#0000FF¨»r«/mi»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»+«/mo»«msub»«mi mathvariant=¨bold¨ mathcolor=¨#0000FF¨»R«/mi»«mi mathvariant=¨bold¨ mathcolor=¨#0000FF¨»X«/mi»«/msub»«mspace linebreak=¨newline¨/»«msub»«mi mathvariant=¨bold¨ mathcolor=¨#0000FF¨»R«/mi»«mi mathvariant=¨bold¨ mathcolor=¨#0000FF¨»X«/mi»«/msub»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»=«/mo»«msub»«mi mathvariant=¨bold¨ mathcolor=¨#0000FF¨»R«/mi»«mi mathvariant=¨bold¨ mathcolor=¨#0000FF¨»T«/mi»«/msub»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»-«/mo»«msub»«mi mathvariant=¨bold¨ mathcolor=¨#0000FF¨»R«/mi»«mi mathvariant=¨bold¨ mathcolor=¨#0000FF¨»L«/mi»«/msub»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»-«/mo»«mi mathvariant=¨bold¨ mathcolor=¨#0000FF¨»r«/mi»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»=«/mo»«mn mathvariant=¨bold¨ mathcolor=¨#0000FF¨»37«/mn»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨».«/mo»«mn mathvariant=¨bold¨ mathcolor=¨#0000FF¨»94«/mn»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»-«/mo»«mn mathvariant=¨bold¨ mathcolor=¨#0000FF¨»10«/mn»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»-«/mo»«mn mathvariant=¨bold¨ mathcolor=¨#0000FF¨»2«/mn»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»=«/mo»«mn mathvariant=¨bold¨ mathcolor=¨#0000FF¨»25«/mn»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨».«/mo»«mn mathvariant=¨bold¨ mathcolor=¨#0000FF¨»94«/mn»«mi mathvariant=¨bold-italic¨ mathcolor=¨#0000FF¨»§#937;«/mi»«/mstyle»«/math»
«math style=¨font-family:Tahoma¨ xmlns=¨http://www.w3.org/1998/Math/MathML¨»«mstyle mathsize=¨20px¨»«mi mathvariant=¨bold¨ mathcolor=¨#0000FF¨»I«/mi»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»=«/mo»«mfrac mathcolor=¨#0000FF¨»«mi mathvariant=¨normal¨»U«/mi»«mi mathvariant=¨bold¨»R«/mi»«/mfrac»«mspace linebreak=¨newline¨/»«mspace linebreak=¨newline¨/»«msub»«mi mathvariant=¨bold¨ mathcolor=¨#0000FF¨»U«/mi»«mi mathvariant=¨bold¨ mathcolor=¨#0000FF¨»L«/mi»«/msub»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»=«/mo»«mi mathvariant=¨bold¨ mathcolor=¨#0000FF¨»I«/mi»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»§#183;«/mo»«msub»«mi mathvariant=¨bold¨ mathcolor=¨#0000FF¨»R«/mi»«mi mathvariant=¨bold¨ mathcolor=¨#0000FF¨»L«/mi»«/msub»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»=«/mo»«mn mathvariant=¨bold¨ mathcolor=¨#0000FF¨»0«/mn»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨».«/mo»«mn mathvariant=¨bold¨ mathcolor=¨#0000FF¨»316«/mn»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»§#183;«/mo»«mn mathvariant=¨bold¨ mathcolor=¨#0000FF¨»10«/mn»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»=«/mo»«mn mathvariant=¨bold¨ mathcolor=¨#0000FF¨»3«/mn»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨».«/mo»«mn mathvariant=¨bold¨ mathcolor=¨#0000FF¨»16«/mn»«mi mathvariant=¨bold¨ mathcolor=¨#0000FF¨»V«/mi»«/mstyle»«/math»
د- يؤدي تغيير موقع نقطة التماس المتحرك إلى زيادة التيار. عندما يزداد التيار، تزداد قدرة المصباح وتزداد قدرة المصدر أيضًا.
تزداد قدرة المصباح بشكل ملحوظ أكثر من قدرة المصدر لأن قدرة المصباح تتناسب مع مربع التيار «math style=¨font-family:Tahoma¨ xmlns=¨http://www.w3.org/1998/Math/MathML¨»«mstyle mathsize=¨20px¨»«msub»«mi mathvariant=¨bold¨ mathcolor=¨#0000FF¨»P«/mi»«mi mathvariant=¨bold¨ mathcolor=¨#0000FF¨»RL«/mi»«/msub»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»=«/mo»«msup»«mi mathvariant=¨bold¨ mathcolor=¨#0000FF¨»I«/mi»«mn mathvariant=¨bold¨ mathcolor=¨#0000FF¨»2«/mn»«/msup»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»§#183;«/mo»«msub»«mi mathvariant=¨bold¨ mathcolor=¨#0000FF¨»R«/mi»«mi mathvariant=¨bold¨ mathcolor=¨#0000FF¨»L«/mi»«/msub»«/mstyle»«/math»
بينما قدرة المصباح تتناسب طرديًا مع شدة التيار : «math style=¨font-family:Tahoma¨ xmlns=¨http://www.w3.org/1998/Math/MathML¨»«mstyle mathsize=¨20px¨»«mmultiscripts»«mi mathvariant=¨bold¨ mathcolor=¨#0000FF¨»P«/mi»«mprescripts/»«mi mathvariant=¨bold¨ mathcolor=¨#0000FF¨»§#1605;§#1589;§#1583;§#1585;«/mi»«none/»«/mmultiscripts»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»=«/mo»«mi mathvariant=¨bold¨ mathcolor=¨#0000FF¨»§#949;«/mi»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»§#183;«/mo»«mi mathvariant=¨bold¨ mathcolor=¨#0000FF¨»I«/mi»«mspace linebreak=¨newline¨/»«/mstyle»«/math»
نظرًا لأن الكفاءة تتعلق على النسبة بين قدرة المصباح وقدرة المصدر، يمكن القول أن زيادة التيار يؤدي إلى زيادة الكفاءة.
هـ- نحسب كفاءة الدائرة بعد تحريك نقطة التماس المتحركة:
«math style=¨font-family:Tahoma¨ xmlns=¨http://www.w3.org/1998/Math/MathML¨»«mstyle mathsize=¨20px¨»«mi mathvariant=¨bold¨ mathcolor=¨#0000FF¨»§#951;«/mi»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»=«/mo»«mfrac mathcolor=¨#0000FF¨»«mi mathvariant=¨bold¨»Peff«/mi»«mi mathvariant=¨bold¨»Pin«/mi»«/mfrac»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»§#183;«/mo»«mn mathvariant=¨bold¨ mathcolor=¨#0000FF¨»100«/mn»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»%«/mo»«mspace linebreak=¨newline¨/»«mi mathvariant=¨bold¨ mathcolor=¨#0000FF¨»§#951;«/mi»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»=«/mo»«mfrac mathcolor=¨#0000FF¨»«msub»«mi mathvariant=¨bold¨»P«/mi»«mi mathvariant=¨bold¨»RL«/mi»«/msub»«mmultiscripts»«mi mathvariant=¨bold¨»P«/mi»«mprescripts/»«mi mathvariant=¨bold¨»§#1605;§#1589;§#1583;§#1585;«/mi»«none/»«/mmultiscripts»«/mfrac»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»§#183;«/mo»«mn mathvariant=¨bold¨ mathcolor=¨#0000FF¨»100«/mn»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»%«/mo»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»=«/mo»«mfrac mathcolor=¨#0000FF¨»«mrow»«msup»«mi mathvariant=¨bold¨»I«/mi»«mn mathvariant=¨bold¨»2«/mn»«/msup»«mo mathvariant=¨bold¨»§#183;«/mo»«msub»«mi mathvariant=¨bold¨»R«/mi»«mi mathvariant=¨bold¨»L«/mi»«/msub»«/mrow»«mrow»«mi mathvariant=¨bold¨»§#949;«/mi»«mo mathvariant=¨bold¨»§#183;«/mo»«mi mathvariant=¨bold¨»I«/mi»«/mrow»«/mfrac»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»§#183;«/mo»«mn mathvariant=¨bold¨ mathcolor=¨#0000FF¨»100«/mn»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»%«/mo»«mspace linebreak=¨newline¨/»«mspace linebreak=¨newline¨/»«mi mathvariant=¨bold¨ mathcolor=¨#0000FF¨»§#951;«/mi»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»=«/mo»«mfrac mathcolor=¨#0000FF¨»«mrow»«msup»«mi mathvariant=¨bold¨»I«/mi»«mn mathvariant=¨bold¨»2«/mn»«/msup»«mo mathvariant=¨bold¨»§#183;«/mo»«msub»«mi mathvariant=¨bold¨»R«/mi»«mi mathvariant=¨bold¨»L«/mi»«/msub»«/mrow»«mrow»«mi mathvariant=¨bold¨»§#949;«/mi»«mo mathvariant=¨bold¨»§#183;«/mo»«mi mathvariant=¨bold¨»I«/mi»«/mrow»«/mfrac»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»§#183;«/mo»«mn mathvariant=¨bold¨ mathcolor=¨#0000FF¨»100«/mn»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»%«/mo»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»=«/mo»«mfrac mathcolor=¨#0000FF¨»«mrow»«mn mathvariant=¨bold¨»0«/mn»«mo mathvariant=¨bold¨».«/mo»«msup»«mn mathvariant=¨bold¨»316«/mn»«mn mathvariant=¨bold¨»2«/mn»«/msup»«mo mathvariant=¨bold¨»§#183;«/mo»«mn mathvariant=¨bold¨»10«/mn»«/mrow»«mrow»«mn mathvariant=¨bold¨»12«/mn»«mo mathvariant=¨bold¨»§#183;«/mo»«mn mathvariant=¨bold¨»0«/mn»«mo mathvariant=¨bold¨».«/mo»«mn mathvariant=¨bold¨»316«/mn»«/mrow»«/mfrac»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»§#183;«/mo»«mn mathvariant=¨bold¨ mathcolor=¨#0000FF¨»100«/mn»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»%«/mo»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»=«/mo»«mn mathvariant=¨bold¨ mathcolor=¨#0000FF¨»26«/mn»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨».«/mo»«mn mathvariant=¨bold¨ mathcolor=¨#0000FF¨»33«/mn»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»%«/mo»«mspace linebreak=¨newline¨/»«/mstyle»«/math»
39. ה.7
أ- يتسبب شغل المقاومة الداخلية لتسخين البطارية. قيمة الشغل للمقاومة الداخلية تساوي قيمة الحرارة المطوّرة في البطارية.
لا تؤدي إضافة قاطع الدائرة الكهربائية إلى تغيير شدة التيار، ففي السؤال 5 وجدنا أن قدرة المقاومة الداخلية للبطارية مقدارها 0.18 واط.
نحسب شغل المقاومة الداخلية لمدة ثلاث دقائق، نستخدم تعريف القدرة:
«math xmlns=¨http://www.w3.org/1998/Math/MathML¨»«mstyle mathsize=¨20px¨»«mi mathvariant=¨bold¨ mathcolor=¨#0000FF¨»P«/mi»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»=«/mo»«mfrac mathcolor=¨#0000FF¨»«mi mathvariant=¨bold¨»W«/mi»«mi mathvariant=¨bold¨»t«/mi»«/mfrac»«mspace linebreak=¨newline¨/»«mi mathcolor=¨#0000FF¨»Q«/mi»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»=«/mo»«msub»«mi mathvariant=¨bold¨ mathcolor=¨#0000FF¨»W«/mi»«mi mathvariant=¨bold¨ mathcolor=¨#0000FF¨»r«/mi»«/msub»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»=«/mo»«msub»«mi mathvariant=¨bold¨ mathcolor=¨#0000FF¨»P«/mi»«mi mathvariant=¨bold¨ mathcolor=¨#0000FF¨»r«/mi»«/msub»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»§#183;«/mo»«mi mathvariant=¨bold¨ mathcolor=¨#0000FF¨»t«/mi»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»=«/mo»«mn mathvariant=¨bold¨ mathcolor=¨#0000FF¨»0«/mn»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨».«/mo»«mn mathvariant=¨bold¨ mathcolor=¨#0000FF¨»18«/mn»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»§#183;«/mo»«mn mathvariant=¨bold¨ mathcolor=¨#0000FF¨»3«/mn»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»§#183;«/mo»«mn mathvariant=¨bold¨ mathcolor=¨#0000FF¨»60«/mn»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»=«/mo»«mn mathvariant=¨bold¨ mathcolor=¨#0000FF¨»32«/mn»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨».«/mo»«mn mathvariant=¨bold¨ mathcolor=¨#0000FF¨»4«/mn»«mi mathvariant=¨bold¨ mathcolor=¨#0000FF¨»J«/mi»«/mstyle»«/math»
ب- يتسبب شغل المقاوم المتغير لتسخينه.
في السؤال 5 وجدنا أن قدرة المقاومة الداخلية للبطارية 2.52 واط.
نحسب شغل المقاوم المتغير لمدة ثلاث دقائق، نستخدم تعريف القدرة:
«math xmlns=¨http://www.w3.org/1998/Math/MathML¨»«mstyle mathsize=¨20px¨»«mi mathvariant=¨bold¨ mathcolor=¨#0000FF¨»P«/mi»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»=«/mo»«mfrac mathcolor=¨#0000FF¨»«mi mathvariant=¨bold¨»W«/mi»«mi mathvariant=¨bold¨»t«/mi»«/mfrac»«mspace linebreak=¨newline¨/»«msub»«mi mathvariant=¨bold¨ mathcolor=¨#0000FF¨»Q«/mi»«msub mathcolor=¨#0000FF¨»«mi mathvariant=¨bold¨»R«/mi»«mi mathvariant=¨bold¨»X«/mi»«/msub»«/msub»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»=«/mo»«msub»«mi mathvariant=¨bold¨ mathcolor=¨#0000FF¨»W«/mi»«msub»«mi mathvariant=¨bold¨ mathcolor=¨#0000FF¨»R«/mi»«mi mathvariant=¨bold¨ mathcolor=¨#0000FF¨»X«/mi»«/msub»«/msub»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»=«/mo»«msub»«mi mathvariant=¨bold¨ mathcolor=¨#0000FF¨»P«/mi»«msub»«mi mathvariant=¨bold¨ mathcolor=¨#0000FF¨»R«/mi»«mi mathvariant=¨bold¨ mathcolor=¨#0000FF¨»X«/mi»«/msub»«/msub»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»§#183;«/mo»«mi mathvariant=¨bold¨ mathcolor=¨#0000FF¨»t«/mi»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»=«/mo»«mn mathvariant=¨bold¨ mathcolor=¨#0000FF¨»2«/mn»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨».«/mo»«mn mathvariant=¨bold¨ mathcolor=¨#0000FF¨»52«/mn»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»§#183;«/mo»«mn mathvariant=¨bold¨ mathcolor=¨#0000FF¨»3«/mn»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»§#183;«/mo»«mn mathvariant=¨bold¨ mathcolor=¨#0000FF¨»60«/mn»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»=«/mo»«mn mathvariant=¨bold¨ mathcolor=¨#0000FF¨»453«/mn»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨».«/mo»«mn mathvariant=¨bold¨ mathcolor=¨#0000FF¨»6«/mn»«mi mathvariant=¨bold¨ mathcolor=¨#0000FF¨»J«/mi»«/mstyle»«/math»
ج- مُعطى أن قدرة المصباح 0.9 واط ، نستخدم تعريف القدرة لحساب شغل المصباح خلال مدة 3 دقائق.
«math xmlns=¨http://www.w3.org/1998/Math/MathML¨»«mstyle mathsize=¨20px¨»«mi mathvariant=¨bold¨ mathcolor=¨#0000FF¨»P«/mi»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»=«/mo»«mfrac mathcolor=¨#0000FF¨»«mi mathvariant=¨bold¨»W«/mi»«mi mathvariant=¨bold¨»t«/mi»«/mfrac»«mspace linebreak=¨newline¨/»«msub»«mi mathvariant=¨bold¨ mathcolor=¨#0000FF¨»W«/mi»«msub»«mi mathvariant=¨bold¨ mathcolor=¨#0000FF¨»R«/mi»«mi mathvariant=¨bold¨ mathcolor=¨#0000FF¨»L«/mi»«/msub»«/msub»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»=«/mo»«msub»«mi mathvariant=¨bold¨ mathcolor=¨#0000FF¨»P«/mi»«msub»«mi mathvariant=¨bold¨ mathcolor=¨#0000FF¨»R«/mi»«mi mathvariant=¨bold¨ mathcolor=¨#0000FF¨»L«/mi»«/msub»«/msub»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»§#183;«/mo»«mi mathvariant=¨bold¨ mathcolor=¨#0000FF¨»t«/mi»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»=«/mo»«mn mathvariant=¨bold¨ mathcolor=¨#0000FF¨»0«/mn»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨».«/mo»«mn mathvariant=¨bold¨ mathcolor=¨#0000FF¨»9«/mn»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»§#183;«/mo»«mn mathvariant=¨bold¨ mathcolor=¨#0000FF¨»3«/mn»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»§#183;«/mo»«mn mathvariant=¨bold¨ mathcolor=¨#0000FF¨»60«/mn»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»=«/mo»«mn mathvariant=¨bold¨ mathcolor=¨#0000FF¨»162«/mn»«mi mathvariant=¨bold¨ mathcolor=¨#0000FF¨»J«/mi»«/mstyle»«/math»
ד- من السؤال 5 وجدنا أن قدرة مصدر فرق الجهد هي 3.6 واط، نستخدم تعريف الطاقة لحساب شغل المصباح خلال مدة 3 دقائق.
«math xmlns=¨http://www.w3.org/1998/Math/MathML¨»«mstyle mathsize=¨20px¨»«mi mathvariant=¨bold¨ mathcolor=¨#0000FF¨»P«/mi»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»=«/mo»«mfrac mathcolor=¨#0000FF¨»«mi mathvariant=¨bold¨»W«/mi»«mi mathvariant=¨bold¨»t«/mi»«/mfrac»«mspace linebreak=¨newline¨/»«mmultiscripts»«mi mathvariant=¨bold¨ mathcolor=¨#0000FF¨»W«/mi»«mprescripts/»«mi mathvariant=¨bold¨ mathcolor=¨#0000FF¨»§#1605;§#1589;§#1583;§#1585;«/mi»«none/»«/mmultiscripts»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»=«/mo»«mmultiscripts»«mi mathvariant=¨bold¨ mathcolor=¨#0000FF¨»P«/mi»«mprescripts/»«mi mathvariant=¨bold¨ mathcolor=¨#0000FF¨»§#1605;§#1589;§#1583;§#1585;«/mi»«none/»«/mmultiscripts»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»§#183;«/mo»«mi mathvariant=¨bold¨ mathcolor=¨#0000FF¨»t«/mi»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»=«/mo»«mn mathvariant=¨bold¨ mathcolor=¨#0000FF¨»3«/mn»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨».«/mo»«mn mathvariant=¨bold¨ mathcolor=¨#0000FF¨»6«/mn»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»§#183;«/mo»«mn mathvariant=¨bold¨ mathcolor=¨#0000FF¨»3«/mn»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»§#183;«/mo»«mn mathvariant=¨bold¨ mathcolor=¨#0000FF¨»60«/mn»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»=«/mo»«mn mathvariant=¨bold¨ mathcolor=¨#0000FF¨»648«/mn»«mi mathvariant=¨bold¨ mathcolor=¨#0000FF¨»J«/mi»«/mstyle»«/math»
40. ה.8
أ- في الدائرة على التوالي، تكون شدة التيار عبر جميع المصابيح هي نفسها وتساوي تيار المصدر.
نحسب مقدار التيار المطلوب حتى يضيء المصباح في ضوءه الكامل، نستخدم قانون أوم في المصباح:
«math style=¨font-family:Tahoma¨ xmlns=¨http://www.w3.org/1998/Math/MathML¨»«mstyle mathsize=¨20px¨»«mi mathvariant=¨bold¨ mathcolor=¨#0000FF¨»I«/mi»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»=«/mo»«mfrac mathcolor=¨#0000FF¨»«mi mathvariant=¨normal¨»U«/mi»«mi mathvariant=¨bold¨»R«/mi»«/mfrac»«mspace linebreak=¨newline¨/»«mspace linebreak=¨newline¨/»«mi mathvariant=¨bold¨ mathcolor=¨#0000FF¨»I«/mi»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»=«/mo»«mfrac mathcolor=¨#0000FF¨»«msub»«mi mathvariant=¨bold¨»U«/mi»«mi mathvariant=¨bold¨»L«/mi»«/msub»«msub»«mi mathvariant=¨bold¨»R«/mi»«mi mathvariant=¨bold¨»L«/mi»«/msub»«/mfrac»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»=«/mo»«mfrac mathcolor=¨#0000FF¨»«mn mathvariant=¨bold¨»3«/mn»«mrow»«mn mathvariant=¨bold¨»1«/mn»«mo mathvariant=¨bold¨».«/mo»«mn mathvariant=¨bold¨»5«/mn»«/mrow»«/mfrac»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»=«/mo»«mn mathvariant=¨bold¨ mathcolor=¨#0000FF¨»2«/mn»«mi mathvariant=¨bold¨ mathcolor=¨#0000FF¨»A«/mi»«/mstyle»«/math»
نحسب بواسطة قانون أوم للدائرة بأكملها المقاومة المحصلة بحيث يكون التيار في الدائرة 2 أمبير.
«math style=¨font-family:Tahoma¨ xmlns=¨http://www.w3.org/1998/Math/MathML¨»«mstyle mathsize=¨20px¨»«mi mathvariant=¨bold¨ mathcolor=¨#0000FF¨»I«/mi»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»=«/mo»«mfrac mathcolor=¨#0000FF¨»«mi mathvariant=¨normal¨»§#949;«/mi»«msub»«mi mathvariant=¨bold¨»R«/mi»«mi mathvariant=¨bold¨»T«/mi»«/msub»«/mfrac»«mspace linebreak=¨newline¨/»«mspace linebreak=¨newline¨/»«msub»«mi mathvariant=¨bold¨ mathcolor=¨#0000FF¨»R«/mi»«mi mathvariant=¨bold¨ mathcolor=¨#0000FF¨»T«/mi»«/msub»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»=«/mo»«mfrac mathcolor=¨#0000FF¨»«mi mathvariant=¨bold¨»§#949;«/mi»«mi mathvariant=¨bold¨»I«/mi»«/mfrac»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»=«/mo»«mfrac mathcolor=¨#0000FF¨»«mn mathvariant=¨bold¨»12«/mn»«mn mathvariant=¨bold¨»2«/mn»«/mfrac»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»=«/mo»«mn mathvariant=¨bold¨ mathcolor=¨#0000FF¨»6«/mn»«mi mathvariant=¨bold¨ mathcolor=¨#0000FF¨»§#937;«/mi»«/mstyle»«/math»
نحسب عدد المصابيح - n عندما تكون المقاومة المحصلة للدائرة 6 أوم.
«math style=¨font-family:Tahoma¨ xmlns=¨http://www.w3.org/1998/Math/MathML¨»«mstyle mathsize=¨20px¨»«msub»«mi mathvariant=¨bold¨ mathcolor=¨#0000FF¨»R«/mi»«mi mathvariant=¨bold¨ mathcolor=¨#0000FF¨»T«/mi»«/msub»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»=«/mo»«mi mathvariant=¨bold¨ mathcolor=¨#0000FF¨»n«/mi»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»§#183;«/mo»«msub»«mi mathvariant=¨bold¨ mathcolor=¨#0000FF¨»R«/mi»«mi mathvariant=¨bold¨ mathcolor=¨#0000FF¨»L«/mi»«/msub»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»+«/mo»«mi mathvariant=¨bold¨ mathcolor=¨#0000FF¨»r«/mi»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»=«/mo»«mn mathvariant=¨bold¨ mathcolor=¨#0000FF¨»6«/mn»«mspace linebreak=¨newline¨/»«mi mathvariant=¨bold¨ mathcolor=¨#0000FF¨»n«/mi»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»=«/mo»«mfrac mathcolor=¨#0000FF¨»«mrow»«mn mathvariant=¨bold¨»6«/mn»«mo mathvariant=¨bold¨»-«/mo»«mi mathvariant=¨bold¨»r«/mi»«/mrow»«msub»«mi mathvariant=¨bold¨»R«/mi»«mi mathvariant=¨bold¨»L«/mi»«/msub»«/mfrac»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»=«/mo»«mfrac mathcolor=¨#0000FF¨»«mrow»«mn mathvariant=¨bold¨»6«/mn»«mo mathvariant=¨bold¨»-«/mo»«mn mathvariant=¨bold¨»1«/mn»«mo mathvariant=¨bold¨».«/mo»«mn mathvariant=¨bold¨»5«/mn»«/mrow»«mrow»«mn mathvariant=¨bold¨»1«/mn»«mo mathvariant=¨bold¨».«/mo»«mn mathvariant=¨bold¨»5«/mn»«/mrow»«/mfrac»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»=«/mo»«mfrac mathcolor=¨#0000FF¨»«mrow»«mn mathvariant=¨bold¨»4«/mn»«mo mathvariant=¨bold¨».«/mo»«mn mathvariant=¨bold¨»5«/mn»«/mrow»«mrow»«mn mathvariant=¨bold¨»1«/mn»«mo mathvariant=¨bold¨».«/mo»«mn mathvariant=¨bold¨»5«/mn»«/mrow»«/mfrac»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»=«/mo»«mn mathvariant=¨bold¨ mathcolor=¨#0000FF¨»3«/mn»«mspace linebreak=¨newline¨/»«/mstyle»«/math»
لذلك ، إذا قمنا بتوصيل ثلاثة مصابيح على التوالي بمصدر فرق الجهد غير المثالي، فإن المصابيح الثلاثة ستضيء بضوءها الكامل.
ب- في الدائرة على التوازي، يكون فرق الجهد على المصابيح هو نفسه ويساوي فرق جهد الأقطاب للبطارية.
نحسب بواسطة تعبير فرق جهد الأقطاب شدة تيار بالمصدر عندما يكون فرق جهد الأقطاب 3 فولط (جهد المصباح).
«math style=¨font-family:Tahoma¨ xmlns=¨http://www.w3.org/1998/Math/MathML¨»«mi mathvariant=¨bold¨ mathcolor=¨#0000FF¨ mathsize=¨20px¨»Vab«/mi»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨ mathsize=¨20px¨»=«/mo»«mi mathvariant=¨bold¨ mathcolor=¨#0000FF¨ mathsize=¨20px¨»§#949;«/mi»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨ mathsize=¨20px¨»-«/mo»«mi mathvariant=¨bold¨ mathcolor=¨#0000FF¨ mathsize=¨20px¨»I«/mi»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨ mathsize=¨20px¨»§#183;«/mo»«mi mathvariant=¨bold¨ mathcolor=¨#0000FF¨ mathsize=¨20px¨»r«/mi»«mspace linebreak=¨newline¨/»«mspace linebreak=¨newline¨/»«mi mathvariant=¨bold¨ mathcolor=¨#0000FF¨ mathsize=¨20px¨»I«/mi»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨ mathsize=¨20px¨»§#183;«/mo»«mi mathvariant=¨bold¨ mathcolor=¨#0000FF¨ mathsize=¨20px¨»r«/mi»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨ mathsize=¨20px¨»=«/mo»«mi mathvariant=¨bold¨ mathcolor=¨#0000FF¨ mathsize=¨20px¨»Vab«/mi»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨ mathsize=¨20px¨»-«/mo»«mi mathvariant=¨bold¨ mathcolor=¨#0000FF¨ mathsize=¨20px¨»§#949;«/mi»«mspace linebreak=¨newline¨/»«mspace linebreak=¨newline¨/»«mi mathvariant=¨bold¨ mathcolor=¨#0000FF¨ mathsize=¨20px¨»I«/mi»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨ mathsize=¨20px¨»=«/mo»«mfrac mathcolor=¨#0000FF¨»«mrow»«mi mathvariant=¨bold¨ mathsize=¨20px¨»§#949;«/mi»«mo mathvariant=¨bold¨ mathsize=¨20px¨»-«/mo»«mi mathvariant=¨bold¨ mathsize=¨20px¨»Vab«/mi»«/mrow»«mi mathvariant=¨bold¨ mathsize=¨20px¨»r«/mi»«/mfrac»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨ mathsize=¨20px¨»=«/mo»«mfrac mathcolor=¨#0000FF¨»«mrow»«mn mathvariant=¨bold¨ mathsize=¨20px¨»12«/mn»«mo mathvariant=¨bold¨ mathsize=¨20px¨»-«/mo»«mn mathvariant=¨bold¨ mathsize=¨20px¨»3«/mn»«/mrow»«mrow»«mn mathvariant=¨bold¨ mathsize=¨20px¨»1«/mn»«mo mathvariant=¨bold¨ mathsize=¨20px¨».«/mo»«mn mathvariant=¨bold¨ mathsize=¨20px¨»5«/mn»«/mrow»«/mfrac»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨ mathsize=¨20px¨»=«/mo»«mfrac mathcolor=¨#0000FF¨»«mn mathvariant=¨bold¨ mathsize=¨20px¨»9«/mn»«mrow»«mn mathvariant=¨bold¨ mathsize=¨20px¨»1«/mn»«mo mathvariant=¨bold¨ mathsize=¨20px¨».«/mo»«mn mathvariant=¨bold¨ mathsize=¨20px¨»5«/mn»«/mrow»«/mfrac»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨ mathsize=¨20px¨»=«/mo»«mn mathvariant=¨bold¨ mathcolor=¨#0000FF¨ mathsize=¨20px¨»6«/mn»«mi mathvariant=¨bold¨ mathcolor=¨#0000FF¨ mathsize=¨20px¨»A«/mi»«mspace linebreak=¨newline¨/»«/math»
يجب أن يكون التيار عبر كل مصباح 2 أمبير. نظرًا لأن تيار المصدر يجب أن يكون 6 أمبير، يجب توصيل ثلاثة مصابيح على التوازي.
ج- في كل دائرة من الدائرتين، القدرة المستهلكة هي مجموع القدرات للمصابيح الثلاثة. والقدرة المبذولة هي قدرة مصدر فرق الجهد.
نحسب كفاءة الدائرة الموصولة على التوالي:
«math style=¨font-family:Tahoma¨ xmlns=¨http://www.w3.org/1998/Math/MathML¨»«mstyle mathsize=¨20px¨»«mi mathvariant=¨bold¨ mathcolor=¨#0000FF¨»§#951;«/mi»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»=«/mo»«mfrac mathcolor=¨#0000FF¨»«mi mathvariant=¨bold¨»Peff«/mi»«mi mathvariant=¨bold¨»Pin«/mi»«/mfrac»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»§#183;«/mo»«mn mathvariant=¨bold¨ mathcolor=¨#0000FF¨»100«/mn»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»%«/mo»«mspace linebreak=¨newline¨/»«mi mathvariant=¨bold¨ mathcolor=¨#0000FF¨»§#951;«/mi»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»=«/mo»«mfrac mathcolor=¨#0000FF¨»«mrow»«mn mathvariant=¨bold¨»3«/mn»«mo mathvariant=¨bold¨»§#183;«/mo»«msub»«mi mathvariant=¨bold¨»P«/mi»«mi mathvariant=¨bold¨»L«/mi»«/msub»«/mrow»«mmultiscripts»«mi mathvariant=¨bold¨»P«/mi»«mprescripts/»«mi mathvariant=¨bold¨»§#1605;§#1589;§#1583;§#1585;«/mi»«none/»«/mmultiscripts»«/mfrac»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»§#183;«/mo»«mn mathvariant=¨bold¨ mathcolor=¨#0000FF¨»100«/mn»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»%«/mo»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»=«/mo»«mfrac mathcolor=¨#0000FF¨»«mrow»«mn mathvariant=¨bold¨»3«/mn»«mo mathvariant=¨bold¨»§#183;«/mo»«mstyle displaystyle=¨true¨»«mfrac»«msup»«msub»«mi mathvariant=¨bold¨»U«/mi»«msub»«mi mathvariant=¨bold¨»R«/mi»«mi mathvariant=¨bold¨»L«/mi»«/msub»«/msub»«mn mathvariant=¨bold¨»2«/mn»«/msup»«msub»«mi mathvariant=¨bold¨»R«/mi»«mi mathvariant=¨bold¨»L«/mi»«/msub»«/mfrac»«/mstyle»«/mrow»«mrow»«mi mathvariant=¨bold¨»§#949;«/mi»«mo mathvariant=¨bold¨»§#183;«/mo»«mi mathvariant=¨bold¨»I«/mi»«/mrow»«/mfrac»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»§#183;«/mo»«mn mathvariant=¨bold¨ mathcolor=¨#0000FF¨»100«/mn»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»%«/mo»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»=«/mo»«mfrac mathcolor=¨#0000FF¨»«mrow»«mn mathvariant=¨bold¨»3«/mn»«mo mathvariant=¨bold¨»§#183;«/mo»«mstyle mathvariant=¨bold¨ displaystyle=¨true¨»«mfrac»«msup»«mn»3«/mn»«mn»2«/mn»«/msup»«mrow»«mn»1«/mn»«mo».«/mo»«mn»5«/mn»«/mrow»«/mfrac»«/mstyle»«/mrow»«mrow»«mn mathvariant=¨bold¨»12«/mn»«mo mathvariant=¨bold¨»§#183;«/mo»«mn mathvariant=¨bold¨»2«/mn»«/mrow»«/mfrac»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»§#183;«/mo»«mn mathvariant=¨bold¨ mathcolor=¨#0000FF¨»100«/mn»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»%«/mo»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»=«/mo»«mfrac mathcolor=¨#0000FF¨»«mn mathvariant=¨bold¨»18«/mn»«mn mathvariant=¨bold¨»24«/mn»«/mfrac»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»§#183;«/mo»«mn mathvariant=¨bold¨ mathcolor=¨#0000FF¨»100«/mn»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»%«/mo»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»=«/mo»«mn mathvariant=¨bold¨ mathcolor=¨#0000FF¨»75«/mn»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»%«/mo»«/mstyle»«/math»
نحسب كفاءة الدائرة الموصولة على التوازي:
«math style=¨font-family:Tahoma¨ xmlns=¨http://www.w3.org/1998/Math/MathML¨»«mstyle mathsize=¨20px¨»«mi mathvariant=¨bold¨ mathcolor=¨#0000FF¨»§#951;«/mi»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»=«/mo»«mfrac mathcolor=¨#0000FF¨»«mi mathvariant=¨bold¨»Peff«/mi»«mi mathvariant=¨bold¨»Pin«/mi»«/mfrac»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»§#183;«/mo»«mn mathvariant=¨bold¨ mathcolor=¨#0000FF¨»100«/mn»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»%«/mo»«mspace linebreak=¨newline¨/»«mi mathvariant=¨bold¨ mathcolor=¨#0000FF¨»§#951;«/mi»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»=«/mo»«mfrac mathcolor=¨#0000FF¨»«mrow»«mn mathvariant=¨bold¨»3«/mn»«mo mathvariant=¨bold¨»§#183;«/mo»«msub»«mi mathvariant=¨bold¨»P«/mi»«mi mathvariant=¨bold¨»L«/mi»«/msub»«/mrow»«mmultiscripts»«mi mathvariant=¨bold¨»P«/mi»«mprescripts/»«mi mathvariant=¨bold¨»§#1605;§#1589;§#1583;§#1585;«/mi»«none/»«/mmultiscripts»«/mfrac»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»§#183;«/mo»«mn mathvariant=¨bold¨ mathcolor=¨#0000FF¨»100«/mn»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»%«/mo»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»=«/mo»«mfrac mathcolor=¨#0000FF¨»«mrow»«mn mathvariant=¨bold¨»3«/mn»«mo mathvariant=¨bold¨»§#183;«/mo»«mstyle displaystyle=¨true¨»«mfrac»«msup»«msub»«mi mathvariant=¨bold¨»U«/mi»«msub»«mi mathvariant=¨bold¨»R«/mi»«mi mathvariant=¨bold¨»L«/mi»«/msub»«/msub»«mn mathvariant=¨bold¨»2«/mn»«/msup»«msub»«mi mathvariant=¨bold¨»R«/mi»«mi mathvariant=¨bold¨»L«/mi»«/msub»«/mfrac»«/mstyle»«/mrow»«mrow»«mi mathvariant=¨bold¨»§#949;«/mi»«mo mathvariant=¨bold¨»§#183;«/mo»«mi mathvariant=¨bold¨»I«/mi»«/mrow»«/mfrac»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»§#183;«/mo»«mn mathvariant=¨bold¨ mathcolor=¨#0000FF¨»100«/mn»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»%«/mo»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»=«/mo»«mfrac mathcolor=¨#0000FF¨»«mrow»«mn mathvariant=¨bold¨»3«/mn»«mo mathvariant=¨bold¨»§#183;«/mo»«mstyle mathvariant=¨bold¨ displaystyle=¨true¨»«mfrac»«msup»«mn»3«/mn»«mn»2«/mn»«/msup»«mrow»«mn»1«/mn»«mo».«/mo»«mn»5«/mn»«/mrow»«/mfrac»«/mstyle»«/mrow»«mrow»«mn mathvariant=¨bold¨»12«/mn»«mo mathvariant=¨bold¨»§#183;«/mo»«mn mathvariant=¨bold¨»6«/mn»«/mrow»«/mfrac»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»§#183;«/mo»«mn mathvariant=¨bold¨ mathcolor=¨#0000FF¨»100«/mn»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»%«/mo»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»=«/mo»«mfrac mathcolor=¨#0000FF¨»«mn mathvariant=¨bold¨»18«/mn»«mn mathvariant=¨bold¨»72«/mn»«/mfrac»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»§#183;«/mo»«mn mathvariant=¨bold¨ mathcolor=¨#0000FF¨»100«/mn»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»%«/mo»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»=«/mo»«mn mathvariant=¨bold¨ mathcolor=¨#0000FF¨»25«/mn»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»%«/mo»«/mstyle»«/math»
41. ו.1
أ- يتدفق التيار خارج مصدر فرق الجهد من الجهد العالي إلى الجهد المنخفض، لذا فإن المصدر 1 يُكوّن تيارًا في اتجاه عقارب الساعة. يقوم المصدر 2 أيضًا بتكوين تيار في اتجاه عقارب الساعة.
لذلك، يعمل كل من المصدران تيار في نفس الاتجاه.
ب- نظرًا لأن كلا مصدري فرق الجهد يعمل كل منهما تيارًا في اتجاه عقارب الساعة، فسوف يتدفق تيار في اتجاه عقارب الساعة في الدائرة.
ج- نجد التيار في الدائرة باستخدام قوانين كيرخوف.
يعمل كل من المصدرين تيارًا في اتجاه عقارب الساعة، ويتدفق كل من التيارين في نفس الاتجاه. نشير إلى التيار في الدائرة بواسطة I.
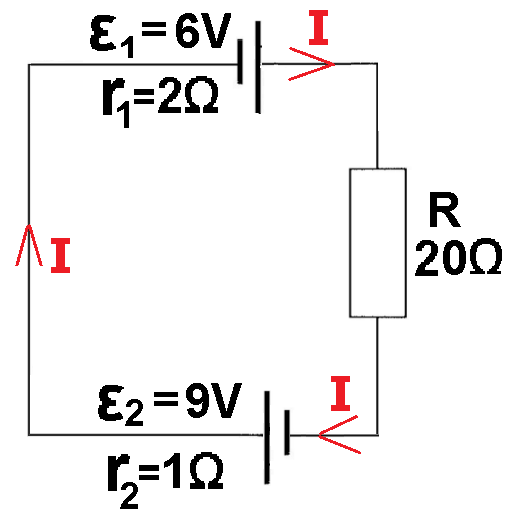
من قانون كيرخوف لفرق الجهد، فإن مجموع فروق الجهد في حلقة مغلقة يساوي صفرًا.
لا يوجد سوى حلقة واحدة في الدائرة، نكتب معادلة فروق الجهد.
قبل كتابة المعادلة، نضيف المقاومات الداخلية إلى الدائرة. وأسهم تمثل فروق الجهد لجميع مكونات الدائرة (نضع رؤوس الأسهم في الجهد العالي).
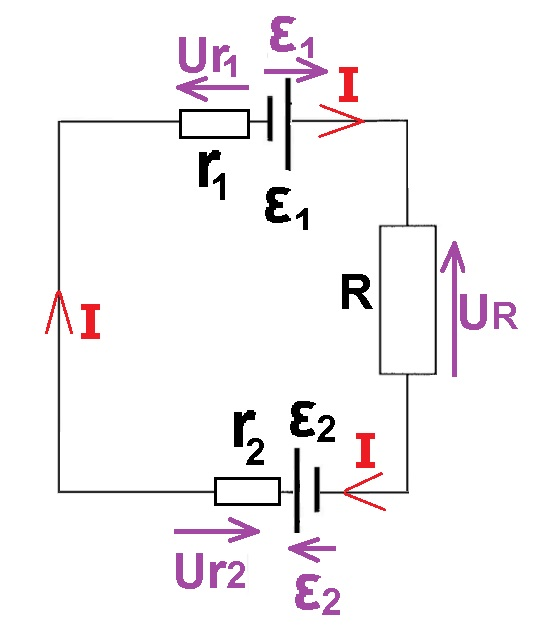
من قانون فروق الجهد لكيرخوف ، فإن مجموع فروق الجهد في كل حلقة مغلقة يساوي صفرًا.
دعنا نجمع فروق الجهد في الحلقة، بدءًا من القطب الموجب للمصدر 1:
«math style=¨font-family:Tahoma¨ xmlns=¨http://www.w3.org/1998/Math/MathML¨»«mstyle mathsize=¨24px¨»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»§#160;«/mo»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»-«/mo»«msub»«mi mathvariant=¨bold¨ mathcolor=¨#0000FF¨»U«/mi»«mi mathvariant=¨bold¨ mathcolor=¨#0000FF¨»R«/mi»«/msub»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»+«/mo»«msub»«mi mathvariant=¨bold¨ mathcolor=¨#0000FF¨»§#949;«/mi»«mn mathvariant=¨bold¨ mathcolor=¨#0000FF¨»2«/mn»«/msub»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»-«/mo»«msub»«mi mathvariant=¨bold¨ mathcolor=¨#0000FF¨»U«/mi»«msub mathcolor=¨#0000FF¨»«mi mathvariant=¨bold¨»r«/mi»«mn mathvariant=¨bold¨»2«/mn»«/msub»«/msub»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»-«/mo»«msub»«mi mathvariant=¨bold¨ mathcolor=¨#0000FF¨»U«/mi»«msub mathcolor=¨#0000FF¨»«mi mathvariant=¨bold¨»r«/mi»«mn mathvariant=¨bold¨»1«/mn»«/msub»«/msub»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»+«/mo»«msub»«mi mathvariant=¨bold¨ mathcolor=¨#0000FF¨»§#949;«/mi»«mn mathvariant=¨bold¨ mathcolor=¨#0000FF¨»1«/mn»«/msub»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»=«/mo»«mn mathvariant=¨bold¨ mathcolor=¨#0000FF¨»0«/mn»«/mstyle»«/math»
نعبر عن معادلات فروق الجهد باستخدام التيار في الدائرة والقوى الكهربائية الدافعة والمقاومة الداخلية:
«math style=¨font-family:Tahoma¨ xmlns=¨http://www.w3.org/1998/Math/MathML¨»«mstyle mathsize=¨24px¨»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»§#160;«/mo»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»-«/mo»«msub»«mi mathvariant=¨bold¨ mathcolor=¨#0000FF¨»U«/mi»«mi mathvariant=¨bold¨ mathcolor=¨#0000FF¨»R«/mi»«/msub»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»+«/mo»«msub»«mi mathvariant=¨bold¨ mathcolor=¨#0000FF¨»§#949;«/mi»«mn mathvariant=¨bold¨ mathcolor=¨#0000FF¨»2«/mn»«/msub»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»-«/mo»«msub»«mi mathvariant=¨bold¨ mathcolor=¨#0000FF¨»U«/mi»«msub mathcolor=¨#0000FF¨»«mi mathvariant=¨bold¨»r«/mi»«mn mathvariant=¨bold¨»2«/mn»«/msub»«/msub»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»-«/mo»«msub»«mi mathvariant=¨bold¨ mathcolor=¨#0000FF¨»U«/mi»«msub mathcolor=¨#0000FF¨»«mi mathvariant=¨bold¨»r«/mi»«mn mathvariant=¨bold¨»1«/mn»«/msub»«/msub»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»+«/mo»«msub»«mi mathvariant=¨bold¨ mathcolor=¨#0000FF¨»§#949;«/mi»«mn mathvariant=¨bold¨ mathcolor=¨#0000FF¨»1«/mn»«/msub»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»=«/mo»«mn mathvariant=¨bold¨ mathcolor=¨#0000FF¨»0«/mn»«mspace linebreak=¨newline¨/»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»-«/mo»«mi mathvariant=¨bold¨ mathcolor=¨#0000FF¨»I«/mi»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»§#183;«/mo»«mi mathvariant=¨bold¨ mathcolor=¨#0000FF¨»R«/mi»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»+«/mo»«msub»«mi mathvariant=¨bold¨ mathcolor=¨#0000FF¨»§#949;«/mi»«mn mathvariant=¨bold¨ mathcolor=¨#0000FF¨»2«/mn»«/msub»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»-«/mo»«mi mathvariant=¨bold¨ mathcolor=¨#0000FF¨»I«/mi»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»§#183;«/mo»«msub»«mi mathvariant=¨bold¨ mathcolor=¨#0000FF¨»r«/mi»«mn mathvariant=¨bold¨ mathcolor=¨#0000FF¨»2«/mn»«/msub»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»-«/mo»«mi mathvariant=¨bold¨ mathcolor=¨#0000FF¨»I«/mi»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»§#183;«/mo»«msub»«mi mathvariant=¨bold¨ mathcolor=¨#0000FF¨»r«/mi»«mn mathvariant=¨bold¨ mathcolor=¨#0000FF¨»1«/mn»«/msub»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»+«/mo»«msub»«mi mathvariant=¨bold¨ mathcolor=¨#0000FF¨»§#949;«/mi»«mn mathvariant=¨bold¨ mathcolor=¨#0000FF¨»1«/mn»«/msub»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»=«/mo»«mn mathvariant=¨bold¨ mathcolor=¨#0000FF¨»0«/mn»«mspace linebreak=¨newline¨/»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»-«/mo»«mi mathvariant=¨bold¨ mathcolor=¨#0000FF¨»I«/mi»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»§#183;«/mo»«mn mathvariant=¨bold¨ mathcolor=¨#0000FF¨»20«/mn»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»+«/mo»«mn mathvariant=¨bold¨ mathcolor=¨#0000FF¨»9«/mn»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»-«/mo»«mi mathvariant=¨bold¨ mathcolor=¨#0000FF¨»I«/mi»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»§#183;«/mo»«mn mathvariant=¨bold¨ mathcolor=¨#0000FF¨»1«/mn»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»-«/mo»«mi mathvariant=¨bold¨ mathcolor=¨#0000FF¨»I«/mi»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»§#183;«/mo»«mn mathvariant=¨bold¨ mathcolor=¨#0000FF¨»2«/mn»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»+«/mo»«mn mathvariant=¨bold¨ mathcolor=¨#0000FF¨»6«/mn»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»=«/mo»«mn mathvariant=¨bold¨ mathcolor=¨#0000FF¨»0«/mn»«/mstyle»«/math»
نجد من هذه المعادلة التيار في الدائرة:
«math style=¨font-family:Tahoma¨ xmlns=¨http://www.w3.org/1998/Math/MathML¨»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨ mathsize=¨24px¨»-«/mo»«mi mathvariant=¨bold¨ mathcolor=¨#0000FF¨ mathsize=¨24px¨»I«/mi»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨ mathsize=¨24px¨»§#183;«/mo»«mn mathvariant=¨bold¨ mathcolor=¨#0000FF¨ mathsize=¨24px¨»20«/mn»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨ mathsize=¨24px¨»+«/mo»«mn mathvariant=¨bold¨ mathcolor=¨#0000FF¨ mathsize=¨24px¨»9«/mn»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨ mathsize=¨24px¨»-«/mo»«mi mathvariant=¨bold¨ mathcolor=¨#0000FF¨ mathsize=¨24px¨»I«/mi»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨ mathsize=¨24px¨»§#183;«/mo»«mn mathvariant=¨bold¨ mathcolor=¨#0000FF¨ mathsize=¨24px¨»1«/mn»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨ mathsize=¨24px¨»-«/mo»«mi mathvariant=¨bold¨ mathcolor=¨#0000FF¨ mathsize=¨24px¨»I«/mi»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨ mathsize=¨24px¨»§#183;«/mo»«mn mathvariant=¨bold¨ mathcolor=¨#0000FF¨ mathsize=¨24px¨»2«/mn»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨ mathsize=¨24px¨»+«/mo»«mn mathvariant=¨bold¨ mathcolor=¨#0000FF¨ mathsize=¨24px¨»6«/mn»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨ mathsize=¨24px¨»=«/mo»«mn mathvariant=¨bold¨ mathcolor=¨#0000FF¨ mathsize=¨24px¨»0«/mn»«mspace linebreak=¨newline¨/»«mspace linebreak=¨newline¨/»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨ mathsize=¨24px¨»-«/mo»«mi mathvariant=¨bold¨ mathcolor=¨#0000FF¨ mathsize=¨24px¨»I«/mi»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨ mathsize=¨24px¨»§#183;«/mo»«mn mathvariant=¨bold¨ mathcolor=¨#0000FF¨ mathsize=¨24px¨»23«/mn»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨ mathsize=¨24px¨»=«/mo»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨ mathsize=¨24px¨»-«/mo»«mn mathvariant=¨bold¨ mathcolor=¨#0000FF¨ mathsize=¨24px¨»15«/mn»«mspace linebreak=¨newline¨/»«mspace linebreak=¨newline¨/»«mi mathvariant=¨bold¨ mathcolor=¨#0000FF¨ mathsize=¨24px¨»I«/mi»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨ mathsize=¨24px¨»=«/mo»«mfrac mathcolor=¨#0000FF¨»«mrow»«mo mathvariant=¨bold¨ mathsize=¨24px¨»-«/mo»«mn mathvariant=¨bold¨ mathsize=¨24px¨»15«/mn»«/mrow»«mrow»«mo mathvariant=¨bold¨ mathsize=¨24px¨»-«/mo»«mn mathvariant=¨bold¨ mathsize=¨24px¨»23«/mn»«/mrow»«/mfrac»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨ mathsize=¨24px¨»=«/mo»«mn mathvariant=¨bold¨ mathcolor=¨#0000FF¨ mathsize=¨24px¨»0«/mn»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨ mathsize=¨24px¨».«/mo»«mn mathvariant=¨bold¨ mathcolor=¨#0000FF¨ mathsize=¨24px¨»65«/mn»«mi mathvariant=¨bold¨ mathcolor=¨#0000FF¨ mathsize=¨24px¨»A«/mi»«mspace linebreak=¨newline¨/»«mspace linebreak=¨newline¨/»«/math»
لذلك ، فإن شدة التيار في الدائرة هو 0.65 أمبير.
42. ו.2
نجد التيار في الدائرة باستخدام مبدأ التراكب.
المرحلة أ- عندما يكون المصدر 1 نشطًا ويكون المصدر 2 في حالة تماس.
الدائرة في هذه الحالة موصوفة في الشكل التالي :
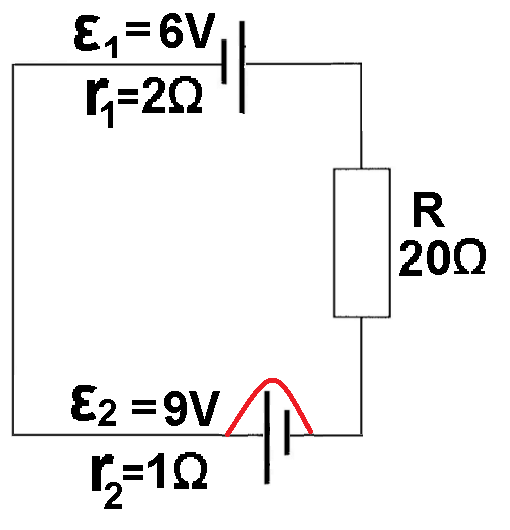
نشير للتيار في هذه الحالة بواسطة 'I ونحسب قيمته باستخدام قانون أوم:
«math style=¨font-family:Tahoma¨ xmlns=¨http://www.w3.org/1998/Math/MathML¨»«mstyle mathsize=¨24px¨»«mi mathvariant=¨bold¨ mathcolor=¨#0000FF¨»I«/mi»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»`«/mo»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»=«/mo»«mfrac mathcolor=¨#0000FF¨»«mi mathvariant=¨bold¨»§#949;«/mi»«msub»«mi mathvariant=¨bold¨»R«/mi»«mi mathvariant=¨bold¨»T«/mi»«/msub»«/mfrac»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»=«/mo»«mfrac mathcolor=¨#0000FF¨»«msub»«mi mathvariant=¨bold¨»§#949;«/mi»«mn mathvariant=¨bold¨»1«/mn»«/msub»«mrow»«mi mathvariant=¨bold¨»R«/mi»«mo mathvariant=¨bold¨»+«/mo»«msub»«mi mathvariant=¨bold¨»r«/mi»«mn mathvariant=¨bold¨»1«/mn»«/msub»«mo mathvariant=¨bold¨»+«/mo»«mi mathvariant=¨bold¨»r«/mi»«mn mathvariant=¨bold¨»2«/mn»«/mrow»«/mfrac»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»=«/mo»«mfrac mathcolor=¨#0000FF¨»«mn mathvariant=¨bold¨»6«/mn»«mrow»«mn mathvariant=¨bold¨»20«/mn»«mo mathvariant=¨bold¨»+«/mo»«mn mathvariant=¨bold¨»2«/mn»«mo mathvariant=¨bold¨»+«/mo»«mn mathvariant=¨bold¨»1«/mn»«/mrow»«/mfrac»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»=«/mo»«mn mathvariant=¨bold¨ mathcolor=¨#0000FF¨»0«/mn»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨».«/mo»«mn mathvariant=¨bold¨ mathcolor=¨#0000FF¨»26«/mn»«mi mathvariant=¨bold¨ mathcolor=¨#0000FF¨»A«/mi»«/mstyle»«/math»
المرحلة ب- عندما يكون المصدر 2 نشطًا ويكون المصدر 1 في حالة تماس.
الدائرة في هذا الوضع موصوفة في الشكل التالي:
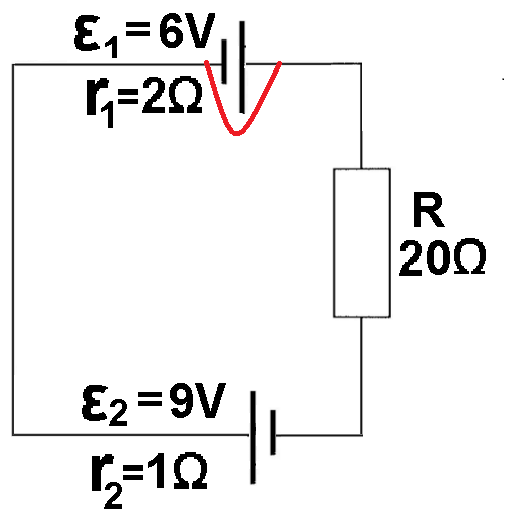
نشير للتيار الناتج في هذه الحالة بـ ''I ونحسب قيمته باستخدام قانون أوم:
«math style=¨font-family:Tahoma¨ xmlns=¨http://www.w3.org/1998/Math/MathML¨»«mstyle mathsize=¨24px¨»«mi mathvariant=¨bold¨ mathcolor=¨#0000FF¨»I«/mi»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»`«/mo»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»`«/mo»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»=«/mo»«mfrac mathcolor=¨#0000FF¨»«mi mathvariant=¨bold¨»§#949;«/mi»«msub»«mi mathvariant=¨bold¨»R«/mi»«mi mathvariant=¨bold¨»T«/mi»«/msub»«/mfrac»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»=«/mo»«mfrac mathcolor=¨#0000FF¨»«msub»«mi mathvariant=¨bold¨»§#949;«/mi»«mn mathvariant=¨bold¨»2«/mn»«/msub»«mrow»«mi mathvariant=¨bold¨»R«/mi»«mo mathvariant=¨bold¨»+«/mo»«msub»«mi mathvariant=¨bold¨»r«/mi»«mn mathvariant=¨bold¨»1«/mn»«/msub»«mo mathvariant=¨bold¨»+«/mo»«mi mathvariant=¨bold¨»r«/mi»«mn mathvariant=¨bold¨»2«/mn»«/mrow»«/mfrac»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»=«/mo»«mfrac mathcolor=¨#0000FF¨»«mn mathvariant=¨bold¨»9«/mn»«mrow»«mn mathvariant=¨bold¨»20«/mn»«mo mathvariant=¨bold¨»+«/mo»«mn mathvariant=¨bold¨»2«/mn»«mo mathvariant=¨bold¨»+«/mo»«mn mathvariant=¨bold¨»1«/mn»«/mrow»«/mfrac»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»=«/mo»«mn mathvariant=¨bold¨ mathcolor=¨#0000FF¨»0«/mn»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨».«/mo»«mn mathvariant=¨bold¨ mathcolor=¨#0000FF¨»39«/mn»«mi mathvariant=¨bold¨ mathcolor=¨#0000FF¨»A«/mi»«/mstyle»«/math»
يعمل كل من مصدري الجهد تياران في نفس الاتجاه، والتيار الناتج عن المصدر 2 أكبر من التيار الناتج عن المصدر 1.
نحسب التيار الناتج في الدائرة عندما يعمل كلا المصدرين:«math style=¨font-family:Tahoma¨ xmlns=¨http://www.w3.org/1998/Math/MathML¨»«mstyle mathsize=¨20px¨»«mi mathvariant=¨bold¨ mathcolor=¨#0000FF¨»I«/mi»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»=«/mo»«mi mathvariant=¨bold¨ mathcolor=¨#0000FF¨»I«/mi»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»`«/mo»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»`«/mo»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»-«/mo»«mi mathvariant=¨bold¨ mathcolor=¨#0000FF¨»I«/mi»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»`«/mo»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»=«/mo»«mn mathvariant=¨bold¨ mathcolor=¨#0000FF¨»0«/mn»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨».«/mo»«mn mathvariant=¨bold¨ mathcolor=¨#0000FF¨»39«/mn»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»+«/mo»«mn mathvariant=¨bold¨ mathcolor=¨#0000FF¨»0«/mn»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨».«/mo»«mn mathvariant=¨bold¨ mathcolor=¨#0000FF¨»26«/mn»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»=«/mo»«mn mathvariant=¨bold¨ mathcolor=¨#0000FF¨»0«/mn»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨».«/mo»«mn mathvariant=¨bold¨ mathcolor=¨#0000FF¨»65«/mn»«mi mathvariant=¨bold¨ mathcolor=¨#0000FF¨»A«/mi»«/mstyle»«/math»
لذلك ، فإن شدة التيار في هذه الدائرة هو 0.65 أمبير.
43. ו.3
أ- المصدر 1 يعمل تيار في اتجاه عقارب الساعة. المصدر 2 يعمل تيارًا عكس اتجاه عقارب الساعة.
لذلك، يعمل المصدران تياران في اتجاهين متعاكسين.
ب- لأن المصدر 2 يعمل تيارًا عكس اتجاه عقارب الساعة وقوته الكهربائية الدافعة أكبر، سيتدفق تيار عكس اتجاه عقارب الساعة في الدائرة.
ج- نشير للتيار بالدائرة بـ I.
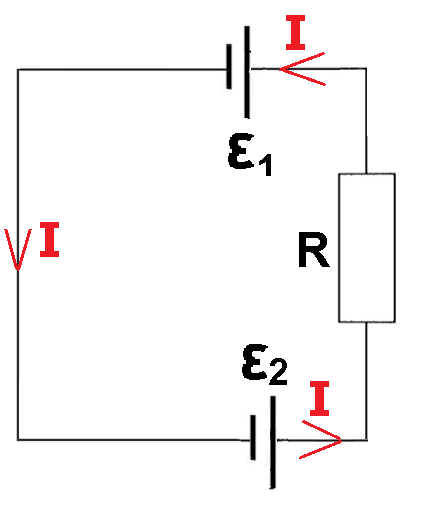
من قانون كيرخوف لفرق الجهد، فإن مجموع فروق الجهد في حلقة مغلقة يساوي صفرًا.
لا يوجد سوى حلقة واحدة في الدائرة، نكتب معادلة فروق الجهد.
قبل كتابة المعادلة، نضيف المقاومات الداخلية إلى الدائرة. وأسهم تمثل فروق الجهد لجميع مكونات الدائرة (نضع رؤوس الأسهم في الجهود العالية).
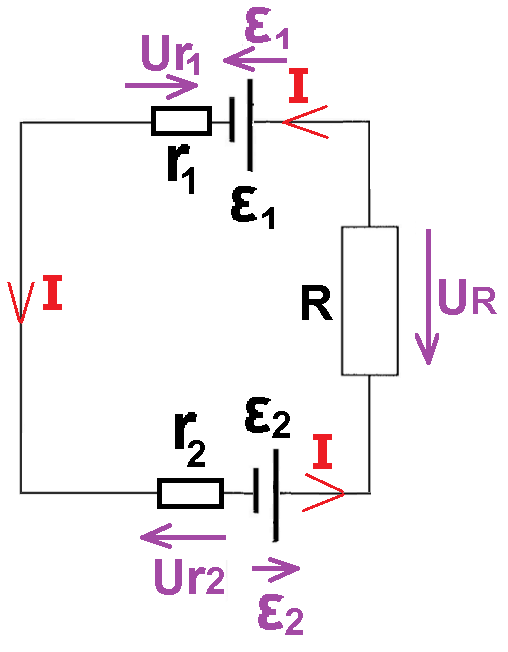
من قانون فروق الجهد لكيرخوف مجموع فروق الجهد في أي حلقة مغلقة يساوي صفر.
نجمع فروق الجهد في الحلقة، بدءًا من القطب الموجب للمصدر 1، نجمع فروق الجهد في اتجاه عقارب الساعة (يمكن أيضًا جمعها في الاتجاه المعاكس):
«math style=¨font-family:Tahoma¨ xmlns=¨http://www.w3.org/1998/Math/MathML¨»«mstyle mathsize=¨24px¨»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»§#160;«/mo»«msub»«mi mathvariant=¨bold¨ mathcolor=¨#0000FF¨»U«/mi»«mi mathvariant=¨bold¨ mathcolor=¨#0000FF¨»R«/mi»«/msub»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»-«/mo»«msub»«mi mathvariant=¨bold¨ mathcolor=¨#0000FF¨»§#949;«/mi»«mn mathvariant=¨bold¨ mathcolor=¨#0000FF¨»2«/mn»«/msub»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»+«/mo»«msub»«mi mathvariant=¨bold¨ mathcolor=¨#0000FF¨»U«/mi»«msub mathcolor=¨#0000FF¨»«mi mathvariant=¨bold¨»r«/mi»«mn mathvariant=¨bold¨»2«/mn»«/msub»«/msub»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»+«/mo»«msub»«mi mathvariant=¨bold¨ mathcolor=¨#0000FF¨»U«/mi»«msub mathcolor=¨#0000FF¨»«mi mathvariant=¨bold¨»r«/mi»«mn mathvariant=¨bold¨»1«/mn»«/msub»«/msub»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»+«/mo»«msub»«mi mathvariant=¨bold¨ mathcolor=¨#0000FF¨»§#949;«/mi»«mn mathvariant=¨bold¨ mathcolor=¨#0000FF¨»1«/mn»«/msub»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»=«/mo»«mn mathvariant=¨bold¨ mathcolor=¨#0000FF¨»0«/mn»«/mstyle»«/math»
نعبر عن معادلات فروق الجهد باستخدام التيار في الدائرة والقوى الكهربائية الدافعة والمقاومة الداخلية:
«math style=¨font-family:Tahoma¨ xmlns=¨http://www.w3.org/1998/Math/MathML¨»«mstyle mathsize=¨24px¨»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»§#160;«/mo»«msub»«mi mathvariant=¨bold¨ mathcolor=¨#0000FF¨»U«/mi»«mi mathvariant=¨bold¨ mathcolor=¨#0000FF¨»R«/mi»«/msub»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»-«/mo»«msub»«mi mathvariant=¨bold¨ mathcolor=¨#0000FF¨»§#949;«/mi»«mn mathvariant=¨bold¨ mathcolor=¨#0000FF¨»2«/mn»«/msub»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»+«/mo»«msub»«mi mathvariant=¨bold¨ mathcolor=¨#0000FF¨»U«/mi»«msub mathcolor=¨#0000FF¨»«mi mathvariant=¨bold¨»r«/mi»«mn mathvariant=¨bold¨»2«/mn»«/msub»«/msub»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»+«/mo»«msub»«mi mathvariant=¨bold¨ mathcolor=¨#0000FF¨»U«/mi»«msub mathcolor=¨#0000FF¨»«mi mathvariant=¨bold¨»r«/mi»«mn mathvariant=¨bold¨»1«/mn»«/msub»«/msub»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»+«/mo»«msub»«mi mathvariant=¨bold¨ mathcolor=¨#0000FF¨»§#949;«/mi»«mn mathvariant=¨bold¨ mathcolor=¨#0000FF¨»1«/mn»«/msub»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»=«/mo»«mn mathvariant=¨bold¨ mathcolor=¨#0000FF¨»0«/mn»«mspace linebreak=¨newline¨/»«mi mathvariant=¨bold¨ mathcolor=¨#0000FF¨»I«/mi»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»§#183;«/mo»«mi mathvariant=¨bold¨ mathcolor=¨#0000FF¨»R«/mi»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»-«/mo»«msub»«mi mathvariant=¨bold¨ mathcolor=¨#0000FF¨»§#949;«/mi»«mn mathvariant=¨bold¨ mathcolor=¨#0000FF¨»2«/mn»«/msub»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»+«/mo»«mi mathvariant=¨bold¨ mathcolor=¨#0000FF¨»I«/mi»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»§#183;«/mo»«msub»«mi mathvariant=¨bold¨ mathcolor=¨#0000FF¨»r«/mi»«mn mathvariant=¨bold¨ mathcolor=¨#0000FF¨»2«/mn»«/msub»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»+«/mo»«mi mathvariant=¨bold¨ mathcolor=¨#0000FF¨»I«/mi»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»§#183;«/mo»«msub»«mi mathvariant=¨bold¨ mathcolor=¨#0000FF¨»r«/mi»«mn mathvariant=¨bold¨ mathcolor=¨#0000FF¨»1«/mn»«/msub»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»+«/mo»«msub»«mi mathvariant=¨bold¨ mathcolor=¨#0000FF¨»§#949;«/mi»«mn mathvariant=¨bold¨ mathcolor=¨#0000FF¨»1«/mn»«/msub»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»=«/mo»«mn mathvariant=¨bold¨ mathcolor=¨#0000FF¨»0«/mn»«mspace linebreak=¨newline¨/»«mi mathvariant=¨bold¨ mathcolor=¨#0000FF¨»I«/mi»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»§#183;«/mo»«mn mathvariant=¨bold¨ mathcolor=¨#0000FF¨»20«/mn»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»-«/mo»«mn mathvariant=¨bold¨ mathcolor=¨#0000FF¨»9«/mn»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»+«/mo»«mi mathvariant=¨bold¨ mathcolor=¨#0000FF¨»I«/mi»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»§#183;«/mo»«mn mathvariant=¨bold¨ mathcolor=¨#0000FF¨»1«/mn»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»+«/mo»«mi mathvariant=¨bold¨ mathcolor=¨#0000FF¨»I«/mi»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»§#183;«/mo»«mn mathvariant=¨bold¨ mathcolor=¨#0000FF¨»2«/mn»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»+«/mo»«mn mathvariant=¨bold¨ mathcolor=¨#0000FF¨»6«/mn»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»=«/mo»«mn mathvariant=¨bold¨ mathcolor=¨#0000FF¨»0«/mn»«/mstyle»«/math»
نجد من هذه المعادلة للتيار في الدائرة:
«math style=¨font-family:Tahoma¨ xmlns=¨http://www.w3.org/1998/Math/MathML¨»«mstyle mathsize=¨24px¨»«mi mathvariant=¨bold¨ mathcolor=¨#0000FF¨»I«/mi»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»§#183;«/mo»«mn mathvariant=¨bold¨ mathcolor=¨#0000FF¨»20«/mn»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»-«/mo»«mn mathvariant=¨bold¨ mathcolor=¨#0000FF¨»9«/mn»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»+«/mo»«mi mathvariant=¨bold¨ mathcolor=¨#0000FF¨»I«/mi»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»§#183;«/mo»«mn mathvariant=¨bold¨ mathcolor=¨#0000FF¨»1«/mn»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»+«/mo»«mi mathvariant=¨bold¨ mathcolor=¨#0000FF¨»I«/mi»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»§#183;«/mo»«mn mathvariant=¨bold¨ mathcolor=¨#0000FF¨»2«/mn»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»+«/mo»«mn mathvariant=¨bold¨ mathcolor=¨#0000FF¨»6«/mn»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»=«/mo»«mn mathvariant=¨bold¨ mathcolor=¨#0000FF¨»0«/mn»«mspace linebreak=¨newline¨/»«mspace linebreak=¨newline¨/»«mi mathvariant=¨bold¨ mathcolor=¨#0000FF¨»I«/mi»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»§#183;«/mo»«mn mathvariant=¨bold¨ mathcolor=¨#0000FF¨»23«/mn»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»=«/mo»«mn mathvariant=¨bold¨ mathcolor=¨#0000FF¨»3«/mn»«mspace linebreak=¨newline¨/»«mspace linebreak=¨newline¨/»«mi mathvariant=¨bold¨ mathcolor=¨#0000FF¨»I«/mi»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»=«/mo»«mfrac mathcolor=¨#0000FF¨»«mn mathvariant=¨bold¨»3«/mn»«mn mathvariant=¨bold¨»23«/mn»«/mfrac»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»=«/mo»«mn mathvariant=¨bold¨ mathcolor=¨#0000FF¨»0«/mn»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨».«/mo»«mn mathvariant=¨bold¨ mathcolor=¨#0000FF¨»13«/mn»«mi mathvariant=¨bold¨ mathcolor=¨#0000FF¨»A«/mi»«mspace linebreak=¨newline¨/»«mspace linebreak=¨newline¨/»«/mstyle»«/math»
لذلك ، فإن شدة التيار في الدائرة هو 0.13 أمبير.
44. ו.4
نجد شدة التيار في الدائرة باستخدام مبدأ التراكب.
المرحلة أ- عندما يكون مصدر فرق الجهد 1 نشطًا ومصدر فرق الجهد 2 في حالة تماس .
الدائرة في هذا الوضع موصوفة في الشكل التالي:
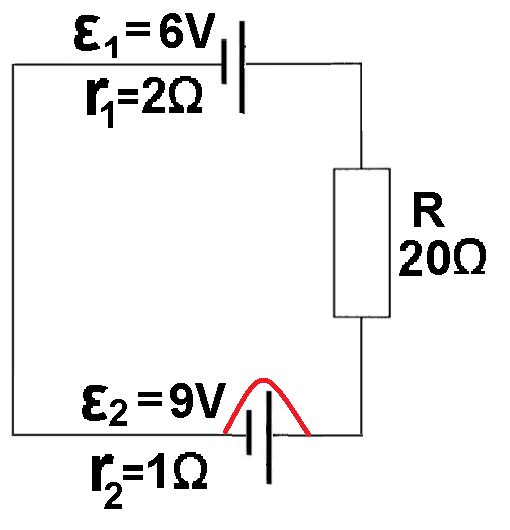
نشير للتيار الذي تم تكوينه في هذه الحالة بواسطة 'I ونحسب قيمته باستخدام قانون أوم:
«math style=¨font-family:Tahoma¨ xmlns=¨http://www.w3.org/1998/Math/MathML¨»«mstyle mathsize=¨24px¨»«mi mathvariant=¨bold¨ mathcolor=¨#0000FF¨»I«/mi»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»`«/mo»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»=«/mo»«mfrac mathcolor=¨#0000FF¨»«mi mathvariant=¨bold¨»§#949;«/mi»«msub»«mi mathvariant=¨bold¨»R«/mi»«mi mathvariant=¨bold¨»T«/mi»«/msub»«/mfrac»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»=«/mo»«mfrac mathcolor=¨#0000FF¨»«msub»«mi mathvariant=¨bold¨»§#949;«/mi»«mn mathvariant=¨bold¨»1«/mn»«/msub»«mrow»«mi mathvariant=¨bold¨»R«/mi»«mo mathvariant=¨bold¨»+«/mo»«msub»«mi mathvariant=¨bold¨»r«/mi»«mn mathvariant=¨bold¨»1«/mn»«/msub»«mo mathvariant=¨bold¨»+«/mo»«mi mathvariant=¨bold¨»r«/mi»«mn mathvariant=¨bold¨»2«/mn»«/mrow»«/mfrac»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»=«/mo»«mfrac mathcolor=¨#0000FF¨»«mn mathvariant=¨bold¨»6«/mn»«mrow»«mn mathvariant=¨bold¨»20«/mn»«mo mathvariant=¨bold¨»+«/mo»«mn mathvariant=¨bold¨»2«/mn»«mo mathvariant=¨bold¨»+«/mo»«mn mathvariant=¨bold¨»1«/mn»«/mrow»«/mfrac»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»=«/mo»«mn mathvariant=¨bold¨ mathcolor=¨#0000FF¨»0«/mn»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨».«/mo»«mn mathvariant=¨bold¨ mathcolor=¨#0000FF¨»26«/mn»«mi mathvariant=¨bold¨ mathcolor=¨#0000FF¨»A«/mi»«/mstyle»«/math»
المرحلة ب- عندما يكون مصدر فرق الجهد 2 نشطًا ومصدر فرق الجهد 1 في حالة تماس .
الدائرة في هذا الوضع موصوفة في الشكل التالي:
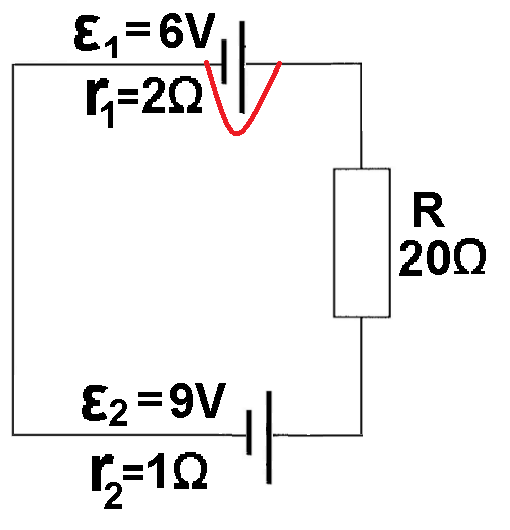
نشير للتيار المتكون في هذه الحالة بـ "I ونحسب قيمته باستخدام قانون أوم:
«math style=¨font-family:Tahoma¨ xmlns=¨http://www.w3.org/1998/Math/MathML¨»«mstyle mathsize=¨24px¨»«mi mathvariant=¨bold¨ mathcolor=¨#0000FF¨»I«/mi»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»`«/mo»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»`«/mo»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»=«/mo»«mfrac mathcolor=¨#0000FF¨»«mi mathvariant=¨bold¨»§#949;«/mi»«msub»«mi mathvariant=¨bold¨»R«/mi»«mi mathvariant=¨bold¨»T«/mi»«/msub»«/mfrac»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»=«/mo»«mfrac mathcolor=¨#0000FF¨»«msub»«mi mathvariant=¨bold¨»§#949;«/mi»«mn mathvariant=¨bold¨»2«/mn»«/msub»«mrow»«mi mathvariant=¨bold¨»R«/mi»«mo mathvariant=¨bold¨»+«/mo»«msub»«mi mathvariant=¨bold¨»r«/mi»«mn mathvariant=¨bold¨»1«/mn»«/msub»«mo mathvariant=¨bold¨»+«/mo»«mi mathvariant=¨bold¨»r«/mi»«mn mathvariant=¨bold¨»2«/mn»«/mrow»«/mfrac»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»=«/mo»«mfrac mathcolor=¨#0000FF¨»«mn mathvariant=¨bold¨»9«/mn»«mrow»«mn mathvariant=¨bold¨»20«/mn»«mo mathvariant=¨bold¨»+«/mo»«mn mathvariant=¨bold¨»2«/mn»«mo mathvariant=¨bold¨»+«/mo»«mn mathvariant=¨bold¨»1«/mn»«/mrow»«/mfrac»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»=«/mo»«mn mathvariant=¨bold¨ mathcolor=¨#0000FF¨»0«/mn»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨».«/mo»«mn mathvariant=¨bold¨ mathcolor=¨#0000FF¨»39«/mn»«mi mathvariant=¨bold¨ mathcolor=¨#0000FF¨»A«/mi»«/mstyle»«/math»
يعمل مصدري الجهد تياران في اتجاهان متعاكسة، والتيار الناتج من المصدر 2 أكبر من التيار الناتج من المصدر 1. نحسب التيار الناتج في الدائرة عندما يعمل كلا المصدرين:
«math style=¨font-family:Tahoma¨ xmlns=¨http://www.w3.org/1998/Math/MathML¨»«mstyle mathsize=¨20px¨»«mi mathvariant=¨bold¨ mathcolor=¨#0000FF¨»I«/mi»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»=«/mo»«mi mathvariant=¨bold¨ mathcolor=¨#0000FF¨»I«/mi»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»`«/mo»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»`«/mo»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»-«/mo»«mi mathvariant=¨bold¨ mathcolor=¨#0000FF¨»I«/mi»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»`«/mo»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»=«/mo»«mn mathvariant=¨bold¨ mathcolor=¨#0000FF¨»0«/mn»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨».«/mo»«mn mathvariant=¨bold¨ mathcolor=¨#0000FF¨»39«/mn»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»-«/mo»«mn mathvariant=¨bold¨ mathcolor=¨#0000FF¨»0«/mn»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨».«/mo»«mn mathvariant=¨bold¨ mathcolor=¨#0000FF¨»26«/mn»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»=«/mo»«mn mathvariant=¨bold¨ mathcolor=¨#0000FF¨»0«/mn»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨».«/mo»«mn mathvariant=¨bold¨ mathcolor=¨#0000FF¨»13«/mn»«mi mathvariant=¨bold¨ mathcolor=¨#0000FF¨»A«/mi»«/mstyle»«/math»
لذلك، فإن شدة التيار في هذه الدائرة هو 0.13 أمبير.
45. ו.5
أ- نشير للتيار الذي تم إنشاؤه بواسطة المصدر 1 في I1، التيار الذي تم إنشاؤه بواسطة المصدر 2 في I2 والتيار عبر المقاوم R بـ I.
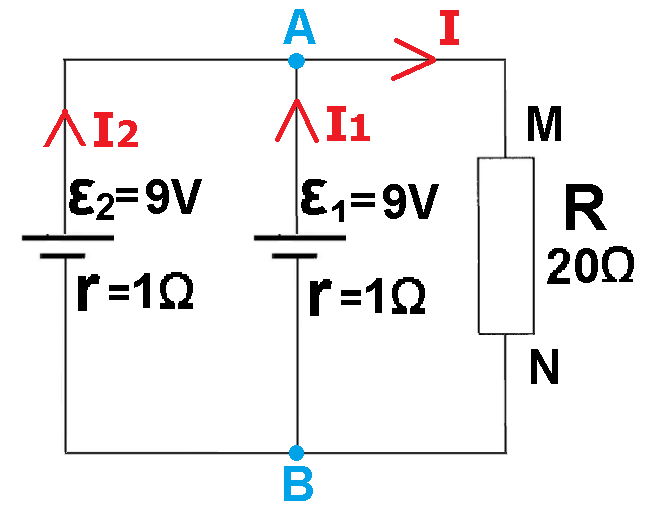
نظرًا لأن كلا التيارين I1 و I2 يدخلان العقدة A ، فإن التيارI يترك العقدة ويتدفق عبر المقاوم R من النقطة M إلى النقطة N.
ب- سنستخدم قانون العقدة ونكتب معادلة التيارات للعقدة A:
«math style=¨font-family:Tahoma¨ xmlns=¨http://www.w3.org/1998/Math/MathML¨»«mstyle mathsize=¨20px¨»«menclose mathcolor=¨#0000FF¨ notation=¨box¨»«msub»«mi mathvariant=¨bold¨»I«/mi»«mn mathvariant=¨bold¨»1«/mn»«/msub»«mo mathvariant=¨bold¨»+«/mo»«msub»«mi mathvariant=¨bold¨»I«/mi»«mn mathvariant=¨bold¨»2«/mn»«/msub»«mo mathvariant=¨bold¨»=«/mo»«mi mathvariant=¨bold¨»I«/mi»«/menclose»«/mstyle»«/math»
من قانون كيرخوف لفروق الجهد، فإن مجموع فروق الجهد في حلقة مغلقة يساوي صفرًا.
يوجد في الدائرة حلقتان، سنكتب معادلة الجهد لكل من الحلقتين.
قبل كتابة معادلات فروق الجهد، نضيف المقاومات الداخلية إلى الدائرة. ونضيف أسهم فروق الجهد إلى جميع مكونات الدائرة، نضع رؤوس الأسهم في الجهود العالية.
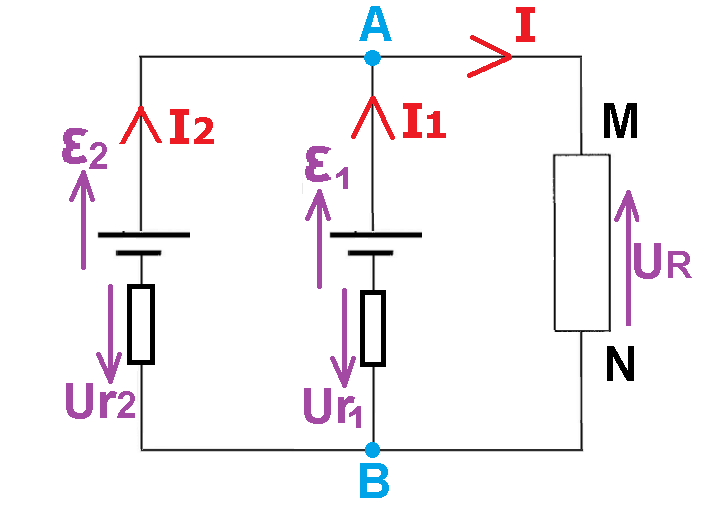
من قانون فروق الجهد لكيرخوف مجموع فروق الجهد في أي حلقة مغلقة يساوي الصفر.
نجمع فروق الجهد في الحلقة اليسرى، بدءًا من القطب السالب للمصدر 2:
«math xmlns=¨http://www.w3.org/1998/Math/MathML¨»«mstyle mathsize=¨24px¨»«menclose mathcolor=¨#0000FF¨ notation=¨circle¨»«mn mathvariant=¨bold¨»1«/mn»«/menclose»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»§#160;«/mo»«msub»«mi mathvariant=¨bold¨ mathcolor=¨#0000FF¨»§#949;«/mi»«mn mathvariant=¨bold¨ mathcolor=¨#0000FF¨»2«/mn»«/msub»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»-«/mo»«msub»«mi mathvariant=¨bold¨ mathcolor=¨#0000FF¨»§#949;«/mi»«mn mathvariant=¨bold¨ mathcolor=¨#0000FF¨»1«/mn»«/msub»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»+«/mo»«msub»«mi mathvariant=¨bold¨ mathcolor=¨#0000FF¨»U«/mi»«msub mathcolor=¨#0000FF¨»«mi mathvariant=¨bold¨»r«/mi»«mn mathvariant=¨bold¨»1«/mn»«/msub»«/msub»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»-«/mo»«msub»«mi mathvariant=¨bold¨ mathcolor=¨#0000FF¨»U«/mi»«msub mathcolor=¨#0000FF¨»«mi mathvariant=¨bold¨»r«/mi»«mn mathvariant=¨bold¨»2«/mn»«/msub»«/msub»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»=«/mo»«mn mathvariant=¨bold¨ mathcolor=¨#0000FF¨»0«/mn»«/mstyle»«/math»
نجمع فروق الجهد في الحلقة الأيمن، بدءًا من القطب السالب للمصدر 1:
«math xmlns=¨http://www.w3.org/1998/Math/MathML¨»«mstyle mathsize=¨24px¨»«menclose mathcolor=¨#0000FF¨ notation=¨circle¨»«mn mathvariant=¨bold¨»2«/mn»«/menclose»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»§#160;«/mo»«msub»«mi mathvariant=¨bold¨ mathcolor=¨#0000FF¨»§#949;«/mi»«mn mathvariant=¨bold¨ mathcolor=¨#0000FF¨»1«/mn»«/msub»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»-«/mo»«msub»«mi mathvariant=¨bold¨ mathcolor=¨#0000FF¨»U«/mi»«mi mathvariant=¨normal¨ mathcolor=¨#0000FF¨»R«/mi»«/msub»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»-«/mo»«msub»«mi mathvariant=¨bold¨ mathcolor=¨#0000FF¨»U«/mi»«msub mathcolor=¨#0000FF¨»«mi mathvariant=¨bold¨»r«/mi»«mn mathvariant=¨bold¨»1«/mn»«/msub»«/msub»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»=«/mo»«mn mathvariant=¨bold¨ mathcolor=¨#0000FF¨»0«/mn»«/mstyle»«/math»
نعبر عن كل من معادلات فروق الجهد باستخدام التيارات في الدائرة وقيم التيار والمقاومة الداخلية:
«math style=¨font-family:Tahoma¨ xmlns=¨http://www.w3.org/1998/Math/MathML¨»«mstyle mathsize=¨24px¨»«menclose mathcolor=¨#0000FF¨ notation=¨circle¨»«mn mathvariant=¨bold¨»1«/mn»«/menclose»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»§#160;«/mo»«msub»«mi mathvariant=¨bold¨ mathcolor=¨#0000FF¨»§#949;«/mi»«mn mathvariant=¨bold¨ mathcolor=¨#0000FF¨»2«/mn»«/msub»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»-«/mo»«msub»«mi mathvariant=¨bold¨ mathcolor=¨#0000FF¨»§#949;«/mi»«mn mathvariant=¨bold¨ mathcolor=¨#0000FF¨»1«/mn»«/msub»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»+«/mo»«msub»«mi mathvariant=¨bold¨ mathcolor=¨#0000FF¨»U«/mi»«msub mathcolor=¨#0000FF¨»«mi mathvariant=¨bold¨»r«/mi»«mn mathvariant=¨bold¨»1«/mn»«/msub»«/msub»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»-«/mo»«msub»«mi mathvariant=¨bold¨ mathcolor=¨#0000FF¨»U«/mi»«msub mathcolor=¨#0000FF¨»«mi mathvariant=¨bold¨»r«/mi»«mn mathvariant=¨bold¨»2«/mn»«/msub»«/msub»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»=«/mo»«mn mathvariant=¨bold¨ mathcolor=¨#0000FF¨»0«/mn»«mspace linebreak=¨newline¨/»«msub»«mi mathvariant=¨bold¨ mathcolor=¨#0000FF¨»§#949;«/mi»«mn mathvariant=¨bold¨ mathcolor=¨#0000FF¨»2«/mn»«/msub»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»-«/mo»«msub»«mi mathvariant=¨bold¨ mathcolor=¨#0000FF¨»§#949;«/mi»«mn mathvariant=¨bold¨ mathcolor=¨#0000FF¨»1«/mn»«/msub»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»+«/mo»«msub»«mi mathvariant=¨bold¨ mathcolor=¨#0000FF¨»I«/mi»«mn mathvariant=¨bold¨ mathcolor=¨#0000FF¨»1«/mn»«/msub»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»§#183;«/mo»«msub»«mi mathvariant=¨bold¨ mathcolor=¨#0000FF¨»r«/mi»«mn mathvariant=¨bold¨ mathcolor=¨#0000FF¨»1«/mn»«/msub»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»-«/mo»«msub»«mi mathvariant=¨bold¨ mathcolor=¨#0000FF¨»I«/mi»«mn mathvariant=¨bold¨ mathcolor=¨#0000FF¨»2«/mn»«/msub»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»§#183;«/mo»«msub»«mi mathvariant=¨bold¨ mathcolor=¨#0000FF¨»r«/mi»«mn mathvariant=¨bold¨ mathcolor=¨#0000FF¨»1«/mn»«/msub»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»=«/mo»«mn mathvariant=¨bold¨ mathcolor=¨#0000FF¨»0«/mn»«mspace linebreak=¨newline¨/»«mn mathvariant=¨bold¨ mathcolor=¨#0000FF¨»9«/mn»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»-«/mo»«mn mathvariant=¨bold¨ mathcolor=¨#0000FF¨»9«/mn»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»+«/mo»«msub»«mi mathvariant=¨bold¨ mathcolor=¨#0000FF¨»I«/mi»«mn mathvariant=¨bold¨ mathcolor=¨#0000FF¨»1«/mn»«/msub»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»§#183;«/mo»«mn mathvariant=¨bold¨ mathcolor=¨#0000FF¨»1«/mn»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»-«/mo»«msub»«mi mathvariant=¨bold¨ mathcolor=¨#0000FF¨»I«/mi»«mn mathvariant=¨bold¨ mathcolor=¨#0000FF¨»2«/mn»«/msub»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»§#183;«/mo»«mn mathvariant=¨bold¨ mathcolor=¨#0000FF¨»1«/mn»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»=«/mo»«mn mathvariant=¨bold¨ mathcolor=¨#0000FF¨»0«/mn»«mspace linebreak=¨newline¨/»«menclose mathcolor=¨#0000FF¨ notation=¨box¨»«msub»«mi mathvariant=¨bold¨»I«/mi»«mn mathvariant=¨bold¨»1«/mn»«/msub»«mo mathvariant=¨bold¨»=«/mo»«msub»«mi mathvariant=¨bold¨»I«/mi»«mn mathvariant=¨bold¨»2«/mn»«/msub»«/menclose»«mspace linebreak=¨newline¨/»«/mstyle»«/math»
«math style=¨font-family:Tahoma¨ xmlns=¨http://www.w3.org/1998/Math/MathML¨»«mstyle mathsize=¨24px¨»«menclose mathcolor=¨#0000FF¨ notation=¨circle¨»«mn mathvariant=¨bold¨»2«/mn»«/menclose»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»§#160;«/mo»«msub»«mi mathvariant=¨bold¨ mathcolor=¨#0000FF¨»§#949;«/mi»«mn mathvariant=¨bold¨ mathcolor=¨#0000FF¨»1«/mn»«/msub»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»-«/mo»«msub»«mi mathvariant=¨bold¨ mathcolor=¨#0000FF¨»U«/mi»«mi mathvariant=¨normal¨ mathcolor=¨#0000FF¨»R«/mi»«/msub»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»-«/mo»«msub»«mi mathvariant=¨bold¨ mathcolor=¨#0000FF¨»U«/mi»«msub mathcolor=¨#0000FF¨»«mi mathvariant=¨bold¨»r«/mi»«mn mathvariant=¨bold¨»1«/mn»«/msub»«/msub»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»=«/mo»«mn mathvariant=¨bold¨ mathcolor=¨#0000FF¨»0«/mn»«mspace linebreak=¨newline¨/»«msub»«mi mathvariant=¨bold¨ mathcolor=¨#0000FF¨»§#949;«/mi»«mn mathvariant=¨bold¨ mathcolor=¨#0000FF¨»1«/mn»«/msub»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»-«/mo»«mi mathvariant=¨bold¨ mathcolor=¨#0000FF¨»I«/mi»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»§#183;«/mo»«mi mathvariant=¨bold¨ mathcolor=¨#0000FF¨»R«/mi»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»-«/mo»«msub»«mi mathvariant=¨bold¨ mathcolor=¨#0000FF¨»I«/mi»«mn mathvariant=¨bold¨ mathcolor=¨#0000FF¨»1«/mn»«/msub»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»§#183;«/mo»«msub»«mi mathvariant=¨bold¨ mathcolor=¨#0000FF¨»r«/mi»«mn mathvariant=¨bold¨ mathcolor=¨#0000FF¨»1«/mn»«/msub»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»=«/mo»«mn mathvariant=¨bold¨ mathcolor=¨#0000FF¨»0«/mn»«mspace linebreak=¨newline¨/»«mn mathvariant=¨bold¨ mathcolor=¨#0000FF¨»9«/mn»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»-«/mo»«mi mathvariant=¨bold¨ mathcolor=¨#0000FF¨»I«/mi»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»§#183;«/mo»«mn mathvariant=¨bold¨ mathcolor=¨#0000FF¨»20«/mn»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»-«/mo»«msub»«mi mathvariant=¨bold¨ mathcolor=¨#0000FF¨»I«/mi»«mn mathvariant=¨bold¨ mathcolor=¨#0000FF¨»1«/mn»«/msub»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»§#183;«/mo»«mn mathvariant=¨bold¨ mathcolor=¨#0000FF¨»1«/mn»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»=«/mo»«mn mathvariant=¨bold¨ mathcolor=¨#0000FF¨»0«/mn»«mspace linebreak=¨newline¨/»«menclose mathcolor=¨#0000FF¨ notation=¨box¨»«mn mathvariant=¨bold¨»9«/mn»«mo mathvariant=¨bold¨»=«/mo»«mi mathvariant=¨bold¨»I«/mi»«mo mathvariant=¨bold¨»§#183;«/mo»«mn mathvariant=¨bold¨»20«/mn»«mo mathvariant=¨bold¨»+«/mo»«msub»«mi mathvariant=¨bold¨»I«/mi»«mn mathvariant=¨bold¨»1«/mn»«/msub»«mo mathvariant=¨bold¨»§#183;«/mo»«mn mathvariant=¨bold¨»1«/mn»«/menclose»«/mstyle»«/math»
حصلنا على ثلاث معادلات للتيار، معادلة واحدة من كيرخوف للتيارات، ومعادلتين أخريين لفروق الجهد.
نكتب المعادلات الثلاث ونجد منها شدة التيار عبر المستهلك:معادلة التيار التي تم الحصول عليها من قانون العقدة (كيرخوف للتيارات): «math style=¨font-family:Tahoma¨ xmlns=¨http://www.w3.org/1998/Math/MathML¨»«mstyle mathsize=¨20px¨»«menclose mathcolor=¨#0000FF¨ notation=¨circle¨»«mn mathvariant=¨bold¨»1«/mn»«/menclose»«mo»§#160;«/mo»«menclose mathcolor=¨#0000FF¨ notation=¨box¨»«msub»«mi mathvariant=¨bold¨»I«/mi»«mn mathvariant=¨bold¨»1«/mn»«/msub»«mo mathvariant=¨bold¨»+«/mo»«msub»«mi mathvariant=¨bold¨»I«/mi»«mn mathvariant=¨bold¨»2«/mn»«/msub»«mo mathvariant=¨bold¨»=«/mo»«mi mathvariant=¨bold¨»I«/mi»«/menclose»«/mstyle»«/math»
معادلات فروق الجهد التي تم الحصول عليها من كيرخوف للفروق الجهد:
«math style=¨font-family:Tahoma¨ xmlns=¨http://www.w3.org/1998/Math/MathML¨»«mstyle mathsize=¨24px¨»«menclose mathcolor=¨#0000FF¨ notation=¨circle¨»«mn mathvariant=¨bold¨»2«/mn»«/menclose»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»§#160;«/mo»«menclose mathcolor=¨#0000FF¨ notation=¨box¨»«msub»«mi mathvariant=¨bold¨»I«/mi»«mn mathvariant=¨bold¨»1«/mn»«/msub»«mo mathvariant=¨bold¨»=«/mo»«msub»«mi mathvariant=¨bold¨»I«/mi»«mn mathvariant=¨bold¨»2«/mn»«/msub»«/menclose»«/mstyle»«/math»
«math style=¨font-family:Tahoma¨ xmlns=¨http://www.w3.org/1998/Math/MathML¨»«mstyle mathsize=¨24px¨»«menclose mathcolor=¨#0000FF¨ notation=¨circle¨»«mn mathvariant=¨bold¨»3«/mn»«/menclose»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»§#160;«/mo»«menclose mathcolor=¨#0000FF¨ notation=¨box¨»«mn mathvariant=¨bold¨»9«/mn»«mo mathvariant=¨bold¨»=«/mo»«mi mathvariant=¨bold¨»I«/mi»«mo mathvariant=¨bold¨»§#183;«/mo»«mn mathvariant=¨bold¨»20«/mn»«mo mathvariant=¨bold¨»+«/mo»«msub»«mi mathvariant=¨bold¨»I«/mi»«mn mathvariant=¨bold¨»1«/mn»«/msub»«mo mathvariant=¨bold¨»§#183;«/mo»«mn mathvariant=¨bold¨»1«/mn»«/menclose»«/mstyle»«/math»
نعوّض المعادلتين 1 و- 2 بالمعادلة 3:
«math style=¨font-family:Tahoma¨ xmlns=¨http://www.w3.org/1998/Math/MathML¨»«mstyle mathsize=¨24px¨»«mn mathvariant=¨bold¨ mathcolor=¨#0000FF¨»9«/mn»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»=«/mo»«mstyle mathvariant=¨bold¨ mathcolor=¨#FF0000¨»«mo stretchy=¨true¨»(«/mo»«mrow»«msub»«mi»I«/mi»«mn»1«/mn»«/msub»«mo»+«/mo»«msub»«mi»I«/mi»«mn»2«/mn»«/msub»«/mrow»«mo stretchy=¨true¨»)«/mo»«/mstyle»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»§#183;«/mo»«mn mathvariant=¨bold¨ mathcolor=¨#0000FF¨»20«/mn»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»+«/mo»«msub»«mi mathvariant=¨bold¨ mathcolor=¨#0000FF¨»I«/mi»«mn mathvariant=¨bold¨ mathcolor=¨#0000FF¨»1«/mn»«/msub»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»§#183;«/mo»«mn mathvariant=¨bold¨ mathcolor=¨#0000FF¨»1«/mn»«mspace linebreak=¨newline¨/»«mn mathvariant=¨bold¨ mathcolor=¨#0000FF¨»9«/mn»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»=«/mo»«mstyle mathvariant=¨bold¨ mathcolor=¨#FF0000¨»«mo stretchy=¨true¨»(«/mo»«msub»«mi»I«/mi»«mn»1«/mn»«/msub»«mo»+«/mo»«msub»«mi mathcolor=¨#007F00¨»I«/mi»«mn mathcolor=¨#007F00¨»1«/mn»«/msub»«mo stretchy=¨true¨»)«/mo»«/mstyle»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»§#183;«/mo»«mn mathvariant=¨bold¨ mathcolor=¨#0000FF¨»20«/mn»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»+«/mo»«msub»«mi mathvariant=¨bold¨ mathcolor=¨#0000FF¨»I«/mi»«mn mathvariant=¨bold¨ mathcolor=¨#0000FF¨»1«/mn»«/msub»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»§#183;«/mo»«mn mathvariant=¨bold¨ mathcolor=¨#0000FF¨»1«/mn»«mspace linebreak=¨newline¨/»«mn mathvariant=¨bold¨ mathcolor=¨#0000FF¨»9«/mn»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»=«/mo»«mn mathvariant=¨bold¨ mathcolor=¨#0000FF¨»20«/mn»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»§#183;«/mo»«mn mathvariant=¨bold¨ mathcolor=¨#0000FF¨»2«/mn»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»§#183;«/mo»«msub»«mi mathvariant=¨bold¨ mathcolor=¨#0000FF¨»I«/mi»«mn mathvariant=¨bold¨ mathcolor=¨#0000FF¨»1«/mn»«/msub»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»+«/mo»«msub»«mi mathvariant=¨bold¨ mathcolor=¨#0000FF¨»I«/mi»«mn mathvariant=¨bold¨ mathcolor=¨#0000FF¨»1«/mn»«/msub»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»§#183;«/mo»«mn mathvariant=¨bold¨ mathcolor=¨#0000FF¨»1«/mn»«mspace linebreak=¨newline¨/»«mn mathvariant=¨bold¨ mathcolor=¨#0000FF¨»9«/mn»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»=«/mo»«mn mathvariant=¨bold¨ mathcolor=¨#0000FF¨»40«/mn»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»§#183;«/mo»«msub»«mi mathvariant=¨bold¨ mathcolor=¨#0000FF¨»I«/mi»«mn mathvariant=¨bold¨ mathcolor=¨#0000FF¨»1«/mn»«/msub»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»+«/mo»«msub»«mi mathvariant=¨bold¨ mathcolor=¨#0000FF¨»I«/mi»«mn mathvariant=¨bold¨ mathcolor=¨#0000FF¨»1«/mn»«/msub»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»§#183;«/mo»«mn mathvariant=¨bold¨ mathcolor=¨#0000FF¨»1«/mn»«mspace linebreak=¨newline¨/»«mn mathvariant=¨bold¨ mathcolor=¨#0000FF¨»9«/mn»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»=«/mo»«mn mathvariant=¨bold¨ mathcolor=¨#0000FF¨»41«/mn»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»§#183;«/mo»«msub»«mi mathvariant=¨bold¨ mathcolor=¨#0000FF¨»I«/mi»«mn mathvariant=¨bold¨ mathcolor=¨#0000FF¨»1«/mn»«/msub»«mspace linebreak=¨newline¨/»«mspace linebreak=¨newline¨/»«msub»«mi mathvariant=¨bold¨ mathcolor=¨#0000FF¨»I«/mi»«mn mathvariant=¨bold¨ mathcolor=¨#0000FF¨»1«/mn»«/msub»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»=«/mo»«mfrac mathcolor=¨#0000FF¨»«mn mathvariant=¨bold¨»9«/mn»«mn mathvariant=¨bold¨»41«/mn»«/mfrac»«mi mathvariant=¨bold¨ mathcolor=¨#0000FF¨»A«/mi»«/mstyle»«/math»
نعوض I1 بالمعادلة 3, ونجد شدة I:
«math style=¨font-family:Tahoma¨ xmlns=¨http://www.w3.org/1998/Math/MathML¨»«mstyle mathsize=¨24px¨»«mn mathvariant=¨bold¨ mathcolor=¨#0000FF¨»9«/mn»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»=«/mo»«mi mathvariant=¨bold¨ mathcolor=¨#0000FF¨»I«/mi»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»§#183;«/mo»«mn mathvariant=¨bold¨ mathcolor=¨#0000FF¨»20«/mn»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»+«/mo»«msub»«mi mathvariant=¨bold¨ mathcolor=¨#0000FF¨»I«/mi»«mn mathvariant=¨bold¨ mathcolor=¨#0000FF¨»1«/mn»«/msub»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»§#183;«/mo»«mn mathvariant=¨bold¨ mathcolor=¨#0000FF¨»1«/mn»«mspace linebreak=¨newline¨/»«mn mathvariant=¨bold¨ mathcolor=¨#0000FF¨»9«/mn»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»=«/mo»«mi mathvariant=¨bold¨ mathcolor=¨#0000FF¨»I«/mi»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»§#183;«/mo»«mn mathvariant=¨bold¨ mathcolor=¨#0000FF¨»20«/mn»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»+«/mo»«mfrac mathcolor=¨#0000FF¨»«mn mathvariant=¨bold¨»9«/mn»«mn mathvariant=¨bold¨»41«/mn»«/mfrac»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»§#183;«/mo»«mn mathvariant=¨bold¨ mathcolor=¨#0000FF¨»1«/mn»«mspace linebreak=¨newline¨/»«mn mathvariant=¨bold¨ mathcolor=¨#0000FF¨»20«/mn»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»§#183;«/mo»«mi mathvariant=¨bold-italic¨ mathcolor=¨#0000FF¨»I«/mi»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»=«/mo»«mn mathvariant=¨bold¨ mathcolor=¨#0000FF¨»9«/mn»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»-«/mo»«mfrac mathcolor=¨#0000FF¨»«mn mathvariant=¨bold¨»9«/mn»«mn mathvariant=¨bold¨»41«/mn»«/mfrac»«mspace linebreak=¨newline¨/»«mn mathvariant=¨bold¨ mathcolor=¨#0000FF¨»20«/mn»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»§#183;«/mo»«mi mathvariant=¨bold¨ mathcolor=¨#0000FF¨»I«/mi»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»=«/mo»«mn mathvariant=¨bold¨ mathcolor=¨#0000FF¨»8«/mn»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨».«/mo»«mn mathvariant=¨bold¨ mathcolor=¨#0000FF¨»78«/mn»«mspace linebreak=¨newline¨/»«mi mathvariant=¨bold¨ mathcolor=¨#0000FF¨»I«/mi»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»=«/mo»«mfrac mathcolor=¨#0000FF¨»«mrow»«mn mathvariant=¨bold¨»8«/mn»«mo mathvariant=¨bold¨».«/mo»«mn mathvariant=¨bold¨»78«/mn»«/mrow»«mn mathvariant=¨bold¨»20«/mn»«/mfrac»«mspace linebreak=¨newline¨/»«menclose mathcolor=¨#0000FF¨ notation=¨circle¨»«mi mathvariant=¨bold¨»I«/mi»«mo mathvariant=¨bold¨»=«/mo»«mn mathvariant=¨bold¨»0«/mn»«mo mathvariant=¨bold¨».«/mo»«mn mathvariant=¨bold¨»44«/mn»«mi mathvariant=¨bold¨»A«/mi»«/menclose»«/mstyle»«/math»
لذلك، التيار عبر المستهلك هو 0.44 أمبير.
46. ו.6
نجد التيار عبر المستهلك باستخدام مبدأ التراكب.
المرحلة أ- عندما يكون المصدر 2 نشطًا ويكون المصدر 1 في حالة تماس. يتم الحصول على دائرة على التوازي.
نحدد التيارات في الدائرة في هذه الحالة:
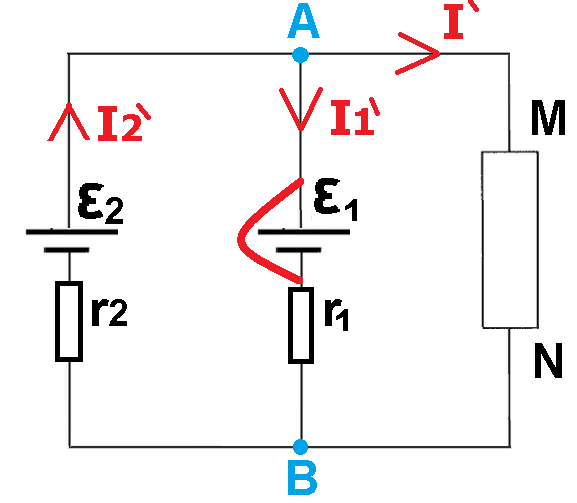
نحسب المقاومة المحصلة:
«math xmlns=¨http://www.w3.org/1998/Math/MathML¨»«mstyle mathsize=¨24px¨»«msub»«mi mathvariant=¨bold¨ mathcolor=¨#0000FF¨»R«/mi»«mi mathvariant=¨bold¨ mathcolor=¨#0000FF¨»T«/mi»«/msub»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»=«/mo»«mstyle mathvariant=¨bold¨ mathcolor=¨#0000FF¨»«mo stretchy=¨true¨»(«/mo»«mrow»«mi»R«/mi»«mo»|«/mo»«mo»|«/mo»«msub»«mi»r«/mi»«mn»1«/mn»«/msub»«/mrow»«mo stretchy=¨true¨»)«/mo»«/mstyle»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»+«/mo»«msub»«mi mathvariant=¨bold¨ mathcolor=¨#0000FF¨»r«/mi»«mn mathvariant=¨bold¨ mathcolor=¨#0000FF¨»2«/mn»«/msub»«mspace linebreak=¨newline¨/»«msub»«mi mathvariant=¨bold¨ mathcolor=¨#0000FF¨»R«/mi»«mi mathvariant=¨bold¨ mathcolor=¨#0000FF¨»T«/mi»«/msub»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»=«/mo»«mfrac mathcolor=¨#0000FF¨»«mrow»«mi mathvariant=¨bold¨»R«/mi»«mo mathvariant=¨bold¨»§#183;«/mo»«msub»«mi mathvariant=¨bold¨»r«/mi»«mn mathvariant=¨bold¨»1«/mn»«/msub»«/mrow»«mrow»«mi mathvariant=¨bold¨»R«/mi»«mo mathvariant=¨bold¨»+«/mo»«msub»«mi mathvariant=¨bold¨»r«/mi»«mn mathvariant=¨bold¨»1«/mn»«/msub»«/mrow»«/mfrac»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»+«/mo»«msub»«mi mathvariant=¨bold¨ mathcolor=¨#0000FF¨»r«/mi»«mn mathvariant=¨bold¨ mathcolor=¨#0000FF¨»2«/mn»«/msub»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»=«/mo»«mfrac mathcolor=¨#0000FF¨»«mrow»«mn mathvariant=¨bold¨»20«/mn»«mo mathvariant=¨bold¨»§#183;«/mo»«mn mathvariant=¨bold¨»1«/mn»«/mrow»«mrow»«mn mathvariant=¨bold¨»20«/mn»«mo mathvariant=¨bold¨»+«/mo»«mn mathvariant=¨bold¨»1«/mn»«/mrow»«/mfrac»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»+«/mo»«mn mathvariant=¨bold¨ mathcolor=¨#0000FF¨»1«/mn»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»=«/mo»«mn mathvariant=¨bold¨ mathcolor=¨#0000FF¨»1«/mn»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨».«/mo»«mn mathvariant=¨bold¨ mathcolor=¨#0000FF¨»95«/mn»«mi mathvariant=¨bold¨ mathcolor=¨#0000FF¨»§#937;«/mi»«/mstyle»«/math»
نحسب تيار المصدر المتولد في المصدر 2 في هذه الحالة باستخدام قانون أوم:
«math style=¨font-family:Tahoma¨ xmlns=¨http://www.w3.org/1998/Math/MathML¨»«mstyle mathsize=¨24px¨»«msub»«mi mathvariant=¨bold¨ mathcolor=¨#0000FF¨»I«/mi»«mn mathvariant=¨bold¨ mathcolor=¨#0000FF¨»2«/mn»«/msub»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»`«/mo»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»=«/mo»«mfrac mathcolor=¨#0000FF¨»«mi mathvariant=¨bold¨»§#949;«/mi»«msub»«mi mathvariant=¨bold¨»R«/mi»«mi mathvariant=¨bold¨»T«/mi»«/msub»«/mfrac»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»=«/mo»«mfrac mathcolor=¨#0000FF¨»«msub»«mi mathvariant=¨bold¨»§#949;«/mi»«mn mathvariant=¨bold¨»2«/mn»«/msub»«msub»«mi mathvariant=¨bold¨»R«/mi»«mi mathvariant=¨bold¨»T«/mi»«/msub»«/mfrac»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»=«/mo»«mfrac mathcolor=¨#0000FF¨»«mn mathvariant=¨bold¨»9«/mn»«mrow»«mn mathvariant=¨bold¨»1«/mn»«mo mathvariant=¨bold¨».«/mo»«mn mathvariant=¨bold¨»95«/mn»«/mrow»«/mfrac»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»=«/mo»«mn mathvariant=¨bold¨ mathcolor=¨#0000FF¨»4«/mn»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨».«/mo»«mn mathvariant=¨bold¨ mathcolor=¨#0000FF¨»61«/mn»«mi mathvariant=¨bold¨ mathcolor=¨#0000FF¨»A«/mi»«/mstyle»«/math»
نحسب التيار I الذي يتدفق عبر المستهلك R عندما يكون المصدر 1 في حالة تماس.
ينقسم التيار القادم من المصدر 2 في العقدة A ، بحيث تكون نسبة التيارين المنقسمين عكسية لنسبة المقاومتين، ويتحقق:
«math style=¨font-family:Tahoma¨ xmlns=¨http://www.w3.org/1998/Math/MathML¨»«mstyle mathsize=¨24px¨»«mfrac mathcolor=¨#0000FF¨»«mrow»«mi mathvariant=¨bold¨»I«/mi»«mo mathvariant=¨bold¨»`«/mo»«/mrow»«mrow»«msub»«mi mathvariant=¨bold¨»I«/mi»«mn mathvariant=¨bold¨»1«/mn»«/msub»«mo mathvariant=¨bold¨»`«/mo»«/mrow»«/mfrac»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»=«/mo»«mfrac mathcolor=¨#0000FF¨»«msub»«mi mathvariant=¨bold¨»r«/mi»«mn mathvariant=¨bold¨»1«/mn»«/msub»«mi mathvariant=¨bold¨»R«/mi»«/mfrac»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»=«/mo»«mfrac mathcolor=¨#0000FF¨»«mn mathvariant=¨bold¨»1«/mn»«mn mathvariant=¨bold¨»20«/mn»«/mfrac»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»§#160;«/mo»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»§#160;«/mo»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»§#8594;«/mo»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»§#160;«/mo»«menclose mathcolor=¨#0000FF¨ notation=¨box¨»«msub»«mi mathvariant=¨bold¨»I«/mi»«mn mathvariant=¨bold¨»1«/mn»«/msub»«mo mathvariant=¨bold¨»`«/mo»«mo mathvariant=¨bold¨»=«/mo»«mn mathvariant=¨bold¨»20«/mn»«mo mathvariant=¨bold¨»§#183;«/mo»«mi mathvariant=¨bold¨»I«/mi»«mo mathvariant=¨bold¨»`«/mo»«/menclose»«/mstyle»«/math»
نكتب معادلة تيارات أخرى من قانون العقدة ، للعقدة A:
«math style=¨font-family:Tahoma¨ xmlns=¨http://www.w3.org/1998/Math/MathML¨»«mstyle mathsize=¨20px¨»«msub»«mi mathvariant=¨bold¨ mathcolor=¨#0000FF¨»I«/mi»«mn mathvariant=¨bold¨ mathcolor=¨#0000FF¨»2«/mn»«/msub»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»`«/mo»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»=«/mo»«mi mathvariant=¨bold¨ mathcolor=¨#0000FF¨»I«/mi»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»`«/mo»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»+«/mo»«msub»«mi mathvariant=¨bold¨ mathcolor=¨#0000FF¨»I«/mi»«mn mathvariant=¨bold¨ mathcolor=¨#0000FF¨»1«/mn»«/msub»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»`«/mo»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»§#160;«/mo»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»§#8594;«/mo»«menclose mathcolor=¨#0000FF¨ notation=¨box¨»«mn mathvariant=¨bold¨»4«/mn»«mo mathvariant=¨bold¨».«/mo»«mn mathvariant=¨bold¨»61«/mn»«mo mathvariant=¨bold¨»=«/mo»«mi mathvariant=¨bold¨»I«/mi»«mo mathvariant=¨bold¨»`«/mo»«mo mathvariant=¨bold¨»+«/mo»«msub»«mi mathvariant=¨bold¨»I«/mi»«mn mathvariant=¨bold¨»1«/mn»«/msub»«mo mathvariant=¨bold¨»`«/mo»«mo mathvariant=¨bold¨»§#160;«/mo»«/menclose»«/mstyle»«/math»
نحل هيئة المعادلات ونجد التيار عبر المستهلك I، عندما يكون المصدر 1 في حالة تماس:
«math style=¨font-family:Tahoma¨ xmlns=¨http://www.w3.org/1998/Math/MathML¨»«mstyle mathsize=¨24px¨»«menclose mathcolor=¨#0000FF¨ notation=¨box¨»«msub»«mi mathvariant=¨bold¨»I«/mi»«mn mathvariant=¨bold¨»1«/mn»«/msub»«mo mathvariant=¨bold¨»=«/mo»«mn mathvariant=¨bold¨»20«/mn»«mo mathvariant=¨bold¨»§#183;«/mo»«mi mathvariant=¨bold¨»I«/mi»«mo mathvariant=¨bold¨»`«/mo»«/menclose»«mspace linebreak=¨newline¨/»«mspace linebreak=¨newline¨/»«menclose mathcolor=¨#0000FF¨ notation=¨box¨»«mn mathvariant=¨bold¨ mathsize=¨20px¨»4«/mn»«mo mathvariant=¨bold¨ mathsize=¨20px¨».«/mo»«mn mathvariant=¨bold¨ mathsize=¨20px¨»61«/mn»«mo mathvariant=¨bold¨ mathsize=¨20px¨»=«/mo»«mi mathvariant=¨bold¨»I«/mi»«mo mathvariant=¨bold¨»`«/mo»«mo mathvariant=¨bold¨ mathsize=¨20px¨»+«/mo»«msub»«mi mathvariant=¨bold¨»I«/mi»«mn mathvariant=¨bold¨ mathsize=¨20px¨»1«/mn»«/msub»«mo mathvariant=¨bold¨ mathsize=¨20px¨»§#160;«/mo»«/menclose»«mspace linebreak=¨newline¨/»«mspace linebreak=¨newline¨/»«mn mathvariant=¨bold¨ mathcolor=¨#0000FF¨»4«/mn»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨».«/mo»«mn mathvariant=¨bold¨ mathcolor=¨#0000FF¨»61«/mn»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»=«/mo»«mi mathvariant=¨bold¨ mathcolor=¨#0000FF¨»I«/mi»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»`«/mo»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»+«/mo»«mn mathvariant=¨bold¨ mathcolor=¨#0000FF¨»20«/mn»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»§#183;«/mo»«mi mathvariant=¨bold¨ mathcolor=¨#0000FF¨»I«/mi»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»`«/mo»«mspace linebreak=¨newline¨/»«mn mathvariant=¨bold¨ mathcolor=¨#0000FF¨»21«/mn»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»§#183;«/mo»«mi mathvariant=¨bold¨ mathcolor=¨#0000FF¨»I«/mi»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»`«/mo»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»=«/mo»«mn mathvariant=¨bold¨ mathcolor=¨#0000FF¨»4«/mn»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨».«/mo»«mn mathvariant=¨bold¨ mathcolor=¨#0000FF¨»61«/mn»«mspace linebreak=¨newline¨/»«mspace linebreak=¨newline¨/»«mi mathvariant=¨bold¨ mathcolor=¨#0000FF¨»I«/mi»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»`«/mo»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»=«/mo»«mfrac mathcolor=¨#0000FF¨»«mrow»«mn mathvariant=¨bold¨»4«/mn»«mo mathvariant=¨bold¨».«/mo»«mn mathvariant=¨bold¨»61«/mn»«/mrow»«mn mathvariant=¨bold¨»21«/mn»«/mfrac»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»=«/mo»«mn mathvariant=¨bold¨ mathcolor=¨#0000FF¨»0«/mn»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨».«/mo»«mn mathvariant=¨bold¨ mathcolor=¨#0000FF¨»22«/mn»«mi mathvariant=¨bold¨ mathcolor=¨#0000FF¨»A«/mi»«mspace linebreak=¨newline¨/»«mspace linebreak=¨newline¨/»«/mstyle»«/math»
المرحلة أ- عندما يكون المصدر 1 نشطًا ويكون المصدر 2 في حالة تماس.
نحدد التيارات في الدائرة في هذه الحالة:
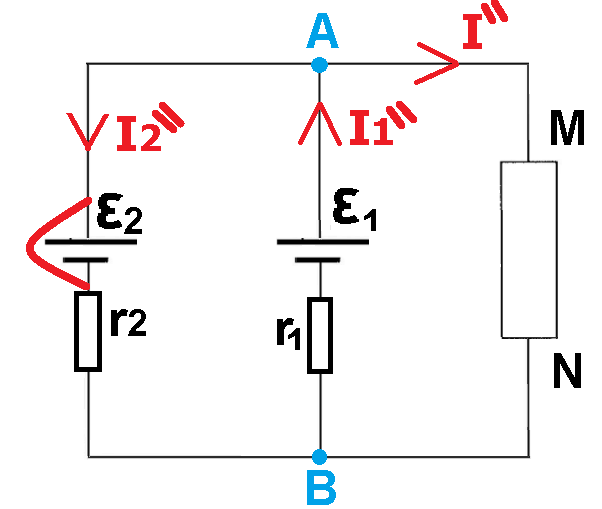
نظرًا لأن المصدرين متشابهين، فإن شدة التيار الذي سيتدفق عبر المستهلك في هذه الحالة ستكون نفس شدة التيار في الوضع السابق ويتحقق: «math style=¨font-family:Tahoma¨ xmlns=¨http://www.w3.org/1998/Math/MathML¨»«mstyle mathsize=¨24px¨»«mi mathvariant=¨bold¨ mathcolor=¨#0000FF¨»I«/mi»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»`«/mo»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»`«/mo»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»=«/mo»«mi mathvariant=¨bold¨ mathcolor=¨#0000FF¨»I«/mi»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»`«/mo»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»=«/mo»«mn mathvariant=¨bold¨ mathcolor=¨#0000FF¨»0«/mn»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨».«/mo»«mn mathvariant=¨bold¨ mathcolor=¨#0000FF¨»22«/mn»«mi mathvariant=¨bold¨ mathcolor=¨#0000FF¨»A«/mi»«/mstyle»«/math»
من مبدأ التراكب، يتحقق أن شدة التيار من خلال المستهلك عندما يعمل كلا المصدرين تساوي مجموع التيارات في المستهلك عندما يعمل كل من المصدرين بمفرده.
نحسب شدة التيار وفقًا لمبدأ التراكب من خلال:
«math style=¨font-family:Tahoma¨ xmlns=¨http://www.w3.org/1998/Math/MathML¨»«mstyle mathsize=¨24px¨»«mi mathvariant=¨bold¨ mathcolor=¨#0000FF¨»I«/mi»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»=«/mo»«mi mathvariant=¨bold¨ mathcolor=¨#0000FF¨»I«/mi»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»`«/mo»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»+«/mo»«mi mathvariant=¨bold¨ mathcolor=¨#0000FF¨»I«/mi»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»`«/mo»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»`«/mo»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»=«/mo»«mn mathvariant=¨bold¨ mathcolor=¨#0000FF¨»0«/mn»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨».«/mo»«mn mathvariant=¨bold¨ mathcolor=¨#0000FF¨»22«/mn»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»+«/mo»«mn mathvariant=¨bold¨ mathcolor=¨#0000FF¨»0«/mn»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨».«/mo»«mn mathvariant=¨bold¨ mathcolor=¨#0000FF¨»22«/mn»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»=«/mo»«mn mathvariant=¨bold¨ mathcolor=¨#0000FF¨»0«/mn»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨».«/mo»«mn mathvariant=¨bold¨ mathcolor=¨#0000FF¨»44«/mn»«mi mathvariant=¨bold¨ mathcolor=¨#0000FF¨»A«/mi»«/mstyle»«/math»
لذلك، شدة التيار من خلال المستهلك هو 0.44 أمبير.
47. ו.7
نشير للتيارات في الدائرة:

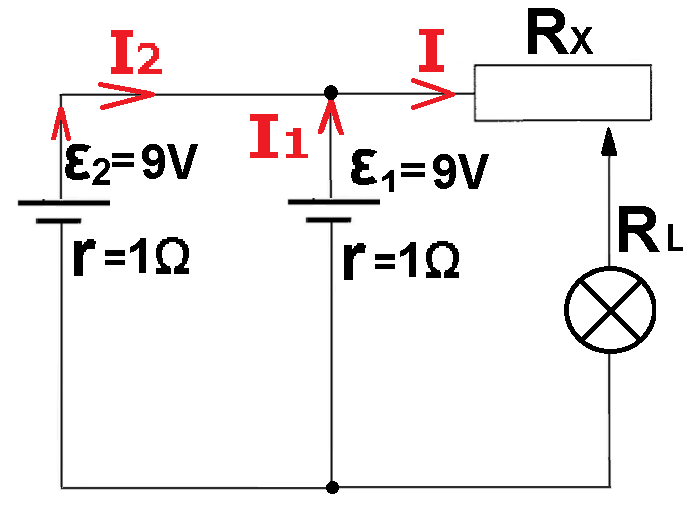
نحسب مقاومة المصباح وفقًا لقيم فرق الجهد وقدرة المصباح:
«math xmlns=¨http://www.w3.org/1998/Math/MathML¨»«mstyle mathsize=¨20px¨»«mi mathvariant=¨bold¨ mathcolor=¨#0000FF¨»R«/mi»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»=«/mo»«mfrac mathcolor=¨#0000FF¨»«msup»«mi mathvariant=¨bold¨»U«/mi»«mn mathvariant=¨bold¨»2«/mn»«/msup»«mi mathvariant=¨bold¨»P«/mi»«/mfrac»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»=«/mo»«mfrac mathcolor=¨#0000FF¨»«msup»«mn mathvariant=¨bold¨»3«/mn»«mn mathvariant=¨bold¨»2«/mn»«/msup»«mrow»«mn mathvariant=¨bold¨»0«/mn»«mo mathvariant=¨bold¨».«/mo»«mn mathvariant=¨bold¨»9«/mn»«/mrow»«/mfrac»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»=«/mo»«mfrac mathcolor=¨#0000FF¨»«mn mathvariant=¨bold¨»9«/mn»«mrow»«mn mathvariant=¨bold¨»0«/mn»«mo mathvariant=¨bold¨».«/mo»«mn mathvariant=¨bold¨»9«/mn»«/mrow»«/mfrac»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»=«/mo»«mn mathvariant=¨bold¨ mathcolor=¨#0000FF¨»10«/mn»«mi mathvariant=¨bold¨ mathcolor=¨#0000FF¨»§#937;«/mi»«mspace linebreak=¨newline¨/»«/mstyle»«/math»
لايجاد مقاومة المقاوم المتغير RX بحيث يضيء المصباح في ضوء كامل، نجد شدة التيار في المصباح عندما يضيء في إضاءته الكاملة:
«math style=¨font-family:Tahoma¨ xmlns=¨http://www.w3.org/1998/Math/MathML¨»«mstyle mathsize=¨20px¨»«mi mathvariant=¨bold¨ mathcolor=¨#0000FF¨»I«/mi»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»=«/mo»«mfrac mathcolor=¨#0000FF¨»«mi mathvariant=¨bold¨»U«/mi»«mi mathvariant=¨bold¨»R«/mi»«/mfrac»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»=«/mo»«mfrac mathcolor=¨#0000FF¨»«mn mathvariant=¨bold¨»3«/mn»«mn mathvariant=¨bold¨»10«/mn»«/mfrac»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»=«/mo»«mn mathvariant=¨bold¨ mathcolor=¨#0000FF¨»0«/mn»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨».«/mo»«mn mathvariant=¨bold¨ mathcolor=¨#0000FF¨»3«/mn»«mi mathvariant=¨bold¨ mathcolor=¨#0000FF¨»A«/mi»«/mstyle»«/math»
كلا مصدري فرق الجهد متماثلان. لذلك يعمل كل منهما تياران متطابقان.
نستخدم قانون العقدة ونجد االتيار عبر كل مصدر من مصدري فرق الجهد:
«math style=¨font-family:Tahoma¨ xmlns=¨http://www.w3.org/1998/Math/MathML¨»«mstyle mathsize=¨20px¨»«mi mathvariant=¨bold¨ mathcolor=¨#0000FF¨»I«/mi»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»=«/mo»«msub»«mi mathvariant=¨bold¨ mathcolor=¨#0000FF¨»I«/mi»«mn mathvariant=¨bold¨ mathcolor=¨#0000FF¨»1«/mn»«/msub»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»+«/mo»«msub»«mi mathvariant=¨bold¨ mathcolor=¨#0000FF¨»I«/mi»«mn mathvariant=¨bold¨ mathcolor=¨#0000FF¨»2«/mn»«/msub»«mspace linebreak=¨newline¨/»«mi mathvariant=¨bold¨ mathcolor=¨#0000FF¨»I«/mi»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»=«/mo»«mn mathvariant=¨bold¨ mathcolor=¨#0000FF¨»2«/mn»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»§#183;«/mo»«msub»«mi mathvariant=¨bold¨ mathcolor=¨#0000FF¨»I«/mi»«mn mathvariant=¨bold¨ mathcolor=¨#0000FF¨»1«/mn»«/msub»«mspace linebreak=¨newline¨/»«msub»«mi mathvariant=¨bold¨ mathcolor=¨#0000FF¨»I«/mi»«mn mathvariant=¨bold¨ mathcolor=¨#0000FF¨»1«/mn»«/msub»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»=«/mo»«msub»«mi mathvariant=¨bold¨ mathcolor=¨#0000FF¨»I«/mi»«mn mathvariant=¨bold¨ mathcolor=¨#0000FF¨»2«/mn»«/msub»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»=«/mo»«mfrac mathcolor=¨#0000FF¨»«mi mathvariant=¨bold¨»I«/mi»«mn mathvariant=¨bold¨»2«/mn»«/mfrac»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»=«/mo»«mfrac mathcolor=¨#0000FF¨»«mrow»«mn mathvariant=¨bold¨»0«/mn»«mo mathvariant=¨bold¨».«/mo»«mn mathvariant=¨bold¨»3«/mn»«/mrow»«mn mathvariant=¨bold¨»2«/mn»«/mfrac»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»=«/mo»«mn mathvariant=¨bold¨ mathcolor=¨#0000FF¨»0«/mn»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨».«/mo»«mn mathvariant=¨bold¨ mathcolor=¨#0000FF¨»15«/mn»«mi mathvariant=¨bold¨ mathcolor=¨#0000FF¨»A«/mi»«mspace linebreak=¨newline¨/»«/mstyle»«/math»
كلا مصدري فرق الجهد لهما نفس فرق جهد الأقطاب، نحسب فرق جهد الأقطاب:
«math style=¨font-family:Tahoma¨ xmlns=¨http://www.w3.org/1998/Math/MathML¨»«mstyle mathsize=¨20px¨»«mi mathvariant=¨bold¨ mathcolor=¨#0000FF¨»Veff«/mi»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»=«/mo»«mi mathvariant=¨bold¨ mathcolor=¨#0000FF¨»§#949;«/mi»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»-«/mo»«mi mathvariant=¨bold¨ mathcolor=¨#0000FF¨»I«/mi»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»§#183;«/mo»«mi mathvariant=¨bold¨ mathcolor=¨#0000FF¨»r«/mi»«mspace linebreak=¨newline¨/»«mi mathvariant=¨bold¨ mathcolor=¨#0000FF¨»Veff«/mi»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»=«/mo»«mn mathvariant=¨bold¨ mathcolor=¨#0000FF¨»9«/mn»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»-«/mo»«mn mathvariant=¨bold¨ mathcolor=¨#0000FF¨»0«/mn»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨».«/mo»«mn mathvariant=¨bold¨ mathcolor=¨#0000FF¨»15«/mn»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»§#183;«/mo»«mn mathvariant=¨bold¨ mathcolor=¨#0000FF¨»1«/mn»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»=«/mo»«mn mathvariant=¨bold¨ mathcolor=¨#0000FF¨»8«/mn»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨».«/mo»«mn mathvariant=¨bold¨ mathcolor=¨#0000FF¨»85«/mn»«mi mathvariant=¨bold¨ mathcolor=¨#0000FF¨»V«/mi»«/mstyle»«/math»
مجموع فرقي الجهد على المقاوم المتغير والمصباح يساوي فرق جهد المصدر. نكتب معادلة فروق الجهد ونعبر عن فرق الجهد على RX منها:
«math style=¨font-family:Tahoma¨ xmlns=¨http://www.w3.org/1998/Math/MathML¨»«mstyle mathsize=¨20px¨»«mi mathvariant=¨bold¨ mathcolor=¨#0000FF¨»Veff«/mi»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»=«/mo»«msub»«mi mathvariant=¨bold¨ mathcolor=¨#0000FF¨»U«/mi»«mi mathvariant=¨bold¨ mathcolor=¨#0000FF¨»RX«/mi»«/msub»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»+«/mo»«msub»«mi mathvariant=¨bold¨ mathcolor=¨#0000FF¨»U«/mi»«mi mathvariant=¨bold¨ mathcolor=¨#0000FF¨»RL«/mi»«/msub»«mspace linebreak=¨newline¨/»«msub»«mi mathvariant=¨bold¨ mathcolor=¨#0000FF¨»U«/mi»«mi mathvariant=¨bold¨ mathcolor=¨#0000FF¨»RX«/mi»«/msub»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»=«/mo»«mi mathvariant=¨bold¨ mathcolor=¨#0000FF¨»Veff«/mi»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»-«/mo»«msub»«mi mathvariant=¨bold¨ mathcolor=¨#0000FF¨»U«/mi»«mi mathvariant=¨bold¨ mathcolor=¨#0000FF¨»RL«/mi»«/msub»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»=«/mo»«mn mathvariant=¨bold¨ mathcolor=¨#0000FF¨»8«/mn»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨».«/mo»«mn mathvariant=¨bold¨ mathcolor=¨#0000FF¨»85«/mn»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»-«/mo»«mn mathvariant=¨bold¨ mathcolor=¨#0000FF¨»3«/mn»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»=«/mo»«mn mathvariant=¨bold¨ mathcolor=¨#0000FF¨»5«/mn»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨».«/mo»«mn mathvariant=¨bold¨ mathcolor=¨#0000FF¨»85«/mn»«mi mathvariant=¨bold¨ mathcolor=¨#0000FF¨»V«/mi»«mspace linebreak=¨newline¨/»«mspace linebreak=¨newline¨/»«/mstyle»«/math»
نجد المقاومة RX بواسطة قانون أوم:
«math style=¨font-family:Tahoma¨ xmlns=¨http://www.w3.org/1998/Math/MathML¨»«mstyle mathsize=¨20px¨»«msub»«mi mathvariant=¨bold¨ mathcolor=¨#0000FF¨»R«/mi»«mi mathvariant=¨bold¨ mathcolor=¨#0000FF¨»X«/mi»«/msub»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»=«/mo»«mfrac mathcolor=¨#0000FF¨»«msub»«mi mathvariant=¨bold¨»U«/mi»«msub»«mi mathvariant=¨bold¨»R«/mi»«mi mathvariant=¨bold¨»X«/mi»«/msub»«/msub»«mi mathvariant=¨bold¨»I«/mi»«/mfrac»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»=«/mo»«mfrac mathcolor=¨#0000FF¨»«mrow»«mn mathvariant=¨bold¨»5«/mn»«mo mathvariant=¨bold¨».«/mo»«mn mathvariant=¨bold¨»85«/mn»«/mrow»«mrow»«mn mathvariant=¨bold¨»0«/mn»«mo mathvariant=¨bold¨».«/mo»«mn mathvariant=¨bold¨»3«/mn»«/mrow»«/mfrac»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»=«/mo»«mn mathvariant=¨bold¨ mathcolor=¨#0000FF¨»19«/mn»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨».«/mo»«mn mathvariant=¨bold¨ mathcolor=¨#0000FF¨»5«/mn»«mi mathvariant=¨bold¨ mathcolor=¨#0000FF¨»§#937;«/mi»«/mstyle»«/math»
لذلك ، لكي يضيء المصباح في ضوءه الكامل، يجب أن تكون مقاومة المقاوم المتغير 19.5 أوم.
يمكن حل السؤال بمساعدة قوانين كيرخوف، طريقة التراكب ليست مناسبة لحل هذا السؤال.