...
لا يتحرك الجسم، معامل الاحتكاك الساكن كبير بما يكفي بحيث يكون مركّب قوة الجاذبية WX الذي يعمل على تحريك الجسم أصغر من قوة الاحتكاك الساكنة القصوى.
הגוף לא זז , מקדם החיכוך הסטטי מספיק גדול כך שרכיב כוח הכובד WX הפועל להנעת הגוף , קטן מכוח החיכוך הסטטי מקסימאלי.
הגוף לא זז , מקדם החיכוך הסטטי מספיק גדול כך שרכיב כוח הכובד WX הפועל להנעת הגוף , קטן מכוח החיכוך הסטטי מקסימאלי.
הגוף לא זז , מכיוון שרכיב כוח הכובד WX הפועל להנעת הגוף קטן מכוח החיכוך הסטטי מקסימאלי.
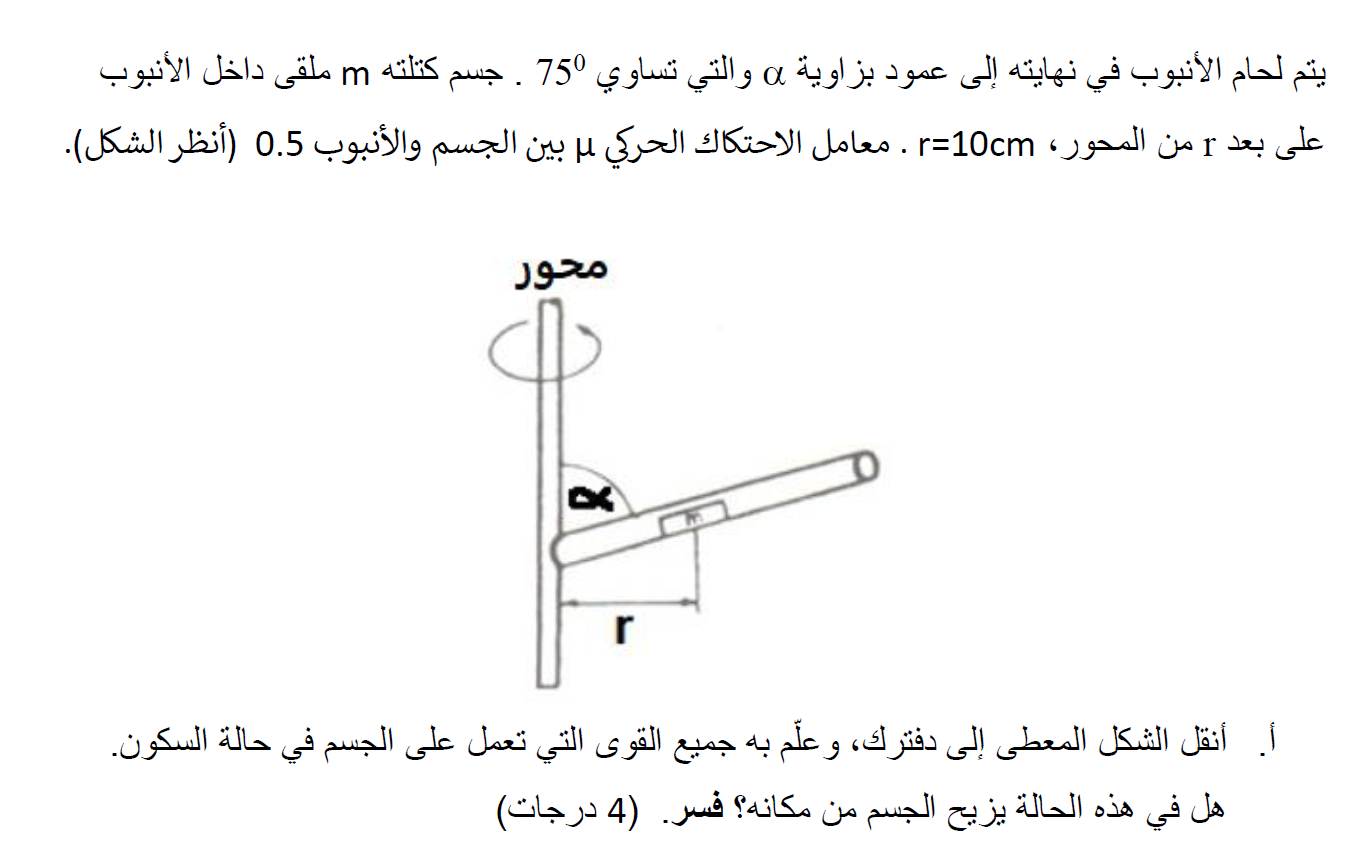
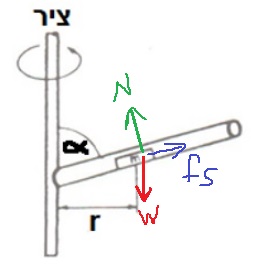
تحديد القوى المؤثرة على الجسم ورسم مخطط للقوى المؤثرة على الجسم.
لمعرفة ما إذا كان الجسم يتحرك في هذه الحالة ، يمكن كتابة معادلات الحركة في وشك الحركة، ومعرفة قيمة معامل الاحتكاك الساكن في حالة وشك الحركة.
إذا كان معامل الاحتكاك الساكن المحسوب أقل من قيمة معامل الاحتكاك الساكن المعطى في السؤال ، فإن الجسم لا يتحرك.
طريق اخر:
لكي يتحرك الجسم ، يجب أن تكون القوة المؤثرة لتحريكه أكبر من قوة الاحتكاك الساكنة القصوى.
من الممكن مقارنة أقصى قوة احتكاك ساكن مع مركّب الجاذبية WX.
כדי לדעת אם הגוף זז במקרה זה , ניתן לכתוב את משוואות התנועה לסף תנועה, ולמצוא מהם את ערכו של מקדם החיכוך הסטטי במצב של סף תנועה.
אם מקדם החיכוך שהסטטי המחושב קטן מערכו של מקדם החיכוך הסטטי הנתון בשאלה הגוף לא זז.
דרך נוספת:
כדי שהגוף יזוז הכוח הפועל להנעתו צריך להיות גדול מכוח החיכוך הסטטי מקסימאלי.
אפשר להשוות בין כוח החיכוך הסטטי מקסימאלי לבין רכיב כוח הכובד WX.
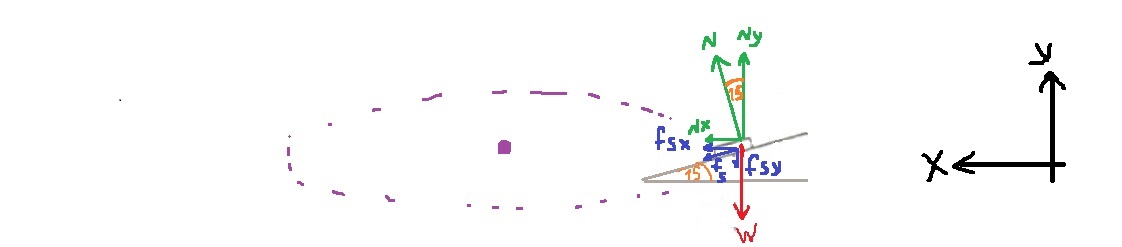
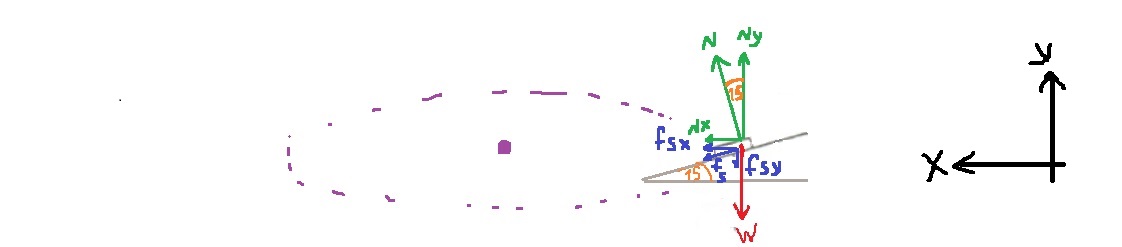
عندما يستقر الجسم في هذا الوضع ، تعمل عليه ثلاث قوى: قوة الجاذبية ، والقوة العمودية ، وقوة الاحتكاك الساكن.
نقوم بعمل مخطّط للقوى المؤثرة على الجسم:
لمعرفة ما إذا كان الجسم سيتحرك من مكانه، نتطرق إلى الحالة الحدّية، عندما يكون الجسم على وشك الحركة ، (تعمل القوة القصوى للاحتكاك الساكن)
نجد قيمة معامل الاحتكاك الساكن في حالة وشك الحركة.
في هذا القسم لا تدور المجموعة، نتطرق إلى الجسم داخل الأنبوب كجسم ملقى على مستوى مائل ، وزاوية ميله: «math xmlns=¨http://www.w3.org/1998/Math/MathML¨»«mn mathvariant=¨bold¨ mathcolor=¨#0000FF¨»90«/mn»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»-«/mo»«mi mathvariant=¨bold¨ mathcolor=¨#0000FF¨»§#945;«/mi»«/math».
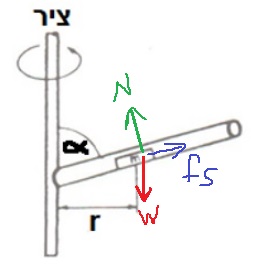
نقوم بعمل مخطط قوى جديد بمستوى مائل ، ونحلل قوة الجاذبية:
نكتب معادلات الحركة
«math xmlns=¨http://www.w3.org/1998/Math/MathML¨»«msub»«mi mathvariant=¨bold¨ mathcolor=¨#0000FF¨»§#931;F«/mi»«mi mathvariant=¨bold¨ mathcolor=¨#0000FF¨»y«/mi»«/msub»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»=«/mo»«mn mathvariant=¨bold¨ mathcolor=¨#0000FF¨»0«/mn»«mspace linebreak=¨newline¨»«/mspace»«mi mathvariant=¨bold¨ mathcolor=¨#0000FF¨»N«/mi»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»=«/mo»«msub»«mi mathvariant=¨bold¨ mathcolor=¨#0000FF¨»W«/mi»«mi mathvariant=¨bold¨ mathcolor=¨#0000FF¨»Y«/mi»«/msub»«mspace linebreak=¨newline¨»«/mspace»«menclose mathcolor=¨#0000FF¨ notation=¨box¨»«mi mathvariant=¨bold¨»N«/mi»«mo mathvariant=¨bold¨»=«/mo»«mi mathvariant=¨bold¨»mg«/mi»«mo mathvariant=¨bold¨»§#183;«/mo»«mi mathvariant=¨bold¨»cos«/mi»«mo mathvariant=¨bold¨»(«/mo»«mn mathvariant=¨bold¨»15«/mn»«mo mathvariant=¨bold¨»)«/mo»«/menclose»«/math» «math xmlns=¨http://www.w3.org/1998/Math/MathML¨»«msub»«mi mathvariant=¨bold¨ mathcolor=¨#0000FF¨»§#931;F«/mi»«mi mathvariant=¨bold¨ mathcolor=¨#0000FF¨»X«/mi»«/msub»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»=«/mo»«mn mathvariant=¨bold¨ mathcolor=¨#0000FF¨»0«/mn»«mspace linebreak=¨newline¨»«/mspace»«msub»«mi mathvariant=¨bold¨ mathcolor=¨#0000FF¨»W«/mi»«mi mathvariant=¨bold¨ mathcolor=¨#0000FF¨»x«/mi»«/msub»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»=«/mo»«msub»«mi mathvariant=¨bold¨ mathcolor=¨#0000FF¨»f«/mi»«msub mathcolor=¨#0000FF¨»«mi mathvariant=¨bold¨»s«/mi»«mi mathvariant=¨bold¨»max«/mi»«/msub»«/msub»«mspace linebreak=¨newline¨»«/mspace»«menclose mathcolor=¨#0000FF¨ notation=¨box¨»«mi mathvariant=¨bold¨»mg«/mi»«mo mathvariant=¨bold¨»§#183;«/mo»«mi mathvariant=¨bold¨»sin«/mi»«mo mathvariant=¨bold¨»(«/mo»«mn mathvariant=¨bold¨»15«/mn»«mo mathvariant=¨bold¨»)«/mo»«mo mathvariant=¨bold¨»=«/mo»«msub»«mi mathvariant=¨bold¨»§#956;«/mi»«mi mathvariant=¨bold¨»s«/mi»«/msub»«mo mathvariant=¨bold¨»§#183;«/mo»«mi mathvariant=¨bold¨»N«/mi»«/menclose»«mspace linebreak=¨newline¨»«/mspace»«/math»
نقسم المعادلات ونجد معامل الاحتكاك الساكن:
«math xmlns=¨http://www.w3.org/1998/Math/MathML¨»«mfrac mathcolor=¨#0000FF¨»«mrow»«menclose notation=¨updiagonalstrike¨»«mi mathvariant=¨bold¨»mg«/mi»«/menclose»«mo mathvariant=¨bold¨»§#183;«/mo»«mi mathvariant=¨bold¨»sin«/mi»«mo mathvariant=¨bold¨»(«/mo»«mn mathvariant=¨bold¨»15«/mn»«mo mathvariant=¨bold¨»)«/mo»«/mrow»«mrow»«menclose notation=¨updiagonalstrike¨»«mi mathvariant=¨bold¨»mg«/mi»«/menclose»«mo mathvariant=¨bold¨»§#183;«/mo»«mi mathvariant=¨bold¨»cos«/mi»«mo mathvariant=¨bold¨»(«/mo»«mn mathvariant=¨bold¨»15«/mn»«mo mathvariant=¨bold¨»)«/mo»«/mrow»«/mfrac»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»=«/mo»«mfrac mathcolor=¨#0000FF¨»«mrow»«msub»«mi mathvariant=¨bold¨»§#956;«/mi»«mi mathvariant=¨bold¨»s«/mi»«/msub»«mo mathvariant=¨bold¨»§#183;«/mo»«menclose notation=¨downdiagonalstrike¨»«mi mathvariant=¨bold¨»N«/mi»«/menclose»«/mrow»«menclose notation=¨downdiagonalstrike¨»«mi mathvariant=¨bold¨»N«/mi»«/menclose»«/mfrac»«mspace linebreak=¨newline¨»«/mspace»«mspace linebreak=¨newline¨»«/mspace»«msub»«mi mathvariant=¨bold¨ mathcolor=¨#0000FF¨»§#956;«/mi»«mi mathvariant=¨bold¨ mathcolor=¨#0000FF¨»s«/mi»«/msub»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»=«/mo»«mi mathvariant=¨bold¨ mathcolor=¨#0000FF¨»tan«/mi»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»(«/mo»«mn mathvariant=¨bold¨ mathcolor=¨#0000FF¨»15«/mn»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»)«/mo»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»=«/mo»«mn mathvariant=¨bold¨ mathcolor=¨#0000FF¨»0«/mn»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨».«/mo»«mn mathvariant=¨bold¨ mathcolor=¨#0000FF¨»26«/mn»«/math»
لذلك ، إذا كان مقدار معامل الاحتكاك 0.26 ، فإن الجسم كان على وشك الحركة ، لأن قيمة معامل الاحتكاك هي 0.5 ، فإن الجسم لم يتحرك.
طريقة أخرى للتحقق مما إذا كان الجسم يتحرك:
لكي يتحرك الجسم ، يجب أن يكون مركّب الجاذبية WX أكبر من الحد الأقصى لقوة الاحتكاك الساكن:
نكتب تعبير لـ WX : «math xmlns=¨http://www.w3.org/1998/Math/MathML¨»«menclose mathcolor=¨#0000FF¨ notation=¨bottom¨»«msub»«mi mathvariant=¨bold¨»W«/mi»«mi mathvariant=¨bold¨»x«/mi»«/msub»«/menclose»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»=«/mo»«mi mathvariant=¨bold¨ mathcolor=¨#0000FF¨»mg«/mi»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»§#183;«/mo»«mi mathvariant=¨bold¨ mathcolor=¨#0000FF¨»sin«/mi»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»(«/mo»«mn mathvariant=¨bold¨ mathcolor=¨#0000FF¨»15«/mn»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»)«/mo»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»=«/mo»«menclose mathcolor=¨#0000FF¨ notation=¨bottom¨»«mn mathvariant=¨bold¨»2«/mn»«mo mathvariant=¨bold¨».«/mo»«mn mathvariant=¨bold¨»58«/mn»«mi mathvariant=¨bold¨»m«/mi»«/menclose»«mspace linebreak=¨newline¨»«/mspace»«/math»
نكتب تعبير لـ fsmax: «math xmlns=¨http://www.w3.org/1998/Math/MathML¨»«mspace linebreak=¨newline¨»«/mspace»«menclose mathcolor=¨#0000FF¨ notation=¨bottom¨»«msub»«mi mathvariant=¨bold¨»f«/mi»«msub»«mi mathvariant=¨bold¨»s«/mi»«mi mathvariant=¨bold¨»max«/mi»«/msub»«/msub»«/menclose»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»=«/mo»«msub»«mi mathvariant=¨bold¨ mathcolor=¨#0000FF¨»§#956;«/mi»«mi mathvariant=¨bold¨ mathcolor=¨#0000FF¨»s«/mi»«/msub»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»§#183;«/mo»«mi mathvariant=¨bold¨ mathcolor=¨#0000FF¨»N«/mi»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»=«/mo»«msub»«mi mathvariant=¨bold¨ mathcolor=¨#0000FF¨»§#956;«/mi»«mi mathvariant=¨bold¨ mathcolor=¨#0000FF¨»s«/mi»«/msub»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»§#183;«/mo»«mi mathvariant=¨bold¨ mathcolor=¨#0000FF¨»mg«/mi»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»§#183;«/mo»«mi mathvariant=¨bold¨ mathcolor=¨#0000FF¨»cos«/mi»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»(«/mo»«mn mathvariant=¨bold¨ mathcolor=¨#0000FF¨»15«/mn»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»)«/mo»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»=«/mo»«menclose mathcolor=¨#0000FF¨ notation=¨bottom¨»«mn mathvariant=¨bold¨»4«/mn»«mo mathvariant=¨bold¨».«/mo»«mn mathvariant=¨bold¨»83«/mn»«mi mathvariant=¨bold¨»m«/mi»«/menclose»«mspace linebreak=¨newline¨»«/mspace»«mspace linebreak=¨newline¨»«/mspace»«/math»
نظرًا لأن مركّب قوة الجاذبية WX أصغر من أقصى قوة احتكاك ساكنة ، فإن الجسم لا يتحرك.
נערוך תרשים כוחות לכוחות הפועלים על הגוף:
1. يوجد في الشكل علامة في الجزء العلوي من المحور تصف دوران المجموعة ، ولكن في هذا القسم لا تدور المجموعة.
2. عادة ما يكفي رسم مربع يمثل الجسم ورسم القوى عليه ، وفي هذا القسم يوجد تعليمات لنسخ الرسم التخطيطي.
4. يمكن أن نتعامل مع الأنبوب على أنه مستوى مائل ، وزاوية α المعطاة ليست زاوية ميل المستوى.
5. تمت صياغة هذا السؤال بطريقة سيئة ومضللة ، في أسئلة البجروت اليوم ، صياغة أكثر نجاحًا.
2. לרוב מספיק לשרטט ריבוע המייצג את הגוף ולסמן עליו את הכוחות , בסעיף זה קיימת הנחייה להעתיק את התרשים.
3. יש לסמן את הכוחות במצב של מנוחה , לא ברור אם הגוף נח , יתרה מכך שואלים אם הגוף נח.
4. שאלה זו מנוסחת בצורה לא טובה ומטעה , בשאלות הבגרות כיום הניסוחים יותר מוצלחים.
...
في الاتجاه لأعلى المستوى ، قبل الانفصال ، تعمل قوة الاحتكاك الساكن لأسفل.
حدّد اتجاه عمل أقصى قوة احتكاك ساكن قبل أن ينفصل الجسم ، وبناءً عليه تعرف لأي اتجاه سيتحرك فيه الجسم عندما ينفصل.
عند سرعات الدوران العالية، ستعمل قوة الاحتكاك الساكن القصوى في الاتجاه نحو الأسفل بحيث يكون لها مركّب في اتجاه مركز الدوران.
مجموع مركّب القوة الساكنة والمركّب العمودي في اتجاه مركز الدوران هو القوة الجاذبة نحو المركز.
ينفصل الجسم عندما تكون قوة الاحتكاك الساكن القصوى التي تعمل في اتجاه المنحدر أقل من اللازم ، وفي هذه الحالة ينزلق الجسم في الاتجاه المعاكس لعمل القوة الساكنة قبل الانفصال ، وبالتالي نتيجة للانفصال يتحرك الجسم في الاتجاه نحو أعلى المستوى المائل.
סכום רכיב כוח סטטי זה ורכיב הנורמל בכיוון מרכז הסיבוב הוא הכוח הצנטריפטלי .
הגוף יינתק כאשר כוח החיכוך הסטטי מקסימאלי הפועל בכיוון המורד יהיה קטן מהדרוש , במצב זה הגוף יחליק בכיוון נגדי לכיוון פעולת הכוח הסטטי לפני ההתנתקות, לכן כתוצאה מההתנתקות הגוף ינוע בכיוון מעלה המישור המשופע.
1. قوة الاحتكاك الساكن هي القوة التي "تلائم نفسها" ، بحيث لا ينزلق الجسم (لا يتحرك). يمكن أن يتغير في المقدار والاتجاه.
عندما كانت المجموعة في حالة سكون وكان الجسم ساكنًا داخل الأنبوب ، كان اتجاه قوة الاحتكاك الساكن لأعلى المستوى المائل
وعندما بدأت المجوعة بالدوران ، كما هو الحال في أي حركة دائرية ، كان الجسم يميل إلى أن "يُقذف منه". لذلك فإن الاحتكاك الساكن
يعمل في اتجاه أسفل الأنبوب.
2. إذا كانت القوة المؤثرة لتحريك الجسم أكبر من أقصى قوة احتكاك ساكنة ، فإن الجسم سينفصل ، ويتحرك في الاتجاه المعاكس لقوة الاحتكاك الساكن قبل الانفصال.
כאשר המערכת הייתה במנוחה והגוף נח בתוך הצינור , כיוון כוח החיכוך הסטטי היה בכיוון מעלה המישור המשופע
וכאשר המערכת התחילה להסתובב כמו בכל תנועה מעגלית היית לגוף נטייה "להיזרק" החוצה. לכן החיכוך הסטטי
פעל בכיוון מורד הצינור.
2. אם הכוח הפועל להנעת הגוף גדול מכוח החיכוך הסטטי מקסימאלי הגוף ינתק , וינוע בכיוון נגדי לכיוון פעולת כוח החיכוך הסטטי לפני ההתנתקות.
...
أصغر سرعة زاوية مطلوبة لتحرك الجسم من موضعه هي 9.44 راديان في الثانية.
من الضروري أن نفهم كيف يبدو مستوى الحركة ، لفهم من هي (أو هم) قوة الجاذبة نحو المركز ، ورسم مخطّط القوى.
كتابة معادلات الحركة في حالة وشك الحركة، وإيجاد السرعة الزاوية في حالة وشك الحركة.
כתיבת משוואות התנועה לסף תנועה , מציאת המהירות הזוויתית בסף תנועה.
الآن يتحرك الجسم في حركة دائرية في مستوى أفقي ، نرسم مستوى الحركة ونقطة مركز الدوران ،
ونرسم مخطط القوة للقوى المؤثرة على الجسم في هذه الحالة:
لا يوجد مركّب لقوة الجاذبية موجّه نحو مركز الدوران ، للقوة العمودية يوجد مركّب، وكذلك لقوة الاحتكاك الساكن يوجد مركّب.
لقد اخترنا هيئة محاور حيث يكون اتجاه المحور X أفقيًا ، ومتجّه نحو نقطة مركز الدوران. واتجاه المحور Y عمودي ومعاكس لقوة الجاذبية.
نحلل القوة العمودية وقوة الاحتكاك الساكن نسبة لهيئة المحاور هذا :
هندسيًا ، زاوية ميل المستوى تساوي الزاوية بين N و NY ، وتساوي أيضًا الزاوية بين fs و fsx.
لإيجاد السرعة الزاوية الصغرى، نتطرق إلى حالة وشك الحركة ، عندما يكون الاحتكاك الساكن المؤثر على الجسم مساويًا لأقصى احتكاك ساكن.
نكتب معادلات الحركة في الاتجاهين الرأسي والأفقي:
«math xmlns=¨http://www.w3.org/1998/Math/MathML¨»«msub»«mi mathvariant=¨bold¨ mathcolor=¨#0000FF¨»§#931;F«/mi»«mi mathvariant=¨bold¨ mathcolor=¨#0000FF¨»y«/mi»«/msub»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»=«/mo»«mn mathvariant=¨bold¨ mathcolor=¨#0000FF¨»0«/mn»«mspace linebreak=¨newline¨/»«msub»«mi mathvariant=¨bold¨ mathcolor=¨#0000FF¨»N«/mi»«mi mathvariant=¨bold¨ mathcolor=¨#0000FF¨»Y«/mi»«/msub»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»=«/mo»«mi mathvariant=¨bold¨ mathcolor=¨#0000FF¨»W«/mi»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»+«/mo»«msub»«mi mathvariant=¨bold¨ mathcolor=¨#0000FF¨»fs«/mi»«msub mathcolor=¨#0000FF¨»«mi mathvariant=¨bold¨»max«/mi»«mi mathvariant=¨bold¨»y«/mi»«/msub»«/msub»«mspace linebreak=¨newline¨/»«menclose mathcolor=¨#0000FF¨ notation=¨box¨»«mi mathvariant=¨bold¨»N«/mi»«mo mathvariant=¨bold¨»§#183;«/mo»«mi mathvariant=¨bold¨»cos«/mi»«mo mathvariant=¨bold¨»(«/mo»«mn mathvariant=¨bold¨»15«/mn»«mo mathvariant=¨bold¨»)«/mo»«mo mathvariant=¨bold¨»=«/mo»«mi mathvariant=¨bold¨»mg«/mi»«mo mathvariant=¨bold¨»+«/mo»«msub»«mi mathvariant=¨bold¨»§#956;«/mi»«mi mathvariant=¨bold¨»s«/mi»«/msub»«mo mathvariant=¨bold¨»§#183;«/mo»«mi mathvariant=¨bold¨»N«/mi»«mo mathvariant=¨bold¨»§#183;«/mo»«mi mathvariant=¨bold¨»sin«/mi»«mo mathvariant=¨bold¨»(«/mo»«mn mathvariant=¨bold¨»15«/mn»«mo mathvariant=¨bold¨»)«/mo»«/menclose»«/math» «math xmlns=¨http://www.w3.org/1998/Math/MathML¨»«msub»«mi mathvariant=¨bold¨ mathcolor=¨#0000FF¨»§#931;F«/mi»«mi mathvariant=¨bold¨ mathcolor=¨#0000FF¨»R«/mi»«/msub»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»=«/mo»«mi mathvariant=¨bold¨ mathcolor=¨#0000FF¨»m«/mi»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»§#183;«/mo»«msup»«msub»«mi mathvariant=¨bold¨ mathcolor=¨#0000FF¨»§#969;«/mi»«mi mathvariant=¨bold¨ mathcolor=¨#0000FF¨»min«/mi»«/msub»«mn mathvariant=¨bold¨ mathcolor=¨#0000FF¨»2«/mn»«/msup»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»§#183;«/mo»«mi mathvariant=¨bold¨ mathcolor=¨#0000FF¨»R«/mi»«mspace linebreak=¨newline¨»«/mspace»«msub»«mi mathvariant=¨bold¨ mathcolor=¨#0000FF¨»N«/mi»«mi mathvariant=¨bold¨ mathcolor=¨#0000FF¨»x«/mi»«/msub»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»+«/mo»«msub»«mi mathvariant=¨bold¨ mathcolor=¨#0000FF¨»f«/mi»«msub mathcolor=¨#0000FF¨»«mi mathvariant=¨bold¨»S«/mi»«msub»«mi mathvariant=¨bold¨»MAX«/mi»«mi mathvariant=¨bold¨»X«/mi»«/msub»«/msub»«/msub»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»=«/mo»«mi mathvariant=¨bold¨ mathcolor=¨#0000FF¨»m«/mi»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»§#183;«/mo»«msup»«msub»«mi mathvariant=¨bold¨ mathcolor=¨#0000FF¨»§#969;«/mi»«mi mathvariant=¨bold¨ mathcolor=¨#0000FF¨»min«/mi»«/msub»«mn mathvariant=¨bold¨ mathcolor=¨#0000FF¨»2«/mn»«/msup»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»§#183;«/mo»«mi mathvariant=¨bold¨ mathcolor=¨#0000FF¨»R«/mi»«mspace linebreak=¨newline¨»«/mspace»«menclose mathcolor=¨#0000FF¨ notation=¨box¨»«mi mathvariant=¨bold¨»N«/mi»«mo mathvariant=¨bold¨»§#183;«/mo»«mi mathvariant=¨bold¨»sin«/mi»«mo mathvariant=¨bold¨»(«/mo»«mn mathvariant=¨bold¨»15«/mn»«mo mathvariant=¨bold¨»)«/mo»«mo mathvariant=¨bold¨»+«/mo»«msub»«mi mathvariant=¨bold¨»§#956;«/mi»«mi mathvariant=¨bold¨»s«/mi»«/msub»«mo mathvariant=¨bold¨»§#183;«/mo»«mi mathvariant=¨bold¨»N«/mi»«mo mathvariant=¨bold¨»§#183;«/mo»«mi mathvariant=¨bold¨»cos«/mi»«mo mathvariant=¨bold¨»(«/mo»«mn mathvariant=¨bold¨»15«/mn»«mo mathvariant=¨bold¨»)«/mo»«mo mathvariant=¨bold¨»=«/mo»«mi mathvariant=¨bold¨»m«/mi»«mo mathvariant=¨bold¨»§#183;«/mo»«msup»«msub»«mi mathvariant=¨bold¨»§#969;«/mi»«mi mathvariant=¨bold¨»min«/mi»«/msub»«mn mathvariant=¨bold¨»2«/mn»«/msup»«mo mathvariant=¨bold¨»§#183;«/mo»«mi mathvariant=¨bold¨»R«/mi»«/menclose»«mspace linebreak=¨newline¨»«/mspace»«/math»
نكتب المعادلات بحيث يتم تقليل اختزال القوة العمودية بعد قسمة المعادلتين:
«math xmlns=¨http://www.w3.org/1998/Math/MathML¨»«mi mathvariant=¨bold¨ mathcolor=¨#0000FF¨»N«/mi»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»§#183;«/mo»«mi mathvariant=¨bold¨ mathcolor=¨#0000FF¨»cos«/mi»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»(«/mo»«mn mathvariant=¨bold¨ mathcolor=¨#0000FF¨»15«/mn»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»)«/mo»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»=«/mo»«mi mathvariant=¨bold¨ mathcolor=¨#0000FF¨»mg«/mi»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»+«/mo»«msub»«mi mathvariant=¨bold¨ mathcolor=¨#0000FF¨»§#956;«/mi»«mi mathvariant=¨bold¨ mathcolor=¨#0000FF¨»s«/mi»«/msub»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»§#183;«/mo»«mi mathvariant=¨bold¨ mathcolor=¨#0000FF¨»N«/mi»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»§#183;«/mo»«mi mathvariant=¨bold¨ mathcolor=¨#0000FF¨»sin«/mi»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»(«/mo»«mn mathvariant=¨bold¨ mathcolor=¨#0000FF¨»15«/mn»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»)«/mo»«mspace linebreak=¨newline¨»«/mspace»«menclose mathcolor=¨#0000FF¨ notation=¨box¨»«mi mathvariant=¨bold¨»N«/mi»«mo mathvariant=¨bold¨»§#183;«/mo»«mfenced open=¨[¨ close=¨]¨»«mrow»«mi mathvariant=¨bold¨»cos«/mi»«mo mathvariant=¨bold¨»(«/mo»«mn mathvariant=¨bold¨»15«/mn»«mo mathvariant=¨bold¨»)«/mo»«mo mathvariant=¨bold¨»-«/mo»«msub»«mi mathvariant=¨bold¨»§#956;«/mi»«mi mathvariant=¨bold¨»s«/mi»«/msub»«mo mathvariant=¨bold¨»§#183;«/mo»«mi mathvariant=¨bold¨»sin«/mi»«mo mathvariant=¨bold¨»(«/mo»«mn mathvariant=¨bold¨»15«/mn»«mo mathvariant=¨bold¨»)«/mo»«/mrow»«/mfenced»«mo mathvariant=¨bold¨»=«/mo»«mi mathvariant=¨bold¨»mg«/mi»«/menclose»«/math» «math xmlns=¨http://www.w3.org/1998/Math/MathML¨»«mi mathvariant=¨bold¨ mathcolor=¨#0000FF¨»N«/mi»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»§#183;«/mo»«mi mathvariant=¨bold¨ mathcolor=¨#0000FF¨»sin«/mi»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»(«/mo»«mn mathvariant=¨bold¨ mathcolor=¨#0000FF¨»15«/mn»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»)«/mo»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»+«/mo»«msub»«mi mathvariant=¨bold¨ mathcolor=¨#0000FF¨»§#956;«/mi»«mi mathvariant=¨bold¨ mathcolor=¨#0000FF¨»s«/mi»«/msub»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»§#183;«/mo»«mi mathvariant=¨bold¨ mathcolor=¨#0000FF¨»N«/mi»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»§#183;«/mo»«mi mathvariant=¨bold¨ mathcolor=¨#0000FF¨»cos«/mi»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»(«/mo»«mn mathvariant=¨bold¨ mathcolor=¨#0000FF¨»15«/mn»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»)«/mo»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»=«/mo»«mi mathvariant=¨bold¨ mathcolor=¨#0000FF¨»m«/mi»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»§#183;«/mo»«msup»«msub»«mi mathvariant=¨bold¨ mathcolor=¨#0000FF¨»§#969;«/mi»«mi mathvariant=¨bold¨ mathcolor=¨#0000FF¨»min«/mi»«/msub»«mn mathvariant=¨bold¨ mathcolor=¨#0000FF¨»2«/mn»«/msup»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»§#183;«/mo»«mi mathvariant=¨bold¨ mathcolor=¨#0000FF¨»R«/mi»«mspace linebreak=¨newline¨»«/mspace»«menclose mathcolor=¨#0000FF¨ notation=¨box¨»«mi mathvariant=¨bold¨»N«/mi»«mo mathvariant=¨bold¨»§#183;«/mo»«mfenced open=¨[¨ close=¨]¨»«mrow»«mi mathvariant=¨bold¨»sin«/mi»«mo mathvariant=¨bold¨»(«/mo»«mn mathvariant=¨bold¨»15«/mn»«mo mathvariant=¨bold¨»)«/mo»«mo mathvariant=¨bold¨»+«/mo»«msub»«mi mathvariant=¨bold¨»§#956;«/mi»«mi mathvariant=¨bold¨»s«/mi»«/msub»«mo mathvariant=¨bold¨»§#183;«/mo»«mi mathvariant=¨bold¨»cos«/mi»«mo mathvariant=¨bold¨»(«/mo»«mn mathvariant=¨bold¨»15«/mn»«mo mathvariant=¨bold¨»)«/mo»«/mrow»«/mfenced»«mo mathvariant=¨bold¨»=«/mo»«mi mathvariant=¨bold¨»m«/mi»«mo mathvariant=¨bold¨»§#183;«/mo»«msup»«msub»«mi mathvariant=¨bold¨»§#969;«/mi»«mi mathvariant=¨bold¨»min«/mi»«/msub»«mn mathvariant=¨bold¨»2«/mn»«/msup»«mo mathvariant=¨bold¨»§#183;«/mo»«mi mathvariant=¨bold¨»R«/mi»«/menclose»«/math»
نقسم المعادلتين :
«math xmlns=¨http://www.w3.org/1998/Math/MathML¨»«mfrac mathcolor=¨#0000FF¨»«mrow»«menclose notation=¨updiagonalstrike¨»«mi mathvariant=¨bold¨»N«/mi»«/menclose»«mo mathvariant=¨bold¨»§#183;«/mo»«mfenced open=¨[¨ close=¨]¨»«mrow»«mi mathvariant=¨bold¨»sin«/mi»«mo mathvariant=¨bold¨»(«/mo»«mn mathvariant=¨bold¨»15«/mn»«mo mathvariant=¨bold¨»)«/mo»«mo mathvariant=¨bold¨»+«/mo»«msub»«mi mathvariant=¨bold¨»§#956;«/mi»«mi mathvariant=¨bold¨»s«/mi»«/msub»«mo mathvariant=¨bold¨»§#183;«/mo»«mi mathvariant=¨bold¨»cos«/mi»«mo mathvariant=¨bold¨»(«/mo»«mn mathvariant=¨bold¨»15«/mn»«mo mathvariant=¨bold¨»)«/mo»«/mrow»«/mfenced»«mo mathvariant=¨bold¨»§#160;«/mo»«/mrow»«mrow»«menclose notation=¨updiagonalstrike¨»«mi mathvariant=¨bold¨»N«/mi»«/menclose»«mo mathvariant=¨bold¨»§#183;«/mo»«mfenced open=¨[¨ close=¨]¨»«mrow»«mi mathvariant=¨bold¨»cos«/mi»«mo mathvariant=¨bold¨»(«/mo»«mn mathvariant=¨bold¨»15«/mn»«mo mathvariant=¨bold¨»)«/mo»«mo mathvariant=¨bold¨»-«/mo»«msub»«mi mathvariant=¨bold¨»§#956;«/mi»«mi mathvariant=¨bold¨»s«/mi»«/msub»«mo mathvariant=¨bold¨»§#183;«/mo»«mi mathvariant=¨bold¨»sin«/mi»«mo mathvariant=¨bold¨»(«/mo»«mn mathvariant=¨bold¨»15«/mn»«mo mathvariant=¨bold¨»)«/mo»«/mrow»«/mfenced»«/mrow»«/mfrac»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»=«/mo»«mfrac mathcolor=¨#0000FF¨»«mrow»«menclose notation=¨downdiagonalstrike¨»«mi mathvariant=¨bold¨»m«/mi»«/menclose»«mo mathvariant=¨bold¨»§#183;«/mo»«msup»«msub»«mi mathvariant=¨bold¨»§#969;«/mi»«mi mathvariant=¨bold¨»min«/mi»«/msub»«mn mathvariant=¨bold¨»2«/mn»«/msup»«mo mathvariant=¨bold¨»§#183;«/mo»«mi mathvariant=¨bold¨»R«/mi»«/mrow»«mrow»«menclose notation=¨downdiagonalstrike¨»«mi mathvariant=¨bold¨»m«/mi»«/menclose»«mo mathvariant=¨bold¨»§#183;«/mo»«mi mathvariant=¨bold¨»g«/mi»«/mrow»«/mfrac»«mspace linebreak=¨newline¨»«/mspace»«/math»
نعبّر عن السرعة الزاوية من التعبير الذي تم الحصول عليه:
«math xmlns=¨http://www.w3.org/1998/Math/MathML¨»«msub»«mi mathvariant=¨bold¨ mathcolor=¨#0000FF¨»§#969;«/mi»«mi mathvariant=¨bold¨ mathcolor=¨#0000FF¨»min«/mi»«/msub»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»=«/mo»«msqrt mathcolor=¨#0000FF¨»«mfrac»«mrow»«mi mathvariant=¨bold¨»g«/mi»«mo mathvariant=¨bold¨»§#183;«/mo»«mfenced open=¨[¨ close=¨]¨»«mrow»«mi mathvariant=¨bold¨»sin«/mi»«mo mathvariant=¨bold¨»(«/mo»«mn mathvariant=¨bold¨»15«/mn»«mo mathvariant=¨bold¨»)«/mo»«mo mathvariant=¨bold¨»+«/mo»«msub»«mi mathvariant=¨bold¨»§#956;«/mi»«mi mathvariant=¨bold¨»s«/mi»«/msub»«mo mathvariant=¨bold¨»§#183;«/mo»«mi mathvariant=¨bold¨»cos«/mi»«mo mathvariant=¨bold¨»(«/mo»«mn mathvariant=¨bold¨»15«/mn»«mo mathvariant=¨bold¨»)«/mo»«/mrow»«/mfenced»«mo mathvariant=¨bold¨»§#160;«/mo»«/mrow»«mrow»«mi mathvariant=¨bold¨»r«/mi»«mo mathvariant=¨bold¨»§#183;«/mo»«mfenced open=¨[¨ close=¨]¨»«mrow»«mi mathvariant=¨bold¨»cos«/mi»«mo mathvariant=¨bold¨»(«/mo»«mn mathvariant=¨bold¨»15«/mn»«mo mathvariant=¨bold¨»)«/mo»«mo mathvariant=¨bold¨»-«/mo»«msub»«mi mathvariant=¨bold¨»§#956;«/mi»«mi mathvariant=¨bold¨»s«/mi»«/msub»«mo mathvariant=¨bold¨»§#183;«/mo»«mi mathvariant=¨bold¨»sin«/mi»«mo mathvariant=¨bold¨»(«/mo»«mn mathvariant=¨bold¨»15«/mn»«mo mathvariant=¨bold¨»)«/mo»«/mrow»«/mfenced»«/mrow»«/mfrac»«/msqrt»«mspace linebreak=¨newline¨»«/mspace»«/math»
نعوّض المعطيات ونوجد الحد الأدنى للسرعة الزاوية التي ينفصل بها الجسم عن موقعه:
«math xmlns=¨http://www.w3.org/1998/Math/MathML¨»«msub»«mi mathvariant=¨bold¨ mathcolor=¨#0000FF¨»§#969;«/mi»«mi mathvariant=¨bold¨ mathcolor=¨#0000FF¨»min«/mi»«/msub»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»=«/mo»«msqrt mathcolor=¨#0000FF¨»«mfrac»«mrow»«mi mathvariant=¨bold¨»g«/mi»«mo mathvariant=¨bold¨»§#183;«/mo»«mfenced open=¨[¨ close=¨]¨»«mrow»«mi mathvariant=¨bold¨»sin«/mi»«mo mathvariant=¨bold¨»(«/mo»«mn mathvariant=¨bold¨»15«/mn»«mo mathvariant=¨bold¨»)«/mo»«mo mathvariant=¨bold¨»+«/mo»«msub»«mi mathvariant=¨bold¨»§#956;«/mi»«mi mathvariant=¨bold¨»s«/mi»«/msub»«mo mathvariant=¨bold¨»§#183;«/mo»«mi mathvariant=¨bold¨»cos«/mi»«mo mathvariant=¨bold¨»(«/mo»«mn mathvariant=¨bold¨»15«/mn»«mo mathvariant=¨bold¨»)«/mo»«/mrow»«/mfenced»«mo mathvariant=¨bold¨»§#160;«/mo»«/mrow»«mrow»«mi mathvariant=¨bold¨»r«/mi»«mo mathvariant=¨bold¨»§#183;«/mo»«mfenced open=¨[¨ close=¨]¨»«mrow»«mi mathvariant=¨bold¨»cos«/mi»«mo mathvariant=¨bold¨»(«/mo»«mn mathvariant=¨bold¨»15«/mn»«mo mathvariant=¨bold¨»)«/mo»«mo mathvariant=¨bold¨»-«/mo»«msub»«mi mathvariant=¨bold¨»§#956;«/mi»«mi mathvariant=¨bold¨»s«/mi»«/msub»«mo mathvariant=¨bold¨»§#183;«/mo»«mi mathvariant=¨bold¨»sin«/mi»«mo mathvariant=¨bold¨»(«/mo»«mn mathvariant=¨bold¨»25«/mn»«mo mathvariant=¨bold¨»)«/mo»«/mrow»«/mfenced»«/mrow»«/mfrac»«/msqrt»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»=«/mo»«msqrt mathcolor=¨#0000FF¨»«mfrac»«mrow»«mn mathvariant=¨bold¨»10«/mn»«mo mathvariant=¨bold¨»§#183;«/mo»«mfenced open=¨[¨ close=¨]¨»«mrow»«mi mathvariant=¨bold¨»sin«/mi»«mo mathvariant=¨bold¨»(«/mo»«mn mathvariant=¨bold¨»15«/mn»«mo mathvariant=¨bold¨»)«/mo»«mo mathvariant=¨bold¨»+«/mo»«mn mathvariant=¨bold¨»0«/mn»«mo mathvariant=¨bold¨».«/mo»«mn mathvariant=¨bold¨»5«/mn»«mo mathvariant=¨bold¨»§#183;«/mo»«mi mathvariant=¨bold¨»cos«/mi»«mo mathvariant=¨bold¨»(«/mo»«mn mathvariant=¨bold¨»15«/mn»«mo mathvariant=¨bold¨»)«/mo»«/mrow»«/mfenced»«mo mathvariant=¨bold¨»§#160;«/mo»«/mrow»«mrow»«mn mathvariant=¨bold¨»0«/mn»«mo mathvariant=¨bold¨».«/mo»«mn mathvariant=¨bold¨»1«/mn»«mo mathvariant=¨bold¨»§#183;«/mo»«mfenced open=¨[¨ close=¨]¨»«mrow»«mi mathvariant=¨bold¨»cos«/mi»«mo mathvariant=¨bold¨»(«/mo»«mn mathvariant=¨bold¨»15«/mn»«mo mathvariant=¨bold¨»)«/mo»«mo mathvariant=¨bold¨»-«/mo»«mn mathvariant=¨bold¨»0«/mn»«mo mathvariant=¨bold¨».«/mo»«mn mathvariant=¨bold¨»5«/mn»«mo mathvariant=¨bold¨»§#183;«/mo»«mi mathvariant=¨bold¨»sin«/mi»«mo mathvariant=¨bold¨»(«/mo»«mn mathvariant=¨bold¨»15«/mn»«mo mathvariant=¨bold¨»)«/mo»«/mrow»«/mfenced»«/mrow»«/mfrac»«/msqrt»«mspace linebreak=¨newline¨»«/mspace»«msub»«mi mathvariant=¨bold¨ mathcolor=¨#0000FF¨»§#969;«/mi»«mi mathvariant=¨bold¨ mathcolor=¨#0000FF¨»min«/mi»«/msub»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»=«/mo»«msqrt mathcolor=¨#0000FF¨»«mfrac»«mrow»«mn mathvariant=¨bold¨»10«/mn»«mo mathvariant=¨bold¨»§#183;«/mo»«mfenced open=¨[¨ close=¨]¨»«mrow»«mn mathvariant=¨bold¨»0«/mn»«mo mathvariant=¨bold¨».«/mo»«mn mathvariant=¨bold¨»258«/mn»«mo mathvariant=¨bold¨»+«/mo»«mn mathvariant=¨bold¨»0«/mn»«mo mathvariant=¨bold¨».«/mo»«mn mathvariant=¨bold¨»48«/mn»«/mrow»«/mfenced»«mo mathvariant=¨bold¨»§#160;«/mo»«/mrow»«mrow»«mn mathvariant=¨bold¨»0«/mn»«mo mathvariant=¨bold¨».«/mo»«mn mathvariant=¨bold¨»1«/mn»«mo mathvariant=¨bold¨»§#183;«/mo»«mfenced open=¨[¨ close=¨]¨»«mrow»«mn mathvariant=¨bold¨»0«/mn»«mo mathvariant=¨bold¨».«/mo»«mn mathvariant=¨bold¨»96«/mn»«mo mathvariant=¨bold¨»-«/mo»«mn mathvariant=¨bold¨»0«/mn»«mo mathvariant=¨bold¨».«/mo»«mn mathvariant=¨bold¨»129«/mn»«/mrow»«/mfenced»«/mrow»«/mfrac»«/msqrt»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»=«/mo»«msqrt mathcolor=¨#0000FF¨»«mfrac»«mrow»«mn mathvariant=¨bold¨»7«/mn»«mo mathvariant=¨bold¨».«/mo»«mn mathvariant=¨bold¨»41«/mn»«/mrow»«mrow»«mn mathvariant=¨bold¨»0«/mn»«mo mathvariant=¨bold¨».«/mo»«mn mathvariant=¨bold¨»0831«/mn»«/mrow»«/mfrac»«/msqrt»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»=«/mo»«msqrt mathcolor=¨#0000FF¨»«mn mathvariant=¨bold¨»89«/mn»«mo mathvariant=¨bold¨».«/mo»«mn mathvariant=¨bold¨»17«/mn»«/msqrt»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»=«/mo»«mn mathvariant=¨bold¨ mathcolor=¨#0000FF¨»9«/mn»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨».«/mo»«mn mathvariant=¨bold¨ mathcolor=¨#0000FF¨»44«/mn»«mfrac mathcolor=¨#0000FF¨»«mrow»«mi mathvariant=¨bold¨»r«/mi»«mi mathvariant=¨bold¨»a«/mi»«mi mathvariant=¨bold¨»d«/mi»«/mrow»«mi mathvariant=¨bold¨»s«/mi»«/mfrac»«mspace linebreak=¨newline¨»«/mspace»«/math»
لذلك ، فإن أقل سرعة زاوية مطلوبة لتحرك الجسم من موقعه هي 9.44 راديان في الثانية.
כעת הגוף נע בתנועה מעגלית במישור אופקי, נסמן את מישור התנועה ואת נקודת מרכז הסיבוב,
ונערוך תרשים כוחות לכוחות הפועלים על הגוף במצב זה:
לכוח הכובד אין רכיב הפונה אל נקודת מרכז הסיבוב , לכוח הנורמל יש , וגם לכוח החיכוך הסטטי יש.
נבחר מערכת צירים שבה כיוון ציר X הוא אופקי, פונה אל נקודת מרכז הסיבוב . וכיוון ציר Y אנכי נגדי לכוח הכובד.
נבצע הפרדה ישרת זווית בהתאם למערכת צירים זו, לכוח הנורמל ולכוח החיכוך הסטטי:
גיאומטרית , זווית נטיית המישור , שווה לזווית שבין N ל NY , ושווה גם לזווית שבין fs לבין fsx.
כדי למצוא את המהירות הזוויתית המינימאלית , נתייחס למקרה של סף תנועה ,כאשר החיכוך הסטטי הפועל על הגוף שווה לחיכוך הסטטי מקסימאלי.
נכתוב את משוואות התנועה לכיוון האנכי ולכיוון האופקי:
«math xmlns=¨http://www.w3.org/1998/Math/MathML¨»«msub»«mi mathvariant=¨bold¨ mathcolor=¨#0000FF¨»§#931;F«/mi»«mi mathvariant=¨bold¨ mathcolor=¨#0000FF¨»y«/mi»«/msub»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»=«/mo»«mn mathvariant=¨bold¨ mathcolor=¨#0000FF¨»0«/mn»«mspace linebreak=¨newline¨»«/mspace»«msub»«mi mathvariant=¨bold¨ mathcolor=¨#0000FF¨»N«/mi»«mi mathvariant=¨bold¨ mathcolor=¨#0000FF¨»Y«/mi»«/msub»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»=«/mo»«mi mathvariant=¨bold¨ mathcolor=¨#0000FF¨»W«/mi»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»+«/mo»«msub»«mi mathvariant=¨bold¨ mathcolor=¨#0000FF¨»fs«/mi»«msub mathcolor=¨#0000FF¨»«mi mathvariant=¨bold¨»max«/mi»«mi mathvariant=¨bold¨»y«/mi»«/msub»«/msub»«mspace linebreak=¨newline¨»«/mspace»«menclose mathcolor=¨#0000FF¨ notation=¨box¨»«mi mathvariant=¨bold¨»N«/mi»«mo mathvariant=¨bold¨»§#183;«/mo»«mi mathvariant=¨bold¨»cos«/mi»«mo mathvariant=¨bold¨»(«/mo»«mn mathvariant=¨bold¨»25«/mn»«mo mathvariant=¨bold¨»)«/mo»«mo mathvariant=¨bold¨»=«/mo»«mi mathvariant=¨bold¨»mg«/mi»«mo mathvariant=¨bold¨»+«/mo»«msub»«mi mathvariant=¨bold¨»§#956;«/mi»«mi mathvariant=¨bold¨»s«/mi»«/msub»«mo mathvariant=¨bold¨»§#183;«/mo»«mi mathvariant=¨bold¨»N«/mi»«mo mathvariant=¨bold¨»§#183;«/mo»«mi mathvariant=¨bold¨»sin«/mi»«mo mathvariant=¨bold¨»(«/mo»«mn mathvariant=¨bold¨»25«/mn»«mo mathvariant=¨bold¨»)«/mo»«/menclose»«/math» «math xmlns=¨http://www.w3.org/1998/Math/MathML¨»«msub»«mi mathvariant=¨bold¨ mathcolor=¨#0000FF¨»§#931;F«/mi»«mi mathvariant=¨bold¨ mathcolor=¨#0000FF¨»R«/mi»«/msub»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»=«/mo»«mi mathvariant=¨bold¨ mathcolor=¨#0000FF¨»m«/mi»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»§#183;«/mo»«msup»«mi mathvariant=¨bold¨ mathcolor=¨#0000FF¨»§#969;«/mi»«mn mathvariant=¨bold¨ mathcolor=¨#0000FF¨»2«/mn»«/msup»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»§#183;«/mo»«mi mathvariant=¨bold¨ mathcolor=¨#0000FF¨»R«/mi»«mspace linebreak=¨newline¨»«/mspace»«msub»«mi mathvariant=¨bold¨ mathcolor=¨#0000FF¨»N«/mi»«mi mathvariant=¨bold¨ mathcolor=¨#0000FF¨»x«/mi»«/msub»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»+«/mo»«msub»«mi mathvariant=¨bold¨ mathcolor=¨#0000FF¨»f«/mi»«msub mathcolor=¨#0000FF¨»«mi mathvariant=¨bold¨»S«/mi»«msub»«mi mathvariant=¨bold¨»MAX«/mi»«mi mathvariant=¨bold¨»X«/mi»«/msub»«/msub»«/msub»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»=«/mo»«mi mathvariant=¨bold¨ mathcolor=¨#0000FF¨»m«/mi»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»§#183;«/mo»«msup»«mi mathvariant=¨bold¨ mathcolor=¨#0000FF¨»§#969;«/mi»«mn mathvariant=¨bold¨ mathcolor=¨#0000FF¨»2«/mn»«/msup»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»§#183;«/mo»«mi mathvariant=¨bold¨ mathcolor=¨#0000FF¨»R«/mi»«mspace linebreak=¨newline¨»«/mspace»«menclose mathcolor=¨#0000FF¨ notation=¨box¨»«mi mathvariant=¨bold¨»N«/mi»«mo mathvariant=¨bold¨»§#183;«/mo»«mi mathvariant=¨bold¨»sin«/mi»«mo mathvariant=¨bold¨»(«/mo»«mn mathvariant=¨bold¨»25«/mn»«mo mathvariant=¨bold¨»)«/mo»«mo mathvariant=¨bold¨»+«/mo»«msub»«mi mathvariant=¨bold¨»§#956;«/mi»«mi mathvariant=¨bold¨»s«/mi»«/msub»«mo mathvariant=¨bold¨»§#183;«/mo»«mi mathvariant=¨bold¨»N«/mi»«mo mathvariant=¨bold¨»§#183;«/mo»«mi mathvariant=¨bold¨»cos«/mi»«mo mathvariant=¨bold¨»(«/mo»«mi mathvariant=¨bold¨»§#945;«/mi»«mo mathvariant=¨bold¨»)«/mo»«mo mathvariant=¨bold¨»=«/mo»«mi mathvariant=¨bold¨»m«/mi»«mo mathvariant=¨bold¨»§#183;«/mo»«msup»«mi mathvariant=¨bold¨»§#969;«/mi»«mn mathvariant=¨bold¨»2«/mn»«/msup»«mo mathvariant=¨bold¨»§#183;«/mo»«mi mathvariant=¨bold¨»R«/mi»«/menclose»«mspace linebreak=¨newline¨»«/mspace»«/math»
נכתוב את המשוואות כך שלאחר חילוק משוואה במשוואה הנורמל יצטמצם :
«math xmlns=¨http://www.w3.org/1998/Math/MathML¨»«mi mathvariant=¨bold¨ mathcolor=¨#0000FF¨»N«/mi»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»§#183;«/mo»«mi mathvariant=¨bold¨ mathcolor=¨#0000FF¨»cos«/mi»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»(«/mo»«mn mathvariant=¨bold¨ mathcolor=¨#0000FF¨»25«/mn»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»)«/mo»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»=«/mo»«mi mathvariant=¨bold¨ mathcolor=¨#0000FF¨»mg«/mi»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»+«/mo»«msub»«mi mathvariant=¨bold¨ mathcolor=¨#0000FF¨»§#956;«/mi»«mi mathvariant=¨bold¨ mathcolor=¨#0000FF¨»s«/mi»«/msub»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»§#183;«/mo»«mi mathvariant=¨bold¨ mathcolor=¨#0000FF¨»N«/mi»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»§#183;«/mo»«mi mathvariant=¨bold¨ mathcolor=¨#0000FF¨»sin«/mi»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»(«/mo»«mn mathvariant=¨bold¨ mathcolor=¨#0000FF¨»25«/mn»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»)«/mo»«mspace linebreak=¨newline¨»«/mspace»«menclose mathcolor=¨#0000FF¨ notation=¨box¨»«mi mathvariant=¨bold¨»N«/mi»«mo mathvariant=¨bold¨»§#183;«/mo»«mfenced open=¨[¨ close=¨]¨»«mrow»«mi mathvariant=¨bold¨»cos«/mi»«mo mathvariant=¨bold¨»(«/mo»«mn mathvariant=¨bold¨»25«/mn»«mo mathvariant=¨bold¨»)«/mo»«mo mathvariant=¨bold¨»-«/mo»«msub»«mi mathvariant=¨bold¨»§#956;«/mi»«mi mathvariant=¨bold¨»s«/mi»«/msub»«mo mathvariant=¨bold¨»§#183;«/mo»«mi mathvariant=¨bold¨»sin«/mi»«mo mathvariant=¨bold¨»(«/mo»«mn mathvariant=¨bold¨»25«/mn»«mo mathvariant=¨bold¨»)«/mo»«/mrow»«/mfenced»«mo mathvariant=¨bold¨»=«/mo»«mi mathvariant=¨bold¨»mg«/mi»«/menclose»«/math» «math xmlns=¨http://www.w3.org/1998/Math/MathML¨»«mi mathvariant=¨bold¨ mathcolor=¨#0000FF¨»N«/mi»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»§#183;«/mo»«mi mathvariant=¨bold¨ mathcolor=¨#0000FF¨»sin«/mi»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»(«/mo»«mn mathvariant=¨bold¨ mathcolor=¨#0000FF¨»25«/mn»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»)«/mo»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»+«/mo»«msub»«mi mathvariant=¨bold¨ mathcolor=¨#0000FF¨»§#956;«/mi»«mi mathvariant=¨bold¨ mathcolor=¨#0000FF¨»s«/mi»«/msub»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»§#183;«/mo»«mi mathvariant=¨bold¨ mathcolor=¨#0000FF¨»N«/mi»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»§#183;«/mo»«mi mathvariant=¨bold¨ mathcolor=¨#0000FF¨»cos«/mi»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»(«/mo»«mi mathvariant=¨bold¨ mathcolor=¨#0000FF¨»§#945;«/mi»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»)«/mo»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»=«/mo»«mi mathvariant=¨bold¨ mathcolor=¨#0000FF¨»m«/mi»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»§#183;«/mo»«msup»«mi mathvariant=¨bold¨ mathcolor=¨#0000FF¨»§#969;«/mi»«mn mathvariant=¨bold¨ mathcolor=¨#0000FF¨»2«/mn»«/msup»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»§#183;«/mo»«mi mathvariant=¨bold¨ mathcolor=¨#0000FF¨»R«/mi»«mspace linebreak=¨newline¨»«/mspace»«menclose mathcolor=¨#0000FF¨ notation=¨box¨»«mi mathvariant=¨bold¨»N«/mi»«mo mathvariant=¨bold¨»§#183;«/mo»«mfenced open=¨[¨ close=¨]¨»«mrow»«mi mathvariant=¨bold¨»sin«/mi»«mo mathvariant=¨bold¨»(«/mo»«mn mathvariant=¨bold¨»25«/mn»«mo mathvariant=¨bold¨»)«/mo»«mo mathvariant=¨bold¨»+«/mo»«msub»«mi mathvariant=¨bold¨»§#956;«/mi»«mi mathvariant=¨bold¨»s«/mi»«/msub»«mo mathvariant=¨bold¨»§#183;«/mo»«mi mathvariant=¨bold¨»cos«/mi»«mo mathvariant=¨bold¨»(«/mo»«mi mathvariant=¨bold¨»§#945;«/mi»«mo mathvariant=¨bold¨»)«/mo»«/mrow»«/mfenced»«mo mathvariant=¨bold¨»=«/mo»«mi mathvariant=¨bold¨»m«/mi»«mo mathvariant=¨bold¨»§#183;«/mo»«msup»«mi mathvariant=¨bold¨»§#969;«/mi»«mn mathvariant=¨bold¨»2«/mn»«/msup»«mo mathvariant=¨bold¨»§#183;«/mo»«mi mathvariant=¨bold¨»R«/mi»«/menclose»«/math»
נחלק את המשוואות :
«math xmlns=¨http://www.w3.org/1998/Math/MathML¨»«mfrac mathcolor=¨#0000FF¨»«mrow»«menclose notation=¨updiagonalstrike¨»«mi mathvariant=¨bold¨»N«/mi»«/menclose»«mo mathvariant=¨bold¨»§#183;«/mo»«mfenced open=¨[¨ close=¨]¨»«mrow»«mi mathvariant=¨bold¨»sin«/mi»«mo mathvariant=¨bold¨»(«/mo»«mn mathvariant=¨bold¨»25«/mn»«mo mathvariant=¨bold¨»)«/mo»«mo mathvariant=¨bold¨»+«/mo»«msub»«mi mathvariant=¨bold¨»§#956;«/mi»«mi mathvariant=¨bold¨»s«/mi»«/msub»«mo mathvariant=¨bold¨»§#183;«/mo»«mi mathvariant=¨bold¨»cos«/mi»«mo mathvariant=¨bold¨»(«/mo»«mi mathvariant=¨bold¨»§#945;«/mi»«mo mathvariant=¨bold¨»)«/mo»«/mrow»«/mfenced»«mo mathvariant=¨bold¨»§#160;«/mo»«/mrow»«mrow»«menclose notation=¨updiagonalstrike¨»«mi mathvariant=¨bold¨»N«/mi»«/menclose»«mo mathvariant=¨bold¨»§#183;«/mo»«mfenced open=¨[¨ close=¨]¨»«mrow»«mi mathvariant=¨bold¨»cos«/mi»«mo mathvariant=¨bold¨»(«/mo»«mn mathvariant=¨bold¨»25«/mn»«mo mathvariant=¨bold¨»)«/mo»«mo mathvariant=¨bold¨»-«/mo»«msub»«mi mathvariant=¨bold¨»§#956;«/mi»«mi mathvariant=¨bold¨»s«/mi»«/msub»«mo mathvariant=¨bold¨»§#183;«/mo»«mi mathvariant=¨bold¨»sin«/mi»«mo mathvariant=¨bold¨»(«/mo»«mn mathvariant=¨bold¨»25«/mn»«mo mathvariant=¨bold¨»)«/mo»«/mrow»«/mfenced»«/mrow»«/mfrac»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»=«/mo»«mfrac mathcolor=¨#0000FF¨»«mrow»«menclose notation=¨downdiagonalstrike¨»«mi mathvariant=¨bold¨»m«/mi»«/menclose»«mo mathvariant=¨bold¨»§#183;«/mo»«msup»«mi mathvariant=¨bold¨»§#969;«/mi»«mn mathvariant=¨bold¨»2«/mn»«/msup»«mo mathvariant=¨bold¨»§#183;«/mo»«mi mathvariant=¨bold¨»R«/mi»«/mrow»«mrow»«menclose notation=¨downdiagonalstrike¨»«mi mathvariant=¨bold¨»m«/mi»«/menclose»«mo mathvariant=¨bold¨»§#183;«/mo»«mi mathvariant=¨bold¨»g«/mi»«/mrow»«/mfrac»«mspace linebreak=¨newline¨»«/mspace»«/math»
1. عندما لا تدور المجموعة ، تكون قوة الجاذبية أكبر من القوة العمودية.
وعندما تدور المجموعة ، يكون مقدار مركّب القوة العمودية مساويًا لمقدار قوة الجاذبية.
نتيجة لدوران المجموعة، تتغير القوى، يجب رسم مخطّط قوى جديد.
2. من حيث المبادئ الفيزيائية ، فإن هذه المجموعة يشبه السيارة التي تكون على مستوى دائري مائل.
عندما لا تتحرك السيارة ، تكون القوة العمودية أقل من قوة الجاذبية ، وعندما تتحرك السيارة في حركة دائرية ، تكون القوة العمودية أكبر من قوة الجاذبية.
3. قبل البدء في تحليل الحركة الدائرية، من المهم أن نفهم كيف يبدو مستوى الحركة وأين تقع نقطة مركز الدوران.
4. الجسم على عمود مائل ، لكن مستوى الحركة أفقي
5. من وجهة نظرنا ، فإن السرعة الدنيا للدوران التي ينفصل بها الجسم تساوي السرعة القصوى التي يمكن للجسم أن يتحرك بها دون أن ينفصل.
6. في أي حركة دائرية ، المحور X موجّه نحو النقطة المركزية للدوران ، ويكون المحور Y متعامدًا عليه. ووفقًا لهذه المحاور فقط ، يجب تحليل القوى المؤثرة على الجسم ، والتي ليست على أحد المحاور.
7. يمكنك استخدام الزاوية المعطاة في السؤال ، أو حساب زاوية ميل الأنبوب ، واستخدام هذه الزاوية بشكل مشابه لمستوى مائل.
8. يوصى بشدة بالتدرب على حل هذا السؤال ، والخطأ والتصحيح ، والخطأ والتصحيح ، حتى تصل إلى الحل الصحيح.
وبعد أسبوع ، حاول حلها مرة أخرى.
וכאשר המערכת מסתובבת הגודל של רכיב הנורמל שווה לגודל כוח הכובד.
כתוצאה מסיבוב המערכת , הכוחות משתנים , חובה לערוך תרשים כוחות חדש.
2. מבחינת העקרונות הפיזיקליים, מערכת זו דומה למכונית הנמצאת על מישור מעגלי נטוי .
כאשר המכונית לא זזה כוח הנורמל קטן מכוח הכובד, וכאשר המכונית נעה בתנועה מעגלית כוח הנורמל גדול מכוח הכובד.
3. לפני שמתחילים לנתח את התנועה המעגלית , חשוב להבין כיצד נראה מישור התנועה והיכן נמצאת נקודת מרכז הסיבוב.
4. הגוף נמצא על מוט נטוי, אך מישור התנועה הוא אופקי
5. מבחינתנו, מהירות הסיבוב המינימאלית שבה הגוף ניתק, שווה למהירות המקסימאלית שבה הגוף יכול לנוע בלי להינתק.
6. בכל תנועה מעגלית , ציר X פונה לנקודת מרכז הסיבוב , ציר Y מאונך לו. ורק בהתאם לצירים אלו יש לבצע הפרדה ישרת זווית
על הכוחות הפועלים על הגוף,שאינם נמצאים על אחד הצירים.
7. אפשר להשתמש בזווית הנתונה בשאלה, או לחשב את זווית נטיית הצינור , ולהשתמש בזווית זו בדומה למישור משופע.
8. מאוד מומלץ לתרגל פתרון של שאלה זו, לטעות לתקן , לטעות ולתקן, עד שמגיעים לפתרון הנכון.
וכעבור שבוע , לנסות לפתור שוב.
9. מאוד לא מומלץ לפתור שאלה כזו במבחן הבגרות, מטעויות בתרגול מרוויחים. על טעויות במבחן מפסידים נקודות.
__________________________________________________________________
_________________