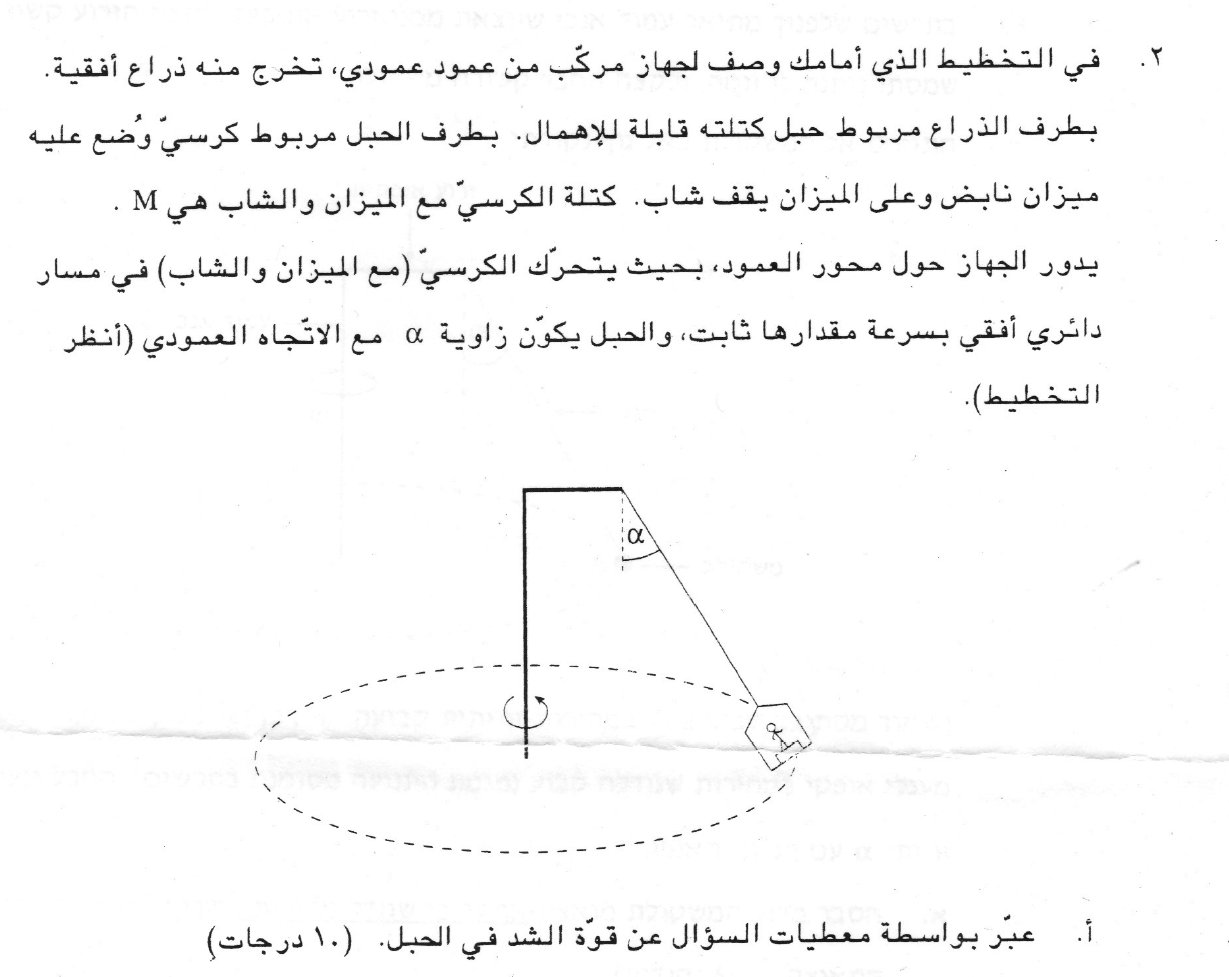
حلول ومنتديات لـ"ألبوم الحلول" – الحركة الدائرية المنتظمة.: 1997,2-بندول مع ذراع أفقي

9. 1997,2-بندول مع ذراع أفقي

______________________________________________________________________________________

...

«math xmlns=¨http://www.w3.org/1998/Math/MathML¨»«mi mathvariant=¨bold¨»T«/mi»«mo mathvariant=¨bold¨»=«/mo»«mfrac»«mrow»«mi mathvariant=¨bold¨»M«/mi»«mo mathvariant=¨bold¨»§#183;«/mo»«mi mathvariant=¨bold¨»g«/mi»«/mrow»«mrow»«mi mathvariant=¨bold¨»cos«/mi»«mo mathvariant=¨bold¨»(«/mo»«mi mathvariant=¨bold¨»§#945;«/mi»«mo mathvariant=¨bold¨»)«/mo»«/mrow»«/mfrac»«/math»

التعامل مع الكرسي والشخص والميزان كجسم واحد. رسم مخطّط القوى المؤثرة على الجسم وكتابة معادلات الحركة والتعبير عن قوة الشد من معادلات الحركة.

نتعامل مع الكرسي والشخص والميزان كجسم واحد ، يتحرك في حركة دائرية منتظمة ، في مستوى أفقي.

لا يوجد مركّب لقوة الجاذبية في الاتجاه الأفقي. القوة الجاذبة نحو المركز هي أحد مركّبات قوة الشد في الاتجاه الأفقي.

نرسم مخطّط للقوى التي تؤثر على الجسم ، ونحلل قوة التوتر إلى مركبتيها:

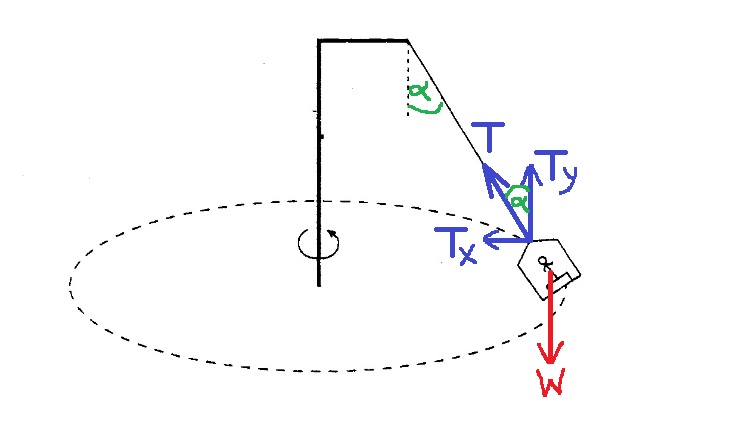
سنكتب معادلة الحركة بالنسبة للمحور الموجه إلى نقطة مركز الدائرة. ومعادلة الحركة العمودية بالنسبة للمحور الرأسي الموجه لأعلى:

«math xmlns=¨http://www.w3.org/1998/Math/MathML¨»«msub»«mi mathvariant=¨bold¨ mathcolor=¨#0000FF¨»§#931;F«/mi»«mi mathvariant=¨bold¨ mathcolor=¨#0000FF¨»R«/mi»«/msub»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»=«/mo»«mi mathvariant=¨bold¨ mathcolor=¨#0000FF¨»M«/mi»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»§#183;«/mo»«msup»«mi mathvariant=¨bold¨ mathcolor=¨#0000FF¨»§#969;«/mi»«mn mathvariant=¨bold¨ mathcolor=¨#0000FF¨»2«/mn»«/msup»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»§#183;«/mo»«mi mathvariant=¨bold¨ mathcolor=¨#0000FF¨»R«/mi»«mspace linebreak=¨newline¨»«/mspace»«msub»«mi mathvariant=¨bold¨ mathcolor=¨#0000FF¨»T«/mi»«mi mathvariant=¨bold¨ mathcolor=¨#0000FF¨»X«/mi»«/msub»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»=«/mo»«mi mathvariant=¨bold¨ mathcolor=¨#0000FF¨»M«/mi»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»§#183;«/mo»«msup»«mi mathvariant=¨bold¨ mathcolor=¨#0000FF¨»§#969;«/mi»«mn mathvariant=¨bold¨ mathcolor=¨#0000FF¨»2«/mn»«/msup»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»§#183;«/mo»«mi mathvariant=¨bold¨ mathcolor=¨#0000FF¨»R«/mi»«mspace linebreak=¨newline¨»«/mspace»«menclose mathcolor=¨#0000FF¨ notation=¨box¨»«mi mathvariant=¨bold¨»T«/mi»«mo mathvariant=¨bold¨»§#183;«/mo»«mi mathvariant=¨bold¨»sin«/mi»«mo mathvariant=¨bold¨»(«/mo»«mi mathvariant=¨bold¨»§#945;«/mi»«mo mathvariant=¨bold¨»)«/mo»«mo mathvariant=¨bold¨»=«/mo»«mi mathvariant=¨bold¨»M«/mi»«mo mathvariant=¨bold¨»§#183;«/mo»«msup»«mi mathvariant=¨bold¨»§#969;«/mi»«mn mathvariant=¨bold¨»2«/mn»«/msup»«mo mathvariant=¨bold¨»§#183;«/mo»«mi mathvariant=¨bold¨»R«/mi»«/menclose»«/math» «math xmlns=¨http://www.w3.org/1998/Math/MathML¨»«msub»«mi mathvariant=¨bold¨ mathcolor=¨#0000FF¨»§#931;F«/mi»«mi mathvariant=¨bold¨ mathcolor=¨#0000FF¨»Y«/mi»«/msub»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»=«/mo»«mn mathvariant=¨bold¨ mathcolor=¨#0000FF¨»0«/mn»«mspace linebreak=¨newline¨»«/mspace»«msub»«mi mathvariant=¨bold¨ mathcolor=¨#0000FF¨»T«/mi»«mi mathvariant=¨bold¨ mathcolor=¨#0000FF¨»Y«/mi»«/msub»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»=«/mo»«mi mathvariant=¨bold¨ mathcolor=¨#0000FF¨»W«/mi»«mspace linebreak=¨newline¨»«/mspace»«menclose mathcolor=¨#0000FF¨ notation=¨box¨»«mi mathvariant=¨bold¨»T«/mi»«mo mathvariant=¨bold¨»§#183;«/mo»«mi mathvariant=¨bold¨»cos«/mi»«mo mathvariant=¨bold¨»(«/mo»«mi mathvariant=¨bold¨»§#945;«/mi»«mo mathvariant=¨bold¨»)«/mo»«mo mathvariant=¨bold¨»=«/mo»«mi mathvariant=¨bold¨»M«/mi»«mo mathvariant=¨bold¨»§#183;«/mo»«mi mathvariant=¨bold¨»g«/mi»«/menclose»«/math»

نعبّر عن قوة الشد من معادلة الحركة العمودية:

«math xmlns=¨http://www.w3.org/1998/Math/MathML¨»«mi mathvariant=¨bold¨ mathcolor=¨#0000FF¨»T«/mi»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»§#183;«/mo»«mi mathvariant=¨bold¨ mathcolor=¨#0000FF¨»cos«/mi»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»(«/mo»«mi mathvariant=¨bold¨ mathcolor=¨#0000FF¨»§#945;«/mi»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»)«/mo»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»=«/mo»«mi mathvariant=¨bold¨ mathcolor=¨#0000FF¨»M«/mi»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»§#183;«/mo»«mi mathvariant=¨bold¨ mathcolor=¨#0000FF¨»g«/mi»«mspace linebreak=¨newline¨»«/mspace»«menclose mathcolor=¨#0000FF¨ notation=¨circle¨»«mi mathvariant=¨bold¨»T«/mi»«mo mathvariant=¨bold¨»=«/mo»«mfrac»«mrow»«mi mathvariant=¨bold¨»M«/mi»«mo mathvariant=¨bold¨»§#183;«/mo»«mi mathvariant=¨bold¨»g«/mi»«/mrow»«mrow»«mi mathvariant=¨bold¨»cos«/mi»«mo mathvariant=¨bold¨»(«/mo»«mi mathvariant=¨bold¨»§#945;«/mi»«mo mathvariant=¨bold¨»)«/mo»«/mrow»«/mfrac»«/menclose»«/math»

הגוף נע בתנועה מעגלית קצובה במישור אופקי. אין לכוח הכובד רכיב בכיוון האופקי.

הכוח הצנטריפטאלי הוא כוח רכיב כוח המתיחות בכיוון האופקי.

נערוך תרשים כוחות לגוף, נבצע הפרדה ישרת זווית לכוח המתיחות:

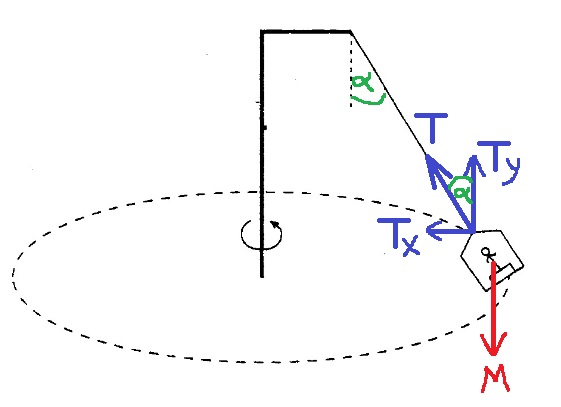
נכתוב את משוואת התנועה הרדיאלית ביחס לציר שכיוונו אל נקודת מרכז המעגל. ואת משוואה התנועה האנכית ביחס לציר אנכי שכיוונו כלפי מעלה:

נבטא את כוח המתיחות ממשוואת התנועה האנכית:

1. لكي تظهر قوة التوتر في معادلات الحركة ، كما هو مكتوب ، من المهم في السؤال التعامل مع الكرسي والشخص والميزان كجسم واحد.
إذا قمنا برسم مخطّط القوى التي تعمل فقط على ا لشخص (أو الميزان) وكتبنا معادلات الحركة وفقًا لذلك ، فلن تظهر قوة التوتر في معادلات الحركة.
إذا قمنا بعمل رسم تخطيطي للقوة للكرسي فقط ، فسيظهر قوة الشد ، لكن علينا إيجاد القوة التي شغّلها الميزان عليه.

2. يجب التعبير عن قوة الشد "باستخدام معطيات السؤال" ، فمعطيات السؤال هي جميع المقادير الفيزيائية المذكورة في مقدمة السؤال.
يمكنك أيضًا استخدام جميع الثوابت، حتى لو لم تظهر في السؤال ، لذا يمكنك استخدام g.

3. تتضمن معادلة الحركة نحو المركز أيضًا السرعة الزاوية ونصف قطر المسار الذي لا يظهر في السؤال.
معادلة الحركة العمودية توضح قوة الشد والمعطيات في السؤال ، لذلك يجب استخدام معادلة الحركة العمودية للتعبير عن قوة الشد.

4.لمعادلة الحركة الدائرية يوجد شكلين ، أحدهما معبر عنها بواسطة السرعة الزاوية والآخر بواسطة السرعة الخطية.
لتوفير العمليات الجبرية غير الضرورية ، من المهم اختيار المعادلة المناسبة. يجب أن يتطابق الاختيار ليس مع القسم الأول فحسب ، بل يجب أن يتطابق مع جميع أقسام السؤال.
في هذه الحالة ، على غير العادة ، لا يوجد تفضيل لشكل على الآخر.

2. יש לבטא את המתיחות "באמצעות נתוני השאלה" , נתוני השאלה הם כל הגדלים הפיזיקליים במופיעים בפתיח לשאלה .

וכל הקבועים גם אם הם לא מופיעים בשאלה ,לכן אפשר להשתמש ב g .

3. משוואת התנועה הרדיאלית כוללת גם את המהירות הזוויתית ורדיוס המסלול שלא מופיע בשאלה. הם לא מופיעים במשוואת התנועה האנכית .

לכן, יש להשתמש דווקא במשוואת התנועה האנכית כדי לבטא את המתיחות.

4. למשוואת התנועה המעגלית יש שתי צורות , אחת עם מהירות זוויתית ואחת עם מהירות קווית.

כדי לחסוך פעולות אלגבריות מיותרות , חשוב לבחור במשוואה המתאימה. בחירה צריכה להתאים לא רק לסעיף הראשון אלא לכל סעיפי השאלה.

במקרה זה , באופן מאוד חריג , אין עדיפות לצורה אחת על פני השנייה.

______________________________________________________________________________________

...

«math xmlns=¨http://www.w3.org/1998/Math/MathML¨»«msub»«mi mathvariant=¨bold¨»a«/mi»«mi mathvariant=¨bold¨»R«/mi»«/msub»«mo mathvariant=¨bold¨»=«/mo»«mi mathvariant=¨bold¨»g«/mi»«mo mathvariant=¨bold¨»§#183;«/mo»«mi mathvariant=¨bold¨»tan«/mi»«mo mathvariant=¨bold¨»(«/mo»«mi mathvariant=¨bold¨»§#945;«/mi»«mo mathvariant=¨bold¨»)«/mo»«/math»

كتابة معادلة الحركة في الصورة العامة باستخدام التسارع.

يتحرك الكرسي بحركة دائرية منتظمة. له تسارع نحو المركز ، وليس لديه تسارع مماسي.

الكرسي هو جزء من الجسم الذي كتلته M. تسارع الكرسي هو نفسه تسارع الجسم.

لنكتب معادلة الحركة الدائرية للجسم:

نقوم بتعويض تعبير الشد من القسم السابق في تعبير التسارع:

«math xmlns=¨http://www.w3.org/1998/Math/MathML¨»«msub»«mi mathvariant=¨bold¨ mathcolor=¨#0000FF¨»§#931;F«/mi»«mi mathvariant=¨bold¨ mathcolor=¨#0000FF¨»R«/mi»«/msub»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»=«/mo»«mi mathvariant=¨bold¨ mathcolor=¨#0000FF¨»M«/mi»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»§#183;«/mo»«msub»«mi mathvariant=¨bold¨ mathcolor=¨#0000FF¨»a«/mi»«mi mathvariant=¨bold¨ mathcolor=¨#0000FF¨»R«/mi»«/msub»«mspace linebreak=¨newline¨»«/mspace»«msub»«mi mathvariant=¨bold¨ mathcolor=¨#0000FF¨»T«/mi»«mi mathvariant=¨bold¨ mathcolor=¨#0000FF¨»X«/mi»«/msub»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»=«/mo»«mi mathvariant=¨bold¨ mathcolor=¨#0000FF¨»M«/mi»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»§#183;«/mo»«msub»«mi mathvariant=¨bold¨ mathcolor=¨#0000FF¨»a«/mi»«mi mathvariant=¨bold¨ mathcolor=¨#0000FF¨»R«/mi»«/msub»«mspace linebreak=¨newline¨»«/mspace»«mi mathvariant=¨bold¨ mathcolor=¨#0000FF¨»T«/mi»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»§#183;«/mo»«mi mathvariant=¨bold¨ mathcolor=¨#0000FF¨»sin«/mi»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»(«/mo»«mi mathvariant=¨bold¨ mathcolor=¨#0000FF¨»§#945;«/mi»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»)«/mo»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»=«/mo»«mi mathvariant=¨bold¨ mathcolor=¨#0000FF¨»M«/mi»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»§#183;«/mo»«msub»«mi mathvariant=¨bold¨ mathcolor=¨#0000FF¨»a«/mi»«mi mathvariant=¨bold¨ mathcolor=¨#0000FF¨»R«/mi»«/msub»«mspace linebreak=¨newline¨»«/mspace»«mspace linebreak=¨newline¨»«/mspace»«msub»«mi mathvariant=¨bold¨ mathcolor=¨#0000FF¨»a«/mi»«mi mathvariant=¨bold¨ mathcolor=¨#0000FF¨»R«/mi»«/msub»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»=«/mo»«mfrac mathcolor=¨#0000FF¨»«mrow»«mi mathvariant=¨bold¨ mathcolor=¨#FF0000¨»T«/mi»«mo mathvariant=¨bold¨»§#183;«/mo»«mi mathvariant=¨bold¨»sin«/mi»«mo mathvariant=¨bold¨»(«/mo»«mi mathvariant=¨bold¨»§#945;«/mi»«mo mathvariant=¨bold¨»)«/mo»«/mrow»«mi mathvariant=¨bold¨»M«/mi»«/mfrac»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»=«/mo»«mfrac mathcolor=¨#0000FF¨»«mrow»«mfrac mathcolor=¨#FF0000¨»«mrow»«menclose notation=¨updiagonalstrike¨»«mi mathvariant=¨bold¨»M«/mi»«/menclose»«mo mathvariant=¨bold¨»§#183;«/mo»«mi mathvariant=¨bold¨»g«/mi»«/mrow»«mrow»«mi mathvariant=¨bold¨»cos«/mi»«mo mathvariant=¨bold¨»(«/mo»«mi mathvariant=¨bold¨»§#945;«/mi»«mo mathvariant=¨bold¨»)«/mo»«/mrow»«/mfrac»«mo mathvariant=¨bold¨»§#183;«/mo»«mi mathvariant=¨bold¨»sin«/mi»«mo mathvariant=¨bold¨»(«/mo»«mi mathvariant=¨bold¨»§#945;«/mi»«mo mathvariant=¨bold¨»)«/mo»«/mrow»«menclose notation=¨updiagonalstrike¨»«mi mathvariant=¨bold¨»M«/mi»«/menclose»«/mfrac»«mspace linebreak=¨newline¨»«/mspace»«mspace linebreak=¨newline¨»«/mspace»«menclose mathcolor=¨#0000FF¨ notation=¨circle¨»«msub»«mi mathvariant=¨bold¨»a«/mi»«mi mathvariant=¨bold¨»R«/mi»«/msub»«mo mathvariant=¨bold¨»=«/mo»«mi mathvariant=¨bold¨»g«/mi»«mo mathvariant=¨bold¨»§#183;«/mo»«mi mathvariant=¨bold¨»tan«/mi»«mo mathvariant=¨bold¨»(«/mo»«mi mathvariant=¨bold¨»§#945;«/mi»«mo mathvariant=¨bold¨»)«/mo»«/menclose»«/math»

هذا التسارع هو تسارع الجسم كله الذي كتلة M ، والكرسي جزء من هذا الجسم ، وبالتالي فهو أيضًا تسارع الكرسي.

يتعامل هذا القسم مع حركة الكرسي ، لذلك بشكل عام يجب عليك رسم مخطط القوة على الكرسي وكتابة معادلة حركة الكرسي.

يتأثر الكرسي بقوة الجاذبية وقوة الشد والقوة التي يشغّلها الميزان على الكرسي في الاتجاه المعاكس لقوة الشد.

كتلة الكرسي غير معطاة في السؤال، كما أن القوة التي يشغّلها الميزان على الكرسي غير معطاة.

تسارع الكرسي هو نفس تسارع الجسم كله، يجب أن ترسم مخططًا للقوى التي تعمل على الجسم كله ، وتجد تسارع الجسم كله.

وتشير في النهاية أن تسارع الكرسي هو نفسه تسارع جسم الكتلة M.

על הכיסא פועל כוח הכובד , כוח המתיחות , וכוח שהמאזניים מפעילים על הכיסא בכיוון נגדי לכיוון כוח המתיחות.

מסת הכיסא לא נתונה , הכוח שהמאזניים מפעילים על הכיסא גם לא נתון.

תאוצת הכיסא זהה לתאוצת הגוף כולו , יש לערוך תרשים כוחות על הגוף כולו, לערוך תרשים כוחות , למצוא את התאוצה של כל הגוף.

ולציין בסוף שתאוצת הכיסא זהה לתאוצת הגוף שמסתו M.

______________________________________________________________________________________

...

تؤثر قوتان على الولد: القوة العمودية - التي يشغّلها السطح الذي يقف عليه الصبي.
قوة الجاذبية - تشغّلها الكرة الأرضية.

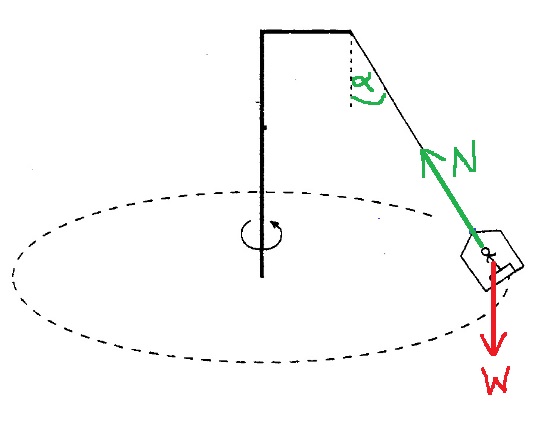
כוח הכובד - מופעל ע"י כדור הארץ.

التعرف على القوى المؤثرة على الجسم ومعرفة مشغليها.

تؤثر قوتان على الصبي ، القوة العمودية N التي يشغّلها الميزان على الشخص لأعلى.
ووزنه (قوة الجاذبية) يؤثر عليه إلى أسفل ، قوة الجاذبية تشغّلها الكرة الأرضية.

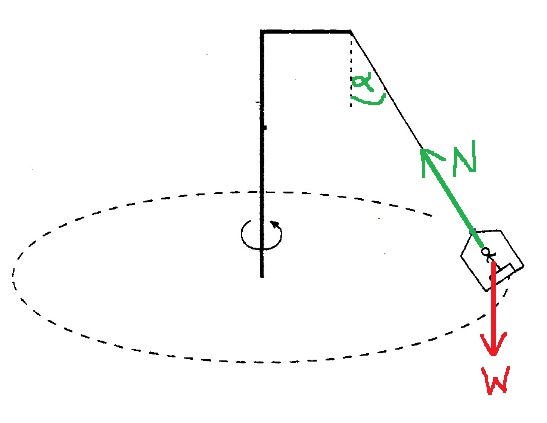
ומשקל הנער(כוח הכובד) הפועל עליו כלפי מטה , את כוח הכובד מפעיל כדור הארץ.

القوة العمودية المؤثرة على الصبي يشغّلها الميزان وليس الكرسي. الولد لا يلمس الكرسي.
يشغّل الصبي قوة على الميزان ، من قانون نيوتن الثالث ،فإن الميزان سيؤثر عليه بقوة متساوية في المقدار ومعاكسة في الاتجاه.

הנער מפעיל כוח על המאזניים , מהחוק השלישי של ניוטון גם המאזניים מפעילים אליו כוח זהה בגודלו ומנוגד בכיוונו.

______________________________________________________________________________________

...

القوة العمودية أكبر من mg. لأن المركّب الطبيعي يساوي mg.

يرسم مخطّط القوى ، وكتابة معادلات الحركة ، والتعبير عن القوة الطبيعية من معادلة الحركة.

من أجل أن يتحرك الشخص في حركة دائرية منتظمة، فإن المركّب للقوة العمودية N_X هو قوة الجاذبة نحو المركز.

نرسم مخططًا للقوى، ونحلل القوة العمودية إلى مركباتها.

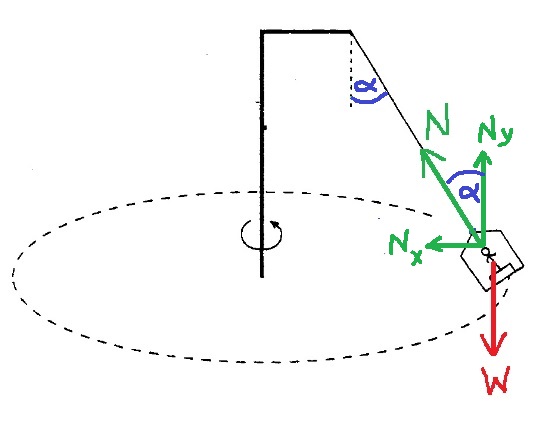
نكتب معادلات الحركة في الاتجاه العمودي بالنسبة للمحور الذي تم تحديده نحو الأعلى. ومعادلة للحركة بالنسبة للمحور الموجّه في اتجاه نقطة مركز الدوران.

«math xmlns=¨http://www.w3.org/1998/Math/MathML¨»«msub»«mi mathvariant=¨bold¨ mathcolor=¨#0000FF¨»§#931;F«/mi»«mi mathvariant=¨bold¨ mathcolor=¨#0000FF¨»R«/mi»«/msub»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»=«/mo»«mi mathvariant=¨bold¨ mathcolor=¨#0000FF¨»m«/mi»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»§#183;«/mo»«msup»«mi mathvariant=¨bold¨ mathcolor=¨#0000FF¨»§#969;«/mi»«mn mathvariant=¨bold¨ mathcolor=¨#0000FF¨»2«/mn»«/msup»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»§#183;«/mo»«mi mathvariant=¨bold¨ mathcolor=¨#0000FF¨»R«/mi»«mspace linebreak=¨newline¨»«/mspace»«msub»«mi mathvariant=¨bold¨ mathcolor=¨#0000FF¨»N«/mi»«mi mathvariant=¨bold¨ mathcolor=¨#0000FF¨»X«/mi»«/msub»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»=«/mo»«mi mathvariant=¨bold¨ mathcolor=¨#0000FF¨»m«/mi»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»§#183;«/mo»«msup»«mi mathvariant=¨bold¨ mathcolor=¨#0000FF¨»§#969;«/mi»«mn mathvariant=¨bold¨ mathcolor=¨#0000FF¨»2«/mn»«/msup»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»§#183;«/mo»«mi mathvariant=¨bold¨ mathcolor=¨#0000FF¨»R«/mi»«mspace linebreak=¨newline¨»«/mspace»«menclose mathcolor=¨#0000FF¨ notation=¨box¨»«mi mathvariant=¨bold¨»N«/mi»«mo mathvariant=¨bold¨»§#183;«/mo»«mi mathvariant=¨bold¨»sin«/mi»«mo mathvariant=¨bold¨»(«/mo»«mi mathvariant=¨bold¨»§#945;«/mi»«mo mathvariant=¨bold¨»)«/mo»«mo mathvariant=¨bold¨»=«/mo»«mi mathvariant=¨bold¨»m«/mi»«mo mathvariant=¨bold¨»§#183;«/mo»«msup»«mi mathvariant=¨bold¨»§#969;«/mi»«mn mathvariant=¨bold¨»2«/mn»«/msup»«mo mathvariant=¨bold¨»§#183;«/mo»«mi mathvariant=¨bold¨»R«/mi»«/menclose»«/math» «math xmlns=¨http://www.w3.org/1998/Math/MathML¨»«msub»«mi mathvariant=¨bold¨ mathcolor=¨#0000FF¨»§#931;F«/mi»«mi mathvariant=¨bold¨ mathcolor=¨#0000FF¨»Y«/mi»«/msub»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»=«/mo»«mn mathvariant=¨bold¨ mathcolor=¨#0000FF¨»0«/mn»«mspace linebreak=¨newline¨»«/mspace»«msub»«mi mathvariant=¨bold¨ mathcolor=¨#0000FF¨»N«/mi»«mi mathvariant=¨bold¨ mathcolor=¨#0000FF¨»Y«/mi»«/msub»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»=«/mo»«mi mathvariant=¨bold¨ mathcolor=¨#0000FF¨»W«/mi»«mspace linebreak=¨newline¨»«/mspace»«menclose mathcolor=¨#0000FF¨ notation=¨box¨»«mi mathvariant=¨bold¨»N«/mi»«mo mathvariant=¨bold¨»§#183;«/mo»«mi mathvariant=¨bold¨»cos«/mi»«mo mathvariant=¨bold¨»(«/mo»«mi mathvariant=¨bold¨»§#945;«/mi»«mo mathvariant=¨bold¨»)«/mo»«mo mathvariant=¨bold¨»=«/mo»«mi mathvariant=¨bold¨»mg«/mi»«/menclose»«/math»

نعبّر عن القوة العمودية من معادلة الحركة العمودية:

«math xmlns=¨http://www.w3.org/1998/Math/MathML¨»«mi mathvariant=¨bold¨ mathcolor=¨#0000FF¨»N«/mi»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»§#183;«/mo»«mi mathvariant=¨bold¨ mathcolor=¨#0000FF¨»cos«/mi»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»(«/mo»«mi mathvariant=¨bold¨ mathcolor=¨#0000FF¨»§#945;«/mi»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»)«/mo»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»=«/mo»«mi mathvariant=¨bold¨ mathcolor=¨#0000FF¨»mg«/mi»«mspace linebreak=¨newline¨»«/mspace»«mspace linebreak=¨newline¨»«/mspace»«menclose mathcolor=¨#0000FF¨ notation=¨circle¨»«mi mathvariant=¨bold¨»N«/mi»«mo mathvariant=¨bold¨»=«/mo»«mfrac»«mi mathvariant=¨bold¨»mg«/mi»«mrow»«mi mathvariant=¨bold¨»cos«/mi»«mo mathvariant=¨bold¨»(«/mo»«mi mathvariant=¨bold¨»§#945;«/mi»«mo mathvariant=¨bold¨»)«/mo»«/mrow»«/mfrac»«/menclose»«/math»

من التعبير يمكنك أن ترى أنه لأي زاوية ميل أكبر من الصفر ، تكون قيمة جيب التمام للزاوية أقل من 1 ، والقوة العمودية تكون أكبر من mg.

נערוך תרשים כוחות, ונבצע הפרדה ישרת זווית לכוח הנורמל.

נכתוב את משוואות התנועה לכיוון האנכי ביחס לציר שכיוונו כלפי מעלה. ומשוואת תנועה רדיאלי ביחס לציר שכיוונו בכיוון נקודת מרכז הסיבוב.

«math xmlns=¨http://www.w3.org/1998/Math/MathML¨»«msub»«mi mathvariant=¨bold¨ mathcolor=¨#0000FF¨»§#931;F«/mi»«mi mathvariant=¨bold¨ mathcolor=¨#0000FF¨»R«/mi»«/msub»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»=«/mo»«mi mathvariant=¨bold¨ mathcolor=¨#0000FF¨»m«/mi»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»§#183;«/mo»«msup»«mi mathvariant=¨bold¨ mathcolor=¨#0000FF¨»§#969;«/mi»«mn mathvariant=¨bold¨ mathcolor=¨#0000FF¨»2«/mn»«/msup»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»§#183;«/mo»«mi mathvariant=¨bold¨ mathcolor=¨#0000FF¨»R«/mi»«mspace linebreak=¨newline¨»«/mspace»«msub»«mi mathvariant=¨bold¨ mathcolor=¨#0000FF¨»N«/mi»«mi mathvariant=¨bold¨ mathcolor=¨#0000FF¨»X«/mi»«/msub»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»=«/mo»«mi mathvariant=¨bold¨ mathcolor=¨#0000FF¨»m«/mi»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»§#183;«/mo»«msup»«mi mathvariant=¨bold¨ mathcolor=¨#0000FF¨»§#969;«/mi»«mn mathvariant=¨bold¨ mathcolor=¨#0000FF¨»2«/mn»«/msup»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»§#183;«/mo»«mi mathvariant=¨bold¨ mathcolor=¨#0000FF¨»R«/mi»«mspace linebreak=¨newline¨»«/mspace»«menclose mathcolor=¨#0000FF¨ notation=¨box¨»«mi mathvariant=¨bold¨»N«/mi»«mo mathvariant=¨bold¨»§#183;«/mo»«mi mathvariant=¨bold¨»sin«/mi»«mo mathvariant=¨bold¨»(«/mo»«mi mathvariant=¨bold¨»§#945;«/mi»«mo mathvariant=¨bold¨»)«/mo»«mo mathvariant=¨bold¨»=«/mo»«mi mathvariant=¨bold¨»m«/mi»«mo mathvariant=¨bold¨»§#183;«/mo»«msup»«mi mathvariant=¨bold¨»§#969;«/mi»«mn mathvariant=¨bold¨»2«/mn»«/msup»«mo mathvariant=¨bold¨»§#183;«/mo»«mi mathvariant=¨bold¨»R«/mi»«/menclose»«/math» «math xmlns=¨http://www.w3.org/1998/Math/MathML¨»«msub»«mi mathvariant=¨bold¨ mathcolor=¨#0000FF¨»§#931;F«/mi»«mi mathvariant=¨bold¨ mathcolor=¨#0000FF¨»Y«/mi»«/msub»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»=«/mo»«mn mathvariant=¨bold¨ mathcolor=¨#0000FF¨»0«/mn»«mspace linebreak=¨newline¨»«/mspace»«msub»«mi mathvariant=¨bold¨ mathcolor=¨#0000FF¨»N«/mi»«mi mathvariant=¨bold¨ mathcolor=¨#0000FF¨»Y«/mi»«/msub»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»=«/mo»«mi mathvariant=¨bold¨ mathcolor=¨#0000FF¨»W«/mi»«mspace linebreak=¨newline¨»«/mspace»«menclose mathcolor=¨#0000FF¨ notation=¨box¨»«mi mathvariant=¨bold¨»N«/mi»«mo mathvariant=¨bold¨»§#183;«/mo»«mi mathvariant=¨bold¨»cos«/mi»«mo mathvariant=¨bold¨»(«/mo»«mi mathvariant=¨bold¨»§#945;«/mi»«mo mathvariant=¨bold¨»)«/mo»«mo mathvariant=¨bold¨»=«/mo»«mi mathvariant=¨bold¨»mg«/mi»«/menclose»«/math»

נבטא את הנורמל ממשוואת התנועה האנכית:

מהביטוי ניתן לראות שעבור כל זווית נטייה גדולה מאפס ,ערך קוסינוס הזווית קטן מ 1 , והנורמל גדול מ mg.

1. السؤال يتعلق بصبي ، لذلك يجب رسم مخطّط القوى التي تعمل على الصبي .
2. نظرًا لأن قيمة القوة العمودية أكبر من قيمة mg ، فستكون قراءة الميزان هي وزن خيالي.

2. מכיוון שערך הנורמל גדול יותר מערך mg, המשקל המוצג יהיה משקל מדומה.

______________________________________________________________________________________