______________________________________________________________________________________
...
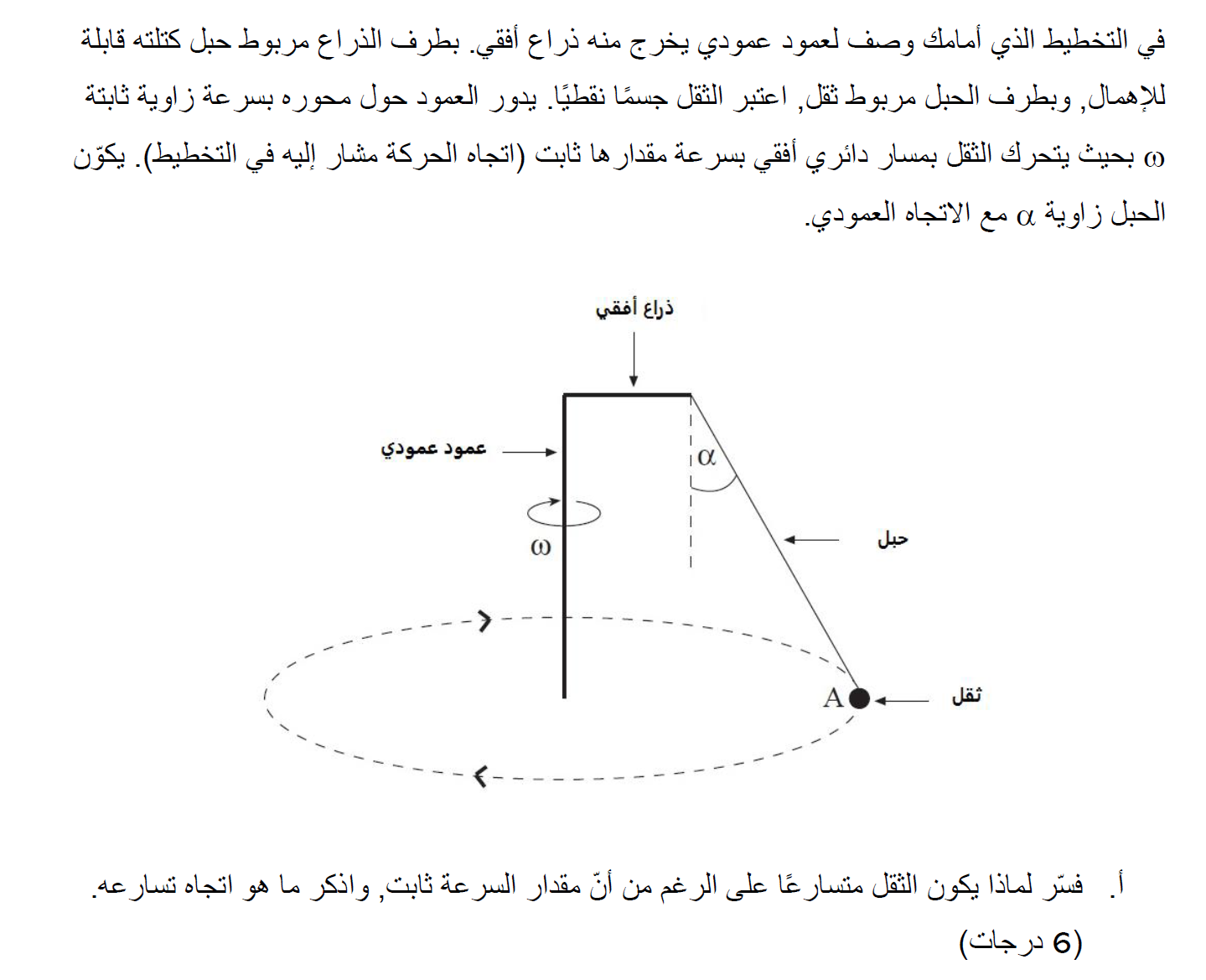
الحركة بتسارع لأن السرعة متغيرة الاتجاه، واتجاه التسارع نحو لمركز الدوران.
معرفة تعريف التسارع والخاصة المتجهة للسرعة. معرفة اتجاه التسارع المركزي في حركة دائرية منتظمة.
يتم تعريف التسارع على أنه وتيرة التغير في السرعة.
السرعة عبارة عن مقدار متجهي ، حتى لو تغير اتجاه السرعة فقط أو تغير مقدار السرعة فقط ، فإنها تعتبر تغيرًا في السرعة وهناك تسارع.
في هذه الحالة يغير الثقل اتجاه حركته في كل لحظة، وبالتالي يتحرك في حركة متسارعة.
يتحرك الثقل بحركة دائرية منتظمة، في كل حركة دائرية ثابتة يكون اتجاه التسارع نحو مركز الدوران.
لذلك ، يكون اتجاه تسارع الثقل نحو مركز الدوران.
המהירות היא גודל ווקטורי , גם אם רק כיוון המהירות משתנה או רק גודל המהירות משתנה , זה נחשב שינוי במהירות ויש תאוצה.
במקרה זה המשקולת משנה את כיוון תנועתה בכל רגע , לכן היא נעה בתנועה מואצת.
המהירות היא גודל ווקטורי יש לה גודל ויש לה כיוון. מספיק שיש שינוי רק בכיוון של המהירות או רק בגודלה זה אומר שיש תאוצה.
1. لكي تكون هناك حركة دائرية منتظمة ، يجب أن تكون هناك قوة جاذبة نحو المركز ، من القانون الثاني لنيوتن إذا كانت هناك قوة جاذبية نحو المركز ، فهناك أيضًا تسارع جاذب نحو المركز.
2. تعمل القوة الجاذبة نحو المركز باتجاه عمودي على الحركة، وأي قوة تعمل بشكل عمودي على الحركة تغير اتجاه الحركة ولكنها لا تغير مقدار السرعة.
3. اتجاه متجه السرعة هو اتجاه الحركة.
4. اذا استعملنا تعريف التسارع «math xmlns=¨http://www.w3.org/1998/Math/MathML¨»«mover mathcolor=¨#FF0000¨»«mi mathvariant=¨bold¨»a«/mi»«mo mathvariant=¨bold¨»§#8594;«/mo»«/mover»«mo mathvariant=¨bold¨ mathcolor=¨#FF0000¨»=«/mo»«mfrac mathcolor=¨#FF0000¨»«mover»«mrow»«mo mathvariant=¨bold¨»§#8710;«/mo»«mi mathvariant=¨bold¨»v«/mi»«/mrow»«mo mathvariant=¨bold¨»§#8594;«/mo»«/mover»«mrow»«mo mathvariant=¨bold¨»§#8710;«/mo»«mi mathvariant=¨bold¨»t«/mi»«/mrow»«/mfrac»«/math» لحركة دائرية منتظمة , نجد مقدار واتجاه التسارع.
2. הכוח הצנטריפטלי פועל בניצב לתנועה, כל כוח הפועל בניצב לתנועה משנה את כיוון התנועה אך הוא לא משנה את גודל המהירות.
______________________________________________________________________________________

______________________________________________________________________________________
...
الحركة متسارعة، وبالتالي فإن القوة المحصلة على اللثقل لا يساوي الصفر ، واتجاه القوة المحصلةة هو نفس اتجاه التسارع ، في اتجاه نحو نقطة مركز الدوران.
القانون الثاني لنيوتن.
طالما يوجد تسارع ، يجب أن تكون القوة المحصلة لا تساوي صفر. نظرًا لأن الثقل يتحرك في حركة متسارعة ، فإن مجموع القوى المؤثرة على الوزن يختلف عن الصفر.
اتجاه تأثير القوة المحصلة هو نفس اتجاه التسارع ، نحو نقطة مركز الدوران.
כיוון פעולתו של הכוח השקול הוא ככיוון התאוצה , אל נקודת מרכז הסיבוב.
نظرًا لأن مقدارالسرعة لا يتغير ، يمكن أن نُخطئ ونقول أنه لا توجد قوة مؤثرة. لكن القوة تعمل أيضًا عندما يكون هناك تغيير فقط في اتجاه الحركة.
في كثير من الأحيان ، يأتي الفهم الأفضل من الحالات البسيطة .......
إذا كان الجسم يتحرك في الفضاء بسرعة معينة ، في خط مستقيم دون تأثير الجاذبية أو قوى الاحتكاك. وفجأة في لحظة معينة قام بتغيير اتجاه حركته دون تغيير مقدار السرعة ، هل كانت هناك قوة في هذه اللحظة؟ نعم! لا يغير الجسم اتجاه حركته دون سبب. اتجاه الحركة يتغير لأن هناك قوة تؤتر على الجسم!
הרבה פעמים, ההבנה הכי טובה מגיעה מהמקרים הפשוטים.......
אם גוף נע בחלל במהירות מסוימת , בקו ישר ללא השפעת כוח כבידה או כוחות חיכוך. ופתאום ברגע מסוים הוא משנה את כיוון תנועתו , מבלי לשנות את גודל המהירות , האם ברגע זה פעל כוח? כן! גוף לא סתם משנה את כיוון תנועתו . כיוון התנועה משתנה מכיוון שכוח פועל על הגוף!
______________________________________________________________________________________

______________________________________________________________________________________
...
يكون اتجاه متجه السرعة مماسًا للمسار ، عند النقطة A يكون اتجاه متجه السرعة إلى الخارج من الصفحة نحو اللقارئ.
معرفة متجه السرعة.
اتجاه السرعة هو نفس اتجاه الحركة ، أي مماس لمسار الحركة.
إذا كان مستوى الحركة عموديًا على مستوى الصفحة ، فبمجرد مرور الثقل بالنقطة A ، يكون اتجاه متجه السرعة إلى خارج الصفحة.
אם מישור התנועה ניצב למישור הדף, ברגע שהמשקולת חולפת בנקודה A כיוון ווקטור המהירות הוא החוצה מהדף.
1. اتجاه الحركة في أي لحظة باتجاه الازاحة في تلك اللحظة ، حسب تعريف السرعة: «math xmlns=¨http://www.w3.org/1998/Math/MathML¨»«mover mathcolor=¨#FF0000¨»«mi mathvariant=¨bold¨»V«/mi»«mo mathvariant=¨bold¨»§#8594;«/mo»«/mover»«mo mathvariant=¨bold¨ mathcolor=¨#FF0000¨»=«/mo»«mfrac mathcolor=¨#FF0000¨»«mover»«mrow»«mo mathvariant=¨bold¨»§#8710;«/mo»«mi mathvariant=¨bold¨»x«/mi»«/mrow»«mo mathvariant=¨bold¨»§#8594;«/mo»«/mover»«mrow»«mo mathvariant=¨bold¨»§#8710;«/mo»«mi mathvariant=¨bold¨»t«/mi»«/mrow»«/mfrac»«/math» اتجاه متجه السرعة هو نفس اتجاه متجه الازاحة.
2. عندما يتحرك الجسم على طول مسار معين ، تكون السرعة باتجاه مماس للمسار.
3. من المهم التمييز ما إذا كان الجسم يتحرك في اتجاه عقارب الساعة أو عكس اتجاه عقارب الساعة.
2. כאשר גוף נע לאורך מסלול כלשהו , המהירות משיקה למסלול.
3. חשוב להבחין אם הגוף נע בכיוון השעון ,או נגד כיוון השעון.
______________________________________________________________________________________

______________________________________________________________________________________
...
«math xmlns=¨http://www.w3.org/1998/Math/MathML¨»«mi mathvariant=¨bold¨»R«/mi»«mo mathvariant=¨bold¨»=«/mo»«mfrac»«mrow»«mi mathvariant=¨bold¨»tan«/mi»«mo mathvariant=¨bold¨»(«/mo»«mi mathvariant=¨bold¨»§#945;«/mi»«mo mathvariant=¨bold¨»)«/mo»«mo mathvariant=¨bold¨»§#183;«/mo»«mi mathvariant=¨bold¨»g«/mi»«/mrow»«msup»«mi mathvariant=¨bold¨»§#969;«/mi»«mn mathvariant=¨bold¨»2«/mn»«/msup»«/mfrac»«/math»
رسم مخطّط القوى التي تعمل على الثقل ، كتابة معادلات الحركة.
نرسم رسم تخطيطي للقوى المؤثرة على الثقل:
نكتب معادلات الحركة في الاتجاه العمودي، وفي الاتجاه نحو مركز الدوران.
«math xmlns=¨http://www.w3.org/1998/Math/MathML¨»«msub»«mi mathvariant=¨bold¨ mathcolor=¨#0000FF¨»§#931;F«/mi»«mi mathvariant=¨bold¨ mathcolor=¨#0000FF¨»R«/mi»«/msub»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»=«/mo»«mi mathvariant=¨bold¨ mathcolor=¨#0000FF¨»m«/mi»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»§#183;«/mo»«msup»«mi mathvariant=¨bold¨ mathcolor=¨#0000FF¨»§#969;«/mi»«mn mathvariant=¨bold¨ mathcolor=¨#0000FF¨»2«/mn»«/msup»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»§#183;«/mo»«mi mathvariant=¨bold¨ mathcolor=¨#0000FF¨»R«/mi»«mspace linebreak=¨newline¨»«/mspace»«msub»«mi mathvariant=¨bold¨ mathcolor=¨#0000FF¨»T«/mi»«mi mathvariant=¨bold¨ mathcolor=¨#0000FF¨»X«/mi»«/msub»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»=«/mo»«mi mathvariant=¨bold¨ mathcolor=¨#0000FF¨»m«/mi»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»§#183;«/mo»«msup»«mi mathvariant=¨bold¨ mathcolor=¨#0000FF¨»§#969;«/mi»«mn mathvariant=¨bold¨ mathcolor=¨#0000FF¨»2«/mn»«/msup»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»§#183;«/mo»«mi mathvariant=¨bold¨ mathcolor=¨#0000FF¨»R«/mi»«mspace linebreak=¨newline¨»«/mspace»«menclose mathcolor=¨#0000FF¨ notation=¨box¨»«mi mathvariant=¨bold¨»T«/mi»«mo mathvariant=¨bold¨»§#183;«/mo»«mi mathvariant=¨bold¨»sin«/mi»«mo mathvariant=¨bold¨»(«/mo»«mi mathvariant=¨bold¨»§#945;«/mi»«mo mathvariant=¨bold¨»)«/mo»«mo mathvariant=¨bold¨»=«/mo»«mi mathvariant=¨bold¨»m«/mi»«mo mathvariant=¨bold¨»§#183;«/mo»«msup»«mi mathvariant=¨bold¨»§#969;«/mi»«mn mathvariant=¨bold¨»2«/mn»«/msup»«mo mathvariant=¨bold¨»§#183;«/mo»«mi mathvariant=¨bold¨»R«/mi»«/menclose»«/math» «math xmlns=¨http://www.w3.org/1998/Math/MathML¨»«msub»«mi mathvariant=¨bold¨ mathcolor=¨#0000FF¨»§#931;F«/mi»«mi mathvariant=¨bold¨ mathcolor=¨#0000FF¨»Y«/mi»«/msub»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»=«/mo»«mn mathvariant=¨bold¨ mathcolor=¨#0000FF¨»0«/mn»«mspace linebreak=¨newline¨»«/mspace»«msub»«mi mathvariant=¨bold¨ mathcolor=¨#0000FF¨»T«/mi»«mi mathvariant=¨bold¨ mathcolor=¨#0000FF¨»Y«/mi»«/msub»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»=«/mo»«mi mathvariant=¨bold¨ mathcolor=¨#0000FF¨»W«/mi»«mspace linebreak=¨newline¨»«/mspace»«menclose mathcolor=¨#0000FF¨ notation=¨box¨»«mi mathvariant=¨bold¨»T«/mi»«mo mathvariant=¨bold¨»§#183;«/mo»«mi mathvariant=¨bold¨»cos«/mi»«mo mathvariant=¨bold¨»(«/mo»«mi mathvariant=¨bold¨»§#945;«/mi»«mo mathvariant=¨bold¨»)«/mo»«mo mathvariant=¨bold¨»=«/mo»«mi mathvariant=¨bold¨»mg«/mi»«/menclose»«/math»
نجري عملية قسمة ، بين معادلات الحركة ، ونعبر عن نصف قطر المسار الدائري:
«math xmlns=¨http://www.w3.org/1998/Math/MathML¨»«mfrac mathcolor=¨#0000FF¨»«mrow»«menclose notation=¨downdiagonalstrike¨»«mi mathvariant=¨bold¨»T«/mi»«/menclose»«mo mathvariant=¨bold¨»§#183;«/mo»«mi mathvariant=¨bold¨»sin«/mi»«mo mathvariant=¨bold¨»(«/mo»«mi mathvariant=¨bold¨»§#945;«/mi»«mo mathvariant=¨bold¨»)«/mo»«/mrow»«mrow»«menclose notation=¨downdiagonalstrike¨»«mi mathvariant=¨bold¨»T«/mi»«/menclose»«mo mathvariant=¨bold¨»§#183;«/mo»«mi mathvariant=¨bold¨»cos«/mi»«mo mathvariant=¨bold¨»(«/mo»«mi mathvariant=¨bold¨»§#945;«/mi»«mo mathvariant=¨bold¨»)«/mo»«/mrow»«/mfrac»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»=«/mo»«mfrac mathcolor=¨#0000FF¨»«mrow»«menclose notation=¨updiagonalstrike¨»«mi mathvariant=¨bold¨»m«/mi»«/menclose»«mo mathvariant=¨bold¨»§#183;«/mo»«msup»«mi mathvariant=¨bold¨»§#969;«/mi»«mn mathvariant=¨bold¨»2«/mn»«/msup»«mo mathvariant=¨bold¨»§#183;«/mo»«mi mathvariant=¨bold¨»R«/mi»«/mrow»«mrow»«menclose notation=¨updiagonalstrike¨»«mi mathvariant=¨bold¨»m«/mi»«/menclose»«mo mathvariant=¨bold¨»§#183;«/mo»«mi mathvariant=¨bold¨»g«/mi»«/mrow»«/mfrac»«mspace linebreak=¨newline¨»«/mspace»«mspace linebreak=¨newline¨»«/mspace»«mi mathvariant=¨bold¨ mathcolor=¨#0000FF¨»tan«/mi»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»(«/mo»«mi mathvariant=¨bold¨ mathcolor=¨#0000FF¨»§#945;«/mi»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»)«/mo»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»=«/mo»«mfrac mathcolor=¨#0000FF¨»«mrow»«msup»«mi mathvariant=¨bold¨»§#969;«/mi»«mn mathvariant=¨bold¨»2«/mn»«/msup»«mo mathvariant=¨bold¨»§#183;«/mo»«mi mathvariant=¨bold¨»R«/mi»«/mrow»«mi mathvariant=¨bold¨»g«/mi»«/mfrac»«mspace linebreak=¨newline¨»«/mspace»«mspace linebreak=¨newline¨»«/mspace»«menclose mathcolor=¨#0000FF¨ notation=¨circle¨»«mi mathvariant=¨bold¨»R«/mi»«mo mathvariant=¨bold¨»=«/mo»«mfrac»«mrow»«mi mathvariant=¨bold¨»tan«/mi»«mo mathvariant=¨bold¨»(«/mo»«mi mathvariant=¨bold¨»§#945;«/mi»«mo mathvariant=¨bold¨»)«/mo»«mo mathvariant=¨bold¨»§#183;«/mo»«mi mathvariant=¨bold¨»g«/mi»«/mrow»«msup»«mi mathvariant=¨bold¨»§#969;«/mi»«mn mathvariant=¨bold¨»2«/mn»«/msup»«/mfrac»«/menclose»«mspace linebreak=¨newline¨»«/mspace»«mspace linebreak=¨newline¨»«/mspace»«/math»
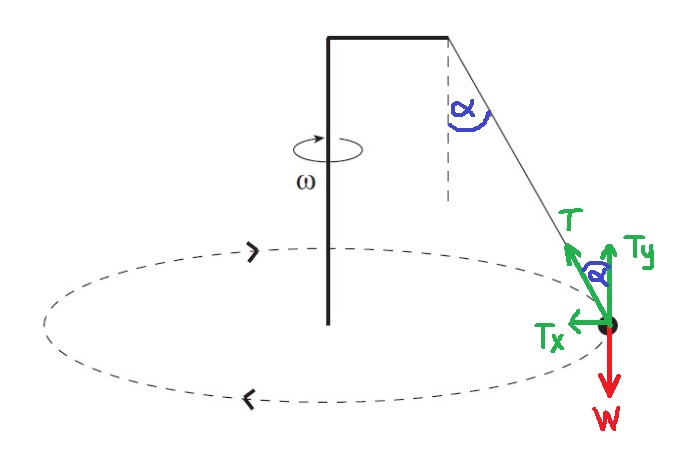
נכתוב את משוואות התנועה לכיוון האנכי, ביחס לציר שכיוונו כלפי מעלה. ולכיוון הרדיאלי ביחס לציר שכיוונו אל מרכז המעגל.
«math xmlns=¨http://www.w3.org/1998/Math/MathML¨»«msub»«mi mathvariant=¨bold¨ mathcolor=¨#0000FF¨»§#931;F«/mi»«mi mathvariant=¨bold¨ mathcolor=¨#0000FF¨»R«/mi»«/msub»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»=«/mo»«mi mathvariant=¨bold¨ mathcolor=¨#0000FF¨»m«/mi»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»§#183;«/mo»«msup»«mi mathvariant=¨bold¨ mathcolor=¨#0000FF¨»§#969;«/mi»«mn mathvariant=¨bold¨ mathcolor=¨#0000FF¨»2«/mn»«/msup»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»§#183;«/mo»«mi mathvariant=¨bold¨ mathcolor=¨#0000FF¨»R«/mi»«mspace linebreak=¨newline¨»«/mspace»«msub»«mi mathvariant=¨bold¨ mathcolor=¨#0000FF¨»T«/mi»«mi mathvariant=¨bold¨ mathcolor=¨#0000FF¨»X«/mi»«/msub»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»=«/mo»«mi mathvariant=¨bold¨ mathcolor=¨#0000FF¨»m«/mi»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»§#183;«/mo»«msup»«mi mathvariant=¨bold¨ mathcolor=¨#0000FF¨»§#969;«/mi»«mn mathvariant=¨bold¨ mathcolor=¨#0000FF¨»2«/mn»«/msup»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»§#183;«/mo»«mi mathvariant=¨bold¨ mathcolor=¨#0000FF¨»R«/mi»«mspace linebreak=¨newline¨»«/mspace»«menclose mathcolor=¨#0000FF¨ notation=¨box¨»«mi mathvariant=¨bold¨»T«/mi»«mo mathvariant=¨bold¨»§#183;«/mo»«mi mathvariant=¨bold¨»sin«/mi»«mo mathvariant=¨bold¨»(«/mo»«mi mathvariant=¨bold¨»§#945;«/mi»«mo mathvariant=¨bold¨»)«/mo»«mo mathvariant=¨bold¨»=«/mo»«mi mathvariant=¨bold¨»m«/mi»«mo mathvariant=¨bold¨»§#183;«/mo»«msup»«mi mathvariant=¨bold¨»§#969;«/mi»«mn mathvariant=¨bold¨»2«/mn»«/msup»«mo mathvariant=¨bold¨»§#183;«/mo»«mi mathvariant=¨bold¨»R«/mi»«/menclose»«/math» «math xmlns=¨http://www.w3.org/1998/Math/MathML¨»«msub»«mi mathvariant=¨bold¨ mathcolor=¨#0000FF¨»§#931;F«/mi»«mi mathvariant=¨bold¨ mathcolor=¨#0000FF¨»Y«/mi»«/msub»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»=«/mo»«mn mathvariant=¨bold¨ mathcolor=¨#0000FF¨»0«/mn»«mspace linebreak=¨newline¨»«/mspace»«msub»«mi mathvariant=¨bold¨ mathcolor=¨#0000FF¨»T«/mi»«mi mathvariant=¨bold¨ mathcolor=¨#0000FF¨»Y«/mi»«/msub»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»=«/mo»«mi mathvariant=¨bold¨ mathcolor=¨#0000FF¨»W«/mi»«mspace linebreak=¨newline¨»«/mspace»«menclose mathcolor=¨#0000FF¨ notation=¨box¨»«mi mathvariant=¨bold¨»T«/mi»«mo mathvariant=¨bold¨»§#183;«/mo»«mi mathvariant=¨bold¨»cos«/mi»«mo mathvariant=¨bold¨»(«/mo»«mi mathvariant=¨bold¨»§#945;«/mi»«mo mathvariant=¨bold¨»)«/mo»«mo mathvariant=¨bold¨»=«/mo»«mi mathvariant=¨bold¨»mg«/mi»«/menclose»«/math»
נבצע פעולת חילוק , בין משוואות התנועה ,ונבטא את רדיוס המסלול המעגלי :
«math xmlns=¨http://www.w3.org/1998/Math/MathML¨»«mfrac mathcolor=¨#0000FF¨»«mrow»«menclose notation=¨downdiagonalstrike¨»«mi mathvariant=¨bold¨»T«/mi»«/menclose»«mo mathvariant=¨bold¨»§#183;«/mo»«mi mathvariant=¨bold¨»sin«/mi»«mo mathvariant=¨bold¨»(«/mo»«mi mathvariant=¨bold¨»§#945;«/mi»«mo mathvariant=¨bold¨»)«/mo»«/mrow»«mrow»«menclose notation=¨downdiagonalstrike¨»«mi mathvariant=¨bold¨»T«/mi»«/menclose»«mo mathvariant=¨bold¨»§#183;«/mo»«mi mathvariant=¨bold¨»cos«/mi»«mo mathvariant=¨bold¨»(«/mo»«mi mathvariant=¨bold¨»§#945;«/mi»«mo mathvariant=¨bold¨»)«/mo»«/mrow»«/mfrac»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»=«/mo»«mfrac mathcolor=¨#0000FF¨»«mrow»«menclose notation=¨updiagonalstrike¨»«mi mathvariant=¨bold¨»m«/mi»«/menclose»«mo mathvariant=¨bold¨»§#183;«/mo»«msup»«mi mathvariant=¨bold¨»§#969;«/mi»«mn mathvariant=¨bold¨»2«/mn»«/msup»«mo mathvariant=¨bold¨»§#183;«/mo»«mi mathvariant=¨bold¨»R«/mi»«/mrow»«mrow»«menclose notation=¨updiagonalstrike¨»«mi mathvariant=¨bold¨»m«/mi»«/menclose»«mo mathvariant=¨bold¨»§#183;«/mo»«mi mathvariant=¨bold¨»g«/mi»«/mrow»«/mfrac»«mspace linebreak=¨newline¨»«/mspace»«mspace linebreak=¨newline¨»«/mspace»«mi mathvariant=¨bold¨ mathcolor=¨#0000FF¨»tan«/mi»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»(«/mo»«mi mathvariant=¨bold¨ mathcolor=¨#0000FF¨»§#945;«/mi»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»)«/mo»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»=«/mo»«mfrac mathcolor=¨#0000FF¨»«mrow»«msup»«mi mathvariant=¨bold¨»§#969;«/mi»«mn mathvariant=¨bold¨»2«/mn»«/msup»«mo mathvariant=¨bold¨»§#183;«/mo»«mi mathvariant=¨bold¨»R«/mi»«/mrow»«mi mathvariant=¨bold¨»g«/mi»«/mfrac»«mspace linebreak=¨newline¨»«/mspace»«mspace linebreak=¨newline¨»«/mspace»«menclose mathcolor=¨#0000FF¨ notation=¨circle¨»«mi mathvariant=¨bold¨»R«/mi»«mo mathvariant=¨bold¨»=«/mo»«mfrac»«mrow»«mi mathvariant=¨bold¨»tan«/mi»«mo mathvariant=¨bold¨»(«/mo»«mi mathvariant=¨bold¨»§#945;«/mi»«mo mathvariant=¨bold¨»)«/mo»«mo mathvariant=¨bold¨»§#183;«/mo»«mi mathvariant=¨bold¨»g«/mi»«/mrow»«msup»«mi mathvariant=¨bold¨»§#969;«/mi»«mn mathvariant=¨bold¨»2«/mn»«/msup»«/mfrac»«/menclose»«mspace linebreak=¨newline¨»«/mspace»«mspace linebreak=¨newline¨»«/mspace»«/math»
1. ليس من الممكن معرفة كيفية تطوير التعبير عن نصف قطر المسار مسبقًا بناءً على السرعة الزاوية وزاوية ميل الخيط.
كالعادة ، ارسم مخطّط القوى التي تعمل على الثقل، واكتب معادلات الحركة. توقف ، وفكر كيف يمكن رياضيًا الوصول إلى التعبير المطلوب.
2. لا فرق بين مجرى الحل والتعبير الناتج. بين هذه الحالة وحالة بندول مخروطي بدون قضيب أفقي.
כמו תמיד יש לערוך תרשים כוחות , לכתוב את משוואות התנועה . לעצור , ולחשוב כיצד מתמטית ניתן להגיע לביטוי המבוקש.
2. אין הבדל בין מהלך הפתרון, והביטוי המתקבל. בין מקרה זה למקרה של מטוטלת קונית ללא מוט אופקי .
______________________________________________________________________________________

______________________________________________________________________________________
...
لكي يكون التسارع نحو المركز مساوٍ لـ g ، يجب أن تكون زاوية ميل الخيط 45 درجة.
باستخدام تعبير التسارع المركزي ، وتعبير نصف القطر.
يتحرك الثقل بحركة دائرية ثابتة، وله تسارع فقط نحو المركز، والتعبير عن تسارع المركزي هو:
«math xmlns=¨http://www.w3.org/1998/Math/MathML¨»«msub»«mi mathvariant=¨bold¨ mathcolor=¨#0000FF¨»a«/mi»«mi mathvariant=¨bold¨ mathcolor=¨#0000FF¨»R«/mi»«/msub»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»=«/mo»«msup»«mi mathvariant=¨bold-italic¨ mathcolor=¨#0000FF¨»§#969;«/mi»«mn mathvariant=¨bold¨ mathcolor=¨#0000FF¨»2«/mn»«/msup»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»§#183;«/mo»«mi mathvariant=¨bold-italic¨ mathcolor=¨#0000FF¨»R«/mi»«/math»
نقوم بتعويض التعبير عن نصف القطر من القسم السابق ، في تعبير التسارع نحو المركز:
«math xmlns=¨http://www.w3.org/1998/Math/MathML¨»«msub»«mi mathvariant=¨bold¨ mathcolor=¨#0000FF¨»a«/mi»«mi mathvariant=¨bold¨ mathcolor=¨#0000FF¨»R«/mi»«/msub»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»=«/mo»«msup»«mi mathvariant=¨bold-italic¨ mathcolor=¨#0000FF¨»§#969;«/mi»«mn mathvariant=¨bold¨ mathcolor=¨#0000FF¨»2«/mn»«/msup»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»§#183;«/mo»«mi mathvariant=¨bold¨ mathcolor=¨#FF0000¨»R«/mi»«mspace linebreak=¨newline¨»«/mspace»«mspace linebreak=¨newline¨»«/mspace»«msub»«mi mathvariant=¨bold¨ mathcolor=¨#0000FF¨»a«/mi»«mi mathvariant=¨bold¨ mathcolor=¨#0000FF¨»R«/mi»«/msub»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»=«/mo»«menclose mathcolor=¨#0000FF¨ notation=¨updiagonalstrike¨»«msup»«mi mathvariant=¨bold¨»§#969;«/mi»«mn mathvariant=¨bold¨»2«/mn»«/msup»«/menclose»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»§#183;«/mo»«mfrac mathcolor=¨#FF0000¨»«mrow»«mi mathvariant=¨bold¨»tan«/mi»«mo mathvariant=¨bold¨»(«/mo»«mi mathvariant=¨bold¨»§#945;«/mi»«mo mathvariant=¨bold¨»)«/mo»«mo mathvariant=¨bold¨»§#183;«/mo»«mi mathvariant=¨bold¨»g«/mi»«/mrow»«menclose notation=¨updiagonalstrike¨»«msup»«mi mathvariant=¨bold¨»§#969;«/mi»«mn mathvariant=¨bold¨»2«/mn»«/msup»«/menclose»«/mfrac»«mspace linebreak=¨newline¨»«/mspace»«mspace linebreak=¨newline¨»«/mspace»«msub»«mi mathvariant=¨bold¨ mathcolor=¨#0000FF¨»a«/mi»«mi mathvariant=¨bold¨ mathcolor=¨#0000FF¨»R«/mi»«/msub»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»=«/mo»«mi mathvariant=¨bold¨ mathcolor=¨#0000FF¨»tan«/mi»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»(«/mo»«mi mathvariant=¨bold¨ mathcolor=¨#0000FF¨»§#945;«/mi»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»)«/mo»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»§#183;«/mo»«mi mathvariant=¨bold¨ mathcolor=¨#0000FF¨»g«/mi»«mspace linebreak=¨newline¨»«/mspace»«mspace linebreak=¨newline¨»«/mspace»«/math»
ونجد قيمة زاوية ميل الخيط عندما يكون مقدار التسارع المركزي مساويًا لمقدار تسارع الجاذبية g:
«math xmlns=¨http://www.w3.org/1998/Math/MathML¨»«msub»«mi mathvariant=¨bold¨ mathcolor=¨#0000FF¨»a«/mi»«mi mathvariant=¨bold¨ mathcolor=¨#0000FF¨»R«/mi»«/msub»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»=«/mo»«mi mathvariant=¨bold¨ mathcolor=¨#0000FF¨»tan«/mi»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»(«/mo»«mi mathvariant=¨bold¨ mathcolor=¨#0000FF¨»§#945;«/mi»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»)«/mo»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»§#183;«/mo»«mi mathvariant=¨bold¨ mathcolor=¨#0000FF¨»g«/mi»«mspace linebreak=¨newline¨»«/mspace»«mi mathvariant=¨bold¨ mathcolor=¨#0000FF¨»§#945;«/mi»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»=«/mo»«mi mathvariant=¨bold¨ mathcolor=¨#0000FF¨»shift«/mi»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»§#160;«/mo»«mi mathvariant=¨bold¨ mathcolor=¨#0000FF¨»tan«/mi»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»(«/mo»«mfrac mathcolor=¨#0000FF¨»«msub»«mi mathvariant=¨bold¨»a«/mi»«mi mathvariant=¨bold¨»R«/mi»«/msub»«mi mathvariant=¨bold¨»g«/mi»«/mfrac»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»)«/mo»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»=«/mo»«mi mathvariant=¨bold¨ mathcolor=¨#0000FF¨»shift«/mi»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»§#160;«/mo»«mi mathvariant=¨bold¨ mathcolor=¨#0000FF¨»tan«/mi»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»(«/mo»«mfrac mathcolor=¨#0000FF¨»«mi mathvariant=¨bold¨»g«/mi»«mi mathvariant=¨bold¨»g«/mi»«/mfrac»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»)«/mo»«mspace linebreak=¨newline¨»«/mspace»«mi mathvariant=¨bold¨ mathcolor=¨#0000FF¨»§#945;«/mi»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»=«/mo»«mi mathvariant=¨bold¨ mathcolor=¨#0000FF¨»shift«/mi»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»§#160;«/mo»«mi mathvariant=¨bold¨ mathcolor=¨#0000FF¨»tan«/mi»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»(«/mo»«mn mathvariant=¨bold¨ mathcolor=¨#0000FF¨»1«/mn»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»)«/mo»«mspace linebreak=¨newline¨»«/mspace»«mspace linebreak=¨newline¨»«/mspace»«mi mathvariant=¨bold¨ mathcolor=¨#0000FF¨»§#945;«/mi»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»=«/mo»«mn mathvariant=¨bold¨ mathcolor=¨#0000FF¨»45«/mn»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»§#176;«/mo»«mspace linebreak=¨newline¨»«/mspace»«mspace linebreak=¨newline¨»«/mspace»«mspace linebreak=¨newline¨»«/mspace»«/math»
لكي يكون التسارع نحو المركز مساوٍ لـ g ، يجب أن تكون زاوية ميل الخيط 45 درجة.
«math xmlns=¨http://www.w3.org/1998/Math/MathML¨»«msub»«mi mathvariant=¨bold¨ mathcolor=¨#0000FF¨»a«/mi»«mi mathvariant=¨bold¨ mathcolor=¨#0000FF¨»R«/mi»«/msub»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»=«/mo»«mfrac mathcolor=¨#0000FF¨»«msup»«mi mathvariant=¨bold¨»V«/mi»«mn mathvariant=¨bold¨»2«/mn»«/msup»«mi mathvariant=¨bold¨»R«/mi»«/mfrac»«/math»
תאוצת המשקולת היא תאוצה צנטריפטלית , נציב את ביטוי הרדיוס מהסעיף הקודם , בביטוי התאוצה הצנטריפטלית :
الحل هو من خلال التعبير عن تسارع نحو مركز الدوران، في السؤال لا يبدو أن التسارع هو التسارع نحو المركز.
من المهم أن نتذكر أن التسارع نحو المركز. تذكر استخدام تعبير التسارع نحو المركز.
חשוב לזכור שהתאוצה היא צנטריפטלית. כדי לזכור להשתמש בביטוי התאוצה הצנטריפטאלית .
______________________________________________________________________________________






