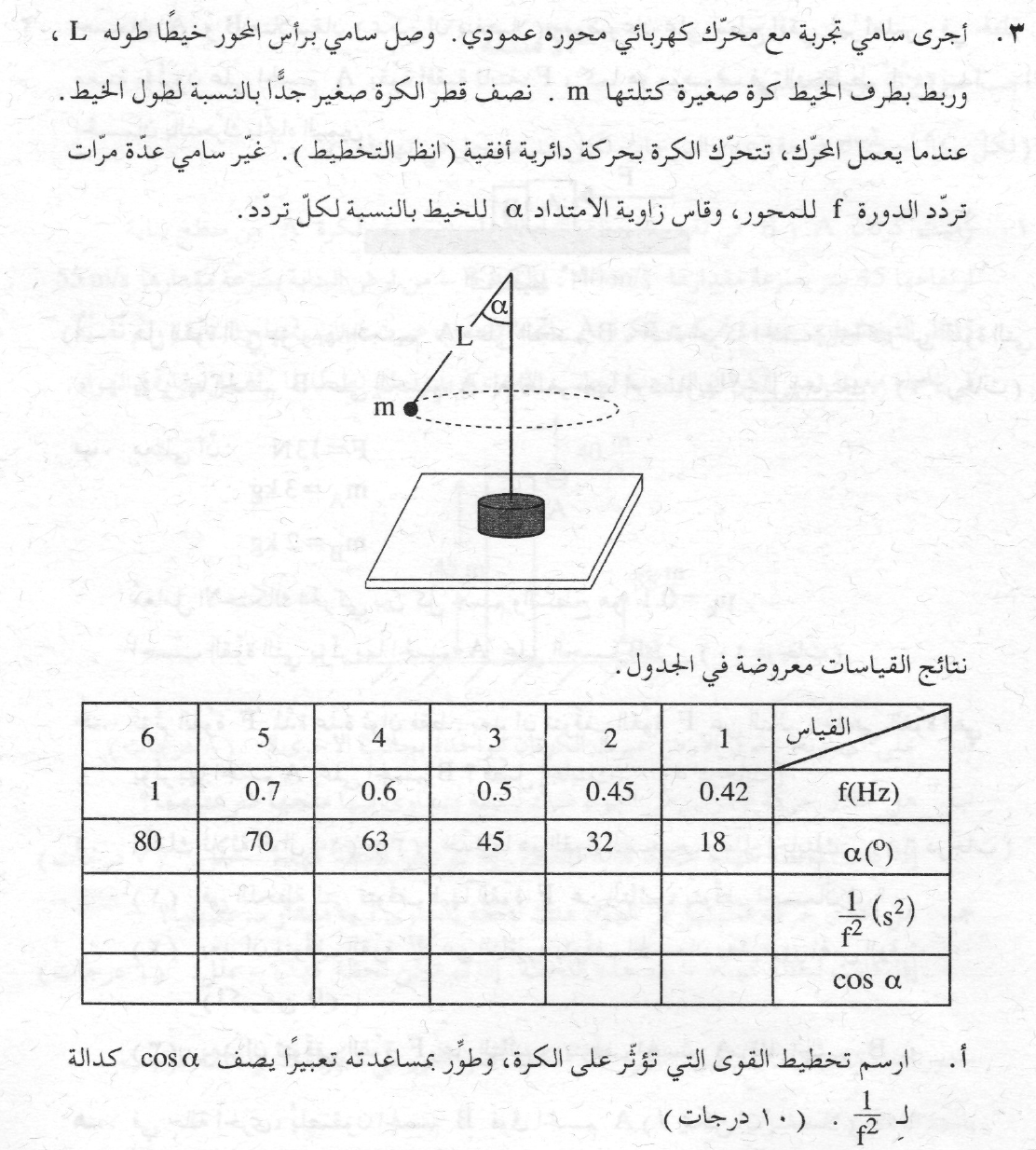
5. 2009,3 - البندول المخروطي
______________________________________________________________________________________
...
«math xmlns=¨http://www.w3.org/1998/Math/MathML¨»«mi mathvariant=¨bold¨»cos«/mi»«mo mathvariant=¨bold¨»(«/mo»«mi mathvariant=¨bold¨»§#945;«/mi»«mo mathvariant=¨bold¨»)«/mo»«mo mathvariant=¨bold¨»=«/mo»«mfrac»«mi mathvariant=¨bold¨»g«/mi»«mrow»«mn mathvariant=¨bold¨»4«/mn»«mo mathvariant=¨bold¨»§#183;«/mo»«msup»«mi mathvariant=¨bold¨»§#960;«/mi»«mn mathvariant=¨bold¨»2«/mn»«/msup»«mo mathvariant=¨bold¨»§#183;«/mo»«mi mathvariant=¨bold¨»L«/mi»«/mrow»«/mfrac»«mo mathvariant=¨bold¨»§#183;«/mo»«mfrac»«mn mathvariant=¨bold¨»1«/mn»«msup»«mi mathvariant=¨bold¨»f«/mi»«mn mathvariant=¨bold¨»2«/mn»«/msup»«/mfrac»«/math»
رسم مخطّط القوى المؤثرة على الجسم، كتابة معادلات الحركة. بالإضافة إلى ذلك ، يجب كتابة تعبير هندسي عن نصف قطر المسار
ونعبر من هذا التعبير ومن معادلات الحركة عن التعبير المطلوب.
ולבטא מביטוי זה וממשוואות התנועה את הביטוי המבוקש.
تؤثر قوتان على الكرة: قوة الجاذبية وقوة التوتر.
حسب مستوى الحركة ، بالنسبة لموقع مركز الدوران ، فإن قوة الجاذبية نحو المركز هي المركب الأفقي لقوة التوتر.
نرسم مخططًا للقوى المؤثرة على الكرة:
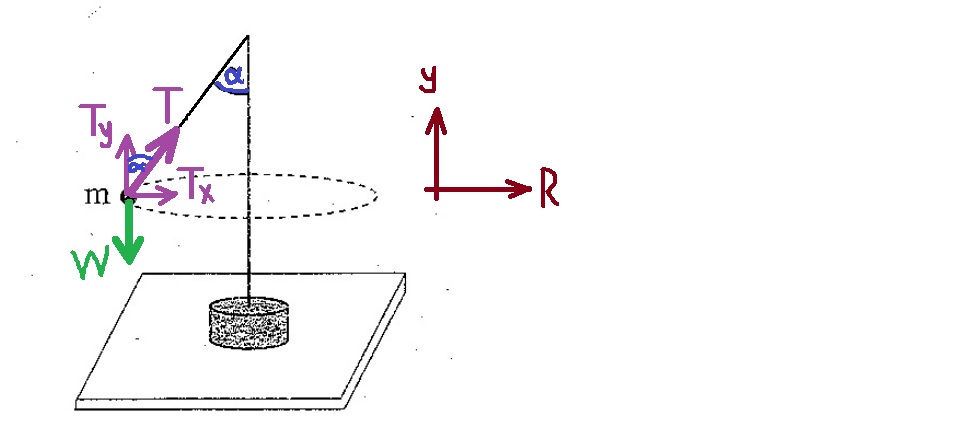
نكتب معادلة الحركة الدائرية بالنسبة للمحور الموجّه نحو المركز، ومعادلة الحركة العمودية بالنسبة للمحور الرأسي الموجّه لأعلى:
«math xmlns=¨http://www.w3.org/1998/Math/MathML¨»«msub»«mi mathvariant=¨bold¨ mathcolor=¨#0000FF¨»§#931;F«/mi»«mi mathvariant=¨bold¨ mathcolor=¨#0000FF¨»R«/mi»«/msub»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»=«/mo»«mi mathvariant=¨bold¨ mathcolor=¨#0000FF¨»m«/mi»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»§#183;«/mo»«msup»«mi mathvariant=¨bold¨ mathcolor=¨#0000FF¨»§#969;«/mi»«mn mathvariant=¨bold¨ mathcolor=¨#0000FF¨»2«/mn»«/msup»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»§#183;«/mo»«mi mathvariant=¨bold¨ mathcolor=¨#0000FF¨»R«/mi»«mspace linebreak=¨newline¨»«/mspace»«msub»«mi mathvariant=¨bold¨ mathcolor=¨#0000FF¨»T«/mi»«mi mathvariant=¨bold¨ mathcolor=¨#0000FF¨»X«/mi»«/msub»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»=«/mo»«mi mathvariant=¨bold¨ mathcolor=¨#0000FF¨»m«/mi»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»§#183;«/mo»«msup»«mi mathvariant=¨bold¨ mathcolor=¨#0000FF¨»§#969;«/mi»«mn mathvariant=¨bold¨ mathcolor=¨#0000FF¨»2«/mn»«/msup»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»§#183;«/mo»«mi mathvariant=¨bold¨ mathcolor=¨#0000FF¨»R«/mi»«mspace linebreak=¨newline¨»«/mspace»«menclose mathcolor=¨#0000FF¨ notation=¨box¨»«mi mathvariant=¨bold¨»T«/mi»«mo mathvariant=¨bold¨»§#183;«/mo»«mi mathvariant=¨bold¨»sin«/mi»«mo mathvariant=¨bold¨»(«/mo»«mi mathvariant=¨bold¨»§#945;«/mi»«mo mathvariant=¨bold¨»)«/mo»«mo mathvariant=¨bold¨»=«/mo»«mi mathvariant=¨bold¨»m«/mi»«mo mathvariant=¨bold¨»§#183;«/mo»«msup»«mi mathvariant=¨bold¨»§#969;«/mi»«mn mathvariant=¨bold¨»2«/mn»«/msup»«mo mathvariant=¨bold¨»§#183;«/mo»«mi mathvariant=¨bold¨»R«/mi»«/menclose»«/math» «math xmlns=¨http://www.w3.org/1998/Math/MathML¨»«msub»«mi mathvariant=¨bold¨ mathcolor=¨#0000FF¨»§#931;F«/mi»«mi mathvariant=¨bold¨ mathcolor=¨#0000FF¨»Y«/mi»«/msub»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»=«/mo»«mn mathvariant=¨bold¨ mathcolor=¨#0000FF¨»0«/mn»«mspace linebreak=¨newline¨»«/mspace»«msub»«mi mathvariant=¨bold¨ mathcolor=¨#0000FF¨»T«/mi»«mi mathvariant=¨bold¨ mathcolor=¨#0000FF¨»Y«/mi»«/msub»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»=«/mo»«mi mathvariant=¨bold¨ mathcolor=¨#0000FF¨»W«/mi»«mspace linebreak=¨newline¨»«/mspace»«menclose mathcolor=¨#0000FF¨ notation=¨box¨»«mi mathvariant=¨bold¨»T«/mi»«mo mathvariant=¨bold¨»§#183;«/mo»«mi mathvariant=¨bold¨»cos«/mi»«mo mathvariant=¨bold¨»(«/mo»«mi mathvariant=¨bold¨»§#945;«/mi»«mo mathvariant=¨bold¨»)«/mo»«mo mathvariant=¨bold¨»=«/mo»«mi mathvariant=¨bold¨»mg«/mi»«/menclose»«/math»
إذا قسمنا معادلات الحركة ، فسنحصل على معادلة بظل زاوية ميل الخيط. وليس مع جيب التمام (cos).
للحصول على معادلة مع جيب التمام (cos) ، نعبر عن نصف قطر المسار في معادلة الحركة الدائرية باستخدام دالة الجيب sin ، ونختزل دالة الجيب
وبعد ذلك فقط نجري عملية قسمة بين معادلات الحركة.
«math xmlns=¨http://www.w3.org/1998/Math/MathML¨»«mi mathvariant=¨bold¨ mathcolor=¨#0000FF¨»sin«/mi»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»(«/mo»«mi mathvariant=¨bold¨ mathcolor=¨#0000FF¨»§#945;«/mi»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»)«/mo»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»=«/mo»«mfrac mathcolor=¨#0000FF¨»«mi mathvariant=¨bold¨»R«/mi»«mi mathvariant=¨bold¨»L«/mi»«/mfrac»«mspace linebreak=¨newline¨»«/mspace»«mspace linebreak=¨newline¨»«/mspace»«menclose mathcolor=¨#0000FF¨ notation=¨circle¨»«mi mathvariant=¨bold¨»R«/mi»«mo mathvariant=¨bold¨»=«/mo»«mi mathvariant=¨bold¨»L«/mi»«mo mathvariant=¨bold¨»§#183;«/mo»«mi mathvariant=¨bold¨»sin«/mi»«mo mathvariant=¨bold¨»(«/mo»«mi mathvariant=¨bold¨»§#945;«/mi»«mo mathvariant=¨bold¨»)«/mo»«/menclose»«/math» 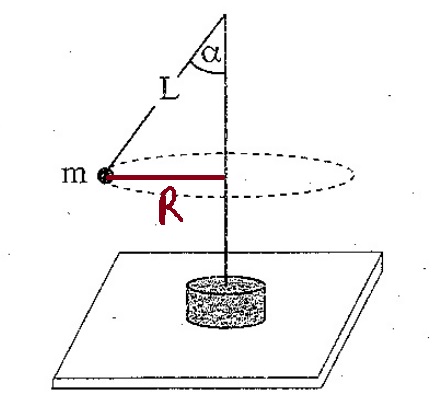

نعوّض التعبير عن نصف قطر المسار في معادلة الحركة الدائرية:
«math xmlns=¨http://www.w3.org/1998/Math/MathML¨»«menclose mathcolor=¨#0000FF¨ notation=¨box¨»«mi mathvariant=¨bold¨»T«/mi»«mo mathvariant=¨bold¨»§#183;«/mo»«mi mathvariant=¨bold¨»sin«/mi»«mo mathvariant=¨bold¨»(«/mo»«mi mathvariant=¨bold¨»§#945;«/mi»«mo mathvariant=¨bold¨»)«/mo»«mo mathvariant=¨bold¨»=«/mo»«mi mathvariant=¨bold¨»m«/mi»«mo mathvariant=¨bold¨»§#183;«/mo»«msup»«mi mathvariant=¨bold¨»§#969;«/mi»«mn mathvariant=¨bold¨»2«/mn»«/msup»«mo mathvariant=¨bold¨»§#183;«/mo»«mi mathvariant=¨bold¨ mathcolor=¨#FF0000¨»R«/mi»«/menclose»«mspace linebreak=¨newline¨»«/mspace»«mspace linebreak=¨newline¨»«/mspace»«mi mathvariant=¨bold¨ mathcolor=¨#0000FF¨»T«/mi»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»§#183;«/mo»«menclose mathcolor=¨#0000FF¨ notation=¨updiagonalstrike¨»«mi mathvariant=¨bold¨»sin«/mi»«mo mathvariant=¨bold¨»(«/mo»«mi mathvariant=¨bold¨»§#945;«/mi»«mo mathvariant=¨bold¨»)«/mo»«/menclose»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»=«/mo»«mi mathvariant=¨bold¨ mathcolor=¨#0000FF¨»m«/mi»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»§#183;«/mo»«msup»«mi mathvariant=¨bold¨ mathcolor=¨#0000FF¨»§#969;«/mi»«mn mathvariant=¨bold¨ mathcolor=¨#0000FF¨»2«/mn»«/msup»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»§#183;«/mo»«mi mathvariant=¨bold¨ mathcolor=¨#FF0000¨»L«/mi»«mo mathvariant=¨bold¨ mathcolor=¨#FF0000¨»§#183;«/mo»«menclose mathcolor=¨#FF0000¨ notation=¨updiagonalstrike¨»«mi mathvariant=¨bold¨»sin«/mi»«mo mathvariant=¨bold¨»(«/mo»«mi mathvariant=¨bold¨»§#945;«/mi»«mo mathvariant=¨bold¨»)«/mo»«/menclose»«mspace linebreak=¨newline¨»«/mspace»«mspace linebreak=¨newline¨»«/mspace»«mi mathvariant=¨bold¨ mathcolor=¨#0000FF¨»T«/mi»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»=«/mo»«mi mathvariant=¨bold¨ mathcolor=¨#0000FF¨»m«/mi»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»§#183;«/mo»«msup»«mi mathvariant=¨bold¨ mathcolor=¨#0000FF¨»§#969;«/mi»«mn mathcolor=¨#0000FF¨ mathvariant=¨bold¨»2«/mn»«/msup»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»§#183;«/mo»«mi mathvariant=¨bold¨ mathcolor=¨#0000FF¨»L«/mi»«mspace linebreak=¨newline¨»«/mspace»«mspace linebreak=¨newline¨»«/mspace»«mi mathvariant=¨bold¨ mathcolor=¨#0000FF¨»T«/mi»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»=«/mo»«mi mathvariant=¨bold¨ mathcolor=¨#0000FF¨»m«/mi»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»§#183;«/mo»«msup»«mfenced mathcolor=¨#0000FF¨»«mrow»«mn mathvariant=¨bold¨»2«/mn»«mo mathvariant=¨bold¨»§#183;«/mo»«mi mathvariant=¨bold¨»§#960;«/mi»«mo mathvariant=¨bold¨»§#183;«/mo»«mi mathvariant=¨bold¨»f«/mi»«/mrow»«/mfenced»«mn mathvariant=¨bold¨ mathcolor=¨#0000FF¨»2«/mn»«/msup»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»§#183;«/mo»«mi mathvariant=¨bold¨ mathcolor=¨#0000FF¨»L«/mi»«mspace linebreak=¨newline¨»«/mspace»«mspace linebreak=¨newline¨»«/mspace»«menclose mathcolor=¨#0000FF¨ notation=¨box¨»«mi mathvariant=¨bold¨»T«/mi»«mo mathvariant=¨bold¨»=«/mo»«mi mathvariant=¨bold¨»m«/mi»«mo mathvariant=¨bold¨»§#183;«/mo»«mn mathvariant=¨bold¨»4«/mn»«mo mathvariant=¨bold¨»§#183;«/mo»«msup»«mi mathvariant=¨bold¨»§#960;«/mi»«mn mathvariant=¨bold¨»2«/mn»«/msup»«mo mathvariant=¨bold¨»§#183;«/mo»«msup»«mi mathvariant=¨bold¨»f«/mi»«mn mathvariant=¨bold¨»2«/mn»«/msup»«mo mathvariant=¨bold¨»§#183;«/mo»«mi mathvariant=¨bold¨»L«/mi»«/menclose»«/math»
نقسم بين معادلات الحركة العمودية لمستوى الدوران ومعادلة الحركة الدائرية ، ونعبّر عن جيب التمام لزاوية ميل الخيط كدالة لمقلوب مربع التردد:
«math xmlns=¨http://www.w3.org/1998/Math/MathML¨»«mfrac mathcolor=¨#0000FF¨»«mrow»«menclose notation=¨updiagonalstrike¨»«mi mathvariant=¨bold¨»T«/mi»«/menclose»«mo mathvariant=¨bold¨»§#183;«/mo»«mi mathvariant=¨bold¨»cos«/mi»«mo mathvariant=¨bold¨»(«/mo»«mi mathvariant=¨bold¨»§#945;«/mi»«mo mathvariant=¨bold¨»)«/mo»«/mrow»«menclose notation=¨updiagonalstrike¨»«mi mathvariant=¨bold¨»T«/mi»«/menclose»«/mfrac»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»=«/mo»«mfrac mathcolor=¨#0000FF¨»«mrow»«menclose notation=¨downdiagonalstrike¨»«mi mathvariant=¨bold¨»m«/mi»«/menclose»«mi mathvariant=¨bold¨»g«/mi»«/mrow»«mrow»«menclose notation=¨downdiagonalstrike¨»«mi mathvariant=¨bold¨»m«/mi»«/menclose»«mo mathvariant=¨bold¨»§#183;«/mo»«mn mathvariant=¨bold¨»4«/mn»«mo mathvariant=¨bold¨»§#183;«/mo»«msup»«mi mathvariant=¨bold¨»§#960;«/mi»«mn mathvariant=¨bold¨»2«/mn»«/msup»«mo mathvariant=¨bold¨»§#183;«/mo»«msup»«mi mathvariant=¨bold¨»f«/mi»«mn mathvariant=¨bold¨»2«/mn»«/msup»«mo mathvariant=¨bold¨»§#183;«/mo»«mi mathvariant=¨bold¨»L«/mi»«/mrow»«/mfrac»«mspace linebreak=¨newline¨»«/mspace»«mspace linebreak=¨newline¨»«/mspace»«menclose mathcolor=¨#0000FF¨ notation=¨circle¨»«mi mathvariant=¨bold¨»cos«/mi»«mo mathvariant=¨bold¨»(«/mo»«mi mathvariant=¨bold¨»§#945;«/mi»«mo mathvariant=¨bold¨»)«/mo»«mo mathvariant=¨bold¨»=«/mo»«mfrac»«mi mathvariant=¨bold¨»g«/mi»«mrow»«mn mathvariant=¨bold¨»4«/mn»«mo mathvariant=¨bold¨»§#183;«/mo»«msup»«mi mathvariant=¨bold¨»§#960;«/mi»«mn mathvariant=¨bold¨»2«/mn»«/msup»«mo mathvariant=¨bold¨»§#183;«/mo»«mi mathvariant=¨bold¨»L«/mi»«/mrow»«/mfrac»«mo mathvariant=¨bold¨»§#183;«/mo»«mfrac»«mn mathvariant=¨bold¨»1«/mn»«msup»«mi mathvariant=¨bold¨»f«/mi»«mn mathvariant=¨bold¨»2«/mn»«/msup»«/mfrac»«/menclose»«mspace linebreak=¨newline¨»«/mspace»«/math»
בהתאם למישור התנועה, למיקום נקודת מרכז הסיבוב ,הכוח הצנטריפטלי הוא הרכיב האופקי של כוח המתיחות.
נערוך תרשים כוחות לכוחות הפועלים על הכדור:

נכתוב את משוואת התנועה המעגלית ביחס לציר רדיאלי , ואת משוואת התנועה האנכית ביחס לציר אנכי שכיוונו כלפי מעלה:
«math xmlns=¨http://www.w3.org/1998/Math/MathML¨»«msub»«mi mathvariant=¨bold¨ mathcolor=¨#0000FF¨»§#931;F«/mi»«mi mathvariant=¨bold¨ mathcolor=¨#0000FF¨»R«/mi»«/msub»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»=«/mo»«msup»«mi mathvariant=¨bold¨ mathcolor=¨#0000FF¨»m§#969;«/mi»«mn mathvariant=¨bold¨ mathcolor=¨#0000FF¨»2«/mn»«/msup»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»§#183;«/mo»«mi mathvariant=¨bold¨ mathcolor=¨#0000FF¨»R«/mi»«mspace linebreak=¨newline¨»«/mspace»«msub»«mi mathvariant=¨bold¨ mathcolor=¨#0000FF¨»f«/mi»«msub mathcolor=¨#0000FF¨»«mi mathvariant=¨bold¨»s«/mi»«mi mathvariant=¨bold¨»max«/mi»«/msub»«/msub»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»=«/mo»«msup»«mi mathvariant=¨bold¨ mathcolor=¨#0000FF¨»m§#969;«/mi»«mn mathvariant=¨bold¨ mathcolor=¨#0000FF¨»2«/mn»«/msup»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»§#183;«/mo»«mi mathvariant=¨bold¨ mathcolor=¨#0000FF¨»R«/mi»«mspace linebreak=¨newline¨»«/mspace»«menclose mathcolor=¨#0000FF¨ notation=¨box¨»«msub»«mi mathvariant=¨bold¨»§#956;«/mi»«mi mathvariant=¨bold¨»s«/mi»«/msub»«mo mathvariant=¨bold¨»§#183;«/mo»«mi mathvariant=¨bold¨»N«/mi»«mo mathvariant=¨bold¨»=«/mo»«msup»«mi mathvariant=¨bold¨»m§#969;«/mi»«mn mathvariant=¨bold¨»2«/mn»«/msup»«mo mathvariant=¨bold¨»§#183;«/mo»«mi mathvariant=¨bold¨»R«/mi»«/menclose»«/math» «math xmlns=¨http://www.w3.org/1998/Math/MathML¨»«msub»«mi mathvariant=¨bold¨ mathcolor=¨#0000FF¨»§#931;F«/mi»«mi mathvariant=¨bold¨ mathcolor=¨#0000FF¨»Y«/mi»«/msub»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»=«/mo»«mn mathvariant=¨bold¨ mathcolor=¨#0000FF¨»0«/mn»«mspace linebreak=¨newline¨»«/mspace»«mi mathvariant=¨bold¨ mathcolor=¨#0000FF¨»N«/mi»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»=«/mo»«mi mathvariant=¨bold¨ mathcolor=¨#0000FF¨»W«/mi»«mspace linebreak=¨newline¨»«/mspace»«menclose mathcolor=¨#0000FF¨ notation=¨box¨»«mi mathvariant=¨bold¨»N«/mi»«mo mathvariant=¨bold¨»=«/mo»«mi mathvariant=¨bold¨»mg«/mi»«/menclose»«/math»
1. في كل من معادلات الحركة ، لا يظهر تردد وجيب تمام (cos) الزاوية.
من قسمة معادلات الحركة تعبيرًا بظل (tan) الزاوية والتردد ، وليس بجيب تمام (cos) الزاوية.
عندما لا تحتوي معادلات الحركة على المقدار الفيزيائي المطلوب ، يجب استخدام تعبير إضافي (عادة هندسي) للوصول إلى التعبير المطلوب.
2. يجب أن نستخدم التعبير عن نصف قطر المسار «math xmlns=¨http://www.w3.org/1998/Math/MathML¨»«mi mathvariant=¨bold¨ mathcolor=¨#FF0000¨»R«/mi»«mo mathvariant=¨bold¨ mathcolor=¨#FF0000¨»=«/mo»«mi mathvariant=¨bold¨ mathcolor=¨#FF0000¨»L«/mi»«mo mathvariant=¨bold¨ mathcolor=¨#FF0000¨»§#183;«/mo»«mi mathvariant=¨bold¨ mathcolor=¨#FF0000¨»sin«/mi»«mo mathvariant=¨bold¨ mathcolor=¨#FF0000¨»(«/mo»«mi mathvariant=¨bold¨ mathcolor=¨#FF0000¨»§#945;«/mi»«mo mathvariant=¨bold¨ mathcolor=¨#FF0000¨»)«/mo»«/math», بالإضافة لمعادلات الحركة.
3. هناك عدة طرق جبرية للوصول إلى التعبير المطلوب من معادلات الحركة و تعبير نصف قطر المسار ، وكل الطرق تؤدي إلى التعبير المطلوب.
כאשר משוואות התנועה לא מכילות את הגודל הפיזיקלי המבוקש יש להשתמש בביטוי נוסף (לרוב גיאומטרי) , כדי להגיע לביטוי המבוקש.
2. כשם שביטוי של X , לא יכול להיות לוי תלוי בצורתו הסופית ב X.
כך, ביטוי קוסינוס הזווית לא יכול להיות תלוי בסינוס הזווית או בטנגנס הזווית.
חייבים במקרה זה להיעזר בביטוי רדיוס המסלול, בנוסף למשוואות התנועה.
3.
______________________________________________________________________________________

______________________________________________________________________________________
...
قيم الجدول:
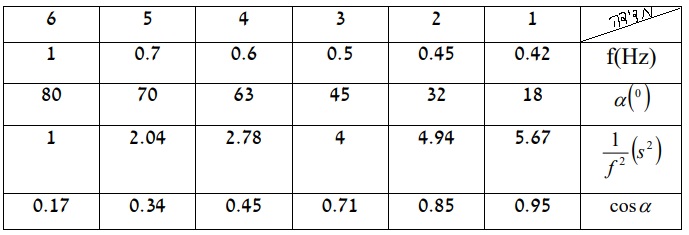
نرسم رسمًا بيانيًا لجيب تمام (cos) زاوية ميل الخيط ، اعتمادًا على مقلوب مربع التردد:
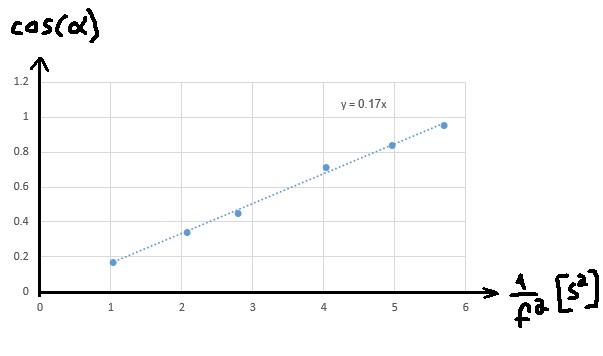

נסרטט גרף של קוסינוס זווית נטיית החוט ,בתלות בהפכי של ריבוע התדירות:

يجب إكمال قيم الجدول وفقًا لتردد وزاوية ميل الخيط. واستخدم قيم الجدول للوصف المطلوب.
نملأ الجدول وفقًا لقيم التردد وزاوية ميل الخيط:
نرسم رسمًا بيانيًا لجيب تمام (cos) الزاوية كدالة لمقلوب مربع التردد:
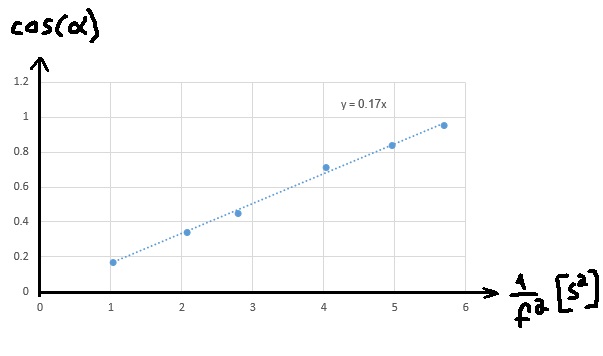
נמלא את הטבלה בהתאם לערכי התדירות וזווית נטיית החוט:

נסרטט גרף של קוסינוס הזווית בתלות בהופכי של ריבוע התדירות:

1. هناك تعليمات لتقريب النتائج إلى نقطتين بعد الفاصلة العشرية. يجب كتابة قيم الجدول وفقًا للتعليمات.
2. من المهم الإشارة إلى أسماء المحاور ووحداتها. وحدات التردد هي هرتز ، والتي تساوي «math xmlns=¨http://www.w3.org/1998/Math/MathML¨»«mfrac mathcolor=¨#FF0000¨»«mn»1«/mn»«mi»s«/mi»«/mfrac»«/math» .
لذلك ، وحدات مقلوب التردد هي الثانية.
2. חשוב לציין את שמות הצירים ויחידותיהם. היחידות של תדירות הם הרץ , השקולים לאחד חלקי שנייה .
לכן, היחידות של ההופכי של התדירות הם שנייה.
______________________________________________________________________________________

______________________________________________________________________________________
...
طول الخيط 1.5 متر.
نقارن قيمة الميل في الرسم البياني بتعبير الميل.
من تعبير جيب التمام (cos) لزاوية ميل الخيط كدالة لمقلوب مربع التردد «math xmlns=¨http://www.w3.org/1998/Math/MathML¨»«mi mathvariant=¨bold¨ mathcolor=¨#0000FF¨»cos«/mi»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»(«/mo»«mi mathvariant=¨bold¨ mathcolor=¨#0000FF¨»§#945;«/mi»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»)«/mo»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»=«/mo»«mfrac mathcolor=¨#0000FF¨»«mi mathvariant=¨bold¨»g«/mi»«mrow»«mn mathvariant=¨bold¨»4«/mn»«mo mathvariant=¨bold¨»§#183;«/mo»«msup»«mi mathvariant=¨bold¨»§#960;«/mi»«mn mathvariant=¨bold¨»2«/mn»«/msup»«mo mathvariant=¨bold¨»§#183;«/mo»«mi mathvariant=¨bold¨»L«/mi»«/mrow»«/mfrac»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»§#183;«/mo»«mfrac mathcolor=¨#0000FF¨»«mn mathvariant=¨bold¨»1«/mn»«msup»«mi mathvariant=¨bold¨»f«/mi»«mn mathvariant=¨bold¨»2«/mn»«/msup»«/mfrac»«/math» معنى ميل الرسم البياني: «math xmlns=¨http://www.w3.org/1998/Math/MathML¨»«mfrac mathcolor=¨#0000FF¨»«mi mathvariant=¨bold¨»g«/mi»«mrow»«mn mathvariant=¨bold¨»4«/mn»«mo mathvariant=¨bold¨»§#183;«/mo»«msup»«mi mathvariant=¨bold¨»§#960;«/mi»«mn mathvariant=¨bold¨»2«/mn»«/msup»«mo mathvariant=¨bold¨»§#183;«/mo»«mi mathvariant=¨bold¨»L«/mi»«/mrow»«/mfrac»«/math»
نجد قيمة ميل الدالة في الرسم البياني لنقطتين على خط المتجّه، وسنشير إلى النقطتين الأولى والخامسة:
«math xmlns=¨http://www.w3.org/1998/Math/MathML¨»«mi mathvariant=¨bold-italic¨ mathcolor=¨#0000FF¨»§#1575;§#1604;§#1605;§#1610;§#1604;«/mi»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»=«/mo»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»§#160;«/mo»«mfrac mathcolor=¨#0000FF¨»«mrow»«mo mathvariant=¨bold¨»§#8710;«/mo»«mi mathvariant=¨bold¨»c«/mi»«mi mathvariant=¨bold¨»o«/mi»«mi mathvariant=¨bold¨»s«/mi»«mo mathvariant=¨bold¨»(«/mo»«mi mathvariant=¨bold¨»§#945;«/mi»«mo mathvariant=¨bold¨»)«/mo»«/mrow»«mrow»«mo mathvariant=¨bold¨»§#8710;«/mo»«mstyle displaystyle=¨true¨»«mfrac»«mn mathvariant=¨bold¨»1«/mn»«msup»«mi mathvariant=¨bold¨»f«/mi»«mn mathvariant=¨bold¨»2«/mn»«/msup»«/mfrac»«/mstyle»«/mrow»«/mfrac»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»=«/mo»«mfrac mathcolor=¨#0000FF¨»«mrow»«mn mathvariant=¨bold¨»0«/mn»«mo mathvariant=¨bold¨».«/mo»«mn mathvariant=¨bold¨»95«/mn»«mo mathvariant=¨bold¨»-«/mo»«mn mathvariant=¨bold¨»0«/mn»«mo mathvariant=¨bold¨».«/mo»«mn mathvariant=¨bold¨»34«/mn»«/mrow»«mrow»«mn mathvariant=¨bold¨»5«/mn»«mo mathvariant=¨bold¨».«/mo»«mn mathvariant=¨bold¨»67«/mn»«mo mathvariant=¨bold¨»-«/mo»«mn mathvariant=¨bold¨»2«/mn»«mo mathvariant=¨bold¨».«/mo»«mn mathvariant=¨bold¨»04«/mn»«/mrow»«/mfrac»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»=«/mo»«mfrac mathcolor=¨#0000FF¨»«mrow»«mn mathvariant=¨bold¨»0«/mn»«mo mathvariant=¨bold¨».«/mo»«mn mathvariant=¨bold¨»61«/mn»«/mrow»«mrow»«mn mathvariant=¨bold¨»3«/mn»«mo mathvariant=¨bold¨».«/mo»«mn mathvariant=¨bold¨»63«/mn»«/mrow»«/mfrac»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»=«/mo»«mn mathvariant=¨bold¨ mathcolor=¨#0000FF¨»0«/mn»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨».«/mo»«mn mathvariant=¨bold¨ mathcolor=¨#0000FF¨»168«/mn»«mfrac mathcolor=¨#0000FF¨»«mn mathvariant=¨bold¨»1«/mn»«msup»«mi mathvariant=¨bold¨»s«/mi»«mn mathvariant=¨bold¨»2«/mn»«/msup»«/mfrac»«/math»
نقارن تعبير الميل من التعبير بقيمته المحسوبة من الرسم البياني.
«math xmlns=¨http://www.w3.org/1998/Math/MathML¨»«mfrac mathcolor=¨#0000FF¨»«mi mathvariant=¨bold¨»g«/mi»«mrow»«mn mathvariant=¨bold¨»4«/mn»«mo mathvariant=¨bold¨»§#183;«/mo»«msup»«mi mathvariant=¨bold¨»§#960;«/mi»«mn mathvariant=¨bold¨»2«/mn»«/msup»«mo mathvariant=¨bold¨»§#183;«/mo»«mi mathvariant=¨bold¨»L«/mi»«/mrow»«/mfrac»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»=«/mo»«mi mathvariant=¨bold¨ mathcolor=¨#0000FF¨»§#1513;§#1497;§#1508;§#1493;§#1506;«/mi»«mspace linebreak=¨newline¨»«/mspace»«mspace linebreak=¨newline¨»«/mspace»«mfrac mathcolor=¨#0000FF¨»«mi mathvariant=¨bold¨»g«/mi»«mrow»«mn mathvariant=¨bold¨»4«/mn»«mo mathvariant=¨bold¨»§#183;«/mo»«msup»«mi mathvariant=¨bold¨»§#960;«/mi»«mn mathvariant=¨bold¨»2«/mn»«/msup»«mo mathvariant=¨bold¨»§#183;«/mo»«mi mathvariant=¨bold¨»L«/mi»«/mrow»«/mfrac»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»=«/mo»«mn mathvariant=¨bold¨ mathcolor=¨#0000FF¨»0«/mn»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨».«/mo»«mn mathvariant=¨bold¨ mathcolor=¨#0000FF¨»168«/mn»«mspace linebreak=¨newline¨»«/mspace»«mspace linebreak=¨newline¨»«/mspace»«mi mathvariant=¨bold¨ mathcolor=¨#0000FF¨»L«/mi»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»=«/mo»«mfrac mathcolor=¨#0000FF¨»«mi mathvariant=¨bold¨»g«/mi»«mrow»«mn mathvariant=¨bold¨»4«/mn»«mo mathvariant=¨bold¨»§#183;«/mo»«msup»«mi mathvariant=¨bold¨»§#960;«/mi»«mn mathvariant=¨bold¨»2«/mn»«/msup»«mo mathvariant=¨bold¨»§#183;«/mo»«mn mathvariant=¨bold¨»0«/mn»«mo mathvariant=¨bold¨».«/mo»«mn mathvariant=¨bold¨»168«/mn»«/mrow»«/mfrac»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»=«/mo»«mfrac mathcolor=¨#0000FF¨»«mn mathvariant=¨bold¨»10«/mn»«mrow»«mn mathvariant=¨bold¨»4«/mn»«mo mathvariant=¨bold¨»§#183;«/mo»«msup»«mi mathvariant=¨bold¨»§#960;«/mi»«mn mathvariant=¨bold¨»2«/mn»«/msup»«mo mathvariant=¨bold¨»§#183;«/mo»«mn mathvariant=¨bold¨»0«/mn»«mo mathvariant=¨bold¨».«/mo»«mn mathvariant=¨bold¨»168«/mn»«/mrow»«/mfrac»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»=«/mo»«mn mathvariant=¨bold¨ mathcolor=¨#0000FF¨»1«/mn»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨».«/mo»«mn mathvariant=¨bold¨ mathcolor=¨#0000FF¨»5«/mn»«mi mathvariant=¨bold¨ mathcolor=¨#0000FF¨»m«/mi»«mspace linebreak=¨newline¨»«/mspace»«mspace linebreak=¨newline¨»«/mspace»«/math»
لذلك ، يبلغ طول الخيط 1.5 متر.
נמצא את ערך שיפוע הפונקציה בגרף משתי נקודות הנמצאות על הישר המסתבר ביותר:
1. في هذا القسم مكتوب في السؤال كيف تجد طول الخيط. في معظم الأحيان ، لا تحتوي الأسئلة على مثل هذه التعليمات.
بشكل عام ، في أي سؤال يحتوي على وصف بياني لدالة خطية ، يمكن إيجاد المطلوب من ميل الرسم البياني.
2. أثناء الحل ، يتم استخدام قيمة الميل، وفي كل مرة تكتب قيمة الميل، يجب عليك تحديد وحداته.
3. يجب حساب طول الخيط بمساعدة ميل الرسم البياني وليس بمساعدة معادلات الحركة.
בד"כ בכל שאלה המכילה תיאור גרפי של פונקציה ליניארית, משיפוע הגרף ניתן למצוא את התשובה הדרושה.
2. במהלך הפתרון נעשה שימוש בערכו של השיפוע , בכל פעם שכותבים את ערכו של השיפוע יש לציין את יחידותיו.
3. יש לחשב את אורך החוט דווקא בעזרת שיפוע הגרף, ולא בעזרת משוואות התנועה.
______________________________________________________________________________________

______________________________________________________________________________________
...
الحد الأدنى للتردد هو 0.4 هرتز.
لجيب تمام (cos) الزاوية له قيمة قصوى ، وبالتالي فإن التردد له قيمة دنيا.
الحد الأقصى لقيمة جيب التمام (cos) الزاوية هو 1 ، من الرسم البياني يمكنك إيجاد الحد الأدنى للتردد الذي تكون قيمة جيب التمام (cos) له 1.
הערך המקסימאלי של קוסינוס הזווית הוא 1, מהגרף ניתן למצוא את התדירות המינמאלית עבורה ערך הקוסינוס הוא 1.
يصف الرسم البياني العلاقة بين التردد وجيب تمام (cos) الزاوية.
أكبر قيمة ممكنة لجيب التمام (cos) هي واحد.
الحد الأدنى للتردد هو التردد الذي تساوي فيه قيمة جيب التمام للزاوية (cos) واحدًا.
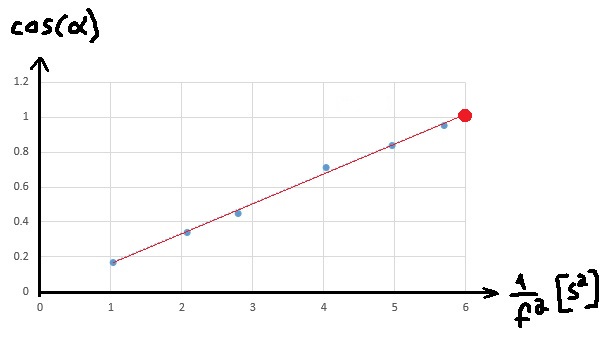
من الرسم البياني يمكن ملاحظة ذلك عندما «math xmlns=¨http://www.w3.org/1998/Math/MathML¨»«mi mathvariant=¨bold¨ mathcolor=¨#0000FF¨»cos«/mi»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»(«/mo»«mi mathvariant=¨bold¨ mathcolor=¨#0000FF¨»§#945;«/mi»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»)«/mo»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»=«/mo»«mn mathvariant=¨bold¨ mathcolor=¨#0000FF¨»1«/mn»«/math» قيمة المقدار «math xmlns=¨http://www.w3.org/1998/Math/MathML¨»«mfrac mathcolor=¨#0000FF¨»«mn mathvariant=¨bold¨»1«/mn»«msup»«msub»«mi mathvariant=¨bold¨»f«/mi»«mi mathvariant=¨bold¨»min«/mi»«/msub»«mn mathvariant=¨bold¨»2«/mn»«/msup»«/mfrac»«/math» 6 ثواني تربيع.
نجد fmin:
«math xmlns=¨http://www.w3.org/1998/Math/MathML¨»«mfrac mathcolor=¨#0000FF¨»«mn mathvariant=¨bold¨»1«/mn»«msup»«msub»«mi mathvariant=¨bold¨»f«/mi»«mi mathvariant=¨bold¨»min«/mi»«/msub»«mn mathvariant=¨bold¨»2«/mn»«/msup»«/mfrac»«mo mathcolor=¨#0000FF¨»=«/mo»«mn mathcolor=¨#0000FF¨»6«/mn»«mspace linebreak=¨newline¨»«/mspace»«mspace linebreak=¨newline¨»«/mspace»«msup»«msub»«mi mathvariant=¨bold¨ mathcolor=¨#0000FF¨»f«/mi»«mi mathvariant=¨bold¨ mathcolor=¨#0000FF¨»min«/mi»«/msub»«mn mathvariant=¨bold¨ mathcolor=¨#0000FF¨»2«/mn»«/msup»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»=«/mo»«mfrac mathcolor=¨#0000FF¨»«mn mathvariant=¨bold¨»1«/mn»«mn mathvariant=¨bold¨»6«/mn»«/mfrac»«mspace linebreak=¨newline¨»«/mspace»«mspace linebreak=¨newline¨»«/mspace»«msub»«mi mathvariant=¨bold¨ mathcolor=¨#0000FF¨»f«/mi»«mi mathvariant=¨bold¨ mathcolor=¨#0000FF¨»min«/mi»«/msub»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»=«/mo»«msqrt mathcolor=¨#0000FF¨»«mfrac»«mn mathvariant=¨bold¨»1«/mn»«mn mathvariant=¨bold¨»6«/mn»«/mfrac»«/msqrt»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»=«/mo»«mn mathvariant=¨bold¨ mathcolor=¨#0000FF¨»0«/mn»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨».«/mo»«msub»«mn mathvariant=¨bold¨ mathcolor=¨#0000FF¨»4«/mn»«mi mathvariant=¨bold¨ mathcolor=¨#0000FF¨»HZ«/mi»«/msub»«mspace linebreak=¨newline¨»«/mspace»«mspace linebreak=¨newline¨»«/mspace»«/math»
يجب تدوير المحور بتردد لا يقل عن 0.4 هرتز. عند تردد أصغر من هذا التردد لن يكون هناك حركة دائرية ، ستكون هناك حركة عشوائية.
ערך קוסינוס הזווית הגדול ביותר האפשרי הוא אחד.
התדירות המינימלית היא התדירות עבורה ערך קוסינוס הזווית שווה לאחד.

מהגרף ניתן לראות שכאשר «math xmlns=¨http://www.w3.org/1998/Math/MathML¨»«mi mathvariant=¨bold¨ mathcolor=¨#0000FF¨»cos«/mi»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»(«/mo»«mi mathvariant=¨bold¨ mathcolor=¨#0000FF¨»§#945;«/mi»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»)«/mo»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»=«/mo»«mn mathvariant=¨bold¨ mathcolor=¨#0000FF¨»1«/mn»«/math» ערכו של «math xmlns=¨http://www.w3.org/1998/Math/MathML¨»«mfrac mathcolor=¨#0000FF¨»«mn mathvariant=¨bold¨»1«/mn»«msup»«msub»«mi mathvariant=¨bold¨»f«/mi»«mi mathvariant=¨bold¨»min«/mi»«/msub»«mn mathvariant=¨bold¨»2«/mn»«/msup»«/mfrac»«/math» הוא 6 שניות בריבוע.
נמצא את fmin:
«math xmlns=¨http://www.w3.org/1998/Math/MathML¨»«mfrac mathcolor=¨#0000FF¨»«mn mathvariant=¨bold¨»1«/mn»«msup»«msub»«mi mathvariant=¨bold¨»f«/mi»«mi mathvariant=¨bold¨»min«/mi»«/msub»«mn mathvariant=¨bold¨»2«/mn»«/msup»«/mfrac»«mo mathcolor=¨#0000FF¨»=«/mo»«mn mathcolor=¨#0000FF¨»6«/mn»«mspace linebreak=¨newline¨»«/mspace»«mspace linebreak=¨newline¨»«/mspace»«msup»«msub»«mi mathvariant=¨bold¨ mathcolor=¨#0000FF¨»f«/mi»«mi mathvariant=¨bold¨ mathcolor=¨#0000FF¨»min«/mi»«/msub»«mn mathvariant=¨bold¨ mathcolor=¨#0000FF¨»2«/mn»«/msup»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»=«/mo»«mfrac mathcolor=¨#0000FF¨»«mn mathvariant=¨bold¨»1«/mn»«mn mathvariant=¨bold¨»6«/mn»«/mfrac»«mspace linebreak=¨newline¨»«/mspace»«mspace linebreak=¨newline¨»«/mspace»«msub»«mi mathvariant=¨bold¨ mathcolor=¨#0000FF¨»f«/mi»«mi mathvariant=¨bold¨ mathcolor=¨#0000FF¨»min«/mi»«/msub»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»=«/mo»«msqrt mathcolor=¨#0000FF¨»«mfrac»«mn mathvariant=¨bold¨»1«/mn»«mn mathvariant=¨bold¨»6«/mn»«/mfrac»«/msqrt»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»=«/mo»«mn mathvariant=¨bold¨ mathcolor=¨#0000FF¨»0«/mn»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨».«/mo»«msub»«mn mathvariant=¨bold¨ mathcolor=¨#0000FF¨»4«/mn»«mi mathvariant=¨bold¨ mathcolor=¨#0000FF¨»HZ«/mi»«/msub»«mspace linebreak=¨newline¨»«/mspace»«mspace linebreak=¨newline¨»«/mspace»«/math»
יש לסובב את הציר בתדירות של לפחות 0.4 הרץ. בתדירות קטנה מתדירות זו לא תהיה תנועה מעגלית, תהיה תנועה אקראית.
1. تُقتصر قيمة دالتَي جيب التمام (cos) وجيب sin الزاوية على واحد. لا يمكن أن تكون قيمتها أكبر من واحد أو أقل من ناقص واحد.
ولكي لا تكون قيمة الجيب أو جيب التمام أكبر من واحد في كل تعبير يظهر فيهما يجب أن يكون هناك قيد آخر.
على سبيل المثال ، في مثلث قائم الزاوية يتحقق: «math xmlns=¨http://www.w3.org/1998/Math/MathML¨»«mi mathvariant=¨bold¨ mathcolor=¨#FF0000¨»sin«/mi»«mo mathvariant=¨bold¨ mathcolor=¨#FF0000¨»(«/mo»«mi mathvariant=¨bold¨ mathcolor=¨#FF0000¨»§#945;«/mi»«mo mathvariant=¨bold¨ mathcolor=¨#FF0000¨»)«/mo»«mo mathvariant=¨bold¨ mathcolor=¨#FF0000¨»=«/mo»«mfrac mathcolor=¨#FF0000¨»«mrow»«mo mathvariant=¨bold¨»§#160;«/mo»«mo mathvariant=¨bold¨»§#160;«/mo»«mi mathvariant=¨bold¨»§#1604;§#1604;§#1586;§#1575;§#1608;§#1610;§#1577;«/mi»«mo mathvariant=¨bold¨»§#160;«/mo»«mi mathvariant=¨bold¨»§#1575;§#1604;§#1605;§#1602;§#1575;§#1576;§#1604;«/mi»«mo mathvariant=¨bold¨»§#160;«/mo»«mi mathvariant=¨bold¨»§#1575;§#1604;§#1590;§#1604;§#1593;«/mi»«/mrow»«mi mathvariant=¨bold¨»§#1575;§#1604;§#1608;§#1578;§#1585;«/mi»«/mfrac»«/math» , القيمة القصوى لـ «math xmlns=¨http://www.w3.org/1998/Math/MathML¨»«mi mathvariant=¨bold¨ mathcolor=¨#FF0000¨»sin«/mi»«mo mathvariant=¨bold¨ mathcolor=¨#FF0000¨»(«/mo»«mi mathvariant=¨bold¨ mathcolor=¨#FF0000¨»§#945;«/mi»«mo mathvariant=¨bold¨ mathcolor=¨#FF0000¨»)«/mo»«/math» هو واحد.
القيمة القصوى لـ «math xmlns=¨http://www.w3.org/1998/Math/MathML¨»«mfrac mathcolor=¨#FF0000¨»«mrow»«mo mathvariant=¨bold¨»§#160;«/mo»«mi mathvariant=¨bold¨»§#1604;§#1604;§#1586;§#1575;§#1608;§#1610;§#1577;«/mi»«mo mathvariant=¨bold¨»§#160;«/mo»«mi mathvariant=¨bold¨»§#1575;§#1604;§#1605;§#1602;§#1575;§#1576;§#1604;«/mi»«mo mathvariant=¨bold¨»§#160;«/mo»«mi mathvariant=¨bold¨»§#1575;§#1604;§#1590;§#1604;§#1593;«/mi»«/mrow»«mi mathvariant=¨bold¨»§#1575;§#1604;§#1608;§#1578;§#1585;«/mi»«/mfrac»«/math» يجب أن يكون هناك أيضًا واحدًا ، وهذا صحيح لأن الضلع العمودي المقابل للزاوية محدود ، ولا يمكن أن يكون أكبر من الوتر.
2. بالرغم من وجود قيود في مقدار فيزيائي واحدة على الأقل في كل تعبير يظهر فيه الجيب أو جيب التمام ، إلا أنه في معظم الأحيان لا يتم التعمق في هذه القيود.
3. لإيجاد القيمة القصوى المحتملة للمقدار الفيزيائي المحدود ، يجب مقارنة قيمة الجيب أو جيب التمام بواحد.
4. لا يصف التعبير الرياضي العلاقة بين المقادير الفيزيائية فحسب، بل يصف أيضًا بشكل غير مباشر القيمة القصوى أو الدنيا.
5. ما وراء القيود الرياضية ، هناك دائما منطق فيزيائي لهذه القيود.
في هذه الحالة ، عندما يدور المحور بتردد قليل، ستكون الكرة قريبة من القضيب.
عندما يزيد تردد الدوران ، تنفصل الكرة عن القضيب لكنها لن تتحرك في حركة دائرية.
فقط عندما يدور القضيب بتردد أكبر من 0.4 هرتز ستكون هناك حركة دائرية.
6. لا تقتصر دالة الظل (tan) على أي قيمة ، ولكنها غير معرّفة عند 90 درجة.
في أي تعبير تظهر فيه دالة الظل ، لا توجد احتمالية رياضية أن تكون زاوية الظل 90 درجة.
في أي حالة من هذا القبيل ، يوجد منطق فيزيائي للزاوية ألا تكون 90. (كما في الجسم المعلق يستخدم كمقياس تسارع).
וכדי שערך הסינוס או הקוסינוס לא יהיה גדול מאחד בכל ביטוי בו הם מופיעים קיימת מוגבלות גם בגדלים אחרים .
לדוגמה במשולש ישר זווית מתקיים: «math xmlns=¨http://www.w3.org/1998/Math/MathML¨»«mi mathvariant=¨bold¨ mathcolor=¨#FF0000¨»sin«/mi»«mo mathvariant=¨bold¨ mathcolor=¨#FF0000¨»(«/mo»«mi mathvariant=¨bold¨ mathcolor=¨#FF0000¨»§#945;«/mi»«mo mathvariant=¨bold¨ mathcolor=¨#FF0000¨»)«/mo»«mo mathvariant=¨bold¨ mathcolor=¨#FF0000¨»=«/mo»«mfrac mathcolor=¨#FF0000¨»«mrow»«mo mathvariant=¨bold¨»§#160;«/mo»«mi mathvariant=¨bold¨»§#1492;§#1494;§#1493;§#1493;§#1497;§#1514;«/mi»«mo mathvariant=¨bold¨»§#160;«/mo»«mi mathvariant=¨bold¨»§#1502;§#1493;§#1500;«/mi»«mo mathvariant=¨bold¨»§#160;«/mo»«mi mathvariant=¨bold¨»§#1504;§#1497;§#1510;§#1489;«/mi»«/mrow»«mi mathvariant=¨bold¨»§#1497;§#1514;§#1512;«/mi»«/mfrac»«/math» , ערכו המקסימאלי «math xmlns=¨http://www.w3.org/1998/Math/MathML¨»«mi mathvariant=¨bold¨ mathcolor=¨#FF0000¨»sin«/mi»«mo mathvariant=¨bold¨ mathcolor=¨#FF0000¨»(«/mo»«mi mathvariant=¨bold¨ mathcolor=¨#FF0000¨»§#945;«/mi»«mo mathvariant=¨bold¨ mathcolor=¨#FF0000¨»)«/mo»«/math» הוא אחד.
הערך המקסימאלי של «math xmlns=¨http://www.w3.org/1998/Math/MathML¨»«mfrac mathcolor=¨#FF0000¨»«mrow»«mo mathvariant=¨bold¨»§#160;«/mo»«mi mathvariant=¨bold¨»§#1492;§#1494;§#1493;§#1493;§#1497;§#1514;«/mi»«mo mathvariant=¨bold¨»§#160;«/mo»«mi mathvariant=¨bold¨»§#1502;§#1493;§#1500;«/mi»«mo mathvariant=¨bold¨»§#160;«/mo»«mi mathvariant=¨bold¨»§#1504;§#1497;§#1510;§#1489;«/mi»«/mrow»«mi mathvariant=¨bold¨»§#1497;§#1514;§#1512;«/mi»«/mfrac»«/math» גם חייב להיות אחד, וזה מתקיים מכיוון שהניצב מול הזווית לא יכול להיות גדול מהיתר.
2. למרות שבכל ביטוי בו מופיע סינוס או קוסינוס קיימת מוגבלות לפחות בגודל פיזיקלי אחד , לרוב לא מתעמקים במגבלות זאת.
כדי למצוא את ערכו הקיצוני האפשרי של הגודל הפיזיקלי המוגבל יש להשוות את ערך הסינוס או הקוסינוס לאחד.
3. הביטוי המתמטי לא מתאר רק את הקשר בין הגדלים הפיזיקליים הוא מתאר את ערכם המקסימאלי או המינימאלי.
4. מעבר למוגבלות המתמטית , תמיד קיים גם היגיון פיזיקלי למוגבלות זאת.
במקרה זה , כאשר הציר מסתובב במהירות קטנה מידי הכדור יהיה צמוד למוט .
כאשר תדירות הסיבוב תגדל הכדור יתנתק מהמוט אך הוא לא ינוע בתנועה מעגלית. רק בתדירות גדולה מ 0.4 הרץ תתקיים תנועה מעגלית.
5. פונקציית הטנגנס לא מוגבלת לערך כלשהו , אך היא לא מוגדרת ב 90 מעלות. בכל ביטוי בו מופיע פונקציית הטנגנס אין משמעות לזווית של 90 מעלות.
בכל מקרה כזה יש היגיון פיזיקלי לכך שהזווית לא תהיה 90 . (כמו בגוף תלוי המשמש כמד תאוצה).
______________________________________________________________________________________