______________________________________________________________________________________
...
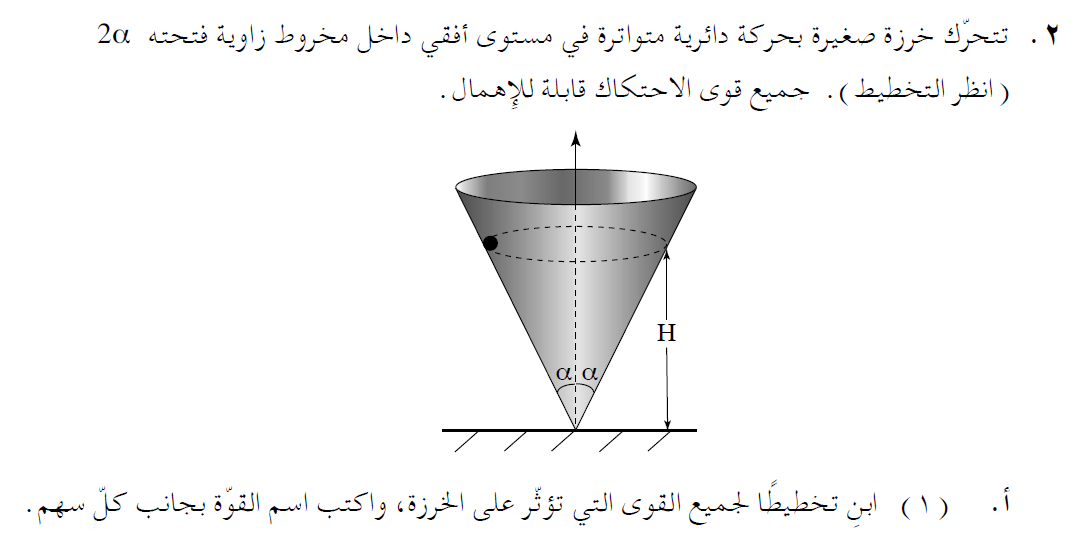
معرفة القوة العمودية وقوة الجاذبية.
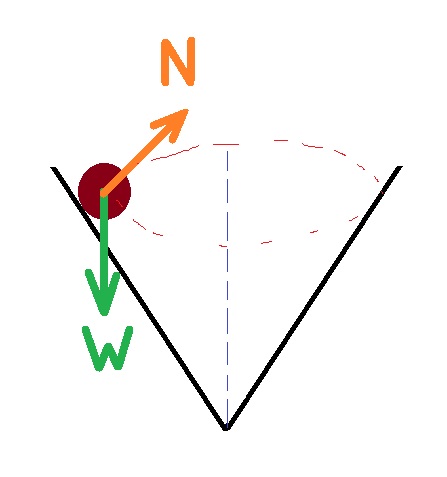
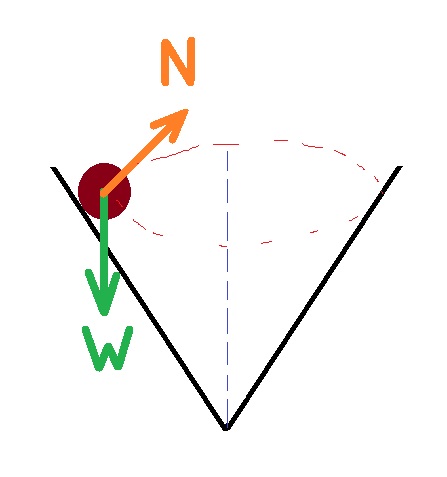
تؤثر قوتان على الخرزة ، قوة الجاذبية والقوة العمودية.
نقوم برسم مخطّط للقوى المؤثرة على الخرزة:
נערוך תרשים כוחות לכוחות הפועלים על החרוז:
لا يكفي الإشارة إلى الحرف الذي يمثل اسم القوة ، بل يجب أيضًا كتابة اسمها الكامل في سياق الحل.
______________________________________________________________________________________
أ. 
______________________________________________________________________________________
...
يشغّل السطح القوة العمودية ، والأرض تشغّل قوة الجاذبية.
معرفة القوة العمودية وقوة الجاذبية.
يشغّل السطح القوة العمودية ، والأرض تشغّل قوة الجاذبية.
كل تأثير بين جسمين هو تأثير متبادل، لذلك دائمًا يوجد جسم تعمل عليه القوة ، والجسم الآخر يشغّل هذه القوة.
______________________________________________________________________________________

______________________________________________________________________________________
...
«math xmlns=¨http://www.w3.org/1998/Math/MathML¨»«menclose notation=¨box¨»«mi mathvariant=¨bold¨»N«/mi»«mo mathvariant=¨bold¨»§#183;«/mo»«mi mathvariant=¨bold¨»cos«/mi»«mo mathvariant=¨bold¨»(«/mo»«mi mathvariant=¨bold¨»§#945;«/mi»«mo mathvariant=¨bold¨»)«/mo»«mo mathvariant=¨bold¨»=«/mo»«msup»«mi mathvariant=¨bold¨»m§#969;«/mi»«mn mathvariant=¨bold¨»2«/mn»«/msup»«mo mathvariant=¨bold¨»§#183;«/mo»«mi mathvariant=¨bold¨»R«/mi»«/menclose»«/math» «math xmlns=¨http://www.w3.org/1998/Math/MathML¨»«menclose notation=¨box¨»«mi mathvariant=¨bold¨»N«/mi»«mo mathvariant=¨bold¨»§#183;«/mo»«mi mathvariant=¨bold¨»sin«/mi»«mo mathvariant=¨bold¨»(«/mo»«mi mathvariant=¨bold¨»§#945;«/mi»«mo mathvariant=¨bold¨»)«/mo»«mo mathvariant=¨bold¨»=«/mo»«mi mathvariant=¨bold¨»mg«/mi»«/menclose»«/math»
«math xmlns=¨http://www.w3.org/1998/Math/MathML¨»«msub»«mi mathvariant=¨bold¨ mathcolor=¨#0000FF¨»§#931;F«/mi»«mi mathvariant=¨bold¨ mathcolor=¨#0000FF¨»R«/mi»«/msub»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»=«/mo»«mfrac mathcolor=¨#0000FF¨»«mrow»«mi mathvariant=¨bold¨»m«/mi»«mo mathvariant=¨bold¨»§#183;«/mo»«msup»«mi mathvariant=¨bold¨»V«/mi»«mn mathvariant=¨bold¨»2«/mn»«/msup»«/mrow»«mi mathvariant=¨bold¨»R«/mi»«/mfrac»«mspace linebreak=¨newline¨»«/mspace»«msub»«mi mathvariant=¨bold¨ mathcolor=¨#0000FF¨»N«/mi»«mi mathvariant=¨bold¨ mathcolor=¨#0000FF¨»X«/mi»«/msub»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»=«/mo»«mfrac mathcolor=¨#0000FF¨»«mrow»«mi mathvariant=¨bold¨»m«/mi»«mo mathvariant=¨bold¨»§#183;«/mo»«msup»«mi mathvariant=¨bold¨»V«/mi»«mn mathvariant=¨bold¨»2«/mn»«/msup»«/mrow»«mi mathvariant=¨bold¨»R«/mi»«/mfrac»«mspace linebreak=¨newline¨»«/mspace»«menclose mathcolor=¨#0000FF¨ notation=¨box¨»«mi mathvariant=¨bold¨»N«/mi»«mo mathvariant=¨bold¨»§#183;«/mo»«mi mathvariant=¨bold¨»cos«/mi»«mo mathvariant=¨bold¨»(«/mo»«mi mathvariant=¨bold¨»§#945;«/mi»«mo mathvariant=¨bold¨»)«/mo»«mo mathvariant=¨bold¨»=«/mo»«msup»«mi mathvariant=¨bold¨»m§#969;«/mi»«mn mathvariant=¨bold¨»2«/mn»«/msup»«mo mathvariant=¨bold¨»§#183;«/mo»«mi mathvariant=¨bold¨»R«/mi»«/menclose»«/math» «math xmlns=¨http://www.w3.org/1998/Math/MathML¨»«msub»«mi mathvariant=¨bold¨ mathcolor=¨#0000FF¨»§#931;F«/mi»«mi mathvariant=¨bold¨ mathcolor=¨#0000FF¨»Y«/mi»«/msub»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»=«/mo»«mn mathvariant=¨bold¨ mathcolor=¨#0000FF¨»0«/mn»«mspace linebreak=¨newline¨»«/mspace»«msub»«mi mathvariant=¨bold¨ mathcolor=¨#0000FF¨»N«/mi»«mi mathvariant=¨bold¨ mathcolor=¨#0000FF¨»Y«/mi»«/msub»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»=«/mo»«mi mathvariant=¨bold¨ mathcolor=¨#0000FF¨»W«/mi»«mspace linebreak=¨newline¨»«/mspace»«menclose mathcolor=¨#0000FF¨ notation=¨box¨»«mi mathvariant=¨bold¨»N«/mi»«mo mathvariant=¨bold¨»§#183;«/mo»«mi mathvariant=¨bold¨»sin«/mi»«mo mathvariant=¨bold¨»(«/mo»«mi mathvariant=¨bold¨»§#945;«/mi»«mo mathvariant=¨bold¨»)«/mo»«mo mathvariant=¨bold¨»=«/mo»«mi mathvariant=¨bold¨»mg«/mi»«/menclose»«/math»
«math xmlns=¨http://www.w3.org/1998/Math/MathML¨»«msub»«mi mathvariant=¨bold¨ mathcolor=¨#0000FF¨»§#931;F«/mi»«mi mathvariant=¨bold¨ mathcolor=¨#0000FF¨»R«/mi»«/msub»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»=«/mo»«mfrac mathcolor=¨#0000FF¨»«mrow»«mi mathvariant=¨bold¨»m«/mi»«mo mathvariant=¨bold¨»§#183;«/mo»«msup»«mi mathvariant=¨bold¨»V«/mi»«mn mathvariant=¨bold¨»2«/mn»«/msup»«/mrow»«mi mathvariant=¨bold¨»R«/mi»«/mfrac»«mspace linebreak=¨newline¨»«/mspace»«msub»«mi mathvariant=¨bold¨ mathcolor=¨#0000FF¨»N«/mi»«mi mathvariant=¨bold¨ mathcolor=¨#0000FF¨»X«/mi»«/msub»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»=«/mo»«mfrac mathcolor=¨#0000FF¨»«mrow»«mi mathvariant=¨bold¨»m«/mi»«mo mathvariant=¨bold¨»§#183;«/mo»«msup»«mi mathvariant=¨bold¨»V«/mi»«mn mathvariant=¨bold¨»2«/mn»«/msup»«/mrow»«mi mathvariant=¨bold¨»R«/mi»«/mfrac»«mspace linebreak=¨newline¨»«/mspace»«menclose mathcolor=¨#0000FF¨ notation=¨box¨»«mi mathvariant=¨bold¨»N«/mi»«mo mathvariant=¨bold¨»§#183;«/mo»«mi mathvariant=¨bold¨»cos«/mi»«mo mathvariant=¨bold¨»(«/mo»«mi mathvariant=¨bold¨»§#945;«/mi»«mo mathvariant=¨bold¨»)«/mo»«mo mathvariant=¨bold¨»=«/mo»«msup»«mi mathvariant=¨bold¨»m§#969;«/mi»«mn mathvariant=¨bold¨»2«/mn»«/msup»«mo mathvariant=¨bold¨»§#183;«/mo»«mi mathvariant=¨bold¨»R«/mi»«/menclose»«/math» «math xmlns=¨http://www.w3.org/1998/Math/MathML¨»«msub»«mi mathvariant=¨bold¨ mathcolor=¨#0000FF¨»§#931;F«/mi»«mi mathvariant=¨bold¨ mathcolor=¨#0000FF¨»Y«/mi»«/msub»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»=«/mo»«mn mathvariant=¨bold¨ mathcolor=¨#0000FF¨»0«/mn»«mspace linebreak=¨newline¨»«/mspace»«msub»«mi mathvariant=¨bold¨ mathcolor=¨#0000FF¨»N«/mi»«mi mathvariant=¨bold¨ mathcolor=¨#0000FF¨»Y«/mi»«/msub»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»=«/mo»«mi mathvariant=¨bold¨ mathcolor=¨#0000FF¨»W«/mi»«mspace linebreak=¨newline¨»«/mspace»«menclose mathcolor=¨#0000FF¨ notation=¨box¨»«mi mathvariant=¨bold¨»N«/mi»«mo mathvariant=¨bold¨»§#183;«/mo»«mi mathvariant=¨bold¨»sin«/mi»«mo mathvariant=¨bold¨»(«/mo»«mi mathvariant=¨bold¨»§#945;«/mi»«mo mathvariant=¨bold¨»)«/mo»«mo mathvariant=¨bold¨»=«/mo»«mi mathvariant=¨bold¨»mg«/mi»«/menclose»«/math»
رسم مخطّط القوى على الجسم وتحديد القوة الجاذبة نحو المركز وكتابة معادلات الحركة.
تتحرك الخرزة في حركة دائرية ، يجب أن تكون هناك قوة جاذبة تعمل في اتجاه مركز الحركة.
وفقًا لمستوى الحركة واتجاه القوة الجاذبة نحو المركز اللازمة ، يكون مركب القوة العمودية في الاتجاه الأفقي هو قوة الجاذبية المركزية.
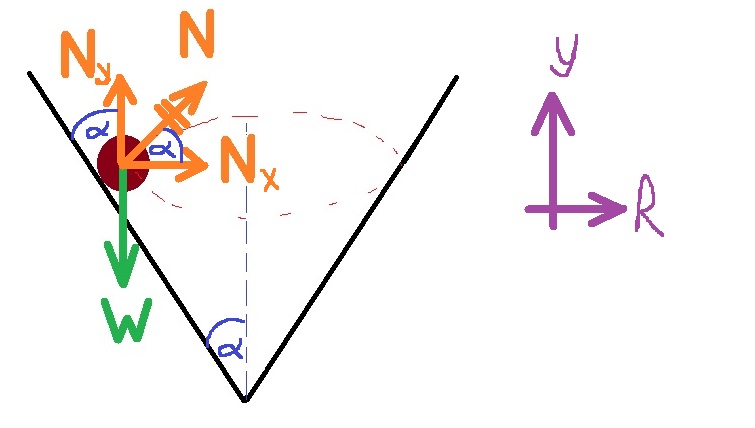
نحلل القوة العمودية إلى مركباتها.
من ناحية هندسية الزاوية α هي الزاوية بين المركب NY والمستوى ، وهي الزاوية بين N و NX ، نضيف الزاوية α إلى الرسم التخطيطي:
نكتب معادلات الحركة في اتجاه مركز الدوران.
ومعادلة الحركة العمودية بالنسبة للمحور الرأسي الموجّه لأعلى.
«math xmlns=¨http://www.w3.org/1998/Math/MathML¨»«msub»«mi mathvariant=¨bold¨ mathcolor=¨#0000FF¨»§#931;F«/mi»«mi mathvariant=¨bold¨ mathcolor=¨#0000FF¨»R«/mi»«/msub»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»=«/mo»«mfrac mathcolor=¨#0000FF¨»«mrow»«mi mathvariant=¨bold¨»m«/mi»«mo mathvariant=¨bold¨»§#183;«/mo»«msup»«mi mathvariant=¨bold¨»V«/mi»«mn mathvariant=¨bold¨»2«/mn»«/msup»«/mrow»«mi mathvariant=¨bold¨»R«/mi»«/mfrac»«mspace linebreak=¨newline¨»«/mspace»«msub»«mi mathvariant=¨bold¨ mathcolor=¨#0000FF¨»N«/mi»«mi mathvariant=¨bold¨ mathcolor=¨#0000FF¨»X«/mi»«/msub»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»=«/mo»«mfrac mathcolor=¨#0000FF¨»«mrow»«mi mathvariant=¨bold¨»m«/mi»«mo mathvariant=¨bold¨»§#183;«/mo»«msup»«mi mathvariant=¨bold¨»V«/mi»«mn mathvariant=¨bold¨»2«/mn»«/msup»«/mrow»«mi mathvariant=¨bold¨»R«/mi»«/mfrac»«mspace linebreak=¨newline¨»«/mspace»«menclose mathcolor=¨#0000FF¨ notation=¨box¨»«mi mathvariant=¨bold¨»N«/mi»«mo mathvariant=¨bold¨»§#183;«/mo»«mi mathvariant=¨bold¨»cos«/mi»«mo mathvariant=¨bold¨»(«/mo»«mi mathvariant=¨bold¨»§#945;«/mi»«mo mathvariant=¨bold¨»)«/mo»«mo mathvariant=¨bold¨»=«/mo»«msup»«mi mathvariant=¨bold¨»m§#969;«/mi»«mn mathvariant=¨bold¨»2«/mn»«/msup»«mo mathvariant=¨bold¨»§#183;«/mo»«mi mathvariant=¨bold¨»R«/mi»«/menclose»«/math» «math xmlns=¨http://www.w3.org/1998/Math/MathML¨»«msub»«mi mathvariant=¨bold¨ mathcolor=¨#0000FF¨»§#931;F«/mi»«mi mathvariant=¨bold¨ mathcolor=¨#0000FF¨»Y«/mi»«/msub»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»=«/mo»«mn mathvariant=¨bold¨ mathcolor=¨#0000FF¨»0«/mn»«mspace linebreak=¨newline¨»«/mspace»«msub»«mi mathvariant=¨bold¨ mathcolor=¨#0000FF¨»N«/mi»«mi mathvariant=¨bold¨ mathcolor=¨#0000FF¨»Y«/mi»«/msub»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»=«/mo»«mi mathvariant=¨bold¨ mathcolor=¨#0000FF¨»W«/mi»«mspace linebreak=¨newline¨»«/mspace»«menclose mathcolor=¨#0000FF¨ notation=¨box¨»«mi mathvariant=¨bold¨»N«/mi»«mo mathvariant=¨bold¨»§#183;«/mo»«mi mathvariant=¨bold¨»sin«/mi»«mo mathvariant=¨bold¨»(«/mo»«mi mathvariant=¨bold¨»§#945;«/mi»«mo mathvariant=¨bold¨»)«/mo»«mo mathvariant=¨bold¨»=«/mo»«mi mathvariant=¨bold¨»mg«/mi»«/menclose»«/math»
בהתאם למישור התנועה ,
1. تعمل قوة الجاذبية تجاه نقطة الدوران المركزية ، لذلك من المهم التمييز بين مستوى الحركة. قبل تحديد القوة الجاذبة نحو المركز .
2. مستوى الحركة أفقي ، وتعمل القوة الجاذبة نحو مركز الدوران في اتجاه أفقي، وليس لقوة الجاذبية أي مركب في الاتجاه الأفقي، فقط القوة العمودية لها مركب في الاتجاه الأفقي.
لذلك ، فإن مركب القوة العمودية في الاتجاه الأفقي NX هو قوة الجاذبية.
3. بعد تحديد القوة الجاذبة نحو المركز، يكون من الأسهل تحديد القوة التي يجب أن نقوم بتحليلها إلى مركباتها قوة الجاذبية أو القوة العمودية.
2. מישור התנועה הוא אופקי, והכוח הצנטריפטלי פועל בכיוון אופקי, אין לכוח הכובד רכיב בכיוון אופקי, רק לכוח הנורמל יש רכיב בכיוון אופקי.
לכן , רכיב כוח הנורמל בכיוון האופקי NX הוא הכוח הצנטריפטאלי.
3. לאחר זיהוי הכוח הצנטריפטאלי יותר קל להחליט לאיזה כוח לבצע הפרדה ישרת זווית, לכוח הכובד או לכוח הנורמל.
______________________________________________________________________________________

______________________________________________________________________________________
...
«math xmlns=¨http://www.w3.org/1998/Math/MathML¨»«mi mathvariant=¨bold¨»H«/mi»«mo mathvariant=¨bold¨»=«/mo»«mfrac»«msup»«mi mathvariant=¨bold¨»V«/mi»«mn mathvariant=¨bold¨»2«/mn»«/msup»«mi mathvariant=¨bold¨»g«/mi»«/mfrac»«/math»
التعبير عن نصف قطر المسار عندما يكون ارتفاع مستوى الحركة H .
تعويض تعبير نصف القطر في معادلة الحركة. والتعبير H من معادلات الحركة.
تتحرك الخرزة في حركة دائرية ، يجب أن تكون هناك قوة جاذبة تعمل في اتجاه مركز الحركة.
وفقًا لمستوى الحركة واتجاه القوة الجاذبة نحو المركز اللازمة ، يكون مركب القوة العمودية في الاتجاه الأفقي هو قوة الجاذبية المركزية.
نحلل القوة العمودية إلى مركباتها.
من ناحية هندسية الزاوية α هي الزاوية بين المركب NY والمستوى ، وهي الزاوية بين N و NX ، نضيف الزاوية α إلى الرسم التخطيطي:
نكتب معادلات الحركة في اتجاه مركز الدوران.
ومعادلة الحركة العمودية بالنسبة للمحور الرأسي الموجّه لأعلى.
«math xmlns=¨http://www.w3.org/1998/Math/MathML¨»«menclose mathcolor=¨#0000FF¨ notation=¨box¨»«mi mathvariant=¨bold¨»N«/mi»«mo mathvariant=¨bold¨»§#183;«/mo»«mi mathvariant=¨bold¨»cos«/mi»«mo mathvariant=¨bold¨»(«/mo»«mi mathvariant=¨bold¨»§#945;«/mi»«mo mathvariant=¨bold¨»)«/mo»«mo mathvariant=¨bold¨»=«/mo»«mfrac»«mrow»«mi mathvariant=¨bold¨»m«/mi»«mo mathvariant=¨bold¨»§#183;«/mo»«msup»«mi mathvariant=¨bold¨»V«/mi»«mn mathvariant=¨bold¨»2«/mn»«/msup»«/mrow»«mi mathcolor=¨#FF0000¨ mathvariant=¨bold¨»R«/mi»«/mfrac»«/menclose»«mspace linebreak=¨newline¨»«/mspace»«mi mathvariant=¨bold¨ mathcolor=¨#0000FF¨»N«/mi»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»§#183;«/mo»«mi mathvariant=¨bold¨ mathcolor=¨#0000FF¨»cos«/mi»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»(«/mo»«mi mathvariant=¨bold¨ mathcolor=¨#0000FF¨»§#945;«/mi»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»)«/mo»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»=«/mo»«mfrac mathcolor=¨#0000FF¨»«mrow»«mi mathvariant=¨bold¨»m«/mi»«mo mathvariant=¨bold¨»§#183;«/mo»«msup»«mi mathvariant=¨bold¨»V«/mi»«mn mathvariant=¨bold¨»2«/mn»«/msup»«/mrow»«mrow»«mi mathcolor=¨#FF0000¨ mathvariant=¨bold¨»H«/mi»«mo mathcolor=¨#FF0000¨ mathvariant=¨bold¨»§#183;«/mo»«mi mathcolor=¨#FF0000¨ mathvariant=¨bold¨»tan«/mi»«mo mathcolor=¨#FF0000¨ mathvariant=¨bold¨»(«/mo»«mi mathcolor=¨#FF0000¨ mathvariant=¨bold¨»§#945;«/mi»«mo mathcolor=¨#FF0000¨ mathvariant=¨bold¨»)«/mo»«/mrow»«/mfrac»«/math» «math xmlns=¨http://www.w3.org/1998/Math/MathML¨»«menclose mathcolor=¨#0000FF¨ notation=¨box¨»«mi mathvariant=¨bold¨»N«/mi»«mo mathvariant=¨bold¨»§#183;«/mo»«mi mathvariant=¨bold¨»sin«/mi»«mo mathvariant=¨bold¨»(«/mo»«mi mathvariant=¨bold¨»§#945;«/mi»«mo mathvariant=¨bold¨»)«/mo»«mo mathvariant=¨bold¨»=«/mo»«mi mathvariant=¨bold¨»mg«/mi»«/menclose»«/math»
نقسم المعادلتين , ونعبّر عن H:
«math xmlns=¨http://www.w3.org/1998/Math/MathML¨»«mfrac mathcolor=¨#0000FF¨»«mrow»«menclose notation=¨updiagonalstrike¨»«mi mathvariant=¨bold¨»N«/mi»«/menclose»«mo mathvariant=¨bold¨»§#183;«/mo»«mi mathvariant=¨bold¨»cos«/mi»«mo mathvariant=¨bold¨»(«/mo»«mi mathvariant=¨bold¨»§#945;«/mi»«mo mathvariant=¨bold¨»)«/mo»«/mrow»«mrow»«menclose notation=¨updiagonalstrike¨»«mi mathvariant=¨bold¨»N«/mi»«/menclose»«mo mathvariant=¨bold¨»§#183;«/mo»«mi mathvariant=¨bold¨»sin«/mi»«mo mathvariant=¨bold¨»(«/mo»«mi mathvariant=¨bold¨»§#945;«/mi»«mo mathvariant=¨bold¨»)«/mo»«/mrow»«/mfrac»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»=«/mo»«mfrac mathcolor=¨#0000FF¨»«mfrac»«mrow»«menclose notation=¨downdiagonalstrike¨»«mi mathvariant=¨bold¨»m«/mi»«/menclose»«mo mathvariant=¨bold¨»§#183;«/mo»«msup»«mi mathvariant=¨bold¨»V«/mi»«mn mathvariant=¨bold¨»2«/mn»«/msup»«/mrow»«mrow»«mi mathvariant=¨bold¨»H«/mi»«mo mathvariant=¨bold¨»§#183;«/mo»«mi mathvariant=¨bold¨»tan«/mi»«mo mathvariant=¨bold¨»(«/mo»«mi mathvariant=¨bold¨»§#945;«/mi»«mo mathvariant=¨bold¨»)«/mo»«mo mathvariant=¨bold¨»§#160;«/mo»«/mrow»«/mfrac»«mrow»«menclose notation=¨downdiagonalstrike¨»«mi mathvariant=¨bold¨»m«/mi»«/menclose»«mo mathvariant=¨bold¨»§#183;«/mo»«mi mathvariant=¨bold¨»g«/mi»«/mrow»«/mfrac»«mspace linebreak=¨newline¨»«/mspace»«mspace linebreak=¨newline¨»«/mspace»«mfrac mathcolor=¨#0000FF¨»«mn mathvariant=¨bold¨»1«/mn»«menclose notation=¨updiagonalstrike¨»«mi mathvariant=¨bold¨»tan«/mi»«mo mathvariant=¨bold¨»(«/mo»«mi mathvariant=¨bold¨»§#945;«/mi»«mo mathvariant=¨bold¨»)«/mo»«/menclose»«/mfrac»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»=«/mo»«mfrac mathcolor=¨#0000FF¨»«msup»«mi mathvariant=¨bold¨»V«/mi»«mn mathvariant=¨bold¨»2«/mn»«/msup»«mrow»«mi mathvariant=¨bold¨»g«/mi»«mo mathvariant=¨bold¨»§#183;«/mo»«mi mathvariant=¨bold¨»H«/mi»«mo mathvariant=¨bold¨»§#183;«/mo»«menclose notation=¨updiagonalstrike¨»«mi mathvariant=¨bold¨»tan«/mi»«mo mathvariant=¨bold¨»(«/mo»«mi mathvariant=¨bold¨»§#945;«/mi»«mo mathvariant=¨bold¨»)«/mo»«/menclose»«/mrow»«/mfrac»«mspace linebreak=¨newline¨»«/mspace»«mspace linebreak=¨newline¨»«/mspace»«msup»«mi mathvariant=¨bold¨ mathcolor=¨#0000FF¨»V«/mi»«mn mathvariant=¨bold¨ mathcolor=¨#0000FF¨»2«/mn»«/msup»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»=«/mo»«mi mathvariant=¨bold¨ mathcolor=¨#0000FF¨»g«/mi»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»§#183;«/mo»«mi mathvariant=¨bold¨ mathcolor=¨#0000FF¨»H«/mi»«mspace linebreak=¨newline¨»«/mspace»«mspace linebreak=¨newline¨»«/mspace»«menclose mathcolor=¨#0000FF¨ notation=¨circle¨»«mi mathvariant=¨bold¨»H«/mi»«mo mathvariant=¨bold¨»=«/mo»«mfrac»«msup»«mi mathvariant=¨bold¨»V«/mi»«mn mathvariant=¨bold¨»2«/mn»«/msup»«mi mathvariant=¨bold¨»g«/mi»«/mfrac»«/menclose»«mspace linebreak=¨newline¨»«/mspace»«/math»
1. نتعامل بشكل عام مع أجسام نقطية ، لذا فإن نصف قطر الخرزة يساوي صفرًا. يقع نصف قطر مسار الخرزة بين نقطة الدوران المركزية وجانب المخروط.
2. عند تحليل القوة إلى مركباتها تحليل قائم الزاوية، يوجد في معادلة حركة واحدة جيب الزاوية (sin)، وفي معادلة ثانية للحركة يوجد جيب تمام الزاوية نفسها (cos) ، عدة مرات
في مثل هذه الحالة ، من عملية قسمة المعادلات ، يتم الحصول على الظل (tan) ، وهناك اختزال في الكتلة ، والقوة العمودية ، وما إلى ذلك.
2. חילוק המשוואות טנגנס
2. חילוק המשוואות טנגנס.
3.
______________________________________________________________________________________

______________________________________________________________________________________
...
يعني فقدان الطاقة الحركية تقليل السرعة. من تعبير الارتفاع الذي طوّرناه في القسم السابق:«math xmlns=¨http://www.w3.org/1998/Math/MathML¨»«mi mathvariant=¨bold¨»H«/mi»«mo mathvariant=¨bold¨»=«/mo»«mfrac»«msup»«mi mathvariant=¨bold¨»V«/mi»«mn mathvariant=¨bold¨»2«/mn»«/msup»«mi mathvariant=¨bold¨»g«/mi»«/mfrac»«/math» عندما تقل السرعة يقل الارتفاع أيضًا.
معرفة علاقة الطاقة الحركية بالسرعة ، واستخدام تعبير الارتفاع من القسم السابق.
يعني فقدان الطاقة الحركية تقليل السرعة. من تعبير الارتفاع الذي طوّرناه في القسم السابق:«math xmlns=¨http://www.w3.org/1998/Math/MathML¨»«mi mathvariant=¨bold¨»H«/mi»«mo mathvariant=¨bold¨»=«/mo»«mfrac»«msup»«mi mathvariant=¨bold¨»V«/mi»«mn mathvariant=¨bold¨»2«/mn»«/msup»«mi mathvariant=¨bold¨»g«/mi»«/mfrac»«/math» عندما تقل السرعة يقل الارتفاع أيضًا.
1. يتم تضمين الطاقة الحركية في المنهاج الدراسي ، وسيتم دراستها لاحقًا. تعبير الطاقة الحركية هو: «math xmlns=¨http://www.w3.org/1998/Math/MathML¨»«msub»«mi mathvariant=¨bold¨ mathcolor=¨#FF0000¨»E«/mi»«mi mathvariant=¨bold¨ mathcolor=¨#FF0000¨»K«/mi»«/msub»«mo mathvariant=¨bold¨ mathcolor=¨#FF0000¨»=«/mo»«mfrac mathcolor=¨#FF0000¨»«mn mathvariant=¨bold¨»1«/mn»«mn mathvariant=¨bold¨»2«/mn»«/mfrac»«mo mathvariant=¨bold¨ mathcolor=¨#FF0000¨»§#183;«/mo»«mi mathvariant=¨bold¨ mathcolor=¨#FF0000¨»m«/mi»«mo mathvariant=¨bold¨ mathcolor=¨#FF0000¨»§#183;«/mo»«msup»«mi mathvariant=¨bold¨ mathcolor=¨#FF0000¨»V«/mi»«mn mathvariant=¨bold¨ mathcolor=¨#FF0000¨»2«/mn»«/msup»«/math».
2. بالنسبة للجزء الأكبر من امتحانات البجروت ، يتعامل كل سؤال مع مجال معين، وهناك أسئلة حول الكينماتيكا، وأسئلة حول الديناميكا ، ولكن هناك أيضًا أسئلة فردية تتناول مجالات متعددة.
3. الاختبارات الداخلية ، بالطبع ، تتعامل فقط مع الموضوعات التي تدّرس ، بحيث لا توجد إشارة إلى الطاقة في اختبار الديناميكا.
2. לרוב במבחני הבגרות, כל שאלה עוסקת בתחום מסוים , יש שאלות בקינמטיקה , ושאלות בדינמיקה .אך יש גם שאלות בודדות העוסקות במספר תחומים .
3. המבחנים הפנימיים עוסקים כמובן רק בנושאים שנלמדו , כך שעל מבחן בדינמיקה לא תהיה התייחסות כל שהיא לאנרגיה.
______________________________________________________________________________________

______________________________________________________________________________________
...
السرعة الخطية للخرزة 1.41 متر في الثانية.
إيجاد السرعة من تعبير الارتفاع.
نعبّر عن السرعة الخطية للخرزة ، من تعبير ارتفاع مستوى الحركة H :
«math xmlns=¨http://www.w3.org/1998/Math/MathML¨»«mi mathvariant=¨bold¨ mathcolor=¨#0000FF¨»H«/mi»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»=«/mo»«mfrac mathcolor=¨#0000FF¨»«msup»«mi mathvariant=¨bold¨»V«/mi»«mn mathvariant=¨bold¨»2«/mn»«/msup»«mi mathvariant=¨bold¨»g«/mi»«/mfrac»«mspace linebreak=¨newline¨»«/mspace»«mi mathvariant=¨bold¨ mathcolor=¨#0000FF¨»V«/mi»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»=«/mo»«msqrt mathcolor=¨#0000FF¨»«mi mathvariant=¨bold¨»H«/mi»«mo mathvariant=¨bold¨»§#183;«/mo»«mi mathvariant=¨bold¨»g«/mi»«/msqrt»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»§#160;«/mo»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»=«/mo»«msqrt mathcolor=¨#0000FF¨»«mn mathvariant=¨bold¨»0«/mn»«mo mathvariant=¨bold¨».«/mo»«mn mathvariant=¨bold¨»2«/mn»«mo mathvariant=¨bold¨»§#183;«/mo»«mn mathvariant=¨bold¨»10«/mn»«/msqrt»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»=«/mo»«msqrt mathcolor=¨#0000FF¨»«mn mathvariant=¨bold¨»2«/mn»«/msqrt»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»=«/mo»«mn mathvariant=¨bold¨ mathcolor=¨#0000FF¨»1«/mn»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨».«/mo»«mn mathvariant=¨bold¨ mathcolor=¨#0000FF¨»41«/mn»«mfrac mathcolor=¨#0000FF¨»«mi mathvariant=¨bold¨»m«/mi»«mi mathvariant=¨bold¨»s«/mi»«/mfrac»«/math»
السرعة الخطية للخرزة 1.41 متر في الثانية.
«math xmlns=¨http://www.w3.org/1998/Math/MathML¨»«mi mathvariant=¨bold¨ mathcolor=¨#0000FF¨»H«/mi»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»=«/mo»«mfrac mathcolor=¨#0000FF¨»«msup»«mi mathvariant=¨bold¨»V«/mi»«mn mathvariant=¨bold¨»2«/mn»«/msup»«mi mathvariant=¨bold¨»g«/mi»«/mfrac»«mspace linebreak=¨newline¨»«/mspace»«mi mathvariant=¨bold¨ mathcolor=¨#0000FF¨»V«/mi»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»=«/mo»«msqrt mathcolor=¨#0000FF¨»«mi mathvariant=¨bold¨»H«/mi»«mo mathvariant=¨bold¨»§#183;«/mo»«mi mathvariant=¨bold¨»g«/mi»«/msqrt»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»§#160;«/mo»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»=«/mo»«msqrt mathcolor=¨#0000FF¨»«mn mathvariant=¨bold¨»0«/mn»«mo mathvariant=¨bold¨».«/mo»«mn mathvariant=¨bold¨»2«/mn»«mo mathvariant=¨bold¨»§#183;«/mo»«mn mathvariant=¨bold¨»10«/mn»«/msqrt»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»=«/mo»«msqrt mathcolor=¨#0000FF¨»«mn mathvariant=¨bold¨»2«/mn»«/msqrt»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»=«/mo»«mn mathvariant=¨bold¨ mathcolor=¨#0000FF¨»1«/mn»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨».«/mo»«mn mathvariant=¨bold¨ mathcolor=¨#0000FF¨»41«/mn»«mfrac mathcolor=¨#0000FF¨»«mi mathvariant=¨bold¨»m«/mi»«mi mathvariant=¨bold¨»s«/mi»«/mfrac»«/math»
המהירות הקווית של החרוז היא 1.41 מטר לשנייה.
هناك أسئلة بسيطة ، سطرين كافيان لحلها بحل صحيح وكامل.
______________________________________________________________________________________
هـ.

______________________________________________________________________________________
...
«math xmlns=¨http://www.w3.org/1998/Math/MathML¨»«mi mathvariant=¨bold¨»T«/mi»«mo mathvariant=¨bold¨»=«/mo»«mn mathvariant=¨bold¨»0«/mn»«mo mathvariant=¨bold¨».«/mo»«mn mathvariant=¨bold¨»51«/mn»«mi mathvariant=¨bold¨»S«/mi»«/math»
خيار أول: استخدام تعبير «math xmlns=¨http://www.w3.org/1998/Math/MathML¨»«mstyle mathsize=¨20px¨»«mrow»«mi mathvariant=¨bold¨ mathcolor=¨#FF6600¨»V«/mi»«mo mathvariant=¨bold¨ mathcolor=¨#FF6600¨»=«/mo»«mi mathvariant=¨bold¨ mathcolor=¨#FF6600¨»§#969;«/mi»«mo mathvariant=¨bold¨ mathcolor=¨#FF6600¨»§#183;«/mo»«mi mathvariant=¨bold¨ mathcolor=¨#FF6600¨»R«/mi»«/mrow»«/mstyle»«/math» وفي التعبيرات المطورة ، لإيجاد زمن الدورة.
خيار آخر: كتابة معادلة الحركة الدائرية بالسرعة الزاوية.
אפשרות נוספת: כתיבת משוואת התנועה המעגלית , עם המהירות הזוויתית .
نعوّض تعبير السرعة «math xmlns=¨http://www.w3.org/1998/Math/MathML¨»«mi mathvariant=¨bold¨ mathcolor=¨#0000FF¨»V«/mi»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»=«/mo»«mi mathvariant=¨bold¨ mathcolor=¨#0000FF¨»§#969;«/mi»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»§#183;«/mo»«mi mathvariant=¨bold¨ mathcolor=¨#0000FF¨»R«/mi»«/math» , في التعبير عن ارتفاع مستوى الحركة ، نعبر عن زمن الدورة:
«math xmlns=¨http://www.w3.org/1998/Math/MathML¨»«mi mathvariant=¨bold¨ mathcolor=¨#0000FF¨»H«/mi»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»=«/mo»«mfrac mathcolor=¨#0000FF¨»«msup»«mi mathvariant=¨bold¨ mathcolor=¨#FF0000¨»V«/mi»«mn mathvariant=¨bold¨»2«/mn»«/msup»«mi mathvariant=¨bold¨»g«/mi»«/mfrac»«mspace linebreak=¨newline¨»«/mspace»«mspace linebreak=¨newline¨»«/mspace»«mi mathvariant=¨bold¨ mathcolor=¨#0000FF¨»H«/mi»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»=«/mo»«mfrac mathcolor=¨#0000FF¨»«msup»«mfenced mathcolor=¨#FF0000¨»«mrow»«mi mathvariant=¨bold¨»§#969;«/mi»«mo mathvariant=¨bold¨»§#183;«/mo»«mi mathvariant=¨bold¨»R«/mi»«/mrow»«/mfenced»«mn mathvariant=¨bold¨»2«/mn»«/msup»«mi mathvariant=¨bold¨»g«/mi»«/mfrac»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»=«/mo»«mfrac mathcolor=¨#0000FF¨»«mrow»«msup»«mi mathvariant=¨bold¨ mathcolor=¨#7F007F¨»§#969;«/mi»«mn mathvariant=¨bold¨»2«/mn»«/msup»«mo mathvariant=¨bold¨»§#183;«/mo»«msup»«mi mathvariant=¨bold¨»R«/mi»«mn mathvariant=¨bold¨»2«/mn»«/msup»«/mrow»«mi mathvariant=¨bold¨»g«/mi»«/mfrac»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»=«/mo»«mfrac mathcolor=¨#0000FF¨»«mrow»«msup»«mfenced mathcolor=¨#7F007F¨»«mfrac»«mrow»«mn mathvariant=¨bold¨»2«/mn»«mo mathvariant=¨bold¨»§#183;«/mo»«mi mathvariant=¨bold¨»§#960;«/mi»«/mrow»«mi mathvariant=¨bold¨»T«/mi»«/mfrac»«/mfenced»«mn mathcolor=¨#7F007F¨ mathvariant=¨bold¨»2«/mn»«/msup»«mo mathvariant=¨bold¨»§#183;«/mo»«msup»«mi mathvariant=¨bold¨»R«/mi»«mn mathvariant=¨bold¨»2«/mn»«/msup»«/mrow»«mi mathvariant=¨bold¨»g«/mi»«/mfrac»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»=«/mo»«mfrac mathcolor=¨#0000FF¨»«mrow»«mfrac mathcolor=¨#7F007F¨»«mrow»«mn mathvariant=¨bold¨»4«/mn»«mo mathvariant=¨bold¨»§#183;«/mo»«msup»«mi mathvariant=¨bold¨»§#960;«/mi»«mn mathvariant=¨bold¨»2«/mn»«/msup»«/mrow»«msup»«mi mathvariant=¨bold¨»T«/mi»«mn mathvariant=¨bold¨»2«/mn»«/msup»«/mfrac»«mo mathvariant=¨bold¨»§#183;«/mo»«msup»«mi mathvariant=¨bold¨»R«/mi»«mn mathvariant=¨bold¨»2«/mn»«/msup»«/mrow»«mi mathvariant=¨bold¨»g«/mi»«/mfrac»«mspace linebreak=¨newline¨»«/mspace»«mspace linebreak=¨newline¨»«/mspace»«mi mathvariant=¨bold¨ mathcolor=¨#0000FF¨»H«/mi»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»=«/mo»«mfrac mathcolor=¨#0000FF¨»«mrow»«mn mathvariant=¨bold¨»4«/mn»«mo mathvariant=¨bold¨»§#183;«/mo»«msup»«mi mathvariant=¨bold¨»§#960;«/mi»«mn mathvariant=¨bold¨»2«/mn»«/msup»«mo mathvariant=¨bold¨»§#183;«/mo»«msup»«mi mathvariant=¨bold¨»R«/mi»«mn mathvariant=¨bold¨»2«/mn»«/msup»«/mrow»«mrow»«msup»«mi mathvariant=¨bold¨»T«/mi»«mn mathvariant=¨bold¨»2«/mn»«/msup»«mo mathvariant=¨bold¨»§#183;«/mo»«mi mathvariant=¨bold¨»g«/mi»«/mrow»«/mfrac»«mspace linebreak=¨newline¨»«/mspace»«mspace linebreak=¨newline¨»«/mspace»«msup»«mi mathvariant=¨bold¨ mathcolor=¨#0000FF¨»T«/mi»«mn mathvariant=¨bold¨ mathcolor=¨#0000FF¨»2«/mn»«/msup»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»=«/mo»«mfrac mathcolor=¨#0000FF¨»«mrow»«mn mathvariant=¨bold¨»4«/mn»«mo mathvariant=¨bold¨»§#183;«/mo»«msup»«mi mathvariant=¨bold¨»§#960;«/mi»«mn mathvariant=¨bold¨»2«/mn»«/msup»«mo mathvariant=¨bold¨»§#183;«/mo»«msup»«mi mathvariant=¨bold¨»R«/mi»«mn mathvariant=¨bold¨»2«/mn»«/msup»«/mrow»«mrow»«mi mathvariant=¨bold¨»H«/mi»«mo mathvariant=¨bold¨»§#183;«/mo»«mi mathvariant=¨bold¨»g«/mi»«/mrow»«/mfrac»«mspace linebreak=¨newline¨»«/mspace»«mspace linebreak=¨newline¨»«/mspace»«mspace linebreak=¨newline¨»«/mspace»«/math»
سنضع في المعادلة التعبير عن نصف قطر المسار «math xmlns=¨http://www.w3.org/1998/Math/MathML¨»«mi mathvariant=¨bold-italic¨ mathcolor=¨#FF0000¨»R«/mi»«mo mathvariant=¨bold¨ mathcolor=¨#FF0000¨»=«/mo»«mi mathvariant=¨bold¨ mathcolor=¨#FF0000¨»H«/mi»«mo mathvariant=¨bold¨ mathcolor=¨#FF0000¨»§#183;«/mo»«mi mathvariant=¨bold¨ mathcolor=¨#FF0000¨»tan«/mi»«mo mathvariant=¨bold¨ mathcolor=¨#FF0000¨»(«/mo»«mi mathvariant=¨bold¨ mathcolor=¨#FF0000¨»§#945;«/mi»«mo mathvariant=¨bold¨ mathcolor=¨#FF0000¨»)«/mo»«/math» :
«math xmlns=¨http://www.w3.org/1998/Math/MathML¨»«msup»«mi mathvariant=¨bold¨ mathcolor=¨#0000FF¨»T«/mi»«mn mathvariant=¨bold¨ mathcolor=¨#0000FF¨»2«/mn»«/msup»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»=«/mo»«mfrac mathcolor=¨#0000FF¨»«mrow»«mn mathvariant=¨bold¨»4«/mn»«mo mathvariant=¨bold¨»§#183;«/mo»«msup»«mi mathvariant=¨bold¨»§#960;«/mi»«mn mathvariant=¨bold¨»2«/mn»«/msup»«mo mathvariant=¨bold¨»§#183;«/mo»«msup»«mi mathvariant=¨bold¨ mathcolor=¨#FF0000¨»R«/mi»«mn mathvariant=¨bold¨»2«/mn»«/msup»«/mrow»«mrow»«mi mathvariant=¨bold¨»H«/mi»«mo mathvariant=¨bold¨»§#183;«/mo»«mi mathvariant=¨bold¨»g«/mi»«/mrow»«/mfrac»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»=«/mo»«mfrac mathcolor=¨#0000FF¨»«mrow»«mn mathvariant=¨bold¨»4«/mn»«mo mathvariant=¨bold¨»§#183;«/mo»«msup»«mi mathvariant=¨bold¨»§#960;«/mi»«mn mathvariant=¨bold¨»2«/mn»«/msup»«mo mathvariant=¨bold¨»§#183;«/mo»«msup»«mi mathcolor=¨#FF0000¨ mathvariant=¨bold¨»H«/mi»«menclose notation=¨downdiagonalstrike¨ mathcolor=¨#FF0000¨»«mn mathvariant=¨bold¨»2«/mn»«/menclose»«/msup»«mo mathcolor=¨#FF0000¨ mathvariant=¨bold¨»§#183;«/mo»«msup»«mi mathcolor=¨#FF0000¨ mathvariant=¨bold¨»tan«/mi»«mn mathvariant=¨bold¨ mathcolor=¨#FF0000¨»2«/mn»«/msup»«mo mathcolor=¨#FF0000¨ mathvariant=¨bold¨»(«/mo»«mi mathcolor=¨#FF0000¨ mathvariant=¨bold¨»§#945;«/mi»«mo mathcolor=¨#FF0000¨ mathvariant=¨bold¨»)«/mo»«/mrow»«mrow»«menclose notation=¨downdiagonalstrike¨»«mi mathvariant=¨bold¨»H«/mi»«/menclose»«mo mathvariant=¨bold¨»§#183;«/mo»«mi mathvariant=¨bold¨»g«/mi»«/mrow»«/mfrac»«mspace linebreak=¨newline¨»«/mspace»«mspace linebreak=¨newline¨»«/mspace»«mi mathvariant=¨bold¨ mathcolor=¨#0000FF¨»T«/mi»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»=«/mo»«msqrt mathcolor=¨#0000FF¨»«mfrac»«mrow»«mn mathvariant=¨bold¨»4«/mn»«mo mathvariant=¨bold¨»§#183;«/mo»«msup»«mi mathvariant=¨bold¨»§#960;«/mi»«mn mathvariant=¨bold¨»2«/mn»«/msup»«mo mathvariant=¨bold¨»§#183;«/mo»«mi mathvariant=¨bold¨»H«/mi»«mo mathvariant=¨bold¨»§#183;«/mo»«msup»«mi mathvariant=¨bold¨»tan«/mi»«mn mathvariant=¨bold¨»2«/mn»«/msup»«mo mathvariant=¨bold¨»(«/mo»«mi mathvariant=¨bold¨»§#945;«/mi»«mo mathvariant=¨bold¨»)«/mo»«/mrow»«mi mathvariant=¨bold¨»g«/mi»«/mfrac»«/msqrt»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»=«/mo»«msqrt mathcolor=¨#0000FF¨»«mfrac»«mrow»«mn mathvariant=¨bold¨»4«/mn»«mo mathvariant=¨bold¨»§#183;«/mo»«msup»«mi mathvariant=¨bold¨»§#960;«/mi»«mn mathvariant=¨bold¨»2«/mn»«/msup»«mo mathvariant=¨bold¨»§#183;«/mo»«mn mathvariant=¨bold¨»0«/mn»«mo mathvariant=¨bold¨».«/mo»«mn mathvariant=¨bold¨»2«/mn»«mo mathvariant=¨bold¨»§#183;«/mo»«msup»«mi mathvariant=¨bold¨»tan«/mi»«mn mathvariant=¨bold¨»2«/mn»«/msup»«mo mathvariant=¨bold¨»(«/mo»«mn mathvariant=¨bold¨»30«/mn»«mo mathvariant=¨bold¨»)«/mo»«/mrow»«mi mathvariant=¨bold¨»g«/mi»«/mfrac»«/msqrt»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»=«/mo»«msqrt mathcolor=¨#0000FF¨»«mfrac»«mrow»«mn mathvariant=¨bold¨»2«/mn»«mo mathvariant=¨bold¨».«/mo»«mn mathvariant=¨bold¨»63«/mn»«/mrow»«mn mathvariant=¨bold¨»10«/mn»«/mfrac»«/msqrt»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»=«/mo»«mn mathvariant=¨bold¨ mathcolor=¨#0000FF¨»0«/mn»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨».«/mo»«mn mathvariant=¨bold¨ mathcolor=¨#0000FF¨»51«/mn»«mi mathvariant=¨bold-italic¨ mathcolor=¨#0000FF¨»s«/mi»«mspace linebreak=¨newline¨»«/mspace»«mspace linebreak=¨newline¨»«/mspace»«mspace linebreak=¨newline¨»«/mspace»«/math»
«math xmlns=¨http://www.w3.org/1998/Math/MathML¨»«mi mathvariant=¨bold¨ mathcolor=¨#0000FF¨»H«/mi»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»=«/mo»«mfrac mathcolor=¨#0000FF¨»«msup»«mi mathvariant=¨bold¨ mathcolor=¨#FF0000¨»V«/mi»«mn mathvariant=¨bold¨»2«/mn»«/msup»«mi mathvariant=¨bold¨»g«/mi»«/mfrac»«mspace linebreak=¨newline¨»«/mspace»«mspace linebreak=¨newline¨»«/mspace»«mi mathvariant=¨bold¨ mathcolor=¨#0000FF¨»H«/mi»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»=«/mo»«mfrac mathcolor=¨#0000FF¨»«msup»«mfenced mathcolor=¨#FF0000¨»«mrow»«mi mathvariant=¨bold¨»§#969;«/mi»«mo mathvariant=¨bold¨»§#183;«/mo»«mi mathvariant=¨bold¨»R«/mi»«/mrow»«/mfenced»«mn mathvariant=¨bold¨»2«/mn»«/msup»«mi mathvariant=¨bold¨»g«/mi»«/mfrac»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»=«/mo»«mfrac mathcolor=¨#0000FF¨»«mrow»«msup»«mi mathvariant=¨bold¨ mathcolor=¨#7F007F¨»§#969;«/mi»«mn mathvariant=¨bold¨»2«/mn»«/msup»«mo mathvariant=¨bold¨»§#183;«/mo»«msup»«mi mathvariant=¨bold¨»R«/mi»«mn mathvariant=¨bold¨»2«/mn»«/msup»«/mrow»«mi mathvariant=¨bold¨»g«/mi»«/mfrac»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»=«/mo»«mfrac mathcolor=¨#0000FF¨»«mrow»«msup»«mfenced mathcolor=¨#7F007F¨»«mfrac»«mrow»«mn mathvariant=¨bold¨»2«/mn»«mo mathvariant=¨bold¨»§#183;«/mo»«mi mathvariant=¨bold¨»§#960;«/mi»«/mrow»«mi mathvariant=¨bold¨»T«/mi»«/mfrac»«/mfenced»«mn mathcolor=¨#7F007F¨ mathvariant=¨bold¨»2«/mn»«/msup»«mo mathvariant=¨bold¨»§#183;«/mo»«msup»«mi mathvariant=¨bold¨»R«/mi»«mn mathvariant=¨bold¨»2«/mn»«/msup»«/mrow»«mi mathvariant=¨bold¨»g«/mi»«/mfrac»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»=«/mo»«mfrac mathcolor=¨#0000FF¨»«mrow»«mfrac mathcolor=¨#7F007F¨»«mrow»«mn mathvariant=¨bold¨»4«/mn»«mo mathvariant=¨bold¨»§#183;«/mo»«msup»«mi mathvariant=¨bold¨»§#960;«/mi»«mn mathvariant=¨bold¨»2«/mn»«/msup»«/mrow»«msup»«mi mathvariant=¨bold¨»T«/mi»«mn mathvariant=¨bold¨»2«/mn»«/msup»«/mfrac»«mo mathvariant=¨bold¨»§#183;«/mo»«msup»«mi mathvariant=¨bold¨»R«/mi»«mn mathvariant=¨bold¨»2«/mn»«/msup»«/mrow»«mi mathvariant=¨bold¨»g«/mi»«/mfrac»«mspace linebreak=¨newline¨»«/mspace»«mspace linebreak=¨newline¨»«/mspace»«mi mathvariant=¨bold¨ mathcolor=¨#0000FF¨»H«/mi»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»=«/mo»«mfrac mathcolor=¨#0000FF¨»«mrow»«mn mathvariant=¨bold¨»4«/mn»«mo mathvariant=¨bold¨»§#183;«/mo»«msup»«mi mathvariant=¨bold¨»§#960;«/mi»«mn mathvariant=¨bold¨»2«/mn»«/msup»«mo mathvariant=¨bold¨»§#183;«/mo»«msup»«mi mathvariant=¨bold¨»R«/mi»«mn mathvariant=¨bold¨»2«/mn»«/msup»«/mrow»«mrow»«msup»«mi mathvariant=¨bold¨»T«/mi»«mn mathvariant=¨bold¨»2«/mn»«/msup»«mo mathvariant=¨bold¨»§#183;«/mo»«mi mathvariant=¨bold¨»g«/mi»«/mrow»«/mfrac»«mspace linebreak=¨newline¨»«/mspace»«mspace linebreak=¨newline¨»«/mspace»«msup»«mi mathvariant=¨bold¨ mathcolor=¨#0000FF¨»T«/mi»«mn mathvariant=¨bold¨ mathcolor=¨#0000FF¨»2«/mn»«/msup»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»=«/mo»«mfrac mathcolor=¨#0000FF¨»«mrow»«mn mathvariant=¨bold¨»4«/mn»«mo mathvariant=¨bold¨»§#183;«/mo»«msup»«mi mathvariant=¨bold¨»§#960;«/mi»«mn mathvariant=¨bold¨»2«/mn»«/msup»«mo mathvariant=¨bold¨»§#183;«/mo»«msup»«mi mathvariant=¨bold¨»R«/mi»«mn mathvariant=¨bold¨»2«/mn»«/msup»«/mrow»«mrow»«mi mathvariant=¨bold¨»H«/mi»«mo mathvariant=¨bold¨»§#183;«/mo»«mi mathvariant=¨bold¨»g«/mi»«/mrow»«/mfrac»«mspace linebreak=¨newline¨»«/mspace»«mspace linebreak=¨newline¨»«/mspace»«mspace linebreak=¨newline¨»«/mspace»«/math»
נציב במשוואה את ביטוי רדיוס המסלול
يمكن حل الغالبية العظمى من أسئلة الحركة الدائرية بمساعدة تعبيرات الحركة الدائرية ومعادلات الحركة ، والعمليات المطلوبة هي عمليات جبرية.
______________________________________________________________________________________