3. 2012,5- قطعة نقديّة على قرص
______________________________________________________________________________________
...
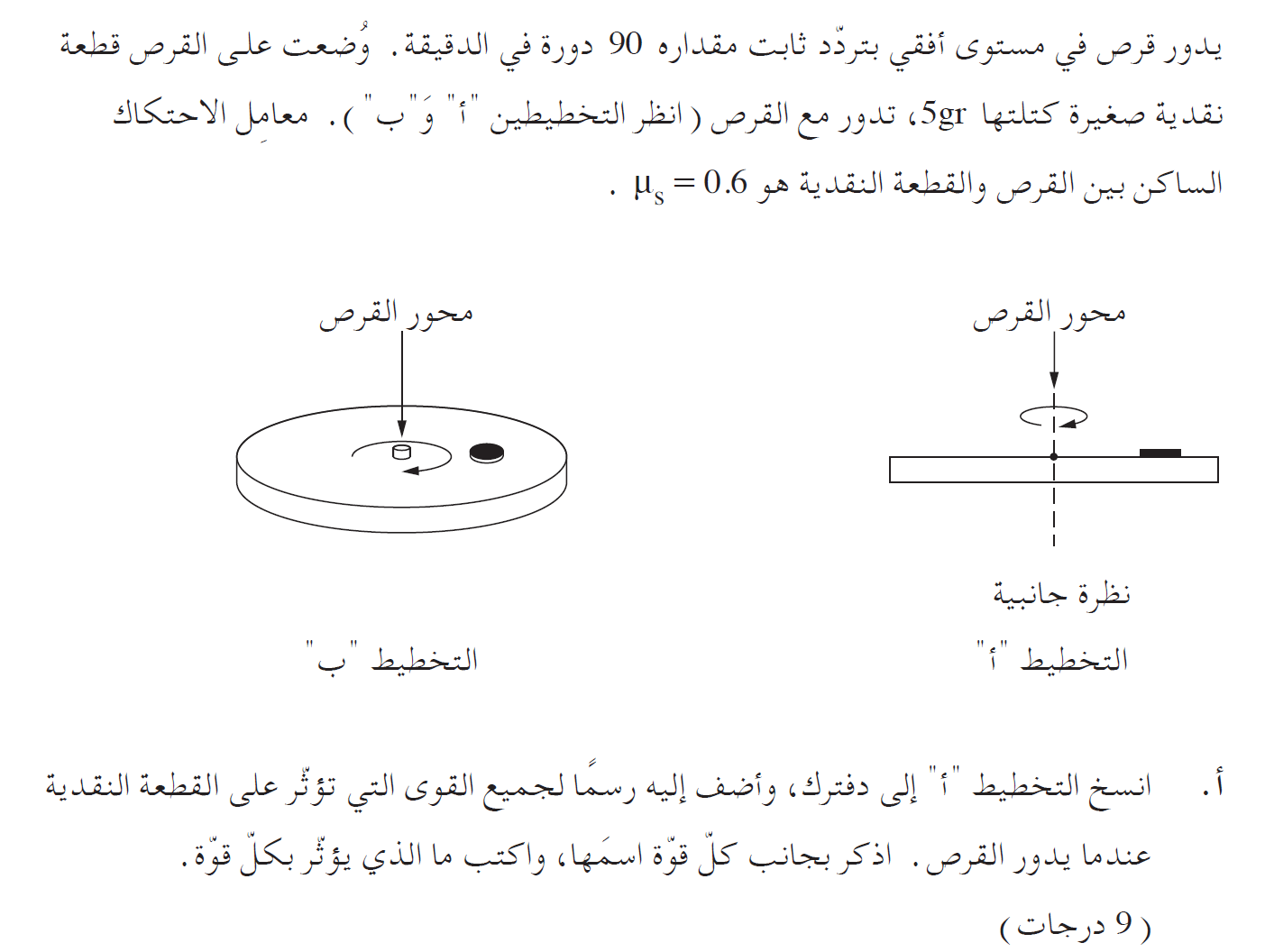
N- القوة العمودية , يشغّلها سطح القرص.
W- قوة الجاذبية، تشغّلها الكرة الأرضية.
fs- قوة الاحتكاك الساكنי , يشغّلها سطح القرص.
N- כוח הנורמל , מופעל ע"י המישור האופקי.
W- כוח הכובד , מופעל ע"י כדור הארץ.
fs- כוח חיכוך סטטי , מופעל ע"י השולחן.
معرفة القوة العمودية وقوة الاحتكاك الساكن وقوة الجاذبية.
تؤثر ثلاث قوى على القطعة النقدية: القوة العمودية وقوة الجاذبية وقوة الاحتكاك الساكن.
نرسم مخطّط القوى ونشير من يشغّل كل قوة.

N- القوة العمودية , يشغّلها سطح القرص.
W- قوة الجاذبية، تشغّلها الكرة الأرضية.
fs- قوة الاحتكاك الساكنי , يشغّلها سطح القرص.
قوة الجاذبية تعمل دائمًا، ولا يمكنك نسيانها ، عندما ترى جسمًا ملقى على سطح ما ، عادة ما تتذكر القوة العمودية ، لكن من السهل نسيان قوة الاحتكاك الساكن.
حقيقة وجود قوة جذب مركزية في كل حركة دائرية ، تساعدنا في هذه الحالة ، على ألا ننسى قوة الاحتكاك الساكن.
העובדה שבכל תנועה מעגלית יש כוח צנטריטאלי , עוזרת לנו במקרה זה , לא לשכוח את כוח החיכוך הסטטי .
______________________________________________________________________________________

______________________________________________________________________________________
...
أقصى بعد ممكن حتى تبقى القطعة النقدية بحالة سكون على القرص هي 6.7 سم.
الإشارة إلى عتبة الحركة، ورسم مخطط القوة ، وكتابة معادلة الحركة.
نصف قطر المسار عندما تكون القطعة النقدية على وشك الحركة هو البعد المطلوب، يجب كتابة تعبير لنصف قطر المسار من معادلات الحركة.
רדיוס המסלול בסף תנועה הוא המרחק המבוקש, יש לכתוב ביטוי רדיוס המסלול ממשוואות התנועה.
عندما تكون القطعة النقدية في أقصى بعد ممكن حتى تبقى في حالة سكون، فإنها تكون على وشك الحركة. القوة المؤثرة عليها هي أقصى قوة احتكاك ساكن.
البعد من محور القرص هو نصف قطر المسار ، نكتب معادلات الحركة عند تعمل أقصى احتكاك ساكن.
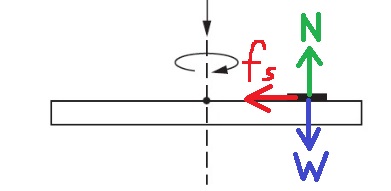
نكتب معادلة القوى نحو مركز الدوران ، ومعادلة القوى على القرص نسبة للمحور الرأسي الموجّه لأعلى ، كما هو موضّح في الرسم البياني التالي:
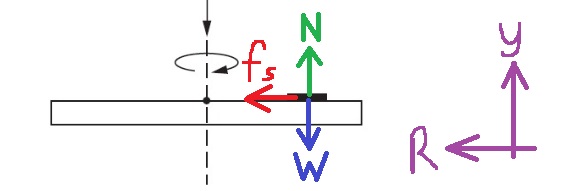
«math xmlns=¨http://www.w3.org/1998/Math/MathML¨»«msub»«mi mathvariant=¨bold¨ mathcolor=¨#0000FF¨»§#931;F«/mi»«mi mathvariant=¨bold¨ mathcolor=¨#0000FF¨»R«/mi»«/msub»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»=«/mo»«msup»«mi mathvariant=¨bold¨ mathcolor=¨#0000FF¨»m§#969;«/mi»«mn mathvariant=¨bold¨ mathcolor=¨#0000FF¨»2«/mn»«/msup»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»§#183;«/mo»«mi mathvariant=¨bold¨ mathcolor=¨#0000FF¨»R«/mi»«mspace linebreak=¨newline¨»«/mspace»«msub»«mi mathvariant=¨bold¨ mathcolor=¨#0000FF¨»f«/mi»«msub mathcolor=¨#0000FF¨»«mi mathvariant=¨bold¨»s«/mi»«mi mathvariant=¨bold¨»max«/mi»«/msub»«/msub»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»=«/mo»«msup»«mi mathvariant=¨bold¨ mathcolor=¨#0000FF¨»m§#969;«/mi»«mn mathvariant=¨bold¨ mathcolor=¨#0000FF¨»2«/mn»«/msup»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»§#183;«/mo»«mi mathvariant=¨bold¨ mathcolor=¨#0000FF¨»R«/mi»«mspace linebreak=¨newline¨»«/mspace»«menclose mathcolor=¨#0000FF¨ notation=¨box¨»«msub»«mi mathvariant=¨bold¨»§#956;«/mi»«mi mathvariant=¨bold¨»s«/mi»«/msub»«mo mathvariant=¨bold¨»§#183;«/mo»«mi mathvariant=¨bold¨»N«/mi»«mo mathvariant=¨bold¨»=«/mo»«msup»«mi mathvariant=¨bold¨»m§#969;«/mi»«mn mathvariant=¨bold¨»2«/mn»«/msup»«mo mathvariant=¨bold¨»§#183;«/mo»«mi mathvariant=¨bold¨»R«/mi»«/menclose»«/math» «math xmlns=¨http://www.w3.org/1998/Math/MathML¨»«msub»«mi mathvariant=¨bold¨ mathcolor=¨#0000FF¨»§#931;F«/mi»«mi mathvariant=¨bold¨ mathcolor=¨#0000FF¨»Y«/mi»«/msub»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»=«/mo»«mn mathvariant=¨bold¨ mathcolor=¨#0000FF¨»0«/mn»«mspace linebreak=¨newline¨»«/mspace»«mi mathvariant=¨bold¨ mathcolor=¨#0000FF¨»N«/mi»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»=«/mo»«mi mathvariant=¨bold¨ mathcolor=¨#0000FF¨»W«/mi»«mspace linebreak=¨newline¨»«/mspace»«menclose mathcolor=¨#0000FF¨ notation=¨box¨»«mi mathvariant=¨bold¨»N«/mi»«mo mathvariant=¨bold¨»=«/mo»«mi mathvariant=¨bold¨»mg«/mi»«/menclose»«/math»
نعوّض القوة العمودية من معادلة الحركة العمودية في معادلة الحركة نحو المركز ونعبّر عن نصف قطر مسار الحركة:
«math xmlns=¨http://www.w3.org/1998/Math/MathML¨»«menclose mathcolor=¨#0000FF¨ notation=¨box¨»«msub»«mi mathvariant=¨bold¨»§#956;«/mi»«mi mathvariant=¨bold¨»s«/mi»«/msub»«mo mathvariant=¨bold¨»§#183;«/mo»«mi mathvariant=¨bold¨ mathcolor=¨#FF0000¨»N«/mi»«mo mathvariant=¨bold¨»=«/mo»«msup»«mi mathvariant=¨bold¨»m§#969;«/mi»«mn mathvariant=¨bold¨»2«/mn»«/msup»«mo mathvariant=¨bold¨»§#183;«/mo»«mi mathvariant=¨bold¨»R«/mi»«/menclose»«mspace linebreak=¨newline¨»«/mspace»«mspace linebreak=¨newline¨»«/mspace»«msub»«mi mathvariant=¨bold¨ mathcolor=¨#0000FF¨»§#956;«/mi»«mi mathvariant=¨bold¨ mathcolor=¨#0000FF¨»s«/mi»«/msub»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»§#183;«/mo»«menclose mathcolor=¨#FF0000¨ notation=¨updiagonalstrike¨»«mi mathvariant=¨bold¨»m«/mi»«/menclose»«mo mathvariant=¨bold¨ mathcolor=¨#FF0000¨»§#183;«/mo»«mi mathvariant=¨bold¨ mathcolor=¨#FF0000¨»g«/mi»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»=«/mo»«menclose mathcolor=¨#0000FF¨ notation=¨updiagonalstrike¨»«mi mathvariant=¨bold¨»m«/mi»«mo mathvariant=¨bold¨»§#183;«/mo»«/menclose»«msup»«mi mathvariant=¨bold¨ mathcolor=¨#0000FF¨»§#969;«/mi»«mn mathvariant=¨bold¨ mathcolor=¨#0000FF¨»2«/mn»«/msup»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»§#183;«/mo»«mi mathvariant=¨bold¨ mathcolor=¨#0000FF¨»R«/mi»«mspace linebreak=¨newline¨»«/mspace»«mspace linebreak=¨newline¨»«/mspace»«mi mathvariant=¨bold¨ mathcolor=¨#0000FF¨»R«/mi»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»=«/mo»«mfrac mathcolor=¨#0000FF¨»«mrow»«msub»«mi mathvariant=¨bold¨»§#956;«/mi»«mi mathvariant=¨bold¨»s«/mi»«/msub»«mo mathvariant=¨bold¨»§#183;«/mo»«mi mathvariant=¨bold¨»g«/mi»«/mrow»«msup»«mi mathvariant=¨bold¨»§#969;«/mi»«mn mathvariant=¨bold¨»2«/mn»«/msup»«/mfrac»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»=«/mo»«mfrac mathcolor=¨#0000FF¨»«mrow»«mn mathvariant=¨bold¨»0«/mn»«mo mathvariant=¨bold¨».«/mo»«mn mathvariant=¨bold¨»6«/mn»«mo mathvariant=¨bold¨»§#183;«/mo»«mn mathvariant=¨bold¨»10«/mn»«/mrow»«msup»«mfenced»«mrow»«mn mathvariant=¨bold¨»2«/mn»«mo mathvariant=¨bold¨»§#183;«/mo»«mi mathvariant=¨bold¨»§#960;«/mi»«mo mathvariant=¨bold¨»§#183;«/mo»«mi mathvariant=¨bold¨»f«/mi»«/mrow»«/mfenced»«mn mathvariant=¨bold¨»2«/mn»«/msup»«/mfrac»«mspace linebreak=¨newline¨»«/mspace»«mi mathvariant=¨bold¨ mathcolor=¨#0000FF¨»R«/mi»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»=«/mo»«mfrac mathcolor=¨#0000FF¨»«mn mathvariant=¨bold¨»6«/mn»«mrow»«mn mathvariant=¨bold¨»4«/mn»«mo mathvariant=¨bold¨»§#183;«/mo»«msup»«mi mathvariant=¨bold¨»§#960;«/mi»«mn mathvariant=¨bold¨»2«/mn»«/msup»«mo mathvariant=¨bold¨»§#183;«/mo»«msup»«mi mathvariant=¨bold¨»f«/mi»«mn mathvariant=¨bold¨»2«/mn»«/msup»«/mrow»«/mfrac»«/math»
القطعة النقدية تدور مع القرص، تردّد القرص 90 دورة في الدقيقة. RPM هي وحدات غير قياسية.
الوحدات القياسية للتردد هي هرتز ، عدد الدورات في الثانية.
في دقيقة واحدة ، يكمل القرص 90 دورة ، وفي الثانية يكمل عددًا أقل من الدورات بـ 60 مرة ، وتردّد القطعة النقدية في الوحدات القياسية هو 1.5 هرتز.
نعوض التردّد بالوحدات القياسية في تعبير نصف القطر:
«math xmlns=¨http://www.w3.org/1998/Math/MathML¨»«mi mathvariant=¨bold¨ mathcolor=¨#0000FF¨»R«/mi»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»=«/mo»«mfrac mathcolor=¨#0000FF¨»«mn mathvariant=¨bold¨»6«/mn»«mrow»«mn mathvariant=¨bold¨»4«/mn»«mo mathvariant=¨bold¨»§#183;«/mo»«msup»«mi mathvariant=¨bold¨»§#960;«/mi»«mn mathvariant=¨bold¨»2«/mn»«/msup»«mo mathvariant=¨bold¨»§#183;«/mo»«msup»«mi mathvariant=¨bold¨»f«/mi»«mn mathvariant=¨bold¨»2«/mn»«/msup»«/mrow»«/mfrac»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»=«/mo»«mfrac mathcolor=¨#0000FF¨»«mn mathvariant=¨bold¨»6«/mn»«mrow»«mn mathvariant=¨bold¨»4«/mn»«mo mathvariant=¨bold¨»§#183;«/mo»«msup»«mi mathvariant=¨bold¨»§#960;«/mi»«mn mathvariant=¨bold¨»2«/mn»«/msup»«mo mathvariant=¨bold¨»§#183;«/mo»«mn mathvariant=¨bold¨»1«/mn»«mo mathvariant=¨bold¨».«/mo»«msup»«mn mathvariant=¨bold¨»5«/mn»«mn mathvariant=¨bold¨»2«/mn»«/msup»«/mrow»«/mfrac»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»=«/mo»«mfrac mathcolor=¨#0000FF¨»«mn mathvariant=¨bold¨»6«/mn»«mrow»«mn mathvariant=¨bold¨»88«/mn»«mo mathvariant=¨bold¨».«/mo»«mn mathvariant=¨bold¨»82«/mn»«/mrow»«/mfrac»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»=«/mo»«mn mathvariant=¨bold¨ mathcolor=¨#0000FF¨»0«/mn»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨».«/mo»«mn mathvariant=¨bold¨ mathcolor=¨#0000FF¨»067«/mn»«mi mathvariant=¨bold¨ mathcolor=¨#0000FF¨»m«/mi»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»=«/mo»«mn mathvariant=¨bold¨ mathcolor=¨#0000FF¨»6«/mn»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨».«/mo»«mn mathvariant=¨bold¨ mathcolor=¨#0000FF¨»75«/mn»«mi mathvariant=¨bold¨ mathcolor=¨#0000FF¨»cm«/mi»«/math»
أقصى بعد بين القطعة النقدية ومحور القرص، بحيث تبقى القطعة النقدية في حالة سكون ، هو 6.7 سم.
המרחק מציר הדיסקה הוא רדיוס המסלול , נכתוב את משוואות התנועה כאשר פועל חיכוך סטטי מקסימאלי .
נכתוב את משוואת התנועה הרדיאלית ביחס לציר שכיוונו אל נקודת מרכז הסיבוב , וציר אנכי שכיוונו כלפי מעלה , כמוראה בתרשים הבא:

«math xmlns=¨http://www.w3.org/1998/Math/MathML¨»«msub»«mi mathvariant=¨bold¨ mathcolor=¨#0000FF¨»§#931;F«/mi»«mi mathvariant=¨bold¨ mathcolor=¨#0000FF¨»R«/mi»«/msub»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»=«/mo»«msup»«mi mathvariant=¨bold¨ mathcolor=¨#0000FF¨»m§#969;«/mi»«mn mathvariant=¨bold¨ mathcolor=¨#0000FF¨»2«/mn»«/msup»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»§#183;«/mo»«mi mathvariant=¨bold¨ mathcolor=¨#0000FF¨»R«/mi»«mspace linebreak=¨newline¨»«/mspace»«msub»«mi mathvariant=¨bold¨ mathcolor=¨#0000FF¨»f«/mi»«msub mathcolor=¨#0000FF¨»«mi mathvariant=¨bold¨»s«/mi»«mi mathvariant=¨bold¨»max«/mi»«/msub»«/msub»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»=«/mo»«msup»«mi mathvariant=¨bold¨ mathcolor=¨#0000FF¨»m§#969;«/mi»«mn mathvariant=¨bold¨ mathcolor=¨#0000FF¨»2«/mn»«/msup»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»§#183;«/mo»«mi mathvariant=¨bold¨ mathcolor=¨#0000FF¨»R«/mi»«mspace linebreak=¨newline¨»«/mspace»«menclose mathcolor=¨#0000FF¨ notation=¨box¨»«msub»«mi mathvariant=¨bold¨»§#956;«/mi»«mi mathvariant=¨bold¨»s«/mi»«/msub»«mo mathvariant=¨bold¨»§#183;«/mo»«mi mathvariant=¨bold¨»N«/mi»«mo mathvariant=¨bold¨»=«/mo»«msup»«mi mathvariant=¨bold¨»m§#969;«/mi»«mn mathvariant=¨bold¨»2«/mn»«/msup»«mo mathvariant=¨bold¨»§#183;«/mo»«mi mathvariant=¨bold¨»R«/mi»«/menclose»«/math» «math xmlns=¨http://www.w3.org/1998/Math/MathML¨»«msub»«mi mathvariant=¨bold¨ mathcolor=¨#0000FF¨»§#931;F«/mi»«mi mathvariant=¨bold¨ mathcolor=¨#0000FF¨»Y«/mi»«/msub»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»=«/mo»«mn mathvariant=¨bold¨ mathcolor=¨#0000FF¨»0«/mn»«mspace linebreak=¨newline¨»«/mspace»«mi mathvariant=¨bold¨ mathcolor=¨#0000FF¨»N«/mi»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»=«/mo»«mi mathvariant=¨bold¨ mathcolor=¨#0000FF¨»W«/mi»«mspace linebreak=¨newline¨»«/mspace»«menclose mathcolor=¨#0000FF¨ notation=¨box¨»«mi mathvariant=¨bold¨»N«/mi»«mo mathvariant=¨bold¨»=«/mo»«mi mathvariant=¨bold¨»mg«/mi»«/menclose»«/math»
נציב את הנורמל ממשוואת התנועה האנכית במשוואת התנועה רדיאלית ונבטא את רדיוס מסלול התנועה:
«math xmlns=¨http://www.w3.org/1998/Math/MathML¨»«menclose mathcolor=¨#0000FF¨ notation=¨box¨»«msub»«mi mathvariant=¨bold¨»§#956;«/mi»«mi mathvariant=¨bold¨»s«/mi»«/msub»«mo mathvariant=¨bold¨»§#183;«/mo»«mi mathvariant=¨bold¨ mathcolor=¨#FF0000¨»N«/mi»«mo mathvariant=¨bold¨»=«/mo»«msup»«mi mathvariant=¨bold¨»m§#969;«/mi»«mn mathvariant=¨bold¨»2«/mn»«/msup»«mo mathvariant=¨bold¨»§#183;«/mo»«mi mathvariant=¨bold¨»R«/mi»«/menclose»«mspace linebreak=¨newline¨»«/mspace»«mspace linebreak=¨newline¨»«/mspace»«msub»«mi mathvariant=¨bold¨ mathcolor=¨#0000FF¨»§#956;«/mi»«mi mathvariant=¨bold¨ mathcolor=¨#0000FF¨»s«/mi»«/msub»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»§#183;«/mo»«menclose mathcolor=¨#FF0000¨ notation=¨updiagonalstrike¨»«mi mathvariant=¨bold¨»m«/mi»«/menclose»«mo mathvariant=¨bold¨ mathcolor=¨#FF0000¨»§#183;«/mo»«mi mathvariant=¨bold¨ mathcolor=¨#FF0000¨»g«/mi»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»=«/mo»«menclose mathcolor=¨#0000FF¨ notation=¨updiagonalstrike¨»«mi mathvariant=¨bold¨»m«/mi»«mo mathvariant=¨bold¨»§#183;«/mo»«/menclose»«msup»«mi mathvariant=¨bold¨ mathcolor=¨#0000FF¨»§#969;«/mi»«mn mathvariant=¨bold¨ mathcolor=¨#0000FF¨»2«/mn»«/msup»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»§#183;«/mo»«mi mathvariant=¨bold¨ mathcolor=¨#0000FF¨»R«/mi»«mspace linebreak=¨newline¨»«/mspace»«mspace linebreak=¨newline¨»«/mspace»«mi mathvariant=¨bold¨ mathcolor=¨#0000FF¨»R«/mi»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»=«/mo»«mfrac mathcolor=¨#0000FF¨»«mrow»«msub»«mi mathvariant=¨bold¨»§#956;«/mi»«mi mathvariant=¨bold¨»s«/mi»«/msub»«mo mathvariant=¨bold¨»§#183;«/mo»«mi mathvariant=¨bold¨»g«/mi»«/mrow»«msup»«mi mathvariant=¨bold¨»§#969;«/mi»«mn mathvariant=¨bold¨»2«/mn»«/msup»«/mfrac»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»=«/mo»«mfrac mathcolor=¨#0000FF¨»«mrow»«mn mathvariant=¨bold¨»0«/mn»«mo mathvariant=¨bold¨».«/mo»«mn mathvariant=¨bold¨»6«/mn»«mo mathvariant=¨bold¨»§#183;«/mo»«mn mathvariant=¨bold¨»10«/mn»«/mrow»«msup»«mfenced»«mrow»«mn mathvariant=¨bold¨»2«/mn»«mo mathvariant=¨bold¨»§#183;«/mo»«mi mathvariant=¨bold¨»§#960;«/mi»«mo mathvariant=¨bold¨»§#183;«/mo»«mi mathvariant=¨bold¨»f«/mi»«/mrow»«/mfenced»«mn mathvariant=¨bold¨»2«/mn»«/msup»«/mfrac»«mspace linebreak=¨newline¨»«/mspace»«mi mathvariant=¨bold¨ mathcolor=¨#0000FF¨»R«/mi»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»=«/mo»«mfrac mathcolor=¨#0000FF¨»«mn mathvariant=¨bold¨»6«/mn»«mrow»«mn mathvariant=¨bold¨»4«/mn»«mo mathvariant=¨bold¨»§#183;«/mo»«msup»«mi mathvariant=¨bold¨»§#960;«/mi»«mn mathvariant=¨bold¨»2«/mn»«/msup»«mo mathvariant=¨bold¨»§#183;«/mo»«msup»«mi mathvariant=¨bold¨»f«/mi»«mn mathvariant=¨bold¨»2«/mn»«/msup»«/mrow»«/mfrac»«/math»
המטבע מסתובב עם הדיסקה , תדירות הדסקה היא 90 סיבובים לדקה . סל"ד הם יחידות לא תקניות.
יחידות התדירות התקניות הם הרץ , מספר הסיבובים בשנייה.
בדקה הדסקה משלימה 90 סיבובים , בשניה היא מבצעת פי 60 פחות סיבובים , תדירות המטבע ביחידות התקניות היא 1.5 הרץ.
נציב את תדירות ביחידות התקניות בביטוי הרדיוס :
«math xmlns=¨http://www.w3.org/1998/Math/MathML¨»«mi mathvariant=¨bold¨ mathcolor=¨#0000FF¨»R«/mi»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»=«/mo»«mfrac mathcolor=¨#0000FF¨»«mn mathvariant=¨bold¨»6«/mn»«mrow»«mn mathvariant=¨bold¨»4«/mn»«mo mathvariant=¨bold¨»§#183;«/mo»«msup»«mi mathvariant=¨bold¨»§#960;«/mi»«mn mathvariant=¨bold¨»2«/mn»«/msup»«mo mathvariant=¨bold¨»§#183;«/mo»«msup»«mi mathvariant=¨bold¨»f«/mi»«mn mathvariant=¨bold¨»2«/mn»«/msup»«/mrow»«/mfrac»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»=«/mo»«mfrac mathcolor=¨#0000FF¨»«mn mathvariant=¨bold¨»6«/mn»«mrow»«mn mathvariant=¨bold¨»4«/mn»«mo mathvariant=¨bold¨»§#183;«/mo»«msup»«mi mathvariant=¨bold¨»§#960;«/mi»«mn mathvariant=¨bold¨»2«/mn»«/msup»«mo mathvariant=¨bold¨»§#183;«/mo»«mn mathvariant=¨bold¨»1«/mn»«mo mathvariant=¨bold¨».«/mo»«msup»«mn mathvariant=¨bold¨»5«/mn»«mn mathvariant=¨bold¨»2«/mn»«/msup»«/mrow»«/mfrac»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»=«/mo»«mfrac mathcolor=¨#0000FF¨»«mn mathvariant=¨bold¨»6«/mn»«mrow»«mn mathvariant=¨bold¨»88«/mn»«mo mathvariant=¨bold¨».«/mo»«mn mathvariant=¨bold¨»82«/mn»«/mrow»«/mfrac»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»=«/mo»«mn mathvariant=¨bold¨ mathcolor=¨#0000FF¨»0«/mn»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨».«/mo»«mn mathvariant=¨bold¨ mathcolor=¨#0000FF¨»067«/mn»«mi mathvariant=¨bold¨ mathcolor=¨#0000FF¨»m«/mi»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»=«/mo»«mn mathvariant=¨bold¨ mathcolor=¨#0000FF¨»6«/mn»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨».«/mo»«mn mathvariant=¨bold¨ mathcolor=¨#0000FF¨»75«/mn»«mi mathvariant=¨bold¨ mathcolor=¨#0000FF¨»cm«/mi»«/math»
המרחק בין המרבי בין המטבע לציר הדסקה ,בו המטבע עדיין נמצא במנוחה הוא 6.7 ס"מ.
1. كلما ابتعدت القطعة النقدية، لا تتغير السرعة الزاوية ، يزداد نصف قطر المسار.
وتكون قوة الجاذبية نحو المركز المطلوبة للقطعة النقدية لتستمر في التحرك في حركة دائرية أكبر.
قوة الجاذبية نحو المركز هي قوة الاحتكاك الساكن، وهناك قيمة قصوى لقوة الاحتكاك الساكن ، وبالتالي يوجد أقصى بعد ممكن للقطعة النقدية من محور الدوران.
2. لا يوجد تعبير لقوة الاحتكاك الساكن ، هناك تعبير عن أقصى قوة احتكاك ساكن، لذلك فإن العديد من الأسئلة تتناول حالة وشك الحركة.
3. من المهم فهم معنى وحدات التردد rpm و hertz بحيث يمكنك الانتقال من rpm إلى hertz.
غالبًا ما يؤدي تعويض القيم في وحدات غير قياسية إلى إجابات غير منطقية.
لذلك ، عند تلقي إجابة غير منطقية أو متطرفة ، يجب عليك التحقق مما إذا كانت جميع الوحدات الموضوعة وحدات قياسية.
4. يمكن استخدام تحليل الأبعاد للتحقق من صحة التعبير الذي وصلنا إليه.
והכוח הצנטריפטלי הנדרש כדי שהמטבע ימשיך לנוע בתנועה מעגלית ,הוא גדול יותר.
הכוח הצנטריפטאלי הוא כוח החיכוך הסטטי , יש ערך מקסימאלי לכוח החיכוך הסטטי לכן יש מרחק מקסימאלי אפשרי למטבע מציר הסיבוב.
2. אין ביטוי לכוח החיכוך הסטטי , יש ביטוי לכוח החיכוך הסטטי המקסימאלי , לכן שאלות רבות עוסקות בסף תנועה.
3. חשבות להבין את משמעות יחידות התדירות סל"ד , והרץ . כדי שניתן יהיה לעבור מסל"ד להרץ.
הצבת ערכים ביחידות לא תקניות מובילה פעמים רבות לתשובות אל הגיוניות.
לכן כשמתקבלת תשובה לא הגיונית ,או קיצונית כדאי לבדוק אם כל היחידות שהוצבו הן יחידות תקניות.
4. אפשר להשתמש באנליזת מימדים, כדי לבדוק את תקפותו של הביטוי אליו הגענו.
______________________________________________________________________________________

______________________________________________________________________________________
...
احداث النقطة B هو 0.03 نيوتن. واحداث النقطة A هو 2.25 هرتز تربيع.
قيمة النقطة B - هي أقصى قيمة قوة احتكاك ساكن. قيمة النقطة A- هي قيمة التردد عندما يكون الاحتكاك الساكن له الحد الأقصى.
قيمة النقطة B تساوي قيمة أقصى قوة احتكاك ساكن. نجد هذه القيمة:
«math xmlns=¨http://www.w3.org/1998/Math/MathML¨»«msub»«mi mathvariant=¨bold¨ mathcolor=¨#0000FF¨»f«/mi»«msub mathcolor=¨#0000FF¨»«mi mathvariant=¨bold¨»s«/mi»«mi mathvariant=¨bold¨»max«/mi»«/msub»«/msub»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»=«/mo»«msub»«mi mathvariant=¨bold¨ mathcolor=¨#0000FF¨»§#956;«/mi»«mi mathvariant=¨bold¨ mathcolor=¨#0000FF¨»s«/mi»«/msub»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»§#183;«/mo»«mi mathvariant=¨bold¨ mathcolor=¨#0000FF¨»N«/mi»«mspace linebreak=¨newline¨»«/mspace»«msub»«mi mathvariant=¨bold¨ mathcolor=¨#0000FF¨»f«/mi»«msub mathcolor=¨#0000FF¨»«mi mathvariant=¨bold¨»s«/mi»«mi mathvariant=¨bold¨»max«/mi»«/msub»«/msub»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»=«/mo»«msub»«mi mathvariant=¨bold¨ mathcolor=¨#0000FF¨»§#956;«/mi»«mi mathvariant=¨bold¨ mathcolor=¨#0000FF¨»s«/mi»«/msub»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»§#183;«/mo»«mi mathvariant=¨bold¨ mathcolor=¨#0000FF¨»m«/mi»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»§#183;«/mo»«mi mathvariant=¨bold¨ mathcolor=¨#0000FF¨»g«/mi»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»=«/mo»«mn mathvariant=¨bold¨ mathcolor=¨#0000FF¨»0«/mn»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨».«/mo»«mn mathvariant=¨bold¨ mathcolor=¨#0000FF¨»6«/mn»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»§#183;«/mo»«mn mathvariant=¨bold¨ mathcolor=¨#0000FF¨»0«/mn»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨».«/mo»«mn mathvariant=¨bold¨ mathcolor=¨#0000FF¨»005«/mn»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»§#183;«/mo»«mn mathvariant=¨bold¨ mathcolor=¨#0000FF¨»10«/mn»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»=«/mo»«mn mathvariant=¨bold¨ mathcolor=¨#0000FF¨»0«/mn»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨».«/mo»«mn mathvariant=¨bold¨ mathcolor=¨#0000FF¨»03«/mn»«mi mathvariant=¨bold¨ mathcolor=¨#0000FF¨»N«/mi»«/math»
قيمة النقطة A تساوي مربع التردد الذي تكون فيه القطعة النقدية على وشك الحركة.
«math xmlns=¨http://www.w3.org/1998/Math/MathML¨»«msup»«mi mathvariant=¨bold¨ mathcolor=¨#0000FF¨»f«/mi»«mn mathvariant=¨bold¨ mathcolor=¨#0000FF¨»2«/mn»«/msup»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»=«/mo»«mn mathvariant=¨bold¨ mathcolor=¨#0000FF¨»1«/mn»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨».«/mo»«msup»«mn mathvariant=¨bold¨ mathcolor=¨#0000FF¨»5«/mn»«mn mathvariant=¨bold¨ mathcolor=¨#0000FF¨»2«/mn»«/msup»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»=«/mo»«mn mathvariant=¨bold¨ mathcolor=¨#0000FF¨»2«/mn»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨».«/mo»«msub»«mn mathvariant=¨bold¨ mathcolor=¨#0000FF¨»25«/mn»«msup mathcolor=¨#0000FF¨»«mi mathvariant=¨bold¨»HZ«/mi»«mn mathvariant=¨bold¨»2«/mn»«/msup»«/msub»«/math»
«math xmlns=¨http://www.w3.org/1998/Math/MathML¨»«msub»«mi mathvariant=¨bold¨ mathcolor=¨#0000FF¨»f«/mi»«msub mathcolor=¨#0000FF¨»«mi mathvariant=¨bold¨»s«/mi»«mi mathvariant=¨bold¨»max«/mi»«/msub»«/msub»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»=«/mo»«msub»«mi mathvariant=¨bold¨ mathcolor=¨#0000FF¨»§#956;«/mi»«mi mathvariant=¨bold¨ mathcolor=¨#0000FF¨»s«/mi»«/msub»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»§#183;«/mo»«mi mathvariant=¨bold¨ mathcolor=¨#0000FF¨»N«/mi»«mspace linebreak=¨newline¨»«/mspace»«msub»«mi mathvariant=¨bold¨ mathcolor=¨#0000FF¨»f«/mi»«msub mathcolor=¨#0000FF¨»«mi mathvariant=¨bold¨»s«/mi»«mi mathvariant=¨bold¨»max«/mi»«/msub»«/msub»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»=«/mo»«msub»«mi mathvariant=¨bold¨ mathcolor=¨#0000FF¨»§#956;«/mi»«mi mathvariant=¨bold¨ mathcolor=¨#0000FF¨»s«/mi»«/msub»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»§#183;«/mo»«mi mathvariant=¨bold¨ mathcolor=¨#0000FF¨»m«/mi»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»§#183;«/mo»«mi mathvariant=¨bold¨ mathcolor=¨#0000FF¨»g«/mi»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»=«/mo»«mn mathvariant=¨bold¨ mathcolor=¨#0000FF¨»0«/mn»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨».«/mo»«mn mathvariant=¨bold¨ mathcolor=¨#0000FF¨»6«/mn»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»§#183;«/mo»«mn mathvariant=¨bold¨ mathcolor=¨#0000FF¨»0«/mn»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨».«/mo»«mn mathvariant=¨bold¨ mathcolor=¨#0000FF¨»005«/mn»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»§#183;«/mo»«mn mathvariant=¨bold¨ mathcolor=¨#0000FF¨»10«/mn»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»=«/mo»«mn mathvariant=¨bold¨ mathcolor=¨#0000FF¨»0«/mn»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨».«/mo»«mn mathvariant=¨bold¨ mathcolor=¨#0000FF¨»03«/mn»«mi mathvariant=¨bold¨ mathcolor=¨#0000FF¨»N«/mi»«/math»
ערך הנקודה A , שווה לריבוע התדירות בה המטבע בסף תנועה.
«math xmlns=¨http://www.w3.org/1998/Math/MathML¨»«msup»«mi mathvariant=¨bold¨ mathcolor=¨#0000FF¨»f«/mi»«mn mathvariant=¨bold¨ mathcolor=¨#0000FF¨»2«/mn»«/msup»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»=«/mo»«mn mathvariant=¨bold¨ mathcolor=¨#0000FF¨»1«/mn»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨».«/mo»«msup»«mn mathvariant=¨bold¨ mathcolor=¨#0000FF¨»5«/mn»«mn mathvariant=¨bold¨ mathcolor=¨#0000FF¨»2«/mn»«/msup»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»=«/mo»«mn mathvariant=¨bold¨ mathcolor=¨#0000FF¨»2«/mn»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨».«/mo»«msub»«mn mathvariant=¨bold¨ mathcolor=¨#0000FF¨»25«/mn»«msup mathcolor=¨#0000FF¨»«mi mathvariant=¨bold¨»HZ«/mi»«mn mathvariant=¨bold¨»2«/mn»«/msup»«/msub»«/math»
1. هناك قوة احتكاك ساكن وقوة احتكاك حركي وهما قوتان مختلفتان ، والرسم البياني بشكل عام يدور حول قوة الاحتكاك ، لأنه يصف كل من قوى الاحتكاك.
2. قوة الاحتكاك الحركي هي قوة ثابتة المقدار، و قوة الاحتكاك الساكن متغيرة المقدار، وتتعلق بالقوة المؤثرة لتحريك الجسم.
عادة ما يكون معامل الاحتكاك الحركي أصغر من معامل الاحتكاك الساكن.
من المهم أن نفهم تمامًا موضوع الاحتكاك الساكن والحركي. حتى نفهم من شكل الرسم البياني في أي تردّد يعمل الاحتكاك الساكن والترددات التي يعمل فيها الاحتكاك الحركي.
2. כוח החיכוך הקינטי הוא כוח קבוע בגודלו , כוח החיכוך הסטטי משתנה בגודלו, בהתאם לכוח הפועל להנעת הגוף.
מקדם החיכוך הקינטי לרוב קטן ממקדם החיכוך הסטטי.
חשוב להבין היטב את נושא החיכוך הסטטי והקינטי. כדי להבין מצורת הגרף באילו תדירויות פועל החיכוך הסטטי ובאילו תדירויות פועל חיכוך קינטי.
______________________________________________________________________________________

______________________________________________________________________________________
...
إذا زادت قطعة القطعة النقدية سيتغير الرسم البياني.
فهم قوى الاحتكاك الساكن وقوى الاحتكاك الساكن القصوى والحركي .
يتعلق الحد الأقصى لقوة الاحتكاك الساكن على الكتلة ، وفقًا لـ: «math xmlns=¨http://www.w3.org/1998/Math/MathML¨»«msub»«mi mathvariant=¨bold¨ mathcolor=¨#0000FF¨»f«/mi»«msub mathcolor=¨#0000FF¨»«mi mathvariant=¨bold¨»s«/mi»«mi mathvariant=¨bold¨»max«/mi»«/msub»«/msub»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»=«/mo»«msub»«mi mathvariant=¨bold¨ mathcolor=¨#0000FF¨»§#956;«/mi»«mi mathvariant=¨bold¨ mathcolor=¨#0000FF¨»s«/mi»«/msub»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»§#183;«/mo»«mi mathvariant=¨bold¨ mathcolor=¨#0000FF¨»m«/mi»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»§#183;«/mo»«mi mathvariant=¨bold¨ mathcolor=¨#0000FF¨»g«/mi»«/math»
بالإضافة إلى ذلك ، تتعلق قوة الاحتكاك الحركي أيضًا بالكتلة ، وفقًا لما يلي: «math xmlns=¨http://www.w3.org/1998/Math/MathML¨»«msub»«mi mathvariant=¨bold¨ mathcolor=¨#0000FF¨»f«/mi»«mi mathvariant=¨bold¨ mathcolor=¨#0000FF¨»K«/mi»«/msub»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»=«/mo»«msub»«mi mathvariant=¨bold¨ mathcolor=¨#0000FF¨»§#956;«/mi»«mi mathvariant=¨bold¨ mathcolor=¨#0000FF¨»K«/mi»«/msub»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»§#183;«/mo»«mi mathvariant=¨bold-italic¨ mathcolor=¨#0000FF¨»m«/mi»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»§#183;«/mo»«mi mathvariant=¨bold-italic¨ mathcolor=¨#0000FF¨»g«/mi»«/math»
لذلك عندما تتغير الكتلة ، سيتغير الرسم البياني أيضًا.
ובנוסף, גם כוח החיכוך הקינטי תלוי במסה , לפי: «math xmlns=¨http://www.w3.org/1998/Math/MathML¨»«msub»«mi mathvariant=¨bold¨ mathcolor=¨#0000FF¨»f«/mi»«mi mathvariant=¨bold¨ mathcolor=¨#0000FF¨»K«/mi»«/msub»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»=«/mo»«msub»«mi mathvariant=¨bold¨ mathcolor=¨#0000FF¨»§#956;«/mi»«mi mathvariant=¨bold¨ mathcolor=¨#0000FF¨»K«/mi»«/msub»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»§#183;«/mo»«mi mathvariant=¨bold-italic¨ mathcolor=¨#0000FF¨»m«/mi»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»§#183;«/mo»«mi mathvariant=¨bold-italic¨ mathcolor=¨#0000FF¨»g«/mi»«/math»
לכן כאשר המסה תשתנה , גם הגרף ישתנה.
ليست هناك حاجة للتفكير حول كيفية تغيير الرسم البياني بالضبط ، والسؤال الوحيد هو ما إذا كان الرسم البياني سيتغير.
يجب عليك كتابة ما إذا كان الرسم البياني سيتغير أم لا وإعطاء وتفسير ذلك.
______________________________________________________________________________________