______________________________________________________________________________________
...
72 ק"ג
فهم معنى الرسم البياني. والاستخدام الصحيح للرسم البياني.
يتعلق زمن الدورة بكتلة رائد الفضاء.
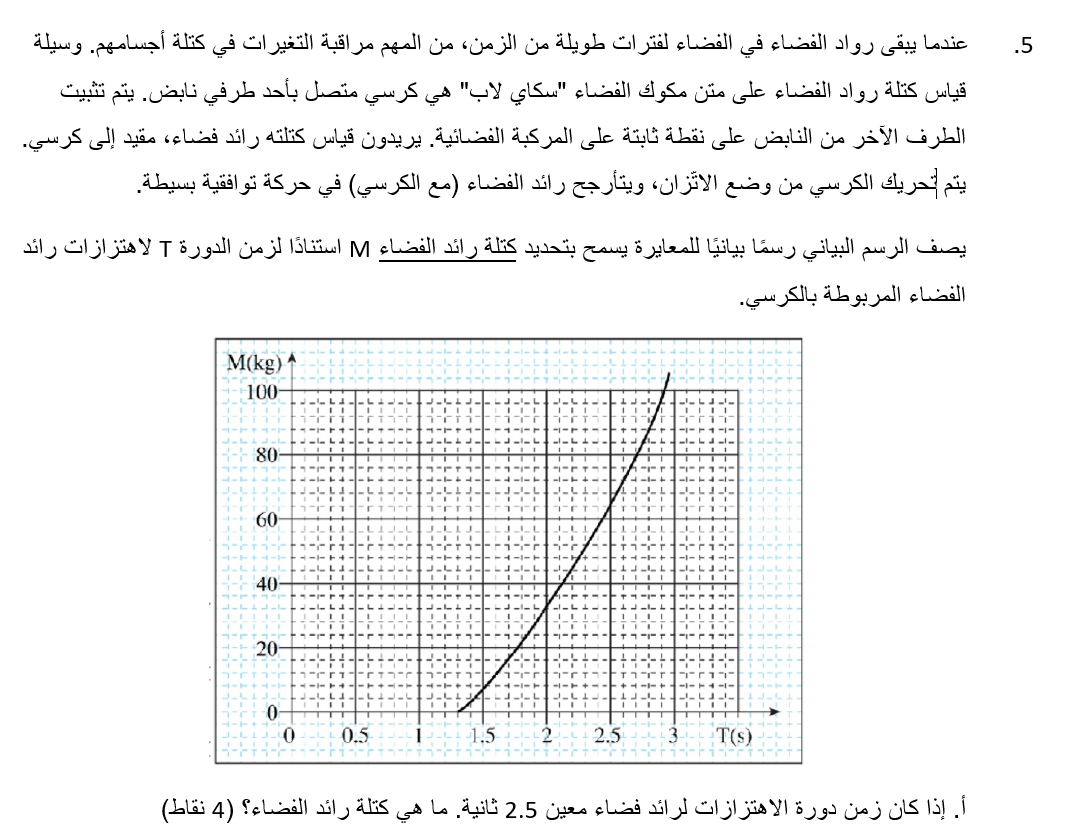
من الرسم البياني، يمكنك أن ترى أن زمن الدورة البالغ 2.6 ثانية يلائم رائد فضاء كتلته 72 كغم.
מהגרף ניתן לראות שזמן מחזור של 2.6 שניות מתאים לאסטרונאוט שמסתו 72 ק"ג.
1. لا يمكنك الحصول على قدر كبير من الدقة من الرسم البياني. يجب تحديد قيمة الكتلة بشكل معقول.
2. يشير السؤال إلى مصطلح "رسم بياني للمعايرة". المعايرة هي عملية لتحديد قيم القياس لجهاز القياس.
حتى لو كنت غير معتاد ولا تعرف ما هو الرسم البياني للمعايرة، فمن المهم عدم الانفعال وفهم الفكرة العامة.
2. בשאלה מופיע המושג "גרף כיול" , כיול היא פעולה לקביעת ערכי מדידה של מכשיר מדידה.
בעזרת גרף זה ניתן למשל לקבוע את ערכי המדידה האפשריים של מכשיר למדידת מסה הפועל בחלל.
3.
______________________________________________________________________________________

______________________________________________________________________________________
...
«math xmlns=¨http://www.w3.org/1998/Math/MathML¨»«mi mathvariant=¨bold¨»T«/mi»«mo mathvariant=¨bold¨»=«/mo»«mn mathvariant=¨bold¨»2«/mn»«mo mathvariant=¨bold¨».«/mo»«mn mathvariant=¨bold¨»6«/mn»«mi mathvariant=¨bold¨»s«/mi»«/math»
فهم الحركة التوافقية.
لا يتعلق زمن تذبذب أي تذبذب توافقي بسيط على السعة. كما يمكن رؤيته ذلك في صيغة زمن الدورة:
«math xmlns=¨http://www.w3.org/1998/Math/MathML¨»«mstyle mathsize=¨20px¨»«mrow»«mi mathvariant=¨bold¨ mathcolor=¨#0000FF¨»T«/mi»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»=«/mo»«mn mathvariant=¨bold¨ mathcolor=¨#0000FF¨»2«/mn»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»§#183;«/mo»«mi mathvariant=¨bold¨ mathcolor=¨#0000FF¨»§#960;«/mi»«msqrt mathcolor=¨#0000FF¨»«mfrac»«mi mathvariant=¨bold¨»m«/mi»«mi mathvariant=¨bold¨»k«/mi»«/mfrac»«/msqrt»«/mrow»«/mstyle»«/math»
كلما زادت السعة، زادت المسافة التي يتحركها الجسم ذهابًا وإيابًا، ولكن سرعته في كل نقطة تكون أكبر.
لذلك، فإن السعة لا تؤثر على زمن الدورة.
ככל שהמשרעת גדולה יותר הגוף נע הלוך ושוב במרחק גדול יותר , אך מהירותו בכל נקודה גדולה יותר.
לכן המשרעת לא משפיעה על זמן המחזור.
1. من تعبير زمن الدورة في الحركة التوافقية البسيطة، يمكن ملاحظة أن زمن الدورة يتعلق فقط على الكتلة وثابت النابض، وليس على أي شيء آخر، ولا حتى على السعة.
2. أحد الأشياء التي يرغبون في إبرازها أكثر من غيرها هو: استقلال زمن دورة التذبذب في الحركة التوافقية عن سعة التذبذبات.
גם לא במשרעת.
2. אחד הדברים שהכי אוהבים להדגים זה: אי תלות זמן מחזור של תנודה הרמונית במשרעת התנודות.
______________________________________________________________________________________

______________________________________________________________________________________
...
«math xmlns=¨http://www.w3.org/1998/Math/MathML¨»«mi mathvariant=¨bold¨»T«/mi»«mo mathvariant=¨bold¨»=«/mo»«mn mathvariant=¨bold¨»1«/mn»«mo mathvariant=¨bold¨».«/mo»«mn mathvariant=¨bold¨»3«/mn»«mi mathvariant=¨bold¨»s«/mi»«/math»
استخدام تعبير زمن الدورة للحركة التوافقية البسيطة.
يتحرك الجسم بحركة توافقية بسيطة، من تعبير زمن الدورة: «math xmlns=¨http://www.w3.org/1998/Math/MathML¨»«mi mathvariant=¨bold¨ mathcolor=¨#0000FF¨»T«/mi»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»=«/mo»«mn mathvariant=¨bold¨ mathcolor=¨#0000FF¨»2«/mn»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»§#183;«/mo»«mi mathvariant=¨bold¨ mathcolor=¨#0000FF¨»§#960;«/mi»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»§#183;«/mo»«msqrt mathcolor=¨#0000FF¨»«mfrac»«mi mathvariant=¨bold¨»m«/mi»«mi mathvariant=¨bold¨»k«/mi»«/mfrac»«/msqrt»«/math»
عندما يزداد ثابت النابض بـ 4 مرات، يقل زمن الدورة بـ 2 مرة.
זמן המחזור קטן פי 2.
إذا كان هناك تخبطًا رياضيًا حول كيفية تغير كمية فيزيائية في بعض التعبيرات عندما تتغير كمية فيزيائية أخرى.
من المستحسن وضع الأرقام في نفس النمط الرياضي. حتى الأرقام ليست هي نفسها تمامًا كما هو موضح في السؤال.
على سبيل المثال، سنكتب تعبيرًا عامًا، بنفس الصيغة الرياضية:
«math xmlns=¨http://www.w3.org/1998/Math/MathML¨»«mn mathvariant=¨bold¨ mathcolor=¨#FF0000¨»2«/mn»«mo mathvariant=¨bold¨ mathcolor=¨#FF0000¨»§#183;«/mo»«mi mathvariant=¨bold¨ mathcolor=¨#FF0000¨»§#960;«/mi»«mo mathvariant=¨bold¨ mathcolor=¨#FF0000¨»§#183;«/mo»«msqrt mathcolor=¨#FF0000¨»«mfrac»«mn mathvariant=¨bold¨»100«/mn»«mn mathvariant=¨bold¨ mathcolor=¨#007F00¨»5«/mn»«/mfrac»«/msqrt»«mo mathvariant=¨bold¨ mathcolor=¨#FF0000¨»=«/mo»«mn mathvariant=¨bold¨ mathcolor=¨#FF0000¨»28«/mn»«mo mathvariant=¨bold¨ mathcolor=¨#FF0000¨».«/mo»«mn mathvariant=¨bold¨ mathcolor=¨#FF0000¨»09«/mn»«/math»
نزيد قيمة الرقم 5 بمقدار 4 مرات :
«math xmlns=¨http://www.w3.org/1998/Math/MathML¨»«mn mathvariant=¨bold¨ mathcolor=¨#FF0000¨»2«/mn»«mo mathvariant=¨bold¨ mathcolor=¨#FF0000¨»§#183;«/mo»«mi mathvariant=¨bold¨ mathcolor=¨#FF0000¨»§#960;«/mi»«mo mathvariant=¨bold¨ mathcolor=¨#FF0000¨»§#183;«/mo»«msqrt mathcolor=¨#FF0000¨»«mfrac»«mn mathvariant=¨bold¨»100«/mn»«mn mathvariant=¨bold¨ mathcolor=¨#007F00¨»20«/mn»«/mfrac»«/msqrt»«mo mathvariant=¨bold¨ mathcolor=¨#FF0000¨»=«/mo»«mn mathvariant=¨bold¨ mathcolor=¨#FF0000¨»14«/mn»«mo mathvariant=¨bold¨ mathcolor=¨#FF0000¨».«/mo»«mn mathvariant=¨bold¨ mathcolor=¨#FF0000¨»04«/mn»«/math»
نرى أن قيمة التعبير صغر بمرتين، لذلك حتى لو قمنا بزيادة قيمة ثابت النابض في تعبير زمن الدورة بمقدار 4 مرات، فسنحصل على زمن دورة أصغر بمرتين.
بهذه الطريقة يمكن إيجاد قيمة زمن الدورة رياضيا، حتى ولو لم يتم إعطاء قيمة ثابت النابض!
מומלץ להציב מספרים באותה תבנית מתמטית. אפילו לא דווקא את אותם המספרים המוצגים בשאלה.
לדוגמה: «math xmlns=¨http://www.w3.org/1998/Math/MathML¨»«mn mathvariant=¨bold¨ mathcolor=¨#FF0000¨»2«/mn»«mo mathvariant=¨bold¨ mathcolor=¨#FF0000¨»§#183;«/mo»«mi mathvariant=¨bold¨ mathcolor=¨#FF0000¨»§#960;«/mi»«mo mathvariant=¨bold¨ mathcolor=¨#FF0000¨»§#183;«/mo»«msqrt mathcolor=¨#FF0000¨»«mfrac»«mn mathvariant=¨bold¨»100«/mn»«mn mathvariant=¨bold¨»5«/mn»«/mfrac»«/msqrt»«mo mathvariant=¨bold¨ mathcolor=¨#FF0000¨»=«/mo»«mn mathvariant=¨bold¨ mathcolor=¨#FF0000¨»28«/mn»«mo mathvariant=¨bold¨ mathcolor=¨#FF0000¨».«/mo»«mn mathvariant=¨bold¨ mathcolor=¨#FF0000¨»09«/mn»«/math»
נגדיל את ערך הספרה 5 פי 4 :
______________________________________________________________________________________

______________________________________________________________________________________
...
«math xmlns=¨http://www.w3.org/1998/Math/MathML¨»«mi mathvariant=¨bold¨»T«/mi»«mo mathvariant=¨bold¨»=«/mo»«mn mathvariant=¨bold¨»2«/mn»«mo mathvariant=¨bold¨»§#183;«/mo»«mi mathvariant=¨bold¨»§#960;«/mi»«msqrt»«mfrac»«mrow»«mi mathvariant=¨bold¨»M«/mi»«mo mathvariant=¨bold¨»+«/mo»«mi mathvariant=¨bold¨»m«/mi»«/mrow»«mi mathvariant=¨bold¨»K«/mi»«/mfrac»«/msqrt»«mspace linebreak=¨newline¨»«/mspace»«msup»«mi mathvariant=¨bold¨»T«/mi»«mn mathvariant=¨bold¨»2«/mn»«/msup»«mo mathvariant=¨bold¨»=«/mo»«msup»«mn mathvariant=¨bold¨»2«/mn»«mn mathvariant=¨bold¨»2«/mn»«/msup»«mo mathvariant=¨bold¨»§#183;«/mo»«msup»«mi mathvariant=¨bold¨»§#960;«/mi»«mn mathvariant=¨bold¨»2«/mn»«/msup»«mrow»«mo mathvariant=¨bold¨»(«/mo»«mfrac»«mrow»«mi mathvariant=¨bold¨»M«/mi»«mo mathvariant=¨bold¨»+«/mo»«mi mathvariant=¨bold¨»m«/mi»«/mrow»«mi mathvariant=¨bold¨»K«/mi»«/mfrac»«mo mathvariant=¨bold¨»)«/mo»«/mrow»«mspace linebreak=¨newline¨»«/mspace»«mfrac»«mrow»«msup»«mi mathvariant=¨bold¨»T«/mi»«mn mathvariant=¨bold¨»2«/mn»«/msup»«mo mathvariant=¨bold¨»§#183;«/mo»«mi mathvariant=¨bold¨»K«/mi»«/mrow»«mrow»«mn mathvariant=¨bold¨»4«/mn»«mo mathvariant=¨bold¨»§#183;«/mo»«msup»«mi mathvariant=¨bold¨»§#960;«/mi»«mn mathvariant=¨bold¨»2«/mn»«/msup»«/mrow»«/mfrac»«mo mathvariant=¨bold¨»=«/mo»«mi mathvariant=¨bold¨»M«/mi»«mo mathvariant=¨bold¨»+«/mo»«mi mathvariant=¨bold¨»m«/mi»«mspace linebreak=¨newline¨»«/mspace»«mspace linebreak=¨newline¨»«/mspace»«menclose notation=¨circle¨»«mi mathvariant=¨bold¨»M«/mi»«mo mathvariant=¨bold¨»=«/mo»«mfrac»«mrow»«msup»«mi mathvariant=¨bold¨»T«/mi»«mn mathvariant=¨bold¨»2«/mn»«/msup»«mo mathvariant=¨bold¨»§#183;«/mo»«mi mathvariant=¨bold¨»K«/mi»«/mrow»«mrow»«mn mathvariant=¨bold¨»4«/mn»«mo mathvariant=¨bold¨»§#183;«/mo»«msup»«mi mathvariant=¨bold¨»§#960;«/mi»«mn mathvariant=¨bold¨»2«/mn»«/msup»«/mrow»«/mfrac»«mo mathvariant=¨bold¨»-«/mo»«mi mathvariant=¨bold¨»m«/mi»«/menclose»«/math»
العمليات الجبرية على تعبير زمن الدورة، حيث كتلة الجسم المتذبذب تساوي مجموع كتلة الكرسي وكتلة رائد الفضاء.
نكتب تعبيرًا لزمن الدورة عندما تكون الكتلة المتذبذبة هي كتلة الكرسي ورائد الفضاء:
«math xmlns=¨http://www.w3.org/1998/Math/MathML¨»«mi mathvariant=¨bold¨ mathcolor=¨#0000FF¨»T«/mi»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»=«/mo»«mn mathvariant=¨bold¨ mathcolor=¨#0000FF¨»2«/mn»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»§#183;«/mo»«mi mathvariant=¨bold¨ mathcolor=¨#0000FF¨»§#960;«/mi»«msqrt mathcolor=¨#0000FF¨»«mfrac»«mrow»«mi mathvariant=¨bold¨»M«/mi»«mo mathvariant=¨bold¨»+«/mo»«mi mathvariant=¨bold¨»m«/mi»«/mrow»«mi mathvariant=¨bold¨»K«/mi»«/mfrac»«/msqrt»«/math»
نعبر عن كتلة الشخص من خلال تعبير زمن الدورة:
«math xmlns=¨http://www.w3.org/1998/Math/MathML¨»«mi mathvariant=¨bold¨ mathcolor=¨#0000FF¨»T«/mi»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»=«/mo»«mn mathvariant=¨bold¨ mathcolor=¨#0000FF¨»2«/mn»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»§#183;«/mo»«mi mathvariant=¨bold¨ mathcolor=¨#0000FF¨»§#960;«/mi»«msqrt mathcolor=¨#0000FF¨»«mfrac»«mrow»«mi mathvariant=¨bold¨»M«/mi»«mo mathvariant=¨bold¨»+«/mo»«mi mathvariant=¨bold¨»m«/mi»«/mrow»«mi mathvariant=¨bold¨»K«/mi»«/mfrac»«/msqrt»«mspace linebreak=¨newline¨»«/mspace»«msup»«mi mathvariant=¨bold¨ mathcolor=¨#0000FF¨»T«/mi»«mn mathvariant=¨bold¨ mathcolor=¨#0000FF¨»2«/mn»«/msup»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»=«/mo»«msup»«mn mathvariant=¨bold¨ mathcolor=¨#0000FF¨»2«/mn»«mn mathvariant=¨bold¨ mathcolor=¨#0000FF¨»2«/mn»«/msup»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»§#183;«/mo»«msup»«mi mathvariant=¨bold¨ mathcolor=¨#0000FF¨»§#960;«/mi»«mn mathvariant=¨bold¨ mathcolor=¨#0000FF¨»2«/mn»«/msup»«mrow mathcolor=¨#0000FF¨»«mo mathvariant=¨bold¨»(«/mo»«mfrac»«mrow»«mi mathvariant=¨bold¨»M«/mi»«mo mathvariant=¨bold¨»+«/mo»«mi mathvariant=¨bold¨»m«/mi»«/mrow»«mi mathvariant=¨bold¨»K«/mi»«/mfrac»«mo mathvariant=¨bold¨»)«/mo»«/mrow»«mspace linebreak=¨newline¨»«/mspace»«mfrac mathcolor=¨#0000FF¨»«mrow»«msup»«mi mathvariant=¨bold¨»T«/mi»«mn mathvariant=¨bold¨»2«/mn»«/msup»«mo mathvariant=¨bold¨»§#183;«/mo»«mi mathvariant=¨bold¨»K«/mi»«/mrow»«mrow»«mn mathvariant=¨bold¨»4«/mn»«mo mathvariant=¨bold¨»§#183;«/mo»«msup»«mi mathvariant=¨bold¨»§#960;«/mi»«mn mathvariant=¨bold¨»2«/mn»«/msup»«/mrow»«/mfrac»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»=«/mo»«mi mathvariant=¨bold¨ mathcolor=¨#0000FF¨»M«/mi»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»+«/mo»«mi mathvariant=¨bold¨ mathcolor=¨#0000FF¨»m«/mi»«mspace linebreak=¨newline¨»«/mspace»«mspace linebreak=¨newline¨»«/mspace»«menclose mathcolor=¨#0000FF¨ notation=¨circle¨»«mi mathvariant=¨bold¨»M«/mi»«mo mathvariant=¨bold¨»=«/mo»«mfrac»«mrow»«msup»«mi mathvariant=¨bold¨»T«/mi»«mn mathvariant=¨bold¨»2«/mn»«/msup»«mo mathvariant=¨bold¨»§#183;«/mo»«mi mathvariant=¨bold¨»K«/mi»«/mrow»«mrow»«mn mathvariant=¨bold¨»4«/mn»«mo mathvariant=¨bold¨»§#183;«/mo»«msup»«mi mathvariant=¨bold¨»§#960;«/mi»«mn mathvariant=¨bold¨»2«/mn»«/msup»«/mrow»«/mfrac»«mo mathvariant=¨bold¨»-«/mo»«mi mathvariant=¨bold¨»m«/mi»«/menclose»«/math»
«math xmlns=¨http://www.w3.org/1998/Math/MathML¨»«mi mathvariant=¨bold¨ mathcolor=¨#0000FF¨»T«/mi»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»=«/mo»«mn mathvariant=¨bold¨ mathcolor=¨#0000FF¨»2«/mn»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»§#183;«/mo»«mi mathvariant=¨bold¨ mathcolor=¨#0000FF¨»§#960;«/mi»«msqrt mathcolor=¨#0000FF¨»«mfrac»«mrow»«mi mathvariant=¨bold¨»M«/mi»«mo mathvariant=¨bold¨»+«/mo»«mi mathvariant=¨bold¨»m«/mi»«/mrow»«mi mathvariant=¨bold¨»K«/mi»«/mfrac»«/msqrt»«/math»
נבטא את מסת האדם , מביטוי זמן המחזור:
«math xmlns=¨http://www.w3.org/1998/Math/MathML¨»«mi mathvariant=¨bold¨ mathcolor=¨#0000FF¨»T«/mi»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»=«/mo»«mn mathvariant=¨bold¨ mathcolor=¨#0000FF¨»2«/mn»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»§#183;«/mo»«mi mathvariant=¨bold¨ mathcolor=¨#0000FF¨»§#960;«/mi»«msqrt mathcolor=¨#0000FF¨»«mfrac»«mrow»«mi mathvariant=¨bold¨»M«/mi»«mo mathvariant=¨bold¨»+«/mo»«mi mathvariant=¨bold¨»m«/mi»«/mrow»«mi mathvariant=¨bold¨»K«/mi»«/mfrac»«/msqrt»«mspace linebreak=¨newline¨»«/mspace»«msup»«mi mathvariant=¨bold¨ mathcolor=¨#0000FF¨»T«/mi»«mn mathvariant=¨bold¨ mathcolor=¨#0000FF¨»2«/mn»«/msup»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»=«/mo»«msup»«mn mathvariant=¨bold¨ mathcolor=¨#0000FF¨»2«/mn»«mn mathvariant=¨bold¨ mathcolor=¨#0000FF¨»2«/mn»«/msup»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»§#183;«/mo»«msup»«mi mathvariant=¨bold¨ mathcolor=¨#0000FF¨»§#960;«/mi»«mn mathvariant=¨bold¨ mathcolor=¨#0000FF¨»2«/mn»«/msup»«mrow mathcolor=¨#0000FF¨»«mo mathvariant=¨bold¨»(«/mo»«mfrac»«mrow»«mi mathvariant=¨bold¨»M«/mi»«mo mathvariant=¨bold¨»+«/mo»«mi mathvariant=¨bold¨»m«/mi»«/mrow»«mi mathvariant=¨bold¨»K«/mi»«/mfrac»«mo mathvariant=¨bold¨»)«/mo»«/mrow»«mspace linebreak=¨newline¨»«/mspace»«mfrac mathcolor=¨#0000FF¨»«mrow»«msup»«mi mathvariant=¨bold¨»T«/mi»«mn mathvariant=¨bold¨»2«/mn»«/msup»«mo mathvariant=¨bold¨»§#183;«/mo»«mi mathvariant=¨bold¨»K«/mi»«/mrow»«mrow»«mn mathvariant=¨bold¨»4«/mn»«mo mathvariant=¨bold¨»§#183;«/mo»«msup»«mi mathvariant=¨bold¨»§#960;«/mi»«mn mathvariant=¨bold¨»2«/mn»«/msup»«/mrow»«/mfrac»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»=«/mo»«mi mathvariant=¨bold¨ mathcolor=¨#0000FF¨»M«/mi»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»+«/mo»«mi mathvariant=¨bold¨ mathcolor=¨#0000FF¨»m«/mi»«mspace linebreak=¨newline¨»«/mspace»«mspace linebreak=¨newline¨»«/mspace»«menclose mathcolor=¨#0000FF¨ notation=¨circle¨»«mi mathvariant=¨bold¨»M«/mi»«mo mathvariant=¨bold¨»=«/mo»«mfrac»«mrow»«msup»«mi mathvariant=¨bold¨»T«/mi»«mn mathvariant=¨bold¨»2«/mn»«/msup»«mo mathvariant=¨bold¨»§#183;«/mo»«mi mathvariant=¨bold¨»K«/mi»«/mrow»«mrow»«mn mathvariant=¨bold¨»4«/mn»«mo mathvariant=¨bold¨»§#183;«/mo»«msup»«mi mathvariant=¨bold¨»§#960;«/mi»«mn mathvariant=¨bold¨»2«/mn»«/msup»«/mrow»«/mfrac»«mo mathvariant=¨bold¨»-«/mo»«mi mathvariant=¨bold¨»m«/mi»«/menclose»«/math»
الغرض من المنظومة هو قياس كتلة رائد الفضاء، ولكن ليس فقط رائد الفضاء يتحرك في تذبذبات، بل يتحرك الكرسي أيضًا في تذبذبات.
يتحرك رائد الفضاء والكرسي معًا. ينبغي التعامل مع حركتهم كحركة جسم واحد كتلته M+m.
האסטרונאוט והכיסא נעים יחד יש להתייחס לתנועתם כאל תנועת גוף אחד שמסתו M+m.
______________________________________________________________________________________

______________________________________________________________________________________
...
كتلة الكرسي هي 25.68 كغم.
قم بالتعبير عن كتلة الكرسي من المعادلة التي تم الحصول عليها في البند السابق، باستخدام ثابت النابض وعوض إحدى النقاط في الرسم البياني.
نعبر عن كتلة الكرسي بواسطة التعبير عن كتلة رائد الفضاء، ونجد كتلة الكرسي من زمن دورة مقداره 1.3 ثانية.
بالنسبة لهذا زمن الدورة، كتلة رائد الفضاء تساوي صفرًا. والاهتزازات هي فقط من الكرسي.
«math xmlns=¨http://www.w3.org/1998/Math/MathML¨»«mi mathvariant=¨bold¨ mathcolor=¨#0000FF¨»M«/mi»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»=«/mo»«mfrac mathcolor=¨#0000FF¨»«mrow»«msup»«mi mathvariant=¨bold¨»T«/mi»«mn mathvariant=¨bold¨»2«/mn»«/msup»«mo mathvariant=¨bold¨»§#183;«/mo»«mi mathvariant=¨bold¨»K«/mi»«/mrow»«mrow»«mn mathvariant=¨bold¨»4«/mn»«mo mathvariant=¨bold¨»§#183;«/mo»«msup»«mi mathvariant=¨bold¨»§#960;«/mi»«mn mathvariant=¨bold¨»2«/mn»«/msup»«/mrow»«/mfrac»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»-«/mo»«mi mathvariant=¨bold¨ mathcolor=¨#0000FF¨»m«/mi»«mspace linebreak=¨newline¨»«/mspace»«mspace linebreak=¨newline¨»«/mspace»«mi mathvariant=¨bold¨ mathcolor=¨#0000FF¨»m«/mi»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»=«/mo»«mfrac mathcolor=¨#0000FF¨»«mrow»«msup»«mi mathvariant=¨bold¨»T«/mi»«mn mathvariant=¨bold¨»2«/mn»«/msup»«mo mathvariant=¨bold¨»§#183;«/mo»«mi mathvariant=¨bold¨»K«/mi»«/mrow»«mrow»«mn mathvariant=¨bold¨»4«/mn»«mo mathvariant=¨bold¨»§#183;«/mo»«msup»«mi mathvariant=¨bold¨»§#960;«/mi»«mn mathvariant=¨bold¨»2«/mn»«/msup»«/mrow»«/mfrac»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»-«/mo»«mi mathvariant=¨bold¨ mathcolor=¨#0000FF¨»M«/mi»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»=«/mo»«mfrac mathcolor=¨#0000FF¨»«mrow»«mn mathvariant=¨bold¨»1«/mn»«mo mathvariant=¨bold¨».«/mo»«msup»«mn mathvariant=¨bold¨»3«/mn»«mn mathvariant=¨bold¨»2«/mn»«/msup»«mo mathvariant=¨bold¨»§#183;«/mo»«mn mathvariant=¨bold¨»600«/mn»«/mrow»«mrow»«mn mathvariant=¨bold¨»4«/mn»«mo mathvariant=¨bold¨»§#183;«/mo»«msup»«mi mathvariant=¨bold¨»§#960;«/mi»«mn mathvariant=¨bold¨»2«/mn»«/msup»«/mrow»«/mfrac»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»-«/mo»«mn mathvariant=¨bold¨ mathcolor=¨#0000FF¨»0«/mn»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»=«/mo»«mfrac mathcolor=¨#0000FF¨»«mn mathvariant=¨bold¨»1014«/mn»«mrow»«mn mathvariant=¨bold¨»4«/mn»«mo mathvariant=¨bold¨»§#183;«/mo»«msup»«mi mathvariant=¨bold¨»§#960;«/mi»«mn mathvariant=¨bold¨»2«/mn»«/msup»«/mrow»«/mfrac»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»=«/mo»«mn mathvariant=¨bold¨ mathcolor=¨#0000FF¨»25«/mn»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨».«/mo»«mn mathvariant=¨bold¨ mathcolor=¨#0000FF¨»68«/mn»«mi mathvariant=¨bold¨ mathcolor=¨#0000FF¨»kg«/mi»«/math»
وبالتالي فإن كتلة الكرسي هي 25.68 كغم.
כאשר מסת האסטרונאוט היא אפס, התנודות הן רק של הכיסא.
«math xmlns=¨http://www.w3.org/1998/Math/MathML¨»«mi mathvariant=¨bold¨ mathcolor=¨#0000FF¨»M«/mi»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»=«/mo»«mfrac mathcolor=¨#0000FF¨»«mrow»«msup»«mi mathvariant=¨bold¨»T«/mi»«mn mathvariant=¨bold¨»2«/mn»«/msup»«mo mathvariant=¨bold¨»§#183;«/mo»«mi mathvariant=¨bold¨»K«/mi»«/mrow»«mrow»«mn mathvariant=¨bold¨»4«/mn»«mo mathvariant=¨bold¨»§#183;«/mo»«msup»«mi mathvariant=¨bold¨»§#960;«/mi»«mn mathvariant=¨bold¨»2«/mn»«/msup»«/mrow»«/mfrac»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»-«/mo»«mi mathvariant=¨bold¨ mathcolor=¨#0000FF¨»m«/mi»«mspace linebreak=¨newline¨»«/mspace»«mspace linebreak=¨newline¨»«/mspace»«mi mathvariant=¨bold¨ mathcolor=¨#0000FF¨»m«/mi»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»=«/mo»«mfrac mathcolor=¨#0000FF¨»«mrow»«msup»«mi mathvariant=¨bold¨»T«/mi»«mn mathvariant=¨bold¨»2«/mn»«/msup»«mo mathvariant=¨bold¨»§#183;«/mo»«mi mathvariant=¨bold¨»K«/mi»«/mrow»«mrow»«mn mathvariant=¨bold¨»4«/mn»«mo mathvariant=¨bold¨»§#183;«/mo»«msup»«mi mathvariant=¨bold¨»§#960;«/mi»«mn mathvariant=¨bold¨»2«/mn»«/msup»«/mrow»«/mfrac»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»-«/mo»«mi mathvariant=¨bold¨ mathcolor=¨#0000FF¨»M«/mi»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»=«/mo»«mfrac mathcolor=¨#0000FF¨»«mrow»«mn mathvariant=¨bold¨»1«/mn»«mo mathvariant=¨bold¨».«/mo»«msup»«mn mathvariant=¨bold¨»3«/mn»«mn mathvariant=¨bold¨»2«/mn»«/msup»«mo mathvariant=¨bold¨»§#183;«/mo»«mn mathvariant=¨bold¨»600«/mn»«/mrow»«mrow»«mn mathvariant=¨bold¨»4«/mn»«mo mathvariant=¨bold¨»§#183;«/mo»«msup»«mi mathvariant=¨bold¨»§#960;«/mi»«mn mathvariant=¨bold¨»2«/mn»«/msup»«/mrow»«/mfrac»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»-«/mo»«mn mathvariant=¨bold¨ mathcolor=¨#0000FF¨»0«/mn»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»=«/mo»«mfrac mathcolor=¨#0000FF¨»«mn mathvariant=¨bold¨»1014«/mn»«mrow»«mn mathvariant=¨bold¨»4«/mn»«mo mathvariant=¨bold¨»§#183;«/mo»«msup»«mi mathvariant=¨bold¨»§#960;«/mi»«mn mathvariant=¨bold¨»2«/mn»«/msup»«/mrow»«/mfrac»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»=«/mo»«mn mathvariant=¨bold¨ mathcolor=¨#0000FF¨»25«/mn»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨».«/mo»«mn mathvariant=¨bold¨ mathcolor=¨#0000FF¨»68«/mn»«mi mathvariant=¨bold¨ mathcolor=¨#0000FF¨»kg«/mi»«/math»
לכן, מסת הכיסא היא 25.68 ק"ג.
1. يمكن حساب كتلة الكرسي باستخدام أي نقطة أخرى على الرسم البياني. وليس فقط استخدام النقطة التي تتقاطع فيها الدالة مع المحور الأفقي.
2. في كل تجربة هناك عدة قياسات. للوصول إلى استنتاج من جميع القياسات، يجب استخدام دالة خطية ذات الخط الأكثر احتمالا (خط الاتجاه).
في دالة غير خطية مثل هذه الحالة، إذا كنت تريد الوصول إلى نتيجة من الرسم البياني كما هو مذكور في السؤال: "جد بواسطة الرسم البياني"
ليس هناك خيار سوى استخدام نقطة واحدة فقط.
إذا كان الرسم البياني خطيًا وتوصل الطالب إلى استنتاج بناءً على قياس واحد وليس حسب ميل الرسم البياني. يكون جوابه صحيحا جزئيا.
3. بسبب عدم الدقة الناتج عن الاعتماد على قياس واحد، فإذا اخترنا نقاطًا أخرى فسوف نحصل على إجابات مختلفة.
على سبيل المثال، إذا كررنا نفس العمليات لـ T=2.6S M=72kg، فسنحصل على كتلة مقدارها حوالي 30 كجم.
«math xmlns=¨http://www.w3.org/1998/Math/MathML¨»«mstyle mathsize=¨20px¨»«mi mathvariant=¨bold¨ mathcolor=¨#FF0000¨»M«/mi»«mo mathvariant=¨bold¨ mathcolor=¨#FF0000¨»=«/mo»«mfrac mathcolor=¨#FF0000¨»«mrow»«mi mathvariant=¨bold¨»k«/mi»«mo mathvariant=¨bold¨»§#183;«/mo»«msup»«mi mathvariant=¨bold¨»T«/mi»«mn mathvariant=¨bold¨»2«/mn»«/msup»«/mrow»«mrow»«mn mathvariant=¨bold¨»4«/mn»«mo mathvariant=¨bold¨»§#183;«/mo»«msup»«mi mathvariant=¨bold¨»§#960;«/mi»«mn mathvariant=¨bold¨»2«/mn»«/msup»«/mrow»«/mfrac»«mo mathvariant=¨bold¨ mathcolor=¨#FF0000¨»-«/mo»«mi mathvariant=¨bold¨ mathcolor=¨#FF0000¨»m«/mi»«mspace linebreak=¨newline¨»«/mspace»«mspace linebreak=¨newline¨»«/mspace»«mi mathvariant=¨bold¨ mathcolor=¨#FF0000¨»m«/mi»«mo mathvariant=¨bold¨ mathcolor=¨#FF0000¨»=«/mo»«mfrac mathcolor=¨#FF0000¨»«mrow»«mi mathvariant=¨bold¨»k«/mi»«mo mathvariant=¨bold¨»§#183;«/mo»«msup»«mi mathvariant=¨bold¨»T«/mi»«mn mathvariant=¨bold¨»2«/mn»«/msup»«/mrow»«mrow»«mn mathvariant=¨bold¨»4«/mn»«mo mathvariant=¨bold¨»§#183;«/mo»«msup»«mi mathvariant=¨bold¨»§#960;«/mi»«mn mathvariant=¨bold¨»2«/mn»«/msup»«/mrow»«/mfrac»«mo mathvariant=¨bold¨ mathcolor=¨#FF0000¨»-«/mo»«mi mathvariant=¨bold¨ mathcolor=¨#FF0000¨»M«/mi»«mo mathvariant=¨bold¨ mathcolor=¨#FF0000¨»=«/mo»«mfrac mathcolor=¨#FF0000¨»«mrow»«mn mathvariant=¨bold¨»600«/mn»«mo mathvariant=¨bold¨»§#183;«/mo»«mn mathvariant=¨bold¨»2«/mn»«mo mathvariant=¨bold¨».«/mo»«msup»«mn mathvariant=¨bold¨»6«/mn»«mn mathvariant=¨bold¨»2«/mn»«/msup»«/mrow»«mrow»«mn mathvariant=¨bold¨»4«/mn»«mo mathvariant=¨bold¨»§#183;«/mo»«msup»«mi mathvariant=¨bold¨»§#960;«/mi»«mn mathvariant=¨bold¨»2«/mn»«/msup»«/mrow»«/mfrac»«mo mathvariant=¨bold¨ mathcolor=¨#FF0000¨»-«/mo»«mn mathvariant=¨bold¨ mathcolor=¨#FF0000¨»72«/mn»«mo mathvariant=¨bold¨ mathcolor=¨#FF0000¨»=«/mo»«mn mathvariant=¨bold¨ mathcolor=¨#FF0000¨»102«/mn»«mo mathvariant=¨bold¨ mathcolor=¨#FF0000¨».«/mo»«mn mathvariant=¨bold¨ mathcolor=¨#FF0000¨»74«/mn»«mo mathvariant=¨bold¨ mathcolor=¨#FF0000¨»-«/mo»«mn mathvariant=¨bold¨ mathcolor=¨#FF0000¨»72«/mn»«mo mathvariant=¨bold¨ mathcolor=¨#FF0000¨»=«/mo»«mn mathvariant=¨bold¨ mathcolor=¨#FF0000¨»30«/mn»«mo mathvariant=¨bold¨ mathcolor=¨#FF0000¨».«/mo»«mn mathvariant=¨bold¨ mathcolor=¨#FF0000¨»74«/mn»«mi mathvariant=¨bold¨ mathcolor=¨#FF0000¨»kg«/mi»«/mstyle»«/math»
2. בכל ניסוי יש מספר מדידות כדי להגיע למסקנה מכל המדידות יש להשתמש בפונקציה ליניארית בישר המסתבר ביותר.
בפונקציה לא ליניארית כמו במקרה הזה , אם רוצים להגיע למסקנה מהגרף כפי שכתוב בשאלה: "מצא בעזרת הגרף"
אין ברירה אלא להשתמש בנקודה אחת בלבד.
אם הגרף היה ליניארי ותלמיד היה כותב תשובה המבוססת על ממדידה אחת , ולא על השיפוע . תשובתו הייתה נכונה חלקית.
______________________________________________________________________________________

______________________________________________________________________________________
...
يتحرك رائد الفضاء داخل قمر اصطناعي يتحرك بنفس حركة القمر الاصطناعي تمامًا، لذا فهو "يطفو" داخل القمر الاصطناعي.
يتحرك القمر الاصطناعي ورائد الفضاء في حركات متطابقة، غير متعلقة الواحدة بالأخرى.
يتحرك القمر الاصطناعي في حركة قمر اصطناعي، ويتحرك رائد الفضاء الموجود بداخله أيضًا في حركة قمر اصطناعي، وبالتالي يطفو رائد الفضاء داخل القمر الاصطناعي ويكون عديم الوزن.
1. عندما يقف شخص على ميزان زنبركي داخل مصعد يسقط سقوطًا حرًا (لنفترض أن الكابل الذي يحمل المصعد ينقطع)
الشخص لا يضغط على سطح الميزان، القوة العمودية تساوي صفر. هناك وزن وهمي.
وذلك لأن الشخص والمصعد يتحركان في نفس الحركة - في سقوط حر.
يمكن أن يكون السقوط الحر حركة في خط مستقيم، أو يمكن أن يكون حركة دائرية، كما هو الحال في حركة القمر الاصطناعي.
2. حتى عندما يركب الشخص دراجة نارية. تتحرك الدراجة النارية والراكب في نفس الحركة، لكن الراكب لا يحوم فوق الدراجة النارية.
الفرق هو أن الشخص داخل القمر الاصطناعي يتحرك "بفضل نفسه" في حركة القمر الاصطناعي، بينما يتحرك راكب الدراجة النارية "بواسطة" الدراجة النارية.
3. في فصل الجاذبية، سنناقش بالتفصيل حركة الأقمار الاصطناعية.
4. رائد الفضاء ليس عديم الوزن حقًا، بل هو فقط يشعر أنه عديم الوزن.
האדם לא מעיק על המאזניים הנורמל שווה לאפס. יש משקל מדומה .
זה נובע מכך שהאדם והמעלית נעים באותה תנועה - בנפילה חופשית.
נפילה חופשית יכולה להיות תנועה בקו ישר , ויכולה להיות תנועה מעגלית כמו בתנועת לוויין.
2. גם כאשר אדם רוכב על אופנוע. האופנוע והרוכב נעים באותה תנועה , אך הרוכב לא מרחף על האופנוע .
ההבדל הוא שאדם הנמצא בתוך לוויין נע "בזכות עצמו" בתנועה לוויינית , רוכב האופנוע נע "בזכות" האופנוע.
3. בפרק הכבידה נעסוק בהרחבה בנושא תנועת לוויינים .
______________________________________________________________________________________





