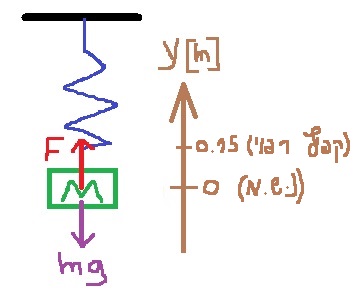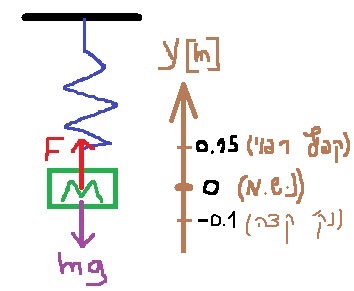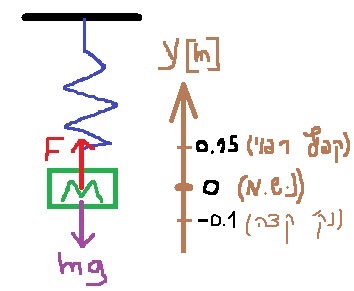______________________________________________________________________________________
...
الحركة التوافقية البسيطة هي الحركة التي فيها القوة المحصلة هي قوة مُعيدة وقيمتها تتناسب طرديًا مع موقع الجسم عن نقطة الاتّزان.
معرفة تعريف الحركة التوافقية البسيطة.
الحركة التوافقية البسيطة هي الحركة التي فيها القوة المحصلة هي قوة مُعيدة وقيمتها تتناسب طرديًا مع موقع الجسم عن نقطة الاتّزان.
في أي حركة، القوة المحصلة هي التي تحدد طبيعة الحركة.
اعتمادًا على القوة المحصلة ومعطيات الحركة الابتدائية، من الممكن التعرف على كل تفاصيل الحركة في كل لحظة.
כך למשל אם מצמידים גוף לקפיץ אופקי המונח על משטח חלק. לאחר שחרור הגוף הקפיץ יפעיל כוח משתנה על הגוף.
מרגע שחרור הגוף ועד שהגוף ניתק מהקפיץ הגוף נע בתנועה הרמונית פשוטה , שהיא לא מחזורית.
______________________________________________________________________________________
أ.
_ _____________________________________________________________________________________
_____________________________________________________________________________________
...
لا، هناك العديد من الحركات الدورية التي لا تندرج تحت الحركة التوافقية البسيطة.
تتحرك الكرة المرنة التي ترتد عموديًا في حركة دورية، ولكن ليس في حركة توافقية بسيطة.
כדור אלסטי המקפץ בתנועה אנכית נע בתנועה מחזורית, אך לא בתה"פ.
معرفة تعريف الحركة التوافقية البسيطة.
ليست كل حركة دورية هي حركة توافقية بسيطة.
فقط الحركة التي تتناسب فيها القوة المحصلة طرديًا على موقع الجسم من نقطة الاتّزان هي حركة توافقية بسيطة.
على سبيل المثال، تتحرك الكرة على سطح أفقي أملس بين جدارين بسرعات ثابتة، ذهابًا وإيابًا، في حركة دورية.
لكن القوة المحصلة لا تتناسب طرديًا على موقع الكرة، وبالتالي فهذه ليست حركة توافقية بسيطة.
רק תנועה שבה הכוח השקול תלוי ליניארית במיקום הגוף היא תנועה הרמונית פשוטה.
כדור הארץ נע סביב השמש בתנועה מחזורית , אך תנועת כדוה"א איננה תנועתה הרמונית פשוטה.
نحن عادة نتعامل مع الحركة التوافقية البسيطة الدورية، ولكن الجسم يمكن أن يتحرك أيضًا في حركة توافقية بسيطة غير دورية.
على سبيل المثال، إذا تم ربط جسم بنابض أفقي موضوع على سطح أملس. بعد تحرير الجسم، سوف يعمل النابض قوة متفاوتة على الجسم.
منذ لحظة تحرير الجسم حتى انفصاله عن النابض، يتحرك الجسم بحركة توافقية بسيطة، وهي غير دورية.
______________________________________________________________________________________

______________________________________________________________________________________
...
مدة الدورة هي 0.77 ثانية.
استخدام صيغة زمن الدورة، وإيجاد ثابت النابض باستخدام معادلة الحركة من نقطة الاتّزان.
إيجاد زمن الدورة باستخدام صيغة زمن الدورة:
«math xmlns=¨http://www.w3.org/1998/Math/MathML¨»«mi mathvariant=¨bold-italic¨ mathcolor=¨#0000FF¨»T«/mi»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»=«/mo»«mn mathvariant=¨bold¨ mathcolor=¨#0000FF¨»2«/mn»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»§#183;«/mo»«mi mathvariant=¨bold¨ mathcolor=¨#0000FF¨»§#960;«/mi»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»§#183;«/mo»«msqrt mathcolor=¨#0000FF¨»«mfrac»«mi mathvariant=¨bold¨»m«/mi»«mi mathvariant=¨bold¨»k«/mi»«/mfrac»«/msqrt»«/math»
قيمة الكتلة معطاة في السؤال. نجد ثابت النابض باستخدام معادلة الحركة من لحظة وصول الثقل إلى نقطة الاتّزان.
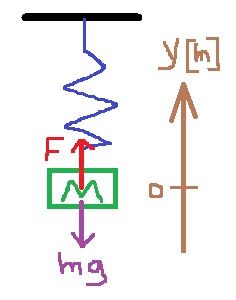
نرسم مخطط القوى المؤثرة على الثقل، للحظة وجوده في نقطة الاتّزان.
نقوم بتحديد محور الحركة الذي يبدأ في نقطة الاتّزان ويتجه نحو الأعلى:
سنكتب معادلة الحركة، ونرمز إلى استطالة النابض من حالة الاسترخاء إلى نقطة الاتّزان بـ «math xmlns=¨http://www.w3.org/1998/Math/MathML¨»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»§#8710;«/mo»«mi mathvariant=¨bold¨ mathcolor=¨#0000FF¨»y«/mi»«/math»
من المعطيات الموجودة في السؤال، هذا الطول يساوي 15 سم:
«math xmlns=¨http://www.w3.org/1998/Math/MathML¨»«msub»«mi mathvariant=¨bold¨ mathcolor=¨#0000FF¨»§#931;F«/mi»«mi mathvariant=¨bold¨ mathcolor=¨#0000FF¨»Y«/mi»«/msub»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»=«/mo»«mn mathvariant=¨bold¨ mathcolor=¨#0000FF¨»0«/mn»«mspace linebreak=¨newline¨»«/mspace»«mi mathvariant=¨bold¨ mathcolor=¨#0000FF¨»F«/mi»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»=«/mo»«mi mathvariant=¨bold¨ mathcolor=¨#0000FF¨»m«/mi»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»§#183;«/mo»«mi mathvariant=¨bold¨ mathcolor=¨#0000FF¨»g«/mi»«mspace linebreak=¨newline¨»«/mspace»«mi mathvariant=¨bold¨ mathcolor=¨#0000FF¨»K«/mi»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»§#183;«/mo»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»§#8710;«/mo»«mi mathvariant=¨bold¨ mathcolor=¨#0000FF¨»Y«/mi»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»=«/mo»«mi mathvariant=¨bold¨ mathcolor=¨#0000FF¨»m«/mi»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»§#183;«/mo»«mi mathvariant=¨bold¨ mathcolor=¨#0000FF¨»g«/mi»«mspace linebreak=¨newline¨»«/mspace»«mi mathvariant=¨bold¨ mathcolor=¨#0000FF¨»K«/mi»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»=«/mo»«mfrac mathcolor=¨#0000FF¨»«mrow»«mi mathvariant=¨bold¨»m«/mi»«mo mathvariant=¨bold¨»§#183;«/mo»«mi mathvariant=¨bold¨»g«/mi»«/mrow»«mrow»«mo mathvariant=¨bold¨»§#8710;«/mo»«mi mathvariant=¨bold¨»Y«/mi»«/mrow»«/mfrac»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»=«/mo»«mfrac mathcolor=¨#0000FF¨»«mrow»«mn mathvariant=¨bold¨»0«/mn»«mo mathvariant=¨bold¨».«/mo»«mn mathvariant=¨bold¨»6«/mn»«mo mathvariant=¨bold¨»§#183;«/mo»«mn mathvariant=¨bold¨»10«/mn»«/mrow»«mrow»«mn mathvariant=¨bold¨»0«/mn»«mo mathvariant=¨bold¨».«/mo»«mn mathvariant=¨bold¨»15«/mn»«/mrow»«/mfrac»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»=«/mo»«mfrac mathcolor=¨#0000FF¨»«mn mathvariant=¨bold¨»6«/mn»«mrow»«mn mathvariant=¨bold¨»0«/mn»«mo mathvariant=¨bold¨».«/mo»«mn mathvariant=¨bold¨»15«/mn»«/mrow»«/mfrac»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»=«/mo»«mn mathvariant=¨bold¨ mathcolor=¨#0000FF¨»40«/mn»«mfrac mathcolor=¨#0000FF¨»«mi mathvariant=¨bold¨»N«/mi»«mi mathvariant=¨bold¨»m«/mi»«/mfrac»«mspace linebreak=¨newline¨»«/mspace»«/math»
سنقوم باستبدال قيمة ثابت النابض في تعبير زمن الدورة:
«math xmlns=¨http://www.w3.org/1998/Math/MathML¨»«mi mathvariant=¨bold¨ mathcolor=¨#0000FF¨»T«/mi»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»=«/mo»«mn mathvariant=¨bold¨ mathcolor=¨#0000FF¨»2«/mn»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»§#183;«/mo»«mi mathvariant=¨bold¨ mathcolor=¨#0000FF¨»§#960;«/mi»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»§#183;«/mo»«msqrt mathcolor=¨#0000FF¨»«mfrac»«mi mathvariant=¨bold¨»m«/mi»«mi mathvariant=¨bold¨»k«/mi»«/mfrac»«/msqrt»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»=«/mo»«mn mathvariant=¨bold¨ mathcolor=¨#0000FF¨»2«/mn»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»§#183;«/mo»«mi mathvariant=¨bold¨ mathcolor=¨#0000FF¨»§#960;«/mi»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»§#183;«/mo»«msqrt mathcolor=¨#0000FF¨»«mfrac»«mrow»«mn mathvariant=¨bold¨»0«/mn»«mo mathvariant=¨bold¨».«/mo»«mn mathvariant=¨bold¨»6«/mn»«/mrow»«mn mathvariant=¨bold¨»40«/mn»«/mfrac»«/msqrt»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»=«/mo»«mn mathvariant=¨bold¨ mathcolor=¨#0000FF¨»0«/mn»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨».«/mo»«mn mathvariant=¨bold¨ mathcolor=¨#0000FF¨»77«/mn»«mi mathvariant=¨bold¨ mathcolor=¨#0000FF¨»s«/mi»«/math»
زمن دورة الاهتزازات هي 0.77 ثانية.
«math xmlns=¨http://www.w3.org/1998/Math/MathML¨»«mi mathvariant=¨bold-italic¨ mathcolor=¨#0000FF¨»T«/mi»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»=«/mo»«mn mathvariant=¨bold¨ mathcolor=¨#0000FF¨»2«/mn»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»§#183;«/mo»«mi mathvariant=¨bold¨ mathcolor=¨#0000FF¨»§#960;«/mi»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»§#183;«/mo»«msqrt mathcolor=¨#0000FF¨»«mfrac»«mi mathvariant=¨bold¨»m«/mi»«mi mathvariant=¨bold¨»k«/mi»«/mfrac»«/msqrt»«/math»
ערך המסה נתון בשאלה. נמצא את קבוע הקפיץ בעזרת משוואת התנועה מהרגע בו המשקולת נמצאת בנקודת שיווי המשקל.
נערוך תרשים כוחות למשקולת , עבור הרגע שבו היא נמצאת בנקודת שיווי המשקל.
נגדיר ציר תנועה שראשיתו בנקודת שיווי המשקל וכיוונו כלפי מעלה:
נכתוב את משוואת התנועה, נסמן את התארכות הקפיץ מהמצב הרפוי לנקודת שיווי המשקל ב «math xmlns=¨http://www.w3.org/1998/Math/MathML¨»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»§#8710;«/mo»«mi mathvariant=¨bold¨ mathcolor=¨#0000FF¨»y«/mi»«/math»
מהנתון בשאלה אורך זה שווה ל 15 ס"מ:
«math xmlns=¨http://www.w3.org/1998/Math/MathML¨»«msub»«mi mathvariant=¨bold¨ mathcolor=¨#0000FF¨»§#931;F«/mi»«mi mathvariant=¨bold¨ mathcolor=¨#0000FF¨»Y«/mi»«/msub»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»=«/mo»«mn mathvariant=¨bold¨ mathcolor=¨#0000FF¨»0«/mn»«mspace linebreak=¨newline¨»«/mspace»«mi mathvariant=¨bold¨ mathcolor=¨#0000FF¨»F«/mi»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»=«/mo»«mi mathvariant=¨bold¨ mathcolor=¨#0000FF¨»m«/mi»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»§#183;«/mo»«mi mathvariant=¨bold¨ mathcolor=¨#0000FF¨»g«/mi»«mspace linebreak=¨newline¨»«/mspace»«mi mathvariant=¨bold¨ mathcolor=¨#0000FF¨»K«/mi»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»§#183;«/mo»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»§#8710;«/mo»«mi mathvariant=¨bold¨ mathcolor=¨#0000FF¨»Y«/mi»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»=«/mo»«mi mathvariant=¨bold¨ mathcolor=¨#0000FF¨»m«/mi»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»§#183;«/mo»«mi mathvariant=¨bold¨ mathcolor=¨#0000FF¨»g«/mi»«mspace linebreak=¨newline¨»«/mspace»«mi mathvariant=¨bold¨ mathcolor=¨#0000FF¨»K«/mi»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»=«/mo»«mfrac mathcolor=¨#0000FF¨»«mrow»«mi mathvariant=¨bold¨»m«/mi»«mo mathvariant=¨bold¨»§#183;«/mo»«mi mathvariant=¨bold¨»g«/mi»«/mrow»«mrow»«mo mathvariant=¨bold¨»§#8710;«/mo»«mi mathvariant=¨bold¨»Y«/mi»«/mrow»«/mfrac»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»=«/mo»«mfrac mathcolor=¨#0000FF¨»«mrow»«mn mathvariant=¨bold¨»0«/mn»«mo mathvariant=¨bold¨».«/mo»«mn mathvariant=¨bold¨»6«/mn»«mo mathvariant=¨bold¨»§#183;«/mo»«mn mathvariant=¨bold¨»10«/mn»«/mrow»«mrow»«mn mathvariant=¨bold¨»0«/mn»«mo mathvariant=¨bold¨».«/mo»«mn mathvariant=¨bold¨»15«/mn»«/mrow»«/mfrac»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»=«/mo»«mfrac mathcolor=¨#0000FF¨»«mn mathvariant=¨bold¨»6«/mn»«mrow»«mn mathvariant=¨bold¨»0«/mn»«mo mathvariant=¨bold¨».«/mo»«mn mathvariant=¨bold¨»15«/mn»«/mrow»«/mfrac»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»=«/mo»«mn mathvariant=¨bold¨ mathcolor=¨#0000FF¨»40«/mn»«mfrac mathcolor=¨#0000FF¨»«mi mathvariant=¨bold¨»N«/mi»«mi mathvariant=¨bold¨»m«/mi»«/mfrac»«mspace linebreak=¨newline¨»«/mspace»«/math»
נציב את ערכו של קבוע הקפיץ בביטוי זמן המחזור:
«math xmlns=¨http://www.w3.org/1998/Math/MathML¨»«mi mathvariant=¨bold¨ mathcolor=¨#0000FF¨»T«/mi»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»=«/mo»«mn mathvariant=¨bold¨ mathcolor=¨#0000FF¨»2«/mn»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»§#183;«/mo»«mi mathvariant=¨bold¨ mathcolor=¨#0000FF¨»§#960;«/mi»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»§#183;«/mo»«msqrt mathcolor=¨#0000FF¨»«mfrac»«mi mathvariant=¨bold¨»m«/mi»«mi mathvariant=¨bold¨»k«/mi»«/mfrac»«/msqrt»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»=«/mo»«mn mathvariant=¨bold¨ mathcolor=¨#0000FF¨»2«/mn»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»§#183;«/mo»«mi mathvariant=¨bold¨ mathcolor=¨#0000FF¨»§#960;«/mi»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»§#183;«/mo»«msqrt mathcolor=¨#0000FF¨»«mfrac»«mrow»«mn mathvariant=¨bold¨»0«/mn»«mo mathvariant=¨bold¨».«/mo»«mn mathvariant=¨bold¨»6«/mn»«/mrow»«mn mathvariant=¨bold¨»40«/mn»«/mfrac»«/msqrt»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»=«/mo»«mn mathvariant=¨bold¨ mathcolor=¨#0000FF¨»0«/mn»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨».«/mo»«mn mathvariant=¨bold¨ mathcolor=¨#0000FF¨»77«/mn»«mi mathvariant=¨bold¨ mathcolor=¨#0000FF¨»s«/mi»«/math»
זמן מחזור התנודות הוא 0.77 שניות.
1. السؤال لا يتضمن رسمًا بيانيًا. من المهم جدًا رسم مخطط في بداية الحل وتنظيم المعطيات.
2. السؤال لا ينص صراحة على أن النقطة O هي نقطة الاتّزان. صيغة السؤال ليست جيدة بما فيه الكفاية.
يجب عليك أن تعرف كيفية التعامل مع مثل هذه الصيغ. من المستحسن أن تكتب كيف فهمت السؤال وتحله وفقًا لذلك.
2. בשאלה לא כתוב בצורה מפורשת שהנקודה O היא נקודת שיווי המשקל. הניסוח לא מספיק טוב .
צריך לדעת להתמודד עם ניסוחים כאלו , מומלץ לכתוב כיצד אתם הבנתם את השאלה ולפתור בהתאם.
______________________________________________________________________________________
ب.

______________________________________________________________________________________
...
يعمل النابض قوة لأعلى مقدارها 10 نيوتن في النقطة M.
قانون هوك.
النقطة M تقع على بعد 10 سم أسفل نقطة الاتّزان، سنضيفها كنقطة طرف الحركة في الرسم التخطيطي:
من قانون هوك، فإن القوة التي يؤثر بها النابض تتناسب طرديًا مع استطالة النابض بالنسبة لحالة الاسترخاء.
عندما يكون الثقل في نقطة النهاية السفلية، فإن استطالة النابض تكون 0.25 متر.
نحسب القوة المؤثرة بواسطة النابض:
«math xmlns=¨http://www.w3.org/1998/Math/MathML¨»«mi mathvariant=¨bold¨ mathcolor=¨#0000FF¨»F«/mi»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»=«/mo»«mi mathvariant=¨bold¨ mathcolor=¨#0000FF¨»K«/mi»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»§#183;«/mo»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»§#8710;«/mo»«mi mathvariant=¨bold¨ mathcolor=¨#0000FF¨»X«/mi»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»=«/mo»«mn mathvariant=¨bold¨ mathcolor=¨#0000FF¨»40«/mn»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»§#183;«/mo»«mn mathvariant=¨bold¨ mathcolor=¨#0000FF¨»0«/mn»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨».«/mo»«mn mathvariant=¨bold¨ mathcolor=¨#0000FF¨»25«/mn»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»=«/mo»«mn mathvariant=¨bold¨ mathcolor=¨#0000FF¨»10«/mn»«mfrac mathcolor=¨#0000FF¨»«mi mathvariant=¨bold¨»N«/mi»«mi mathvariant=¨bold¨»m«/mi»«/mfrac»«/math»
عندما يكون النابض في نقطة نهايته السفلية، يؤثر النابض قوة مقدارها 10 نيوتن إلى الأعلى.
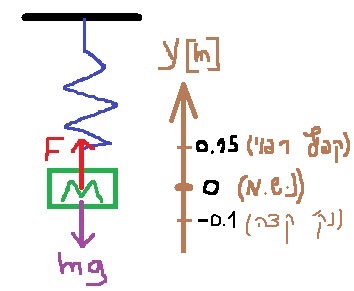
מחוק הוק, הכוח שהקפיץ מפעיל תלוי בהתארכות הקפיץ ביחס למצב הרפוי .
כאשר המשקולת נמצאת בנקודת הקצה התחתונה , התארכות הקפיץ שווה 0.25 מטר.
נחשב את הכוח שהקפיץ מפעיל:
«math xmlns=¨http://www.w3.org/1998/Math/MathML¨»«mi mathvariant=¨bold¨ mathcolor=¨#0000FF¨»F«/mi»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»=«/mo»«mi mathvariant=¨bold¨ mathcolor=¨#0000FF¨»K«/mi»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»§#183;«/mo»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»§#8710;«/mo»«mi mathvariant=¨bold¨ mathcolor=¨#0000FF¨»X«/mi»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»=«/mo»«mn mathvariant=¨bold¨ mathcolor=¨#0000FF¨»40«/mn»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»§#183;«/mo»«mn mathvariant=¨bold¨ mathcolor=¨#0000FF¨»0«/mn»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨».«/mo»«mn mathvariant=¨bold¨ mathcolor=¨#0000FF¨»25«/mn»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»=«/mo»«mn mathvariant=¨bold¨ mathcolor=¨#0000FF¨»10«/mn»«mfrac mathcolor=¨#0000FF¨»«mi mathvariant=¨bold¨»N«/mi»«mi mathvariant=¨bold¨»m«/mi»«/mfrac»«/math»
כאשר הקפיץ נמצא בנקודת הקצה התחתונה , הקפיץ מפעיל כוח של 10 ניוטון כלפי מעלה.
1. في الحركة التوافقية البسيطة في نابض رأسي، لاستخدام دوال الحركة التوافقية البسيطة، يجب تعيين أصل المحور في نقطة الاتّزان.
لاستخدام الطاقة الوضعية الكلية، يجب أيضًا تحديد أصل المحور في نقطة الاتّزان.
ومن ناحية أخرى، لإيجاد الطاقة الوضعية المرنة والقوة المؤثرة بواسطة النابض.
يجب استخدام محور يبدأ من النقطة التي يكون فيها النابض مرتخيًا.
إذن ماذا نفعل عندما نسأل عن الطاقة الوضعية الكلية والطاقة المرنة أيضًا؟ أين يقع بداية المحور؟
من المستحسن وضع المحور في نقطة الاتّزان وحساب القوة والطاقة الوضعية المرنة.
بدلالة استطالة النابض من حالة الاسترخاء.
2. عند كتابة الإجابة يجب الإشارة إلى اتجاه شغل قوة النابض أيضًا.
כדי להשתמש באנרגיה פוטנציאלית כוללת חייבים למקם את ראשית הציר גם בנקודת שיווי המשקל.
לעומת זאת כדי למצוא את האנרגיה פוטנציאלית אלסטית ואת הכוח שהקפיץ מפעיל
יש להשתמש בציר שראשיתו בנקודה בה הקפיץ רפוי.
אז מה עושים כשושאלים על האנרגיה הפוטנציאלית הכוללת וגם האלסטית ? היכן ממקמים את ראשית הציר?
מומלץ למקם את הציר בנקודת שיווי משקל ולחשב את הכוח והאנרגיה הפוטנציאלית אלסטית
בהתאם להתארכות מהמצב הרפוי.
2. בכתיבת התשובה יש לציין גם את כיוון פעולת כוח הקפיץ.
______________________________________________________________________________________
ب.

______________________________________________________________________________________
...
עבודת התלמיד שווה ל 0.2 ג'אול.
ביטוי עבודת כוח לא משמר.
הכוח שהתלמיד הפעיל הוא לא כוח משמר , עבודתו גרמה לשינוי באנרגיה המכנית.
מביטוי עבודת הכוח הלא משמר, עבודת הכוח הלא משמר שווה לשינוי באנרגיה המכנית הכוללת.
נמצא את העבודה שעשה התלמיד במשיכת המשקולת מנקודה O לנקודה M.
האנרגיה המכנית הכוללת שווה לסכום האנרגיה הקינטית, האנרגיה הפוטנציאלית כובדית והאנרגיה הפוטנציאלית אלסטית.
נתאר את האנרגיה המכנית בעזרת האנרגיה הפוטנציאלית הכוללת:
«math xmlns=¨http://www.w3.org/1998/Math/MathML¨»«mstyle mathsize=¨16px¨»«mrow»«mi mathvariant=¨bold¨ mathcolor=¨#0000FF¨»W«/mi»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»=«/mo»«mi mathvariant=¨bold¨ mathcolor=¨#0000FF¨»§#916;E«/mi»«mspace linebreak=¨newline¨»«/mspace»«mspace linebreak=¨newline¨»«/mspace»«mi mathvariant=¨bold¨ mathcolor=¨#0000FF¨»W«/mi»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»=«/mo»«msub»«mi mathvariant=¨bold¨ mathcolor=¨#0000FF¨»E«/mi»«mi mathvariant=¨bold¨ mathcolor=¨#0000FF¨»M«/mi»«/msub»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»-«/mo»«msub»«mi mathvariant=¨bold¨ mathcolor=¨#0000FF¨»E«/mi»«mi mathvariant=¨bold¨ mathcolor=¨#0000FF¨»O«/mi»«/msub»«mspace linebreak=¨newline¨»«/mspace»«mspace linebreak=¨newline¨»«/mspace»«mi mathvariant=¨bold¨ mathcolor=¨#0000FF¨»W«/mi»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»=«/mo»«msub»«msub»«mi mathvariant=¨bold¨ mathcolor=¨#0000FF¨»E«/mi»«mi mathvariant=¨bold¨ mathcolor=¨#0000FF¨»K«/mi»«/msub»«mi mathvariant=¨bold¨ mathcolor=¨#0000FF¨»M«/mi»«/msub»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»+«/mo»«msub»«mi mathvariant=¨bold¨ mathcolor=¨#0000FF¨»U«/mi»«msub mathcolor=¨#0000FF¨»«mi mathvariant=¨bold¨»T«/mi»«mi mathvariant=¨bold¨»M«/mi»«/msub»«/msub»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»-«/mo»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»(«/mo»«msub»«msub»«mi mathvariant=¨bold¨ mathcolor=¨#0000FF¨»E«/mi»«mi mathvariant=¨bold¨ mathcolor=¨#0000FF¨»K«/mi»«/msub»«mi mathvariant=¨bold¨ mathcolor=¨#0000FF¨»O«/mi»«/msub»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»+«/mo»«msub»«mi mathvariant=¨bold¨ mathcolor=¨#0000FF¨»U«/mi»«msub mathcolor=¨#0000FF¨»«mi mathvariant=¨bold¨»T«/mi»«mi mathvariant=¨bold¨»O«/mi»«/msub»«/msub»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»)«/mo»«mspace linebreak=¨newline¨»«/mspace»«/mrow»«/mstyle»«/math»
התלמיד מושך את המשקולת מנקודת לנקודה , בכל נקודה מהירות המשקולת היא אפס:
«math xmlns=¨http://www.w3.org/1998/Math/MathML¨»«mrow»«mi mathvariant=¨bold¨ mathcolor=¨#0000FF¨»W«/mi»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»=«/mo»«msub»«msub»«mi mathvariant=¨bold¨ mathcolor=¨#0000FF¨»E«/mi»«mi mathvariant=¨bold¨ mathcolor=¨#0000FF¨»K«/mi»«/msub»«mi mathvariant=¨bold¨ mathcolor=¨#0000FF¨»M«/mi»«/msub»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»+«/mo»«msub»«mi mathvariant=¨bold¨ mathcolor=¨#0000FF¨»U«/mi»«msub mathcolor=¨#0000FF¨»«mi mathvariant=¨bold¨»T«/mi»«mi mathvariant=¨bold¨»M«/mi»«/msub»«/msub»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»-«/mo»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»(«/mo»«msub»«msub»«mi mathvariant=¨bold¨ mathcolor=¨#0000FF¨»E«/mi»«mi mathvariant=¨bold¨ mathcolor=¨#0000FF¨»K«/mi»«/msub»«mi mathvariant=¨bold¨ mathcolor=¨#0000FF¨»O«/mi»«/msub»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»+«/mo»«msub»«mi mathvariant=¨bold¨ mathcolor=¨#0000FF¨»U«/mi»«msub mathcolor=¨#0000FF¨»«mi mathvariant=¨bold¨»T«/mi»«mi mathvariant=¨bold¨»O«/mi»«/msub»«/msub»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»)«/mo»«mspace linebreak=¨newline¨»«/mspace»«/mrow»«mspace linebreak=¨newline¨»«/mspace»«mi mathvariant=¨bold¨ mathcolor=¨#0000FF¨»W«/mi»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»=«/mo»«menclose mathcolor=¨#0000FF¨ notation=¨updiagonalstrike¨»«msub»«msub»«mi mathvariant=¨bold¨»E«/mi»«mi mathvariant=¨bold¨»K«/mi»«/msub»«mi mathvariant=¨bold¨»M«/mi»«/msub»«/menclose»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»+«/mo»«msub»«mi mathvariant=¨bold¨ mathcolor=¨#0000FF¨»U«/mi»«msub mathcolor=¨#0000FF¨»«mi mathvariant=¨bold¨»T«/mi»«mi mathvariant=¨bold¨»M«/mi»«/msub»«/msub»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»-«/mo»«menclose mathcolor=¨#0000FF¨ notation=¨updiagonalstrike¨»«msub»«msub»«mi mathvariant=¨bold¨»E«/mi»«mi mathvariant=¨bold¨»K«/mi»«/msub»«mi mathvariant=¨bold¨»O«/mi»«/msub»«/menclose»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»-«/mo»«msub»«mi mathvariant=¨bold¨ mathcolor=¨#0000FF¨»U«/mi»«msub mathcolor=¨#0000FF¨»«mi mathvariant=¨bold¨»T«/mi»«mi mathvariant=¨bold¨»O«/mi»«/msub»«/msub»«mspace linebreak=¨newline¨»«/mspace»«mspace linebreak=¨newline¨»«/mspace»«mi mathvariant=¨bold¨ mathcolor=¨#0000FF¨»W«/mi»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»=«/mo»«msub»«mi mathvariant=¨bold¨ mathcolor=¨#0000FF¨»U«/mi»«msub mathcolor=¨#0000FF¨»«mi mathvariant=¨bold¨»T«/mi»«mi mathvariant=¨bold¨»M«/mi»«/msub»«/msub»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»-«/mo»«msub»«mi mathvariant=¨bold¨ mathcolor=¨#0000FF¨»U«/mi»«msub mathcolor=¨#0000FF¨»«mi mathvariant=¨bold¨»T«/mi»«mi mathvariant=¨bold¨»O«/mi»«/msub»«/msub»«mspace linebreak=¨newline¨»«/mspace»«mi mathvariant=¨bold¨ mathcolor=¨#0000FF¨»W«/mi»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»=«/mo»«mfrac mathcolor=¨#0000FF¨»«mn mathvariant=¨bold¨»1«/mn»«mn mathvariant=¨bold¨»2«/mn»«/mfrac»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»§#183;«/mo»«mi mathvariant=¨bold¨ mathcolor=¨#0000FF¨»K«/mi»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»§#183;«/mo»«msup»«msub»«mi mathvariant=¨bold¨ mathcolor=¨#0000FF¨»X«/mi»«mi mathvariant=¨bold¨ mathcolor=¨#0000FF¨»M«/mi»«/msub»«mn mathvariant=¨bold¨ mathcolor=¨#0000FF¨»2«/mn»«/msup»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»-«/mo»«mfrac mathcolor=¨#0000FF¨»«mn mathvariant=¨bold¨»1«/mn»«mn mathvariant=¨bold¨»2«/mn»«/mfrac»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»§#183;«/mo»«mi mathvariant=¨bold¨ mathcolor=¨#0000FF¨»K«/mi»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»§#183;«/mo»«msup»«msub»«mi mathvariant=¨bold¨ mathcolor=¨#0000FF¨»X«/mi»«mi mathvariant=¨bold¨ mathcolor=¨#0000FF¨»M«/mi»«/msub»«mn mathvariant=¨bold¨ mathcolor=¨#0000FF¨»2«/mn»«/msup»«mspace linebreak=¨newline¨»«/mspace»«mi mathvariant=¨bold¨ mathcolor=¨#0000FF¨»W«/mi»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»=«/mo»«mfrac mathcolor=¨#0000FF¨»«mn mathvariant=¨bold¨»1«/mn»«mn mathvariant=¨bold¨»2«/mn»«/mfrac»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»§#183;«/mo»«mn mathvariant=¨bold¨ mathcolor=¨#0000FF¨»40«/mn»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»§#183;«/mo»«mn mathvariant=¨bold¨ mathcolor=¨#0000FF¨»0«/mn»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨».«/mo»«msup»«mn mathvariant=¨bold¨ mathcolor=¨#0000FF¨»1«/mn»«mn mathvariant=¨bold¨ mathcolor=¨#0000FF¨»2«/mn»«/msup»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»-«/mo»«mfrac mathcolor=¨#0000FF¨»«mn mathvariant=¨bold¨»1«/mn»«mn mathvariant=¨bold¨»2«/mn»«/mfrac»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»§#183;«/mo»«mn mathvariant=¨bold¨ mathcolor=¨#0000FF¨»40«/mn»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»§#183;«/mo»«msup»«mn mathvariant=¨bold¨ mathcolor=¨#0000FF¨»0«/mn»«mn mathvariant=¨bold¨ mathcolor=¨#0000FF¨»2«/mn»«/msup»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»=«/mo»«mn mathvariant=¨bold¨ mathcolor=¨#0000FF¨»0«/mn»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨».«/mo»«mn mathvariant=¨bold¨ mathcolor=¨#0000FF¨»2«/mn»«mi mathvariant=¨bold¨ mathcolor=¨#0000FF¨»J«/mi»«mspace linebreak=¨newline¨»«/mspace»«/math»
עבודת התלמיד היא 0.2 בהנעת המשקולת מהנקודה O לנקודה M היא 0.2 ג'אול.
מביטוי עבודת הכוח הלא משמר, עבודת הכוח הלא משמר שווה לשינוי באנרגיה המכנית הכוללת.
נמצא את העבודה שעשה התלמיד במשיכת המשקולת מנקודה O לנקודה M.
האנרגיה המכנית הכוללת שווה לסכום האנרגיה הקינטית, האנרגיה הפוטנציאלית כובדית והאנרגיה הפוטנציאלית אלסטית.
נתאר את האנרגיה המכנית בעזרת האנרגיה הפוטנציאלית הכוללת:
«math xmlns=¨http://www.w3.org/1998/Math/MathML¨»«mstyle mathsize=¨16px¨»«mrow»«mi mathvariant=¨bold¨ mathcolor=¨#0000FF¨»W«/mi»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»=«/mo»«mi mathvariant=¨bold¨ mathcolor=¨#0000FF¨»§#916;E«/mi»«mspace linebreak=¨newline¨»«/mspace»«mspace linebreak=¨newline¨»«/mspace»«mi mathvariant=¨bold¨ mathcolor=¨#0000FF¨»W«/mi»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»=«/mo»«msub»«mi mathvariant=¨bold¨ mathcolor=¨#0000FF¨»E«/mi»«mi mathvariant=¨bold¨ mathcolor=¨#0000FF¨»M«/mi»«/msub»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»-«/mo»«msub»«mi mathvariant=¨bold¨ mathcolor=¨#0000FF¨»E«/mi»«mi mathvariant=¨bold¨ mathcolor=¨#0000FF¨»O«/mi»«/msub»«mspace linebreak=¨newline¨»«/mspace»«mspace linebreak=¨newline¨»«/mspace»«mi mathvariant=¨bold¨ mathcolor=¨#0000FF¨»W«/mi»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»=«/mo»«msub»«msub»«mi mathvariant=¨bold¨ mathcolor=¨#0000FF¨»E«/mi»«mi mathvariant=¨bold¨ mathcolor=¨#0000FF¨»K«/mi»«/msub»«mi mathvariant=¨bold¨ mathcolor=¨#0000FF¨»M«/mi»«/msub»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»+«/mo»«msub»«mi mathvariant=¨bold¨ mathcolor=¨#0000FF¨»U«/mi»«msub mathcolor=¨#0000FF¨»«mi mathvariant=¨bold¨»T«/mi»«mi mathvariant=¨bold¨»M«/mi»«/msub»«/msub»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»-«/mo»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»(«/mo»«msub»«msub»«mi mathvariant=¨bold¨ mathcolor=¨#0000FF¨»E«/mi»«mi mathvariant=¨bold¨ mathcolor=¨#0000FF¨»K«/mi»«/msub»«mi mathvariant=¨bold¨ mathcolor=¨#0000FF¨»O«/mi»«/msub»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»+«/mo»«msub»«mi mathvariant=¨bold¨ mathcolor=¨#0000FF¨»U«/mi»«msub mathcolor=¨#0000FF¨»«mi mathvariant=¨bold¨»T«/mi»«mi mathvariant=¨bold¨»O«/mi»«/msub»«/msub»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»)«/mo»«mspace linebreak=¨newline¨»«/mspace»«/mrow»«/mstyle»«/math»
התלמיד מושך את המשקולת מנקודת לנקודה , בכל נקודה מהירות המשקולת היא אפס:
«math xmlns=¨http://www.w3.org/1998/Math/MathML¨»«mrow»«mi mathvariant=¨bold¨ mathcolor=¨#0000FF¨»W«/mi»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»=«/mo»«msub»«msub»«mi mathvariant=¨bold¨ mathcolor=¨#0000FF¨»E«/mi»«mi mathvariant=¨bold¨ mathcolor=¨#0000FF¨»K«/mi»«/msub»«mi mathvariant=¨bold¨ mathcolor=¨#0000FF¨»M«/mi»«/msub»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»+«/mo»«msub»«mi mathvariant=¨bold¨ mathcolor=¨#0000FF¨»U«/mi»«msub mathcolor=¨#0000FF¨»«mi mathvariant=¨bold¨»T«/mi»«mi mathvariant=¨bold¨»M«/mi»«/msub»«/msub»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»-«/mo»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»(«/mo»«msub»«msub»«mi mathvariant=¨bold¨ mathcolor=¨#0000FF¨»E«/mi»«mi mathvariant=¨bold¨ mathcolor=¨#0000FF¨»K«/mi»«/msub»«mi mathvariant=¨bold¨ mathcolor=¨#0000FF¨»O«/mi»«/msub»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»+«/mo»«msub»«mi mathvariant=¨bold¨ mathcolor=¨#0000FF¨»U«/mi»«msub mathcolor=¨#0000FF¨»«mi mathvariant=¨bold¨»T«/mi»«mi mathvariant=¨bold¨»O«/mi»«/msub»«/msub»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»)«/mo»«mspace linebreak=¨newline¨»«/mspace»«/mrow»«mspace linebreak=¨newline¨»«/mspace»«mi mathvariant=¨bold¨ mathcolor=¨#0000FF¨»W«/mi»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»=«/mo»«menclose mathcolor=¨#0000FF¨ notation=¨updiagonalstrike¨»«msub»«msub»«mi mathvariant=¨bold¨»E«/mi»«mi mathvariant=¨bold¨»K«/mi»«/msub»«mi mathvariant=¨bold¨»M«/mi»«/msub»«/menclose»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»+«/mo»«msub»«mi mathvariant=¨bold¨ mathcolor=¨#0000FF¨»U«/mi»«msub mathcolor=¨#0000FF¨»«mi mathvariant=¨bold¨»T«/mi»«mi mathvariant=¨bold¨»M«/mi»«/msub»«/msub»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»-«/mo»«menclose mathcolor=¨#0000FF¨ notation=¨updiagonalstrike¨»«msub»«msub»«mi mathvariant=¨bold¨»E«/mi»«mi mathvariant=¨bold¨»K«/mi»«/msub»«mi mathvariant=¨bold¨»O«/mi»«/msub»«/menclose»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»-«/mo»«msub»«mi mathvariant=¨bold¨ mathcolor=¨#0000FF¨»U«/mi»«msub mathcolor=¨#0000FF¨»«mi mathvariant=¨bold¨»T«/mi»«mi mathvariant=¨bold¨»O«/mi»«/msub»«/msub»«mspace linebreak=¨newline¨»«/mspace»«mspace linebreak=¨newline¨»«/mspace»«mi mathvariant=¨bold¨ mathcolor=¨#0000FF¨»W«/mi»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»=«/mo»«msub»«mi mathvariant=¨bold¨ mathcolor=¨#0000FF¨»U«/mi»«msub mathcolor=¨#0000FF¨»«mi mathvariant=¨bold¨»T«/mi»«mi mathvariant=¨bold¨»M«/mi»«/msub»«/msub»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»-«/mo»«msub»«mi mathvariant=¨bold¨ mathcolor=¨#0000FF¨»U«/mi»«msub mathcolor=¨#0000FF¨»«mi mathvariant=¨bold¨»T«/mi»«mi mathvariant=¨bold¨»O«/mi»«/msub»«/msub»«mspace linebreak=¨newline¨»«/mspace»«mi mathvariant=¨bold¨ mathcolor=¨#0000FF¨»W«/mi»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»=«/mo»«mfrac mathcolor=¨#0000FF¨»«mn mathvariant=¨bold¨»1«/mn»«mn mathvariant=¨bold¨»2«/mn»«/mfrac»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»§#183;«/mo»«mi mathvariant=¨bold¨ mathcolor=¨#0000FF¨»K«/mi»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»§#183;«/mo»«msup»«msub»«mi mathvariant=¨bold¨ mathcolor=¨#0000FF¨»X«/mi»«mi mathvariant=¨bold¨ mathcolor=¨#0000FF¨»M«/mi»«/msub»«mn mathvariant=¨bold¨ mathcolor=¨#0000FF¨»2«/mn»«/msup»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»-«/mo»«mfrac mathcolor=¨#0000FF¨»«mn mathvariant=¨bold¨»1«/mn»«mn mathvariant=¨bold¨»2«/mn»«/mfrac»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»§#183;«/mo»«mi mathvariant=¨bold¨ mathcolor=¨#0000FF¨»K«/mi»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»§#183;«/mo»«msup»«msub»«mi mathvariant=¨bold¨ mathcolor=¨#0000FF¨»X«/mi»«mi mathvariant=¨bold¨ mathcolor=¨#0000FF¨»M«/mi»«/msub»«mn mathvariant=¨bold¨ mathcolor=¨#0000FF¨»2«/mn»«/msup»«mspace linebreak=¨newline¨»«/mspace»«mi mathvariant=¨bold¨ mathcolor=¨#0000FF¨»W«/mi»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»=«/mo»«mfrac mathcolor=¨#0000FF¨»«mn mathvariant=¨bold¨»1«/mn»«mn mathvariant=¨bold¨»2«/mn»«/mfrac»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»§#183;«/mo»«mn mathvariant=¨bold¨ mathcolor=¨#0000FF¨»40«/mn»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»§#183;«/mo»«mn mathvariant=¨bold¨ mathcolor=¨#0000FF¨»0«/mn»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨».«/mo»«msup»«mn mathvariant=¨bold¨ mathcolor=¨#0000FF¨»1«/mn»«mn mathvariant=¨bold¨ mathcolor=¨#0000FF¨»2«/mn»«/msup»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»-«/mo»«mfrac mathcolor=¨#0000FF¨»«mn mathvariant=¨bold¨»1«/mn»«mn mathvariant=¨bold¨»2«/mn»«/mfrac»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»§#183;«/mo»«mn mathvariant=¨bold¨ mathcolor=¨#0000FF¨»40«/mn»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»§#183;«/mo»«msup»«mn mathvariant=¨bold¨ mathcolor=¨#0000FF¨»0«/mn»«mn mathvariant=¨bold¨ mathcolor=¨#0000FF¨»2«/mn»«/msup»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»=«/mo»«mn mathvariant=¨bold¨ mathcolor=¨#0000FF¨»0«/mn»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨».«/mo»«mn mathvariant=¨bold¨ mathcolor=¨#0000FF¨»2«/mn»«mi mathvariant=¨bold¨ mathcolor=¨#0000FF¨»J«/mi»«mspace linebreak=¨newline¨»«/mspace»«/math»
עבודת התלמיד היא 0.2 בהנעת המשקולת מהנקודה O לנקודה M היא 0.2 ג'אול.
1. אם רק כוחות משמרים עושים עבודה - האנרגיה המכנית נשמרת , אפשר לכתוב את משוואת שימור האנרגיה.
אם יש עבודה של כוח לא משמר , האנרגיה המכנית לא נשמרת. אפשר לכתוב את ביטוי עבודת הכוח הלא משמר.
זה מזכיר קצת את החוק הראשון והשני של ניוטון ... או שהשקול כוחות שווה לאפס או שהוא שונה מאפס.
אם רק כוחות משמרים עושים עבודה השינוי באנרגיה המכנית שווה לאפס.
אם כוחות לא משמרים עושים עבודה השינוי באנרגיה המכנית שונה מאפס .
2. התלמיד מגדיל את האנרגיה המכנית הכוללת , לכן הוא עושה עבודה חיובית.
3. אפשר למצוא את עבודת התלמיד בעזרת האנרגיה הפוטנציאלית כובדית והאנרגיה פוטנציאלית אלסטית .
במקום עם האנרגיה הפוטנציאלית הכוללת.
נתייחס לאנרגיה הפוטנציאלית אלסטית ביחס למצב הרפוי ונקבע את מישור התנועה בגובה בו נמצאת הנקודה M
(במבחן לא מומלץ לפתור בשתי דרכים שונות, אני רק מראה כאן בקצרה שאפשר,לחידוד ולתרגול )
«math xmlns=¨http://www.w3.org/1998/Math/MathML¨»«mrow mathcolor=¨#FF0000¨»«mi mathvariant=¨bold¨»W«/mi»«mo mathvariant=¨bold¨»=«/mo»«mi mathvariant=¨bold¨»§#916;E«/mi»«mspace linebreak=¨newline¨»«/mspace»«mspace linebreak=¨newline¨»«/mspace»«mi mathvariant=¨bold¨»W«/mi»«mo mathvariant=¨bold¨»=«/mo»«msub»«mi mathvariant=¨bold¨»E«/mi»«mi mathvariant=¨bold¨»M«/mi»«/msub»«mo mathvariant=¨bold¨»-«/mo»«msub»«mi mathvariant=¨bold¨»E«/mi»«mi mathvariant=¨bold¨»O«/mi»«/msub»«mspace linebreak=¨newline¨»«/mspace»«mspace linebreak=¨newline¨»«/mspace»«mi mathvariant=¨bold¨»W«/mi»«mo mathvariant=¨bold¨»=«/mo»«msub»«msub»«mi mathvariant=¨bold¨»E«/mi»«mi mathvariant=¨bold¨»K«/mi»«/msub»«mi mathvariant=¨bold¨»M«/mi»«/msub»«mo mathvariant=¨bold¨»+«/mo»«msub»«mi mathvariant=¨bold¨»U«/mi»«msub»«mi mathvariant=¨bold¨»sp«/mi»«mi mathvariant=¨bold¨»M«/mi»«/msub»«/msub»«mo mathvariant=¨bold¨»+«/mo»«msub»«mi mathvariant=¨bold¨»U«/mi»«mrow»«mi mathvariant=¨bold¨»G«/mi»«mi mathvariant=¨bold¨»M«/mi»«/mrow»«/msub»«mo mathvariant=¨bold¨»-«/mo»«mo mathvariant=¨bold¨»(«/mo»«msub»«msub»«mi mathvariant=¨bold¨»E«/mi»«mi mathvariant=¨bold¨»K«/mi»«/msub»«mi mathvariant=¨bold¨»O«/mi»«/msub»«mo mathvariant=¨bold¨»+«/mo»«msub»«mi mathvariant=¨bold¨»U«/mi»«msub»«mi mathvariant=¨bold¨»sp«/mi»«mi mathvariant=¨bold¨»O«/mi»«/msub»«/msub»«mo mathvariant=¨bold¨»+«/mo»«msub»«mi mathvariant=¨bold¨»U«/mi»«mi mathvariant=¨bold¨»GO«/mi»«/msub»«mo mathvariant=¨bold¨»)«/mo»«mspace linebreak=¨newline¨»«/mspace»«/mrow»«/math»
בנקודה M האנרגיה הקינטית והפוטנציאלית כובדית שוות לאפס.
בנקודה O האנרגיה הפוטנציאלית אלסטית שווה לאפס.
«math xmlns=¨http://www.w3.org/1998/Math/MathML¨»«mrow mathcolor=¨#FF0000¨»«mspace linebreak=¨newline¨»«/mspace»«mi mathvariant=¨bold¨»W«/mi»«mo mathvariant=¨bold¨»=«/mo»«msub»«msub»«mi mathvariant=¨bold¨»E«/mi»«mi mathvariant=¨bold¨»K«/mi»«/msub»«mi mathvariant=¨bold¨»M«/mi»«/msub»«mo mathvariant=¨bold¨»+«/mo»«msub»«mi mathvariant=¨bold¨»U«/mi»«msub»«mi mathvariant=¨bold¨»sp«/mi»«mi mathvariant=¨bold¨»M«/mi»«/msub»«/msub»«mo mathvariant=¨bold¨»+«/mo»«msub»«mi mathvariant=¨bold¨»U«/mi»«mi mathvariant=¨bold¨»GM«/mi»«/msub»«mo mathvariant=¨bold¨»-«/mo»«mo mathvariant=¨bold¨»(«/mo»«msub»«msub»«mi mathvariant=¨bold¨»E«/mi»«mi mathvariant=¨bold¨»K«/mi»«/msub»«mi mathvariant=¨bold¨»O«/mi»«/msub»«mo mathvariant=¨bold¨»+«/mo»«msub»«mi mathvariant=¨bold¨»U«/mi»«msub»«mi mathvariant=¨bold¨»sp«/mi»«mi mathvariant=¨bold¨»O«/mi»«/msub»«/msub»«mo mathvariant=¨bold¨»+«/mo»«msub»«mi mathvariant=¨bold¨»U«/mi»«mi mathvariant=¨bold¨»GO«/mi»«/msub»«mo mathvariant=¨bold¨»)«/mo»«mspace linebreak=¨newline¨»«/mspace»«/mrow»«mspace linebreak=¨newline¨»«/mspace»«mspace linebreak=¨newline¨»«/mspace»«mi mathvariant=¨bold¨ mathcolor=¨#FF0000¨»W«/mi»«mo mathvariant=¨bold¨ mathcolor=¨#FF0000¨»=«/mo»«menclose mathcolor=¨#FF0000¨ notation=¨updiagonalstrike¨»«msub»«msub»«mi mathvariant=¨bold¨»E«/mi»«mi mathvariant=¨bold¨»K«/mi»«/msub»«mi mathvariant=¨bold¨»M«/mi»«/msub»«/menclose»«mo mathvariant=¨bold¨ mathcolor=¨#FF0000¨»+«/mo»«msub»«mi mathvariant=¨bold¨ mathcolor=¨#FF0000¨»U«/mi»«msub mathcolor=¨#FF0000¨»«mi mathvariant=¨bold¨»sp«/mi»«mi mathvariant=¨bold¨»M«/mi»«/msub»«/msub»«mo mathvariant=¨bold¨ mathcolor=¨#FF0000¨»+«/mo»«menclose mathcolor=¨#FF0000¨ notation=¨updiagonalstrike¨»«msub»«mi mathvariant=¨bold¨»U«/mi»«mi mathvariant=¨bold¨»GM«/mi»«/msub»«/menclose»«mo mathvariant=¨bold¨ mathcolor=¨#FF0000¨»-«/mo»«menclose mathcolor=¨#FF0000¨ notation=¨updiagonalstrike¨»«msub»«msub»«mi mathvariant=¨bold¨»E«/mi»«mi mathvariant=¨bold¨»K«/mi»«/msub»«mi mathvariant=¨bold¨»O«/mi»«/msub»«/menclose»«mo mathvariant=¨bold¨ mathcolor=¨#FF0000¨»-«/mo»«msub»«mi mathvariant=¨bold¨ mathcolor=¨#FF0000¨»U«/mi»«msub mathcolor=¨#FF0000¨»«mi mathvariant=¨bold¨»sp«/mi»«mi mathvariant=¨bold¨»O«/mi»«/msub»«/msub»«mo mathvariant=¨bold¨ mathcolor=¨#FF0000¨»-«/mo»«msub»«mi mathvariant=¨bold¨ mathcolor=¨#FF0000¨»U«/mi»«mi mathvariant=¨bold¨ mathcolor=¨#FF0000¨»GO«/mi»«/msub»«mspace linebreak=¨newline¨»«/mspace»«mspace linebreak=¨newline¨»«/mspace»«mi mathvariant=¨bold¨ mathcolor=¨#FF0000¨»W«/mi»«mo mathvariant=¨bold¨ mathcolor=¨#FF0000¨»=«/mo»«mfrac mathcolor=¨#FF0000¨»«mn mathvariant=¨bold¨»1«/mn»«mn mathvariant=¨bold¨»2«/mn»«/mfrac»«mo mathvariant=¨bold¨ mathcolor=¨#FF0000¨»§#183;«/mo»«mi mathvariant=¨bold¨ mathcolor=¨#FF0000¨»K«/mi»«mo mathvariant=¨bold¨ mathcolor=¨#FF0000¨»§#183;«/mo»«msup»«msub»«mi mathvariant=¨bold¨ mathcolor=¨#FF0000¨»X«/mi»«mi mathvariant=¨bold¨ mathcolor=¨#FF0000¨»M«/mi»«/msub»«mn mathvariant=¨bold¨ mathcolor=¨#FF0000¨»2«/mn»«/msup»«mo mathvariant=¨bold¨ mathcolor=¨#FF0000¨»-«/mo»«mfrac mathcolor=¨#FF0000¨»«mn mathvariant=¨bold¨»1«/mn»«mn mathvariant=¨bold¨»2«/mn»«/mfrac»«mo mathvariant=¨bold¨ mathcolor=¨#FF0000¨»§#183;«/mo»«mi mathvariant=¨bold¨ mathcolor=¨#FF0000¨»K«/mi»«mo mathvariant=¨bold¨ mathcolor=¨#FF0000¨»§#183;«/mo»«msup»«msub»«mi mathvariant=¨bold¨ mathcolor=¨#FF0000¨»X«/mi»«mi mathvariant=¨bold¨ mathcolor=¨#FF0000¨»o«/mi»«/msub»«mn mathvariant=¨bold¨ mathcolor=¨#FF0000¨»2«/mn»«/msup»«mo mathvariant=¨bold¨ mathcolor=¨#FF0000¨»-«/mo»«mi mathvariant=¨bold¨ mathcolor=¨#FF0000¨»m«/mi»«mo mathvariant=¨bold¨ mathcolor=¨#FF0000¨»§#183;«/mo»«mi mathvariant=¨bold¨ mathcolor=¨#FF0000¨»g«/mi»«mo mathvariant=¨bold¨ mathcolor=¨#FF0000¨»§#183;«/mo»«msub»«mi mathvariant=¨bold¨ mathcolor=¨#FF0000¨»h«/mi»«mn mathvariant=¨bold¨ mathcolor=¨#FF0000¨»0«/mn»«/msub»«mspace linebreak=¨newline¨»«/mspace»«mi mathvariant=¨bold¨ mathcolor=¨#FF0000¨»W«/mi»«mo mathvariant=¨bold¨ mathcolor=¨#FF0000¨»=«/mo»«mfrac mathcolor=¨#FF0000¨»«mn mathvariant=¨bold¨»1«/mn»«mn mathvariant=¨bold¨»2«/mn»«/mfrac»«mo mathvariant=¨bold¨ mathcolor=¨#FF0000¨»§#183;«/mo»«mn mathvariant=¨bold¨ mathcolor=¨#FF0000¨»40«/mn»«mo mathvariant=¨bold¨ mathcolor=¨#FF0000¨»§#183;«/mo»«mn mathvariant=¨bold¨ mathcolor=¨#FF0000¨»0«/mn»«mo mathvariant=¨bold¨ mathcolor=¨#FF0000¨».«/mo»«msup»«mn mathvariant=¨bold¨ mathcolor=¨#FF0000¨»25«/mn»«mn mathvariant=¨bold¨ mathcolor=¨#FF0000¨»2«/mn»«/msup»«mo mathvariant=¨bold¨ mathcolor=¨#FF0000¨»-«/mo»«mfrac mathcolor=¨#FF0000¨»«mn mathvariant=¨bold¨»1«/mn»«mn mathvariant=¨bold¨»2«/mn»«/mfrac»«mo mathvariant=¨bold¨ mathcolor=¨#FF0000¨»§#183;«/mo»«mn mathvariant=¨bold¨ mathcolor=¨#FF0000¨»40«/mn»«mo mathvariant=¨bold¨ mathcolor=¨#FF0000¨»§#183;«/mo»«mn mathvariant=¨bold¨ mathcolor=¨#FF0000¨»0«/mn»«mo mathvariant=¨bold¨ mathcolor=¨#FF0000¨».«/mo»«msup»«mn mathvariant=¨bold¨ mathcolor=¨#FF0000¨»15«/mn»«mn mathvariant=¨bold¨ mathcolor=¨#FF0000¨»2«/mn»«/msup»«mo mathvariant=¨bold¨ mathcolor=¨#FF0000¨»-«/mo»«mn mathvariant=¨bold¨ mathcolor=¨#FF0000¨»0«/mn»«mo mathvariant=¨bold¨ mathcolor=¨#FF0000¨».«/mo»«mn mathvariant=¨bold¨ mathcolor=¨#FF0000¨»6«/mn»«mo mathvariant=¨bold¨ mathcolor=¨#FF0000¨»§#183;«/mo»«mn mathvariant=¨bold¨ mathcolor=¨#FF0000¨»10«/mn»«mo mathvariant=¨bold¨ mathcolor=¨#FF0000¨»§#183;«/mo»«mn mathvariant=¨bold¨ mathcolor=¨#FF0000¨»0«/mn»«mo mathvariant=¨bold¨ mathcolor=¨#FF0000¨».«/mo»«mn mathvariant=¨bold¨ mathcolor=¨#FF0000¨»1«/mn»«mo mathvariant=¨bold¨ mathcolor=¨#FF0000¨»=«/mo»«mn mathvariant=¨bold¨ mathcolor=¨#FF0000¨»0«/mn»«mo mathvariant=¨bold¨ mathcolor=¨#FF0000¨».«/mo»«mn mathvariant=¨bold¨ mathcolor=¨#FF0000¨»2«/mn»«mi mathvariant=¨bold¨ mathcolor=¨#FF0000¨»J«/mi»«mspace linebreak=¨newline¨»«/mspace»«/math»
אם יש עבודה של כוח לא משמר , האנרגיה המכנית לא נשמרת. אפשר לכתוב את ביטוי עבודת הכוח הלא משמר.
זה מזכיר קצת את החוק הראשון והשני של ניוטון ... או שהשקול כוחות שווה לאפס או שהוא שונה מאפס.
אם רק כוחות משמרים עושים עבודה השינוי באנרגיה המכנית שווה לאפס.
אם כוחות לא משמרים עושים עבודה השינוי באנרגיה המכנית שונה מאפס .
2. התלמיד מגדיל את האנרגיה המכנית הכוללת , לכן הוא עושה עבודה חיובית.
3. אפשר למצוא את עבודת התלמיד בעזרת האנרגיה הפוטנציאלית כובדית והאנרגיה פוטנציאלית אלסטית .
במקום עם האנרגיה הפוטנציאלית הכוללת.
______________________________________________________________________________________

 _____________________________________________________________________________________
_____________________________________________________________________________________