23. 1980,3
______________________________________________________________________________________
...
حركة توافقية بسيطة.
لتحديد طبيعة الحركة، يجب مقارنة تعبير القوة المحصّلة المؤثرة على الكتلة مع تعبير القوة المحصّلة للحركة التوافقية.
نكتب تعبيرًا للقوة المحصّلة المؤثرة على الجسم.
هناك ثلاث قوى تؤثر على الجسم: الجاذبية، والقوة العمودية، وقوة النابض. نرسم مخطط القوى للقوى المؤثرة على الجسم في لحظة تحريره:
في الاتجاه الرأسي الجسم موجود في حالة اتّزان، محصّلة القوى المؤثرة على الجسم يساوي قوة النابض F. ويتحقق: «math xmlns=¨http://www.w3.org/1998/Math/MathML¨»«mstyle mathsize=¨20px¨»«mi mathvariant=¨bold¨ mathcolor=¨#0000FF¨»§#931;F«/mi»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»=«/mo»«mi mathvariant=¨bold¨ mathcolor=¨#0000FF¨»K«/mi»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»§#183;«/mo»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»§#8710;«/mo»«mi mathvariant=¨bold¨ mathcolor=¨#0000FF¨»X«/mi»«/mstyle»«/math»
نعبر عن القوة المحصّلة بالنسبة لمحور الحركة الذي نقطة أصله في النقطة التي يكون فيها النابض مسترخيًا.
بالنسبة لهذا المحور، تعمل قوة النابض كقوة معيدة، ويتحقق: «math xmlns=¨http://www.w3.org/1998/Math/MathML¨»«mstyle mathsize=¨20px¨»«mi mathvariant=¨bold¨ mathcolor=¨#0000FF¨»§#931;F«/mi»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»=«/mo»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»-«/mo»«mi mathvariant=¨bold¨ mathcolor=¨#0000FF¨»K«/mi»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»§#183;«/mo»«mi mathvariant=¨bold¨ mathcolor=¨#0000FF¨»X«/mi»«/mstyle»«/math».
الحركة التوافقية البسيطة هي حركة في خط مستقيم التي فيها القوة المحصلة تتناسب طرديًا مع موقع الجسم، وبالنسبة للمحور الذي نقطة أصله
أين يكون الجسم عندما يكون النابض مرتخيًا، فإن تعبير القوة الحصّلة هو: «math xmlns=¨http://www.w3.org/1998/Math/MathML¨»«mstyle mathsize=¨20px¨»«mi mathvariant=¨bold¨ mathcolor=¨#0000FF¨»§#931;F«/mi»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»=«/mo»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»-«/mo»«mi mathvariant=¨bold¨ mathcolor=¨#0000FF¨»C«/mi»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»§#183;«/mo»«mi mathvariant=¨bold¨ mathcolor=¨#0000FF¨»X«/mi»«/mstyle»«/math»
لذلك يتحرك الجسم بحركة توافقية بسيطة.
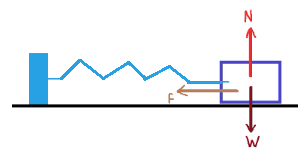
בכיוון האנכי הגוף מתמיד בתנועתו, שקול הכוחות הפועלים על הגוף שווה לכוח הקפיץ F. ומתקיים: «math xmlns=¨http://www.w3.org/1998/Math/MathML¨»«mstyle mathsize=¨20px¨»«mi mathvariant=¨bold¨ mathcolor=¨#0000FF¨»§#931;F«/mi»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»=«/mo»«mi mathvariant=¨bold¨ mathcolor=¨#0000FF¨»K«/mi»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»§#183;«/mo»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»§#8710;«/mo»«mi mathvariant=¨bold¨ mathcolor=¨#0000FF¨»X«/mi»«/mstyle»«/math»
נבטא את הכוח השקול ביחס לציר תנועה שראשיתו בנקודה בה הגוף נמצא כאשר הקפיץ רפוי.
ביחס לציר זה כוח הקפיץ פועל ככוח מחזיר, ומתקיים: «math xmlns=¨http://www.w3.org/1998/Math/MathML¨»«mstyle mathsize=¨20px¨»«mi mathvariant=¨bold¨ mathcolor=¨#0000FF¨»§#931;F«/mi»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»=«/mo»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»-«/mo»«mi mathvariant=¨bold¨ mathcolor=¨#0000FF¨»K«/mi»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»§#183;«/mo»«mi mathvariant=¨bold¨ mathcolor=¨#0000FF¨»X«/mi»«/mstyle»«/math».
תנועה הרמונית פשוטה היא תנועה בקו ישר שבה הכוח השקול תלוי ביחס ישר במיקום הגוף, וביחס לציר שראשיתו בנקודה
בה נמצא הגוף כאשר הקפיץ רפוי ביטוי הכוח השקול הוא: «math xmlns=¨http://www.w3.org/1998/Math/MathML¨»«mstyle mathsize=¨20px¨»«mi mathvariant=¨bold¨ mathcolor=¨#0000FF¨»§#931;F«/mi»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»=«/mo»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»-«/mo»«mi mathvariant=¨bold¨ mathcolor=¨#0000FF¨»C«/mi»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»§#183;«/mo»«mi mathvariant=¨bold¨ mathcolor=¨#0000FF¨»X«/mi»«/mstyle»«/math»
לכן הגוף נע בתנועה הרמונית פשוטה.
1. يتضمن السؤال عبارة "طبيعة الحركة"، والتي تشير إلى نوع الحركة.
2. تتطرق العديد من الأسئلة في الحركة التوافقية البسيطة إلى الشرط لنوع الحركة كحركة توافقية بسيطة.
من المهم معرفة الحالة. (القوة المحصّلة تتناسب طرديًا مع موقع الجسم.)
(القوة المكافئة تعتمد بشكل مباشر على موضع الجسم.)
3. أي حركة في خط مستقيم حيث تتناسب فيها القوة المحصّلة تناسبًا طرديًا مع موقع الجسم هي حركة توافقية بسيطة.
3. أي حركة في خط مستقيم حيث تتناسب فيها القوة المحصّلة تناسبًا طرديًا مع موقع الجسم هي حركة توافقية بسيطة.
يمكن استخدام كافة دوال الحركة التوافقية البسيطة لوصف الحركة.
2. שאלות רבות בתנועה הרמונית פשוטה עוסקות בתנאי לקביעת סוג התנועה כתנועה הרמונית פשוטה.
חשוב להכיר את התנאי. (כוח שקול תלוי ביחס ישר במיקום הגוף).
3. בכל תנועה בקו ישר שבה הכוח השקול תלוי ביחס ישר במיקום הגוף היא תנועה הרמונית פשוטה.
ניתן להשתמש בכל פונקציות התה"פ לתיאור התנועה.
______________________________________________________________________________________
______________________________________________________________________________________
...
«math xmlns=¨http://www.w3.org/1998/Math/MathML¨»«mstyle mathsize=¨20px¨»«mi mathvariant=¨bold¨»V«/mi»«mo mathvariant=¨bold¨»=«/mo»«mn mathvariant=¨bold¨»1«/mn»«mfrac»«mi mathvariant=¨bold¨»m«/mi»«mi mathvariant=¨bold¨»s«/mi»«/mfrac»«/mstyle»«/math»
يمكن التعبير عن السرعة القصوى من خلال تعبير السرعة كدالة للزمن، عندما تكون قيمة دالة sin قصوى (تساوي 1).
من دالة السرعة كدالة للزمن «math xmlns=¨http://www.w3.org/1998/Math/MathML¨»«mi mathvariant=¨bold¨ mathcolor=¨#0000FF¨»V«/mi»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»(«/mo»«mi mathvariant=¨bold¨ mathcolor=¨#0000FF¨»t«/mi»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»)«/mo»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»=«/mo»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»-«/mo»«mi mathvariant=¨bold¨ mathcolor=¨#0000FF¨»§#969;A«/mi»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»§#183;«/mo»«mi mathvariant=¨bold¨ mathcolor=¨#0000FF¨»sin«/mi»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»(«/mo»«mi mathvariant=¨bold¨ mathcolor=¨#0000FF¨»§#969;t«/mi»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»+«/mo»«msub»«mi mathvariant=¨bold¨ mathcolor=¨#0000FF¨»§#1012;«/mi»«mn mathvariant=¨bold¨ mathcolor=¨#0000FF¨»0«/mn»«/msub»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»)«/mo»«/math» يمكن تحديد قيمة السرعة القصوى : «math xmlns=¨http://www.w3.org/1998/Math/MathML¨»«mstyle mathsize=¨20px¨»«msub»«mi mathvariant=¨bold¨ mathcolor=¨#0000FF¨»V«/mi»«mi mathvariant=¨bold¨ mathcolor=¨#0000FF¨»max«/mi»«/msub»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»=«/mo»«mi mathvariant=¨bold¨ mathcolor=¨#0000FF¨»§#969;«/mi»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»§#183;«/mo»«mi mathvariant=¨bold¨ mathcolor=¨#0000FF¨»A«/mi»«/mstyle»«/math»
نحسب التردد الزاوي:
«math xmlns=¨http://www.w3.org/1998/Math/MathML¨»«mstyle mathsize=¨20px¨»«mi mathvariant=¨bold¨ mathcolor=¨#0000FF¨»T«/mi»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»=«/mo»«mn mathvariant=¨bold¨ mathcolor=¨#0000FF¨»2«/mn»«mi mathvariant=¨bold¨ mathcolor=¨#0000FF¨»§#960;«/mi»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»§#183;«/mo»«msqrt mathcolor=¨#0000FF¨»«mfrac»«mi mathvariant=¨bold¨»m«/mi»«mi mathvariant=¨bold¨»k«/mi»«/mfrac»«/msqrt»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»§#160;«/mo»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»§#160;«/mo»«mspace linebreak=¨newline¨/»«mi mathvariant=¨bold¨ mathcolor=¨#0000FF¨»§#969;«/mi»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»=«/mo»«mfrac mathcolor=¨#0000FF¨»«mrow»«mn mathvariant=¨bold¨»2«/mn»«mi mathvariant=¨bold¨»§#960;«/mi»«/mrow»«mi mathvariant=¨bold¨»T«/mi»«/mfrac»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»=«/mo»«mfrac mathcolor=¨#0000FF¨»«mrow»«mn mathvariant=¨bold¨»2«/mn»«mi mathvariant=¨bold¨»§#960;«/mi»«/mrow»«mrow»«mn mathvariant=¨bold¨»2«/mn»«mi mathvariant=¨bold¨»§#960;«/mi»«mo mathvariant=¨bold¨»§#183;«/mo»«msqrt»«mfrac»«mi mathvariant=¨bold¨»m«/mi»«mi mathvariant=¨bold¨»k«/mi»«/mfrac»«/msqrt»«/mrow»«/mfrac»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»=«/mo»«msqrt mathcolor=¨#0000FF¨»«mfrac»«mi mathvariant=¨bold¨»k«/mi»«mi mathvariant=¨bold¨»m«/mi»«/mfrac»«/msqrt»«/mstyle»«/math»
نحسب قيمة ثابت النابض بناءً على القوة المؤثرة على النابض واستطالته.
يتم تشغيل قوة مقدارها 20 نيوتن على النابض، فيزداد طوله بمقدار 10 سم. يمكن حساب قيمة ثابت النابض من قانون هوك:
«math xmlns=¨http://www.w3.org/1998/Math/MathML¨»«mstyle mathsize=¨20px¨»«mi mathvariant=¨bold¨ mathcolor=¨#0000FF¨»F«/mi»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»=«/mo»«mi mathvariant=¨bold¨ mathcolor=¨#0000FF¨»K«/mi»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»§#183;«/mo»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»§#8710;«/mo»«mi mathvariant=¨bold¨ mathcolor=¨#0000FF¨»X«/mi»«mspace linebreak=¨newline¨/»«mspace linebreak=¨newline¨/»«mi mathvariant=¨bold¨ mathcolor=¨#0000FF¨»K«/mi»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»=«/mo»«mfrac mathcolor=¨#0000FF¨»«mi mathvariant=¨bold¨»F«/mi»«mrow»«mo mathvariant=¨bold¨»§#8710;«/mo»«mi mathvariant=¨bold¨»X«/mi»«/mrow»«/mfrac»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»=«/mo»«mfrac mathcolor=¨#0000FF¨»«mn mathvariant=¨bold¨»20«/mn»«mrow»«mn mathvariant=¨bold¨»0«/mn»«mo mathvariant=¨bold¨».«/mo»«mn mathvariant=¨bold¨»1«/mn»«/mrow»«/mfrac»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»=«/mo»«mn mathvariant=¨bold¨ mathcolor=¨#0000FF¨»200«/mn»«mfrac mathcolor=¨#0000FF¨»«mi mathvariant=¨bold¨»N«/mi»«mi mathvariant=¨bold¨»m«/mi»«/mfrac»«/mstyle»«/math»
نعبر عن مقدار السرعة القصوى ونحسب قيمتها:
«math xmlns=¨http://www.w3.org/1998/Math/MathML¨»«mstyle mathsize=¨20px¨»«msub»«mi mathvariant=¨bold¨ mathcolor=¨#0000FF¨»V«/mi»«mi mathvariant=¨bold¨ mathcolor=¨#0000FF¨»max«/mi»«/msub»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»=«/mo»«mi mathvariant=¨bold¨ mathcolor=¨#0000FF¨»§#969;«/mi»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»§#183;«/mo»«mi mathvariant=¨bold¨ mathcolor=¨#0000FF¨»A«/mi»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»=«/mo»«msqrt mathcolor=¨#0000FF¨»«mfrac»«mi mathvariant=¨bold¨»k«/mi»«mi mathvariant=¨bold¨»m«/mi»«/mfrac»«/msqrt»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»§#183;«/mo»«mi mathvariant=¨bold¨ mathcolor=¨#0000FF¨»A«/mi»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»=«/mo»«msqrt mathcolor=¨#0000FF¨»«mfrac»«mn mathvariant=¨bold¨»200«/mn»«mn mathvariant=¨bold¨»2«/mn»«/mfrac»«/msqrt»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»§#183;«/mo»«mn mathvariant=¨bold¨ mathcolor=¨#0000FF¨»0«/mn»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨».«/mo»«mn mathvariant=¨bold¨ mathcolor=¨#0000FF¨»1«/mn»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»=«/mo»«msqrt mathcolor=¨#0000FF¨»«mn mathvariant=¨bold¨»100«/mn»«/msqrt»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»§#183;«/mo»«mn mathvariant=¨bold¨ mathcolor=¨#0000FF¨»0«/mn»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨».«/mo»«mn mathvariant=¨bold¨ mathcolor=¨#0000FF¨»1«/mn»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»=«/mo»«mn mathvariant=¨bold¨ mathcolor=¨#0000FF¨»10«/mn»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»§#183;«/mo»«mn mathvariant=¨bold¨ mathcolor=¨#0000FF¨»0«/mn»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨».«/mo»«mn mathvariant=¨bold¨ mathcolor=¨#0000FF¨»1«/mn»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»=«/mo»«mn mathvariant=¨bold¨ mathcolor=¨#0000FF¨»1«/mn»«mfrac mathcolor=¨#0000FF¨»«mi mathvariant=¨bold¨»m«/mi»«mi mathvariant=¨bold¨»s«/mi»«/mfrac»«/mstyle»«/math»
1. من القانون الثالث لنيوتن، عندما يتم تشغيل قوة مقدارها 20 نيوتن على النابض، فإن النابض سيؤثر بقوة مساوية في الاتجاه المعاكس.
2. من الجدير بالذكر أن مقدار السرعة القصوى يساوي حاصل الضرب «math xmlns=¨http://www.w3.org/1998/Math/MathML¨»«mi mathvariant=¨bold¨ mathcolor=¨#FF0000¨»§#969;«/mi»«mo mathvariant=¨bold¨ mathcolor=¨#FF0000¨»§#183;«/mo»«mi mathvariant=¨bold¨ mathcolor=¨#FF0000¨»A«/mi»«/math» ومقدار التسارع الأقصى يساوي «math xmlns=¨http://www.w3.org/1998/Math/MathML¨»«msup»«mi mathvariant=¨bold¨ mathcolor=¨#FF0000¨»§#969;«/mi»«mn mathvariant=¨bold¨ mathcolor=¨#FF0000¨»2«/mn»«/msup»«mo mathvariant=¨bold¨ mathcolor=¨#FF0000¨»§#183;«/mo»«mi mathvariant=¨bold¨ mathcolor=¨#FF0000¨»A«/mi»«/math».
3. يمكن التعبير عن مقدار السرعة القصوى والتسارع الأقصى من الدالتين v(t) وa(t).
يمكن أيضًا استخدام الدالتين v(x) وa(x) لهذا الغرض.
עם הכוח שהקפיץ מפעיל ניתן להשתמש בחוק הוק.
2. כדאי לזכור שגודל המהירות המקסימאלית שווה למכפלה «math xmlns=¨http://www.w3.org/1998/Math/MathML¨»«mi mathvariant=¨bold¨ mathcolor=¨#FF0000¨»§#969;«/mi»«mo mathvariant=¨bold¨ mathcolor=¨#FF0000¨»§#183;«/mo»«mi mathvariant=¨bold¨ mathcolor=¨#FF0000¨»A«/mi»«/math» וגודל התאוצה המקסימאלית שווה «math xmlns=¨http://www.w3.org/1998/Math/MathML¨»«msup»«mi mathvariant=¨bold¨ mathcolor=¨#FF0000¨»§#969;«/mi»«mn mathvariant=¨bold¨ mathcolor=¨#FF0000¨»2«/mn»«/msup»«mo mathvariant=¨bold¨ mathcolor=¨#FF0000¨»§#183;«/mo»«mi mathvariant=¨bold¨ mathcolor=¨#FF0000¨»A«/mi»«/math».
3. ניתן לבטא את גודל המהירות המקסימאלית והתאוצה המקסימאלית מפונקציות v(t) ו- a(t) .
ניתן להשתמש לשם כך גם בפונקציות v(x) ו- a(x).
______________________________________________________________________________________
______________________________________________________________________________________
...
«math xmlns=¨http://www.w3.org/1998/Math/MathML¨»«mstyle mathsize=¨20px¨»«mi mathvariant=¨bold¨»t«/mi»«mo mathvariant=¨bold¨»=«/mo»«mn mathvariant=¨bold¨»0«/mn»«mo mathvariant=¨bold¨».«/mo»«mn mathvariant=¨bold¨»157«/mn»«mi mathvariant=¨bold¨»s«/mi»«/mstyle»«/math»
من مبادئ الحركة التوافقية البسيطة، يتم قياس أقصى سرعة للجسم عندما يمر الجسم عبر نقطة أصل المحور (نقطة الاتّزان).
نصف حركة الجسم بالنسبة لمحور نقطة أصله في النقطة التي يقع فيها الجسم عندما يكون النابض مسترخياً، ويتجه إلى اليمين.
ستصل الكتلة إلى أقصى سرعتها عندما تمر في نقطة أصل المحور، بعد ربع زمن دورة.
نحسب زمن الدورة:
«math xmlns=¨http://www.w3.org/1998/Math/MathML¨»«mstyle mathsize=¨20px¨»«mi mathvariant=¨bold¨ mathcolor=¨#0000FF¨»T«/mi»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»=«/mo»«mn mathvariant=¨bold¨ mathcolor=¨#0000FF¨»2«/mn»«mi mathvariant=¨bold¨ mathcolor=¨#0000FF¨»§#960;«/mi»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»§#183;«/mo»«msqrt mathcolor=¨#0000FF¨»«mfrac»«mi mathvariant=¨bold¨»m«/mi»«mi mathvariant=¨bold¨»k«/mi»«/mfrac»«/msqrt»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»=«/mo»«mn mathvariant=¨bold¨ mathcolor=¨#0000FF¨»2«/mn»«mi mathvariant=¨bold¨ mathcolor=¨#0000FF¨»§#960;«/mi»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»§#183;«/mo»«msqrt mathcolor=¨#0000FF¨»«mfrac»«mn mathvariant=¨bold¨»2«/mn»«mn mathvariant=¨bold¨»200«/mn»«/mfrac»«/msqrt»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»=«/mo»«mn mathvariant=¨bold¨ mathcolor=¨#0000FF¨»2«/mn»«mi mathvariant=¨bold¨ mathcolor=¨#0000FF¨»§#960;«/mi»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»§#183;«/mo»«msqrt mathcolor=¨#0000FF¨»«mn mathvariant=¨bold¨»0«/mn»«mo mathvariant=¨bold¨».«/mo»«mn mathvariant=¨bold¨»01«/mn»«/msqrt»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»=«/mo»«mn mathvariant=¨bold¨ mathcolor=¨#0000FF¨»0«/mn»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨».«/mo»«mn mathvariant=¨bold¨ mathcolor=¨#0000FF¨»628«/mn»«mi mathvariant=¨bold¨ mathcolor=¨#0000FF¨»s«/mi»«/mstyle»«/math»
نحسب زمن حركة الجسم من لحظة تحريره حتى وصوله إلى نقطة الأصل للمحور:
«math xmlns=¨http://www.w3.org/1998/Math/MathML¨»«mstyle mathsize=¨20px¨»«mi mathvariant=¨bold¨ mathcolor=¨#0000FF¨»t«/mi»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»=«/mo»«mfrac mathcolor=¨#0000FF¨»«mi mathvariant=¨bold¨»T«/mi»«mn mathvariant=¨bold¨»4«/mn»«/mfrac»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»=«/mo»«mfrac mathcolor=¨#0000FF¨»«mrow»«mn mathvariant=¨bold¨»0«/mn»«mo mathvariant=¨bold¨».«/mo»«mn mathvariant=¨bold¨»628«/mn»«/mrow»«mn mathvariant=¨bold¨»4«/mn»«/mfrac»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»=«/mo»«mn mathvariant=¨bold¨ mathcolor=¨#0000FF¨»0«/mn»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨».«/mo»«mn mathvariant=¨bold¨ mathcolor=¨#0000FF¨»157«/mn»«mi mathvariant=¨bold¨ mathcolor=¨#0000FF¨»S«/mi»«/mstyle»«/math»
המסה תגיע לגודל המהירות המקסימאלית כאשר היא תגיע לנקודת ראשית הציר, לאחר רבע זמן מחזור.
נחשב את זמן המחזור:
«math xmlns=¨http://www.w3.org/1998/Math/MathML¨»«mstyle mathsize=¨20px¨»«mi mathvariant=¨bold¨ mathcolor=¨#0000FF¨»T«/mi»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»=«/mo»«mn mathvariant=¨bold¨ mathcolor=¨#0000FF¨»2«/mn»«mi mathvariant=¨bold¨ mathcolor=¨#0000FF¨»§#960;«/mi»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»§#183;«/mo»«msqrt mathcolor=¨#0000FF¨»«mfrac»«mi mathvariant=¨bold¨»m«/mi»«mi mathvariant=¨bold¨»k«/mi»«/mfrac»«/msqrt»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»=«/mo»«mn mathvariant=¨bold¨ mathcolor=¨#0000FF¨»2«/mn»«mi mathvariant=¨bold¨ mathcolor=¨#0000FF¨»§#960;«/mi»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»§#183;«/mo»«msqrt mathcolor=¨#0000FF¨»«mfrac»«mn mathvariant=¨bold¨»2«/mn»«mn mathvariant=¨bold¨»200«/mn»«/mfrac»«/msqrt»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»=«/mo»«mn mathvariant=¨bold¨ mathcolor=¨#0000FF¨»2«/mn»«mi mathvariant=¨bold¨ mathcolor=¨#0000FF¨»§#960;«/mi»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»§#183;«/mo»«msqrt mathcolor=¨#0000FF¨»«mn mathvariant=¨bold¨»0«/mn»«mo mathvariant=¨bold¨».«/mo»«mn mathvariant=¨bold¨»01«/mn»«/msqrt»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»=«/mo»«mn mathvariant=¨bold¨ mathcolor=¨#0000FF¨»0«/mn»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨».«/mo»«mn mathvariant=¨bold¨ mathcolor=¨#0000FF¨»628«/mn»«mi mathvariant=¨bold¨ mathcolor=¨#0000FF¨»s«/mi»«/mstyle»«/math»
נחשב את זמן תנועת הגוף מרגע שחרורו ועד שהוא מגיע לנקודת ראשית הציר:
«math xmlns=¨http://www.w3.org/1998/Math/MathML¨»«mstyle mathsize=¨20px¨»«mi mathvariant=¨bold¨ mathcolor=¨#0000FF¨»t«/mi»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»=«/mo»«mfrac mathcolor=¨#0000FF¨»«mi mathvariant=¨bold¨»T«/mi»«mn mathvariant=¨bold¨»4«/mn»«/mfrac»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»=«/mo»«mfrac mathcolor=¨#0000FF¨»«mrow»«mn mathvariant=¨bold¨»0«/mn»«mo mathvariant=¨bold¨».«/mo»«mn mathvariant=¨bold¨»628«/mn»«/mrow»«mn mathvariant=¨bold¨»4«/mn»«/mfrac»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»=«/mo»«mn mathvariant=¨bold¨ mathcolor=¨#0000FF¨»0«/mn»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨».«/mo»«mn mathvariant=¨bold¨ mathcolor=¨#0000FF¨»157«/mn»«mi mathvariant=¨bold¨ mathcolor=¨#0000FF¨»S«/mi»«/mstyle»«/math»
1. قبل استخدام مبادئ الحركة التوافقية البسيطة، يجب تحديد المحور الذي يبدأ في النقطة التي يقع فيها الجسم عندما يكون النابض مسترخيًا.
2. يتكون زمن الدورة الكاملة لأي حركة توافقية من أربع فترات متساوية المدة (ربع دورة).
زمن ربع الدورة الأول: من لحظة تحرير الجسم حتى وصوله إلى نقطة أصل المحور للمرة الأولى.
زمن ربع الدورة الثانية: من لحظة مرور الجسم بأصل المحور للمرة الأولى حتى يصل إلى نقطة الطرف السالبة.
زمن ربع الدورة الثالث: من لحظة وصول الجسم إلى نقطة الطرق السالبة حتى يمر بأصل المحور للمرة الثانية.
ربع الدورة هو الزمن اللازم من لحظة مرور الجسم بأصل المحور للمرة الثانية حتى يعود الجسم إلى نقطة الطرف الموجبة.
3. يمكن حساب زمن الدورة دون تحديد أصل المحور. لفهم الحركة ووصفها بشكل جيد، من المهم تحديد محور الحركة.
4. طريقة أخرى: يمكن حساب زمن الحركة باستخدام دالة الموقع كدالة للزمن:
يتم اختيار محور يشير إلى اليمين، بحيث يكون الجسم في نقطة الطرف الموجبة في لحظة بدء الحركة، وستكون زاوية الطور الأولية صفرًا.
«math xmlns=¨http://www.w3.org/1998/Math/MathML¨»«mstyle mathsize=¨20px¨»«mi mathvariant=¨bold¨ mathcolor=¨#FF0000¨»x«/mi»«mo mathvariant=¨bold¨ mathcolor=¨#FF0000¨»(«/mo»«mi mathvariant=¨bold¨ mathcolor=¨#FF0000¨»t«/mi»«mo mathvariant=¨bold¨ mathcolor=¨#FF0000¨»)«/mo»«mo mathvariant=¨bold¨ mathcolor=¨#FF0000¨»=«/mo»«mi mathvariant=¨bold¨ mathcolor=¨#FF0000¨»A«/mi»«mo mathvariant=¨bold¨ mathcolor=¨#FF0000¨»§#183;«/mo»«mi mathvariant=¨bold¨ mathcolor=¨#FF0000¨»cos«/mi»«mo mathvariant=¨bold¨ mathcolor=¨#FF0000¨»(«/mo»«mi mathvariant=¨bold¨ mathcolor=¨#FF0000¨»§#969;t«/mi»«mo mathvariant=¨bold¨ mathcolor=¨#FF0000¨»)«/mo»«mspace linebreak=¨newline¨/»«mn mathvariant=¨bold¨ mathcolor=¨#FF0000¨»0«/mn»«mo mathvariant=¨bold¨ mathcolor=¨#FF0000¨»=«/mo»«mn mathvariant=¨bold¨ mathcolor=¨#FF0000¨»0«/mn»«mo mathvariant=¨bold¨ mathcolor=¨#FF0000¨».«/mo»«mn mathvariant=¨bold¨ mathcolor=¨#FF0000¨»1«/mn»«mo mathvariant=¨bold¨ mathcolor=¨#FF0000¨»§#183;«/mo»«mi mathvariant=¨bold¨ mathcolor=¨#FF0000¨»cos«/mi»«mo mathvariant=¨bold¨ mathcolor=¨#FF0000¨»(«/mo»«mi mathvariant=¨bold¨ mathcolor=¨#FF0000¨»§#969;t«/mi»«mo mathvariant=¨bold¨ mathcolor=¨#FF0000¨»)«/mo»«mspace linebreak=¨newline¨/»«mn mathvariant=¨bold¨ mathcolor=¨#FF0000¨»0«/mn»«mo mathvariant=¨bold¨ mathcolor=¨#FF0000¨»=«/mo»«mi mathvariant=¨bold¨ mathcolor=¨#FF0000¨»cos«/mi»«mo mathvariant=¨bold¨ mathcolor=¨#FF0000¨»(«/mo»«mi mathvariant=¨bold¨ mathcolor=¨#FF0000¨»§#969;t«/mi»«mo mathvariant=¨bold¨ mathcolor=¨#FF0000¨»)«/mo»«mspace linebreak=¨newline¨/»«mspace linebreak=¨newline¨/»«mi mathvariant=¨bold¨ mathcolor=¨#FF0000¨»shift«/mi»«mo mathvariant=¨bold¨ mathcolor=¨#FF0000¨»§#160;«/mo»«mi mathvariant=¨bold¨ mathcolor=¨#FF0000¨»cos«/mi»«mo mathvariant=¨bold¨ mathcolor=¨#FF0000¨»(«/mo»«mn mathvariant=¨bold¨ mathcolor=¨#FF0000¨»0«/mn»«mo mathvariant=¨bold¨ mathcolor=¨#FF0000¨»)«/mo»«mo mathvariant=¨bold¨ mathcolor=¨#FF0000¨»=«/mo»«mi mathvariant=¨bold¨ mathcolor=¨#FF0000¨»§#969;«/mi»«mo mathvariant=¨bold¨ mathcolor=¨#FF0000¨»§#183;«/mo»«mi mathvariant=¨bold¨ mathcolor=¨#FF0000¨»t«/mi»«mo mathvariant=¨bold¨ mathcolor=¨#FF0000¨»=«/mo»«mfrac mathcolor=¨#FF0000¨»«mrow»«mn mathvariant=¨bold¨»2«/mn»«mo mathvariant=¨bold¨»§#183;«/mo»«mi mathvariant=¨bold¨»§#960;«/mi»«/mrow»«mi mathvariant=¨bold¨»T«/mi»«/mfrac»«mo mathvariant=¨bold¨ mathcolor=¨#FF0000¨»§#183;«/mo»«mi mathvariant=¨bold¨ mathcolor=¨#FF0000¨»t«/mi»«mspace linebreak=¨newline¨/»«mspace linebreak=¨newline¨/»«mn mathvariant=¨bold¨ mathcolor=¨#FF0000¨»1«/mn»«mo mathvariant=¨bold¨ mathcolor=¨#FF0000¨».«/mo»«msub»«mn mathvariant=¨bold¨ mathcolor=¨#FF0000¨»57«/mn»«mi mathvariant=¨bold¨ mathcolor=¨#FF0000¨»rad«/mi»«/msub»«mo mathvariant=¨bold¨ mathcolor=¨#FF0000¨»=«/mo»«mfrac mathcolor=¨#FF0000¨»«mrow»«mn mathvariant=¨bold¨»2«/mn»«mo mathvariant=¨bold¨»§#183;«/mo»«mi mathvariant=¨bold¨»§#960;«/mi»«/mrow»«mrow»«mn mathvariant=¨bold¨»0«/mn»«mo mathvariant=¨bold¨».«/mo»«mn mathvariant=¨bold¨»628«/mn»«/mrow»«/mfrac»«mo mathvariant=¨bold¨ mathcolor=¨#FF0000¨»§#183;«/mo»«mi mathvariant=¨bold¨ mathcolor=¨#FF0000¨»t«/mi»«mspace linebreak=¨newline¨/»«mspace linebreak=¨newline¨/»«mi mathvariant=¨bold¨ mathcolor=¨#FF0000¨»t«/mi»«mo mathvariant=¨bold¨ mathcolor=¨#FF0000¨»=«/mo»«mfrac mathcolor=¨#FF0000¨»«mrow»«mn mathvariant=¨bold¨»1«/mn»«mo mathvariant=¨bold¨».«/mo»«mn mathvariant=¨bold¨»57«/mn»«mo mathvariant=¨bold¨»§#183;«/mo»«mn mathvariant=¨bold¨»0«/mn»«mo mathvariant=¨bold¨».«/mo»«mn mathvariant=¨bold¨»628«/mn»«/mrow»«mrow»«mn mathvariant=¨bold¨»2«/mn»«mo mathvariant=¨bold¨»§#183;«/mo»«mi mathvariant=¨bold¨»§#960;«/mi»«/mrow»«/mfrac»«mo mathvariant=¨bold¨ mathcolor=¨#FF0000¨»=«/mo»«mfrac mathcolor=¨#FF0000¨»«mrow»«mn mathvariant=¨bold¨»0«/mn»«mo mathvariant=¨bold¨».«/mo»«mn mathvariant=¨bold¨»985«/mn»«/mrow»«mrow»«mn mathvariant=¨bold¨»6«/mn»«mo mathvariant=¨bold¨».«/mo»«mn mathvariant=¨bold¨»28«/mn»«/mrow»«/mfrac»«mo mathvariant=¨bold¨ mathcolor=¨#FF0000¨»=«/mo»«mn mathvariant=¨bold¨ mathcolor=¨#FF0000¨»0«/mn»«mo mathvariant=¨bold¨ mathcolor=¨#FF0000¨».«/mo»«mn mathvariant=¨bold¨ mathcolor=¨#FF0000¨»157«/mn»«mi mathvariant=¨bold-italic¨ mathcolor=¨#FF0000¨»s«/mi»«mspace linebreak=¨newline¨/»«/mstyle»«/math»
لا يمكن استخدام دالة الموقع كدالة للزمن دون تحديد محور الحركة.
2. כדי שזווית המופע ההתחלתית תהיה אפס יש לקבוע את כיוון הציר כך שהגוף יתחיל לנוע מנקודת הקצה החיובית.
3. זמן מחזור תנועה שלם של כל תנועה הרמונית מורכב מארבעה רבעי מחזור בעלי זמן זהה.
רבע זמן מחזור ראשון: מרגע שחרור הגוף ועד שהוא מגיע לנקודת ראשית הציר בפעם הראשונה.
רבע זמן מחזור שני: מרגע שהגוף חולף בפעם הראשונה בנקודת ראשית הציר ועד שהוא מגיע לנקודת הקצה השלילית.
רבע זמן מחזור שלישי: מרגע שהגוף נמצא בנקודת הקצה השלילית ועד שהוא חולף בנקודת ראשית הציר בפעם השנייה.
רבע זמן מחזור ראשון: מרגע שחרור הגוף ועד שהוא מגיע לנקודת ראשית הציר בפעם הראשונה.
רבע זמן מחזור שני: מרגע שהגוף חולף בפעם הראשונה בנקודת ראשית הציר ועד שהוא מגיע לנקודת הקצה השלילית.
רבע זמן מחזור שלישי: מרגע שהגוף נמצא בנקודת הקצה השלילית ועד שהוא חולף בנקודת ראשית הציר בפעם השנייה.
רבע זמן מחזור רביעי מרגע שהגוף חולף בנקודת ראשית הציר בפעם השנייה ועד שהגוף מגיע חזרה לנקודת הקצה החיובית.
4. במקום להגדיר
______________________________________________________________________________________
______________________________________________________________________________________
...
في الحظة t=0s أيكون قصى تسارع في المقدار.
سرعة الكتلة في هذه اللحظة تساوي صفر.
מהירות המסה ברגע זה היא אפס.
من القانون الثاني لنيوتن ، يكون أقص تسارع في المقدار عندما يكون مقدار القوة المحصّلة قصوى.
في نقطتي طرفي الحركة، يغير الجسم اتجاه حركته؛ سرعتها في هذه النقاط تساوي صفرًا.
בנקודות הקצה הגוף משנה את כיוון תנועתו, מהירותו בנקודות אלו היא אפס.
من القانون الثاني لنيوتن، تكون أقصى قيمة للتسارع (بالقيمة المطلقة) عندما تكون القوة المحصّلة المؤثرة على الجسم قصوى.
نظرًا لأن القوة المحصّلة المؤثرة على الجسم تساوي قوة النابض، فكلما كان الجسم أبعد من أصل المحور (نقطة الاتّزان)، كلما كانت القوة المحصّلة أكبر.
لذلك، فإن تسارع الجسم يكون ذو قيمة قصوى (في القيمة المطلقة) عندما يكون الجسم في طرفي الحركة. يبدأ الجسم بالتحرك من نقطة طرف الحركة الموجبة، لذا في اللحظة t=0s سيكون للكتلة أكبر تسارع (بالقيمة المطلقة).
في نقاط الطرف تكون سرعة الكتلة صفرًا.
כיוון שהכוח השקול הפועל על הגוף שווה לכוח הקפיץ, ככל שהגוף רחוק מנקודת ראשית הציר (נקודת שיווי המשקל) כך הכוח השקול יהיה גדול יותר.
לכן תאוצת הגוף היא הגדולה ביותר בערכה המוחלט כאשר הגוף נמצא בנקודות הקצה. הגוף מתחיל לנוע מנקודת הקצה החיובית לכן ברגע t=0s תהיה למסה תאוצה הגדולה ביותר (בערכה המוחלט).
בנקודות הקצה מהירות המסה היא אפס.
1.قد تكون هناك لحظة حيث يكون التسارع أقصى ما يمكن والسرعة تساوي الصفر. لا يوجد تناقض هنا.
يصف التسارع معدل التغير في السرعة.
ومن الأمثلة التوضيحية على ذلك حساب بنكي بمليارات الشواقل وفي لحظة معينة لا يحدث أي تغيير في قيمة الأموال الموجودة في الحساب. 2. في السؤال مكتوب "نحرّر النابض". والمقصود تحريره من حالة السكون، لا رميه.
لذلك، في اللحظة التي تبدأ فيها الحركة، تكون الكتلة في أحدى طرفي الحركة، وسرعتها تساوي صفرًا.
3. جميع بنود السؤال يتعلق بحركة الجسم في طرف الحركة أو في نقطة الأصل. يمكن الإجابة على الأسئلة من خلال فهم الحركة التوافقية.
بدون استخدام الحركة التوافقية الكاملة. 4. في الحل المقترح هنا لهذه المسألة، اخترنا محور الحركة الموجه نحو اليمين، بحيث يكون الجسم في نقطة طرف الحركة الموجبة.
بالنسبة لهذا المحور، القوة المحصّلة سالبة والتسارع سالب. السؤال يتعلق بالقيمة المطلقة للتسارع، وليس التسارع نفسه.
5. من دالة التسارع كدالة للزمن: «math xmlns=¨http://www.w3.org/1998/Math/MathML¨»«mstyle mathsize=¨20px¨»«mi mathvariant=¨bold¨ mathcolor=¨#FF0000¨»a«/mi»«mo mathvariant=¨bold¨ mathcolor=¨#FF0000¨»(«/mo»«mi mathvariant=¨bold¨ mathcolor=¨#FF0000¨»t«/mi»«mo mathvariant=¨bold¨ mathcolor=¨#FF0000¨»)«/mo»«mo mathvariant=¨bold¨ mathcolor=¨#FF0000¨»=«/mo»«mo mathvariant=¨bold¨ mathcolor=¨#FF0000¨»-«/mo»«msup»«mi mathvariant=¨bold¨ mathcolor=¨#FF0000¨»§#969;«/mi»«mn mathvariant=¨bold¨ mathcolor=¨#FF0000¨»2«/mn»«/msup»«mi mathvariant=¨bold¨ mathcolor=¨#FF0000¨»A«/mi»«mo mathvariant=¨bold¨ mathcolor=¨#FF0000¨»§#183;«/mo»«mi mathvariant=¨bold¨ mathcolor=¨#FF0000¨»cos«/mi»«mo mathvariant=¨bold¨ mathcolor=¨#FF0000¨»(«/mo»«mi mathvariant=¨bold¨ mathcolor=¨#FF0000¨»§#969;t«/mi»«mo mathvariant=¨bold¨ mathcolor=¨#FF0000¨»)«/mo»«/mstyle»«/math» يمكن ملاحظة أنه في اللحظة t=0 تكون قيمة cos مساوية 1 (الحد الأقصى)
وتكون قيمة التسارع قصوى.
وتكون قيمة التسارع قصوى.
6.من دالة التسارع كدالة للموقع: «math xmlns=¨http://www.w3.org/1998/Math/MathML¨»«mstyle mathsize=¨20px¨»«mi mathvariant=¨bold¨ mathcolor=¨#FF0000¨»a«/mi»«mo mathvariant=¨bold¨ mathcolor=¨#FF0000¨»(«/mo»«mi mathvariant=¨bold-italic¨ mathcolor=¨#FF0000¨»x«/mi»«mo mathvariant=¨bold¨ mathcolor=¨#FF0000¨»)«/mo»«mo mathvariant=¨bold¨ mathcolor=¨#FF0000¨»=«/mo»«mo mathvariant=¨bold¨ mathcolor=¨#FF0000¨»-«/mo»«msup»«mi mathvariant=¨bold¨ mathcolor=¨#FF0000¨»§#969;«/mi»«mn mathvariant=¨bold¨ mathcolor=¨#FF0000¨»2«/mn»«/msup»«mo mathvariant=¨bold¨ mathcolor=¨#FF0000¨»§#183;«/mo»«mi mathvariant=¨bold-italic¨ mathcolor=¨#FF0000¨»x«/mi»«/mstyle»«/math» يمكن ملاحظة أنه عندما يكون الجسم في نقطة الطرف، تكون قيمة X مساوية لـ
سعة الاهتزاز هي (القيمة القصوى) ومقدار التسارع هو الحد الأقصى.
سعة الاهتزاز هي (القيمة القصوى) ومقدار التسارع هو الحد الأقصى.
7. الدالة v(x) عندما يكون الجسم في نقطة الطرف فإن سرعته تساوي صفرًا:
«math xmlns=¨http://www.w3.org/1998/Math/MathML¨»«mstyle mathsize=¨20px¨»«mi mathvariant=¨bold¨ mathcolor=¨#FF0000¨»V«/mi»«mo mathvariant=¨bold¨ mathcolor=¨#FF0000¨»(«/mo»«mi mathvariant=¨bold¨ mathcolor=¨#FF0000¨»X«/mi»«mo mathvariant=¨bold¨ mathcolor=¨#FF0000¨»)«/mo»«mo mathvariant=¨bold¨ mathcolor=¨#FF0000¨»=«/mo»«mo mathvariant=¨bold¨ mathcolor=¨#FF0000¨»§#177;«/mo»«mi mathvariant=¨bold¨ mathcolor=¨#FF0000¨»§#969;«/mi»«mroot mathcolor=¨#FF0000¨»«mrow»«mo mathvariant=¨bold¨»(«/mo»«msup»«mi mathvariant=¨bold¨»A«/mi»«mn mathvariant=¨bold¨»2«/mn»«/msup»«mo mathvariant=¨bold¨»-«/mo»«msup»«mi mathvariant=¨bold¨»X«/mi»«mn mathvariant=¨bold¨»2«/mn»«/msup»«mo mathvariant=¨bold¨»)«/mo»«/mrow»«mrow/»«/mroot»«mspace linebreak=¨newline¨/»«mspace linebreak=¨newline¨/»«mi mathvariant=¨bold¨ mathcolor=¨#FF0000¨»V«/mi»«mo mathvariant=¨bold¨ mathcolor=¨#FF0000¨»(«/mo»«mi mathvariant=¨bold¨ mathcolor=¨#FF0000¨»A«/mi»«mo mathvariant=¨bold¨ mathcolor=¨#FF0000¨»)«/mo»«mo mathvariant=¨bold¨ mathcolor=¨#FF0000¨»=«/mo»«mo mathvariant=¨bold¨ mathcolor=¨#FF0000¨»§#177;«/mo»«mi mathvariant=¨bold¨ mathcolor=¨#FF0000¨»§#969;«/mi»«mroot mathcolor=¨#FF0000¨»«mrow»«mo mathvariant=¨bold¨»(«/mo»«msup»«mi mathvariant=¨bold¨»A«/mi»«mn mathvariant=¨bold¨»2«/mn»«/msup»«mo mathvariant=¨bold¨»-«/mo»«msup»«mi mathvariant=¨bold¨»A«/mi»«mn mathvariant=¨bold¨»2«/mn»«/msup»«mo mathvariant=¨bold¨»)«/mo»«/mrow»«mrow/»«/mroot»«mo mathvariant=¨bold¨ mathcolor=¨#FF0000¨»=«/mo»«mn mathvariant=¨bold¨ mathcolor=¨#FF0000¨»0«/mn»«mfrac mathcolor=¨#FF0000¨»«mi mathvariant=¨bold¨»m«/mi»«mi mathvariant=¨bold¨»s«/mi»«/mfrac»«mspace linebreak=¨newline¨/»«/mstyle»«/math»
8. من الدالة v(t) باللحظة t=0s تكون سرعة الجسم:
«math xmlns=¨http://www.w3.org/1998/Math/MathML¨»«mstyle mathsize=¨20px¨»«mi mathvariant=¨bold¨ mathcolor=¨#FF0000¨»V«/mi»«mo mathvariant=¨bold¨ mathcolor=¨#FF0000¨»(«/mo»«mi mathvariant=¨bold¨ mathcolor=¨#FF0000¨»t«/mi»«mo mathvariant=¨bold¨ mathcolor=¨#FF0000¨»)«/mo»«mo mathvariant=¨bold¨ mathcolor=¨#FF0000¨»=«/mo»«mo mathvariant=¨bold¨ mathcolor=¨#FF0000¨»-«/mo»«mi mathvariant=¨bold¨ mathcolor=¨#FF0000¨»§#969;A«/mi»«mo mathvariant=¨bold¨ mathcolor=¨#FF0000¨»§#183;«/mo»«mi mathvariant=¨bold¨ mathcolor=¨#FF0000¨»sin«/mi»«mo mathvariant=¨bold¨ mathcolor=¨#FF0000¨»(«/mo»«mi mathvariant=¨bold¨ mathcolor=¨#FF0000¨»§#969;«/mi»«mo mathvariant=¨bold¨ mathcolor=¨#FF0000¨»§#183;«/mo»«mi mathvariant=¨bold¨ mathcolor=¨#FF0000¨»t«/mi»«mo mathvariant=¨bold¨ mathcolor=¨#FF0000¨»)«/mo»«mspace linebreak=¨newline¨/»«mi mathvariant=¨bold¨ mathcolor=¨#FF0000¨»V«/mi»«mo mathvariant=¨bold¨ mathcolor=¨#FF0000¨»(«/mo»«mn mathvariant=¨bold¨ mathcolor=¨#FF0000¨»0«/mn»«mo mathvariant=¨bold¨ mathcolor=¨#FF0000¨»)«/mo»«mo mathvariant=¨bold¨ mathcolor=¨#FF0000¨»=«/mo»«mo mathvariant=¨bold¨ mathcolor=¨#FF0000¨»-«/mo»«mi mathvariant=¨bold¨ mathcolor=¨#FF0000¨»§#969;A«/mi»«mo mathvariant=¨bold¨ mathcolor=¨#FF0000¨»§#183;«/mo»«mi mathvariant=¨bold¨ mathcolor=¨#FF0000¨»sin«/mi»«mo mathvariant=¨bold¨ mathcolor=¨#FF0000¨»(«/mo»«mi mathvariant=¨bold¨ mathcolor=¨#FF0000¨»§#969;«/mi»«mo mathvariant=¨bold¨ mathcolor=¨#FF0000¨»§#183;«/mo»«mn mathvariant=¨bold¨ mathcolor=¨#FF0000¨»0«/mn»«mo mathvariant=¨bold¨ mathcolor=¨#FF0000¨»)«/mo»«mo mathvariant=¨bold¨ mathcolor=¨#FF0000¨»§#160;«/mo»«mo mathvariant=¨bold¨ mathcolor=¨#FF0000¨»=«/mo»«mo mathvariant=¨bold¨ mathcolor=¨#FF0000¨»-«/mo»«mi mathvariant=¨bold¨ mathcolor=¨#FF0000¨»§#969;A«/mi»«mo mathvariant=¨bold¨ mathcolor=¨#FF0000¨»§#183;«/mo»«mi mathvariant=¨bold¨ mathcolor=¨#FF0000¨»sin«/mi»«mo mathvariant=¨bold¨ mathcolor=¨#FF0000¨»(«/mo»«mn mathvariant=¨bold¨ mathcolor=¨#FF0000¨»0«/mn»«mo mathvariant=¨bold¨ mathcolor=¨#FF0000¨»)«/mo»«mo mathvariant=¨bold¨ mathcolor=¨#FF0000¨»=«/mo»«mo mathvariant=¨bold¨ mathcolor=¨#FF0000¨»-«/mo»«mi mathvariant=¨bold¨ mathcolor=¨#FF0000¨»§#969;A«/mi»«mo mathvariant=¨bold¨ mathcolor=¨#FF0000¨»§#183;«/mo»«mn mathvariant=¨bold¨ mathcolor=¨#FF0000¨»0«/mn»«mo mathvariant=¨bold¨ mathcolor=¨#FF0000¨»=«/mo»«mn mathvariant=¨bold¨ mathcolor=¨#FF0000¨»0«/mn»«mfrac mathcolor=¨#FF0000¨»«mi mathvariant=¨bold¨»m«/mi»«mi mathvariant=¨bold¨»s«/mi»«/mfrac»«/mstyle»«/math»
התאוצה מתארת את קצב השינוי במהירות.
דוגמה להמחשה, יכול להיות חשבון בנק עם מיליארדי שקלים וברגע מסוים אין שינוי בערך הכסף בחשבון.
דוגמה להמחשה, יכול להיות חשבון בנק עם מיליארדי שקלים וברגע מסוים אין שינוי בערך הכסף בחשבון.
2. בשאלה כתוב "משחררים את הקפיץ" הכוונה היא שמשחררים ממנוחה לא זורקים.
לכן ברגע תחילת התנועה המסה נמצאת בנקודת קצה, מהירותה אפס.
3. כל סעיפי השאלה עוסקים בתנעת הגוף בנקודת קצה או בנקודת הראשית , ניתן לענות על השאלות מהבנת התנועה הרמונית
3. כל סעיפי השאלה עוסקים בתנעת הגוף בנקודת קצה או בנקודת הראשית , ניתן לענות על השאלות מהבנת התנועה הרמונית
בלי להשתמש בפונקציות התה"פ במלואן.
4. בפתרון המוצע כאן לשאלה זו, בחרנו ציר תנועה שכיוונו ימינה, כך שהגוף ימצא בנקודת הקצה החיובית.
ביחס לציר זה הכוח השקול שלילי והתאוצה שלילית. השאלה עוסקת בערכה המוחלט של התאוצה ולא בתאוצה.
5. מפונקציית התאוצה כתלות בזמן: «math xmlns=¨http://www.w3.org/1998/Math/MathML¨»«mstyle mathsize=¨20px¨»«mi mathvariant=¨bold¨ mathcolor=¨#FF0000¨»a«/mi»«mo mathvariant=¨bold¨ mathcolor=¨#FF0000¨»(«/mo»«mi mathvariant=¨bold¨ mathcolor=¨#FF0000¨»t«/mi»«mo mathvariant=¨bold¨ mathcolor=¨#FF0000¨»)«/mo»«mo mathvariant=¨bold¨ mathcolor=¨#FF0000¨»=«/mo»«mo mathvariant=¨bold¨ mathcolor=¨#FF0000¨»-«/mo»«msup»«mi mathvariant=¨bold¨ mathcolor=¨#FF0000¨»§#969;«/mi»«mn mathvariant=¨bold¨ mathcolor=¨#FF0000¨»2«/mn»«/msup»«mi mathvariant=¨bold¨ mathcolor=¨#FF0000¨»A«/mi»«mo mathvariant=¨bold¨ mathcolor=¨#FF0000¨»§#183;«/mo»«mi mathvariant=¨bold¨ mathcolor=¨#FF0000¨»cos«/mi»«mo mathvariant=¨bold¨ mathcolor=¨#FF0000¨»(«/mo»«mi mathvariant=¨bold¨ mathcolor=¨#FF0000¨»§#969;t«/mi»«mo mathvariant=¨bold¨ mathcolor=¨#FF0000¨»)«/mo»«/mstyle»«/math» ניתן לראות שברגע t=0 ערך הקוסינוס הוא 1 (מקסימאלי)
וגודל התאוצה הוא מקסימאלי.
6. מפונקציית התאוצה כתלות במקום: «math xmlns=¨http://www.w3.org/1998/Math/MathML¨»«mstyle mathsize=¨20px¨»«mi mathvariant=¨bold¨ mathcolor=¨#FF0000¨»a«/mi»«mo mathvariant=¨bold¨ mathcolor=¨#FF0000¨»(«/mo»«mi mathvariant=¨bold-italic¨ mathcolor=¨#FF0000¨»x«/mi»«mo mathvariant=¨bold¨ mathcolor=¨#FF0000¨»)«/mo»«mo mathvariant=¨bold¨ mathcolor=¨#FF0000¨»=«/mo»«mo mathvariant=¨bold¨ mathcolor=¨#FF0000¨»-«/mo»«msup»«mi mathvariant=¨bold¨ mathcolor=¨#FF0000¨»§#969;«/mi»«mn mathvariant=¨bold¨ mathcolor=¨#FF0000¨»2«/mn»«/msup»«mo mathvariant=¨bold¨ mathcolor=¨#FF0000¨»§#183;«/mo»«mi mathvariant=¨bold-italic¨ mathcolor=¨#FF0000¨»x«/mi»«/mstyle»«/math» ניתן לראות שכאשר הגוף נמצא בנקודת הקצה, ערכו של X שווה
לערך משרעת התנודה , (ערך מקסימאלי) וגדול התאוצה הוא מקסימאלי.
7. מפונקציית v(x) כאשר הגוף נמצא בנקודת המשרעת מהירותו שווה לאפס:
«math xmlns=¨http://www.w3.org/1998/Math/MathML¨»«mstyle mathsize=¨20px¨»«mi mathvariant=¨bold¨ mathcolor=¨#FF0000¨»V«/mi»«mo mathvariant=¨bold¨ mathcolor=¨#FF0000¨»(«/mo»«mi mathvariant=¨bold¨ mathcolor=¨#FF0000¨»X«/mi»«mo mathvariant=¨bold¨ mathcolor=¨#FF0000¨»)«/mo»«mo mathvariant=¨bold¨ mathcolor=¨#FF0000¨»=«/mo»«mo mathvariant=¨bold¨ mathcolor=¨#FF0000¨»§#177;«/mo»«mi mathvariant=¨bold¨ mathcolor=¨#FF0000¨»§#969;«/mi»«mroot mathcolor=¨#FF0000¨»«mrow»«mo mathvariant=¨bold¨»(«/mo»«msup»«mi mathvariant=¨bold¨»A«/mi»«mn mathvariant=¨bold¨»2«/mn»«/msup»«mo mathvariant=¨bold¨»-«/mo»«msup»«mi mathvariant=¨bold¨»X«/mi»«mn mathvariant=¨bold¨»2«/mn»«/msup»«mo mathvariant=¨bold¨»)«/mo»«/mrow»«mrow/»«/mroot»«mspace linebreak=¨newline¨/»«mspace linebreak=¨newline¨/»«mi mathvariant=¨bold¨ mathcolor=¨#FF0000¨»V«/mi»«mo mathvariant=¨bold¨ mathcolor=¨#FF0000¨»(«/mo»«mi mathvariant=¨bold¨ mathcolor=¨#FF0000¨»A«/mi»«mo mathvariant=¨bold¨ mathcolor=¨#FF0000¨»)«/mo»«mo mathvariant=¨bold¨ mathcolor=¨#FF0000¨»=«/mo»«mo mathvariant=¨bold¨ mathcolor=¨#FF0000¨»§#177;«/mo»«mi mathvariant=¨bold¨ mathcolor=¨#FF0000¨»§#969;«/mi»«mroot mathcolor=¨#FF0000¨»«mrow»«mo mathvariant=¨bold¨»(«/mo»«msup»«mi mathvariant=¨bold¨»A«/mi»«mn mathvariant=¨bold¨»2«/mn»«/msup»«mo mathvariant=¨bold¨»-«/mo»«msup»«mi mathvariant=¨bold¨»A«/mi»«mn mathvariant=¨bold¨»2«/mn»«/msup»«mo mathvariant=¨bold¨»)«/mo»«/mrow»«mrow/»«/mroot»«mo mathvariant=¨bold¨ mathcolor=¨#FF0000¨»=«/mo»«mn mathvariant=¨bold¨ mathcolor=¨#FF0000¨»0«/mn»«mfrac mathcolor=¨#FF0000¨»«mi mathvariant=¨bold¨»m«/mi»«mi mathvariant=¨bold¨»s«/mi»«/mfrac»«mspace linebreak=¨newline¨/»«/mstyle»«/math»
8. מפונקציית v(t) ברגע t=0s מהירות הגוף שווה לאפס:
«math xmlns=¨http://www.w3.org/1998/Math/MathML¨»«mstyle mathsize=¨20px¨»«mi mathvariant=¨bold¨ mathcolor=¨#FF0000¨»V«/mi»«mo mathvariant=¨bold¨ mathcolor=¨#FF0000¨»(«/mo»«mi mathvariant=¨bold¨ mathcolor=¨#FF0000¨»t«/mi»«mo mathvariant=¨bold¨ mathcolor=¨#FF0000¨»)«/mo»«mo mathvariant=¨bold¨ mathcolor=¨#FF0000¨»=«/mo»«mo mathvariant=¨bold¨ mathcolor=¨#FF0000¨»-«/mo»«mi mathvariant=¨bold¨ mathcolor=¨#FF0000¨»§#969;A«/mi»«mo mathvariant=¨bold¨ mathcolor=¨#FF0000¨»§#183;«/mo»«mi mathvariant=¨bold¨ mathcolor=¨#FF0000¨»sin«/mi»«mo mathvariant=¨bold¨ mathcolor=¨#FF0000¨»(«/mo»«mi mathvariant=¨bold¨ mathcolor=¨#FF0000¨»§#969;«/mi»«mo mathvariant=¨bold¨ mathcolor=¨#FF0000¨»§#183;«/mo»«mi mathvariant=¨bold¨ mathcolor=¨#FF0000¨»t«/mi»«mo mathvariant=¨bold¨ mathcolor=¨#FF0000¨»)«/mo»«mspace linebreak=¨newline¨/»«mi mathvariant=¨bold¨ mathcolor=¨#FF0000¨»V«/mi»«mo mathvariant=¨bold¨ mathcolor=¨#FF0000¨»(«/mo»«mn mathvariant=¨bold¨ mathcolor=¨#FF0000¨»0«/mn»«mo mathvariant=¨bold¨ mathcolor=¨#FF0000¨»)«/mo»«mo mathvariant=¨bold¨ mathcolor=¨#FF0000¨»=«/mo»«mo mathvariant=¨bold¨ mathcolor=¨#FF0000¨»-«/mo»«mi mathvariant=¨bold¨ mathcolor=¨#FF0000¨»§#969;A«/mi»«mo mathvariant=¨bold¨ mathcolor=¨#FF0000¨»§#183;«/mo»«mi mathvariant=¨bold¨ mathcolor=¨#FF0000¨»sin«/mi»«mo mathvariant=¨bold¨ mathcolor=¨#FF0000¨»(«/mo»«mi mathvariant=¨bold¨ mathcolor=¨#FF0000¨»§#969;«/mi»«mo mathvariant=¨bold¨ mathcolor=¨#FF0000¨»§#183;«/mo»«mn mathvariant=¨bold¨ mathcolor=¨#FF0000¨»0«/mn»«mo mathvariant=¨bold¨ mathcolor=¨#FF0000¨»)«/mo»«mo mathvariant=¨bold¨ mathcolor=¨#FF0000¨»§#160;«/mo»«mo mathvariant=¨bold¨ mathcolor=¨#FF0000¨»=«/mo»«mo mathvariant=¨bold¨ mathcolor=¨#FF0000¨»-«/mo»«mi mathvariant=¨bold¨ mathcolor=¨#FF0000¨»§#969;A«/mi»«mo mathvariant=¨bold¨ mathcolor=¨#FF0000¨»§#183;«/mo»«mi mathvariant=¨bold¨ mathcolor=¨#FF0000¨»sin«/mi»«mo mathvariant=¨bold¨ mathcolor=¨#FF0000¨»(«/mo»«mn mathvariant=¨bold¨ mathcolor=¨#FF0000¨»0«/mn»«mo mathvariant=¨bold¨ mathcolor=¨#FF0000¨»)«/mo»«mo mathvariant=¨bold¨ mathcolor=¨#FF0000¨»=«/mo»«mo mathvariant=¨bold¨ mathcolor=¨#FF0000¨»-«/mo»«mi mathvariant=¨bold¨ mathcolor=¨#FF0000¨»§#969;A«/mi»«mo mathvariant=¨bold¨ mathcolor=¨#FF0000¨»§#183;«/mo»«mn mathvariant=¨bold¨ mathcolor=¨#FF0000¨»0«/mn»«mo mathvariant=¨bold¨ mathcolor=¨#FF0000¨»=«/mo»«mn mathvariant=¨bold¨ mathcolor=¨#FF0000¨»0«/mn»«mfrac mathcolor=¨#FF0000¨»«mi mathvariant=¨bold¨»m«/mi»«mi mathvariant=¨bold¨»s«/mi»«/mfrac»«/mstyle»«/math»
______________________________________________________________________________________