______________________________________________________________________________________
...
زمن حركة الجسم من لحظة بدء حركته حتى وصوله إلى النقطة B هو 0.785 ثانية.
مبادئ الحركة التوافقية البسيطة.
القوة الوحيدة المؤثرة على الجسم A منذ لحظة إطلاقه هي قوة النابض. قوة النابض هي القوة المحصّلة، وهي تتناسب طرديًا مع الموقع.
لذلك يتحرك الجسم A في حركة توافقية بسيطة.
من مبادئ الحركة التوافقية البسيطة، من لحظة بدء الجسم A في الحركة حتى يصل إلى نقطة الاتّزان، يمر ربع دورة زمنية.
نجد زمن حركة الجسم A من لحظة بدء حركته حتى يصل إلى النقطة B، باستخدام صيغة زمن الدورة الملائمة لحركة توافقية بسيطة:
«math xmlns=¨http://www.w3.org/1998/Math/MathML¨»«mi mathvariant=¨bold-italic¨ mathcolor=¨#0000FF¨»t«/mi»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»=«/mo»«mfrac mathcolor=¨#0000FF¨»«mi mathvariant=¨bold¨»T«/mi»«mn mathvariant=¨bold¨»4«/mn»«/mfrac»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»=«/mo»«mfrac mathcolor=¨#0000FF¨»«mrow»«mn mathvariant=¨bold¨»2«/mn»«mo mathvariant=¨bold¨»§#183;«/mo»«mi mathvariant=¨bold¨»§#960;«/mi»«mo mathvariant=¨bold¨»§#183;«/mo»«msqrt»«mstyle displaystyle=¨true¨ mathvariant=¨bold¨»«mfrac»«mi»m«/mi»«mi»k«/mi»«/mfrac»«/mstyle»«/msqrt»«/mrow»«mn mathvariant=¨bold¨»4«/mn»«/mfrac»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»=«/mo»«mfrac mathcolor=¨#0000FF¨»«mrow»«mi mathvariant=¨bold¨»§#960;«/mi»«mo mathvariant=¨bold¨»§#183;«/mo»«msqrt»«mstyle displaystyle=¨true¨ mathvariant=¨bold¨»«mfrac»«mrow»«mn»7«/mn»«mo».«/mo»«mn»5«/mn»«/mrow»«mn»30«/mn»«/mfrac»«/mstyle»«/msqrt»«/mrow»«mn mathvariant=¨bold¨»2«/mn»«/mfrac»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»=«/mo»«mn mathvariant=¨bold¨ mathcolor=¨#0000FF¨»0«/mn»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨».«/mo»«mn mathvariant=¨bold¨ mathcolor=¨#0000FF¨»785«/mn»«mi mathvariant=¨bold-italic¨ mathcolor=¨#0000FF¨»s«/mi»«/math»
وبالتالي فإن زمن حركة الجسم من لحظة بدء حركته حتى وصوله إلى النقطة B هو 0.785 ثانية.
לכן גוף A נע בתנועה הרמונית פשוטה .
מעקרונות התה"פ , מרגע שגוף A מתחיל לנוע ועד שהוא מגיע לנקודת שיווי המשקל עובר רבע זמן מחזור.
נמצא את זמן תנועת גוף A מרגע תחילת תנועתו ועד פגיעתו בנקודה B ,בעזרת נוסחת זמן המחזור המתאים לתה"פ:
«math xmlns=¨http://www.w3.org/1998/Math/MathML¨»«mi mathvariant=¨bold-italic¨ mathcolor=¨#0000FF¨»t«/mi»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»=«/mo»«mfrac mathcolor=¨#0000FF¨»«mi mathvariant=¨bold¨»T«/mi»«mn mathvariant=¨bold¨»4«/mn»«/mfrac»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»=«/mo»«mfrac mathcolor=¨#0000FF¨»«mrow»«mn mathvariant=¨bold¨»2«/mn»«mo mathvariant=¨bold¨»§#183;«/mo»«mi mathvariant=¨bold¨»§#960;«/mi»«mo mathvariant=¨bold¨»§#183;«/mo»«msqrt»«mstyle displaystyle=¨true¨ mathvariant=¨bold¨»«mfrac»«mi»m«/mi»«mi»k«/mi»«/mfrac»«/mstyle»«/msqrt»«/mrow»«mn mathvariant=¨bold¨»4«/mn»«/mfrac»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»=«/mo»«mfrac mathcolor=¨#0000FF¨»«mrow»«mi mathvariant=¨bold¨»§#960;«/mi»«mo mathvariant=¨bold¨»§#183;«/mo»«msqrt»«mstyle displaystyle=¨true¨ mathvariant=¨bold¨»«mfrac»«mrow»«mn»7«/mn»«mo».«/mo»«mn»5«/mn»«/mrow»«mn»30«/mn»«/mfrac»«/mstyle»«/msqrt»«/mrow»«mn mathvariant=¨bold¨»2«/mn»«/mfrac»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»=«/mo»«mn mathvariant=¨bold¨ mathcolor=¨#0000FF¨»0«/mn»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨».«/mo»«mn mathvariant=¨bold¨ mathcolor=¨#0000FF¨»785«/mn»«mi mathvariant=¨bold-italic¨ mathcolor=¨#0000FF¨»s«/mi»«/math»
לכן , זמן תנועת הגוף מרגע תחילת תנועתו ועד שהוא מגיע לנקודה B הוא 0.785 שניות.
.1 الوقت المطلوب لا يتعلق بالجسم B والنابض الأيمن.2. نقطة الاتّزان هي نقطة، ويجب التعامل مع كلا الجسمين كجسمين نقطيين (صغيرين جدًا)
حتى يتمكنوا من الوصول إلى نقطة الاتّزان. 2. נקודת שיווי המשקל היא נקודה , יש להתייחס לשני הגופים כאל גופים נקודתיים(מאוד קטנים)
כדי שהם יוכלו להיות בנקודת שיווי המשקל.
______________________________________________________________________________________

______________________________________________________________________________________
...
السرعة المشتركة للجسمين 0.1 متر في الثانية.
مبادئ الحركية التوافقية البسيطة وحفظ كمية الحركة.
ב.1-لإيجاد السرعة الكلية للجسمين بعد الاصطدام. نجد سرعة الجسمA قبل الاصطدام مباشرة.
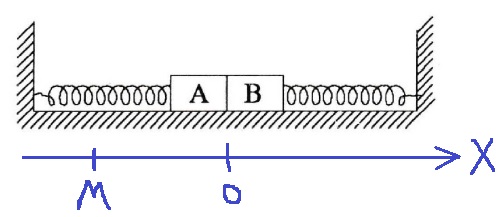
سنقوم بوصف حركة الجسمين بالنسبة للمحور الذي يشير إلى اليمين.
نُشير إلى النقطة التي يتم فيها تحرير الجسم بـ M، ونقطة الاتّزان بـ O.
أوجد سرعة الجسم عند النقطة O باستخدام دالة الموقع كدالة للزمكن:
«math xmlns=¨http://www.w3.org/1998/Math/MathML¨»«mi mathvariant=¨bold¨ mathcolor=¨#0000FF¨»V«/mi»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»(«/mo»«mi mathvariant=¨bold¨ mathcolor=¨#0000FF¨»x«/mi»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»)«/mo»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»=«/mo»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»§#177;«/mo»«mi mathvariant=¨bold¨ mathcolor=¨#0000FF¨»§#969;«/mi»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»§#183;«/mo»«msqrt mathcolor=¨#0000FF¨»«msup»«mi mathvariant=¨bold¨»A«/mi»«mn mathvariant=¨bold¨»2«/mn»«/msup»«mo mathvariant=¨bold¨»-«/mo»«msup»«mi mathvariant=¨bold¨»X«/mi»«mn mathvariant=¨bold¨»2«/mn»«/msup»«/msqrt»«mspace linebreak=¨newline¨»«/mspace»«mi mathvariant=¨bold¨ mathcolor=¨#0000FF¨»V«/mi»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»(«/mo»«mn mathvariant=¨bold¨ mathcolor=¨#0000FF¨»0«/mn»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»)«/mo»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»=«/mo»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»§#177;«/mo»«mi mathvariant=¨bold¨ mathcolor=¨#0000FF¨»§#969;«/mi»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»§#183;«/mo»«msqrt mathcolor=¨#0000FF¨»«msup»«mi mathvariant=¨bold¨»A«/mi»«mn mathvariant=¨bold¨»2«/mn»«/msup»«mo mathvariant=¨bold¨»-«/mo»«msup»«mn mathvariant=¨bold¨»0«/mn»«mn mathvariant=¨bold¨»2«/mn»«/msup»«/msqrt»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»=«/mo»«mfrac mathcolor=¨#0000FF¨»«mrow»«mn mathvariant=¨bold¨»2«/mn»«mo mathvariant=¨bold¨»§#183;«/mo»«mi mathvariant=¨bold¨»§#960;«/mi»«/mrow»«mi mathvariant=¨bold¨»T«/mi»«/mfrac»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»§#183;«/mo»«mi mathvariant=¨bold¨ mathcolor=¨#0000FF¨»A«/mi»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»=«/mo»«mfrac mathcolor=¨#0000FF¨»«mrow»«mn mathvariant=¨bold¨»2«/mn»«mo mathvariant=¨bold¨»§#183;«/mo»«mi mathvariant=¨bold¨»§#960;«/mi»«/mrow»«mrow»«mn mathvariant=¨bold¨»2«/mn»«mo mathvariant=¨bold¨»§#183;«/mo»«mi mathvariant=¨bold¨»§#960;«/mi»«mo mathvariant=¨bold¨»§#183;«/mo»«msqrt»«mstyle displaystyle=¨true¨»«mfrac»«mi mathvariant=¨bold¨»m«/mi»«mi mathvariant=¨bold¨»K«/mi»«/mfrac»«/mstyle»«/msqrt»«/mrow»«/mfrac»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»§#183;«/mo»«mi mathvariant=¨bold¨ mathcolor=¨#0000FF¨»A«/mi»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»=«/mo»«msqrt mathcolor=¨#0000FF¨»«mfrac»«mi mathvariant=¨bold¨»K«/mi»«mi mathvariant=¨bold¨»m«/mi»«/mfrac»«/msqrt»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»§#183;«/mo»«mi mathvariant=¨bold¨ mathcolor=¨#0000FF¨»A«/mi»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»=«/mo»«msqrt mathcolor=¨#0000FF¨»«mfrac»«mn mathvariant=¨bold¨»30«/mn»«mrow»«mn mathvariant=¨bold¨»7«/mn»«mo mathvariant=¨bold¨».«/mo»«mn mathvariant=¨bold¨»5«/mn»«/mrow»«/mfrac»«/msqrt»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»§#183;«/mo»«mn mathvariant=¨bold¨ mathcolor=¨#0000FF¨»0«/mn»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨».«/mo»«mn mathvariant=¨bold¨ mathcolor=¨#0000FF¨»1«/mn»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»=«/mo»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»§#177;«/mo»«mn mathvariant=¨bold¨ mathcolor=¨#0000FF¨»0«/mn»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨».«/mo»«mn mathvariant=¨bold¨ mathcolor=¨#0000FF¨»2«/mn»«mfrac mathcolor=¨#0000FF¨»«mi mathvariant=¨bold¨»m«/mi»«mi mathvariant=¨bold¨»s«/mi»«/mfrac»«/math»
عندما يصل الجسم A إلى النقطة O، يتحرك الجسم في اتجاه المحور وتكون سرعته موجبة.
أثناء الاصطدام، يكون النابضان مرتخيان، وقوة الجاذبية المؤثرة على كل جسم تساوي القوة العمودية على كلمنهما.
عندما يكون الجسمان في نقطة الاتزان، فإن حركتها تتأثر فقط بالقوى الداخلية. يتم حفظ كمبة الحركة الزخم الإجمالي.
نكتب معادلة حفظ كمية الحركة الملاءمة للاصطدام اللدن:
نرمز للسرعة المشتركة للجسمين بعد الاصطدام بـ U.
«math xmlns=¨http://www.w3.org/1998/Math/MathML¨»«msub»«mi mathvariant=¨bold¨ mathcolor=¨#0000FF¨»m«/mi»«mi mathvariant=¨bold¨ mathcolor=¨#0000FF¨»A«/mi»«/msub»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»§#183;«/mo»«msub»«mi mathvariant=¨bold¨ mathcolor=¨#0000FF¨»V«/mi»«mi mathvariant=¨bold¨ mathcolor=¨#0000FF¨»A«/mi»«/msub»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»+«/mo»«msub»«mi mathvariant=¨bold¨ mathcolor=¨#0000FF¨»m«/mi»«mi mathvariant=¨bold¨ mathcolor=¨#0000FF¨»B«/mi»«/msub»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»§#183;«/mo»«msub»«mi mathvariant=¨bold¨ mathcolor=¨#0000FF¨»V«/mi»«mi mathvariant=¨bold¨ mathcolor=¨#0000FF¨»B«/mi»«/msub»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»=«/mo»«mrow mathcolor=¨#0000FF¨»«mo mathvariant=¨bold¨»(«/mo»«msub»«mi mathvariant=¨bold¨»m«/mi»«mi mathvariant=¨bold¨»A«/mi»«/msub»«mo mathvariant=¨bold¨»+«/mo»«msub»«mi mathvariant=¨bold¨»m«/mi»«mi mathvariant=¨bold¨»B«/mi»«/msub»«mo mathvariant=¨bold¨»)«/mo»«/mrow»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»§#183;«/mo»«mi mathvariant=¨bold¨ mathcolor=¨#0000FF¨»U«/mi»«/math»
سرعة الجسم ب قبل الاصطدام تساوي صفرًا. نعبر عن السرعة المشتركة U:
«math xmlns=¨http://www.w3.org/1998/Math/MathML¨»«msub»«mi mathvariant=¨bold¨ mathcolor=¨#0000FF¨»m«/mi»«mi mathvariant=¨bold¨ mathcolor=¨#0000FF¨»A«/mi»«/msub»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»§#183;«/mo»«msub»«mi mathvariant=¨bold¨ mathcolor=¨#0000FF¨»V«/mi»«mi mathvariant=¨bold¨ mathcolor=¨#0000FF¨»A«/mi»«/msub»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»+«/mo»«msub»«mi mathvariant=¨bold¨ mathcolor=¨#0000FF¨»m«/mi»«mi mathvariant=¨bold¨ mathcolor=¨#0000FF¨»B«/mi»«/msub»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»§#183;«/mo»«menclose mathcolor=¨#0000FF¨ notation=¨updiagonalstrike¨»«msub»«mi mathvariant=¨bold¨»V«/mi»«mi mathvariant=¨bold¨»B«/mi»«/msub»«/menclose»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»=«/mo»«mrow mathcolor=¨#0000FF¨»«mo mathvariant=¨bold¨»(«/mo»«msub»«mi mathvariant=¨bold¨»m«/mi»«mi mathvariant=¨bold¨»A«/mi»«/msub»«mo mathvariant=¨bold¨»+«/mo»«msub»«mi mathvariant=¨bold¨»m«/mi»«mi mathvariant=¨bold¨»B«/mi»«/msub»«mo mathvariant=¨bold¨»)«/mo»«/mrow»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»§#183;«/mo»«mi mathvariant=¨bold¨ mathcolor=¨#0000FF¨»U«/mi»«mspace linebreak=¨newline¨»«/mspace»«mspace linebreak=¨newline¨»«/mspace»«mi mathvariant=¨bold¨ mathcolor=¨#0000FF¨»U«/mi»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»=«/mo»«mfrac mathcolor=¨#0000FF¨»«mrow»«msub»«mi mathvariant=¨bold¨»m«/mi»«mi mathvariant=¨bold¨»A«/mi»«/msub»«mo mathvariant=¨bold¨»§#183;«/mo»«msub»«mi mathvariant=¨bold¨»V«/mi»«mi mathvariant=¨bold¨»A«/mi»«/msub»«/mrow»«mrow»«msub»«mi mathvariant=¨bold¨»m«/mi»«mi mathvariant=¨bold¨»A«/mi»«/msub»«mo mathvariant=¨bold¨»+«/mo»«msub»«mi mathvariant=¨bold¨»m«/mi»«mi mathvariant=¨bold¨»B«/mi»«/msub»«/mrow»«/mfrac»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»=«/mo»«mfrac mathcolor=¨#0000FF¨»«mrow»«msub»«mi mathvariant=¨bold¨»m«/mi»«mi mathvariant=¨bold¨»A«/mi»«/msub»«mo mathvariant=¨bold¨»§#183;«/mo»«msub»«mi mathvariant=¨bold¨»V«/mi»«mi mathvariant=¨bold¨»A«/mi»«/msub»«/mrow»«mrow»«msub»«mi mathvariant=¨bold¨»m«/mi»«mi mathvariant=¨bold¨»A«/mi»«/msub»«mo mathvariant=¨bold¨»+«/mo»«msub»«mi mathvariant=¨bold¨»m«/mi»«mi mathvariant=¨bold¨»B«/mi»«/msub»«/mrow»«/mfrac»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»=«/mo»«mfrac mathcolor=¨#0000FF¨»«mrow»«mn mathvariant=¨bold¨»7«/mn»«mo mathvariant=¨bold¨».«/mo»«mn mathvariant=¨bold¨»5«/mn»«mo mathvariant=¨bold¨»§#183;«/mo»«mn mathvariant=¨bold¨»0«/mn»«mo mathvariant=¨bold¨».«/mo»«mn mathvariant=¨bold¨»2«/mn»«/mrow»«mrow»«mn mathvariant=¨bold¨»7«/mn»«mo mathvariant=¨bold¨».«/mo»«mn mathvariant=¨bold¨»5«/mn»«mo mathvariant=¨bold¨»+«/mo»«mn mathvariant=¨bold¨»7«/mn»«mo mathvariant=¨bold¨».«/mo»«mn mathvariant=¨bold¨»5«/mn»«/mrow»«/mfrac»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»=«/mo»«mn mathvariant=¨bold¨ mathcolor=¨#0000FF¨»0«/mn»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨».«/mo»«mn mathvariant=¨bold¨ mathcolor=¨#0000FF¨»1«/mn»«mfrac mathcolor=¨#0000FF¨»«mi mathvariant=¨bold¨»m«/mi»«mi mathvariant=¨bold¨»s«/mi»«/mfrac»«/math»
يتحرك الجسمان معًا بسرعة 0.1 متر في الثانية.
נתאר את תנועת הגופים ביחס לציר שכיוונו ימינה.
נסמן את הנקודה בה הגוף משוחרר ב M , ואת נקודת שיווי המשקל ב O.
נמצא את מהירות הגוף בנקודה O , בעזרת פונקציית מקום זמן:
«math xmlns=¨http://www.w3.org/1998/Math/MathML¨»«mi mathvariant=¨bold¨ mathcolor=¨#0000FF¨»V«/mi»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»(«/mo»«mi mathvariant=¨bold¨ mathcolor=¨#0000FF¨»x«/mi»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»)«/mo»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»=«/mo»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»§#177;«/mo»«mi mathvariant=¨bold¨ mathcolor=¨#0000FF¨»§#969;«/mi»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»§#183;«/mo»«msqrt mathcolor=¨#0000FF¨»«msup»«mi mathvariant=¨bold¨»A«/mi»«mn mathvariant=¨bold¨»2«/mn»«/msup»«mo mathvariant=¨bold¨»-«/mo»«msup»«mi mathvariant=¨bold¨»X«/mi»«mn mathvariant=¨bold¨»2«/mn»«/msup»«/msqrt»«mspace linebreak=¨newline¨»«/mspace»«mi mathvariant=¨bold¨ mathcolor=¨#0000FF¨»V«/mi»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»(«/mo»«mn mathvariant=¨bold¨ mathcolor=¨#0000FF¨»0«/mn»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»)«/mo»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»=«/mo»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»§#177;«/mo»«mi mathvariant=¨bold¨ mathcolor=¨#0000FF¨»§#969;«/mi»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»§#183;«/mo»«msqrt mathcolor=¨#0000FF¨»«msup»«mi mathvariant=¨bold¨»A«/mi»«mn mathvariant=¨bold¨»2«/mn»«/msup»«mo mathvariant=¨bold¨»-«/mo»«msup»«mn mathvariant=¨bold¨»0«/mn»«mn mathvariant=¨bold¨»2«/mn»«/msup»«/msqrt»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»=«/mo»«mfrac mathcolor=¨#0000FF¨»«mrow»«mn mathvariant=¨bold¨»2«/mn»«mo mathvariant=¨bold¨»§#183;«/mo»«mi mathvariant=¨bold¨»§#960;«/mi»«/mrow»«mi mathvariant=¨bold¨»T«/mi»«/mfrac»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»§#183;«/mo»«mi mathvariant=¨bold¨ mathcolor=¨#0000FF¨»A«/mi»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»=«/mo»«mfrac mathcolor=¨#0000FF¨»«mrow»«mn mathvariant=¨bold¨»2«/mn»«mo mathvariant=¨bold¨»§#183;«/mo»«mi mathvariant=¨bold¨»§#960;«/mi»«/mrow»«mrow»«mn mathvariant=¨bold¨»2«/mn»«mo mathvariant=¨bold¨»§#183;«/mo»«mi mathvariant=¨bold¨»§#960;«/mi»«mo mathvariant=¨bold¨»§#183;«/mo»«msqrt»«mstyle displaystyle=¨true¨»«mfrac»«mi mathvariant=¨bold¨»m«/mi»«mi mathvariant=¨bold¨»K«/mi»«/mfrac»«/mstyle»«/msqrt»«/mrow»«/mfrac»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»§#183;«/mo»«mi mathvariant=¨bold¨ mathcolor=¨#0000FF¨»A«/mi»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»=«/mo»«msqrt mathcolor=¨#0000FF¨»«mfrac»«mi mathvariant=¨bold¨»K«/mi»«mi mathvariant=¨bold¨»m«/mi»«/mfrac»«/msqrt»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»§#183;«/mo»«mi mathvariant=¨bold¨ mathcolor=¨#0000FF¨»A«/mi»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»=«/mo»«msqrt mathcolor=¨#0000FF¨»«mfrac»«mn mathvariant=¨bold¨»30«/mn»«mrow»«mn mathvariant=¨bold¨»7«/mn»«mo mathvariant=¨bold¨».«/mo»«mn mathvariant=¨bold¨»5«/mn»«/mrow»«/mfrac»«/msqrt»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»§#183;«/mo»«mn mathvariant=¨bold¨ mathcolor=¨#0000FF¨»0«/mn»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨».«/mo»«mn mathvariant=¨bold¨ mathcolor=¨#0000FF¨»1«/mn»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»=«/mo»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»§#177;«/mo»«mn mathvariant=¨bold¨ mathcolor=¨#0000FF¨»0«/mn»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨».«/mo»«mn mathvariant=¨bold¨ mathcolor=¨#0000FF¨»2«/mn»«mfrac mathcolor=¨#0000FF¨»«mi mathvariant=¨bold¨»m«/mi»«mi mathvariant=¨bold¨»s«/mi»«/mfrac»«/math»
כאשר גוף A מגיע לנקודה O , הגוף נע בכיוון הציר מהירותו חיובית.
בזמן ההתנגשות הקפיצים רפויים , כוח הכובד הפועל על כל גוף מתקזז עם כוח הנורמל.
כאשר הגופים נמצאים בנקודת שיווי המשקל תנועתם מושפעת מכוחות פנימיים בלבד. התנע הכולל נשמר.
נכתוב את משוואת שימור התנע המתאימה להתנגשות פלסטית:
נסמן את מהירות שני הגופים יחד אחרי ההתנגשות ב U.
«math xmlns=¨http://www.w3.org/1998/Math/MathML¨»«msub»«mi mathvariant=¨bold¨ mathcolor=¨#0000FF¨»m«/mi»«mi mathvariant=¨bold¨ mathcolor=¨#0000FF¨»A«/mi»«/msub»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»§#183;«/mo»«msub»«mi mathvariant=¨bold¨ mathcolor=¨#0000FF¨»V«/mi»«mi mathvariant=¨bold¨ mathcolor=¨#0000FF¨»A«/mi»«/msub»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»+«/mo»«msub»«mi mathvariant=¨bold¨ mathcolor=¨#0000FF¨»m«/mi»«mi mathvariant=¨bold¨ mathcolor=¨#0000FF¨»B«/mi»«/msub»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»§#183;«/mo»«msub»«mi mathvariant=¨bold¨ mathcolor=¨#0000FF¨»V«/mi»«mi mathvariant=¨bold¨ mathcolor=¨#0000FF¨»B«/mi»«/msub»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»=«/mo»«mrow mathcolor=¨#0000FF¨»«mo mathvariant=¨bold¨»(«/mo»«msub»«mi mathvariant=¨bold¨»m«/mi»«mi mathvariant=¨bold¨»A«/mi»«/msub»«mo mathvariant=¨bold¨»+«/mo»«msub»«mi mathvariant=¨bold¨»m«/mi»«mi mathvariant=¨bold¨»B«/mi»«/msub»«mo mathvariant=¨bold¨»)«/mo»«/mrow»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»§#183;«/mo»«mi mathvariant=¨bold¨ mathcolor=¨#0000FF¨»U«/mi»«/math»
מהירות גוף B לפני ההתנגשות שווה לאפס. נבטא את המהירות המשותפת U:
«math xmlns=¨http://www.w3.org/1998/Math/MathML¨»«msub»«mi mathvariant=¨bold¨ mathcolor=¨#0000FF¨»m«/mi»«mi mathvariant=¨bold¨ mathcolor=¨#0000FF¨»A«/mi»«/msub»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»§#183;«/mo»«msub»«mi mathvariant=¨bold¨ mathcolor=¨#0000FF¨»V«/mi»«mi mathvariant=¨bold¨ mathcolor=¨#0000FF¨»A«/mi»«/msub»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»+«/mo»«msub»«mi mathvariant=¨bold¨ mathcolor=¨#0000FF¨»m«/mi»«mi mathvariant=¨bold¨ mathcolor=¨#0000FF¨»B«/mi»«/msub»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»§#183;«/mo»«menclose mathcolor=¨#0000FF¨ notation=¨updiagonalstrike¨»«msub»«mi mathvariant=¨bold¨»V«/mi»«mi mathvariant=¨bold¨»B«/mi»«/msub»«/menclose»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»=«/mo»«mrow mathcolor=¨#0000FF¨»«mo mathvariant=¨bold¨»(«/mo»«msub»«mi mathvariant=¨bold¨»m«/mi»«mi mathvariant=¨bold¨»A«/mi»«/msub»«mo mathvariant=¨bold¨»+«/mo»«msub»«mi mathvariant=¨bold¨»m«/mi»«mi mathvariant=¨bold¨»B«/mi»«/msub»«mo mathvariant=¨bold¨»)«/mo»«/mrow»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»§#183;«/mo»«mi mathvariant=¨bold¨ mathcolor=¨#0000FF¨»U«/mi»«mspace linebreak=¨newline¨»«/mspace»«mspace linebreak=¨newline¨»«/mspace»«mi mathvariant=¨bold¨ mathcolor=¨#0000FF¨»U«/mi»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»=«/mo»«mfrac mathcolor=¨#0000FF¨»«mrow»«msub»«mi mathvariant=¨bold¨»m«/mi»«mi mathvariant=¨bold¨»A«/mi»«/msub»«mo mathvariant=¨bold¨»§#183;«/mo»«msub»«mi mathvariant=¨bold¨»V«/mi»«mi mathvariant=¨bold¨»A«/mi»«/msub»«/mrow»«mrow»«msub»«mi mathvariant=¨bold¨»m«/mi»«mi mathvariant=¨bold¨»A«/mi»«/msub»«mo mathvariant=¨bold¨»+«/mo»«msub»«mi mathvariant=¨bold¨»m«/mi»«mi mathvariant=¨bold¨»B«/mi»«/msub»«/mrow»«/mfrac»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»=«/mo»«mfrac mathcolor=¨#0000FF¨»«mrow»«msub»«mi mathvariant=¨bold¨»m«/mi»«mi mathvariant=¨bold¨»A«/mi»«/msub»«mo mathvariant=¨bold¨»§#183;«/mo»«msub»«mi mathvariant=¨bold¨»V«/mi»«mi mathvariant=¨bold¨»A«/mi»«/msub»«/mrow»«mrow»«msub»«mi mathvariant=¨bold¨»m«/mi»«mi mathvariant=¨bold¨»A«/mi»«/msub»«mo mathvariant=¨bold¨»+«/mo»«msub»«mi mathvariant=¨bold¨»m«/mi»«mi mathvariant=¨bold¨»B«/mi»«/msub»«/mrow»«/mfrac»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»=«/mo»«mfrac mathcolor=¨#0000FF¨»«mrow»«mn mathvariant=¨bold¨»7«/mn»«mo mathvariant=¨bold¨».«/mo»«mn mathvariant=¨bold¨»5«/mn»«mo mathvariant=¨bold¨»§#183;«/mo»«mn mathvariant=¨bold¨»0«/mn»«mo mathvariant=¨bold¨».«/mo»«mn mathvariant=¨bold¨»2«/mn»«/mrow»«mrow»«mn mathvariant=¨bold¨»7«/mn»«mo mathvariant=¨bold¨».«/mo»«mn mathvariant=¨bold¨»5«/mn»«mo mathvariant=¨bold¨»+«/mo»«mn mathvariant=¨bold¨»7«/mn»«mo mathvariant=¨bold¨».«/mo»«mn mathvariant=¨bold¨»5«/mn»«/mrow»«/mfrac»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»=«/mo»«mn mathvariant=¨bold¨ mathcolor=¨#0000FF¨»0«/mn»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨».«/mo»«mn mathvariant=¨bold¨ mathcolor=¨#0000FF¨»1«/mn»«mfrac mathcolor=¨#0000FF¨»«mi mathvariant=¨bold¨»m«/mi»«mi mathvariant=¨bold¨»s«/mi»«/mfrac»«/math»
שני הגופים נעים יחד במהירות 0.1 מטר לשנייה.
1. يمكن إيجاد سرعة الجسم A قبل الاصطدام مباشرة باستخدام دالة السرعة-الزمن.
اعتمادًا على المحور المختار في الحل، يجب إضافة زاوية طور ابتدائية مقدارها «math xmlns=¨http://www.w3.org/1998/Math/MathML¨»«mtext mathvariant=¨bold¨ mathcolor=¨#FF0000¨»§#960;«/mtext»«/math» راديان.
2. ينبغي أن نفترض أن مدة الاصطدام قصير جدًا، بحيث تبقى النوابض مرتخية طوال الاصطدام.
والأجسام لا تتأثر إلا بالقوى الداخلية أثناء الاصطدام.
בהתאם הציר הנבחר בפתרון יש להוסיף זווית מופע התחלתית של פאי רדיאן.
2. בזמן ההתנגשות הקפיצים רפויים ,בזמן ההתנגשות הגופים מושפעים רק מהכוחות הפנימיים.
______________________________________________________________________________________
ب.
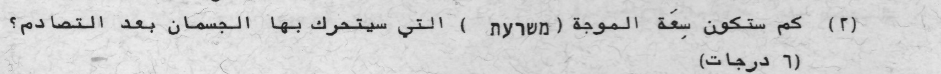
______________________________________________________________________________________
...
«math xmlns=¨http://www.w3.org/1998/Math/MathML¨»«mi mathvariant=¨bold¨»A«/mi»«mo mathvariant=¨bold¨»=«/mo»«mn mathvariant=¨bold¨»0«/mn»«mo mathvariant=¨bold¨».«/mo»«mn mathvariant=¨bold¨»05«/mn»«mi mathvariant=¨bold¨»m«/mi»«/math»
مبادئ الحركة التوافقية. التعامل مع الجسمين كجسم واحد والنابضين كنابض واحد.
بعد الاصطدام، يتحرك الجسمان معًا كجسم واحد.
عندما يتحرك الجسمان معًا متر واحد إلى اليمين، ينكمش النابض الأيمن بمقدار متر واحد ويُشغل قوة مقدارها 30 نيوتن لكل متر على الجسم الأيسر.
من ناحية أخرى، يتم تمدّد النابض الأيسر بمقدار متر ويُشغل أيضًا قوة إلى اليسار مقدارها 30 نيوتن لكل متر.
يمكن التعامل مع النابضين كنابض واحد مع ثابت نابض 60 نيوتن لكل متر.
نستخدم دالة السرعة كدالة للموقع، في اللحظة التي يمر فيها الجسم بنقطة الاتّزان.
نعبر من هذا التعبير عن السعة، وفقًا للكتلة المشتركة. ومعامل النابض المحصّل مقداره 60 نيوتن لكل متر:
«math xmlns=¨http://www.w3.org/1998/Math/MathML¨»«mi mathvariant=¨bold¨ mathcolor=¨#0000FF¨»V«/mi»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»(«/mo»«mi mathvariant=¨bold¨ mathcolor=¨#0000FF¨»x«/mi»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»)«/mo»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»=«/mo»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»§#177;«/mo»«mi mathvariant=¨bold¨ mathcolor=¨#0000FF¨»§#969;«/mi»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»§#183;«/mo»«msqrt mathcolor=¨#0000FF¨»«msup»«mi mathvariant=¨bold¨»A«/mi»«mn mathvariant=¨bold¨»2«/mn»«/msup»«mo mathvariant=¨bold¨»-«/mo»«msup»«mi mathvariant=¨bold¨»X«/mi»«mn mathvariant=¨bold¨»2«/mn»«/msup»«/msqrt»«mspace linebreak=¨newline¨»«/mspace»«mspace linebreak=¨newline¨»«/mspace»«mi mathvariant=¨bold¨ mathcolor=¨#0000FF¨»V«/mi»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»(«/mo»«mn mathvariant=¨bold¨ mathcolor=¨#0000FF¨»0«/mn»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»)«/mo»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»=«/mo»«mi mathvariant=¨bold¨ mathcolor=¨#0000FF¨»§#969;«/mi»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»§#183;«/mo»«mi mathvariant=¨bold¨ mathcolor=¨#0000FF¨»A«/mi»«mspace linebreak=¨newline¨»«/mspace»«mspace linebreak=¨newline¨»«/mspace»«mi mathvariant=¨bold¨ mathcolor=¨#0000FF¨»A«/mi»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»=«/mo»«mfrac mathcolor=¨#0000FF¨»«mrow»«mi mathvariant=¨bold¨»V«/mi»«mo mathvariant=¨bold¨»(«/mo»«mn mathvariant=¨bold¨»0«/mn»«mo mathvariant=¨bold¨»)«/mo»«/mrow»«mi mathvariant=¨bold¨»§#969;«/mi»«/mfrac»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»=«/mo»«mfrac mathcolor=¨#0000FF¨»«mrow»«mi mathvariant=¨bold¨»V«/mi»«mo mathvariant=¨bold¨»(«/mo»«mn mathvariant=¨bold¨»0«/mn»«mo mathvariant=¨bold¨»)«/mo»«/mrow»«mstyle displaystyle=¨true¨»«mfrac»«menclose notation=¨updiagonalstrike¨»«mn mathvariant=¨bold¨»2«/mn»«mo mathvariant=¨bold¨»§#183;«/mo»«mi mathvariant=¨bold¨»§#960;«/mi»«/menclose»«mrow»«menclose notation=¨updiagonalstrike¨»«mn mathvariant=¨bold¨»2«/mn»«mo mathvariant=¨bold¨»§#183;«/mo»«mi mathvariant=¨bold¨»§#960;«/mi»«/menclose»«mo mathvariant=¨bold¨»§#183;«/mo»«msqrt»«mstyle mathvariant=¨bold¨»«mfrac»«msub»«mi»m«/mi»«mi»T«/mi»«/msub»«msub»«mi»K«/mi»«mi»T«/mi»«/msub»«/mfrac»«/mstyle»«/msqrt»«/mrow»«/mfrac»«/mstyle»«/mfrac»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»=«/mo»«mi mathvariant=¨bold¨ mathcolor=¨#0000FF¨»V«/mi»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»(«/mo»«mn mathvariant=¨bold¨ mathcolor=¨#0000FF¨»0«/mn»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»)«/mo»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»§#183;«/mo»«msqrt mathcolor=¨#0000FF¨»«mfrac»«msub»«mi mathvariant=¨bold¨»K«/mi»«mi mathvariant=¨bold¨»T«/mi»«/msub»«msub»«mi mathvariant=¨bold¨»m«/mi»«mi mathvariant=¨bold¨»T«/mi»«/msub»«/mfrac»«/msqrt»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»=«/mo»«mn mathvariant=¨bold¨ mathcolor=¨#0000FF¨»0«/mn»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨».«/mo»«mn mathvariant=¨bold¨ mathcolor=¨#0000FF¨»1«/mn»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»§#183;«/mo»«msqrt mathcolor=¨#0000FF¨»«mstyle mathvariant=¨bold¨»«mfrac»«mn»15«/mn»«mn»60«/mn»«/mfrac»«/mstyle»«/msqrt»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»=«/mo»«mn mathvariant=¨bold¨ mathcolor=¨#0000FF¨»0«/mn»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨».«/mo»«mn mathvariant=¨bold¨ mathcolor=¨#0000FF¨»05«/mn»«mi mathvariant=¨bold¨ mathcolor=¨#0000FF¨»m«/mi»«/math»
سيتحرك الجسمان بسعة مقدارها 5 سم.
يبدو أن النابضين موصلان على التوالي، ولكن ميكانيكيًا لا يمكن التعامل معهما كنوابض موصولة على التوالي.
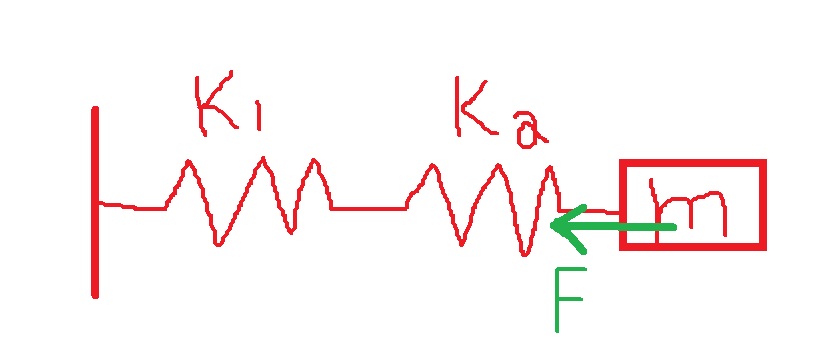
إذا قمنا بربط نابضين متطابقين بجسم ثابت النابض لكل منهما هو 30 نيوتن على التوالي، وحركنا الجسم مسافة متر واحد.
ستؤثر قوة على الجسم بالصورة التالية:
القوة المؤثرة على الجسم ستكون أقل من 30 نيوتن. حسب توصيل النوابض على التوالي:
«math xmlns=¨http://www.w3.org/1998/Math/MathML¨»«mi mathvariant=¨bold¨ mathcolor=¨#FF0000¨»F«/mi»«mo mathvariant=¨bold¨ mathcolor=¨#FF0000¨»=«/mo»«msub»«mi mathvariant=¨bold¨ mathcolor=¨#FF0000¨»K«/mi»«mi mathvariant=¨bold¨ mathcolor=¨#FF0000¨»T«/mi»«/msub»«mo mathvariant=¨bold¨ mathcolor=¨#FF0000¨»§#183;«/mo»«mo mathvariant=¨bold¨ mathcolor=¨#FF0000¨»§#8710;«/mo»«mi mathvariant=¨bold¨ mathcolor=¨#FF0000¨»L«/mi»«mspace linebreak=¨newline¨»«/mspace»«mspace linebreak=¨newline¨»«/mspace»«mi mathvariant=¨bold¨ mathcolor=¨#FF0000¨»F«/mi»«mo mathvariant=¨bold¨ mathcolor=¨#FF0000¨»=«/mo»«mfrac mathcolor=¨#FF0000¨»«mrow»«msub»«mi mathvariant=¨bold¨»K«/mi»«mn mathvariant=¨bold¨»1«/mn»«/msub»«mo mathvariant=¨bold¨»§#183;«/mo»«msub»«mi mathvariant=¨bold¨»K«/mi»«mn mathvariant=¨bold¨»2«/mn»«/msub»«/mrow»«mrow»«msub»«mi mathvariant=¨bold¨»K«/mi»«mn mathvariant=¨bold¨»1«/mn»«/msub»«mo mathvariant=¨bold¨»+«/mo»«msub»«mi mathvariant=¨bold¨»K«/mi»«mn mathvariant=¨bold¨»2«/mn»«/msub»«/mrow»«/mfrac»«mo mathvariant=¨bold¨ mathcolor=¨#FF0000¨»§#183;«/mo»«mo mathvariant=¨bold¨ mathcolor=¨#FF0000¨»§#8710;«/mo»«mi mathvariant=¨bold¨ mathcolor=¨#FF0000¨»L«/mi»«mo mathvariant=¨bold¨ mathcolor=¨#FF0000¨»=«/mo»«mfrac mathcolor=¨#FF0000¨»«mrow»«mn mathvariant=¨bold¨»30«/mn»«mo mathvariant=¨bold¨»§#183;«/mo»«mn mathvariant=¨bold¨»30«/mn»«/mrow»«mrow»«mn mathvariant=¨bold¨»30«/mn»«mo mathvariant=¨bold¨»+«/mo»«mn mathvariant=¨bold¨»30«/mn»«/mrow»«/mfrac»«mo mathvariant=¨bold¨ mathcolor=¨#FF0000¨»§#183;«/mo»«mn mathvariant=¨bold¨ mathcolor=¨#FF0000¨»1«/mn»«mo mathvariant=¨bold¨ mathcolor=¨#FF0000¨»=«/mo»«mn mathvariant=¨bold¨ mathcolor=¨#FF0000¨»15«/mn»«mi mathvariant=¨bold¨ mathcolor=¨#FF0000¨»N«/mi»«/math»
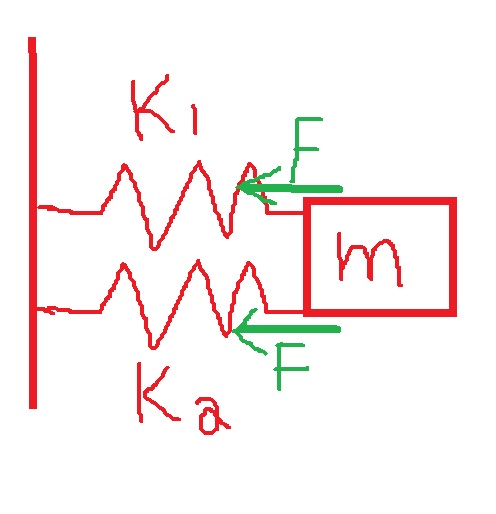
إذا قمنا بربط هذين النابضين على التوازي مع نفس الجسم، وحركنا الجسم مسافة متر. كل من النابضين سوف يُشغل قوة على الجسم، على النحو التالي:
القوة المؤثرة على الجسم ستكون 60 نيوتن. وفقًا لمبادئ توصيل النوابض على التوازي:
«math xmlns=¨http://www.w3.org/1998/Math/MathML¨»«mi mathvariant=¨bold¨ mathcolor=¨#FF0000¨»F«/mi»«mo mathvariant=¨bold¨ mathcolor=¨#FF0000¨»=«/mo»«msub»«mi mathvariant=¨bold¨ mathcolor=¨#FF0000¨»K«/mi»«mi mathvariant=¨bold¨ mathcolor=¨#FF0000¨»T«/mi»«/msub»«mo mathvariant=¨bold¨ mathcolor=¨#FF0000¨»§#183;«/mo»«mo mathvariant=¨bold¨ mathcolor=¨#FF0000¨»§#8710;«/mo»«mi mathvariant=¨bold¨ mathcolor=¨#FF0000¨»L«/mi»«mspace linebreak=¨newline¨»«/mspace»«mspace linebreak=¨newline¨»«/mspace»«mi mathvariant=¨bold¨ mathcolor=¨#FF0000¨»F«/mi»«mo mathvariant=¨bold¨ mathcolor=¨#FF0000¨»=«/mo»«mrow mathcolor=¨#FF0000¨»«mo mathvariant=¨bold¨»(«/mo»«msub»«mi mathvariant=¨bold¨»K«/mi»«mn mathvariant=¨bold¨»1«/mn»«/msub»«mo mathvariant=¨bold¨»+«/mo»«msub»«mi mathvariant=¨bold¨»K«/mi»«mn mathvariant=¨bold¨»2«/mn»«/msub»«mo mathvariant=¨bold¨»)«/mo»«/mrow»«mo mathvariant=¨bold¨ mathcolor=¨#FF0000¨»§#183;«/mo»«mo mathvariant=¨bold¨ mathcolor=¨#FF0000¨»§#8710;«/mo»«mi mathvariant=¨bold¨ mathcolor=¨#FF0000¨»L«/mi»«mo mathvariant=¨bold¨ mathcolor=¨#FF0000¨»=«/mo»«mrow mathcolor=¨#FF0000¨»«mo mathvariant=¨bold¨»(«/mo»«mn mathvariant=¨bold¨»30«/mn»«mo mathvariant=¨bold¨»+«/mo»«mn mathvariant=¨bold¨»30«/mn»«mo mathvariant=¨bold¨»)«/mo»«/mrow»«mo mathvariant=¨bold¨ mathcolor=¨#FF0000¨»§#183;«/mo»«mn mathvariant=¨bold¨ mathcolor=¨#FF0000¨»1«/mn»«mo mathvariant=¨bold¨ mathcolor=¨#FF0000¨»=«/mo»«mn mathvariant=¨bold¨ mathcolor=¨#FF0000¨»60«/mn»«mi mathvariant=¨bold¨ mathcolor=¨#FF0000¨»N«/mi»«/math»
باختصار: القوى التي تؤثر بها النوابض على الجسم في الحالة الموضحة في السؤال مناسبة لتوصيل النوابض على التوازي.
وليس لتوصيل النوابض على التوالي.
אם נחבר לגוף שני קפיצים זהים בעלי קבוע קפיץ של 30 ניוטון בטור, ונסיט את הגוף במטר.
יפעל על הגוף כוח באופן הבא:
הכוח הפועל על הגוף יהיה קטן מ 30 ניוטון. בהתאם לחיבור קפיצים בטור:
«math xmlns=¨http://www.w3.org/1998/Math/MathML¨»«mi mathvariant=¨bold¨ mathcolor=¨#FF0000¨»F«/mi»«mo mathvariant=¨bold¨ mathcolor=¨#FF0000¨»=«/mo»«msub»«mi mathvariant=¨bold¨ mathcolor=¨#FF0000¨»K«/mi»«mi mathvariant=¨bold¨ mathcolor=¨#FF0000¨»T«/mi»«/msub»«mo mathvariant=¨bold¨ mathcolor=¨#FF0000¨»§#183;«/mo»«mo mathvariant=¨bold¨ mathcolor=¨#FF0000¨»§#8710;«/mo»«mi mathvariant=¨bold¨ mathcolor=¨#FF0000¨»L«/mi»«mspace linebreak=¨newline¨»«/mspace»«mspace linebreak=¨newline¨»«/mspace»«mi mathvariant=¨bold¨ mathcolor=¨#FF0000¨»F«/mi»«mo mathvariant=¨bold¨ mathcolor=¨#FF0000¨»=«/mo»«mfrac mathcolor=¨#FF0000¨»«mrow»«msub»«mi mathvariant=¨bold¨»K«/mi»«mn mathvariant=¨bold¨»1«/mn»«/msub»«mo mathvariant=¨bold¨»§#183;«/mo»«msub»«mi mathvariant=¨bold¨»K«/mi»«mn mathvariant=¨bold¨»2«/mn»«/msub»«/mrow»«mrow»«msub»«mi mathvariant=¨bold¨»K«/mi»«mn mathvariant=¨bold¨»1«/mn»«/msub»«mo mathvariant=¨bold¨»+«/mo»«msub»«mi mathvariant=¨bold¨»K«/mi»«mn mathvariant=¨bold¨»2«/mn»«/msub»«/mrow»«/mfrac»«mo mathvariant=¨bold¨ mathcolor=¨#FF0000¨»§#183;«/mo»«mo mathvariant=¨bold¨ mathcolor=¨#FF0000¨»§#8710;«/mo»«mi mathvariant=¨bold¨ mathcolor=¨#FF0000¨»L«/mi»«mo mathvariant=¨bold¨ mathcolor=¨#FF0000¨»=«/mo»«mfrac mathcolor=¨#FF0000¨»«mrow»«mn mathvariant=¨bold¨»30«/mn»«mo mathvariant=¨bold¨»§#183;«/mo»«mn mathvariant=¨bold¨»30«/mn»«/mrow»«mrow»«mn mathvariant=¨bold¨»30«/mn»«mo mathvariant=¨bold¨»+«/mo»«mn mathvariant=¨bold¨»30«/mn»«/mrow»«/mfrac»«mo mathvariant=¨bold¨ mathcolor=¨#FF0000¨»§#183;«/mo»«mn mathvariant=¨bold¨ mathcolor=¨#FF0000¨»1«/mn»«mo mathvariant=¨bold¨ mathcolor=¨#FF0000¨»=«/mo»«mn mathvariant=¨bold¨ mathcolor=¨#FF0000¨»15«/mn»«mi mathvariant=¨bold¨ mathcolor=¨#FF0000¨»N«/mi»«/math»
אם נחבר את אותם שני הקפיצים במקביל לאותו הגוף ,ונסיט את הגוף במטר. כל אחד משני הקפיצים
יפעיל כוח על הגוף, באופן הבא:
הכוח שיפעל על הגוף יהיה 60 ניוטון. בהתאם לעקרונות חיבור קפיצים במקביל:
«math xmlns=¨http://www.w3.org/1998/Math/MathML¨»«mi mathvariant=¨bold¨ mathcolor=¨#FF0000¨»F«/mi»«mo mathvariant=¨bold¨ mathcolor=¨#FF0000¨»=«/mo»«msub»«mi mathvariant=¨bold¨ mathcolor=¨#FF0000¨»K«/mi»«mi mathvariant=¨bold¨ mathcolor=¨#FF0000¨»T«/mi»«/msub»«mo mathvariant=¨bold¨ mathcolor=¨#FF0000¨»§#183;«/mo»«mo mathvariant=¨bold¨ mathcolor=¨#FF0000¨»§#8710;«/mo»«mi mathvariant=¨bold¨ mathcolor=¨#FF0000¨»L«/mi»«mspace linebreak=¨newline¨»«/mspace»«mspace linebreak=¨newline¨»«/mspace»«mi mathvariant=¨bold¨ mathcolor=¨#FF0000¨»F«/mi»«mo mathvariant=¨bold¨ mathcolor=¨#FF0000¨»=«/mo»«mrow mathcolor=¨#FF0000¨»«mo mathvariant=¨bold¨»(«/mo»«msub»«mi mathvariant=¨bold¨»K«/mi»«mn mathvariant=¨bold¨»1«/mn»«/msub»«mo mathvariant=¨bold¨»+«/mo»«msub»«mi mathvariant=¨bold¨»K«/mi»«mn mathvariant=¨bold¨»2«/mn»«/msub»«mo mathvariant=¨bold¨»)«/mo»«/mrow»«mo mathvariant=¨bold¨ mathcolor=¨#FF0000¨»§#183;«/mo»«mo mathvariant=¨bold¨ mathcolor=¨#FF0000¨»§#8710;«/mo»«mi mathvariant=¨bold¨ mathcolor=¨#FF0000¨»L«/mi»«mo mathvariant=¨bold¨ mathcolor=¨#FF0000¨»=«/mo»«mrow mathcolor=¨#FF0000¨»«mo mathvariant=¨bold¨»(«/mo»«mn mathvariant=¨bold¨»30«/mn»«mo mathvariant=¨bold¨»+«/mo»«mn mathvariant=¨bold¨»30«/mn»«mo mathvariant=¨bold¨»)«/mo»«/mrow»«mo mathvariant=¨bold¨ mathcolor=¨#FF0000¨»§#183;«/mo»«mn mathvariant=¨bold¨ mathcolor=¨#FF0000¨»1«/mn»«mo mathvariant=¨bold¨ mathcolor=¨#FF0000¨»=«/mo»«mn mathvariant=¨bold¨ mathcolor=¨#FF0000¨»60«/mn»«mi mathvariant=¨bold¨ mathcolor=¨#FF0000¨»N«/mi»«/math»
לסיכום: הכוחות שהקפיצים מפעילים על הגוף במקרה המתואר בשאלה מתאימים לחיבור קפיצים במקביל
ולא לחיבור קפיצים בטור.
______________________________________________________________________________________

______________________________________________________________________________________
...
سوف يلتقي الجسمين في نقطة الاتّزان. وسيكون البعد بينهما وبين نقطة الاتّزان صفرًا.
مبادئ الحركة التوافقية البسيطة.
زمن الدورة لجسم مربوط بنابض ويتحرك حركة توافقية بسيطة، يتعلق فقط على كتلة الجسم وثابت النابض.
كلا الجسمين لهما نفس الكتلة، وهما موصلان بنابضين متطابقين. لذلك، زمن الدورة هو نفسه.
من لحظة بدء حركة الجسمين حتى وصولهما إلى نقطة الاتزان، يمر ربع دورة زمنية.
نظرًا لأن زمن الدورة هو نفسه، فإن الجسمين سوف يصطدمان في نقطة الاتّزان.
ويكون البعد بين الجسمين في نقطة الاتّزان في لحظة الاصطدام صفرًا.
לשני הגופים מסה זהה , והם מחוברים לקפיצים זהים . לכן זמני המחזור זהים.
מרגע שהגופים מתחילים לנוע ועד שהם מגיעים לנקודת שיווי המשקל ,עובר רבע זמן מחזור. מכיוון שזמני המחזור זהים , הגופים יתנגשו בנקודת שיווי המשקל. מרחק הגופים מנקודת שיווי המשקל ברגע ההתנגשות הוא אפס.
1.من المثير للدهشة أنه في الحركة التوافقية البسيطة، لا يتعلق زمن الدورة على السعة.
ليس من المستغرب أن محرري امتحان البجروت يحبون السؤال عن علاقة زمن الدورة بالسعة.
2. عندما تكون السعة كبيرة، يكون البعد بين طرفي الحركة أكبر، ولكن السرعة في كل نقطة تكون أيضًا أكبر.
وبالتالي فإن زمن الدورة لا يتعلق بسعة الاهتزاز.
3. هناك عدد لا بأس به من النقاط "المفاجئة" في المنهاج الدراسي، يجب عليك التركيز عليها وفهمها جيدًا. ومن الجدير أن نتذكر أيضًا...
ولا تتفاجأوا من أسئلة البجروت.
أمثلة أخرى: زاوية ميل الخيط المستخدم كمقياس تسارع لا تتعلق على الكتلة. إن تسارع الجاذبية لجميع الأجسام على الأرض هو نفسه.
سرعة الجسم المتحرك على مسار رأسي أملس لا تتعلق على شكل المسار.
يمكن لأي شخص أن يقف على ميزان عادي ويرى أن القيمة المعروضة تختلف عن القيمة الحقيقية (وزن وهمي). באופן לא מפתיע עורכי שאלות הבגרות אוהבים לשאול על זמן המחזור בתלות במשרעת.
2. כאשר המשרעת גדולה מרחק התנועה מנקודת קצה לנקודת קצה הוא גדול יותר, אך גם המהירות בכל נקודה גדולה יותר.
כך שזמן המחזור לא תלוי במשרעת התנודה.
3. בתכנית הלימודים יש לא מעט דברים "מפתיעים" , יש להתמקד בהם, להבין אותם היטב . וכדאי גם לזכור...
ולא להיות מופתע משאלות הבגרות.
דוגמאות נוספות : זווית נטיית חוט המשמש כמד תאוצה לא תלויה במסה .
תאוצת הכובד של כל הגופים על פני כדור הארץ היא זהה.
מהירותו של גוף הנע במסילה אנכית חלקה לא תלויה בצורת המסילה.
אדם יכול לעמוד על משקל תקין ולראות שהערך המוצג שונה מהערך האמתי (משקל מדומה).
______________________________________________________________________________________