18. 1987,4 - جسم مربوط بنابض أفقي ويتحرك في حركة توافقية بسيطة

______________________________________________________________________________________
...
السرعة القصوى هي 1.58 متر في الثانية.
حفظ الطاقة.
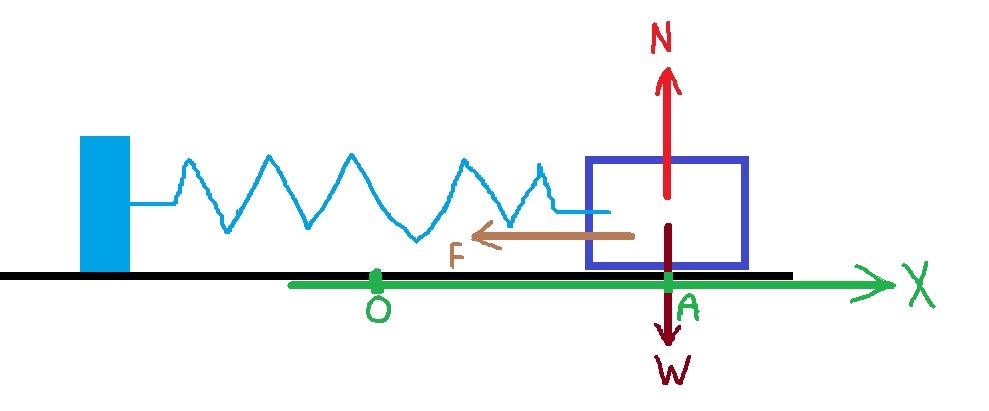
سنرسم مخطط القوى، ونحدد محور الحركة الذي يبدأ في نقطة الاتّزان، ونحدد الموقع الابتدائي للجسم في نقطة الطرف الموجبة للحركة.
نُشير لنقطة الطرف الموجبة للحركة بـ A، ونقطة الاتّزان بـ O. ونضيف إلى الرسم التخطيطي القوى المؤثرة على الجسم.
من مبادئ الحركة التوافقية البسيطة، فإن السرعة القصوى للجسم تساوي سرعة الجسم عندما يمر بنقطة الاتّزان.
القوة الوحيدة التي تعمل على الجسم هي قوة النابض، وبالتالي فإنه سوف يتحقق حفظ الطاقة الميكانيكية.
أينما يقع الجسم، فإن الطاقة الميكانيكية الكلية تساوي 1 جول.
نكتب معادلة حفظ الطاقة لحظة مرور الجسم بالنقطة O:
«math xmlns=¨http://www.w3.org/1998/Math/MathML¨»«msub»«mi mathvariant=¨bold¨ mathcolor=¨#0000FF¨»E«/mi»«mrow mathcolor=¨#0000FF¨»«mi mathvariant=¨bold¨»O«/mi»«mo mathvariant=¨bold¨»§#160;«/mo»«/mrow»«/msub»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»=«/mo»«msub»«mi mathvariant=¨bold¨ mathcolor=¨#0000FF¨»E«/mi»«msub mathcolor=¨#0000FF¨»«mi mathvariant=¨bold¨»K«/mi»«mi mathvariant=¨bold¨»o«/mi»«/msub»«/msub»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»+«/mo»«msub»«mi mathvariant=¨bold¨ mathcolor=¨#0000FF¨»U«/mi»«mi mathvariant=¨bold¨ mathcolor=¨#0000FF¨»o«/mi»«/msub»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»=«/mo»«mn mathvariant=¨bold¨ mathcolor=¨#0000FF¨»1«/mn»«mspace linebreak=¨newline¨»«/mspace»«mspace linebreak=¨newline¨»«/mspace»«mspace linebreak=¨newline¨»«/mspace»«/math»
عندما يمر الجسم بالنقطة o، يصبح النابض مسترخياً. وطاقته الوضعية المرنة تساوي صفرًا.
«math xmlns=¨http://www.w3.org/1998/Math/MathML¨»«msub»«mi mathvariant=¨bold¨ mathcolor=¨#0000FF¨»E«/mi»«msub mathcolor=¨#0000FF¨»«mi mathvariant=¨bold¨»K«/mi»«mi mathvariant=¨bold¨»o«/mi»«/msub»«/msub»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»+«/mo»«menclose mathcolor=¨#0000FF¨ notation=¨updiagonalstrike¨»«msub»«mi mathvariant=¨bold¨»U«/mi»«mi mathvariant=¨bold¨»o«/mi»«/msub»«/menclose»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»=«/mo»«mn mathvariant=¨bold¨ mathcolor=¨#0000FF¨»1«/mn»«mspace linebreak=¨newline¨»«/mspace»«mspace linebreak=¨newline¨»«/mspace»«mfrac mathcolor=¨#0000FF¨»«mn mathvariant=¨bold¨»1«/mn»«mn mathvariant=¨bold¨»2«/mn»«/mfrac»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»§#183;«/mo»«mi mathvariant=¨bold-italic¨ mathcolor=¨#0000FF¨»m«/mi»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»§#183;«/mo»«msup»«msub»«mi mathvariant=¨bold-italic¨ mathcolor=¨#0000FF¨»V«/mi»«mi mathvariant=¨bold¨ mathcolor=¨#0000FF¨»o«/mi»«/msub»«mn mathvariant=¨bold¨ mathcolor=¨#0000FF¨»2«/mn»«/msup»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»=«/mo»«mn mathvariant=¨bold¨ mathcolor=¨#0000FF¨»1«/mn»«mspace linebreak=¨newline¨»«/mspace»«msub»«mi mathvariant=¨bold-italic¨ mathcolor=¨#0000FF¨»V«/mi»«mi mathvariant=¨bold¨ mathcolor=¨#0000FF¨»o«/mi»«/msub»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»=«/mo»«msub»«mi mathvariant=¨bold-italic¨ mathcolor=¨#0000FF¨»V«/mi»«mrow mathcolor=¨#0000FF¨»«mi mathvariant=¨bold¨»m«/mi»«mi mathvariant=¨bold¨»a«/mi»«mi mathvariant=¨bold¨»x«/mi»«/mrow»«/msub»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»=«/mo»«msqrt mathcolor=¨#0000FF¨»«mfrac»«mn mathvariant=¨bold¨»2«/mn»«mi mathvariant=¨bold¨»m«/mi»«/mfrac»«/msqrt»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»=«/mo»«msqrt mathcolor=¨#0000FF¨»«mfrac»«mn mathvariant=¨bold¨»2«/mn»«mrow»«mn mathvariant=¨bold¨»0«/mn»«mo mathvariant=¨bold¨».«/mo»«mn mathvariant=¨bold¨»8«/mn»«/mrow»«/mfrac»«/msqrt»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»=«/mo»«msqrt mathcolor=¨#0000FF¨»«mn mathvariant=¨bold¨»2«/mn»«mo mathvariant=¨bold¨».«/mo»«mn mathvariant=¨bold¨»5«/mn»«/msqrt»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»=«/mo»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»§#177;«/mo»«mn mathvariant=¨bold¨ mathcolor=¨#0000FF¨»1«/mn»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨».«/mo»«mn mathvariant=¨bold¨ mathcolor=¨#0000FF¨»58«/mn»«mfrac mathcolor=¨#0000FF¨»«mi mathvariant=¨bold¨»m«/mi»«mi mathvariant=¨bold¨»s«/mi»«/mfrac»«mspace linebreak=¨newline¨»«/mspace»«mspace linebreak=¨newline¨»«/mspace»«mspace linebreak=¨newline¨»«/mspace»«/math»
هناك حلين رياضيين، وكلاهما له أهمية فيزيائية. القيمة الموجبة للسرعة تلائم الحركة في اتجاه المحور.
القيمة السالبة تلائم الحركة عكس اتجاه المحور.
السرعة القصوى هي 1.58 متر في الثانية.
נסמן את נקודת הקצה החיובית ב A , ואת נקודת שיווי המשקל ב O. ונוסיף לתרשים את הכוחות הפועלים על הגוף.

מעקרונות התה"פ מהירותו המקסימאלית של הגוף שווה למהירות הגוף כאשר הוא חולף בנקודת שיווי המשקל.
רק כוח הקפיץ מבצע עבודה על הגוף,לכן האנרגיה המכנית נשמרת.
בכל מקום בו נמצא הגוף האנרגיה המכנית הכוללת שווה 1 ג'אול.
נכתוב את משוואת שימור האנרגיה לרגע בו חולף הגוף בנקודה O:
«math xmlns=¨http://www.w3.org/1998/Math/MathML¨»«msub»«mi mathvariant=¨bold¨ mathcolor=¨#0000FF¨»E«/mi»«mrow mathcolor=¨#0000FF¨»«mi mathvariant=¨bold¨»O«/mi»«mo mathvariant=¨bold¨»§#160;«/mo»«/mrow»«/msub»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»=«/mo»«msub»«mi mathvariant=¨bold¨ mathcolor=¨#0000FF¨»E«/mi»«msub mathcolor=¨#0000FF¨»«mi mathvariant=¨bold¨»K«/mi»«mi mathvariant=¨bold¨»o«/mi»«/msub»«/msub»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»+«/mo»«msub»«mi mathvariant=¨bold¨ mathcolor=¨#0000FF¨»U«/mi»«mi mathvariant=¨bold¨ mathcolor=¨#0000FF¨»o«/mi»«/msub»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»=«/mo»«mn mathvariant=¨bold¨ mathcolor=¨#0000FF¨»1«/mn»«mspace linebreak=¨newline¨»«/mspace»«mspace linebreak=¨newline¨»«/mspace»«mspace linebreak=¨newline¨»«/mspace»«/math»
כאשר הגוף חולף בנקודה o , הקפיץ רפוי . האנרגיה הפוטנציאלית אלסטית שלו שווה לאפס.
«math xmlns=¨http://www.w3.org/1998/Math/MathML¨»«msub»«mi mathvariant=¨bold¨ mathcolor=¨#0000FF¨»E«/mi»«msub mathcolor=¨#0000FF¨»«mi mathvariant=¨bold¨»K«/mi»«mi mathvariant=¨bold¨»o«/mi»«/msub»«/msub»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»+«/mo»«menclose mathcolor=¨#0000FF¨ notation=¨updiagonalstrike¨»«msub»«mi mathvariant=¨bold¨»U«/mi»«mi mathvariant=¨bold¨»o«/mi»«/msub»«/menclose»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»=«/mo»«mn mathvariant=¨bold¨ mathcolor=¨#0000FF¨»1«/mn»«mspace linebreak=¨newline¨»«/mspace»«mspace linebreak=¨newline¨»«/mspace»«mfrac mathcolor=¨#0000FF¨»«mn mathvariant=¨bold¨»1«/mn»«mn mathvariant=¨bold¨»2«/mn»«/mfrac»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»§#183;«/mo»«mi mathvariant=¨bold-italic¨ mathcolor=¨#0000FF¨»m«/mi»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»§#183;«/mo»«msup»«msub»«mi mathvariant=¨bold-italic¨ mathcolor=¨#0000FF¨»V«/mi»«mi mathvariant=¨bold¨ mathcolor=¨#0000FF¨»o«/mi»«/msub»«mn mathvariant=¨bold¨ mathcolor=¨#0000FF¨»2«/mn»«/msup»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»=«/mo»«mn mathvariant=¨bold¨ mathcolor=¨#0000FF¨»1«/mn»«mspace linebreak=¨newline¨»«/mspace»«msub»«mi mathvariant=¨bold-italic¨ mathcolor=¨#0000FF¨»V«/mi»«mi mathvariant=¨bold¨ mathcolor=¨#0000FF¨»o«/mi»«/msub»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»=«/mo»«msub»«mi mathvariant=¨bold-italic¨ mathcolor=¨#0000FF¨»V«/mi»«mrow mathcolor=¨#0000FF¨»«mi mathvariant=¨bold¨»m«/mi»«mi mathvariant=¨bold¨»a«/mi»«mi mathvariant=¨bold¨»x«/mi»«/mrow»«/msub»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»=«/mo»«msqrt mathcolor=¨#0000FF¨»«mfrac»«mn mathvariant=¨bold¨»2«/mn»«mi mathvariant=¨bold¨»m«/mi»«/mfrac»«/msqrt»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»=«/mo»«msqrt mathcolor=¨#0000FF¨»«mfrac»«mn mathvariant=¨bold¨»2«/mn»«mrow»«mn mathvariant=¨bold¨»0«/mn»«mo mathvariant=¨bold¨».«/mo»«mn mathvariant=¨bold¨»8«/mn»«/mrow»«/mfrac»«/msqrt»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»=«/mo»«msqrt mathcolor=¨#0000FF¨»«mn mathvariant=¨bold¨»2«/mn»«mo mathvariant=¨bold¨».«/mo»«mn mathvariant=¨bold¨»5«/mn»«/msqrt»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»=«/mo»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»§#177;«/mo»«mn mathvariant=¨bold¨ mathcolor=¨#0000FF¨»1«/mn»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨».«/mo»«mn mathvariant=¨bold¨ mathcolor=¨#0000FF¨»58«/mn»«mfrac mathcolor=¨#0000FF¨»«mi mathvariant=¨bold¨»m«/mi»«mi mathvariant=¨bold¨»s«/mi»«/mfrac»«mspace linebreak=¨newline¨»«/mspace»«mspace linebreak=¨newline¨»«/mspace»«mspace linebreak=¨newline¨»«/mspace»«/math»
לכן, גודל המהירות המקסימאלית 1.58 מטר לשנייה.
1. عند كتابة معادلة حفظ الطاقة. ليس من الضروري دائمًا مقارنة قيم الطاقة في مكانين مختلفين.
يمكن مقارنة قيمة الطاقة الميكانيكية الكلية بتعبير الطاقة في نقطة ما.
يمكن مقارنة قيمة الطاقة الميكانيكية الكلية بتعبير الطاقة في نقطة ما.
2. من دالة السرعة كدالة للموقع، يمكن ملاحظة أنه في نقطة الاتّزان، حيث X = 0 متر
سرعة الجسم القصوى:
«math xmlns=¨http://www.w3.org/1998/Math/MathML¨»«mi mathvariant=¨bold¨ mathcolor=¨#FF0000¨»V«/mi»«mo mathvariant=¨bold¨ mathcolor=¨#FF0000¨»(«/mo»«mi mathvariant=¨bold¨ mathcolor=¨#FF0000¨»x«/mi»«mo mathvariant=¨bold¨ mathcolor=¨#FF0000¨»)«/mo»«mo mathvariant=¨bold¨ mathcolor=¨#FF0000¨»=«/mo»«mo mathvariant=¨bold¨ mathcolor=¨#FF0000¨»-«/mo»«mi mathvariant=¨bold¨ mathcolor=¨#FF0000¨»§#969;«/mi»«mo mathvariant=¨bold¨ mathcolor=¨#FF0000¨»§#183;«/mo»«msqrt mathcolor=¨#FF0000¨»«msup»«mi mathvariant=¨bold¨»A«/mi»«mn mathvariant=¨bold¨»2«/mn»«/msup»«mo mathvariant=¨bold¨»-«/mo»«msup»«mi mathvariant=¨bold¨»X«/mi»«mn mathvariant=¨bold¨»2«/mn»«/msup»«/msqrt»«mspace linebreak=¨newline¨»«/mspace»«mspace linebreak=¨newline¨»«/mspace»«msub»«mi mathvariant=¨bold¨ mathcolor=¨#FF0000¨»V«/mi»«mrow mathcolor=¨#FF0000¨»«mi mathvariant=¨bold¨»max«/mi»«mo mathvariant=¨bold¨»=«/mo»«/mrow»«/msub»«mi mathvariant=¨bold¨ mathcolor=¨#FF0000¨»V«/mi»«mo mathvariant=¨bold¨ mathcolor=¨#FF0000¨»(«/mo»«mn mathvariant=¨bold¨ mathcolor=¨#FF0000¨»0«/mn»«mo mathvariant=¨bold¨ mathcolor=¨#FF0000¨»)«/mo»«mo mathvariant=¨bold¨ mathcolor=¨#FF0000¨»=«/mo»«mo mathvariant=¨bold¨ mathcolor=¨#FF0000¨»-«/mo»«mi mathvariant=¨bold¨ mathcolor=¨#FF0000¨»§#969;«/mi»«mo mathvariant=¨bold¨ mathcolor=¨#FF0000¨»§#183;«/mo»«msqrt mathcolor=¨#FF0000¨»«msup»«mi mathvariant=¨bold¨»A«/mi»«mn mathvariant=¨bold¨»2«/mn»«/msup»«mo mathvariant=¨bold¨»-«/mo»«msup»«mn mathvariant=¨bold¨»0«/mn»«mn mathvariant=¨bold¨»2«/mn»«/msup»«/msqrt»«mo mathvariant=¨bold¨ mathcolor=¨#FF0000¨»=«/mo»«mo mathvariant=¨bold¨ mathcolor=¨#FF0000¨»§#177;«/mo»«mi mathvariant=¨bold¨ mathcolor=¨#FF0000¨»§#969;«/mi»«mo mathvariant=¨bold¨ mathcolor=¨#FF0000¨»§#183;«/mo»«mi mathvariant=¨bold¨ mathcolor=¨#FF0000¨»A«/mi»«/math»
ניתן להשוות בין ערך האנרגיה המכנית הכוללת לביטוי האנרגיה בנקודה כלשהי.
2. מפונקציית המהירות בתלות במקום ניתן לראות שבנקודת שיווי המשקל , כאשר X=0m
מהירות הגוף היא מקסימאלית:
«math xmlns=¨http://www.w3.org/1998/Math/MathML¨»«mi mathvariant=¨bold¨ mathcolor=¨#FF0000¨»V«/mi»«mo mathvariant=¨bold¨ mathcolor=¨#FF0000¨»(«/mo»«mi mathvariant=¨bold¨ mathcolor=¨#FF0000¨»x«/mi»«mo mathvariant=¨bold¨ mathcolor=¨#FF0000¨»)«/mo»«mo mathvariant=¨bold¨ mathcolor=¨#FF0000¨»=«/mo»«mo mathvariant=¨bold¨ mathcolor=¨#FF0000¨»-«/mo»«mi mathvariant=¨bold¨ mathcolor=¨#FF0000¨»§#969;«/mi»«mo mathvariant=¨bold¨ mathcolor=¨#FF0000¨»§#183;«/mo»«msqrt mathcolor=¨#FF0000¨»«msup»«mi mathvariant=¨bold¨»A«/mi»«mn mathvariant=¨bold¨»2«/mn»«/msup»«mo mathvariant=¨bold¨»-«/mo»«msup»«mi mathvariant=¨bold¨»X«/mi»«mn mathvariant=¨bold¨»2«/mn»«/msup»«/msqrt»«mspace linebreak=¨newline¨»«/mspace»«mspace linebreak=¨newline¨»«/mspace»«msub»«mi mathvariant=¨bold¨ mathcolor=¨#FF0000¨»V«/mi»«mrow mathcolor=¨#FF0000¨»«mi mathvariant=¨bold¨»max«/mi»«mo mathvariant=¨bold¨»=«/mo»«/mrow»«/msub»«mi mathvariant=¨bold¨ mathcolor=¨#FF0000¨»V«/mi»«mo mathvariant=¨bold¨ mathcolor=¨#FF0000¨»(«/mo»«mn mathvariant=¨bold¨ mathcolor=¨#FF0000¨»0«/mn»«mo mathvariant=¨bold¨ mathcolor=¨#FF0000¨»)«/mo»«mo mathvariant=¨bold¨ mathcolor=¨#FF0000¨»=«/mo»«mo mathvariant=¨bold¨ mathcolor=¨#FF0000¨»-«/mo»«mi mathvariant=¨bold¨ mathcolor=¨#FF0000¨»§#969;«/mi»«mo mathvariant=¨bold¨ mathcolor=¨#FF0000¨»§#183;«/mo»«msqrt mathcolor=¨#FF0000¨»«msup»«mi mathvariant=¨bold¨»A«/mi»«mn mathvariant=¨bold¨»2«/mn»«/msup»«mo mathvariant=¨bold¨»-«/mo»«msup»«mn mathvariant=¨bold¨»0«/mn»«mn mathvariant=¨bold¨»2«/mn»«/msup»«/msqrt»«mo mathvariant=¨bold¨ mathcolor=¨#FF0000¨»=«/mo»«mo mathvariant=¨bold¨ mathcolor=¨#FF0000¨»§#177;«/mo»«mi mathvariant=¨bold¨ mathcolor=¨#FF0000¨»§#969;«/mi»«mo mathvariant=¨bold¨ mathcolor=¨#FF0000¨»§#183;«/mo»«mi mathvariant=¨bold¨ mathcolor=¨#FF0000¨»A«/mi»«/math»
______________________________________________________________________________________

______________________________________________________________________________________
...
قيمة ثابت النابض هي 31.58 نيوتن لكل متر.
يتم الحصول على ثابت النابض من قانون زمن الدورة.
نعبر عن ثابت النابض من تعبير زمن الدورة:
«math xmlns=¨http://www.w3.org/1998/Math/MathML¨»«mi mathvariant=¨bold-italic¨ mathcolor=¨#0000FF¨»T«/mi»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»=«/mo»«mn mathvariant=¨bold¨ mathcolor=¨#0000FF¨»2«/mn»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»§#183;«/mo»«mi mathvariant=¨bold¨ mathcolor=¨#0000FF¨»§#960;«/mi»«msqrt mathcolor=¨#0000FF¨»«mfrac»«mi mathvariant=¨bold¨»m«/mi»«mi mathvariant=¨bold¨»K«/mi»«/mfrac»«/msqrt»«mspace linebreak=¨newline¨»«/mspace»«mspace linebreak=¨newline¨»«/mspace»«msup»«mi mathvariant=¨bold¨ mathcolor=¨#0000FF¨»T«/mi»«mn mathvariant=¨bold¨ mathcolor=¨#0000FF¨»2«/mn»«/msup»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»=«/mo»«mn mathvariant=¨bold¨ mathcolor=¨#0000FF¨»4«/mn»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»§#183;«/mo»«msup»«mi mathvariant=¨bold¨ mathcolor=¨#0000FF¨»§#960;«/mi»«mn mathvariant=¨bold¨ mathcolor=¨#0000FF¨»2«/mn»«/msup»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»§#183;«/mo»«mfrac mathcolor=¨#0000FF¨»«mi mathvariant=¨bold¨»m«/mi»«mi mathvariant=¨bold¨»K«/mi»«/mfrac»«mspace linebreak=¨newline¨»«/mspace»«mspace linebreak=¨newline¨»«/mspace»«mi mathvariant=¨bold¨ mathcolor=¨#0000FF¨»K«/mi»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»=«/mo»«mfrac mathcolor=¨#0000FF¨»«mrow»«mn mathvariant=¨bold¨»4«/mn»«mo mathvariant=¨bold¨»§#183;«/mo»«msup»«mi mathvariant=¨bold¨»§#960;«/mi»«mn mathvariant=¨bold¨»2«/mn»«/msup»«mo mathvariant=¨bold¨»§#183;«/mo»«mi mathvariant=¨bold¨»m«/mi»«/mrow»«msup»«mi mathvariant=¨bold¨»T«/mi»«mn mathvariant=¨bold¨»2«/mn»«/msup»«/mfrac»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»=«/mo»«mfrac mathcolor=¨#0000FF¨»«mrow»«mn mathvariant=¨bold¨»4«/mn»«mo mathvariant=¨bold¨»§#183;«/mo»«msup»«mi mathvariant=¨bold¨»§#960;«/mi»«mn mathvariant=¨bold¨»2«/mn»«/msup»«mo mathvariant=¨bold¨»§#183;«/mo»«mi mathvariant=¨bold¨»m«/mi»«/mrow»«msup»«mi mathvariant=¨bold¨»T«/mi»«mn mathvariant=¨bold¨»2«/mn»«/msup»«/mfrac»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»=«/mo»«mfrac mathcolor=¨#0000FF¨»«mrow»«mn mathvariant=¨bold¨»4«/mn»«mo mathvariant=¨bold¨»§#183;«/mo»«msup»«mi mathvariant=¨bold¨»§#960;«/mi»«mn mathvariant=¨bold¨»2«/mn»«/msup»«mo mathvariant=¨bold¨»§#183;«/mo»«mn mathvariant=¨bold¨»0«/mn»«mo mathvariant=¨bold¨».«/mo»«mn mathvariant=¨bold¨»8«/mn»«/mrow»«msup»«mn mathvariant=¨bold¨»1«/mn»«mn mathvariant=¨bold¨»2«/mn»«/msup»«/mfrac»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»=«/mo»«mn mathvariant=¨bold¨ mathcolor=¨#0000FF¨»31«/mn»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨».«/mo»«mn mathvariant=¨bold¨ mathcolor=¨#0000FF¨»58«/mn»«mfrac mathcolor=¨#0000FF¨»«mi mathvariant=¨bold¨»N«/mi»«mi mathvariant=¨bold¨»m«/mi»«/mfrac»«mspace linebreak=¨newline¨»«/mspace»«mspace linebreak=¨newline¨»«/mspace»«/math»
قيمة ثابت الزنبرك هي 31.58 نيوتن لكل متر.
«math xmlns=¨http://www.w3.org/1998/Math/MathML¨»«mi mathvariant=¨bold-italic¨ mathcolor=¨#0000FF¨»T«/mi»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»=«/mo»«mn mathvariant=¨bold¨ mathcolor=¨#0000FF¨»2«/mn»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»§#183;«/mo»«mi mathvariant=¨bold¨ mathcolor=¨#0000FF¨»§#960;«/mi»«msqrt mathcolor=¨#0000FF¨»«mfrac»«mi mathvariant=¨bold¨»m«/mi»«mi mathvariant=¨bold¨»K«/mi»«/mfrac»«/msqrt»«mspace linebreak=¨newline¨»«/mspace»«mspace linebreak=¨newline¨»«/mspace»«msup»«mi mathvariant=¨bold¨ mathcolor=¨#0000FF¨»T«/mi»«mn mathvariant=¨bold¨ mathcolor=¨#0000FF¨»2«/mn»«/msup»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»=«/mo»«mn mathvariant=¨bold¨ mathcolor=¨#0000FF¨»4«/mn»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»§#183;«/mo»«msup»«mi mathvariant=¨bold¨ mathcolor=¨#0000FF¨»§#960;«/mi»«mn mathvariant=¨bold¨ mathcolor=¨#0000FF¨»2«/mn»«/msup»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»§#183;«/mo»«mfrac mathcolor=¨#0000FF¨»«mi mathvariant=¨bold¨»m«/mi»«mi mathvariant=¨bold¨»K«/mi»«/mfrac»«mspace linebreak=¨newline¨»«/mspace»«mspace linebreak=¨newline¨»«/mspace»«mi mathvariant=¨bold¨ mathcolor=¨#0000FF¨»K«/mi»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»=«/mo»«mfrac mathcolor=¨#0000FF¨»«mrow»«mn mathvariant=¨bold¨»4«/mn»«mo mathvariant=¨bold¨»§#183;«/mo»«msup»«mi mathvariant=¨bold¨»§#960;«/mi»«mn mathvariant=¨bold¨»2«/mn»«/msup»«mo mathvariant=¨bold¨»§#183;«/mo»«mi mathvariant=¨bold¨»m«/mi»«/mrow»«msup»«mi mathvariant=¨bold¨»T«/mi»«mn mathvariant=¨bold¨»2«/mn»«/msup»«/mfrac»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»=«/mo»«mfrac mathcolor=¨#0000FF¨»«mrow»«mn mathvariant=¨bold¨»4«/mn»«mo mathvariant=¨bold¨»§#183;«/mo»«msup»«mi mathvariant=¨bold¨»§#960;«/mi»«mn mathvariant=¨bold¨»2«/mn»«/msup»«mo mathvariant=¨bold¨»§#183;«/mo»«mi mathvariant=¨bold¨»m«/mi»«/mrow»«msup»«mi mathvariant=¨bold¨»T«/mi»«mn mathvariant=¨bold¨»2«/mn»«/msup»«/mfrac»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»=«/mo»«mfrac mathcolor=¨#0000FF¨»«mrow»«mn mathvariant=¨bold¨»4«/mn»«mo mathvariant=¨bold¨»§#183;«/mo»«msup»«mi mathvariant=¨bold¨»§#960;«/mi»«mn mathvariant=¨bold¨»2«/mn»«/msup»«mo mathvariant=¨bold¨»§#183;«/mo»«mn mathvariant=¨bold¨»0«/mn»«mo mathvariant=¨bold¨».«/mo»«mn mathvariant=¨bold¨»8«/mn»«/mrow»«msup»«mn mathvariant=¨bold¨»1«/mn»«mn mathvariant=¨bold¨»2«/mn»«/msup»«/mfrac»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»=«/mo»«mn mathvariant=¨bold¨ mathcolor=¨#0000FF¨»31«/mn»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨».«/mo»«mn mathvariant=¨bold¨ mathcolor=¨#0000FF¨»58«/mn»«mfrac mathcolor=¨#0000FF¨»«mi mathvariant=¨bold¨»N«/mi»«mi mathvariant=¨bold¨»m«/mi»«/mfrac»«mspace linebreak=¨newline¨»«/mspace»«mspace linebreak=¨newline¨»«/mspace»«/math»
ערכו של קבוע הקפיץ הוא 31.58 ניוטון למטר.
السؤال ينص على أن الجسم يتحرك حركة توافقية بسيطة، لذلك ليست هناك حاجة لإثبات أن الحركة هي حركة توافقية بسيطة قبل استخدام دوال الحركة التوافقية البسيطة.
______________________________________________________________________________________

______________________________________________________________________________________
...
سعة الاهتزاز هي 0.25 متر.
قوانين الحركة التوافقية البسيطة.
من تعبير السرعة كدالة للزمن لحركة التوافقية البسيطة الملائمة لجسم يتحرك من نقطة النهاية الموجبة:
السرعة القصوى هي: «math xmlns=¨http://www.w3.org/1998/Math/MathML¨»«msub»«mi mathvariant=¨bold-italic¨ mathcolor=¨#0000FF¨»V«/mi»«mrow mathcolor=¨#0000FF¨»«mi mathvariant=¨bold¨»m«/mi»«mi mathvariant=¨bold¨»a«/mi»«mi mathvariant=¨bold¨»x«/mi»«/mrow»«/msub»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»=«/mo»«mi mathvariant=¨bold-italic¨ mathcolor=¨#0000FF¨»§#969;«/mi»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»§#183;«/mo»«mi mathvariant=¨bold-italic¨ mathcolor=¨#0000FF¨»A«/mi»«/math»
نعبر عن السعة من خلال تعبير السرعة القصوى:
«math xmlns=¨http://www.w3.org/1998/Math/MathML¨»«mi mathvariant=¨bold-italic¨ mathcolor=¨#0000FF¨»A«/mi»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»=«/mo»«mfrac mathcolor=¨#0000FF¨»«msub»«mi mathvariant=¨bold¨»V«/mi»«mi mathvariant=¨bold¨»max«/mi»«/msub»«mi mathvariant=¨bold¨»§#969;«/mi»«/mfrac»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»=«/mo»«mfrac mathcolor=¨#0000FF¨»«msub»«mi mathvariant=¨bold¨»V«/mi»«mi mathvariant=¨bold¨»max«/mi»«/msub»«mstyle displaystyle=¨true¨»«mfrac»«mrow»«mn mathvariant=¨bold¨»2«/mn»«mo mathvariant=¨bold¨»§#183;«/mo»«mi mathvariant=¨bold¨»§#960;«/mi»«/mrow»«mi mathvariant=¨bold¨»T«/mi»«/mfrac»«/mstyle»«/mfrac»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»=«/mo»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»§#160;«/mo»«mfrac mathcolor=¨#0000FF¨»«mrow»«msub»«mi mathvariant=¨bold¨»V«/mi»«mi mathvariant=¨bold¨»max«/mi»«/msub»«mo mathvariant=¨bold¨»§#183;«/mo»«mi mathvariant=¨bold¨»T«/mi»«/mrow»«mstyle displaystyle=¨true¨ mathvariant=¨bold¨»«mn»2«/mn»«mo»§#183;«/mo»«mi»§#960;«/mi»«/mstyle»«/mfrac»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»=«/mo»«mfrac mathcolor=¨#0000FF¨»«mrow»«mn mathvariant=¨bold¨»1«/mn»«mo mathvariant=¨bold¨».«/mo»«mn mathvariant=¨bold¨»58«/mn»«mo mathvariant=¨bold¨»§#183;«/mo»«mn mathvariant=¨bold¨»1«/mn»«/mrow»«mrow»«mn mathvariant=¨bold¨»2«/mn»«mo mathvariant=¨bold¨»§#183;«/mo»«mi mathvariant=¨bold¨»§#960;«/mi»«/mrow»«/mfrac»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»=«/mo»«mn mathvariant=¨bold¨ mathcolor=¨#0000FF¨»0«/mn»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨».«/mo»«mn mathvariant=¨bold¨ mathcolor=¨#0000FF¨»25«/mn»«mi mathvariant=¨bold-italic¨ mathcolor=¨#0000FF¨»m«/mi»«/math»
سعة الهتزاز هي 0.25 متر.
המהירות המקסימאלית היא: «math xmlns=¨http://www.w3.org/1998/Math/MathML¨»«msub»«mi mathvariant=¨bold-italic¨ mathcolor=¨#0000FF¨»V«/mi»«mrow mathcolor=¨#0000FF¨»«mi mathvariant=¨bold¨»m«/mi»«mi mathvariant=¨bold¨»a«/mi»«mi mathvariant=¨bold¨»x«/mi»«/mrow»«/msub»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»=«/mo»«mi mathvariant=¨bold-italic¨ mathcolor=¨#0000FF¨»§#969;«/mi»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»§#183;«/mo»«mi mathvariant=¨bold-italic¨ mathcolor=¨#0000FF¨»A«/mi»«/math»
נבטא מביטוי המהירות המקסימאלית את המשרעת :
«math xmlns=¨http://www.w3.org/1998/Math/MathML¨»«mi mathvariant=¨bold-italic¨ mathcolor=¨#0000FF¨»A«/mi»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»=«/mo»«mfrac mathcolor=¨#0000FF¨»«msub»«mi mathvariant=¨bold¨»V«/mi»«mi mathvariant=¨bold¨»max«/mi»«/msub»«mi mathvariant=¨bold¨»§#969;«/mi»«/mfrac»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»=«/mo»«mfrac mathcolor=¨#0000FF¨»«msub»«mi mathvariant=¨bold¨»V«/mi»«mi mathvariant=¨bold¨»max«/mi»«/msub»«mstyle displaystyle=¨true¨»«mfrac»«mrow»«mn mathvariant=¨bold¨»2«/mn»«mo mathvariant=¨bold¨»§#183;«/mo»«mi mathvariant=¨bold¨»§#960;«/mi»«/mrow»«mi mathvariant=¨bold¨»T«/mi»«/mfrac»«/mstyle»«/mfrac»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»=«/mo»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»§#160;«/mo»«mfrac mathcolor=¨#0000FF¨»«mrow»«msub»«mi mathvariant=¨bold¨»V«/mi»«mi mathvariant=¨bold¨»max«/mi»«/msub»«mo mathvariant=¨bold¨»§#183;«/mo»«mi mathvariant=¨bold¨»T«/mi»«/mrow»«mstyle displaystyle=¨true¨ mathvariant=¨bold¨»«mn»2«/mn»«mo»§#183;«/mo»«mi»§#960;«/mi»«/mstyle»«/mfrac»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»=«/mo»«mfrac mathcolor=¨#0000FF¨»«mrow»«mn mathvariant=¨bold¨»1«/mn»«mo mathvariant=¨bold¨».«/mo»«mn mathvariant=¨bold¨»58«/mn»«mo mathvariant=¨bold¨»§#183;«/mo»«mn mathvariant=¨bold¨»1«/mn»«/mrow»«mrow»«mn mathvariant=¨bold¨»2«/mn»«mo mathvariant=¨bold¨»§#183;«/mo»«mi mathvariant=¨bold¨»§#960;«/mi»«/mrow»«/mfrac»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»=«/mo»«mn mathvariant=¨bold¨ mathcolor=¨#0000FF¨»0«/mn»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨».«/mo»«mn mathvariant=¨bold¨ mathcolor=¨#0000FF¨»25«/mn»«mi mathvariant=¨bold-italic¨ mathcolor=¨#0000FF¨»m«/mi»«/math»
גודל משרעת התנודה 0.25 מטר.
في أي حركة توافقية بسيطة، تكون سرعة الجسم أثناء مروره عبر نقطة الاتّزان هي السرعة القصوى.
ويكون مساويًا لحاصل ضرب السرعة الزاوية في سعة الاهتزاز.
והיא שווה למכפלת המהירות הזוויתית במשרעת התנודה.
______________________________________________________________________________________

______________________________________________________________________________________
...
البعد هو 0.178 متر.
معادلة حفظ الطاقة، حيث تكون قيمة الطاقة الحركية مساوية للطاقة الوضعية.
سوف يتم حفظ الطاقة الميكانيكية، مجموع الطاقة الحركية والطاقة الوضعية المرنة ثابت ويساوي الطاقة الميكانيكية الكلية ET .
«math xmlns=¨http://www.w3.org/1998/Math/MathML¨»«mstyle mathsize=¨24px¨»«msub»«mi mathvariant=¨bold¨ mathcolor=¨#0000FF¨»E«/mi»«mi mathvariant=¨bold¨ mathcolor=¨#0000FF¨»K«/mi»«/msub»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»+«/mo»«msub»«mi mathvariant=¨bold¨ mathcolor=¨#0000FF¨»U«/mi»«mi mathvariant=¨bold¨ mathcolor=¨#0000FF¨»sp«/mi»«/msub»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»=«/mo»«msub»«mi mathvariant=¨bold¨ mathcolor=¨#0000FF¨»E«/mi»«mi mathvariant=¨bold¨ mathcolor=¨#0000FF¨»T«/mi»«/msub»«/mstyle»«/math»
في النقطة التي تتساوى فيها الطاقة الحركية مع الطاقة الوضعية. يتحقق أن ضعف قيمة الطاقة الوضعية تساوي
القيمة الكلية للطاقة الميكانيكية هي:
«math xmlns=¨http://www.w3.org/1998/Math/MathML¨»«mstyle mathsize=¨24px¨»«mn mathvariant=¨bold¨ mathcolor=¨#0000FF¨»2«/mn»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»§#183;«/mo»«msub»«mi mathvariant=¨bold¨ mathcolor=¨#0000FF¨»U«/mi»«mrow»«mi mathvariant=¨bold-italic¨ mathcolor=¨#0000FF¨»s«/mi»«mi mathvariant=¨bold-italic¨ mathcolor=¨#0000FF¨»p«/mi»«/mrow»«/msub»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»=«/mo»«msub»«mi mathvariant=¨bold¨ mathcolor=¨#0000FF¨»E«/mi»«mi mathvariant=¨bold¨ mathcolor=¨#0000FF¨»T«/mi»«/msub»«/mstyle»«/math»
تتحقق هذه المعادلة فقط عندما تكون قيمة الطاقة الحركية مساوية لطاقة الوضع المرنة.
نرمز لهذا المكان بـ 'X.
نكتب قيمة الطاقة الوضعية المرنة بصورة صريحة، ونجد الموقع 'X:
«math xmlns=¨http://www.w3.org/1998/Math/MathML¨»«mn mathvariant=¨bold¨ mathcolor=¨#0000FF¨»2«/mn»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»§#183;«/mo»«msub»«mi mathvariant=¨bold¨ mathcolor=¨#0000FF¨»U«/mi»«mrow»«mi mathvariant=¨bold-italic¨ mathcolor=¨#0000FF¨»s«/mi»«mi mathvariant=¨bold-italic¨ mathcolor=¨#0000FF¨»p«/mi»«/mrow»«/msub»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»=«/mo»«msub»«mi mathvariant=¨bold¨ mathcolor=¨#0000FF¨»E«/mi»«mi mathvariant=¨bold¨ mathcolor=¨#0000FF¨»T«/mi»«/msub»«mspace linebreak=¨newline¨»«/mspace»«mn mathvariant=¨bold¨ mathcolor=¨#0000FF¨»2«/mn»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»§#183;«/mo»«mfrac mathcolor=¨#0000FF¨»«mn mathvariant=¨bold¨»1«/mn»«mn mathvariant=¨bold¨»2«/mn»«/mfrac»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»§#183;«/mo»«mi mathvariant=¨bold¨ mathcolor=¨#0000FF¨»K«/mi»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»§#183;«/mo»«mi mathvariant=¨bold¨ mathcolor=¨#0000FF¨»X«/mi»«msup»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»`«/mo»«mn mathvariant=¨bold¨ mathcolor=¨#0000FF¨»2«/mn»«/msup»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»=«/mo»«msub»«mi mathvariant=¨bold¨ mathcolor=¨#0000FF¨»E«/mi»«mi mathvariant=¨bold¨ mathcolor=¨#0000FF¨»T«/mi»«/msub»«mspace linebreak=¨newline¨»«/mspace»«mspace linebreak=¨newline¨»«/mspace»«mi mathvariant=¨bold¨ mathcolor=¨#0000FF¨»X«/mi»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»`«/mo»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»=«/mo»«msqrt mathcolor=¨#0000FF¨»«mfrac»«msub»«mi mathvariant=¨bold¨»E«/mi»«mi mathvariant=¨bold¨»T«/mi»«/msub»«mi mathvariant=¨bold¨»K«/mi»«/mfrac»«/msqrt»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»=«/mo»«msqrt mathcolor=¨#0000FF¨»«mfrac»«mn mathvariant=¨bold¨»1«/mn»«mrow»«mn mathvariant=¨bold¨»31«/mn»«mo mathvariant=¨bold¨».«/mo»«mn mathvariant=¨bold¨»58«/mn»«/mrow»«/mfrac»«/msqrt»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»=«/mo»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»§#177;«/mo»«mn mathvariant=¨bold¨ mathcolor=¨#0000FF¨»0«/mn»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨».«/mo»«mn mathvariant=¨bold¨ mathcolor=¨#0000FF¨»178«/mn»«mi mathvariant=¨bold¨ mathcolor=¨#0000FF¨»m«/mi»«/math»
هناك نقطتان يتحقق فيهما الشرط:«math xmlns=¨http://www.w3.org/1998/Math/MathML¨»«mi mathvariant=¨bold¨ mathcolor=¨#0000FF¨»X«/mi»«msub»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»`«/mo»«mn mathvariant=¨bold¨ mathcolor=¨#0000FF¨»1«/mn»«/msub»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»=«/mo»«mn mathvariant=¨bold¨ mathcolor=¨#0000FF¨»0«/mn»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨».«/mo»«mn mathvariant=¨bold¨ mathcolor=¨#0000FF¨»178«/mn»«mi mathvariant=¨bold¨ mathcolor=¨#0000FF¨»m«/mi»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»§#160;«/mo»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»§#160;«/mo»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»§#160;«/mo»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»-«/mo»«mi mathvariant=¨bold¨ mathcolor=¨#0000FF¨»§#1493;«/mi»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»§#160;«/mo»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»§#160;«/mo»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»§#160;«/mo»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»§#160;«/mo»«mi mathvariant=¨bold¨ mathcolor=¨#0000FF¨»X«/mi»«msub»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»`«/mo»«mn mathvariant=¨bold¨ mathcolor=¨#0000FF¨»2«/mn»«/msub»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»=«/mo»«mn mathvariant=¨bold¨ mathcolor=¨#0000FF¨»0«/mn»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨».«/mo»«mn mathvariant=¨bold¨ mathcolor=¨#0000FF¨»178«/mn»«mi mathvariant=¨bold¨ mathcolor=¨#0000FF¨»m«/mi»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»§#160;«/mo»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»§#160;«/mo»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»§#160;«/mo»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»§#160;«/mo»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»§#160;«/mo»«/math» .
كلتا النقطتين تبعدان بقدار 0.178 متر عن نقطة الاتّزان.
لذا فإن البُعد من نقطة الاتّزان حيث تساوي قيمة الطاقة الحركية قيمة الطاقة الكامنة المرنة هي 0.178 متر.
«math xmlns=¨http://www.w3.org/1998/Math/MathML¨»«mstyle mathsize=¨24px¨»«msub»«mi mathvariant=¨bold¨ mathcolor=¨#0000FF¨»E«/mi»«mi mathvariant=¨bold¨ mathcolor=¨#0000FF¨»K«/mi»«/msub»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»+«/mo»«msub»«mi mathvariant=¨bold¨ mathcolor=¨#0000FF¨»U«/mi»«mi mathvariant=¨bold¨ mathcolor=¨#0000FF¨»sp«/mi»«/msub»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»=«/mo»«msub»«mi mathvariant=¨bold¨ mathcolor=¨#0000FF¨»E«/mi»«mi mathvariant=¨bold¨ mathcolor=¨#0000FF¨»T«/mi»«/msub»«/mstyle»«/math»
בנקודה בה האנרגיה הקינטית שווה לאנרגיה הפוטנציאלית. מתקיים שפעמיים ערך האנרגיה הפוטנציאלית שווה
לערך האנרגיה המכנית הכוללת :
«math xmlns=¨http://www.w3.org/1998/Math/MathML¨»«mstyle mathsize=¨24px¨»«mn mathvariant=¨bold¨ mathcolor=¨#0000FF¨»2«/mn»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»§#183;«/mo»«msub»«mi mathvariant=¨bold¨ mathcolor=¨#0000FF¨»U«/mi»«mrow»«mi mathvariant=¨bold-italic¨ mathcolor=¨#0000FF¨»s«/mi»«mi mathvariant=¨bold-italic¨ mathcolor=¨#0000FF¨»p«/mi»«/mrow»«/msub»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»=«/mo»«msub»«mi mathvariant=¨bold¨ mathcolor=¨#0000FF¨»E«/mi»«mi mathvariant=¨bold¨ mathcolor=¨#0000FF¨»T«/mi»«/msub»«/mstyle»«/math»
משוואה זו מתקיימת רק במקום שבו ערך האנרגיה הקינטית שווה לאנרגיה הפוטנציאלית אלסטית.
נסמן מקום זה כ 'X.
נכתוב את ערך האנרגיה הפוטנציאלית אלסטית במפורש , ונמצא את המקום 'X:
«math xmlns=¨http://www.w3.org/1998/Math/MathML¨»«mn mathvariant=¨bold¨ mathcolor=¨#0000FF¨»2«/mn»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»§#183;«/mo»«msub»«mi mathvariant=¨bold¨ mathcolor=¨#0000FF¨»U«/mi»«mrow»«mi mathvariant=¨bold-italic¨ mathcolor=¨#0000FF¨»s«/mi»«mi mathvariant=¨bold-italic¨ mathcolor=¨#0000FF¨»p«/mi»«/mrow»«/msub»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»=«/mo»«msub»«mi mathvariant=¨bold¨ mathcolor=¨#0000FF¨»E«/mi»«mi mathvariant=¨bold¨ mathcolor=¨#0000FF¨»T«/mi»«/msub»«mspace linebreak=¨newline¨»«/mspace»«mn mathvariant=¨bold¨ mathcolor=¨#0000FF¨»2«/mn»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»§#183;«/mo»«mfrac mathcolor=¨#0000FF¨»«mn mathvariant=¨bold¨»1«/mn»«mn mathvariant=¨bold¨»2«/mn»«/mfrac»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»§#183;«/mo»«mi mathvariant=¨bold¨ mathcolor=¨#0000FF¨»K«/mi»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»§#183;«/mo»«mi mathvariant=¨bold¨ mathcolor=¨#0000FF¨»X«/mi»«msup»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»`«/mo»«mn mathvariant=¨bold¨ mathcolor=¨#0000FF¨»2«/mn»«/msup»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»=«/mo»«msub»«mi mathvariant=¨bold¨ mathcolor=¨#0000FF¨»E«/mi»«mi mathvariant=¨bold¨ mathcolor=¨#0000FF¨»T«/mi»«/msub»«mspace linebreak=¨newline¨»«/mspace»«mspace linebreak=¨newline¨»«/mspace»«mi mathvariant=¨bold¨ mathcolor=¨#0000FF¨»X«/mi»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»`«/mo»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»=«/mo»«msqrt mathcolor=¨#0000FF¨»«mfrac»«msub»«mi mathvariant=¨bold¨»E«/mi»«mi mathvariant=¨bold¨»T«/mi»«/msub»«mi mathvariant=¨bold¨»K«/mi»«/mfrac»«/msqrt»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»=«/mo»«msqrt mathcolor=¨#0000FF¨»«mfrac»«mn mathvariant=¨bold¨»1«/mn»«mrow»«mn mathvariant=¨bold¨»31«/mn»«mo mathvariant=¨bold¨».«/mo»«mn mathvariant=¨bold¨»58«/mn»«/mrow»«/mfrac»«/msqrt»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»=«/mo»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»§#177;«/mo»«mn mathvariant=¨bold¨ mathcolor=¨#0000FF¨»0«/mn»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨».«/mo»«mn mathvariant=¨bold¨ mathcolor=¨#0000FF¨»178«/mn»«mi mathvariant=¨bold¨ mathcolor=¨#0000FF¨»m«/mi»«/math»
יש שתי נקודות בהן התנאי המתקיים: «math xmlns=¨http://www.w3.org/1998/Math/MathML¨»«mi mathvariant=¨bold¨ mathcolor=¨#0000FF¨»X«/mi»«msub»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»`«/mo»«mn mathvariant=¨bold¨ mathcolor=¨#0000FF¨»1«/mn»«/msub»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»=«/mo»«mn mathvariant=¨bold¨ mathcolor=¨#0000FF¨»0«/mn»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨».«/mo»«mn mathvariant=¨bold¨ mathcolor=¨#0000FF¨»178«/mn»«mi mathvariant=¨bold¨ mathcolor=¨#0000FF¨»m«/mi»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»§#160;«/mo»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»§#160;«/mo»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»§#160;«/mo»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»-«/mo»«mi mathvariant=¨bold¨ mathcolor=¨#0000FF¨»§#1493;«/mi»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»§#160;«/mo»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»§#160;«/mo»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»§#160;«/mo»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»§#160;«/mo»«mi mathvariant=¨bold¨ mathcolor=¨#0000FF¨»X«/mi»«msub»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»`«/mo»«mn mathvariant=¨bold¨ mathcolor=¨#0000FF¨»2«/mn»«/msub»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»=«/mo»«mn mathvariant=¨bold¨ mathcolor=¨#0000FF¨»0«/mn»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨».«/mo»«mn mathvariant=¨bold¨ mathcolor=¨#0000FF¨»178«/mn»«mi mathvariant=¨bold¨ mathcolor=¨#0000FF¨»m«/mi»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»§#160;«/mo»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»§#160;«/mo»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»§#160;«/mo»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»§#160;«/mo»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»§#160;«/mo»«/math»
שתי הנקודות רחוקות 0.178 מטר מנקודת שיווי המשקל.
לכן המרחק מנקודת שיווי המשקל שבו ערך האנרגיה הקינטית שווה לערך האנרגיה הפוטנצילית אלסטית הוא 0.178 מטר.
1. يتناول السؤال البعد من نقطة الاّتزان إلى النقطة التي يتحقق فيها الشرط.
إذا كان السؤال هو ما هو المكان الذي يتحقق فيه الشرط، فسيكون هناك إجابتان صحيحتان.
إذا كان السؤال هو ما هو المكان الذي يتحقق فيه الشرط، فسيكون هناك إجابتان صحيحتان.
2. يمكن أن تكون الازاحة قيمة سالبة، ولا يمكن أن تكون للمسافة قيمة سالبة.
3. كما يمكن القول أن قيمة الطاقة الوضعية المضاعفة تساوي قيمة الطاقة الميكانيكية الكلية.
يمكن القول أن قيمة الطاقة الحركية المضاعفة تساوي قيمة الطاقة الميكانيكية، ولكن من هذا التعبير لا نستطيع أن نتعلم عن الموضع.
كل خطوة من خطوات الحل تعتمد على المبادئ الفيزيائية. بعض العمليات الحسابية وقليل من التدريبات الصحيحة.
אם השאלה הייתה מה הוא המיקום בו התנאי מתקיים היו שתי תשובות נכונות.
2. להעתק יכול להיות ערך שלילי , למרחק לא יכול להיות ערך שלילי.
3. כשם שניתן לומר שפעמיים ערך האנרגיה פוטנציאלית שווה לערך האנרגיה המכנית הכוללת .
ניתן לומר שפעמיים ערך האנרגיה הקינטית שווה לערך האנרגיה המכנית , אך מביטוי זה לא ניתן ללמוד על המיקום.
כל פתרון מבוסס על העקרונות הפיזיקליים . מעט פעולות מתמטיות ומעט.. תמרון נכון.
______________________________________________________________________________________