17. 1988,4- خرزة داخل طوق

______________________________________________________________________________________
...
سوف تتحرك الخرزة بتسارع متغير.
يتم تحديد طبيعة الحركة حسب القوة المحصّلة، والتي تتعلق بالجاذبية والقوة العمودية.
تتحرك الخرزة بحركة دائرية. لتحديد طبيعة الحركة، سيتم رسم مخطط القوى.
هناك قوتان تؤثران على الخرزة، قوة الجاذبية للأسفل والقوة العمودية التي يُشغلها الطوق:
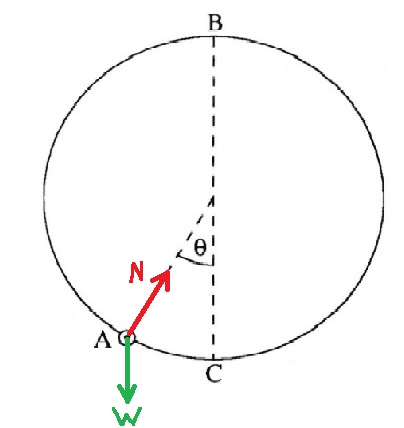
قوة الجاذبية لا تتغير في المقدار أو في الاتجاه طوال الحركة.
تختلف القوة العمودية في المقدار والاتجاه حسب موقع الجسم وسرعته، وذلك حسب معادلات الحركة.
وبالتالي فإن القوة المحصّلة المؤثرة على الخرزة تتغير في المقدار والاتجاه، ومن قانون نيوتن الثاني يمكن القول أن التسارع يتغير أيضًا في المقدار والاتجاه.
על החרוז פועלים שני כוחות , כוח הכובד כלפי מטה וכוח הנורמל שהחישוק מפעיל:

כוח הכובד לא משתנה בגודלו ובכיוונו כל זמן התנועה.
כוח הנורמל משתנה בגודלו ובכיוונו בתלות במיקום הגוף ובתלות במהירות הגוף ,בהתאם למשוואות התנועה.
לכן הכוח השקול משתנה בגודלו ובכיוונו במהלך תנועת החרוז, ומהחוק השני של ניוטון ניתן לומר שגם התאוצה משתנה בגודלה ובכיוונה.
1. حركة الخرزة تشبه حركة البندول البسيط.
القوة العمودية تؤثر على الخرزة بشكل مشابه لقوة الشد المؤثرة على الجسم المتحرك في منظومة البندول البسيط.
القوة العمودية تؤثر على الخرزة بشكل مشابه لقوة الشد المؤثرة على الجسم المتحرك في منظومة البندول البسيط.
2. يعرف كاتب السؤال أن الطلاب على دراية بالبندول البسيط، ويتوقع منهم أن يفهموا أن حركة البندول هي نفسها
لحركة الجسم المتحرك في حركة البندول البسيطة.
هذه حركات مختلفة في حالات مختلفة، لذلك لكي يتمكن الطالب من الربط بين الحركتين، يجب عليه أن يفهم موضوع البندول البسيط تمامًا.
3. إذا كانت الزاوية «math xmlns=¨http://www.w3.org/1998/Math/MathML¨»«mi mathvariant=¨bold¨ mathcolor=¨#FF0000¨»§#952;«/mi»«/math» صغيرة، فيمكن القول أن الخرزة تتحرك بحركة توافقية بسيطة، وهي أيضًا حركة ذات تسارع متغير.
4. من معادلات الحركة، يمكن كتابة تعبير للتسارع المماسي والشعاعي (الراديالي). وإظهار بالضبط كيف يتغير كل من التسارعات
اعتمادا على الزاوية «math xmlns=¨http://www.w3.org/1998/Math/MathML¨»«mi mathvariant=¨bold¨ mathcolor=¨#FF0000¨»§#952;«/mi»«/math». لكن السؤال عام، فيكفي أن نكتب جواباً عاماً، دون تعبير دقيق.
כוח הנורמל פועל על החרוז בדומה לכוח המתיחות הפועל על הגוף הנע במערכת מטוטלת פשוטה.
2. כותב השאלה יודע שהתלמידים מכירים את המטוטלת הפשוטה, והוא מצפה שהם יבינו שתנועת החרוז זהה
לתנועתו של גוף הנע בתנועת מטוטלת פשוטה.
3. אם הזווית «math xmlns=¨http://www.w3.org/1998/Math/MathML¨»«mi mathvariant=¨bold¨ mathcolor=¨#FF0000¨»§#952;«/mi»«/math» הייתה קטנה , ניתן היה לומר שהחרוז נע בתה"פ ,גם היא תנועה בתאוצה משתנה.
______________________________________________________________________________________

______________________________________________________________________________________
...
«math xmlns=¨http://www.w3.org/1998/Math/MathML¨»«mi mathvariant=¨bold¨»T«/mi»«mo mathvariant=¨bold¨»=«/mo»«mn mathvariant=¨bold¨»2«/mn»«mi mathvariant=¨bold¨»§#960;«/mi»«mo mathvariant=¨bold¨»§#183;«/mo»«msqrt»«mfrac»«mi mathvariant=¨bold¨»R«/mi»«mi mathvariant=¨bold¨»g«/mi»«/mfrac»«/msqrt»«/math»
التطرق لحركة الخرزة كحركة بندول بسيطة يتحرك بزوايا صغيرة. واستخدام مبادئ الحركة التوافقية البسيطة.
نتعامل مع حركة الخرزة كحركة جسم يتحرك في حركة البندول البسيطة.
من مبادئ البندول البسيط، عندما تكون الزاوية «math xmlns=¨http://www.w3.org/1998/Math/MathML¨»«mi mathvariant=¨bold¨ mathcolor=¨#0000FF¨»§#920;«/mi»«/math» صغيرة، يمكن اعتبار حركة الخرزة كحركة توافقية بسيطة.
سوف نستخدم قانون زمن الدورة الملائمة لحركة البندول البسيط:
«math xmlns=¨http://www.w3.org/1998/Math/MathML¨»«mi mathvariant=¨bold¨ mathcolor=¨#0000FF¨»T«/mi»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»=«/mo»«mn mathvariant=¨bold¨ mathcolor=¨#0000FF¨»2«/mn»«mi mathvariant=¨bold¨ mathcolor=¨#0000FF¨»§#960;«/mi»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»§#183;«/mo»«msqrt mathcolor=¨#0000FF¨»«mfrac»«mi mathvariant=¨bold¨»L«/mi»«mi mathvariant=¨bold¨»g«/mi»«/mfrac»«/msqrt»«mspace linebreak=¨newline¨»«/mspace»«mspace linebreak=¨newline¨»«/mspace»«mi mathvariant=¨bold¨ mathcolor=¨#0000FF¨»T«/mi»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»=«/mo»«mn mathvariant=¨bold¨ mathcolor=¨#0000FF¨»2«/mn»«mi mathvariant=¨bold¨ mathcolor=¨#0000FF¨»§#960;«/mi»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»§#183;«/mo»«msqrt mathcolor=¨#0000FF¨»«mfrac»«mi mathvariant=¨bold¨»R«/mi»«mi mathvariant=¨bold¨»g«/mi»«/mfrac»«/msqrt»«/math»
لذلك، فإن التعبير لزمن الدورة هو: «math xmlns=¨http://www.w3.org/1998/Math/MathML¨»«mi mathvariant=¨bold¨ mathcolor=¨#0000FF¨»T«/mi»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»=«/mo»«mn mathvariant=¨bold¨ mathcolor=¨#0000FF¨»2«/mn»«mi mathvariant=¨bold¨ mathcolor=¨#0000FF¨»§#960;«/mi»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»§#183;«/mo»«msqrt mathcolor=¨#0000FF¨»«mfrac»«mi mathvariant=¨bold¨»R«/mi»«mi mathvariant=¨bold¨»g«/mi»«/mfrac»«/msqrt»«/math».
מעקרונות מטוטלת פשוטה, כאשר הזווית «math xmlns=¨http://www.w3.org/1998/Math/MathML¨»«mi mathvariant=¨bold¨ mathcolor=¨#0000FF¨»§#920;«/mi»«/math» היא קטנה ,ניתן להתייחס לתנועת החרוז כאל תנועה הרמונית פשוטה.
נשתמש בנוסחת זמן המחזור המתאימה לתנועת מטוטלת פשוטה:
«math xmlns=¨http://www.w3.org/1998/Math/MathML¨»«mi mathvariant=¨bold¨ mathcolor=¨#0000FF¨»T«/mi»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»=«/mo»«mn mathvariant=¨bold¨ mathcolor=¨#0000FF¨»2«/mn»«mi mathvariant=¨bold¨ mathcolor=¨#0000FF¨»§#960;«/mi»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»§#183;«/mo»«msqrt mathcolor=¨#0000FF¨»«mfrac»«mi mathvariant=¨bold¨»L«/mi»«mi mathvariant=¨bold¨»g«/mi»«/mfrac»«/msqrt»«mspace linebreak=¨newline¨»«/mspace»«mspace linebreak=¨newline¨»«/mspace»«mi mathvariant=¨bold¨ mathcolor=¨#0000FF¨»T«/mi»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»=«/mo»«mn mathvariant=¨bold¨ mathcolor=¨#0000FF¨»2«/mn»«mi mathvariant=¨bold¨ mathcolor=¨#0000FF¨»§#960;«/mi»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»§#183;«/mo»«msqrt mathcolor=¨#0000FF¨»«mfrac»«mi mathvariant=¨bold¨»R«/mi»«mi mathvariant=¨bold¨»g«/mi»«/mfrac»«/msqrt»«/math»
לכן ביטוי זמן המחזור הוא: «math xmlns=¨http://www.w3.org/1998/Math/MathML¨»«mi mathvariant=¨bold¨ mathcolor=¨#0000FF¨»T«/mi»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»=«/mo»«mn mathvariant=¨bold¨ mathcolor=¨#0000FF¨»2«/mn»«mi mathvariant=¨bold¨ mathcolor=¨#0000FF¨»§#960;«/mi»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»§#183;«/mo»«msqrt mathcolor=¨#0000FF¨»«mfrac»«mi mathvariant=¨bold¨»R«/mi»«mi mathvariant=¨bold¨»g«/mi»«/mfrac»«/msqrt»«/math»
في حالة البندول البسيط، يوجد خيط، ويظهر طوله في تعبير زمن الدورة.
هنا لا يوجد خيط، ولكن دلالة طول الخيط لا تزال موجودة، وتظهر في التعبير عن زمن الدورة كنصف قطر الحركة الدائرية.
כאן אין חוט אך משמעות אורך החוט עדיין קיימת, והיא מופיעה בביטוי זמן המחזור כרדיוס התנועה המעגלית.
______________________________________________________________________________________

______________________________________________________________________________________
...
«math xmlns=¨http://www.w3.org/1998/Math/MathML¨»«mi mathvariant=¨bold¨»§#969;«/mi»«mo mathvariant=¨bold¨»=«/mo»«mn mathvariant=¨bold¨»6«/mn»«mo mathvariant=¨bold¨».«/mo»«mn mathvariant=¨bold¨»2«/mn»«mfrac»«mi mathvariant=¨bold¨»Rad«/mi»«mi mathvariant=¨bold¨»s«/mi»«/mfrac»«/math»
حدّد مستوى الحركة الدائرية الجديد. رسم مخطط القوى، وكتابة معادلات الحركة، والتعبير عن السرعة الزاوية من معادلات الحركة.
ونتيجة لدوران الطوق تتحرك الخرزة بحركة مختلفة عن حركتها السابقة؛ ويتحرك الآن بحركة دائرية منتظمة.
وتؤثر أيضًا قوة الجاذبية والقوة العمودية في هذه الحركة.
سنقوم بتحديد مركز الدوران ومستوى الحركة في الشكل:
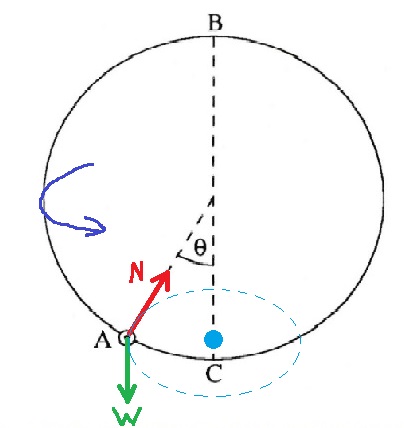
في هذه الحركة، لا يوجد لقوة الجاذبية أي مركبة في الاتجاه الشعاعي؛ القوة الشعاعية هي أحد مركبات القوة العمودية.
نقوم بإجراء تحليل قائم الزاوية للقوة العمودية، مع الإشارة إلى المحور X موجهًا أفقيًا نحو مركز الدوران، والمحور Y باعتباره موجهًا رأسيًا إلى الأعلى:
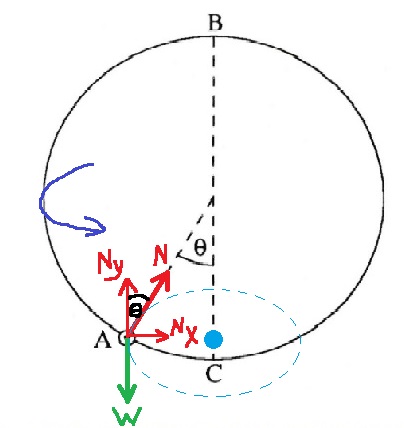
لإيجاد السرعة الزاوية، نكتب معادلات الحركة في اتجاه المحور X، وفي اتجاه المحور Y. سنرمز لنصف قطر الحركة الدائرية الجديدة بالرمز r.
«math xmlns=¨http://www.w3.org/1998/Math/MathML¨»«msub»«mi mathvariant=¨bold¨ mathcolor=¨#0000FF¨»§#931;F«/mi»«mi mathvariant=¨bold¨ mathcolor=¨#0000FF¨»x«/mi»«/msub»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»=«/mo»«msub»«mi mathvariant=¨bold¨ mathcolor=¨#0000FF¨»§#931;F«/mi»«mi mathvariant=¨bold¨ mathcolor=¨#0000FF¨»R«/mi»«/msub»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»=«/mo»«mi mathvariant=¨bold¨ mathcolor=¨#0000FF¨»m«/mi»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»§#183;«/mo»«msup»«mi mathvariant=¨bold¨ mathcolor=¨#0000FF¨»§#969;«/mi»«mn mathvariant=¨bold¨ mathcolor=¨#0000FF¨»2«/mn»«/msup»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»§#183;«/mo»«mi mathvariant=¨bold¨ mathcolor=¨#0000FF¨»r«/mi»«mspace linebreak=¨newline¨»«/mspace»«msub»«mi mathvariant=¨bold¨ mathcolor=¨#0000FF¨»N«/mi»«mi mathvariant=¨bold¨ mathcolor=¨#0000FF¨»X«/mi»«/msub»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»=«/mo»«mi mathvariant=¨bold¨ mathcolor=¨#0000FF¨»m«/mi»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»§#183;«/mo»«msup»«mi mathvariant=¨bold¨ mathcolor=¨#0000FF¨»§#969;«/mi»«mn mathvariant=¨bold¨ mathcolor=¨#0000FF¨»2«/mn»«/msup»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»§#183;«/mo»«mi mathvariant=¨bold¨ mathcolor=¨#0000FF¨»r«/mi»«mspace linebreak=¨newline¨»«/mspace»«menclose mathcolor=¨#0000FF¨ notation=¨box¨»«mi mathvariant=¨bold¨»N«/mi»«mo mathvariant=¨bold¨»§#183;«/mo»«mi mathvariant=¨bold¨»sin«/mi»«mo mathvariant=¨bold¨»(«/mo»«mi mathvariant=¨bold¨»§#920;«/mi»«mo mathvariant=¨bold¨»)«/mo»«mo mathvariant=¨bold¨»=«/mo»«mi mathvariant=¨bold¨»m«/mi»«mo mathvariant=¨bold¨»§#183;«/mo»«msup»«mi mathvariant=¨bold¨»§#969;«/mi»«mn mathvariant=¨bold¨»2«/mn»«/msup»«mo mathvariant=¨bold¨»§#183;«/mo»«mi mathvariant=¨bold¨»r«/mi»«/menclose»«/math» «math xmlns=¨http://www.w3.org/1998/Math/MathML¨»«msub»«mi mathvariant=¨bold¨ mathcolor=¨#0000FF¨»§#931;F«/mi»«mi mathvariant=¨bold¨ mathcolor=¨#0000FF¨»Y«/mi»«/msub»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»=«/mo»«mn mathvariant=¨bold¨ mathcolor=¨#0000FF¨»0«/mn»«mspace linebreak=¨newline¨»«/mspace»«msub»«mi mathvariant=¨bold¨ mathcolor=¨#0000FF¨»N«/mi»«mi mathvariant=¨bold¨ mathcolor=¨#0000FF¨»Y«/mi»«/msub»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»=«/mo»«mi mathvariant=¨bold¨ mathcolor=¨#0000FF¨»W«/mi»«mspace linebreak=¨newline¨»«/mspace»«menclose mathcolor=¨#0000FF¨ notation=¨box¨»«mi mathvariant=¨bold¨»N«/mi»«mo mathvariant=¨bold¨»§#183;«/mo»«mi mathvariant=¨bold¨»cos«/mi»«mo mathvariant=¨bold¨»(«/mo»«mi mathvariant=¨bold¨»§#920;«/mi»«mo mathvariant=¨bold¨»)«/mo»«mo mathvariant=¨bold¨»=«/mo»«mi mathvariant=¨bold¨»mg«/mi»«/menclose»«/math»
نقسم معادلاتي الحركة على بعضهما البعض:
«math xmlns=¨http://www.w3.org/1998/Math/MathML¨»«mfrac mathcolor=¨#0000FF¨»«mrow»«menclose notation=¨downdiagonalstrike¨»«mi mathvariant=¨bold¨»N«/mi»«/menclose»«mo mathvariant=¨bold¨»§#183;«/mo»«mi mathvariant=¨bold¨»sin«/mi»«mo mathvariant=¨bold¨»(«/mo»«mi mathvariant=¨bold¨»§#920;«/mi»«mo mathvariant=¨bold¨»)«/mo»«/mrow»«mrow»«mi mathvariant=¨bold¨»N«/mi»«menclose notation=¨downdiagonalstrike¨»«/menclose»«mo mathvariant=¨bold¨»§#183;«/mo»«mi mathvariant=¨bold¨»cos«/mi»«mo mathvariant=¨bold¨»(«/mo»«mi mathvariant=¨bold¨»§#920;«/mi»«mo mathvariant=¨bold¨»)«/mo»«/mrow»«/mfrac»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»=«/mo»«mfrac mathcolor=¨#0000FF¨»«mrow»«menclose notation=¨updiagonalstrike¨»«mi mathvariant=¨bold¨»m«/mi»«/menclose»«mo mathvariant=¨bold¨»§#183;«/mo»«msup»«mi mathvariant=¨bold¨»§#969;«/mi»«mn mathvariant=¨bold¨»2«/mn»«/msup»«mo mathvariant=¨bold¨»§#183;«/mo»«mi mathvariant=¨bold¨»r«/mi»«/mrow»«mrow»«menclose notation=¨updiagonalstrike¨»«mi mathvariant=¨bold¨»m«/mi»«/menclose»«mi mathvariant=¨bold¨»g«/mi»«/mrow»«/mfrac»«mspace linebreak=¨newline¨»«/mspace»«mspace linebreak=¨newline¨»«/mspace»«mi mathvariant=¨bold¨ mathcolor=¨#0000FF¨»tan«/mi»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»(«/mo»«mi mathvariant=¨bold¨ mathcolor=¨#0000FF¨»§#920;«/mi»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»)«/mo»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»=«/mo»«mfrac mathcolor=¨#0000FF¨»«mrow»«msup»«mi mathvariant=¨bold¨»§#969;«/mi»«mn mathvariant=¨bold¨»2«/mn»«/msup»«mo mathvariant=¨bold¨»§#183;«/mo»«mi mathvariant=¨bold¨»r«/mi»«/mrow»«mi mathvariant=¨bold¨»g«/mi»«/mfrac»«mspace linebreak=¨newline¨»«/mspace»«mspace linebreak=¨newline¨»«/mspace»«mi mathvariant=¨bold¨ mathcolor=¨#0000FF¨»§#969;«/mi»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»=«/mo»«msqrt mathcolor=¨#0000FF¨»«mfrac»«mrow»«mi mathvariant=¨bold¨»g«/mi»«mo mathvariant=¨bold¨»§#183;«/mo»«mi mathvariant=¨bold¨»tan«/mi»«mo mathvariant=¨bold¨»(«/mo»«mi mathvariant=¨bold¨»§#920;«/mi»«mo mathvariant=¨bold¨»)«/mo»«/mrow»«mi mathvariant=¨bold¨»r«/mi»«/mfrac»«/msqrt»«mspace linebreak=¨newline¨»«/mspace»«mspace linebreak=¨newline¨»«/mspace»«mspace linebreak=¨newline¨»«/mspace»«/math»
نعبر هندسيًا عن نصف قطر مسار الحركة الدائرية الجديد r كدالة لنصف قطر الطوق R:
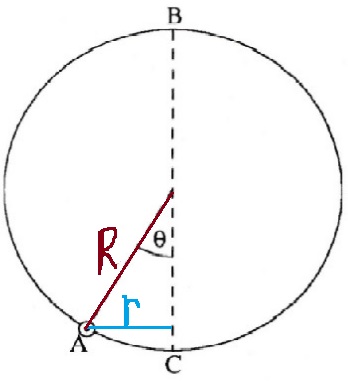
«math xmlns=¨http://www.w3.org/1998/Math/MathML¨»«mstyle mathsize=¨28px¨»«mrow»«mi mathvariant=¨bold¨ mathcolor=¨#0000FF¨»sin«/mi»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»(«/mo»«mi mathvariant=¨bold¨ mathcolor=¨#0000FF¨»§#952;«/mi»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»)«/mo»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»=«/mo»«mfrac mathcolor=¨#0000FF¨»«mi mathvariant=¨bold¨»r«/mi»«mi mathvariant=¨bold¨»R«/mi»«/mfrac»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»§#160;«/mo»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»§#8658;«/mo»«mi mathvariant=¨bold¨ mathcolor=¨#0000FF¨»r«/mi»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»=«/mo»«mi mathvariant=¨bold¨ mathcolor=¨#0000FF¨»R«/mi»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»§#183;«/mo»«mi mathvariant=¨bold¨ mathcolor=¨#0000FF¨»sin«/mi»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»(«/mo»«mi mathvariant=¨bold¨ mathcolor=¨#0000FF¨»§#952;«/mi»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»)«/mo»«/mrow»«/mstyle»«/math»
نستبدل تعبير نصف قطر الحركة الدائرية الجديدة في تعبير السرعة الزاوية، ونحسب مقدارها عندما «math xmlns=¨http://www.w3.org/1998/Math/MathML¨»«mi mathvariant=¨bold¨ mathcolor=¨#0000FF¨»§#952;«/mi»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»=«/mo»«mn mathvariant=¨bold¨ mathcolor=¨#0000FF¨»30«/mn»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»§#176;«/mo»«/math»:
«math xmlns=¨http://www.w3.org/1998/Math/MathML¨»«mspace linebreak=¨newline¨»«/mspace»«mi mathvariant=¨bold¨ mathcolor=¨#0000FF¨»§#969;«/mi»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»=«/mo»«msqrt mathcolor=¨#0000FF¨»«mfrac»«mrow»«mi mathvariant=¨bold¨»g«/mi»«mo mathvariant=¨bold¨»§#183;«/mo»«mi mathvariant=¨bold¨»tan«/mi»«mo mathvariant=¨bold¨»(«/mo»«mi mathvariant=¨bold¨»§#920;«/mi»«mo mathvariant=¨bold¨»)«/mo»«/mrow»«mi mathvariant=¨bold¨»r«/mi»«/mfrac»«/msqrt»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»§#160;«/mo»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»=«/mo»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»§#160;«/mo»«msqrt mathcolor=¨#0000FF¨»«mfrac»«mrow»«mi mathvariant=¨bold¨»g«/mi»«mo mathvariant=¨bold¨»§#183;«/mo»«mi mathcolor=¨#007F00¨ mathvariant=¨bold¨»tan«/mi»«mo mathcolor=¨#007F00¨ mathvariant=¨bold¨»(«/mo»«mi mathcolor=¨#007F00¨ mathvariant=¨bold¨»§#920;«/mi»«mo mathcolor=¨#007F00¨ mathvariant=¨bold¨»)«/mo»«/mrow»«mrow»«mi mathvariant=¨bold¨»R«/mi»«mo mathvariant=¨bold¨»§#183;«/mo»«mi mathvariant=¨bold¨»sin«/mi»«mo mathvariant=¨bold¨»(«/mo»«mi mathvariant=¨bold¨»§#920;«/mi»«mo mathvariant=¨bold¨»)«/mo»«/mrow»«/mfrac»«/msqrt»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»§#160;«/mo»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»=«/mo»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»§#160;«/mo»«msqrt mathcolor=¨#0000FF¨»«mfrac»«mrow»«mi mathvariant=¨bold¨»g«/mi»«mo mathvariant=¨bold¨»§#183;«/mo»«menclose mathcolor=¨#007F00¨ notation=¨updiagonalstrike¨»«mi mathvariant=¨bold¨»sin«/mi»«mo mathvariant=¨bold¨»(«/mo»«mi mathvariant=¨bold¨»§#920;«/mi»«mo mathvariant=¨bold¨»)«/mo»«/menclose»«/mrow»«mrow»«mi mathvariant=¨bold¨»R«/mi»«mo mathvariant=¨bold¨»§#183;«/mo»«mi mathcolor=¨#007F00¨ mathvariant=¨bold¨»c«/mi»«mi mathcolor=¨#007F00¨ mathvariant=¨bold¨»o«/mi»«mi mathcolor=¨#007F00¨ mathvariant=¨bold¨»s«/mi»«mo mathvariant=¨bold¨»(«/mo»«mi mathcolor=¨#007F00¨ mathvariant=¨bold¨»§#920;«/mi»«mo mathcolor=¨#007F00¨ mathvariant=¨bold¨»)«/mo»«mo mathcolor=¨#007F00¨ mathvariant=¨bold¨»§#183;«/mo»«menclose notation=¨updiagonalstrike¨»«mi mathvariant=¨bold¨»sin«/mi»«mo mathvariant=¨bold¨»(«/mo»«mi mathvariant=¨bold¨»§#920;«/mi»«mo mathvariant=¨bold¨»)«/mo»«/menclose»«/mrow»«/mfrac»«/msqrt»«mspace linebreak=¨newline¨»«/mspace»«mspace linebreak=¨newline¨»«/mspace»«mi mathvariant=¨bold¨ mathcolor=¨#0000FF¨»§#969;«/mi»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»=«/mo»«msqrt mathcolor=¨#0000FF¨»«mfrac»«mi mathvariant=¨bold¨»g«/mi»«mrow»«mi mathvariant=¨bold¨»R«/mi»«mo mathvariant=¨bold¨»§#183;«/mo»«mi mathvariant=¨bold¨»cos«/mi»«mo mathvariant=¨bold¨»(«/mo»«mi mathvariant=¨bold¨»§#920;«/mi»«mo mathvariant=¨bold¨»)«/mo»«/mrow»«/mfrac»«/msqrt»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»=«/mo»«msqrt mathcolor=¨#0000FF¨»«mfrac»«mn mathvariant=¨bold¨»10«/mn»«mrow»«mn mathvariant=¨bold¨»0«/mn»«mo mathvariant=¨bold¨».«/mo»«mn mathvariant=¨bold¨»3«/mn»«mo mathvariant=¨bold¨»§#183;«/mo»«mi mathvariant=¨bold¨»cos«/mi»«mo mathvariant=¨bold¨»(«/mo»«mn mathvariant=¨bold¨»30«/mn»«mo mathvariant=¨bold¨»)«/mo»«/mrow»«/mfrac»«/msqrt»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»=«/mo»«msqrt mathcolor=¨#0000FF¨»«mn mathvariant=¨bold¨»38«/mn»«mo mathvariant=¨bold¨».«/mo»«mn mathvariant=¨bold¨»49«/mn»«mo mathvariant=¨bold¨»§#160;«/mo»«/msqrt»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»=«/mo»«mn mathvariant=¨bold¨ mathcolor=¨#0000FF¨»6«/mn»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨».«/mo»«mn mathvariant=¨bold¨ mathcolor=¨#0000FF¨»2«/mn»«mfrac mathcolor=¨#0000FF¨»«mrow»«mi mathvariant=¨bold¨»R«/mi»«mi mathvariant=¨bold¨»A«/mi»«mi mathvariant=¨bold¨»D«/mi»«/mrow»«mi mathvariant=¨bold¨»S«/mi»«/mfrac»«mspace linebreak=¨newline¨»«/mspace»«/math»
لكي ترتفع الخرزة إلى النقطة A، يجب أن يدور الطوق بسرعة زاوية مقدارها 6.2 راديان في الثانية.
גם בתנועה זו פועלים כוח הכובד וכוח הנורמל.
נסמן באיור את נקודת מרכז הסיבוב , ואת מישור התנועה:

בתנועה זו אין לכוח הכובד רכיב בכיוון הרדיאלי , הכוח הרדיאלי הוא רכיב של כוח הנורמל.
נבצע הפרדה ישרת זווית לכוח הנורמל , נתייחס לציר X שכיוונו אופקי רדיאלי, ולציר Y שכיוונו אנכי כלפי מעלה:

כדי למצוא את המהירות הזוויתית , נכתוב את משוואות התנועה בכיוון ציר X , ובכיוון ציר Y. נסמן את רדיוס התנועה המעגלית החדשה ב r.
«math xmlns=¨http://www.w3.org/1998/Math/MathML¨»«msub»«mi mathvariant=¨bold¨ mathcolor=¨#0000FF¨»§#931;F«/mi»«mi mathvariant=¨bold¨ mathcolor=¨#0000FF¨»x«/mi»«/msub»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»=«/mo»«msub»«mi mathvariant=¨bold¨ mathcolor=¨#0000FF¨»§#931;F«/mi»«mi mathvariant=¨bold¨ mathcolor=¨#0000FF¨»R«/mi»«/msub»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»=«/mo»«mi mathvariant=¨bold¨ mathcolor=¨#0000FF¨»m«/mi»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»§#183;«/mo»«msup»«mi mathvariant=¨bold¨ mathcolor=¨#0000FF¨»§#969;«/mi»«mn mathvariant=¨bold¨ mathcolor=¨#0000FF¨»2«/mn»«/msup»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»§#183;«/mo»«mi mathvariant=¨bold¨ mathcolor=¨#0000FF¨»r«/mi»«mspace linebreak=¨newline¨»«/mspace»«msub»«mi mathvariant=¨bold¨ mathcolor=¨#0000FF¨»N«/mi»«mi mathvariant=¨bold¨ mathcolor=¨#0000FF¨»X«/mi»«/msub»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»=«/mo»«mi mathvariant=¨bold¨ mathcolor=¨#0000FF¨»m«/mi»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»§#183;«/mo»«msup»«mi mathvariant=¨bold¨ mathcolor=¨#0000FF¨»§#969;«/mi»«mn mathvariant=¨bold¨ mathcolor=¨#0000FF¨»2«/mn»«/msup»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»§#183;«/mo»«mi mathvariant=¨bold¨ mathcolor=¨#0000FF¨»r«/mi»«mspace linebreak=¨newline¨»«/mspace»«menclose mathcolor=¨#0000FF¨ notation=¨box¨»«mi mathvariant=¨bold¨»N«/mi»«mo mathvariant=¨bold¨»§#183;«/mo»«mi mathvariant=¨bold¨»sin«/mi»«mo mathvariant=¨bold¨»(«/mo»«mi mathvariant=¨bold¨»§#920;«/mi»«mo mathvariant=¨bold¨»)«/mo»«mo mathvariant=¨bold¨»=«/mo»«mi mathvariant=¨bold¨»m«/mi»«mo mathvariant=¨bold¨»§#183;«/mo»«msup»«mi mathvariant=¨bold¨»§#969;«/mi»«mn mathvariant=¨bold¨»2«/mn»«/msup»«mo mathvariant=¨bold¨»§#183;«/mo»«mi mathvariant=¨bold¨»r«/mi»«/menclose»«/math» «math xmlns=¨http://www.w3.org/1998/Math/MathML¨»«msub»«mi mathvariant=¨bold¨ mathcolor=¨#0000FF¨»§#931;F«/mi»«mi mathvariant=¨bold¨ mathcolor=¨#0000FF¨»Y«/mi»«/msub»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»=«/mo»«mn mathvariant=¨bold¨ mathcolor=¨#0000FF¨»0«/mn»«mspace linebreak=¨newline¨»«/mspace»«msub»«mi mathvariant=¨bold¨ mathcolor=¨#0000FF¨»N«/mi»«mi mathvariant=¨bold¨ mathcolor=¨#0000FF¨»Y«/mi»«/msub»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»=«/mo»«mi mathvariant=¨bold¨ mathcolor=¨#0000FF¨»W«/mi»«mspace linebreak=¨newline¨»«/mspace»«menclose mathcolor=¨#0000FF¨ notation=¨box¨»«mi mathvariant=¨bold¨»N«/mi»«mo mathvariant=¨bold¨»§#183;«/mo»«mi mathvariant=¨bold¨»cos«/mi»«mo mathvariant=¨bold¨»(«/mo»«mi mathvariant=¨bold¨»§#920;«/mi»«mo mathvariant=¨bold¨»)«/mo»«mo mathvariant=¨bold¨»=«/mo»«mi mathvariant=¨bold¨»mg«/mi»«/menclose»«/math»
נבצע פעולת חילוק בין משוואות התנועה:
«math xmlns=¨http://www.w3.org/1998/Math/MathML¨»«mfrac mathcolor=¨#0000FF¨»«mrow»«menclose notation=¨downdiagonalstrike¨»«mi mathvariant=¨bold¨»N«/mi»«/menclose»«mo mathvariant=¨bold¨»§#183;«/mo»«mi mathvariant=¨bold¨»sin«/mi»«mo mathvariant=¨bold¨»(«/mo»«mi mathvariant=¨bold¨»§#920;«/mi»«mo mathvariant=¨bold¨»)«/mo»«/mrow»«mrow»«mi mathvariant=¨bold¨»N«/mi»«menclose notation=¨downdiagonalstrike¨»«/menclose»«mo mathvariant=¨bold¨»§#183;«/mo»«mi mathvariant=¨bold¨»cos«/mi»«mo mathvariant=¨bold¨»(«/mo»«mi mathvariant=¨bold¨»§#920;«/mi»«mo mathvariant=¨bold¨»)«/mo»«/mrow»«/mfrac»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»=«/mo»«mfrac mathcolor=¨#0000FF¨»«mrow»«menclose notation=¨updiagonalstrike¨»«mi mathvariant=¨bold¨»m«/mi»«/menclose»«mo mathvariant=¨bold¨»§#183;«/mo»«msup»«mi mathvariant=¨bold¨»§#969;«/mi»«mn mathvariant=¨bold¨»2«/mn»«/msup»«mo mathvariant=¨bold¨»§#183;«/mo»«mi mathvariant=¨bold¨»r«/mi»«/mrow»«mrow»«menclose notation=¨updiagonalstrike¨»«mi mathvariant=¨bold¨»m«/mi»«/menclose»«mi mathvariant=¨bold¨»g«/mi»«/mrow»«/mfrac»«mspace linebreak=¨newline¨»«/mspace»«mspace linebreak=¨newline¨»«/mspace»«mi mathvariant=¨bold¨ mathcolor=¨#0000FF¨»tan«/mi»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»(«/mo»«mi mathvariant=¨bold¨ mathcolor=¨#0000FF¨»§#920;«/mi»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»)«/mo»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»=«/mo»«mfrac mathcolor=¨#0000FF¨»«mrow»«msup»«mi mathvariant=¨bold¨»§#969;«/mi»«mn mathvariant=¨bold¨»2«/mn»«/msup»«mo mathvariant=¨bold¨»§#183;«/mo»«mi mathvariant=¨bold¨»r«/mi»«/mrow»«mi mathvariant=¨bold¨»g«/mi»«/mfrac»«mspace linebreak=¨newline¨»«/mspace»«mspace linebreak=¨newline¨»«/mspace»«mi mathvariant=¨bold¨ mathcolor=¨#0000FF¨»§#969;«/mi»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»=«/mo»«msqrt mathcolor=¨#0000FF¨»«mfrac»«mrow»«mi mathvariant=¨bold¨»g«/mi»«mo mathvariant=¨bold¨»§#183;«/mo»«mi mathvariant=¨bold¨»tan«/mi»«mo mathvariant=¨bold¨»(«/mo»«mi mathvariant=¨bold¨»§#920;«/mi»«mo mathvariant=¨bold¨»)«/mo»«/mrow»«mi mathvariant=¨bold¨»r«/mi»«/mfrac»«/msqrt»«mspace linebreak=¨newline¨»«/mspace»«mspace linebreak=¨newline¨»«/mspace»«mspace linebreak=¨newline¨»«/mspace»«/math»
נבטא גיאומטרית את רדיוס מסלול התנועה המעגלית החדשה r בתלות ברדיוס החישוק R:

«math xmlns=¨http://www.w3.org/1998/Math/MathML¨»«mstyle mathsize=¨28px¨»«mrow»«mi mathvariant=¨bold¨ mathcolor=¨#0000FF¨»sin«/mi»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»(«/mo»«mi mathvariant=¨bold¨ mathcolor=¨#0000FF¨»§#952;«/mi»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»)«/mo»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»=«/mo»«mfrac mathcolor=¨#0000FF¨»«mi mathvariant=¨bold¨»r«/mi»«mi mathvariant=¨bold¨»R«/mi»«/mfrac»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»§#160;«/mo»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»§#8658;«/mo»«mi mathvariant=¨bold¨ mathcolor=¨#0000FF¨»r«/mi»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»=«/mo»«mi mathvariant=¨bold¨ mathcolor=¨#0000FF¨»R«/mi»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»§#183;«/mo»«mi mathvariant=¨bold¨ mathcolor=¨#0000FF¨»sin«/mi»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»(«/mo»«mi mathvariant=¨bold¨ mathcolor=¨#0000FF¨»§#952;«/mi»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»)«/mo»«/mrow»«/mstyle»«/math»
נציב את ביטוי רדיוס התנועה המעגלית החדשה בביטוי המהירות הזוויתית , ונחשב את גודלה כאשר «math xmlns=¨http://www.w3.org/1998/Math/MathML¨»«mi mathvariant=¨bold¨ mathcolor=¨#0000FF¨»§#952;«/mi»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»=«/mo»«mn mathvariant=¨bold¨ mathcolor=¨#0000FF¨»30«/mn»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»§#176;«/mo»«/math»:
«math xmlns=¨http://www.w3.org/1998/Math/MathML¨»«mspace linebreak=¨newline¨»«/mspace»«mi mathvariant=¨bold¨ mathcolor=¨#0000FF¨»§#969;«/mi»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»=«/mo»«msqrt mathcolor=¨#0000FF¨»«mfrac»«mrow»«mi mathvariant=¨bold¨»g«/mi»«mo mathvariant=¨bold¨»§#183;«/mo»«mi mathvariant=¨bold¨»tan«/mi»«mo mathvariant=¨bold¨»(«/mo»«mi mathvariant=¨bold¨»§#920;«/mi»«mo mathvariant=¨bold¨»)«/mo»«/mrow»«mi mathvariant=¨bold¨»r«/mi»«/mfrac»«/msqrt»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»§#160;«/mo»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»=«/mo»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»§#160;«/mo»«msqrt mathcolor=¨#0000FF¨»«mfrac»«mrow»«mi mathvariant=¨bold¨»g«/mi»«mo mathvariant=¨bold¨»§#183;«/mo»«mi mathcolor=¨#007F00¨ mathvariant=¨bold¨»tan«/mi»«mo mathcolor=¨#007F00¨ mathvariant=¨bold¨»(«/mo»«mi mathcolor=¨#007F00¨ mathvariant=¨bold¨»§#920;«/mi»«mo mathcolor=¨#007F00¨ mathvariant=¨bold¨»)«/mo»«/mrow»«mrow»«mi mathvariant=¨bold¨»R«/mi»«mo mathvariant=¨bold¨»§#183;«/mo»«mi mathvariant=¨bold¨»sin«/mi»«mo mathvariant=¨bold¨»(«/mo»«mi mathvariant=¨bold¨»§#920;«/mi»«mo mathvariant=¨bold¨»)«/mo»«/mrow»«/mfrac»«/msqrt»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»§#160;«/mo»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»=«/mo»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»§#160;«/mo»«msqrt mathcolor=¨#0000FF¨»«mfrac»«mrow»«mi mathvariant=¨bold¨»g«/mi»«mo mathvariant=¨bold¨»§#183;«/mo»«menclose mathcolor=¨#007F00¨ notation=¨updiagonalstrike¨»«mi mathvariant=¨bold¨»sin«/mi»«mo mathvariant=¨bold¨»(«/mo»«mi mathvariant=¨bold¨»§#920;«/mi»«mo mathvariant=¨bold¨»)«/mo»«/menclose»«/mrow»«mrow»«mi mathvariant=¨bold¨»R«/mi»«mo mathvariant=¨bold¨»§#183;«/mo»«mi mathcolor=¨#007F00¨ mathvariant=¨bold¨»c«/mi»«mi mathcolor=¨#007F00¨ mathvariant=¨bold¨»o«/mi»«mi mathcolor=¨#007F00¨ mathvariant=¨bold¨»s«/mi»«mo mathvariant=¨bold¨»(«/mo»«mi mathcolor=¨#007F00¨ mathvariant=¨bold¨»§#920;«/mi»«mo mathcolor=¨#007F00¨ mathvariant=¨bold¨»)«/mo»«mo mathcolor=¨#007F00¨ mathvariant=¨bold¨»§#183;«/mo»«menclose notation=¨updiagonalstrike¨»«mi mathvariant=¨bold¨»sin«/mi»«mo mathvariant=¨bold¨»(«/mo»«mi mathvariant=¨bold¨»§#920;«/mi»«mo mathvariant=¨bold¨»)«/mo»«/menclose»«/mrow»«/mfrac»«/msqrt»«mspace linebreak=¨newline¨»«/mspace»«mspace linebreak=¨newline¨»«/mspace»«mi mathvariant=¨bold¨ mathcolor=¨#0000FF¨»§#969;«/mi»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»=«/mo»«msqrt mathcolor=¨#0000FF¨»«mfrac»«mi mathvariant=¨bold¨»g«/mi»«mrow»«mi mathvariant=¨bold¨»R«/mi»«mo mathvariant=¨bold¨»§#183;«/mo»«mi mathvariant=¨bold¨»cos«/mi»«mo mathvariant=¨bold¨»(«/mo»«mi mathvariant=¨bold¨»§#920;«/mi»«mo mathvariant=¨bold¨»)«/mo»«/mrow»«/mfrac»«/msqrt»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»=«/mo»«msqrt mathcolor=¨#0000FF¨»«mfrac»«mn mathvariant=¨bold¨»10«/mn»«mrow»«mn mathvariant=¨bold¨»0«/mn»«mo mathvariant=¨bold¨».«/mo»«mn mathvariant=¨bold¨»3«/mn»«mo mathvariant=¨bold¨»§#183;«/mo»«mi mathvariant=¨bold¨»cos«/mi»«mo mathvariant=¨bold¨»(«/mo»«mn mathvariant=¨bold¨»30«/mn»«mo mathvariant=¨bold¨»)«/mo»«/mrow»«/mfrac»«/msqrt»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»=«/mo»«msqrt mathcolor=¨#0000FF¨»«mn mathvariant=¨bold¨»38«/mn»«mo mathvariant=¨bold¨».«/mo»«mn mathvariant=¨bold¨»49«/mn»«mo mathvariant=¨bold¨»§#160;«/mo»«/msqrt»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»=«/mo»«mn mathvariant=¨bold¨ mathcolor=¨#0000FF¨»6«/mn»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨».«/mo»«mn mathvariant=¨bold¨ mathcolor=¨#0000FF¨»2«/mn»«mfrac mathcolor=¨#0000FF¨»«mrow»«mi mathvariant=¨bold¨»R«/mi»«mi mathvariant=¨bold¨»A«/mi»«mi mathvariant=¨bold¨»D«/mi»«/mrow»«mi mathvariant=¨bold¨»S«/mi»«/mfrac»«mspace linebreak=¨newline¨»«/mspace»«/math»
כדי שהחרוז יעלה עד לנקודה A , יש לסובב את החישוק במהירות זוויתית שגודלה 6.2 רדיאן לשנייה.
1. تنص الفقرة على أن الخرزة ترتفع أولا إلى النقطة A، لكنها لا تنص كيف ترتفع.
فقط في نهاية البند، بعد طرح السؤال، قيل أن الطوق يدور حول محوره الرأسي BC.
من المهم قراءة حتى نهاية البند والعودة إلى بدايته لفهم المطلوب.
هنالك إشكالية في صياغة السؤال، وهذا ما يحدث في أسئلة البجروت. يجب عليك قراءته مرارًا وتكرارًا ومحاولة فهم نية المؤلف.
2. يؤدي تدوير الطوق حول محوره الرأسي إلى تغيير الحركة، قبل رسم مخطط القوى وكتابة معادلات الحركة.
يجب عليك أن تفهم أين يقع مركز الدوران - لمعرفة ما هي القوة المركزية.
ولكي نعرف أين يقع مركز الدوران، لا بد من فهم أين يقع مستوى الحركة الدائرية.
يبدأ كل تحليل للحركة الدائرية بتحديد مستوى الحركة الدائرية. 3. تغيرت الحركة الدائرية. لم يعد نصف قطر مسار الحركة الدائرية الجديد هو نصف قطر الطوق.
هذا خطأ متكرر. من المهم العمل ببطء والانتباه للأشياء.
4. في الحركة الدائرية الأولى، هناك قوة خارجية ترفع الخرزة إلى النقطة A.
في الحركة الدائرية الجديدة، تستقر الخرزة "لوحدها" في النقطة A بحيث يكون نصف قطر مسار الحركة والقوة المركزية تحققان معادلات الحركة.
على غرار الكرة التي تتحرك في حركة دائرية داخل مخروط، يتغير نصف قطر المسار اعتمادًا على سرعة الكرة.
5. في الحركة الدائرية الأولى، تعمل القوة العمودية في الاتجاه الشعاعي، باتجاه مركز الدوران.
وتعمل مركبة القوة الجاذبية في الاتجاه الشعاعي المعاكس للاتجاه العمودي.
في الحركة الدائرية الجديدة، تعمل مركبة القوة العمودية في الاتجاه الشعاعي. وقوة الجاذبية ليس لها مركب في الاتجاه الشعاعي.
6. في كلتا الحركتين الدائريتين، فقط قوة الجاذبية والقوة العمودية تؤثران على الخرزة. القوة هي نفسها في كلتا الحالتين.
القوة العمودية تتغير.
في الحركة الأولى في النقطة A، القوة العمودية أصغر من قوة الجاذبية. في الحركة الجديدة، القوة العمودية أكبر من قوة الجاذبية.
7. في النقطة C في الحركة الأولى، تكون القوة العمودية أكبر من قوة الجاذبية.
רק בסוף הסעיף אחרי שנשאלת השאלה כתוב שמסובבים את החישוק סביב צירו האנכי BC .
חשוב לקרוא את סוף הסעיף ,לחזור לתחילת הסעיף כדי להבין את הסיטואציה.
הניסוח הוא בעייתי , וזה קורה בשאלות הבגרות. צריך לקרוא שוב ושוב ולנסות להבין את כוונת כותב השאלה.
2. סיבוב החישוק סביב צירו האנכי משנה את התנועה , לפני עריכת תרשים כוחות וכתיבת משוואות התנועה
יש להבין היכן נמצאת נקודת מרכז הסיבוב - כדי לדעת מי הוא הכוח הצנטריפטאלי.
וכדי לדעת היכן ממוקמת נקודת מרכז הסיבוב יש להבין היכן ממוקם מישור התנועה המעגלית.
כל ניתוח תנועה מעגלית מתחיל באיתור מיקום מישור התנועה המעגלית.
3. התנועה המעגלית השתנתה. רדיוס מסלול התנועה המעגלית החדשה הוא כבר לא רדיוס החישוק.
זאת טעות שחוזרת על עצמה. חשוב לעבוד לאט ולשים לב לדברים.
4. בתנועה המעגלית הראשונה יש כוח חיצוני המעלה את החרוז לנקודה A .
בתנועה המעגלית החדשה החרוז מתמקם "לבד" בנקודה A כך שרדיוס מסלול התנועה
והכוח הצנטריפטלי יקיימו את משוואות התנועה.
בדומה לכדור הנע בתנועה מעגלית בקונוס , רדיוס המסלול משתנה בהתאם למהירות הכדור.
5.בתנועה המעגלית הראשונה כוח הנורמל פועל בכיוון הרדיאלי ,אל נקודת מרכז הסיבוב.
ורכיב כוח הכובד פועל בכיוון הרדיאלי הפוך לנורמל.
בתנועה המעגלית החדשה רכיב כוח הנורמל פועל בכיוון הרדיאלי. ואין לכוח הכובד רכיב בכיוון רדיאלי.
6. בתנועה הראשונה כוח הנורמל גדול מכוח הכובד , בתנועה החדשה כוח הנורמל
______________________________________________________________________________________