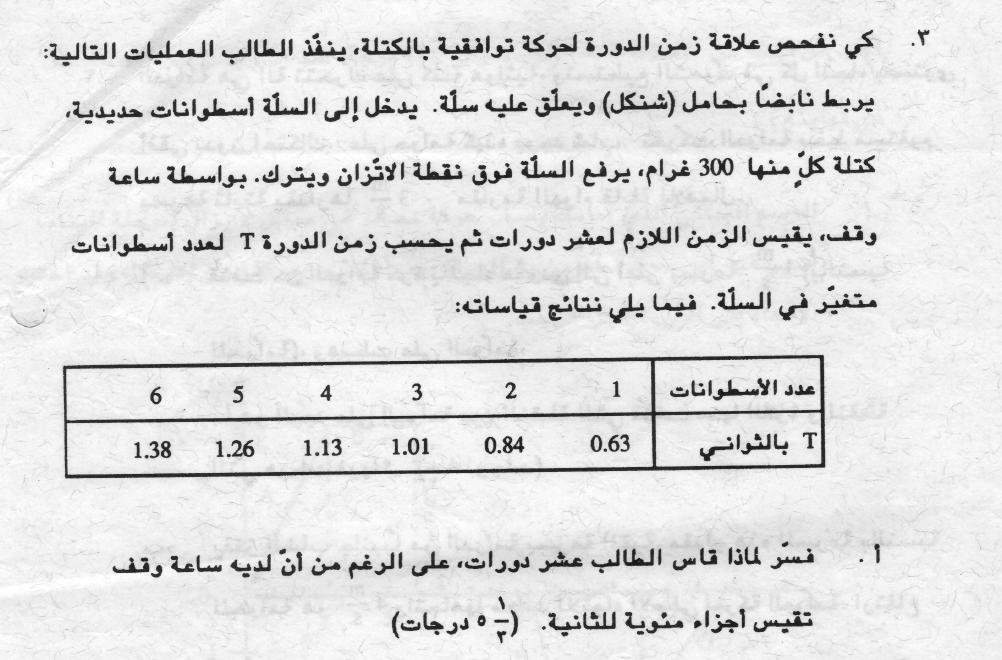
14. 1992,3- سلة مع أوزان تتحرك في حركة توافقية بسيطة
______________________________________________________________________________________
...
عند قياس زمن الحركة لعشر دورات، كلما كان الخطأ النسبي أصغر، كلما كانت جودة القياس أعلى.
خطأ القياس والخطأ النسبي.
تقيس ساعة الوقف جزءًا مئويًا من الثانية، لكن خطأ القياس يتعلق أيضًا على زمن رد فعل الطالب.
تتعلق جودة القياس على خطأ القياس والكمية المقاسة. كلما كانت قيمة الكمية المقاسة أكبر، كلما كانت جودة القياس أعلى، لذلك قام الطالب بقياس عشر دورات. وليس دورة واحدة.
ככל שערכו של הגודל הנמדד גדול יותר כך המדידה נחשבת איכותית יותר, לכן התלמיד מדד עשרה מחזורים. ולא מחזור אחד.
يجب الإجابة على السؤال بشكل عام، ولكن من المهم فهم الفرق بين خطأ القياس والخطأ النسبي والعلاقة بينهما.
خطأ القياس - كل جهاز لديه خطأ في القياس، بغض النظر عن قيمة الكمية المقاسة. خطأ القياس يساوي أصغر قيمة يمكن قياسها باستخدام أداة القياس. على سبيل المثال، خطأ قياس المسطرة هو 1 مليمتر.
لخطأ النسبي - تتناسب جودة القياس عكسيا على المقدار الذي يتم قياسه. إذا قمنا بقياس ارتفاع مبنى وكان خطأ القياس مليمتر واحد فإن جودة القياس تعتبر عالية، أما إذا قمنا بقياس سمك الشعرة وكان خطأ القياس مليمتر واحد فإن جودة القياس تعتبر رديئة جداً.
يتم تعريف جودة القياس على أنها الخطأ النسبي، ويتم تعريفها على النحو التالي:
«math xmlns=¨http://www.w3.org/1998/Math/MathML¨»«mi mathvariant=¨bold¨ mathcolor=¨#FF0000¨»§#1575;§#1604;§#1606;§#1587;§#1576;§#1610;«/mi»«mo mathvariant=¨bold¨ mathcolor=¨#FF0000¨»§#160;«/mo»«mi mathvariant=¨bold¨ mathcolor=¨#FF0000¨»§#1575;§#1604;§#1582;§#1591;§#1571;«/mi»«mo mathvariant=¨bold¨ mathcolor=¨#FF0000¨»=«/mo»«mo mathvariant=¨bold¨ mathcolor=¨#FF0000¨»§#160;«/mo»«mfrac mathcolor=¨#FF0000¨»«mrow»«mi mathvariant=¨bold¨»§#1575;§#1604;§#1602;§#1610;§#1575;§#1587;«/mi»«mo mathvariant=¨bold¨»§#160;«/mo»«mi mathvariant=¨bold¨»§#1582;§#1591;§#1571;«/mi»«mo mathvariant=¨bold¨»§#160;«/mo»«/mrow»«mrow»«mi mathvariant=¨bold¨»§#1575;§#1604;§#1605;§#1602;§#1575;§#1587;«/mi»«mo mathvariant=¨bold¨»§#160;«/mo»«mi mathvariant=¨bold¨»§#1575;§#1604;§#1605;§#1602;§#1583;§#1575;§#1585;«/mi»«/mrow»«/mfrac»«mo mathvariant=¨bold¨ mathcolor=¨#FF0000¨»§#183;«/mo»«mn mathvariant=¨bold¨ mathcolor=¨#FF0000¨»100«/mn»«mo mathvariant=¨bold¨ mathcolor=¨#FF0000¨»%«/mo»«/math»
يريد الطالب إيجاد زمن الحركة لدورة واحدة من الحركة. إن زمن الدورة الواحدة صغير، فإذا قام الطالب بقياس زمن حركة دورة واحدة فإن الخطأ النسبي سيكون صغيراً، ولن تكون جودة القياس جيدة بما فيه الكفاية.
قام الطالب بقياس عشر دورات حركة بنفس الجهاز بحيث يكون خطأ القياس متساويا ولكن الكمية المقاسة أكبر بعشر مرات، والخطأ النسبي أصغر بعشر مرات. جودة القياس أفضل بكثير.
שגיאת מדידה - לכל מכשיר יש שגיאת מדידה , לא משנה מה ערכו של הגודל הנמדד. שגיאת המדידה שווה לאערך הקטן ביותר שניתן למדוד בעזרת מכשיר המדידה. כך למשל שגיאת המדידה של סרגל היא 1 מילי מטר.
שגיאה יחסית - איכות המדידה תלויה ביחס הפוך בגודל הנמדד , אם נמדוד גובה של בניין ושגיאת המדידה תהיה מלימטר המדידה נחשבת איכותית, אך אם נמדוד עובי שערה בשגיאת מדידה של מילי מטר - איכות המדידה נחשבת מאוד לא איכותית.
איכות המדידה מוגדרת כשגיאה יחסית , והיא מוגדרת באופן הבא:
«math xmlns=¨http://www.w3.org/1998/Math/MathML¨»«mi mathvariant=¨bold¨ mathcolor=¨#FF0000¨»§#1497;§#1495;§#1505;§#1497;§#1514;«/mi»«mo mathvariant=¨bold¨ mathcolor=¨#FF0000¨»§#160;«/mo»«mi mathvariant=¨bold¨ mathcolor=¨#FF0000¨»§#1513;§#1490;§#1497;§#1488;§#1492;«/mi»«mo mathvariant=¨bold¨ mathcolor=¨#FF0000¨»=«/mo»«mo mathvariant=¨bold¨ mathcolor=¨#FF0000¨»§#160;«/mo»«mfrac mathcolor=¨#FF0000¨»«mrow»«mi mathvariant=¨bold¨»§#1502;§#1491;§#1497;§#1491;§#1492;«/mi»«mo mathvariant=¨bold¨»§#160;«/mo»«mi mathvariant=¨bold¨»§#1513;§#1490;§#1497;§#1488;§#1514;«/mi»«mo mathvariant=¨bold¨»§#160;«/mo»«/mrow»«mrow»«mi mathvariant=¨bold¨»§#1504;§#1502;§#1491;§#1491;«/mi»«mo mathvariant=¨bold¨»§#160;«/mo»«mi mathvariant=¨bold¨»§#1490;§#1493;§#1491;§#1500;«/mi»«/mrow»«/mfrac»«mo mathvariant=¨bold¨ mathcolor=¨#FF0000¨»§#183;«/mo»«mn mathvariant=¨bold¨ mathcolor=¨#FF0000¨»100«/mn»«mo mathvariant=¨bold¨ mathcolor=¨#FF0000¨»%«/mo»«/math»
______________________________________________________________________________________

______________________________________________________________________________________
...
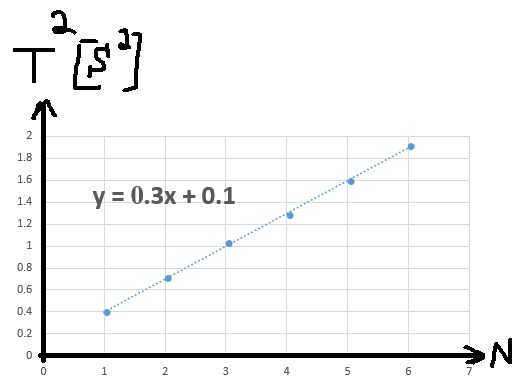
إضافة عمود مربع زمن الدورة، ورسم الرسم البياني لمربع زمن الدورة كدالة لعدد الأسطوانات.
نضيف عمودًا يحتوي على مربع زمن الدورة إلى الجدول الموجود:
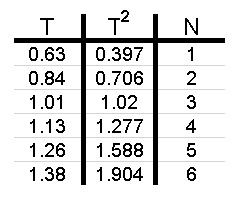
نرسم رسمًا بيانيًا لمربع زمن الدورة كدالة لعدد الأسطوانات N:
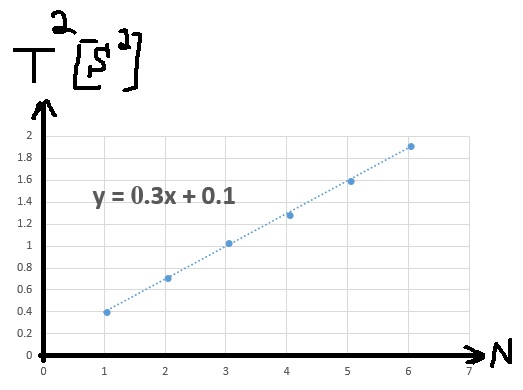

נערוך גרף של ריבוע זמן המחזור בתלות במספר הגלילים N:

1.وحدات المحاور ليست وحدات قياسية. وحدات المحور الرأسي هي الثواني المربعة، أما المحور الأفقي فلا يحتوي على وحدات.
2. الغرض من الرسم البياني غير واضح. سيتم استخدام الرسم البياني في البنود التالية.
2. לא ברורה מטרתו של הגרף, בסעיפים הבאים יעשה שימוש בגרף.
2. בסעיף זה עדיין לא ברור מה המטרה של הגרף, לרוב הגרף משמש הכנה לסעיפים הבאים.
______________________________________________________________________________________

______________________________________________________________________________________
...
الدالة لا تمر عبر نقطة الأصل.
تمثل النقطة التي تتقاطع فيها الدالة مع المحور الرأسي قيمة مربع زمن الدورة عندما يكون عدد الأوزان في السّلة مساويًا للصفر.
تمثل النقطة التي تتقاطع فيها الدالة مع المحور الأفقي عدد الأوزان عندما يكون زمن الدورة صفرًا.
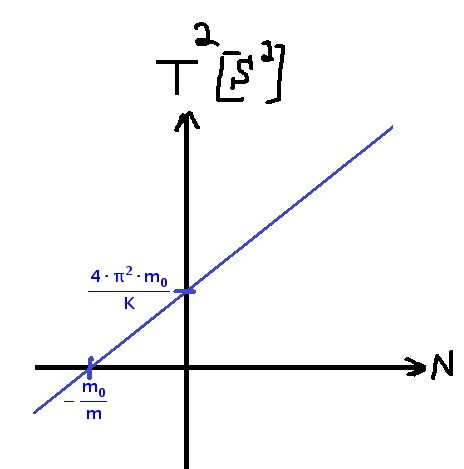
נקודת חיתוך הפונקציה את הציר האנכי מייצגת את ערך ריבוע זמן המחזור כשמספר המשקולות בסל שווה לאפס.
נקודת חיתוך הפונקציה את הציר האופקי מייצגת את מספר המשקולות כשזמן המחזור הוא אפס.
تطوير تعبير لزمن الدورة وإيجاد النقاط التي تتقاطع فيها الدالة مع المحاور من التعبير.
نمد الخط المستقيم على استقامته ونرى ما إذا كان يمر عبر نقطة الأصل:
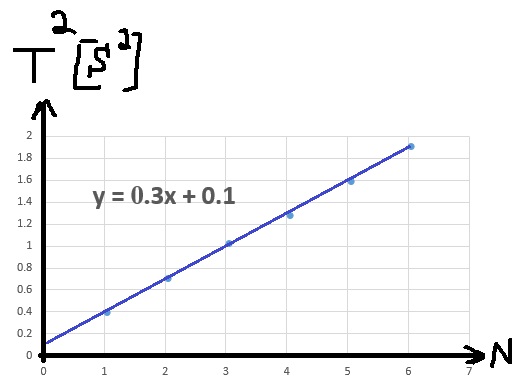
الدالة لا تمر عبر الأصل. وتقطع المحور الرأسي في 0.1 ثانية مربعة.
لإيجاد معنى نقاط التقاطع مع كل من المحاور، سنكتب تعبيرًا لمربع زمن الدورة كدالة لعدد الأسطوانات.
فلنرمز لكتلة السلة بـ m0، ولعدد الأسطوانات في السلة بـ N، ولكتلة كل أسطوانة بـ m.
«math xmlns=¨http://www.w3.org/1998/Math/MathML¨»«mi mathvariant=¨bold-italic¨ mathcolor=¨#0000FF¨»T«/mi»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»=«/mo»«mn mathvariant=¨bold¨ mathcolor=¨#0000FF¨»2«/mn»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»§#183;«/mo»«mi mathvariant=¨bold¨ mathcolor=¨#0000FF¨»§#960;«/mi»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»§#183;«/mo»«msqrt mathcolor=¨#0000FF¨»«mfrac»«mi mathvariant=¨bold¨»m«/mi»«mi mathvariant=¨bold¨»k«/mi»«/mfrac»«/msqrt»«mspace linebreak=¨newline¨»«/mspace»«mspace linebreak=¨newline¨»«/mspace»«mi mathvariant=¨bold-italic¨ mathcolor=¨#0000FF¨»T«/mi»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»=«/mo»«mn mathvariant=¨bold¨ mathcolor=¨#0000FF¨»2«/mn»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»§#183;«/mo»«mi mathvariant=¨bold¨ mathcolor=¨#0000FF¨»§#960;«/mi»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»§#183;«/mo»«msqrt mathcolor=¨#0000FF¨»«mfrac»«mrow»«msub»«mi mathvariant=¨bold¨»m«/mi»«mn mathvariant=¨bold¨»0«/mn»«/msub»«mo mathvariant=¨bold¨»+«/mo»«mi mathvariant=¨bold¨»N«/mi»«mo mathvariant=¨bold¨»§#183;«/mo»«mi mathvariant=¨bold¨»m«/mi»«/mrow»«mi mathvariant=¨bold¨»k«/mi»«/mfrac»«/msqrt»«mspace linebreak=¨newline¨»«/mspace»«mspace linebreak=¨newline¨»«/mspace»«msup»«mi mathvariant=¨bold-italic¨ mathcolor=¨#0000FF¨»T«/mi»«mn mathvariant=¨bold¨ mathcolor=¨#0000FF¨»2«/mn»«/msup»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»=«/mo»«mn mathvariant=¨bold¨ mathcolor=¨#0000FF¨»4«/mn»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»§#183;«/mo»«msup»«mi mathvariant=¨bold¨ mathcolor=¨#0000FF¨»§#960;«/mi»«mn mathvariant=¨bold¨ mathcolor=¨#0000FF¨»2«/mn»«/msup»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»§#183;«/mo»«mrow mathcolor=¨#0000FF¨»«mo mathvariant=¨bold¨»(«/mo»«mfrac»«mrow»«msub»«mi mathvariant=¨bold¨»m«/mi»«mn mathvariant=¨bold¨»0«/mn»«/msub»«mo mathvariant=¨bold¨»+«/mo»«mi mathvariant=¨bold¨»N«/mi»«mo mathvariant=¨bold¨»§#183;«/mo»«mi mathvariant=¨bold¨»m«/mi»«/mrow»«mi mathvariant=¨bold¨»k«/mi»«/mfrac»«mo mathvariant=¨bold¨»)«/mo»«/mrow»«mspace linebreak=¨newline¨»«/mspace»«mspace linebreak=¨newline¨»«/mspace»«menclose mathcolor=¨#0000FF¨ notation=¨circle¨»«msup»«mi mathvariant=¨bold¨»T«/mi»«mn mathvariant=¨bold¨»2«/mn»«/msup»«mo mathvariant=¨bold¨»=«/mo»«mo mathvariant=¨bold¨»§#160;«/mo»«mo mathvariant=¨bold¨»§#160;«/mo»«mfrac»«mrow»«mn mathvariant=¨bold¨»4«/mn»«mo mathvariant=¨bold¨»§#183;«/mo»«msup»«mi mathvariant=¨bold¨»§#960;«/mi»«mn mathvariant=¨bold¨»2«/mn»«/msup»«mo mathvariant=¨bold¨»§#183;«/mo»«msub»«mi mathvariant=¨bold¨»m«/mi»«mn mathvariant=¨bold¨»0«/mn»«/msub»«/mrow»«mi mathvariant=¨bold¨»K«/mi»«/mfrac»«mo mathvariant=¨bold¨»+«/mo»«mfrac»«mrow»«mn mathvariant=¨bold¨»4«/mn»«mo mathvariant=¨bold¨»§#183;«/mo»«msup»«mi mathvariant=¨bold¨»§#960;«/mi»«mn mathvariant=¨bold¨»2«/mn»«/msup»«mo mathvariant=¨bold¨»§#183;«/mo»«mi mathvariant=¨bold¨»N«/mi»«mo mathvariant=¨bold¨»§#183;«/mo»«mi mathvariant=¨bold¨»m«/mi»«/mrow»«mi mathvariant=¨bold¨»K«/mi»«/mfrac»«/menclose»«/math»
نقطة تقاطع الدالة مع المحور الرأسي:
نقطة تقاطع الدالة مع المحور الرأسي تتوافق مع قيمة الدالة عندما تكون قيمة N مساوية للصفر.
ومن العبارة يتبين أنه عندما يكون عدد الأسطوانات يساوي صفرًا فإن قيمة مربع الزمن تساوي «math xmlns=¨http://www.w3.org/1998/Math/MathML¨»«msup»«mi mathvariant=¨bold¨ mathcolor=¨#0000FF¨»T«/mi»«mn mathvariant=¨bold¨ mathcolor=¨#0000FF¨»2«/mn»«/msup»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»=«/mo»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»§#160;«/mo»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»§#160;«/mo»«mfrac mathcolor=¨#0000FF¨»«mrow»«mn mathvariant=¨bold¨»4«/mn»«mo mathvariant=¨bold¨»§#183;«/mo»«msup»«mi mathvariant=¨bold¨»§#960;«/mi»«mn mathvariant=¨bold¨»2«/mn»«/msup»«mo mathvariant=¨bold¨»§#183;«/mo»«msub»«mi mathvariant=¨bold¨»m«/mi»«mn mathvariant=¨bold¨»0«/mn»«/msub»«/mrow»«mi mathvariant=¨bold¨»K«/mi»«/mfrac»«/math»
عندما لا توجد أوزان داخل السّلة، يمكن أن تكون هناك حركة توافقية بسيطة، وفي هذه الحالة تكون الحركة للسّلة نفسها. من النقطة التي تتقاطع فيها الدالة مع المحور الرأسي، يمكننا أن نتعلم عن زمن دورة السّلة عندما تكون فارغة.
נקודת חציית הפונקציה את הציר האופקי:
נקודת חציית הפונקציה את הציר האופקי מתאים לערך של מספר הגלילים כאשר ריבוע זמן המחזור שווה לאפס.
«math xmlns=¨http://www.w3.org/1998/Math/MathML¨»«msup»«mi mathvariant=¨bold¨ mathcolor=¨#0000FF¨»T«/mi»«mn mathvariant=¨bold¨ mathcolor=¨#0000FF¨»2«/mn»«/msup»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»=«/mo»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»§#160;«/mo»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»§#160;«/mo»«mfrac mathcolor=¨#0000FF¨»«mrow»«mn mathvariant=¨bold¨»4«/mn»«mo mathvariant=¨bold¨»§#183;«/mo»«msup»«mi mathvariant=¨bold¨»§#960;«/mi»«mn mathvariant=¨bold¨»2«/mn»«/msup»«mo mathvariant=¨bold¨»§#183;«/mo»«msub»«mi mathvariant=¨bold¨»m«/mi»«mn mathvariant=¨bold¨»0«/mn»«/msub»«/mrow»«mi mathvariant=¨bold¨»K«/mi»«/mfrac»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»+«/mo»«mfrac mathcolor=¨#0000FF¨»«mrow»«mn mathvariant=¨bold¨»4«/mn»«mo mathvariant=¨bold¨»§#183;«/mo»«msup»«mi mathvariant=¨bold¨»§#960;«/mi»«mn mathvariant=¨bold¨»2«/mn»«/msup»«mo mathvariant=¨bold¨»§#183;«/mo»«mi mathvariant=¨bold¨»N«/mi»«mo mathvariant=¨bold¨»§#183;«/mo»«mi mathvariant=¨bold¨»m«/mi»«/mrow»«mi mathvariant=¨bold¨»K«/mi»«/mfrac»«mspace linebreak=¨newline¨»«/mspace»«mspace linebreak=¨newline¨»«/mspace»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»-«/mo»«mfrac mathcolor=¨#0000FF¨»«mrow»«menclose notation=¨updiagonalstrike¨»«mn mathvariant=¨bold¨»4«/mn»«mo mathvariant=¨bold¨»§#183;«/mo»«msup»«mi mathvariant=¨bold¨»§#960;«/mi»«mn mathvariant=¨bold¨»2«/mn»«/msup»«/menclose»«mo mathvariant=¨bold¨»§#183;«/mo»«mi mathvariant=¨bold¨»N«/mi»«mo mathvariant=¨bold¨»§#183;«/mo»«mi mathvariant=¨bold¨»m«/mi»«/mrow»«menclose notation=¨downdiagonalstrike¨»«mi mathvariant=¨bold¨»K«/mi»«/menclose»«/mfrac»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»=«/mo»«mfrac mathcolor=¨#0000FF¨»«mrow»«menclose notation=¨updiagonalstrike¨»«mn mathvariant=¨bold¨»4«/mn»«mo mathvariant=¨bold¨»§#183;«/mo»«msup»«mi mathvariant=¨bold¨»§#960;«/mi»«mn mathvariant=¨bold¨»2«/mn»«/msup»«/menclose»«mo mathvariant=¨bold¨»§#183;«/mo»«msub»«mi mathvariant=¨bold¨»m«/mi»«mn mathvariant=¨bold¨»0«/mn»«/msub»«/mrow»«menclose notation=¨downdiagonalstrike¨»«mi mathvariant=¨bold¨»K«/mi»«/menclose»«/mfrac»«mspace linebreak=¨newline¨»«/mspace»«mspace linebreak=¨newline¨»«/mspace»«menclose mathcolor=¨#0000FF¨ notation=¨circle¨»«mi mathvariant=¨bold¨»N«/mi»«mo mathvariant=¨bold¨»=«/mo»«mo mathvariant=¨bold¨»-«/mo»«mfrac»«msub»«mi mathvariant=¨bold¨»m«/mi»«mn mathvariant=¨bold¨»0«/mn»«/msub»«mi mathvariant=¨bold¨»m«/mi»«/mfrac»«/menclose»«/math»
כאשר מספר הגלילים שווה ל «math xmlns=¨http://www.w3.org/1998/Math/MathML¨»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»-«/mo»«mfrac mathcolor=¨#0000FF¨»«msub»«mi mathvariant=¨bold¨»m«/mi»«mn mathvariant=¨bold¨»0«/mn»«/msub»«mi mathvariant=¨bold¨»m«/mi»«/mfrac»«/math» אז זמן המחזור שווה לאפס , וזו נקודת חציית הפונקציה את הציר האופקי .
אין משמעות פיזיקלית לזמן מחזור אפס, או למספר גלילים שלילי.
נתאר בגרף את ערכי נקודות החצייה:
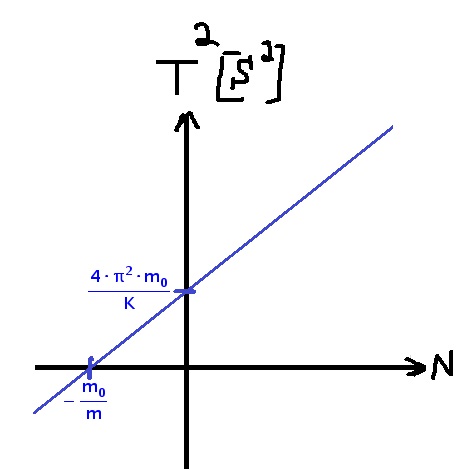

הפונקציה לא עוברת דרך ראשית הצירים. היא חוצה את הציר האנכי ב 0.1 שנייה בריבוע.
כדי למצוא את המשמעות של נקודות החיתוך עם כל אחד מהצירים , נכתוב ביטוי לריבוע זמן המחזור בלות במספר הגלילים.
נסמן את מסת הסל ........
«math xmlns=¨http://www.w3.org/1998/Math/MathML¨»«mi mathvariant=¨bold-italic¨ mathcolor=¨#0000FF¨»T«/mi»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»=«/mo»«mn mathvariant=¨bold¨ mathcolor=¨#0000FF¨»2«/mn»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»§#183;«/mo»«mi mathvariant=¨bold¨ mathcolor=¨#0000FF¨»§#960;«/mi»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»§#183;«/mo»«msqrt mathcolor=¨#0000FF¨»«mfrac»«mi mathvariant=¨bold¨»m«/mi»«mi mathvariant=¨bold¨»k«/mi»«/mfrac»«/msqrt»«/math»
המשמעות היא שגם כאשר אין משקולות בתוך הסל יכולה להיות תנועה הרמונית פשוטה , במקרה זה התנועה היא של הסל עצמו.
تشير نقطة تقاطع الدالة مع المحور الأفقي إلى الحالة التي يكون فيها زمن الدورة صفرًا.
من مربع تعبير زمن الدورة، رياضيا لكي يكون زمن الدورة صفرًا يجب أن يكون عدد الأوزان سالبا، وهو أمر غير واقعي.
حقيقة أن النقطة التي تتقاطع فيها الدالة مع المحور الأفقي ليس لها معنى فيزيئي لا يعني أن نقطة التقاطع لا تمثل شيئًا.
מביטוי ריבוע זמן המחזור ,מתמטית כדי שזמן המחזור יהיה אפס מספר המשקולות צריך להיות שלילי וזה לא מציאותי.
העובדה שאין משמעות פיזיקלית לנקודת חיתוך הפונקציה את הציר האופקי לא אומרת שנקודת החצייה לא מייצגת משהו.
______________________________________________________________________________________

______________________________________________________________________________________
...
قيمة ثابت النابض هو 39.47 نيوتن لكل متر.
إيجاد ثابت النابض من ميل خط الاتجاه.
سوف نستخدم تعبير الدالة الموصوفة في الرسم البياني، الدالة خطية، الثابت N يساوي ميل الرسم البياني:
«math xmlns=¨http://www.w3.org/1998/Math/MathML¨»«msup»«mi mathvariant=¨bold¨ mathcolor=¨#0000FF¨»T«/mi»«mn mathvariant=¨bold¨ mathcolor=¨#0000FF¨»2«/mn»«/msup»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»=«/mo»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»§#160;«/mo»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»§#160;«/mo»«mfrac mathcolor=¨#0000FF¨»«mrow»«mn mathvariant=¨bold¨»4«/mn»«mo mathvariant=¨bold¨»§#183;«/mo»«msup»«mi mathvariant=¨bold¨»§#960;«/mi»«mn mathvariant=¨bold¨»2«/mn»«/msup»«mo mathvariant=¨bold¨»§#183;«/mo»«msub»«mi mathvariant=¨bold¨»m«/mi»«mn mathvariant=¨bold¨»0«/mn»«/msub»«/mrow»«mi mathvariant=¨bold¨»K«/mi»«/mfrac»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»+«/mo»«menclose mathcolor=¨#0000FF¨ notation=¨circle¨»«mfrac»«mrow»«mn mathvariant=¨bold¨»4«/mn»«mo mathvariant=¨bold¨»§#183;«/mo»«msup»«mi mathvariant=¨bold¨»§#960;«/mi»«mn mathvariant=¨bold¨»2«/mn»«/msup»«mo mathvariant=¨bold¨»§#183;«/mo»«mi mathvariant=¨bold¨»m«/mi»«/mrow»«mi mathvariant=¨bold¨»K«/mi»«/mfrac»«/menclose»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»§#183;«/mo»«mi mathvariant=¨bold¨ mathcolor=¨#0000FF¨»N«/mi»«/math»
نقوم بإيجاد ميل خط الاتجاه، مع الأخذ بعين الاعتبار النقطة الأخيرة والثانية:
«math xmlns=¨http://www.w3.org/1998/Math/MathML¨»«mi mathvariant=¨bold¨ mathcolor=¨#0000FF¨»§#1575;§#1604;§#1605;§#1610;§#1604;«/mi»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»§#160;«/mo»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»=«/mo»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»§#160;«/mo»«mfrac mathcolor=¨#0000FF¨»«mrow»«mo mathvariant=¨bold¨»§#8710;«/mo»«msup»«mi mathvariant=¨bold¨»T«/mi»«mn mathvariant=¨bold¨»2«/mn»«/msup»«/mrow»«mrow»«mo mathvariant=¨bold¨»§#8710;«/mo»«mi mathvariant=¨bold¨»N«/mi»«/mrow»«/mfrac»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»=«/mo»«mfrac mathcolor=¨#0000FF¨»«mrow»«mn mathvariant=¨bold¨»1«/mn»«mo mathvariant=¨bold¨».«/mo»«mn mathvariant=¨bold¨»904«/mn»«mo mathvariant=¨bold¨»-«/mo»«mn mathvariant=¨bold¨»0«/mn»«mo mathvariant=¨bold¨».«/mo»«mn mathvariant=¨bold¨»706«/mn»«/mrow»«mrow»«mn mathvariant=¨bold¨»6«/mn»«mo mathvariant=¨bold¨»-«/mo»«mn mathvariant=¨bold¨»2«/mn»«/mrow»«/mfrac»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»=«/mo»«mn mathvariant=¨bold¨ mathcolor=¨#0000FF¨»0«/mn»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨».«/mo»«mn mathvariant=¨bold¨ mathcolor=¨#0000FF¨»3«/mn»«msup»«mi mathvariant=¨bold¨ mathcolor=¨#0000FF¨»s«/mi»«mn mathvariant=¨bold¨ mathcolor=¨#0000FF¨»2«/mn»«/msup»«/math»
نقوم بمقارنة تعبير الميل مع قيمته، ونحصل على ثابت النابض:
«math xmlns=¨http://www.w3.org/1998/Math/MathML¨»«mfrac mathcolor=¨#0000FF¨»«mrow»«mn mathvariant=¨bold¨»4«/mn»«mo mathvariant=¨bold¨»§#183;«/mo»«msup»«mi mathvariant=¨bold¨»§#960;«/mi»«mn mathvariant=¨bold¨»2«/mn»«/msup»«mo mathvariant=¨bold¨»§#183;«/mo»«mi mathvariant=¨bold¨»m«/mi»«/mrow»«mi mathvariant=¨bold¨»K«/mi»«/mfrac»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»=«/mo»«mn mathvariant=¨bold¨ mathcolor=¨#0000FF¨»0«/mn»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨».«/mo»«mn mathvariant=¨bold¨ mathcolor=¨#0000FF¨»3«/mn»«mspace linebreak=¨newline¨»«/mspace»«mspace linebreak=¨newline¨»«/mspace»«mi mathvariant=¨bold¨ mathcolor=¨#0000FF¨»K«/mi»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»=«/mo»«mfrac mathcolor=¨#0000FF¨»«mrow»«mn mathvariant=¨bold¨»4«/mn»«mo mathvariant=¨bold¨»§#183;«/mo»«msup»«mi mathvariant=¨bold¨»§#960;«/mi»«mn mathvariant=¨bold¨»2«/mn»«/msup»«mo mathvariant=¨bold¨»§#183;«/mo»«mi mathvariant=¨bold¨»m«/mi»«/mrow»«mrow»«mn mathvariant=¨bold¨»0«/mn»«mo mathvariant=¨bold¨».«/mo»«mn mathvariant=¨bold¨»3«/mn»«/mrow»«/mfrac»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»=«/mo»«mfrac mathcolor=¨#0000FF¨»«mrow»«mn mathvariant=¨bold¨»4«/mn»«mo mathvariant=¨bold¨»§#183;«/mo»«msup»«mi mathvariant=¨bold¨»§#960;«/mi»«mn mathvariant=¨bold¨»2«/mn»«/msup»«mo mathvariant=¨bold¨»§#183;«/mo»«mn mathvariant=¨bold¨»0«/mn»«mo mathvariant=¨bold¨».«/mo»«mn mathvariant=¨bold¨»3«/mn»«/mrow»«mrow»«mn mathvariant=¨bold¨»0«/mn»«mo mathvariant=¨bold¨».«/mo»«mn mathvariant=¨bold¨»3«/mn»«/mrow»«/mfrac»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»=«/mo»«mn mathvariant=¨bold¨ mathcolor=¨#0000FF¨»39«/mn»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨».«/mo»«mn mathvariant=¨bold¨ mathcolor=¨#0000FF¨»47«/mn»«mfrac mathcolor=¨#0000FF¨»«mi mathvariant=¨bold¨»N«/mi»«mi mathvariant=¨bold¨»m«/mi»«/mfrac»«/math»
قيمة ثابت النابض هو 39.47 نيوتن لكل متر.
«math xmlns=¨http://www.w3.org/1998/Math/MathML¨»«msup»«mi mathvariant=¨bold¨ mathcolor=¨#0000FF¨»T«/mi»«mn mathvariant=¨bold¨ mathcolor=¨#0000FF¨»2«/mn»«/msup»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»=«/mo»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»§#160;«/mo»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»§#160;«/mo»«mfrac mathcolor=¨#0000FF¨»«mrow»«mn mathvariant=¨bold¨»4«/mn»«mo mathvariant=¨bold¨»§#183;«/mo»«msup»«mi mathvariant=¨bold¨»§#960;«/mi»«mn mathvariant=¨bold¨»2«/mn»«/msup»«mo mathvariant=¨bold¨»§#183;«/mo»«msub»«mi mathvariant=¨bold¨»m«/mi»«mn mathvariant=¨bold¨»0«/mn»«/msub»«/mrow»«mi mathvariant=¨bold¨»K«/mi»«/mfrac»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»+«/mo»«menclose mathcolor=¨#0000FF¨ notation=¨circle¨»«mfrac»«mrow»«mn mathvariant=¨bold¨»4«/mn»«mo mathvariant=¨bold¨»§#183;«/mo»«msup»«mi mathvariant=¨bold¨»§#960;«/mi»«mn mathvariant=¨bold¨»2«/mn»«/msup»«mo mathvariant=¨bold¨»§#183;«/mo»«mi mathvariant=¨bold¨»m«/mi»«/mrow»«mi mathvariant=¨bold¨»K«/mi»«/mfrac»«/menclose»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»§#183;«/mo»«mi mathvariant=¨bold¨ mathcolor=¨#0000FF¨»N«/mi»«/math»
נמצא את ערך השיפוע של הישר המסתבר ביותר , נתייחס לנקודה האחרונה והשנייה:
«math xmlns=¨http://www.w3.org/1998/Math/MathML¨»«mi mathvariant=¨bold¨ mathcolor=¨#0000FF¨»§#1513;§#1497;§#1508;§#1493;§#1506;«/mi»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»§#160;«/mo»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»=«/mo»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»§#160;«/mo»«mfrac mathcolor=¨#0000FF¨»«mrow»«mo mathvariant=¨bold¨»§#8710;«/mo»«msup»«mi mathvariant=¨bold¨»T«/mi»«mn mathvariant=¨bold¨»2«/mn»«/msup»«/mrow»«mrow»«mo mathvariant=¨bold¨»§#8710;«/mo»«mi mathvariant=¨bold¨»N«/mi»«/mrow»«/mfrac»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»=«/mo»«mfrac mathcolor=¨#0000FF¨»«mrow»«mn mathvariant=¨bold¨»1«/mn»«mo mathvariant=¨bold¨».«/mo»«mn mathvariant=¨bold¨»904«/mn»«mo mathvariant=¨bold¨»-«/mo»«mn mathvariant=¨bold¨»0«/mn»«mo mathvariant=¨bold¨».«/mo»«mn mathvariant=¨bold¨»706«/mn»«/mrow»«mrow»«mn mathvariant=¨bold¨»6«/mn»«mo mathvariant=¨bold¨»-«/mo»«mn mathvariant=¨bold¨»2«/mn»«/mrow»«/mfrac»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»=«/mo»«mn mathvariant=¨bold¨ mathcolor=¨#0000FF¨»0«/mn»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨».«/mo»«mn mathvariant=¨bold¨ mathcolor=¨#0000FF¨»3«/mn»«msup»«mi mathvariant=¨bold¨ mathcolor=¨#0000FF¨»s«/mi»«mn mathvariant=¨bold¨ mathcolor=¨#0000FF¨»2«/mn»«/msup»«/math»
נשווה בין ביטוי השיפוע לערכו , ונמצא את קבוע הקפיץ:
«math xmlns=¨http://www.w3.org/1998/Math/MathML¨»«mfrac mathcolor=¨#0000FF¨»«mrow»«mn mathvariant=¨bold¨»4«/mn»«mo mathvariant=¨bold¨»§#183;«/mo»«msup»«mi mathvariant=¨bold¨»§#960;«/mi»«mn mathvariant=¨bold¨»2«/mn»«/msup»«mo mathvariant=¨bold¨»§#183;«/mo»«mi mathvariant=¨bold¨»m«/mi»«/mrow»«mi mathvariant=¨bold¨»K«/mi»«/mfrac»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»=«/mo»«mn mathvariant=¨bold¨ mathcolor=¨#0000FF¨»0«/mn»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨».«/mo»«mn mathvariant=¨bold¨ mathcolor=¨#0000FF¨»3«/mn»«mspace linebreak=¨newline¨»«/mspace»«mspace linebreak=¨newline¨»«/mspace»«mi mathvariant=¨bold¨ mathcolor=¨#0000FF¨»K«/mi»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»=«/mo»«mfrac mathcolor=¨#0000FF¨»«mrow»«mn mathvariant=¨bold¨»4«/mn»«mo mathvariant=¨bold¨»§#183;«/mo»«msup»«mi mathvariant=¨bold¨»§#960;«/mi»«mn mathvariant=¨bold¨»2«/mn»«/msup»«mo mathvariant=¨bold¨»§#183;«/mo»«mi mathvariant=¨bold¨»m«/mi»«/mrow»«mrow»«mn mathvariant=¨bold¨»0«/mn»«mo mathvariant=¨bold¨».«/mo»«mn mathvariant=¨bold¨»3«/mn»«/mrow»«/mfrac»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»=«/mo»«mfrac mathcolor=¨#0000FF¨»«mrow»«mn mathvariant=¨bold¨»4«/mn»«mo mathvariant=¨bold¨»§#183;«/mo»«msup»«mi mathvariant=¨bold¨»§#960;«/mi»«mn mathvariant=¨bold¨»2«/mn»«/msup»«mo mathvariant=¨bold¨»§#183;«/mo»«mn mathvariant=¨bold¨»0«/mn»«mo mathvariant=¨bold¨».«/mo»«mn mathvariant=¨bold¨»3«/mn»«/mrow»«mrow»«mn mathvariant=¨bold¨»0«/mn»«mo mathvariant=¨bold¨».«/mo»«mn mathvariant=¨bold¨»3«/mn»«/mrow»«/mfrac»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»=«/mo»«mn mathvariant=¨bold¨ mathcolor=¨#0000FF¨»39«/mn»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨».«/mo»«mn mathvariant=¨bold¨ mathcolor=¨#0000FF¨»47«/mn»«mfrac mathcolor=¨#0000FF¨»«mi mathvariant=¨bold¨»N«/mi»«mi mathvariant=¨bold¨»m«/mi»«/mfrac»«/math»
ערכו של קבוע הקפיץ הוא 39.47 ניוטון למטר.
1. عند حساب ميل الرسم البياني، يجب علينا أن نأخذ بعين الاعتبار النقاط التي تقع على خط الاتجاه.
2. هناك وحدات لقيمة الميل، ومن المهم الإشارة لها.
3. يمكن القول أن هذا السؤال يتضمن إيجاد ثابت النابض باستخدام ميزان رأسي مع سلة وأوزان.
2. יש יחידות לערך השיפוע, חשוב לציין אותן.
______________________________________________________________________________________