______________________________________________________________________________________
...
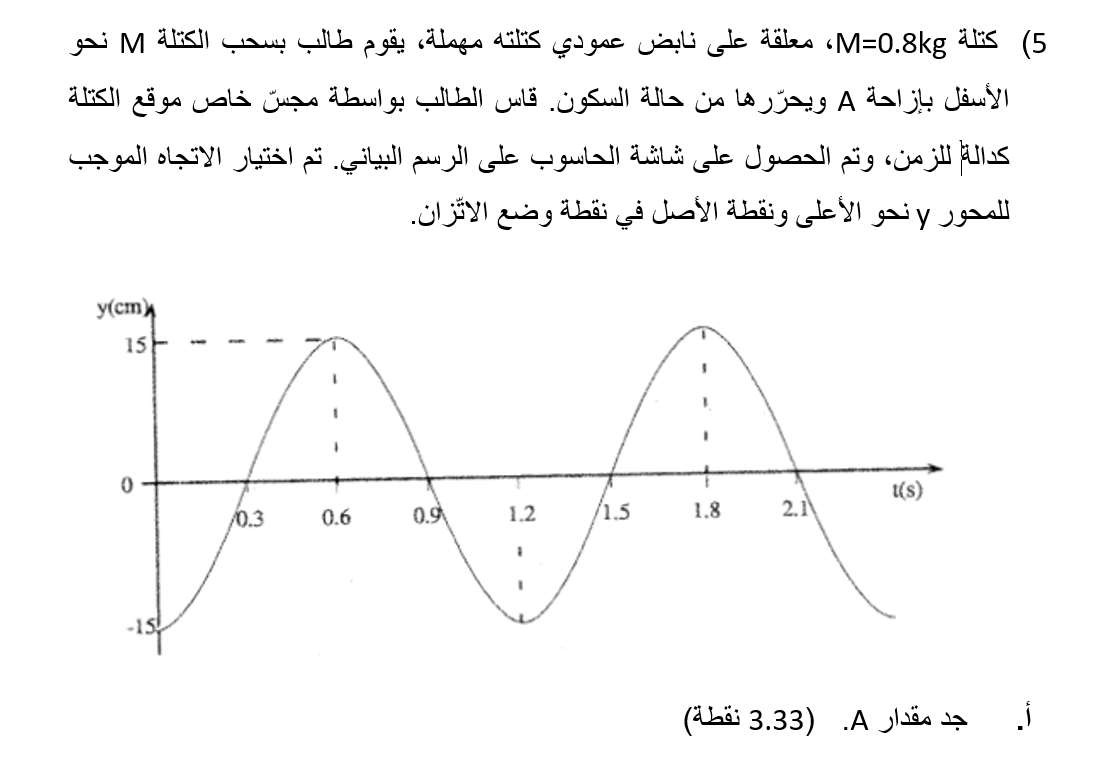
«math xmlns=¨http://www.w3.org/1998/Math/MathML¨»«mi mathvariant=¨bold¨»A«/mi»«mo mathvariant=¨bold¨»=«/mo»«mn mathvariant=¨bold¨»15«/mn»«mi mathvariant=¨bold¨»cm«/mi»«/math»
فهم معنى السعة. وإيجاد السعة من الرسم البياني.
السعة تساوي البعد بين نقطة التوازن ونقطة النهاية. من الرسم البياني، هذا البعد يساوي 15 سم.
1. القيم على المحور الرأسي معطاة بوحدات السنتيمتر، وليس بالوحدات القياسية.
2. الرسم البياني للموقع كدالة للزمن، والرسم البياني للسرعة كدالة للزمن، والرسم البياني للتسارع كدالة للزمن، لها أيضًا شكل موجة.
فقط في الرسم البياني للموقع يكون زمن سعة الموجة مساويًا لسعة الحركة.
2. לגרף מקום זמן ,גרף מהירות זמן, וגם גרף תאוצה זמן יש צורה של גל.
רק בגרף המקום זמן משרעת הגל שווה למשרעת התנועה.
______________________________________________________________________________________

______________________________________________________________________________________
...
«math xmlns=¨http://www.w3.org/1998/Math/MathML¨»«mi mathvariant=¨bold¨»T«/mi»«mo mathvariant=¨bold¨»=«/mo»«mn mathvariant=¨bold¨»1«/mn»«mo mathvariant=¨bold¨».«/mo»«mn mathvariant=¨bold¨»2«/mn»«mi mathvariant=¨bold¨»s«/mi»«mo mathvariant=¨bold¨»§#160;«/mo»«mspace linebreak=¨newline¨»«/mspace»«mi mathvariant=¨bold¨»f«/mi»«mo mathvariant=¨bold¨»=«/mo»«mn mathvariant=¨bold¨»0«/mn»«mo mathvariant=¨bold¨».«/mo»«mn mathvariant=¨bold¨»83«/mn»«msub»«mi mathvariant=¨bold¨»H«/mi»«mi mathvariant=¨bold¨»Z«/mi»«/msub»«/math»
إيجاد زمن الدورة من الرسم البياني، واستخدام تعبير التردد.
زمن الدورة يساوي أقصر وقت تتكرر فيه الحركة الدورية.
في هذه الحالة، من الرسم البياني لدالة الموقع كدالة للزمن المعطاة، يمكننا أن نرى أن زمن الدورة هو 1.2 ثانية.
نجد التردد:
«math xmlns=¨http://www.w3.org/1998/Math/MathML¨»«mi mathvariant=¨bold¨ mathcolor=¨#0000FF¨»f«/mi»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»=«/mo»«mfrac mathcolor=¨#0000FF¨»«mn mathvariant=¨bold¨»1«/mn»«mi mathvariant=¨bold¨»T«/mi»«/mfrac»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»=«/mo»«mfrac mathcolor=¨#0000FF¨»«mn mathvariant=¨bold¨»1«/mn»«mn mathvariant=¨bold¨»12«/mn»«/mfrac»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»=«/mo»«mn mathvariant=¨bold¨ mathcolor=¨#0000FF¨»0«/mn»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨».«/mo»«mn mathvariant=¨bold¨ mathcolor=¨#0000FF¨»83«/mn»«msub»«mi mathvariant=¨bold¨ mathcolor=¨#0000FF¨»H«/mi»«mi mathvariant=¨bold¨ mathcolor=¨#0000FF¨»Z«/mi»«/msub»«/math»
زمن الدورة يساوي 1.2 ثانية، والتردد يساوي 0.83 هرتز.
במקרה זה מהגרף מקום זמן הנתון ניתן לראות שזמן המחזור הוא 1.2 שניות.
נמצא את התדירות :
«math xmlns=¨http://www.w3.org/1998/Math/MathML¨»«mi mathvariant=¨bold¨ mathcolor=¨#0000FF¨»f«/mi»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»=«/mo»«mfrac mathcolor=¨#0000FF¨»«mn mathvariant=¨bold¨»1«/mn»«mi mathvariant=¨bold¨»T«/mi»«/mfrac»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»=«/mo»«mfrac mathcolor=¨#0000FF¨»«mn mathvariant=¨bold¨»1«/mn»«mn mathvariant=¨bold¨»12«/mn»«/mfrac»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»=«/mo»«mn mathvariant=¨bold¨ mathcolor=¨#0000FF¨»0«/mn»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨».«/mo»«mn mathvariant=¨bold¨ mathcolor=¨#0000FF¨»83«/mn»«msub»«mi mathvariant=¨bold¨ mathcolor=¨#0000FF¨»H«/mi»«mi mathvariant=¨bold¨ mathcolor=¨#0000FF¨»Z«/mi»«/msub»«/math»
זמן המחזור שווה ל 1.2 שניות, והתדירות שווה ל 0.83 הרץ.
بالنسبة لجميع الموجات الثلاث، يصف الرسم البياني الموقع كدالة للزمن، السرعة كدالة للزمن، والتسارع كدالة للزمن. لها فترة تساوي فترة الحركة التوافقية البسيطة.
______________________________________________________________________________________
______________________________________________________________________________________
...
ثابت النابض يساوي 21.93 نيوتن لكل متر.
استخدام صيغة زمن الدورة.
الرسم البياني يلائم الحركة التوافقية البسيطة. نعبر عن ثابت النابض من صيغة زمن الدورة للحركة التوافقية البسيطة.
«math xmlns=¨http://www.w3.org/1998/Math/MathML¨»«mi mathvariant=¨bold-italic¨ mathcolor=¨#0000FF¨»T«/mi»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»=«/mo»«mn mathvariant=¨bold¨ mathcolor=¨#0000FF¨»2«/mn»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»§#183;«/mo»«mi mathvariant=¨bold¨ mathcolor=¨#0000FF¨»§#960;«/mi»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»§#183;«/mo»«msqrt mathcolor=¨#0000FF¨»«mfrac»«mi mathvariant=¨bold¨»m«/mi»«mi mathvariant=¨bold¨»k«/mi»«/mfrac»«/msqrt»«mspace linebreak=¨newline¨»«/mspace»«msup»«mi mathvariant=¨bold¨ mathcolor=¨#0000FF¨»T«/mi»«mn mathvariant=¨bold¨ mathcolor=¨#0000FF¨»2«/mn»«/msup»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»=«/mo»«mn mathvariant=¨bold¨ mathcolor=¨#0000FF¨»4«/mn»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»§#183;«/mo»«msup»«mi mathvariant=¨bold¨ mathcolor=¨#0000FF¨»§#960;«/mi»«mn mathvariant=¨bold¨ mathcolor=¨#0000FF¨»2«/mn»«/msup»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»§#183;«/mo»«mfrac mathcolor=¨#0000FF¨»«mi mathvariant=¨bold¨»m«/mi»«mi mathvariant=¨bold¨»k«/mi»«/mfrac»«mspace linebreak=¨newline¨»«/mspace»«mi mathvariant=¨bold¨ mathcolor=¨#0000FF¨»k«/mi»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»=«/mo»«mfrac mathcolor=¨#0000FF¨»«mrow»«mn mathvariant=¨bold¨»4«/mn»«mo mathvariant=¨bold¨»§#183;«/mo»«msup»«mi mathvariant=¨bold¨»§#960;«/mi»«mn mathvariant=¨bold¨»2«/mn»«/msup»«mo mathvariant=¨bold¨»§#183;«/mo»«mi mathvariant=¨bold¨»m«/mi»«/mrow»«msup»«mi mathvariant=¨bold¨»T«/mi»«mn mathvariant=¨bold¨»2«/mn»«/msup»«/mfrac»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»=«/mo»«mfrac mathcolor=¨#0000FF¨»«mrow»«mn mathvariant=¨bold¨»4«/mn»«mo mathvariant=¨bold¨»§#183;«/mo»«msup»«mi mathvariant=¨bold¨»§#960;«/mi»«mn mathvariant=¨bold¨»2«/mn»«/msup»«mo mathvariant=¨bold¨»§#183;«/mo»«mn mathvariant=¨bold¨»0«/mn»«mo mathvariant=¨bold¨».«/mo»«mn mathvariant=¨bold¨»8«/mn»«/mrow»«mrow»«mn mathvariant=¨bold¨»1«/mn»«mo mathvariant=¨bold¨».«/mo»«msup»«mn mathvariant=¨bold¨»2«/mn»«mn mathvariant=¨bold¨»2«/mn»«/msup»«/mrow»«/mfrac»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»=«/mo»«mn mathvariant=¨bold¨ mathcolor=¨#0000FF¨»21«/mn»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨».«/mo»«mn mathvariant=¨bold¨ mathcolor=¨#0000FF¨»93«/mn»«mfrac mathcolor=¨#0000FF¨»«mi mathvariant=¨bold¨»N«/mi»«mi mathvariant=¨bold¨»m«/mi»«/mfrac»«/math»
ثابت النابض يساوي 21.93 نيوتن لكل متر.
«math xmlns=¨http://www.w3.org/1998/Math/MathML¨»«mi mathvariant=¨bold-italic¨ mathcolor=¨#0000FF¨»T«/mi»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»=«/mo»«mn mathvariant=¨bold¨ mathcolor=¨#0000FF¨»2«/mn»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»§#183;«/mo»«mi mathvariant=¨bold¨ mathcolor=¨#0000FF¨»§#960;«/mi»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»§#183;«/mo»«msqrt mathcolor=¨#0000FF¨»«mfrac»«mi mathvariant=¨bold¨»m«/mi»«mi mathvariant=¨bold¨»k«/mi»«/mfrac»«/msqrt»«mspace linebreak=¨newline¨»«/mspace»«msup»«mi mathvariant=¨bold¨ mathcolor=¨#0000FF¨»T«/mi»«mn mathvariant=¨bold¨ mathcolor=¨#0000FF¨»2«/mn»«/msup»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»=«/mo»«mn mathvariant=¨bold¨ mathcolor=¨#0000FF¨»4«/mn»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»§#183;«/mo»«msup»«mi mathvariant=¨bold¨ mathcolor=¨#0000FF¨»§#960;«/mi»«mn mathvariant=¨bold¨ mathcolor=¨#0000FF¨»2«/mn»«/msup»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»§#183;«/mo»«mfrac mathcolor=¨#0000FF¨»«mi mathvariant=¨bold¨»m«/mi»«mi mathvariant=¨bold¨»k«/mi»«/mfrac»«mspace linebreak=¨newline¨»«/mspace»«mi mathvariant=¨bold¨ mathcolor=¨#0000FF¨»k«/mi»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»=«/mo»«mfrac mathcolor=¨#0000FF¨»«mrow»«mn mathvariant=¨bold¨»4«/mn»«mo mathvariant=¨bold¨»§#183;«/mo»«msup»«mi mathvariant=¨bold¨»§#960;«/mi»«mn mathvariant=¨bold¨»2«/mn»«/msup»«mo mathvariant=¨bold¨»§#183;«/mo»«mi mathvariant=¨bold¨»m«/mi»«/mrow»«msup»«mi mathvariant=¨bold¨»T«/mi»«mn mathvariant=¨bold¨»2«/mn»«/msup»«/mfrac»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»=«/mo»«mfrac mathcolor=¨#0000FF¨»«mrow»«mn mathvariant=¨bold¨»4«/mn»«mo mathvariant=¨bold¨»§#183;«/mo»«msup»«mi mathvariant=¨bold¨»§#960;«/mi»«mn mathvariant=¨bold¨»2«/mn»«/msup»«mo mathvariant=¨bold¨»§#183;«/mo»«mn mathvariant=¨bold¨»0«/mn»«mo mathvariant=¨bold¨».«/mo»«mn mathvariant=¨bold¨»8«/mn»«/mrow»«mrow»«mn mathvariant=¨bold¨»1«/mn»«mo mathvariant=¨bold¨».«/mo»«msup»«mn mathvariant=¨bold¨»2«/mn»«mn mathvariant=¨bold¨»2«/mn»«/msup»«/mrow»«/mfrac»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»=«/mo»«mn mathvariant=¨bold¨ mathcolor=¨#0000FF¨»21«/mn»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨».«/mo»«mn mathvariant=¨bold¨ mathcolor=¨#0000FF¨»93«/mn»«mfrac mathcolor=¨#0000FF¨»«mi mathvariant=¨bold¨»N«/mi»«mi mathvariant=¨bold¨»m«/mi»«/mfrac»«/math»
קבוע הקפיץ שווה ל 21.93 ניוטון למטר.
قبل استخدام قوانين الحركة التوافقية، لا بد من تفسير أو شرح سبب كون الحركة توافقية بسيطة.
______________________________________________________________________________________

______________________________________________________________________________________
...
الأزمنة التي تكون فيها السرعة صفر هي: t=0.6s ו- t=1.2s .
يجب أن يكون الشخص على دراية بالحركة التوافقية، لمعرفة متى تصبح سرعة الجسم المتحرك بحركة توافقية بسيطة صفرًا.
في الحركة التوافقية البسيطة، تكون السرعة صفرًا في طرفي الحركة.
وفقًا للرسم البياني للوقت، فإن الأزمنة التي تصل فيها السرعة إلى الصفر هي: t=0.6s ו- t=1.2s .
בהתאם לגרף בזמנים הזמנים בהם המהירות מתאפסת הם: t=0.6s ו- t=1.2s .
في الرسم البياني للموقع كدالة للزمن، يكون ميل الرسم البياني مساويًا لسرعة الجسم؛ في نقاط النهاية، يكون ميل الرسم البياني مساويًا للصفر.
______________________________________________________________________________________
______________________________________________________________________________________
...
يكون التسارع مساويًا لصفر في بعض الأزمنة t=0.3s و- t=0.9s.
نقطة الاتّزان هي النقطة التي تكون فيها محصل القوى مساويًا للصفر.
في الحركة التوافقية البسيطة، يكون التسارع صفرًا عندما يكون الجسم في نقطة الاتّزان.
في الحركة الموضحة في الرسم البياني، يصبح التسارع صفرًا في اللحظتين t=0.3s و- t=0.9s.
בתנועה המתוארת בגרף ,התאוצה מתאפסת בזמנים t=0.3s ו- t=0.9s.
من خلال الرسم البياني للموقع كدالة للزمن، يمكنك معرفة السرعة، ولكن لا يمكنك معرفة التسارع.
______________________________________________________________________________________

______________________________________________________________________________________
...
القوة المحصلة تعمل نحو الأعلى.
القوة المحصلة في حالة الحركة التوافقية البسيطة هي قوة معيدة، والتي تعمل باتجاه نقطة الاتّزان.
في اللحظة t=1s يكون موقع الجسم سالبًا بالنسبة للمحور، ويكون الجسم أسفل نقطة الاتّزان.
في الحركة التوافقية البسيطة، تعمل القوة المحصّلة باتجاه نقطة الاتّزان، لذا يكون اتجاه القوة نحو الأعلى.
בתנועה הרמונית פשוטה הכוח פועל לכיוון נקודת שיווי המשקל, לכן כיוון הכוח הוא כלפי מעלה.
في الحركة التوافقية البسيطة، فإن اتجاه القوة المحصّلة تعمل نحو نقطة الاتّزان وليس نحو النقطة التي يكون فيها النابض مرتخيًا.
اتجاه قوة النابض تؤثر نحو النقطة التي يكون فيها النابض مرتخيًا وليس نحو نقطة التوازن.
כיוון כוח הקפיץ פועל לכיוון הנקודה בה הקפיץ רפוי ולא לנקודת שיווי המשקל.
______________________________________________________________________________________