حلول ومنتديات لألبوم الحلول – الحركة التوافقية البسيطة: 1993,3 -رصاصة تخترق جسمًا ويتحركان بحركة بندول بسيط.

13. 1993,3 -رصاصة تخترق جسمًا ويتحركان بحركة بندول بسيط.

______________________________________________________________________________________

...

لا يتم حفظ الطاقة الميكانيكية، والاصطدام اصطدامًا لدنًا.

يتم حفظ الطاقة الميكانيكية في عملية الاصطدام فقط إذا لم يتم تحويل الطاقة إلى أي شكل آخر غير الطاقة الميكانيكية.
الطاقات الميكانيكية هي: الطاقة الحركية، وطاقة الوضع المرنة، وطاقة وضع الجاذبية.

האנרגיות המכניות הן: אנרגיה קינטית, אנרגיה פוטנציאלית אלסטית, ואנרגיה פוטנציאלית כובדית.

عندما تصطدم الرصاصة بكتلة الخشب، يحدث احتكاك بين الرصاصة وكتلة الخشب، مما يتسبب في تحويل الطاقة الحركية إلى حرارة.

بالإضافة إلى ذلك، يمكن الافتراض أنه في لحظة الاصطدام، يُسمع صوت الرصاصة وهي تضرب جذع الشجرة، حيث يتم تحويل الطاقة الحركية إلى موجات صوتية.

لذلك، لا يتم حفظ الطاقة الميكانيكية .

בנוסף, אפשר להניח שבזמן הפגיעה נשמע קול פגיעת הקליע בבול העץ , אנרגיה קינטית מומרת לגלי קול.

לכן, האנרגיה המכנית לא נשמרת.

1. لكي يتحقق حفظ الطاقة الميكانيكية أثناء الاصطدام، يجب استيفاء الشروط التالية:
- تعود الأجسام المصطدمة إلى شكلها الأصلي (يجب أن تكون الأجسام مصنوعة من مواد مرنة).

- أثناء الاصطدام لم يسمع أي صوت على الإطلاق.

- لا تسخن الأجسام نتيجة الاصطدام.

2. يسمى الاصطدام الذي تُحفظ فيه الطاقة الميكانيكية بالاصطدام المرن.

3. في الواقع، لا يكون الاصطدام المرن ممكنًا إلا في حالات خاصة من الاصطدامات بين الجسيمات.

4. في أسئلة البجروت التي تنص على أن الاصطدام مرن، يتم إهمال جميع أشكال فقدان الطاقة الميكانيكية.

5. في كل اصطدام لدن، تتشوه الأجسام ولا يتم حفظ الطاقة الميكانيكية.

- הגופים המתנגשים חוזרים לצורתם המקורית (הגופים חייבים להיות עשויים מחומרים אלסטיים).

- בזמן ההתנגשות כלל לא נשמע קול .

- הגופים לא מתחממים כתוצאה מההתנגשות.

2. התנגשות שבה האנרגיה המכנית נשמרת נקראת התנגשות אלסטית.

3. במציאות התנגשות אלסטית אפשרית רק במקרים מיוחדים בהתנגשות בין חלקיקים.

4. בשאלות הבגרות בהן כתוב שההתנגשות היא אלסטית , מזניחים את כל צורות איבודי האנרגיה המכנית.

______________________________________________________________________________________

...

«math xmlns=¨http://www.w3.org/1998/Math/MathML¨»«msub»«mi mathvariant=¨bold¨»h«/mi»«mi mathvariant=¨bold¨»max«/mi»«/msub»«mo mathvariant=¨bold¨»=«/mo»«mn mathvariant=¨bold¨»5«/mn»«mi mathvariant=¨bold¨»cm«/mi»«/math»

حفظ كمية الحركة في لإيجاد سرعة الصندوق والقذيفة بعد الاصطدام.
وحفظ الطاقة الميكانيكية لإيجاد أقصى ارتفاع.

ושימור אנרגיה מכנית למציאת הגובה המקסימאלי .

سنرسم مخططًا ونضع علامة على الارتفاع الذي يصل إليه الصندوق، نُشير لكتلة الرصاصة على أنها الجسم 1، وكتلة الصندوق على أنها الجسم 2:

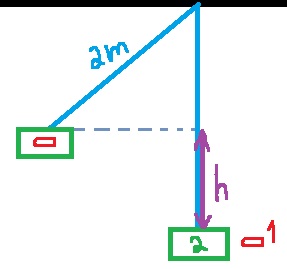
يتعلق الارتفاع الذي يصل إليه الصندوق بسرعة الصندوق بعد أن تستقر الرصاصة يداخله.

أثناء اصطدام الرصاصة بالصندوق، فإن القوى الداخلية فقط هي التي تعمل في الاتجاه الأفقي، وبالتالي فإن كمية الحركة في الاتجاه الأفقي سوف يُحفظ.

نكتب معادلة حفظ الزخم في الاتجاه الأفقي:

«math xmlns=¨http://www.w3.org/1998/Math/MathML¨»«msub»«mi mathvariant=¨bold¨ mathcolor=¨#0000FF¨»m«/mi»«mn mathvariant=¨bold¨ mathcolor=¨#0000FF¨»1«/mn»«/msub»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»§#183;«/mo»«msub»«mi mathvariant=¨bold¨ mathcolor=¨#0000FF¨»V«/mi»«mn mathvariant=¨bold¨ mathcolor=¨#0000FF¨»1«/mn»«/msub»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»+«/mo»«msub»«mi mathvariant=¨bold¨ mathcolor=¨#0000FF¨»m«/mi»«mn mathvariant=¨bold¨ mathcolor=¨#0000FF¨»2«/mn»«/msub»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»§#183;«/mo»«msub»«mi mathvariant=¨bold¨ mathcolor=¨#0000FF¨»V«/mi»«mn mathvariant=¨bold¨ mathcolor=¨#0000FF¨»2«/mn»«/msub»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»=«/mo»«mrow mathcolor=¨#0000FF¨»«mo mathvariant=¨bold¨»(«/mo»«msub»«mi mathvariant=¨bold¨»m«/mi»«mn mathvariant=¨bold¨»1«/mn»«/msub»«mo mathvariant=¨bold¨»+«/mo»«msub»«mi mathvariant=¨bold¨»m«/mi»«mn mathvariant=¨bold¨»2«/mn»«/msub»«mo mathvariant=¨bold¨»)«/mo»«/mrow»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»§#183;«/mo»«mi mathvariant=¨bold¨ mathcolor=¨#0000FF¨»U«/mi»«mspace linebreak=¨newline¨»«/mspace»«mspace linebreak=¨newline¨»«/mspace»«mi mathvariant=¨bold¨ mathcolor=¨#0000FF¨»U«/mi»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»=«/mo»«mfrac mathcolor=¨#0000FF¨»«mrow»«msub»«mi mathvariant=¨bold¨»m«/mi»«mn mathvariant=¨bold¨»1«/mn»«/msub»«mo mathvariant=¨bold¨»§#183;«/mo»«msub»«mi mathvariant=¨bold¨»V«/mi»«mn mathvariant=¨bold¨»1«/mn»«/msub»«mo mathvariant=¨bold¨»+«/mo»«msub»«mi mathvariant=¨bold¨»m«/mi»«mn mathvariant=¨bold¨»2«/mn»«/msub»«mo mathvariant=¨bold¨»§#183;«/mo»«msub»«mi mathvariant=¨bold¨»V«/mi»«mn mathvariant=¨bold¨»2«/mn»«/msub»«/mrow»«mrow»«msub»«mi mathvariant=¨bold¨»m«/mi»«mn mathvariant=¨bold¨»1«/mn»«/msub»«mo mathvariant=¨bold¨»+«/mo»«msub»«mi mathvariant=¨bold¨»m«/mi»«mn mathvariant=¨bold¨»2«/mn»«/msub»«/mrow»«/mfrac»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»=«/mo»«mfrac mathcolor=¨#0000FF¨»«mrow»«mn mathvariant=¨bold¨»0«/mn»«mo mathvariant=¨bold¨».«/mo»«mn mathvariant=¨bold¨»02«/mn»«mo mathvariant=¨bold¨»§#183;«/mo»«mn mathvariant=¨bold¨»500«/mn»«mo mathvariant=¨bold¨»+«/mo»«mn mathvariant=¨bold¨»9«/mn»«mo mathvariant=¨bold¨».«/mo»«mn mathvariant=¨bold¨»98«/mn»«mo mathvariant=¨bold¨»§#183;«/mo»«mn mathvariant=¨bold¨»0«/mn»«/mrow»«mrow»«mn mathvariant=¨bold¨»0«/mn»«mo mathvariant=¨bold¨».«/mo»«mn mathvariant=¨bold¨»02«/mn»«mo mathvariant=¨bold¨»+«/mo»«mn mathvariant=¨bold¨»9«/mn»«mo mathvariant=¨bold¨».«/mo»«mn mathvariant=¨bold¨»98«/mn»«/mrow»«/mfrac»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»=«/mo»«mfrac mathcolor=¨#0000FF¨»«mn mathvariant=¨bold¨»1«/mn»«mn mathvariant=¨bold¨»1«/mn»«/mfrac»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»=«/mo»«mn mathvariant=¨bold¨ mathcolor=¨#0000FF¨»1«/mn»«mfrac mathcolor=¨#0000FF¨»«mi mathvariant=¨bold¨»m«/mi»«mi mathvariant=¨bold¨»s«/mi»«/mfrac»«/math»

في حركة الصندوق والرصاصة من أدنى نقطة إلى أعلى نقطة، الجاذبية فقط هي التي تعمل.

قوة الشد تعمل بشكل عمودي على الحركة، ولا تبذل شغلاً.

سوف نحدد أدنى نقطة بالنقطة A وأعلى نقطة بالنقطة B.

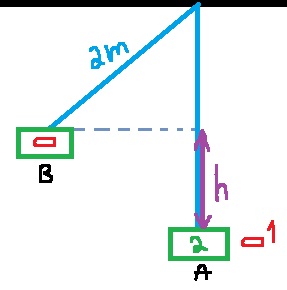
نكتب معادلة حفظ الطاقة، مع تحديد المستوى المرجعي في ارتفاع النقطة A:

«math xmlns=¨http://www.w3.org/1998/Math/MathML¨»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»§#160;«/mo»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»§#160;«/mo»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»§#160;«/mo»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»§#160;«/mo»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»§#160;«/mo»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»§#160;«/mo»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»§#160;«/mo»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»§#160;«/mo»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»§#160;«/mo»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»§#160;«/mo»«msub»«mi mathvariant=¨bold¨ mathcolor=¨#0000FF¨»E«/mi»«mi mathvariant=¨bold¨ mathcolor=¨#0000FF¨»A«/mi»«/msub»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»=«/mo»«msub»«mi mathvariant=¨bold¨ mathcolor=¨#0000FF¨»E«/mi»«mi mathvariant=¨bold¨ mathcolor=¨#0000FF¨»B«/mi»«/msub»«mspace linebreak=¨newline¨»«/mspace»«mspace linebreak=¨newline¨»«/mspace»«msub»«mi mathvariant=¨bold¨ mathcolor=¨#0000FF¨»E«/mi»«msub mathcolor=¨#0000FF¨»«mi mathvariant=¨bold¨»K«/mi»«mi mathvariant=¨bold¨»A«/mi»«/msub»«/msub»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»+«/mo»«msub»«mi mathvariant=¨bold¨ mathcolor=¨#0000FF¨»U«/mi»«mi mathvariant=¨bold¨ mathcolor=¨#0000FF¨»A«/mi»«/msub»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»=«/mo»«msub»«mi mathvariant=¨bold¨ mathcolor=¨#0000FF¨»E«/mi»«msub mathcolor=¨#0000FF¨»«mi mathvariant=¨bold¨»K«/mi»«mi mathvariant=¨bold¨»B«/mi»«/msub»«/msub»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»+«/mo»«msub»«mi mathvariant=¨bold¨ mathcolor=¨#0000FF¨»U«/mi»«mi mathvariant=¨bold¨ mathcolor=¨#0000FF¨»B«/mi»«/msub»«/math»

في النقطة A يكون ارتفاع الجسم بالنسبة للمستوى المرجعي مساويًا للصفر. لا توجد طاقة وضع جاذبية في النقطة A.

في النقطة B توقف الجسم توقفًا لحظيًا، الجسم ليس لديه طاقة حركية في النقطة B:

«math xmlns=¨http://www.w3.org/1998/Math/MathML¨»«msub»«mi mathvariant=¨bold¨ mathcolor=¨#0000FF¨»E«/mi»«msub mathcolor=¨#0000FF¨»«mi mathvariant=¨bold¨»K«/mi»«mi mathvariant=¨bold¨»A«/mi»«/msub»«/msub»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»+«/mo»«menclose mathcolor=¨#0000FF¨ notation=¨updiagonalstrike¨»«msub»«mi mathvariant=¨bold¨»U«/mi»«mi mathvariant=¨bold¨»A«/mi»«/msub»«/menclose»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»=«/mo»«menclose mathcolor=¨#0000FF¨ notation=¨updiagonalstrike¨»«msub»«mi mathvariant=¨bold¨»E«/mi»«msub»«mi mathvariant=¨bold¨»K«/mi»«mi mathvariant=¨bold¨»B«/mi»«/msub»«/msub»«/menclose»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»+«/mo»«msub»«mi mathvariant=¨bold¨ mathcolor=¨#0000FF¨»U«/mi»«mi mathvariant=¨bold¨ mathcolor=¨#0000FF¨»B«/mi»«/msub»«mspace linebreak=¨newline¨»«/mspace»«mspace linebreak=¨newline¨»«/mspace»«mfrac mathcolor=¨#0000FF¨»«mn mathvariant=¨bold¨»1«/mn»«mn mathvariant=¨bold¨»2«/mn»«/mfrac»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»§#183;«/mo»«menclose mathcolor=¨#0000FF¨ notation=¨updiagonalstrike¨»«mi mathvariant=¨bold¨»m«/mi»«/menclose»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»§#183;«/mo»«msup»«msub»«mi mathvariant=¨bold¨ mathcolor=¨#0000FF¨»V«/mi»«mi mathvariant=¨bold¨ mathcolor=¨#0000FF¨»A«/mi»«/msub»«mn mathvariant=¨bold¨ mathcolor=¨#0000FF¨»2«/mn»«/msup»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»=«/mo»«menclose mathcolor=¨#0000FF¨ notation=¨updiagonalstrike¨»«mi mathvariant=¨bold¨»m«/mi»«/menclose»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»§#183;«/mo»«mi mathvariant=¨bold¨ mathcolor=¨#0000FF¨»g«/mi»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»§#183;«/mo»«msub»«mi mathvariant=¨bold¨ mathcolor=¨#0000FF¨»h«/mi»«mi mathvariant=¨bold¨ mathcolor=¨#0000FF¨»B«/mi»«/msub»«mspace linebreak=¨newline¨»«/mspace»«mspace linebreak=¨newline¨»«/mspace»«msub»«mi mathvariant=¨bold¨ mathcolor=¨#0000FF¨»h«/mi»«mi mathvariant=¨bold¨ mathcolor=¨#0000FF¨»B«/mi»«/msub»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»=«/mo»«mfrac mathcolor=¨#0000FF¨»«msup»«msub»«mi mathvariant=¨bold¨»V«/mi»«mi mathvariant=¨bold¨»A«/mi»«/msub»«mn mathvariant=¨bold¨»2«/mn»«/msup»«mrow»«mn mathvariant=¨bold¨»2«/mn»«mo mathvariant=¨bold¨»§#183;«/mo»«mi mathvariant=¨bold¨»g«/mi»«/mrow»«/mfrac»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»=«/mo»«mfrac mathcolor=¨#0000FF¨»«msup»«mn mathvariant=¨bold¨»1«/mn»«mn mathvariant=¨bold¨»2«/mn»«/msup»«mrow»«mn mathvariant=¨bold¨»2«/mn»«mo mathvariant=¨bold¨»§#183;«/mo»«mn mathvariant=¨bold¨»10«/mn»«/mrow»«/mfrac»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»=«/mo»«mfrac mathcolor=¨#0000FF¨»«mn mathvariant=¨bold¨»1«/mn»«mn mathvariant=¨bold¨»20«/mn»«/mfrac»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»=«/mo»«mn mathvariant=¨bold¨ mathcolor=¨#0000FF¨»0«/mn»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨».«/mo»«mn mathvariant=¨bold¨ mathcolor=¨#0000FF¨»05«/mn»«mi mathvariant=¨bold¨ mathcolor=¨#0000FF¨»m«/mi»«/math»

أقصى ارتفاع يصل إليه الصندوق مع الرصاصة هو 5 سم فوق أدنى نقطة.

הגובה אליו מגיע בול העץ תלוי במהירות בול העץ לאחר פגיעת הקליע.

בזמן התנגשות הקליע בבול העץ , בכיוון האופקי פועלים רק כוחות פנימיים , לכן התנע בכיוון האופקי נשמר.

נכתוב את משוואת שימור התנע לכיוון האופקי:

בתנועת בול העץ והקליע מהנקודה הנמוכה ביותר לנקודה הגבוה ביותר , רק כוח הכבידה עושה עבודה.

כוח המתיחות פועל בניצב לתנועה, הוא לא מבצע עבודה.

נסמן את הנקודה הנמוכה ביותר כנקודה A ואת הנקודה הגבוהה ביותר כנקודה B.

נכתוב את משוואת שימור האנרגיה , נגדיר את מישור הייחוס בגובה הנקודה A:

בנקודה A גובה הגוף ביחס למישור הייחוס שווה לאפס. אין אנרגיה פוטנציאלית כובדית בנקודה A.

בנקודה B הגוף עצר רגעית, אין לגוף אנרגיה קינטית בנקודה B:

הגובה המרבי אליו מגיע בול העץ עם הקליע הוא 5 ס"מ מעל הנקודה הנמוכה ביותר.

1. في السؤال، يتم الإشارة إلى الكتل بواسطة M و m، وهذا الترميز غير عملي لمعادلة كمية الحركة والطاقة.
الحل الأفضل هو الإشارة لكل من الكتلتين بـ m1 m2 وبالتالي V1،V2،U1،U2.

2. إن مدة اختراق الرصاصة للصندوق قصيرة؛ لا يرتفع الصندوق أثناء انغراس الرصاصة فيه.
وبالتالي هناك مرحلتين مختلفتين، مرحلة الاصطدام التي يكون فيها حفظ لكمية الحركة . ومرحلة الحركة التي يتم فيها حفظ الطاقة.

3. تعتبر أبعاد الصندوق الخشبي صغيرة نسبيًا مقارنة بطول الخيط، لذلك ليست هناك حاجة إلى الأخذ في الحسبان مركز كتلة الصندوق.
على سبيل المثال، نصف قطر الدوران يساوي طول الخيط، وليس طول الخيط بالإضافة إلى البعد بين طرف الخيط ومركز الصندوق.

4. من المُتبع استخدام الحرف U كطاقة وضعية وسرعة بعد الاصطدام. من المهم أن نبقى مركزين ولا نخلط بين الاثنين.

5. السرعة المشتركة للرصاصة والصندوق الناتجة من معادلة حفظ كمية الحركة U
هي سرعة الصندوق والرصاصة في النقطة A، ويشار إليها بـ VA.

6.مذكور في السؤال : "احسب الارتفاع الأقصى". لم يذكر نسبة لأي ارتفاع. المقصود هنا إلى التغيير في الارتفاع.

עדיף פתרון לסמן את המסות ב m1 m2 ובהתאמה V1,V2,U1,U2 .

2. זמן חדירת הקליע לבול העץ הוא קצר , בול העץ לא עולה בזמן שקליע ננעץ בו.

כך יש שני שלבים שונים שלב ההתנגשות שבו התנע נשמר. ושלב התנועה שבו האנרגיה נשמרת.

3. ממדי בול העץ קטנים ביחס לאורך החוט , אין צורך להתייחס למרכז המסה של בול העץ .

כך למשל רדיוס הסיבוב שווה לאורך החוט ולא לאורך החוט בתוספת המרחק שבין קצה החוט למרכז בול העץ.

4. מקובל להשתמש באות U כאנרגיה פוטנציאלית וכמהירות אחרי ההתנגשות. חשוב להיות מרוכזים ולא לבלבל בין השניים.

5. המהירות המשותפת של הקליע ובול העץ המתקבלת ממשוואת שימור התנע U

היא מהירות בול העץ והקליע בנקודה A המסומנת כ VA.

6. כתוב בשאלה: "חשב את הגובה המירבי" לא כתוב ביחס לאיזה גובה . הכוונה היא לשינוי בגובה.

______________________________________________________________________________________

...

شغل قوة الشد يساوي صفرًا.

تعريف الشغل.

قوة الشد تعمل بشكل عمودي على الحركة. بحسب تعريف الشغل، فإن قوة الشد لا تبذل شغلاً.

«math xmlns=¨http://www.w3.org/1998/Math/MathML¨»«mi mathvariant=¨bold¨ mathcolor=¨#0000FF¨»W«/mi»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»=«/mo»«mrow mathcolor=¨#0000FF¨»«mo mathvariant=¨bold¨»|«/mo»«mi mathvariant=¨bold¨»F«/mi»«mo mathvariant=¨bold¨»|«/mo»«/mrow»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»§#183;«/mo»«mrow mathcolor=¨#0000FF¨»«mo mathvariant=¨bold¨»|«/mo»«mo mathvariant=¨bold¨»§#8710;«/mo»«mi mathvariant=¨bold¨»X«/mi»«mo mathvariant=¨bold¨»|«/mo»«/mrow»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»§#183;«/mo»«mi mathvariant=¨bold¨ mathcolor=¨#0000FF¨»cos«/mi»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»(«/mo»«mi mathvariant=¨bold¨ mathcolor=¨#0000FF¨»§#945;«/mi»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»)«/mo»«mspace linebreak=¨newline¨»«/mspace»«mspace linebreak=¨newline¨»«/mspace»«mi mathvariant=¨bold¨ mathcolor=¨#0000FF¨»W«/mi»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»=«/mo»«mrow mathcolor=¨#0000FF¨»«mo mathvariant=¨bold¨»|«/mo»«mi mathvariant=¨bold¨»T«/mi»«mo mathvariant=¨bold¨»|«/mo»«/mrow»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»§#183;«/mo»«mrow mathcolor=¨#0000FF¨»«mo mathvariant=¨bold¨»|«/mo»«mo mathvariant=¨bold¨»§#8710;«/mo»«mi mathvariant=¨bold¨»X«/mi»«mo mathvariant=¨bold¨»|«/mo»«/mrow»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»§#183;«/mo»«mi mathvariant=¨bold¨ mathcolor=¨#0000FF¨»cos«/mi»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»(«/mo»«mn mathvariant=¨bold¨ mathcolor=¨#0000FF¨»90«/mn»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»)«/mo»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»=«/mo»«mn mathvariant=¨bold¨ mathcolor=¨#0000FF¨»0«/mn»«/math»

شغل قوة الشد يساوي صفرًا.

עבודת כוח המתיחות שווה לאפס.

1. لا تعمل قوة الشد دائمًا بشكل عمودي على الحركة. هناك حالات يكون فيها اتجاه قوة الشد في اتجاه الحركة.
حتى القوة العمودية المؤثرة على السطح لا تؤثر دائمًا بشكل عمودي على الحركة. يجب فحص كل حالة على حدة.

2. من المهم كتابة تعبير الشغل، وإظهار أنه عندما تعمل القوة بشكل عمودي على الحركة، فإن شغلها يساوي صفرًا.

גם כוח הנורמל הפועל בניצב למשטח לא תמיד פועל בניצב לתנועה.

2. תלמיד שיכתוב : כוח המתיחות פועל בניצב לתנועה לכן הוא לא עושה עבודה . לא יקבל את מלא הנקודות.

חייבים להתייחס גם להגדרת העבודה. יש להסביר מדוע כוח ניצב לא מבצע עבודה.

______________________________________________________________________________________

...

«math xmlns=¨http://www.w3.org/1998/Math/MathML¨»«mi mathvariant=¨bold¨»t«/mi»«mo mathvariant=¨bold¨»=«/mo»«mn mathvariant=¨bold¨»0«/mn»«mo mathvariant=¨bold¨».«/mo»«mn mathvariant=¨bold¨»7«/mn»«mi mathvariant=¨bold¨»s«/mi»«/math»

التطرق إلى حركة البندول كحركة توافقية بسيطة.

بعد أن أصابت الرصاصة الصندوق الخشبي. تتحرك الرصاصة والصندوق في حركة البندول البسيطة.

يعتبر التغيير في ارتفاع الصندوق صغيرًا نسبيًا مقارنة بطول الخيط. يتحرك الصندوق بحركة البندول البسيطة بزوايا صغيرة.

نقوم بحساب قيمة أقصى زاوية ميل للخيط، ونرمز للارتفاع بـ X، البُعد الرأسي بين النقطة B والسقف:

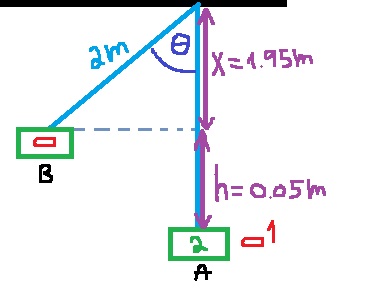
نستخدم نسبة cos :

«math xmlns=¨http://www.w3.org/1998/Math/MathML¨»«mi mathvariant=¨bold-italic¨ mathcolor=¨#0000FF¨»c«/mi»«mi mathvariant=¨bold-italic¨ mathcolor=¨#0000FF¨»o«/mi»«mi mathvariant=¨bold-italic¨ mathcolor=¨#0000FF¨»s«/mi»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»(«/mo»«mi mathvariant=¨bold-italic¨ mathcolor=¨#0000FF¨»§#952;«/mi»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»)«/mo»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»=«/mo»«mfrac mathcolor=¨#0000FF¨»«mi mathvariant=¨bold¨»X«/mi»«mi mathvariant=¨bold¨»L«/mi»«/mfrac»«mspace linebreak=¨newline¨»«/mspace»«mi mathvariant=¨bold-italic¨ mathcolor=¨#0000FF¨»§#952;«/mi»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»=«/mo»«mi mathvariant=¨bold-italic¨ mathcolor=¨#0000FF¨»s«/mi»«mi mathvariant=¨bold-italic¨ mathcolor=¨#0000FF¨»h«/mi»«mi mathvariant=¨bold-italic¨ mathcolor=¨#0000FF¨»i«/mi»«mi mathvariant=¨bold-italic¨ mathcolor=¨#0000FF¨»f«/mi»«mi mathvariant=¨bold-italic¨ mathcolor=¨#0000FF¨»t«/mi»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»§#160;«/mo»«mi mathvariant=¨bold-italic¨ mathcolor=¨#0000FF¨»c«/mi»«mi mathvariant=¨bold-italic¨ mathcolor=¨#0000FF¨»o«/mi»«mi mathvariant=¨bold-italic¨ mathcolor=¨#0000FF¨»s«/mi»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»(«/mo»«mfrac mathcolor=¨#0000FF¨»«mi mathvariant=¨bold¨»X«/mi»«mi mathvariant=¨bold¨»L«/mi»«/mfrac»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»)«/mo»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»=«/mo»«mi mathvariant=¨bold-italic¨ mathcolor=¨#0000FF¨»s«/mi»«mi mathvariant=¨bold-italic¨ mathcolor=¨#0000FF¨»h«/mi»«mi mathvariant=¨bold-italic¨ mathcolor=¨#0000FF¨»i«/mi»«mi mathvariant=¨bold-italic¨ mathcolor=¨#0000FF¨»f«/mi»«mi mathvariant=¨bold-italic¨ mathcolor=¨#0000FF¨»t«/mi»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»§#160;«/mo»«mi mathvariant=¨bold-italic¨ mathcolor=¨#0000FF¨»c«/mi»«mi mathvariant=¨bold-italic¨ mathcolor=¨#0000FF¨»o«/mi»«mi mathvariant=¨bold-italic¨ mathcolor=¨#0000FF¨»s«/mi»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»(«/mo»«mfrac mathcolor=¨#0000FF¨»«mrow»«mn mathvariant=¨bold¨»1«/mn»«mo mathvariant=¨bold¨».«/mo»«mn mathvariant=¨bold¨»95«/mn»«/mrow»«mn mathvariant=¨bold¨»2«/mn»«/mfrac»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»)«/mo»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»=«/mo»«mn mathvariant=¨bold¨ mathcolor=¨#0000FF¨»12«/mn»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨».«/mo»«msup»«mn mathvariant=¨bold¨ mathcolor=¨#0000FF¨»83«/mn»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»§#176;«/mo»«/msup»«/math»

نتعامل مع حركة البندول البسيطة كحركة توافقية بسيطة.

يمكننا إيجاد زمن الحركة باستخدام قانون زمن الدورة لحركة البندول البسيط المتحرك بزوايا صغيرة:

«math xmlns=¨http://www.w3.org/1998/Math/MathML¨»«mi mathvariant=¨bold¨ mathcolor=¨#0000FF¨»T«/mi»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»=«/mo»«mn mathvariant=¨bold¨ mathcolor=¨#0000FF¨»2«/mn»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»§#183;«/mo»«mi mathvariant=¨bold¨ mathcolor=¨#0000FF¨»§#960;«/mi»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»§#183;«/mo»«msqrt mathcolor=¨#0000FF¨»«mfrac»«mi mathvariant=¨bold¨»L«/mi»«mi mathvariant=¨bold¨»g«/mi»«/mfrac»«/msqrt»«mspace linebreak=¨newline¨»«/mspace»«mi mathvariant=¨bold¨ mathcolor=¨#0000FF¨»T«/mi»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»=«/mo»«mn mathvariant=¨bold¨ mathcolor=¨#0000FF¨»2«/mn»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»§#183;«/mo»«mi mathvariant=¨bold¨ mathcolor=¨#0000FF¨»§#960;«/mi»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»§#183;«/mo»«msqrt mathcolor=¨#0000FF¨»«mfrac»«mn mathvariant=¨bold¨»2«/mn»«mn mathvariant=¨bold¨»10«/mn»«/mfrac»«/msqrt»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»=«/mo»«mn mathvariant=¨bold¨ mathcolor=¨#0000FF¨»6«/mn»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨».«/mo»«mn mathvariant=¨bold¨ mathcolor=¨#0000FF¨»28«/mn»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»§#183;«/mo»«msqrt mathcolor=¨#0000FF¨»«mn mathvariant=¨bold¨»0«/mn»«mo mathvariant=¨bold¨».«/mo»«mn mathvariant=¨bold¨»2«/mn»«/msqrt»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»§#160;«/mo»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»=«/mo»«mn mathvariant=¨bold¨ mathcolor=¨#0000FF¨»2«/mn»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨».«/mo»«mn mathvariant=¨bold¨ mathcolor=¨#0000FF¨»8«/mn»«mi mathvariant=¨bold¨ mathcolor=¨#0000FF¨»s«/mi»«/math»

من لحظة بدء تحرك الصندوق حتى وصوله إلى نقطة النهاية، يمر ربع دورة زمنية. احسب زمن حركة الصندوق:

«math xmlns=¨http://www.w3.org/1998/Math/MathML¨»«mi mathvariant=¨bold¨ mathcolor=¨#0000FF¨»t«/mi»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»=«/mo»«mfrac mathcolor=¨#0000FF¨»«mi mathvariant=¨bold¨»T«/mi»«mn mathvariant=¨bold¨»4«/mn»«/mfrac»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»=«/mo»«mfrac mathcolor=¨#0000FF¨»«mrow»«mn mathvariant=¨bold¨»2«/mn»«mo mathvariant=¨bold¨».«/mo»«mn mathvariant=¨bold¨»8«/mn»«/mrow»«mn mathvariant=¨bold¨»4«/mn»«/mfrac»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»=«/mo»«mn mathvariant=¨bold¨ mathcolor=¨#0000FF¨»0«/mn»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨».«/mo»«mn mathvariant=¨bold¨ mathcolor=¨#0000FF¨»7«/mn»«mi mathvariant=¨bold¨ mathcolor=¨#0000FF¨»s«/mi»«/math»

بعد مضي 0.7 ثانية، يصل الصندوق والرصاصة الموجودة بداخله إلى أقصى ارتفاع.

השינוי בגובה בול העץ קטן ביחס לאורך החוט . בול העץ נע בתנועת מטוטלת פשוטה בזוויות קטנות.

נתייחס לתנועת המטוטלת הפשוטה כאל תנועה הרמונית פשוטה.

נמצא את זמן מחזור התנועה , בעזרת נוסחת זמן המחזור לתנועת מטוטלת פשוטה הנעה בזוויות קטנות:

מרגע תחילת תנועת בול העץ ועד שבול העץ מגיע לנקודת הקצה עובר רבע זמן מחזור . נחשב זמן תנועת בול העץ:

כעבור 0.7 שניות מגיע בול העץ והקליע בתוכו לגובה מירבי.

1. في تعبير القوة الأفقية المؤثرة على جسم يتحرك في حركة بندول بسيطة، يوجد تقريب للزوايا الصغيرة وفقًا: «math xmlns=¨http://www.w3.org/1998/Math/MathML¨»«mi mathvariant=¨bold¨ mathcolor=¨#FF0000¨»sin«/mi»«mo mathvariant=¨bold¨ mathcolor=¨#FF0000¨»(«/mo»«msub»«mi mathvariant=¨bold¨ mathcolor=¨#FF0000¨»§#952;«/mi»«mi mathvariant=¨bold¨ mathcolor=¨#FF0000¨»rad«/mi»«/msub»«mo mathvariant=¨bold¨ mathcolor=¨#FF0000¨»)«/mo»«mo mathvariant=¨bold¨ mathcolor=¨#FF0000¨»=«/mo»«msub»«mi mathvariant=¨bold¨ mathcolor=¨#FF0000¨»§#952;«/mi»«mi mathvariant=¨bold¨ mathcolor=¨#FF0000¨»rad«/mi»«/msub»«/math»

يحتوي الجدول التالي على قيم جيب الزاوية والزاوية بالراديان على التوالي:

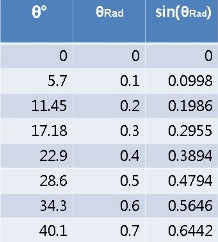
وبشكل عام، يمكن اعتبار الحركة بزاوية أقل من 30 درجة حركة توافقية بسيطة.
في الحالة المذكورة في السؤال، أقصى زاوية ميل للخيط هي 12.8 درجة، وبالتالي يمكن اعتبار حركة البندول بمثابة بندول.

2. قبل استخدام قوانين الحركة التوافقية البسيطة، تجدر الإشارة إلى أن البندول يتحرك بزوايا ميل صغيرة.

הטבלה הבאה מכילה את ערכי סינוס הזווית והזווית ברדיאן ,בהתאמה:

באופן כללי ,בזווית קטנה מ 30 מעלות אפשר להתייחס לתנועה כאל תנועה הרמונית פשוטה.

במקרה המתואר בשאלה זווית נטיית החוט המקסימאלית היא 12.8 מעלות, לכן ניתן להתייחס לתנועת המטוטלת כתה"פ.

2. לפני התייחסות המטוטלת כאל תנועה הרמונית פשוטה , יש לציין שמטוטלת נעה בזוויות נטייה קטנות.

הטבלה הבאה מכילה את ערכי סינוס הזווית לצד ערכי הזווית בהתאמה:

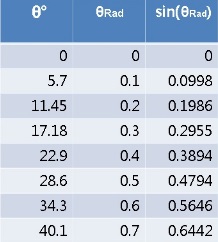
מהטבלה אפשר לראות שעד 30 מעלות , אפשר להגיד שבקירוב סינוס הזווית ברדיאן שווה לערך הזווית.

2. בול העץ מחובר לחוט שאורכו 2 מטרים. בול העץ עולה רק ב 5 ס"מ , זווית נטיית החוט המקסימאלית קטנה.

______________________________________________________________________________________