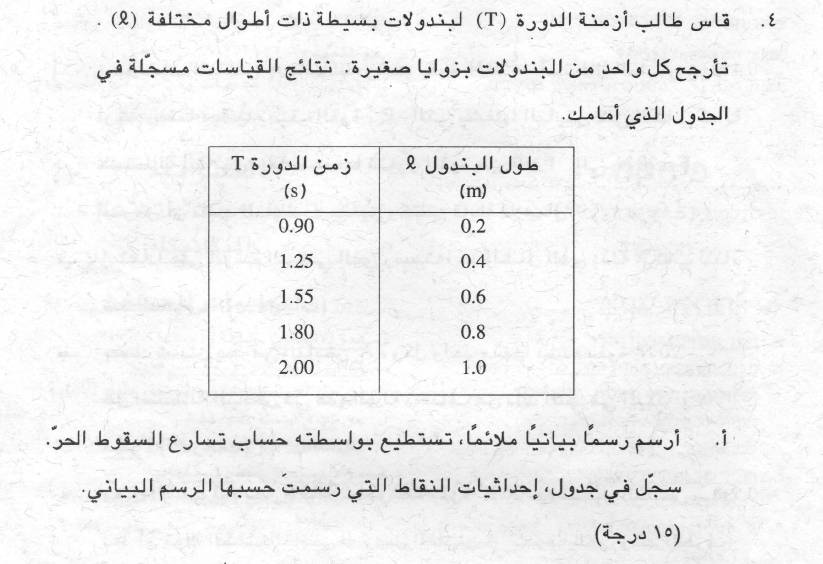
10. 1998,4- ايجاد g بواسطة البندول الرياضي
______________________________________________________________________________________
...
نضيف عمودًا إلى الجدول لمربع زمن الدورة:
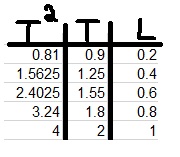
نرسم رسمًا بيانيًا لمربع زمن الدورة كدالة لطول البندول:
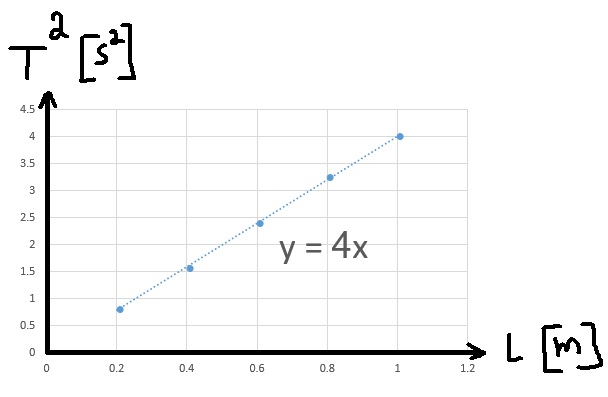

נערוך גרף ריבוע זמן מחזור בתלות באורך המטוטלת:

فهم تعبير زمن دورة البندول البسيط المتأرجح بزوايا صغيرة، ورسم بياني.
لإيجاد ثابت الجاذبية، بناءً على التعبير والكميات التي تظهر في الجدول: زمن الدورة وطول الخيط.
למציאת קבוע גרביטציה, המבוסס על הביטוי ועל הגדלים המופיעים בטבלה :זמן המחזור ואורך החוט.
يصف الجدول أزمنة دورة البندول، في أطوال مختلفة.
مُعطى العلاقة بين زمن الدورة وطول الخيط حسب تعبير زمن الدورة: «math xmlns=¨http://www.w3.org/1998/Math/MathML¨»«mi mathvariant=¨bold-italic¨ mathcolor=¨#0000FF¨»T«/mi»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»=«/mo»«mn mathvariant=¨bold¨ mathcolor=¨#0000FF¨»2«/mn»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»§#183;«/mo»«mi mathvariant=¨bold¨ mathcolor=¨#0000FF¨»§#960;«/mi»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»§#183;«/mo»«msqrt mathcolor=¨#0000FF¨»«mfrac»«mi mathvariant=¨bold¨»L«/mi»«mi mathvariant=¨bold¨»g«/mi»«/mfrac»«/msqrt»«/math»
لإيجاد تسارع السقوط الحر، نرسم رسمًا بيانيًا لمربع زمن الدورة كدالة لطول الخيط.
ومن ثم، من ميل الدالة، يمكننا إيجاد ثابت الجاذبية:
«math xmlns=¨http://www.w3.org/1998/Math/MathML¨»«msup»«mi mathvariant=¨bold-italic¨ mathcolor=¨#0000FF¨»T«/mi»«mn mathvariant=¨bold¨ mathcolor=¨#0000FF¨»2«/mn»«/msup»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»=«/mo»«munder mathcolor=¨#0000FF¨»«menclose notation=¨circle¨»«mfrac»«mrow»«mn mathvariant=¨bold¨»4«/mn»«mo mathvariant=¨bold¨»§#183;«/mo»«msup»«mi mathvariant=¨bold¨»§#960;«/mi»«mn mathvariant=¨bold¨»2«/mn»«/msup»«/mrow»«mi mathvariant=¨bold¨»g«/mi»«/mfrac»«/menclose»«mi mathvariant=¨bold¨»§#1575;§#1604;§#1605;§#1610;§#1604;«/mi»«/munder»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»§#183;«/mo»«mi mathvariant=¨bold-italic¨ mathcolor=¨#0000FF¨»L«/mi»«/math»
نضيف عمودًا إلى الجدول لمربع زمن الدورة:
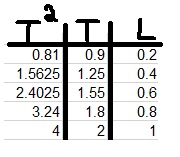
نرسم مربع زمن الدورة كدالة لطول البندول:
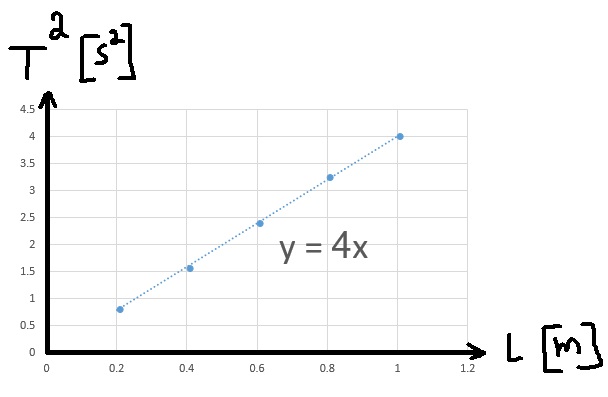
הקשר שבין זמן המחזור לאורך החוט נתון בביטוי זמן המחזור: «math xmlns=¨http://www.w3.org/1998/Math/MathML¨»«mi mathvariant=¨bold-italic¨ mathcolor=¨#0000FF¨»T«/mi»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»=«/mo»«mn mathvariant=¨bold¨ mathcolor=¨#0000FF¨»2«/mn»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»§#183;«/mo»«mi mathvariant=¨bold¨ mathcolor=¨#0000FF¨»§#960;«/mi»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»§#183;«/mo»«msqrt mathcolor=¨#0000FF¨»«mfrac»«mi mathvariant=¨bold¨»L«/mi»«mi mathvariant=¨bold¨»g«/mi»«/mfrac»«/msqrt»«/math»
כדי למצוא את תאוצת הנפילה החופשית, נשרטט גרף של ריבוע זמן המחזור בתלות באורך החוט.
כך שמשיפוע הפונקציה נוכל למצוא את קבוע הגרביטציה:
«math xmlns=¨http://www.w3.org/1998/Math/MathML¨»«msup»«mi mathvariant=¨bold-italic¨ mathcolor=¨#0000FF¨»T«/mi»«mn mathvariant=¨bold¨ mathcolor=¨#0000FF¨»2«/mn»«/msup»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»=«/mo»«munder mathcolor=¨#0000FF¨»«menclose notation=¨circle¨»«mfrac»«mrow»«mn mathvariant=¨bold¨»4«/mn»«mo mathvariant=¨bold¨»§#183;«/mo»«msup»«mi mathvariant=¨bold¨»§#960;«/mi»«mn mathvariant=¨bold¨»2«/mn»«/msup»«/mrow»«mi mathvariant=¨bold¨»g«/mi»«/mfrac»«/menclose»«mi mathvariant=¨bold¨»§#1513;§#1497;§#1508;§#1493;§#1506;«/mi»«/munder»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»§#183;«/mo»«mi mathvariant=¨bold-italic¨ mathcolor=¨#0000FF¨»L«/mi»«/math»
נוסיף לטבלה עמודה של ריבוע זמן המחזור:

נתאר בגרף את ריבוע זמן המחזור בתלות באורך המטוטלת:

1. في هذا القسم، ليس من الضروري إيجاد ثابت الجاذبية. فقط قم بوصف الخطوات في عملية ايجاد ثابت الجاذبية.
2. تعبير زمن الدورة مناسب فقط للبندول الذي يتأرجح بزوايا صغيرة.
السؤال ينص على أنه في كل حالة تكون التذبذبات بزاوية صغيرة، لذا يمكن استخدام تعبير الفترة للبندول البسيط.
2. ביטוי זמן המחזור מתאים רק למטוטלת המתנודדת בזוויות קטנות.
בשאלה כתוב שבכל אחד מהמקרים התנודות הן בזווית קטנות לכן ניתן להשתמש בביטוי זמן המחזור למטוטלת פשוטה.
______________________________________________________________________________________

______________________________________________________________________________________
...
«math xmlns=¨http://www.w3.org/1998/Math/MathML¨»«mi mathvariant=¨bold¨»g«/mi»«mo mathvariant=¨bold¨»=«/mo»«mn mathvariant=¨bold¨»9«/mn»«mo mathvariant=¨bold¨».«/mo»«mn mathvariant=¨bold¨»87«/mn»«mfrac»«mi mathvariant=¨bold¨»m«/mi»«msup»«mi mathvariant=¨bold¨»s«/mi»«mn mathvariant=¨bold¨»2«/mn»«/msup»«/mfrac»«/math»
إيجاد ثابت الجاذبية من ميل الرسم البياني.
نحسب ميل الرسم البياني من نقطتين تقعان على خط الاتجاه:
«math xmlns=¨http://www.w3.org/1998/Math/MathML¨»«mi mathvariant=¨bold¨ mathcolor=¨#0000FF¨»§#1575;§#1604;§#1605;§#1610;§#1604;«/mi»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»=«/mo»«mfrac mathcolor=¨#0000FF¨»«mrow»«mo mathvariant=¨bold¨»§#8710;«/mo»«msup»«mi mathvariant=¨bold¨»T«/mi»«mn mathvariant=¨bold¨»2«/mn»«/msup»«/mrow»«mrow»«mo mathvariant=¨bold¨»§#8710;«/mo»«mi mathvariant=¨bold¨»L«/mi»«/mrow»«/mfrac»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»=«/mo»«mfrac mathcolor=¨#0000FF¨»«mrow»«mn mathvariant=¨bold¨»4«/mn»«mo mathvariant=¨bold¨»-«/mo»«mn mathvariant=¨bold¨»0«/mn»«mo mathvariant=¨bold¨».«/mo»«mn mathvariant=¨bold¨»81«/mn»«/mrow»«mrow»«mn mathvariant=¨bold¨»1«/mn»«mo mathvariant=¨bold¨»-«/mo»«mn mathvariant=¨bold¨»0«/mn»«mo mathvariant=¨bold¨».«/mo»«mn mathvariant=¨bold¨»2«/mn»«/mrow»«/mfrac»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»=«/mo»«mfrac mathcolor=¨#0000FF¨»«mrow»«mn mathvariant=¨bold¨»3«/mn»«mo mathvariant=¨bold¨».«/mo»«mn mathvariant=¨bold¨»19«/mn»«/mrow»«mrow»«mn mathvariant=¨bold¨»0«/mn»«mo mathvariant=¨bold¨».«/mo»«mn mathvariant=¨bold¨»8«/mn»«/mrow»«/mfrac»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»=«/mo»«mn mathvariant=¨bold¨ mathcolor=¨#0000FF¨»4«/mn»«mfrac mathcolor=¨#0000FF¨»«msup»«mi mathvariant=¨bold¨»s«/mi»«mn mathvariant=¨bold¨»2«/mn»«/msup»«mi mathvariant=¨bold¨»m«/mi»«/mfrac»«/math»
يمكننا إيجاد قيمة ثابت الجاذبية عن طريق مقارنة قيمة الميل بتعبير الميل من دالة مربع زمن كدالة لطول الخيط:
«math xmlns=¨http://www.w3.org/1998/Math/MathML¨»«mfrac mathcolor=¨#0000FF¨»«mrow»«mn mathvariant=¨bold¨»4«/mn»«mo mathvariant=¨bold¨»§#183;«/mo»«msup»«mi mathvariant=¨bold¨»§#960;«/mi»«mn mathvariant=¨bold¨»2«/mn»«/msup»«/mrow»«mi mathvariant=¨bold¨»g«/mi»«/mfrac»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»=«/mo»«mn mathvariant=¨bold¨ mathcolor=¨#0000FF¨»4«/mn»«mspace linebreak=¨newline¨»«/mspace»«mspace linebreak=¨newline¨»«/mspace»«mi mathvariant=¨bold-italic¨ mathcolor=¨#0000FF¨»g«/mi»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»=«/mo»«mfrac mathcolor=¨#0000FF¨»«mrow»«mn mathvariant=¨bold¨»4«/mn»«mo mathvariant=¨bold¨»§#183;«/mo»«msup»«mi mathvariant=¨bold¨»§#960;«/mi»«mn mathvariant=¨bold¨»2«/mn»«/msup»«/mrow»«mn mathvariant=¨bold¨»4«/mn»«/mfrac»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»=«/mo»«msup»«mi mathvariant=¨bold¨ mathcolor=¨#0000FF¨»§#960;«/mi»«mn mathvariant=¨bold¨ mathcolor=¨#0000FF¨»2«/mn»«/msup»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»=«/mo»«mn mathvariant=¨bold¨ mathcolor=¨#0000FF¨»9«/mn»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨».«/mo»«mn mathvariant=¨bold¨ mathcolor=¨#0000FF¨»87«/mn»«mfrac mathcolor=¨#0000FF¨»«mi mathvariant=¨bold¨»m«/mi»«msup»«mi mathvariant=¨bold¨»s«/mi»«mn mathvariant=¨bold¨»2«/mn»«/msup»«/mfrac»«/math»
وبالتالي فإن القيمة المحسوبة لثابت الجاذبية هي 9.87 متر في الثانية تربيع.
«math xmlns=¨http://www.w3.org/1998/Math/MathML¨»«mi mathvariant=¨bold¨ mathcolor=¨#0000FF¨»§#1513;§#1497;§#1508;§#1493;§#1506;«/mi»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»=«/mo»«mfrac mathcolor=¨#0000FF¨»«mrow»«mo mathvariant=¨bold¨»§#8710;«/mo»«msup»«mi mathvariant=¨bold¨»T«/mi»«mn mathvariant=¨bold¨»2«/mn»«/msup»«/mrow»«mrow»«mo mathvariant=¨bold¨»§#8710;«/mo»«mi mathvariant=¨bold¨»L«/mi»«/mrow»«/mfrac»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»=«/mo»«mfrac mathcolor=¨#0000FF¨»«mrow»«mn mathvariant=¨bold¨»4«/mn»«mo mathvariant=¨bold¨»-«/mo»«mn mathvariant=¨bold¨»0«/mn»«mo mathvariant=¨bold¨».«/mo»«mn mathvariant=¨bold¨»81«/mn»«/mrow»«mrow»«mn mathvariant=¨bold¨»1«/mn»«mo mathvariant=¨bold¨»-«/mo»«mn mathvariant=¨bold¨»0«/mn»«mo mathvariant=¨bold¨».«/mo»«mn mathvariant=¨bold¨»2«/mn»«/mrow»«/mfrac»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»=«/mo»«mfrac mathcolor=¨#0000FF¨»«mrow»«mn mathvariant=¨bold¨»3«/mn»«mo mathvariant=¨bold¨».«/mo»«mn mathvariant=¨bold¨»19«/mn»«/mrow»«mrow»«mn mathvariant=¨bold¨»0«/mn»«mo mathvariant=¨bold¨».«/mo»«mn mathvariant=¨bold¨»8«/mn»«/mrow»«/mfrac»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»=«/mo»«mn mathvariant=¨bold¨ mathcolor=¨#0000FF¨»4«/mn»«mfrac mathcolor=¨#0000FF¨»«msup»«mi mathvariant=¨bold¨»s«/mi»«mn mathvariant=¨bold¨»2«/mn»«/msup»«mi mathvariant=¨bold¨»m«/mi»«/mfrac»«/math»
נמצא את ערך קבוע הגרביטציה , מהשוואת ערך השיפוע לביטוי השיפוע מפונקציית ריבוע זמן המחזור בתלות באורך החוט:
«math xmlns=¨http://www.w3.org/1998/Math/MathML¨»«mfrac mathcolor=¨#0000FF¨»«mrow»«mn mathvariant=¨bold¨»4«/mn»«mo mathvariant=¨bold¨»§#183;«/mo»«msup»«mi mathvariant=¨bold¨»§#960;«/mi»«mn mathvariant=¨bold¨»2«/mn»«/msup»«/mrow»«mi mathvariant=¨bold¨»g«/mi»«/mfrac»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»=«/mo»«mn mathvariant=¨bold¨ mathcolor=¨#0000FF¨»4«/mn»«mspace linebreak=¨newline¨»«/mspace»«mspace linebreak=¨newline¨»«/mspace»«mi mathvariant=¨bold-italic¨ mathcolor=¨#0000FF¨»g«/mi»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»=«/mo»«mfrac mathcolor=¨#0000FF¨»«mrow»«mn mathvariant=¨bold¨»4«/mn»«mo mathvariant=¨bold¨»§#183;«/mo»«msup»«mi mathvariant=¨bold¨»§#960;«/mi»«mn mathvariant=¨bold¨»2«/mn»«/msup»«/mrow»«mn mathvariant=¨bold¨»4«/mn»«/mfrac»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»=«/mo»«msup»«mi mathvariant=¨bold¨ mathcolor=¨#0000FF¨»§#960;«/mi»«mn mathvariant=¨bold¨ mathcolor=¨#0000FF¨»2«/mn»«/msup»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»=«/mo»«mn mathvariant=¨bold¨ mathcolor=¨#0000FF¨»9«/mn»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨».«/mo»«mn mathvariant=¨bold¨ mathcolor=¨#0000FF¨»87«/mn»«mfrac mathcolor=¨#0000FF¨»«mi mathvariant=¨bold¨»m«/mi»«msup»«mi mathvariant=¨bold¨»s«/mi»«mn mathvariant=¨bold¨»2«/mn»«/msup»«/mfrac»«/math»
לכן, ערך קבוע הגרביטציה המחושב הוא 9.87 מטר לשנייה בריבוע.
1. عند حساب الميل، من المهم تحديد وحدات قيمة الميل.
2. في الممارسة العملية، يتم الحصول على نتائج جيدة في تجربة لإيجاد ثابت الجاذبية.
نظرًا لأن التجربة يتم إجراؤها بزوايا ميل صغيرة، فإن السرعات صغيرة .
2. באופן מעשי בניסוי למציאת קבוע הגרביטציה מתקבלים תוצאות טובות.
מכיוון שהניסוי מתבצע בזוויות נטייה קטנות ,המהירות קטנות וכוח החיכוך זניח.
______________________________________________________________________________________
______________________________________________________________________________________
...
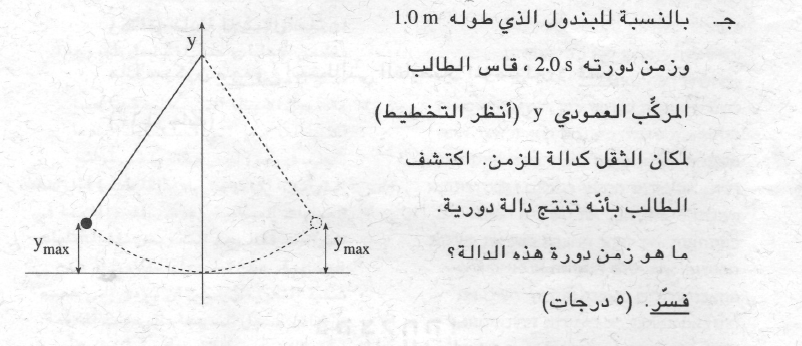
زمن دورة الحركة الرأسية ثانية واحدة.
اعتمادًا على عدد دورات الحركة الرأسية التي تحدث في الحركة الدورية الواحدة للبندول
يمكن حساب زمن دورة الحركة الرأسية.
ניתן לחשב את זמן המחזור של התנועה האנכית.
في دورة واحدة من حركة البندول، هناك دورتان من الحركة الرأسية. وبالتالي فإن زمن الحركة الرأسية يساوي نصف زمن حركة البندول. وبالتالي فإن زمن دورة الحركة الرأسية هو ثانية واحدة.
من المستحسن عمل جدول ووصف الموقع الرأسي للبندول على مدى عدة دورات.
ومن ثم من الجدول نحدد بوضوح زمن دورة الحركة الرأسية.
في بعض الأحيان يتردد الطلاب لفترة طويلة، ويقررون قبل أن يقتنعوا... من الأفضل إعداد جدول.
ולאחר מכן מתוך הטבלה לזהות בבירור את זמן מחזור התנועה האנכית.
לפעמים תלמידים מתלבטים לא מעט זמן, ומחליטים לפני שהשתכנעו ... עדיף להכין טבלה.
______________________________________________________________________________________