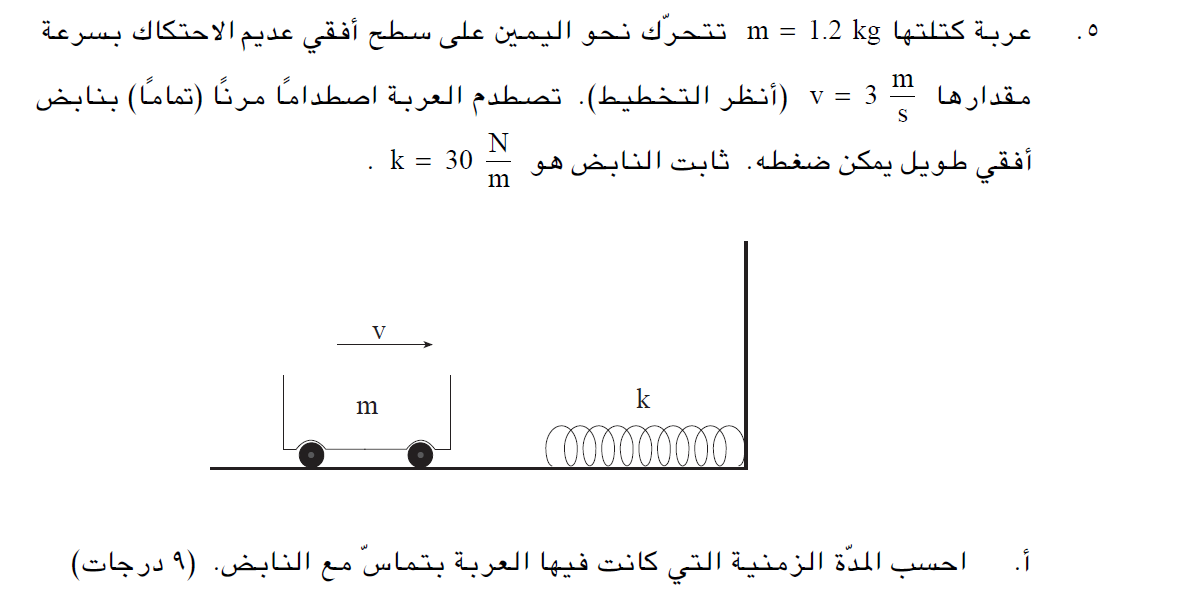
8. 2002,5 - عربة تصطدم بنابض أفقي.
______________________________________________________________________________________
...
«math xmlns=¨http://www.w3.org/1998/Math/MathML¨»«mi mathvariant=¨bold¨»t«/mi»«mo mathvariant=¨bold¨»=«/mo»«mn mathvariant=¨bold¨»0«/mn»«mo mathvariant=¨bold¨».«/mo»«mn mathvariant=¨bold¨»628«/mn»«mi mathvariant=¨bold¨»s«/mi»«/math»
من مبادئ الحركة التوافقية البسيطة، يمكن إيجاد زمن الدورة، ووفقًا للطبيعة جزئية الحركة من زمن الدورة الكامل، يمكن إيجاد زمن الحركة.
تتحرك العربة على سطح أفقي أملس. القوة المحصلة المؤثرة على العربة هي قوة النابض.
نظرًا لأن القوة المحصلة تتناسب طرديًا على الموقع، تتحرك العربة في حركة توافقية بسيطة بواسطة نابض أفقي.
نقطة الاتّزان هي النقطة التي تلامس فيها العربة النابض.
يمكننا إيجاد زمن الحركة باستخدام صيغة زمن الدورة للحركة التوافقية البسيطة:
«math xmlns=¨http://www.w3.org/1998/Math/MathML¨»«mi mathvariant=¨bold¨ mathcolor=¨#0000FF¨»T«/mi»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»=«/mo»«mn mathvariant=¨bold¨ mathcolor=¨#0000FF¨»2«/mn»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»§#183;«/mo»«mi mathvariant=¨bold¨ mathcolor=¨#0000FF¨»§#960;«/mi»«msqrt mathcolor=¨#0000FF¨»«mfrac»«mi mathvariant=¨bold¨»m«/mi»«mi mathvariant=¨bold¨»k«/mi»«/mfrac»«/msqrt»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»=«/mo»«mn mathvariant=¨bold¨ mathcolor=¨#0000FF¨»2«/mn»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»§#183;«/mo»«mi mathvariant=¨bold¨ mathcolor=¨#0000FF¨»§#960;«/mi»«msqrt mathcolor=¨#0000FF¨»«mfrac»«mrow»«mn mathvariant=¨bold¨»1«/mn»«mo mathvariant=¨bold¨».«/mo»«mn mathvariant=¨bold¨»2«/mn»«/mrow»«mn mathvariant=¨bold¨»30«/mn»«/mfrac»«/msqrt»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»=«/mo»«mn mathvariant=¨bold¨ mathcolor=¨#0000FF¨»1«/mn»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨».«/mo»«mn mathvariant=¨bold¨ mathcolor=¨#0000FF¨»256«/mn»«mi mathvariant=¨bold¨ mathcolor=¨#0000FF¨»s«/mi»«/math»
بعد أن تعود العربة إلى النقطة التي يصبح فيها النابض مرتخيًا، تستمر في الحركة بسرعة ثابتة. النابض مثبت بالحائط ولا يستمر في الحركة من هذه النقطة مع العربة، لذلك عندما تعود العربة إلى النقطة التي يكون فيها النابض في حالة استرخاء، فإنها ستنفصل عن النابض.
الزمن الكلي الذي تبقى فيها العربة على اتصال بالنابض هو نصف زمن الدورة، ويتم حساب هذا الزمن على النحو التالي:
«math xmlns=¨http://www.w3.org/1998/Math/MathML¨»«mi mathvariant=¨bold¨ mathcolor=¨#0000FF¨»t«/mi»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»=«/mo»«mfrac mathcolor=¨#0000FF¨»«mi mathvariant=¨bold¨»T«/mi»«mn mathvariant=¨bold¨»2«/mn»«/mfrac»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»=«/mo»«mfrac mathcolor=¨#0000FF¨»«mrow»«mn mathvariant=¨bold¨»1«/mn»«mo mathvariant=¨bold¨».«/mo»«mn mathvariant=¨bold¨»256«/mn»«/mrow»«mn mathvariant=¨bold¨»2«/mn»«/mfrac»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»=«/mo»«mn mathvariant=¨bold¨ mathcolor=¨#0000FF¨»0«/mn»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨».«/mo»«mn mathvariant=¨bold¨ mathcolor=¨#0000FF¨»628«/mn»«mi mathvariant=¨bold¨ mathcolor=¨#0000FF¨»s«/mi»«/math»
وبالتالي، تتحرك العربة لمدة 0.628 ثانية بحركة توافقية بسيطة. خلال هذه الفترة الزمنية، تلامس العربة النابض.
מכיוון שהכוח השקול תלוי לניארית במקום העגלה נעה בתנועה הרמונית פשוטה בקפיץ אופקי.
נקודת שיווי המשקל היא הנקודה בה נוגעת העגלה בקפיץ.
נמצא את זמן מחזור התנועה ,בעזרת נוסחת זמן מחזור לתנועה הרמונית פשוטה:
«math xmlns=¨http://www.w3.org/1998/Math/MathML¨»«mi mathvariant=¨bold¨ mathcolor=¨#0000FF¨»T«/mi»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»=«/mo»«mn mathvariant=¨bold¨ mathcolor=¨#0000FF¨»2«/mn»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»§#183;«/mo»«mi mathvariant=¨bold¨ mathcolor=¨#0000FF¨»§#960;«/mi»«msqrt mathcolor=¨#0000FF¨»«mfrac»«mi mathvariant=¨bold¨»m«/mi»«mi mathvariant=¨bold¨»k«/mi»«/mfrac»«/msqrt»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»=«/mo»«mn mathvariant=¨bold¨ mathcolor=¨#0000FF¨»2«/mn»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»§#183;«/mo»«mi mathvariant=¨bold¨ mathcolor=¨#0000FF¨»§#960;«/mi»«msqrt mathcolor=¨#0000FF¨»«mfrac»«mrow»«mn mathvariant=¨bold¨»1«/mn»«mo mathvariant=¨bold¨».«/mo»«mn mathvariant=¨bold¨»2«/mn»«/mrow»«mn mathvariant=¨bold¨»30«/mn»«/mfrac»«/msqrt»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»=«/mo»«mn mathvariant=¨bold¨ mathcolor=¨#0000FF¨»1«/mn»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨».«/mo»«mn mathvariant=¨bold¨ mathcolor=¨#0000FF¨»256«/mn»«mi mathvariant=¨bold¨ mathcolor=¨#0000FF¨»s«/mi»«/math»
לאחר חזרת העגלה לנקודה בה הקפיץ רפוי ,היא ממשיכה לנוע במהירות קבועה , הקפיץ מחובר לקיר הוא לא ממשיך לנוע מנקודה זו במהירות קבועה, לכן כאשר העגלה חוזרת לנקודה בה הקפיץ רפוי היא מתנתקת מהקפיץ.
סה"כ הקרונית נמצאת במגע עם הקפיץ במשך חצי זמן מחזור, נחשב זמן זה:
«math xmlns=¨http://www.w3.org/1998/Math/MathML¨»«mi mathvariant=¨bold¨ mathcolor=¨#0000FF¨»t«/mi»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»=«/mo»«mfrac mathcolor=¨#0000FF¨»«mi mathvariant=¨bold¨»T«/mi»«mn mathvariant=¨bold¨»2«/mn»«/mfrac»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»=«/mo»«mfrac mathcolor=¨#0000FF¨»«mrow»«mn mathvariant=¨bold¨»1«/mn»«mo mathvariant=¨bold¨».«/mo»«mn mathvariant=¨bold¨»256«/mn»«/mrow»«mn mathvariant=¨bold¨»2«/mn»«/mfrac»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»=«/mo»«mn mathvariant=¨bold¨ mathcolor=¨#0000FF¨»0«/mn»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨».«/mo»«mn mathvariant=¨bold¨ mathcolor=¨#0000FF¨»628«/mn»«mi mathvariant=¨bold¨ mathcolor=¨#0000FF¨»s«/mi»«/math»
לכן, העגלה נעה במשך 0.628 שניות בתה"פ. בכל זמן זה היא נוגעת בקפיץ.
1. قبل استخدام صيغة زمن الدورة، من الضروري توضيح سبب تحرك العربة في حركة توافقية بسيطة (تتناسب القوة المحصلة طرديًا مع الموقع).
2. العربة لا تتحرك بحركة دورية، ولكن حركتها هي جزء من دورة لحركة توافقية بسيطة. ينبغي التعامل مع حركتها باعتبارها حركة توافقية بسيطة.
3. تتحرك العربة في ربع دورة من لحظة اصطدامها بالنابض (عندما يكون النابض في حالة استرخاء) إلى أقصى انقباض له.
وربع دورة أخرى من لحظة أقصى انقباض للنابض حتى يصبح النابض مرتخيًا مرة أخرى، الزمن الكلي يكون ربعي دورة.
4. لو التصقت العربة بالنابض في لحظة اصطدام العربة بالنابض، فسوف تكون هناك دورات كاملة من الحركة التوافقية، الحركة التوافقية البسيطة الطبيعية العادية.
2. העגלה לא נעה בתנועה מחזורית,אך תנועתה היא חלק ממחזור תנועה של תה"פ. יש להתייחס לתנועתה כאל תה"פ.
3. העגלה נע ברבע מחזור תנועה מרגע פגיעתה בקפיץ (כשהוא רפוי) ועד לכיווץ מקסימאלי
וברבע מחזור נוסף מרגע שהקפיץ מכיווץ מקסימאלי ועד שהקפיץ חוזר להיות רפוי , סה"כ 2 רבעי מחזור.
4. אם בזמן התנגשות העגלה בקפיץ העגלה והקפיץ היו מתחברים , היו מחזורי תנועה הרמונית שלמים . תה"פ רגילה.
______________________________________________________________________________________

______________________________________________________________________________________
...
الحد الأقصى للانقباض هو 0.6 متر.
الطريقة أ: حفظ الطاقة.
الطريقة ب: مبادئ الحركة التوافقية البسيطة.
דרך ב': עקרונות התה"פ.
طوال الوقت الذي تتحرك فيه العربة، القوة الوحيدة التي تبذل شغل على العربة هي قوة النابض. قوة النابض هي قوة حافظة، لذا فإنه سيتم حفظ الطاقة الميكانيكية.
سنقوم بتحديد محور الحركة الذي يبدأ في النقطة التي يكون فيها النابض في حالة استرخاء، نرمز لنقطة البداية بـ A، والنقطة التي تتوقف فيها العربة بـ B:
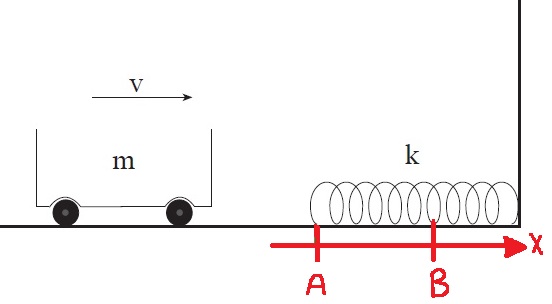
نكتب معادلة حفظ الطاقة، نقارن الطاقة الميكانيكية الكلية في النقطة A بالطاقة الميكانيكية الكلية في النقطة B.
ومن معادلة حفظ الطاقة يتم التعبير عن موقع النقطة B:
«math xmlns=¨http://www.w3.org/1998/Math/MathML¨»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»§#160;«/mo»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»§#160;«/mo»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»§#160;«/mo»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»§#160;«/mo»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»§#160;«/mo»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»§#160;«/mo»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»§#160;«/mo»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»§#160;«/mo»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»§#160;«/mo»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»§#160;«/mo»«msub»«mi mathvariant=¨bold¨ mathcolor=¨#0000FF¨»E«/mi»«mi mathvariant=¨bold¨ mathcolor=¨#0000FF¨»A«/mi»«/msub»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»=«/mo»«msub»«mi mathvariant=¨bold¨ mathcolor=¨#0000FF¨»E«/mi»«mi mathvariant=¨bold¨ mathcolor=¨#0000FF¨»B«/mi»«/msub»«mspace linebreak=¨newline¨»«/mspace»«msub»«mi mathvariant=¨bold¨ mathcolor=¨#0000FF¨»E«/mi»«msub mathcolor=¨#0000FF¨»«mi mathvariant=¨bold¨»K«/mi»«mi mathvariant=¨bold¨»A«/mi»«/msub»«/msub»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»+«/mo»«msub»«mi mathvariant=¨bold¨ mathcolor=¨#0000FF¨»U«/mi»«mi mathvariant=¨bold¨ mathcolor=¨#0000FF¨»A«/mi»«/msub»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»=«/mo»«msub»«mi mathvariant=¨bold¨ mathcolor=¨#0000FF¨»E«/mi»«msub mathcolor=¨#0000FF¨»«mi mathvariant=¨bold¨»K«/mi»«mi mathvariant=¨bold¨»B«/mi»«/msub»«/msub»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»+«/mo»«msub»«mi mathvariant=¨bold¨ mathcolor=¨#0000FF¨»U«/mi»«mi mathvariant=¨bold¨ mathcolor=¨#0000FF¨»B«/mi»«/msub»«/math»
في النقطة B تتوقف العربة، الطاقة الحركية للعربة في النقطة B تساوي صفرًا.
في النقطة A يكون النابض في حالة استرخاء، ولا يكون للنابض طاقة وضعية مرنة في النقطة A.
«math xmlns=¨http://www.w3.org/1998/Math/MathML¨»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»§#160;«/mo»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»§#160;«/mo»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»§#160;«/mo»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»§#160;«/mo»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»§#160;«/mo»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»§#160;«/mo»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»§#160;«/mo»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»§#160;«/mo»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»§#160;«/mo»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»§#160;«/mo»«msub»«mi mathvariant=¨bold¨ mathcolor=¨#0000FF¨»E«/mi»«mi mathvariant=¨bold¨ mathcolor=¨#0000FF¨»A«/mi»«/msub»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»=«/mo»«msub»«mi mathvariant=¨bold¨ mathcolor=¨#0000FF¨»E«/mi»«mi mathvariant=¨bold¨ mathcolor=¨#0000FF¨»B«/mi»«/msub»«mspace linebreak=¨newline¨»«/mspace»«msub»«mi mathvariant=¨bold¨ mathcolor=¨#0000FF¨»E«/mi»«msub mathcolor=¨#0000FF¨»«mi mathvariant=¨bold¨»K«/mi»«mi mathvariant=¨bold¨»A«/mi»«/msub»«/msub»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»+«/mo»«menclose mathcolor=¨#0000FF¨ notation=¨updiagonalstrike¨»«msub»«mi mathvariant=¨bold¨»U«/mi»«mi mathvariant=¨bold¨»A«/mi»«/msub»«/menclose»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»=«/mo»«menclose mathcolor=¨#0000FF¨ notation=¨updiagonalstrike¨»«msub»«mi mathvariant=¨bold¨»E«/mi»«msub»«mi mathvariant=¨bold¨»K«/mi»«mi mathvariant=¨bold¨»B«/mi»«/msub»«/msub»«/menclose»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»+«/mo»«msub»«mi mathvariant=¨bold¨ mathcolor=¨#0000FF¨»U«/mi»«mi mathvariant=¨bold¨ mathcolor=¨#0000FF¨»B«/mi»«/msub»«mspace linebreak=¨newline¨»«/mspace»«menclose mathcolor=¨#0000FF¨ notation=¨downdiagonalstrike¨»«mfrac»«mn mathvariant=¨bold¨»1«/mn»«mn mathvariant=¨bold¨»2«/mn»«/mfrac»«/menclose»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»§#183;«/mo»«mi mathvariant=¨bold¨ mathcolor=¨#0000FF¨»m«/mi»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»§#183;«/mo»«msup»«msub»«mi mathvariant=¨bold¨ mathcolor=¨#0000FF¨»V«/mi»«mi mathvariant=¨bold¨ mathcolor=¨#0000FF¨»A«/mi»«/msub»«mn mathvariant=¨bold¨ mathcolor=¨#0000FF¨»2«/mn»«/msup»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»=«/mo»«menclose mathcolor=¨#0000FF¨ notation=¨downdiagonalstrike¨»«mfrac»«mn mathvariant=¨bold¨»1«/mn»«mn mathvariant=¨bold¨»2«/mn»«/mfrac»«/menclose»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»§#183;«/mo»«mi mathvariant=¨bold¨ mathcolor=¨#0000FF¨»K«/mi»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»§#183;«/mo»«msup»«msub»«mi mathvariant=¨bold¨ mathcolor=¨#0000FF¨»X«/mi»«mi mathvariant=¨bold¨ mathcolor=¨#0000FF¨»B«/mi»«/msub»«mn mathvariant=¨bold¨ mathcolor=¨#0000FF¨»2«/mn»«/msup»«mspace linebreak=¨newline¨»«/mspace»«mspace linebreak=¨newline¨»«/mspace»«msub»«mi mathvariant=¨bold¨ mathcolor=¨#0000FF¨»X«/mi»«mi mathvariant=¨bold¨ mathcolor=¨#0000FF¨»B«/mi»«/msub»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»=«/mo»«msqrt mathcolor=¨#0000FF¨»«mfrac»«mrow»«mi mathvariant=¨bold¨»m«/mi»«mo mathvariant=¨bold¨»§#183;«/mo»«msup»«msub»«mi mathvariant=¨bold¨»V«/mi»«mi mathvariant=¨bold¨»A«/mi»«/msub»«mn mathvariant=¨bold¨»2«/mn»«/msup»«/mrow»«mi mathvariant=¨bold¨»K«/mi»«/mfrac»«/msqrt»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»=«/mo»«msqrt mathcolor=¨#0000FF¨»«mfrac»«mrow»«mn mathvariant=¨bold¨»1«/mn»«mo mathvariant=¨bold¨».«/mo»«mn mathvariant=¨bold¨»2«/mn»«mo mathvariant=¨bold¨»§#183;«/mo»«msup»«mn mathvariant=¨bold¨»3«/mn»«mn mathvariant=¨bold¨»2«/mn»«/msup»«/mrow»«mn mathvariant=¨bold¨»30«/mn»«/mfrac»«/msqrt»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»=«/mo»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»§#177;«/mo»«mn mathvariant=¨bold¨ mathcolor=¨#0000FF¨»0«/mn»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨».«/mo»«mn mathvariant=¨bold¨ mathcolor=¨#0000FF¨»6«/mn»«mi mathvariant=¨bold¨ mathcolor=¨#0000FF¨»m«/mi»«/math»
بالنسبة للمحور المعطى، فإن موقع الجسم في أقصى انقباض هو زائد 0.6 متر، ومقدار الانقباض الأقصى هو 0.6 متر.
طريقة أخرى: من مبادئ الحركة التوافقية البسيطة.
من تعبير السرعة كدالة للزمن وتعبير السرعة كدالة للمكان، فإن تعبير السرعة القصوى في التوافقية البسيطة هو:
«math xmlns=¨http://www.w3.org/1998/Math/MathML¨»«msub»«mi mathvariant=¨bold¨ mathcolor=¨#0000FF¨»V«/mi»«mi mathvariant=¨bold¨ mathcolor=¨#0000FF¨»max«/mi»«/msub»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»=«/mo»«mi mathvariant=¨bold¨ mathcolor=¨#0000FF¨»§#969;«/mi»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»§#183;«/mo»«mi mathvariant=¨bold¨ mathcolor=¨#0000FF¨»A«/mi»«/math»
السرعة القصوى في الحركة التوافقية البسيطة هي سرعة الجسم عندما يكون في نقطة الاتّزان، وفي هذه الحالة تكون السرعة القصوى هي السرعة التي تضرب بها العربة النابض.
نجد سعة الحركة:
«math xmlns=¨http://www.w3.org/1998/Math/MathML¨»«msub»«mi mathvariant=¨bold¨ mathcolor=¨#0000FF¨»V«/mi»«mi mathvariant=¨bold¨ mathcolor=¨#0000FF¨»max«/mi»«/msub»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»=«/mo»«mi mathvariant=¨bold¨ mathcolor=¨#0000FF¨»§#969;«/mi»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»§#183;«/mo»«mi mathvariant=¨bold¨ mathcolor=¨#0000FF¨»A«/mi»«mspace linebreak=¨newline¨»«/mspace»«mspace linebreak=¨newline¨»«/mspace»«mi mathvariant=¨bold¨ mathcolor=¨#0000FF¨»A«/mi»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»=«/mo»«mfrac mathcolor=¨#0000FF¨»«msub»«mi mathvariant=¨bold¨»V«/mi»«mi mathvariant=¨bold¨»max«/mi»«/msub»«mi mathvariant=¨bold¨»§#969;«/mi»«/mfrac»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»=«/mo»«mfrac mathcolor=¨#0000FF¨»«msub»«mi mathvariant=¨bold¨»V«/mi»«mi mathvariant=¨bold¨»max«/mi»«/msub»«mstyle displaystyle=¨true¨»«mfrac»«mrow»«mn mathvariant=¨bold¨»2«/mn»«mo mathvariant=¨bold¨»§#183;«/mo»«mi mathvariant=¨bold¨»§#960;«/mi»«/mrow»«mi mathvariant=¨bold¨»T«/mi»«/mfrac»«/mstyle»«/mfrac»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»=«/mo»«mfrac mathcolor=¨#0000FF¨»«mrow»«msub»«mi mathvariant=¨bold¨»V«/mi»«mi mathvariant=¨bold¨»max«/mi»«/msub»«mo mathvariant=¨bold¨»§#183;«/mo»«mi mathvariant=¨bold¨»T«/mi»«/mrow»«mstyle displaystyle=¨true¨ mathvariant=¨bold¨»«mn»2«/mn»«mo»§#183;«/mo»«mi»§#960;«/mi»«/mstyle»«/mfrac»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»=«/mo»«mfrac mathcolor=¨#0000FF¨»«mrow»«mn mathvariant=¨bold¨»3«/mn»«mo mathvariant=¨bold¨»§#183;«/mo»«mn mathvariant=¨bold¨»1«/mn»«mo mathvariant=¨bold¨».«/mo»«mn mathvariant=¨bold¨»256«/mn»«/mrow»«mrow»«mn mathvariant=¨bold¨»2«/mn»«mo mathvariant=¨bold¨»§#183;«/mo»«mi mathvariant=¨bold¨»§#960;«/mi»«/mrow»«/mfrac»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»=«/mo»«mn mathvariant=¨bold¨ mathcolor=¨#0000FF¨»0«/mn»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨».«/mo»«mn mathvariant=¨bold¨ mathcolor=¨#0000FF¨»6«/mn»«mi mathvariant=¨bold¨ mathcolor=¨#0000FF¨»m«/mi»«/math»
נגדיר ציר תנועה שראשיתו בנקודה בה הקפיץ רפוי , נסמן את נקודת הראשית ב A , ואת הנקודה בה נעצרת העגלה ב B:

נכתוב את משוואת שימור האנרגיה, נשווה בין האנרגיה המכנית הכוללת בנקודה A לאנרגיה המכנית הכוללת בנקודה B
ונבטא ממשוואת שימור האנרגיה מיקום הנקודה B:
«math xmlns=¨http://www.w3.org/1998/Math/MathML¨»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»§#160;«/mo»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»§#160;«/mo»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»§#160;«/mo»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»§#160;«/mo»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»§#160;«/mo»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»§#160;«/mo»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»§#160;«/mo»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»§#160;«/mo»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»§#160;«/mo»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»§#160;«/mo»«msub»«mi mathvariant=¨bold¨ mathcolor=¨#0000FF¨»E«/mi»«mi mathvariant=¨bold¨ mathcolor=¨#0000FF¨»A«/mi»«/msub»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»=«/mo»«msub»«mi mathvariant=¨bold¨ mathcolor=¨#0000FF¨»E«/mi»«mi mathvariant=¨bold¨ mathcolor=¨#0000FF¨»B«/mi»«/msub»«mspace linebreak=¨newline¨»«/mspace»«msub»«mi mathvariant=¨bold¨ mathcolor=¨#0000FF¨»E«/mi»«msub mathcolor=¨#0000FF¨»«mi mathvariant=¨bold¨»K«/mi»«mi mathvariant=¨bold¨»A«/mi»«/msub»«/msub»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»+«/mo»«msub»«mi mathvariant=¨bold¨ mathcolor=¨#0000FF¨»U«/mi»«mi mathvariant=¨bold¨ mathcolor=¨#0000FF¨»A«/mi»«/msub»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»=«/mo»«msub»«mi mathvariant=¨bold¨ mathcolor=¨#0000FF¨»E«/mi»«msub mathcolor=¨#0000FF¨»«mi mathvariant=¨bold¨»K«/mi»«mi mathvariant=¨bold¨»B«/mi»«/msub»«/msub»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»+«/mo»«msub»«mi mathvariant=¨bold¨ mathcolor=¨#0000FF¨»U«/mi»«mi mathvariant=¨bold¨ mathcolor=¨#0000FF¨»B«/mi»«/msub»«/math»
בנקודה B העגלה נעצרת , האנרגיה הקינטית של העגלה בנקודה B שווה לאפס.
בנקודה A הקפיץ רפוי ,אין אנרגיה פוטנציאלית אלסטית לקפיץ בנקודה A.
«math xmlns=¨http://www.w3.org/1998/Math/MathML¨»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»§#160;«/mo»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»§#160;«/mo»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»§#160;«/mo»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»§#160;«/mo»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»§#160;«/mo»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»§#160;«/mo»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»§#160;«/mo»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»§#160;«/mo»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»§#160;«/mo»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»§#160;«/mo»«msub»«mi mathvariant=¨bold¨ mathcolor=¨#0000FF¨»E«/mi»«mi mathvariant=¨bold¨ mathcolor=¨#0000FF¨»A«/mi»«/msub»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»=«/mo»«msub»«mi mathvariant=¨bold¨ mathcolor=¨#0000FF¨»E«/mi»«mi mathvariant=¨bold¨ mathcolor=¨#0000FF¨»B«/mi»«/msub»«mspace linebreak=¨newline¨»«/mspace»«msub»«mi mathvariant=¨bold¨ mathcolor=¨#0000FF¨»E«/mi»«msub mathcolor=¨#0000FF¨»«mi mathvariant=¨bold¨»K«/mi»«mi mathvariant=¨bold¨»A«/mi»«/msub»«/msub»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»+«/mo»«menclose mathcolor=¨#0000FF¨ notation=¨updiagonalstrike¨»«msub»«mi mathvariant=¨bold¨»U«/mi»«mi mathvariant=¨bold¨»A«/mi»«/msub»«/menclose»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»=«/mo»«menclose mathcolor=¨#0000FF¨ notation=¨updiagonalstrike¨»«msub»«mi mathvariant=¨bold¨»E«/mi»«msub»«mi mathvariant=¨bold¨»K«/mi»«mi mathvariant=¨bold¨»B«/mi»«/msub»«/msub»«/menclose»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»+«/mo»«msub»«mi mathvariant=¨bold¨ mathcolor=¨#0000FF¨»U«/mi»«mi mathvariant=¨bold¨ mathcolor=¨#0000FF¨»B«/mi»«/msub»«mspace linebreak=¨newline¨»«/mspace»«menclose mathcolor=¨#0000FF¨ notation=¨downdiagonalstrike¨»«mfrac»«mn mathvariant=¨bold¨»1«/mn»«mn mathvariant=¨bold¨»2«/mn»«/mfrac»«/menclose»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»§#183;«/mo»«mi mathvariant=¨bold¨ mathcolor=¨#0000FF¨»m«/mi»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»§#183;«/mo»«msup»«msub»«mi mathvariant=¨bold¨ mathcolor=¨#0000FF¨»V«/mi»«mi mathvariant=¨bold¨ mathcolor=¨#0000FF¨»A«/mi»«/msub»«mn mathvariant=¨bold¨ mathcolor=¨#0000FF¨»2«/mn»«/msup»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»=«/mo»«menclose mathcolor=¨#0000FF¨ notation=¨downdiagonalstrike¨»«mfrac»«mn mathvariant=¨bold¨»1«/mn»«mn mathvariant=¨bold¨»2«/mn»«/mfrac»«/menclose»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»§#183;«/mo»«mi mathvariant=¨bold¨ mathcolor=¨#0000FF¨»K«/mi»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»§#183;«/mo»«msup»«msub»«mi mathvariant=¨bold¨ mathcolor=¨#0000FF¨»X«/mi»«mi mathvariant=¨bold¨ mathcolor=¨#0000FF¨»B«/mi»«/msub»«mn mathvariant=¨bold¨ mathcolor=¨#0000FF¨»2«/mn»«/msup»«mspace linebreak=¨newline¨»«/mspace»«mspace linebreak=¨newline¨»«/mspace»«msub»«mi mathvariant=¨bold¨ mathcolor=¨#0000FF¨»X«/mi»«mi mathvariant=¨bold¨ mathcolor=¨#0000FF¨»B«/mi»«/msub»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»=«/mo»«msqrt mathcolor=¨#0000FF¨»«mfrac»«mrow»«mi mathvariant=¨bold¨»m«/mi»«mo mathvariant=¨bold¨»§#183;«/mo»«msup»«msub»«mi mathvariant=¨bold¨»V«/mi»«mi mathvariant=¨bold¨»A«/mi»«/msub»«mn mathvariant=¨bold¨»2«/mn»«/msup»«/mrow»«mi mathvariant=¨bold¨»K«/mi»«/mfrac»«/msqrt»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»=«/mo»«msqrt mathcolor=¨#0000FF¨»«mfrac»«mrow»«mn mathvariant=¨bold¨»1«/mn»«mo mathvariant=¨bold¨».«/mo»«mn mathvariant=¨bold¨»2«/mn»«mo mathvariant=¨bold¨»§#183;«/mo»«msup»«mn mathvariant=¨bold¨»3«/mn»«mn mathvariant=¨bold¨»2«/mn»«/msup»«/mrow»«mn mathvariant=¨bold¨»30«/mn»«/mfrac»«/msqrt»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»=«/mo»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»§#177;«/mo»«mn mathvariant=¨bold¨ mathcolor=¨#0000FF¨»0«/mn»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨».«/mo»«mn mathvariant=¨bold¨ mathcolor=¨#0000FF¨»6«/mn»«mi mathvariant=¨bold¨ mathcolor=¨#0000FF¨»m«/mi»«/math»
ביחס לציר הנתון מיקום הגוף בכיווץ מקסימאלי הוא פלוס 0.6 מטר, שיעור הכיווץ המרבי הוא 0.6 מטר.
דרך נוספת: מעקרונות התה"פ.
מביטוי המהירות בתלות בזמן וביטוי המהירות בתלות במקום , ביטוי המהירות המקסימאלית בתה"פ הוא:
«math xmlns=¨http://www.w3.org/1998/Math/MathML¨»«msub»«mi mathvariant=¨bold¨ mathcolor=¨#0000FF¨»V«/mi»«mi mathvariant=¨bold¨ mathcolor=¨#0000FF¨»max«/mi»«/msub»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»=«/mo»«mi mathvariant=¨bold¨ mathcolor=¨#0000FF¨»§#969;«/mi»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»§#183;«/mo»«mi mathvariant=¨bold¨ mathcolor=¨#0000FF¨»A«/mi»«/math»
המהירות המקסימאלית בתה"פ היא מהירות הגוף כאשר הוא נמצא בנקודת שיווי משקל ,במקרה זה המהירות המקסימאלית היא מהירות פגיעת העגלה בקפיץ.
נמצא את משרעת התנועה:
«math xmlns=¨http://www.w3.org/1998/Math/MathML¨»«msub»«mi mathvariant=¨bold¨ mathcolor=¨#0000FF¨»V«/mi»«mi mathvariant=¨bold¨ mathcolor=¨#0000FF¨»max«/mi»«/msub»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»=«/mo»«mi mathvariant=¨bold¨ mathcolor=¨#0000FF¨»§#969;«/mi»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»§#183;«/mo»«mi mathvariant=¨bold¨ mathcolor=¨#0000FF¨»A«/mi»«mspace linebreak=¨newline¨»«/mspace»«mspace linebreak=¨newline¨»«/mspace»«mi mathvariant=¨bold¨ mathcolor=¨#0000FF¨»A«/mi»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»=«/mo»«mfrac mathcolor=¨#0000FF¨»«msub»«mi mathvariant=¨bold¨»V«/mi»«mi mathvariant=¨bold¨»max«/mi»«/msub»«mi mathvariant=¨bold¨»§#969;«/mi»«/mfrac»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»=«/mo»«mfrac mathcolor=¨#0000FF¨»«msub»«mi mathvariant=¨bold¨»V«/mi»«mi mathvariant=¨bold¨»max«/mi»«/msub»«mstyle displaystyle=¨true¨»«mfrac»«mrow»«mn mathvariant=¨bold¨»2«/mn»«mo mathvariant=¨bold¨»§#183;«/mo»«mi mathvariant=¨bold¨»§#960;«/mi»«/mrow»«mi mathvariant=¨bold¨»T«/mi»«/mfrac»«/mstyle»«/mfrac»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»=«/mo»«mfrac mathcolor=¨#0000FF¨»«mrow»«msub»«mi mathvariant=¨bold¨»V«/mi»«mi mathvariant=¨bold¨»max«/mi»«/msub»«mo mathvariant=¨bold¨»§#183;«/mo»«mi mathvariant=¨bold¨»T«/mi»«/mrow»«mstyle displaystyle=¨true¨ mathvariant=¨bold¨»«mn»2«/mn»«mo»§#183;«/mo»«mi»§#960;«/mi»«/mstyle»«/mfrac»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»=«/mo»«mfrac mathcolor=¨#0000FF¨»«mrow»«mn mathvariant=¨bold¨»3«/mn»«mo mathvariant=¨bold¨»§#183;«/mo»«mn mathvariant=¨bold¨»1«/mn»«mo mathvariant=¨bold¨».«/mo»«mn mathvariant=¨bold¨»256«/mn»«/mrow»«mrow»«mn mathvariant=¨bold¨»2«/mn»«mo mathvariant=¨bold¨»§#183;«/mo»«mi mathvariant=¨bold¨»§#960;«/mi»«/mrow»«/mfrac»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»=«/mo»«mn mathvariant=¨bold¨ mathcolor=¨#0000FF¨»0«/mn»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨».«/mo»«mn mathvariant=¨bold¨ mathcolor=¨#0000FF¨»6«/mn»«mi mathvariant=¨bold¨ mathcolor=¨#0000FF¨»m«/mi»«/math»
1. لا تتطلب الاعتبارات المتعلقة بالطاقة محور حركة، ولكن بعض دوال الحركة التوافقية تتطلب ذلك.
2. تبدأ العربة بالتحرك من نقطة الاتّزان وليس من نقطة الطرف الموجبة.
حسب اتجاه حركة العربة بالنسبة للمحور، تكون العربة إما ربع دورة للخلف أو ثلاثة أرباع دورة للأمام.
لذلك، فإن دالة الموقع كدالة للزمن الملائمة للحركة يمكن أن تكون واحدة من اثنتين: «math xmlns=¨http://www.w3.org/1998/Math/MathML¨»«mi mathvariant=¨bold¨ mathcolor=¨#FF0000¨»X«/mi»«mo mathvariant=¨bold¨ mathcolor=¨#FF0000¨»(«/mo»«mi mathvariant=¨bold¨ mathcolor=¨#FF0000¨»t«/mi»«mo mathvariant=¨bold¨ mathcolor=¨#FF0000¨»)«/mo»«mo mathvariant=¨bold¨ mathcolor=¨#FF0000¨»=«/mo»«mi mathvariant=¨bold¨ mathcolor=¨#FF0000¨»A«/mi»«mo mathvariant=¨bold¨ mathcolor=¨#FF0000¨»§#183;«/mo»«mi mathvariant=¨bold¨ mathcolor=¨#FF0000¨»cos«/mi»«mo mathvariant=¨bold¨ mathcolor=¨#FF0000¨»(«/mo»«mi mathvariant=¨bold¨ mathcolor=¨#FF0000¨»§#969;«/mi»«mo mathvariant=¨bold¨ mathcolor=¨#FF0000¨»§#183;«/mo»«mi mathvariant=¨bold¨ mathcolor=¨#FF0000¨»t«/mi»«mo mathvariant=¨bold¨ mathcolor=¨#FF0000¨»-«/mo»«mfrac mathcolor=¨#FF0000¨»«mi mathvariant=¨bold¨»§#960;«/mi»«mn mathvariant=¨bold¨»2«/mn»«/mfrac»«mo mathvariant=¨bold¨ mathcolor=¨#FF0000¨»)«/mo»«mo mathvariant=¨bold¨ mathcolor=¨#FF0000¨»§#160;«/mo»«mo mathvariant=¨bold¨ mathcolor=¨#FF0000¨»§#160;«/mo»«mo mathvariant=¨bold¨ mathcolor=¨#FF0000¨»§#160;«/mo»«mo mathvariant=¨bold¨ mathcolor=¨#FF0000¨»§#160;«/mo»«mo mathvariant=¨bold¨ mathcolor=¨#FF0000¨»§#160;«/mo»«mo mathvariant=¨bold¨ mathcolor=¨#FF0000¨»§#160;«/mo»«mo mathvariant=¨bold¨ mathcolor=¨#FF0000¨»§#160;«/mo»«mo mathvariant=¨bold¨ mathcolor=¨#FF0000¨»§#160;«/mo»«mo mathvariant=¨bold¨ mathcolor=¨#FF0000¨»§#160;«/mo»«mo mathvariant=¨bold¨ mathcolor=¨#FF0000¨»§#160;«/mo»«mo mathvariant=¨bold¨ mathcolor=¨#FF0000¨»§#160;«/mo»«mo mathvariant=¨bold¨ mathcolor=¨#FF0000¨»§#160;«/mo»«mo mathvariant=¨bold¨ mathcolor=¨#FF0000¨»§#160;«/mo»«mo mathvariant=¨bold¨ mathcolor=¨#FF0000¨»§#160;«/mo»«mo mathvariant=¨bold¨ mathcolor=¨#FF0000¨»§#160;«/mo»«mo mathvariant=¨bold¨ mathcolor=¨#FF0000¨»§#160;«/mo»«mo mathvariant=¨bold¨ mathcolor=¨#FF0000¨»§#160;«/mo»«mo mathvariant=¨bold¨ mathcolor=¨#FF0000¨»§#160;«/mo»«mo mathvariant=¨bold¨ mathcolor=¨#FF0000¨»§#160;«/mo»«mi mathvariant=¨bold¨ mathcolor=¨#FF0000¨»X«/mi»«mo mathvariant=¨bold¨ mathcolor=¨#FF0000¨»(«/mo»«mi mathvariant=¨bold¨ mathcolor=¨#FF0000¨»t«/mi»«mo mathvariant=¨bold¨ mathcolor=¨#FF0000¨»)«/mo»«mo mathvariant=¨bold¨ mathcolor=¨#FF0000¨»=«/mo»«mi mathvariant=¨bold¨ mathcolor=¨#FF0000¨»A«/mi»«mo mathvariant=¨bold¨ mathcolor=¨#FF0000¨»§#183;«/mo»«mi mathvariant=¨bold¨ mathcolor=¨#FF0000¨»cos«/mi»«mo mathvariant=¨bold¨ mathcolor=¨#FF0000¨»(«/mo»«mi mathvariant=¨bold¨ mathcolor=¨#FF0000¨»§#969;«/mi»«mo mathvariant=¨bold¨ mathcolor=¨#FF0000¨»§#183;«/mo»«mi mathvariant=¨bold¨ mathcolor=¨#FF0000¨»t«/mi»«mo mathvariant=¨bold¨ mathcolor=¨#FF0000¨»+«/mo»«mfrac mathcolor=¨#FF0000¨»«mrow»«mn mathvariant=¨bold¨»3«/mn»«mi mathvariant=¨bold¨»§#960;«/mi»«/mrow»«mn mathvariant=¨bold¨»2«/mn»«/mfrac»«mo mathvariant=¨bold¨ mathcolor=¨#FF0000¨»)«/mo»«/math»
يجب إضافة زاوية الطور الابتدائية إلى كل من دالة السرعة كدالة للزمن ودالة التسارع كدالة للزمن.
نظرًا لأن الحل يعتمد على السرعة القصوى، فليس من الضروري استخدام زاوية الطور أثناء الحل، ولكن من الجيد معرفتها.
يمكنك التعرف على زاوية الطور الابتدائية في اليوكيوب 29:
2. העגלה מתחילה לנוע מנקודת שיווי המשקל ולא מנקודת הקצה החיובית.
בהתאם לכיוון תנועת העגלה ביחס לציר, העגלה מאחרת ברבע מחזור או מקדימה ב שלושת רבעי מחזור .
לכן, פונקציית המקום זמן המתאימה לתנועה יכולה להיות אחת מהשתיים :
«math xmlns=¨http://www.w3.org/1998/Math/MathML¨»«mi mathvariant=¨bold¨ mathcolor=¨#FF0000¨»X«/mi»«mo mathvariant=¨bold¨ mathcolor=¨#FF0000¨»(«/mo»«mi mathvariant=¨bold¨ mathcolor=¨#FF0000¨»t«/mi»«mo mathvariant=¨bold¨ mathcolor=¨#FF0000¨»)«/mo»«mo mathvariant=¨bold¨ mathcolor=¨#FF0000¨»=«/mo»«mi mathvariant=¨bold¨ mathcolor=¨#FF0000¨»A«/mi»«mo mathvariant=¨bold¨ mathcolor=¨#FF0000¨»§#183;«/mo»«mi mathvariant=¨bold¨ mathcolor=¨#FF0000¨»cos«/mi»«mo mathvariant=¨bold¨ mathcolor=¨#FF0000¨»(«/mo»«mi mathvariant=¨bold¨ mathcolor=¨#FF0000¨»§#969;«/mi»«mo mathvariant=¨bold¨ mathcolor=¨#FF0000¨»§#183;«/mo»«mi mathvariant=¨bold¨ mathcolor=¨#FF0000¨»t«/mi»«mo mathvariant=¨bold¨ mathcolor=¨#FF0000¨»-«/mo»«mfrac mathcolor=¨#FF0000¨»«mi mathvariant=¨bold¨»§#960;«/mi»«mn mathvariant=¨bold¨»2«/mn»«/mfrac»«mo mathvariant=¨bold¨ mathcolor=¨#FF0000¨»)«/mo»«mo mathvariant=¨bold¨ mathcolor=¨#FF0000¨»§#160;«/mo»«mo mathvariant=¨bold¨ mathcolor=¨#FF0000¨»§#160;«/mo»«mo mathvariant=¨bold¨ mathcolor=¨#FF0000¨»§#160;«/mo»«mo mathvariant=¨bold¨ mathcolor=¨#FF0000¨»§#160;«/mo»«mo mathvariant=¨bold¨ mathcolor=¨#FF0000¨»§#160;«/mo»«mo mathvariant=¨bold¨ mathcolor=¨#FF0000¨»§#160;«/mo»«mo mathvariant=¨bold¨ mathcolor=¨#FF0000¨»§#160;«/mo»«mo mathvariant=¨bold¨ mathcolor=¨#FF0000¨»§#160;«/mo»«mo mathvariant=¨bold¨ mathcolor=¨#FF0000¨»§#160;«/mo»«mo mathvariant=¨bold¨ mathcolor=¨#FF0000¨»§#160;«/mo»«mo mathvariant=¨bold¨ mathcolor=¨#FF0000¨»§#160;«/mo»«mo mathvariant=¨bold¨ mathcolor=¨#FF0000¨»§#160;«/mo»«mo mathvariant=¨bold¨ mathcolor=¨#FF0000¨»§#160;«/mo»«mo mathvariant=¨bold¨ mathcolor=¨#FF0000¨»§#160;«/mo»«mo mathvariant=¨bold¨ mathcolor=¨#FF0000¨»§#160;«/mo»«mo mathvariant=¨bold¨ mathcolor=¨#FF0000¨»§#160;«/mo»«mo mathvariant=¨bold¨ mathcolor=¨#FF0000¨»§#160;«/mo»«mo mathvariant=¨bold¨ mathcolor=¨#FF0000¨»§#160;«/mo»«mo mathvariant=¨bold¨ mathcolor=¨#FF0000¨»§#160;«/mo»«mi mathvariant=¨bold¨ mathcolor=¨#FF0000¨»X«/mi»«mo mathvariant=¨bold¨ mathcolor=¨#FF0000¨»(«/mo»«mi mathvariant=¨bold¨ mathcolor=¨#FF0000¨»t«/mi»«mo mathvariant=¨bold¨ mathcolor=¨#FF0000¨»)«/mo»«mo mathvariant=¨bold¨ mathcolor=¨#FF0000¨»=«/mo»«mi mathvariant=¨bold¨ mathcolor=¨#FF0000¨»A«/mi»«mo mathvariant=¨bold¨ mathcolor=¨#FF0000¨»§#183;«/mo»«mi mathvariant=¨bold¨ mathcolor=¨#FF0000¨»cos«/mi»«mo mathvariant=¨bold¨ mathcolor=¨#FF0000¨»(«/mo»«mi mathvariant=¨bold¨ mathcolor=¨#FF0000¨»§#969;«/mi»«mo mathvariant=¨bold¨ mathcolor=¨#FF0000¨»§#183;«/mo»«mi mathvariant=¨bold¨ mathcolor=¨#FF0000¨»t«/mi»«mo mathvariant=¨bold¨ mathcolor=¨#FF0000¨»+«/mo»«mfrac mathcolor=¨#FF0000¨»«mrow»«mn mathvariant=¨bold¨»3«/mn»«mi mathvariant=¨bold¨»§#960;«/mi»«/mrow»«mn mathvariant=¨bold¨»2«/mn»«/mfrac»«mo mathvariant=¨bold¨ mathcolor=¨#FF0000¨»)«/mo»«/math»
יש להוסיף את זווית המופע ההתחלתי גם לפונקציית המהירות זמן , וגם לפונקציית התאוצה זמן.
מכיוון שהפתרון מבוסס על המהירות המקסימאלית , אין צורך להשתמש בזווית המופע במהלך הפתרון, אך כדאי לדעת.
ניתן ללמוד ב קיוב 29 על זווית המופע ההתחלתי :
______________________________________________________________________________________

______________________________________________________________________________________
...
شغل النابض يساوي صفرًا. من قانون الشغل والطاقة، لا يوجد تغيير في الطاقة الحركية، وبالتالي فإن الشغل يساوي صفرًا.
قانون الشغل والطاقة، شغل القوة الحافظة.
الاصطدام مرن. وبالتالي فإن الطاقة الحركية في بداية الاصطدام تساوي الطاقة الحركية في نهاية الاصطدام.
القوة الوحيدة التي تعمل هي قوة النابض، من قانون الشغل والطاقة: «math xmlns=¨http://www.w3.org/1998/Math/MathML¨»«mi mathvariant=¨bold-italic¨ mathcolor=¨#0000FF¨»W«/mi»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»=«/mo»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»§#8710;«/mo»«msub»«mi mathvariant=¨bold-italic¨ mathcolor=¨#0000FF¨»E«/mi»«mi mathvariant=¨bold¨ mathcolor=¨#0000FF¨»K«/mi»«/msub»«/math» ، نظرًا لعدم وجود تغيير في الطاقة الحركية، فإن الشغل الذي يبذله النابض يساوي صفرًا.
הכוח היחיד שעושה עבודה הוא כוח הקפיץ, ממשפט עבודה אנרגיה: «math xmlns=¨http://www.w3.org/1998/Math/MathML¨»«mi mathvariant=¨bold-italic¨ mathcolor=¨#0000FF¨»W«/mi»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»=«/mo»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»§#8710;«/mo»«msub»«mi mathvariant=¨bold-italic¨ mathcolor=¨#0000FF¨»E«/mi»«mi mathvariant=¨bold¨ mathcolor=¨#0000FF¨»K«/mi»«/msub»«/math» , מכיוון שאין שינוי באנרגיה הקינטית עבודת הקפיץ שווה לאפס.
1. قوة النابض هي قوة حافظة، وشغل أي قوة حافظة في مسار مغلق (في نهاية الحركة يعود الجسم إلى نقطة بداية الحركة) يساوي صفر.
2. من لحظة الاصطدام حتى الانقباض الأقصى، تعمل قوة النابض عكس اتجاه الحركة. حسب تعريف الشغل، فإن النابض يبذل شغل سالب.
من لحظة الانقباض الأقصى حتى نهاية الاصطدام، تعمل قوة النابض في اتجاه الحركة، وتبذل شغل موجب.
إن الشغل المحصل الذي يبذله النابض من لحظة بدء الاصطدام إلى لحظة انتهاء الاصطدام يساوي صفرًا.
3. الشغل يساوي التغير في الطاقة الحركية. الطاقة الحركية هي كمية قياسية، ولا يوجد معنى للاتجاه.
التغيير الوحيد في حركة العربة قبل وبعد الاصطدام هو في اتجاه الحركة، وليس في مقدار السرعة.
(בסוף התנועה הגוף חוזר לנקודת תחילת התנועה) שווה לאפס .
2. מרגע הפגיעה ועד לכיווץ מקסימאלי כוח הקפיץ פועל נגד כיוון התנועה , מהגדרת העבודה הקפיץ עושה עבודה שלילית.
מרגע הכיווץ המקסימאלי ועד לסיום ההתנגשות ,כוח הקפיץ פועל בכיוון התנועה הוא עושה עבודה חיובית.
סה"כ עבודת הקפיץ מרגע תחילת ההתנגשות ועד לסיום ההתנגשות שווה לאפס.
______________________________________________________________________________________

______________________________________________________________________________________
...
إن كمية الدفع الذي يؤثر به النابض على العربة تختلف عن الصفر. من قانون الدفع وكمية الحركة، هناك تغير في كمية الحركة، وبالتالي فإن الدفع يختلف عن الصفر.
قانون الدفع وكمية الحركة.
من قانون الدفع وكمية الحركة، فإن كمية الدفع تساوي التغير في كمية الحركة : «math xmlns=¨http://www.w3.org/1998/Math/MathML¨»«mover mathcolor=¨#0000FF¨»«mi mathvariant=¨bold¨»J«/mi»«mo mathvariant=¨bold¨»§#8594;«/mo»«/mover»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»=«/mo»«mover mathcolor=¨#0000FF¨»«mrow»«mo mathvariant=¨bold¨»§#8710;«/mo»«mi mathvariant=¨bold¨»P«/mi»«/mrow»«mo mathvariant=¨bold¨»§#8594;«/mo»«/mover»«/math»
إن كمية الحركة قبل الاصطدام يختلف في الاتجاه عن كمية الحركة بعد الاصطدام، وبالتالي فإن الدافع يختلف عن الصفر.
«math xmlns=¨http://www.w3.org/1998/Math/MathML¨»«mover mathcolor=¨#0000FF¨»«mrow»«mi mathvariant=¨bold¨»P«/mi»«mo mathvariant=¨bold¨»`«/mo»«/mrow»«mo mathvariant=¨bold¨»§#8594;«/mo»«/mover»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»§#8800;«/mo»«mover mathcolor=¨#0000FF¨»«msub»«mi mathvariant=¨bold¨»P«/mi»«mn mathvariant=¨bold¨»0«/mn»«/msub»«mo mathvariant=¨bold¨»§#8594;«/mo»«/mover»«mspace linebreak=¨newline¨»«/mspace»«mspace linebreak=¨newline¨»«/mspace»«mover mathcolor=¨#0000FF¨»«mrow»«mo mathvariant=¨bold¨»§#8710;«/mo»«mi mathvariant=¨bold¨»P«/mi»«/mrow»«mo mathvariant=¨bold¨»§#8594;«/mo»«/mover»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»=«/mo»«mover mathcolor=¨#0000FF¨»«mrow»«mi mathvariant=¨bold¨»P«/mi»«mo mathvariant=¨bold¨»`«/mo»«/mrow»«mo mathvariant=¨bold¨»§#8594;«/mo»«/mover»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»-«/mo»«mover mathcolor=¨#0000FF¨»«msub»«mi mathvariant=¨bold¨»P«/mi»«mn mathvariant=¨bold¨»0«/mn»«/msub»«mo mathvariant=¨bold¨»§#8594;«/mo»«/mover»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»§#8800;«/mo»«mn mathvariant=¨bold¨ mathcolor=¨#0000FF¨»0«/mn»«mspace linebreak=¨newline¨»«/mspace»«/math»
התנע לפני ההתנגשות שונה בכיוונו מהתנע בתום ההתנגשות לכן המתקף שונה מאפס.
1. على عكس الطاقة الحركية، كمية الحركة هو متجه، وبالتالي فإن كمية الحركة قبل الاصطدام يختلف عن كمية الحركة قبل الاصطدام.
تتغير كمية الحركة بالتالي وفقًا لقانون كمية الحركة ، حيث تكون كمية الحركة مختلفًا عن الصفر.
2. يتم تعريف كمية الدفع المؤثر على أنه حاصل ضرب القوة في الزمن الذي تؤثر فيه القوة. من لحظة بدء الاصطدام حتى نهايته يكون اتجاه القوة إلى اليسار.
اتجاه القوة لا يتغير
إن كمية الدفع من لحظة بداية الاصطدام إلى الانقباض الأقصى هي نفس كمية الدفع من لحظة الانقباض الأقصى إلى نهاية الاصطدام.
لذلك فإن كمية الحركة من لحظة بدء الاصطدام إلى نهايته يختلف عن الصفر.
התנע משתנה לכן ממשפט תנע מתקף המתקף שונה מאפס.
2. המתקף מוגדר כמכפלת הכוח בזמן פעולת הכוח, מרגע תחילת ההתנגשות ועד סיומה כיוון הכוח הוא שמאלה.
כיוון הכוח לא משתנה .
המתקף מרגע תחילת ההתנגשות ועד לכיווץ המקסיאמלי זהה למתקף מרגע כיווץ מקסימאלי ועד לסיום ההתנגשות.
לכן המתקף מרגע תחילת ההתנגשות ועד סיומה שונה מאפס.
______________________________________________________________________________________