6. 2003,4 - ثلاث كرات وثلاثة رسوم بيانية
______________________________________________________________________________________
...
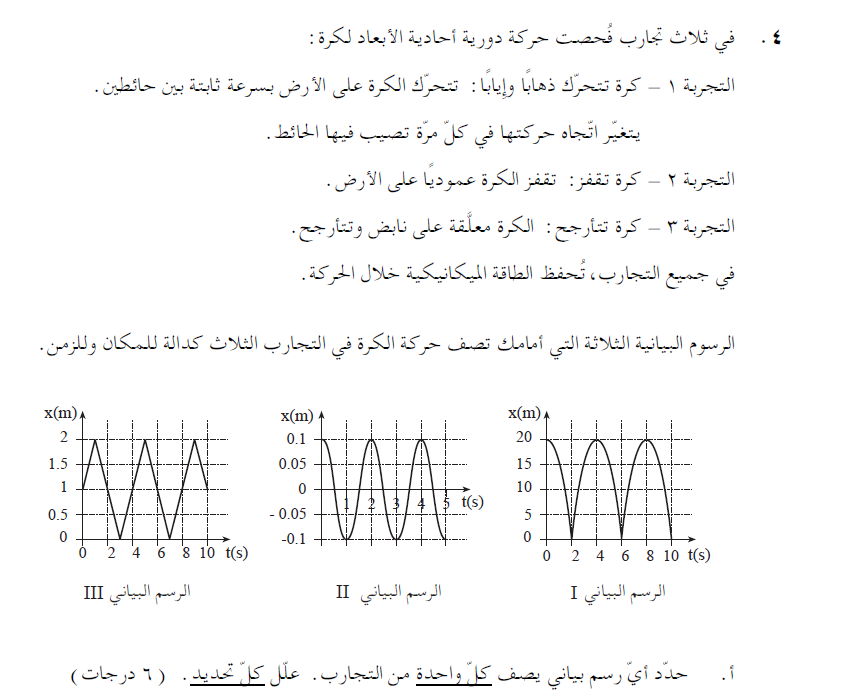
الرسم البياني 1 - لكرة تقفز.
الرسم البياني 2 - الكرة المتأرجحة.
الكرة 3 - كرة تتحرك ذهابًا وإيابًا.
גרף 2- כדור מתנודד.
כדור 3- כדור מתרוצץ.
فهم كل حركة من الحركات الثلاث وفهم الرسوم البياني للمكان كدالة للزمن.
مُعطى ثلاثة رسوم بيانية للمكان كدالة للزمن، فإن ميل الدالة في الرسم البياني للمكان كدالة للزمن يساوي السرعة.
الكرة المتحركة ذهابًا وإيابًا - تتحرك الكرة بسرعة ثابتة في اتجاه المحور، وتصطدم بالحائط وتتحرك بنفس السرعة عكس اتجاه المحور.
في فترة من الزمن يكون الميل ثابتًا وموجبًا. وفي فترة أخرى يكون الميل سالبًا ثابتًا - والرسم البياني الملائم هو الرسم البياني 3.
في فترة من الزمن يكون الميل ثابتًا وموجبًا. وفي فترة أخرى يكون الميل سالبًا ثابتًا - والرسم البياني الملائم هو الرسم البياني 3.
الكرة التي تقفز - تتحرك الكرة في سقوط حر، وتزداد سرعتها حتى تصطدم بالأرض،
في لحظة الاصطدام، تغير الكرة اتجاه حركتها، وتغير السرعة إشارتها - والرسم البياني الملائم هو الرسم البياني 1.
في لحظة الاصطدام، تغير الكرة اتجاه حركتها، وتغير السرعة إشارتها - والرسم البياني الملائم هو الرسم البياني 1.
الكرة المتأرجحة - تتحرك الكرة في تذبذبات. بالنسبة لجسم يتحرك في تذبذبات في حركة توافقية بسيطة، فإن دالة الموقع-الزمن هي دالة
شكله العام دالة جيب التمام، والرسم البياني الملائم هو الرسم البياني 2.
شكله العام دالة جيب التمام، والرسم البياني الملائم هو الرسم البياني 2.
כדור מתרוצץ- הכדור נע במהירות קבועה בכיוון הציר , מתנגש בקיר ונע באותה המהירות נגד כיוון הציר.
חלק מהזמן השיפוע קבוע וחיובי. וחלק מהזמן השיפוע קבוע שלילי - הגרף המתאים הוא גרף 3.
כדור מקפץ- הכדור נע בנפילה חופשית , מהירותו הולכת וגדלה עד שהוא פוגע בקרקע ,
ברגע הפגיעה הכדור משנה את כיוון תנועתו , המהירות משנה את סימנה - הגרף המתאים גרף 1.
כדור מתנודד- הכדור נע בתנודות. לגוף הנע בתנודות בתה"פ פונקצית המקום זמן היא פונקציה
שצורתה הכללית דומה לפונקציית הקוסינוס , הגרף המתרים הוא גרף 2.
1. لكل حركة محور حركة، حتى لو لم تظهر بشكل واضح. لكي يكون هناك تطابق بين حركة الكرة والرسم البياني، يجب أن تعرف اتجاه المحور في كل من الحركات.
في الكرة التي تقفز - اتجاه محور الحركة هو إلى الأعلى.
في الكرة المتأرجحة - اتجاه المحور هو عكس الاتجاه الابتدائي للحركة.
في الكرة المتحركة ذهابًا وإيابًا- اتجاه المحور هو نفس اتجاه الحركة الابتدائي. 2. من المهم أن نتذكر أنه عندما يكون الميل موجبًا، تكون السرعة موجبة، ويتحرك الجسم في اتجاه المحور.
وعندما يكون الميل سالبًا، تكون السرعة سالبة، يتحرك الجسم عكس اتجاه المحور.
3. بما أن السؤال يتناول بالتلائم بين ثلاث حركات وثلاثة رسوم بيانية، فمن السهل أن تضيع.
من المستحسن أن تبدأ بالحركة الأكثر وضوحًا بالنسبة لك، ثم ملائمتها مع الرسم البياني المناسب.
4. وفقًا للسؤال، يجب عليك كتابة سبب لكل ملائمة.
5. يمكنك التفسير بطريقة النفي (שלילה)، على سبيل المثال: في الرسم البياني 1 والرسم البياني 2 يتغير الميل باستمرار ولكن الكرة المتحركة ذهابًا وإيابًا تتحرك بسرعات ثابتة، والرسم البياني الملائم هو الرسم البياني 3.
בכדור המקפץ- כיוון ציר התנועה כלפי מעלה.
בכדור המתנודד- כיוון הציר הפוך לכיוון התנועה ההתחלתי.
בכדור המתרוצץ- כיוון הציר הוא ככיוון התנועה ההתחלתי.
2. חשוב לזכור כאשר השיפוע חיובי המהירות חיובית הגוף נע בכיוון הציר.
וכאשר השיפוע שלילי המהירות שלילית הגוף נע נגד כיוון הציר.
3. בגלל שהשאלה עוסקת בהתאמה בין שלוש תנועות ולשלושה גרפים , ניתן בקלות ללכת לאיבוד.
מומלץ להתחיל מהתנועה הכי ברורה לכם, ולהתאים לה את הגרף המתאים .
4. בהתאם לכתוב בשאלה בשאלה , חייבים לכתוב נימוק לכל התאמה .
5. אפשר לנמק בדרך השלילה, לדוגמה: בגרף 1 ובגרף 2 השיפוע כל הזמן משתנה אך הכדור המתרוצץ נע במהירויות קבועות, הגרף המתאים הוא גרף 3.
______________________________________________________________________________________
______________________________________________________________________________________
...
زمن دورة الكرة المتحركة ذهابًا وإيابًا هي 4 ثواني.
زمن دورة الكرة المتأرجحة هي 2 ثانية.
زمن دورة الكرة التي تقفز هي 4 ثواني.
זמן המחזור של הכדור המתנודד - 2 שניות.
זמן המחזור של הכדור המנתר - 4 שניות.
זמן המחזור של הכדור המתנודד- 2 שניות.
זמן המחזור של הכדור המנתר- 4 שניות.
فهم معنى زمن الدورة.
في الحركة الدورية، الزمن الدوري هو أقصر زمن يمر أثناء الحركة من لحظة بدء الجسم في الحركة من نقطة معينة حتى يعود الجسم إلى نفس النقطة وفي نفس الحركة.
في الكرة المتحركة ذهابًا وإيابًا (الرسم البياني 3) - تبدأ الكرة في التحرك من الموقع x=1m وبعد 4 ثواني تصل إلى الموقع x=1m وتتحرك بنفس السرعة
وبالتالي فإن زمن دورة الكرة المتحركة ذهابًا وإيابًا هو 4 ثوان.
في الكرة المتأرجحة (الشكل 2) - تبدأ الكرة في الحركة من الموقع x=0.1m وتعود إلى الموقع x=0.1m بعد ثانيتين، وتتحرك بنفس الحركة. وبالتالي فإن زمن دورة الكرة المتأرجحة هو 2 ثانية.
في الكرة التي تقفز (الرسم البياني 1) - تصطدم الكرة بالأرض في الموقع x = 0 متر في اللحظة t = 2s وتعود إلى الموقع x = 0 متر وفي نفس الحركة في اللحظة t = 6s .
لذلك فإن زمن الدورة هو 4 ثوان.
1.يصف زمن الدورة دورية الحركة؛ لا يكفي أن يعود الجسم إلى نفس الموقع.
على سبيل المثال، في الكرة المتحركة ذهابًا وإيابًا، تصل الكرة إلى نفس النقطة كل ثانية، ولكن زمن الدورة هو ثانيتين.
على سبيل المثال، في الكرة المتحركة ذهابًا وإيابًا، تصل الكرة إلى نفس النقطة كل ثانية، ولكن زمن الدورة هو ثانيتين.
2. زمن الدورة هو أقصر فترة زمنية تتكرر فيها الحركة.
تعود الكرة التي تقفز إلى نفس الحركة ونفس النقطة بعد ثماني ثوانٍ، ولكن زمن الدورة هو 4 ثوانٍ، وليس 8 ثوانٍ.
3. يمكنك الكتابة في الحل: "زمن دورة الكرة المتحركة ذهابًا وإيابًا هو 4 ثوانٍ كما هو موضح في الرسم البياني 3". من الأفضل أن تُفصّل.
4. لإيجاد زمن الدورة، يجب فحص الحركة بأكملها، والتأكد من أن الدورية صحيحة بالفعل للحركة بأكملها.
כך למשל בכדור המתרוצץ הכדור בכל שניה מגיע לאותה הנקודה , אך זמן המחזור הוא 2 שניות.
2. זמן המחזור הוא פרק הזמן הקצר ביותר שבו התנועה חוזרת על עצמה .
הכדור המתרוצץ חוזר לאותה תנועה ובאותה נקודה כעבור שמונה שניות, אך זמן המחזור הוא 4 שניות ולא 8 שניות.
3. אפשר לכתוב בפתרון:" זמן המחזור של הכדור המתרוצץ הוא 4 שניות כפי שניתן לראות בגרף 3" עדיף לפרט.
4. כדי למצוא את זמן המחזור יש לבחון את כל התנועה, ולראות שאכן המחזוריות נכונה לכל התנועה.
______________________________________________________________________________________
______________________________________________________________________________________
...
السرعة القصوى للكرة المتحركة ذهابًا وإيابًا: 1 متر في الثانية.
السرعة القصوى للكرة التي تقفز: 20 متراً في الثانية.
السرعة القصوى للكرة المتأرجحة: 0.314 متر في الثانية.
המהירות המקסימאלית של הכדור המנתר : 20 מטר לשנייה.
המהירות המקסימאלית של הכדור המתנודד : 0.314 מטר לשנייה.
تتحرك كل كرة بحركات مختلفة. يتعين عليك أن تجد السرعة القصوى بطريقة مختلفة.
تتحرك الكرة المتحركة ذهابًا وإيابًا بسرعة ثابتة؛ يمكن إيجاد سرعتها باستخدام الكينيماتيكا. من الرسم البياني أو تعريف السرعة.
تتحرك الكرة التي تقفز بحركات بالستية - حركية.
تتحرك الكرة المتأرجحة في اهتزازات - سوف نشير إليها بالاهتزازات التوافقية البسيطة.
הכדור המתרוצץ נע במהירות קבועה , אפשר למצוא את מהירותו בעזרת קינמטיקה . מהגרף או מהגדרת המהירות.
הכדור המקפץ נע בתנועות בליסטיות- קינמטיקה.
הכדור המתנודד נע בתנודות- נתייחס אליהן כאל תנודות הרמוניות פשוטות.
تتحرك الكرات بحركات مختلفة، نجد سرعة كل كرة حسب نوع الحركة:
أقصى سرعة للكرة المتحركة ذهابًا وإيابًا، التجربة 1
تتحرك الكرة بسرعات ثابتة، وسوف نستخدم تعريف السرعة في الثانية الأولى:
«math xmlns=¨http://www.w3.org/1998/Math/MathML¨»«msub»«mi mathvariant=¨bold¨ mathcolor=¨#0000FF¨»V«/mi»«msub mathcolor=¨#0000FF¨»«mi mathvariant=¨bold¨»max«/mi»«mn mathvariant=¨bold¨»1«/mn»«/msub»«/msub»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»=«/mo»«mfrac mathcolor=¨#0000FF¨»«mrow»«mo mathvariant=¨bold¨»§#8710;«/mo»«mi mathvariant=¨bold¨»X«/mi»«/mrow»«mrow»«mo mathvariant=¨bold¨»§#8710;«/mo»«mi mathvariant=¨bold¨»t«/mi»«/mrow»«/mfrac»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»=«/mo»«mfrac mathcolor=¨#0000FF¨»«mrow»«mn mathvariant=¨bold¨»2«/mn»«mo mathvariant=¨bold¨»-«/mo»«mn mathvariant=¨bold¨»1«/mn»«/mrow»«mrow»«mn mathvariant=¨bold¨»1«/mn»«mo mathvariant=¨bold¨»-«/mo»«mn mathvariant=¨bold¨»0«/mn»«/mrow»«/mfrac»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»=«/mo»«mfrac mathcolor=¨#0000FF¨»«mn mathvariant=¨bold¨»1«/mn»«mn mathvariant=¨bold¨»1«/mn»«/mfrac»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»=«/mo»«mn mathvariant=¨bold¨ mathcolor=¨#0000FF¨»1«/mn»«mfrac mathcolor=¨#0000FF¨»«mi mathvariant=¨bold¨»m«/mi»«mi mathvariant=¨bold¨»s«/mi»«/mfrac»«/math»
لذلك فإن السرعة القصوى للكرة المتحركة ذهابًا وإيابًا هي 1 متر في الثانية.
أقصى سرعة للكرة التي تقفز، التجربة 2
الكرة تسقط سقوطا حرا من ارتفاع 20 مترا وتصل إلى الأرض بعد ثانيتين من بدء حركتها.
من الرسم البياني 1، يبدو أن الكرة بدأت بالتحرك من حالة السكون.
نستخدم دالة السرعة-الزمن الملائمة للحركة بتسارع ثابت:
«math xmlns=¨http://www.w3.org/1998/Math/MathML¨»«mi mathvariant=¨bold-italic¨ mathcolor=¨#0000FF¨»V«/mi»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»(«/mo»«mi mathvariant=¨bold-italic¨ mathcolor=¨#0000FF¨»t«/mi»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»)«/mo»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»=«/mo»«msub»«mi mathvariant=¨bold-italic¨ mathcolor=¨#0000FF¨»V«/mi»«mn mathvariant=¨bold¨ mathcolor=¨#0000FF¨»0«/mn»«/msub»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»+«/mo»«mi mathvariant=¨bold-italic¨ mathcolor=¨#0000FF¨»a«/mi»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»§#183;«/mo»«mi mathvariant=¨bold-italic¨ mathcolor=¨#0000FF¨»t«/mi»«mspace linebreak=¨newline¨»«/mspace»«msub»«mi mathvariant=¨bold-italic¨ mathcolor=¨#0000FF¨»V«/mi»«mrow mathcolor=¨#0000FF¨»«mi mathvariant=¨bold¨»m«/mi»«mi mathvariant=¨bold¨»a«/mi»«msub»«mi mathvariant=¨bold¨»x«/mi»«mn mathvariant=¨bold¨»2«/mn»«/msub»«/mrow»«/msub»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»=«/mo»«mi mathvariant=¨bold-italic¨ mathcolor=¨#0000FF¨»V«/mi»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»(«/mo»«mn mathvariant=¨bold¨ mathcolor=¨#0000FF¨»2«/mn»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»)«/mo»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»=«/mo»«mn mathvariant=¨bold¨ mathcolor=¨#0000FF¨»0«/mn»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»+«/mo»«mn mathvariant=¨bold¨ mathcolor=¨#0000FF¨»10«/mn»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»§#183;«/mo»«mn mathvariant=¨bold¨ mathcolor=¨#0000FF¨»2«/mn»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»=«/mo»«mn mathvariant=¨bold¨ mathcolor=¨#0000FF¨»20«/mn»«mfrac mathcolor=¨#0000FF¨»«mi mathvariant=¨bold¨»m«/mi»«mi mathvariant=¨bold¨»s«/mi»«/mfrac»«/math»
ومن الممكن أيضًا استخدام تعبير مربع السرعات:
«math xmlns=¨http://www.w3.org/1998/Math/MathML¨»«msup»«mi mathvariant=¨bold¨ mathcolor=¨#0000FF¨»V«/mi»«mn mathvariant=¨bold¨ mathcolor=¨#0000FF¨»2«/mn»«/msup»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»=«/mo»«msup»«msub»«mi mathvariant=¨bold¨ mathcolor=¨#0000FF¨»V«/mi»«mn mathvariant=¨bold¨ mathcolor=¨#0000FF¨»0«/mn»«/msub»«mn mathvariant=¨bold¨ mathcolor=¨#0000FF¨»2«/mn»«/msup»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»+«/mo»«mn mathvariant=¨bold¨ mathcolor=¨#0000FF¨»2«/mn»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»§#183;«/mo»«mi mathvariant=¨bold¨ mathcolor=¨#0000FF¨»a«/mi»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»§#183;«/mo»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»§#8710;«/mo»«mi mathvariant=¨bold¨ mathcolor=¨#0000FF¨»y«/mi»«mspace linebreak=¨newline¨»«/mspace»«msub»«mi mathvariant=¨bold¨ mathcolor=¨#0000FF¨»V«/mi»«msub mathcolor=¨#0000FF¨»«mi mathvariant=¨bold¨»max«/mi»«mn mathvariant=¨bold¨»3«/mn»«/msub»«/msub»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»=«/mo»«msqrt mathcolor=¨#0000FF¨»«msup»«msub»«mi mathvariant=¨bold¨»V«/mi»«mn mathvariant=¨bold¨»0«/mn»«/msub»«mn mathvariant=¨bold¨»2«/mn»«/msup»«mo mathvariant=¨bold¨»+«/mo»«mn mathvariant=¨bold¨»2«/mn»«mo mathvariant=¨bold¨»§#183;«/mo»«mi mathvariant=¨bold¨»a«/mi»«mo mathvariant=¨bold¨»§#183;«/mo»«mo mathvariant=¨bold¨»§#8710;«/mo»«mi mathvariant=¨bold¨»y«/mi»«/msqrt»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»=«/mo»«msqrt mathcolor=¨#0000FF¨»«msup»«mn mathvariant=¨bold¨»0«/mn»«mn mathvariant=¨bold¨»2«/mn»«/msup»«mo mathvariant=¨bold¨»+«/mo»«mn mathvariant=¨bold¨»2«/mn»«mo mathvariant=¨bold¨»§#183;«/mo»«mn mathvariant=¨bold¨»10«/mn»«mo mathvariant=¨bold¨»§#183;«/mo»«mn mathvariant=¨bold¨»20«/mn»«/msqrt»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»=«/mo»«msqrt mathcolor=¨#0000FF¨»«mn mathvariant=¨bold¨»400«/mn»«/msqrt»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»§#160;«/mo»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»=«/mo»«mn mathvariant=¨bold¨ mathcolor=¨#0000FF¨»20«/mn»«mfrac mathcolor=¨#0000FF¨»«mi mathvariant=¨bold¨»m«/mi»«mi mathvariant=¨bold¨»s«/mi»«/mfrac»«/math»
لذلك فإن السرعة القصوى للكرة المرتدة هي 20 متراً في الثانية.
أقصى سرعة للكرة المتأرجحة، التجربة 3
لنفترض أن الكرة المتذبذبة تتحرك بحركة توافقية بسيطة. وسوف نستخدم دالة السرعة كدالة للزمن الملائمة لحركة توافقية بسيطة.
السرعة القصوى للكرة هي بعد مرور ربع دورة من لحظة بدء الحركة:
«math xmlns=¨http://www.w3.org/1998/Math/MathML¨»«mi mathvariant=¨bold¨ mathcolor=¨#0000FF¨»V«/mi»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»(«/mo»«mi mathvariant=¨bold¨ mathcolor=¨#0000FF¨»t«/mi»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»)«/mo»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»=«/mo»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»-«/mo»«mi mathvariant=¨bold¨ mathcolor=¨#0000FF¨»§#969;«/mi»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»§#183;«/mo»«mi mathvariant=¨bold¨ mathcolor=¨#0000FF¨»A«/mi»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»§#183;«/mo»«mi mathvariant=¨bold¨ mathcolor=¨#0000FF¨»sin«/mi»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»(«/mo»«mi mathvariant=¨bold¨ mathcolor=¨#0000FF¨»§#969;«/mi»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»§#183;«/mo»«mi mathvariant=¨bold¨ mathcolor=¨#0000FF¨»t«/mi»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»)«/mo»«mspace linebreak=¨newline¨»«/mspace»«mspace linebreak=¨newline¨»«/mspace»«mi mathvariant=¨bold¨ mathcolor=¨#0000FF¨»V«/mi»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»(«/mo»«mi mathvariant=¨bold¨ mathcolor=¨#0000FF¨»t«/mi»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»)«/mo»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»=«/mo»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»-«/mo»«mfrac mathcolor=¨#0000FF¨»«mrow»«mn mathvariant=¨bold¨»2«/mn»«mo mathvariant=¨bold¨»§#183;«/mo»«mi mathvariant=¨bold¨»§#960;«/mi»«/mrow»«mi mathvariant=¨bold¨»T«/mi»«/mfrac»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»§#183;«/mo»«mi mathvariant=¨bold¨ mathcolor=¨#0000FF¨»A«/mi»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»§#183;«/mo»«mi mathvariant=¨bold¨ mathcolor=¨#0000FF¨»sin«/mi»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»(«/mo»«mfrac mathcolor=¨#0000FF¨»«mrow»«mn mathvariant=¨bold¨»2«/mn»«mo mathvariant=¨bold¨»§#183;«/mo»«mi mathvariant=¨bold¨»§#960;«/mi»«/mrow»«mi mathvariant=¨bold¨»T«/mi»«/mfrac»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»§#183;«/mo»«mi mathvariant=¨bold¨ mathcolor=¨#0000FF¨»t«/mi»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»)«/mo»«mspace linebreak=¨newline¨»«/mspace»«mi mathvariant=¨bold¨ mathcolor=¨#0000FF¨»V«/mi»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»(«/mo»«mfrac mathcolor=¨#0000FF¨»«mi mathvariant=¨bold¨»T«/mi»«mn mathvariant=¨bold¨»4«/mn»«/mfrac»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»)«/mo»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»=«/mo»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»-«/mo»«mfrac mathcolor=¨#0000FF¨»«mrow»«mn mathvariant=¨bold¨»2«/mn»«mo mathvariant=¨bold¨»§#183;«/mo»«mi mathvariant=¨bold¨»§#960;«/mi»«/mrow»«mi mathvariant=¨bold¨»T«/mi»«/mfrac»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»§#183;«/mo»«mn mathvariant=¨bold¨ mathcolor=¨#0000FF¨»0«/mn»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨».«/mo»«mn mathvariant=¨bold¨ mathcolor=¨#0000FF¨»1«/mn»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»§#183;«/mo»«mi mathvariant=¨bold¨ mathcolor=¨#0000FF¨»sin«/mi»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»(«/mo»«mfrac mathcolor=¨#0000FF¨»«mrow»«mn mathvariant=¨bold¨»2«/mn»«mo mathvariant=¨bold¨»§#183;«/mo»«mi mathvariant=¨bold¨»§#960;«/mi»«/mrow»«mi mathvariant=¨bold¨»T«/mi»«/mfrac»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»§#183;«/mo»«mfrac mathcolor=¨#0000FF¨»«mi mathvariant=¨bold¨»T«/mi»«mn mathvariant=¨bold¨»4«/mn»«/mfrac»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»)«/mo»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»=«/mo»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»-«/mo»«mfrac mathcolor=¨#0000FF¨»«mrow»«mn mathvariant=¨bold¨»2«/mn»«mo mathvariant=¨bold¨»§#183;«/mo»«mi mathvariant=¨bold¨»§#960;«/mi»«/mrow»«mn mathvariant=¨bold¨»2«/mn»«/mfrac»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»§#183;«/mo»«mn mathvariant=¨bold¨ mathcolor=¨#0000FF¨»0«/mn»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨».«/mo»«mn mathvariant=¨bold¨ mathcolor=¨#0000FF¨»1«/mn»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»§#183;«/mo»«mi mathvariant=¨bold¨ mathcolor=¨#0000FF¨»sin«/mi»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»(«/mo»«mfrac mathcolor=¨#0000FF¨»«mrow»«mn mathvariant=¨bold¨»2«/mn»«mo mathvariant=¨bold¨»§#183;«/mo»«mi mathvariant=¨bold¨»§#960;«/mi»«/mrow»«mn mathvariant=¨bold¨»2«/mn»«/mfrac»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»§#183;«/mo»«mfrac mathcolor=¨#0000FF¨»«mn mathvariant=¨bold¨»2«/mn»«mn mathvariant=¨bold¨»4«/mn»«/mfrac»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»)«/mo»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»=«/mo»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»-«/mo»«mn mathvariant=¨bold¨ mathcolor=¨#0000FF¨»0«/mn»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨».«/mo»«mn mathvariant=¨bold¨ mathcolor=¨#0000FF¨»314«/mn»«mfrac mathcolor=¨#0000FF¨»«mi mathvariant=¨bold¨»m«/mi»«mi mathvariant=¨bold¨»s«/mi»«/mfrac»«mspace linebreak=¨newline¨»«/mspace»«/math»
وبالتالي فإن السرعة القصوى للكرة المتأرجحة هي 0.314 متر في الثانية.
מהירותו המרבית של הכדור המתרוצץ, ניסוי 1
הכדור נע במהירויות קבועות , נשתמש בהגדרת המהירות לשנייה הראשונה:
«math xmlns=¨http://www.w3.org/1998/Math/MathML¨»«msub»«mi mathvariant=¨bold¨ mathcolor=¨#0000FF¨»V«/mi»«msub mathcolor=¨#0000FF¨»«mi mathvariant=¨bold¨»max«/mi»«mn mathvariant=¨bold¨»1«/mn»«/msub»«/msub»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»=«/mo»«mfrac mathcolor=¨#0000FF¨»«mrow»«mo mathvariant=¨bold¨»§#8710;«/mo»«mi mathvariant=¨bold¨»X«/mi»«/mrow»«mrow»«mo mathvariant=¨bold¨»§#8710;«/mo»«mi mathvariant=¨bold¨»t«/mi»«/mrow»«/mfrac»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»=«/mo»«mfrac mathcolor=¨#0000FF¨»«mrow»«mn mathvariant=¨bold¨»2«/mn»«mo mathvariant=¨bold¨»-«/mo»«mn mathvariant=¨bold¨»1«/mn»«/mrow»«mrow»«mn mathvariant=¨bold¨»1«/mn»«mo mathvariant=¨bold¨»-«/mo»«mn mathvariant=¨bold¨»0«/mn»«/mrow»«/mfrac»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»=«/mo»«mfrac mathcolor=¨#0000FF¨»«mn mathvariant=¨bold¨»1«/mn»«mn mathvariant=¨bold¨»1«/mn»«/mfrac»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»=«/mo»«mn mathvariant=¨bold¨ mathcolor=¨#0000FF¨»1«/mn»«mfrac mathcolor=¨#0000FF¨»«mi mathvariant=¨bold¨»m«/mi»«mi mathvariant=¨bold¨»s«/mi»«/mfrac»«/math»
לכן מהירותו המקסימאלית של הכדור המתרוצף היא 1 מטר לשנייה.
מהירותו המרבית של הכדור המקפץ,ניסוי 2
הכדור נע בנפילה חופשית מגובה 20 מטר והוא מגיע לקרקע 2 שניות מרגע תחילת תנועתו.
מגרף 1 , נראה שהכדור התחיל לנוע ממנוחה.
נשתמש בפונקציית מהירות זמן המתאימה לתנועה בתאוצה קבועה:
«math xmlns=¨http://www.w3.org/1998/Math/MathML¨»«mi mathvariant=¨bold-italic¨ mathcolor=¨#0000FF¨»V«/mi»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»(«/mo»«mi mathvariant=¨bold-italic¨ mathcolor=¨#0000FF¨»t«/mi»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»)«/mo»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»=«/mo»«msub»«mi mathvariant=¨bold-italic¨ mathcolor=¨#0000FF¨»V«/mi»«mn mathvariant=¨bold¨ mathcolor=¨#0000FF¨»0«/mn»«/msub»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»+«/mo»«mi mathvariant=¨bold-italic¨ mathcolor=¨#0000FF¨»a«/mi»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»§#183;«/mo»«mi mathvariant=¨bold-italic¨ mathcolor=¨#0000FF¨»t«/mi»«mspace linebreak=¨newline¨»«/mspace»«msub»«mi mathvariant=¨bold-italic¨ mathcolor=¨#0000FF¨»V«/mi»«mrow mathcolor=¨#0000FF¨»«mi mathvariant=¨bold¨»m«/mi»«mi mathvariant=¨bold¨»a«/mi»«msub»«mi mathvariant=¨bold¨»x«/mi»«mn mathvariant=¨bold¨»2«/mn»«/msub»«/mrow»«/msub»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»=«/mo»«mi mathvariant=¨bold-italic¨ mathcolor=¨#0000FF¨»V«/mi»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»(«/mo»«mn mathvariant=¨bold¨ mathcolor=¨#0000FF¨»2«/mn»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»)«/mo»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»=«/mo»«mn mathvariant=¨bold¨ mathcolor=¨#0000FF¨»0«/mn»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»+«/mo»«mn mathvariant=¨bold¨ mathcolor=¨#0000FF¨»10«/mn»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»§#183;«/mo»«mn mathvariant=¨bold¨ mathcolor=¨#0000FF¨»2«/mn»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»=«/mo»«mn mathvariant=¨bold¨ mathcolor=¨#0000FF¨»20«/mn»«mfrac mathcolor=¨#0000FF¨»«mi mathvariant=¨bold¨»m«/mi»«mi mathvariant=¨bold¨»s«/mi»«/mfrac»«/math»
אפשר גם עם ביטוי ריבוע המהירויות :
«math xmlns=¨http://www.w3.org/1998/Math/MathML¨»«msup»«mi mathvariant=¨bold¨ mathcolor=¨#0000FF¨»V«/mi»«mn mathvariant=¨bold¨ mathcolor=¨#0000FF¨»2«/mn»«/msup»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»=«/mo»«msup»«msub»«mi mathvariant=¨bold¨ mathcolor=¨#0000FF¨»V«/mi»«mn mathvariant=¨bold¨ mathcolor=¨#0000FF¨»0«/mn»«/msub»«mn mathvariant=¨bold¨ mathcolor=¨#0000FF¨»2«/mn»«/msup»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»+«/mo»«mn mathvariant=¨bold¨ mathcolor=¨#0000FF¨»2«/mn»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»§#183;«/mo»«mi mathvariant=¨bold¨ mathcolor=¨#0000FF¨»a«/mi»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»§#183;«/mo»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»§#8710;«/mo»«mi mathvariant=¨bold¨ mathcolor=¨#0000FF¨»y«/mi»«mspace linebreak=¨newline¨»«/mspace»«msub»«mi mathvariant=¨bold¨ mathcolor=¨#0000FF¨»V«/mi»«msub mathcolor=¨#0000FF¨»«mi mathvariant=¨bold¨»max«/mi»«mn mathvariant=¨bold¨»3«/mn»«/msub»«/msub»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»=«/mo»«msqrt mathcolor=¨#0000FF¨»«msup»«msub»«mi mathvariant=¨bold¨»V«/mi»«mn mathvariant=¨bold¨»0«/mn»«/msub»«mn mathvariant=¨bold¨»2«/mn»«/msup»«mo mathvariant=¨bold¨»+«/mo»«mn mathvariant=¨bold¨»2«/mn»«mo mathvariant=¨bold¨»§#183;«/mo»«mi mathvariant=¨bold¨»a«/mi»«mo mathvariant=¨bold¨»§#183;«/mo»«mo mathvariant=¨bold¨»§#8710;«/mo»«mi mathvariant=¨bold¨»y«/mi»«/msqrt»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»=«/mo»«msqrt mathcolor=¨#0000FF¨»«msup»«mn mathvariant=¨bold¨»0«/mn»«mn mathvariant=¨bold¨»2«/mn»«/msup»«mo mathvariant=¨bold¨»+«/mo»«mn mathvariant=¨bold¨»2«/mn»«mo mathvariant=¨bold¨»§#183;«/mo»«mn mathvariant=¨bold¨»10«/mn»«mo mathvariant=¨bold¨»§#183;«/mo»«mn mathvariant=¨bold¨»20«/mn»«/msqrt»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»=«/mo»«msqrt mathcolor=¨#0000FF¨»«mn mathvariant=¨bold¨»400«/mn»«/msqrt»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»§#160;«/mo»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»=«/mo»«mn mathvariant=¨bold¨ mathcolor=¨#0000FF¨»20«/mn»«mfrac mathcolor=¨#0000FF¨»«mi mathvariant=¨bold¨»m«/mi»«mi mathvariant=¨bold¨»s«/mi»«/mfrac»«/math»
לכן מהירותו המקסימאלית של הכדור המקפץ היא 20 מטר לשניה.
מהירותו המרבית של הכדור המתנודד, ניסוי 3
נניח שהכדור המתנודד נע בתנועה הרמונית פשוטה . ונשתמש בפונקציית המהירות בתלות בזמן המתאימה לתה"פ.
מהירות הכדור מקסימאלית כעבור רבע זמן מחזור מרגע תחילת התנועה:
«math xmlns=¨http://www.w3.org/1998/Math/MathML¨»«mi mathvariant=¨bold¨ mathcolor=¨#0000FF¨»V«/mi»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»(«/mo»«mi mathvariant=¨bold¨ mathcolor=¨#0000FF¨»t«/mi»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»)«/mo»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»=«/mo»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»-«/mo»«mi mathvariant=¨bold¨ mathcolor=¨#0000FF¨»§#969;«/mi»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»§#183;«/mo»«mi mathvariant=¨bold¨ mathcolor=¨#0000FF¨»A«/mi»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»§#183;«/mo»«mi mathvariant=¨bold¨ mathcolor=¨#0000FF¨»sin«/mi»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»(«/mo»«mi mathvariant=¨bold¨ mathcolor=¨#0000FF¨»§#969;«/mi»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»§#183;«/mo»«mi mathvariant=¨bold¨ mathcolor=¨#0000FF¨»t«/mi»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»)«/mo»«mspace linebreak=¨newline¨»«/mspace»«mspace linebreak=¨newline¨»«/mspace»«mi mathvariant=¨bold¨ mathcolor=¨#0000FF¨»V«/mi»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»(«/mo»«mi mathvariant=¨bold¨ mathcolor=¨#0000FF¨»t«/mi»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»)«/mo»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»=«/mo»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»-«/mo»«mfrac mathcolor=¨#0000FF¨»«mrow»«mn mathvariant=¨bold¨»2«/mn»«mo mathvariant=¨bold¨»§#183;«/mo»«mi mathvariant=¨bold¨»§#960;«/mi»«/mrow»«mi mathvariant=¨bold¨»T«/mi»«/mfrac»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»§#183;«/mo»«mi mathvariant=¨bold¨ mathcolor=¨#0000FF¨»A«/mi»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»§#183;«/mo»«mi mathvariant=¨bold¨ mathcolor=¨#0000FF¨»sin«/mi»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»(«/mo»«mfrac mathcolor=¨#0000FF¨»«mrow»«mn mathvariant=¨bold¨»2«/mn»«mo mathvariant=¨bold¨»§#183;«/mo»«mi mathvariant=¨bold¨»§#960;«/mi»«/mrow»«mi mathvariant=¨bold¨»T«/mi»«/mfrac»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»§#183;«/mo»«mi mathvariant=¨bold¨ mathcolor=¨#0000FF¨»t«/mi»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»)«/mo»«mspace linebreak=¨newline¨»«/mspace»«mi mathvariant=¨bold¨ mathcolor=¨#0000FF¨»V«/mi»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»(«/mo»«mfrac mathcolor=¨#0000FF¨»«mi mathvariant=¨bold¨»T«/mi»«mn mathvariant=¨bold¨»4«/mn»«/mfrac»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»)«/mo»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»=«/mo»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»-«/mo»«mfrac mathcolor=¨#0000FF¨»«mrow»«mn mathvariant=¨bold¨»2«/mn»«mo mathvariant=¨bold¨»§#183;«/mo»«mi mathvariant=¨bold¨»§#960;«/mi»«/mrow»«mi mathvariant=¨bold¨»T«/mi»«/mfrac»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»§#183;«/mo»«mn mathvariant=¨bold¨ mathcolor=¨#0000FF¨»0«/mn»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨».«/mo»«mn mathvariant=¨bold¨ mathcolor=¨#0000FF¨»1«/mn»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»§#183;«/mo»«mi mathvariant=¨bold¨ mathcolor=¨#0000FF¨»sin«/mi»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»(«/mo»«mfrac mathcolor=¨#0000FF¨»«mrow»«mn mathvariant=¨bold¨»2«/mn»«mo mathvariant=¨bold¨»§#183;«/mo»«mi mathvariant=¨bold¨»§#960;«/mi»«/mrow»«mi mathvariant=¨bold¨»T«/mi»«/mfrac»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»§#183;«/mo»«mfrac mathcolor=¨#0000FF¨»«mi mathvariant=¨bold¨»T«/mi»«mn mathvariant=¨bold¨»4«/mn»«/mfrac»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»)«/mo»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»=«/mo»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»-«/mo»«mfrac mathcolor=¨#0000FF¨»«mrow»«mn mathvariant=¨bold¨»2«/mn»«mo mathvariant=¨bold¨»§#183;«/mo»«mi mathvariant=¨bold¨»§#960;«/mi»«/mrow»«mn mathvariant=¨bold¨»2«/mn»«/mfrac»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»§#183;«/mo»«mn mathvariant=¨bold¨ mathcolor=¨#0000FF¨»0«/mn»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨».«/mo»«mn mathvariant=¨bold¨ mathcolor=¨#0000FF¨»1«/mn»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»§#183;«/mo»«mi mathvariant=¨bold¨ mathcolor=¨#0000FF¨»sin«/mi»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»(«/mo»«mfrac mathcolor=¨#0000FF¨»«mrow»«mn mathvariant=¨bold¨»2«/mn»«mo mathvariant=¨bold¨»§#183;«/mo»«mi mathvariant=¨bold¨»§#960;«/mi»«/mrow»«mn mathvariant=¨bold¨»2«/mn»«/mfrac»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»§#183;«/mo»«mfrac mathcolor=¨#0000FF¨»«mn mathvariant=¨bold¨»2«/mn»«mn mathvariant=¨bold¨»4«/mn»«/mfrac»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»)«/mo»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»=«/mo»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»-«/mo»«mn mathvariant=¨bold¨ mathcolor=¨#0000FF¨»0«/mn»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨».«/mo»«mn mathvariant=¨bold¨ mathcolor=¨#0000FF¨»314«/mn»«mfrac mathcolor=¨#0000FF¨»«mi mathvariant=¨bold¨»m«/mi»«mi mathvariant=¨bold¨»s«/mi»«/mfrac»«mspace linebreak=¨newline¨»«/mspace»«/math»
לכן מהירותו המקסימאלית של הכדור המתנודד היא 0.314 מטר לשנייה.
1. لم يتم ذكر أن الكرة المتأرجحة تتحرك في حركة توافقية، ولكن من شكل الرسم البياني يمكن افتراض أنها تتحرك في حركة توافقية.
وبعد ذلك فقط يمكنك استخدام دوال الحركة التوافقية البسيطة.
وبعد ذلك فقط يمكنك استخدام دوال الحركة التوافقية البسيطة.
2. السؤال ينص على: "احسب أقصى مقدار لسرعة الكرة..." اتجاه الحركة ليس مهمًا، وبالتالي فإن إشارة السرعة ليست مهمة.
3. تتحرك الكرة التي تقفز عموديًا. يتم تمثيل المحور الرأسي في الرسم البياني كمحور X. من الأفضل استخدام الصيغة التقليدية ووصف الموقع الرأسي للكرة في الدوال باستخدام Y.
ורק לאחר מכן להשתמש בפונקציות התה"פ.
2. בשאלה כתוב: " חשב את הגודל המרבי של מהירות הכדור.." אין חשיבות לכיוון התנועה , לכן אין חשיבות לסימן המהירות.
3.הכדור המנתר נע בתנועה אנכית, הציר האנכי בגרף מתואר כציר X , עדיף להשתמש בסימונים המקובלים ולתאר את המיקום האנכי של הכדור בפונקציות בעזרת Y.
______________________________________________________________________________________

______________________________________________________________________________________
...
الرسم البياني 2 - الحركة التوافقية البسيطة في نقاط الأطراف.
الرسم البياني 1 - الحركات الباليستية العمودية، في نقاط الارتفاع القصوى.
גרף 1- תנועות בליסטיות אנכיות,בנקודות שיא הגובה.
فهم معنى التسارع ومعنى السرعة.
يوضح الرسم البياني 2 الحركة التوافقية البسيطة. في أي حركة توافقية بسيطة، عندما يكون الجسم في نقاط أطراف الحركة، تكون سرعته صفرًا ولكن تسارعه يكون أقصى ما يمكن. ويحدث هذا كل ثانية منذ لحظة بدء الحركة.
يوضح الرسم البياني رقم 1 الحركة الرأسية. عندما يصل الجسم إلى قمة الارتفاع فإن سرعة الجسم تكون صفرًا، ولكن تسارع الجسم يكون دائمًا g.
حتى لو توقف الجسم للحظة..
בגרף 1 מתוארת תנועה אנכית , בכל פעם שהגוף מגיע לנקודת שיא הגובה מהירות הגוף אפס, אך תאוצת הגוף היא תמיד g
גם כאשר הגוף נעצר רגעית.
يتم تعريف التسارع باستخدام السرعة وفقًا لـ : «math xmlns=¨http://www.w3.org/1998/Math/MathML¨»«mi mathvariant=¨bold¨ mathcolor=¨#FF0000¨»a«/mi»«mo mathvariant=¨bold¨ mathcolor=¨#FF0000¨»=«/mo»«mfrac mathcolor=¨#FF0000¨»«mrow»«mo mathvariant=¨bold¨»§#8710;«/mo»«mi mathvariant=¨bold¨»V«/mi»«/mrow»«mrow»«mo mathvariant=¨bold¨»§#8710;«/mo»«mi mathvariant=¨bold¨»t«/mi»«/mrow»«/mfrac»«/math»
ولكن حتى عندما لا توجد سرعة، يمكن أن يكون هناك تسارع، لأن التسارع لا يعتمد على السرعة ولكن على التغير في السرعة!!!
سأخبرك بمثل...
لتحقيق الربح في سوق الأوراق المالية، عليك شراء الأسهم عندما تكون قيمتها منخفضة وبيعها عندما تكون قيمتها مرتفعة.
تعتمد الربحية على التغير في قيمة السهم وليس سعر السهم. قد يكون السهم ذو قيمة كبيرة من المال ولكنه ليس مربحًا. ربما يكون الأمر ذو قيمة قليلة، لكنه مربح.
لنفترض أن شخصًا ما اشترى سهمًا بقيمة سالبة (ولنفترض أن هذا ممكن)، واستمر السهم في الارتفاع، حتى وصلت قيمة السهم في أحد الأيام إلى الصفر.
إن كون قيمة السهم تساوي صفرًا لا يعني أن ربحية السهم تساوي صفرًا. إن ربحية السهم لا تعتمد على قيمة السهم بل على التغير في قيمة السهم.
وبالمثل، يعتمد التسارع على التغير في السرعة وليس السرعة، حتى عندما تكون السرعة صفرًا، لا يزال من الممكن أن يكون هناك تسارع. لأن التسارع يعتمد على التغير في السرعة وليس السرعة.
«math xmlns=¨http://www.w3.org/1998/Math/MathML¨»«mi mathvariant=¨bold¨ mathcolor=¨#FF0000¨»a«/mi»«mo mathvariant=¨bold¨ mathcolor=¨#FF0000¨»=«/mo»«mfrac mathcolor=¨#FF0000¨»«mrow»«mo mathvariant=¨bold¨»§#8710;«/mo»«mi mathvariant=¨bold¨»V«/mi»«/mrow»«mrow»«mo mathvariant=¨bold¨»§#8710;«/mo»«mi mathvariant=¨bold¨»t«/mi»«/mrow»«/mfrac»«/math»
אך גם כאשר אין מהירות יכולה להיות תאוצה , כי התאוצה לא תלויה במהירות אלא בשינוי המהירות!!!
אמשול לכם משל...
כדי להרוויח בבורסה צריך לקנות מניות כאשר ערכם קטן ולמכור אותם כאשר ערכם גדול.
הרווחיות תלויה בשינוי בערך המניה ולא בערך המניה. יכול להיות שמניה שווה הרבה מאוד כסף אך היא לא רווחית . יכול להיות שהיא שווה מעט אך היא רווחית.
נניח שמשהו רכש מניה בערך שלילי (ונניח שזה אפשרי) , והמניה כל הזמן עלתה , עד שיום אחד ערך המניה הגיע לאפס.
העובדה שערך המניה שווה לאפס לא אומרת שרווחיות המניה היא אפס. רווחיות המניה לא תלויה בערך המניה אלא בשינוי בערך המניה.
באופן דומה , התאוצה תלויה בשינוי במהירות ולא במהירות , גם כאשר המהירות שווה אפס יכול להיות שתהיה תאוצה. מכיוון שהתאוצה תלויה בשינוי במהירות ולא במהירות.
______________________________________________________________________________________