______________________________________________________________________________________
...
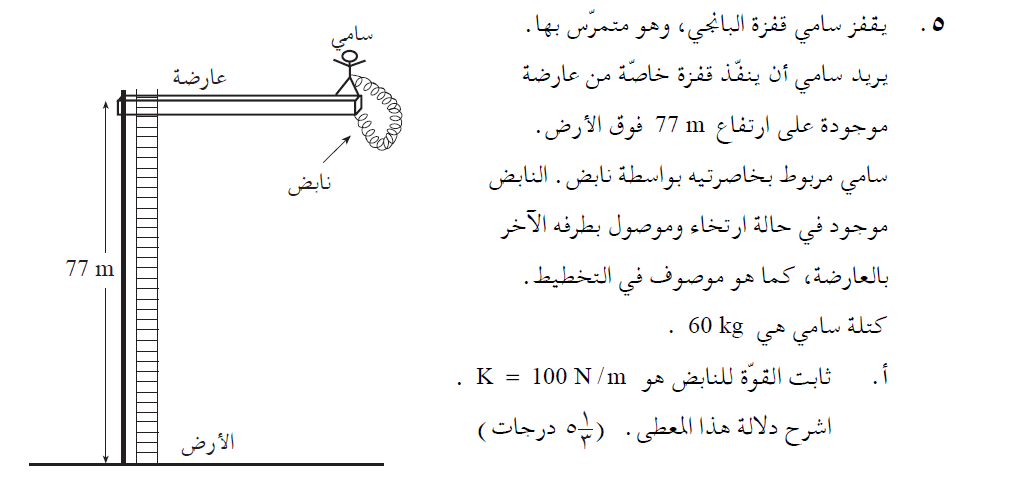
ثابت النابض هو الذي يحدد صلابة النابض؛ يصف مقدار القوة المطلوبة لتمديد أو ضغط النابض بمتر واحد شرط أن يبقى النابض في مجال مرونته.
لتغيير طول هذا النابض بمسافة متر واحد، يجب تأثير قوة مقدارها 100 نيوتن.
כדי לשנות את אורכו של קפיץ זה במטר אחד יש להפעיל כוח של 100 ניוטון.
ثابت النابض هو الذي يحدد صلابة النابض؛ يصف مقدار القوة المطلوبة لتمديد أو ضغط النابض بمتر واحد شرط أن يبقى النابض في مجال مرونته.
لتغيير طول هذا النابض بمسافة متر واحد، يجب تأثير قوة مقدارها 100 نيوتن.
1. لكل مقدار فيزيائي له معنى. إن فهم معنى المقادير الفيزيائية هو الأساس لفهم التعبيرات والفيزياء بشكل عام.2. من وحدات المقدار الفيزيائي يمكن فهم معنى المقدار الفيزيائي.
وحدات ثابت النابض هو نيوتن لكل متر، وثابت النابض يصف القوة المطلوبة لتمديد النابض. 2. מהיחידות של הגודל הפיזיקלי ,ניתן להבין את המשמעות של הגודל הפיזיקלי .
היחידות של קבוע הקפיץ הן ניוטון למטר , וקבוע הקפיץ מתאר את הכוח הנדרש ל הארכת הקפיץ .
______________________________________________________________________________________

______________________________________________________________________________________
...
طول النابض في حالته المرخية 45 متراً.
اعتبارات الطاقة لإيجاد استطالة النابض. اعتمادًا على الطول النهائي للنابض واستطالته، يمكن حساب طوله في حالة الاسترخاء.
منذ اللحظة التي يقفز فيها سامي حتى يعيده النابض إلى الأعلى، فإن قوة الجاذبية وقوة النابض فقط هما اللذان يعملان على سامي.
هاتين القوتان هما قوتان حافظتان، لذا فإن الطاقة الميكانيكية سوف تُحفظ.
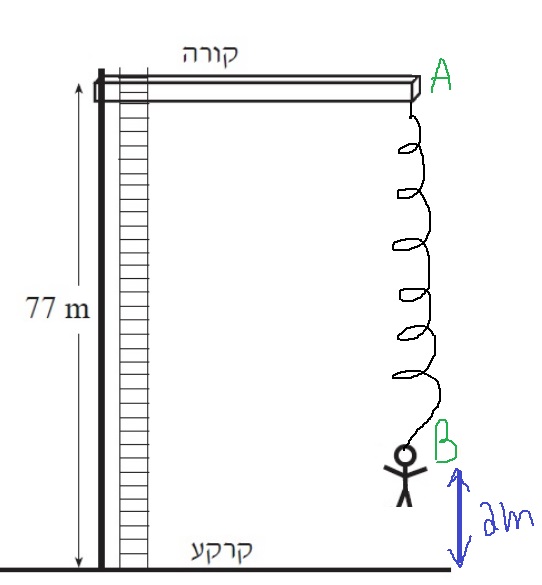
نرسم مخططًا عامًا، نرمز إلى النقطة التي يقفز منها سامي بـ A والنقطة التي يعود منها سامي إلى القمة بـ B.
يتحقق حفظ الطاقة الميكانيكية ، نكتب معادلة حفظ الطاقة، ونحسب الطاقة الوضعية الجاذبية بالنسبة للأرض.
والطاقة الوضعية المرنة بالنسبة للحالة التي يكون فيها النابض مسترخي.
«math xmlns=¨http://www.w3.org/1998/Math/MathML¨»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»§#160;«/mo»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»§#160;«/mo»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»§#160;«/mo»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»§#160;«/mo»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»§#160;«/mo»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»§#160;«/mo»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»§#160;«/mo»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»§#160;«/mo»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»§#160;«/mo»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»§#160;«/mo»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»§#160;«/mo»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»§#160;«/mo»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»§#160;«/mo»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»§#160;«/mo»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»§#160;«/mo»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»§#160;«/mo»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»§#160;«/mo»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»§#160;«/mo»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»§#160;«/mo»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»§#160;«/mo»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»§#160;«/mo»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»§#160;«/mo»«msub»«mi mathvariant=¨bold¨ mathcolor=¨#0000FF¨»E«/mi»«mi mathvariant=¨bold¨ mathcolor=¨#0000FF¨»A«/mi»«/msub»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»=«/mo»«msub»«mi mathvariant=¨bold¨ mathcolor=¨#0000FF¨»E«/mi»«mi mathvariant=¨bold¨ mathcolor=¨#0000FF¨»B«/mi»«/msub»«mspace linebreak=¨newline¨»«/mspace»«msub»«mi mathvariant=¨bold¨ mathcolor=¨#0000FF¨»E«/mi»«msub mathcolor=¨#0000FF¨»«mi mathvariant=¨bold¨»K«/mi»«mi mathvariant=¨bold¨»A«/mi»«/msub»«/msub»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»+«/mo»«msub»«mi mathvariant=¨bold¨ mathcolor=¨#0000FF¨»U«/mi»«msub mathcolor=¨#0000FF¨»«mi mathvariant=¨bold¨»SP«/mi»«mi mathvariant=¨bold¨»A«/mi»«/msub»«/msub»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»+«/mo»«msub»«mi mathvariant=¨bold¨ mathcolor=¨#0000FF¨»U«/mi»«msub mathcolor=¨#0000FF¨»«mi mathvariant=¨bold¨»G«/mi»«mi mathvariant=¨bold¨»A«/mi»«/msub»«/msub»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»=«/mo»«msub»«mi mathvariant=¨bold¨ mathcolor=¨#0000FF¨»E«/mi»«msub mathcolor=¨#0000FF¨»«mi mathvariant=¨bold¨»K«/mi»«mi mathvariant=¨bold¨»A«/mi»«/msub»«/msub»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»+«/mo»«msub»«mi mathvariant=¨bold¨ mathcolor=¨#0000FF¨»U«/mi»«msub mathcolor=¨#0000FF¨»«mi mathvariant=¨bold¨»SP«/mi»«mi mathvariant=¨bold¨»A«/mi»«/msub»«/msub»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»+«/mo»«msub»«mi mathvariant=¨bold¨ mathcolor=¨#0000FF¨»U«/mi»«msub mathcolor=¨#0000FF¨»«mi mathvariant=¨bold¨»G«/mi»«mi mathvariant=¨bold¨»A«/mi»«/msub»«/msub»«/math»
لنفترض أن السرعة الابتدائية لسامي في النقطة A هي صفر، وبالتالي فإن الطاقة الحركية لسامي في النقطة A هي صفر.
في لحظة القفزة، يكون النابض في حالة استرخاء. لا يوجد للنابض طاقة وضع مرنة عندما يكون سامي في النقطة A.
عندما يصل سامي إلى النقطة B، تنخفض سرعته إلى الصفر ولا يكون له طاقة حركية في هذه النقطة.
نكتب معادلة حفظ الطاقة وفقًا لذلك:
«math xmlns=¨http://www.w3.org/1998/Math/MathML¨»«menclose mathcolor=¨#0000FF¨ notation=¨updiagonalstrike¨»«msub»«mi mathvariant=¨bold¨»E«/mi»«msub»«mi mathvariant=¨bold¨»K«/mi»«mi mathvariant=¨bold¨»A«/mi»«/msub»«/msub»«/menclose»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»+«/mo»«menclose mathcolor=¨#0000FF¨ notation=¨updiagonalstrike¨»«msub»«mi mathvariant=¨bold¨»U«/mi»«msub»«mi mathvariant=¨bold¨»SP«/mi»«mi mathvariant=¨bold¨»A«/mi»«/msub»«/msub»«/menclose»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»+«/mo»«msub»«mi mathvariant=¨bold¨ mathcolor=¨#0000FF¨»U«/mi»«msub mathcolor=¨#0000FF¨»«mi mathvariant=¨bold¨»G«/mi»«mi mathvariant=¨bold¨»A«/mi»«/msub»«/msub»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»=«/mo»«menclose mathcolor=¨#0000FF¨ notation=¨updiagonalstrike¨»«msub»«mi mathvariant=¨bold¨»E«/mi»«msub»«mi mathvariant=¨bold¨»K«/mi»«mi mathvariant=¨bold¨»B«/mi»«/msub»«/msub»«/menclose»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»+«/mo»«msub»«mi mathvariant=¨bold¨ mathcolor=¨#0000FF¨»U«/mi»«msub mathcolor=¨#0000FF¨»«mi mathvariant=¨bold¨»SP«/mi»«mi mathvariant=¨bold¨»B«/mi»«/msub»«/msub»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»+«/mo»«msub»«mi mathvariant=¨bold¨ mathcolor=¨#0000FF¨»U«/mi»«msub mathcolor=¨#0000FF¨»«mi mathvariant=¨bold¨»G«/mi»«mi mathvariant=¨bold¨»B«/mi»«/msub»«/msub»«mspace linebreak=¨newline¨»«/mspace»«mspace linebreak=¨newline¨»«/mspace»«mi mathvariant=¨bold¨ mathcolor=¨#0000FF¨»m«/mi»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»§#183;«/mo»«mi mathvariant=¨bold¨ mathcolor=¨#0000FF¨»g«/mi»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»§#183;«/mo»«msub»«mi mathvariant=¨bold¨ mathcolor=¨#0000FF¨»h«/mi»«mi mathvariant=¨bold¨ mathcolor=¨#0000FF¨»A«/mi»«/msub»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»=«/mo»«mfrac mathcolor=¨#0000FF¨»«mn mathvariant=¨bold¨»1«/mn»«mn mathvariant=¨bold¨»2«/mn»«/mfrac»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»§#183;«/mo»«mi mathvariant=¨bold¨ mathcolor=¨#0000FF¨»K«/mi»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»§#183;«/mo»«msup»«mrow mathcolor=¨#0000FF¨»«mo mathvariant=¨bold¨»(«/mo»«mo mathvariant=¨bold¨»§#8710;«/mo»«mi mathvariant=¨bold¨»L«/mi»«mo mathvariant=¨bold¨»)«/mo»«/mrow»«mn mathvariant=¨bold¨ mathcolor=¨#0000FF¨»2«/mn»«/msup»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»+«/mo»«mi mathvariant=¨bold¨ mathcolor=¨#0000FF¨»m«/mi»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»§#183;«/mo»«mi mathvariant=¨bold¨ mathcolor=¨#0000FF¨»g«/mi»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»§#183;«/mo»«msub»«mi mathvariant=¨bold¨ mathcolor=¨#0000FF¨»h«/mi»«mi mathvariant=¨bold¨ mathcolor=¨#0000FF¨»B«/mi»«/msub»«mspace linebreak=¨newline¨»«/mspace»«mspace linebreak=¨newline¨»«/mspace»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»§#8710;«/mo»«mi mathvariant=¨bold¨ mathcolor=¨#0000FF¨»L«/mi»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»=«/mo»«msqrt mathcolor=¨#0000FF¨»«mfrac»«mrow»«mn mathvariant=¨bold¨»2«/mn»«mo mathvariant=¨bold¨»§#183;«/mo»«mi mathvariant=¨bold¨»m«/mi»«mo mathvariant=¨bold¨»§#183;«/mo»«mi mathvariant=¨bold¨»g«/mi»«mo mathvariant=¨bold¨»§#183;«/mo»«mrow»«mo mathvariant=¨bold¨»(«/mo»«msub»«mi mathvariant=¨bold¨»h«/mi»«mi mathvariant=¨bold¨»A«/mi»«/msub»«mo mathvariant=¨bold¨»-«/mo»«msub»«mi mathvariant=¨bold¨»h«/mi»«mi mathvariant=¨bold¨»B«/mi»«/msub»«mo mathvariant=¨bold¨»)«/mo»«/mrow»«/mrow»«mi mathvariant=¨bold¨»K«/mi»«/mfrac»«/msqrt»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»=«/mo»«msqrt mathcolor=¨#0000FF¨»«mfrac»«mrow»«mn mathvariant=¨bold¨»2«/mn»«mo mathvariant=¨bold¨»§#183;«/mo»«mn mathvariant=¨bold¨»60«/mn»«mo mathvariant=¨bold¨»§#183;«/mo»«mn mathvariant=¨bold¨»10«/mn»«mo mathvariant=¨bold¨»§#183;«/mo»«mrow»«mo mathvariant=¨bold¨»(«/mo»«mn mathvariant=¨bold¨»77«/mn»«mo mathvariant=¨bold¨»-«/mo»«mn mathvariant=¨bold¨»2«/mn»«mo mathvariant=¨bold¨»)«/mo»«/mrow»«/mrow»«mn mathvariant=¨bold¨»100«/mn»«/mfrac»«/msqrt»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»=«/mo»«msqrt mathcolor=¨#0000FF¨»«mn mathvariant=¨bold¨»900«/mn»«/msqrt»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»§#160;«/mo»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»=«/mo»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»§#160;«/mo»«mn mathvariant=¨bold¨ mathcolor=¨#0000FF¨»30«/mn»«mi mathvariant=¨bold¨ mathcolor=¨#0000FF¨»m«/mi»«/math»
الطول الكلي للنابض عندما يكون سامي في النقطة B هو 75 مترًا. يبلغ طول استطالة النابض 30 متراً.
ولذلك طول النابض في حالته المسترخية 45 متراً.
שני כוחות אלו הם כוחות משמרים , לכן האנרגיה המכנית נשמרת.
נערוך תרשים כללי , נסמן את הנקודה ממנה יצחק קופץ ב A ואת הנקודה בה יצחק חוזר למעלה ב B.
האנרגיה המכנית נשמרת, נכתוב את משוואת שימור האנרגיה , נתאר את האנרגיה הפוטנצאילית כובדית ביחס לקרקע.
ואת האנרגיה הפוטנציאלית אלסטית ביחס למצב בו הקפיץ רפוי.
«math xmlns=¨http://www.w3.org/1998/Math/MathML¨»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»§#160;«/mo»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»§#160;«/mo»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»§#160;«/mo»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»§#160;«/mo»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»§#160;«/mo»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»§#160;«/mo»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»§#160;«/mo»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»§#160;«/mo»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»§#160;«/mo»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»§#160;«/mo»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»§#160;«/mo»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»§#160;«/mo»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»§#160;«/mo»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»§#160;«/mo»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»§#160;«/mo»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»§#160;«/mo»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»§#160;«/mo»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»§#160;«/mo»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»§#160;«/mo»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»§#160;«/mo»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»§#160;«/mo»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»§#160;«/mo»«msub»«mi mathvariant=¨bold¨ mathcolor=¨#0000FF¨»E«/mi»«mi mathvariant=¨bold¨ mathcolor=¨#0000FF¨»A«/mi»«/msub»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»=«/mo»«msub»«mi mathvariant=¨bold¨ mathcolor=¨#0000FF¨»E«/mi»«mi mathvariant=¨bold¨ mathcolor=¨#0000FF¨»B«/mi»«/msub»«mspace linebreak=¨newline¨»«/mspace»«msub»«mi mathvariant=¨bold¨ mathcolor=¨#0000FF¨»E«/mi»«msub mathcolor=¨#0000FF¨»«mi mathvariant=¨bold¨»K«/mi»«mi mathvariant=¨bold¨»A«/mi»«/msub»«/msub»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»+«/mo»«msub»«mi mathvariant=¨bold¨ mathcolor=¨#0000FF¨»U«/mi»«msub mathcolor=¨#0000FF¨»«mi mathvariant=¨bold¨»SP«/mi»«mi mathvariant=¨bold¨»A«/mi»«/msub»«/msub»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»+«/mo»«msub»«mi mathvariant=¨bold¨ mathcolor=¨#0000FF¨»U«/mi»«msub mathcolor=¨#0000FF¨»«mi mathvariant=¨bold¨»G«/mi»«mi mathvariant=¨bold¨»A«/mi»«/msub»«/msub»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»=«/mo»«msub»«mi mathvariant=¨bold¨ mathcolor=¨#0000FF¨»E«/mi»«msub mathcolor=¨#0000FF¨»«mi mathvariant=¨bold¨»K«/mi»«mi mathvariant=¨bold¨»A«/mi»«/msub»«/msub»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»+«/mo»«msub»«mi mathvariant=¨bold¨ mathcolor=¨#0000FF¨»U«/mi»«msub mathcolor=¨#0000FF¨»«mi mathvariant=¨bold¨»SP«/mi»«mi mathvariant=¨bold¨»A«/mi»«/msub»«/msub»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»+«/mo»«msub»«mi mathvariant=¨bold¨ mathcolor=¨#0000FF¨»U«/mi»«msub mathcolor=¨#0000FF¨»«mi mathvariant=¨bold¨»G«/mi»«mi mathvariant=¨bold¨»A«/mi»«/msub»«/msub»«/math»
נניח כי מהירותו ההתחלתית של יצחק בנקודה A היא אפס , לכן האנרגיה הקינטית של יצחק בנקודה A היא אפס.
ברגע הקפיצה הקפיץ רפוי אין אנרגיה פוטנציאלית אלסטית לקפיץ כאשר יצחק נימצא בנקודה A.
כאשר יצחק מגיע לנקודה B מהירותו מתאפסת אין לו אנרגיה קינטית בנקודה זו.
נכתוב בהתאם את משוואת שימור האנרגיה:
«math xmlns=¨http://www.w3.org/1998/Math/MathML¨»«menclose mathcolor=¨#0000FF¨ notation=¨updiagonalstrike¨»«msub»«mi mathvariant=¨bold¨»E«/mi»«msub»«mi mathvariant=¨bold¨»K«/mi»«mi mathvariant=¨bold¨»A«/mi»«/msub»«/msub»«/menclose»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»+«/mo»«menclose mathcolor=¨#0000FF¨ notation=¨updiagonalstrike¨»«msub»«mi mathvariant=¨bold¨»U«/mi»«msub»«mi mathvariant=¨bold¨»SP«/mi»«mi mathvariant=¨bold¨»A«/mi»«/msub»«/msub»«/menclose»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»+«/mo»«msub»«mi mathvariant=¨bold¨ mathcolor=¨#0000FF¨»U«/mi»«msub mathcolor=¨#0000FF¨»«mi mathvariant=¨bold¨»G«/mi»«mi mathvariant=¨bold¨»A«/mi»«/msub»«/msub»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»=«/mo»«menclose mathcolor=¨#0000FF¨ notation=¨updiagonalstrike¨»«msub»«mi mathvariant=¨bold¨»E«/mi»«msub»«mi mathvariant=¨bold¨»K«/mi»«mi mathvariant=¨bold¨»B«/mi»«/msub»«/msub»«/menclose»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»+«/mo»«msub»«mi mathvariant=¨bold¨ mathcolor=¨#0000FF¨»U«/mi»«msub mathcolor=¨#0000FF¨»«mi mathvariant=¨bold¨»SP«/mi»«mi mathvariant=¨bold¨»B«/mi»«/msub»«/msub»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»+«/mo»«msub»«mi mathvariant=¨bold¨ mathcolor=¨#0000FF¨»U«/mi»«msub mathcolor=¨#0000FF¨»«mi mathvariant=¨bold¨»G«/mi»«mi mathvariant=¨bold¨»B«/mi»«/msub»«/msub»«mspace linebreak=¨newline¨»«/mspace»«mspace linebreak=¨newline¨»«/mspace»«mi mathvariant=¨bold¨ mathcolor=¨#0000FF¨»m«/mi»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»§#183;«/mo»«mi mathvariant=¨bold¨ mathcolor=¨#0000FF¨»g«/mi»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»§#183;«/mo»«msub»«mi mathvariant=¨bold¨ mathcolor=¨#0000FF¨»h«/mi»«mi mathvariant=¨bold¨ mathcolor=¨#0000FF¨»A«/mi»«/msub»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»=«/mo»«mfrac mathcolor=¨#0000FF¨»«mn mathvariant=¨bold¨»1«/mn»«mn mathvariant=¨bold¨»2«/mn»«/mfrac»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»§#183;«/mo»«mi mathvariant=¨bold¨ mathcolor=¨#0000FF¨»K«/mi»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»§#183;«/mo»«msup»«mrow mathcolor=¨#0000FF¨»«mo mathvariant=¨bold¨»(«/mo»«mo mathvariant=¨bold¨»§#8710;«/mo»«mi mathvariant=¨bold¨»L«/mi»«mo mathvariant=¨bold¨»)«/mo»«/mrow»«mn mathvariant=¨bold¨ mathcolor=¨#0000FF¨»2«/mn»«/msup»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»+«/mo»«mi mathvariant=¨bold¨ mathcolor=¨#0000FF¨»m«/mi»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»§#183;«/mo»«mi mathvariant=¨bold¨ mathcolor=¨#0000FF¨»g«/mi»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»§#183;«/mo»«msub»«mi mathvariant=¨bold¨ mathcolor=¨#0000FF¨»h«/mi»«mi mathvariant=¨bold¨ mathcolor=¨#0000FF¨»B«/mi»«/msub»«mspace linebreak=¨newline¨»«/mspace»«mspace linebreak=¨newline¨»«/mspace»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»§#8710;«/mo»«mi mathvariant=¨bold¨ mathcolor=¨#0000FF¨»L«/mi»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»=«/mo»«msqrt mathcolor=¨#0000FF¨»«mfrac»«mrow»«mn mathvariant=¨bold¨»2«/mn»«mo mathvariant=¨bold¨»§#183;«/mo»«mi mathvariant=¨bold¨»m«/mi»«mo mathvariant=¨bold¨»§#183;«/mo»«mi mathvariant=¨bold¨»g«/mi»«mo mathvariant=¨bold¨»§#183;«/mo»«mrow»«mo mathvariant=¨bold¨»(«/mo»«msub»«mi mathvariant=¨bold¨»h«/mi»«mi mathvariant=¨bold¨»A«/mi»«/msub»«mo mathvariant=¨bold¨»-«/mo»«msub»«mi mathvariant=¨bold¨»h«/mi»«mi mathvariant=¨bold¨»B«/mi»«/msub»«mo mathvariant=¨bold¨»)«/mo»«/mrow»«/mrow»«mi mathvariant=¨bold¨»K«/mi»«/mfrac»«/msqrt»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»=«/mo»«msqrt mathcolor=¨#0000FF¨»«mfrac»«mrow»«mn mathvariant=¨bold¨»2«/mn»«mo mathvariant=¨bold¨»§#183;«/mo»«mn mathvariant=¨bold¨»60«/mn»«mo mathvariant=¨bold¨»§#183;«/mo»«mn mathvariant=¨bold¨»10«/mn»«mo mathvariant=¨bold¨»§#183;«/mo»«mrow»«mo mathvariant=¨bold¨»(«/mo»«mn mathvariant=¨bold¨»77«/mn»«mo mathvariant=¨bold¨»-«/mo»«mn mathvariant=¨bold¨»2«/mn»«mo mathvariant=¨bold¨»)«/mo»«/mrow»«/mrow»«mn mathvariant=¨bold¨»100«/mn»«/mfrac»«/msqrt»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»=«/mo»«msqrt mathcolor=¨#0000FF¨»«mn mathvariant=¨bold¨»900«/mn»«/msqrt»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»§#160;«/mo»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»=«/mo»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»§#160;«/mo»«mn mathvariant=¨bold¨ mathcolor=¨#0000FF¨»30«/mn»«mi mathvariant=¨bold¨ mathcolor=¨#0000FF¨»m«/mi»«/math»
האורך הכולל של הקפיץ כאשר יצחק נמצא בנקודה B הוא 75 מטר . התארכות הקפיץ 30 מטר .
לכן אורכו של הקפיץ במצבו הרפוי הוא 45 מטרים.
1. مكتوب في السؤال يقول أن سامي يسقط سقوطا حرا، أي حركة تحت تأثير الجاذبية هي سقوط حر.
حتى لو قفز إلى أسفل أو إلى أعلى، فهو لا يزال سقوطًا حرًا. ومن المفترض أن القصد هو أنه بدأ التحرك من السكون.
2. يمكن وصف الطاقة الوضعية الجاذبية بالنسبة لأي مستوى مرجعي.
تتعلق الطاقة الوضعية المرنة باستطالة النابض بالنسبة لحالته المرخية.
3. لا يحدد السؤال في مكان ارتخاء النابض، في وصف قوة النابض وطاقة الوضع المرنة
من الأفضل استخدام الاستطالة بدلاً من الموقع بالنسبة للمحور (مثل القوة المعيدة).
גם אם הוא קפץ למטה או למעלה זו עדיין נפילה חופשית. יש להניח שהכוונה היא שהוא התחיל לנוע ממנוחה.
2. אנרגיה פוטנציאלית כובדית אפשר לתאר ביחס לכל מישור ייחוס נבחר.
אנרגיה פוטנצאילית אלסטית תלויה בהתארכות הקפיץ ביחס למצבו הרפוי.
3. בשאלה לא נתון המקום בו הקפיץ רפוי , בתיאור כוח הקפיץ והאנרגיה הפוטנציאלית אלסטית
עדיף להשתמש בהתארכות ולא במיקום ביחס לציר (כמו כוח מחזיר).
______________________________________________________________________________________

______________________________________________________________________________________
...
القوة المحصلة المؤثرة على سامي عندما يكون على ارتفاع 2 متر فوق سطح الأرض هي 2400 نيوتن وتتجه إلى الأعلى.
رسم مخطط القوى وإيجاد القوة المحصلة.
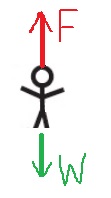
عندما يكون سامي في النقطة B، فإن قوة الجاذبية تؤثر عليه إلى الأسفل، وقوة النابض تؤثر عليه إلى الأعلى.
نرسم مخطط القوى التي تعمل على سامي:
نجد القوة المحصلة المؤثرة على سامي في هذا الموقف:
«math xmlns=¨http://www.w3.org/1998/Math/MathML¨»«mi mathvariant=¨bold¨ mathcolor=¨#0000FF¨»§#931;F«/mi»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»=«/mo»«mi mathvariant=¨bold¨ mathcolor=¨#0000FF¨»F«/mi»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»-«/mo»«mi mathvariant=¨bold¨ mathcolor=¨#0000FF¨»mg«/mi»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»=«/mo»«mi mathvariant=¨bold¨ mathcolor=¨#0000FF¨»K«/mi»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»§#183;«/mo»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»§#8710;«/mo»«mi mathvariant=¨bold¨ mathcolor=¨#0000FF¨»L«/mi»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»-«/mo»«mi mathvariant=¨bold¨ mathcolor=¨#0000FF¨»mg«/mi»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»=«/mo»«mn mathvariant=¨bold¨ mathcolor=¨#0000FF¨»100«/mn»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»§#183;«/mo»«mn mathvariant=¨bold¨ mathcolor=¨#0000FF¨»30«/mn»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»-«/mo»«mn mathvariant=¨bold¨ mathcolor=¨#0000FF¨»60«/mn»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»§#183;«/mo»«mn mathvariant=¨bold¨ mathcolor=¨#0000FF¨»10«/mn»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»=«/mo»«mn mathvariant=¨bold¨ mathcolor=¨#0000FF¨»2400«/mn»«mi mathvariant=¨bold¨ mathcolor=¨#0000FF¨»N«/mi»«mspace linebreak=¨newline¨»«/mspace»«/math»
القوة المحصلة المؤثرة على سامي عندما يكون على ارتفاع 2 متر فوق سطح الأرض هي 2400 نيوتن وتتجه إلى الأعلى.
נערוך תרשים כוחות על יצחק:
נמצא את הכוח השקול הפועל על יצחק במצב זה:
«math xmlns=¨http://www.w3.org/1998/Math/MathML¨»«mi mathvariant=¨bold¨ mathcolor=¨#0000FF¨»§#931;F«/mi»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»=«/mo»«mi mathvariant=¨bold¨ mathcolor=¨#0000FF¨»F«/mi»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»-«/mo»«mi mathvariant=¨bold¨ mathcolor=¨#0000FF¨»mg«/mi»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»=«/mo»«mi mathvariant=¨bold¨ mathcolor=¨#0000FF¨»K«/mi»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»§#183;«/mo»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»§#8710;«/mo»«mi mathvariant=¨bold¨ mathcolor=¨#0000FF¨»L«/mi»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»-«/mo»«mi mathvariant=¨bold¨ mathcolor=¨#0000FF¨»mg«/mi»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»=«/mo»«mn mathvariant=¨bold¨ mathcolor=¨#0000FF¨»100«/mn»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»§#183;«/mo»«mn mathvariant=¨bold¨ mathcolor=¨#0000FF¨»30«/mn»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»-«/mo»«mn mathvariant=¨bold¨ mathcolor=¨#0000FF¨»60«/mn»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»§#183;«/mo»«mn mathvariant=¨bold¨ mathcolor=¨#0000FF¨»10«/mn»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»=«/mo»«mn mathvariant=¨bold¨ mathcolor=¨#0000FF¨»2400«/mn»«mi mathvariant=¨bold¨ mathcolor=¨#0000FF¨»N«/mi»«mspace linebreak=¨newline¨»«/mspace»«/math»
1. عندما يصل سامي إلى ارتفاع 2 متر فوق الأرض، فإنه يتوقف للحظة. القوة المحصلة عليه لا تساوي الصفر.
2. بعد التوقف، يتحرك سامي إلى الأعلى، وبالتالي فإن القوة المحصلة تعمل إلى الأعلى في لحظة التوقف.
2. לאחר העצירה יצחק נע כלפי מעלה ,מכאן שהכוח השקול פועל ברגע העצירה כלפי מעלה.
______________________________________________________________________________________

______________________________________________________________________________________
...
عندما تكون القوة المحصلة المؤثرة على سامي تساوي صفرًا، فإنه يكون على ارتفاع 26 مترًا فوق سطح الأرض.
إيجاد استطالة النابض في هذا الوضع من معادلة الحركة. حسب الطول النهائي وارتفاع العارضة، يمكن إيجاد الارتفاع المطلوب.
سنكتب معادلة الحركة، ونعبر منها عن استطالة النابض من حالة الاسترخاء: «math xmlns=¨http://www.w3.org/1998/Math/MathML¨»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»§#8710;«/mo»«mi mathvariant=¨bold¨ mathcolor=¨#0000FF¨»L«/mi»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»`«/mo»«/math» عندما تكون محصلة القوى المؤثرة على سامي يساوي صفرًا.
«math xmlns=¨http://www.w3.org/1998/Math/MathML¨»«msub»«mi mathvariant=¨bold¨ mathcolor=¨#0000FF¨»§#931;F«/mi»«mi mathvariant=¨bold¨ mathcolor=¨#0000FF¨»Y«/mi»«/msub»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»=«/mo»«mn mathvariant=¨bold¨ mathcolor=¨#0000FF¨»0«/mn»«mspace linebreak=¨newline¨»«/mspace»«mi mathvariant=¨bold¨ mathcolor=¨#0000FF¨»F«/mi»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»-«/mo»«mi mathvariant=¨bold¨ mathcolor=¨#0000FF¨»m«/mi»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»§#183;«/mo»«mi mathvariant=¨bold¨ mathcolor=¨#0000FF¨»g«/mi»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»=«/mo»«mn mathvariant=¨bold¨ mathcolor=¨#0000FF¨»0«/mn»«mspace linebreak=¨newline¨»«/mspace»«mi mathvariant=¨bold¨ mathcolor=¨#0000FF¨»K«/mi»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»§#183;«/mo»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»§#8710;«/mo»«mi mathvariant=¨bold¨ mathcolor=¨#0000FF¨»L«/mi»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»`«/mo»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»-«/mo»«mi mathvariant=¨bold¨ mathcolor=¨#0000FF¨»m«/mi»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»§#183;«/mo»«mi mathvariant=¨bold¨ mathcolor=¨#0000FF¨»g«/mi»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»=«/mo»«mn mathvariant=¨bold¨ mathcolor=¨#0000FF¨»0«/mn»«mspace linebreak=¨newline¨»«/mspace»«mi mathvariant=¨bold¨ mathcolor=¨#0000FF¨»K«/mi»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»§#183;«/mo»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»§#8710;«/mo»«mi mathvariant=¨bold¨ mathcolor=¨#0000FF¨»L«/mi»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»`«/mo»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»=«/mo»«mi mathvariant=¨bold¨ mathcolor=¨#0000FF¨»m«/mi»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»§#183;«/mo»«mi mathvariant=¨bold¨ mathcolor=¨#0000FF¨»g«/mi»«mspace linebreak=¨newline¨»«/mspace»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»§#8710;«/mo»«mi mathvariant=¨bold¨ mathcolor=¨#0000FF¨»L«/mi»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»`«/mo»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»=«/mo»«mfrac mathcolor=¨#0000FF¨»«mrow»«mi mathvariant=¨bold¨»m«/mi»«mo mathvariant=¨bold¨»§#183;«/mo»«mi mathvariant=¨bold¨»g«/mi»«/mrow»«mi mathvariant=¨bold¨»K«/mi»«/mfrac»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»=«/mo»«mfrac mathcolor=¨#0000FF¨»«mrow»«mn mathvariant=¨bold¨»60«/mn»«mo mathvariant=¨bold¨»§#183;«/mo»«mn mathvariant=¨bold¨»10«/mn»«/mrow»«mn mathvariant=¨bold¨»100«/mn»«/mfrac»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»=«/mo»«mn mathvariant=¨bold¨ mathcolor=¨#0000FF¨»6«/mn»«mi mathvariant=¨bold¨ mathcolor=¨#0000FF¨»m«/mi»«/math»
يستطيل النابض ستة أمتار من حالة الاسترخاء. يبلغ طول النابض في حالة الاسترخاء 45 متراً.
الطول الكلي للنابض عندما تكون القوة المحصلة المؤثرة على سامي تساوي صفرًا هو 51 مترًا.
يبلغ ارتفاع العارضة عن الأرض 77 متراً، بينما يبلغ طول النابض 51 متراً. ارتفاع سامي عن الأرض هو 26 متراً.
שקול הכוחות הפועלים על יצחק שווה לאפס.
«math xmlns=¨http://www.w3.org/1998/Math/MathML¨»«msub»«mi mathvariant=¨bold¨ mathcolor=¨#0000FF¨»§#931;F«/mi»«mi mathvariant=¨bold¨ mathcolor=¨#0000FF¨»Y«/mi»«/msub»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»=«/mo»«mn mathvariant=¨bold¨ mathcolor=¨#0000FF¨»0«/mn»«mspace linebreak=¨newline¨»«/mspace»«mi mathvariant=¨bold¨ mathcolor=¨#0000FF¨»F«/mi»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»-«/mo»«mi mathvariant=¨bold¨ mathcolor=¨#0000FF¨»m«/mi»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»§#183;«/mo»«mi mathvariant=¨bold¨ mathcolor=¨#0000FF¨»g«/mi»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»=«/mo»«mn mathvariant=¨bold¨ mathcolor=¨#0000FF¨»0«/mn»«mspace linebreak=¨newline¨»«/mspace»«mi mathvariant=¨bold¨ mathcolor=¨#0000FF¨»K«/mi»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»§#183;«/mo»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»§#8710;«/mo»«mi mathvariant=¨bold¨ mathcolor=¨#0000FF¨»L«/mi»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»`«/mo»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»-«/mo»«mi mathvariant=¨bold¨ mathcolor=¨#0000FF¨»m«/mi»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»§#183;«/mo»«mi mathvariant=¨bold¨ mathcolor=¨#0000FF¨»g«/mi»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»=«/mo»«mn mathvariant=¨bold¨ mathcolor=¨#0000FF¨»0«/mn»«mspace linebreak=¨newline¨»«/mspace»«mi mathvariant=¨bold¨ mathcolor=¨#0000FF¨»K«/mi»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»§#183;«/mo»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»§#8710;«/mo»«mi mathvariant=¨bold¨ mathcolor=¨#0000FF¨»L«/mi»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»`«/mo»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»=«/mo»«mi mathvariant=¨bold¨ mathcolor=¨#0000FF¨»m«/mi»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»§#183;«/mo»«mi mathvariant=¨bold¨ mathcolor=¨#0000FF¨»g«/mi»«mspace linebreak=¨newline¨»«/mspace»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»§#8710;«/mo»«mi mathvariant=¨bold¨ mathcolor=¨#0000FF¨»L«/mi»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»`«/mo»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»=«/mo»«mfrac mathcolor=¨#0000FF¨»«mrow»«mi mathvariant=¨bold¨»m«/mi»«mo mathvariant=¨bold¨»§#183;«/mo»«mi mathvariant=¨bold¨»g«/mi»«/mrow»«mi mathvariant=¨bold¨»K«/mi»«/mfrac»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»=«/mo»«mfrac mathcolor=¨#0000FF¨»«mrow»«mn mathvariant=¨bold¨»60«/mn»«mo mathvariant=¨bold¨»§#183;«/mo»«mn mathvariant=¨bold¨»10«/mn»«/mrow»«mn mathvariant=¨bold¨»100«/mn»«/mfrac»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»=«/mo»«mn mathvariant=¨bold¨ mathcolor=¨#0000FF¨»6«/mn»«mi mathvariant=¨bold¨ mathcolor=¨#0000FF¨»m«/mi»«/math»
הקפיץ מתארך שישה מטרים ממצבו הרפוי . אורך הקפיץ במצב הרפוי הוא 45 מטרים.
סה"כ אורכו של הקפיץ כאשר שקול הכוחות הפועלים על יצחק הוא אפס הוא 51 מטרים.
גובה הקורה מעל הקרקע הוא 77 מטרים , כאשר אורכו של הקפיץ 51 מטרים גובהו של יצחק מעל פני הקרקע 26 מטרים.
هناك العديد من الأطوال لهذا السؤال:
طول النابض عندما يكون مسترخياً، الاستطالة إلى نقطة نهاية سفلية، الاستطالة إلى النقطة التي يكون فيها محصلة القوة صفراً.
هناك ارتفاع سامي بالنسبة للأرض وارتفاع العارضة.
من الممكن أن تحدث أخطاء في الأطوال، ومن المهم العمل بطريقة منظمة. شيئا فشيئا...
אורך הקפיץ כשהוא רפוי , התארכות עד לנקודת קצה תחתונה, התארכות עד לנקודה בה שקול הכוחות שווה לאפס.
יש את גובה יצחק ביחס לקרקע ואת גובה הקורה.
אפשר לטעות באורכים, חשוב לעבוד בצורה מסודרת. לאט לאט...
______________________________________________________________________________________

______________________________________________________________________________________
...
«math xmlns=¨http://www.w3.org/1998/Math/MathML¨»«mi mathvariant=¨bold¨»t«/mi»«mo mathvariant=¨bold¨»=«/mo»«mn mathvariant=¨bold¨»2«/mn»«mo mathvariant=¨bold¨».«/mo»«mn mathvariant=¨bold¨»43«/mn»«mi mathvariant=¨bold¨»s«/mi»«/math»
يرتفع سامي من أدنى نقطة ويتحرك في اتجاه عمودي. يمكنك استخدام دوال الحركة التوافقية البسيطة.
الزمن المطلوب يساوي زمن الحركة التوافقية البسيطة من نقطة طرف الحركة إلى أخرى.
הזמן המבוקש שווה לזמן תנועה הרמונית פשוטה מנקודת קצה אחת לנקודת קצה שנייה.
منذ اللحظة التي يرتفع فيها سامي من أدنى نقطة، فإنه يتحرك في تذبذبات.
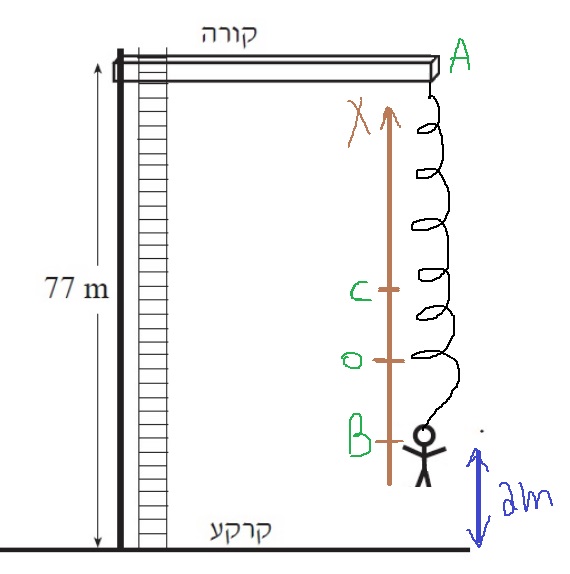
نرسم مخططًا يحتوي على نقطة الطرف العلوية C، ومحور يبدأ من نقطة الاتّزان ويتجه نحو الأعلى.
نكتب تعبيرًا للقوة المحصلة المؤثرة على سامي: «math xmlns=¨http://www.w3.org/1998/Math/MathML¨»«mi mathvariant=¨bold¨ mathcolor=¨#0000FF¨»§#931;F«/mi»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»=«/mo»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»-«/mo»«mi mathvariant=¨bold¨ mathcolor=¨#0000FF¨»K«/mi»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»§#183;«/mo»«mi mathvariant=¨bold¨ mathcolor=¨#0000FF¨»X«/mi»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»-«/mo»«mi mathvariant=¨bold¨ mathcolor=¨#0000FF¨»m«/mi»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»§#183;«/mo»«mi mathvariant=¨bold¨ mathcolor=¨#0000FF¨»g«/mi»«/math» , تتناسب القوة المحصلة خطيًا على الموقع، لذا فإن حركة سامي هي حركة توافقية بسيطة.
يتحرك سامي في حركة توافقية بسيطة عموديًا بين نقطة النهاية B ونقطة النهاية C.
نجد زمن الدورة لهذه التذبذبات:
«math xmlns=¨http://www.w3.org/1998/Math/MathML¨»«mi mathvariant=¨bold¨ mathcolor=¨#0000FF¨»T«/mi»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»=«/mo»«mn mathvariant=¨bold¨ mathcolor=¨#0000FF¨»2«/mn»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»§#183;«/mo»«mi mathvariant=¨bold¨ mathcolor=¨#0000FF¨»§#960;«/mi»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»§#183;«/mo»«msqrt mathcolor=¨#0000FF¨»«mfrac»«mi mathvariant=¨bold¨»m«/mi»«mi mathvariant=¨bold¨»K«/mi»«/mfrac»«/msqrt»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»=«/mo»«mn mathvariant=¨bold¨ mathcolor=¨#0000FF¨»2«/mn»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»§#183;«/mo»«mi mathvariant=¨bold¨ mathcolor=¨#0000FF¨»§#960;«/mi»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»§#183;«/mo»«msqrt mathcolor=¨#0000FF¨»«mfrac»«mn mathvariant=¨bold¨»60«/mn»«mn mathvariant=¨bold¨»100«/mn»«/mfrac»«/msqrt»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»=«/mo»«mn mathvariant=¨bold¨ mathcolor=¨#0000FF¨»4«/mn»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨».«/mo»«mn mathvariant=¨bold¨ mathcolor=¨#0000FF¨»86«/mn»«mi mathvariant=¨bold¨ mathcolor=¨#0000FF¨»s«/mi»«/math»
الزمن الذي يمر من لحظة بدء سامي في التحرك من أدنى نقطة B حتى وصوله إلى أعلى نقطة C يساوي نصف زمن دورة.
وبالتالي فإن الزمن الذي يحتاجه سامي للانتقال من أدنى نقطة إلى أعلى نقطة هو 2.43 ثانية.
נערוך תרשים המכיל את נקודת הקצה העליונה C , וציר שראשיתו בנקודת שיווי המשקל וכיוונו כלפי מעלה.
יצחק נע בתנועה הרמונית פשוטה אנכית בין נקודת הקצה B לנקודת הקצה C.
נמצא את זמן המחזור של תנודות אלו:
«math xmlns=¨http://www.w3.org/1998/Math/MathML¨»«mi mathvariant=¨bold¨ mathcolor=¨#0000FF¨»T«/mi»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»=«/mo»«mn mathvariant=¨bold¨ mathcolor=¨#0000FF¨»2«/mn»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»§#183;«/mo»«mi mathvariant=¨bold¨ mathcolor=¨#0000FF¨»§#960;«/mi»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»§#183;«/mo»«msqrt mathcolor=¨#0000FF¨»«mfrac»«mi mathvariant=¨bold¨»m«/mi»«mi mathvariant=¨bold¨»K«/mi»«/mfrac»«/msqrt»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»=«/mo»«mn mathvariant=¨bold¨ mathcolor=¨#0000FF¨»2«/mn»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»§#183;«/mo»«mi mathvariant=¨bold¨ mathcolor=¨#0000FF¨»§#960;«/mi»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»§#183;«/mo»«msqrt mathcolor=¨#0000FF¨»«mfrac»«mn mathvariant=¨bold¨»60«/mn»«mn mathvariant=¨bold¨»100«/mn»«/mfrac»«/msqrt»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»=«/mo»«mn mathvariant=¨bold¨ mathcolor=¨#0000FF¨»4«/mn»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨».«/mo»«mn mathvariant=¨bold¨ mathcolor=¨#0000FF¨»86«/mn»«mi mathvariant=¨bold¨ mathcolor=¨#0000FF¨»s«/mi»«/math»
הזמן שעובר מרגע שיצחק מתחיל לנוע מהנקודה הנמוכה ביותר B ועד שהוא מגיע לנקודה הגבוה ביותר C
שווה ל חצי זמן מחזור.
לכן, זמן תנועת יצחק מהנקודה הנמוכה ביותר לנקודה הגבוה ביותר הוא 2.43 שניות.
1. في أغلب الأسئلة، تبدأ الحركة التوافقية نتيجة انحراف الجسم من نقطة الاتّزان.
يمكن أن تؤدي قفزة البانجي أيضًا إلى حدوث حركة توافقية بسيطة. أي حركة تتناسب فيها القوة المحصلة بالموقع تناسبًا طرديًا هي حركة توافقية بسيطة.
2. في البداية، يتحرك سامي في سقوط حر، وخلال هذه الفترة تؤثر قوة ثابتة mg، ولا يتحرك سامي في حركة توافقية بسيطة.
3. يتم حفظ الطاقة الميكانيكية من لحظة القفزة وطوال الحركة التوافقية البسيطة بأكملها.
4. تتناول المسألة زمن الحركة، ولا تتطرق الاعتبارات المتعلقة بالطاقة بالزمن. الحل يجب أن يكون انطلاقا من مبادئ الحركة التوافقية البسيطة.
5. قد يبدو السؤال مختلفًا ومعقدًا بعض الشيء، ولكن بمجرد فهمك له، ستكتشف أنه كان في الواقع على ما يرام...
تبدو جميع الأسئلة في امتحان البجروت مختلفة ومعقدة بعض الشيء، لكن الطلاب يقولون بعد ذلك في المنزل إنها كانت سهلة بالفعل.
السؤال هو ماذا يحدث في هذه الأثناء... إلى أي مدى يتمكن الطلاب من الاسترخاء، والإيمان بأنفسهم، ومعرفة أنهم قادرون على النجاح، وينجحون!
גם קפיצת בנג'י יכולה לגרום לתנעה הרמונית פשוטה. כל תנועה שבה הכוח השקול תלוי ליניארית במיקום היא תה"פ.
2. בתחילה יצחק נע בנפילה חופשית , בזמן זה פועל כוח קבוע mg , ויצחק לא נע בתנועה הרמונית.
3. האנרגיה המכנית נשמרת מרגע הקפיצה וכל זמן תנועת התה"פ .
4. השאלה עוסקת בזמן תנועה ואין בשיקולי אנרגיה התייחסות לזמן. הפתרון חייב להיות מעקרונות התה"פ.
5. השאלה נראית מעט שונה ומסובכת , אך תמונה אחרי שמבינים מגלים שהיא דווקא הייתה בסדר...
כל השאלות בבגרות נראות קצת שונות ומורכבות , אח"כ בבית תלמידים אומרים דווקא היה קל.
השאלה מה קורה בין לבין.. עד כמה התלמידים מצליחים להירגע להאמין בעצמם, לדעת שהם יכולים להצליח ,ולהצליח!
______________________________________________________________________________________