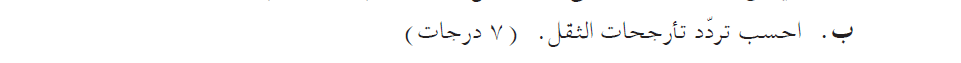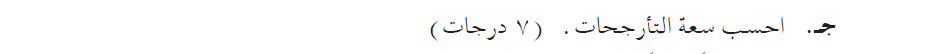
______________________________________________________________________________________
...
الطالب "أ" على حق.
من خلال الرسم البياني للسرعة كدالة للزمن المعطى واتجاه محور الحركة، من الممكن فهم كيفية تحرك الثقل
من الموقع الابتدائي، يمكننا معرفة الطول الابتدائي للنابض.
מהמיקום ההתחלתי ניתן לדעת מה אורך הקפיץ ההתחלתי.
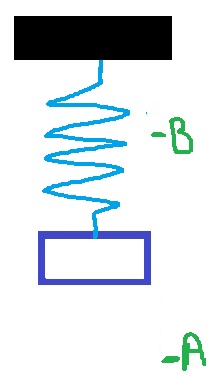
نرسم مخططًا عامًا للثقل ونقطتي النهاية للحركة. نقوم بتحديد نقطة النهاية السفلية في A ونقطة النهاية العلوية في B.
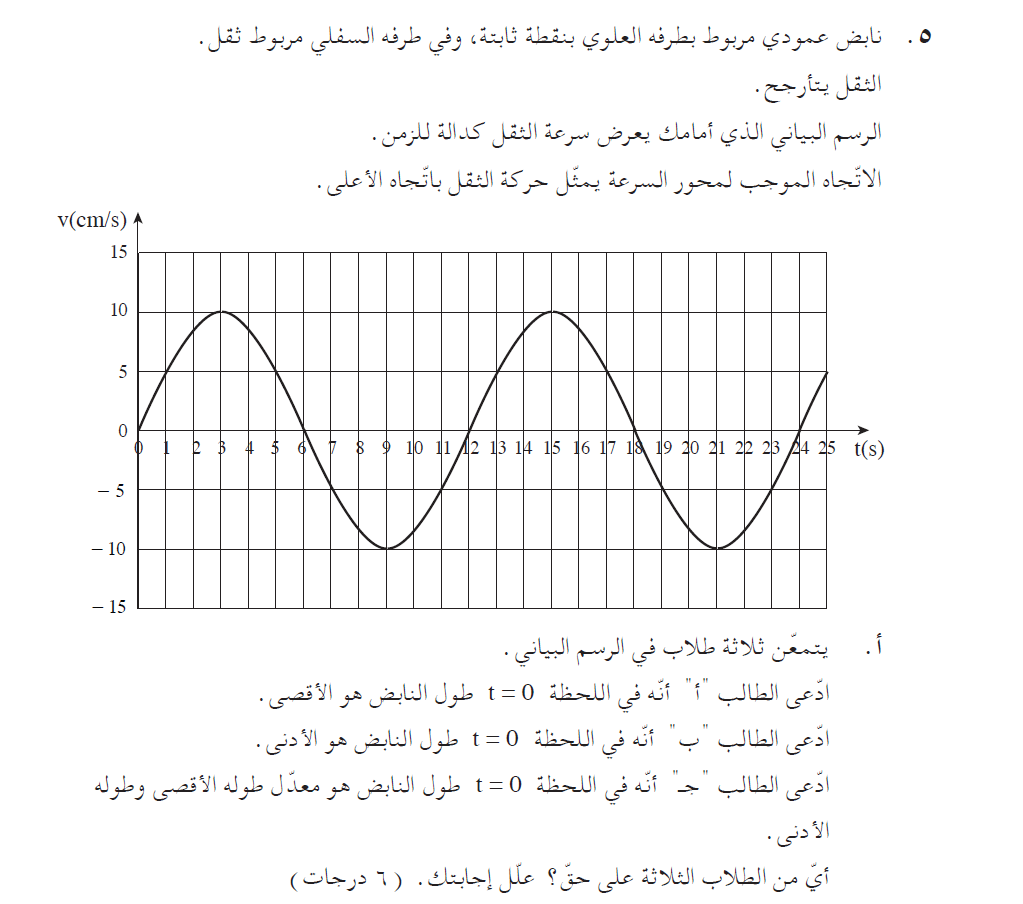
من الرسم البياني، يمكننا أن نرى أنه في اللحظة التي تبدأ فيها الحركة، تكون سرعة الثقل صفرًا. هناك مكانين فقط حيث تكون سرعة الجسم صفرًا في نقطة النهاية العلوية أو نقطة النهاية السفلية.
في بداية الحركة تكون السرعة موجبة، وهذا يعني أن الثقل يتحرك في اتجاه المحور. يكون اتجاه المحور نحو الأعلى، لذا يتحرك الثقل في البداية نحو الأعلى.
وبما أن الوزن يتحرك في البداية نحو الأعلى، فمن الممكن تحديد أنه يبدأ في التحرك من نقطة النهاية السفلية. لذلك فإن الطالب (أ) على حق.
מהגרף ניתן לראות שברגע תחילת התנועה מהירות המשקולת היא אפס. יש רק שתי מקומות בהן מהירות הגוף היא אפס בנקודת הקצה העליונה או בנקודת הקצה התחתונה.
בתחילת התנועה המהירות חיובית, זה אומר שהמשקולת נעה בכיוון הציר . כיוון הציר הוא כלפי מעלה לכן המשקולת נעה בתחילה כלפי מעלה.
מכיוון שהמשקולת נעה בהתחלה כלפי מעלה ניתן לקבוע שהיא מתחילה לנוע מנקודת הקצה התחתונה. לכן תלמיד א' צודק.
1. النص: "الاتجاه الموجب لمحور السرعة يمثل حركة الثقل نحو الأعلى." إنه نص أقل شيوعًا.
المقصود أنه عندما تكون قيمة السرعة موجبة، يتحرك الثقل إلى الأعلى.:
2. لم يذكر في السؤال صراحة أن الحركة هي حركة توافقية بسيطة. ليس هناك حاجة لإثبات أن الحركة توافقية.
يعتمد التفسير على الرسم البياني واتجاه المحور، وليس على دوال الحركة التوافقية البسيطة.
הכוונה שכאשר ערך המהירות חיובי המשקולת נעה כלפי מעלה .
2. לא כתוב במפורש בשאלה שהתנועה היא תנועה הרמונית פשוטה. אין צורך להוכיח שהתנועה היא הרמונית.
הנימוק מבוסס על הגרף ועל כיוון הציר ולא על הפונקציות של תה"פ.
______________________________________________________________________________________
______________________________________________________________________________________
...
«math xmlns=¨http://www.w3.org/1998/Math/MathML¨»«mi mathvariant=¨bold¨»f«/mi»«mo mathvariant=¨bold¨»=«/mo»«mn mathvariant=¨bold¨»0«/mn»«mo mathvariant=¨bold¨».«/mo»«mn mathvariant=¨bold¨»083«/mn»«mi mathvariant=¨bold¨»Hz«/mi»«/math»
يتم تعريف التردد على أنه واحد مقسوم على زمن الدورة. من خلال الرسم البياني، يمكنك التعرف على زمن الدورة.
ومن الرسم البياني يمكننا أن نرى أن زمن الدورة هو 12 ثانية. نحسب تردد تذبذبات الثقل:
«math xmlns=¨http://www.w3.org/1998/Math/MathML¨»«mi mathvariant=¨bold¨ mathcolor=¨#0000FF¨»f«/mi»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»=«/mo»«mfrac mathcolor=¨#0000FF¨»«mn mathvariant=¨bold¨»1«/mn»«mi mathvariant=¨bold¨»T«/mi»«/mfrac»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»=«/mo»«mfrac mathcolor=¨#0000FF¨»«mn mathvariant=¨bold¨»1«/mn»«mn mathvariant=¨bold¨»12«/mn»«/mfrac»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»=«/mo»«mn mathvariant=¨bold¨ mathcolor=¨#0000FF¨»0«/mn»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨».«/mo»«mn mathvariant=¨bold¨ mathcolor=¨#0000FF¨»083«/mn»«mi mathvariant=¨bold¨ mathcolor=¨#0000FF¨»Hz«/mi»«/math»
تردد التذبذبات هو 0.083 هرتز.
«math xmlns=¨http://www.w3.org/1998/Math/MathML¨»«mi mathvariant=¨bold¨ mathcolor=¨#0000FF¨»f«/mi»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»=«/mo»«mfrac mathcolor=¨#0000FF¨»«mn mathvariant=¨bold¨»1«/mn»«mi mathvariant=¨bold¨»T«/mi»«/mfrac»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»=«/mo»«mfrac mathcolor=¨#0000FF¨»«mn mathvariant=¨bold¨»1«/mn»«mn mathvariant=¨bold¨»12«/mn»«/mfrac»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»=«/mo»«mn mathvariant=¨bold¨ mathcolor=¨#0000FF¨»0«/mn»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨».«/mo»«mn mathvariant=¨bold¨ mathcolor=¨#0000FF¨»083«/mn»«mi mathvariant=¨bold¨ mathcolor=¨#0000FF¨»Hz«/mi»«/math»
תדירות התנודות היא 0.083 הרץ.
يصف زمن الدورة الزمن الذي تستغرقه الحركة لتكرار نفسها. يجب عليك أن تتعلم عن دورية الحركة.
من دالة الموقع كدالة للزمن.
في جميع دوال الحركة التوافقية الثلاث، الموقع كدالة للزمن، السرعة كدالة للزمن والتسارع كدالة للزمن يكون معامل t هو ω، لذا فإن هذه الدوال الثلاث لها
نفس زمن الدورة. دورية دالة السرعة-الزمن هي نفس دورية دالة الموقع-الزمن.
لذلك، يمكن إيجاد زمن الدورة من الرسم البياني للسرعة كدالة للزمن للحركة التوافقية البسيطة.
מפונקציית המקום בתלות בזמן .
בכל שלושת פונקציות התה"פ מקום זמן מהירות זמן ותאוצה זמן המקדם של t הוא ω , לכן לשלושת פונקציות אלו זמן
מחזור זהה. מחזוריות פונקציית המהירות זמן זהה למחזוריות פונקציית המקום זמן.
לכן ניתן למצוא את זמן המחזור מגרף מהירות זמן של תנועה הרמונית פשוטה.
______________________________________________________________________________________
______________________________________________________________________________________
...
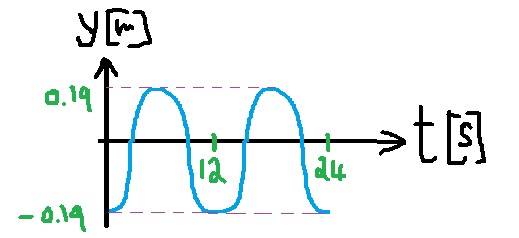
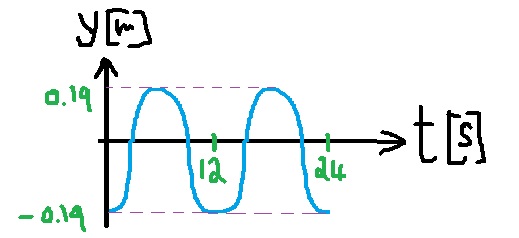
«math xmlns=¨http://www.w3.org/1998/Math/MathML¨»«mi mathvariant=¨bold¨»A«/mi»«mo mathvariant=¨bold¨»=«/mo»«mn mathvariant=¨bold¨»0«/mn»«mo mathvariant=¨bold¨».«/mo»«mn mathvariant=¨bold¨»19«/mn»«mi mathvariant=¨bold¨»m«/mi»«/math»
استخدام دوال الحركة التوافقية البسيطة.
يبدو شكل الرسم البياني للسرعة كدالة للزمن دالة sin. على غرار الرسم البياني للسرعة كدالة للزمن لجسم يتحرك في حركة توافقية بسيطة.
لنفترض أن الثقل يتحرك بحركة توافقية بسيطة.
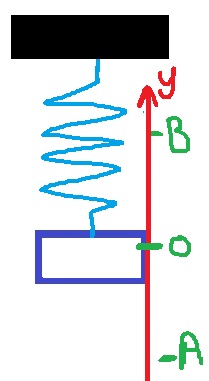
في بداية الحركة تكون السرعة موجبة، ويتحرك الثقل من نقطة النهاية السفلية إلى الأعلى في اتجاه المحور.
ومن ثم، فإن اتجاه محور الحركة المختار هو نحو الأعلى.
سنضيف محور الحركة، قبل استخدام دوال الحركة التوافقية:
نستخدم دالة السرعة كدالة للزمن:
«math xmlns=¨http://www.w3.org/1998/Math/MathML¨»«mstyle mathsize=¨20px¨»«mrow»«mi mathvariant=¨bold¨ mathcolor=¨#0000FF¨»V«/mi»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»(«/mo»«mi mathvariant=¨bold¨ mathcolor=¨#0000FF¨»t«/mi»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»)«/mo»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»=«/mo»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»-«/mo»«mi mathvariant=¨bold¨ mathcolor=¨#0000FF¨»§#969;«/mi»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»§#183;«/mo»«mi mathvariant=¨bold¨ mathcolor=¨#0000FF¨»A«/mi»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»§#183;«/mo»«mi mathvariant=¨bold¨ mathcolor=¨#0000FF¨»sin«/mi»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»(«/mo»«mi mathvariant=¨bold¨ mathcolor=¨#0000FF¨»§#969;«/mi»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»§#183;«/mo»«mi mathvariant=¨bold¨ mathcolor=¨#0000FF¨»t«/mi»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»)«/mo»«/mrow»«/mstyle»«/math»
تتراوح دالة الجيب بين 1 و- 1. يتم تحديد السرعة القصوى بواسطة:
«math xmlns=¨http://www.w3.org/1998/Math/MathML¨»«mstyle mathsize=¨24px¨»«mrow»«msub»«mi mathvariant=¨bold¨ mathcolor=¨#0000FF¨»V«/mi»«mi mathvariant=¨bold¨ mathcolor=¨#0000FF¨»max«/mi»«/msub»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»=«/mo»«mi mathvariant=¨bold¨ mathcolor=¨#0000FF¨»§#969;«/mi»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»§#183;«/mo»«mi mathvariant=¨bold¨ mathcolor=¨#0000FF¨»A«/mi»«/mrow»«/mstyle»«/math»
يمكننا إيجاد السعة من التعبير عن السرعة القصوى:
«math xmlns=¨http://www.w3.org/1998/Math/MathML¨»«mstyle mathsize=¨20px¨»«msub»«mi mathvariant=¨bold¨ mathcolor=¨#0000FF¨»V«/mi»«mi mathvariant=¨bold¨ mathcolor=¨#0000FF¨»max«/mi»«/msub»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»=«/mo»«mi mathvariant=¨bold¨ mathcolor=¨#0000FF¨»§#969;«/mi»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»§#183;«/mo»«mi mathvariant=¨bold¨ mathcolor=¨#0000FF¨»A«/mi»«mspace linebreak=¨newline¨»«/mspace»«mspace linebreak=¨newline¨»«/mspace»«mi mathvariant=¨bold¨ mathcolor=¨#0000FF¨»A«/mi»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»=«/mo»«mfrac mathcolor=¨#0000FF¨»«msub»«mi mathvariant=¨bold¨»V«/mi»«mi mathvariant=¨bold¨»max«/mi»«/msub»«mi mathvariant=¨bold¨»§#969;«/mi»«/mfrac»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»=«/mo»«mfrac mathcolor=¨#0000FF¨»«msub»«mi mathvariant=¨bold¨»V«/mi»«mi mathvariant=¨bold¨»max«/mi»«/msub»«mrow»«mn mathvariant=¨bold¨»2«/mn»«mo mathvariant=¨bold¨»§#183;«/mo»«mi mathvariant=¨bold¨»§#960;«/mi»«mo mathvariant=¨bold¨»§#183;«/mo»«mi mathvariant=¨bold¨»f«/mi»«/mrow»«/mfrac»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»=«/mo»«mfrac mathcolor=¨#0000FF¨»«mrow»«mn mathvariant=¨bold¨»0«/mn»«mo mathvariant=¨bold¨».«/mo»«mn mathvariant=¨bold¨»1«/mn»«/mrow»«mrow»«mn mathvariant=¨bold¨»2«/mn»«mo mathvariant=¨bold¨»§#183;«/mo»«mi mathvariant=¨bold¨»§#960;«/mi»«mo mathvariant=¨bold¨»§#183;«/mo»«mn mathvariant=¨bold¨»0«/mn»«mo mathvariant=¨bold¨».«/mo»«mn mathvariant=¨bold¨»083«/mn»«/mrow»«/mfrac»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»=«/mo»«mn mathvariant=¨bold¨ mathcolor=¨#0000FF¨»0«/mn»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨».«/mo»«mn mathvariant=¨bold¨ mathcolor=¨#0000FF¨»19«/mn»«mi mathvariant=¨bold¨ mathcolor=¨#0000FF¨»m«/mi»«/mstyle»«/math»
سعة الحركة هي 0.19 متر.
נניח שהמשקולת נעה בתנועה הרמונית פשוטה.
בתחילת התנועה המהירות חיובית , המשקולת נעה מנקודת הקצה התחתונה כלפי מעלה בכיוון הציר.
מכאן שכיוון ציר התנועה הנבחר הוא כלפי מעלה.
נוסיף את ציר התנועה ,לפני שנשתמש בפונקציות התה"פ:
נשתמש בפונקציית המהירות בתלות בזמן:
«math xmlns=¨http://www.w3.org/1998/Math/MathML¨»«mi mathvariant=¨bold¨ mathcolor=¨#0000FF¨»V«/mi»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»(«/mo»«mi mathvariant=¨bold¨ mathcolor=¨#0000FF¨»t«/mi»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»)«/mo»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»=«/mo»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»-«/mo»«mi mathvariant=¨bold¨ mathcolor=¨#0000FF¨»§#969;«/mi»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»§#183;«/mo»«mi mathvariant=¨bold¨ mathcolor=¨#0000FF¨»A«/mi»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»§#183;«/mo»«mi mathvariant=¨bold¨ mathcolor=¨#0000FF¨»sin«/mi»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»(«/mo»«mi mathvariant=¨bold¨ mathcolor=¨#0000FF¨»§#969;«/mi»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»§#183;«/mo»«mi mathvariant=¨bold¨ mathcolor=¨#0000FF¨»t«/mi»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»)«/mo»«/math»
בתחילת התנועה המהירות חיובית יש לבצע התאמה לפונקציית המהירות להוסיף זווית מופע של פאי רדיאן(חצי מחזור).
או להוריד את המינוס.
1. يبدأ الثقل بالتحرك من نقطة النهاية السالبة. يجب إضافة زاوية طور Π راديان.
أو اضرب دالة الموقع-الزمن، والسرعة-الزمن، والتسارع-الزمن في ناقص واحد.
2. هناك نقطة نهاية موجبة ونقطة نهاية سالبة ولكن لا يوجد شيء مثل السعة السالبة. السعة دائما موجبة
3.الوحدات الموجودة في الرسم البياني ليست قياسية.
4. هناك خطأ شائع يقع فيه الطلاب عندما يتطرقون إلى الرسم البياني للسرعة والزمن على أنه رسم بياني للمكان كدالة للزمن.
وفي هذه الحالة نحدد أن قيمة السعة هي 10 سم.
______________________________________________________________________________________

______________________________________________________________________________________
...
وصف دالة المكان كدالة للزمن للحركة التوافقية، اعتمادًا على السعة، زمن الدورة والموقع الابتدائي.
يتحرك الثقل من نقطة النهاية السالبة، من الموقع X= - 0.19 متر، في زمن دورة مدتها 12 ثانية.
نقوم بوصف حركة الثقل في اهتزازتين.
נתאר את תנועת המשקולת בשתי תנודות.
1. المقصود بالتأرجح إلى دورة كاملة من الحركة وليس إلى الحركة من البداية إلى النهاية.2. إذا كنت لا تعرف ما معنى التأرجح، فمن الجيد أن تكتب كيف تفهم معنى كلمة التأرجح، وتحل وفقًا لذلك.
3. من المهم معرفة الرسوم البيانية الثلاثة المتبعة في الحركة التوافقية البسيطة: المكان - الزمن، والسرعة-الزمن، والتسارع-الزمن.
واعرف كيفية تحرير الثلاثة وفقًا لذلك. 2. אם אתם לא יודעים מה המשמעות של תנודה , כדאי לכתוב כיצד אתם מבינים את משמעות המילה תנודה, ולפתור בהתאם.
3. חשוב להכיר את שלושת הגרפים הנפוצים בתה"פ : מקום זמן, מהירות זמן, ותאוצה זמן.
ולדעת לערוך את שלושתם בהתאמה.
______________________________________________________________________________________

______________________________________________________________________________________
...
التعبير مناسب للحركة ذات التسارع الثابت. الحركة التوافقية البسيطة هي حركة ذات تسارع متغير.
معرفة معادلة مربع السرعة وصلاحيتها. والتعرف على الحركة التوافقية البسيطة.
تعبير تربيع السرعة يلائم الحركة بتسارع ثابت.
الحركة التوافقية البسيطة هي حركة ذات تسارع متغير، لذا فإن حساب الطالب غير صحيح.
תנועה הרמונית פשוטה היא תנועה בתאוצה משתנה , לכן דרך החישוב של התלמיד היא שגויה.
1. أولئك الذين يدرسون مع يوكيوب على دراية بمفهوم "تعبير مربع السرعة ". ولكن ليس الجميع يسمون هذا التعبير بهذا الاسم.
2. في الكنيماتيكا، تعاملنا مع الحركة بسرعة ثابتة أو الحركة بتسارع ثابت.
الحركة التوافقية البسيطة هي حالة خاصة للحركة ذات التسارع المتغير. .
3. كل تعبير له صلاحية يتم تحديدها وفقًا لصلاحية الصيغ والتعبيرات التي تم تطوير التعبير منها.
يعتمد تعبير تربيع السرعة على دالة المكان كدالة للزمن ودالة السرعة-الزمن المناسبة للحركة ذات التسارع الثابت فقط.
لذلك، فإن تعبير مربع السرعات مناسب أيضًا فقط للحركة ذات التسارع الثابت.
4. ويمكن أيضًا تقييم صلاحية التعبير وفقًا لوجود معنى لكل من الكميات الفيزيائية في التعبير.إذا تحرك جسم من نقطة إلى أخرى في حركة توافقية بسيطة، فإن هناك قيمة مقابلة للسرعة الابتدائية وقيمة مقابلة للسرعة النهائية، وهناك أيضًا قيمة مقابلة للإزاحة. ولكن لا توجد قيمة مناسبة للتسارع لأن تسارع الجسم يتغير في كل نقطة.
نظرًا لعدم وجود قيمة مناسبة للتسارع، فإن التعبير بأكمله غير مناسب.
هناك شيء أساسي هنا. دعونا نحسن الأمر قليلاً... يزعم آدم أن كمية المصابيح الموجودة في السوق يمكن حسابها بناءً على كمية الطماطم المعروضة للبيع في السوق. كيف؟ ويزعم أن عدد المصابيح أقل بألف مرة من عدد الطماطم.
يمكنك العد ومعرفة ما إذا كان هذا صحيحًا ...
ويمكن رفض الصيغة من حيث المبدأ... فكمية الطماطم المعروضة للبيع تختلف، في حين أن كمية المصابيح لا تتغير، وبالتالي فإن الصيغة لا يمكن أن تكون مناسبة.
نفس الشيء تمامًا... لا يمكن لمعادلة مربع السرعات أن تستوعب الحركة ذات التسارع المتغير
2. בכל קינמטיקה עסקנו בתנועה במהירות קבועה או תנועה בתאוצה קבועה .
תה"פ היא מקרה מיוחד של תנועה בתאוצה משתנה.
______________________________________________________________________________________