2. 2018,5- حركة توافقية بسيطة لعربة مربوطة بنابض
______________________________________________________________________________________
...
«math xmlns=¨http://www.w3.org/1998/Math/MathML¨»«mi mathvariant=¨bold¨»T«/mi»«mo mathvariant=¨bold¨»=«/mo»«mn mathvariant=¨bold¨»2«/mn»«mi mathvariant=¨bold¨»s«/mi»«mo mathvariant=¨bold¨»§#160;«/mo»«mo mathvariant=¨bold¨»,«/mo»«mo mathvariant=¨bold¨»§#160;«/mo»«mo mathvariant=¨bold¨»§#160;«/mo»«mi mathvariant=¨bold¨»A«/mi»«mo mathvariant=¨bold¨»=«/mo»«mn mathvariant=¨bold¨»0«/mn»«mo mathvariant=¨bold¨».«/mo»«mn mathvariant=¨bold¨»2«/mn»«mi mathvariant=¨bold¨»m«/mi»«/math»
زمن الدورة في الحركة التوافقية البسيطة هو الزمن الذي يمر من لحظة بدء الجسم في الحركة حتى يعود إلى نقطة بداية الحركة، وهو الزمن ذهابًا وإيابًا.
السعة تساوي بعد نقطة احدى طرفي الحركة عن نقطة الاتزان.
زمن الدورة هو الزمن الذي يمر من لحظة بدء الحركة حتى عودة الجسم إلى نقطة بداية الحركة.
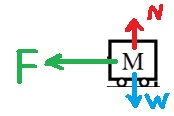
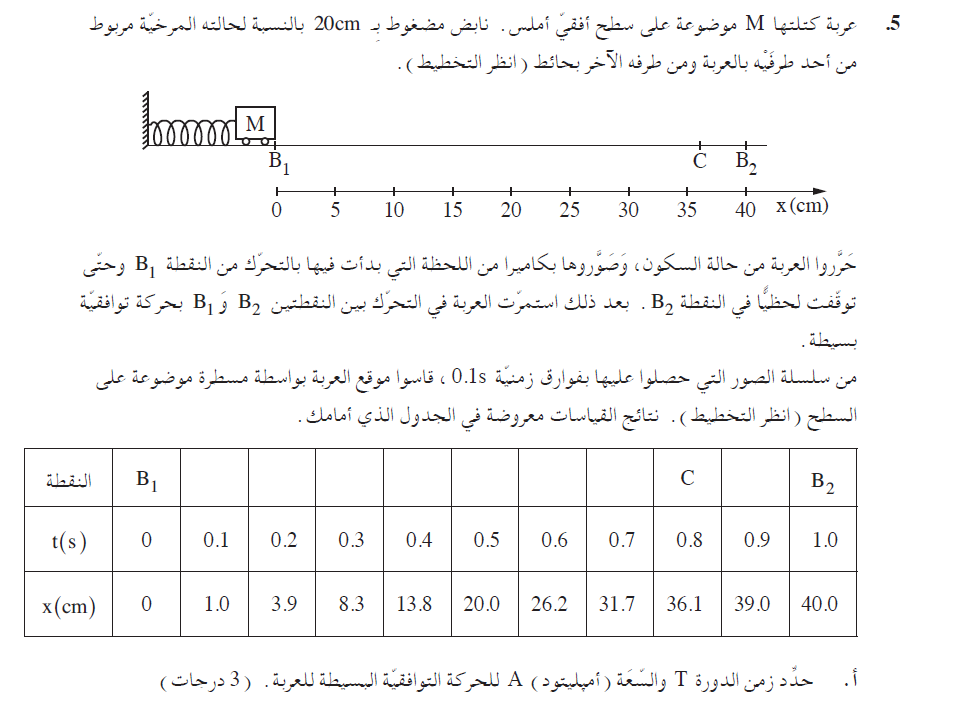
ومن الجدول يمكن فهم أن الزمن الذي يمر من لحظة بدء الحركة عند نقطة النهاية اليسرى حتى يصل الجسم إلى نقطة النهاية اليمنى هو ثانية واحدة، وبالتالي فإن الزمن الذي يمر من لحظة بدء الحركة حتى عودة العربة إلى نقطة بداية الحركة هو ثانيتين.
السعة تساوي البعد بين نقطة الاتزان وإحدى نقاط طرفي الحركة. يتم ضغط النابض بمقدار 20 سم، وبالتالي فإن النقطة التي يسترخي فيها النابض هي x=20cm، ويتحرك الجسم بين نقطة النهاية اليسرى x=0cm وx=40cm.
البعد بين نقطة الاتزان ونقطة النهاية هي 20 سم. هذا البعد هو سعة الحركة.
1. بحسب السؤال، ليست هناك حاجة للتفسير، حتى لو كتب الطالب الإجابات النهائية بدون تفسير، إذا كانت الإجابات صحيحة. سيحصل على النقاط الكاملة، ولكن إذا كانت الإجابات غير صحيحة، فلن يحصل على أي نقاط على إجاباته. لذلك فمن المستحسن أن تكتب تفسيرًا مختصرًا حتى لو لم يكن التفسير مطلوبًا.
2. يتم إعطاء القيم في الجدول بوحدات غير قياسية. يمكن وصف الحركة بوحدات غير قياسية، ولكن لا يمكن استخدام الوحدات غير القياسية في التعبيرات الفيزيائية.
______________________________________________________________________________________
______________________________________________________________________________________
...
«math xmlns=¨http://www.w3.org/1998/Math/MathML¨»«mi mathvariant=¨bold¨»V«/mi»«mo mathvariant=¨bold¨»=«/mo»«mn mathvariant=¨bold¨»0«/mn»«mo mathvariant=¨bold¨».«/mo»«mn mathvariant=¨bold¨»62«/mn»«mfrac»«mi mathvariant=¨bold¨»m«/mi»«mi mathvariant=¨bold¨»s«/mi»«/mfrac»«/math»
تحديد اللحظة التي تكون فيها السرعة قصوى، واستخدام تعريف السرعة المتوسطة لتقدير السرعة اللحظية في منتصف زمن الحركة.
تتحرك العربة بحركة توافقية بسيطة. في أي حركة توافقية بسيطة، تكون السرعة القصوى هي سرعة الجسم عندما يكون في نقطة الاتزان.
نقطة الاتزان هي نقطة المنتصف بين نقطتي طرفي الحركة، وفقًا للمحور الموصوف في السؤال. تقع هذه النقطة في x=20سم.
السرعة القصوى في اللحظة t=0.5 ثانية.
لإيجاد السرعة اللحظية في اللحظة t=0.5 ثانية، نحسب متوسط سرعة حركة العربة بين اللحظة t=0.4 ثانية واللحظة t=0.6 ثانية حسب المعطيات الموجودة في الجدول:
«math xmlns=¨http://www.w3.org/1998/Math/MathML¨»«mover mathcolor=¨#0000FF¨»«mi mathvariant=¨bold¨»V«/mi»«mo mathvariant=¨bold¨»§#175;«/mo»«/mover»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»=«/mo»«mfrac mathcolor=¨#0000FF¨»«mrow»«mo mathvariant=¨bold¨»§#8710;«/mo»«mi mathvariant=¨bold¨»X«/mi»«/mrow»«mrow»«mo mathvariant=¨bold¨»§#8710;«/mo»«mi mathvariant=¨bold¨»t«/mi»«/mrow»«/mfrac»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»=«/mo»«mfrac mathcolor=¨#0000FF¨»«mrow»«mi mathvariant=¨bold¨»X«/mi»«mo mathvariant=¨bold¨»(«/mo»«mn mathvariant=¨bold¨»0«/mn»«mo mathvariant=¨bold¨».«/mo»«mn mathvariant=¨bold¨»6«/mn»«mo mathvariant=¨bold¨»)«/mo»«mo mathvariant=¨bold¨»-«/mo»«mi mathvariant=¨bold¨»X«/mi»«mo mathvariant=¨bold¨»(«/mo»«mn mathvariant=¨bold¨»0«/mn»«mo mathvariant=¨bold¨».«/mo»«mn mathvariant=¨bold¨»4«/mn»«mo mathvariant=¨bold¨»)«/mo»«/mrow»«mrow»«mn mathvariant=¨bold¨»0«/mn»«mo mathvariant=¨bold¨».«/mo»«mn mathvariant=¨bold¨»6«/mn»«mo mathvariant=¨bold¨»-«/mo»«mn mathvariant=¨bold¨»0«/mn»«mo mathvariant=¨bold¨».«/mo»«mn mathvariant=¨bold¨»4«/mn»«/mrow»«/mfrac»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»=«/mo»«mfrac mathcolor=¨#0000FF¨»«mrow»«mn mathvariant=¨bold¨»0«/mn»«mo mathvariant=¨bold¨».«/mo»«mn mathvariant=¨bold¨»262«/mn»«mo mathvariant=¨bold¨»-«/mo»«mn mathvariant=¨bold¨»0«/mn»«mo mathvariant=¨bold¨».«/mo»«mn mathvariant=¨bold¨»138«/mn»«/mrow»«mrow»«mn mathvariant=¨bold¨»0«/mn»«mo mathvariant=¨bold¨».«/mo»«mn mathvariant=¨bold¨»2«/mn»«/mrow»«/mfrac»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»=«/mo»«mfrac mathcolor=¨#0000FF¨»«mrow»«mn mathvariant=¨bold¨»0«/mn»«mo mathvariant=¨bold¨».«/mo»«mn mathvariant=¨bold¨»124«/mn»«/mrow»«mrow»«mn mathvariant=¨bold¨»0«/mn»«mo mathvariant=¨bold¨».«/mo»«mn mathvariant=¨bold¨»2«/mn»«/mrow»«/mfrac»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»=«/mo»«mn mathvariant=¨bold¨ mathcolor=¨#0000FF¨»0«/mn»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨».«/mo»«mn mathvariant=¨bold¨ mathcolor=¨#0000FF¨»62«/mn»«mfrac mathcolor=¨#0000FF¨»«mi mathvariant=¨bold¨»m«/mi»«mi mathvariant=¨bold¨»s«/mi»«/mfrac»«/math»
هذه السرعة المتوسطة تساوي تقريبًا السرعة في منتصف الحركة في اللحظة t=0.5 ثانية، لذا فهي تقريبًا السرعة القصوى.
נקודת שיווי המשקל היא נקודת האמצע שבין שתי נקודות הקצה ,בהתאם לציר המתואר בשאלה הנקודה הזאת נמצאת ב x=20cm.
נשתמש בהגדרת המהירות הרגעית תנועה שבין רגע לפני ורגע אחרי שהעגלה בנקודת שיווי המשקל.
בהתאם לנתוני הטבלה:
«math xmlns=¨http://www.w3.org/1998/Math/MathML¨»«mi mathvariant=¨bold¨ mathcolor=¨#0000FF¨»V«/mi»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»=«/mo»«mfrac mathcolor=¨#0000FF¨»«mrow»«mo mathvariant=¨bold¨»§#8710;«/mo»«mi mathvariant=¨bold¨»X«/mi»«/mrow»«mrow»«mo mathvariant=¨bold¨»§#8710;«/mo»«mi mathvariant=¨bold¨»t«/mi»«/mrow»«/mfrac»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»=«/mo»«mfrac mathcolor=¨#0000FF¨»«mrow»«mi mathvariant=¨bold¨»X«/mi»«mo mathvariant=¨bold¨»(«/mo»«mn mathvariant=¨bold¨»0«/mn»«mo mathvariant=¨bold¨».«/mo»«mn mathvariant=¨bold¨»6«/mn»«mo mathvariant=¨bold¨»)«/mo»«mo mathvariant=¨bold¨»-«/mo»«mi mathvariant=¨bold¨»X«/mi»«mo mathvariant=¨bold¨»(«/mo»«mn mathvariant=¨bold¨»0«/mn»«mo mathvariant=¨bold¨».«/mo»«mn mathvariant=¨bold¨»4«/mn»«mo mathvariant=¨bold¨»)«/mo»«/mrow»«mrow»«mn mathvariant=¨bold¨»0«/mn»«mo mathvariant=¨bold¨».«/mo»«mn mathvariant=¨bold¨»6«/mn»«mo mathvariant=¨bold¨»-«/mo»«mn mathvariant=¨bold¨»0«/mn»«mo mathvariant=¨bold¨».«/mo»«mn mathvariant=¨bold¨»4«/mn»«/mrow»«/mfrac»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»=«/mo»«mfrac mathcolor=¨#0000FF¨»«mrow»«mn mathvariant=¨bold¨»0«/mn»«mo mathvariant=¨bold¨».«/mo»«mn mathvariant=¨bold¨»262«/mn»«mo mathvariant=¨bold¨»-«/mo»«mn mathvariant=¨bold¨»0«/mn»«mo mathvariant=¨bold¨».«/mo»«mn mathvariant=¨bold¨»138«/mn»«/mrow»«mrow»«mn mathvariant=¨bold¨»0«/mn»«mo mathvariant=¨bold¨».«/mo»«mn mathvariant=¨bold¨»2«/mn»«/mrow»«/mfrac»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»=«/mo»«mfrac mathcolor=¨#0000FF¨»«mrow»«mn mathvariant=¨bold¨»0«/mn»«mo mathvariant=¨bold¨».«/mo»«mn mathvariant=¨bold¨»124«/mn»«/mrow»«mrow»«mn mathvariant=¨bold¨»0«/mn»«mo mathvariant=¨bold¨».«/mo»«mn mathvariant=¨bold¨»2«/mn»«/mrow»«/mfrac»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»=«/mo»«mn mathvariant=¨bold¨ mathcolor=¨#0000FF¨»0«/mn»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨».«/mo»«mn mathvariant=¨bold¨ mathcolor=¨#0000FF¨»62«/mn»«mfrac mathcolor=¨#0000FF¨»«mi mathvariant=¨bold¨»m«/mi»«mi mathvariant=¨bold¨»s«/mi»«/mfrac»«/math»
1. من دالة السرعة كدالة للزمن ودالة السرعة كدالة للموقع للحركة التوافقية البسيطة: مقدار السرعة القصوى
يساوي حاصل ضرب السرعة الزاوية في السعة:
يساوي حاصل ضرب السرعة الزاوية في السعة:
«math xmlns=¨http://www.w3.org/1998/Math/MathML¨»«mi mathvariant=¨bold¨ mathcolor=¨#FF0000¨»V«/mi»«mo mathvariant=¨bold¨ mathcolor=¨#FF0000¨»=«/mo»«mi mathvariant=¨bold¨ mathcolor=¨#FF0000¨»§#969;«/mi»«mo mathvariant=¨bold¨ mathcolor=¨#FF0000¨»§#183;«/mo»«mi mathvariant=¨bold¨ mathcolor=¨#FF0000¨»A«/mi»«mo mathvariant=¨bold¨ mathcolor=¨#FF0000¨»=«/mo»«mfrac mathcolor=¨#FF0000¨»«mrow»«mn mathvariant=¨bold¨»2«/mn»«mo mathvariant=¨bold¨»§#183;«/mo»«mi mathvariant=¨bold¨»§#960;«/mi»«/mrow»«mi mathvariant=¨bold¨»T«/mi»«/mfrac»«mo mathvariant=¨bold¨ mathcolor=¨#FF0000¨»§#183;«/mo»«mi mathvariant=¨bold¨ mathcolor=¨#FF0000¨»A«/mi»«mo mathvariant=¨bold¨ mathcolor=¨#FF0000¨»=«/mo»«mfrac mathcolor=¨#FF0000¨»«mrow»«mn mathvariant=¨bold¨»2«/mn»«mo mathvariant=¨bold¨»§#183;«/mo»«mi mathvariant=¨bold¨»§#960;«/mi»«/mrow»«mn mathvariant=¨bold¨»2«/mn»«/mfrac»«mo mathvariant=¨bold¨ mathcolor=¨#FF0000¨»§#183;«/mo»«mn mathvariant=¨bold¨ mathcolor=¨#FF0000¨»0«/mn»«mo mathvariant=¨bold¨ mathcolor=¨#FF0000¨».«/mo»«mn mathvariant=¨bold¨ mathcolor=¨#FF0000¨»2«/mn»«mo mathvariant=¨bold¨ mathcolor=¨#FF0000¨»=«/mo»«mn mathvariant=¨bold¨ mathcolor=¨#FF0000¨»0«/mn»«mo mathvariant=¨bold¨ mathcolor=¨#FF0000¨».«/mo»«mn mathvariant=¨bold¨ mathcolor=¨#FF0000¨»628«/mn»«mfrac mathcolor=¨#FF0000¨»«mi mathvariant=¨bold¨»m«/mi»«mi mathvariant=¨bold¨»s«/mi»«/mfrac»«/math»
هذه الإجابة أكثر دقة، ولكن السؤال يطلب إيجاد السرعة القصوى باستخدام الجدول.
2. السرعة اللحظية تساوي السرعة في منتصف الحركة فقط إذا كان الجسم يتحرك في حركة بتسارع ثابت.
في الحركة التوافقية البسيطة، لا يتحرك الجسم بتسارع ثابت، لذا فإن الإجابة ليست دقيقة (بالإضافة إلى أننا اعتمدنا على نتائج القياس).
في الحركة التوافقية البسيطة، لا يتحرك الجسم بتسارع ثابت، لذا فإن الإجابة ليست دقيقة (بالإضافة إلى أننا اعتمدنا على نتائج القياس).
3. إتجاه الحركة ليس مهما في هذا السؤال. السؤال يتعلق بالقيمة المطلقة للسرعة.
שווה למכפלת המהירות הזוויתית במשרעת:
«math xmlns=¨http://www.w3.org/1998/Math/MathML¨»«mi mathvariant=¨bold¨ mathcolor=¨#FF0000¨»V«/mi»«mo mathvariant=¨bold¨ mathcolor=¨#FF0000¨»=«/mo»«mi mathvariant=¨bold¨ mathcolor=¨#FF0000¨»§#969;«/mi»«mo mathvariant=¨bold¨ mathcolor=¨#FF0000¨»§#183;«/mo»«mi mathvariant=¨bold¨ mathcolor=¨#FF0000¨»A«/mi»«mo mathvariant=¨bold¨ mathcolor=¨#FF0000¨»=«/mo»«mfrac mathcolor=¨#FF0000¨»«mrow»«mn mathvariant=¨bold¨»2«/mn»«mo mathvariant=¨bold¨»§#183;«/mo»«mi mathvariant=¨bold¨»§#960;«/mi»«/mrow»«mi mathvariant=¨bold¨»T«/mi»«/mfrac»«mo mathvariant=¨bold¨ mathcolor=¨#FF0000¨»§#183;«/mo»«mi mathvariant=¨bold¨ mathcolor=¨#FF0000¨»A«/mi»«mo mathvariant=¨bold¨ mathcolor=¨#FF0000¨»=«/mo»«mfrac mathcolor=¨#FF0000¨»«mrow»«mn mathvariant=¨bold¨»2«/mn»«mo mathvariant=¨bold¨»§#183;«/mo»«mi mathvariant=¨bold¨»§#960;«/mi»«/mrow»«mn mathvariant=¨bold¨»2«/mn»«/mfrac»«mo mathvariant=¨bold¨ mathcolor=¨#FF0000¨»§#183;«/mo»«mn mathvariant=¨bold¨ mathcolor=¨#FF0000¨»0«/mn»«mo mathvariant=¨bold¨ mathcolor=¨#FF0000¨».«/mo»«mn mathvariant=¨bold¨ mathcolor=¨#FF0000¨»2«/mn»«mo mathvariant=¨bold¨ mathcolor=¨#FF0000¨»=«/mo»«mn mathvariant=¨bold¨ mathcolor=¨#FF0000¨»0«/mn»«mo mathvariant=¨bold¨ mathcolor=¨#FF0000¨».«/mo»«mn mathvariant=¨bold¨ mathcolor=¨#FF0000¨»628«/mn»«mfrac mathcolor=¨#FF0000¨»«mi mathvariant=¨bold¨»m«/mi»«mi mathvariant=¨bold¨»s«/mi»«/mfrac»«/math»
התשובה הזאת יותר מדויקת , אך בשאלה בקשו למצוא את המהירות המרבית בעזרת הטבלה.
2. כדי לפתור את השאלה בעזרת נתוני הטבלה חייבים לדעת מתי בתה"פ מהירות הגוף מקסימאלית.
3. אין חשיבות לכיוון התנועה בשאלה זאת. השאלה מתייחסת לערך המוחלט של המהירות.
______________________________________________________________________________________
______________________________________________________________________________________
...
«math xmlns=¨http://www.w3.org/1998/Math/MathML¨»«mi mathvariant=¨bold¨»K«/mi»«mo mathvariant=¨bold¨»=«/mo»«mn mathvariant=¨bold¨»29«/mn»«mo mathvariant=¨bold¨».«/mo»«mn mathvariant=¨bold¨»6«/mn»«mfrac»«mi mathvariant=¨bold¨»N«/mi»«mi mathvariant=¨bold¨»m«/mi»«/mfrac»«/math»
تعبير ثابت النابض من صيغة زمن الدورة لـلحركة التوافقية البسيطة
نستخدم الصيغة لإيجاد زمن دورة الجسم الموصول بنابض ويتحرك بحركة توافقية بسيطة:
«math xmlns=¨http://www.w3.org/1998/Math/MathML¨»«mi mathvariant=¨bold-italic¨ mathcolor=¨#0000FF¨»T«/mi»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»=«/mo»«mn mathvariant=¨bold¨ mathcolor=¨#0000FF¨»2«/mn»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»§#183;«/mo»«mi mathvariant=¨bold¨ mathcolor=¨#0000FF¨»§#960;«/mi»«msqrt mathcolor=¨#0000FF¨»«mfrac»«mi mathvariant=¨bold¨»m«/mi»«mi mathvariant=¨bold¨»k«/mi»«/mfrac»«/msqrt»«mspace linebreak=¨newline¨»«/mspace»«mspace linebreak=¨newline¨»«/mspace»«msup»«mi mathvariant=¨bold¨ mathcolor=¨#0000FF¨»T«/mi»«mn mathvariant=¨bold¨ mathcolor=¨#0000FF¨»2«/mn»«/msup»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»=«/mo»«msup»«mn mathvariant=¨bold¨ mathcolor=¨#0000FF¨»2«/mn»«mn mathvariant=¨bold¨ mathcolor=¨#0000FF¨»2«/mn»«/msup»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»§#183;«/mo»«msup»«mi mathvariant=¨bold¨ mathcolor=¨#0000FF¨»§#960;«/mi»«mn mathvariant=¨bold¨ mathcolor=¨#0000FF¨»2«/mn»«/msup»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»§#183;«/mo»«mfrac mathcolor=¨#0000FF¨»«mi mathvariant=¨bold¨»m«/mi»«mi mathvariant=¨bold¨»k«/mi»«/mfrac»«mspace linebreak=¨newline¨»«/mspace»«mi mathvariant=¨bold¨ mathcolor=¨#0000FF¨»k«/mi»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»=«/mo»«mfrac mathcolor=¨#0000FF¨»«mrow»«mn mathvariant=¨bold¨»4«/mn»«mo mathvariant=¨bold¨»§#183;«/mo»«msup»«mi mathvariant=¨bold¨»§#960;«/mi»«mn mathvariant=¨bold¨»2«/mn»«/msup»«mo mathvariant=¨bold¨»§#183;«/mo»«mi mathvariant=¨bold¨»m«/mi»«/mrow»«msup»«mi mathvariant=¨bold¨»T«/mi»«mn mathvariant=¨bold¨»2«/mn»«/msup»«/mfrac»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»=«/mo»«mfrac mathcolor=¨#0000FF¨»«mrow»«mn mathvariant=¨bold¨»4«/mn»«mo mathvariant=¨bold¨»§#183;«/mo»«msup»«mi mathvariant=¨bold¨»§#960;«/mi»«mn mathvariant=¨bold¨»2«/mn»«/msup»«mo mathvariant=¨bold¨»§#183;«/mo»«mn mathvariant=¨bold¨»3«/mn»«/mrow»«msup»«mn mathvariant=¨bold¨»2«/mn»«mn mathvariant=¨bold¨»2«/mn»«/msup»«/mfrac»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»=«/mo»«mn mathvariant=¨bold¨ mathcolor=¨#0000FF¨»29«/mn»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨».«/mo»«mn mathvariant=¨bold¨ mathcolor=¨#0000FF¨»6«/mn»«mfrac mathcolor=¨#0000FF¨»«mi mathvariant=¨bold¨»N«/mi»«mi mathvariant=¨bold¨»m«/mi»«/mfrac»«/math»
وبالتالي فإن مقدار ثابت النابض يساوي 29.6 نيوتن لكل متر.
«math xmlns=¨http://www.w3.org/1998/Math/MathML¨»«mi mathvariant=¨bold-italic¨ mathcolor=¨#0000FF¨»T«/mi»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»=«/mo»«mn mathvariant=¨bold¨ mathcolor=¨#0000FF¨»2«/mn»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»§#183;«/mo»«mi mathvariant=¨bold¨ mathcolor=¨#0000FF¨»§#960;«/mi»«msqrt mathcolor=¨#0000FF¨»«mfrac»«mi mathvariant=¨bold¨»m«/mi»«mi mathvariant=¨bold¨»k«/mi»«/mfrac»«/msqrt»«mspace linebreak=¨newline¨»«/mspace»«mspace linebreak=¨newline¨»«/mspace»«msup»«mi mathvariant=¨bold¨ mathcolor=¨#0000FF¨»T«/mi»«mn mathvariant=¨bold¨ mathcolor=¨#0000FF¨»2«/mn»«/msup»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»=«/mo»«msup»«mn mathvariant=¨bold¨ mathcolor=¨#0000FF¨»2«/mn»«mn mathvariant=¨bold¨ mathcolor=¨#0000FF¨»2«/mn»«/msup»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»§#183;«/mo»«msup»«mi mathvariant=¨bold¨ mathcolor=¨#0000FF¨»§#960;«/mi»«mn mathvariant=¨bold¨ mathcolor=¨#0000FF¨»2«/mn»«/msup»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»§#183;«/mo»«mfrac mathcolor=¨#0000FF¨»«mi mathvariant=¨bold¨»m«/mi»«mi mathvariant=¨bold¨»k«/mi»«/mfrac»«mspace linebreak=¨newline¨»«/mspace»«mi mathvariant=¨bold¨ mathcolor=¨#0000FF¨»k«/mi»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»=«/mo»«mfrac mathcolor=¨#0000FF¨»«mrow»«mn mathvariant=¨bold¨»4«/mn»«mo mathvariant=¨bold¨»§#183;«/mo»«msup»«mi mathvariant=¨bold¨»§#960;«/mi»«mn mathvariant=¨bold¨»2«/mn»«/msup»«mo mathvariant=¨bold¨»§#183;«/mo»«mi mathvariant=¨bold¨»m«/mi»«/mrow»«msup»«mi mathvariant=¨bold¨»T«/mi»«mn mathvariant=¨bold¨»2«/mn»«/msup»«/mfrac»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»=«/mo»«mfrac mathcolor=¨#0000FF¨»«mrow»«mn mathvariant=¨bold¨»4«/mn»«mo mathvariant=¨bold¨»§#183;«/mo»«msup»«mi mathvariant=¨bold¨»§#960;«/mi»«mn mathvariant=¨bold¨»2«/mn»«/msup»«mo mathvariant=¨bold¨»§#183;«/mo»«mn mathvariant=¨bold¨»3«/mn»«/mrow»«msup»«mn mathvariant=¨bold¨»2«/mn»«mn mathvariant=¨bold¨»2«/mn»«/msup»«/mfrac»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»=«/mo»«mn mathvariant=¨bold¨ mathcolor=¨#0000FF¨»29«/mn»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨».«/mo»«mn mathvariant=¨bold¨ mathcolor=¨#0000FF¨»6«/mn»«mfrac mathcolor=¨#0000FF¨»«mi mathvariant=¨bold¨»N«/mi»«mi mathvariant=¨bold¨»m«/mi»«/mfrac»«/math»
לכן גודלו של קבוע הקפיץ הוא 29.6 ניוטון למטר.
1. إن تعبير زمن الدورة مناسب لكل من الحركة التوافقية في نابض أفقي وTAF في نابض رأسي.
2. ليس في كل حركة توافقية تكون القوة التوافقية هي القوة التي يؤثر بها النابض. لكل حركة توافقية يوجد ثابت حركة توافقية C.
ويتعلق زمن الدورة على C وفقًا لـلتعبير:
ويتعلق زمن الدورة على C وفقًا لـلتعبير:
«math xmlns=¨http://www.w3.org/1998/Math/MathML¨»«mstyle mathsize=¨20px¨»«mrow»«mi mathvariant=¨bold¨ mathcolor=¨#FF0000¨»T«/mi»«mo mathvariant=¨bold¨ mathcolor=¨#FF0000¨»=«/mo»«mn mathvariant=¨bold¨ mathcolor=¨#FF0000¨»2«/mn»«mo mathvariant=¨bold¨ mathcolor=¨#FF0000¨»§#183;«/mo»«mi mathvariant=¨bold¨ mathcolor=¨#FF0000¨»§#960;«/mi»«mo mathvariant=¨bold¨ mathcolor=¨#FF0000¨»§#183;«/mo»«msqrt mathcolor=¨#FF0000¨»«mfrac»«mi mathvariant=¨bold¨»m«/mi»«mi mathvariant=¨bold¨»C«/mi»«/mfrac»«/msqrt»«mspace linebreak=¨newline¨»«/mspace»«mspace linebreak=¨newline¨»«/mspace»«/mrow»«/mstyle»«/math»
C هو المعامل الذي يظهر في تعبير القوة المحصلة في الحركة التوافقية البسيطة: «math xmlns=¨http://www.w3.org/1998/Math/MathML¨»«mi mathvariant=¨bold¨ mathcolor=¨#FF0000¨»§#931;F«/mi»«mo mathvariant=¨bold¨ mathcolor=¨#FF0000¨»=«/mo»«mo mathvariant=¨bold¨ mathcolor=¨#FF0000¨»-«/mo»«mi mathvariant=¨bold¨ mathcolor=¨#FF0000¨»C«/mi»«mo mathvariant=¨bold¨ mathcolor=¨#FF0000¨»§#183;«/mo»«mi mathvariant=¨bold¨ mathcolor=¨#FF0000¨»X«/mi»«/math» , في حالة الحركة التوافقية البسيطة لجسم مربوط بنابض، C هو ثابت النابض.
2. לא בכל תנועה הרמונית הכוח ההרמוני הוא כוח המופעל על ידי קפיץ. לכל תנועה הרמונית קיים קבועה תנועה הרמונית.
______________________________________________________________________________________
______________________________________________________________________________________
...
ד.1-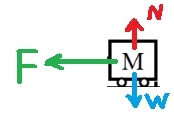 
ד.2- «math xmlns=¨http://www.w3.org/1998/Math/MathML¨»«mi mathvariant=¨bold¨»§#931;F«/mi»«mo mathvariant=¨bold¨»=«/mo»«mn mathvariant=¨bold¨»4«/mn»«mo mathvariant=¨bold¨».«/mo»«mn mathvariant=¨bold¨»73«/mn»«mi mathvariant=¨bold¨»N«/mi»«/math»
ד.3- «math xmlns=¨http://www.w3.org/1998/Math/MathML¨»«msub»«mi mathvariant=¨bold¨»t«/mi»«mn mathvariant=¨bold¨»2«/mn»«/msub»«mo mathvariant=¨bold¨»=«/mo»«mn mathvariant=¨bold¨»1«/mn»«mo mathvariant=¨bold¨».«/mo»«mn mathvariant=¨bold¨»2«/mn»«mi mathvariant=¨bold¨»s«/mi»«/math»
ד.2- «math xmlns=¨http://www.w3.org/1998/Math/MathML¨»«mi mathvariant=¨bold¨»§#931;F«/mi»«mo mathvariant=¨bold¨»=«/mo»«mn mathvariant=¨bold¨»4«/mn»«mo mathvariant=¨bold¨».«/mo»«mn mathvariant=¨bold¨»73«/mn»«mi mathvariant=¨bold¨»N«/mi»«/math»
ד.2-
د.1- معرفة القوى المؤثرة على العربة: الجاذبية العمودية وقوة النابض.
د.2- تحديد محور حركة جديد، وإيجاد موقع العربة في اللحظة t=0.8s، وبالتالي إيجاد قوة النابض من تعبير القوة المعيدة.
د.3- تعمل على العربة قوة مختلفة في كل موقع. نجد الزمن الذي تستغرقه العربة للعودة إلى النقطة C.
ד.2- הגדרת ציר תנועה חדש, מציאת מיקום העגלה ברגע t=0.8s , ובהתאם מציאת כוח הקפיץ מביטוי הכוח המחזיר.
ד.3- בכל מקום יש לעגלה כוח שונה, יש למצוא את הזמן שעובר עד שהעגלה תחזור שוב לנקודה C.
د.1- هناك ثلاث قوى تؤثر على العربة: قوة الجاذبية، والقوة العمودية، وقوة النابض التي تعمل كقوة معيدة لنقطة الاتزان.
نرسم مخطط القوى:
نرسم مخطط القوى:
د.2- العربة لا تتحرك في الاتجاه العمودي. محصلة القوى في الاتجاه الرأسي يساوي صفرًا. القوة المحصلة المؤثرة على العربة هي قوة النابض.
لإيجاد قوة النابض واستخدام دوال الحركة التوافقية البسيطة، سنقوم بتحديد محور حركة جديد يبدأ في نقطة الاتزان.
لإيجاد قوة النابض واستخدام دوال الحركة التوافقية البسيطة، سنقوم بتحديد محور حركة جديد يبدأ في نقطة الاتزان.
نجد موقع العربة بعد 0.8 ثانية من بدء حركتها بالنسبة لمحور الحركة الجديد.
نستخدم دالة الموقع كدالة للزمن الملائمة للحركة التوافقية البسيطة: العربة 0.8 ثانية بعد بدء حركتها بالنسبة لمحور الحركة الجديد.
سوف نستخدم دالة الموقع كدالة للزمن الملائمة للحركة التوافقية البسيطة:
سوف نستخدم دالة الموقع كدالة للزمن الملائمة للحركة التوافقية البسيطة:
«math xmlns=¨http://www.w3.org/1998/Math/MathML¨»«mi mathvariant=¨bold¨ mathcolor=¨#0000FF¨»X«/mi»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»(«/mo»«mi mathvariant=¨bold¨ mathcolor=¨#0000FF¨»t«/mi»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»)«/mo»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»=«/mo»«mi mathvariant=¨bold¨ mathcolor=¨#0000FF¨»A«/mi»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»§#183;«/mo»«mi mathvariant=¨bold¨ mathcolor=¨#0000FF¨»cos«/mi»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»(«/mo»«mi mathvariant=¨bold¨ mathcolor=¨#0000FF¨»§#969;t«/mi»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»)«/mo»«mspace linebreak=¨newline¨»«/mspace»«mi mathvariant=¨bold¨ mathcolor=¨#0000FF¨»X«/mi»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»(«/mo»«mn mathvariant=¨bold¨ mathcolor=¨#0000FF¨»0«/mn»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨».«/mo»«mn mathvariant=¨bold¨ mathcolor=¨#0000FF¨»8«/mn»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»)«/mo»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»=«/mo»«mn mathvariant=¨bold¨ mathcolor=¨#0000FF¨»0«/mn»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨».«/mo»«mn mathvariant=¨bold¨ mathcolor=¨#0000FF¨»2«/mn»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»§#183;«/mo»«mi mathvariant=¨bold¨ mathcolor=¨#0000FF¨»cos«/mi»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»(«/mo»«mfrac mathcolor=¨#0000FF¨»«mrow»«mn mathvariant=¨bold¨»2«/mn»«mo mathvariant=¨bold¨»§#183;«/mo»«mi mathvariant=¨bold¨»§#960;«/mi»«/mrow»«mn mathvariant=¨bold¨»2«/mn»«/mfrac»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»§#183;«/mo»«mn mathvariant=¨bold¨ mathcolor=¨#0000FF¨»0«/mn»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨».«/mo»«mn mathvariant=¨bold¨ mathcolor=¨#0000FF¨»8«/mn»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»)«/mo»«mspace linebreak=¨newline¨»«/mspace»«mi mathvariant=¨bold¨ mathcolor=¨#0000FF¨»X«/mi»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»(«/mo»«mn mathvariant=¨bold¨ mathcolor=¨#0000FF¨»0«/mn»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨».«/mo»«mn mathvariant=¨bold¨ mathcolor=¨#0000FF¨»8«/mn»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»)«/mo»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»=«/mo»«mn mathvariant=¨bold¨ mathcolor=¨#0000FF¨»0«/mn»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨».«/mo»«mn mathvariant=¨bold¨ mathcolor=¨#0000FF¨»2«/mn»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»§#183;«/mo»«mi mathvariant=¨bold¨ mathcolor=¨#0000FF¨»cos«/mi»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»(«/mo»«mfrac mathcolor=¨#0000FF¨»«mrow»«mn mathvariant=¨bold¨»2«/mn»«mo mathvariant=¨bold¨»§#183;«/mo»«mi mathvariant=¨bold¨»§#960;«/mi»«/mrow»«mn mathvariant=¨bold¨»2«/mn»«/mfrac»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»§#183;«/mo»«mn mathvariant=¨bold¨ mathcolor=¨#0000FF¨»0«/mn»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨».«/mo»«mn mathvariant=¨bold¨ mathcolor=¨#0000FF¨»8«/mn»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»)«/mo»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»=«/mo»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»-«/mo»«mn mathvariant=¨bold¨ mathcolor=¨#0000FF¨»0«/mn»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨».«/mo»«mn mathvariant=¨bold¨ mathcolor=¨#0000FF¨»16«/mn»«mi mathvariant=¨bold¨ mathcolor=¨#0000FF¨»m«/mi»«mspace linebreak=¨newline¨»«/mspace»«/math»
نجد قوة النابض باستخدام تعبير القوة المعيدة:
«math xmlns=¨http://www.w3.org/1998/Math/MathML¨»«mi mathvariant=¨bold¨ mathcolor=¨#0000FF¨»F«/mi»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»=«/mo»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»-«/mo»«mi mathvariant=¨bold¨ mathcolor=¨#0000FF¨»K«/mi»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»§#183;«/mo»«mi mathvariant=¨bold¨ mathcolor=¨#0000FF¨»X«/mi»«mspace linebreak=¨newline¨»«/mspace»«mi mathvariant=¨bold¨ mathcolor=¨#0000FF¨»F«/mi»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»=«/mo»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»-«/mo»«mn mathvariant=¨bold¨ mathcolor=¨#0000FF¨»29«/mn»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨».«/mo»«mn mathvariant=¨bold¨ mathcolor=¨#0000FF¨»6«/mn»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»§#183;«/mo»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»(«/mo»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»-«/mo»«mn mathvariant=¨bold¨ mathcolor=¨#0000FF¨»0«/mn»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨».«/mo»«mn mathvariant=¨bold¨ mathcolor=¨#0000FF¨»16«/mn»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»)«/mo»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»=«/mo»«mn mathvariant=¨bold¨ mathcolor=¨#0000FF¨»4«/mn»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨».«/mo»«mn mathvariant=¨bold¨ mathcolor=¨#0000FF¨»73«/mn»«mi mathvariant=¨bold¨ mathcolor=¨#0000FF¨»N«/mi»«/math»
القوة المحصّلة هي قوة النابض، لذا فإن مقدار القوة المحصلة هو 4.73 نيوتن واتجاهها هو نفس اتجاه المحور إلى اليسار.
د.3- تتعلق القوة على الموقع، وفقًا لتعبير القوة المعيدة، في كل نقطة يقع فيها الجسم، تؤثر قوة مختلفة.
خلال نصف وقت الدورة، تتحرك العربة من نقطة النهاية اليسرى إلى نقطة النهاية اليمنى (لمدة ثانية واحدة).
في المرة التالية التي تمر فيها العربة بالنقطة C، سوف تؤثر عليها قوة بنفس المقدار والاتجاه.
يمر الجسم بالنقطة C للمرة الأولى بعد 0.8 ثانية من بدء الحركة.
نحسب الزمن 't الذي يمر من لحظة تحرك العربة من النقطة C حتى وصولها إلى نقطة الطرف اليمنى للحركة: «math xmlns=¨http://www.w3.org/1998/Math/MathML¨»«mi mathvariant=¨bold¨ mathcolor=¨#0000FF¨»t«/mi»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»`«/mo»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»=«/mo»«mn mathvariant=¨bold¨ mathcolor=¨#0000FF¨»1«/mn»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»-«/mo»«mn mathvariant=¨bold¨ mathcolor=¨#0000FF¨»0«/mn»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨».«/mo»«mn mathvariant=¨bold¨ mathcolor=¨#0000FF¨»8«/mn»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»=«/mo»«mn mathvariant=¨bold¨ mathcolor=¨#0000FF¨»0«/mn»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨».«/mo»«mn mathvariant=¨bold¨ mathcolor=¨#0000FF¨»2«/mn»«mi mathvariant=¨bold¨ mathcolor=¨#0000FF¨»S«/mi»«/math»
يمر نفس المقدار من الوقت من لحظة خروج العربة من نقطة الطرف اليمنى حتى تمر بالنقطة C للمرة الثانية.
وبالتالي فإن الزمن الكلي الذي يمر من لحظة بدء الحركة حتى مرور العربة بالنقطة C للمرة الثانية هو 1.2 ثانية.
נערוך תרשים כוחות:
ד.2- העגלה לא נעה בכיוון האנכי שקול הכוחות בכיוון האנכי מתאפס. הכוח השקול הפועל על העגלה הוא כוח הקפיץ.
כדי למצוא את כוח הקפיץ ולהשתמש בפונקציות התה"פ נגדיר ציר תנועה חדש שראשיתו בנקודת שיווי המשקל.
נמצא את מיקום העגלה כעבור 0.8 שניות מרגע תחילת תנועתה ביחס לציר התנועה החדש.
נשתמש בפונקציית המקום זמן המתאימה לתה"פ:
«math xmlns=¨http://www.w3.org/1998/Math/MathML¨»«mi mathvariant=¨bold¨ mathcolor=¨#0000FF¨»X«/mi»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»(«/mo»«mi mathvariant=¨bold¨ mathcolor=¨#0000FF¨»t«/mi»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»)«/mo»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»=«/mo»«mi mathvariant=¨bold¨ mathcolor=¨#0000FF¨»A«/mi»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»§#183;«/mo»«mi mathvariant=¨bold¨ mathcolor=¨#0000FF¨»cos«/mi»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»(«/mo»«mi mathvariant=¨bold¨ mathcolor=¨#0000FF¨»§#969;t«/mi»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»)«/mo»«mspace linebreak=¨newline¨»«/mspace»«mi mathvariant=¨bold¨ mathcolor=¨#0000FF¨»X«/mi»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»(«/mo»«mn mathvariant=¨bold¨ mathcolor=¨#0000FF¨»0«/mn»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨».«/mo»«mn mathvariant=¨bold¨ mathcolor=¨#0000FF¨»8«/mn»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»)«/mo»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»=«/mo»«mn mathvariant=¨bold¨ mathcolor=¨#0000FF¨»0«/mn»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨».«/mo»«mn mathvariant=¨bold¨ mathcolor=¨#0000FF¨»2«/mn»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»§#183;«/mo»«mi mathvariant=¨bold¨ mathcolor=¨#0000FF¨»cos«/mi»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»(«/mo»«mfrac mathcolor=¨#0000FF¨»«mrow»«mn mathvariant=¨bold¨»2«/mn»«mo mathvariant=¨bold¨»§#183;«/mo»«mi mathvariant=¨bold¨»§#960;«/mi»«/mrow»«mn mathvariant=¨bold¨»2«/mn»«/mfrac»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»§#183;«/mo»«mn mathvariant=¨bold¨ mathcolor=¨#0000FF¨»0«/mn»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨».«/mo»«mn mathvariant=¨bold¨ mathcolor=¨#0000FF¨»8«/mn»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»)«/mo»«mspace linebreak=¨newline¨»«/mspace»«mi mathvariant=¨bold¨ mathcolor=¨#0000FF¨»X«/mi»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»(«/mo»«mn mathvariant=¨bold¨ mathcolor=¨#0000FF¨»0«/mn»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨».«/mo»«mn mathvariant=¨bold¨ mathcolor=¨#0000FF¨»8«/mn»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»)«/mo»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»=«/mo»«mn mathvariant=¨bold¨ mathcolor=¨#0000FF¨»0«/mn»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨».«/mo»«mn mathvariant=¨bold¨ mathcolor=¨#0000FF¨»2«/mn»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»§#183;«/mo»«mi mathvariant=¨bold¨ mathcolor=¨#0000FF¨»cos«/mi»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»(«/mo»«mfrac mathcolor=¨#0000FF¨»«mrow»«mn mathvariant=¨bold¨»2«/mn»«mo mathvariant=¨bold¨»§#183;«/mo»«mi mathvariant=¨bold¨»§#960;«/mi»«/mrow»«mn mathvariant=¨bold¨»2«/mn»«/mfrac»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»§#183;«/mo»«mn mathvariant=¨bold¨ mathcolor=¨#0000FF¨»0«/mn»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨».«/mo»«mn mathvariant=¨bold¨ mathcolor=¨#0000FF¨»8«/mn»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»)«/mo»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»=«/mo»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»-«/mo»«mn mathvariant=¨bold¨ mathcolor=¨#0000FF¨»0«/mn»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨».«/mo»«mn mathvariant=¨bold¨ mathcolor=¨#0000FF¨»16«/mn»«mi mathvariant=¨bold¨ mathcolor=¨#0000FF¨»m«/mi»«mspace linebreak=¨newline¨»«/mspace»«/math»
נמצא את כוח הקפיץ בעזרת ביטוי הכוח המחזיר:
«math xmlns=¨http://www.w3.org/1998/Math/MathML¨»«mi mathvariant=¨bold¨ mathcolor=¨#0000FF¨»F«/mi»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»=«/mo»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»-«/mo»«mi mathvariant=¨bold¨ mathcolor=¨#0000FF¨»K«/mi»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»§#183;«/mo»«mi mathvariant=¨bold¨ mathcolor=¨#0000FF¨»X«/mi»«mspace linebreak=¨newline¨»«/mspace»«mi mathvariant=¨bold¨ mathcolor=¨#0000FF¨»F«/mi»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»=«/mo»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»-«/mo»«mn mathvariant=¨bold¨ mathcolor=¨#0000FF¨»29«/mn»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨».«/mo»«mn mathvariant=¨bold¨ mathcolor=¨#0000FF¨»6«/mn»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»§#183;«/mo»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»(«/mo»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»-«/mo»«mn mathvariant=¨bold¨ mathcolor=¨#0000FF¨»0«/mn»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨».«/mo»«mn mathvariant=¨bold¨ mathcolor=¨#0000FF¨»16«/mn»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»)«/mo»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»=«/mo»«mn mathvariant=¨bold¨ mathcolor=¨#0000FF¨»4«/mn»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨».«/mo»«mn mathvariant=¨bold¨ mathcolor=¨#0000FF¨»73«/mn»«mi mathvariant=¨bold¨ mathcolor=¨#0000FF¨»N«/mi»«/math»
הכוח השקול הוא כוח הקפיץ, לכן גודלו של הכוח השקול הוא 4.73 ניוטון וכיוונו ככיוון הציר שמאלה.
ד.3- הכוח תלוי במיקום בהתאם לביטוי הכוח המחזיר ,בכל נקודה בה נמצא הגוף פעול כוח שונה.
בפעם הבאה שהעגלה תחלוף בנקודה C יפעל כוח זהה בגודלו ובכיוונו.
הגוף חולף בפעם הראשונה בנקודה C כעבור 0.8 שניות מרגע תחילת התנועה .
במשך חצי זמן מחזור העגלה נעה מנקודת הקצה השמאלית לנקודת הקצה הימנית(במשך שנייה אחת).
נחשב את הזמן 't שעובר מרגע שהעגלה נעה מנקודה C ועד שהיא מגיעה לנקודת הקצה הימנית: «math xmlns=¨http://www.w3.org/1998/Math/MathML¨»«mi mathvariant=¨bold¨ mathcolor=¨#0000FF¨»t«/mi»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»`«/mo»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»=«/mo»«mn mathvariant=¨bold¨ mathcolor=¨#0000FF¨»1«/mn»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»-«/mo»«mn mathvariant=¨bold¨ mathcolor=¨#0000FF¨»0«/mn»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨».«/mo»«mn mathvariant=¨bold¨ mathcolor=¨#0000FF¨»8«/mn»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»=«/mo»«mn mathvariant=¨bold¨ mathcolor=¨#0000FF¨»0«/mn»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨».«/mo»«mn mathvariant=¨bold¨ mathcolor=¨#0000FF¨»2«/mn»«mi mathvariant=¨bold¨ mathcolor=¨#0000FF¨»S«/mi»«/math»
זמן זהה עובר מרגע שהעגלה יוצאת מנקודת הקצה הימנית ועד שהיא חולפת בנקודה C בפעם השנייה.
לכן סה"כ הזמן שעובר מרגע תחילת התנועה ועד שהעגלה חולפת בפעם השנייה בנקודה C הוא 1.2 שניות.
1. لا يمكن استخدام تعبير القوة المعيدة، وجميع دوال الحركة التوافقية البسيطة، باستخدام المحور المُعطى في السؤال.
يجب تحديد محور جديد، بدءًا من النقطة التي يكون فيها الجسم في حالة اتزان.
يجب تحديد محور جديد، بدءًا من النقطة التي يكون فيها الجسم في حالة اتزان.
2. من المستحسن تحديد اتجاه المحور الجديد إلى اليسار، بحيث تبدأ الحركة من نقطة الطرف الموجبة.
وسيكون من الممكن استخدام دوال الحركة التوافقية البسيطة بدون زاوية طور ابتدائية.
وسيكون من الممكن استخدام دوال الحركة التوافقية البسيطة بدون زاوية طور ابتدائية.
3. لم يتم تحديد الزمن t2 بشكل واضح في السؤال. يشير هذا إلى الزمن الذي يمر منذ لحظة بدء الحركة.
4. إذا قمنا بتعويض الزمن t1 أو الزمن t2 في دالة الموقع-الزمن، فسنحصل على نفس الموقع.
5. في كل دورة حركة، يمر الجسم بنفس النقطة مرتين.
إن الزمن الذي يمر بين لحظة مرور الجسم بنقطة ما للمرة الأولى والمرة الثانية عبر تلك النقطة ليس زمن دورة ولا نصف دورة.
إن الزمن الذي يمر بين لحظة مرور الجسم بنقطة ما للمرة الأولى والمرة الثانية عبر تلك النقطة ليس زمن دورة ولا نصف دورة.
יש להגדיר ציר חדש , שראשיתו בנקודה בה הגוף נמצא בשיווי משקל.
2. מומלץ להגדיר את כיוון הציר החדש שמאלה,כך שתחילת התנועה תהיה מנקודת הקצה החיובית
וניתן יהיה להשתמש בפונקציות התה"פ ללא זווית מופע התחלתית.
3. הזמן t2 לא מוגדר בצורה ברורה בשאלה. הכוונה היא לזמן שעובר מרגע תחילת התנועה.
4. אם נציב בפונקציית המקום זמן את זמן t1 או את זמן t2 , נקבל מיקום זהה.
5. בכל מחזור תנועה הגוף חולף פעמיים דרך אותה נקודה.
הזמן שעובר בין הרגע שבו הגוף חולף בפעם הראשונה בנקודה לפעם השנייה בנקודה הוא לא זמן מחזור ולא חצי זמן מחזור.
______________________________________________________________________________________
______________________________________________________________________________________
...
هـ.1- سوف يزداد زمن الدورة.
هـ.2- لن يتغير زمن الدورة.
هـ.3- سوف يقل زمن الدورة.
ה.2- זמן המחזור לא ישתנה.
ה.3- זמן המחזור יקטן.
صيغة زمن الدورة للحركة التوافقية البسيطة.
نستخدم تعبير زمن الدورة «math xmlns=¨http://www.w3.org/1998/Math/MathML¨»«mi mathvariant=¨bold-italic¨ mathcolor=¨#0000FF¨»T«/mi»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»=«/mo»«mn mathvariant=¨bold¨ mathcolor=¨#0000FF¨»2«/mn»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»§#183;«/mo»«mi mathvariant=¨bold¨ mathcolor=¨#0000FF¨»§#960;«/mi»«msqrt mathcolor=¨#0000FF¨»«mfrac»«mi mathvariant=¨bold¨»m«/mi»«mi mathvariant=¨bold¨»k«/mi»«/mfrac»«/msqrt»«/math» لتحديد كيف يتغير زمن الدورة في كل حالة.
1. ومن خلال التعبير، يمكننا أن نرى أنه مع زيادة كتلة العربة، يزداد زمن الدورة أيضًا.
2. يؤدي تغيير ضغط النابض فقط إلى تغيير سعة الحركة؛ ومن خلال التعبير يمكننا أن نرى أن زمن الدورة لا يتعلق بسعة الحركة.
3. كلما كان ثابت النابض أكبر، كلما كان زمن الدورة أقصر. كما يتضح من التعبير.
1. מהביטוי ניתן לראות שככל שמסת העגלה גדלה , גם זמן המחזור גדל.
2. שינוי כיווץ הקפיץ משנה את משרעת התנועה בלבד, מהביטוי ניתן לראות שזמן המחזור לא תלוי במשרעת התנועה.
3. ככל שקבוע הקפיץ גדול יותר כך זמן מחזור התנועה קטן יותר. כפי שניתן לראות מהביטוי.
1. في بعض الأحيان يكون من الأسهل والأصح الاعتماد على تعبير ما لمعرفة الإجابة والتعليل باستخدام التعبير.
هناك تعبيرات "غير محدودة"، ويجب فحص العلاقة لكل من الكميات الفيزيائية التي تظهر في التعبير.
هناك تعبيرات "غير محدودة"، ويجب فحص العلاقة لكل من الكميات الفيزيائية التي تظهر في التعبير.
2. إلى جانب الصيغ، من المهم الاعتماد على المنطق...
لا يتعلق زمن الدورة على السعة - فكلما زادت السعة، زاد زمن الحركة من البداية إلى النهاية.
من ناحية أخرى، يتحرك الجسم بسرعات أكبر، وبشكل عام، لا تؤثر السعة على زمن الدورة.
يتعلق زمن الدورة على الكتلة - فكلما زادت الكتلة، قل التسارع في كل نقطة، وبالتالي يتحرك الجسم بسرعات أقل.
وسوف تكون زمن الدورة أطول. من التعبير، عندما تزيد الكتلة بمقدار 2 مرات، يزداد زمن الدورة بمقدار الجذر التربيعي لـ 2.
يتعلق زمن الدورة على ثابت النابض - فكلما كان ثابت النابض أكبر، كلما زاد تسارع الجسم في كل نقطة، وسيتحرك الجسم بسرعات أكبر.
ستكون زمن الدورة أقصر. من التعبير، عندما يكون ثابت النابض أكبر بمرتين، يكون زمن الدورة أقل بمرتين.
3. لا تحتاج الإجابة إلى تحديد كيفية تغير زمن الدورة بشكل دقيق. فقط إذا كان يكبر يصغر أو لا يتغير.
4. ليست هناك حاجة لتطوير تعبير زمن الدورة، حيث أنّ التعبير موجود في أوراق القوانين.
יש ביטויים שהם "לא סופיים" , יש לבחון את התלות של כל אחד מהגדלים הפיזיקלים המופיעים בביטוי.
2. מעבר לנוסחאות חשוב להתחבר להיגיון ...
זמן המחזור לא תלוי במשרעת - ככל שהמשרעת גדולה יותר כך זמן התנועה מקצה לקצה גדול יותר
מצד שני הגוף נע במהירויות גדולות יותר ,ובסך הכל אין למשרעת השפעה על זמן המחזור.
זמן המחזור תלוי במסה- ככל שהמסה גדולה יותר כך התאוצה בכל נקודה תהיה קטנה יותר, הגוף ינוע במהירויות יותר קטנות.
וזמן המחזור יהיה יותר גדול. מהביטוי כאשר המסה גדלה פי 2 זמן המחזור גדל פי שורש 2.
זמן המחזור תלוי בקבוע הקפיץ- ככל שקבוע הקפיץ גדול יותר , תאוצת הגוף בכל נקודה תהיה גדולה יותר ,והגוף ינוע במהירויות גדולות יותר.
זמן המחזור יהיה יותר קטן. מהביטוי כאשר קבוע הקפיץ גדול פי 2 , זמן המחזור קטן פי שורש 2.
______________________________________________________________________________________