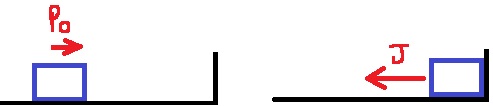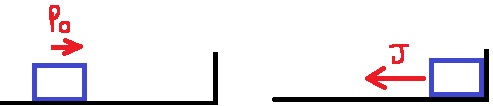
______________________________________________________________________________________
...
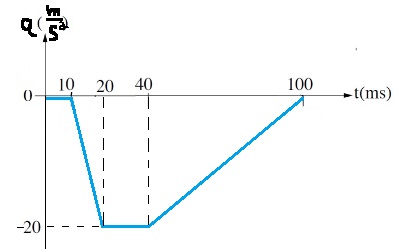
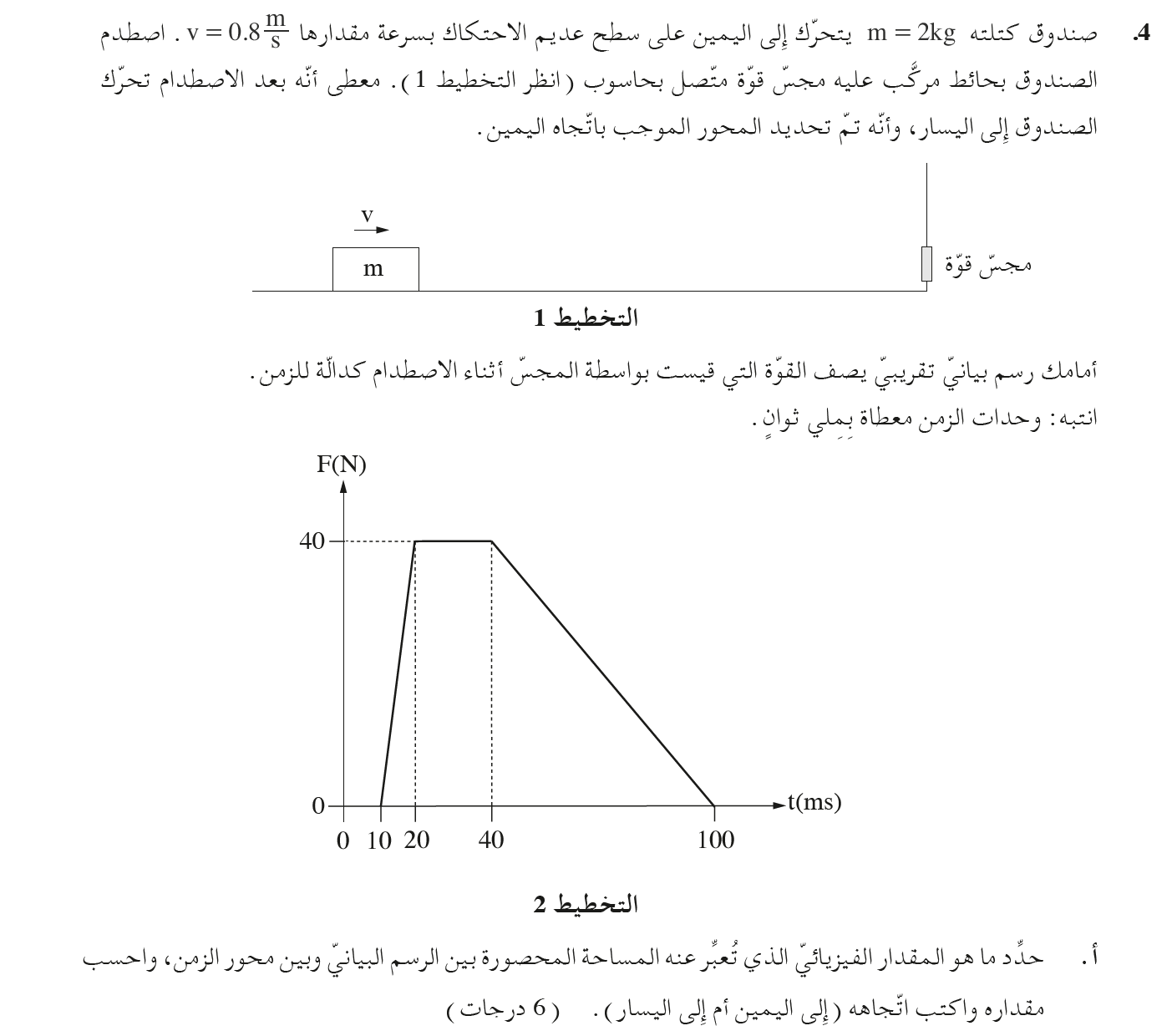
المساحة المحصورة بين الرسم البياني ومحور الزمن تُعبّر عن كمية الدفع التي عملت على المجس ، واتجاه كمية الدفع هذه نحو اليمين ، وومقدار كمية الدفع هذه 2.2NS.
معرفة معنى المساحة المحصورة في الرسم البياني للقوة كدالة للزمن.
حسب تعريف كمية الدفع: «math xmlns=¨http://www.w3.org/1998/Math/MathML¨»«mover mathcolor=¨#0000FF¨»«mi mathvariant=¨bold¨»J«/mi»«mo mathvariant=¨bold¨»§#8594;«/mo»«/mover»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»=«/mo»«mover mathcolor=¨#0000FF¨»«mi mathvariant=¨bold¨»F«/mi»«mo mathvariant=¨bold¨»§#8594;«/mo»«/mover»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»§#183;«/mo»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»§#8710;«/mo»«mi mathvariant=¨bold¨ mathcolor=¨#0000FF¨»t«/mi»«/math» , المساحة المحصورة بين الرسم البياني للقوة كدالة للزمن ومحور الزمن تساوي كمية الدفع.
القوة الموضحة في الرسم البياني موجبة واتجاه المحور إلى اليمين. لذلك فإن الرسم البياني يعبر عن كمية الدفع التي تعمل على المجس.
احسب مقدار كمية الدفع عن طريق حساب المساحة المحصورة المحصورة تحت شبه المنحرف:
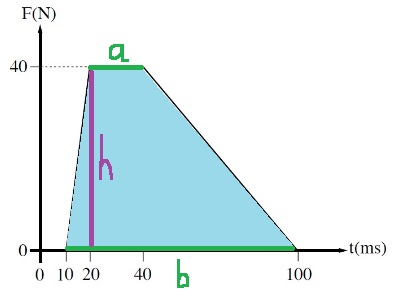
«math xmlns=¨http://www.w3.org/1998/Math/MathML¨»«mi mathvariant=¨bold¨ mathcolor=¨#0000FF¨»J«/mi»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»=«/mo»«mfrac mathcolor=¨#0000FF¨»«mrow»«mrow»«mo mathvariant=¨bold¨»(«/mo»«mi mathvariant=¨bold¨»a«/mi»«mo mathvariant=¨bold¨»+«/mo»«mi mathvariant=¨bold¨»b«/mi»«mo mathvariant=¨bold¨»)«/mo»«/mrow»«mo mathvariant=¨bold¨»§#183;«/mo»«mi mathvariant=¨bold¨»h«/mi»«/mrow»«mn mathvariant=¨bold¨»2«/mn»«/mfrac»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»=«/mo»«mfrac mathcolor=¨#0000FF¨»«mrow»«mrow»«mo mathvariant=¨bold¨»(«/mo»«mn mathvariant=¨bold¨»20«/mn»«mo mathvariant=¨bold¨»§#183;«/mo»«msup»«mn mathvariant=¨bold¨»10«/mn»«mrow»«mo mathvariant=¨bold¨»-«/mo»«mn mathvariant=¨bold¨»3«/mn»«/mrow»«/msup»«mo mathvariant=¨bold¨»+«/mo»«mn mathvariant=¨bold¨»90«/mn»«mo mathvariant=¨bold¨»§#183;«/mo»«msup»«mn mathvariant=¨bold¨»10«/mn»«mrow»«mo mathvariant=¨bold¨»-«/mo»«mn mathvariant=¨bold¨»3«/mn»«/mrow»«/msup»«mo mathvariant=¨bold¨»)«/mo»«/mrow»«mo mathvariant=¨bold¨»§#183;«/mo»«mn mathvariant=¨bold¨»40«/mn»«/mrow»«mn mathvariant=¨bold¨»2«/mn»«/mfrac»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»=«/mo»«mfrac mathcolor=¨#0000FF¨»«mrow»«mn mathvariant=¨bold¨»4«/mn»«mo mathvariant=¨bold¨».«/mo»«mn mathvariant=¨bold¨»4«/mn»«/mrow»«mn mathvariant=¨bold¨»2«/mn»«/mfrac»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»=«/mo»«mn mathvariant=¨bold¨ mathcolor=¨#0000FF¨»2«/mn»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨».«/mo»«mn mathvariant=¨bold¨ mathcolor=¨#0000FF¨»2«/mn»«mi mathvariant=¨bold¨ mathcolor=¨#0000FF¨»N«/mi»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»§#183;«/mo»«mi mathvariant=¨bold¨ mathcolor=¨#0000FF¨»s«/mi»«/math»
لذلك ، تعبّر المساحة عن كمية دفع مقدارها 2.2NS وموجهة إلى اليمين.
נחשב את המתקף בעזרת חישוב השטח התחום בטרפז:

«math xmlns=¨http://www.w3.org/1998/Math/MathML¨»«mi mathvariant=¨bold¨ mathcolor=¨#0000FF¨»J«/mi»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»=«/mo»«mfrac mathcolor=¨#0000FF¨»«mrow»«mrow»«mo mathvariant=¨bold¨»(«/mo»«mi mathvariant=¨bold¨»a«/mi»«mo mathvariant=¨bold¨»+«/mo»«mi mathvariant=¨bold¨»b«/mi»«mo mathvariant=¨bold¨»)«/mo»«/mrow»«mo mathvariant=¨bold¨»§#183;«/mo»«mi mathvariant=¨bold¨»h«/mi»«/mrow»«mn mathvariant=¨bold¨»2«/mn»«/mfrac»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»=«/mo»«mfrac mathcolor=¨#0000FF¨»«mrow»«mrow»«mo mathvariant=¨bold¨»(«/mo»«mn mathvariant=¨bold¨»20«/mn»«mo mathvariant=¨bold¨»§#183;«/mo»«msup»«mn mathvariant=¨bold¨»10«/mn»«mrow»«mo mathvariant=¨bold¨»-«/mo»«mn mathvariant=¨bold¨»3«/mn»«/mrow»«/msup»«mo mathvariant=¨bold¨»+«/mo»«mn mathvariant=¨bold¨»90«/mn»«mo mathvariant=¨bold¨»§#183;«/mo»«msup»«mn mathvariant=¨bold¨»10«/mn»«mrow»«mo mathvariant=¨bold¨»-«/mo»«mn mathvariant=¨bold¨»3«/mn»«/mrow»«/msup»«mo mathvariant=¨bold¨»)«/mo»«/mrow»«mo mathvariant=¨bold¨»§#183;«/mo»«mn mathvariant=¨bold¨»40«/mn»«/mrow»«mn mathvariant=¨bold¨»2«/mn»«/mfrac»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»=«/mo»«mfrac mathcolor=¨#0000FF¨»«mrow»«mn mathvariant=¨bold¨»4«/mn»«mo mathvariant=¨bold¨».«/mo»«mn mathvariant=¨bold¨»4«/mn»«/mrow»«mn mathvariant=¨bold¨»2«/mn»«/mfrac»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»=«/mo»«mn mathvariant=¨bold¨ mathcolor=¨#0000FF¨»2«/mn»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨».«/mo»«mn mathvariant=¨bold¨ mathcolor=¨#0000FF¨»2«/mn»«mi mathvariant=¨bold¨ mathcolor=¨#0000FF¨»N«/mi»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»§#183;«/mo»«mi mathvariant=¨bold¨ mathcolor=¨#0000FF¨»s«/mi»«/math»
המתקף מופעל בזמן ההתנגשות על ידי הקיר , כיוון הכוח שהקיר מפעיל הוא שמאלה.
מהגדרת המתקף «math xmlns=¨http://www.w3.org/1998/Math/MathML¨»«mover mathcolor=¨#0000FF¨»«mi mathvariant=¨bold¨»J«/mi»«mo mathvariant=¨bold¨»§#8594;«/mo»«/mover»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»=«/mo»«mover mathcolor=¨#0000FF¨»«mi mathvariant=¨bold¨»F«/mi»«mo mathvariant=¨bold¨»§#8594;«/mo»«/mover»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»§#183;«/mo»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»§#8710;«/mo»«mi mathvariant=¨bold¨ mathcolor=¨#0000FF¨»t«/mi»«/math» כיוון המתקף הוא ככיוון הכוח- שמאלה .
לכן, גודלו של המתקף 2.2 ניוטון כפול שניה וכיוונו שמאלה.
1. الرسم البياني للقوة كدالة للزمن هو رسم بياني دارج في كمية الدفع وكمية الحركة، من المهم معرفة الرسم البياني ومعنى المساحة المحصورة بين الرسم البياني ومحور الزمن.
2. أثناء اصطدام الصندوق بالحائط ، هناك قوتان: القوة التي يشغّلها الصندوق على المجس والقوة التي يشغّلها المجس على الصندوق.
لتحديد معنى المساحة المحصورة بشكل صحيح ، يجب أن تفهم أي من القوتين التي يتطرق لها الرسم البياني.
2. ביחס לציר הכוח שלילי והמתקף שלילי . בשאלה כתוב "הגרף מתאר את הכוח שנמדד באמצעות החיישן"
ולא את גודל הכוח הנמדד, אין טעות בשאלה, החיישן לא "מכיר" את הציר הוא תמיד מציג כוח חיובי.
יש לתאר את הגדלים הפיזיקליים ביחס לציר הנבחר. גם אם החיישן לא מתאר את הכוח ביחס לציר.
______________________________________________________________________________________

______________________________________________________________________________________
...
تعريف كمية الحركة وتعريف كمية الدفع.
تسبب كمية الدفع التي تعمل على الصندوق تغييرًا في الاتجاه، وبالتالي تكون كمية الدفع أكبر من كمية الحركة الابتدائية.
نصف متّجه كمية الحركة ومتوسط متّجه كمية الحركة الذي يعمل أثناء الاصطدام.
يوضّح الشكل الأيمن متّجه القوة الذي يعمل أثناء الاصطدام ويوضح الشكل الأيسر متّجه كمية الحركة قبل الاصطدام:
يعمل متّجه كمية الدفع في اتجاه القوة إلى اليسار ويكون أكبر من متّجه كمية الحركة الابتدائي. اتجاه متّجه كمية الحركة الابتدائي هو اتجاه الحركة إلى اليسار.
נתאר את וקטור התנע ואת וקטור המתקף הממוצע הפועל במהלך ההתנגשות.
1. مكتوب في السؤال أنه يجب الحرص على النسبة بين طولَي المتّجهين ، وبعبارة أخرى ، من المهم معرفة أي من المتّجهات أكبر.
2. كمية الدفع تساوي التغيير في كمية الحركة. إذا تسبب الدفع في تغيير الجسم لاتجاه حركته ، فيمكن تحديد أن كمية الدفع أكبر من كمية الحركة الابتدائية.
من الممكن أيضًا مقدار كمية الدفع ومقدار كمية الحركة ومقارنتها.
وجدنا في القسم السابق أن مقدار متّجه كمية الدفع يساوي 2.2NS. نحسب كمية الحركة الابتدائية:
«math xmlns=¨http://www.w3.org/1998/Math/MathML¨»«msub»«mi mathvariant=¨bold¨ mathcolor=¨#0000FF¨»P«/mi»«mn mathvariant=¨bold¨ mathcolor=¨#0000FF¨»0«/mn»«/msub»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»=«/mo»«mi mathvariant=¨bold¨ mathcolor=¨#0000FF¨»m«/mi»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»§#183;«/mo»«msub»«mi mathvariant=¨bold¨ mathcolor=¨#0000FF¨»V«/mi»«mn mathvariant=¨bold¨ mathcolor=¨#0000FF¨»0«/mn»«/msub»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»=«/mo»«mn mathvariant=¨bold¨ mathcolor=¨#0000FF¨»2«/mn»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»§#183;«/mo»«mn mathvariant=¨bold¨ mathcolor=¨#0000FF¨»0«/mn»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨».«/mo»«mn mathvariant=¨bold¨ mathcolor=¨#0000FF¨»8«/mn»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»=«/mo»«mn mathvariant=¨bold¨ mathcolor=¨#0000FF¨»1«/mn»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨».«/mo»«mn mathvariant=¨bold¨ mathcolor=¨#0000FF¨»6«/mn»«mi mathvariant=¨bold¨ mathcolor=¨#0000FF¨»N«/mi»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»§#183;«/mo»«mi mathvariant=¨bold¨ mathcolor=¨#0000FF¨»s«/mi»«/math»
ومن ثم فإن مقدار كمية الدفع أكبر من مقدار كمية الحركة الابتدائية .
2. המתקף שווה לשינוי בתנע. אם המתקף גורם לגוף לשנות את כיוון תנועתו ניתן לקבוע שהמתקף גדול מהתנע ההתחלתי.
אפשר גם למצוא את ערך המתקף ואת ערך התנע ההתחלתי ולהשוות ביניהם.
בסעיף הקודם מצאנו שגודל ווקטור המתקף שווה 2.2 ניוטון כפול שניה . נחשב את התנע ההתחלתי:
«math xmlns=¨http://www.w3.org/1998/Math/MathML¨»«msub»«mi mathvariant=¨bold¨ mathcolor=¨#0000FF¨»P«/mi»«mn mathvariant=¨bold¨ mathcolor=¨#0000FF¨»0«/mn»«/msub»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»=«/mo»«mi mathvariant=¨bold¨ mathcolor=¨#0000FF¨»m«/mi»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»§#183;«/mo»«msub»«mi mathvariant=¨bold¨ mathcolor=¨#0000FF¨»V«/mi»«mn mathvariant=¨bold¨ mathcolor=¨#0000FF¨»0«/mn»«/msub»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»=«/mo»«mn mathvariant=¨bold¨ mathcolor=¨#0000FF¨»2«/mn»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»§#183;«/mo»«mn mathvariant=¨bold¨ mathcolor=¨#0000FF¨»0«/mn»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨».«/mo»«mn mathvariant=¨bold¨ mathcolor=¨#0000FF¨»8«/mn»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»=«/mo»«mn mathvariant=¨bold¨ mathcolor=¨#0000FF¨»1«/mn»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨».«/mo»«mn mathvariant=¨bold¨ mathcolor=¨#0000FF¨»6«/mn»«mi mathvariant=¨bold¨ mathcolor=¨#0000FF¨»N«/mi»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»§#183;«/mo»«mi mathvariant=¨bold¨ mathcolor=¨#0000FF¨»s«/mi»«/math»
מכאן שגודלו של המתקף גדול יותר מגודל התנע ההתחלתי.
______________________________________________________________________________________
______________________________________________________________________________________
...
«math xmlns=¨http://www.w3.org/1998/Math/MathML¨»«mi mathvariant=¨bold¨ mathcolor=¨#0000FF¨»V«/mi»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»`«/mo»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»=«/mo»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»-«/mo»«mn mathvariant=¨bold¨ mathcolor=¨#0000FF¨»0«/mn»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨».«/mo»«mn mathvariant=¨bold¨ mathcolor=¨#0000FF¨»3«/mn»«mfrac mathcolor=¨#0000FF¨»«mi mathvariant=¨bold¨»m«/mi»«mi mathvariant=¨bold¨»s«/mi»«/mfrac»«/math»
قانون كمية الدفع وكمية الحركة.
نجد سرعة الصندوق بعد الاصطدام باستخدام قانون كمية الدفع وكمية الحركة بالنسبة للمحور المحدد:
«math xmlns=¨http://www.w3.org/1998/Math/MathML¨»«mi mathvariant=¨bold¨ mathcolor=¨#0000FF¨»J«/mi»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»=«/mo»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»§#8710;«/mo»«mi mathvariant=¨bold¨ mathcolor=¨#0000FF¨»P«/mi»«mspace linebreak=¨newline¨/»«mi mathvariant=¨bold¨ mathcolor=¨#0000FF¨»J«/mi»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»=«/mo»«mi mathvariant=¨bold¨ mathcolor=¨#0000FF¨»P«/mi»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»`«/mo»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»-«/mo»«msub»«mi mathvariant=¨bold¨ mathcolor=¨#0000FF¨»P«/mi»«mn mathvariant=¨bold¨ mathcolor=¨#0000FF¨»0«/mn»«/msub»«mspace linebreak=¨newline¨/»«mi mathvariant=¨bold¨ mathcolor=¨#0000FF¨»P«/mi»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»`«/mo»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»=«/mo»«mi mathvariant=¨bold¨ mathcolor=¨#0000FF¨»J«/mi»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»+«/mo»«msub»«mi mathvariant=¨bold¨ mathcolor=¨#0000FF¨»P«/mi»«mn mathvariant=¨bold¨ mathcolor=¨#0000FF¨»0«/mn»«/msub»«mspace linebreak=¨newline¨/»«mi mathvariant=¨bold¨ mathcolor=¨#0000FF¨»m«/mi»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»§#183;«/mo»«mi mathvariant=¨bold¨ mathcolor=¨#0000FF¨»V«/mi»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»`«/mo»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»=«/mo»«mi mathvariant=¨bold¨ mathcolor=¨#0000FF¨»J«/mi»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»+«/mo»«msub»«mi mathvariant=¨bold¨ mathcolor=¨#0000FF¨»P«/mi»«mn mathvariant=¨bold¨ mathcolor=¨#0000FF¨»0«/mn»«/msub»«mspace linebreak=¨newline¨/»«mi mathvariant=¨bold¨ mathcolor=¨#0000FF¨»V«/mi»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»`«/mo»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»=«/mo»«mfrac mathcolor=¨#0000FF¨»«mrow»«mi mathvariant=¨bold¨»J«/mi»«mo mathvariant=¨bold¨»+«/mo»«msub»«mi mathvariant=¨bold¨»P«/mi»«mn mathvariant=¨bold¨»0«/mn»«/msub»«/mrow»«mi mathvariant=¨bold¨»m«/mi»«/mfrac»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»=«/mo»«mfrac mathcolor=¨#0000FF¨»«mrow»«mi mathvariant=¨bold¨»J«/mi»«mo mathvariant=¨bold¨»+«/mo»«mi mathvariant=¨bold¨»m«/mi»«mo mathvariant=¨bold¨»§#183;«/mo»«msub»«mi mathvariant=¨bold¨»V«/mi»«mn mathvariant=¨bold¨»0«/mn»«/msub»«/mrow»«mi mathvariant=¨bold¨»m«/mi»«/mfrac»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»=«/mo»«mfrac mathcolor=¨#0000FF¨»«mrow»«mo mathvariant=¨bold¨»-«/mo»«mn mathvariant=¨bold¨»2«/mn»«mo mathvariant=¨bold¨».«/mo»«mn mathvariant=¨bold¨»2«/mn»«mo mathvariant=¨bold¨»+«/mo»«mn mathvariant=¨bold¨»2«/mn»«mo mathvariant=¨bold¨»§#183;«/mo»«mn mathvariant=¨bold¨»0«/mn»«mo mathvariant=¨bold¨».«/mo»«mn mathvariant=¨bold¨»8«/mn»«/mrow»«mn mathvariant=¨bold¨»2«/mn»«/mfrac»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»=«/mo»«mfrac mathcolor=¨#0000FF¨»«mrow»«mo mathvariant=¨bold¨»-«/mo»«mn mathvariant=¨bold¨»0«/mn»«mo mathvariant=¨bold¨».«/mo»«mn mathvariant=¨bold¨»6«/mn»«/mrow»«mn mathvariant=¨bold¨»2«/mn»«/mfrac»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»=«/mo»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»-«/mo»«mn mathvariant=¨bold¨ mathcolor=¨#0000FF¨»0«/mn»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨».«/mo»«mn mathvariant=¨bold¨ mathcolor=¨#0000FF¨»3«/mn»«mfrac mathcolor=¨#0000FF¨»«mi mathvariant=¨bold¨»m«/mi»«mi mathvariant=¨bold¨»s«/mi»«/mfrac»«/math»
لذلك ، فإن سرعة الصندوق بعد الاصطدام تساوي 0.3 متر في الثانية. اتجاه حركة الصندوق إلى اليسار.
«math xmlns=¨http://www.w3.org/1998/Math/MathML¨»«mi mathvariant=¨bold¨ mathcolor=¨#0000FF¨»J«/mi»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»=«/mo»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»§#8710;«/mo»«mi mathvariant=¨bold¨ mathcolor=¨#0000FF¨»P«/mi»«mspace linebreak=¨newline¨/»«mi mathvariant=¨bold¨ mathcolor=¨#0000FF¨»J«/mi»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»=«/mo»«mi mathvariant=¨bold¨ mathcolor=¨#0000FF¨»P«/mi»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»`«/mo»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»-«/mo»«msub»«mi mathvariant=¨bold¨ mathcolor=¨#0000FF¨»P«/mi»«mn mathvariant=¨bold¨ mathcolor=¨#0000FF¨»0«/mn»«/msub»«mspace linebreak=¨newline¨/»«mi mathvariant=¨bold¨ mathcolor=¨#0000FF¨»P«/mi»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»`«/mo»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»=«/mo»«mi mathvariant=¨bold¨ mathcolor=¨#0000FF¨»J«/mi»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»+«/mo»«msub»«mi mathvariant=¨bold¨ mathcolor=¨#0000FF¨»P«/mi»«mn mathvariant=¨bold¨ mathcolor=¨#0000FF¨»0«/mn»«/msub»«mspace linebreak=¨newline¨/»«mi mathvariant=¨bold¨ mathcolor=¨#0000FF¨»m«/mi»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»§#183;«/mo»«mi mathvariant=¨bold¨ mathcolor=¨#0000FF¨»V«/mi»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»`«/mo»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»=«/mo»«mi mathvariant=¨bold¨ mathcolor=¨#0000FF¨»J«/mi»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»+«/mo»«msub»«mi mathvariant=¨bold¨ mathcolor=¨#0000FF¨»P«/mi»«mn mathvariant=¨bold¨ mathcolor=¨#0000FF¨»0«/mn»«/msub»«mspace linebreak=¨newline¨/»«mi mathvariant=¨bold¨ mathcolor=¨#0000FF¨»V«/mi»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»`«/mo»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»=«/mo»«mfrac mathcolor=¨#0000FF¨»«mrow»«mi mathvariant=¨bold¨»J«/mi»«mo mathvariant=¨bold¨»+«/mo»«msub»«mi mathvariant=¨bold¨»P«/mi»«mn mathvariant=¨bold¨»0«/mn»«/msub»«/mrow»«mi mathvariant=¨bold¨»m«/mi»«/mfrac»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»=«/mo»«mfrac mathcolor=¨#0000FF¨»«mrow»«mi mathvariant=¨bold¨»J«/mi»«mo mathvariant=¨bold¨»+«/mo»«mi mathvariant=¨bold¨»m«/mi»«mo mathvariant=¨bold¨»§#183;«/mo»«msub»«mi mathvariant=¨bold¨»V«/mi»«mn mathvariant=¨bold¨»0«/mn»«/msub»«/mrow»«mi mathvariant=¨bold¨»m«/mi»«/mfrac»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»=«/mo»«mfrac mathcolor=¨#0000FF¨»«mrow»«mo mathvariant=¨bold¨»-«/mo»«mn mathvariant=¨bold¨»2«/mn»«mo mathvariant=¨bold¨».«/mo»«mn mathvariant=¨bold¨»2«/mn»«mo mathvariant=¨bold¨»+«/mo»«mn mathvariant=¨bold¨»2«/mn»«mo mathvariant=¨bold¨»§#183;«/mo»«mn mathvariant=¨bold¨»0«/mn»«mo mathvariant=¨bold¨».«/mo»«mn mathvariant=¨bold¨»8«/mn»«/mrow»«mn mathvariant=¨bold¨»2«/mn»«/mfrac»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»=«/mo»«mfrac mathcolor=¨#0000FF¨»«mrow»«mo mathvariant=¨bold¨»-«/mo»«mn mathvariant=¨bold¨»0«/mn»«mo mathvariant=¨bold¨».«/mo»«mn mathvariant=¨bold¨»6«/mn»«/mrow»«mn mathvariant=¨bold¨»2«/mn»«/mfrac»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»=«/mo»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»-«/mo»«mn mathvariant=¨bold¨ mathcolor=¨#0000FF¨»0«/mn»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨».«/mo»«mn mathvariant=¨bold¨ mathcolor=¨#0000FF¨»3«/mn»«mfrac mathcolor=¨#0000FF¨»«mi mathvariant=¨bold¨»m«/mi»«mi mathvariant=¨bold¨»s«/mi»«/mfrac»«/math»
לכן, גודל מהירות התיבה לאחר ההתנגשות היא 0.3 מטר לשנייה. כיוון תנועת התיבה שמאלה.
1. بعد الاصطدام ، يتحرك الصندوق إلى اليسار ، عكس اتجاه المحور. لذلك يجب أن تكون سرعة الصندوق بالنسبة للمحور سالبة.
2. منذ اللحظة التي وجدنا فيها كمية الحركة، لم يعد الرسم البياني مستخدمًا لإيجاد سرعة الصندوق بعد الاصطدام.
3. يجب ايجاد سرعة الصندوق بعد الاصطدام مباشرة. لم يتم تحديد سرعة الصندوق في اللحظة التي تلي الاصطدام.
يتم تحديد السرعة وفقًا لتأثير القوة طوال فترة الاصطدام.
2. מרגע שמצאנו את המתקף אין עוד שימוש בגרף למציאת מהירות התיבה לאחר ההתנגשות.
3. יש למצוא את מהירות התיבה רגע לאחר ההתנגשות. מהירות התיבה לא נקבעת ברגע שלאחר ההתנגשות.
המהירות נקבעת בהתאם לפעולת הכוח כל זמן ההתנגשות.
______________________________________________________________________________________

______________________________________________________________________________________
...
القانون الثاني لنيوتن.
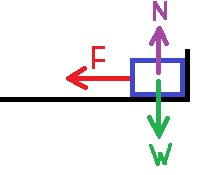
تعمل ثلاث قوى على الصندوق: القوة العمودية. قوة الجاذبية لأسفل. والقوة التي يشغّلها المجس إلى اليسار.
نرسم مخطّط للقوى المؤثرة على الصندوق:
القوى الرأسية تُبطل احداهما الأخرى ، القوة المحصلة المؤثرة على الصندوق تساوي القوة F التي يشغّلها المجس على الصندوق.
من القانون الثاني لنيوتن، تسارع الصندوق يساوي النسبة بين القوة المحصلة وكتلة الجسم:
«math xmlns=¨http://www.w3.org/1998/Math/MathML¨»«mi mathvariant=¨bold¨ mathcolor=¨#0000FF¨»§#931;F«/mi»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»=«/mo»«mi mathvariant=¨bold¨ mathcolor=¨#0000FF¨»m«/mi»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»§#183;«/mo»«mi mathvariant=¨bold¨ mathcolor=¨#0000FF¨»a«/mi»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»§#160;«/mo»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»§#160;«/mo»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»§#8658;«/mo»«mi mathvariant=¨bold¨ mathcolor=¨#0000FF¨»a«/mi»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»=«/mo»«mfrac mathcolor=¨#0000FF¨»«mi mathvariant=¨bold¨»§#931;F«/mi»«mi mathvariant=¨bold¨»m«/mi»«/mfrac»«mspace linebreak=¨newline¨/»«/math»
بالإضافة إلى ذلك ، يكون اتجاه القوة المحصلة عكس اتجاه المحور - وبالتالي يكون التسارع سالبًا.
נערוך תרשים כוחות:
הכוחות האנכיים מתקזזים, הכוח השקול הפועל על התיבה שווה לכוח F שהקיר מפעיל על התיבה.
מהחוק השני של ניוטון תאוצת התיבה שווה ליחס שבין הכוח השקול למסת הגוף:
«math xmlns=¨http://www.w3.org/1998/Math/MathML¨»«mi mathvariant=¨bold¨ mathcolor=¨#0000FF¨»§#931;F«/mi»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»=«/mo»«mi mathvariant=¨bold¨ mathcolor=¨#0000FF¨»m«/mi»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»§#183;«/mo»«mi mathvariant=¨bold¨ mathcolor=¨#0000FF¨»a«/mi»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»§#160;«/mo»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»§#160;«/mo»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»§#8658;«/mo»«mi mathvariant=¨bold¨ mathcolor=¨#0000FF¨»a«/mi»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»=«/mo»«mfrac mathcolor=¨#0000FF¨»«mi mathvariant=¨bold¨»§#931;F«/mi»«mi mathvariant=¨bold¨»m«/mi»«/mfrac»«mspace linebreak=¨newline¨/»«/math»
לכן, ערך התאוצה קטן פי ערך המסה .
בנוסף, כיוון הכוח השקול הוא נגד כיוון הציר - לכן התאוצה שלילית.
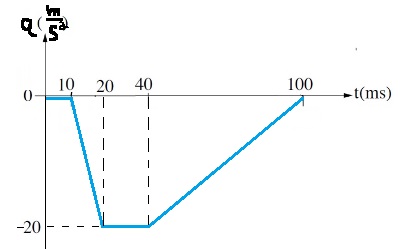
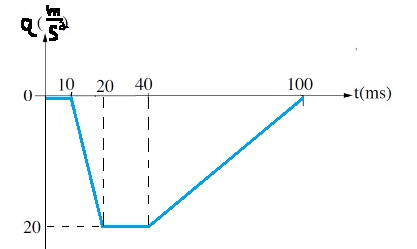
1. في الأسئلة التي لا يلزم فيها إضافة قيم كمية ، يُطلب في السؤال في شكل صريح: أرسم رسم بياني كيفي، أو صِف نوعياً.
في هذه الحالة ، يقول فقط أن هناك رسمًا بيانيًا يتم رسمه، لذا يجب إضافة قيم كمية مهمة إلى الرسم البياني، مثل الحد الأدنى لقيمة تسارع الصندوق.
2. إذا كان مكتوبًا في السؤال: "ارسم رسمًا بيانيًا يصف مقدار تسارع الصندوق" ، فيمكن وصف التسارع كتسارع موجب.
لكن في هذه الحالة ، تعمل القوة عكس اتجاه المحور ، ومطلوب رسم بياني للتسارع . لذلك يجب أن يكون التسارع سالبًا.
في الرسم البياني الموضح في السؤال ، القوة موجبة. لكن هذا الرسم البياني ليس الرسم البياني للقوة. هذا الرسم البياني هو الرسم البياني الذي تم قياسه بواسطة المجس.
במקרה זה כתוב רק שיש לסרטט גרף גרף, לכן יש להוסיף לגרף ערכים כמותיים חשובים, כמו ערך תאוצת התיבה המינימאלי.
2. אם היה כתוב בשאלה " סרטט גרף המתאר את גודל תאוצת התיבה" ניתן היה לתאר את התאוצה כתאוצה חיובית.
אך במקרה זה הכוח פועל נגד כיוון הציר , וכתוב רק סרטט גרף של התאוצה. לכן התאוצה חייבת להיות שלילית.
בגרף הנתון בשאלה הכוח חיובי. אך גרף זה איננו גרף הכוח . גרף זה הוא הגרף הנמדד על ידי החיישן.
3. לתלמיד המצליח במבחן להתמודד עם שאלה זו היטב , מומלץ ללמוד פיזיקה בהתמחות משפטים 
______________________________________________________________________________________

______________________________________________________________________________________
...
مقدار القوة الثابتة 24.44 نيوتن.
قانون كمية الدفع وكمية الحركة.
نستخدم قانون كمية الدفع وكمية الحركة، ونتطرق إلى كمية الحركة الابتدائية والنهائية التي تظهر في السؤال.
وفقًا للرسم البياني، استمر زمن الاصطدام 90 جزء من الألف من الثانية فقط.
«math xmlns=¨http://www.w3.org/1998/Math/MathML¨»«mi mathvariant=¨bold¨ mathcolor=¨#0000FF¨»J«/mi»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»=«/mo»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»§#8710;«/mo»«mi mathvariant=¨bold¨ mathcolor=¨#0000FF¨»P«/mi»«mspace linebreak=¨newline¨/»«mspace linebreak=¨newline¨/»«mi mathvariant=¨bold¨ mathcolor=¨#0000FF¨»F«/mi»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»§#183;«/mo»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»§#8710;«/mo»«mi mathvariant=¨bold¨ mathcolor=¨#0000FF¨»t«/mi»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»=«/mo»«mi mathvariant=¨bold¨ mathcolor=¨#0000FF¨»P«/mi»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»`«/mo»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»-«/mo»«msub»«mi mathvariant=¨bold¨ mathcolor=¨#0000FF¨»P«/mi»«mn mathvariant=¨bold¨ mathcolor=¨#0000FF¨»0«/mn»«/msub»«mspace linebreak=¨newline¨/»«mspace linebreak=¨newline¨/»«mi mathvariant=¨bold¨ mathcolor=¨#0000FF¨»F«/mi»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»=«/mo»«mfrac mathcolor=¨#0000FF¨»«mrow»«mi mathvariant=¨bold¨»P«/mi»«mo mathvariant=¨bold¨»`«/mo»«mo mathvariant=¨bold¨»-«/mo»«msub»«mi mathvariant=¨bold¨»P«/mi»«mn mathvariant=¨bold¨»0«/mn»«/msub»«/mrow»«mrow»«mo mathvariant=¨bold¨»§#8710;«/mo»«mi mathvariant=¨bold¨»t«/mi»«/mrow»«/mfrac»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»=«/mo»«mfrac mathcolor=¨#0000FF¨»«mrow»«mi mathvariant=¨bold¨»m«/mi»«mo mathvariant=¨bold¨»§#183;«/mo»«mi mathvariant=¨bold¨»V«/mi»«mo mathvariant=¨bold¨»`«/mo»«mo mathvariant=¨bold¨»-«/mo»«mi mathvariant=¨bold¨»m«/mi»«mo mathvariant=¨bold¨»§#183;«/mo»«msub»«mi mathvariant=¨bold¨»V«/mi»«mn mathvariant=¨bold¨»0«/mn»«/msub»«/mrow»«mrow»«mo mathvariant=¨bold¨»§#8710;«/mo»«mi mathvariant=¨bold¨»t«/mi»«/mrow»«/mfrac»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»=«/mo»«mfrac mathcolor=¨#0000FF¨»«mrow»«mn mathvariant=¨bold¨»2«/mn»«mo mathvariant=¨bold¨»§#183;«/mo»«mo mathvariant=¨bold¨»(«/mo»«mo mathvariant=¨bold¨»-«/mo»«mn mathvariant=¨bold¨»0«/mn»«mo mathvariant=¨bold¨».«/mo»«mn mathvariant=¨bold¨»3«/mn»«mo mathvariant=¨bold¨»)«/mo»«mo mathvariant=¨bold¨»-«/mo»«mn mathvariant=¨bold¨»2«/mn»«mo mathvariant=¨bold¨»§#183;«/mo»«mn mathvariant=¨bold¨»0«/mn»«mo mathvariant=¨bold¨».«/mo»«mn mathvariant=¨bold¨»8«/mn»«/mrow»«mrow»«mn mathvariant=¨bold¨»90«/mn»«mo mathvariant=¨bold¨»§#183;«/mo»«msup»«mn mathvariant=¨bold¨»10«/mn»«mrow»«mo mathvariant=¨bold¨»-«/mo»«mn mathvariant=¨bold¨»3«/mn»«/mrow»«/msup»«/mrow»«/mfrac»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»=«/mo»«mfrac mathcolor=¨#0000FF¨»«mrow»«mo mathvariant=¨bold¨»-«/mo»«mn mathvariant=¨bold¨»2«/mn»«mo mathvariant=¨bold¨».«/mo»«mn mathvariant=¨bold¨»2«/mn»«/mrow»«mrow»«mn mathvariant=¨bold¨»90«/mn»«mo mathvariant=¨bold¨»§#183;«/mo»«msup»«mn mathvariant=¨bold¨»10«/mn»«mrow»«mo mathvariant=¨bold¨»-«/mo»«mn mathvariant=¨bold¨»3«/mn»«/mrow»«/msup»«/mrow»«/mfrac»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»=«/mo»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»-«/mo»«mn mathvariant=¨bold¨ mathcolor=¨#0000FF¨»24«/mn»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨».«/mo»«mn mathvariant=¨bold¨ mathcolor=¨#0000FF¨»44«/mn»«mi mathvariant=¨bold¨ mathcolor=¨#0000FF¨»N«/mi»«mspace linebreak=¨newline¨/»«/math»
إذن ، مقدار القوة الثابتة هو 24.44 نيوتن.
בהתאם לגרף זמן ההתנגשות נמשך 90 אלפיות שניה בלבד.
«math xmlns=¨http://www.w3.org/1998/Math/MathML¨»«mi mathvariant=¨bold¨ mathcolor=¨#0000FF¨»J«/mi»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»=«/mo»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»§#8710;«/mo»«mi mathvariant=¨bold¨ mathcolor=¨#0000FF¨»P«/mi»«mspace linebreak=¨newline¨/»«mspace linebreak=¨newline¨/»«mi mathvariant=¨bold¨ mathcolor=¨#0000FF¨»F«/mi»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»§#183;«/mo»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»§#8710;«/mo»«mi mathvariant=¨bold¨ mathcolor=¨#0000FF¨»t«/mi»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»=«/mo»«mi mathvariant=¨bold¨ mathcolor=¨#0000FF¨»P«/mi»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»`«/mo»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»-«/mo»«msub»«mi mathvariant=¨bold¨ mathcolor=¨#0000FF¨»P«/mi»«mn mathvariant=¨bold¨ mathcolor=¨#0000FF¨»0«/mn»«/msub»«mspace linebreak=¨newline¨/»«mspace linebreak=¨newline¨/»«mi mathvariant=¨bold¨ mathcolor=¨#0000FF¨»F«/mi»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»=«/mo»«mfrac mathcolor=¨#0000FF¨»«mrow»«mi mathvariant=¨bold¨»P«/mi»«mo mathvariant=¨bold¨»`«/mo»«mo mathvariant=¨bold¨»-«/mo»«msub»«mi mathvariant=¨bold¨»P«/mi»«mn mathvariant=¨bold¨»0«/mn»«/msub»«/mrow»«mrow»«mo mathvariant=¨bold¨»§#8710;«/mo»«mi mathvariant=¨bold¨»t«/mi»«/mrow»«/mfrac»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»=«/mo»«mfrac mathcolor=¨#0000FF¨»«mrow»«mi mathvariant=¨bold¨»m«/mi»«mo mathvariant=¨bold¨»§#183;«/mo»«mi mathvariant=¨bold¨»V«/mi»«mo mathvariant=¨bold¨»`«/mo»«mo mathvariant=¨bold¨»-«/mo»«mi mathvariant=¨bold¨»m«/mi»«mo mathvariant=¨bold¨»§#183;«/mo»«msub»«mi mathvariant=¨bold¨»V«/mi»«mn mathvariant=¨bold¨»0«/mn»«/msub»«/mrow»«mrow»«mo mathvariant=¨bold¨»§#8710;«/mo»«mi mathvariant=¨bold¨»t«/mi»«/mrow»«/mfrac»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»=«/mo»«mfrac mathcolor=¨#0000FF¨»«mrow»«mn mathvariant=¨bold¨»2«/mn»«mo mathvariant=¨bold¨»§#183;«/mo»«mo mathvariant=¨bold¨»(«/mo»«mo mathvariant=¨bold¨»-«/mo»«mn mathvariant=¨bold¨»0«/mn»«mo mathvariant=¨bold¨».«/mo»«mn mathvariant=¨bold¨»3«/mn»«mo mathvariant=¨bold¨»)«/mo»«mo mathvariant=¨bold¨»-«/mo»«mn mathvariant=¨bold¨»2«/mn»«mo mathvariant=¨bold¨»§#183;«/mo»«mn mathvariant=¨bold¨»0«/mn»«mo mathvariant=¨bold¨».«/mo»«mn mathvariant=¨bold¨»8«/mn»«/mrow»«mrow»«mn mathvariant=¨bold¨»90«/mn»«mo mathvariant=¨bold¨»§#183;«/mo»«msup»«mn mathvariant=¨bold¨»10«/mn»«mrow»«mo mathvariant=¨bold¨»-«/mo»«mn mathvariant=¨bold¨»3«/mn»«/mrow»«/msup»«/mrow»«/mfrac»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»=«/mo»«mfrac mathcolor=¨#0000FF¨»«mrow»«mo mathvariant=¨bold¨»-«/mo»«mn mathvariant=¨bold¨»2«/mn»«mo mathvariant=¨bold¨».«/mo»«mn mathvariant=¨bold¨»2«/mn»«/mrow»«mrow»«mn mathvariant=¨bold¨»90«/mn»«mo mathvariant=¨bold¨»§#183;«/mo»«msup»«mn mathvariant=¨bold¨»10«/mn»«mrow»«mo mathvariant=¨bold¨»-«/mo»«mn mathvariant=¨bold¨»3«/mn»«/mrow»«/msup»«/mrow»«/mfrac»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»=«/mo»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»-«/mo»«mn mathvariant=¨bold¨ mathcolor=¨#0000FF¨»24«/mn»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨».«/mo»«mn mathvariant=¨bold¨ mathcolor=¨#0000FF¨»44«/mn»«mi mathvariant=¨bold¨ mathcolor=¨#0000FF¨»N«/mi»«mspace linebreak=¨newline¨/»«/math»
לכן גודל הכוח הקבוע הוא 24.44 ניוטון.
1. القوة الثابتة هي القوة المتوسطة للقوة المتغيرة في الرسم البياني.
2. بعد حساب القوة الثابتة، من المفضل معرفة ما إذا كانت قيمة القوة المحسوبة ، وفقًا للرسم البياني ، مناسبة بشكل عام لتكون متوسط القوة في الرسم البياني.
3. في أول عشرة آلاف من الثانية ، القوة تساوي صفرًا ، ولم يبدأ الاصطدام بعد ، لذلك عند حساب وقت الاصطدام
يجب تحديد وقت الحركة على 90 مللي ثانية وليس 100 مللي ثانية.
2. לאחר חישוב הכוח הקבוע כדאי לראות אם בהתאם לגרף ערך הכוח המחושב מתאים באופן כללי להיות ממוצע לכוח בגרף.
3. בעשר אלפיות השנייה הראשונות, הכוח שווה לאפס, עדיין לא התחילה ההתנגשות, לכן בחישוב זמן ההתנגשות
יש לקבוע זמן תנועה של 90ms ולא 100ms.
______________________________________________________________________________________