8. 2013,5- שדה מגנטי משתנה בתוך כריכה
______________________________________________________________________________________
...
(1)בזמן: «math xmlns=¨http://www.w3.org/1998/Math/MathML¨»«mstyle mathsize=¨20px¨»«mn mathvariant=¨bold¨»0«/mn»«mo mathvariant=¨bold¨»§#10877;«/mo»«mi mathvariant=¨bold¨»t«/mi»«mo mathvariant=¨bold¨»§#10877;«/mo»«mn mathvariant=¨bold¨»0«/mn»«mo mathvariant=¨bold¨».«/mo»«mn mathvariant=¨bold¨»1«/mn»«mi mathvariant=¨bold¨»s«/mi»«/mstyle»«/math» : קצב שינוי השטף קבוע , לכן מחוק פארדיי נוצר בכריכה כא"מ קבוע בגודלו.
(2) בזמן: «math xmlns=¨http://www.w3.org/1998/Math/MathML¨»«mn mathvariant=¨bold¨ mathsize=¨20px¨»0«/mn»«mo mathvariant=¨bold¨ mathsize=¨20px¨».«/mo»«mn mathvariant=¨bold¨ mathsize=¨20px¨»14«/mn»«mi mathvariant=¨bold-italic¨ mathsize=¨20px¨»s«/mi»«mo mathvariant=¨bold¨ mathsize=¨20px¨»§#10877;«/mo»«mi mathvariant=¨bold¨ mathsize=¨20px¨»t«/mi»«mo mathvariant=¨bold¨ mathsize=¨20px¨»§#10877;«/mo»«mn mathvariant=¨bold¨ mathsize=¨20px¨»0«/mn»«mo mathvariant=¨bold¨ mathsize=¨20px¨».«/mo»«mn mathvariant=¨bold¨ mathsize=¨20px¨»3«/mn»«mi mathvariant=¨bold¨ mathsize=¨20px¨»s«/mi»«/math» : קצב שינוי השטף הולך וגדל, מחוק פארדיי נוצר בכריכה כא"מ הולך וגדל .
(1)בזמן: «math xmlns=¨http://www.w3.org/1998/Math/MathML¨»«mstyle mathsize=¨20px¨»«mn mathvariant=¨bold¨»0«/mn»«mo mathvariant=¨bold¨»§#10877;«/mo»«mi mathvariant=¨bold¨»t«/mi»«mo mathvariant=¨bold¨»§#10877;«/mo»«mn mathvariant=¨bold¨»0«/mn»«mo mathvariant=¨bold¨».«/mo»«mn mathvariant=¨bold¨»1«/mn»«mi mathvariant=¨bold¨»s«/mi»«/mstyle»«/math» : קצב שינוי השטף קבוע , לכן מחוק פארדיי נוצר בכריכה כא"מ קבוע בגודלו.
(2) בזמן: «math xmlns=¨http://www.w3.org/1998/Math/MathML¨»«mn mathvariant=¨bold¨ mathsize=¨20px¨»0«/mn»«mo mathvariant=¨bold¨ mathsize=¨20px¨».«/mo»«mn mathvariant=¨bold¨ mathsize=¨20px¨»14«/mn»«mi mathvariant=¨bold-italic¨ mathsize=¨20px¨»s«/mi»«mo mathvariant=¨bold¨ mathsize=¨20px¨»§#10877;«/mo»«mi mathvariant=¨bold¨ mathsize=¨20px¨»t«/mi»«mo mathvariant=¨bold¨ mathsize=¨20px¨»§#10877;«/mo»«mn mathvariant=¨bold¨ mathsize=¨20px¨»0«/mn»«mo mathvariant=¨bold¨ mathsize=¨20px¨».«/mo»«mn mathvariant=¨bold¨ mathsize=¨20px¨»3«/mn»«mi mathvariant=¨bold¨ mathsize=¨20px¨»s«/mi»«/math» : קצב שינוי השטף הולך וגדל, מחוק פארדיי נוצר בכריכה כא"מ הולך וגדל .
חוק פארדיי.
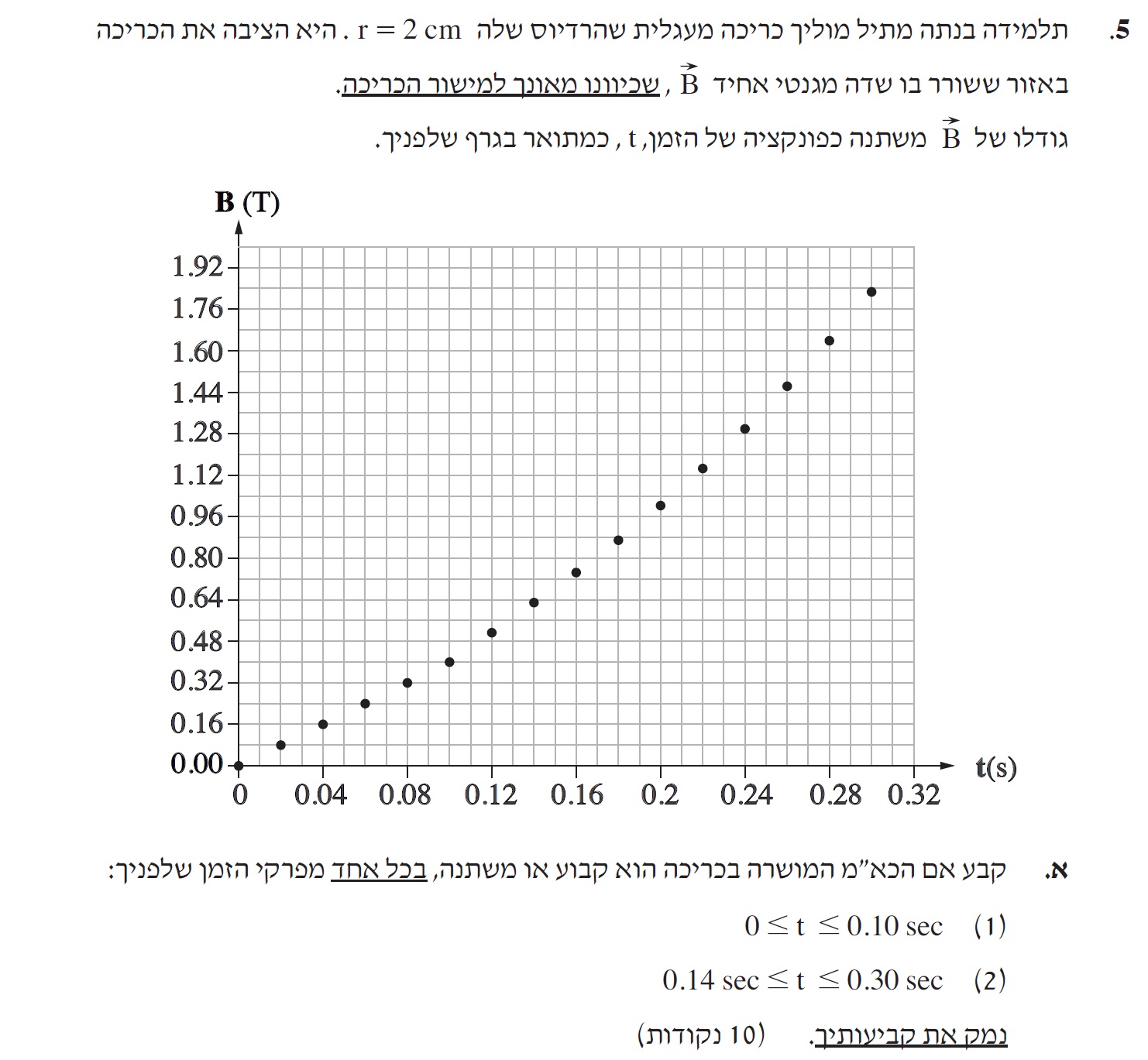
מהגרף ניתן לראות שעוצמת השדה המגנטי בכריכה משתנה. בהתאם לשינוי בעוצמת השדה משתנה גם השטף בכריכה.
ומחוק פארדיי קצב השינוי בשטף שווה לגודל הכא"מ המושרה בכריכה.
נשתמש בחוק פארדיי: «math xmlns=¨http://www.w3.org/1998/Math/MathML¨»«mstyle mathsize=¨20px¨»«mrow»«mi mathvariant=¨bold¨ mathcolor=¨#0000FF¨»§#949;«/mi»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»=«/mo»«mfrac mathcolor=¨#0000FF¨»«mrow»«mo mathvariant=¨bold¨»§#8710;«/mo»«mi mathvariant=¨bold¨»§#981;«/mi»«/mrow»«mrow»«mo mathvariant=¨bold¨»§#8710;«/mo»«mi mathvariant=¨bold¨»t«/mi»«/mrow»«/mfrac»«/mrow»«/mstyle»«/math» ובהגדרת השטף: «math xmlns=¨http://www.w3.org/1998/Math/MathML¨»«mi mathvariant=¨bold¨ mathcolor=¨#0000FF¨»§#981;«/mi»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»=«/mo»«mi mathvariant=¨bold¨ mathcolor=¨#0000FF¨»B«/mi»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»§#183;«/mo»«mi mathvariant=¨bold¨ mathcolor=¨#0000FF¨»A«/mi»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»§#183;«/mo»«mi mathvariant=¨bold¨ mathcolor=¨#0000FF¨»cos«/mi»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»(«/mo»«mi mathvariant=¨bold¨ mathcolor=¨#0000FF¨»§#945;«/mi»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»)«/mo»«/math» כדי לבטא את הכא"מ המושרה בתלות בקצב השינוי בעוצמת השדה המגנטי.
«math xmlns=¨http://www.w3.org/1998/Math/MathML¨»«mstyle mathsize=¨20px¨»«mi mathvariant=¨bold¨ mathcolor=¨#0000FF¨»§#949;«/mi»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»=«/mo»«mfrac mathcolor=¨#0000FF¨»«mrow»«mo mathvariant=¨bold¨»§#8710;«/mo»«mi mathvariant=¨bold¨»§#981;«/mi»«/mrow»«mrow»«mo mathvariant=¨bold¨»§#8710;«/mo»«mi mathvariant=¨bold¨»t«/mi»«/mrow»«/mfrac»«mspace linebreak=¨newline¨»«/mspace»«mspace linebreak=¨newline¨»«/mspace»«mi mathvariant=¨bold¨ mathcolor=¨#0000FF¨»§#949;«/mi»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»=«/mo»«mfrac mathcolor=¨#0000FF¨»«mrow»«mo mathvariant=¨bold¨»§#8710;«/mo»«mi mathvariant=¨bold¨»§#981;«/mi»«/mrow»«mrow»«mo mathvariant=¨bold¨»§#8710;«/mo»«mi mathvariant=¨bold¨»t«/mi»«/mrow»«/mfrac»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»=«/mo»«mfrac mathcolor=¨#0000FF¨»«mrow»«mo mathvariant=¨bold¨»§#8710;«/mo»«mo mathvariant=¨bold¨»[«/mo»«mi mathvariant=¨bold¨»B«/mi»«mo mathvariant=¨bold¨»§#183;«/mo»«mi mathvariant=¨bold¨»A«/mi»«mo mathvariant=¨bold¨»§#183;«/mo»«mi mathvariant=¨bold¨»cos«/mi»«mo mathvariant=¨bold¨»(«/mo»«mi mathvariant=¨bold¨»§#945;«/mi»«mo mathvariant=¨bold¨»)«/mo»«mo mathvariant=¨bold¨»]«/mo»«/mrow»«mrow»«mo mathvariant=¨bold¨»§#8710;«/mo»«mi mathvariant=¨bold¨»t«/mi»«/mrow»«/mfrac»«mspace linebreak=¨newline¨»«/mspace»«mspace linebreak=¨newline¨»«/mspace»«mi mathvariant=¨bold¨ mathcolor=¨#0000FF¨»§#949;«/mi»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»=«/mo»«mfrac mathcolor=¨#0000FF¨»«mrow»«mo mathvariant=¨bold¨»§#8710;«/mo»«mi mathvariant=¨bold¨»§#981;«/mi»«/mrow»«mrow»«mo mathvariant=¨bold¨»§#8710;«/mo»«mi mathvariant=¨bold¨»t«/mi»«/mrow»«/mfrac»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»=«/mo»«mi mathvariant=¨bold¨ mathcolor=¨#0000FF¨»A«/mi»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»§#183;«/mo»«mi mathvariant=¨bold¨ mathcolor=¨#0000FF¨»cos«/mi»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»(«/mo»«mi mathvariant=¨bold¨ mathcolor=¨#0000FF¨»§#945;«/mi»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»)«/mo»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»§#183;«/mo»«mfrac mathcolor=¨#0000FF¨»«mrow»«mo mathvariant=¨bold¨»§#8710;«/mo»«mi mathvariant=¨bold¨»B«/mi»«/mrow»«mrow»«mo mathvariant=¨bold¨»§#8710;«/mo»«mi mathvariant=¨bold¨»t«/mi»«/mrow»«/mfrac»«mspace linebreak=¨newline¨»«/mspace»«/mstyle»«/math»
כיוון השדה המגנטי ניצב למישור הכריכה בדומה לכיוון וקטור שטח הכריכה , לכן : «math xmlns=¨http://www.w3.org/1998/Math/MathML¨»«mstyle mathsize=¨20px¨»«mrow»«mi mathvariant=¨bold¨ mathcolor=¨#0000FF¨»§#945;«/mi»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»=«/mo»«mn mathvariant=¨bold¨ mathcolor=¨#0000FF¨»0«/mn»«/mrow»«/mstyle»«/math».
«math xmlns=¨http://www.w3.org/1998/Math/MathML¨»«mstyle mathsize=¨20px¨»«mrow»«mi mathvariant=¨bold¨ mathcolor=¨#0000FF¨»§#949;«/mi»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»=«/mo»«mfrac mathcolor=¨#0000FF¨»«mrow»«mo mathvariant=¨bold¨»§#8710;«/mo»«mi mathvariant=¨bold¨»§#981;«/mi»«/mrow»«mrow»«mo mathvariant=¨bold¨»§#8710;«/mo»«mi mathvariant=¨bold¨»t«/mi»«/mrow»«/mfrac»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»=«/mo»«mi mathvariant=¨bold¨ mathcolor=¨#0000FF¨»A«/mi»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»§#183;«/mo»«mi mathvariant=¨bold¨ mathcolor=¨#0000FF¨»cos«/mi»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»(«/mo»«mn mathvariant=¨bold¨ mathcolor=¨#0000FF¨»0«/mn»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»)«/mo»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»§#183;«/mo»«mfrac mathcolor=¨#0000FF¨»«mrow»«mo mathvariant=¨bold¨»§#8710;«/mo»«mi mathvariant=¨bold¨»B«/mi»«/mrow»«mrow»«mo mathvariant=¨bold¨»§#8710;«/mo»«mi mathvariant=¨bold¨»t«/mi»«/mrow»«/mfrac»«mspace linebreak=¨newline¨»«/mspace»«/mrow»«mspace linebreak=¨newline¨»«/mspace»«menclose mathcolor=¨#0000FF¨ notation=¨circle¨»«mi mathvariant=¨bold¨»§#949;«/mi»«mo mathvariant=¨bold¨»=«/mo»«mfrac»«mrow»«mo mathvariant=¨bold¨»§#8710;«/mo»«mi mathvariant=¨bold¨»§#981;«/mi»«/mrow»«mrow»«mo mathvariant=¨bold¨»§#8710;«/mo»«mi mathvariant=¨bold¨»t«/mi»«/mrow»«/mfrac»«mo mathvariant=¨bold¨»=«/mo»«mi mathvariant=¨bold¨»A«/mi»«mo mathvariant=¨bold¨»§#183;«/mo»«mfrac»«mrow»«mo mathvariant=¨bold¨»§#8710;«/mo»«mi mathvariant=¨bold¨»B«/mi»«/mrow»«mrow»«mo mathvariant=¨bold¨»§#8710;«/mo»«mi mathvariant=¨bold¨»t«/mi»«/mrow»«/mfrac»«/menclose»«mspace linebreak=¨newline¨»«/mspace»«/mstyle»«/math»
בזמן «math xmlns=¨http://www.w3.org/1998/Math/MathML¨»«mstyle mathsize=¨20px¨»«mrow»«mn mathvariant=¨bold¨ mathcolor=¨#0000FF¨»0«/mn»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»§#10877;«/mo»«mi mathvariant=¨bold¨ mathcolor=¨#0000FF¨»t«/mi»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»§#10877;«/mo»«mn mathvariant=¨bold¨ mathcolor=¨#0000FF¨»0«/mn»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨».«/mo»«mn mathvariant=¨bold¨ mathcolor=¨#0000FF¨»1«/mn»«mi mathvariant=¨bold¨ mathcolor=¨#0000FF¨»s«/mi»«/mrow»«/mstyle»«/math» - קצב השינוי בשדה המגנטי «math xmlns=¨http://www.w3.org/1998/Math/MathML¨»«mfrac mathcolor=¨#0000FF¨»«mrow»«mo mathvariant=¨bold¨»§#8710;«/mo»«mi mathvariant=¨bold¨»B«/mi»«/mrow»«mrow»«mo mathvariant=¨bold¨»§#8710;«/mo»«mi mathvariant=¨bold¨»t«/mi»«/mrow»«/mfrac»«/math»הוא קבוע . לכן בזמן זה הכא"מ המושרה בכריכה הוא קבוע.
בזמן «math xmlns=¨http://www.w3.org/1998/Math/MathML¨»«mstyle mathsize=¨20px¨»«mn mathvariant=¨bold¨ mathcolor=¨#0000FF¨»0«/mn»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨».«/mo»«mn mathvariant=¨bold¨ mathcolor=¨#0000FF¨»14«/mn»«mi mathvariant=¨bold-italic¨ mathcolor=¨#0000FF¨»s«/mi»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»§#10877;«/mo»«mi mathvariant=¨bold¨ mathcolor=¨#0000FF¨»t«/mi»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»§#10877;«/mo»«mn mathvariant=¨bold¨ mathcolor=¨#0000FF¨»0«/mn»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨».«/mo»«mn mathvariant=¨bold¨ mathcolor=¨#0000FF¨»3«/mn»«mi mathvariant=¨bold¨ mathcolor=¨#0000FF¨»s«/mi»«/mstyle»«/math» - קצב השינוי בשדה המגנטי «math xmlns=¨http://www.w3.org/1998/Math/MathML¨»«mfrac mathcolor=¨#0000FF¨»«mrow»«mo mathvariant=¨bold¨»§#8710;«/mo»«mi mathvariant=¨bold¨»B«/mi»«/mrow»«mrow»«mo mathvariant=¨bold¨»§#8710;«/mo»«mi mathvariant=¨bold¨»t«/mi»«/mrow»«/mfrac»«/math»משתנה, הוא הולך וגדל. לכן בזמן זה הכא"מ המושרה משתנה.
מהגרף ניתן לראות שעוצמת השדה המגנטי בכריכה משתנה. בהתאם לשינוי בעוצמת השדה משתנה גם השטף בכריכה.
ומחוק פארדיי קצב השינוי בשטף שווה לגודל הכא"מ המושרה בכריכה.
נשתמש בחוק פארדיי: «math xmlns=¨http://www.w3.org/1998/Math/MathML¨»«mstyle mathsize=¨20px¨»«mrow»«mi mathvariant=¨bold¨ mathcolor=¨#0000FF¨»§#949;«/mi»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»=«/mo»«mfrac mathcolor=¨#0000FF¨»«mrow»«mo mathvariant=¨bold¨»§#8710;«/mo»«mi mathvariant=¨bold¨»§#981;«/mi»«/mrow»«mrow»«mo mathvariant=¨bold¨»§#8710;«/mo»«mi mathvariant=¨bold¨»t«/mi»«/mrow»«/mfrac»«/mrow»«/mstyle»«/math» ובהגדרת השטף: «math xmlns=¨http://www.w3.org/1998/Math/MathML¨»«mi mathvariant=¨bold¨ mathcolor=¨#0000FF¨»§#981;«/mi»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»=«/mo»«mi mathvariant=¨bold¨ mathcolor=¨#0000FF¨»B«/mi»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»§#183;«/mo»«mi mathvariant=¨bold¨ mathcolor=¨#0000FF¨»A«/mi»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»§#183;«/mo»«mi mathvariant=¨bold¨ mathcolor=¨#0000FF¨»cos«/mi»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»(«/mo»«mi mathvariant=¨bold¨ mathcolor=¨#0000FF¨»§#945;«/mi»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»)«/mo»«/math» כדי לבטא את הכא"מ המושרה בתלות בקצב השינוי בעוצמת השדה המגנטי.
«math xmlns=¨http://www.w3.org/1998/Math/MathML¨»«mstyle mathsize=¨20px¨»«mi mathvariant=¨bold¨ mathcolor=¨#0000FF¨»§#949;«/mi»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»=«/mo»«mfrac mathcolor=¨#0000FF¨»«mrow»«mo mathvariant=¨bold¨»§#8710;«/mo»«mi mathvariant=¨bold¨»§#981;«/mi»«/mrow»«mrow»«mo mathvariant=¨bold¨»§#8710;«/mo»«mi mathvariant=¨bold¨»t«/mi»«/mrow»«/mfrac»«mspace linebreak=¨newline¨»«/mspace»«mspace linebreak=¨newline¨»«/mspace»«mi mathvariant=¨bold¨ mathcolor=¨#0000FF¨»§#949;«/mi»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»=«/mo»«mfrac mathcolor=¨#0000FF¨»«mrow»«mo mathvariant=¨bold¨»§#8710;«/mo»«mi mathvariant=¨bold¨»§#981;«/mi»«/mrow»«mrow»«mo mathvariant=¨bold¨»§#8710;«/mo»«mi mathvariant=¨bold¨»t«/mi»«/mrow»«/mfrac»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»=«/mo»«mfrac mathcolor=¨#0000FF¨»«mrow»«mo mathvariant=¨bold¨»§#8710;«/mo»«mo mathvariant=¨bold¨»[«/mo»«mi mathvariant=¨bold¨»B«/mi»«mo mathvariant=¨bold¨»§#183;«/mo»«mi mathvariant=¨bold¨»A«/mi»«mo mathvariant=¨bold¨»§#183;«/mo»«mi mathvariant=¨bold¨»cos«/mi»«mo mathvariant=¨bold¨»(«/mo»«mi mathvariant=¨bold¨»§#945;«/mi»«mo mathvariant=¨bold¨»)«/mo»«mo mathvariant=¨bold¨»]«/mo»«/mrow»«mrow»«mo mathvariant=¨bold¨»§#8710;«/mo»«mi mathvariant=¨bold¨»t«/mi»«/mrow»«/mfrac»«mspace linebreak=¨newline¨»«/mspace»«mspace linebreak=¨newline¨»«/mspace»«mi mathvariant=¨bold¨ mathcolor=¨#0000FF¨»§#949;«/mi»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»=«/mo»«mfrac mathcolor=¨#0000FF¨»«mrow»«mo mathvariant=¨bold¨»§#8710;«/mo»«mi mathvariant=¨bold¨»§#981;«/mi»«/mrow»«mrow»«mo mathvariant=¨bold¨»§#8710;«/mo»«mi mathvariant=¨bold¨»t«/mi»«/mrow»«/mfrac»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»=«/mo»«mi mathvariant=¨bold¨ mathcolor=¨#0000FF¨»A«/mi»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»§#183;«/mo»«mi mathvariant=¨bold¨ mathcolor=¨#0000FF¨»cos«/mi»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»(«/mo»«mi mathvariant=¨bold¨ mathcolor=¨#0000FF¨»§#945;«/mi»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»)«/mo»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»§#183;«/mo»«mfrac mathcolor=¨#0000FF¨»«mrow»«mo mathvariant=¨bold¨»§#8710;«/mo»«mi mathvariant=¨bold¨»B«/mi»«/mrow»«mrow»«mo mathvariant=¨bold¨»§#8710;«/mo»«mi mathvariant=¨bold¨»t«/mi»«/mrow»«/mfrac»«mspace linebreak=¨newline¨»«/mspace»«/mstyle»«/math»
כיוון השדה המגנטי ניצב למישור הכריכה בדומה לכיוון וקטור שטח הכריכה , לכן : «math xmlns=¨http://www.w3.org/1998/Math/MathML¨»«mstyle mathsize=¨20px¨»«mrow»«mi mathvariant=¨bold¨ mathcolor=¨#0000FF¨»§#945;«/mi»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»=«/mo»«mn mathvariant=¨bold¨ mathcolor=¨#0000FF¨»0«/mn»«/mrow»«/mstyle»«/math».
«math xmlns=¨http://www.w3.org/1998/Math/MathML¨»«mstyle mathsize=¨20px¨»«mrow»«mi mathvariant=¨bold¨ mathcolor=¨#0000FF¨»§#949;«/mi»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»=«/mo»«mfrac mathcolor=¨#0000FF¨»«mrow»«mo mathvariant=¨bold¨»§#8710;«/mo»«mi mathvariant=¨bold¨»§#981;«/mi»«/mrow»«mrow»«mo mathvariant=¨bold¨»§#8710;«/mo»«mi mathvariant=¨bold¨»t«/mi»«/mrow»«/mfrac»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»=«/mo»«mi mathvariant=¨bold¨ mathcolor=¨#0000FF¨»A«/mi»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»§#183;«/mo»«mi mathvariant=¨bold¨ mathcolor=¨#0000FF¨»cos«/mi»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»(«/mo»«mn mathvariant=¨bold¨ mathcolor=¨#0000FF¨»0«/mn»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»)«/mo»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»§#183;«/mo»«mfrac mathcolor=¨#0000FF¨»«mrow»«mo mathvariant=¨bold¨»§#8710;«/mo»«mi mathvariant=¨bold¨»B«/mi»«/mrow»«mrow»«mo mathvariant=¨bold¨»§#8710;«/mo»«mi mathvariant=¨bold¨»t«/mi»«/mrow»«/mfrac»«mspace linebreak=¨newline¨»«/mspace»«/mrow»«mspace linebreak=¨newline¨»«/mspace»«menclose mathcolor=¨#0000FF¨ notation=¨circle¨»«mi mathvariant=¨bold¨»§#949;«/mi»«mo mathvariant=¨bold¨»=«/mo»«mfrac»«mrow»«mo mathvariant=¨bold¨»§#8710;«/mo»«mi mathvariant=¨bold¨»§#981;«/mi»«/mrow»«mrow»«mo mathvariant=¨bold¨»§#8710;«/mo»«mi mathvariant=¨bold¨»t«/mi»«/mrow»«/mfrac»«mo mathvariant=¨bold¨»=«/mo»«mi mathvariant=¨bold¨»A«/mi»«mo mathvariant=¨bold¨»§#183;«/mo»«mfrac»«mrow»«mo mathvariant=¨bold¨»§#8710;«/mo»«mi mathvariant=¨bold¨»B«/mi»«/mrow»«mrow»«mo mathvariant=¨bold¨»§#8710;«/mo»«mi mathvariant=¨bold¨»t«/mi»«/mrow»«/mfrac»«/menclose»«mspace linebreak=¨newline¨»«/mspace»«/mstyle»«/math»
בזמן «math xmlns=¨http://www.w3.org/1998/Math/MathML¨»«mstyle mathsize=¨20px¨»«mrow»«mn mathvariant=¨bold¨ mathcolor=¨#0000FF¨»0«/mn»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»§#10877;«/mo»«mi mathvariant=¨bold¨ mathcolor=¨#0000FF¨»t«/mi»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»§#10877;«/mo»«mn mathvariant=¨bold¨ mathcolor=¨#0000FF¨»0«/mn»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨».«/mo»«mn mathvariant=¨bold¨ mathcolor=¨#0000FF¨»1«/mn»«mi mathvariant=¨bold¨ mathcolor=¨#0000FF¨»s«/mi»«/mrow»«/mstyle»«/math» - קצב השינוי בשדה המגנטי «math xmlns=¨http://www.w3.org/1998/Math/MathML¨»«mfrac mathcolor=¨#0000FF¨»«mrow»«mo mathvariant=¨bold¨»§#8710;«/mo»«mi mathvariant=¨bold¨»B«/mi»«/mrow»«mrow»«mo mathvariant=¨bold¨»§#8710;«/mo»«mi mathvariant=¨bold¨»t«/mi»«/mrow»«/mfrac»«/math»הוא קבוע . לכן בזמן זה הכא"מ המושרה בכריכה הוא קבוע.
בזמן «math xmlns=¨http://www.w3.org/1998/Math/MathML¨»«mstyle mathsize=¨20px¨»«mn mathvariant=¨bold¨ mathcolor=¨#0000FF¨»0«/mn»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨».«/mo»«mn mathvariant=¨bold¨ mathcolor=¨#0000FF¨»14«/mn»«mi mathvariant=¨bold-italic¨ mathcolor=¨#0000FF¨»s«/mi»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»§#10877;«/mo»«mi mathvariant=¨bold¨ mathcolor=¨#0000FF¨»t«/mi»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»§#10877;«/mo»«mn mathvariant=¨bold¨ mathcolor=¨#0000FF¨»0«/mn»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨».«/mo»«mn mathvariant=¨bold¨ mathcolor=¨#0000FF¨»3«/mn»«mi mathvariant=¨bold¨ mathcolor=¨#0000FF¨»s«/mi»«/mstyle»«/math» - קצב השינוי בשדה המגנטי «math xmlns=¨http://www.w3.org/1998/Math/MathML¨»«mfrac mathcolor=¨#0000FF¨»«mrow»«mo mathvariant=¨bold¨»§#8710;«/mo»«mi mathvariant=¨bold¨»B«/mi»«/mrow»«mrow»«mo mathvariant=¨bold¨»§#8710;«/mo»«mi mathvariant=¨bold¨»t«/mi»«/mrow»«/mfrac»«/math»משתנה, הוא הולך וגדל. לכן בזמן זה הכא"מ המושרה משתנה.
1. נוצר כא"מ מושרה בכריכה רק כתוצאה מהשינוי בשטף בתוך הכריכה. מהגדרת השטף יש שלוש סיבות לשינוי בשטף:
א- שינוי בעוצמת השדה המגנטי בכריכה.
ב- שינוי בגודל בשטח הכריכה.
ג- שינוי בגודל הזווית שבין ווקטור השטח למישור הכריכה.
לפני שעונים על שאלה כל שהיא בכא"מ מושרה חשוב לזהות את הסיבה ליצירת הכא"מ המושרה בכריכה.
2. אפשר לענות על שאלה זו באופן מילולי גם בלי לפתח את הביטוי לכא"מ בתלות בקצב השינוי בשדה המגנטי.
3. השאלה עוסקת בשני פרקי זמן שונים, לכן סביר שתתקבל תשובה שונה לכל פרק זמן.
4. קצב שינוי השדה המגנטי «math xmlns=¨http://www.w3.org/1998/Math/MathML¨»«mfrac mathcolor=¨#FF0000¨»«mrow»«mo mathvariant=¨bold¨»§#8710;«/mo»«mi mathvariant=¨bold¨»B«/mi»«/mrow»«mrow»«mo mathvariant=¨bold¨»§#8710;«/mo»«mi mathvariant=¨bold¨»t«/mi»«/mrow»«/mfrac»«/math» שווה לשיפוע הפונקציה.
5. כדי לזהות בגרף אם השיפוע הוא קבוע או משתנה מומלץ להשתמש בסרגל לכל אחד מפרקי הזמן.
6. הכא"מ תלוי בשיפוע הגרף ולא בערך הגרף. בפרק הזמן הראשון עוצמת השדה גדלה והשטף גדל אך הכא"מ הוא קבוע.
א- שינוי בעוצמת השדה המגנטי בכריכה.
ב- שינוי בגודל בשטח הכריכה.
ג- שינוי בגודל הזווית שבין ווקטור השטח למישור הכריכה.
לפני שעונים על שאלה כל שהיא בכא"מ מושרה חשוב לזהות את הסיבה ליצירת הכא"מ המושרה בכריכה.
2. אפשר לענות על שאלה זו באופן מילולי גם בלי לפתח את הביטוי לכא"מ בתלות בקצב השינוי בשדה המגנטי.
3. השאלה עוסקת בשני פרקי זמן שונים, לכן סביר שתתקבל תשובה שונה לכל פרק זמן.
4. קצב שינוי השדה המגנטי «math xmlns=¨http://www.w3.org/1998/Math/MathML¨»«mfrac mathcolor=¨#FF0000¨»«mrow»«mo mathvariant=¨bold¨»§#8710;«/mo»«mi mathvariant=¨bold¨»B«/mi»«/mrow»«mrow»«mo mathvariant=¨bold¨»§#8710;«/mo»«mi mathvariant=¨bold¨»t«/mi»«/mrow»«/mfrac»«/math» שווה לשיפוע הפונקציה.
5. כדי לזהות בגרף אם השיפוע הוא קבוע או משתנה מומלץ להשתמש בסרגל לכל אחד מפרקי הזמן.
6. הכא"מ תלוי בשיפוע הגרף ולא בערך הגרף. בפרק הזמן הראשון עוצמת השדה גדלה והשטף גדל אך הכא"מ הוא קבוע.
______________________________________________________________________________________
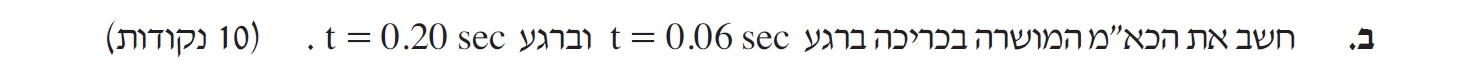
______________________________________________________________________________________
...
«math xmlns=¨http://www.w3.org/1998/Math/MathML¨»«mstyle mathsize=¨20px¨»«mrow»«mi mathvariant=¨bold¨»V«/mi»«mo mathvariant=¨bold¨»(«/mo»«mn mathvariant=¨bold¨»0«/mn»«mo mathvariant=¨bold¨».«/mo»«mn mathvariant=¨bold¨»06«/mn»«mo mathvariant=¨bold¨»)«/mo»«mo mathvariant=¨bold¨»=«/mo»«mn mathvariant=¨bold¨»5«/mn»«mo mathvariant=¨bold¨».«/mo»«mn mathvariant=¨bold¨»02«/mn»«mo mathvariant=¨bold¨»§#183;«/mo»«msup»«mn mathvariant=¨bold¨»10«/mn»«mrow»«mo mathvariant=¨bold¨»-«/mo»«mn mathvariant=¨bold¨»3«/mn»«/mrow»«/msup»«mi mathvariant=¨bold¨»V«/mi»«mspace linebreak=¨newline¨/»«mspace linebreak=¨newline¨/»«mi mathvariant=¨bold¨»V«/mi»«mo mathvariant=¨bold¨»(«/mo»«mn mathvariant=¨bold¨»0«/mn»«mo mathvariant=¨bold¨».«/mo»«mn mathvariant=¨bold¨»2«/mn»«mo mathvariant=¨bold¨»)«/mo»«mo mathvariant=¨bold¨»=«/mo»«mn mathvariant=¨bold¨»8«/mn»«mo mathvariant=¨bold¨».«/mo»«mn mathvariant=¨bold¨»79«/mn»«mo mathvariant=¨bold¨»§#183;«/mo»«msup»«mn mathvariant=¨bold¨»10«/mn»«mrow»«mo mathvariant=¨bold¨»-«/mo»«mn mathvariant=¨bold¨»3«/mn»«/mrow»«/msup»«mi mathvariant=¨bold¨»V«/mi»«mspace linebreak=¨newline¨/»«/mrow»«/mstyle»«/math»
מציאת קצב שינוי השדה «math xmlns=¨http://www.w3.org/1998/Math/MathML¨»«mstyle mathsize=¨20px¨»«mfrac mathcolor=¨#FF6600¨»«mrow»«mo mathvariant=¨bold¨»§#8710;«/mo»«mi mathvariant=¨bold¨»B«/mi»«/mrow»«mrow»«mo mathvariant=¨bold¨»§#8710;«/mo»«mi mathvariant=¨bold¨»t«/mi»«/mrow»«/mfrac»«/mstyle»«/math» משיפוע המשיק לפונקציה באותו רגע.
הכא"מ תלוי בקצב השינוי בשדה המגנטי:
«math xmlns=¨http://www.w3.org/1998/Math/MathML¨»«mstyle mathsize=¨20px¨»«mi mathvariant=¨bold¨ mathcolor=¨#0000FF¨»§#949;«/mi»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»=«/mo»«mi mathvariant=¨bold¨ mathcolor=¨#0000FF¨»A«/mi»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»§#183;«/mo»«mfrac mathcolor=¨#0000FF¨»«mrow»«mo mathvariant=¨bold¨»§#8710;«/mo»«mi mathvariant=¨bold¨»B«/mi»«/mrow»«mrow»«mo mathvariant=¨bold¨»§#8710;«/mo»«mi mathvariant=¨bold¨»t«/mi»«/mrow»«/mfrac»«/mstyle»«/math»
מחוק פארדי קצב השינוי בעוצמת השדה שווה לשיפוע הפונקציה בגרף.
נחשב את השטח של הכריכה:
«math xmlns=¨http://www.w3.org/1998/Math/MathML¨»«mstyle mathsize=¨20px¨»«mi mathvariant=¨bold¨ mathcolor=¨#0000FF¨»A«/mi»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»=«/mo»«mi mathvariant=¨bold¨ mathcolor=¨#0000FF¨»§#960;«/mi»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»§#183;«/mo»«msup»«mi mathvariant=¨bold¨ mathcolor=¨#0000FF¨»r«/mi»«mn mathvariant=¨bold¨ mathcolor=¨#0000FF¨»2«/mn»«/msup»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»=«/mo»«mi mathvariant=¨bold¨ mathcolor=¨#0000FF¨»§#960;«/mi»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»§#183;«/mo»«mn mathvariant=¨bold¨ mathcolor=¨#0000FF¨»0«/mn»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨».«/mo»«msup»«mn mathvariant=¨bold¨ mathcolor=¨#0000FF¨»02«/mn»«mn mathvariant=¨bold¨ mathcolor=¨#0000FF¨»2«/mn»«/msup»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»=«/mo»«mn mathvariant=¨bold¨ mathcolor=¨#0000FF¨»1«/mn»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨».«/mo»«mn mathvariant=¨bold¨ mathcolor=¨#0000FF¨»256«/mn»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»§#183;«/mo»«msup»«mn mathvariant=¨bold¨ mathcolor=¨#0000FF¨»10«/mn»«mrow mathcolor=¨#0000FF¨»«mo mathvariant=¨bold¨»-«/mo»«mn mathvariant=¨bold¨»3«/mn»«/mrow»«/msup»«msup»«mi mathvariant=¨bold¨ mathcolor=¨#0000FF¨»m«/mi»«mn mathvariant=¨bold¨ mathcolor=¨#0000FF¨»2«/mn»«/msup»«/mstyle»«/math»
נמצא את הכא"מ המושרה בכל אחד משני הרגעים מסוים בהתאם לערך שיפוע הפונקציה סביב אותו רגע.
«math xmlns=¨http://www.w3.org/1998/Math/MathML¨»«mstyle mathsize=¨20px¨»«mrow mathcolor=¨#0000FF¨»«mi mathvariant=¨bold¨»§#949;«/mi»«mo mathvariant=¨bold¨»(«/mo»«mn mathvariant=¨bold¨»0«/mn»«mo mathvariant=¨bold¨».«/mo»«mn mathvariant=¨bold¨»06«/mn»«mo mathvariant=¨bold¨»)«/mo»«mo mathvariant=¨bold¨»=«/mo»«mi mathvariant=¨bold¨»A«/mi»«mo mathvariant=¨bold¨»§#183;«/mo»«mfrac»«mrow»«mo mathvariant=¨bold¨»§#8710;«/mo»«mi mathvariant=¨bold¨»B«/mi»«/mrow»«mrow»«mo mathvariant=¨bold¨»§#8710;«/mo»«mi mathvariant=¨bold¨»t«/mi»«/mrow»«/mfrac»«mo mathvariant=¨bold¨»=«/mo»«mi mathvariant=¨bold¨»A«/mi»«mo mathvariant=¨bold¨»§#183;«/mo»«mfrac»«mrow»«mi mathvariant=¨bold¨»B«/mi»«mo mathvariant=¨bold¨»(«/mo»«mn mathvariant=¨bold¨»0«/mn»«mo mathvariant=¨bold¨».«/mo»«mn mathvariant=¨bold¨»08«/mn»«mo mathvariant=¨bold¨»)«/mo»«mo mathvariant=¨bold¨»-«/mo»«mi mathvariant=¨bold¨»B«/mi»«mo mathvariant=¨bold¨»(«/mo»«mn mathvariant=¨bold¨»0«/mn»«mo mathvariant=¨bold¨».«/mo»«mn mathvariant=¨bold¨»04«/mn»«mo mathvariant=¨bold¨»)«/mo»«/mrow»«mrow»«mn mathvariant=¨bold¨»0«/mn»«mo mathvariant=¨bold¨».«/mo»«mn mathvariant=¨bold¨»08«/mn»«mo mathvariant=¨bold¨»-«/mo»«mn mathvariant=¨bold¨»0«/mn»«mo mathvariant=¨bold¨».«/mo»«mn mathvariant=¨bold¨»04«/mn»«/mrow»«/mfrac»«/mrow»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»=«/mo»«mn mathvariant=¨bold¨ mathcolor=¨#0000FF¨»1«/mn»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨».«/mo»«mn mathvariant=¨bold¨ mathcolor=¨#0000FF¨»256«/mn»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»§#183;«/mo»«msup»«mn mathvariant=¨bold¨ mathcolor=¨#0000FF¨»10«/mn»«mrow mathcolor=¨#0000FF¨»«mo mathvariant=¨bold¨»-«/mo»«mn mathvariant=¨bold¨»3«/mn»«/mrow»«/msup»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»§#183;«/mo»«mfrac mathcolor=¨#0000FF¨»«mrow»«mn mathvariant=¨bold¨»0«/mn»«mo mathvariant=¨bold¨».«/mo»«mn mathvariant=¨bold¨»32«/mn»«mo mathvariant=¨bold¨»-«/mo»«mn mathvariant=¨bold¨»0«/mn»«mo mathvariant=¨bold¨».«/mo»«mn mathvariant=¨bold¨»16«/mn»«/mrow»«mrow»«mn mathvariant=¨bold¨»0«/mn»«mo mathvariant=¨bold¨».«/mo»«mn mathvariant=¨bold¨»04«/mn»«/mrow»«/mfrac»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»=«/mo»«mn mathvariant=¨bold¨ mathcolor=¨#0000FF¨»5«/mn»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨».«/mo»«mn mathvariant=¨bold¨ mathcolor=¨#0000FF¨»02«/mn»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»§#183;«/mo»«msup»«mn mathvariant=¨bold¨ mathcolor=¨#0000FF¨»10«/mn»«mrow mathcolor=¨#0000FF¨»«mo mathvariant=¨bold¨»-«/mo»«mn mathvariant=¨bold¨»3«/mn»«/mrow»«/msup»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»§#160;«/mo»«mi mathvariant=¨bold¨ mathcolor=¨#0000FF¨»V«/mi»«mspace linebreak=¨newline¨/»«mspace linebreak=¨newline¨/»«mrow mathcolor=¨#0000FF¨»«mi mathvariant=¨bold¨»§#949;«/mi»«mo mathvariant=¨bold¨»(«/mo»«mn mathvariant=¨bold¨»0«/mn»«mo mathvariant=¨bold¨».«/mo»«mn mathvariant=¨bold¨»2«/mn»«mo mathvariant=¨bold¨»)«/mo»«mo mathvariant=¨bold¨»=«/mo»«mi mathvariant=¨bold¨»A«/mi»«mo mathvariant=¨bold¨»§#183;«/mo»«mfrac»«mrow»«mo mathvariant=¨bold¨»§#8710;«/mo»«mi mathvariant=¨bold¨»B«/mi»«/mrow»«mrow»«mo mathvariant=¨bold¨»§#8710;«/mo»«mi mathvariant=¨bold¨»t«/mi»«/mrow»«/mfrac»«mo mathvariant=¨bold¨»=«/mo»«mi mathvariant=¨bold¨»A«/mi»«mo mathvariant=¨bold¨»§#183;«/mo»«mfrac»«mrow»«mi mathvariant=¨bold¨»B«/mi»«mo mathvariant=¨bold¨»(«/mo»«mn mathvariant=¨bold¨»0«/mn»«mo mathvariant=¨bold¨».«/mo»«mn mathvariant=¨bold¨»22«/mn»«mo mathvariant=¨bold¨»)«/mo»«mo mathvariant=¨bold¨»-«/mo»«mi mathvariant=¨bold¨»B«/mi»«mo mathvariant=¨bold¨»(«/mo»«mn mathvariant=¨bold¨»0«/mn»«mo mathvariant=¨bold¨».«/mo»«mn mathvariant=¨bold¨»18«/mn»«mo mathvariant=¨bold¨»)«/mo»«/mrow»«mrow»«mn mathvariant=¨bold¨»0«/mn»«mo mathvariant=¨bold¨».«/mo»«mn mathvariant=¨bold¨»22«/mn»«mo mathvariant=¨bold¨»-«/mo»«mn mathvariant=¨bold¨»0«/mn»«mo mathvariant=¨bold¨».«/mo»«mn mathvariant=¨bold¨»18«/mn»«/mrow»«/mfrac»«/mrow»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»=«/mo»«mn mathvariant=¨bold¨ mathcolor=¨#0000FF¨»1«/mn»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨».«/mo»«mn mathvariant=¨bold¨ mathcolor=¨#0000FF¨»256«/mn»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»§#183;«/mo»«msup»«mn mathvariant=¨bold¨ mathcolor=¨#0000FF¨»10«/mn»«mrow mathcolor=¨#0000FF¨»«mo mathvariant=¨bold¨»-«/mo»«mn mathvariant=¨bold¨»3«/mn»«/mrow»«/msup»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»§#183;«/mo»«mfrac mathcolor=¨#0000FF¨»«mrow»«mn mathvariant=¨bold¨»1«/mn»«mo mathvariant=¨bold¨».«/mo»«mn mathvariant=¨bold¨»14«/mn»«mo mathvariant=¨bold¨»-«/mo»«mn mathvariant=¨bold¨»0«/mn»«mo mathvariant=¨bold¨».«/mo»«mn mathvariant=¨bold¨»86«/mn»«/mrow»«mrow»«mn mathvariant=¨bold¨»0«/mn»«mo mathvariant=¨bold¨».«/mo»«mn mathvariant=¨bold¨»04«/mn»«/mrow»«/mfrac»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»=«/mo»«mn mathvariant=¨bold¨ mathcolor=¨#0000FF¨»8«/mn»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨».«/mo»«mn mathvariant=¨bold¨ mathcolor=¨#0000FF¨»79«/mn»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»§#183;«/mo»«msup»«mn mathvariant=¨bold¨ mathcolor=¨#0000FF¨»10«/mn»«mrow mathcolor=¨#0000FF¨»«mo mathvariant=¨bold¨»-«/mo»«mn mathvariant=¨bold¨»3«/mn»«/mrow»«/msup»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»§#160;«/mo»«mi mathvariant=¨bold¨ mathcolor=¨#0000FF¨»V«/mi»«/mstyle»«/math»
ערך הכא"מ המושרה ברגע t=0.06s הוא 5.02 מילי וולט.
וערך הכא"מ המושרה ברגע t=0.2s הוא 8.79 מילי וולט.
כדי למצוא את הכא"מ המושרה ברגע מסוים נמצא את שיפוע הפונקציה סביב אותו רגע.
נמצא את הכא"מ המושרה ברגע t=0.06s :
«math xmlns=¨http://www.w3.org/1998/Math/MathML¨»«mstyle mathsize=¨20px¨»«mrow»«mi mathvariant=¨bold¨ mathcolor=¨#0000FF¨»§#949;«/mi»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»=«/mo»«mfrac mathcolor=¨#0000FF¨»«mrow»«mo mathvariant=¨bold¨»§#8710;«/mo»«mi mathvariant=¨bold¨»§#981;«/mi»«/mrow»«mrow»«mo mathvariant=¨bold¨»§#8710;«/mo»«mi mathvariant=¨bold¨»t«/mi»«/mrow»«/mfrac»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»=«/mo»«mi mathvariant=¨bold¨ mathcolor=¨#0000FF¨»A«/mi»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»§#183;«/mo»«mi mathvariant=¨bold¨ mathcolor=¨#0000FF¨»cos«/mi»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»(«/mo»«mn mathvariant=¨bold¨ mathcolor=¨#0000FF¨»0«/mn»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»)«/mo»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»§#183;«/mo»«mfrac mathcolor=¨#0000FF¨»«mrow»«mo mathvariant=¨bold¨»§#8710;«/mo»«mi mathvariant=¨bold¨»B«/mi»«/mrow»«mrow»«mo mathvariant=¨bold¨»§#8710;«/mo»«mi mathvariant=¨bold¨»t«/mi»«/mrow»«/mfrac»«mspace linebreak=¨newline¨»«/mspace»«/mrow»«mspace linebreak=¨newline¨»«/mspace»«menclose mathcolor=¨#0000FF¨ notation=¨circle¨»«mi mathvariant=¨bold¨»§#949;«/mi»«mo mathvariant=¨bold¨»=«/mo»«mfrac»«mrow»«mo mathvariant=¨bold¨»§#8710;«/mo»«mi mathvariant=¨bold¨»§#981;«/mi»«/mrow»«mrow»«mo mathvariant=¨bold¨»§#8710;«/mo»«mi mathvariant=¨bold¨»t«/mi»«/mrow»«/mfrac»«mo mathvariant=¨bold¨»=«/mo»«mi mathvariant=¨bold¨»A«/mi»«mo mathvariant=¨bold¨»§#183;«/mo»«mfrac»«mrow»«mo mathvariant=¨bold¨»§#8710;«/mo»«mi mathvariant=¨bold¨»B«/mi»«/mrow»«mrow»«mo mathvariant=¨bold¨»§#8710;«/mo»«mi mathvariant=¨bold¨»t«/mi»«/mrow»«/mfrac»«/menclose»«mspace linebreak=¨newline¨»«/mspace»«/mstyle»«/math»
1. בחישוב שטח הכריכה יש לבטא את רדיוס הכריכה ביחידות תקניות של מטר , כדי שהשטח יתקבל במטר בריבוע
כך גם יחידות הכא"מ המושרה יהיו תקניות (וולט).
2. ניתן לקרא מהגרף במדויק את ערכי הנקודות בפרק הזמן הראשון.
אך לא ניתן ללמוד מהגרף במדויק על ערכי הנקודות בפרק הזמן השני , יש לבצע הערכה סבירה לערכי הנקודות.
3. בפרק הזמן הראשון הפונקציה שיפוע הפונקציה הוא קבוע, ערך שיפוע הפונקציה המחושב שווה בדיוק
לשיפוע הפונקציה ברגע t=0.06s.
בפרק הזמן השני ערך שיפוע הפונקציה משתנה, מחישוב שיפוע הפונקציה בין שתי הנקודות מתקבל שיפוע ממוצע
השווה בקירוב לערך שיפוע הפונקציה ברגע t=0.2s. אך לא במדויק.
כך גם יחידות הכא"מ המושרה יהיו תקניות (וולט).
2. ניתן לקרא מהגרף במדויק את ערכי הנקודות בפרק הזמן הראשון.
אך לא ניתן ללמוד מהגרף במדויק על ערכי הנקודות בפרק הזמן השני , יש לבצע הערכה סבירה לערכי הנקודות.
3. בפרק הזמן הראשון הפונקציה שיפוע הפונקציה הוא קבוע, ערך שיפוע הפונקציה המחושב שווה בדיוק
לשיפוע הפונקציה ברגע t=0.06s.
בפרק הזמן השני ערך שיפוע הפונקציה משתנה, מחישוב שיפוע הפונקציה בין שתי הנקודות מתקבל שיפוע ממוצע
השווה בקירוב לערך שיפוע הפונקציה ברגע t=0.2s. אך לא במדויק.
______________________________________________________________________________________

______________________________________________________________________________________
...
מחוק לנץ , כיוון השדה המגנטי שהזרם המושרה יוצר הפוך לכיוון השדה המגנטי «math xmlns=¨http://www.w3.org/1998/Math/MathML¨»«mstyle mathsize=¨20px¨»«mover»«mi mathvariant=¨bold¨»B«/mi»«mo mathvariant=¨bold¨»§#8594;«/mo»«/mover»«/mstyle»«/math» בו נמצאת הכריכה.
חוק לנץ.
עפ"י חוק לנץ הזרם המושרה מתנגד לסיבה להיווצרותו.
מהגרף ניתן לראות שעוצמת השדה המגנטי בכריכה הולכת וגדלה. חוק לנץ קובע שהזרם המושרה יתנגד למגמת שינוי זאת.
לכן, השדה המגנטי הנוצר מהזרם המושרה בכריכה פועל בכיוון נגדי לכיוון השדה המגנטי בו נמצאת הכריכה.
מהגרף ניתן לראות שעוצמת השדה המגנטי בכריכה הולכת וגדלה. חוק לנץ קובע שהזרם המושרה יתנגד למגמת שינוי זאת.
לכן, השדה המגנטי הנוצר מהזרם המושרה בכריכה פועל בכיוון נגדי לכיוון השדה המגנטי בו נמצאת הכריכה.
1. יש למצוא את כיוון השדה המגנטי הנוצר מהזרם המושרה ביחס לשדה המגנטי הנתון בכריכה.
לא נתון כיוון השדה המגנטי בכריכה,
2. חוק לנץ לא קובע שהשדה המגנטי הנוצר מהזרם המושרה הפוך לכיוון השדה המגנטי הנתון בכריכה.
הוא קובע שכיוון השדה הנוצר מהזרם המושרה הפוך למגמת שינוי השדה המגנטי בכריכה.
אם השדה המגנטי הנתון בכריכה היה הולך וקטן בעוצמתו, הזרם המושרה היה מתנגד למגמת השינוי ויוצר שדה מגנטי
בכיוון זהה לכיוון השדה המגנטי הנתון בכריכה.
לא נתון כיוון השדה המגנטי בכריכה,
2. חוק לנץ לא קובע שהשדה המגנטי הנוצר מהזרם המושרה הפוך לכיוון השדה המגנטי הנתון בכריכה.
הוא קובע שכיוון השדה הנוצר מהזרם המושרה הפוך למגמת שינוי השדה המגנטי בכריכה.
אם השדה המגנטי הנתון בכריכה היה הולך וקטן בעוצמתו, הזרם המושרה היה מתנגד למגמת השינוי ויוצר שדה מגנטי
בכיוון זהה לכיוון השדה המגנטי הנתון בכריכה.
______________________________________________________________________________________

______________________________________________________________________________________
...
«math xmlns=¨http://www.w3.org/1998/Math/MathML¨»«mstyle mathsize=¨20px¨»«mrow»«mi mathvariant=¨bold¨»§#949;«/mi»«mo mathvariant=¨bold¨»=«/mo»«mn mathvariant=¨bold¨»0«/mn»«mi mathvariant=¨bold¨»V«/mi»«/mrow»«/mstyle»«/math»
חוק פארדי.
הזווית בין כיוון וקטור השדה המגנטי B לכיוון וקטור השטח A היא 90 מעלות.
מהגדרת השטף המגנטי: «math xmlns=¨http://www.w3.org/1998/Math/MathML¨»«mi mathvariant=¨bold¨ mathcolor=¨#0000FF¨»§#981;«/mi»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»=«/mo»«mi mathvariant=¨bold¨ mathcolor=¨#0000FF¨»B«/mi»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»§#183;«/mo»«mi mathvariant=¨bold¨ mathcolor=¨#0000FF¨»A«/mi»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»§#183;«/mo»«mi mathvariant=¨bold¨ mathcolor=¨#0000FF¨»cos«/mi»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»(«/mo»«mi mathvariant=¨bold¨ mathcolor=¨#0000FF¨»§#945;«/mi»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»)«/mo»«/math» עוצמת השטף בכריכה היא אפס . עוצמת השטף בכריכה לא משתנה
גם כאשר עוצמת השדה המגנטי משתנה.
מחוק פארדיי מכיוון שאין שינוי בגודל השטף בכריכה לא נוצר כא"מ מושרה .
גודל הכא"מ המושרה המתקבל בכריכה ברגע t=0.06s או בכל רגע אחר הוא אפס וולט.
מהגדרת השטף המגנטי: «math xmlns=¨http://www.w3.org/1998/Math/MathML¨»«mi mathvariant=¨bold¨ mathcolor=¨#0000FF¨»§#981;«/mi»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»=«/mo»«mi mathvariant=¨bold¨ mathcolor=¨#0000FF¨»B«/mi»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»§#183;«/mo»«mi mathvariant=¨bold¨ mathcolor=¨#0000FF¨»A«/mi»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»§#183;«/mo»«mi mathvariant=¨bold¨ mathcolor=¨#0000FF¨»cos«/mi»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»(«/mo»«mi mathvariant=¨bold¨ mathcolor=¨#0000FF¨»§#945;«/mi»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»)«/mo»«/math» עוצמת השטף בכריכה היא אפס . עוצמת השטף בכריכה לא משתנה
גם כאשר עוצמת השדה המגנטי משתנה.
מחוק פארדיי מכיוון שאין שינוי בגודל השטף בכריכה לא נוצר כא"מ מושרה .
גודל הכא"מ המושרה המתקבל בכריכה ברגע t=0.06s או בכל רגע אחר הוא אפס וולט.
הכא"מ המושרה שווה לאפס וולט לא בגלל שהשטף המגנטי שווה לאפס וובר , אלא רק בגלל שהשטף המגנטי לא משתנה.
______________________________________________________________________________________