7. 2014,4- מסגרת משוחררת ממנוחה נכנסת ויוצאת משדה

______________________________________________________________________________________
...
בשלב ראשון- פועל כוח הכובד וכוח מגנטי הולך וגדל - הכוח השקול הולך וקטן.
בשלב השני- פועל רק כוח הכובד, הכוח השקול לא משתנה.
בשלב השלישי- פועל כוח הכובד וכוח מגנטי הולך וגדל - הכוח השקול הולך וקטן.
בשלב השני- פועל רק כוח הכובד, הכוח השקול לא משתנה.
בשלב השלישי- פועל כוח הכובד וכוח מגנטי הולך וגדל - הכוח השקול הולך וקטן.
יש לקשר בין תנועת המסגרת לכוח המגנטי.
שלב 1 - המסגרת נכנסת לשדה המגנטי.
בהתאם לתנועת המסגרת, יש יותר קווי שדה פנימה בתוך המסגרת.
מחוק לנץ הזרם המושרה יוצר שדה מגנטי בתוך הכריכה בכיוון החוצה, לכן מכלל יד ימין יזרום זרם נגד כיוון השעון.
וכל עוד לא כל המסגרת נכנסה לשדה יפעל כוח מגנטי על המסגרת כלפי מעלה .
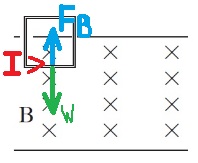
מהירות המסגרת הולכת וגדלה, קצב שינוי השטף הולך וגדל. עוצמת הזרם הולכת וגדלה ובהתאם הכוח המגנטי הולך וגדל.
על המסגרת פועל כוח הכובד כלפי מטה וכוח מגנטי הולך וגדל כלפי מעלה. הכוח השקול הפועל על המסגרת הולכת וקטן.
שלב 2- המסגרת נמצאת כולה בתוך השדה המגנטי.
בשלב זה כל המסגרת נמצאת בתוך השדה המגנטי:
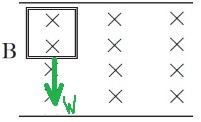
מכיוון שכל המסגרת נמצאת בתוך השדה אין שינוי במספר קווי השדה בכריכה. השטף בכריכה הוא קבוע.
לא נוצר כא"מ מושרה, לא זורם זרם בכריכה ולא פועל כוח מגנטי.
הכוח היחיד הפועל על הכריכה הוא כוח הכובד, הכוח השקול לא משתנה והוא שווה למשקל הכריכה.
שלב 3- המסגרת יוצאת מהשדה.
בהתאם לתנועת המסגרת, יש פחות קווי שדה פנימה בתוך המסגרת.
מחוק לנץ הזרם המושרה יוצר שדה מגנטי בתוך הכריכה בכיוון פנימה, לכן מכלל יד ימין יזרום זרם בכיוון השעון.
וכל עוד לא כל המסגרת יצאה משדה יפעל כוח מגנטי על המסגרת כלפי מעלה, הולך וגדל .
בנוסף, יפעל על המסגרת כוח הכובד כלפי מטה.
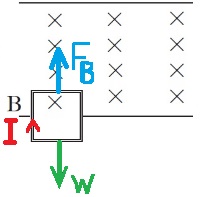
על הכריכה פועל כוח הכובד כלפי מטה וכוח מגנטי כלפי מעלה הולך וגדל, לכן הכוח השקול הפועל על המסגרת הולך וקטן.
בהתאם לתנועת המסגרת, יש יותר קווי שדה פנימה בתוך המסגרת.
מחוק לנץ הזרם המושרה יוצר שדה מגנטי בתוך הכריכה בכיוון החוצה, לכן מכלל יד ימין יזרום זרם נגד כיוון השעון.
וכל עוד לא כל המסגרת נכנסה לשדה יפעל כוח מגנטי על המסגרת כלפי מעלה .

מהירות המסגרת הולכת וגדלה, קצב שינוי השטף הולך וגדל. עוצמת הזרם הולכת וגדלה ובהתאם הכוח המגנטי הולך וגדל.
על המסגרת פועל כוח הכובד כלפי מטה וכוח מגנטי הולך וגדל כלפי מעלה. הכוח השקול הפועל על המסגרת הולכת וקטן.
שלב 2- המסגרת נמצאת כולה בתוך השדה המגנטי.
בשלב זה כל המסגרת נמצאת בתוך השדה המגנטי:

מכיוון שכל המסגרת נמצאת בתוך השדה אין שינוי במספר קווי השדה בכריכה. השטף בכריכה הוא קבוע.
לא נוצר כא"מ מושרה, לא זורם זרם בכריכה ולא פועל כוח מגנטי.
הכוח היחיד הפועל על הכריכה הוא כוח הכובד, הכוח השקול לא משתנה והוא שווה למשקל הכריכה.
שלב 3- המסגרת יוצאת מהשדה.
בהתאם לתנועת המסגרת, יש פחות קווי שדה פנימה בתוך המסגרת.
מחוק לנץ הזרם המושרה יוצר שדה מגנטי בתוך הכריכה בכיוון פנימה, לכן מכלל יד ימין יזרום זרם בכיוון השעון.
וכל עוד לא כל המסגרת יצאה משדה יפעל כוח מגנטי על המסגרת כלפי מעלה, הולך וגדל .
בנוסף, יפעל על המסגרת כוח הכובד כלפי מטה.

על הכריכה פועל כוח הכובד כלפי מטה וכוח מגנטי כלפי מעלה הולך וגדל, לכן הכוח השקול הפועל על המסגרת הולך וקטן.
1. אפשר לענות על השאלה בעזרת ביטוי הכא"מ המושרה במוט הנע בשדה מגנטי.
המסגרת מורכבת מארבעה מוליכים ישרים, שניים אופקיים ושניים אנכיים. הקיטוב הנוצר במוליכים האנכיים הוא זניח.
כאשר מוליך אופקי נע בתוך השדה המגנטי נוצר בו כאמ מושרה.
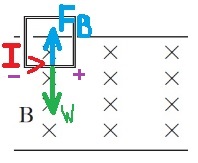
בשלב הראשון - המוט האופקי התחתון נכנס לשדה המגנטי, נוצר כא"מ מושרה במוט. בקצה הימני של המוט יש פוטנציאל חיובי.
בקצה השמאלי הפוטנציאל שלילי, בהתאם לכיוון הזרם מכלל יד שמאל פועל כוח מגנטי כלפי מעלה
על המוט האופקי התחתון.
מהירות המוט הולכת וגדלה לכן הכא"מ גדל, עוצמת הזרם גדלה. והכוח המגנטי הולך וגדל.
כוח הכובד קבוע מכיוון שהכוח המגנטי גדל, הכוח השקול הולך וקטן.
 \
\בשלב השני - שני המוטות האופקיים נמצאים בתוך השדה המגנטי. נוצר כא"מ מושרה במוט העליון, וכא"מ מושרה זהה במוט
התחתון. נוצרים שני זרמים זהים בגודלם והפוכים בכיוונם.
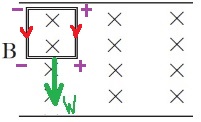
בשלב השלישי - המוט האופקי התחתון יוצא מהשדה המגנטי, נוצר כא"מ מושרה רק במוט העליון .
בקצה הימני של המוט יש פוטנציאל חיובי. בקצה השמאלי הפוטנציאל שלילי.
בהתאם לכיוון הזרם מכלל יד שמאל פועל כוח מגנטי כלפי מעלה על המוט האופקי העליון.
מהירות המוט הולכת וגדלה לכן הכא"מ גדל, עוצמת הזרם גדלה. והכוח המגנטי הולך וגדל.
כוח הכובד קבוע מכיוון שהכוח המגנטי גדל, הכוח השקול הולך וקטן.
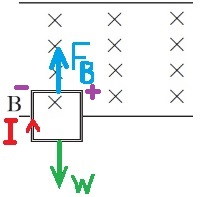
2. השלב השלישי מעט מטעה, הכריכה נעה בתאוצה הולכת וקטנה, אך המהירות הולכת וגדלה.
הכא"מ המושרה תלוי במהירות הכריכה ולא בתאוצתה.
3. בשלב הראשון הכריכה נכנסת לשדה , ובשלב השלישי היא יוצאת מהשדה ,אך בשני המקרים הכוח השקול הולך וקטן.
זה נובע מכך שבשני המקרים כיוון הזרם במוט האופקי הנמצא בתוך השדה הוא זהה . ובשני המקרים מהירות הכריכה גדלה.
המסגרת מורכבת מארבעה מוליכים ישרים, שניים אופקיים ושניים אנכיים. הקיטוב הנוצר במוליכים האנכיים הוא זניח.
כאשר מוליך אופקי נע בתוך השדה המגנטי נוצר בו כאמ מושרה.
בשלב הראשון - המוט האופקי התחתון נכנס לשדה המגנטי, נוצר כא"מ מושרה במוט. בקצה הימני של המוט יש פוטנציאל חיובי.
בקצה השמאלי הפוטנציאל שלילי, בהתאם לכיוון הזרם פועל כוח מגנטי כלפי מעלה על המוט האופקי התחתון.
מהירות המוט הולכת וגדלה לכן הכא"מ גדל, עוצמת הזרם גדלה. והכוח המגנטי הולך וגדל.
כוח הכובד קבוע מכיוון שבכוח המגנטי גדל, הכוח השקול הולך וקטן.

בשלב השני - שני המוטות האופקיים נמצאים בתוך השדה המגנטי. נוצר כא"מ מושרה במוט העליון, וכא"מ מושרה זהה במוט
התחתון. נוצרים שני זרמים זהים בגודלם והפוכים בכיוונם.
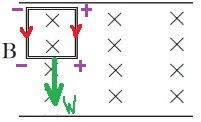
בשלב השלישי - המוט האופקי התחתון נכנס לשדה המגנטי, נוצר כא"מ מושרה במוט. בקצה הימני של המוט יש פוטנציאל חיובי.
בקצה השמאלי הפוטנציאל שלילי, בהתאם לכיוון הזרם פועל כוח מגנטי כלפי מעלה על המוט האופקי התחתון.
מהירות המוט הולכת וגדלה לכן הכא"מ גדל, עוצמת הזרם גדלה. והכוח המגנטי הולך וגדל.
כוח הכובד קבוע מכיוון שבכוח המגנטי גדל, הכוח השקול הולך וקטן.
______________________________________________________________________________________

______________________________________________________________________________________
...
שלב 1- יש זרם, בכיוון נגדי לכיוון השעון.
שלב 2- אין זרם.
שלב 3- יש זרם, בכיוון השעון.
שלב 2- אין זרם.
שלב 3- יש זרם, בכיוון השעון.
חוק פארדי וחוק לנץ.
שלה 1- יש שינוי בשטף בתוך המסגרת. מחוק פארדי נוצר כא"מ מושרה. הכא"מ גורם לזרם מושרה במסגרת.
בזמן תנועת המסגרת מספר קווי השדה פנימה בתוך המסגרת הולך וגדל,מחוק לנץ הזרם המושרה ייצר שדה מגנטי
בתוך הכריכה שכיוונו החוצה מהדף, מכלל יד ימין כיוון הזרם המושרה יהיה נגד כיוון השעון.
שלב 2- אין שינוי בשטף בכריכה לכן לא נוצר כא"מ ולא יזרום זרם מושרה במסגרת.
שלב 3- יש שינוי בשטף בתוך המסגרת. מחוק פארדי נוצר כא"מ מושרה. הכא"מ גורם לזרם מושרה במסגרת.
בזמן תנועת המסגרת מספר קווי השדה פנימה בתוך המסגרת הולך וקטן, מחוק לנץ הזרם המושרה ייצר שדה מגנטי
בתוך הכריכה שכיוונו פנימה לתוך הדף, מכלל יד ימין כיוון הזרם המושרה יהיה בכיוון השעון.
בזמן תנועת המסגרת מספר קווי השדה פנימה בתוך המסגרת הולך וגדל,מחוק לנץ הזרם המושרה ייצר שדה מגנטי
בתוך הכריכה שכיוונו החוצה מהדף, מכלל יד ימין כיוון הזרם המושרה יהיה נגד כיוון השעון.
שלב 2- אין שינוי בשטף בכריכה לכן לא נוצר כא"מ ולא יזרום זרם מושרה במסגרת.
שלב 3- יש שינוי בשטף בתוך המסגרת. מחוק פארדי נוצר כא"מ מושרה. הכא"מ גורם לזרם מושרה במסגרת.
בזמן תנועת המסגרת מספר קווי השדה פנימה בתוך המסגרת הולך וקטן, מחוק לנץ הזרם המושרה ייצר שדה מגנטי
בתוך הכריכה שכיוונו פנימה לתוך הדף, מכלל יד ימין כיוון הזרם המושרה יהיה בכיוון השעון.
כדי לענות על הסעיף הקודם יש לדעת אם פועל זרם או לא ואם כן מה כיוונו. היה עדיף לשנות את סדר הסעיפים.
______________________________________________________________________________________

______________________________________________________________________________________
...
«math style=¨font-family:`Times New Roman`¨ xmlns=¨http://www.w3.org/1998/Math/MathML¨»«mstyle mathsize=¨24px¨»«mrow»«mi mathvariant=¨bold¨»I«/mi»«mo mathvariant=¨bold¨»=«/mo»«mn mathvariant=¨bold¨»4«/mn»«mi mathvariant=¨bold¨»A«/mi»«/mrow»«/mstyle»«/math»
ביטוי כוח מגנטי הפועל על מוליך נושא זרם.
המסגרת נעה בתאוצה שגודלה אפס, מכאן שפועל כוח מגנטי על אחד מהמוליכים האופקיים כלפי מעלה.
נבטא את הזרם מביטוי הכוח המגנטי הפועל על מוליך נושא זרם:
«math style=¨font-family:`Times New Roman`¨ xmlns=¨http://www.w3.org/1998/Math/MathML¨»«mstyle mathsize=¨24px¨»«mrow»«mi mathvariant=¨bold¨ mathcolor=¨#0000FF¨»F«/mi»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»=«/mo»«mi mathvariant=¨bold¨ mathcolor=¨#0000FF¨»B«/mi»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»§#183;«/mo»«mi mathvariant=¨bold¨ mathcolor=¨#0000FF¨»L«/mi»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»§#183;«/mo»«mi mathvariant=¨bold¨ mathcolor=¨#0000FF¨»I«/mi»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»§#183;«/mo»«mi mathvariant=¨bold¨ mathcolor=¨#0000FF¨»sin«/mi»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»(«/mo»«mi mathvariant=¨bold¨ mathcolor=¨#0000FF¨»§#945;«/mi»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»)«/mo»«mspace linebreak=¨newline¨»«/mspace»«mspace linebreak=¨newline¨»«/mspace»«mi mathvariant=¨bold¨ mathcolor=¨#0000FF¨»I«/mi»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»=«/mo»«mfrac mathcolor=¨#0000FF¨»«mi mathvariant=¨bold¨»F«/mi»«mrow»«mi mathvariant=¨bold¨»B«/mi»«mo mathvariant=¨bold¨»§#183;«/mo»«mi mathvariant=¨bold¨»L«/mi»«mo mathvariant=¨bold¨»§#183;«/mo»«mi mathvariant=¨bold¨»sin«/mi»«mo mathvariant=¨bold¨»(«/mo»«mi mathvariant=¨bold¨»§#945;«/mi»«mo mathvariant=¨bold¨»)«/mo»«/mrow»«/mfrac»«/mrow»«/mstyle»«/math»
תאוצת המסגרת שווה לאפס, מהחוק השני של ניוטון שקול הכוחות שווה לאפס. לכן, הכוח המגנטי שווה בגודלו לכוח הכובד.
המסגרת נעה בניצב לשדה: «math xmlns=¨http://www.w3.org/1998/Math/MathML¨»«mi mathvariant=¨bold¨ mathcolor=¨#0000FF¨»§#945;«/mi»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»=«/mo»«mn mathvariant=¨bold¨ mathcolor=¨#0000FF¨»0«/mn»«/math». נמצא בהתאם את עוצמת הזרם:
«math style=¨font-family:`Times New Roman`¨ xmlns=¨http://www.w3.org/1998/Math/MathML¨»«mstyle mathsize=¨24px¨»«mi mathvariant=¨bold¨ mathcolor=¨#0000FF¨»I«/mi»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»=«/mo»«mfrac mathcolor=¨#0000FF¨»«mi mathvariant=¨bold¨»F«/mi»«mrow»«mi mathvariant=¨bold¨»B«/mi»«mo mathvariant=¨bold¨»§#183;«/mo»«mi mathvariant=¨bold¨»L«/mi»«mo mathvariant=¨bold¨»§#183;«/mo»«mi mathvariant=¨bold¨»sin«/mi»«mo mathvariant=¨bold¨»(«/mo»«mi mathvariant=¨bold¨»§#945;«/mi»«mo mathvariant=¨bold¨»)«/mo»«/mrow»«/mfrac»«mspace linebreak=¨newline¨»«/mspace»«mspace linebreak=¨newline¨»«/mspace»«mi mathvariant=¨bold¨ mathcolor=¨#0000FF¨»I«/mi»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»=«/mo»«mfrac mathcolor=¨#0000FF¨»«mi mathvariant=¨bold¨»mg«/mi»«mrow»«mi mathvariant=¨bold¨»B«/mi»«mo mathvariant=¨bold¨»§#183;«/mo»«mi mathvariant=¨bold¨»L«/mi»«mo mathvariant=¨bold¨»§#183;«/mo»«mi mathvariant=¨bold¨»sin«/mi»«mo mathvariant=¨bold¨»(«/mo»«mi mathvariant=¨bold¨»§#945;«/mi»«mo mathvariant=¨bold¨»)«/mo»«/mrow»«/mfrac»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»=«/mo»«mfrac mathcolor=¨#0000FF¨»«mrow»«mn mathvariant=¨bold¨»0«/mn»«mo mathvariant=¨bold¨».«/mo»«mn mathvariant=¨bold¨»1«/mn»«mo mathvariant=¨bold¨»§#183;«/mo»«mn mathvariant=¨bold¨»10«/mn»«/mrow»«mrow»«mn mathvariant=¨bold¨»0«/mn»«mo mathvariant=¨bold¨».«/mo»«mn mathvariant=¨bold¨»5«/mn»«mo mathvariant=¨bold¨»§#183;«/mo»«mn mathvariant=¨bold¨»0«/mn»«mo mathvariant=¨bold¨».«/mo»«mn mathvariant=¨bold¨»5«/mn»«mo mathvariant=¨bold¨»§#183;«/mo»«mi mathvariant=¨bold¨»sin«/mi»«mo mathvariant=¨bold¨»(«/mo»«mn mathvariant=¨bold¨»90«/mn»«mo mathvariant=¨bold¨»)«/mo»«/mrow»«/mfrac»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»=«/mo»«mfrac mathcolor=¨#0000FF¨»«mn mathvariant=¨bold¨»1«/mn»«mrow»«mn mathvariant=¨bold¨»0«/mn»«mo mathvariant=¨bold¨».«/mo»«mn mathvariant=¨bold¨»25«/mn»«/mrow»«/mfrac»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»=«/mo»«mn mathvariant=¨bold¨ mathcolor=¨#0000FF¨»4«/mn»«mi mathvariant=¨bold¨ mathcolor=¨#0000FF¨»A«/mi»«mspace linebreak=¨newline¨»«/mspace»«/mstyle»«/math»
לכן, עוצמת הזרם במסגרת היא 4 אמפר.
נבטא את הזרם מביטוי הכוח המגנטי הפועל על מוליך נושא זרם:
«math style=¨font-family:`Times New Roman`¨ xmlns=¨http://www.w3.org/1998/Math/MathML¨»«mstyle mathsize=¨24px¨»«mrow»«mi mathvariant=¨bold¨ mathcolor=¨#0000FF¨»F«/mi»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»=«/mo»«mi mathvariant=¨bold¨ mathcolor=¨#0000FF¨»B«/mi»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»§#183;«/mo»«mi mathvariant=¨bold¨ mathcolor=¨#0000FF¨»L«/mi»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»§#183;«/mo»«mi mathvariant=¨bold¨ mathcolor=¨#0000FF¨»I«/mi»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»§#183;«/mo»«mi mathvariant=¨bold¨ mathcolor=¨#0000FF¨»sin«/mi»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»(«/mo»«mi mathvariant=¨bold¨ mathcolor=¨#0000FF¨»§#945;«/mi»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»)«/mo»«mspace linebreak=¨newline¨»«/mspace»«mspace linebreak=¨newline¨»«/mspace»«mi mathvariant=¨bold¨ mathcolor=¨#0000FF¨»I«/mi»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»=«/mo»«mfrac mathcolor=¨#0000FF¨»«mi mathvariant=¨bold¨»F«/mi»«mrow»«mi mathvariant=¨bold¨»B«/mi»«mo mathvariant=¨bold¨»§#183;«/mo»«mi mathvariant=¨bold¨»L«/mi»«mo mathvariant=¨bold¨»§#183;«/mo»«mi mathvariant=¨bold¨»sin«/mi»«mo mathvariant=¨bold¨»(«/mo»«mi mathvariant=¨bold¨»§#945;«/mi»«mo mathvariant=¨bold¨»)«/mo»«/mrow»«/mfrac»«/mrow»«/mstyle»«/math»
תאוצת המסגרת שווה לאפס, מהחוק השני של ניוטון שקול הכוחות שווה לאפס. לכן, הכוח המגנטי שווה בגודלו לכוח הכובד.
המסגרת נעה בניצב לשדה: «math xmlns=¨http://www.w3.org/1998/Math/MathML¨»«mi mathvariant=¨bold¨ mathcolor=¨#0000FF¨»§#945;«/mi»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»=«/mo»«mn mathvariant=¨bold¨ mathcolor=¨#0000FF¨»0«/mn»«/math». נמצא בהתאם את עוצמת הזרם:
«math style=¨font-family:`Times New Roman`¨ xmlns=¨http://www.w3.org/1998/Math/MathML¨»«mstyle mathsize=¨24px¨»«mi mathvariant=¨bold¨ mathcolor=¨#0000FF¨»I«/mi»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»=«/mo»«mfrac mathcolor=¨#0000FF¨»«mi mathvariant=¨bold¨»F«/mi»«mrow»«mi mathvariant=¨bold¨»B«/mi»«mo mathvariant=¨bold¨»§#183;«/mo»«mi mathvariant=¨bold¨»L«/mi»«mo mathvariant=¨bold¨»§#183;«/mo»«mi mathvariant=¨bold¨»sin«/mi»«mo mathvariant=¨bold¨»(«/mo»«mi mathvariant=¨bold¨»§#945;«/mi»«mo mathvariant=¨bold¨»)«/mo»«/mrow»«/mfrac»«mspace linebreak=¨newline¨»«/mspace»«mspace linebreak=¨newline¨»«/mspace»«mi mathvariant=¨bold¨ mathcolor=¨#0000FF¨»I«/mi»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»=«/mo»«mfrac mathcolor=¨#0000FF¨»«mi mathvariant=¨bold¨»mg«/mi»«mrow»«mi mathvariant=¨bold¨»B«/mi»«mo mathvariant=¨bold¨»§#183;«/mo»«mi mathvariant=¨bold¨»L«/mi»«mo mathvariant=¨bold¨»§#183;«/mo»«mi mathvariant=¨bold¨»sin«/mi»«mo mathvariant=¨bold¨»(«/mo»«mi mathvariant=¨bold¨»§#945;«/mi»«mo mathvariant=¨bold¨»)«/mo»«/mrow»«/mfrac»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»=«/mo»«mfrac mathcolor=¨#0000FF¨»«mrow»«mn mathvariant=¨bold¨»0«/mn»«mo mathvariant=¨bold¨».«/mo»«mn mathvariant=¨bold¨»1«/mn»«mo mathvariant=¨bold¨»§#183;«/mo»«mn mathvariant=¨bold¨»10«/mn»«/mrow»«mrow»«mn mathvariant=¨bold¨»0«/mn»«mo mathvariant=¨bold¨».«/mo»«mn mathvariant=¨bold¨»5«/mn»«mo mathvariant=¨bold¨»§#183;«/mo»«mn mathvariant=¨bold¨»0«/mn»«mo mathvariant=¨bold¨».«/mo»«mn mathvariant=¨bold¨»5«/mn»«mo mathvariant=¨bold¨»§#183;«/mo»«mi mathvariant=¨bold¨»sin«/mi»«mo mathvariant=¨bold¨»(«/mo»«mn mathvariant=¨bold¨»90«/mn»«mo mathvariant=¨bold¨»)«/mo»«/mrow»«/mfrac»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»=«/mo»«mfrac mathcolor=¨#0000FF¨»«mn mathvariant=¨bold¨»1«/mn»«mrow»«mn mathvariant=¨bold¨»0«/mn»«mo mathvariant=¨bold¨».«/mo»«mn mathvariant=¨bold¨»25«/mn»«/mrow»«/mfrac»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»=«/mo»«mn mathvariant=¨bold¨ mathcolor=¨#0000FF¨»4«/mn»«mi mathvariant=¨bold¨ mathcolor=¨#0000FF¨»A«/mi»«mspace linebreak=¨newline¨»«/mspace»«/mstyle»«/math»
לכן, עוצמת הזרם במסגרת היא 4 אמפר.
לא ניתן לקבוע אם ברגע המסוים שבו התאוצה שווה לאפס המסגרת נכנסת לשדה או יוצאת ממנו.
______________________________________________________________________________________
______________________________________________________________________________________
...
«math xmlns=¨http://www.w3.org/1998/Math/MathML¨»«mi mathvariant=¨bold¨»V«/mi»«mo mathvariant=¨bold¨»=«/mo»«mn mathvariant=¨bold¨»4«/mn»«mfrac»«mi mathvariant=¨bold¨»m«/mi»«mi mathvariant=¨bold¨»s«/mi»«/mfrac»«/math»
ביטוי כא"מ המושרה במוט . חוק אום.
נשתמש בביטוי הכא"מ המושרה במוט, ונבטא ממנו את מהירות המוט:
«math xmlns=¨http://www.w3.org/1998/Math/MathML¨»«mi mathvariant=¨bold¨ mathcolor=¨#0000FF¨»§#949;«/mi»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»=«/mo»«mi mathvariant=¨bold¨ mathcolor=¨#0000FF¨»B«/mi»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»§#183;«/mo»«mi mathvariant=¨bold¨ mathcolor=¨#0000FF¨»V«/mi»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»§#183;«/mo»«mi mathvariant=¨bold¨ mathcolor=¨#0000FF¨»L«/mi»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»§#183;«/mo»«mi mathvariant=¨bold¨ mathcolor=¨#0000FF¨»sin«/mi»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»(«/mo»«mi mathvariant=¨bold¨ mathcolor=¨#0000FF¨»§#945;«/mi»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»)«/mo»«mspace linebreak=¨newline¨»«/mspace»«mspace linebreak=¨newline¨»«/mspace»«mi mathvariant=¨bold¨ mathcolor=¨#0000FF¨»V«/mi»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»=«/mo»«mfrac mathcolor=¨#0000FF¨»«mi mathvariant=¨bold¨»§#949;«/mi»«mrow»«mi mathvariant=¨bold¨»B«/mi»«mo mathvariant=¨bold¨»§#183;«/mo»«mi mathvariant=¨bold¨»L«/mi»«mo mathvariant=¨bold¨»§#183;«/mo»«mi mathvariant=¨bold¨»sin«/mi»«mo mathvariant=¨bold¨»(«/mo»«mi mathvariant=¨bold¨»§#945;«/mi»«mo mathvariant=¨bold¨»)«/mo»«/mrow»«/mfrac»«/math»
נבטא את הכא"מ בתלות בהתנגדות המסגרת והזרם לפי חוק אום:
«math style=¨font-family:`Times New Roman`¨ xmlns=¨http://www.w3.org/1998/Math/MathML¨»«mstyle mathsize=¨20px¨»«mrow»«mi mathvariant=¨bold¨ mathcolor=¨#0000FF¨»I«/mi»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»=«/mo»«mfrac mathcolor=¨#0000FF¨»«mi mathvariant=¨bold¨»§#949;«/mi»«mi mathvariant=¨bold¨»R«/mi»«/mfrac»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»§#160;«/mo»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»§#8658;«/mo»«mi mathvariant=¨bold¨ mathcolor=¨#0000FF¨»§#949;«/mi»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»=«/mo»«mi mathvariant=¨bold¨ mathcolor=¨#0000FF¨»I«/mi»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»§#183;«/mo»«mi mathvariant=¨bold¨ mathcolor=¨#0000FF¨»R«/mi»«mspace linebreak=¨newline¨»«/mspace»«/mrow»«/mstyle»«/math»
נציב את ביטוי הכא"מ ונחשב את המהירות:
«math style=¨font-family:`Times New Roman`¨ xmlns=¨http://www.w3.org/1998/Math/MathML¨»«mstyle mathsize=¨20px¨»«mrow»«mi mathvariant=¨bold¨ mathcolor=¨#0000FF¨»V«/mi»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»=«/mo»«mfrac mathcolor=¨#0000FF¨»«mi mathvariant=¨bold¨»§#949;«/mi»«mrow»«mi mathvariant=¨bold¨»B«/mi»«mo mathvariant=¨bold¨»§#183;«/mo»«mi mathvariant=¨bold¨»L«/mi»«mo mathvariant=¨bold¨»§#183;«/mo»«mi mathvariant=¨bold¨»sin«/mi»«mo mathvariant=¨bold¨»(«/mo»«mi mathvariant=¨bold¨»§#945;«/mi»«mo mathvariant=¨bold¨»)«/mo»«/mrow»«/mfrac»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»=«/mo»«mfrac mathcolor=¨#0000FF¨»«mrow»«mi mathvariant=¨bold¨»I«/mi»«mo mathvariant=¨bold¨»§#183;«/mo»«mi mathvariant=¨bold¨»R«/mi»«/mrow»«mrow»«mi mathvariant=¨bold¨»B«/mi»«mo mathvariant=¨bold¨»§#183;«/mo»«mi mathvariant=¨bold¨»L«/mi»«mo mathvariant=¨bold¨»§#183;«/mo»«mi mathvariant=¨bold¨»sin«/mi»«mo mathvariant=¨bold¨»(«/mo»«mi mathvariant=¨bold¨»§#945;«/mi»«mo mathvariant=¨bold¨»)«/mo»«/mrow»«/mfrac»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»=«/mo»«mfrac mathcolor=¨#0000FF¨»«mrow»«mn mathvariant=¨bold¨»4«/mn»«mo mathvariant=¨bold¨»§#183;«/mo»«mn mathvariant=¨bold¨»1«/mn»«/mrow»«mrow»«mn mathvariant=¨bold¨»0«/mn»«mo mathvariant=¨bold¨».«/mo»«mn mathvariant=¨bold¨»5«/mn»«mo mathvariant=¨bold¨»§#183;«/mo»«mn mathvariant=¨bold¨»0«/mn»«mo mathvariant=¨bold¨».«/mo»«mn mathvariant=¨bold¨»5«/mn»«mo mathvariant=¨bold¨»§#183;«/mo»«mi mathvariant=¨bold¨»sin«/mi»«mo mathvariant=¨bold¨»(«/mo»«mn mathvariant=¨bold¨»90«/mn»«mo mathvariant=¨bold¨»)«/mo»«/mrow»«/mfrac»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»=«/mo»«mfrac mathcolor=¨#0000FF¨»«mn mathvariant=¨bold¨»4«/mn»«mrow»«mn mathvariant=¨bold¨»0«/mn»«mo mathvariant=¨bold¨».«/mo»«mn mathvariant=¨bold¨»25«/mn»«/mrow»«/mfrac»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»=«/mo»«mn mathvariant=¨bold¨ mathcolor=¨#0000FF¨»16«/mn»«mfrac mathcolor=¨#0000FF¨»«mi mathvariant=¨bold¨»m«/mi»«mi mathvariant=¨bold¨»s«/mi»«/mfrac»«mspace linebreak=¨newline¨/»«/mrow»«/mstyle»«/math»
מהירות המסגרת היא 4 מטר לשנייה.
«math xmlns=¨http://www.w3.org/1998/Math/MathML¨»«mi mathvariant=¨bold¨ mathcolor=¨#0000FF¨»§#949;«/mi»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»=«/mo»«mi mathvariant=¨bold¨ mathcolor=¨#0000FF¨»B«/mi»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»§#183;«/mo»«mi mathvariant=¨bold¨ mathcolor=¨#0000FF¨»V«/mi»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»§#183;«/mo»«mi mathvariant=¨bold¨ mathcolor=¨#0000FF¨»L«/mi»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»§#183;«/mo»«mi mathvariant=¨bold¨ mathcolor=¨#0000FF¨»sin«/mi»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»(«/mo»«mi mathvariant=¨bold¨ mathcolor=¨#0000FF¨»§#945;«/mi»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»)«/mo»«mspace linebreak=¨newline¨»«/mspace»«mspace linebreak=¨newline¨»«/mspace»«mi mathvariant=¨bold¨ mathcolor=¨#0000FF¨»V«/mi»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»=«/mo»«mfrac mathcolor=¨#0000FF¨»«mi mathvariant=¨bold¨»§#949;«/mi»«mrow»«mi mathvariant=¨bold¨»B«/mi»«mo mathvariant=¨bold¨»§#183;«/mo»«mi mathvariant=¨bold¨»L«/mi»«mo mathvariant=¨bold¨»§#183;«/mo»«mi mathvariant=¨bold¨»sin«/mi»«mo mathvariant=¨bold¨»(«/mo»«mi mathvariant=¨bold¨»§#945;«/mi»«mo mathvariant=¨bold¨»)«/mo»«/mrow»«/mfrac»«/math»
נבטא את הכא"מ בתלות בהתנגדות המסגרת והזרם לפי חוק אום:
«math style=¨font-family:`Times New Roman`¨ xmlns=¨http://www.w3.org/1998/Math/MathML¨»«mstyle mathsize=¨20px¨»«mrow»«mi mathvariant=¨bold¨ mathcolor=¨#0000FF¨»I«/mi»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»=«/mo»«mfrac mathcolor=¨#0000FF¨»«mi mathvariant=¨bold¨»§#949;«/mi»«mi mathvariant=¨bold¨»R«/mi»«/mfrac»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»§#160;«/mo»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»§#8658;«/mo»«mi mathvariant=¨bold¨ mathcolor=¨#0000FF¨»§#949;«/mi»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»=«/mo»«mi mathvariant=¨bold¨ mathcolor=¨#0000FF¨»I«/mi»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»§#183;«/mo»«mi mathvariant=¨bold¨ mathcolor=¨#0000FF¨»R«/mi»«mspace linebreak=¨newline¨»«/mspace»«/mrow»«/mstyle»«/math»
נציב את ביטוי הכא"מ ונחשב את המהירות:
«math style=¨font-family:`Times New Roman`¨ xmlns=¨http://www.w3.org/1998/Math/MathML¨»«mstyle mathsize=¨20px¨»«mrow»«mi mathvariant=¨bold¨ mathcolor=¨#0000FF¨»V«/mi»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»=«/mo»«mfrac mathcolor=¨#0000FF¨»«mi mathvariant=¨bold¨»§#949;«/mi»«mrow»«mi mathvariant=¨bold¨»B«/mi»«mo mathvariant=¨bold¨»§#183;«/mo»«mi mathvariant=¨bold¨»L«/mi»«mo mathvariant=¨bold¨»§#183;«/mo»«mi mathvariant=¨bold¨»sin«/mi»«mo mathvariant=¨bold¨»(«/mo»«mi mathvariant=¨bold¨»§#945;«/mi»«mo mathvariant=¨bold¨»)«/mo»«/mrow»«/mfrac»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»=«/mo»«mfrac mathcolor=¨#0000FF¨»«mrow»«mi mathvariant=¨bold¨»I«/mi»«mo mathvariant=¨bold¨»§#183;«/mo»«mi mathvariant=¨bold¨»R«/mi»«/mrow»«mrow»«mi mathvariant=¨bold¨»B«/mi»«mo mathvariant=¨bold¨»§#183;«/mo»«mi mathvariant=¨bold¨»L«/mi»«mo mathvariant=¨bold¨»§#183;«/mo»«mi mathvariant=¨bold¨»sin«/mi»«mo mathvariant=¨bold¨»(«/mo»«mi mathvariant=¨bold¨»§#945;«/mi»«mo mathvariant=¨bold¨»)«/mo»«/mrow»«/mfrac»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»=«/mo»«mfrac mathcolor=¨#0000FF¨»«mrow»«mn mathvariant=¨bold¨»4«/mn»«mo mathvariant=¨bold¨»§#183;«/mo»«mn mathvariant=¨bold¨»1«/mn»«/mrow»«mrow»«mn mathvariant=¨bold¨»0«/mn»«mo mathvariant=¨bold¨».«/mo»«mn mathvariant=¨bold¨»5«/mn»«mo mathvariant=¨bold¨»§#183;«/mo»«mn mathvariant=¨bold¨»0«/mn»«mo mathvariant=¨bold¨».«/mo»«mn mathvariant=¨bold¨»5«/mn»«mo mathvariant=¨bold¨»§#183;«/mo»«mi mathvariant=¨bold¨»sin«/mi»«mo mathvariant=¨bold¨»(«/mo»«mn mathvariant=¨bold¨»90«/mn»«mo mathvariant=¨bold¨»)«/mo»«/mrow»«/mfrac»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»=«/mo»«mfrac mathcolor=¨#0000FF¨»«mn mathvariant=¨bold¨»4«/mn»«mrow»«mn mathvariant=¨bold¨»0«/mn»«mo mathvariant=¨bold¨».«/mo»«mn mathvariant=¨bold¨»25«/mn»«/mrow»«/mfrac»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»=«/mo»«mn mathvariant=¨bold¨ mathcolor=¨#0000FF¨»16«/mn»«mfrac mathcolor=¨#0000FF¨»«mi mathvariant=¨bold¨»m«/mi»«mi mathvariant=¨bold¨»s«/mi»«/mfrac»«mspace linebreak=¨newline¨/»«/mrow»«/mstyle»«/math»
מהירות המסגרת היא 4 מטר לשנייה.
1. בפיזיקה ובמיוחד בחשמל יש רצף של גדלים פיזיקליים התלויים אחד בשני , השאלה הזאת היא דוגמה טובה לכך.
מהעובדה שהמוט מתמיד בתנועתו - ניתן לקבוע הכוח המגנטי שווה לכוח הכובד (חוק ראשון של ניוטון).
בהתאם לכוח המגנטי - ניתן למצוא את הזרם במסגרת (ביטוי כוח מגנטי הפועל על מוליך נושא זרם).
בהתאם לזרם - אפשר למצוא את מהירות המסגרת(ביטוי כא"מ הנוצר במוט וחוק אום)
2. בשאלה מעורבים הרבה עקרונות, זה יוצא מעט קושי , מצריך תמרון וגישוש.
מומלץ לנסות למצוא את המהלך הנכון בדף טיוטה.
מהעובדה שהמוט מתמיד בתנועתו - ניתן לקבוע הכוח המגנטי שווה לכוח הכובד (חוק ראשון של ניוטון).
בהתאם לכוח המגנטי - ניתן למצוא את הזרם במסגרת (ביטוי כוח מגנטי הפועל על מוליך נושא זרם).
בהתאם לזרם - אפשר למצוא את מהירות המסגרת(ביטוי כא"מ הנוצר במוט וחוק אום)
2. בשאלה מעורבים הרבה עקרונות, זה יוצא מעט קושי , מצריך תמרון וגישוש.
מומלץ לנסות למצוא את המהלך הנכון בדף טיוטה.
______________________________________________________________________________________