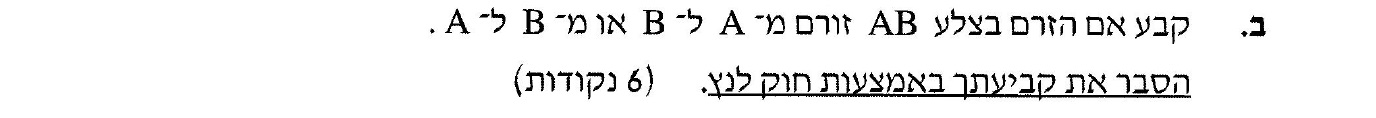
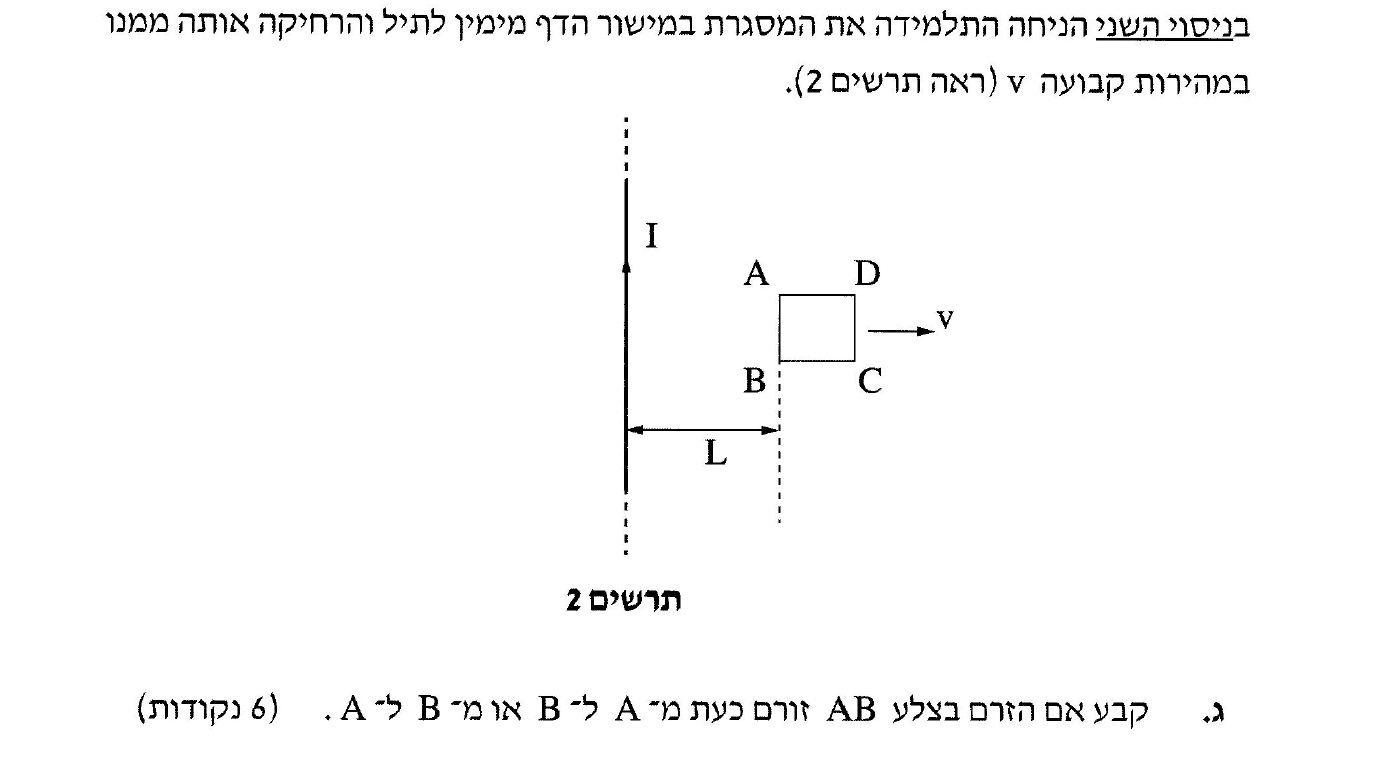
______________________________________________________________________________________
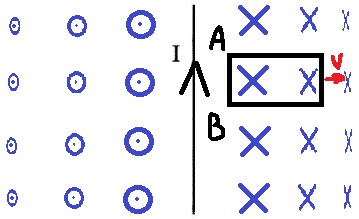
...
החוצה מהדף.
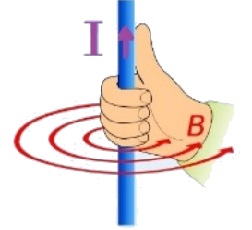
כלל יד ימין.
בהתאם לכלל יד ימין, כיוון השדה המגנטי משמאל לתיל הוא החוצה מהדף.
1. בשימוש בכלל יד ימין ,כאשר כיוון האגודל של יד ימין הוא בכיוון הזרם כיוון ארבעת האצבעות בכיוון השדה המגנטי.
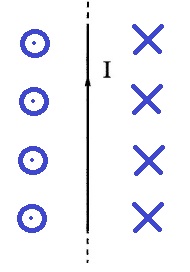
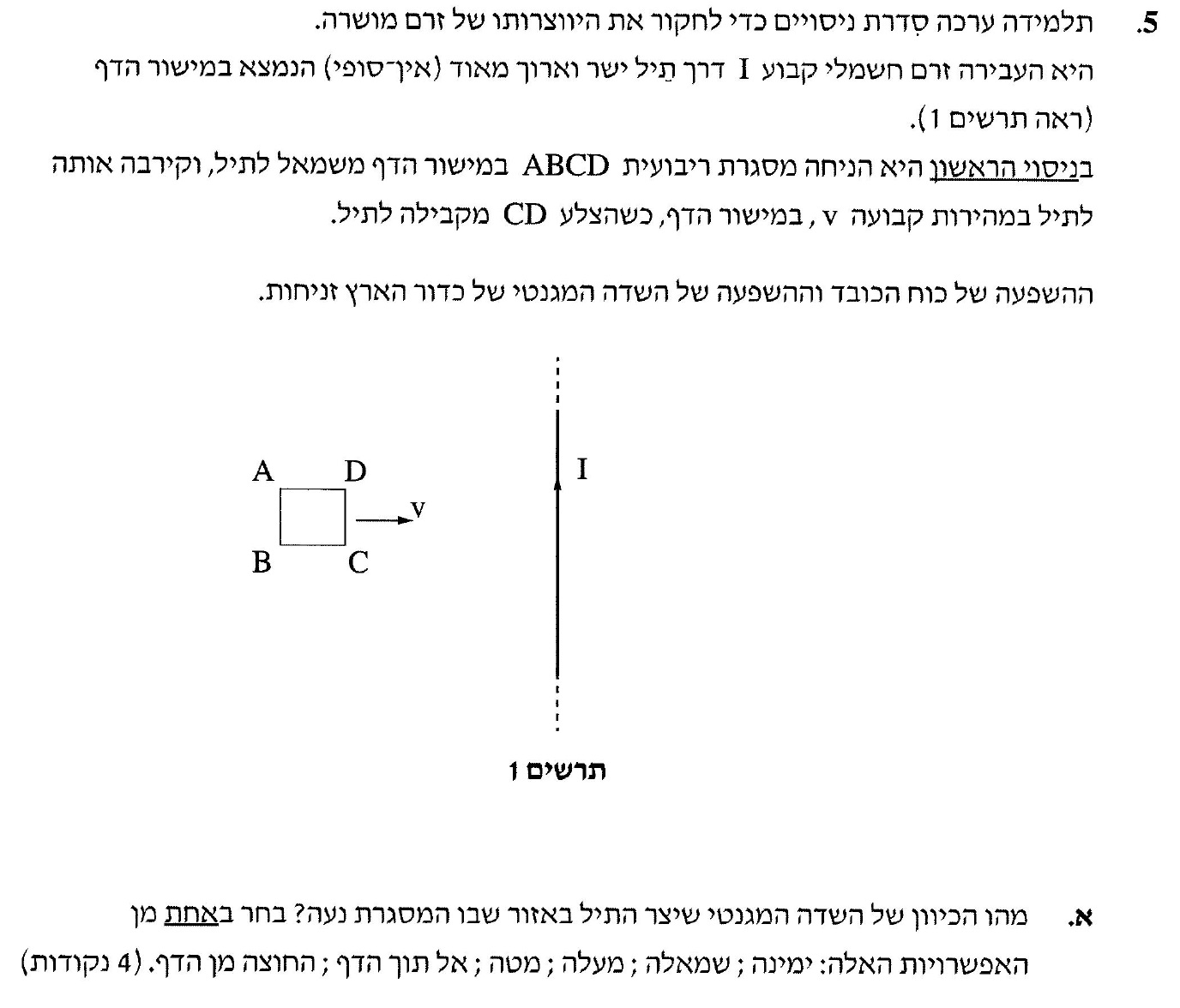
מצד שמאל של המוליך, במישור הדף, כיוון קווי השדה הוא החוצה מהדף, כפי שניתן לראות האיור הבא:
2. כאשר נושא זרם מונח על מישור, תמיד בצד אחד של המוליך יש קווי שדה פנימה ובצד השני קווי שדה החוצה.
כמוראה באיור הבא:
מצד שמאל של המוליך, במישור הדף, כיוון קווי השדה הוא החוצה מהדף, כפי שניתן לראות האיור הבא:
2. כאשר נושא זרם מונח על מישור, תמיד בצד אחד של המוליך יש קווי שדה פנימה ובצד השני קווי שדה החוצה.
______________________________________________________________________________________
______________________________________________________________________________________
...
כיוון הזרם המושרה בכריכה הוא מנקודה B לנקודה A.
חוק לנץ.
מחוק לנץ הזרם המושרה מתנגד לסיבה להיווצרותו (למגמת השינוי בשטף המגנטי בכריכה).
כיוון השטף בכריכה הוא החוצה מהדף והוא הולך וגדל, הזרם המושרה מתנגד לשינוי זה, הוא ייצר בכריכה שדה שכיוונו פנימה.
מכלל יד ימין כיוון הזרם המושרה יהיה מנקודה B לנקודה A, כך שבתוך הכריכה כיוון השדה המגנטי יהיה לתוך הדף.
שטח המסגרת קבוע , מביטוי השטף «math xmlns=¨http://www.w3.org/1998/Math/MathML¨»«mi mathvariant=¨bold¨ mathcolor=¨#0000FF¨»§#981;«/mi»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»=«/mo»«mi mathvariant=¨bold¨ mathcolor=¨#0000FF¨»B«/mi»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»§#183;«/mo»«mi mathvariant=¨bold¨ mathcolor=¨#0000FF¨»A«/mi»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»§#183;«/mo»«mi mathvariant=¨bold¨ mathcolor=¨#0000FF¨»cos«/mi»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»(«/mo»«mi mathvariant=¨bold¨ mathcolor=¨#0000FF¨»§#945;«/mi»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»)«/mo»«/math» ניתן לומר שהשטף הולך וגדל .
מחוק לנץ הזרם המושרה מתנגד לסיבה להיווצרותו (למגמת השינוי בשטף המגנטי בכריכה).
כיוון השטף בכריכה הוא החוצה מהדף והוא הולך וגדל, הזרם המושרה מתנגד לשינוי זה, הוא ייצר בכריכה שדה שכיוונו פנימה.
מכלל יד ימין כיוון הזרם המושרה יהיה מנקודה B לנקודה A, כך שבתוך הכריכה כיוון השדה המגנטי יהיה לתוך הדף.
1. שטח המסגרת קבוע, כאשר המסגרת מתקרבת למוליך עוצמת השדה המגנטי גדלה .
מביטוי השטף «math xmlns=¨http://www.w3.org/1998/Math/MathML¨»«mi mathvariant=¨bold¨ mathcolor=¨#0000FF¨»§#981;«/mi»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»=«/mo»«mi mathvariant=¨bold¨ mathcolor=¨#0000FF¨»B«/mi»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»§#183;«/mo»«mi mathvariant=¨bold¨ mathcolor=¨#0000FF¨»A«/mi»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»§#183;«/mo»«mi mathvariant=¨bold¨ mathcolor=¨#0000FF¨»cos«/mi»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»(«/mo»«mi mathvariant=¨bold¨ mathcolor=¨#0000FF¨»§#945;«/mi»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»)«/mo»«/math» ניתן לומר שהשטף הולך וגדל.
2. השטף הוא תיאור כמותי , קווי השדה הם תיאור חזותי , השטף וקווי השדה מתארים את אותו רעיון בצורה שונה .
חוק פראדיי מוגדר בעזרת השטף. ניתן להשתמש בחוק לנץ בתיאור החזותי בקווי השדה, במקום בשטף.
במקרה זה, ניתן לומר שכאשר המסגרת נעה ימינה , יש יותר קווי שדה החוצה, הזרם מתנגד לשינוי זה
הוא יצור שדה מגנטי שכיווני במסגרת לתוך הדף. מכלל יד ימין כיוון הזרם יהיה מ B ל A.
3. באופן כללי מקובל לתאר את כיוון הזרם בכריכה ביחס לכיוון השעון (בכיוון השעון או נגד כיוון השעון).
סעיף זה עוסק בכיוון הזרם בין שתי נקודות , אין חשיבות מיוחדת דווקא לשתי נקודות אלו.
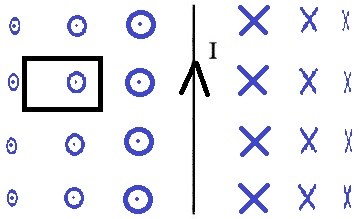
4. כדי שיהיה נוח לחשוב על הפתרון מומלץ לסמן את האזור שבו יש שדה חזק בסימון גדול
ואת האזור שבו השדה המגנטי חלש בסימון קטן. ורק לאחר מכן לחשוב על מגמת השינוי בקווי השדה המגנטי בכריכה.
כמוראה באיור הבא:
______________________________________________________________________________________
______________________________________________________________________________________
...
כיוון הזרם המושרה בכריכה הוא מנקודה B לנקודה A.
חוק לנץ
מכלל יד ימין, מצדו הימני של המוליך כיוון קווי השדה הם לתוך הדף.
כפי שניתן לראות באיור הבא:
ככל שהמסגרת מתרחקת מהמוליך השטף בכריכה הולך וקטן. מחוק לזנץ הזרם מתנגד לשינוי זה , הזרם המושרה יגרום לשדה מגנטי לתוך הדף. לכן כיוון הזרם בכריכה יהיה מנקודה B לנקודה A.
כפי שניתן לראות באיור הבא:
ככל שהמסגרת מתרחקת מהמוליך השטף בכריכה הולך וקטן. מחוק לזנץ הזרם מתנגד לשינוי זה , הזרם המושרה יגרום לשדה מגנטי לתוך הדף. לכן כיוון הזרם בכריכה יהיה מנקודה B לנקודה A.
1. קיימים שני שינויים בין תנועת המוליך משמאל למוליך לתנועתו מימין למוליך:
א- באזור השמאלי כיוון השדה המגנטי הוא החוצה מהדף ובאזור הימני כיוון השדה המגנטי הוא לתוך הדף.
ב- בתנועת המסגרת משמאל למוליך השטף גדל. ובתנועת המסגרת מימין למוליך השטף קטן.
כל אחד משני שינויים אלו גורם להיפוך כיוון הזרם המושרה. מכיוון שיש שני שינויים כיוון הזרם לא משתנה כתוצאה
ממעבר הכריכה מהאזור השמאלי לימני.
2. כיוון הזרם קבוע, אך עוצמת הזרם איננה קבועה.
א- באזור השמאלי כיוון השדה המגנטי הוא החוצה מהדף ובאזור הימני כיוון השדה המגנטי הוא לתוך הדף.
ב- בתנועת המסגרת משמאל למוליך השטף גדל. ובתנועת המסגרת מימין למוליך השטף קטן.
כל אחד משני שינויים אלו גורם להיפוך כיוון הזרם המושרה. מכיוון שיש שני שינויים כיוון הזרם לא משתנה כתוצאה
ממעבר הכריכה מהאזור השמאלי לימני.
2. כיוון הזרם קבוע, אך עוצמת הזרם איננה קבועה.
______________________________________________________________________________________

______________________________________________________________________________________
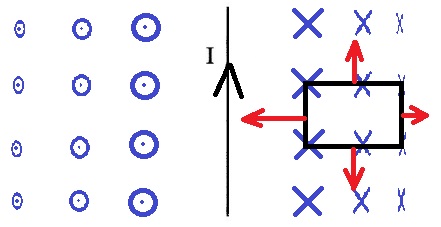
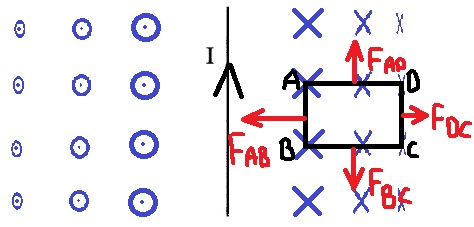
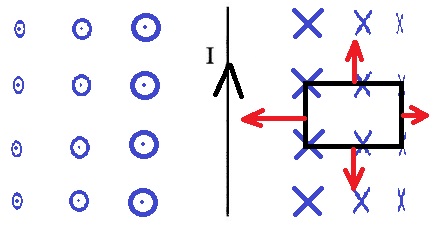
...
כלל יש שמאל וביטוי הכוח המגנטי: «math style=¨font-family:`Times New Roman`¨ xmlns=¨http://www.w3.org/1998/Math/MathML¨»«mstyle mathsize=¨20px¨»«mrow»«mi mathvariant=¨bold¨ mathcolor=¨#FF6600¨»F«/mi»«mo mathvariant=¨bold¨ mathcolor=¨#FF6600¨»=«/mo»«mi mathvariant=¨bold¨ mathcolor=¨#FF6600¨»B«/mi»«mo mathvariant=¨bold¨ mathcolor=¨#FF6600¨»§#183;«/mo»«mi mathvariant=¨bold¨ mathcolor=¨#FF6600¨»L«/mi»«mo mathvariant=¨bold¨ mathcolor=¨#FF6600¨»§#183;«/mo»«mi mathvariant=¨bold¨ mathcolor=¨#FF6600¨»I«/mi»«mo mathvariant=¨bold¨ mathcolor=¨#FF6600¨»§#183;«/mo»«mi mathvariant=¨bold¨ mathcolor=¨#FF6600¨»sin«/mi»«mo mathvariant=¨bold¨ mathcolor=¨#FF6600¨»(«/mo»«mi mathvariant=¨bold¨ mathcolor=¨#FF6600¨»§#945;«/mi»«mo mathvariant=¨bold¨ mathcolor=¨#FF6600¨»)«/mo»«/mrow»«/mstyle»«/math».
כיוון הכוח המגנטי הפועל על כל צלע נקבע בהתאם לכלל יד שמאל.
גודלו תלוי בביטוי הכוח המגנטי הפועל על מוליך נושא זרם השרוי בתוך שדה מגנטי: «math style=¨font-family:`Times New Roman`¨ xmlns=¨http://www.w3.org/1998/Math/MathML¨»«mi mathvariant=¨bold¨ mathcolor=¨#0000FF¨»F«/mi»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»=«/mo»«mi mathvariant=¨bold¨ mathcolor=¨#0000FF¨»B«/mi»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»§#183;«/mo»«mi mathvariant=¨bold¨ mathcolor=¨#0000FF¨»L«/mi»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»§#183;«/mo»«mi mathvariant=¨bold¨ mathcolor=¨#0000FF¨»I«/mi»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»§#183;«/mo»«mi mathvariant=¨bold¨ mathcolor=¨#0000FF¨»sin«/mi»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»(«/mo»«mi mathvariant=¨bold¨ mathcolor=¨#0000FF¨»§#945;«/mi»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»)«/mo»«/math»
נסמן בהתאם את כיוון הכוח על כל צלע:
גודלו תלוי בביטוי הכוח המגנטי הפועל על מוליך נושא זרם השרוי בתוך שדה מגנטי: «math style=¨font-family:`Times New Roman`¨ xmlns=¨http://www.w3.org/1998/Math/MathML¨»«mi mathvariant=¨bold¨ mathcolor=¨#0000FF¨»F«/mi»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»=«/mo»«mi mathvariant=¨bold¨ mathcolor=¨#0000FF¨»B«/mi»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»§#183;«/mo»«mi mathvariant=¨bold¨ mathcolor=¨#0000FF¨»L«/mi»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»§#183;«/mo»«mi mathvariant=¨bold¨ mathcolor=¨#0000FF¨»I«/mi»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»§#183;«/mo»«mi mathvariant=¨bold¨ mathcolor=¨#0000FF¨»sin«/mi»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»(«/mo»«mi mathvariant=¨bold¨ mathcolor=¨#0000FF¨»§#945;«/mi»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»)«/mo»«/math»
נסמן בהתאם את כיוון הכוח על כל צלע:
1. עוצמת השדה המגנטי לאורך צלע AB ולאורך צלע DC היא קבועה.
לעומת זאת, לאורך צלעות AD ו-BC פועל שדה מגנטי משתנה, הולך וקטן בגודלו, בהתאם משתנה גם
הכוח המגנטי הפועל על צלעות אלו, הכוח המסומן על הצלעות הוא כוח ממוצע.
2. גם אם לא היה כתוב בשאלה להקפיד על אורכי החצים , היה צריך להקפיד על האורך היחסי של הכוחות המגנטיים.
לעומת זאת, לאורך צלעות AD ו-BC פועל שדה מגנטי משתנה, הולך וקטן בגודלו, בהתאם משתנה גם
הכוח המגנטי הפועל על צלעות אלו, הכוח המסומן על הצלעות הוא כוח ממוצע.
2. גם אם לא היה כתוב בשאלה להקפיד על אורכי החצים , היה צריך להקפיד על האורך היחסי של הכוחות המגנטיים.
______________________________________________________________________________________
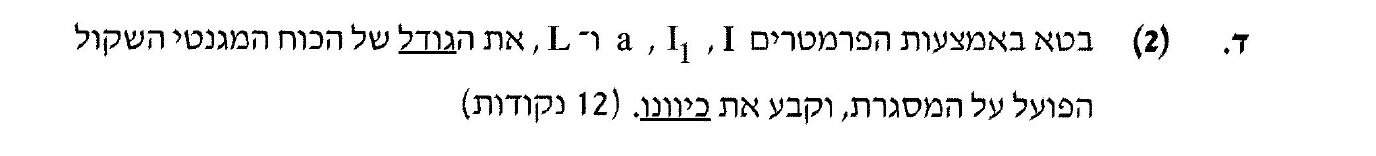
______________________________________________________________________________________
...
ביטוי גודלו של הכוח השקול הוא: «math xmlns=¨http://www.w3.org/1998/Math/MathML¨»«mrow»«mo mathvariant=¨bold¨»|«/mo»«mi mathvariant=¨bold¨»§#931;F«/mi»«mo mathvariant=¨bold¨»|«/mo»«/mrow»«mo mathvariant=¨bold¨»=«/mo»«mo mathvariant=¨bold¨»§#160;«/mo»«mfrac»«mrow»«msub»«mi mathvariant=¨bold¨ mathsize=¨20px¨»§#956;«/mi»«mn mathvariant=¨bold¨ mathsize=¨20px¨»0«/mn»«/msub»«mo mathvariant=¨bold¨ mathsize=¨20px¨»§#183;«/mo»«mi mathvariant=¨bold¨ mathsize=¨20px¨»I«/mi»«mo mathvariant=¨bold¨ mathsize=¨20px¨»§#183;«/mo»«msub»«mi mathvariant=¨bold¨ mathsize=¨20px¨»I«/mi»«mn mathvariant=¨bold¨ mathsize=¨20px¨»1«/mn»«/msub»«mo mathvariant=¨bold¨ mathsize=¨20px¨»§#183;«/mo»«mi mathvariant=¨bold¨ mathsize=¨20px¨»a«/mi»«/mrow»«mrow»«mn mathvariant=¨bold¨ mathsize=¨20px¨»2«/mn»«mo mathvariant=¨bold¨ mathsize=¨20px¨»§#183;«/mo»«mi mathvariant=¨bold¨ mathsize=¨20px¨»§#960;«/mi»«/mrow»«/mfrac»«mo mathvariant=¨bold¨»§#183;«/mo»«mrow»«mo mathvariant=¨bold¨»(«/mo»«mfrac»«mn mathvariant=¨bold¨»1«/mn»«mi mathvariant=¨bold¨»L«/mi»«/mfrac»«mo mathvariant=¨bold¨»-«/mo»«mfrac»«mn mathvariant=¨bold¨ mathsize=¨20px¨»1«/mn»«mstyle mathvariant=¨bold¨ mathsize=¨20px¨»«mo»(«/mo»«mi»L«/mi»«mo»+«/mo»«mi»a«/mi»«mo»)«/mo»«/mstyle»«/mfrac»«mo mathvariant=¨bold¨»)«/mo»«/mrow»«/math»
כיוונו של הכוח השקול הוא שמאלה.
כיוונו של הכוח השקול הוא שמאלה.
שימוש בביטוי הכוח המגנטי הפועל בין מוליכים נושאי זרם.
הכוח המגנטי השקול הפועל על המסגרת שווה לסכום ארבעת הכוחות הפועלים על צלעות המסגרת.
הכוחות המגנטיים הפועלים על הצלעות האופקיות AD ו- BC זהים בגודלם והפוכים בכיוונם, לכן הם מתקזזים.
נבטא את הכוחות הפועלים על הצלעות האופקיות בעזרת ביטוי הכוח המגנטי הפועל בין שני מוליכים נושאי זרם:
«math style=¨font-family:Tahoma¨ xmlns=¨http://www.w3.org/1998/Math/MathML¨»«mfrac mathcolor=¨#0000FF¨»«mi mathvariant=¨bold¨»F«/mi»«mi mathvariant=¨bold¨»§#8467;«/mi»«/mfrac»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»=«/mo»«mfrac mathcolor=¨#0000FF¨»«mrow»«msub»«mi mathvariant=¨bold¨»§#956;«/mi»«mn mathvariant=¨bold¨»0«/mn»«/msub»«mo mathvariant=¨bold¨»§#183;«/mo»«msub»«mi mathvariant=¨bold¨»I«/mi»«mn mathvariant=¨bold¨»1«/mn»«/msub»«mo mathvariant=¨bold¨»§#183;«/mo»«msub»«mi mathvariant=¨bold¨»I«/mi»«mn mathvariant=¨bold¨»2«/mn»«/msub»«/mrow»«mrow»«mn mathvariant=¨bold¨»2«/mn»«mo mathvariant=¨bold¨»§#183;«/mo»«mi mathvariant=¨bold¨»§#960;«/mi»«mo mathvariant=¨bold¨»§#183;«/mo»«mi mathvariant=¨bold¨»d«/mi»«/mrow»«/mfrac»«/math»
נבטא את הכוח המגנטי הפועל על צלע AB:
«math style=¨font-family:`Times New Roman`¨ xmlns=¨http://www.w3.org/1998/Math/MathML¨»«mstyle mathsize=¨20px¨»«mfrac mathcolor=¨#0000FF¨»«msub»«mi mathvariant=¨bold¨»F«/mi»«mi mathvariant=¨bold¨»AB«/mi»«/msub»«mi mathvariant=¨bold¨»a«/mi»«/mfrac»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»=«/mo»«mfrac mathcolor=¨#0000FF¨»«mrow»«msub»«mi mathvariant=¨bold¨»§#956;«/mi»«mn mathvariant=¨bold¨»0«/mn»«/msub»«mo mathvariant=¨bold¨»§#183;«/mo»«mi mathvariant=¨bold¨»I«/mi»«mo mathvariant=¨bold¨»§#183;«/mo»«msub»«mi mathvariant=¨bold¨»I«/mi»«mn mathvariant=¨bold¨»1«/mn»«/msub»«/mrow»«mrow»«mn mathvariant=¨bold¨»2«/mn»«mo mathvariant=¨bold¨»§#183;«/mo»«mi mathvariant=¨bold¨»§#960;«/mi»«mo mathvariant=¨bold¨»§#183;«/mo»«mi mathvariant=¨bold¨»L«/mi»«/mrow»«/mfrac»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»§#160;«/mo»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»§#160;«/mo»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»§#8658;«/mo»«msub»«mi mathvariant=¨bold¨ mathcolor=¨#0000FF¨»F«/mi»«mi mathvariant=¨bold¨ mathcolor=¨#0000FF¨»AB«/mi»«/msub»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»=«/mo»«mfrac mathcolor=¨#0000FF¨»«mrow»«msub»«mi mathvariant=¨bold¨»§#956;«/mi»«mn mathvariant=¨bold¨»0«/mn»«/msub»«mo mathvariant=¨bold¨»§#183;«/mo»«mi mathvariant=¨bold¨»I«/mi»«mo mathvariant=¨bold¨»§#183;«/mo»«msub»«mi mathvariant=¨bold¨»I«/mi»«mn mathvariant=¨bold¨»1«/mn»«/msub»«mo mathvariant=¨bold¨»§#183;«/mo»«mi mathvariant=¨bold¨»a«/mi»«/mrow»«mrow»«mn mathvariant=¨bold¨»2«/mn»«mo mathvariant=¨bold¨»§#183;«/mo»«mi mathvariant=¨bold¨»§#960;«/mi»«mo mathvariant=¨bold¨»§#183;«/mo»«mi mathvariant=¨bold¨»L«/mi»«/mrow»«/mfrac»«/mstyle»«/math»
המרחק בין הצלע CD למוליך נושא הזרם הוא «math xmlns=¨http://www.w3.org/1998/Math/MathML¨»«mi mathvariant=¨bold¨ mathcolor=¨#0000FF¨»L«/mi»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»+«/mo»«mi mathvariant=¨bold¨ mathcolor=¨#0000FF¨»a«/mi»«/math» .
נבטא בהתאם את הכוח המגנטי הפועל על צלע CD:
«math style=¨font-family:`Times New Roman`¨ xmlns=¨http://www.w3.org/1998/Math/MathML¨»«mstyle mathsize=¨20px¨»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»§#160;«/mo»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»§#160;«/mo»«msub»«mi mathvariant=¨bold¨ mathcolor=¨#0000FF¨»F«/mi»«mi mathvariant=¨bold¨ mathcolor=¨#0000FF¨»CD«/mi»«/msub»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»=«/mo»«mfrac mathcolor=¨#0000FF¨»«mrow»«msub»«mi mathvariant=¨bold¨»§#956;«/mi»«mn mathvariant=¨bold¨»0«/mn»«/msub»«mo mathvariant=¨bold¨»§#183;«/mo»«mi mathvariant=¨bold¨»I«/mi»«mo mathvariant=¨bold¨»§#183;«/mo»«msub»«mi mathvariant=¨bold¨»I«/mi»«mn mathvariant=¨bold¨»1«/mn»«/msub»«mo mathvariant=¨bold¨»§#183;«/mo»«mi mathvariant=¨bold¨»a«/mi»«/mrow»«mrow»«mn mathvariant=¨bold¨»2«/mn»«mo mathvariant=¨bold¨»§#183;«/mo»«mi mathvariant=¨bold¨»§#960;«/mi»«mo mathvariant=¨bold¨»§#183;«/mo»«mo mathvariant=¨bold¨»(«/mo»«mi mathvariant=¨bold¨»L«/mi»«mo mathvariant=¨bold¨»+«/mo»«mi mathvariant=¨bold¨»a«/mi»«mo mathvariant=¨bold¨»)«/mo»«/mrow»«/mfrac»«/mstyle»«/math»
על צלעות המסגרת האנכיות פועלים כוחות נגדיים, שונים בגודלם. הכוח הפועל על צלע CD גדול יותר.
נבטא את הכוח השקול:
«math style=¨font-family:Tahoma¨ xmlns=¨http://www.w3.org/1998/Math/MathML¨»«mover mathcolor=¨#0000FF¨»«mi mathvariant=¨bold¨»§#931;F«/mi»«mo mathvariant=¨bold¨»§#8594;«/mo»«/mover»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»=«/mo»«mover mathcolor=¨#0000FF¨»«msub»«mi mathvariant=¨bold¨»F«/mi»«mi mathvariant=¨bold¨»AB«/mi»«/msub»«mo mathvariant=¨bold¨»§#8594;«/mo»«/mover»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»-«/mo»«mover mathcolor=¨#0000FF¨»«msub»«mi mathvariant=¨bold¨»F«/mi»«mi mathvariant=¨bold¨»DC«/mi»«/msub»«mo mathvariant=¨bold¨»§#8594;«/mo»«/mover»«mspace linebreak=¨newline¨»«/mspace»«mspace linebreak=¨newline¨»«/mspace»«mrow mathcolor=¨#0000FF¨»«mo mathvariant=¨bold¨»|«/mo»«mi mathvariant=¨bold¨»§#931;F«/mi»«mo mathvariant=¨bold¨»|«/mo»«/mrow»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»=«/mo»«mrow mathcolor=¨#0000FF¨»«mo mathvariant=¨bold¨»|«/mo»«msub»«mi mathvariant=¨bold¨»F«/mi»«mi mathvariant=¨bold¨»AB«/mi»«/msub»«mo mathvariant=¨bold¨»|«/mo»«/mrow»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»-«/mo»«mrow mathcolor=¨#0000FF¨»«mo mathvariant=¨bold¨»|«/mo»«msub»«mi mathvariant=¨bold¨»F«/mi»«mi mathvariant=¨bold¨»DC«/mi»«/msub»«mo mathvariant=¨bold¨»|«/mo»«/mrow»«mspace linebreak=¨newline¨»«/mspace»«mspace linebreak=¨newline¨»«/mspace»«mspace linebreak=¨newline¨»«/mspace»«mrow mathcolor=¨#0000FF¨»«mo mathvariant=¨bold¨»|«/mo»«mi mathvariant=¨bold¨»§#931;F«/mi»«mo mathvariant=¨bold¨»|«/mo»«/mrow»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»=«/mo»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»§#160;«/mo»«mfrac mathcolor=¨#0000FF¨»«mrow»«msub»«mi mathvariant=¨bold¨ mathsize=¨20px¨»§#956;«/mi»«mn mathvariant=¨bold¨ mathsize=¨20px¨»0«/mn»«/msub»«mo mathvariant=¨bold¨ mathsize=¨20px¨»§#183;«/mo»«mi mathvariant=¨bold¨ mathsize=¨20px¨»I«/mi»«mo mathvariant=¨bold¨ mathsize=¨20px¨»§#183;«/mo»«msub»«mi mathvariant=¨bold¨ mathsize=¨20px¨»I«/mi»«mn mathvariant=¨bold¨ mathsize=¨20px¨»1«/mn»«/msub»«mo mathvariant=¨bold¨ mathsize=¨20px¨»§#183;«/mo»«mi mathvariant=¨bold¨ mathsize=¨20px¨»a«/mi»«/mrow»«mrow»«mn mathvariant=¨bold¨ mathsize=¨20px¨»2«/mn»«mo mathvariant=¨bold¨ mathsize=¨20px¨»§#183;«/mo»«mi mathvariant=¨bold¨ mathsize=¨20px¨»§#960;«/mi»«mo mathvariant=¨bold¨ mathsize=¨20px¨»§#183;«/mo»«mi mathvariant=¨bold¨ mathsize=¨20px¨»L«/mi»«/mrow»«/mfrac»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»-«/mo»«mfrac mathcolor=¨#0000FF¨»«mrow»«msub»«mi mathvariant=¨bold¨ mathsize=¨20px¨»§#956;«/mi»«mn mathvariant=¨bold¨ mathsize=¨20px¨»0«/mn»«/msub»«mo mathvariant=¨bold¨ mathsize=¨20px¨»§#183;«/mo»«mi mathvariant=¨bold¨ mathsize=¨20px¨»I«/mi»«mo mathvariant=¨bold¨ mathsize=¨20px¨»§#183;«/mo»«msub»«mi mathvariant=¨bold¨ mathsize=¨20px¨»I«/mi»«mn mathvariant=¨bold¨ mathsize=¨20px¨»1«/mn»«/msub»«mo mathvariant=¨bold¨ mathsize=¨20px¨»§#183;«/mo»«mi mathvariant=¨bold¨ mathsize=¨20px¨»a«/mi»«/mrow»«mrow»«mn mathvariant=¨bold¨ mathsize=¨20px¨»2«/mn»«mo mathvariant=¨bold¨ mathsize=¨20px¨»§#183;«/mo»«mi mathvariant=¨bold¨ mathsize=¨20px¨»§#960;«/mi»«mo mathvariant=¨bold¨ mathsize=¨20px¨»§#183;«/mo»«mstyle mathvariant=¨bold¨ mathsize=¨20px¨»«mo»(«/mo»«mi»L«/mi»«mo»+«/mo»«mi»a«/mi»«mo»)«/mo»«/mstyle»«/mrow»«/mfrac»«mspace linebreak=¨newline¨»«/mspace»«mspace linebreak=¨newline¨»«/mspace»«menclose mathcolor=¨#0000FF¨ notation=¨circle¨»«mrow»«mo mathvariant=¨bold¨»|«/mo»«mi mathvariant=¨bold¨»§#931;F«/mi»«mo mathvariant=¨bold¨»|«/mo»«/mrow»«mo mathvariant=¨bold¨»=«/mo»«mo mathvariant=¨bold¨»§#160;«/mo»«mfrac»«mrow»«msub»«mi mathsize=¨20px¨ mathvariant=¨bold¨»§#956;«/mi»«mn mathsize=¨20px¨ mathvariant=¨bold¨»0«/mn»«/msub»«mo mathsize=¨20px¨ mathvariant=¨bold¨»§#183;«/mo»«mi mathsize=¨20px¨ mathvariant=¨bold¨»I«/mi»«mo mathsize=¨20px¨ mathvariant=¨bold¨»§#183;«/mo»«msub»«mi mathsize=¨20px¨ mathvariant=¨bold¨»I«/mi»«mn mathsize=¨20px¨ mathvariant=¨bold¨»1«/mn»«/msub»«mo mathsize=¨20px¨ mathvariant=¨bold¨»§#183;«/mo»«mi mathsize=¨20px¨ mathvariant=¨bold¨»a«/mi»«/mrow»«mrow»«mn mathsize=¨20px¨ mathvariant=¨bold¨»2«/mn»«mo mathsize=¨20px¨ mathvariant=¨bold¨»§#183;«/mo»«mi mathsize=¨20px¨ mathvariant=¨bold¨»§#960;«/mi»«/mrow»«/mfrac»«mo mathvariant=¨bold¨»§#183;«/mo»«mrow»«mo mathvariant=¨bold¨»(«/mo»«mfrac»«mn mathvariant=¨bold¨»1«/mn»«mi mathvariant=¨bold¨»L«/mi»«/mfrac»«mo mathvariant=¨bold¨»-«/mo»«mfrac»«mn mathsize=¨20px¨ mathvariant=¨bold¨»1«/mn»«mstyle mathsize=¨20px¨ mathvariant=¨bold¨»«mo»(«/mo»«mi»L«/mi»«mo»+«/mo»«mi»a«/mi»«mo»)«/mo»«/mstyle»«/mfrac»«mo mathvariant=¨bold¨»)«/mo»«/mrow»«/menclose»«/math»
כיוון הכוח השקול הוא בכיוון הכוח הגדול FAB שמאלה.
הכוחות המגנטיים הפועלים על הצלעות האופקיות AD ו- BC זהים בגודלם והפוכים בכיוונם, לכן הם מתקזזים.
נבטא את הכוחות הפועלים על הצלעות האופקיות בעזרת ביטוי הכוח המגנטי הפועל בין שני מוליכים נושאי זרם:
«math style=¨font-family:Tahoma¨ xmlns=¨http://www.w3.org/1998/Math/MathML¨»«mfrac mathcolor=¨#0000FF¨»«mi mathvariant=¨bold¨»F«/mi»«mi mathvariant=¨bold¨»§#8467;«/mi»«/mfrac»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»=«/mo»«mfrac mathcolor=¨#0000FF¨»«mrow»«msub»«mi mathvariant=¨bold¨»§#956;«/mi»«mn mathvariant=¨bold¨»0«/mn»«/msub»«mo mathvariant=¨bold¨»§#183;«/mo»«msub»«mi mathvariant=¨bold¨»I«/mi»«mn mathvariant=¨bold¨»1«/mn»«/msub»«mo mathvariant=¨bold¨»§#183;«/mo»«msub»«mi mathvariant=¨bold¨»I«/mi»«mn mathvariant=¨bold¨»2«/mn»«/msub»«/mrow»«mrow»«mn mathvariant=¨bold¨»2«/mn»«mo mathvariant=¨bold¨»§#183;«/mo»«mi mathvariant=¨bold¨»§#960;«/mi»«mo mathvariant=¨bold¨»§#183;«/mo»«mi mathvariant=¨bold¨»d«/mi»«/mrow»«/mfrac»«/math»
נבטא את הכוח המגנטי הפועל על צלע AB:
«math style=¨font-family:`Times New Roman`¨ xmlns=¨http://www.w3.org/1998/Math/MathML¨»«mstyle mathsize=¨20px¨»«mfrac mathcolor=¨#0000FF¨»«msub»«mi mathvariant=¨bold¨»F«/mi»«mi mathvariant=¨bold¨»AB«/mi»«/msub»«mi mathvariant=¨bold¨»a«/mi»«/mfrac»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»=«/mo»«mfrac mathcolor=¨#0000FF¨»«mrow»«msub»«mi mathvariant=¨bold¨»§#956;«/mi»«mn mathvariant=¨bold¨»0«/mn»«/msub»«mo mathvariant=¨bold¨»§#183;«/mo»«mi mathvariant=¨bold¨»I«/mi»«mo mathvariant=¨bold¨»§#183;«/mo»«msub»«mi mathvariant=¨bold¨»I«/mi»«mn mathvariant=¨bold¨»1«/mn»«/msub»«/mrow»«mrow»«mn mathvariant=¨bold¨»2«/mn»«mo mathvariant=¨bold¨»§#183;«/mo»«mi mathvariant=¨bold¨»§#960;«/mi»«mo mathvariant=¨bold¨»§#183;«/mo»«mi mathvariant=¨bold¨»L«/mi»«/mrow»«/mfrac»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»§#160;«/mo»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»§#160;«/mo»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»§#8658;«/mo»«msub»«mi mathvariant=¨bold¨ mathcolor=¨#0000FF¨»F«/mi»«mi mathvariant=¨bold¨ mathcolor=¨#0000FF¨»AB«/mi»«/msub»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»=«/mo»«mfrac mathcolor=¨#0000FF¨»«mrow»«msub»«mi mathvariant=¨bold¨»§#956;«/mi»«mn mathvariant=¨bold¨»0«/mn»«/msub»«mo mathvariant=¨bold¨»§#183;«/mo»«mi mathvariant=¨bold¨»I«/mi»«mo mathvariant=¨bold¨»§#183;«/mo»«msub»«mi mathvariant=¨bold¨»I«/mi»«mn mathvariant=¨bold¨»1«/mn»«/msub»«mo mathvariant=¨bold¨»§#183;«/mo»«mi mathvariant=¨bold¨»a«/mi»«/mrow»«mrow»«mn mathvariant=¨bold¨»2«/mn»«mo mathvariant=¨bold¨»§#183;«/mo»«mi mathvariant=¨bold¨»§#960;«/mi»«mo mathvariant=¨bold¨»§#183;«/mo»«mi mathvariant=¨bold¨»L«/mi»«/mrow»«/mfrac»«/mstyle»«/math»
המרחק בין הצלע CD למוליך נושא הזרם הוא «math xmlns=¨http://www.w3.org/1998/Math/MathML¨»«mi mathvariant=¨bold¨ mathcolor=¨#0000FF¨»L«/mi»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»+«/mo»«mi mathvariant=¨bold¨ mathcolor=¨#0000FF¨»a«/mi»«/math» .
נבטא בהתאם את הכוח המגנטי הפועל על צלע CD:
«math style=¨font-family:`Times New Roman`¨ xmlns=¨http://www.w3.org/1998/Math/MathML¨»«mstyle mathsize=¨20px¨»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»§#160;«/mo»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»§#160;«/mo»«msub»«mi mathvariant=¨bold¨ mathcolor=¨#0000FF¨»F«/mi»«mi mathvariant=¨bold¨ mathcolor=¨#0000FF¨»CD«/mi»«/msub»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»=«/mo»«mfrac mathcolor=¨#0000FF¨»«mrow»«msub»«mi mathvariant=¨bold¨»§#956;«/mi»«mn mathvariant=¨bold¨»0«/mn»«/msub»«mo mathvariant=¨bold¨»§#183;«/mo»«mi mathvariant=¨bold¨»I«/mi»«mo mathvariant=¨bold¨»§#183;«/mo»«msub»«mi mathvariant=¨bold¨»I«/mi»«mn mathvariant=¨bold¨»1«/mn»«/msub»«mo mathvariant=¨bold¨»§#183;«/mo»«mi mathvariant=¨bold¨»a«/mi»«/mrow»«mrow»«mn mathvariant=¨bold¨»2«/mn»«mo mathvariant=¨bold¨»§#183;«/mo»«mi mathvariant=¨bold¨»§#960;«/mi»«mo mathvariant=¨bold¨»§#183;«/mo»«mo mathvariant=¨bold¨»(«/mo»«mi mathvariant=¨bold¨»L«/mi»«mo mathvariant=¨bold¨»+«/mo»«mi mathvariant=¨bold¨»a«/mi»«mo mathvariant=¨bold¨»)«/mo»«/mrow»«/mfrac»«/mstyle»«/math»
על צלעות המסגרת האנכיות פועלים כוחות נגדיים, שונים בגודלם. הכוח הפועל על צלע CD גדול יותר.
נבטא את הכוח השקול:
«math style=¨font-family:Tahoma¨ xmlns=¨http://www.w3.org/1998/Math/MathML¨»«mover mathcolor=¨#0000FF¨»«mi mathvariant=¨bold¨»§#931;F«/mi»«mo mathvariant=¨bold¨»§#8594;«/mo»«/mover»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»=«/mo»«mover mathcolor=¨#0000FF¨»«msub»«mi mathvariant=¨bold¨»F«/mi»«mi mathvariant=¨bold¨»AB«/mi»«/msub»«mo mathvariant=¨bold¨»§#8594;«/mo»«/mover»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»-«/mo»«mover mathcolor=¨#0000FF¨»«msub»«mi mathvariant=¨bold¨»F«/mi»«mi mathvariant=¨bold¨»DC«/mi»«/msub»«mo mathvariant=¨bold¨»§#8594;«/mo»«/mover»«mspace linebreak=¨newline¨»«/mspace»«mspace linebreak=¨newline¨»«/mspace»«mrow mathcolor=¨#0000FF¨»«mo mathvariant=¨bold¨»|«/mo»«mi mathvariant=¨bold¨»§#931;F«/mi»«mo mathvariant=¨bold¨»|«/mo»«/mrow»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»=«/mo»«mrow mathcolor=¨#0000FF¨»«mo mathvariant=¨bold¨»|«/mo»«msub»«mi mathvariant=¨bold¨»F«/mi»«mi mathvariant=¨bold¨»AB«/mi»«/msub»«mo mathvariant=¨bold¨»|«/mo»«/mrow»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»-«/mo»«mrow mathcolor=¨#0000FF¨»«mo mathvariant=¨bold¨»|«/mo»«msub»«mi mathvariant=¨bold¨»F«/mi»«mi mathvariant=¨bold¨»DC«/mi»«/msub»«mo mathvariant=¨bold¨»|«/mo»«/mrow»«mspace linebreak=¨newline¨»«/mspace»«mspace linebreak=¨newline¨»«/mspace»«mspace linebreak=¨newline¨»«/mspace»«mrow mathcolor=¨#0000FF¨»«mo mathvariant=¨bold¨»|«/mo»«mi mathvariant=¨bold¨»§#931;F«/mi»«mo mathvariant=¨bold¨»|«/mo»«/mrow»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»=«/mo»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»§#160;«/mo»«mfrac mathcolor=¨#0000FF¨»«mrow»«msub»«mi mathvariant=¨bold¨ mathsize=¨20px¨»§#956;«/mi»«mn mathvariant=¨bold¨ mathsize=¨20px¨»0«/mn»«/msub»«mo mathvariant=¨bold¨ mathsize=¨20px¨»§#183;«/mo»«mi mathvariant=¨bold¨ mathsize=¨20px¨»I«/mi»«mo mathvariant=¨bold¨ mathsize=¨20px¨»§#183;«/mo»«msub»«mi mathvariant=¨bold¨ mathsize=¨20px¨»I«/mi»«mn mathvariant=¨bold¨ mathsize=¨20px¨»1«/mn»«/msub»«mo mathvariant=¨bold¨ mathsize=¨20px¨»§#183;«/mo»«mi mathvariant=¨bold¨ mathsize=¨20px¨»a«/mi»«/mrow»«mrow»«mn mathvariant=¨bold¨ mathsize=¨20px¨»2«/mn»«mo mathvariant=¨bold¨ mathsize=¨20px¨»§#183;«/mo»«mi mathvariant=¨bold¨ mathsize=¨20px¨»§#960;«/mi»«mo mathvariant=¨bold¨ mathsize=¨20px¨»§#183;«/mo»«mi mathvariant=¨bold¨ mathsize=¨20px¨»L«/mi»«/mrow»«/mfrac»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»-«/mo»«mfrac mathcolor=¨#0000FF¨»«mrow»«msub»«mi mathvariant=¨bold¨ mathsize=¨20px¨»§#956;«/mi»«mn mathvariant=¨bold¨ mathsize=¨20px¨»0«/mn»«/msub»«mo mathvariant=¨bold¨ mathsize=¨20px¨»§#183;«/mo»«mi mathvariant=¨bold¨ mathsize=¨20px¨»I«/mi»«mo mathvariant=¨bold¨ mathsize=¨20px¨»§#183;«/mo»«msub»«mi mathvariant=¨bold¨ mathsize=¨20px¨»I«/mi»«mn mathvariant=¨bold¨ mathsize=¨20px¨»1«/mn»«/msub»«mo mathvariant=¨bold¨ mathsize=¨20px¨»§#183;«/mo»«mi mathvariant=¨bold¨ mathsize=¨20px¨»a«/mi»«/mrow»«mrow»«mn mathvariant=¨bold¨ mathsize=¨20px¨»2«/mn»«mo mathvariant=¨bold¨ mathsize=¨20px¨»§#183;«/mo»«mi mathvariant=¨bold¨ mathsize=¨20px¨»§#960;«/mi»«mo mathvariant=¨bold¨ mathsize=¨20px¨»§#183;«/mo»«mstyle mathvariant=¨bold¨ mathsize=¨20px¨»«mo»(«/mo»«mi»L«/mi»«mo»+«/mo»«mi»a«/mi»«mo»)«/mo»«/mstyle»«/mrow»«/mfrac»«mspace linebreak=¨newline¨»«/mspace»«mspace linebreak=¨newline¨»«/mspace»«menclose mathcolor=¨#0000FF¨ notation=¨circle¨»«mrow»«mo mathvariant=¨bold¨»|«/mo»«mi mathvariant=¨bold¨»§#931;F«/mi»«mo mathvariant=¨bold¨»|«/mo»«/mrow»«mo mathvariant=¨bold¨»=«/mo»«mo mathvariant=¨bold¨»§#160;«/mo»«mfrac»«mrow»«msub»«mi mathsize=¨20px¨ mathvariant=¨bold¨»§#956;«/mi»«mn mathsize=¨20px¨ mathvariant=¨bold¨»0«/mn»«/msub»«mo mathsize=¨20px¨ mathvariant=¨bold¨»§#183;«/mo»«mi mathsize=¨20px¨ mathvariant=¨bold¨»I«/mi»«mo mathsize=¨20px¨ mathvariant=¨bold¨»§#183;«/mo»«msub»«mi mathsize=¨20px¨ mathvariant=¨bold¨»I«/mi»«mn mathsize=¨20px¨ mathvariant=¨bold¨»1«/mn»«/msub»«mo mathsize=¨20px¨ mathvariant=¨bold¨»§#183;«/mo»«mi mathsize=¨20px¨ mathvariant=¨bold¨»a«/mi»«/mrow»«mrow»«mn mathsize=¨20px¨ mathvariant=¨bold¨»2«/mn»«mo mathsize=¨20px¨ mathvariant=¨bold¨»§#183;«/mo»«mi mathsize=¨20px¨ mathvariant=¨bold¨»§#960;«/mi»«/mrow»«/mfrac»«mo mathvariant=¨bold¨»§#183;«/mo»«mrow»«mo mathvariant=¨bold¨»(«/mo»«mfrac»«mn mathvariant=¨bold¨»1«/mn»«mi mathvariant=¨bold¨»L«/mi»«/mfrac»«mo mathvariant=¨bold¨»-«/mo»«mfrac»«mn mathsize=¨20px¨ mathvariant=¨bold¨»1«/mn»«mstyle mathsize=¨20px¨ mathvariant=¨bold¨»«mo»(«/mo»«mi»L«/mi»«mo»+«/mo»«mi»a«/mi»«mo»)«/mo»«/mstyle»«/mfrac»«mo mathvariant=¨bold¨»)«/mo»«/mrow»«/menclose»«/math»
כיוון הכוח השקול הוא בכיוון הכוח הגדול FAB שמאלה.
מהחוק השלישי של ניוטון, הכוח שהמסגרת מפעילה על המוליך הישר שווה לכוח שהמוליך הישר מפעיל על המסגרת.
במקום למצוא את הכוח השקול הפועל על המסגרת אפשר למצוא את הכוח המגנטי הפועל על המוליך הישר.
השדה המגנטי נוצר סביב המוליך, לכן הצלעות האופקיות של המסגרת לא יוצרות שדה מגנטי במקום בו נמצא המוליך הישר.
המוליך הישר מושפע רק מהצלעות האנכיות של המסגרת.
נבטא את גודל השדה המגנטי שיוצרים כל אחת משתי הצלעות האנכיות במקום בו נמצא המוליך הישר:
«math style=¨font-family:Tahoma¨ xmlns=¨http://www.w3.org/1998/Math/MathML¨»«mi mathvariant=¨bold¨ mathcolor=¨#0000FF¨»B«/mi»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»=«/mo»«mfrac mathcolor=¨#0000FF¨»«mrow»«msub»«mi mathvariant=¨bold¨»§#956;«/mi»«mn mathvariant=¨bold¨»0«/mn»«/msub»«mo mathvariant=¨bold¨»§#183;«/mo»«mi mathvariant=¨bold¨»I«/mi»«/mrow»«mrow»«mn mathvariant=¨bold¨»2«/mn»«mo mathvariant=¨bold¨»§#183;«/mo»«mi mathvariant=¨bold¨»§#960;«/mi»«mo mathvariant=¨bold¨»§#183;«/mo»«mi mathvariant=¨bold¨»d«/mi»«/mrow»«/mfrac»«mspace linebreak=¨newline¨»«/mspace»«mspace linebreak=¨newline¨»«/mspace»«msub»«mi mathvariant=¨bold¨ mathcolor=¨#0000FF¨»B«/mi»«mi mathvariant=¨bold¨ mathcolor=¨#0000FF¨»AB«/mi»«/msub»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»=«/mo»«mfrac mathcolor=¨#0000FF¨»«mrow»«msub»«mi mathvariant=¨bold¨»§#956;«/mi»«mn mathvariant=¨bold¨»0«/mn»«/msub»«mo mathvariant=¨bold¨»§#183;«/mo»«msub»«mi mathvariant=¨bold¨»I«/mi»«mn mathvariant=¨bold¨»1«/mn»«/msub»«/mrow»«mrow»«mn mathvariant=¨bold¨»2«/mn»«mo mathvariant=¨bold¨»§#183;«/mo»«mi mathvariant=¨bold¨»§#960;«/mi»«mo mathvariant=¨bold¨»§#183;«/mo»«mi mathvariant=¨bold¨»L«/mi»«/mrow»«/mfrac»«mspace linebreak=¨newline¨»«/mspace»«mspace linebreak=¨newline¨»«/mspace»«msub»«mi mathvariant=¨bold¨ mathcolor=¨#0000FF¨»B«/mi»«mi mathvariant=¨bold¨ mathcolor=¨#0000FF¨»DC«/mi»«/msub»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»=«/mo»«mfrac mathcolor=¨#0000FF¨»«mrow»«msub»«mi mathvariant=¨bold¨»§#956;«/mi»«mn mathvariant=¨bold¨»0«/mn»«/msub»«mo mathvariant=¨bold¨»§#183;«/mo»«msub»«mi mathvariant=¨bold¨»I«/mi»«mn mathvariant=¨bold¨»1«/mn»«/msub»«/mrow»«mrow»«mn mathvariant=¨bold¨»2«/mn»«mo mathvariant=¨bold¨»§#183;«/mo»«mi mathvariant=¨bold¨»§#960;«/mi»«mo mathvariant=¨bold¨»§#183;«/mo»«mrow»«mo mathvariant=¨bold¨»(«/mo»«mi mathvariant=¨bold¨»L«/mi»«mo mathvariant=¨bold¨»+«/mo»«mi mathvariant=¨bold¨»a«/mi»«mo mathvariant=¨bold¨»)«/mo»«/mrow»«/mrow»«/mfrac»«/math»
הצלע AB יוצרת במקום בו נמצא המוליך שדה מגנטי כלפי מעלה. הצלע DC יוצרת שדה מגנטי על המוליך כלפי מטה.
נבטא את השדה המגנטי BT הנוצר משתי הצלעות האנכיות במקום בו נמצא המוליך הישר:
«math style=¨font-family:Tahoma¨ xmlns=¨http://www.w3.org/1998/Math/MathML¨»«msub»«mi mathvariant=¨bold¨ mathcolor=¨#0000FF¨»B«/mi»«mi mathvariant=¨bold¨ mathcolor=¨#0000FF¨»T«/mi»«/msub»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»=«/mo»«msub»«mi mathvariant=¨bold¨ mathcolor=¨#0000FF¨»B«/mi»«mi mathvariant=¨bold¨ mathcolor=¨#0000FF¨»AB«/mi»«/msub»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»-«/mo»«msub»«mi mathvariant=¨bold¨ mathcolor=¨#0000FF¨»B«/mi»«mi mathvariant=¨bold¨ mathcolor=¨#0000FF¨»DC«/mi»«/msub»«mspace linebreak=¨newline¨»«/mspace»«mspace linebreak=¨newline¨»«/mspace»«msub»«mi mathvariant=¨bold¨ mathcolor=¨#0000FF¨»B«/mi»«mi mathvariant=¨bold¨ mathcolor=¨#0000FF¨»T«/mi»«/msub»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»=«/mo»«mfrac mathcolor=¨#0000FF¨»«mrow»«msub»«mi mathvariant=¨bold¨»§#956;«/mi»«mn mathvariant=¨bold¨»0«/mn»«/msub»«mo mathvariant=¨bold¨»§#183;«/mo»«msub»«mi mathvariant=¨bold¨»I«/mi»«mn mathvariant=¨bold¨»1«/mn»«/msub»«/mrow»«mrow»«mn mathvariant=¨bold¨»2«/mn»«mo mathvariant=¨bold¨»§#183;«/mo»«mi mathvariant=¨bold¨»§#960;«/mi»«mo mathvariant=¨bold¨»§#183;«/mo»«mi mathvariant=¨bold¨»L«/mi»«/mrow»«/mfrac»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»-«/mo»«mfrac mathcolor=¨#0000FF¨»«mrow»«msub»«mi mathvariant=¨bold¨»§#956;«/mi»«mn mathvariant=¨bold¨»0«/mn»«/msub»«mo mathvariant=¨bold¨»§#183;«/mo»«msub»«mi mathvariant=¨bold¨»I«/mi»«mn mathvariant=¨bold¨»1«/mn»«/msub»«/mrow»«mrow»«mn mathvariant=¨bold¨»2«/mn»«mo mathvariant=¨bold¨»§#183;«/mo»«mi mathvariant=¨bold¨»§#960;«/mi»«mo mathvariant=¨bold¨»§#183;«/mo»«mrow»«mo mathvariant=¨bold¨»(«/mo»«mi mathvariant=¨bold¨»L«/mi»«mo mathvariant=¨bold¨»+«/mo»«mi mathvariant=¨bold¨»a«/mi»«mo mathvariant=¨bold¨»)«/mo»«/mrow»«/mrow»«/mfrac»«mspace linebreak=¨newline¨»«/mspace»«mspace linebreak=¨newline¨»«/mspace»«msub»«mi mathvariant=¨bold¨ mathcolor=¨#0000FF¨»B«/mi»«mi mathvariant=¨bold¨ mathcolor=¨#0000FF¨»T«/mi»«/msub»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»=«/mo»«mfrac mathcolor=¨#0000FF¨»«mrow»«msub»«mi mathvariant=¨bold¨»§#956;«/mi»«mn mathvariant=¨bold¨»0«/mn»«/msub»«mo mathvariant=¨bold¨»§#183;«/mo»«msub»«mi mathvariant=¨bold¨»I«/mi»«mn mathvariant=¨bold¨»1«/mn»«/msub»«/mrow»«mrow»«mn mathvariant=¨bold¨»2«/mn»«mo mathvariant=¨bold¨»§#183;«/mo»«mi mathvariant=¨bold¨»§#960;«/mi»«/mrow»«/mfrac»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»§#183;«/mo»«mrow mathcolor=¨#0000FF¨»«mo mathvariant=¨bold¨»(«/mo»«mfrac»«mn mathvariant=¨bold¨»1«/mn»«mi mathvariant=¨bold¨»L«/mi»«/mfrac»«mo mathvariant=¨bold¨»-«/mo»«mfrac»«mn mathvariant=¨bold¨»1«/mn»«mrow»«mi mathvariant=¨bold¨»L«/mi»«mo mathvariant=¨bold¨»+«/mo»«mi mathvariant=¨bold¨»a«/mi»«/mrow»«/mfrac»«mo mathvariant=¨bold¨»)«/mo»«/mrow»«mspace linebreak=¨newline¨»«/mspace»«mspace linebreak=¨newline¨»«/mspace»«/math»
נמצא את גודל הכוח המגנטי הפועל על המוליך הישר:
«math style=¨font-family:`Times New Roman`¨ xmlns=¨http://www.w3.org/1998/Math/MathML¨»«mstyle mathsize=¨20px¨»«mrow»«mi mathvariant=¨bold¨ mathcolor=¨#0000FF¨»F«/mi»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»=«/mo»«mi mathvariant=¨bold¨ mathcolor=¨#0000FF¨»B«/mi»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»§#183;«/mo»«mi mathvariant=¨bold¨ mathcolor=¨#0000FF¨»L«/mi»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»§#183;«/mo»«mi mathvariant=¨bold¨ mathcolor=¨#0000FF¨»I«/mi»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»§#183;«/mo»«mi mathvariant=¨bold¨ mathcolor=¨#0000FF¨»sin«/mi»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»(«/mo»«mi mathvariant=¨bold¨ mathcolor=¨#0000FF¨»§#945;«/mi»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»)«/mo»«mspace linebreak=¨newline¨/»«mspace linebreak=¨newline¨/»«mi mathvariant=¨bold¨ mathcolor=¨#0000FF¨»F«/mi»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»=«/mo»«mfrac mathcolor=¨#0000FF¨»«mrow»«msub»«mi mathvariant=¨bold¨»§#956;«/mi»«mn mathvariant=¨bold¨»0«/mn»«/msub»«mo mathvariant=¨bold¨»§#183;«/mo»«msub»«mi mathvariant=¨bold¨»I«/mi»«mn mathvariant=¨bold¨»1«/mn»«/msub»«/mrow»«mrow»«mn mathvariant=¨bold¨»2«/mn»«mo mathvariant=¨bold¨»§#183;«/mo»«mi mathvariant=¨bold¨»§#960;«/mi»«/mrow»«/mfrac»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»§#183;«/mo»«mrow mathcolor=¨#0000FF¨»«mo mathvariant=¨bold¨»(«/mo»«mfrac»«mn mathvariant=¨bold¨»1«/mn»«mi mathvariant=¨bold¨»L«/mi»«/mfrac»«mo mathvariant=¨bold¨»-«/mo»«mfrac»«mn mathvariant=¨bold¨»1«/mn»«mrow»«mi mathvariant=¨bold¨»L«/mi»«mo mathvariant=¨bold¨»+«/mo»«mi mathvariant=¨bold¨»a«/mi»«/mrow»«/mfrac»«mo mathvariant=¨bold¨»)«/mo»«/mrow»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»§#183;«/mo»«mi mathvariant=¨bold-italic¨ mathcolor=¨#0000FF¨»a«/mi»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»§#183;«/mo»«mi mathvariant=¨bold-italic¨ mathcolor=¨#0000FF¨»I«/mi»«mspace linebreak=¨newline¨/»«/mrow»«mspace linebreak=¨newline¨/»«menclose mathcolor=¨#0000FF¨ notation=¨circle¨»«mi mathvariant=¨bold¨»F«/mi»«mo mathvariant=¨bold¨»=«/mo»«mfrac»«mrow»«msub»«mi mathvariant=¨bold¨»§#956;«/mi»«mn mathvariant=¨bold¨»0«/mn»«/msub»«mo mathvariant=¨bold¨»§#183;«/mo»«msub»«mi mathvariant=¨bold¨»I«/mi»«mn mathvariant=¨bold¨»1«/mn»«/msub»«mo mathvariant=¨bold¨»§#183;«/mo»«mi mathvariant=¨bold¨»I«/mi»«mo mathvariant=¨bold¨»§#183;«/mo»«mi mathvariant=¨bold¨»a«/mi»«/mrow»«mrow»«mn mathvariant=¨bold¨»2«/mn»«mo mathvariant=¨bold¨»§#183;«/mo»«mi mathvariant=¨bold¨»§#960;«/mi»«/mrow»«/mfrac»«mo mathvariant=¨bold¨»§#183;«/mo»«mrow»«mo mathvariant=¨bold¨»(«/mo»«mfrac»«mn mathvariant=¨bold¨»1«/mn»«mi mathvariant=¨bold¨»L«/mi»«/mfrac»«mo mathvariant=¨bold¨»-«/mo»«mfrac»«mn mathvariant=¨bold¨»1«/mn»«mrow»«mi mathvariant=¨bold¨»L«/mi»«mo mathvariant=¨bold¨»+«/mo»«mi mathvariant=¨bold¨»a«/mi»«/mrow»«/mfrac»«mo mathvariant=¨bold¨»)«/mo»«/mrow»«/menclose»«/mstyle»«/math»
במקום למצוא את הכוח השקול הפועל על המסגרת אפשר למצוא את הכוח המגנטי הפועל על המוליך הישר.
השדה המגנטי נוצר סביב המוליך, לכן הצלעות האופקיות של המסגרת לא יוצרות שדה מגנטי במקום בו נמצא המוליך הישר.
המוליך הישר מושפע רק מהצלעות האנכיות של המסגרת.
נבטא את גודל השדה המגנטי שיוצרים כל אחת משתי הצלעות האנכיות במקום בו נמצא המוליך הישר:
«math style=¨font-family:Tahoma¨ xmlns=¨http://www.w3.org/1998/Math/MathML¨»«mi mathvariant=¨bold¨ mathcolor=¨#0000FF¨»B«/mi»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»=«/mo»«mfrac mathcolor=¨#0000FF¨»«mrow»«msub»«mi mathvariant=¨bold¨»§#956;«/mi»«mn mathvariant=¨bold¨»0«/mn»«/msub»«mo mathvariant=¨bold¨»§#183;«/mo»«mi mathvariant=¨bold¨»I«/mi»«/mrow»«mrow»«mn mathvariant=¨bold¨»2«/mn»«mo mathvariant=¨bold¨»§#183;«/mo»«mi mathvariant=¨bold¨»§#960;«/mi»«mo mathvariant=¨bold¨»§#183;«/mo»«mi mathvariant=¨bold¨»d«/mi»«/mrow»«/mfrac»«mspace linebreak=¨newline¨»«/mspace»«mspace linebreak=¨newline¨»«/mspace»«msub»«mi mathvariant=¨bold¨ mathcolor=¨#0000FF¨»B«/mi»«mi mathvariant=¨bold¨ mathcolor=¨#0000FF¨»AB«/mi»«/msub»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»=«/mo»«mfrac mathcolor=¨#0000FF¨»«mrow»«msub»«mi mathvariant=¨bold¨»§#956;«/mi»«mn mathvariant=¨bold¨»0«/mn»«/msub»«mo mathvariant=¨bold¨»§#183;«/mo»«msub»«mi mathvariant=¨bold¨»I«/mi»«mn mathvariant=¨bold¨»1«/mn»«/msub»«/mrow»«mrow»«mn mathvariant=¨bold¨»2«/mn»«mo mathvariant=¨bold¨»§#183;«/mo»«mi mathvariant=¨bold¨»§#960;«/mi»«mo mathvariant=¨bold¨»§#183;«/mo»«mi mathvariant=¨bold¨»L«/mi»«/mrow»«/mfrac»«mspace linebreak=¨newline¨»«/mspace»«mspace linebreak=¨newline¨»«/mspace»«msub»«mi mathvariant=¨bold¨ mathcolor=¨#0000FF¨»B«/mi»«mi mathvariant=¨bold¨ mathcolor=¨#0000FF¨»DC«/mi»«/msub»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»=«/mo»«mfrac mathcolor=¨#0000FF¨»«mrow»«msub»«mi mathvariant=¨bold¨»§#956;«/mi»«mn mathvariant=¨bold¨»0«/mn»«/msub»«mo mathvariant=¨bold¨»§#183;«/mo»«msub»«mi mathvariant=¨bold¨»I«/mi»«mn mathvariant=¨bold¨»1«/mn»«/msub»«/mrow»«mrow»«mn mathvariant=¨bold¨»2«/mn»«mo mathvariant=¨bold¨»§#183;«/mo»«mi mathvariant=¨bold¨»§#960;«/mi»«mo mathvariant=¨bold¨»§#183;«/mo»«mrow»«mo mathvariant=¨bold¨»(«/mo»«mi mathvariant=¨bold¨»L«/mi»«mo mathvariant=¨bold¨»+«/mo»«mi mathvariant=¨bold¨»a«/mi»«mo mathvariant=¨bold¨»)«/mo»«/mrow»«/mrow»«/mfrac»«/math»
הצלע AB יוצרת במקום בו נמצא המוליך שדה מגנטי כלפי מעלה. הצלע DC יוצרת שדה מגנטי על המוליך כלפי מטה.
נבטא את השדה המגנטי BT הנוצר משתי הצלעות האנכיות במקום בו נמצא המוליך הישר:
«math style=¨font-family:Tahoma¨ xmlns=¨http://www.w3.org/1998/Math/MathML¨»«msub»«mi mathvariant=¨bold¨ mathcolor=¨#0000FF¨»B«/mi»«mi mathvariant=¨bold¨ mathcolor=¨#0000FF¨»T«/mi»«/msub»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»=«/mo»«msub»«mi mathvariant=¨bold¨ mathcolor=¨#0000FF¨»B«/mi»«mi mathvariant=¨bold¨ mathcolor=¨#0000FF¨»AB«/mi»«/msub»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»-«/mo»«msub»«mi mathvariant=¨bold¨ mathcolor=¨#0000FF¨»B«/mi»«mi mathvariant=¨bold¨ mathcolor=¨#0000FF¨»DC«/mi»«/msub»«mspace linebreak=¨newline¨»«/mspace»«mspace linebreak=¨newline¨»«/mspace»«msub»«mi mathvariant=¨bold¨ mathcolor=¨#0000FF¨»B«/mi»«mi mathvariant=¨bold¨ mathcolor=¨#0000FF¨»T«/mi»«/msub»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»=«/mo»«mfrac mathcolor=¨#0000FF¨»«mrow»«msub»«mi mathvariant=¨bold¨»§#956;«/mi»«mn mathvariant=¨bold¨»0«/mn»«/msub»«mo mathvariant=¨bold¨»§#183;«/mo»«msub»«mi mathvariant=¨bold¨»I«/mi»«mn mathvariant=¨bold¨»1«/mn»«/msub»«/mrow»«mrow»«mn mathvariant=¨bold¨»2«/mn»«mo mathvariant=¨bold¨»§#183;«/mo»«mi mathvariant=¨bold¨»§#960;«/mi»«mo mathvariant=¨bold¨»§#183;«/mo»«mi mathvariant=¨bold¨»L«/mi»«/mrow»«/mfrac»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»-«/mo»«mfrac mathcolor=¨#0000FF¨»«mrow»«msub»«mi mathvariant=¨bold¨»§#956;«/mi»«mn mathvariant=¨bold¨»0«/mn»«/msub»«mo mathvariant=¨bold¨»§#183;«/mo»«msub»«mi mathvariant=¨bold¨»I«/mi»«mn mathvariant=¨bold¨»1«/mn»«/msub»«/mrow»«mrow»«mn mathvariant=¨bold¨»2«/mn»«mo mathvariant=¨bold¨»§#183;«/mo»«mi mathvariant=¨bold¨»§#960;«/mi»«mo mathvariant=¨bold¨»§#183;«/mo»«mrow»«mo mathvariant=¨bold¨»(«/mo»«mi mathvariant=¨bold¨»L«/mi»«mo mathvariant=¨bold¨»+«/mo»«mi mathvariant=¨bold¨»a«/mi»«mo mathvariant=¨bold¨»)«/mo»«/mrow»«/mrow»«/mfrac»«mspace linebreak=¨newline¨»«/mspace»«mspace linebreak=¨newline¨»«/mspace»«msub»«mi mathvariant=¨bold¨ mathcolor=¨#0000FF¨»B«/mi»«mi mathvariant=¨bold¨ mathcolor=¨#0000FF¨»T«/mi»«/msub»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»=«/mo»«mfrac mathcolor=¨#0000FF¨»«mrow»«msub»«mi mathvariant=¨bold¨»§#956;«/mi»«mn mathvariant=¨bold¨»0«/mn»«/msub»«mo mathvariant=¨bold¨»§#183;«/mo»«msub»«mi mathvariant=¨bold¨»I«/mi»«mn mathvariant=¨bold¨»1«/mn»«/msub»«/mrow»«mrow»«mn mathvariant=¨bold¨»2«/mn»«mo mathvariant=¨bold¨»§#183;«/mo»«mi mathvariant=¨bold¨»§#960;«/mi»«/mrow»«/mfrac»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»§#183;«/mo»«mrow mathcolor=¨#0000FF¨»«mo mathvariant=¨bold¨»(«/mo»«mfrac»«mn mathvariant=¨bold¨»1«/mn»«mi mathvariant=¨bold¨»L«/mi»«/mfrac»«mo mathvariant=¨bold¨»-«/mo»«mfrac»«mn mathvariant=¨bold¨»1«/mn»«mrow»«mi mathvariant=¨bold¨»L«/mi»«mo mathvariant=¨bold¨»+«/mo»«mi mathvariant=¨bold¨»a«/mi»«/mrow»«/mfrac»«mo mathvariant=¨bold¨»)«/mo»«/mrow»«mspace linebreak=¨newline¨»«/mspace»«mspace linebreak=¨newline¨»«/mspace»«/math»
נמצא את גודל הכוח המגנטי הפועל על המוליך הישר:
«math style=¨font-family:`Times New Roman`¨ xmlns=¨http://www.w3.org/1998/Math/MathML¨»«mstyle mathsize=¨20px¨»«mrow»«mi mathvariant=¨bold¨ mathcolor=¨#0000FF¨»F«/mi»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»=«/mo»«mi mathvariant=¨bold¨ mathcolor=¨#0000FF¨»B«/mi»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»§#183;«/mo»«mi mathvariant=¨bold¨ mathcolor=¨#0000FF¨»L«/mi»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»§#183;«/mo»«mi mathvariant=¨bold¨ mathcolor=¨#0000FF¨»I«/mi»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»§#183;«/mo»«mi mathvariant=¨bold¨ mathcolor=¨#0000FF¨»sin«/mi»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»(«/mo»«mi mathvariant=¨bold¨ mathcolor=¨#0000FF¨»§#945;«/mi»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»)«/mo»«mspace linebreak=¨newline¨/»«mspace linebreak=¨newline¨/»«mi mathvariant=¨bold¨ mathcolor=¨#0000FF¨»F«/mi»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»=«/mo»«mfrac mathcolor=¨#0000FF¨»«mrow»«msub»«mi mathvariant=¨bold¨»§#956;«/mi»«mn mathvariant=¨bold¨»0«/mn»«/msub»«mo mathvariant=¨bold¨»§#183;«/mo»«msub»«mi mathvariant=¨bold¨»I«/mi»«mn mathvariant=¨bold¨»1«/mn»«/msub»«/mrow»«mrow»«mn mathvariant=¨bold¨»2«/mn»«mo mathvariant=¨bold¨»§#183;«/mo»«mi mathvariant=¨bold¨»§#960;«/mi»«/mrow»«/mfrac»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»§#183;«/mo»«mrow mathcolor=¨#0000FF¨»«mo mathvariant=¨bold¨»(«/mo»«mfrac»«mn mathvariant=¨bold¨»1«/mn»«mi mathvariant=¨bold¨»L«/mi»«/mfrac»«mo mathvariant=¨bold¨»-«/mo»«mfrac»«mn mathvariant=¨bold¨»1«/mn»«mrow»«mi mathvariant=¨bold¨»L«/mi»«mo mathvariant=¨bold¨»+«/mo»«mi mathvariant=¨bold¨»a«/mi»«/mrow»«/mfrac»«mo mathvariant=¨bold¨»)«/mo»«/mrow»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»§#183;«/mo»«mi mathvariant=¨bold-italic¨ mathcolor=¨#0000FF¨»a«/mi»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»§#183;«/mo»«mi mathvariant=¨bold-italic¨ mathcolor=¨#0000FF¨»I«/mi»«mspace linebreak=¨newline¨/»«/mrow»«mspace linebreak=¨newline¨/»«menclose mathcolor=¨#0000FF¨ notation=¨circle¨»«mi mathvariant=¨bold¨»F«/mi»«mo mathvariant=¨bold¨»=«/mo»«mfrac»«mrow»«msub»«mi mathvariant=¨bold¨»§#956;«/mi»«mn mathvariant=¨bold¨»0«/mn»«/msub»«mo mathvariant=¨bold¨»§#183;«/mo»«msub»«mi mathvariant=¨bold¨»I«/mi»«mn mathvariant=¨bold¨»1«/mn»«/msub»«mo mathvariant=¨bold¨»§#183;«/mo»«mi mathvariant=¨bold¨»I«/mi»«mo mathvariant=¨bold¨»§#183;«/mo»«mi mathvariant=¨bold¨»a«/mi»«/mrow»«mrow»«mn mathvariant=¨bold¨»2«/mn»«mo mathvariant=¨bold¨»§#183;«/mo»«mi mathvariant=¨bold¨»§#960;«/mi»«/mrow»«/mfrac»«mo mathvariant=¨bold¨»§#183;«/mo»«mrow»«mo mathvariant=¨bold¨»(«/mo»«mfrac»«mn mathvariant=¨bold¨»1«/mn»«mi mathvariant=¨bold¨»L«/mi»«/mfrac»«mo mathvariant=¨bold¨»-«/mo»«mfrac»«mn mathvariant=¨bold¨»1«/mn»«mrow»«mi mathvariant=¨bold¨»L«/mi»«mo mathvariant=¨bold¨»+«/mo»«mi mathvariant=¨bold¨»a«/mi»«/mrow»«/mfrac»«mo mathvariant=¨bold¨»)«/mo»«/mrow»«/menclose»«/mstyle»«/math»
______________________________________________________________________________________
______________________________________________________________________________________
...
לא זורם זרם בצלע AB מכיוון שאין שינוי בשטף בכריכה.
חוק פארדי.
המסגרת נעה לאורך המוליך הישר. היא לא מתקרבת ולא מתרחקת לכן אין שינוי בשטף בכריכה .
לפי חוק פארדי לא נוצר כא"מ מושרה בכריכה, לכן לא זורם זרם בצלע AB.
לפי חוק פארדי לא נוצר כא"מ מושרה בכריכה, לכן לא זורם זרם בצלע AB.
אפשר להסביר מדוע לא נוצר זרם במסגרת גם בעזרת ביטוי הכא"מ במוט הנע בשדה מגנטי.
הקיטוב בצלעות האנכיות הוא זניח, הקיטוב בצלעות האופקיות הוא זהה . ומתקבל המעגל הבא:
במעגל זה מקורות המתח יוצרים זרמים זהם בגודלם ומנוגדים בכיוונם , לכן הזרם השקול יהיה אפס אמפר.
הקיטוב בצלעות האנכיות הוא זניח, הקיטוב בצלעות האופקיות הוא זהה . ומתקבל המעגל הבא:
במעגל זה מקורות המתח יוצרים זרמים זהם בגודלם ומנוגדים בכיוונם , לכן הזרם השקול יהיה אפס אמפר.
______________________________________________________________________________________