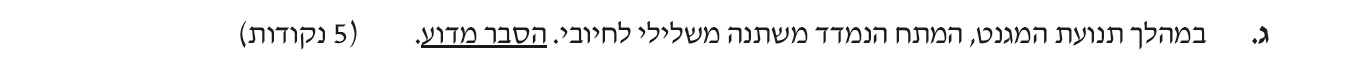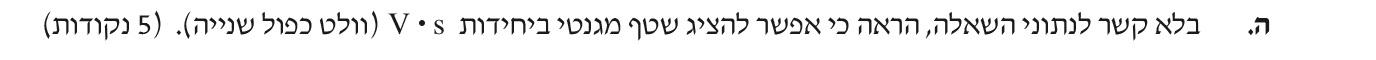
______________________________________________________________________________________
...
תוך כדי התקרבות המגנט השטף בכריכה גדל, בהתאם לחוק פראדיי נוצר כא"מ מושרה בכריכה.
חוק פראדיי.
כאשר המגנט מתקרב לכריכה מספר קווי השדה שכיוונם כלפי מטה בתוך הכריכה הולך וגדל.
תוך כדי תנועת המגנט יש שינוי בשטף, בהתאם לחוק פראדיי «math xmlns=¨http://www.w3.org/1998/Math/MathML¨»«mi mathvariant=¨bold¨ mathcolor=¨#0000FF¨»§#949;«/mi»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»=«/mo»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»-«/mo»«mfrac mathcolor=¨#0000FF¨»«mrow»«mo mathvariant=¨bold¨»§#8710;«/mo»«mi mathvariant=¨bold¨»§#934;«/mi»«/mrow»«mrow»«mo mathvariant=¨bold¨»§#8710;«/mo»«mi mathvariant=¨bold¨»t«/mi»«/mrow»«/mfrac»«/math» נוצר כא"מ מושרה בכריכה.
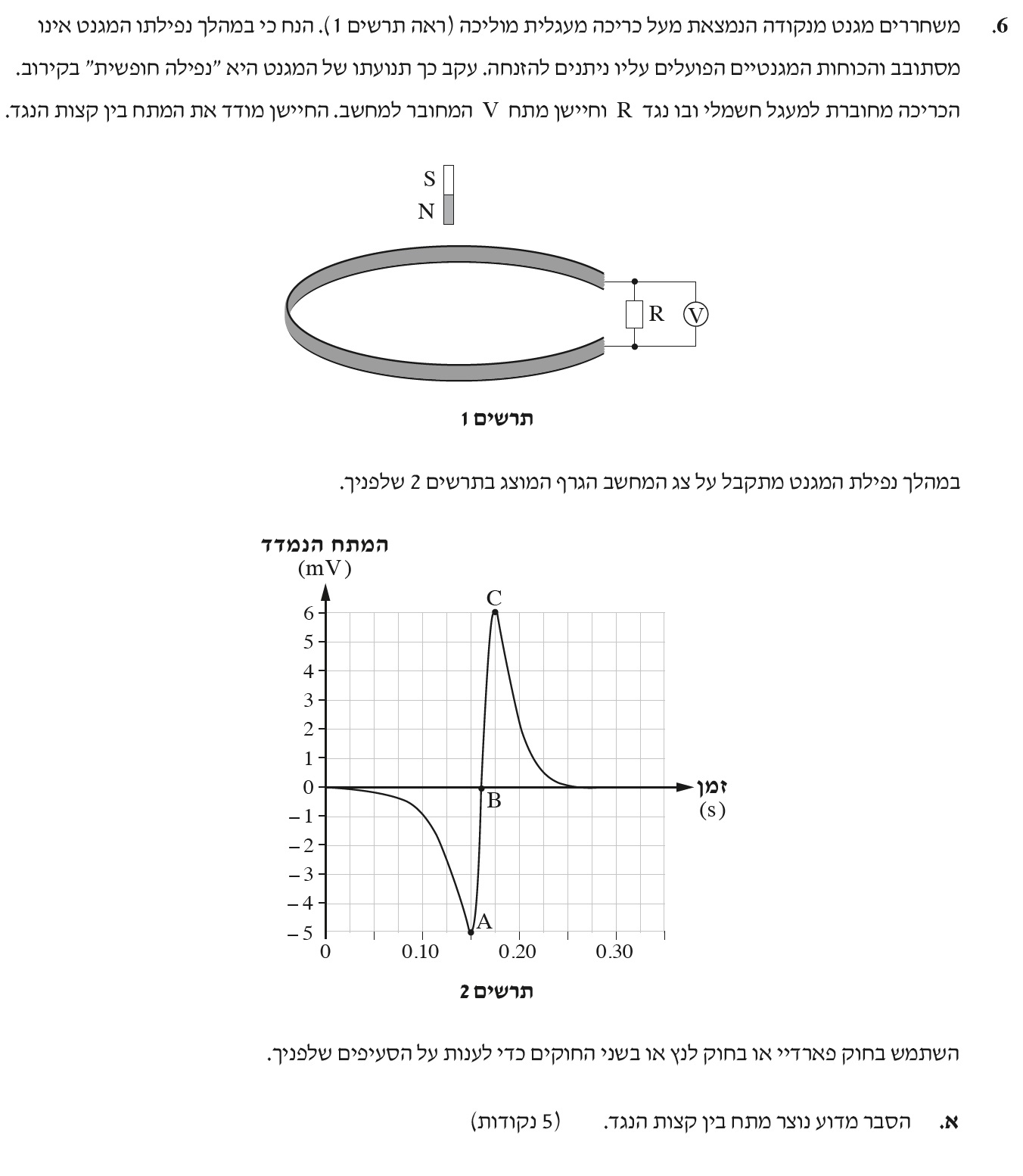
כא"מ זה שווה למתח בין קצות הנגד.
תוך כדי תנועת המגנט יש שינוי בשטף, בהתאם לחוק פראדיי «math xmlns=¨http://www.w3.org/1998/Math/MathML¨»«mi mathvariant=¨bold¨ mathcolor=¨#0000FF¨»§#949;«/mi»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»=«/mo»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»-«/mo»«mfrac mathcolor=¨#0000FF¨»«mrow»«mo mathvariant=¨bold¨»§#8710;«/mo»«mi mathvariant=¨bold¨»§#934;«/mi»«/mrow»«mrow»«mo mathvariant=¨bold¨»§#8710;«/mo»«mi mathvariant=¨bold¨»t«/mi»«/mrow»«/mfrac»«/math» נוצר כא"מ מושרה בכריכה , כא"מ זה שווה למתח בין קצות הנגד.
1. חוק פראדיי מסביר מדוע נוצר כא"מ מושרה בכריכה, לא מדוע נוצר מתח בין הדקי הנגד.
הנגד מחובר בתוך הכריכה ,בטור לכריכה, זרם זהה זורם דרך הכריכה ודרך הנגד.
יש להניח כי התנגדות הכריכה זניחה ביחס להתנגדות הנגד, כך שהמתח בין הדקי הנגד שווה לכא"מ המושרה.
2. יש לענות על סעיף זה באופן כללי , ללא כל קשר לגרף הנתון בשאלה.
הנגד מחובר בתוך הכריכה ,בטור לכריכה, זרם זהה זורם דרך הכריכה ודרך הנגד.
יש להניח כי התנגדות הכריכה זניחה ביחס להתנגדות הנגד, כך שהמתח בין הדקי הנגד שווה לכא"מ המושרה.
2. יש לענות על סעיף זה באופן כללי , ללא כל קשר לגרף הנתון בשאלה.
______________________________________________________________________________________

______________________________________________________________________________________
...
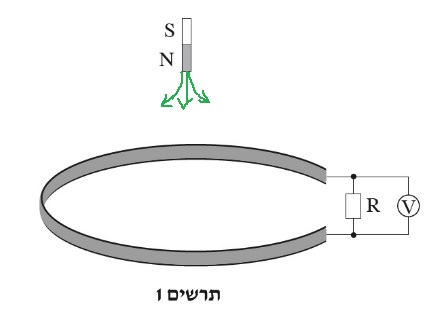
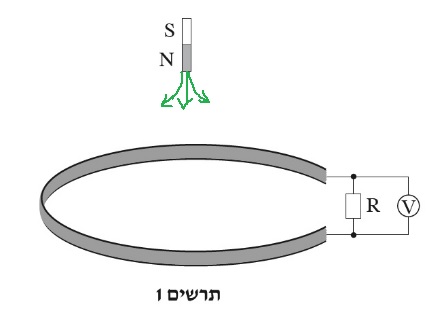
כאשר המוט מתקרב לכריכה יש יותר קווי שדה כלפי מטה , מחוק לנץ ייווצר שדה מושרה בכריכה כלפי מעלה.
חוץ לנץ.
כאשר המגנט נע כלפי מטה הקוטב הצפוני "N" של המגנט מתקרב לכריכה ויש יותר קווי שדה כלפי מטה בתוך הכריכה.
חוק לנץ קובע שהזרם המושרה מתנגד לסיבה להיווצרותו, לכן כיוון השדה המושרה יהיה כלפי מעלה.
חוק לנץ קובע שהזרם המושרה מתנגד לסיבה להיווצרותו, לכן כיוון השדה המושרה יהיה כלפי מעלה.
מחוק לנץ קובע שהזרם המושרה מתנגד לסיבה להיווצרותו ,
1. בזמן תנועת המגנט גם לקוטב הדרומי "S" יש השפעה על השטף בכריכה אך השפעה זו זניחה ביחס
להשפעת הקוטב הצפוני "N".
2. המוט נע בתאוצה , גם אם הוא היה נע במהירות קבועה היה שינוי בשטף בשטף בכריכה.
3. השדה המגנטי המושרה בכריכה הוא השדה המגנטי הנוצר מהזרם המושרה.
4. חוק לנץ מתאר את כיוון הזרם המושרה בכריכה , בשאלה זו אין צורה למצוא את כיוון הזרם המושרה בכריכה.
5. כדי לענות נכון על שאלה זו חשוב לזכור שקווי השדה המגנטי יוצאים מהקוטב הצפוני "N" של המגנט.
להשפעת הקוטב הצפוני"N".
______________________________________________________________________________________
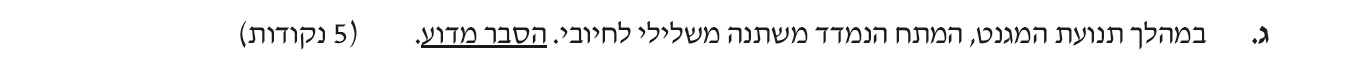
______________________________________________________________________________________
...
כיוון הזרם המושרה משתנה לכן גם קוטביות המתח משתנה.
הזרם נע מפוטנציאל גבוה לנמוך, לכן קוטביות המתח הנמדד תלויה בכיוון הזרם.
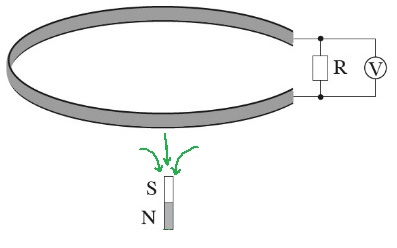
כאשר המגנט נמצא מעל הכריכה והוא נע כלפי מטה יש יותר קווי שדה כלפי מטה בכריכה היוצאים מהקוטב הצפוני.
מחוק לנץ הזרם המושרה יוצר שדה מגנטי בתוך הכריכה כלפי מעלה, מכלל יד ימין כיוון הזרם דרך הנגד יהיה כלפי מעלה.
כאשר המגנט נמצא מתחת לכריכה והוא נע כלפי מטה יש בכריכה פחות קווי שדה כלפי מטה הנכנסים לקוטב הדרומי.
מחוק לנץ הזרם המושרה יוצר שדה מגנטי בתוך הכריכה כלפי מטה, מכלל יד ימין כיוון הזרם בנגד יהיה כלפי מטה.
במעבר המגנט מתחת למישור הכריכה כיוון הזרם בכריכה מתחלף.
באופן כללי, הזרם נע מפוטנציאל גבוה לפוטנציאל נמוך כאשר כיוון הזרם משתנה קוטביות המתח משתנה.
המתח הנמדד משתנה משלילי לחיובי.
מחוק לנץ הזרם המושרה יוצר שדה מגנטי בכריכה כלפי מעלה , מכלל יד ימין כיוון הזרם דרך הנגד יהיה כלפי מעלה .
וכאשר המגנט נע מתחת לכריכה יש פחות קווי שדה כלפי מעלה הנכנסים לקוטב הדרומי.
הזרם נע מפוטנציאל גבוה לפוטנציאל נמוך. כאשר כיוון הזרם משתנה קוטביות המתח משתנה.
1. מומלץ לסמן את קווי השדה המגנטי בקטבים לפני מציאת מגמת שינוי השדה המגנטי בכריכה.
אחרת, קל מאוד לשכוח את העובדה שקווי השדה נכנסים לקוטב הדרומי.
2. מישור הכריכה ניצב לדף לא נוח לתאר את כיוון הזרם בעזרת הכריכה. עדיף לתאר את כיוון הזרם הכריכה ביחס לנגד.
3. המתח משתנה משלילי לחיובי ולא ההיפך מחיובי לשלילי בהתאם לחיבור הדקי מד המתח .
מד המתח מציג את ההפרש שבין הפוטנציאל במוליך האדום לפוטנציאל במוליך השחור .
באיור הבא מתואר מד המתח והזרמים , הזרם I1 המסומן בירוק מתאר את הזרם המושרה כאשר המגנט נע מעל הכריכה.
והזרם I2 המסומן בכחול מתאר את הזרם המושרה כאשר המגנט נע מתחת לכריכה.
אחרת, קל מאוד לשכוח את העובדה שקווי השדה נכנסים לקוטב הדרומי.
2.
______________________________________________________________________________________

______________________________________________________________________________________
...
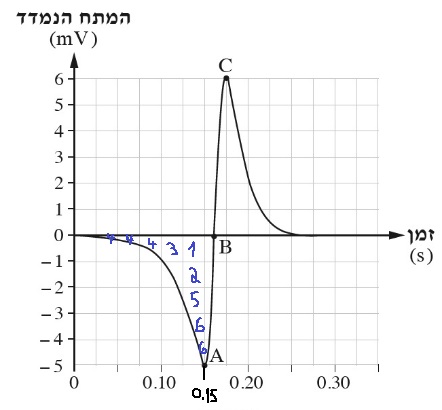
כאשר המגנט עובר את מישור הכריכה מהירותו גדולה יותר והשינוי בשטף יהיה יותר גדול.
מחוק פראדיי הכא"מ גדול יותר בנקודה C.
מחוק פראדיי הכא"מ גדול יותר בנקודה C.
חוק פראדיי.
המתח הנמדד על ידי מד המתח שווה למתח הכא"מ המושרה.
מחוק פארדיי גודל הכא"מ המושרה תלוי בגודל שינוי השטף בכריכה.
המגנט נע בתאוצת הכובד. מהירותו בנקודה C גדולה יותר ממהירותו בנקודה A,
שינוי השטף בכריכה יהיה יותר גדול כאשר המגנט יחלוף בנקודה C.
לכן, מחוק פארדיי הכא"מ הנוצר בכריכה יהיה גדול יותר כאשר הממגנט יחלוף בנקודה C.
מחוק פארדיי גודל הכא"מ המושרה תלוי בגודל שינוי השטף בכריכה.
ככל שמהירות המגנט גדולה יותר כך שינוי השטף בכריכה גדול יותר.
המגנט נע בתאוצת הכובד מהירותו גדולה יותר לאחר שהוא עובר את מישור הכריכה, לכן המתח המקסימאלי הנמדד ביציאת המגנט מהכריכה הוא גדול יותר .
1. יש לענות על סעיף זה בהיגיון כללי ולא בצורה כמותית.
2. יש שלוש נקודות שבהן הכא"מ שווה לאפס וולט:
א- בתחילת התנועה - בנקודה זו המהירות שווה לאפס, אין שינויי בשטף.
ב- כאשר המגנט חולף במישור הכריכה - הזרם משנה את כיוונו ,בדיוק ברגע זה הזרם שווה לאפס , אין כא"מ מושרה.
ג- כאשר המגנט מרוחק מהכריכה - עוצמת השדה המגנטי בכריכה קטנה , השינוי בשדה המגנטי בכריכה שואף לאפס. אין כא"מ.
3. לא נכון לומר שגודל הכא"מ תלוי רק במהירות המגנט, כך למשל כאשר המגנט עובר את מישור הכריכה והוא מאוד מרוחק ממנה
מהירותו מאוד גדולה אך הכא"מ שווה לאפס.
2. יש שלוש נקודות שבהן הכא"מ שווה לאפס וולט
א- בתחילת התנועה - בנקודה זו המהירות שווה לאפס, אין שינויי בשטף.
ב- כאשר המגנט חולף במישור הכריכה - הזרם משנה את כיוונו ,בדיוק ברגע זה הזרם שווה לאפס , אין כא"מ מושרה.
ג- כאשר המגנט מרוחק מהכריכה - עוצמת השדה המגנטי בכריכה קטנה , השינוי בשדה המגנטי בכריכה שואף לאפס. אין כא"מ.
3. לא נכון לומר שגודל הכא"מ תלוי רק במהירות המגנט, כך למשל כאשר המגנט עובר את מישור הכריכה והוא מאוד מרוחק ממנה
מהירותו מאוד גדולה אך הכא"מ שווה לאפס.
______________________________________________________________________________________
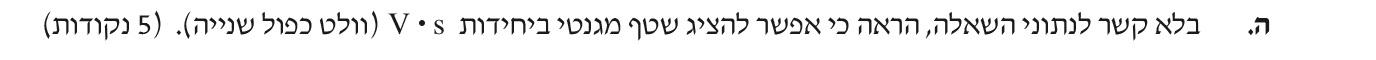
______________________________________________________________________________________
...
מחוק פארדיי ניתן לבטא את שינוי השטף באופן הבא: «math xmlns=¨http://www.w3.org/1998/Math/MathML¨»«mo mathvariant=¨bold¨»§#8710;«/mo»«mi mathvariant=¨bold¨»§#934;«/mi»«mo mathvariant=¨bold¨»=«/mo»«mo mathvariant=¨bold¨»-«/mo»«mi mathvariant=¨bold¨»§#949;«/mi»«mo mathvariant=¨bold¨»§#183;«/mo»«mo mathvariant=¨bold¨»§#8710;«/mo»«mi mathvariant=¨bold¨»t«/mi»«/math». מביטוי זה יחידות השטף הן וולט כפול שנייה.
שימוש בביטוי העוסק בגדלים הפיזיקליים: מתח , זמן, ושטף מגנטי. או ביטוי היחידות הנתונות בתלות ביחידות הבסיסיות.
נשתמש בחוק פארדיי:
«math xmlns=¨http://www.w3.org/1998/Math/MathML¨»«mi mathvariant=¨bold¨ mathcolor=¨#0000FF¨»§#949;«/mi»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»=«/mo»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»-«/mo»«mfrac mathcolor=¨#0000FF¨»«mrow»«mo mathvariant=¨bold¨»§#8710;«/mo»«mi mathvariant=¨bold¨»§#934;«/mi»«/mrow»«mrow»«mo mathvariant=¨bold¨»§#8710;«/mo»«mi mathvariant=¨bold¨»t«/mi»«/mrow»«/mfrac»«/math»
נבטא את שינוי השטף בתלות בכא"מ ובזמן:
«math xmlns=¨http://www.w3.org/1998/Math/MathML¨»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»§#8710;«/mo»«mi mathvariant=¨bold¨ mathcolor=¨#0000FF¨»§#934;«/mi»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»=«/mo»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»-«/mo»«mi mathvariant=¨bold¨ mathcolor=¨#0000FF¨»§#949;«/mi»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»§#183;«/mo»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»§#8710;«/mo»«mi mathvariant=¨bold¨ mathcolor=¨#0000FF¨»t«/mi»«/math»
מביטוי זה ניתן לראות שיחידות השטף המגנטי הן וולט כפול שנייה.
«math xmlns=¨http://www.w3.org/1998/Math/MathML¨»«mi mathvariant=¨bold¨ mathcolor=¨#0000FF¨»§#949;«/mi»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»=«/mo»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»-«/mo»«mfrac mathcolor=¨#0000FF¨»«mrow»«mo mathvariant=¨bold¨»§#8710;«/mo»«mi mathvariant=¨bold¨»§#934;«/mi»«/mrow»«mrow»«mo mathvariant=¨bold¨»§#8710;«/mo»«mi mathvariant=¨bold¨»t«/mi»«/mrow»«/mfrac»«/math»
נבטא את שינוי השטף בתלות בכא"מ ובזמן:
«math xmlns=¨http://www.w3.org/1998/Math/MathML¨»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»§#8710;«/mo»«mi mathvariant=¨bold¨ mathcolor=¨#0000FF¨»§#934;«/mi»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»=«/mo»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»-«/mo»«mi mathvariant=¨bold¨ mathcolor=¨#0000FF¨»§#949;«/mi»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»§#183;«/mo»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»§#8710;«/mo»«mi mathvariant=¨bold¨ mathcolor=¨#0000FF¨»t«/mi»«/math»
מביטוי זה ניתן לראות שיחידות השטף המגנטי הן וולט כפול שנייה.
1. היחידות המופיעות בסעיף זה הן של שלושת הגדלים המופיעים בחוק פארדיי.
לכן מומלץ לנסות להשתמש בחוק פארדיי כדי לפתור את השאלה.
2. אם לא קיים ביטוי או שלא מוצאים ביטוי העוסק רק ביחידות הרלוונטיות תמיד ניתן לבטא כל אחת מהיחידות בעזרת היחידות הבסיסיות: מטר, ק"ג , שנייה, וקולון.
«math xmlns=¨http://www.w3.org/1998/Math/MathML¨»«mi mathvariant=¨bold¨ mathcolor=¨#FF0000¨»§#934;«/mi»«mo mathvariant=¨bold¨ mathcolor=¨#FF0000¨»=«/mo»«mi mathvariant=¨bold¨ mathcolor=¨#0000FF¨»B«/mi»«mo mathvariant=¨bold¨ mathcolor=¨#FF0000¨»§#183;«/mo»«mi mathvariant=¨bold¨ mathcolor=¨#007F00¨»A«/mi»«mo mathvariant=¨bold¨ mathcolor=¨#FF0000¨»=«/mo»«mfrac mathcolor=¨#0000FF¨»«mi mathvariant=¨bold¨»F«/mi»«mrow»«mi mathvariant=¨bold¨»q«/mi»«mo mathvariant=¨bold¨»§#183;«/mo»«mi mathvariant=¨bold¨»V«/mi»«mo mathvariant=¨bold¨»§#183;«/mo»«mi mathvariant=¨bold¨»sin«/mi»«mo mathvariant=¨bold¨»(«/mo»«mi mathvariant=¨bold¨»§#945;«/mi»«mo mathvariant=¨bold¨»)«/mo»«/mrow»«/mfrac»«mo mathvariant=¨bold¨ mathcolor=¨#FF0000¨»§#183;«/mo»«mi mathvariant=¨bold¨ mathcolor=¨#007F00¨»A«/mi»«mo mathvariant=¨bold¨ mathcolor=¨#FF0000¨»=«/mo»«mfrac mathcolor=¨#0000FF¨»«mstyle mathvariant=¨bold¨»«mo»[«/mo»«mi»N«/mi»«mo»]«/mo»«/mstyle»«mrow»«mrow»«mo mathvariant=¨bold¨»[«/mo»«mi mathvariant=¨bold¨»C«/mi»«mo mathvariant=¨bold¨»]«/mo»«/mrow»«mo mathvariant=¨bold¨»§#183;«/mo»«mrow»«mo mathvariant=¨bold¨»[«/mo»«mstyle displaystyle=¨true¨ mathvariant=¨bold¨»«mfrac»«mi»m«/mi»«mi»s«/mi»«/mfrac»«/mstyle»«mo mathvariant=¨bold¨»]«/mo»«/mrow»«/mrow»«/mfrac»«mo mathvariant=¨bold¨ mathcolor=¨#FF0000¨»§#183;«/mo»«mrow»«mo mathvariant=¨bold¨»[«/mo»«msup»«mi mathvariant=¨bold¨»m«/mi»«mn mathvariant=¨bold¨»2«/mn»«/msup»«mo mathvariant=¨bold¨»]«/mo»«/mrow»«mo mathvariant=¨bold¨ mathcolor=¨#FF0000¨»=«/mo»«mfrac mathcolor=¨#FF0000¨»«mrow»«mrow mathcolor=¨#0000FF¨»«mo mathvariant=¨bold¨»[«/mo»«mi mathvariant=¨bold¨»N«/mi»«mo mathvariant=¨bold¨»]«/mo»«/mrow»«mo mathvariant=¨bold¨»§#183;«/mo»«mrow mathcolor=¨#007F00¨»«mo mathvariant=¨bold¨»[«/mo»«mi mathvariant=¨bold¨»m«/mi»«menclose notation=¨updiagonalstrike¨»«msup»«mrow»«/mrow»«mn mathvariant=¨bold¨»2«/mn»«/msup»«/menclose»«mo mathvariant=¨bold¨»]«/mo»«/mrow»«mo mathvariant=¨bold¨»§#183;«/mo»«mrow»«mo mathvariant=¨bold¨»[«/mo»«mi mathvariant=¨bold¨»s«/mi»«mo mathvariant=¨bold¨»]«/mo»«/mrow»«/mrow»«mrow»«mrow mathcolor=¨#0000FF¨»«mo mathvariant=¨bold¨»[«/mo»«mi mathvariant=¨bold¨»C«/mi»«mo mathvariant=¨bold¨»]«/mo»«/mrow»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»§#183;«/mo»«menclose mathcolor=¨#0000FF¨ notation=¨updiagonalstrike¨»«mo mathvariant=¨bold¨»[«/mo»«mi mathvariant=¨bold¨»m«/mi»«mo mathvariant=¨bold¨»]«/mo»«/menclose»«/mrow»«/mfrac»«mo mathvariant=¨bold¨ mathcolor=¨#FF0000¨»=«/mo»«mfrac mathcolor=¨#FF0000¨»«mrow»«mrow mathcolor=¨#0000FF¨»«mo mathvariant=¨bold¨»[«/mo»«mi mathvariant=¨bold¨»N«/mi»«mo mathvariant=¨bold¨»]«/mo»«/mrow»«mo mathvariant=¨bold¨»§#183;«/mo»«mrow mathcolor=¨#007F00¨»«mo mathvariant=¨bold¨»[«/mo»«mi mathvariant=¨bold¨»m«/mi»«mo mathvariant=¨bold¨»]«/mo»«/mrow»«mo mathvariant=¨bold¨»§#183;«/mo»«mrow»«mo mathvariant=¨bold¨»[«/mo»«mi mathvariant=¨bold¨»s«/mi»«mo mathvariant=¨bold¨»]«/mo»«/mrow»«/mrow»«mrow mathcolor=¨#0000FF¨»«mo mathvariant=¨bold¨»[«/mo»«mi mathvariant=¨bold¨»C«/mi»«mo mathvariant=¨bold¨»]«/mo»«/mrow»«/mfrac»«mspace linebreak=¨newline¨»«/mspace»«mo mathvariant=¨bold¨ mathcolor=¨#FF0000¨»=«/mo»«mfrac mathcolor=¨#FF0000¨»«mrow»«mrow mathcolor=¨#0000FF¨»«mo mathvariant=¨bold¨»[«/mo»«mstyle displaystyle=¨true¨»«mfrac»«mrow»«mi mathvariant=¨bold¨»kg«/mi»«mo mathvariant=¨bold¨»§#183;«/mo»«mi mathvariant=¨bold¨»m«/mi»«/mrow»«msup»«mi mathvariant=¨bold¨»s«/mi»«mn mathvariant=¨bold¨»2«/mn»«/msup»«/mfrac»«/mstyle»«mo mathvariant=¨bold¨»]«/mo»«/mrow»«mo mathvariant=¨bold¨»§#183;«/mo»«mrow mathcolor=¨#0000FF¨»«mo mathvariant=¨bold¨»[«/mo»«mi mathvariant=¨bold¨»m«/mi»«mo mathvariant=¨bold¨»]«/mo»«/mrow»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»§#183;«/mo»«mrow mathcolor=¨#0000FF¨»«mo mathvariant=¨bold¨»[«/mo»«mi mathvariant=¨bold¨»s«/mi»«mo mathvariant=¨bold¨»]«/mo»«/mrow»«/mrow»«mrow mathcolor=¨#0000FF¨»«mo mathvariant=¨bold¨»[«/mo»«mi mathvariant=¨bold¨»C«/mi»«mo mathvariant=¨bold¨»]«/mo»«/mrow»«/mfrac»«mo mathvariant=¨bold¨ mathcolor=¨#FF0000¨»=«/mo»«mfrac mathcolor=¨#FF0000¨»«mrow»«mrow mathcolor=¨#0000FF¨»«mo mathvariant=¨bold¨»[«/mo»«mstyle mathvariant=¨bold¨ displaystyle=¨true¨»«mi»kg«/mi»«/mstyle»«mo mathvariant=¨bold¨»]«/mo»«/mrow»«mo mathvariant=¨bold¨»§#183;«/mo»«mrow mathcolor=¨#0000FF¨»«mo mathvariant=¨bold¨»[«/mo»«msup»«mi mathvariant=¨bold¨»m«/mi»«mn mathvariant=¨bold¨»2«/mn»«/msup»«mo mathvariant=¨bold¨»]«/mo»«/mrow»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»§#183;«/mo»«menclose mathcolor=¨#0000FF¨ notation=¨updiagonalstrike¨»«mo mathvariant=¨bold¨»[«/mo»«mi mathvariant=¨bold¨»s«/mi»«mo mathvariant=¨bold¨»]«/mo»«/menclose»«/mrow»«mrow mathcolor=¨#0000FF¨»«mrow»«mo mathvariant=¨bold¨»[«/mo»«mi mathvariant=¨bold¨»s«/mi»«menclose notation=¨updiagonalstrike¨»«msup»«mrow»«/mrow»«mn mathvariant=¨bold¨»2«/mn»«/msup»«/menclose»«mo mathvariant=¨bold¨»]«/mo»«/mrow»«mo mathvariant=¨bold¨ mathcolor=¨#FF0000¨»§#183;«/mo»«mo mathvariant=¨bold¨»[«/mo»«mi mathvariant=¨bold¨»C«/mi»«mo mathvariant=¨bold¨»]«/mo»«/mrow»«/mfrac»«mo mathvariant=¨bold¨ mathcolor=¨#FF0000¨»=«/mo»«mfrac mathcolor=¨#FF0000¨»«mrow»«mrow mathcolor=¨#0000FF¨»«mo mathvariant=¨bold¨»[«/mo»«mstyle mathvariant=¨bold¨ displaystyle=¨true¨»«mi»kg«/mi»«/mstyle»«mo mathvariant=¨bold¨»]«/mo»«/mrow»«mo mathvariant=¨bold¨»§#183;«/mo»«mrow mathcolor=¨#0000FF¨»«mo mathvariant=¨bold¨»[«/mo»«msup»«mi mathvariant=¨bold¨»m«/mi»«mn mathvariant=¨bold¨»2«/mn»«/msup»«mo mathvariant=¨bold¨»]«/mo»«/mrow»«/mrow»«mrow mathcolor=¨#0000FF¨»«mrow»«mo mathvariant=¨bold¨»[«/mo»«mi mathvariant=¨bold¨»s«/mi»«mo mathvariant=¨bold¨»]«/mo»«/mrow»«mo mathvariant=¨bold¨ mathcolor=¨#FF0000¨»§#183;«/mo»«mo mathvariant=¨bold¨»[«/mo»«mi mathvariant=¨bold¨»C«/mi»«mo mathvariant=¨bold¨»]«/mo»«/mrow»«/mfrac»«mspace linebreak=¨newline¨»«/mspace»«mspace linebreak=¨newline¨»«/mspace»«mspace linebreak=¨newline¨»«/mspace»«mspace linebreak=¨newline¨»«/mspace»«mrow»«mo mathvariant=¨bold¨»[«/mo»«mi mathvariant=¨bold¨»V«/mi»«mo mathvariant=¨bold¨»]«/mo»«/mrow»«mo mathvariant=¨bold¨ mathcolor=¨#FF0000¨»§#183;«/mo»«mrow»«mo mathvariant=¨bold¨»[«/mo»«mi mathvariant=¨bold¨»S«/mi»«mo mathvariant=¨bold¨»]«/mo»«/mrow»«mo mathvariant=¨bold¨ mathcolor=¨#FF0000¨»=«/mo»«mrow»«mo mathvariant=¨bold¨»[«/mo»«mfrac»«mi mathvariant=¨bold¨»J«/mi»«mi mathvariant=¨bold¨»C«/mi»«/mfrac»«mo mathvariant=¨bold¨»]«/mo»«/mrow»«mo mathvariant=¨bold¨ mathcolor=¨#FF0000¨»§#183;«/mo»«mrow mathcolor=¨#FF0000¨»«mo mathvariant=¨bold¨»[«/mo»«mi mathvariant=¨bold¨»S«/mi»«mo mathvariant=¨bold¨»]«/mo»«/mrow»«mo mathvariant=¨bold¨ mathcolor=¨#FF0000¨»=«/mo»«mrow mathcolor=¨#FF0000¨»«mo mathvariant=¨bold¨»[«/mo»«mfrac»«mrow»«mi mathvariant=¨bold¨»N«/mi»«mo mathvariant=¨bold¨»§#183;«/mo»«mi mathvariant=¨bold¨»m«/mi»«/mrow»«mi mathvariant=¨bold¨»C«/mi»«/mfrac»«mo mathvariant=¨bold¨»]«/mo»«/mrow»«mo mathvariant=¨bold¨ mathcolor=¨#FF0000¨»§#183;«/mo»«mrow mathcolor=¨#FF0000¨»«mo mathvariant=¨bold¨»[«/mo»«mi mathvariant=¨bold¨»S«/mi»«mo mathvariant=¨bold¨»]«/mo»«mo mathvariant=¨bold¨»=«/mo»«/mrow»«mfrac mathcolor=¨#FF0000¨»«mrow»«mrow mathcolor=¨#0000FF¨»«mo mathvariant=¨bold¨»[«/mo»«mstyle mathvariant=¨bold¨ displaystyle=¨true¨»«mfrac»«mrow»«mi»kg«/mi»«mo»§#183;«/mo»«mi»m«/mi»«/mrow»«msup»«mi»s«/mi»«mn»2«/mn»«/msup»«/mfrac»«/mstyle»«mo mathvariant=¨bold¨»]«/mo»«/mrow»«mo mathvariant=¨bold¨»§#183;«/mo»«mrow mathcolor=¨#0000FF¨»«mo mathvariant=¨bold¨»[«/mo»«mi mathvariant=¨bold¨»m«/mi»«mo mathvariant=¨bold¨»]«/mo»«/mrow»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»§#183;«/mo»«mrow mathcolor=¨#0000FF¨»«mo mathvariant=¨bold¨»[«/mo»«mi mathvariant=¨bold¨»s«/mi»«mo mathvariant=¨bold¨»]«/mo»«/mrow»«/mrow»«mrow mathcolor=¨#0000FF¨»«mo mathvariant=¨bold¨»[«/mo»«mi mathvariant=¨bold¨»C«/mi»«mo mathvariant=¨bold¨»]«/mo»«/mrow»«/mfrac»«mo mathvariant=¨bold¨ mathcolor=¨#FF0000¨»=«/mo»«mfrac mathcolor=¨#FF0000¨»«mrow»«mrow mathcolor=¨#0000FF¨»«mo mathvariant=¨bold¨»[«/mo»«mstyle mathvariant=¨bold¨ displaystyle=¨true¨»«mi»kg«/mi»«/mstyle»«mo mathvariant=¨bold¨»]«/mo»«/mrow»«mo mathvariant=¨bold¨»§#183;«/mo»«mrow mathcolor=¨#0000FF¨»«mo mathvariant=¨bold¨»[«/mo»«msup»«mi mathvariant=¨bold¨»m«/mi»«mn mathvariant=¨bold¨»2«/mn»«/msup»«mo mathvariant=¨bold¨»]«/mo»«/mrow»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»§#183;«/mo»«menclose mathcolor=¨#0000FF¨ notation=¨updiagonalstrike¨»«mo mathvariant=¨bold¨»[«/mo»«mi mathvariant=¨bold¨»s«/mi»«mo mathvariant=¨bold¨»]«/mo»«/menclose»«/mrow»«mrow mathcolor=¨#0000FF¨»«mrow»«mo mathvariant=¨bold¨»[«/mo»«mi mathvariant=¨bold¨»s«/mi»«menclose notation=¨updiagonalstrike¨»«msup»«mrow»«/mrow»«mn mathvariant=¨bold¨»2«/mn»«/msup»«/menclose»«mo mathvariant=¨bold¨»]«/mo»«/mrow»«mo mathvariant=¨bold¨ mathcolor=¨#FF0000¨»§#183;«/mo»«mo mathvariant=¨bold¨»[«/mo»«mi mathvariant=¨bold¨»C«/mi»«mo mathvariant=¨bold¨»]«/mo»«/mrow»«/mfrac»«mo mathvariant=¨bold¨ mathcolor=¨#FF0000¨»=«/mo»«mfrac mathcolor=¨#FF0000¨»«mrow»«mrow mathcolor=¨#0000FF¨»«mo mathvariant=¨bold¨»[«/mo»«mstyle mathvariant=¨bold¨ displaystyle=¨true¨»«mi»kg«/mi»«/mstyle»«mo mathvariant=¨bold¨»]«/mo»«/mrow»«mo mathvariant=¨bold¨»§#183;«/mo»«mrow mathcolor=¨#0000FF¨»«mo mathvariant=¨bold¨»[«/mo»«msup»«mi mathvariant=¨bold¨»m«/mi»«mn mathvariant=¨bold¨»2«/mn»«/msup»«mo mathvariant=¨bold¨»]«/mo»«/mrow»«/mrow»«mrow mathcolor=¨#0000FF¨»«mrow»«mo mathvariant=¨bold¨»[«/mo»«mi mathvariant=¨bold¨»s«/mi»«mo mathvariant=¨bold¨»]«/mo»«/mrow»«mo mathvariant=¨bold¨ mathcolor=¨#FF0000¨»§#183;«/mo»«mo mathvariant=¨bold¨»[«/mo»«mi mathvariant=¨bold¨»C«/mi»«mo mathvariant=¨bold¨»]«/mo»«/mrow»«/mfrac»«mspace linebreak=¨newline¨»«/mspace»«mspace linebreak=¨newline¨»«/mspace»«/math»
לכן מומלץ לנסות להשתמש בחוק פארדיי כדי לפתור את השאלה.
2. אם לא קיים ביטוי או שלא מוצאים ביטוי העוסק רק ביחידות הרלוונטיות תמיד ניתן לבטא כל אחת מהיחידות בעזרת היחידות הבסיסיות: מטר, ק"ג , שנייה, וקולון.
«math xmlns=¨http://www.w3.org/1998/Math/MathML¨»«mi mathvariant=¨bold¨ mathcolor=¨#FF0000¨»§#934;«/mi»«mo mathvariant=¨bold¨ mathcolor=¨#FF0000¨»=«/mo»«mi mathvariant=¨bold¨ mathcolor=¨#0000FF¨»B«/mi»«mo mathvariant=¨bold¨ mathcolor=¨#FF0000¨»§#183;«/mo»«mi mathvariant=¨bold¨ mathcolor=¨#007F00¨»A«/mi»«mo mathvariant=¨bold¨ mathcolor=¨#FF0000¨»=«/mo»«mfrac mathcolor=¨#0000FF¨»«mi mathvariant=¨bold¨»F«/mi»«mrow»«mi mathvariant=¨bold¨»q«/mi»«mo mathvariant=¨bold¨»§#183;«/mo»«mi mathvariant=¨bold¨»V«/mi»«mo mathvariant=¨bold¨»§#183;«/mo»«mi mathvariant=¨bold¨»sin«/mi»«mo mathvariant=¨bold¨»(«/mo»«mi mathvariant=¨bold¨»§#945;«/mi»«mo mathvariant=¨bold¨»)«/mo»«/mrow»«/mfrac»«mo mathvariant=¨bold¨ mathcolor=¨#FF0000¨»§#183;«/mo»«mi mathvariant=¨bold¨ mathcolor=¨#007F00¨»A«/mi»«mo mathvariant=¨bold¨ mathcolor=¨#FF0000¨»=«/mo»«mfrac mathcolor=¨#0000FF¨»«mstyle mathvariant=¨bold¨»«mo»[«/mo»«mi»N«/mi»«mo»]«/mo»«/mstyle»«mrow»«mrow»«mo mathvariant=¨bold¨»[«/mo»«mi mathvariant=¨bold¨»C«/mi»«mo mathvariant=¨bold¨»]«/mo»«/mrow»«mo mathvariant=¨bold¨»§#183;«/mo»«mrow»«mo mathvariant=¨bold¨»[«/mo»«mstyle displaystyle=¨true¨ mathvariant=¨bold¨»«mfrac»«mi»m«/mi»«mi»s«/mi»«/mfrac»«/mstyle»«mo mathvariant=¨bold¨»]«/mo»«/mrow»«/mrow»«/mfrac»«mo mathvariant=¨bold¨ mathcolor=¨#FF0000¨»§#183;«/mo»«mrow»«mo mathvariant=¨bold¨»[«/mo»«msup»«mi mathvariant=¨bold¨»m«/mi»«mn mathvariant=¨bold¨»2«/mn»«/msup»«mo mathvariant=¨bold¨»]«/mo»«/mrow»«mo mathvariant=¨bold¨ mathcolor=¨#FF0000¨»=«/mo»«mfrac mathcolor=¨#FF0000¨»«mrow»«mrow mathcolor=¨#0000FF¨»«mo mathvariant=¨bold¨»[«/mo»«mi mathvariant=¨bold¨»N«/mi»«mo mathvariant=¨bold¨»]«/mo»«/mrow»«mo mathvariant=¨bold¨»§#183;«/mo»«mrow mathcolor=¨#007F00¨»«mo mathvariant=¨bold¨»[«/mo»«mi mathvariant=¨bold¨»m«/mi»«menclose notation=¨updiagonalstrike¨»«msup»«mrow»«/mrow»«mn mathvariant=¨bold¨»2«/mn»«/msup»«/menclose»«mo mathvariant=¨bold¨»]«/mo»«/mrow»«mo mathvariant=¨bold¨»§#183;«/mo»«mrow»«mo mathvariant=¨bold¨»[«/mo»«mi mathvariant=¨bold¨»s«/mi»«mo mathvariant=¨bold¨»]«/mo»«/mrow»«/mrow»«mrow»«mrow mathcolor=¨#0000FF¨»«mo mathvariant=¨bold¨»[«/mo»«mi mathvariant=¨bold¨»C«/mi»«mo mathvariant=¨bold¨»]«/mo»«/mrow»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»§#183;«/mo»«menclose mathcolor=¨#0000FF¨ notation=¨updiagonalstrike¨»«mo mathvariant=¨bold¨»[«/mo»«mi mathvariant=¨bold¨»m«/mi»«mo mathvariant=¨bold¨»]«/mo»«/menclose»«/mrow»«/mfrac»«mo mathvariant=¨bold¨ mathcolor=¨#FF0000¨»=«/mo»«mfrac mathcolor=¨#FF0000¨»«mrow»«mrow mathcolor=¨#0000FF¨»«mo mathvariant=¨bold¨»[«/mo»«mi mathvariant=¨bold¨»N«/mi»«mo mathvariant=¨bold¨»]«/mo»«/mrow»«mo mathvariant=¨bold¨»§#183;«/mo»«mrow mathcolor=¨#007F00¨»«mo mathvariant=¨bold¨»[«/mo»«mi mathvariant=¨bold¨»m«/mi»«mo mathvariant=¨bold¨»]«/mo»«/mrow»«mo mathvariant=¨bold¨»§#183;«/mo»«mrow»«mo mathvariant=¨bold¨»[«/mo»«mi mathvariant=¨bold¨»s«/mi»«mo mathvariant=¨bold¨»]«/mo»«/mrow»«/mrow»«mrow mathcolor=¨#0000FF¨»«mo mathvariant=¨bold¨»[«/mo»«mi mathvariant=¨bold¨»C«/mi»«mo mathvariant=¨bold¨»]«/mo»«/mrow»«/mfrac»«mspace linebreak=¨newline¨»«/mspace»«mo mathvariant=¨bold¨ mathcolor=¨#FF0000¨»=«/mo»«mfrac mathcolor=¨#FF0000¨»«mrow»«mrow mathcolor=¨#0000FF¨»«mo mathvariant=¨bold¨»[«/mo»«mstyle displaystyle=¨true¨»«mfrac»«mrow»«mi mathvariant=¨bold¨»kg«/mi»«mo mathvariant=¨bold¨»§#183;«/mo»«mi mathvariant=¨bold¨»m«/mi»«/mrow»«msup»«mi mathvariant=¨bold¨»s«/mi»«mn mathvariant=¨bold¨»2«/mn»«/msup»«/mfrac»«/mstyle»«mo mathvariant=¨bold¨»]«/mo»«/mrow»«mo mathvariant=¨bold¨»§#183;«/mo»«mrow mathcolor=¨#0000FF¨»«mo mathvariant=¨bold¨»[«/mo»«mi mathvariant=¨bold¨»m«/mi»«mo mathvariant=¨bold¨»]«/mo»«/mrow»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»§#183;«/mo»«mrow mathcolor=¨#0000FF¨»«mo mathvariant=¨bold¨»[«/mo»«mi mathvariant=¨bold¨»s«/mi»«mo mathvariant=¨bold¨»]«/mo»«/mrow»«/mrow»«mrow mathcolor=¨#0000FF¨»«mo mathvariant=¨bold¨»[«/mo»«mi mathvariant=¨bold¨»C«/mi»«mo mathvariant=¨bold¨»]«/mo»«/mrow»«/mfrac»«mo mathvariant=¨bold¨ mathcolor=¨#FF0000¨»=«/mo»«mfrac mathcolor=¨#FF0000¨»«mrow»«mrow mathcolor=¨#0000FF¨»«mo mathvariant=¨bold¨»[«/mo»«mstyle mathvariant=¨bold¨ displaystyle=¨true¨»«mi»kg«/mi»«/mstyle»«mo mathvariant=¨bold¨»]«/mo»«/mrow»«mo mathvariant=¨bold¨»§#183;«/mo»«mrow mathcolor=¨#0000FF¨»«mo mathvariant=¨bold¨»[«/mo»«msup»«mi mathvariant=¨bold¨»m«/mi»«mn mathvariant=¨bold¨»2«/mn»«/msup»«mo mathvariant=¨bold¨»]«/mo»«/mrow»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»§#183;«/mo»«menclose mathcolor=¨#0000FF¨ notation=¨updiagonalstrike¨»«mo mathvariant=¨bold¨»[«/mo»«mi mathvariant=¨bold¨»s«/mi»«mo mathvariant=¨bold¨»]«/mo»«/menclose»«/mrow»«mrow mathcolor=¨#0000FF¨»«mrow»«mo mathvariant=¨bold¨»[«/mo»«mi mathvariant=¨bold¨»s«/mi»«menclose notation=¨updiagonalstrike¨»«msup»«mrow»«/mrow»«mn mathvariant=¨bold¨»2«/mn»«/msup»«/menclose»«mo mathvariant=¨bold¨»]«/mo»«/mrow»«mo mathvariant=¨bold¨ mathcolor=¨#FF0000¨»§#183;«/mo»«mo mathvariant=¨bold¨»[«/mo»«mi mathvariant=¨bold¨»C«/mi»«mo mathvariant=¨bold¨»]«/mo»«/mrow»«/mfrac»«mo mathvariant=¨bold¨ mathcolor=¨#FF0000¨»=«/mo»«mfrac mathcolor=¨#FF0000¨»«mrow»«mrow mathcolor=¨#0000FF¨»«mo mathvariant=¨bold¨»[«/mo»«mstyle mathvariant=¨bold¨ displaystyle=¨true¨»«mi»kg«/mi»«/mstyle»«mo mathvariant=¨bold¨»]«/mo»«/mrow»«mo mathvariant=¨bold¨»§#183;«/mo»«mrow mathcolor=¨#0000FF¨»«mo mathvariant=¨bold¨»[«/mo»«msup»«mi mathvariant=¨bold¨»m«/mi»«mn mathvariant=¨bold¨»2«/mn»«/msup»«mo mathvariant=¨bold¨»]«/mo»«/mrow»«/mrow»«mrow mathcolor=¨#0000FF¨»«mrow»«mo mathvariant=¨bold¨»[«/mo»«mi mathvariant=¨bold¨»s«/mi»«mo mathvariant=¨bold¨»]«/mo»«/mrow»«mo mathvariant=¨bold¨ mathcolor=¨#FF0000¨»§#183;«/mo»«mo mathvariant=¨bold¨»[«/mo»«mi mathvariant=¨bold¨»C«/mi»«mo mathvariant=¨bold¨»]«/mo»«/mrow»«/mfrac»«mspace linebreak=¨newline¨»«/mspace»«mspace linebreak=¨newline¨»«/mspace»«mspace linebreak=¨newline¨»«/mspace»«mspace linebreak=¨newline¨»«/mspace»«mrow»«mo mathvariant=¨bold¨»[«/mo»«mi mathvariant=¨bold¨»V«/mi»«mo mathvariant=¨bold¨»]«/mo»«/mrow»«mo mathvariant=¨bold¨ mathcolor=¨#FF0000¨»§#183;«/mo»«mrow»«mo mathvariant=¨bold¨»[«/mo»«mi mathvariant=¨bold¨»S«/mi»«mo mathvariant=¨bold¨»]«/mo»«/mrow»«mo mathvariant=¨bold¨ mathcolor=¨#FF0000¨»=«/mo»«mrow»«mo mathvariant=¨bold¨»[«/mo»«mfrac»«mi mathvariant=¨bold¨»J«/mi»«mi mathvariant=¨bold¨»C«/mi»«/mfrac»«mo mathvariant=¨bold¨»]«/mo»«/mrow»«mo mathvariant=¨bold¨ mathcolor=¨#FF0000¨»§#183;«/mo»«mrow mathcolor=¨#FF0000¨»«mo mathvariant=¨bold¨»[«/mo»«mi mathvariant=¨bold¨»S«/mi»«mo mathvariant=¨bold¨»]«/mo»«/mrow»«mo mathvariant=¨bold¨ mathcolor=¨#FF0000¨»=«/mo»«mrow mathcolor=¨#FF0000¨»«mo mathvariant=¨bold¨»[«/mo»«mfrac»«mrow»«mi mathvariant=¨bold¨»N«/mi»«mo mathvariant=¨bold¨»§#183;«/mo»«mi mathvariant=¨bold¨»m«/mi»«/mrow»«mi mathvariant=¨bold¨»C«/mi»«/mfrac»«mo mathvariant=¨bold¨»]«/mo»«/mrow»«mo mathvariant=¨bold¨ mathcolor=¨#FF0000¨»§#183;«/mo»«mrow mathcolor=¨#FF0000¨»«mo mathvariant=¨bold¨»[«/mo»«mi mathvariant=¨bold¨»S«/mi»«mo mathvariant=¨bold¨»]«/mo»«mo mathvariant=¨bold¨»=«/mo»«/mrow»«mfrac mathcolor=¨#FF0000¨»«mrow»«mrow mathcolor=¨#0000FF¨»«mo mathvariant=¨bold¨»[«/mo»«mstyle mathvariant=¨bold¨ displaystyle=¨true¨»«mfrac»«mrow»«mi»kg«/mi»«mo»§#183;«/mo»«mi»m«/mi»«/mrow»«msup»«mi»s«/mi»«mn»2«/mn»«/msup»«/mfrac»«/mstyle»«mo mathvariant=¨bold¨»]«/mo»«/mrow»«mo mathvariant=¨bold¨»§#183;«/mo»«mrow mathcolor=¨#0000FF¨»«mo mathvariant=¨bold¨»[«/mo»«mi mathvariant=¨bold¨»m«/mi»«mo mathvariant=¨bold¨»]«/mo»«/mrow»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»§#183;«/mo»«mrow mathcolor=¨#0000FF¨»«mo mathvariant=¨bold¨»[«/mo»«mi mathvariant=¨bold¨»s«/mi»«mo mathvariant=¨bold¨»]«/mo»«/mrow»«/mrow»«mrow mathcolor=¨#0000FF¨»«mo mathvariant=¨bold¨»[«/mo»«mi mathvariant=¨bold¨»C«/mi»«mo mathvariant=¨bold¨»]«/mo»«/mrow»«/mfrac»«mo mathvariant=¨bold¨ mathcolor=¨#FF0000¨»=«/mo»«mfrac mathcolor=¨#FF0000¨»«mrow»«mrow mathcolor=¨#0000FF¨»«mo mathvariant=¨bold¨»[«/mo»«mstyle mathvariant=¨bold¨ displaystyle=¨true¨»«mi»kg«/mi»«/mstyle»«mo mathvariant=¨bold¨»]«/mo»«/mrow»«mo mathvariant=¨bold¨»§#183;«/mo»«mrow mathcolor=¨#0000FF¨»«mo mathvariant=¨bold¨»[«/mo»«msup»«mi mathvariant=¨bold¨»m«/mi»«mn mathvariant=¨bold¨»2«/mn»«/msup»«mo mathvariant=¨bold¨»]«/mo»«/mrow»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»§#183;«/mo»«menclose mathcolor=¨#0000FF¨ notation=¨updiagonalstrike¨»«mo mathvariant=¨bold¨»[«/mo»«mi mathvariant=¨bold¨»s«/mi»«mo mathvariant=¨bold¨»]«/mo»«/menclose»«/mrow»«mrow mathcolor=¨#0000FF¨»«mrow»«mo mathvariant=¨bold¨»[«/mo»«mi mathvariant=¨bold¨»s«/mi»«menclose notation=¨updiagonalstrike¨»«msup»«mrow»«/mrow»«mn mathvariant=¨bold¨»2«/mn»«/msup»«/menclose»«mo mathvariant=¨bold¨»]«/mo»«/mrow»«mo mathvariant=¨bold¨ mathcolor=¨#FF0000¨»§#183;«/mo»«mo mathvariant=¨bold¨»[«/mo»«mi mathvariant=¨bold¨»C«/mi»«mo mathvariant=¨bold¨»]«/mo»«/mrow»«/mfrac»«mo mathvariant=¨bold¨ mathcolor=¨#FF0000¨»=«/mo»«mfrac mathcolor=¨#FF0000¨»«mrow»«mrow mathcolor=¨#0000FF¨»«mo mathvariant=¨bold¨»[«/mo»«mstyle mathvariant=¨bold¨ displaystyle=¨true¨»«mi»kg«/mi»«/mstyle»«mo mathvariant=¨bold¨»]«/mo»«/mrow»«mo mathvariant=¨bold¨»§#183;«/mo»«mrow mathcolor=¨#0000FF¨»«mo mathvariant=¨bold¨»[«/mo»«msup»«mi mathvariant=¨bold¨»m«/mi»«mn mathvariant=¨bold¨»2«/mn»«/msup»«mo mathvariant=¨bold¨»]«/mo»«/mrow»«/mrow»«mrow mathcolor=¨#0000FF¨»«mrow»«mo mathvariant=¨bold¨»[«/mo»«mi mathvariant=¨bold¨»s«/mi»«mo mathvariant=¨bold¨»]«/mo»«/mrow»«mo mathvariant=¨bold¨ mathcolor=¨#FF0000¨»§#183;«/mo»«mo mathvariant=¨bold¨»[«/mo»«mi mathvariant=¨bold¨»C«/mi»«mo mathvariant=¨bold¨»]«/mo»«/mrow»«/mfrac»«mspace linebreak=¨newline¨»«/mspace»«mspace linebreak=¨newline¨»«/mspace»«/math»
______________________________________________________________________________________

______________________________________________________________________________________
...
«math xmlns=¨http://www.w3.org/1998/Math/MathML¨»«mo mathvariant=¨bold¨»§#8710;«/mo»«mi mathvariant=¨bold¨»§#934;«/mi»«mo mathvariant=¨bold¨»=«/mo»«mo mathvariant=¨bold¨»-«/mo»«mn mathvariant=¨bold¨»1«/mn»«mo mathvariant=¨bold¨».«/mo»«mn mathvariant=¨bold¨»5«/mn»«mo mathvariant=¨bold¨»§#183;«/mo»«msup»«mn mathvariant=¨bold¨»10«/mn»«mrow»«mo mathvariant=¨bold¨»-«/mo»«mn mathvariant=¨bold¨»4«/mn»«/mrow»«/msup»«mi mathvariant=¨bold¨»wb«/mi»«/math»
חוק פראדיי, ניתוח גרפי.
מחוק פארדיי «math xmlns=¨http://www.w3.org/1998/Math/MathML¨»«mi mathvariant=¨bold¨ mathcolor=¨#0000FF¨»§#949;«/mi»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»=«/mo»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»-«/mo»«mfrac mathcolor=¨#0000FF¨»«mrow»«mo mathvariant=¨bold¨»§#8710;«/mo»«mi mathvariant=¨bold¨»§#934;«/mi»«/mrow»«mrow»«mo mathvariant=¨bold¨»§#8710;«/mo»«mi mathvariant=¨bold¨»t«/mi»«/mrow»«/mfrac»«/math» מכפלת ערך הכא"מ בזמן שווה לשינוי השטף. בגרף המתאר את הכא"מ בתלות בזמן השטח התחום שווה לשינוי בשטף.
נחשב את גודל שינוי השטף המיוצג בשטח משבצת אחת:
«math xmlns=¨http://www.w3.org/1998/Math/MathML¨»«mmultiscripts»«mrow mathcolor=¨#0000FF¨»«mo mathvariant=¨bold¨»§#8710;«/mo»«mi mathvariant=¨bold¨»§#934;«/mi»«/mrow»«mprescripts»«/mprescripts»«mrow mathcolor=¨#0000FF¨»«mi mathvariant=¨bold¨»§#1488;§#1495;§#1514;«/mi»«mo mathvariant=¨bold¨»§#160;«/mo»«mi mathvariant=¨bold¨»§#1502;§#1513;§#1489;§#1510;§#1514;«/mi»«mo mathvariant=¨bold¨»§#160;«/mo»«/mrow»«none»«/none»«/mmultiscripts»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»=«/mo»«mn mathvariant=¨bold¨ mathcolor=¨#0000FF¨»1«/mn»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»§#183;«/mo»«msup»«mn mathvariant=¨bold¨ mathcolor=¨#0000FF¨»10«/mn»«mrow mathcolor=¨#0000FF¨»«mo mathvariant=¨bold¨»-«/mo»«mn mathvariant=¨bold¨»3«/mn»«/mrow»«/msup»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»§#183;«/mo»«mn mathvariant=¨bold¨ mathcolor=¨#0000FF¨»0«/mn»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨».«/mo»«mn mathvariant=¨bold¨ mathcolor=¨#0000FF¨»025«/mn»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»=«/mo»«mn mathvariant=¨bold¨ mathcolor=¨#0000FF¨»0«/mn»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨».«/mo»«mn mathvariant=¨bold¨ mathcolor=¨#0000FF¨»025«/mn»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»§#183;«/mo»«msup»«mn mathvariant=¨bold¨ mathcolor=¨#0000FF¨»10«/mn»«mrow mathcolor=¨#0000FF¨»«mo mathvariant=¨bold¨»-«/mo»«mn mathvariant=¨bold¨»3«/mn»«/mrow»«/msup»«mi mathvariant=¨bold¨ mathcolor=¨#0000FF¨»Wb«/mi»«/math»
נספור את מספר המשבצות התחומות בפונקציה:
בקירוב תחומות 6 משבצות בקירוב ב 0.15 השניות הראשונות. נחשב את השינוי בשטף בהתאם :
«math xmlns=¨http://www.w3.org/1998/Math/MathML¨»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»§#8710;«/mo»«mi mathvariant=¨bold¨ mathcolor=¨#0000FF¨»§#934;«/mi»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»=«/mo»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»-«/mo»«mn mathvariant=¨bold¨ mathcolor=¨#0000FF¨»6«/mn»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»§#183;«/mo»«mn mathvariant=¨bold¨ mathcolor=¨#0000FF¨»0«/mn»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨».«/mo»«mn mathvariant=¨bold¨ mathcolor=¨#0000FF¨»025«/mn»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»§#183;«/mo»«msup»«mn mathvariant=¨bold¨ mathcolor=¨#0000FF¨»10«/mn»«mrow mathcolor=¨#0000FF¨»«mo mathvariant=¨bold¨»-«/mo»«mn mathvariant=¨bold¨»3«/mn»«/mrow»«/msup»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»=«/mo»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»-«/mo»«mn mathvariant=¨bold¨ mathcolor=¨#0000FF¨»1«/mn»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨».«/mo»«mn mathvariant=¨bold¨ mathcolor=¨#0000FF¨»5«/mn»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»§#183;«/mo»«msup»«mn mathvariant=¨bold¨ mathcolor=¨#0000FF¨»10«/mn»«mrow mathcolor=¨#0000FF¨»«mo mathvariant=¨bold¨»-«/mo»«mn mathvariant=¨bold¨»4«/mn»«/mrow»«/msup»«mi mathvariant=¨bold¨ mathcolor=¨#0000FF¨»wb«/mi»«/math»
לכן, השטף המגנטי קטן ב «math xmlns=¨http://www.w3.org/1998/Math/MathML¨»«mn mathvariant=¨bold¨ mathcolor=¨#0000FF¨»1«/mn»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨».«/mo»«mn mathvariant=¨bold¨ mathcolor=¨#0000FF¨»5«/mn»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»§#183;«/mo»«msup»«mn mathvariant=¨bold¨ mathcolor=¨#0000FF¨»10«/mn»«mrow mathcolor=¨#0000FF¨»«mo mathvariant=¨bold¨»-«/mo»«mn mathvariant=¨bold¨»4«/mn»«/mrow»«/msup»«mi mathvariant=¨bold¨ mathcolor=¨#0000FF¨»wb«/mi»«/math» ב 0.15 השניות הראשונות.
נחשב את גודל שינוי השטף המיוצג בשטח משבצת אחת:
«math xmlns=¨http://www.w3.org/1998/Math/MathML¨»«mmultiscripts»«mrow mathcolor=¨#0000FF¨»«mo mathvariant=¨bold¨»§#8710;«/mo»«mi mathvariant=¨bold¨»§#934;«/mi»«/mrow»«mprescripts»«/mprescripts»«mrow mathcolor=¨#0000FF¨»«mi mathvariant=¨bold¨»§#1488;§#1495;§#1514;«/mi»«mo mathvariant=¨bold¨»§#160;«/mo»«mi mathvariant=¨bold¨»§#1502;§#1513;§#1489;§#1510;§#1514;«/mi»«mo mathvariant=¨bold¨»§#160;«/mo»«/mrow»«none»«/none»«/mmultiscripts»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»=«/mo»«mn mathvariant=¨bold¨ mathcolor=¨#0000FF¨»1«/mn»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»§#183;«/mo»«msup»«mn mathvariant=¨bold¨ mathcolor=¨#0000FF¨»10«/mn»«mrow mathcolor=¨#0000FF¨»«mo mathvariant=¨bold¨»-«/mo»«mn mathvariant=¨bold¨»3«/mn»«/mrow»«/msup»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»§#183;«/mo»«mn mathvariant=¨bold¨ mathcolor=¨#0000FF¨»0«/mn»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨».«/mo»«mn mathvariant=¨bold¨ mathcolor=¨#0000FF¨»025«/mn»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»=«/mo»«mn mathvariant=¨bold¨ mathcolor=¨#0000FF¨»0«/mn»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨».«/mo»«mn mathvariant=¨bold¨ mathcolor=¨#0000FF¨»025«/mn»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»§#183;«/mo»«msup»«mn mathvariant=¨bold¨ mathcolor=¨#0000FF¨»10«/mn»«mrow mathcolor=¨#0000FF¨»«mo mathvariant=¨bold¨»-«/mo»«mn mathvariant=¨bold¨»3«/mn»«/mrow»«/msup»«mi mathvariant=¨bold¨ mathcolor=¨#0000FF¨»Wb«/mi»«/math»
נספור את מספר המשבצות התחומות בפונקציה:
בקירוב תחומות 6 משבצות בקירוב ב 0.15 השניות הראשונות. נחשב את השינוי בשטף בהתאם :
«math xmlns=¨http://www.w3.org/1998/Math/MathML¨»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»§#8710;«/mo»«mi mathvariant=¨bold¨ mathcolor=¨#0000FF¨»§#934;«/mi»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»=«/mo»«mn mathvariant=¨bold¨ mathcolor=¨#0000FF¨»6«/mn»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»§#183;«/mo»«mn mathvariant=¨bold¨ mathcolor=¨#0000FF¨»0«/mn»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨».«/mo»«mn mathvariant=¨bold¨ mathcolor=¨#0000FF¨»025«/mn»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»§#183;«/mo»«msup»«mn mathvariant=¨bold¨ mathcolor=¨#0000FF¨»10«/mn»«mrow mathcolor=¨#0000FF¨»«mo mathvariant=¨bold¨»-«/mo»«mn mathvariant=¨bold¨»3«/mn»«/mrow»«/msup»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»=«/mo»«mn mathvariant=¨bold¨ mathcolor=¨#0000FF¨»1«/mn»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨».«/mo»«mn mathvariant=¨bold¨ mathcolor=¨#0000FF¨»5«/mn»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»§#183;«/mo»«msup»«mn mathvariant=¨bold¨ mathcolor=¨#0000FF¨»10«/mn»«mrow mathcolor=¨#0000FF¨»«mo mathvariant=¨bold¨»-«/mo»«mn mathvariant=¨bold¨»4«/mn»«/mrow»«/msup»«mi mathvariant=¨bold¨ mathcolor=¨#0000FF¨»wb«/mi»«/math»
לכן, השטף המגנטי קטן ב «math xmlns=¨http://www.w3.org/1998/Math/MathML¨»«mn mathvariant=¨bold¨ mathcolor=¨#0000FF¨»1«/mn»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨».«/mo»«mn mathvariant=¨bold¨ mathcolor=¨#0000FF¨»5«/mn»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»§#183;«/mo»«msup»«mn mathvariant=¨bold¨ mathcolor=¨#0000FF¨»10«/mn»«mrow mathcolor=¨#0000FF¨»«mo mathvariant=¨bold¨»-«/mo»«mn mathvariant=¨bold¨»4«/mn»«/mrow»«/msup»«mi mathvariant=¨bold¨ mathcolor=¨#0000FF¨»wb«/mi»«/math» ב 0.15 השניות הראשונות.
1. מאוד קל לטעות בחישוב גודל השטח המיוצג על ידי משבצת אחת. יש לשים לב היטב לערכים בשנתות ולמקדמים בצירים.
2. מהביטוי «math xmlns=¨http://www.w3.org/1998/Math/MathML¨»«mo mathvariant=¨bold¨ mathcolor=¨#FF0000¨»§#8710;«/mo»«mi mathvariant=¨bold¨ mathcolor=¨#FF0000¨»X«/mi»«mo mathvariant=¨bold¨ mathcolor=¨#FF0000¨»=«/mo»«mi mathvariant=¨bold¨ mathcolor=¨#FF0000¨»V«/mi»«mo mathvariant=¨bold¨ mathcolor=¨#FF0000¨»§#183;«/mo»«mi mathvariant=¨bold¨ mathcolor=¨#FF0000¨»t«/mi»«/math» ניתן לומר שבגרף המתאר את המהירות בתלות בזמן השטח התחום שווה לשינוי במיקום- להעתק התנועה.
באופן דומה מהביטוי: «math xmlns=¨http://www.w3.org/1998/Math/MathML¨»«mo mathvariant=¨bold¨ mathcolor=¨#FF0000¨»§#8710;«/mo»«mi mathvariant=¨bold¨ mathcolor=¨#FF0000¨»§#934;«/mi»«mo mathvariant=¨bold¨ mathcolor=¨#FF0000¨»=«/mo»«mi mathvariant=¨bold¨ mathcolor=¨#FF0000¨»§#949;«/mi»«mo mathvariant=¨bold¨ mathcolor=¨#FF0000¨»§#183;«/mo»«mo mathvariant=¨bold¨ mathcolor=¨#FF0000¨»§#8710;«/mo»«mi mathvariant=¨bold¨ mathcolor=¨#FF0000¨»t«/mi»«/math» בגרף המתאר את הכא"מ בתלות בזמן השטח התחום שווה לשינוי בשטף.
3. השינוי בשטף הוא שלילי , השטף קטן.
2. מהביטוי «math xmlns=¨http://www.w3.org/1998/Math/MathML¨»«mo mathvariant=¨bold¨ mathcolor=¨#FF0000¨»§#8710;«/mo»«mi mathvariant=¨bold¨ mathcolor=¨#FF0000¨»X«/mi»«mo mathvariant=¨bold¨ mathcolor=¨#FF0000¨»=«/mo»«mi mathvariant=¨bold¨ mathcolor=¨#FF0000¨»V«/mi»«mo mathvariant=¨bold¨ mathcolor=¨#FF0000¨»§#183;«/mo»«mi mathvariant=¨bold¨ mathcolor=¨#FF0000¨»t«/mi»«/math» ניתן לומר שבגרף המתאר את המהירות בתלות בזמן השטח התחום שווה לשינוי במיקום- להעתק התנועה.
באופן דומה מהביטוי: «math xmlns=¨http://www.w3.org/1998/Math/MathML¨»«mo mathvariant=¨bold¨ mathcolor=¨#FF0000¨»§#8710;«/mo»«mi mathvariant=¨bold¨ mathcolor=¨#FF0000¨»§#934;«/mi»«mo mathvariant=¨bold¨ mathcolor=¨#FF0000¨»=«/mo»«mi mathvariant=¨bold¨ mathcolor=¨#FF0000¨»§#949;«/mi»«mo mathvariant=¨bold¨ mathcolor=¨#FF0000¨»§#183;«/mo»«mo mathvariant=¨bold¨ mathcolor=¨#FF0000¨»§#8710;«/mo»«mi mathvariant=¨bold¨ mathcolor=¨#FF0000¨»t«/mi»«/math» בגרף המתאר את הכא"מ בתלות בזמן השטח התחום שווה לשינוי בשטף.
______________________________________________________________________________________