حلول ومنتديات لـ"ألبوم الحلول" – الدوائر الكهربائية: 1983,19- دائرة بوتانسيومتر، ودائرة مع مقاومة متغيرة - ريوستات

10. 1983,19- دائرة بوتانسيومتر، ودائرة مع مقاومة متغيرة - ريوستات

______________________________________________________________________________________

...

التيار في الدائرة (أ) أكبر بمقدار 0.144 أمبير من التيار في الدائرة (ب).

لإيجاد شدة تيار المصدر في الدائرة (أ)، يجب التعبير عن تيار المصدر من قانون أوم على الدائرة بأكملها وقانون أوم على جزء المقاومة المتغيرة التي يتدفق من خلالها تيار المصدر.

لايجاد شدة التيار بالمصدر في الدائرة (ب)، يجب ايجاد شدة التيار الذي يمر عبر المصباح.

بعد حساب شدتي تياري المصدر في كل من الدائرتين، يجب حساب الفرق بين هذين التيارين.

כדי למצוא את עוצמת המקור במעגל ב' יש למצוא את הזרם דרך הנורה.

לאחר חישוב זרמי המקור בכל אחד משני המעגלים יש לחשב את ההפרש בין זרמים אלו.

لايجاد فرق التيار بين الدائرتين، نحسب شدة التيار في كل دائرة عندما يكون المصباح مضاءً بكامل إضاءته:

احسب مقاومة المصباح اعتمادًا على فرق الجهد المخصص له وقدرته:
«math xmlns=¨http://www.w3.org/1998/Math/MathML¨»«mi mathvariant=¨bold¨ mathcolor=¨#0000FF¨»P«/mi»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»=«/mo»«mfrac mathcolor=¨#0000FF¨»«msup»«mi mathvariant=¨bold¨»U«/mi»«mn mathvariant=¨bold¨»2«/mn»«/msup»«mi mathvariant=¨bold¨»R«/mi»«/mfrac»«mspace linebreak=¨newline¨»«/mspace»«mspace linebreak=¨newline¨»«/mspace»«mi mathvariant=¨bold¨ mathcolor=¨#0000FF¨»R«/mi»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»=«/mo»«mfrac mathcolor=¨#0000FF¨»«msup»«mi mathvariant=¨bold¨»U«/mi»«mn mathvariant=¨bold¨»2«/mn»«/msup»«mi mathvariant=¨bold¨»P«/mi»«/mfrac»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»=«/mo»«mfrac mathcolor=¨#0000FF¨»«msup»«mn mathvariant=¨bold¨»4«/mn»«mn mathvariant=¨bold¨»2«/mn»«/msup»«mn mathvariant=¨bold¨»1«/mn»«/mfrac»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»=«/mo»«mn mathvariant=¨bold¨ mathcolor=¨#0000FF¨»16«/mn»«mi mathvariant=¨bold¨ mathcolor=¨#0000FF¨»§#937;«/mi»«/math»

نحسب شدة تيار المصدر في الدائرة (أ):

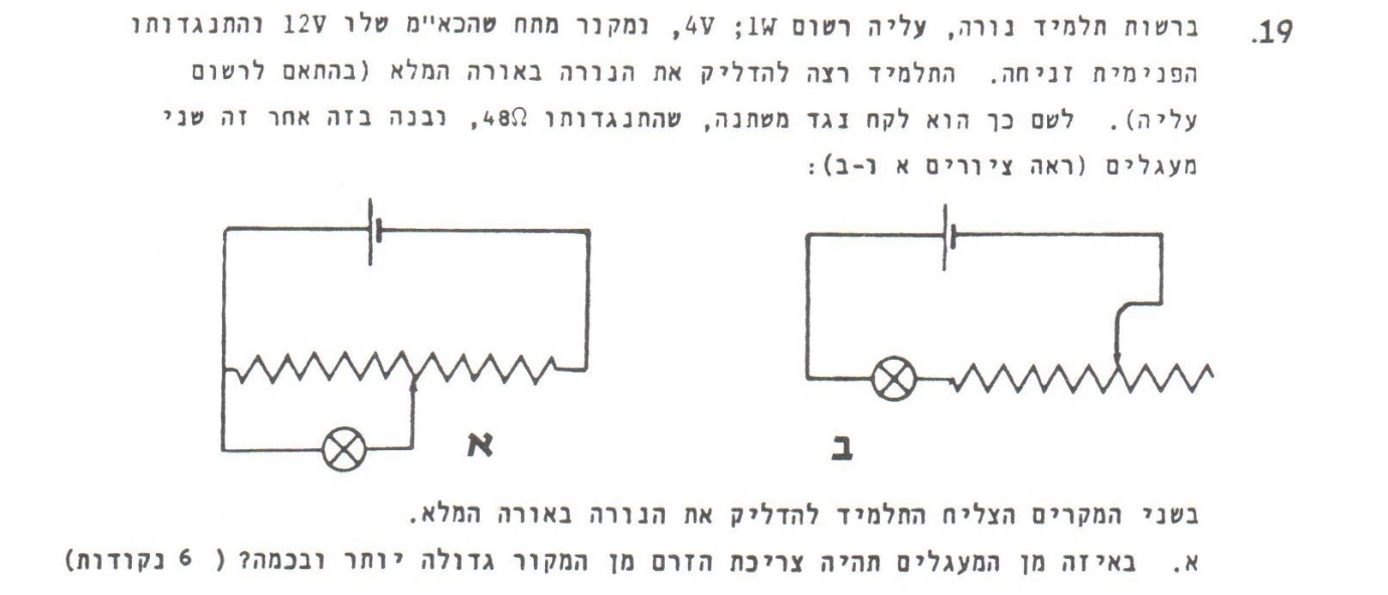
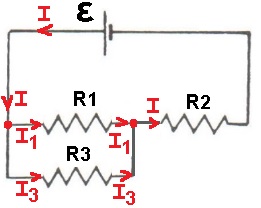
الدائرة عبارة عن دائرة مزدوجة، نقطة التماس المتحرك تُشكِّل نقطة مفترق كهربائية التي تقسم المقاومة المتغيرة إلى مقاومتين، نُشير لهاتين المقاومتين بـ R₁ و R₂. ولمقاومة المصباح بـ R₃.

نرسم الدائرة المختلطة ونضيف التيارات فيها:

يتم توصيل المقاومة R1 على التوازي مع المصباح R3، وبالتالي فإن فرق الجهد عليهما هو نفسه ويتحقق: «math xmlns=¨http://www.w3.org/1998/Math/MathML¨»«msub»«mi mathvariant=¨bold¨ mathcolor=¨#0000FF¨»U«/mi»«msub mathcolor=¨#0000FF¨»«mi mathvariant=¨bold¨»R«/mi»«mn mathvariant=¨bold¨»1«/mn»«/msub»«/msub»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»=«/mo»«msub»«mi mathvariant=¨bold¨ mathcolor=¨#0000FF¨»U«/mi»«msub mathcolor=¨#0000FF¨»«mi mathvariant=¨bold¨»R«/mi»«mn mathvariant=¨bold¨»3«/mn»«/msub»«/msub»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»=«/mo»«mn mathvariant=¨bold¨ mathcolor=¨#0000FF¨»4«/mn»«mi mathvariant=¨bold¨ mathcolor=¨#0000FF¨»V«/mi»«/math».

مجموع مقاومتي المقاومتين R1 و- R2 هو 48 أوم: «math xmlns=¨http://www.w3.org/1998/Math/MathML¨»«msub»«mi mathvariant=¨bold¨ mathcolor=¨#0000FF¨»R«/mi»«mn mathvariant=¨bold¨ mathcolor=¨#0000FF¨»1«/mn»«/msub»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»+«/mo»«msub»«mi mathvariant=¨bold¨ mathcolor=¨#0000FF¨»R«/mi»«mn mathvariant=¨bold¨ mathcolor=¨#0000FF¨»2«/mn»«/msub»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»=«/mo»«mn mathvariant=¨bold¨ mathcolor=¨#0000FF¨»48«/mn»«mi mathvariant=¨bold¨ mathcolor=¨#0000FF¨»§#937;«/mi»«/math»

ومجموع مقاومتي المقاومتين R1 و- R2 هو 12 فولط: «math xmlns=¨http://www.w3.org/1998/Math/MathML¨»«msub»«mi mathvariant=¨bold¨ mathcolor=¨#0000FF¨»U«/mi»«msub mathcolor=¨#0000FF¨»«mi mathvariant=¨bold¨»R«/mi»«mn mathvariant=¨bold¨»1«/mn»«/msub»«/msub»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»+«/mo»«msub»«mi mathvariant=¨bold¨ mathcolor=¨#0000FF¨»U«/mi»«msub mathcolor=¨#0000FF¨»«mi mathvariant=¨bold¨»R«/mi»«mn mathvariant=¨bold¨»2«/mn»«/msub»«/msub»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»=«/mo»«mn mathvariant=¨bold¨ mathcolor=¨#0000FF¨»12«/mn»«mi mathvariant=¨bold¨ mathcolor=¨#0000FF¨»V«/mi»«/math»

نحسب شدة التيار المار بالمقاومة R3 : «math style=¨font-family:`Times New Roman`¨ xmlns=¨http://www.w3.org/1998/Math/MathML¨»«mstyle mathsize=¨20px¨»«mrow»«msub»«mi mathvariant=¨bold¨ mathcolor=¨#0000FF¨»I«/mi»«mn mathvariant=¨bold¨ mathcolor=¨#0000FF¨»3«/mn»«/msub»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»=«/mo»«mfrac mathcolor=¨#0000FF¨»«msub»«mi mathvariant=¨bold¨»P«/mi»«mn mathvariant=¨bold¨»3«/mn»«/msub»«mrow»«mi mathvariant=¨bold¨»U«/mi»«msub»«mi mathvariant=¨bold¨»R«/mi»«mn mathvariant=¨bold¨»3«/mn»«/msub»«/mrow»«/mfrac»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»=«/mo»«mfrac mathcolor=¨#0000FF¨»«mn mathvariant=¨bold¨»1«/mn»«mn mathvariant=¨bold¨»4«/mn»«/mfrac»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»=«/mo»«mn mathvariant=¨bold¨ mathcolor=¨#0000FF¨»0«/mn»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨».«/mo»«mn mathvariant=¨bold¨ mathcolor=¨#0000FF¨»25«/mn»«mi mathvariant=¨bold¨ mathcolor=¨#0000FF¨»A«/mi»«/mrow»«/mstyle»«/math»

يتدفق تيار المصدر خلال R2، ونعبر عن تيار المصدر من قانون أوم على R2: :

«math style=¨font-family:`Times New Roman`¨ xmlns=¨http://www.w3.org/1998/Math/MathML¨»«mstyle mathsize=¨20px¨»«mrow»«mi mathvariant=¨bold¨ mathcolor=¨#0000FF¨»I«/mi»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»=«/mo»«mfrac mathcolor=¨#0000FF¨»«msub»«mi mathvariant=¨bold¨»U«/mi»«msub»«mi mathvariant=¨bold¨»R«/mi»«mn mathvariant=¨bold¨»2«/mn»«/msub»«/msub»«msub»«mi mathvariant=¨bold¨»R«/mi»«mn mathvariant=¨bold¨»2«/mn»«/msub»«/mfrac»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»=«/mo»«mfrac mathcolor=¨#0000FF¨»«mrow»«mn mathvariant=¨bold¨»12«/mn»«mo mathvariant=¨bold¨»-«/mo»«msub»«mi mathvariant=¨bold¨»U«/mi»«msub»«mi mathvariant=¨bold¨»R«/mi»«mn mathvariant=¨bold¨»1«/mn»«/msub»«/msub»«/mrow»«msub»«mi mathvariant=¨bold¨»R«/mi»«mn mathvariant=¨bold¨»2«/mn»«/msub»«/mfrac»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»=«/mo»«mfrac mathcolor=¨#0000FF¨»«mrow»«mn mathvariant=¨bold¨»12«/mn»«mo mathvariant=¨bold¨»-«/mo»«msub»«mi mathvariant=¨bold¨»U«/mi»«msub»«mi mathvariant=¨bold¨»R«/mi»«mn mathvariant=¨bold¨»3«/mn»«/msub»«/msub»«/mrow»«msub»«mi mathvariant=¨bold¨»R«/mi»«mn mathvariant=¨bold¨»2«/mn»«/msub»«/mfrac»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»=«/mo»«mfrac mathcolor=¨#0000FF¨»«mrow»«mn mathvariant=¨bold¨»12«/mn»«mo mathvariant=¨bold¨»-«/mo»«mn mathvariant=¨bold¨»4«/mn»«/mrow»«msub»«mi mathvariant=¨bold¨»R«/mi»«mn mathvariant=¨bold¨»2«/mn»«/msub»«/mfrac»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»=«/mo»«mfrac mathcolor=¨#0000FF¨»«mn mathvariant=¨bold¨»8«/mn»«msub»«mi mathvariant=¨bold¨»R«/mi»«mn mathvariant=¨bold¨»2«/mn»«/msub»«/mfrac»«/mrow»«/mstyle»«/math»

«math style=¨font-family:`Times New Roman`¨ xmlns=¨http://www.w3.org/1998/Math/MathML¨»«mstyle mathsize=¨20px¨»«menclose mathcolor=¨#0000FF¨ notation=¨box¨»«mi mathvariant=¨bold¨»I«/mi»«mo mathvariant=¨bold¨»=«/mo»«mfrac»«mn mathvariant=¨bold¨»8«/mn»«msub»«mi mathvariant=¨bold¨»R«/mi»«mn mathvariant=¨bold¨»2«/mn»«/msub»«/mfrac»«/menclose»«/mstyle»«/math»

نعبر عن تيار المصدر من قانون أوم للدائرة بأكملها:

نعبر عن المقاومة المحصلة أولاً::
«math xmlns=¨http://www.w3.org/1998/Math/MathML¨»«msub»«mi mathvariant=¨bold¨ mathcolor=¨#0000FF¨»R«/mi»«mi mathvariant=¨bold¨ mathcolor=¨#0000FF¨»T«/mi»«/msub»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»=«/mo»«mrow mathcolor=¨#0000FF¨»«mo mathvariant=¨bold¨»(«/mo»«msub»«mi mathvariant=¨bold¨»R«/mi»«mn mathvariant=¨bold¨»1«/mn»«/msub»«mo mathvariant=¨bold¨»§#8741;«/mo»«msub»«mi mathvariant=¨bold¨»R«/mi»«mn mathvariant=¨bold¨»3«/mn»«/msub»«mo mathvariant=¨bold¨»)«/mo»«/mrow»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»+«/mo»«msub»«mi mathvariant=¨bold¨ mathcolor=¨#0000FF¨»R«/mi»«mn mathvariant=¨bold¨ mathcolor=¨#0000FF¨»2«/mn»«/msub»«mspace linebreak=¨newline¨»«/mspace»«mspace linebreak=¨newline¨»«/mspace»«msub»«mi mathvariant=¨bold¨ mathcolor=¨#0000FF¨»R«/mi»«mi mathvariant=¨bold¨ mathcolor=¨#0000FF¨»T«/mi»«/msub»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»=«/mo»«mfrac mathcolor=¨#0000FF¨»«mrow»«msub»«mi mathvariant=¨bold¨»R«/mi»«mn mathvariant=¨bold¨»1«/mn»«/msub»«mo mathvariant=¨bold¨»§#183;«/mo»«msub»«mi mathvariant=¨bold¨»R«/mi»«mn mathvariant=¨bold¨»3«/mn»«/msub»«/mrow»«mrow»«msub»«mi mathvariant=¨bold¨»R«/mi»«mn mathvariant=¨bold¨»1«/mn»«/msub»«mo mathvariant=¨bold¨»+«/mo»«msub»«mi mathvariant=¨bold¨»R«/mi»«mn mathvariant=¨bold¨»3«/mn»«/msub»«/mrow»«/mfrac»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»+«/mo»«msub»«mi mathvariant=¨bold¨ mathcolor=¨#0000FF¨»R«/mi»«mn mathvariant=¨bold¨ mathcolor=¨#0000FF¨»2«/mn»«/msub»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»=«/mo»«mfrac mathcolor=¨#0000FF¨»«mrow»«msub»«mi mathvariant=¨bold¨»R«/mi»«mn mathvariant=¨bold¨»1«/mn»«/msub»«mo mathvariant=¨bold¨»§#183;«/mo»«mn mathvariant=¨bold¨»16«/mn»«/mrow»«mrow»«msub»«mi mathvariant=¨bold¨»R«/mi»«mn mathvariant=¨bold¨»1«/mn»«/msub»«mo mathvariant=¨bold¨»+«/mo»«mn mathvariant=¨bold¨»16«/mn»«/mrow»«/mfrac»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»+«/mo»«msub»«mi mathvariant=¨bold¨ mathcolor=¨#0000FF¨»R«/mi»«mn mathvariant=¨bold¨ mathcolor=¨#0000FF¨»2«/mn»«/msub»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»=«/mo»«mfrac mathcolor=¨#0000FF¨»«mrow»«mrow»«mo mathvariant=¨bold¨»(«/mo»«mn mathvariant=¨bold¨»48«/mn»«mo mathvariant=¨bold¨»-«/mo»«msub»«mi mathvariant=¨bold¨»R«/mi»«mn mathvariant=¨bold¨»2«/mn»«/msub»«mo mathvariant=¨bold¨»)«/mo»«/mrow»«mo mathvariant=¨bold¨»§#183;«/mo»«mn mathvariant=¨bold¨»16«/mn»«/mrow»«mrow»«mrow»«mo mathvariant=¨bold¨»(«/mo»«mn mathvariant=¨bold¨»48«/mn»«mo mathvariant=¨bold¨»-«/mo»«msub»«mi mathvariant=¨bold¨»R«/mi»«mn mathvariant=¨bold¨»2«/mn»«/msub»«mo mathvariant=¨bold¨»)«/mo»«/mrow»«mo mathvariant=¨bold¨»+«/mo»«mn mathvariant=¨bold¨»16«/mn»«/mrow»«/mfrac»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»+«/mo»«msub»«mi mathvariant=¨bold¨ mathcolor=¨#0000FF¨»R«/mi»«mn mathvariant=¨bold¨ mathcolor=¨#0000FF¨»2«/mn»«/msub»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»=«/mo»«mfrac mathcolor=¨#0000FF¨»«mrow»«mn mathvariant=¨bold¨»768«/mn»«mo mathvariant=¨bold¨»-«/mo»«mn mathvariant=¨bold¨»16«/mn»«mo mathvariant=¨bold¨»§#183;«/mo»«msub»«mi mathvariant=¨bold¨»R«/mi»«mn mathvariant=¨bold¨»2«/mn»«/msub»«/mrow»«mrow»«mn mathvariant=¨bold¨»64«/mn»«mo mathvariant=¨bold¨»-«/mo»«msub»«mi mathvariant=¨bold¨»R«/mi»«mn mathvariant=¨bold¨»2«/mn»«/msub»«/mrow»«/mfrac»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»+«/mo»«msub»«mi mathvariant=¨bold¨ mathcolor=¨#0000FF¨»R«/mi»«mn mathvariant=¨bold¨ mathcolor=¨#0000FF¨»2«/mn»«/msub»«mspace linebreak=¨newline¨»«/mspace»«/math»

نكتب قانون أوم على الدائرة بأكملها:

«math style=¨font-family:`Times New Roman`¨ xmlns=¨http://www.w3.org/1998/Math/MathML¨»«mstyle mathsize=¨20px¨»«mi mathvariant=¨bold¨ mathcolor=¨#0000FF¨»I«/mi»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»=«/mo»«mfrac mathcolor=¨#0000FF¨»«mi mathvariant=¨bold¨»§#949;«/mi»«msub»«mi mathvariant=¨bold¨»R«/mi»«mi mathvariant=¨bold-italic¨»T«/mi»«/msub»«/mfrac»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»=«/mo»«mfrac mathcolor=¨#0000FF¨»«mi mathvariant=¨bold¨»§#949;«/mi»«mrow»«mo mathvariant=¨bold¨»§#160;«/mo»«mstyle displaystyle=¨true¨»«mfrac»«mrow»«mn mathvariant=¨bold¨»768«/mn»«mo mathvariant=¨bold¨»-«/mo»«mn mathvariant=¨bold¨»16«/mn»«mo mathvariant=¨bold¨»§#183;«/mo»«msub»«mi mathvariant=¨bold¨»R«/mi»«mn mathvariant=¨bold¨»2«/mn»«/msub»«/mrow»«mrow»«mn mathvariant=¨bold¨»64«/mn»«mo mathvariant=¨bold¨»-«/mo»«msub»«mi mathvariant=¨bold¨»R«/mi»«mn mathvariant=¨bold¨»2«/mn»«/msub»«/mrow»«/mfrac»«/mstyle»«mo mathvariant=¨bold¨»+«/mo»«msub»«mi mathvariant=¨bold-italic¨»R«/mi»«mn mathvariant=¨bold¨»2«/mn»«/msub»«/mrow»«/mfrac»«mspace linebreak=¨newline¨»«/mspace»«mspace linebreak=¨newline¨»«/mspace»«mfrac mathcolor=¨#0000FF¨»«mrow»«mn mathvariant=¨bold¨»768«/mn»«mo mathvariant=¨bold¨»-«/mo»«mn mathvariant=¨bold¨»16«/mn»«mo mathvariant=¨bold¨»§#183;«/mo»«msub»«mi mathvariant=¨bold¨»R«/mi»«mn mathvariant=¨bold¨»2«/mn»«/msub»«/mrow»«mrow»«mn mathvariant=¨bold¨»64«/mn»«mo mathvariant=¨bold¨»-«/mo»«msub»«mi mathvariant=¨bold¨»R«/mi»«mn mathvariant=¨bold¨»2«/mn»«/msub»«/mrow»«/mfrac»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»+«/mo»«msub»«mi mathvariant=¨bold-italic¨ mathcolor=¨#0000FF¨»R«/mi»«mn mathvariant=¨bold¨ mathcolor=¨#0000FF¨»2«/mn»«/msub»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»=«/mo»«mfrac mathcolor=¨#0000FF¨»«mi mathvariant=¨bold¨»§#949;«/mi»«mi mathvariant=¨bold¨»I«/mi»«/mfrac»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»=«/mo»«mfrac mathcolor=¨#0000FF¨»«mn mathvariant=¨bold¨»12«/mn»«mi mathvariant=¨bold¨»I«/mi»«/mfrac»«mspace linebreak=¨newline¨»«/mspace»«mspace linebreak=¨newline¨»«/mspace»«menclose mathcolor=¨#0000FF¨ notation=¨box¨»«mfrac»«mrow»«mn mathvariant=¨bold¨»768«/mn»«mo mathvariant=¨bold¨»-«/mo»«mn mathvariant=¨bold¨»16«/mn»«mo mathvariant=¨bold¨»§#183;«/mo»«msub»«mi mathvariant=¨bold¨»R«/mi»«mn mathvariant=¨bold¨»2«/mn»«/msub»«/mrow»«mrow»«mn mathvariant=¨bold¨»64«/mn»«mo mathvariant=¨bold¨»-«/mo»«msub»«mi mathvariant=¨bold¨»R«/mi»«mn mathvariant=¨bold¨»2«/mn»«/msub»«/mrow»«/mfrac»«mo mathvariant=¨bold¨»+«/mo»«msub»«mi mathvariant=¨bold¨»R«/mi»«mn mathvariant=¨bold¨»2«/mn»«/msub»«mo mathvariant=¨bold¨»=«/mo»«mfrac»«mn mathvariant=¨bold¨»12«/mn»«mi mathvariant=¨bold¨»I«/mi»«/mfrac»«/menclose»«mspace linebreak=¨newline¨»«/mspace»«mspace linebreak=¨newline¨»«/mspace»«/mstyle»«/math»

حصلنا على معادلتين في مجهولين، سنقوم بإيجاد تيار المصدر من خلال حل هذه المعادلات:

«math style=¨font-family:`Times New Roman`¨ xmlns=¨http://www.w3.org/1998/Math/MathML¨»«mstyle mathsize=¨20px¨»«menclose mathcolor=¨#0000FF¨ notation=¨box¨»«mfrac»«mrow»«mn mathvariant=¨bold¨»768«/mn»«mo mathvariant=¨bold¨»-«/mo»«mn mathvariant=¨bold¨»16«/mn»«mo mathvariant=¨bold¨»§#183;«/mo»«msub»«mi mathvariant=¨bold¨»R«/mi»«mn mathvariant=¨bold¨»2«/mn»«/msub»«/mrow»«mrow»«mn mathvariant=¨bold¨»64«/mn»«mo mathvariant=¨bold¨»-«/mo»«msub»«mi mathvariant=¨bold¨»R«/mi»«mn mathvariant=¨bold¨»2«/mn»«/msub»«/mrow»«/mfrac»«mo mathvariant=¨bold¨»+«/mo»«msub»«mi mathvariant=¨bold¨»R«/mi»«mn mathvariant=¨bold¨»2«/mn»«/msub»«mo mathvariant=¨bold¨»=«/mo»«mfrac»«mn mathvariant=¨bold¨»12«/mn»«mi mathvariant=¨bold¨»I«/mi»«/mfrac»«/menclose»«mspace linebreak=¨newline¨»«/mspace»«mspace linebreak=¨newline¨»«/mspace»«menclose mathcolor=¨#0000FF¨ notation=¨box¨»«mi mathvariant=¨bold¨»I«/mi»«mo mathvariant=¨bold¨»=«/mo»«mfrac»«mn mathvariant=¨bold¨»8«/mn»«msub»«mi mathvariant=¨bold¨»R«/mi»«mn mathvariant=¨bold¨»2«/mn»«/msub»«/mfrac»«/menclose»«mo»§#160;«/mo»«mo»§#8658;«/mo»«msub»«mi mathvariant=¨bold¨ mathcolor=¨#FF0000¨»R«/mi»«mn mathvariant=¨bold¨ mathcolor=¨#FF0000¨»2«/mn»«/msub»«mo mathvariant=¨bold¨ mathcolor=¨#FF0000¨»=«/mo»«mfrac mathcolor=¨#FF0000¨»«mn mathvariant=¨bold¨»8«/mn»«mi mathvariant=¨bold¨»I«/mi»«/mfrac»«mspace linebreak=¨newline¨»«/mspace»«mspace linebreak=¨newline¨»«/mspace»«mspace linebreak=¨newline¨»«/mspace»«mfrac mathcolor=¨#0000FF¨»«mrow»«mn mathvariant=¨bold¨»768«/mn»«mo mathvariant=¨bold¨»-«/mo»«mn mathvariant=¨bold¨»16«/mn»«mo mathvariant=¨bold¨»§#183;«/mo»«mfrac mathcolor=¨#FF0000¨»«mn mathvariant=¨bold¨»8«/mn»«mi mathvariant=¨bold¨»I«/mi»«/mfrac»«/mrow»«mrow»«mn mathvariant=¨bold¨»64«/mn»«mo mathvariant=¨bold¨»-«/mo»«mfrac mathcolor=¨#FF0000¨»«mn mathvariant=¨bold¨»8«/mn»«mi mathvariant=¨bold¨»I«/mi»«/mfrac»«/mrow»«/mfrac»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»+«/mo»«mfrac mathcolor=¨#FF0000¨»«mn mathvariant=¨bold¨»8«/mn»«mi mathvariant=¨bold¨»I«/mi»«/mfrac»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»=«/mo»«mfrac mathcolor=¨#0000FF¨»«mn mathvariant=¨bold¨»12«/mn»«mi mathvariant=¨bold¨»I«/mi»«/mfrac»«/mstyle»«/math»
نضرب كل من البسط والمقام في تيار المصدر:

«math style=¨font-family:`Times New Roman`¨ xmlns=¨http://www.w3.org/1998/Math/MathML¨»«mstyle mathsize=¨20px¨»«mfrac mathcolor=¨#0000FF¨»«mrow»«mn mathvariant=¨bold¨»768«/mn»«mo mathvariant=¨bold¨»§#183;«/mo»«mi mathvariant=¨bold¨»I«/mi»«mo mathvariant=¨bold¨»-«/mo»«mn mathvariant=¨bold¨»16«/mn»«mo mathvariant=¨bold¨»§#183;«/mo»«mn mathvariant=¨bold¨»8«/mn»«/mrow»«mrow»«mn mathvariant=¨bold¨»64«/mn»«mo mathvariant=¨bold¨»§#183;«/mo»«mi mathvariant=¨bold¨»I«/mi»«mo mathvariant=¨bold¨»-«/mo»«mn mathvariant=¨bold¨»8«/mn»«/mrow»«/mfrac»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»+«/mo»«mfrac mathcolor=¨#0000FF¨»«mn mathvariant=¨bold¨»8«/mn»«mi mathvariant=¨bold¨»I«/mi»«/mfrac»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»=«/mo»«mfrac mathcolor=¨#0000FF¨»«mn mathvariant=¨bold¨»12«/mn»«mi mathvariant=¨bold¨»I«/mi»«/mfrac»«mspace linebreak=¨newline¨»«/mspace»«mspace linebreak=¨newline¨»«/mspace»«mfrac mathcolor=¨#0000FF¨»«mrow»«mn mathvariant=¨bold¨»768«/mn»«mo mathvariant=¨bold¨»§#183;«/mo»«mi mathvariant=¨bold¨»I«/mi»«mo mathvariant=¨bold¨»-«/mo»«mn mathvariant=¨bold¨»128«/mn»«/mrow»«mrow»«mn mathvariant=¨bold¨»64«/mn»«mo mathvariant=¨bold¨»§#183;«/mo»«mi mathvariant=¨bold¨»I«/mi»«mo mathvariant=¨bold¨»-«/mo»«mn mathvariant=¨bold¨»8«/mn»«/mrow»«/mfrac»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»+«/mo»«mfrac mathcolor=¨#0000FF¨»«mn mathvariant=¨bold¨»8«/mn»«mi mathvariant=¨bold¨»I«/mi»«/mfrac»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»=«/mo»«mfrac mathcolor=¨#0000FF¨»«mn mathvariant=¨bold¨»12«/mn»«mi mathvariant=¨bold¨»I«/mi»«/mfrac»«/mstyle»«/math»

نضرب كل المعادلة في تيار المصدر:

«math style=¨font-family:`Times New Roman`¨ xmlns=¨http://www.w3.org/1998/Math/MathML¨»«mstyle mathsize=¨20px¨»«mspace linebreak=¨newline¨»«/mspace»«mfrac mathcolor=¨#0000FF¨»«mrow»«mi mathvariant=¨bold¨»I«/mi»«mo mathvariant=¨bold¨»§#183;«/mo»«mrow»«mo mathvariant=¨bold¨»(«/mo»«mn mathvariant=¨bold¨»768«/mn»«mo mathvariant=¨bold¨»§#183;«/mo»«mi mathvariant=¨bold¨»I«/mi»«mo mathvariant=¨bold¨»-«/mo»«mn mathvariant=¨bold¨»128«/mn»«mo mathvariant=¨bold¨»)«/mo»«/mrow»«/mrow»«mrow»«mn mathvariant=¨bold¨»64«/mn»«mo mathvariant=¨bold¨»§#183;«/mo»«mi mathvariant=¨bold¨»I«/mi»«mo mathvariant=¨bold¨»-«/mo»«mn mathvariant=¨bold¨»8«/mn»«/mrow»«/mfrac»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»+«/mo»«mn mathvariant=¨bold¨ mathcolor=¨#0000FF¨»8«/mn»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»=«/mo»«mn mathvariant=¨bold¨ mathcolor=¨#0000FF¨»12«/mn»«mspace linebreak=¨newline¨»«/mspace»«mi mathvariant=¨bold¨ mathcolor=¨#0000FF¨»I«/mi»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»§#183;«/mo»«mrow mathcolor=¨#0000FF¨»«mo mathvariant=¨bold¨»(«/mo»«mn mathvariant=¨bold¨»768«/mn»«mo mathvariant=¨bold¨»§#183;«/mo»«mi mathvariant=¨bold¨»I«/mi»«mo mathvariant=¨bold¨»-«/mo»«mn mathvariant=¨bold¨»128«/mn»«mo mathvariant=¨bold¨»)«/mo»«/mrow»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»=«/mo»«mn mathvariant=¨bold¨ mathcolor=¨#0000FF¨»4«/mn»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»§#183;«/mo»«mrow mathcolor=¨#0000FF¨»«mo mathvariant=¨bold¨»(«/mo»«mn mathvariant=¨bold¨»64«/mn»«mo mathvariant=¨bold¨»§#183;«/mo»«mi mathvariant=¨bold¨»I«/mi»«mo mathvariant=¨bold¨»-«/mo»«mn mathvariant=¨bold¨»8«/mn»«mo mathvariant=¨bold¨»)«/mo»«/mrow»«mspace linebreak=¨newline¨»«/mspace»«mspace linebreak=¨newline¨»«/mspace»«mn mathvariant=¨bold¨ mathcolor=¨#0000FF¨»768«/mn»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»§#183;«/mo»«msup»«mi mathvariant=¨bold¨ mathcolor=¨#0000FF¨»I«/mi»«mn mathvariant=¨bold¨ mathcolor=¨#0000FF¨»2«/mn»«/msup»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»-«/mo»«mn mathvariant=¨bold¨ mathcolor=¨#0000FF¨»128«/mn»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»§#183;«/mo»«mi mathvariant=¨bold¨ mathcolor=¨#0000FF¨»I«/mi»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»=«/mo»«mn mathvariant=¨bold¨ mathcolor=¨#0000FF¨»256«/mn»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»§#183;«/mo»«mi mathvariant=¨bold¨ mathcolor=¨#0000FF¨»I«/mi»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»-«/mo»«mn mathvariant=¨bold¨ mathcolor=¨#0000FF¨»32«/mn»«mspace linebreak=¨newline¨»«/mspace»«mspace linebreak=¨newline¨»«/mspace»«mn mathvariant=¨bold¨ mathcolor=¨#0000FF¨»768«/mn»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»§#183;«/mo»«msup»«mi mathvariant=¨bold¨ mathcolor=¨#0000FF¨»I«/mi»«mn mathvariant=¨bold¨ mathcolor=¨#0000FF¨»2«/mn»«/msup»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»-«/mo»«mn mathvariant=¨bold¨ mathcolor=¨#0000FF¨»384«/mn»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»§#183;«/mo»«mi mathvariant=¨bold¨ mathcolor=¨#0000FF¨»I«/mi»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»+«/mo»«mn mathvariant=¨bold¨ mathcolor=¨#0000FF¨»32«/mn»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»=«/mo»«mn mathvariant=¨bold¨ mathcolor=¨#0000FF¨»0«/mn»«/mstyle»«/math»

حصلنا على معادلة تربيعية، وسوف نقوم بحل المعادلة:

«math style=¨font-family:`Times New Roman`¨ xmlns=¨http://www.w3.org/1998/Math/MathML¨»«mstyle mathsize=¨20px¨»«mn mathvariant=¨bold¨ mathcolor=¨#0000FF¨»768«/mn»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»§#183;«/mo»«msup»«mi mathvariant=¨bold¨ mathcolor=¨#0000FF¨»I«/mi»«mn mathvariant=¨bold¨ mathcolor=¨#0000FF¨»2«/mn»«/msup»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»-«/mo»«mn mathvariant=¨bold¨ mathcolor=¨#0000FF¨»384«/mn»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»§#183;«/mo»«mi mathvariant=¨bold¨ mathcolor=¨#0000FF¨»I«/mi»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»+«/mo»«mn mathvariant=¨bold¨ mathcolor=¨#0000FF¨»32«/mn»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»=«/mo»«mn mathvariant=¨bold¨ mathcolor=¨#0000FF¨»0«/mn»«mspace linebreak=¨newline¨»«/mspace»«mspace linebreak=¨newline¨»«/mspace»«msub»«mi mathvariant=¨bold¨ mathcolor=¨#0000FF¨»I«/mi»«mrow mathcolor=¨#0000FF¨»«mn mathvariant=¨bold¨»1«/mn»«mo mathvariant=¨bold¨»,«/mo»«mn mathvariant=¨bold¨»2«/mn»«/mrow»«/msub»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»=«/mo»«mfrac mathcolor=¨#0000FF¨»«mrow»«mn mathvariant=¨bold¨»384«/mn»«mo mathvariant=¨bold¨»§#177;«/mo»«msqrt»«msup»«mn mathvariant=¨bold¨»384«/mn»«mn mathvariant=¨bold¨»2«/mn»«/msup»«mo mathvariant=¨bold¨»-«/mo»«mn mathvariant=¨bold¨»4«/mn»«mo mathvariant=¨bold¨»§#183;«/mo»«mn mathvariant=¨bold¨»768«/mn»«mo mathvariant=¨bold¨»§#183;«/mo»«mn mathvariant=¨bold¨»32«/mn»«/msqrt»«/mrow»«mrow»«mn mathvariant=¨bold¨»2«/mn»«mo mathvariant=¨bold¨»§#183;«/mo»«mn mathvariant=¨bold¨»768«/mn»«/mrow»«/mfrac»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»=«/mo»«mfrac mathcolor=¨#0000FF¨»«mrow»«mn mathvariant=¨bold¨»384«/mn»«mo mathvariant=¨bold¨»§#177;«/mo»«msqrt»«mn mathvariant=¨bold¨»49«/mn»«mo mathvariant=¨bold¨»,«/mo»«mn mathvariant=¨bold¨»152«/mn»«/msqrt»«/mrow»«mrow»«mn mathvariant=¨bold¨»2«/mn»«mo mathvariant=¨bold¨»§#183;«/mo»«mn mathvariant=¨bold¨»768«/mn»«/mrow»«/mfrac»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»=«/mo»«mfrac mathcolor=¨#0000FF¨»«mrow»«mn mathvariant=¨bold¨»384«/mn»«mo mathvariant=¨bold¨»§#177;«/mo»«mn mathvariant=¨bold¨»221«/mn»«mo mathvariant=¨bold¨».«/mo»«mn mathvariant=¨bold¨»7«/mn»«/mrow»«mn mathvariant=¨bold¨»1536«/mn»«/mfrac»«mspace linebreak=¨newline¨»«/mspace»«mspace linebreak=¨newline¨»«/mspace»«msub»«mi mathvariant=¨bold¨ mathcolor=¨#0000FF¨»I«/mi»«mn mathvariant=¨bold¨ mathcolor=¨#0000FF¨»1«/mn»«/msub»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»=«/mo»«mn mathvariant=¨bold¨ mathcolor=¨#0000FF¨»0«/mn»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨».«/mo»«mn mathvariant=¨bold¨ mathcolor=¨#0000FF¨»394«/mn»«mi mathvariant=¨bold¨ mathcolor=¨#0000FF¨»A«/mi»«mspace linebreak=¨newline¨»«/mspace»«mspace linebreak=¨newline¨»«/mspace»«msub»«mi mathvariant=¨bold¨ mathcolor=¨#0000FF¨»I«/mi»«mn mathvariant=¨bold¨ mathcolor=¨#0000FF¨»2«/mn»«/msub»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»=«/mo»«mn mathvariant=¨bold¨ mathcolor=¨#0000FF¨»0«/mn»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨».«/mo»«mn mathvariant=¨bold¨ mathcolor=¨#0000FF¨»1«/mn»«mi mathvariant=¨bold¨ mathcolor=¨#0000FF¨»A«/mi»«/mstyle»«/math»

التيار المار عبر المصباح هو 0.25A (محسوب في بداية الحل). يجب أن يكون تيارالمصدر أكبر.
وبالتالي فإن شدة تيار المصدر في الدائرة "أ" هي 0.394A.

نحسب شدة التيار المار في الدائرة "ب".
الدائرة "ب" عبارة عن دائرة على التوالي، عندما يُضاء المصباح بكامل الإضاءة، يكون التيار المار عبره 0.25A، وهو التيار المار عبر المصدر في الدائرة "أ".

نحسب الفرق في تياري المصدر للدائرتين:
«math style=¨font-family:`Times New Roman`¨ xmlns=¨http://www.w3.org/1998/Math/MathML¨»«mstyle mathsize=¨20px¨»«mrow»«msub»«mi mathvariant=¨bold¨ mathcolor=¨#0000FF¨»I«/mi»«mi mathvariant=¨bold¨ mathcolor=¨#0000FF¨»§#1489;«/mi»«/msub»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»-«/mo»«msub»«mi mathvariant=¨bold¨ mathcolor=¨#0000FF¨»I«/mi»«mi mathvariant=¨bold¨ mathcolor=¨#0000FF¨»§#1488;«/mi»«/msub»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»=«/mo»«mn mathvariant=¨bold¨ mathcolor=¨#0000FF¨»0«/mn»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨».«/mo»«mn mathvariant=¨bold¨ mathcolor=¨#0000FF¨»394«/mn»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»-«/mo»«mn mathvariant=¨bold¨ mathcolor=¨#0000FF¨»0«/mn»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨».«/mo»«mn mathvariant=¨bold¨ mathcolor=¨#0000FF¨»25«/mn»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»=«/mo»«mn mathvariant=¨bold¨ mathcolor=¨#0000FF¨»0«/mn»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨».«/mo»«mn mathvariant=¨bold¨ mathcolor=¨#0000FF¨»144«/mn»«mi mathvariant=¨bold¨ mathcolor=¨#0000FF¨»A«/mi»«/mrow»«/mstyle»«/math»

خلاصة القول، التيار في الدائرة "أ" أكبر بمقدار 0.144 أمبير من التيار في الدائرة "ب".

נחשב את התנגדות הנורה, בהתאם למתח אליו היא מיועדת ולהספקה:

«math xmlns=¨http://www.w3.org/1998/Math/MathML¨»«mi mathvariant=¨bold¨ mathcolor=¨#0000FF¨»P«/mi»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»=«/mo»«mfrac mathcolor=¨#0000FF¨»«msup»«mi mathvariant=¨bold¨»U«/mi»«mn mathvariant=¨bold¨»2«/mn»«/msup»«mi mathvariant=¨bold¨»R«/mi»«/mfrac»«mspace linebreak=¨newline¨»«/mspace»«mspace linebreak=¨newline¨»«/mspace»«mi mathvariant=¨bold¨ mathcolor=¨#0000FF¨»R«/mi»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»=«/mo»«mfrac mathcolor=¨#0000FF¨»«msup»«mi mathvariant=¨bold¨»U«/mi»«mn mathvariant=¨bold¨»2«/mn»«/msup»«mi mathvariant=¨bold¨»P«/mi»«/mfrac»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»=«/mo»«mfrac mathcolor=¨#0000FF¨»«msup»«mn mathvariant=¨bold¨»4«/mn»«mn mathvariant=¨bold¨»2«/mn»«/msup»«mn mathvariant=¨bold¨»1«/mn»«/mfrac»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»=«/mo»«mn mathvariant=¨bold¨ mathcolor=¨#0000FF¨»16«/mn»«mi mathvariant=¨bold¨ mathcolor=¨#0000FF¨»§#937;«/mi»«/math»

נמצא את עוצמת זרם המקור במעגל א':

המעגל הוא מעגל מעורב נקודת חיבור הגררה היא נקודת צומת חשמלית המחלקת את הנגד המשתנה לשני נגדים , נגדיר נגדים אלו כ R1 ו- R2. ואת הנורה כנגד R3.

נסרטט את המעגל המעורב ונוסיף בו את הזרמים :

הנגד R1 מחובר במקביל לנורה R3, לכן המתח עליהם הוא זהה ומתקיים : «math xmlns=¨http://www.w3.org/1998/Math/MathML¨»«msub»«mi mathvariant=¨bold¨ mathcolor=¨#0000FF¨»U«/mi»«msub mathcolor=¨#0000FF¨»«mi mathvariant=¨bold¨»R«/mi»«mn mathvariant=¨bold¨»1«/mn»«/msub»«/msub»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»=«/mo»«msub»«mi mathvariant=¨bold¨ mathcolor=¨#0000FF¨»U«/mi»«msub mathcolor=¨#0000FF¨»«mi mathvariant=¨bold¨»R«/mi»«mn mathvariant=¨bold¨»3«/mn»«/msub»«/msub»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»=«/mo»«mn mathvariant=¨bold¨ mathcolor=¨#0000FF¨»4«/mn»«mi mathvariant=¨bold¨ mathcolor=¨#0000FF¨»V«/mi»«/math».

סכום התנגדויות הנגדים R1 ו- R2 הוא 48 אום: «math xmlns=¨http://www.w3.org/1998/Math/MathML¨»«msub»«mi mathvariant=¨bold¨ mathcolor=¨#0000FF¨»R«/mi»«mn mathvariant=¨bold¨ mathcolor=¨#0000FF¨»1«/mn»«/msub»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»+«/mo»«msub»«mi mathvariant=¨bold¨ mathcolor=¨#0000FF¨»R«/mi»«mn mathvariant=¨bold¨ mathcolor=¨#0000FF¨»2«/mn»«/msub»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»=«/mo»«mn mathvariant=¨bold¨ mathcolor=¨#0000FF¨»48«/mn»«mi mathvariant=¨bold¨ mathcolor=¨#0000FF¨»§#937;«/mi»«/math»

וסכום המתחים על נגדים R1 ו- R2 הוא 12 וולט: «math xmlns=¨http://www.w3.org/1998/Math/MathML¨»«msub»«mi mathvariant=¨bold¨ mathcolor=¨#0000FF¨»U«/mi»«msub mathcolor=¨#0000FF¨»«mi mathvariant=¨bold¨»R«/mi»«mn mathvariant=¨bold¨»1«/mn»«/msub»«/msub»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»+«/mo»«msub»«mi mathvariant=¨bold¨ mathcolor=¨#0000FF¨»U«/mi»«msub mathcolor=¨#0000FF¨»«mi mathvariant=¨bold¨»R«/mi»«mn mathvariant=¨bold¨»2«/mn»«/msub»«/msub»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»=«/mo»«mn mathvariant=¨bold¨ mathcolor=¨#0000FF¨»12«/mn»«mi mathvariant=¨bold¨ mathcolor=¨#0000FF¨»V«/mi»«/math»

נחשב את הזרם דרך R3 : «math style=¨font-family:`Times New Roman`¨ xmlns=¨http://www.w3.org/1998/Math/MathML¨»«mstyle mathsize=¨20px¨»«mrow»«msub»«mi mathvariant=¨bold¨ mathcolor=¨#0000FF¨»I«/mi»«mn mathvariant=¨bold¨ mathcolor=¨#0000FF¨»3«/mn»«/msub»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»=«/mo»«mfrac mathcolor=¨#0000FF¨»«msub»«mi mathvariant=¨bold¨»P«/mi»«mn mathvariant=¨bold¨»3«/mn»«/msub»«mrow»«mi mathvariant=¨bold¨»U«/mi»«msub»«mi mathvariant=¨bold¨»R«/mi»«mn mathvariant=¨bold¨»3«/mn»«/msub»«/mrow»«/mfrac»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»=«/mo»«mfrac mathcolor=¨#0000FF¨»«mn mathvariant=¨bold¨»1«/mn»«mn mathvariant=¨bold¨»4«/mn»«/mfrac»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»=«/mo»«mn mathvariant=¨bold¨ mathcolor=¨#0000FF¨»0«/mn»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨».«/mo»«mn mathvariant=¨bold¨ mathcolor=¨#0000FF¨»25«/mn»«mi mathvariant=¨bold¨ mathcolor=¨#0000FF¨»A«/mi»«/mrow»«/mstyle»«/math»

זרם המקור זורם דרך R2 , נבטא את זרם המקור מחוק אום על R2:

«math style=¨font-family:`Times New Roman`¨ xmlns=¨http://www.w3.org/1998/Math/MathML¨»«mstyle mathsize=¨20px¨»«mrow»«mi mathvariant=¨bold¨ mathcolor=¨#0000FF¨»I«/mi»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»=«/mo»«mfrac mathcolor=¨#0000FF¨»«msub»«mi mathvariant=¨bold¨»U«/mi»«msub»«mi mathvariant=¨bold¨»R«/mi»«mn mathvariant=¨bold¨»2«/mn»«/msub»«/msub»«msub»«mi mathvariant=¨bold¨»R«/mi»«mn mathvariant=¨bold¨»2«/mn»«/msub»«/mfrac»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»=«/mo»«mfrac mathcolor=¨#0000FF¨»«mrow»«mn mathvariant=¨bold¨»12«/mn»«mo mathvariant=¨bold¨»-«/mo»«msub»«mi mathvariant=¨bold¨»U«/mi»«msub»«mi mathvariant=¨bold¨»R«/mi»«mn mathvariant=¨bold¨»1«/mn»«/msub»«/msub»«/mrow»«msub»«mi mathvariant=¨bold¨»R«/mi»«mn mathvariant=¨bold¨»2«/mn»«/msub»«/mfrac»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»=«/mo»«mfrac mathcolor=¨#0000FF¨»«mrow»«mn mathvariant=¨bold¨»12«/mn»«mo mathvariant=¨bold¨»-«/mo»«msub»«mi mathvariant=¨bold¨»U«/mi»«msub»«mi mathvariant=¨bold¨»R«/mi»«mn mathvariant=¨bold¨»3«/mn»«/msub»«/msub»«/mrow»«msub»«mi mathvariant=¨bold¨»R«/mi»«mn mathvariant=¨bold¨»2«/mn»«/msub»«/mfrac»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»=«/mo»«mfrac mathcolor=¨#0000FF¨»«mrow»«mn mathvariant=¨bold¨»12«/mn»«mo mathvariant=¨bold¨»-«/mo»«mn mathvariant=¨bold¨»4«/mn»«/mrow»«msub»«mi mathvariant=¨bold¨»R«/mi»«mn mathvariant=¨bold¨»2«/mn»«/msub»«/mfrac»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»=«/mo»«mfrac mathcolor=¨#0000FF¨»«mn mathvariant=¨bold¨»8«/mn»«msub»«mi mathvariant=¨bold¨»R«/mi»«mn mathvariant=¨bold¨»2«/mn»«/msub»«/mfrac»«/mrow»«/mstyle»«/math»

נבטא את זרם המקור מחוק אום על כל המעגל:

נבטא תחילה את ההתנגדות השקולה:

«math xmlns=¨http://www.w3.org/1998/Math/MathML¨»«msub»«mi mathvariant=¨bold¨ mathcolor=¨#0000FF¨»R«/mi»«mi mathvariant=¨bold¨ mathcolor=¨#0000FF¨»T«/mi»«/msub»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»=«/mo»«mrow mathcolor=¨#0000FF¨»«mo mathvariant=¨bold¨»(«/mo»«msub»«mi mathvariant=¨bold¨»R«/mi»«mn mathvariant=¨bold¨»1«/mn»«/msub»«mo mathvariant=¨bold¨»§#8741;«/mo»«msub»«mi mathvariant=¨bold¨»R«/mi»«mn mathvariant=¨bold¨»3«/mn»«/msub»«mo mathvariant=¨bold¨»)«/mo»«/mrow»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»+«/mo»«msub»«mi mathvariant=¨bold¨ mathcolor=¨#0000FF¨»R«/mi»«mn mathvariant=¨bold¨ mathcolor=¨#0000FF¨»2«/mn»«/msub»«mspace linebreak=¨newline¨»«/mspace»«mspace linebreak=¨newline¨»«/mspace»«msub»«mi mathvariant=¨bold¨ mathcolor=¨#0000FF¨»R«/mi»«mi mathvariant=¨bold¨ mathcolor=¨#0000FF¨»T«/mi»«/msub»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»=«/mo»«mfrac mathcolor=¨#0000FF¨»«mrow»«msub»«mi mathvariant=¨bold¨»R«/mi»«mn mathvariant=¨bold¨»1«/mn»«/msub»«mo mathvariant=¨bold¨»§#183;«/mo»«msub»«mi mathvariant=¨bold¨»R«/mi»«mn mathvariant=¨bold¨»3«/mn»«/msub»«/mrow»«mrow»«msub»«mi mathvariant=¨bold¨»R«/mi»«mn mathvariant=¨bold¨»1«/mn»«/msub»«mo mathvariant=¨bold¨»+«/mo»«msub»«mi mathvariant=¨bold¨»R«/mi»«mn mathvariant=¨bold¨»3«/mn»«/msub»«/mrow»«/mfrac»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»+«/mo»«msub»«mi mathvariant=¨bold¨ mathcolor=¨#0000FF¨»R«/mi»«mn mathvariant=¨bold¨ mathcolor=¨#0000FF¨»2«/mn»«/msub»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»=«/mo»«mfrac mathcolor=¨#0000FF¨»«mrow»«msub»«mi mathvariant=¨bold¨»R«/mi»«mn mathvariant=¨bold¨»1«/mn»«/msub»«mo mathvariant=¨bold¨»§#183;«/mo»«mn mathvariant=¨bold¨»16«/mn»«/mrow»«mrow»«msub»«mi mathvariant=¨bold¨»R«/mi»«mn mathvariant=¨bold¨»1«/mn»«/msub»«mo mathvariant=¨bold¨»+«/mo»«mn mathvariant=¨bold¨»16«/mn»«/mrow»«/mfrac»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»+«/mo»«msub»«mi mathvariant=¨bold¨ mathcolor=¨#0000FF¨»R«/mi»«mn mathvariant=¨bold¨ mathcolor=¨#0000FF¨»2«/mn»«/msub»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»=«/mo»«mfrac mathcolor=¨#0000FF¨»«mrow»«mrow»«mo mathvariant=¨bold¨»(«/mo»«mn mathvariant=¨bold¨»48«/mn»«mo mathvariant=¨bold¨»-«/mo»«msub»«mi mathvariant=¨bold¨»R«/mi»«mn mathvariant=¨bold¨»2«/mn»«/msub»«mo mathvariant=¨bold¨»)«/mo»«/mrow»«mo mathvariant=¨bold¨»§#183;«/mo»«mn mathvariant=¨bold¨»16«/mn»«/mrow»«mrow»«mrow»«mo mathvariant=¨bold¨»(«/mo»«mn mathvariant=¨bold¨»48«/mn»«mo mathvariant=¨bold¨»-«/mo»«msub»«mi mathvariant=¨bold¨»R«/mi»«mn mathvariant=¨bold¨»2«/mn»«/msub»«mo mathvariant=¨bold¨»)«/mo»«/mrow»«mo mathvariant=¨bold¨»+«/mo»«mn mathvariant=¨bold¨»16«/mn»«/mrow»«/mfrac»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»+«/mo»«msub»«mi mathvariant=¨bold¨ mathcolor=¨#0000FF¨»R«/mi»«mn mathvariant=¨bold¨ mathcolor=¨#0000FF¨»2«/mn»«/msub»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»=«/mo»«mfrac mathcolor=¨#0000FF¨»«mrow»«mn mathvariant=¨bold¨»768«/mn»«mo mathvariant=¨bold¨»-«/mo»«mn mathvariant=¨bold¨»16«/mn»«mo mathvariant=¨bold¨»§#183;«/mo»«msub»«mi mathvariant=¨bold¨»R«/mi»«mn mathvariant=¨bold¨»2«/mn»«/msub»«/mrow»«mrow»«mn mathvariant=¨bold¨»64«/mn»«mo mathvariant=¨bold¨»-«/mo»«msub»«mi mathvariant=¨bold¨»R«/mi»«mn mathvariant=¨bold¨»2«/mn»«/msub»«/mrow»«/mfrac»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»+«/mo»«msub»«mi mathvariant=¨bold¨ mathcolor=¨#0000FF¨»R«/mi»«mn mathvariant=¨bold¨ mathcolor=¨#0000FF¨»2«/mn»«/msub»«mspace linebreak=¨newline¨»«/mspace»«/math»

נכתוב את חוק אום על כל המעגל:

«math style=¨font-family:`Times New Roman`¨ xmlns=¨http://www.w3.org/1998/Math/MathML¨»«mstyle mathsize=¨20px¨»«mi mathvariant=¨bold¨ mathcolor=¨#0000FF¨»I«/mi»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»=«/mo»«mfrac mathcolor=¨#0000FF¨»«mi mathvariant=¨bold¨»§#949;«/mi»«msub»«mi mathvariant=¨bold¨»R«/mi»«mi mathvariant=¨bold-italic¨»T«/mi»«/msub»«/mfrac»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»=«/mo»«mfrac mathcolor=¨#0000FF¨»«mi mathvariant=¨bold¨»§#949;«/mi»«mrow»«mo mathvariant=¨bold¨»§#160;«/mo»«mstyle displaystyle=¨true¨»«mfrac»«mrow»«mn mathvariant=¨bold¨»768«/mn»«mo mathvariant=¨bold¨»-«/mo»«mn mathvariant=¨bold¨»16«/mn»«mo mathvariant=¨bold¨»§#183;«/mo»«msub»«mi mathvariant=¨bold¨»R«/mi»«mn mathvariant=¨bold¨»2«/mn»«/msub»«/mrow»«mrow»«mn mathvariant=¨bold¨»64«/mn»«mo mathvariant=¨bold¨»-«/mo»«msub»«mi mathvariant=¨bold¨»R«/mi»«mn mathvariant=¨bold¨»2«/mn»«/msub»«/mrow»«/mfrac»«/mstyle»«mo mathvariant=¨bold¨»+«/mo»«msub»«mi mathvariant=¨bold-italic¨»R«/mi»«mn mathvariant=¨bold¨»2«/mn»«/msub»«/mrow»«/mfrac»«mspace linebreak=¨newline¨»«/mspace»«mspace linebreak=¨newline¨»«/mspace»«mfrac mathcolor=¨#0000FF¨»«mrow»«mn mathvariant=¨bold¨»768«/mn»«mo mathvariant=¨bold¨»-«/mo»«mn mathvariant=¨bold¨»16«/mn»«mo mathvariant=¨bold¨»§#183;«/mo»«msub»«mi mathvariant=¨bold¨»R«/mi»«mn mathvariant=¨bold¨»2«/mn»«/msub»«/mrow»«mrow»«mn mathvariant=¨bold¨»64«/mn»«mo mathvariant=¨bold¨»-«/mo»«msub»«mi mathvariant=¨bold¨»R«/mi»«mn mathvariant=¨bold¨»2«/mn»«/msub»«/mrow»«/mfrac»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»+«/mo»«msub»«mi mathvariant=¨bold-italic¨ mathcolor=¨#0000FF¨»R«/mi»«mn mathvariant=¨bold¨ mathcolor=¨#0000FF¨»2«/mn»«/msub»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»=«/mo»«mfrac mathcolor=¨#0000FF¨»«mi mathvariant=¨bold¨»§#949;«/mi»«mi mathvariant=¨bold¨»I«/mi»«/mfrac»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»=«/mo»«mfrac mathcolor=¨#0000FF¨»«mn mathvariant=¨bold¨»12«/mn»«mi mathvariant=¨bold¨»I«/mi»«/mfrac»«mspace linebreak=¨newline¨»«/mspace»«mspace linebreak=¨newline¨»«/mspace»«menclose mathcolor=¨#0000FF¨ notation=¨box¨»«mfrac»«mrow»«mn mathvariant=¨bold¨»768«/mn»«mo mathvariant=¨bold¨»-«/mo»«mn mathvariant=¨bold¨»16«/mn»«mo mathvariant=¨bold¨»§#183;«/mo»«msub»«mi mathvariant=¨bold¨»R«/mi»«mn mathvariant=¨bold¨»2«/mn»«/msub»«/mrow»«mrow»«mn mathvariant=¨bold¨»64«/mn»«mo mathvariant=¨bold¨»-«/mo»«msub»«mi mathvariant=¨bold¨»R«/mi»«mn mathvariant=¨bold¨»2«/mn»«/msub»«/mrow»«/mfrac»«mo mathvariant=¨bold¨»+«/mo»«msub»«mi mathvariant=¨bold¨»R«/mi»«mn mathvariant=¨bold¨»2«/mn»«/msub»«mo mathvariant=¨bold¨»=«/mo»«mfrac»«mn mathvariant=¨bold¨»12«/mn»«mi mathvariant=¨bold¨»I«/mi»«/mfrac»«/menclose»«mspace linebreak=¨newline¨»«/mspace»«mspace linebreak=¨newline¨»«/mspace»«/mstyle»«/math»

קבלנו שתי משוואות בשני נעלמים , נמצא את זרם המקור מפתרון משוואות אלו:

«math style=¨font-family:`Times New Roman`¨ xmlns=¨http://www.w3.org/1998/Math/MathML¨»«mstyle mathsize=¨20px¨»«menclose mathcolor=¨#0000FF¨ notation=¨box¨»«mfrac»«mrow»«mn mathvariant=¨bold¨»768«/mn»«mo mathvariant=¨bold¨»-«/mo»«mn mathvariant=¨bold¨»16«/mn»«mo mathvariant=¨bold¨»§#183;«/mo»«msub»«mi mathvariant=¨bold¨»R«/mi»«mn mathvariant=¨bold¨»2«/mn»«/msub»«/mrow»«mrow»«mn mathvariant=¨bold¨»64«/mn»«mo mathvariant=¨bold¨»-«/mo»«msub»«mi mathvariant=¨bold¨»R«/mi»«mn mathvariant=¨bold¨»2«/mn»«/msub»«/mrow»«/mfrac»«mo mathvariant=¨bold¨»+«/mo»«msub»«mi mathvariant=¨bold¨»R«/mi»«mn mathvariant=¨bold¨»2«/mn»«/msub»«mo mathvariant=¨bold¨»=«/mo»«mfrac»«mn mathvariant=¨bold¨»12«/mn»«mi mathvariant=¨bold¨»I«/mi»«/mfrac»«/menclose»«mspace linebreak=¨newline¨»«/mspace»«mspace linebreak=¨newline¨»«/mspace»«menclose mathcolor=¨#0000FF¨ notation=¨box¨»«mi mathvariant=¨bold¨»I«/mi»«mo mathvariant=¨bold¨»=«/mo»«mfrac»«mn mathvariant=¨bold¨»8«/mn»«msub»«mi mathvariant=¨bold¨»R«/mi»«mn mathvariant=¨bold¨»2«/mn»«/msub»«/mfrac»«/menclose»«mo»§#160;«/mo»«mo»§#8658;«/mo»«msub»«mi mathvariant=¨bold¨ mathcolor=¨#FF0000¨»R«/mi»«mn mathvariant=¨bold¨ mathcolor=¨#FF0000¨»2«/mn»«/msub»«mo mathvariant=¨bold¨ mathcolor=¨#FF0000¨»=«/mo»«mfrac mathcolor=¨#FF0000¨»«mn mathvariant=¨bold¨»8«/mn»«mi mathvariant=¨bold¨»I«/mi»«/mfrac»«mspace linebreak=¨newline¨»«/mspace»«mspace linebreak=¨newline¨»«/mspace»«mspace linebreak=¨newline¨»«/mspace»«mfrac mathcolor=¨#0000FF¨»«mrow»«mn mathvariant=¨bold¨»768«/mn»«mo mathvariant=¨bold¨»-«/mo»«mn mathvariant=¨bold¨»16«/mn»«mo mathvariant=¨bold¨»§#183;«/mo»«mfrac mathcolor=¨#FF0000¨»«mn mathvariant=¨bold¨»8«/mn»«mi mathvariant=¨bold¨»I«/mi»«/mfrac»«/mrow»«mrow»«mn mathvariant=¨bold¨»64«/mn»«mo mathvariant=¨bold¨»-«/mo»«mfrac mathcolor=¨#FF0000¨»«mn mathvariant=¨bold¨»8«/mn»«mi mathvariant=¨bold¨»I«/mi»«/mfrac»«/mrow»«/mfrac»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»+«/mo»«mfrac mathcolor=¨#FF0000¨»«mn mathvariant=¨bold¨»8«/mn»«mi mathvariant=¨bold¨»I«/mi»«/mfrac»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»=«/mo»«mfrac mathcolor=¨#0000FF¨»«mn mathvariant=¨bold¨»12«/mn»«mi mathvariant=¨bold¨»I«/mi»«/mfrac»«/mstyle»«/math»

נכפיל את המונה והמכנה בזרם המקור:

«math style=¨font-family:`Times New Roman`¨ xmlns=¨http://www.w3.org/1998/Math/MathML¨»«mstyle mathsize=¨20px¨»«mfrac mathcolor=¨#0000FF¨»«mrow»«mn mathvariant=¨bold¨»768«/mn»«mo mathvariant=¨bold¨»§#183;«/mo»«mi mathvariant=¨bold¨»I«/mi»«mo mathvariant=¨bold¨»-«/mo»«mn mathvariant=¨bold¨»16«/mn»«mo mathvariant=¨bold¨»§#183;«/mo»«mn mathvariant=¨bold¨»8«/mn»«/mrow»«mrow»«mn mathvariant=¨bold¨»64«/mn»«mo mathvariant=¨bold¨»§#183;«/mo»«mi mathvariant=¨bold¨»I«/mi»«mo mathvariant=¨bold¨»-«/mo»«mn mathvariant=¨bold¨»8«/mn»«/mrow»«/mfrac»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»+«/mo»«mfrac mathcolor=¨#0000FF¨»«mn mathvariant=¨bold¨»8«/mn»«mi mathvariant=¨bold¨»I«/mi»«/mfrac»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»=«/mo»«mfrac mathcolor=¨#0000FF¨»«mn mathvariant=¨bold¨»12«/mn»«mi mathvariant=¨bold¨»I«/mi»«/mfrac»«mspace linebreak=¨newline¨»«/mspace»«mspace linebreak=¨newline¨»«/mspace»«mfrac mathcolor=¨#0000FF¨»«mrow»«mn mathvariant=¨bold¨»768«/mn»«mo mathvariant=¨bold¨»§#183;«/mo»«mi mathvariant=¨bold¨»I«/mi»«mo mathvariant=¨bold¨»-«/mo»«mn mathvariant=¨bold¨»128«/mn»«/mrow»«mrow»«mn mathvariant=¨bold¨»64«/mn»«mo mathvariant=¨bold¨»§#183;«/mo»«mi mathvariant=¨bold¨»I«/mi»«mo mathvariant=¨bold¨»-«/mo»«mn mathvariant=¨bold¨»8«/mn»«/mrow»«/mfrac»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»+«/mo»«mfrac mathcolor=¨#0000FF¨»«mn mathvariant=¨bold¨»8«/mn»«mi mathvariant=¨bold¨»I«/mi»«/mfrac»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»=«/mo»«mfrac mathcolor=¨#0000FF¨»«mn mathvariant=¨bold¨»12«/mn»«mi mathvariant=¨bold¨»I«/mi»«/mfrac»«/mstyle»«/math»

נכפיל את כל המשוואה בזרם המקור:

«math style=¨font-family:`Times New Roman`¨ xmlns=¨http://www.w3.org/1998/Math/MathML¨»«mstyle mathsize=¨20px¨»«mspace linebreak=¨newline¨»«/mspace»«mfrac mathcolor=¨#0000FF¨»«mrow»«mi mathvariant=¨bold¨»I«/mi»«mo mathvariant=¨bold¨»§#183;«/mo»«mrow»«mo mathvariant=¨bold¨»(«/mo»«mn mathvariant=¨bold¨»768«/mn»«mo mathvariant=¨bold¨»§#183;«/mo»«mi mathvariant=¨bold¨»I«/mi»«mo mathvariant=¨bold¨»-«/mo»«mn mathvariant=¨bold¨»128«/mn»«mo mathvariant=¨bold¨»)«/mo»«/mrow»«/mrow»«mrow»«mn mathvariant=¨bold¨»64«/mn»«mo mathvariant=¨bold¨»§#183;«/mo»«mi mathvariant=¨bold¨»I«/mi»«mo mathvariant=¨bold¨»-«/mo»«mn mathvariant=¨bold¨»8«/mn»«/mrow»«/mfrac»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»+«/mo»«mn mathvariant=¨bold¨ mathcolor=¨#0000FF¨»8«/mn»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»=«/mo»«mn mathvariant=¨bold¨ mathcolor=¨#0000FF¨»12«/mn»«mspace linebreak=¨newline¨»«/mspace»«mi mathvariant=¨bold¨ mathcolor=¨#0000FF¨»I«/mi»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»§#183;«/mo»«mrow mathcolor=¨#0000FF¨»«mo mathvariant=¨bold¨»(«/mo»«mn mathvariant=¨bold¨»768«/mn»«mo mathvariant=¨bold¨»§#183;«/mo»«mi mathvariant=¨bold¨»I«/mi»«mo mathvariant=¨bold¨»-«/mo»«mn mathvariant=¨bold¨»128«/mn»«mo mathvariant=¨bold¨»)«/mo»«/mrow»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»=«/mo»«mn mathvariant=¨bold¨ mathcolor=¨#0000FF¨»4«/mn»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»§#183;«/mo»«mrow mathcolor=¨#0000FF¨»«mo mathvariant=¨bold¨»(«/mo»«mn mathvariant=¨bold¨»64«/mn»«mo mathvariant=¨bold¨»§#183;«/mo»«mi mathvariant=¨bold¨»I«/mi»«mo mathvariant=¨bold¨»-«/mo»«mn mathvariant=¨bold¨»8«/mn»«mo mathvariant=¨bold¨»)«/mo»«/mrow»«mspace linebreak=¨newline¨»«/mspace»«mspace linebreak=¨newline¨»«/mspace»«mn mathvariant=¨bold¨ mathcolor=¨#0000FF¨»768«/mn»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»§#183;«/mo»«msup»«mi mathvariant=¨bold¨ mathcolor=¨#0000FF¨»I«/mi»«mn mathvariant=¨bold¨ mathcolor=¨#0000FF¨»2«/mn»«/msup»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»-«/mo»«mn mathvariant=¨bold¨ mathcolor=¨#0000FF¨»128«/mn»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»§#183;«/mo»«mi mathvariant=¨bold¨ mathcolor=¨#0000FF¨»I«/mi»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»=«/mo»«mn mathvariant=¨bold¨ mathcolor=¨#0000FF¨»256«/mn»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»§#183;«/mo»«mi mathvariant=¨bold¨ mathcolor=¨#0000FF¨»I«/mi»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»-«/mo»«mn mathvariant=¨bold¨ mathcolor=¨#0000FF¨»32«/mn»«mspace linebreak=¨newline¨»«/mspace»«mspace linebreak=¨newline¨»«/mspace»«mn mathvariant=¨bold¨ mathcolor=¨#0000FF¨»768«/mn»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»§#183;«/mo»«msup»«mi mathvariant=¨bold¨ mathcolor=¨#0000FF¨»I«/mi»«mn mathvariant=¨bold¨ mathcolor=¨#0000FF¨»2«/mn»«/msup»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»-«/mo»«mn mathvariant=¨bold¨ mathcolor=¨#0000FF¨»384«/mn»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»§#183;«/mo»«mi mathvariant=¨bold¨ mathcolor=¨#0000FF¨»I«/mi»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»+«/mo»«mn mathvariant=¨bold¨ mathcolor=¨#0000FF¨»32«/mn»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»=«/mo»«mn mathvariant=¨bold¨ mathcolor=¨#0000FF¨»0«/mn»«/mstyle»«/math»

קבלנו משוואה ריבועית , נפתור את המשוואה:

«math style=¨font-family:`Times New Roman`¨ xmlns=¨http://www.w3.org/1998/Math/MathML¨»«mstyle mathsize=¨20px¨»«mn mathvariant=¨bold¨ mathcolor=¨#0000FF¨»768«/mn»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»§#183;«/mo»«msup»«mi mathvariant=¨bold¨ mathcolor=¨#0000FF¨»I«/mi»«mn mathvariant=¨bold¨ mathcolor=¨#0000FF¨»2«/mn»«/msup»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»-«/mo»«mn mathvariant=¨bold¨ mathcolor=¨#0000FF¨»384«/mn»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»§#183;«/mo»«mi mathvariant=¨bold¨ mathcolor=¨#0000FF¨»I«/mi»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»+«/mo»«mn mathvariant=¨bold¨ mathcolor=¨#0000FF¨»32«/mn»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»=«/mo»«mn mathvariant=¨bold¨ mathcolor=¨#0000FF¨»0«/mn»«mspace linebreak=¨newline¨»«/mspace»«mspace linebreak=¨newline¨»«/mspace»«msub»«mi mathvariant=¨bold¨ mathcolor=¨#0000FF¨»I«/mi»«mrow mathcolor=¨#0000FF¨»«mn mathvariant=¨bold¨»1«/mn»«mo mathvariant=¨bold¨»,«/mo»«mn mathvariant=¨bold¨»2«/mn»«/mrow»«/msub»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»=«/mo»«mfrac mathcolor=¨#0000FF¨»«mrow»«mn mathvariant=¨bold¨»384«/mn»«mo mathvariant=¨bold¨»§#177;«/mo»«msqrt»«msup»«mn mathvariant=¨bold¨»384«/mn»«mn mathvariant=¨bold¨»2«/mn»«/msup»«mo mathvariant=¨bold¨»-«/mo»«mn mathvariant=¨bold¨»4«/mn»«mo mathvariant=¨bold¨»§#183;«/mo»«mn mathvariant=¨bold¨»768«/mn»«mo mathvariant=¨bold¨»§#183;«/mo»«mn mathvariant=¨bold¨»32«/mn»«/msqrt»«/mrow»«mrow»«mn mathvariant=¨bold¨»2«/mn»«mo mathvariant=¨bold¨»§#183;«/mo»«mn mathvariant=¨bold¨»768«/mn»«/mrow»«/mfrac»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»=«/mo»«mfrac mathcolor=¨#0000FF¨»«mrow»«mn mathvariant=¨bold¨»384«/mn»«mo mathvariant=¨bold¨»§#177;«/mo»«msqrt»«mn mathvariant=¨bold¨»49«/mn»«mo mathvariant=¨bold¨»,«/mo»«mn mathvariant=¨bold¨»152«/mn»«/msqrt»«/mrow»«mrow»«mn mathvariant=¨bold¨»2«/mn»«mo mathvariant=¨bold¨»§#183;«/mo»«mn mathvariant=¨bold¨»768«/mn»«/mrow»«/mfrac»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»=«/mo»«mfrac mathcolor=¨#0000FF¨»«mrow»«mn mathvariant=¨bold¨»384«/mn»«mo mathvariant=¨bold¨»§#177;«/mo»«mn mathvariant=¨bold¨»221«/mn»«mo mathvariant=¨bold¨».«/mo»«mn mathvariant=¨bold¨»7«/mn»«/mrow»«mn mathvariant=¨bold¨»1536«/mn»«/mfrac»«mspace linebreak=¨newline¨»«/mspace»«mspace linebreak=¨newline¨»«/mspace»«msub»«mi mathvariant=¨bold¨ mathcolor=¨#0000FF¨»I«/mi»«mn mathvariant=¨bold¨ mathcolor=¨#0000FF¨»1«/mn»«/msub»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»=«/mo»«mn mathvariant=¨bold¨ mathcolor=¨#0000FF¨»0«/mn»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨».«/mo»«mn mathvariant=¨bold¨ mathcolor=¨#0000FF¨»394«/mn»«mi mathvariant=¨bold¨ mathcolor=¨#0000FF¨»A«/mi»«mspace linebreak=¨newline¨»«/mspace»«mspace linebreak=¨newline¨»«/mspace»«msub»«mi mathvariant=¨bold¨ mathcolor=¨#0000FF¨»I«/mi»«mn mathvariant=¨bold¨ mathcolor=¨#0000FF¨»2«/mn»«/msub»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»=«/mo»«mn mathvariant=¨bold¨ mathcolor=¨#0000FF¨»0«/mn»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨».«/mo»«mn mathvariant=¨bold¨ mathcolor=¨#0000FF¨»1«/mn»«mi mathvariant=¨bold¨ mathcolor=¨#0000FF¨»A«/mi»«/mstyle»«/math»

הזרם דרך הנורה הוא 0.25A (מחושב בתחילת הפתרון). זרם המקור חייב להיות גדול יותר לכן הפתרון הנכון הוא 0.394A .

מעגל א- הוא מעגל טורי , כאשר הנורה דולקת באורה המלא עוצמת הזרם דרכה 0.25A , זה הזרם דרך המקור במעגל א'.

נחשב את ההפרש בזרמי המקור של שני המעגלים:

«math style=¨font-family:`Times New Roman`¨ xmlns=¨http://www.w3.org/1998/Math/MathML¨»«mstyle mathsize=¨20px¨»«mrow»«msub»«mi mathvariant=¨bold¨ mathcolor=¨#0000FF¨»I«/mi»«mi mathvariant=¨bold¨ mathcolor=¨#0000FF¨»§#1489;«/mi»«/msub»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»-«/mo»«msub»«mi mathvariant=¨bold¨ mathcolor=¨#0000FF¨»I«/mi»«mi mathvariant=¨bold¨ mathcolor=¨#0000FF¨»§#1488;«/mi»«/msub»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»=«/mo»«mn mathvariant=¨bold¨ mathcolor=¨#0000FF¨»0«/mn»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨».«/mo»«mn mathvariant=¨bold¨ mathcolor=¨#0000FF¨»394«/mn»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»-«/mo»«mn mathvariant=¨bold¨ mathcolor=¨#0000FF¨»0«/mn»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨».«/mo»«mn mathvariant=¨bold¨ mathcolor=¨#0000FF¨»25«/mn»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»=«/mo»«mn mathvariant=¨bold¨ mathcolor=¨#0000FF¨»0«/mn»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨».«/mo»«mn mathvariant=¨bold¨ mathcolor=¨#0000FF¨»144«/mn»«mi mathvariant=¨bold¨ mathcolor=¨#0000FF¨»A«/mi»«/mrow»«/mstyle»«/math»

לסיכום הזרם במעגל ב' גדול ב 0.144 אמפר מהזרם במעגל א'.

1. من السهل جدًا حساب شدة تيار المصدر في الدائرة (ب)، وليس من السهل حساب شدة تيار المصدر في الدائرة (أ).

2. في الدائرة (أ)، فرق الجهد على R1 يساوي فرق الجهد على R3، لكن مقاومتهما مختلفة.

3. في الدائرة (أ) يتم الحصول على دائرة مختلطة، قيمة المقاومتين فيها غير معروفة، وبالتالي فإن عملية الحل طويلة ومعقدة.
من الأفضل حل الأسئلة الطويلة والمعقدة من خلال التدريب في المنزل، وليس في الاختبار.

4. تيار المصدر في الدائرة "ب" يساوي التيار المار عبر المصباح في الدائرة "أ":

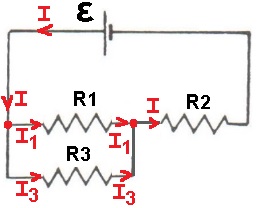
الفرق بين تيار المصدر في الدائرة "ب" والتيار المصدر في الدائرة "أ". يساوي الفرق بين التيارين: «math style=¨font-family:`Times New Roman`¨ xmlns=¨http://www.w3.org/1998/Math/MathML¨»«mstyle mathsize=¨20px¨»«mrow»«mi mathvariant=¨bold¨ mathcolor=¨#FF0000¨»I«/mi»«mo mathvariant=¨bold¨ mathcolor=¨#FF0000¨»-«/mo»«msub»«mi mathvariant=¨bold¨ mathcolor=¨#FF0000¨»I«/mi»«mn mathvariant=¨bold¨ mathcolor=¨#FF0000¨»3«/mn»«/msub»«/mrow»«/mstyle»«/math».
من قانون العقدة يتحقق: «math style=¨font-family:`Times New Roman`¨ xmlns=¨http://www.w3.org/1998/Math/MathML¨»«mstyle mathsize=¨20px¨»«mrow»«mi mathvariant=¨bold¨ mathcolor=¨#FF0000¨»I«/mi»«mo mathvariant=¨bold¨ mathcolor=¨#FF0000¨»=«/mo»«msub»«mi mathvariant=¨bold¨ mathcolor=¨#FF0000¨»I«/mi»«mn mathvariant=¨bold¨ mathcolor=¨#FF0000¨»1«/mn»«/msub»«mo mathvariant=¨bold¨ mathcolor=¨#FF0000¨»+«/mo»«msub»«mi mathvariant=¨bold¨ mathcolor=¨#FF0000¨»I«/mi»«mn mathvariant=¨bold¨ mathcolor=¨#FF0000¨»3«/mn»«/msub»«/mrow»«/mstyle»«/math».

القيمة التي تم الحصول عليها من الفرق بين التيارين : «math style=¨font-family:`Times New Roman`¨ xmlns=¨http://www.w3.org/1998/Math/MathML¨»«mstyle mathsize=¨20px¨»«mrow»«mi mathvariant=¨bold¨ mathcolor=¨#FF0000¨»I«/mi»«mo mathvariant=¨bold¨ mathcolor=¨#FF0000¨»-«/mo»«msub»«mi mathvariant=¨bold¨ mathcolor=¨#FF0000¨»I«/mi»«mn mathvariant=¨bold¨ mathcolor=¨#FF0000¨»3«/mn»«/msub»«/mrow»«/mstyle»«/math» هو «math style=¨font-family:`Times New Roman`¨ xmlns=¨http://www.w3.org/1998/Math/MathML¨»«mstyle mathsize=¨20px¨»«msub»«mi mathvariant=¨bold¨ mathcolor=¨#FF0000¨»I«/mi»«mn mathvariant=¨bold¨ mathcolor=¨#FF0000¨»1«/mn»«/msub»«/mstyle»«/math».

لذلك يمكننا القول أن الفرق بين التيارين بالمصدر في الدائرتين يساوي التيار المار عبر R1 في الدائرة "أ".

2. במעגל א' מתקבל מעגל מעורב ,ערך שני הנגדים בו אינם ידועים, לכן מהלך הפתרון ארוך ומורכב.

שאלות ארוכות ומורכבות עדיף לפתור כתרגול בבית ולא במבחן.

______________________________________________________________________________________

______________________________________________________________________________________

...

في الدائرة (أ)، في التوصيل البوتانسيومتري، يمكن تقليل فرق الجهد إلى صفر فولط.

معرفة التوصيل البوتانسيومتري والتوصيل الريئوستاتي.

في الدائرة (أ) يتم توصيل المقاومة المتغيرة في توصيل بوتانسيومتري، إذا قام الطالب بتحريك التماس المتحرك إلى اليسار في الدائرة (أ)، فإن شدة إضاءة المصباح الكهربائي ستنخفض. وعندما تصل نقطة التماسّ المتحركة إلى الحافة اليسرى لن يكون هناك فرق جهد بين طرفي المصباح الكهربائي وسينطفأ المصباح الكهربائي بشكل تام.

في الدائرة (ب)، يتم توصيل المقاومة المتغيرة بتوصيل ريئوستاتي، وفي أي نقطة يتم فيها وضع التماسّ المتحرك، سوف يتدفق تيار في الدائرة.

ولذلك فإن الدائرة التي سيتمكن الطالب من إضعاف شدة الإضاءة فيها حتى تنطفئ هي الدائرة (أ).

במעגל ב' הנגד המשתנה מחובר בחיבור אלקטרוסטט, בכל נקודה בה תמוקם הגררה יזרום זרם במעגל.

לכן , המעגל בו התלמיד יוכל להחליש את עוצמת ההארה עד לכיבויה הוא מעגל א'.

1. عندما يكون التماسّ المتحرك في الطرف الأيمن في الدائرة (ب)، ستكون شدة التيار صغيرة ولكن ليست صفراً، نحسب شدة التيار في هذه الحالة:

«math style=¨font-family:`Times New Roman`¨ xmlns=¨http://www.w3.org/1998/Math/MathML¨»«mstyle mathsize=¨20px¨»«mrow»«mi mathvariant=¨bold¨ mathcolor=¨#FF0000¨»I«/mi»«mo mathvariant=¨bold¨ mathcolor=¨#FF0000¨»=«/mo»«mfrac mathcolor=¨#FF0000¨»«mi mathvariant=¨bold¨»§#949;«/mi»«msub»«mi mathvariant=¨bold¨»R«/mi»«mi mathvariant=¨bold¨»T«/mi»«/msub»«/mfrac»«mo mathvariant=¨bold¨ mathcolor=¨#FF0000¨»=«/mo»«mfrac mathcolor=¨#FF0000¨»«mi mathvariant=¨bold¨»§#949;«/mi»«mrow»«msub»«mi mathvariant=¨bold¨»R«/mi»«mi mathvariant=¨bold¨»X«/mi»«/msub»«mo mathvariant=¨bold¨»+«/mo»«msub»«mi mathvariant=¨bold¨»R«/mi»«mi mathvariant=¨bold¨»max«/mi»«/msub»«/mrow»«/mfrac»«mo mathvariant=¨bold¨ mathcolor=¨#FF0000¨»=«/mo»«mfrac mathcolor=¨#FF0000¨»«mn mathvariant=¨bold¨»12«/mn»«mrow»«mn mathvariant=¨bold¨»16«/mn»«mo mathvariant=¨bold¨»+«/mo»«mn mathvariant=¨bold¨»48«/mn»«/mrow»«/mfrac»«mo mathvariant=¨bold¨ mathcolor=¨#FF0000¨»=«/mo»«mn mathvariant=¨bold¨ mathcolor=¨#FF0000¨»0«/mn»«mo mathvariant=¨bold¨ mathcolor=¨#FF0000¨».«/mo»«mn mathvariant=¨bold¨ mathcolor=¨#FF0000¨»1875«/mn»«mi mathvariant=¨bold¨ mathcolor=¨#FF0000¨»A«/mi»«/mrow»«/mstyle»«/math»

نحسب شدة التيار المار بالمصباح عندما يعمل بكامل الإضاءة:

«math style=¨font-family:`Times New Roman`¨ xmlns=¨http://www.w3.org/1998/Math/MathML¨»«mstyle mathsize=¨20px¨»«mi mathvariant=¨bold¨ mathcolor=¨#FF0000¨»I«/mi»«mo mathvariant=¨bold¨ mathcolor=¨#FF0000¨»=«/mo»«mfrac mathcolor=¨#FF0000¨»«mi mathvariant=¨bold¨»P«/mi»«mi mathvariant=¨bold¨»U«/mi»«/mfrac»«mo mathvariant=¨bold¨ mathcolor=¨#FF0000¨»=«/mo»«mfrac mathcolor=¨#FF0000¨»«mn mathvariant=¨bold¨»1«/mn»«mn mathvariant=¨bold¨»4«/mn»«/mfrac»«mo mathvariant=¨bold¨ mathcolor=¨#FF0000¨»=«/mo»«mn mathvariant=¨bold¨ mathcolor=¨#FF0000¨»0«/mn»«mo mathvariant=¨bold¨ mathcolor=¨#FF0000¨».«/mo»«mn mathvariant=¨bold¨ mathcolor=¨#FF0000¨»25«/mn»«mi mathvariant=¨bold¨ mathcolor=¨#FF0000¨»A«/mi»«/mstyle»«/math»

وفقًا لقيم التيار هذه، عندما يكون التماسّ المتحرك في الدائرة (أ) في الطرف الأيمن، تنخفض شدة التيار بنسبة 25 بالمائة، ولن يتم إطفاءه بالكامل.

2. عندما يكون التماسّ المتحرك في الدائرة (أ) في الطرف الأيسر، ستكون شدة التيار القصوى، نحسب الحد الأقصى لشدة التيار:

«math style=¨font-family:`Times New Roman`¨ xmlns=¨http://www.w3.org/1998/Math/MathML¨»«mstyle mathsize=¨20px¨»«mi mathvariant=¨bold¨ mathcolor=¨#FF0000¨»I«/mi»«mo mathvariant=¨bold¨ mathcolor=¨#FF0000¨»=«/mo»«mfrac mathcolor=¨#FF0000¨»«mi mathvariant=¨bold¨»§#949;«/mi»«msub»«mi mathvariant=¨bold¨»R«/mi»«mi mathvariant=¨bold¨»T«/mi»«/msub»«/mfrac»«mo mathvariant=¨bold¨ mathcolor=¨#FF0000¨»=«/mo»«mfrac mathcolor=¨#FF0000¨»«mi mathvariant=¨bold¨»§#949;«/mi»«msub»«mi mathvariant=¨bold¨»R«/mi»«mi mathvariant=¨bold¨»X«/mi»«/msub»«/mfrac»«mo mathvariant=¨bold¨ mathcolor=¨#FF0000¨»=«/mo»«mfrac mathcolor=¨#FF0000¨»«mn mathvariant=¨bold¨»12«/mn»«mn mathvariant=¨bold¨»16«/mn»«/mfrac»«mo mathvariant=¨bold¨ mathcolor=¨#FF0000¨»=«/mo»«mn mathvariant=¨bold¨ mathcolor=¨#FF0000¨»0«/mn»«mo mathvariant=¨bold¨ mathcolor=¨#FF0000¨».«/mo»«mn mathvariant=¨bold¨ mathcolor=¨#FF0000¨»75«/mn»«mi mathvariant=¨bold¨ mathcolor=¨#FF0000¨»A«/mi»«/mstyle»«/math»

شدة التيار القصوى أكبر بثلاث مرات من شدة التيار اللازم لإضاءة المصباح بكامل إضائءته.

في هذه الحالة، سوف يحترق المصباح وينطفئ ولكن لن يتم إطفاءه بشكل متواصل.

נחשב את עוצמת הזרם דרך הנורה כאשר היא פועלת באורה המלא:

בהתאם לערכי זרם אלו, כאשר הגררה נמצאת במעגל א' בקצה הימני עוצמת הזרם קטנה ב 25 אחוז, היא לא תהיה כבויה לחלוטין.

2. כאשר הגררה במעגל א' תהיה בקצה השמאלי עוצמת הזרם תהיה מקסימאלית, נחשב את עוצמת הזרם המקסימאלית:

«math style=¨font-family:`Times New Roman`¨ xmlns=¨http://www.w3.org/1998/Math/MathML¨»«mstyle mathsize=¨20px¨»«mi mathvariant=¨bold¨ mathcolor=¨#FF0000¨»I«/mi»«mo mathvariant=¨bold¨ mathcolor=¨#FF0000¨»=«/mo»«mfrac mathcolor=¨#FF0000¨»«mi mathvariant=¨bold¨»§#949;«/mi»«msub»«mi mathvariant=¨bold¨»R«/mi»«mi mathvariant=¨bold¨»T«/mi»«/msub»«/mfrac»«mo mathvariant=¨bold¨ mathcolor=¨#FF0000¨»=«/mo»«mfrac mathcolor=¨#FF0000¨»«mi mathvariant=¨bold¨»§#949;«/mi»«msub»«mi mathvariant=¨bold¨»R«/mi»«mi mathvariant=¨bold¨»X«/mi»«/msub»«/mfrac»«mo mathvariant=¨bold¨ mathcolor=¨#FF0000¨»=«/mo»«mfrac mathcolor=¨#FF0000¨»«mn mathvariant=¨bold¨»12«/mn»«mn mathvariant=¨bold¨»16«/mn»«/mfrac»«mo mathvariant=¨bold¨ mathcolor=¨#FF0000¨»=«/mo»«mn mathvariant=¨bold¨ mathcolor=¨#FF0000¨»0«/mn»«mo mathvariant=¨bold¨ mathcolor=¨#FF0000¨».«/mo»«mn mathvariant=¨bold¨ mathcolor=¨#FF0000¨»75«/mn»«mi mathvariant=¨bold¨ mathcolor=¨#FF0000¨»A«/mi»«/mstyle»«/math»

עוצמת הזרם המקסימאלית גדולה פי 3 מעוצמת הזרם הדרושה להארת הנורה באורה המלא.

במקרה זה הנורה תישרף ותיכבה אך הכיבוי לא יהיה מדורג .

______________________________________________________________________________________

...

ميزة الدائرة (أ) - يمكن إطفاء المصباح بالكامل.

ميزة الدائرة (ب) - في نفس إضاءة المصباح، يتدفق تيار أقل، وتكون الدائرة أكثر نجاعة.

יתרון מעגל ב' -

יתרונות מעגל ב' -

التعرف على خصائص دوائر التيار والمصباح الكهربائي: كفاءة الدائرة، كيفية إطفاء المصباح الكهربائي.

ميزة الدائرة (أ) - يمكن إطفاء المصباح بالكامل.

ميزة الدائرة (ب) - في نفس إضاءة المصباح، يتدفق تيار أقل، وتكون الدائرة أكثر نجاعة.

יתרון מעגל ב' - באותה עוצמת ההארה של הנורה זורם פחות זרם, המעגל יותר חסכוני.

1. من الإجابة على البند أ، يمكن أن نفهم أن الدائرة (ب) أكثر كفاءة من حيث الطاقة.

من الإجابة على البند ب يمكن أن نفهم أنه من الممكن أن نُطفئ المصباح بالكامل في الدائرة (أ).

لا تحتاج إلى أن تكون خبيرًا في مزايا المصابيح والدوائر الكهربائية للإجابة على البند ج. ويكفي أن نفهم البندين السابقين.

2. ميزة أخرى للدائرة (ب) - عندما يحترق المصباح (يحدث لكل مصباح)، ستستمر البطارية الموجودة في الدائرة (أ) في العمل.

في الدائرة (ب)، من ناحية أخرى، بعد احتراق المصباح، سيكون هناك انقطاع في الدائرة. لن تستمر البطارية في العمل.

3. ليست هناك حاجة لشرح المزايا فقط لذكر مزايا كل طريقة توصيل.

מהתשובה על סעיף ב' ניתן להבין שאפשר להגיע לכיבוי מלא במעגל א'.

לא צריך להיות מומחה ביתרונות של נורות ומעגלי זרם כדי לענות על סעיף ג' . מספיק להבין את שני הסעיפים הקודמים.

2. יתרון נוסף למעגל ב' - כאשר הנורה נשרפת (קורה לכל נורה) , הסוללה במעגל א' תמשיך לעבוד .

במעגל ב' לעומת זאת לאחר שריפת הנורה יהיה נתק במעגל. הסוללה לא תמשיך לעבודה.

______________________________________________________________________________________