7. 2000,3 رسم بياني لمقلوب التيار كدالة لطول السلك
______________________________________________________________________________________
...
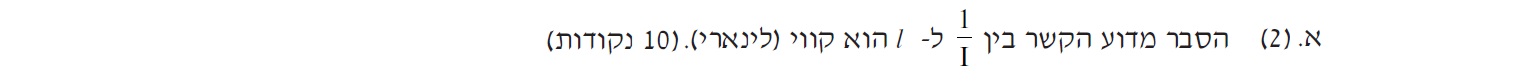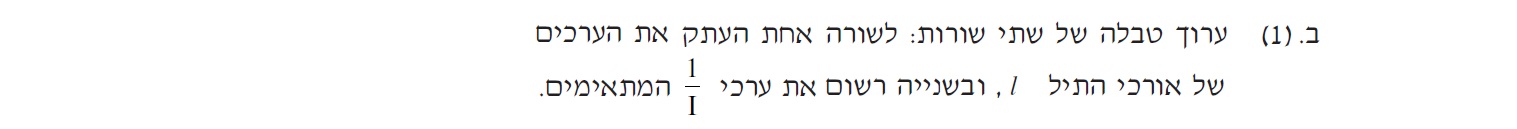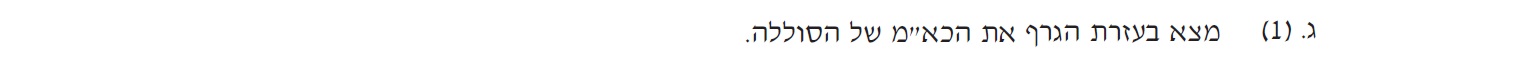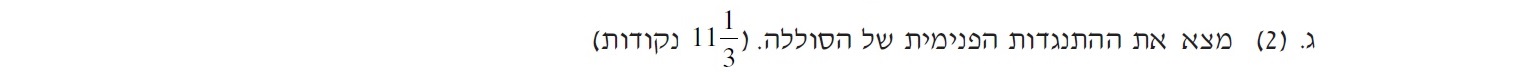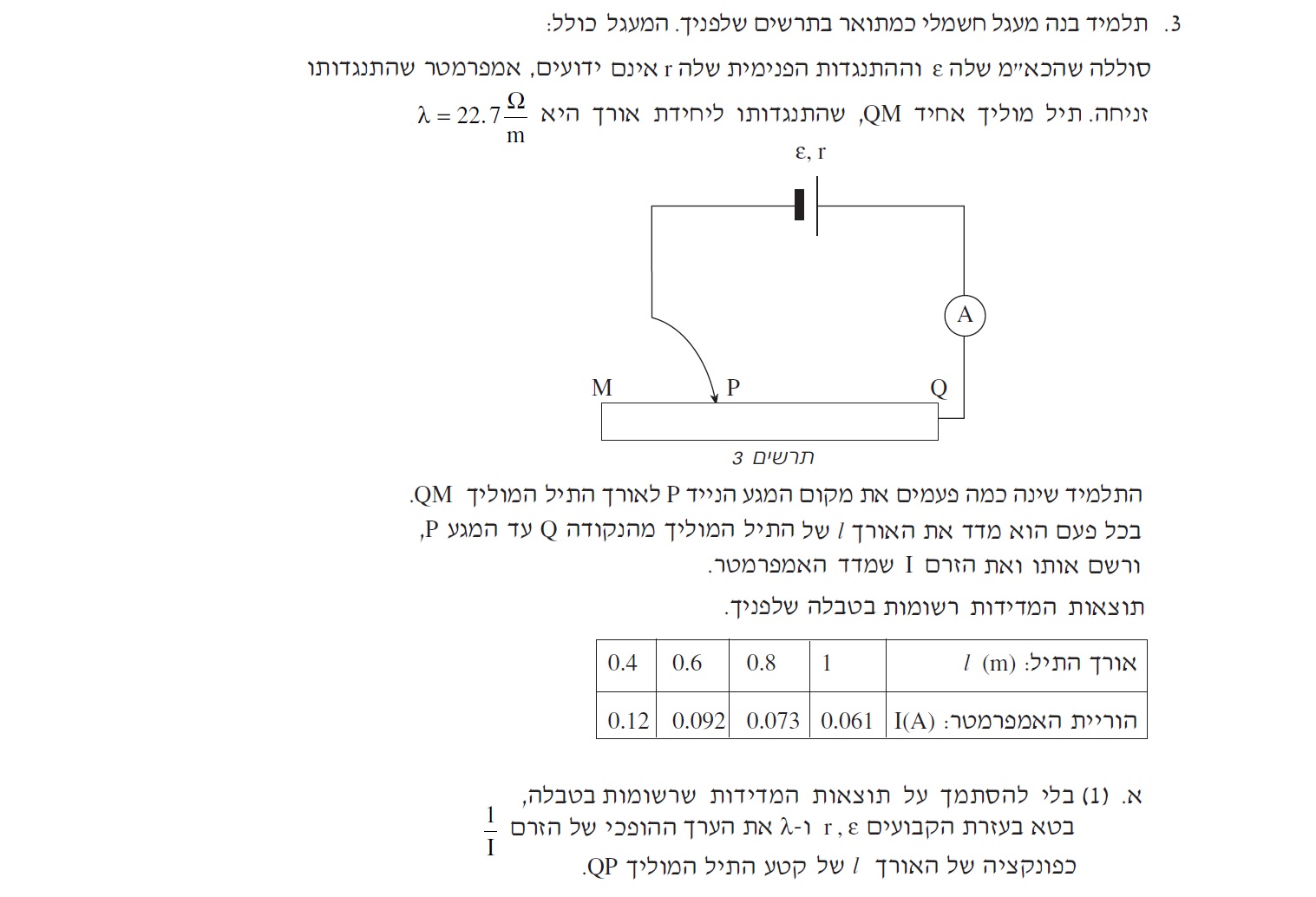
«math style=¨font-family:`Times New Roman`¨ xmlns=¨http://www.w3.org/1998/Math/MathML¨»«mfrac»«mn mathvariant=¨bold¨ mathsize=¨20px¨»1«/mn»«mi mathvariant=¨bold¨ mathsize=¨20px¨»I«/mi»«/mfrac»«mo mathvariant=¨bold¨ mathsize=¨20px¨»(«/mo»«mi mathvariant=¨bold¨ mathsize=¨20px¨»L«/mi»«mo mathvariant=¨bold¨ mathsize=¨20px¨»)«/mo»«mo mathvariant=¨bold¨ mathsize=¨20px¨»=«/mo»«mfrac»«mi mathvariant=¨bold¨ mathsize=¨20px¨»r«/mi»«mi mathvariant=¨bold¨ mathsize=¨20px¨»§#949;«/mi»«/mfrac»«mo mathvariant=¨bold¨ mathsize=¨20px¨»+«/mo»«mfrac»«mi mathvariant=¨bold¨ mathsize=¨20px¨»§#955;«/mi»«mi mathvariant=¨bold¨ mathsize=¨20px¨»§#949;«/mi»«/mfrac»«mo mathvariant=¨bold¨ mathsize=¨20px¨»§#183;«/mo»«mi mathvariant=¨bold¨ mathsize=¨20px¨»L«/mi»«/math»
قانون أوم للدائرة بأكملها والتعبير عن مقاومة السلك الموصل كدالة للمقاومة لكل وحدة طول.
المقاومة لكل وحدة طول السلك.«math xmlns=¨http://www.w3.org/1998/Math/MathML¨»«mi mathvariant=¨bold¨ mathcolor=¨#0000FF¨»§#955;«/mi»«/math» تساوي النسبة بين مقاومة السلك الموصل وطوله«math xmlns=¨http://www.w3.org/1998/Math/MathML¨»«mi mathvariant=¨bold¨ mathcolor=¨#0000FF¨»§#955;«/mi»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»=«/mo»«mfrac mathcolor=¨#0000FF¨»«mi mathvariant=¨bold¨»R«/mi»«mi mathvariant=¨bold¨»L«/mi»«/mfrac»«/math» .
السلك موصول بتوصيل ريئوستاتي. سنعبر عن التيار باستخدام قانون أوم للدائرة بأكملها:
«math style=¨font-family:`Times New Roman`¨ xmlns=¨http://www.w3.org/1998/Math/MathML¨»«mstyle mathsize=¨20px¨»«mi mathvariant=¨bold¨ mathcolor=¨#0000FF¨»I«/mi»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»=«/mo»«mfrac mathcolor=¨#0000FF¨»«mi mathvariant=¨bold¨»§#949;«/mi»«msub»«mi mathvariant=¨bold¨»R«/mi»«mi mathvariant=¨bold¨»T«/mi»«/msub»«/mfrac»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»=«/mo»«mfrac mathcolor=¨#0000FF¨»«mi mathvariant=¨bold¨»§#949;«/mi»«mrow»«mi mathvariant=¨bold¨»r«/mi»«mo mathvariant=¨bold¨»+«/mo»«mi mathvariant=¨bold¨»R«/mi»«/mrow»«/mfrac»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»=«/mo»«mfrac mathcolor=¨#0000FF¨»«mi mathvariant=¨bold¨»§#949;«/mi»«mrow»«mi mathvariant=¨bold¨»r«/mi»«mo mathvariant=¨bold¨»+«/mo»«mi mathvariant=¨bold¨»§#955;«/mi»«mo mathvariant=¨bold¨»§#183;«/mo»«mi mathvariant=¨bold¨»L«/mi»«/mrow»«/mfrac»«/mstyle»«/math»
يجب كتابة تعبير لمقلوب التيار. سنقوم بقلب البسط والمقام بالمعادلة:
«math style=¨font-family:`Times New Roman`¨ xmlns=¨http://www.w3.org/1998/Math/MathML¨»«mstyle mathsize=¨20px¨»«mfrac mathcolor=¨#0000FF¨»«mn mathvariant=¨bold¨»1«/mn»«mi mathvariant=¨bold¨»I«/mi»«/mfrac»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»=«/mo»«mfrac mathcolor=¨#0000FF¨»«mrow»«mi mathvariant=¨bold¨»r«/mi»«mo mathvariant=¨bold¨»+«/mo»«mi mathvariant=¨bold¨»§#955;«/mi»«mo mathvariant=¨bold¨»§#183;«/mo»«mi mathvariant=¨bold¨»L«/mi»«/mrow»«mi mathvariant=¨bold¨»§#949;«/mi»«/mfrac»«/mstyle»«/math»
لوصف مقلوب شدة التيار كدالة لطول السلك الموصل L، نصف الجانب الأيمن كمجموع كسرين:
«math style=¨font-family:`Times New Roman`¨ xmlns=¨http://www.w3.org/1998/Math/MathML¨»«mstyle mathsize=¨20px¨»«menclose mathcolor=¨#0000FF¨ notation=¨circle¨»«mfrac»«mn mathvariant=¨bold¨»1«/mn»«mi mathvariant=¨bold¨»I«/mi»«/mfrac»«mo mathvariant=¨bold¨»(«/mo»«mi mathvariant=¨bold¨»L«/mi»«mo mathvariant=¨bold¨»)«/mo»«mo mathvariant=¨bold¨»=«/mo»«mfrac»«mi mathvariant=¨bold¨»r«/mi»«mi mathvariant=¨bold¨»§#949;«/mi»«/mfrac»«mo mathvariant=¨bold¨»+«/mo»«mfrac»«mi mathvariant=¨bold¨»§#955;«/mi»«mi mathvariant=¨bold¨»§#949;«/mi»«/mfrac»«mo mathvariant=¨bold¨»§#183;«/mo»«mi mathvariant=¨bold¨»L«/mi»«/menclose»«/mstyle»«/math»
ההתנגדות ליחידת אורך «math xmlns=¨http://www.w3.org/1998/Math/MathML¨»«mi mathvariant=¨bold¨ mathcolor=¨#0000FF¨»§#955;«/mi»«/math» שווה ליחס בין אורך המוליך להתנגדותו «math xmlns=¨http://www.w3.org/1998/Math/MathML¨»«mi mathvariant=¨bold¨ mathcolor=¨#0000FF¨»§#955;«/mi»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»=«/mo»«mfrac mathcolor=¨#0000FF¨»«mi mathvariant=¨bold¨»R«/mi»«mi mathvariant=¨bold¨»L«/mi»«/mfrac»«/math»
במקרה זה «math xmlns=¨http://www.w3.org/1998/Math/MathML¨»«mi mathvariant=¨bold¨ mathcolor=¨#0000FF¨»§#955;«/mi»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»=«/mo»«mn mathvariant=¨bold¨ mathcolor=¨#0000FF¨»22«/mn»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨».«/mo»«mn mathvariant=¨bold¨ mathcolor=¨#0000FF¨»7«/mn»«mfrac mathcolor=¨#0000FF¨»«mi mathvariant=¨bold¨»§#937;«/mi»«mi mathvariant=¨bold¨»m«/mi»«/mfrac»«/math» לכל מטר מוליך ההתנגדות היא 22.7 אום.
את היחס בין התנגדות המוליך לאורכו.
נבטא את התנגדות התיל בתלות באורכו ובהתנגדות המוליך ליחידת אורך:
נבטא את הזרם בעזרת חוק אום על כל המעגל:
התנגד
«math style=¨font-family:`Times New Roman`¨ xmlns=¨http://www.w3.org/1998/Math/MathML¨»«mstyle mathsize=¨20px¨»«mrow»«mi mathvariant=¨bold¨ mathcolor=¨#0000FF¨»I«/mi»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»=«/mo»«mfrac mathcolor=¨#0000FF¨»«mi mathvariant=¨bold¨»§#949;«/mi»«msub»«mi mathvariant=¨bold¨»R«/mi»«mi mathvariant=¨bold¨»T«/mi»«/msub»«/mfrac»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»=«/mo»«mfrac mathcolor=¨#0000FF¨»«mi mathvariant=¨bold¨»§#949;«/mi»«mrow»«mi mathvariant=¨bold¨»r«/mi»«mo mathvariant=¨bold¨»+«/mo»«mi mathvariant=¨bold¨»R«/mi»«/mrow»«/mfrac»«/mrow»«/mstyle»«/math»
1. ليس من الواضح كيفية التوصل إلى التعبير، فقانون أوم في الدائرة يعطي تعبيراً للتيار ومقاومة السلك الموصل.
ولهذا السبب يعد قانون أوم خيارًا جيدًا للبدء منه.
2. من تعبير مقاومة السلك الموصل «math xmlns=¨http://www.w3.org/1998/Math/MathML¨»«mi mathvariant=¨bold¨ mathcolor=¨#FF0000¨»R«/mi»«mo mathvariant=¨bold¨ mathcolor=¨#FF0000¨»=«/mo»«mfrac mathcolor=¨#FF0000¨»«mrow»«mi mathvariant=¨bold¨»§#961;«/mi»«mo mathvariant=¨bold¨»§#183;«/mo»«mi mathvariant=¨bold¨»L«/mi»«/mrow»«mi mathvariant=¨bold¨»A«/mi»«/mfrac»«/math» النسبة بين مقاومة السلك الموصل وطوله تساوي النسبة بين المقاومة النوعية ومساحة مقطعه: «math xmlns=¨http://www.w3.org/1998/Math/MathML¨»«mfrac mathcolor=¨#FF0000¨»«mi mathvariant=¨bold¨»R«/mi»«mi mathvariant=¨bold¨»L«/mi»«/mfrac»«mo mathvariant=¨bold¨ mathcolor=¨#FF0000¨»=«/mo»«mfrac mathcolor=¨#FF0000¨»«mi mathvariant=¨bold¨»§#961;«/mi»«mi mathvariant=¨bold¨»A«/mi»«/mfrac»«/math»
3. المقاومة لكل وحدة طوالتي تصف مقاومة الموصل لكل متر.
في هذه الحالة «math xmlns=¨http://www.w3.org/1998/Math/MathML¨»«mi mathvariant=¨bold¨ mathcolor=¨#FF0000¨»§#955;«/mi»«mo mathvariant=¨bold¨ mathcolor=¨#FF0000¨»=«/mo»«mn mathvariant=¨bold¨ mathcolor=¨#FF0000¨»22«/mn»«mo mathvariant=¨bold¨ mathcolor=¨#FF0000¨».«/mo»«mn mathvariant=¨bold¨ mathcolor=¨#FF0000¨»7«/mn»«mfrac mathcolor=¨#FF0000¨»«mi mathvariant=¨bold¨»§#937;«/mi»«mi mathvariant=¨bold¨»m«/mi»«/mfrac»«/math» وهذا يعني أن مقاومة السلك الموصل لكل متر هي 22.7 أوم.
في هذه الحالة «math xmlns=¨http://www.w3.org/1998/Math/MathML¨»«mi mathvariant=¨bold¨ mathcolor=¨#FF0000¨»§#955;«/mi»«mo mathvariant=¨bold¨ mathcolor=¨#FF0000¨»=«/mo»«mn mathvariant=¨bold¨ mathcolor=¨#FF0000¨»22«/mn»«mo mathvariant=¨bold¨ mathcolor=¨#FF0000¨».«/mo»«mn mathvariant=¨bold¨ mathcolor=¨#FF0000¨»7«/mn»«mfrac mathcolor=¨#FF0000¨»«mi mathvariant=¨bold¨»§#937;«/mi»«mi mathvariant=¨bold¨»m«/mi»«/mfrac»«/math» وهذا يعني أن مقاومة السلك الموصل لكل متر هي 22.7 أوم.
4. في تطوير الدوال، عادة ما يكون من غير الواضح ما هي الطريقة الصحيحة لتطوير الدالة.
يوصى بإجراء التطوير على المسودة ثم كتابة الإجابة في ورقة الاختبار بطريقة مرتّبة .
______________________________________________________________________________________
______________________________________________________________________________________
...
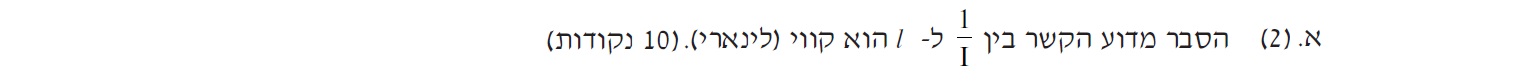
الدالة «math style=¨font-family:`Times New Roman`¨ xmlns=¨http://www.w3.org/1998/Math/MathML¨»«mfrac»«mn mathvariant=¨bold¨ mathsize=¨20px¨»1«/mn»«mi mathvariant=¨bold¨ mathsize=¨20px¨»I«/mi»«/mfrac»«mo mathvariant=¨bold¨ mathsize=¨20px¨»(«/mo»«mi mathvariant=¨bold¨ mathsize=¨20px¨»L«/mi»«mo mathvariant=¨bold¨ mathsize=¨20px¨»)«/mo»«mo mathvariant=¨bold¨ mathsize=¨20px¨»=«/mo»«mfrac»«mi mathvariant=¨bold¨ mathsize=¨20px¨»r«/mi»«mi mathvariant=¨bold¨ mathsize=¨20px¨»§#949;«/mi»«/mfrac»«mo mathvariant=¨bold¨ mathsize=¨20px¨»+«/mo»«mfrac»«mi mathvariant=¨bold¨ mathsize=¨20px¨»§#955;«/mi»«mi mathvariant=¨bold¨ mathsize=¨20px¨»§#949;«/mi»«/mfrac»«mo mathvariant=¨bold¨ mathsize=¨20px¨»§#183;«/mo»«mi mathvariant=¨bold¨ mathsize=¨20px¨»L«/mi»«/math» هي دالة خطية. لذلك العلاقة خطية.
تفسير رياضي حسب الدالة التي تم الحصول عليها في القسم السابق.
رياضيًا، من التعبير الذي حصلنا عليه «math style=¨font-family:`Times New Roman`¨ xmlns=¨http://www.w3.org/1998/Math/MathML¨»«mfrac mathcolor=¨#0000FF¨»«mn mathvariant=¨bold¨ mathsize=¨20px¨»1«/mn»«mi mathvariant=¨bold¨ mathsize=¨20px¨»I«/mi»«/mfrac»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨ mathsize=¨20px¨»(«/mo»«mi mathvariant=¨bold¨ mathcolor=¨#0000FF¨ mathsize=¨20px¨»L«/mi»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨ mathsize=¨20px¨»)«/mo»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨ mathsize=¨20px¨»=«/mo»«mfrac mathcolor=¨#0000FF¨»«mi mathvariant=¨bold¨ mathsize=¨20px¨»r«/mi»«mi mathvariant=¨bold¨ mathsize=¨20px¨»§#949;«/mi»«/mfrac»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨ mathsize=¨20px¨»+«/mo»«mfrac mathcolor=¨#0000FF¨»«mi mathvariant=¨bold¨ mathsize=¨20px¨»§#955;«/mi»«mi mathvariant=¨bold¨ mathsize=¨20px¨»§#949;«/mi»«/mfrac»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨ mathsize=¨20px¨»§#183;«/mo»«mi mathvariant=¨bold¨ mathcolor=¨#0000FF¨ mathsize=¨20px¨»L«/mi»«/math»يتم الحصول على دالة خطية (قوة L واحدة)، وبالتالي فإن العلاقة خطية.
1. يجب إثبات أن هناك علاقة خطية، وليس مطلوبًا تفسير سبب كون العلاقة خطية فيزيائياً. الصياغة مضللة بعض الشيء.
في مثل هذه الحالة، يوصى بكتابة كيف فهمت السؤال وحله وفقًا لذلك.
2. في الأسئلة التي يجب ايجاددالة معينة فيها، دائمًا تقريبًا، إجابات الأقسام التي تظهر لاحقًا في السؤال تكون في الدالة.
במקרה כזה, מומלץ לכתוב כיצד הבנתם את השאלה, ולפתור בהתאם.
2. בשאלות בהן יש למצוא פונקציה מסוימת , כמעט תמיד, התשובות לסעיפים המופיעים בהמשך השאלה נמצאות בפונקציה.
______________________________________________________________________________________
______________________________________________________________________________________
...
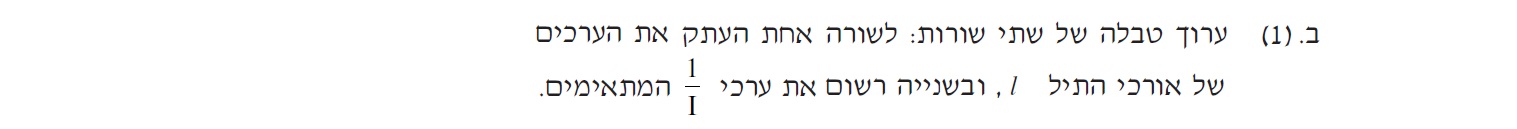
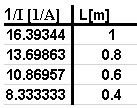
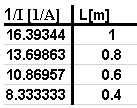
حساب القيمة العكسية للتيار، وإعداد جدول جديد.
حسب قيم التيار نحسب قيم مقلوب التيار، ونصف هذه القيمة بدلالة طول السلك في الجدول:
1. في بعض الأحيان تكون هناك أسئلة بسيطة، وعادة ما تكون الأسئلة البسيطة بمثابة خطوة تمهيدية للبنود التالية.
2. يمكنك كتابة ثلاثة أعمدة، ويمكنك أيضًا كتابة صفوف.
2. אפשר לכתוב שלוש עמודות, אפשר גם לכתוב שורות.
______________________________________________________________________________________
______________________________________________________________________________________
...
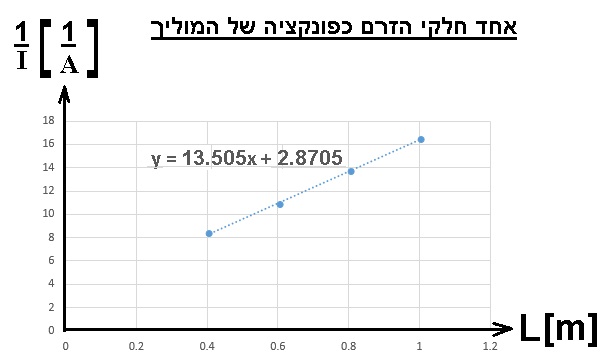
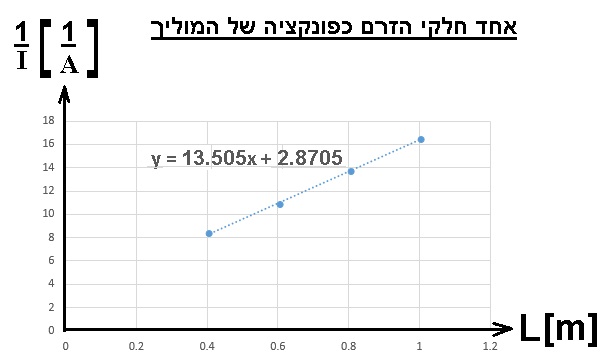
رسم الرسم البياني وفقا للبيانات الموجودة في الجدول.
نرسم رسمًا بيانيًا لمقلوب التيار كدالة لطول السلك الموصل، وفقًا للبيانات الموجودة في الجدول:
من المهم الانتباه إلى الوحدات الموجودة على المحاور، الوحدات الموجودة على المحور الرأسي هي واحد على الأمبير.
______________________________________________________________________________________
______________________________________________________________________________________
...
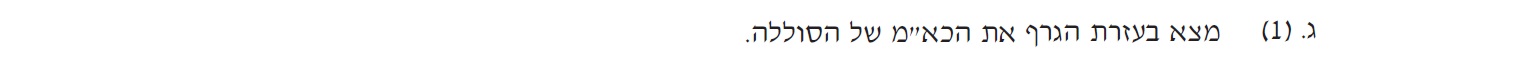
«math xmlns=¨http://www.w3.org/1998/Math/MathML¨»«mi mathvariant=¨bold¨»§#949;«/mi»«mo mathvariant=¨bold¨»=«/mo»«mn mathvariant=¨bold¨»1«/mn»«mo mathvariant=¨bold¨».«/mo»«mn mathvariant=¨bold¨»68«/mn»«mi mathvariant=¨bold¨»V«/mi»«/math»
ميل الدالة .
من التعبير عن الدالة الموصوفة في الرسم البياني: «math style=¨font-family:`Times New Roman`¨ xmlns=¨http://www.w3.org/1998/Math/MathML¨»«mfrac mathcolor=¨#0000FF¨»«mn mathvariant=¨bold¨ mathsize=¨20px¨»1«/mn»«mi mathvariant=¨bold¨ mathsize=¨20px¨»I«/mi»«/mfrac»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨ mathsize=¨20px¨»(«/mo»«mi mathvariant=¨bold¨ mathcolor=¨#0000FF¨ mathsize=¨20px¨»L«/mi»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨ mathsize=¨20px¨»)«/mo»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨ mathsize=¨20px¨»=«/mo»«mfrac mathcolor=¨#0000FF¨»«mi mathvariant=¨bold¨ mathsize=¨20px¨»r«/mi»«mi mathvariant=¨bold¨ mathsize=¨20px¨»§#949;«/mi»«/mfrac»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨ mathsize=¨20px¨»+«/mo»«mfrac mathcolor=¨#0000FF¨»«mi mathvariant=¨bold¨ mathsize=¨20px¨»§#955;«/mi»«mi mathvariant=¨bold¨ mathsize=¨20px¨»§#949;«/mi»«/mfrac»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨ mathsize=¨20px¨»§#183;«/mo»«mi mathvariant=¨bold¨ mathcolor=¨#0000FF¨ mathsize=¨20px¨»L«/mi»«/math» فإن ميل الرسم البياني: «math style=¨font-family:`Times New Roman`¨ xmlns=¨http://www.w3.org/1998/Math/MathML¨»«mstyle mathsize=¨20px¨»«mfrac mathcolor=¨#0000FF¨»«mi mathvariant=¨bold¨»§#955;«/mi»«mi mathvariant=¨bold¨»§#949;«/mi»«/mfrac»«/mstyle»«/math»
من معادلة الخط المستقيم «math xmlns=¨http://www.w3.org/1998/Math/MathML¨»«mi mathvariant=¨bold¨ mathcolor=¨#0000FF¨»y«/mi»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»=«/mo»«mn mathvariant=¨bold¨ mathcolor=¨#0000FF¨»13«/mn»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨».«/mo»«mn mathvariant=¨bold¨ mathcolor=¨#0000FF¨»5«/mn»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»§#183;«/mo»«mi mathvariant=¨bold¨ mathcolor=¨#0000FF¨»X«/mi»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»+«/mo»«mn mathvariant=¨bold¨ mathcolor=¨#0000FF¨»2«/mn»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨».«/mo»«mn mathvariant=¨bold¨ mathcolor=¨#0000FF¨»87«/mn»«/math» ميل الخط «math xmlns=¨http://www.w3.org/1998/Math/MathML¨»«mn mathvariant=¨bold¨ mathcolor=¨#0000FF¨»13«/mn»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨».«/mo»«mn mathvariant=¨bold¨ mathcolor=¨#0000FF¨»5«/mn»«mfrac mathcolor=¨#0000FF¨»«mn mathvariant=¨bold¨»1«/mn»«mrow»«mi mathvariant=¨bold¨»A«/mi»«mo mathvariant=¨bold¨»§#183;«/mo»«mi mathvariant=¨bold¨»m«/mi»«/mrow»«/mfrac»«/math».
نقارن تعبير الميل في الدالة بقيمته في الرسم البياني، ونجد القوة الكهربائية الدافعة للبطارية:
«math style=¨font-family:`Times New Roman`¨ xmlns=¨http://www.w3.org/1998/Math/MathML¨»«mstyle mathsize=¨20px¨»«mfrac mathcolor=¨#0000FF¨»«mi mathvariant=¨bold¨»§#955;«/mi»«mi mathvariant=¨bold¨»§#949;«/mi»«/mfrac»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»=«/mo»«mn mathvariant=¨bold¨ mathcolor=¨#0000FF¨»13«/mn»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨».«/mo»«mn mathvariant=¨bold¨ mathcolor=¨#0000FF¨»5«/mn»«mspace linebreak=¨newline¨»«/mspace»«mspace linebreak=¨newline¨»«/mspace»«mi mathvariant=¨bold¨ mathcolor=¨#0000FF¨»§#949;«/mi»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»=«/mo»«mfrac mathcolor=¨#0000FF¨»«mi mathvariant=¨bold¨»§#955;«/mi»«mrow»«mn mathvariant=¨bold¨»13«/mn»«mo mathvariant=¨bold¨».«/mo»«mn mathvariant=¨bold¨»5«/mn»«/mrow»«/mfrac»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»=«/mo»«mfrac mathcolor=¨#0000FF¨»«mrow»«mn mathvariant=¨bold¨»22«/mn»«mo mathvariant=¨bold¨».«/mo»«mn mathvariant=¨bold¨»7«/mn»«/mrow»«mrow»«mn mathvariant=¨bold¨»13«/mn»«mo mathvariant=¨bold¨».«/mo»«mn mathvariant=¨bold¨»5«/mn»«/mrow»«/mfrac»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»=«/mo»«mn mathvariant=¨bold¨ mathcolor=¨#0000FF¨»1«/mn»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨».«/mo»«mn mathvariant=¨bold¨ mathcolor=¨#0000FF¨»68«/mn»«mi mathvariant=¨bold¨ mathcolor=¨#0000FF¨»V«/mi»«mspace linebreak=¨newline¨»«/mspace»«/mstyle»«/math»
ومن ثم فإن القوة الكهربائية الدافعة للبطارية يساوي 1.68 فولط.
ממשוואת הישר «math xmlns=¨http://www.w3.org/1998/Math/MathML¨»«mi mathvariant=¨bold¨ mathcolor=¨#0000FF¨»y«/mi»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»=«/mo»«mn mathvariant=¨bold¨ mathcolor=¨#0000FF¨»13«/mn»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨».«/mo»«mn mathvariant=¨bold¨ mathcolor=¨#0000FF¨»5«/mn»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»§#183;«/mo»«mi mathvariant=¨bold¨ mathcolor=¨#0000FF¨»X«/mi»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»+«/mo»«mn mathvariant=¨bold¨ mathcolor=¨#0000FF¨»2«/mn»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨».«/mo»«mn mathvariant=¨bold¨ mathcolor=¨#0000FF¨»87«/mn»«/math» שיפוע הישר שווה «math xmlns=¨http://www.w3.org/1998/Math/MathML¨»«mn mathvariant=¨bold¨ mathcolor=¨#0000FF¨»13«/mn»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨».«/mo»«mn mathvariant=¨bold¨ mathcolor=¨#0000FF¨»5«/mn»«mfrac mathcolor=¨#0000FF¨»«mn mathvariant=¨bold¨»1«/mn»«mrow»«mi mathvariant=¨bold¨»A«/mi»«mo mathvariant=¨bold¨»§#183;«/mo»«mi mathvariant=¨bold¨»m«/mi»«/mrow»«/mfrac»«/math».
נשווה בין ביטוי השיפוע בפונקציה לערכו בגרף , ונמצא את כא"מ הסוללה:
«math style=¨font-family:`Times New Roman`¨ xmlns=¨http://www.w3.org/1998/Math/MathML¨»«mstyle mathsize=¨20px¨»«mfrac mathcolor=¨#0000FF¨»«mi mathvariant=¨bold¨»§#955;«/mi»«mi mathvariant=¨bold¨»§#949;«/mi»«/mfrac»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»=«/mo»«mn mathvariant=¨bold¨ mathcolor=¨#0000FF¨»13«/mn»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨».«/mo»«mn mathvariant=¨bold¨ mathcolor=¨#0000FF¨»5«/mn»«mspace linebreak=¨newline¨»«/mspace»«mspace linebreak=¨newline¨»«/mspace»«mi mathvariant=¨bold¨ mathcolor=¨#0000FF¨»§#949;«/mi»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»=«/mo»«mfrac mathcolor=¨#0000FF¨»«mi mathvariant=¨bold¨»§#955;«/mi»«mrow»«mn mathvariant=¨bold¨»13«/mn»«mo mathvariant=¨bold¨».«/mo»«mn mathvariant=¨bold¨»5«/mn»«/mrow»«/mfrac»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»=«/mo»«mfrac mathcolor=¨#0000FF¨»«mrow»«mn mathvariant=¨bold¨»22«/mn»«mo mathvariant=¨bold¨».«/mo»«mn mathvariant=¨bold¨»7«/mn»«/mrow»«mrow»«mn mathvariant=¨bold¨»13«/mn»«mo mathvariant=¨bold¨».«/mo»«mn mathvariant=¨bold¨»5«/mn»«/mrow»«/mfrac»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»=«/mo»«mn mathvariant=¨bold¨ mathcolor=¨#0000FF¨»1«/mn»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨».«/mo»«mn mathvariant=¨bold¨ mathcolor=¨#0000FF¨»68«/mn»«mi mathvariant=¨bold¨ mathcolor=¨#0000FF¨»V«/mi»«mspace linebreak=¨newline¨»«/mspace»«/mstyle»«/math»
מכאן שכא"מ הסוללה שווה ל 1.68 וולט.
1. قيمة القوة الكهربائية الدافعة للبطارية العادية هي 1.5 فولط، أما البطارية الجديدة فلها قوة كهربائية دافعة أكبر قليلًا.
2. في دفتر الامتحان يجب حساب الميل على أساس نقطتين تقعان على خط الاتجاه.
3. في كل مرة تكتب فيها قيمة مقدار فيزيائي، يجب عليك كتابة الوحدات، ويعتبر ميل الدالة في الرسم البياني أيضًا قيمة فيزيائية.
يجب كتابة الوحدات المناسبة بجانب قيمة الميل.
2. במחברת הבחינה יש לחשב את השיפוע על פי שתי נקודות הנמצאות על הישר המסתבר ביותר.
______________________________________________________________________________________
______________________________________________________________________________________
...
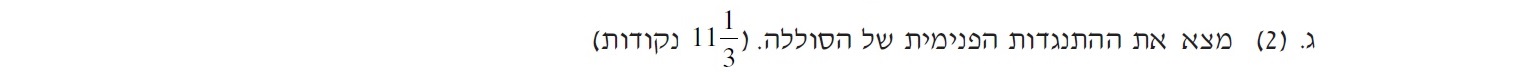
«math xmlns=¨http://www.w3.org/1998/Math/MathML¨»«mstyle mathsize=¨20px¨»«mrow»«mi mathvariant=¨bold¨»r«/mi»«mo mathvariant=¨bold¨»=«/mo»«mn mathvariant=¨bold¨»4«/mn»«mo mathvariant=¨bold¨».«/mo»«mn mathvariant=¨bold¨»82«/mn»«mi mathvariant=¨bold¨»§#937;«/mi»«/mrow»«/mstyle»«/math»
نقطة التقاطع.
من تعبير الدالة الموصوفة في الرسم البياني: «math style=¨font-family:`Times New Roman`¨ xmlns=¨http://www.w3.org/1998/Math/MathML¨»«mfrac mathcolor=¨#0000FF¨»«mn mathvariant=¨bold¨ mathsize=¨20px¨»1«/mn»«mi mathvariant=¨bold¨ mathsize=¨20px¨»I«/mi»«/mfrac»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨ mathsize=¨20px¨»(«/mo»«mi mathvariant=¨bold¨ mathcolor=¨#0000FF¨ mathsize=¨20px¨»L«/mi»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨ mathsize=¨20px¨»)«/mo»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨ mathsize=¨20px¨»=«/mo»«mfrac mathcolor=¨#0000FF¨»«mi mathvariant=¨bold¨ mathsize=¨20px¨»r«/mi»«mi mathvariant=¨bold¨ mathsize=¨20px¨»§#949;«/mi»«/mfrac»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨ mathsize=¨20px¨»+«/mo»«mfrac mathcolor=¨#0000FF¨»«mi mathvariant=¨bold¨ mathsize=¨20px¨»§#955;«/mi»«mi mathvariant=¨bold¨ mathsize=¨20px¨»§#949;«/mi»«/mfrac»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨ mathsize=¨20px¨»§#183;«/mo»«mi mathvariant=¨bold¨ mathcolor=¨#0000FF¨ mathsize=¨20px¨»L«/mi»«/math» تُمثِّل نقطة التقاطع: «math style=¨font-family:`Times New Roman`¨ xmlns=¨http://www.w3.org/1998/Math/MathML¨»«mfrac mathcolor=¨#0000FF¨»«mi mathvariant=¨bold¨ mathsize=¨20px¨»r«/mi»«mi mathvariant=¨bold¨ mathsize=¨20px¨»§#949;«/mi»«/mfrac»«/math»
من معادلة الخط المستقيم «math xmlns=¨http://www.w3.org/1998/Math/MathML¨»«mi mathvariant=¨bold¨ mathcolor=¨#0000FF¨»y«/mi»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»=«/mo»«mn mathvariant=¨bold¨ mathcolor=¨#0000FF¨»13«/mn»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨».«/mo»«mn mathvariant=¨bold¨ mathcolor=¨#0000FF¨»5«/mn»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»§#183;«/mo»«mi mathvariant=¨bold¨ mathcolor=¨#0000FF¨»X«/mi»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»+«/mo»«mn mathvariant=¨bold¨ mathcolor=¨#0000FF¨»2«/mn»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨».«/mo»«mn mathvariant=¨bold¨ mathcolor=¨#0000FF¨»87«/mn»«/math» قيمة نقطة تقاطع الدالة مع المحور العمودي هي «math xmlns=¨http://www.w3.org/1998/Math/MathML¨»«mn mathvariant=¨bold¨ mathcolor=¨#0000FF¨»2«/mn»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨».«/mo»«mn mathvariant=¨bold¨ mathcolor=¨#0000FF¨»87«/mn»«mfrac mathcolor=¨#0000FF¨»«mn mathvariant=¨bold¨»1«/mn»«mi mathvariant=¨bold¨»A«/mi»«/mfrac»«/math».
نقارن عبارة نقطة التقاطع من معادلة الخط بقيمة نقطة تقاطع الدالة مع المحور العمودي:
«math style=¨font-family:`Times New Roman`¨ xmlns=¨http://www.w3.org/1998/Math/MathML¨»«mstyle mathsize=¨20px¨»«mrow»«mfrac mathcolor=¨#0000FF¨»«mi mathvariant=¨bold¨»r«/mi»«mi mathvariant=¨bold¨»§#949;«/mi»«/mfrac»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»=«/mo»«mn mathvariant=¨bold¨ mathcolor=¨#0000FF¨»2«/mn»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨».«/mo»«mn mathvariant=¨bold¨ mathcolor=¨#0000FF¨»87«/mn»«mspace linebreak=¨newline¨/»«mi mathvariant=¨bold¨ mathcolor=¨#0000FF¨»r«/mi»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»=«/mo»«mn mathvariant=¨bold¨ mathcolor=¨#0000FF¨»2«/mn»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨».«/mo»«mn mathvariant=¨bold¨ mathcolor=¨#0000FF¨»87«/mn»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»§#183;«/mo»«mi mathvariant=¨bold¨ mathcolor=¨#0000FF¨»§#949;«/mi»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»=«/mo»«mn mathvariant=¨bold¨ mathcolor=¨#0000FF¨»2«/mn»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨».«/mo»«mn mathvariant=¨bold¨ mathcolor=¨#0000FF¨»87«/mn»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»§#183;«/mo»«mn mathvariant=¨bold¨ mathcolor=¨#0000FF¨»1«/mn»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨».«/mo»«mn mathvariant=¨bold¨ mathcolor=¨#0000FF¨»68«/mn»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»=«/mo»«mn mathvariant=¨bold¨ mathcolor=¨#0000FF¨»4«/mn»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨».«/mo»«mn mathvariant=¨bold¨ mathcolor=¨#0000FF¨»82«/mn»«mi mathvariant=¨bold¨ mathcolor=¨#0000FF¨»§#937;«/mi»«/mrow»«/mstyle»«/math»
قيمة المقاومة الداخلية 4.82 أوم.
ממשוואת הישר «math xmlns=¨http://www.w3.org/1998/Math/MathML¨»«mi mathvariant=¨bold¨ mathcolor=¨#0000FF¨»y«/mi»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»=«/mo»«mn mathvariant=¨bold¨ mathcolor=¨#0000FF¨»13«/mn»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨».«/mo»«mn mathvariant=¨bold¨ mathcolor=¨#0000FF¨»5«/mn»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»§#183;«/mo»«mi mathvariant=¨bold¨ mathcolor=¨#0000FF¨»X«/mi»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»+«/mo»«mn mathvariant=¨bold¨ mathcolor=¨#0000FF¨»2«/mn»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨».«/mo»«mn mathvariant=¨bold¨ mathcolor=¨#0000FF¨»87«/mn»«/math» ערך נקודת החיתוך של הפונקציה עם הציר האנכי הוא «math xmlns=¨http://www.w3.org/1998/Math/MathML¨»«mn mathvariant=¨bold¨ mathcolor=¨#0000FF¨»2«/mn»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨».«/mo»«mn mathvariant=¨bold¨ mathcolor=¨#0000FF¨»87«/mn»«mfrac mathcolor=¨#0000FF¨»«mn mathvariant=¨bold¨»1«/mn»«mi mathvariant=¨bold¨»A«/mi»«/mfrac»«/math».
נשווה בין ביטוי נקודת החיתוך ממשוואת הישר לערך נקודת החיתוך ממשוואת הישר:
«math style=¨font-family:`Times New Roman`¨ xmlns=¨http://www.w3.org/1998/Math/MathML¨»«mstyle mathsize=¨20px¨»«mrow»«mfrac mathcolor=¨#0000FF¨»«mi mathvariant=¨bold¨»r«/mi»«mi mathvariant=¨bold¨»§#949;«/mi»«/mfrac»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»=«/mo»«mn mathvariant=¨bold¨ mathcolor=¨#0000FF¨»2«/mn»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨».«/mo»«mn mathvariant=¨bold¨ mathcolor=¨#0000FF¨»87«/mn»«mspace linebreak=¨newline¨/»«mi mathvariant=¨bold¨ mathcolor=¨#0000FF¨»r«/mi»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»=«/mo»«mn mathvariant=¨bold¨ mathcolor=¨#0000FF¨»2«/mn»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨».«/mo»«mn mathvariant=¨bold¨ mathcolor=¨#0000FF¨»87«/mn»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»§#183;«/mo»«mi mathvariant=¨bold¨ mathcolor=¨#0000FF¨»§#949;«/mi»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»=«/mo»«mn mathvariant=¨bold¨ mathcolor=¨#0000FF¨»2«/mn»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨».«/mo»«mn mathvariant=¨bold¨ mathcolor=¨#0000FF¨»87«/mn»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»§#183;«/mo»«mn mathvariant=¨bold¨ mathcolor=¨#0000FF¨»1«/mn»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨».«/mo»«mn mathvariant=¨bold¨ mathcolor=¨#0000FF¨»68«/mn»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»=«/mo»«mn mathvariant=¨bold¨ mathcolor=¨#0000FF¨»4«/mn»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨».«/mo»«mn mathvariant=¨bold¨ mathcolor=¨#0000FF¨»82«/mn»«mi mathvariant=¨bold¨ mathcolor=¨#0000FF¨»§#937;«/mi»«/mrow»«/mstyle»«/math»
ערך ההתנגדות הפנימית הוא 4.82 אום.
1. في دفتر الامتحان، يمكنك مَد خط الاتجاه على استقامته بمساعدة المسطرة، وتقدير نقطة التقاطع.
يمكنك إيجاد معادلة الخط بواسطة نقطتين تقعان على خط الاتجاه.
2. عند كتابة قيمة نقطة التقاطع، يجب أيضًا كتابة الوحدات، في هذه الحالة تكون واحد على الأمبير.
3. قيمة المقاومة الداخلية بالنسبة للبطارية كبيرة بعض الشيء، وكان النموذج منذ أكثر من 20 عامًا، ويبدو أن البطاريات حينه كانت أقل كفاءة.
אפשר למצוא את משוואת הישר לפי שתי נקודות הנמצאות על הישר המסתבר ביותר.
2. בכתיבת ערך נקודת החיתוך יש לכתוב גם את היחידות, במקרה זה אחד חלקי אמפר.
3. ערך ההתנגדות הפנימית יחסית לסוללה יצא קצת גדול, השאלון לפני יותר מ 20 שנה כנראה הסוללות אז היו פחות יעילות.
______________________________________________________________________________________