3. 2012,2-مقاومة السلك الموصل بدلالة بياناته
______________________________________________________________________________________
...
يحقق السلك لقانون أوم، ومقاومته: «math xmlns=¨http://www.w3.org/1998/Math/MathML¨»«mstyle mathsize=¨16px¨»«mi mathvariant=¨bold-italic¨»R«/mi»«mo mathvariant=¨bold¨»=«/mo»«mn mathvariant=¨bold¨»5«/mn»«mo mathvariant=¨bold¨».«/mo»«mn mathvariant=¨bold¨»15«/mn»«mi mathvariant=¨bold-italic¨»§#937;«/mi»«/mstyle»«/math»
התיל מקיים את חוק אוהם, התנגדותו : «math xmlns=¨http://www.w3.org/1998/Math/MathML¨»«mstyle mathsize=¨16px¨»«mi mathvariant=¨bold-italic¨»R«/mi»«mo mathvariant=¨bold¨»=«/mo»«mn mathvariant=¨bold¨»5«/mn»«mo mathvariant=¨bold¨».«/mo»«mn mathvariant=¨bold¨»15«/mn»«mi mathvariant=¨bold-italic¨»§#937;«/mi»«/mstyle»«/math»
התיל מקיים את חוק אוהם, התנגדותו : «math xmlns=¨http://www.w3.org/1998/Math/MathML¨»«mstyle mathsize=¨16px¨»«mi mathvariant=¨bold-italic¨»R«/mi»«mo mathvariant=¨bold¨»=«/mo»«mn mathvariant=¨bold¨»5«/mn»«mo mathvariant=¨bold¨».«/mo»«mn mathvariant=¨bold¨»15«/mn»«mi mathvariant=¨bold-italic¨»§#937;«/mi»«/mstyle»«/math»
התיל מקיים את חוק אוהם, התנגדותו : «math xmlns=¨http://www.w3.org/1998/Math/MathML¨»«mstyle mathsize=¨16px¨»«mi mathvariant=¨bold-italic¨»R«/mi»«mo mathvariant=¨bold¨»=«/mo»«mn mathvariant=¨bold¨»5«/mn»«mo mathvariant=¨bold¨».«/mo»«mn mathvariant=¨bold¨»15«/mn»«mi mathvariant=¨bold-italic¨»§#937;«/mi»«/mstyle»«/math»
התיל מקיים את חוק אוהם, התנגדותו : «math xmlns=¨http://www.w3.org/1998/Math/MathML¨»«mstyle mathsize=¨16px¨»«mi mathvariant=¨bold-italic¨»R«/mi»«mo mathvariant=¨bold¨»=«/mo»«mn mathvariant=¨bold¨»5«/mn»«mo mathvariant=¨bold¨».«/mo»«mn mathvariant=¨bold¨»15«/mn»«mi mathvariant=¨bold-italic¨»§#937;«/mi»«/mstyle»«/math»
התיל מקיים את חוק אוהם, התנגדותו : «math xmlns=¨http://www.w3.org/1998/Math/MathML¨»«mstyle mathsize=¨16px¨»«mi mathvariant=¨bold-italic¨»R«/mi»«mo mathvariant=¨bold¨»=«/mo»«mn mathvariant=¨bold¨»5«/mn»«mo mathvariant=¨bold¨».«/mo»«mn mathvariant=¨bold¨»15«/mn»«mi mathvariant=¨bold-italic¨»§#937;«/mi»«/mstyle»«/math»
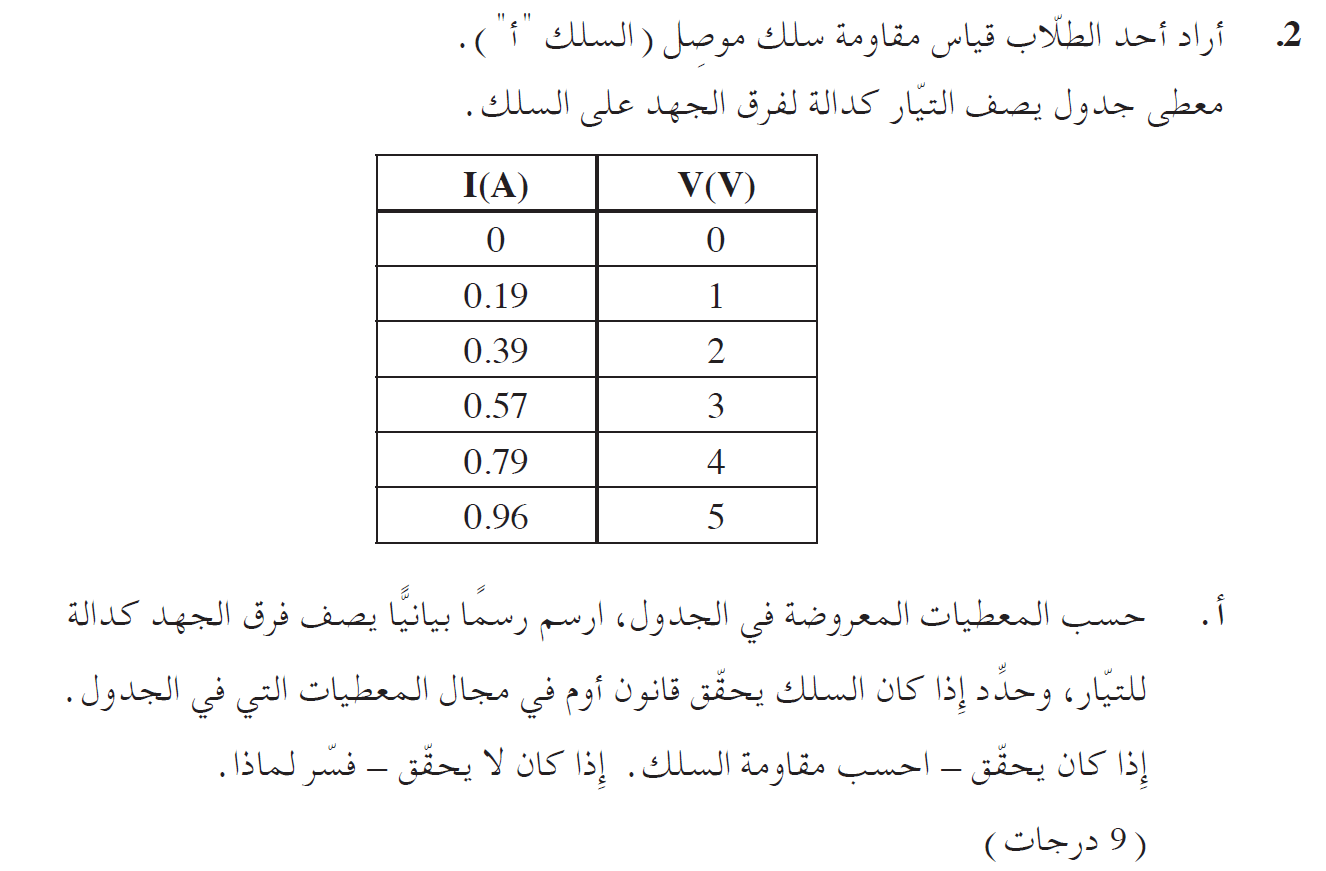
يجب رسم رسمًا بيانيًا لفرق الجهد كدالة للتيار، وفقًا للبيانات الموجودة في الجدول.
نصف الرسم البياني لفرق الجهد كدالة للتيارللبيانات الموجودة بالجدول .
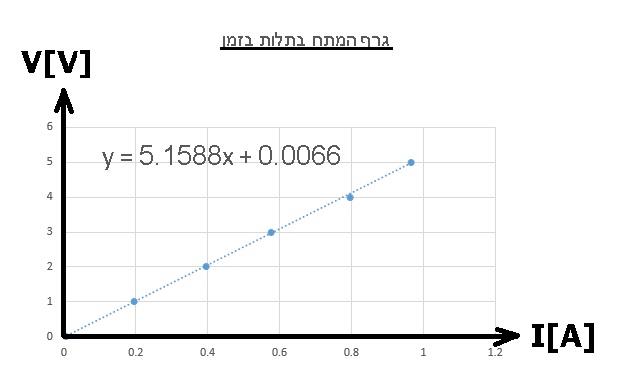
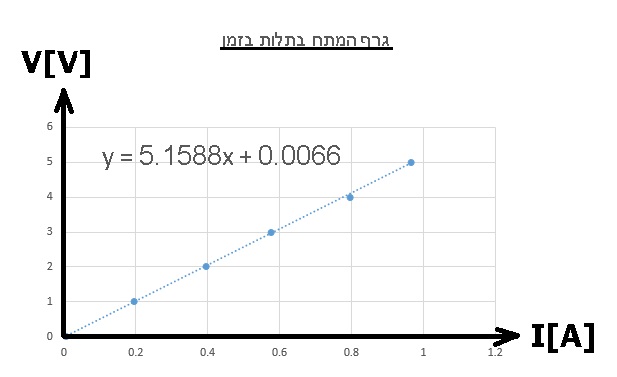
من الرسم البياني يمكن أن ترى أن النسبة بين فرق الجهد والتيار ثابتة. ولذلك فإن السلك يحقق قانون أوم.
من قانون أوم: «math style=¨font-family:Tahoma¨ xmlns=¨http://www.w3.org/1998/Math/MathML¨»«mi mathvariant=¨bold¨ mathcolor=¨#0000FF¨»V«/mi»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»=«/mo»«mi mathvariant=¨bold¨ mathcolor=¨#0000FF¨»I«/mi»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»§#183;«/mo»«mi mathvariant=¨bold¨ mathcolor=¨#0000FF¨»R«/mi»«/math», يمكن تحديد أنه في الرسم البياني الذي يصف فرق الجهد كدالة للتيار، فإن ميل الرسم البياني يساوي مقاومة السلك الموصل.
وبالتالي فإن مقاومة السلك الموصل هي: «math xmlns=¨http://www.w3.org/1998/Math/MathML¨»«mi mathvariant=¨bold¨ mathcolor=¨#0000FF¨»R«/mi»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»=«/mo»«mn mathvariant=¨bold¨ mathcolor=¨#0000FF¨»5«/mn»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨».«/mo»«mn mathvariant=¨bold¨ mathcolor=¨#0000FF¨»15«/mn»«mi mathvariant=¨bold¨ mathcolor=¨#0000FF¨»§#937;«/mi»«/math»

1. يصف الجدول التيار كدالة لفرق الجهد. وهذا وصف منطقي لأن التيار يتعلق بفرق الجهد.
الرسم البياني يصف فرق الجهد بدلالة التيار، وهو وصف أقل منطقية لأن فرق الجهد لا يتعلق بالتيار.
2. من المهم عدم ارتكاب الأخطاء في وصف رسم بياني لفرق الجهد كدالة للتيار وليس العكس.
הגרף מתאר את המתח בתלות בזרם, זה תיאור פחות הגיוני מכיוון שהמתח לא תלוי בזרם.
2. חשוב לא לטעות , לתאר גרף של המתח בתלות בזרם ולא ההיפך.
______________________________________________________________________________________

______________________________________________________________________________________
...
«math xmlns=¨http://www.w3.org/1998/Math/MathML¨»«mi mathvariant=¨bold¨»§#961;«/mi»«mo mathvariant=¨bold¨»=«/mo»«mn mathvariant=¨bold¨»10«/mn»«mo mathvariant=¨bold¨»§#183;«/mo»«msup»«mn mathvariant=¨bold¨»10«/mn»«mrow»«mo mathvariant=¨bold¨»-«/mo»«mn mathvariant=¨bold¨»7«/mn»«/mrow»«/msup»«mi mathvariant=¨bold¨»§#937;«/mi»«mo mathvariant=¨bold¨»§#183;«/mo»«mi mathvariant=¨bold¨»m«/mi»«/math»
تعبير مقاومة السلك الموصل وفقا لبياناته.
سوف نستخدم تعبيرًا لمقاومة سلك موصل بدلالة بياناته، وسنعبر عن مقاومته النوعية من التعبير
«math xmlns=¨http://www.w3.org/1998/Math/MathML¨»«mi mathvariant=¨bold¨ mathcolor=¨#0000FF¨»R«/mi»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»=«/mo»«mfrac mathcolor=¨#0000FF¨»«mrow»«mi mathvariant=¨bold¨»§#961;«/mi»«mo mathvariant=¨bold¨»§#183;«/mo»«mi mathvariant=¨bold¨»L«/mi»«/mrow»«mi mathvariant=¨bold¨»A«/mi»«/mfrac»«mspace linebreak=¨newline¨»«/mspace»«mspace linebreak=¨newline¨»«/mspace»«mi mathvariant=¨bold¨ mathcolor=¨#0000FF¨»§#961;«/mi»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»=«/mo»«mfrac mathcolor=¨#0000FF¨»«mrow»«mi mathvariant=¨bold¨»R«/mi»«mo mathvariant=¨bold¨»§#183;«/mo»«mi mathvariant=¨bold¨»A«/mi»«/mrow»«mi mathvariant=¨bold¨»L«/mi»«/mfrac»«/math»
قانون أوم، الميل في الرسم البياني للجهد كدالة للتيار يساوي المقاومة، «math style=¨font-family:Tahoma¨ xmlns=¨http://www.w3.org/1998/Math/MathML¨»«mi mathvariant=¨bold¨ mathcolor=¨#0000FF¨»V«/mi»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»=«/mo»«munder mathcolor=¨#FF0000¨»«munder»«mi mathvariant=¨bold¨»R«/mi»«mo mathvariant=¨bold¨»§#9183;«/mo»«/munder»«mi mathvariant=¨bold¨»§#1575;§#1604;§#1605;§#1610;§#1604;«/mi»«/munder»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»§#183;«/mo»«mi mathvariant=¨bold¨ mathcolor=¨#0000FF¨»I«/mi»«/math» . من دالة الخط المستقيم تكون قيمة الميل 5.15 أوم.
نحسب مساحة المقطع حسب قطر مساحة المقطع الوارد في السؤال:
«math xmlns=¨http://www.w3.org/1998/Math/MathML¨»«mi mathvariant=¨bold-italic¨ mathcolor=¨#0000FF¨»A«/mi»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»=«/mo»«mi mathvariant=¨bold¨ mathcolor=¨#0000FF¨»§#960;«/mi»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»§#183;«/mo»«msup»«mi mathvariant=¨bold¨ mathcolor=¨#0000FF¨»r«/mi»«mn mathvariant=¨bold¨ mathcolor=¨#0000FF¨»2«/mn»«/msup»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»=«/mo»«mi mathvariant=¨bold¨ mathcolor=¨#0000FF¨»§#960;«/mi»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»§#183;«/mo»«msup»«mrow mathcolor=¨#0000FF¨»«mo mathvariant=¨bold¨»(«/mo»«mn mathvariant=¨bold¨»0«/mn»«mo mathvariant=¨bold¨».«/mo»«mn mathvariant=¨bold¨»25«/mn»«mo mathvariant=¨bold¨»§#183;«/mo»«msup»«mn mathvariant=¨bold¨»10«/mn»«mrow»«mo mathvariant=¨bold¨»-«/mo»«mn mathvariant=¨bold¨»3«/mn»«/mrow»«/msup»«mo mathvariant=¨bold¨»)«/mo»«/mrow»«mn mathvariant=¨bold¨ mathcolor=¨#0000FF¨»2«/mn»«/msup»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»=«/mo»«mn mathvariant=¨bold¨ mathcolor=¨#0000FF¨»1«/mn»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨».«/mo»«mn mathvariant=¨bold¨ mathcolor=¨#0000FF¨»96«/mn»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»§#183;«/mo»«msup»«mn mathvariant=¨bold¨ mathcolor=¨#0000FF¨»10«/mn»«mrow mathcolor=¨#0000FF¨»«mo mathvariant=¨bold¨»-«/mo»«mn mathvariant=¨bold¨»7«/mn»«/mrow»«/msup»«msup»«mi mathvariant=¨bold¨ mathcolor=¨#0000FF¨»m«/mi»«mn mathvariant=¨bold¨ mathcolor=¨#0000FF¨»2«/mn»«/msup»«/math»
نُعوّض مقاومة السلك الموصل ومساحة مقطعه في تعبير المقاومة النوعية:
«math xmlns=¨http://www.w3.org/1998/Math/MathML¨»«mi mathvariant=¨bold¨ mathcolor=¨#0000FF¨»§#961;«/mi»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»=«/mo»«mfrac mathcolor=¨#0000FF¨»«mrow»«mi mathvariant=¨bold¨»R«/mi»«mo mathvariant=¨bold¨»§#183;«/mo»«mi mathvariant=¨bold¨»A«/mi»«/mrow»«mi mathvariant=¨bold¨»L«/mi»«/mfrac»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»=«/mo»«mfrac mathcolor=¨#0000FF¨»«mrow»«mn mathvariant=¨bold¨»5«/mn»«mo mathvariant=¨bold¨».«/mo»«mn mathvariant=¨bold¨»1«/mn»«mo mathvariant=¨bold¨»§#183;«/mo»«mn mathvariant=¨bold¨»1«/mn»«mo mathvariant=¨bold¨».«/mo»«mn mathvariant=¨bold¨»96«/mn»«mo mathvariant=¨bold¨»§#183;«/mo»«msup»«mn mathvariant=¨bold¨»10«/mn»«mrow»«mo mathvariant=¨bold¨»-«/mo»«mn mathvariant=¨bold¨»7«/mn»«/mrow»«/msup»«/mrow»«mn mathvariant=¨bold¨»1«/mn»«/mfrac»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»=«/mo»«mn mathvariant=¨bold¨ mathcolor=¨#0000FF¨»10«/mn»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»§#183;«/mo»«msup»«mn mathvariant=¨bold¨ mathcolor=¨#0000FF¨»10«/mn»«mrow mathcolor=¨#0000FF¨»«mo mathvariant=¨bold¨»-«/mo»«mn mathvariant=¨bold¨»7«/mn»«/mrow»«/msup»«mi mathvariant=¨bold¨ mathcolor=¨#0000FF¨»§#937;«/mi»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»§#183;«/mo»«mi mathvariant=¨bold¨ mathcolor=¨#0000FF¨»m«/mi»«/math»
وبالتالي فإن المقاومة النوعية هي: «math xmlns=¨http://www.w3.org/1998/Math/MathML¨»«mn mathvariant=¨bold¨ mathcolor=¨#0000FF¨»10«/mn»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»§#183;«/mo»«msup»«mn mathvariant=¨bold¨ mathcolor=¨#0000FF¨»10«/mn»«mrow mathcolor=¨#0000FF¨»«mo mathvariant=¨bold¨»-«/mo»«mn mathvariant=¨bold¨»7«/mn»«/mrow»«/msup»«mi mathvariant=¨bold¨ mathcolor=¨#0000FF¨»§#937;«/mi»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»§#183;«/mo»«mi mathvariant=¨bold¨ mathcolor=¨#0000FF¨»m«/mi»«/math».
«math xmlns=¨http://www.w3.org/1998/Math/MathML¨»«mi mathvariant=¨bold¨ mathcolor=¨#0000FF¨»R«/mi»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»=«/mo»«mfrac mathcolor=¨#0000FF¨»«mrow»«mi mathvariant=¨bold¨»§#961;«/mi»«mo mathvariant=¨bold¨»§#183;«/mo»«mi mathvariant=¨bold¨»L«/mi»«/mrow»«mi mathvariant=¨bold¨»A«/mi»«/mfrac»«mspace linebreak=¨newline¨»«/mspace»«mspace linebreak=¨newline¨»«/mspace»«mi mathvariant=¨bold¨ mathcolor=¨#0000FF¨»§#961;«/mi»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»=«/mo»«mfrac mathcolor=¨#0000FF¨»«mrow»«mi mathvariant=¨bold¨»R«/mi»«mo mathvariant=¨bold¨»§#183;«/mo»«mi mathvariant=¨bold¨»A«/mi»«/mrow»«mi mathvariant=¨bold¨»L«/mi»«/mfrac»«/math»
מחוק אום , השיפוע בגרף מתח בתלות בזרם שווה להתנגדות, «math style=¨font-family:Tahoma¨ xmlns=¨http://www.w3.org/1998/Math/MathML¨»«mi mathvariant=¨bold¨ mathcolor=¨#0000FF¨»V«/mi»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»=«/mo»«munder mathcolor=¨#FF0000¨»«munder»«mi mathvariant=¨bold¨»R«/mi»«mo mathvariant=¨bold¨»§#9183;«/mo»«/munder»«mi mathvariant=¨bold¨»§#1513;§#1497;§#1508;§#1493;§#1506;«/mi»«/munder»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»§#183;«/mo»«mi mathvariant=¨bold¨ mathcolor=¨#0000FF¨»I«/mi»«/math» . מפונקצית הישר ערך השיפוע הוא 5.15 אום.
נחשב את שטח החתך בהתאם לקוטר שטח החתך הנתון בשאלה :
«math xmlns=¨http://www.w3.org/1998/Math/MathML¨»«mi mathvariant=¨bold-italic¨ mathcolor=¨#0000FF¨»A«/mi»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»=«/mo»«mi mathvariant=¨bold¨ mathcolor=¨#0000FF¨»§#960;«/mi»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»§#183;«/mo»«msup»«mi mathvariant=¨bold¨ mathcolor=¨#0000FF¨»r«/mi»«mn mathvariant=¨bold¨ mathcolor=¨#0000FF¨»2«/mn»«/msup»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»=«/mo»«mi mathvariant=¨bold¨ mathcolor=¨#0000FF¨»§#960;«/mi»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»§#183;«/mo»«msup»«mrow mathcolor=¨#0000FF¨»«mo mathvariant=¨bold¨»(«/mo»«mn mathvariant=¨bold¨»0«/mn»«mo mathvariant=¨bold¨».«/mo»«mn mathvariant=¨bold¨»25«/mn»«mo mathvariant=¨bold¨»§#183;«/mo»«msup»«mn mathvariant=¨bold¨»10«/mn»«mrow»«mo mathvariant=¨bold¨»-«/mo»«mn mathvariant=¨bold¨»3«/mn»«/mrow»«/msup»«mo mathvariant=¨bold¨»)«/mo»«/mrow»«mn mathvariant=¨bold¨ mathcolor=¨#0000FF¨»2«/mn»«/msup»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»=«/mo»«mn mathvariant=¨bold¨ mathcolor=¨#0000FF¨»1«/mn»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨».«/mo»«mn mathvariant=¨bold¨ mathcolor=¨#0000FF¨»96«/mn»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»§#183;«/mo»«msup»«mn mathvariant=¨bold¨ mathcolor=¨#0000FF¨»10«/mn»«mrow mathcolor=¨#0000FF¨»«mo mathvariant=¨bold¨»-«/mo»«mn mathvariant=¨bold¨»7«/mn»«/mrow»«/msup»«msup»«mi mathvariant=¨bold¨ mathcolor=¨#0000FF¨»m«/mi»«mn mathvariant=¨bold¨ mathcolor=¨#0000FF¨»2«/mn»«/msup»«/math»
נציב את התנגדות המוליך ואת שטח החתך בביטוי ההתנגדות הסגולית:
«math xmlns=¨http://www.w3.org/1998/Math/MathML¨»«mi mathvariant=¨bold¨ mathcolor=¨#0000FF¨»§#961;«/mi»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»=«/mo»«mfrac mathcolor=¨#0000FF¨»«mrow»«mi mathvariant=¨bold¨»R«/mi»«mo mathvariant=¨bold¨»§#183;«/mo»«mi mathvariant=¨bold¨»A«/mi»«/mrow»«mi mathvariant=¨bold¨»L«/mi»«/mfrac»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»=«/mo»«mfrac mathcolor=¨#0000FF¨»«mrow»«mn mathvariant=¨bold¨»5«/mn»«mo mathvariant=¨bold¨».«/mo»«mn mathvariant=¨bold¨»1«/mn»«mo mathvariant=¨bold¨»§#183;«/mo»«mn mathvariant=¨bold¨»1«/mn»«mo mathvariant=¨bold¨».«/mo»«mn mathvariant=¨bold¨»96«/mn»«mo mathvariant=¨bold¨»§#183;«/mo»«msup»«mn mathvariant=¨bold¨»10«/mn»«mrow»«mo mathvariant=¨bold¨»-«/mo»«mn mathvariant=¨bold¨»7«/mn»«/mrow»«/msup»«/mrow»«mn mathvariant=¨bold¨»1«/mn»«/mfrac»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»=«/mo»«mn mathvariant=¨bold¨ mathcolor=¨#0000FF¨»10«/mn»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»§#183;«/mo»«msup»«mn mathvariant=¨bold¨ mathcolor=¨#0000FF¨»10«/mn»«mrow mathcolor=¨#0000FF¨»«mo mathvariant=¨bold¨»-«/mo»«mn mathvariant=¨bold¨»7«/mn»«/mrow»«/msup»«mi mathvariant=¨bold¨ mathcolor=¨#0000FF¨»§#937;«/mi»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»§#183;«/mo»«mi mathvariant=¨bold¨ mathcolor=¨#0000FF¨»m«/mi»«/math»
לכן, ההתנגדות הסגולית היא: «math xmlns=¨http://www.w3.org/1998/Math/MathML¨»«mn mathvariant=¨bold¨ mathcolor=¨#0000FF¨»10«/mn»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»§#183;«/mo»«msup»«mn mathvariant=¨bold¨ mathcolor=¨#0000FF¨»10«/mn»«mrow mathcolor=¨#0000FF¨»«mo mathvariant=¨bold¨»-«/mo»«mn mathvariant=¨bold¨»7«/mn»«/mrow»«/msup»«mi mathvariant=¨bold¨ mathcolor=¨#0000FF¨»§#937;«/mi»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»§#183;«/mo»«mi mathvariant=¨bold¨ mathcolor=¨#0000FF¨»m«/mi»«/math».
1. عادة ما يكون هناك قسم يتعامل فقط مع الاستنتاجات التي تنتج من ميل الرسم البياني.
في هذا القسم، يعد حساب المقاومة من الميل هذا مجرد مُعطى آخر أثناء الحل لإيجاد المقاومة المحددة.
2. مساحة المقطع للسلك تتعلق بنصف قطر المقطع . في السؤال تم إعطاء قطر السلك الموصل.
3. يُقاس القطر بوحدات المليمتر، كما هو الحال دائمًا، يجب استخدام الوحدات القياسية فقط.
4. من الناحية النظرية، وفقا لقانون أوم، فإن خط الاتجاه يجب أن يمر عبر نقطة أصل المحاور. يتم الحصول على انحراف صغير في Excel
الناشئة عن أخطاء القياس.
בסעיף זה חישוב ההתנגדות מהשיפוע , זה רק עוד נתון במהלך הפתרון למציאת ההתנגדות הסגולית.
2. שטח החתך תלוי ברדיוס החתך ולא בקוטר. בשאלה נתון הקוטר של המוליך. הרדיוס שווה למחצית הקוטר.
3. הקוטר נתון ביחידות של מילימטר, יש להשתמש כמו תמיד רק ביחידות תקניות.
4. באופן תיאורטי, בהתאם לחוק אום , הישר המסתבר ביותר צריך לעבור דרך ראשית הצירים. באקסל מתקבלת סטייה קטנה
הנובעת משגיאות מדידה.
______________________________________________________________________________________

______________________________________________________________________________________
...
مقاومة السلك "ب" أصغر.
التعبير عن مقاومة السلك الموصل وفقا لبياناته.
من تعبير مقاومة السلك الموصل «math xmlns=¨http://www.w3.org/1998/Math/MathML¨»«mi mathvariant=¨bold¨ mathcolor=¨#0000FF¨»R«/mi»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»=«/mo»«mfrac mathcolor=¨#0000FF¨»«mrow»«mi mathvariant=¨bold¨»§#961;«/mi»«mo mathvariant=¨bold¨»§#183;«/mo»«mi mathvariant=¨bold¨»L«/mi»«/mrow»«mi mathvariant=¨bold¨»A«/mi»«/mfrac»«/math» , كلما زادت مساحة المقطع للسلك للموصل، قلت مقاومته.
ولذلك فإن مقاومة السلك "ب" أقل من مقاومة الموصل "أ".
في الرسم البياني لفرق الجهد كدالة للتيار، يكون الميل مساويًا للمقاومة. المقاومة أصغر، وبالتالي يجب أن يكون الميل أصغر أيضًا.
نضيف إلى الرسم البياني دالة جديدة تلائم السلك الموصل "ب".
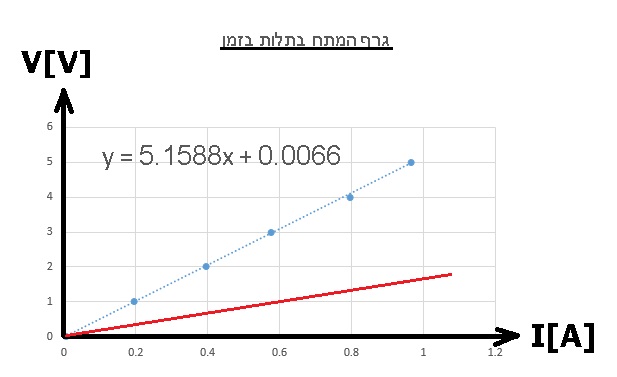
לכן, התנגדותו של תיל ב' קטנה מההתנגדות של מוליך א'.
1. كلما زادت مساحة مقطع السلك للموصل، كلما زاد عدد الإلكترونات التي تتحرك في مساحة مقطع السلك الموصل، كلما زاد التيار.
من قانون أوم، كلما زاد التيار (بنفس فرق الجهد)، قلت المقاومة.
2. في نهاية القسم ج هناك إضافة صغيرة: "لإضافة رسم بياني كيفي مناسب للسلك ب" عليك الانتباه والإجابة على هذه الإضافة أيضًا.
3. مكتوب في السؤال أنه يجب إضافة رسم بياني، أي إضافة دالة أخرى في نفس الرسم البياني.
4. الرسم البياني النوعي هو رسم بياني غير كمي، وهو وصف عام ومبدئي فقط بدون قيم كمية.
لا يمكن إضافة دالة تصف السلك "ب" كميًا لأنه لا يُعطى مقدار مساحة مقطع السلك "ب" أكبر من مساحة مقطع السطح
للسلك أ.
5. على الرغم من أن الدالة الملائمة للسلك الموصل "ب" هي دالة نوعية فقط، فمن المهم أن تمر في نقطة الأصل.
في أي سلك موصل، عندما يكون فرق الجهد بين طرفيه صفر فولط، فإن التيار المار عبره سيكون أيضًا صفر أمبير.
מחוק אום ,ככל שהזרם גדל (באותו הפרש פוטנציאלים) ההתנגדות קטנה יותר.
2. בסוף סעיף ג' יש תוספת קטנה: "להוסיף גרף איכותי המתאים לתיל ב' " צריך לשים לב ולענות גם על התוספת הזאת.
3. כאשר אומרים איכותי ,הכוונה לא כמותי. תיאור כללי ועקרוני בלבד.
______________________________________________________________________________________
______________________________________________________________________________________
...
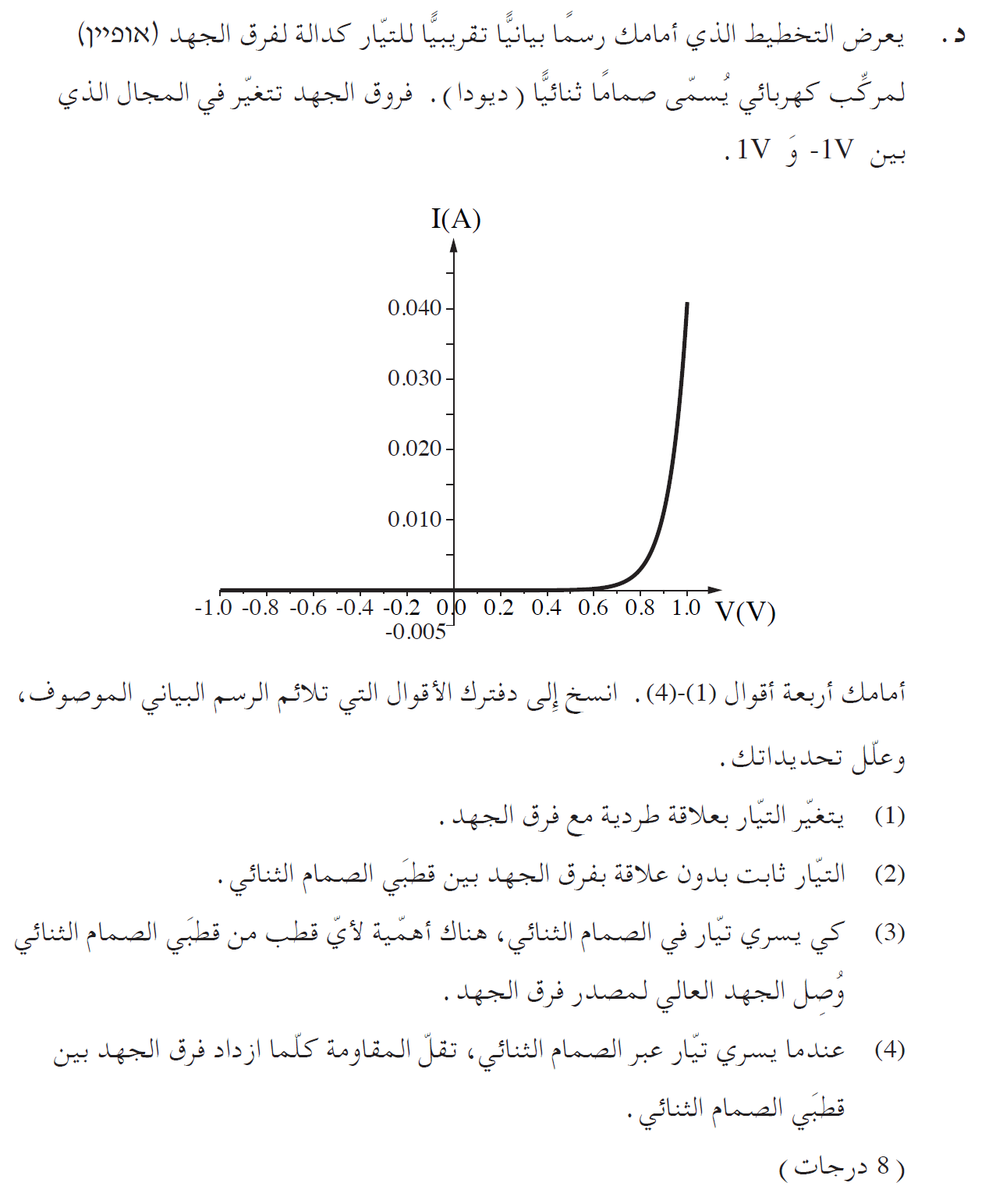
العبارات الصحيحة هي 3 و- 4.
استخلاص النتائج بناءً على الرسم البياني، وفهم معنى الميل وقيمة فرق الجهد السالب.
العبارة 1 - عبارة خاطئة. الدالة في الرسم البياني ليست خطية.
العبارة 2 - عبارة خاطئة. بفروق جهد مختلفة لها تيارات مختلفة.
العبارة 3- عبارة صحيحة. في فرق جهد 0.8 فولط يوجد تيار، إذا قمنا بعكس توصيل الصمام الثنائي (الجهد ناقص 0.8 فولط) فلن يكون هناك تيار.
لذلك، من المهم أن يتم توصيل طرفي الصمام الثنائي ذات الجهد العالي.
العبارة 4- في الرسم البياني للتيار كدالة لفرق الجهد، يكون الميل مساويًا لمقلوب المقاومة. عندما يزداد فرق الجهد، ويتجاوز 0.6 فولط هناك تيار،
يزداد ميل الدالة وبالتالي تقل المقاومة مع زيادة فرق الجهد عندما يتدفق التيار عبر الصمام الثنائي.
היגד 2- היגד לא נכון. במתחים שונים יש זרם שונה.
היגד 3- היגד נכון. במתח של 0.8 וולט יש זרם , אם נהפוך את חיבור הדיודה (מתח מינוס 0.8 וולט) לא יהיה זרם.
לכן, יש חשיבות לאיזה מהדקי הדיודה מחובר הפוטנציאל הגבוה.
היגד 4- בגרף זרם בתלות במתח, השיפוע שווה לאחד חלקי ההתנגדות. כאשר המתח הולך וגדל ,מעבר ל 0.6 וולט יש זרם,
השיפוע של הפונקציה הולך וגדל מכאן שההתנגדות הולכת וקטנה ככל שמתח גדל כאשר זורם זרם דרך הדיודה.
1. لا يشترط على الطالب معرفة الديودة للإجابة على السؤال، يمكن الإجابة على السؤال بالاعتماد على الرسم البياني فقط.
يجب أن يكتسب الطالب ما يكفي من الثقة بالنفس حتى يتمكن من الإجابة على الأسئلة المتعلقة بالمكونات الإلكترونية التي لم يسمع عنها من قبل.
2. الرسم البياني في القسم (أ) يتعامل مع فرق الجهد كدالة للتيار،يمثل الميل في الرسم البياني المقاومة.
ويتناول الرسم البياني في هذا القسم التيار بدلالة فرق الجهد ومعنى الميل في هذا الرسم البياني هو مقلوب المقاومة.
عليك أن تكون يقظًا ومركزًا بدرجة كافية حتى لا تخطئ في معنى الميل.
תלמיד צריך להגיע עם ביטחון עצמי מספיק כך שיוכל לענות על שאלות העוסקות ברכיבים אלקטרוניים שהוא מעולם לא
שמע עליהם.
2. הגרף בסעיף א' עוסק במתח בתלות בזרם משמעות השיפוע בגרף היא ההתנגדות.
הגרף בסעיף זה עוסק בזרם בתלות במתח משמעות
______________________________________________________________________________________