7.3
نرسم مخططًا للقوى المؤثرة على q3 ونُشير للبعد بين q1 و q3 بـ r1,3 والبعد بين q2 و q3 بـ r2,3.
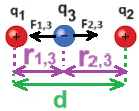
محصّلة القوى المؤثرة في هذه الحالة على q3 تساوي صفرًا. لنكتب معادلة الحركة:
«math xmlns=¨http://www.w3.org/1998/Math/MathML¨»«mstyle mathsize=¨22px¨»«mi mathvariant=¨bold-italic¨ mathcolor=¨#0000FF¨»§#931;«/mi»«mi mathvariant=¨bold-italic¨ mathcolor=¨#0000FF¨»F«/mi»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»=«/mo»«mn mathvariant=¨bold¨ mathcolor=¨#0000FF¨»0«/mn»«mspace linebreak=¨newline¨/»«mspace linebreak=¨newline¨/»«msub»«mi mathvariant=¨bold-italic¨ mathcolor=¨#0000FF¨»F«/mi»«mrow mathcolor=¨#0000FF¨»«mn mathvariant=¨bold¨»1«/mn»«mo mathvariant=¨bold¨»,«/mo»«mn mathvariant=¨bold¨»3«/mn»«/mrow»«/msub»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»=«/mo»«msub»«mi mathvariant=¨bold-italic¨ mathcolor=¨#0000FF¨»F«/mi»«mrow mathcolor=¨#0000FF¨»«mn mathvariant=¨bold¨»2«/mn»«mo mathvariant=¨bold¨»,«/mo»«mn mathvariant=¨bold¨»3«/mn»«/mrow»«/msub»«mspace linebreak=¨newline¨/»«mspace linebreak=¨newline¨/»«mfrac mathcolor=¨#0000FF¨»«mrow»«mi mathvariant=¨bold¨»K«/mi»«mo mathvariant=¨bold¨»§#183;«/mo»«msub»«mi mathvariant=¨bold¨»q«/mi»«mn mathvariant=¨bold¨»1«/mn»«/msub»«mo mathvariant=¨bold¨»§#183;«/mo»«msub»«mi mathvariant=¨bold¨»q«/mi»«mn mathvariant=¨bold¨»3«/mn»«/msub»«/mrow»«msup»«msub»«mi mathvariant=¨bold¨»r«/mi»«mrow»«mn mathvariant=¨bold¨»1«/mn»«mo mathvariant=¨bold¨»,«/mo»«mn mathvariant=¨bold¨»3«/mn»«/mrow»«/msub»«mn mathvariant=¨bold¨»2«/mn»«/msup»«/mfrac»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»=«/mo»«mfrac mathcolor=¨#0000FF¨»«mrow»«mi mathvariant=¨bold¨»K«/mi»«mo mathvariant=¨bold¨»§#183;«/mo»«msub»«mi mathvariant=¨bold¨»q«/mi»«mn mathvariant=¨bold¨»2«/mn»«/msub»«mo mathvariant=¨bold¨»§#183;«/mo»«msub»«mi mathvariant=¨bold¨»q«/mi»«mn mathvariant=¨bold¨»3«/mn»«/msub»«/mrow»«msup»«msub»«mi mathvariant=¨bold¨»r«/mi»«mrow»«mn mathvariant=¨bold¨»2«/mn»«mo mathvariant=¨bold¨»,«/mo»«mn mathvariant=¨bold¨»3«/mn»«/mrow»«/msub»«mn mathvariant=¨bold¨»2«/mn»«/msup»«/mfrac»«/mstyle»«/math»
نقوم بإجراء عمليات اختزال ونعوض قيم الشحنات:
«math xmlns=¨http://www.w3.org/1998/Math/MathML¨»«mfrac mathcolor=¨#0000FF¨»«mrow»«menclose notation=¨updiagonalstrike¨»«mi mathvariant=¨bold¨ mathsize=¨22px¨»K«/mi»«/menclose»«mo mathvariant=¨bold¨ mathsize=¨22px¨»§#183;«/mo»«msub»«mi mathvariant=¨bold¨ mathsize=¨22px¨»q«/mi»«mn mathvariant=¨bold¨ mathsize=¨22px¨»1«/mn»«/msub»«mo mathvariant=¨bold¨ mathsize=¨22px¨»§#183;«/mo»«menclose notation=¨downdiagonalstrike¨»«msub»«mi mathvariant=¨bold¨ mathsize=¨22px¨»q«/mi»«mn mathvariant=¨bold¨ mathsize=¨22px¨»3«/mn»«/msub»«/menclose»«/mrow»«msup»«msub»«mi mathvariant=¨bold¨ mathsize=¨22px¨»r«/mi»«mrow»«mn mathvariant=¨bold¨ mathsize=¨22px¨»1«/mn»«mo mathvariant=¨bold¨ mathsize=¨22px¨»,«/mo»«mn mathvariant=¨bold¨ mathsize=¨22px¨»3«/mn»«/mrow»«/msub»«mn mathvariant=¨bold¨ mathsize=¨22px¨»2«/mn»«/msup»«/mfrac»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨ mathsize=¨22px¨»=«/mo»«mfrac mathcolor=¨#0000FF¨»«mrow»«menclose notation=¨updiagonalstrike¨»«mi mathvariant=¨bold¨ mathsize=¨22px¨»K«/mi»«/menclose»«mo mathvariant=¨bold¨ mathsize=¨22px¨»§#183;«/mo»«msub»«mi mathvariant=¨bold¨ mathsize=¨22px¨»q«/mi»«mn mathvariant=¨bold¨ mathsize=¨22px¨»2«/mn»«/msub»«mo mathvariant=¨bold¨ mathsize=¨22px¨»§#183;«/mo»«menclose notation=¨downdiagonalstrike¨»«msub»«mi mathvariant=¨bold¨ mathsize=¨22px¨»q«/mi»«mn mathvariant=¨bold¨ mathsize=¨22px¨»3«/mn»«/msub»«/menclose»«/mrow»«msup»«msub»«mi mathvariant=¨bold¨ mathsize=¨22px¨»r«/mi»«mrow»«mn mathvariant=¨bold¨ mathsize=¨22px¨»2«/mn»«mo mathvariant=¨bold¨ mathsize=¨22px¨»,«/mo»«mn mathvariant=¨bold¨ mathsize=¨22px¨»3«/mn»«/mrow»«/msub»«mn mathvariant=¨bold¨ mathsize=¨22px¨»2«/mn»«/msup»«/mfrac»«mspace linebreak=¨newline¨/»«mspace linebreak=¨newline¨/»«mfrac mathcolor=¨#0000FF¨»«msub»«mi mathvariant=¨bold¨ mathsize=¨22px¨»q«/mi»«mn mathvariant=¨bold¨ mathsize=¨22px¨»1«/mn»«/msub»«msup»«msub»«mi mathvariant=¨bold¨ mathsize=¨22px¨»r«/mi»«mrow»«mn mathvariant=¨bold¨ mathsize=¨22px¨»1«/mn»«mo mathvariant=¨bold¨ mathsize=¨22px¨»,«/mo»«mn mathvariant=¨bold¨ mathsize=¨22px¨»3«/mn»«/mrow»«/msub»«mn mathvariant=¨bold¨ mathsize=¨22px¨»2«/mn»«/msup»«/mfrac»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨ mathsize=¨22px¨»=«/mo»«mfrac mathcolor=¨#0000FF¨»«msub»«mi mathvariant=¨bold¨ mathsize=¨22px¨»q«/mi»«mn mathvariant=¨bold¨ mathsize=¨22px¨»2«/mn»«/msub»«msup»«msub»«mi mathvariant=¨bold¨ mathsize=¨22px¨»r«/mi»«mrow»«mn mathvariant=¨bold¨ mathsize=¨22px¨»2«/mn»«mo mathvariant=¨bold¨ mathsize=¨22px¨»,«/mo»«mn mathvariant=¨bold¨ mathsize=¨22px¨»3«/mn»«/mrow»«/msub»«mn mathvariant=¨bold¨ mathsize=¨22px¨»2«/mn»«/msup»«/mfrac»«mspace linebreak=¨newline¨/»«mspace linebreak=¨newline¨/»«mfrac mathcolor=¨#0000FF¨»«mrow»«mn mathvariant=¨bold¨ mathsize=¨22px¨»5«/mn»«mo mathvariant=¨bold¨ mathsize=¨22px¨»§#183;«/mo»«msup»«mn mathvariant=¨bold¨ mathsize=¨22px¨»10«/mn»«mrow»«mo mathvariant=¨bold¨ mathsize=¨22px¨»-«/mo»«mn mathvariant=¨bold¨ mathsize=¨22px¨»9«/mn»«/mrow»«/msup»«/mrow»«msup»«msub»«mi mathvariant=¨bold¨ mathsize=¨22px¨»r«/mi»«mrow»«mn mathvariant=¨bold¨ mathsize=¨22px¨»1«/mn»«mo mathvariant=¨bold¨ mathsize=¨22px¨»,«/mo»«mn mathvariant=¨bold¨ mathsize=¨22px¨»3«/mn»«/mrow»«/msub»«mn mathvariant=¨bold¨ mathsize=¨22px¨»2«/mn»«/msup»«/mfrac»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨ mathsize=¨22px¨»=«/mo»«mfrac mathcolor=¨#0000FF¨»«mrow»«mn mathvariant=¨bold¨ mathsize=¨22px¨»7«/mn»«mo mathvariant=¨bold¨ mathsize=¨22px¨»§#183;«/mo»«msup»«mn mathvariant=¨bold¨ mathsize=¨22px¨»10«/mn»«mrow»«mo mathvariant=¨bold¨ mathsize=¨22px¨»-«/mo»«mn mathvariant=¨bold¨ mathsize=¨22px¨»9«/mn»«/mrow»«/msup»«/mrow»«msup»«msub»«mi mathvariant=¨bold¨ mathsize=¨22px¨»r«/mi»«mrow»«mn mathvariant=¨bold¨ mathsize=¨22px¨»2«/mn»«mo mathvariant=¨bold¨ mathsize=¨22px¨»,«/mo»«mn mathvariant=¨bold¨ mathsize=¨22px¨»3«/mn»«/mrow»«/msub»«mn mathvariant=¨bold¨ mathsize=¨22px¨»2«/mn»«/msup»«/mfrac»«mspace linebreak=¨newline¨/»«mspace linebreak=¨newline¨/»«mfrac mathcolor=¨#0000FF¨»«msup»«msub»«mi mathvariant=¨bold¨ mathsize=¨22px¨»r«/mi»«mrow»«mn mathvariant=¨bold¨ mathsize=¨22px¨»2«/mn»«mo mathvariant=¨bold¨ mathsize=¨22px¨»,«/mo»«mn mathvariant=¨bold¨ mathsize=¨22px¨»3«/mn»«/mrow»«/msub»«mn mathvariant=¨bold¨ mathsize=¨22px¨»2«/mn»«/msup»«msup»«msub»«mi mathvariant=¨bold¨ mathsize=¨22px¨»r«/mi»«mrow»«mn mathvariant=¨bold¨ mathsize=¨22px¨»1«/mn»«mo mathvariant=¨bold¨ mathsize=¨22px¨»,«/mo»«mn mathvariant=¨bold¨ mathsize=¨22px¨»3«/mn»«/mrow»«/msub»«mn mathvariant=¨bold¨ mathsize=¨22px¨»2«/mn»«/msup»«/mfrac»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨ mathsize=¨22px¨»=«/mo»«mfrac mathcolor=¨#0000FF¨»«mrow»«mn mathvariant=¨bold¨ mathsize=¨22px¨»7«/mn»«mo mathvariant=¨bold¨ mathsize=¨22px¨»§#183;«/mo»«msup»«mn mathvariant=¨bold¨ mathsize=¨22px¨»10«/mn»«mrow»«mo mathvariant=¨bold¨ mathsize=¨22px¨»-«/mo»«mn mathvariant=¨bold¨ mathsize=¨22px¨»9«/mn»«/mrow»«/msup»«/mrow»«mrow»«mn mathvariant=¨bold¨ mathsize=¨22px¨»5«/mn»«mo mathvariant=¨bold¨ mathsize=¨22px¨»§#183;«/mo»«msup»«mn mathvariant=¨bold¨ mathsize=¨22px¨»10«/mn»«mrow»«mo mathvariant=¨bold¨ mathsize=¨22px¨»-«/mo»«mn mathvariant=¨bold¨ mathsize=¨22px¨»9«/mn»«/mrow»«/msup»«/mrow»«/mfrac»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨ mathsize=¨22px¨»=«/mo»«mn mathvariant=¨bold¨ mathcolor=¨#0000FF¨ mathsize=¨22px¨»1«/mn»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨ mathsize=¨22px¨».«/mo»«mn mathvariant=¨bold¨ mathcolor=¨#0000FF¨ mathsize=¨22px¨»4«/mn»«mspace linebreak=¨newline¨/»«mspace linebreak=¨newline¨/»«menclose mathcolor=¨#0000FF¨ notation=¨box¨»«mfrac»«msub»«mi mathvariant=¨bold¨ mathsize=¨22px¨»r«/mi»«mrow»«mn mathvariant=¨bold¨ mathsize=¨22px¨»2«/mn»«mo mathvariant=¨bold¨ mathsize=¨22px¨»,«/mo»«mn mathvariant=¨bold¨ mathsize=¨22px¨»3«/mn»«/mrow»«/msub»«msub»«mi mathvariant=¨bold¨ mathsize=¨22px¨»r«/mi»«mrow»«mn mathvariant=¨bold¨ mathsize=¨22px¨»1«/mn»«mo mathvariant=¨bold¨ mathsize=¨22px¨»,«/mo»«mn mathvariant=¨bold¨ mathsize=¨22px¨»3«/mn»«/mrow»«/msub»«/mfrac»«mo mathvariant=¨bold¨ mathsize=¨22px¨»=«/mo»«msqrt»«mn mathvariant=¨bold¨ mathsize=¨22px¨»1«/mn»«mo mathvariant=¨bold¨ mathsize=¨22px¨».«/mo»«mn mathvariant=¨bold¨ mathsize=¨22px¨»4«/mn»«/msqrt»«/menclose»«/math»
مجموع البعدين r2,3 و r1,3 يساوي البعد d الذي قيمته 2 متر.
وعليه نكتب معادلة أخرى بنفس المتغيرين: r2,3 و r1,3. .
«math xmlns=¨http://www.w3.org/1998/Math/MathML¨»«menclose mathcolor=¨#0000FF¨ notation=¨box¨»«msub»«mi mathvariant=¨bold¨ mathsize=¨22px¨»r«/mi»«mrow»«mn mathvariant=¨bold¨ mathsize=¨22px¨»1«/mn»«mo mathvariant=¨bold¨ mathsize=¨22px¨»,«/mo»«mn mathvariant=¨bold¨ mathsize=¨22px¨»3«/mn»«/mrow»«/msub»«mo mathvariant=¨bold¨ mathsize=¨22px¨»+«/mo»«msub»«mi mathvariant=¨bold¨ mathsize=¨22px¨»r«/mi»«mrow»«mn mathvariant=¨bold¨ mathsize=¨22px¨»2«/mn»«mo mathvariant=¨bold¨ mathsize=¨22px¨»,«/mo»«mn mathvariant=¨bold¨ mathsize=¨22px¨»3«/mn»«/mrow»«/msub»«mo mathvariant=¨bold¨ mathsize=¨22px¨»=«/mo»«mn mathvariant=¨bold¨ mathsize=¨22px¨»2«/mn»«/menclose»«mspace linebreak=¨newline¨/»«mspace linebreak=¨newline¨/»«/math»
نُعبر عن البعد اللازم r1,3 من المعادلتين :
«math xmlns=¨http://www.w3.org/1998/Math/MathML¨»«mstyle mathsize=¨20px¨»«menclose mathcolor=¨#0000FF¨ notation=¨box¨»«msub»«mi mathvariant=¨bold¨»r«/mi»«mrow»«mn mathvariant=¨bold¨»1«/mn»«mo mathvariant=¨bold¨»,«/mo»«mn mathvariant=¨bold¨»3«/mn»«/mrow»«/msub»«mo mathvariant=¨bold¨»+«/mo»«msub»«mi mathvariant=¨bold¨»r«/mi»«mrow»«mn mathvariant=¨bold¨»2«/mn»«mo mathvariant=¨bold¨»,«/mo»«mn mathvariant=¨bold¨»3«/mn»«/mrow»«/msub»«mo mathvariant=¨bold¨»=«/mo»«mn mathvariant=¨bold¨»2«/mn»«/menclose»«mo»§#160;«/mo»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»§#8658;«/mo»«msub»«mi mathvariant=¨bold¨ mathcolor=¨#0000FF¨»r«/mi»«mrow mathcolor=¨#0000FF¨»«mn mathvariant=¨bold¨»2«/mn»«mo mathvariant=¨bold¨»,«/mo»«mn mathvariant=¨bold¨»3«/mn»«/mrow»«/msub»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»=«/mo»«mn mathvariant=¨bold¨ mathcolor=¨#0000FF¨»2«/mn»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»-«/mo»«msub»«mi mathvariant=¨bold¨ mathcolor=¨#0000FF¨»r«/mi»«mrow mathcolor=¨#0000FF¨»«mn mathvariant=¨bold¨»1«/mn»«mo mathvariant=¨bold¨»,«/mo»«mn mathvariant=¨bold¨»3«/mn»«/mrow»«/msub»«mspace linebreak=¨newline¨/»«mspace linebreak=¨newline¨/»«/mstyle»«/math»
«math xmlns=¨http://www.w3.org/1998/Math/MathML¨»«mstyle mathsize=¨22px¨»«mspace linebreak=¨newline¨/»«menclose mathcolor=¨#0000FF¨ notation=¨box¨»«mfrac»«msub»«mi mathvariant=¨bold¨ mathcolor=¨#FF0000¨»r«/mi»«mrow mathcolor=¨#FF0000¨»«mn mathvariant=¨bold¨»2«/mn»«mo mathvariant=¨bold¨»,«/mo»«mn mathvariant=¨bold¨»3«/mn»«/mrow»«/msub»«msub»«mi mathvariant=¨bold¨»r«/mi»«mrow»«mn mathvariant=¨bold¨»1«/mn»«mo mathvariant=¨bold¨»,«/mo»«mn mathvariant=¨bold¨»3«/mn»«/mrow»«/msub»«/mfrac»«mo mathvariant=¨bold¨»=«/mo»«msqrt»«mn mathvariant=¨bold¨»1«/mn»«mo mathvariant=¨bold¨».«/mo»«mn mathvariant=¨bold¨»4«/mn»«/msqrt»«/menclose»«mo»§#160;«/mo»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»§#8658;«/mo»«mfrac mathcolor=¨#0000FF¨»«mrow»«mn mathvariant=¨bold¨ mathcolor=¨#FF0000¨»2«/mn»«mo mathvariant=¨bold¨ mathcolor=¨#FF0000¨»-«/mo»«msub»«mi mathvariant=¨bold¨ mathcolor=¨#FF0000¨»r«/mi»«mrow mathcolor=¨#FF0000¨»«mn mathvariant=¨bold¨»1«/mn»«mo mathvariant=¨bold¨»,«/mo»«mn mathvariant=¨bold¨»3«/mn»«/mrow»«/msub»«/mrow»«msub»«mi mathvariant=¨bold¨»r«/mi»«mrow»«mn mathvariant=¨bold¨»1«/mn»«mo mathvariant=¨bold¨»,«/mo»«mn mathvariant=¨bold¨»3«/mn»«/mrow»«/msub»«/mfrac»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»=«/mo»«msqrt mathcolor=¨#0000FF¨»«mn mathvariant=¨bold¨»1«/mn»«mo mathvariant=¨bold¨».«/mo»«mn mathvariant=¨bold¨»4«/mn»«/msqrt»«/mstyle»«/math»
نُعبر عن البعد r1,3:
«math xmlns=¨http://www.w3.org/1998/Math/MathML¨»«mstyle mathsize=¨22px¨»«mfrac mathcolor=¨#0000FF¨»«mrow»«mn mathvariant=¨bold¨»2«/mn»«mo mathvariant=¨bold¨»-«/mo»«msub»«mi mathvariant=¨bold¨»r«/mi»«mrow»«mn mathvariant=¨bold¨»1«/mn»«mo mathvariant=¨bold¨»,«/mo»«mn mathvariant=¨bold¨»3«/mn»«/mrow»«/msub»«/mrow»«msub»«mi mathvariant=¨bold¨»r«/mi»«mrow»«mn mathvariant=¨bold¨»1«/mn»«mo mathvariant=¨bold¨»,«/mo»«mn mathvariant=¨bold¨»3«/mn»«/mrow»«/msub»«/mfrac»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»=«/mo»«msqrt mathcolor=¨#0000FF¨»«mn mathvariant=¨bold¨»1«/mn»«mo mathvariant=¨bold¨».«/mo»«mn mathvariant=¨bold¨»4«/mn»«/msqrt»«mspace linebreak=¨newline¨/»«mspace linebreak=¨newline¨/»«mn mathvariant=¨bold¨ mathcolor=¨#0000FF¨»2«/mn»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»-«/mo»«msub»«mi mathvariant=¨bold¨ mathcolor=¨#0000FF¨»r«/mi»«mrow mathcolor=¨#0000FF¨»«mn mathvariant=¨bold¨»1«/mn»«mo mathvariant=¨bold¨»,«/mo»«mn mathvariant=¨bold¨»3«/mn»«/mrow»«/msub»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»=«/mo»«msub»«mi mathvariant=¨bold¨ mathcolor=¨#0000FF¨»r«/mi»«mrow mathcolor=¨#0000FF¨»«mn mathvariant=¨bold¨»1«/mn»«mo mathvariant=¨bold¨»,«/mo»«mn mathvariant=¨bold¨»3«/mn»«/mrow»«/msub»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»§#183;«/mo»«msqrt mathcolor=¨#0000FF¨»«mn mathvariant=¨bold¨»1«/mn»«mo mathvariant=¨bold¨».«/mo»«mn mathvariant=¨bold¨»4«/mn»«/msqrt»«mspace linebreak=¨newline¨/»«mspace linebreak=¨newline¨/»«mn mathvariant=¨bold¨ mathcolor=¨#0000FF¨»2«/mn»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»=«/mo»«msub»«mi mathvariant=¨bold¨ mathcolor=¨#0000FF¨»r«/mi»«mrow mathcolor=¨#0000FF¨»«mn mathvariant=¨bold¨»1«/mn»«mo mathvariant=¨bold¨»,«/mo»«mn mathvariant=¨bold¨»3«/mn»«/mrow»«/msub»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»+«/mo»«msub»«mi mathvariant=¨bold¨ mathcolor=¨#0000FF¨»r«/mi»«mrow mathcolor=¨#0000FF¨»«mn mathvariant=¨bold¨»1«/mn»«mo mathvariant=¨bold¨»,«/mo»«mn mathvariant=¨bold¨»3«/mn»«/mrow»«/msub»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»§#183;«/mo»«msqrt mathcolor=¨#0000FF¨»«mn mathvariant=¨bold¨»1«/mn»«mo mathvariant=¨bold¨».«/mo»«mn mathvariant=¨bold¨»4«/mn»«/msqrt»«mspace linebreak=¨newline¨/»«mspace linebreak=¨newline¨/»«mn mathvariant=¨bold¨ mathcolor=¨#0000FF¨»2«/mn»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»=«/mo»«msub»«mi mathvariant=¨bold¨ mathcolor=¨#0000FF¨»r«/mi»«mrow mathcolor=¨#0000FF¨»«mn mathvariant=¨bold¨»1«/mn»«mo mathvariant=¨bold¨»,«/mo»«mn mathvariant=¨bold¨»3«/mn»«/mrow»«/msub»«mrow mathcolor=¨#0000FF¨»«mo mathvariant=¨bold¨ stretchy=¨true¨»(«/mo»«mn mathvariant=¨bold¨»1«/mn»«mo mathvariant=¨bold¨»+«/mo»«msqrt»«mn mathvariant=¨bold¨»1«/mn»«mo mathvariant=¨bold¨».«/mo»«mn mathvariant=¨bold¨»4«/mn»«/msqrt»«mo mathvariant=¨bold¨ stretchy=¨true¨»)«/mo»«/mrow»«mspace linebreak=¨newline¨/»«mspace linebreak=¨newline¨/»«msub»«mi mathvariant=¨bold¨ mathcolor=¨#0000FF¨»r«/mi»«mrow mathcolor=¨#0000FF¨»«mn mathvariant=¨bold¨»1«/mn»«mo mathvariant=¨bold¨»,«/mo»«mn mathvariant=¨bold¨»3«/mn»«/mrow»«/msub»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»=«/mo»«mfrac mathcolor=¨#0000FF¨»«mn mathvariant=¨bold¨»2«/mn»«mrow»«mn mathvariant=¨bold¨»1«/mn»«mo mathvariant=¨bold¨»+«/mo»«msqrt»«mn mathvariant=¨bold¨»1«/mn»«mo mathvariant=¨bold¨».«/mo»«mn mathvariant=¨bold¨»4«/mn»«/msqrt»«/mrow»«/mfrac»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»=«/mo»«mfrac mathcolor=¨#0000FF¨»«mn mathvariant=¨bold¨»2«/mn»«mrow»«mn mathvariant=¨bold¨»2«/mn»«mo mathvariant=¨bold¨».«/mo»«mn mathvariant=¨bold¨»18«/mn»«/mrow»«/mfrac»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»=«/mo»«mn mathvariant=¨bold¨ mathcolor=¨#0000FF¨»0«/mn»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨».«/mo»«mn mathvariant=¨bold¨ mathcolor=¨#0000FF¨»91«/mn»«mi mathvariant=¨bold-italic¨ mathcolor=¨#0000FF¨»m«/mi»«/mstyle»«/math»
لتلخيص ذلك: عندما تكون الشحنة q2 تساوي 7nC والشحنة q1 تساوي 5nC، فإن النقطة التي يجب أن توضع فيها الشحنة q3 وتكون محصلة القوى عليها صفرًا، تتوجد على بعد 91 سم على يسار q1.