حلول التدريبات العملية 1 في الكهروستاتيكا

الموقع:	YouCube
المقرر:	אלקטרוסטטיקה - ערבית
كتاب:	حلول التدريبات العملية 1 في الكهروستاتيكا

طبع بواسطة:	משתמש אורח
التاريخ:	الأربعاء، 4 فبراير 2026، 2:37 AM

جدول المحتويات

1.1
1.2
1.3
2.1
2.2
3.1
3.2
3.3
4.1
4.2
5.1
5.2
5.3
5.4
6.1
6.2
6.3
7.1
7.2
7.3
7.4
8.1
8.2
8.3
9
10.1
10.2
11
12
13.1
13.2
13.3
13.4
14.1
14.2
14.3
14.4
15.1
15.2
15.3
16.1
16.2
17
18
19.1
19.2
19.3
20.1
20.2
20.3
20.4
21.1
21.2,3
21.4
21.5
21.6
22.1
22.2
22.3
23.1
23.2
23.3
24.1
24.2
24.3
24.4
25.1
25.2
25.3
25.4
26.1
26.2
26.3
27.1
27.2
27.3
27.4
27.5
27.6
28.1
28.2
28.3
28.4
28.5

1.1

بعد إضافة الإلكترونات، تحتوي الكرة على إلكترونين فائضين، شحنة الكرة تساوي شحنة الإلكترونين.

نحسب شحنة الكرة :

«math xmlns=¨http://www.w3.org/1998/Math/MathML¨»«mstyle mathsize=¨22px¨»«mi mathvariant=¨bold¨ mathcolor=¨#0000FF¨»Q«/mi»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»=«/mo»«msub»«mi mathvariant=¨bold¨ mathcolor=¨#0000FF¨»q«/mi»«mi mathvariant=¨bold¨ mathcolor=¨#0000FF¨»e«/mi»«/msub»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»§#183;«/mo»«mi mathvariant=¨bold¨ mathcolor=¨#0000FF¨»N«/mi»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»=«/mo»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»-«/mo»«mn mathvariant=¨bold¨ mathcolor=¨#0000FF¨»1«/mn»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨».«/mo»«mn mathvariant=¨bold¨ mathcolor=¨#0000FF¨»6«/mn»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»§#183;«/mo»«msup»«mn mathvariant=¨bold¨ mathcolor=¨#0000FF¨»10«/mn»«mrow mathcolor=¨#0000FF¨»«mo mathvariant=¨bold¨»-«/mo»«mn mathvariant=¨bold¨»19«/mn»«/mrow»«/msup»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»§#183;«/mo»«mn mathvariant=¨bold¨ mathcolor=¨#0000FF¨»2«/mn»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»=«/mo»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»-«/mo»«mn mathvariant=¨bold¨ mathcolor=¨#0000FF¨»3«/mn»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨».«/mo»«mn mathvariant=¨bold¨ mathcolor=¨#0000FF¨»2«/mn»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»§#183;«/mo»«msup»«mn mathvariant=¨bold¨ mathcolor=¨#0000FF¨»10«/mn»«mrow mathcolor=¨#0000FF¨»«mo mathvariant=¨bold¨»-«/mo»«mn mathvariant=¨bold¨»19«/mn»«/mrow»«/msup»«mi mathvariant=¨bold¨ mathcolor=¨#0000FF¨»C«/mi»«/mstyle»«/math»

1.2

بعد نزع ثلاثة إلكترونات من الكرة المحايدة، تحتوي الكرة على ثلاثة بروتونات فائضة، لذا شحنة الكرة تساوي شحنة البروتونات الثلاثة.

نحسب شحنة الكرة :

«math xmlns=¨http://www.w3.org/1998/Math/MathML¨»«mstyle mathsize=¨22px¨»«mi mathvariant=¨bold¨ mathcolor=¨#0000FF¨»Q«/mi»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»=«/mo»«msub»«mi mathvariant=¨bold¨ mathcolor=¨#0000FF¨»q«/mi»«mi mathvariant=¨bold¨ mathcolor=¨#0000FF¨»p«/mi»«/msub»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»§#183;«/mo»«mi mathvariant=¨bold¨ mathcolor=¨#0000FF¨»N«/mi»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»=«/mo»«mn mathvariant=¨bold¨ mathcolor=¨#0000FF¨»1«/mn»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨».«/mo»«mn mathvariant=¨bold¨ mathcolor=¨#0000FF¨»6«/mn»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»§#183;«/mo»«msup»«mn mathvariant=¨bold¨ mathcolor=¨#0000FF¨»10«/mn»«mrow mathcolor=¨#0000FF¨»«mo mathvariant=¨bold¨»-«/mo»«mn mathvariant=¨bold¨»19«/mn»«/mrow»«/msup»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»§#183;«/mo»«mn mathvariant=¨bold¨ mathcolor=¨#0000FF¨»3«/mn»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»=«/mo»«mn mathvariant=¨bold¨ mathcolor=¨#0000FF¨»4«/mn»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨».«/mo»«mn mathvariant=¨bold¨ mathcolor=¨#0000FF¨»8«/mn»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»§#183;«/mo»«msup»«mn mathvariant=¨bold¨ mathcolor=¨#0000FF¨»10«/mn»«mrow mathcolor=¨#0000FF¨»«mo mathvariant=¨bold¨»-«/mo»«mn mathvariant=¨bold¨»19«/mn»«/mrow»«/msup»«mi mathvariant=¨bold¨ mathcolor=¨#0000FF¨»C«/mi»«/mstyle»«/math»

1.3

بعد نزع ثلاثة ملياردات إلكترونات من الكرة المحايدة، تحتوي الكرة على ثلاثة ملياردات بروتونات فائضة، لذا شحنة الكرة تساوي شحنة الثلاثة ملياردات من البروتونات.

نحسب شحنة الكرة :

«math xmlns=¨http://www.w3.org/1998/Math/MathML¨»«mstyle mathsize=¨22px¨»«mi mathvariant=¨bold¨ mathcolor=¨#0000FF¨»Q«/mi»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»=«/mo»«msub»«mi mathvariant=¨bold¨ mathcolor=¨#0000FF¨»q«/mi»«mi mathvariant=¨bold¨ mathcolor=¨#0000FF¨»p«/mi»«/msub»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»§#183;«/mo»«mi mathvariant=¨bold¨ mathcolor=¨#0000FF¨»N«/mi»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»=«/mo»«mn mathvariant=¨bold¨ mathcolor=¨#0000FF¨»1«/mn»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨».«/mo»«mn mathvariant=¨bold¨ mathcolor=¨#0000FF¨»6«/mn»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»§#183;«/mo»«msup»«mn mathvariant=¨bold¨ mathcolor=¨#0000FF¨»10«/mn»«mrow mathcolor=¨#0000FF¨»«mo mathvariant=¨bold¨»-«/mo»«mn mathvariant=¨bold¨»19«/mn»«/mrow»«/msup»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»§#183;«/mo»«mn mathvariant=¨bold¨ mathcolor=¨#0000FF¨»3«/mn»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»§#183;«/mo»«msup»«mn mathvariant=¨bold¨ mathcolor=¨#0000FF¨»10«/mn»«mn mathvariant=¨bold¨ mathcolor=¨#0000FF¨»9«/mn»«/msup»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»§#160;«/mo»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»=«/mo»«mn mathvariant=¨bold¨ mathcolor=¨#0000FF¨»4«/mn»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨».«/mo»«mn mathvariant=¨bold¨ mathcolor=¨#0000FF¨»8«/mn»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»§#183;«/mo»«msup»«mn mathvariant=¨bold¨ mathcolor=¨#0000FF¨»10«/mn»«mrow mathcolor=¨#0000FF¨»«mo mathvariant=¨bold¨»-«/mo»«mn mathvariant=¨bold¨»10«/mn»«/mrow»«/msup»«mi mathvariant=¨bold¨ mathcolor=¨#0000FF¨»C«/mi»«/mstyle»«/math»

2.1

بعد إضافة الإلكترونات، تحتوي الكرة على إلكترونين فائضين، شحنة الكرة تساوي شحنة الإلكترونين.

نحسب شحنة الكرة :

شحنة الكرة تساوي شحنة الإلكترونات الزائدة في الكرة. ولا تتعلق على كمية الإلكترونات الكلية الموجودة في الجسم (وبالتالي شحنة الجسم لا تتعلق على حجم الجسم).

2.2

تتناسب شحنة القطعة النقدية Q تناسبًا طرديًا مع عدد الإلكترونات المنزوعة من القطعة النقدية N (هذا العدد هو نفس البروتونات الزائدة في القطعة النقدية) وقيمة شحنة كل بروتون «math xmlns=¨http://www.w3.org/1998/Math/MathML¨»«mstyle mathsize=¨22px¨»«msub»«mi mathvariant=¨bold¨»q«/mi»«mi mathvariant=¨bold¨»p«/mi»«/msub»«/mstyle»«/math».

العلاقة بين Q ,N و- «math xmlns=¨http://www.w3.org/1998/Math/MathML¨»«mstyle mathsize=¨22px¨»«msub»«mi mathvariant=¨bold¨»q«/mi»«mi mathvariant=¨bold¨»p«/mi»«/msub»«/mstyle»«/math» , هي :«math xmlns=¨http://www.w3.org/1998/Math/MathML¨»«mstyle mathsize=¨26px¨»«mi mathvariant=¨bold¨ mathcolor=¨#0000FF¨»Q«/mi»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»=«/mo»«msub»«mi mathvariant=¨bold¨ mathcolor=¨#0000FF¨»q«/mi»«mi mathvariant=¨bold¨ mathcolor=¨#0000FF¨»p«/mi»«/msub»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»§#183;«/mo»«mi mathvariant=¨bold¨ mathcolor=¨#0000FF¨»N«/mi»«/mstyle»«/math»

نُعبر عن عدد البروتونات الموجودة في القطعة النقدية من هذه العلاقة، بحيث تكون شحنة القطعة النقدية 1 كولون.

«math xmlns=¨http://www.w3.org/1998/Math/MathML¨»«mstyle mathsize=¨26px¨»«mi mathvariant=¨bold¨ mathcolor=¨#0000FF¨»Q«/mi»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»=«/mo»«msub»«mi mathvariant=¨bold¨ mathcolor=¨#0000FF¨»q«/mi»«mi mathvariant=¨bold¨ mathcolor=¨#0000FF¨»p«/mi»«/msub»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»§#183;«/mo»«mi mathvariant=¨bold¨ mathcolor=¨#0000FF¨»N«/mi»«mspace linebreak=¨newline¨/»«mi mathvariant=¨bold¨ mathcolor=¨#0000FF¨»N«/mi»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»=«/mo»«mfrac mathcolor=¨#0000FF¨»«mi mathvariant=¨bold¨»Q«/mi»«msub»«mi mathvariant=¨bold¨»q«/mi»«mi mathvariant=¨bold¨»p«/mi»«/msub»«/mfrac»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»=«/mo»«mfrac mathcolor=¨#0000FF¨»«mn mathvariant=¨bold¨»1«/mn»«mrow»«mn mathvariant=¨bold¨»1«/mn»«mo mathvariant=¨bold¨».«/mo»«mn mathvariant=¨bold¨»6«/mn»«mo mathvariant=¨bold¨»§#183;«/mo»«msup»«mn mathvariant=¨bold¨»10«/mn»«mrow»«mo mathvariant=¨bold¨»-«/mo»«mn mathvariant=¨bold¨»19«/mn»«/mrow»«/msup»«/mrow»«/mfrac»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»=«/mo»«mn mathvariant=¨bold¨ mathcolor=¨#0000FF¨»6«/mn»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨».«/mo»«mn mathvariant=¨bold¨ mathcolor=¨#0000FF¨»25«/mn»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»§#183;«/mo»«msup»«mn mathvariant=¨bold¨ mathcolor=¨#0000FF¨»10«/mn»«mn mathvariant=¨bold¨ mathcolor=¨#0000FF¨»18«/mn»«/msup»«/mstyle»«/math»

3.1

الكرة اليمنى مشحونة بـ 4 ميكرو كولون، مع العلم أن نصف الشحنة التي كانت في الكرة اليمنى قبل التوصيل تنتقل إلى الكرة اليسرى.
وبالتالي فإن كمية الشحنة التي تنتقل إلى الشحنة اليسرى هي 2 ميكرو كولون.

3.2

الكرة اليمنى مشحونة بشحنة موجبة والكرة اليسرى محايدة. هناك نقص في الإلكترونات في الكرة اليمنى، وبالتالي ستنتقل الإلكترونات من الكرة اليسرى إلى الكرة اليمنى.

3.3

نتيجة لتوصيل السلك الموصل، تنتقل الإلكترونات من الكرة اليسرى إلى الكرة اليمنى.

كمية الشحنة التي تنتقل من الكرة اليسرى إلى الكرة اليمنى هي: «math xmlns=¨http://www.w3.org/1998/Math/MathML¨»«mstyle mathsize=¨20px¨»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»-«/mo»«mn mathvariant=¨bold¨ mathcolor=¨#0000FF¨»2«/mn»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»§#183;«/mo»«msup»«mn mathvariant=¨bold¨ mathcolor=¨#0000FF¨»10«/mn»«mrow mathcolor=¨#0000FF¨»«mo mathvariant=¨bold¨»-«/mo»«mn mathvariant=¨bold¨»6«/mn»«/mrow»«/msup»«mi mathvariant=¨bold¨ mathcolor=¨#0000FF¨»C«/mi»«/mstyle»«/math»

نستخدم التعبير «math xmlns=¨http://www.w3.org/1998/Math/MathML¨»«mstyle mathsize=¨20px¨»«mi mathvariant=¨bold¨ mathcolor=¨#0000FF¨»Q«/mi»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»=«/mo»«mi mathvariant=¨bold¨ mathcolor=¨#0000FF¨»N«/mi»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»§#183;«/mo»«msub»«mi mathvariant=¨bold¨ mathcolor=¨#0000FF¨»q«/mi»«mi mathvariant=¨bold¨ mathcolor=¨#0000FF¨»e«/mi»«/msub»«/mstyle»«/math» ونحسب كمية الإلكترونات التي انتقلت من الكرة اليسرى إلى الكرة اليمنى.

«math xmlns=¨http://www.w3.org/1998/Math/MathML¨»«mstyle mathsize=¨20px¨»«mi mathvariant=¨bold¨ mathcolor=¨#0000FF¨»N«/mi»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»=«/mo»«mfrac mathcolor=¨#0000FF¨»«mi mathvariant=¨bold¨»Q«/mi»«msub»«mi mathvariant=¨bold¨»q«/mi»«mi mathvariant=¨bold¨»e«/mi»«/msub»«/mfrac»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»=«/mo»«mfrac mathcolor=¨#0000FF¨»«mrow»«mo mathvariant=¨bold¨»-«/mo»«mn mathvariant=¨bold¨»2«/mn»«mo mathvariant=¨bold¨»§#183;«/mo»«msup»«mn mathvariant=¨bold¨»10«/mn»«mrow»«mo mathvariant=¨bold¨»-«/mo»«mn mathvariant=¨bold¨»6«/mn»«/mrow»«/msup»«/mrow»«mrow»«mo mathvariant=¨bold¨»-«/mo»«mn mathvariant=¨bold¨»1«/mn»«mo mathvariant=¨bold¨».«/mo»«mn mathvariant=¨bold¨»6«/mn»«mo mathvariant=¨bold¨»§#183;«/mo»«msup»«mn mathvariant=¨bold¨»10«/mn»«mrow»«mo mathvariant=¨bold¨»-«/mo»«mn mathvariant=¨bold¨»19«/mn»«/mrow»«/msup»«/mrow»«/mfrac»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»=«/mo»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»§#160;«/mo»«mn mathvariant=¨bold¨ mathcolor=¨#0000FF¨»1«/mn»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨».«/mo»«mn mathvariant=¨bold¨ mathcolor=¨#0000FF¨»25«/mn»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»§#183;«/mo»«msup»«mn mathvariant=¨bold¨ mathcolor=¨#0000FF¨»10«/mn»«mn mathvariant=¨bold¨ mathcolor=¨#0000FF¨»13«/mn»«/msup»«/mstyle»«/math»

4.1

الكرة اليمنى مشحونة بشحنة سالبة، وفيها فائض من الإلكترونات، والكرة اليسرى غير مشحونة. نتيجة لتوصيل السلك الموصل، تتحرك الإلكترونات في السلك الموصل من الكرة اليمنى إلى الكرة اليسرى.

4.2

مُعطى أن ربع شحنة الكرة الكبيرة تذهب إلى الكرة الصغيرة. شحنة الكرة الكبيرة هي «math xmlns=¨http://www.w3.org/1998/Math/MathML¨»«mstyle mathsize=¨20px¨»«mo mathvariant=¨bold¨»-«/mo»«mn mathvariant=¨bold¨»4«/mn»«mi mathvariant=¨bold¨»nC«/mi»«/mstyle»«/math».

وبالتالي فإن الشحنة تنتقل من الكرة الكبيرة إلى الكرة الصغيرة «math xmlns=¨http://www.w3.org/1998/Math/MathML¨»«mstyle mathsize=¨20px¨»«mo mathvariant=¨bold¨»-«/mo»«mn mathvariant=¨bold¨»1«/mn»«mi mathvariant=¨bold¨»nC«/mi»«/mstyle»«/math».

نستخدم التعبير «math xmlns=¨http://www.w3.org/1998/Math/MathML¨»«mstyle mathsize=¨20px¨»«mi mathvariant=¨bold¨ mathcolor=¨#0000FF¨»Q«/mi»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»=«/mo»«mi mathvariant=¨bold¨ mathcolor=¨#0000FF¨»N«/mi»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»§#183;«/mo»«msub»«mi mathvariant=¨bold¨ mathcolor=¨#0000FF¨»q«/mi»«mi mathvariant=¨bold¨ mathcolor=¨#0000FF¨»e«/mi»«/msub»«/mstyle»«/math» ونحسب عدد الإلكترونات N التي انتقلت من الكرة الكبيرة إلى الصغيرة.

«math xmlns=¨http://www.w3.org/1998/Math/MathML¨»«mstyle mathsize=¨20px¨»«mi mathvariant=¨bold¨ mathcolor=¨#0000FF¨»N«/mi»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»=«/mo»«mfrac mathcolor=¨#0000FF¨»«mi mathvariant=¨bold¨»Q«/mi»«msub»«mi mathvariant=¨bold¨»q«/mi»«mi mathvariant=¨bold¨»e«/mi»«/msub»«/mfrac»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»=«/mo»«mfrac mathcolor=¨#0000FF¨»«mrow»«mo mathvariant=¨bold¨»-«/mo»«mn mathvariant=¨bold¨»1«/mn»«mo mathvariant=¨bold¨»§#183;«/mo»«msup»«mn mathvariant=¨bold¨»10«/mn»«mrow»«mo mathvariant=¨bold¨»-«/mo»«mn mathvariant=¨bold¨»9«/mn»«/mrow»«/msup»«/mrow»«mrow»«mo mathvariant=¨bold¨»-«/mo»«mn mathvariant=¨bold¨»1«/mn»«mo mathvariant=¨bold¨».«/mo»«mn mathvariant=¨bold¨»6«/mn»«mo mathvariant=¨bold¨»§#183;«/mo»«msup»«mn mathvariant=¨bold¨»10«/mn»«mrow»«mo mathvariant=¨bold¨»-«/mo»«mn mathvariant=¨bold¨»19«/mn»«/mrow»«/msup»«/mrow»«/mfrac»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»=«/mo»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»§#160;«/mo»«mn mathvariant=¨bold¨ mathcolor=¨#0000FF¨»6«/mn»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨».«/mo»«mn mathvariant=¨bold¨ mathcolor=¨#0000FF¨»25«/mn»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»§#183;«/mo»«msup»«mn mathvariant=¨bold¨ mathcolor=¨#0000FF¨»10«/mn»«mn mathvariant=¨bold¨ mathcolor=¨#0000FF¨»9«/mn»«/msup»«/mstyle»«/math»

5.1

توجد قوة تنافر بين الشحنتين التي لها نفس الإشارة.

وبما أن كلا الجسمين مشحونان بشحنات موجبة، فسوف تعمل قوة تنافر بينهما.

5.2

يصف قانون كولون مقدار القوة المؤثرة على كل من الجسمين المشحونين.

«math xmlns=¨http://www.w3.org/1998/Math/MathML¨»«mstyle mathsize=¨22px¨»«msub»«mi mathvariant=¨bold¨ mathcolor=¨#0000FF¨»F«/mi»«mrow mathcolor=¨#0000FF¨»«mn mathvariant=¨bold¨»1«/mn»«mo mathvariant=¨bold¨»,«/mo»«mn mathvariant=¨bold¨»2«/mn»«/mrow»«/msub»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»=«/mo»«mfrac mathcolor=¨#0000FF¨»«mrow»«mi mathvariant=¨bold¨»K«/mi»«mo mathvariant=¨bold¨»§#183;«/mo»«msub»«mi mathvariant=¨bold¨»q«/mi»«mn mathvariant=¨bold¨»1«/mn»«/msub»«mo mathvariant=¨bold¨»§#183;«/mo»«msub»«mi mathvariant=¨bold¨»q«/mi»«mn mathvariant=¨bold¨»2«/mn»«/msub»«/mrow»«msup»«mi mathvariant=¨bold¨»r«/mi»«mn mathvariant=¨bold¨»2«/mn»«/msup»«/mfrac»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»=«/mo»«mfrac mathcolor=¨#0000FF¨»«mrow»«mn mathvariant=¨bold¨»9«/mn»«mo mathvariant=¨bold¨»§#183;«/mo»«msup»«mn mathvariant=¨bold¨»10«/mn»«mn mathvariant=¨bold¨»9«/mn»«/msup»«mo mathvariant=¨bold¨»§#183;«/mo»«mn mathvariant=¨bold¨»8«/mn»«mo mathvariant=¨bold¨»§#183;«/mo»«msup»«mn mathvariant=¨bold¨»10«/mn»«mrow»«mo mathvariant=¨bold¨»-«/mo»«mn mathvariant=¨bold¨»9«/mn»«/mrow»«/msup»«mo mathvariant=¨bold¨»§#183;«/mo»«mn mathvariant=¨bold¨»8«/mn»«mo mathvariant=¨bold¨»§#183;«/mo»«msup»«mn mathvariant=¨bold¨»10«/mn»«mrow»«mo mathvariant=¨bold¨»-«/mo»«mn mathvariant=¨bold¨»9«/mn»«/mrow»«/msup»«/mrow»«msup»«mn mathvariant=¨bold¨»3«/mn»«mn mathvariant=¨bold¨»2«/mn»«/msup»«/mfrac»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»=«/mo»«mfrac mathcolor=¨#0000FF¨»«mrow»«mn mathvariant=¨bold¨»5«/mn»«mo mathvariant=¨bold¨».«/mo»«mn mathvariant=¨bold¨»76«/mn»«mo mathvariant=¨bold¨»§#183;«/mo»«msup»«mn mathvariant=¨bold¨»10«/mn»«mrow»«mo mathvariant=¨bold¨»-«/mo»«mn mathvariant=¨bold¨»7«/mn»«/mrow»«/msup»«/mrow»«mn mathvariant=¨bold¨»9«/mn»«/mfrac»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»=«/mo»«mn mathvariant=¨bold¨ mathcolor=¨#0000FF¨»6«/mn»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨».«/mo»«mn mathvariant=¨bold¨ mathcolor=¨#0000FF¨»4«/mn»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»§#183;«/mo»«msup»«mn mathvariant=¨bold¨ mathcolor=¨#0000FF¨»10«/mn»«mrow mathcolor=¨#0000FF¨»«mo mathvariant=¨bold¨»-«/mo»«mn mathvariant=¨bold¨»8«/mn»«/mrow»«/msup»«mi mathvariant=¨bold¨ mathcolor=¨#0000FF¨»N«/mi»«/mstyle»«/math»

5.3

نحسب بمساعدة قانون كولون مقدار القوة الكهربائية المؤثرة بين الشحنتين:

«math xmlns=¨http://www.w3.org/1998/Math/MathML¨»«mstyle mathsize=¨22px¨»«msub»«mi mathvariant=¨bold¨ mathcolor=¨#0000FF¨»F«/mi»«mrow mathcolor=¨#0000FF¨»«mn mathvariant=¨bold¨»2«/mn»«mo mathvariant=¨bold¨»,«/mo»«mn mathvariant=¨bold¨»1«/mn»«/mrow»«/msub»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»=«/mo»«mfrac mathcolor=¨#0000FF¨»«mrow»«mi mathvariant=¨bold¨»K«/mi»«mo mathvariant=¨bold¨»§#183;«/mo»«msub»«mi mathvariant=¨bold¨»q«/mi»«mn mathvariant=¨bold¨»2«/mn»«/msub»«mo mathvariant=¨bold¨»§#183;«/mo»«msub»«mi mathvariant=¨bold¨»q«/mi»«mn mathvariant=¨bold¨»1«/mn»«/msub»«/mrow»«msup»«mi mathvariant=¨bold¨»r«/mi»«mn mathvariant=¨bold¨»2«/mn»«/msup»«/mfrac»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»=«/mo»«mfrac mathcolor=¨#0000FF¨»«mrow»«mn mathvariant=¨bold¨»9«/mn»«mo mathvariant=¨bold¨»§#183;«/mo»«msup»«mn mathvariant=¨bold¨»10«/mn»«mn mathvariant=¨bold¨»9«/mn»«/msup»«mo mathvariant=¨bold¨»§#183;«/mo»«mn mathvariant=¨bold¨»8«/mn»«mo mathvariant=¨bold¨»§#183;«/mo»«msup»«mn mathvariant=¨bold¨»10«/mn»«mrow»«mo mathvariant=¨bold¨»-«/mo»«mn mathvariant=¨bold¨»9«/mn»«/mrow»«/msup»«mo mathvariant=¨bold¨»§#183;«/mo»«mn mathvariant=¨bold¨»8«/mn»«mo mathvariant=¨bold¨»§#183;«/mo»«msup»«mn mathvariant=¨bold¨»10«/mn»«mrow»«mo mathvariant=¨bold¨»-«/mo»«mn mathvariant=¨bold¨»9«/mn»«/mrow»«/msup»«/mrow»«msup»«mn mathvariant=¨bold¨»3«/mn»«mn mathvariant=¨bold¨»2«/mn»«/msup»«/mfrac»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»=«/mo»«mfrac mathcolor=¨#0000FF¨»«mrow»«mn mathvariant=¨bold¨»5«/mn»«mo mathvariant=¨bold¨».«/mo»«mn mathvariant=¨bold¨»76«/mn»«mo mathvariant=¨bold¨»§#183;«/mo»«msup»«mn mathvariant=¨bold¨»10«/mn»«mrow»«mo mathvariant=¨bold¨»-«/mo»«mn mathvariant=¨bold¨»7«/mn»«/mrow»«/msup»«/mrow»«mn mathvariant=¨bold¨»9«/mn»«/mfrac»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»=«/mo»«mn mathvariant=¨bold¨ mathcolor=¨#0000FF¨»6«/mn»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨».«/mo»«mn mathvariant=¨bold¨ mathcolor=¨#0000FF¨»4«/mn»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»§#183;«/mo»«msup»«mn mathvariant=¨bold¨ mathcolor=¨#0000FF¨»10«/mn»«mrow mathcolor=¨#0000FF¨»«mo mathvariant=¨bold¨»-«/mo»«mn mathvariant=¨bold¨»8«/mn»«/mrow»«/msup»«mi mathvariant=¨bold¨ mathcolor=¨#0000FF¨»N«/mi»«/mstyle»«/math»

5.4

حسب قانون كولون : «math xmlns=¨http://www.w3.org/1998/Math/MathML¨»«mstyle mathsize=¨22px¨»«mi mathvariant=¨bold¨ mathcolor=¨#0000FF¨»F«/mi»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»=«/mo»«mfrac mathcolor=¨#0000FF¨»«mrow»«mi mathvariant=¨bold¨»K«/mi»«mo mathvariant=¨bold¨»§#183;«/mo»«msub»«mi mathvariant=¨bold¨»q«/mi»«mn mathvariant=¨bold¨»1«/mn»«/msub»«mo mathvariant=¨bold¨»§#183;«/mo»«msub»«mi mathvariant=¨bold¨»q«/mi»«mn mathvariant=¨bold¨»2«/mn»«/msub»«/mrow»«msup»«mi mathvariant=¨bold¨»r«/mi»«mn mathvariant=¨bold¨»2«/mn»«/msup»«/mfrac»«/mstyle»«/math» يمكن ملاحظة أن القوة الكهربائية تتناسب عكسيا مع مربع البعد بين الشحنتين.

لذلك، عندما يزيد البعد بين الشحنتين بمقدار مرتين، تصبح القوة الكهربائية أصغر بأربع مرات.

ويمكنك أيضًا حساب القوة في الحالة الجديدة، عندما يكون البعد بين الشحنتين ستة أمتار:

«math xmlns=¨http://www.w3.org/1998/Math/MathML¨»«mstyle mathsize=¨22px¨»«msub»«mi mathvariant=¨bold¨ mathcolor=¨#0000FF¨»F«/mi»«mrow mathcolor=¨#0000FF¨»«mn mathvariant=¨bold¨»1«/mn»«mo mathvariant=¨bold¨»,«/mo»«mn mathvariant=¨bold¨»2«/mn»«/mrow»«/msub»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»=«/mo»«mfrac mathcolor=¨#0000FF¨»«mrow»«mi mathvariant=¨bold¨»K«/mi»«mo mathvariant=¨bold¨»§#183;«/mo»«msub»«mi mathvariant=¨bold¨»q«/mi»«mn mathvariant=¨bold¨»1«/mn»«/msub»«mo mathvariant=¨bold¨»§#183;«/mo»«msub»«mi mathvariant=¨bold¨»q«/mi»«mn mathvariant=¨bold¨»2«/mn»«/msub»«/mrow»«msup»«mi mathvariant=¨bold¨»r«/mi»«mn mathvariant=¨bold¨»2«/mn»«/msup»«/mfrac»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»=«/mo»«mfrac mathcolor=¨#0000FF¨»«mrow»«mn mathvariant=¨bold¨»9«/mn»«mo mathvariant=¨bold¨»§#183;«/mo»«msup»«mn mathvariant=¨bold¨»10«/mn»«mn mathvariant=¨bold¨»9«/mn»«/msup»«mo mathvariant=¨bold¨»§#183;«/mo»«mn mathvariant=¨bold¨»8«/mn»«mo mathvariant=¨bold¨»§#183;«/mo»«msup»«mn mathvariant=¨bold¨»10«/mn»«mrow»«mo mathvariant=¨bold¨»-«/mo»«mn mathvariant=¨bold¨»9«/mn»«/mrow»«/msup»«mo mathvariant=¨bold¨»§#183;«/mo»«mn mathvariant=¨bold¨»8«/mn»«mo mathvariant=¨bold¨»§#183;«/mo»«msup»«mn mathvariant=¨bold¨»10«/mn»«mrow»«mo mathvariant=¨bold¨»-«/mo»«mn mathvariant=¨bold¨»9«/mn»«/mrow»«/msup»«/mrow»«msup»«mn mathvariant=¨bold¨»6«/mn»«mn mathvariant=¨bold¨»2«/mn»«/msup»«/mfrac»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»=«/mo»«mfrac mathcolor=¨#0000FF¨»«mrow»«mn mathvariant=¨bold¨»5«/mn»«mo mathvariant=¨bold¨».«/mo»«mn mathvariant=¨bold¨»76«/mn»«mo mathvariant=¨bold¨»§#183;«/mo»«msup»«mn mathvariant=¨bold¨»10«/mn»«mrow»«mo mathvariant=¨bold¨»-«/mo»«mn mathvariant=¨bold¨»7«/mn»«/mrow»«/msup»«/mrow»«mn mathvariant=¨bold¨»36«/mn»«/mfrac»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»=«/mo»«mn mathvariant=¨bold¨ mathcolor=¨#0000FF¨»1«/mn»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨».«/mo»«mn mathvariant=¨bold¨ mathcolor=¨#0000FF¨»6«/mn»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»§#183;«/mo»«msup»«mn mathvariant=¨bold¨ mathcolor=¨#0000FF¨»10«/mn»«mrow mathcolor=¨#0000FF¨»«mo mathvariant=¨bold¨»-«/mo»«mn mathvariant=¨bold¨»8«/mn»«/mrow»«/msup»«mi mathvariant=¨bold¨ mathcolor=¨#0000FF¨»N«/mi»«/mstyle»«/math»

عندما كان البعد بين الشحنتين 3 أمتار، يكون مقدار القوة الكهربائية: «math xmlns=¨http://www.w3.org/1998/Math/MathML¨»«mstyle mathsize=¨20px¨»«mn mathvariant=¨bold¨ mathcolor=¨#0000FF¨»6«/mn»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨».«/mo»«mn mathvariant=¨bold¨ mathcolor=¨#0000FF¨»4«/mn»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»§#183;«/mo»«msup»«mn mathvariant=¨bold¨ mathcolor=¨#0000FF¨»10«/mn»«mrow mathcolor=¨#0000FF¨»«mo mathvariant=¨bold¨»-«/mo»«mn mathvariant=¨bold¨»8«/mn»«/mrow»«/msup»«mi mathvariant=¨bold¨ mathcolor=¨#0000FF¨»N«/mi»«/mstyle»«/math» .

والآن وجدنا أنه عندما يكون البعد بين الشحنتين 36 متراً يكون مقدار القوة الكهربائية: «math xmlns=¨http://www.w3.org/1998/Math/MathML¨»«mstyle mathsize=¨22px¨»«mn mathvariant=¨bold¨ mathcolor=¨#0000FF¨»1«/mn»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨».«/mo»«mn mathvariant=¨bold¨ mathcolor=¨#0000FF¨»6«/mn»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»§#183;«/mo»«msup»«mn mathvariant=¨bold¨ mathcolor=¨#0000FF¨»10«/mn»«mrow mathcolor=¨#0000FF¨»«mo mathvariant=¨bold¨»-«/mo»«mn mathvariant=¨bold¨»8«/mn»«/mrow»«/msup»«mi mathvariant=¨bold¨ mathcolor=¨#0000FF¨»N«/mi»«/mstyle»«/math».

يمكن ملاحظة أن زيادة البعد بمقدار مرتين يؤدي إلى انخفاض القوة الكهربائية بمقدار 4 مرات.

6.1

نحسب بمساعدة قانون كولون مقدار القوة الكهربائية المؤثرة بين الشحنتين:

«math xmlns=¨http://www.w3.org/1998/Math/MathML¨»«mstyle mathsize=¨22px¨»«msub»«mi mathvariant=¨bold¨ mathcolor=¨#0000FF¨»F«/mi»«mrow mathcolor=¨#0000FF¨»«mn mathvariant=¨bold¨»2«/mn»«mo mathvariant=¨bold¨»,«/mo»«mn mathvariant=¨bold¨»1«/mn»«/mrow»«/msub»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»=«/mo»«mfrac mathcolor=¨#0000FF¨»«mrow»«mi mathvariant=¨bold¨»K«/mi»«mo mathvariant=¨bold¨»§#183;«/mo»«msub»«mi mathvariant=¨bold¨»q«/mi»«mn mathvariant=¨bold¨»2«/mn»«/msub»«mo mathvariant=¨bold¨»§#183;«/mo»«msub»«mi mathvariant=¨bold¨»q«/mi»«mn mathvariant=¨bold¨»1«/mn»«/msub»«/mrow»«msup»«mi mathvariant=¨bold¨»r«/mi»«mn mathvariant=¨bold¨»2«/mn»«/msup»«/mfrac»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»=«/mo»«mfrac mathcolor=¨#0000FF¨»«mrow»«mn mathvariant=¨bold¨»9«/mn»«mo mathvariant=¨bold¨»§#183;«/mo»«msup»«mn mathvariant=¨bold¨»10«/mn»«mn mathvariant=¨bold¨»9«/mn»«/msup»«mo mathvariant=¨bold¨»§#183;«/mo»«mn mathvariant=¨bold¨»800«/mn»«mo mathvariant=¨bold¨»§#183;«/mo»«msup»«mn mathvariant=¨bold¨»10«/mn»«mrow»«mo mathvariant=¨bold¨»-«/mo»«mn mathvariant=¨bold¨»9«/mn»«/mrow»«/msup»«mo mathvariant=¨bold¨»§#183;«/mo»«mn mathvariant=¨bold¨»8«/mn»«mo mathvariant=¨bold¨»§#183;«/mo»«msup»«mn mathvariant=¨bold¨»10«/mn»«mrow»«mo mathvariant=¨bold¨»-«/mo»«mn mathvariant=¨bold¨»9«/mn»«/mrow»«/msup»«/mrow»«msup»«mn mathvariant=¨bold¨»3«/mn»«mn mathvariant=¨bold¨»2«/mn»«/msup»«/mfrac»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»=«/mo»«mfrac mathcolor=¨#0000FF¨»«mrow»«mn mathvariant=¨bold¨»5«/mn»«mo mathvariant=¨bold¨».«/mo»«mn mathvariant=¨bold¨»76«/mn»«mo mathvariant=¨bold¨»§#183;«/mo»«msup»«mn mathvariant=¨bold¨»10«/mn»«mrow»«mo mathvariant=¨bold¨»-«/mo»«mn mathvariant=¨bold¨»5«/mn»«/mrow»«/msup»«/mrow»«mn mathvariant=¨bold¨»9«/mn»«/mfrac»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»=«/mo»«mn mathvariant=¨bold¨ mathcolor=¨#0000FF¨»6«/mn»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨».«/mo»«mn mathvariant=¨bold¨ mathcolor=¨#0000FF¨»4«/mn»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»§#183;«/mo»«msup»«mn mathvariant=¨bold¨ mathcolor=¨#0000FF¨»10«/mn»«mrow mathcolor=¨#0000FF¨»«mo mathvariant=¨bold¨»-«/mo»«mn mathvariant=¨bold¨»6«/mn»«/mrow»«/msup»«mi mathvariant=¨bold¨ mathcolor=¨#0000FF¨»N«/mi»«/mstyle»«/math»

6.2

نحسب بمساعدة قانون كولون مقدار القوة الكهربائية المؤثرة بين الشحنتين:

«math xmlns=¨http://www.w3.org/1998/Math/MathML¨»«mstyle mathsize=¨22px¨»«msub»«mi mathvariant=¨bold¨ mathcolor=¨#0000FF¨»F«/mi»«mrow mathcolor=¨#0000FF¨»«mn mathvariant=¨bold¨»1«/mn»«mo mathvariant=¨bold¨»,«/mo»«mn mathvariant=¨bold¨»2«/mn»«/mrow»«/msub»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»=«/mo»«mfrac mathcolor=¨#0000FF¨»«mrow»«mi mathvariant=¨bold¨»K«/mi»«mo mathvariant=¨bold¨»§#183;«/mo»«msub»«mi mathvariant=¨bold¨»q«/mi»«mn mathvariant=¨bold¨»1«/mn»«/msub»«mo mathvariant=¨bold¨»§#183;«/mo»«msub»«mi mathvariant=¨bold¨»q«/mi»«mn mathvariant=¨bold¨»2«/mn»«/msub»«/mrow»«msup»«mi mathvariant=¨bold¨»r«/mi»«mn mathvariant=¨bold¨»2«/mn»«/msup»«/mfrac»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»=«/mo»«mfrac mathcolor=¨#0000FF¨»«mrow»«mn mathvariant=¨bold¨»9«/mn»«mo mathvariant=¨bold¨»§#183;«/mo»«msup»«mn mathvariant=¨bold¨»10«/mn»«mn mathvariant=¨bold¨»9«/mn»«/msup»«mo mathvariant=¨bold¨»§#183;«/mo»«mn mathvariant=¨bold¨»8«/mn»«mo mathvariant=¨bold¨»§#183;«/mo»«msup»«mn mathvariant=¨bold¨»10«/mn»«mrow»«mo mathvariant=¨bold¨»-«/mo»«mn mathvariant=¨bold¨»9«/mn»«/mrow»«/msup»«mo mathvariant=¨bold¨»§#183;«/mo»«mn mathvariant=¨bold¨»800«/mn»«mo mathvariant=¨bold¨»§#183;«/mo»«msup»«mn mathvariant=¨bold¨»10«/mn»«mrow»«mo mathvariant=¨bold¨»-«/mo»«mn mathvariant=¨bold¨»9«/mn»«/mrow»«/msup»«/mrow»«msup»«mn mathvariant=¨bold¨»3«/mn»«mn mathvariant=¨bold¨»2«/mn»«/msup»«/mfrac»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»=«/mo»«mfrac mathcolor=¨#0000FF¨»«mrow»«mn mathvariant=¨bold¨»5«/mn»«mo mathvariant=¨bold¨».«/mo»«mn mathvariant=¨bold¨»76«/mn»«mo mathvariant=¨bold¨»§#183;«/mo»«msup»«mn mathvariant=¨bold¨»10«/mn»«mrow»«mo mathvariant=¨bold¨»-«/mo»«mn mathvariant=¨bold¨»5«/mn»«/mrow»«/msup»«/mrow»«mn mathvariant=¨bold¨»9«/mn»«/mfrac»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»=«/mo»«mn mathvariant=¨bold¨ mathcolor=¨#0000FF¨»6«/mn»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨».«/mo»«mn mathvariant=¨bold¨ mathcolor=¨#0000FF¨»4«/mn»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»§#183;«/mo»«msup»«mn mathvariant=¨bold¨ mathcolor=¨#0000FF¨»10«/mn»«mrow mathcolor=¨#0000FF¨»«mo mathvariant=¨bold¨»-«/mo»«mn mathvariant=¨bold¨»6«/mn»«/mrow»«/msup»«mi mathvariant=¨bold¨ mathcolor=¨#0000FF¨»N«/mi»«/mstyle»«/math»

6.3

نُعبر عن البعد بين الجسمين r من قانون كولون:

«math xmlns=¨http://www.w3.org/1998/Math/MathML¨»«mstyle mathsize=¨22px¨»«mi mathvariant=¨bold¨ mathcolor=¨#0000FF¨»F«/mi»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»=«/mo»«mfrac mathcolor=¨#0000FF¨»«mrow»«mi mathvariant=¨bold¨»K«/mi»«mo mathvariant=¨bold¨»§#183;«/mo»«msub»«mi mathvariant=¨bold¨»q«/mi»«mn mathvariant=¨bold¨»1«/mn»«/msub»«mo mathvariant=¨bold¨»§#183;«/mo»«msub»«mi mathvariant=¨bold¨»q«/mi»«mn mathvariant=¨bold¨»2«/mn»«/msub»«/mrow»«msup»«mi mathvariant=¨bold¨»r«/mi»«mn mathvariant=¨bold¨»2«/mn»«/msup»«/mfrac»«mspace linebreak=¨newline¨/»«mspace linebreak=¨newline¨/»«msup»«mi mathvariant=¨bold¨ mathcolor=¨#0000FF¨»r«/mi»«mn mathvariant=¨bold¨ mathcolor=¨#0000FF¨»2«/mn»«/msup»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»=«/mo»«mfrac mathcolor=¨#0000FF¨»«mrow»«mi mathvariant=¨bold¨»K«/mi»«mo mathvariant=¨bold¨»§#183;«/mo»«msub»«mi mathvariant=¨bold¨»q«/mi»«mn mathvariant=¨bold¨»1«/mn»«/msub»«mo mathvariant=¨bold¨»§#183;«/mo»«msub»«mi mathvariant=¨bold¨»q«/mi»«mn mathvariant=¨bold¨»2«/mn»«/msub»«/mrow»«mi mathvariant=¨bold¨»F«/mi»«/mfrac»«mspace linebreak=¨newline¨/»«mspace linebreak=¨newline¨/»«menclose mathcolor=¨#0000FF¨ notation=¨circle¨»«mi mathvariant=¨bold¨»r«/mi»«mo mathvariant=¨bold¨»=«/mo»«msqrt»«mfrac»«mrow»«mi mathvariant=¨bold¨»K«/mi»«mo mathvariant=¨bold¨»§#183;«/mo»«msub»«mi mathvariant=¨bold¨»q«/mi»«mn mathvariant=¨bold¨»1«/mn»«/msub»«mo mathvariant=¨bold¨»§#183;«/mo»«msub»«mi mathvariant=¨bold¨»q«/mi»«mn mathvariant=¨bold¨»2«/mn»«/msub»«/mrow»«mi mathvariant=¨bold¨»F«/mi»«/mfrac»«/msqrt»«/menclose»«mspace linebreak=¨newline¨/»«mspace linebreak=¨newline¨/»«mspace linebreak=¨newline¨/»«/mstyle»«/math»

نُعوّض معطيات السؤال في تعبير البعد ونُعوض مقدار القوة F 1 نيوتن.

«math xmlns=¨http://www.w3.org/1998/Math/MathML¨»«mstyle mathsize=¨22px¨»«mspace linebreak=¨newline¨/»«mspace linebreak=¨newline¨/»«mi mathvariant=¨bold¨ mathcolor=¨#0000FF¨»r«/mi»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»=«/mo»«msqrt mathcolor=¨#0000FF¨»«mfrac»«mrow»«mi mathvariant=¨bold¨»K«/mi»«mo mathvariant=¨bold¨»§#183;«/mo»«msub»«mi mathvariant=¨bold¨»q«/mi»«mn mathvariant=¨bold¨»1«/mn»«/msub»«mo mathvariant=¨bold¨»§#183;«/mo»«msub»«mi mathvariant=¨bold¨»q«/mi»«mn mathvariant=¨bold¨»2«/mn»«/msub»«/mrow»«mi mathvariant=¨bold¨»F«/mi»«/mfrac»«/msqrt»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»=«/mo»«msqrt mathcolor=¨#0000FF¨»«mfrac»«mrow»«mn mathvariant=¨bold¨»9«/mn»«mo mathvariant=¨bold¨»§#183;«/mo»«msup»«mn mathvariant=¨bold¨»10«/mn»«mn mathvariant=¨bold¨»9«/mn»«/msup»«mo mathvariant=¨bold¨»§#183;«/mo»«mn mathvariant=¨bold¨»8«/mn»«mo mathvariant=¨bold¨»§#183;«/mo»«msup»«mn mathvariant=¨bold¨»10«/mn»«mrow»«mo mathvariant=¨bold¨»-«/mo»«mn mathvariant=¨bold¨»9«/mn»«/mrow»«/msup»«mo mathvariant=¨bold¨»§#183;«/mo»«mn mathvariant=¨bold¨»800«/mn»«mo mathvariant=¨bold¨»§#183;«/mo»«msup»«mn mathvariant=¨bold¨»10«/mn»«mrow»«mo mathvariant=¨bold¨»-«/mo»«mn mathvariant=¨bold¨»9«/mn»«/mrow»«/msup»«/mrow»«mn mathvariant=¨bold¨»1«/mn»«/mfrac»«/msqrt»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»=«/mo»«msqrt mathcolor=¨#0000FF¨»«mn mathvariant=¨bold¨»5«/mn»«mo mathvariant=¨bold¨».«/mo»«mn mathvariant=¨bold¨»76«/mn»«mo mathvariant=¨bold¨»§#183;«/mo»«msup»«mn mathvariant=¨bold¨»10«/mn»«mrow»«mo mathvariant=¨bold¨»-«/mo»«mn mathvariant=¨bold¨»5«/mn»«/mrow»«/msup»«/msqrt»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»=«/mo»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»§#160;«/mo»«mn mathvariant=¨bold¨ mathcolor=¨#0000FF¨»7«/mn»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨».«/mo»«mn mathvariant=¨bold¨ mathcolor=¨#0000FF¨»58«/mn»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»§#183;«/mo»«msup»«mn mathvariant=¨bold¨ mathcolor=¨#0000FF¨»10«/mn»«mrow mathcolor=¨#0000FF¨»«mo mathvariant=¨bold¨»-«/mo»«mn mathvariant=¨bold¨»3«/mn»«/mrow»«/msup»«mi mathvariant=¨bold¨ mathcolor=¨#0000FF¨»m«/mi»«mspace linebreak=¨newline¨/»«/mstyle»«/math»

الكرتان مشحونتان بشحنات صغيرة، لذلك لكي تعمل قوة كهربائية مقدارها 1 نيوتن، يجب أن تكون الشحنتان على بعد حوالي 7 ملم.

7.1

نُشير إلى البعد بين الشحنة q₃ والشحنة q₁ بـ r_1,3

نُشير إلى البعد بين الشحنة q₃ والشحنة q₂ بـ - r_2,3

نرسم مخطط القوى للقوى المؤثرة على q₃.

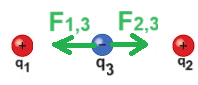
إذا كان البعد بين الشحنتين q₁ وq₂ يساوي 2m.

بما أن الشحنة q₃ تقع في المنتصف، فإن البعد بين الشحنة q₃ وكل من الشحنتين الآخرتين هي 1 متر.

احسب بمساعدة قانون كولون القوى الكهربائية المؤثرة على الشحنة q₃:

«math xmlns=¨http://www.w3.org/1998/Math/MathML¨»«mstyle mathsize=¨22px¨»«msub»«mi mathvariant=¨bold¨ mathcolor=¨#0000FF¨»F«/mi»«mrow mathcolor=¨#0000FF¨»«mn mathvariant=¨bold¨»1«/mn»«mo mathvariant=¨bold¨»,«/mo»«mn mathvariant=¨bold¨»3«/mn»«/mrow»«/msub»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»=«/mo»«mfrac mathcolor=¨#0000FF¨»«mrow»«mi mathvariant=¨bold¨»K«/mi»«mo mathvariant=¨bold¨»§#183;«/mo»«msub»«mi mathvariant=¨bold¨»q«/mi»«mn mathvariant=¨bold¨»1«/mn»«/msub»«mo mathvariant=¨bold¨»§#183;«/mo»«msub»«mi mathvariant=¨bold¨»q«/mi»«mn mathvariant=¨bold¨»3«/mn»«/msub»«/mrow»«msup»«msub»«mi mathvariant=¨bold¨»r«/mi»«mrow»«mn mathvariant=¨bold¨»1«/mn»«mo mathvariant=¨bold¨»,«/mo»«mn mathvariant=¨bold¨»3«/mn»«/mrow»«/msub»«mn mathvariant=¨bold¨»2«/mn»«/msup»«/mfrac»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»=«/mo»«mfrac mathcolor=¨#0000FF¨»«mrow»«mn mathvariant=¨bold¨»9«/mn»«mo mathvariant=¨bold¨»§#183;«/mo»«msup»«mn mathvariant=¨bold¨»10«/mn»«mn mathvariant=¨bold¨»9«/mn»«/msup»«mo mathvariant=¨bold¨»§#183;«/mo»«mn mathvariant=¨bold¨»5«/mn»«mo mathvariant=¨bold¨»§#183;«/mo»«msup»«mn mathvariant=¨bold¨»10«/mn»«mrow»«mo mathvariant=¨bold¨»-«/mo»«mn mathvariant=¨bold¨»9«/mn»«/mrow»«/msup»«mo mathvariant=¨bold¨»§#183;«/mo»«mn mathvariant=¨bold¨»5«/mn»«mo mathvariant=¨bold¨»§#183;«/mo»«msup»«mn mathvariant=¨bold¨»10«/mn»«mrow»«mo mathvariant=¨bold¨»-«/mo»«mn mathvariant=¨bold¨»9«/mn»«/mrow»«/msup»«/mrow»«msup»«mn mathvariant=¨bold¨»1«/mn»«mn mathvariant=¨bold¨»2«/mn»«/msup»«/mfrac»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»=«/mo»«mn mathvariant=¨bold¨ mathcolor=¨#0000FF¨»2«/mn»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨».«/mo»«mn mathvariant=¨bold¨ mathcolor=¨#0000FF¨»25«/mn»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»§#183;«/mo»«msup»«mn mathvariant=¨bold¨ mathcolor=¨#0000FF¨»10«/mn»«mrow mathcolor=¨#0000FF¨»«mo mathvariant=¨bold¨»-«/mo»«mn mathvariant=¨bold¨»7«/mn»«/mrow»«/msup»«mi mathvariant=¨bold¨ mathcolor=¨#0000FF¨»N«/mi»«/mstyle»«/math»

«math xmlns=¨http://www.w3.org/1998/Math/MathML¨»«mstyle mathsize=¨22px¨»«msub»«mi mathvariant=¨bold¨ mathcolor=¨#0000FF¨»F«/mi»«mrow mathcolor=¨#0000FF¨»«mn mathvariant=¨bold¨»2«/mn»«mo mathvariant=¨bold¨»,«/mo»«mn mathvariant=¨bold¨»3«/mn»«/mrow»«/msub»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»=«/mo»«mfrac mathcolor=¨#0000FF¨»«mrow»«mi mathvariant=¨bold¨»K«/mi»«mo mathvariant=¨bold¨»§#183;«/mo»«msub»«mi mathvariant=¨bold¨»q«/mi»«mn mathvariant=¨bold¨»2«/mn»«/msub»«mo mathvariant=¨bold¨»§#183;«/mo»«msub»«mi mathvariant=¨bold¨»q«/mi»«mn mathvariant=¨bold¨»3«/mn»«/msub»«/mrow»«msup»«msub»«mi mathvariant=¨bold¨»r«/mi»«mrow»«mn mathvariant=¨bold¨»2«/mn»«mo mathvariant=¨bold¨»,«/mo»«mn mathvariant=¨bold¨»3«/mn»«/mrow»«/msub»«mn mathvariant=¨bold¨»2«/mn»«/msup»«/mfrac»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»=«/mo»«mfrac mathcolor=¨#0000FF¨»«mrow»«mn mathvariant=¨bold¨»9«/mn»«mo mathvariant=¨bold¨»§#183;«/mo»«msup»«mn mathvariant=¨bold¨»10«/mn»«mn mathvariant=¨bold¨»9«/mn»«/msup»«mo mathvariant=¨bold¨»§#183;«/mo»«mn mathvariant=¨bold¨»5«/mn»«mo mathvariant=¨bold¨»§#183;«/mo»«msup»«mn mathvariant=¨bold¨»10«/mn»«mrow»«mo mathvariant=¨bold¨»-«/mo»«mn mathvariant=¨bold¨»9«/mn»«/mrow»«/msup»«mo mathvariant=¨bold¨»§#183;«/mo»«mn mathvariant=¨bold¨»5«/mn»«mo mathvariant=¨bold¨»§#183;«/mo»«msup»«mn mathvariant=¨bold¨»10«/mn»«mrow»«mo mathvariant=¨bold¨»-«/mo»«mn mathvariant=¨bold¨»9«/mn»«/mrow»«/msup»«/mrow»«msup»«mn mathvariant=¨bold¨»1«/mn»«mn mathvariant=¨bold¨»2«/mn»«/msup»«/mfrac»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»=«/mo»«mn mathvariant=¨bold¨ mathcolor=¨#0000FF¨»2«/mn»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨».«/mo»«mn mathvariant=¨bold¨ mathcolor=¨#0000FF¨»25«/mn»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»§#183;«/mo»«msup»«mn mathvariant=¨bold¨ mathcolor=¨#0000FF¨»10«/mn»«mrow mathcolor=¨#0000FF¨»«mo mathvariant=¨bold¨»-«/mo»«mn mathvariant=¨bold¨»7«/mn»«/mrow»«/msup»«mi mathvariant=¨bold¨ mathcolor=¨#0000FF¨»N«/mi»«/mstyle»«/math»

بما أن القوتين متساويتين في المقدار ومتعاكستين في الاتجاه، فأن محصلة القوى الكهربائية المؤثرة على q₃ تساوي صفرًا.

7.2

نرسم مخطط القوى للقوى الكهربائية المؤثرة على q₃، عندما تكون الشحنة في كل من المجالات الثلاثة:

يمكن ملاحظة أن القوى الكهربائية تعمل في اتجاهين متعاكسين فقط في المجال (ب). لذلك، في هذا المجال فقط، يمكن أن يكون محصلة القوى المؤثرة على q₃ صفرًا.

7.3

نرسم مخططًا للقوى المؤثرة على q₃ ونُشير للبعد بين q₁ و q₃ بـ r_1,3 والبعد بين q₂ و q₃ بـ r_2,3.

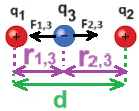
محصّلة القوى المؤثرة في هذه الحالة على q₃ تساوي صفرًا. لنكتب معادلة الحركة:

«math xmlns=¨http://www.w3.org/1998/Math/MathML¨»«mstyle mathsize=¨22px¨»«mi mathvariant=¨bold-italic¨ mathcolor=¨#0000FF¨»§#931;«/mi»«mi mathvariant=¨bold-italic¨ mathcolor=¨#0000FF¨»F«/mi»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»=«/mo»«mn mathvariant=¨bold¨ mathcolor=¨#0000FF¨»0«/mn»«mspace linebreak=¨newline¨/»«mspace linebreak=¨newline¨/»«msub»«mi mathvariant=¨bold-italic¨ mathcolor=¨#0000FF¨»F«/mi»«mrow mathcolor=¨#0000FF¨»«mn mathvariant=¨bold¨»1«/mn»«mo mathvariant=¨bold¨»,«/mo»«mn mathvariant=¨bold¨»3«/mn»«/mrow»«/msub»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»=«/mo»«msub»«mi mathvariant=¨bold-italic¨ mathcolor=¨#0000FF¨»F«/mi»«mrow mathcolor=¨#0000FF¨»«mn mathvariant=¨bold¨»2«/mn»«mo mathvariant=¨bold¨»,«/mo»«mn mathvariant=¨bold¨»3«/mn»«/mrow»«/msub»«mspace linebreak=¨newline¨/»«mspace linebreak=¨newline¨/»«mfrac mathcolor=¨#0000FF¨»«mrow»«mi mathvariant=¨bold¨»K«/mi»«mo mathvariant=¨bold¨»§#183;«/mo»«msub»«mi mathvariant=¨bold¨»q«/mi»«mn mathvariant=¨bold¨»1«/mn»«/msub»«mo mathvariant=¨bold¨»§#183;«/mo»«msub»«mi mathvariant=¨bold¨»q«/mi»«mn mathvariant=¨bold¨»3«/mn»«/msub»«/mrow»«msup»«msub»«mi mathvariant=¨bold¨»r«/mi»«mrow»«mn mathvariant=¨bold¨»1«/mn»«mo mathvariant=¨bold¨»,«/mo»«mn mathvariant=¨bold¨»3«/mn»«/mrow»«/msub»«mn mathvariant=¨bold¨»2«/mn»«/msup»«/mfrac»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»=«/mo»«mfrac mathcolor=¨#0000FF¨»«mrow»«mi mathvariant=¨bold¨»K«/mi»«mo mathvariant=¨bold¨»§#183;«/mo»«msub»«mi mathvariant=¨bold¨»q«/mi»«mn mathvariant=¨bold¨»2«/mn»«/msub»«mo mathvariant=¨bold¨»§#183;«/mo»«msub»«mi mathvariant=¨bold¨»q«/mi»«mn mathvariant=¨bold¨»3«/mn»«/msub»«/mrow»«msup»«msub»«mi mathvariant=¨bold¨»r«/mi»«mrow»«mn mathvariant=¨bold¨»2«/mn»«mo mathvariant=¨bold¨»,«/mo»«mn mathvariant=¨bold¨»3«/mn»«/mrow»«/msub»«mn mathvariant=¨bold¨»2«/mn»«/msup»«/mfrac»«/mstyle»«/math»

نقوم بإجراء عمليات اختزال ونعوض قيم الشحنات:

«math xmlns=¨http://www.w3.org/1998/Math/MathML¨»«mfrac mathcolor=¨#0000FF¨»«mrow»«menclose notation=¨updiagonalstrike¨»«mi mathvariant=¨bold¨ mathsize=¨22px¨»K«/mi»«/menclose»«mo mathvariant=¨bold¨ mathsize=¨22px¨»§#183;«/mo»«msub»«mi mathvariant=¨bold¨ mathsize=¨22px¨»q«/mi»«mn mathvariant=¨bold¨ mathsize=¨22px¨»1«/mn»«/msub»«mo mathvariant=¨bold¨ mathsize=¨22px¨»§#183;«/mo»«menclose notation=¨downdiagonalstrike¨»«msub»«mi mathvariant=¨bold¨ mathsize=¨22px¨»q«/mi»«mn mathvariant=¨bold¨ mathsize=¨22px¨»3«/mn»«/msub»«/menclose»«/mrow»«msup»«msub»«mi mathvariant=¨bold¨ mathsize=¨22px¨»r«/mi»«mrow»«mn mathvariant=¨bold¨ mathsize=¨22px¨»1«/mn»«mo mathvariant=¨bold¨ mathsize=¨22px¨»,«/mo»«mn mathvariant=¨bold¨ mathsize=¨22px¨»3«/mn»«/mrow»«/msub»«mn mathvariant=¨bold¨ mathsize=¨22px¨»2«/mn»«/msup»«/mfrac»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨ mathsize=¨22px¨»=«/mo»«mfrac mathcolor=¨#0000FF¨»«mrow»«menclose notation=¨updiagonalstrike¨»«mi mathvariant=¨bold¨ mathsize=¨22px¨»K«/mi»«/menclose»«mo mathvariant=¨bold¨ mathsize=¨22px¨»§#183;«/mo»«msub»«mi mathvariant=¨bold¨ mathsize=¨22px¨»q«/mi»«mn mathvariant=¨bold¨ mathsize=¨22px¨»2«/mn»«/msub»«mo mathvariant=¨bold¨ mathsize=¨22px¨»§#183;«/mo»«menclose notation=¨downdiagonalstrike¨»«msub»«mi mathvariant=¨bold¨ mathsize=¨22px¨»q«/mi»«mn mathvariant=¨bold¨ mathsize=¨22px¨»3«/mn»«/msub»«/menclose»«/mrow»«msup»«msub»«mi mathvariant=¨bold¨ mathsize=¨22px¨»r«/mi»«mrow»«mn mathvariant=¨bold¨ mathsize=¨22px¨»2«/mn»«mo mathvariant=¨bold¨ mathsize=¨22px¨»,«/mo»«mn mathvariant=¨bold¨ mathsize=¨22px¨»3«/mn»«/mrow»«/msub»«mn mathvariant=¨bold¨ mathsize=¨22px¨»2«/mn»«/msup»«/mfrac»«mspace linebreak=¨newline¨/»«mspace linebreak=¨newline¨/»«mfrac mathcolor=¨#0000FF¨»«msub»«mi mathvariant=¨bold¨ mathsize=¨22px¨»q«/mi»«mn mathvariant=¨bold¨ mathsize=¨22px¨»1«/mn»«/msub»«msup»«msub»«mi mathvariant=¨bold¨ mathsize=¨22px¨»r«/mi»«mrow»«mn mathvariant=¨bold¨ mathsize=¨22px¨»1«/mn»«mo mathvariant=¨bold¨ mathsize=¨22px¨»,«/mo»«mn mathvariant=¨bold¨ mathsize=¨22px¨»3«/mn»«/mrow»«/msub»«mn mathvariant=¨bold¨ mathsize=¨22px¨»2«/mn»«/msup»«/mfrac»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨ mathsize=¨22px¨»=«/mo»«mfrac mathcolor=¨#0000FF¨»«msub»«mi mathvariant=¨bold¨ mathsize=¨22px¨»q«/mi»«mn mathvariant=¨bold¨ mathsize=¨22px¨»2«/mn»«/msub»«msup»«msub»«mi mathvariant=¨bold¨ mathsize=¨22px¨»r«/mi»«mrow»«mn mathvariant=¨bold¨ mathsize=¨22px¨»2«/mn»«mo mathvariant=¨bold¨ mathsize=¨22px¨»,«/mo»«mn mathvariant=¨bold¨ mathsize=¨22px¨»3«/mn»«/mrow»«/msub»«mn mathvariant=¨bold¨ mathsize=¨22px¨»2«/mn»«/msup»«/mfrac»«mspace linebreak=¨newline¨/»«mspace linebreak=¨newline¨/»«mfrac mathcolor=¨#0000FF¨»«mrow»«mn mathvariant=¨bold¨ mathsize=¨22px¨»5«/mn»«mo mathvariant=¨bold¨ mathsize=¨22px¨»§#183;«/mo»«msup»«mn mathvariant=¨bold¨ mathsize=¨22px¨»10«/mn»«mrow»«mo mathvariant=¨bold¨ mathsize=¨22px¨»-«/mo»«mn mathvariant=¨bold¨ mathsize=¨22px¨»9«/mn»«/mrow»«/msup»«/mrow»«msup»«msub»«mi mathvariant=¨bold¨ mathsize=¨22px¨»r«/mi»«mrow»«mn mathvariant=¨bold¨ mathsize=¨22px¨»1«/mn»«mo mathvariant=¨bold¨ mathsize=¨22px¨»,«/mo»«mn mathvariant=¨bold¨ mathsize=¨22px¨»3«/mn»«/mrow»«/msub»«mn mathvariant=¨bold¨ mathsize=¨22px¨»2«/mn»«/msup»«/mfrac»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨ mathsize=¨22px¨»=«/mo»«mfrac mathcolor=¨#0000FF¨»«mrow»«mn mathvariant=¨bold¨ mathsize=¨22px¨»7«/mn»«mo mathvariant=¨bold¨ mathsize=¨22px¨»§#183;«/mo»«msup»«mn mathvariant=¨bold¨ mathsize=¨22px¨»10«/mn»«mrow»«mo mathvariant=¨bold¨ mathsize=¨22px¨»-«/mo»«mn mathvariant=¨bold¨ mathsize=¨22px¨»9«/mn»«/mrow»«/msup»«/mrow»«msup»«msub»«mi mathvariant=¨bold¨ mathsize=¨22px¨»r«/mi»«mrow»«mn mathvariant=¨bold¨ mathsize=¨22px¨»2«/mn»«mo mathvariant=¨bold¨ mathsize=¨22px¨»,«/mo»«mn mathvariant=¨bold¨ mathsize=¨22px¨»3«/mn»«/mrow»«/msub»«mn mathvariant=¨bold¨ mathsize=¨22px¨»2«/mn»«/msup»«/mfrac»«mspace linebreak=¨newline¨/»«mspace linebreak=¨newline¨/»«mfrac mathcolor=¨#0000FF¨»«msup»«msub»«mi mathvariant=¨bold¨ mathsize=¨22px¨»r«/mi»«mrow»«mn mathvariant=¨bold¨ mathsize=¨22px¨»2«/mn»«mo mathvariant=¨bold¨ mathsize=¨22px¨»,«/mo»«mn mathvariant=¨bold¨ mathsize=¨22px¨»3«/mn»«/mrow»«/msub»«mn mathvariant=¨bold¨ mathsize=¨22px¨»2«/mn»«/msup»«msup»«msub»«mi mathvariant=¨bold¨ mathsize=¨22px¨»r«/mi»«mrow»«mn mathvariant=¨bold¨ mathsize=¨22px¨»1«/mn»«mo mathvariant=¨bold¨ mathsize=¨22px¨»,«/mo»«mn mathvariant=¨bold¨ mathsize=¨22px¨»3«/mn»«/mrow»«/msub»«mn mathvariant=¨bold¨ mathsize=¨22px¨»2«/mn»«/msup»«/mfrac»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨ mathsize=¨22px¨»=«/mo»«mfrac mathcolor=¨#0000FF¨»«mrow»«mn mathvariant=¨bold¨ mathsize=¨22px¨»7«/mn»«mo mathvariant=¨bold¨ mathsize=¨22px¨»§#183;«/mo»«msup»«mn mathvariant=¨bold¨ mathsize=¨22px¨»10«/mn»«mrow»«mo mathvariant=¨bold¨ mathsize=¨22px¨»-«/mo»«mn mathvariant=¨bold¨ mathsize=¨22px¨»9«/mn»«/mrow»«/msup»«/mrow»«mrow»«mn mathvariant=¨bold¨ mathsize=¨22px¨»5«/mn»«mo mathvariant=¨bold¨ mathsize=¨22px¨»§#183;«/mo»«msup»«mn mathvariant=¨bold¨ mathsize=¨22px¨»10«/mn»«mrow»«mo mathvariant=¨bold¨ mathsize=¨22px¨»-«/mo»«mn mathvariant=¨bold¨ mathsize=¨22px¨»9«/mn»«/mrow»«/msup»«/mrow»«/mfrac»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨ mathsize=¨22px¨»=«/mo»«mn mathvariant=¨bold¨ mathcolor=¨#0000FF¨ mathsize=¨22px¨»1«/mn»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨ mathsize=¨22px¨».«/mo»«mn mathvariant=¨bold¨ mathcolor=¨#0000FF¨ mathsize=¨22px¨»4«/mn»«mspace linebreak=¨newline¨/»«mspace linebreak=¨newline¨/»«menclose mathcolor=¨#0000FF¨ notation=¨box¨»«mfrac»«msub»«mi mathvariant=¨bold¨ mathsize=¨22px¨»r«/mi»«mrow»«mn mathvariant=¨bold¨ mathsize=¨22px¨»2«/mn»«mo mathvariant=¨bold¨ mathsize=¨22px¨»,«/mo»«mn mathvariant=¨bold¨ mathsize=¨22px¨»3«/mn»«/mrow»«/msub»«msub»«mi mathvariant=¨bold¨ mathsize=¨22px¨»r«/mi»«mrow»«mn mathvariant=¨bold¨ mathsize=¨22px¨»1«/mn»«mo mathvariant=¨bold¨ mathsize=¨22px¨»,«/mo»«mn mathvariant=¨bold¨ mathsize=¨22px¨»3«/mn»«/mrow»«/msub»«/mfrac»«mo mathvariant=¨bold¨ mathsize=¨22px¨»=«/mo»«msqrt»«mn mathvariant=¨bold¨ mathsize=¨22px¨»1«/mn»«mo mathvariant=¨bold¨ mathsize=¨22px¨».«/mo»«mn mathvariant=¨bold¨ mathsize=¨22px¨»4«/mn»«/msqrt»«/menclose»«/math»

مجموع البعدين r_2,3 و r_1,3 يساوي البعد d الذي قيمته 2 متر.

وعليه نكتب معادلة أخرى بنفس المتغيرين: r_2,3 و r_1,3. .

«math xmlns=¨http://www.w3.org/1998/Math/MathML¨»«menclose mathcolor=¨#0000FF¨ notation=¨box¨»«msub»«mi mathvariant=¨bold¨ mathsize=¨22px¨»r«/mi»«mrow»«mn mathvariant=¨bold¨ mathsize=¨22px¨»1«/mn»«mo mathvariant=¨bold¨ mathsize=¨22px¨»,«/mo»«mn mathvariant=¨bold¨ mathsize=¨22px¨»3«/mn»«/mrow»«/msub»«mo mathvariant=¨bold¨ mathsize=¨22px¨»+«/mo»«msub»«mi mathvariant=¨bold¨ mathsize=¨22px¨»r«/mi»«mrow»«mn mathvariant=¨bold¨ mathsize=¨22px¨»2«/mn»«mo mathvariant=¨bold¨ mathsize=¨22px¨»,«/mo»«mn mathvariant=¨bold¨ mathsize=¨22px¨»3«/mn»«/mrow»«/msub»«mo mathvariant=¨bold¨ mathsize=¨22px¨»=«/mo»«mn mathvariant=¨bold¨ mathsize=¨22px¨»2«/mn»«/menclose»«mspace linebreak=¨newline¨/»«mspace linebreak=¨newline¨/»«/math»

نُعبر عن البعد اللازم r_1,3 من المعادلتين :

«math xmlns=¨http://www.w3.org/1998/Math/MathML¨»«mstyle mathsize=¨20px¨»«menclose mathcolor=¨#0000FF¨ notation=¨box¨»«msub»«mi mathvariant=¨bold¨»r«/mi»«mrow»«mn mathvariant=¨bold¨»1«/mn»«mo mathvariant=¨bold¨»,«/mo»«mn mathvariant=¨bold¨»3«/mn»«/mrow»«/msub»«mo mathvariant=¨bold¨»+«/mo»«msub»«mi mathvariant=¨bold¨»r«/mi»«mrow»«mn mathvariant=¨bold¨»2«/mn»«mo mathvariant=¨bold¨»,«/mo»«mn mathvariant=¨bold¨»3«/mn»«/mrow»«/msub»«mo mathvariant=¨bold¨»=«/mo»«mn mathvariant=¨bold¨»2«/mn»«/menclose»«mo»§#160;«/mo»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»§#8658;«/mo»«msub»«mi mathvariant=¨bold¨ mathcolor=¨#0000FF¨»r«/mi»«mrow mathcolor=¨#0000FF¨»«mn mathvariant=¨bold¨»2«/mn»«mo mathvariant=¨bold¨»,«/mo»«mn mathvariant=¨bold¨»3«/mn»«/mrow»«/msub»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»=«/mo»«mn mathvariant=¨bold¨ mathcolor=¨#0000FF¨»2«/mn»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»-«/mo»«msub»«mi mathvariant=¨bold¨ mathcolor=¨#0000FF¨»r«/mi»«mrow mathcolor=¨#0000FF¨»«mn mathvariant=¨bold¨»1«/mn»«mo mathvariant=¨bold¨»,«/mo»«mn mathvariant=¨bold¨»3«/mn»«/mrow»«/msub»«mspace linebreak=¨newline¨/»«mspace linebreak=¨newline¨/»«/mstyle»«/math»

«math xmlns=¨http://www.w3.org/1998/Math/MathML¨»«mstyle mathsize=¨22px¨»«mspace linebreak=¨newline¨/»«menclose mathcolor=¨#0000FF¨ notation=¨box¨»«mfrac»«msub»«mi mathvariant=¨bold¨ mathcolor=¨#FF0000¨»r«/mi»«mrow mathcolor=¨#FF0000¨»«mn mathvariant=¨bold¨»2«/mn»«mo mathvariant=¨bold¨»,«/mo»«mn mathvariant=¨bold¨»3«/mn»«/mrow»«/msub»«msub»«mi mathvariant=¨bold¨»r«/mi»«mrow»«mn mathvariant=¨bold¨»1«/mn»«mo mathvariant=¨bold¨»,«/mo»«mn mathvariant=¨bold¨»3«/mn»«/mrow»«/msub»«/mfrac»«mo mathvariant=¨bold¨»=«/mo»«msqrt»«mn mathvariant=¨bold¨»1«/mn»«mo mathvariant=¨bold¨».«/mo»«mn mathvariant=¨bold¨»4«/mn»«/msqrt»«/menclose»«mo»§#160;«/mo»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»§#8658;«/mo»«mfrac mathcolor=¨#0000FF¨»«mrow»«mn mathvariant=¨bold¨ mathcolor=¨#FF0000¨»2«/mn»«mo mathvariant=¨bold¨ mathcolor=¨#FF0000¨»-«/mo»«msub»«mi mathvariant=¨bold¨ mathcolor=¨#FF0000¨»r«/mi»«mrow mathcolor=¨#FF0000¨»«mn mathvariant=¨bold¨»1«/mn»«mo mathvariant=¨bold¨»,«/mo»«mn mathvariant=¨bold¨»3«/mn»«/mrow»«/msub»«/mrow»«msub»«mi mathvariant=¨bold¨»r«/mi»«mrow»«mn mathvariant=¨bold¨»1«/mn»«mo mathvariant=¨bold¨»,«/mo»«mn mathvariant=¨bold¨»3«/mn»«/mrow»«/msub»«/mfrac»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»=«/mo»«msqrt mathcolor=¨#0000FF¨»«mn mathvariant=¨bold¨»1«/mn»«mo mathvariant=¨bold¨».«/mo»«mn mathvariant=¨bold¨»4«/mn»«/msqrt»«/mstyle»«/math»

نُعبر عن البعد r_1,3:

«math xmlns=¨http://www.w3.org/1998/Math/MathML¨»«mstyle mathsize=¨22px¨»«mfrac mathcolor=¨#0000FF¨»«mrow»«mn mathvariant=¨bold¨»2«/mn»«mo mathvariant=¨bold¨»-«/mo»«msub»«mi mathvariant=¨bold¨»r«/mi»«mrow»«mn mathvariant=¨bold¨»1«/mn»«mo mathvariant=¨bold¨»,«/mo»«mn mathvariant=¨bold¨»3«/mn»«/mrow»«/msub»«/mrow»«msub»«mi mathvariant=¨bold¨»r«/mi»«mrow»«mn mathvariant=¨bold¨»1«/mn»«mo mathvariant=¨bold¨»,«/mo»«mn mathvariant=¨bold¨»3«/mn»«/mrow»«/msub»«/mfrac»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»=«/mo»«msqrt mathcolor=¨#0000FF¨»«mn mathvariant=¨bold¨»1«/mn»«mo mathvariant=¨bold¨».«/mo»«mn mathvariant=¨bold¨»4«/mn»«/msqrt»«mspace linebreak=¨newline¨/»«mspace linebreak=¨newline¨/»«mn mathvariant=¨bold¨ mathcolor=¨#0000FF¨»2«/mn»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»-«/mo»«msub»«mi mathvariant=¨bold¨ mathcolor=¨#0000FF¨»r«/mi»«mrow mathcolor=¨#0000FF¨»«mn mathvariant=¨bold¨»1«/mn»«mo mathvariant=¨bold¨»,«/mo»«mn mathvariant=¨bold¨»3«/mn»«/mrow»«/msub»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»=«/mo»«msub»«mi mathvariant=¨bold¨ mathcolor=¨#0000FF¨»r«/mi»«mrow mathcolor=¨#0000FF¨»«mn mathvariant=¨bold¨»1«/mn»«mo mathvariant=¨bold¨»,«/mo»«mn mathvariant=¨bold¨»3«/mn»«/mrow»«/msub»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»§#183;«/mo»«msqrt mathcolor=¨#0000FF¨»«mn mathvariant=¨bold¨»1«/mn»«mo mathvariant=¨bold¨».«/mo»«mn mathvariant=¨bold¨»4«/mn»«/msqrt»«mspace linebreak=¨newline¨/»«mspace linebreak=¨newline¨/»«mn mathvariant=¨bold¨ mathcolor=¨#0000FF¨»2«/mn»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»=«/mo»«msub»«mi mathvariant=¨bold¨ mathcolor=¨#0000FF¨»r«/mi»«mrow mathcolor=¨#0000FF¨»«mn mathvariant=¨bold¨»1«/mn»«mo mathvariant=¨bold¨»,«/mo»«mn mathvariant=¨bold¨»3«/mn»«/mrow»«/msub»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»+«/mo»«msub»«mi mathvariant=¨bold¨ mathcolor=¨#0000FF¨»r«/mi»«mrow mathcolor=¨#0000FF¨»«mn mathvariant=¨bold¨»1«/mn»«mo mathvariant=¨bold¨»,«/mo»«mn mathvariant=¨bold¨»3«/mn»«/mrow»«/msub»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»§#183;«/mo»«msqrt mathcolor=¨#0000FF¨»«mn mathvariant=¨bold¨»1«/mn»«mo mathvariant=¨bold¨».«/mo»«mn mathvariant=¨bold¨»4«/mn»«/msqrt»«mspace linebreak=¨newline¨/»«mspace linebreak=¨newline¨/»«mn mathvariant=¨bold¨ mathcolor=¨#0000FF¨»2«/mn»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»=«/mo»«msub»«mi mathvariant=¨bold¨ mathcolor=¨#0000FF¨»r«/mi»«mrow mathcolor=¨#0000FF¨»«mn mathvariant=¨bold¨»1«/mn»«mo mathvariant=¨bold¨»,«/mo»«mn mathvariant=¨bold¨»3«/mn»«/mrow»«/msub»«mrow mathcolor=¨#0000FF¨»«mo mathvariant=¨bold¨ stretchy=¨true¨»(«/mo»«mn mathvariant=¨bold¨»1«/mn»«mo mathvariant=¨bold¨»+«/mo»«msqrt»«mn mathvariant=¨bold¨»1«/mn»«mo mathvariant=¨bold¨».«/mo»«mn mathvariant=¨bold¨»4«/mn»«/msqrt»«mo mathvariant=¨bold¨ stretchy=¨true¨»)«/mo»«/mrow»«mspace linebreak=¨newline¨/»«mspace linebreak=¨newline¨/»«msub»«mi mathvariant=¨bold¨ mathcolor=¨#0000FF¨»r«/mi»«mrow mathcolor=¨#0000FF¨»«mn mathvariant=¨bold¨»1«/mn»«mo mathvariant=¨bold¨»,«/mo»«mn mathvariant=¨bold¨»3«/mn»«/mrow»«/msub»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»=«/mo»«mfrac mathcolor=¨#0000FF¨»«mn mathvariant=¨bold¨»2«/mn»«mrow»«mn mathvariant=¨bold¨»1«/mn»«mo mathvariant=¨bold¨»+«/mo»«msqrt»«mn mathvariant=¨bold¨»1«/mn»«mo mathvariant=¨bold¨».«/mo»«mn mathvariant=¨bold¨»4«/mn»«/msqrt»«/mrow»«/mfrac»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»=«/mo»«mfrac mathcolor=¨#0000FF¨»«mn mathvariant=¨bold¨»2«/mn»«mrow»«mn mathvariant=¨bold¨»2«/mn»«mo mathvariant=¨bold¨».«/mo»«mn mathvariant=¨bold¨»18«/mn»«/mrow»«/mfrac»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»=«/mo»«mn mathvariant=¨bold¨ mathcolor=¨#0000FF¨»0«/mn»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨».«/mo»«mn mathvariant=¨bold¨ mathcolor=¨#0000FF¨»91«/mn»«mi mathvariant=¨bold-italic¨ mathcolor=¨#0000FF¨»m«/mi»«/mstyle»«/math»

لتلخيص ذلك: عندما تكون الشحنة q2 تساوي 7nC والشحنة q1 تساوي 5nC، فإن النقطة التي يجب أن توضع فيها الشحنة q₃ وتكون محصلة القوى عليها صفرًا، تتوجد على بعد 91 سم على يسار q₁.

7.4

نرسم مخططًا للقوى المؤثرة على q₃ عندما تكون محصلة القوى المؤثرة على q₃ تساوي صفرًا.

نُشير للبعد بين q₁ و q₃ بـ r_1,3 والبعد بين q₂ و q₃ بـ r_2,3.

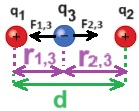
محصّلة القوى المؤثرة في هذه الحالة على q₃ تساوي صفرًا. لنكتب معادلة الحركة:

نعمل عمليات اختزال :

«math xmlns=¨http://www.w3.org/1998/Math/MathML¨»«mfrac mathcolor=¨#0000FF¨»«mrow»«menclose notation=¨updiagonalstrike¨»«mi mathvariant=¨bold¨ mathsize=¨22px¨»K«/mi»«/menclose»«mo mathvariant=¨bold¨ mathsize=¨22px¨»§#183;«/mo»«msub»«mi mathvariant=¨bold¨ mathsize=¨22px¨»q«/mi»«mn mathvariant=¨bold¨ mathsize=¨22px¨»1«/mn»«/msub»«mo mathvariant=¨bold¨ mathsize=¨22px¨»§#183;«/mo»«menclose notation=¨downdiagonalstrike¨»«msub»«mi mathvariant=¨bold¨ mathsize=¨22px¨»q«/mi»«mn mathvariant=¨bold¨ mathsize=¨22px¨»3«/mn»«/msub»«/menclose»«/mrow»«msup»«msub»«mi mathvariant=¨bold¨ mathsize=¨22px¨»r«/mi»«mrow»«mn mathvariant=¨bold¨ mathsize=¨22px¨»1«/mn»«mo mathvariant=¨bold¨ mathsize=¨22px¨»,«/mo»«mn mathvariant=¨bold¨ mathsize=¨22px¨»3«/mn»«/mrow»«/msub»«mn mathvariant=¨bold¨ mathsize=¨22px¨»2«/mn»«/msup»«/mfrac»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨ mathsize=¨22px¨»=«/mo»«mfrac mathcolor=¨#0000FF¨»«mrow»«menclose notation=¨updiagonalstrike¨»«mi mathvariant=¨bold¨ mathsize=¨22px¨»K«/mi»«/menclose»«mo mathvariant=¨bold¨ mathsize=¨22px¨»§#183;«/mo»«msub»«mi mathvariant=¨bold¨ mathsize=¨22px¨»q«/mi»«mn mathvariant=¨bold¨ mathsize=¨22px¨»2«/mn»«/msub»«mo mathvariant=¨bold¨ mathsize=¨22px¨»§#183;«/mo»«menclose notation=¨downdiagonalstrike¨»«msub»«mi mathvariant=¨bold¨ mathsize=¨22px¨»q«/mi»«mn mathvariant=¨bold¨ mathsize=¨22px¨»3«/mn»«/msub»«/menclose»«/mrow»«msup»«msub»«mi mathvariant=¨bold¨ mathsize=¨22px¨»r«/mi»«mrow»«mn mathvariant=¨bold¨ mathsize=¨22px¨»2«/mn»«mo mathvariant=¨bold¨ mathsize=¨22px¨»,«/mo»«mn mathvariant=¨bold¨ mathsize=¨22px¨»3«/mn»«/mrow»«/msub»«mn mathvariant=¨bold¨ mathsize=¨22px¨»2«/mn»«/msup»«/mfrac»«mspace linebreak=¨newline¨/»«mspace linebreak=¨newline¨/»«mfrac mathcolor=¨#0000FF¨»«msub»«mi mathvariant=¨bold¨ mathsize=¨22px¨»q«/mi»«mn mathvariant=¨bold¨ mathsize=¨22px¨»1«/mn»«/msub»«msup»«msub»«mi mathvariant=¨bold¨ mathsize=¨22px¨»r«/mi»«mrow»«mn mathvariant=¨bold¨ mathsize=¨22px¨»1«/mn»«mo mathvariant=¨bold¨ mathsize=¨22px¨»,«/mo»«mn mathvariant=¨bold¨ mathsize=¨22px¨»3«/mn»«/mrow»«/msub»«mn mathvariant=¨bold¨ mathsize=¨22px¨»2«/mn»«/msup»«/mfrac»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨ mathsize=¨22px¨»=«/mo»«mfrac mathcolor=¨#0000FF¨»«msub»«mi mathvariant=¨bold¨ mathsize=¨22px¨»q«/mi»«mn mathvariant=¨bold¨ mathsize=¨22px¨»2«/mn»«/msub»«msup»«msub»«mi mathvariant=¨bold¨ mathsize=¨22px¨»r«/mi»«mrow»«mn mathvariant=¨bold¨ mathsize=¨22px¨»2«/mn»«mo mathvariant=¨bold¨ mathsize=¨22px¨»,«/mo»«mn mathvariant=¨bold¨ mathsize=¨22px¨»3«/mn»«/mrow»«/msub»«mn mathvariant=¨bold¨ mathsize=¨22px¨»2«/mn»«/msup»«/mfrac»«mspace linebreak=¨newline¨/»«mspace linebreak=¨newline¨/»«mfrac mathcolor=¨#0000FF¨»«msup»«msub»«mi mathvariant=¨bold¨ mathsize=¨22px¨»r«/mi»«mrow»«mn mathvariant=¨bold¨ mathsize=¨22px¨»2«/mn»«mo mathvariant=¨bold¨ mathsize=¨22px¨»,«/mo»«mn mathvariant=¨bold¨ mathsize=¨22px¨»3«/mn»«/mrow»«/msub»«mn mathvariant=¨bold¨ mathsize=¨22px¨»2«/mn»«/msup»«msup»«msub»«mi mathvariant=¨bold¨ mathsize=¨22px¨»r«/mi»«mrow»«mn mathvariant=¨bold¨ mathsize=¨22px¨»1«/mn»«mo mathvariant=¨bold¨ mathsize=¨22px¨»,«/mo»«mn mathvariant=¨bold¨ mathsize=¨22px¨»3«/mn»«/mrow»«/msub»«mn mathvariant=¨bold¨ mathsize=¨22px¨»2«/mn»«/msup»«/mfrac»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨ mathsize=¨22px¨»=«/mo»«mfrac mathcolor=¨#0000FF¨»«msub»«mi mathvariant=¨bold¨ mathsize=¨22px¨»q«/mi»«mn mathvariant=¨bold¨ mathsize=¨22px¨»2«/mn»«/msub»«msub»«mi mathvariant=¨bold¨ mathsize=¨22px¨»q«/mi»«mn mathvariant=¨bold¨ mathsize=¨22px¨»1«/mn»«/msub»«/mfrac»«mspace linebreak=¨newline¨/»«mspace linebreak=¨newline¨/»«menclose mathcolor=¨#0000FF¨ notation=¨box¨»«mfrac»«msub»«mi mathvariant=¨bold¨ mathsize=¨22px¨»r«/mi»«mrow»«mn mathvariant=¨bold¨ mathsize=¨22px¨»2«/mn»«mo mathvariant=¨bold¨ mathsize=¨22px¨»,«/mo»«mn mathvariant=¨bold¨ mathsize=¨22px¨»3«/mn»«/mrow»«/msub»«msub»«mi mathvariant=¨bold¨ mathsize=¨22px¨»r«/mi»«mrow»«mn mathvariant=¨bold¨ mathsize=¨22px¨»1«/mn»«mo mathvariant=¨bold¨ mathsize=¨22px¨»,«/mo»«mn mathvariant=¨bold¨ mathsize=¨22px¨»3«/mn»«/mrow»«/msub»«/mfrac»«mo mathvariant=¨bold¨ mathsize=¨22px¨»=«/mo»«msqrt»«mfrac»«msub»«mi mathvariant=¨bold¨ mathsize=¨22px¨»q«/mi»«mn mathvariant=¨bold¨ mathsize=¨22px¨»2«/mn»«/msub»«msub»«mi mathvariant=¨bold¨ mathsize=¨22px¨»q«/mi»«mn mathvariant=¨bold¨ mathsize=¨22px¨»1«/mn»«/msub»«/mfrac»«/msqrt»«/menclose»«/math»

مجموع البعدين r_2,3 و r_1,3 يساوي البعد d. ووفقًا لذلك نكتب معادلة أخرى بنفس المتغيرين: r_2,3 و r1,3

«math xmlns=¨http://www.w3.org/1998/Math/MathML¨»«menclose mathcolor=¨#0000FF¨ notation=¨box¨»«msub»«mi mathvariant=¨bold¨ mathsize=¨22px¨»r«/mi»«mrow»«mn mathvariant=¨bold¨ mathsize=¨22px¨»1«/mn»«mo mathvariant=¨bold¨ mathsize=¨22px¨»,«/mo»«mn mathvariant=¨bold¨ mathsize=¨22px¨»3«/mn»«/mrow»«/msub»«mo mathvariant=¨bold¨ mathsize=¨22px¨»+«/mo»«msub»«mi mathvariant=¨bold¨ mathsize=¨22px¨»r«/mi»«mrow»«mn mathvariant=¨bold¨ mathsize=¨22px¨»2«/mn»«mo mathvariant=¨bold¨ mathsize=¨22px¨»,«/mo»«mn mathvariant=¨bold¨ mathsize=¨22px¨»3«/mn»«/mrow»«/msub»«mo mathvariant=¨bold¨ mathsize=¨22px¨»=«/mo»«mi mathvariant=¨bold¨ mathsize=¨22px¨»d«/mi»«/menclose»«mspace linebreak=¨newline¨/»«mspace linebreak=¨newline¨/»«/math»

نُعبر عن البعد اللازم r_1,3من المعادلتين :

«math xmlns=¨http://www.w3.org/1998/Math/MathML¨»«mstyle mathsize=¨20px¨»«menclose mathcolor=¨#0000FF¨ notation=¨box¨»«msub»«mi mathvariant=¨bold¨»r«/mi»«mrow»«mn mathvariant=¨bold¨»1«/mn»«mo mathvariant=¨bold¨»,«/mo»«mn mathvariant=¨bold¨»3«/mn»«/mrow»«/msub»«mo mathvariant=¨bold¨»+«/mo»«msub»«mi mathvariant=¨bold¨»r«/mi»«mrow»«mn mathvariant=¨bold¨»2«/mn»«mo mathvariant=¨bold¨»,«/mo»«mn mathvariant=¨bold¨»3«/mn»«/mrow»«/msub»«mo mathvariant=¨bold¨»=«/mo»«mi mathvariant=¨bold¨»d«/mi»«/menclose»«mo»§#160;«/mo»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»§#8658;«/mo»«msub»«mi mathvariant=¨bold¨ mathcolor=¨#0000FF¨»r«/mi»«mrow mathcolor=¨#0000FF¨»«mn mathvariant=¨bold¨»2«/mn»«mo mathvariant=¨bold¨»,«/mo»«mn mathvariant=¨bold¨»3«/mn»«/mrow»«/msub»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»=«/mo»«mi mathvariant=¨bold¨ mathcolor=¨#0000FF¨»d«/mi»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»-«/mo»«msub»«mi mathvariant=¨bold¨ mathcolor=¨#0000FF¨»r«/mi»«mrow mathcolor=¨#0000FF¨»«mn mathvariant=¨bold¨»1«/mn»«mo mathvariant=¨bold¨»,«/mo»«mn mathvariant=¨bold¨»3«/mn»«/mrow»«/msub»«mspace linebreak=¨newline¨/»«mspace linebreak=¨newline¨/»«/mstyle»«/math»

«math xmlns=¨http://www.w3.org/1998/Math/MathML¨»«mstyle mathsize=¨22px¨»«mspace linebreak=¨newline¨/»«menclose mathcolor=¨#0000FF¨ notation=¨box¨»«mfrac»«msub»«mi mathvariant=¨bold¨ mathcolor=¨#FF0000¨»r«/mi»«mrow mathcolor=¨#FF0000¨»«mn mathvariant=¨bold¨»2«/mn»«mo mathvariant=¨bold¨»,«/mo»«mn mathvariant=¨bold¨»3«/mn»«/mrow»«/msub»«msub»«mi mathvariant=¨bold¨»r«/mi»«mrow»«mn mathvariant=¨bold¨»1«/mn»«mo mathvariant=¨bold¨»,«/mo»«mn mathvariant=¨bold¨»3«/mn»«/mrow»«/msub»«/mfrac»«mo mathvariant=¨bold¨»=«/mo»«msqrt»«mfrac»«msub»«mi mathvariant=¨bold¨»q«/mi»«mn mathvariant=¨bold¨»2«/mn»«/msub»«msub»«mi mathvariant=¨bold¨»q«/mi»«mn mathvariant=¨bold¨»1«/mn»«/msub»«/mfrac»«/msqrt»«/menclose»«mo»§#160;«/mo»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»§#8658;«/mo»«mfrac mathcolor=¨#0000FF¨»«mrow»«mi mathcolor=¨#FF0000¨ mathvariant=¨bold¨»d«/mi»«mo mathcolor=¨#FF0000¨ mathvariant=¨bold¨»-«/mo»«msub»«mi mathcolor=¨#FF0000¨ mathvariant=¨bold¨»r«/mi»«mrow mathcolor=¨#FF0000¨»«mn mathvariant=¨bold¨»1«/mn»«mo mathvariant=¨bold¨»,«/mo»«mn mathvariant=¨bold¨»3«/mn»«/mrow»«/msub»«/mrow»«msub»«mi mathvariant=¨bold¨»r«/mi»«mrow»«mn mathvariant=¨bold¨»1«/mn»«mo mathvariant=¨bold¨»,«/mo»«mn mathvariant=¨bold¨»3«/mn»«/mrow»«/msub»«/mfrac»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»=«/mo»«msqrt mathcolor=¨#0000FF¨»«mfrac»«msub»«mi mathvariant=¨bold¨»q«/mi»«mn mathvariant=¨bold¨»2«/mn»«/msub»«msub»«mi mathvariant=¨bold¨»q«/mi»«mn mathvariant=¨bold¨»1«/mn»«/msub»«/mfrac»«/msqrt»«/mstyle»«/math»

نُعبر عن البعد r_1,3:

«math xmlns=¨http://www.w3.org/1998/Math/MathML¨»«mstyle mathsize=¨22px¨»«mfrac mathcolor=¨#0000FF¨»«mrow»«mi mathvariant=¨bold¨»d«/mi»«mo mathvariant=¨bold¨»-«/mo»«msub»«mi mathvariant=¨bold¨»r«/mi»«mrow»«mn mathvariant=¨bold¨»1«/mn»«mo mathvariant=¨bold¨»,«/mo»«mn mathvariant=¨bold¨»3«/mn»«/mrow»«/msub»«/mrow»«msub»«mi mathvariant=¨bold¨»r«/mi»«mrow»«mn mathvariant=¨bold¨»1«/mn»«mo mathvariant=¨bold¨»,«/mo»«mn mathvariant=¨bold¨»3«/mn»«/mrow»«/msub»«/mfrac»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»=«/mo»«msqrt mathcolor=¨#0000FF¨»«mfrac»«msub»«mi mathvariant=¨bold¨»q«/mi»«mn mathvariant=¨bold¨»2«/mn»«/msub»«msub»«mi mathvariant=¨bold¨»q«/mi»«mn mathvariant=¨bold¨»1«/mn»«/msub»«/mfrac»«/msqrt»«mspace linebreak=¨newline¨/»«mspace linebreak=¨newline¨/»«mi mathvariant=¨bold¨ mathcolor=¨#0000FF¨»d«/mi»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»-«/mo»«msub»«mi mathvariant=¨bold¨ mathcolor=¨#0000FF¨»r«/mi»«mrow mathcolor=¨#0000FF¨»«mn mathvariant=¨bold¨»1«/mn»«mo mathvariant=¨bold¨»,«/mo»«mn mathvariant=¨bold¨»3«/mn»«/mrow»«/msub»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»=«/mo»«msub»«mi mathvariant=¨bold¨ mathcolor=¨#0000FF¨»r«/mi»«mrow mathcolor=¨#0000FF¨»«mn mathvariant=¨bold¨»1«/mn»«mo mathvariant=¨bold¨»,«/mo»«mn mathvariant=¨bold¨»3«/mn»«/mrow»«/msub»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»§#183;«/mo»«msqrt mathcolor=¨#0000FF¨»«mfrac»«msub»«mi mathvariant=¨bold¨»q«/mi»«mn mathvariant=¨bold¨»2«/mn»«/msub»«msub»«mi mathvariant=¨bold¨»q«/mi»«mn mathvariant=¨bold¨»1«/mn»«/msub»«/mfrac»«/msqrt»«mspace linebreak=¨newline¨/»«mspace linebreak=¨newline¨/»«mi mathvariant=¨bold¨ mathcolor=¨#0000FF¨»d«/mi»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»=«/mo»«msub»«mi mathvariant=¨bold¨ mathcolor=¨#0000FF¨»r«/mi»«mrow mathcolor=¨#0000FF¨»«mn mathvariant=¨bold¨»1«/mn»«mo mathvariant=¨bold¨»,«/mo»«mn mathvariant=¨bold¨»3«/mn»«/mrow»«/msub»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»+«/mo»«msub»«mi mathvariant=¨bold¨ mathcolor=¨#0000FF¨»r«/mi»«mrow mathcolor=¨#0000FF¨»«mn mathvariant=¨bold¨»1«/mn»«mo mathvariant=¨bold¨»,«/mo»«mn mathvariant=¨bold¨»3«/mn»«/mrow»«/msub»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»§#183;«/mo»«msqrt mathcolor=¨#0000FF¨»«mfrac»«msub»«mi mathvariant=¨bold¨»q«/mi»«mn mathvariant=¨bold¨»2«/mn»«/msub»«msub»«mi mathvariant=¨bold¨»q«/mi»«mn mathvariant=¨bold¨»1«/mn»«/msub»«/mfrac»«/msqrt»«mspace linebreak=¨newline¨/»«mspace linebreak=¨newline¨/»«mi mathvariant=¨bold¨ mathcolor=¨#0000FF¨»d«/mi»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»=«/mo»«msub»«mi mathvariant=¨bold¨ mathcolor=¨#0000FF¨»r«/mi»«mrow mathcolor=¨#0000FF¨»«mn mathvariant=¨bold¨»1«/mn»«mo mathvariant=¨bold¨»,«/mo»«mn mathvariant=¨bold¨»3«/mn»«/mrow»«/msub»«mstyle mathvariant=¨bold¨ mathcolor=¨#0000FF¨»«mo stretchy=¨true¨»(«/mo»«mrow»«mn»1«/mn»«mo»+«/mo»«msqrt»«mfrac»«msub»«mi»q«/mi»«mn»2«/mn»«/msub»«msub»«mi»q«/mi»«mn»1«/mn»«/msub»«/mfrac»«/msqrt»«/mrow»«mo stretchy=¨true¨»)«/mo»«/mstyle»«mspace linebreak=¨newline¨/»«mspace linebreak=¨newline¨/»«menclose mathcolor=¨#0000FF¨ notation=¨circle¨»«msub»«mi mathvariant=¨bold¨»r«/mi»«mrow»«mn mathvariant=¨bold¨»1«/mn»«mo mathvariant=¨bold¨»,«/mo»«mn mathvariant=¨bold¨»3«/mn»«/mrow»«/msub»«mo mathvariant=¨bold¨»=«/mo»«mfrac»«mi mathvariant=¨bold¨»d«/mi»«mrow»«mn mathvariant=¨bold¨»1«/mn»«mo mathvariant=¨bold¨»+«/mo»«msqrt»«mfrac»«msub»«mi mathvariant=¨bold¨»q«/mi»«mn mathvariant=¨bold¨»2«/mn»«/msub»«msub»«mi mathvariant=¨bold¨»q«/mi»«mn mathvariant=¨bold¨»1«/mn»«/msub»«/mfrac»«/msqrt»«/mrow»«/mfrac»«/menclose»«mspace linebreak=¨newline¨/»«mspace linebreak=¨newline¨/»«mspace linebreak=¨newline¨/»«/mstyle»«/math»

8.1

نرسم مخطط القوى للقوى الكهربائية المؤثرة على q₃، عندما تكون الشحنة في كل من المجالات الثلاثة:

يمكن ملاحظة أن القوى تعمل في اتجاهين متعاكسين عندما تكون الشحنتان في المجالين א' و ג'.

الشحنة q₁ أكبر من الشحنة q₂ (بالقيمة المطلقة). لكي تكون القوى الكهربائية المؤثرة على q₃ متساوية في المقدار، يجب وضع q₃ بعيدًا عن q₁ وقريبًا من q₂. لذلك، لكي نكون محصّلة القوى المؤثرة على q₃ مساويًا للصفر، يجب وضع الشحنة في المجال א'.

8.2

نرسم مخطط القوى للقوى المؤثرة على الشحنة q₃

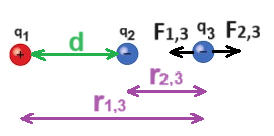
محصّلة القوى المؤثرة في هذه الحالة على q₃ تساوي صفرًا. لنكتب معادلة الحركة:

نقوم بإجراء عمليات إختزال وتعويض قيم الشحنات:

«math xmlns=¨http://www.w3.org/1998/Math/MathML¨»«mfrac mathcolor=¨#0000FF¨»«mrow»«menclose notation=¨updiagonalstrike¨»«mi mathvariant=¨bold¨ mathsize=¨22px¨»K«/mi»«/menclose»«mo mathvariant=¨bold¨ mathsize=¨22px¨»§#183;«/mo»«msub»«mi mathvariant=¨bold¨ mathsize=¨22px¨»q«/mi»«mn mathvariant=¨bold¨ mathsize=¨22px¨»1«/mn»«/msub»«mo mathvariant=¨bold¨ mathsize=¨22px¨»§#183;«/mo»«menclose notation=¨downdiagonalstrike¨»«msub»«mi mathvariant=¨bold¨ mathsize=¨22px¨»q«/mi»«mn mathvariant=¨bold¨ mathsize=¨22px¨»3«/mn»«/msub»«/menclose»«/mrow»«msup»«msub»«mi mathvariant=¨bold¨ mathsize=¨22px¨»r«/mi»«mrow»«mn mathvariant=¨bold¨ mathsize=¨22px¨»1«/mn»«mo mathvariant=¨bold¨ mathsize=¨22px¨»,«/mo»«mn mathvariant=¨bold¨ mathsize=¨22px¨»3«/mn»«/mrow»«/msub»«mn mathvariant=¨bold¨ mathsize=¨22px¨»2«/mn»«/msup»«/mfrac»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨ mathsize=¨22px¨»=«/mo»«mfrac mathcolor=¨#0000FF¨»«mrow»«menclose notation=¨updiagonalstrike¨»«mi mathvariant=¨bold¨ mathsize=¨22px¨»K«/mi»«/menclose»«mo mathvariant=¨bold¨ mathsize=¨22px¨»§#183;«/mo»«msub»«mi mathvariant=¨bold¨ mathsize=¨22px¨»q«/mi»«mn mathvariant=¨bold¨ mathsize=¨22px¨»2«/mn»«/msub»«mo mathvariant=¨bold¨ mathsize=¨22px¨»§#183;«/mo»«menclose notation=¨downdiagonalstrike¨»«msub»«mi mathvariant=¨bold¨ mathsize=¨22px¨»q«/mi»«mn mathvariant=¨bold¨ mathsize=¨22px¨»3«/mn»«/msub»«/menclose»«/mrow»«msup»«msub»«mi mathvariant=¨bold¨ mathsize=¨22px¨»r«/mi»«mrow»«mn mathvariant=¨bold¨ mathsize=¨22px¨»2«/mn»«mo mathvariant=¨bold¨ mathsize=¨22px¨»,«/mo»«mn mathvariant=¨bold¨ mathsize=¨22px¨»3«/mn»«/mrow»«/msub»«mn mathvariant=¨bold¨ mathsize=¨22px¨»2«/mn»«/msup»«/mfrac»«mspace linebreak=¨newline¨/»«mspace linebreak=¨newline¨/»«mfrac mathcolor=¨#0000FF¨»«msub»«mi mathvariant=¨bold¨ mathsize=¨22px¨»q«/mi»«mn mathvariant=¨bold¨ mathsize=¨22px¨»1«/mn»«/msub»«msup»«msub»«mi mathvariant=¨bold¨ mathsize=¨22px¨»r«/mi»«mrow»«mn mathvariant=¨bold¨ mathsize=¨22px¨»1«/mn»«mo mathvariant=¨bold¨ mathsize=¨22px¨»,«/mo»«mn mathvariant=¨bold¨ mathsize=¨22px¨»3«/mn»«/mrow»«/msub»«mn mathvariant=¨bold¨ mathsize=¨22px¨»2«/mn»«/msup»«/mfrac»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨ mathsize=¨22px¨»=«/mo»«mfrac mathcolor=¨#0000FF¨»«msub»«mi mathvariant=¨bold¨ mathsize=¨22px¨»q«/mi»«mn mathvariant=¨bold¨ mathsize=¨22px¨»2«/mn»«/msub»«msup»«msub»«mi mathvariant=¨bold¨ mathsize=¨22px¨»r«/mi»«mrow»«mn mathvariant=¨bold¨ mathsize=¨22px¨»2«/mn»«mo mathvariant=¨bold¨ mathsize=¨22px¨»,«/mo»«mn mathvariant=¨bold¨ mathsize=¨22px¨»3«/mn»«/mrow»«/msub»«mn mathvariant=¨bold¨ mathsize=¨22px¨»2«/mn»«/msup»«/mfrac»«mspace linebreak=¨newline¨/»«mspace linebreak=¨newline¨/»«mfrac mathcolor=¨#0000FF¨»«mrow»«mn mathvariant=¨bold¨ mathsize=¨22px¨»5«/mn»«mo mathvariant=¨bold¨ mathsize=¨22px¨»§#183;«/mo»«msup»«mn mathvariant=¨bold¨ mathsize=¨22px¨»10«/mn»«mrow»«mo mathvariant=¨bold¨ mathsize=¨22px¨»-«/mo»«mn mathvariant=¨bold¨ mathsize=¨22px¨»9«/mn»«/mrow»«/msup»«/mrow»«msup»«msub»«mi mathvariant=¨bold¨ mathsize=¨22px¨»r«/mi»«mrow»«mn mathvariant=¨bold¨ mathsize=¨22px¨»1«/mn»«mo mathvariant=¨bold¨ mathsize=¨22px¨»,«/mo»«mn mathvariant=¨bold¨ mathsize=¨22px¨»3«/mn»«/mrow»«/msub»«mn mathvariant=¨bold¨ mathsize=¨22px¨»2«/mn»«/msup»«/mfrac»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨ mathsize=¨22px¨»=«/mo»«mfrac mathcolor=¨#0000FF¨»«mrow»«mn mathvariant=¨bold¨ mathsize=¨22px¨»2«/mn»«mo mathvariant=¨bold¨ mathsize=¨22px¨»§#183;«/mo»«msup»«mn mathvariant=¨bold¨ mathsize=¨22px¨»10«/mn»«mrow»«mo mathvariant=¨bold¨ mathsize=¨22px¨»-«/mo»«mn mathvariant=¨bold¨ mathsize=¨22px¨»9«/mn»«/mrow»«/msup»«/mrow»«msup»«msub»«mi mathvariant=¨bold¨ mathsize=¨22px¨»r«/mi»«mrow»«mn mathvariant=¨bold¨ mathsize=¨22px¨»2«/mn»«mo mathvariant=¨bold¨ mathsize=¨22px¨»,«/mo»«mn mathvariant=¨bold¨ mathsize=¨22px¨»3«/mn»«/mrow»«/msub»«mn mathvariant=¨bold¨ mathsize=¨22px¨»2«/mn»«/msup»«/mfrac»«mspace linebreak=¨newline¨/»«mspace linebreak=¨newline¨/»«mfrac mathcolor=¨#0000FF¨»«msup»«msub»«mi mathvariant=¨bold¨ mathsize=¨22px¨»r«/mi»«mrow»«mn mathvariant=¨bold¨ mathsize=¨22px¨»2«/mn»«mo mathvariant=¨bold¨ mathsize=¨22px¨»,«/mo»«mn mathvariant=¨bold¨ mathsize=¨22px¨»3«/mn»«/mrow»«/msub»«mn mathvariant=¨bold¨ mathsize=¨22px¨»2«/mn»«/msup»«msup»«msub»«mi mathvariant=¨bold¨ mathsize=¨22px¨»r«/mi»«mrow»«mn mathvariant=¨bold¨ mathsize=¨22px¨»1«/mn»«mo mathvariant=¨bold¨ mathsize=¨22px¨»,«/mo»«mn mathvariant=¨bold¨ mathsize=¨22px¨»3«/mn»«/mrow»«/msub»«mn mathvariant=¨bold¨ mathsize=¨22px¨»2«/mn»«/msup»«/mfrac»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨ mathsize=¨22px¨»=«/mo»«mfrac mathcolor=¨#0000FF¨»«mrow»«mn mathvariant=¨bold¨ mathsize=¨22px¨»2«/mn»«mo mathvariant=¨bold¨ mathsize=¨22px¨»§#183;«/mo»«msup»«mn mathvariant=¨bold¨ mathsize=¨22px¨»10«/mn»«mrow»«mo mathvariant=¨bold¨ mathsize=¨22px¨»-«/mo»«mn mathvariant=¨bold¨ mathsize=¨22px¨»9«/mn»«/mrow»«/msup»«/mrow»«mrow»«mn mathvariant=¨bold¨ mathsize=¨22px¨»5«/mn»«mo mathvariant=¨bold¨ mathsize=¨22px¨»§#183;«/mo»«msup»«mn mathvariant=¨bold¨ mathsize=¨22px¨»10«/mn»«mrow»«mo mathvariant=¨bold¨ mathsize=¨22px¨»-«/mo»«mn mathvariant=¨bold¨ mathsize=¨22px¨»9«/mn»«/mrow»«/msup»«/mrow»«/mfrac»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨ mathsize=¨22px¨»=«/mo»«mn mathvariant=¨bold¨ mathcolor=¨#0000FF¨ mathsize=¨22px¨»0«/mn»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨ mathsize=¨22px¨».«/mo»«mn mathvariant=¨bold¨ mathcolor=¨#0000FF¨ mathsize=¨22px¨»4«/mn»«mspace linebreak=¨newline¨/»«mspace linebreak=¨newline¨/»«menclose mathcolor=¨#0000FF¨ notation=¨box¨»«mfrac»«msub»«mi mathvariant=¨bold¨ mathsize=¨22px¨»r«/mi»«mrow»«mn mathvariant=¨bold¨ mathsize=¨22px¨»2«/mn»«mo mathvariant=¨bold¨ mathsize=¨22px¨»,«/mo»«mn mathvariant=¨bold¨ mathsize=¨22px¨»3«/mn»«/mrow»«/msub»«msub»«mi mathvariant=¨bold¨ mathsize=¨22px¨»r«/mi»«mrow»«mn mathvariant=¨bold¨ mathsize=¨22px¨»1«/mn»«mo mathvariant=¨bold¨ mathsize=¨22px¨»,«/mo»«mn mathvariant=¨bold¨ mathsize=¨22px¨»3«/mn»«/mrow»«/msub»«/mfrac»«mo mathvariant=¨bold¨ mathsize=¨22px¨»=«/mo»«msqrt»«mn mathvariant=¨bold¨ mathsize=¨22px¨»0«/mn»«mo mathvariant=¨bold¨ mathsize=¨22px¨».«/mo»«mn mathvariant=¨bold¨ mathsize=¨22px¨»4«/mn»«/msqrt»«/menclose»«/math»

وبناء على ذلك سوف نكتب معادلة أخرى مع المجاهيل: r_2,3 r_1,3 و- d.

«math xmlns=¨http://www.w3.org/1998/Math/MathML¨»«menclose mathcolor=¨#0000FF¨ notation=¨box¨»«msub»«mi mathvariant=¨bold¨ mathsize=¨22px¨»r«/mi»«mrow»«mn mathvariant=¨bold¨ mathsize=¨22px¨»2«/mn»«mo mathvariant=¨bold¨ mathsize=¨22px¨»,«/mo»«mn mathvariant=¨bold¨ mathsize=¨22px¨»3«/mn»«/mrow»«/msub»«mo mathvariant=¨bold¨ mathsize=¨22px¨»+«/mo»«mi mathvariant=¨bold¨ mathsize=¨22px¨»d«/mi»«mo mathvariant=¨bold¨ mathsize=¨22px¨»=«/mo»«msub»«mi mathvariant=¨bold¨ mathsize=¨22px¨»r«/mi»«mrow»«mn mathvariant=¨bold¨ mathsize=¨22px¨»1«/mn»«mo mathvariant=¨bold¨ mathsize=¨22px¨»,«/mo»«mn mathvariant=¨bold¨ mathsize=¨22px¨»3«/mn»«/mrow»«/msub»«/menclose»«mspace linebreak=¨newline¨/»«mspace linebreak=¨newline¨/»«/math»

نُعبر عن البعد اللمطلوب r_1,3 من المعادلتين :

«math xmlns=¨http://www.w3.org/1998/Math/MathML¨»«mstyle mathsize=¨22px¨»«menclose mathcolor=¨#0000FF¨ notation=¨box¨»«msub»«mi mathvariant=¨bold¨»r«/mi»«mrow»«mn mathvariant=¨bold¨»2«/mn»«mo mathvariant=¨bold¨»,«/mo»«mn mathvariant=¨bold¨»3«/mn»«/mrow»«/msub»«mo mathvariant=¨bold¨»+«/mo»«mi mathvariant=¨bold¨»d«/mi»«mo mathvariant=¨bold¨»=«/mo»«msub»«mi mathvariant=¨bold¨»r«/mi»«mrow»«mn mathvariant=¨bold¨»1«/mn»«mo mathvariant=¨bold¨»,«/mo»«mn mathvariant=¨bold¨»3«/mn»«/mrow»«/msub»«/menclose»«mo»§#160;«/mo»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»§#8658;«/mo»«mo»§#160;«/mo»«msub»«mi mathvariant=¨bold¨ mathcolor=¨#0000FF¨»r«/mi»«mrow mathcolor=¨#0000FF¨»«mn mathvariant=¨bold¨»2«/mn»«mo mathvariant=¨bold¨»,«/mo»«mn mathvariant=¨bold¨»3«/mn»«/mrow»«/msub»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»=«/mo»«msub»«mi mathvariant=¨bold¨ mathcolor=¨#0000FF¨»r«/mi»«mrow mathcolor=¨#0000FF¨»«mn mathvariant=¨bold¨»1«/mn»«mo mathvariant=¨bold¨»,«/mo»«mn mathvariant=¨bold¨»3«/mn»«/mrow»«/msub»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»-«/mo»«mi mathvariant=¨bold¨ mathcolor=¨#0000FF¨»d«/mi»«/mstyle»«/math»

«math xmlns=¨http://www.w3.org/1998/Math/MathML¨»«mstyle mathsize=¨22px¨»«mspace linebreak=¨newline¨/»«menclose mathcolor=¨#0000FF¨ notation=¨box¨»«mfrac»«msub»«mi mathvariant=¨bold¨ mathcolor=¨#FF0000¨»r«/mi»«mrow mathcolor=¨#FF0000¨»«mn mathvariant=¨bold¨»2«/mn»«mo mathvariant=¨bold¨»,«/mo»«mn mathvariant=¨bold¨»3«/mn»«/mrow»«/msub»«msub»«mi mathvariant=¨bold¨»r«/mi»«mrow»«mn mathvariant=¨bold¨»1«/mn»«mo mathvariant=¨bold¨»,«/mo»«mn mathvariant=¨bold¨»3«/mn»«/mrow»«/msub»«/mfrac»«mo mathvariant=¨bold¨»=«/mo»«msqrt»«mn mathvariant=¨bold¨»0«/mn»«mo mathvariant=¨bold¨».«/mo»«mn mathvariant=¨bold¨»4«/mn»«/msqrt»«/menclose»«mo»§#160;«/mo»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»§#8658;«/mo»«mfrac mathcolor=¨#0000FF¨»«mrow»«msub»«mi mathvariant=¨bold¨ mathcolor=¨#FF0000¨»r«/mi»«mrow mathcolor=¨#FF0000¨»«mn mathvariant=¨bold¨»1«/mn»«mo mathvariant=¨bold¨»,«/mo»«mn mathvariant=¨bold¨»3«/mn»«/mrow»«/msub»«mo mathvariant=¨bold¨ mathcolor=¨#FF0000¨»-«/mo»«mi mathvariant=¨bold¨ mathcolor=¨#FF0000¨»d«/mi»«/mrow»«msub»«mi mathvariant=¨bold¨»r«/mi»«mrow»«mn mathvariant=¨bold¨»1«/mn»«mo mathvariant=¨bold¨»,«/mo»«mn mathvariant=¨bold¨»3«/mn»«/mrow»«/msub»«/mfrac»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»=«/mo»«msqrt mathcolor=¨#0000FF¨»«mn mathvariant=¨bold¨»0«/mn»«mo mathvariant=¨bold¨».«/mo»«mn mathvariant=¨bold¨»4«/mn»«/msqrt»«/mstyle»«/math»

نُعبر عن البعد r_1,3:

«math xmlns=¨http://www.w3.org/1998/Math/MathML¨»«mstyle mathsize=¨22px¨»«mfrac mathcolor=¨#0000FF¨»«mrow»«msub»«mi mathvariant=¨bold¨»r«/mi»«mrow»«mn mathvariant=¨bold¨»1«/mn»«mo mathvariant=¨bold¨»,«/mo»«mn mathvariant=¨bold¨»3«/mn»«/mrow»«/msub»«mo mathvariant=¨bold¨»-«/mo»«mi mathvariant=¨bold¨»d«/mi»«/mrow»«msub»«mi mathvariant=¨bold¨»r«/mi»«mrow»«mn mathvariant=¨bold¨»1«/mn»«mo mathvariant=¨bold¨»,«/mo»«mn mathvariant=¨bold¨»3«/mn»«/mrow»«/msub»«/mfrac»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»=«/mo»«msqrt mathcolor=¨#0000FF¨»«mn mathvariant=¨bold¨»0«/mn»«mo mathvariant=¨bold¨».«/mo»«mn mathvariant=¨bold¨»4«/mn»«/msqrt»«mspace linebreak=¨newline¨/»«mspace linebreak=¨newline¨/»«msub»«mi mathvariant=¨bold¨ mathcolor=¨#0000FF¨»r«/mi»«mrow mathcolor=¨#0000FF¨»«mn mathvariant=¨bold¨»1«/mn»«mo mathvariant=¨bold¨»,«/mo»«mn mathvariant=¨bold¨»3«/mn»«/mrow»«/msub»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»-«/mo»«mi mathvariant=¨bold¨ mathcolor=¨#0000FF¨»d«/mi»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»=«/mo»«msub»«mi mathvariant=¨bold¨ mathcolor=¨#0000FF¨»r«/mi»«mrow mathcolor=¨#0000FF¨»«mn mathvariant=¨bold¨»1«/mn»«mo mathvariant=¨bold¨»,«/mo»«mn mathvariant=¨bold¨»3«/mn»«/mrow»«/msub»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»§#183;«/mo»«msqrt mathcolor=¨#0000FF¨»«mn mathvariant=¨bold¨»0«/mn»«mo mathvariant=¨bold¨».«/mo»«mn mathvariant=¨bold¨»4«/mn»«/msqrt»«mspace linebreak=¨newline¨/»«mspace linebreak=¨newline¨/»«msub»«mi mathvariant=¨bold¨ mathcolor=¨#0000FF¨»r«/mi»«mrow mathcolor=¨#0000FF¨»«mn mathvariant=¨bold¨»1«/mn»«mo mathvariant=¨bold¨»,«/mo»«mn mathvariant=¨bold¨»3«/mn»«/mrow»«/msub»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»-«/mo»«msub»«mi mathvariant=¨bold¨ mathcolor=¨#0000FF¨»r«/mi»«mrow mathcolor=¨#0000FF¨»«mn mathvariant=¨bold¨»1«/mn»«mo mathvariant=¨bold¨»,«/mo»«mn mathvariant=¨bold¨»3«/mn»«/mrow»«/msub»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»§#183;«/mo»«msqrt mathcolor=¨#0000FF¨»«mn mathvariant=¨bold¨»0«/mn»«mo mathvariant=¨bold¨».«/mo»«mn mathvariant=¨bold¨»4«/mn»«/msqrt»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»=«/mo»«mi mathvariant=¨bold¨ mathcolor=¨#0000FF¨»d«/mi»«mspace linebreak=¨newline¨/»«mspace linebreak=¨newline¨/»«msub»«mi mathvariant=¨bold¨ mathcolor=¨#0000FF¨»r«/mi»«mrow mathcolor=¨#0000FF¨»«mn mathvariant=¨bold¨»1«/mn»«mo mathvariant=¨bold¨»,«/mo»«mn mathvariant=¨bold¨»3«/mn»«/mrow»«/msub»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»(«/mo»«mn mathvariant=¨bold¨ mathcolor=¨#0000FF¨»1«/mn»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»-«/mo»«msqrt mathcolor=¨#0000FF¨»«mn mathvariant=¨bold¨»0«/mn»«mo mathvariant=¨bold¨».«/mo»«mn mathvariant=¨bold¨»4«/mn»«/msqrt»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»)«/mo»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»=«/mo»«mi mathvariant=¨bold¨ mathcolor=¨#0000FF¨»d«/mi»«mspace linebreak=¨newline¨/»«mspace linebreak=¨newline¨/»«msub»«mi mathvariant=¨bold¨ mathcolor=¨#0000FF¨»r«/mi»«mrow mathcolor=¨#0000FF¨»«mn mathvariant=¨bold¨»1«/mn»«mo mathvariant=¨bold¨»,«/mo»«mn mathvariant=¨bold¨»3«/mn»«/mrow»«/msub»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»=«/mo»«mfrac mathcolor=¨#0000FF¨»«mi mathvariant=¨bold¨»d«/mi»«mrow»«mn mathvariant=¨bold¨»1«/mn»«mo mathvariant=¨bold¨»-«/mo»«msqrt»«mn mathvariant=¨bold¨»0«/mn»«mo mathvariant=¨bold¨».«/mo»«mn mathvariant=¨bold¨»4«/mn»«/msqrt»«/mrow»«/mfrac»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»=«/mo»«mfrac mathcolor=¨#0000FF¨»«mn mathvariant=¨bold¨»2«/mn»«mrow»«mn mathvariant=¨bold¨»1«/mn»«mo mathvariant=¨bold¨»-«/mo»«mn mathvariant=¨bold¨»0«/mn»«mo mathvariant=¨bold¨».«/mo»«mn mathvariant=¨bold¨»632«/mn»«/mrow»«/mfrac»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»=«/mo»«mfrac mathcolor=¨#0000FF¨»«mn mathvariant=¨bold¨»2«/mn»«mrow»«mn mathvariant=¨bold¨»0«/mn»«mo mathvariant=¨bold¨».«/mo»«mn mathvariant=¨bold¨»367«/mn»«/mrow»«/mfrac»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»=«/mo»«mn mathvariant=¨bold¨ mathcolor=¨#0000FF¨»5«/mn»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨».«/mo»«mn mathvariant=¨bold¨ mathcolor=¨#0000FF¨»44«/mn»«mi mathvariant=¨bold¨ mathcolor=¨#0000FF¨»m«/mi»«mspace linebreak=¨newline¨/»«/mstyle»«/math»

للتلخيص: عندما تكون الشحنة q₂ تساوي 2nC- والشحنة q₁ تساوي 5nC فإن النقطة التي يجب أن توضع فيها الشحنة q₃ وتكون محصّل القوى عليها صفراً هي 5.44 متر على يسار q₁.

8.3

نرسم مخططًا للقوى المؤثرة على الشحنة q₃، عندما تكون محصّلة القوى المؤثرة عليها يساوي صفرًا.

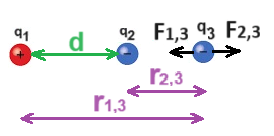
نكتب معادلة الحركة:

نقوم بإجراء عمليات اختزال ونُعبرعن نسبة البعدين:

«math xmlns=¨http://www.w3.org/1998/Math/MathML¨»«mfrac mathcolor=¨#0000FF¨»«mrow»«menclose notation=¨updiagonalstrike¨»«mi mathvariant=¨bold¨ mathsize=¨22px¨»K«/mi»«/menclose»«mo mathvariant=¨bold¨ mathsize=¨22px¨»§#183;«/mo»«msub»«mi mathvariant=¨bold¨ mathsize=¨22px¨»q«/mi»«mn mathvariant=¨bold¨ mathsize=¨22px¨»1«/mn»«/msub»«mo mathvariant=¨bold¨ mathsize=¨22px¨»§#183;«/mo»«menclose notation=¨downdiagonalstrike¨»«msub»«mi mathvariant=¨bold¨ mathsize=¨22px¨»q«/mi»«mn mathvariant=¨bold¨ mathsize=¨22px¨»3«/mn»«/msub»«/menclose»«/mrow»«msup»«msub»«mi mathvariant=¨bold¨ mathsize=¨22px¨»r«/mi»«mrow»«mn mathvariant=¨bold¨ mathsize=¨22px¨»1«/mn»«mo mathvariant=¨bold¨ mathsize=¨22px¨»,«/mo»«mn mathvariant=¨bold¨ mathsize=¨22px¨»3«/mn»«/mrow»«/msub»«mn mathvariant=¨bold¨ mathsize=¨22px¨»2«/mn»«/msup»«/mfrac»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨ mathsize=¨22px¨»=«/mo»«mfrac mathcolor=¨#0000FF¨»«mrow»«menclose notation=¨updiagonalstrike¨»«mi mathvariant=¨bold¨ mathsize=¨22px¨»K«/mi»«/menclose»«mo mathvariant=¨bold¨ mathsize=¨22px¨»§#183;«/mo»«msub»«mi mathvariant=¨bold¨ mathsize=¨22px¨»q«/mi»«mn mathvariant=¨bold¨ mathsize=¨22px¨»2«/mn»«/msub»«mo mathvariant=¨bold¨ mathsize=¨22px¨»§#183;«/mo»«menclose notation=¨downdiagonalstrike¨»«msub»«mi mathvariant=¨bold¨ mathsize=¨22px¨»q«/mi»«mn mathvariant=¨bold¨ mathsize=¨22px¨»3«/mn»«/msub»«/menclose»«/mrow»«msup»«msub»«mi mathvariant=¨bold¨ mathsize=¨22px¨»r«/mi»«mrow»«mn mathvariant=¨bold¨ mathsize=¨22px¨»2«/mn»«mo mathvariant=¨bold¨ mathsize=¨22px¨»,«/mo»«mn mathvariant=¨bold¨ mathsize=¨22px¨»3«/mn»«/mrow»«/msub»«mn mathvariant=¨bold¨ mathsize=¨22px¨»2«/mn»«/msup»«/mfrac»«mspace linebreak=¨newline¨/»«mspace linebreak=¨newline¨/»«mfrac mathcolor=¨#0000FF¨»«msub»«mi mathvariant=¨bold¨ mathsize=¨22px¨»q«/mi»«mn mathvariant=¨bold¨ mathsize=¨22px¨»1«/mn»«/msub»«msup»«msub»«mi mathvariant=¨bold¨ mathsize=¨22px¨»r«/mi»«mrow»«mn mathvariant=¨bold¨ mathsize=¨22px¨»1«/mn»«mo mathvariant=¨bold¨ mathsize=¨22px¨»,«/mo»«mn mathvariant=¨bold¨ mathsize=¨22px¨»3«/mn»«/mrow»«/msub»«mn mathvariant=¨bold¨ mathsize=¨22px¨»2«/mn»«/msup»«/mfrac»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨ mathsize=¨22px¨»=«/mo»«mfrac mathcolor=¨#0000FF¨»«msub»«mi mathvariant=¨bold¨ mathsize=¨22px¨»q«/mi»«mn mathvariant=¨bold¨ mathsize=¨22px¨»2«/mn»«/msub»«msup»«msub»«mi mathvariant=¨bold¨ mathsize=¨22px¨»r«/mi»«mrow»«mn mathvariant=¨bold¨ mathsize=¨22px¨»2«/mn»«mo mathvariant=¨bold¨ mathsize=¨22px¨»,«/mo»«mn mathvariant=¨bold¨ mathsize=¨22px¨»3«/mn»«/mrow»«/msub»«mn mathvariant=¨bold¨ mathsize=¨22px¨»2«/mn»«/msup»«/mfrac»«mspace linebreak=¨newline¨/»«mspace linebreak=¨newline¨/»«mfrac mathcolor=¨#0000FF¨»«mrow»«mn mathvariant=¨bold¨ mathsize=¨22px¨»5«/mn»«mo mathvariant=¨bold¨ mathsize=¨22px¨»§#183;«/mo»«msup»«mn mathvariant=¨bold¨ mathsize=¨22px¨»10«/mn»«mrow»«mo mathvariant=¨bold¨ mathsize=¨22px¨»-«/mo»«mn mathvariant=¨bold¨ mathsize=¨22px¨»9«/mn»«/mrow»«/msup»«/mrow»«msup»«msub»«mi mathvariant=¨bold¨ mathsize=¨22px¨»r«/mi»«mrow»«mn mathvariant=¨bold¨ mathsize=¨22px¨»1«/mn»«mo mathvariant=¨bold¨ mathsize=¨22px¨»,«/mo»«mn mathvariant=¨bold¨ mathsize=¨22px¨»3«/mn»«/mrow»«/msub»«mn mathvariant=¨bold¨ mathsize=¨22px¨»2«/mn»«/msup»«/mfrac»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨ mathsize=¨22px¨»=«/mo»«mfrac mathcolor=¨#0000FF¨»«mrow»«mn mathvariant=¨bold¨ mathsize=¨22px¨»2«/mn»«mo mathvariant=¨bold¨ mathsize=¨22px¨»§#183;«/mo»«msup»«mn mathvariant=¨bold¨ mathsize=¨22px¨»10«/mn»«mrow»«mo mathvariant=¨bold¨ mathsize=¨22px¨»-«/mo»«mn mathvariant=¨bold¨ mathsize=¨22px¨»9«/mn»«/mrow»«/msup»«/mrow»«msup»«msub»«mi mathvariant=¨bold¨ mathsize=¨22px¨»r«/mi»«mrow»«mn mathvariant=¨bold¨ mathsize=¨22px¨»2«/mn»«mo mathvariant=¨bold¨ mathsize=¨22px¨»,«/mo»«mn mathvariant=¨bold¨ mathsize=¨22px¨»3«/mn»«/mrow»«/msub»«mn mathvariant=¨bold¨ mathsize=¨22px¨»2«/mn»«/msup»«/mfrac»«mspace linebreak=¨newline¨/»«mspace linebreak=¨newline¨/»«mfrac mathcolor=¨#0000FF¨»«msup»«msub»«mi mathvariant=¨bold¨ mathsize=¨22px¨»r«/mi»«mrow»«mn mathvariant=¨bold¨ mathsize=¨22px¨»2«/mn»«mo mathvariant=¨bold¨ mathsize=¨22px¨»,«/mo»«mn mathvariant=¨bold¨ mathsize=¨22px¨»3«/mn»«/mrow»«/msub»«mn mathvariant=¨bold¨ mathsize=¨22px¨»2«/mn»«/msup»«msup»«msub»«mi mathvariant=¨bold¨ mathsize=¨22px¨»r«/mi»«mrow»«mn mathvariant=¨bold¨ mathsize=¨22px¨»1«/mn»«mo mathvariant=¨bold¨ mathsize=¨22px¨»,«/mo»«mn mathvariant=¨bold¨ mathsize=¨22px¨»3«/mn»«/mrow»«/msub»«mn mathvariant=¨bold¨ mathsize=¨22px¨»2«/mn»«/msup»«/mfrac»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨ mathsize=¨22px¨»=«/mo»«mfrac mathcolor=¨#0000FF¨»«msub»«mi mathvariant=¨bold¨ mathsize=¨22px¨»q«/mi»«mn mathvariant=¨bold¨ mathsize=¨22px¨»2«/mn»«/msub»«msub»«mi mathvariant=¨bold¨ mathsize=¨22px¨»q«/mi»«mn mathvariant=¨bold¨ mathsize=¨22px¨»1«/mn»«/msub»«/mfrac»«mspace linebreak=¨newline¨/»«mspace linebreak=¨newline¨/»«menclose mathcolor=¨#0000FF¨ notation=¨box¨»«mfrac»«msub»«mi mathvariant=¨bold¨ mathsize=¨22px¨»r«/mi»«mrow»«mn mathvariant=¨bold¨ mathsize=¨22px¨»2«/mn»«mo mathvariant=¨bold¨ mathsize=¨22px¨»,«/mo»«mn mathvariant=¨bold¨ mathsize=¨22px¨»3«/mn»«/mrow»«/msub»«msub»«mi mathvariant=¨bold¨ mathsize=¨22px¨»r«/mi»«mrow»«mn mathvariant=¨bold¨ mathsize=¨22px¨»1«/mn»«mo mathvariant=¨bold¨ mathsize=¨22px¨»,«/mo»«mn mathvariant=¨bold¨ mathsize=¨22px¨»3«/mn»«/mrow»«/msub»«/mfrac»«mo mathvariant=¨bold¨ mathsize=¨22px¨»=«/mo»«msqrt»«mfrac»«msub»«mi mathvariant=¨bold¨ mathsize=¨22px¨»q«/mi»«mn mathvariant=¨bold¨ mathsize=¨22px¨»2«/mn»«/msub»«msub»«mi mathvariant=¨bold¨ mathsize=¨22px¨»q«/mi»«mn mathvariant=¨bold¨ mathsize=¨22px¨»1«/mn»«/msub»«/mfrac»«/msqrt»«/menclose»«/math»

وبناء على ذلك نكتب معادلة أخرى بدلالة المجاهيل : r_2,3 r_1,3 و- d.

«math xmlns=¨http://www.w3.org/1998/Math/MathML¨»«menclose mathcolor=¨#0000FF¨ notation=¨box¨»«msub»«mi mathvariant=¨bold¨ mathsize=¨22px¨»r«/mi»«mrow»«mn mathvariant=¨bold¨ mathsize=¨22px¨»2«/mn»«mo mathvariant=¨bold¨ mathsize=¨22px¨»,«/mo»«mn mathvariant=¨bold¨ mathsize=¨22px¨»3«/mn»«/mrow»«/msub»«mo mathvariant=¨bold¨ mathsize=¨22px¨»+«/mo»«mi mathvariant=¨bold¨ mathsize=¨22px¨»d«/mi»«mo mathvariant=¨bold¨ mathsize=¨22px¨»=«/mo»«msub»«mi mathvariant=¨bold¨ mathsize=¨22px¨»r«/mi»«mrow»«mn mathvariant=¨bold¨ mathsize=¨22px¨»1«/mn»«mo mathvariant=¨bold¨ mathsize=¨22px¨»,«/mo»«mn mathvariant=¨bold¨ mathsize=¨22px¨»3«/mn»«/mrow»«/msub»«/menclose»«mspace linebreak=¨newline¨/»«mspace linebreak=¨newline¨/»«/math»

عبر عن البعد اللازم r_1,3 من المعادلتين :

«math xmlns=¨http://www.w3.org/1998/Math/MathML¨»«mstyle mathsize=¨22px¨»«mspace linebreak=¨newline¨/»«menclose mathcolor=¨#0000FF¨ notation=¨box¨»«mfrac»«msub»«mi mathvariant=¨bold¨ mathcolor=¨#FF0000¨»r«/mi»«mrow mathcolor=¨#FF0000¨»«mn mathvariant=¨bold¨»2«/mn»«mo mathvariant=¨bold¨»,«/mo»«mn mathvariant=¨bold¨»3«/mn»«/mrow»«/msub»«msub»«mi mathvariant=¨bold¨»r«/mi»«mrow»«mn mathvariant=¨bold¨»1«/mn»«mo mathvariant=¨bold¨»,«/mo»«mn mathvariant=¨bold¨»3«/mn»«/mrow»«/msub»«/mfrac»«mo mathvariant=¨bold¨»=«/mo»«msqrt»«mfrac»«msub»«mi mathvariant=¨bold¨»q«/mi»«mn mathvariant=¨bold¨»2«/mn»«/msub»«msub»«mi mathvariant=¨bold¨»q«/mi»«mn mathvariant=¨bold¨»1«/mn»«/msub»«/mfrac»«/msqrt»«/menclose»«mo»§#160;«/mo»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»§#8658;«/mo»«mfrac mathcolor=¨#0000FF¨»«mrow»«msub»«mi mathvariant=¨bold¨ mathcolor=¨#FF0000¨»r«/mi»«mrow mathcolor=¨#FF0000¨»«mn mathvariant=¨bold¨»1«/mn»«mo mathvariant=¨bold¨»,«/mo»«mn mathvariant=¨bold¨»3«/mn»«/mrow»«/msub»«mo mathvariant=¨bold¨ mathcolor=¨#FF0000¨»-«/mo»«mi mathvariant=¨bold¨ mathcolor=¨#FF0000¨»d«/mi»«/mrow»«msub»«mi mathvariant=¨bold¨»r«/mi»«mrow»«mn mathvariant=¨bold¨»1«/mn»«mo mathvariant=¨bold¨»,«/mo»«mn mathvariant=¨bold¨»3«/mn»«/mrow»«/msub»«/mfrac»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»=«/mo»«msqrt mathcolor=¨#0000FF¨»«mfrac»«msub»«mi mathvariant=¨bold¨»q«/mi»«mn mathvariant=¨bold¨»2«/mn»«/msub»«msub»«mi mathvariant=¨bold¨»q«/mi»«mn mathvariant=¨bold¨»1«/mn»«/msub»«/mfrac»«/msqrt»«/mstyle»«/math»

نُعبر عن البعد r_1,3:

«math xmlns=¨http://www.w3.org/1998/Math/MathML¨»«mstyle mathsize=¨22px¨»«mfrac mathcolor=¨#0000FF¨»«mrow»«msub»«mi mathvariant=¨bold¨»r«/mi»«mrow»«mn mathvariant=¨bold¨»1«/mn»«mo mathvariant=¨bold¨»,«/mo»«mn mathvariant=¨bold¨»3«/mn»«/mrow»«/msub»«mo mathvariant=¨bold¨»-«/mo»«mi mathvariant=¨bold¨»d«/mi»«/mrow»«msub»«mi mathvariant=¨bold¨»r«/mi»«mrow»«mn mathvariant=¨bold¨»1«/mn»«mo mathvariant=¨bold¨»,«/mo»«mn mathvariant=¨bold¨»3«/mn»«/mrow»«/msub»«/mfrac»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»=«/mo»«msqrt mathcolor=¨#0000FF¨»«mfrac»«msub»«mi mathvariant=¨bold¨»q«/mi»«mn mathvariant=¨bold¨»2«/mn»«/msub»«msub»«mi mathvariant=¨bold¨»q«/mi»«mn mathvariant=¨bold¨»1«/mn»«/msub»«/mfrac»«/msqrt»«mspace linebreak=¨newline¨/»«mspace linebreak=¨newline¨/»«msub»«mi mathvariant=¨bold¨ mathcolor=¨#0000FF¨»r«/mi»«mrow mathcolor=¨#0000FF¨»«mn mathvariant=¨bold¨»1«/mn»«mo mathvariant=¨bold¨»,«/mo»«mn mathvariant=¨bold¨»3«/mn»«/mrow»«/msub»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»-«/mo»«mi mathvariant=¨bold¨ mathcolor=¨#0000FF¨»d«/mi»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»=«/mo»«msub»«mi mathvariant=¨bold¨ mathcolor=¨#0000FF¨»r«/mi»«mrow mathcolor=¨#0000FF¨»«mn mathvariant=¨bold¨»1«/mn»«mo mathvariant=¨bold¨»,«/mo»«mn mathvariant=¨bold¨»3«/mn»«/mrow»«/msub»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»§#183;«/mo»«msqrt mathcolor=¨#0000FF¨»«mfrac»«msub»«mi mathvariant=¨bold¨»q«/mi»«mn mathvariant=¨bold¨»2«/mn»«/msub»«msub»«mi mathvariant=¨bold¨»q«/mi»«mn mathvariant=¨bold¨»1«/mn»«/msub»«/mfrac»«/msqrt»«mspace linebreak=¨newline¨/»«mspace linebreak=¨newline¨/»«msub»«mi mathvariant=¨bold¨ mathcolor=¨#0000FF¨»r«/mi»«mrow mathcolor=¨#0000FF¨»«mn mathvariant=¨bold¨»1«/mn»«mo mathvariant=¨bold¨»,«/mo»«mn mathvariant=¨bold¨»3«/mn»«/mrow»«/msub»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»-«/mo»«msub»«mi mathvariant=¨bold¨ mathcolor=¨#0000FF¨»r«/mi»«mrow mathcolor=¨#0000FF¨»«mn mathvariant=¨bold¨»1«/mn»«mo mathvariant=¨bold¨»,«/mo»«mn mathvariant=¨bold¨»3«/mn»«/mrow»«/msub»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»§#183;«/mo»«msqrt mathcolor=¨#0000FF¨»«mfrac»«msub»«mi mathvariant=¨bold¨»q«/mi»«mn mathvariant=¨bold¨»2«/mn»«/msub»«msub»«mi mathvariant=¨bold¨»q«/mi»«mn mathvariant=¨bold¨»1«/mn»«/msub»«/mfrac»«/msqrt»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»=«/mo»«mi mathvariant=¨bold¨ mathcolor=¨#0000FF¨»d«/mi»«mspace linebreak=¨newline¨/»«mspace linebreak=¨newline¨/»«msub»«mi mathvariant=¨bold¨ mathcolor=¨#0000FF¨»r«/mi»«mrow mathcolor=¨#0000FF¨»«mn mathvariant=¨bold¨»1«/mn»«mo mathvariant=¨bold¨»,«/mo»«mn mathvariant=¨bold¨»3«/mn»«/mrow»«/msub»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»(«/mo»«mn mathvariant=¨bold¨ mathcolor=¨#0000FF¨»1«/mn»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»-«/mo»«msqrt mathcolor=¨#0000FF¨»«mfrac»«msub»«mi mathvariant=¨bold¨»q«/mi»«mn mathvariant=¨bold¨»2«/mn»«/msub»«msub»«mi mathvariant=¨bold¨»q«/mi»«mn mathvariant=¨bold¨»1«/mn»«/msub»«/mfrac»«/msqrt»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»)«/mo»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»=«/mo»«mi mathvariant=¨bold¨ mathcolor=¨#0000FF¨»d«/mi»«mspace linebreak=¨newline¨/»«mspace linebreak=¨newline¨/»«menclose mathcolor=¨#0000FF¨ notation=¨circle¨»«msub»«mi mathvariant=¨bold¨»r«/mi»«mrow»«mn mathvariant=¨bold¨»1«/mn»«mo mathvariant=¨bold¨»,«/mo»«mn mathvariant=¨bold¨»3«/mn»«/mrow»«/msub»«mo mathvariant=¨bold¨»=«/mo»«mfrac»«mi mathvariant=¨bold¨»d«/mi»«mrow»«mn mathvariant=¨bold¨»1«/mn»«mo mathvariant=¨bold¨»-«/mo»«msqrt»«mfrac»«msub»«mi mathvariant=¨bold¨»q«/mi»«mn mathvariant=¨bold¨»2«/mn»«/msub»«msub»«mi mathvariant=¨bold¨»q«/mi»«mn mathvariant=¨bold¨»1«/mn»«/msub»«/mfrac»«/msqrt»«/mrow»«/mfrac»«/menclose»«mspace linebreak=¨newline¨/»«/mstyle»«/math»

9

تؤثر قوتان جاذبتان على الشحنة q₃، القوة التي تؤثر بها الشحنة q₂ عليها والقوة التي تؤثر بها q₁ عليها.

المثلث متساوي الأضلاع، وبالتالي فإن جميع زوايا المثلث متساوية وتساوي 60 درجة.

نرسم مخطط القوى للقوى المؤثرة على q₃.

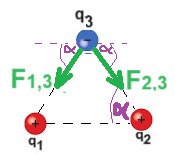
نُحلل القوى الكهربائية المؤثرة على q₃، نستخدم المحور X الأفقي والمحور Y العمودي:

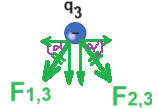
«math xmlns=¨http://www.w3.org/1998/Math/MathML¨»«mstyle mathsize=¨20px¨»«msub»«mi mathvariant=¨bold¨ mathcolor=¨#0000FF¨»F«/mi»«msub mathcolor=¨#0000FF¨»«mrow»«mn mathvariant=¨bold¨»1«/mn»«mo mathvariant=¨bold¨»,«/mo»«mn mathvariant=¨bold¨»3«/mn»«/mrow»«mi mathvariant=¨bold¨»X«/mi»«/msub»«/msub»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»=«/mo»«msub»«mi mathvariant=¨bold¨ mathcolor=¨#0000FF¨»F«/mi»«mrow mathcolor=¨#0000FF¨»«mn mathvariant=¨bold¨»1«/mn»«mo mathvariant=¨bold¨»,«/mo»«mn mathvariant=¨bold¨»3«/mn»«/mrow»«/msub»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»§#183;«/mo»«mi mathvariant=¨bold¨ mathcolor=¨#0000FF¨»cos«/mi»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»(«/mo»«mi mathvariant=¨bold¨ mathcolor=¨#0000FF¨»§#945;«/mi»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»)«/mo»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»=«/mo»«mfrac mathcolor=¨#0000FF¨»«mrow»«mi mathvariant=¨bold¨»K«/mi»«mo mathvariant=¨bold¨»§#183;«/mo»«msub»«mi mathvariant=¨bold¨»q«/mi»«mn mathvariant=¨bold¨»1«/mn»«/msub»«mo mathvariant=¨bold¨»§#183;«/mo»«msub»«mi mathvariant=¨bold¨»q«/mi»«mn mathvariant=¨bold¨»3«/mn»«/msub»«/mrow»«msup»«mi mathvariant=¨bold¨»d«/mi»«mn mathvariant=¨bold¨»2«/mn»«/msup»«/mfrac»«mrow mathcolor=¨#0000FF¨»«mo mathvariant=¨bold¨»§#183;«/mo»«mi mathvariant=¨bold¨»cos«/mi»«mo mathvariant=¨bold¨»(«/mo»«mn mathvariant=¨bold¨»60«/mn»«mo mathvariant=¨bold¨»)«/mo»«/mrow»«mspace linebreak=¨newline¨/»«mrow mathcolor=¨#0000FF¨»«msub»«mi mathvariant=¨bold¨»F«/mi»«msub»«mrow»«mn mathvariant=¨bold¨»1«/mn»«mo mathvariant=¨bold¨»,«/mo»«mn mathvariant=¨bold¨»3«/mn»«/mrow»«mi mathvariant=¨bold¨»Y«/mi»«/msub»«/msub»«mo mathvariant=¨bold¨»=«/mo»«msub»«mi mathvariant=¨bold¨»F«/mi»«mrow»«mn mathvariant=¨bold¨»1«/mn»«mo mathvariant=¨bold¨»,«/mo»«mn mathvariant=¨bold¨»3«/mn»«/mrow»«/msub»«mo mathvariant=¨bold¨»§#183;«/mo»«mi mathvariant=¨bold¨»sin«/mi»«mo mathvariant=¨bold¨»(«/mo»«mi mathvariant=¨bold¨»§#945;«/mi»«mo mathvariant=¨bold¨»)«/mo»«mo mathvariant=¨bold¨»=«/mo»«mfrac»«mrow»«mi mathvariant=¨bold¨»K«/mi»«mo mathvariant=¨bold¨»§#183;«/mo»«msub»«mi mathvariant=¨bold¨»q«/mi»«mn mathvariant=¨bold¨»1«/mn»«/msub»«mo mathvariant=¨bold¨»§#183;«/mo»«msub»«mi mathvariant=¨bold¨»q«/mi»«mn mathvariant=¨bold¨»3«/mn»«/msub»«/mrow»«msup»«mi mathvariant=¨bold¨»d«/mi»«mn mathvariant=¨bold¨»2«/mn»«/msup»«/mfrac»«mrow»«mo mathvariant=¨bold¨»§#183;«/mo»«mi mathvariant=¨bold¨»sin«/mi»«mo mathvariant=¨bold¨»(«/mo»«mn mathvariant=¨bold¨»60«/mn»«mo mathvariant=¨bold¨»)«/mo»«/mrow»«/mrow»«mspace linebreak=¨newline¨/»«mspace linebreak=¨newline¨/»«mrow mathcolor=¨#0000FF¨»«msub»«mi mathvariant=¨bold¨»F«/mi»«msub»«mrow»«mn mathvariant=¨bold¨»2«/mn»«mo mathvariant=¨bold¨»,«/mo»«mn mathvariant=¨bold¨»3«/mn»«/mrow»«mi mathvariant=¨bold¨»X«/mi»«/msub»«/msub»«mo mathvariant=¨bold¨»=«/mo»«msub»«mi mathvariant=¨bold¨»F«/mi»«mrow»«mn mathvariant=¨bold¨»2«/mn»«mo mathvariant=¨bold¨»,«/mo»«mn mathvariant=¨bold¨»3«/mn»«/mrow»«/msub»«mo mathvariant=¨bold¨»§#183;«/mo»«mi mathvariant=¨bold¨»cos«/mi»«mo mathvariant=¨bold¨»(«/mo»«mi mathvariant=¨bold¨»§#945;«/mi»«mo mathvariant=¨bold¨»)«/mo»«mo mathvariant=¨bold¨»=«/mo»«mfrac»«mrow»«mi mathvariant=¨bold¨»K«/mi»«mo mathvariant=¨bold¨»§#183;«/mo»«msub»«mi mathvariant=¨bold¨»q«/mi»«mn mathvariant=¨bold¨»2«/mn»«/msub»«mo mathvariant=¨bold¨»§#183;«/mo»«msub»«mi mathvariant=¨bold¨»q«/mi»«mn mathvariant=¨bold¨»3«/mn»«/msub»«/mrow»«msup»«mi mathvariant=¨bold¨»d«/mi»«mn mathvariant=¨bold¨»2«/mn»«/msup»«/mfrac»«mrow»«mo mathvariant=¨bold¨»§#183;«/mo»«mi mathvariant=¨bold¨»cos«/mi»«mo mathvariant=¨bold¨»(«/mo»«mn mathvariant=¨bold¨»60«/mn»«mo mathvariant=¨bold¨»)«/mo»«/mrow»«mspace linebreak=¨newline¨/»«mrow»«msub»«mi mathvariant=¨bold¨»F«/mi»«msub»«mrow»«mn mathvariant=¨bold¨»2«/mn»«mo mathvariant=¨bold¨»,«/mo»«mn mathvariant=¨bold¨»3«/mn»«/mrow»«mi mathvariant=¨bold¨»Y«/mi»«/msub»«/msub»«mo mathvariant=¨bold¨»=«/mo»«msub»«mi mathvariant=¨bold¨»F«/mi»«mrow»«mn mathvariant=¨bold¨»2«/mn»«mo mathvariant=¨bold¨»,«/mo»«mn mathvariant=¨bold¨»3«/mn»«/mrow»«/msub»«mo mathvariant=¨bold¨»§#183;«/mo»«mi mathvariant=¨bold¨»sin«/mi»«mo mathvariant=¨bold¨»(«/mo»«mi mathvariant=¨bold¨»§#945;«/mi»«mo mathvariant=¨bold¨»)«/mo»«mo mathvariant=¨bold¨»=«/mo»«mfrac»«mrow»«mi mathvariant=¨bold¨»K«/mi»«mo mathvariant=¨bold¨»§#183;«/mo»«msub»«mi mathvariant=¨bold¨»q«/mi»«mn mathvariant=¨bold¨»2«/mn»«/msub»«mo mathvariant=¨bold¨»§#183;«/mo»«msub»«mi mathvariant=¨bold¨»q«/mi»«mn mathvariant=¨bold¨»3«/mn»«/msub»«/mrow»«msup»«mi mathvariant=¨bold¨»d«/mi»«mn mathvariant=¨bold¨»2«/mn»«/msup»«/mfrac»«mrow»«mo mathvariant=¨bold¨»§#183;«/mo»«mi mathvariant=¨bold¨»sin«/mi»«mo mathvariant=¨bold¨»(«/mo»«mn mathvariant=¨bold¨»60«/mn»«mo mathvariant=¨bold¨»)«/mo»«/mrow»«/mrow»«/mrow»«/mstyle»«/math»

تعمل مركبات القوى في اتجاه المحور X في اتجاهين متعاكسين وتكونا متساويتان في المقدار، وبالتالي سوف تُبطل احداهما الأخرى.

تعمل مركبتي القوى في اتجاه المحور Y في نفس الاتجاه، والقوة المحصّلة تساوي مجموعهما. نُعبر عن القوة المحصّلة وفقًا لذلك:

«math xmlns=¨http://www.w3.org/1998/Math/MathML¨»«mstyle mathsize=¨20px¨»«mi mathvariant=¨bold¨ mathcolor=¨#0000FF¨»§#931;F«/mi»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»=«/mo»«msub»«mi mathvariant=¨bold¨ mathcolor=¨#0000FF¨»F«/mi»«msub mathcolor=¨#0000FF¨»«mrow»«mn mathvariant=¨bold¨»1«/mn»«mo mathvariant=¨bold¨»,«/mo»«mn mathvariant=¨bold¨»3«/mn»«/mrow»«mi mathvariant=¨bold¨»Y«/mi»«/msub»«/msub»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»+«/mo»«msub»«mi mathvariant=¨bold¨ mathcolor=¨#0000FF¨»F«/mi»«msub mathcolor=¨#0000FF¨»«mrow»«mn mathvariant=¨bold¨»2«/mn»«mo mathvariant=¨bold¨»,«/mo»«mn mathvariant=¨bold¨»3«/mn»«/mrow»«mi mathvariant=¨bold¨»Y«/mi»«/msub»«/msub»«mspace linebreak=¨newline¨/»«mspace linebreak=¨newline¨/»«mi mathvariant=¨bold¨ mathcolor=¨#0000FF¨»§#931;F«/mi»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»=«/mo»«mfrac mathcolor=¨#0000FF¨»«mrow»«mi mathvariant=¨bold¨»K«/mi»«mo mathvariant=¨bold¨»§#183;«/mo»«msub»«mi mathvariant=¨bold¨»q«/mi»«mn mathvariant=¨bold¨»1«/mn»«/msub»«mo mathvariant=¨bold¨»§#183;«/mo»«msub»«mi mathvariant=¨bold¨»q«/mi»«mn mathvariant=¨bold¨»3«/mn»«/msub»«/mrow»«msup»«mi mathvariant=¨bold¨»d«/mi»«mn mathvariant=¨bold¨»2«/mn»«/msup»«/mfrac»«mrow mathcolor=¨#0000FF¨»«mo mathvariant=¨bold¨»§#183;«/mo»«mi mathvariant=¨bold¨»sin«/mi»«mo mathvariant=¨bold¨»(«/mo»«mn mathvariant=¨bold¨»60«/mn»«mo mathvariant=¨bold¨»)«/mo»«/mrow»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»+«/mo»«mfrac mathcolor=¨#0000FF¨»«mrow»«mi mathvariant=¨bold¨»K«/mi»«mo mathvariant=¨bold¨»§#183;«/mo»«msub»«mi mathvariant=¨bold¨»q«/mi»«mn mathvariant=¨bold¨»2«/mn»«/msub»«mo mathvariant=¨bold¨»§#183;«/mo»«msub»«mi mathvariant=¨bold¨»q«/mi»«mn mathvariant=¨bold¨»3«/mn»«/msub»«/mrow»«msup»«mi mathvariant=¨bold¨»d«/mi»«mn mathvariant=¨bold¨»2«/mn»«/msup»«/mfrac»«mrow mathcolor=¨#0000FF¨»«mo mathvariant=¨bold¨»§#183;«/mo»«mi mathvariant=¨bold¨»sin«/mi»«mo mathvariant=¨bold¨»(«/mo»«mn mathvariant=¨bold¨»60«/mn»«mo mathvariant=¨bold¨»)«/mo»«/mrow»«mspace linebreak=¨newline¨/»«mspace linebreak=¨newline¨/»«mspace linebreak=¨newline¨/»«menclose mathcolor=¨#0000FF¨ notation=¨circle¨»«mi mathvariant=¨bold¨»§#931;F«/mi»«mo mathvariant=¨bold¨»=«/mo»«mfrac»«mrow»«mi mathvariant=¨bold¨»K«/mi»«mo mathvariant=¨bold¨»§#183;«/mo»«msub»«mi mathvariant=¨bold¨»q«/mi»«mn mathvariant=¨bold¨»3«/mn»«/msub»«mo mathvariant=¨bold¨»§#183;«/mo»«mi mathvariant=¨bold¨»sin«/mi»«mo mathvariant=¨bold¨»(«/mo»«mn mathvariant=¨bold¨»60«/mn»«mo mathvariant=¨bold¨»)«/mo»«mo mathvariant=¨bold¨»§#183;«/mo»«mo mathvariant=¨bold¨»(«/mo»«msub»«mi mathvariant=¨bold¨»q«/mi»«mn mathvariant=¨bold¨»1«/mn»«/msub»«mo mathvariant=¨bold¨»+«/mo»«msub»«mi mathvariant=¨bold¨»q«/mi»«mn mathvariant=¨bold¨»2«/mn»«/msub»«mo mathvariant=¨bold¨»)«/mo»«/mrow»«msup»«mi mathvariant=¨bold¨»d«/mi»«mn mathvariant=¨bold¨»2«/mn»«/msup»«/mfrac»«/menclose»«mspace linebreak=¨newline¨/»«/mstyle»«/math»

10.1

تؤثر ثلاث قوى على الشحنة q₁: قوة الشد. القوة الكهربائية وقوة الجاذبية.

نرسم مخطط القوى للقوى المؤثرة على q₁.

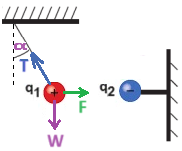
نُحلل قوة الشد لمركبتيها المتعامدتين:

«math xmlns=¨http://www.w3.org/1998/Math/MathML¨»«mstyle mathsize=¨22px¨»«msub»«mi mathvariant=¨bold¨ mathcolor=¨#0000FF¨»T«/mi»«mi mathvariant=¨bold¨ mathcolor=¨#0000FF¨»X«/mi»«/msub»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»=«/mo»«mi mathvariant=¨bold¨ mathcolor=¨#0000FF¨»T«/mi»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»§#183;«/mo»«mi mathvariant=¨bold¨ mathcolor=¨#0000FF¨»sin«/mi»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»(«/mo»«mi mathvariant=¨bold¨ mathcolor=¨#0000FF¨»§#945;«/mi»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»)«/mo»«mspace linebreak=¨newline¨/»«mrow mathcolor=¨#0000FF¨»«msub»«mi mathvariant=¨bold¨»T«/mi»«mi mathvariant=¨bold¨»Y«/mi»«/msub»«mo mathvariant=¨bold¨»=«/mo»«mi mathvariant=¨bold¨»T«/mi»«mo mathvariant=¨bold¨»§#183;«/mo»«mi mathvariant=¨bold¨»cos«/mi»«mo mathvariant=¨bold¨»(«/mo»«mi mathvariant=¨bold¨»§#945;«/mi»«mo mathvariant=¨bold¨»)«/mo»«/mrow»«/mstyle»«/math»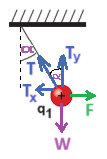

الشحنة q₁ لا تتحرك، نكتب معادلتي الحركة بالنسبة للمحور X الأفقي، والمحور Y الرأسي.

«math xmlns=¨http://www.w3.org/1998/Math/MathML¨»«mstyle mathsize=¨22px¨»«mrow»«msub»«mi mathvariant=¨bold¨ mathcolor=¨#0000FF¨»§#931;F«/mi»«mi mathvariant=¨bold¨ mathcolor=¨#0000FF¨»Y«/mi»«/msub»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»=«/mo»«mn mathvariant=¨bold¨ mathcolor=¨#0000FF¨»0«/mn»«mspace linebreak=¨newline¨/»«msub»«mi mathvariant=¨bold¨ mathcolor=¨#0000FF¨»T«/mi»«mi mathvariant=¨bold¨ mathcolor=¨#0000FF¨»Y«/mi»«/msub»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»=«/mo»«mi mathvariant=¨bold¨ mathcolor=¨#0000FF¨»W«/mi»«mspace linebreak=¨newline¨/»«menclose mathcolor=¨#0000FF¨ notation=¨box¨»«mi mathvariant=¨bold¨»T«/mi»«mo mathvariant=¨bold¨»§#183;«/mo»«mi mathvariant=¨bold¨»cos«/mi»«mo mathvariant=¨bold¨»(«/mo»«mi mathvariant=¨bold¨»§#945;«/mi»«mo mathvariant=¨bold¨»)«/mo»«mo mathvariant=¨bold¨»=«/mo»«mi mathvariant=¨bold¨»m«/mi»«mo mathvariant=¨bold¨»§#183;«/mo»«mi mathvariant=¨bold¨»g«/mi»«/menclose»«/mrow»«mspace linebreak=¨newline¨/»«/mstyle»«/math» «math xmlns=¨http://www.w3.org/1998/Math/MathML¨»«mstyle mathsize=¨22px¨»«msub»«mi mathvariant=¨bold¨ mathcolor=¨#0000FF¨»§#931;F«/mi»«mi mathvariant=¨bold¨ mathcolor=¨#0000FF¨»X«/mi»«/msub»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»=«/mo»«mn mathvariant=¨bold¨ mathcolor=¨#0000FF¨»0«/mn»«mspace linebreak=¨newline¨/»«msub»«mi mathvariant=¨bold¨ mathcolor=¨#0000FF¨»T«/mi»«mi mathvariant=¨bold¨ mathcolor=¨#0000FF¨»X«/mi»«/msub»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»=«/mo»«mi mathvariant=¨bold¨ mathcolor=¨#0000FF¨»F«/mi»«mspace linebreak=¨newline¨/»«menclose mathcolor=¨#0000FF¨ notation=¨box¨»«mi mathvariant=¨bold¨»T«/mi»«mo mathvariant=¨bold¨»§#183;«/mo»«mi mathvariant=¨bold¨»sin«/mi»«mo mathvariant=¨bold¨»(«/mo»«mi mathvariant=¨bold¨»§#945;«/mi»«mo mathvariant=¨bold¨»)«/mo»«mo mathvariant=¨bold¨»=«/mo»«mfrac»«mrow»«mi mathvariant=¨bold¨»K«/mi»«mo mathvariant=¨bold¨»§#183;«/mo»«msub»«mi mathvariant=¨bold¨»q«/mi»«mn mathvariant=¨bold¨»1«/mn»«/msub»«mo mathvariant=¨bold¨»§#183;«/mo»«msub»«mi mathvariant=¨bold¨»q«/mi»«mn mathvariant=¨bold¨»2«/mn»«/msub»«/mrow»«msup»«mi mathvariant=¨bold¨»d«/mi»«mn mathvariant=¨bold¨»2«/mn»«/msup»«/mfrac»«/menclose»«/mstyle»«/math»

نقوم بقسمة المعادلتين:

«math xmlns=¨http://www.w3.org/1998/Math/MathML¨»«mstyle mathsize=¨22px¨»«mfrac mathcolor=¨#0000FF¨»«mrow»«mi mathvariant=¨bold¨»T«/mi»«mo mathvariant=¨bold¨»§#183;«/mo»«mi mathvariant=¨bold¨»sin«/mi»«mo mathvariant=¨bold¨»(«/mo»«mi mathvariant=¨bold¨»§#945;«/mi»«mo mathvariant=¨bold¨»)«/mo»«/mrow»«mrow»«mi mathvariant=¨bold¨»T«/mi»«mo mathvariant=¨bold¨»§#183;«/mo»«mi mathvariant=¨bold¨»cos«/mi»«mo mathvariant=¨bold¨»(«/mo»«mi mathvariant=¨bold¨»§#945;«/mi»«mo mathvariant=¨bold¨»)«/mo»«/mrow»«/mfrac»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»=«/mo»«mfrac mathcolor=¨#0000FF¨»«mfrac»«mrow»«mi mathvariant=¨bold¨»K«/mi»«mo mathvariant=¨bold¨»§#183;«/mo»«msub»«mi mathvariant=¨bold¨»q«/mi»«mn mathvariant=¨bold¨»1«/mn»«/msub»«mo mathvariant=¨bold¨»§#183;«/mo»«msub»«mi mathvariant=¨bold¨»q«/mi»«mn mathvariant=¨bold¨»2«/mn»«/msub»«/mrow»«msup»«mi mathvariant=¨bold¨»d«/mi»«mn mathvariant=¨bold¨»2«/mn»«/msup»«/mfrac»«mrow»«mi mathvariant=¨bold¨»m«/mi»«mo mathvariant=¨bold¨»§#183;«/mo»«mi mathvariant=¨bold¨»g«/mi»«/mrow»«/mfrac»«mspace linebreak=¨newline¨/»«mspace linebreak=¨newline¨/»«mfrac mathcolor=¨#0000FF¨»«mrow»«menclose notation=¨downdiagonalstrike¨»«mi mathvariant=¨bold¨»T«/mi»«/menclose»«mo mathvariant=¨bold¨»§#183;«/mo»«mi mathvariant=¨bold¨»sin«/mi»«mo mathvariant=¨bold¨»(«/mo»«mi mathvariant=¨bold¨»§#945;«/mi»«mo mathvariant=¨bold¨»)«/mo»«/mrow»«mrow»«menclose notation=¨downdiagonalstrike¨»«mi mathvariant=¨bold¨»T«/mi»«/menclose»«mo mathvariant=¨bold¨»§#183;«/mo»«mi mathvariant=¨bold¨»cos«/mi»«mo mathvariant=¨bold¨»(«/mo»«mi mathvariant=¨bold¨»§#945;«/mi»«mo mathvariant=¨bold¨»)«/mo»«/mrow»«/mfrac»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»=«/mo»«mfrac mathcolor=¨#0000FF¨»«mrow»«mi mathvariant=¨bold¨»K«/mi»«mo mathvariant=¨bold¨»§#183;«/mo»«msub»«mi mathvariant=¨bold¨»q«/mi»«mn mathvariant=¨bold¨»1«/mn»«/msub»«mo mathvariant=¨bold¨»§#183;«/mo»«msub»«mi mathvariant=¨bold¨»q«/mi»«mn mathvariant=¨bold¨»2«/mn»«/msub»«/mrow»«mrow»«mi mathvariant=¨bold¨»m«/mi»«mo mathvariant=¨bold¨»§#183;«/mo»«mi mathvariant=¨bold¨»g«/mi»«mo mathvariant=¨bold¨»§#183;«/mo»«msup»«mi mathvariant=¨bold¨»d«/mi»«mn mathvariant=¨bold¨»2«/mn»«/msup»«/mrow»«/mfrac»«mspace linebreak=¨newline¨/»«mspace linebreak=¨newline¨/»«menclose mathcolor=¨#0000FF¨ notation=¨circle¨»«mi mathvariant=¨bold¨»tan«/mi»«mo mathvariant=¨bold¨»(«/mo»«mi mathvariant=¨bold¨»§#945;«/mi»«mo mathvariant=¨bold¨»)«/mo»«mo mathvariant=¨bold¨»=«/mo»«mfrac»«mrow»«mi mathvariant=¨bold¨»K«/mi»«mo mathvariant=¨bold¨»§#183;«/mo»«msub»«mi mathvariant=¨bold¨»q«/mi»«mn mathvariant=¨bold¨»1«/mn»«/msub»«mo mathvariant=¨bold¨»§#183;«/mo»«msub»«mi mathvariant=¨bold¨»q«/mi»«mn mathvariant=¨bold¨»2«/mn»«/msub»«/mrow»«mrow»«mi mathvariant=¨bold¨»m«/mi»«mo mathvariant=¨bold¨»§#183;«/mo»«mi mathvariant=¨bold¨»g«/mi»«mo mathvariant=¨bold¨»§#183;«/mo»«msup»«mi mathvariant=¨bold¨»d«/mi»«mn mathvariant=¨bold¨»2«/mn»«/msup»«/mrow»«/mfrac»«/menclose»«mspace linebreak=¨newline¨/»«mspace linebreak=¨newline¨/»«/mstyle»«/math»

10.2

تؤثر ثلاث قوى على الشحنة q₁: قوة الشد. القوة الكهربائية والجاذبية.

نرسم مخطط القوى للقوى المؤثرة على q₁.

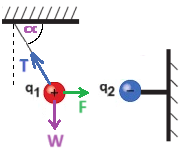
نقوم بتحليل قوة التوتر لمركبتيها المتعامدتين:

«math xmlns=¨http://www.w3.org/1998/Math/MathML¨»«mstyle mathsize=¨22px¨»«msub»«mi mathvariant=¨bold¨ mathcolor=¨#0000FF¨»T«/mi»«mi mathvariant=¨bold¨ mathcolor=¨#0000FF¨»Y«/mi»«/msub»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»=«/mo»«mi mathvariant=¨bold¨ mathcolor=¨#0000FF¨»T«/mi»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»§#183;«/mo»«mi mathvariant=¨bold¨ mathcolor=¨#0000FF¨»sin«/mi»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»(«/mo»«mi mathvariant=¨bold¨ mathcolor=¨#0000FF¨»§#945;«/mi»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»)«/mo»«mspace linebreak=¨newline¨/»«mrow mathcolor=¨#0000FF¨»«msub»«mi mathvariant=¨bold¨»T«/mi»«mi mathvariant=¨bold¨»X«/mi»«/msub»«mo mathvariant=¨bold¨»=«/mo»«mi mathvariant=¨bold¨»T«/mi»«mo mathvariant=¨bold¨»§#183;«/mo»«mi mathvariant=¨bold¨»cos«/mi»«mo mathvariant=¨bold¨»(«/mo»«mi mathvariant=¨bold¨»§#945;«/mi»«mo mathvariant=¨bold¨»)«/mo»«/mrow»«/mstyle»«/math»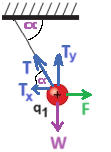

الشحنة q₁ لا تتحرك،نكتب معادلتي الحركة بالنسبة للمحور X الأفقي، والمحور Y الرأسي.

«math xmlns=¨http://www.w3.org/1998/Math/MathML¨»«mstyle mathsize=¨22px¨»«msub»«mi mathvariant=¨bold¨ mathcolor=¨#0000FF¨»§#931;F«/mi»«mi mathvariant=¨bold¨ mathcolor=¨#0000FF¨»Y«/mi»«/msub»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»=«/mo»«mn mathvariant=¨bold¨ mathcolor=¨#0000FF¨»0«/mn»«mspace linebreak=¨newline¨/»«msub»«mi mathvariant=¨bold¨ mathcolor=¨#0000FF¨»T«/mi»«mi mathvariant=¨bold¨ mathcolor=¨#0000FF¨»Y«/mi»«/msub»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»=«/mo»«mi mathvariant=¨bold¨ mathcolor=¨#0000FF¨»W«/mi»«mspace linebreak=¨newline¨/»«menclose mathcolor=¨#0000FF¨ notation=¨box¨»«mi mathvariant=¨bold¨»T«/mi»«mo mathvariant=¨bold¨»§#183;«/mo»«mi mathvariant=¨bold¨»sin«/mi»«mo mathvariant=¨bold¨»(«/mo»«mi mathvariant=¨bold¨»§#945;«/mi»«mo mathvariant=¨bold¨»)«/mo»«mo mathvariant=¨bold¨»=«/mo»«mi mathvariant=¨bold¨»m«/mi»«mo mathvariant=¨bold¨»§#183;«/mo»«mi mathvariant=¨bold¨»g«/mi»«/menclose»«mspace linebreak=¨newline¨/»«/mstyle»«/math» «math xmlns=¨http://www.w3.org/1998/Math/MathML¨»«mstyle mathsize=¨22px¨»«msub»«mi mathvariant=¨bold¨ mathcolor=¨#0000FF¨»§#931;F«/mi»«mi mathvariant=¨bold¨ mathcolor=¨#0000FF¨»X«/mi»«/msub»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»=«/mo»«mn mathvariant=¨bold¨ mathcolor=¨#0000FF¨»0«/mn»«mspace linebreak=¨newline¨/»«msub»«mi mathvariant=¨bold¨ mathcolor=¨#0000FF¨»T«/mi»«mi mathvariant=¨bold¨ mathcolor=¨#0000FF¨»X«/mi»«/msub»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»=«/mo»«mi mathvariant=¨bold¨ mathcolor=¨#0000FF¨»F«/mi»«mspace linebreak=¨newline¨/»«menclose mathcolor=¨#0000FF¨ notation=¨box¨»«mi mathvariant=¨bold¨»T«/mi»«mo mathvariant=¨bold¨»§#183;«/mo»«mi mathvariant=¨bold¨»cos«/mi»«mo mathvariant=¨bold¨»(«/mo»«mi mathvariant=¨bold¨»§#945;«/mi»«mo mathvariant=¨bold¨»)«/mo»«mo mathvariant=¨bold¨»=«/mo»«mfrac»«mrow»«mi mathvariant=¨bold¨»K«/mi»«mo mathvariant=¨bold¨»§#183;«/mo»«msub»«mi mathvariant=¨bold¨»q«/mi»«mn mathvariant=¨bold¨»1«/mn»«/msub»«mo mathvariant=¨bold¨»§#183;«/mo»«msub»«mi mathvariant=¨bold¨»q«/mi»«mn mathvariant=¨bold¨»2«/mn»«/msub»«/mrow»«msup»«mi mathvariant=¨bold¨»d«/mi»«mn mathvariant=¨bold¨»2«/mn»«/msup»«/mfrac»«/menclose»«/mstyle»«/math»

نقسم المعادلتين:

«math xmlns=¨http://www.w3.org/1998/Math/MathML¨»«mstyle mathsize=¨22px¨»«mfrac mathcolor=¨#0000FF¨»«mrow»«mi mathvariant=¨bold¨»T«/mi»«mo mathvariant=¨bold¨»§#183;«/mo»«mi mathvariant=¨bold¨»sin«/mi»«mo mathvariant=¨bold¨»(«/mo»«mi mathvariant=¨bold¨»§#945;«/mi»«mo mathvariant=¨bold¨»)«/mo»«/mrow»«mrow»«mi mathvariant=¨bold¨»T«/mi»«mo mathvariant=¨bold¨»§#183;«/mo»«mi mathvariant=¨bold¨»cos«/mi»«mo mathvariant=¨bold¨»(«/mo»«mi mathvariant=¨bold¨»§#945;«/mi»«mo mathvariant=¨bold¨»)«/mo»«/mrow»«/mfrac»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»=«/mo»«mfrac mathcolor=¨#0000FF¨»«mrow»«mi mathvariant=¨bold¨»m«/mi»«mo mathvariant=¨bold¨»§#183;«/mo»«mi mathvariant=¨bold¨»g«/mi»«/mrow»«mfrac»«mrow»«mi mathvariant=¨bold¨»K«/mi»«mo mathvariant=¨bold¨»§#183;«/mo»«msub»«mi mathvariant=¨bold¨»q«/mi»«mn mathvariant=¨bold¨»1«/mn»«/msub»«mo mathvariant=¨bold¨»§#183;«/mo»«msub»«mi mathvariant=¨bold¨»q«/mi»«mn mathvariant=¨bold¨»2«/mn»«/msub»«/mrow»«msup»«mi mathvariant=¨bold¨»d«/mi»«mn mathvariant=¨bold¨»2«/mn»«/msup»«/mfrac»«/mfrac»«mspace linebreak=¨newline¨/»«mspace linebreak=¨newline¨/»«mfrac mathcolor=¨#0000FF¨»«mrow»«menclose notation=¨downdiagonalstrike¨»«mi mathvariant=¨bold¨»T«/mi»«/menclose»«mo mathvariant=¨bold¨»§#183;«/mo»«mi mathvariant=¨bold¨»sin«/mi»«mo mathvariant=¨bold¨»(«/mo»«mi mathvariant=¨bold¨»§#945;«/mi»«mo mathvariant=¨bold¨»)«/mo»«/mrow»«mrow»«menclose notation=¨downdiagonalstrike¨»«mi mathvariant=¨bold¨»T«/mi»«/menclose»«mo mathvariant=¨bold¨»§#183;«/mo»«mi mathvariant=¨bold¨»cos«/mi»«mo mathvariant=¨bold¨»(«/mo»«mi mathvariant=¨bold¨»§#945;«/mi»«mo mathvariant=¨bold¨»)«/mo»«/mrow»«/mfrac»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»=«/mo»«mfrac mathcolor=¨#0000FF¨»«mrow»«mi mathvariant=¨bold¨»m«/mi»«mo mathvariant=¨bold¨»§#183;«/mo»«mi mathvariant=¨bold¨»g«/mi»«mo mathvariant=¨bold¨»§#183;«/mo»«msup»«mi mathvariant=¨bold¨»d«/mi»«mn mathvariant=¨bold¨»2«/mn»«/msup»«/mrow»«mrow»«mi mathvariant=¨bold¨»K«/mi»«mo mathvariant=¨bold¨»§#183;«/mo»«msub»«mi mathvariant=¨bold¨»q«/mi»«mn mathvariant=¨bold¨»1«/mn»«/msub»«mo mathvariant=¨bold¨»§#183;«/mo»«msub»«mi mathvariant=¨bold¨»q«/mi»«mn mathvariant=¨bold¨»2«/mn»«/msub»«/mrow»«/mfrac»«mspace linebreak=¨newline¨/»«mspace linebreak=¨newline¨/»«menclose mathcolor=¨#0000FF¨ notation=¨circle¨»«mi mathvariant=¨bold¨»tan«/mi»«mo mathvariant=¨bold¨»(«/mo»«mi mathvariant=¨bold¨»§#945;«/mi»«mo mathvariant=¨bold¨»)«/mo»«mo mathvariant=¨bold¨»=«/mo»«mfrac»«mrow»«mi mathvariant=¨bold¨»m«/mi»«mo mathvariant=¨bold¨»§#183;«/mo»«mi mathvariant=¨bold¨»g«/mi»«mo mathvariant=¨bold¨»§#183;«/mo»«msup»«mi mathvariant=¨bold¨»d«/mi»«mn mathvariant=¨bold¨»2«/mn»«/msup»«/mrow»«mrow»«mi mathvariant=¨bold¨»K«/mi»«mo mathvariant=¨bold¨»§#183;«/mo»«msub»«mi mathvariant=¨bold¨»q«/mi»«mn mathvariant=¨bold¨»1«/mn»«/msub»«mo mathvariant=¨bold¨»§#183;«/mo»«msub»«mi mathvariant=¨bold¨»q«/mi»«mn mathvariant=¨bold¨»2«/mn»«/msub»«/mrow»«/mfrac»«/menclose»«mspace linebreak=¨newline¨/»«mspace linebreak=¨newline¨/»«/mstyle»«/math»

11

يتحرك الجسم 2 في حركة دائرية منتظمة، والقوة الجاذبة المركزية المؤثرة عليه هي القوة الكهربائية.

نُشير للقوة الكهربائية في الرسم التخطيطي بـ F .

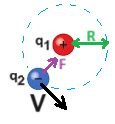
لنكتب معادلة الحركة الدائرية:

«math xmlns=¨http://www.w3.org/1998/Math/MathML¨»«mstyle mathsize=¨22px¨»«msub»«mi mathvariant=¨bold¨ mathcolor=¨#0000FF¨»§#931;F«/mi»«mi mathvariant=¨bold¨ mathcolor=¨#0000FF¨»R«/mi»«/msub»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»=«/mo»«mfrac mathcolor=¨#0000FF¨»«mrow»«msub»«mi mathvariant=¨bold¨»m«/mi»«mn mathvariant=¨bold¨»2«/mn»«/msub»«mo mathvariant=¨bold¨»§#183;«/mo»«msup»«mi mathvariant=¨bold¨»V«/mi»«mn mathvariant=¨bold¨»2«/mn»«/msup»«/mrow»«mi mathvariant=¨bold¨»R«/mi»«/mfrac»«mspace linebreak=¨newline¨/»«mi mathvariant=¨bold¨ mathcolor=¨#0000FF¨»F«/mi»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»=«/mo»«mfrac mathcolor=¨#0000FF¨»«mrow»«msub»«mi mathvariant=¨bold¨»m«/mi»«mn mathvariant=¨bold¨»2«/mn»«/msub»«mo mathvariant=¨bold¨»§#183;«/mo»«msup»«mi mathvariant=¨bold¨»V«/mi»«mn mathvariant=¨bold¨»2«/mn»«/msup»«/mrow»«mi mathvariant=¨bold¨»R«/mi»«/mfrac»«mspace linebreak=¨newline¨/»«mspace linebreak=¨newline¨/»«mfrac mathcolor=¨#0000FF¨»«mrow»«mi mathvariant=¨bold¨»K«/mi»«mo mathvariant=¨bold¨»§#183;«/mo»«msub»«mi mathvariant=¨bold¨»q«/mi»«mn mathvariant=¨bold¨»1«/mn»«/msub»«mo mathvariant=¨bold¨»§#183;«/mo»«msub»«mi mathvariant=¨bold¨»q«/mi»«mn mathvariant=¨bold¨»2«/mn»«/msub»«/mrow»«msup»«mi mathvariant=¨bold¨»R«/mi»«menclose notation=¨downdiagonalstrike¨»«mn mathvariant=¨bold¨»2«/mn»«/menclose»«/msup»«/mfrac»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»=«/mo»«mfrac mathcolor=¨#0000FF¨»«mrow»«msub»«mi mathvariant=¨bold¨»m«/mi»«mn mathvariant=¨bold¨»2«/mn»«/msub»«mo mathvariant=¨bold¨»§#183;«/mo»«msup»«mi mathvariant=¨bold¨»V«/mi»«mn mathvariant=¨bold¨»2«/mn»«/msup»«/mrow»«menclose notation=¨downdiagonalstrike¨»«mi mathvariant=¨bold¨»R«/mi»«/menclose»«/mfrac»«mspace linebreak=¨newline¨/»«mspace linebreak=¨newline¨/»«menclose mathcolor=¨#0000FF¨ notation=¨circle¨»«mi mathvariant=¨bold¨»V«/mi»«mo mathvariant=¨bold¨»=«/mo»«msqrt»«mfrac»«mrow»«mi mathvariant=¨bold¨»K«/mi»«mo mathvariant=¨bold¨»§#183;«/mo»«msub»«mi mathvariant=¨bold¨»q«/mi»«mn mathvariant=¨bold¨»1«/mn»«/msub»«mo mathvariant=¨bold¨»§#183;«/mo»«msub»«mi mathvariant=¨bold¨»q«/mi»«mn mathvariant=¨bold¨»2«/mn»«/msub»«/mrow»«mrow»«msub»«mi mathvariant=¨bold¨»m«/mi»«mn mathvariant=¨bold¨»2«/mn»«/msub»«mo mathvariant=¨bold¨»§#183;«/mo»«mi mathvariant=¨bold¨»R«/mi»«/mrow»«/mfrac»«/msqrt»«/menclose»«/mstyle»«/math»

12

القوة الجاذبة المركزية المؤثرة على الإلكترون هي القوة الكهربائية المؤثرة بين شحنة الإلكترون ونواة الذرة.

نرسم مخطط للقوى:

نكتب معادلة الحركة الدائرية لحركة الإلكترون ونُعبر عن سرعة الإلكترون من معادلة الحركة:

نُشير إلى شحنة الإلكترون بالرمز q ولشحنة النواة بالرمز Q.

«math xmlns=¨http://www.w3.org/1998/Math/MathML¨»«mi mathvariant=¨bold-italic¨ mathcolor=¨#0000FF¨»§#931;«/mi»«msub»«mi mathvariant=¨bold-italic¨ mathcolor=¨#0000FF¨»F«/mi»«mi mathvariant=¨bold¨ mathcolor=¨#0000FF¨»R«/mi»«/msub»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»=«/mo»«mfrac mathcolor=¨#0000FF¨»«mrow»«mi mathvariant=¨bold¨»m«/mi»«mo mathvariant=¨bold¨»§#183;«/mo»«msup»«mi mathvariant=¨bold¨»V«/mi»«mn mathvariant=¨bold¨»2«/mn»«/msup»«/mrow»«mi mathvariant=¨bold¨»R«/mi»«/mfrac»«mspace linebreak=¨newline¨/»«mfrac mathcolor=¨#0000FF¨»«mrow»«mi mathvariant=¨bold¨»K«/mi»«mo mathvariant=¨bold¨»§#183;«/mo»«msub»«mi mathvariant=¨bold¨»q«/mi»«mi mathvariant=¨bold¨»e«/mi»«/msub»«mo mathvariant=¨bold¨»§#183;«/mo»«mi mathvariant=¨bold¨»Q«/mi»«/mrow»«msup»«mi mathvariant=¨bold¨»R«/mi»«menclose notation=¨downdiagonalstrike¨»«mn mathvariant=¨bold¨»2«/mn»«/menclose»«/msup»«/mfrac»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»=«/mo»«mfrac mathcolor=¨#0000FF¨»«mrow»«msub»«mi mathvariant=¨bold¨»m«/mi»«mi mathvariant=¨bold¨»e«/mi»«/msub»«mo mathvariant=¨bold¨»§#183;«/mo»«msup»«mi mathvariant=¨bold¨»V«/mi»«mn mathvariant=¨bold¨»2«/mn»«/msup»«/mrow»«menclose notation=¨downdiagonalstrike¨»«mi mathvariant=¨bold¨»R«/mi»«/menclose»«/mfrac»«mspace linebreak=¨newline¨/»«mspace linebreak=¨newline¨/»«mi mathvariant=¨bold-italic¨ mathcolor=¨#0000FF¨»V«/mi»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»=«/mo»«msqrt mathcolor=¨#0000FF¨»«mfrac»«mrow»«mi mathvariant=¨bold¨»K«/mi»«mo mathvariant=¨bold¨»§#183;«/mo»«msub»«mi mathvariant=¨bold¨»q«/mi»«mi mathvariant=¨bold¨»e«/mi»«/msub»«mo mathvariant=¨bold¨»§#183;«/mo»«mi mathvariant=¨bold¨ mathcolor=¨#FF0000¨»Q«/mi»«/mrow»«mrow»«msub»«mi mathvariant=¨bold¨»m«/mi»«mi mathvariant=¨bold¨»e«/mi»«/msub»«mo mathvariant=¨bold¨»§#183;«/mo»«mi mathvariant=¨bold¨»R«/mi»«/mrow»«/mfrac»«/msqrt»«mspace linebreak=¨newline¨/»«mspace linebreak=¨newline¨/»«menclose mathcolor=¨#0000FF¨ notation=¨circle¨»«mi mathvariant=¨bold¨»V«/mi»«mo mathvariant=¨bold¨»=«/mo»«msqrt»«mfrac»«mrow»«mi mathvariant=¨bold¨»K«/mi»«mo mathvariant=¨bold¨»§#183;«/mo»«msub»«mi mathvariant=¨bold¨»q«/mi»«mi mathvariant=¨bold¨»e«/mi»«/msub»«mo mathvariant=¨bold¨»§#183;«/mo»«mn mathvariant=¨bold¨ mathcolor=¨#FF0000¨»2«/mn»«mo mathvariant=¨bold¨ mathcolor=¨#FF0000¨»§#183;«/mo»«msub»«mi mathvariant=¨bold¨ mathcolor=¨#FF0000¨»q«/mi»«mi mathvariant=¨bold¨ mathcolor=¨#FF0000¨»P«/mi»«/msub»«/mrow»«mrow»«msub»«mi mathvariant=¨bold¨»m«/mi»«mi mathvariant=¨bold¨»e«/mi»«/msub»«mo mathvariant=¨bold¨»§#183;«/mo»«mi mathvariant=¨bold¨»R«/mi»«/mrow»«/mfrac»«/msqrt»«/menclose»«mspace linebreak=¨newline¨/»«mspace linebreak=¨newline¨/»«mspace linebreak=¨newline¨/»«/math»

نعوّض المعطيات ونحسب سرعة الإلكترون:

«math xmlns=¨http://www.w3.org/1998/Math/MathML¨»«mi mathvariant=¨bold-italic¨ mathcolor=¨#0000FF¨»V«/mi»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»=«/mo»«msqrt mathcolor=¨#0000FF¨»«mfrac»«mrow»«mn mathvariant=¨bold¨»9«/mn»«mo mathvariant=¨bold¨»§#183;«/mo»«msup»«mn mathvariant=¨bold¨»10«/mn»«mn mathvariant=¨bold¨»9«/mn»«/msup»«mo mathvariant=¨bold¨»§#183;«/mo»«mrow»«mo mathvariant=¨bold¨ stretchy=¨true¨»|«/mo»«mo mathvariant=¨bold¨»-«/mo»«mn mathvariant=¨bold¨»1«/mn»«mo mathvariant=¨bold¨».«/mo»«mn mathvariant=¨bold¨»6«/mn»«mo mathvariant=¨bold¨»§#183;«/mo»«msup»«mn mathvariant=¨bold¨»10«/mn»«mrow»«mo mathvariant=¨bold¨»-«/mo»«mn mathvariant=¨bold¨»19«/mn»«/mrow»«/msup»«mo mathvariant=¨bold¨ stretchy=¨true¨»|«/mo»«/mrow»«mo mathvariant=¨bold¨»§#183;«/mo»«mn mathvariant=¨bold¨»2«/mn»«mo mathvariant=¨bold¨»§#183;«/mo»«mn mathvariant=¨bold¨»1«/mn»«mo mathvariant=¨bold¨».«/mo»«mn mathvariant=¨bold¨»6«/mn»«mo mathvariant=¨bold¨»§#183;«/mo»«msup»«mn mathvariant=¨bold¨»10«/mn»«mrow»«mo mathvariant=¨bold¨»-«/mo»«mn mathvariant=¨bold¨»19«/mn»«/mrow»«/msup»«/mrow»«mrow»«mn mathvariant=¨bold¨»9«/mn»«mo mathvariant=¨bold¨».«/mo»«mn mathvariant=¨bold¨»11«/mn»«mo mathvariant=¨bold¨»§#183;«/mo»«msup»«mn mathvariant=¨bold¨»10«/mn»«mrow»«mo mathvariant=¨bold¨»-«/mo»«mn mathvariant=¨bold¨»31«/mn»«/mrow»«/msup»«mo mathvariant=¨bold¨»§#183;«/mo»«mn mathvariant=¨bold¨»140«/mn»«mo mathvariant=¨bold¨»§#183;«/mo»«msup»«mn mathvariant=¨bold¨»10«/mn»«mrow»«mo mathvariant=¨bold¨»-«/mo»«mn mathvariant=¨bold¨»12«/mn»«/mrow»«/msup»«/mrow»«/mfrac»«/msqrt»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»=«/mo»«msqrt mathcolor=¨#0000FF¨»«mfrac»«mrow»«mn mathvariant=¨bold¨»4«/mn»«mo mathvariant=¨bold¨».«/mo»«mn mathvariant=¨bold¨»608«/mn»«mo mathvariant=¨bold¨»§#183;«/mo»«msup»«mn mathvariant=¨bold¨»10«/mn»«mrow»«mo mathvariant=¨bold¨»-«/mo»«mn mathvariant=¨bold¨»28«/mn»«/mrow»«/msup»«/mrow»«mrow»«mn mathvariant=¨bold¨»1«/mn»«mo mathvariant=¨bold¨».«/mo»«mn mathvariant=¨bold¨»275«/mn»«mo mathvariant=¨bold¨»§#183;«/mo»«msup»«mn mathvariant=¨bold¨»10«/mn»«mrow»«mo mathvariant=¨bold¨»-«/mo»«mn mathvariant=¨bold¨»40«/mn»«/mrow»«/msup»«/mrow»«/mfrac»«/msqrt»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»=«/mo»«msqrt mathcolor=¨#0000FF¨»«mn mathvariant=¨bold¨»3«/mn»«mo mathvariant=¨bold¨».«/mo»«mn mathvariant=¨bold¨»612«/mn»«mo mathvariant=¨bold¨»§#183;«/mo»«msup»«mn mathvariant=¨bold¨»10«/mn»«mn mathvariant=¨bold¨»12«/mn»«/msup»«/msqrt»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»=«/mo»«mn mathvariant=¨bold¨ mathcolor=¨#0000FF¨»1«/mn»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨».«/mo»«mn mathvariant=¨bold¨ mathcolor=¨#0000FF¨»9«/mn»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»§#183;«/mo»«msup»«mn mathvariant=¨bold¨ mathcolor=¨#0000FF¨»10«/mn»«mn mathvariant=¨bold¨ mathcolor=¨#0000FF¨»6«/mn»«/msup»«mfrac mathcolor=¨#0000FF¨»«mi mathvariant=¨bold¨»m«/mi»«mi mathvariant=¨bold¨»s«/mi»«/mfrac»«mspace linebreak=¨newline¨/»«/math»

13.1

نحسب مقدار القوة الكهربائية المؤثرة على شحنة الفحص في النقطة A.

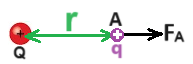
«math xmlns=¨http://www.w3.org/1998/Math/MathML¨»«mi mathvariant=¨bold¨ mathcolor=¨#0000FF¨»F«/mi»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»=«/mo»«mfrac mathcolor=¨#0000FF¨»«mrow»«mi mathvariant=¨bold¨»K«/mi»«mo mathvariant=¨bold¨»§#183;«/mo»«mi mathvariant=¨bold¨»Q«/mi»«mo mathvariant=¨bold¨»§#183;«/mo»«mi mathvariant=¨bold¨»q«/mi»«/mrow»«msup»«mi mathvariant=¨bold¨»r«/mi»«mn mathvariant=¨bold¨»2«/mn»«/msup»«/mfrac»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»=«/mo»«mfrac mathcolor=¨#0000FF¨»«mrow»«mn mathvariant=¨bold¨»9«/mn»«mo mathvariant=¨bold¨»§#183;«/mo»«msup»«mn mathvariant=¨bold¨»10«/mn»«mn mathvariant=¨bold¨»9«/mn»«/msup»«mo mathvariant=¨bold¨»§#183;«/mo»«mn mathvariant=¨bold¨»4«/mn»«mo mathvariant=¨bold¨»§#183;«/mo»«msup»«mn mathvariant=¨bold¨»10«/mn»«mrow»«mo mathvariant=¨bold¨»-«/mo»«mn mathvariant=¨bold¨»6«/mn»«/mrow»«/msup»«mo mathvariant=¨bold¨»§#183;«/mo»«mn mathvariant=¨bold¨»1«/mn»«mo mathvariant=¨bold¨»§#183;«/mo»«msup»«mn mathvariant=¨bold¨»10«/mn»«mrow»«mo mathvariant=¨bold¨»-«/mo»«mn mathvariant=¨bold¨»9«/mn»«/mrow»«/msup»«/mrow»«msup»«mn mathvariant=¨bold¨»2«/mn»«mn mathvariant=¨bold¨»2«/mn»«/msup»«/mfrac»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»=«/mo»«mn mathvariant=¨bold¨ mathcolor=¨#0000FF¨»9«/mn»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»§#183;«/mo»«msup»«mn mathvariant=¨bold¨ mathcolor=¨#0000FF¨»10«/mn»«mrow mathcolor=¨#0000FF¨»«mo mathvariant=¨bold¨»-«/mo»«mn mathvariant=¨bold¨»6«/mn»«/mrow»«/msup»«mi mathvariant=¨bold¨ mathcolor=¨#0000FF¨»N«/mi»«/math»

13.2

معادلة الحقل الكهربائي هي معادلة متجهة.

«math xmlns=¨http://www.w3.org/1998/Math/MathML¨»«mstyle mathsize=¨24px¨»«mover mathcolor=¨#0000FF¨»«mi mathvariant=¨bold¨»E«/mi»«mo mathvariant=¨bold¨»§#8594;«/mo»«/mover»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»=«/mo»«mfrac mathcolor=¨#0000FF¨»«mover»«mi mathvariant=¨bold¨»F«/mi»«mo mathvariant=¨bold¨»§#8594;«/mo»«/mover»«mi mathvariant=¨bold¨»q«/mi»«/mfrac»«/mstyle»«/math»

يتم تعريف الحقل على أنه النسبة بين القوة المؤثرة على شحنة الفحص (مقدار متجه) وقيمة شحنة الفحص (قيمة عددية).

عند قسمة متجهًا بمقدار عددي، تحصل على متجه اتجاهه هو في اتجاه المتجه المقسوم.

وبالتالي فإن اتجاه الحقل الكهربائي هو في اتجاه القوة الكهربائية المؤثرة على شحنة الفحص الموجبة.

في هذه الحالة تؤثر قوة كهربائية على شحنة الفحص إلى اليمين، وبالتالي فإن اتجاه الحقل الكهربائي إلى اليمين كما هو موضح في الشكل التالي:

13.3

نستخدم تعريف الحقل الكهربائي لحساب شدة الحقل الكهربائي الناتج عن الشحنة Q الموجودة في النقطة A:

«math xmlns=¨http://www.w3.org/1998/Math/MathML¨»«mstyle mathsize=¨24px¨»«mi mathvariant=¨bold¨ mathcolor=¨#0000FF¨»E«/mi»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»=«/mo»«mfrac mathcolor=¨#0000FF¨»«mi mathvariant=¨bold¨»F«/mi»«mi mathvariant=¨bold¨»q«/mi»«/mfrac»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»=«/mo»«mfrac mathcolor=¨#0000FF¨»«mrow»«mn mathvariant=¨bold¨»9«/mn»«mo mathvariant=¨bold¨»§#183;«/mo»«msup»«mn mathvariant=¨bold¨»10«/mn»«mrow»«mo mathvariant=¨bold¨»-«/mo»«mn mathvariant=¨bold¨»6«/mn»«/mrow»«/msup»«/mrow»«mrow»«mn mathvariant=¨bold¨»1«/mn»«mo mathvariant=¨bold¨»§#183;«/mo»«msup»«mn mathvariant=¨bold¨»10«/mn»«mrow»«mo mathvariant=¨bold¨»-«/mo»«mn mathvariant=¨bold¨»9«/mn»«/mrow»«/msup»«/mrow»«/mfrac»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»=«/mo»«mn mathvariant=¨bold¨ mathcolor=¨#0000FF¨»9«/mn»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»§#183;«/mo»«msup»«mn mathvariant=¨bold¨ mathcolor=¨#0000FF¨»10«/mn»«mn mathvariant=¨bold¨ mathcolor=¨#0000FF¨»3«/mn»«/msup»«mfrac mathcolor=¨#0000FF¨»«mi mathvariant=¨bold¨»N«/mi»«mi mathvariant=¨bold¨»C«/mi»«/mfrac»«/mstyle»«/math»

13.4

الشحنة التي تُكوّن الحقل الكهربائي هي شحنة نقطية.

نحسب مقدار الحقل الكهربائي باستخدام تعبير الحقل الكهربائي الناتج حول شحنة نقطية.

14.1

نحسب بمساعدة قانون كولون مقدار القوة الكهربائية المؤثرة على شحنة الفحص في النقطة A.

نأخذ في قانون كولون القيمة المطلقة للشحنة Q.

«math xmlns=¨http://www.w3.org/1998/Math/MathML¨»«mstyle mathsize=¨22px¨»«mi mathvariant=¨bold¨ mathcolor=¨#0000FF¨»F«/mi»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»=«/mo»«mfrac mathcolor=¨#0000FF¨»«mrow»«mi mathvariant=¨bold¨»K«/mi»«mo mathvariant=¨bold¨»§#183;«/mo»«mi mathvariant=¨bold¨»Q«/mi»«mo mathvariant=¨bold¨»§#183;«/mo»«mi mathvariant=¨bold¨»q«/mi»«/mrow»«msup»«mi mathvariant=¨bold¨»r«/mi»«mn mathvariant=¨bold¨»2«/mn»«/msup»«/mfrac»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»=«/mo»«mfrac mathcolor=¨#0000FF¨»«mrow»«mn mathvariant=¨bold¨»9«/mn»«mo mathvariant=¨bold¨»§#183;«/mo»«msup»«mn mathvariant=¨bold¨»10«/mn»«mn mathvariant=¨bold¨»9«/mn»«/msup»«mo mathvariant=¨bold¨»§#183;«/mo»«mrow»«mo stretchy=¨true¨ mathvariant=¨bold¨»|«/mo»«mo mathvariant=¨bold¨»-«/mo»«mn mathvariant=¨bold¨»4«/mn»«mo mathvariant=¨bold¨»§#183;«/mo»«msup»«mn mathvariant=¨bold¨»10«/mn»«mrow»«mo mathvariant=¨bold¨»-«/mo»«mn mathvariant=¨bold¨»6«/mn»«/mrow»«/msup»«mo stretchy=¨true¨ mathvariant=¨bold¨»|«/mo»«/mrow»«mo mathvariant=¨bold¨»§#183;«/mo»«mn mathvariant=¨bold¨»1«/mn»«mo mathvariant=¨bold¨»§#183;«/mo»«msup»«mn mathvariant=¨bold¨»10«/mn»«mrow»«mo mathvariant=¨bold¨»-«/mo»«mn mathvariant=¨bold¨»9«/mn»«/mrow»«/msup»«/mrow»«msup»«mn mathvariant=¨bold¨»2«/mn»«mn mathvariant=¨bold¨»2«/mn»«/msup»«/mfrac»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»=«/mo»«mn mathvariant=¨bold¨ mathcolor=¨#0000FF¨»9«/mn»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»§#183;«/mo»«msup»«mn mathvariant=¨bold¨ mathcolor=¨#0000FF¨»10«/mn»«mrow mathcolor=¨#0000FF¨»«mo mathvariant=¨bold¨»-«/mo»«mn mathvariant=¨bold¨»6«/mn»«/mrow»«/msup»«mi mathvariant=¨bold¨ mathcolor=¨#0000FF¨»N«/mi»«/mstyle»«/math»

14.2

ومن تعريف الحقل الكهربائي فإن اتجاه الحقل الكهربائي هو اتجاه القوة الكهربائية التي تعمل على شحنة موجبة.
اتجاه القوة المؤثرة على شحنة الفحص هو إلى اليسار، وبالتالي فإن اتجاه الحقل الكهربائي في النقطة A هو إلى اليسار. كما هو مبين في الشكل التالي:

14.3

نستخدم تعريف الحقل الكهربائي لحساب شدة الحقل الكهربائي الناتج عن الشحنة Q في النقطة A:

14.4

نحسب مقدار الحقل الكهربائي باستخدام تعبيرالحقل الكهربائي حول شحنة نقطية.

نأخذ القيمة المطلقة للشحنة Q.

«math xmlns=¨http://www.w3.org/1998/Math/MathML¨»«mstyle mathsize=¨22px¨»«mi mathvariant=¨bold¨ mathcolor=¨#0000FF¨»E«/mi»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»=«/mo»«mfrac mathcolor=¨#0000FF¨»«mrow»«mi mathvariant=¨bold¨»K«/mi»«mo mathvariant=¨bold¨»§#183;«/mo»«mi mathvariant=¨bold¨»Q«/mi»«/mrow»«msup»«mi mathvariant=¨bold¨»R«/mi»«mn mathvariant=¨bold¨»2«/mn»«/msup»«/mfrac»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»=«/mo»«mfrac mathcolor=¨#0000FF¨»«mrow»«mn mathvariant=¨bold¨»9«/mn»«mo mathvariant=¨bold¨»§#183;«/mo»«msup»«mn mathvariant=¨bold¨»10«/mn»«mn mathvariant=¨bold¨»9«/mn»«/msup»«mo mathvariant=¨bold¨»§#183;«/mo»«mstyle mathvariant=¨bold¨»«mo stretchy=¨true¨»|«/mo»«mrow»«mo»-«/mo»«mn»4«/mn»«mo»§#183;«/mo»«msup»«mn»10«/mn»«mrow»«mo»-«/mo»«mn»6«/mn»«/mrow»«/msup»«/mrow»«mo stretchy=¨true¨»|«/mo»«/mstyle»«/mrow»«msup»«mn mathvariant=¨bold¨»2«/mn»«mn mathvariant=¨bold¨»2«/mn»«/msup»«/mfrac»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»=«/mo»«mn mathvariant=¨bold¨ mathcolor=¨#0000FF¨»9«/mn»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»§#183;«/mo»«msup»«mn mathvariant=¨bold¨ mathcolor=¨#0000FF¨»10«/mn»«mn mathvariant=¨bold¨ mathcolor=¨#0000FF¨»3«/mn»«/msup»«mfrac mathcolor=¨#0000FF¨»«mi mathvariant=¨bold¨»N«/mi»«mi mathvariant=¨bold¨»C«/mi»«/mfrac»«/mstyle»«/math»

15.1

يتم تعريف متجه الحقل الكهربائي في كل نقطة وفقًا للقوة الكهربائية المؤثرة على شحنة الفحص في تلك النقطة:

في أي نقطة حول الشحنة الموجبة حيث نضع شحنة االفحص، ستعمل قوة تنافر كهربائية على شحنة الفحص.

ولذلك فإن اتجاه متّجه الحقل الكهربائي يكون شعاعيًا (راديالي) نحو الخارج.

كلما كانت النقطة أبعد عن الشحنة الكهربائية (شحنة المصدر)، كلما كانت القوة الكهربائية التي تؤثر على شحنة الفحص الموضوعة في النقطة أصغر.

ولذلك، كلما كانت النقطة أبعد عن الشحنة الكهربائية، كلما كان متّجه الحقل الكهربائي أصغر في النقطة.

يصف الشكل التالي متّجه الحقل الكهربائي حول الشحنة الموجبة:

15.2

خطوط الحقل هي خطوط وهمية متواصلة، اتجاه خط الحقل (اتجاه المماس) في نقطة معينة يمثل اتجاه الحقل في تلك النقطة.

وصف خطوط الحقل هو وصف مرئي يصف الحقل بشكل عام بطريقة غير كمية. اتجاه خط الحقل في أي نقطة هو اتجاه القوة الكهربائية المؤثرة على شحنة الفحص في تلك النقطة.

15.3

تمثل كثافة خطوط الحقل شدة الحقل. لذلك، كلما كانت الشحنة أكبر، كلما زاد عدد خطوط الحقل الخارجة من الشحنة.

(عندما يتم وصف الحقل الكهربائي حول الشحنة بمساعدة متّجه الحقل، فإن طول المتجه يمثل شدة الحقل الكهربائي.

عند استخدام خطوط الحقل، لا توجد متجهات تصف شدة الحقل، يتم تمثيل شدة الحقل بواسطة كثافة خطوط الحقل).

16.1

يتم تعريف متجه الحقل الكهربائي في كل نقطة وفقًا لاتجاه القوة الكهربائية المؤثرة على شحنة الفحص في النقطة:

في أي نقطة حول الشحنة السالبة حيث نضع شحنة الفحص، ستؤثر قوة جذب كهربائية على شحنة الفحص.

ولذلك فإن اتجاه متّجه الحقل الكهربائي يكون شعاعياً (راديالي) نحو الداخل.

كلما كانت النقطة أبعد من الشحنة الكهربائية، كلما كانت القوة الكهربائية التي تؤثر على شحنة الفحص الموضوعة في النقطة أصغر.

ولذلك، كلما كانت النقطة أبعد عن الشحنة الكهربائية، كلما كان متّجه الحقل الكهربائي أصغر في النقطة.

يصف الشكل التالي متّجه الحقل حول الشحنة السالبة:

16.2

اتجاه خطوط الحقل بالقرب من شحنة النقطية السالبة يكون شعاعيًا نحو الداخل. كما ترون في الشكل التالي:

17

تترك خطوط الحقل الشحنة الموجبة وتدخل الشحنة السالبة.

وبما أن الشحنات متساوية في المقدار، فإن كمية خطوط الحقل الخارجة من الشحنة الموجبة هو نفس كمية خطوط الحقل الداخلة نحو الشحنة السالبة.

يحتوي الشكل التالي على اقتراح لإجابة محتملة مع ستة عشر خط حقل يخرج من الشحنة الموجبة وستة عشر خط حقل يدخل إلى الشحنة السالبة.

(يمكن وصف الرسم التخطيطي بعدد مماثل من خطوط الحقل التي تدخل/تخرج من الشحنتين).

18

كلتا الشحنتين موجبة ومتطابقتان في المقدار والإشارة.

وفي النقطة الواقعة في منتصف البعد بين الشحنتين، تكون شدة الحقل الكهربائي تساوي صفرًا.

ولذلك فإن كثافة خطوط الحقل في نقطة المنتصف تساوي الصفر، وتكون خطوط الحقل منحنية بحيث لا تمر في منتصف البعد بين الشحنتين.

يظهر الحل الممكن في الشكل التالي:

19.1

تنبعث خطوط الحقل من الشحنة Q1 وبالتالي تكون الشحنة Q1 موجبة.

ومن ناحية أخرى تدخل خطوط الحقل باستثناء Q2 وبالتالي تكون الشحنة Q2 سالبة.

19.2

يتناسب عدد خطوط الحقل التي تدخل أو تخرج من الشحنات تناسبًا طرديًا على مقدار الشحنة.

من التخطيط يمكنك أن ترى أن هناك 23 خط حقل يخرج من الشحنة Q1 و12 خط حقل يدخل الشحنة Q2.

نسبة الشحنة تساوي نسبة عدد خطوط الحقل.

«math xmlns=¨http://www.w3.org/1998/Math/MathML¨»«mstyle mathsize=¨22px¨»«mfenced mathcolor=¨#0000FF¨ open=¨|¨ close=¨|¨»«mfrac»«mstyle mathvariant=¨bold¨»«msub»«mi»Q«/mi»«mn»1«/mn»«/msub»«/mstyle»«mstyle mathvariant=¨bold¨»«msub»«mi»Q«/mi»«mn»2«/mn»«/msub»«/mstyle»«/mfrac»«/mfenced»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»=«/mo»«mfrac mathcolor=¨#0000FF¨»«mn mathvariant=¨bold¨»23«/mn»«mn mathvariant=¨bold¨»12«/mn»«/mfrac»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»=«/mo»«mn mathvariant=¨bold¨ mathcolor=¨#0000FF¨»1«/mn»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨».«/mo»«mn mathvariant=¨bold¨ mathcolor=¨#0000FF¨»91«/mn»«mspace linebreak=¨newline¨/»«mspace linebreak=¨newline¨/»«/mstyle»«/math»

19.3

تمثل كثافة خطوط الحقل شدة الحقل.

من التخطيط يمكن أن ترى أن كثافة خطوط الحقل في النقطة A أكبر.

ولذلك فإن شدة الحقل الكهربائي في النقطة A أكبر من شدة الحقل الكهربائي في النقطة B.

20.1

في الرسم البياني يمكن أن نرى أن خطوط الحقل تخرج من الشحنات الثلاث، لذلك يمكن تحديد أن الشحنات الثلاث مشحونة بشحنة موجبة.

20.2

لترتيب مقدار الشحنات، نحسب عدد خطوط الحقل الخارجة من كل شحنة من الشحنات الثلاث.

12 خط حقل يخرج من الشحنة Q₁.

24 خط حقل يخرج من الشحنة Q₂.

6 خطوط حقل تخرج من الشحنة Q₃.

حسب كمية خطوط الحقل الخارجة من الشحنات، فإن ترتيب الشحنات هو:

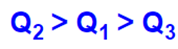
20.3

في مخطط خطوط الحقل، يمكن التمييز بين منطقتين حيث شدة الحقل تساوي الصفر.

تم الإشارة لهذه المناطق في التخطيط التالي باللون الأصفر:

وتساوي شدة الحقل صفرًا فقط في نقطة واحدة في كل منطقة.

20.4

في أي نقطة على خط الحقل، يكون اتجاه القوة الكهربائية المؤثرة على شحنة موجبة هو في اتجاه خط الحقل، حسب تعريف الحقل.

اتجاه القوة المؤثرة على الشحنة السالبة يكون عكس اتجاه الحقل.

في هذه الحالة، يكون اتجاه القوة المؤثرة على q معاكسًا لاتجاه الحقل، وبالتالي فإن شحنة الشحنة q تكون سالبة.

طريقة أخرى: خطوط الحقل تخرج من الشحنة Q₁، وبالتالي تكون الشحنة Q₁ موجبة.

وبما أن الشحنة q تنجذب إلى الشحنة Q₁ فإن شحنة q سالبة.

21.1

اللوح مشحون بشحنة موجبة، لذلك تخرج خطوط الحقل من اللوح (من كلا الجانبين).

تخرج خطوط الحقل من بشكل عمودي من سطح اللوح، وبالتالي تكون خطوط الحقل متوازية، كما هو موضح في الشكل التالي:

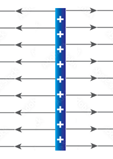
21.2,3

نحسب شدة الحقل المتجانس باستخدام التعبير عن شدة الحقل الكهربائي بالقرب من لوحة مشحونة لا نهائية:

«math xmlns=¨http://www.w3.org/1998/Math/MathML¨»«mi mathvariant=¨bold¨ mathcolor=¨#0000FF¨»E«/mi»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»=«/mo»«mfrac mathcolor=¨#0000FF¨»«mi mathvariant=¨bold¨»§#963;«/mi»«mrow»«mn mathvariant=¨bold¨»2«/mn»«mo mathvariant=¨bold¨»§#183;«/mo»«msub»«mi mathvariant=¨bold¨»§#949;«/mi»«mn mathvariant=¨bold¨»0«/mn»«/msub»«/mrow»«/mfrac»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»=«/mo»«mfrac mathcolor=¨#0000FF¨»«mrow»«mn mathvariant=¨bold¨»5«/mn»«mo mathvariant=¨bold¨»§#183;«/mo»«msup»«mn mathvariant=¨bold¨»10«/mn»«mrow»«mo mathvariant=¨bold¨»-«/mo»«mn mathvariant=¨bold¨»9«/mn»«/mrow»«/msup»«/mrow»«mrow»«mn mathvariant=¨bold¨»2«/mn»«mo mathvariant=¨bold¨»§#183;«/mo»«mn mathvariant=¨bold¨»8«/mn»«mo mathvariant=¨bold¨».«/mo»«mn mathvariant=¨bold¨»85«/mn»«mo mathvariant=¨bold¨»§#183;«/mo»«msup»«mn mathvariant=¨bold¨»10«/mn»«mrow»«mo mathvariant=¨bold¨»-«/mo»«mn mathvariant=¨bold¨»12«/mn»«/mrow»«/msup»«/mrow»«/mfrac»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»=«/mo»«mfrac mathcolor=¨#0000FF¨»«mrow»«mn mathvariant=¨bold¨»5«/mn»«mo mathvariant=¨bold¨»§#183;«/mo»«msup»«mn mathvariant=¨bold¨»10«/mn»«mrow»«mo mathvariant=¨bold¨»-«/mo»«mn mathvariant=¨bold¨»9«/mn»«/mrow»«/msup»«/mrow»«mrow»«mn mathvariant=¨bold¨»1«/mn»«mo mathvariant=¨bold¨».«/mo»«mn mathvariant=¨bold¨»77«/mn»«mo mathvariant=¨bold¨»§#183;«/mo»«msup»«mn mathvariant=¨bold¨»10«/mn»«mrow»«mo mathvariant=¨bold¨»-«/mo»«mn mathvariant=¨bold¨»11«/mn»«/mrow»«/msup»«/mrow»«/mfrac»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»=«/mo»«mn mathvariant=¨bold¨ mathcolor=¨#0000FF¨»282«/mn»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨».«/mo»«mn mathvariant=¨bold¨ mathcolor=¨#0000FF¨»48«/mn»«mfrac mathcolor=¨#0000FF¨»«mi mathvariant=¨bold¨»N«/mi»«mi mathvariant=¨bold¨»C«/mi»«/mfrac»«/math»

لذلك فإن شدة الحقل الكهربائي في أي نقطة حول اللوح هي 282.48 نيوتن لكل كولون، وبما أن الحقل متجانس، فهذه هي شدة الحقل في النقطة A وفي النقطة B.

21.4

نحسب مقدار القوة الكهربائية المؤثرة على البروتون، ونستخدم تعريف الحقل:

«math xmlns=¨http://www.w3.org/1998/Math/MathML¨»«mstyle mathsize=¨22px¨»«mover mathcolor=¨#0000FF¨»«mi mathvariant=¨bold¨»E«/mi»«mo mathvariant=¨bold¨»§#8594;«/mo»«/mover»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»=«/mo»«mfrac mathcolor=¨#0000FF¨»«mover»«mi mathvariant=¨bold¨»F«/mi»«mo mathvariant=¨bold¨»§#8594;«/mo»«/mover»«mi mathvariant=¨bold¨»q«/mi»«/mfrac»«/mstyle»«/math»

أ- نعبر عن القوة الكهربائية بدلالة الحقل، نستخدم تعبير الحقل الموجود بالقرب من لوح مشحون:

«math xmlns=¨http://www.w3.org/1998/Math/MathML¨»«mstyle mathsize=¨22px¨»«mi mathvariant=¨bold¨ mathcolor=¨#0000FF¨ mathsize=¨24px¨»F«/mi»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨ mathsize=¨24px¨»=«/mo»«mi mathvariant=¨bold¨ mathcolor=¨#FF0000¨ mathsize=¨24px¨»E«/mi»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨ mathsize=¨24px¨»§#183;«/mo»«mi mathvariant=¨bold¨ mathcolor=¨#0000FF¨ mathsize=¨24px¨»q«/mi»«mspace linebreak=¨newline¨/»«mi mathvariant=¨bold¨ mathcolor=¨#0000FF¨ mathsize=¨24px¨»F«/mi»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨ mathsize=¨24px¨»=«/mo»«mfrac mathcolor=¨#FF0000¨»«mi mathvariant=¨bold¨ mathsize=¨24px¨»§#963;«/mi»«mrow»«mn mathvariant=¨bold¨ mathsize=¨24px¨»2«/mn»«mo mathvariant=¨bold¨ mathsize=¨24px¨»§#183;«/mo»«msub»«mi mathvariant=¨bold¨ mathsize=¨24px¨»§#949;«/mi»«mn mathvariant=¨bold¨ mathsize=¨24px¨»0«/mn»«/msub»«/mrow»«/mfrac»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»§#183;«/mo»«msub»«mi mathvariant=¨bold¨ mathcolor=¨#0000FF¨»q«/mi»«mi mathvariant=¨bold¨ mathcolor=¨#0000FF¨»P«/mi»«/msub»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»=«/mo»«mfrac mathcolor=¨#0000FF¨»«mrow»«mi mathvariant=¨bold¨»§#963;«/mi»«mo mathvariant=¨bold¨»§#183;«/mo»«msub»«mi mathvariant=¨bold¨»q«/mi»«mi mathvariant=¨bold¨»P«/mi»«/msub»«/mrow»«mrow»«mn mathvariant=¨bold¨»2«/mn»«mo mathvariant=¨bold¨»§#183;«/mo»«msub»«mi mathvariant=¨bold¨»§#949;«/mi»«mn mathvariant=¨bold¨»0«/mn»«/msub»«/mrow»«/mfrac»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»=«/mo»«mfrac mathcolor=¨#0000FF¨»«mrow»«mn mathvariant=¨bold¨»5«/mn»«mo mathvariant=¨bold¨»§#183;«/mo»«msup»«mn mathvariant=¨bold¨»10«/mn»«mrow»«mo mathvariant=¨bold¨»-«/mo»«mn mathvariant=¨bold¨»9«/mn»«/mrow»«/msup»«mo mathvariant=¨bold¨»§#183;«/mo»«mn mathvariant=¨bold¨»1«/mn»«mo mathvariant=¨bold¨».«/mo»«mn mathvariant=¨bold¨»6«/mn»«mo mathvariant=¨bold¨»§#183;«/mo»«msup»«mn mathvariant=¨bold¨»10«/mn»«mrow»«mo mathvariant=¨bold¨»-«/mo»«mn mathvariant=¨bold¨»19«/mn»«/mrow»«/msup»«/mrow»«mrow»«mn mathvariant=¨bold¨»2«/mn»«mo mathvariant=¨bold¨»§#183;«/mo»«mn mathvariant=¨bold¨»8«/mn»«mo mathvariant=¨bold¨».«/mo»«mn mathvariant=¨bold¨»85«/mn»«mo mathvariant=¨bold¨»§#183;«/mo»«msup»«mn mathvariant=¨bold¨»10«/mn»«mrow»«mo mathvariant=¨bold¨»-«/mo»«mn mathvariant=¨bold¨»12«/mn»«/mrow»«/msup»«/mrow»«/mfrac»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»=«/mo»«mfrac mathcolor=¨#0000FF¨»«mrow»«mn mathvariant=¨bold¨»8«/mn»«mo mathvariant=¨bold¨»§#183;«/mo»«msup»«mn mathvariant=¨bold¨»10«/mn»«mrow»«mo mathvariant=¨bold¨»-«/mo»«mn mathvariant=¨bold¨»28«/mn»«/mrow»«/msup»«/mrow»«mrow»«mn mathvariant=¨bold¨»1«/mn»«mo mathvariant=¨bold¨».«/mo»«mn mathvariant=¨bold¨»77«/mn»«mo mathvariant=¨bold¨»§#183;«/mo»«msup»«mn mathvariant=¨bold¨»10«/mn»«mrow»«mo mathvariant=¨bold¨»-«/mo»«mn mathvariant=¨bold¨»11«/mn»«/mrow»«/msup»«/mrow»«/mfrac»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»=«/mo»«mn mathvariant=¨bold¨ mathcolor=¨#0000FF¨»4«/mn»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨».«/mo»«mn mathvariant=¨bold¨ mathcolor=¨#0000FF¨»519«/mn»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»§#183;«/mo»«msup»«mn mathvariant=¨bold¨ mathcolor=¨#0000FF¨»10«/mn»«mrow mathcolor=¨#0000FF¨»«mo mathvariant=¨bold¨»-«/mo»«mn mathvariant=¨bold¨»17«/mn»«/mrow»«/msup»«mi mathvariant=¨bold¨ mathcolor=¨#0000FF¨»N«/mi»«mspace linebreak=¨newline¨/»«/mstyle»«/math»

ب - نحسب مقدار قوة الجاذبية المؤثرة على البروتون:

«math xmlns=¨http://www.w3.org/1998/Math/MathML¨»«mstyle mathsize=¨22px¨»«mi mathvariant=¨bold¨ mathcolor=¨#0000FF¨»W«/mi»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»=«/mo»«msub»«mi mathvariant=¨bold¨ mathcolor=¨#0000FF¨»m«/mi»«mi mathvariant=¨bold¨ mathcolor=¨#0000FF¨»P«/mi»«/msub»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»§#183;«/mo»«mi mathvariant=¨bold¨ mathcolor=¨#0000FF¨»g«/mi»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»=«/mo»«mn mathvariant=¨bold¨ mathcolor=¨#0000FF¨»1«/mn»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨».«/mo»«mn mathvariant=¨bold¨ mathcolor=¨#0000FF¨»67«/mn»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»§#183;«/mo»«msup»«mn mathvariant=¨bold¨ mathcolor=¨#0000FF¨»10«/mn»«mrow mathcolor=¨#0000FF¨»«mo mathvariant=¨bold¨»-«/mo»«mn mathvariant=¨bold¨»27«/mn»«/mrow»«/msup»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»§#183;«/mo»«mn mathvariant=¨bold¨ mathcolor=¨#0000FF¨»10«/mn»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»=«/mo»«mn mathvariant=¨bold¨ mathcolor=¨#0000FF¨»1«/mn»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨».«/mo»«mn mathvariant=¨bold¨ mathcolor=¨#0000FF¨»67«/mn»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»§#183;«/mo»«msup»«mn mathvariant=¨bold¨ mathcolor=¨#0000FF¨»10«/mn»«mrow mathcolor=¨#0000FF¨»«mo mathvariant=¨bold¨»-«/mo»«mn mathvariant=¨bold¨»26«/mn»«/mrow»«/msup»«mi mathvariant=¨bold¨ mathcolor=¨#0000FF¨»N«/mi»«/mstyle»«/math»

ج- نحسب كم مرة تزيد القوة الكهربائية عن قوة الجاذبية:

«math xmlns=¨http://www.w3.org/1998/Math/MathML¨»«mstyle mathsize=¨22px¨»«mfrac mathcolor=¨#0000FF¨»«mi mathvariant=¨bold¨»F«/mi»«mi mathvariant=¨bold¨»W«/mi»«/mfrac»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»=«/mo»«mfrac mathcolor=¨#0000FF¨»«mrow»«mn mathvariant=¨bold¨»4«/mn»«mo mathvariant=¨bold¨».«/mo»«mn mathvariant=¨bold¨»519«/mn»«mo mathvariant=¨bold¨»§#183;«/mo»«msup»«mn mathvariant=¨bold¨»10«/mn»«mrow»«mo mathvariant=¨bold¨»-«/mo»«mn mathvariant=¨bold¨»17«/mn»«/mrow»«/msup»«/mrow»«mrow»«mn mathvariant=¨bold¨»1«/mn»«mo mathvariant=¨bold¨».«/mo»«mn mathvariant=¨bold¨»67«/mn»«mo mathvariant=¨bold¨»§#183;«/mo»«msup»«mn mathvariant=¨bold¨»10«/mn»«mrow»«mo mathvariant=¨bold¨»-«/mo»«mn mathvariant=¨bold¨»26«/mn»«/mrow»«/msup»«/mrow»«/mfrac»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»=«/mo»«mn mathvariant=¨bold¨ mathcolor=¨#0000FF¨»2«/mn»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨».«/mo»«mn mathvariant=¨bold¨ mathcolor=¨#0000FF¨»706«/mn»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»§#183;«/mo»«msup»«mn mathvariant=¨bold¨ mathcolor=¨#0000FF¨»10«/mn»«mn mathvariant=¨bold¨ mathcolor=¨#0000FF¨»9«/mn»«/msup»«mspace linebreak=¨newline¨/»«mspace linebreak=¨newline¨/»«/mstyle»«/math»

لذلك فإن القوة الكهربائية المؤثرة على البروتون أكبر بحوالي 270 مليار مرة من قوة الجاذبية المؤثرة على البروتون. قوة الجاذبية المؤثرة على الشحنات مهملة مقارنة بالقوة الكهربائية.

21.5

قوة الجاذبية المؤثرة على البروتون مهملة مقارنة بالقوة الكهربائية المؤثرة عليه.

نرسم رسمًا تخطيطيًا يصف الحقل الكهربائي حول اللوح والقوة الكهربائية المؤثرة على الإلكترون:

نُشير لشحنة البروتون بـ «math xmlns=¨http://www.w3.org/1998/Math/MathML¨»«msub»«mi mathvariant=¨bold¨»q«/mi»«mi mathvariant=¨bold¨»p«/mi»«/msub»«/math» , يتحرك البروتون بتسارع ثابت، نكتب معادلة الحركة بالنسبة إلى المحور X الذي أشرنا إليه باتجاه الحركة:

«math xmlns=¨http://www.w3.org/1998/Math/MathML¨»«mstyle mathsize=¨24px¨»«mi mathvariant=¨bold¨ mathcolor=¨#0000FF¨»§#931;F«/mi»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»=«/mo»«mi mathvariant=¨bold¨ mathcolor=¨#0000FF¨»m«/mi»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»§#183;«/mo»«mi mathvariant=¨bold¨ mathcolor=¨#0000FF¨»a«/mi»«/mstyle»«/math»

نعبر عن القوة الكهربائية F كدالة لشدة الحقل E باستخدام تعريف الحقل الكهربائي «math xmlns=¨http://www.w3.org/1998/Math/MathML¨»«mstyle mathsize=¨18px¨»«mover mathcolor=¨#0000FF¨»«mi mathvariant=¨bold¨»E«/mi»«mo mathvariant=¨bold¨»§#8594;«/mo»«/mover»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»=«/mo»«mfrac mathcolor=¨#0000FF¨»«mover»«mi mathvariant=¨bold¨»F«/mi»«mo mathvariant=¨bold¨»§#8594;«/mo»«/mover»«mi mathvariant=¨bold¨»q«/mi»«/mfrac»«/mstyle»«/math»:

«math xmlns=¨http://www.w3.org/1998/Math/MathML¨»«mstyle mathsize=¨24px¨»«mi mathvariant=¨bold¨ mathcolor=¨#FF0000¨»F«/mi»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»=«/mo»«msub»«mi mathvariant=¨bold¨ mathcolor=¨#0000FF¨»m«/mi»«mi mathvariant=¨bold¨ mathcolor=¨#0000FF¨»p«/mi»«/msub»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»§#183;«/mo»«mi mathvariant=¨bold¨ mathcolor=¨#0000FF¨»a«/mi»«mspace linebreak=¨newline¨/»«mi mathvariant=¨bold¨ mathcolor=¨#FF0000¨»E«/mi»«mo mathvariant=¨bold¨ mathcolor=¨#FF0000¨»§#183;«/mo»«msub»«mi mathvariant=¨bold¨ mathcolor=¨#FF0000¨»q«/mi»«mi mathvariant=¨bold¨ mathcolor=¨#FF0000¨»p«/mi»«/msub»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»=«/mo»«msub»«mi mathvariant=¨bold¨ mathcolor=¨#0000FF¨»m«/mi»«mi mathvariant=¨bold¨ mathcolor=¨#0000FF¨»p«/mi»«/msub»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»§#183;«/mo»«mi mathvariant=¨bold¨ mathcolor=¨#0000FF¨»a«/mi»«/mstyle»«/math»

نُعبر عن شدة الحقل الكهربائي E، باستخدام التعبير عن الحقل بالقرب من لوح مشحون «math xmlns=¨http://www.w3.org/1998/Math/MathML¨»«mstyle mathsize=¨18px¨»«mi mathvariant=¨bold¨ mathcolor=¨#0000FF¨»E«/mi»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»=«/mo»«mfrac mathcolor=¨#0000FF¨»«mi mathvariant=¨bold¨»§#963;«/mi»«mrow»«mn mathvariant=¨bold¨»2«/mn»«mo mathvariant=¨bold¨»§#183;«/mo»«msub»«mi mathvariant=¨bold¨»§#949;«/mi»«mn mathvariant=¨bold¨»0«/mn»«/msub»«/mrow»«/mfrac»«mspace linebreak=¨newline¨/»«/mstyle»«/math» :

«math xmlns=¨http://www.w3.org/1998/Math/MathML¨»«mstyle mathsize=¨22px¨»«mi mathvariant=¨bold¨ mathcolor=¨#FF0000¨ mathsize=¨24px¨»E«/mi»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨ mathsize=¨24px¨»§#183;«/mo»«msub»«mi mathvariant=¨bold¨ mathcolor=¨#0000FF¨ mathsize=¨24px¨»q«/mi»«mi mathvariant=¨bold¨ mathcolor=¨#0000FF¨ mathsize=¨24px¨»p«/mi»«/msub»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨ mathsize=¨24px¨»=«/mo»«msub»«mi mathvariant=¨bold¨ mathcolor=¨#0000FF¨ mathsize=¨24px¨»m«/mi»«mi mathvariant=¨bold¨ mathsize=¨24px¨ mathcolor=¨#0000FF¨»p«/mi»«/msub»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨ mathsize=¨24px¨»§#183;«/mo»«mi mathvariant=¨bold¨ mathcolor=¨#0000FF¨ mathsize=¨24px¨»a«/mi»«mspace linebreak=¨newline¨/»«mfrac mathcolor=¨#FF0000¨»«mi mathvariant=¨bold¨»§#963;«/mi»«mrow»«mn mathvariant=¨bold¨»2«/mn»«mo mathvariant=¨bold¨»§#183;«/mo»«msub»«mi mathvariant=¨bold¨»§#949;«/mi»«mn mathvariant=¨bold¨»0«/mn»«/msub»«/mrow»«/mfrac»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»§#183;«/mo»«msub»«mi mathvariant=¨bold¨ mathcolor=¨#0000FF¨»q«/mi»«mi mathvariant=¨bold¨ mathcolor=¨#0000FF¨»p«/mi»«/msub»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»=«/mo»«msub»«mi mathvariant=¨bold¨ mathcolor=¨#0000FF¨»m«/mi»«mi mathvariant=¨bold¨ mathcolor=¨#0000FF¨»p«/mi»«/msub»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»§#183;«/mo»«mi mathvariant=¨bold¨ mathcolor=¨#0000FF¨»a«/mi»«/mstyle»«/math»

نُعبر عن تسارع البروتون من معادلة الحركة:

21.6

يتحرك الجسم بتسارع ثابت، ولقد وجدنا تعبيراً للتسارع في البند السابق.

نُشير إلى حركة الجسم من النقطة A إلى النقطة B، ونستخدم تعبير مربع السرعة من قوانين الحركة، ونعبر عن سرعة الجسم في النقطة B.

بدأ الجسم في الحركة من حالة السكون، لذا فإن سرعته الابتدائية تساوي صفرًا.

«math xmlns=¨http://www.w3.org/1998/Math/MathML¨»«mstyle mathsize=¨22px¨»«msup»«mi mathvariant=¨bold¨ mathcolor=¨#0000FF¨»V«/mi»«mn mathvariant=¨bold¨ mathcolor=¨#0000FF¨»2«/mn»«/msup»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»=«/mo»«msup»«msub»«mi mathvariant=¨bold¨ mathcolor=¨#0000FF¨»V«/mi»«mn mathvariant=¨bold¨ mathcolor=¨#0000FF¨»0«/mn»«/msub»«mn mathvariant=¨bold¨ mathcolor=¨#0000FF¨»2«/mn»«/msup»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»+«/mo»«mn mathvariant=¨bold¨ mathcolor=¨#0000FF¨»2«/mn»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»§#183;«/mo»«mi mathvariant=¨bold¨ mathcolor=¨#0000FF¨»a«/mi»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»§#183;«/mo»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»§#8710;«/mo»«mi mathvariant=¨bold¨ mathcolor=¨#0000FF¨»X«/mi»«mspace linebreak=¨newline¨/»«mspace linebreak=¨newline¨/»«msub»«mi mathvariant=¨bold¨ mathcolor=¨#0000FF¨»V«/mi»«mi mathvariant=¨bold¨ mathcolor=¨#0000FF¨»B«/mi»«/msub»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»=«/mo»«msqrt mathcolor=¨#0000FF¨»«msup»«msub»«mi mathvariant=¨bold¨»V«/mi»«mi mathvariant=¨bold¨»A«/mi»«/msub»«mn mathvariant=¨bold¨»2«/mn»«/msup»«mo mathvariant=¨bold¨»+«/mo»«mn mathvariant=¨bold¨»2«/mn»«mo mathvariant=¨bold¨»§#183;«/mo»«mi mathvariant=¨bold¨ mathcolor=¨#FF0000¨»a«/mi»«mo mathvariant=¨bold¨»§#183;«/mo»«mo mathvariant=¨bold¨»§#8710;«/mo»«mi mathvariant=¨bold¨»X«/mi»«/msqrt»«mspace linebreak=¨newline¨/»«mspace linebreak=¨newline¨/»«msub»«mi mathvariant=¨bold¨ mathcolor=¨#0000FF¨»V«/mi»«mi mathvariant=¨bold¨ mathcolor=¨#0000FF¨»B«/mi»«/msub»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»=«/mo»«msqrt mathcolor=¨#0000FF¨»«msup»«msub»«mi mathvariant=¨bold¨»V«/mi»«mi mathvariant=¨bold¨»A«/mi»«/msub»«mn mathvariant=¨bold¨»2«/mn»«/msup»«mo mathvariant=¨bold¨»+«/mo»«menclose notation=¨updiagonalstrike¨»«mn mathvariant=¨bold¨»2«/mn»«/menclose»«mo mathvariant=¨bold¨»§#183;«/mo»«mfrac mathcolor=¨#FF0000¨»«mrow»«mi mathvariant=¨bold¨»§#963;«/mi»«mo mathvariant=¨bold¨»§#183;«/mo»«msub»«mi mathvariant=¨bold¨»q«/mi»«mi mathvariant=¨bold¨»p«/mi»«/msub»«/mrow»«mrow»«menclose notation=¨updiagonalstrike¨»«mn mathvariant=¨bold¨»2«/mn»«/menclose»«mo mathvariant=¨bold¨»§#183;«/mo»«msub»«mi mathvariant=¨bold¨»§#949;«/mi»«mn mathvariant=¨bold¨»0«/mn»«/msub»«mo mathvariant=¨bold¨»§#183;«/mo»«msub»«mi mathvariant=¨bold¨»m«/mi»«mi mathvariant=¨bold¨»p«/mi»«/msub»«/mrow»«/mfrac»«mo mathvariant=¨bold¨»§#183;«/mo»«mo mathvariant=¨bold¨»§#8710;«/mo»«mi mathvariant=¨bold¨»X«/mi»«/msqrt»«mspace linebreak=¨newline¨/»«mspace linebreak=¨newline¨/»«menclose mathcolor=¨#0000FF¨ notation=¨circle¨»«msub»«mi mathvariant=¨bold¨»V«/mi»«mi mathvariant=¨bold¨»B«/mi»«/msub»«mo mathvariant=¨bold¨»=«/mo»«msqrt»«msup»«msub»«mi mathvariant=¨bold¨»V«/mi»«mi mathvariant=¨bold¨»A«/mi»«/msub»«mn mathvariant=¨bold¨»2«/mn»«/msup»«mo mathvariant=¨bold¨»+«/mo»«mfrac»«mrow»«mi mathvariant=¨bold¨»§#963;«/mi»«mo mathvariant=¨bold¨»§#183;«/mo»«msub»«mi mathvariant=¨bold¨»q«/mi»«mi mathvariant=¨bold¨»p«/mi»«/msub»«mo mathvariant=¨bold¨»§#183;«/mo»«mo mathvariant=¨bold¨»§#8710;«/mo»«mi mathvariant=¨bold¨»X«/mi»«/mrow»«mrow»«msub»«mi mathvariant=¨bold¨»§#949;«/mi»«mn mathvariant=¨bold¨»0«/mn»«/msub»«mo mathvariant=¨bold¨»§#183;«/mo»«msub»«mi mathvariant=¨bold¨»m«/mi»«mi mathvariant=¨bold¨»p«/mi»«/msub»«/mrow»«/mfrac»«/msqrt»«/menclose»«/mstyle»«/math»

نُعوّض المعطيات في التعبير، ونحسب سرعة الجسم في النقطة B:

«math xmlns=¨http://www.w3.org/1998/Math/MathML¨»«mstyle mathsize=¨22px¨»«msub»«mi mathvariant=¨bold¨ mathcolor=¨#0000FF¨»V«/mi»«mi mathvariant=¨bold¨ mathcolor=¨#0000FF¨»B«/mi»«/msub»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»=«/mo»«msqrt mathcolor=¨#0000FF¨»«msup»«msub»«mi mathvariant=¨bold¨»V«/mi»«mi mathvariant=¨bold¨»A«/mi»«/msub»«mn mathvariant=¨bold¨»2«/mn»«/msup»«mo mathvariant=¨bold¨»+«/mo»«mfrac»«mrow»«mi mathvariant=¨bold¨»§#963;«/mi»«mo mathvariant=¨bold¨»§#183;«/mo»«msub»«mi mathvariant=¨bold¨»q«/mi»«mi mathvariant=¨bold¨»p«/mi»«/msub»«mo mathvariant=¨bold¨»§#183;«/mo»«mo mathvariant=¨bold¨»§#8710;«/mo»«mi mathvariant=¨bold¨»X«/mi»«/mrow»«mrow»«msub»«mi mathvariant=¨bold¨»§#949;«/mi»«mn mathvariant=¨bold¨»0«/mn»«/msub»«mo mathvariant=¨bold¨»§#183;«/mo»«msub»«mi mathvariant=¨bold¨»m«/mi»«mi mathvariant=¨bold¨»p«/mi»«/msub»«/mrow»«/mfrac»«/msqrt»«mspace linebreak=¨newline¨/»«msub»«mi mathvariant=¨bold¨ mathcolor=¨#0000FF¨»V«/mi»«mi mathvariant=¨bold¨ mathcolor=¨#0000FF¨»B«/mi»«/msub»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»=«/mo»«msqrt mathcolor=¨#0000FF¨»«msup»«mn mathvariant=¨bold¨»0«/mn»«mn mathvariant=¨bold¨»2«/mn»«/msup»«mo mathvariant=¨bold¨»+«/mo»«mfrac»«mrow»«mn mathvariant=¨bold¨»5«/mn»«mo mathvariant=¨bold¨»§#183;«/mo»«msup»«mn mathvariant=¨bold¨»10«/mn»«mrow»«mo mathvariant=¨bold¨»-«/mo»«mn mathvariant=¨bold¨»9«/mn»«/mrow»«/msup»«mo mathvariant=¨bold¨»§#183;«/mo»«mn mathvariant=¨bold¨»1«/mn»«mo mathvariant=¨bold¨».«/mo»«mn mathvariant=¨bold¨»6«/mn»«mo mathvariant=¨bold¨»§#183;«/mo»«msup»«mn mathvariant=¨bold¨»10«/mn»«mrow»«mo mathvariant=¨bold¨»-«/mo»«mn mathvariant=¨bold¨»19«/mn»«/mrow»«/msup»«mo mathvariant=¨bold¨»§#183;«/mo»«mn mathvariant=¨bold¨»3«/mn»«/mrow»«mrow»«mn mathvariant=¨bold¨»8«/mn»«mo mathvariant=¨bold¨».«/mo»«mn mathvariant=¨bold¨»85«/mn»«mo mathvariant=¨bold¨»§#183;«/mo»«msup»«mn mathvariant=¨bold¨»10«/mn»«mrow»«mo mathvariant=¨bold¨»-«/mo»«mn mathvariant=¨bold¨»12«/mn»«/mrow»«/msup»«mo mathvariant=¨bold¨»§#183;«/mo»«mn mathvariant=¨bold¨»1«/mn»«mo mathvariant=¨bold¨».«/mo»«mn mathvariant=¨bold¨»67«/mn»«mo mathvariant=¨bold¨»§#183;«/mo»«msup»«mn mathvariant=¨bold¨»10«/mn»«mrow»«mo mathvariant=¨bold¨»-«/mo»«mn mathvariant=¨bold¨»27«/mn»«/mrow»«/msup»«/mrow»«/mfrac»«/msqrt»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»=«/mo»«msqrt mathcolor=¨#0000FF¨»«mfrac»«mrow»«mn mathvariant=¨bold¨»2«/mn»«mo mathvariant=¨bold¨».«/mo»«mn mathvariant=¨bold¨»4«/mn»«mo mathvariant=¨bold¨»§#183;«/mo»«msup»«mn mathvariant=¨bold¨»10«/mn»«mrow»«mo mathvariant=¨bold¨»-«/mo»«mn mathvariant=¨bold¨»27«/mn»«/mrow»«/msup»«/mrow»«mrow»«mn mathvariant=¨bold¨»1«/mn»«mo mathvariant=¨bold¨».«/mo»«mn mathvariant=¨bold¨»477«/mn»«mo mathvariant=¨bold¨»§#183;«/mo»«msup»«mn mathvariant=¨bold¨»10«/mn»«mrow»«mo mathvariant=¨bold¨»-«/mo»«mn mathvariant=¨bold¨»38«/mn»«/mrow»«/msup»«/mrow»«/mfrac»«/msqrt»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»=«/mo»«msqrt mathcolor=¨#0000FF¨»«mn mathvariant=¨bold¨»1«/mn»«mo mathvariant=¨bold¨».«/mo»«mn mathvariant=¨bold¨»62«/mn»«mo mathvariant=¨bold¨»§#183;«/mo»«msup»«mn mathvariant=¨bold¨»10«/mn»«mn mathvariant=¨bold¨»11«/mn»«/msup»«/msqrt»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»§#160;«/mo»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»=«/mo»«mn mathvariant=¨bold¨ mathcolor=¨#0000FF¨»402«/mn»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨».«/mo»«mn mathvariant=¨bold¨ mathcolor=¨#0000FF¨»49«/mn»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»§#183;«/mo»«msup»«mn mathvariant=¨bold¨ mathcolor=¨#0000FF¨»10«/mn»«mn mathvariant=¨bold¨ mathcolor=¨#0000FF¨»3«/mn»«/msup»«mfrac mathcolor=¨#0000FF¨»«mi mathvariant=¨bold¨»m«/mi»«mi mathvariant=¨bold¨»s«/mi»«/mfrac»«/mstyle»«/math»

ومقدار سرعة البروتون في النقطة B حوالي 400 ألف متر في الثانية.

22.1

اللوح مشحون بشحنة سالبة، وبالتالي تخرج خطوط الحقل من اللوح (في كلا الجانبين).

تخرج خطوط الحقل من اللوح بشكل عمودي من سطح اللوح، وبالتالي فإن خطوط الحقل تكون متوازية، والحقل الناتج من اللوح هو حقل متجانس. كما مبين في الشكل التالي:

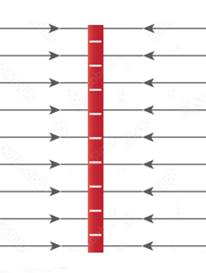
22.2

نحسب شدة الحقل المتجانس باستخدام التعبير لشدة الحقل الكهربائي بالقرب من لوح مشحون لا نهائي.

نأخذ القيمة المطلقة لكثافة الشحنة:

«math xmlns=¨http://www.w3.org/1998/Math/MathML¨»«mstyle mathsize=¨22px¨»«mi mathvariant=¨bold¨ mathcolor=¨#0000FF¨»E«/mi»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»=«/mo»«mfrac mathcolor=¨#0000FF¨»«mi mathvariant=¨bold¨»§#963;«/mi»«mrow»«mn mathvariant=¨bold¨»2«/mn»«mo mathvariant=¨bold¨»§#183;«/mo»«msub»«mi mathvariant=¨bold¨»§#949;«/mi»«mn mathvariant=¨bold¨»0«/mn»«/msub»«/mrow»«/mfrac»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»=«/mo»«mfrac mathcolor=¨#0000FF¨»«mstyle mathvariant=¨bold¨»«mo stretchy=¨true¨»|«/mo»«mo»-«/mo»«mn»5«/mn»«mo»§#183;«/mo»«msup»«mn»10«/mn»«mrow»«mo»-«/mo»«mn»9«/mn»«/mrow»«/msup»«mo stretchy=¨true¨»|«/mo»«/mstyle»«mrow»«mn mathvariant=¨bold¨»2«/mn»«mo mathvariant=¨bold¨»§#183;«/mo»«mn mathvariant=¨bold¨»8«/mn»«mo mathvariant=¨bold¨».«/mo»«mn mathvariant=¨bold¨»85«/mn»«mo mathvariant=¨bold¨»§#183;«/mo»«msup»«mn mathvariant=¨bold¨»10«/mn»«mrow»«mo mathvariant=¨bold¨»-«/mo»«mn mathvariant=¨bold¨»12«/mn»«/mrow»«/msup»«/mrow»«/mfrac»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»=«/mo»«mfrac mathcolor=¨#0000FF¨»«mrow»«mn mathvariant=¨bold¨»5«/mn»«mo mathvariant=¨bold¨»§#183;«/mo»«msup»«mn mathvariant=¨bold¨»10«/mn»«mrow»«mo mathvariant=¨bold¨»-«/mo»«mn mathvariant=¨bold¨»9«/mn»«/mrow»«/msup»«/mrow»«mrow»«mn mathvariant=¨bold¨»1«/mn»«mo mathvariant=¨bold¨».«/mo»«mn mathvariant=¨bold¨»77«/mn»«mo mathvariant=¨bold¨»§#183;«/mo»«msup»«mn mathvariant=¨bold¨»10«/mn»«mrow»«mo mathvariant=¨bold¨»-«/mo»«mn mathvariant=¨bold¨»11«/mn»«/mrow»«/msup»«/mrow»«/mfrac»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»=«/mo»«mn mathvariant=¨bold¨ mathcolor=¨#0000FF¨»282«/mn»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨».«/mo»«mn mathvariant=¨bold¨ mathcolor=¨#0000FF¨»48«/mn»«mfrac mathcolor=¨#0000FF¨»«mi mathvariant=¨bold¨»N«/mi»«mi mathvariant=¨bold¨»C«/mi»«/mfrac»«/mstyle»«/math»

وبما أن الحقل متجانس، فهذه هي شدة الحقل في النقطة A وفي أي نقطة أخرى داخل الحقل.

22.3

يتحرك الجسم المشحون تحت تأثير القوة الكهربائية فقط.

نرسم مخططًا يصف القوة الكهربائية المؤثرة على الجسم المشحون:

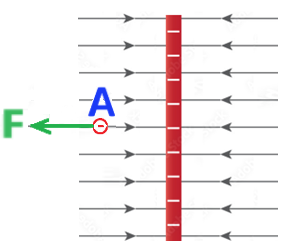
نكتب معادلة الحركة بالنسبة للمحور X الذي تم اختياره في اتجاه الحركة:

نُشير إلى شحنة الجسم المشحون بـ «math xmlns=¨http://www.w3.org/1998/Math/MathML¨»«mi mathvariant=¨bold¨»q«/mi»«/math» .

نُعبر عن القوة الكهربائية F كدالة لشدة الحقل E باستخدام تعريف الحقل الكهربائي «math xmlns=¨http://www.w3.org/1998/Math/MathML¨»«mstyle mathsize=¨20px¨»«mover mathcolor=¨#0000FF¨»«mi mathvariant=¨bold¨»E«/mi»«mo mathvariant=¨bold¨»§#8594;«/mo»«/mover»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»=«/mo»«mfrac mathcolor=¨#0000FF¨»«mover»«mi mathvariant=¨bold¨»F«/mi»«mo mathvariant=¨bold¨»§#8594;«/mo»«/mover»«mi mathvariant=¨bold¨»q«/mi»«/mfrac»«/mstyle»«/math»:

«math xmlns=¨http://www.w3.org/1998/Math/MathML¨»«mstyle mathsize=¨24px¨»«mi mathvariant=¨bold¨ mathcolor=¨#FF0000¨»F«/mi»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»=«/mo»«mi mathvariant=¨bold¨ mathcolor=¨#0000FF¨»m«/mi»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»§#183;«/mo»«mi mathvariant=¨bold¨ mathcolor=¨#0000FF¨»a«/mi»«mspace linebreak=¨newline¨/»«mi mathvariant=¨bold¨ mathcolor=¨#FF0000¨»E«/mi»«mo mathvariant=¨bold¨ mathcolor=¨#FF0000¨»§#183;«/mo»«mi mathvariant=¨bold¨ mathcolor=¨#FF0000¨»q«/mi»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»=«/mo»«mi mathvariant=¨bold¨ mathcolor=¨#0000FF¨»m«/mi»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»§#183;«/mo»«mi mathvariant=¨bold¨ mathcolor=¨#0000FF¨»a«/mi»«/mstyle»«/math»

نُعبر عن شدة الحقل الكهربائي E، باستخدام التعبير عن الحقل بالقرب من لوح مشحون: «math xmlns=¨http://www.w3.org/1998/Math/MathML¨»«mstyle mathsize=¨20px¨»«mi mathvariant=¨bold¨ mathcolor=¨#0000FF¨»E«/mi»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»=«/mo»«mfrac mathcolor=¨#0000FF¨»«mi mathvariant=¨bold¨»§#963;«/mi»«mrow»«mn mathvariant=¨bold¨»2«/mn»«mo mathvariant=¨bold¨»§#183;«/mo»«msub»«mi mathvariant=¨bold¨»§#949;«/mi»«mn mathvariant=¨bold¨»0«/mn»«/msub»«/mrow»«/mfrac»«mspace linebreak=¨newline¨/»«/mstyle»«/math» .

«math xmlns=¨http://www.w3.org/1998/Math/MathML¨»«mstyle mathsize=¨22px¨»«mi mathvariant=¨bold¨ mathcolor=¨#0000FF¨ mathsize=¨24px¨»E«/mi»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨ mathsize=¨24px¨»§#183;«/mo»«mi mathvariant=¨bold¨ mathcolor=¨#0000FF¨ mathsize=¨24px¨»q«/mi»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨ mathsize=¨24px¨»=«/mo»«mi mathvariant=¨bold¨ mathcolor=¨#0000FF¨ mathsize=¨24px¨»m«/mi»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨ mathsize=¨24px¨»§#183;«/mo»«mi mathvariant=¨bold¨ mathcolor=¨#0000FF¨ mathsize=¨24px¨»a«/mi»«mspace linebreak=¨newline¨/»«menclose mathcolor=¨#0000FF¨ notation=¨box¨»«mfrac»«mi mathvariant=¨bold¨»§#963;«/mi»«mrow»«mn mathvariant=¨bold¨»2«/mn»«mo mathvariant=¨bold¨»§#183;«/mo»«msub»«mi mathvariant=¨bold¨»§#949;«/mi»«mn mathvariant=¨bold¨»0«/mn»«/msub»«/mrow»«/mfrac»«mo mathvariant=¨bold¨»§#183;«/mo»«mi mathvariant=¨bold¨»q«/mi»«mo mathvariant=¨bold¨»=«/mo»«mi mathvariant=¨bold¨»m«/mi»«mo mathvariant=¨bold¨»§#183;«/mo»«mi mathvariant=¨bold¨»a«/mi»«/menclose»«/mstyle»«/math»

نُعبر عن تسارع الإلكترون من معادلة الحركة:

«math xmlns=¨http://www.w3.org/1998/Math/MathML¨»«mstyle mathsize=¨22px¨»«mfrac mathcolor=¨#0000FF¨»«mi mathvariant=¨bold¨»§#963;«/mi»«mrow»«mn mathvariant=¨bold¨»2«/mn»«mo mathvariant=¨bold¨»§#183;«/mo»«msub»«mi mathvariant=¨bold¨»§#949;«/mi»«mn mathvariant=¨bold¨»0«/mn»«/msub»«/mrow»«/mfrac»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»§#183;«/mo»«mi mathvariant=¨bold¨ mathcolor=¨#0000FF¨»q«/mi»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»=«/mo»«mi mathvariant=¨bold¨ mathcolor=¨#0000FF¨»m«/mi»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»§#183;«/mo»«mi mathvariant=¨bold¨ mathcolor=¨#0000FF¨»a«/mi»«mspace linebreak=¨newline¨/»«mspace linebreak=¨newline¨/»«mi mathvariant=¨bold¨ mathcolor=¨#0000FF¨»a«/mi»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»=«/mo»«mfrac mathcolor=¨#0000FF¨»«mrow»«mi mathvariant=¨bold¨»§#963;«/mi»«mo mathvariant=¨bold¨»§#183;«/mo»«mi mathvariant=¨bold¨»q«/mi»«/mrow»«mrow»«mn mathvariant=¨bold¨»2«/mn»«mo mathvariant=¨bold¨»§#183;«/mo»«msub»«mi mathvariant=¨bold¨»§#949;«/mi»«mn mathvariant=¨bold¨»0«/mn»«/msub»«mo mathvariant=¨bold¨»§#183;«/mo»«mi mathvariant=¨bold¨»m«/mi»«/mrow»«/mfrac»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»=«/mo»«mfrac mathcolor=¨#0000FF¨»«mrow»«mrow»«mo stretchy=¨true¨ mathvariant=¨bold¨»|«/mo»«mo mathvariant=¨bold¨»-«/mo»«mn mathvariant=¨bold¨»5«/mn»«mo mathvariant=¨bold¨»§#183;«/mo»«msup»«mn mathvariant=¨bold¨»10«/mn»«mrow»«mo mathvariant=¨bold¨»-«/mo»«mn mathvariant=¨bold¨»9«/mn»«/mrow»«/msup»«mo stretchy=¨true¨ mathvariant=¨bold¨»|«/mo»«/mrow»«mo mathvariant=¨bold¨»§#183;«/mo»«mrow»«mo stretchy=¨true¨ mathvariant=¨bold¨»|«/mo»«mo mathvariant=¨bold¨»-«/mo»«mn mathvariant=¨bold¨»1«/mn»«mo mathvariant=¨bold¨»§#183;«/mo»«msup»«mn mathvariant=¨bold¨»10«/mn»«mrow»«mo mathvariant=¨bold¨»-«/mo»«mn mathvariant=¨bold¨»9«/mn»«/mrow»«/msup»«mo stretchy=¨true¨ mathvariant=¨bold¨»|«/mo»«/mrow»«/mrow»«mrow»«mn mathvariant=¨bold¨»2«/mn»«mo mathvariant=¨bold¨»§#183;«/mo»«mn mathvariant=¨bold¨»8«/mn»«mo mathvariant=¨bold¨».«/mo»«mn mathvariant=¨bold¨»85«/mn»«mo mathvariant=¨bold¨»§#183;«/mo»«msup»«mn mathvariant=¨bold¨»10«/mn»«mrow»«mo mathvariant=¨bold¨»-«/mo»«mn mathvariant=¨bold¨»12«/mn»«/mrow»«/msup»«mo mathvariant=¨bold¨»§#183;«/mo»«mn mathvariant=¨bold¨»5«/mn»«mo mathvariant=¨bold¨»§#183;«/mo»«msup»«mn mathvariant=¨bold¨»10«/mn»«mrow»«mo mathvariant=¨bold¨»-«/mo»«mn mathvariant=¨bold¨»6«/mn»«/mrow»«/msup»«/mrow»«/mfrac»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»=«/mo»«mfrac mathcolor=¨#0000FF¨»«mrow»«mn mathvariant=¨bold¨»5«/mn»«mo mathvariant=¨bold¨»§#183;«/mo»«msup»«mn mathvariant=¨bold¨»10«/mn»«mrow»«mo mathvariant=¨bold¨»-«/mo»«mn mathvariant=¨bold¨»18«/mn»«/mrow»«/msup»«/mrow»«mrow»«mn mathvariant=¨bold¨»8«/mn»«mo mathvariant=¨bold¨».«/mo»«mn mathvariant=¨bold¨»85«/mn»«mo mathvariant=¨bold¨»§#183;«/mo»«msup»«mn mathvariant=¨bold¨»10«/mn»«mrow»«mo mathvariant=¨bold¨»-«/mo»«mn mathvariant=¨bold¨»17«/mn»«/mrow»«/msup»«/mrow»«/mfrac»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»=«/mo»«mn mathvariant=¨bold¨ mathcolor=¨#0000FF¨»0«/mn»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨».«/mo»«mn mathvariant=¨bold¨ mathcolor=¨#0000FF¨»056«/mn»«mfrac mathcolor=¨#0000FF¨»«mi mathvariant=¨bold¨»m«/mi»«msup»«mi mathvariant=¨bold¨»s«/mi»«mn mathvariant=¨bold¨»2«/mn»«/msup»«/mfrac»«/mstyle»«/math»

23.1

يتم رمي الجسم المشحون في اتجاه موازٍ للوح، وتؤثر عليه قوة كهربائية ثابتة F، في اتجاه عمودي على الاتجاه الابتدائي للحركة. كما هو مُبيّنن في الشكل التالي:

في اتجاه رمي الجسم، لا تؤثر أي قوة على الجسم - في هذا الاتجاه يستمر الجسم في حركته.

في الاتجاه العمودي على اللوح، تؤثر القوة الكهربائية F فقط على الجسم - وفي هذا الاتجاه يتحرك الجسم بتسارع ثابت.

حركة الجسم تشبه حركة جسم يتحرك في حركة باليستية في رمي أفقي، وسوف نصف حسب القوة الكهربائية وسرعة الرمي مسار حركة الجسم:

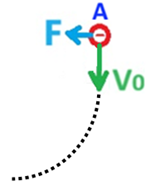
23.2

القوة الوحيدة المؤثرة على الإلكترون هي القوة الكهربائية، وهذه القوة تجعل الإلكترون يتحرك بتسارع في اتجاه عمودي نسبة للوح المشحون.

نختار محور الحركة Y في الاتجاه العمودي على اللوح ، ونحسب تسارع الإلكترون في هذا الاتجاه:

لإيجاد التسارع نكتب معادلة الحركة في اتجاه المحور Y:

«math xmlns=¨http://www.w3.org/1998/Math/MathML¨»«mstyle mathsize=¨24px¨»«msub»«mi mathvariant=¨bold¨ mathcolor=¨#0000FF¨»§#931;F«/mi»«mi mathvariant=¨bold¨ mathcolor=¨#0000FF¨»Y«/mi»«/msub»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»=«/mo»«mi mathvariant=¨bold¨ mathcolor=¨#0000FF¨»m«/mi»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»§#183;«/mo»«mi mathvariant=¨bold¨ mathcolor=¨#0000FF¨»a«/mi»«/mstyle»«/math»

في اتجاه المحور Y تعمل فقط القوة F. وسوف نعبر عن القوة الكهربائية F اعتماداً على شدة الحقل E باستخدام تعريف الحقل الكهربائي «math xmlns=¨http://www.w3.org/1998/Math/MathML¨»«mstyle mathsize=¨18px¨»«mover mathcolor=¨#0000FF¨»«mi mathvariant=¨bold¨»E«/mi»«mo mathvariant=¨bold¨»§#8594;«/mo»«/mover»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»=«/mo»«mfrac mathcolor=¨#0000FF¨»«mover»«mi mathvariant=¨bold¨»F«/mi»«mo mathvariant=¨bold¨»§#8594;«/mo»«/mover»«mi mathvariant=¨bold¨»q«/mi»«/mfrac»«/mstyle»«/math»:

«math xmlns=¨http://www.w3.org/1998/Math/MathML¨»«mstyle mathsize=¨24px¨»«mi mathvariant=¨bold¨ mathcolor=¨#FF0000¨»F«/mi»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»=«/mo»«msub»«mi mathvariant=¨bold¨ mathcolor=¨#0000FF¨»m«/mi»«mi mathvariant=¨bold¨ mathcolor=¨#0000FF¨»e«/mi»«/msub»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»§#183;«/mo»«mi mathvariant=¨bold¨ mathcolor=¨#0000FF¨»a«/mi»«mspace linebreak=¨newline¨/»«mi mathvariant=¨bold¨ mathcolor=¨#FF0000¨»E«/mi»«mo mathvariant=¨bold¨ mathcolor=¨#FF0000¨»§#183;«/mo»«msub»«mi mathvariant=¨bold¨ mathcolor=¨#FF0000¨»q«/mi»«mi mathvariant=¨bold¨ mathcolor=¨#FF0000¨»e«/mi»«/msub»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»=«/mo»«msub»«mi mathvariant=¨bold¨ mathcolor=¨#0000FF¨»m«/mi»«mi mathvariant=¨bold¨ mathcolor=¨#0000FF¨»e«/mi»«/msub»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»§#183;«/mo»«mi mathvariant=¨bold¨ mathcolor=¨#0000FF¨»a«/mi»«/mstyle»«/math»

«math xmlns=¨http://www.w3.org/1998/Math/MathML¨»«mstyle mathsize=¨22px¨»«mi mathvariant=¨bold¨ mathcolor=¨#FF0000¨ mathsize=¨24px¨»E«/mi»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨ mathsize=¨24px¨»§#183;«/mo»«msub»«mi mathvariant=¨bold¨ mathcolor=¨#0000FF¨ mathsize=¨24px¨»q«/mi»«mi mathvariant=¨bold¨ mathcolor=¨#0000FF¨ mathsize=¨24px¨»e«/mi»«/msub»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨ mathsize=¨24px¨»=«/mo»«msub»«mi mathvariant=¨bold¨ mathcolor=¨#0000FF¨ mathsize=¨24px¨»m«/mi»«mi mathvariant=¨bold¨ mathcolor=¨#0000FF¨ mathsize=¨24px¨»e«/mi»«/msub»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨ mathsize=¨24px¨»§#183;«/mo»«mi mathvariant=¨bold¨ mathcolor=¨#0000FF¨ mathsize=¨24px¨»a«/mi»«mspace linebreak=¨newline¨/»«mfrac mathcolor=¨#FF0000¨»«mi mathvariant=¨bold¨»§#963;«/mi»«mrow»«mn mathvariant=¨bold¨»2«/mn»«mo mathvariant=¨bold¨»§#183;«/mo»«msub»«mi mathvariant=¨bold¨»§#949;«/mi»«mn mathvariant=¨bold¨»0«/mn»«/msub»«/mrow»«/mfrac»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»§#183;«/mo»«msub»«mi mathvariant=¨bold¨ mathcolor=¨#0000FF¨»q«/mi»«mi mathvariant=¨bold¨ mathcolor=¨#0000FF¨»e«/mi»«/msub»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»=«/mo»«msub»«mi mathvariant=¨bold¨ mathcolor=¨#0000FF¨»m«/mi»«mi mathvariant=¨bold¨ mathcolor=¨#0000FF¨»e«/mi»«/msub»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»§#183;«/mo»«mi mathvariant=¨bold¨ mathcolor=¨#0000FF¨»a«/mi»«/mstyle»«/math»

نُعبر عن تسارع الإلكترون من معادلة الحركة:

نُعوض معطيات السؤال ونجد التسارع:

«math xmlns=¨http://www.w3.org/1998/Math/MathML¨»«mstyle mathsize=¨22px¨»«mi mathvariant=¨bold¨ mathcolor=¨#0000FF¨»a«/mi»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»=«/mo»«mfrac mathcolor=¨#0000FF¨»«mrow»«mi mathvariant=¨bold¨»§#963;«/mi»«mo mathvariant=¨bold¨»§#183;«/mo»«msub»«mi mathvariant=¨bold¨»q«/mi»«mi mathvariant=¨bold¨»e«/mi»«/msub»«/mrow»«mrow»«mn mathvariant=¨bold¨»2«/mn»«mo mathvariant=¨bold¨»§#183;«/mo»«msub»«mi mathvariant=¨bold¨»§#949;«/mi»«mn mathvariant=¨bold¨»0«/mn»«/msub»«mo mathvariant=¨bold¨»§#183;«/mo»«msub»«mi mathvariant=¨bold¨»m«/mi»«mi mathvariant=¨bold¨»e«/mi»«/msub»«/mrow»«/mfrac»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»=«/mo»«mfrac mathcolor=¨#0000FF¨»«mrow»«mstyle mathvariant=¨bold¨»«mo stretchy=¨true¨»|«/mo»«mrow»«mo»-«/mo»«mn»5«/mn»«mo»§#183;«/mo»«msup»«mn»10«/mn»«mrow»«mo»-«/mo»«mn»15«/mn»«/mrow»«/msup»«/mrow»«mo stretchy=¨true¨»|«/mo»«/mstyle»«mo mathvariant=¨bold¨»§#183;«/mo»«mstyle mathvariant=¨bold¨»«mo stretchy=¨true¨»|«/mo»«mrow»«mo»-«/mo»«mn»1«/mn»«mo».«/mo»«mn»6«/mn»«mo»§#183;«/mo»«msup»«mn»10«/mn»«mrow»«mo»-«/mo»«mn»19«/mn»«/mrow»«/msup»«/mrow»«mo stretchy=¨true¨»|«/mo»«/mstyle»«/mrow»«mrow»«mn mathvariant=¨bold¨»2«/mn»«mo mathvariant=¨bold¨»§#183;«/mo»«mn mathvariant=¨bold¨»8«/mn»«mo mathvariant=¨bold¨».«/mo»«mn mathvariant=¨bold¨»85«/mn»«mo mathvariant=¨bold¨»§#183;«/mo»«msup»«mn mathvariant=¨bold¨»10«/mn»«mrow»«mo mathvariant=¨bold¨»-«/mo»«mn mathvariant=¨bold¨»12«/mn»«/mrow»«/msup»«mo mathvariant=¨bold¨»§#183;«/mo»«mn mathvariant=¨bold¨»9«/mn»«mo mathvariant=¨bold¨».«/mo»«mn mathvariant=¨bold¨»11«/mn»«mo mathvariant=¨bold¨»§#183;«/mo»«msup»«mn mathvariant=¨bold¨»10«/mn»«mrow»«mo mathvariant=¨bold¨»-«/mo»«mn mathvariant=¨bold¨»31«/mn»«/mrow»«/msup»«/mrow»«/mfrac»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»=«/mo»«mfrac mathcolor=¨#0000FF¨»«mrow»«mn mathvariant=¨bold¨»8«/mn»«mo mathvariant=¨bold¨»§#183;«/mo»«msup»«mn mathvariant=¨bold¨»10«/mn»«mrow»«mo mathvariant=¨bold¨»-«/mo»«mn mathvariant=¨bold¨»34«/mn»«/mrow»«/msup»«/mrow»«mrow»«mn mathvariant=¨bold¨»1«/mn»«mo mathvariant=¨bold¨».«/mo»«mn mathvariant=¨bold¨»61«/mn»«mo mathvariant=¨bold¨»§#183;«/mo»«msup»«mn mathvariant=¨bold¨»10«/mn»«mrow»«mo mathvariant=¨bold¨»-«/mo»«mn mathvariant=¨bold¨»41«/mn»«/mrow»«/msup»«/mrow»«/mfrac»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»=«/mo»«mn mathvariant=¨bold¨ mathcolor=¨#0000FF¨»49«/mn»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨».«/mo»«mn mathvariant=¨bold¨ mathcolor=¨#0000FF¨»61«/mn»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»§#183;«/mo»«msup»«mn mathvariant=¨bold¨ mathcolor=¨#0000FF¨»10«/mn»«mn mathvariant=¨bold¨ mathcolor=¨#0000FF¨»6«/mn»«/msup»«mfrac mathcolor=¨#0000FF¨»«mi mathvariant=¨bold¨»m«/mi»«msup»«mi mathvariant=¨bold¨»s«/mi»«mn mathvariant=¨bold¨»2«/mn»«/msup»«/mfrac»«/mstyle»«/math»

23.3

يتحرك الجسم المشحون في حركة ثنائية الأبعاد (حركة في مستوى)، سوف نَصِف حركة الجسم بالنسبة لمحور X الموجه في اتجاه رمي الجسم والمحور Y الموجه في اتجاه تأثير القوة F، كما هو موضح في الشكل التالي:

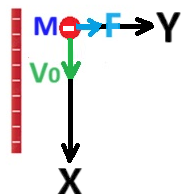
في اتجاه المحور X - لا تؤثر أي قوة على الجسم - في هذا الاتجاه يكون الجسم في في حالة استمرارية، وسرعته ثابتة ومساوية لسرعة الرمي:

في اتجاه المحور Y - تعمل قوة كهربائية ثابتة (F) على الجسم - في هذا الاتجاه يتحرك الجسم بتسارع ثابت. والذي وجدناه في البند السابق:

«math xmlns=¨http://www.w3.org/1998/Math/MathML¨»«mstyle mathsize=¨22px¨»«mi mathvariant=¨bold¨ mathcolor=¨#0000FF¨»a«/mi»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»=«/mo»«mn mathvariant=¨bold¨ mathcolor=¨#0000FF¨»0«/mn»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨».«/mo»«mn mathvariant=¨bold¨ mathcolor=¨#0000FF¨»056«/mn»«mfrac mathcolor=¨#0000FF¨»«mi mathvariant=¨bold¨»m«/mi»«msup»«mi mathvariant=¨bold¨»s«/mi»«mn mathvariant=¨bold¨»2«/mn»«/msup»«/mfrac»«/mstyle»«/math»

نحسب سرعة الجسم في اتجاه المحور Y بعد ثانيتين من لحظة الرمي :

يوضح الشكل التالي سرعة الجسم (V) ومركبات السرعتان ( «math xmlns=¨http://www.w3.org/1998/Math/MathML¨»«mstyle mathsize=¨22px¨»«msub»«mi mathvariant=¨bold¨»V«/mi»«mi mathvariant=¨bold¨»X«/mi»«/msub»«mo mathvariant=¨bold¨»-«/mo»«mi mathvariant=¨bold¨»§#1608;«/mi»«mo mathvariant=¨bold¨»§#160;«/mo»«msub»«mi mathvariant=¨bold¨»V«/mi»«mi mathvariant=¨bold¨»Y«/mi»«/msub»«/mstyle»«/math») :

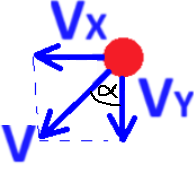
نحسب بالاعتماد على «math xmlns=¨http://www.w3.org/1998/Math/MathML¨»«mstyle mathsize=¨22px¨»«msub»«mi mathvariant=¨bold¨»V«/mi»«mi mathvariant=¨bold¨»X«/mi»«/msub»«mo mathvariant=¨bold¨»-«/mo»«mi mathvariant=¨bold¨»§#1608;«/mi»«mo mathvariant=¨bold¨»§#160;«/mo»«msub»«mi mathvariant=¨bold¨»V«/mi»«mi mathvariant=¨bold¨»Y«/mi»«/msub»«/mstyle»«/math» مقدار سرعة الجسم بعد مرور ثانيتين من لحظة القذف :

«math xmlns=¨http://www.w3.org/1998/Math/MathML¨»«mstyle mathsize=¨20px¨»«msup»«mi mathvariant=¨bold¨ mathcolor=¨#0000FF¨»V«/mi»«mn mathvariant=¨bold¨ mathcolor=¨#0000FF¨»2«/mn»«/msup»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»=«/mo»«msup»«msub»«mi mathvariant=¨bold¨ mathcolor=¨#0000FF¨»V«/mi»«mi mathvariant=¨bold¨ mathcolor=¨#0000FF¨»X«/mi»«/msub»«mn mathvariant=¨bold¨ mathcolor=¨#0000FF¨»2«/mn»«/msup»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»+«/mo»«msup»«msub»«mi mathvariant=¨bold¨ mathcolor=¨#0000FF¨»V«/mi»«mi mathvariant=¨bold¨ mathcolor=¨#0000FF¨»Y«/mi»«/msub»«mn mathvariant=¨bold¨ mathcolor=¨#0000FF¨»2«/mn»«/msup»«mspace linebreak=¨newline¨/»«mi mathvariant=¨bold¨ mathcolor=¨#0000FF¨»V«/mi»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»=«/mo»«msqrt mathcolor=¨#0000FF¨»«msup»«msub»«mi mathvariant=¨bold¨»V«/mi»«mi mathvariant=¨bold¨»X«/mi»«/msub»«mn mathvariant=¨bold¨»2«/mn»«/msup»«mo mathvariant=¨bold¨»+«/mo»«msup»«msub»«mi mathvariant=¨bold¨»V«/mi»«mi mathvariant=¨bold¨»Y«/mi»«/msub»«mn mathvariant=¨bold¨»2«/mn»«/msup»«/msqrt»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»=«/mo»«msqrt mathcolor=¨#0000FF¨»«mn mathvariant=¨bold¨»0«/mn»«mo mathvariant=¨bold¨».«/mo»«msup»«mn mathvariant=¨bold¨»2«/mn»«mn mathvariant=¨bold¨»2«/mn»«/msup»«mo mathvariant=¨bold¨»+«/mo»«msup»«mrow»«mn mathvariant=¨bold¨»0«/mn»«mo mathvariant=¨bold¨».«/mo»«mn mathvariant=¨bold¨»112«/mn»«/mrow»«mn mathvariant=¨bold¨»2«/mn»«/msup»«/msqrt»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»=«/mo»«msqrt mathcolor=¨#0000FF¨»«mn mathvariant=¨bold¨»0«/mn»«mo mathvariant=¨bold¨».«/mo»«mn mathvariant=¨bold¨»052«/mn»«/msqrt»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»=«/mo»«mn mathvariant=¨bold¨ mathcolor=¨#0000FF¨»0«/mn»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨».«/mo»«mn mathvariant=¨bold¨ mathcolor=¨#0000FF¨»229«/mn»«mfrac mathcolor=¨#0000FF¨»«mi mathvariant=¨bold¨»m«/mi»«mi mathvariant=¨bold¨»s«/mi»«/mfrac»«/mstyle»«/math»

نحسب بالاعتماد على «math xmlns=¨http://www.w3.org/1998/Math/MathML¨»«mstyle mathsize=¨22px¨»«msub»«mi mathvariant=¨bold¨»V«/mi»«mi mathvariant=¨bold¨»X«/mi»«/msub»«mo mathvariant=¨bold¨»-«/mo»«mi mathvariant=¨bold¨»§#1608;«/mi»«mo mathvariant=¨bold¨»§#160;«/mo»«msub»«mi mathvariant=¨bold¨»V«/mi»«mi mathvariant=¨bold¨»Y«/mi»«/msub»«/mstyle»«/math» قيمة الزاوية α:

«math xmlns=¨http://www.w3.org/1998/Math/MathML¨»«mstyle mathsize=¨22px¨»«mrow mathcolor=¨#0000FF¨»«mi mathvariant=¨bold¨»tan«/mi»«mo mathvariant=¨bold¨»(«/mo»«mi mathvariant=¨bold¨»§#945;«/mi»«mo mathvariant=¨bold¨»)«/mo»«/mrow»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»=«/mo»«mfrac mathcolor=¨#0000FF¨»«msub»«mi mathvariant=¨bold¨»V«/mi»«mi mathvariant=¨bold¨»X«/mi»«/msub»«msub»«mi mathvariant=¨bold¨»V«/mi»«mi mathvariant=¨bold¨»Y«/mi»«/msub»«/mfrac»«mspace linebreak=¨newline¨/»«mspace linebreak=¨newline¨/»«mi mathvariant=¨bold¨ mathcolor=¨#0000FF¨»§#945;«/mi»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»=«/mo»«mi mathvariant=¨bold¨ mathcolor=¨#0000FF¨»shift«/mi»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»§#160;«/mo»«mi mathvariant=¨bold¨ mathcolor=¨#0000FF¨»tan«/mi»«mrow mathcolor=¨#0000FF¨»«mo mathvariant=¨bold¨ stretchy=¨true¨»(«/mo»«mfrac»«msub»«mi mathvariant=¨bold¨»V«/mi»«mi mathvariant=¨bold¨»X«/mi»«/msub»«msub»«mi mathvariant=¨bold¨»V«/mi»«mi mathvariant=¨bold¨»Y«/mi»«/msub»«/mfrac»«mo mathvariant=¨bold¨ stretchy=¨true¨»)«/mo»«/mrow»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»=«/mo»«mi mathvariant=¨bold¨ mathcolor=¨#0000FF¨»shift«/mi»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»§#160;«/mo»«mi mathvariant=¨bold¨ mathcolor=¨#0000FF¨»tan«/mi»«mrow mathcolor=¨#0000FF¨»«mo mathvariant=¨bold¨ stretchy=¨true¨»(«/mo»«mfrac»«mrow»«mn mathvariant=¨bold¨»0«/mn»«mo mathvariant=¨bold¨».«/mo»«mn mathvariant=¨bold¨»2«/mn»«/mrow»«mrow»«mn mathvariant=¨bold¨»0«/mn»«mo mathvariant=¨bold¨».«/mo»«mn mathvariant=¨bold¨»112«/mn»«/mrow»«/mfrac»«mo mathvariant=¨bold¨ stretchy=¨true¨»)«/mo»«/mrow»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»=«/mo»«mi mathvariant=¨bold¨ mathcolor=¨#0000FF¨»shift«/mi»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»§#160;«/mo»«mi mathvariant=¨bold¨ mathcolor=¨#0000FF¨»tan«/mi»«mrow mathcolor=¨#0000FF¨»«mo mathvariant=¨bold¨ stretchy=¨true¨»(«/mo»«mn mathvariant=¨bold¨»1«/mn»«mo mathvariant=¨bold¨».«/mo»«mn mathvariant=¨bold¨»78«/mn»«mo mathvariant=¨bold¨ stretchy=¨true¨»)«/mo»«/mrow»«mspace linebreak=¨newline¨/»«mspace linebreak=¨newline¨/»«mi mathvariant=¨bold¨ mathcolor=¨#0000FF¨»§#945;«/mi»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»=«/mo»«mn mathvariant=¨bold¨ mathcolor=¨#0000FF¨»60«/mn»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨».«/mo»«mn mathvariant=¨bold¨ mathcolor=¨#0000FF¨»75«/mn»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»§#176;«/mo»«mspace linebreak=¨newline¨/»«mspace linebreak=¨newline¨/»«mspace linebreak=¨newline¨/»«mspace linebreak=¨newline¨/»«mspace linebreak=¨newline¨/»«/mstyle»«/math»

24.1

نحسب شدة الحقل المتجانس باستخدام التعبير لشدة الحقل الكهربائي بالقرب من لوح مشحون لا نهائي.

«math xmlns=¨http://www.w3.org/1998/Math/MathML¨»«mstyle mathsize=¨22px¨»«mi mathvariant=¨bold¨ mathcolor=¨#0000FF¨»E«/mi»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»=«/mo»«mfrac mathcolor=¨#0000FF¨»«mi mathvariant=¨bold¨»§#963;«/mi»«mrow»«mn mathvariant=¨bold¨»2«/mn»«mo mathvariant=¨bold¨»§#183;«/mo»«msub»«mi mathvariant=¨bold¨»§#949;«/mi»«mn mathvariant=¨bold¨»0«/mn»«/msub»«/mrow»«/mfrac»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»=«/mo»«mfrac mathcolor=¨#0000FF¨»«mstyle mathvariant=¨bold¨»«mn»8«/mn»«mo»§#183;«/mo»«msup»«mn»10«/mn»«mrow»«mo»-«/mo»«mn»9«/mn»«/mrow»«/msup»«/mstyle»«mrow»«mn mathvariant=¨bold¨»2«/mn»«mo mathvariant=¨bold¨»§#183;«/mo»«mn mathvariant=¨bold¨»8«/mn»«mo mathvariant=¨bold¨».«/mo»«mn mathvariant=¨bold¨»85«/mn»«mo mathvariant=¨bold¨»§#183;«/mo»«msup»«mn mathvariant=¨bold¨»10«/mn»«mrow»«mo mathvariant=¨bold¨»-«/mo»«mn mathvariant=¨bold¨»12«/mn»«/mrow»«/msup»«/mrow»«/mfrac»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»=«/mo»«mfrac mathcolor=¨#0000FF¨»«mrow»«mn mathvariant=¨bold¨»8«/mn»«mo mathvariant=¨bold¨»§#183;«/mo»«msup»«mn mathvariant=¨bold¨»10«/mn»«mrow»«mo mathvariant=¨bold¨»-«/mo»«mn mathvariant=¨bold¨»9«/mn»«/mrow»«/msup»«/mrow»«mrow»«mn mathvariant=¨bold¨»1«/mn»«mo mathvariant=¨bold¨».«/mo»«mn mathvariant=¨bold¨»77«/mn»«mo mathvariant=¨bold¨»§#183;«/mo»«msup»«mn mathvariant=¨bold¨»10«/mn»«mrow»«mo mathvariant=¨bold¨»-«/mo»«mn mathvariant=¨bold¨»11«/mn»«/mrow»«/msup»«/mrow»«/mfrac»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»=«/mo»«mn mathvariant=¨bold¨ mathcolor=¨#0000FF¨»451«/mn»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨».«/mo»«mn mathvariant=¨bold¨ mathcolor=¨#0000FF¨»977«/mn»«mfrac mathcolor=¨#0000FF¨»«mi mathvariant=¨bold¨»N«/mi»«mi mathvariant=¨bold¨»C«/mi»«/mfrac»«/mstyle»«/math»

شدة الحقل الكهربائي المحسوبة هي شدة الحقل التي يُكونها كل لوح في كلا الجانبين.

24.2

كلا اللوحين مشحون بشحنة موجبة، وبالتالي فإن اتجاه الحقل الكهربائي الناتج عن كل لوح يكون باتجاه خارج من اللوح.

ويصف الشكل التالي اتجاه الحقل في كل منطقة من المناطق الثلاثة:

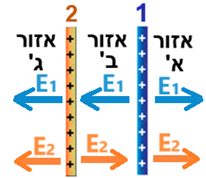
24.3

لأن اللوحان لهما نفس كثافة الشحنة. يُكوّن كل من اللوحين حقلًا متجانسًا وبنفس الشدة،

بالمنطقتين א' و- ג' يعمل الحقلان الكهربائيان في نفس الاتجاه.

بالمنطقة ב' ، يعمل الحقلان في اتجاهين متعاكسين، نظرًا لأنهما متساويان في المقدار، فإن شدة الحقل المحصّل في المنطقة ב' يساوي صفرًا.

يصف الشكل التالي شدة الحقل الكهربائي في كل منطقة من المناطق الثلاث:

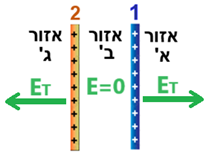
24.4

في المنطقة א'، يعمل الحقلان في نفس الاتجاه إلى اليمين، نحسب شدة الحقل الناتجة بواسطة كل لوح في البند 24.1.

نحسب وفقًا لذلك شدة الحقل المحصّل في المنطقة א':

«math xmlns=¨http://www.w3.org/1998/Math/MathML¨»«mstyle mathsize=¨20px¨»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»§#160;«/mo»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»`«/mo»«mi mathvariant=¨bold¨ mathcolor=¨#0000FF¨»§#1488;«/mi»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»§#160;«/mo»«mi mathvariant=¨bold¨ mathcolor=¨#0000FF¨»§#1488;§#1494;§#1493;§#1512;«/mi»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»§#160;«/mo»«msub»«mi mathvariant=¨bold¨ mathcolor=¨#0000FF¨»E«/mi»«mi mathvariant=¨bold¨ mathcolor=¨#0000FF¨»T«/mi»«/msub»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»=«/mo»«msub»«mi mathvariant=¨bold¨ mathcolor=¨#0000FF¨»E«/mi»«mn mathvariant=¨bold¨ mathcolor=¨#0000FF¨»1«/mn»«/msub»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»+«/mo»«msub»«mi mathvariant=¨bold¨ mathcolor=¨#0000FF¨»E«/mi»«mn mathvariant=¨bold¨ mathcolor=¨#0000FF¨»2«/mn»«/msub»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»=«/mo»«mn mathvariant=¨bold¨ mathcolor=¨#0000FF¨»451«/mn»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨».«/mo»«mn mathvariant=¨bold¨ mathcolor=¨#0000FF¨»977«/mn»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»+«/mo»«mn mathvariant=¨bold¨ mathcolor=¨#0000FF¨»451«/mn»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨».«/mo»«mn mathvariant=¨bold¨ mathcolor=¨#0000FF¨»977«/mn»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»=«/mo»«mn mathvariant=¨bold¨ mathcolor=¨#0000FF¨»903«/mn»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨».«/mo»«mn mathvariant=¨bold¨ mathcolor=¨#0000FF¨»954«/mn»«mfrac mathcolor=¨#0000FF¨»«mi mathvariant=¨bold¨»N«/mi»«mi mathvariant=¨bold¨»C«/mi»«/mfrac»«/mstyle»«/math»

في المنطقة ב' يعمل الحقلان في اتجاهين متعاكسين، نحسب شدة الحقل المحصّل في المنطقة ב':

«math xmlns=¨http://www.w3.org/1998/Math/MathML¨»«mstyle mathsize=¨20px¨»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»§#160;«/mo»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»`«/mo»«mi mathvariant=¨bold¨ mathcolor=¨#0000FF¨»§#1489;«/mi»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»§#160;«/mo»«mi mathvariant=¨bold¨ mathcolor=¨#0000FF¨»§#1488;§#1494;§#1493;§#1512;«/mi»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»§#160;«/mo»«msub»«mi mathvariant=¨bold¨ mathcolor=¨#0000FF¨»E«/mi»«mi mathvariant=¨bold¨ mathcolor=¨#0000FF¨»T«/mi»«/msub»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»=«/mo»«msub»«mi mathvariant=¨bold¨ mathcolor=¨#0000FF¨»E«/mi»«mn mathvariant=¨bold¨ mathcolor=¨#0000FF¨»1«/mn»«/msub»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»-«/mo»«msub»«mi mathvariant=¨bold¨ mathcolor=¨#0000FF¨»E«/mi»«mn mathvariant=¨bold¨ mathcolor=¨#0000FF¨»2«/mn»«/msub»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»=«/mo»«mn mathvariant=¨bold¨ mathcolor=¨#0000FF¨»451«/mn»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨».«/mo»«mn mathvariant=¨bold¨ mathcolor=¨#0000FF¨»977«/mn»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»-«/mo»«mn mathvariant=¨bold¨ mathcolor=¨#0000FF¨»451«/mn»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨».«/mo»«mn mathvariant=¨bold¨ mathcolor=¨#0000FF¨»977«/mn»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»=«/mo»«mn mathvariant=¨bold¨ mathcolor=¨#0000FF¨»0«/mn»«mfrac mathcolor=¨#0000FF¨»«mi mathvariant=¨bold¨»N«/mi»«mi mathvariant=¨bold¨»C«/mi»«/mfrac»«/mstyle»«/math»

في المنطقة ג' يعمل الحقلان في نفس الاتجاه إلى اليسار، نحسب شدة الحقل المحصّل في المنطقة ג':

«math xmlns=¨http://www.w3.org/1998/Math/MathML¨»«mstyle mathsize=¨20px¨»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»§#160;«/mo»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»`«/mo»«mi mathvariant=¨bold¨ mathcolor=¨#0000FF¨»§#1490;«/mi»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»§#160;«/mo»«mi mathvariant=¨bold¨ mathcolor=¨#0000FF¨»§#1488;§#1494;§#1493;§#1512;«/mi»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»§#160;«/mo»«msub»«mi mathvariant=¨bold¨ mathcolor=¨#0000FF¨»E«/mi»«mi mathvariant=¨bold¨ mathcolor=¨#0000FF¨»T«/mi»«/msub»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»=«/mo»«msub»«mi mathvariant=¨bold¨ mathcolor=¨#0000FF¨»E«/mi»«mn mathvariant=¨bold¨ mathcolor=¨#0000FF¨»1«/mn»«/msub»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»+«/mo»«msub»«mi mathvariant=¨bold¨ mathcolor=¨#0000FF¨»E«/mi»«mn mathvariant=¨bold¨ mathcolor=¨#0000FF¨»2«/mn»«/msub»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»=«/mo»«mn mathvariant=¨bold¨ mathcolor=¨#0000FF¨»451«/mn»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨».«/mo»«mn mathvariant=¨bold¨ mathcolor=¨#0000FF¨»977«/mn»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»+«/mo»«mn mathvariant=¨bold¨ mathcolor=¨#0000FF¨»451«/mn»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨».«/mo»«mn mathvariant=¨bold¨ mathcolor=¨#0000FF¨»977«/mn»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»=«/mo»«mn mathvariant=¨bold¨ mathcolor=¨#0000FF¨»903«/mn»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨».«/mo»«mn mathvariant=¨bold¨ mathcolor=¨#0000FF¨»954«/mn»«mfrac mathcolor=¨#0000FF¨»«mi mathvariant=¨bold¨»N«/mi»«mi mathvariant=¨bold¨»C«/mi»«/mfrac»«/mstyle»«/math»

25.1

نحسب شدة الحقل الكهربائي المتجانس باستخدام التعبير الملائم لشدة الحقل الكهربائي بالقرب من لوح مشحون لا نهائي.

«math xmlns=¨http://www.w3.org/1998/Math/MathML¨»«mstyle mathsize=¨22px¨»«mi mathvariant=¨bold¨ mathcolor=¨#0000FF¨»E«/mi»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»=«/mo»«mfrac mathcolor=¨#0000FF¨»«mi mathvariant=¨bold¨»§#963;«/mi»«mrow»«mn mathvariant=¨bold¨»2«/mn»«mo mathvariant=¨bold¨»§#183;«/mo»«msub»«mi mathvariant=¨bold¨»§#949;«/mi»«mn mathvariant=¨bold¨»0«/mn»«/msub»«/mrow»«/mfrac»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»=«/mo»«mfrac mathcolor=¨#0000FF¨»«mstyle mathvariant=¨bold¨»«mn»8«/mn»«mo»§#183;«/mo»«msup»«mn»10«/mn»«mrow»«mo»-«/mo»«mn»9«/mn»«/mrow»«/msup»«/mstyle»«mrow»«mn mathvariant=¨bold¨»2«/mn»«mo mathvariant=¨bold¨»§#183;«/mo»«mn mathvariant=¨bold¨»8«/mn»«mo mathvariant=¨bold¨».«/mo»«mn mathvariant=¨bold¨»85«/mn»«mo mathvariant=¨bold¨»§#183;«/mo»«msup»«mn mathvariant=¨bold¨»10«/mn»«mrow»«mo mathvariant=¨bold¨»-«/mo»«mn mathvariant=¨bold¨»12«/mn»«/mrow»«/msup»«/mrow»«/mfrac»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»=«/mo»«mfrac mathcolor=¨#0000FF¨»«mrow»«mn mathvariant=¨bold¨»8«/mn»«mo mathvariant=¨bold¨»§#183;«/mo»«msup»«mn mathvariant=¨bold¨»10«/mn»«mrow»«mo mathvariant=¨bold¨»-«/mo»«mn mathvariant=¨bold¨»9«/mn»«/mrow»«/msup»«/mrow»«mrow»«mn mathvariant=¨bold¨»1«/mn»«mo mathvariant=¨bold¨».«/mo»«mn mathvariant=¨bold¨»77«/mn»«mo mathvariant=¨bold¨»§#183;«/mo»«msup»«mn mathvariant=¨bold¨»10«/mn»«mrow»«mo mathvariant=¨bold¨»-«/mo»«mn mathvariant=¨bold¨»11«/mn»«/mrow»«/msup»«/mrow»«/mfrac»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»=«/mo»«mn mathvariant=¨bold¨ mathcolor=¨#0000FF¨»451«/mn»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»,«/mo»«mn mathvariant=¨bold¨ mathcolor=¨#0000FF¨»977«/mn»«mfrac mathcolor=¨#0000FF¨»«mi mathvariant=¨bold¨»N«/mi»«mi mathvariant=¨bold¨»C«/mi»«/mfrac»«/mstyle»«/math»

شدة الحقل الكهربائي المحسوبة هي شدة الحقل التي يُكوّنها كل لوح في كلا الجانبين.

25.2

اللوحان مشحونان بشحنات مختلفة، اللوح 1 مشحون بشحنة موجبة، واتجاه الحقل الكهربائي في المنطقة المجاورة له هو من اللوح نحو الخارج. اللوح 2 مشحون بشحنة سالبة، واتجاه الحقل الكهربائي بالقرب من اللوح 2 يكون في اتجاه نحو اللوح.

يصف الشكل التالي الحقول التي يُكوّنها اللوحان في كل منطقة من المناطق الثلاث:

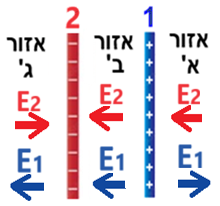
25.3

للوحين نفس كثافة الشحنة من حيث القيمة المطلقة، وبالتالي يتم إنشاء حقل متجانس بنفس المقدار من كلا اللوحين.

في المنطقتين א' و- ג' ، يعمل الحقلان الكهربائيان في اتجاهين متعاكسين، وشدة الحقل في تلك المنطقتين تساوي صفر نيوتن لكل كولون.

في المنطقة ב' يعمل الحقلان الكهربائيان في نفس الاتجاه، وشدة الحقل الكهربائي في المنطقة B تساوي محصلة الحقلين الناتجين من اللوحين.

ويصف الشكل التالي شدة الحقل الكهربائي في كل منطقة من المناطق الثلاث:

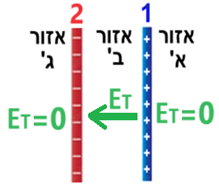
25.4

ينتج كل من اللوحين حقلًا كهربائيًا متجانسًا له نفس المقدار.

في المنطقتين א' و- ג' يعمل الحقلان في اتجاهين متعاكسين. وبما أن الحقلان متساويان في المقدار، فإن شدة الحقل الكهربائي في هاتين المنطقتين تساوي صفر نيوتن لكل كولون.

في المنطقة ב' ، يعمل الحقلان إلى اليسار، بنفس الاتجاه. قمنا بحساب شدة الحقل الناتج عن كل لوح في البند 25.1، وقمنا بحساب شدة الحقل الكهربائي المحصّل في المنطقة ב'.

«math xmlns=¨http://www.w3.org/1998/Math/MathML¨»«mstyle mathsize=¨20px¨»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»§#160;«/mo»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»`«/mo»«mi mathvariant=¨bold¨ mathcolor=¨#0000FF¨»§#1489;«/mi»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»§#160;«/mo»«mi mathvariant=¨bold¨ mathcolor=¨#0000FF¨»§#1488;§#1494;§#1493;§#1512;«/mi»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»§#160;«/mo»«msub»«mi mathvariant=¨bold¨ mathcolor=¨#0000FF¨»E«/mi»«mi mathvariant=¨bold¨ mathcolor=¨#0000FF¨»T«/mi»«/msub»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»=«/mo»«msub»«mi mathvariant=¨bold¨ mathcolor=¨#0000FF¨»E«/mi»«mn mathvariant=¨bold¨ mathcolor=¨#0000FF¨»1«/mn»«/msub»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»+«/mo»«msub»«mi mathvariant=¨bold¨ mathcolor=¨#0000FF¨»E«/mi»«mn mathvariant=¨bold¨ mathcolor=¨#0000FF¨»2«/mn»«/msub»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»=«/mo»«mn mathvariant=¨bold¨ mathcolor=¨#0000FF¨»451«/mn»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»,«/mo»«mn mathvariant=¨bold¨ mathcolor=¨#0000FF¨»977«/mn»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»+«/mo»«mn mathvariant=¨bold¨ mathcolor=¨#0000FF¨»451«/mn»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»,«/mo»«mn mathvariant=¨bold¨ mathcolor=¨#0000FF¨»977«/mn»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»=«/mo»«mn mathvariant=¨bold¨ mathcolor=¨#0000FF¨»903«/mn»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»,«/mo»«mn mathvariant=¨bold¨ mathcolor=¨#0000FF¨»954«/mn»«mfrac mathcolor=¨#0000FF¨»«mi mathvariant=¨bold¨»N«/mi»«mi mathvariant=¨bold¨»C«/mi»«/mfrac»«/mstyle»«/math»

26.1

ينتج حقلان كهربائيان في النقطة M : الحقل الناتج بواسطة اللوح المشحون والحقل الناتج بواسطة الشحنة النقطية.

نرسم رسمًا تخطيطيًا لمتجهات الحقل الكهربائي في النقطة M:

نُشير إلى الحقلين في النقطة M: الحقل الناتج من الشحنة Q بواسطة E1، والحقل الناتج من اللوح بواسطة E2.

مُعطى أن الحقل المحصّل في النقطة M يساوي 8 نيوتن لكل كولون.

«math xmlns=¨http://www.w3.org/1998/Math/MathML¨»«mstyle mathsize=¨22px¨»«msub»«mi mathvariant=¨bold¨ mathcolor=¨#0000FF¨»E«/mi»«mn mathvariant=¨bold¨ mathcolor=¨#0000FF¨»1«/mn»«/msub»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»+«/mo»«msub»«mi mathvariant=¨bold¨ mathcolor=¨#0000FF¨»E«/mi»«mn mathvariant=¨bold¨ mathcolor=¨#0000FF¨»2«/mn»«/msub»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»=«/mo»«mn mathvariant=¨bold¨ mathcolor=¨#0000FF¨»8«/mn»«/mstyle»«/math»

نُعبر عن شدة الحقلين الناتجين من اللوح والشحنة النقطية في النقطة M:

«math xmlns=¨http://www.w3.org/1998/Math/MathML¨»«mstyle mathsize=¨24px¨»«msub»«mi mathvariant=¨bold¨ mathcolor=¨#0000FF¨»E«/mi»«mn mathvariant=¨bold¨ mathcolor=¨#0000FF¨»1«/mn»«/msub»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»+«/mo»«msub»«mi mathvariant=¨bold¨ mathcolor=¨#0000FF¨»E«/mi»«mn mathvariant=¨bold¨ mathcolor=¨#0000FF¨»2«/mn»«/msub»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»=«/mo»«mn mathvariant=¨bold¨ mathcolor=¨#0000FF¨»8«/mn»«mspace linebreak=¨newline¨/»«mspace linebreak=¨newline¨/»«mfrac mathcolor=¨#0000FF¨»«mrow»«mi mathvariant=¨bold¨»K«/mi»«mo mathvariant=¨bold¨»§#183;«/mo»«msub»«mi mathvariant=¨bold¨»Q«/mi»«mn mathvariant=¨bold¨»1«/mn»«/msub»«/mrow»«msup»«msub»«mi mathvariant=¨bold¨»d«/mi»«mn mathvariant=¨bold¨»1«/mn»«/msub»«mn mathvariant=¨bold¨»2«/mn»«/msup»«/mfrac»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»+«/mo»«mfrac mathcolor=¨#0000FF¨»«mi mathvariant=¨bold¨»§#963;«/mi»«mrow»«mn mathvariant=¨bold¨»2«/mn»«mo mathvariant=¨bold¨»§#183;«/mo»«msub»«mi mathvariant=¨bold¨»§#949;«/mi»«mn mathvariant=¨bold¨»0«/mn»«/msub»«/mrow»«/mfrac»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»=«/mo»«mn mathvariant=¨bold¨ mathcolor=¨#0000FF¨»8«/mn»«/mstyle»«/math»

نكتب تعبيرًا لكثافة الشحنة على اللوح:

«math xmlns=¨http://www.w3.org/1998/Math/MathML¨»«mstyle mathsize=¨24px¨»«mfrac mathcolor=¨#0000FF¨»«mrow»«mi mathvariant=¨bold¨»K«/mi»«mo mathvariant=¨bold¨»§#183;«/mo»«msub»«mi mathvariant=¨bold¨»Q«/mi»«mn mathvariant=¨bold¨»1«/mn»«/msub»«/mrow»«msup»«msub»«mi mathvariant=¨bold¨»d«/mi»«mn mathvariant=¨bold¨»1«/mn»«/msub»«mn mathvariant=¨bold¨»2«/mn»«/msup»«/mfrac»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»+«/mo»«mfrac mathcolor=¨#0000FF¨»«mi mathvariant=¨bold¨»§#963;«/mi»«mrow»«mn mathvariant=¨bold¨»2«/mn»«mo mathvariant=¨bold¨»§#183;«/mo»«msub»«mi mathvariant=¨bold¨»§#949;«/mi»«mn mathvariant=¨bold¨»0«/mn»«/msub»«/mrow»«/mfrac»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»=«/mo»«mn mathvariant=¨bold¨ mathcolor=¨#0000FF¨»8«/mn»«mspace linebreak=¨newline¨/»«mspace linebreak=¨newline¨/»«mfrac mathcolor=¨#0000FF¨»«mi mathvariant=¨bold¨»§#963;«/mi»«mrow»«mn mathvariant=¨bold¨»2«/mn»«mo mathvariant=¨bold¨»§#183;«/mo»«msub»«mi mathvariant=¨bold¨»§#949;«/mi»«mn mathvariant=¨bold¨»0«/mn»«/msub»«/mrow»«/mfrac»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»=«/mo»«mn mathvariant=¨bold¨ mathcolor=¨#0000FF¨»8«/mn»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»-«/mo»«mfrac mathcolor=¨#0000FF¨»«mrow»«mi mathvariant=¨bold¨»K«/mi»«mo mathvariant=¨bold¨»§#183;«/mo»«msub»«mi mathvariant=¨bold¨»Q«/mi»«mn mathvariant=¨bold¨»1«/mn»«/msub»«/mrow»«msup»«msub»«mi mathvariant=¨bold¨»d«/mi»«mn mathvariant=¨bold¨»1«/mn»«/msub»«mn mathvariant=¨bold¨»2«/mn»«/msup»«/mfrac»«mspace linebreak=¨newline¨/»«mspace linebreak=¨newline¨/»«mi mathvariant=¨bold¨ mathcolor=¨#0000FF¨»§#963;«/mi»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»=«/mo»«mn mathvariant=¨bold¨ mathcolor=¨#0000FF¨»2«/mn»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»§#183;«/mo»«msub»«mi mathvariant=¨bold¨ mathcolor=¨#0000FF¨»§#949;«/mi»«mn mathvariant=¨bold¨ mathcolor=¨#0000FF¨»0«/mn»«/msub»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»§#183;«/mo»«mstyle mathvariant=¨bold¨ mathcolor=¨#0000FF¨»«mo stretchy=¨true¨»(«/mo»«mrow»«mn»8«/mn»«mo»-«/mo»«mfrac»«mrow»«mi»K«/mi»«mo»§#183;«/mo»«msub»«mi»Q«/mi»«mn»1«/mn»«/msub»«/mrow»«msup»«msub»«mi»d«/mi»«mn»1«/mn»«/msub»«mn»2«/mn»«/msup»«/mfrac»«/mrow»«mo stretchy=¨true¨»)«/mo»«/mstyle»«/mstyle»«/math»

نُعوّض مُعطيات السؤال ونحسب كثافة الشحنة:

«math xmlns=¨http://www.w3.org/1998/Math/MathML¨»«mstyle mathsize=¨24px¨»«mspace linebreak=¨newline¨/»«mi mathvariant=¨bold¨ mathcolor=¨#0000FF¨»§#963;«/mi»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»=«/mo»«mn mathvariant=¨bold¨ mathcolor=¨#0000FF¨»2«/mn»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»§#183;«/mo»«msub»«mi mathvariant=¨bold¨ mathcolor=¨#0000FF¨»§#949;«/mi»«mn mathvariant=¨bold¨ mathcolor=¨#0000FF¨»0«/mn»«/msub»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»§#183;«/mo»«mrow mathcolor=¨#0000FF¨»«mo mathvariant=¨bold¨ stretchy=¨true¨»(«/mo»«mn mathvariant=¨bold¨»8«/mn»«mo mathvariant=¨bold¨»-«/mo»«mfrac»«mrow»«mi mathvariant=¨bold¨»K«/mi»«mo mathvariant=¨bold¨»§#183;«/mo»«msub»«mi mathvariant=¨bold¨»Q«/mi»«mn mathvariant=¨bold¨»1«/mn»«/msub»«/mrow»«msup»«msub»«mi mathvariant=¨bold¨»d«/mi»«mn mathvariant=¨bold¨»1«/mn»«/msub»«mn mathvariant=¨bold¨»2«/mn»«/msup»«/mfrac»«mo mathvariant=¨bold¨ stretchy=¨true¨»)«/mo»«mo mathvariant=¨bold¨»=«/mo»«mn mathvariant=¨bold¨»2«/mn»«mo mathvariant=¨bold¨»§#183;«/mo»«mn mathvariant=¨bold¨»8«/mn»«mo mathvariant=¨bold¨».«/mo»«mn mathvariant=¨bold¨»85«/mn»«mo mathvariant=¨bold¨»§#183;«/mo»«msup»«mn mathvariant=¨bold¨»10«/mn»«mrow»«mo mathvariant=¨bold¨»-«/mo»«mn mathvariant=¨bold¨»12«/mn»«/mrow»«/msup»«mo mathvariant=¨bold¨»§#183;«/mo»«mrow»«mo mathvariant=¨bold¨ stretchy=¨true¨»(«/mo»«mn mathvariant=¨bold¨»8«/mn»«mo mathvariant=¨bold¨»-«/mo»«mfrac»«mrow»«mn mathvariant=¨bold¨»9«/mn»«mo mathvariant=¨bold¨»§#183;«/mo»«msup»«mn mathvariant=¨bold¨»10«/mn»«mn mathvariant=¨bold¨»9«/mn»«/msup»«mo mathvariant=¨bold¨»§#183;«/mo»«mn mathvariant=¨bold¨»5«/mn»«mo mathvariant=¨bold¨»§#183;«/mo»«msup»«mn mathvariant=¨bold¨»10«/mn»«mrow»«mo mathvariant=¨bold¨»-«/mo»«mn mathvariant=¨bold¨»9«/mn»«/mrow»«/msup»«/mrow»«msup»«mn mathvariant=¨bold¨»3«/mn»«mn mathvariant=¨bold¨»2«/mn»«/msup»«/mfrac»«mo mathvariant=¨bold¨ stretchy=¨true¨»)«/mo»«mo mathvariant=¨bold¨»=«/mo»«mn mathvariant=¨bold¨»2«/mn»«mo mathvariant=¨bold¨»§#183;«/mo»«mn mathvariant=¨bold¨»8«/mn»«mo mathvariant=¨bold¨».«/mo»«mn mathvariant=¨bold¨»85«/mn»«mo mathvariant=¨bold¨»§#183;«/mo»«msup»«mn mathvariant=¨bold¨»10«/mn»«mrow»«mo mathvariant=¨bold¨»-«/mo»«mn mathvariant=¨bold¨»12«/mn»«/mrow»«/msup»«mo mathvariant=¨bold¨»§#183;«/mo»«mrow»«mo mathvariant=¨bold¨ stretchy=¨true¨»(«/mo»«mn mathvariant=¨bold¨»8«/mn»«mo mathvariant=¨bold¨»-«/mo»«mn mathvariant=¨bold¨»5«/mn»«mo mathvariant=¨bold¨ stretchy=¨true¨»)«/mo»«/mrow»«/mrow»«/mrow»«mspace linebreak=¨newline¨/»«mi mathvariant=¨bold¨ mathcolor=¨#0000FF¨»§#963;«/mi»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»=«/mo»«mn mathvariant=¨bold¨ mathcolor=¨#0000FF¨»2«/mn»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»§#183;«/mo»«mn mathvariant=¨bold¨ mathcolor=¨#0000FF¨»8«/mn»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨».«/mo»«mn mathvariant=¨bold¨ mathcolor=¨#0000FF¨»85«/mn»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»§#183;«/mo»«msup»«mn mathvariant=¨bold¨ mathcolor=¨#0000FF¨»10«/mn»«mrow mathcolor=¨#0000FF¨»«mo mathvariant=¨bold¨»-«/mo»«mn mathvariant=¨bold¨»12«/mn»«/mrow»«/msup»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»§#183;«/mo»«mn mathvariant=¨bold¨ mathcolor=¨#0000FF¨»3«/mn»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»=«/mo»«mn mathvariant=¨bold¨ mathcolor=¨#0000FF¨»5«/mn»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨».«/mo»«mn mathvariant=¨bold¨ mathcolor=¨#0000FF¨»31«/mn»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»§#183;«/mo»«msup»«mn mathvariant=¨bold¨ mathcolor=¨#0000FF¨»10«/mn»«mrow mathcolor=¨#0000FF¨»«mo mathvariant=¨bold¨»-«/mo»«mn mathvariant=¨bold¨»11«/mn»«/mrow»«/msup»«mfrac mathcolor=¨#0000FF¨»«mi mathvariant=¨bold¨»C«/mi»«msup»«mi mathvariant=¨bold¨»m«/mi»«mn mathvariant=¨bold¨»2«/mn»«/msup»«/mfrac»«/mstyle»«/math»

26.2

حسب تعريف شدة الحقل«math xmlns=¨http://www.w3.org/1998/Math/MathML¨»«mstyle mathsize=¨22px¨»«mover mathcolor=¨#0000FF¨»«mi mathvariant=¨bold¨»E«/mi»«mo mathvariant=¨bold¨»§#8594;«/mo»«/mover»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»=«/mo»«mfrac mathcolor=¨#0000FF¨»«mover»«mi mathvariant=¨bold¨»F«/mi»«mo mathvariant=¨bold¨»§#8594;«/mo»«/mover»«mi mathvariant=¨bold¨»q«/mi»«/mfrac»«/mstyle»«/math» النقطة التي تكون فيها شدة الحقل تساوي صفرًا هي النقطة التي تكون فيها القوة الكهربائية المحصّلة المؤثرة على شحنة الفحص تساوي صفرًا.

النقطة التي تكون فيها محصّلة القوى الكهربائية التي تعمل على شحنة الفحص مساوية للصفر، تقع في المنطقة الواقعة بين اللوح والشحنة النقطية.

فقط في هذا المنطقة تعمل القوى الكهربائية في اتجاهين متعاكسين.

نُشير للبعد بين شحنة الفحص q والشحنة النقطية Q بـ «math xmlns=¨http://www.w3.org/1998/Math/MathML¨»«mstyle mathsize=¨24px¨»«msub»«mi mathvariant=¨bold¨»r«/mi»«mn mathvariant=¨bold¨»1«/mn»«/msub»«/mstyle»«/math» .

يتم وصف البعد «math xmlns=¨http://www.w3.org/1998/Math/MathML¨»«mstyle mathsize=¨24px¨»«msub»«mi mathvariant=¨bold¨»r«/mi»«mn mathvariant=¨bold¨»1«/mn»«/msub»«/mstyle»«/math» والقوى الكهربائية في الشكل التالي:

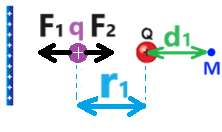
نكتب معادلة الحركة، عندما تكون شحنة الفحص في النقطة التي تكون فيها محصّلة القوى المؤثرة عليها يساوي صفرًا.

«math xmlns=¨http://www.w3.org/1998/Math/MathML¨»«mstyle mathsize=¨22px¨»«mi mathvariant=¨bold¨ mathcolor=¨#0000FF¨»§#931;F«/mi»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»=«/mo»«mn mathvariant=¨bold¨ mathcolor=¨#0000FF¨»0«/mn»«mspace linebreak=¨newline¨/»«mspace linebreak=¨newline¨/»«msub»«mi mathvariant=¨bold¨ mathcolor=¨#0000FF¨»F«/mi»«mn mathvariant=¨bold¨ mathcolor=¨#0000FF¨»1«/mn»«/msub»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»=«/mo»«msub»«mi mathvariant=¨bold¨ mathcolor=¨#0000FF¨»F«/mi»«mn mathvariant=¨bold¨ mathcolor=¨#0000FF¨»2«/mn»«/msub»«mspace linebreak=¨newline¨/»«mspace linebreak=¨newline¨/»«mfrac mathcolor=¨#0000FF¨»«mrow»«mi mathvariant=¨bold¨»K«/mi»«mo mathvariant=¨bold¨»§#183;«/mo»«msub»«mi mathvariant=¨bold¨»Q«/mi»«mn mathvariant=¨bold¨»1«/mn»«/msub»«mo mathvariant=¨bold¨»§#183;«/mo»«mi mathvariant=¨bold¨»q«/mi»«/mrow»«msup»«msub»«mi mathvariant=¨bold¨»r«/mi»«mn mathvariant=¨bold¨»1«/mn»«/msub»«mn mathvariant=¨bold¨»2«/mn»«/msup»«/mfrac»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»=«/mo»«mi mathvariant=¨bold¨ mathcolor=¨#0000FF¨»E«/mi»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»§#183;«/mo»«mi mathvariant=¨bold¨ mathcolor=¨#0000FF¨»q«/mi»«mspace linebreak=¨newline¨/»«mspace linebreak=¨newline¨/»«mfrac mathcolor=¨#0000FF¨»«mrow»«mi mathvariant=¨bold¨»K«/mi»«mo mathvariant=¨bold¨»§#183;«/mo»«msub»«mi mathvariant=¨bold¨»Q«/mi»«mn mathvariant=¨bold¨»1«/mn»«/msub»«mo mathvariant=¨bold¨»§#183;«/mo»«menclose notation=¨updiagonalstrike¨»«mi mathvariant=¨bold¨»q«/mi»«/menclose»«/mrow»«msup»«msub»«mi mathvariant=¨bold¨»r«/mi»«mn mathvariant=¨bold¨»1«/mn»«/msub»«mn mathvariant=¨bold¨»2«/mn»«/msup»«/mfrac»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»=«/mo»«mfrac mathcolor=¨#0000FF¨»«mi mathvariant=¨bold¨»§#963;«/mi»«mrow»«mn mathvariant=¨bold¨»2«/mn»«mo mathvariant=¨bold¨»§#183;«/mo»«msub»«mi mathvariant=¨bold¨»§#949;«/mi»«mn mathvariant=¨bold¨»0«/mn»«/msub»«/mrow»«/mfrac»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»§#183;«/mo»«menclose mathcolor=¨#0000FF¨ notation=¨updiagonalstrike¨»«mi mathvariant=¨bold¨»q«/mi»«/menclose»«mspace linebreak=¨newline¨/»«mspace linebreak=¨newline¨/»«menclose mathcolor=¨#0000FF¨ notation=¨circle¨»«mfrac»«mrow»«mi mathvariant=¨bold¨»K«/mi»«mo mathvariant=¨bold¨»§#183;«/mo»«msub»«mi mathvariant=¨bold¨»Q«/mi»«mn mathvariant=¨bold¨»1«/mn»«/msub»«/mrow»«msup»«msub»«mi mathvariant=¨bold¨»r«/mi»«mn mathvariant=¨bold¨»1«/mn»«/msub»«mn mathvariant=¨bold¨»2«/mn»«/msup»«/mfrac»«mo mathvariant=¨bold¨»=«/mo»«mfrac»«mi mathvariant=¨bold¨»§#963;«/mi»«mrow»«mn mathvariant=¨bold¨»2«/mn»«mo mathvariant=¨bold¨»§#183;«/mo»«msub»«mi mathvariant=¨bold¨»§#949;«/mi»«mn mathvariant=¨bold¨»0«/mn»«/msub»«/mrow»«/mfrac»«/menclose»«/mstyle»«/math»

نُعبّر عن «math xmlns=¨http://www.w3.org/1998/Math/MathML¨»«mstyle mathsize=¨24px¨»«msub»«mi mathvariant=¨bold¨»r«/mi»«mn mathvariant=¨bold¨»1«/mn»«/msub»«/mstyle»«/math» من معادلة القوى:

«math xmlns=¨http://www.w3.org/1998/Math/MathML¨»«mstyle mathsize=¨22px¨»«mfrac mathcolor=¨#0000FF¨»«mrow»«mi mathvariant=¨bold¨»K«/mi»«mo mathvariant=¨bold¨»§#183;«/mo»«msub»«mi mathvariant=¨bold¨»Q«/mi»«mn mathvariant=¨bold¨»1«/mn»«/msub»«/mrow»«msup»«msub»«mi mathvariant=¨bold¨»r«/mi»«mn mathvariant=¨bold¨»1«/mn»«/msub»«mn mathvariant=¨bold¨»2«/mn»«/msup»«/mfrac»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»=«/mo»«mfrac mathcolor=¨#0000FF¨»«mi mathvariant=¨bold¨»§#963;«/mi»«mrow»«mn mathvariant=¨bold¨»2«/mn»«mo mathvariant=¨bold¨»§#183;«/mo»«msub»«mi mathvariant=¨bold¨»§#949;«/mi»«mn mathvariant=¨bold¨»0«/mn»«/msub»«/mrow»«/mfrac»«mspace linebreak=¨newline¨/»«mspace linebreak=¨newline¨/»«msub»«mi mathvariant=¨bold¨ mathcolor=¨#0000FF¨»r«/mi»«mn mathvariant=¨bold¨ mathcolor=¨#0000FF¨»1«/mn»«/msub»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»=«/mo»«msqrt mathcolor=¨#0000FF¨»«mfrac»«mrow»«mi mathvariant=¨bold¨»K«/mi»«mo mathvariant=¨bold¨»§#183;«/mo»«msub»«mi mathvariant=¨bold¨»Q«/mi»«mn mathvariant=¨bold¨»1«/mn»«/msub»«mo mathvariant=¨bold¨»§#183;«/mo»«mn mathvariant=¨bold¨»2«/mn»«mo mathvariant=¨bold¨»§#183;«/mo»«msub»«mi mathvariant=¨bold¨»§#949;«/mi»«mn mathvariant=¨bold¨»0«/mn»«/msub»«/mrow»«mi mathvariant=¨bold¨»§#963;«/mi»«/mfrac»«/msqrt»«/mstyle»«/math»

نُعوّض معطيات السؤال ونحسب البعد «math xmlns=¨http://www.w3.org/1998/Math/MathML¨»«mstyle mathsize=¨24px¨»«msub»«mi mathvariant=¨bold¨»r«/mi»«mn mathvariant=¨bold¨»1«/mn»«/msub»«/mstyle»«/math»:

«math xmlns=¨http://www.w3.org/1998/Math/MathML¨»«msub»«mi mathvariant=¨bold¨ mathcolor=¨#0000FF¨ mathsize=¨22px¨»r«/mi»«mn mathvariant=¨bold¨ mathcolor=¨#0000FF¨ mathsize=¨22px¨»1«/mn»«/msub»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨ mathsize=¨22px¨»=«/mo»«msqrt mathcolor=¨#0000FF¨»«mfrac»«mrow»«mi mathvariant=¨bold¨ mathsize=¨22px¨»K«/mi»«mo mathvariant=¨bold¨ mathsize=¨22px¨»§#183;«/mo»«msub»«mi mathvariant=¨bold¨ mathsize=¨22px¨»Q«/mi»«mn mathvariant=¨bold¨ mathsize=¨22px¨»1«/mn»«/msub»«mo mathvariant=¨bold¨ mathsize=¨22px¨»§#183;«/mo»«mn mathvariant=¨bold¨ mathsize=¨22px¨»2«/mn»«mo mathvariant=¨bold¨ mathsize=¨22px¨»§#183;«/mo»«msub»«mi mathvariant=¨bold¨ mathsize=¨22px¨»§#949;«/mi»«mn mathvariant=¨bold¨ mathsize=¨22px¨»0«/mn»«/msub»«/mrow»«mi mathvariant=¨bold¨ mathsize=¨22px¨»§#963;«/mi»«/mfrac»«/msqrt»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨ mathsize=¨22px¨»=«/mo»«msqrt mathcolor=¨#0000FF¨»«mfrac»«mrow»«mn mathvariant=¨bold¨ mathsize=¨22px¨»9«/mn»«mo mathvariant=¨bold¨ mathsize=¨22px¨»§#183;«/mo»«msup»«mn mathvariant=¨bold¨ mathsize=¨22px¨»10«/mn»«mn mathvariant=¨bold¨ mathsize=¨22px¨»9«/mn»«/msup»«mo mathvariant=¨bold¨ mathsize=¨22px¨»§#183;«/mo»«mn mathvariant=¨bold¨ mathsize=¨22px¨»5«/mn»«mo mathvariant=¨bold¨ mathsize=¨22px¨»§#183;«/mo»«msup»«mn mathvariant=¨bold¨ mathsize=¨22px¨»10«/mn»«mrow»«mo mathvariant=¨bold¨ mathsize=¨22px¨»-«/mo»«mn mathvariant=¨bold¨ mathsize=¨22px¨»9«/mn»«/mrow»«/msup»«mo mathvariant=¨bold¨ mathsize=¨22px¨»§#183;«/mo»«mn mathvariant=¨bold¨ mathsize=¨22px¨»2«/mn»«mo mathvariant=¨bold¨ mathsize=¨22px¨»§#183;«/mo»«mn mathvariant=¨bold¨ mathsize=¨22px¨»8«/mn»«mo mathvariant=¨bold¨ mathsize=¨22px¨».«/mo»«mn mathvariant=¨bold¨ mathsize=¨22px¨»85«/mn»«mo mathvariant=¨bold¨ mathsize=¨22px¨»§#183;«/mo»«msup»«mn mathvariant=¨bold¨ mathsize=¨22px¨»10«/mn»«mrow»«mo mathvariant=¨bold¨ mathsize=¨22px¨»-«/mo»«mn mathvariant=¨bold¨ mathsize=¨22px¨»12«/mn»«/mrow»«/msup»«/mrow»«mrow»«mn mathvariant=¨bold¨ mathsize=¨22px¨»5«/mn»«mo mathvariant=¨bold¨ mathsize=¨22px¨».«/mo»«mn mathvariant=¨bold¨ mathsize=¨22px¨»31«/mn»«mo mathvariant=¨bold¨ mathsize=¨22px¨»§#183;«/mo»«msup»«mn mathvariant=¨bold¨ mathsize=¨22px¨»10«/mn»«mrow»«mo mathvariant=¨bold¨ mathsize=¨22px¨»-«/mo»«mn mathvariant=¨bold¨ mathsize=¨22px¨»11«/mn»«/mrow»«/msup»«/mrow»«/mfrac»«/msqrt»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨ mathsize=¨22px¨»=«/mo»«msqrt mathcolor=¨#0000FF¨»«mfrac»«mrow»«mn mathvariant=¨bold¨ mathsize=¨22px¨»7«/mn»«mo mathvariant=¨bold¨ mathsize=¨22px¨».«/mo»«mn mathvariant=¨bold¨ mathsize=¨22px¨»965«/mn»«mo mathvariant=¨bold¨ mathsize=¨22px¨»§#183;«/mo»«msup»«mn mathvariant=¨bold¨ mathsize=¨22px¨»10«/mn»«mrow»«mo mathvariant=¨bold¨ mathsize=¨22px¨»-«/mo»«mn mathvariant=¨bold¨ mathsize=¨22px¨»10«/mn»«/mrow»«/msup»«/mrow»«mrow»«mn mathvariant=¨bold¨ mathsize=¨22px¨»5«/mn»«mo mathvariant=¨bold¨ mathsize=¨22px¨».«/mo»«mn mathvariant=¨bold¨ mathsize=¨22px¨»31«/mn»«mo mathvariant=¨bold¨ mathsize=¨22px¨»§#183;«/mo»«msup»«mn mathvariant=¨bold¨ mathsize=¨22px¨»10«/mn»«mrow»«mo mathvariant=¨bold¨ mathsize=¨22px¨»-«/mo»«mn mathvariant=¨bold¨ mathsize=¨22px¨»11«/mn»«/mrow»«/msup»«/mrow»«/mfrac»«/msqrt»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨ mathsize=¨22px¨»=«/mo»«msqrt mathcolor=¨#0000FF¨»«mn mathvariant=¨bold¨ mathsize=¨22px¨»15«/mn»«/msqrt»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨ mathsize=¨22px¨»=«/mo»«mn mathvariant=¨bold¨ mathcolor=¨#0000FF¨ mathsize=¨22px¨»3«/mn»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨ mathsize=¨22px¨».«/mo»«mn mathvariant=¨bold¨ mathcolor=¨#0000FF¨ mathsize=¨22px¨»87«/mn»«mi mathvariant=¨bold¨ mathcolor=¨#0000FF¨ mathsize=¨22px¨»m«/mi»«/math»

26.3

عندما يتم نقل النقطة M إلى اليسار، فإن شدة الحقل الكهربائي الناتج عن اللوح المشحون في النقطة M لا تتغير.

لكي لا يتغير الحقل المحصّل في النقطة M، يجب ألا تتغير شدة الحقل الناتج عن الشحنة النقطية في النقطة M.

وبالتالي فإن قيمة d2 هي نفس قيمة d1.

شكل آخر للحل:

وبعد تحريك النقطة M إلى اليسار، تصبح محصّلة الحقلين مساوية لـ 8 نيوتن لكل كولون. ويتحقق:

«math xmlns=¨http://www.w3.org/1998/Math/MathML¨»«mstyle mathsize=¨24px¨»«msub»«mi mathvariant=¨bold¨ mathcolor=¨#0000FF¨»E«/mi»«mn mathvariant=¨bold¨ mathcolor=¨#0000FF¨»1«/mn»«/msub»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»+«/mo»«msub»«mi mathvariant=¨bold¨ mathcolor=¨#0000FF¨»E«/mi»«mn mathvariant=¨bold¨ mathcolor=¨#0000FF¨»2«/mn»«/msub»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»=«/mo»«mn mathvariant=¨bold¨ mathcolor=¨#0000FF¨»8«/mn»«mspace linebreak=¨newline¨/»«mspace linebreak=¨newline¨/»«mfrac mathcolor=¨#0000FF¨»«mrow»«mi mathvariant=¨bold¨»K«/mi»«mo mathvariant=¨bold¨»§#183;«/mo»«msub»«mi mathvariant=¨bold¨»Q«/mi»«mn mathvariant=¨bold¨»1«/mn»«/msub»«/mrow»«msup»«msub»«mi mathvariant=¨bold¨»d«/mi»«mn mathvariant=¨bold¨»2«/mn»«/msub»«mn mathvariant=¨bold¨»2«/mn»«/msup»«/mfrac»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»+«/mo»«mfrac mathcolor=¨#0000FF¨»«mi mathvariant=¨bold¨»§#963;«/mi»«mrow»«mn mathvariant=¨bold¨»2«/mn»«mo mathvariant=¨bold¨»§#183;«/mo»«msub»«mi mathvariant=¨bold¨»§#949;«/mi»«mn mathvariant=¨bold¨»0«/mn»«/msub»«/mrow»«/mfrac»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»=«/mo»«mn mathvariant=¨bold¨ mathcolor=¨#0000FF¨»8«/mn»«/mstyle»«/math»

كل قيم المقادير الظاهرة بالمعادلة: «math xmlns=¨http://www.w3.org/1998/Math/MathML¨»«mstyle mathsize=¨22px¨»«mi mathvariant=¨bold¨ mathcolor=¨#0000FF¨»K«/mi»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»,«/mo»«msub»«mi mathvariant=¨bold¨ mathcolor=¨#0000FF¨»Q«/mi»«mn mathvariant=¨bold¨ mathcolor=¨#0000FF¨»1«/mn»«/msub»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»,«/mo»«mi mathvariant=¨bold¨ mathcolor=¨#0000FF¨»§#963;«/mi»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»,«/mo»«msub»«mi mathvariant=¨bold¨ mathcolor=¨#0000FF¨»§#949;«/mi»«mn mathvariant=¨bold¨ mathcolor=¨#0000FF¨»0«/mn»«/msub»«/mstyle»«/math» في الحالة السابقة نفس القيم في هذه الحالة ، لذلك: «math xmlns=¨http://www.w3.org/1998/Math/MathML¨»«mstyle mathsize=¨24px¨»«msub»«mi mathvariant=¨bold¨ mathcolor=¨#0000FF¨»d«/mi»«mn mathvariant=¨bold¨ mathcolor=¨#0000FF¨»2«/mn»«/msub»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»=«/mo»«msub»«mi mathvariant=¨bold¨ mathcolor=¨#0000FF¨»d«/mi»«mn mathvariant=¨bold¨ mathcolor=¨#0000FF¨»1«/mn»«/msub»«/mstyle»«/math»

27.1

في النقطة A، يعمل حقلان: الحقل E1 الناتج من اللوح 1 والحقل E2 الناتج من اللوح 2.

نُشير لشدة الحقل المحصّل لهذين الحقلين بـ - EA , كما هو مبين في الشكل:

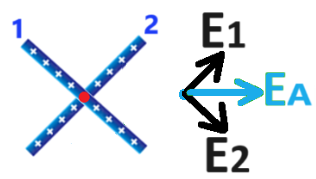
في النقطة B، يعمل حقلان مماثلان للحقلين العاملين في النقطة A، ولكن في اتجاهاين مختلفين. نُشير إلى الحقل المحصّل في النقطة B بـ E_B:

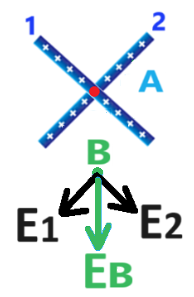
نصف متجهات الحقل بالنقطتين A و- B:

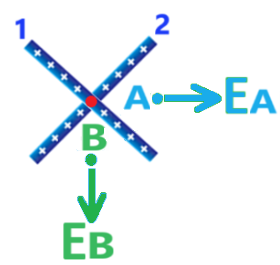
27.2

لحساب شدة الحقل المحصّل في النقطة A، نقوم بإجراء تحليل قائم الزاوية للحقلين E₁ وE₂.

نختار هيئة محاور بحيث يكون اتجاه المحور X أفقيًا، واتجاه المحور Y عموديًا.

من التخطيط التالي يمكنك أن ترى أن الزاوية α هي الزاوية المحصورة بين E_1Y وE₁.

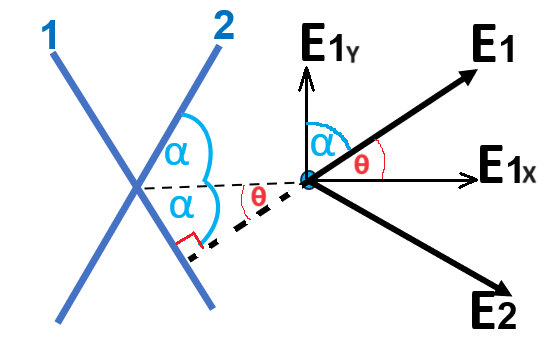
نقوم بتحليل قائم الزاوية للحقل E1:

«math xmlns=¨http://www.w3.org/1998/Math/MathML¨»«mstyle mathsize=¨20px¨»«msub»«mi mathvariant=¨bold¨ mathcolor=¨#0000FF¨»E«/mi»«msub mathcolor=¨#0000FF¨»«mn mathvariant=¨bold¨»1«/mn»«mi mathvariant=¨bold¨»Y«/mi»«/msub»«/msub»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»=«/mo»«msub»«mi mathvariant=¨bold¨ mathcolor=¨#0000FF¨»E«/mi»«mn mathvariant=¨bold¨ mathcolor=¨#0000FF¨»1«/mn»«/msub»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»§#183;«/mo»«mi mathvariant=¨bold¨ mathcolor=¨#0000FF¨»cos«/mi»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»(«/mo»«mi mathvariant=¨bold¨ mathcolor=¨#0000FF¨»§#945;«/mi»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»)«/mo»«mspace linebreak=¨newline¨/»«mrow mathcolor=¨#0000FF¨»«msub»«mi mathvariant=¨bold¨»E«/mi»«msub»«mn mathvariant=¨bold¨»1«/mn»«mi mathvariant=¨bold¨»X«/mi»«/msub»«/msub»«mo mathvariant=¨bold¨»=«/mo»«msub»«mi mathvariant=¨bold¨»E«/mi»«mn mathvariant=¨bold¨»1«/mn»«/msub»«mo mathvariant=¨bold¨»§#183;«/mo»«mi mathvariant=¨bold¨»sin«/mi»«mo mathvariant=¨bold¨»(«/mo»«mi mathvariant=¨bold¨»§#945;«/mi»«mo mathvariant=¨bold¨»)«/mo»«/mrow»«/mstyle»«/math»

وبالمثل الزاوية المحصورة بين E2Y و E2 تساوي الزاوية α:

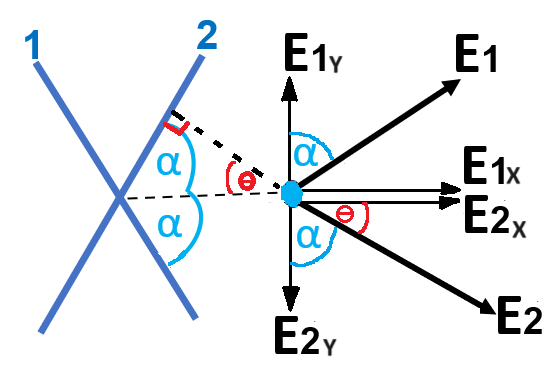
نقوم بتحليل قائم الزاوية للحقل E2:

«math xmlns=¨http://www.w3.org/1998/Math/MathML¨»«mstyle mathsize=¨20px¨»«msub»«mi mathvariant=¨bold¨ mathcolor=¨#0000FF¨»E«/mi»«msub mathcolor=¨#0000FF¨»«mn mathvariant=¨bold¨»2«/mn»«mi mathvariant=¨bold¨»Y«/mi»«/msub»«/msub»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»=«/mo»«msub»«mi mathvariant=¨bold¨ mathcolor=¨#0000FF¨»E«/mi»«mn mathvariant=¨bold¨ mathcolor=¨#0000FF¨»2«/mn»«/msub»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»§#183;«/mo»«mi mathvariant=¨bold¨ mathcolor=¨#0000FF¨»cos«/mi»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»(«/mo»«mi mathvariant=¨bold¨ mathcolor=¨#0000FF¨»§#945;«/mi»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»)«/mo»«mspace linebreak=¨newline¨/»«mrow mathcolor=¨#0000FF¨»«msub»«mi mathvariant=¨bold¨»E«/mi»«msub»«mn mathvariant=¨bold¨»2«/mn»«mi mathvariant=¨bold¨»X«/mi»«/msub»«/msub»«mo mathvariant=¨bold¨»=«/mo»«msub»«mi mathvariant=¨bold¨»E«/mi»«mn mathvariant=¨bold¨»2«/mn»«/msub»«mo mathvariant=¨bold¨»§#183;«/mo»«mi mathvariant=¨bold¨»sin«/mi»«mo mathvariant=¨bold¨»(«/mo»«mi mathvariant=¨bold¨»§#945;«/mi»«mo mathvariant=¨bold¨»)«/mo»«/mrow»«/mstyle»«/math»

في اتجاه المحور Y: الحقلان E1Y وE2Y يلغيان أحدهما الآخر. الحقل المحصّل في النقطة A يساوي مجموع الحقلين E1X و- E2X

نُعبر عن شدة الحقل المحصّل في النقطة A :

«math xmlns=¨http://www.w3.org/1998/Math/MathML¨»«mstyle mathsize=¨20px¨»«msub»«mi mathvariant=¨bold¨ mathcolor=¨#0000FF¨»E«/mi»«mi mathvariant=¨bold¨ mathcolor=¨#0000FF¨»A«/mi»«/msub»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»=«/mo»«msub»«msub»«mi mathvariant=¨bold¨ mathcolor=¨#0000FF¨»E«/mi»«mn mathvariant=¨bold¨ mathcolor=¨#0000FF¨»1«/mn»«/msub»«mi mathvariant=¨bold¨ mathcolor=¨#0000FF¨»X«/mi»«/msub»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»+«/mo»«msub»«mi mathvariant=¨bold¨ mathcolor=¨#0000FF¨»E«/mi»«msub mathcolor=¨#0000FF¨»«mn mathvariant=¨bold¨»2«/mn»«mi mathvariant=¨bold¨»X«/mi»«/msub»«/msub»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»=«/mo»«msub»«mi mathvariant=¨bold¨ mathcolor=¨#0000FF¨»E«/mi»«mn mathvariant=¨bold¨ mathcolor=¨#0000FF¨»1«/mn»«/msub»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»§#183;«/mo»«mi mathvariant=¨bold¨ mathcolor=¨#0000FF¨»sin«/mi»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»(«/mo»«mi mathvariant=¨bold¨ mathcolor=¨#0000FF¨»§#945;«/mi»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»)«/mo»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»+«/mo»«mrow mathcolor=¨#0000FF¨»«msub»«mi mathvariant=¨bold¨»E«/mi»«mn mathvariant=¨bold¨»2«/mn»«/msub»«mo mathvariant=¨bold¨»§#183;«/mo»«mi mathvariant=¨bold¨»sin«/mi»«mo mathvariant=¨bold¨»(«/mo»«mi mathvariant=¨bold¨»§#945;«/mi»«mo mathvariant=¨bold¨»)«/mo»«/mrow»«/mstyle»«/math»

كثافة الشحنة في اللوحين هي نفسها، وبالتالي فإن شدة الحقلين E1 وE2 الناتجين من اللوحين متساويين، ونعبر عن شدة الحقل المحصّل في النقطة A، باستخدام تعبير الحقل الناتج من اللوح المشحون:

«math xmlns=¨http://www.w3.org/1998/Math/MathML¨»«mstyle mathsize=¨20px¨»«mrow»«msub»«mi mathvariant=¨bold¨ mathcolor=¨#0000FF¨»E«/mi»«mi mathvariant=¨bold¨ mathcolor=¨#0000FF¨»A«/mi»«/msub»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»=«/mo»«msub»«mi mathvariant=¨bold¨ mathcolor=¨#0000FF¨»E«/mi»«mn mathvariant=¨bold¨ mathcolor=¨#0000FF¨»1«/mn»«/msub»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»§#183;«/mo»«mi mathvariant=¨bold¨ mathcolor=¨#0000FF¨»sin«/mi»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»(«/mo»«mi mathvariant=¨bold¨ mathcolor=¨#0000FF¨»§#945;«/mi»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»)«/mo»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»+«/mo»«mrow mathcolor=¨#0000FF¨»«msub»«mi mathvariant=¨bold¨»E«/mi»«mn mathvariant=¨bold¨»2«/mn»«/msub»«mo mathvariant=¨bold¨»§#183;«/mo»«mi mathvariant=¨bold¨»sin«/mi»«mo mathvariant=¨bold¨»(«/mo»«mi mathvariant=¨bold¨»§#945;«/mi»«mo mathvariant=¨bold¨»)«/mo»«/mrow»«/mrow»«mspace linebreak=¨newline¨/»«msub»«mi mathvariant=¨bold¨ mathcolor=¨#0000FF¨»E«/mi»«mi mathvariant=¨bold¨ mathcolor=¨#0000FF¨»A«/mi»«/msub»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»=«/mo»«mfrac mathcolor=¨#0000FF¨»«mi mathvariant=¨bold¨»§#963;«/mi»«mrow»«mn mathvariant=¨bold¨»2«/mn»«mo mathvariant=¨bold¨»§#183;«/mo»«msub»«mi mathvariant=¨bold¨»§#949;«/mi»«mn mathvariant=¨bold¨»0«/mn»«/msub»«/mrow»«/mfrac»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»§#183;«/mo»«mi mathvariant=¨bold¨ mathcolor=¨#0000FF¨»sin«/mi»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»(«/mo»«mi mathvariant=¨bold¨ mathcolor=¨#0000FF¨»§#945;«/mi»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»)«/mo»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»+«/mo»«mrow mathcolor=¨#0000FF¨»«mfrac»«mi mathvariant=¨bold¨»§#963;«/mi»«mrow»«mn mathvariant=¨bold¨»2«/mn»«mo mathvariant=¨bold¨»§#183;«/mo»«msub»«mi mathvariant=¨bold¨»§#949;«/mi»«mn mathvariant=¨bold¨»0«/mn»«/msub»«/mrow»«/mfrac»«mo mathvariant=¨bold¨»§#183;«/mo»«mi mathvariant=¨bold¨»sin«/mi»«mo mathvariant=¨bold¨»(«/mo»«mi mathvariant=¨bold¨»§#945;«/mi»«mo mathvariant=¨bold¨»)«/mo»«/mrow»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»=«/mo»«menclose mathcolor=¨#0000FF¨ notation=¨updiagonalstrike¨»«mn mathvariant=¨bold¨»2«/mn»«/menclose»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»§#183;«/mo»«mfrac mathcolor=¨#0000FF¨»«mi mathvariant=¨bold¨»§#963;«/mi»«mrow»«menclose notation=¨updiagonalstrike¨»«mn mathvariant=¨bold¨»2«/mn»«/menclose»«mo mathvariant=¨bold¨»§#183;«/mo»«msub»«mi mathvariant=¨bold¨»§#949;«/mi»«mn mathvariant=¨bold¨»0«/mn»«/msub»«/mrow»«/mfrac»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»§#183;«/mo»«mi mathvariant=¨bold¨ mathcolor=¨#0000FF¨»sin«/mi»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»(«/mo»«mi mathvariant=¨bold¨ mathcolor=¨#0000FF¨»§#945;«/mi»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»)«/mo»«mspace linebreak=¨newline¨/»«mspace linebreak=¨newline¨/»«menclose mathcolor=¨#0000FF¨ notation=¨circle¨»«msub»«mi mathvariant=¨bold¨»E«/mi»«mi mathvariant=¨bold¨»A«/mi»«/msub»«mo mathvariant=¨bold¨»=«/mo»«mfrac»«mi mathvariant=¨bold¨»§#963;«/mi»«msub»«mi mathvariant=¨bold¨»§#949;«/mi»«mn mathvariant=¨bold¨»0«/mn»«/msub»«/mfrac»«mo mathvariant=¨bold¨»§#183;«/mo»«mi mathvariant=¨bold¨»sin«/mi»«mo mathvariant=¨bold¨»(«/mo»«mi mathvariant=¨bold¨»§#945;«/mi»«mo mathvariant=¨bold¨»)«/mo»«/menclose»«/mstyle»«/math»

27.3

نحسب شدة الحقل في النقطة A باستخدام تعبير الحقل في النقطة A من البند السابق.

«math xmlns=¨http://www.w3.org/1998/Math/MathML¨»«mstyle mathsize=¨20px¨»«msub»«mi mathvariant=¨bold¨ mathcolor=¨#0000FF¨»E«/mi»«mi mathvariant=¨bold¨ mathcolor=¨#0000FF¨»A«/mi»«/msub»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»=«/mo»«mfrac mathcolor=¨#0000FF¨»«mi mathvariant=¨bold¨»§#963;«/mi»«msub»«mi mathvariant=¨bold¨»§#949;«/mi»«mn mathvariant=¨bold¨»0«/mn»«/msub»«/mfrac»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»§#183;«/mo»«mi mathvariant=¨bold¨ mathcolor=¨#0000FF¨»sin«/mi»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»(«/mo»«mi mathvariant=¨bold¨ mathcolor=¨#0000FF¨»§#945;«/mi»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»)«/mo»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»=«/mo»«mfrac mathcolor=¨#0000FF¨»«mrow»«mn mathvariant=¨bold¨»8«/mn»«mo mathvariant=¨bold¨»§#183;«/mo»«msup»«mn mathvariant=¨bold¨»10«/mn»«mrow»«mo mathvariant=¨bold¨»-«/mo»«mn mathvariant=¨bold¨»9«/mn»«/mrow»«/msup»«/mrow»«mrow»«mn mathvariant=¨bold¨»8«/mn»«mo mathvariant=¨bold¨».«/mo»«mn mathvariant=¨bold¨»85«/mn»«mo mathvariant=¨bold¨»§#183;«/mo»«msup»«mn mathvariant=¨bold¨»10«/mn»«mrow»«mo mathvariant=¨bold¨»-«/mo»«mn mathvariant=¨bold¨»12«/mn»«/mrow»«/msup»«/mrow»«/mfrac»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»§#183;«/mo»«mi mathvariant=¨bold¨ mathcolor=¨#0000FF¨»sin«/mi»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»(«/mo»«mn mathvariant=¨bold¨ mathcolor=¨#0000FF¨»40«/mn»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»)«/mo»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»=«/mo»«mn mathvariant=¨bold¨ mathcolor=¨#0000FF¨»581«/mn»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨».«/mo»«mn mathvariant=¨bold¨ mathcolor=¨#0000FF¨»05«/mn»«mfrac mathcolor=¨#0000FF¨»«mi mathvariant=¨bold¨»N«/mi»«mi mathvariant=¨bold¨»C«/mi»«/mfrac»«/mstyle»«/math»

27.4

يُكوّن كل لوح مشحون حقلًا متجانسًا، والحقل المحصّل لحقلين متجانسين هو أيضًا حقل متجانس. ولذلك فإن شدة الحقل في النقطة M تساوي شدة الحقل في النقطة A.

نحسب شدة الحقل الكهربائي في النقطة M باستخدام تعبير الحقل في النقطة A:

27.5

حسب الزوايا بين اللوحين في كل منطقة، تكون شدة الحقل في المنطقة A هي نفس شدة الحقل في المنطقة ג'

شدة الحقل في المجال ב' تساوي شدة الحقل في المنطقة ד'.

قيمة الزاوية α في المنطقتين א' و- ג' هي 30 درجة، احسب بناء على ذلك شدة الحقل في المنطقتين א' و- ג' :

«math xmlns=¨http://www.w3.org/1998/Math/MathML¨»«mstyle mathsize=¨20px¨»«mmultiscripts»«mi mathvariant=¨bold¨ mathcolor=¨#0000FF¨»E«/mi»«mprescripts/»«mrow mathcolor=¨#0000FF¨»«mo mathvariant=¨bold¨»`«/mo»«mi mathvariant=¨bold¨»§#1490;«/mi»«mo mathvariant=¨bold¨»§#160;«/mo»«mi mathvariant=¨bold¨»§#1605;§#1606;§#1591;§#1602;§#1577;«/mi»«/mrow»«none/»«/mmultiscripts»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»=«/mo»«mrow»«mmultiscripts»«mi mathvariant=¨bold¨ mathcolor=¨#0000FF¨»E«/mi»«mprescripts/»«mrow mathcolor=¨#0000FF¨»«mo mathvariant=¨bold¨»`«/mo»«mi mathvariant=¨bold¨»§#1488;«/mi»«mo mathvariant=¨bold¨»§#160;«/mo»«mi mathvariant=¨bold¨»§#1605;§#1606;§#1591;§#1602;§#1577;«/mi»«/mrow»«none/»«/mmultiscripts»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»=«/mo»«mfrac mathcolor=¨#0000FF¨»«mi mathvariant=¨bold¨»§#963;«/mi»«msub»«mi mathvariant=¨bold¨»§#949;«/mi»«mn mathvariant=¨bold¨»0«/mn»«/msub»«/mfrac»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»§#183;«/mo»«mi mathvariant=¨bold¨ mathcolor=¨#0000FF¨»sin«/mi»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»(«/mo»«mi mathvariant=¨bold¨ mathcolor=¨#0000FF¨»§#945;«/mi»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»)«/mo»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»=«/mo»«mfrac mathcolor=¨#0000FF¨»«mrow»«mn mathvariant=¨bold¨»8«/mn»«mo mathvariant=¨bold¨»§#183;«/mo»«msup»«mn mathvariant=¨bold¨»10«/mn»«mrow»«mo mathvariant=¨bold¨»-«/mo»«mn mathvariant=¨bold¨»9«/mn»«/mrow»«/msup»«/mrow»«mrow»«mn mathvariant=¨bold¨»8«/mn»«mo mathvariant=¨bold¨».«/mo»«mn mathvariant=¨bold¨»85«/mn»«mo mathvariant=¨bold¨»§#183;«/mo»«msup»«mn mathvariant=¨bold¨»10«/mn»«mrow»«mo mathvariant=¨bold¨»-«/mo»«mn mathvariant=¨bold¨»12«/mn»«/mrow»«/msup»«/mrow»«/mfrac»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»§#183;«/mo»«mi mathvariant=¨bold¨ mathcolor=¨#0000FF¨»sin«/mi»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»(«/mo»«mn mathvariant=¨bold¨ mathcolor=¨#0000FF¨»30«/mn»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»)«/mo»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»=«/mo»«mn mathvariant=¨bold¨ mathcolor=¨#0000FF¨»451«/mn»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨».«/mo»«mn mathvariant=¨bold¨ mathcolor=¨#0000FF¨»97«/mn»«mfrac mathcolor=¨#0000FF¨»«mi mathvariant=¨bold¨»N«/mi»«mi mathvariant=¨bold¨»C«/mi»«/mfrac»«/mrow»«/mstyle»«/math»

نُشير إلى الزاوية المقابلة للزاوية α في المنطقتين ב' و- ד' بـ β، وفي الشكل التالي يتم وصف الزاويتين في المناطق الأربع:

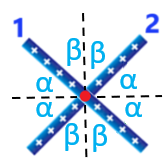
نحسب قيمة الزاوية β:

«math xmlns=¨http://www.w3.org/1998/Math/MathML¨»«mstyle mathsize=¨20px¨»«mn mathvariant=¨bold¨ mathcolor=¨#0000FF¨»4«/mn»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»§#183;«/mo»«mi mathvariant=¨bold¨ mathcolor=¨#0000FF¨»§#945;«/mi»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»+«/mo»«mn mathvariant=¨bold¨ mathcolor=¨#0000FF¨»4«/mn»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»§#183;«/mo»«mi mathvariant=¨bold¨ mathcolor=¨#0000FF¨»§#946;«/mi»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»=«/mo»«mn mathvariant=¨bold¨ mathcolor=¨#0000FF¨»360«/mn»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»§#176;«/mo»«mspace linebreak=¨newline¨/»«mspace linebreak=¨newline¨/»«mi mathvariant=¨bold¨ mathcolor=¨#0000FF¨»§#946;«/mi»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»=«/mo»«mfrac mathcolor=¨#0000FF¨»«mrow»«mn mathvariant=¨bold¨»360«/mn»«mo mathvariant=¨bold¨»-«/mo»«mn mathvariant=¨bold¨»4«/mn»«mo mathvariant=¨bold¨»§#183;«/mo»«mi mathvariant=¨bold¨»§#945;«/mi»«/mrow»«mn mathvariant=¨bold¨»4«/mn»«/mfrac»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»=«/mo»«mfrac mathcolor=¨#0000FF¨»«mrow»«mn mathvariant=¨bold¨»360«/mn»«mo mathvariant=¨bold¨»-«/mo»«mn mathvariant=¨bold¨»4«/mn»«mo mathvariant=¨bold¨»§#183;«/mo»«mn mathvariant=¨bold¨»30«/mn»«/mrow»«mn mathvariant=¨bold¨»4«/mn»«/mfrac»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»=«/mo»«mfrac mathcolor=¨#0000FF¨»«mn mathvariant=¨bold¨»240«/mn»«mn mathvariant=¨bold¨»4«/mn»«/mfrac»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»=«/mo»«mn mathvariant=¨bold¨ mathcolor=¨#0000FF¨»60«/mn»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»§#176;«/mo»«/mstyle»«/math»

نحسب شدة الحقل الكهربائي بالمنطقتين ב' و- ד':

«math xmlns=¨http://www.w3.org/1998/Math/MathML¨»«mstyle mathsize=¨20px¨»«mmultiscripts»«mi mathvariant=¨bold¨ mathcolor=¨#0000FF¨»E«/mi»«mprescripts/»«mrow mathcolor=¨#0000FF¨»«mo mathvariant=¨bold¨»`«/mo»«mi mathvariant=¨bold¨»§#1491;«/mi»«mo mathvariant=¨bold¨»§#160;«/mo»«mi mathvariant=¨bold¨»§#1605;§#1606;§#1591;§#1602;§#1577;«/mi»«/mrow»«none/»«/mmultiscripts»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»=«/mo»«mrow»«mmultiscripts»«mi mathvariant=¨bold¨ mathcolor=¨#0000FF¨»E«/mi»«mprescripts/»«mrow mathcolor=¨#0000FF¨»«mo mathvariant=¨bold¨»`«/mo»«mi mathvariant=¨bold¨»§#1489;«/mi»«mo mathvariant=¨bold¨»§#160;«/mo»«mi mathvariant=¨bold¨»§#1605;§#1606;§#1591;§#1602;§#1577;«/mi»«/mrow»«none/»«/mmultiscripts»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»=«/mo»«mfrac mathcolor=¨#0000FF¨»«mi mathvariant=¨bold¨»§#963;«/mi»«msub»«mi mathvariant=¨bold¨»§#949;«/mi»«mn mathvariant=¨bold¨»0«/mn»«/msub»«/mfrac»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»§#183;«/mo»«mi mathvariant=¨bold¨ mathcolor=¨#0000FF¨»sin«/mi»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»(«/mo»«mi mathvariant=¨bold¨ mathcolor=¨#0000FF¨»§#945;«/mi»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»)«/mo»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»=«/mo»«mfrac mathcolor=¨#0000FF¨»«mrow»«mn mathvariant=¨bold¨»8«/mn»«mo mathvariant=¨bold¨»§#183;«/mo»«msup»«mn mathvariant=¨bold¨»10«/mn»«mrow»«mo mathvariant=¨bold¨»-«/mo»«mn mathvariant=¨bold¨»9«/mn»«/mrow»«/msup»«/mrow»«mrow»«mn mathvariant=¨bold¨»8«/mn»«mo mathvariant=¨bold¨».«/mo»«mn mathvariant=¨bold¨»85«/mn»«mo mathvariant=¨bold¨»§#183;«/mo»«msup»«mn mathvariant=¨bold¨»10«/mn»«mrow»«mo mathvariant=¨bold¨»-«/mo»«mn mathvariant=¨bold¨»12«/mn»«/mrow»«/msup»«/mrow»«/mfrac»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»§#183;«/mo»«mi mathvariant=¨bold¨ mathcolor=¨#0000FF¨»sin«/mi»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»(«/mo»«mn mathvariant=¨bold¨ mathcolor=¨#0000FF¨»60«/mn»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»)«/mo»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»=«/mo»«mn mathvariant=¨bold¨ mathcolor=¨#0000FF¨»782«/mn»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨».«/mo»«mn mathvariant=¨bold¨ mathcolor=¨#0000FF¨»84«/mn»«mfrac mathcolor=¨#0000FF¨»«mi mathvariant=¨bold¨»N«/mi»«mi mathvariant=¨bold¨»C«/mi»«/mfrac»«/mrow»«/mstyle»«/math»

27.6

اتجاه خطوط الحقل في أي نقطة هو اتجاه القوة الكهربائية المحصّلة المؤثرة على شحنة الفحص الموجودة في هذه النقطة.

في المنطقتين ב' و- ד' شدة الحقل أكبر من شدة الحقل في المنطقتين א' و- ג'. ولذلك، في المناطق ב' و- ד' ، تكون كثافة خطوط الحقل أكبر.

ينبغي وصف خطوط الحقل بشكل عام فقط.

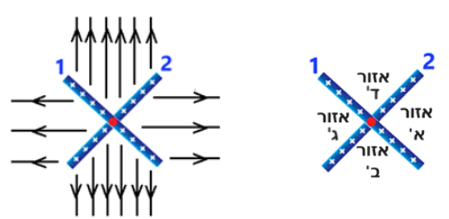
28.1

نحسب شحنة الكرة حسب كمية الإلكترونات الزائدة وشحنة الإلكترون:

«math xmlns=¨http://www.w3.org/1998/Math/MathML¨»«mi mathvariant=¨bold¨ mathcolor=¨#0000FF¨»Q«/mi»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»=«/mo»«mi mathvariant=¨bold¨ mathcolor=¨#0000FF¨»N«/mi»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»§#183;«/mo»«msub»«mi mathvariant=¨bold¨ mathcolor=¨#0000FF¨»q«/mi»«mi mathvariant=¨bold¨ mathcolor=¨#0000FF¨»e«/mi»«/msub»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»=«/mo»«mn mathvariant=¨bold¨ mathcolor=¨#0000FF¨»3«/mn»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»§#183;«/mo»«msup»«mn mathvariant=¨bold¨ mathcolor=¨#0000FF¨»10«/mn»«mn mathvariant=¨bold¨ mathcolor=¨#0000FF¨»9«/mn»«/msup»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»§#183;«/mo»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»(«/mo»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»-«/mo»«mn mathvariant=¨bold¨ mathcolor=¨#0000FF¨»1«/mn»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨».«/mo»«mn mathvariant=¨bold¨ mathcolor=¨#0000FF¨»6«/mn»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»§#183;«/mo»«msup»«mn mathvariant=¨bold¨ mathcolor=¨#0000FF¨»10«/mn»«mrow mathcolor=¨#0000FF¨»«mo mathvariant=¨bold¨»-«/mo»«mn mathvariant=¨bold¨»19«/mn»«/mrow»«/msup»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»)«/mo»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»=«/mo»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»-«/mo»«mn mathvariant=¨bold¨ mathcolor=¨#0000FF¨»4«/mn»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨».«/mo»«mn mathvariant=¨bold¨ mathcolor=¨#0000FF¨»8«/mn»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»§#183;«/mo»«msup»«mn mathvariant=¨bold¨ mathcolor=¨#0000FF¨»10«/mn»«mrow mathcolor=¨#0000FF¨»«mo mathvariant=¨bold¨»-«/mo»«mn mathvariant=¨bold¨»10«/mn»«/mrow»«/msup»«mi mathvariant=¨bold¨ mathcolor=¨#0000FF¨»C«/mi»«/math»

28.2

لايجاد شدة الحقل الكهربائي في نقطة ما، ضع شحنة فحص في هذه النقطة واحسب النسبة بين القوة الكهربائية المؤثرة على شحنة الفحص ومقدار شحنة الفحص، وفقًا لتعريف الحقل.

لايجاد شدة الحقل الكهربائي في نقطة مركز الكرة المشحونة، يتم وضع شحنة فحص في النقطة المركزية للكرة.

وبما أن الشحنة الزائدة تتوزع على سطح الكرة في توزيع متجانس للشحنة، فإن محصّل القوى المؤثرة على شحنة الفحص الموجودة في النقطة المركزية للكرة المشحونة سيكون مساوياً للصفر.

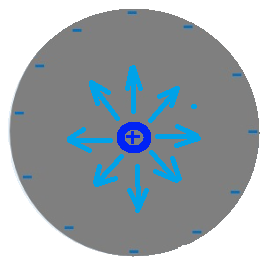
ولذلك، ومن تعريف الحقل الكهربائي، فإن شدة الحقل الكهربائي في مركز الكرة تساوي صفرًا.

28.3

نتطرق إلى نقطة تبعد 10 سم في الجزء العلوي من الكرة، ونضع شحنة فحص في هذه النقطة.

على شحنة الفحص ستعمل القليل من القوى القوية في اتجاه الجزء العلوي من الكرة وستعمل الكثير من القوى الضعيفة في اتجاه الجزء السفلي من الكرة. كما هو موضح في الشكل التالي:

في أي نقطة داخل الكرة المشحونة، يكون مقدار القوة الكهربائية المحصّلئة المؤثرة على شحنة الفحص صفرًا. ولذلك فمن تعريف الحقل الكهربائي فإن شدة الحقل الكهربائي داخل الكرة المشحونة تساوي صفرًا. ليس فقط في مركز الكرة.

28.4

لحساب شدة الحقل الكهربائي الناتج عن الكرة المشحونة في نقطة خارج الكرة، يجب استخدام التعبير عن الحقل الكهربائي بالقرب من شحنة نقطية. نتعامل مع شحنة الكرة المشحونة على أنها شحنة نقطية تقع في مركز الكرة:

«math xmlns=¨http://www.w3.org/1998/Math/MathML¨»«mstyle mathsize=¨22px¨»«msub»«mi mathvariant=¨bold¨ mathcolor=¨#0000FF¨»E«/mi»«mi mathvariant=¨bold¨ mathcolor=¨#0000FF¨»C«/mi»«/msub»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»=«/mo»«mfrac mathcolor=¨#0000FF¨»«mrow»«mi mathvariant=¨bold¨»K«/mi»«mo mathvariant=¨bold¨»§#183;«/mo»«mi mathvariant=¨bold¨»Q«/mi»«/mrow»«msup»«mi mathvariant=¨bold¨»R«/mi»«mn mathvariant=¨bold¨»2«/mn»«/msup»«/mfrac»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»=«/mo»«mfrac mathcolor=¨#0000FF¨»«mrow»«mn mathvariant=¨bold¨»9«/mn»«mo mathvariant=¨bold¨»§#183;«/mo»«msup»«mn mathvariant=¨bold¨»10«/mn»«mn mathvariant=¨bold¨»9«/mn»«/msup»«mo mathvariant=¨bold¨»§#183;«/mo»«mo mathvariant=¨bold¨»-«/mo»«mn mathvariant=¨bold¨»4«/mn»«mo mathvariant=¨bold¨».«/mo»«mn mathvariant=¨bold¨»8«/mn»«mo mathvariant=¨bold¨»§#183;«/mo»«msup»«mn mathvariant=¨bold¨»10«/mn»«mrow»«mo mathvariant=¨bold¨»-«/mo»«mn mathvariant=¨bold¨»10«/mn»«/mrow»«/msup»«/mrow»«mrow»«mn mathvariant=¨bold¨»0«/mn»«mo mathvariant=¨bold¨».«/mo»«msup»«mn mathvariant=¨bold¨»2«/mn»«mn mathvariant=¨bold¨»2«/mn»«/msup»«/mrow»«/mfrac»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»=«/mo»«mfrac mathcolor=¨#0000FF¨»«mrow»«mn mathvariant=¨bold¨»4«/mn»«mo mathvariant=¨bold¨».«/mo»«mn mathvariant=¨bold¨»32«/mn»«/mrow»«mrow»«mn mathvariant=¨bold¨»0«/mn»«mo mathvariant=¨bold¨».«/mo»«mn mathvariant=¨bold¨»04«/mn»«/mrow»«/mfrac»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»=«/mo»«mn mathvariant=¨bold¨ mathcolor=¨#0000FF¨»108«/mn»«mfrac mathcolor=¨#0000FF¨»«mi mathvariant=¨bold¨»N«/mi»«mi mathvariant=¨bold¨»C«/mi»«/mfrac»«/mstyle»«/math»

28.5

النقطة الواقعة على سطح الكرة تعتبر نقطة تقع خارج الكرة. نحسب شدة الحقل الكهربائي في النقطة D باستخدام صيغة حساب شدة الحقل بالقرب من شحنة نقطية.

نتعامل مع شحنة الكرة كشحنة نقطية متمركزة في نقطة مركز الكرة:

«math xmlns=¨http://www.w3.org/1998/Math/MathML¨»«mstyle mathsize=¨22px¨»«msub»«mi mathvariant=¨bold¨ mathcolor=¨#0000FF¨»E«/mi»«mi mathvariant=¨bold¨ mathcolor=¨#0000FF¨»D«/mi»«/msub»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»=«/mo»«mfrac mathcolor=¨#0000FF¨»«mrow»«mi mathvariant=¨bold¨»K«/mi»«mo mathvariant=¨bold¨»§#183;«/mo»«mi mathvariant=¨bold¨»Q«/mi»«/mrow»«msup»«mi mathvariant=¨bold¨»R«/mi»«mn mathvariant=¨bold¨»2«/mn»«/msup»«/mfrac»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»=«/mo»«mfrac mathcolor=¨#0000FF¨»«mrow»«mn mathvariant=¨bold¨»9«/mn»«mo mathvariant=¨bold¨»§#183;«/mo»«msup»«mn mathvariant=¨bold¨»10«/mn»«mn mathvariant=¨bold¨»9«/mn»«/msup»«mo mathvariant=¨bold¨»§#183;«/mo»«mo mathvariant=¨bold¨»-«/mo»«mn mathvariant=¨bold¨»4«/mn»«mo mathvariant=¨bold¨».«/mo»«mn mathvariant=¨bold¨»8«/mn»«mo mathvariant=¨bold¨»§#183;«/mo»«msup»«mn mathvariant=¨bold¨»10«/mn»«mrow»«mo mathvariant=¨bold¨»-«/mo»«mn mathvariant=¨bold¨»10«/mn»«/mrow»«/msup»«/mrow»«mrow»«mn mathvariant=¨bold¨»0«/mn»«mo mathvariant=¨bold¨».«/mo»«msup»«mn mathvariant=¨bold¨»15«/mn»«mn mathvariant=¨bold¨»2«/mn»«/msup»«/mrow»«/mfrac»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»=«/mo»«mfrac mathcolor=¨#0000FF¨»«mrow»«mn mathvariant=¨bold¨»4«/mn»«mo mathvariant=¨bold¨».«/mo»«mn mathvariant=¨bold¨»32«/mn»«/mrow»«mrow»«mn mathvariant=¨bold¨»0«/mn»«mo mathvariant=¨bold¨».«/mo»«mn mathvariant=¨bold¨»0225«/mn»«/mrow»«/mfrac»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»=«/mo»«mn mathvariant=¨bold¨ mathcolor=¨#0000FF¨»192«/mn»«mfrac mathcolor=¨#0000FF¨»«mi mathvariant=¨bold¨»N«/mi»«mi mathvariant=¨bold¨»C«/mi»«/mfrac»«/mstyle»«/math»