7.4
نرسم مخططًا للقوى المؤثرة على q3 عندما تكون محصلة القوى المؤثرة على q3 تساوي صفرًا.
نُشير للبعد بين q1 و q3 بـ r1,3 والبعد بين q2 و q3 بـ r2,3.
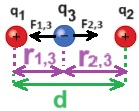
محصّلة القوى المؤثرة في هذه الحالة على q3 تساوي صفرًا. لنكتب معادلة الحركة:
«math xmlns=¨http://www.w3.org/1998/Math/MathML¨»«mstyle mathsize=¨22px¨»«mi mathvariant=¨bold-italic¨ mathcolor=¨#0000FF¨»§#931;«/mi»«mi mathvariant=¨bold-italic¨ mathcolor=¨#0000FF¨»F«/mi»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»=«/mo»«mn mathvariant=¨bold¨ mathcolor=¨#0000FF¨»0«/mn»«mspace linebreak=¨newline¨/»«mspace linebreak=¨newline¨/»«msub»«mi mathvariant=¨bold-italic¨ mathcolor=¨#0000FF¨»F«/mi»«mrow mathcolor=¨#0000FF¨»«mn mathvariant=¨bold¨»1«/mn»«mo mathvariant=¨bold¨»,«/mo»«mn mathvariant=¨bold¨»3«/mn»«/mrow»«/msub»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»=«/mo»«msub»«mi mathvariant=¨bold-italic¨ mathcolor=¨#0000FF¨»F«/mi»«mrow mathcolor=¨#0000FF¨»«mn mathvariant=¨bold¨»2«/mn»«mo mathvariant=¨bold¨»,«/mo»«mn mathvariant=¨bold¨»3«/mn»«/mrow»«/msub»«mspace linebreak=¨newline¨/»«mspace linebreak=¨newline¨/»«mfrac mathcolor=¨#0000FF¨»«mrow»«mi mathvariant=¨bold¨»K«/mi»«mo mathvariant=¨bold¨»§#183;«/mo»«msub»«mi mathvariant=¨bold¨»q«/mi»«mn mathvariant=¨bold¨»1«/mn»«/msub»«mo mathvariant=¨bold¨»§#183;«/mo»«msub»«mi mathvariant=¨bold¨»q«/mi»«mn mathvariant=¨bold¨»3«/mn»«/msub»«/mrow»«msup»«msub»«mi mathvariant=¨bold¨»r«/mi»«mrow»«mn mathvariant=¨bold¨»1«/mn»«mo mathvariant=¨bold¨»,«/mo»«mn mathvariant=¨bold¨»3«/mn»«/mrow»«/msub»«mn mathvariant=¨bold¨»2«/mn»«/msup»«/mfrac»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»=«/mo»«mfrac mathcolor=¨#0000FF¨»«mrow»«mi mathvariant=¨bold¨»K«/mi»«mo mathvariant=¨bold¨»§#183;«/mo»«msub»«mi mathvariant=¨bold¨»q«/mi»«mn mathvariant=¨bold¨»2«/mn»«/msub»«mo mathvariant=¨bold¨»§#183;«/mo»«msub»«mi mathvariant=¨bold¨»q«/mi»«mn mathvariant=¨bold¨»3«/mn»«/msub»«/mrow»«msup»«msub»«mi mathvariant=¨bold¨»r«/mi»«mrow»«mn mathvariant=¨bold¨»2«/mn»«mo mathvariant=¨bold¨»,«/mo»«mn mathvariant=¨bold¨»3«/mn»«/mrow»«/msub»«mn mathvariant=¨bold¨»2«/mn»«/msup»«/mfrac»«/mstyle»«/math»
نعمل عمليات اختزال :
«math xmlns=¨http://www.w3.org/1998/Math/MathML¨»«mfrac mathcolor=¨#0000FF¨»«mrow»«menclose notation=¨updiagonalstrike¨»«mi mathvariant=¨bold¨ mathsize=¨22px¨»K«/mi»«/menclose»«mo mathvariant=¨bold¨ mathsize=¨22px¨»§#183;«/mo»«msub»«mi mathvariant=¨bold¨ mathsize=¨22px¨»q«/mi»«mn mathvariant=¨bold¨ mathsize=¨22px¨»1«/mn»«/msub»«mo mathvariant=¨bold¨ mathsize=¨22px¨»§#183;«/mo»«menclose notation=¨downdiagonalstrike¨»«msub»«mi mathvariant=¨bold¨ mathsize=¨22px¨»q«/mi»«mn mathvariant=¨bold¨ mathsize=¨22px¨»3«/mn»«/msub»«/menclose»«/mrow»«msup»«msub»«mi mathvariant=¨bold¨ mathsize=¨22px¨»r«/mi»«mrow»«mn mathvariant=¨bold¨ mathsize=¨22px¨»1«/mn»«mo mathvariant=¨bold¨ mathsize=¨22px¨»,«/mo»«mn mathvariant=¨bold¨ mathsize=¨22px¨»3«/mn»«/mrow»«/msub»«mn mathvariant=¨bold¨ mathsize=¨22px¨»2«/mn»«/msup»«/mfrac»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨ mathsize=¨22px¨»=«/mo»«mfrac mathcolor=¨#0000FF¨»«mrow»«menclose notation=¨updiagonalstrike¨»«mi mathvariant=¨bold¨ mathsize=¨22px¨»K«/mi»«/menclose»«mo mathvariant=¨bold¨ mathsize=¨22px¨»§#183;«/mo»«msub»«mi mathvariant=¨bold¨ mathsize=¨22px¨»q«/mi»«mn mathvariant=¨bold¨ mathsize=¨22px¨»2«/mn»«/msub»«mo mathvariant=¨bold¨ mathsize=¨22px¨»§#183;«/mo»«menclose notation=¨downdiagonalstrike¨»«msub»«mi mathvariant=¨bold¨ mathsize=¨22px¨»q«/mi»«mn mathvariant=¨bold¨ mathsize=¨22px¨»3«/mn»«/msub»«/menclose»«/mrow»«msup»«msub»«mi mathvariant=¨bold¨ mathsize=¨22px¨»r«/mi»«mrow»«mn mathvariant=¨bold¨ mathsize=¨22px¨»2«/mn»«mo mathvariant=¨bold¨ mathsize=¨22px¨»,«/mo»«mn mathvariant=¨bold¨ mathsize=¨22px¨»3«/mn»«/mrow»«/msub»«mn mathvariant=¨bold¨ mathsize=¨22px¨»2«/mn»«/msup»«/mfrac»«mspace linebreak=¨newline¨/»«mspace linebreak=¨newline¨/»«mfrac mathcolor=¨#0000FF¨»«msub»«mi mathvariant=¨bold¨ mathsize=¨22px¨»q«/mi»«mn mathvariant=¨bold¨ mathsize=¨22px¨»1«/mn»«/msub»«msup»«msub»«mi mathvariant=¨bold¨ mathsize=¨22px¨»r«/mi»«mrow»«mn mathvariant=¨bold¨ mathsize=¨22px¨»1«/mn»«mo mathvariant=¨bold¨ mathsize=¨22px¨»,«/mo»«mn mathvariant=¨bold¨ mathsize=¨22px¨»3«/mn»«/mrow»«/msub»«mn mathvariant=¨bold¨ mathsize=¨22px¨»2«/mn»«/msup»«/mfrac»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨ mathsize=¨22px¨»=«/mo»«mfrac mathcolor=¨#0000FF¨»«msub»«mi mathvariant=¨bold¨ mathsize=¨22px¨»q«/mi»«mn mathvariant=¨bold¨ mathsize=¨22px¨»2«/mn»«/msub»«msup»«msub»«mi mathvariant=¨bold¨ mathsize=¨22px¨»r«/mi»«mrow»«mn mathvariant=¨bold¨ mathsize=¨22px¨»2«/mn»«mo mathvariant=¨bold¨ mathsize=¨22px¨»,«/mo»«mn mathvariant=¨bold¨ mathsize=¨22px¨»3«/mn»«/mrow»«/msub»«mn mathvariant=¨bold¨ mathsize=¨22px¨»2«/mn»«/msup»«/mfrac»«mspace linebreak=¨newline¨/»«mspace linebreak=¨newline¨/»«mfrac mathcolor=¨#0000FF¨»«msup»«msub»«mi mathvariant=¨bold¨ mathsize=¨22px¨»r«/mi»«mrow»«mn mathvariant=¨bold¨ mathsize=¨22px¨»2«/mn»«mo mathvariant=¨bold¨ mathsize=¨22px¨»,«/mo»«mn mathvariant=¨bold¨ mathsize=¨22px¨»3«/mn»«/mrow»«/msub»«mn mathvariant=¨bold¨ mathsize=¨22px¨»2«/mn»«/msup»«msup»«msub»«mi mathvariant=¨bold¨ mathsize=¨22px¨»r«/mi»«mrow»«mn mathvariant=¨bold¨ mathsize=¨22px¨»1«/mn»«mo mathvariant=¨bold¨ mathsize=¨22px¨»,«/mo»«mn mathvariant=¨bold¨ mathsize=¨22px¨»3«/mn»«/mrow»«/msub»«mn mathvariant=¨bold¨ mathsize=¨22px¨»2«/mn»«/msup»«/mfrac»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨ mathsize=¨22px¨»=«/mo»«mfrac mathcolor=¨#0000FF¨»«msub»«mi mathvariant=¨bold¨ mathsize=¨22px¨»q«/mi»«mn mathvariant=¨bold¨ mathsize=¨22px¨»2«/mn»«/msub»«msub»«mi mathvariant=¨bold¨ mathsize=¨22px¨»q«/mi»«mn mathvariant=¨bold¨ mathsize=¨22px¨»1«/mn»«/msub»«/mfrac»«mspace linebreak=¨newline¨/»«mspace linebreak=¨newline¨/»«menclose mathcolor=¨#0000FF¨ notation=¨box¨»«mfrac»«msub»«mi mathvariant=¨bold¨ mathsize=¨22px¨»r«/mi»«mrow»«mn mathvariant=¨bold¨ mathsize=¨22px¨»2«/mn»«mo mathvariant=¨bold¨ mathsize=¨22px¨»,«/mo»«mn mathvariant=¨bold¨ mathsize=¨22px¨»3«/mn»«/mrow»«/msub»«msub»«mi mathvariant=¨bold¨ mathsize=¨22px¨»r«/mi»«mrow»«mn mathvariant=¨bold¨ mathsize=¨22px¨»1«/mn»«mo mathvariant=¨bold¨ mathsize=¨22px¨»,«/mo»«mn mathvariant=¨bold¨ mathsize=¨22px¨»3«/mn»«/mrow»«/msub»«/mfrac»«mo mathvariant=¨bold¨ mathsize=¨22px¨»=«/mo»«msqrt»«mfrac»«msub»«mi mathvariant=¨bold¨ mathsize=¨22px¨»q«/mi»«mn mathvariant=¨bold¨ mathsize=¨22px¨»2«/mn»«/msub»«msub»«mi mathvariant=¨bold¨ mathsize=¨22px¨»q«/mi»«mn mathvariant=¨bold¨ mathsize=¨22px¨»1«/mn»«/msub»«/mfrac»«/msqrt»«/menclose»«/math»
مجموع البعدين r2,3 و r1,3 يساوي البعد d. ووفقًا لذلك نكتب معادلة أخرى بنفس المتغيرين: r2,3 و r1,3
«math xmlns=¨http://www.w3.org/1998/Math/MathML¨»«menclose mathcolor=¨#0000FF¨ notation=¨box¨»«msub»«mi mathvariant=¨bold¨ mathsize=¨22px¨»r«/mi»«mrow»«mn mathvariant=¨bold¨ mathsize=¨22px¨»1«/mn»«mo mathvariant=¨bold¨ mathsize=¨22px¨»,«/mo»«mn mathvariant=¨bold¨ mathsize=¨22px¨»3«/mn»«/mrow»«/msub»«mo mathvariant=¨bold¨ mathsize=¨22px¨»+«/mo»«msub»«mi mathvariant=¨bold¨ mathsize=¨22px¨»r«/mi»«mrow»«mn mathvariant=¨bold¨ mathsize=¨22px¨»2«/mn»«mo mathvariant=¨bold¨ mathsize=¨22px¨»,«/mo»«mn mathvariant=¨bold¨ mathsize=¨22px¨»3«/mn»«/mrow»«/msub»«mo mathvariant=¨bold¨ mathsize=¨22px¨»=«/mo»«mi mathvariant=¨bold¨ mathsize=¨22px¨»d«/mi»«/menclose»«mspace linebreak=¨newline¨/»«mspace linebreak=¨newline¨/»«/math»
نُعبر عن البعد اللازم r1,3 من المعادلتين :
«math xmlns=¨http://www.w3.org/1998/Math/MathML¨»«mstyle mathsize=¨20px¨»«menclose mathcolor=¨#0000FF¨ notation=¨box¨»«msub»«mi mathvariant=¨bold¨»r«/mi»«mrow»«mn mathvariant=¨bold¨»1«/mn»«mo mathvariant=¨bold¨»,«/mo»«mn mathvariant=¨bold¨»3«/mn»«/mrow»«/msub»«mo mathvariant=¨bold¨»+«/mo»«msub»«mi mathvariant=¨bold¨»r«/mi»«mrow»«mn mathvariant=¨bold¨»2«/mn»«mo mathvariant=¨bold¨»,«/mo»«mn mathvariant=¨bold¨»3«/mn»«/mrow»«/msub»«mo mathvariant=¨bold¨»=«/mo»«mi mathvariant=¨bold¨»d«/mi»«/menclose»«mo»§#160;«/mo»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»§#8658;«/mo»«msub»«mi mathvariant=¨bold¨ mathcolor=¨#0000FF¨»r«/mi»«mrow mathcolor=¨#0000FF¨»«mn mathvariant=¨bold¨»2«/mn»«mo mathvariant=¨bold¨»,«/mo»«mn mathvariant=¨bold¨»3«/mn»«/mrow»«/msub»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»=«/mo»«mi mathvariant=¨bold¨ mathcolor=¨#0000FF¨»d«/mi»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»-«/mo»«msub»«mi mathvariant=¨bold¨ mathcolor=¨#0000FF¨»r«/mi»«mrow mathcolor=¨#0000FF¨»«mn mathvariant=¨bold¨»1«/mn»«mo mathvariant=¨bold¨»,«/mo»«mn mathvariant=¨bold¨»3«/mn»«/mrow»«/msub»«mspace linebreak=¨newline¨/»«mspace linebreak=¨newline¨/»«/mstyle»«/math»
«math xmlns=¨http://www.w3.org/1998/Math/MathML¨»«mstyle mathsize=¨22px¨»«mspace linebreak=¨newline¨/»«menclose mathcolor=¨#0000FF¨ notation=¨box¨»«mfrac»«msub»«mi mathvariant=¨bold¨ mathcolor=¨#FF0000¨»r«/mi»«mrow mathcolor=¨#FF0000¨»«mn mathvariant=¨bold¨»2«/mn»«mo mathvariant=¨bold¨»,«/mo»«mn mathvariant=¨bold¨»3«/mn»«/mrow»«/msub»«msub»«mi mathvariant=¨bold¨»r«/mi»«mrow»«mn mathvariant=¨bold¨»1«/mn»«mo mathvariant=¨bold¨»,«/mo»«mn mathvariant=¨bold¨»3«/mn»«/mrow»«/msub»«/mfrac»«mo mathvariant=¨bold¨»=«/mo»«msqrt»«mfrac»«msub»«mi mathvariant=¨bold¨»q«/mi»«mn mathvariant=¨bold¨»2«/mn»«/msub»«msub»«mi mathvariant=¨bold¨»q«/mi»«mn mathvariant=¨bold¨»1«/mn»«/msub»«/mfrac»«/msqrt»«/menclose»«mo»§#160;«/mo»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»§#8658;«/mo»«mfrac mathcolor=¨#0000FF¨»«mrow»«mi mathcolor=¨#FF0000¨ mathvariant=¨bold¨»d«/mi»«mo mathcolor=¨#FF0000¨ mathvariant=¨bold¨»-«/mo»«msub»«mi mathcolor=¨#FF0000¨ mathvariant=¨bold¨»r«/mi»«mrow mathcolor=¨#FF0000¨»«mn mathvariant=¨bold¨»1«/mn»«mo mathvariant=¨bold¨»,«/mo»«mn mathvariant=¨bold¨»3«/mn»«/mrow»«/msub»«/mrow»«msub»«mi mathvariant=¨bold¨»r«/mi»«mrow»«mn mathvariant=¨bold¨»1«/mn»«mo mathvariant=¨bold¨»,«/mo»«mn mathvariant=¨bold¨»3«/mn»«/mrow»«/msub»«/mfrac»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»=«/mo»«msqrt mathcolor=¨#0000FF¨»«mfrac»«msub»«mi mathvariant=¨bold¨»q«/mi»«mn mathvariant=¨bold¨»2«/mn»«/msub»«msub»«mi mathvariant=¨bold¨»q«/mi»«mn mathvariant=¨bold¨»1«/mn»«/msub»«/mfrac»«/msqrt»«/mstyle»«/math»
نُعبر عن البعد r1,3:
«math xmlns=¨http://www.w3.org/1998/Math/MathML¨»«mstyle mathsize=¨22px¨»«mfrac mathcolor=¨#0000FF¨»«mrow»«mi mathvariant=¨bold¨»d«/mi»«mo mathvariant=¨bold¨»-«/mo»«msub»«mi mathvariant=¨bold¨»r«/mi»«mrow»«mn mathvariant=¨bold¨»1«/mn»«mo mathvariant=¨bold¨»,«/mo»«mn mathvariant=¨bold¨»3«/mn»«/mrow»«/msub»«/mrow»«msub»«mi mathvariant=¨bold¨»r«/mi»«mrow»«mn mathvariant=¨bold¨»1«/mn»«mo mathvariant=¨bold¨»,«/mo»«mn mathvariant=¨bold¨»3«/mn»«/mrow»«/msub»«/mfrac»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»=«/mo»«msqrt mathcolor=¨#0000FF¨»«mfrac»«msub»«mi mathvariant=¨bold¨»q«/mi»«mn mathvariant=¨bold¨»2«/mn»«/msub»«msub»«mi mathvariant=¨bold¨»q«/mi»«mn mathvariant=¨bold¨»1«/mn»«/msub»«/mfrac»«/msqrt»«mspace linebreak=¨newline¨/»«mspace linebreak=¨newline¨/»«mi mathvariant=¨bold¨ mathcolor=¨#0000FF¨»d«/mi»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»-«/mo»«msub»«mi mathvariant=¨bold¨ mathcolor=¨#0000FF¨»r«/mi»«mrow mathcolor=¨#0000FF¨»«mn mathvariant=¨bold¨»1«/mn»«mo mathvariant=¨bold¨»,«/mo»«mn mathvariant=¨bold¨»3«/mn»«/mrow»«/msub»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»=«/mo»«msub»«mi mathvariant=¨bold¨ mathcolor=¨#0000FF¨»r«/mi»«mrow mathcolor=¨#0000FF¨»«mn mathvariant=¨bold¨»1«/mn»«mo mathvariant=¨bold¨»,«/mo»«mn mathvariant=¨bold¨»3«/mn»«/mrow»«/msub»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»§#183;«/mo»«msqrt mathcolor=¨#0000FF¨»«mfrac»«msub»«mi mathvariant=¨bold¨»q«/mi»«mn mathvariant=¨bold¨»2«/mn»«/msub»«msub»«mi mathvariant=¨bold¨»q«/mi»«mn mathvariant=¨bold¨»1«/mn»«/msub»«/mfrac»«/msqrt»«mspace linebreak=¨newline¨/»«mspace linebreak=¨newline¨/»«mi mathvariant=¨bold¨ mathcolor=¨#0000FF¨»d«/mi»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»=«/mo»«msub»«mi mathvariant=¨bold¨ mathcolor=¨#0000FF¨»r«/mi»«mrow mathcolor=¨#0000FF¨»«mn mathvariant=¨bold¨»1«/mn»«mo mathvariant=¨bold¨»,«/mo»«mn mathvariant=¨bold¨»3«/mn»«/mrow»«/msub»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»+«/mo»«msub»«mi mathvariant=¨bold¨ mathcolor=¨#0000FF¨»r«/mi»«mrow mathcolor=¨#0000FF¨»«mn mathvariant=¨bold¨»1«/mn»«mo mathvariant=¨bold¨»,«/mo»«mn mathvariant=¨bold¨»3«/mn»«/mrow»«/msub»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»§#183;«/mo»«msqrt mathcolor=¨#0000FF¨»«mfrac»«msub»«mi mathvariant=¨bold¨»q«/mi»«mn mathvariant=¨bold¨»2«/mn»«/msub»«msub»«mi mathvariant=¨bold¨»q«/mi»«mn mathvariant=¨bold¨»1«/mn»«/msub»«/mfrac»«/msqrt»«mspace linebreak=¨newline¨/»«mspace linebreak=¨newline¨/»«mi mathvariant=¨bold¨ mathcolor=¨#0000FF¨»d«/mi»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»=«/mo»«msub»«mi mathvariant=¨bold¨ mathcolor=¨#0000FF¨»r«/mi»«mrow mathcolor=¨#0000FF¨»«mn mathvariant=¨bold¨»1«/mn»«mo mathvariant=¨bold¨»,«/mo»«mn mathvariant=¨bold¨»3«/mn»«/mrow»«/msub»«mstyle mathvariant=¨bold¨ mathcolor=¨#0000FF¨»«mo stretchy=¨true¨»(«/mo»«mrow»«mn»1«/mn»«mo»+«/mo»«msqrt»«mfrac»«msub»«mi»q«/mi»«mn»2«/mn»«/msub»«msub»«mi»q«/mi»«mn»1«/mn»«/msub»«/mfrac»«/msqrt»«/mrow»«mo stretchy=¨true¨»)«/mo»«/mstyle»«mspace linebreak=¨newline¨/»«mspace linebreak=¨newline¨/»«menclose mathcolor=¨#0000FF¨ notation=¨circle¨»«msub»«mi mathvariant=¨bold¨»r«/mi»«mrow»«mn mathvariant=¨bold¨»1«/mn»«mo mathvariant=¨bold¨»,«/mo»«mn mathvariant=¨bold¨»3«/mn»«/mrow»«/msub»«mo mathvariant=¨bold¨»=«/mo»«mfrac»«mi mathvariant=¨bold¨»d«/mi»«mrow»«mn mathvariant=¨bold¨»1«/mn»«mo mathvariant=¨bold¨»+«/mo»«msqrt»«mfrac»«msub»«mi mathvariant=¨bold¨»q«/mi»«mn mathvariant=¨bold¨»2«/mn»«/msub»«msub»«mi mathvariant=¨bold¨»q«/mi»«mn mathvariant=¨bold¨»1«/mn»«/msub»«/mfrac»«/msqrt»«/mrow»«/mfrac»«/menclose»«mspace linebreak=¨newline¨/»«mspace linebreak=¨newline¨/»«mspace linebreak=¨newline¨/»«/mstyle»«/math»