7. أ.7- الثبات في نقطة بين الكرة الأرضية والقمر.
نشير للكرة الأرضية بالجسم 1، والقمر بالجسم 2. نضع جسمًا في النقطة "O" ، نشير لهذا الجسم على أنه الجسم رقم 3.
البعد المطلوب هو البعد بين الجسم 3 ومركز الأرض، ونشير إلى هذه البعد بـ OM.
نرسم مخطط للقوى المؤثرةعلى الجسم 3:
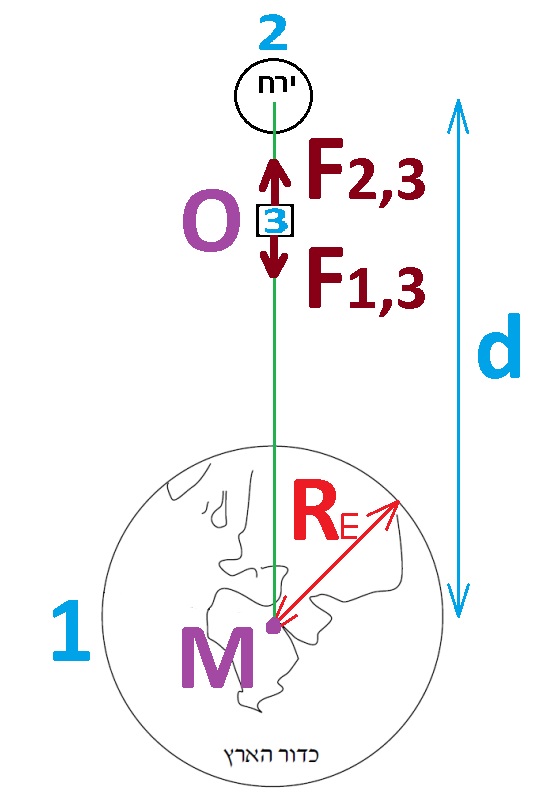
نكتب معادلة القوى على الجسم 3:
«math xmlns=¨http://www.w3.org/1998/Math/MathML¨»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»§#160;«/mo»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»§#160;«/mo»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»§#160;«/mo»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»§#160;«/mo»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»§#160;«/mo»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»§#160;«/mo»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»§#160;«/mo»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»§#160;«/mo»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»§#160;«/mo»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»§#160;«/mo»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»§#160;«/mo»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»§#160;«/mo»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»§#160;«/mo»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»§#160;«/mo»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»§#160;«/mo»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»§#160;«/mo»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»§#160;«/mo»«mi mathvariant=¨bold¨ mathcolor=¨#0000FF¨»§#931;F«/mi»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»=«/mo»«mn mathvariant=¨bold¨ mathcolor=¨#0000FF¨»0«/mn»«mspace linebreak=¨newline¨/»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»§#160;«/mo»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»§#160;«/mo»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»§#160;«/mo»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»§#160;«/mo»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»§#160;«/mo»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»§#160;«/mo»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»§#160;«/mo»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»§#160;«/mo»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»§#160;«/mo»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»§#160;«/mo»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»§#160;«/mo»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»§#160;«/mo»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»§#160;«/mo»«mi mathvariant=¨bold¨ mathcolor=¨#0000FF¨»F«/mi»«mn mathvariant=¨bold¨ mathcolor=¨#0000FF¨»1«/mn»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»,«/mo»«mn mathvariant=¨bold¨ mathcolor=¨#0000FF¨»3«/mn»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»=«/mo»«mi mathvariant=¨bold¨ mathcolor=¨#0000FF¨»F«/mi»«mn mathvariant=¨bold¨ mathcolor=¨#0000FF¨»2«/mn»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»,«/mo»«mn mathvariant=¨bold¨ mathcolor=¨#0000FF¨»3«/mn»«mspace linebreak=¨newline¨/»«mfrac mathcolor=¨#0000FF¨»«mrow»«mi mathvariant=¨bold¨»G«/mi»«mo mathvariant=¨bold¨»§#183;«/mo»«msub»«mi mathvariant=¨bold¨»m«/mi»«mn mathvariant=¨bold¨»1«/mn»«/msub»«mo mathvariant=¨bold¨»§#183;«/mo»«mi mathvariant=¨bold¨»m«/mi»«mn mathvariant=¨bold¨»3«/mn»«/mrow»«msup»«mi mathvariant=¨bold¨»OM«/mi»«mn mathvariant=¨bold¨»2«/mn»«/msup»«/mfrac»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»=«/mo»«mfrac mathcolor=¨#0000FF¨»«mrow»«mi mathvariant=¨bold¨»G«/mi»«mo mathvariant=¨bold¨»§#183;«/mo»«msub»«mi mathvariant=¨bold¨»m«/mi»«mn mathvariant=¨bold¨»2«/mn»«/msub»«mo mathvariant=¨bold¨»§#183;«/mo»«mi mathvariant=¨bold¨»m«/mi»«mn mathvariant=¨bold¨»3«/mn»«/mrow»«msup»«mfenced»«mrow»«mi mathvariant=¨bold¨»d«/mi»«mo mathvariant=¨bold¨»-«/mo»«mi mathvariant=¨bold¨»OM«/mi»«/mrow»«/mfenced»«mn mathvariant=¨bold¨»2«/mn»«/msup»«/mfrac»«/math»
للتعبير عن البعد X بدلالة نصف قطر الكرة الأرضية R. نعبر عن d بدلالة R. و m2 بدلالة m1:
«math xmlns=¨http://www.w3.org/1998/Math/MathML¨»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»§#160;«/mo»«mfrac mathcolor=¨#0000FF¨»«mrow»«mi mathvariant=¨bold¨»G«/mi»«mo mathvariant=¨bold¨»§#183;«/mo»«msub»«mi mathvariant=¨bold¨»m«/mi»«mn mathvariant=¨bold¨»1«/mn»«/msub»«mo mathvariant=¨bold¨»§#183;«/mo»«mi mathvariant=¨bold¨»m«/mi»«mn mathvariant=¨bold¨»3«/mn»«/mrow»«msup»«mi mathvariant=¨bold¨»OM«/mi»«mn mathvariant=¨bold¨»2«/mn»«/msup»«/mfrac»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»=«/mo»«mfrac mathcolor=¨#0000FF¨»«mrow»«mi mathvariant=¨bold¨»G«/mi»«mo mathvariant=¨bold¨»§#183;«/mo»«msub»«mi mathvariant=¨bold¨ mathcolor=¨#FF0000¨»m«/mi»«mn mathvariant=¨bold¨ mathcolor=¨#FF0000¨»2«/mn»«/msub»«mo mathvariant=¨bold¨»§#183;«/mo»«mi mathvariant=¨bold¨»m«/mi»«mn mathvariant=¨bold¨»3«/mn»«/mrow»«msup»«mfenced»«mrow»«mi mathvariant=¨bold¨»d«/mi»«mo mathvariant=¨bold¨»-«/mo»«mi mathvariant=¨bold¨»OM«/mi»«/mrow»«/mfenced»«mn mathvariant=¨bold¨»2«/mn»«/msup»«/mfrac»«mspace linebreak=¨newline¨/»«mspace linebreak=¨newline¨/»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»§#160;«/mo»«mfrac mathcolor=¨#0000FF¨»«mrow»«mi mathvariant=¨bold¨»G«/mi»«mo mathvariant=¨bold¨»§#183;«/mo»«msub»«mi mathvariant=¨bold¨»m«/mi»«mn mathvariant=¨bold¨»1«/mn»«/msub»«mo mathvariant=¨bold¨»§#183;«/mo»«mi mathvariant=¨bold¨»m«/mi»«mn mathvariant=¨bold¨»3«/mn»«/mrow»«msup»«mi mathvariant=¨bold¨»OM«/mi»«mn mathvariant=¨bold¨»2«/mn»«/msup»«/mfrac»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»=«/mo»«mfrac mathcolor=¨#0000FF¨»«mrow»«mi mathvariant=¨bold¨»G«/mi»«mo mathvariant=¨bold¨»§#183;«/mo»«msub»«mi mathvariant=¨bold¨ mathcolor=¨#FF0000¨»m«/mi»«mn mathvariant=¨bold¨ mathcolor=¨#FF0000¨»1«/mn»«/msub»«mo mathvariant=¨bold¨»§#183;«/mo»«mi mathvariant=¨bold¨»m«/mi»«mn mathvariant=¨bold¨»3«/mn»«/mrow»«mrow»«mn mathvariant=¨bold¨ mathcolor=¨#FF0000¨»81«/mn»«mo mathvariant=¨bold¨»§#183;«/mo»«msup»«mfenced»«mrow»«mn mathvariant=¨bold¨»60«/mn»«mi mathvariant=¨bold¨»R«/mi»«mo mathvariant=¨bold¨»-«/mo»«mi mathvariant=¨bold¨»OM«/mi»«/mrow»«/mfenced»«mn mathvariant=¨bold¨»2«/mn»«/msup»«/mrow»«/mfrac»«mspace linebreak=¨newline¨/»«mspace linebreak=¨newline¨/»«mfrac mathcolor=¨#0000FF¨»«mrow»«menclose notation=¨updiagonalstrike¨»«mi mathvariant=¨bold¨»G«/mi»«/menclose»«mo mathvariant=¨bold¨»§#183;«/mo»«menclose notation=¨horizontalstrike¨»«msub»«mi mathvariant=¨bold¨»m«/mi»«mn mathvariant=¨bold¨»1«/mn»«/msub»«/menclose»«mo mathvariant=¨bold¨»§#183;«/mo»«menclose notation=¨downdiagonalstrike¨»«mi mathvariant=¨bold¨»m«/mi»«mn mathvariant=¨bold¨»3«/mn»«/menclose»«/mrow»«msup»«mi mathvariant=¨bold¨»OM«/mi»«mn mathvariant=¨bold¨»2«/mn»«/msup»«/mfrac»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»=«/mo»«mfrac mathcolor=¨#0000FF¨»«mrow»«menclose notation=¨updiagonalstrike¨»«mi mathvariant=¨bold¨»G«/mi»«/menclose»«mo mathvariant=¨bold¨»§#183;«/mo»«menclose notation=¨horizontalstrike¨»«msub»«mi mathvariant=¨bold¨»m«/mi»«mn mathvariant=¨bold¨»1«/mn»«/msub»«/menclose»«mo mathvariant=¨bold¨»§#183;«/mo»«menclose notation=¨downdiagonalstrike¨»«mi mathvariant=¨bold¨»m«/mi»«mn mathvariant=¨bold¨»3«/mn»«/menclose»«/mrow»«mrow»«mn mathvariant=¨bold¨»81«/mn»«mo mathvariant=¨bold¨»§#183;«/mo»«msup»«mstyle mathvariant=¨bold¨»«mo stretchy=¨true¨»(«/mo»«mrow»«mn»60«/mn»«mi»R«/mi»«mo»-«/mo»«mi»OM«/mi»«/mrow»«mo stretchy=¨true¨»)«/mo»«/mstyle»«mn mathvariant=¨bold¨»2«/mn»«/msup»«/mrow»«/mfrac»«mspace linebreak=¨newline¨/»«mspace linebreak=¨newline¨/»«mfrac mathcolor=¨#0000FF¨»«mn mathvariant=¨bold¨»1«/mn»«msup»«mi mathvariant=¨bold¨»OM«/mi»«mn mathvariant=¨bold¨»2«/mn»«/msup»«/mfrac»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»=«/mo»«mfrac mathcolor=¨#0000FF¨»«mn mathvariant=¨bold¨»1«/mn»«mrow»«mn mathvariant=¨bold¨»81«/mn»«mo mathvariant=¨bold¨»§#183;«/mo»«msup»«mrow»«mo stretchy=¨true¨ mathvariant=¨bold¨»(«/mo»«mn mathvariant=¨bold¨»60«/mn»«mi mathvariant=¨bold¨»R«/mi»«mo mathvariant=¨bold¨»-«/mo»«mi mathvariant=¨bold¨»OM«/mi»«mo stretchy=¨true¨ mathvariant=¨bold¨»)«/mo»«/mrow»«mn mathvariant=¨bold¨»2«/mn»«/msup»«/mrow»«/mfrac»«mspace linebreak=¨newline¨/»«mspace linebreak=¨newline¨/»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»§#160;«/mo»«mfrac mathcolor=¨#0000FF¨»«msup»«mfenced»«mrow»«mn mathvariant=¨bold¨»60«/mn»«mi mathvariant=¨bold¨»R«/mi»«mo mathvariant=¨bold¨»-«/mo»«mi mathvariant=¨bold¨»OM«/mi»«/mrow»«/mfenced»«mn mathvariant=¨bold¨»2«/mn»«/msup»«msup»«mi mathvariant=¨bold¨»OM«/mi»«mn mathvariant=¨bold¨»2«/mn»«/msup»«/mfrac»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»=«/mo»«mfrac mathcolor=¨#0000FF¨»«mn mathvariant=¨bold¨»1«/mn»«mn mathvariant=¨bold¨»81«/mn»«/mfrac»«mspace linebreak=¨newline¨/»«mspace linebreak=¨newline¨/»«msqrt mathcolor=¨#0000FF¨»«mfrac»«msup»«mfenced»«mrow»«mn mathvariant=¨bold¨»60«/mn»«mi mathvariant=¨bold¨»R«/mi»«mo mathvariant=¨bold¨»-«/mo»«mi mathvariant=¨bold¨»OM«/mi»«/mrow»«/mfenced»«mn mathvariant=¨bold¨»2«/mn»«/msup»«msup»«mi mathvariant=¨bold¨»OM«/mi»«mn mathvariant=¨bold¨»2«/mn»«/msup»«/mfrac»«/msqrt»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»=«/mo»«msqrt mathcolor=¨#0000FF¨»«mfrac»«mn mathvariant=¨bold¨»1«/mn»«mn mathvariant=¨bold¨»81«/mn»«/mfrac»«/msqrt»«mspace linebreak=¨newline¨/»«mspace linebreak=¨newline¨/»«mspace linebreak=¨newline¨/»«mfrac mathcolor=¨#0000FF¨»«mfenced»«mrow»«mn mathvariant=¨bold¨»60«/mn»«mi mathvariant=¨bold¨»R«/mi»«mo mathvariant=¨bold¨»-«/mo»«mi mathvariant=¨bold¨»OM«/mi»«/mrow»«/mfenced»«mi mathvariant=¨bold¨»OM«/mi»«/mfrac»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»=«/mo»«mfrac mathcolor=¨#0000FF¨»«mn mathvariant=¨bold¨»1«/mn»«mn mathvariant=¨bold¨»9«/mn»«/mfrac»«mspace linebreak=¨newline¨/»«mspace linebreak=¨newline¨/»«mi mathvariant=¨bold¨ mathcolor=¨#0000FF¨»OM«/mi»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»=«/mo»«mn mathvariant=¨bold¨ mathcolor=¨#0000FF¨»9«/mn»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»§#183;«/mo»«mfenced mathcolor=¨#0000FF¨»«mrow»«mn mathvariant=¨bold¨»60«/mn»«mi mathvariant=¨bold¨»R«/mi»«mo mathvariant=¨bold¨»-«/mo»«mi mathvariant=¨bold¨»OM«/mi»«/mrow»«/mfenced»«mspace linebreak=¨newline¨/»«mi mathvariant=¨bold¨ mathcolor=¨#0000FF¨»OM«/mi»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»=«/mo»«mn mathvariant=¨bold¨ mathcolor=¨#0000FF¨»540«/mn»«mi mathvariant=¨bold¨ mathcolor=¨#0000FF¨»R«/mi»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»-«/mo»«mn mathvariant=¨bold¨ mathcolor=¨#0000FF¨»9«/mn»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»§#183;«/mo»«mi mathvariant=¨bold¨ mathcolor=¨#0000FF¨»OM«/mi»«mspace linebreak=¨newline¨/»«mspace linebreak=¨newline¨/»«mn mathvariant=¨bold¨ mathcolor=¨#0000FF¨»10«/mn»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»§#183;«/mo»«mi mathvariant=¨bold¨ mathcolor=¨#0000FF¨»OM«/mi»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»=«/mo»«mn mathvariant=¨bold¨ mathcolor=¨#0000FF¨»540«/mn»«mi mathvariant=¨bold¨ mathcolor=¨#0000FF¨»R«/mi»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»§#160;«/mo»«mspace linebreak=¨newline¨/»«/math»
لذلك فإن التعبير عن البعد OM هو:
«math xmlns=¨http://www.w3.org/1998/Math/MathML¨»«mstyle mathsize=¨20px¨»«mspace linebreak=¨newline¨/»«mspace linebreak=¨newline¨/»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»§#160;«/mo»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»§#160;«/mo»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»§#160;«/mo»«menclose mathcolor=¨#0000FF¨ notation=¨circle¨»«mi mathvariant=¨bold¨»OM«/mi»«mo mathvariant=¨bold¨»=«/mo»«mn mathvariant=¨bold¨»54«/mn»«mo mathvariant=¨bold¨»§#183;«/mo»«mi mathvariant=¨bold¨»R«/mi»«/menclose»«/mstyle»«/math»