حلول التدريبات العملية الجاذبية - ديناميكا (دون الطاقة)

1. أ.1- تسارع الجاذبية على سطح كوكب

افترض أن الجسم قريب من سطح الكوكب ، بحيث يكون البعد بين الجسم ومركز الكوكب مساويًا لنصف قطر الكوكب.

تؤثر على الجسم فقط قوة الجاذبية العامة.

نرسم مخطط القوى التي تؤثر على الجسم:

نكتب معادلة الحركة، ونشير إلى تسارع الجسم بـ *g:

«math xmlns=¨http://www.w3.org/1998/Math/MathML¨»«mi mathvariant=¨bold¨ mathcolor=¨#0000FF¨»§#931;F«/mi»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»=«/mo»«mi mathvariant=¨bold¨ mathcolor=¨#0000FF¨»m«/mi»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»§#183;«/mo»«mi mathvariant=¨bold-italic¨ mathcolor=¨#0000FF¨»a«/mi»«mspace linebreak=¨newline¨/»«mspace linebreak=¨newline¨/»«msub»«mi mathvariant=¨bold¨ mathcolor=¨#0000FF¨»F«/mi»«mi mathvariant=¨bold¨ mathcolor=¨#0000FF¨»g«/mi»«/msub»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»=«/mo»«mi mathvariant=¨bold¨ mathcolor=¨#0000FF¨»m«/mi»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»§#183;«/mo»«mi mathvariant=¨bold-italic¨ mathcolor=¨#0000FF¨»g«/mi»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»*«/mo»«mspace linebreak=¨newline¨/»«mspace linebreak=¨newline¨/»«mfrac mathcolor=¨#0000FF¨»«mrow»«mi mathvariant=¨bold¨»G«/mi»«mo mathvariant=¨bold¨»§#183;«/mo»«msub»«mi mathvariant=¨bold¨»M«/mi»«mi mathvariant=¨bold¨»x«/mi»«/msub»«mo mathvariant=¨bold¨»§#183;«/mo»«menclose notation=¨updiagonalstrike¨»«mi mathvariant=¨bold¨»m«/mi»«/menclose»«/mrow»«msup»«msub»«mi mathvariant=¨bold¨»R«/mi»«mi mathvariant=¨bold¨»x«/mi»«/msub»«mn mathvariant=¨bold¨»2«/mn»«/msup»«/mfrac»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»=«/mo»«menclose mathcolor=¨#0000FF¨ notation=¨updiagonalstrike¨»«mi mathvariant=¨bold¨»m«/mi»«/menclose»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»§#183;«/mo»«mi mathvariant=¨bold¨ mathcolor=¨#0000FF¨»g«/mi»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»*«/mo»«/math»

لذلك فإن تعبير تسارع الجاذبية على سطح الأرض هو:

«math xmlns=¨http://www.w3.org/1998/Math/MathML¨»«mspace linebreak=¨newline¨/»«menclose mathcolor=¨#0000FF¨ notation=¨circle¨»«mi mathvariant=¨bold¨»g«/mi»«mo mathvariant=¨bold¨»*«/mo»«mo mathvariant=¨bold¨»=«/mo»«mfrac»«mrow»«mi mathvariant=¨bold¨»G«/mi»«mo mathvariant=¨bold¨»§#183;«/mo»«msub»«mi mathvariant=¨bold¨»M«/mi»«mi mathvariant=¨bold¨»x«/mi»«/msub»«/mrow»«msup»«msub»«mi mathvariant=¨bold¨»R«/mi»«mi mathvariant=¨bold¨»x«/mi»«/msub»«mn mathvariant=¨bold¨»2«/mn»«/msup»«/mfrac»«/menclose»«/math»

2. أ.2- حساب تسارع الجاذبية على سطح الكرة الأرضية

فقط قوة الجاذبية العامة هي التي تؤثر على الجسم. نشير إلى هذه القوة بـ Fg.

نرسم مخطط للقوى المؤثرة على الجسم:

نكتب معادلة الحركة، نشير إلى تسارع الجسم بـ g:

«math xmlns=¨http://www.w3.org/1998/Math/MathML¨»«mi mathvariant=¨bold¨ mathcolor=¨#0000FF¨»§#931;F«/mi»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»=«/mo»«mi mathvariant=¨bold¨ mathcolor=¨#0000FF¨»m«/mi»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»§#183;«/mo»«mi mathvariant=¨bold-italic¨ mathcolor=¨#0000FF¨»a«/mi»«mspace linebreak=¨newline¨/»«mspace linebreak=¨newline¨/»«msub»«mi mathvariant=¨bold¨ mathcolor=¨#0000FF¨»F«/mi»«mi mathvariant=¨bold¨ mathcolor=¨#0000FF¨»g«/mi»«/msub»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»=«/mo»«mi mathvariant=¨bold¨ mathcolor=¨#0000FF¨»m«/mi»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»§#183;«/mo»«mi mathvariant=¨bold-italic¨ mathcolor=¨#0000FF¨»g«/mi»«mspace linebreak=¨newline¨/»«mspace linebreak=¨newline¨/»«mfrac mathcolor=¨#0000FF¨»«mrow»«mi mathvariant=¨bold¨»G«/mi»«mo mathvariant=¨bold¨»§#183;«/mo»«msub»«mi mathvariant=¨bold¨»M«/mi»«mi mathvariant=¨bold¨»E«/mi»«/msub»«mo mathvariant=¨bold¨»§#183;«/mo»«menclose notation=¨updiagonalstrike¨»«mi mathvariant=¨bold¨»m«/mi»«/menclose»«/mrow»«msup»«msub»«mi mathvariant=¨bold¨»R«/mi»«mi mathvariant=¨bold¨»E«/mi»«/msub»«mn mathvariant=¨bold¨»2«/mn»«/msup»«/mfrac»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»=«/mo»«menclose mathcolor=¨#0000FF¨ notation=¨updiagonalstrike¨»«mi mathvariant=¨bold¨»m«/mi»«/menclose»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»§#183;«/mo»«msup»«mi mathvariant=¨bold¨ mathcolor=¨#0000FF¨»g«/mi»«mrow/»«/msup»«/math»

لذلك فإن التعبير عن تسارع الجاذبية على سطح الأرض هو:

«math xmlns=¨http://www.w3.org/1998/Math/MathML¨»«mspace linebreak=¨newline¨/»«menclose mathcolor=¨#0000FF¨ notation=¨circle¨»«mi mathvariant=¨bold¨»g«/mi»«mo mathvariant=¨bold¨»=«/mo»«mfrac»«mrow»«mi mathvariant=¨bold¨»G«/mi»«mo mathvariant=¨bold¨»§#183;«/mo»«msub»«mi mathvariant=¨bold¨»M«/mi»«mi mathvariant=¨bold¨»E«/mi»«/msub»«/mrow»«msup»«msub»«mi mathvariant=¨bold¨»R«/mi»«mi mathvariant=¨bold¨»E«/mi»«/msub»«mn mathvariant=¨bold¨»2«/mn»«/msup»«/mfrac»«/menclose»«/math»

نعوّض كتلة الكرة الأرضية M_E، ونصف قطر الكرة الأرضية وقيمة ثابت الجاذبية G. ونجد قيمة تسارع الجاذبية:

«math xmlns=¨http://www.w3.org/1998/Math/MathML¨»«mi mathvariant=¨bold¨ mathcolor=¨#0000FF¨»g«/mi»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»=«/mo»«mfrac mathcolor=¨#0000FF¨»«mrow»«mi mathvariant=¨bold¨»G«/mi»«mo mathvariant=¨bold¨»§#183;«/mo»«msub»«mi mathvariant=¨bold¨»M«/mi»«mi mathvariant=¨bold¨»E«/mi»«/msub»«/mrow»«msup»«msub»«mi mathvariant=¨bold¨»R«/mi»«mi mathvariant=¨bold¨»E«/mi»«/msub»«mn mathvariant=¨bold¨»2«/mn»«/msup»«/mfrac»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»=«/mo»«mfrac mathcolor=¨#0000FF¨»«mrow»«mn mathvariant=¨bold¨»6«/mn»«mo mathvariant=¨bold¨».«/mo»«mn mathvariant=¨bold¨»67«/mn»«mo mathvariant=¨bold¨»§#183;«/mo»«msup»«mn mathvariant=¨bold¨»10«/mn»«mrow»«mo mathvariant=¨bold¨»-«/mo»«mn mathvariant=¨bold¨»11«/mn»«/mrow»«/msup»«mo mathvariant=¨bold¨»§#183;«/mo»«mn mathvariant=¨bold¨»5«/mn»«mo mathvariant=¨bold¨».«/mo»«mn mathvariant=¨bold¨»974«/mn»«mo mathvariant=¨bold¨»§#183;«/mo»«msup»«mn mathvariant=¨bold¨»10«/mn»«mn mathvariant=¨bold¨»24«/mn»«/msup»«/mrow»«msup»«mstyle mathvariant=¨bold¨»«mo stretchy=¨true¨»(«/mo»«mrow»«mn»6«/mn»«mo».«/mo»«mn»38«/mn»«mo»§#183;«/mo»«msup»«mn»10«/mn»«mn»6«/mn»«/msup»«/mrow»«mo stretchy=¨true¨»)«/mo»«/mstyle»«mn mathvariant=¨bold¨»2«/mn»«/msup»«/mfrac»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»=«/mo»«mfrac mathcolor=¨#0000FF¨»«mrow»«mn mathvariant=¨bold¨»3«/mn»«mo mathvariant=¨bold¨».«/mo»«mn mathvariant=¨bold¨»984658«/mn»«mo mathvariant=¨bold¨»§#183;«/mo»«msup»«mn mathvariant=¨bold¨»10«/mn»«mn mathvariant=¨bold¨»14«/mn»«/msup»«/mrow»«mrow»«mn mathvariant=¨bold¨»4«/mn»«mo mathvariant=¨bold¨».«/mo»«mn mathvariant=¨bold¨»07044«/mn»«mo mathvariant=¨bold¨»§#183;«/mo»«msup»«mn mathvariant=¨bold¨»10«/mn»«mn mathvariant=¨bold¨»13«/mn»«/msup»«/mrow»«/mfrac»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»=«/mo»«mn mathvariant=¨bold¨ mathcolor=¨#0000FF¨»9«/mn»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨».«/mo»«mn mathvariant=¨bold¨ mathcolor=¨#0000FF¨»789«/mn»«mfrac mathcolor=¨#0000FF¨»«mi mathvariant=¨bold¨»m«/mi»«msup»«mi mathvariant=¨bold¨»s«/mi»«mn mathvariant=¨bold¨»2«/mn»«/msup»«/mfrac»«/math»

3. أ.3- مقدار تسارع الجاذبية على القمر.

نستخدم تعبير تسارع الجاذبية على سطح كوكب لحساب تسارع الجاذبية على القمر:

«math xmlns=¨http://www.w3.org/1998/Math/MathML¨»«mi mathvariant=¨bold¨ mathcolor=¨#0000FF¨»g«/mi»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»*«/mo»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»=«/mo»«mfrac mathcolor=¨#0000FF¨»«mrow»«mi mathvariant=¨bold¨»G«/mi»«mo mathvariant=¨bold¨»§#183;«/mo»«msub»«mi mathvariant=¨bold¨»M«/mi»«mi mathvariant=¨bold¨»m«/mi»«/msub»«/mrow»«msup»«msub»«mi mathvariant=¨bold¨»R«/mi»«mi mathvariant=¨bold¨»m«/mi»«/msub»«mn mathvariant=¨bold¨»2«/mn»«/msup»«/mfrac»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»=«/mo»«mfrac mathcolor=¨#0000FF¨»«mrow»«mn mathvariant=¨bold¨»6«/mn»«mo mathvariant=¨bold¨».«/mo»«mn mathvariant=¨bold¨»67«/mn»«mo mathvariant=¨bold¨»§#183;«/mo»«msup»«mn mathvariant=¨bold¨»10«/mn»«mrow»«mo mathvariant=¨bold¨»-«/mo»«mn mathvariant=¨bold¨»11«/mn»«/mrow»«/msup»«mo mathvariant=¨bold¨»§#183;«/mo»«mn mathvariant=¨bold¨»7«/mn»«mo mathvariant=¨bold¨».«/mo»«mn mathvariant=¨bold¨»35«/mn»«mo mathvariant=¨bold¨»§#183;«/mo»«msup»«mn mathvariant=¨bold¨»10«/mn»«mn mathvariant=¨bold¨»22«/mn»«/msup»«/mrow»«msup»«mstyle mathvariant=¨bold¨»«mo stretchy=¨true¨»(«/mo»«mrow»«mn»1«/mn»«mo».«/mo»«mn»74«/mn»«mo»§#183;«/mo»«msup»«mn»10«/mn»«mn»6«/mn»«/msup»«/mrow»«mo stretchy=¨true¨»)«/mo»«/mstyle»«mn mathvariant=¨bold¨»2«/mn»«/msup»«/mfrac»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»=«/mo»«mfrac mathcolor=¨#0000FF¨»«mrow»«mn mathvariant=¨bold¨»4«/mn»«mo mathvariant=¨bold¨».«/mo»«mn mathvariant=¨bold¨»9«/mn»«mo mathvariant=¨bold¨»§#183;«/mo»«msup»«mn mathvariant=¨bold¨»10«/mn»«mn mathvariant=¨bold¨»12«/mn»«/msup»«/mrow»«mrow»«mn mathvariant=¨bold¨»1«/mn»«mo mathvariant=¨bold¨».«/mo»«mn mathvariant=¨bold¨»74«/mn»«mo mathvariant=¨bold¨»§#183;«/mo»«msup»«mn mathvariant=¨bold¨»10«/mn»«mn mathvariant=¨bold¨»6«/mn»«/msup»«/mrow»«/mfrac»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»=«/mo»«mn mathvariant=¨bold¨ mathcolor=¨#0000FF¨»1«/mn»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨».«/mo»«mn mathvariant=¨bold¨ mathcolor=¨#0000FF¨»6«/mn»«mfrac mathcolor=¨#0000FF¨»«mi mathvariant=¨bold¨»m«/mi»«msup»«mi mathvariant=¨bold¨»s«/mi»«mn mathvariant=¨bold¨»2«/mn»«/msup»«/mfrac»«/math»

4. أ.4- تسارع الجاذبية على ارتفاع h فوق سطح الكرة الأرضية.

تؤثر على الجسم فقط قوة الجاذبية العامة. نشير إلى هذه القوة بـ Fg.

نرسم مخطط للقوى المؤثرة على الجسم:

نكتب معادلة الحركة ، نظرًا للبعد الكبير، يختلف التسارع عن تسارع الجاذبية على سطح الأرض.

نشير إلى هذا التسارع بواسطة *g:

«math xmlns=¨http://www.w3.org/1998/Math/MathML¨»«mi mathvariant=¨bold¨ mathcolor=¨#0000FF¨»§#931;F«/mi»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»=«/mo»«mi mathvariant=¨bold¨ mathcolor=¨#0000FF¨»m«/mi»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»§#183;«/mo»«mi mathvariant=¨bold-italic¨ mathcolor=¨#0000FF¨»a«/mi»«mspace linebreak=¨newline¨/»«mspace linebreak=¨newline¨/»«msub»«mi mathvariant=¨bold¨ mathcolor=¨#0000FF¨»F«/mi»«mi mathvariant=¨bold¨ mathcolor=¨#0000FF¨»g«/mi»«/msub»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»=«/mo»«mi mathvariant=¨bold¨ mathcolor=¨#0000FF¨»m«/mi»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»§#183;«/mo»«mi mathvariant=¨bold-italic¨ mathcolor=¨#0000FF¨»g«/mi»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»*«/mo»«mspace linebreak=¨newline¨/»«mspace linebreak=¨newline¨/»«mfrac mathcolor=¨#0000FF¨»«mrow»«mi mathvariant=¨bold¨»G«/mi»«mo mathvariant=¨bold¨»§#183;«/mo»«msub»«mi mathvariant=¨bold¨»M«/mi»«mi mathvariant=¨bold¨»E«/mi»«/msub»«mo mathvariant=¨bold¨»§#183;«/mo»«menclose notation=¨updiagonalstrike¨»«mi mathvariant=¨bold¨»m«/mi»«/menclose»«/mrow»«msup»«mfenced»«mrow»«msub»«mi mathvariant=¨bold¨»R«/mi»«mi mathvariant=¨bold¨»E«/mi»«/msub»«mo mathvariant=¨bold¨»+«/mo»«mi mathvariant=¨bold¨»h«/mi»«/mrow»«/mfenced»«mn mathvariant=¨bold¨»2«/mn»«/msup»«/mfrac»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»=«/mo»«menclose mathcolor=¨#0000FF¨ notation=¨updiagonalstrike¨»«mi mathvariant=¨bold¨»m«/mi»«/menclose»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»§#183;«/mo»«mi mathvariant=¨bold¨ mathcolor=¨#0000FF¨»g«/mi»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»*«/mo»«mspace linebreak=¨newline¨/»«mspace linebreak=¨newline¨/»«/math»

لذلك فإن التعبير عن تسارع الجاذبية على ارتفاع h فوق سطح الأرض هو:

«math xmlns=¨http://www.w3.org/1998/Math/MathML¨»«menclose mathcolor=¨#0000FF¨ notation=¨circle¨»«mi mathvariant=¨bold¨»g«/mi»«mo mathvariant=¨bold¨»*«/mo»«mo mathvariant=¨bold¨»=«/mo»«mfrac»«mrow»«mi mathvariant=¨bold¨»G«/mi»«mo mathvariant=¨bold¨»§#183;«/mo»«msub»«mi mathvariant=¨bold¨»M«/mi»«mi mathvariant=¨bold¨»E«/mi»«/msub»«/mrow»«msup»«mrow»«mo stretchy=¨true¨ mathvariant=¨bold¨»(«/mo»«msub»«mi mathvariant=¨bold¨»R«/mi»«mi mathvariant=¨bold¨»E«/mi»«/msub»«mo mathvariant=¨bold¨»+«/mo»«mi mathvariant=¨bold¨»h«/mi»«mo stretchy=¨true¨ mathvariant=¨bold¨»)«/mo»«/mrow»«mn mathvariant=¨bold¨»2«/mn»«/msup»«/mfrac»«/menclose»«/math»

من التعبير يمكن ملاحظة أنه كلما زاد الارتفاع h ، كلما كان تسارع الجاذبية *g أصغر.

ملاحظات هامة:

1. من التعبير يمكن ملاحظة أنه كان h مهمل نسبة لـ R_E ، فإن تسارع الجسم هو g.

2. فقط في اللانهاية يكون تسارع الجاذبية بسبب الكرة الأرضية صفر. رواد الفضاء في الفضاء يسبحون لأنهم يتحركون في حركة قمر اصطناعي داخل مكوك دفع ساتلي. ليس لأنهم وصلوا إلى مكان تساوي فيه تسارع الجاذبية صفرًا.

5. أ.5- يتعلق تسارع الجاذبية على سطحه بكتلة الكوكب

حتى نعبّ تسارع الجاذبية على سطح كوكب بدلالة كتلة الكوكب.

نتطرّق إلى الجسم المحرر من حالة السكون على سطح الكوكب.

القوة الوحيدة المؤثرة على الجسم هي قوة الجاذبية العامة. نشير إلى هذه القوة بـ Fg.

نرسم مخطط القوى المؤثرة على الجسم :

نكتب معادلة الحركة، ونستخدم الرموز التالية:

*g - التسارع على الكوكب السيار.

m - كتلة الجسم.

MX - كتلة الكوكب.

RX- نصف قطر الكوكب.

«math xmlns=¨http://www.w3.org/1998/Math/MathML¨»«mstyle mathsize=¨24px¨»«mi mathvariant=¨bold¨ mathcolor=¨#0000FF¨»§#931;F«/mi»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»=«/mo»«mi mathvariant=¨bold¨ mathcolor=¨#0000FF¨»m«/mi»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»§#183;«/mo»«mi mathvariant=¨bold-italic¨ mathcolor=¨#0000FF¨»a«/mi»«mspace linebreak=¨newline¨/»«mspace linebreak=¨newline¨/»«msub»«mi mathvariant=¨bold¨ mathcolor=¨#0000FF¨»F«/mi»«mi mathvariant=¨bold¨ mathcolor=¨#0000FF¨»g«/mi»«/msub»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»=«/mo»«mi mathvariant=¨bold¨ mathcolor=¨#0000FF¨»m«/mi»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»§#183;«/mo»«mi mathvariant=¨bold-italic¨ mathcolor=¨#0000FF¨»g«/mi»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»*«/mo»«mspace linebreak=¨newline¨/»«mspace linebreak=¨newline¨/»«mfrac mathcolor=¨#0000FF¨»«mrow»«mi mathvariant=¨bold¨»G«/mi»«mo mathvariant=¨bold¨»§#183;«/mo»«msub»«mi mathvariant=¨bold¨»M«/mi»«mi mathvariant=¨bold¨»X«/mi»«/msub»«mo mathvariant=¨bold¨»§#183;«/mo»«menclose notation=¨updiagonalstrike¨»«mi mathvariant=¨bold¨»m«/mi»«/menclose»«/mrow»«msup»«msub»«mi mathvariant=¨bold¨»R«/mi»«mi mathvariant=¨bold¨»X«/mi»«/msub»«mn mathvariant=¨bold¨»2«/mn»«/msup»«/mfrac»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»=«/mo»«menclose mathcolor=¨#0000FF¨ notation=¨updiagonalstrike¨»«mi mathvariant=¨bold¨»m«/mi»«/menclose»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»§#183;«/mo»«msup»«mi mathvariant=¨bold¨ mathcolor=¨#0000FF¨»g«/mi»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»*«/mo»«/msup»«/mstyle»«/math»

نعبر عن كتلة الكوكب M من معادلة الحركة:

«math xmlns=¨http://www.w3.org/1998/Math/MathML¨»«mstyle mathsize=¨24px¨»«menclose mathcolor=¨#0000FF¨ notation=¨circle¨»«msub»«mi mathvariant=¨bold¨»M«/mi»«mi mathvariant=¨bold¨»X«/mi»«/msub»«mo mathvariant=¨bold¨»=«/mo»«mfrac»«mrow»«msup»«msub»«mi mathvariant=¨bold¨»R«/mi»«mi mathvariant=¨bold¨»X«/mi»«/msub»«mn mathvariant=¨bold¨»2«/mn»«/msup»«mo mathvariant=¨bold¨»§#183;«/mo»«mi mathvariant=¨bold¨»g«/mi»«mo mathvariant=¨bold¨»*«/mo»«/mrow»«mi mathvariant=¨bold¨»G«/mi»«/mfrac»«/menclose»«/mstyle»«/math»

6. أ.6- حساب كتلة الكرة الارضية

«math xmlns=¨http://www.w3.org/1998/Math/MathML¨»«mstyle mathsize=¨24px¨»«msub»«mi mathvariant=¨bold¨ mathcolor=¨#0000FF¨»M«/mi»«mi mathvariant=¨bold¨ mathcolor=¨#0000FF¨»E«/mi»«/msub»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»=«/mo»«mfrac mathcolor=¨#0000FF¨»«mrow»«msup»«msub»«mi mathvariant=¨bold¨»R«/mi»«mi mathvariant=¨bold¨»E«/mi»«/msub»«mn mathvariant=¨bold¨»2«/mn»«/msup»«mo mathvariant=¨bold¨»§#183;«/mo»«mi mathvariant=¨bold¨»g«/mi»«/mrow»«mi mathvariant=¨bold¨»G«/mi»«/mfrac»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»=«/mo»«mfrac mathcolor=¨#0000FF¨»«mrow»«msup»«mrow»«mo stretchy=¨true¨ mathvariant=¨bold¨»(«/mo»«mn mathvariant=¨bold¨»6«/mn»«mo mathvariant=¨bold¨».«/mo»«mn mathvariant=¨bold¨»38«/mn»«mo mathvariant=¨bold¨»§#183;«/mo»«msup»«mn mathvariant=¨bold¨»10«/mn»«mn mathvariant=¨bold¨»6«/mn»«/msup»«mo stretchy=¨true¨ mathvariant=¨bold¨»)«/mo»«/mrow»«mn mathvariant=¨bold¨»2«/mn»«/msup»«mo mathvariant=¨bold¨»§#183;«/mo»«mn mathvariant=¨bold¨»9«/mn»«mo mathvariant=¨bold¨».«/mo»«mn mathvariant=¨bold¨»789«/mn»«/mrow»«mrow»«mn mathvariant=¨bold¨»6«/mn»«mo mathvariant=¨bold¨».«/mo»«mn mathvariant=¨bold¨»67«/mn»«mo mathvariant=¨bold¨»§#183;«/mo»«msup»«mn mathvariant=¨bold¨»10«/mn»«mrow»«mo mathvariant=¨bold¨»-«/mo»«mn mathvariant=¨bold¨»11«/mn»«/mrow»«/msup»«/mrow»«/mfrac»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»=«/mo»«mn mathvariant=¨bold¨ mathcolor=¨#0000FF¨»5«/mn»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨».«/mo»«mn mathvariant=¨bold¨ mathcolor=¨#0000FF¨»97«/mn»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»§#183;«/mo»«msup»«mn mathvariant=¨bold¨ mathcolor=¨#0000FF¨»10«/mn»«mn mathvariant=¨bold¨ mathcolor=¨#0000FF¨»24«/mn»«/msup»«mi mathvariant=¨bold¨ mathcolor=¨#0000FF¨»kg«/mi»«/mstyle»«/math»

7. أ.7- الثبات في نقطة بين الكرة الأرضية والقمر.

نشير للكرة الأرضية بالجسم 1، والقمر بالجسم 2. نضع جسمًا في النقطة "O" ، نشير لهذا الجسم على أنه الجسم رقم 3.

البعد المطلوب هو البعد بين الجسم 3 ومركز الأرض، ونشير إلى هذه البعد بـ OM.

نرسم مخطط للقوى المؤثرةعلى الجسم 3:

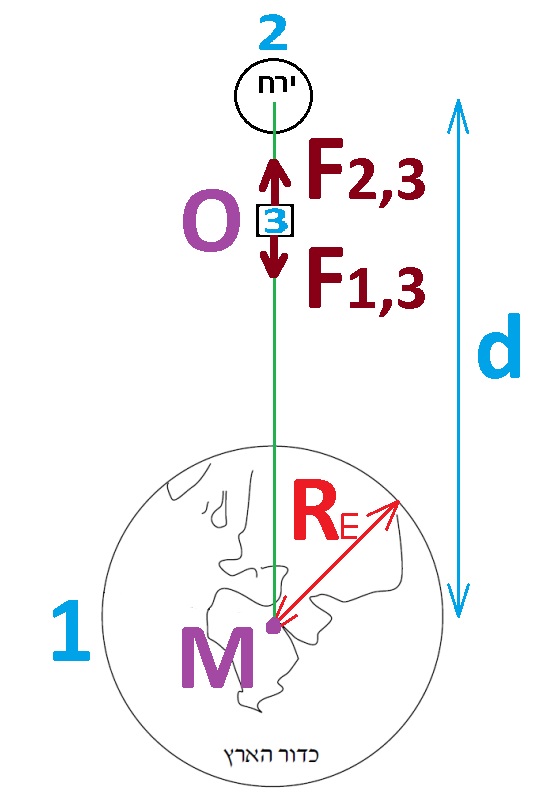
نكتب معادلة القوى على الجسم 3:

«math xmlns=¨http://www.w3.org/1998/Math/MathML¨»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»§#160;«/mo»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»§#160;«/mo»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»§#160;«/mo»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»§#160;«/mo»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»§#160;«/mo»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»§#160;«/mo»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»§#160;«/mo»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»§#160;«/mo»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»§#160;«/mo»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»§#160;«/mo»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»§#160;«/mo»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»§#160;«/mo»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»§#160;«/mo»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»§#160;«/mo»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»§#160;«/mo»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»§#160;«/mo»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»§#160;«/mo»«mi mathvariant=¨bold¨ mathcolor=¨#0000FF¨»§#931;F«/mi»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»=«/mo»«mn mathvariant=¨bold¨ mathcolor=¨#0000FF¨»0«/mn»«mspace linebreak=¨newline¨/»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»§#160;«/mo»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»§#160;«/mo»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»§#160;«/mo»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»§#160;«/mo»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»§#160;«/mo»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»§#160;«/mo»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»§#160;«/mo»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»§#160;«/mo»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»§#160;«/mo»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»§#160;«/mo»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»§#160;«/mo»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»§#160;«/mo»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»§#160;«/mo»«mi mathvariant=¨bold¨ mathcolor=¨#0000FF¨»F«/mi»«mn mathvariant=¨bold¨ mathcolor=¨#0000FF¨»1«/mn»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»,«/mo»«mn mathvariant=¨bold¨ mathcolor=¨#0000FF¨»3«/mn»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»=«/mo»«mi mathvariant=¨bold¨ mathcolor=¨#0000FF¨»F«/mi»«mn mathvariant=¨bold¨ mathcolor=¨#0000FF¨»2«/mn»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»,«/mo»«mn mathvariant=¨bold¨ mathcolor=¨#0000FF¨»3«/mn»«mspace linebreak=¨newline¨/»«mfrac mathcolor=¨#0000FF¨»«mrow»«mi mathvariant=¨bold¨»G«/mi»«mo mathvariant=¨bold¨»§#183;«/mo»«msub»«mi mathvariant=¨bold¨»m«/mi»«mn mathvariant=¨bold¨»1«/mn»«/msub»«mo mathvariant=¨bold¨»§#183;«/mo»«mi mathvariant=¨bold¨»m«/mi»«mn mathvariant=¨bold¨»3«/mn»«/mrow»«msup»«mi mathvariant=¨bold¨»OM«/mi»«mn mathvariant=¨bold¨»2«/mn»«/msup»«/mfrac»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»=«/mo»«mfrac mathcolor=¨#0000FF¨»«mrow»«mi mathvariant=¨bold¨»G«/mi»«mo mathvariant=¨bold¨»§#183;«/mo»«msub»«mi mathvariant=¨bold¨»m«/mi»«mn mathvariant=¨bold¨»2«/mn»«/msub»«mo mathvariant=¨bold¨»§#183;«/mo»«mi mathvariant=¨bold¨»m«/mi»«mn mathvariant=¨bold¨»3«/mn»«/mrow»«msup»«mfenced»«mrow»«mi mathvariant=¨bold¨»d«/mi»«mo mathvariant=¨bold¨»-«/mo»«mi mathvariant=¨bold¨»OM«/mi»«/mrow»«/mfenced»«mn mathvariant=¨bold¨»2«/mn»«/msup»«/mfrac»«/math»

للتعبير عن البعد X بدلالة نصف قطر الكرة الأرضية R. نعبر عن d بدلالة R. و m₂ بدلالة m₁:

«math xmlns=¨http://www.w3.org/1998/Math/MathML¨»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»§#160;«/mo»«mfrac mathcolor=¨#0000FF¨»«mrow»«mi mathvariant=¨bold¨»G«/mi»«mo mathvariant=¨bold¨»§#183;«/mo»«msub»«mi mathvariant=¨bold¨»m«/mi»«mn mathvariant=¨bold¨»1«/mn»«/msub»«mo mathvariant=¨bold¨»§#183;«/mo»«mi mathvariant=¨bold¨»m«/mi»«mn mathvariant=¨bold¨»3«/mn»«/mrow»«msup»«mi mathvariant=¨bold¨»OM«/mi»«mn mathvariant=¨bold¨»2«/mn»«/msup»«/mfrac»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»=«/mo»«mfrac mathcolor=¨#0000FF¨»«mrow»«mi mathvariant=¨bold¨»G«/mi»«mo mathvariant=¨bold¨»§#183;«/mo»«msub»«mi mathvariant=¨bold¨ mathcolor=¨#FF0000¨»m«/mi»«mn mathvariant=¨bold¨ mathcolor=¨#FF0000¨»2«/mn»«/msub»«mo mathvariant=¨bold¨»§#183;«/mo»«mi mathvariant=¨bold¨»m«/mi»«mn mathvariant=¨bold¨»3«/mn»«/mrow»«msup»«mfenced»«mrow»«mi mathvariant=¨bold¨»d«/mi»«mo mathvariant=¨bold¨»-«/mo»«mi mathvariant=¨bold¨»OM«/mi»«/mrow»«/mfenced»«mn mathvariant=¨bold¨»2«/mn»«/msup»«/mfrac»«mspace linebreak=¨newline¨/»«mspace linebreak=¨newline¨/»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»§#160;«/mo»«mfrac mathcolor=¨#0000FF¨»«mrow»«mi mathvariant=¨bold¨»G«/mi»«mo mathvariant=¨bold¨»§#183;«/mo»«msub»«mi mathvariant=¨bold¨»m«/mi»«mn mathvariant=¨bold¨»1«/mn»«/msub»«mo mathvariant=¨bold¨»§#183;«/mo»«mi mathvariant=¨bold¨»m«/mi»«mn mathvariant=¨bold¨»3«/mn»«/mrow»«msup»«mi mathvariant=¨bold¨»OM«/mi»«mn mathvariant=¨bold¨»2«/mn»«/msup»«/mfrac»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»=«/mo»«mfrac mathcolor=¨#0000FF¨»«mrow»«mi mathvariant=¨bold¨»G«/mi»«mo mathvariant=¨bold¨»§#183;«/mo»«msub»«mi mathvariant=¨bold¨ mathcolor=¨#FF0000¨»m«/mi»«mn mathvariant=¨bold¨ mathcolor=¨#FF0000¨»1«/mn»«/msub»«mo mathvariant=¨bold¨»§#183;«/mo»«mi mathvariant=¨bold¨»m«/mi»«mn mathvariant=¨bold¨»3«/mn»«/mrow»«mrow»«mn mathvariant=¨bold¨ mathcolor=¨#FF0000¨»81«/mn»«mo mathvariant=¨bold¨»§#183;«/mo»«msup»«mfenced»«mrow»«mn mathvariant=¨bold¨»60«/mn»«mi mathvariant=¨bold¨»R«/mi»«mo mathvariant=¨bold¨»-«/mo»«mi mathvariant=¨bold¨»OM«/mi»«/mrow»«/mfenced»«mn mathvariant=¨bold¨»2«/mn»«/msup»«/mrow»«/mfrac»«mspace linebreak=¨newline¨/»«mspace linebreak=¨newline¨/»«mfrac mathcolor=¨#0000FF¨»«mrow»«menclose notation=¨updiagonalstrike¨»«mi mathvariant=¨bold¨»G«/mi»«/menclose»«mo mathvariant=¨bold¨»§#183;«/mo»«menclose notation=¨horizontalstrike¨»«msub»«mi mathvariant=¨bold¨»m«/mi»«mn mathvariant=¨bold¨»1«/mn»«/msub»«/menclose»«mo mathvariant=¨bold¨»§#183;«/mo»«menclose notation=¨downdiagonalstrike¨»«mi mathvariant=¨bold¨»m«/mi»«mn mathvariant=¨bold¨»3«/mn»«/menclose»«/mrow»«msup»«mi mathvariant=¨bold¨»OM«/mi»«mn mathvariant=¨bold¨»2«/mn»«/msup»«/mfrac»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»=«/mo»«mfrac mathcolor=¨#0000FF¨»«mrow»«menclose notation=¨updiagonalstrike¨»«mi mathvariant=¨bold¨»G«/mi»«/menclose»«mo mathvariant=¨bold¨»§#183;«/mo»«menclose notation=¨horizontalstrike¨»«msub»«mi mathvariant=¨bold¨»m«/mi»«mn mathvariant=¨bold¨»1«/mn»«/msub»«/menclose»«mo mathvariant=¨bold¨»§#183;«/mo»«menclose notation=¨downdiagonalstrike¨»«mi mathvariant=¨bold¨»m«/mi»«mn mathvariant=¨bold¨»3«/mn»«/menclose»«/mrow»«mrow»«mn mathvariant=¨bold¨»81«/mn»«mo mathvariant=¨bold¨»§#183;«/mo»«msup»«mstyle mathvariant=¨bold¨»«mo stretchy=¨true¨»(«/mo»«mrow»«mn»60«/mn»«mi»R«/mi»«mo»-«/mo»«mi»OM«/mi»«/mrow»«mo stretchy=¨true¨»)«/mo»«/mstyle»«mn mathvariant=¨bold¨»2«/mn»«/msup»«/mrow»«/mfrac»«mspace linebreak=¨newline¨/»«mspace linebreak=¨newline¨/»«mfrac mathcolor=¨#0000FF¨»«mn mathvariant=¨bold¨»1«/mn»«msup»«mi mathvariant=¨bold¨»OM«/mi»«mn mathvariant=¨bold¨»2«/mn»«/msup»«/mfrac»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»=«/mo»«mfrac mathcolor=¨#0000FF¨»«mn mathvariant=¨bold¨»1«/mn»«mrow»«mn mathvariant=¨bold¨»81«/mn»«mo mathvariant=¨bold¨»§#183;«/mo»«msup»«mrow»«mo stretchy=¨true¨ mathvariant=¨bold¨»(«/mo»«mn mathvariant=¨bold¨»60«/mn»«mi mathvariant=¨bold¨»R«/mi»«mo mathvariant=¨bold¨»-«/mo»«mi mathvariant=¨bold¨»OM«/mi»«mo stretchy=¨true¨ mathvariant=¨bold¨»)«/mo»«/mrow»«mn mathvariant=¨bold¨»2«/mn»«/msup»«/mrow»«/mfrac»«mspace linebreak=¨newline¨/»«mspace linebreak=¨newline¨/»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»§#160;«/mo»«mfrac mathcolor=¨#0000FF¨»«msup»«mfenced»«mrow»«mn mathvariant=¨bold¨»60«/mn»«mi mathvariant=¨bold¨»R«/mi»«mo mathvariant=¨bold¨»-«/mo»«mi mathvariant=¨bold¨»OM«/mi»«/mrow»«/mfenced»«mn mathvariant=¨bold¨»2«/mn»«/msup»«msup»«mi mathvariant=¨bold¨»OM«/mi»«mn mathvariant=¨bold¨»2«/mn»«/msup»«/mfrac»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»=«/mo»«mfrac mathcolor=¨#0000FF¨»«mn mathvariant=¨bold¨»1«/mn»«mn mathvariant=¨bold¨»81«/mn»«/mfrac»«mspace linebreak=¨newline¨/»«mspace linebreak=¨newline¨/»«msqrt mathcolor=¨#0000FF¨»«mfrac»«msup»«mfenced»«mrow»«mn mathvariant=¨bold¨»60«/mn»«mi mathvariant=¨bold¨»R«/mi»«mo mathvariant=¨bold¨»-«/mo»«mi mathvariant=¨bold¨»OM«/mi»«/mrow»«/mfenced»«mn mathvariant=¨bold¨»2«/mn»«/msup»«msup»«mi mathvariant=¨bold¨»OM«/mi»«mn mathvariant=¨bold¨»2«/mn»«/msup»«/mfrac»«/msqrt»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»=«/mo»«msqrt mathcolor=¨#0000FF¨»«mfrac»«mn mathvariant=¨bold¨»1«/mn»«mn mathvariant=¨bold¨»81«/mn»«/mfrac»«/msqrt»«mspace linebreak=¨newline¨/»«mspace linebreak=¨newline¨/»«mspace linebreak=¨newline¨/»«mfrac mathcolor=¨#0000FF¨»«mfenced»«mrow»«mn mathvariant=¨bold¨»60«/mn»«mi mathvariant=¨bold¨»R«/mi»«mo mathvariant=¨bold¨»-«/mo»«mi mathvariant=¨bold¨»OM«/mi»«/mrow»«/mfenced»«mi mathvariant=¨bold¨»OM«/mi»«/mfrac»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»=«/mo»«mfrac mathcolor=¨#0000FF¨»«mn mathvariant=¨bold¨»1«/mn»«mn mathvariant=¨bold¨»9«/mn»«/mfrac»«mspace linebreak=¨newline¨/»«mspace linebreak=¨newline¨/»«mi mathvariant=¨bold¨ mathcolor=¨#0000FF¨»OM«/mi»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»=«/mo»«mn mathvariant=¨bold¨ mathcolor=¨#0000FF¨»9«/mn»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»§#183;«/mo»«mfenced mathcolor=¨#0000FF¨»«mrow»«mn mathvariant=¨bold¨»60«/mn»«mi mathvariant=¨bold¨»R«/mi»«mo mathvariant=¨bold¨»-«/mo»«mi mathvariant=¨bold¨»OM«/mi»«/mrow»«/mfenced»«mspace linebreak=¨newline¨/»«mi mathvariant=¨bold¨ mathcolor=¨#0000FF¨»OM«/mi»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»=«/mo»«mn mathvariant=¨bold¨ mathcolor=¨#0000FF¨»540«/mn»«mi mathvariant=¨bold¨ mathcolor=¨#0000FF¨»R«/mi»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»-«/mo»«mn mathvariant=¨bold¨ mathcolor=¨#0000FF¨»9«/mn»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»§#183;«/mo»«mi mathvariant=¨bold¨ mathcolor=¨#0000FF¨»OM«/mi»«mspace linebreak=¨newline¨/»«mspace linebreak=¨newline¨/»«mn mathvariant=¨bold¨ mathcolor=¨#0000FF¨»10«/mn»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»§#183;«/mo»«mi mathvariant=¨bold¨ mathcolor=¨#0000FF¨»OM«/mi»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»=«/mo»«mn mathvariant=¨bold¨ mathcolor=¨#0000FF¨»540«/mn»«mi mathvariant=¨bold¨ mathcolor=¨#0000FF¨»R«/mi»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»§#160;«/mo»«mspace linebreak=¨newline¨/»«/math»

لذلك فإن التعبير عن البعد OM هو:

«math xmlns=¨http://www.w3.org/1998/Math/MathML¨»«mstyle mathsize=¨20px¨»«mspace linebreak=¨newline¨/»«mspace linebreak=¨newline¨/»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»§#160;«/mo»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»§#160;«/mo»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»§#160;«/mo»«menclose mathcolor=¨#0000FF¨ notation=¨circle¨»«mi mathvariant=¨bold¨»OM«/mi»«mo mathvariant=¨bold¨»=«/mo»«mn mathvariant=¨bold¨»54«/mn»«mo mathvariant=¨bold¨»§#183;«/mo»«mi mathvariant=¨bold¨»R«/mi»«/menclose»«/mstyle»«/math»

8. ب.1- قمر اصطناعي يتحرك حول كوكب سيار (R)T

يتحرك القمر الاصطناعي في حركة دائرية تحت تأثير قوة الجاذبية فقط (سقوط حر).

نشير إلى القوة الجاذبة نحو المركز بـ Fg.

نرسم مخطط للقوى المؤثرة على الجسم:

نكتب معادلة الحركة الدائرية.

«math xmlns=¨http://www.w3.org/1998/Math/MathML¨»«msub»«mi mathvariant=¨bold¨ mathcolor=¨#0000FF¨»§#931;F«/mi»«mi mathvariant=¨bold¨ mathcolor=¨#0000FF¨»R«/mi»«/msub»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»=«/mo»«mi mathvariant=¨bold¨ mathcolor=¨#0000FF¨»m«/mi»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»§#183;«/mo»«msup»«mi mathvariant=¨bold¨ mathcolor=¨#0000FF¨»§#969;«/mi»«mn mathvariant=¨bold¨ mathcolor=¨#0000FF¨»2«/mn»«/msup»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»§#183;«/mo»«mi mathvariant=¨bold¨ mathcolor=¨#0000FF¨»R«/mi»«mspace linebreak=¨newline¨/»«mspace linebreak=¨newline¨/»«mfrac mathcolor=¨#0000FF¨»«mrow»«mi mathvariant=¨bold¨»G«/mi»«mo mathvariant=¨bold¨»§#183;«/mo»«msub»«mi mathvariant=¨bold¨»M«/mi»«mi mathvariant=¨bold¨»X«/mi»«/msub»«mo mathvariant=¨bold¨»§#183;«/mo»«menclose notation=¨updiagonalstrike¨»«mi mathvariant=¨bold¨»m«/mi»«/menclose»«/mrow»«msup»«mi mathvariant=¨bold¨»R«/mi»«mn mathvariant=¨bold¨»2«/mn»«/msup»«/mfrac»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»=«/mo»«menclose mathcolor=¨#0000FF¨ notation=¨updiagonalstrike¨»«mi mathvariant=¨bold¨»m«/mi»«/menclose»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»§#183;«/mo»«msup»«mi mathvariant=¨bold¨ mathcolor=¨#0000FF¨»§#969;«/mi»«mn mathvariant=¨bold¨ mathcolor=¨#0000FF¨»2«/mn»«/msup»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»§#183;«/mo»«mi mathvariant=¨bold¨ mathcolor=¨#0000FF¨»R«/mi»«mspace linebreak=¨newline¨/»«mspace linebreak=¨newline¨/»«mfrac mathcolor=¨#0000FF¨»«mrow»«mi mathvariant=¨bold¨»G«/mi»«mo mathvariant=¨bold¨»§#183;«/mo»«msub»«mi mathvariant=¨bold¨»M«/mi»«mi mathvariant=¨bold¨»X«/mi»«/msub»«mo mathvariant=¨bold¨»§#183;«/mo»«menclose notation=¨updiagonalstrike¨»«mi mathvariant=¨bold¨»m«/mi»«/menclose»«/mrow»«msup»«mi mathvariant=¨bold¨»R«/mi»«mn mathvariant=¨bold¨»2«/mn»«/msup»«/mfrac»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»=«/mo»«menclose mathcolor=¨#0000FF¨ notation=¨updiagonalstrike¨»«mi mathvariant=¨bold¨»m«/mi»«/menclose»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»§#183;«/mo»«msup»«mrow mathcolor=¨#0000FF¨»«mo stretchy=¨true¨ mathvariant=¨bold¨»(«/mo»«mfrac»«mrow»«mn mathvariant=¨bold¨»2«/mn»«mi mathvariant=¨bold¨»§#960;«/mi»«/mrow»«mi mathvariant=¨bold¨»T«/mi»«/mfrac»«mo stretchy=¨true¨ mathvariant=¨bold¨»)«/mo»«/mrow»«mn mathvariant=¨bold¨ mathcolor=¨#0000FF¨»2«/mn»«/msup»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»§#183;«/mo»«mi mathvariant=¨bold¨ mathcolor=¨#0000FF¨»R«/mi»«mspace linebreak=¨newline¨/»«mspace linebreak=¨newline¨/»«mfrac mathcolor=¨#0000FF¨»«mrow»«mi mathvariant=¨bold¨»G«/mi»«mo mathvariant=¨bold¨»§#183;«/mo»«msub»«mi mathvariant=¨bold¨»M«/mi»«mi mathvariant=¨bold¨»X«/mi»«/msub»«mo mathvariant=¨bold¨»§#183;«/mo»«menclose notation=¨updiagonalstrike¨»«mi mathvariant=¨bold¨»m«/mi»«/menclose»«/mrow»«msup»«mi mathvariant=¨bold¨»R«/mi»«mn mathvariant=¨bold¨»2«/mn»«/msup»«/mfrac»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»=«/mo»«menclose mathcolor=¨#0000FF¨ notation=¨updiagonalstrike¨»«mi mathvariant=¨bold¨»m«/mi»«/menclose»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»§#183;«/mo»«mfrac mathcolor=¨#0000FF¨»«mrow»«mn mathvariant=¨bold¨»4«/mn»«mo mathvariant=¨bold¨»§#183;«/mo»«msup»«mi mathvariant=¨bold¨»§#960;«/mi»«mn mathvariant=¨bold¨»2«/mn»«/msup»«/mrow»«msup»«mi mathvariant=¨bold¨»T«/mi»«mn mathvariant=¨bold¨»2«/mn»«/msup»«/mfrac»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»§#183;«/mo»«mi mathvariant=¨bold¨ mathcolor=¨#0000FF¨»R«/mi»«mspace linebreak=¨newline¨/»«mspace linebreak=¨newline¨/»«msup»«mi mathvariant=¨bold¨ mathcolor=¨#0000FF¨»T«/mi»«mn mathvariant=¨bold¨ mathcolor=¨#0000FF¨»2«/mn»«/msup»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»=«/mo»«mfrac mathcolor=¨#0000FF¨»«mrow»«mn mathvariant=¨bold¨»4«/mn»«mo mathvariant=¨bold¨»§#183;«/mo»«msup»«mi mathvariant=¨bold¨»§#960;«/mi»«mn mathvariant=¨bold¨»2«/mn»«/msup»«mo mathvariant=¨bold¨»§#183;«/mo»«msup»«mi mathvariant=¨bold¨»R«/mi»«mn mathvariant=¨bold¨»3«/mn»«/msup»«/mrow»«mrow»«mi mathvariant=¨bold¨»G«/mi»«mo mathvariant=¨bold¨»§#183;«/mo»«msub»«mi mathvariant=¨bold¨»M«/mi»«mi mathvariant=¨bold¨»X«/mi»«/msub»«/mrow»«/mfrac»«mspace linebreak=¨newline¨/»«mspace linebreak=¨newline¨/»«mspace linebreak=¨newline¨/»«/math»

لذلك ، فإن التعبير عن زمن الدورة كدالة لنصف قطر المدار هو:

«math xmlns=¨http://www.w3.org/1998/Math/MathML¨»«mstyle mathsize=¨24px¨»«menclose mathcolor=¨#0000FF¨ notation=¨circle¨»«mi mathvariant=¨bold¨»T«/mi»«mo mathvariant=¨bold¨»=«/mo»«msqrt»«mfrac»«mrow»«mn mathvariant=¨bold¨»4«/mn»«mo mathvariant=¨bold¨»§#183;«/mo»«msup»«mi mathvariant=¨bold¨»§#960;«/mi»«mn mathvariant=¨bold¨»2«/mn»«/msup»«mo mathvariant=¨bold¨»§#183;«/mo»«msup»«mi mathvariant=¨bold¨»R«/mi»«mn mathvariant=¨bold¨»3«/mn»«/msup»«/mrow»«mrow»«mi mathvariant=¨bold¨»G«/mi»«mo mathvariant=¨bold¨»§#183;«/mo»«msub»«mi mathvariant=¨bold¨»M«/mi»«mi mathvariant=¨bold¨»X«/mi»«/msub»«/mrow»«/mfrac»«/msqrt»«/menclose»«/mstyle»«/math»

9. ب.2- حساب زمن دورة حركة الكرة الأرضية.

نستخدم التعبير لزمن دورة حركة القمر الاصطناعي، لحركة الكرة الأرضية حول الشمس.

«math xmlns=¨http://www.w3.org/1998/Math/MathML¨»«mstyle mathsize=¨24px¨»«mi mathvariant=¨bold¨ mathcolor=¨#0000FF¨»T«/mi»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»=«/mo»«msqrt mathcolor=¨#0000FF¨»«mfrac»«mrow»«mn mathvariant=¨bold¨»4«/mn»«mo mathvariant=¨bold¨»§#183;«/mo»«msup»«mi mathvariant=¨bold¨»§#960;«/mi»«mn mathvariant=¨bold¨»2«/mn»«/msup»«mo mathvariant=¨bold¨»§#183;«/mo»«msup»«mi mathvariant=¨bold¨»R«/mi»«mn mathvariant=¨bold¨»3«/mn»«/msup»«/mrow»«mrow»«mi mathvariant=¨bold¨»G«/mi»«mo mathvariant=¨bold¨»§#183;«/mo»«mi mathvariant=¨bold¨»M«/mi»«/mrow»«/mfrac»«/msqrt»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»=«/mo»«msqrt mathcolor=¨#0000FF¨»«mfrac»«mrow»«mn mathvariant=¨bold¨»4«/mn»«mo mathvariant=¨bold¨»§#183;«/mo»«msup»«mi mathvariant=¨bold¨»§#960;«/mi»«mn mathvariant=¨bold¨»2«/mn»«/msup»«mo mathvariant=¨bold¨»§#183;«/mo»«msup»«mstyle mathvariant=¨bold¨»«mo stretchy=¨true¨»(«/mo»«mrow»«mn»149«/mn»«mo».«/mo»«mn»6«/mn»«mo»§#183;«/mo»«msup»«mn»10«/mn»«mn»9«/mn»«/msup»«/mrow»«mo stretchy=¨true¨»)«/mo»«/mstyle»«mn mathvariant=¨bold¨»3«/mn»«/msup»«/mrow»«mrow»«mn mathvariant=¨bold¨»6«/mn»«mo mathvariant=¨bold¨».«/mo»«mn mathvariant=¨bold¨»67«/mn»«mo mathvariant=¨bold¨»§#183;«/mo»«msup»«mn mathvariant=¨bold¨»10«/mn»«mrow»«mo mathvariant=¨bold¨»-«/mo»«mn mathvariant=¨bold¨»11«/mn»«/mrow»«/msup»«mo mathvariant=¨bold¨»§#183;«/mo»«mn mathvariant=¨bold¨»1«/mn»«mo mathvariant=¨bold¨».«/mo»«mn mathvariant=¨bold¨»99«/mn»«mo mathvariant=¨bold¨»§#183;«/mo»«msup»«mn mathvariant=¨bold¨»10«/mn»«mn mathvariant=¨bold¨»30«/mn»«/msup»«/mrow»«/mfrac»«mo mathvariant=¨bold¨»=«/mo»«/msqrt»«msqrt mathcolor=¨#0000FF¨»«mfrac»«mrow»«mn mathvariant=¨bold¨»1«/mn»«mo mathvariant=¨bold¨».«/mo»«mn mathvariant=¨bold¨»321«/mn»«mo mathvariant=¨bold¨»§#183;«/mo»«msup»«mn mathvariant=¨bold¨»10«/mn»«mn mathvariant=¨bold¨»35«/mn»«/msup»«/mrow»«mrow»«mn mathvariant=¨bold¨»1«/mn»«mo mathvariant=¨bold¨».«/mo»«mn mathvariant=¨bold¨»327«/mn»«mo mathvariant=¨bold¨»§#183;«/mo»«msup»«mn mathvariant=¨bold¨»10«/mn»«mn mathvariant=¨bold¨»20«/mn»«/msup»«/mrow»«/mfrac»«/msqrt»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»=«/mo»«msqrt mathcolor=¨#0000FF¨»«mn mathvariant=¨bold¨»9«/mn»«mo mathvariant=¨bold¨».«/mo»«mn mathvariant=¨bold¨»952«/mn»«mo mathvariant=¨bold¨»§#183;«/mo»«msup»«mn mathvariant=¨bold¨»10«/mn»«mn mathvariant=¨bold¨»14«/mn»«/msup»«mo mathvariant=¨bold¨»=«/mo»«/msqrt»«mn mathvariant=¨bold¨ mathcolor=¨#0000FF¨»31«/mn»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨».«/mo»«mn mathvariant=¨bold¨ mathcolor=¨#0000FF¨»55«/mn»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»§#183;«/mo»«msup»«mn mathvariant=¨bold¨ mathcolor=¨#0000FF¨»10«/mn»«mn mathvariant=¨bold¨ mathcolor=¨#0000FF¨»6«/mn»«/msup»«mi mathvariant=¨bold-italic¨ mathcolor=¨#0000FF¨»S«/mi»«mspace linebreak=¨newline¨/»«/mstyle»«/math»

نعبر عن زمن الدورة بالساعات والأيام:

«math xmlns=¨http://www.w3.org/1998/Math/MathML¨»«mstyle mathsize=¨24px¨»«mi mathvariant=¨bold¨ mathcolor=¨#0000FF¨»T«/mi»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»=«/mo»«mfrac mathcolor=¨#0000FF¨»«mrow»«mn mathvariant=¨bold¨»31«/mn»«mo mathvariant=¨bold¨».«/mo»«mn mathvariant=¨bold¨»55«/mn»«mo mathvariant=¨bold¨»§#183;«/mo»«msup»«mn mathvariant=¨bold¨»10«/mn»«mn mathvariant=¨bold¨»6«/mn»«/msup»«/mrow»«mrow»«mn mathvariant=¨bold¨»3«/mn»«mo mathvariant=¨bold¨»,«/mo»«mn mathvariant=¨bold¨»600«/mn»«/mrow»«/mfrac»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»=«/mo»«mn mathvariant=¨bold¨ mathcolor=¨#0000FF¨»8763«/mn»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨».«/mo»«mn mathvariant=¨bold¨ mathcolor=¨#0000FF¨»88«/mn»«mi mathvariant=¨bold¨ mathcolor=¨#0000FF¨»h«/mi»«mspace linebreak=¨newline¨/»«mspace linebreak=¨newline¨/»«mi mathvariant=¨bold¨ mathcolor=¨#0000FF¨»T«/mi»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»=«/mo»«mfrac mathcolor=¨#0000FF¨»«mrow»«mn mathvariant=¨bold¨»8763«/mn»«mo mathvariant=¨bold¨».«/mo»«mn mathvariant=¨bold¨»88«/mn»«/mrow»«mn mathvariant=¨bold¨»24«/mn»«/mfrac»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»=«/mo»«mn mathvariant=¨bold¨ mathcolor=¨#0000FF¨»365«/mn»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨».«/mo»«mn mathvariant=¨bold¨ mathcolor=¨#0000FF¨»16«/mn»«mi mathvariant=¨bold¨ mathcolor=¨#0000FF¨»day«/mi»«mspace linebreak=¨newline¨/»«mspace linebreak=¨newline¨/»«mspace linebreak=¨newline¨/»«/mstyle»«/math»

10. ب.3- حساب زمن دورة حركة القمر.

نستخدم التعبير لزمن دورة حركة القمر الاصطناعي ، لحركة القمر حول الكرة الأرضية.

«math xmlns=¨http://www.w3.org/1998/Math/MathML¨»«mstyle mathsize=¨24px¨»«mi mathvariant=¨bold¨ mathcolor=¨#0000FF¨»T«/mi»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»=«/mo»«msqrt mathcolor=¨#0000FF¨»«mfrac»«mrow»«mn mathvariant=¨bold¨»4«/mn»«mo mathvariant=¨bold¨»§#183;«/mo»«msup»«mi mathvariant=¨bold¨»§#960;«/mi»«mn mathvariant=¨bold¨»2«/mn»«/msup»«mo mathvariant=¨bold¨»§#183;«/mo»«msup»«mi mathvariant=¨bold¨»R«/mi»«mn mathvariant=¨bold¨»3«/mn»«/msup»«/mrow»«mrow»«mi mathvariant=¨bold¨»G«/mi»«mo mathvariant=¨bold¨»§#183;«/mo»«msub»«mi mathvariant=¨bold¨»M«/mi»«mi mathvariant=¨bold¨»E«/mi»«/msub»«/mrow»«/mfrac»«/msqrt»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»=«/mo»«msqrt mathcolor=¨#0000FF¨»«mfrac»«mrow»«mn mathvariant=¨bold¨»4«/mn»«mo mathvariant=¨bold¨»§#183;«/mo»«msup»«mi mathvariant=¨bold¨»§#960;«/mi»«mn mathvariant=¨bold¨»2«/mn»«/msup»«mo mathvariant=¨bold¨»§#183;«/mo»«msup»«mrow»«mo mathvariant=¨bold¨ stretchy=¨true¨»(«/mo»«mn mathvariant=¨bold¨»3«/mn»«mo mathvariant=¨bold¨».«/mo»«mn mathvariant=¨bold¨»84«/mn»«mo mathvariant=¨bold¨»§#183;«/mo»«msup»«mn mathvariant=¨bold¨»10«/mn»«mn mathvariant=¨bold¨»8«/mn»«/msup»«mo mathvariant=¨bold¨ stretchy=¨true¨»)«/mo»«/mrow»«mn mathvariant=¨bold¨»3«/mn»«/msup»«/mrow»«mrow»«mn mathvariant=¨bold¨»6«/mn»«mo mathvariant=¨bold¨».«/mo»«mn mathvariant=¨bold¨»67«/mn»«mo mathvariant=¨bold¨»§#183;«/mo»«msup»«mn mathvariant=¨bold¨»10«/mn»«mrow»«mo mathvariant=¨bold¨»-«/mo»«mn mathvariant=¨bold¨»11«/mn»«/mrow»«/msup»«mo mathvariant=¨bold¨»§#183;«/mo»«mn mathvariant=¨bold¨»5«/mn»«mo mathvariant=¨bold¨».«/mo»«mn mathvariant=¨bold¨»974«/mn»«mo mathvariant=¨bold¨»§#183;«/mo»«msup»«mn mathvariant=¨bold¨»10«/mn»«mn mathvariant=¨bold¨»24«/mn»«/msup»«/mrow»«/mfrac»«mo mathvariant=¨bold¨»=«/mo»«/msqrt»«msqrt mathcolor=¨#0000FF¨»«mfrac»«mrow»«mn mathvariant=¨bold¨»2«/mn»«mo mathvariant=¨bold¨».«/mo»«mn mathvariant=¨bold¨»23«/mn»«mo mathvariant=¨bold¨»§#183;«/mo»«msup»«mn mathvariant=¨bold¨»10«/mn»«mn mathvariant=¨bold¨»27«/mn»«/msup»«/mrow»«mrow»«mn mathvariant=¨bold¨»3«/mn»«mo mathvariant=¨bold¨».«/mo»«mn mathvariant=¨bold¨»98«/mn»«mo mathvariant=¨bold¨»§#183;«/mo»«msup»«mn mathvariant=¨bold¨»10«/mn»«mn mathvariant=¨bold¨»14«/mn»«/msup»«/mrow»«/mfrac»«/msqrt»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»=«/mo»«msqrt mathcolor=¨#0000FF¨»«mn mathvariant=¨bold¨»5«/mn»«mo mathvariant=¨bold¨».«/mo»«mn mathvariant=¨bold¨»596«/mn»«mo mathvariant=¨bold¨»§#183;«/mo»«msup»«mn mathvariant=¨bold¨»10«/mn»«mn mathvariant=¨bold¨»12«/mn»«/msup»«mo mathvariant=¨bold¨»=«/mo»«/msqrt»«mn mathvariant=¨bold¨ mathcolor=¨#0000FF¨»2«/mn»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨».«/mo»«mn mathvariant=¨bold¨ mathcolor=¨#0000FF¨»36«/mn»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»§#183;«/mo»«msup»«mn mathvariant=¨bold¨ mathcolor=¨#0000FF¨»10«/mn»«mn mathvariant=¨bold¨ mathcolor=¨#0000FF¨»6«/mn»«/msup»«mi mathvariant=¨bold-italic¨ mathcolor=¨#0000FF¨»S«/mi»«mspace linebreak=¨newline¨/»«/mstyle»«/math»

نبر عن زمن الدورة بالساعات والأيام:

«math xmlns=¨http://www.w3.org/1998/Math/MathML¨»«mstyle mathsize=¨24px¨»«mi mathvariant=¨bold¨ mathcolor=¨#0000FF¨»T«/mi»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»=«/mo»«mfrac mathcolor=¨#0000FF¨»«mrow»«mn mathvariant=¨bold¨»2«/mn»«mo mathvariant=¨bold¨».«/mo»«mn mathvariant=¨bold¨»36«/mn»«mo mathvariant=¨bold¨»§#183;«/mo»«msup»«mn mathvariant=¨bold¨»10«/mn»«mn mathvariant=¨bold¨»6«/mn»«/msup»«/mrow»«mrow»«mn mathvariant=¨bold¨»3«/mn»«mo mathvariant=¨bold¨»,«/mo»«mn mathvariant=¨bold¨»600«/mn»«/mrow»«/mfrac»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»=«/mo»«mn mathvariant=¨bold¨ mathcolor=¨#0000FF¨»657«/mn»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨».«/mo»«mn mathvariant=¨bold¨ mathcolor=¨#0000FF¨»13«/mn»«mi mathvariant=¨bold¨ mathcolor=¨#0000FF¨»h«/mi»«mspace linebreak=¨newline¨/»«mspace linebreak=¨newline¨/»«mi mathvariant=¨bold¨ mathcolor=¨#0000FF¨»T«/mi»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»=«/mo»«mfrac mathcolor=¨#0000FF¨»«mrow»«mn mathvariant=¨bold¨»657«/mn»«mo mathvariant=¨bold¨».«/mo»«mn mathvariant=¨bold¨»13«/mn»«/mrow»«mn mathvariant=¨bold¨»24«/mn»«/mfrac»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»=«/mo»«mn mathvariant=¨bold¨ mathcolor=¨#0000FF¨»27«/mn»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨».«/mo»«mn mathvariant=¨bold¨ mathcolor=¨#0000FF¨»38«/mn»«mi mathvariant=¨bold¨ mathcolor=¨#0000FF¨»day«/mi»«mspace linebreak=¨newline¨/»«mspace linebreak=¨newline¨/»«mspace linebreak=¨newline¨/»«/mstyle»«/math»

11. ب.4- قمر اصطناعي يدور حول كوكب (R)V

يتحرك القمر الاصطناعي في حركة دائرية تحت تأثير قوة الجاذبية فقط (سقوط حر).
نشير إلى القوة الجاذبة نحو المركز بـ Fg.

نرسم مخطط للقوى المؤثرة على الجسم:

نكتب معادلة الحركة الدائرية.

«math xmlns=¨http://www.w3.org/1998/Math/MathML¨»«msub»«mi mathvariant=¨bold¨ mathcolor=¨#0000FF¨»§#931;F«/mi»«mi mathvariant=¨bold¨ mathcolor=¨#0000FF¨»R«/mi»«/msub»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»=«/mo»«mfrac mathcolor=¨#0000FF¨»«mrow»«mi mathvariant=¨bold¨»m«/mi»«mo mathvariant=¨bold¨»§#183;«/mo»«msup»«mi mathvariant=¨bold¨»V«/mi»«mn mathvariant=¨bold¨»2«/mn»«/msup»«/mrow»«mi mathvariant=¨bold¨»R«/mi»«/mfrac»«mspace linebreak=¨newline¨/»«mspace linebreak=¨newline¨/»«mfrac mathcolor=¨#0000FF¨»«mrow»«mi mathvariant=¨bold¨»G«/mi»«mo mathvariant=¨bold¨»§#183;«/mo»«msub»«mi mathvariant=¨bold¨»M«/mi»«mi mathvariant=¨bold¨»X«/mi»«/msub»«mo mathvariant=¨bold¨»§#183;«/mo»«menclose notation=¨updiagonalstrike¨»«mi mathvariant=¨bold¨»m«/mi»«/menclose»«/mrow»«msup»«mi mathvariant=¨bold¨»R«/mi»«menclose notation=¨downdiagonalstrike¨»«mn mathvariant=¨bold¨»2«/mn»«/menclose»«/msup»«/mfrac»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»=«/mo»«mfrac mathcolor=¨#0000FF¨»«mrow»«menclose notation=¨updiagonalstrike¨»«mi mathvariant=¨bold¨»m«/mi»«/menclose»«mo mathvariant=¨bold¨»§#183;«/mo»«msup»«mi mathvariant=¨bold¨»V«/mi»«mn mathvariant=¨bold¨»2«/mn»«/msup»«/mrow»«menclose notation=¨downdiagonalstrike¨»«mi mathvariant=¨bold¨»R«/mi»«/menclose»«/mfrac»«mspace linebreak=¨newline¨/»«mspace linebreak=¨newline¨/»«msup»«mi mathvariant=¨bold¨ mathcolor=¨#0000FF¨»V«/mi»«mn mathvariant=¨bold¨ mathcolor=¨#0000FF¨»2«/mn»«/msup»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»=«/mo»«mfrac mathcolor=¨#0000FF¨»«mrow»«mi mathvariant=¨bold¨»G«/mi»«mo mathvariant=¨bold¨»§#183;«/mo»«msub»«mi mathvariant=¨bold¨»M«/mi»«mi mathvariant=¨bold¨»X«/mi»«/msub»«/mrow»«mi mathvariant=¨bold¨»R«/mi»«/mfrac»«mspace linebreak=¨newline¨/»«mspace linebreak=¨newline¨/»«/math»

لذلك، فإن التعبير عن سرعة القمر الاصطناعي كدالة لنصف قطر المدار هو:

«math xmlns=¨http://www.w3.org/1998/Math/MathML¨»«mstyle mathsize=¨24px¨»«menclose mathcolor=¨#0000FF¨ notation=¨circle¨»«mi mathvariant=¨bold¨»V«/mi»«mo mathvariant=¨bold¨»=«/mo»«msqrt»«mfrac»«mrow»«mi mathvariant=¨bold¨»G«/mi»«mo mathvariant=¨bold¨»§#183;«/mo»«msub»«mi mathvariant=¨bold¨»M«/mi»«mi mathvariant=¨bold¨»X«/mi»«/msub»«/mrow»«mi mathvariant=¨bold¨»R«/mi»«/mfrac»«/msqrt»«/menclose»«/mstyle»«/math»

12. ب.5- حساب سرعة قمر اصطناعي يتحرك حول الكرة الأرضية.

«math xmlns=¨http://www.w3.org/1998/Math/MathML¨»«mstyle mathsize=¨24px¨»«mi mathvariant=¨bold¨ mathcolor=¨#0000FF¨»V«/mi»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»=«/mo»«msqrt mathcolor=¨#0000FF¨»«mfrac»«mrow»«mi mathvariant=¨bold¨»G«/mi»«mo mathvariant=¨bold¨»§#183;«/mo»«msub»«mi mathvariant=¨bold¨»M«/mi»«mi mathvariant=¨bold¨»E«/mi»«/msub»«/mrow»«mrow»«msub»«mi mathvariant=¨bold¨»R«/mi»«mi mathvariant=¨bold¨»E«/mi»«/msub»«mo mathvariant=¨bold¨»+«/mo»«mi mathvariant=¨bold¨»h«/mi»«/mrow»«/mfrac»«/msqrt»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»=«/mo»«msqrt mathcolor=¨#0000FF¨»«mfrac»«mrow»«mn mathvariant=¨bold¨»6«/mn»«mo mathvariant=¨bold¨».«/mo»«mn mathvariant=¨bold¨»67«/mn»«mo mathvariant=¨bold¨»§#183;«/mo»«msup»«mn mathvariant=¨bold¨»10«/mn»«mrow»«mo mathvariant=¨bold¨»-«/mo»«mn mathvariant=¨bold¨»11«/mn»«/mrow»«/msup»«mo mathvariant=¨bold¨»§#183;«/mo»«mn mathvariant=¨bold¨»5«/mn»«mo mathvariant=¨bold¨».«/mo»«mn mathvariant=¨bold¨»974«/mn»«mo mathvariant=¨bold¨»§#183;«/mo»«msup»«mn mathvariant=¨bold¨»10«/mn»«mn mathvariant=¨bold¨»24«/mn»«/msup»«/mrow»«mrow»«mn mathvariant=¨bold¨»6«/mn»«mo mathvariant=¨bold¨».«/mo»«mn mathvariant=¨bold¨»38«/mn»«mo mathvariant=¨bold¨»§#183;«/mo»«msup»«mn mathvariant=¨bold¨»10«/mn»«mn mathvariant=¨bold¨»6«/mn»«/msup»«mo mathvariant=¨bold¨»+«/mo»«mn mathvariant=¨bold¨»6«/mn»«mo mathvariant=¨bold¨»§#183;«/mo»«msup»«mn mathvariant=¨bold¨»10«/mn»«mn mathvariant=¨bold¨»6«/mn»«/msup»«/mrow»«/mfrac»«/msqrt»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»=«/mo»«msqrt mathcolor=¨#0000FF¨»«mfrac»«mrow»«mn mathvariant=¨bold¨»3«/mn»«mo mathvariant=¨bold¨».«/mo»«mn mathvariant=¨bold¨»984«/mn»«mo mathvariant=¨bold¨»§#183;«/mo»«msup»«mn mathvariant=¨bold¨»10«/mn»«mn mathvariant=¨bold¨»14«/mn»«/msup»«/mrow»«mrow»«mn mathvariant=¨bold¨»12«/mn»«mo mathvariant=¨bold¨».«/mo»«mn mathvariant=¨bold¨»38«/mn»«mo mathvariant=¨bold¨»§#183;«/mo»«msup»«mn mathvariant=¨bold¨»10«/mn»«mn mathvariant=¨bold¨»6«/mn»«/msup»«/mrow»«/mfrac»«/msqrt»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»=«/mo»«msqrt mathcolor=¨#0000FF¨»«mn mathvariant=¨bold¨»32«/mn»«mo mathvariant=¨bold¨».«/mo»«mn mathvariant=¨bold¨»18«/mn»«mo mathvariant=¨bold¨»§#183;«/mo»«msup»«mn mathvariant=¨bold¨»10«/mn»«mn mathvariant=¨bold¨»6«/mn»«/msup»«/msqrt»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»=«/mo»«mn mathvariant=¨bold¨ mathcolor=¨#0000FF¨»5«/mn»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨».«/mo»«mn mathvariant=¨bold¨ mathcolor=¨#0000FF¨»67«/mn»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»§#183;«/mo»«msup»«mn mathvariant=¨bold¨ mathcolor=¨#0000FF¨»10«/mn»«mn mathvariant=¨bold¨ mathcolor=¨#0000FF¨»3«/mn»«/msup»«mfrac mathcolor=¨#0000FF¨»«mi mathvariant=¨bold¨»m«/mi»«mi mathvariant=¨bold¨»s«/mi»«/mfrac»«/mstyle»«/math»

13. ب.6- تعبير التسارع الرديالي (aR(V,R

في أي حركة دائرية منتظمة، يتعلق التسارع الرديالي (نحو المركز) بالسرعة الخطية وفقًا لما يلي:

«math xmlns=¨http://www.w3.org/1998/Math/MathML¨»«mstyle mathsize=¨22px¨»«menclose mathcolor=¨#0000FF¨ notation=¨circle¨»«msub»«mi mathvariant=¨bold¨»a«/mi»«mi mathvariant=¨bold¨»R«/mi»«/msub»«mo mathvariant=¨bold¨»=«/mo»«mfrac»«msup»«mi mathvariant=¨bold¨»V«/mi»«mn mathvariant=¨bold¨»2«/mn»«/msup»«mi mathvariant=¨bold¨»R«/mi»«/mfrac»«/menclose»«/mstyle»«/math»

14. ب.7- حساب التسارع الرديالي

نحسب التسارع الرديالي على ارتفاع 6000 كم وفقًا لسرعة الجسم في هذا الارتفاع (محسوبًا في البند ب 5):

«math xmlns=¨http://www.w3.org/1998/Math/MathML¨»«mstyle mathsize=¨20px¨»«msub»«mi mathvariant=¨bold¨ mathcolor=¨#0000FF¨»a«/mi»«mi mathvariant=¨bold¨ mathcolor=¨#0000FF¨»R«/mi»«/msub»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»=«/mo»«mfrac mathcolor=¨#0000FF¨»«msup»«mi mathvariant=¨bold¨»V«/mi»«mn mathvariant=¨bold¨»2«/mn»«/msup»«mi mathvariant=¨bold¨»R«/mi»«/mfrac»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»=«/mo»«mfrac mathcolor=¨#0000FF¨»«msup»«mi mathvariant=¨bold¨»V«/mi»«mn mathvariant=¨bold¨»2«/mn»«/msup»«mrow»«msub»«mi mathvariant=¨bold¨»R«/mi»«mi mathvariant=¨bold¨»E«/mi»«/msub»«mo mathvariant=¨bold¨»+«/mo»«mi mathvariant=¨bold¨»h«/mi»«/mrow»«/mfrac»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»=«/mo»«mfrac mathcolor=¨#0000FF¨»«msup»«mstyle mathvariant=¨bold¨»«mo stretchy=¨true¨»(«/mo»«mrow»«mn»5«/mn»«mo».«/mo»«mn»67«/mn»«mo»§#183;«/mo»«msup»«mn»10«/mn»«mn»3«/mn»«/msup»«/mrow»«mo stretchy=¨true¨»)«/mo»«/mstyle»«mn mathvariant=¨bold¨»2«/mn»«/msup»«mrow»«mn mathvariant=¨bold¨»6«/mn»«mo mathvariant=¨bold¨».«/mo»«mn mathvariant=¨bold¨»38«/mn»«mo mathvariant=¨bold¨»§#183;«/mo»«msup»«mn mathvariant=¨bold¨»10«/mn»«mn mathvariant=¨bold¨»6«/mn»«/msup»«mo mathvariant=¨bold¨»+«/mo»«mn mathvariant=¨bold¨»6«/mn»«mo mathvariant=¨bold¨»§#183;«/mo»«msup»«mn mathvariant=¨bold¨»10«/mn»«mn mathvariant=¨bold¨»6«/mn»«/msup»«/mrow»«/mfrac»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»=«/mo»«mfrac mathcolor=¨#0000FF¨»«mrow»«mn mathvariant=¨bold¨»32«/mn»«mo mathvariant=¨bold¨».«/mo»«mn mathvariant=¨bold¨»148«/mn»«mo mathvariant=¨bold¨»§#183;«/mo»«msup»«mn mathvariant=¨bold¨»10«/mn»«mn mathvariant=¨bold¨»6«/mn»«/msup»«/mrow»«mrow»«mn mathvariant=¨bold¨»12«/mn»«mo mathvariant=¨bold¨».«/mo»«mn mathvariant=¨bold¨»38«/mn»«mo mathvariant=¨bold¨»§#183;«/mo»«msup»«mn mathvariant=¨bold¨»10«/mn»«mn mathvariant=¨bold¨»6«/mn»«/msup»«/mrow»«/mfrac»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»=«/mo»«mn mathvariant=¨bold¨ mathcolor=¨#0000FF¨»2«/mn»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨».«/mo»«mn mathvariant=¨bold¨ mathcolor=¨#0000FF¨»59«/mn»«mfrac mathcolor=¨#0000FF¨»«mi mathvariant=¨bold¨»m«/mi»«msup»«mi mathvariant=¨bold¨»s«/mi»«mn mathvariant=¨bold¨»2«/mn»«/msup»«/mfrac»«/mstyle»«/math»

15. ب.8- تعبير تسارع الجاذبية

نتطرق إلى الجسم المتحرر من حالة السكون على سطح الكوكب.

القوة الوحيدة المؤثرة على الجسم هي قوة الجاذبية العامة. نشير إلى هذه القوة بـ Fg.

نرسم مخطط للقوى المؤثرة على الجسم:

نكتب معادلة الحركة، ونستخدم الرموز التالية:

*g - تسارع الجاذبية في نقطة تحرير الجسم.

m - كتلة الجسم.

ME - كتلة الكوكب.

RE- نصف قطر الكوكب.

«math xmlns=¨http://www.w3.org/1998/Math/MathML¨»«mstyle mathsize=¨24px¨»«mi mathvariant=¨bold¨ mathcolor=¨#0000FF¨»§#931;F«/mi»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»=«/mo»«mi mathvariant=¨bold¨ mathcolor=¨#0000FF¨»m«/mi»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»§#183;«/mo»«mi mathvariant=¨bold-italic¨ mathcolor=¨#0000FF¨»a«/mi»«mspace linebreak=¨newline¨/»«mspace linebreak=¨newline¨/»«msub»«mi mathvariant=¨bold¨ mathcolor=¨#0000FF¨»F«/mi»«mi mathvariant=¨bold¨ mathcolor=¨#0000FF¨»g«/mi»«/msub»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»=«/mo»«mi mathvariant=¨bold¨ mathcolor=¨#0000FF¨»m«/mi»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»§#183;«/mo»«mi mathvariant=¨bold-italic¨ mathcolor=¨#0000FF¨»g«/mi»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»*«/mo»«mspace linebreak=¨newline¨/»«mspace linebreak=¨newline¨/»«mfrac mathcolor=¨#0000FF¨»«mrow»«mi mathvariant=¨bold¨»G«/mi»«mo mathvariant=¨bold¨»§#183;«/mo»«msub»«mi mathvariant=¨bold¨»M«/mi»«mi mathvariant=¨bold¨»X«/mi»«/msub»«mo mathvariant=¨bold¨»§#183;«/mo»«menclose notation=¨updiagonalstrike¨»«mi mathvariant=¨bold¨»m«/mi»«/menclose»«/mrow»«msup»«mstyle mathvariant=¨bold¨»«mo stretchy=¨true¨»(«/mo»«mrow»«msub»«mi»R«/mi»«mi»E«/mi»«/msub»«mo»+«/mo»«mi»h«/mi»«/mrow»«mo stretchy=¨true¨»)«/mo»«/mstyle»«mn mathvariant=¨bold¨»2«/mn»«/msup»«/mfrac»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»=«/mo»«menclose mathcolor=¨#0000FF¨ notation=¨updiagonalstrike¨»«mi mathvariant=¨bold¨»m«/mi»«/menclose»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»§#183;«/mo»«msup»«mi mathvariant=¨bold¨ mathcolor=¨#0000FF¨»g«/mi»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»*«/mo»«/msup»«/mstyle»«/math»

نعبر عن تسارع الجاذبية من معادلة الحركة، ونحسب قيمة تسارع الجاذبية للجسم لحظة تحريره من حالة السكون من ارتفاع 6000 كم.

«math xmlns=¨http://www.w3.org/1998/Math/MathML¨»«mstyle mathsize=¨24px¨»«mspace linebreak=¨newline¨/»«msup»«mi mathvariant=¨bold¨ mathcolor=¨#0000FF¨»g«/mi»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»*«/mo»«/msup»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»=«/mo»«mfrac mathcolor=¨#0000FF¨»«mrow»«mi mathvariant=¨bold¨»G«/mi»«mo mathvariant=¨bold¨»§#183;«/mo»«msub»«mi mathvariant=¨bold¨»M«/mi»«mi mathvariant=¨bold¨»E«/mi»«/msub»«/mrow»«msup»«mrow»«mo stretchy=¨true¨ mathvariant=¨bold¨»(«/mo»«msub»«mi mathvariant=¨bold¨»R«/mi»«mi mathvariant=¨bold¨»E«/mi»«/msub»«mo mathvariant=¨bold¨»+«/mo»«mi mathvariant=¨bold¨»h«/mi»«mo stretchy=¨true¨ mathvariant=¨bold¨»)«/mo»«/mrow»«mn mathvariant=¨bold¨»2«/mn»«/msup»«/mfrac»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»=«/mo»«mfrac mathcolor=¨#0000FF¨»«mrow»«mn mathvariant=¨bold¨»6«/mn»«mo mathvariant=¨bold¨».«/mo»«mn mathvariant=¨bold¨»67«/mn»«mo mathvariant=¨bold¨»§#183;«/mo»«msup»«mn mathvariant=¨bold¨»10«/mn»«mrow»«mo mathvariant=¨bold¨»-«/mo»«mn mathvariant=¨bold¨»11«/mn»«/mrow»«/msup»«mo mathvariant=¨bold¨»§#183;«/mo»«mn mathvariant=¨bold¨»5«/mn»«mo mathvariant=¨bold¨».«/mo»«mn mathvariant=¨bold¨»974«/mn»«mo mathvariant=¨bold¨»§#183;«/mo»«msup»«mn mathvariant=¨bold¨»10«/mn»«mn mathvariant=¨bold¨»24«/mn»«/msup»«/mrow»«msup»«mstyle mathvariant=¨bold¨»«mo stretchy=¨true¨»(«/mo»«mrow»«mn»6«/mn»«mo».«/mo»«mn»38«/mn»«mo»§#183;«/mo»«msup»«mn»10«/mn»«mn»6«/mn»«/msup»«mo»+«/mo»«mn»6«/mn»«mo»§#183;«/mo»«msup»«mn»10«/mn»«mn»6«/mn»«/msup»«/mrow»«mo stretchy=¨true¨»)«/mo»«/mstyle»«mn mathvariant=¨bold¨»2«/mn»«/msup»«/mfrac»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»=«/mo»«mfrac mathcolor=¨#0000FF¨»«mrow»«mn mathvariant=¨bold¨»3«/mn»«mo mathvariant=¨bold¨».«/mo»«mn mathvariant=¨bold¨»984«/mn»«mo mathvariant=¨bold¨»§#183;«/mo»«msup»«mn mathvariant=¨bold¨»10«/mn»«mn mathvariant=¨bold¨»14«/mn»«/msup»«/mrow»«mrow»«mn mathvariant=¨bold¨»1«/mn»«mo mathvariant=¨bold¨».«/mo»«mn mathvariant=¨bold¨»532«/mn»«mo mathvariant=¨bold¨»§#183;«/mo»«msup»«mn mathvariant=¨bold¨»10«/mn»«mn mathvariant=¨bold¨»14«/mn»«/msup»«/mrow»«/mfrac»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»=«/mo»«mn mathvariant=¨bold¨ mathcolor=¨#0000FF¨»2«/mn»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨».«/mo»«mn mathvariant=¨bold¨ mathcolor=¨#0000FF¨»59«/mn»«mfrac mathcolor=¨#0000FF¨»«mi mathvariant=¨bold¨»m«/mi»«msup»«mi mathvariant=¨bold¨»s«/mi»«mn mathvariant=¨bold¨»2«/mn»«/msup»«/mfrac»«/mstyle»«/math»

16. ب.9- التعبير عن ارتفاع القمر الاصطناعي كدالة لنصف قطر الكوكب

نستخدم تعريف الجيب للزاوية BCO .

«math xmlns=¨http://www.w3.org/1998/Math/MathML¨»«mstyle mathsize=¨20px¨»«mi mathvariant=¨bold¨ mathcolor=¨#0000FF¨»sin«/mi»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»(«/mo»«mn mathvariant=¨bold¨ mathcolor=¨#0000FF¨»30«/mn»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»)«/mo»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»=«/mo»«mfrac mathcolor=¨#0000FF¨»«mi mathvariant=¨bold¨»OB«/mi»«mi mathvariant=¨bold¨»OC«/mi»«/mfrac»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»=«/mo»«mfrac mathcolor=¨#0000FF¨»«mi mathvariant=¨bold¨»R«/mi»«mrow»«mi mathvariant=¨bold¨»R«/mi»«mo mathvariant=¨bold¨»+«/mo»«mi mathvariant=¨bold¨»H«/mi»«/mrow»«/mfrac»«/mstyle»«/math»

نعبر عن ارتفاع القمر الاصطناعي كدالة لنصف القطر:

«math xmlns=¨http://www.w3.org/1998/Math/MathML¨»«mstyle mathsize=¨20px¨»«mn mathvariant=¨bold¨ mathcolor=¨#0000FF¨»0«/mn»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨».«/mo»«mn mathvariant=¨bold¨ mathcolor=¨#0000FF¨»5«/mn»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»=«/mo»«mfrac mathcolor=¨#0000FF¨»«mi mathvariant=¨bold¨»R«/mi»«mrow»«mi mathvariant=¨bold¨»R«/mi»«mo mathvariant=¨bold¨»+«/mo»«mi mathvariant=¨bold¨»H«/mi»«/mrow»«/mfrac»«mspace linebreak=¨newline¨/»«mspace linebreak=¨newline¨/»«mn mathvariant=¨bold¨ mathcolor=¨#0000FF¨»0«/mn»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨».«/mo»«mn mathvariant=¨bold¨ mathcolor=¨#0000FF¨»5«/mn»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»§#183;«/mo»«mstyle mathvariant=¨bold¨ mathcolor=¨#0000FF¨»«mo stretchy=¨true¨»(«/mo»«mrow»«mi»R«/mi»«mo»+«/mo»«mi»H«/mi»«/mrow»«mo stretchy=¨true¨»)«/mo»«/mstyle»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»=«/mo»«mi mathvariant=¨bold¨ mathcolor=¨#0000FF¨»R«/mi»«mspace linebreak=¨newline¨/»«mspace linebreak=¨newline¨/»«mn mathvariant=¨bold¨ mathcolor=¨#0000FF¨»0«/mn»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨».«/mo»«mn mathvariant=¨bold¨ mathcolor=¨#0000FF¨»5«/mn»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»§#183;«/mo»«mstyle mathvariant=¨bold¨ mathcolor=¨#0000FF¨»«mi»R«/mi»«mo»+«/mo»«/mstyle»«mn mathvariant=¨bold¨ mathcolor=¨#0000FF¨»0«/mn»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨».«/mo»«mn mathvariant=¨bold¨ mathcolor=¨#0000FF¨»5«/mn»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»§#183;«/mo»«mi mathvariant=¨bold¨ mathcolor=¨#0000FF¨»H«/mi»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»=«/mo»«mi mathvariant=¨bold¨ mathcolor=¨#0000FF¨»R«/mi»«mspace linebreak=¨newline¨/»«mspace linebreak=¨newline¨/»«mn mathvariant=¨bold¨ mathcolor=¨#0000FF¨»0«/mn»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨».«/mo»«mn mathvariant=¨bold¨ mathcolor=¨#0000FF¨»5«/mn»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»§#183;«/mo»«mi mathvariant=¨bold¨ mathcolor=¨#0000FF¨»H«/mi»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»=«/mo»«mi mathvariant=¨bold¨ mathcolor=¨#0000FF¨»R«/mi»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»-«/mo»«mn mathvariant=¨bold¨ mathcolor=¨#0000FF¨»0«/mn»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨».«/mo»«mn mathvariant=¨bold¨ mathcolor=¨#0000FF¨»5«/mn»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»§#183;«/mo»«mi mathvariant=¨bold¨ mathcolor=¨#0000FF¨»R«/mi»«mspace linebreak=¨newline¨/»«mspace linebreak=¨newline¨/»«mn mathvariant=¨bold¨ mathcolor=¨#0000FF¨»0«/mn»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨».«/mo»«mn mathvariant=¨bold¨ mathcolor=¨#0000FF¨»5«/mn»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»§#183;«/mo»«mi mathvariant=¨bold¨ mathcolor=¨#0000FF¨»H«/mi»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»=«/mo»«mn mathvariant=¨bold¨ mathcolor=¨#0000FF¨»0«/mn»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨».«/mo»«mn mathvariant=¨bold¨ mathcolor=¨#0000FF¨»5«/mn»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»§#183;«/mo»«mi mathvariant=¨bold¨ mathcolor=¨#0000FF¨»R«/mi»«mspace linebreak=¨newline¨/»«mspace linebreak=¨newline¨/»«menclose mathcolor=¨#0000FF¨ notation=¨circle¨»«mi mathvariant=¨bold¨»H«/mi»«mo mathvariant=¨bold¨»=«/mo»«mi mathvariant=¨bold¨»R«/mi»«/menclose»«/mstyle»«/math»

لذلك ، فإن ارتفاع القمر الاصطناعي فوق الكوكب يساوي نصف قطر الكوكب.

17. ب.10- التعبير عن القوة العمودية على شخص موجود داخل القمر الاصطناعي.

نرسم مخطط للقوى للشخص والقمر الاصطناعي بشكل منفصل:

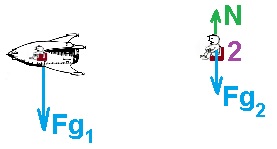
نكتب معادلات الحركة للقمر الاصطناعي والشخص، كلاهما يتحركان في نفس المدار وبنفس السرعة.
نشير إلى سرعتهما بواسطة V ونصف قطر مدارهما بواسطة R:
«math xmlns=¨http://www.w3.org/1998/Math/MathML¨»«msub mathcolor=¨#0000FF¨»«mi mathvariant=¨bold¨ mathcolor=¨#0000FF¨»§#931;F«/mi»«msub»«mi mathvariant=¨bold¨»R«/mi»«mn mathvariant=¨bold¨»2«/mn»«/msub»«/msub»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»=«/mo»«mfrac mathcolor=¨#0000FF¨»«mrow»«msub»«mi mathvariant=¨bold¨»m«/mi»«mn mathvariant=¨bold¨»2«/mn»«/msub»«mo mathvariant=¨bold¨»§#183;«/mo»«msup»«mi mathvariant=¨bold¨»V«/mi»«mn mathvariant=¨bold¨»2«/mn»«/msup»«/mrow»«mi mathvariant=¨bold¨»R«/mi»«/mfrac»«mspace linebreak=¨newline¨»«/mspace»«mfrac mathcolor=¨#0000FF¨»«mrow»«mi mathvariant=¨bold¨»G«/mi»«mo mathvariant=¨bold¨»§#183;«/mo»«msub»«mi mathvariant=¨bold¨»M«/mi»«mi mathvariant=¨bold¨»E«/mi»«/msub»«mo mathvariant=¨bold¨»§#183;«/mo»«msub»«mi mathvariant=¨bold¨»m«/mi»«mn mathvariant=¨bold¨»2«/mn»«/msub»«/mrow»«msup»«mi mathvariant=¨bold¨»R«/mi»«mn mathvariant=¨bold¨»2«/mn»«/msup»«/mfrac»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»-«/mo»«mi mathvariant=¨bold¨ mathcolor=¨#0000FF¨»N«/mi»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»=«/mo»«mfrac mathcolor=¨#0000FF¨»«mrow»«msub»«mi mathvariant=¨bold¨»m«/mi»«mn mathvariant=¨bold¨»2«/mn»«/msub»«mo mathvariant=¨bold¨»§#183;«/mo»«msup»«mi mathvariant=¨bold¨»V«/mi»«mn mathvariant=¨bold¨»2«/mn»«/msup»«/mrow»«mi mathvariant=¨bold¨»R«/mi»«/mfrac»«/math» «math xmlns=¨http://www.w3.org/1998/Math/MathML¨»«msub mathcolor=¨#0000FF¨»«mi mathvariant=¨bold¨ mathcolor=¨#0000FF¨»§#931;F«/mi»«msub»«mi mathvariant=¨bold¨»R«/mi»«mn mathvariant=¨bold¨»1«/mn»«/msub»«/msub»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»=«/mo»«mfrac mathcolor=¨#0000FF¨»«mrow»«msub»«mi mathvariant=¨bold¨»m«/mi»«mn mathvariant=¨bold¨»1«/mn»«/msub»«mo mathvariant=¨bold¨»§#183;«/mo»«msup»«mi mathvariant=¨bold¨»V«/mi»«mn mathvariant=¨bold¨»2«/mn»«/msup»«/mrow»«mi mathvariant=¨bold¨»R«/mi»«/mfrac»«mspace linebreak=¨newline¨»«/mspace»«mfrac mathcolor=¨#0000FF¨»«mrow»«mi mathvariant=¨bold¨»G«/mi»«mo mathvariant=¨bold¨»§#183;«/mo»«msub»«mi mathvariant=¨bold¨»M«/mi»«mi mathvariant=¨bold¨»E«/mi»«/msub»«mo mathvariant=¨bold¨»§#183;«/mo»«msub»«mi mathvariant=¨bold¨»m«/mi»«mn mathvariant=¨bold¨»1«/mn»«/msub»«/mrow»«msup»«mi mathvariant=¨bold¨»R«/mi»«mn mathvariant=¨bold¨»2«/mn»«/msup»«/mfrac»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»=«/mo»«mfrac mathcolor=¨#0000FF¨»«mrow»«msub»«mi mathvariant=¨bold¨»m«/mi»«mn mathvariant=¨bold¨»1«/mn»«/msub»«mo mathvariant=¨bold¨»§#183;«/mo»«msup»«mi mathvariant=¨bold¨»V«/mi»«mn mathvariant=¨bold¨»2«/mn»«/msup»«/mrow»«mi mathvariant=¨bold¨»R«/mi»«/mfrac»«/math»

نعبر عن النسبة بين مربع السرعة ونصف قطر المدار من معادلة حركة القمر الاصطناعي:

«math xmlns=¨http://www.w3.org/1998/Math/MathML¨»«msub mathcolor=¨#0000FF¨»«mi mathvariant=¨bold¨ mathcolor=¨#0000FF¨»§#931;F«/mi»«msub»«mi mathvariant=¨bold¨»R«/mi»«mn mathvariant=¨bold¨»1«/mn»«/msub»«/msub»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»=«/mo»«mfrac mathcolor=¨#0000FF¨»«mrow»«msub»«mi mathvariant=¨bold¨»m«/mi»«mn mathvariant=¨bold¨»1«/mn»«/msub»«mo mathvariant=¨bold¨»§#183;«/mo»«msup»«mi mathvariant=¨bold¨»V«/mi»«mn mathvariant=¨bold¨»2«/mn»«/msup»«/mrow»«mi mathvariant=¨bold¨»R«/mi»«/mfrac»«mspace linebreak=¨newline¨»«/mspace»«mfrac mathcolor=¨#0000FF¨»«mrow»«mi mathvariant=¨bold¨»G«/mi»«mo mathvariant=¨bold¨»§#183;«/mo»«msub»«mi mathvariant=¨bold¨»M«/mi»«mi mathvariant=¨bold¨»E«/mi»«/msub»«mo mathvariant=¨bold¨»§#183;«/mo»«menclose notation=¨updiagonalstrike¨»«msub»«mi mathvariant=¨bold¨»m«/mi»«mn mathvariant=¨bold¨»1«/mn»«/msub»«/menclose»«/mrow»«msup»«mi mathvariant=¨bold¨»R«/mi»«mn mathvariant=¨bold¨»2«/mn»«/msup»«/mfrac»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»=«/mo»«mfrac mathcolor=¨#0000FF¨»«mrow»«menclose notation=¨updiagonalstrike¨»«msub»«mi mathvariant=¨bold¨»m«/mi»«mn mathvariant=¨bold¨»1«/mn»«/msub»«/menclose»«mo mathvariant=¨bold¨»§#183;«/mo»«msup»«mi mathvariant=¨bold¨»V«/mi»«mn mathvariant=¨bold¨»2«/mn»«/msup»«/mrow»«mi mathvariant=¨bold¨»R«/mi»«/mfrac»«mspace linebreak=¨newline¨»«/mspace»«mspace linebreak=¨newline¨»«/mspace»«mfrac mathcolor=¨#FF0000¨»«msup»«mi mathvariant=¨bold¨»V«/mi»«mn mathvariant=¨bold¨»2«/mn»«/msup»«mi mathvariant=¨bold¨»R«/mi»«/mfrac»«mo mathvariant=¨bold¨ mathcolor=¨#FF0000¨»=«/mo»«mfrac mathcolor=¨#FF0000¨»«mrow»«mi mathvariant=¨bold¨»G«/mi»«mo mathvariant=¨bold¨»§#183;«/mo»«msub»«mi mathvariant=¨bold¨»M«/mi»«mi mathvariant=¨bold¨»E«/mi»«/msub»«/mrow»«msup»«mi mathvariant=¨bold¨»R«/mi»«mn mathvariant=¨bold¨»2«/mn»«/msup»«/mfrac»«/math»
نعوّض هذه العلاقة في معادلة حركة الشخص:

«math xmlns=¨http://www.w3.org/1998/Math/MathML¨»«msub mathcolor=¨#0000FF¨»«mi mathvariant=¨bold¨ mathcolor=¨#0000FF¨»§#931;F«/mi»«msub»«mi mathvariant=¨bold¨»R«/mi»«mn mathvariant=¨bold¨»2«/mn»«/msub»«/msub»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»=«/mo»«mfrac mathcolor=¨#0000FF¨»«mrow»«msub»«mi mathvariant=¨bold¨»m«/mi»«mn mathvariant=¨bold¨»2«/mn»«/msub»«mo mathvariant=¨bold¨»§#183;«/mo»«msup»«mi mathvariant=¨bold¨»V«/mi»«mn mathvariant=¨bold¨»2«/mn»«/msup»«/mrow»«mi mathvariant=¨bold¨»R«/mi»«/mfrac»«mspace linebreak=¨newline¨»«/mspace»«mfrac mathcolor=¨#0000FF¨»«mrow»«mi mathvariant=¨bold¨»G«/mi»«mo mathvariant=¨bold¨»§#183;«/mo»«msub»«mi mathvariant=¨bold¨»M«/mi»«mi mathvariant=¨bold¨»E«/mi»«/msub»«mo mathvariant=¨bold¨»§#183;«/mo»«msub»«mi mathvariant=¨bold¨»m«/mi»«mn mathvariant=¨bold¨»2«/mn»«/msub»«/mrow»«msup»«mi mathvariant=¨bold¨»R«/mi»«mn mathvariant=¨bold¨»2«/mn»«/msup»«/mfrac»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»-«/mo»«mi mathvariant=¨bold¨ mathcolor=¨#0000FF¨»N«/mi»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»=«/mo»«mfrac mathcolor=¨#0000FF¨»«mrow»«msub»«mi mathvariant=¨bold¨»m«/mi»«mn mathvariant=¨bold¨»2«/mn»«/msub»«mo mathvariant=¨bold¨»§#183;«/mo»«msup mathcolor=¨#FF0000¨»«mi mathvariant=¨bold¨ mathcolor=¨#FF0000¨»V«/mi»«mn mathvariant=¨bold¨»2«/mn»«/msup»«/mrow»«mi mathvariant=¨bold¨ mathcolor=¨#FF0000¨»R«/mi»«/mfrac»«mspace linebreak=¨newline¨»«/mspace»«mfrac mathcolor=¨#0000FF¨»«mrow»«mi mathvariant=¨bold¨»G«/mi»«mo mathvariant=¨bold¨»§#183;«/mo»«msub»«mi mathvariant=¨bold¨»M«/mi»«mi mathvariant=¨bold¨»E«/mi»«/msub»«mo mathvariant=¨bold¨»§#183;«/mo»«msub»«mi mathvariant=¨bold¨»m«/mi»«mn mathvariant=¨bold¨»2«/mn»«/msub»«/mrow»«msup»«mi mathvariant=¨bold¨»R«/mi»«mn mathvariant=¨bold¨»2«/mn»«/msup»«/mfrac»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»-«/mo»«mi mathvariant=¨bold¨ mathcolor=¨#0000FF¨»N«/mi»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»=«/mo»«msub mathcolor=¨#0000FF¨»«mi mathvariant=¨bold¨ mathcolor=¨#0000FF¨»m«/mi»«mn mathvariant=¨bold¨»2«/mn»«/msub»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»§#183;«/mo»«mfrac mathcolor=¨#FF0000¨»«mrow»«mi mathvariant=¨bold¨»G«/mi»«mo mathvariant=¨bold¨»§#183;«/mo»«msub»«mi mathvariant=¨bold¨»M«/mi»«mi mathvariant=¨bold¨»E«/mi»«/msub»«/mrow»«msup»«mi mathvariant=¨bold¨»R«/mi»«mn mathvariant=¨bold¨»2«/mn»«/msup»«/mfrac»«mspace linebreak=¨newline¨»«/mspace»«mspace linebreak=¨newline¨»«/mspace»«mi mathvariant=¨bold¨ mathcolor=¨#0000FF¨»N«/mi»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»=«/mo»«mfrac mathcolor=¨#0000FF¨»«mrow»«mi mathvariant=¨bold¨»G«/mi»«mo mathvariant=¨bold¨»§#183;«/mo»«msub»«mi mathvariant=¨bold¨»M«/mi»«mi mathvariant=¨bold¨»E«/mi»«/msub»«mo mathvariant=¨bold¨»§#183;«/mo»«msub»«mi mathvariant=¨bold¨»m«/mi»«mn mathvariant=¨bold¨»2«/mn»«/msub»«/mrow»«msup»«mi mathvariant=¨bold¨»R«/mi»«mn mathvariant=¨bold¨»2«/mn»«/msup»«/mfrac»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»-«/mo»«mfrac mathcolor=¨#0000FF¨»«mrow»«mi mathvariant=¨bold¨»G«/mi»«mo mathvariant=¨bold¨»§#183;«/mo»«msub»«mi mathvariant=¨bold¨»M«/mi»«mi mathvariant=¨bold¨»E«/mi»«/msub»«mo mathvariant=¨bold¨»§#183;«/mo»«msub»«mi mathvariant=¨bold¨»m«/mi»«mn mathvariant=¨bold¨»2«/mn»«/msub»«/mrow»«msup»«mi mathvariant=¨bold¨»R«/mi»«mn mathvariant=¨bold¨»2«/mn»«/msup»«/mfrac»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»=«/mo»«mn mathvariant=¨bold¨ mathcolor=¨#0000FF¨»0«/mn»«/math»

لذلك ، فإن القوة العمودية التي يشغلها القمر الاصطناعي على الشخص هي صفر. الشخص لا يضغط على القمر الاصطناعي ، إنه "يطفو" بداخله.

18. ب.11- القوة العمودية التي تؤثر على جسم في حالة سكون.

تؤثر قوتان على السيارة، القوة العمودية وقوة الجاذبية (وهي قوة الجاذبية العامة).

نرسم مخطط للقوى المؤثرة على السيارة:

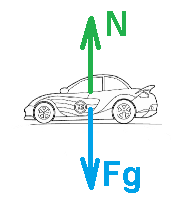
الجسم ثابت ، نكتب معادلة الحركة:

«math xmlns=¨http://www.w3.org/1998/Math/MathML¨»«mstyle mathsize=¨20px¨»«mi mathvariant=¨bold¨ mathcolor=¨#0000FF¨»§#931;F«/mi»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»=«/mo»«mn mathvariant=¨bold¨ mathcolor=¨#0000FF¨»0«/mn»«mspace linebreak=¨newline¨/»«mspace linebreak=¨newline¨/»«mi mathvariant=¨bold¨ mathcolor=¨#0000FF¨»N«/mi»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»=«/mo»«msub»«mi mathvariant=¨bold¨ mathcolor=¨#0000FF¨»F«/mi»«mi mathvariant=¨bold¨ mathcolor=¨#0000FF¨»g«/mi»«/msub»«mspace linebreak=¨newline¨/»«mspace linebreak=¨newline¨/»«menclose mathcolor=¨#0000FF¨ notation=¨circle¨»«mi mathvariant=¨bold¨»N«/mi»«mo mathvariant=¨bold¨»=«/mo»«mfrac»«mrow»«mi mathvariant=¨bold¨»G«/mi»«mo mathvariant=¨bold¨»§#183;«/mo»«msub»«mi mathvariant=¨bold¨»M«/mi»«mi mathvariant=¨bold¨»x«/mi»«/msub»«mo mathvariant=¨bold¨»§#183;«/mo»«mi mathvariant=¨bold¨»m«/mi»«/mrow»«msup»«msub»«mi mathvariant=¨bold¨»R«/mi»«mi mathvariant=¨bold¨»x«/mi»«/msub»«mn mathvariant=¨bold¨»2«/mn»«/msup»«/mfrac»«/menclose»«mspace linebreak=¨newline¨/»«/mstyle»«/math»

19. ب 12 - القوة العمودية المؤثرة على جسم متحرك.

تتحرك السيارة في حركة دائرية ، القوة الجاذبة نحو المركزهي القوة المحصّلة للقوة العمودية ووزن الجسم.

لكي تكون القوة الجاذبة نحو المركز مختلفة عن الصفر ، يجب أن تكون القوة العمودية أقل من وزن الجسم.

نرسم مخطط القوى على السيارة:

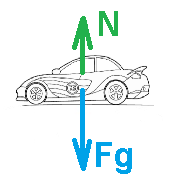
نكتب معادلة الحركة الدائرية:

«math xmlns=¨http://www.w3.org/1998/Math/MathML¨»«mstyle mathsize=¨20px¨»«msub»«mi mathvariant=¨bold¨ mathcolor=¨#0000FF¨»§#931;F«/mi»«mi mathvariant=¨bold¨ mathcolor=¨#0000FF¨»R«/mi»«/msub»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»=«/mo»«mfrac mathcolor=¨#0000FF¨»«mrow»«mi mathvariant=¨bold¨»m«/mi»«mo mathvariant=¨bold¨»§#183;«/mo»«msup»«mi mathvariant=¨bold¨»V«/mi»«mn mathvariant=¨bold¨»2«/mn»«/msup»«/mrow»«mi mathvariant=¨bold¨»R«/mi»«/mfrac»«mspace linebreak=¨newline¨/»«mspace linebreak=¨newline¨/»«msub»«mi mathvariant=¨bold¨ mathcolor=¨#0000FF¨»F«/mi»«mi mathvariant=¨bold¨ mathcolor=¨#0000FF¨»g«/mi»«/msub»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»-«/mo»«mi mathvariant=¨bold¨ mathcolor=¨#0000FF¨»N«/mi»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»=«/mo»«mfrac mathcolor=¨#0000FF¨»«mrow»«mi mathvariant=¨bold¨»m«/mi»«mo mathvariant=¨bold¨»§#183;«/mo»«msup»«mi mathvariant=¨bold¨»V«/mi»«mn mathvariant=¨bold¨»2«/mn»«/msup»«/mrow»«msub»«mi mathvariant=¨bold¨»R«/mi»«mi mathvariant=¨bold¨»X«/mi»«/msub»«/mfrac»«mspace linebreak=¨newline¨/»«mspace linebreak=¨newline¨/»«mi mathvariant=¨bold¨ mathcolor=¨#0000FF¨»N«/mi»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»=«/mo»«msub»«mi mathvariant=¨bold¨ mathcolor=¨#0000FF¨»F«/mi»«mi mathvariant=¨bold¨ mathcolor=¨#0000FF¨»g«/mi»«/msub»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»-«/mo»«mfrac mathcolor=¨#0000FF¨»«mrow»«mi mathvariant=¨bold¨»m«/mi»«mo mathvariant=¨bold¨»§#183;«/mo»«msup»«mi mathvariant=¨bold¨»V«/mi»«mn mathvariant=¨bold¨»2«/mn»«/msup»«/mrow»«msub»«mi mathvariant=¨bold¨»R«/mi»«mi mathvariant=¨bold¨»X«/mi»«/msub»«/mfrac»«mspace linebreak=¨newline¨/»«mspace linebreak=¨newline¨/»«menclose mathcolor=¨#0000FF¨ notation=¨circle¨»«mi mathvariant=¨bold¨»N«/mi»«mo mathvariant=¨bold¨»=«/mo»«mfrac»«mrow»«mi mathvariant=¨bold¨»G«/mi»«mo mathvariant=¨bold¨»§#183;«/mo»«msub»«mi mathvariant=¨bold¨»M«/mi»«mi mathvariant=¨bold¨»x«/mi»«/msub»«mo mathvariant=¨bold¨»§#183;«/mo»«mi mathvariant=¨bold¨»m«/mi»«/mrow»«msup»«msub»«mi mathvariant=¨bold¨»R«/mi»«mi mathvariant=¨bold¨»x«/mi»«/msub»«mn mathvariant=¨bold¨»2«/mn»«/msup»«/mfrac»«mo mathvariant=¨bold¨»-«/mo»«mfrac»«mrow»«mi mathvariant=¨bold¨»m«/mi»«mo mathvariant=¨bold¨»§#183;«/mo»«msup»«mi mathvariant=¨bold¨»V«/mi»«mn mathvariant=¨bold¨»2«/mn»«/msup»«/mrow»«msub»«mi mathvariant=¨bold¨»R«/mi»«mi mathvariant=¨bold¨»X«/mi»«/msub»«/mfrac»«/menclose»«mspace linebreak=¨newline¨/»«/mstyle»«/math»

20. ب.13- سرعة الجسم التي تكون بها القوة العمودية مساوية صفر.

نستخدم التعبير للقوة العمودية من القسم السابق.

نعوّض قيمة القوة العمودية بصفر ونعبر عن سرعة السيارة.

«math xmlns=¨http://www.w3.org/1998/Math/MathML¨»«mstyle mathsize=¨20px¨»«mi mathvariant=¨bold¨ mathcolor=¨#0000FF¨»N«/mi»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»=«/mo»«mfrac mathcolor=¨#0000FF¨»«mrow»«mi mathvariant=¨bold¨»G«/mi»«mo mathvariant=¨bold¨»§#183;«/mo»«msub»«mi mathvariant=¨bold¨»M«/mi»«mi mathvariant=¨bold¨»x«/mi»«/msub»«mo mathvariant=¨bold¨»§#183;«/mo»«mi mathvariant=¨bold¨»m«/mi»«/mrow»«msup»«msub»«mi mathvariant=¨bold¨»R«/mi»«mi mathvariant=¨bold¨»x«/mi»«/msub»«mn mathvariant=¨bold¨»2«/mn»«/msup»«/mfrac»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»-«/mo»«mfrac mathcolor=¨#0000FF¨»«mrow»«mi mathvariant=¨bold¨»m«/mi»«mo mathvariant=¨bold¨»§#183;«/mo»«msup»«mi mathvariant=¨bold¨»V«/mi»«mn mathvariant=¨bold¨»2«/mn»«/msup»«/mrow»«msub»«mi mathvariant=¨bold¨»R«/mi»«mi mathvariant=¨bold¨»X«/mi»«/msub»«/mfrac»«mspace linebreak=¨newline¨/»«mspace linebreak=¨newline¨/»«mn mathvariant=¨bold¨ mathcolor=¨#0000FF¨»0«/mn»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»=«/mo»«mfrac mathcolor=¨#0000FF¨»«mrow»«mi mathvariant=¨bold¨»G«/mi»«mo mathvariant=¨bold¨»§#183;«/mo»«msub»«mi mathvariant=¨bold¨»M«/mi»«mi mathvariant=¨bold¨»x«/mi»«/msub»«mo mathvariant=¨bold¨»§#183;«/mo»«mi mathvariant=¨bold¨»m«/mi»«/mrow»«msup»«msub»«mi mathvariant=¨bold¨»R«/mi»«mi mathvariant=¨bold¨»x«/mi»«/msub»«mn mathvariant=¨bold¨»2«/mn»«/msup»«/mfrac»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»-«/mo»«mfrac mathcolor=¨#0000FF¨»«mrow»«mi mathvariant=¨bold¨»m«/mi»«mo mathvariant=¨bold¨»§#183;«/mo»«msup»«mi mathvariant=¨bold¨»V«/mi»«mn mathvariant=¨bold¨»2«/mn»«/msup»«/mrow»«msub»«mi mathvariant=¨bold¨»R«/mi»«mi mathvariant=¨bold¨»X«/mi»«/msub»«/mfrac»«mspace linebreak=¨newline¨/»«mspace linebreak=¨newline¨/»«mfrac mathcolor=¨#0000FF¨»«mrow»«menclose notation=¨updiagonalstrike¨»«mi mathvariant=¨bold¨»m«/mi»«/menclose»«mo mathvariant=¨bold¨»§#183;«/mo»«msup»«mi mathvariant=¨bold¨»V«/mi»«mn mathvariant=¨bold¨»2«/mn»«/msup»«/mrow»«menclose notation=¨downdiagonalstrike¨»«msub»«mi mathvariant=¨bold¨»R«/mi»«mi mathvariant=¨bold¨»X«/mi»«/msub»«/menclose»«/mfrac»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»=«/mo»«mfrac mathcolor=¨#0000FF¨»«mrow»«mi mathvariant=¨bold¨»G«/mi»«mo mathvariant=¨bold¨»§#183;«/mo»«msub»«mi mathvariant=¨bold¨»M«/mi»«mi mathvariant=¨bold¨»x«/mi»«/msub»«mo mathvariant=¨bold¨»§#183;«/mo»«menclose notation=¨updiagonalstrike¨»«mi mathvariant=¨bold¨»m«/mi»«/menclose»«/mrow»«msup»«msub»«mi mathvariant=¨bold¨»R«/mi»«mi mathvariant=¨bold¨»x«/mi»«/msub»«menclose notation=¨downdiagonalstrike¨»«mn mathvariant=¨bold¨»2«/mn»«/menclose»«/msup»«/mfrac»«mspace linebreak=¨newline¨/»«mspace linebreak=¨newline¨/»«menclose mathcolor=¨#0000FF¨ notation=¨circle¨»«mi mathvariant=¨bold¨»V«/mi»«mo mathvariant=¨bold¨»=«/mo»«msqrt»«mfrac»«mrow»«mi mathvariant=¨bold¨»G«/mi»«mo mathvariant=¨bold¨»§#183;«/mo»«msub»«mi mathvariant=¨bold¨»M«/mi»«mi mathvariant=¨bold¨»x«/mi»«/msub»«/mrow»«msub»«mi mathvariant=¨bold¨»R«/mi»«mi mathvariant=¨bold¨»x«/mi»«/msub»«/mfrac»«/msqrt»«/menclose»«/mstyle»«/math»

21. ب.14 السرعة التي تتحرك بها السيارة في حركة قمر اصطناعي.

نستخدم تعبير السرعة من القسم السابق لسيارة تتحرك على سطح الأرض:

«math xmlns=¨http://www.w3.org/1998/Math/MathML¨»«mstyle mathsize=¨20px¨»«mi mathvariant=¨bold¨ mathcolor=¨#0000FF¨»V«/mi»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»=«/mo»«msqrt mathcolor=¨#0000FF¨»«mfrac»«mrow»«mi mathvariant=¨bold¨»G«/mi»«mo mathvariant=¨bold¨»§#183;«/mo»«msub»«mi mathvariant=¨bold¨»M«/mi»«mi mathvariant=¨bold¨»E«/mi»«/msub»«/mrow»«msub»«mi mathvariant=¨bold¨»R«/mi»«mi mathvariant=¨bold¨»E«/mi»«/msub»«/mfrac»«/msqrt»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»=«/mo»«msqrt mathcolor=¨#0000FF¨»«mfrac»«mrow»«mn mathvariant=¨bold¨»6«/mn»«mo mathvariant=¨bold¨».«/mo»«mn mathvariant=¨bold¨»67«/mn»«mo mathvariant=¨bold¨»§#183;«/mo»«msup»«mn mathvariant=¨bold¨»10«/mn»«mrow»«mo mathvariant=¨bold¨»-«/mo»«mn mathvariant=¨bold¨»11«/mn»«/mrow»«/msup»«mo mathvariant=¨bold¨»§#183;«/mo»«mn mathvariant=¨bold¨»5«/mn»«mo mathvariant=¨bold¨».«/mo»«mn mathvariant=¨bold¨»974«/mn»«mo mathvariant=¨bold¨»§#183;«/mo»«msup»«mn mathvariant=¨bold¨»10«/mn»«mn mathvariant=¨bold¨»24«/mn»«/msup»«/mrow»«mrow»«mn mathvariant=¨bold¨»6«/mn»«mo mathvariant=¨bold¨».«/mo»«mn mathvariant=¨bold¨»38«/mn»«mo mathvariant=¨bold¨»§#183;«/mo»«msup»«mn mathvariant=¨bold¨»10«/mn»«mn mathvariant=¨bold¨»6«/mn»«/msup»«/mrow»«/mfrac»«/msqrt»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»=«/mo»«msqrt mathcolor=¨#0000FF¨»«mfrac»«mrow»«mn mathvariant=¨bold¨»3«/mn»«mo mathvariant=¨bold¨».«/mo»«mn mathvariant=¨bold¨»98«/mn»«mo mathvariant=¨bold¨»§#183;«/mo»«msup»«mn mathvariant=¨bold¨»10«/mn»«mn mathvariant=¨bold¨»14«/mn»«/msup»«/mrow»«mrow»«mn mathvariant=¨bold¨»6«/mn»«mo mathvariant=¨bold¨».«/mo»«mn mathvariant=¨bold¨»38«/mn»«mo mathvariant=¨bold¨»§#183;«/mo»«msup»«mn mathvariant=¨bold¨»10«/mn»«mn mathvariant=¨bold¨»6«/mn»«/msup»«/mrow»«/mfrac»«/msqrt»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»=«/mo»«msqrt mathcolor=¨#0000FF¨»«mn mathvariant=¨bold¨»62«/mn»«mo mathvariant=¨bold¨».«/mo»«mn mathvariant=¨bold¨»38«/mn»«mo mathvariant=¨bold¨»§#183;«/mo»«msup»«mn mathvariant=¨bold¨»10«/mn»«mn mathvariant=¨bold¨»6«/mn»«/msup»«/msqrt»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»=«/mo»«mn mathvariant=¨bold¨ mathcolor=¨#0000FF¨»7«/mn»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»,«/mo»«mn mathvariant=¨bold¨ mathcolor=¨#0000FF¨»898«/mn»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨».«/mo»«mn mathvariant=¨bold¨ mathcolor=¨#0000FF¨»25«/mn»«mfrac mathcolor=¨#0000FF¨»«mi mathvariant=¨bold¨»m«/mi»«mi mathvariant=¨bold¨»s«/mi»«/mfrac»«/mstyle»«/math»

لذلك، إذا تحركت سيارة على الأرض بسرعة حوالي 28 ألف كم / ساعة ، فسوف تنفصل السيارة عن الأرض وتتحرك في حركة قمر اصطناعي.

22. ب.15- التعبير عن القوة العمودية على خط الاستواء

تؤثر قوتان على الشخص: قوة الجاذبية العامة التي تعمل نحو اتجاه نقطة مركز الكرة الأرضية ، والقوة العمودية.

نرسم مخطط القوى المؤثرة على الشخص.

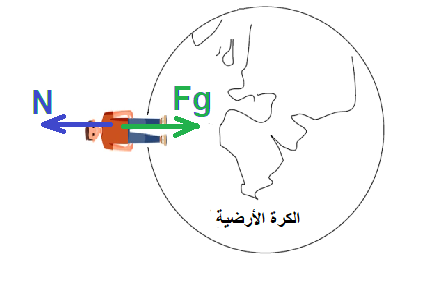
نكتب معادلة الحركة الدائرية:

«math xmlns=¨http://www.w3.org/1998/Math/MathML¨»«mstyle mathsize=¨20px¨»«msub»«mi mathvariant=¨bold¨ mathcolor=¨#0000FF¨»§#931;F«/mi»«mi mathvariant=¨bold¨ mathcolor=¨#0000FF¨»R«/mi»«/msub»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»=«/mo»«mi mathvariant=¨bold¨ mathcolor=¨#0000FF¨»m«/mi»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»§#183;«/mo»«msup»«mi mathvariant=¨bold-italic¨ mathcolor=¨#0000FF¨»§#969;«/mi»«mn mathvariant=¨bold¨ mathcolor=¨#0000FF¨»2«/mn»«/msup»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»§#183;«/mo»«mi mathvariant=¨bold¨ mathcolor=¨#0000FF¨»R«/mi»«mspace linebreak=¨newline¨/»«mspace linebreak=¨newline¨/»«msub»«mi mathvariant=¨bold¨ mathcolor=¨#0000FF¨»F«/mi»«mi mathvariant=¨bold¨ mathcolor=¨#0000FF¨»g«/mi»«/msub»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»-«/mo»«mi mathvariant=¨bold¨ mathcolor=¨#0000FF¨»N«/mi»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»=«/mo»«mi mathvariant=¨bold¨ mathcolor=¨#0000FF¨»m«/mi»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»§#183;«/mo»«msup»«mi mathvariant=¨bold-italic¨ mathcolor=¨#0000FF¨»§#969;«/mi»«mn mathvariant=¨bold¨ mathcolor=¨#0000FF¨»2«/mn»«/msup»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»§#183;«/mo»«mi mathvariant=¨bold¨ mathcolor=¨#0000FF¨»R«/mi»«/mstyle»«/math»

نعبر عن القوة العمودية من معادلة الحركة:

«math xmlns=¨http://www.w3.org/1998/Math/MathML¨»«mstyle mathsize=¨20px¨»«msub»«mi mathvariant=¨bold¨ mathcolor=¨#0000FF¨»F«/mi»«mi mathvariant=¨bold¨ mathcolor=¨#0000FF¨»g«/mi»«/msub»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»-«/mo»«mi mathvariant=¨bold¨ mathcolor=¨#0000FF¨»N«/mi»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»=«/mo»«mi mathvariant=¨bold¨ mathcolor=¨#0000FF¨»m«/mi»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»§#183;«/mo»«msup»«mi mathvariant=¨bold-italic¨ mathcolor=¨#0000FF¨»§#969;«/mi»«mn mathvariant=¨bold¨ mathcolor=¨#0000FF¨»2«/mn»«/msup»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»§#183;«/mo»«mi mathvariant=¨bold¨ mathcolor=¨#0000FF¨»R«/mi»«mspace linebreak=¨newline¨/»«mspace linebreak=¨newline¨/»«mi mathvariant=¨bold¨ mathcolor=¨#0000FF¨»N«/mi»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»=«/mo»«msub»«mi mathvariant=¨bold¨ mathcolor=¨#0000FF¨»F«/mi»«mi mathvariant=¨bold¨ mathcolor=¨#0000FF¨»g«/mi»«/msub»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»-«/mo»«mi mathvariant=¨bold¨ mathcolor=¨#0000FF¨»m«/mi»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»§#183;«/mo»«msup»«mi mathvariant=¨bold¨ mathcolor=¨#0000FF¨»§#969;«/mi»«mn mathvariant=¨bold¨ mathcolor=¨#0000FF¨»2«/mn»«/msup»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»§#183;«/mo»«mi mathvariant=¨bold¨ mathcolor=¨#0000FF¨»R«/mi»«/mstyle»«/math»

الشخص موجود على سطح الأرض، قوة الجاذبية العامة المؤثرة عليه هي قوة الجاذبية mg.

«math xmlns=¨http://www.w3.org/1998/Math/MathML¨»«mstyle mathsize=¨20px¨»«mi mathvariant=¨bold¨ mathcolor=¨#0000FF¨»N«/mi»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»=«/mo»«msub»«mi mathvariant=¨bold¨ mathcolor=¨#0000FF¨»F«/mi»«mi mathvariant=¨bold¨ mathcolor=¨#0000FF¨»g«/mi»«/msub»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»-«/mo»«mi mathvariant=¨bold¨ mathcolor=¨#0000FF¨»m«/mi»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»§#183;«/mo»«msup»«mi mathvariant=¨bold¨ mathcolor=¨#0000FF¨»§#969;«/mi»«mn mathvariant=¨bold¨ mathcolor=¨#0000FF¨»2«/mn»«/msup»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»§#183;«/mo»«msub»«mi mathvariant=¨bold¨ mathcolor=¨#0000FF¨»R«/mi»«mi mathvariant=¨bold¨ mathcolor=¨#0000FF¨»E«/mi»«/msub»«mspace linebreak=¨newline¨/»«mspace linebreak=¨newline¨/»«mi mathvariant=¨bold¨ mathcolor=¨#0000FF¨»N«/mi»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»=«/mo»«mi mathvariant=¨bold¨ mathcolor=¨#0000FF¨»m«/mi»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»§#183;«/mo»«mi mathvariant=¨bold¨ mathcolor=¨#0000FF¨»g«/mi»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»-«/mo»«mi mathvariant=¨bold¨ mathcolor=¨#0000FF¨»m«/mi»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»§#183;«/mo»«msup»«mstyle mathvariant=¨bold¨ mathcolor=¨#0000FF¨»«mo stretchy=¨true¨»(«/mo»«mfrac»«mrow»«mn»2«/mn»«mo»§#183;«/mo»«mi»§#960;«/mi»«/mrow»«mi»T«/mi»«/mfrac»«mo stretchy=¨true¨»)«/mo»«/mstyle»«mn mathvariant=¨bold¨ mathcolor=¨#0000FF¨»2«/mn»«/msup»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»§#183;«/mo»«msub»«mi mathvariant=¨bold¨ mathcolor=¨#0000FF¨»R«/mi»«mi mathvariant=¨bold¨ mathcolor=¨#0000FF¨»E«/mi»«/msub»«mspace linebreak=¨newline¨/»«mspace linebreak=¨newline¨/»«mi mathvariant=¨bold¨ mathcolor=¨#0000FF¨»N«/mi»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»=«/mo»«mi mathvariant=¨bold¨ mathcolor=¨#0000FF¨»m«/mi»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»§#183;«/mo»«mi mathvariant=¨bold¨ mathcolor=¨#0000FF¨»g«/mi»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»-«/mo»«mi mathvariant=¨bold¨ mathcolor=¨#0000FF¨»m«/mi»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»§#183;«/mo»«msup»«mfrac mathcolor=¨#0000FF¨»«mrow»«mn mathvariant=¨bold¨»4«/mn»«mo mathvariant=¨bold¨»§#183;«/mo»«mi mathvariant=¨bold¨»§#960;«/mi»«/mrow»«msup»«mi mathvariant=¨bold¨»T«/mi»«mn mathvariant=¨bold¨»2«/mn»«/msup»«/mfrac»«mn mathvariant=¨bold¨ mathcolor=¨#0000FF¨»2«/mn»«/msup»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»§#183;«/mo»«msub»«mi mathvariant=¨bold¨ mathcolor=¨#0000FF¨»R«/mi»«mi mathvariant=¨bold¨ mathcolor=¨#0000FF¨»E«/mi»«/msub»«/mstyle»«/math»

نعوّض قيمة نصف قطر الكرة الأرضية وزمن حركة الكرة الأرضية حول محورها:

«math xmlns=¨http://www.w3.org/1998/Math/MathML¨»«mstyle mathsize=¨20px¨»«mi mathvariant=¨bold¨ mathcolor=¨#0000FF¨»N«/mi»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»=«/mo»«mi mathvariant=¨bold¨ mathcolor=¨#0000FF¨»m«/mi»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»§#183;«/mo»«mi mathvariant=¨bold¨ mathcolor=¨#0000FF¨»g«/mi»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»-«/mo»«mi mathvariant=¨bold¨ mathcolor=¨#0000FF¨»m«/mi»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»§#183;«/mo»«msup»«mfrac mathcolor=¨#0000FF¨»«mrow»«mn mathvariant=¨bold¨»4«/mn»«mo mathvariant=¨bold¨»§#183;«/mo»«mi mathvariant=¨bold¨»§#960;«/mi»«/mrow»«msup»«mi mathvariant=¨bold¨»T«/mi»«mn mathvariant=¨bold¨»2«/mn»«/msup»«/mfrac»«mn mathvariant=¨bold¨ mathcolor=¨#0000FF¨»2«/mn»«/msup»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»§#183;«/mo»«msub»«mi mathvariant=¨bold¨ mathcolor=¨#0000FF¨»R«/mi»«mi mathvariant=¨bold¨ mathcolor=¨#0000FF¨»E«/mi»«/msub»«mspace linebreak=¨newline¨/»«mspace linebreak=¨newline¨/»«mi mathvariant=¨bold¨ mathcolor=¨#0000FF¨»N«/mi»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»=«/mo»«mi mathvariant=¨bold¨ mathcolor=¨#0000FF¨»m«/mi»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»§#183;«/mo»«mi mathvariant=¨bold¨ mathcolor=¨#0000FF¨»g«/mi»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»-«/mo»«mi mathvariant=¨bold¨ mathcolor=¨#0000FF¨»m«/mi»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»§#183;«/mo»«mfrac mathcolor=¨#0000FF¨»«mrow»«mn mathvariant=¨bold¨»4«/mn»«mo mathvariant=¨bold¨»§#183;«/mo»«msup»«mi mathvariant=¨bold¨»§#960;«/mi»«mn mathvariant=¨bold¨»2«/mn»«/msup»«/mrow»«msup»«mstyle mathvariant=¨bold¨»«mo stretchy=¨true¨»(«/mo»«mrow»«mn»24«/mn»«mo»§#183;«/mo»«mn»3«/mn»«mo»,«/mo»«mn»600«/mn»«/mrow»«mo stretchy=¨true¨»)«/mo»«/mstyle»«mn mathvariant=¨bold¨»2«/mn»«/msup»«/mfrac»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»§#183;«/mo»«mn mathvariant=¨bold¨ mathcolor=¨#0000FF¨»6«/mn»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨».«/mo»«mn mathvariant=¨bold¨ mathcolor=¨#0000FF¨»38«/mn»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»§#183;«/mo»«msup»«mn mathvariant=¨bold¨ mathcolor=¨#0000FF¨»10«/mn»«mn mathvariant=¨bold¨ mathcolor=¨#0000FF¨»6«/mn»«/msup»«mspace linebreak=¨newline¨/»«mspace linebreak=¨newline¨/»«mi mathvariant=¨bold¨ mathcolor=¨#0000FF¨»N«/mi»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»=«/mo»«mi mathvariant=¨bold¨ mathcolor=¨#0000FF¨»m«/mi»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»§#183;«/mo»«mi mathvariant=¨bold¨ mathcolor=¨#0000FF¨»g«/mi»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»-«/mo»«mi mathvariant=¨bold¨ mathcolor=¨#0000FF¨»m«/mi»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»§#183;«/mo»«mfrac mathcolor=¨#0000FF¨»«mrow»«mn mathvariant=¨bold¨»251«/mn»«mo mathvariant=¨bold¨».«/mo»«mn mathvariant=¨bold¨»87«/mn»«mo mathvariant=¨bold¨»§#183;«/mo»«msup»«mn mathvariant=¨bold¨»10«/mn»«mn mathvariant=¨bold¨»6«/mn»«/msup»«/mrow»«mstyle mathvariant=¨bold¨»«mn»7«/mn»«mo».«/mo»«mn»46«/mn»«mo»§#183;«/mo»«msup»«mn»10«/mn»«mn»9«/mn»«/msup»«/mstyle»«/mfrac»«mspace linebreak=¨newline¨/»«mspace linebreak=¨newline¨/»«menclose mathcolor=¨#0000FF¨ notation=¨circle¨»«mi mathvariant=¨bold¨»N«/mi»«mo mathvariant=¨bold¨»=«/mo»«mi mathvariant=¨bold¨»m«/mi»«mo mathvariant=¨bold¨»§#183;«/mo»«mi mathvariant=¨bold¨»g«/mi»«mo mathvariant=¨bold¨»-«/mo»«mi mathvariant=¨bold¨»m«/mi»«mo mathvariant=¨bold¨»§#183;«/mo»«mn mathvariant=¨bold¨»0«/mn»«mo mathvariant=¨bold¨».«/mo»«mn mathvariant=¨bold¨»033«/mn»«/menclose»«/mstyle»«/math»

من التعبير يمكن ملاحظة أن القوة العمودية أقل بقليل من mg نتيجة لقوة الجاذبية.

23. ب.16- حساب زمن دورة الكرة الأرضية في حالة N=0.

«math xmlns=¨http://www.w3.org/1998/Math/MathML¨»«mstyle mathsize=¨20px¨»«mi mathvariant=¨bold¨ mathcolor=¨#0000FF¨»T«/mi»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»*«/mo»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»=«/mo»«mn mathvariant=¨bold¨ mathcolor=¨#0000FF¨»2«/mn»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»§#183;«/mo»«mi mathvariant=¨bold¨ mathcolor=¨#0000FF¨»§#960;«/mi»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»§#183;«/mo»«msqrt mathcolor=¨#0000FF¨»«mfrac»«msup»«msub»«mi mathvariant=¨bold¨»R«/mi»«mi mathvariant=¨bold¨»E«/mi»«/msub»«mn mathvariant=¨bold¨»3«/mn»«/msup»«mrow»«mi mathvariant=¨bold¨»G«/mi»«mo mathvariant=¨bold¨»§#183;«/mo»«msub»«mi mathvariant=¨bold¨»M«/mi»«mi mathvariant=¨bold¨»E«/mi»«/msub»«/mrow»«/mfrac»«/msqrt»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»=«/mo»«mn mathvariant=¨bold¨ mathcolor=¨#0000FF¨»2«/mn»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»§#183;«/mo»«mi mathvariant=¨bold¨ mathcolor=¨#0000FF¨»§#960;«/mi»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»§#183;«/mo»«msqrt mathcolor=¨#0000FF¨»«mfrac»«msup»«mrow»«mo mathvariant=¨bold¨ stretchy=¨true¨»(«/mo»«mn mathvariant=¨bold¨»6«/mn»«mo mathvariant=¨bold¨».«/mo»«mn mathvariant=¨bold¨»38«/mn»«mo mathvariant=¨bold¨»§#183;«/mo»«msup»«mn mathvariant=¨bold¨»10«/mn»«mn mathvariant=¨bold¨»6«/mn»«/msup»«mo mathvariant=¨bold¨ stretchy=¨true¨»)«/mo»«/mrow»«mn mathvariant=¨bold¨»3«/mn»«/msup»«mrow»«mn mathvariant=¨bold¨»6«/mn»«mo mathvariant=¨bold¨».«/mo»«mn mathvariant=¨bold¨»67«/mn»«mo mathvariant=¨bold¨»§#183;«/mo»«msup»«mn mathvariant=¨bold¨»10«/mn»«mrow»«mo mathvariant=¨bold¨»-«/mo»«mn mathvariant=¨bold¨»11«/mn»«/mrow»«/msup»«mo mathvariant=¨bold¨»§#183;«/mo»«mn mathvariant=¨bold¨»5«/mn»«mo mathvariant=¨bold¨».«/mo»«mn mathvariant=¨bold¨»974«/mn»«mo mathvariant=¨bold¨»§#183;«/mo»«msup»«mn mathvariant=¨bold¨»10«/mn»«mn mathvariant=¨bold¨»24«/mn»«/msup»«/mrow»«/mfrac»«/msqrt»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»=«/mo»«mn mathvariant=¨bold¨ mathcolor=¨#0000FF¨»2«/mn»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»§#183;«/mo»«mi mathvariant=¨bold¨ mathcolor=¨#0000FF¨»§#960;«/mi»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»§#183;«/mo»«msqrt mathcolor=¨#0000FF¨»«mfrac»«mrow»«mn mathvariant=¨bold¨»2«/mn»«mo mathvariant=¨bold¨».«/mo»«mn mathvariant=¨bold¨»59«/mn»«mo mathvariant=¨bold¨»§#183;«/mo»«msup»«mn mathvariant=¨bold¨»10«/mn»«mn mathvariant=¨bold¨»20«/mn»«/msup»«/mrow»«mrow»«mn mathvariant=¨bold¨»3«/mn»«mo mathvariant=¨bold¨».«/mo»«mn mathvariant=¨bold¨»98«/mn»«mo mathvariant=¨bold¨»§#183;«/mo»«msup»«mn mathvariant=¨bold¨»10«/mn»«mn mathvariant=¨bold¨»14«/mn»«/msup»«/mrow»«/mfrac»«/msqrt»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»=«/mo»«mn mathvariant=¨bold¨ mathcolor=¨#0000FF¨»2«/mn»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»§#183;«/mo»«mi mathvariant=¨bold¨ mathcolor=¨#0000FF¨»§#960;«/mi»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»§#183;«/mo»«msqrt mathcolor=¨#0000FF¨»«mn mathvariant=¨bold¨»649«/mn»«mo mathvariant=¨bold¨».«/mo»«mn mathvariant=¨bold¨»99«/mn»«mo mathvariant=¨bold¨»§#183;«/mo»«msup»«mn mathvariant=¨bold¨»10«/mn»«mn mathvariant=¨bold¨»3«/mn»«/msup»«/msqrt»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»=«/mo»«mn mathvariant=¨bold¨ mathcolor=¨#0000FF¨»5065«/mn»«mi mathvariant=¨bold-italic¨ mathcolor=¨#0000FF¨»S«/mi»«/mstyle»«/math»

إذا أكملت الكرة الأرضية دورة في حوالي ساعة و- 41 دقيقة تقريبًا (بدلاً من 24 ساعة) ، فلن يشعر الشخص على خط الاستواء بقوة الجاذبية على الإطلاق.

24. ب.17- التعبير للقوة العمودية، رجل يقف على برج في كوكب لا يدور.

تؤثر قوتان على الشخص، القوة العمودية وقوة الجاذبية Fg:

الشخص ساكن، نكتب معادلة الحركة، ونعبر عن القوة العمودية منها:

«math xmlns=¨http://www.w3.org/1998/Math/MathML¨»«mstyle mathsize=¨24px¨»«mi mathvariant=¨bold¨ mathcolor=¨#0000FF¨»§#931;F«/mi»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»=«/mo»«mn mathvariant=¨bold¨ mathcolor=¨#0000FF¨»0«/mn»«mspace linebreak=¨newline¨/»«mspace linebreak=¨newline¨/»«mi mathvariant=¨bold¨ mathcolor=¨#0000FF¨»N«/mi»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»=«/mo»«msub»«mi mathvariant=¨bold¨ mathcolor=¨#0000FF¨»F«/mi»«mi mathvariant=¨bold¨ mathcolor=¨#0000FF¨»g«/mi»«/msub»«mspace linebreak=¨newline¨/»«mspace linebreak=¨newline¨/»«menclose mathcolor=¨#0000FF¨ notation=¨circle¨»«mi mathvariant=¨bold¨»N«/mi»«mo mathvariant=¨bold¨»=«/mo»«mfrac»«mrow»«mi mathvariant=¨bold¨»G«/mi»«mo mathvariant=¨bold¨»§#183;«/mo»«msub»«mi mathvariant=¨bold¨»M«/mi»«mi mathvariant=¨bold¨»X«/mi»«/msub»«mo mathvariant=¨bold¨»§#183;«/mo»«mi mathvariant=¨bold¨»m«/mi»«/mrow»«msup»«mrow»«mo mathvariant=¨bold¨ stretchy=¨true¨»(«/mo»«msub»«mi mathvariant=¨bold¨»R«/mi»«mi mathvariant=¨bold¨»X«/mi»«/msub»«mo mathvariant=¨bold¨»+«/mo»«mi mathvariant=¨bold¨»h«/mi»«mo mathvariant=¨bold¨ stretchy=¨true¨»)«/mo»«/mrow»«mn mathvariant=¨bold¨»2«/mn»«/msup»«/mfrac»«/menclose»«/mstyle»«/math»

25. ب.18- تعبير القوة العمودية التيي تعمل على شخصيجلس على برج موجود كوكب يدور.

تؤثر قوتان على الشخص، القوة العمودية وقوة الجاذبية Fg:

يتحرك الشخص في حركة دائرية ، نكتب معادلة الحركة ونعبر عن القوة العمودية منها:

«math xmlns=¨http://www.w3.org/1998/Math/MathML¨»«mstyle mathsize=¨20px¨»«msub»«mi mathvariant=¨bold¨ mathcolor=¨#0000FF¨»§#931;F«/mi»«mi mathvariant=¨bold¨ mathcolor=¨#0000FF¨»R«/mi»«/msub»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»=«/mo»«mi mathvariant=¨bold¨ mathcolor=¨#0000FF¨»m«/mi»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»§#183;«/mo»«msup»«mi mathvariant=¨bold-italic¨ mathcolor=¨#0000FF¨»§#969;«/mi»«mn mathvariant=¨bold¨ mathcolor=¨#0000FF¨»2«/mn»«/msup»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»§#183;«/mo»«mi mathvariant=¨bold¨ mathcolor=¨#0000FF¨»R«/mi»«mspace linebreak=¨newline¨/»«mspace linebreak=¨newline¨/»«msub»«mi mathvariant=¨bold¨ mathcolor=¨#0000FF¨»F«/mi»«mi mathvariant=¨bold¨ mathcolor=¨#0000FF¨»g«/mi»«/msub»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»-«/mo»«mi mathvariant=¨bold¨ mathcolor=¨#0000FF¨»N«/mi»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»=«/mo»«mi mathvariant=¨bold¨ mathcolor=¨#0000FF¨»m«/mi»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»§#183;«/mo»«msup»«mi mathvariant=¨bold-italic¨ mathcolor=¨#0000FF¨»§#969;«/mi»«mn mathvariant=¨bold¨ mathcolor=¨#0000FF¨»2«/mn»«/msup»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»§#183;«/mo»«mi mathvariant=¨bold¨ mathcolor=¨#0000FF¨»R«/mi»«mspace linebreak=¨newline¨/»«mspace linebreak=¨newline¨/»«mi mathvariant=¨bold¨ mathcolor=¨#0000FF¨»N«/mi»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»=«/mo»«msub»«mi mathvariant=¨bold¨ mathcolor=¨#0000FF¨»F«/mi»«mi mathvariant=¨bold¨ mathcolor=¨#0000FF¨»g«/mi»«/msub»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»-«/mo»«mi mathvariant=¨bold¨ mathcolor=¨#0000FF¨»m«/mi»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»§#183;«/mo»«msup»«mi mathvariant=¨bold¨ mathcolor=¨#0000FF¨»§#969;«/mi»«mn mathvariant=¨bold¨ mathcolor=¨#0000FF¨»2«/mn»«/msup»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»§#183;«/mo»«mi mathvariant=¨bold¨ mathcolor=¨#0000FF¨»R«/mi»«/mstyle»«/math»

نستخدم قوة الجاذبية العامة ونعبر عن نصف قطر المدار R وفقًا للارتفاع الذي يكون فيه الشخص على ارتفاع h من سطح الكوكب ونصف قطر الكوكب R_X.

«math xmlns=¨http://www.w3.org/1998/Math/MathML¨»«mstyle mathsize=¨20px¨»«mi mathvariant=¨bold¨ mathcolor=¨#0000FF¨»N«/mi»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»=«/mo»«mfrac mathcolor=¨#0000FF¨»«mrow»«mi mathvariant=¨bold¨»G«/mi»«mo mathvariant=¨bold¨»§#183;«/mo»«msub»«mi mathvariant=¨bold¨»M«/mi»«mi mathvariant=¨bold¨»X«/mi»«/msub»«mo mathvariant=¨bold¨»§#183;«/mo»«mi mathvariant=¨bold¨»m«/mi»«/mrow»«mstyle mathvariant=¨bold¨»«msup»«mi»R«/mi»«mn»2«/mn»«/msup»«/mstyle»«/mfrac»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»-«/mo»«mfrac mathcolor=¨#0000FF¨»«mrow»«mi mathvariant=¨bold¨»m«/mi»«mo mathvariant=¨bold¨»§#183;«/mo»«msup»«mi mathvariant=¨bold¨»V«/mi»«mn mathvariant=¨bold¨»2«/mn»«/msup»«/mrow»«mi mathvariant=¨bold¨»R«/mi»«/mfrac»«mspace linebreak=¨newline¨/»«mspace linebreak=¨newline¨/»«menclose mathcolor=¨#0000FF¨ notation=¨circle¨»«mspace linebreak=¨newline¨/»«mi mathvariant=¨bold¨»N«/mi»«mo mathvariant=¨bold¨»=«/mo»«mfrac»«mrow»«mi mathvariant=¨bold¨»G«/mi»«mo mathvariant=¨bold¨»§#183;«/mo»«msub»«mi mathvariant=¨bold¨»M«/mi»«mi mathvariant=¨bold¨»X«/mi»«/msub»«mo mathvariant=¨bold¨»§#183;«/mo»«mi mathvariant=¨bold¨»m«/mi»«/mrow»«msup»«mstyle mathvariant=¨bold¨»«mo stretchy=¨true¨»(«/mo»«mrow»«msub»«mi»R«/mi»«mi»X«/mi»«/msub»«mo»+«/mo»«mi»h«/mi»«/mrow»«mo stretchy=¨true¨»)«/mo»«/mstyle»«mn mathvariant=¨bold¨»2«/mn»«/msup»«/mfrac»«mo mathvariant=¨bold¨»-«/mo»«mfrac»«mrow»«mi mathvariant=¨bold¨»m«/mi»«mo mathvariant=¨bold¨»§#183;«/mo»«msup»«mi mathvariant=¨bold¨»V«/mi»«mn mathvariant=¨bold¨»2«/mn»«/msup»«/mrow»«mrow»«msub»«mi mathvariant=¨bold¨»R«/mi»«mi mathvariant=¨bold¨»X«/mi»«/msub»«mo mathvariant=¨bold¨»+«/mo»«mi mathvariant=¨bold¨»h«/mi»«/mrow»«/mfrac»«/menclose»«mspace linebreak=¨newline¨/»«mspace linebreak=¨newline¨/»«/mstyle»«/math»

26. ب.19- التعبير عن زمن دورة شخص يجلس على برج موجود على سطح كوكب يدور حول محوره.

نرسم مخطط للقوى المؤثرة على الشخص:

نكتب معادلة الحركة الدائرية، ونعبر عن زمن الدورة T عندما تكون القوة العمودية مساوية لصفر.

«math xmlns=¨http://www.w3.org/1998/Math/MathML¨»«mstyle mathsize=¨20px¨»«msub»«mi mathvariant=¨bold¨ mathcolor=¨#0000FF¨»F«/mi»«mi mathvariant=¨bold¨ mathcolor=¨#0000FF¨»g«/mi»«/msub»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»-«/mo»«mi mathvariant=¨bold¨ mathcolor=¨#0000FF¨»N«/mi»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»=«/mo»«mi mathvariant=¨bold¨ mathcolor=¨#0000FF¨»m«/mi»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»§#183;«/mo»«msup»«mi mathvariant=¨bold-italic¨ mathcolor=¨#0000FF¨»§#969;«/mi»«mn mathvariant=¨bold¨ mathcolor=¨#0000FF¨»2«/mn»«/msup»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»§#183;«/mo»«mi mathvariant=¨bold¨ mathcolor=¨#0000FF¨»R«/mi»«mspace linebreak=¨newline¨/»«mspace linebreak=¨newline¨/»«mfrac mathcolor=¨#0000FF¨»«mrow»«mi mathvariant=¨bold¨»G«/mi»«mo mathvariant=¨bold¨»§#183;«/mo»«msub»«mi mathvariant=¨bold¨»M«/mi»«mi mathvariant=¨bold¨»X«/mi»«/msub»«mo mathvariant=¨bold¨»§#183;«/mo»«mi mathvariant=¨bold¨»m«/mi»«/mrow»«msup»«mi mathvariant=¨bold¨»R«/mi»«mn mathvariant=¨bold¨»2«/mn»«/msup»«/mfrac»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»-«/mo»«mn mathvariant=¨bold¨ mathcolor=¨#0000FF¨»0«/mn»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»=«/mo»«mi mathvariant=¨bold¨ mathcolor=¨#0000FF¨»m«/mi»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»§#183;«/mo»«msup»«mrow mathcolor=¨#0000FF¨»«mo mathvariant=¨bold¨ stretchy=¨true¨»(«/mo»«mfrac»«mrow»«mn mathvariant=¨bold¨»2«/mn»«mo mathvariant=¨bold¨»§#183;«/mo»«mi mathvariant=¨bold¨»§#960;«/mi»«/mrow»«mi mathvariant=¨bold¨»T«/mi»«/mfrac»«mo mathvariant=¨bold¨ stretchy=¨true¨»)«/mo»«/mrow»«mn mathvariant=¨bold¨ mathcolor=¨#0000FF¨»2«/mn»«/msup»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»§#183;«/mo»«mi mathvariant=¨bold¨ mathcolor=¨#0000FF¨»R«/mi»«mspace linebreak=¨newline¨/»«mspace linebreak=¨newline¨/»«mfrac mathcolor=¨#0000FF¨»«mrow»«mi mathvariant=¨bold¨»G«/mi»«mo mathvariant=¨bold¨»§#183;«/mo»«msub»«mi mathvariant=¨bold¨»M«/mi»«mi mathvariant=¨bold¨»X«/mi»«/msub»«mo mathvariant=¨bold¨»§#183;«/mo»«menclose notation=¨downdiagonalstrike¨»«mi mathvariant=¨bold¨»m«/mi»«/menclose»«/mrow»«msup»«mi mathvariant=¨bold¨»R«/mi»«mn mathvariant=¨bold¨»2«/mn»«/msup»«/mfrac»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»=«/mo»«menclose mathcolor=¨#0000FF¨ notation=¨downdiagonalstrike¨»«mi mathvariant=¨bold¨»m«/mi»«/menclose»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»§#183;«/mo»«mfrac mathcolor=¨#0000FF¨»«mrow»«mn mathvariant=¨bold¨»4«/mn»«mo mathvariant=¨bold¨»§#183;«/mo»«msup»«mi mathvariant=¨bold¨»§#960;«/mi»«mn mathvariant=¨bold¨»2«/mn»«/msup»«/mrow»«msup»«mi mathvariant=¨bold¨»T«/mi»«mn mathvariant=¨bold¨»2«/mn»«/msup»«/mfrac»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»§#183;«/mo»«mi mathvariant=¨bold¨ mathcolor=¨#0000FF¨»R«/mi»«mspace linebreak=¨newline¨/»«mspace linebreak=¨newline¨/»«mi mathvariant=¨bold¨ mathcolor=¨#0000FF¨»T«/mi»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»=«/mo»«msqrt mathcolor=¨#0000FF¨»«mfrac»«mrow»«mn mathvariant=¨bold¨»4«/mn»«mo mathvariant=¨bold¨»§#183;«/mo»«msup»«mi mathvariant=¨bold¨»§#960;«/mi»«mn mathvariant=¨bold¨»2«/mn»«/msup»«mo mathvariant=¨bold¨»§#183;«/mo»«msup»«mi mathvariant=¨bold¨»R«/mi»«mn mathvariant=¨bold¨»3«/mn»«/msup»«/mrow»«mrow»«mi mathvariant=¨bold¨»G«/mi»«mo mathvariant=¨bold¨»§#183;«/mo»«msub»«mi mathvariant=¨bold¨»M«/mi»«mi mathvariant=¨bold¨»X«/mi»«/msub»«/mrow»«/mfrac»«/msqrt»«mspace linebreak=¨newline¨/»«mi mathvariant=¨bold-italic¨ mathcolor=¨#0000FF¨»R«/mi»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»=«/mo»«msub»«mi mathvariant=¨bold-italic¨ mathcolor=¨#0000FF¨»R«/mi»«mi mathvariant=¨bold¨ mathcolor=¨#0000FF¨»x«/mi»«/msub»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»+«/mo»«mi mathvariant=¨bold-italic¨ mathcolor=¨#0000FF¨»h«/mi»«mspace linebreak=¨newline¨/»«mspace linebreak=¨newline¨/»«menclose mathcolor=¨#0000FF¨ notation=¨circle¨»«mi mathvariant=¨bold¨»T«/mi»«mo mathvariant=¨bold¨»=«/mo»«mn mathvariant=¨bold¨»2«/mn»«mo mathvariant=¨bold¨»§#183;«/mo»«mi mathvariant=¨bold¨»§#960;«/mi»«msqrt»«mfrac»«msup»«mstyle mathvariant=¨bold¨»«mo stretchy=¨true¨»(«/mo»«mrow»«msub»«mi»R«/mi»«mi»X«/mi»«/msub»«mo»+«/mo»«mi»h«/mi»«/mrow»«mo stretchy=¨true¨»)«/mo»«/mstyle»«mn mathvariant=¨bold¨»3«/mn»«/msup»«mrow»«mi mathvariant=¨bold¨»G«/mi»«mo mathvariant=¨bold¨»§#183;«/mo»«msub»«mi mathvariant=¨bold¨»M«/mi»«mi mathvariant=¨bold¨»X«/mi»«/msub»«/mrow»«/mfrac»«/msqrt»«/menclose»«mspace linebreak=¨newline¨/»«mspace linebreak=¨newline¨/»«/mstyle»«/math»

27. ب.20- تعبير لنصف قطر المدار لقمر اصطناعي للاتصالات .

القوة الوحيدة المؤثرة على القمر الاصطناعي هي قوة الجاذبية العامة.

نكتب معادلة الحركة الدائرية:

«math xmlns=¨http://www.w3.org/1998/Math/MathML¨»«mstyle mathsize=¨20px¨»«msub»«mi mathvariant=¨bold¨ mathcolor=¨#0000FF¨»§#931;F«/mi»«mi mathvariant=¨bold¨ mathcolor=¨#0000FF¨»R«/mi»«/msub»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»=«/mo»«mi mathvariant=¨bold¨ mathcolor=¨#0000FF¨»m«/mi»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»§#183;«/mo»«msup»«mi mathvariant=¨bold¨ mathcolor=¨#0000FF¨»§#969;«/mi»«mn mathvariant=¨bold¨ mathcolor=¨#0000FF¨»2«/mn»«/msup»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»§#183;«/mo»«mi mathvariant=¨bold¨ mathcolor=¨#0000FF¨»R«/mi»«mspace linebreak=¨newline¨/»«mspace linebreak=¨newline¨/»«msub»«mi mathvariant=¨bold¨ mathcolor=¨#0000FF¨»F«/mi»«mi mathvariant=¨bold¨ mathcolor=¨#0000FF¨»g«/mi»«/msub»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»=«/mo»«mi mathvariant=¨bold¨ mathcolor=¨#0000FF¨»m«/mi»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»§#183;«/mo»«msup»«mi mathvariant=¨bold¨ mathcolor=¨#0000FF¨»§#969;«/mi»«mn mathvariant=¨bold¨ mathcolor=¨#0000FF¨»2«/mn»«/msup»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»§#183;«/mo»«mi mathvariant=¨bold¨ mathcolor=¨#0000FF¨»R«/mi»«mspace linebreak=¨newline¨/»«mspace linebreak=¨newline¨/»«mfrac mathcolor=¨#0000FF¨»«mrow»«mi mathvariant=¨bold¨»G«/mi»«mo mathvariant=¨bold¨»§#183;«/mo»«msub»«mi mathvariant=¨bold¨»M«/mi»«mi mathvariant=¨bold¨»x«/mi»«/msub»«mo mathvariant=¨bold¨»§#183;«/mo»«menclose notation=¨updiagonalstrike¨»«mi mathvariant=¨bold¨»m«/mi»«/menclose»«/mrow»«msup»«mi mathvariant=¨bold¨»R«/mi»«mn mathvariant=¨bold¨»2«/mn»«/msup»«/mfrac»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»=«/mo»«menclose mathcolor=¨#0000FF¨ notation=¨updiagonalstrike¨»«mi mathvariant=¨bold¨»m«/mi»«/menclose»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»§#183;«/mo»«msup»«mfrac mathcolor=¨#0000FF¨»«mrow»«mn mathvariant=¨bold¨»4«/mn»«mo mathvariant=¨bold¨»§#183;«/mo»«mi mathvariant=¨bold¨»§#960;«/mi»«/mrow»«msup»«mi mathvariant=¨bold¨»T«/mi»«mn mathvariant=¨bold¨»2«/mn»«/msup»«/mfrac»«mn mathvariant=¨bold¨ mathcolor=¨#0000FF¨»2«/mn»«/msup»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»§#183;«/mo»«mi mathvariant=¨bold¨ mathcolor=¨#0000FF¨»R«/mi»«mspace linebreak=¨newline¨/»«mspace linebreak=¨newline¨/»«msup»«mi mathvariant=¨bold¨ mathcolor=¨#0000FF¨»R«/mi»«mn mathvariant=¨bold¨ mathcolor=¨#0000FF¨»3«/mn»«/msup»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»=«/mo»«mfrac mathcolor=¨#0000FF¨»«mrow»«mi mathvariant=¨bold¨»G«/mi»«mo mathvariant=¨bold¨»§#183;«/mo»«msub»«mi mathvariant=¨bold¨»M«/mi»«mi mathvariant=¨bold¨»x«/mi»«/msub»«mo mathvariant=¨bold¨»§#183;«/mo»«msup»«mi mathvariant=¨bold¨»T«/mi»«mn mathvariant=¨bold¨»2«/mn»«/msup»«/mrow»«mrow»«mn mathvariant=¨bold¨»4«/mn»«mo mathvariant=¨bold¨»§#183;«/mo»«msup»«mi mathvariant=¨bold¨»§#960;«/mi»«mn mathvariant=¨bold¨»2«/mn»«/msup»«/mrow»«/mfrac»«mspace linebreak=¨newline¨/»«mspace linebreak=¨newline¨/»«menclose mathcolor=¨#0000FF¨ notation=¨circle¨»«mi mathvariant=¨bold¨»R«/mi»«mo mathvariant=¨bold¨»=«/mo»«msup»«mstyle mathvariant=¨bold¨»«mo stretchy=¨true¨»(«/mo»«mfrac»«mrow»«mi»G«/mi»«mo»§#183;«/mo»«msub»«mi»M«/mi»«mi»x«/mi»«/msub»«mo»§#183;«/mo»«msup»«mi»T«/mi»«mn»2«/mn»«/msup»«/mrow»«mrow»«mn»4«/mn»«mo»§#183;«/mo»«msup»«mi»§#960;«/mi»«mn»2«/mn»«/msup»«/mrow»«/mfrac»«mo stretchy=¨true¨»)«/mo»«/mstyle»«mfrac»«mn mathvariant=¨bold¨»1«/mn»«mn mathvariant=¨bold¨»3«/mn»«/mfrac»«/msup»«/menclose»«mspace linebreak=¨newline¨/»«mspace linebreak=¨newline¨/»«mspace linebreak=¨newline¨/»«mspace linebreak=¨newline¨/»«/mstyle»«/math»

28. ب.21- زمن دورة حركة القمر الاصطناعي حول الكرة الأرضية.

تتحرك كل نقطة على سطح الكرة الأرضية في حركة دائرية منتظمة بزمن دورة مدته 24 ساعة.

يكون القمر الاصطناعي للاتصالات فوق نقطة ثابتة بشكل دائم، وبالتالي يتحرك القمر الاصطناعي في حركة دائرية خلال دورة مدتها 24 ساعة.

29. بב.22- ارتفاع أقمار الاتصالات.

القوة الوحيدة المؤثرة على القمر الاصطناعي هي قوة الجاذبية العامة.

نكتب معادلة الحركة الدائرية:

«math xmlns=¨http://www.w3.org/1998/Math/MathML¨»«mstyle mathsize=¨20px¨»«msub»«mi mathvariant=¨bold¨ mathcolor=¨#0000FF¨»§#931;F«/mi»«mi mathvariant=¨bold¨ mathcolor=¨#0000FF¨»R«/mi»«/msub»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»=«/mo»«mi mathvariant=¨bold¨ mathcolor=¨#0000FF¨»m«/mi»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»§#183;«/mo»«msup»«mi mathvariant=¨bold¨ mathcolor=¨#0000FF¨»§#969;«/mi»«mn mathvariant=¨bold¨ mathcolor=¨#0000FF¨»2«/mn»«/msup»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»§#183;«/mo»«mi mathvariant=¨bold¨ mathcolor=¨#0000FF¨»R«/mi»«mspace linebreak=¨newline¨/»«mspace linebreak=¨newline¨/»«msub»«mi mathvariant=¨bold¨ mathcolor=¨#0000FF¨»F«/mi»«mi mathvariant=¨bold¨ mathcolor=¨#0000FF¨»g«/mi»«/msub»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»=«/mo»«mi mathvariant=¨bold¨ mathcolor=¨#0000FF¨»m«/mi»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»§#183;«/mo»«msup»«mi mathvariant=¨bold¨ mathcolor=¨#0000FF¨»§#969;«/mi»«mn mathvariant=¨bold¨ mathcolor=¨#0000FF¨»2«/mn»«/msup»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»§#183;«/mo»«mi mathvariant=¨bold¨ mathcolor=¨#0000FF¨»R«/mi»«mspace linebreak=¨newline¨/»«mspace linebreak=¨newline¨/»«mfrac mathcolor=¨#0000FF¨»«mrow»«mi mathvariant=¨bold¨»G«/mi»«mo mathvariant=¨bold¨»§#183;«/mo»«msub»«mi mathvariant=¨bold¨»M«/mi»«mi mathvariant=¨bold¨»E«/mi»«/msub»«mo mathvariant=¨bold¨»§#183;«/mo»«menclose notation=¨updiagonalstrike¨»«mi mathvariant=¨bold¨»m«/mi»«/menclose»«/mrow»«msup»«mi mathvariant=¨bold¨»R«/mi»«mn mathvariant=¨bold¨»2«/mn»«/msup»«/mfrac»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»=«/mo»«menclose mathcolor=¨#0000FF¨ notation=¨updiagonalstrike¨»«mi mathvariant=¨bold¨»m«/mi»«/menclose»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»§#183;«/mo»«msup»«mfrac mathcolor=¨#0000FF¨»«mrow»«mn mathvariant=¨bold¨»4«/mn»«mo mathvariant=¨bold¨»§#183;«/mo»«mi mathvariant=¨bold¨»§#960;«/mi»«/mrow»«msup»«mi mathvariant=¨bold¨»T«/mi»«mn mathvariant=¨bold¨»2«/mn»«/msup»«/mfrac»«mn mathvariant=¨bold¨ mathcolor=¨#0000FF¨»2«/mn»«/msup»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»§#183;«/mo»«mi mathvariant=¨bold¨ mathcolor=¨#0000FF¨»R«/mi»«mspace linebreak=¨newline¨/»«mspace linebreak=¨newline¨/»«mi mathvariant=¨bold¨ mathcolor=¨#0000FF¨»G«/mi»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»§#183;«/mo»«msub»«mi mathvariant=¨bold¨ mathcolor=¨#0000FF¨»M«/mi»«mi mathvariant=¨bold¨ mathcolor=¨#0000FF¨»E«/mi»«/msub»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»=«/mo»«msup»«mfrac mathcolor=¨#0000FF¨»«mrow»«mn mathvariant=¨bold¨»4«/mn»«mo mathvariant=¨bold¨»§#183;«/mo»«mi mathvariant=¨bold¨»§#960;«/mi»«/mrow»«msup»«mi mathvariant=¨bold¨»T«/mi»«mn mathvariant=¨bold¨»2«/mn»«/msup»«/mfrac»«mn mathvariant=¨bold¨ mathcolor=¨#0000FF¨»2«/mn»«/msup»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»§#183;«/mo»«msup»«mi mathvariant=¨bold¨ mathcolor=¨#0000FF¨»R«/mi»«mn mathvariant=¨bold¨ mathcolor=¨#0000FF¨»3«/mn»«/msup»«mspace linebreak=¨newline¨/»«mspace linebreak=¨newline¨/»«/mstyle»«/math»

نعبر عن نصف قطر مدار القمر الاصطناعي كمجموع نصف قطر الكرة الأرضية وارتفاع القمر الاصطناعي فوق سطح الأرض.

«math xmlns=¨http://www.w3.org/1998/Math/MathML¨»«mstyle mathsize=¨20px¨»«mi mathvariant=¨bold¨ mathcolor=¨#0000FF¨»G«/mi»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»§#183;«/mo»«msub»«mi mathvariant=¨bold¨ mathcolor=¨#0000FF¨»M«/mi»«mi mathvariant=¨bold¨ mathcolor=¨#0000FF¨»E«/mi»«/msub»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»=«/mo»«msup»«mfrac mathcolor=¨#0000FF¨»«mrow»«mn mathvariant=¨bold¨»4«/mn»«mo mathvariant=¨bold¨»§#183;«/mo»«mi mathvariant=¨bold¨»§#960;«/mi»«/mrow»«msup»«mi mathvariant=¨bold¨»T«/mi»«mn mathvariant=¨bold¨»2«/mn»«/msup»«/mfrac»«mn mathvariant=¨bold¨ mathcolor=¨#0000FF¨»2«/mn»«/msup»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»§#183;«/mo»«msup»«mi mathvariant=¨bold¨ mathcolor=¨#0000FF¨»R«/mi»«mn mathvariant=¨bold¨ mathcolor=¨#0000FF¨»3«/mn»«/msup»«mspace linebreak=¨newline¨/»«mspace linebreak=¨newline¨/»«mi mathvariant=¨bold¨ mathcolor=¨#0000FF¨»G«/mi»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»§#183;«/mo»«msub»«mi mathvariant=¨bold¨ mathcolor=¨#0000FF¨»M«/mi»«mi mathvariant=¨bold¨ mathcolor=¨#0000FF¨»E«/mi»«/msub»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»=«/mo»«msup»«mfrac mathcolor=¨#0000FF¨»«mrow»«mn mathvariant=¨bold¨»4«/mn»«mo mathvariant=¨bold¨»§#183;«/mo»«mi mathvariant=¨bold¨»§#960;«/mi»«/mrow»«msup»«mi mathvariant=¨bold¨»T«/mi»«mn mathvariant=¨bold¨»2«/mn»«/msup»«/mfrac»«mn mathvariant=¨bold¨ mathcolor=¨#0000FF¨»2«/mn»«/msup»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»§#183;«/mo»«msup»«mrow mathcolor=¨#0000FF¨»«mo stretchy=¨true¨ mathvariant=¨bold¨»(«/mo»«msub»«mi mathvariant=¨bold¨»R«/mi»«mi mathvariant=¨bold¨»E«/mi»«/msub»«mo mathvariant=¨bold¨»+«/mo»«mi mathvariant=¨bold¨»h«/mi»«mo stretchy=¨true¨ mathvariant=¨bold¨»)«/mo»«/mrow»«mn mathvariant=¨bold¨ mathcolor=¨#0000FF¨»3«/mn»«/msup»«mspace linebreak=¨newline¨/»«mspace linebreak=¨newline¨/»«msup»«mrow mathcolor=¨#0000FF¨»«mo mathvariant=¨bold¨ stretchy=¨true¨»(«/mo»«msub»«mi mathvariant=¨bold¨»R«/mi»«mi mathvariant=¨bold¨»E«/mi»«/msub»«mo mathvariant=¨bold¨»+«/mo»«mi mathvariant=¨bold¨»h«/mi»«mo mathvariant=¨bold¨ stretchy=¨true¨»)«/mo»«/mrow»«mn mathvariant=¨bold¨ mathcolor=¨#0000FF¨»3«/mn»«/msup»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»=«/mo»«mfrac mathcolor=¨#0000FF¨»«mrow»«mi mathvariant=¨bold¨»G«/mi»«mo mathvariant=¨bold¨»§#183;«/mo»«msub»«mi mathvariant=¨bold¨»M«/mi»«mi mathvariant=¨bold¨»E«/mi»«/msub»«mo mathvariant=¨bold¨»§#183;«/mo»«msup»«mi mathvariant=¨bold¨»T«/mi»«mn mathvariant=¨bold¨»2«/mn»«/msup»«/mrow»«mrow»«mn mathvariant=¨bold¨»4«/mn»«mo mathvariant=¨bold¨»§#183;«/mo»«msup»«mi mathvariant=¨bold¨»§#960;«/mi»«mn mathvariant=¨bold¨»2«/mn»«/msup»«/mrow»«/mfrac»«mspace linebreak=¨newline¨/»«mspace linebreak=¨newline¨/»«msub»«mi mathvariant=¨bold¨ mathcolor=¨#0000FF¨»R«/mi»«mi mathvariant=¨bold¨ mathcolor=¨#0000FF¨»E«/mi»«/msub»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»+«/mo»«mi mathvariant=¨bold¨ mathcolor=¨#0000FF¨»h«/mi»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»=«/mo»«msup»«mrow mathcolor=¨#0000FF¨»«mo stretchy=¨true¨ mathvariant=¨bold¨»(«/mo»«mfrac»«mrow»«mi mathvariant=¨bold¨»G«/mi»«mo mathvariant=¨bold¨»§#183;«/mo»«msub»«mi mathvariant=¨bold¨»M«/mi»«mi mathvariant=¨bold¨»E«/mi»«/msub»«mo mathvariant=¨bold¨»§#183;«/mo»«msup»«mi mathvariant=¨bold¨»T«/mi»«mn mathvariant=¨bold¨»2«/mn»«/msup»«/mrow»«mrow»«mn mathvariant=¨bold¨»4«/mn»«mo mathvariant=¨bold¨»§#183;«/mo»«msup»«mi mathvariant=¨bold¨»§#960;«/mi»«mn mathvariant=¨bold¨»2«/mn»«/msup»«/mrow»«/mfrac»«mo stretchy=¨true¨ mathvariant=¨bold¨»)«/mo»«/mrow»«mfrac mathcolor=¨#0000FF¨»«mn mathvariant=¨bold¨»1«/mn»«mn mathvariant=¨bold¨»2«/mn»«/mfrac»«/msup»«mspace linebreak=¨newline¨/»«mspace linebreak=¨newline¨/»«menclose mathcolor=¨#0000FF¨ notation=¨circle¨»«mi mathvariant=¨bold¨»h«/mi»«mo mathvariant=¨bold¨»=«/mo»«msup»«mrow»«mo stretchy=¨true¨ mathvariant=¨bold¨»(«/mo»«mfrac»«mrow»«mi mathvariant=¨bold¨»G«/mi»«mo mathvariant=¨bold¨»§#183;«/mo»«msub»«mi mathvariant=¨bold¨»M«/mi»«mi mathvariant=¨bold¨»E«/mi»«/msub»«mo mathvariant=¨bold¨»§#183;«/mo»«msup»«mi mathvariant=¨bold¨»T«/mi»«mn mathvariant=¨bold¨»2«/mn»«/msup»«/mrow»«mrow»«mn mathvariant=¨bold¨»4«/mn»«mo mathvariant=¨bold¨»§#183;«/mo»«msup»«mi mathvariant=¨bold¨»§#960;«/mi»«mn mathvariant=¨bold¨»2«/mn»«/msup»«/mrow»«/mfrac»«mo stretchy=¨true¨ mathvariant=¨bold¨»)«/mo»«/mrow»«mfrac»«mn mathvariant=¨bold¨»1«/mn»«mn mathvariant=¨bold¨»2«/mn»«/mfrac»«/msup»«mo mathvariant=¨bold¨»-«/mo»«msub»«mi mathvariant=¨bold¨»R«/mi»«mi mathvariant=¨bold¨»E«/mi»«/msub»«/menclose»«/mstyle»«/math»

نحسب ارتفاع القمر الاصطناعي بدلالة نصف قطر الكرة الأرضية وكتلتها.

«math xmlns=¨http://www.w3.org/1998/Math/MathML¨»«mstyle mathsize=¨20px¨»«mi mathvariant=¨bold¨ mathcolor=¨#0000FF¨»h«/mi»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»=«/mo»«msup»«mrow mathcolor=¨#0000FF¨»«mo mathvariant=¨bold¨ stretchy=¨true¨»(«/mo»«mfrac»«mrow»«mi mathvariant=¨bold¨»G«/mi»«mo mathvariant=¨bold¨»§#183;«/mo»«msub»«mi mathvariant=¨bold¨»M«/mi»«mi mathvariant=¨bold¨»E«/mi»«/msub»«mo mathvariant=¨bold¨»§#183;«/mo»«msup»«mi mathvariant=¨bold¨»T«/mi»«mn mathvariant=¨bold¨»2«/mn»«/msup»«/mrow»«mrow»«mn mathvariant=¨bold¨»4«/mn»«mo mathvariant=¨bold¨»§#183;«/mo»«msup»«mi mathvariant=¨bold¨»§#960;«/mi»«mn mathvariant=¨bold¨»2«/mn»«/msup»«/mrow»«/mfrac»«mo mathvariant=¨bold¨ stretchy=¨true¨»)«/mo»«/mrow»«mfrac mathcolor=¨#0000FF¨»«mn mathvariant=¨bold¨»1«/mn»«mn mathvariant=¨bold¨»3«/mn»«/mfrac»«/msup»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»-«/mo»«msub»«mi mathvariant=¨bold¨ mathcolor=¨#0000FF¨»R«/mi»«mi mathvariant=¨bold¨ mathcolor=¨#0000FF¨»E«/mi»«/msub»«mspace linebreak=¨newline¨/»«mspace linebreak=¨newline¨/»«mi mathvariant=¨bold¨ mathcolor=¨#0000FF¨»h«/mi»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»=«/mo»«msup»«mrow mathcolor=¨#0000FF¨»«mo mathvariant=¨bold¨ stretchy=¨true¨»(«/mo»«mfrac»«mrow»«mn mathvariant=¨bold¨»6«/mn»«mo mathvariant=¨bold¨».«/mo»«mn mathvariant=¨bold¨»67«/mn»«mo mathvariant=¨bold¨»§#183;«/mo»«msup»«mn mathvariant=¨bold¨»10«/mn»«mrow»«mo mathvariant=¨bold¨»-«/mo»«mn mathvariant=¨bold¨»11«/mn»«/mrow»«/msup»«mo mathvariant=¨bold¨»§#183;«/mo»«mn mathvariant=¨bold¨»5«/mn»«mo mathvariant=¨bold¨».«/mo»«mn mathvariant=¨bold¨»974«/mn»«mo mathvariant=¨bold¨»§#183;«/mo»«msup»«mn mathvariant=¨bold¨»10«/mn»«mn mathvariant=¨bold¨»24«/mn»«/msup»«mo mathvariant=¨bold¨»§#183;«/mo»«msup»«mrow»«mo stretchy=¨true¨ mathvariant=¨bold¨»(«/mo»«mn mathvariant=¨bold¨»24«/mn»«mo mathvariant=¨bold¨»§#183;«/mo»«mn mathvariant=¨bold¨»3«/mn»«mo mathvariant=¨bold¨»,«/mo»«mn mathvariant=¨bold¨»600«/mn»«mo stretchy=¨true¨ mathvariant=¨bold¨»)«/mo»«/mrow»«mn mathvariant=¨bold¨»2«/mn»«/msup»«/mrow»«mrow»«mn mathvariant=¨bold¨»4«/mn»«mo mathvariant=¨bold¨»§#183;«/mo»«msup»«mi mathvariant=¨bold¨»§#960;«/mi»«mn mathvariant=¨bold¨»2«/mn»«/msup»«/mrow»«/mfrac»«mo mathvariant=¨bold¨ stretchy=¨true¨»)«/mo»«/mrow»«mfrac mathcolor=¨#0000FF¨»«mn mathvariant=¨bold¨»1«/mn»«mn mathvariant=¨bold¨»3«/mn»«/mfrac»«/msup»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»-«/mo»«mn mathvariant=¨bold¨ mathcolor=¨#0000FF¨»6«/mn»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨».«/mo»«mn mathvariant=¨bold¨ mathcolor=¨#0000FF¨»38«/mn»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»§#183;«/mo»«msup»«mn mathvariant=¨bold¨ mathcolor=¨#0000FF¨»10«/mn»«mn mathvariant=¨bold¨ mathcolor=¨#0000FF¨»6«/mn»«/msup»«mspace linebreak=¨newline¨/»«mspace linebreak=¨newline¨/»«mi mathvariant=¨bold¨ mathcolor=¨#0000FF¨»h«/mi»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»=«/mo»«msup»«mrow mathcolor=¨#0000FF¨»«mo mathvariant=¨bold¨ stretchy=¨true¨»(«/mo»«mfrac»«mrow»«mn mathvariant=¨bold¨»6«/mn»«mo mathvariant=¨bold¨».«/mo»«mn mathvariant=¨bold¨»67«/mn»«mo mathvariant=¨bold¨»§#183;«/mo»«msup»«mn mathvariant=¨bold¨»10«/mn»«mrow»«mo mathvariant=¨bold¨»-«/mo»«mn mathvariant=¨bold¨»11«/mn»«/mrow»«/msup»«mo mathvariant=¨bold¨»§#183;«/mo»«mn mathvariant=¨bold¨»5«/mn»«mo mathvariant=¨bold¨».«/mo»«mn mathvariant=¨bold¨»974«/mn»«mo mathvariant=¨bold¨»§#183;«/mo»«msup»«mn mathvariant=¨bold¨»10«/mn»«mn mathvariant=¨bold¨»24«/mn»«/msup»«mo mathvariant=¨bold¨»§#183;«/mo»«msup»«mrow»«mo stretchy=¨true¨ mathvariant=¨bold¨»(«/mo»«mn mathvariant=¨bold¨»86«/mn»«mo mathvariant=¨bold¨»,«/mo»«mn mathvariant=¨bold¨»400«/mn»«mo stretchy=¨true¨ mathvariant=¨bold¨»)«/mo»«/mrow»«mn mathvariant=¨bold¨»2«/mn»«/msup»«/mrow»«mrow»«mn mathvariant=¨bold¨»4«/mn»«mo mathvariant=¨bold¨»§#183;«/mo»«msup»«mi mathvariant=¨bold¨»§#960;«/mi»«mn mathvariant=¨bold¨»2«/mn»«/msup»«/mrow»«/mfrac»«mo mathvariant=¨bold¨ stretchy=¨true¨»)«/mo»«/mrow»«mfrac mathcolor=¨#0000FF¨»«mn mathvariant=¨bold¨»1«/mn»«mn mathvariant=¨bold¨»3«/mn»«/mfrac»«/msup»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»-«/mo»«mn mathvariant=¨bold¨ mathcolor=¨#0000FF¨»6«/mn»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨».«/mo»«mn mathvariant=¨bold¨ mathcolor=¨#0000FF¨»38«/mn»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»§#183;«/mo»«msup»«mn mathvariant=¨bold¨ mathcolor=¨#0000FF¨»10«/mn»«mn mathvariant=¨bold¨ mathcolor=¨#0000FF¨»6«/mn»«/msup»«mspace linebreak=¨newline¨/»«mspace linebreak=¨newline¨/»«mi mathvariant=¨bold¨ mathcolor=¨#0000FF¨»h«/mi»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»=«/mo»«msup»«mrow mathcolor=¨#0000FF¨»«mo mathvariant=¨bold¨ stretchy=¨true¨»(«/mo»«mfrac»«mrow»«mn mathvariant=¨bold¨»2«/mn»«mo mathvariant=¨bold¨».«/mo»«mn mathvariant=¨bold¨»974«/mn»«mo mathvariant=¨bold¨»§#183;«/mo»«msup»«mn mathvariant=¨bold¨»10«/mn»«mn mathvariant=¨bold¨»24«/mn»«/msup»«/mrow»«mrow»«mn mathvariant=¨bold¨»4«/mn»«mo mathvariant=¨bold¨»§#183;«/mo»«msup»«mi mathvariant=¨bold¨»§#960;«/mi»«mn mathvariant=¨bold¨»2«/mn»«/msup»«/mrow»«/mfrac»«mo mathvariant=¨bold¨ stretchy=¨true¨»)«/mo»«/mrow»«mfrac mathcolor=¨#0000FF¨»«mn mathvariant=¨bold¨»1«/mn»«mn mathvariant=¨bold¨»3«/mn»«/mfrac»«/msup»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»-«/mo»«mn mathvariant=¨bold¨ mathcolor=¨#0000FF¨»6«/mn»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨».«/mo»«mn mathvariant=¨bold¨ mathcolor=¨#0000FF¨»38«/mn»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»§#183;«/mo»«msup»«mn mathvariant=¨bold¨ mathcolor=¨#0000FF¨»10«/mn»«mn mathvariant=¨bold¨ mathcolor=¨#0000FF¨»6«/mn»«/msup»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»=«/mo»«msup»«mrow mathcolor=¨#0000FF¨»«mo mathvariant=¨bold¨ stretchy=¨true¨»(«/mo»«mn mathvariant=¨bold¨»7«/mn»«mo mathvariant=¨bold¨».«/mo»«mn mathvariant=¨bold¨»534«/mn»«mo mathvariant=¨bold¨»§#183;«/mo»«msup»«mn mathvariant=¨bold¨»10«/mn»«mn mathvariant=¨bold¨»22«/mn»«/msup»«mo mathvariant=¨bold¨ stretchy=¨true¨»)«/mo»«/mrow»«mfrac mathcolor=¨#0000FF¨»«mn mathvariant=¨bold¨»1«/mn»«mn mathvariant=¨bold¨»3«/mn»«/mfrac»«/msup»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»-«/mo»«mn mathvariant=¨bold¨ mathcolor=¨#0000FF¨»6«/mn»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨».«/mo»«mn mathvariant=¨bold¨ mathcolor=¨#0000FF¨»38«/mn»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»§#183;«/mo»«msup»«mn mathvariant=¨bold¨ mathcolor=¨#0000FF¨»10«/mn»«mn mathvariant=¨bold¨ mathcolor=¨#0000FF¨»6«/mn»«/msup»«mspace linebreak=¨newline¨/»«mspace linebreak=¨newline¨/»«mi mathvariant=¨bold¨ mathcolor=¨#0000FF¨»h«/mi»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»=«/mo»«mn mathvariant=¨bold¨ mathcolor=¨#0000FF¨»42«/mn»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨».«/mo»«mn mathvariant=¨bold¨ mathcolor=¨#0000FF¨»22«/mn»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»§#183;«/mo»«msup»«mn mathvariant=¨bold¨ mathcolor=¨#0000FF¨»10«/mn»«mn mathvariant=¨bold¨ mathcolor=¨#0000FF¨»6«/mn»«/msup»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»-«/mo»«mn mathvariant=¨bold¨ mathcolor=¨#0000FF¨»6«/mn»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨».«/mo»«mn mathvariant=¨bold¨ mathcolor=¨#0000FF¨»38«/mn»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»§#183;«/mo»«msup»«mn mathvariant=¨bold¨ mathcolor=¨#0000FF¨»10«/mn»«mn mathvariant=¨bold¨ mathcolor=¨#0000FF¨»6«/mn»«/msup»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»=«/mo»«mn mathvariant=¨bold¨ mathcolor=¨#0000FF¨»35«/mn»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨».«/mo»«mn mathvariant=¨bold¨ mathcolor=¨#0000FF¨»84«/mn»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»§#183;«/mo»«msup»«mn mathvariant=¨bold¨ mathcolor=¨#0000FF¨»10«/mn»«mn mathvariant=¨bold¨ mathcolor=¨#0000FF¨»6«/mn»«/msup»«mi mathvariant=¨bold¨ mathcolor=¨#0000FF¨»m«/mi»«/mstyle»«/math»

لذلك ، لكي تكون أقمار الاتصالات التي تتحرك حول الكرة الأرضية فوق نقطة ثابتة، يجب أن تتحرك على ارتفاع 35.84 مليون متر فوق سطح الأرض.

30. ب.23- شرح سبب تحرك قمر اصطناعي للاتصالات فوق خط الاستواء.

لكي يتحرك القمر الاصطناعي في حركة دائرية منتظمة فوق نقطة ثابتة، يجب أن تعمل قوة الجاذبية العامة باتجاه نقطة مركز الدوران ، لذلك يجب أن يكون مستوى الحركة فوق خط الاستواء.

في الشكل التالي، يظهر قمر اصطناعي يقع فوق النقطة A (نقطة ليست على خط الاستواء) ، ومستوى الحركة مُصوَّر بخط أحمر متقطع، والنقطة المركزية للحركة مشار لها بالنقطة B.

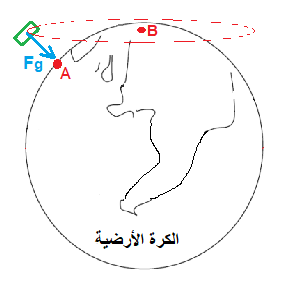
تعمل قوة الجاذبية العامة دائمًا تجاه نقطة مركز الكرة الأرضية.

في هذه الحالة، حسب موقع النقطة A، لا تعمل قوة الجاذبية العامة في اتجاه نقطة مركز الدوران (النقطة B).

حركة القمر الاصطناعي فوق النقطة A غير ممكنة في هذه الحالة.

فقط إذا كان القمر الاصطناعي فوق نقطة تقع على خط الاستواء سيكون اتجاه الجاذبية العامة نحو نقطة مركز الدوران.

يوضح الشكل التالي قمرًا اصطناعيًا يتحرك فوق النقطة A على خط الاستواء:

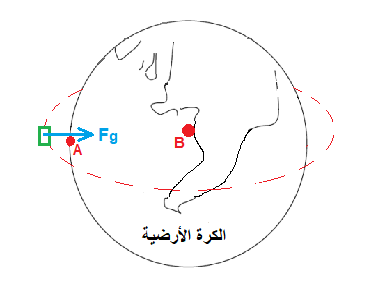
31. ب.24- حساب نصف قطر مدار قمر اتصالات يتحرك حول القمر

القوة الوحيدة المؤثرة على القمر الاصطناعي هي قوة الجاذبية العامة.

نكتب معادلة الحركة الدائرية لحركة القمر الاصطناعي حول القمر:

«math xmlns=¨http://www.w3.org/1998/Math/MathML¨»«mstyle mathsize=¨20px¨»«msub»«mi mathvariant=¨bold¨ mathcolor=¨#0000FF¨»§#931;F«/mi»«mi mathvariant=¨bold¨ mathcolor=¨#0000FF¨»R«/mi»«/msub»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»=«/mo»«mi mathvariant=¨bold¨ mathcolor=¨#0000FF¨»m«/mi»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»§#183;«/mo»«msup»«mi mathvariant=¨bold¨ mathcolor=¨#0000FF¨»§#969;«/mi»«mn mathvariant=¨bold¨ mathcolor=¨#0000FF¨»2«/mn»«/msup»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»§#183;«/mo»«mi mathvariant=¨bold¨ mathcolor=¨#0000FF¨»R«/mi»«mspace linebreak=¨newline¨/»«mspace linebreak=¨newline¨/»«msub»«mi mathvariant=¨bold¨ mathcolor=¨#0000FF¨»F«/mi»«mi mathvariant=¨bold¨ mathcolor=¨#0000FF¨»g«/mi»«/msub»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»=«/mo»«mi mathvariant=¨bold¨ mathcolor=¨#0000FF¨»m«/mi»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»§#183;«/mo»«msup»«mi mathvariant=¨bold¨ mathcolor=¨#0000FF¨»§#969;«/mi»«mn mathvariant=¨bold¨ mathcolor=¨#0000FF¨»2«/mn»«/msup»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»§#183;«/mo»«mi mathvariant=¨bold¨ mathcolor=¨#0000FF¨»R«/mi»«mspace linebreak=¨newline¨/»«mspace linebreak=¨newline¨/»«mfrac mathcolor=¨#0000FF¨»«mrow»«mi mathvariant=¨bold¨»G«/mi»«mo mathvariant=¨bold¨»§#183;«/mo»«msub»«mi mathvariant=¨bold¨»M«/mi»«mi mathvariant=¨bold¨»m«/mi»«/msub»«mo mathvariant=¨bold¨»§#183;«/mo»«menclose notation=¨updiagonalstrike¨»«mi mathvariant=¨bold¨»m«/mi»«/menclose»«/mrow»«msup»«mi mathvariant=¨bold¨»R«/mi»«mn mathvariant=¨bold¨»2«/mn»«/msup»«/mfrac»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»=«/mo»«menclose mathcolor=¨#0000FF¨ notation=¨updiagonalstrike¨»«mi mathvariant=¨bold¨»m«/mi»«/menclose»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»§#183;«/mo»«msup»«mfrac mathcolor=¨#0000FF¨»«mrow»«mn mathvariant=¨bold¨»4«/mn»«mo mathvariant=¨bold¨»§#183;«/mo»«mi mathvariant=¨bold¨»§#960;«/mi»«/mrow»«msup»«msub»«mi mathvariant=¨bold¨»T«/mi»«mi mathvariant=¨bold¨»m«/mi»«/msub»«mn mathvariant=¨bold¨»2«/mn»«/msup»«/mfrac»«mn mathvariant=¨bold¨ mathcolor=¨#0000FF¨»2«/mn»«/msup»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»§#183;«/mo»«mi mathvariant=¨bold¨ mathcolor=¨#0000FF¨»R«/mi»«mspace linebreak=¨newline¨/»«mspace linebreak=¨newline¨/»«mi mathvariant=¨bold¨ mathcolor=¨#0000FF¨»G«/mi»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»§#183;«/mo»«msub»«mi mathvariant=¨bold¨ mathcolor=¨#0000FF¨»M«/mi»«mi mathvariant=¨bold¨ mathcolor=¨#0000FF¨»m«/mi»«/msub»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»=«/mo»«msup»«mfrac mathcolor=¨#0000FF¨»«mrow»«mn mathvariant=¨bold¨»4«/mn»«mo mathvariant=¨bold¨»§#183;«/mo»«mi mathvariant=¨bold¨»§#960;«/mi»«/mrow»«msup»«msub»«mi mathvariant=¨bold¨»T«/mi»«mi mathvariant=¨bold¨»m«/mi»«/msub»«mn mathvariant=¨bold¨»2«/mn»«/msup»«/mfrac»«mn mathvariant=¨bold¨ mathcolor=¨#0000FF¨»2«/mn»«/msup»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»§#183;«/mo»«msup»«mi mathvariant=¨bold¨ mathcolor=¨#0000FF¨»R«/mi»«mn mathvariant=¨bold¨ mathcolor=¨#0000FF¨»3«/mn»«/msup»«mspace linebreak=¨newline¨/»«mspace linebreak=¨newline¨/»«msup»«mi mathvariant=¨bold¨ mathcolor=¨#0000FF¨»R«/mi»«mn mathvariant=¨bold¨ mathcolor=¨#0000FF¨»3«/mn»«/msup»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»=«/mo»«mfrac mathcolor=¨#0000FF¨»«mrow»«mi mathvariant=¨bold¨»G«/mi»«mo mathvariant=¨bold¨»§#183;«/mo»«msub»«mi mathvariant=¨bold¨»M«/mi»«mi mathvariant=¨bold¨»m«/mi»«/msub»«mo mathvariant=¨bold¨»§#183;«/mo»«msup»«msub»«mi mathvariant=¨bold¨»T«/mi»«mi mathvariant=¨bold¨»m«/mi»«/msub»«mn mathvariant=¨bold¨»2«/mn»«/msup»«/mrow»«mrow»«mn mathvariant=¨bold¨»4«/mn»«mo mathvariant=¨bold¨»§#183;«/mo»«msup»«mi mathvariant=¨bold¨»§#960;«/mi»«mn mathvariant=¨bold¨»2«/mn»«/msup»«/mrow»«/mfrac»«mspace linebreak=¨newline¨/»«mspace linebreak=¨newline¨/»«menclose mathcolor=¨#0000FF¨ notation=¨circle¨»«mi mathvariant=¨bold¨»R«/mi»«mo mathvariant=¨bold¨»=«/mo»«msup»«mstyle mathvariant=¨bold¨»«mo stretchy=¨true¨»(«/mo»«mfrac»«mrow»«mi»G«/mi»«mo»§#183;«/mo»«msub»«mi»M«/mi»«mi»m«/mi»«/msub»«mo»§#183;«/mo»«msup»«msub»«mi»T«/mi»«mi»m«/mi»«/msub»«mn»2«/mn»«/msup»«/mrow»«mrow»«mn»4«/mn»«mo»§#183;«/mo»«msup»«mi»§#960;«/mi»«mn»2«/mn»«/msup»«/mrow»«/mfrac»«mo stretchy=¨true¨»)«/mo»«/mstyle»«mfrac»«mn mathvariant=¨bold¨»1«/mn»«mn mathvariant=¨bold¨»3«/mn»«/mfrac»«/msup»«/menclose»«mspace linebreak=¨newline¨/»«mspace linebreak=¨newline¨/»«/mstyle»«/math»

نعوّض معطيات القمر ونجد نصف قطر مدار القمر الاصطناعي.

«math xmlns=¨http://www.w3.org/1998/Math/MathML¨»«mstyle mathsize=¨20px¨»«mi mathvariant=¨bold¨ mathcolor=¨#0000FF¨»R«/mi»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»=«/mo»«msup»«mrow mathcolor=¨#0000FF¨»«mo mathvariant=¨bold¨ stretchy=¨true¨»(«/mo»«mfrac»«mrow»«mi mathvariant=¨bold¨»G«/mi»«mo mathvariant=¨bold¨»§#183;«/mo»«msub»«mi mathvariant=¨bold¨»M«/mi»«mi mathvariant=¨bold¨»m«/mi»«/msub»«mo mathvariant=¨bold¨»§#183;«/mo»«msup»«msub»«mi mathvariant=¨bold¨»T«/mi»«mi mathvariant=¨bold¨»m«/mi»«/msub»«mn mathvariant=¨bold¨»2«/mn»«/msup»«/mrow»«mrow»«mn mathvariant=¨bold¨»4«/mn»«mo mathvariant=¨bold¨»§#183;«/mo»«msup»«mi mathvariant=¨bold¨»§#960;«/mi»«mn mathvariant=¨bold¨»2«/mn»«/msup»«/mrow»«/mfrac»«mo mathvariant=¨bold¨ stretchy=¨true¨»)«/mo»«/mrow»«mfrac mathcolor=¨#0000FF¨»«mn mathvariant=¨bold¨»1«/mn»«mn mathvariant=¨bold¨»3«/mn»«/mfrac»«/msup»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»=«/mo»«msup»«mrow mathcolor=¨#0000FF¨»«mo stretchy=¨true¨ mathvariant=¨bold¨»(«/mo»«mfrac»«mrow»«mn mathvariant=¨bold¨»6«/mn»«mo mathvariant=¨bold¨».«/mo»«mn mathvariant=¨bold¨»67«/mn»«mo mathvariant=¨bold¨»§#183;«/mo»«msup»«mn mathvariant=¨bold¨»10«/mn»«mrow»«mo mathvariant=¨bold¨»-«/mo»«mn mathvariant=¨bold¨»11«/mn»«/mrow»«/msup»«mo mathvariant=¨bold¨»§#183;«/mo»«mn mathvariant=¨bold¨»7«/mn»«mo mathvariant=¨bold¨».«/mo»«mn mathvariant=¨bold¨»35«/mn»«mo mathvariant=¨bold¨»§#183;«/mo»«msup»«mn mathvariant=¨bold¨»10«/mn»«mn mathvariant=¨bold¨»22«/mn»«/msup»«mo mathvariant=¨bold¨»§#183;«/mo»«msup»«mrow»«mo mathvariant=¨bold¨»(«/mo»«mn mathvariant=¨bold¨»27«/mn»«mo mathvariant=¨bold¨».«/mo»«mn mathvariant=¨bold¨»3«/mn»«mo mathvariant=¨bold¨»§#183;«/mo»«mn mathvariant=¨bold¨»24«/mn»«mo mathvariant=¨bold¨»§#183;«/mo»«mn mathvariant=¨bold¨»3600«/mn»«mo mathvariant=¨bold¨»)«/mo»«/mrow»«mn mathvariant=¨bold¨»2«/mn»«/msup»«/mrow»«mrow»«mn mathvariant=¨bold¨»4«/mn»«mo mathvariant=¨bold¨»§#183;«/mo»«msup»«mi mathvariant=¨bold¨»§#960;«/mi»«mn mathvariant=¨bold¨»2«/mn»«/msup»«/mrow»«/mfrac»«mo stretchy=¨true¨ mathvariant=¨bold¨»)«/mo»«/mrow»«mfrac mathcolor=¨#0000FF¨»«mn mathvariant=¨bold¨»1«/mn»«mn mathvariant=¨bold¨»3«/mn»«/mfrac»«/msup»«mspace linebreak=¨newline¨/»«mspace linebreak=¨newline¨/»«mi mathvariant=¨bold¨ mathcolor=¨#0000FF¨»R«/mi»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»=«/mo»«msup»«mstyle mathvariant=¨bold¨ mathcolor=¨#0000FF¨»«mo stretchy=¨true¨»(«/mo»«mfrac»«mrow»«mn»2«/mn»«mo».«/mo»«mn»727«/mn»«mo»§#183;«/mo»«msup»«mn»10«/mn»«mn»25«/mn»«/msup»«/mrow»«mrow»«mn»39«/mn»«mo».«/mo»«mn»47«/mn»«/mrow»«/mfrac»«mo stretchy=¨true¨»)«/mo»«/mstyle»«mfrac mathcolor=¨#0000FF¨»«mn mathvariant=¨bold¨»1«/mn»«mn mathvariant=¨bold¨»3«/mn»«/mfrac»«/msup»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»=«/mo»«msup»«mstyle mathvariant=¨bold¨ mathcolor=¨#0000FF¨»«mo stretchy=¨true¨»(«/mo»«mrow»«mn»6«/mn»«mo».«/mo»«mn»908«/mn»«mo»§#183;«/mo»«msup»«mn»10«/mn»«mn»23«/mn»«/msup»«/mrow»«mo stretchy=¨true¨»)«/mo»«/mstyle»«mfrac mathcolor=¨#0000FF¨»«mn mathvariant=¨bold¨»1«/mn»«mn mathvariant=¨bold¨»3«/mn»«/mfrac»«/msup»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»=«/mo»«mn mathvariant=¨bold¨ mathcolor=¨#0000FF¨»88«/mn»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨».«/mo»«mn mathvariant=¨bold¨ mathcolor=¨#0000FF¨»39«/mn»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»§#183;«/mo»«msup»«mn mathvariant=¨bold¨ mathcolor=¨#0000FF¨»10«/mn»«mn mathvariant=¨bold¨ mathcolor=¨#0000FF¨»6«/mn»«/msup»«mi mathvariant=¨bold-italic¨ mathcolor=¨#0000FF¨»m«/mi»«/mstyle»«/math»

32. ب.25- تطوير القانون الثالث لكبلر.

ينص القانون الثالث لكبلر على أن النسبة بين مربع زمن الدورة ومكعب نصف القطر المداري ثابتة لجميع الكواكب السيارة التي تتحرك في حركة قمر اصطناعي حول نفس النجم.

نعبر عن النسبة التي يتعامل بها القانون الثالث لكبلر «math xmlns=¨http://www.w3.org/1998/Math/MathML¨»«mfrac mathcolor=¨#0000FF¨»«msup»«mi mathvariant=¨bold¨»T«/mi»«mn mathvariant=¨bold¨»2«/mn»«/msup»«msup»«mi mathvariant=¨bold¨»R«/mi»«mn mathvariant=¨bold¨»3«/mn»«/msup»«/mfrac»«/math» ، من معادلة الحركة الدائرية .

نتطرّق إلى كوكب يتحرك حول الشمس تحت تأثير قوة الجاذبية العامة التي تشغلها الشمس عليه.

نكتب معادلة الحركة:

«math xmlns=¨http://www.w3.org/1998/Math/MathML¨»«mstyle mathsize=¨20px¨»«msub»«mi mathvariant=¨bold¨ mathcolor=¨#0000FF¨»§#931;F«/mi»«mi mathvariant=¨bold¨ mathcolor=¨#0000FF¨»R«/mi»«/msub»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»=«/mo»«mi mathvariant=¨bold¨ mathcolor=¨#0000FF¨»m«/mi»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»§#183;«/mo»«msup»«mi mathvariant=¨bold¨ mathcolor=¨#0000FF¨»§#969;«/mi»«mn mathvariant=¨bold¨ mathcolor=¨#0000FF¨»2«/mn»«/msup»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»§#183;«/mo»«mi mathvariant=¨bold¨ mathcolor=¨#0000FF¨»R«/mi»«mspace linebreak=¨newline¨/»«mspace linebreak=¨newline¨/»«msub»«mi mathvariant=¨bold¨ mathcolor=¨#0000FF¨»F«/mi»«mi mathvariant=¨bold¨ mathcolor=¨#0000FF¨»g«/mi»«/msub»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»=«/mo»«mi mathvariant=¨bold¨ mathcolor=¨#0000FF¨»m«/mi»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»§#183;«/mo»«msup»«mi mathvariant=¨bold¨ mathcolor=¨#0000FF¨»§#969;«/mi»«mn mathvariant=¨bold¨ mathcolor=¨#0000FF¨»2«/mn»«/msup»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»§#183;«/mo»«mi mathvariant=¨bold¨ mathcolor=¨#0000FF¨»R«/mi»«mspace linebreak=¨newline¨/»«mspace linebreak=¨newline¨/»«mfrac mathcolor=¨#0000FF¨»«mrow»«mi mathvariant=¨bold¨»G«/mi»«mo mathvariant=¨bold¨»§#183;«/mo»«msub»«mi mathvariant=¨bold¨»M«/mi»«mi mathvariant=¨bold¨»S«/mi»«/msub»«mo mathvariant=¨bold¨»§#183;«/mo»«menclose notation=¨updiagonalstrike¨»«mi mathvariant=¨bold¨»m«/mi»«/menclose»«/mrow»«msup»«mi mathvariant=¨bold¨»R«/mi»«mn mathvariant=¨bold¨»2«/mn»«/msup»«/mfrac»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»=«/mo»«menclose mathcolor=¨#0000FF¨ notation=¨updiagonalstrike¨»«mi mathvariant=¨bold¨»m«/mi»«/menclose»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»§#183;«/mo»«msup»«mfrac mathcolor=¨#0000FF¨»«mrow»«mn mathvariant=¨bold¨»4«/mn»«mo mathvariant=¨bold¨»§#183;«/mo»«mi mathvariant=¨bold¨»§#960;«/mi»«/mrow»«msup»«mi mathvariant=¨bold¨»T«/mi»«mn mathvariant=¨bold¨»2«/mn»«/msup»«/mfrac»«mn mathvariant=¨bold¨ mathcolor=¨#0000FF¨»2«/mn»«/msup»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»§#183;«/mo»«mi mathvariant=¨bold¨ mathcolor=¨#0000FF¨»R«/mi»«mspace linebreak=¨newline¨/»«mspace linebreak=¨newline¨/»«menclose mathcolor=¨#0000FF¨ notation=¨circle¨»«mfrac»«msup»«mi mathvariant=¨bold¨»T«/mi»«mn mathvariant=¨bold¨»2«/mn»«/msup»«msup»«mi mathvariant=¨bold¨»R«/mi»«mn mathvariant=¨bold¨»3«/mn»«/msup»«/mfrac»«mo mathvariant=¨bold¨»=«/mo»«msup»«mfrac»«mrow»«mn mathvariant=¨bold¨»4«/mn»«mo mathvariant=¨bold¨»§#183;«/mo»«mi mathvariant=¨bold¨»§#960;«/mi»«/mrow»«mrow»«mi mathvariant=¨bold¨»G«/mi»«mo mathvariant=¨bold¨»§#183;«/mo»«msub»«mi mathvariant=¨bold¨»M«/mi»«mi mathvariant=¨bold¨»s«/mi»«/msub»«/mrow»«/mfrac»«mn mathvariant=¨bold¨»2«/mn»«/msup»«/menclose»«/mstyle»«/math»

من التعبير الذي تم الحصول عليه يمكن ملاحظة أن النسبة «math xmlns=¨http://www.w3.org/1998/Math/MathML¨»«mfrac mathcolor=¨#0000FF¨»«msup»«mi mathvariant=¨bold¨»T«/mi»«mn mathvariant=¨bold¨»2«/mn»«/msup»«msup»«mi mathvariant=¨bold¨»R«/mi»«mn mathvariant=¨bold¨»3«/mn»«/msup»«/mfrac»«/math» تتعلق فقط بكتلة الشمس.

التعبير عن النسبة «math xmlns=¨http://www.w3.org/1998/Math/MathML¨»«mfrac mathcolor=¨#0000FF¨»«msup»«mi mathvariant=¨bold¨»T«/mi»«mn mathvariant=¨bold¨»2«/mn»«/msup»«msup»«mi mathvariant=¨bold¨»R«/mi»«mn mathvariant=¨bold¨»3«/mn»«/msup»«/mfrac»«/math» يتم الحصول عليها من معادلة حركة كل من الكواكب التي تدور حول الشمس.

لذلك بالنسبة لكوكبين مختلفين: «math xmlns=¨http://www.w3.org/1998/Math/MathML¨»«mstyle mathsize=¨24px¨»«menclose mathcolor=¨#0000FF¨ notation=¨box¨»«mfrac»«msup»«msub»«mi mathvariant=¨bold¨»T«/mi»«mn mathvariant=¨bold¨»1«/mn»«/msub»«mn mathvariant=¨bold¨»2«/mn»«/msup»«msup»«msub»«mi mathvariant=¨bold¨»R«/mi»«mn mathvariant=¨bold¨»1«/mn»«/msub»«mn mathvariant=¨bold¨»3«/mn»«/msup»«/mfrac»«mo mathvariant=¨bold¨»=«/mo»«mfrac»«msup»«msub»«mi mathvariant=¨bold¨»T«/mi»«mn mathvariant=¨bold¨»2«/mn»«/msub»«mn mathvariant=¨bold¨»2«/mn»«/msup»«msup»«msub»«mi mathvariant=¨bold¨»R«/mi»«mn mathvariant=¨bold¨»2«/mn»«/msub»«mn mathvariant=¨bold¨»3«/mn»«/msup»«/mfrac»«/menclose»«/mstyle»«/math»

33. ب.26- قمر اصطناعي يتحرك تحت تأثير الكرة الأرضية والشمس.

من معادلة الحركة الدائرية، يمكن ملاحظة أن القانون الثالث لكبلر يتحقق فقط عندما يتحرك الجسم تحت تأثير النجم الذي يتحرك حوله.

في هذه الحالة يتحرك القمر الاصطناعي حول الشمس ويتحرك تحت تأثير الشمس وتأثير الكرة الأرضية.

نرسم مخطط القوى لهذه الحالة، ونشير للشمس كجسم 1 ، والقمر الاصطناعي كجسم 2 ، والأرض كجسم 3.

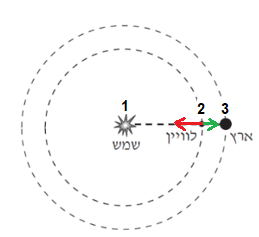
نكتب معادلة الحركة الدائرية لحركة القمر الاصطناعي:

«math xmlns=¨http://www.w3.org/1998/Math/MathML¨»«mstyle mathsize=¨20px¨»«msub»«mi mathvariant=¨bold¨ mathcolor=¨#0000FF¨»§#931;F«/mi»«mi mathvariant=¨bold¨ mathcolor=¨#0000FF¨»R«/mi»«/msub»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»=«/mo»«mi mathvariant=¨bold¨ mathcolor=¨#0000FF¨»m«/mi»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»§#183;«/mo»«msup»«mi mathvariant=¨bold¨ mathcolor=¨#0000FF¨»§#969;«/mi»«mn mathvariant=¨bold¨ mathcolor=¨#0000FF¨»2«/mn»«/msup»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»§#183;«/mo»«mi mathvariant=¨bold¨ mathcolor=¨#0000FF¨»R«/mi»«mspace linebreak=¨newline¨/»«mspace linebreak=¨newline¨/»«msub»«mi mathvariant=¨bold¨ mathcolor=¨#0000FF¨»F«/mi»«mrow»«mn mathvariant=¨bold¨ mathcolor=¨#0000FF¨»1«/mn»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»,«/mo»«mn mathvariant=¨bold¨ mathcolor=¨#0000FF¨»2«/mn»«/mrow»«/msub»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»-«/mo»«msub»«mi mathvariant=¨bold¨ mathcolor=¨#0000FF¨»F«/mi»«mrow mathcolor=¨#0000FF¨»«mn mathvariant=¨bold¨»2«/mn»«mo mathvariant=¨bold¨»,«/mo»«mn mathvariant=¨bold¨»3«/mn»«/mrow»«/msub»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»=«/mo»«mi mathvariant=¨bold¨ mathcolor=¨#0000FF¨»m«/mi»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»§#183;«/mo»«msup»«mi mathvariant=¨bold¨ mathcolor=¨#0000FF¨»§#969;«/mi»«mn mathvariant=¨bold¨ mathcolor=¨#0000FF¨»2«/mn»«/msup»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»§#183;«/mo»«mi mathvariant=¨bold¨ mathcolor=¨#0000FF¨»R«/mi»«mspace linebreak=¨newline¨/»«mspace linebreak=¨newline¨/»«mfrac mathcolor=¨#0000FF¨»«mrow»«mi mathvariant=¨bold¨»G«/mi»«mo mathvariant=¨bold¨»§#183;«/mo»«msub»«mi mathvariant=¨bold¨»m«/mi»«mn mathvariant=¨bold¨»2«/mn»«/msub»«mo mathvariant=¨bold¨»§#183;«/mo»«msub»«mi mathvariant=¨bold¨»m«/mi»«mn mathvariant=¨bold¨»1«/mn»«/msub»«/mrow»«msup»«msub»«mi mathvariant=¨bold¨»R«/mi»«mrow»«mn mathvariant=¨bold¨»2«/mn»«mo mathvariant=¨bold¨»,«/mo»«mn mathvariant=¨bold¨»1«/mn»«/mrow»«/msub»«mn mathvariant=¨bold¨»2«/mn»«/msup»«/mfrac»«mo mathcolor=¨#0000FF¨»-«/mo»«mfrac mathcolor=¨#0000FF¨»«mrow»«mi mathvariant=¨bold¨»G«/mi»«mo mathvariant=¨bold¨»§#183;«/mo»«msub»«mi mathvariant=¨bold¨»m«/mi»«mn mathvariant=¨bold¨»2«/mn»«/msub»«mo mathvariant=¨bold¨»§#183;«/mo»«msub»«mi mathvariant=¨bold¨»m«/mi»«mn mathvariant=¨bold¨»3«/mn»«/msub»«/mrow»«msup»«msub»«mi mathvariant=¨bold¨»R«/mi»«mrow»«mn mathvariant=¨bold¨»2«/mn»«mo mathvariant=¨bold¨»,«/mo»«mn mathvariant=¨bold¨»3«/mn»«/mrow»«/msub»«mn mathvariant=¨bold¨»2«/mn»«/msup»«/mfrac»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»=«/mo»«mi mathvariant=¨bold-italic¨ mathcolor=¨#0000FF¨»m«/mi»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»§#183;«/mo»«msup»«mfrac mathcolor=¨#0000FF¨»«mrow»«mn mathvariant=¨bold¨»4«/mn»«mo mathvariant=¨bold¨»§#183;«/mo»«mi mathvariant=¨bold¨»§#960;«/mi»«/mrow»«msup»«mi mathvariant=¨bold¨»T«/mi»«mn mathvariant=¨bold¨»2«/mn»«/msup»«/mfrac»«mn mathvariant=¨bold¨ mathcolor=¨#0000FF¨»2«/mn»«/msup»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»§#183;«/mo»«msub»«mi mathvariant=¨bold¨ mathcolor=¨#0000FF¨»R«/mi»«mrow mathcolor=¨#0000FF¨»«mn mathvariant=¨bold¨»2«/mn»«mo mathvariant=¨bold¨»,«/mo»«mn mathvariant=¨bold¨»1«/mn»«/mrow»«/msub»«mspace linebreak=¨newline¨/»«mspace linebreak=¨newline¨/»«/mstyle»«/math»

من المعادلة الناتجة، لا يمكن التعبير عن النسبة بين مربع زمن دورة القمر الاصطناعي ومكعب نصف قطر مداره بدلالة كتلة الشمس وحدها.

لذلك لا ينطبق قانون كبلر الثالث في هذه الحالة.

34. ب.27- التعبير عن كتلة النجم من خلال حركة قمر اصطناعي يتحرك حوله.

تعمل قوة الجاذبية العامة فقط على القمر الاصطناعي.

نكتب معادلة الحركة الدائرية ونعبر عن كتلة النجم كدالة لحركة القمر الاصطناعي:

«math xmlns=¨http://www.w3.org/1998/Math/MathML¨»«mstyle mathsize=¨20px¨»«msub»«mi mathvariant=¨bold¨ mathcolor=¨#0000FF¨»F«/mi»«mi mathvariant=¨bold¨ mathcolor=¨#0000FF¨»g«/mi»«/msub»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»=«/mo»«mi mathvariant=¨bold¨ mathcolor=¨#0000FF¨»m«/mi»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»§#183;«/mo»«msup»«mi mathvariant=¨bold-italic¨ mathcolor=¨#0000FF¨»§#969;«/mi»«mn mathvariant=¨bold¨ mathcolor=¨#0000FF¨»2«/mn»«/msup»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»§#183;«/mo»«mi mathvariant=¨bold¨ mathcolor=¨#0000FF¨»R«/mi»«mspace linebreak=¨newline¨/»«mspace linebreak=¨newline¨/»«mfrac mathcolor=¨#0000FF¨»«mrow»«mi mathvariant=¨bold¨»G«/mi»«mo mathvariant=¨bold¨»§#183;«/mo»«msub»«mi mathvariant=¨bold¨»M«/mi»«mi mathvariant=¨bold¨»X«/mi»«/msub»«mo mathvariant=¨bold¨»§#183;«/mo»«mi mathvariant=¨bold¨»m«/mi»«/mrow»«msup»«mi mathvariant=¨bold¨»R«/mi»«mn mathvariant=¨bold¨»2«/mn»«/msup»«/mfrac»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»=«/mo»«mi mathvariant=¨bold¨ mathcolor=¨#0000FF¨»m«/mi»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»§#183;«/mo»«msup»«mrow mathcolor=¨#0000FF¨»«mo mathvariant=¨bold¨ stretchy=¨true¨»(«/mo»«mfrac»«mrow»«mn mathvariant=¨bold¨»2«/mn»«mo mathvariant=¨bold¨»§#183;«/mo»«mi mathvariant=¨bold¨»§#960;«/mi»«/mrow»«mi mathvariant=¨bold¨»T«/mi»«/mfrac»«mo mathvariant=¨bold¨ stretchy=¨true¨»)«/mo»«/mrow»«mn mathvariant=¨bold¨ mathcolor=¨#0000FF¨»2«/mn»«/msup»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»§#183;«/mo»«mi mathvariant=¨bold¨ mathcolor=¨#0000FF¨»R«/mi»«mspace linebreak=¨newline¨/»«mspace linebreak=¨newline¨/»«mfrac mathcolor=¨#0000FF¨»«mrow»«mi mathvariant=¨bold¨»G«/mi»«mo mathvariant=¨bold¨»§#183;«/mo»«msub»«mi mathvariant=¨bold¨»M«/mi»«mi mathvariant=¨bold¨»X«/mi»«/msub»«mo mathvariant=¨bold¨»§#183;«/mo»«menclose notation=¨downdiagonalstrike¨»«mi mathvariant=¨bold¨»m«/mi»«/menclose»«/mrow»«msup»«mi mathvariant=¨bold¨»R«/mi»«mn mathvariant=¨bold¨»2«/mn»«/msup»«/mfrac»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»=«/mo»«menclose mathcolor=¨#0000FF¨ notation=¨downdiagonalstrike¨»«mi mathvariant=¨bold¨»m«/mi»«/menclose»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»§#183;«/mo»«mfrac mathcolor=¨#0000FF¨»«mrow»«mn mathvariant=¨bold¨»4«/mn»«mo mathvariant=¨bold¨»§#183;«/mo»«msup»«mi mathvariant=¨bold¨»§#960;«/mi»«mn mathvariant=¨bold¨»2«/mn»«/msup»«/mrow»«msup»«mi mathvariant=¨bold¨»T«/mi»«mn mathvariant=¨bold¨»2«/mn»«/msup»«/mfrac»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»§#183;«/mo»«mi mathvariant=¨bold¨ mathcolor=¨#0000FF¨»R«/mi»«mspace linebreak=¨newline¨/»«mspace linebreak=¨newline¨/»«mspace linebreak=¨newline¨/»«menclose mathcolor=¨#0000FF¨ notation=¨circle¨»«msub»«mi mathvariant=¨bold¨»M«/mi»«mi mathvariant=¨bold¨»X«/mi»«/msub»«mo mathvariant=¨bold¨»=«/mo»«mfrac»«mrow»«mn mathvariant=¨bold¨»4«/mn»«mo mathvariant=¨bold¨»§#183;«/mo»«msup»«mi mathvariant=¨bold¨»§#960;«/mi»«mn mathvariant=¨bold¨»2«/mn»«/msup»«mo mathvariant=¨bold¨»§#183;«/mo»«msup»«mi mathvariant=¨bold¨»R«/mi»«mn mathvariant=¨bold¨»3«/mn»«/msup»«/mrow»«mrow»«msup»«mi mathvariant=¨bold¨»T«/mi»«mn mathvariant=¨bold¨»2«/mn»«/msup»«mo mathvariant=¨bold¨»§#183;«/mo»«mi mathvariant=¨bold¨»G«/mi»«/mrow»«/mfrac»«/menclose»«mspace linebreak=¨newline¨/»«mspace linebreak=¨newline¨/»«mspace linebreak=¨newline¨/»«/mstyle»«/math»

35. ب.28 - حساب كتلة الكرة الأرضية من خلال حركة القمر حولها.

تعمل قوة الجاذبية العامة فقط على القمر الاصطناعي.

نكتب معادلة الحركة الدائرية ونعبر عن كتلة الكرة الأرضية اعتمادًا على حركة القمر الاصطناعي:

«math xmlns=¨http://www.w3.org/1998/Math/MathML¨»«mstyle mathsize=¨20px¨»«msub»«mi mathvariant=¨bold¨ mathcolor=¨#0000FF¨»F«/mi»«mi mathvariant=¨bold¨ mathcolor=¨#0000FF¨»g«/mi»«/msub»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»=«/mo»«mi mathvariant=¨bold¨ mathcolor=¨#0000FF¨»m«/mi»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»§#183;«/mo»«msup»«mi mathvariant=¨bold¨ mathcolor=¨#0000FF¨»§#969;«/mi»«mn mathvariant=¨bold¨ mathcolor=¨#0000FF¨»2«/mn»«/msup»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»§#183;«/mo»«mi mathvariant=¨bold¨ mathcolor=¨#0000FF¨»R«/mi»«mspace linebreak=¨newline¨/»«mspace linebreak=¨newline¨/»«mfrac mathcolor=¨#0000FF¨»«mrow»«mi mathvariant=¨bold¨»G«/mi»«mo mathvariant=¨bold¨»§#183;«/mo»«msub»«mi mathvariant=¨bold¨»M«/mi»«mi mathvariant=¨bold¨»E«/mi»«/msub»«mo mathvariant=¨bold¨»§#183;«/mo»«mi mathvariant=¨bold¨»m«/mi»«/mrow»«msup»«mi mathvariant=¨bold¨»R«/mi»«mn mathvariant=¨bold¨»2«/mn»«/msup»«/mfrac»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»=«/mo»«mi mathvariant=¨bold¨ mathcolor=¨#0000FF¨»m«/mi»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»§#183;«/mo»«msup»«mrow mathcolor=¨#0000FF¨»«mo mathvariant=¨bold¨ stretchy=¨true¨»(«/mo»«mfrac»«mrow»«mn mathvariant=¨bold¨»2«/mn»«mo mathvariant=¨bold¨»§#183;«/mo»«mi mathvariant=¨bold¨»§#960;«/mi»«/mrow»«mi mathvariant=¨bold¨»T«/mi»«/mfrac»«mo mathvariant=¨bold¨ stretchy=¨true¨»)«/mo»«/mrow»«mn mathvariant=¨bold¨ mathcolor=¨#0000FF¨»2«/mn»«/msup»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»§#183;«/mo»«mi mathvariant=¨bold¨ mathcolor=¨#0000FF¨»R«/mi»«mspace linebreak=¨newline¨/»«mspace linebreak=¨newline¨/»«mfrac mathcolor=¨#0000FF¨»«mrow»«mi mathvariant=¨bold¨»G«/mi»«mo mathvariant=¨bold¨»§#183;«/mo»«msub»«mi mathvariant=¨bold¨»M«/mi»«mi mathvariant=¨bold¨»E«/mi»«/msub»«mo mathvariant=¨bold¨»§#183;«/mo»«menclose notation=¨downdiagonalstrike¨»«mi mathvariant=¨bold¨»m«/mi»«/menclose»«/mrow»«msup»«mi mathvariant=¨bold¨»R«/mi»«mn mathvariant=¨bold¨»2«/mn»«/msup»«/mfrac»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»=«/mo»«menclose mathcolor=¨#0000FF¨ notation=¨downdiagonalstrike¨»«mi mathvariant=¨bold¨»m«/mi»«/menclose»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»§#183;«/mo»«mfrac mathcolor=¨#0000FF¨»«mrow»«mn mathvariant=¨bold¨»4«/mn»«mo mathvariant=¨bold¨»§#183;«/mo»«msup»«mi mathvariant=¨bold¨»§#960;«/mi»«mn mathvariant=¨bold¨»2«/mn»«/msup»«/mrow»«msup»«mi mathvariant=¨bold¨»T«/mi»«mn mathvariant=¨bold¨»2«/mn»«/msup»«/mfrac»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»§#183;«/mo»«mi mathvariant=¨bold¨ mathcolor=¨#0000FF¨»R«/mi»«mspace linebreak=¨newline¨/»«mspace linebreak=¨newline¨/»«mspace linebreak=¨newline¨/»«msub»«mi mathvariant=¨bold¨ mathcolor=¨#0000FF¨»M«/mi»«mi mathvariant=¨bold¨ mathcolor=¨#0000FF¨»E«/mi»«/msub»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»=«/mo»«mfrac mathcolor=¨#0000FF¨»«mrow»«mn mathvariant=¨bold¨»4«/mn»«mo mathvariant=¨bold¨»§#183;«/mo»«msup»«mi mathvariant=¨bold¨»§#960;«/mi»«mn mathvariant=¨bold¨»2«/mn»«/msup»«mo mathvariant=¨bold¨»§#183;«/mo»«msup»«mi mathvariant=¨bold¨»R«/mi»«mn mathvariant=¨bold¨»3«/mn»«/msup»«/mrow»«mrow»«msup»«mi mathvariant=¨bold¨»T«/mi»«mn mathvariant=¨bold¨»2«/mn»«/msup»«mo mathvariant=¨bold¨»§#183;«/mo»«mi mathvariant=¨bold¨»G«/mi»«/mrow»«/mfrac»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»=«/mo»«mfrac mathcolor=¨#0000FF¨»«mrow»«mn mathvariant=¨bold¨»4«/mn»«mo mathvariant=¨bold¨»§#183;«/mo»«msup»«mi mathvariant=¨bold¨»§#960;«/mi»«mn mathvariant=¨bold¨»2«/mn»«/msup»«mo mathvariant=¨bold¨»§#183;«/mo»«msup»«mstyle mathvariant=¨bold¨»«mo stretchy=¨true¨»(«/mo»«mrow»«mn»3«/mn»«mo».«/mo»«mn»84«/mn»«mo»§#183;«/mo»«msup»«mn»10«/mn»«mn»8«/mn»«/msup»«/mrow»«mo stretchy=¨true¨»)«/mo»«/mstyle»«mn mathvariant=¨bold¨»3«/mn»«/msup»«/mrow»«mrow»«msup»«mrow»«mo mathvariant=¨bold¨»(«/mo»«mn mathvariant=¨bold¨»27«/mn»«mo mathvariant=¨bold¨».«/mo»«mn mathvariant=¨bold¨»3«/mn»«mo mathvariant=¨bold¨»§#183;«/mo»«mn mathvariant=¨bold¨»24«/mn»«mo mathvariant=¨bold¨»§#183;«/mo»«mn mathvariant=¨bold¨»3600«/mn»«mo mathvariant=¨bold¨»)«/mo»«/mrow»«mn mathvariant=¨bold¨»2«/mn»«/msup»«mo mathvariant=¨bold¨»§#183;«/mo»«mn mathvariant=¨bold¨»6«/mn»«mo mathvariant=¨bold¨».«/mo»«mn mathvariant=¨bold¨»67«/mn»«mo mathvariant=¨bold¨»§#183;«/mo»«msup»«mn mathvariant=¨bold¨»10«/mn»«mrow mathvariant=¨bold¨»«mo»-«/mo»«mn»11«/mn»«/mrow»«/msup»«/mrow»«/mfrac»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»=«/mo»«mfrac mathcolor=¨#0000FF¨»«mrow»«mn mathvariant=¨bold¨»2«/mn»«mo mathvariant=¨bold¨».«/mo»«mn mathvariant=¨bold¨»235«/mn»«mo mathvariant=¨bold¨»§#183;«/mo»«msup»«mn mathvariant=¨bold¨»10«/mn»«mn mathvariant=¨bold¨»27«/mn»«/msup»«/mrow»«mrow»«mn mathvariant=¨bold¨»371«/mn»«mo mathvariant=¨bold¨».«/mo»«mn mathvariant=¨bold¨»089«/mn»«/mrow»«/mfrac»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»=«/mo»«mn mathvariant=¨bold¨ mathcolor=¨#0000FF¨»6«/mn»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»§#183;«/mo»«msup»«mn mathvariant=¨bold¨ mathcolor=¨#0000FF¨»10«/mn»«mn mathvariant=¨bold¨ mathcolor=¨#0000FF¨»24«/mn»«/msup»«mi mathvariant=¨bold¨ mathcolor=¨#0000FF¨»Kg«/mi»«mspace linebreak=¨newline¨/»«mspace linebreak=¨newline¨/»«mspace linebreak=¨newline¨/»«/mstyle»«/math»

الموقع:	YouCube
المقرر:	כבידה - ערבית
كتاب:	حلول التدريبات العملية الجاذبية - ديناميكا (دون الطاقة)

طبع بواسطة:	משתמש אורח
التاريخ:	الأربعاء، 4 فبراير 2026، 2:40 AM

حلول التدريبات العملية الجاذبية - ديناميكا (دون الطاقة)

جدول المحتويات

1. أ.1- تسارع الجاذبية على سطح كوكب

2. أ.2- حساب تسارع الجاذبية على سطح الكرة الأرضية

3. أ.3- مقدار تسارع الجاذبية على القمر.

4. أ.4- تسارع الجاذبية على ارتفاع h فوق سطح الكرة الأرضية.

5. أ.5- يتعلق تسارع الجاذبية على سطحه بكتلة الكوكب

6. أ.6- حساب كتلة الكرة الارضية

7. أ.7- الثبات في نقطة بين الكرة الأرضية والقمر.

8. ب.1- قمر اصطناعي يتحرك حول كوكب سيار (R)T

9. ب.2- حساب زمن دورة حركة الكرة الأرضية.

10. ب.3- حساب زمن دورة حركة القمر.

11. ب.4- قمر اصطناعي يدور حول كوكب (R)V

12. ب.5- حساب سرعة قمر اصطناعي يتحرك حول الكرة الأرضية.

13. ب.6- تعبير التسارع الرديالي (aR(V,R

14. ب.7- حساب التسارع الرديالي

15. ب.8- تعبير تسارع الجاذبية

16. ب.9- التعبير عن ارتفاع القمر الاصطناعي كدالة لنصف قطر الكوكب

17. ب.10- التعبير عن القوة العمودية على شخص موجود داخل القمر الاصطناعي.

18. ب.11- القوة العمودية التي تؤثر على جسم في حالة سكون.

19. ب 12 - القوة العمودية المؤثرة على جسم متحرك.

20. ب.13- سرعة الجسم التي تكون بها القوة العمودية مساوية صفر.

21. ب.14 السرعة التي تتحرك بها السيارة في حركة قمر اصطناعي.

22. ب.15- التعبير عن القوة العمودية على خط الاستواء

23. ب.16- حساب زمن دورة الكرة الأرضية في حالة N=0.

24. ب.17- التعبير للقوة العمودية، رجل يقف على برج في كوكب لا يدور.

25. ب.18- تعبير القوة العمودية التيي تعمل على شخصيجلس على برج موجود كوكب يدور.

26. ب.19- التعبير عن زمن دورة شخص يجلس على برج موجود على سطح كوكب يدور حول محوره.

27. ب.20- تعبير لنصف قطر المدار لقمر اصطناعي للاتصالات .

28. ب.21- زمن دورة حركة القمر الاصطناعي حول الكرة الأرضية.

29. بב.22- ارتفاع أقمار الاتصالات.

30. ب.23- شرح سبب تحرك قمر اصطناعي للاتصالات فوق خط الاستواء.

31. ب.24- حساب نصف قطر مدار قمر اتصالات يتحرك حول القمر

32. ب.25- تطوير القانون الثالث لكبلر.

33. ب.26- قمر اصطناعي يتحرك تحت تأثير الكرة الأرضية والشمس.

34. ب.27- التعبير عن كتلة النجم من خلال حركة قمر اصطناعي يتحرك حوله.

35. ب.28 - حساب كتلة الكرة الأرضية من خلال حركة القمر حولها.