 ____________________________________________________________________________________
____________________________________________________________________________________
...
مقدار كمية الدفع التي يشغّلها المجس على العربة هي 0.276NS .
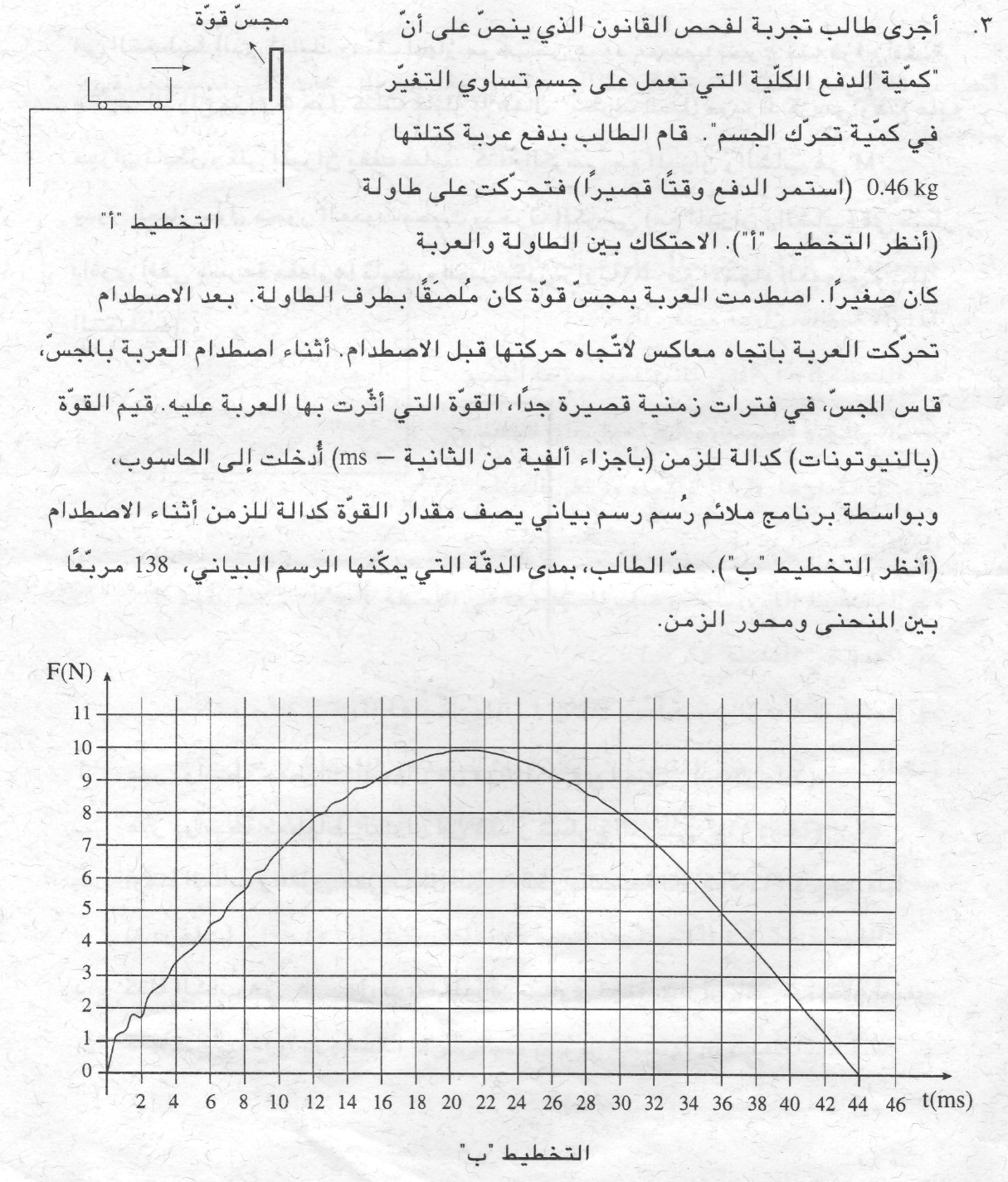
المساحة المحصورة بين الرسم البياني للقوة كدالة للزمن ومحور الزمن تساوي كمية الدفع للقوة .
في الرسم البياني الذي يصف القوة التي تشغّلها العربة على المجس كدالة للزمن، فإن المساحة المحصورة بين الرسم البياني ومحور الزمن مساوية لكمية الدفع .
في السؤال ، هناك 138 مربع بين المنحنى والمحور الزمني. نجد مقدار مساحة المربع الواحد.
«math xmlns=¨http://www.w3.org/1998/Math/MathML¨»«mi mathvariant=¨bold¨ mathcolor=¨#0000FF¨»§#1608;§#1575;§#1581;§#1583;«/mi»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»§#160;«/mo»«mi mathvariant=¨bold¨ mathcolor=¨#0000FF¨»§#1605;§#1585;§#1576;§#1593;«/mi»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»§#160;«/mo»«mi mathvariant=¨bold¨ mathcolor=¨#0000FF¨»J«/mi»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»=«/mo»«mmultiscripts»«mi mathvariant=¨bold¨ mathcolor=¨#0000FF¨»F«/mi»«mprescripts/»«mrow mathcolor=¨#0000FF¨»«mi mathvariant=¨bold¨»§#1608;§#1575;§#1581;§#1583;«/mi»«mo mathvariant=¨bold¨»§#160;«/mo»«mi mathvariant=¨bold¨»§#1605;§#1585;§#1576;§#1593;«/mi»«mo mathvariant=¨bold¨»§#160;«/mo»«/mrow»«none/»«/mmultiscripts»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»§#183;«/mo»«mmultiscripts»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»§#8710;«/mo»«mprescripts/»«mrow mathcolor=¨#0000FF¨»«mi mathvariant=¨bold¨»§#1608;§#1575;§#1581;§#1583;«/mi»«mo mathvariant=¨bold¨»§#160;«/mo»«mi mathvariant=¨bold¨»§#1605;§#1585;§#1576;§#1593;«/mi»«mo mathvariant=¨bold¨»§#160;«/mo»«/mrow»«none/»«/mmultiscripts»«mi mathvariant=¨bold¨ mathcolor=¨#0000FF¨»t«/mi»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»=«/mo»«mn mathvariant=¨bold¨ mathcolor=¨#0000FF¨»1«/mn»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»§#183;«/mo»«mn mathvariant=¨bold¨ mathcolor=¨#0000FF¨»2«/mn»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»§#183;«/mo»«msup»«mn mathvariant=¨bold¨ mathcolor=¨#0000FF¨»10«/mn»«mrow mathcolor=¨#0000FF¨»«mo mathvariant=¨bold¨»-«/mo»«mn mathvariant=¨bold¨»3«/mn»«/mrow»«/msup»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»=«/mo»«mn mathvariant=¨bold¨ mathcolor=¨#0000FF¨»2«/mn»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»§#183;«/mo»«msup»«mn mathvariant=¨bold¨ mathcolor=¨#0000FF¨»10«/mn»«mrow mathcolor=¨#0000FF¨»«mo mathvariant=¨bold¨»-«/mo»«mn mathvariant=¨bold¨»3«/mn»«/mrow»«/msup»«mi mathvariant=¨bold¨ mathcolor=¨#0000FF¨»N«/mi»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»§#183;«/mo»«mi mathvariant=¨bold¨ mathcolor=¨#0000FF¨»S«/mi»«/math»
اعتمادًا على عدد المربعات المحصورة بين المنحنى والمحور الزمني ، نحسب كمية الدفع الذي شغّله المجس على العربة:
«math xmlns=¨http://www.w3.org/1998/Math/MathML¨»«mi mathvariant=¨bold¨ mathcolor=¨#0000FF¨»J«/mi»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»=«/mo»«mn mathvariant=¨bold¨ mathcolor=¨#0000FF¨»138«/mn»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»§#183;«/mo»«mmultiscripts»«mi mathvariant=¨bold¨ mathcolor=¨#0000FF¨»J«/mi»«mprescripts/»«mrow mathcolor=¨#0000FF¨»«mi mathvariant=¨bold¨»§#1608;§#1575;§#1581;§#1583;«/mi»«mo mathvariant=¨bold¨»§#160;«/mo»«mi mathvariant=¨bold¨»§#1605;§#1585;§#1576;§#1593;«/mi»«mo mathvariant=¨bold¨»§#160;«/mo»«/mrow»«none/»«/mmultiscripts»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»=«/mo»«mn mathvariant=¨bold¨ mathcolor=¨#0000FF¨»138«/mn»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»§#183;«/mo»«mn mathvariant=¨bold¨ mathcolor=¨#0000FF¨»2«/mn»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»§#183;«/mo»«msup»«mn mathvariant=¨bold¨ mathcolor=¨#0000FF¨»10«/mn»«mrow mathcolor=¨#0000FF¨»«mo mathvariant=¨bold¨»-«/mo»«mn mathvariant=¨bold¨»3«/mn»«/mrow»«/msup»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»=«/mo»«mn mathvariant=¨bold¨ mathcolor=¨#0000FF¨»0«/mn»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨».«/mo»«mn mathvariant=¨bold¨ mathcolor=¨#0000FF¨»276«/mn»«mi mathvariant=¨bold¨ mathcolor=¨#0000FF¨»N«/mi»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»§#183;«/mo»«mi mathvariant=¨bold¨ mathcolor=¨#0000FF¨»S«/mi»«/math»
لذلك ، فإن مقدار كمية الدفع التي عملتها العربة على المجس هو 0.276 نيوتن في الثانية.
من القانون الثالث لنيوتن، كمية الدفع التي يشغلها المجس على العربة هو نفس كمية الدفع التي تشغّلها العربة على المجس.
مقدار كمية الدفع التي عملها المجس على العربة هي 0.276 نيوتن في الثانية.
בשאלה נתון שבין העקומה לציר הזמן יש 138 משבצות. נמצא את גודל המתקף של שטח משבצת אחת.
«math xmlns=¨http://www.w3.org/1998/Math/MathML¨»«mmultiscripts»«mi mathvariant=¨bold¨ mathcolor=¨#0000FF¨»J«/mi»«mprescripts»«/mprescripts»«mrow mathcolor=¨#0000FF¨»«mi mathvariant=¨bold¨»§#1488;§#1495;§#1514;«/mi»«mo mathvariant=¨bold¨»§#160;«/mo»«mi mathvariant=¨bold¨»§#1502;§#1513;§#1489;§#1510;§#1514;«/mi»«/mrow»«none»«/none»«/mmultiscripts»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»=«/mo»«mmultiscripts»«mi mathvariant=¨bold¨ mathcolor=¨#0000FF¨»F«/mi»«mprescripts»«/mprescripts»«mrow mathcolor=¨#0000FF¨»«mi mathvariant=¨bold¨»§#1488;§#1495;§#1514;«/mi»«mo mathvariant=¨bold¨»§#160;«/mo»«mi mathvariant=¨bold¨»§#1502;§#1513;§#1489;§#1510;§#1514;«/mi»«/mrow»«none»«/none»«/mmultiscripts»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»§#183;«/mo»«mmultiscripts»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»§#8710;«/mo»«mprescripts»«/mprescripts»«mrow mathcolor=¨#0000FF¨»«mi mathvariant=¨bold¨»§#1488;§#1495;§#1514;«/mi»«mo mathvariant=¨bold¨»§#160;«/mo»«mi mathvariant=¨bold¨»§#1502;§#1513;§#1489;§#1510;§#1514;«/mi»«/mrow»«none»«/none»«/mmultiscripts»«mi mathvariant=¨bold¨ mathcolor=¨#0000FF¨»t«/mi»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»=«/mo»«mn mathvariant=¨bold¨ mathcolor=¨#0000FF¨»1«/mn»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»§#183;«/mo»«mn mathvariant=¨bold¨ mathcolor=¨#0000FF¨»2«/mn»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»§#183;«/mo»«msup»«mn mathvariant=¨bold¨ mathcolor=¨#0000FF¨»10«/mn»«mrow mathcolor=¨#0000FF¨»«mo mathvariant=¨bold¨»-«/mo»«mn mathvariant=¨bold¨»3«/mn»«/mrow»«/msup»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»=«/mo»«mn mathvariant=¨bold¨ mathcolor=¨#0000FF¨»2«/mn»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»§#183;«/mo»«msup»«mn mathvariant=¨bold¨ mathcolor=¨#0000FF¨»10«/mn»«mrow mathcolor=¨#0000FF¨»«mo mathvariant=¨bold¨»-«/mo»«mn mathvariant=¨bold¨»3«/mn»«/mrow»«/msup»«mi mathvariant=¨bold¨ mathcolor=¨#0000FF¨»N«/mi»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»§#183;«/mo»«mi mathvariant=¨bold¨ mathcolor=¨#0000FF¨»S«/mi»«/math»
בהתאם למספר המשבצות התחומות בין העקומה לציר הזמן , נחשב את המתקף שהחיישן הפעיל על הקרונית:
«math xmlns=¨http://www.w3.org/1998/Math/MathML¨»«mi mathvariant=¨bold¨ mathcolor=¨#0000FF¨»J«/mi»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»=«/mo»«mn mathvariant=¨bold¨ mathcolor=¨#0000FF¨»138«/mn»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»§#183;«/mo»«mmultiscripts»«mi mathvariant=¨bold¨ mathcolor=¨#0000FF¨»J«/mi»«mprescripts/»«mrow mathcolor=¨#0000FF¨»«mi mathvariant=¨bold¨»§#1488;§#1495;§#1514;«/mi»«mo mathvariant=¨bold¨»§#160;«/mo»«mi mathvariant=¨bold¨»§#1502;§#1513;§#1489;§#1510;§#1514;«/mi»«/mrow»«none/»«/mmultiscripts»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»=«/mo»«mn mathvariant=¨bold¨ mathcolor=¨#0000FF¨»138«/mn»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»§#183;«/mo»«mn mathvariant=¨bold¨ mathcolor=¨#0000FF¨»2«/mn»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»§#183;«/mo»«msup»«mn mathvariant=¨bold¨ mathcolor=¨#0000FF¨»10«/mn»«mrow mathcolor=¨#0000FF¨»«mo mathvariant=¨bold¨»-«/mo»«mn mathvariant=¨bold¨»3«/mn»«/mrow»«/msup»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»=«/mo»«mn mathvariant=¨bold¨ mathcolor=¨#0000FF¨»0«/mn»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨».«/mo»«mn mathvariant=¨bold¨ mathcolor=¨#0000FF¨»276«/mn»«mi mathvariant=¨bold¨ mathcolor=¨#0000FF¨»N«/mi»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»§#183;«/mo»«mi mathvariant=¨bold¨ mathcolor=¨#0000FF¨»S«/mi»«/math»
לכן גודל המתקף שהקרונית הפעילה על החיישן הוא 0.276 ניוטון כפול שנייה.
מהחוק השלישי של ניוטון , גודל המתקף שהחיישן הפעיל על הקרונית זהה לגודל המתקף שהקרונית הפעילה על החיישן.
גודל המתקף החיישן הפעיל על הקרונית הוא 0.276 ניוטון כפול שנייה.
1.
الوحدات الزمنية على المحور الأفقي معطاة بالألف من الثانية وليست بوحدات
الثانية.
قبل استخلاص
النتائج من الرسم البياني، يجب فحص وحدات المحاور في الرسم البياني.
2. يجب حساب مقدار
كمية الدفع لمربع واحد، وعندها فقط احسب مقدار كمية الدفع لجميع المربعات الـ 138.
3. يصف الرسم
البياني القوة التي تشغّلها الشاحنة على المجس، لذا معنى المساحة في هذا الرسم
البياني مقدار كمية الدفع التي تشغّلها الشاحنة على المجس.
السؤال عن كمية
الدفع الذي قام بتشغيله جهاز الاستشعار على العربة.
لذلك من
المهم أن نلاحظ وفقًا للقانون الثالث لنيوتن أن مقداري كمية الدفع متماثلان متساويان.
4. يتعامل السؤال
مع مقدار كمية الدفع الذي قام المجس بتشغيله. لا داعي للإشارة إلى اتجاه كمية
الدفع.
5. تبدو الدالة
في الرسم البياني مشوهة بعض الشيء، خاصة في بداية الرسم البياني. الرسم البياني هو
تجربة حقيقية، في كل تجربة حقيقية هناك اضطرابات.
من حيث مسار
الحل، الشيء المهم هو أن هناك 138 خانة زمنية بين الدالة والمحور الزمني.
לפני הסקת מסקנות מגרף חייבים לבחון את יחידות הצירים בגרף.
2. יש לחשב את המתקף של משבצת אחרת , ורק לאחר מכן לחשב את המתקף של כל 138 המשבצות.
3. הגרף מתאר את הכוח שהקרונית מפעילה על החיישן משמעות השטח בגרף זה היא המתקף שהקרונית מפעילה על החיישן.
השאלה היא על המתקף שהחיישן הפעיל על הקרונית.
לכן חשוב לציין לפי החוק השלישי של ניוטון ששני מתקפים אלו זהים בגודלם.
4. השאלה עוסקת בגודל המתקף שהחיישן הפעיל . אין צורך להתייחס לכיוונו של המתקף .
5. הפונקציה בגרף נראית משובשת מעט , במיוחד בתחילת הגרף. הגרף הוא של ניסוי אמיתי , בכל ניסוי אמיתי קיימים הפרעות.
מבחינת מהלך הפתרון הדבר החשוב הוא שיש 138 משבצות בין הפונקציה לציר הזמן.
______________________________________________________________________________________

______________________________________________________________________________________
...
نتيجة الاصطدام ، تنخفض كمية حركة العربة بمقدار 0.287 نيوتن في الثانية.
بمساعدة معطيات حركة العربة قبل الاصطدام وبعده، من الممكن حساب السرعة قبل الاصطدام وبعده.
ووفقًا لهاتين السرعتين، يمكن حساب التغيّر في كمية الحركة.
ובהתאם למהירויות אלו ניתן לחשב את שינוי התנע.
لايجاد التغيير في كمية الحركة، نحسب كمية الحركة قبل الاصطدام وبعده باستخدام معطيات حركة العربة قبل الاصطدام وبعده:
بما أن حركة العربة بعد اصطدامها بالمجس تكون معاكسة لاتجاه حركتها قبل الاصطدام ، تكون إحدى السرعتي موجبة والأخرى سالبة.
تشغّل العربة قوة على المجس في الاتجاه الصحيح. توصف هذه القوة في الرسم البياني بأنها قوة موجبة، وبالتالي يكون اتجاه محور الحركة جهة اليمين.
قبل الاصطدام ، تتحرك السيارة إلى اليمين في اتجاه محور الازاحة، وبالتالي تكون الازاحة موجبة.
بعد الاصطدام ، تتحرك العربة عكس اتجاه المحور، وتكون إزاحتها سالبة.
نحسب سرعة العربة قبل الاصطدام:
«math xmlns=¨http://www.w3.org/1998/Math/MathML¨»«mi mathvariant=¨bold¨ mathcolor=¨#0000FF¨»V«/mi»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»=«/mo»«mfrac mathcolor=¨#0000FF¨»«mrow»«mo mathvariant=¨bold¨»§#8710;«/mo»«mi mathvariant=¨bold¨»X«/mi»«/mrow»«mrow»«mo mathvariant=¨bold¨»§#8710;«/mo»«mi mathvariant=¨bold¨»t«/mi»«/mrow»«/mfrac»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»=«/mo»«mfrac mathcolor=¨#0000FF¨»«mrow»«mn mathvariant=¨bold¨»0«/mn»«mo mathvariant=¨bold¨».«/mo»«mn mathvariant=¨bold¨»03«/mn»«/mrow»«mrow»«mn mathvariant=¨bold¨»0«/mn»«mo mathvariant=¨bold¨».«/mo»«mn mathvariant=¨bold¨»09«/mn»«/mrow»«/mfrac»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»=«/mo»«mn mathvariant=¨bold¨ mathcolor=¨#0000FF¨»0«/mn»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨».«/mo»«mn mathvariant=¨bold¨ mathcolor=¨#0000FF¨»33«/mn»«mfrac mathcolor=¨#0000FF¨»«mi mathvariant=¨bold¨»m«/mi»«mi mathvariant=¨bold¨»s«/mi»«/mfrac»«/math»
نحسب سرعة العربة بعد الاصطدام:
«math xmlns=¨http://www.w3.org/1998/Math/MathML¨»«mi mathvariant=¨bold¨ mathcolor=¨#0000FF¨»U«/mi»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»=«/mo»«mfrac mathcolor=¨#0000FF¨»«mrow»«mo mathvariant=¨bold¨»§#8710;«/mo»«mi mathvariant=¨bold¨»X«/mi»«mo mathvariant=¨bold¨»`«/mo»«/mrow»«mrow»«mo mathvariant=¨bold¨»§#8710;«/mo»«mi mathvariant=¨bold¨»t«/mi»«mo mathvariant=¨bold¨»`«/mo»«/mrow»«/mfrac»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»=«/mo»«mfrac mathcolor=¨#0000FF¨»«mrow»«mo mathvariant=¨bold¨»-«/mo»«mn mathvariant=¨bold¨»0«/mn»«mo mathvariant=¨bold¨».«/mo»«mn mathvariant=¨bold¨»03«/mn»«/mrow»«mrow»«mn mathvariant=¨bold¨»0«/mn»«mo mathvariant=¨bold¨».«/mo»«mn mathvariant=¨bold¨»102«/mn»«/mrow»«/mfrac»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»=«/mo»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»-«/mo»«mn mathvariant=¨bold¨ mathcolor=¨#0000FF¨»0«/mn»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨».«/mo»«mn mathvariant=¨bold¨ mathcolor=¨#0000FF¨»294«/mn»«mfrac mathcolor=¨#0000FF¨»«mi mathvariant=¨bold¨»m«/mi»«mi mathvariant=¨bold¨»s«/mi»«/mfrac»«/math»
نحسب التغير في كمية الحركة للعربة بعد الاصطدام:«math xmlns=¨http://www.w3.org/1998/Math/MathML¨»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»§#8710;«/mo»«mi mathvariant=¨bold¨ mathcolor=¨#0000FF¨»P«/mi»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»=«/mo»«mi mathvariant=¨bold¨ mathcolor=¨#0000FF¨»m«/mi»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»§#183;«/mo»«mi mathvariant=¨bold¨ mathcolor=¨#0000FF¨»U«/mi»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»-«/mo»«mi mathvariant=¨bold¨ mathcolor=¨#0000FF¨»m«/mi»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»§#183;«/mo»«mi mathvariant=¨bold¨ mathcolor=¨#0000FF¨»V«/mi»«mspace linebreak=¨newline¨/»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»§#8710;«/mo»«mi mathvariant=¨bold¨ mathcolor=¨#0000FF¨»P«/mi»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»=«/mo»«mn mathvariant=¨bold¨ mathcolor=¨#0000FF¨»0«/mn»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨».«/mo»«mn mathvariant=¨bold¨ mathcolor=¨#0000FF¨»46«/mn»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»§#183;«/mo»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»(«/mo»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»-«/mo»«mn mathvariant=¨bold¨ mathcolor=¨#0000FF¨»0«/mn»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨».«/mo»«mn mathvariant=¨bold¨ mathcolor=¨#0000FF¨»294«/mn»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»)«/mo»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»-«/mo»«mn mathvariant=¨bold¨ mathcolor=¨#0000FF¨»0«/mn»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨».«/mo»«mn mathvariant=¨bold¨ mathcolor=¨#0000FF¨»46«/mn»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»§#183;«/mo»«mn mathvariant=¨bold¨ mathcolor=¨#0000FF¨»0«/mn»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨».«/mo»«mn mathvariant=¨bold¨ mathcolor=¨#0000FF¨»33«/mn»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»=«/mo»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»-«/mo»«mn mathvariant=¨bold¨ mathcolor=¨#0000FF¨»0«/mn»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨».«/mo»«mn mathvariant=¨bold¨ mathcolor=¨#0000FF¨»287«/mn»«mi mathvariant=¨bold¨ mathcolor=¨#0000FF¨»N«/mi»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»§#183;«/mo»«mi mathvariant=¨bold¨ mathcolor=¨#0000FF¨»S«/mi»«/math»
نتيجة الاصطدام ، تنخفض كمية الحركة للعربة بمقدار 0.287 نيوتن في الثانية.
1.
تتحرك السيارة في اتجاهين متعاكسين قبل الاصطدام وبعده.
من المهم أن نعرف
ما هو اتجاه محور الحركة، بحيث يمكن تحديد متى تكون السرعة سالبة.
في هذا
السؤال، اتجاه القوة التي تشغّلها الشاحنة على المجس هو لجهة اليسار، وفي الرسم
البياني ، توصف هذه القوة بأنها قوة موجبة، وبالتالي يكون اتجاه المحور جهة
اليمين.
2. إذا لم يتم
وصف القوة في السؤال، ولم يكن هناك أي قيود على اتجاه معين لمحور الحركة، فيجب
تحديد اتجاه المحور بشكل اعتباطي
وحدد جميع معطيات
السؤال وفقًا للاتجاه المختار.
3. قبل الاصطدام،
تحركت العربة نحو اليمين، في اتجاه المحور، وكانت كمية الحركة للعربة موجبًا.
بعد
الاصطدام، تتحرك السيارة إلى اليسار عكس اتجاه المحور لذلك كمية الحركة للعربة يكون
سالبًا.
فيما يتعلق
بمحور الحركة الموجه إلى اليمين، فإن كمية الحركة يقل. لذلك فإن قيمة تغير كمية
الحركة سالبة.
4. كما هو مكتوب
في السؤال، يجب حساب التغيير في كمية الحركة وليس مقدار التغيير في كمية الحركة.
يجب أن تشير
الإجابة إلى إشارة تغيّر كمية الحركة وإلى اتجاه محور الحركة المختار.
5. في القسم أ ،
كُتب "أوجد مقدار كمية الدفع" ، وفي القسم ب مكتوب "أوجد التغيير
في كمية الحركة ".
لذلك فإن
الإجابة على القسم أ موجبة والإجابة على القسم ب سالبة.
6. من قانون كمية
الدفع وكمية الحركة، متجه التغيُّر في كمية الحركة يساوي لمتّجه كمية الدفع. في
القسم (أ) حصلنا على كمية دفع مقداره 0.276NS.
في القسم ب
حصلنا على تغيير في كمية الحركة قدره 0.287NS.
القسم التالي يناقش هذا الاختلاف.
بشكل عام، أي
اختلاف بين مقدار التغيير في كمية الحركة ومقدار كمية الدفع يتطلب الفحص.
חשוב להבין מה הוא כיוון ציר התנועה , כדי שניתן יהיה לקבוע מתי המהירות שלילית.
בשאלה זו כיוון הכוח שהקרונית מפעילה על החיישן הוא שמאלה , בגרף כוח זה מתואר ככוח חיובי , לכן כיוון הציר ימינה.
2. במידה והכוח לא מתואר בשאלה, ואין אילוץ לכיוון מסוים של ציר התנועה, יש לקבוע את כיוון הציר באופן שרירותי
ולהגדיר את כל נתוני השאלה בהתאם לכיוון הנבחר.
3. בהתאם לכתוב בשאלה , יש לחשב את השינוי בתנע ולא את גודל השינוי התנע .
התשובה צריכה להתייחס לסימן שינוי התנע, ולכיוון ציר התנועה הנבחר.
4. בסעיף א' כתוב "מצא את גודל המתקף" , בסעיף ב' כתוב "מצא את השינוי בתנע" .
לכן התשובה לסעיף א' חיובית והתשובה לסעיף ב' שלילית.
5. ממשפט תנע מתקף, וקטור השינוי בתנע שווה לווקטור המתקף . בסעיף א' קבלנו מתקף שגודלו 0.276 ניוטון כפול שנייה.
בסעיף ב' קבלנו שינוי תנע שגודלו 0.287 ניוטון כפול שנייה. הסעיף הבא דן בהפרש זה.
באופן כללי , כל הפרש בין גודל שינוי תנע לגודל המתקף מצריך בדיקה .
______________________________________________________________________________________

______________________________________________________________________________________
...
الأسباب المحتملة لعدم الدقة:
1. عدم دقة مجس القياس.
2. عدم دقة الطالب في قياس الازاحة وأوقات حركة العربة.
3. يختلف عدد المربعات عن 138.
4. قوى الاحتكاك ليست مهملة.
1. חוסר דיוק של חיישן המדידה.
2. חוסר דיוק של התלמיד במדידת העתקים וזמני התנועה של הקרונית.
3. מספר משבצות שונה מ 138 .
4. כוחות חיכוך לא זניחים.
1. קע
2. גע
يمكن أن ينتج خطأ بسيط عن أخطاء القياس. أو من عدم الدقة في الافتراضات التي استندت إليها التجربة.
في كل تجربة ، هناك أخطاء ناتجة عن أدوات القياس أو الافتراضات التي ليست دقيقة تمامًا.
الأسباب المحتملة لعدم الدقة:
1. مثل أي جهاز قياس ، فإن دقة المجس ليست مطلقة.
2. قد لا يكون عدد المربعات التي قيست ليست بالضبط 138 مربعًا.
3. ينتج التغيير في كمية الحركة من جميع القوى المؤثرة على الجسم، من الرسم البياني يمكنك فقط معرفة القوة التي قام المجس بتشغيلها.
من الواضح أن قوى الاحتكاك ليست مهملة تمامًا.
4. قياسات الطالب ليست دقيقة تماما.
גורמים אפשריים לחוסר דיוק:
1. כמו כל מכשיר מדידה דיוק החיישן איננו מוחלט .
2. יכול להיות שמספר המשבצות הוא לא בדיוק 138.
3. השינוי בתנע נובע מכלל הכוחות הפועלים על הגוף , מהגרף ניתן ללמוד רק על הכוח שהחיישן הפעיל .
כככל הנראה כוחות החיכוך אינם זניחים לחלוטין.
4. מדידותיו של התלמיד אינן מדויקות לחלוטין.
1.
مكتوب في السؤال: "عدّ الطالب عدد المربعات بين الرسم البياني ومحور
الزمن بمدى الدقة الذي يسمح به بـ 138 مربعًا." هذا يعني أنه يوجد خطأ في تحديد عدد المربعات.
ومن ثم فإن
قيمة عدد المربعات ليست دقيقة تمامًا.
2. مكتوب في
السؤال: "الاحتكاك بين الطاولة والعربة صغير"، وبالتالي فإن الاحتكاك
ليس مهملاً تمامًا. في حساب كمية الدفع، أخذنا بالحسبان فقط إلى الرسم البياني.
من الرسم
البياني، يمكنك فقط التعرف على كمية الدفع الذي شَغّله المجس على العربة. وإذا اعتمدنا
فقط على التمثيل البياني، فإننا نفترض أنه لا يوجد احتكاك.
3. لم يُكتب كيف
قاس الطالب الازاحة وزمن الحركة بأي طريقة يختارها الطالب لن تكون قيم القياس
دقيقة تمامًا.
4. هناك ادعاءات
عامة بعدم الدقة، وليس لها إشارة محددة إلى شكل عدم الدقة، مثل خطأ القياس.
طالما يوجد
خطأ في القياس، يمكن أن تكون القيمة الحقيقية أكبر أو أقل من القيمة المقاسة.
هناك ادعاءات
بعدم الدقة ليست عامة ولا تناسب كل حالة. على سبيل المثال، إذا كانت السرعة منخفضة
جدًا لا يمكن تفسير ذلك بسبب عدم مراعاة قوة الاحتكاك. فإذا أخذنا في الاعتبار
الاحتكاك، فستكون السرعة أقل.
5. في هذا
السؤال، عدم الدقة ضئيل، لذا يمكن الافتراض أنه نابع من العوامل المذكورة في
الإجابة، وليس من مشكلة خطيرة أو خلل في إجراء التجربة.
6. من المستحسن
أن تتذكر أن كل جهاز قياس به خطأ في القياس، واستخدام هذه الحجة لشرح عدم الدقة الصغيرة
في كل تجربة.
מכאן שערך מספר המשבצות איננו מדויק לחלטין.
2. כתוב בשאלה:" החיכוך בין השולחן לקרונית קטן" , מכאן שהחיכוך לא זניח לחלוטין. בחישוב המתקף התייחסנו רק לגרף.
מהגרף אפשר ללמוד רק על המתקף שהחיישן הפעיל על הקרונית. ואם הסתמכנו רק על הגרף הרי שהנחנו שאין חיכוך .
3. לא כתוב איך התלמיד מדד את ההעתקים ואת זמני התנועה , בכל דרך שהתלמיד יבחר לעשות זאת
ערכי המדידות לא יהיו מדויקים לחלוטין.
בהתאם לסעיפים הקודמים , היה נכון יותר לשאול על ההפרש בין גודל התנע לגודל שינוי התנע.
______________________________________________________________________________________

______________________________________________________________________________________
...
في اللحظة التي تغير فيها العربة اتجاه حركتها تكون سرعتها صفرًا (توقّف لحظي).
من الرسم البياني للقوة كدالة للزمن، يمكنك معرفة اتجاه حركة العربة. إذا تغير اتجاه حركة العربة، فهناك لحظة تكون فيها سرعةالعربة صفر.
تصطدم العربة بالمجس وتؤثر عليه بقوة. في البداية، تتزايد هذه القوة لأن العربة تقترب أكثر فأكثر من المجس. من اللحظة t = 21ms تصبح هذه القوة أصغر وتتحرك السيارة بعيدًا عن المجس. وفي اللحظة t = 44ms تنفصل العربة عن المجس وتتحرك يسارًا.
أثناء الاصطدام ، غيرت السيارة اتجاه حركتها ، لذلك توجد بالضرورة لحظة أثناء الاصطدام تكون فيها سرعة السيارة مساوية للصفر.
בתחילה כוח זה הולך וגדל מכיוון שהקרונית מתקרבת יותר ויותר לחיישן . מרגע t=21ms כוח זה הולך וקטן הקרונית מתרחקת מהחיישן ברגע t=44ms הקרונית ניתקת מהחיישן והיא נעה שמאלה .
אם הקרונית כל הזמן הייתה נעה רק ימינה הכוח שהיא הייתה מפעילה על החיישן היה כל הזמן הולך וגדל. בגרף ניתן לראות שהכוח שהקרונית מפעילה גדל ולאחר מכן קטן, לכן הקרונית מתקרבת לחיישן ולאחר מכן מתרחקת ממנו.
בהתאם לגרף הכוח ,ניתן להבין שבזמן ההתנגשות הקרונית שינתה את כיוון תנועתה,
לכן בהכרח יש רגע שבו מהירותה שווה לאפס.
1.
إذا كانت العربة تتحرك باستمرار إلى اليمين فقط، فإن القوة التي تشغّلها
على المجس سوف تتزايد باستمرار.
من الرسم
البياني يمكنك أن ترى أن القوة تأخذ بالنقصان حتى تصبح صفر، لذلك أثناء الاصطدام تأخذ
العربة بالابتعاد عن المجس.
2. لحظة قبل الاصطدام،
تتحرك العربة إلى اليمين ولحظة بعد الاصطدام، تتحرك العربة إلى اليسار.
بين هاتين
اللحظتين (أثناء الاصطدام) يجب أن تكون هناك لحظة تغير فيها العربة اتجاه حركتها،
في هذه اللحظة تكون سرعة العربة صفراً!
3. من الممكن
ارتكاب خطأ في هذا السؤال، والاعتقاد أنه إذا لم تُغير القوة المؤثرة على العربة
اتجاهها ، فإن السيارة لا تُغير اتجاهها أيضًا.
على الرغم من
أن اتجاه القوة التي يشغّلها المجس على العربة لا يتغير (موجهًا دائمًا إلى
اليسار) ، يتغير اتجاه حركة العربة.
على غرار
الرمي نحو الأعلى، يكون اتجاه الجاذبية دائمًا لأسفل، وجزء من الزمن يتحرك فيه
الجسم لأعلى وجزء من الزمن لأسفل.
القوة تسبب
تغييرا في الحركة ولكن القوة وحدها لا تحدد اتجاه الحركة، يتم تحديد اتجاه الحركة
حسب معطيات الحركة الابتدئية !!
تحت تأثير
الجاذبية وحدها، يمكن أن تكون هناك حركة في خط مستقيم أو حركة بقطع مكافئ أو حركة
دائرية.
2. רגע לפני ההתנגשות נעה הקרונית ימינה רגע אחרי ההתנגשות נעה הקרונית שמאלה .
בין שני רגעים אלו בזמן ההתנגשות קיים רגע בו הקרונית משנה את כיוון תנועה, ברגע זה מהירות הקרונית אפס!
3. כיוון הכוח שהחיישן מפעיל על הקרונית לא משתנה (תמיד כיוונו שמאלה), כיוון תנועת הקרונית משתנה .
בדומה לזריקה כלפי מעלה, תמיד כיוון כוח הכובד הוא כלפי מטה , חלק מהזמן הגוף נע כלפי מעלה וחלק מהזמן כלפי מטה.
הכוח גורם לשינוי בתנועה , אך הכוח לבדו לא קובע את כיוון התנועה , כיוון התנועה נקבע בהתאם לנתוני התנועה ההתחלתיים!!
בהשפעת כוח הכובד בלבד , יכולה להיות תנועה בקו ישר, תנועה פרבולית או תנועה מעגלית.
______________________________________________________________________________________

 ____________________________________________________________________________________
____________________________________________________________________________________

