______________________________________________________________________________________
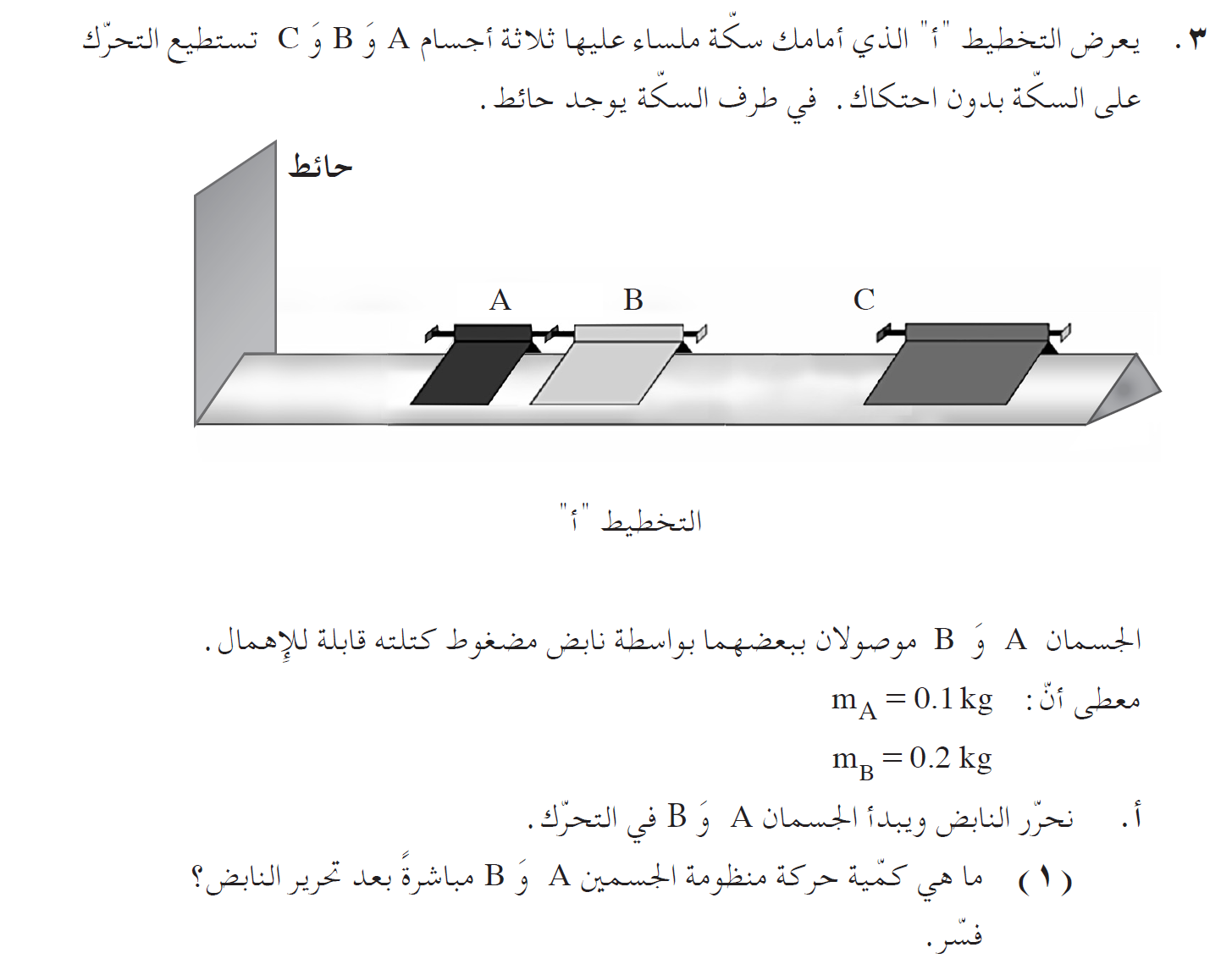
...
كمية الحركة لمنظمة الجسمين بعد تحرير النابض هو صفر.
يتحقق حفظ كمية الحركة المحصّلة، ومجموع كمية الحركة قبل تحرير النابض يساوي مجموع كمية الحركة بعد تحرير النابض .
يشغّل النابض نفس القوة في كلا الطرفين ، لذلك في كل لحظة يتأثر الجسمان بقوى متساوية في المقدار ومعاكسة في الاتجاه ، بصورة مماثلة للقوى الداخلية. نظرًا لأن المسار أملس ، وبافتراض أنه أفقي ، فلا توجد قوى خارجية ، تُحفظ كمية الحركة!
وقانون حفظ كمية الحركة: كمية الحركة المحصّلة للجسمين قبل تحرير النابض تساوي كمية الحركة المحصّلة للجسمين بعد تحريره.
كمية الحركة المحصّلة للجسمين قبل تحرير النابض تساوي صفرًا ، وبالتالي فإن كمية الحركة المحصّلة للجسمين بعد تحرير النابض يساوي صفرًا.
ומחוק שימור התנע :סכום התנעים של שני הגופים לאחר שחרור הקפיץ שווה לסכום התנעים של שני הגופים לאחר השחרור .
התנע הכולל של שני הגופים לפני שחרור הקפיץ שווה לאפס , לכן התנע הכולל של שני הגופים אחרי שחרור הקפיץ שווה לאפס.
1.يمكن
اعتبار المنظومة على أنها منظومة تتكون من ثلاث أجسام: الجسمان A و B والنابض.
تُشغّل الأجسام الثلاثة قوى داخلية فقط على
بعضها البعض، وبالتالي يتحقق حفظ كمية الحركة المحصّلة للأجسام الثلاثة.
2. يمكنك أن
تسأل نفس السؤال بالضبط، مع جسمين مرنين (مثل الكرات المطاطية) ملتصقان ببعض، متحرران من
حالة السكون.
שלושת הגופים מפעילים אחד על השני כוחות פנימיים בלבד , לכן התנע הכולל של שלושת הגופים נשמר.
2. אפשר לשאול בדיוק את אותה שאלה , עם שני גופים אלסטיים(כמו כדורי גומי) צמודים , המשוחררים ממנוחה.
______________________________________________________________________________________

______________________________________________________________________________________
...
بعد تحرير النابض، يتحرك الجسم B إلى اليمين بسرعة 0.3 متر في الثانية.
يتم حفظ كمية الحركة، من خلال حفظ كمية الحركة يمكن التعبير عن سرعة الجسم B بعد الاصطدام.
لا توجد قوى خارجية تعمل على الأجسام، يتحقق حفظ كمية الحركة. لنكتب معادلة حفظ كمية الحركة:
نصف حركة الأجسام بالنسبة لمحور الحركة الموجّه إلى اليسار.
نحدد سرعة الأجسام قبل الاصطدام بـ V ، وسرعتهم بعده بـ U.
«math xmlns=¨http://www.w3.org/1998/Math/MathML¨»«msub»«mi mathvariant=¨bold¨ mathcolor=¨#0000FF¨»m«/mi»«mi mathvariant=¨bold¨ mathcolor=¨#0000FF¨»A«/mi»«/msub»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»§#183;«/mo»«msub»«mi mathvariant=¨bold¨ mathcolor=¨#0000FF¨»V«/mi»«mi mathvariant=¨bold¨ mathcolor=¨#0000FF¨»A«/mi»«/msub»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»+«/mo»«msub»«mi mathvariant=¨bold¨ mathcolor=¨#0000FF¨»m«/mi»«mi mathvariant=¨bold¨ mathcolor=¨#0000FF¨»B«/mi»«/msub»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»§#183;«/mo»«msub»«mi mathvariant=¨bold¨ mathcolor=¨#0000FF¨»V«/mi»«mi mathvariant=¨bold¨ mathcolor=¨#0000FF¨»B«/mi»«/msub»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»=«/mo»«msub»«mi mathvariant=¨bold¨ mathcolor=¨#0000FF¨»m«/mi»«mi mathvariant=¨bold¨ mathcolor=¨#0000FF¨»A«/mi»«/msub»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»§#183;«/mo»«msub»«mi mathvariant=¨bold¨ mathcolor=¨#0000FF¨»U«/mi»«mi mathvariant=¨bold¨ mathcolor=¨#0000FF¨»A«/mi»«/msub»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»+«/mo»«msub»«mi mathvariant=¨bold¨ mathcolor=¨#0000FF¨»m«/mi»«mi mathvariant=¨bold¨ mathcolor=¨#0000FF¨»B«/mi»«/msub»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»§#183;«/mo»«msub»«mi mathvariant=¨bold¨ mathcolor=¨#0000FF¨»U«/mi»«mi mathvariant=¨bold¨ mathcolor=¨#0000FF¨»B«/mi»«/msub»«/math»
نُعبّر عن سرعة الجسم B بعد تحرير النابض بـ UB من قانون حفظ كمية الحركة:
«math xmlns=¨http://www.w3.org/1998/Math/MathML¨»«msub»«mi mathvariant=¨bold¨ mathcolor=¨#0000FF¨»U«/mi»«mi mathvariant=¨bold¨ mathcolor=¨#0000FF¨»B«/mi»«/msub»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»=«/mo»«mfrac mathcolor=¨#0000FF¨»«mrow»«msub»«mi mathvariant=¨bold¨»m«/mi»«mi mathvariant=¨bold¨»A«/mi»«/msub»«mo mathvariant=¨bold¨»§#183;«/mo»«msub»«mi mathvariant=¨bold¨»V«/mi»«mi mathvariant=¨bold¨»A«/mi»«/msub»«mo mathvariant=¨bold¨»+«/mo»«msub»«mi mathvariant=¨bold¨»m«/mi»«mi mathvariant=¨bold¨»B«/mi»«/msub»«mo mathvariant=¨bold¨»§#183;«/mo»«msub»«mi mathvariant=¨bold¨»V«/mi»«mi mathvariant=¨bold¨»B«/mi»«/msub»«mo mathvariant=¨bold¨»-«/mo»«msub»«mi mathvariant=¨bold¨»m«/mi»«mi mathvariant=¨bold¨»A«/mi»«/msub»«mo mathvariant=¨bold¨»§#183;«/mo»«msub»«mi mathvariant=¨bold¨»U«/mi»«mi mathvariant=¨bold¨»A«/mi»«/msub»«/mrow»«msub»«mi mathvariant=¨bold¨»m«/mi»«mi mathvariant=¨bold¨»B«/mi»«/msub»«/mfrac»«/math»
قبل تحرير النابض، تكون سرعة كلا الجسمين صفرًا.
بعد تحرير النابض، يتحرك الجسم أ إلى اليسار في اتجاه المحور، وبالتالي فإن سرعته موجبة.
نعوّض كتل الأجسام ونجد السرعة UB بالنسبة للمحور المحدّد:
«math xmlns=¨http://www.w3.org/1998/Math/MathML¨»«msub»«mi mathvariant=¨bold¨ mathcolor=¨#0000FF¨»U«/mi»«mi mathvariant=¨bold¨ mathcolor=¨#0000FF¨»B«/mi»«/msub»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»=«/mo»«mfrac mathcolor=¨#0000FF¨»«mrow»«msub»«mi mathvariant=¨bold¨»m«/mi»«mi mathvariant=¨bold¨»A«/mi»«/msub»«mo mathvariant=¨bold¨»§#183;«/mo»«msub»«mi mathvariant=¨bold¨»V«/mi»«mi mathvariant=¨bold¨»A«/mi»«/msub»«mo mathvariant=¨bold¨»+«/mo»«msub»«mi mathvariant=¨bold¨»m«/mi»«mi mathvariant=¨bold¨»B«/mi»«/msub»«mo mathvariant=¨bold¨»§#183;«/mo»«msub»«mi mathvariant=¨bold¨»V«/mi»«mi mathvariant=¨bold¨»B«/mi»«/msub»«mo mathvariant=¨bold¨»-«/mo»«msub»«mi mathvariant=¨bold¨»m«/mi»«mi mathvariant=¨bold¨»A«/mi»«/msub»«mo mathvariant=¨bold¨»§#183;«/mo»«msub»«mi mathvariant=¨bold¨»U«/mi»«mi mathvariant=¨bold¨»A«/mi»«/msub»«/mrow»«msub»«mi mathvariant=¨bold¨»m«/mi»«mi mathvariant=¨bold¨»B«/mi»«/msub»«/mfrac»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»=«/mo»«mfrac mathcolor=¨#0000FF¨»«mrow»«mn mathvariant=¨bold¨»0«/mn»«mo mathvariant=¨bold¨».«/mo»«mn mathvariant=¨bold¨»1«/mn»«mo mathvariant=¨bold¨»§#183;«/mo»«mn mathvariant=¨bold¨»0«/mn»«mo mathvariant=¨bold¨»+«/mo»«mn mathvariant=¨bold¨»0«/mn»«mo mathvariant=¨bold¨».«/mo»«mn mathvariant=¨bold¨»2«/mn»«mo mathvariant=¨bold¨»§#183;«/mo»«mn mathvariant=¨bold¨»0«/mn»«mo mathvariant=¨bold¨»-«/mo»«mn mathvariant=¨bold¨»0«/mn»«mo mathvariant=¨bold¨».«/mo»«mn mathvariant=¨bold¨»1«/mn»«mo mathvariant=¨bold¨»§#183;«/mo»«mn mathvariant=¨bold¨»0«/mn»«mo mathvariant=¨bold¨».«/mo»«mn mathvariant=¨bold¨»6«/mn»«/mrow»«mrow»«mn mathvariant=¨bold¨»0«/mn»«mo mathvariant=¨bold¨».«/mo»«mn mathvariant=¨bold¨»2«/mn»«/mrow»«/mfrac»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»=«/mo»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»-«/mo»«mn mathvariant=¨bold¨ mathcolor=¨#0000FF¨»0«/mn»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨».«/mo»«mn mathvariant=¨bold¨ mathcolor=¨#0000FF¨»3«/mn»«mfrac mathcolor=¨#0000FF¨»«mi mathvariant=¨bold¨»m«/mi»«mi mathvariant=¨bold¨»s«/mi»«/mfrac»«/math»
ومن ثم ، بعد تحرير النابض، يتحرك الجسم B إلى اليمين بسرعة 0.3 متر في الثانية.
נתאר את תנועת הגופים ביחס לציר תנועה שכיוונו שמאלה.
נסמן את מהירות הגופים לפני ב V , ואת מהירותם אחרי ב U.
«math xmlns=¨http://www.w3.org/1998/Math/MathML¨»«msub»«mi mathvariant=¨bold¨ mathcolor=¨#0000FF¨»m«/mi»«mi mathvariant=¨bold¨ mathcolor=¨#0000FF¨»A«/mi»«/msub»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»§#183;«/mo»«msub»«mi mathvariant=¨bold¨ mathcolor=¨#0000FF¨»V«/mi»«mi mathvariant=¨bold¨ mathcolor=¨#0000FF¨»A«/mi»«/msub»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»+«/mo»«msub»«mi mathvariant=¨bold¨ mathcolor=¨#0000FF¨»m«/mi»«mi mathvariant=¨bold¨ mathcolor=¨#0000FF¨»B«/mi»«/msub»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»§#183;«/mo»«msub»«mi mathvariant=¨bold¨ mathcolor=¨#0000FF¨»V«/mi»«mi mathvariant=¨bold¨ mathcolor=¨#0000FF¨»B«/mi»«/msub»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»=«/mo»«msub»«mi mathvariant=¨bold¨ mathcolor=¨#0000FF¨»m«/mi»«mi mathvariant=¨bold¨ mathcolor=¨#0000FF¨»A«/mi»«/msub»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»§#183;«/mo»«msub»«mi mathvariant=¨bold¨ mathcolor=¨#0000FF¨»U«/mi»«mi mathvariant=¨bold¨ mathcolor=¨#0000FF¨»A«/mi»«/msub»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»+«/mo»«msub»«mi mathvariant=¨bold¨ mathcolor=¨#0000FF¨»m«/mi»«mi mathvariant=¨bold¨ mathcolor=¨#0000FF¨»B«/mi»«/msub»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»§#183;«/mo»«msub»«mi mathvariant=¨bold¨ mathcolor=¨#0000FF¨»U«/mi»«mi mathvariant=¨bold¨ mathcolor=¨#0000FF¨»B«/mi»«/msub»«/math»
נבטא מחוק שימור התנע את מהירות גוף B אחרי שחרור הקפיץ:
«math xmlns=¨http://www.w3.org/1998/Math/MathML¨»«msub»«mi mathvariant=¨bold¨ mathcolor=¨#0000FF¨»m«/mi»«mi mathvariant=¨bold¨ mathcolor=¨#0000FF¨»A«/mi»«/msub»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»§#183;«/mo»«msub»«mi mathvariant=¨bold¨ mathcolor=¨#0000FF¨»V«/mi»«mi mathvariant=¨bold¨ mathcolor=¨#0000FF¨»A«/mi»«/msub»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»+«/mo»«msub»«mi mathvariant=¨bold¨ mathcolor=¨#0000FF¨»m«/mi»«mi mathvariant=¨bold¨ mathcolor=¨#0000FF¨»B«/mi»«/msub»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»§#183;«/mo»«msub»«mi mathvariant=¨bold¨ mathcolor=¨#0000FF¨»V«/mi»«mi mathvariant=¨bold¨ mathcolor=¨#0000FF¨»B«/mi»«/msub»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»=«/mo»«msub»«mi mathvariant=¨bold¨ mathcolor=¨#0000FF¨»m«/mi»«mi mathvariant=¨bold¨ mathcolor=¨#0000FF¨»A«/mi»«/msub»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»§#183;«/mo»«msub»«mi mathvariant=¨bold¨ mathcolor=¨#0000FF¨»U«/mi»«mi mathvariant=¨bold¨ mathcolor=¨#0000FF¨»A«/mi»«/msub»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»+«/mo»«msub»«mi mathvariant=¨bold¨ mathcolor=¨#0000FF¨»m«/mi»«mi mathvariant=¨bold¨ mathcolor=¨#0000FF¨»B«/mi»«/msub»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»§#183;«/mo»«msub»«mi mathvariant=¨bold¨ mathcolor=¨#0000FF¨»U«/mi»«mi mathvariant=¨bold¨ mathcolor=¨#0000FF¨»B«/mi»«/msub»«/math»
1. في الحالات التي يتم فيها حفظ كمية الحركة،
يجب كتابة واستخدام معادلة حفظ كمية الحركة. أي
حل آخر يعتمد على المنطق يؤدي بسهولة إلى استنتاجات غير صحيحة.
2. لم يتم تحديد محور الحركة في السؤال، قبل
استخدام قانون حفظ كمية الحركة، يجب تحديد المحور، للإشارة بشكل صحيح إلى إشارة السرعة.
3. في إجابة هذا السؤال، من الممكن أن نكتب أن
الجسم يتحرك إلى اليمين، ومن الممكن أيضًا أن نكتب أن سرعته سالبة بالنسبة للمحور
الذي يشير إلى اليسار.
2. בתשובה לשאלה זו ניתן לכתוב שהגוף נע ימינה , ניתן גם לכתוב שמהירותו שלילית ביחס לציר שכיוונו שמאלה.
______________________________________________________________________________________

*يتناول هذا القسم موضوع الطاقة ، وهذا الموضوع هو الموضوع التالي ، فلا داعي للإجابة على هذا السؤال في الوقت الحالي.

*في حالة الاصطدام المرن ، لا يتغير مقدار سرعة الجسم ، سنناقش الاصطدام المرن بالتفصيل في الفصل التالي. وسنعرف التعريف الدقيق للطاقة الحركية.
______________________________________________________________________________________
...
يشغّل الجدار كمية دفع مقدارها 0.12 نيوتن في الثانية ، واتجاهها يمينًا.
قانون كمية الدفع وكمية الحركة.
من قانون كمية الدفع وكمية الحركة، فإن كمية الدفع الذي يشغّله الحائط على الجسم A يساوي التغير في كمية حركة الجسم A.
نجد الزاوية بالنسبة للمحور الذي اتجاهه إلى اليسار:
«math xmlns=¨http://www.w3.org/1998/Math/MathML¨»«mi mathvariant=¨bold¨ mathcolor=¨#0000FF¨»J«/mi»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»=«/mo»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»§#8710;«/mo»«mi mathvariant=¨bold¨ mathcolor=¨#0000FF¨»P«/mi»«mspace linebreak=¨newline¨/»«mi mathvariant=¨bold¨ mathcolor=¨#0000FF¨»J«/mi»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»=«/mo»«mi mathvariant=¨bold¨ mathcolor=¨#0000FF¨»P«/mi»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»`«/mo»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»-«/mo»«msub»«mi mathvariant=¨bold¨ mathcolor=¨#0000FF¨»P«/mi»«mn mathvariant=¨bold¨ mathcolor=¨#0000FF¨»0«/mn»«/msub»«mspace linebreak=¨newline¨/»«mi mathvariant=¨bold¨ mathcolor=¨#0000FF¨»J«/mi»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»=«/mo»«msub»«mi mathvariant=¨bold¨ mathcolor=¨#0000FF¨»m«/mi»«mi mathvariant=¨bold¨ mathcolor=¨#0000FF¨»A«/mi»«/msub»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»§#183;«/mo»«msub»«mi mathvariant=¨bold¨ mathcolor=¨#0000FF¨»U«/mi»«mi mathvariant=¨bold¨ mathcolor=¨#0000FF¨»A«/mi»«/msub»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»-«/mo»«msub»«mi mathvariant=¨bold¨ mathcolor=¨#0000FF¨»m«/mi»«mi mathvariant=¨bold¨ mathcolor=¨#0000FF¨»A«/mi»«/msub»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»§#183;«/mo»«msub»«mi mathvariant=¨bold¨ mathcolor=¨#0000FF¨»V«/mi»«mi mathvariant=¨bold¨ mathcolor=¨#0000FF¨»A«/mi»«/msub»«mspace linebreak=¨newline¨/»«mi mathvariant=¨bold¨ mathcolor=¨#0000FF¨»J«/mi»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»=«/mo»«mn mathvariant=¨bold¨ mathcolor=¨#0000FF¨»0«/mn»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨».«/mo»«mn mathvariant=¨bold¨ mathcolor=¨#0000FF¨»1«/mn»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»§#183;«/mo»«mfenced mathcolor=¨#0000FF¨»«mrow»«mo mathvariant=¨bold¨»-«/mo»«mn mathvariant=¨bold¨»0«/mn»«mo mathvariant=¨bold¨».«/mo»«mn mathvariant=¨bold¨»6«/mn»«/mrow»«/mfenced»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»-«/mo»«mn mathvariant=¨bold¨ mathcolor=¨#0000FF¨»0«/mn»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨».«/mo»«mn mathvariant=¨bold¨ mathcolor=¨#0000FF¨»1«/mn»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»§#183;«/mo»«mn mathvariant=¨bold¨ mathcolor=¨#0000FF¨»0«/mn»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨».«/mo»«mn mathvariant=¨bold¨ mathcolor=¨#0000FF¨»6«/mn»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»=«/mo»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»-«/mo»«mn mathvariant=¨bold¨ mathcolor=¨#0000FF¨»0«/mn»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨».«/mo»«mn mathvariant=¨bold¨ mathcolor=¨#0000FF¨»06«/mn»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»-«/mo»«mn mathvariant=¨bold¨ mathcolor=¨#0000FF¨»0«/mn»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨».«/mo»«mn mathvariant=¨bold¨ mathcolor=¨#0000FF¨»06«/mn»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»=«/mo»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»-«/mo»«mn mathvariant=¨bold¨ mathcolor=¨#0000FF¨»0«/mn»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨».«/mo»«mn mathvariant=¨bold¨ mathcolor=¨#0000FF¨»12«/mn»«mi mathvariant=¨bold¨ mathcolor=¨#0000FF¨»N«/mi»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»§#183;«/mo»«mi mathvariant=¨bold¨ mathcolor=¨#0000FF¨»S«/mi»«mspace linebreak=¨newline¨/»«/math»
لذلك ، أثناء الاصطدام ، يشغّل الحائط على الجسم A كمية دفع مقدارها 0.12 نيوتن في الثانية ، موجهة إلى اليمين، عكس اتجاه المحور.
נמצא את המתקף ביחס לציר שכיוונו שמאלה:
«math xmlns=¨http://www.w3.org/1998/Math/MathML¨»«mi mathvariant=¨bold¨ mathcolor=¨#0000FF¨»J«/mi»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»=«/mo»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»§#8710;«/mo»«mi mathvariant=¨bold¨ mathcolor=¨#0000FF¨»P«/mi»«mspace linebreak=¨newline¨»«/mspace»«mi mathvariant=¨bold¨ mathcolor=¨#0000FF¨»J«/mi»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»=«/mo»«mi mathvariant=¨bold¨ mathcolor=¨#0000FF¨»P«/mi»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»`«/mo»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»-«/mo»«msub»«mi mathvariant=¨bold¨ mathcolor=¨#0000FF¨»P«/mi»«mn mathvariant=¨bold¨ mathcolor=¨#0000FF¨»0«/mn»«/msub»«mspace linebreak=¨newline¨»«/mspace»«mi mathvariant=¨bold¨ mathcolor=¨#0000FF¨»J«/mi»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»=«/mo»«msub»«mi mathvariant=¨bold¨ mathcolor=¨#0000FF¨»m«/mi»«mi mathvariant=¨bold¨ mathcolor=¨#0000FF¨»A«/mi»«/msub»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»§#183;«/mo»«msub»«mi mathvariant=¨bold¨ mathcolor=¨#0000FF¨»U«/mi»«mi mathvariant=¨bold¨ mathcolor=¨#0000FF¨»A«/mi»«/msub»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»-«/mo»«msub»«mi mathvariant=¨bold¨ mathcolor=¨#0000FF¨»m«/mi»«mi mathvariant=¨bold¨ mathcolor=¨#0000FF¨»A«/mi»«/msub»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»§#183;«/mo»«msub»«mi mathvariant=¨bold¨ mathcolor=¨#0000FF¨»V«/mi»«mi mathvariant=¨bold¨ mathcolor=¨#0000FF¨»A«/mi»«/msub»«mspace linebreak=¨newline¨»«/mspace»«mi mathvariant=¨bold¨ mathcolor=¨#0000FF¨»J«/mi»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»=«/mo»«mn mathvariant=¨bold¨ mathcolor=¨#0000FF¨»0«/mn»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨».«/mo»«mn mathvariant=¨bold¨ mathcolor=¨#0000FF¨»1«/mn»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»§#183;«/mo»«mfenced mathcolor=¨#0000FF¨»«mrow»«mo mathvariant=¨bold¨»-«/mo»«mn mathvariant=¨bold¨»0«/mn»«mo mathvariant=¨bold¨».«/mo»«mn mathvariant=¨bold¨»6«/mn»«/mrow»«/mfenced»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»-«/mo»«mn mathvariant=¨bold¨ mathcolor=¨#0000FF¨»0«/mn»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨».«/mo»«mn mathvariant=¨bold¨ mathcolor=¨#0000FF¨»1«/mn»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»§#183;«/mo»«mn mathvariant=¨bold¨ mathcolor=¨#0000FF¨»0«/mn»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨».«/mo»«mn mathvariant=¨bold¨ mathcolor=¨#0000FF¨»6«/mn»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»=«/mo»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»-«/mo»«mn mathvariant=¨bold¨ mathcolor=¨#0000FF¨»0«/mn»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨».«/mo»«mn mathvariant=¨bold¨ mathcolor=¨#0000FF¨»6«/mn»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»-«/mo»«mn mathvariant=¨bold¨ mathcolor=¨#0000FF¨»0«/mn»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨».«/mo»«mn mathvariant=¨bold¨ mathcolor=¨#0000FF¨»6«/mn»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»=«/mo»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»-«/mo»«mn mathvariant=¨bold¨ mathcolor=¨#0000FF¨»1«/mn»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨».«/mo»«mn mathvariant=¨bold¨ mathcolor=¨#0000FF¨»2«/mn»«mi mathvariant=¨bold¨ mathcolor=¨#0000FF¨»N«/mi»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»§#183;«/mo»«mi mathvariant=¨bold¨ mathcolor=¨#0000FF¨»S«/mi»«mspace linebreak=¨newline¨»«/mspace»«/math»
לכן , בזמן ההתנגשות , הקיר מפעיל על גוף A מתקף שגודלו 1.2 ניוטון שנייה , וכיוונה ימינה ,נגד כיוון הציר.
قانون كمية الدفع وكمية الحركة هو قانون متّجه. في هذه الحالة ، نظرًا لأن الجسم A يتحرك في حركة أحادية البعد ، في الاتجاه الذي يشغّل فيه الجدار قوة ، فمن الأنسب استخدامه لوصف كمية الدفع والحركة بالنسبة لمحور حركة محدّد.
بالطبع ، يمكن أيضًا ايجاد كمية الدفع في صورة متّجهية.
כמובן, ניתן למצוא את המתקף גם בצורה ווקטורית.
______________________________________________________________________________________

______________________________________________________________________________________
...
كمية الدفع التي يشغّلها الحائط على الجسم A.
معرفة تعريف كمية الحركة وفهم معنى المساحة المحصورة في الرسم البياني للقوة كدالة للزمن.
من تعريف كمية الدفع «math xmlns=¨http://www.w3.org/1998/Math/MathML¨»«mover mathcolor=¨#0000FF¨»«mi mathvariant=¨bold¨»J«/mi»«mo mathvariant=¨bold¨»§#8594;«/mo»«/mover»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»=«/mo»«mover mathcolor=¨#0000FF¨»«mi mathvariant=¨bold¨»F«/mi»«mo mathvariant=¨bold¨»§#8594;«/mo»«/mover»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»§#183;«/mo»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»§#8710;«/mo»«mi mathvariant=¨bold¨ mathcolor=¨#0000FF¨»t«/mi»«/math» حاصل ضرب القوة بزمن تأثيرها يساوي كمية الدفع.
للحصول على المساحة التي يحصرها الرسم البياني للقوة كدالة للزمن، يجب ضرب القوة بالزمن، وبالتالي فإن مقدار المساحة المحصورة بين الدالة ومحور الزمن يساوي مقدار كمية الدفع.
כדי לקבל את השטח התחום בגרף כוח בתלות בזמן זה יש להכפיל כוח בזמן , לכן גודל השטח התחום בין הפונקציה לציר הזמן שווה לגודל המתקף.
في
هذه الحالة تكون كمية الدفع موجبة، وهذا يعني أن اتجاه المحور الذي تم اختياره في
هذا القسم هو إلى اليمين وليس إلى اليسار.
حتى
إذا قمت بحل الأقسام السابقة باستخدام محور يشير إلى اليسار، فلا داعي لتغيير
الحل في الأقسام السابقة.
من
المهم دائمًا فهم اتجاه المحور الذي تم اختياره.
גם אם בסעיפים קודמים פתרתם עם ציר שכיוונו שמאלה, אין צורך לשנות את הפתרון בסעיפים קודמים.
חשוב תמיד להבין מה כיוון הציר הנבחר.
______________________________________________________________________________________

______________________________________________________________________________________
...
مقدار القوة القصوى 3 نيوتن.
اعتمادًا على معنى المساحة المحصورة في الرسم البياني ، يمكن إيجاد مقدار القوة القصوى هندسيًا.
في الرسم البياني للقوة كدالة للزمن، يكون مقدار المساحة المحصورة مساويًا لمقدار كمية الدفع. وجدنا أن مقدار كمية الدفع التي يشغّلها الحائط على الجسم A تساوي 0.12NS .
نعبر هندسيًا عن المساحة المحصورة ، في أول 0.08 ثانية بدلالة الحد الأقصى للقوة ، ونقارن هذه المساحة بكمية الدفع:
«math xmlns=¨http://www.w3.org/1998/Math/MathML¨»«mi mathvariant=¨bold¨ mathcolor=¨#0000FF¨»J«/mi»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»=«/mo»«mfrac mathcolor=¨#0000FF¨»«mrow»«mn mathvariant=¨bold¨»0«/mn»«mo mathvariant=¨bold¨».«/mo»«mn mathvariant=¨bold¨»08«/mn»«mo mathvariant=¨bold¨»§#183;«/mo»«msub»«mi mathvariant=¨bold¨»F«/mi»«mi mathvariant=¨bold¨»max«/mi»«/msub»«/mrow»«mn mathvariant=¨bold¨»2«/mn»«/mfrac»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»=«/mo»«mn mathvariant=¨bold¨ mathcolor=¨#0000FF¨»0«/mn»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨».«/mo»«mn mathvariant=¨bold¨ mathcolor=¨#0000FF¨»12«/mn»«mi mathvariant=¨bold¨ mathcolor=¨#0000FF¨»N«/mi»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»§#183;«/mo»«mi mathvariant=¨bold¨ mathcolor=¨#0000FF¨»S«/mi»«/math»
نجد القوة القصوى من هذا التعبير:
«math xmlns=¨http://www.w3.org/1998/Math/MathML¨»«mi mathvariant=¨bold¨ mathcolor=¨#0000FF¨»J«/mi»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»=«/mo»«mfrac mathcolor=¨#0000FF¨»«mrow»«mn mathvariant=¨bold¨»0«/mn»«mo mathvariant=¨bold¨».«/mo»«mn mathvariant=¨bold¨»08«/mn»«mo mathvariant=¨bold¨»§#183;«/mo»«msub»«mi mathvariant=¨bold¨»F«/mi»«mi mathvariant=¨bold¨»max«/mi»«/msub»«/mrow»«mn mathvariant=¨bold¨»2«/mn»«/mfrac»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»=«/mo»«mn mathvariant=¨bold¨ mathcolor=¨#0000FF¨»0«/mn»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨».«/mo»«mn mathvariant=¨bold¨ mathcolor=¨#0000FF¨»12«/mn»«mi mathvariant=¨bold¨ mathcolor=¨#0000FF¨»N«/mi»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»§#183;«/mo»«mi mathvariant=¨bold¨ mathcolor=¨#0000FF¨»S«/mi»«mspace linebreak=¨newline¨»«/mspace»«mspace linebreak=¨newline¨»«/mspace»«msub»«mi mathvariant=¨bold¨ mathcolor=¨#0000FF¨»F«/mi»«mi mathvariant=¨bold¨ mathcolor=¨#0000FF¨»max«/mi»«/msub»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»=«/mo»«mfrac mathcolor=¨#0000FF¨»«mrow»«mn mathvariant=¨bold¨»2«/mn»«mo mathvariant=¨bold¨»§#183;«/mo»«mn mathvariant=¨bold¨»0«/mn»«mo mathvariant=¨bold¨».«/mo»«mn mathvariant=¨bold¨»12«/mn»«/mrow»«mrow»«mn mathvariant=¨bold¨»0«/mn»«mo mathvariant=¨bold¨».«/mo»«mn mathvariant=¨bold¨»08«/mn»«/mrow»«/mfrac»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»=«/mo»«mn mathvariant=¨bold¨ mathcolor=¨#0000FF¨»3«/mn»«mi mathvariant=¨bold¨ mathcolor=¨#0000FF¨»N«/mi»«/math»
إذن ، مقدار القوة القصوى 3 نيوتن.
נבטא גיאומטרית את השטח התחום , ב 0.08 שניות הראשונות בתלות בכוח המקסימאלי , ונשווה שטח זה למתקף:
«math xmlns=¨http://www.w3.org/1998/Math/MathML¨»«mi mathvariant=¨bold¨ mathcolor=¨#0000FF¨»J«/mi»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»=«/mo»«mfrac mathcolor=¨#0000FF¨»«mrow»«mn mathvariant=¨bold¨»0«/mn»«mo mathvariant=¨bold¨».«/mo»«mn mathvariant=¨bold¨»08«/mn»«mo mathvariant=¨bold¨»§#183;«/mo»«msub»«mi mathvariant=¨bold¨»F«/mi»«mi mathvariant=¨bold¨»max«/mi»«/msub»«/mrow»«mn mathvariant=¨bold¨»2«/mn»«/mfrac»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»=«/mo»«mn mathvariant=¨bold¨ mathcolor=¨#0000FF¨»0«/mn»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨».«/mo»«mn mathvariant=¨bold¨ mathcolor=¨#0000FF¨»12«/mn»«mi mathvariant=¨bold¨ mathcolor=¨#0000FF¨»N«/mi»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»§#183;«/mo»«mi mathvariant=¨bold¨ mathcolor=¨#0000FF¨»S«/mi»«/math»
נמצא מביטוי זה את הכוח המקסימאלי:
«math xmlns=¨http://www.w3.org/1998/Math/MathML¨»«mi mathvariant=¨bold¨ mathcolor=¨#0000FF¨»J«/mi»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»=«/mo»«mfrac mathcolor=¨#0000FF¨»«mrow»«mn mathvariant=¨bold¨»0«/mn»«mo mathvariant=¨bold¨».«/mo»«mn mathvariant=¨bold¨»08«/mn»«mo mathvariant=¨bold¨»§#183;«/mo»«msub»«mi mathvariant=¨bold¨»F«/mi»«mi mathvariant=¨bold¨»max«/mi»«/msub»«/mrow»«mn mathvariant=¨bold¨»2«/mn»«/mfrac»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»=«/mo»«mn mathvariant=¨bold¨ mathcolor=¨#0000FF¨»0«/mn»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨».«/mo»«mn mathvariant=¨bold¨ mathcolor=¨#0000FF¨»12«/mn»«mi mathvariant=¨bold¨ mathcolor=¨#0000FF¨»N«/mi»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»§#183;«/mo»«mi mathvariant=¨bold¨ mathcolor=¨#0000FF¨»S«/mi»«/math»
هناك
العديد من الأسئلة التي "تبني خطوة"، كما في هذا السؤال. أولاً ، يوجد
قسم يتناول كمية الدفع، ثم هناك قسم يتناول معنى كمية الدفع في الرسم البياني. ثم
قسم يعتمد على هذين القسمين السابقين لحساب القوة القصوى هندسيًا.
من
المهم رؤية الفكرة العامة لأقسام السؤال انظر كيف يبنون هذه الخطوة.
وإذا
كان هناك سؤال لا يبدو لك أن لديه أي فكرة واضحة، فابحث عن الفكرة (أو مفتاح الحل)
في الأقسام السابقة.
חשוב לראות את הרעיון הכללי של סעיפי השאלה . לראות כיצד הם בונים את המהלך .
ואם יש שאלה שלא נראה לכם שיש בה איזה שהוא רעיון ברור , חפשו את הרעיון (או הרמז לפתרון) בסעיפים הקודמים.
______________________________________________________________________________________

______________________________________________________________________________________
...
قبل الاصطدام يتحرك الجسم C إلى اليسار في اتجاه المحور بسرعة 0.15 متر في الثانية.
حفظ كمية الحركة في الاصطدام اللدن .
نتطرق إلى اصطدام الجسمين كاصطدام لدن. لا توجد قوى خارجية تعمل على الأجسام ، لذلك يتم حفظ كمية الحركة.
لنكتب معادلة حفظ كمية الحركة:
«math xmlns=¨http://www.w3.org/1998/Math/MathML¨»«msub»«mi mathvariant=¨bold¨ mathcolor=¨#0000FF¨»m«/mi»«mi mathvariant=¨bold¨ mathcolor=¨#0000FF¨»B«/mi»«/msub»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»§#183;«/mo»«msub»«mi mathvariant=¨bold¨ mathcolor=¨#0000FF¨»V«/mi»«mi mathvariant=¨bold¨ mathcolor=¨#0000FF¨»B«/mi»«/msub»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»+«/mo»«msub»«mi mathvariant=¨bold¨ mathcolor=¨#0000FF¨»m«/mi»«mi mathvariant=¨bold¨ mathcolor=¨#0000FF¨»C«/mi»«/msub»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»§#183;«/mo»«msub»«mi mathvariant=¨bold¨ mathcolor=¨#0000FF¨»V«/mi»«mi mathvariant=¨bold¨ mathcolor=¨#0000FF¨»C«/mi»«/msub»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»=«/mo»«mfenced mathcolor=¨#0000FF¨»«mrow»«msub»«mi mathvariant=¨bold¨»m«/mi»«mi mathvariant=¨bold¨»B«/mi»«/msub»«mo mathvariant=¨bold¨»+«/mo»«msub»«mi mathvariant=¨bold¨»m«/mi»«mi mathvariant=¨bold¨»C«/mi»«/msub»«/mrow»«/mfenced»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»§#183;«/mo»«mi mathvariant=¨bold¨ mathcolor=¨#0000FF¨»U«/mi»«/math»
السرعة المشتركة لكلا الجسمين بعد الاصطدام تساوي صفرًا. نجد سرعة الجسم C قبل الاصطدام:
«math xmlns=¨http://www.w3.org/1998/Math/MathML¨»«msub»«mi mathvariant=¨bold¨ mathcolor=¨#0000FF¨»m«/mi»«mi mathvariant=¨bold¨ mathcolor=¨#0000FF¨»B«/mi»«/msub»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»§#183;«/mo»«msub»«mi mathvariant=¨bold¨ mathcolor=¨#0000FF¨»V«/mi»«mi mathvariant=¨bold¨ mathcolor=¨#0000FF¨»B«/mi»«/msub»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»+«/mo»«msub»«mi mathvariant=¨bold¨ mathcolor=¨#0000FF¨»m«/mi»«mi mathvariant=¨bold¨ mathcolor=¨#0000FF¨»C«/mi»«/msub»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»§#183;«/mo»«msub»«mi mathvariant=¨bold¨ mathcolor=¨#0000FF¨»V«/mi»«mi mathvariant=¨bold¨ mathcolor=¨#0000FF¨»C«/mi»«/msub»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»=«/mo»«mfenced mathcolor=¨#0000FF¨»«mrow»«msub»«mi mathvariant=¨bold¨»m«/mi»«mi mathvariant=¨bold¨»B«/mi»«/msub»«mo mathvariant=¨bold¨»+«/mo»«msub»«mi mathvariant=¨bold¨»m«/mi»«mi mathvariant=¨bold¨»C«/mi»«/msub»«/mrow»«/mfenced»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»§#183;«/mo»«mn mathvariant=¨bold¨ mathcolor=¨#0000FF¨»0«/mn»«mspace linebreak=¨newline¨»«/mspace»«msub»«mi mathvariant=¨bold¨ mathcolor=¨#0000FF¨»m«/mi»«mi mathvariant=¨bold¨ mathcolor=¨#0000FF¨»B«/mi»«/msub»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»§#183;«/mo»«msub»«mi mathvariant=¨bold¨ mathcolor=¨#0000FF¨»V«/mi»«mi mathvariant=¨bold¨ mathcolor=¨#0000FF¨»B«/mi»«/msub»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»+«/mo»«msub»«mi mathvariant=¨bold¨ mathcolor=¨#0000FF¨»m«/mi»«mi mathvariant=¨bold¨ mathcolor=¨#0000FF¨»C«/mi»«/msub»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»§#183;«/mo»«msub»«mi mathvariant=¨bold¨ mathcolor=¨#0000FF¨»V«/mi»«mi mathvariant=¨bold¨ mathcolor=¨#0000FF¨»C«/mi»«/msub»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»=«/mo»«mn mathvariant=¨bold¨ mathcolor=¨#0000FF¨»0«/mn»«mspace linebreak=¨newline¨»«/mspace»«msub»«mi mathvariant=¨bold¨ mathcolor=¨#0000FF¨»V«/mi»«mi mathvariant=¨bold¨ mathcolor=¨#0000FF¨»C«/mi»«/msub»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»=«/mo»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»-«/mo»«mfrac mathcolor=¨#0000FF¨»«mrow»«msub»«mi mathvariant=¨bold¨»m«/mi»«mi mathvariant=¨bold¨»B«/mi»«/msub»«mo mathvariant=¨bold¨»§#183;«/mo»«msub»«mi mathvariant=¨bold¨»V«/mi»«mi mathvariant=¨bold¨»B«/mi»«/msub»«/mrow»«msub»«mi mathvariant=¨bold¨»m«/mi»«mi mathvariant=¨bold¨»C«/mi»«/msub»«/mfrac»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»=«/mo»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»-«/mo»«mfrac mathcolor=¨#0000FF¨»«mrow»«mn mathvariant=¨bold¨»0«/mn»«mo mathvariant=¨bold¨».«/mo»«mn mathvariant=¨bold¨»2«/mn»«mo mathvariant=¨bold¨»§#183;«/mo»«mo mathvariant=¨bold¨»(«/mo»«mo mathvariant=¨bold¨»-«/mo»«mn mathvariant=¨bold¨»0«/mn»«mo mathvariant=¨bold¨».«/mo»«mn mathvariant=¨bold¨»3«/mn»«mo mathvariant=¨bold¨»)«/mo»«/mrow»«mrow»«mn mathvariant=¨bold¨»0«/mn»«mo mathvariant=¨bold¨».«/mo»«mn mathvariant=¨bold¨»4«/mn»«/mrow»«/mfrac»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»=«/mo»«mfrac mathcolor=¨#0000FF¨»«mrow»«mn mathvariant=¨bold¨»0«/mn»«mo mathvariant=¨bold¨».«/mo»«mn mathvariant=¨bold¨»06«/mn»«/mrow»«mrow»«mn mathvariant=¨bold¨»0«/mn»«mo mathvariant=¨bold¨».«/mo»«mn mathvariant=¨bold¨»4«/mn»«/mrow»«/mfrac»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»=«/mo»«mn mathvariant=¨bold¨ mathcolor=¨#0000FF¨»0«/mn»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨».«/mo»«mn mathvariant=¨bold¨ mathcolor=¨#0000FF¨»15«/mn»«mfrac mathcolor=¨#0000FF¨»«mi mathvariant=¨bold¨»m«/mi»«mi mathvariant=¨bold¨»s«/mi»«/mfrac»«/math»
قبل الاصطدام يتحرك الجسم C إلى اليسار في اتجاه المحور بسرعة 0.15 متر في الثانية.
נכתוב את משוואת שימור התנע:
1.
الاصطدام اللدن هو اصطدام يتحرك فيه الجسمان المتصادمان معًا كجسم
واحد.
على الرغم
من أن الجسمين في هذه الحالة لا تتحرك بعد الاصطدام، إلا أنه لا يزال اصطدامًا لدنًا.
2. إذا قمنا
بحساب كمية الحركة لكل من الجسمين قبل الاصطدام ...
«math xmlns=¨http://www.w3.org/1998/Math/MathML¨»«msub»«mi mathvariant=¨bold¨ mathcolor=¨#FF0000¨»P«/mi»«mi mathvariant=¨bold¨ mathcolor=¨#FF0000¨»B«/mi»«/msub»«mo mathvariant=¨bold¨ mathcolor=¨#FF0000¨»=«/mo»«msub»«mi mathvariant=¨bold¨ mathcolor=¨#FF0000¨»m«/mi»«mi mathvariant=¨bold¨ mathcolor=¨#FF0000¨»B«/mi»«/msub»«mo mathvariant=¨bold¨ mathcolor=¨#FF0000¨»§#183;«/mo»«msub»«mi mathvariant=¨bold¨ mathcolor=¨#FF0000¨»V«/mi»«mi mathvariant=¨bold¨ mathcolor=¨#FF0000¨»B«/mi»«/msub»«mo mathvariant=¨bold¨ mathcolor=¨#FF0000¨»=«/mo»«mn mathvariant=¨bold¨ mathcolor=¨#FF0000¨»0«/mn»«mo mathvariant=¨bold¨ mathcolor=¨#FF0000¨».«/mo»«mn mathvariant=¨bold¨ mathcolor=¨#FF0000¨»2«/mn»«mo mathvariant=¨bold¨ mathcolor=¨#FF0000¨»§#183;«/mo»«mo mathvariant=¨bold¨ mathcolor=¨#FF0000¨»(«/mo»«mo mathvariant=¨bold¨ mathcolor=¨#FF0000¨»-«/mo»«mn mathvariant=¨bold¨ mathcolor=¨#FF0000¨»0«/mn»«mo mathvariant=¨bold¨ mathcolor=¨#FF0000¨».«/mo»«mn mathvariant=¨bold¨ mathcolor=¨#FF0000¨»3«/mn»«mo mathvariant=¨bold¨ mathcolor=¨#FF0000¨»)«/mo»«mo mathvariant=¨bold¨ mathcolor=¨#FF0000¨»=«/mo»«mo mathvariant=¨bold¨ mathcolor=¨#FF0000¨»-«/mo»«mn mathvariant=¨bold¨ mathcolor=¨#FF0000¨»0«/mn»«mo mathvariant=¨bold¨ mathcolor=¨#FF0000¨».«/mo»«mn mathvariant=¨bold¨ mathcolor=¨#FF0000¨»06«/mn»«mi mathvariant=¨bold¨ mathcolor=¨#FF0000¨»N«/mi»«mo mathvariant=¨bold¨ mathcolor=¨#FF0000¨»§#183;«/mo»«mi mathvariant=¨bold¨ mathcolor=¨#FF0000¨»S«/mi»«mspace linebreak=¨newline¨»«/mspace»«msub»«mi mathvariant=¨bold¨ mathcolor=¨#FF0000¨»P«/mi»«mi mathvariant=¨bold¨ mathcolor=¨#FF0000¨»C«/mi»«/msub»«mo mathvariant=¨bold¨ mathcolor=¨#FF0000¨»=«/mo»«msub»«mi mathvariant=¨bold¨ mathcolor=¨#FF0000¨»m«/mi»«mi mathvariant=¨bold¨ mathcolor=¨#FF0000¨»C«/mi»«/msub»«mo mathvariant=¨bold¨ mathcolor=¨#FF0000¨»§#183;«/mo»«msub»«mi mathvariant=¨bold¨ mathcolor=¨#FF0000¨»V«/mi»«mi mathvariant=¨bold¨ mathcolor=¨#FF0000¨»C«/mi»«/msub»«mo mathvariant=¨bold¨ mathcolor=¨#FF0000¨»=«/mo»«mn mathvariant=¨bold¨ mathcolor=¨#FF0000¨»0«/mn»«mo mathvariant=¨bold¨ mathcolor=¨#FF0000¨».«/mo»«mn mathvariant=¨bold¨ mathcolor=¨#FF0000¨»4«/mn»«mo mathvariant=¨bold¨ mathcolor=¨#FF0000¨»§#183;«/mo»«mn mathvariant=¨bold¨ mathcolor=¨#FF0000¨»0«/mn»«mo mathvariant=¨bold¨ mathcolor=¨#FF0000¨».«/mo»«mn mathvariant=¨bold¨ mathcolor=¨#FF0000¨»15«/mn»«mo mathvariant=¨bold¨ mathcolor=¨#FF0000¨»=«/mo»«mn mathvariant=¨bold¨ mathcolor=¨#FF0000¨»0«/mn»«mo mathvariant=¨bold¨ mathcolor=¨#FF0000¨».«/mo»«mn mathvariant=¨bold¨ mathcolor=¨#FF0000¨»06«/mn»«mi mathvariant=¨bold¨ mathcolor=¨#FF0000¨»N«/mi»«mo mathvariant=¨bold¨ mathcolor=¨#FF0000¨»§#183;«/mo»«mi mathvariant=¨bold¨ mathcolor=¨#FF0000¨»S«/mi»«/math»
يبدو
أن كمية الحركة المحصّلة قبل الاصطدام تساوي صفرًا. نظرًا لتحقق حفظ كمية الحركة حتى بعد
الاصطدام، فإن كمية الحركة المحصّلة تساوي صفرًا.
لذلك
تم توقُف الجسمين.
למרות שבמקרה זה הגופים לא נעים לאחר ההתנגשות , זו עדיין התנגשות פלסטית.
______________________________________________________________________________________

______________________________________________________________________________________
...
يتحرك الجسمان إلى اليمين.
فهم مبدأ حفظ كمية الحركة .
إذا كانت سرعة الجسم C أصغر ، فسيكون مقداركمية حركة الجسم C أصغر من مقدار كمية حركة الجسم B ، ولن تختلف مقدا كمية الحركة قبل الاصطدام عن الصفر ، وسيكون اتجاهه إلى اليمين باتجاه كمية الحركة الكبرى.
من قانون حفظ كمية الحركة، حتى بعد الاصطدام، لن تتغيركمية الحركة المحصّلة سواء من حيث المقدار أو الاتجاه ، وبالتالي سيتحرك الجسمان معًا إلى اليمين.
משימור תנע , גם אחרי ההתנגשות התנע הכולל לא ישתנה לא בגודלו ולא בכיוונו , לכן הגופים ינועו יחד ימינה.
1.
السؤال نوعي وليس كميًا، علاوة على أنه مكتوب في السؤال "تحديد بدون
حساب"، للإجابة على هذا السؤال يجب فهم معنى حفظ كمية الحركة.
إذا كنت لا تشعر بالثقة في أنك تعرف الإجابة، فمن
المستحسن أن تحدد على ورقة مسودة سرعة أصغر للجسم C، وكتابة
معادلة حفظ كمية الحركة، ومعرفة اتجاه حركة الجسم C ، وبعد ذلك
فقط فكر في معنى حفظ كمية الحركة وتفسير السبب في دفتر الامتحان.
2. السؤال من
ثمانية أقسام، وقت الامتحان مكلف. مثل هذا السؤال مفيد للتمرن، ولا يوصى باختيار
أسئلة طويلة في اختبار البجروت.
אם אתם לא מרגישים בטוחים שאתם יודעים את התשובה, מומלץ לקבוע בדף טיוטה מהירות קטנה יותר לגוף C , ולכתוב את משוואת שימור התנע , לגלות את כיוון תנועת גוף C, ורק לאחר מכן לחשוב על משמעות שימור התנע , ולנמק במחברת הבחינה.
2. בשאלה יש שמונה סעיפים , זמן הבחינה יקר . שאלה כזו טובה לתרגול פחות מומלץ לבחור בשאלות ארוכות במבחן הבגרות.
______________________________________________________________________________________
+
-







