...
«math xmlns=¨http://www.w3.org/1998/Math/MathML¨»«mfrac»«mrow»«mo mathvariant=¨bold¨ mathsize=¨20px¨»§#8710;«/mo»«mfenced»«mrow»«mi mathvariant=¨bold¨ mathsize=¨20px¨»m«/mi»«mo mathvariant=¨bold¨ mathsize=¨20px¨»§#183;«/mo»«mover»«mi mathvariant=¨bold¨ mathsize=¨20px¨»V«/mi»«mo mathvariant=¨bold¨ mathsize=¨20px¨»§#8594;«/mo»«/mover»«/mrow»«/mfenced»«/mrow»«mrow»«mo mathvariant=¨bold¨ mathsize=¨20px¨»§#8710;«/mo»«mi mathvariant=¨bold¨ mathsize=¨20px¨»t«/mi»«/mrow»«/mfrac»«mo mathsize=¨20px¨»=«/mo»«mfrac»«mrow»«mi mathvariant=¨bold¨ mathsize=¨20px¨»m«/mi»«mo mathvariant=¨bold¨ mathsize=¨20px¨»§#183;«/mo»«mo mathvariant=¨bold¨ mathsize=¨20px¨»§#8710;«/mo»«mfenced»«mover»«mi mathvariant=¨bold¨ mathsize=¨20px¨»V«/mi»«mo mathvariant=¨bold¨ mathsize=¨20px¨»§#8594;«/mo»«/mover»«/mfenced»«/mrow»«mrow»«mo mathvariant=¨bold¨ mathsize=¨20px¨»§#8710;«/mo»«mi mathvariant=¨bold¨ mathsize=¨20px¨»t«/mi»«/mrow»«/mfrac»«mo mathsize=¨20px¨»=«/mo»«mi mathvariant=¨bold¨ mathsize=¨20px¨»m«/mi»«mo mathvariant=¨bold¨ mathsize=¨20px¨»§#183;«/mo»«mfrac»«mrow»«mo mathvariant=¨bold¨ mathsize=¨20px¨»§#8710;«/mo»«mfenced»«mover»«mi mathvariant=¨bold¨ mathsize=¨20px¨»V«/mi»«mo mathvariant=¨bold¨ mathsize=¨20px¨»§#8594;«/mo»«/mover»«/mfenced»«/mrow»«mrow»«mo mathvariant=¨bold¨ mathsize=¨20px¨»§#8710;«/mo»«mi mathvariant=¨bold¨ mathsize=¨20px¨»t«/mi»«/mrow»«/mfrac»«mo mathvariant=¨bold¨ mathsize=¨20px¨»=«/mo»«mi mathvariant=¨bold¨ mathsize=¨20px¨»m«/mi»«mo mathvariant=¨bold¨ mathsize=¨20px¨»§#183;«/mo»«mover»«mi mathvariant=¨bold¨ mathsize=¨20px¨»a«/mi»«mo mathvariant=¨bold¨ mathsize=¨20px¨»§#8594;«/mo»«/mover»«/math»
«math xmlns=¨http://www.w3.org/1998/Math/MathML¨»«mstyle mathsize=¨20px¨»«mfrac mathcolor=¨#0000FF¨»«mrow»«mo mathvariant=¨bold¨»§#8710;«/mo»«mfenced»«mrow»«mi mathvariant=¨bold¨»m«/mi»«mo mathvariant=¨bold¨»§#183;«/mo»«mover»«mi mathvariant=¨bold¨»V«/mi»«mo mathvariant=¨bold¨»§#8594;«/mo»«/mover»«/mrow»«/mfenced»«/mrow»«mrow»«mo mathvariant=¨bold¨»§#8710;«/mo»«mi mathvariant=¨bold¨»t«/mi»«/mrow»«/mfrac»«/mstyle»«/math»
«math xmlns=¨http://www.w3.org/1998/Math/MathML¨»«mstyle mathsize=¨20px¨»«mfrac mathcolor=¨#0000FF¨»«mrow»«mo mathvariant=¨bold¨»§#8710;«/mo»«mfenced»«mrow»«mi mathvariant=¨bold¨»m«/mi»«mo mathvariant=¨bold¨»§#183;«/mo»«mover»«mi mathvariant=¨bold¨»V«/mi»«mo mathvariant=¨bold¨»§#8594;«/mo»«/mover»«/mrow»«/mfenced»«/mrow»«mrow»«mo mathvariant=¨bold¨»§#8710;«/mo»«mi mathvariant=¨bold¨»t«/mi»«/mrow»«/mfrac»«/mstyle»«/math»
باستخدام تعبير كمية الحركة وتعبير التسارع ، للانتقال من الطرف الأيسر للمعادلة إلى التعبير المطابق للتعبير الوارد في الطرف الأيمن.
إمكانية أخرى ، الرجوع للخلف ... للانتقال من التعبير المعطى في الطرف الأيمن بمساعدة كمية الحركة والتسارع إلى التعبير المعطى في الطرف الأيسر.
نُعبّر عن كمية الحركة في الطرف الأيسر:
«math xmlns=¨http://www.w3.org/1998/Math/MathML¨»«mstyle mathsize=¨20px¨»«mfrac mathcolor=¨#0000FF¨»«mrow»«mo mathvariant=¨bold¨»§#8710;«/mo»«mfenced»«mrow»«mi mathvariant=¨bold¨»m«/mi»«mo mathvariant=¨bold¨»§#183;«/mo»«mover»«mi mathvariant=¨bold¨»V«/mi»«mo mathvariant=¨bold¨»§#8594;«/mo»«/mover»«/mrow»«/mfenced»«/mrow»«mrow»«mo mathvariant=¨bold¨»§#8710;«/mo»«mi mathvariant=¨bold¨»t«/mi»«/mrow»«/mfrac»«/mstyle»«/math»
كما هو مذكور في السؤال ، فإن الكتلة ثابتة ، لذلك نُخرِج الكتلة من دالة دلتا:
«math xmlns=¨http://www.w3.org/1998/Math/MathML¨»«mstyle mathsize=¨20px¨»«mfrac mathcolor=¨#0000FF¨»«mrow»«mi mathvariant=¨bold¨»m«/mi»«mo mathvariant=¨bold¨»§#183;«/mo»«mo mathvariant=¨bold¨»§#8710;«/mo»«mfenced»«mover»«mi mathvariant=¨bold¨»V«/mi»«mo mathvariant=¨bold¨»§#8594;«/mo»«/mover»«/mfenced»«/mrow»«mrow»«mo mathvariant=¨bold¨»§#8710;«/mo»«mi mathvariant=¨bold¨»t«/mi»«/mrow»«/mfrac»«/mstyle»«/math»
وحسب تعريف التسارع : «math xmlns=¨http://www.w3.org/1998/Math/MathML¨»«mstyle mathsize=¨20px¨»«mrow»«mi mathvariant=¨bold¨ mathcolor=¨#0000FF¨»a«/mi»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»=«/mo»«mfrac mathcolor=¨#0000FF¨»«mrow»«mo mathvariant=¨bold¨»§#8710;«/mo»«mover»«mi mathvariant=¨bold¨»V«/mi»«mo mathvariant=¨bold¨»§#8594;«/mo»«/mover»«/mrow»«mrow»«mo mathvariant=¨bold¨»§#8710;«/mo»«mi mathvariant=¨bold¨»t«/mi»«/mrow»«/mfrac»«/mrow»«/mstyle»«/math»
ونحصل في الطرف الأيسر: «math xmlns=¨http://www.w3.org/1998/Math/MathML¨»«mstyle mathsize=¨20px¨»«mi mathvariant=¨bold¨ mathcolor=¨#0000FF¨»m«/mi»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»§#183;«/mo»«mover mathcolor=¨#0000FF¨»«mi mathvariant=¨bold¨»a«/mi»«mo mathvariant=¨bold¨»§#8594;«/mo»«/mover»«/mstyle»«/math» كما يظهر في الطرف الأيمن.
1. أن نفهم جيدًا أنه
يمكن إخراج الكتلة من الدلتا عندما تكون الكتلة ثابتة.
نكتب تعبيرًا
مناسبًا لحالة عامة حيث تتغير الكتلة أيضًا، وسنشير إلى الكتلة النهائية بـ والسرعة النهائية «math xmlns=¨http://www.w3.org/1998/Math/MathML¨»«mi mathvariant=¨bold-italic¨ mathcolor=¨#FF0000¨»V«/mi»«mo mathvariant=¨bold¨ mathcolor=¨#FF0000¨»`«/mo»«/math» :
«math xmlns=¨http://www.w3.org/1998/Math/MathML¨»«mstyle mathsize=¨20px¨»«mrow»«mo mathvariant=¨bold¨ mathcolor=¨#FF0000¨»§#8710;«/mo»«mo mathvariant=¨bold¨ mathcolor=¨#FF0000¨»(«/mo»«mi mathvariant=¨bold¨ mathcolor=¨#FF0000¨»m«/mi»«mo mathvariant=¨bold¨ mathcolor=¨#FF0000¨»§#183;«/mo»«mi mathvariant=¨bold¨ mathcolor=¨#FF0000¨»V«/mi»«mo mathvariant=¨bold¨ mathcolor=¨#FF0000¨»)«/mo»«mo mathvariant=¨bold¨ mathcolor=¨#FF0000¨»=«/mo»«mi mathvariant=¨bold¨ mathcolor=¨#FF0000¨»m«/mi»«mo mathvariant=¨bold¨ mathcolor=¨#FF0000¨»`«/mo»«mo mathvariant=¨bold¨ mathcolor=¨#FF0000¨»§#183;«/mo»«mi mathvariant=¨bold¨ mathcolor=¨#FF0000¨»V«/mi»«mo mathvariant=¨bold¨ mathcolor=¨#FF0000¨»`«/mo»«mo mathvariant=¨bold¨ mathcolor=¨#FF0000¨»-«/mo»«msub»«mi mathvariant=¨bold¨ mathcolor=¨#FF0000¨»m«/mi»«mn mathvariant=¨bold¨ mathcolor=¨#FF0000¨»0«/mn»«/msub»«mo mathvariant=¨bold¨ mathcolor=¨#FF0000¨»§#183;«/mo»«msub»«mi mathvariant=¨bold¨ mathcolor=¨#FF0000¨»V«/mi»«mn mathvariant=¨bold¨ mathcolor=¨#FF0000¨»0«/mn»«/msub»«/mrow»«/mstyle»«/math»
نظرًا لأن الكتلة ثابتة، يمكن اخراجها كعامل مشترك:
«math xmlns=¨http://www.w3.org/1998/Math/MathML¨»«mstyle mathsize=¨20px¨»«mo mathvariant=¨bold¨ mathcolor=¨#FF0000¨»§#8710;«/mo»«mo mathvariant=¨bold¨ mathcolor=¨#FF0000¨»(«/mo»«mi mathvariant=¨bold¨ mathcolor=¨#FF0000¨»m«/mi»«mo mathvariant=¨bold¨ mathcolor=¨#FF0000¨»§#183;«/mo»«mi mathvariant=¨bold¨ mathcolor=¨#FF0000¨»V«/mi»«mo mathvariant=¨bold¨ mathcolor=¨#FF0000¨»)«/mo»«mo mathvariant=¨bold¨ mathcolor=¨#FF0000¨»=«/mo»«mi mathvariant=¨bold¨ mathcolor=¨#FF0000¨»m«/mi»«mo mathvariant=¨bold¨ mathcolor=¨#FF0000¨»§#183;«/mo»«mi mathvariant=¨bold¨ mathcolor=¨#FF0000¨»V«/mi»«mo mathvariant=¨bold¨ mathcolor=¨#FF0000¨»`«/mo»«mo mathvariant=¨bold¨ mathcolor=¨#FF0000¨»-«/mo»«mi mathvariant=¨bold¨ mathcolor=¨#FF0000¨»m«/mi»«mo mathvariant=¨bold¨ mathcolor=¨#FF0000¨»§#183;«/mo»«msub»«mi mathvariant=¨bold¨ mathcolor=¨#FF0000¨»V«/mi»«mn mathvariant=¨bold¨ mathcolor=¨#FF0000¨»0«/mn»«/msub»«mo mathvariant=¨bold¨ mathcolor=¨#FF0000¨»=«/mo»«mi mathvariant=¨bold¨ mathcolor=¨#FF0000¨»m«/mi»«mo mathvariant=¨bold¨ mathcolor=¨#FF0000¨»§#183;«/mo»«mfenced mathcolor=¨#FF0000¨»«mrow»«mi mathvariant=¨bold¨»V«/mi»«mo mathvariant=¨bold¨»`«/mo»«mo mathvariant=¨bold¨»-«/mo»«msub»«mi mathvariant=¨bold¨»V«/mi»«mn mathvariant=¨bold¨»0«/mn»«/msub»«/mrow»«/mfenced»«/mstyle»«/math»
يمكنك استخدام دالة دلتا وكتابة:
«math xmlns=¨http://www.w3.org/1998/Math/MathML¨»«mstyle mathsize=¨20px¨»«mo mathvariant=¨bold¨ mathcolor=¨#FF0000¨»§#8710;«/mo»«mo mathvariant=¨bold¨ mathcolor=¨#FF0000¨»(«/mo»«mi mathvariant=¨bold¨ mathcolor=¨#FF0000¨»m«/mi»«mo mathvariant=¨bold¨ mathcolor=¨#FF0000¨»§#183;«/mo»«mi mathvariant=¨bold¨ mathcolor=¨#FF0000¨»V«/mi»«mo mathvariant=¨bold¨ mathcolor=¨#FF0000¨»)«/mo»«mo mathvariant=¨bold¨ mathcolor=¨#FF0000¨»=«/mo»«mi mathvariant=¨bold¨ mathcolor=¨#FF0000¨»m«/mi»«mo mathvariant=¨bold¨ mathcolor=¨#FF0000¨»§#183;«/mo»«mfenced mathcolor=¨#FF0000¨»«mrow»«mi mathvariant=¨bold¨»V«/mi»«mo mathvariant=¨bold¨»`«/mo»«mo mathvariant=¨bold¨»-«/mo»«msub»«mi mathvariant=¨bold¨»V«/mi»«mn mathvariant=¨bold¨»0«/mn»«/msub»«/mrow»«/mfenced»«mo mathvariant=¨bold¨ mathcolor=¨#FF0000¨»=«/mo»«mi mathvariant=¨bold¨ mathcolor=¨#FF0000¨»m«/mi»«mo mathvariant=¨bold¨ mathcolor=¨#FF0000¨»§#183;«/mo»«mo mathvariant=¨bold¨ mathcolor=¨#FF0000¨»§#8710;«/mo»«mi mathvariant=¨bold¨ mathcolor=¨#FF0000¨»V«/mi»«/mstyle»«/math»
لذلك ، إذا كان هناك حد ثابت داخل الدلتا ، فمن المتبع إخراجه من الدلتا.
2. إذا كان هناك حاصل ضرب حدود داخل الدلتا بدلاً من مجموع حدود ، فلن يكون من الممكن إخراج الحد الثابت من دلتا.
3. التعبير في السؤال هو الشكل الأصلي لقانون نيوتن الثاني. كما صاغه نيوتن.
...
نتيجة لتأثير القوة ، تزداد كمية الحركة بمقدار 2 نيوتن في الثانية.
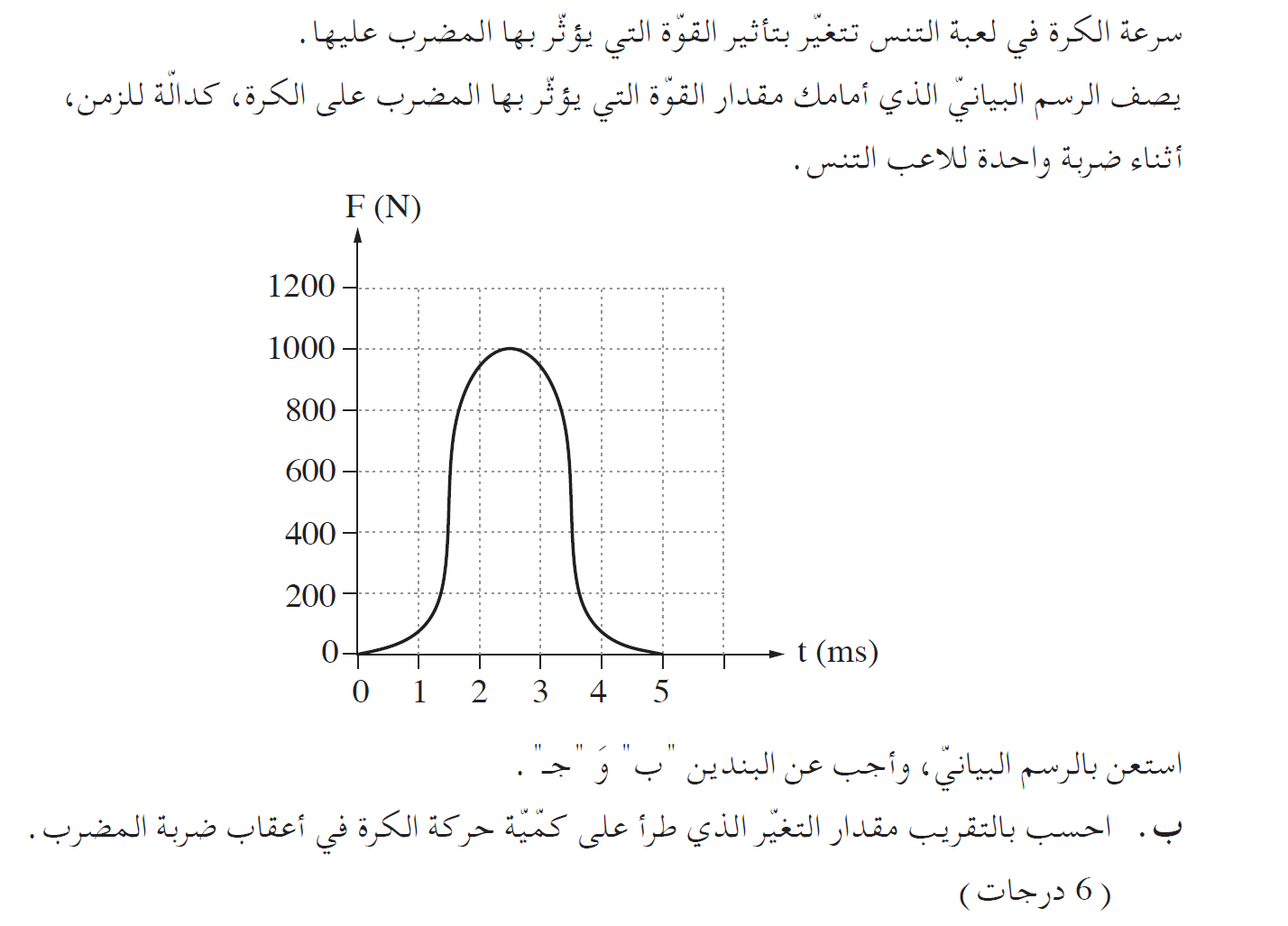
في الرسم البياني للقوة كدالة للزمن، تكونمقدار المساحة المحصورة بين الدالة ومحور الزمن مساويًا لمقدار كمية الدفع.
من قانون كمية الدفع وكمية الحركة، مقدار كمية الدفع يساوي مقدار تغير كمية الحركة.
ממשפט תנע מתנע גודל המתקף שווה לגודל שינוי התנע.
بالنظر إلى الرسم البياني الذي يصف القوة كدالة للزمن، في هذا الرسم البياني ، فإن مقدار المساحة التي يحدها الرسم البياني تساوي مقدار كمية الدفع للقوة المؤثرة على الكرة.
من قانون كمية الدفع وكمية الحركة «math xmlns=¨http://www.w3.org/1998/Math/MathML¨»«mover mathcolor=¨#0000FF¨»«mi mathvariant=¨bold¨»J«/mi»«mo mathvariant=¨bold¨»§#8594;«/mo»«/mover»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»=«/mo»«mover mathcolor=¨#0000FF¨»«mrow»«mo mathvariant=¨bold¨»§#8710;«/mo»«mi mathvariant=¨bold¨»P«/mi»«/mrow»«mo mathvariant=¨bold¨»§#8594;«/mo»«/mover»«/math» , كمية الدفع هذه تساوي التغيير في كمية حركة الجسم.
لذلك ، لإيجاد التغيير في كمية الحركة، نحسب المساحة المحصورة بين الرسم البياني ومحور الزمن.
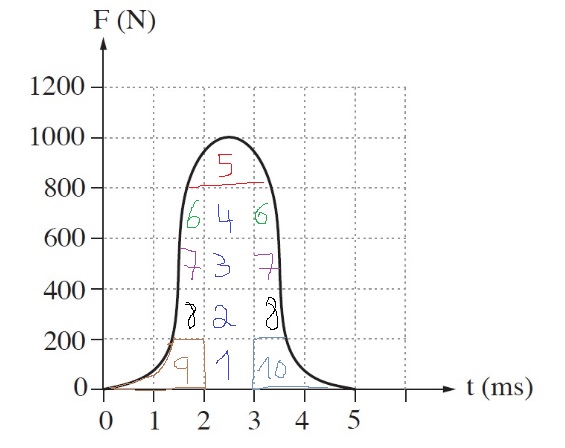
نحسب تقريبًا عدد المربعات المحصورة بين الدالة ومحور الزمن:
تقريبًا ، يمكن القول أن هناك عشر مربعات محصورة بين الدالة والمحور الزمني.
نحسب مقدار كمية الدفع الملائمة لمساحة مربع واحد:
«math xmlns=¨http://www.w3.org/1998/Math/MathML¨»«mi mathvariant=¨bold¨ mathcolor=¨#0000FF¨»§#1608;§#1575;§#1581;§#1583;«/mi»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»§#160;«/mo»«mi mathvariant=¨bold¨ mathcolor=¨#0000FF¨»§#1605;§#1585;§#1576;§#1593;«/mi»«mi mathvariant=¨bold¨ mathcolor=¨#0000FF¨»J«/mi»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»=«/mo»«mn mathvariant=¨bold¨ mathcolor=¨#0000FF¨»200«/mn»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»§#183;«/mo»«mn mathvariant=¨bold¨ mathcolor=¨#0000FF¨»1«/mn»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»§#183;«/mo»«msup»«mn mathvariant=¨bold¨ mathcolor=¨#0000FF¨»10«/mn»«mrow mathcolor=¨#0000FF¨»«mo mathvariant=¨bold¨»-«/mo»«mn mathvariant=¨bold¨»3«/mn»«/mrow»«/msup»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»=«/mo»«mn mathvariant=¨bold¨ mathcolor=¨#0000FF¨»0«/mn»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨».«/mo»«mn mathvariant=¨bold¨ mathcolor=¨#0000FF¨»2«/mn»«mi mathvariant=¨bold¨ mathcolor=¨#0000FF¨»N«/mi»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»§#183;«/mo»«mi mathvariant=¨bold¨ mathcolor=¨#0000FF¨»S«/mi»«/math»
المساحة المحصورة تحوي 10 مربعات , نحسب مقدار كمية الدفع خلال 5 مللي ثانية:
«math xmlns=¨http://www.w3.org/1998/Math/MathML¨»«mstyle mathsize=¨16px¨»«mi mathvariant=¨bold¨ mathcolor=¨#0000FF¨»J«/mi»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»=«/mo»«mi mathvariant=¨bold¨ mathcolor=¨#0000FF¨»§#1608;§#1575;§#1581;§#1583;«/mi»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»§#160;«/mo»«mi mathvariant=¨bold¨ mathcolor=¨#0000FF¨»§#1605;§#1585;§#1576;§#1593;«/mi»«mi mathvariant=¨bold¨ mathcolor=¨#0000FF¨»J«/mi»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»§#183;«/mo»«mn mathvariant=¨bold¨ mathcolor=¨#0000FF¨»10«/mn»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»=«/mo»«mn mathvariant=¨bold¨ mathcolor=¨#0000FF¨»0«/mn»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨».«/mo»«mn mathvariant=¨bold¨ mathcolor=¨#0000FF¨»2«/mn»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»§#183;«/mo»«mn mathvariant=¨bold¨ mathcolor=¨#0000FF¨»10«/mn»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»=«/mo»«mn mathvariant=¨bold¨ mathcolor=¨#0000FF¨»2«/mn»«mi mathvariant=¨bold¨ mathcolor=¨#0000FF¨»N«/mi»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»§#183;«/mo»«mi mathvariant=¨bold¨ mathcolor=¨#0000FF¨»S«/mi»«/mstyle»«/math»
من قانون كمية الدفع وكمية الحركة «math xmlns=¨http://www.w3.org/1998/Math/MathML¨»«mover mathcolor=¨#0000FF¨»«mi mathvariant=¨bold¨»J«/mi»«mo mathvariant=¨bold¨»§#8594;«/mo»«/mover»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»=«/mo»«mover mathcolor=¨#0000FF¨»«mrow»«mo mathvariant=¨bold¨»§#8710;«/mo»«mi mathvariant=¨bold¨»P«/mi»«/mrow»«mo mathvariant=¨bold¨»§#8594;«/mo»«/mover»«/math» مقدار كمية الدفع مسوي مقدار تغير كمية الحركة، وبالتالي نتيجة لتأثير القوة ، تزداد كمية الحركة بمقدار 2 نيوتن في الثانية.
ממשפט תנע מתקף «math xmlns=¨http://www.w3.org/1998/Math/MathML¨»«mover mathcolor=¨#0000FF¨»«mi mathvariant=¨bold¨»J«/mi»«mo mathvariant=¨bold¨»§#8594;«/mo»«/mover»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»=«/mo»«mover mathcolor=¨#0000FF¨»«mrow»«mo mathvariant=¨bold¨»§#8710;«/mo»«mi mathvariant=¨bold¨»P«/mi»«/mrow»«mo mathvariant=¨bold¨»§#8594;«/mo»«/mover»«/math» , מתקף זה שווה לשינוי בתנע של הגוף.
לכן כדי למצוא את שינוי התנע , נחשב את המתקף מהשטח התחום בגרף.
נספור את מספר המשבצות התחומות בין הפונקציה לציר הזמן:
בקירוב , ניתן לומר שיש עשר משבצות התחומות בין הפונקציה לציר הזמן:
נחשב את ערך המ המתקף
1. ليس من الممكن حساب عدد المربعات المحصورة بدقة بين الدالة والمحور الزمني.
2. من السهل ارتكاب خطأ والاعتقاد بأن القيم في المحور الزمني بوحدات الثانية، والوحدات هي ميلي ثانية.
3. وحدات كمية الحركة هي : «math xmlns=¨http://www.w3.org/1998/Math/MathML¨»«mo mathvariant=¨bold¨ mathcolor=¨#FF0000¨»[«/mo»«mfrac mathcolor=¨#FF0000¨»«mrow»«mi mathvariant=¨bold¨»Kg«/mi»«mo mathvariant=¨bold¨»§#183;«/mo»«mi mathvariant=¨bold¨»m«/mi»«/mrow»«mi mathvariant=¨bold¨»s«/mi»«/mfrac»«mo mathvariant=¨bold¨ mathcolor=¨#FF0000¨»]«/mo»«/math» ووحدات كمية الدفع هي: «math xmlns=¨http://www.w3.org/1998/Math/MathML¨»«mo mathvariant=¨bold¨ mathcolor=¨#FF0000¨»[«/mo»«mi mathvariant=¨bold¨ mathcolor=¨#FF0000¨»N«/mi»«mo mathvariant=¨bold¨ mathcolor=¨#FF0000¨»§#183;«/mo»«mi mathvariant=¨bold¨ mathcolor=¨#FF0000¨»S«/mi»«mo mathvariant=¨bold¨ mathcolor=¨#FF0000¨»]«/mo»«/math» .
يمكن إثبات أن وحدات كمية الدفع هي نفس وحدات كمية الحركة:
«math xmlns=¨http://www.w3.org/1998/Math/MathML¨»«mo mathvariant=¨bold¨ mathcolor=¨#FF0000¨»[«/mo»«mi mathvariant=¨bold-italic¨ mathcolor=¨#007F00¨»N«/mi»«mo mathvariant=¨bold¨ mathcolor=¨#FF0000¨»§#183;«/mo»«mi mathvariant=¨bold-italic¨ mathcolor=¨#FF0000¨»S«/mi»«mo mathvariant=¨bold¨ mathcolor=¨#FF0000¨»]«/mo»«mo mathvariant=¨bold¨ mathcolor=¨#FF0000¨»=«/mo»«mo mathvariant=¨bold¨ mathcolor=¨#FF0000¨»[«/mo»«mfrac mathcolor=¨#007F00¨»«mrow»«mi mathvariant=¨bold¨»Kg«/mi»«mo mathvariant=¨bold¨»§#183;«/mo»«mi mathvariant=¨bold¨»m«/mi»«/mrow»«msup»«mi mathvariant=¨bold¨»s«/mi»«mn mathvariant=¨bold¨»2«/mn»«/msup»«/mfrac»«mo mathvariant=¨bold¨ mathcolor=¨#FF0000¨»§#183;«/mo»«mi mathvariant=¨bold-italic¨ mathcolor=¨#FF0000¨»S«/mi»«mo mathvariant=¨bold¨ mathcolor=¨#FF0000¨»]«/mo»«mo mathvariant=¨bold¨ mathcolor=¨#FF0000¨»=«/mo»«mo mathvariant=¨bold¨ mathcolor=¨#FF0000¨»[«/mo»«mfrac mathcolor=¨#FF0000¨»«mrow»«mi mathvariant=¨bold¨»Kg«/mi»«mo mathvariant=¨bold¨»§#183;«/mo»«mi mathvariant=¨bold¨»m«/mi»«/mrow»«mi mathvariant=¨bold¨»s«/mi»«/mfrac»«mo mathvariant=¨bold¨ mathcolor=¨#FF0000¨»]«/mo»«/math»
لذلك ، على الرغم من أن السؤال يتعلق بتغيير كمية الحركة، يمكن كتابة الإجابة بوحدات كمية الدفع.
2. קל לטעות ולחשוב שהערכים בציר הזמן הם ביחידות של שנייה, היחידות הן אלפית שנייה.
...
بعد الضربة ، تتحرك الكرة بسرعة 33.7 مترًا في الثانية ، في اتجاه 8.53 درجة فوق الأفق.
تُغير الضربة الأفقية فقط السرعة الأفقية، حسب مقدار تغير كمية الحركة من القسم السابق، يمكن حساب السرعة الأفقية للكرة بعد الضربة.
وحسب السرعة الأفقية والسرعة الرأسية بعد الضربة ، من الممكن حساب مقدار واتجاه سرعة الكرة بشكل متجهي بعد الضربة.
ובהתאם למהירות האופקית והמהירות האנכית לאחר החבטה, ניתן ווקטורית לחשב את גודל וכיוון מהירות הכדור לאחר החבטה.
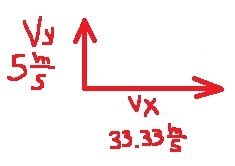
قبل الضربة ، تتحرك الكرة عموديًا لأعلى بسرعة 5 أمتار في الثانية ، وليس للكرة سرعة أفقية.
يضرب اللاعب الكرة في اتجاه أفقي ، تزداد السرعة الأفقية وفقًا لقيمة تغير كمية الحركة.
باستخدام مقدار التغير في كمية الحركة، نجد مقدار سرعة الكرة الأفقية بعد الضربة:
«math xmlns=¨http://www.w3.org/1998/Math/MathML¨»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»§#8710;«/mo»«msub»«mi mathvariant=¨bold¨ mathcolor=¨#0000FF¨»P«/mi»«mi mathvariant=¨bold¨ mathcolor=¨#0000FF¨»X«/mi»«/msub»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»=«/mo»«mn mathvariant=¨bold¨ mathcolor=¨#0000FF¨»2«/mn»«mi mathvariant=¨bold¨ mathcolor=¨#0000FF¨»NS«/mi»«mspace linebreak=¨newline¨»«/mspace»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»§#8710;«/mo»«msub»«mi mathvariant=¨bold¨ mathcolor=¨#0000FF¨»P«/mi»«mi mathvariant=¨bold¨ mathcolor=¨#0000FF¨»X«/mi»«/msub»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»=«/mo»«mi mathvariant=¨bold¨ mathcolor=¨#0000FF¨»m«/mi»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»§#183;«/mo»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»§#8710;«/mo»«msub»«mi mathvariant=¨bold¨ mathcolor=¨#0000FF¨»V«/mi»«mi mathvariant=¨bold¨ mathcolor=¨#0000FF¨»X«/mi»«/msub»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»=«/mo»«mi mathvariant=¨bold¨ mathcolor=¨#0000FF¨»m«/mi»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»§#183;«/mo»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»(«/mo»«msub»«mi mathvariant=¨bold¨ mathcolor=¨#0000FF¨»V«/mi»«mi mathvariant=¨bold¨ mathcolor=¨#0000FF¨»X«/mi»«/msub»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»-«/mo»«msub»«mi mathvariant=¨bold¨ mathcolor=¨#0000FF¨»V«/mi»«msub mathcolor=¨#0000FF¨»«mn mathvariant=¨bold¨»0«/mn»«mi mathvariant=¨bold¨»X«/mi»«/msub»«/msub»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»)«/mo»«mspace linebreak=¨newline¨»«/mspace»«/math»
السرعة الأفقية للكرة قبل الاصطدام تساوي صفر متر في الثانية.
نجد السرعة الأفقية للكرة بعد الضربة:
«math xmlns=¨http://www.w3.org/1998/Math/MathML¨»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»§#8710;«/mo»«msub»«mi mathvariant=¨bold¨ mathcolor=¨#0000FF¨»P«/mi»«mi mathvariant=¨bold¨ mathcolor=¨#0000FF¨»X«/mi»«/msub»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»=«/mo»«mi mathvariant=¨bold¨ mathcolor=¨#0000FF¨»m«/mi»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»§#183;«/mo»«msub»«mi mathvariant=¨bold¨ mathcolor=¨#0000FF¨»V«/mi»«mi mathvariant=¨bold¨ mathcolor=¨#0000FF¨»X«/mi»«/msub»«mspace linebreak=¨newline¨/»«msub»«mi mathvariant=¨bold¨ mathcolor=¨#0000FF¨»V«/mi»«mi mathvariant=¨bold¨ mathcolor=¨#0000FF¨»X«/mi»«/msub»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»=«/mo»«mfrac mathcolor=¨#0000FF¨»«mrow»«mo mathvariant=¨bold¨»§#8710;«/mo»«msub»«mi mathvariant=¨bold¨»P«/mi»«mi mathvariant=¨bold¨»X«/mi»«/msub»«/mrow»«mi mathvariant=¨bold¨»m«/mi»«/mfrac»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»=«/mo»«mfrac mathcolor=¨#0000FF¨»«mn mathvariant=¨bold¨»2«/mn»«mrow»«mn mathvariant=¨bold¨»0«/mn»«mo mathvariant=¨bold¨».«/mo»«mn mathvariant=¨bold¨»06«/mn»«/mrow»«/mfrac»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»=«/mo»«mn mathvariant=¨bold¨ mathcolor=¨#0000FF¨»33«/mn»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨».«/mo»«mn mathvariant=¨bold¨ mathcolor=¨#0000FF¨»33«/mn»«mfrac mathcolor=¨#0000FF¨»«mi mathvariant=¨bold¨»m«/mi»«mi mathvariant=¨bold¨»s«/mi»«/mfrac»«mspace linebreak=¨newline¨/»«/math»
لا تؤثر الضربة على السرعة العمودية.
نجد سرعة الكرة بعد الضربة باستخدام السرعة العمودية والسرعة الأفقية:
نحدد اتجاه حركة الكرة بعد الضربة بالنسبة إلى الأفق بزاوية ألفا.
نجد سرعة الكرة بعد ضربها باستخدام فيثاغورس:
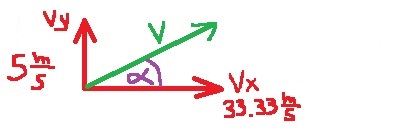
«math xmlns=¨http://www.w3.org/1998/Math/MathML¨»«msup»«mi mathvariant=¨bold¨ mathcolor=¨#0000FF¨»V«/mi»«mn mathvariant=¨bold¨ mathcolor=¨#0000FF¨»2«/mn»«/msup»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»=«/mo»«msup»«msub»«mi mathvariant=¨bold¨ mathcolor=¨#0000FF¨»V«/mi»«mi mathvariant=¨bold¨ mathcolor=¨#0000FF¨»X«/mi»«/msub»«mn mathvariant=¨bold¨ mathcolor=¨#0000FF¨»2«/mn»«/msup»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»+«/mo»«msup»«msub»«mi mathvariant=¨bold¨ mathcolor=¨#0000FF¨»V«/mi»«mi mathvariant=¨bold¨ mathcolor=¨#0000FF¨»Y«/mi»«/msub»«mn mathvariant=¨bold¨ mathcolor=¨#0000FF¨»2«/mn»«/msup»«mspace linebreak=¨newline¨/»«mi mathvariant=¨bold¨ mathcolor=¨#0000FF¨»V«/mi»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»=«/mo»«msqrt mathcolor=¨#0000FF¨»«msup»«msub»«mi mathvariant=¨bold¨»V«/mi»«mi mathvariant=¨bold¨»X«/mi»«/msub»«mn mathvariant=¨bold¨»2«/mn»«/msup»«mo mathvariant=¨bold¨»+«/mo»«msup»«msub»«mi mathvariant=¨bold¨»V«/mi»«mi mathvariant=¨bold¨»Y«/mi»«/msub»«mn mathvariant=¨bold¨»2«/mn»«/msup»«/msqrt»«mspace linebreak=¨newline¨/»«mi mathvariant=¨bold¨ mathcolor=¨#0000FF¨»V«/mi»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»=«/mo»«msqrt mathcolor=¨#0000FF¨»«mn mathvariant=¨bold¨»33«/mn»«mo mathvariant=¨bold¨».«/mo»«msup»«mn mathvariant=¨bold¨»33«/mn»«mn mathvariant=¨bold¨»2«/mn»«/msup»«mo mathvariant=¨bold¨»+«/mo»«msup»«mn mathvariant=¨bold¨»5«/mn»«mn mathvariant=¨bold¨»2«/mn»«/msup»«/msqrt»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»=«/mo»«msqrt mathcolor=¨#0000FF¨»«mn mathvariant=¨bold¨»1135«/mn»«mo mathvariant=¨bold¨».«/mo»«mn mathvariant=¨bold¨»88«/mn»«/msqrt»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»§#160;«/mo»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»=«/mo»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»§#160;«/mo»«mn mathvariant=¨bold¨ mathcolor=¨#0000FF¨»33«/mn»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨».«/mo»«mn mathvariant=¨bold¨ mathcolor=¨#0000FF¨»7«/mn»«mfrac mathcolor=¨#0000FF¨»«mi mathvariant=¨bold¨»m«/mi»«mi mathvariant=¨bold¨»s«/mi»«/mfrac»«/math»
نجد اتجاه حركة الكرة بعد الضربة باستخدام نسبة الظل (tan):
«math xmlns=¨http://www.w3.org/1998/Math/MathML¨»«mi mathvariant=¨bold¨ mathcolor=¨#0000FF¨»tan«/mi»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»(«/mo»«mi mathvariant=¨bold¨ mathcolor=¨#0000FF¨»§#945;«/mi»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»)«/mo»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»=«/mo»«mfrac mathcolor=¨#0000FF¨»«msub»«mi mathvariant=¨bold¨»V«/mi»«mi mathvariant=¨bold¨»Y«/mi»«/msub»«msub»«mi mathvariant=¨bold¨»V«/mi»«mi mathvariant=¨bold¨»X«/mi»«/msub»«/mfrac»«mspace linebreak=¨newline¨/»«mspace linebreak=¨newline¨/»«mi mathvariant=¨bold¨ mathcolor=¨#0000FF¨»§#945;«/mi»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»=«/mo»«mi mathvariant=¨bold¨ mathcolor=¨#0000FF¨»shift«/mi»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»§#160;«/mo»«mi mathvariant=¨bold¨ mathcolor=¨#0000FF¨»tan«/mi»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»(«/mo»«mfrac mathcolor=¨#0000FF¨»«msub»«mi mathvariant=¨bold¨»V«/mi»«mi mathvariant=¨bold¨»Y«/mi»«/msub»«msub»«mi mathvariant=¨bold¨»V«/mi»«mi mathvariant=¨bold¨»X«/mi»«/msub»«/mfrac»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»)«/mo»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»=«/mo»«mi mathvariant=¨bold¨ mathcolor=¨#0000FF¨»shift«/mi»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»§#160;«/mo»«mi mathvariant=¨bold¨ mathcolor=¨#0000FF¨»tan«/mi»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»(«/mo»«mfrac mathcolor=¨#0000FF¨»«mn mathvariant=¨bold¨»5«/mn»«mrow»«mn mathvariant=¨bold¨»33«/mn»«mo mathvariant=¨bold¨».«/mo»«mn mathvariant=¨bold¨»33«/mn»«/mrow»«/mfrac»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»)«/mo»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»=«/mo»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»=«/mo»«mi mathvariant=¨bold¨ mathcolor=¨#0000FF¨»shift«/mi»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»§#160;«/mo»«mi mathvariant=¨bold¨ mathcolor=¨#0000FF¨»tan«/mi»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»(«/mo»«mn mathvariant=¨bold¨ mathcolor=¨#0000FF¨»0«/mn»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨».«/mo»«mn mathvariant=¨bold¨ mathcolor=¨#0000FF¨»15«/mn»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»)«/mo»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»=«/mo»«mn mathvariant=¨bold¨ mathcolor=¨#0000FF¨»8«/mn»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨».«/mo»«mn mathvariant=¨bold¨ mathcolor=¨#0000FF¨»53«/mn»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»§#176;«/mo»«/math»
بعد الضربة ، تتحرك الكرة بسرعة 33.7 مترًا في الثانية ، في اتجاه 8.53 درجة فوق الأفق.
השחקן חובט בכדור בכיוון אופקי , המהירות האופקית גדלה , בהתאם לערך שינוי התנע.
נמצא בעזרת גודל שינוי התנע , את גודל מהירותו האופקית של הכדור לאחר החבטה:
«math xmlns=¨http://www.w3.org/1998/Math/MathML¨»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»§#8710;«/mo»«msub»«mi mathvariant=¨bold¨ mathcolor=¨#0000FF¨»P«/mi»«mi mathvariant=¨bold¨ mathcolor=¨#0000FF¨»X«/mi»«/msub»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»=«/mo»«mn mathvariant=¨bold¨ mathcolor=¨#0000FF¨»2«/mn»«mi mathvariant=¨bold¨ mathcolor=¨#0000FF¨»NS«/mi»«mspace linebreak=¨newline¨»«/mspace»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»§#8710;«/mo»«msub»«mi mathvariant=¨bold¨ mathcolor=¨#0000FF¨»P«/mi»«mi mathvariant=¨bold¨ mathcolor=¨#0000FF¨»X«/mi»«/msub»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»=«/mo»«mi mathvariant=¨bold¨ mathcolor=¨#0000FF¨»m«/mi»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»§#183;«/mo»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»§#8710;«/mo»«msub»«mi mathvariant=¨bold¨ mathcolor=¨#0000FF¨»V«/mi»«mi mathvariant=¨bold¨ mathcolor=¨#0000FF¨»X«/mi»«/msub»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»=«/mo»«mi mathvariant=¨bold¨ mathcolor=¨#0000FF¨»m«/mi»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»§#183;«/mo»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»(«/mo»«msub»«mi mathvariant=¨bold¨ mathcolor=¨#0000FF¨»V«/mi»«mi mathvariant=¨bold¨ mathcolor=¨#0000FF¨»X«/mi»«/msub»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»-«/mo»«msub»«mi mathvariant=¨bold¨ mathcolor=¨#0000FF¨»V«/mi»«msub mathcolor=¨#0000FF¨»«mn mathvariant=¨bold¨»0«/mn»«mi mathvariant=¨bold¨»X«/mi»«/msub»«/msub»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»)«/mo»«mspace linebreak=¨newline¨»«/mspace»«/math»
המהירות האופקית של הכדור לפני החבטה היא אפס מטר לשנייה.
נמצא את מהירותו האופקית של הכדור לאחר החבטה:
«math xmlns=¨http://www.w3.org/1998/Math/MathML¨»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»§#8710;«/mo»«msub»«mi mathvariant=¨bold¨ mathcolor=¨#0000FF¨»P«/mi»«mi mathvariant=¨bold¨ mathcolor=¨#0000FF¨»X«/mi»«/msub»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»=«/mo»«mi mathvariant=¨bold¨ mathcolor=¨#0000FF¨»m«/mi»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»§#183;«/mo»«msub»«mi mathvariant=¨bold¨ mathcolor=¨#0000FF¨»V«/mi»«mi mathvariant=¨bold¨ mathcolor=¨#0000FF¨»X«/mi»«/msub»«mspace linebreak=¨newline¨/»«msub»«mi mathvariant=¨bold¨ mathcolor=¨#0000FF¨»V«/mi»«mi mathvariant=¨bold¨ mathcolor=¨#0000FF¨»X«/mi»«/msub»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»=«/mo»«mfrac mathcolor=¨#0000FF¨»«mrow»«mo mathvariant=¨bold¨»§#8710;«/mo»«msub»«mi mathvariant=¨bold¨»P«/mi»«mi mathvariant=¨bold¨»X«/mi»«/msub»«/mrow»«mi mathvariant=¨bold¨»m«/mi»«/mfrac»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»=«/mo»«mfrac mathcolor=¨#0000FF¨»«mn mathvariant=¨bold¨»2«/mn»«mrow»«mn mathvariant=¨bold¨»0«/mn»«mo mathvariant=¨bold¨».«/mo»«mn mathvariant=¨bold¨»06«/mn»«/mrow»«/mfrac»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»=«/mo»«mn mathvariant=¨bold¨ mathcolor=¨#0000FF¨»33«/mn»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨».«/mo»«mn mathvariant=¨bold¨ mathcolor=¨#0000FF¨»33«/mn»«mfrac mathcolor=¨#0000FF¨»«mi mathvariant=¨bold¨»m«/mi»«mi mathvariant=¨bold¨»s«/mi»«/mfrac»«mspace linebreak=¨newline¨/»«/math»
החבטה לא משפיעה על המהירות האנכית.
נמצא את מהירות הכדור לאחר החבטה בעזרת המהירות האנכית והמהירות האופקית:
נגדיר את כיוון תנועת הכדור לאחר החבטה ביחס לאופק בזווית אלפא.
נמצא את מהירות הכדור לאחר החבטה בעזרת פיתגורס:
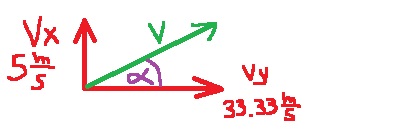
«math xmlns=¨http://www.w3.org/1998/Math/MathML¨»«msup»«mi mathvariant=¨bold¨ mathcolor=¨#0000FF¨»V«/mi»«mn mathvariant=¨bold¨ mathcolor=¨#0000FF¨»2«/mn»«/msup»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»=«/mo»«msup»«msub»«mi mathvariant=¨bold¨ mathcolor=¨#0000FF¨»V«/mi»«mi mathvariant=¨bold¨ mathcolor=¨#0000FF¨»X«/mi»«/msub»«mn mathvariant=¨bold¨ mathcolor=¨#0000FF¨»2«/mn»«/msup»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»+«/mo»«msup»«msub»«mi mathvariant=¨bold¨ mathcolor=¨#0000FF¨»V«/mi»«mi mathvariant=¨bold¨ mathcolor=¨#0000FF¨»Y«/mi»«/msub»«mn mathvariant=¨bold¨ mathcolor=¨#0000FF¨»2«/mn»«/msup»«mspace linebreak=¨newline¨/»«mi mathvariant=¨bold¨ mathcolor=¨#0000FF¨»V«/mi»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»=«/mo»«msqrt mathcolor=¨#0000FF¨»«msup»«msub»«mi mathvariant=¨bold¨»V«/mi»«mi mathvariant=¨bold¨»X«/mi»«/msub»«mn mathvariant=¨bold¨»2«/mn»«/msup»«mo mathvariant=¨bold¨»+«/mo»«msup»«msub»«mi mathvariant=¨bold¨»V«/mi»«mi mathvariant=¨bold¨»Y«/mi»«/msub»«mn mathvariant=¨bold¨»2«/mn»«/msup»«/msqrt»«mspace linebreak=¨newline¨/»«mi mathvariant=¨bold¨ mathcolor=¨#0000FF¨»V«/mi»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»=«/mo»«msqrt mathcolor=¨#0000FF¨»«mn mathvariant=¨bold¨»33«/mn»«mo mathvariant=¨bold¨».«/mo»«msup»«mn mathvariant=¨bold¨»33«/mn»«mn mathvariant=¨bold¨»2«/mn»«/msup»«mo mathvariant=¨bold¨»+«/mo»«msup»«mn mathvariant=¨bold¨»5«/mn»«mn mathvariant=¨bold¨»2«/mn»«/msup»«/msqrt»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»=«/mo»«msqrt mathcolor=¨#0000FF¨»«mn mathvariant=¨bold¨»1135«/mn»«mo mathvariant=¨bold¨».«/mo»«mn mathvariant=¨bold¨»88«/mn»«/msqrt»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»§#160;«/mo»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»=«/mo»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»§#160;«/mo»«mn mathvariant=¨bold¨ mathcolor=¨#0000FF¨»33«/mn»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨».«/mo»«mn mathvariant=¨bold¨ mathcolor=¨#0000FF¨»7«/mn»«mfrac mathcolor=¨#0000FF¨»«mi mathvariant=¨bold¨»m«/mi»«mi mathvariant=¨bold¨»s«/mi»«/mfrac»«/math»
נמצא את כיוון תנועת הכדור לאחר החבטה , בעזרת זהות הטנגנס :
«math xmlns=¨http://www.w3.org/1998/Math/MathML¨»«mi mathvariant=¨bold¨ mathcolor=¨#0000FF¨»tan«/mi»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»(«/mo»«mi mathvariant=¨bold¨ mathcolor=¨#0000FF¨»§#945;«/mi»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»)«/mo»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»=«/mo»«mfrac mathcolor=¨#0000FF¨»«msub»«mi mathvariant=¨bold¨»V«/mi»«mi mathvariant=¨bold¨»Y«/mi»«/msub»«msub»«mi mathvariant=¨bold¨»V«/mi»«mi mathvariant=¨bold¨»X«/mi»«/msub»«/mfrac»«mspace linebreak=¨newline¨/»«mspace linebreak=¨newline¨/»«mi mathvariant=¨bold¨ mathcolor=¨#0000FF¨»§#945;«/mi»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»=«/mo»«mi mathvariant=¨bold¨ mathcolor=¨#0000FF¨»shift«/mi»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»§#160;«/mo»«mi mathvariant=¨bold¨ mathcolor=¨#0000FF¨»tan«/mi»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»(«/mo»«mfrac mathcolor=¨#0000FF¨»«msub»«mi mathvariant=¨bold¨»V«/mi»«mi mathvariant=¨bold¨»Y«/mi»«/msub»«msub»«mi mathvariant=¨bold¨»V«/mi»«mi mathvariant=¨bold¨»X«/mi»«/msub»«/mfrac»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»)«/mo»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»=«/mo»«mi mathvariant=¨bold¨ mathcolor=¨#0000FF¨»shift«/mi»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»§#160;«/mo»«mi mathvariant=¨bold¨ mathcolor=¨#0000FF¨»tan«/mi»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»(«/mo»«mfrac mathcolor=¨#0000FF¨»«mn mathvariant=¨bold¨»5«/mn»«mrow»«mn mathvariant=¨bold¨»33«/mn»«mo mathvariant=¨bold¨».«/mo»«mn mathvariant=¨bold¨»33«/mn»«/mrow»«/mfrac»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»)«/mo»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»=«/mo»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»=«/mo»«mi mathvariant=¨bold¨ mathcolor=¨#0000FF¨»shift«/mi»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»§#160;«/mo»«mi mathvariant=¨bold¨ mathcolor=¨#0000FF¨»tan«/mi»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»(«/mo»«mn mathvariant=¨bold¨ mathcolor=¨#0000FF¨»0«/mn»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨».«/mo»«mn mathvariant=¨bold¨ mathcolor=¨#0000FF¨»15«/mn»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»)«/mo»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»=«/mo»«mn mathvariant=¨bold¨ mathcolor=¨#0000FF¨»8«/mn»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨».«/mo»«mn mathvariant=¨bold¨ mathcolor=¨#0000FF¨»53«/mn»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»§#176;«/mo»«/math»
לאחר החבטה הכדור נע במהירות 33.7 מטר לשנייה , בכיוון 8.53 מעלות מעל האופק.
1. نظرًا لأن الضربة
أفقية، فإن قوة الضربة ليس لها أي تأثير على الاتجاه الرأسي.
إذا كانت الضربة في أي زاوية بالنسبة إلى
الأفق، فسيكون للضربة أيضًا تأثير على السرعة الرأسية.
في مثل هذه الحالة، يجب إجراء تحليل قائم الزاوية
لقوة الضربة وحساب تغير الزخم في كل اتجاه على حدة.
2. مُعطى أن
اللاعب يضرب الكرة في اتجاه أفقي، وليس في أي اتجاه، يمكنك اختيار أي اتجاه أفقي
بشكل اعتباطي.
3. أثناء الضربة،
تؤثر قوة الجاذبية أيضًا على الكرة، لكنها مهملة مقارنة بقوة الضربة. لهذا السبب
لم نأخذها في الاعتبار في الحل.
من المفضل الإشارة أن قوة الجاذبية تعمل
أيضًا، والاشارة على أنها مهملة.
4. في هذه
الحالة، بعد الضربة، تتحرك الكرة في حركة باليستية، في رمي بزاوية.
2. נתון שהשחקן חובט בכדור בכיוון אופקי , לא נתון באיזה כיוון , אפשר לבחור שרירותית כל כיוון אופקי.
3. בזמן החבטה גם כוח הכובד משפיעה על הכדור ,אך הוא זניח ביחס לכוח החבטה. לכן לא התייחסנו אליו בפתרון. כדאי לציין את העובדה שגם כוח הכובד פועל , ולציין שהוא זניח .
4. במקרה זה , לאחר החבטה הכדור נע בתנועה בליסטית ,בזריקה בזווית.
...
1- صحيح.
2- غير صحيح.
3- غير صحيح.
2- לא נכון.
3- לא נכון.
2- לא נכון.
3
كمية الحركة هي كمية متّجهة إذا كان هناك تغيير في اتجاه الحركة هناك تغيير في كمية الحركة.
الطاقة الحركية هي كمية عددية (سكلار)، والتغيير في اتجاه الحركة وحده لا يغير الطاقة الحركية.
האנרגיה הקינטית היא גודל סקלארי , שינוי בכיוון התנועה בלבד לא משנה את האנרגיה הקינטית.
1- صحيح - لكن التغيير في كمية حركة الأرض ضئيل لأن كتلتها كبيرة جدًا.
التفسير: مقدار سرعة الكرة لا يتغير ، لكن اتجاه حركتها ، الزخم متجه ، وبالتالي فإن اتجاهها مهم.
2- غير صحيح - هناك تغيير ولكنه ضئيل.
التفسير: يمكن اعتبار كتلة الأرض وكتلة الكرة جسمين متصادمين.
بغض النظر عن القوى التي يشغلها الجسمان على بعضهما البعض، لا توجد قوى خارجية تعمل عليهما، لذا تُحفظ كمية الحركة الكلية، ولا تحفظ كمية الحركة لكل منهما.
3- غير صحيح - فالطاقة الحركية لا تتغير.
التفسير: الطاقة الحركية ، مثل كل الطاقة ، هي كمية عددية (سكلار)، تغيرت السرعة في الاتجاه ، وليس في المقدار ، وبالتالي لا يوجد تغيير في الطاقة الحركية.
נימוק: גודל המהירות של הכדור לא משתנה , אך כיוון תנועתו , התנע הוא ווקטור , לכן יש חשיבות לכיוונו.
2- לא נכון - חל שינוי אך הוא זניח.
נימוק: אפשר להתייחס למסת כדור הארץ ולמסת הכדור כאל שני גופים המתנגשים.
מלבד הכוחות שהם מפעילים אחד על השני לא פועלים כוחות חיצוניים, התנע הכולל נשמר, התנע של כול אחד מהם לא נשמר.
3- לא נכון - האנרגיה הקינטית לא משתנה.
נימוק: אנרגיה קינטית כמו כל אנרגיה היא גודל סקלרי , המהירות שונה בכיוונה לא בגודלה , לכן אין שינוי באנרגיה הקינטית.
يمكنك القول أن كمية الحركة للكرة الأرضية لا يتغير لأن كتلتها كبيرة جدًا. وثم ...
1- غير صحيح.
2- صحيح.
3- غير صحيح.
ويمكنك القول أن كمية الحركة للكرة الأرضية يتغير بالفعل ، لكن التغيير مهمل.
1- صحيح.
2- غير صحيح.
3- غير صحيح.
1- לא נכון.
2-נכון.
3- לא נכון .
אפשר להגיד שהתנע של כדור הארץ כן משתנה אך השינוי הוא זניח.
1- נכון.
2- לא נכון.
3- לא נכון.






 ____________________________________________________________________________
____________________________________________________________________________