41. 1986,1- حركة تحت تأثير قوة متغيرة

______________________________________________________________________________________
...
يتحرك الجسم بتسارع متغيرة آخذ بالازدياد.
رسم مخطط القوى ، وكتابة معادلات الحركة ، والتعبير عن التسارع من معادلات الحركة. من التعبير عن التسارع يمكن أن نفهم طبيعة الحركة.
نرسم مخطط القوى المؤثرة على الجسم:
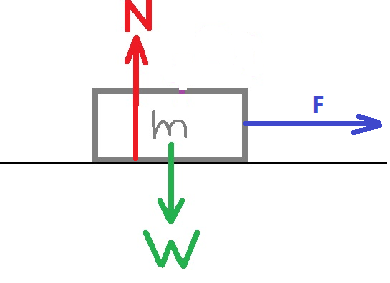
نكتب معادلات الحركة في الاتجاه الأفقي وفي الاتجاه العمودي:
«math xmlns=¨http://www.w3.org/1998/Math/MathML¨»«mstyle mathsize=¨20px¨»«msub»«mi mathvariant=¨bold¨ mathcolor=¨#0000FF¨»§#931;F«/mi»«mi mathvariant=¨bold¨ mathcolor=¨#0000FF¨»y«/mi»«/msub»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»=«/mo»«mn mathvariant=¨bold¨ mathcolor=¨#0000FF¨»0«/mn»«mspace linebreak=¨newline¨»«/mspace»«mi mathvariant=¨bold¨ mathcolor=¨#0000FF¨»N«/mi»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»=«/mo»«mi mathvariant=¨bold¨ mathcolor=¨#0000FF¨»W«/mi»«mspace linebreak=¨newline¨»«/mspace»«menclose mathcolor=¨#0000FF¨ notation=¨box¨»«mi mathvariant=¨bold¨»N«/mi»«mo mathvariant=¨bold¨»=«/mo»«mi mathvariant=¨bold¨»m«/mi»«mo mathvariant=¨bold¨»§#183;«/mo»«mi mathvariant=¨bold¨»g«/mi»«/menclose»«/mstyle»«/math» «math xmlns=¨http://www.w3.org/1998/Math/MathML¨»«mstyle mathsize=¨20px¨»«msub»«mi mathvariant=¨bold¨ mathcolor=¨#0000FF¨»§#931;F«/mi»«mi mathvariant=¨bold¨ mathcolor=¨#0000FF¨»X«/mi»«/msub»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»=«/mo»«mi mathvariant=¨bold¨ mathcolor=¨#0000FF¨»m«/mi»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»§#183;«/mo»«mi mathvariant=¨bold¨ mathcolor=¨#0000FF¨»a«/mi»«mspace linebreak=¨newline¨»«/mspace»«menclose mathcolor=¨#0000FF¨ notation=¨box¨»«mi mathvariant=¨bold¨»F«/mi»«mo mathvariant=¨bold¨»=«/mo»«mi mathvariant=¨bold¨»m«/mi»«mo mathvariant=¨bold¨»§#183;«/mo»«mi mathvariant=¨bold¨»a«/mi»«/menclose»«mspace linebreak=¨newline¨»«/mspace»«mspace linebreak=¨newline¨»«/mspace»«mspace linebreak=¨newline¨»«/mspace»«/mstyle»«/math»
نعبر عن التسارع من معادلة الحركة الأفقية:
«math xmlns=¨http://www.w3.org/1998/Math/MathML¨»«mstyle mathsize=¨20px¨»«menclose mathcolor=¨#0000FF¨ notation=¨box¨»«mi mathvariant=¨bold¨»F«/mi»«mo mathvariant=¨bold¨»=«/mo»«mi mathvariant=¨bold¨»m«/mi»«mo mathvariant=¨bold¨»§#183;«/mo»«mi mathvariant=¨bold¨»a«/mi»«/menclose»«mspace linebreak=¨newline¨»«/mspace»«mi mathvariant=¨bold¨ mathcolor=¨#0000FF¨»a«/mi»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»=«/mo»«mfrac mathcolor=¨#0000FF¨»«mi mathvariant=¨bold¨»F«/mi»«mi mathvariant=¨bold¨»m«/mi»«/mfrac»«mspace linebreak=¨newline¨»«/mspace»«mspace linebreak=¨newline¨»«/mspace»«mspace linebreak=¨newline¨»«/mspace»«/mstyle»«/math»
القوة الأفقية المؤثرة على الجسم تزداد بوتيرة ثابته في الثواني الأربع الأولى.
من تعبير التسارع ، يزداد التسارع أيضًا في هذه الثواني الأربع. لذلك ، يتحرك الجسم بتسارع متغيرة F
عندما تؤثر قوة ثابتة على جسم ، فإنه يتحرك بسرعة تزداد بوتيرة ثابتة، تسارع ثابت.
حتى عندما تؤثر قوة متزايدة على الجسم ، تزداد سرعته ، ولكن بوتيرة متزايدة ، تسارع آخذ بالازدياد.
لذلك ، عندما يتحرك الجسم بسرعة متغيرة ،نميّز حركته بالتسارع وليس بالسرعة.
גם כאשר פועל על גוף כוח הולך וגדל ,מהירותו הולכת וגדלה, אך בקצב הולך וגדל, בתאוצה הולכת וגדלה.
לכן , כאשר גוף נע במהירות משתנה ,תנועתו מאופיינת על ידי התאוצה ולא ע"י המהירות.
______________________________________________________________________________________

______________________________________________________________________________________
...
«math xmlns=¨http://www.w3.org/1998/Math/MathML¨»«mi mathvariant=¨bold¨»a«/mi»«mo mathvariant=¨bold¨»(«/mo»«mn mathvariant=¨bold¨»4«/mn»«mo mathvariant=¨bold¨»)«/mo»«mo mathvariant=¨bold¨»=«/mo»«mn mathvariant=¨bold¨»3«/mn»«mfrac»«mi mathvariant=¨bold¨»m«/mi»«msup»«mi mathvariant=¨bold¨»s«/mi»«mn mathvariant=¨bold¨»2«/mn»«/msup»«/mfrac»«mo mathvariant=¨bold¨»§#160;«/mo»«mo mathvariant=¨bold¨»§#160;«/mo»«mo mathvariant=¨bold¨»§#160;«/mo»«mo mathvariant=¨bold¨»§#160;«/mo»«mo mathvariant=¨bold¨»§#160;«/mo»«mo mathvariant=¨bold¨»§#160;«/mo»«mo mathvariant=¨bold¨»§#160;«/mo»«mo mathvariant=¨bold¨»§#160;«/mo»«mo mathvariant=¨bold¨»§#160;«/mo»«mo mathvariant=¨bold¨»§#160;«/mo»«mo mathvariant=¨bold¨»§#160;«/mo»«mo mathvariant=¨bold¨»§#160;«/mo»«mo mathvariant=¨bold¨»§#160;«/mo»«mo mathvariant=¨bold¨»§#160;«/mo»«mi mathvariant=¨bold¨»V«/mi»«mo mathvariant=¨bold¨»(«/mo»«mn mathvariant=¨bold¨»4«/mn»«mo mathvariant=¨bold¨»)«/mo»«mo mathvariant=¨bold¨»=«/mo»«mn mathvariant=¨bold¨»9«/mn»«mfrac»«mi mathvariant=¨bold¨»m«/mi»«mi mathvariant=¨bold¨»s«/mi»«/mfrac»«mo mathvariant=¨bold¨»§#160;«/mo»«mo mathvariant=¨bold¨»§#160;«/mo»«mo mathvariant=¨bold¨»§#160;«/mo»«mo mathvariant=¨bold¨»§#160;«/mo»«mo mathvariant=¨bold¨»§#160;«/mo»«mo mathvariant=¨bold¨»§#160;«/mo»«/math»
إيجاد التسارع في اللحظة t = 4s باستخدام تعبير التسارع الناتج من معادلة الحركة.
إيجاد السرعة في اللحظة t = 4s بمساعدة دالة سرعة للزمن المناسبة لتسارع ثابت ، باستخدام متوسط التسارع.
מציאת המהירות ברגע t=4s בעזרת פונקציית מהירות זמן המתאימה לתאוצה קבועה , באמצעות התאוצה הממוצעת.
لنفترض أن الجسم يتحرك إلى اليمين، ونصف حركة الجسم بالنسبة لمحور الحركة الذي اتجاهه في اتجاه الحركة إلى اليمين.
تسارع الجسم في اللحظة t = 4s يتعلق فقط على القوة المؤثرة على الجسم في اللحظة t = 4s وكتلة الجسم.
يمكن أن نرى من الرسم البياني أن مقدار القوة المؤثرة على الجسم في اللحظة t = 4s يساوي 6 نيوتن.
نجد التسارع في اللحظة t = 4s باستخدام تعبير التسارع من القسم السابق :
«math xmlns=¨http://www.w3.org/1998/Math/MathML¨»«mstyle mathsize=¨20px¨»«mi mathvariant=¨bold¨ mathcolor=¨#0000FF¨»a«/mi»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»(«/mo»«mi mathvariant=¨bold-italic¨ mathcolor=¨#0000FF¨»t«/mi»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»)«/mo»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»=«/mo»«mfrac mathcolor=¨#0000FF¨»«mrow»«mi mathvariant=¨bold¨»F«/mi»«mo mathvariant=¨bold¨»(«/mo»«mi mathvariant=¨bold-italic¨»t«/mi»«mo mathvariant=¨bold¨»)«/mo»«/mrow»«mi mathvariant=¨bold¨»m«/mi»«/mfrac»«mspace linebreak=¨newline¨»«/mspace»«mi mathvariant=¨bold¨ mathcolor=¨#0000FF¨»a«/mi»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»(«/mo»«mn mathvariant=¨bold¨ mathcolor=¨#0000FF¨»4«/mn»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»)«/mo»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»=«/mo»«mfrac mathcolor=¨#0000FF¨»«mrow»«mi mathvariant=¨bold¨»F«/mi»«mo mathvariant=¨bold¨»(«/mo»«mn mathvariant=¨bold¨»4«/mn»«mo mathvariant=¨bold¨»)«/mo»«/mrow»«mi mathvariant=¨bold¨»m«/mi»«/mfrac»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»=«/mo»«mfrac mathcolor=¨#0000FF¨»«mn mathvariant=¨bold¨»6«/mn»«mn mathvariant=¨bold¨»2«/mn»«/mfrac»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»=«/mo»«mn mathvariant=¨bold¨ mathcolor=¨#0000FF¨»3«/mn»«mfrac mathcolor=¨#0000FF¨»«mi mathvariant=¨bold¨»m«/mi»«msup»«mi mathvariant=¨bold¨»s«/mi»«mn mathvariant=¨bold¨»2«/mn»«/msup»«/mfrac»«mspace linebreak=¨newline¨»«/mspace»«mspace linebreak=¨newline¨»«/mspace»«mspace linebreak=¨newline¨»«/mspace»«/mstyle»«/math»
تسارع لجسم في اللحظة t = 4s تساوي 3m/s2، والتسارع موجب وموجه إلى اليمين.
نجد سرعة الجسم في اللحظة t = 4s.
يتحرك الجسم بتسارع متغير، فلا يمكن استخدام تعبير السرعة كدالة للزمن التي تلائم تسارعًا ثابتًا.
يتزايد التسارع بوتيرة ثابتة، ومن الممكن حساب متوسط التسارع في الثواني الأربع الأولى وفقًا لمتوسط حسابي بسيط.
«math xmlns=¨http://www.w3.org/1998/Math/MathML¨»«menclose mathcolor=¨#0000FF¨ notation=¨top¨»«mi mathvariant=¨bold¨»a«/mi»«/menclose»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»=«/mo»«mfrac mathcolor=¨#0000FF¨»«mrow»«mi mathvariant=¨bold¨»a«/mi»«mo mathvariant=¨bold¨»(«/mo»«mn mathvariant=¨bold¨»0«/mn»«mo mathvariant=¨bold¨»)«/mo»«mo mathvariant=¨bold¨»+«/mo»«mi mathvariant=¨bold¨»a«/mi»«mo mathvariant=¨bold¨»(«/mo»«mn mathvariant=¨bold¨»4«/mn»«mo mathvariant=¨bold¨»)«/mo»«/mrow»«mn mathvariant=¨bold¨»2«/mn»«/mfrac»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»=«/mo»«mfrac mathcolor=¨#0000FF¨»«mrow»«mn mathvariant=¨bold¨»0«/mn»«mo mathvariant=¨bold¨»+«/mo»«mn mathvariant=¨bold¨»3«/mn»«/mrow»«mn mathvariant=¨bold¨»2«/mn»«/mfrac»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»=«/mo»«mn mathvariant=¨bold¨ mathcolor=¨#0000FF¨»1«/mn»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨».«/mo»«mn mathvariant=¨bold¨ mathcolor=¨#0000FF¨»5«/mn»«mfrac mathcolor=¨#0000FF¨»«mi mathvariant=¨bold¨»m«/mi»«msup»«mi mathvariant=¨bold¨»s«/mi»«mn mathvariant=¨bold¨»2«/mn»«/msup»«/mfrac»«/math»
نستخدم دالة السرعة كدالة للزمن المناسبة لتسارع ثابت ، ونجد سرعة الجسم في اللحظة t = 4s باستخدام متوسط التسارع.
«math xmlns=¨http://www.w3.org/1998/Math/MathML¨»«mi mathvariant=¨bold¨ mathcolor=¨#0000FF¨»V«/mi»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»(«/mo»«mi mathvariant=¨bold¨ mathcolor=¨#0000FF¨»t«/mi»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»)«/mo»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»=«/mo»«msub»«mi mathvariant=¨bold¨ mathcolor=¨#0000FF¨»V«/mi»«mn mathvariant=¨bold¨ mathcolor=¨#0000FF¨»0«/mn»«/msub»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»+«/mo»«menclose mathcolor=¨#0000FF¨ notation=¨top¨»«mi mathvariant=¨bold¨»a«/mi»«/menclose»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»§#183;«/mo»«mi mathvariant=¨bold¨ mathcolor=¨#0000FF¨»t«/mi»«mspace linebreak=¨newline¨»«/mspace»«mi mathvariant=¨bold¨ mathcolor=¨#0000FF¨»V«/mi»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»(«/mo»«mn mathvariant=¨bold¨ mathcolor=¨#0000FF¨»4«/mn»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»)«/mo»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»=«/mo»«mn mathvariant=¨bold¨ mathcolor=¨#0000FF¨»3«/mn»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»+«/mo»«mn mathvariant=¨bold¨ mathcolor=¨#0000FF¨»1«/mn»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨».«/mo»«mn mathvariant=¨bold¨ mathcolor=¨#0000FF¨»5«/mn»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»§#183;«/mo»«mn mathvariant=¨bold¨ mathcolor=¨#0000FF¨»4«/mn»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»=«/mo»«mn mathvariant=¨bold¨ mathcolor=¨#0000FF¨»9«/mn»«mfrac mathcolor=¨#0000FF¨»«mi mathvariant=¨bold¨»m«/mi»«mi mathvariant=¨bold¨»s«/mi»«/mfrac»«mspace linebreak=¨newline¨»«/mspace»«/math»
מהגרף ניתן לראות שגודלו של הכוח הפועל על הגוף ברגע t=4d הוא 6 ניוטון.
נמצא את התאוצה ברגע t=4s , בעזרת ביטוי התאוצה מהסעיף הקודם:
1. من المهم تحديد محور الحركة قبل كتابة الحل ، وتحديد السرعة والتسارع بالنسبة للمحور المحدّد.
2. في السؤال لم يتم كتابة ما هو بالضبط اتجاه حركة الجسم ، فمن الممكن أن نفترض أن الجسم يتحرك في اتجاه معين وحل السؤال وفقا لذلك.
في هذا القسم ، يجب أن يكون اتجاه القوة هو نفسه اتجاه الحركة.
3. بعد إيجاد مقدار السرعة والتسارع ، يجب أيضًا الإشارة لاتجاههما.
2. לאחר מציאת גודלם של המהירות והתאוצה , יש לציין גם את כיוון המהירות וכיוון התאוצה.
______________________________________________________________________________________

...
«math xmlns=¨http://www.w3.org/1998/Math/MathML¨»«mi mathvariant=¨bold¨»a«/mi»«mo mathvariant=¨bold¨»(«/mo»«mn mathvariant=¨bold¨»4«/mn»«mo mathvariant=¨bold¨»)«/mo»«mo mathvariant=¨bold¨»=«/mo»«mo mathvariant=¨bold¨»-«/mo»«mn mathvariant=¨bold¨»3«/mn»«mfrac»«mi mathvariant=¨bold¨»m«/mi»«msup»«mi mathvariant=¨bold¨»s«/mi»«mn mathvariant=¨bold¨»2«/mn»«/msup»«/mfrac»«mo mathvariant=¨bold¨»§#160;«/mo»«mo mathvariant=¨bold¨»§#160;«/mo»«mo mathvariant=¨bold¨»§#160;«/mo»«mo mathvariant=¨bold¨»§#160;«/mo»«mo mathvariant=¨bold¨»§#160;«/mo»«mo mathvariant=¨bold¨»§#160;«/mo»«mo mathvariant=¨bold¨»§#160;«/mo»«mo mathvariant=¨bold¨»§#160;«/mo»«mo mathvariant=¨bold¨»§#160;«/mo»«mo mathvariant=¨bold¨»§#160;«/mo»«mo mathvariant=¨bold¨»§#160;«/mo»«mo mathvariant=¨bold¨»§#160;«/mo»«mo mathvariant=¨bold¨»§#160;«/mo»«mo mathvariant=¨bold¨»§#160;«/mo»«mi mathvariant=¨bold¨»V«/mi»«mo mathvariant=¨bold¨»(«/mo»«mn mathvariant=¨bold¨»4«/mn»«mo mathvariant=¨bold¨»)«/mo»«mo mathvariant=¨bold¨»=«/mo»«mo mathvariant=¨bold¨»-«/mo»«mn mathvariant=¨bold¨»3«/mn»«mfrac»«mi mathvariant=¨bold¨»m«/mi»«mi mathvariant=¨bold¨»s«/mi»«/mfrac»«mo mathvariant=¨bold¨»§#160;«/mo»«mo mathvariant=¨bold¨»§#160;«/mo»«mo mathvariant=¨bold¨»§#160;«/mo»«mo mathvariant=¨bold¨»§#160;«/mo»«mo mathvariant=¨bold¨»§#160;«/mo»«mo mathvariant=¨bold¨»§#160;«/mo»«/math»
يتغير اتجاه القوة. تتغير إشارة القوة بالنسبة للمحور المحدّد.
تعمل القوة في الاتجاه المعاكس للحركة، بالنسبة إلى المحور المحدّد ، والقوة سالبة ، ووفقًا للقانون الثاني لنيوتن، فإن تسارعها سالب أيضًا.
لا يتغير مقدار التسارع، وبالتالي فإن التسارع هو «math xmlns=¨http://www.w3.org/1998/Math/MathML¨»«mi mathvariant=¨bold-italic¨ mathcolor=¨#0000FF¨»a«/mi»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»=«/mo»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»-«/mo»«mn mathvariant=¨bold¨ mathcolor=¨#0000FF¨»3«/mn»«mfrac mathcolor=¨#0000FF¨»«mi mathvariant=¨bold¨»m«/mi»«msup»«mi mathvariant=¨bold¨»s«/mi»«mn mathvariant=¨bold¨»2«/mn»«/msup»«/mfrac»«/math» , اتجاهه باتجاه القوة ، إلى اليسار.
نجد سرعة الجسم في اللحظة t = 4s باستخدام دالة السرعة كدالة للزمن:
لا يتغير مقدار متوسط التسارع فقط تتغير إشارته: «math xmlns=¨http://www.w3.org/1998/Math/MathML¨»«menclose mathcolor=¨#0000FF¨ notation=¨top¨»«mi mathvariant=¨bold¨»a«/mi»«/menclose»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»=«/mo»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»-«/mo»«mn mathvariant=¨bold¨ mathcolor=¨#0000FF¨»1«/mn»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨».«/mo»«mn mathvariant=¨bold¨ mathcolor=¨#0000FF¨»5«/mn»«mfrac mathcolor=¨#0000FF¨»«mi mathvariant=¨bold¨»m«/mi»«msup»«mi mathvariant=¨bold¨»s«/mi»«mn mathvariant=¨bold¨»2«/mn»«/msup»«/mfrac»«/math».
«math xmlns=¨http://www.w3.org/1998/Math/MathML¨»«mi mathvariant=¨bold¨ mathcolor=¨#0000FF¨»V«/mi»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»(«/mo»«mi mathvariant=¨bold¨ mathcolor=¨#0000FF¨»t«/mi»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»)«/mo»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»=«/mo»«msub»«mi mathvariant=¨bold¨ mathcolor=¨#0000FF¨»V«/mi»«mn mathvariant=¨bold¨ mathcolor=¨#0000FF¨»0«/mn»«/msub»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»+«/mo»«menclose mathcolor=¨#0000FF¨ notation=¨top¨»«mi mathvariant=¨bold¨»a«/mi»«/menclose»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»§#183;«/mo»«mi mathvariant=¨bold¨ mathcolor=¨#0000FF¨»t«/mi»«mspace linebreak=¨newline¨»«/mspace»«mi mathvariant=¨bold¨ mathcolor=¨#0000FF¨»V«/mi»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»(«/mo»«mn mathvariant=¨bold¨ mathcolor=¨#0000FF¨»4«/mn»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»)«/mo»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»=«/mo»«mn mathvariant=¨bold¨ mathcolor=¨#0000FF¨»3«/mn»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»-«/mo»«mn mathvariant=¨bold¨ mathcolor=¨#0000FF¨»1«/mn»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨».«/mo»«mn mathvariant=¨bold¨ mathcolor=¨#0000FF¨»5«/mn»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»§#183;«/mo»«mn mathvariant=¨bold¨ mathcolor=¨#0000FF¨»4«/mn»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»=«/mo»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»-«/mo»«mn mathvariant=¨bold¨ mathcolor=¨#0000FF¨»3«/mn»«mfrac mathcolor=¨#0000FF¨»«mi mathvariant=¨bold¨»m«/mi»«mi mathvariant=¨bold¨»s«/mi»«/mfrac»«mspace linebreak=¨newline¨»«/mspace»«/math»
في هذه الحالة ، في اللحظة t = 4s ، يكون مقدار السرعة 3 أمتار في الثانية ، واتجاهها إلى اليسار ، عكس اتجاه المحور.
גודל התאוצה לא משתנה , לכן התאוצה היא «math xmlns=¨http://www.w3.org/1998/Math/MathML¨»«mi mathvariant=¨bold-italic¨ mathcolor=¨#0000FF¨»a«/mi»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»=«/mo»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»-«/mo»«mn mathvariant=¨bold¨ mathcolor=¨#0000FF¨»3«/mn»«mfrac mathcolor=¨#0000FF¨»«mi mathvariant=¨bold¨»m«/mi»«msup»«mi mathvariant=¨bold¨»s«/mi»«mn mathvariant=¨bold¨»2«/mn»«/msup»«/mfrac»«/math» , כיוון ככיוון הכוח שמאלה.
נמצא את מהירות הגוף ברגע t=4s בעזרת פונקציית המהירות בתלות בזמן:
התאוצה הממוצעת לא משתנה בגודלה רק בסימונה: «math xmlns=¨http://www.w3.org/1998/Math/MathML¨»«menclose mathcolor=¨#0000FF¨ notation=¨top¨»«mi mathvariant=¨bold¨»a«/mi»«/menclose»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»=«/mo»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»-«/mo»«mn mathvariant=¨bold¨ mathcolor=¨#0000FF¨»1«/mn»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨».«/mo»«mn mathvariant=¨bold¨ mathcolor=¨#0000FF¨»5«/mn»«mfrac mathcolor=¨#0000FF¨»«mi mathvariant=¨bold¨»m«/mi»«msup»«mi mathvariant=¨bold¨»s«/mi»«mn mathvariant=¨bold¨»2«/mn»«/msup»«/mfrac»«/math».
من حيث المبدأ، من الممكن اختيار اتجاه محور حركة مختلف لكل قسم ، لتجنب حدوث ارتباك لا داعي له ، يوصى بعدم استخدام نفس محور الحركة في جميع الحالات.
______________________________________________________________________________________

______________________________________________________________________________________
...
يكون تسارع الجسم صفرًا ، يستمر في التحرك إلى اليمين بسرعة ابتدائية مقدارها 3 أمتار في الثانية.
مخطط القوى، القانون الأول لنيوتن.
نرسم مخطط القوى للحالة الجديدة:
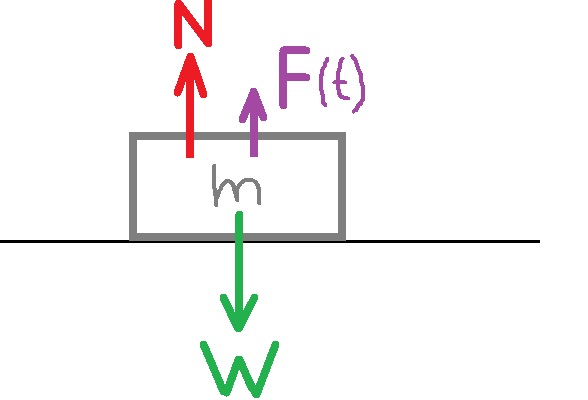
لا تعمل أي قوة في الاتجاه الأفقي ، ومحصلة القوى في الاتجاه الأفقي هي صفر ، من القانون الأول لنيوتن، يكون الجسم متزنًا، وسيكون تسارع الجسم صفرًا.
سيستمر الجسم في التحرك إلى اليمين بسرعة ابتدائية V0 وهي 3 أمتار في الثانية.
وزن الجسم 20 نيوتن وأقصى مقدار للقوة F يساوي 6 نيوتن. القوة لا ترفع F الجسم عن الأرض.
משקל הגוף הוא 20 ניוטון גודלו המקסימאלי של הכוח F הוא 6 ניוטון. הכוח F לא מרים את הגוף מהקרקע .
1. حتى إذا كان هناك تغيير طفيف "فقط" في إحدى القوى ، فمن المهم جدًا بدء الحل من خلال رسم مخطط قوى جديد.
2. التأثير الوحيد للقوة F سيكون على القوة العمودية. مجموع القوى في الاتجاه العمودي هو صفر ، عندما تزيد القوة F تقل القوة العمودية.