حلول ومنتديات لألبوم الحلول - الديناميكا في خط مستقيم

______________________________________________________________________________________

• مجلد
• الجواب النهائي
• استراتيجية
• الحل الكامل
• انتبهوا

...

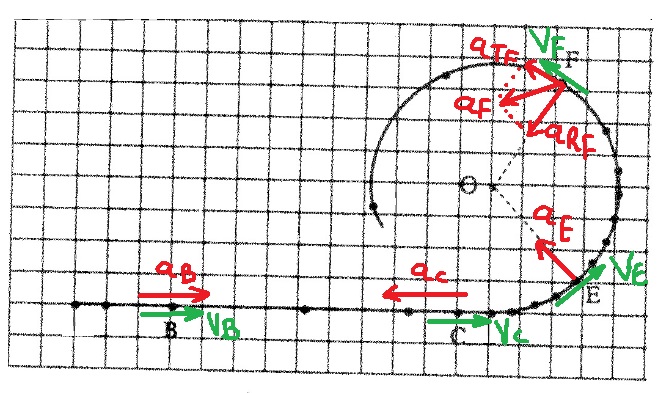
في الشكل التالي ، تم تمثيل متجهات السرعة بأسهم خضراء ، ومتجهات التسارع معروضة بأسهم حمراء.

وفقًا للسؤال ، تصف المتجهات الاتجاه فقط.

במקרה זה ,בהתאם לשאלה ,הווקטורים מתארים את הכיוון בלבד.

من تعريف السرعة ، اتجاه السرعة هو اتجاه الحركة ، من القانون الثاني اتجاه تسارع الجسم هو اتجاه محصلة القوى . 

من تعريف السرعة ، يكون اتجاه متجّه السرعة هو اتجاه الحركة. لهذا فإن اتجاه السرعة مماس دائمًا للمسار.

في الشكل التالي ، تم تحديد متجهات السرعة الأربعة باللون الأخضر في كل نقطة من النقاط الأربع ،وفقًا لاتجاه الحركة في كل نقطة. 

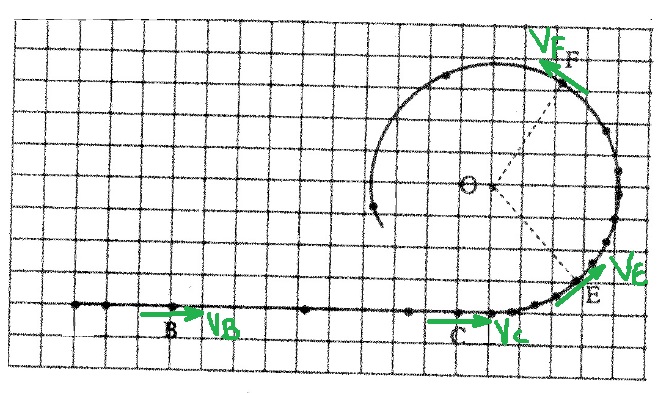
* في هذه الحالة ، بناءً على السؤال ، تصف المتجهات الاتجاه فقط.

اتجاه متجه التسارع هو نفس اتجاه متجّه القوة المحصّلة.

في النقطة B - من توزيع النقاط ، يمكن ملاحظة أنه في النقطة B تزداد السرعة ، واتجاه القوة المحصّلة هو نفس اتجاه الحركة إلى اليمين ، واتجاه تسارع الجسم هو إلى اليمين.

في النقطة C - من توزيع النقاط ، تقل  السرعة في النقطة C ، واتجاه القوة المحصّلة في الاتجاه المعاكس للحركة ، واتجاه التسارع إلى اليسار.

في النقطة E - من توزيع النقاط ، لا يوجد تغيير في مقدار السرعة فقط اتجاه الحركة يتغير، تعمل القوة في اتجاه عمودي على الحركة نحو مركز الدوران ،

                اتجاه التسارع نحو مركز الدائرة ، وهذا التسارع يسمى تسارع مركزي - תאוצה צנטריפטאלית .

في النقطة F- تتغير السرعة في المقدار، وبالتالي هناك تسارع مماسي ، ولكن هناك أيضًا تغيير في اتجاه الحركة، وبالتالي هناك أيضًا تسارع مركزي.

                لذلك ، هناك مركّب للقوة المحصّلة في الاتجاه مماس للمسار الذي يسبب التسارع المماسي ، وهناك مركّب للقوة المحصّلة في الاتجاه المركزي الذي يسبب التسارع المركزي.

                اتجاه التسارع في اتجاه القوة المحصّلة. (يُظهر الرسم البياني أيضًا التسارع المركزي والماسي في النقطة F).

نُضيف متجهات التسارع في النقاط الأربع باللون الأحمر.

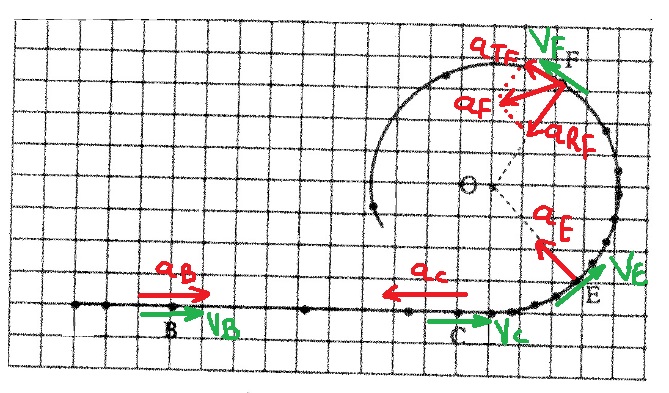
في أي تعريف أو قانون معروض في معادلة متجّهيه ، يجب الانتباه إلى اتجاهات المقادير الفيزيائية التي تظهر في التعبير.

يعتمد حل هذا السؤال على رؤيتين مهمتين:

1. من تعريف السرعة ، يكون اتجاه متجّه السرعة هو نفسه اتجاه متجّه الازاحة ، وبالتالي يكون اتجاه متجّه السرعة هو نفسه اتجاه الحركة.

2. من القانون الثاني لنيوتن، اتجاه تسارع الجسم ، باتجاه القوة المحصّلة المؤثرة على الجسم.

______________________________________________________________________________________

______________________________________________________________________________________

• مجلد
• الجواب النهائي
• استراتيجية
• الحل الكامل
• انتبهوا

...

السرعة عند النقطة B أكبر من السرعة في النقطة C.  

السرعة اللحظية في نقطة معينة تساوي تقريبًا متوسط ​​السرعة في مقطع الحركة بين نقطة قبل النقطة المعينة ونقطة بعد تلك النقطة المعينة.

باستخدام متوسط ​​السرعات يمكنك معرفة السرعات اللحظية.

יש להשוות בין המהירויות הממוצעות , ומהשוואה זו להגיע למסקנה על המהירויות הרגעיות.  

כדי להשוות בין המהירויות הרגעיות בשתי נקודות יש להשוות בין המהירויות הממוצעות של התנועות סביב אותן נקודות. 

نُشير للنقطة قبل النقطة  B على أنها النقطة B₀ ، والنقطة بعد النقطة B على أنها B.

وبالمثل ، نُشير للنقطة قبل النقطة D على أنها D₀ ، والنقطة بعد النقطة D على أنها D.

هذه النقاط موضحة في الشكل التالي: 

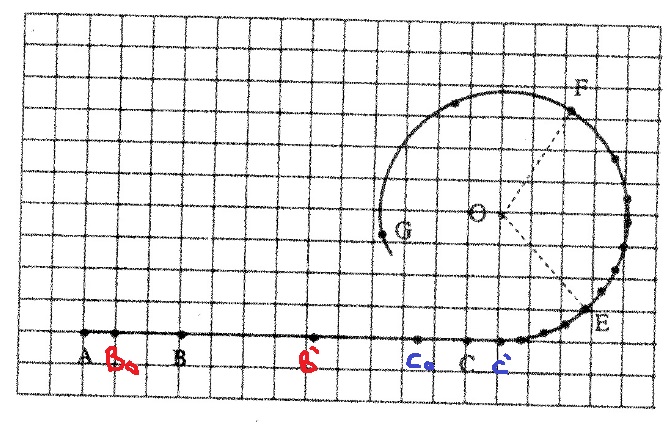
يتم تحديد متوسط ​​السرعة من خلال النسبة بين الازاحة الكلية وزمن الحركة الكلي

في أزمنة حركية قصيرة، يكون متوسط ​​السرعة مساويًا تقريبًا للسرعة اللحظية في منتصف الفترة الزمنية:

نستخدم تعريف متوسط ​​السرعة لوصف السرعات في النقطتين B و C:

«math xmlns=¨http://www.w3.org/1998/Math/MathML¨»«msub»«mi mathvariant=¨bold¨ mathcolor=¨#0000FF¨»V«/mi»«mi mathvariant=¨bold¨ mathcolor=¨#0000FF¨»C«/mi»«/msub»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»§#8776;«/mo»«msub»«mover mathcolor=¨#0000FF¨»«mi mathvariant=¨bold¨»V«/mi»«mo mathvariant=¨bold¨»§#175;«/mo»«/mover»«mrow mathcolor=¨#0000FF¨»«msub»«mi mathvariant=¨bold¨»C«/mi»«mn mathvariant=¨bold¨»0«/mn»«/msub»«mo mathvariant=¨bold¨»-«/mo»«mi mathvariant=¨bold¨»C«/mi»«mo mathvariant=¨bold¨»`«/mo»«/mrow»«/msub»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»=«/mo»«mfrac mathcolor=¨#0000FF¨»«mrow»«mo mathvariant=¨bold¨»§#8710;«/mo»«msub»«mi mathvariant=¨bold¨»X«/mi»«msub»«mrow»«/mrow»«mrow»«msub»«mi mathvariant=¨bold¨»C«/mi»«mn mathvariant=¨bold¨»0«/mn»«/msub»«mo mathvariant=¨bold¨»-«/mo»«mi mathvariant=¨bold¨»C«/mi»«mo mathvariant=¨bold¨»`«/mo»«/mrow»«/msub»«/msub»«/mrow»«mrow»«mo mathvariant=¨bold¨»§#8710;«/mo»«msub»«mi mathvariant=¨bold¨»t«/mi»«msub»«mrow»«/mrow»«mrow»«msub»«mi mathvariant=¨bold¨»C«/mi»«mn mathvariant=¨bold¨»0«/mn»«/msub»«mo mathvariant=¨bold¨»-«/mo»«mi mathvariant=¨bold¨»C«/mi»«mo mathvariant=¨bold¨»`«/mo»«/mrow»«/msub»«/msub»«/mrow»«/mfrac»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»§#160;«/mo»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»§#160;«/mo»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»§#160;«/mo»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»§#160;«/mo»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»§#160;«/mo»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»§#160;«/mo»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»§#160;«/mo»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»§#160;«/mo»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»§#160;«/mo»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»§#160;«/mo»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»§#160;«/mo»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»§#160;«/mo»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»§#160;«/mo»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»§#160;«/mo»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»§#160;«/mo»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»§#160;«/mo»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»§#160;«/mo»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»§#160;«/mo»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»§#160;«/mo»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»§#160;«/mo»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»§#160;«/mo»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»§#160;«/mo»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»§#160;«/mo»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»§#160;«/mo»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»§#160;«/mo»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»§#160;«/mo»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»§#160;«/mo»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»§#160;«/mo»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»§#160;«/mo»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»§#160;«/mo»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»§#160;«/mo»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»§#160;«/mo»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»§#160;«/mo»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»§#160;«/mo»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»§#160;«/mo»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»§#160;«/mo»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»§#160;«/mo»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»§#160;«/mo»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»§#160;«/mo»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»§#160;«/mo»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»§#160;«/mo»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»§#160;«/mo»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»§#160;«/mo»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»§#160;«/mo»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»§#160;«/mo»«msub»«mi mathvariant=¨bold¨ mathcolor=¨#0000FF¨»V«/mi»«mi mathvariant=¨bold¨ mathcolor=¨#0000FF¨»B«/mi»«/msub»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»§#8776;«/mo»«msub»«mover mathcolor=¨#0000FF¨»«mi mathvariant=¨bold¨»V«/mi»«mo mathvariant=¨bold¨»§#175;«/mo»«/mover»«mrow mathcolor=¨#0000FF¨»«msub»«mi mathvariant=¨bold¨»B«/mi»«mn mathvariant=¨bold¨»0«/mn»«/msub»«mo mathvariant=¨bold¨»-«/mo»«mi mathvariant=¨bold¨»B«/mi»«mo mathvariant=¨bold¨»`«/mo»«/mrow»«/msub»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»=«/mo»«mfrac mathcolor=¨#0000FF¨»«mrow»«mo mathvariant=¨bold¨»§#8710;«/mo»«msub»«mi mathvariant=¨bold¨»X«/mi»«msub»«mrow»«/mrow»«mrow»«msub»«mi mathvariant=¨bold¨»B«/mi»«mn mathvariant=¨bold¨»0«/mn»«/msub»«mo mathvariant=¨bold¨»-«/mo»«mi mathvariant=¨bold¨»B«/mi»«mo mathvariant=¨bold¨»`«/mo»«/mrow»«/msub»«/msub»«/mrow»«mrow»«mo mathvariant=¨bold¨»§#8710;«/mo»«msub»«mi mathvariant=¨bold¨»t«/mi»«msub»«mrow»«/mrow»«mrow»«msub»«mi mathvariant=¨bold¨»B«/mi»«mn mathvariant=¨bold¨»0«/mn»«/msub»«mo mathvariant=¨bold¨»-«/mo»«mi mathvariant=¨bold¨»B«/mi»«mo mathvariant=¨bold¨»`«/mo»«/mrow»«/msub»«/msub»«/mrow»«/mfrac»«/math»

زمني الحركة  «math xmlns=¨http://www.w3.org/1998/Math/MathML¨»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»§#8710;«/mo»«msub»«mi mathvariant=¨bold¨ mathcolor=¨#0000FF¨»t«/mi»«msub mathcolor=¨#0000FF¨»«mrow»«/mrow»«mrow»«msub»«mi mathvariant=¨bold¨»C«/mi»«mn mathvariant=¨bold¨»0«/mn»«/msub»«mo mathvariant=¨bold¨»-«/mo»«mi mathvariant=¨bold¨»C«/mi»«mo mathvariant=¨bold¨»`«/mo»«/mrow»«/msub»«/msub»«/math» ו- «math xmlns=¨http://www.w3.org/1998/Math/MathML¨»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»§#8710;«/mo»«msub»«mi mathvariant=¨bold¨ mathcolor=¨#0000FF¨»t«/mi»«msub mathcolor=¨#0000FF¨»«mrow»«/mrow»«mrow»«msub»«mi mathvariant=¨bold¨»B«/mi»«mn mathvariant=¨bold¨»0«/mn»«/msub»«mo mathvariant=¨bold¨»-«/mo»«mi mathvariant=¨bold¨»B«/mi»«mo mathvariant=¨bold¨»`«/mo»«/mrow»«/msub»«/msub»«/math» متساويان , لكن الازاحة مختلفة «math xmlns=¨http://www.w3.org/1998/Math/MathML¨»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»§#8710;«/mo»«msub»«mi mathvariant=¨bold¨ mathcolor=¨#0000FF¨»X«/mi»«msub mathcolor=¨#0000FF¨»«mrow»«/mrow»«mrow»«msub»«mi mathvariant=¨bold¨»C«/mi»«mn mathvariant=¨bold¨»0«/mn»«/msub»«mo mathvariant=¨bold¨»-«/mo»«mi mathvariant=¨bold¨»C«/mi»«mo mathvariant=¨bold¨»`«/mo»«/mrow»«/msub»«/msub»«/math» أصغر من «math xmlns=¨http://www.w3.org/1998/Math/MathML¨»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»§#8710;«/mo»«msub»«mi mathvariant=¨bold¨ mathcolor=¨#0000FF¨»X«/mi»«msub mathcolor=¨#0000FF¨»«mrow»«/mrow»«mrow»«msub»«mi mathvariant=¨bold¨»B«/mi»«mn mathvariant=¨bold¨»0«/mn»«/msub»«mo mathvariant=¨bold¨»-«/mo»«mi mathvariant=¨bold¨»B«/mi»«mo mathvariant=¨bold¨»`«/mo»«/mrow»«/msub»«/msub»«/math» لذلك السرعة بالنقطة B أكبر من السرعة في النقطة  C. 

באופן דומה, נסמן את הנקודה שלפני הנקודה D  ב  D0 , ואת הנקודה שאחרי הנקודה D ב 'D.

נקודות אלו מסומנות באיור הבא:

המהירות הממוצעת מוגדרת לפי היחס שבין ההעתק הכולל לזמן התנועה הכולל 

בזמני תנועה קצרים המהירות הממוצעת שווה בקירוב למהירות הרגעית באמצע הזמן:

נשתמש בהגדרת המהירות הממוצעת כדי לתאר את המהירויות בנקודות B ו- C :

«math xmlns=¨http://www.w3.org/1998/Math/MathML¨»«msub»«mi mathvariant=¨bold¨ mathcolor=¨#0000FF¨»V«/mi»«mi mathvariant=¨bold¨ mathcolor=¨#0000FF¨»C«/mi»«/msub»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»§#8776;«/mo»«msub»«mover mathcolor=¨#0000FF¨»«mi mathvariant=¨bold¨»V«/mi»«mo mathvariant=¨bold¨»§#175;«/mo»«/mover»«mrow mathcolor=¨#0000FF¨»«msub»«mi mathvariant=¨bold¨»C«/mi»«mn mathvariant=¨bold¨»0«/mn»«/msub»«mo mathvariant=¨bold¨»-«/mo»«mi mathvariant=¨bold¨»C«/mi»«mo mathvariant=¨bold¨»`«/mo»«/mrow»«/msub»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»=«/mo»«mfrac mathcolor=¨#0000FF¨»«mrow»«mo mathvariant=¨bold¨»§#8710;«/mo»«msub»«mi mathvariant=¨bold¨»X«/mi»«msub»«mrow»«/mrow»«mrow»«msub»«mi mathvariant=¨bold¨»C«/mi»«mn mathvariant=¨bold¨»0«/mn»«/msub»«mo mathvariant=¨bold¨»-«/mo»«mi mathvariant=¨bold¨»C«/mi»«mo mathvariant=¨bold¨»`«/mo»«/mrow»«/msub»«/msub»«/mrow»«mrow»«mo mathvariant=¨bold¨»§#8710;«/mo»«msub»«mi mathvariant=¨bold¨»t«/mi»«msub»«mrow»«/mrow»«mrow»«msub»«mi mathvariant=¨bold¨»C«/mi»«mn mathvariant=¨bold¨»0«/mn»«/msub»«mo mathvariant=¨bold¨»-«/mo»«mi mathvariant=¨bold¨»C«/mi»«mo mathvariant=¨bold¨»`«/mo»«/mrow»«/msub»«/msub»«/mrow»«/mfrac»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»§#160;«/mo»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»§#160;«/mo»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»§#160;«/mo»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»§#160;«/mo»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»§#160;«/mo»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»§#160;«/mo»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»§#160;«/mo»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»§#160;«/mo»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»§#160;«/mo»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»§#160;«/mo»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»§#160;«/mo»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»§#160;«/mo»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»§#160;«/mo»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»§#160;«/mo»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»§#160;«/mo»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»§#160;«/mo»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»§#160;«/mo»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»§#160;«/mo»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»§#160;«/mo»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»§#160;«/mo»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»§#160;«/mo»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»§#160;«/mo»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»§#160;«/mo»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»§#160;«/mo»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»§#160;«/mo»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»§#160;«/mo»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»§#160;«/mo»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»§#160;«/mo»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»§#160;«/mo»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»§#160;«/mo»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»§#160;«/mo»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»§#160;«/mo»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»§#160;«/mo»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»§#160;«/mo»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»§#160;«/mo»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»§#160;«/mo»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»§#160;«/mo»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»§#160;«/mo»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»§#160;«/mo»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»§#160;«/mo»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»§#160;«/mo»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»§#160;«/mo»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»§#160;«/mo»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»§#160;«/mo»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»§#160;«/mo»«msub»«mi mathvariant=¨bold¨ mathcolor=¨#0000FF¨»V«/mi»«mi mathvariant=¨bold¨ mathcolor=¨#0000FF¨»B«/mi»«/msub»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»§#8776;«/mo»«msub»«mover mathcolor=¨#0000FF¨»«mi mathvariant=¨bold¨»V«/mi»«mo mathvariant=¨bold¨»§#175;«/mo»«/mover»«mrow mathcolor=¨#0000FF¨»«msub»«mi mathvariant=¨bold¨»B«/mi»«mn mathvariant=¨bold¨»0«/mn»«/msub»«mo mathvariant=¨bold¨»-«/mo»«mi mathvariant=¨bold¨»B«/mi»«mo mathvariant=¨bold¨»`«/mo»«/mrow»«/msub»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»=«/mo»«mfrac mathcolor=¨#0000FF¨»«mrow»«mo mathvariant=¨bold¨»§#8710;«/mo»«msub»«mi mathvariant=¨bold¨»X«/mi»«msub»«mrow»«/mrow»«mrow»«msub»«mi mathvariant=¨bold¨»B«/mi»«mn mathvariant=¨bold¨»0«/mn»«/msub»«mo mathvariant=¨bold¨»-«/mo»«mi mathvariant=¨bold¨»B«/mi»«mo mathvariant=¨bold¨»`«/mo»«/mrow»«/msub»«/msub»«/mrow»«mrow»«mo mathvariant=¨bold¨»§#8710;«/mo»«msub»«mi mathvariant=¨bold¨»t«/mi»«msub»«mrow»«/mrow»«mrow»«msub»«mi mathvariant=¨bold¨»B«/mi»«mn mathvariant=¨bold¨»0«/mn»«/msub»«mo mathvariant=¨bold¨»-«/mo»«mi mathvariant=¨bold¨»B«/mi»«mo mathvariant=¨bold¨»`«/mo»«/mrow»«/msub»«/msub»«/mrow»«/mfrac»«/math»

זמני התנועה  «math xmlns=¨http://www.w3.org/1998/Math/MathML¨»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»§#8710;«/mo»«msub»«mi mathvariant=¨bold¨ mathcolor=¨#0000FF¨»t«/mi»«msub mathcolor=¨#0000FF¨»«mrow»«/mrow»«mrow»«msub»«mi mathvariant=¨bold¨»C«/mi»«mn mathvariant=¨bold¨»0«/mn»«/msub»«mo mathvariant=¨bold¨»-«/mo»«mi mathvariant=¨bold¨»C«/mi»«mo mathvariant=¨bold¨»`«/mo»«/mrow»«/msub»«/msub»«/math» ו- «math xmlns=¨http://www.w3.org/1998/Math/MathML¨»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»§#8710;«/mo»«msub»«mi mathvariant=¨bold¨ mathcolor=¨#0000FF¨»t«/mi»«msub mathcolor=¨#0000FF¨»«mrow»«/mrow»«mrow»«msub»«mi mathvariant=¨bold¨»B«/mi»«mn mathvariant=¨bold¨»0«/mn»«/msub»«mo mathvariant=¨bold¨»-«/mo»«mi mathvariant=¨bold¨»B«/mi»«mo mathvariant=¨bold¨»`«/mo»«/mrow»«/msub»«/msub»«/math» הם שווים , אך ההעתקים שונים «math xmlns=¨http://www.w3.org/1998/Math/MathML¨»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»§#8710;«/mo»«msub»«mi mathvariant=¨bold¨ mathcolor=¨#0000FF¨»X«/mi»«msub mathcolor=¨#0000FF¨»«mrow»«/mrow»«mrow»«msub»«mi mathvariant=¨bold¨»C«/mi»«mn mathvariant=¨bold¨»0«/mn»«/msub»«mo mathvariant=¨bold¨»-«/mo»«mi mathvariant=¨bold¨»C«/mi»«mo mathvariant=¨bold¨»`«/mo»«/mrow»«/msub»«/msub»«/math» קטן מ «math xmlns=¨http://www.w3.org/1998/Math/MathML¨»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»§#8710;«/mo»«msub»«mi mathvariant=¨bold¨ mathcolor=¨#0000FF¨»X«/mi»«msub mathcolor=¨#0000FF¨»«mrow»«/mrow»«mrow»«msub»«mi mathvariant=¨bold¨»B«/mi»«mn mathvariant=¨bold¨»0«/mn»«/msub»«mo mathvariant=¨bold¨»-«/mo»«mi mathvariant=¨bold¨»B«/mi»«mo mathvariant=¨bold¨»`«/mo»«/mrow»«/msub»«/msub»«/math» לכן המהירות בנקודה B גדולה מהמהירות בנקודה C. 

1. دائمًا ما يكون متوسط ​​السرعة في مقطع حركة معين مساويًا تمامًا للسرعة اللحظية في منتصف الفترة الزمنية لهذه الحركة ، فقط إذا كان الجسم يتحرك بسرعة ثابتة أو بتسارع ثابت.

2. إذا تم حساب متوسط ​​السرعة خلال فترة حركة صغيرة ، فإن السرعة في منتصف الفترة الزمنية تساوي تقريبًا السرعة اللحظية.

3. إذا لم يتحرك الجسم بسرعة ثابتة أو بتسارع ثابت، ولم يكن زمن حركته قصيرًا ، فلا يمكن القول إن متوسط ​​السرعة يساوي السرعة في منتصف الفترة الزمنية.

2. אם המהירות הממוצעת מחושבת בזמן תנועה קטן , המהירות באמצע הזמן שווה בקירוב למהירות הרגעית.

3. אם גוף לא נע במהירות קבועה ולא בתאוצה קבועה, וזמן תנועתו לא קטן, לא ניתן לומר שהמהירות הממוצעת שווה למהירות באמצע הזמן.

______________________________________________________________________________________

          ב. 

______________________________________________________________________________________

• مجلد
• الجواب النهائي
• استراتيجية
• الحل الكامل
• انتبهوا