
______________________________________________________________________________________
...
شكل المسار هو خط مستقيم.
צורת המסלול היא קו ישר.
يمكن أن تتغير السرعة في المقدار ويمكن أن تتغير في الاتجاه.
لكي تتغير السرعة في الاتجاه ، يجب أن يكون هناك تسارع شعاعي (مركزي) ، لذلك يجب أن تكون القوة المحصّلة في الاتجاه الشعاعي مختلفة عن الصفر.
يُلقى الجسم في الاتجاه السالب للمحور X. وتعمل القوة في الاتجاه الموجب للمحور X ، والقوة متعامدة مع الحركة، ولا يوجد مركّب مركزي (شعاعي) للقوة.
لذلك في هذه الحالة ، لن يكون هناك تسارع مركزي، فقط تسارع مماسي.
يتغير مقدار السرعة ، ولن تتغير في الاتجاه. شكل مسار حركة الجسم هو خط مستقيم.
1. غالبًا ما يشعر الطلاب أنهم يعرفون الإجابة وأنهم على حق ، لكنهم يجدون صعوبة في كتابة تفسير جيد ودقيق.
في الغالب ، المنطق السيئ هو التفسير المبني على الأفكار العامة ومنطق قلب الطالب.
من ناحية أخرى ، يعتمد التفسير الجيد على المبادئ والمفاهيم الفيزيائية ، حتى يتمكن الطالب من التفسير بواسطة هذه المبادئ، يحتاج إلى فهم هذه المفاهيم والمبادئ حقًا.
حتى يتمكن من استخدامها في كتابة التعليل.
هذا السؤال هو مثال جيد على كيف أنه ، بالنسبة لأولئك الذين يفهمون معنى التسارع المركزي ، من السهل تفسير سبب تحرك الجسم في خط مستقيم - لأنه لا يوجد تسارع مركزي.
2. من الممكن والمناسب استخدام المفاهيم دون شرح معناها ، ولا داعي لشرح ماهية التسارع المركزي ،
يجب أن تبني الحل ببساطة على التسارع المركزي.
3. يميل الطلاب في البداية إلى عدم استخدام المفاهيم الفيزيائية ، والمفاهيم غريبة عليهم. إنها مسألة وقت وقبل كل شيء قرار.
عليك أن تقرر أنك تستخدم المفاهيم الفيزيائية وليس المنطق العام. يتخذ الطلاب المتميزون مثل هذا القرار في المراحل الأولية ،
الطلاب الذين يعانون هم الطلاب الذين يصرون على عدم استخدام المفاهيم الفيزيائية في كتابة الحلول.
לרוב , נימוק לא טוב הוא נימוק המבוסס על רעיונות כלליים ,ועל היגיון ליבו של התלמיד.
לעומת זאת, נימוק איכותי וטוב מבוסס על העקרונות והמושגים הפיזיקליים, כדי שתלמיד יוכל לנמק בעזרתם הוא צריך ממש להבין את המושגים והעקרונות.
כדי שיוכל להשתמש בהם בכתיבת הנימוק.
שאלה זו היא דוגמה טובה לכך, למי שמבין את משמעות התאוצה הרדיאלית , קל לנמק מדוע הגוף נע בקו ישר - מכיוון שאין תאוצה רדיאלית.
2. אפשר וכדאי להשתמש במושגים בלי להסביר את משמעותם , אין צורך להסביר מה היא תאוצה רדיאלית ,
כדאי פשוט לבסס את הפתרון על התאוצה הרדיאלית.
3. בהתחלה תלמידים נוטים לא להשתמש במושגים הפיזיקליים, המושגים זרים להם. זה עניין של זמן ובעיקר החלטה.
צריך להחליט שמשתמשים במושגים הפיזיקליים ולא בהיגיון כללי . התלמידים המצטיינים מקבלים החלטה כזו בשלבים ראשוניים ,
התלמידים המתקשים הם התלמידים המתעקשים שלא להשתמש במושגים הפיזיקליים בכתיבת הפתרונות.
______________________________________________________________________________________

______________________________________________________________________________________
...
اتجاه متجه التسارع إلى اليمين. وهو لا يتغير.
القانون الثاني لنيوتن .
من مبادئ المتجّه في الرياضيات، ينتج عن ضرب متجّه في قيمة عددية متجه يكون اتجاهه هو اتجاه المتجه المضاعف.
من قانون نيوتن الثاني: «math xmlns=¨http://www.w3.org/1998/Math/MathML¨»«mover mathcolor=¨#0000FF¨»«mi mathvariant=¨bold¨»§#931;F«/mi»«mo mathvariant=¨bold¨»§#8594;«/mo»«/mover»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»=«/mo»«mi mathvariant=¨bold¨ mathcolor=¨#0000FF¨»m«/mi»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»§#183;«/mo»«mover mathcolor=¨#0000FF¨»«mi mathvariant=¨bold¨»a«/mi»«mo mathvariant=¨bold¨»§#8594;«/mo»«/mover»«/math» وفقًا لمبادئ المتجّه ، يمكن القول أن اتجاه متجّه التسارع هو نفس اتجاه متجّه القوة المحصّلة.
في جميع أوقات الحركة ، يكون اتجاه القوة المحصّلة إلى اليمين ، وبالتالي من القانون الثاني لنيوتن، يكون اتجاه التسارع إلى اليمين.
يتغير اتجاه الحركة، لكن اتجاه القوة المحصّلة لا يتغير، لذلك يكون اتجاه التسارع دائمًا إلى اليمين ، حتى عندما يغير الجسم اتجاه حركته.
מהחוק השני של ניוטון: «math xmlns=¨http://www.w3.org/1998/Math/MathML¨»«mover mathcolor=¨#0000FF¨»«mi mathvariant=¨bold¨»§#931;F«/mi»«mo mathvariant=¨bold¨»§#8594;«/mo»«/mover»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»=«/mo»«mi mathvariant=¨bold¨ mathcolor=¨#0000FF¨»m«/mi»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»§#183;«/mo»«mover mathcolor=¨#0000FF¨»«mi mathvariant=¨bold¨»a«/mi»«mo mathvariant=¨bold¨»§#8594;«/mo»«/mover»«/math» בהתאם לעקרונות הווקטוריים, ניתן לומר שכיוון ווקטור התאוצה הוא ככיוון ווקטור הכוח השקול.
בכל זמן התנועה , כיוון הכוח השקול הוא ימינה, לכן מהחוק השני של ניוטון,כיוון התאוצה היא ימינה.
تشبه هذه الحركة حركة الرمي العمودي لأعلى، حيث يتغير اتجاه الحركة ، لكن اتجاه التسارع يكون دائمًا نحو الأسفل.
______________________________________________________________________________________

______________________________________________________________________________________
...
حتى التوقف يقل مقدار السرعة . بعد التوقف، يزداد مقدار السرعة .
إن فهم الحركة وفهم معنى "مقدار السرعة" يشير فقط إلى مقدار السرعة وليس إلى اتجاهها.
بالنسبة لمقدار السرعة (القيمة المطلقة) ، يتحرك الجسم مبدئيًا إلى اليسار بسرعة تقل تدريجيًا حتى يتوقف الجسم توقفًا لحظيًا. بعد ذلك يتحرك الجسم إلى اليمين بسرعة آخذة بالازدياد.
לכן המהירות תמיד גדלה .
בהתייחס לגודל המהירות (לערכה המוחלט) ,הגוף נע בהתחלה שמאלה במהירות הולכת וקטנה בגודלה עד שהגוף נעצר , רגעית. לאחר מכן הגוף נע ימינה במהירות הולכת וגדלה .
1. يتحرك الجسم بالبداية نحو اليسار، عكس اتجاه المحور ، وسرعته سالبة ، وتزداد السرعة حتى تصبح السرعة صفرًا.
يتوقف الجسم توقفًا لحظيًا ثم يتحرك نحو اليمين في اتجاه المحور بسرعة آخذة بالازدياد.
السرعة تزداد دائما. السؤال لا يتناول السرعة ، انما فقط مقدار السرعة ، ولا يوجد أي صلة لاتجاه الحركة غ، نتطرق هنا فقط إلى القيمة المطلقة للسرعة.
لذلك ، حتى التوقف تقل مقدار السرعة ، وبعد التوقف يزداد مقدار السرعة .
2. إذا كان معنى مقدار السرعة غير واضح ، سواء كان يتضمن إشارة السرعة أم لا ، فمن المستحسن وصف الحركة في كلا الخيارين ، وشرح كل خيار على حدة.
______________________________________________________________________________________

______________________________________________________________________________________
...
مسار حركة الجسم هو قطع مكافئ.
تطوير معادلة المسار من تعبيري الموقع كدالة للزمن : «math xmlns=¨http://www.w3.org/1998/Math/MathML¨»«mi mathvariant=¨bold¨ mathcolor=¨#FF6600¨»X«/mi»«mo mathvariant=¨bold¨ mathcolor=¨#FF6600¨»(«/mo»«mi mathvariant=¨bold¨ mathcolor=¨#FF6600¨»t«/mi»«mo mathvariant=¨bold¨ mathcolor=¨#FF6600¨»)«/mo»«mo mathvariant=¨bold¨ mathcolor=¨#FF6600¨»§#160;«/mo»«mo mathvariant=¨bold¨ mathcolor=¨#FF6600¨»,«/mo»«mo mathvariant=¨bold¨ mathcolor=¨#FF6600¨»§#160;«/mo»«mi mathvariant=¨bold¨ mathcolor=¨#FF6600¨»Y«/mi»«mo mathvariant=¨bold¨ mathcolor=¨#FF6600¨»(«/mo»«mi mathvariant=¨bold¨ mathcolor=¨#FF6600¨»t«/mi»«mo mathvariant=¨bold¨ mathcolor=¨#FF6600¨»)«/mo»«/math» .
يكتسب الجسم الثاني سرعة ابتدائية في اتجاه المحور Y ، وتؤثر القوة على الجسم في اتجاه المحور X. تعمل القوة في البداية باتجاه عمودي على اتجاه الحركة ، في اتجاه شعاعي (רדיאלי).
لذلك هناك تسارع شعاعي ، واتجاه الحركة يتغير ، والجسم لا يتحرك على طول خط مستقيم.
لإيجاد شكل مسار حركة الجسم ، نطوّر معادلة المسار.
نكتب معادلة المكان كدالة للزمن في اتجاه المحور X ، وفي اتجاه المحور Y ، في اتجاه المحور X ، يتحرك الجسم بتسارع ثابت ، في اتجاه المحور Y يتحرك الجسم بسرعة ثابتة:
«math xmlns=¨http://www.w3.org/1998/Math/MathML¨»«mi mathvariant=¨bold-italic¨ mathcolor=¨#0000FF¨»y«/mi»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»(«/mo»«mi mathvariant=¨bold-italic¨ mathcolor=¨#0000FF¨»t«/mi»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»)«/mo»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»=«/mo»«msub»«mi mathvariant=¨bold-italic¨ mathcolor=¨#0000FF¨»Y«/mi»«mn mathvariant=¨bold¨ mathcolor=¨#0000FF¨»0«/mn»«/msub»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»+«/mo»«msub»«mi mathvariant=¨bold-italic¨ mathcolor=¨#0000FF¨»V«/mi»«msub mathcolor=¨#0000FF¨»«mn mathvariant=¨bold¨»0«/mn»«mi mathvariant=¨bold¨»Y«/mi»«/msub»«/msub»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»§#183;«/mo»«mi mathvariant=¨bold-italic¨ mathcolor=¨#0000FF¨»t«/mi»«/math» «math xmlns=¨http://www.w3.org/1998/Math/MathML¨»«mi mathvariant=¨bold-italic¨ mathcolor=¨#0000FF¨»X«/mi»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»(«/mo»«mi mathvariant=¨bold-italic¨ mathcolor=¨#0000FF¨»t«/mi»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»)«/mo»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»=«/mo»«msub»«mi mathvariant=¨bold-italic¨ mathcolor=¨#0000FF¨»X«/mi»«mn mathvariant=¨bold¨ mathcolor=¨#0000FF¨»0«/mn»«/msub»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»+«/mo»«msub»«mi mathvariant=¨bold-italic¨ mathcolor=¨#0000FF¨»V«/mi»«msub mathcolor=¨#0000FF¨»«mn mathvariant=¨bold¨»0«/mn»«mi mathvariant=¨bold¨»X«/mi»«/msub»«/msub»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»§#183;«/mo»«mi mathvariant=¨bold-italic¨ mathcolor=¨#0000FF¨»t«/mi»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»§#160;«/mo»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»+«/mo»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»§#160;«/mo»«mfrac mathcolor=¨#0000FF¨»«mn mathvariant=¨bold¨»1«/mn»«mn mathvariant=¨bold¨»2«/mn»«/mfrac»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»§#183;«/mo»«mi mathvariant=¨bold-italic¨ mathcolor=¨#0000FF¨»a«/mi»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»§#183;«/mo»«msup»«mi mathvariant=¨bold-italic¨ mathcolor=¨#0000FF¨»t«/mi»«mn mathvariant=¨bold¨ mathcolor=¨#0000FF¨»2«/mn»«/msup»«/math»
نعبر عن زمن الحركة من دالة المكان كدالة للزمن العمودية ونعوّضها في دالة المكان كدالة للزمن الأفقية.
«math xmlns=¨http://www.w3.org/1998/Math/MathML¨»«mi mathvariant=¨bold-italic¨ mathcolor=¨#0000FF¨»y«/mi»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»(«/mo»«mi mathvariant=¨bold-italic¨ mathcolor=¨#0000FF¨»t«/mi»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»)«/mo»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»=«/mo»«msub»«mi mathvariant=¨bold-italic¨ mathcolor=¨#0000FF¨»Y«/mi»«mn mathvariant=¨bold¨ mathcolor=¨#0000FF¨»0«/mn»«/msub»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»+«/mo»«msub»«mi mathvariant=¨bold-italic¨ mathcolor=¨#0000FF¨»V«/mi»«msub mathcolor=¨#0000FF¨»«mn mathvariant=¨bold¨»0«/mn»«mi mathvariant=¨bold¨»Y«/mi»«/msub»«/msub»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»§#183;«/mo»«mi mathvariant=¨bold-italic¨ mathcolor=¨#0000FF¨»t«/mi»«mspace linebreak=¨newline¨»«/mspace»«mi mathvariant=¨normal¨ mathcolor=¨#FF0000¨»t«/mi»«mo mathvariant=¨bold¨ mathcolor=¨#FF0000¨»=«/mo»«mfrac mathcolor=¨#FF0000¨»«mi mathvariant=¨bold¨»y«/mi»«msub»«mi mathvariant=¨bold¨»V«/mi»«msub»«mn mathvariant=¨bold¨»0«/mn»«mi mathvariant=¨bold¨»Y«/mi»«/msub»«/msub»«/mfrac»«mo mathvariant=¨bold¨ mathcolor=¨#FF0000¨»§#160;«/mo»«/math» «math xmlns=¨http://www.w3.org/1998/Math/MathML¨»«mi mathvariant=¨bold-italic¨ mathcolor=¨#0000FF¨»X«/mi»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»(«/mo»«mi mathvariant=¨bold-italic¨ mathcolor=¨#0000FF¨»t«/mi»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»)«/mo»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»=«/mo»«msub»«mi mathvariant=¨bold-italic¨ mathcolor=¨#0000FF¨»X«/mi»«mn mathvariant=¨bold¨ mathcolor=¨#0000FF¨»0«/mn»«/msub»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»+«/mo»«msub»«mi mathvariant=¨bold-italic¨ mathcolor=¨#0000FF¨»V«/mi»«msub mathcolor=¨#0000FF¨»«mn mathvariant=¨bold¨»0«/mn»«mi mathvariant=¨bold¨»X«/mi»«/msub»«/msub»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»§#183;«/mo»«mi mathvariant=¨bold-italic¨ mathcolor=¨#0000FF¨»t«/mi»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»§#160;«/mo»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»+«/mo»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»§#160;«/mo»«mfrac mathcolor=¨#0000FF¨»«mn mathvariant=¨bold¨»1«/mn»«mn mathvariant=¨bold¨»2«/mn»«/mfrac»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»§#183;«/mo»«mi mathvariant=¨bold-italic¨ mathcolor=¨#0000FF¨»a«/mi»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»§#183;«/mo»«msup»«mi mathvariant=¨bold-italic¨ mathcolor=¨#0000FF¨»t«/mi»«mn mathvariant=¨bold¨ mathcolor=¨#0000FF¨»2«/mn»«/msup»«mspace linebreak=¨newline¨»«/mspace»«mi mathvariant=¨bold-italic¨ mathcolor=¨#0000FF¨»X«/mi»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»(«/mo»«mi mathvariant=¨bold-italic¨ mathcolor=¨#0000FF¨»y«/mi»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»)«/mo»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»=«/mo»«mn mathvariant=¨bold¨ mathcolor=¨#0000FF¨»0«/mn»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»+«/mo»«mn mathvariant=¨bold¨ mathcolor=¨#0000FF¨»0«/mn»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»§#183;«/mo»«mfrac mathcolor=¨#FF0000¨»«mi mathvariant=¨bold¨»y«/mi»«msub»«mi mathvariant=¨bold¨»V«/mi»«msub»«mn mathvariant=¨bold¨»0«/mn»«mi mathvariant=¨bold¨»Y«/mi»«/msub»«/msub»«/mfrac»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»§#160;«/mo»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»+«/mo»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»§#160;«/mo»«mfrac mathcolor=¨#0000FF¨»«mn mathvariant=¨bold¨»1«/mn»«mn mathvariant=¨bold¨»2«/mn»«/mfrac»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»§#183;«/mo»«mi mathvariant=¨bold-italic¨ mathcolor=¨#0000FF¨»a«/mi»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»§#183;«/mo»«mfrac mathcolor=¨#FF0000¨»«msup»«mi mathvariant=¨bold¨»y«/mi»«mn mathvariant=¨bold¨»2«/mn»«/msup»«msup»«msub»«mi mathvariant=¨bold¨»V«/mi»«msub»«mn mathvariant=¨bold¨»0«/mn»«mi mathvariant=¨bold¨»Y«/mi»«/msub»«/msub»«mn mathvariant=¨bold¨»2«/mn»«/msup»«/mfrac»«mspace linebreak=¨newline¨»«/mspace»«menclose mathcolor=¨#0000FF¨ notation=¨circle¨»«mi mathvariant=¨bold¨»X«/mi»«mo mathvariant=¨bold¨»(«/mo»«mi mathvariant=¨bold¨»y«/mi»«mo mathvariant=¨bold¨»)«/mo»«mo mathvariant=¨bold¨»=«/mo»«mo mathvariant=¨bold¨»§#160;«/mo»«mfrac»«mrow»«mi mathvariant=¨bold¨»a«/mi»«mo mathvariant=¨bold¨»§#183;«/mo»«msup»«mi mathvariant=¨bold¨»y«/mi»«mn mathvariant=¨bold¨»2«/mn»«/msup»«/mrow»«mrow»«mn mathvariant=¨bold¨»2«/mn»«mo mathvariant=¨bold¨»§#183;«/mo»«msup»«msub»«mi mathvariant=¨bold¨»V«/mi»«msub»«mn mathvariant=¨bold¨»0«/mn»«mi mathvariant=¨bold¨»Y«/mi»«/msub»«/msub»«mn mathvariant=¨bold¨»2«/mn»«/msup»«/mrow»«/mfrac»«/menclose»«/math»
الصورة الرياضية للدالة هي تلك الخاصة بالقطع المكافئ ، وبالتالي فإن مسار حركة الجسم الثاني هو قطع مكافئ.
לכן קיימת תאוצה רדיאלית , כיוון התנועה משתנה , הגוף לא נע לאורך קו ישר.
כדי למצוא את צורת מסלול תנועת הגוף נפתח את משוואת המסלול .
נכתוב את פונקציות המקום זמן לכיוון ציר X, ולכיוון ציר Y ,בכיוון ציר X הגוף נע בתאוצה קבועה, בכיוון ציר Y הגוף נע במהירות קבועה:
«math xmlns=¨http://www.w3.org/1998/Math/MathML¨»«mi mathvariant=¨bold-italic¨ mathcolor=¨#0000FF¨»y«/mi»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»(«/mo»«mi mathvariant=¨bold-italic¨ mathcolor=¨#0000FF¨»t«/mi»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»)«/mo»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»=«/mo»«msub»«mi mathvariant=¨bold-italic¨ mathcolor=¨#0000FF¨»Y«/mi»«mn mathvariant=¨bold¨ mathcolor=¨#0000FF¨»0«/mn»«/msub»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»+«/mo»«msub»«mi mathvariant=¨bold-italic¨ mathcolor=¨#0000FF¨»V«/mi»«msub mathcolor=¨#0000FF¨»«mn mathvariant=¨bold¨»0«/mn»«mi mathvariant=¨bold¨»Y«/mi»«/msub»«/msub»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»§#183;«/mo»«mi mathvariant=¨bold-italic¨ mathcolor=¨#0000FF¨»t«/mi»«/math» «math xmlns=¨http://www.w3.org/1998/Math/MathML¨»«mi mathvariant=¨bold-italic¨ mathcolor=¨#0000FF¨»X«/mi»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»(«/mo»«mi mathvariant=¨bold-italic¨ mathcolor=¨#0000FF¨»t«/mi»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»)«/mo»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»=«/mo»«msub»«mi mathvariant=¨bold-italic¨ mathcolor=¨#0000FF¨»X«/mi»«mn mathvariant=¨bold¨ mathcolor=¨#0000FF¨»0«/mn»«/msub»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»+«/mo»«msub»«mi mathvariant=¨bold-italic¨ mathcolor=¨#0000FF¨»V«/mi»«msub mathcolor=¨#0000FF¨»«mn mathvariant=¨bold¨»0«/mn»«mi mathvariant=¨bold¨»X«/mi»«/msub»«/msub»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»§#183;«/mo»«mi mathvariant=¨bold-italic¨ mathcolor=¨#0000FF¨»t«/mi»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»§#160;«/mo»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»+«/mo»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»§#160;«/mo»«mfrac mathcolor=¨#0000FF¨»«mn mathvariant=¨bold¨»1«/mn»«mn mathvariant=¨bold¨»2«/mn»«/mfrac»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»§#183;«/mo»«mi mathvariant=¨bold-italic¨ mathcolor=¨#0000FF¨»a«/mi»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»§#183;«/mo»«msup»«mi mathvariant=¨bold-italic¨ mathcolor=¨#0000FF¨»t«/mi»«mn mathvariant=¨bold¨ mathcolor=¨#0000FF¨»2«/mn»«/msup»«/math»
1. تصف معادلة مسار الحركة الباليستية الموقع Y كدالة للموقع X. في هذه الحالة ، لا تعتبر حركة باليستية ، فمن الأنسب رياضيًا وصف الموقع X كدالة للموقع Y.
تصف أيضًا دالة الموقع Y كدالة للموقع X المحل الهندسي لكافة النقاط التي يمر من خلالها الجسم. إذا حددنا جميع النقاط التي تحقق الدالة ، فسنحصل على القطع المكافئ ، وبالتالي شكل
المسار هو قطع مكافئ.
2. من وجهة نظر الشخص الذي يقف على الأرض وينظر لأعلى ، فإن حركة الجسم هي نفس حركة الرمي الأفقي، ومسار حركة الجسم هو نفسه مسار الرمي الأفقي.
المسار هو قطع مكافئ.
גם פונקציה של Y בתלות ב X מתארת את כל אוסף הנקודות דרכם הגוף עובר. אם נסמן את כל הנקודות המקיימות את הפונקציה נקבל פרבולה, לכן צורת
המסלול היא פרבולית.
2. מנקודת מבטו של אדם השוכב על הקרקע ומביט כלפי מעלה , תנועת הגוף זהה לזריקה אופקית, מסלול תנועת הגוף זהה למסלול זריקה אופקית.
המסלול הוא פרבולי.
______________________________________________________________________________________

______________________________________________________________________________________
...
سرعة الجسم الثاني تتزايد.
مبدأ استقلالية الحركات تميز أنواع الحركات. في اتجاه المحور X وفي اتجاه المحور Y. والتعبير عن مقدار السرعة V كدالة لمركبات السرعات VX و VY.
نستخدم مبدأ استقلالية الحركات. نصف السرعة V للجسم كدالة لمركبات السرعة VX و VY.
تؤثر قوة واحدة فقط على الجسم في الاتجاه الأفقي ، ولا توجد قوة تؤثر في الاتجاه العمودي.
لذلك ، يتحرك الجسم في الاتجاه العمودي بسرعة ثابتة. يتحرك الجسم في الاتجاه الأفقي بتسارع ثابت.
من مبادئ الحركة في مستوى ، فإن سرعة الجسم في أي لحظة تكون V مساوية في المقدار لمجموع متجّه السرعة الأفقية Vx والسرعة العمودية Vy: ,
«math xmlns=¨http://www.w3.org/1998/Math/MathML¨»«mstyle mathsize=¨28px¨»«mrow»«mover mathcolor=¨#0000FF¨»«mi mathvariant=¨bold¨»V«/mi»«mo mathvariant=¨bold¨»§#8594;«/mo»«/mover»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»=«/mo»«msub»«mover mathcolor=¨#0000FF¨»«mi mathvariant=¨bold¨»V«/mi»«mo mathvariant=¨bold¨»§#8594;«/mo»«/mover»«mi mathvariant=¨bold¨ mathcolor=¨#0000FF¨»X«/mi»«/msub»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»+«/mo»«msub»«mover mathcolor=¨#0000FF¨»«mi mathvariant=¨bold¨»V«/mi»«mo mathvariant=¨bold¨»§#8594;«/mo»«/mover»«mi mathvariant=¨bold¨ mathcolor=¨#0000FF¨»Y«/mi»«/msub»«/mrow»«/mstyle»«/math» 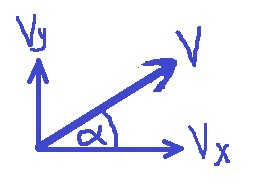
نعبّر عن مقدار السرعة V ، بدلالة مركبات السرعة ، بمساعدة فيثاغورس:
«math xmlns=¨http://www.w3.org/1998/Math/MathML¨»«mstyle mathsize=¨28px¨»«mi mathvariant=¨bold-italic¨ mathcolor=¨#0000FF¨»V«/mi»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»=«/mo»«msqrt mathcolor=¨#0000FF¨»«msup»«msub»«mi mathvariant=¨bold¨»V«/mi»«mi mathvariant=¨bold¨»X«/mi»«/msub»«mn mathvariant=¨bold¨»2«/mn»«/msup»«mo mathvariant=¨bold¨»+«/mo»«msup»«msub»«mi mathvariant=¨bold¨»V«/mi»«mi mathvariant=¨bold¨»Y«/mi»«/msub»«mn mathvariant=¨bold¨»2«/mn»«/msup»«/msqrt»«/mstyle»«/math»
في اتجاه المحور Y ، يتحرك الجسم بسرعة ثابتة - لا تتغير السرعة VY.
في اتجاه المحور X ، يتحرك الجسم بالتسارع - تزداد سرعة VX.
من التعبير عن مقدار سرعة الجسم V ، نظرًا لأن VX يزداد فإن سرعة الجسم ، تزداد أيضًا V.
לכן, בכיוון האנכי הגוף נע במהירות קבועה. בכיוון האופקי הגוף נע בתאוצה קבועה.
מעקרונות התנועה במישור , מהירות הגוף בכל רגע V שווה בגודלה לסכום הווקטורי של המהירות האופקית Vx והמהירות האנכית Vy:
«math xmlns=¨http://www.w3.org/1998/Math/MathML¨»«mstyle mathsize=¨28px¨»«mrow»«mover mathcolor=¨#0000FF¨»«mi mathvariant=¨bold¨»V«/mi»«mo mathvariant=¨bold¨»§#8594;«/mo»«/mover»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»=«/mo»«msub»«mover mathcolor=¨#0000FF¨»«mi mathvariant=¨bold¨»V«/mi»«mo mathvariant=¨bold¨»§#8594;«/mo»«/mover»«mi mathvariant=¨bold¨ mathcolor=¨#0000FF¨»X«/mi»«/msub»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»+«/mo»«msub»«mover mathcolor=¨#0000FF¨»«mi mathvariant=¨bold¨»V«/mi»«mo mathvariant=¨bold¨»§#8594;«/mo»«/mover»«mi mathvariant=¨bold¨ mathcolor=¨#0000FF¨»Y«/mi»«/msub»«/mrow»«/mstyle»«/math» 
נבטא את גודל המהירות V ,בתלות ברכיבי המהירות,בעזרת פיתגורס:
«math xmlns=¨http://www.w3.org/1998/Math/MathML¨»«mstyle mathsize=¨28px¨»«mi mathvariant=¨bold-italic¨ mathcolor=¨#0000FF¨»V«/mi»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»=«/mo»«msqrt mathcolor=¨#0000FF¨»«msup»«msub»«mi mathvariant=¨bold¨»V«/mi»«mi mathvariant=¨bold¨»X«/mi»«/msub»«mn mathvariant=¨bold¨»2«/mn»«/msup»«mo mathvariant=¨bold¨»+«/mo»«msup»«msub»«mi mathvariant=¨bold¨»V«/mi»«mi mathvariant=¨bold¨»Y«/mi»«/msub»«mn mathvariant=¨bold¨»2«/mn»«/msup»«/msqrt»«/mstyle»«/math»
בכיוון ציר X ,הגוף נע בתאוצה - המהירות בכיוון ציר X , הולכת וגדלה. מביטוי גודל מהירות הגוף V, מכיוון שVX גדל גם מהירות הגוף V גדלה.
1. في حركة الجسم الأول ، تقل سرعة الجسم في قيمتها المطلقة حتى التوقف اللحظي. ثم زادت السرعة.
من ناحية أخرى ، في حركة الجسم الثاني ، تشبه الرمي الأفقي. لا توجد لحظة تكون فيها سرعة الجسم مساوية للصفر ، فمنذ لحظة رمي الجسم تزداد سرعة الجسم باستمرار.
2. يعتمد حل هذا السؤال على فهم مبدأ استقلالية الحركات ومبادئ الرمي الأفقي. لكنها صيغت بشكل مختلف.
يُطلب من الطالب أن يفهم المبادئ جيدًا بما يكفي ، حتى يتمكن من التعامل مع الأسئلة بصيغ مختلفة.
לעומת זאת, בתנועת הגוף השני, דומה לזריקה אופקית. אין רגע שבו מהירות הגוף שווה לאפס, מרגע זריקת הגוף, מהירות הגוף הולכת וגדלה כל הזמן .
2. פתרון שאלה זו מבוסס על הבנת עיקרון אי תלות התנועות ועקרונות הזריקה האופקית. אך היא מנוסחת בצורה שונה.
תלמיד נדרש להבין את העקרונות בצורה מספיק טובה , כך שהוא יוכל להתמודד עם שאלות בניסוחים שונים.
______________________________________________________________________________________

______________________________________________________________________________________
...
«math xmlns=¨http://www.w3.org/1998/Math/MathML¨»«mo mathvariant=¨bold¨»(«/mo»«mn mathvariant=¨bold¨»64«/mn»«mi mathvariant=¨bold¨»m«/mi»«mo mathvariant=¨bold¨»,«/mo»«mn mathvariant=¨bold¨»96«/mn»«mi mathvariant=¨bold¨»m«/mi»«mo mathvariant=¨bold¨»)«/mo»«/math»
مبدأ استقلالية الحركات وإيجاد الموقع الأفقي والموقع العمودي بشكل منفصل بمساعدة دوال الموقع كدالة للزمن في الكينماتيكا.
سنستخدم مبدأ استقلالية الحركات ، ونصف موقع الجسم في شكل إحداثي، وسنجد بشكل منفصل الموقع الأفقي والعمودي في اللحظة t = 4s.
نجد الموقع العمودي بمساعدة دالة المكان كدالة للزمن المناسبة للحركة بسرعة ثابتة:
«math xmlns=¨http://www.w3.org/1998/Math/MathML¨»«mi mathvariant=¨bold-italic¨ mathcolor=¨#0000FF¨»y«/mi»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»(«/mo»«mi mathvariant=¨bold-italic¨ mathcolor=¨#0000FF¨»t«/mi»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»)«/mo»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»=«/mo»«msub»«mi mathvariant=¨bold-italic¨ mathcolor=¨#0000FF¨»Y«/mi»«mn mathvariant=¨bold¨ mathcolor=¨#0000FF¨»0«/mn»«/msub»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»+«/mo»«msub»«mi mathvariant=¨bold-italic¨ mathcolor=¨#0000FF¨»V«/mi»«msub mathcolor=¨#0000FF¨»«mn mathvariant=¨bold¨»0«/mn»«mi mathvariant=¨bold¨»Y«/mi»«/msub»«/msub»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»§#183;«/mo»«mi mathvariant=¨bold-italic¨ mathcolor=¨#0000FF¨»t«/mi»«mspace linebreak=¨newline¨»«/mspace»«mi mathvariant=¨bold-italic¨ mathcolor=¨#0000FF¨»y«/mi»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»(«/mo»«mn mathvariant=¨bold¨ mathcolor=¨#0000FF¨»4«/mn»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»)«/mo»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»=«/mo»«mn mathvariant=¨bold¨ mathcolor=¨#0000FF¨»0«/mn»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»+«/mo»«mn mathvariant=¨bold¨ mathcolor=¨#0000FF¨»24«/mn»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»§#183;«/mo»«mn mathvariant=¨bold¨ mathcolor=¨#0000FF¨»4«/mn»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»=«/mo»«mn mathvariant=¨bold¨ mathcolor=¨#0000FF¨»96«/mn»«mi mathvariant=¨bold-italic¨ mathcolor=¨#0000FF¨»m«/mi»«mspace linebreak=¨newline¨»«/mspace»«mi mathvariant=¨bold-italic¨ mathcolor=¨#0000FF¨»y«/mi»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»(«/mo»«mn mathvariant=¨bold¨ mathcolor=¨#0000FF¨»4«/mn»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»)«/mo»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»=«/mo»«mn mathvariant=¨bold¨ mathcolor=¨#0000FF¨»96«/mn»«mi mathvariant=¨bold-italic¨ mathcolor=¨#0000FF¨»m«/mi»«/math»
نجد الموقع الأفقي بمساعدة دالة الموقع كدالة للزمن المناسبة للحركة بتسارع ثابت:
«math xmlns=¨http://www.w3.org/1998/Math/MathML¨»«mi mathvariant=¨bold-italic¨ mathcolor=¨#0000FF¨»X«/mi»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»(«/mo»«mi mathvariant=¨bold-italic¨ mathcolor=¨#0000FF¨»t«/mi»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»)«/mo»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»=«/mo»«msub»«mi mathvariant=¨bold-italic¨ mathcolor=¨#0000FF¨»X«/mi»«mn mathvariant=¨bold¨ mathcolor=¨#0000FF¨»0«/mn»«/msub»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»+«/mo»«msub»«mi mathvariant=¨bold-italic¨ mathcolor=¨#0000FF¨»V«/mi»«msub mathcolor=¨#0000FF¨»«mn mathvariant=¨bold¨»0«/mn»«mi mathvariant=¨bold¨»X«/mi»«/msub»«/msub»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»§#183;«/mo»«mi mathvariant=¨bold-italic¨ mathcolor=¨#0000FF¨»t«/mi»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»§#160;«/mo»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»+«/mo»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»§#160;«/mo»«mfrac mathcolor=¨#0000FF¨»«mn mathvariant=¨bold¨»1«/mn»«mn mathvariant=¨bold¨»2«/mn»«/mfrac»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»§#183;«/mo»«mi mathvariant=¨bold-italic¨ mathcolor=¨#0000FF¨»a«/mi»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»§#183;«/mo»«msup»«mi mathvariant=¨bold-italic¨ mathcolor=¨#0000FF¨»t«/mi»«mn mathvariant=¨bold¨ mathcolor=¨#0000FF¨»2«/mn»«/msup»«mspace linebreak=¨newline¨»«/mspace»«mi mathvariant=¨bold-italic¨ mathcolor=¨#0000FF¨»X«/mi»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»(«/mo»«mn mathvariant=¨bold¨ mathcolor=¨#0000FF¨»4«/mn»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»)«/mo»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»=«/mo»«mn mathvariant=¨bold¨ mathcolor=¨#0000FF¨»0«/mn»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»+«/mo»«mn mathvariant=¨bold¨ mathcolor=¨#0000FF¨»0«/mn»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»§#183;«/mo»«mn mathvariant=¨bold¨ mathcolor=¨#0000FF¨»4«/mn»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»§#160;«/mo»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»+«/mo»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»§#160;«/mo»«mfrac mathcolor=¨#0000FF¨»«mn mathvariant=¨bold¨»1«/mn»«mn mathvariant=¨bold¨»2«/mn»«/mfrac»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»§#183;«/mo»«mi mathvariant=¨bold-italic¨ mathcolor=¨#0000FF¨»a«/mi»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»§#183;«/mo»«msup»«mn mathvariant=¨bold¨ mathcolor=¨#0000FF¨»4«/mn»«mn mathvariant=¨bold¨ mathcolor=¨#0000FF¨»2«/mn»«/msup»«mspace linebreak=¨newline¨»«/mspace»«mi mathvariant=¨bold-italic¨ mathcolor=¨#0000FF¨»X«/mi»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»(«/mo»«mn mathvariant=¨bold¨ mathcolor=¨#0000FF¨»4«/mn»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»)«/mo»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»=«/mo»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»§#160;«/mo»«mn mathvariant=¨bold¨ mathcolor=¨#0000FF¨»8«/mn»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»§#183;«/mo»«mi mathvariant=¨bold-italic¨ mathcolor=¨#0000FF¨»a«/mi»«/math»
نجد تسارع الجسم باستخدام القانون الثاني لنيوتن:
«math xmlns=¨http://www.w3.org/1998/Math/MathML¨»«mi mathvariant=¨bold¨ mathcolor=¨#0000FF¨»F«/mi»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»=«/mo»«mi mathvariant=¨bold¨ mathcolor=¨#0000FF¨»m«/mi»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»§#183;«/mo»«mi mathvariant=¨bold¨ mathcolor=¨#0000FF¨»a«/mi»«mspace linebreak=¨newline¨»«/mspace»«mi mathvariant=¨bold¨ mathcolor=¨#0000FF¨»a«/mi»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»=«/mo»«mfrac mathcolor=¨#0000FF¨»«mi mathvariant=¨bold¨»F«/mi»«mi mathvariant=¨bold¨»m«/mi»«/mfrac»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»=«/mo»«mfrac mathcolor=¨#0000FF¨»«mrow»«mn mathvariant=¨bold¨»1«/mn»«mo mathvariant=¨bold¨».«/mo»«mn mathvariant=¨bold¨»6«/mn»«/mrow»«mrow»«mn mathvariant=¨bold¨»0«/mn»«mo mathvariant=¨bold¨».«/mo»«mn mathvariant=¨bold¨»2«/mn»«/mrow»«/mfrac»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»=«/mo»«mn mathvariant=¨bold¨ mathcolor=¨#0000FF¨»8«/mn»«mfrac mathcolor=¨#0000FF¨»«mi mathvariant=¨bold¨»m«/mi»«msup»«mi mathvariant=¨bold¨»s«/mi»«mn mathvariant=¨bold¨»2«/mn»«/msup»«/mfrac»«/math»
نعوّض التسارع في تعبير المكان الأفقي.
«math xmlns=¨http://www.w3.org/1998/Math/MathML¨»«mi mathvariant=¨bold¨ mathcolor=¨#0000FF¨»X«/mi»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»(«/mo»«mn mathvariant=¨bold¨ mathcolor=¨#0000FF¨»4«/mn»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»)«/mo»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»=«/mo»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»§#160;«/mo»«mn mathvariant=¨bold¨ mathcolor=¨#0000FF¨»8«/mn»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»§#183;«/mo»«mi mathvariant=¨bold¨ mathcolor=¨#0000FF¨»a«/mi»«mspace linebreak=¨newline¨»«/mspace»«mi mathvariant=¨bold¨ mathcolor=¨#0000FF¨»X«/mi»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»(«/mo»«mn mathvariant=¨bold¨ mathcolor=¨#0000FF¨»4«/mn»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»)«/mo»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»=«/mo»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»§#160;«/mo»«mn mathvariant=¨bold¨ mathcolor=¨#0000FF¨»8«/mn»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»§#183;«/mo»«mn mathvariant=¨bold¨ mathcolor=¨#0000FF¨»8«/mn»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»=«/mo»«mn mathvariant=¨bold¨ mathcolor=¨#0000FF¨»64«/mn»«mi mathvariant=¨bold¨ mathcolor=¨#0000FF¨»m«/mi»«/math»
لذلك في اللحظة t = 4s ، يكون الموقع العمودي للجسم y = 96m ، والموقع الأفقي للجسم هو x = 64m.
בצורה הקרטזית , מיקום הגוף ברגע t=4s ,הוא: «math xmlns=¨http://www.w3.org/1998/Math/MathML¨»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»(«/mo»«mn mathvariant=¨bold¨ mathcolor=¨#0000FF¨»64«/mn»«mi mathvariant=¨bold¨ mathcolor=¨#0000FF¨»m«/mi»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»,«/mo»«mn mathvariant=¨bold¨ mathcolor=¨#0000FF¨»96«/mn»«mi mathvariant=¨bold¨ mathcolor=¨#0000FF¨»m«/mi»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»)«/mo»«/math».
נמצא את המיקום האנכי , בעזרת פונקציית המקום בתלות בזמן .
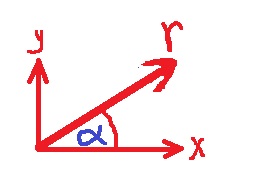
يمكن وصف موقع الجسم في صورة قطبية بواسطة مقدار واتجاه متجّه الموقع r.
نجد مقدار متجّه الموقع:
«math xmlns=¨http://www.w3.org/1998/Math/MathML¨»«mi mathvariant=¨bold¨ mathcolor=¨#FF0000¨»r«/mi»«mo mathvariant=¨bold¨ mathcolor=¨#FF0000¨»=«/mo»«msqrt mathcolor=¨#FF0000¨»«msup»«mi mathvariant=¨bold¨»x«/mi»«mn mathvariant=¨bold¨»2«/mn»«/msup»«mo mathvariant=¨bold¨»+«/mo»«msup»«mi mathvariant=¨bold¨»y«/mi»«mn mathvariant=¨bold¨»2«/mn»«/msup»«/msqrt»«mo mathvariant=¨bold¨ mathcolor=¨#FF0000¨»=«/mo»«msqrt mathcolor=¨#FF0000¨»«msup»«mn mathvariant=¨bold¨»64«/mn»«mn mathvariant=¨bold¨»2«/mn»«/msup»«mo mathvariant=¨bold¨»+«/mo»«msup»«mn mathvariant=¨bold¨»96«/mn»«mn mathvariant=¨bold¨»2«/mn»«/msup»«/msqrt»«mo mathvariant=¨bold¨ mathcolor=¨#FF0000¨»=«/mo»«mn mathvariant=¨bold¨ mathcolor=¨#FF0000¨»115«/mn»«mo mathvariant=¨bold¨ mathcolor=¨#FF0000¨».«/mo»«mn mathvariant=¨bold¨ mathcolor=¨#FF0000¨»37«/mn»«mi mathvariant=¨bold¨ mathcolor=¨#FF0000¨»m«/mi»«/math»
نجد اتجاه متجّه الموقع:
«math xmlns=¨http://www.w3.org/1998/Math/MathML¨»«mi mathvariant=¨bold¨ mathcolor=¨#FF0000¨»tan«/mi»«mo mathvariant=¨bold¨ mathcolor=¨#FF0000¨»(«/mo»«mi mathvariant=¨bold¨ mathcolor=¨#FF0000¨»§#945;«/mi»«mo mathvariant=¨bold¨ mathcolor=¨#FF0000¨»)«/mo»«mo mathvariant=¨bold¨ mathcolor=¨#FF0000¨»=«/mo»«mfrac mathcolor=¨#FF0000¨»«mi mathvariant=¨bold¨»y«/mi»«mi mathvariant=¨bold¨»x«/mi»«/mfrac»«mspace linebreak=¨newline¨»«/mspace»«mspace linebreak=¨newline¨»«/mspace»«mi mathvariant=¨bold¨ mathcolor=¨#FF0000¨»§#945;«/mi»«mo mathvariant=¨bold¨ mathcolor=¨#FF0000¨»=«/mo»«mi mathvariant=¨bold¨ mathcolor=¨#FF0000¨»shift«/mi»«mo mathvariant=¨bold¨ mathcolor=¨#FF0000¨»§#160;«/mo»«mi mathvariant=¨bold¨ mathcolor=¨#FF0000¨»tan«/mi»«mo mathvariant=¨bold¨ mathcolor=¨#FF0000¨»(«/mo»«mfrac mathcolor=¨#FF0000¨»«mi mathvariant=¨bold¨»y«/mi»«mi mathvariant=¨bold¨»x«/mi»«/mfrac»«mo mathvariant=¨bold¨ mathcolor=¨#FF0000¨»)«/mo»«mo mathvariant=¨bold¨ mathcolor=¨#FF0000¨»=«/mo»«mi mathvariant=¨bold¨ mathcolor=¨#FF0000¨»shift«/mi»«mo mathvariant=¨bold¨ mathcolor=¨#FF0000¨»§#160;«/mo»«mi mathvariant=¨bold¨ mathcolor=¨#FF0000¨»tan«/mi»«mo mathvariant=¨bold¨ mathcolor=¨#FF0000¨»(«/mo»«mfrac mathcolor=¨#FF0000¨»«mn mathvariant=¨bold¨»96«/mn»«mn mathvariant=¨bold¨»64«/mn»«/mfrac»«mo mathvariant=¨bold¨ mathcolor=¨#FF0000¨»)«/mo»«mo mathvariant=¨bold¨ mathcolor=¨#FF0000¨»=«/mo»«mn mathvariant=¨bold¨ mathcolor=¨#FF0000¨»56«/mn»«mo mathvariant=¨bold¨ mathcolor=¨#FF0000¨».«/mo»«msup»«mn mathvariant=¨bold¨ mathcolor=¨#FF0000¨»3«/mn»«mo mathvariant=¨bold¨ mathcolor=¨#FF0000¨»§#176;«/mo»«/msup»«/math»
لذلك ، في هذه اللحظة t = 4s ، مقدار ومتجّه الموقع الذي يصف موقع الجسم هو 115.37 مترًا ، والاتجاه 56.3 درجة فوق المحور X.
נמצא את גודלו של ווקטור המיקום:
«math xmlns=¨http://www.w3.org/1998/Math/MathML¨»«mi mathvariant=¨bold¨ mathcolor=¨#FF0000¨»r«/mi»«mo mathvariant=¨bold¨ mathcolor=¨#FF0000¨»=«/mo»«msqrt mathcolor=¨#FF0000¨»«msup»«mi mathvariant=¨bold¨»x«/mi»«mn mathvariant=¨bold¨»2«/mn»«/msup»«mo mathvariant=¨bold¨»+«/mo»«msup»«mi mathvariant=¨bold¨»y«/mi»«mn mathvariant=¨bold¨»2«/mn»«/msup»«/msqrt»«mo mathvariant=¨bold¨ mathcolor=¨#FF0000¨»=«/mo»«msqrt mathcolor=¨#FF0000¨»«msup»«mn mathvariant=¨bold¨»64«/mn»«mn mathvariant=¨bold¨»2«/mn»«/msup»«mo mathvariant=¨bold¨»+«/mo»«msup»«mn mathvariant=¨bold¨»96«/mn»«mn mathvariant=¨bold¨»2«/mn»«/msup»«/msqrt»«mo mathvariant=¨bold¨ mathcolor=¨#FF0000¨»=«/mo»«mn mathvariant=¨bold¨ mathcolor=¨#FF0000¨»115«/mn»«mo mathvariant=¨bold¨ mathcolor=¨#FF0000¨».«/mo»«mn mathvariant=¨bold¨ mathcolor=¨#FF0000¨»37«/mn»«mi mathvariant=¨bold¨ mathcolor=¨#FF0000¨»m«/mi»«/math»
נמצא את כיוונו של ווקטור המיקום:
«math xmlns=¨http://www.w3.org/1998/Math/MathML¨»«mi mathvariant=¨bold¨ mathcolor=¨#FF0000¨»tan«/mi»«mo mathvariant=¨bold¨ mathcolor=¨#FF0000¨»(«/mo»«mi mathvariant=¨bold¨ mathcolor=¨#FF0000¨»§#945;«/mi»«mo mathvariant=¨bold¨ mathcolor=¨#FF0000¨»)«/mo»«mo mathvariant=¨bold¨ mathcolor=¨#FF0000¨»=«/mo»«mfrac mathcolor=¨#FF0000¨»«mi mathvariant=¨bold¨»y«/mi»«mi mathvariant=¨bold¨»x«/mi»«/mfrac»«mspace linebreak=¨newline¨»«/mspace»«mspace linebreak=¨newline¨»«/mspace»«mi mathvariant=¨bold¨ mathcolor=¨#FF0000¨»§#945;«/mi»«mo mathvariant=¨bold¨ mathcolor=¨#FF0000¨»=«/mo»«mi mathvariant=¨bold¨ mathcolor=¨#FF0000¨»shift«/mi»«mo mathvariant=¨bold¨ mathcolor=¨#FF0000¨»§#160;«/mo»«mi mathvariant=¨bold¨ mathcolor=¨#FF0000¨»tan«/mi»«mo mathvariant=¨bold¨ mathcolor=¨#FF0000¨»(«/mo»«mfrac mathcolor=¨#FF0000¨»«mi mathvariant=¨bold¨»y«/mi»«mi mathvariant=¨bold¨»x«/mi»«/mfrac»«mo mathvariant=¨bold¨ mathcolor=¨#FF0000¨»)«/mo»«mo mathvariant=¨bold¨ mathcolor=¨#FF0000¨»=«/mo»«mi mathvariant=¨bold¨ mathcolor=¨#FF0000¨»shift«/mi»«mo mathvariant=¨bold¨ mathcolor=¨#FF0000¨»§#160;«/mo»«mi mathvariant=¨bold¨ mathcolor=¨#FF0000¨»tan«/mi»«mo mathvariant=¨bold¨ mathcolor=¨#FF0000¨»(«/mo»«mfrac mathcolor=¨#FF0000¨»«mn mathvariant=¨bold¨»96«/mn»«mn mathvariant=¨bold¨»64«/mn»«/mfrac»«mo mathvariant=¨bold¨ mathcolor=¨#FF0000¨»)«/mo»«mo mathvariant=¨bold¨ mathcolor=¨#FF0000¨»=«/mo»«mn mathvariant=¨bold¨ mathcolor=¨#FF0000¨»56«/mn»«mo mathvariant=¨bold¨ mathcolor=¨#FF0000¨».«/mo»«msup»«mn mathvariant=¨bold¨ mathcolor=¨#FF0000¨»3«/mn»«mo mathvariant=¨bold¨ mathcolor=¨#FF0000¨»§#176;«/mo»«/msup»«/math»
לכן, ברגע t=4s , גודלו ווקטור המיקום המתאר את מיקום הגוף הוא 115.37 מטר , וכיוון 56.3 מעלות מעל ציר X.
______________________________________________________________________________________









