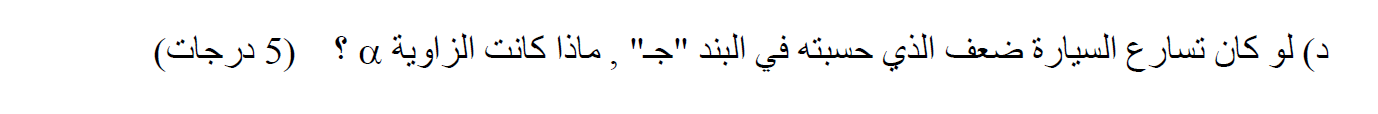
______________________________________________________________________________________________
...
معرفة قوة الشد وقوة الجاذبية.
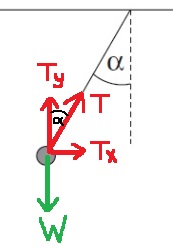
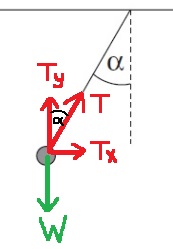
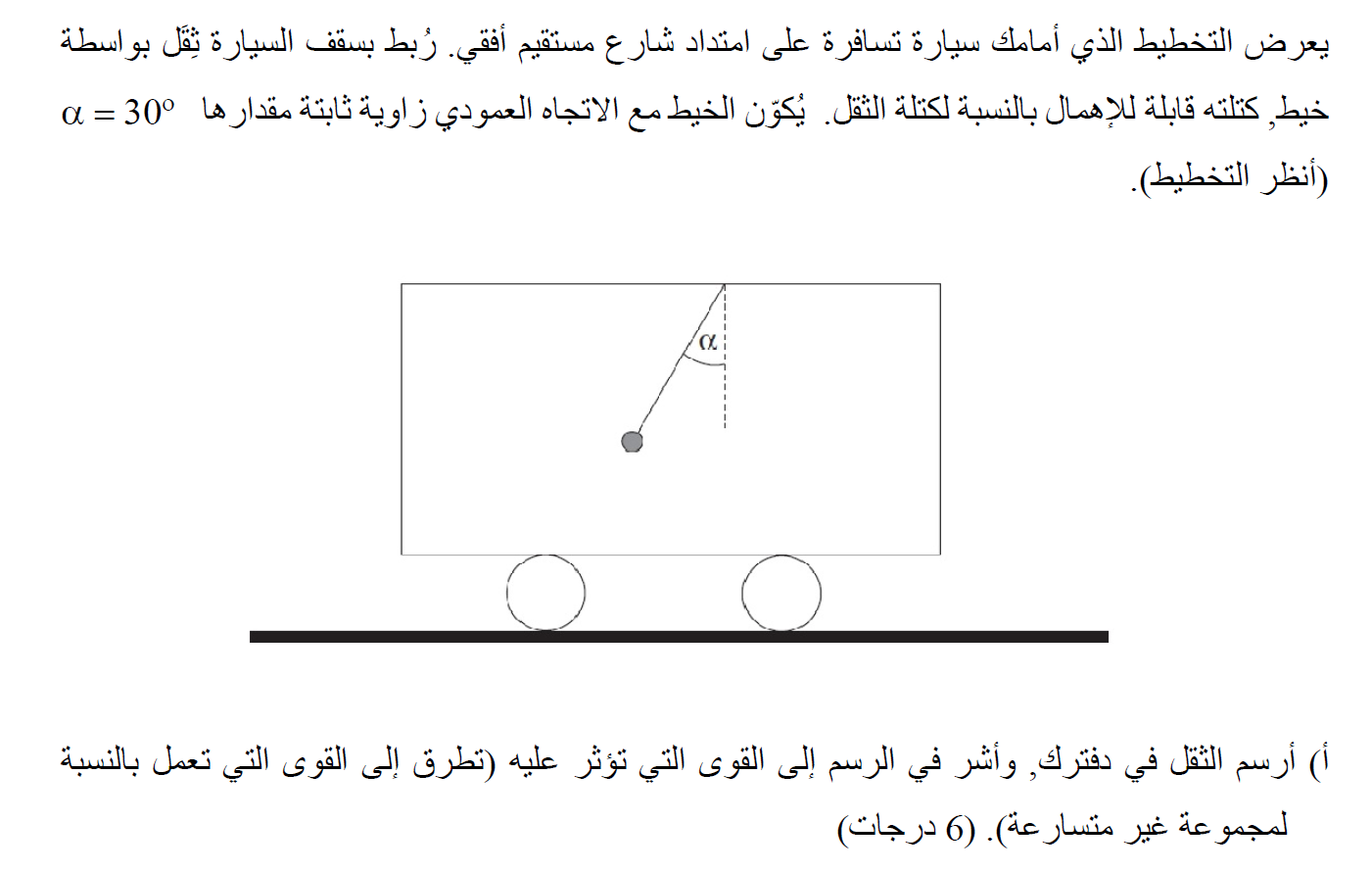
تؤثر قوتان على الثقل: قوة الجاذبية وقوة التوتر. نرسم مخططًا لهذه القوى:
1. تتحرك السيارة بتسارع، والثقل داخلها يتحرك أيضًا بنفس التسارع ، يميل الطلاب إلى إضافة قوة أفقية عن طريق الخطأ غير موجودة.
2. موضوع الهيئة المرجعية خارج المنهاج الدراسي، بشكل عام يجب استخدام معادلات الحركة بالنسبة لمراقب الذي لا يتحرك بتسارع ، القصور الذاتي يعني مستمرًا.
2. נושא מערכות ייחוס יצא מתכנית הלימודים, בגדול יש להשתמש במשוואות התנועה ביחס למתבונן שלא נע בתאוצה , אינרציאלי משמעותו מתמיד.
______________________________________________________________________________________________
______________________________________________________________________________________
...
اتجاه القوة المحصّلة نحو اليمين.
القانون الثاني والأول لنيوتن .
السيارة تكون في حالة سكون في الاتجاه العمودي، وبالتالي فإن محصلة القوى في الاتجاه العمودي يساوي صفرًا. مركّب قوة الشد TY يساوي قوة الجاذبية المؤثرة على الوزن.
وفي الاتجاه الأفقي ، يعمل TX فقط ، وبالتالي فهي محصلة القوى في المقدار والاتجاه. اتجاه محصلة القوى هو اتجاه TX إلى اليمين.
בכיוון האופקי פועל רק TX , לכן הוא הכוח השקול בגודלו ובכיוונו . כיוון הכוח השקול הוא ככיוון TX ימינה.
يتعامل السؤال مع اتجاه القوة المحصّلة ، لكن من المهم أن نفهم ما هي القوة المحصّلة.
______________________________________________________________________________________
______________________________________________________________________________________
...
«math xmlns=¨http://www.w3.org/1998/Math/MathML¨»«mi mathvariant=¨bold-italic¨»a«/mi»«mo mathvariant=¨bold¨»=«/mo»«mn mathvariant=¨bold¨»5«/mn»«mfrac»«mi mathvariant=¨bold¨»m«/mi»«msup»«mi mathvariant=¨bold¨»s«/mi»«mn mathvariant=¨bold¨»2«/mn»«/msup»«/mfrac»«/math» . اتجاه التسارع نحو اليمين.
تسارع الثقل هو نفس تسارع السيارة.
ارسم مخطط القوى على الثقل ، واكتب معادلات الحركة وعبر عن التسارع من معادلات الحركة.
יש לערוך תרשים כוחות על המשקולות, לכתוב את משוואות התנועה ולבטא את התאוצה ממשוואות התנועה.
יש לערוך תרשים כוחות על המשקולת, לכתוב את משוואות תנועה, ולבטא את תאוצת המשקולת ממשוואות התנועה.
حسب مخطط القوى في القسم السابق. نكتب معادلات الحركة في الاتجاه الأفقي وفي الاتجاه العمودي.
نكتب معادلة الحركة في الاتجاه الأفقي بالنسبة لمحور الحركة الأفقي الذي اتجاهه نحو اليمين.
ونكتب معادلة الحركة العمودية بالنسبة لمحور الحركة العمودي الموجّه نحو الأعلى:
«math xmlns=¨http://www.w3.org/1998/Math/MathML¨»«msub»«mi mathvariant=¨bold¨ mathcolor=¨#0000FF¨»§#931;F«/mi»«mi mathvariant=¨bold¨ mathcolor=¨#0000FF¨»Y«/mi»«/msub»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»=«/mo»«mn mathvariant=¨bold¨ mathcolor=¨#0000FF¨»0«/mn»«mspace linebreak=¨newline¨»«/mspace»«mi mathvariant=¨bold¨ mathcolor=¨#0000FF¨»W«/mi»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»=«/mo»«msub»«mi mathvariant=¨bold¨ mathcolor=¨#0000FF¨»T«/mi»«mi mathvariant=¨bold¨ mathcolor=¨#0000FF¨»Y«/mi»«/msub»«mspace linebreak=¨newline¨»«/mspace»«menclose mathcolor=¨#0000FF¨ notation=¨box¨»«mi mathvariant=¨bold¨»m«/mi»«mo mathvariant=¨bold¨»§#183;«/mo»«mi mathvariant=¨bold¨»g«/mi»«mo mathvariant=¨bold¨»=«/mo»«mi mathvariant=¨bold¨»T«/mi»«mo mathvariant=¨bold¨»§#183;«/mo»«mi mathvariant=¨bold¨»cos«/mi»«mo mathvariant=¨bold¨»(«/mo»«mi mathvariant=¨bold¨»§#945;«/mi»«mo mathvariant=¨bold¨»)«/mo»«/menclose»«/math» «math xmlns=¨http://www.w3.org/1998/Math/MathML¨»«msub»«mi mathvariant=¨bold¨ mathcolor=¨#0000FF¨»§#931;F«/mi»«mi mathvariant=¨bold-italic¨ mathcolor=¨#0000FF¨»x«/mi»«/msub»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»=«/mo»«mi mathvariant=¨bold¨ mathcolor=¨#0000FF¨»m«/mi»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»§#183;«/mo»«mi mathvariant=¨bold¨ mathcolor=¨#0000FF¨»a«/mi»«mspace linebreak=¨newline¨»«/mspace»«msub»«mi mathvariant=¨bold¨ mathcolor=¨#0000FF¨»T«/mi»«mi mathvariant=¨bold¨ mathcolor=¨#0000FF¨»x«/mi»«/msub»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»=«/mo»«mi mathvariant=¨bold¨ mathcolor=¨#0000FF¨»m«/mi»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»§#183;«/mo»«mi mathvariant=¨bold¨ mathcolor=¨#0000FF¨»a«/mi»«mspace linebreak=¨newline¨»«/mspace»«menclose mathcolor=¨#0000FF¨ notation=¨box¨»«mi mathvariant=¨bold¨»T«/mi»«mo mathvariant=¨bold¨»§#183;«/mo»«mi mathvariant=¨bold¨»sin«/mi»«mo mathvariant=¨bold¨»(«/mo»«mi mathvariant=¨bold-italic¨»§#945;«/mi»«mo mathvariant=¨bold¨»)«/mo»«mo mathvariant=¨bold¨»=«/mo»«mi mathvariant=¨bold¨»m«/mi»«mo mathvariant=¨bold¨»§#183;«/mo»«mi mathvariant=¨bold¨»a«/mi»«/menclose»«/math»
نعبّر عن التسارع من معادلات الحركة، ونقوم بعملية قسمة بين المعادلتين:
«math xmlns=¨http://www.w3.org/1998/Math/MathML¨»«mspace linebreak=¨newline¨»«/mspace»«mfrac mathcolor=¨#0000FF¨»«mrow»«menclose notation=¨updiagonalstrike¨»«mi mathvariant=¨bold¨»T«/mi»«/menclose»«mo mathvariant=¨bold¨»§#183;«/mo»«mi mathvariant=¨bold¨»sin«/mi»«mo mathvariant=¨bold¨»(«/mo»«mi mathvariant=¨bold¨»§#945;«/mi»«mo mathvariant=¨bold¨»)«/mo»«/mrow»«mrow»«menclose notation=¨updiagonalstrike¨»«mi mathvariant=¨bold¨»T«/mi»«/menclose»«mo mathvariant=¨bold¨»§#183;«/mo»«mi mathvariant=¨bold¨»cos«/mi»«mo mathvariant=¨bold¨»(«/mo»«mi mathvariant=¨bold¨»§#945;«/mi»«mo mathvariant=¨bold¨»)«/mo»«/mrow»«/mfrac»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»=«/mo»«mfrac mathcolor=¨#0000FF¨»«mrow»«menclose notation=¨updiagonalstrike¨»«mi mathvariant=¨bold¨»m«/mi»«/menclose»«mo mathvariant=¨bold¨»§#183;«/mo»«mi mathvariant=¨bold¨»a«/mi»«/mrow»«mrow»«menclose notation=¨updiagonalstrike¨»«mi mathvariant=¨bold¨»m«/mi»«/menclose»«mo mathvariant=¨bold¨»§#183;«/mo»«mi mathvariant=¨bold¨»g«/mi»«/mrow»«/mfrac»«mspace linebreak=¨newline¨»«/mspace»«mspace linebreak=¨newline¨»«/mspace»«mi mathvariant=¨bold¨ mathcolor=¨#0000FF¨»tan«/mi»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»(«/mo»«mi mathvariant=¨bold¨ mathcolor=¨#0000FF¨»§#945;«/mi»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»)«/mo»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»=«/mo»«mfrac mathcolor=¨#0000FF¨»«mi mathvariant=¨bold¨»a«/mi»«mi mathvariant=¨bold¨»g«/mi»«/mfrac»«mspace linebreak=¨newline¨»«/mspace»«menclose mathcolor=¨#0000FF¨ notation=¨circle¨»«mi mathvariant=¨bold¨»a«/mi»«mo mathvariant=¨bold¨»=«/mo»«mi mathvariant=¨bold¨»g«/mi»«mo mathvariant=¨bold¨»§#183;«/mo»«mi mathvariant=¨bold¨»tan«/mi»«mo mathvariant=¨bold¨»(«/mo»«mi mathvariant=¨bold¨»§#945;«/mi»«mo mathvariant=¨bold¨»)«/mo»«/menclose»«mspace linebreak=¨newline¨»«/mspace»«mspace linebreak=¨newline¨»«/mspace»«mi mathvariant=¨bold¨ mathcolor=¨#0000FF¨»a«/mi»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»=«/mo»«mi mathvariant=¨bold¨ mathcolor=¨#0000FF¨»g«/mi»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»§#183;«/mo»«mi mathvariant=¨bold¨ mathcolor=¨#0000FF¨»tan«/mi»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»(«/mo»«mi mathvariant=¨bold¨ mathcolor=¨#0000FF¨»§#945;«/mi»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»)«/mo»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»=«/mo»«mi mathvariant=¨bold¨ mathcolor=¨#0000FF¨»g«/mi»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»§#183;«/mo»«mi mathvariant=¨bold¨ mathcolor=¨#0000FF¨»tan«/mi»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»(«/mo»«mn mathvariant=¨bold¨ mathcolor=¨#0000FF¨»30«/mn»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»)«/mo»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»=«/mo»«mn mathvariant=¨bold¨ mathcolor=¨#0000FF¨»10«/mn»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»§#183;«/mo»«mn mathvariant=¨bold¨ mathcolor=¨#0000FF¨»0«/mn»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨».«/mo»«mn mathvariant=¨bold¨ mathcolor=¨#0000FF¨»577«/mn»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»=«/mo»«mn mathvariant=¨bold¨ mathcolor=¨#0000FF¨»5«/mn»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨».«/mo»«mn mathvariant=¨bold¨ mathcolor=¨#0000FF¨»77«/mn»«mfrac mathcolor=¨#0000FF¨»«mi mathvariant=¨bold¨»m«/mi»«msup»«mi mathvariant=¨bold¨»s«/mi»«mn mathvariant=¨bold¨»2«/mn»«/msup»«/mfrac»«mspace linebreak=¨newline¨»«/mspace»«mspace linebreak=¨newline¨»«/mspace»«/math»
تسارع الثقل 5.77m/s2.
حسب القانون الثاني لنيوتن ، اتجاه التسارع هو في اتجاه محصلة القوى. اتجاه محصلة القوى المؤثرة على الثقل نحو اليمين. لذلك ، فإن اتجاه تسارع الثقل نحو اليمين.
لا توجد حركة نسبية بين الثقل والسيارة ، فتسارع السيارة هو نفس تسارع الثقل في المقدار والاتجاه.
נכתוב את משוואת התנועה לכיוון האופקי ביחס לציר תנועה אופקי שכיוונו ימינה.
ונכתוב את משוואת התנועה האנכית ביחס לציר תנועה אנכי שכיוונו כלפי מעלה:
«math xmlns=¨http://www.w3.org/1998/Math/MathML¨»«msub»«mi mathvariant=¨bold¨ mathcolor=¨#0000FF¨»§#931;F«/mi»«mi mathvariant=¨bold¨ mathcolor=¨#0000FF¨»Y«/mi»«/msub»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»=«/mo»«mn mathvariant=¨bold¨ mathcolor=¨#0000FF¨»0«/mn»«mspace linebreak=¨newline¨»«/mspace»«mi mathvariant=¨bold¨ mathcolor=¨#0000FF¨»W«/mi»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»=«/mo»«msub»«mi mathvariant=¨bold¨ mathcolor=¨#0000FF¨»T«/mi»«mi mathvariant=¨bold¨ mathcolor=¨#0000FF¨»Y«/mi»«/msub»«mspace linebreak=¨newline¨»«/mspace»«menclose mathcolor=¨#0000FF¨ notation=¨box¨»«mi mathvariant=¨bold¨»m«/mi»«mo mathvariant=¨bold¨»§#183;«/mo»«mi mathvariant=¨bold¨»g«/mi»«mo mathvariant=¨bold¨»=«/mo»«mi mathvariant=¨bold¨»T«/mi»«mo mathvariant=¨bold¨»§#183;«/mo»«mi mathvariant=¨bold¨»cos«/mi»«mo mathvariant=¨bold¨»(«/mo»«mi mathvariant=¨bold¨»§#945;«/mi»«mo mathvariant=¨bold¨»)«/mo»«/menclose»«/math» «math xmlns=¨http://www.w3.org/1998/Math/MathML¨»«msub»«mi mathvariant=¨bold¨ mathcolor=¨#0000FF¨»§#931;F«/mi»«mi mathvariant=¨bold-italic¨ mathcolor=¨#0000FF¨»x«/mi»«/msub»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»=«/mo»«mi mathvariant=¨bold¨ mathcolor=¨#0000FF¨»m«/mi»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»§#183;«/mo»«mi mathvariant=¨bold¨ mathcolor=¨#0000FF¨»a«/mi»«mspace linebreak=¨newline¨»«/mspace»«msub»«mi mathvariant=¨bold¨ mathcolor=¨#0000FF¨»T«/mi»«mi mathvariant=¨bold¨ mathcolor=¨#0000FF¨»x«/mi»«/msub»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»=«/mo»«mi mathvariant=¨bold¨ mathcolor=¨#0000FF¨»m«/mi»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»§#183;«/mo»«mi mathvariant=¨bold¨ mathcolor=¨#0000FF¨»a«/mi»«mspace linebreak=¨newline¨»«/mspace»«menclose mathcolor=¨#0000FF¨ notation=¨box¨»«mi mathvariant=¨bold¨»T«/mi»«mo mathvariant=¨bold¨»§#183;«/mo»«mi mathvariant=¨bold¨»sin«/mi»«mo mathvariant=¨bold¨»(«/mo»«mi mathvariant=¨bold-italic¨»§#945;«/mi»«mo mathvariant=¨bold¨»)«/mo»«mo mathvariant=¨bold¨»=«/mo»«mi mathvariant=¨bold¨»m«/mi»«mo mathvariant=¨bold¨»§#183;«/mo»«mi mathvariant=¨bold¨»a«/mi»«/menclose»«/math»
נבטא ממשוואות התנועה את התאוצה, נבצע פעולת חילוק בין המשוואות :
«math xmlns=¨http://www.w3.org/1998/Math/MathML¨»«mspace linebreak=¨newline¨»«/mspace»«mfrac mathcolor=¨#0000FF¨»«mrow»«menclose notation=¨updiagonalstrike¨»«mi mathvariant=¨bold¨»T«/mi»«/menclose»«mo mathvariant=¨bold¨»§#183;«/mo»«mi mathvariant=¨bold¨»sin«/mi»«mo mathvariant=¨bold¨»(«/mo»«mi mathvariant=¨bold¨»§#945;«/mi»«mo mathvariant=¨bold¨»)«/mo»«/mrow»«mrow»«menclose notation=¨updiagonalstrike¨»«mi mathvariant=¨bold¨»T«/mi»«/menclose»«mo mathvariant=¨bold¨»§#183;«/mo»«mi mathvariant=¨bold¨»cos«/mi»«mo mathvariant=¨bold¨»(«/mo»«mi mathvariant=¨bold¨»§#945;«/mi»«mo mathvariant=¨bold¨»)«/mo»«/mrow»«/mfrac»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»=«/mo»«mfrac mathcolor=¨#0000FF¨»«mrow»«menclose notation=¨updiagonalstrike¨»«mi mathvariant=¨bold¨»m«/mi»«/menclose»«mo mathvariant=¨bold¨»§#183;«/mo»«mi mathvariant=¨bold¨»a«/mi»«/mrow»«mrow»«menclose notation=¨updiagonalstrike¨»«mi mathvariant=¨bold¨»m«/mi»«/menclose»«mo mathvariant=¨bold¨»§#183;«/mo»«mi mathvariant=¨bold¨»g«/mi»«/mrow»«/mfrac»«mspace linebreak=¨newline¨»«/mspace»«mspace linebreak=¨newline¨»«/mspace»«mi mathvariant=¨bold¨ mathcolor=¨#0000FF¨»tan«/mi»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»(«/mo»«mi mathvariant=¨bold¨ mathcolor=¨#0000FF¨»§#945;«/mi»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»)«/mo»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»=«/mo»«mfrac mathcolor=¨#0000FF¨»«mi mathvariant=¨bold¨»a«/mi»«mi mathvariant=¨bold¨»g«/mi»«/mfrac»«mspace linebreak=¨newline¨»«/mspace»«menclose mathcolor=¨#0000FF¨ notation=¨circle¨»«mi mathvariant=¨bold¨»a«/mi»«mo mathvariant=¨bold¨»=«/mo»«mi mathvariant=¨bold¨»g«/mi»«mo mathvariant=¨bold¨»§#183;«/mo»«mi mathvariant=¨bold¨»tan«/mi»«mo mathvariant=¨bold¨»(«/mo»«mi mathvariant=¨bold¨»§#945;«/mi»«mo mathvariant=¨bold¨»)«/mo»«/menclose»«mspace linebreak=¨newline¨»«/mspace»«mspace linebreak=¨newline¨»«/mspace»«mi mathvariant=¨bold¨ mathcolor=¨#0000FF¨»a«/mi»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»=«/mo»«mi mathvariant=¨bold¨ mathcolor=¨#0000FF¨»g«/mi»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»§#183;«/mo»«mi mathvariant=¨bold¨ mathcolor=¨#0000FF¨»tan«/mi»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»(«/mo»«mi mathvariant=¨bold¨ mathcolor=¨#0000FF¨»§#945;«/mi»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»)«/mo»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»=«/mo»«mi mathvariant=¨bold¨ mathcolor=¨#0000FF¨»g«/mi»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»§#183;«/mo»«mi mathvariant=¨bold¨ mathcolor=¨#0000FF¨»tan«/mi»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»(«/mo»«mn mathvariant=¨bold¨ mathcolor=¨#0000FF¨»30«/mn»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»)«/mo»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»=«/mo»«mn mathvariant=¨bold¨ mathcolor=¨#0000FF¨»10«/mn»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»§#183;«/mo»«mn mathvariant=¨bold¨ mathcolor=¨#0000FF¨»0«/mn»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨».«/mo»«mn mathvariant=¨bold¨ mathcolor=¨#0000FF¨»577«/mn»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»=«/mo»«mn mathvariant=¨bold¨ mathcolor=¨#0000FF¨»5«/mn»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨».«/mo»«mn mathvariant=¨bold¨ mathcolor=¨#0000FF¨»77«/mn»«mfrac mathcolor=¨#0000FF¨»«mi mathvariant=¨bold¨»m«/mi»«msup»«mi mathvariant=¨bold¨»s«/mi»«mn mathvariant=¨bold¨»2«/mn»«/msup»«/mfrac»«mspace linebreak=¨newline¨»«/mspace»«mspace linebreak=¨newline¨»«/mspace»«/math»
תאוצת המשקולת היא 5.77 מטר לשנייה בריבוע , מכיוון שזווית נטיית החוט היא קבועה , אין תנועה יחסית בין המשקולת למכונית.
תאוצת המכונית זהה לתאוצת המשקולת. תאוצת המכונית היא 5.77 מטר לשנייה בריבוע.
1. في كثير من الحالات ، يتم تنفيذ عملية تحليل القوة إلى مركباتها العمودية. إذن في اتجاه واحد يوجد مركّب واحد من القوة يتعلق بجيب (sin) الزاوية ،
وفي اتجاه آخر مركب من نفس القوة يتعلق بجيب التمام (cos) للزاوية.
في مثل هذه الحالات ، غالبًا من الأسهل الحصول على التعبير المطلوب عن طريق قسمة المعادلات.
2. مخطط القوة ومعادلات الحركة على الثقل.
تعبير التسارع الذي تم الحصول عليه من معادلات الحركة هو تسارع الثقل وليس تسارع السيارة.
لذلك ، من المهم ملاحظة أن الثقل لا يتحرك بالنسبة للسيارة. لذلك فإن تسارع السيارة هو نفس تسارع الثقل.
3. يقوم الطلاب في كثير من الأحيان بكل الأعمال ويجدون التسارع ، ثم ينتقلون إلى القسم التالي
بدون تحديد اتجاه التسارع.
حتى لو لم يتم كتابة المقدار والاتجاه بين قوسين ، نظرًا لعدم كتابة مقدار التسارع ، يجب تحديد اتجاه التسارع.
ובכיוון אחר רכיב של אותו כוח בתלות בקוסינוס של הזווית. במקרים כאלו לרוב, נוח לקבל את הביטוי המבוקש מחילוק המשוואות .
2. תרשים הכוחות ומשוואות התנועה הם על המשקולת , ביטוי התאוצה המתקבל ממשוואות התנועה הוא תאוצת המשקולת ולא תאוצת המכונית.
לכן, חשוב לציין שהמשקולת לא נעה ביחס למכונית. לכן תאוצת המכונית זהה לתאוצת המשקולת.
3. ממשוואות התנועה מתקבל גודל התאוצה , קל לשכוח לציין את כיוון התאוצה. גם אם לא היה כתוב בסוגריים גודל וכיוון , מכיוון שלא כתוב גודל התאוצה , יש למצוא את גודלה וגם את כיוונה.
______________________________________________________________________________________
______________________________________________________________________________________
...
تكون زاوية ميل الخيط 49.08 درجة.
تغيير الصيغة للتعبير عن تسارع الثقل. تعبير الزاوية كدالة للتسارع.
نستخدم تعبير التسارع الذي تم تطويره من معادلات الحركة في القسم السابق، ومن خلاله نعبّر عن زاوية ميل الخيط α:
«math xmlns=¨http://www.w3.org/1998/Math/MathML¨»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»§#160;«/mo»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»§#160;«/mo»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»§#160;«/mo»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»§#160;«/mo»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»§#160;«/mo»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»§#160;«/mo»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»§#160;«/mo»«mi mathvariant=¨bold¨ mathcolor=¨#0000FF¨»a«/mi»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»=«/mo»«mi mathvariant=¨bold¨ mathcolor=¨#0000FF¨»g«/mi»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»§#183;«/mo»«mi mathvariant=¨bold¨ mathcolor=¨#0000FF¨»tan«/mi»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»(«/mo»«mi mathvariant=¨bold¨ mathcolor=¨#0000FF¨»§#945;«/mi»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»)«/mo»«mspace linebreak=¨newline¨»«/mspace»«mspace linebreak=¨newline¨»«/mspace»«menclose mathcolor=¨#0000FF¨ notation=¨circle¨»«mi mathvariant=¨bold¨»§#945;«/mi»«mo mathvariant=¨bold¨»=«/mo»«mi mathvariant=¨bold¨»shift«/mi»«mo mathvariant=¨bold¨»§#160;«/mo»«mi mathvariant=¨bold¨»tan«/mi»«mo mathvariant=¨bold¨»(«/mo»«mfrac»«mi mathvariant=¨bold¨»a«/mi»«mi mathvariant=¨bold¨»g«/mi»«/mfrac»«mo mathvariant=¨bold¨»)«/mo»«/menclose»«/math»
نجد زاوية ميل الخيط، عندما يكون تسارع السيارة أكبر بمرتين ، ويساوي 11.54 مترًا لكل ثانية مربعة:
«math xmlns=¨http://www.w3.org/1998/Math/MathML¨»«mi mathvariant=¨bold¨ mathcolor=¨#0000FF¨»§#945;«/mi»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»=«/mo»«mi mathvariant=¨bold¨ mathcolor=¨#0000FF¨»shift«/mi»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»§#160;«/mo»«mi mathvariant=¨bold¨ mathcolor=¨#0000FF¨»tan«/mi»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»(«/mo»«mfrac mathcolor=¨#0000FF¨»«mi mathvariant=¨bold¨»a«/mi»«mi mathvariant=¨bold¨»g«/mi»«/mfrac»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»)«/mo»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»=«/mo»«mi mathvariant=¨bold¨ mathcolor=¨#0000FF¨»shift«/mi»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»§#160;«/mo»«mi mathvariant=¨bold¨ mathcolor=¨#0000FF¨»tan«/mi»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»(«/mo»«mfrac mathcolor=¨#0000FF¨»«mrow»«mn mathvariant=¨bold¨»11«/mn»«mo mathvariant=¨bold¨».«/mo»«mn mathvariant=¨bold¨»54«/mn»«/mrow»«mn mathvariant=¨bold¨»10«/mn»«/mfrac»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»)«/mo»«mspace linebreak=¨newline¨»«/mspace»«mi mathvariant=¨bold¨ mathcolor=¨#0000FF¨»§#945;«/mi»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»=«/mo»«mn mathvariant=¨bold¨ mathcolor=¨#0000FF¨»49«/mn»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨».«/mo»«mn mathvariant=¨bold¨ mathcolor=¨#0000FF¨»08«/mn»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»§#176;«/mo»«/math»
عندما يتضاعف التسارع، ستكون زاوية ميل الخيط 49.08 درجة.
«math xmlns=¨http://www.w3.org/1998/Math/MathML¨»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»§#160;«/mo»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»§#160;«/mo»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»§#160;«/mo»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»§#160;«/mo»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»§#160;«/mo»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»§#160;«/mo»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»§#160;«/mo»«mi mathvariant=¨bold¨ mathcolor=¨#0000FF¨»a«/mi»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»=«/mo»«mi mathvariant=¨bold¨ mathcolor=¨#0000FF¨»g«/mi»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»§#183;«/mo»«mi mathvariant=¨bold¨ mathcolor=¨#0000FF¨»tan«/mi»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»(«/mo»«mi mathvariant=¨bold¨ mathcolor=¨#0000FF¨»§#945;«/mi»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»)«/mo»«mspace linebreak=¨newline¨»«/mspace»«mspace linebreak=¨newline¨»«/mspace»«menclose mathcolor=¨#0000FF¨ notation=¨circle¨»«mi mathvariant=¨bold¨»§#945;«/mi»«mo mathvariant=¨bold¨»=«/mo»«mi mathvariant=¨bold¨»shift«/mi»«mo mathvariant=¨bold¨»§#160;«/mo»«mi mathvariant=¨bold¨»tan«/mi»«mo mathvariant=¨bold¨»(«/mo»«mfrac»«mi mathvariant=¨bold¨»a«/mi»«mi mathvariant=¨bold¨»g«/mi»«/mfrac»«mo mathvariant=¨bold¨»)«/mo»«/menclose»«/math»
נמצא את זווית נטיית החוט ,כאשר תאוצת המכונית גדולה פי 2 , ושווה ל 11.54 מטר לשנייה בריבוע:
«math xmlns=¨http://www.w3.org/1998/Math/MathML¨»«mi mathvariant=¨bold¨ mathcolor=¨#0000FF¨»§#945;«/mi»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»=«/mo»«mi mathvariant=¨bold¨ mathcolor=¨#0000FF¨»shift«/mi»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»§#160;«/mo»«mi mathvariant=¨bold¨ mathcolor=¨#0000FF¨»tan«/mi»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»(«/mo»«mfrac mathcolor=¨#0000FF¨»«mi mathvariant=¨bold¨»a«/mi»«mi mathvariant=¨bold¨»g«/mi»«/mfrac»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»)«/mo»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»=«/mo»«mi mathvariant=¨bold¨ mathcolor=¨#0000FF¨»shift«/mi»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»§#160;«/mo»«mi mathvariant=¨bold¨ mathcolor=¨#0000FF¨»tan«/mi»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»(«/mo»«mfrac mathcolor=¨#0000FF¨»«mrow»«mn mathvariant=¨bold¨»11«/mn»«mo mathvariant=¨bold¨».«/mo»«mn mathvariant=¨bold¨»54«/mn»«/mrow»«mn mathvariant=¨bold¨»10«/mn»«/mfrac»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»)«/mo»«mspace linebreak=¨newline¨»«/mspace»«mi mathvariant=¨bold¨ mathcolor=¨#0000FF¨»§#945;«/mi»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»=«/mo»«mn mathvariant=¨bold¨ mathcolor=¨#0000FF¨»49«/mn»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨».«/mo»«mn mathvariant=¨bold¨ mathcolor=¨#0000FF¨»08«/mn»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»§#176;«/mo»«/math»
כאשר התאוצה תגדל פי 2 , זווית נטיית החוט תהיה 49.08 מעלות.
1. زاد التسارع مرتين ، لكن زاوية ميل الخيط لم تزداد 1.63 مرة ، وبالتالي فإن زاوية ميل الخيط لا تتناسب طرديًا على التسارع.
2. يتم تحديد زاوية ميل الخيط وفقًا لتسارع السيارة وثابت الجاذبية، وبالتالي يمكن استخدام الثقل المعلق كمقياس تسارع.
2. זווית נטיית החוט נקבעת בהתאם לתאוצת המכונית ולקבוע הגרביטציה בלבד, לכן המשקולת התלויה יכולה לשמש כמד תאוצה.
______________________________________________________________________________________

______________________________________________________________________________________
...
نعم.
فهم جيد لتعريف السرعة وتعريف التسارع.
نعم ، يجب أن يكون التسارع نحو اليمين ، ولكن يمكن أن تكون الحركة في أي اتجاه.
המכונית יכולה לנסוע שמאלה ולבלום, או לנסוע ימינה ולהאיץ. בשני המקרים זווית נטיית החוט היא זהה.
بمساعدة الثقل المعلق الذي يستعمل كمقياس تسارع ، يمكنك معرفة اتجاه التسارع ومقداره. لا يمكن معرفة اتجاه الحركة من متجه التسارع.
اتجاه الحركة هو اتجاه متجه السرعة.
عندما يقذف الجسم نحو الأعلى ، يتحرك الجسم في جزء من الوقت لأعلى وفي جزء آخر من الوقت يتحرك للأسفل ، لكن اتجاه التسارع دائمًا لأسفل.
في الصورة التالية يوجد لاعبان وكرة ، تؤثر قوة الجاذبية على الكرة لأسفل ، وبالتالي يكون تسارع الكرة g لأسفل.
هل يمكن معرفة اتجاه حركة الكرة بمعرفة تسارع الكرة؟ لا!
حتى في حالة الكتلة المعلقة المستخدمة كمقياس تسارع ، يمكن معرفة اتجاه التسارع ، ولكن لا يمكن معرفة اتجاه الحركة.
כיוון התנועה הוא ככיוונו של ווקטור המהירות.
כאשר גוף נזרק כלפי מעלה , חלק מהזמן הוא נע כלפי מעלה וחלק מהזמן הוא נע כלפי מטה, אך כיוון התאוצה הוא תמיד כלפי מטה.
בתמונה הבאה מופיעים שני שחקנים וכדור , כוח הכובד פועל על הכדור כלפי מטה , לכן תאוצת הכדור היא g כלפי מטה .
האם מידיעת תאוצת הכדור ניתן לדעת את כיוון תנועתו? לא!
גם במקרה של מסה תלוי המשמשת כמד תאוצה ניתן לדעת מה כיוון התאוצה אך לא ניתן לדעת מה כיוון התנועה.
______________________________________________________________________________________
______________________________________________________________________________________
...
زاوية ميل الخيط لا تتعلق بكتلة الثقل.
لقد طورنا تعبيرًا لزاوية ميل الخيط ، يجب التفسير بمساعدة هذا التعبير.
من تعبير الزاوية «math xmlns=¨http://www.w3.org/1998/Math/MathML¨»«mi mathvariant=¨bold¨ mathcolor=¨#0000FF¨»§#945;«/mi»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»=«/mo»«mi mathvariant=¨bold¨ mathcolor=¨#0000FF¨»shift«/mi»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»§#160;«/mo»«mi mathvariant=¨bold¨ mathcolor=¨#0000FF¨»tan«/mi»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»(«/mo»«mfrac mathcolor=¨#0000FF¨»«mi mathvariant=¨bold¨»a«/mi»«mi mathvariant=¨bold¨»g«/mi»«/mfrac»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»)«/mo»«mspace linebreak=¨newline¨»«/mspace»«/math» يمكن ملاحظة أن زاوية ميل الخيط لا تتعلق بكتلة الثقل.
من الصعب جدًا الإجابة على مثل هذا السؤال بشكل تام بدون تعبير، فلا حاجة أن تجيب بدون تعبير !!
ببساطة يجب أن نظهر من التعبير أن التسارع لا يتعلق بالكتلة.
لا يتعلق التسارع بالكتلة لأنه كلما زادت الكتلة، زادت قوة التوتر، يزداد مركّب التوتر في اتجاه الحركة. يمكن القول أن القوة المحصّلة المؤثرة على الكتلة تتناسب طرديًا مع مقدار الكتلة. من ناحية أخرى ، من القانون الثاني لنيوتن ، يتناسب التسارع عكسياً مع الكتلة.
نظرًا لأن التسارع يتناسب طرديًا مع الكتلة مرة بشكل طردي ومرة أخرى بشكل عكسي ،تُختزل علاقة التسارع بالكتلة. وعندها التسارع لا يتعلق بالكتلة.
تمامًا مثل تسارع الجاذبية.
יש פשוט להראות מהביטוי שהתאוצה איננה תלויה במסה.
התאוצה לא תלויה במסה מכיוון שככל שהמסה גדולה יותר ,כך כוח המתיחות גדול יותר ,רכיב המתיחות בכיוון התנועה גדול יותר. אפשר להגיד שהכוח השקול הפועל על המסה תלוי ביחס ישר בגודל המסה. מצד שני מהחוק השני של ניוטון התאוצה תלויה במסה ביחס הפוך.
מכיוון שהתאוצה תלויה במסה גם ביחס ישר וגם ביחס הפוך ,תלות התאוצה במסה מתקזז. והתאוצה לא תלויה במסה.
בדיוק כמו תאוצת הכובד.
______________________________________________________________________________________