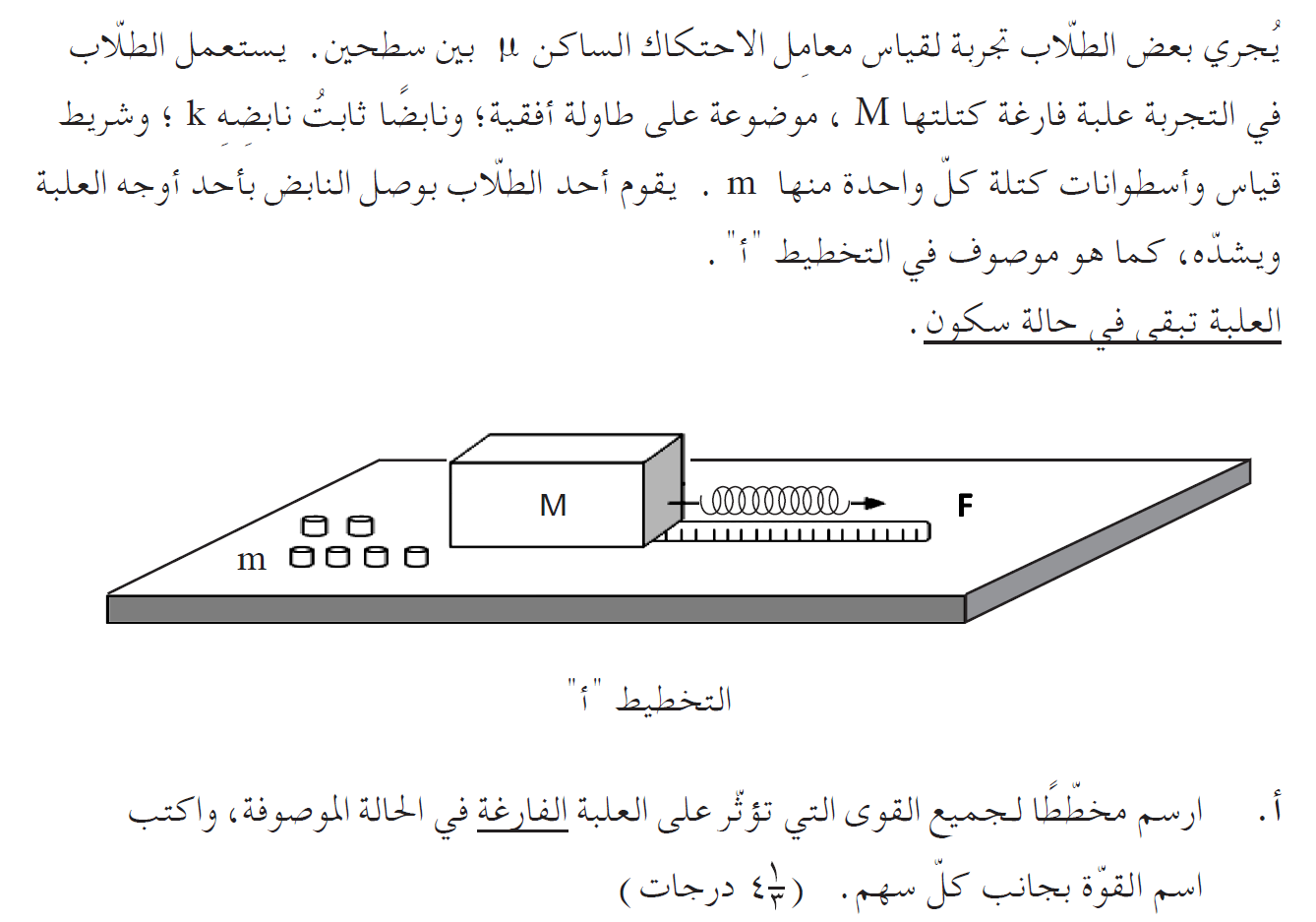
حلول ومنتديات لألبوم الحلول - الديناميكا في خط مستقيم: 2011,2- الاحتكاك الساكن وحافة الحركة

14. 2011,2- الاحتكاك الساكن وحافة الحركة

______________________________________________________________________________________

...

التمييز بين جميع القوى المؤثرة على الصندوق، ومعرفة اتجاه كل واحدة من هذه القوى.

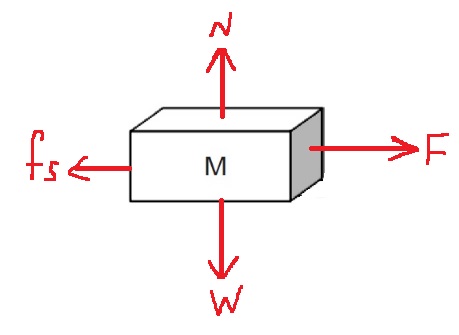
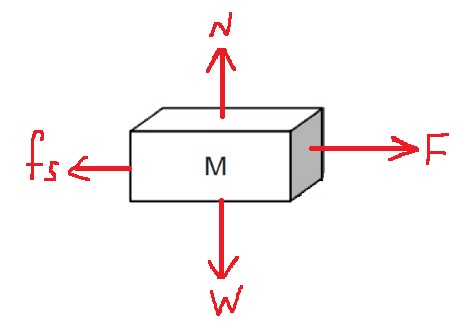
تعمل على الجسم أربع قوى : القوة العمودية N ، قوة الجاذبية W ، قوة الزنبرك F. وقوة الاحتكاك الساكن fs.

نرسم مخطط القوى المؤثرة على الجسم:

נערוך תרשים כוחות ,לכוחות הפועלים על הגוף:

1. يشغّل الطالب قوة على النابض، فهو لا يشغّل قوة على الصندوق لأنه لا يلمس الصندوق. النابض هو الذي يشغّل قوة على الصندوق.

2. قوة النابض تعمل على الصندوق الموجود على اليمين، والصندوق موجود في حالة سكون لذا بالضرورة تعمل عليه قوة احتكاك ساكن نحو اليسار.

3. في الحالات التي تكون فيها قوة الاحتكاك مهملة، نشير في السؤال أن السطح أملس، أو أن الاحتكاك مهمل.
في الحالات التي لا توجد فيها إشارة إلى الاحتكاك في السؤال، فإن الاحتكاك لا يمكن إهماله.

2. כוח הקפיץ פועל על התיבה ימינה ,והתיבה נחה בהכרח פועל כוח חיכוך סטטי שמאלה.

3. במקרים בהם כוח החיכוך זניח , מציינים בשאלה שהמשטח חלק, או שהחיכוך זניח .

במקרים בהם אין התייחסות לחיכוך בשאלה , החיכוך לא לא זניח.

______________________________________________________________________________________

____________________________________________________________________________________

...

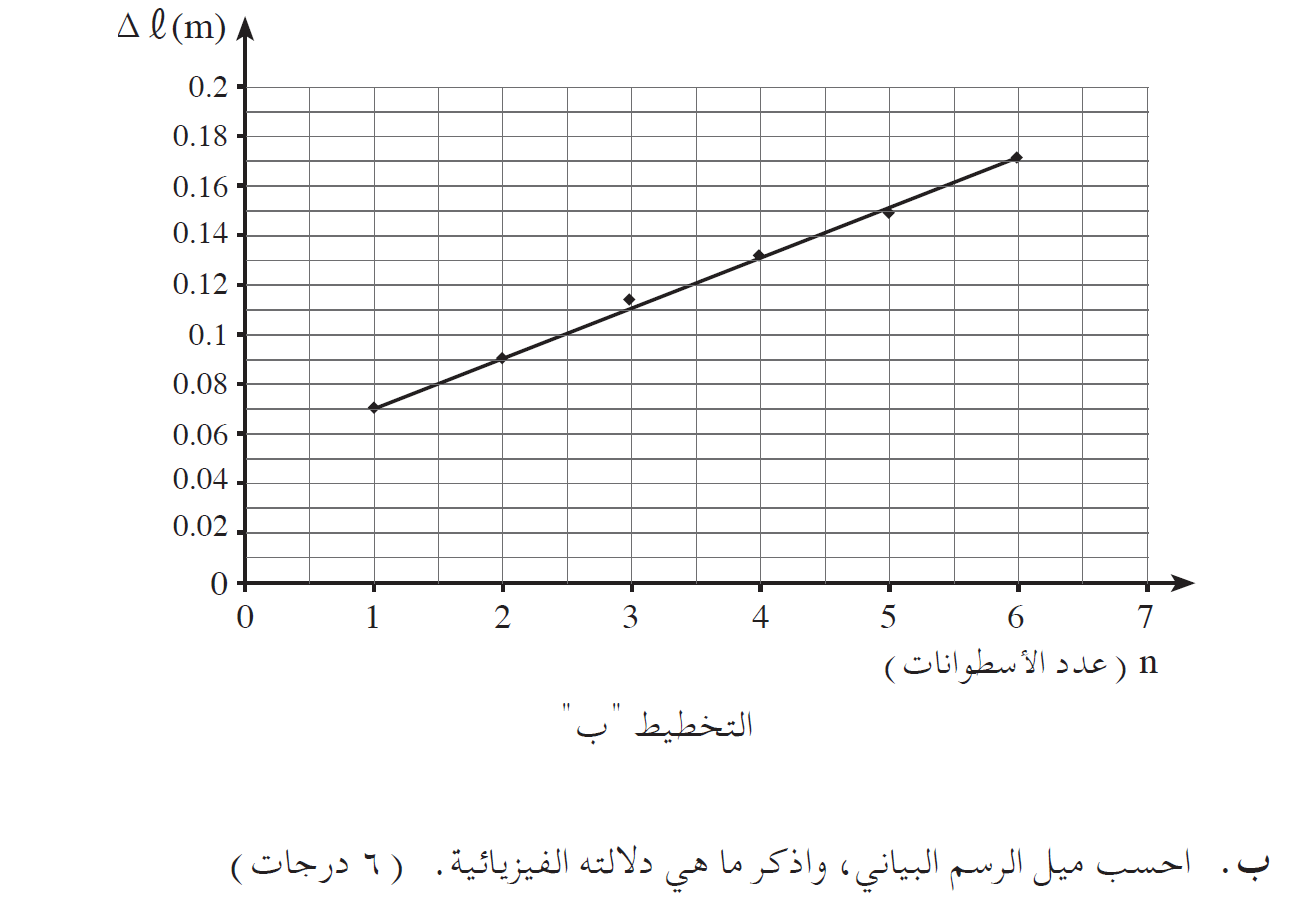
الميل الناتج هو 0.02 متر لكل اسطوانة.
هذا يعني أنه لكل أسطوانة تضاف إلى الصندوق، تلزم استطالة إضافية بمقدار 0.02 متر في طول النابض حتى تكون المجموعة على وشك الحركة.

המשמעות היא שעל כל גליל שנוסף לתיבה , נדרשת תוספת התארכות של 0.2 מטר באורך הקפיץ כדי שהמערכת תהיה בסף תנועה.

يتم حساب ميل الرسم البياني وفقًا للفرق في القيم على المحور العمودي وفرق القيم على المحور الأفقي.
معنى الميل بشكل عام: التغيّر في قيمة المحور العمودي كدالة للتغيّر في قيمة المحور الأفقي.

משמעות השיפוע באופן כללי: השינוי בערך הציר האנכי בתלות בשינוי בערך הציר האופקי.

نحسب ميل الرسم البياني, بواسطة نقطتين موجودتين على الدالة المعطاة في الرسم البياني:

«math xmlns=¨http://www.w3.org/1998/Math/MathML¨»«mi mathvariant=¨bold¨ mathcolor=¨#0000FF¨»§#1575;§#1604;§#1605;§#1610;§#1604;«/mi»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»=«/mo»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»§#160;«/mo»«mfrac mathcolor=¨#0000FF¨»«msub»«mo mathvariant=¨bold¨»§#8710;«/mo»«mrow»«mo mathvariant=¨bold¨»§#8710;«/mo»«mo mathvariant=¨bold¨»§#160;«/mo»«mi mathvariant=¨bold¨»L«/mi»«/mrow»«/msub»«mrow»«mo mathvariant=¨bold¨»§#8710;«/mo»«mi mathvariant=¨bold¨»n«/mi»«/mrow»«/mfrac»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»=«/mo»«mfrac mathcolor=¨#0000FF¨»«mrow»«mn mathvariant=¨bold¨»0«/mn»«mo mathvariant=¨bold¨».«/mo»«mn mathvariant=¨bold¨»09«/mn»«mo mathvariant=¨bold¨»-«/mo»«mn mathvariant=¨bold¨»0«/mn»«mo mathvariant=¨bold¨».«/mo»«mn mathvariant=¨bold¨»07«/mn»«/mrow»«mrow»«mn mathvariant=¨bold¨»2«/mn»«mo mathvariant=¨bold¨»-«/mo»«mn mathvariant=¨bold¨»1«/mn»«/mrow»«/mfrac»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»=«/mo»«mfrac mathcolor=¨#0000FF¨»«mrow»«mn mathvariant=¨bold¨»0«/mn»«mo mathvariant=¨bold¨».«/mo»«mn mathvariant=¨bold¨»02«/mn»«/mrow»«mn mathvariant=¨bold¨»1«/mn»«/mfrac»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»=«/mo»«mn mathvariant=¨bold¨ mathcolor=¨#0000FF¨»0«/mn»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨».«/mo»«mn mathvariant=¨bold¨ mathcolor=¨#0000FF¨»02«/mn»«mi mathvariant=¨bold¨ mathcolor=¨#0000FF¨»m«/mi»«/math»

كلما زادت كتلة الصندوق (مع الأسطوانات)، زادت استطالة النابض عند وشك الحركة.
الميل الذي تم الحصول عليه هو 0.02 متر لكل أسطوانة، مما يعني أنه لكل أسطوانة تضاف إلى الصندوق، تلزم استطالة إضافية بمقدار 0.02 متر في طول النابض حتى تكون المجموعة على وشك الحركة.

«math xmlns=¨http://www.w3.org/1998/Math/MathML¨»«mi mathvariant=¨bold¨ mathcolor=¨#0000FF¨»§#1513;§#1497;§#1508;§#1493;§#1506;«/mi»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»=«/mo»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»§#160;«/mo»«mfrac mathcolor=¨#0000FF¨»«msub»«mo mathvariant=¨bold¨»§#8710;«/mo»«mrow»«mo mathvariant=¨bold¨»§#8710;«/mo»«mo mathvariant=¨bold¨»§#160;«/mo»«mi mathvariant=¨bold¨»L«/mi»«/mrow»«/msub»«mrow»«mo mathvariant=¨bold¨»§#8710;«/mo»«mi mathvariant=¨bold¨»n«/mi»«/mrow»«/mfrac»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»=«/mo»«mfrac mathcolor=¨#0000FF¨»«mrow»«mn mathvariant=¨bold¨»0«/mn»«mo mathvariant=¨bold¨».«/mo»«mn mathvariant=¨bold¨»9«/mn»«mo mathvariant=¨bold¨»-«/mo»«mn mathvariant=¨bold¨»0«/mn»«mo mathvariant=¨bold¨».«/mo»«mn mathvariant=¨bold¨»7«/mn»«/mrow»«mrow»«mn mathvariant=¨bold¨»2«/mn»«mo mathvariant=¨bold¨»-«/mo»«mn mathvariant=¨bold¨»1«/mn»«/mrow»«/mfrac»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»=«/mo»«mfrac mathcolor=¨#0000FF¨»«mrow»«mn mathvariant=¨bold¨»0«/mn»«mo mathvariant=¨bold¨».«/mo»«mn mathvariant=¨bold¨»2«/mn»«/mrow»«mn mathvariant=¨bold¨»1«/mn»«/mfrac»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»=«/mo»«mn mathvariant=¨bold¨ mathcolor=¨#0000FF¨»0«/mn»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨».«/mo»«mn mathvariant=¨bold¨ mathcolor=¨#0000FF¨»2«/mn»«mi mathvariant=¨bold¨ mathcolor=¨#0000FF¨»m«/mi»«/math»

ככל שמסת התיבה (עם הגלילים) , גדולה יותר כך התארכות הקפיץ בסף תנועה תהיה גדולה יותר.

משמעות שיפוע הגרף, על כל תוספת גליל , נדרשת תוספת התארכות של 0.2 מטר באורך הקפיץ כדי שהמערכת תהיה בסף תנועה.

هناك رسوم بيانية شائعة يُعرف فيها معنى الميل، على سبيل المثال في الرسم البياني للمكان كدالة للزمن، فإن معنى الميل هو السرعة. في الرسم البياني للسرعة كدالة للزمن، الميل يعني التسارع.
في الرسوم البيانية الأقل شيوعًا، مثل هذا الرسم البياني. يجب أن تكتب تعبيرًا للميل، من تعبير الميل ووحدات الميل نفهم معنى الميل.

בגרפים פחות נפוצים , כמו גרף זה . יש לכתוב ביטוי לשיפוע , מביטוי השיפוע ויחידות השיפוע להבין את משמעות השיפוע.

______________________________________________________________________________________

...

البرهان موجود في الحل الكامل.

نكتب معادلة الحركة في الاتجاه الأفقي وفي الاتجاه العمودي، في حالة وشك الحركة.

نكتب معادلة الحركة في الاتجاه الأفقي وفي الاتجاه العمودي، في حالة أن الجسم على وشك الحركة.

«math xmlns=¨http://www.w3.org/1998/Math/MathML¨»«msub»«mi mathvariant=¨bold¨ mathcolor=¨#0000FF¨»§#931;F«/mi»«mi mathvariant=¨bold¨ mathcolor=¨#0000FF¨»Y«/mi»«/msub»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»=«/mo»«mn mathvariant=¨bold¨ mathcolor=¨#0000FF¨»0«/mn»«mspace linebreak=¨newline¨»«/mspace»«mi mathvariant=¨bold¨ mathcolor=¨#0000FF¨»N«/mi»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»=«/mo»«mi mathvariant=¨bold¨ mathcolor=¨#0000FF¨»W«/mi»«mspace linebreak=¨newline¨»«/mspace»«menclose mathcolor=¨#0000FF¨ notation=¨box¨»«mi mathvariant=¨bold¨»N«/mi»«mo mathvariant=¨bold¨»=«/mo»«mfenced»«mrow»«mi mathvariant=¨bold¨»M«/mi»«mo mathvariant=¨bold¨»+«/mo»«mi mathvariant=¨bold¨»nm«/mi»«/mrow»«/mfenced»«mo mathvariant=¨bold¨»§#183;«/mo»«mi mathvariant=¨bold¨»g«/mi»«/menclose»«/math» «math xmlns=¨http://www.w3.org/1998/Math/MathML¨»«msub»«mi mathvariant=¨bold¨ mathcolor=¨#0000FF¨»§#931;F«/mi»«mi mathvariant=¨bold¨ mathcolor=¨#0000FF¨»x«/mi»«/msub»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»=«/mo»«mn mathvariant=¨bold¨ mathcolor=¨#0000FF¨»0«/mn»«mspace linebreak=¨newline¨»«/mspace»«msub»«mi mathvariant=¨bold¨ mathcolor=¨#0000FF¨»f«/mi»«msub mathcolor=¨#0000FF¨»«mi mathvariant=¨bold¨»s«/mi»«mi mathvariant=¨bold¨»max«/mi»«/msub»«/msub»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»=«/mo»«mi mathvariant=¨bold¨ mathcolor=¨#0000FF¨»F«/mi»«mspace linebreak=¨newline¨»«/mspace»«menclose mathcolor=¨#0000FF¨ notation=¨box¨»«msub»«mi mathvariant=¨bold¨»§#956;«/mi»«mi mathvariant=¨bold¨»s«/mi»«/msub»«mo mathvariant=¨bold¨»§#183;«/mo»«mi mathvariant=¨bold¨»N«/mi»«mo mathvariant=¨bold¨»=«/mo»«mi mathvariant=¨bold¨»K«/mi»«mo mathvariant=¨bold¨»§#183;«/mo»«mo mathvariant=¨bold¨»§#8710;«/mo»«mi mathvariant=¨bold¨»L«/mi»«/menclose»«/math»

نُعوّض القوة العمودية من معادلة الحركة الأفقية في معادلة الحركة العمودية، ونعبر عن استطالة النابض:

«math xmlns=¨http://www.w3.org/1998/Math/MathML¨»«msub»«mi mathvariant=¨bold¨ mathcolor=¨#0000FF¨»§#956;«/mi»«mi mathvariant=¨bold¨ mathcolor=¨#0000FF¨»s«/mi»«/msub»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»§#183;«/mo»«mi mathvariant=¨bold¨ mathcolor=¨#0000FF¨»N«/mi»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»=«/mo»«mi mathvariant=¨bold¨ mathcolor=¨#0000FF¨»K«/mi»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»§#183;«/mo»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»§#8710;«/mo»«mi mathvariant=¨bold¨ mathcolor=¨#0000FF¨»L«/mi»«mspace linebreak=¨newline¨»«/mspace»«mspace linebreak=¨newline¨»«/mspace»«msub»«mi mathvariant=¨bold¨ mathcolor=¨#0000FF¨»§#956;«/mi»«mi mathvariant=¨bold¨ mathcolor=¨#0000FF¨»s«/mi»«/msub»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»§#183;«/mo»«mfenced mathcolor=¨#0000FF¨»«mrow»«mi mathvariant=¨bold¨»M«/mi»«mo mathvariant=¨bold¨»+«/mo»«mi mathvariant=¨bold¨»nm«/mi»«/mrow»«/mfenced»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»§#183;«/mo»«mi mathvariant=¨bold¨ mathcolor=¨#0000FF¨»g«/mi»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»=«/mo»«mi mathvariant=¨bold¨ mathcolor=¨#0000FF¨»K«/mi»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»§#183;«/mo»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»§#8710;«/mo»«mi mathvariant=¨bold¨ mathcolor=¨#0000FF¨»L«/mi»«mspace linebreak=¨newline¨»«/mspace»«mspace linebreak=¨newline¨»«/mspace»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»§#8710;«/mo»«mi mathvariant=¨bold¨ mathcolor=¨#0000FF¨»L«/mi»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»=«/mo»«mfrac mathcolor=¨#0000FF¨»«mrow»«msub»«mi mathvariant=¨bold¨»§#956;«/mi»«mi mathvariant=¨bold¨»s«/mi»«/msub»«mo mathvariant=¨bold¨»§#183;«/mo»«mfenced»«mrow»«mi mathvariant=¨bold¨»M«/mi»«mo mathvariant=¨bold¨»+«/mo»«mi mathvariant=¨bold¨»nm«/mi»«/mrow»«/mfenced»«mo mathvariant=¨bold¨»§#183;«/mo»«mi mathvariant=¨bold¨»g«/mi»«/mrow»«mi mathvariant=¨bold¨»K«/mi»«/mfrac»«mspace linebreak=¨newline¨»«/mspace»«mspace linebreak=¨newline¨»«/mspace»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»§#8710;«/mo»«mi mathvariant=¨bold¨ mathcolor=¨#0000FF¨»L«/mi»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»=«/mo»«mfrac mathcolor=¨#0000FF¨»«mrow»«msub»«mi mathvariant=¨bold¨»§#956;«/mi»«mi mathvariant=¨bold¨»s«/mi»«/msub»«mo mathvariant=¨bold¨»§#183;«/mo»«mi mathvariant=¨bold¨»M«/mi»«mo mathvariant=¨bold¨»§#183;«/mo»«mi mathvariant=¨bold¨»g«/mi»«/mrow»«mi mathvariant=¨bold¨»K«/mi»«/mfrac»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»+«/mo»«mfrac mathcolor=¨#0000FF¨»«mrow»«msub»«mi mathvariant=¨bold¨»§#956;«/mi»«mi mathvariant=¨bold¨»s«/mi»«/msub»«mo mathvariant=¨bold¨»§#183;«/mo»«mi mathvariant=¨bold¨»nm«/mi»«mo mathvariant=¨bold¨»§#183;«/mo»«mi mathvariant=¨bold¨»g«/mi»«/mrow»«mi mathvariant=¨bold¨»K«/mi»«/mfrac»«mspace linebreak=¨newline¨»«/mspace»«mspace linebreak=¨newline¨»«/mspace»«menclose mathcolor=¨#0000FF¨ notation=¨circle¨»«mo mathvariant=¨bold¨»§#8710;«/mo»«mi mathvariant=¨bold¨»L«/mi»«mo mathvariant=¨bold¨»=«/mo»«mfrac»«mrow»«msub»«mi mathvariant=¨bold¨»§#956;«/mi»«mi mathvariant=¨bold¨»s«/mi»«/msub»«mo mathvariant=¨bold¨»§#183;«/mo»«mi mathvariant=¨bold¨»m«/mi»«mo mathvariant=¨bold¨»§#183;«/mo»«mi mathvariant=¨bold¨»g«/mi»«/mrow»«mi mathvariant=¨bold¨»K«/mi»«/mfrac»«mo mathvariant=¨bold¨»§#183;«/mo»«mi mathvariant=¨bold¨»n«/mi»«mo mathvariant=¨bold¨»+«/mo»«mfrac»«mrow»«msub»«mi mathvariant=¨bold¨»§#956;«/mi»«mi mathvariant=¨bold¨»s«/mi»«/msub»«mo mathvariant=¨bold¨»§#183;«/mo»«mi mathvariant=¨bold¨»M«/mi»«mo mathvariant=¨bold¨»§#183;«/mo»«mi mathvariant=¨bold¨»g«/mi»«/mrow»«mi mathvariant=¨bold¨»K«/mi»«/mfrac»«/menclose»«mspace linebreak=¨newline¨»«/mspace»«mspace linebreak=¨newline¨»«/mspace»«mspace linebreak=¨newline¨»«/mspace»«/math»

1. يتناول التعبير الحالة التي يكون فيها الجسم على وشك الحركة، ومن المهم فهم ذلك وكتابة معادلات الحركة وفقًا لذلك.
2. لا يمكنك معرفة كيفية تطويره بمجرد النظر للتعبير. من المفترض أن يتم تطوير التعبير من معادلات الحركة.
لذلك ، يجب كتابة معادلات الحركة والتعبير عن استطالة النابض من هذه المعادلات.

2. רק מלראות את הביטוי לא ניתן לדעת כיצד לפתח אותו. יש להניח שהביטוי פותח ממשוואות התנועה.

לכן יש לכתוב את משוואות התנועה התנועה ולבטא מהן את התארכות הקפיץ.

______________________________________________________________________________________

...

قيمة معامل الاحتكاك الساكن هي 0.3 .

مقارنة قيمة الميل بمعامل n مع تعبير الاستطالة.

وفقًا للتعبير الظاهر في الرسم البياني السابق، في الرسم البياني الذي يصف الاستطالة كدالة لعدد اللفات، فإن قيمة معامل عدد اللفات تساوي قيمة الميل.

«math xmlns=¨http://www.w3.org/1998/Math/MathML¨»«mi mathvariant=¨bold¨ mathcolor=¨#0000FF¨»§#1513;§#1497;§#1508;§#1493;§#1506;«/mi»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»=«/mo»«mfrac mathcolor=¨#0000FF¨»«mrow»«msub»«mi mathvariant=¨bold¨»§#956;«/mi»«mi mathvariant=¨bold¨»s«/mi»«/msub»«mo mathvariant=¨bold¨»§#183;«/mo»«mi mathvariant=¨bold¨»m«/mi»«mo mathvariant=¨bold¨»§#183;«/mo»«mi mathvariant=¨bold¨»g«/mi»«/mrow»«mi mathvariant=¨bold¨»K«/mi»«/mfrac»«mspace linebreak=¨newline¨»«/mspace»«mspace linebreak=¨newline¨»«/mspace»«mn mathvariant=¨bold¨ mathcolor=¨#0000FF¨»0«/mn»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨».«/mo»«mn mathvariant=¨bold¨ mathcolor=¨#0000FF¨»02«/mn»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»=«/mo»«mfrac mathcolor=¨#0000FF¨»«mstyle displaystyle=¨true¨»«msub»«mi mathvariant=¨bold¨»§#956;«/mi»«mi mathvariant=¨bold¨»s«/mi»«/msub»«mo mathvariant=¨bold¨»§#183;«/mo»«mi mathvariant=¨bold¨»m«/mi»«mo mathvariant=¨bold¨»§#183;«/mo»«mi mathvariant=¨bold¨»g«/mi»«/mstyle»«mstyle displaystyle=¨true¨»«mi mathvariant=¨bold¨»K«/mi»«/mstyle»«/mfrac»«mspace linebreak=¨newline¨»«/mspace»«mspace linebreak=¨newline¨»«/mspace»«msub»«mi mathvariant=¨bold¨ mathcolor=¨#0000FF¨»§#956;«/mi»«mi mathvariant=¨bold¨ mathcolor=¨#0000FF¨»s«/mi»«/msub»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»=«/mo»«mfrac mathcolor=¨#0000FF¨»«mrow»«mn mathvariant=¨bold¨»0«/mn»«mo mathvariant=¨bold¨».«/mo»«mn mathvariant=¨bold¨»02«/mn»«mo mathvariant=¨bold¨»§#183;«/mo»«mi mathvariant=¨bold¨»K«/mi»«/mrow»«mrow»«mi mathvariant=¨bold¨»m«/mi»«mo mathvariant=¨bold¨»§#183;«/mo»«mi mathvariant=¨bold¨»g«/mi»«/mrow»«/mfrac»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»=«/mo»«mfrac mathcolor=¨#0000FF¨»«mstyle displaystyle=¨true¨»«mn mathvariant=¨bold¨»0«/mn»«mo mathvariant=¨bold¨».«/mo»«mn mathvariant=¨bold¨»02«/mn»«mo mathvariant=¨bold¨»§#183;«/mo»«mi mathvariant=¨bold¨»K«/mi»«/mstyle»«mstyle displaystyle=¨true¨»«mi mathvariant=¨bold¨»m«/mi»«mo mathvariant=¨bold¨»§#183;«/mo»«mi mathvariant=¨bold¨»g«/mi»«/mstyle»«/mfrac»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»=«/mo»«mfrac mathcolor=¨#0000FF¨»«mstyle displaystyle=¨true¨ mathvariant=¨bold¨»«mn»0«/mn»«mo».«/mo»«mn»02«/mn»«mo»§#183;«/mo»«mn»12«/mn»«/mstyle»«mstyle displaystyle=¨true¨ mathvariant=¨bold¨»«mn»0«/mn»«mo».«/mo»«mn»08«/mn»«mo»§#183;«/mo»«mn»10«/mn»«/mstyle»«/mfrac»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»=«/mo»«mfrac mathcolor=¨#0000FF¨»«mrow»«mn mathvariant=¨bold¨»0«/mn»«mo mathvariant=¨bold¨».«/mo»«mn mathvariant=¨bold¨»24«/mn»«/mrow»«mrow»«mn mathvariant=¨bold¨»0«/mn»«mo mathvariant=¨bold¨».«/mo»«mn mathvariant=¨bold¨»8«/mn»«/mrow»«/mfrac»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»=«/mo»«mn mathvariant=¨bold¨ mathcolor=¨#0000FF¨»0«/mn»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨».«/mo»«mn mathvariant=¨bold¨ mathcolor=¨#0000FF¨»3«/mn»«/math»

لذلك ، فإن قيمة معامل الاحتكاك الساكن هي 0.3

في معظم الأسئلة التي يكون فيها رسم بياني ، فإن مسار الحل يتعلق على ميل الرسم البياني.

______________________________________________________________________________________

...

كتلة الصندوق هي 0.2 كغم.

مقارنة قيمة النقطة التي تتقاطع فيها الدالة مع المحور العمودي ، بالمعامل الحر في تعبير الاستطالة.

في التعبير عن الاستطالة كدالة لعدد اللفات، تكون الكتلة في المعامل الحر. قيمة المعامل الحر في الدالة الخطية تساوي النقطة التي تتقاطع فيها الدالة مع المحور العمودي، من الرسم البياني يمكنك أن ترى أن قيمة هذه النقطة هي: 0.05 متر.

نقارن هذه القيمة بالمعامل الحر ، في تعبير استطالة النابض:

«math xmlns=¨http://www.w3.org/1998/Math/MathML¨»«mn mathvariant=¨bold¨ mathcolor=¨#0000FF¨»0«/mn»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨».«/mo»«mn mathvariant=¨bold¨ mathcolor=¨#0000FF¨»05«/mn»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»=«/mo»«mfrac mathcolor=¨#0000FF¨»«mrow»«msub»«mi mathvariant=¨bold¨»§#956;«/mi»«mi mathvariant=¨bold¨»s«/mi»«/msub»«mo mathvariant=¨bold¨»§#183;«/mo»«mi mathvariant=¨bold¨»M«/mi»«mo mathvariant=¨bold¨»§#183;«/mo»«mi mathvariant=¨bold¨»g«/mi»«/mrow»«mi mathvariant=¨bold¨»K«/mi»«/mfrac»«mspace linebreak=¨newline¨»«/mspace»«mspace linebreak=¨newline¨»«/mspace»«mi mathvariant=¨bold¨ mathcolor=¨#0000FF¨»M«/mi»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»=«/mo»«mfrac mathcolor=¨#0000FF¨»«mrow»«mn mathvariant=¨bold¨»0«/mn»«mo mathvariant=¨bold¨».«/mo»«mn mathvariant=¨bold¨»05«/mn»«mo mathvariant=¨bold¨»§#183;«/mo»«mi mathvariant=¨bold¨»K«/mi»«/mrow»«mrow»«msub»«mi mathvariant=¨bold¨»§#956;«/mi»«mi mathvariant=¨bold¨»s«/mi»«/msub»«mo mathvariant=¨bold¨»§#183;«/mo»«mi mathvariant=¨bold¨»g«/mi»«/mrow»«/mfrac»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»=«/mo»«mfrac mathcolor=¨#0000FF¨»«mrow»«mn mathvariant=¨bold¨»0«/mn»«mo mathvariant=¨bold¨».«/mo»«mn mathvariant=¨bold¨»05«/mn»«mo mathvariant=¨bold¨»§#183;«/mo»«mn mathvariant=¨bold¨»12«/mn»«/mrow»«mrow»«mn mathvariant=¨bold¨»0«/mn»«mo mathvariant=¨bold¨».«/mo»«mn mathvariant=¨bold¨»3«/mn»«mo mathvariant=¨bold¨»§#183;«/mo»«mn mathvariant=¨bold¨»10«/mn»«/mrow»«/mfrac»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»=«/mo»«mn mathvariant=¨bold¨ mathcolor=¨#0000FF¨»0«/mn»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨».«/mo»«mn mathvariant=¨bold¨ mathcolor=¨#0000FF¨»2«/mn»«mi mathvariant=¨bold¨ mathcolor=¨#0000FF¨»Kg«/mi»«/math»

لذلك ، فإن كتلة الصندوق الفارغ هي 0.2 كغم.

נשווה ערך זה לאיבר החופשי ,בביטוי התארכות הקפיץ:

לכן, מסת התיבה הריקה היא 0.2 ק"ג.

1. تصف الدالة الاستطالة كدالة لعدد اللفات، ومن المهم أن نفهم بالضبط بماذا تتعلق الدالة لمعرفة ما هو الميل وما هو المعامل الحر.
2. في الدوال الخطية، نتعامل بشكل أساسي مع معنى الميل، وأحيانًا أيضًا مع معنى نقطتي تقاطع الدالة مع المحاور.

2. בפונקציות ליניאריות נעסוק בעיקר במשמעות השיפוע , ולעתים גם במשמעות נקודת חציית הפונקציה את הצירים.

______________________________________________________________________________________

...

مقدار قوة الاحتكاك الساكن في هذه الحالة هو 0.24 نيوتن.

عندما تكون القوة التي تعمل على تحريك الجسم أقل من الحد الأقصى لقوة الاحتكاك الساكن، تعمل على الجسم قوة احتكاك ساكن، ويكون الجسم ساكنًا .
ومن القانون الأول لنيوتن (من معادلة الحركة)، فإن مقدار قوة الاحتكاك الساكن مساوية لمقدار القوة التي تعمل على تحريك الجسم.

ומהחוק הראשון של ניוטון , (ממשוואת התנועה), גודלו של כוח החיכוך הסטטי כגודל הכוח הפועל להנעת הגוף.

عندما يكون الصندوق فارغًا، عند استطالة 0.05 متر يكون الصندوق على وشك الحركة. عند استطالة 0.02 متر ، لا يكون الصندوق على وشك الحركة ، ولا تمثل قوة الاحتكاك الساكن التي تعمل عليه أقصى قوة احتكاك ساكن.

حتى في هذه الحالة يكون الصندوق ساكنًا، ومن معادلة الحركة الأفقية - قوة النابض تساوي قوة الاحتكاك الساكن.

«math xmlns=¨http://www.w3.org/1998/Math/MathML¨»«msub»«mi mathvariant=¨bold¨ mathcolor=¨#0000FF¨»§#931;F«/mi»«mi mathvariant=¨bold¨ mathcolor=¨#0000FF¨»X«/mi»«/msub»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»=«/mo»«mn mathvariant=¨bold¨ mathcolor=¨#0000FF¨»0«/mn»«mspace linebreak=¨newline¨»«/mspace»«msub»«mi mathvariant=¨bold¨ mathcolor=¨#0000FF¨»f«/mi»«mi mathvariant=¨bold¨ mathcolor=¨#0000FF¨»s«/mi»«/msub»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»=«/mo»«mi mathvariant=¨bold¨ mathcolor=¨#0000FF¨»F«/mi»«mspace linebreak=¨newline¨»«/mspace»«msub»«mi mathvariant=¨bold¨ mathcolor=¨#0000FF¨»f«/mi»«mi mathvariant=¨bold¨ mathcolor=¨#0000FF¨»s«/mi»«/msub»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»=«/mo»«mi mathvariant=¨bold¨ mathcolor=¨#0000FF¨»K«/mi»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»§#183;«/mo»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»§#8710;«/mo»«mi mathvariant=¨bold¨ mathcolor=¨#0000FF¨»L«/mi»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»=«/mo»«mn mathvariant=¨bold¨ mathcolor=¨#0000FF¨»12«/mn»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»§#183;«/mo»«mn mathvariant=¨bold¨ mathcolor=¨#0000FF¨»0«/mn»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨».«/mo»«mn mathvariant=¨bold¨ mathcolor=¨#0000FF¨»02«/mn»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»=«/mo»«mn mathvariant=¨bold¨ mathcolor=¨#0000FF¨»0«/mn»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨».«/mo»«mn mathvariant=¨bold¨ mathcolor=¨#0000FF¨»24«/mn»«mi mathvariant=¨bold¨ mathcolor=¨#0000FF¨»N«/mi»«mspace linebreak=¨newline¨»«/mspace»«/math»

إذن ، مقدار قوة الاحتكاك الساكن في هذه الحالة هو 0.24 نيوتن.

גם במקרה זה התיבה מתמידה בתנועתה , וממשוואת התנועה האופקית - כוח הקפיץ שווה לכוח החיכוך הסטטי .

לכן, גודלו של כוח החיכוך הסטטי במקרה זה הוא 0.24 ניוטון.

من أجل أن نتطرق بشكل صحيح لقوة الاحتكاك الساكن، في معادلة الحركة الأفقية ، يجب أن نفهم ما إذا كان الجسم على وشك الحركة أم لا.
وفقًا لما ذًكر في السؤال (بالمناسبة) ، يجب أن نفهم الحالة التي يكون فيها الجسم، وبحسب ذلك نتطرق للاحتكاك الساكن في معادلة الحركة.

בהתאם לנאמר בשאלה (כדרך אגב) יש להבין את המצב בו הגוף נמצא , ובהתאם להתייחס לחיכוך הסטטי במשוואת התנועה.

______________________________________________________________________________________