______________________________________________________________________________________
...
«math xmlns=¨http://www.w3.org/1998/Math/MathML¨»«mstyle mathsize=¨20px¨»«mfrac»«mfenced open=¨[¨ close=¨]¨»«mstyle mathvariant=¨bold¨ displaystyle=¨true¨»«mi»N«/mi»«/mstyle»«/mfenced»«mfenced open=¨[¨ close=¨]¨»«mstyle mathvariant=¨bold¨ displaystyle=¨true¨»«mfrac»«msup»«mi»m«/mi»«mn»2«/mn»«/msup»«msup»«mi»s«/mi»«mn»2«/mn»«/msup»«/mfrac»«/mstyle»«/mfenced»«/mfrac»«mo mathvariant=¨bold¨»=«/mo»«mfrac»«mfenced open=¨[¨ close=¨]¨»«mstyle mathvariant=¨bold¨ displaystyle=¨true¨»«mfrac»«mrow»«mi»kg«/mi»«mo»§#183;«/mo»«mi»m«/mi»«/mrow»«msup»«mi»s«/mi»«mn»2«/mn»«/msup»«/mfrac»«/mstyle»«/mfenced»«mfenced open=¨[¨ close=¨]¨»«mstyle mathvariant=¨bold¨ displaystyle=¨true¨»«mfrac»«msup»«mi»m«/mi»«mn»2«/mn»«/msup»«msup»«mi»s«/mi»«mn»2«/mn»«/msup»«/mfrac»«/mstyle»«/mfenced»«/mfrac»«mo mathvariant=¨bold¨»=«/mo»«mfenced open=¨[¨ close=¨]¨»«mfrac»«mi mathvariant=¨bold¨»kg«/mi»«mi mathvariant=¨bold¨»m«/mi»«/mfrac»«/mfenced»«/mstyle»«/math»
يمكن إيجاد وحدات أي كمية فيزيائية باستخدام التعبير لتلك الكمية الفيزيائية.
نكتب تعبيرًا لـ K حسب التعبير الوارد في السؤال:
«math xmlns=¨http://www.w3.org/1998/Math/MathML¨»«mstyle mathsize=¨24px¨»«mrow»«mi mathvariant=¨bold¨ mathcolor=¨#0000FF¨»k«/mi»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»=«/mo»«mfrac mathcolor=¨#0000FF¨»«mi mathvariant=¨bold¨»f«/mi»«msup»«mi mathvariant=¨bold¨»V«/mi»«mn mathvariant=¨bold¨»2«/mn»«/msup»«/mfrac»«/mrow»«/mstyle»«/math»
نجد وحدات K من تعبيره:
«math xmlns=¨http://www.w3.org/1998/Math/MathML¨»«mfrac mathcolor=¨#0000FF¨»«mfenced open=¨[¨ close=¨]¨»«mi mathvariant=¨bold¨»N«/mi»«/mfenced»«mstyle displaystyle=¨true¨»«mfenced open=¨[¨ close=¨]¨»«mfrac»«msup»«mi mathvariant=¨bold¨»m«/mi»«mn mathvariant=¨bold¨»2«/mn»«/msup»«msup»«mi mathvariant=¨bold¨»s«/mi»«mn mathvariant=¨bold¨»2«/mn»«/msup»«/mfrac»«/mfenced»«/mstyle»«/mfrac»«/math»
يمكن كتابة وحدات [N] حسب القانون الثاني لنيوتن:
«math xmlns=¨http://www.w3.org/1998/Math/MathML¨»«mfrac mathcolor=¨#0000FF¨»«mfenced open=¨[¨ close=¨]¨»«mrow»«mi mathvariant=¨bold¨»Kg«/mi»«mo mathvariant=¨bold¨»§#183;«/mo»«mstyle displaystyle=¨true¨»«mfrac»«mi mathvariant=¨bold¨»m«/mi»«msup»«mi mathvariant=¨bold¨»s«/mi»«mn mathvariant=¨bold¨»2«/mn»«/msup»«/mfrac»«/mstyle»«/mrow»«/mfenced»«mstyle displaystyle=¨true¨»«mfenced open=¨[¨ close=¨]¨»«mfrac»«msup»«mi mathvariant=¨bold¨»m«/mi»«mn mathvariant=¨bold¨»2«/mn»«/msup»«msup»«mi mathvariant=¨bold¨»s«/mi»«mn mathvariant=¨bold¨»2«/mn»«/msup»«/mfrac»«/mfenced»«/mstyle»«/mfrac»«/math»
يمكن الاختزال:
«math xmlns=¨http://www.w3.org/1998/Math/MathML¨»«mfrac mathcolor=¨#0000FF¨»«mfenced open=¨[¨ close=¨]¨»«mrow»«mi mathvariant=¨bold¨»Kg«/mi»«mo mathvariant=¨bold¨»§#183;«/mo»«mstyle displaystyle=¨true¨»«mfrac»«menclose notation=¨updiagonalstrike¨»«mi mathvariant=¨bold¨»m«/mi»«/menclose»«menclose notation=¨downdiagonalstrike¨»«msup»«mi mathvariant=¨bold¨»s«/mi»«mn mathvariant=¨bold¨»2«/mn»«/msup»«/menclose»«/mfrac»«/mstyle»«/mrow»«/mfenced»«mstyle displaystyle=¨true¨»«mfenced open=¨[¨ close=¨]¨»«mfrac»«mrow»«mi mathvariant=¨bold¨»m«/mi»«menclose notation=¨updiagonalstrike¨»«msup»«mrow»«/mrow»«mn mathvariant=¨bold¨»2«/mn»«/msup»«/menclose»«/mrow»«menclose notation=¨downdiagonalstrike¨»«msup»«mi mathvariant=¨bold¨»s«/mi»«mn mathvariant=¨bold¨»2«/mn»«/msup»«/menclose»«/mfrac»«/mfenced»«/mstyle»«/mfrac»«mo mathcolor=¨#0000FF¨»=«/mo»«mfenced mathcolor=¨#0000FF¨ open=¨[¨ close=¨]¨»«mfrac»«mi mathvariant=¨bold¨»kg«/mi»«mi mathvariant=¨bold¨»m«/mi»«/mfrac»«/mfenced»«/math»
لذلك فإن وحدات K , هي :
«math xmlns=¨http://www.w3.org/1998/Math/MathML¨»«mstyle mathsize=¨20px¨»«mfrac mathcolor=¨#0000FF¨»«mfenced open=¨[¨ close=¨]¨»«mstyle mathvariant=¨bold¨ displaystyle=¨true¨»«mi»N«/mi»«/mstyle»«/mfenced»«mfenced open=¨[¨ close=¨]¨»«mstyle mathvariant=¨bold¨ displaystyle=¨true¨»«mfrac»«msup»«mi»m«/mi»«mn»2«/mn»«/msup»«msup»«mi»s«/mi»«mn»2«/mn»«/msup»«/mfrac»«/mstyle»«/mfenced»«/mfrac»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»=«/mo»«mfrac mathcolor=¨#0000FF¨»«mfenced open=¨[¨ close=¨]¨»«mstyle mathvariant=¨bold¨ displaystyle=¨true¨»«mfrac»«mrow»«mi»kg«/mi»«mo»§#183;«/mo»«mi»m«/mi»«/mrow»«msup»«mi»s«/mi»«mn»2«/mn»«/msup»«/mfrac»«/mstyle»«/mfenced»«mfenced open=¨[¨ close=¨]¨»«mstyle mathvariant=¨bold¨ displaystyle=¨true¨»«mfrac»«msup»«mi»m«/mi»«mn»2«/mn»«/msup»«msup»«mi»s«/mi»«mn»2«/mn»«/msup»«/mfrac»«/mstyle»«/mfenced»«/mfrac»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»=«/mo»«mfenced mathcolor=¨#0000FF¨ open=¨[¨ close=¨]¨»«mfrac»«mi mathvariant=¨bold¨»kg«/mi»«mi mathvariant=¨bold¨»m«/mi»«/mfrac»«/mfenced»«/mstyle»«/math»
«math xmlns=¨http://www.w3.org/1998/Math/MathML¨»«mstyle mathsize=¨24px¨»«mrow»«mi mathvariant=¨bold¨ mathcolor=¨#0000FF¨»k«/mi»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»=«/mo»«mfrac mathcolor=¨#0000FF¨»«mi mathvariant=¨bold¨»f«/mi»«msup»«mi mathvariant=¨bold¨»V«/mi»«mn mathvariant=¨bold¨»2«/mn»«/msup»«/mfrac»«/mrow»«/mstyle»«/math»
נמצא את היחידות של K , מביטויו:
«math xmlns=¨http://www.w3.org/1998/Math/MathML¨»«mfrac mathcolor=¨#0000FF¨»«mfenced open=¨[¨ close=¨]¨»«mi mathvariant=¨bold¨»N«/mi»«/mfenced»«mstyle displaystyle=¨true¨»«mfenced open=¨[¨ close=¨]¨»«mfrac»«msup»«mi mathvariant=¨bold¨»m«/mi»«mn mathvariant=¨bold¨»2«/mn»«/msup»«msup»«mi mathvariant=¨bold¨»s«/mi»«mn mathvariant=¨bold¨»2«/mn»«/msup»«/mfrac»«/mfenced»«/mstyle»«/mfrac»«/math»
אפשר לכתוב ביטוי ליחידות [N] מהחוק השני של ניוטון :
«math xmlns=¨http://www.w3.org/1998/Math/MathML¨»«mfrac mathcolor=¨#0000FF¨»«mfenced open=¨[¨ close=¨]¨»«mi mathvariant=¨bold¨»N«/mi»«/mfenced»«mstyle displaystyle=¨true¨»«mfenced open=¨[¨ close=¨]¨»«mfrac»«msup»«mi mathvariant=¨bold¨»m«/mi»«mn mathvariant=¨bold¨»2«/mn»«/msup»«msup»«mi mathvariant=¨bold¨»s«/mi»«mn mathvariant=¨bold¨»2«/mn»«/msup»«/mfrac»«/mfenced»«/mstyle»«/mfrac»«/math»
1. ليس من الضروري الوصول إلى الشكل الأكثر اختزالًا لوحدات الثابت K ، الصورة الصحيحة الأولى «math xmlns=¨http://www.w3.org/1998/Math/MathML¨»«mstyle mathsize=¨12px¨»«mfrac mathcolor=¨#FF0000¨»«mfenced open=¨[¨ close=¨]¨»«mstyle mathvariant=¨bold¨ displaystyle=¨true¨»«mi»N«/mi»«/mstyle»«/mfenced»«mfenced open=¨[¨ close=¨]¨»«mstyle mathvariant=¨bold¨ displaystyle=¨true¨»«mfrac»«msup»«mi»m«/mi»«mn»2«/mn»«/msup»«msup»«mi»s«/mi»«mn»2«/mn»«/msup»«/mfrac»«/mstyle»«/mfenced»«/mfrac»«/mstyle»«/math» كافية أيضًا.
2. عند التمرين في البيت يوصى بالاختزال والوصول إلى الشكل النهائي، وهذا في الامتحان يتطلب القليل من الوقت ، ويزيد من احتمالية ارتكاب الخطأ.
لذلك ، في امتحان البجروت، من الأفضل ترك العبارة الأولى التي يتم الحصول عليها كحل نهائي.
בתרגול בבית מומלץ לצמצם ולהגיע לצורה הסופית, במבחן זה דורש מעט זמן , ומגדיל את האפשרות לטעות.
לכן במבחן הבגרות עדיף להשאיר את את הביטוי הראשון שממתקבל כפתרון סופי.
______________________________________________________________________________________

______________________________________________________________________________________
...
السقوط الحر هي حركة بتأثير الجاذبية فقط ، وفي هذه الحالة تعمل قوة الاحتكاك، لذا لا تعتبر الحركة سقوطًا حرًا.
معرفة تعريف السقوط الحر.
السقوط الحر هي حركة بتأثير الجاذبية فقط ، وفي هذه الحالة تعمل قوة الاحتكاك، لذا لا تعتبر الحركة سقوطًا حرًا.
1. السقوط الحر ليس مجرد سقوط من حالة السكون. انما هي حركة تحت تأثير الجاذبية وحدها .
يُعرّف الرمي لأعلى أو الرمي بزاوية أيضًا بالسقوط الحر.
2. يشير السقوط الحر إلى الحركة الحرة من أي قوة باستثناء قوة الجاذبية.
3. السقوط الحر يسمى أيضا الحركة البالستية.
אם גוף לא נע בתאוצה קבועה , המהירות הרגעית שווה למהירות באמצע הזמן , בקירוב בלבד.
המהירות הרגעית באמצע הזמן שווה בדיוק למהירות הממוצעת רק כאשר הגוף נע בתנועה בתאוצה קבועה. אם הגוף לא נע בתאוצה קבועה וקטע התנועה קטן , גם אפשר למצוא את המהירות הרגעית באמצע הזמן בדרך זו, אך התשובה תהיה נכונה בקירוב.
______________________________________________________________________________________

______________________________________________________________________________________
...
تزداد قوة الاحتكاك مع زيادة السرعة، وعندما يكون مقدار قوة الاحتكاك مساويًا لمقدار قوة الجاذبية ، فإن محصلة القوى المؤثرة على الجسم تساوي صفرًا.
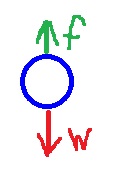
من المهم أن نفهم أن قوة الاحتكاك تتعلق بالسرعة (مكتوبة في السؤال) ، وأن نرسم مخطط القوة لفهم العلاقة بين قوة الاحتكاك ومحصلة القوى.
بالإضافة إلى ذلك ، من المهم فهم القانون الأول لنيوتن.
בנוסף חשוב להבין את החוק הראשון של ניוטון.
تعمل على الجسم قوتان. قوة الجاذبية نحو الأسفل وقوة الاحتكاك التي تعمل ضد اتجاه الحركة.
من التعبير لقوة الاحتكاك، مع زيادة سرعة الجسم، تزداد قوة الاحتكاك.
من الممكن أن يتحرك الجسم لفترة معينة بسرعة ثابتة لأن سرعة الجسم ستكون كبيرة بما يكفي بحيث تكون قوة الاحتكاك مساوية في المقدار لقوة الجاذبية.
في مثل هذه الحالة، سيكون محصلة القوى المؤثرة على الجسم صفرًا. وسيستمر الجسم في حركته.
מביטוי כוח החיכוך, ככל שמהירות הגוף גדלה, כוח החיכוך גדל.
ייתכן שברגע מסויים הגוף ינוע במהירות קבועה מכיוון שייכן ומהירות הגוף תהיה מספיק גדולה כך שכוח החיכוך יהיה שווה בגודלו לכוח הכובד .
במקרה כזה שקול הכוחות הפועלים על הגוף יהיה אפס. והגוף יתמיד בתנועתו.
1.موضوع الاحتكاك مع الهواء خارج المنهاج الدراسي، ولكن السؤال يحتوي على كل المعلومات اللازمة ، فهناك مثل هذه الأسئلة ، فهي متبّعة.
2. الاحتكاك هنا ليس احتكاكًا حركيًا ولا ساكنًا. لهذا السبب نشير له ببساطة بالحرف f.
2. החיכוך כאן הוא לא חיכוך קינטי ולא חיכוך סטטי. לכן כדאי לסמן אותו פשוט באות f.
______________________________________________________________________________________

______________________________________________________________________________________
...
سرعة الجسم في عندما يتحرك بسرعة ثابتة هي 20 مترًا في الثانية.
مخطط القوة ومعادلة الحركة وكتابة تعبير للسرعة من معادلات الحركة.
في اللحظة التي تحرك فيها الجسم بسرعة ثابتة ، فإن محصلة القوى المؤثرة عليه تساوي صفرًا.
لإيجاد هذه اللحظة نكتب معادلة الحركة:
«math xmlns=¨http://www.w3.org/1998/Math/MathML¨»«msub mathcolor=¨#0000FF¨»«mi mathvariant=¨bold¨ mathcolor=¨#0000FF¨»§#931;F«/mi»«mi mathvariant=¨bold¨»y«/mi»«/msub»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»=«/mo»«mn mathvariant=¨bold¨ mathcolor=¨#0000FF¨»0«/mn»«mspace linebreak=¨newline¨»«/mspace»«mi mathvariant=¨bold¨ mathcolor=¨#0000FF¨»f«/mi»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»=«/mo»«mi mathvariant=¨bold¨ mathcolor=¨#0000FF¨»m«/mi»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»§#183;«/mo»«mi mathvariant=¨bold¨ mathcolor=¨#0000FF¨»g«/mi»«mspace linebreak=¨newline¨»«/mspace»«menclose mathcolor=¨#0000FF¨ notation=¨box¨»«mi mathvariant=¨bold¨»k«/mi»«mo mathvariant=¨bold¨»§#183;«/mo»«msup»«mi mathvariant=¨bold¨»V«/mi»«mn mathvariant=¨bold¨»2«/mn»«/msup»«mo mathvariant=¨bold¨»=«/mo»«mi mathvariant=¨bold¨»m«/mi»«mo mathvariant=¨bold¨»§#183;«/mo»«mi mathvariant=¨bold¨»g«/mi»«/menclose»«/math»
نكتب تعبيرًا لسرعة الجسم في اللحظة التي يواصل فيها حركته، من معادلة الحركة:
«math xmlns=¨http://www.w3.org/1998/Math/MathML¨»«menclose mathcolor=¨#0000FF¨ notation=¨circle¨»«mi mathvariant=¨bold-italic¨»V«/mi»«mo mathvariant=¨bold¨»=«/mo»«msqrt»«mfrac»«mrow»«mi mathvariant=¨bold¨»m«/mi»«mo mathvariant=¨bold¨»§#183;«/mo»«mi mathvariant=¨bold¨»g«/mi»«/mrow»«mi mathvariant=¨bold¨»k«/mi»«/mfrac»«/msqrt»«mspace linebreak=¨newline¨»«/mspace»«/menclose»«/math»
نعوّض المعطيات ونجد سرعة الجسم عند تحركه بسرعة ثابتة:
«math xmlns=¨http://www.w3.org/1998/Math/MathML¨»«mi mathvariant=¨bold¨ mathcolor=¨#0000FF¨»V«/mi»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»=«/mo»«msqrt mathcolor=¨#0000FF¨»«mfrac»«mrow»«mi mathvariant=¨bold¨»m«/mi»«mo mathvariant=¨bold¨»§#183;«/mo»«mi mathvariant=¨bold¨»g«/mi»«/mrow»«mi mathvariant=¨bold¨»k«/mi»«/mfrac»«/msqrt»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»=«/mo»«msqrt mathcolor=¨#0000FF¨»«mfrac»«mrow»«mn mathvariant=¨bold¨»10«/mn»«mo mathvariant=¨bold¨»§#183;«/mo»«mn mathvariant=¨bold¨»10«/mn»«/mrow»«mrow»«mn mathvariant=¨bold¨»0«/mn»«mo mathvariant=¨bold¨».«/mo»«mn mathvariant=¨bold¨»25«/mn»«/mrow»«/mfrac»«/msqrt»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»=«/mo»«msqrt mathcolor=¨#0000FF¨»«mn mathvariant=¨bold¨»400«/mn»«/msqrt»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»=«/mo»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»§#160;«/mo»«mn mathvariant=¨bold¨ mathcolor=¨#0000FF¨»20«/mn»«mfrac mathcolor=¨#0000FF¨»«mi mathvariant=¨bold¨»m«/mi»«mi mathvariant=¨bold¨»s«/mi»«/mfrac»«/math»
لذلك ، فإن مقدار سرعة الجسم في اللحظة التي يتحرك فيها الجسم بسرعة ثابتة مساوية 20 مترًا في الثانية.
כדי למצוא רגע זה נכתוב את משוואת התנועה:
«math xmlns=¨http://www.w3.org/1998/Math/MathML¨»«msub mathcolor=¨#0000FF¨»«mi mathvariant=¨bold¨ mathcolor=¨#0000FF¨»§#931;F«/mi»«mi mathvariant=¨bold¨»y«/mi»«/msub»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»=«/mo»«mn mathvariant=¨bold¨ mathcolor=¨#0000FF¨»0«/mn»«mspace linebreak=¨newline¨»«/mspace»«mi mathvariant=¨bold¨ mathcolor=¨#0000FF¨»f«/mi»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»=«/mo»«mi mathvariant=¨bold¨ mathcolor=¨#0000FF¨»m«/mi»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»§#183;«/mo»«mi mathvariant=¨bold¨ mathcolor=¨#0000FF¨»g«/mi»«mspace linebreak=¨newline¨»«/mspace»«menclose mathcolor=¨#0000FF¨ notation=¨box¨»«mi mathvariant=¨bold¨»k«/mi»«mo mathvariant=¨bold¨»§#183;«/mo»«msup»«mi mathvariant=¨bold¨»V«/mi»«mn mathvariant=¨bold¨»2«/mn»«/msup»«mo mathvariant=¨bold¨»=«/mo»«mi mathvariant=¨bold¨»m«/mi»«mo mathvariant=¨bold¨»§#183;«/mo»«mi mathvariant=¨bold¨»g«/mi»«/menclose»«/math»
נכתוב ביטוי למהירות הגוף ברגע שהוא מתמיד בתנועתו , ממשוואת התנועה:
«math xmlns=¨http://www.w3.org/1998/Math/MathML¨»«menclose mathcolor=¨#0000FF¨ notation=¨circle¨»«mi mathvariant=¨bold-italic¨»V«/mi»«mo mathvariant=¨bold¨»=«/mo»«msqrt»«mfrac»«mrow»«mi mathvariant=¨bold¨»m«/mi»«mo mathvariant=¨bold¨»§#183;«/mo»«mi mathvariant=¨bold¨»g«/mi»«/mrow»«mi mathvariant=¨bold¨»k«/mi»«/mfrac»«/msqrt»«mspace linebreak=¨newline¨»«/mspace»«/menclose»«/math»
נציב את את הנתונים ונמצא את מהירות הגוף ברגע שהוא נע במהירות קבועה:
«math xmlns=¨http://www.w3.org/1998/Math/MathML¨»«mi mathvariant=¨bold¨ mathcolor=¨#0000FF¨»V«/mi»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»=«/mo»«msqrt mathcolor=¨#0000FF¨»«mfrac»«mrow»«mi mathvariant=¨bold¨»m«/mi»«mo mathvariant=¨bold¨»§#183;«/mo»«mi mathvariant=¨bold¨»g«/mi»«/mrow»«mi mathvariant=¨bold¨»k«/mi»«/mfrac»«/msqrt»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»=«/mo»«msqrt mathcolor=¨#0000FF¨»«mfrac»«mrow»«mn mathvariant=¨bold¨»10«/mn»«mo mathvariant=¨bold¨»§#183;«/mo»«mn mathvariant=¨bold¨»10«/mn»«/mrow»«mrow»«mn mathvariant=¨bold¨»0«/mn»«mo mathvariant=¨bold¨».«/mo»«mn mathvariant=¨bold¨»25«/mn»«/mrow»«/mfrac»«/msqrt»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»=«/mo»«msqrt mathcolor=¨#0000FF¨»«mn mathvariant=¨bold¨»400«/mn»«/msqrt»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»=«/mo»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»§#160;«/mo»«mn mathvariant=¨bold¨ mathcolor=¨#0000FF¨»20«/mn»«mfrac mathcolor=¨#0000FF¨»«mi mathvariant=¨bold¨»m«/mi»«mi mathvariant=¨bold¨»s«/mi»«/mfrac»«/math»
לכן גודל מהירות הגוף ברגע בו הגוף נע במהירות קבועה הוא 20 מטר לשנייה.
بشكل عام، يجب تحديد اتجاه المقدار الفيزيائي، في هذا السؤال يجب تحديد مقدار السرعة ، وبالتالي لا توجد حاجة لتحديد اتجاه السرعة.
اتجاه السرعة نحو الأسفل ، بالنسبة لمحور الحركة الموجّه نحو الأعلى ، تكون السرعة سالبة.
כיוון המהירות היא כלפי מטה, ביחס לציר תנועה שכיוונו כלפי מעלה המהירות שלילית.
אפשר לכתוב שהמהירות היא 20 מטר לשנייה וכיוונה כלפי מטה. או מינוס 20 מטר לשנייה ביחס לציר שכיוונו כלפי מעלה.
______________________________________________________________________________________

______________________________________________________________________________________
...
من الضروري أن نفهم كيف يتحرك الجسم، وما هي سرعته الابتدائية، وما نوع حركته.
من المهم أيضًا أن نفهم أنه في الرسم البياني للسرعة كدالة للزمن، يكون مقدار الميل مساوٍ لمقدار التسارع.
חשוב גם להבין שבגרף מהירות בתלות בזמן גודל השיפוע כגודל התאוצה.
يبدأ الجسم حركته من حالة السكون ، وسرعته الابتدائية صفر متر في الثانية، من التعبير لقوة الاحتكاك، لا توجد قوة تؤثر على الجسم في اللحظة التي يبدأ فيها الحركة، وبالتالي يتحرك الجسم من اللحظة التي تبدأ فيها الحركة بتسارع الجاذبية.
وفقًا لتعبير قوة الاحتكاك ، كلما زادت سرعة الجسم، تزداد قوة الاحتكاك، ولا تتغير قوة الجاذبية. لذلك ، مع زيادة سرعة الجسم، تقل القوة المحصّلة.
من القانون الثاني لنيوتن، بما أن القوة آخذة بالنقصان، فإن التسارع يقل أيضًا، من قيمة مساوية لتسارع الجاذبية حتى الصفر.
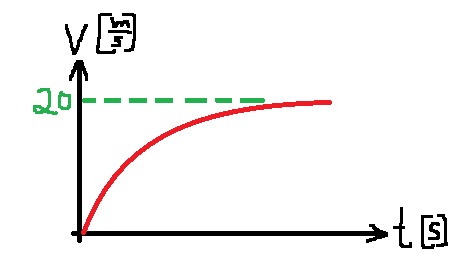
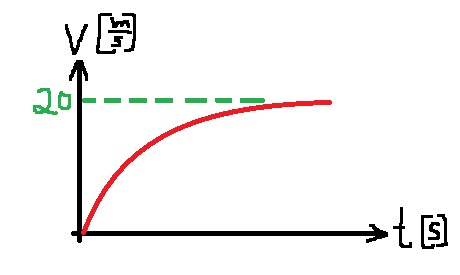
نصف حركة الجسم من لحظة تحريره حتى اللحظة التي يتحرك فيها بسرعة ثابتة في رسم بياني للسرعة كدالة للزمن:
בהתאם לביטוי כוח החיכוך, ככל שמהירות הגוף גדלה כוח החיכוך גדל, כוח הכובד לא משתנה. לכן ככל שמהירות הגוף גדלה הכוח השקול קטן.
מהחוק השני של ניוטון מכיוון שהכוח הולך וקטן גם התאוצה הולכת וקטנה, מתאוצת הכובד ועד שהתאוצה היא אפס.
נתאר את תנועת הגוף מרגע שחרורו ועד לרגע בו הוא נע במהירות קבועה בגרף מהירות בתלות בזמן:
1. التسارع لا يقل بصورة خطية ، في إطار دراستنا في المدرسة الثانوية لا يمكن تحديد الشكل الذي يقل فيه التسارع ، ولا يمكن إيجاد الزمن الذي يمر من اللحظة التي تبدأ فيها الحركة حتى يتحرك الجسم بسرعة ثابتة. لهذا مكتوب في السؤال لا تشر إلى القيم على المحور الزمني ، والقصد هو عدم المحاولة، وعدم مضيعة الوقت فيه.
2. لم يتم كتابته لتحديد القيم على محور السرعة، ولكن للحصول على كامل نقاط في القسم، يجب تحديد قيمة السرعة الثابتة التي وصل إليها الجسم.
2. לא כתוב לציין ערכים בציר המהירות, אך כדי לקבל את מלא הנקודות יש לציין את ערך המהירות הקבועה אליה מגיע הגוף.
______________________________________________________________________________________