
______________________________________________________________________________________
...
قوة الاحتكاك التي يشغّلها الشارع على السيارة.
يجب فهم قوة الاحتكاك بشكل عام، واعلم أن قوة الاحتكاك يمكن أن تسبب الحركة أيضًا.
عندما تبدأ السيارة في السفر، تدفع عجلات السيارة الشارع للخلف بقوة (قوة الاحتكاك).
وحسب القانون الثالث لنيوتن، يعمل الشارع قوة احتكاك على السيارة في اتجاه سيرها، وهذه القوة هي القوة التي تجعل السيارة تتحرك.
القوة المؤثرة على السيارة هي قوة احتكاك ، وتؤثر على الطريق.
מהחוק השלישי של ניוטון הכביש מפעיל כוח חיכוך על המכונית בכיוון הנסיעה, כוח זה הוא הכוח הגורם למכונית לנסוע.
הכוח הפועל על המכונית הוא כוח חיכוך, והוא מופעל על ידי הכביש.
في إطار المنهاج الدراسي، يتم دراسة نوعين من قوى الاحتكاك. قوة الاحتكاك الساكن وقوة الاحتكاك الحركي.
موضوع الاحتكاك الساكن موضوع معقد ويتطلب فهمًا أعمق.
في هذه الحالة، تكون قوة الاحتكاك التي تحرك السيارة هي قوة احتكاك ساكن، وقوة الاحتكاك التي تعمل ضد اتجاه الحركة هي قوة احتكاك تدحرجي.
للإجابة على أسئلة البجروت ، يجب أن يعرف المرء قوة الاحتكاك الحركي ، وقوة الاحتكاك الساكن، وبالطبع الفكرة العامة لقوة الاحتكاك.
כוח החיכוך יותר מורכב והוא דורש הבנה מעמיקה יותר.
במקרה זה כוח החיכוך המניע את המכונית הוא כוח חיכוך סטטי , וכוח החיכוך הפועל נגד כיוון התנועה כוח חיכוך מסוג גלגול.
כדי לענות על שאלות הבגרות, יש להכיר את כוח החיכוך הקינטי , ואת כוח החיכוך הסטטי , וכמובן את הרעיון הכללי של כוח החיכוך.
______________________________________________________________________________________

______________________________________________________________________________________
...
يقلل الجليد من معامل الاحتكاك، تقل قوة الاحتكاك، وبما أن قوة الاحتكاك هي القوة الدافعة للسيارة، لذا سيقل تسارع السيارة أيضًا.
يجب الربط بين إضافة الجليد لقوة الاحتكاك. وبين التغير في قوة الاحتكاك والتغير في التسارع.
إضافة الجليد تقلل من قوة الاحتكاك، حيث تعمل السيارة قوة احتكاك أقل على الطريق. وكرد فعل لذلك، يعمل الشارع قوة احتكاك أقل على السيارة ، وبالتالي يكون تسارع السيارة أصغر.
في بعض الأحيان يكون من السهل فهم المبادئ من الحالات القصوى.
لو كان الشارع أملسًا تمامًا ، فلن تتمكن السيارة من عمل قوة احتكاك على الشارع، وبحسب القانون الثالث لنيوتن لا يمكن للشارع أن يعمل أي قوة على السيارة أيضًا.
لذلك لا يمكن للسيارة الموجودة على سطح أملس تمامًا أن تتحرك.
إذا كان السطح أملسًا قليلاً ، ولكن ليس أملسًا تمامًا ، يمكن للسيارة أن تتحرك ، لكن تسارعها سيكون محدودًا.
אם הכביש היה חלק לחלוטין , המכונית לא הייתה יכולה להפעיל כוח חיכוך על הכביש, ומהחוק השלישי גם הכביש לא היה יכול להפעיל כוח על המכונית.
לכן מכונית הנחה על משטח חלק לחלוטין לא יכולה לנוע.
אם המשטח מעט חלק , אבל לא חלק לחלוטין, המכונית יכולה לנוע , אך תאוצתה תהיה מוגבלת.
______________________________________________________________________________________

______________________________________________________________________________________
...
بالنسبة لمعامل احتكاك 0.1 ، تكون إزاحة الحركة: 312.5 مترًا.
بالنسبة لمعامل احتكاك 0.8 , تكون الإزاحة : 39.06 مترًا.
עבור מקדם שגודלו 0.8 , העתק התנועה הוא : 39.06 מטרים.
يجب رسم مخطط قوى وكتابة معادلات الحركة، من معادلات الحركة قم بتطوير التعبير للمسافة التي تقطعها السيارة، واستخدم هذا التعبير لإيجاد إزاحة الحركة لكل قيمة من قيمتي معامل الاحتكاك.
نطوّر تعبيرًا للمسافة التي تقطعها السيارة كدالة لمعامل الاحتكاك.
لهذا ، نرسم مخططًا للقوى ونكتب معادلات الحركة، ونطوّر التعبير المطلوب بمساعدة معادلات الحركة.
تم اختيار محور أفقي للحركة في اتجاه الحركة.
نكتب معادلات الحركة في الاتجاهين الأفقي والعمودي:
«math xmlns=¨http://www.w3.org/1998/Math/MathML¨»«msub mathcolor=¨#0000FF¨»«mi mathvariant=¨bold¨ mathcolor=¨#0000FF¨»§#931;F«/mi»«mi mathvariant=¨bold¨»y«/mi»«/msub»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»=«/mo»«mn mathvariant=¨bold¨ mathcolor=¨#0000FF¨»0«/mn»«mspace linebreak=¨newline¨»«/mspace»«mi mathvariant=¨bold¨ mathcolor=¨#0000FF¨»N«/mi»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»=«/mo»«mi mathvariant=¨bold¨ mathcolor=¨#0000FF¨»W«/mi»«mspace linebreak=¨newline¨»«/mspace»«menclose mathcolor=¨#0000FF¨ notation=¨box¨»«mi mathvariant=¨bold¨»N«/mi»«mo mathvariant=¨bold¨»=«/mo»«mi mathvariant=¨bold¨»mg«/mi»«/menclose»«/math» «math xmlns=¨http://www.w3.org/1998/Math/MathML¨»«msub mathcolor=¨#0000FF¨»«mi mathvariant=¨bold¨ mathcolor=¨#0000FF¨»§#931;F«/mi»«mi mathvariant=¨bold¨»X«/mi»«/msub»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»=«/mo»«mi mathvariant=¨bold¨ mathcolor=¨#0000FF¨»m«/mi»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»§#183;«/mo»«mi mathvariant=¨bold¨ mathcolor=¨#0000FF¨»a«/mi»«mspace linebreak=¨newline¨»«/mspace»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»-«/mo»«msub mathcolor=¨#0000FF¨»«mi mathvariant=¨bold¨ mathcolor=¨#0000FF¨»f«/mi»«mi mathvariant=¨bold¨»k«/mi»«/msub»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»=«/mo»«mi mathvariant=¨bold¨ mathcolor=¨#0000FF¨»m«/mi»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»§#183;«/mo»«mi mathvariant=¨bold¨ mathcolor=¨#0000FF¨»a«/mi»«mspace linebreak=¨newline¨»«/mspace»«menclose mathcolor=¨#0000FF¨ notation=¨box¨»«mo mathvariant=¨bold¨»-«/mo»«msub»«mi mathvariant=¨bold¨»§#956;«/mi»«mi mathvariant=¨bold¨»k«/mi»«/msub»«mo mathvariant=¨bold¨»§#183;«/mo»«mi mathvariant=¨bold¨»N«/mi»«mo mathvariant=¨bold¨»=«/mo»«mi mathvariant=¨bold¨»m«/mi»«mo mathvariant=¨bold¨»§#183;«/mo»«mi mathvariant=¨bold¨»a«/mi»«/menclose»«/math»
نعوّض القوة العمودية من معادلة الحركة العمودية في معادلة الحركة الأفقية.
«math xmlns=¨http://www.w3.org/1998/Math/MathML¨»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»-«/mo»«msub mathcolor=¨#0000FF¨»«mi mathvariant=¨bold¨ mathcolor=¨#0000FF¨»§#956;«/mi»«mi mathvariant=¨bold¨»k«/mi»«/msub»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»§#183;«/mo»«mi mathvariant=¨bold¨ mathcolor=¨#FF0000¨»N«/mi»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»=«/mo»«mi mathvariant=¨bold¨ mathcolor=¨#0000FF¨»m«/mi»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»§#183;«/mo»«mi mathvariant=¨bold¨ mathcolor=¨#0000FF¨»a«/mi»«mspace linebreak=¨newline¨»«/mspace»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»-«/mo»«msub mathcolor=¨#0000FF¨»«mi mathvariant=¨bold¨ mathcolor=¨#0000FF¨»§#956;«/mi»«mi mathvariant=¨bold¨»k«/mi»«/msub»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»§#183;«/mo»«mi mathvariant=¨bold¨ mathcolor=¨#FF0000¨»m«/mi»«mo mathvariant=¨bold¨ mathcolor=¨#FF0000¨»§#183;«/mo»«mi mathvariant=¨bold¨ mathcolor=¨#FF0000¨»g«/mi»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»=«/mo»«mi mathvariant=¨bold¨ mathcolor=¨#0000FF¨»m«/mi»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»§#183;«/mo»«mi mathvariant=¨bold¨ mathcolor=¨#0000FF¨»a«/mi»«/math»
نعبّر عن التسارع كدالة لمعامل الاحتكاك:
«math xmlns=¨http://www.w3.org/1998/Math/MathML¨»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»-«/mo»«msub mathcolor=¨#0000FF¨»«mi mathvariant=¨bold¨ mathcolor=¨#0000FF¨»§#956;«/mi»«mi mathvariant=¨bold¨»k«/mi»«/msub»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»§#183;«/mo»«menclose mathcolor=¨#0000FF¨ notation=¨downdiagonalstrike¨»«mi mathvariant=¨bold¨»m«/mi»«/menclose»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»§#183;«/mo»«mi mathvariant=¨bold¨ mathcolor=¨#0000FF¨»g«/mi»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»=«/mo»«menclose mathcolor=¨#0000FF¨ notation=¨downdiagonalstrike¨»«mi mathvariant=¨bold¨»m«/mi»«/menclose»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»§#183;«/mo»«mi mathvariant=¨bold¨ mathcolor=¨#0000FF¨»a«/mi»«mspace linebreak=¨newline¨»«/mspace»«mspace linebreak=¨newline¨»«/mspace»«mi mathvariant=¨bold¨ mathcolor=¨#0000FF¨»a«/mi»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»=«/mo»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»-«/mo»«msub mathcolor=¨#0000FF¨»«mi mathvariant=¨bold¨ mathcolor=¨#0000FF¨»§#956;«/mi»«mi mathvariant=¨bold¨»k«/mi»«/msub»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»§#183;«/mo»«mi mathvariant=¨bold¨ mathcolor=¨#0000FF¨»g«/mi»«/math»
مقدار السرعة الابتدائية 90 كم / ساعة أي 25 مترًا في الثانية .
نعبر عن إزاحة السيارة من تعبير مربع السرعات وفقًا للتسارع والسرعة الابتدائية:
«math xmlns=¨http://www.w3.org/1998/Math/MathML¨»«mstyle mathsize=¨20px¨»«mrow»«msup mathcolor=¨#0000FF¨»«mi mathvariant=¨bold¨ mathcolor=¨#0000FF¨»V«/mi»«mn mathvariant=¨bold¨»2«/mn»«/msup»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»=«/mo»«msup mathcolor=¨#0000FF¨»«msub mathcolor=¨#0000FF¨»«mi mathvariant=¨bold¨ mathcolor=¨#0000FF¨»V«/mi»«mn mathvariant=¨bold¨»0«/mn»«/msub»«mn mathvariant=¨bold¨»2«/mn»«/msup»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»+«/mo»«mn mathvariant=¨bold¨ mathcolor=¨#0000FF¨»2«/mn»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»§#183;«/mo»«mi mathvariant=¨bold¨ mathcolor=¨#0000FF¨»a«/mi»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»§#183;«/mo»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»§#8710;«/mo»«mi mathvariant=¨bold¨ mathcolor=¨#0000FF¨»x«/mi»«mspace linebreak=¨newline¨»«/mspace»«mspace linebreak=¨newline¨»«/mspace»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»§#8710;«/mo»«mi mathvariant=¨bold¨ mathcolor=¨#0000FF¨»x«/mi»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»=«/mo»«mfrac mathcolor=¨#0000FF¨»«mrow»«msup»«mi mathvariant=¨bold¨»V«/mi»«mn mathvariant=¨bold¨»2«/mn»«/msup»«mo mathvariant=¨bold¨»-«/mo»«msup»«msub»«mi mathvariant=¨bold¨»V«/mi»«mn mathvariant=¨bold¨»0«/mn»«/msub»«mn mathvariant=¨bold¨»2«/mn»«/msup»«/mrow»«mrow»«mn mathvariant=¨bold¨»2«/mn»«mo mathvariant=¨bold¨»§#183;«/mo»«mi mathvariant=¨bold¨»a«/mi»«/mrow»«/mfrac»«/mrow»«/mstyle»«/math»
في نهاية الحركة ، تكون سرعة السيارة صفرًا. نعوّض تعبير التسارع وقيمة كل من السرعتين:
«math xmlns=¨http://www.w3.org/1998/Math/MathML¨»«mstyle mathsize=¨20px¨»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»§#8710;«/mo»«mi mathvariant=¨bold¨ mathcolor=¨#0000FF¨»x«/mi»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»=«/mo»«mfrac mathcolor=¨#0000FF¨»«mrow»«msup»«mi mathvariant=¨bold¨»V«/mi»«mn mathvariant=¨bold¨»2«/mn»«/msup»«mo mathvariant=¨bold¨»-«/mo»«msup»«msub»«mi mathvariant=¨bold¨»V«/mi»«mn mathvariant=¨bold¨»0«/mn»«/msub»«mn mathvariant=¨bold¨»2«/mn»«/msup»«/mrow»«mrow»«mn mathvariant=¨bold¨»2«/mn»«mo mathvariant=¨bold¨»§#183;«/mo»«mi mathvariant=¨bold¨ mathcolor=¨#FF0000¨»a«/mi»«/mrow»«/mfrac»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»=«/mo»«mfrac mathcolor=¨#0000FF¨»«mrow»«msup»«mn mathvariant=¨bold¨»0«/mn»«mn mathvariant=¨bold¨»2«/mn»«/msup»«mo mathvariant=¨bold¨»-«/mo»«msup»«mn mathvariant=¨bold¨»25«/mn»«mn mathvariant=¨bold¨»2«/mn»«/msup»«/mrow»«mrow»«mn mathvariant=¨bold¨»2«/mn»«mo mathvariant=¨bold¨»§#183;«/mo»«mo mathvariant=¨bold¨»(«/mo»«mo mathvariant=¨bold¨»-«/mo»«mi mathvariant=¨bold¨»§#956;«/mi»«mi mathvariant=¨bold¨»k«/mi»«mo mathvariant=¨bold¨»§#183;«/mo»«mi mathvariant=¨bold¨»g«/mi»«mo mathvariant=¨bold¨»)«/mo»«/mrow»«/mfrac»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»=«/mo»«mfrac mathcolor=¨#0000FF¨»«mrow»«mo mathvariant=¨bold¨»-«/mo»«mn mathvariant=¨bold¨»625«/mn»«/mrow»«mrow»«mo mathvariant=¨bold¨»-«/mo»«mn mathvariant=¨bold¨»2«/mn»«mo mathvariant=¨bold¨»§#183;«/mo»«mi mathvariant=¨bold¨»§#956;k«/mi»«mo mathvariant=¨bold¨»§#183;«/mo»«mi mathvariant=¨bold¨»g«/mi»«/mrow»«/mfrac»«mspace linebreak=¨newline¨»«/mspace»«mspace linebreak=¨newline¨»«/mspace»«menclose mathcolor=¨#0000FF¨ notation=¨circle¨»«mo mathvariant=¨bold¨»§#8710;«/mo»«mi mathvariant=¨bold¨»x«/mi»«mo mathvariant=¨bold¨»=«/mo»«mfrac»«mrow»«mn mathvariant=¨bold¨»312«/mn»«mo mathvariant=¨bold¨».«/mo»«mn mathvariant=¨bold¨»5«/mn»«/mrow»«mrow»«mi mathvariant=¨bold¨»§#956;k«/mi»«mo mathvariant=¨bold¨»§#183;«/mo»«mi mathvariant=¨bold¨»g«/mi»«/mrow»«/mfrac»«/menclose»«mspace linebreak=¨newline¨»«/mspace»«mspace linebreak=¨newline¨»«/mspace»«/mstyle»«/math»
نجد مقدار الازاحة عندما يكون هناك جليد على الشارع ويكون معامل الاحتكاك الحركي مساوٍ لـ 0.1 :
«math xmlns=¨http://www.w3.org/1998/Math/MathML¨»«mstyle mathsize=¨20px¨»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»§#8710;«/mo»«msub mathcolor=¨#0000FF¨»«mi mathvariant=¨bold¨ mathcolor=¨#0000FF¨»x«/mi»«mn mathvariant=¨bold¨»1«/mn»«/msub»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»=«/mo»«mfrac mathcolor=¨#0000FF¨»«mrow»«mn mathvariant=¨bold¨»312«/mn»«mo mathvariant=¨bold¨».«/mo»«mn mathvariant=¨bold¨»5«/mn»«/mrow»«mrow»«mi mathvariant=¨bold¨»§#956;k«/mi»«mo mathvariant=¨bold¨»§#183;«/mo»«mi mathvariant=¨bold¨»g«/mi»«/mrow»«/mfrac»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»=«/mo»«mfrac mathcolor=¨#0000FF¨»«mrow»«mn mathvariant=¨bold¨»312«/mn»«mo mathvariant=¨bold¨».«/mo»«mn mathvariant=¨bold¨»5«/mn»«/mrow»«mrow»«mn mathvariant=¨bold¨»0«/mn»«mo mathvariant=¨bold¨».«/mo»«mn mathvariant=¨bold¨»1«/mn»«mo mathvariant=¨bold¨»§#183;«/mo»«mn mathvariant=¨bold¨»10«/mn»«/mrow»«/mfrac»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»=«/mo»«mn mathvariant=¨bold¨ mathcolor=¨#0000FF¨»312«/mn»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨».«/mo»«mn mathvariant=¨bold¨ mathcolor=¨#0000FF¨»5«/mn»«mi mathvariant=¨bold¨ mathcolor=¨#0000FF¨»m«/mi»«/mstyle»«/math»
نجد مقدار الازاحة عندما يكون هناك جليد على الشارع ويكون معامل الاحتكاك الحركي مساوٍ لـ 0.8 :
«math xmlns=¨http://www.w3.org/1998/Math/MathML¨»«mstyle mathsize=¨20px¨»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»§#8710;«/mo»«msub mathcolor=¨#0000FF¨»«mi mathvariant=¨bold¨ mathcolor=¨#0000FF¨»x«/mi»«mn mathvariant=¨bold¨»2«/mn»«/msub»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»=«/mo»«mfrac mathcolor=¨#0000FF¨»«mrow»«mn mathvariant=¨bold¨»312«/mn»«mo mathvariant=¨bold¨».«/mo»«mn mathvariant=¨bold¨»5«/mn»«/mrow»«mrow»«mn mathvariant=¨bold¨»0«/mn»«mo mathvariant=¨bold¨».«/mo»«mn mathvariant=¨bold¨»8«/mn»«mo mathvariant=¨bold¨»§#183;«/mo»«mn mathvariant=¨bold¨»10«/mn»«/mrow»«/mfrac»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»=«/mo»«mn mathvariant=¨bold¨ mathcolor=¨#0000FF¨»39«/mn»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨».«/mo»«mn mathvariant=¨bold¨ mathcolor=¨#0000FF¨»06«/mn»«mi mathvariant=¨bold¨ mathcolor=¨#0000FF¨»m«/mi»«/mstyle»«/math»
נערוך תרשים כוחות ונכתוב את משוואות התנועה , ונפתח את הביטוי הדרוש ממשוואות התנועה.
נבחר ציר תנועה אופקי שכיוונו ככיוון התנועה.
נכתוב את משוואות התנועה לכיוון האופקי ולכיוון האנכי:
«math xmlns=¨http://www.w3.org/1998/Math/MathML¨»«msub mathcolor=¨#0000FF¨»«mi mathvariant=¨bold¨ mathcolor=¨#0000FF¨»§#931;F«/mi»«mi mathvariant=¨bold¨»y«/mi»«/msub»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»=«/mo»«mn mathvariant=¨bold¨ mathcolor=¨#0000FF¨»0«/mn»«mspace linebreak=¨newline¨»«/mspace»«mi mathvariant=¨bold¨ mathcolor=¨#0000FF¨»N«/mi»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»=«/mo»«mi mathvariant=¨bold¨ mathcolor=¨#0000FF¨»W«/mi»«mspace linebreak=¨newline¨»«/mspace»«menclose mathcolor=¨#0000FF¨ notation=¨box¨»«mi mathvariant=¨bold¨»N«/mi»«mo mathvariant=¨bold¨»=«/mo»«mi mathvariant=¨bold¨»mg«/mi»«/menclose»«/math» «math xmlns=¨http://www.w3.org/1998/Math/MathML¨»«msub mathcolor=¨#0000FF¨»«mi mathvariant=¨bold¨ mathcolor=¨#0000FF¨»§#931;F«/mi»«mi mathvariant=¨bold¨»X«/mi»«/msub»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»=«/mo»«mi mathvariant=¨bold¨ mathcolor=¨#0000FF¨»m«/mi»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»§#183;«/mo»«mi mathvariant=¨bold¨ mathcolor=¨#0000FF¨»a«/mi»«mspace linebreak=¨newline¨»«/mspace»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»-«/mo»«msub mathcolor=¨#0000FF¨»«mi mathvariant=¨bold¨ mathcolor=¨#0000FF¨»f«/mi»«mi mathvariant=¨bold¨»k«/mi»«/msub»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»=«/mo»«mi mathvariant=¨bold¨ mathcolor=¨#0000FF¨»m«/mi»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»§#183;«/mo»«mi mathvariant=¨bold¨ mathcolor=¨#0000FF¨»a«/mi»«mspace linebreak=¨newline¨»«/mspace»«menclose mathcolor=¨#0000FF¨ notation=¨box¨»«mo mathvariant=¨bold¨»-«/mo»«msub»«mi mathvariant=¨bold¨»§#956;«/mi»«mi mathvariant=¨bold¨»k«/mi»«/msub»«mo mathvariant=¨bold¨»§#183;«/mo»«mi mathvariant=¨bold¨»N«/mi»«mo mathvariant=¨bold¨»=«/mo»«mi mathvariant=¨bold¨»m«/mi»«mo mathvariant=¨bold¨»§#183;«/mo»«mi mathvariant=¨bold¨»a«/mi»«/menclose»«/math»
נציב את הנורמל ממשוואת התנועה האנכית במשוואת התנועה האופקית.
«math xmlns=¨http://www.w3.org/1998/Math/MathML¨»«msub mathcolor=¨#0000FF¨»«mi mathvariant=¨bold¨ mathcolor=¨#0000FF¨»§#931;F«/mi»«mi mathvariant=¨bold¨»X«/mi»«/msub»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»=«/mo»«mi mathvariant=¨bold¨ mathcolor=¨#0000FF¨»m«/mi»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»§#183;«/mo»«mi mathvariant=¨bold¨ mathcolor=¨#0000FF¨»a«/mi»«mspace linebreak=¨newline¨»«/mspace»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»-«/mo»«msub mathcolor=¨#0000FF¨»«mi mathvariant=¨bold¨ mathcolor=¨#0000FF¨»f«/mi»«mi mathvariant=¨bold¨»k«/mi»«/msub»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»=«/mo»«mi mathvariant=¨bold¨ mathcolor=¨#0000FF¨»m«/mi»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»§#183;«/mo»«mi mathvariant=¨bold¨ mathcolor=¨#0000FF¨»a«/mi»«mspace linebreak=¨newline¨»«/mspace»«menclose mathcolor=¨#0000FF¨ notation=¨box¨»«mo mathvariant=¨bold¨»-«/mo»«msub»«mi mathvariant=¨bold¨»§#956;«/mi»«mi mathvariant=¨bold¨»k«/mi»«/msub»«mo mathvariant=¨bold¨»§#183;«/mo»«mi mathvariant=¨bold¨»N«/mi»«mo mathvariant=¨bold¨»=«/mo»«mi mathvariant=¨bold¨»m«/mi»«mo mathvariant=¨bold¨»§#183;«/mo»«mi mathvariant=¨bold¨»a«/mi»«/menclose»«/math»
1. السرعة الابتدائية معطاة بوحدات كم / ساعة ، وهذه الوحدات غير قياسية ، ويجب أن تعويض قيمة السرعة بوحدات متر في الثانية.
2. تتحرك السيارة في خط مستقيم حتى تتوقف. المسافة التي تقطعها السيارة تساوي إزاحة الحركة. لذلك ، يجب حساب الازاحة بالنسبة لمحور الحركة الذي تم اختياره.
3. أثناء عملية الكبح ، تتوقف عجلات السيارة ، تنزلق السيارة على الشارع ، لذا يمكنك استخدام تعريف قوة الاحتكاك الحركي ، معامل الاحتكاك المعطى هومعامل الاحتكاك الحركي.
2. המכונית נעה בקו ישר ,עד לעצירתה. המרחק שהמכונית עוברת שווה להעתק התנועה. לכן יש למצוא את ההעתק ביחס לציר תנועה נבחר.
3. בזמן הבלימה גלגלי המכונית נעצרים, המכונית מחליקה על הכביש , לכן אפשר להשתמש בהגדרת כוח החיכוך הקינטי , מקדם החיכוך הנתון הוא של כוח החיכוך הקינטי.
______________________________________________________________________________________
ג.  ______________________________________________________________________________________
______________________________________________________________________________________
...
كلما زادت مسافة الكبح في حالة الفرملة الطارئة ، زادت المسافة التي تقطعها السيارة. وستكون قدرة السائقين على تفادي الحوادث أقل ، وبالتالي يتم إغلاق الطرق.
يجب فهم العلاقة بين مسافة الكبح الكبيرة وإغلاق الشارع بحسب المنطق.
كلما زادت مسافة الكبح في حالة الفرملة الطارئة، زادت المسافة التي تقطعها السيارة. وستكون قدرة السائقين على تفادي الحوادث أقل ، وبالتالي يتم إغلاق الطرق.
هناك أسئلة تكفي أن يجيب عليها منطقيًا. عادة ما تكون هذه الأسئلة بسيطة للغاية.
ليست هناك حاجة لأن تكون مترددًا أو خائفًا. هناك أيضا مثل هذه الأسئلة.
לא צריך להתרגש או לחשוש . יש גם שאלות כאלו.
______________________________________________________________________________________
 ______________________________________________________________________________________
______________________________________________________________________________________
...
التسارع 0.8 متر لكل ثانية مربعة ، واتجاهه في اتجاه محور الحركة.
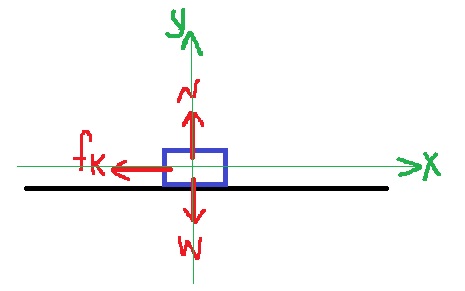
رسم مخطط قوى وكتابة معادلات الحركة.
نرسم مخطط القوى على السيارة ونُشير إلى قوة الاحتكاك التي تعمل في الاتجاه المعاكس ب'fk:

نكتب معادلات الحركة في الاتجاهين الأفقي والعمودي:
«math xmlns=¨http://www.w3.org/1998/Math/MathML¨»«msub mathcolor=¨#0000FF¨»«mi mathvariant=¨bold¨ mathcolor=¨#0000FF¨»§#931;F«/mi»«mi mathvariant=¨bold¨»y«/mi»«/msub»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»=«/mo»«mn mathvariant=¨bold¨ mathcolor=¨#0000FF¨»0«/mn»«mspace linebreak=¨newline¨»«/mspace»«mi mathvariant=¨bold¨ mathcolor=¨#0000FF¨»N«/mi»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»=«/mo»«mi mathvariant=¨bold¨ mathcolor=¨#0000FF¨»W«/mi»«mspace linebreak=¨newline¨»«/mspace»«menclose mathcolor=¨#0000FF¨ notation=¨box¨»«mi mathvariant=¨bold¨»N«/mi»«mo mathvariant=¨bold¨»=«/mo»«mi mathvariant=¨bold¨»mg«/mi»«/menclose»«/math» «math xmlns=¨http://www.w3.org/1998/Math/MathML¨»«msub mathcolor=¨#0000FF¨»«mi mathvariant=¨bold¨ mathcolor=¨#0000FF¨»§#931;F«/mi»«mi mathvariant=¨bold¨»X«/mi»«/msub»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»=«/mo»«mi mathvariant=¨bold¨ mathcolor=¨#0000FF¨»m«/mi»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»§#183;«/mo»«mi mathvariant=¨bold¨ mathcolor=¨#0000FF¨»a«/mi»«mspace linebreak=¨newline¨»«/mspace»«menclose mathcolor=¨#0000FF¨ notation=¨box¨»«mi mathvariant=¨bold¨»F«/mi»«mo mathvariant=¨bold¨»-«/mo»«msub»«mi mathvariant=¨bold¨»f«/mi»«mi mathvariant=¨bold¨»k«/mi»«/msub»«mo mathvariant=¨bold¨»`«/mo»«mo mathvariant=¨bold¨»=«/mo»«mi mathvariant=¨bold¨»m«/mi»«mo mathvariant=¨bold¨»§#183;«/mo»«mi mathvariant=¨bold¨»a«/mi»«/menclose»«/math»
نعبّر عن التسارع من معادلة الحركة الأفقية، ونجد مقدارها وفقًا للمعطيات المعطاة في السؤال:
«math xmlns=¨http://www.w3.org/1998/Math/MathML¨»«mi mathvariant=¨bold¨ mathcolor=¨#0000FF¨»a«/mi»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»=«/mo»«mfrac mathcolor=¨#0000FF¨»«mrow»«mi mathvariant=¨bold¨»F«/mi»«mo mathvariant=¨bold¨»-«/mo»«mi mathvariant=¨bold¨»fk«/mi»«mo mathvariant=¨bold¨»`«/mo»«/mrow»«mi mathvariant=¨bold¨»m«/mi»«/mfrac»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»=«/mo»«mfrac mathcolor=¨#0000FF¨»«mrow»«mn mathvariant=¨bold¨»1200«/mn»«mo mathvariant=¨bold¨»-«/mo»«mn mathvariant=¨bold¨»400«/mn»«/mrow»«mn mathvariant=¨bold¨»1000«/mn»«/mfrac»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨»=«/mo»«mn mathvariant=¨bold¨ mathcolor=¨#0000FF¨»0«/mn»«mo mathvariant=¨bold¨ mathcolor=¨#0000FF¨».«/mo»«mn mathvariant=¨bold¨ mathcolor=¨#0000FF¨»8«/mn»«mfrac mathcolor=¨#0000FF¨»«mi mathvariant=¨bold¨»m«/mi»«msup»«mi mathvariant=¨bold¨»s«/mi»«mn mathvariant=¨bold¨»2«/mn»«/msup»«/mfrac»«/math»
لذلك ، فإن تسارع السيارة تساوي 0.8 متر لكل ثانية مربعة. التسارع موجب، وبالتالي فإن اتجاه التسارع في اتجاه الحركة.
1. بالإضافة إلى إيجاد مقدار التسارع، يجب أيضًا إشارة التسارع وفقًا للاتجاه الذي تم اختياره. الحل الذي يحتوي على قيمة التسارع فقط لا يمكنك الحصول على علامة كاملة.
2. ليس من الضروري دائمًا استخدام جميع معادلات الحركة ، في هذه الحالة استخدمنا معادلة الحركة الأفقية فقط.
من المهم كتابة جميع معادلات الحركة وبعد ذلك فقط تقرر المعادلة التي يجب استخدامها.
2. לא תמיד יש צורך להשתמש בכל משוואות התנועה , במקרה זה השתמשנו במשוואת התנועה האופקית בלבד. חשוב לכתוב את כל משוואות התנועה ורק אחר כך להחליט באיזו משוואה להשתמש.
______________________________________________________________________________________

______________________________________________________________________________________
...
تزداد قوة الاحتكاك مع زيادة السرعة. في سرعة ما تتساوى قوة الاحتكاك مع القوة الدافعة للسيارة ،عندها تكون محصلة القوى المؤثرة على السيارة صفراً. وتستمر السيارة في التحرك ولن تزيد السرعة. لذلك تصل السيارة لسرعة قصوى.
القوة الدافعة للسيارة ثابتة، وتزداد قوة الاحتكاك مع زيادة السرعة.
تزداد قوة الاحتكاك مع زيادة السرعة. في سرعة ما تتساوى قوة الاحتكاك مع القوة الدافعة للسيارة ،عندها تكون محصلة القوى المؤثرة على السيارة صفراً. وتستمر السيارة في التحرك ولن تزيد السرعة. لذلك تصل السيارة لسرعة قصوى.
1. تتعلق حركة الجسم بالقوى المؤثرة على الجسم ، وفي هذه الحالة الخاصة تحدد الحركة (مقدار السرعة) مقدار القوة المؤثرة على السيارة.
2. في هذه الحالة تعمل قوة آخذة بالازدياد ضد اتجاه الحركة ، تزداد السرعة بوتيرة آخذة بالنقصان، التسارع يأخذ بالنقصان، حتى يصبح التسارع صفرًا.
عندها يصل الجسم إلى أقصى سرعة له.
2.בכל מקרה בו פועל כוח הולך וגדל נגד כיוון התנועה , המהירות תגדל בקצב הולך וקטן ,בתאוצה הולכת וקטנה, עד שהתאוצה תהיה אפס .
והגוף יגיע למהירויות המקסימאלית.
3. סעיף זה נשען על הבנת הדינמיקה בסעיפים הקודמים, הרבה פעמים הסעיף האחרון , הוא מסכם בצורה קצת שונה את כל השאלה.
______________________________________________________________________________________




 ______________________________________________________________________________________
______________________________________________________________________________________ ______________________________________________________________________________________
______________________________________________________________________________________
